Bài tập trắc nghiệm nón – trụ – cầu vận dụng cao Toán 12

Tài liệu gồm 65 trang, tuyển chọn các bài tập trắc nghiệm nón – trụ – cầu vận dụng cao, có đáp án và lời giải chi tiết, giúp học sinh lớp 12 tham khảo khi học chương trình Toán 12 phần Hình học chương 2: Mặt Nón – Mặt Trụ – Mặt Cầu.Mời các bạn đón xem.

37 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Mặt nón, mặt trụ, mặt cầu

Môn: Toán 12

Thông tin:

65 trang 8 tháng trước

Tác giả:

Profile Lan Tường
1
NÓN – TRỤ – CẦU
Vận dụng cao
Phần 1. Thể tích và các yếu tố liên quan
Phần 2. Vật thể tròn xoay
Phần 3. Ứng dụng thực tiễn
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Phần 5. Mặt cầu ngoại tiếp khối đa diện
Phần 6. Bài toán cực trị
2
Phần 1. Thể tích và các yếu tố liên quan
Câu 1.
Một chiếc thùng hình trụ có bán kính đáy
20,R
bên
trong đựng một lượng nước. Biết rằng khi nghiêng thùng sao cho
đường sinh của hình trụ tạo với mặt đáy góc
45
cho đến khi
nước lặng thì mặt nước chạm vào hai điểm
A
và
B
nằm trên hai
mặt đáy như hình vẽ bên. Thể tích của thùng đã cho bằng
A.
16000 .
B.
12000 .
C.
D.
Câu 2. Cho hình lăng trụ tứ giác đều
..ABCD EFGH
Tính tỉ số
k
giữa thể tích khối
trụ ngoại tiếp và thể tích khối trụ nội tiếp hình lăng trụ trên.
A.
2.k
B.
2.k
C.
2 2.k
D.
4.k
Câu 3.
Cho một hình trụ tròn xoay và hình vuông
ABCD
cạnh
a
có
hai đỉnh liên tiếp
, AB
nằm trên đường tròn đáy thứ nhất của hình
trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ.
Mặt phẳng
ABCD
tạo với đáy hình trụ góc
45
như hình vẽ. Thể
tích khối trụ bằng
A.
3
.
16
a
B.
3
2
.
16
a
C.
3
3
.
16
a
D.
3
32
.
16
a
Câu 4.
Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không
vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song

,AB A B
mà

6 cmAB A B
. Biết diện tích tứ giác

ABB A
bằng
2
60 cm .
Chiều cao của hình trụ đã cho bằng
A.
43
cm. B.
53
cm. C.
62
cm. D.
82
cm.
Câu 5. Một thùng hình trụ có chiều cao
3m,h
bán kính đường tròn đáy
1mR
chứa một lượng nước. Biết rằng nếu đặt thùng nằm ngang ta được chiều cao mực nước
trong thùng là
0,5m.d
Hỏi thể tích lượng nước có trong thùng gần nhất với kết quả
nào sau đây ?
A.
3
1, 7 5m .
B.
3
1, 8 m .
C.
3
1, 8 5m .
D.
3
1, 9 m .
Câu 6. Cho một hình trụ có bán kính đáy bằng
R
và có chiều cao bằng
3.R
Hai
điểm
, AB
lần lượt nằm trên hai đường tròn đáy sao cho góc giữa
AB
và trục của
hình trụ bằng
0
30
. Khoảng cách giữa
AB
và trục của hình trụ bằng
A.
.R
B.
3.
R
C.
3
.
2
R
D.
3
.
4
R
Câu 7. Cho hình trụ có hai đáy là hai hình tròn
O
và
,O
thiết diện qua trục của
hình trụ là hình vuông. Gọi
, AB
là hai điểm lần lượt nằm trên hai đường tròn
O
và
3
.O
Biết
2AB a
và khoảng cách giữa hai đường thẳng
AB
và
OO
bằng
3
.
2
a
Bán kính đáy của hình trụ bằng
A.
14
.
2
a
B.
14
.
3
a
C.
2
.
4
a
D.
14
.
4
a
Câu 8. Cho hình trụ có đáy là hai đường tròn tâm
O
và
,O
bán kính đáy bằng chiều
cao và bằng
.a
Trên đường tròn tâm
O
lấy điểm
,A
trên đường tròn tâm
O
lấy điểm
B
sao cho
2.AB a
Thể tích của khối tứ diện
OO AB
bằng
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
6
a
D.
3
3
.
12
a
Câu 9. Một hình trụ có bán kính đáy
70cmR
và chiều cao
20cm.h
Một hình vuông
ABCD
có hai cạnh
AB
và
CD
lần
lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng
ABCD
không vuông góc với mặt đáy của hình trụ (tham
khảo hình vẽ). Cạnh của hình vuông
ABCD
có độ dài bằng
A.
80cm.
B.
100cm.
C.
100 2cm.
D.
140cm.
Câu 10.
Cho hình nón có đỉnh
,S
trục
,SO
bán kính
,R
chiều
cao
.h
Dây cung
AB
thuộc đường tròn đáy và cách
O
một
khoảng
2
R
như hình vẽ. Ký hiệu
12
,SS
lần lượt là diện tích
xung quanh của mặt nón và diện tích tam giác
.SAB
Biết
1
2
10
,
33
S
S
mệnh đề nào sau đây đúng ?
A.
5
.
22
hR
B.
11
.
8
hR
C.
21.hR
D.
1
.
3
hR
Câu 11.
Cho hình chóp tam giác đều
..S ABC
Hình nón có đỉnh
S
và có đường tròn đáy là đường tròn nội tiếp tam giác
ABC
gọi là
hình nón nội tiếp hình chóp
.,S ABC
hình nón có đỉnh
S
và có
đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
gọi là hình
nón ngoại tiếp hình chóp
..
S ABC
Tỉ số thể tích của hình nón nội
tiếp và hình nón ngoại tiếp hình chóp đã cho bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
1
.
4
Câu 12. Cho hình nón đỉnh
S
có đáy là hình tròn tâm
.O
Dựng hai đường sinh
SA
và
,SB
biết tam giác
SAB
vuông và có diện tích bằng
2
4.a
Góc tạo bởi giữa trục
SO
và mặt phẳng
SAB
bằng
0
30 .
Đường cao
h
của hình nón bằng
A.
2.ha
B.
3.ha
C.
3
.
2
a
h
D.
6
.
4
a
h
4
Câu 13. Cho hình nón đỉnh
S
có đường cao
.SO
Gọi
, AB
là hai điểm thuộc đường
tròn đáy của hình nón sao cho khoảng cách từ
O
đến
AB
bằng
a
và
0
30 ,SAO
0
60 .SAB
Độ dài đường sinh
của hình nón bằng
A.
.
a
B.
2.a
C.
3.a
D.
2.a
Câu 14. Một cái phễu có dạng hình nón, chiều cao của phễu là
20 cm
(Hình 1). Người
ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu là
10 cm.
Nếu bịt kín miệng phễu rồi lật ngược lên (Hình 2).
Khi đó chiều cao cột nước trong phễu bằng giá trị nào sau đây ?
A.
0,87 cm.
B.
1, 07 cm .
C.
5 cm.
D.
Câu 15. Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng
là một khối nón có chiều cao
10 cm
(mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất
chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất
sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn
5 cm
. Tính
chiều cao
h
của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất
lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao
hụt khi chuyển. Tính gần đúng
h
với sai số không quá
0, 01 cm
).
A.
9, 09 cm .
B.
9,18 cm .
C.
9,56 cm .
D.
9,57 cm .
Câu 16.
Cho một đồng hồ cát gồm
2
hình nón chung đỉnh ghép
lại, trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc
60
như hình bên. Biết rằng chiều cao của đồng hồ là
30cm
và
tổng thể tích của đồng hồ là
3
1000 cm .
Hỏi nếu cho đầy lượng
cát vào phần trên thì khi chảy hết xuống dưới, khi đó tỉ lệ thể
tích lượng cát chiếm chỗ và thể tích phần dưới là bao nhiêu ?
A.
1
.
33
B.
1
.
8
C.
1
.
27
D.
1
.
64
5
Câu 17. Để tính diện tích xung quanh của một khối cầu bằng đá,
người ta thả nó vào trong một chiếc thùng hình trụ có chiều cao
2m,h
bán kính đường tròn đáy bằng
0,5m
R
và chứa một
lượng nước có thể tích bằng
1
8
thể tích khối trụ. Sau khi thả khối
cầu đá vào khối trụ người ta đo được mực nước trong khối trụ cao
gấp ba lần mực nước ban đầu khi chưa thả khối cầu. Hỏi diện tích
xung quanh của khối cầu gần bằng kết quả nào được cho dưới đây ?
A.
2
1, 5m .
B.
2
1, 7 m .
C.
2
2, 6m .
D.
2
3, 4m .
Câu 18. Cho mặt cầu
S
tâm
,O
bán kính
3.
R
Mặt phẳng
P
cách
O
một khoảng bằng
1
và cắt
S
theo giao tuyến là đường
tròn
C
có tâm
.H
Gọi
T
là giao điểm của tia
HO
với
,S
tính
thể tích
V
của khối nón đỉnh
,T
đáy là hình tròn
C
(như hình).
A.
16
.
3
V
B.
32
.
3
V
C.
16 .V
D.
32 .V
Câu 19.
Một bình đựng nước dạng hình nón không nắp đựng đầy
nước. Biết rằng chiều cao của bình gấp
3
lần bán kính đáy của nó.
Người ta thả vào bình đó một khối trụ và đo được thể tích nước trào
ra ngoài là
3
16
dm .
9
Biết rằng một mặt của khối trụ nằm trên mặt
đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của
hình nón (như hình vẽ). Tính bán kính đáy
R
của bình nước.
A.
2 dm.R
B.
3 dm.R
C.
4 dm.R
D.
5 dm.R
Câu 20.
Xét một hình trụ nội tiếp trong hình nón như hình
bên, trong đó
S
là đỉnh hình nón,
O
là tâm đường tròn
mặt đáy. Các đoạn
, AB CD
lần lượt là đường kính của
đường tròn đáy của hình nón và hình trụ. Biết
, AC BD
cắt
nhau tại điểm
M SO
và tỉ số thể tích của hình trụ và
hình nón là
4
.
9
Tỉ số
SM
SO
bằng
A.
2
.
3
B.
4
.
5
C.
5
.
6
D.
7
.
9
Câu 21.
Cắt một hình nón bằng một mặt phẳng song song với đáy
thì phần hình nón nằm giữa mặt phẳng và đáy gọi là hình nón
cụt. Một chiếc cốc có dạng hình nón cụt cao
9cm,
bán kính của
đáy cốc và miệng cốc lần lượt là
3cm
và
4cm.
Hỏi chiếc cốc có thể
chứa được lượng nước tối đa là bao nhiêu trong các lựa chọn sau ?
A.
250 ml.
B.
300 ml.
C.
350 ml.
D.
400 ml.
6
Câu 22. Phần không gian bên trong của chai nước ngọt có hình
dạng như hình vẽ. Biết bán kính đáy và bán kính cổ chai lần lượt
là
5 cm,R
2 cm.r
Thể tích phần không gian bên trong của
chai nước ngọt (giả sử độ dày của vỏ chai không đáng kể) bằng
A.
3
412 cm .
B.
3
462 cm .
C.
3
490 cm .
D.
3
495 cm .
Câu 23.
Để định vị một trụ điện, người ta cần đúc một khối bê
tông có chiều cao
1, 5 m
h
gồm: Phần dưới có dạng hình trụ
bán kính
1mR
và có chiều cao bằng
1
;
3
h
Phần trên có dạng
hình nón bán kính đáy bằng
R
đã bị cắt bỏ bớt một phần hình
nón có bán kính đáy bằng
1
2
R
ở phía trên (người ta gọi hình đó là hình nón cụt);
Phần ở giữa rỗng có dạng hình trụ, bán kính đáy bằng
1
4
R
(tham khảo hình vẽ bên).
Tính thể tích
V
của khối bê tông (làm tròn đến chữ số thập phân thứ ba).
A.
3
2,814 m .V
B.
3
2,815m .V
C.
3
3,109m .V
D.
3
3, 403m .
V
Câu 24. Trong không gian cho một hình cầu
S
tâm
O
có bán kính
R
và một điểm
S
cho trước sao cho
2SO R
. Từ
S
ta kẻ các tiếp tuyến đến mặt cầu với tiếp điểm
thuộc đường tròn
1
.C
Trên mặt phẳng
P
chứa đường tròn
1
C
ta lấy điểm
E
thay
đổi nằm ngoài mặt cầu
.S
Gọi
N
là hình nón có đỉnh là
E
và đáy là đường tròn
2
C
gồm các tiếp điểm của tiếp tuyến kẻ từ
E
đến mặt cầu
.S
Biết rằng hai đường
tròn
1
C
và
2
C
luôn có cùng bán kính, khi đó quỹ tích các điểm
E
là một đường
tròn, đường tròn này có bán kính
R
bằng
A.
3
.
2
R
B.
15
.
2
R
C.
17
.
2
R
D.
15
.
4
R
Câu 25. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông tại
,A
22BC
và
30 .ACB 
Hình chiếu của
S
trên mặt phẳng đáy là trung điểm
H
của
.BC
Giả sử có mặt
cầu tâm
,O
bán kính bằng
1
tiếp xúc với
, SA SB
và tia đối
của
SC
lần lượt tại
111
,,ABC
đồng thời mặt cầu tâm
O
đó
cũng tiếp xúc với mặt phẳng
ABC
(tham khảo hình vẽ).
Thể tích của hình chóp
.S ABC
bằng
A.
32
.
2
B.
3
.
3
C.
22
.
3
D.
23
.
3
7
Phần 2. Vật thể tròn xoay
Câu 1.
Cho tam giác vuông cân
ABC
có
2AB AC a
và hình
chữ nhật
MNPQ
với
2MQ MN
được xếp chồng lên nhau sao cho
,
MN
lần lượt là trung điểm của
,AB AC
(như hình vẽ). Tính thể
tích
V
của vật thể tròn xoay khi quay mô hình trên quanh trục
,
AI
với
I
là trung điểm
.PQ
A.
3
5
.
6
a
V
B.
3
11
.
6
a
V
C.
3
11
.
8
a
V
D.
3
17
.
24
a
V
Câu 2. Cho hình thang
ABCD
vuông
A
và
B
với
.
2
AD
AB BC a
Quay hình
thang và miền trong của nó quanh đường thẳng chứa cạnh
.BC
Tính thể tích
V
của
khối tròn xoay được tạo thành.
A.
3
4
.
3
a
V
B.
3
5
.
3
a
V
C.
3
7
.
3
a
V
D.
3
.Va
Câu 3.
Cho hình bình hành
ABCD
có
2,
AD a
3,AB a
45
BAD

(như hình vẽ). Tính thể tích
V
của khối tròn
xoay nhận được khi quay hình bình hành
ABCD
quanh
trục
.AB
A.
3
5
.
2
a
V
B.
3
9
.
2
a
V
C.
3
5.Va
D.
3
6.Va
Câu 4.
Một cơ sở sản xuất kem chuẩn bị làm
1000
chiếc
kem giống nhau theo đơn đặt hàng. Cốc đựng kem có
dạng hình tròn xoay được tạo thành khi quay hình thang
ABCD
vuông tại
A
và
D
xung quanh trục
AD
(xem
hình vẽ). Chiếc cốc có bề dày không đáng kể, chiều cao
7, 2 cm;
đường kính miệng cốc bằng
6,4 cm;
đường kính
đáy cốc bằng
1,6 cm.
Kem được đổ đầy cốc và dư ra phía
ngoài một lượng có dạng nửa hình cầu, có bán kính bằng
bán kính miệng cốc. Cơ sở đó cần dùng lượng kem gần
nhất với giá trị nào trong các giá trị sau
A.
3
132 dm .
B.
3
170 dm .
C.
3
293 dm .
D.
3
954 dm .
Câu 5. Cho tam giác
SAB
vuông tại
,A
60 ,ABS 
đường phân
giác trong
ABS
cắt
SA
tại
.I
Vẽ nửa đường tròn tâm
I
bán kính
IA
(như hình vẽ). Cho tam giác
SAB
và nửa đường tròn trên cùng
quay quanh
SA
tạo nên khối cầu và khối nón tương ứng có thể
tích là
1
V
và
2
.V
Khẳng định nào sau đây đúng ?
A.
12
3.VV
B.
12
2 3.VV
C.
12
4 9.VV
D.
12
9 4.VV
8
Câu 6. Cho hình vuông
ABCD
nội tiếp đường tròn
,O
bán kính
;r
tam giác đều
MNP
nội tiếp đường tròn đó và
MN
song song
AB
(như hình vẽ). Cho mô hình trên quay quanh đường thẳng
.OP
Kí
hiệu
123
,,VVV
là thể tích khối tròn xoay do hình vuông, hình tròn
và tam giác đều tạo thành. Khẳng định nào sau đây đúng ?
A.
1 23
.VVV
B.
3 21
.
VVV
C.
2
1 23
..V VV
D.
2
3 21
..V VV
Câu 7. Cho tam giác
ABC
vuông tại
A
và có
, 3.
AC a AB a
Gọi
123
,,VVV
là thể
tích các khối tròn xoay sinh bởi tam giác
ABC
kể cả các điểm trong khi lần lượt quay
quanh các cạnh
,,.
AB AC BC
Trong các khẳng định sau, khẳng định nào đúng ?
Hình 1 Hình 2 Hình 3
A.
1 32
1 11
.
V VV

B.
312
1 11
.
V VV

C.
2 22
2 32
1 11
.
V VV

D.
2 22
312
1 11
.
V VV

Câu 8. Cho hình tứ diện
ABCD
có
AD
vuông góc với mặt phẳng
ABC
và tam giác
ABC
vuông tại
.B
Biết
,BC a
3,
AB a
3.AD a
Quay các tam giác
ABC
và
ABD
(bao gồm cả điểm bên trong hai tam giác) xung quanh đường thẳng
AB
ta được
hai khối tròn xoay. Thể tích phần chung của hai khối tròn xoay bằng
A.
3
83
.
3
a
B.
3
33
.
16
a
C.
3
43
.
16
a
D.
3
53
.
16
a
Câu 9. Ban đầu ta có một tam giác đều cạnh bằng
3
như hình 1. Tiếp theo ta chia
mỗi cạnh của tam giác thành
3
đoạn bằng nhau, dựng một tam giác đều về phía bên
ngoài có một cạnh là đoạn giữa, sau đó bỏ đi đoạn giữa ta được hình 2. Khi quay hình
2 xung quanh
d
ta được một khối tròn xoay có thể tích bằng
Hình 1
Hình 2
A.
B.
53
.
3
C.
D.
93
.
8
9
Câu 10. Cho nửa đường tròn đường kính
2AB R
và điểm
C
thay
đổi trên nửa đường tròn đó, đặt
CAB
và gọi
H
là hình chiếu
vuông góc của
C
lên
AB
(như hình vẽ). Tìm
sao cho thể tích vật
thể tròn xoay tạo thành khi quay tam giác
ACH
quanh trục
AB
đạt
giá trị lớn nhất.
A.
45 .

B.
60 .

C.
arctan 2.
D.
1
arctan .
2
Phần 3. Ứng dụng thực tiễn
Câu 1.
Bé Bách có một tấm bìa có chiều dài
20 cm;
chiều rộng
1 cm.
Bé muốn gấp một cái
hộp nhỏ xinh để bỏ kẹp tóc vào hộp đó tặng
quà cho mẹ ngày 20 tháng 10. Anh Siêu đã chỉ
cho bé hai cách gấp hộp. Cách thứ nhất là bé cuốn tấm bìa thành một cái hộp hình trụ
không có hai đáy có thể tích
1
.V
Cách thứ hai là bé gập tấm bìa một hình hộp chữ
nhật có thể tích
2
V
có các kích thước như hình vẽ. Hãy tìm tỉ số thể tích của hai hộp
để biết được gấp theo cách nào sẽ có thể tích lớn hơn.
A.
1
2
4
.
V
V
B.
1
2
.
4
V
V
C.
1
2
1
.
4
V
V
D.
1
2
4.
V
V
Câu 2. Một tấm tôn hình tròn tâm
,O
bán kính
R
được chia thành hai hình
1
H
và
2
H
như hình vẽ. Cho biết góc
90 .
AOB 
Từ hình
1
H
gò tấm tôn để được hình
nón
1
N
không đáy và từ hình
2
H
gò tấm tôn để được hình nón
2
N
không đáy.
Ký hiệu
12
,VV
lần lượt là thể tích của hình nón
12
, .NN
Tỉ số
1
2
V
V
bằng
A.
2.
B.
3.
C.
3 105
.
5
D.
7 105
.
9
Câu 3. Từ cùng một tấm kim loại dẻo hình
quạt (như hình vẽ) có kích thước bán kính
5R
và chu vi của hình quạt là
8 10,P
người ta gò tấm kim loại thành
những chiếc phễu theo hai cách:
Cách 1. Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu.
10
Cách 2. Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung
quanh của hai cái phễu. Gọi
1
V
là thể tích của cái phễu thứ nhất,
2
V
là tổng thể tích
của hai cái phễu ở cách thứ hai. Tỉ số
1
2
V
V
bằng
A.
1
2
2
.
7
V
V
B.
1
2
22
.
7
V
V
C.
1
2
21
.
7
V
V
D.
1
2
2 21
.
7
V
V
Câu 4.
Để làm cống thoát nước cho một khu vực dân cư người ta
cần đúc
500
ống hình trụ có đường kính trong và chiều cao của
mỗi ống bằng
1 m,
độ dày của thành ống là
10 cm.
Chọn mác bê
tông là
250
(tức mỗi khối bê tông là 7 bao ximăng). Hỏi phải
chuẩn bị bao nhiêu bao ximăng để làm đủ số ống nói trên ?
A.
1110 bao .
B.
1200 bao .
C.
1210 bao .
D.
4 210 bao .
Câu 5.
Cắt một miếng tôn hình vuông
cạnh
1m
thành hai hình chữ nhật,
trong đó một hình có chiều rộng
m,x
gọi miếng tôn này là miếng tôn thứ
nhất. Người ta gò miếng tôn thứ nhất
thành một lăng trụ tam giác đều, miếng còn lại gò thành một hình trụ (như hình vẽ).
Tìm
x
để tổng thể tích khối lăng trụ và khối trụ thu được là nhỏ nhất.
A.
9
.
39
x
B.
1
.
33 1
x
C.
9
.
93
x
D.
1
.
3
x
Câu 6. Một tấm tôn hình chữ nhật có chiều dài
4m,
chiều rộng
1m.
Một người thợ
muốn cắt tấm tôn này thành hai phần như hình vẽ. Người thợ gò phần
1
thành hình
trụ có đáy hình vuông và phần
2
thành hình trụ có đáy hình tròn. Tìm
x
để tổng thể
tích của hai khối trụ là nhỏ nhất.
A.
4
.
4
x
B.
8
.
4
x
C.
16
.
4
x
D.
16
.
4
x
Câu 7.
Từ một tấm tôn hình chữ nhật người ta cuộn
thành một chiếc thùng hình trụ không đáy (như hình
vẽ). Biết tâm tôn có chu vi bằng 120 cm. Để chiếc thùng
có thể tích lớn nhất thì chiều dài, rộng của mảnh tôn
lần lượt là
A.
35 cm; 25 cm.
B.
30 cm; 30 cm.
C.
40 cm; 20 cm.
D.
50 cm; 10 cm.
Câu 8. Bạn An có một tấm bìa hình tròn như hình vẽ, An muốn biến hình tròn đó
thành một cái phễu hình nón. Khi đó An phải cắt hình quạt tròn
OAB
rồi dán hai bán
11
kính
,OA OB
lại với nhau. Gọi
là góc ở tâm hình quạt tròn dùng làm phễu. Tìm
để thể tích phễu là lớn nhất.
A.
.
2
B.
.
3
C.
26
.
3
D.
.
4
Câu 9.
Có tấm bìa hình tam giác vuông cân
ABC
có cạnh huyền
BC
bằng
.
a
Người ta
muốn cắt tấm bìa đó thành hình chữ nhật
MNPQ
rồi cuộn lại thành một hình trụ không
đáy như hình vẽ. Diện tích hình chữ nhật đó
bằng bao nhiêu để diện tích xung quanh của hình trụ là lớn nhất ?
A.
2
.
2
a
B.
2
.
4
a
C.
2
.
8
a
D.
2
.
12
a
Câu 10. Cho tấm tôn hình nón có bán kính đáy là
2
,
3
r
độ dài đường sinh
2.
Người ta cắt theo một
đường sinh và trải phẳng ra được một hình quạt. Gọi
,
MN
thứ tự là trung điểm của
,.OA OB
Hỏi khi cắt hình quạt theo hình chữ nhật
MNPQ
(hình vẽ) và tạo thành hình trụ
(không đáy) có đường
PN
trùng
MQ
thì được khối trụ có thể tích bằng
A.
3 13 1
.
4
B.
3 13 1
.
8
C.
13 1
.
9
D.
5 13 1
.
12
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Câu 1.
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng
3
lần đường kính của đáy; Một viên bi và một khối nón đều bằng thủy tinh.
Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước.
Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì
thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại
trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
A.
1
.
2
B.
2
.
3
C.
4
.
9
D.
5
.
9
12
Câu 2. Một cái ống nghiệm hình trụ có bán kính trong lòng ống là
,R
ống
nghiệm đang chứa một lượng nước có chiều cao
.h
Người ta thả
3
viên bi có
cùng bán kính
R
vào ống nghiệm thì mực nước dâng lên vừa đủ phủ kín
viên bi cao nhất như hình vẽ. Khẳng định nào sau đây đúng?
A.
3.
hR
B.
2.hR
C.
2.hR
D.
3
3.hR
Câu 3.
Ba quả bóng dạng hình cầu có bán kính bằng
1
đôi một tiếp
xúc nhau và tiếp xúc với mặt phẳng
.P
Mặt cầu
S
bán kính
bằng
2
tiếp xúc với ba quả bóng trên. Gọi
M
là điểm bất kì trên
,S
MH
là khoảng cách từ
M
đến mặt phẳng
.P
Giá trị lớn
nhất của
MH
bằng
A.
30
3.
2
B.
69
3.
3
C.
123
3.
4
D.
52
.
9
Câu 4. Có một hình nón chứa bốn quả bóng bàn bằng nhau, đường
kính mỗi quả bóng bàn là
4.
Các quả bóng bàn tiếp xúc với nhau, ba
quả tiếp xúc với đáy của hình nón đồng thời bốn quả tiếp xúc với mặt
xung quanh của hình nón như hình vẽ. Chiều cao của hình nón bằng
A.
42
2.
3
B.
4
23 .
3
C.
4
2 3 2.
3

D.
42
2 3 2.
3

Câu 5.
Một khối hộp chữ nhật có kích thước
4 cm 4 cm cmh
chứa
một quả cầu lớn và tám quả cầu nhỏ. Biết quả cầu lớn có bán kính
2 cmR
và quả cầu nhỏ có bán kính
1cmr
; các quả cầu tiếp xúc
nhau và tiếp xúc các mặt của hình hộp (như hình vẽ). Tìm
h
.
A.
21 2 2h 
cm .
B.
21 7
h 
cm .
C.
23 7h 
cm .
D.
8h
cm .
Câu 6. Một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba
khối nón giống nhau có thiết diện qua trục là một tam giác vuông
cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với
nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh
của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với
hai cạnh của đáy bể (tham khảo hình vẽ). Sau đó người ta đặt lên
đỉnh của ba khối nón một khối cầu có bán kính bằng
4
3
lần bán kính đáy của khối
nón. Biết khối cầu vừa đủ ngập trong nước (mặt trên của bể là tiếp diện của mặt cầu)
và lượng nước tràn ra là
3
337
cm .
3
Thể tích lượng nước ban đầu ở trong bể xấp xỉ
A.
3
885,2 cm .
B.
3
1106,2 cm .
C.
3
1174,2 cm .
D.
3
1209,2 cm .
13
Câu 7. Cho hình nón có bán kính đáy
5,Ra
độ dài đường sinh
13 .a
Thể tích
khối cầu nội tiếp hình nón bằng
A.
3
40
.
9
a
B.
3
400
.
27
a
C.
3
4000
.
27
a
D.
3
4000
.
81
a
Câu 8.
Một bình đựng nước dạng hình nón (không có đáy), đựng
đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng
một nửa chiều cao của bình nước và đo được thể tích tràn ra là
3
32
dm .
3
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh
của hình nón và toàn bộ khối cầu chìm trong nước, trong đó mặt
nước là tiết diện của khối cầu (hình vẽ bên). Thể tích nước còn
lại trong bình bằng
A.
3
16
dm .
3
B.
3
32
dm .
3
C.
3
40
dm .
3
D.
3
64
dm .
3
Câu 9.
Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả
vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao
của bình nước và đo được thể tích nước tràn ra ngoài là
.V
Biết rằng
khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng
một nửa khối cầu chìm trong nước như hình vẽ.
Thể tích nước còn lại
trong ly bằng
A.
.V
B.
1
.V
C.
1
.
3
V
D.
1
.
6
V
Câu 10.
Nguời ta đặt được vào trong một hình nón hai khối cầu có
bán kính lần lượt là
a
và
2a
sao cho các khối cầu đều tiếp xúc với
mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và
khối cầu lớn tiếp xúc với đáy của hình nón (tham khảo hình vẽ). Bán
kính đáy của hình nón đã cho bằng
A.
5.
a
B.
2 2.a
C.
3.a
D.
8
.
3
a
Câu 11.
Người ta chế tạo ra một món đồ chơi cho trẻ em theo các
công đoạn như sau: Trước tiên, chế tạo ra một hình nón tròn
xoay có góc ở đỉnh là
2 60

bằng thủy tinh cho trong suốt.
Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ
khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc
với mặt nón, quả cầu lớn tiếp xúc với cả mặt đáy của hình nón
(hình vẽ). Biết rằng chiều cao của hình nón là
9 cm.
Bỏ qua bề
dày của các lớp vỏ thủy tinh, tổng thể tích của hai khối cầu bằng
A.
3
38
cm .
3
B.
3
40
cm .
3
C.
3
100
cm .
3
D.
3
112
cm .
3
14
Câu 12. Một ly nước có dạng như hình vẽ. Phần phía trên chứa
nước có dạng hình nón đỉnh
S
với đường kính đáy và chiều cao
SO
cùng bằng
8cm.
Ban đầu ly chứa lượng nước có chiều cao
4cm
so
với đỉnh
.S
Cho vào ly nước một viên bi sắt hình cầu thì nước dâng
lên vừa phủ kín viên bi. Tính bán kính
r
của viên bi làm tròn đến
hai chữ số thập phân.
A.
1, 23cm.
r
B.
1,28cm.
r
C.
1, 5 3 cm.
r
D.
1, 7 8 c m.r
Câu 13.
Một chiếc chén hình trụ có chiều cao bằng đường kính quả
bóng bàn. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài
của quả bóng có chiều cao bằng
3
4
chiều cao của nó. Gọi
12
, VV
lần
lượt là thể tích của quả bóng và chiếc chén. Khi đó
A.
12
3 2.VV
B.
12
9 8.VV
C.
12
16 9 .
VV
D.
12
27 8 .
VV
Câu 14. Một quả cầu có thể tích
3
256
cm
3
được đặt vào một
chiếc cốc có dạng hình trụ với đường kính đáy là
6 cm
như hình vẽ.
Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến
hàng phần trăm)
A.
2, 00 cm.
B.
4,00 cm.
C.
4,65 cm.
D.
6, 65 cm.
Câu 15. Một hình cầu nội tiếp trong một hình nón cụt. Hình cầu nội
tiếp trong hình nón cụt là hình cầu tiếp xúc với hai đáy của hình nón
cụt và tiếp với mặt xung quanh của hình nón cụt
(tham khảo hình vẽ).
Biết rằng thể tích khối nón cụt gấp đôi thể tích của khối cầu. T
ỉ lệ
giữa bán kính đáy lớn và bán kính đáy nhỏ của hình nón cụt bằng
A.
3.
B.
3
.
2
C.
15
.
2
D.
35
.
2
Phần 5. Mặt cầu ngoại tiếp khối chóp
Câu 1. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
và
.BC a
Cạnh bên
SA
vuông góc với đáy
.ABC
Gọi
, HK
lần lượt là hình chiếu vuông góc
của
A
lên cạnh bên
SB
và
.SC
Thể tích của khối cầu ngoại tiếp chóp
.A HKCB
bằng
A.
3
2.a
B.
3
.
2
a
C.
3
2
.
3
a
D.
3
.
6
a
Câu 2. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
và
.BD a
Hình
chiếu vuông góc của
S
trên mặt phẳng đáy là trung điểm
OD
. Đường thẳng
SD
tạo
với mặt đáy một góc bằng
0
60 .
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
.a
B.
.
2
a
C.
.
3
a
D.
.
4
a
15
Câu 3. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
. Đường
thẳng
SA
vuông góc với đáy
ABCD
và
2.SA a
Gọi
M
là trung điểm
,SC
mặt
phẳng
đi qua hai điểm
A
và
M
đồng thời song song với
BD
cắt
,SB
SD
lần lượt
tại
,E
.F
Bán kính mặt cầu đi qua năm điểm
, , , ,
SAEM F
bằng
A.
a
. B.
2.a
C.
.
2
a
D.
2
.
2
a
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Đường thẳng
SA
vuông góc đáy
.ABCD
Gọi
H
là hình chiếu của
A
trên đường thẳng
SB
. Bán kính
mặt cầu ngoại tiếp tứ diện
bằng
A.
a
. B.
2.a
C.
.
2
a
D.
2
.
2
a
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Tam giác
SAB
vuông tại
S
và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp
hình chóp
.S ABCD
bằng
A.
3
.
3
a
B.
3
2
.
3
a
C.
3
.
6
a
D.
3
11 11
.
162
a
Câu 6. Cho hình chóp
.O ABC
có
,OA OB OC a
60 ,AOB 
90 ,BOC 
120 .COA 
Gọi
S
là trung điểm của
.OB
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
.
2
a
B.
7
.
2
a
C.
.
4
a
D.
7
.
4
a
Câu 7. Cho hình chóp đều
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a
cạnh bên
bằng
23
.
3
a
Gọi
D
là điểm đối xứng của
B
qua
.C
Bán kính của mặt cầu ngoại tiếp
hình chóp
.S ABD
bằng
A.
37
.
6
a
B.
35
.
7
a
C.
36
.
7
a
D.
39
.
7
a
Câu 8. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang cân với
1,AD DC CB 
2.AB
Gọi
O
là giao điểm của
AC
và
,BD
hình chiếu vuông góc
của
S
xuống mặt
ABCD
là trung điểm của
.OA
Đường thẳng
SC
tạo với mặt đáy
ABCD
một góc bằng
60 .
Thể tích khối cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
17 59
.
54
B.
31 61
.
81
C.
31 51
.
162
D.
61 61
.
162
Câu 9. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
,B
1
.
2
AB BC AD a
Cạnh bên
6SA a
và vuông góc với đáy. Gọi
E
là trung điểm
của
.AD
Bán kính mặt cầu ngoại tiếp chóp
bằng
16
A.
114
.
2
a
B.
114
.
4
a
C.
114
.
6
a
D.
114
.
8
a
Câu 10. Cho hình chóp tứ giác đều
.S ABCD
có đáy
ABCD
là hình vuông tâm
,O
cạnh
2.a
Mặt bên tạo với đáy góc
0
60 .
Gọi
H
là hình chiếu vuông góc của
O
trên
.SD
Bán
kính mặt cầu ngoại tiếp tứ diện
HADC
bằng
A.
21
.
3
a
B.
21
.
6
a
C.
11 5
.
20
a
D.
11 5
.
50
a
Câu 11. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
SAD
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
M
và
N
lần lượt là trung
điểm của
BC
và
.CD
Bán kính của mặt cầu ngoại tiếp hình chóp
.S CMN
bằng
A.
37
.
6
a
B.
29
.
8
a
C.
53
.
12
a
D.
93
.
12
a
Câu 12. Cho tứ diện đều
ABCD
có mặt cầu nội tiếp là
1
S
và mặt cầu ngoại tiếp là
2
.S
Một hình lập phương ngoại tiếp
2
S
và nội tiếp mặt cầu
3
.S
Gọi
123
,,rrr
lần
lượt là bán kính các mặt cầu
123
,,.SSS
Khẳng định nào sau đây đúng ?
A.
1
2
2
3
r
r
và
2
3
1
.
3
r
r
B.
1
2
2
3
r
r
và
2
3
1
.
2
r
r
C.
1
2
1
3
r
r
và
2
3
1
.
3
r
r
D.
1
2
1
3
r
r
và
2
3
1
.
33
r
r
Câu 13. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
2
và hình
chiếu của
S
lên mặt phẳng
ABC
là điểm
H
nằm trong tam giác
ABC
sao cho
150 ,AHB 
120 ,BHC 
90 .CHA 
Biết tổng diện tích mặt cầu ngoại tiếp các hình
chóp
.,S HAB
.,
S HBC
.S HCA
là
124
.
3
Thể tích khối chóp
.S ABC
bằng
A.
9
.
2
B.
4
.
3
C.
9
.
4
D.
4.
Câu 14. Cho tứ diện
ABCD
với
,AB a CD b
và các cạnh còn lại có độ dài bằng
nhau. Gọi
, MN
lần lượt là trung điểm của
AB
và
CD
và
.MN m
Biết rằng tồn tại
một mặt cầu tiếp xúc với
6
cạnh của tứ diện đã cho. Hệ thức nào sau đây đúng ?
A.
2
.ab m
B.
2
2.
ab m
C.
2
2.ab m
D.
2
3 2.ab m
Câu 15. Cho hình chóp đều
.S ABC
có cạnh đáy bằng
.a
Gọi
,MN
lần lượt là trung
điểm của
,AB BC
và
P
là điểm thuộc tia đối của
SC
sao cho
3.SC SP
Biết rằng
trong các mặt cầu đi qua
,,AM N
thì mặt cầu ngoại tiếp tứ diện
AMNP
có bán kính
nhỏ nhất. Thể tích của hình chóp
.S ABC
bằng
A.
3
2
.
16
a
B.
3
2
.
32
a
C.
3
2
.
48
a
D.
3
2
.
96
a
17
Phần 6. Bài toán cực trị
Câu 1.
Một hình trụ có thể tích
V
không đổi. Tìm mối quan hệ giữa
bán kính
r
của đáy và chiều cao
h
của hình trụ khi diện tích toàn
phần đạt giá trị nhỏ nhất.
A.
.hr
B.
2.hr
C.
3.hr
D.
2.hr
Câu 2. Một hộp sữa hình trụ có thể tích
V
(không đổi) được làm từ một tấm tôn có
diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa
bán kính đáy
r
và đường cao
h
là
A.
.hr
B.
2.hr
C.
3.
hr
D.
2.hr
Câu 3. Trong số các hình trụ có diện tích toàn phần đều bằng
S
thì
bán kính
r
và chiều cao
h
của khối trụ có thể tích lớn nhất là
A.
1
;.
2 22
SS
rh


B.
;2.
22
SS
rh


C.
1
;.
6 26
SS
rh


D.
;2.
66
SS
rh


Câu 4.
Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có
thể tích
V
không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp
của thùng bằng nhau và đắt gấp
3
lần so với giá vật liệu để làm mặt
xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao
của thùng là
h
và bán kính đáy là
.
r
Tính tỷ số
h
r
sao cho chi phí vật liệu sản xuất
thùng nhỏ nhất.
A.
1.
h
r
B.
2.
h
r
C.
6.
h
r
D.
9.
h
r
Câu 5. Nam muốn xây một bình chứa hình trụ có thể tích
3
72m .
Đáy làm
bằng bêtông giá 100 nghìn đồng
2
/m ,
thành làm bằng tôn giá 90 nghìn đồng
2
/m ,
nắp
bằng nhôm giá 140 nghìn đồng
2
/m .
Vậy đáy của hình trụ có bán kính bằng bao
nhiêu để chi phí xây dựng là thấp nhất ?
A.
3
2
m.
B.
3
3
m.
C.
3
3
m.
D.
3
3
m.
2
Câu 6 Trong tất cả các hình nón có độ dài đường sinh
bằng
.
Hình nón có thể tích lớn nhất bằng
A.
3
3
.
9
B.
3
23
.
9
C.
3
3
.
27
D.
3
23
.
27
18
Câu 7. Trong các hình nón cùng có diện tích toàn phần bằng
.S
Hình nón có thể tích
lớn nhất khi (
, r
lần lượt là bán kính đáy và đường sinh của hình nón)
C.
.r
D.
2.r
B.
2 2.
r
A.
3.r
Câu 8. Cho hình nón đỉnh
S
có đáy là đường tròn tâm
.O
Thiết diện qua trục hình
nón là một tam giác cân với cạnh đáy bằng
a
và có diện tích là
2
.a
Gọi
,AB
là hai
điểm bất kỳ trên đường tròn
.
O
Thể tích khối chóp
.S OAB
đạt giá trị lớn nhất bằng
A.
3
.
2
a
B.
3
.
6
a
C.
3
.
12
a
D.
3
2
.
12
a
Câu 9. Cho mặt cầu
S
bán kính
5 cm.R
Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
C
có chu vi
bằng
8 cm.
Bốn điểm
,,,ABC D
thay đổi sao cho
,,ABC
thuộc đường tròn
C
, điểm
D
thuộc
S
D C
và tam giác
ABC
đều. Thể tích lớn nhất của tứ diện
ABCD
bằng
A.
3
20 3 cm .
B.
3
32 3 cm .
D.
3
60 3 cm .
D.
3
96 3 cm .
Câu 10. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng
9,
hình chóp có thể tích lớn nhất bằng
A.
484.
B.
529.
C.
576.
D.
625.
Câu 11.
Cho hình nón
1
N
có đỉnh
,
S
chiều cao
.h
Một hình
nón
2
N
có đỉnh là tâm của đáy
1
N
và có đáy là một thiết diện
song song với đáy của
1
N
như hình vẽ. Khối nón
2
N
có thể
tích lớn nhất khi chiều cao
x
bằng
A.
.
2
h
B.
.
3
h
C.
2
.
3
h
D.
3
.
3
h
Câu 12.
Cho hình lập phương
.ABCD A B C D

có thể tích
bằng
1.
Gọi
N
là một hình nón có tâm đường tròn đáy
trùng với tâm của hình vuông
,ABCD
đồng thời các điểm
,,,ABC D

nằm trên các đường sinh của hình nón như
hình vẽ. Thể tích khối nón
N
có giá trị nhỏ nhất bằng
A.
2
.
3
B.
3
.
4
C.
9
.
8
D.
9
.
16
19
Câu 13. Trong các hình nón nội tiếp một hình cầu có bán kính
bằng
R
không đổi, tính chiều cao
h
và bán kính mặt đáy
r
của
hình nón có thể tích lớn nhất.
A.
4 22
; .
33
h Rr R
B.
33
; .
4
22
h Rr R

C.
42
; .
33
h Rr R
D.
31
; .
22
h Rr R
Câu 14.
Cho mặt cầu
S
có bán kính
R
không đổi, hình nón
N
bất kì nội tiếp mặt cầu
S
như hình vẽ. Thể tích khối nón
N
là
1
V
; thể tích phần còn lại là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng
A.
32
.
49
B.
32
.
76
C.
49
.
81
D.
32
.
81
Câu 15. Một hạt ngọc trai hình cầu có bán kính
R
được bọc trong
một hộp trang sức dạng hình nón ngoại tiếp mặt cầu như hình vẽ.
Hỏi nhà sản xuất phải thiết kế hộp trang sức hình nón có chiều cao
h
như thế nào để hộp quà đó có thể tích nhỏ nhất.
A.
22.hR
B.
3.
hR
C.
4.hR
D.
5.
hR
Câu 16. Cho nửa hình cầu bán kính
R
không đổi. Một hình
nón có chiều cao
,
h
bán kính đáy là
r
tiếp xúc với nửa hình
cầu như hình vẽ (hai đường tròn đáy là đồng tâm và cùng thuộc
một mặt phẳng). Khi diện tích xung quanh của hình nón là nhỏ
nhất, khẳng định nào sau đây đúng ?
A.
.hr
B.
2.hr
C.
3.hr
D.
2 3.
hr
Câu 17. Cho một hình nón có chiều cao
h
và bán kính của đường
tròn đáy là
.
R
Một mặt phẳng
P
thay đổi song song với mặt
chứa đáy của hình nón và cắt hình nón theo một đường tròn giao
tuyến
.C
Dựng hình trụ
H
có một đáy là đường tròn
C
và
đáy còn lại nằm trên mặt đáy của hình nón như hình vẽ. Khi khối
trụ
H
có thể tích lớn nhất, gọi
h
là chiều cao
của
H
và
R
là bán kính đáy của
.H
Khẳng định nào sau đây đúng ?
A.
11
; .
22
h hR R


B.
12
; .
33
h hR R


C.
13
; .
44
h hR R


D.
31
; .
44
h hR R


20
Câu 18. Cho khối gỗ hình trụ có bán kính
3 cm
và chiều cao
6 cm ,
đáy là hai hình tròn tâm
O
và
.O
Đục khối gỗ này
tạo ra hai khối nón có đỉnh nằm trên
OO
và đáy trùng với
hai đáy của khối gỗ sao cho góc ở đỉnh bằng
0
60
(như hình vẽ)
và
OI x
3 2 3 3.x
Giá trị nhỏ nhất của tổng diện
tích xung quanh hai hình nón đã đục bằng
A.
2
12 cm .
B.
2
14 cm .
C.
2
44 cm .
D.
2
72 cm .
Câu 19.
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh bằng
2.
a
Cạnh bên
4SA a
và vuông góc với
đáy. Gọi
M
là một điểm trên cạnh
SA
(khác
A
và
S
).
Mặt phẳng
qua
M
và vuông góc với
SA
cắt
, , SB SC SD
lần lượt tại
, , .NPQ
Hình trụ
H
có đáy là
đường tròn ngoại tiếp tứ giác
MNPQ
và có một đường
sinh là
MA
như hình vẽ. Khi khối trụ
H
có thể tích lớn nhất thì tỉ số
SM
SA
bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
4
Câu 20. Cho hình trụ có đáy là hai đường tròn
;OR
và
;,OR
chiều cao bằng
đường kính đáy. Trên đường tròn tâm
O
lấy điểm
,A
trên đường tròn tâm
O
lấy
điểm
.B
Thể tích của khối tứ diện
OO AB
có giá trị lớn nhất bằng
A.
3
.
2
R
B.
3
.
3
R
C.
D.
3
.
6
R
---------- HẾT ----------
1
NÓN – TRỤ – CẦU
Vận dụng cao
Phần 1. Thể tích và các yếu tố liên quan
Phần 2. Vật thể tròn xoay
Phần 3. Ứng dụng thực tiễn
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Phần 5. Mặt cầu ngoại tiếp khối đa diện
Phần 6. Bài toán cực trị
2
Phần 1. Thể tích và các yếu tố liên quan
Câu 1.
Một chiếc thùng hình trụ có bán kính đáy
20,R
bên
trong đựng một lượng nước. Biết rằng khi nghiêng thùng sao cho
đường sinh của hình trụ tạo với mặt đáy góc
45
cho đến khi
nước lặng thì mặt nước chạm vào hai điểm
A
và
B
nằm trên hai
mặt đáy như hình vẽ bên. Thể tích của thùng đã cho bằng
A.
16000 .
B.
12000 .
C.
D.
Lời giải.
Xét phần mặt cắt và kí hiệu các điểm như hình vẽ.
Ta có
45BAC 
suy ra
vuông cân nên
40.BC CA
Vậy thể tích thùng nước
2
. 16000 .
2
AC
V BC



Chọn A.
Câu 2. Cho hình lăng trụ tứ giác đều
..ABCD EFGH
Tính tỉ số
k
giữa thể tích khối
trụ ngoại tiếp và thể tích khối trụ nội tiếp hình lăng trụ trên.
A.
2.k
B.
2.
k
C.
2 2.k
D.
4.
k
Lời giải. Hai khối trụ có chung đường cao nên
2
2
2
1
2
2
R
V
R
k
Vr
h
rh



với
2
22
AC AB
R

là bán kính đường tròn ngoại tiếp đáy;
2
AB
r
là bán kính đường tròn nội tiếp đáy. Chọn B.
Câu 3.
Cho một hình trụ tròn xoay và hình vuông
ABCD
cạnh
a
có
hai đỉnh liên tiếp
, AB
nằm trên đường tròn đáy thứ nhất của hình
trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ.
Mặt phẳng
ABCD
tạo với đáy hình trụ góc
45
như hình vẽ. Thể
tích khối trụ bằng
A.
3
.
16
a
B.
3
2
.
16
a
C.
3
3
.
16
a
D.
3
32
.
16
a
Lời giải. Tam giác
IOM
vuông cân có
,
2
a
IM
suy ra
.
22 2
aa
IO OM OO
 
Tam giác cân
,OAB
có
6
.
22
4
a
OM
a
OA OB
AB a

Vậy
3
22
32
..
16
a
V R h OA OO


Chọn D.
3
Câu 4. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không
vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song

,AB A B
mà

6 cmAB A B
. Biết diện tích tứ giác

ABB A
bằng
2
60 cm .
Chiều cao của hình trụ đã cho bằng
A.
43
cm. B.
53
cm. C.
62
cm. D.
82
cm.
Lời giải. Dựng đường sinh
BC
và
'AD
, suy ra tứ giác

ABCD
là
hình chữ nhật. Suy ra
ABCD
là hình bình hành và nội tiếp được
nên là hình chữ nhật. Từ đó chứng minh được
ABB A

là hình chữ
nhật. Do đó
60
. 10 cm
6
ABB A
S AB BB BB



6, 2 8 2
6 2 cm.
AB AC R
BC


Chọn C.
Câu 5. Một thùng hình trụ có chiều cao
3m,
h
bán kính đường tròn đáy
1mR
chứa một lượng nước. Biết rằng nếu đặt thùng nằm ngang ta được chiều cao mực nước
trong thùng là
0,5m.d
Hỏi thể tích lượng nước có trong thùng gần nhất với kết quả
nào sau đây ?
A.
3
1, 7 5m .
B.
3
1, 8 m .
C.
3
1, 8 5m .
D.
3
1, 9 m .
Lời giải. Xét mặt cắt vuông góc với trục của hình trụ và kí hiệu như hình vẽ.
Ta có
00
1
cos 60 120 .
2
OH R d
HOB HOB AOB
OB R

Suy ra
quat
1
3
AOB
S
hình tròn đáy
1
.
3
Suy ra diện phần gạch sọc bằng:
quat
13
.
34
AOB AOB
SS S

Vậy thể tích lượng nước trong thùng:
3
33
. 1, 8 4 m .
4
V Sh

Chọn C.
Câu 6. Cho một hình trụ có bán kính đáy bằng
R
và có chiều cao bằng
3.R
Hai
điểm
, AB
lần lượt nằm trên hai đường tròn đáy sao cho góc giữa
AB
và trục của
hình trụ bằng
0
30
. Khoảng cách giữa
AB
và trục của hình trụ bằng
A.
.
R
B.
3.R
C.
3
.
2
R
D.
3
.
4
R
Lời giải. Kẻ đường sinh
.AA
Suy ra
.OO ABA

Khi đó
, , ,.d OO AB d OO ABA d O ABA


 




Gọi
H
là trung điểm
,AB
ta có
OH AB
O H ABA
O H AA




nên
,.d O ABA O H




Tam giác vuông
,ABA
có
0
tan 30 .
BA AA R


Suy ra tam giác
A BO

đều, có cạnh bằng
R
nên
3
.
2
R
OH
Chọn C.
4
Câu 7. Cho hình trụ có hai đáy là hai hình tròn
O
và
,O
thiết diện qua trục của
hình trụ là hình vuông. Gọi
,
AB
là hai điểm lần lượt nằm trên hai đường tròn
O
và
.
O
Biết
2AB a
và khoảng cách giữa hai đường thẳng
AB
và
OO
bằng
3
.
2
a
Bán kính đáy của hình trụ bằng
A.
14
.
2
a
B.
14
.
3
a
C.
2
.
4
a
D.
14
.
4
a
Lời giải. Đặt
,
OA O B R

suy ra
2.
OO R
Tương tự như bài trước. Kẻ đường sinh
22
4 4.AA BA a R


Xét tam giác cân
,AOB

có
22
14
44 .
4
3
2
A O BO R
a
AB a R R
a
OH



Chọn D.
Câu 8. Cho hình trụ có đáy là hai đường tròn tâm
O
và
,O
bán kính đáy bằng chiều
cao và bằng
.a
Trên đường tròn tâm
O
lấy điểm
,
A
trên đường tròn tâm
O
lấy điểm
B
sao cho
2.
AB a
Thể tích của khối tứ diện
OO AB
bằng
A.
3
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
6
a
D.
3
3
.
12
a
Lời giải.
Kẻ đường sinh
AM
và
BN
như hình vẽ.
Ta có
. . ..
1 12 1
.. . .
2 23 3
OOAB AOOBN AON MOB AON MOB AMOB
VV V V V




Tương tự như bài trước. Tính được
3.MB a
Xét tam giác cân
có
.
2
3
OM OB a
a
OH
MB a



Khi đó
3
.
11 3
. 3. .
3 2 2 12
OOAB AMOB
aa
VV a a




Chọn D.
Câu 9. Một hình trụ có bán kính đáy
70cmR
và chiều cao
20cm.h
Một hình vuông
ABCD
có hai cạnh
AB
và
CD
lần
lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng
ABCD
không vuông góc với mặt đáy của hình trụ (tham
khảo hình vẽ). Cạnh của hình vuông
ABCD
có độ dài bằng
A.
80cm.
B.
100cm.
C.
100 2cm.
D.
140cm.
5
Lời giải. Dựng đường sinh
,
AA
ta có
.
CD AA
CD AA D CD A D
CD AD

 
Suy ra
AC
là đường kính đáy nên
2 140cm.AC R

Tam giác vuông
,AA C
có
22
100 2cm.AC AA A C


Suy ra cạnh hình vuông bằng
100cm.
Chọn B.
Câu 10.
Cho hình nón có đỉnh
,S
trục
,SO
bán kính
,
R
chiều
cao
.h
Dây cung
AB
thuộc đường tròn đáy và cách
O
một
khoảng
2
R
như hình vẽ. Ký hiệu
12
,SS
lần lượt là diện tích
xung quanh của mặt nón và diện tích tam giác
.SAB
Biết
1
2
10
,
33
S
S
mệnh đề nào sau đây đúng ?
A.
5
.
22
hR
B.
11
.
8
hR
C.
21.hR
D.
1
.
3
hR
Lời giải. Đường sinh của hình nón
22
.SB SA R h
Khi đó
22
1
.S R RR h
Pytago, ta được
2
22 2
4
R
SI SO OI h 
và
22
3
3.
2
R
IA OA OI AB R

Khi đó
2
2
2
11
. 3. .
22 4
R
S AB SI R h
Theo đề
2
22 2
1
2
10 3 11
3 3. 10 . . .
24 8
33
S
RR R
RR h h h
S
 
Chọn B.
Câu 11.
Cho hình chóp tam giác đều
..S ABC
Hình nón có đỉnh
S
và có đường tròn đáy là đường tròn nội tiếp tam giác
ABC
gọi là
hình nón nội tiếp hình chóp
.,S ABC
hình nón có đỉnh
S
và có
đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
gọi là hình
nón ngoại tiếp hình chóp
..S ABC
Tỉ số thể tích của hình nón nội
tiếp và hình nón ngoại tiếp hình chóp đã cho bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
1
.
4
Lời giải. Hai hình nón có cùng chiều cao nên tỉ số thể tích bằng tỉ số diện tích mặt
đáy. Vì tam giác
ABC
đều nên bán kính đường tròn ngoại tiếp bằng
2
3
đường cao của
tam giác; bán kính đường tròn nội tiếp bằng
1
3
đường cao của tam giác.
6
Suy ra
11
22
11
.
24
VS
r
R VS

Chọn D.
Câu 12. Cho hình nón đỉnh
S
có đáy là hình tròn tâm
.O
Dựng hai đường sinh
SA
và
,SB
biết tam giác
SAB
vuông và có diện tích bằng
2
4.a
Góc tạo bởi giữa trục
SO
và mặt phẳng
SAB
bằng
0
30 .
Đường cao
h
của hình nón bằng
A.
2.ha
B.
3.
ha
C.
3
.
2
a
h
D.
6
.
4
a
h
Lời giải. Gọi
E
là trung điểm
.AB
Tam giác
SAB
vuông cân tại
S
nên
2.
AB SE
Ta có
2
11
. . 4 .2 . 2 .
22
SAB
S AB SE a SE SE SE a

Dễ dàng xác định được:
0
30 , .SO SAB OSE

Tam giác vuông
,
SOE
có
.cos 3.SO SE OSE a
Chọn B.
Câu 13. Cho hình nón đỉnh
S
có đường cao
.SO
Gọi
,
AB
là hai điểm thuộc đường
tròn đáy của hình nón sao cho khoảng cách từ
O
đến
AB
bằng
a
và
0
30 ,SAO
0
60 .SAB
Độ dài đường sinh
của hình nón bằng
A.
.a
B.
2.a
C.
3.a
D.
2.a
Lời giải. Gọi
I
là trung điểm
,AB
suy ra
OI AB
nên
.OI a
Đặt
0
2
.
cos30
3
SOA
OA R
OA R SA

Tam giác
SAB
cân và có
0
60SAB
nên là tam giác đều.
Suy ra
1
.
2
3
R
AI SA

Trong tam giác vuông
,OIA
ta có
2
2 2 2 22
3
.
3
2
Ra
OA OI IA R a R 
Suy ra
2.SA a
Chọn B.
Câu 14. Một cái phễu có dạng hình nón, chiều cao của phễu là
20 cm
(Hình 1). Người
ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu là
10 cm.
Nếu bịt kín miệng phễu rồi lật ngược lên (Hình 2).
Khi đó chiều cao cột nước trong phễu bằng giá trị nào sau đây ?
A.
0,87 cm.
B.
1, 07 cm .
C.
5 cm.
D.
7
Lời giải. Xét phần mặt cắt và kí hiệu các điểm như hình vẽ.
Gọi
12
,,VV V
lần lượt là thể tích của phễu, của phần chứa
nước, và phần không chứa nước. Ta có
2
2
1
1
.
3
.
1
.
3
V HM AH
V PN AP
Suy ra
33
2
12
2
. 11 7
.
28 8
.
VV
PN AP AP
V AH V
HM AH









Khi lật ngược phễu, ta có
33
2
3
77
. 19,13 cm .
88
V
AK AK
AK AH
V AH AH
 







 
Suy ra
0,87 cm .HK
Chọn A.
Câu 15. Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng
là một khối nón có chiều cao
10 cm
(mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất
chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất
sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn
5 cm
. Tính
chiều cao
h
của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất
lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao
hụt khi chuyển. Tính gần đúng
h
với sai số không quá
0, 01 cm
).
A.
9, 09 cm .
B.
9,18 cm .
C.
9,56 cm .
D.
9,57 cm .
Lời giải. Gọi
1
r
,
2
r
và
3
r
theo thứ tự là bán kính của chiếc ly, bán kính của khối chất
lỏng còn lại trong ly thứ nhất và bán kính của khối chất lỏng trong ly thứ hai (sau khi
chuyển chất lỏng từ ly thứ nhất sang ly thứ hai).
Ta có
21
2
1
1
22
rr
r
r

và
3
1
3
1
.
10 10
r
rh
h
r
r

Thể tích của khối chất lỏng được chuyển từ ly thứ nhất sang ly thứ hai là
22 2
12 1
1 35
.10 .5 .
3 12
V rr r 
1
Mặt khác, ta có
2
2 23
1
31
11 1
.
3 3 10 300
rh
V rh h rh



2
Từ
1
và
2,
ta có
23 2 3
11
1 35
875 9,56 cm .
300 12
rh r h h
 
Chọn C.
8
Câu 16. Cho một đồng hồ cát gồm
2
hình nón chung đỉnh ghép
lại, trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc
60
như hình bên. Biết rằng chiều cao của đồng hồ là
30cm
và
tổng thể tích của đồng hồ là
3
1000 cm .
Hỏi nếu cho đầy lượng
cát vào phần trên thì khi chảy hết xuống dưới, khi đó tỉ lệ thể
tích lượng cát chiếm chỗ và thể tích phần dưới là bao nhiêu ?
A.
1
.
33
B.
1
.
8
C.
1
.
27
D.
1
.
64
Lời giải. Gọi bán kính của hình nón lớn và nón nhỏ lần lượt là
, .xy
Suy ra chiều cao của hình nón lớn và nón nhỏ lần lượt là
3, 3.xy
Theo giả thiết, ta có
22
3 3 30
11
. 3 . 3 1000
33
xy
xx yy



33
10 3
20 3 10 3
,.
33
1000 3
xy
xy
xy



Do hai hình nón đồng dạng nên tỉ số cần tính bằng
3
1
.
8
y
x


Chọn B.
Câu 17. Để tính diện tích xung quanh của một khối cầu bằng đá,
người ta thả nó vào trong một chiếc thùng hình trụ có chiều cao
2m,h
bán kính đường tròn đáy bằng
0,5mR
và chứa một
lượng nước có thể tích bằng
1
8
thể tích khối trụ. Sau khi thả khối
cầu đá vào khối trụ người ta đo được mực nước trong khối trụ cao
gấp ba lần mực nước ban đầu khi chưa thả khối cầu. Hỏi diện tích
xung quanh của khối cầu gần bằng kết quả nào được cho dưới đây ?
A.
2
1, 5m .
B.
2
1, 7 m .
C.
2
2, 6m .
D.
2
3, 4m .
Lời giải. Thể tích khối trụ
2
1
.
2
V Rh
Suy ra thể tích lượng nước
1
.
8 16
V
V

Từ giả thiết suy ra thể tích khối cầu:
3
3
Cau Cau Cau
41 3
22 .
3 16 32
VV R R

Vậy diện tích xung quanh của khối cầu là
22
Cau
4 2,6m .SR

Chọn C.
Câu 18.
Cho mặt cầu
S
tâm
,O
bán kính
3.R
Mặt phẳng
P
cách
O
một khoảng bằng
1
và cắt
S
theo giao tuyến là đường
tròn
C
có tâm
.H
Gọi
T
là giao điểm của tia
HO
với
,S
tính
thể tích
V
của khối nón đỉnh
,T
đáy là hình tròn
C
(như hình).
A.
16
.
3
V
B.
32
.
3
V
C.
16 .V
D.
32 .V
Lời giải. Từ giả thiết suy ra
1.OH
9
Suy ra chiều cao hình nón
3 1 4.
h TO OH 
Bán kính đường tròn đáy hình nón
22
2 2.r AH OA OH
Vậy thể tích khối nón cần tính
2
2
Non
1 1 32
. 2 2 .4 .
33 3
V rh

Chọn B.
Câu 19.
Một bình đựng nước dạng hình nón không nắp đựng đầy
nước. Biết rằng chiều cao của bình gấp
3
lần bán kính đáy của nó.
Người ta thả vào bình đó một khối trụ và đo được thể tích nước trào
ra ngoài là
3
16
dm .
9
Biết rằng một mặt của khối trụ nằm trên mặt
đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của
hình nón (như hình vẽ). Tính bán kính đáy
R
của bình nước.
A.
2 dm.R
B.
3 dm.R
C.
4 dm.R
D.
5 dm.R
Lời giải. Gọi
,
hh
lần lượt là chiều cao của khối nón và khối trụ;
,Rr
lần lượt là bán
kính đáy của khối nón và khối trụ. Khi đó
3, 2.h Rh R

Xét phần mặt cắt và gọi các điểm như hình vẽ.
Theo giả thiết
2
tru
16
.
9
V rh

Ta sẽ chuyển
tru
V
theo
.R
Cụ thể:
2
.
32 1 1
33 3
hR
r SI h h R R
rR
R SO h R


Khi đó
2
tru
16
2 2 dm.
99
R
VRR

Chọn A.
Câu 20. Xét một hình trụ nội tiếp trong hình nón như hình
bên, trong đó
S
là đỉnh hình nón,
O
là tâm đường tròn
mặt đáy. Các đoạn
, AB CD
lần lượt là đường kính của
đường tròn đáy của hình nón và hình trụ. Biết
,
AC BD
cắt
nhau tại điểm
M SO
và tỉ số thể tích của hình trụ và
hình nón là
4
.
9
Tỉ số
SM
SO
bằng
A.
2
.
3
B.
4
.
5
C.
5
.
6
D.
7
.
9
Lời giải.
Gọi
I
là trung điểm
.DC
Đặt
.
1
ID tOA
SI ID IM
t
IO t SO
SO OA MO


Theo giả thiết ta có
22
2
. .1
42
.
1
93
..
3
t OA t SO
t
OA SO

Suy ra
24
.
35
SI IM SM
SO MO SO

Chọn B.
10
Câu 21. Cắt một hình nón bằng một mặt phẳng song song với đáy
thì phần hình nón nằm giữa mặt phẳng và đáy gọi là hình nón
cụt. Một chiếc cốc có dạng hình nón cụt cao
9cm,
bán kính của
đáy cốc và miệng cốc lần lượt là
3cm
và
4cm.
Hỏi chiếc cốc có thể
chứa được lượng nước tối đa là bao nhiêu trong các lựa chọn sau ?
A.
250 ml.
B.
348 ml.
C.
349 ml.
D.
350 ml.
Lời giải. Gọi
, , Rrh
lần lượt là bán kính mặt đáy lớn, bán kính mặt đáy nhỏ và
chiều cao của hình nón cụt. Ta thiết lập được công thức tính thể tích của khối nón cụt
là
22
1
3
V R r Rr h

(lấy khối nón lớn trừ đi khối nón nhỏ).
Áp dụng với
4 cm, 3 cm, 9 cm.
Rrh
Ta được
3
348,7 cm 348,7 ml.V 
Chọn B.
Câu 22.
Phần không gian bên trong của chai nước ngọt có hình
dạng như hình vẽ. Biết bán kính đáy và bán kính cổ chai lần lượt
là
5 cm,
R
2 cm.r
Thể tích phần không gian bên trong của
chai nước ngọt (giả sử độ dày của vỏ chai không đáng kể) bằng
A.
3
412 cm .
B.
3
462 cm .
C.
3
490 cm .
D.
3
495 cm .
Lời giải. Xét phần mặt cắt và kí hiệu như hình vẽ.
Thể tích khối trụ có đường cao
CD
là:
23
1
. 400 cm .
V R CD

Thể tích khối trụ có đường cao
AB
là:
23
2
. 12 cm .V r AB


Thể tích phần nón cụt có đường cao
BC
là:
22 3
1
. 78 cm .
3
V R r Rr BC 
Vậy thể tích chai nước là:
3
123
490 cm .VVV V 
Chọn C.
Câu 23. Để định vị một trụ điện, người ta cần đúc một khối bê
tông có chiều cao
1, 5 m
h
gồm: Phần dưới có dạng hình trụ
bán kính
1mR
và có chiều cao bằng
1
;
3
h
Phần trên có dạng
hình nón bán kính đáy bằng
R
đã bị cắt bỏ bớt một phần hình
nón có bán kính đáy bằng
1
2
R
ở phía trên (người ta gọi hình đó là hình nón cụt);
Phần ở giữa rỗng có dạng hình trụ, bán kính đáy bằng
1
4
R
(tham khảo hình vẽ bên).
Tính thể tích
V
của khối bê tông (làm tròn đến chữ số thập phân thứ ba).
A.
3
2,814 m .V
B.
3
2,815m .V
C.
3
3,109m .V
D.
3
3, 403m .V
11
Lời giải. Thể tích của phần dưới có dạng hình trụ:
23
1
1, 5
.1. m .
3 32
h
VR

Thể tích của phần nón cụt có
1
1,
22
R
Rr 
và chiều cao bằng
2
1
3
h
là
3
2
1 17
1 1. m .
3 4 2 12
V




Thể tích của phần ở giữa rỗng có dạng hình trụ:
2
3
3
3
m.
4 32
R
Vh



Vậy thể tích cần tính
3
123
7 3 95
3,109 m .
2 12 32 96
VVVV

 
Chọn C.
Câu 24. Trong không gian cho một hình cầu
S
tâm
O
có bán kính
R
và một điểm
S
cho trước sao cho
2SO R
. Từ
S
ta kẻ các tiếp tuyến đến mặt cầu với tiếp điểm
thuộc đường tròn
1
.C
Trên mặt phẳng
P
chứa đường tròn
1
C
ta lấy điểm
E
thay
đổi nằm ngoài mặt cầu
.S
Gọi
N
là hình nón có đỉnh là
E
và đáy là đường tròn
2
C
gồm các tiếp điểm của tiếp tuyến kẻ từ
E
đến mặt cầu
.S
Biết rằng hai đường
tròn
1
C
và
2
C
luôn có cùng bán kính, khi đó quỹ tích các điểm
E
là một đường
tròn, đường tròn này có bán kính
R
bằng
A.
3
.
2
R
B.
15
.
2
R
C.
17
.
2
R
D.
15
.
4
R
Lời giải.
Gọi bán kính của
12
, CC
lần lượt là
12
, .rr
Gọi
C
là tâm của
1
C
và
D
là một điểm trên
1
.C
Suy ra
SOD
vuông tại
D
nên ta có
..CD OS DO DS
22 2
1
2
..
1.
DO DS R OS R R
r CD R
OS OS
OS

Tương tự, ta tính được

2
2
2
1.
R
rR
OE
Theo giả thiết:
12
rr
suy ra
2OE OS R
 E
di động trên đường tròn giao
tuyến của mặt cầu tâm
O
bán kính
2R
với mặt phẳng
.P
Lại có:

2
2
OD R
OC
OS

2
22 2
15
4.
42
RR
R OE OC R
Chọn B.
Câu 25. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông tại
,A
22BC
và
30 .ACB 
Hình chiếu của
S
trên mặt phẳng đáy là trung điểm
H
của
.BC
Giả sử có mặt
cầu tâm
,O
bán kính bằng
1
tiếp xúc với
, SA SB
và tia đối
của
SC
lần lượt tại
111
,,ABC
đồng thời mặt cầu tâm
O
đó
cũng tiếp xúc với mặt phẳng
ABC
(tham khảo hình vẽ).
Thể tích của hình chóp
.S ABC
bằng
12
A.
32
.
2
B.
3
.
3
C.
22
.
3
D.
23
.
3
Lời giải. Dựng
là mặt phẳng qua
S
và song
song với
.ABC
Ta chứng minh
.
O
Khi đó
, , 1.d S ABC d O ABC



Suy ra
.
3
.
3
S ABC
V
Thật vậy: • Tam giác
SBC
có
SH
là đường cao và
cũng là đường trung tuyến nên
SH
là đường
phân giác của góc
.BSC
1
• Hai góc
BSC
và
11
C SB
là hai góc kề bù.
2
• Tam giác
11
B SC
cân tại
.S
3
Từ
1,
2
và
3,
suy ra mặt phẳng phân giác của
11
C SB
(cũng là mặt phẳng trung
trực của
11
BC
) đi qua
S
và vuông góc với
SH
. Mặt phẳng này trùng với mặt phẳng
đã dựng ở trên. Vì
11
OB OC
nên suy ra
.O
Chọn B.
Phần 2. Vật thể tròn xoay
Câu 1.
Cho tam giác vuông cân
ABC
có
2
AB AC a
và hình
chữ nhật
MNPQ
với
2
MQ MN
được xếp chồng lên nhau sao cho
,MN
lần lượt là trung điểm của
,AB AC
(như hình vẽ). Tính thể
tích
V
của vật thể tròn xoay khi quay mô hình trên quanh trục
,AI
với
I
là trung điểm
.
PQ
A.
3
5
.
6
a
V
B.
3
11
.
6
a
V
C.
3
11
.
8
a
V
D.
3
17
.
24
a
V
Lời giải. Ta có:
22
2 , 2.BC AB AC a MN a MQ a 
Gọi
,EF
lần lượt là trung điểm
MN
và
.BC
Tính được
3
,.
2 22
BC a
AF a EF IF a 
Khi đó
22 3
1 17
.. .
3 24
V FB AF IQ IF a 
Chọn D.
Câu 2. Cho hình thang
ABCD
vuông
A
và
B
với
.
2
AD
AB BC a
Quay hình
thang và miền trong của nó quanh đường thẳng chứa cạnh
.BC
Tính thể tích
V
của
khối tròn xoay được tạo thành.
A.
3
4
.
3
a
V
B.
3
5
.
3
a
V
C.
3
7
.
3
a
V
D.
3
.Va
13
Lời giải. Thể tích khối tròn xoay tạo thành bằng thể tích hình trụ
có bán kính đáy
AB
và đường sinh
AD
trừ đi phần thể tích hình
nón có bán kính đáy
OD AB
và đường cao
.OC AD BC
Vậy
3
2 22 2
1 15
. . .2 . .
3 33
a
V AB AD OD OC a a a a
 
Chọn B.
Câu 3.
Cho hình bình hành
ABCD
có
2,AD a
3,
AB a
45BAD 
(như hình vẽ). Tính thể tích
V
của khối tròn
xoay nhận được khi quay hình bình hành
ABCD
quanh
trục
.AB
A.
3
5
.
2
a
V
B.
3
9
.
2
a
V
C.
3
5.Va
D.
3
6.Va
Lời giải. Gọi
H
là hình chiếu vuông góc của
D
lên cạnh
AB
2.
DH a
Khối tròn xoay nhận được khi quanh
hình bình hành
ABCD
quanh trục
AB
có thể tích đúng
bằng thể tích khối trụ có đường sinh
DC
và bán kính đáy
DH
(hai hình nón bù trừ nhau).
Vậy
2
22 3
. . 2 .3 6 .
V DH HK DH DC a a a  
Chon D.
Câu 4.
Một cơ sở sản xuất kem chuẩn bị làm
1000
chiếc
kem giống nhau theo đơn đặt hàng. Cốc đựng kem có
dạng hình tròn xoay được tạo thành khi quay hình thang
ABCD
vuông tại
A
và
D
xung quanh trục
AD
(xem
hình vẽ). Chiếc cốc có bề dày không đáng kể, chiều cao
7, 2 cm;
đường kính miệng cốc bằng
6,4 cm;
đường kính
đáy cốc bằng
1,6 cm.
Kem được đổ đầy cốc và dư ra phía
ngoài một lượng có dạng nửa hình cầu, có bán kính bằng
bán kính miệng cốc. Cơ sở đó cần dùng lượng kem gần
nhất với giá trị nào trong các giá trị sau
A.
3
132 dm .
B.
3
170 dm .
C.
3
293 dm .
D.
3
954 dm .
Lời giải. Thể tích của một chiếc kem cần tính bao gồm:
• Thể tích của hình nón cụt có lớn
3, 2 cm,R
0,8 cmr
và
7, 2 cm.h
• Thể tích của nửa khối cầu có bán kính
3, 2 cm.R
Suy ra
2 23 3
12
170 cm .
33
V h R Rr r R 
Vậy thể tích của
1000
chiếc kem là:
33 3
170.10 cm 170 dm .
Chọn B.
14
Câu 5.
Cho tam giác
SAB
vuông tại
,A
60 ,
ABS 
đường phân
giác trong
ABS
cắt
SA
tại
.I
Vẽ nửa đường tròn tâm
I
bán kính
IA
(như hình vẽ). Cho tam giác
SAB
và nửa đường tròn trên cùng
quay quanh
SA
tạo nên khối cầu và khối nón tương ứng có thể
tích là
1
V
và
2
.V
Khẳng định nào sau đây đúng ?
A.
12
3.VV
B.
12
2 3.VV
C.
12
4 9.VV
D.
12
9 4.VV
Lời giải. Ta có
3
33
1
1
2
22 3
2
4 4 43
tan 30
4
3 3 27
.
9
11 3
. . tan 60 .
33 3
V IA AB AB
V
V
V AB SA AB AB AB





Chọn D.
Câu 6. Cho hình vuông
ABCD
nội tiếp đường tròn
,O
bán kính
;r
tam giác đều
MNP
nội tiếp đường tròn đó và
MN
song song
AB
(như hình vẽ). Cho mô hình trên quay quanh đường thẳng
.OP
Kí
hiệu
123
,,VVV
là thể tích khối tròn xoay do hình vuông, hình tròn
và tam giác đều tạo thành. Khẳng định nào sau đây đúng ?
A.
1 23
.
VVV
B.
3 21
.VVV
C.
2
1 23
..V VV
D.
2
3 21
..
V VV
Lời giải. Gọi
,QI
lần lượt là trung điểm của
,.MN AB
Thể tích khối cầu (tạo bởi khi quay hình tròn quanh trục
OP
) là
3
2
4
.
3
r
V
Ta có
2AC r
cạnh hình vuông bằng
2r
nên
2
3
2
1
22
. .2 .
22
rr
V IB BC r




Ta có
3
2
OP r PQ r
cạnh tam giác đều bằng
3r
nên
2
3
2
3
1 1 333
. ..
3 32 2 8
rr r
V QN PQ




Vậy
2
1 23
..V VV
Chọn C.
Câu 7. Cho tam giác
ABC
vuông tại
A
và có
, 3.AC a AB a
Gọi
123
,,VVV
là thể
tích các khối tròn xoay sinh bởi tam giác
ABC
kể cả các điểm trong khi lần lượt quay
quanh các cạnh
,,.AB AC BC
Trong các khẳng định sau, khẳng định nào đúng ?
Hình 1 Hình 2 Hình 3
15
A.
1 32
1 11
.
V VV

B.
312
1 11
.
V VV

C.
2 22
2 32
1 11
.
V VV

D.
2 22
312
1 11
.
V VV

Lời giải. Khi tam giác
ABC
quay quanh cạch
AB
ta được khối nón có chiều cao
1
3h AB a
và có bán kính đáy là
1
R AC a
(Hình 1) nên
23
1 11
13
.
33
V Rh a
Khi tam giác
ABC
quay quanh cạch
AC
ta được khối nón có chiều cao
2
h AC a
và có bán kính đáy là
2
3
R AB a
(Hình 2) nên
23
2 22
1
.
3
V Rh a

Hạ đường cao
AI
của tam giác
ABC
. Khi quay tam giác
ABC
quanh cạnh
BC
ta
được hai khối nón sinh bởi hai tam giác
ABI
và
.ACI
Hai khối nón này có chung
đường tròn đáy có bán kính bằng độ dài đoạn
AI
(Hình 3). Do đó ta có
2
3
222 2
3
1 1 1 1 13
. . 2.
3 3 3 3 32 2
aa
V AI BI AI CI AI BI CI AI BC a




Từ đó suy ra
2 22
312
1 11
.
V VV

Chọn D.
Câu 8. Cho hình tứ diện
ABCD
có
AD
vuông góc với mặt phẳng
ABC
và tam giác
ABC
vuông tại
.B
Biết
,
BC a
3,AB a
3.
AD a
Quay các tam giác
ABC
và
ABD
(bao gồm cả điểm bên trong hai tam giác) xung quanh đường thẳng
AB
ta được
hai khối tròn xoay. Thể tích phần chung của hai khối tròn xoay bằng
A.
3
83
.
3
a
B.
3
33
.
16
a
C.
3
43
.
16
a
D.
3
53
.
16
a
Lời giải.
Khi quay tam giác
ABD
quanh
AB
ta được khối nón đỉnh
B
có đường cao
,BA
đáy là đường tròn bán kính
3.
AD a
Biểu
diễn các điểm như hình vẽ. Gọi
,
I AC BE
.IH AB H AB
Phần chung của hai khối
nón khi quay tam giác
ABC
và tam giác
ABD
quanh
AB
là hai khối nón có đỉnh
A
và đỉnh
,B
có đáy là đường tròn bán kính
.IH
Ta có
IBC IEA∽
1
3.
3
IC BC
IA IC
IA AE

Lại có
3 3. 3
.
4 44
AH IH AI BC a
IH BC IH
AB BC AC

Khi đó thể tích phần chung:
22
11
..
33
V IH AH IH BH
3
22
1 1 33
. ..
3 3 16
a
IH AH BH IH AB
 
Chọn B.
Câu 9. Ban đầu ta có một tam giác đều cạnh bằng
3
như hình 1. Tiếp theo ta chia
mỗi cạnh của tam giác thành
3
đoạn bằng nhau, dựng một tam giác đều về phía bên
16
ngoài có một cạnh là đoạn giữa, sau đó bỏ đi đoạn giữa ta được hình 2. Khi quay hình
2 xung quanh
d
ta được một khối tròn xoay có thể tích bằng
Hình 1
Hình 2
A.
B.
53
.
3
C.
D.
93
.
8
Lời giải. Kí hiệu các điểm như hình vẽ.
Ta có thể tích khối tròn xoay tạo thành bằng
2
lần thể tích nữa trên (hình
SIABK
quay quanh trục
SK
).
Tam giác
SIH
quay quanh trục
SK
tạo thành khối nón có
1
1
,
2
r IH

1
3
2
h SH
nên
2
1 11
1 113 3
.. .
3 3 4 2 24
V rh

Hình thang vuông
HABK
quay quanh trục
HK
tạo thành hình nón cụt có
3
,
2
R AH
1,r BK
3
2
h HK SH 
nên
22
2
19 3
.
3 24
h
V R r Rr


Vậy thể tích khối tròn xoay tọa thành:
12
53
2.
3
V VV

Chọn B.
Câu 10.
Cho nửa đường tròn đường kính
2AB R
và điểm
C
thay
đổi trên nửa đường tròn đó, đặt
CAB
và gọi
H
là hình chiếu
vuông góc của
C
lên
AB
(như hình vẽ). Tìm
sao cho thể tích vật
thể tròn xoay tạo thành khi quay tam giác
ACH
quanh trục
AB
đạt
giá trị lớn nhất.
A.
45 . 
B.
60 . 
C.
arctan 2.
D.
1
arctan .
2
Lời giải. Ta có
2
cos 2 cos
sin 2 cos sin .
cos 2 cos
AC AB R
CH AC R
AH AC R






Vật thể tròn xoay tạo thành khi quay
tam giác
ACH
quanh trục
AB
là một khối nón có bán kính đường tròn đáy
,
r HC
17
chiều cao
h AH
nên
2 32 2 2
14
. .cos .cos . 2 2 cos
33
V CH AH R  
3
22 2
3
3
cos cos 2 2 cos
4 32
..
3 27 81
R
R
 

Dấu
""
xảy ra
2 22
11
cos 2 2 cos tan arctan .
2
2
 
Chọn D.
Phần 3. Ứng dụng thực tiễn
Câu 1.
Bé Bách có một tấm bìa có chiều dài
20 cm;
chiều rộng
1 cm.
Bé muốn gấp một cái
hộp nhỏ xinh để bỏ kẹp tóc vào hộp đó tặng
quà cho mẹ ngày 20 tháng 10. Anh Siêu đã chỉ
cho bé hai cách gấp hộp. Cách thứ nhất là bé cuốn tấm bìa thành một cái hộp hình trụ
không có hai đáy có thể tích
1
.V
Cách thứ hai là bé gập tấm bìa một hình hộp chữ
nhật có thể tích
2
V
có các kích thước như hình vẽ. Hãy tìm tỉ số thể tích của hai hộp
để biết được gấp theo cách nào sẽ có thể tích lớn hơn.
A.
1
2
4
.
V
V
B.
1
2
.
4
V
V
C.
1
2
1
.
4
V
V
D.
1
2
4.
V
V
Lời giải. Chiều dài của tấm bìa là
20 cm,
suy ra
•
10
20 2 .
RR

(
R
là bán kính đường tròn đáy hình trụ).
• Theo đề bài thì hình hộp chữ nhật có đáy là hình vuông (hình vẽ) nên cạnh của hình
vuông bằng
20
5.
4
Khi đó
2
11 1
2
22 2
.1
4
.
.1
5
VS S
R
VS S

Chọn A.
Câu 2. Một tấm tôn hình tròn tâm
,O
bán kính
R
được chia thành hai hình
1
H
và
2
H
như hình vẽ. Cho biết góc
90 .AOB

Từ hình
1
H
gò tấm tôn để được hình
nón
1
N
không đáy và từ hình
2
H
gò tấm tôn để được hình nón
2
N
không đáy.
Ký hiệu
12
,VV
lần lượt là thể tích của hình nón
12
, .NN
Tỉ số
1
2
V
V
bằng
A.
2.
B.
3.
C.
3 105
.
5
D.
7 105
.
9
18
Lời giải. Hai hình nón có độ dài đường sinh bằng nhau:
12
.R
Gọi
12
, rr
lần lượt là bán kính đáy của hình nón
12
, .NN
Ta có
11
22
33
2 .2
44
.
1
2 .2
44
R
r Rr
R
r Rr




Khi đó
22 2
1 11
1
22 2
2
2 22
1
3 105
3
.
1
5
3
rr
V
V
rr

Chọn C.
Câu 3.
Từ cùng một tấm kim loại dẻo hình
quạt (như hình vẽ) có kích thước bán kính
5
R
và chu vi của hình quạt là
8 10,P
người ta gò tấm kim loại thành
những chiếc phễu theo hai cách:
Cách 1. Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu.
Cách 2. Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung
quanh của hai cái phễu. Gọi
1
V
là thể tích của cái phễu thứ nhất,
2
V
là tổng thể tích
của hai cái phễu ở cách thứ hai. Tỉ số
1
2
V
V
bằng
A.
1
2
2
.
7
V
V
B.
1
2
22
.
7
V
V
C.
1
2
21
.
7
V
V
D.
1
2
2 21
.
7
V
V
Lời giải. Chu vi của hình quạt
độ dài cung
2.R
Suy ra độ dài cung tròn
8.
Cách 1: Chu vi đường tròn đáy của cái phễu là
8.
Ta có
22 2
1 11 1 1
1
2 8 4 3 .4 .3 16 .
3
r r h Rr V

Cách 2: Chu vi đường tròn đáy của mỗi phễu nhỏ là
4.
Ta có
22 2
2 22 2 2
1 8 21
2 4 2 21 2 .2 . 21 .
33
r r h Rr V



Vậy
1
2
2 21
.
7
V
V
Chọn D.
Câu 4. Để làm cống thoát nước cho một khu vực dân cư người ta
cần đúc
500
ống hình trụ có đường kính trong và chiều cao của
mỗi ống bằng
1 m,
độ dày của thành ống là
10 cm.
Chọn mác bê
tông là
250
(tức mỗi khối bê tông là 7 bao ximăng). Hỏi phải
chuẩn bị bao nhiêu bao ximăng để làm đủ số ống nói trên ?
A.
1110 bao .
B.
1200 bao .
C.
1210 bao .
D.
4 210 bao .
Lời giải. Thể tích khối trụ có bán kính đáy
0, 6 m
là:
2
2
11
9
0, 6 .1 .
25
V Rh 
Thể tích khối trục có bán kính đáy
0,5 m
là:
2
2
22
1
0,5 .1 .
4
V Rh 
19
Lượng bê tông cho một ống là:
3
12
9 1 11
m.
25 4 100
VVV




Lượng bê tông để làm 500 ống là:
3
11
500 55 m .
100

Vậy số lượng bao ximăng cần chuẩn bị là:
55 .7 1210 bao .
Chọn C.
Câu 5.
Cắt một miếng tôn hình vuông
cạnh
1m
thành hai hình chữ nhật,
trong đó một hình có chiều rộng
m,x
gọi miếng tôn này là miếng tôn thứ
nhất. Người ta gò miếng tôn thứ nhất
thành một lăng trụ tam giác đều, miếng còn lại gò thành một hình trụ (như hình vẽ).
Tìm
x
để tổng thể tích khối lăng trụ và khối trụ thu được là nhỏ nhất.
A.
9
.
39
x
B.
1
.
33 1
x
C.
9
.
93
x
D.
1
.
3
x
Lời giải. Chu vi tam giác đáy của lăng trụ là
,x
mà đáy của lăng trụ là tam giác đều
nên có diện tích bằng
2
3
.
36
x
Gọi
r
là bán kính đáy của hình trụ. Suy ra
1
21 .
2
x
r xr

Tổng thể tích của hai khối:
2
2
2
3 1 31 1 1
.1 .1 .
36 2 36 4 2 4
xx
x x fx






Đây là hàm bậc hai nên
9
, 0;1 .
39
fx f x



Chọn A.
Câu 6. Một tấm tôn hình chữ nhật có chiều dài
4m,
chiều rộng
1m.
Một người thợ
muốn cắt tấm tôn này thành hai phần như hình vẽ. Người thợ gò phần
1
thành hình
trụ có đáy hình vuông và phần
2
thành hình trụ có đáy hình tròn. Tìm
x
để tổng thể
tích của hai khối trụ là nhỏ nhất.
A.
4
.
4
x
B.
8
.
4
x
C.
16
.
4
x
D.
16
.
4
x
Lời giải. Gọi
r
là bán kính đáy của hình trụ. Suy ra
4
24 .
2
x
r xr

Tổng thể tích của hai khối:
22
2
4 11 2 4
.1 .1 .
4 2 16 4
xx
x x fx










20
Đây là hàm bậc hai nên
16
, 0; 4 .
4
fx f x



Chọn C.
Câu 7. Từ một tấm tôn hình chữ nhật người ta cuộn
thành một chiếc thùng hình trụ không đáy (như hình
vẽ). Biết tâm tôn có chu vi bằng 120 cm. Để chiếc thùng
có thể tích lớn nhất thì chiều dài, rộng của mảnh tôn
lần lượt là
A.
35 cm; 25 cm.
B.
30 cm; 30 cm.
C.
40 cm; 20 cm.
D.
50 cm; 10 cm.
Lời giải. Gọi chiều dài tấm tôn là
cmx
0 60 .
x
Suy ra chiều rộng:
60 cm .x
Giả sử quấn cạnh có chiều dài là
x
bán kính đáy
2
x
r
và chiều cao
60 .hx
Khi đó
3
32
Cosi
23
. . 120 2 120 2
60 8000
cm .
4 8 8 .27
xx x x x x
xx
V rh




Dấu
""
xảy ra
120 2 40 cm .
x xx
 
Chọn C.
Câu 8. Bạn An có một tấm bìa hình tròn như hình vẽ, An muốn biến hình tròn đó
thành một cái phễu hình nón. Khi đó An phải cắt hình quạt tròn
OAB
rồi dán hai bán
kính
,OA OB
lại với nhau. Gọi
là góc ở tâm hình quạt tròn dùng làm phễu. Tìm
để thể tích phễu là lớn nhất.
A.
.
2
B.
.
3
C.
26
.
3
D.
.
4
Lời giải. Thể tích của phễu
2 22
11
.
33
V rh R h h

Khảo sát ta thấy
V
đạt GTLN khi
.
3
R
h
Suy ra
2
.
3
R
r
Ta có
AB
chu vi đường tròn đáy của hình nón
26
2.
3
Rr
 
Chọn C.
Câu 9. Có tấm bìa hình tam giác vuông cân
ABC
có cạnh huyền
BC
bằng
.a
Người ta
muốn cắt tấm bìa đó thành hình chữ nhật
MNPQ
rồi cuộn lại thành một hình trụ không
đáy như hình vẽ. Diện tích hình chữ nhật đó
bằng bao nhiêu để diện tích xung quanh của hình trụ là lớn nhất ?
21
A.
2
.
2
a
B.
2
.
4
a
C.
2
.
8
a
D.
2
.
12
a
Lời giải. Kẻ đường cao
AH
cắt
MN
tại
K
như hình vẽ.
Tam giác
ABC
vuông cân nên
.
2
a
AH BH CH
Đặt
MK x
0.
2
a
x



Suy ra
.
2
a
AKMKx KH x  
Chu vi đáy hình trụ bằng
2 2.MK x
Do đó
2
2
xq
2
2. 2. 2 .
2 48
a
xx
aa
S x KH x x






Dấu
'' ''
xảy ra
.
4
a
x
Khi đó
2
2
2
.
8
4
MNPQ
a
MN x
a
S
a
KH


Chọn C.
Nhận xét: Diện tích xung quanh của hình trụ chính là diện tích của hình chữ nhật.
Câu 10. Cho tấm tôn hình nón có bán kính đáy là
2
,
3
r
độ dài đường sinh
2.
Người ta cắt theo một
đường sinh và trải phẳng ra được một hình quạt. Gọi
, MN
thứ tự là trung điểm của
,.OA OB
Hỏi khi cắt hình quạt theo hình chữ nhật
MNPQ
(hình vẽ) và tạo thành hình trụ
(không đáy) có đường
PN
trùng
MQ
thì được khối trụ có thể tích bằng bao nhiêu ?
A.
3 13 1
.
4
B.
3 13 1
.
8
C.
13 1
.
9
D.
5 13 1
.
12
Lời giải. Độ dài cung
AB
bằng chu vi đáy của hình nón và bằng
24
2. .
33
Ta có
0
42
. . 120 30 120 .
33
AB
OA AOB AOB AOB ONM ONP

 
Áp dụng định lí cosin trong tam giác
,OAB
ta được
2 3 3.AB MN
Áp dụng định lí cosin trong tam giác
,ONP
ta được
1 13
.
2
NP

Khi đó hình chữ nhât
MNPQ
được cuốn thành mặt trụ có chiều cao
13 1
2
h NP

,
bán kính đáy
3
.
22
MN
R


Vậy thể tích khối trụ
3 13 1
.
8
V
Chọn B.
22
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Câu 1.
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng
3
lần đường kính của đáy; Một viên bi và một khối nón đều bằng thủy tinh.
Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước.
Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì
thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại
trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
A.
1
.
2
B.
2
.
3
C.
4
.
9
D.
5
.
9
Lời giải. Gọi bán kính đáy của cốc hình trụ là
.R
Suy ra chiều cao của cốc nước hình
trụ là
6;R
bán kính của viên bi là
;R
bán kính đáy hình nón là
;R
chiều cao của
hình nón là
4.
R
Thể tích khối nón là
3
non
4
.
3
VR
Thể tích của viên bi là
3
cau
4
.
3
VR
Thể tích của cốc (thể tích lượng nước ban đầu) là
3
6.VR
Suy ra thể tích nước còn lại:
3
non cau
10
.
3
V VV V R

Vậy
5
.
9
V
V
Chọn D.
Câu 2.
Một cái ống nghiệm hình trụ có bán kính trong lòng ống là
,R
ống
nghiệm đang chứa một lượng nước có chiều cao
.h
Người ta thả
3
viên bi có
cùng bán kính
R
vào ống nghiệm thì mực nước dâng lên vừa đủ phủ kín
viên bi cao nhất như hình vẽ. Khẳng định nào sau đây đúng?
A.
3.hR
B.
2.hR
C.
2.
hR
D.
3
3.hR
Lời giải. Gọi
h
là chiều cao của mực nước trong ống nghiệm sau khi thả
3
viên bi
vào ống nghiệm. Khi đó
6.hR
Thể tích phần trụ có hai đáy là hai mặt nước là:
23
1
6. 6 .V RR R

Thể tích ba viên bi là:
33
2
4
3. 4 .
3
V RR
Suy ra thể tích lượng nước ban đầu trong ống nghiệm là:
3
12
2.VVV R
Mà
2
V hR
nên ta có
23
2 2.hR R h R 
Chọn B.
Câu 3. Ba quả bóng dạng hình cầu có bán kính bằng
1
đôi một tiếp
xúc nhau và tiếp xúc với mặt phẳng
.P
Mặt cầu
S
bán kính
bằng
2
tiếp xúc với ba quả bóng trên. Gọi
M
là điểm bất kì trên
,S
MH
là khoảng cách từ
M
đến mặt phẳng
.P
Giá trị lớn
nhất của
MH
bằng
A.
30
3.
2
B.
69
3.
3
C.
123
3.
4
D.
52
.
9
23
Lời giải. Gọi tâm của ba mặt cầu bé bán kính
1
r
lần lượt
là
,, ;
BC D
tâm của mặt cầu lớn bán kính
2R
là
.A
Do ba mặt cầu bé tiếp xúc với nhau nên tam giác
BCD
đều có
cạnh bằng
2.
Mặt cầu lớn tiếp xúc với ba mặt cầu bé nên tứ diện
ABCD
có
cạnh bên
3.AB AC AD
Khi đó khoảng cách thỏa mãn bài toán là:
,
69
3.
3
A BCD
Rrd




Chọn B.
Câu 4. Có một hình nón chứa bốn quả bóng bàn bằng nhau, đường
kính mỗi quả bóng bàn là
4.
Các quả bóng bàn tiếp xúc với nhau, ba
quả tiếp xúc với đáy của hình nón đồng thời bốn quả tiếp xúc với mặt
xung quanh của hình nón như hình vẽ. Chiều cao của hình nón bằng
A.
42
2.
3
B.
4
23 .
3
C.
4
2 3 2.
3

D.
42
2 3 2.
3

Lời giải. Gọi
,,,ABCS
lần lượt là tâm của bốn quả cầu. Khi đó khối chóp
ABCD
là
tứ diện đều cạnh bằng
4,
gọi
D
là trung điểm của
.BC
Xét phần mặt cắt (mặt cắt là mặt trung trực của
BC
) và kí hiệu
như hình vẽ. Với
M
là đỉnh của hình nón;
I
là chân đường cao
xuất phát từ đỉnh
S
của tứ diện
.;S ABC
,
HK
là hình chiếu vuông
góc của
,SA
trên đường sinh của hình nón.
Vì
.S ABC
là tứ diện đều có cạnh bằng
4
nên suy ra
46
.
3
SI
Ta có
2 3.
SM AS
MHS SIA SM
SH AI
 ∽
Vậy chiều cao của hình nón:
46
2 3 2.
3
h MN SM SI IN 
Chọn D.
Câu 5.
Một khối hộp chữ nhật có kích thước
4 cm 4 cm cmh
chứa
một quả cầu lớn và tám quả cầu nhỏ. Biết quả cầu lớn có bán kính
2 cmR
và quả cầu nhỏ có bán kính
1cmr
; các quả cầu tiếp xúc
nhau và tiếp xúc các mặt của hình hộp (như hình vẽ). Tìm
h
.
A.
21 2 2h 
cm .
B.
21 7h

cm .
C.
23 7
h 
cm .
D.
8
h
cm .
Lời giải. Gọi tâm của quả cầu lớn là
,I
tâm của bốn quả cầu nhỏ nằm bên dưới lần
lượt là
, , , .ABC D
Khi đó
.I ABCD
là hình chóp tứ giác đều và có độ dài các cạnh như
hình vẽ bên dưới.
24
Ta có
2cmCD r r

và
3cm.ID R r

Gọi
.O AC BD
Tính được
7IO
. Vậy
21 7h 
cm .
Chọn B.
Câu 6. Một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba
khối nón giống nhau có thiết diện qua trục là một tam giác vuông
cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với
nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh
của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với
hai cạnh của đáy bể (tham khảo hình vẽ). Sau đó người ta đặt lên
đỉnh của ba khối nón một khối cầu có bán kính bằng
4
3
lần bán kính đáy của khối
nón. Biết khối cầu vừa đủ ngập trong nước (mặt trên của bể là tiếp diện của mặt cầu)
và lượng nước tràn ra là
3
337
cm .
3
Thể tích lượng nước ban đầu ở trong bể xấp xỉ
A.
3
885,2 cm .
B.
3
1106,2 cm .
C.
3
1174,2 cm .
D.
3
1209,2 cm .
Lời giải. Gọi bán kính đường tròn đáy của khối nón là
cm ,r
suy ra chiều cao của
khối nón là
hr
(do thiết diện là tam giác vuông cân) và bán kính mặt cầu là
4
cm .
3
r
Xét mặt đáy và ký hiệu như hình vẽ.
Suy ra chiều dài hình chữ nhật (mặt đáy) là
4 cmr
; chiều rộng
hình chữ nhật (mặt đáy) là
2 2 3 2 3 cm .r CH r r r 
Mặt phẳng
qua ba đỉnh của khối nón, cắt mặt cầu theo thiết
diện là một đường tròn có bán kính bằng bán kính của đường tròn
ngoại tiếp
ABC
nên bằng
23
cm .
3
r
Do đó khoảng cách từ tâm mặt cầu đến mặt
phẳng
bằng
2
2
4 23 2
.
3 33
rr
r





Suy ra chiều cao của hình hộp chữ nhật bằng:
24
3.
33
rr
rr
25
Thể tích ba khối nón và khối cầu
3
gia thiet
33
4 4 337 337
. 3.
3 3 81 3
Vr r r r





Thể khối hình hộp chữ nhật
33 3
12 2 3 324 2 3 1209,2 cm .Vr r 
Chọn D.
Câu 7. Cho hình nón có bán kính đáy
5,Ra
độ dài đường sinh
13 .a
Thể tích
khối cầu nội tiếp hình nón bằng
A.
3
40
.
9
a
B.
3
400
.
27
a
C.
3
4000
.
27
a
D.
3
4000
.
81
a
Lời giải.
Ta cần tìm bán kính của mặt cầu. Xét mặt cắt qua
trục của hình nón và ký hiệu như hình vẽ.
Từ giả thiết, suy ra chiều cao của hình nón
22
12 .h Ra

Ta có
SAB
hR S pr

với
r
là bán kính đường tròn nội tiếp tam
giác
SAB
và cũng là bán kính của hình cầu nội tiếp hình nón,
p
là nửa chu vi tam giác
.SAB
Suy ra
10
.
3
hR a
r
p

Thể tích khối cầu:
3
3
3
4 4 10 4000
.
3 3 3 81
aa
Vr




Chọn D.
Câu 8. Một bình đựng nước dạng hình nón (không có đáy), đựng
đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng
một nửa chiều cao của bình nước và đo được thể tích tràn ra là
3
32
dm .
3
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh
của hình nón và toàn bộ khối cầu chìm trong nước, trong đó mặt
nước là tiết diện của khối cầu (hình vẽ bên). Thể tích nước còn
lại trong bình bằng
A.
3
16
dm .
3
B.
3
32
dm .
3
C.
3
40
dm .
3
D.
3
64
dm .
3
Lời giải.
Xét phần thiết diện qua trục và kí hiệu các điểm như hình.
Gọi
R
là bán kính khối cầu. Theo đề, ta có
3
4 32
2.
33
RR

Khi đó
4 8.OH R
Do
OKI OHA∽
nên
22
62
2 2.
8
OI IK
AH
OA AH AH
AH

Thể tích nước còn lại trong bình:
2
32 32
.. .
3 33
AH OH


Chọn B.
Câu 9. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả
vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao
của bình nước và đo được thể tích nước tràn ra ngoài là
.V
Biết rằng
khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng
một nửa khối cầu chìm trong nước như hình vẽ.
Thể tích nước còn lại
trong ly bằng
26
A.
.
V
B.
1
.V
C.
1
.
3
V
D.
1
.
6
V
Lời giải. Gọi bán kính mặt cầu là
R
, suy ra thể tích khối cầu
3
4
.
3
VR
S
Suy ra thể tích nước tràn ra ngoài:
3
2
.
23
V
VR

S
Xét phần mặt cắt qua trục hình nón và kí hiệu như hình vẽ.
Ta có
2
2
2
22 2
111 4
.
3
OF R
OO R
R
OA
OF OA OO

Suy ra thể tích khối nón:
23
2
1 14 8
. . . .2 .
3 33 9
RR
V OA OO R

N
Vậy thể tích nước còn lại trong ly:
3
2
.
93
V
VV R
N
Chọn C.
Câu 10. Nguời ta đặt được vào trong một hình nón hai khối cầu có
bán kính lần lượt là
a
và
2a
sao cho các khối cầu đều tiếp xúc với
mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và
khối cầu lớn tiếp xúc với đáy của hình nón (tham khảo hình vẽ). Bán
kính đáy của hình nón đã cho bằng
A.
5.
a
B.
2 2.a
C.
3.a
D.
8
.
3
a
Lời giải. Xét phần thiết diện qua trục và kí hiệu các điểm như
hình vẽ, trong đó
A
là đỉnh của hình nón và
BC
là đường kính
đáy của hình nón có tâm đáy là
.I
Gọi
,MN
lần lượt là tâm của
hai khối cầu có bán kính
2, ;aa
,HK
lần lượt là điểm tiếp xúc của
AC
với hai đường tròn tâm
,.MN
Vì
2
MH
NK
và
NK MH
NK 
là đường trung bình trong
tam giác
AMH
suy ra
N
là trung điểm
.AM
Khi đó
2 6 8.AM MN a AI a 
Mặt khác
22
8
2 2.
2
62
IC AI IC a
AIC AHM IC a
HM AH a
aa

∽
Chọn B.
Câu 11. Người ta chế tạo ra một món đồ chơi cho trẻ em theo các
công đoạn như sau: Trước tiên, chế tạo ra một hình nón tròn
xoay có góc ở đỉnh là
2 60 
bằng thủy tinh cho trong suốt.
Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ
khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc
với mặt nón, quả cầu lớn tiếp xúc với cả mặt đáy của hình nón
(hình vẽ). Biết rằng chiều cao của hình nón là
9 cm.
Bỏ qua bề
dày của các lớp vỏ thủy tinh, tổng thể tích của hai khối cầu bằng
27
A.
3
38
cm .
3
B.
3
40
cm .
3
C.
3
100
cm .
3
D.
3
112
cm .
3
Lời giải. Xét phần thiết diện qua trục và kí hiệu như hình vẽ.
Ta có
SAB
đều có chiều cao
9 cmh
nên bán kính đường tròn
nội tiếp
3.
3
h
r 
Tương tự
SEF
đều có chiều cao
92 3hr

nên có bán kính
đường tròn nội tiếp
1.
3
h
r

Thể tích hai khối cầu bằng:
33 3
4 4 112
cm .
33 3
rr


Chọn D.
Cách 2.
(Dùng khi góc ở đỉnh khác
0
60
) Gọi
1
,
Nr
là tâm và bán
kính của quả cầu nhỏ;
2
,Mr
là tâm và bán kính của quả cầu lớn.
Do các mặt cầu tiếp xúc với nhau và tiếp xúc với mặt nón nên
tam giác
SQN
vuông tại
,Q
tam giác
SPM
vuông tại
.P
Hình nón tròn xoay có góc ở đỉnh là
2 60

nên
30 .
ASO

Ta có
0
2 22
11
.sin 30 3;
22
r MP SM SM SO r r 
0
1 12 1
11
.sin 30 2 1.
22
r NQ SN SN SO r r r 
Câu 12.
Một ly nước có dạng như hình vẽ. Phần phía trên chứa
nước có dạng hình nón đỉnh
S
với đường kính đáy và chiều cao
SO
cùng bằng
8cm.
Ban đầu ly chứa lượng nước có chiều cao
4cm
so
với đỉnh
.S
Cho vào ly nước một viên bi sắt hình cầu thì nước dâng
lên vừa phủ kín viên bi. Tính bán kính
r
của viên bi làm tròn đến
hai chữ số thập phân.
A.
1, 23cm.r
B.
1,28cm.r
C.
1, 5 3 cm.
r
D.
1, 7 8 c m.r
Lời giải.
Đặt
bằng nửa góc ở đỉnh của hình nón.
Suy ra
1
tan
2
(do chiều cao bằng đường kính).
Bạn đầu lượng nước có chiều cao
4cm
nên bán kính của đường
tròn giao tuyến (mặt nước với ly) bằng
4.tan 2cm.
Suy ra thể
tích lượng nước ban đầu
2
1
1 16
.2 .4 .
33
V

Thể tích viên bi sắt là:
3
2
4
.
3
Vr
Đặt
SH h
là chiều cao mực nước sau khi thả viên bi, ta có
22
2,
tan
5 1;
IH r
IM
SM r
h SI IH IM SM IH h r


.tan .
2
h
HK SH 
28
Suy ra thể tích ly nước sau khi thả viên bi:
3
23 3
1
. . 15.
3 12 12
V HK SH h r


Ta có:
3
3 3 CASIO
12
16 4
1 5 1, 5 3 cm .
12 3 3
VVV r r x


Chọn C.
Câu 13. Một chiếc chén hình trụ có chiều cao bằng đường kính quả
bóng bàn. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài
của quả bóng có chiều cao bằng
3
4
chiều cao của nó. Gọi
12
, VV
lần
lượt là thể tích của quả bóng và chiếc chén. Khi đó
A.
12
3 2.
VV
B.
12
9 8.
VV
C.
12
16 9 .VV
D.
12
27 8 .
VV
Lời giải. Gọi
h
là chiều cao của hình trụ,
r
là bán kính của chén hình trụ,
R
là bán
kính của quả bóng. Suy ra
2.hR
Xét phần thiết diện qua trục và kí hiệu như hình vẽ.
Ta có
.
2
h
OA OB R 
Từ giả thiết suy ra
.
44
hh
IB OI

Bán kính đáy của chén hình trụ là
22
3
.
4
h
r IA OA OI
Vậy tỉ số thể tích:
3
2
3
1
12
2
2
4
4 38
3
: 9 8 .
32 4 9
R
V
hh
h VV
V
rh






Chọn B.
Câu 14. Một quả cầu có thể tích
3
256
cm
3
được đặt vào một
chiếc cốc có dạng hình trụ với đường kính đáy là
6 cm
như hình vẽ.
Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến
hàng phần trăm)
A.
2, 00 cm.
B.
4,00 cm.
C.
4,65 cm.
D.
6, 65 cm.
Lời giải.
Từ giả thiết suy ra quả cầu có bán kính
4 cm .r
Xét phần thiết diện qua trục và kí hiệu như hình vẽ.
Khi đó
4 cm;OM r
3 cm.BM
Tam giác vuông
,OBM
có
22
7 cm .OB OM MB 
Vậy chiều cao của quả cầu nhô ra khỏi miệng cốc bằng
4 7 cm 6,65 cm .TB TO OB r OB
Chọn D.
Câu 15. Một hình cầu nội tiếp trong một hình nón cụt. Hình cầu nội
tiếp trong hình nón cụt là hình cầu tiếp xúc với hai đáy của hình nón
cụt và tiếp với mặt xung quanh của hình nón cụt
(tham khảo hình vẽ).
Biết rằng thể tích khối nón cụt gấp đôi thể tích của khối cầu. T
ỉ lệ
giữa bán kính đáy lớn và bán kính đáy nhỏ của hình nón cụt bằng
29
A.
3.
B.
3
.
2
C.
15
.
2
D.
35
.
2
Lời giải. Chuẩn hóa bán kính đáy nhỏ của hình nón bằng
1.
Gọi
bán kính đáy lớn của hình nón là
1,R
r
là bán kính của hình
cầu. Suy ra chiều cao của hình nón cụt là
2.hr
Xét mặt cắt qua trục của hình nón cụt và kí hiệu như hình vẽ.
Tam giác vuông
,ABC
có
2 22
222
1 12 .BC AB AC R R r r R 
Thể tích khối cầu:
3
1
44
.
33
RR
Vr

Thể tích khối nón cụt:
22 2
2
2
1 .1 .2 . 1 .
33
V R R r RR R


Theo giả thiết, ta có
21
21
2 8 35
2. 1 .
3 32
R
RR
V V RR R R


Vậy tỉ số cần tính:
35
.
12
R
Chọn D.
Phần 5. Mặt cầu ngoại tiếp khối chóp
Câu 1. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
và
.
BC a
Cạnh bên
SA
vuông góc với đáy
.ABC
Gọi
, HK
lần lượt là hình chiếu vuông góc
của
A
lên cạnh bên
SB
và
.
SC
Thể tích của khối cầu ngoại tiếp chóp
.A HKCB
bằng
A.
3
2.a
B.
3
.
2
a
C.
3
2
.
3
a
D.
3
.
6
a
Lời giải.
Theo giả thiết, ta có
0
90ABC
và
0
90 .
AKC
1
Do
.
do
AH SB
AH HC
AH BC BC SAB


2
Từ
1
và
2,
suy ra ba điểm
, , BHK
cùng nhìn xuống
AC
dưới một góc
0
90
nên
22
.
22 2
AC AB a
R 
Vậy
3
3
42
.
33
a
VR

Chọn C.
Câu 2. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
và
.BD a
Hình
chiếu vuông góc của
S
trên mặt phẳng đáy là trung điểm
OD
. Đường thẳng
SD
tạo
với mặt đáy một góc bằng
0
60 .
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
.a
B.
.
2
a
C.
.
3
a
D.
.
4
a
30
Lời giải. Xác định được
0
60 , .SD ABCD SDH

Tính được
3
;
42
aa
SH SD

và
3
.
2
a
SB
Ta có
2 22 2
.SB SD a BD 
Suy ra tam giác
SBD
vuông
tại
.S
Vậy các đỉnh
, , SAC
cùng nhìn xuống
BD
dưới một
góc vuông nên
1
22
a
R BD
. Chọn B.
Câu 3. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
. Đường
thẳng
SA
vuông góc với đáy
ABCD
và
2.SA a
Gọi
M
là trung điểm
,SC
mặt
phẳng
đi qua hai điểm
A
và
M
đồng thời song song với
BD
cắt
,SB
SD
lần lượt
tại
,E
.F
Bán kính mặt cầu đi qua năm điểm
, , , , SAEM F
bằng
A.
a
. B.
2.
a
C.
.
2
a
D.
2
.
2
a
Lời giải. Dễ thấy
.
EF BD
Mà
.
BD SAC BD SC EF SC 
1
Tam giác
SAC
cân tại
.A AM SC 
2
Từ
1
và
2,
suy ra
.SC SC AE
Lại có
.
BC AB
BC SAB BC AE
BC SA
 
Từ đó suy ra
.AE SBC AE SB 
Tương tự ta cũng có
.AF SD
Vậy các đỉnh
, , EMF
cùng nhìn
SA
dưới một góc
vuông nên
2
.
22
SA a
R 
Chọn D.
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Đường thẳng
SA
vuông góc đáy
.ABCD
Gọi
H
là hình chiếu của
A
trên đường thẳng
SB
. Bán kính
mặt cầu ngoại tiếp tứ diện
bằng
A.
a
. B.
2.
a
C.
.
2
a
D.
2
.
2
a
Lời giải.
Gọi
.O AC BD
Vì
ABCD
là hình vuông
nên
.OB OD OC
1
Dễ dàng chứng minh được
AH HC
nên tam giác
AHC
vuông tại
H
và có
O
là trung điểm cạnh huyền
AC
nên suy ra
.OH OC
2
Từ
1
và
2,
suy ra
2
.
2
a
R OH OB 
Chọn D.
31
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
.a
Tam giác
SAB
vuông tại
S
và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp
hình chóp
.S ABCD
bằng
A.
3
.
3
a
B.
3
2
.
3
a
C.
3
.
6
a
D.
3
11 11
.
162
a
Lời giải. Gọi
.O AC BD
Suy ra
.OA OB OC OD
1
Gọi
M
là trung điểm
,
AB
do tam giác
SAB
vuông tại
S
nên
.MS MA MB
Gọi
H
là hình chiếu của
S
trên
.AB
Từ giả thiết suy ra
.SH ABCD
Ta có
OM AB
OM SAB
OM SH

nên
OM
là trục của tam giác
SAB
, suy ra
.OA OB OS
2
Từ
1
và
2,
ta có
.OS OA OB OC OD

Vậy
O
là tâm mặt cầu ngoại tiếp khối
chóp
.,
S ABCD
bán kính
2
2
a
R OA
nên
3
3
42
.
33
a
VR

Chọn B.
Câu 6. Cho hình chóp
.O ABC
có
,OA OB OC a
60 ,AOB 
90 ,BOC 
120 .COA

Gọi
S
là trung điểm của
.OB
Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
.
2
a
B.
7
.
2
a
C.
.
4
a
D.
7
.
4
a
Lời giải.
Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là
22
R xr

với
r
là bán kính đường tròn ngoại tiếp đa giác đáy.
22
:
2
SO r
x
h
S
là đỉnh hình chóp,
O
là tâm đường tròn ngoại tiếp đa giác đáy,
h
là chiều cao khối chóp.
Xét bài toán. Cho hình chóp
.
S ABCDEF
có đường cao
,SH
tâm đường tròn ngoại tiếp
đáy là
.O
Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho.
•
Qua
O
kẻ đường thẳng
d
song song với
SH
thì
d
là trục đường tròn ngoại tiếp đáy.
• Gọi
I
trên
d
là tâm mặt cầu cần tìm, đặt
.OI x
Khi
0x
thì
OI

và
HS

cùng chiều;
Khi
0x
thì
OI

và
HS

ngược chiều.
• Kẻ
IK SH
thì
,IK OH
.SK SH x
• Ta có
2222
IS IC IK SK OI OC
2
2 22
OH SH x x OC 
32
2 22 22 22
.
2 22
OH SH OC SO OC SO r
xx
SH SH h

 
• Bán kính mặt cầu cần tìm:
2 2 22
.
R x OC x r
 
Áp dụng. Tính được
, 2, 3AB a BC a AC a

nên
tam giác
ABC
vuông tại
.B
Gọi
H
là trung điểm
AC
suy ra
H
là tâm đường tròn
ngoại tiếp tam giác đáy nên
3
.
22
AC a
r 
Từ giả thiết suy ra
OH ABC
và tính được
.
2
a
OH
Gọi
M
là trung điểm
BH
suy ra
SM ABC
và
.
24
OH a
SM 
Trong tam giác vuông
SMH
tính được
.
2
a
SH
Vậy ta có
3
,
24
aa
rh
và
2
a
SH
nên suy ra
7
.
2
a
R
Chọn B.
Câu 7. Cho hình chóp đều
.S ABC
có đáy
ABC
là tam giác đều cạnh
,a
cạnh bên
bằng
23
.
3
a
Gọi
D
là điểm đối xứng của
B
qua
.C
Bán kính của mặt cầu ngoại tiếp
hình chóp
.S ABD
bằng
A.
37
.
6
a
B.
35
.
7
a
C.
36
.
7
a
D.
39
.
7
a
Lời giải. Dễ thấy
C
là tâm đường tròn ngoại tiếp tam
giác
ABD
nên
.r CB a
Tam giác vuông
SHC
có
23
3
a
SC
và
3
a
HC
nên suy ra
.SH a
Vậy
, r ah a
và
23
3
a
SC
nên
37
.
6
R
Chọn A.
Câu 8. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang cân với
1,AD DC CB

2.AB
Gọi
O
là giao điểm của
AC
và
,BD
hình chiếu vuông góc
của
S
xuống mặt
ABCD
là trung điểm của
.OA
Đường thẳng
SC
tạo với mặt đáy
ABCD
một góc bằng
60 .
Thể tích khối cầu ngoại tiếp hình chóp
.S ABCD
bằng
A.
17 59
.
54
B.
31 61
.
81
C.
31 51
.
162
D.
61 61
.
162
33
Lời giải. Gọi
E
là trung điểm
.AB
Dễ thấy
ABCD
là
nửa lục giác đều nội tiếp đường tròn tâm
E
nên
1.r EA
Tam giác
ABC
vuông tại
C
suy ra
0
, 60
2
3 2.
3
SC ABCD
AC HC SH

Ta có
3 13
.
233
3
SHE
BO AC
HE SE

Vậy ta có
1, 2rh

và
13
3
SE
nên suy ra
61 61 61
.
6 162
RV

Chọn D.
Câu 9. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
,B
1
.
2
AB BC AD a
Cạnh bên
6SA a
và vuông góc với đáy. Gọi
E
là trung điểm
của
.AD
Bán kính mặt cầu ngoại tiếp chóp
bằng
A.
114
.
2
a
B.
114
.
4
a
C.
114
.
6
a
D.
114
.
8
a
Lời giải. Tam giác
ECD
vuông tại
E
nên
12
.
22
a
r CD
Chiều cao
6.h SA a
Gọi
N
là trung điểm
.AB
Khi đó
22 2 22
34
.
2
a
SO SA AO SA AN NO
Suy ra
114
.
6
Ra
Chọn C.
Câu 10. Cho hình chóp tứ giác đều
.S ABCD
có đáy
ABCD
là hình vuông tâm
,
O
cạnh
2.a
Mặt bên tạo với đáy góc
0
60 .
Gọi
H
là hình chiếu vuông góc của
O
trên
.SD
Bán
kính mặt cầu ngoại tiếp tứ diện
HADC
bằng
A.
21
.
3
a
B.
21
.
6
a
C.
11 5
.
20
a
D.
11 5
.
50
a
Lời giải. Dễ thấy
O
là tâm đường tròn ngoại tiếp tam giác
ADC
nên
2.r AO a
Gọi
K
là trung điểm
.AB
Xác định được
60 , .SAB ABCD SKO
Suy ra
3 5.SO a SD a 
34
Kẻ
HI OD
suy ra
.HI ADC
Ta có
2
2
2
5
HI HD OD
SO SD
SD

suy ra
23
.
5
a
HI
Trong tam giác vuông
SOD
có
222
1 11 6
.
5
a
OH
OH SO OD

Vậy ta có
23
2,
5
a
ra h
và
6
5
a
OH
nên suy ra
21
.
3
a
R
Chọn A.
Câu 11. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,a
SAD
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
M
và
N
lần lượt là trung
điểm của
BC
và
.CD
Bán kính của mặt cầu ngoại tiếp hình chóp
.S CMN
bằng
A.
37
.
6
a
B.
29
.
8
a
C.
53
.
12
a
D.
93
.
12
a
Lời giải. Đáy là tam giác
CMN
vuông tại
C
nên
11 2
.
24 4
a
r MN BD 
Chiều cao
3
.
2
a
h SH
Tâm
O
của đường tròn ngoại tiếp tam giác
CMN
là
trung điểm
;MN
Áp dụng công thức đường trung tuyến trong tam
giác
HMN
tính được
2
2
5
.
8
a
HO
Trong tam giác vuông
SHO
có
2
222
11
.
8
a
SO SH HO
Vậy ta có
23
,
42
aa
rh

và
2
2
11
8
a
SO
nên suy ra
93
.
12
a
R
Chọn D.
Câu 12. Cho tứ diện đều
ABCD
có mặt cầu nội tiếp là
1
S
và mặt cầu ngoại tiếp là
2
.S
Một hình lập phương ngoại tiếp
2
S
và nội tiếp mặt cầu
3
.S
Gọi
123
,,rrr
lần
lượt là bán kính các mặt cầu
123
,,.SSS
Khẳng định nào sau đây đúng ?
A.
1
2
2
3
r
r
và
2
3
1
.
3
r
r
B.
1
2
2
3
r
r
và
2
3
1
.
2
r
r
C.
1
2
1
3
r
r
và
2
3
1
.
3
r
r
D.
1
2
1
3
r
r
và
2
3
1
.
33
r
r
Lời giải. Tứ diện đều nên suy ra tâm mặt cầu ngoại tiếp, nội
tiếp tứ diện trùng nhau và là trọng tâm của tứ diện. Gọi các
điểm như hình vẽ, khi đó:
12
,.r IK r IA

Ta có
1
2
1
sin .
3
AM DM
r
HM HM
IDK
r AM DM

Mặt cầu ngoại tiếp, mặt cầu nội tiếp hình lập phương đều có
tâm là
.O
Gọi các điểm như hình vẽ, khi đó:
23
,.r OE r OF
35
Ta có
2
3
1
si
3
n.
r
OE
EFO
r OF

Vậy
1
2
1
3
r
r
và
2
3
1
.
3
r
r
Chọn C.
Câu 13. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
2
và hình
chiếu của
S
lên mặt phẳng
ABC
là điểm
H
nằm trong tam giác
ABC
sao cho
150 ,AHB 
120 ,BHC 
90 .CHA 
Biết tổng diện tích mặt cầu ngoại tiếp các hình
chóp
.,S HAB
.,S HBC
.S HCA
là
124
.
3
Thể tích khối chóp
.S ABC
bằng
A.
9
.
2
B.
4
.
3
C.
9
.
4
D.
4.
Lời giải. Gọi
123
,,rrr
lần lượt là bán kính đường tròn ngoại tiếp
các tam giác
,HAB HBC
và
.HCA
Áp dụng định lí hàm số sin, ta tìm được
12 3
23
2; ; 1.
3
rr r
Gọi
123
,,RRR
lần lượt là bán kính mặt cầu ngoại tiếp các hình
chóp
. , .S HAB S HBC
và
..S HCA
Đặt
2 0.SH x

Suy ra
2
22 2 2
11 2 3
4
4, , 1.
43
SH
Rr x R x R x   
Theo đề, ta có
222 2
123
19 124 2 3
444 43 .
33 3
RRR x x




Vậy
14
..
33
ABC
V S SH

Chọn B.
Câu 14. Cho tứ diện
ABCD
với
,AB a CD b
và các cạnh còn lại có độ dài bằng
nhau. Gọi
, MN
lần lượt là trung điểm của
AB
và
CD
và
.MN m
Biết rằng tồn tại
một mặt cầu tiếp xúc với
6
cạnh của tứ diện đã cho. Hệ thức nào sau đây đúng ?
A.
2
.ab m
B.
2
2.ab m
C.
2
2.ab m
D.
2
3 2.ab m
Lời giải. Gọi
I
là trung điểm của
,
MN
E
là hình chiếu của
I
lên
.BC
36
Tam giác
ACD
và
BCD
lần lượt cân tại
A
và
B
nên
.
BN CD
CD MN
AN CD

Tương tự ta cũng có
AB MN
nên
MN
là đoạn vuông góc chung của
AB
và
CD

I
là tâm của mặt cầu thỏa yêu cầu bài toán.
Ta có
IEC INC

2
b
EC CN
và
 .
2
a
BIE BIM BM BE
Suy ra các cạnh còn lại bằng nhau và bằng
.
2
ab
BC BE EC

Ta có:
2
22
2 222222
.
2 44 2
a b a b ab
m MN BN BM BC CN BM



Chọn B.
Câu 15. Cho hình chóp đều
.
S ABC
có cạnh đáy bằng
.a
Gọi
,
MN
lần lượt là trung
điểm của
,AB BC
và
P
là điểm thuộc tia đối của
SC
sao cho
3.SC SP
Biết rằng
trong các mặt cầu đi qua
,,AM N
thì mặt cầu ngoại tiếp tứ diện
AMNP
có bán kính
nhỏ nhất. Thể tích của hình chóp
.S ABC
bằng
A.
3
2
.
16
a
B.
3
2
.
32
a
C.
3
2
.
48
a
D.
3
2
.
96
a
Lời giải. Gọi
0
S
là mặt cầu đường kính
;AC
S
là mặt cầu đi qua
,,AM N
suy ra
S
chứa đường tròn đường kính
.
AC
Trong các mặt cầu chứa đường tròn đường
kính
AC
thì mặt cầu có bán kính nhỏ nhất
chính là mặt cầu
0
.S
Từ giả thiết suy ra
0
.P S CP AP 
Đặt
3.SP x SC x
Trong
APC
có
2 2 22 2
16 ;AP AC CP a x 
APS
có
2 2 22 2
15 .
SA AP SP a x 
Mà
SA SC
nên
2 22 22
66 6
15 9 .
12 4 12
aa a
a x x x SC SO SC CO
Vậy
3
.
12
..
3 48
S ABC ABC
a
V S SO

Chọn C.
37
Phần 6. Bài toán cực trị
Câu 1.
Một hình trụ có thể tích
V
không đổi. Tìm mối quan hệ giữa
bán kính
r
của đáy và chiều cao
h
của hình trụ khi diện tích toàn
phần đạt giá trị nhỏ nhất.
A.
.hr
B.
2.hr
C.
3.hr
D.
2.hr
Lời giải. Ta có
2
2
.
V
V rh h
r

Diện tích toàn phần:
3
2 2 22
tp
2 2 2 2 2 32 .
V VV
S rh r r r V
r rr
 
Dấu
""
xảy ra
2
2 do 2
2 2 2.
V rh
V
r rh r h r
r


Chọn D.
Câu 2. Một hộp sữa hình trụ có thể tích
V
(không đổi) được làm từ một tấm tôn có
diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa
bán kính đáy
r
và đường cao
h
là
A.
.hr
B.
2.hr
C.
3.hr
D.
2.hr
Lời giải. Tương tự như bài trên với chú ý
2
2.S rh r


Chọn A.
Câu 3.
Trong số các hình trụ có diện tích toàn phần đều bằng
S
thì
bán kính
r
và chiều cao
h
của khối trụ có thể tích lớn nhất là
A.
1
;.
2 22
SS
rh


B.
;2.
22
SS
rh


C.
1
;.
6 26
SS
rh


D.
;2.
66
SS
rh


Lời giải. Ta có
2
tp
2
tp
2
22 .
2
Sr
S rh r h
r


Khi đó
2
tp
22 3
tp
2
1
. 2.
22
Sr
V r h r rS r
r


Xét hàm
3
tp
2.f r rS r

Ta có
tp
2
tp
6 ; 0 .
6
S
fr r S fr r


Lập bảng biến thiên ta thấy
max
V
tại
tp
.
6
S
r
Suy ra
tp
2 2.
6
S
hr

Chọn D.
Câu 4. Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có
thể tích
V
không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp
của thùng bằng nhau và đắt gấp
3
lần so với giá vật liệu để làm mặt
xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao
của thùng là
h
và bán kính đáy là
.r
Tính tỷ số
h
r
sao cho chi phí vật liệu sản xuất
thùng nhỏ nhất.
38
A.
1.
h
r
B.
2.
h
r
C.
6.
h
r
D.
9.
h
r
Lời giải. Ta có
2
2
.
V
V rh h
r

Gọi
t
là giá tiền của một đơn vị diện tích vật liệu để làm mặt xung quanh, suy ra giá
tiền của một đơn vị diện tích vật liệu để làm mặt đáy là
3.t
Diện tích mặt xung quanh
1
2.S rh

giá tiền mặt xung quanh là
1
2.T rh t
Diện tích hai mặt đáy
2
2
2Sr

giá tiền hai mặt đáy là
2
2
2 3.T rt
Tổng tiền hoàn thành sản phẩm:
22
12
2 3 23
V
T T T t rh r t r
r




22
3
3
2 3 23 .
22 4
VV
t rt V
rr




Dấu
""
xảy ra
2
2 do
3 6.
2
V rh
V
r hr
r

Chọn C.
Câu 5. Nam muốn xây một bình chứa hình trụ có thể tích
3
72m .
Đáy làm
bằng bêtông giá 100 nghìn đồng
2
/m ,
thành làm bằng tôn giá 90 nghìn đồng
2
/m ,
nắp
bằng nhôm giá 140 nghìn đồng
2
/m .
Vậy đáy của hình trụ có bán kính bằng bao
nhiêu để chi phí xây dựng là thấp nhất ?
A.
3
2
m.
B.
3
3
m.
C.
3
3
m.
D.
3
3
m.
2
Lời giải. Ta có
2
22
72
.
V
V rh h
rr


Tổng chi phí xây dựng là:
2 22
2
72
100 90.2 140 240 90.2 .
Prrhrrr
r

 
22
3
12960 6480 6480
240 240 6480 .
rr
r rr
 
Dấu
""
xảy ra
2
3
6480 3
240 m .rr
r

Chọn C.
Câu 6
Trong tất cả các hình nón có độ dài đường sinh
bằng
.
Hình nón có thể tích lớn nhất bằng
A.
3
3
.
9
B.
3
23
.
9
C.
3
3
.
27
D.
3
23
.
27
Lời giải. Gọi
0hh
là chiều cao hình nón, suy ra bán kính
22
.rh
Suy ra thể tích khối nón là
2 23
11 1
..
33 3
V rh h h f h 
Xét hàm
23
fh h h
trên
0; ,
ta được
3
2
max .
3 33
fh f




39
Vậy
3
max
23
.
27
V
Dấu
""
xảy ra
.
3
h
Chọn D.
Câu 7. Trong các hình nón cùng có diện tích toàn phần bằng
.S
Hình nón có thể tích
lớn nhất khi (
,
r
lần lượt là bán kính đáy và đường sinh của hình nón)
C.
.
r
D.
2.r
B.
2 2.
r
A.
3.
r
Lời giải. Ta có
2
2
.
Sr
Sr r
r



Thể tích
2
2
2 22 2 2 2 2 4
22
11 1 1
2.
33 3 3
Sr
V r h r r r r S Sr r
r

 
Lập bảng biến thiên cho hàm
24
2f r Sr r

trên
0; ,
ta thấy hàm số đạt giá
trị lớn nhất tại
3.
4
S
rr

Chọn D.
Câu 8. Cho hình nón đỉnh
S
có đáy là đường tròn tâm
.O
Thiết diện qua trục hình
nón là một tam giác cân với cạnh đáy bằng
a
và có diện tích là
2
.a
Gọi
,AB
là hai
điểm bất kỳ trên đường tròn
.O
Thể tích khối chóp
.S OAB
đạt giá trị lớn nhất bằng
A.
3
.
2
a
B.
3
.
6
a
C.
3
.
12
a
D.
3
2
.
12
a
Lời giải. Tam giác cân
,SCD
có
2
11
. . 2.
22
SCD
S CD SO a a SO SO a

Khối chóp
.S OAB
có chiều cao
2
SO a
không đổi nên để
thể tích lớn nhất khi và chỉ khi diện tích tam giác
OAB
lớn
nhất. Mà
2
11
. .sin .sin
22
OAB
S OA OB AOB r AOB

(với
r
là
bán kính đường tròn mặt đáy hình nón. Do đó để
OAB
S
lớn
nhất khi
sin 1.AOB
Khi đó
3
max
.
12
a
V
Chọn C.
Câu 9.
Cho mặt cầu
S
bán kính
5 cm.R
Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
C
có chu vi
bằng
8 cm.
Bốn điểm
,,,ABC D
thay đổi sao cho
,,ABC
thuộc đường tròn
C
, điểm
D
thuộc
S
D C
và tam giác
ABC
đều. Thể tích lớn nhất của tứ diện
ABCD
bằng
A.
3
20 3 cm .
B.
3
32 3 cm .
D.
3
60 3 cm .
D.
3
96 3 cm .
Lời giải.
Gọi
H
là hình chiếu của
D
trên mặt phẳng
.P
Đường tròn ngoại tiếp tam giác đều
ABC
có chu vi bằng
8 cm.
Suy ra bán kính đường tròn
8
4 cm .
2
R

Suy ra cạnh của tam giác
ABC
bằng
4 3 cm .
40
Suy ra
2
2
43 3
12 3 cm
4
ABC
S

không đổi.
Do đó thể tích khối tứ diện
ABCD
lớn nhất khi
,
d D ABC


lớn nhất
D
và
O
nằm cùng phía so với mặt phẳng
P
và
, , DOH
thẳng hàng
DH DO OH 
22
5 25 16 8.DO OA AH 
Khi đó
3
max
1
.12 3.8 32 3 cm .
3
V 
Chọn B.
Câu 10. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng
9,
hình chóp có thể tích lớn nhất bằng
A.
484.
B.
529.
C.
576.
D.
625.
Lời giải.
Giả sử hình chóp tứ giác đều là
..S ABCD
Xét phần mặt
cắt qua đường cao và kí hiệu như hình vẽ.
Đặt
AB BC CD DA a

0 92a
và
0 18 .SO h h 
Thể tích khối chóp:
2
2
.
1
..
33
S ABCD
ha
V AB h
Tam giác
SAE
vuông tại
A
nên
2
2
2
. 18 18 .
2
a
AO SO OE h h h h

 

Khi đó
2
.
2
18 .
3
S ABCD
V hh
Xét hàm
2
18fh h h
trên
0;18 ,
ta được
fh
đạt
giá trị lớn nhất tại
12h 
GTLN của
.S ABCD
V
bằng
576.
Chọn C.
Câu 11.
Cho hình nón
1
N
có đỉnh
,S
chiều cao
.h
Một hình
nón
2
N
có đỉnh là tâm của đáy
1
N
và có đáy là một thiết diện
song song với đáy của
1
N
như hình vẽ. Khối nón
2
N
có thể
tích lớn nhất khi chiều cao
x
bằng
A.
.
2
h
B.
.
3
h
C.
2
.
3
h
D.
3
.
3
h
Lời giải.
Xét mặt cắt qua trục hình nón và kí hiệu như hình vẽ.
Với
, OI
lần lượt là tâm đáy của hình nón
12
, ;NN
,Rr
lần
lượt là các bán kính của hai đường tròn đáy của
12
, .NN
Ta có
.
Rh x
SI r h x r
r
SO R h R h

41
Thể tích khối nón
2
N
là:
2
2
2
2
2
2
22
11
.. .
33
3
Rh x
R
V rx x xh x
hh


N
Xét hàm
2
3 22
2f x x h x x hx h x

trên
0; .h
Ta có
22
34 ;f x x hx h

0.
3
xh
fx
h
x

Lập bảng biến thiên tìm được
fx
đạt giá trị lớn nhất trên
khoảng
0;h
tại
.
3
h
x
Chọn B.
Câu 12. Cho hình lập phương
.ABCD A B C D

có thể tích
bằng
1.
Gọi
N
là một hình nón có tâm đường tròn đáy
trùng với tâm của hình vuông
,
ABCD
đồng thời các điểm
,,,ABC D

nằm trên các đường sinh của hình nón như
hình vẽ. Thể tích khối nón
N
có giá trị nhỏ nhất bằng
A.
2
.
3
B.
3
.
4
C.
9
.
8
D.
9
.
16
Lời giải.
Xét phần mặt cắt qua trục hình nón và kí hiệu như hình
vẽ. Với
,IH
lần lượt là tâm của hình vuông
,ABCD A B C D

và
đỉnh
A
nằm trên đường sinh
EF
của hình nón.
Hình lập phương có thể tích bằng
1
nên
2
1, .
2
AA HI A H


Đặt
0.EH x x

Khi đó, ta có
2 21
.
12 2
EH A H x x
FI r
EI FI x FI x



Thể tích khối nón
N
là:
3
2
2
2
1
1 11
1.
36 6
x
x
V r EI x
x
x




N
Xét hàm số
3
2
1x
fx
x
trên
0; .
Ta có

2
3
21
.
xx
fx
x

Lập bảng biến
thiên tìm được
0;
27
min
4
fx

tại
2.x
Suy ra
9
min .
8
V
N
Chọn C.
Câu 13. Trong các hình nón nội tiếp một hình cầu có bán kính
bằng
R
không đổi, tính chiều cao
h
và bán kính mặt đáy
r
của
hình nón có thể tích lớn nhất.
A.
4 22
; .
33
h Rr R
B.
33
; .
4
22
h Rr R
C.
42
; .
33
h Rr R
D.
31
; .
22
h Rr R
42
Lời giải. Xét phần mặt cắt và kí hiệu các điểm như hình vẽ.
Tam giác
AKM
vuông tại
K
nên
22
. 2.IK AI IM r h R h

Thể tích khối nón:
22
11
2.
33
V rh h R h


N
Cách 1. Ta có
3
3
2
1 1 1 4 2 32
2 ..4 2 . .
3 6 6 3 81
hh R h R
h R h hh R h





Dấu
""
xảy ra
4
42 .
3
h Rhh R 
Suy ra
22
3
rR
và
2.
h
r
Cách 2. Xét hàm
2 32
2 2;f h h R h h Rh 
có
2
3 4.f h h Rh

Lập BBT tìm được
fh
đạt GTLN trên khoảng
0;2R
tại
4
.
3
hR
Chọn A.
Câu 14.
Cho mặt cầu
S
có bán kính
R
không đổi, hình nón
N
bất kì nội tiếp mặt cầu
S
như hình vẽ. Thể tích khối nón
N
là
1
V
; thể tích phần còn lại là
2
V
. Giá trị lớn nhất của
1
2
V
V
bằng
A.
32
.
49
B.
32
.
76
C.
49
.
81
D.
32
.
81
Lời giải. Thể tích khối cầu:
3
4
.
3
VR
Ta có
11
21
21
1
1
.
1
VV
V VV
V
V VV
V

Suy ra
1
2
V
V
lớn nhất
1
V
V
nhỏ nhất
1
V
đạt giá trị lớn nhất.
Như bài trên tìm được GTLN của
1
V
bằng
3
32
.
81
R
Khi đó
1
2
32
.
76
V
V
Chọn B.
Câu 15.
Một hạt ngọc trai hình cầu có bán kính
R
được bọc trong
một hộp trang sức dạng hình nón ngoại tiếp mặt cầu như hình vẽ.
Hỏi nhà sản xuất phải thiết kế hộp trang sức hình nón có chiều cao
h
như thế nào để hộp quà đó có thể tích nhỏ nhất.
A.
22.hR
B.
3.hR
C.
4.hR
D.
5.
hR
Lời giải. Xét phần mặt cắt qua trục hình nón và kí hiệu như hình.
Đặt
.SI x x R
Khi đó
h SO x R 
và
22
.SK x R
Ta có
22
.
RR x
SK IK
SKI SOA AO
SO AO
xR

∽
Thể tích khối nón:
22
2
2
2
22
11
.. . ..
33 3
RRx Rx
R
V OA SO x R
xR
xR



N
Xét
2
Rx
fx
xR
trên
;.R 
Ta có
22
2
23
;0 .
3
xR
x Rx R
fx fx
xR
xR




43
Lập BBT tìm được
fx
đạt GTNN trên khoảng
;R 
tại
3.xR
Suy ra
4
h SO R

và bán kính đường tròn đáy
22
2.
RR x
r AO R
xR

Chọn C.
Câu 16.
Cho nửa hình cầu bán kính
R
không đổi. Một hình
nón có chiều cao
,h
bán kính đáy là
r
tiếp xúc với nửa hình
cầu như hình vẽ (hai đường tròn đáy là đồng tâm và cùng thuộc
một mặt phẳng). Khi diện tích xung quanh của hình nón là nhỏ
nhất, khẳng định nào sau đây đúng ?
A.
.hr
B.
2.hr
C.
3.hr
D.
2 3.hr
Lời giải. Xét phần mặt cắt như hình vẽ.
Ta có
22
2
2 2 2 2 22 2 2
1 11 1 11
.
Rr
h
R r h h Rr rR

Gọi
là đường sinh
22
2 22 2
22
.
Rr
hr r
rR

Diện tích xung quanh:
22 3
2
22
22
2
2 2. .
Rr r
Sr r r
rR
rR
 
Xét hàm
3
22
r
fr
rR
trên
;.R 
Ta có
4 22
2222
23
.
r rR
fr
rRrR

Lập BBT tìm được
fr
đạt GTNN trên khoảng
;
R 
tại
3
.
2
rR
Khi đó
22
22
22
3 3.
Rr
h Rh R
rR

Suy ra
2
h
r
hay
2.hr
Chọn B.
Câu 17.
Cho một hình nón có chiều cao
h
và bán kính của đường
tròn đáy là
.R
Một mặt phẳng
P
thay đổi song song với mặt
chứa đáy của hình nón và cắt hình nón theo một đường tròn giao
tuyến
.C
Dựng hình trụ
H
có một đáy là đường tròn
C
và
đáy còn lại nằm trên mặt đáy của hình nón như hình vẽ. Khi khối
trụ
H
có thể tích lớn nhất, gọi
h
là chiều cao
của
H
và
R
là bán kính đáy của
.H
Khẳng định nào sau đây đúng ?
A.
11
; .
22
h hR R


B.
12
; .
33
h hR R


C.
13
; .
44
h hR R


D.
31
; .
44
h hR R


Lời giải. Thể tích
2
.V Rh

H
Ta sẽ biểu diễn
h
theo
R
để xét hàm
Xét phần mặt cắt qua trục và kí hiệu như hình vẽ.
Khi đó
,HC R OD R

và
.OH h
Do
AOD AHC∽
nên có
AO OD AH OH OD
AH HC AH HC

44
..
hh R RR
hh
hR R



Khi đó
3
22
.. .
RR R
V R h hR
RR






H
Xét hàm
3
2
R
fR R
R


trên
0; R
ta
được
fR
đạt GTLN tại
2
..
33
R RR h
R hh
R


Chọn B.
Câu 18. Cho khối gỗ hình trụ có bán kính
3 cm
và chiều cao
6 cm ,
đáy là hai hình tròn tâm
O
và
.O
Đục khối gỗ này
tạo ra hai khối nón có đỉnh nằm trên
OO
và đáy trùng với
hai đáy của khối gỗ sao cho góc ở đỉnh bằng
0
60
(như hình vẽ)
và
OI x
3 2 3 3.x

Giá trị nhỏ nhất của tổng diện
tích xung quanh hai hình nón đã đục bằng
A.
2
12 cm .
B.
2
14 cm .
C.
2
44 cm .
D.
2
72 cm .
Lời giải. Xét tam giác vuông
,IOA
có
0
30
3
x
AIO
OA
IO x

và
2
.
3
x
IA
Suy ra diện tích xung quanh của hình nón này:
2
1
2
.
3
Sx
Tương tự, ta có diện tích xung quanh của hình nón còn lại là:
2
2
2
6.
3
Sx
Khi đó
2
2
22
12
6
22
6 . 12 cm .
3 32
xx
SS x x






≥
Dấu
'' ''
xảy ra
6 3 cm .x xx
Chọn A.
Câu 19.
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh bằng
2.a
Cạnh bên
4SA a
và vuông góc với
đáy. Gọi
M
là một điểm trên cạnh
SA
(khác
A
và
S
).
Mặt phẳng
qua
M
và vuông góc với
SA
cắt
, , SB SC SD
lần lượt tại
, , .NPQ
Hình trụ
H
có đáy là
đường tròn ngoại tiếp tứ giác
MNPQ
và có một đường
sinh là
MA
như hình vẽ. Khi khối trụ
H
có thể tích lớn nhất thì tỉ số
SM
SA
bằng
A.
1
.
2
B.
1
.
3
C.
2
.
3
D.
3
.
4
Lời giải. Chọn
1.a
Đặt
,AM x
suy ra
4.SM x
Vì
.4
.
2
MN SM SM AB x
MN
AB SA SA

Chứng minh được
MNPQ
là hình vuông nên
42
2
.
24
x
MN
R

H
45
Khi đó thể tích khối trụ:
2
2
. 4.
8
V R AM x x

H
Xét hàm
2
4fx x x
trên
0;4 ,
ta được
0;4
256
max
27
fx
tại
4
.
3
x
Khi đó GTLN của
V
H
bằng
3
32 32
27 27
a


và
42
.
43
SM x
SA

Chọn C.
Câu 20. Cho hình trụ có đáy là hai đường tròn
;OR
và
;,OR
chiều cao bằng
đường kính đáy. Trên đường tròn tâm
O
lấy điểm
,
A
trên đường tròn tâm
O
lấy
điểm
.B
Thể tích của khối tứ diện
OO AB
có giá trị lớn nhất bằng
A.
3
.
2
R
B.
3
.
3
R
C.
D.
3
.
6
R
Lời giải. Kẻ đường sinh
AM
và
BN
như hình vẽ.
Đặt
2 2 2.AB x R x R

Ta có
. . ..
1 12 1
.. . .
2 23 3
OOAB AOOBN AON MOB AON MOB AMOB
VV V V V




Tam giác vuông
,
AMB
có
2 2 22
4.
MB AB AM x R 
Tam giác cân
,O MB
tính được
22
8
.
2
Rx
OH
Khi đó
2 2 22
.
1
. . 48 .
36
OOAB AMOB OMB
R
V V S AM x R R x


Khảo sát hàm ta được GTLN của
OO AB
V
bằng
3
3
R
đạt tại
6.xR
Chọn B.
Cách 2. Dùng công thức nhanh
1
. . , .sin , .
6
OO AB
V OO AB d OO AB OO AB

Trong đó
,;d OO AB O H

sin , sin , sin .
MB
OO AB AM AB MAB
AB

| 1/65
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


NÓN – TRỤ – CẦU Vận dụng cao
Phần 1. Thể tích và các yếu tố liên quan
Phần 2. Vật thể tròn xoay
Phần 3. Ứng dụng thực tiễn
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Phần 5. Mặt cầu ngoại tiếp khối đa diện
Phần 6. Bài toán cực trị 1
Phần 1. Thể tích và các yếu tố liên quan
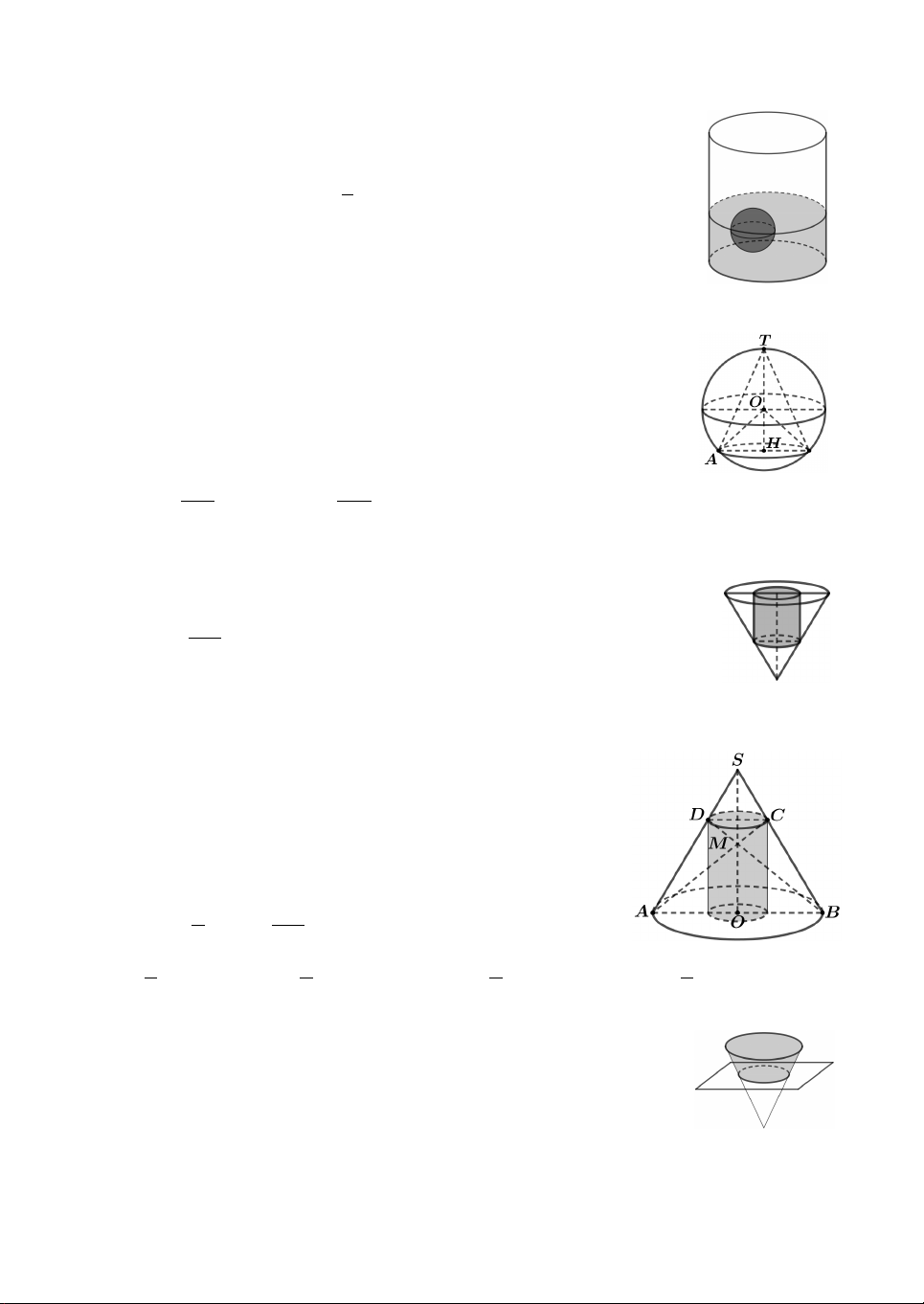
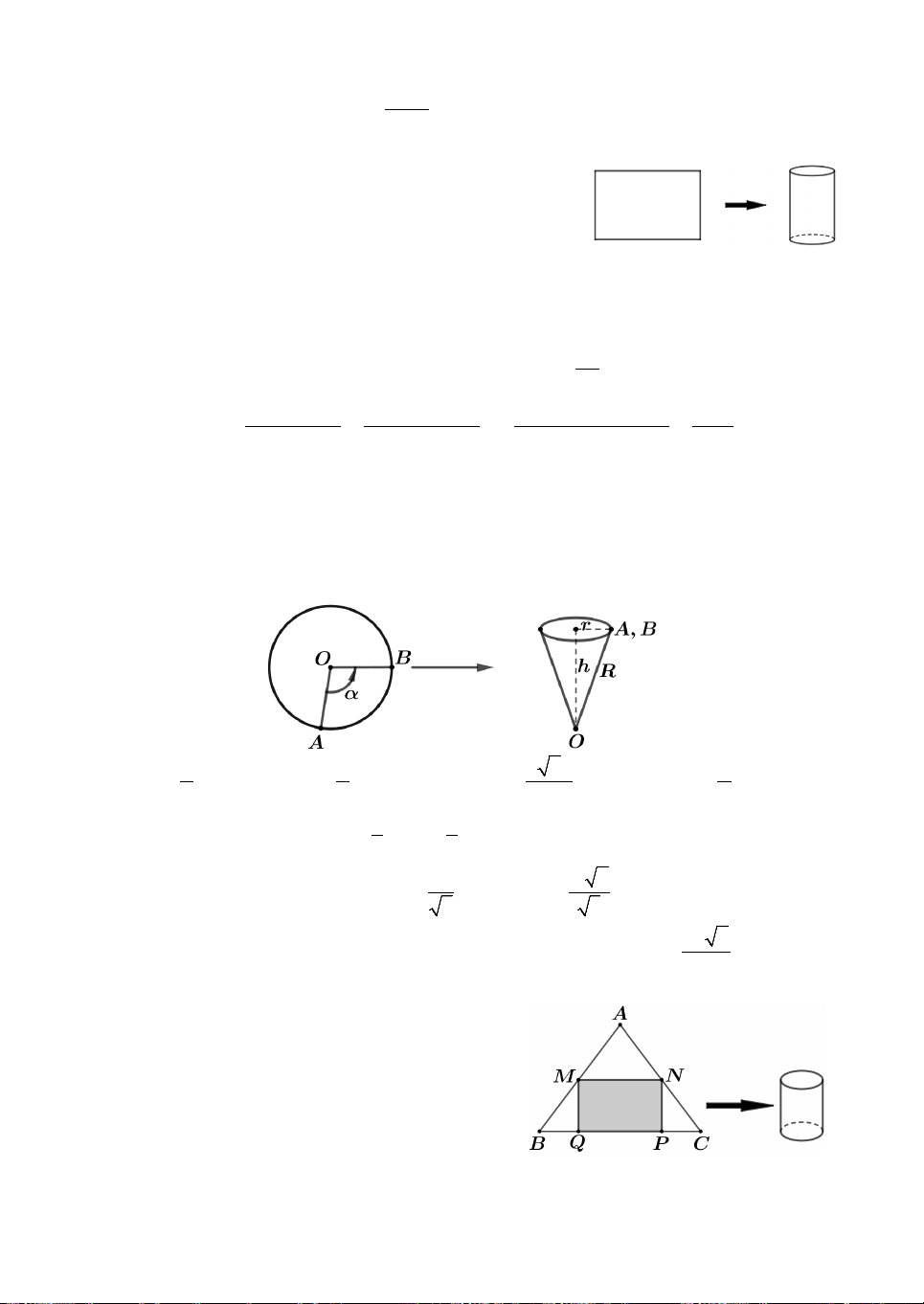
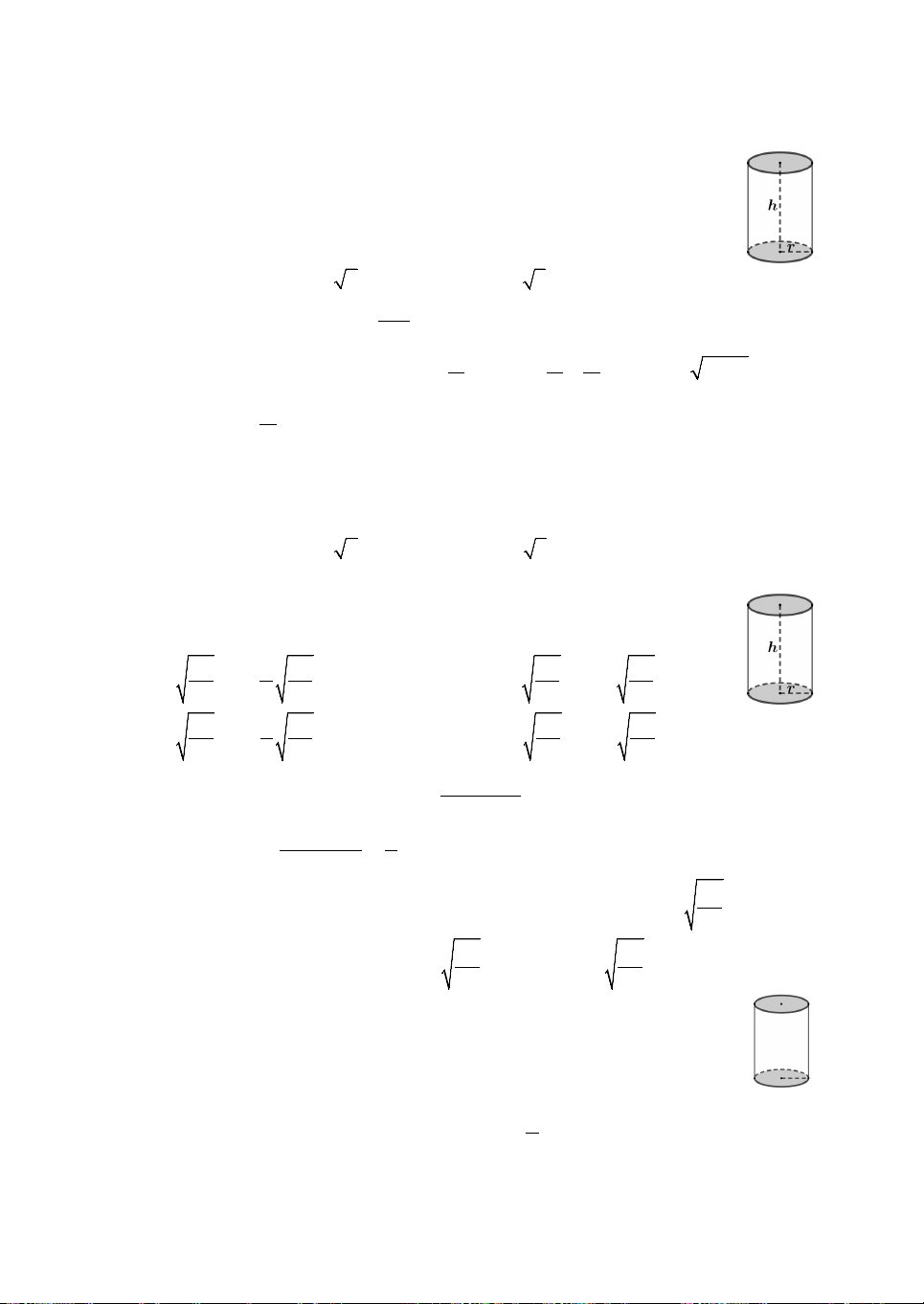
Câu 1. Một chiếc thùng hình trụ có bán kính đáy R  20, bên
trong đựng một lượng nước. Biết rằng khi nghiêng thùng sao cho
đường sinh của hình trụ tạo với mặt đáy góc 45 cho đến khi
nước lặng thì mặt nước chạm vào hai điểm A và B nằm trên hai
mặt đáy như hình vẽ bên. Thể tích của thùng đã cho bằng A. 16000 . B. 12000 . C. 8000 . D. 6000 .
Câu 2. Cho hình lăng trụ tứ giác đều ABCD.EFGH. Tính tỉ số k giữa thể tích khối
trụ ngoại tiếp và thể tích khối trụ nội tiếp hình lăng trụ trên.
A. k  2.
B. k  2.
C. k  2 2.
D. k  4.
Câu 3. Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp ,
A B nằm trên đường tròn đáy thứ nhất của hình
trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ.
Mặt phẳng ABCD tạo với đáy hình trụ góc 45 như hình vẽ. Thể tích khối trụ bằng A. 3 a a a a . B. 3 2 . C. 3 3 . D. 3 3 2 . 16 16 16 16
Câu 4. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không
vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song
AB, AB mà AB AB  6 cm . Biết diện tích tứ giác ABBA bằng 2
60 cm . Chiều cao của hình trụ đã cho bằng A. 4 3 cm. B. 5 3 cm. C. 6 2 cm. D. 8 2 cm.
Câu 5. Một thùng hình trụ có chiều cao h  3m, bán kính đường tròn đáy R  1m
chứa một lượng nước. Biết rằng nếu đặt thùng nằm ngang ta được chiều cao mực nước
trong thùng là d  0,5m. Hỏi thể tích lượng nước có trong thùng gần nhất với kết quả nào sau đây ? A. 3 1,75m . B. 3 1,8m . C. 3 1,85m . D. 3 1,9m .
Câu 6. Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R 3. Hai điểm ,
A B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 0
30 . Khoảng cách giữa AB và trục của hình trụ bằng A. R R . R B. R 3. C. 3 . D. 3 . 2 4
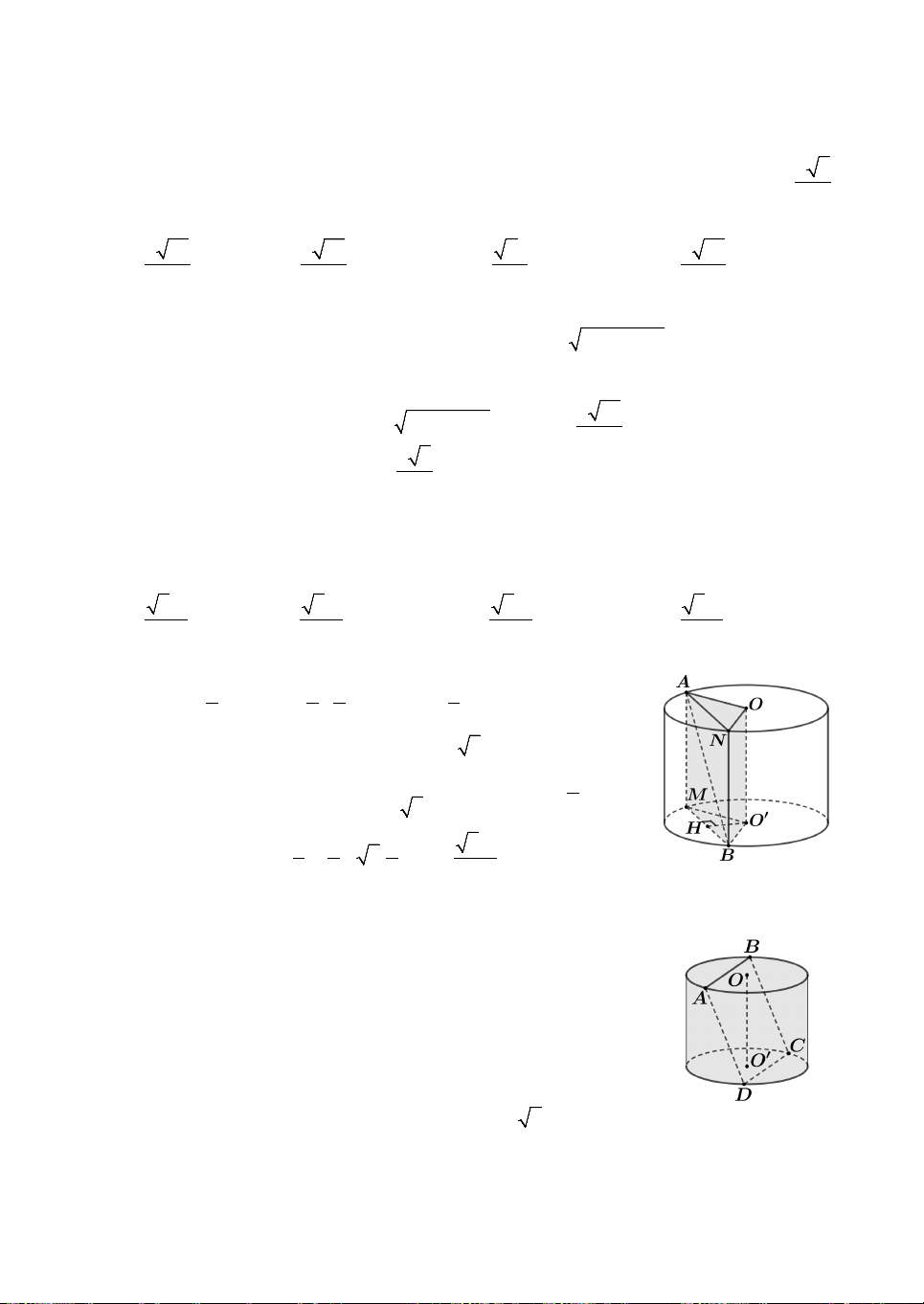
Câu 7. Cho hình trụ có hai đáy là hai hình tròn O và O, thiết diện qua trục của
hình trụ là hình vuông. Gọi ,
A B là hai điểm lần lượt nằm trên hai đường tròn O và 2  a
O. Biết AB  2a và khoảng cách giữa hai đường thẳng AB và OO bằng 3 . 2
Bán kính đáy của hình trụ bằng A. a 14 a a a . B. 14 . C. 2 . D. 14 . 2 3 4 4
Câu 8. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng .
a Trên đường tròn tâm O lấy điểm ,
A trên đường tròn tâm O lấy điểm
B sao cho AB  2 .
a Thể tích của khối tứ diện OO AB bằng 3 3 3 3 A. 3a 3a 3a 3a . B. . C. . D. . 2 4 6 12
Câu 9. Một hình trụ có bán kính đáy R  70cm và chiều cao
h  20cm. Một hình vuông ABCD có hai cạnh AB và CD lần
lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng
ABCD không vuông góc với mặt đáy của hình trụ (tham
khảo hình vẽ). Cạnh của hình vuông ABCD có độ dài bằng A. 80cm. B. 100cm. C. 100 2cm. D. 140cm.
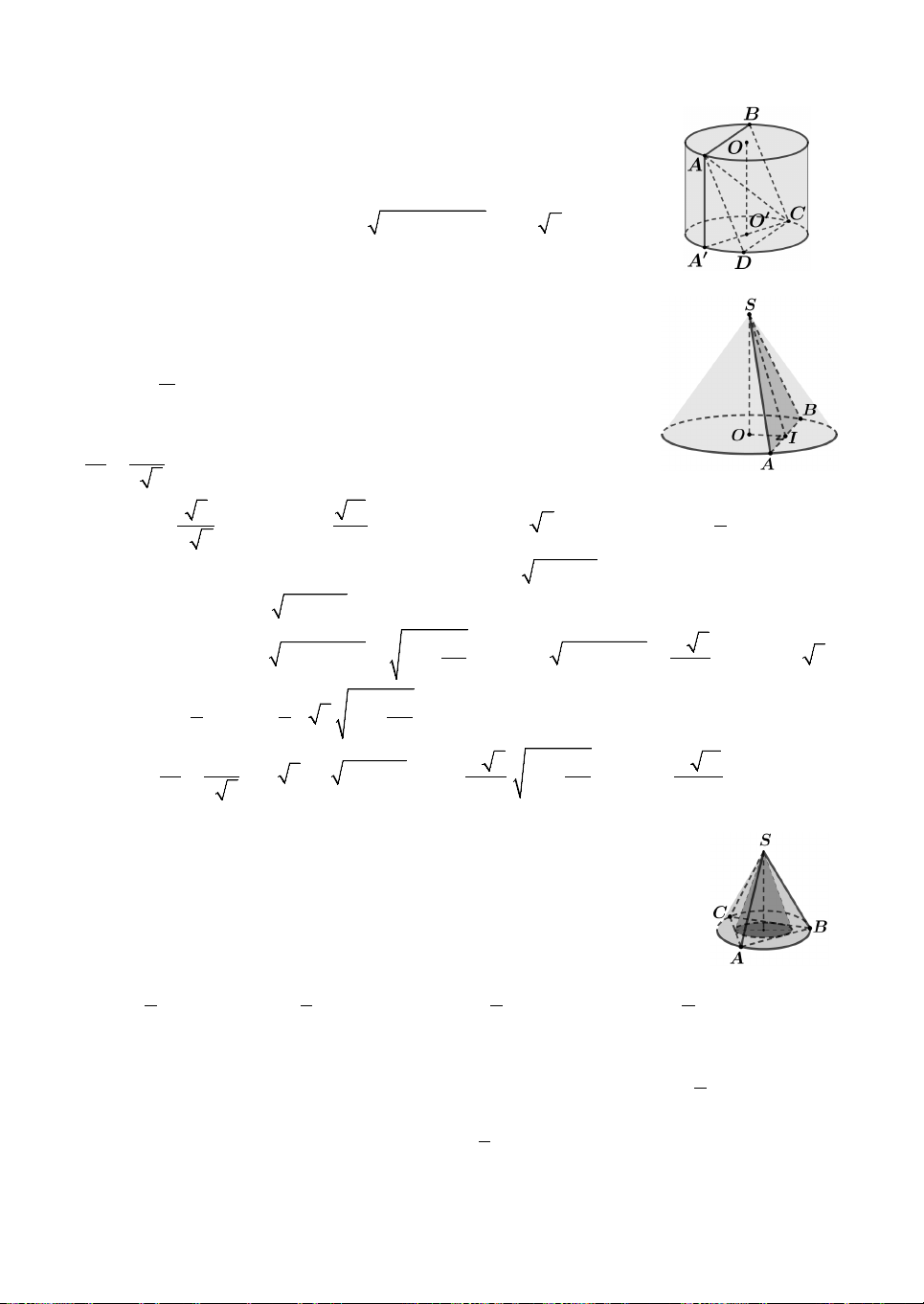
Câu 10. Cho hình nón có đỉnh S, trục SO, bán kính , R chiều cao .
h Dây cung AB thuộc đường tròn đáy và cách O một
khoảng R như hình vẽ. Ký hiệu S , S lần lượt là diện tích 2 1 2
xung quanh của mặt nón và diện tích tam giác SAB. Biết S 10 1 
, mệnh đề nào sau đây đúng ? S2 3 3 A. 5 h  . R B. 11 h  . R
C. h   2   1 . R D. 1 h  . R 2 2 8 3
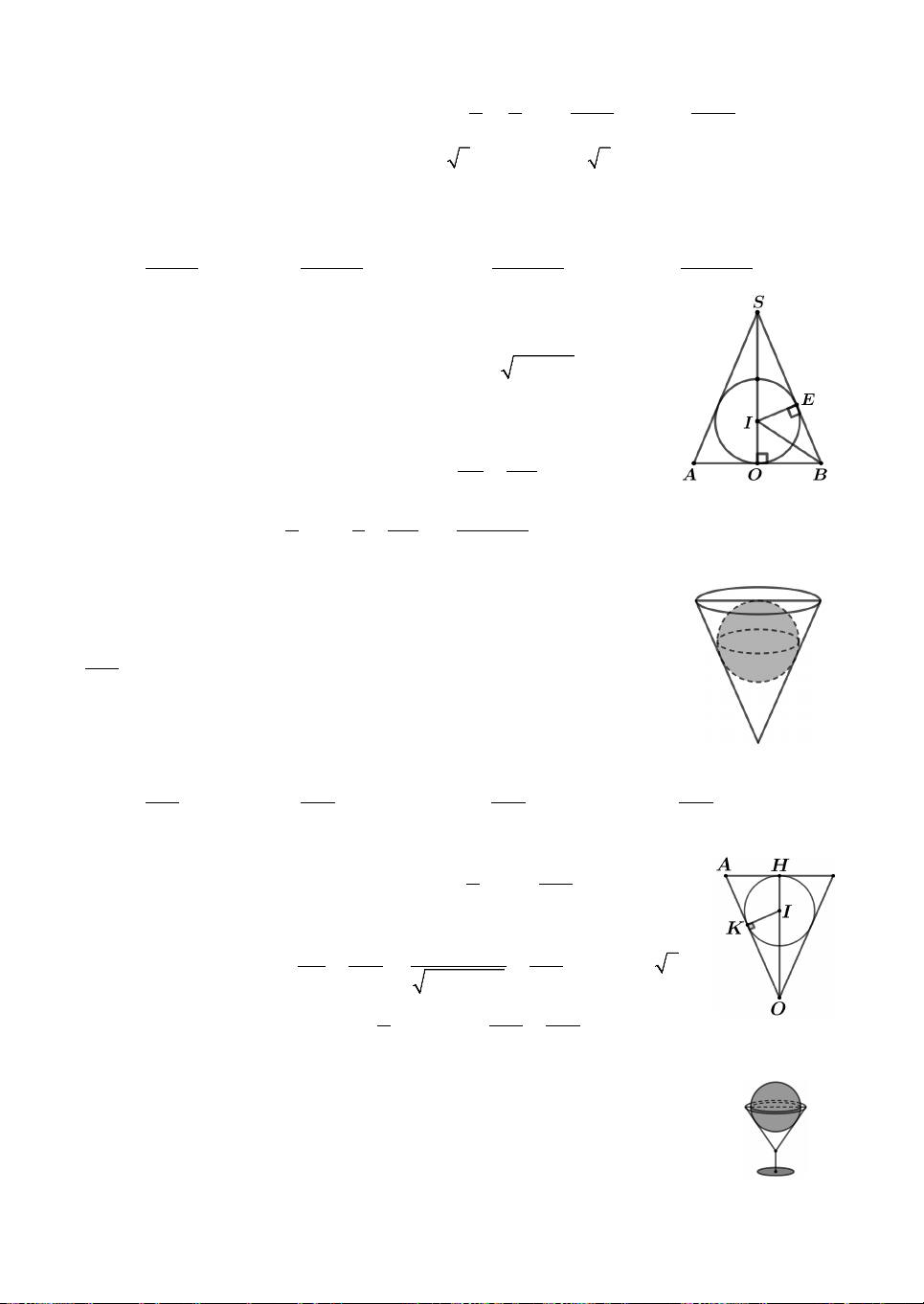
Câu 11. Cho hình chóp tam giác đều S.ABC. Hình nón có đỉnh S
và có đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là
hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có
đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình
nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội
tiếp và hình nón ngoại tiếp hình chóp đã cho bằng A. 1 . B. 1. C. 2 . D. 1 . 2 3 3 4
Câu 12. Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA
và SB, biết tam giác SAB vuông và có diện tích bằng 2
4a . Góc tạo bởi giữa trục SO
và mặt phẳng SAB bằng 0
30 . Đường cao h của hình nón bằng A. a a h a 2.
B. h a 3. C. 3 h  . D. 6 h  . 2 4 3
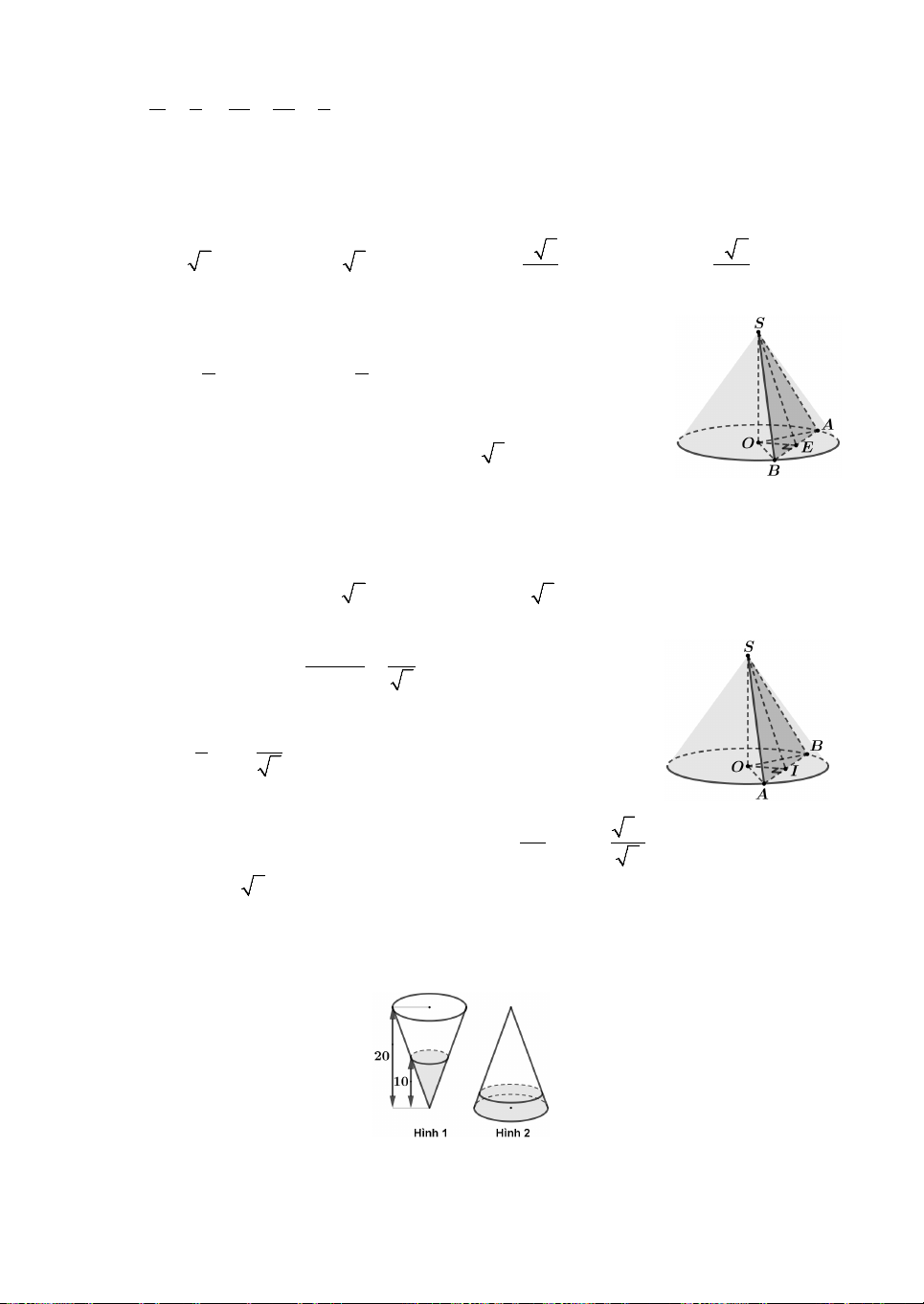
Câu 13. Cho hình nón đỉnh S có đường cao SO. Gọi ,
A B là hai điểm thuộc đường
tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và  0 SAO  30 ,  0
SAB  60 . Độ dài đường sinh  của hình nón bằng A.   . a B.   a 2. C.   a 3. D.   2 . a
Câu 14. Một cái phễu có dạng hình nón, chiều cao của phễu là 20 cm (Hình 1). Người
ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu là 10 cm.
Nếu bịt kín miệng phễu rồi lật ngược lên (Hình 2).
Khi đó chiều cao cột nước trong phễu bằng giá trị nào sau đây ? A. 0,87 cm. B. 1,07 cm. C. 5 cm. D. 10 cm.
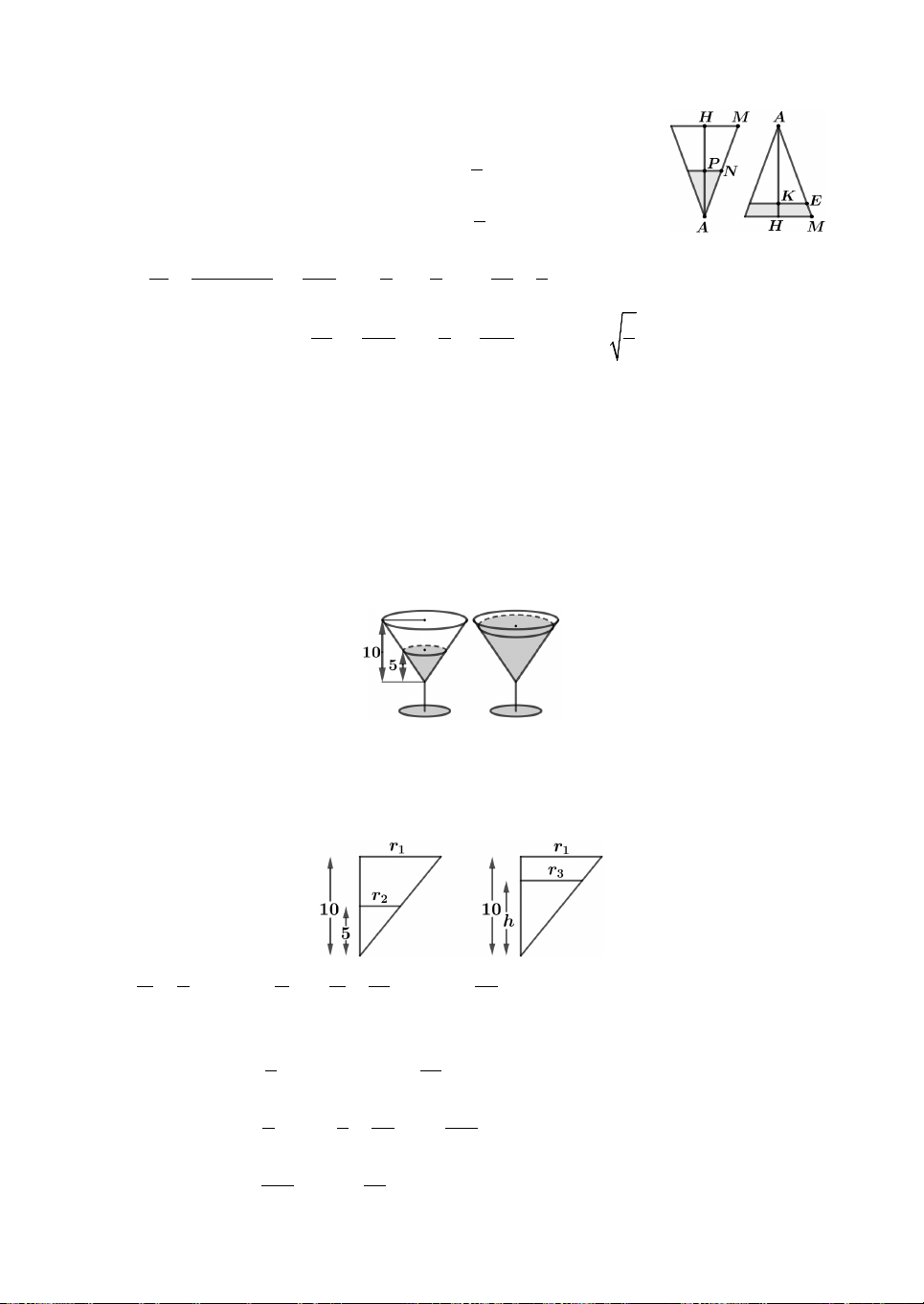
Câu 15. Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng
là một khối nón có chiều cao 10 cm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất
chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất
sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 5 cm . Tính
chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất
lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao
hụt khi chuyển. Tính gần đúng h với sai số không quá 0,01 cm ).
A. 9,09 cm. B. 9,18 cm. C. 9,56 cm. D. 9,57 cm.
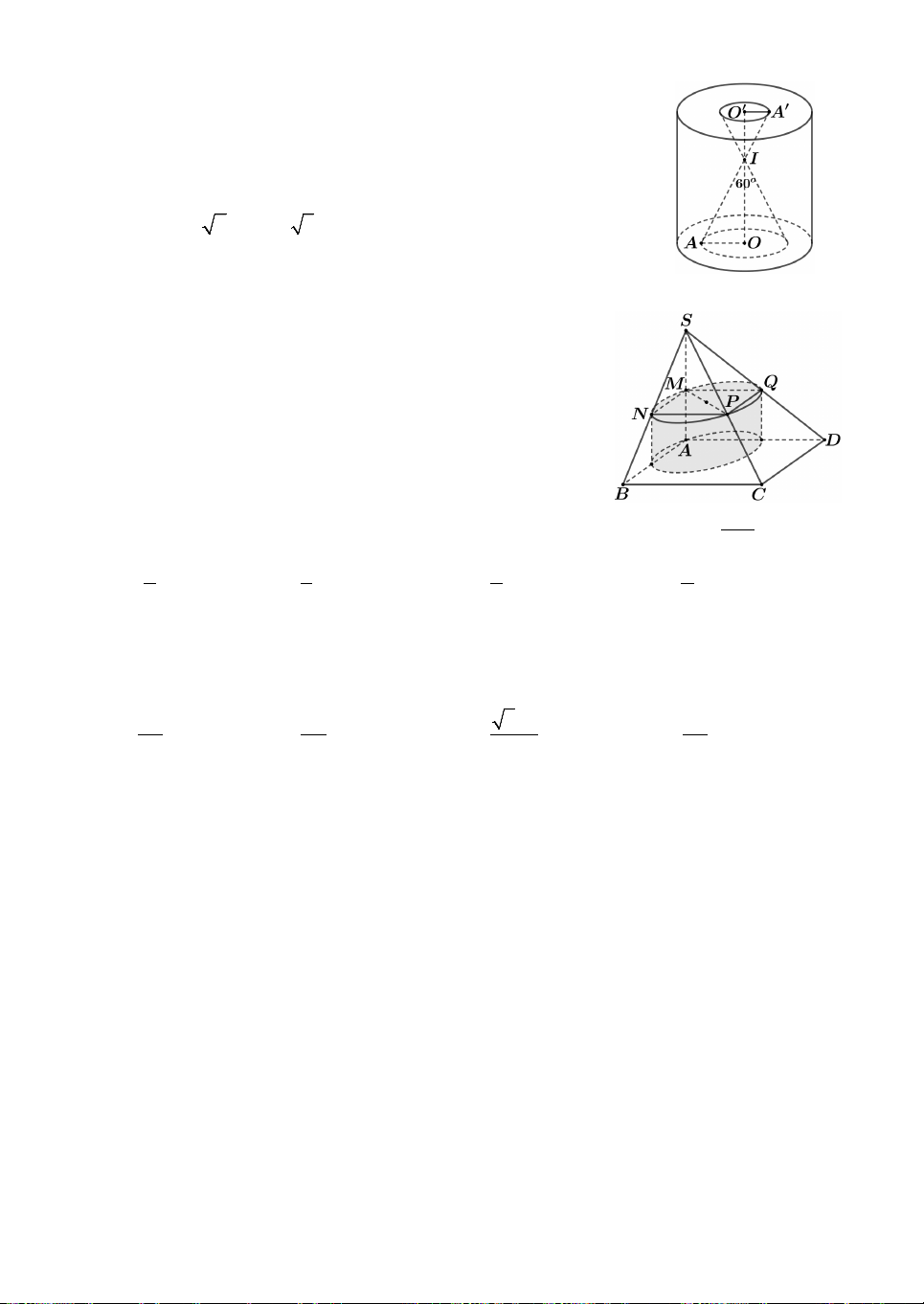
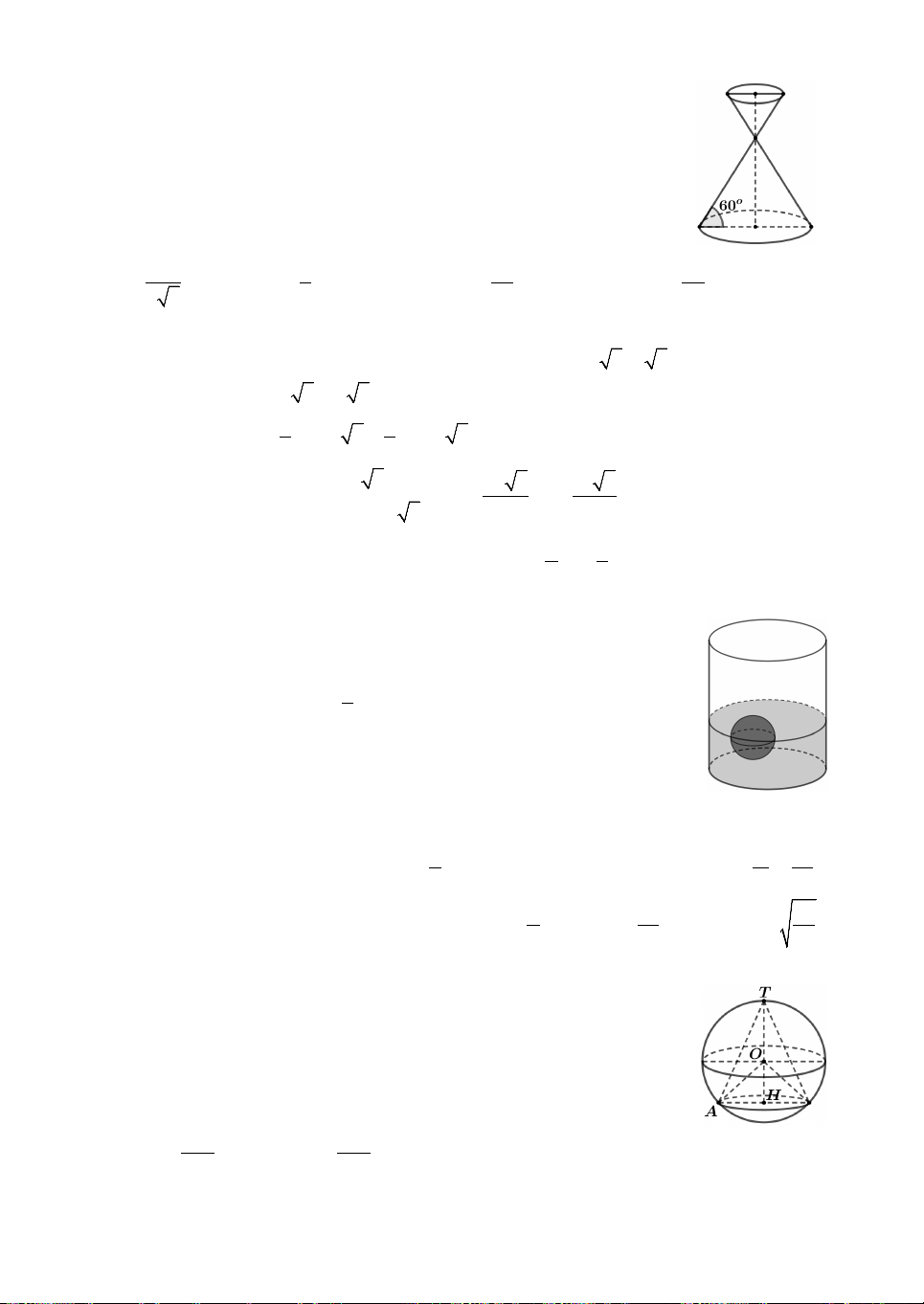
Câu 16. Cho một đồng hồ cát gồm 2 hình nón chung đỉnh ghép
lại, trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc
60 như hình bên. Biết rằng chiều cao của đồng hồ là 30cm và
tổng thể tích của đồng hồ là  3
1000 cm . Hỏi nếu cho đầy lượng
cát vào phần trên thì khi chảy hết xuống dưới, khi đó tỉ lệ thể
tích lượng cát chiếm chỗ và thể tích phần dưới là bao nhiêu ? A. 1 . B. 1 . C. 1 . D. 1 . 3 3 8 27 64 4
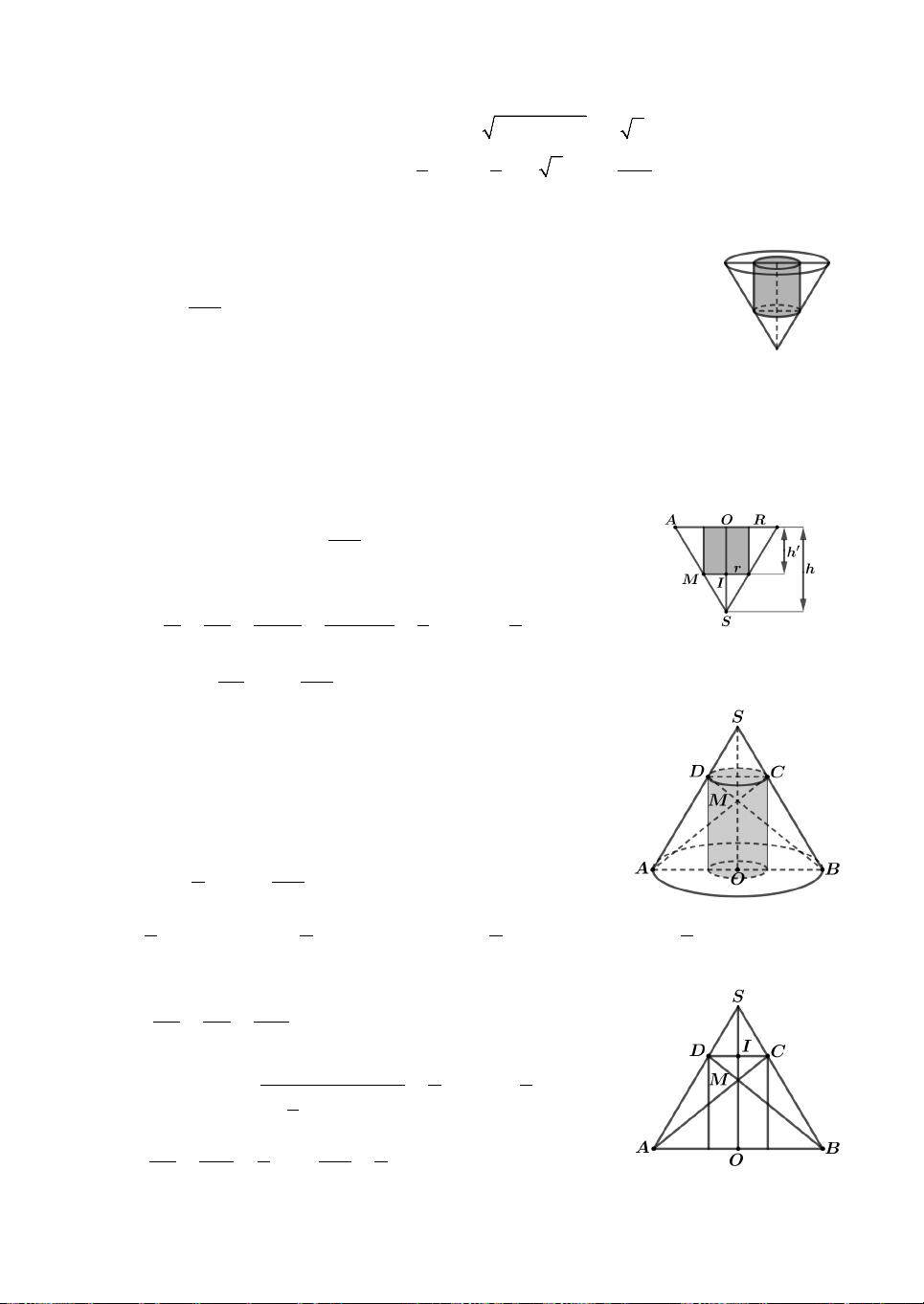
Câu 17. Để tính diện tích xung quanh của một khối cầu bằng đá,
người ta thả nó vào trong một chiếc thùng hình trụ có chiều cao
h  2m, bán kính đường tròn đáy bằng R  0,5m và chứa một
lượng nước có thể tích bằng 1 thể tích khối trụ. Sau khi thả khối 8
cầu đá vào khối trụ người ta đo được mực nước trong khối trụ cao
gấp ba lần mực nước ban đầu khi chưa thả khối cầu. Hỏi diện tích
xung quanh của khối cầu gần bằng kết quả nào được cho dưới đây ? A. 2 1,5m . B. 2 1,7m . C. 2 2,6m . D. 2 3,4m .
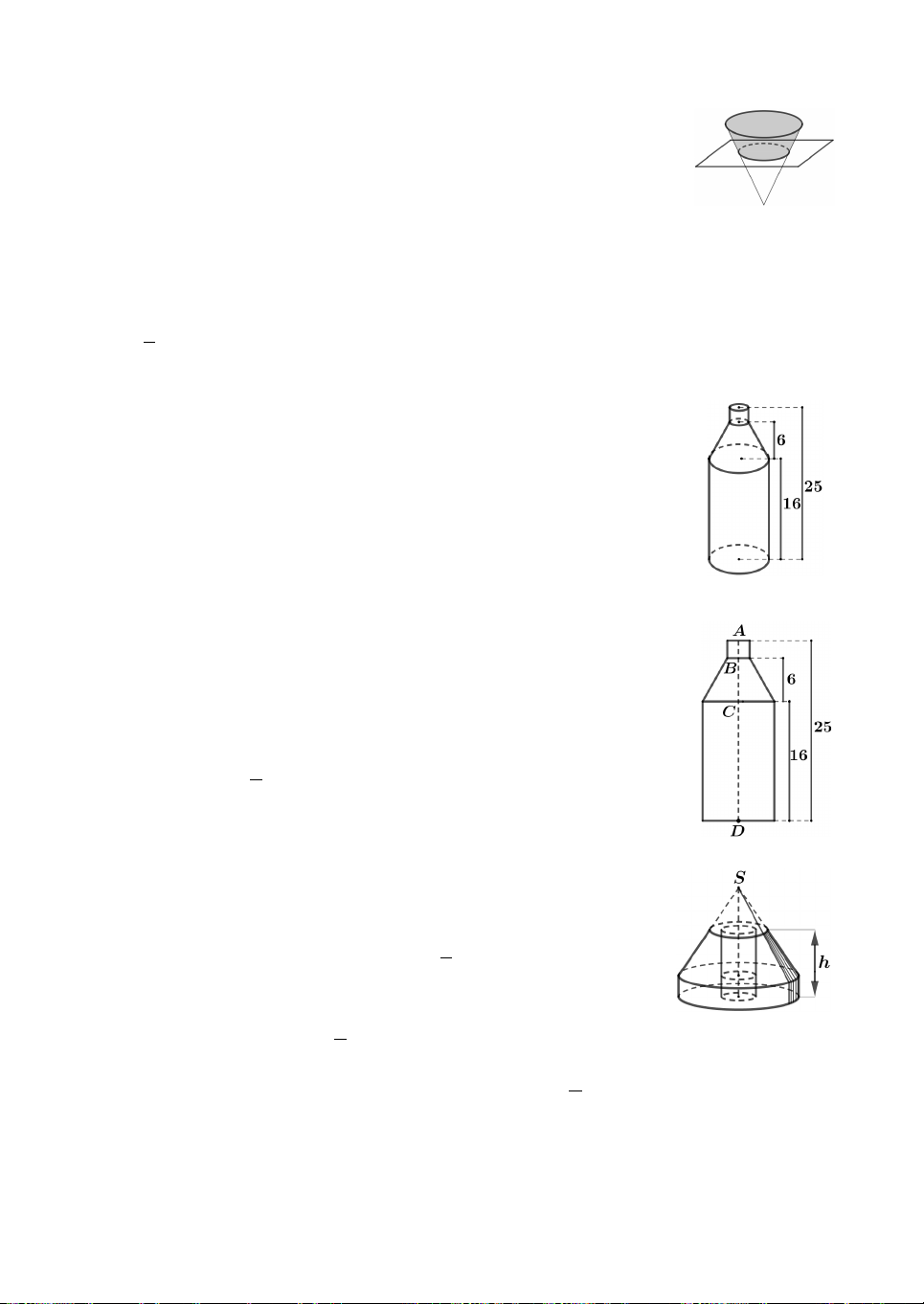
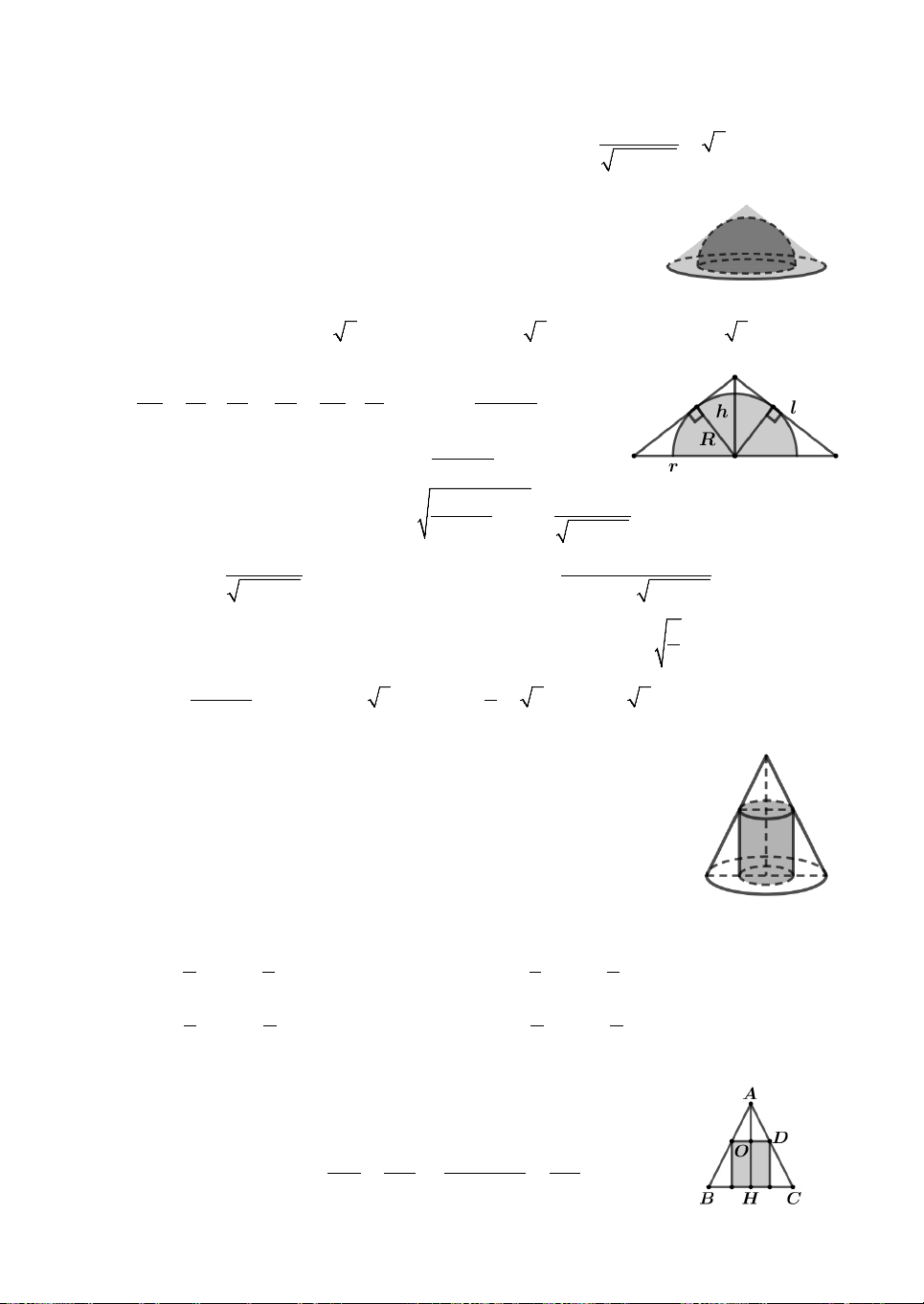
Câu 18. Cho mặt cầu S tâm O, bán kính R  3. Mặt phẳng P
cách O một khoảng bằng 1 và cắt S theo giao tuyến là đường
tròn C có tâm H. Gọi T là giao điểm của tia HO với S, tính
thể tích V của khối nón đỉnh T , đáy là hình tròn C (như hình). A. 16 V  . B. 32 V  . C. V  16 . D. V  32 . 3 3
Câu 19. Một bình đựng nước dạng hình nón không nắp đựng đầy
nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó.
Người ta thả vào bình đó một khối trụ và đo được thể tích nước trào ra ngoài là 16 3
dm . Biết rằng một mặt của khối trụ nằm trên mặt 9
đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của
hình nón (như hình vẽ). Tính bán kính đáy R của bình nước. A. R  2 dm. B. R  3 dm. C. R  4 dm. D. R  5 dm.
Câu 20. Xét một hình trụ nội tiếp trong hình nón như hình
bên, trong đó S là đỉnh hình nón, O là tâm đường tròn
mặt đáy. Các đoạn AB, CD lần lượt là đường kính của
đường tròn đáy của hình nón và hình trụ. Biết AC, BD cắt
nhau tại điểm M SO và tỉ số thể tích của hình trụ và
hình nón là 4 . Tỉ số SM bằng 9 SO A. 2 . B. 4 . C. 5 . D. 7 . 3 5 6 9
Câu 21. Cắt một hình nón bằng một mặt phẳng song song với đáy
thì phần hình nón nằm giữa mặt phẳng và đáy gọi là hình nón
cụt. Một chiếc cốc có dạng hình nón cụt cao 9cm, bán kính của
đáy cốc và miệng cốc lần lượt là 3cm và 4cm. Hỏi chiếc cốc có thể
chứa được lượng nước tối đa là bao nhiêu trong các lựa chọn sau ? A. 250 ml. B. 300 ml. C. 350 ml. D. 400 ml. 5
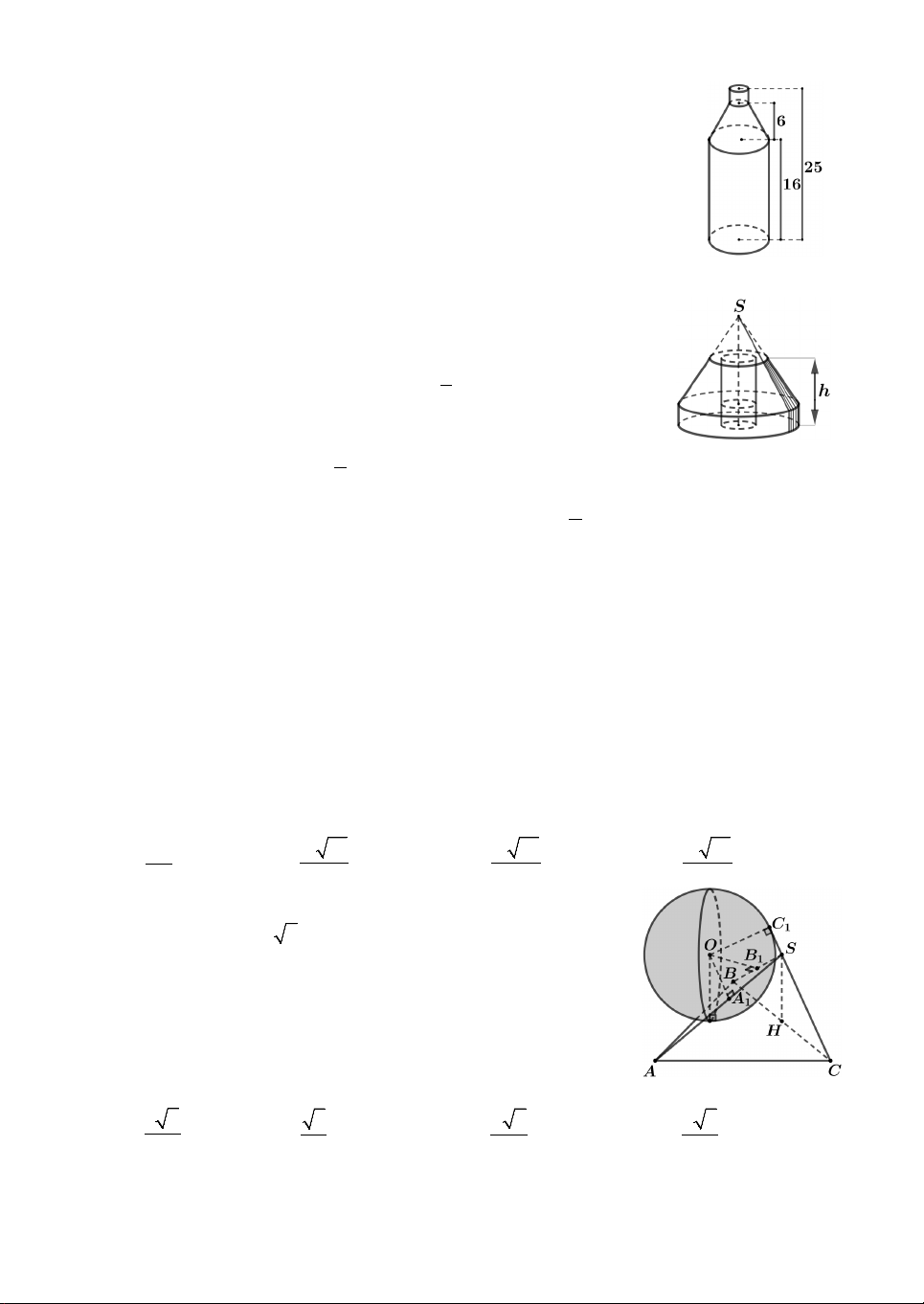
Câu 22. Phần không gian bên trong của chai nước ngọt có hình
dạng như hình vẽ. Biết bán kính đáy và bán kính cổ chai lần lượt
là R  5 cm, r  2 cm. Thể tích phần không gian bên trong của
chai nước ngọt (giả sử độ dày của vỏ chai không đáng kể) bằng A.  3 412 cm . B.  3 462 cm . C.  3 490 cm . D.  3 495 cm .
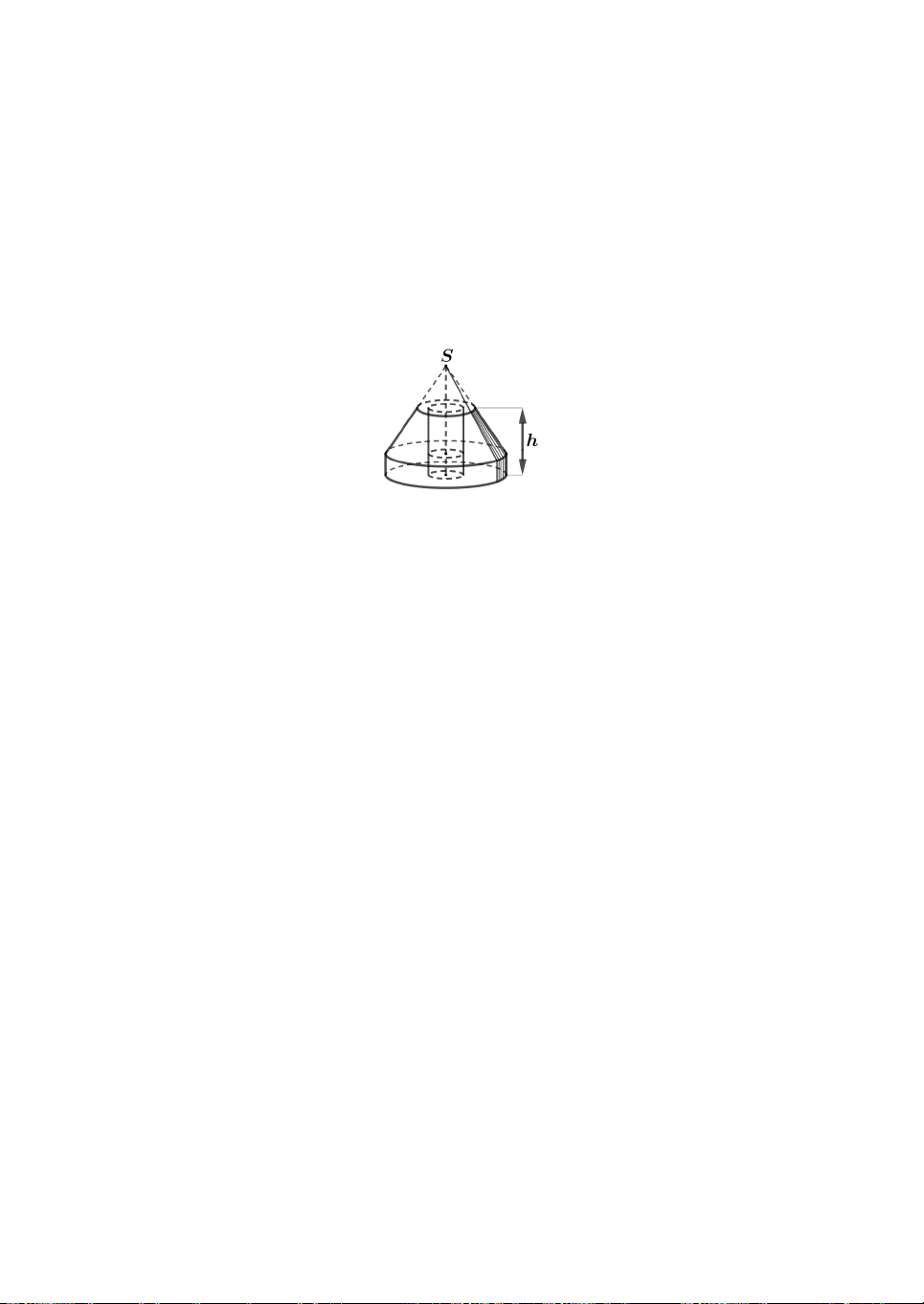
Câu 23. Để định vị một trụ điện, người ta cần đúc một khối bê
tông có chiều cao h  1,5m gồm: Phần dưới có dạng hình trụ
bán kính R  1m và có chiều cao bằng 1 ;
h Phần trên có dạng 3
hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình
nón có bán kính đáy bằng 1 R ở phía trên (người ta gọi hình đó là hình nón cụt); 2
Phần ở giữa rỗng có dạng hình trụ, bán kính đáy bằng 1 R (tham khảo hình vẽ bên). 4
Tính thể tích V của khối bê tông (làm tròn đến chữ số thập phân thứ ba). A. 3
V  2,814 m . B. 3 V  2,815m . C. 3
V  3,109 m . D. 3 V  3,403m .
Câu 24. Trong không gian cho một hình cầu S  tâm O có bán kính R và một điểm
S cho trước sao cho SO  2R . Từ S ta kẻ các tiếp tuyến đến mặt cầu với tiếp điểm
thuộc đường tròn C . Trên mặt phẳng P chứa đường tròn C ta lấy điểm E thay 1  1 
đổi nằm ngoài mặt cầu S . Gọi N  là hình nón có đỉnh là E và đáy là đường tròn
C gồm các tiếp điểm của tiếp tuyến kẻ từ E đến mặt cầu S . Biết rằng hai đường 2 
tròn C và C luôn có cùng bán kính, khi đó quỹ tích các điểm E là một đường 2  1 
tròn, đường tròn này có bán kính R bằng A. 3R R R R . B. 15 . C. 17 . D. 15 . 2 2 2 4
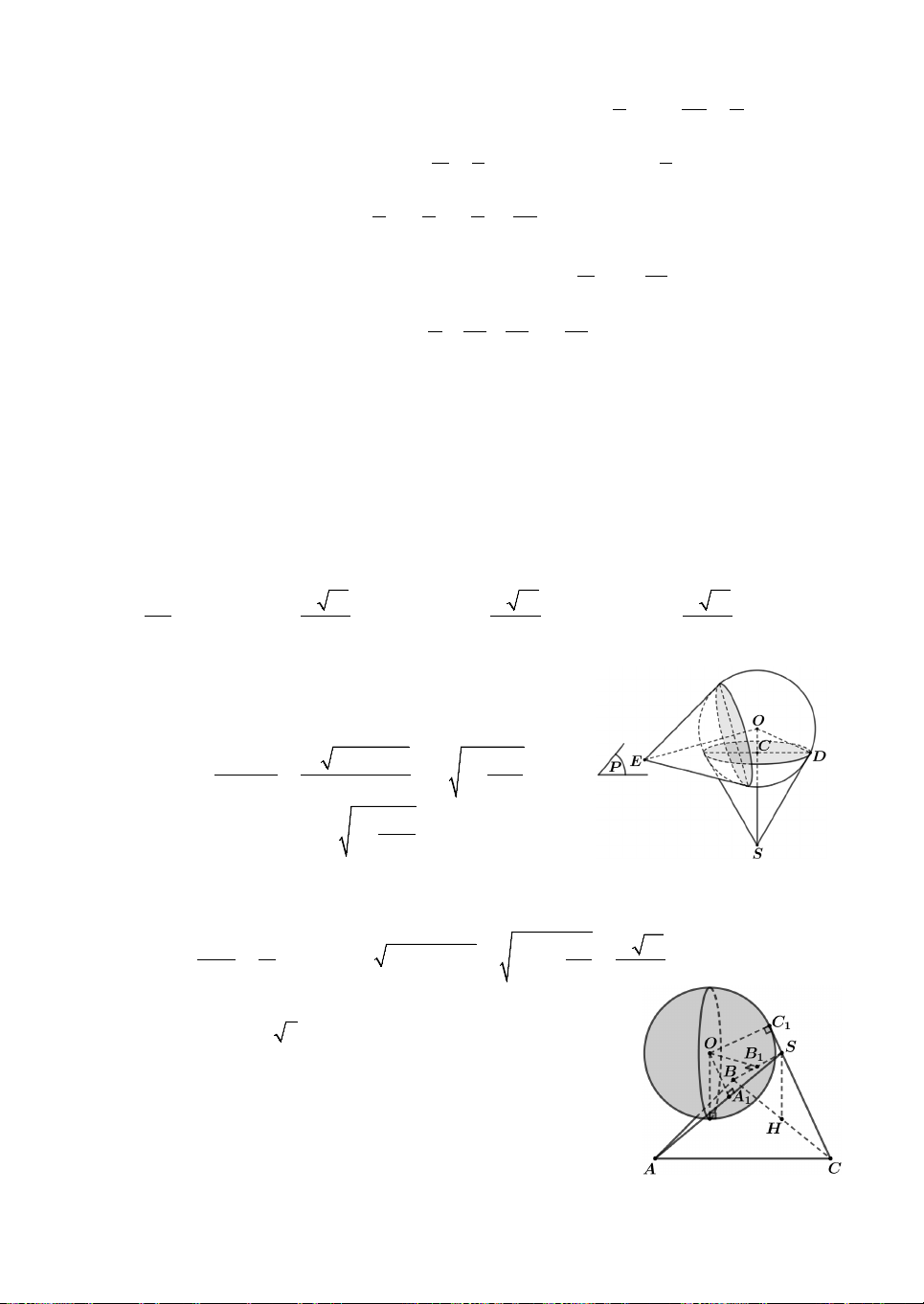
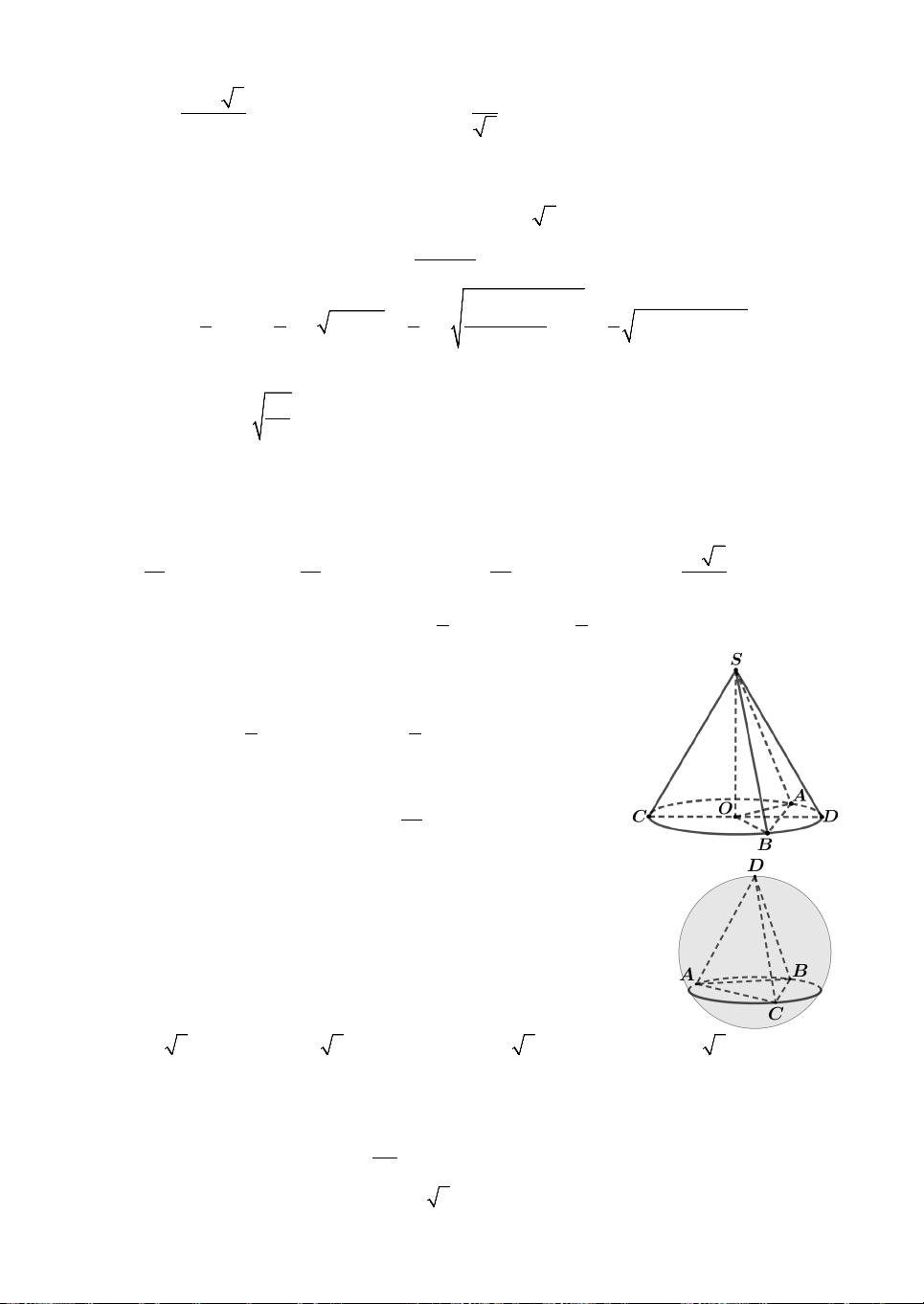
Câu 25. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại ,
A BC  2 2 và 
ACB  30. Hình chiếu của S
trên mặt phẳng đáy là trung điểm H của BC. Giả sử có mặt
cầu tâm O, bán kính bằng 1 tiếp xúc với ,
SA SB và tia đối
của SC lần lượt tại A , B , C đồng thời mặt cầu tâm O đó 1 1 1
cũng tiếp xúc với mặt phẳng ABC (tham khảo hình vẽ).
Thể tích của hình chóp S.ABC bằng A. 3 2 . B. 3 . C. 2 2 . D. 2 3 . 2 3 3 3 6
Phần 2. Vật thể tròn xoay
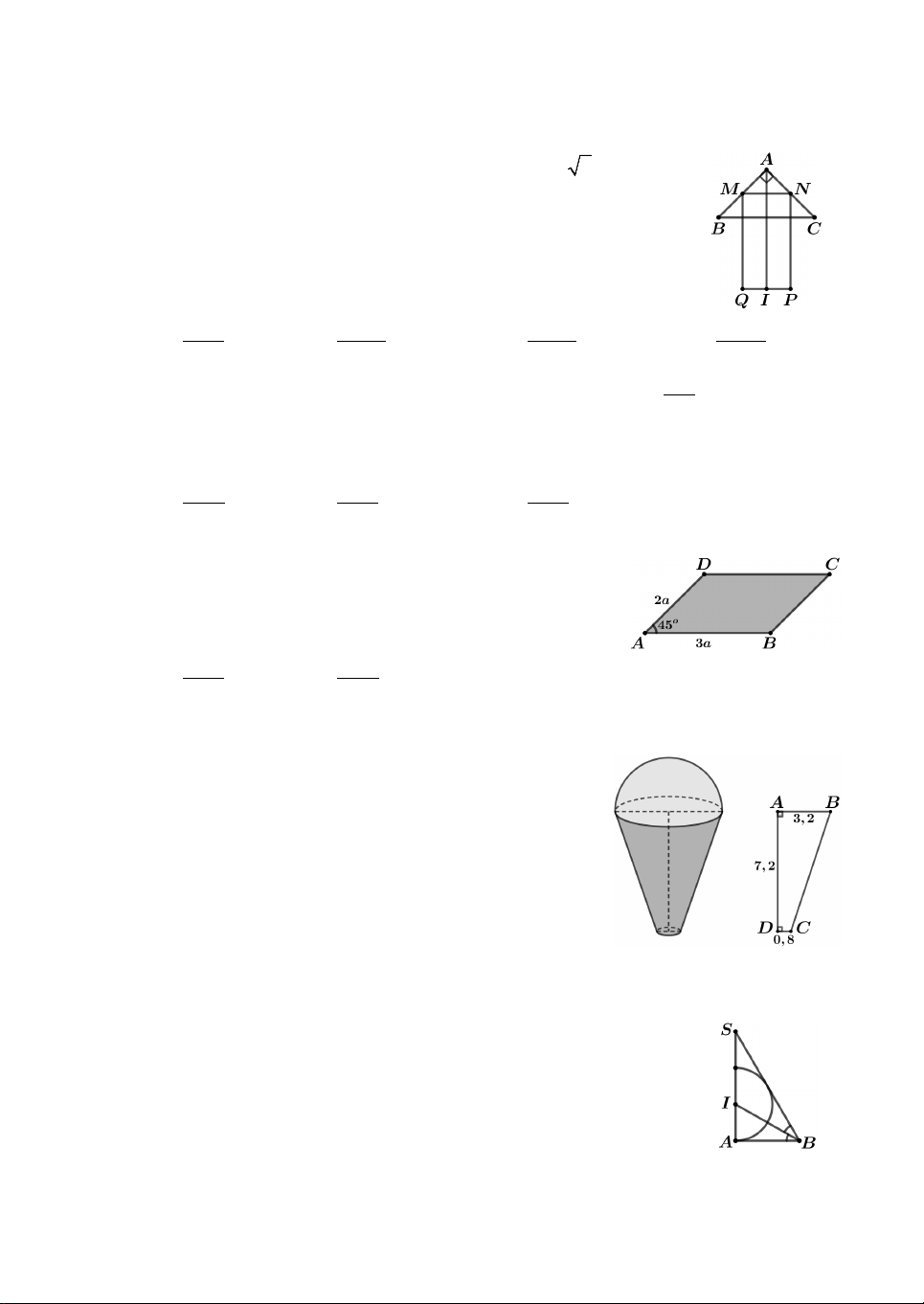
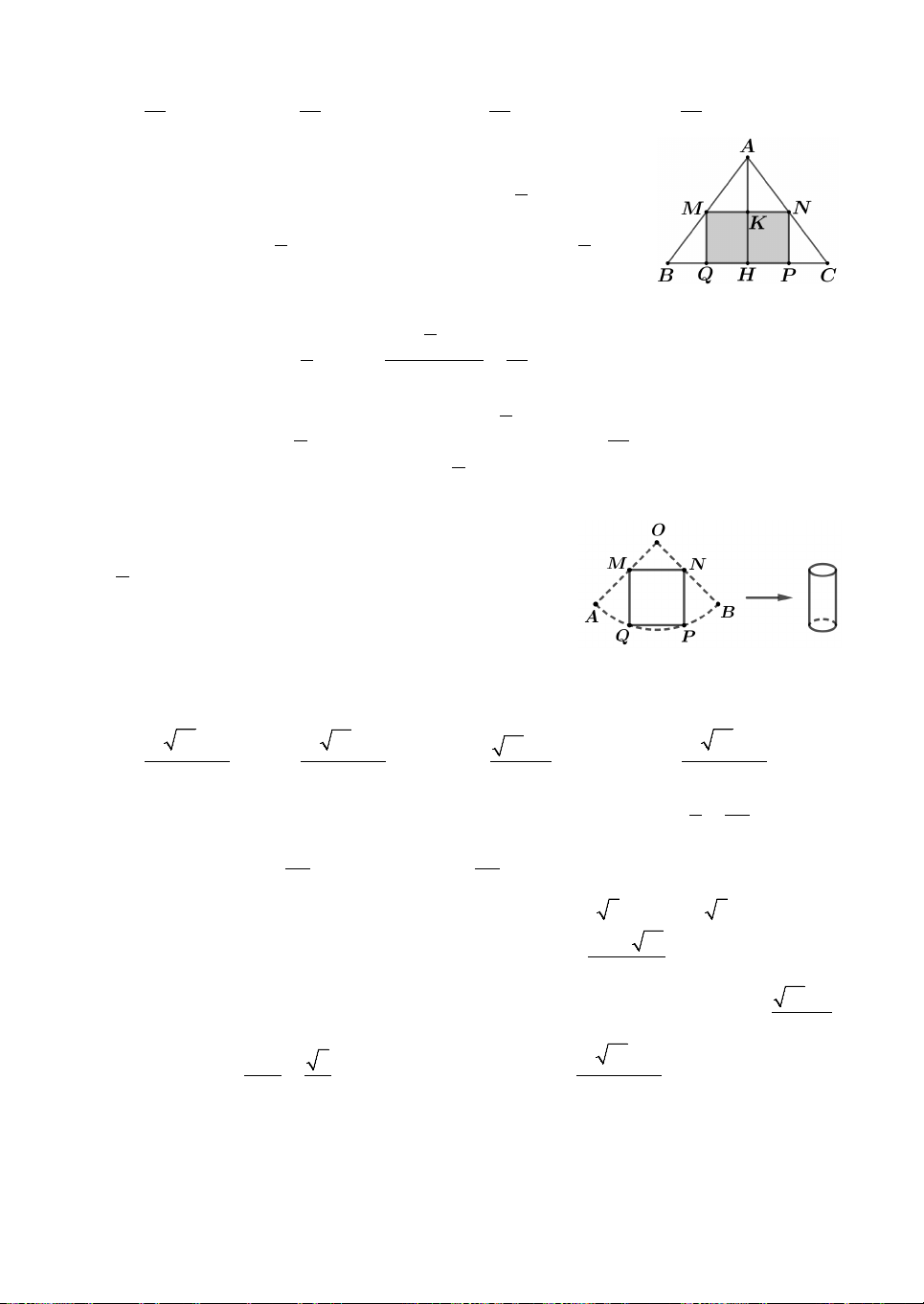
Câu 1. Cho tam giác vuông cân ABC có AB AC a 2 và hình
chữ nhật MNPQ với MQ  2MN được xếp chồng lên nhau sao cho
M , N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể
tích V của vật thể tròn xoay khi quay mô hình trên quanh trục
AI, với I là trung điểm PQ. 3 3 3 3 A. 5a 11a 11a 17a V  . B. V  . C. V  . D. V  . 6 6 8 24
Câu 2. Cho hình thang AD
ABCD vuông A và B với AB BC   . a Quay hình 2
thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của
khối tròn xoay được tạo thành. 3 3 3 A. 4a 5a 7a V  . B. V  . C. V  . D. 3
V a . 3 3 3
Câu 3. Cho hình bình hành ABCD có AD  2 , a AB  3 , a
BAD  45 (như hình vẽ). Tính thể tích V của khối tròn
xoay nhận được khi quay hình bình hành ABCD quanh trục AB. 3 3 A. 5a 9a V  . B. V  . C. 3 V  5a . D. 3 V  6a . 2 2
Câu 4. Một cơ sở sản xuất kem chuẩn bị làm 1000 chiếc
kem giống nhau theo đơn đặt hàng. Cốc đựng kem có
dạng hình tròn xoay được tạo thành khi quay hình thang
ABCD vuông tại A và D xung quanh trục AD (xem
hình vẽ). Chiếc cốc có bề dày không đáng kể, chiều cao
7,2 cm; đường kính miệng cốc bằng 6,4 cm; đường kính
đáy cốc bằng 1,6 cm. Kem được đổ đầy cốc và dư ra phía
ngoài một lượng có dạng nửa hình cầu, có bán kính bằng
bán kính miệng cốc. Cơ sở đó cần dùng lượng kem gần
nhất với giá trị nào trong các giá trị sau A. 3 132 dm . B. 3 170 dm . C. 3 293 dm . D. 3 954 dm .
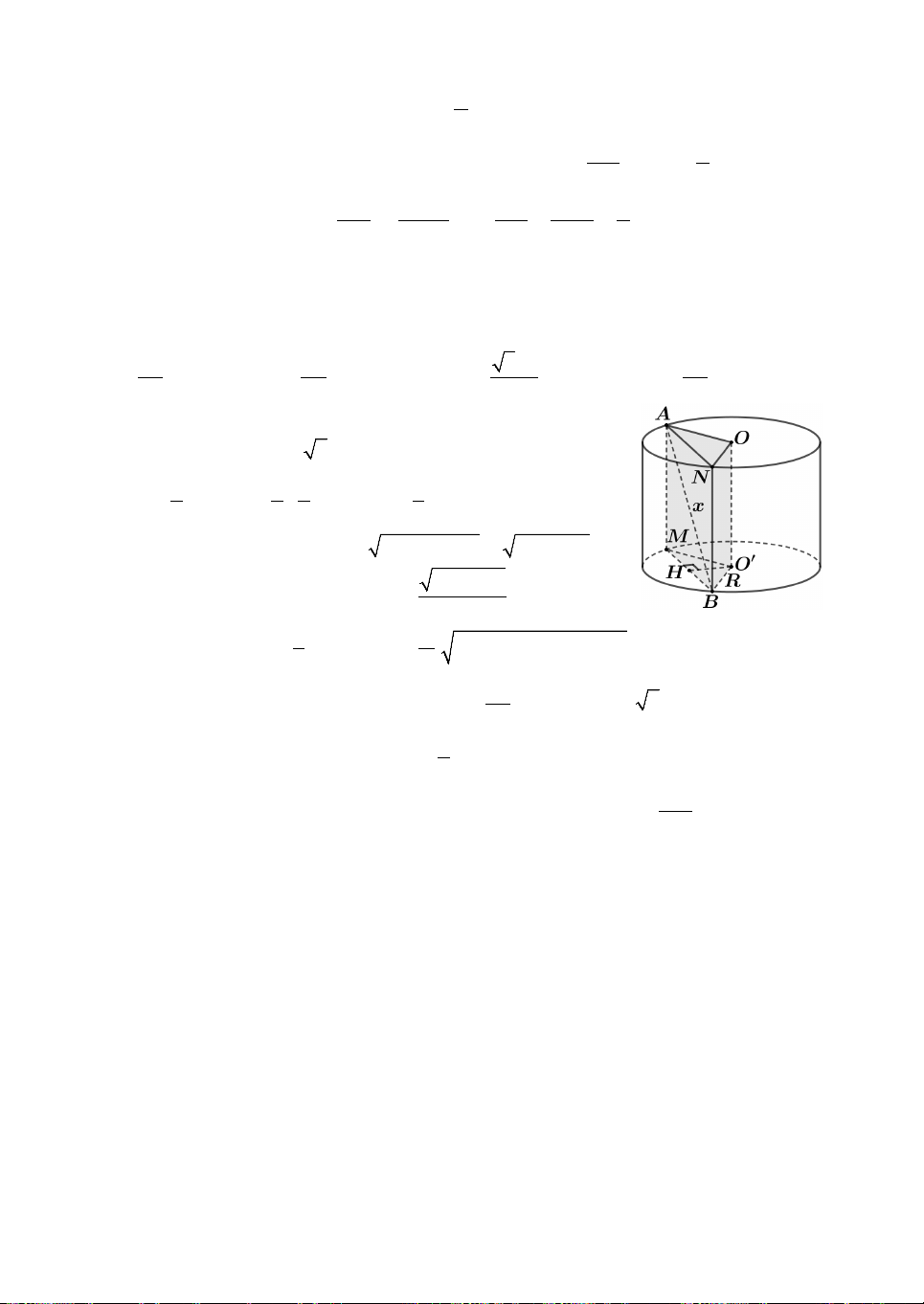
Câu 5. Cho tam giác SAB vuông tại , A ABS  60 ,  đường phân giác trong 
ABS cắt SA tại I. Vẽ nửa đường tròn tâm I bán kính
IA (như hình vẽ). Cho tam giác SAB và nửa đường tròn trên cùng
quay quanh SA tạo nên khối cầu và khối nón tương ứng có thể
tích là V và V . Khẳng định nào sau đây đúng ? 1 2
A. V  3V .
B. 2V  3V .
C. 4V  9V .
D. 9V  4V . 1 2 1 2 1 2 1 2 7
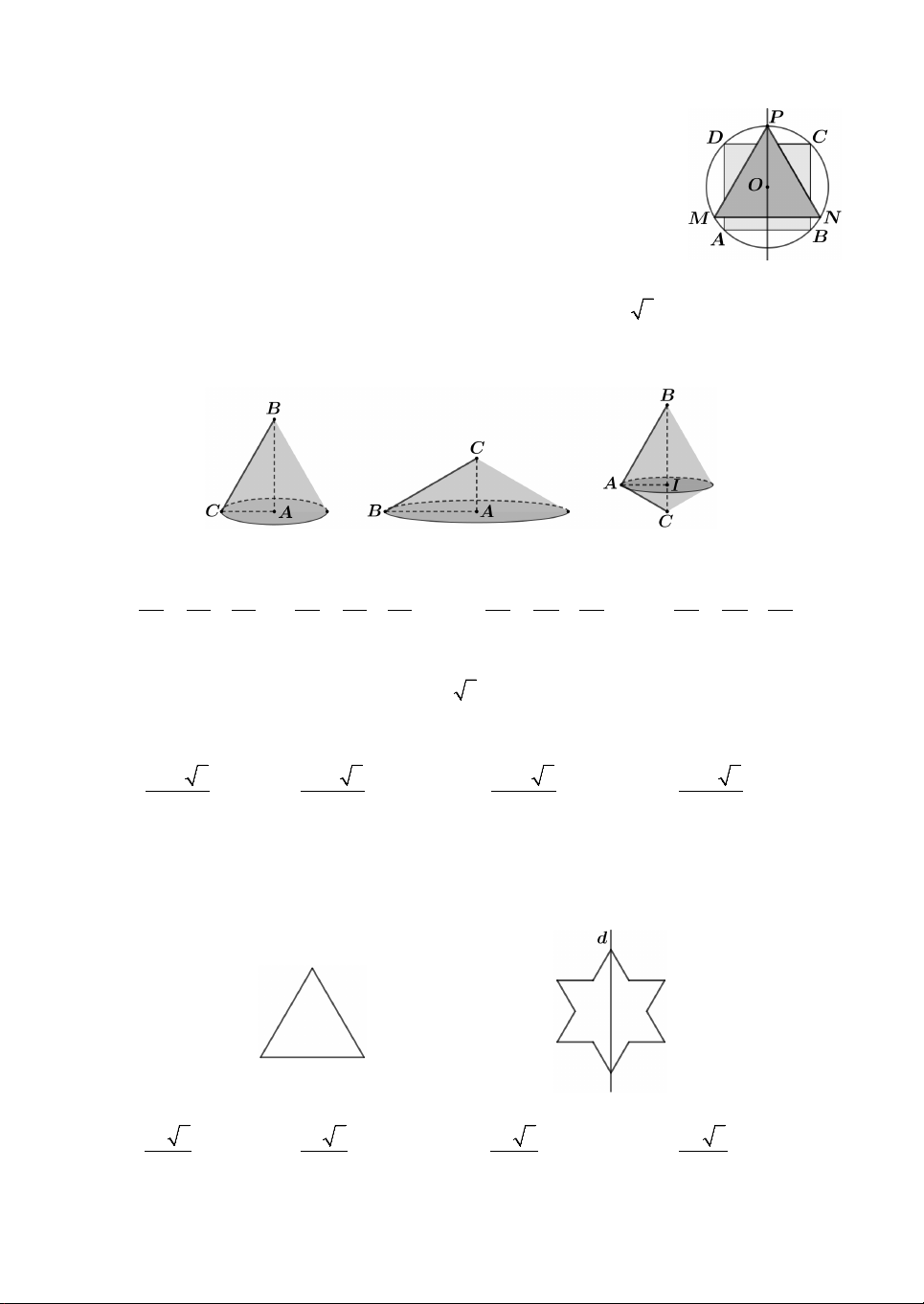
Câu 6. Cho hình vuông ABCD nội tiếp đường tròn O, bán kính r;
tam giác đều MNP nội tiếp đường tròn đó và MN song song AB
(như hình vẽ). Cho mô hình trên quay quanh đường thẳng OP. Kí
hiệu V , V , V là thể tích khối tròn xoay do hình vuông, hình tròn 1 2 3
và tam giác đều tạo thành. Khẳng định nào sau đây đúng ?
A. V V V . B. V V V . C. 2
V V .V . D. 2
V V .V . 1 2 3 3 2 1 1 2 3 3 2 1
Câu 7. Cho tam giác ABC vuông tại A và có AC  ,
a AB a 3. Gọi V , V , V là thể 1 2 3
tích các khối tròn xoay sinh bởi tam giác ABC kể cả các điểm trong khi lần lượt quay
quanh các cạnh AB, AC, BC. Trong các khẳng định sau, khẳng định nào đúng ? Hình 1 Hình 2 Hình 3 A. 1 1 1 1 1 1 1 1 1 1 1 1   . B.   . C.   . D.   . V V V V V V 2 2 2 V V V 2 2 2 V V V 1 3 2 3 1 2 2 3 2 3 1 2
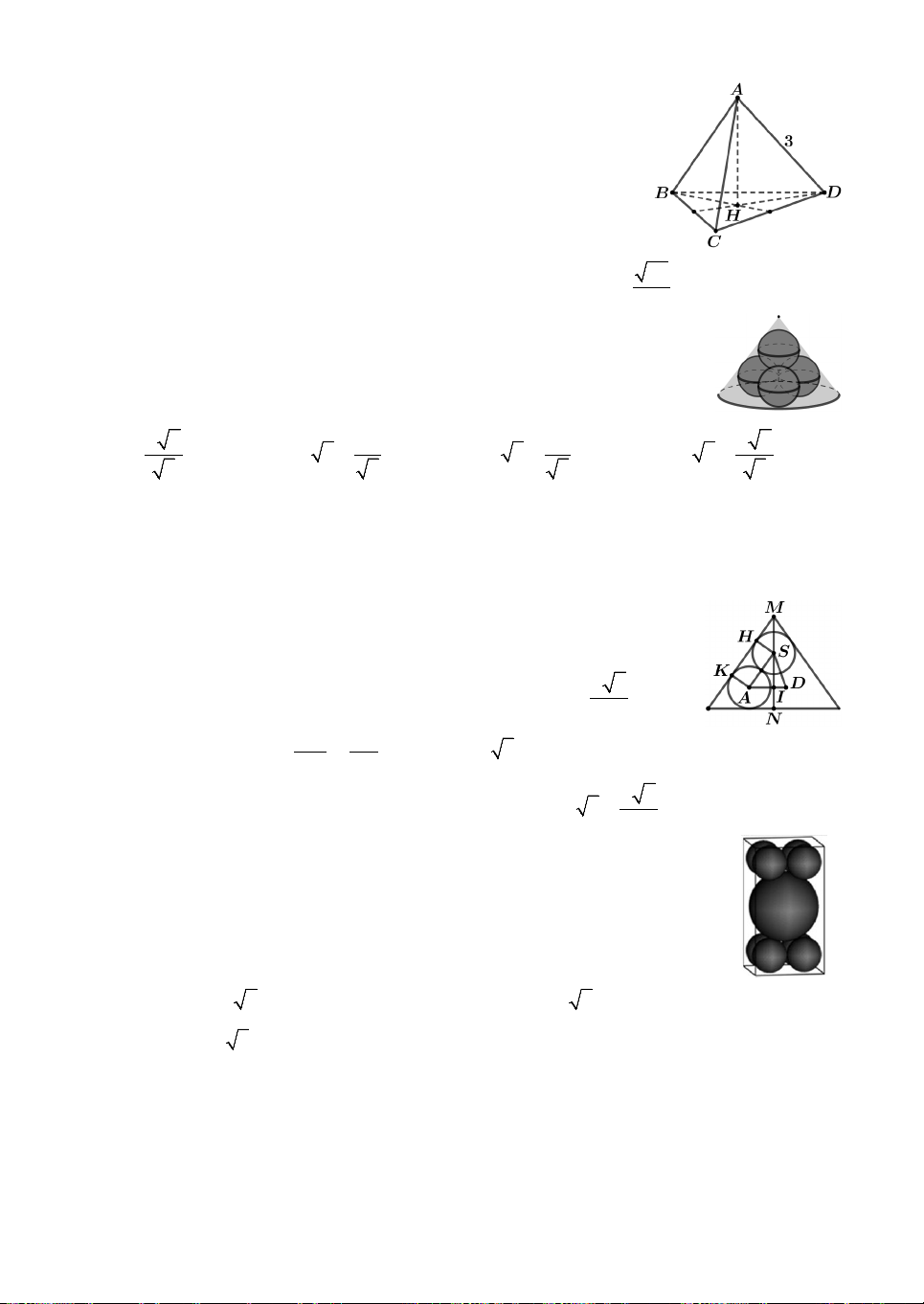
Câu 8. Cho hình tứ diện ABCD có AD vuông góc với mặt phẳng ABC và tam giác
ABC vuông tại B. Biết BC a, AB a 3, AD  3 .
a Quay các tam giác ABC và
ABD (bao gồm cả điểm bên trong hai tam giác) xung quanh đường thẳng AB ta được
hai khối tròn xoay. Thể tích phần chung của hai khối tròn xoay bằng 3 3 3 3 A. 8a  3 3a  3 4a  3 5a  3 . B. . C. . D. . 3 16 16 16
Câu 9. Ban đầu ta có một tam giác đều cạnh bằng 3 như hình 1. Tiếp theo ta chia
mỗi cạnh của tam giác thành 3 đoạn bằng nhau, dựng một tam giác đều về phía bên
ngoài có một cạnh là đoạn giữa, sau đó bỏ đi đoạn giữa ta được hình 2. Khi quay hình
2 xung quanh d ta được một khối tròn xoay có thể tích bằng Hình 1 Hình 2 A. 53 . B. 5 3 . C. 5 3 . D. 9 3 . 2 3 6 8 8
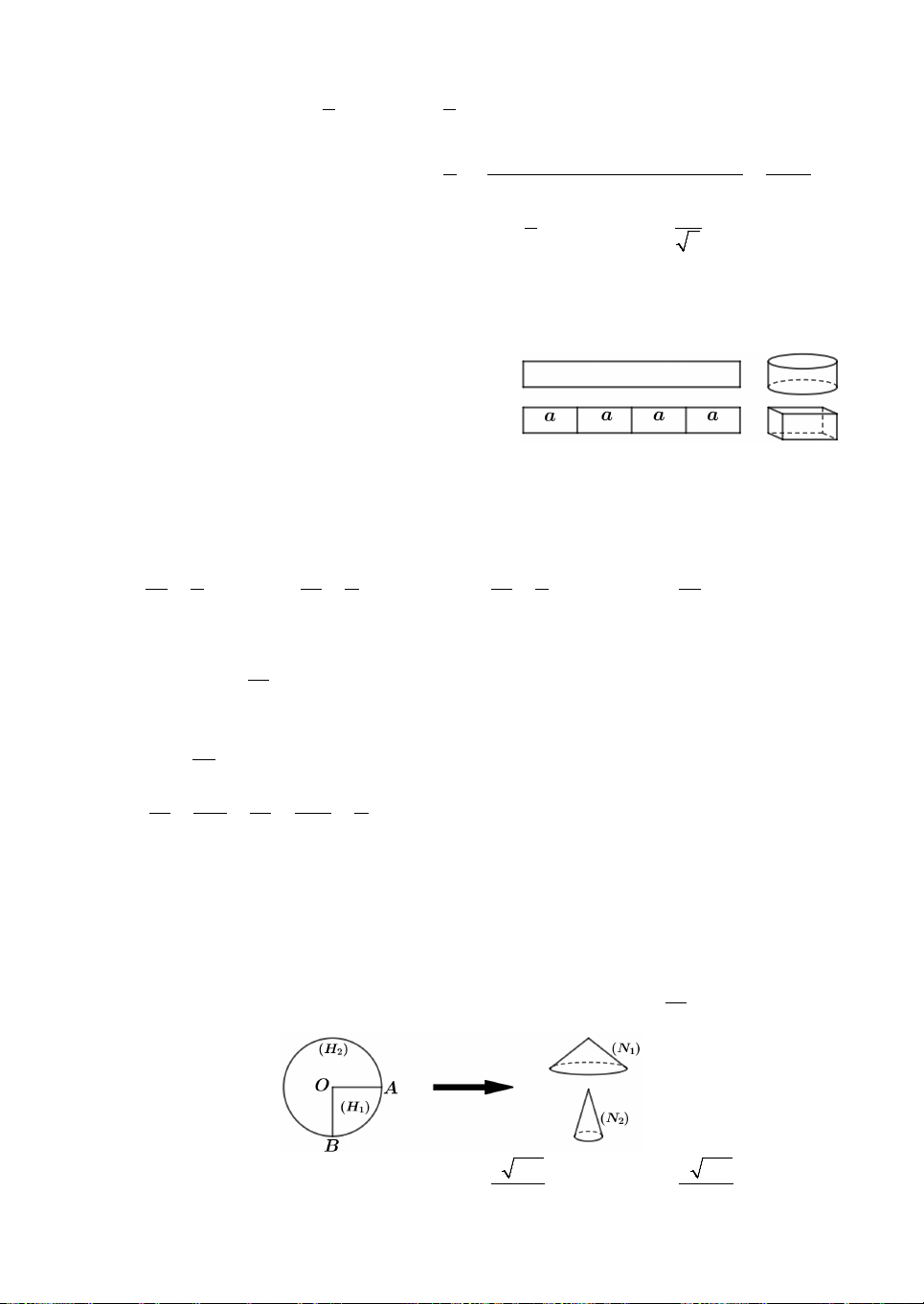
Câu 10. Cho nửa đường tròn đường kính AB  2R và điểm C thay
đổi trên nửa đường tròn đó, đặt 
CAB và gọi H là hình chiếu
vuông góc của C lên AB (như hình vẽ). Tìm sao cho thể tích vật
thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
A.  45.
B.  60. C. arctan 2. D. 1 arctan . 2
Phần 3. Ứng dụng thực tiễn
Câu 1. Bé Bách có một tấm bìa có chiều dài
20 cm; chiều rộng 1 cm. Bé muốn gấp một cái
hộp nhỏ xinh để bỏ kẹp tóc vào hộp đó tặng
quà cho mẹ ngày 20 tháng 10. Anh Siêu đã chỉ
cho bé hai cách gấp hộp. Cách thứ nhất là bé cuốn tấm bìa thành một cái hộp hình trụ
không có hai đáy có thể tích V . Cách thứ hai là bé gập tấm bìa một hình hộp chữ 1
nhật có thể tích V có các kích thước như hình vẽ. Hãy tìm tỉ số thể tích của hai hộp 2
để biết được gấp theo cách nào sẽ có thể tích lớn hơn. A. V 4 V V 1 V 1  . B. 1  . C. 1  . D. 1  4. V V 4 V 4 V 2 2 2 2
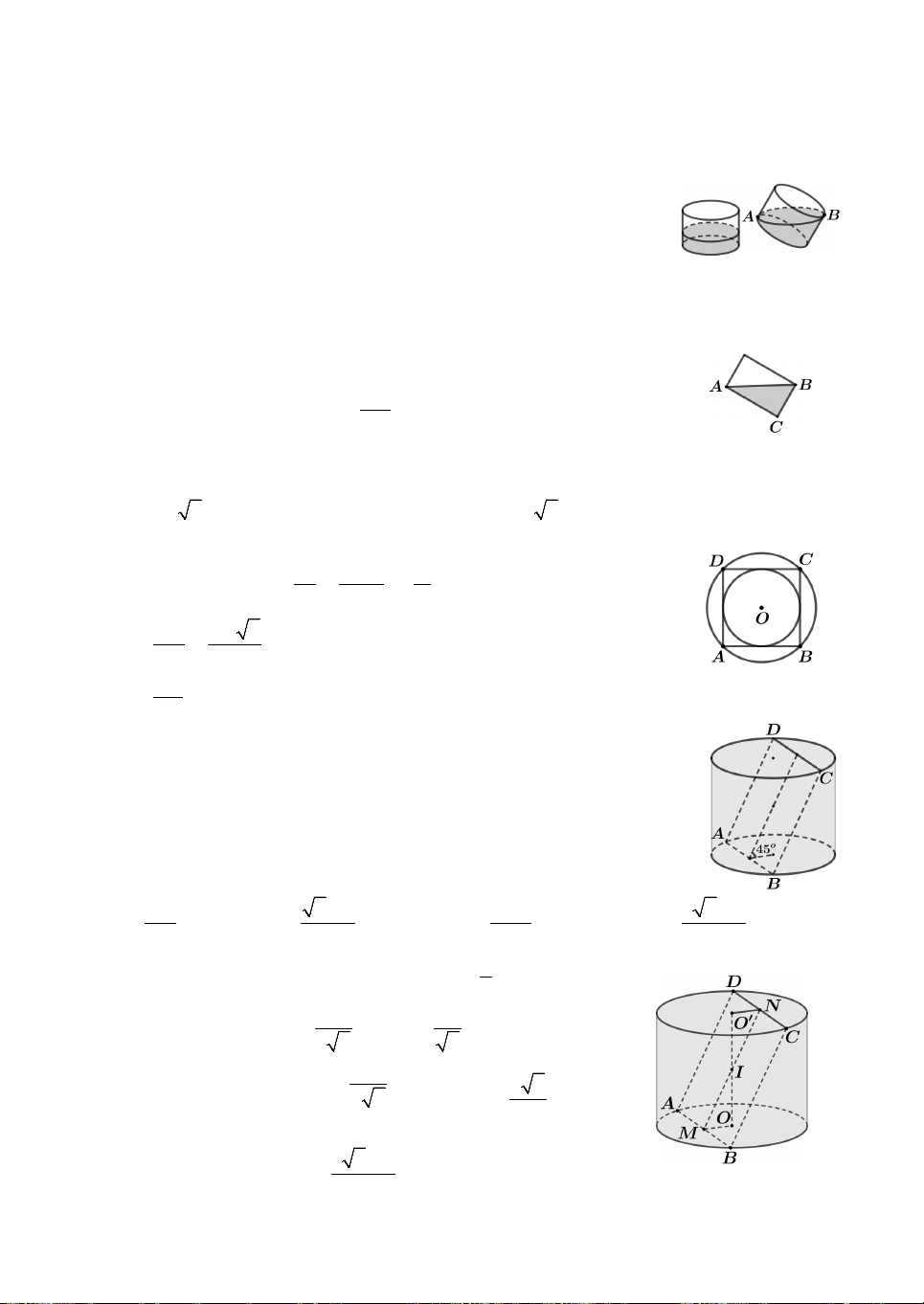
Câu 2. Một tấm tôn hình tròn tâm O, bán kính R được chia thành hai hình H và 1 
H như hình vẽ. Cho biết góc 
AOB  90. Từ hình H gò tấm tôn để được hình 1  2 
nón N không đáy và từ hình H gò tấm tôn để được hình nón N không đáy. 2  2  1  Ký hiệu V
V , V lần lượt là thể tích của hình nón N ,
N . Tỉ số 1 bằng 1   2  1 2 V2 A. 2. B. 3. C. 3 105 . D. 7 105 . 5 9
Câu 3. Từ cùng một tấm kim loại dẻo hình
quạt (như hình vẽ) có kích thước bán kính
R  5 và chu vi của hình quạt là
P  810, người ta gò tấm kim loại thành
những chiếc phễu theo hai cách:
Cách 1. Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu. 9
Cách 2. Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung
quanh của hai cái phễu. Gọi V là thể tích của cái phễu thứ nhất, V là tổng thể tích 1 2
của hai cái phễu ở cách thứ hai. Tỉ số V1 bằng V2 A. V 2 V 2 2 V 21 V 2 21 1  . B. 1  . C. 1  . D. 1  . V 7 V 7 V 7 V 7 2 2 2 2
Câu 4. Để làm cống thoát nước cho một khu vực dân cư người ta
cần đúc 500 ống hình trụ có đường kính trong và chiều cao của
mỗi ống bằng 1 m, độ dày của thành ống là 10 cm. Chọn mác bê
tông là 250 (tức mỗi khối bê tông là 7 bao ximăng). Hỏi phải
chuẩn bị bao nhiêu bao ximăng để làm đủ số ống nói trên ?
A.  1110 bao. B. 1200 bao. C.  1210 bao.
D.  4 210 bao.
Câu 5. Cắt một miếng tôn hình vuông
cạnh 1 m thành hai hình chữ nhật,
trong đó một hình có chiều rộng x m,
gọi miếng tôn này là miếng tôn thứ
nhất. Người ta gò miếng tôn thứ nhất
thành một lăng trụ tam giác đều, miếng còn lại gò thành một hình trụ (như hình vẽ).
Tìm x để tổng thể tích khối lăng trụ và khối trụ thu được là nhỏ nhất. A. 9 x  . B. 1 x  . C. 9 x  . D. 1 x  . 3 9 3 31 9 3  3
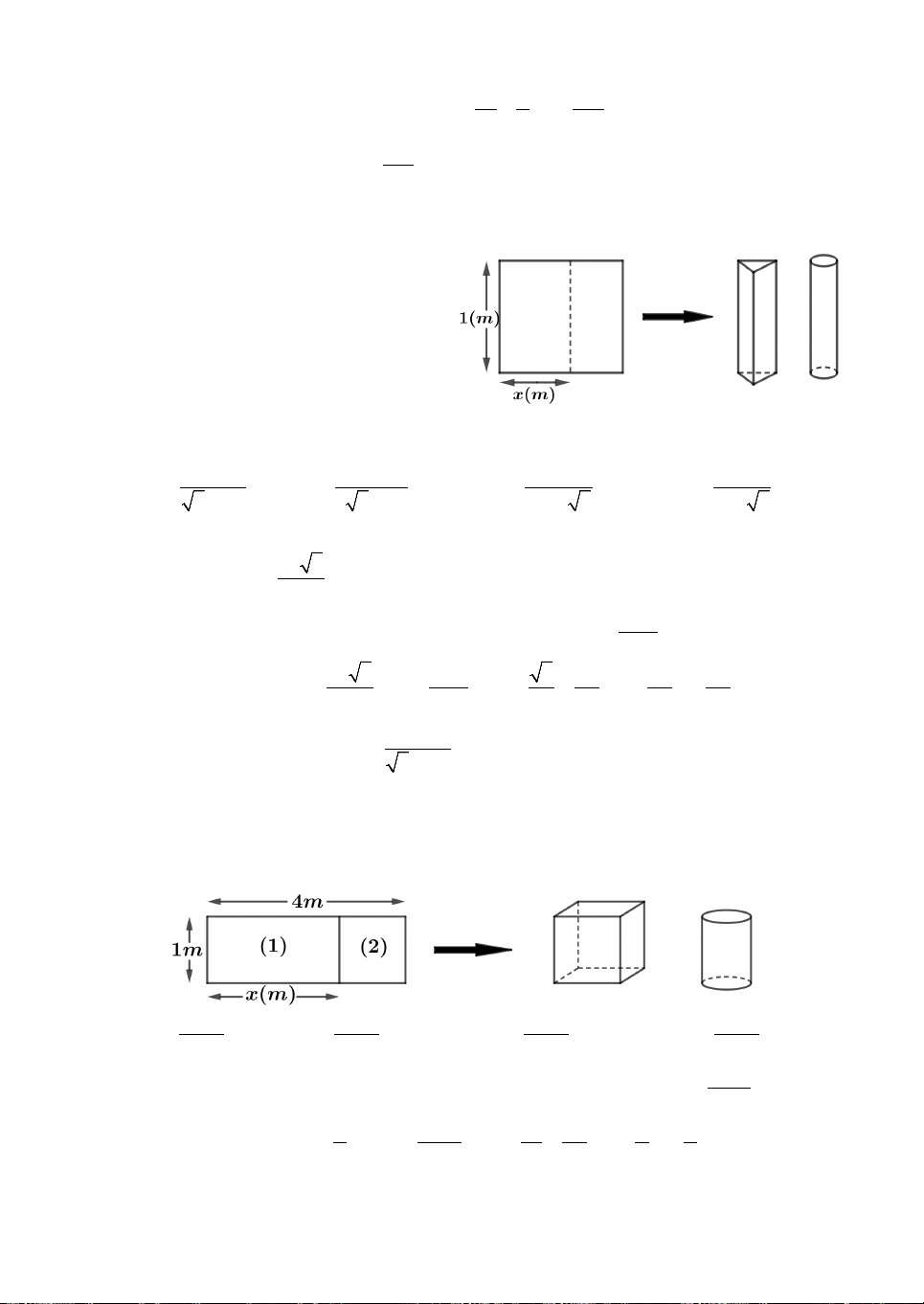
Câu 6. Một tấm tôn hình chữ nhật có chiều dài 4m, chiều rộng 1m. Một người thợ
muốn cắt tấm tôn này thành hai phần như hình vẽ. Người thợ gò phần 1 thành hình
trụ có đáy hình vuông và phần 2 thành hình trụ có đáy hình tròn. Tìm x để tổng thể
tích của hai khối trụ là nhỏ nhất. A. 4 x  . B. 8 x  . C. 16 x  . D. 16 x  .  4  4  4  4
Câu 7. Từ một tấm tôn hình chữ nhật người ta cuộn
thành một chiếc thùng hình trụ không đáy (như hình
vẽ). Biết tâm tôn có chu vi bằng 120 cm. Để chiếc thùng
có thể tích lớn nhất thì chiều dài, rộng của mảnh tôn lần lượt là
A. 35 cm; 25 cm. B. 30 cm; 30 cm. C. 40 cm; 20 cm. D. 50 cm; 10 cm.
Câu 8. Bạn An có một tấm bìa hình tròn như hình vẽ, An muốn biến hình tròn đó
thành một cái phễu hình nón. Khi đó An phải cắt hình quạt tròn OAB rồi dán hai bán 10 kính O ,
A OB lại với nhau. Gọi là góc ở tâm hình quạt tròn dùng làm phễu. Tìm
để thể tích phễu là lớn nhất. A.  . B.  . C. 2 6  . D.  . 2 3 3 4
Câu 9. Có tấm bìa hình tam giác vuông cân
ABC có cạnh huyền BC bằng . a Người ta
muốn cắt tấm bìa đó thành hình chữ nhật
MNPQ rồi cuộn lại thành một hình trụ không
đáy như hình vẽ. Diện tích hình chữ nhật đó
bằng bao nhiêu để diện tích xung quanh của hình trụ là lớn nhất ? 2 2 2 2 A. a a a a . B. . C. . D. . 2 4 8 12
Câu 10. Cho tấm tôn hình nón có bán kính đáy là 2
r  , độ dài đường sinh   2. Người ta cắt theo một 3
đường sinh và trải phẳng ra được một hình quạt. Gọi
M , N thứ tự là trung điểm của O , A OB.
Hỏi khi cắt hình quạt theo hình chữ nhật MNPQ (hình vẽ) và tạo thành hình trụ
(không đáy) có đường PN trùng MQ thì được khối trụ có thể tích bằng 3 13   1 3 13   1 5 13   1 A.  . B. . C. 13 1. D. . 4 8 9 12
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Câu 1. Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng
3 lần đường kính của đáy; Một viên bi và một khối nón đều bằng thủy tinh.
Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước.
Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì
thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại
trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh). A. 1 . B. 2 . C. 4 . D. 5 . 2 3 9 9 11
Câu 2. Một cái ống nghiệm hình trụ có bán kính trong lòng ống là , R ống
nghiệm đang chứa một lượng nước có chiều cao .
h Người ta thả 3 viên bi có
cùng bán kính R vào ống nghiệm thì mực nước dâng lên vừa đủ phủ kín
viên bi cao nhất như hình vẽ. Khẳng định nào sau đây đúng? A. h  3 . R B. h  2 . R C. h  2 . R D. 3 h  3 . R
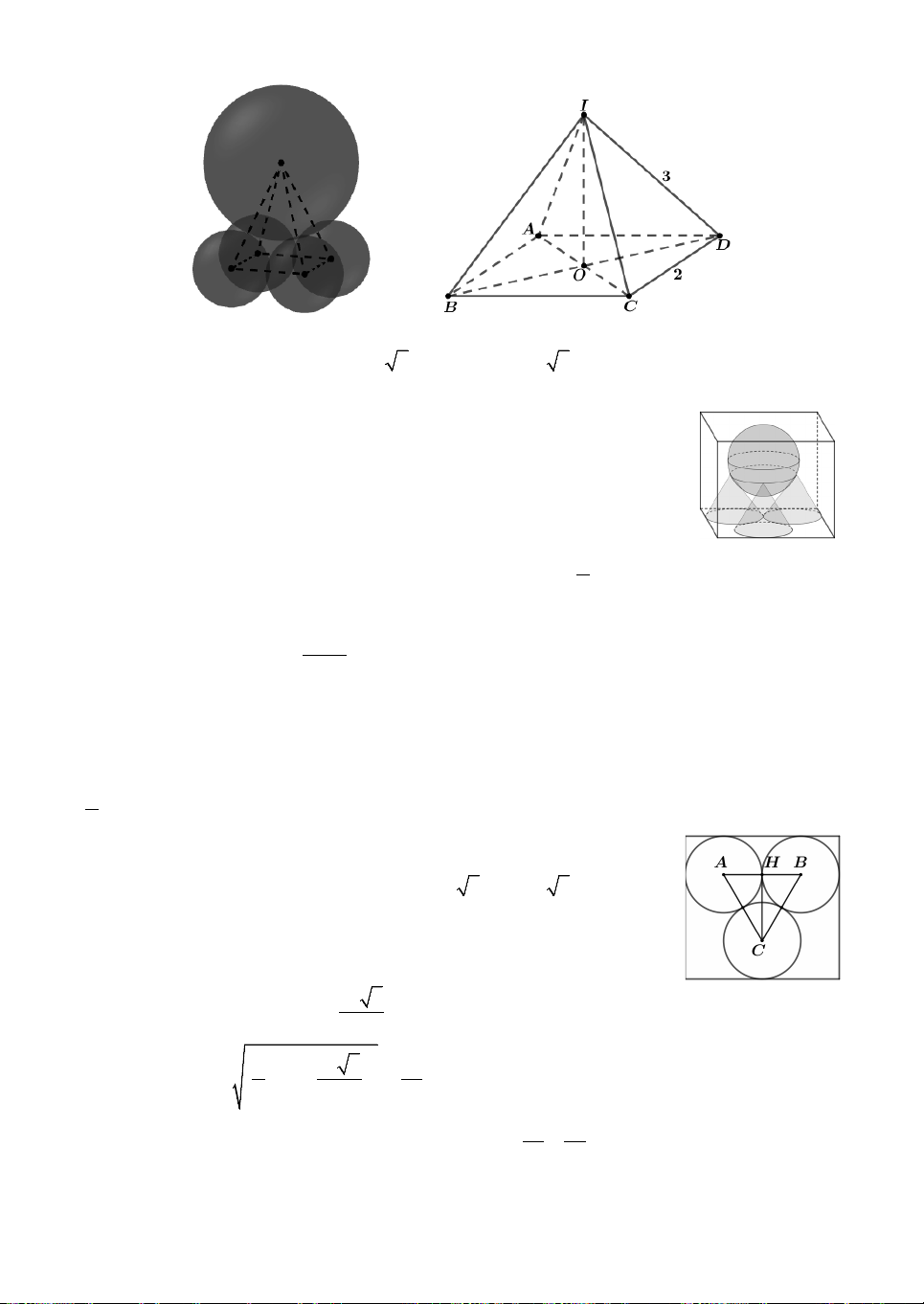
Câu 3. Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp
xúc nhau và tiếp xúc với mặt phẳng P. Mặt cầu S bán kính
bằng 2 tiếp xúc với ba quả bóng trên. Gọi M là điểm bất kì trên
S, MH là khoảng cách từ M đến mặt phẳng P. Giá trị lớn
nhất của MH bằng A. 30 69 123 3  . B. 3 . C. 3 . D. 52 . 2 3 4 9
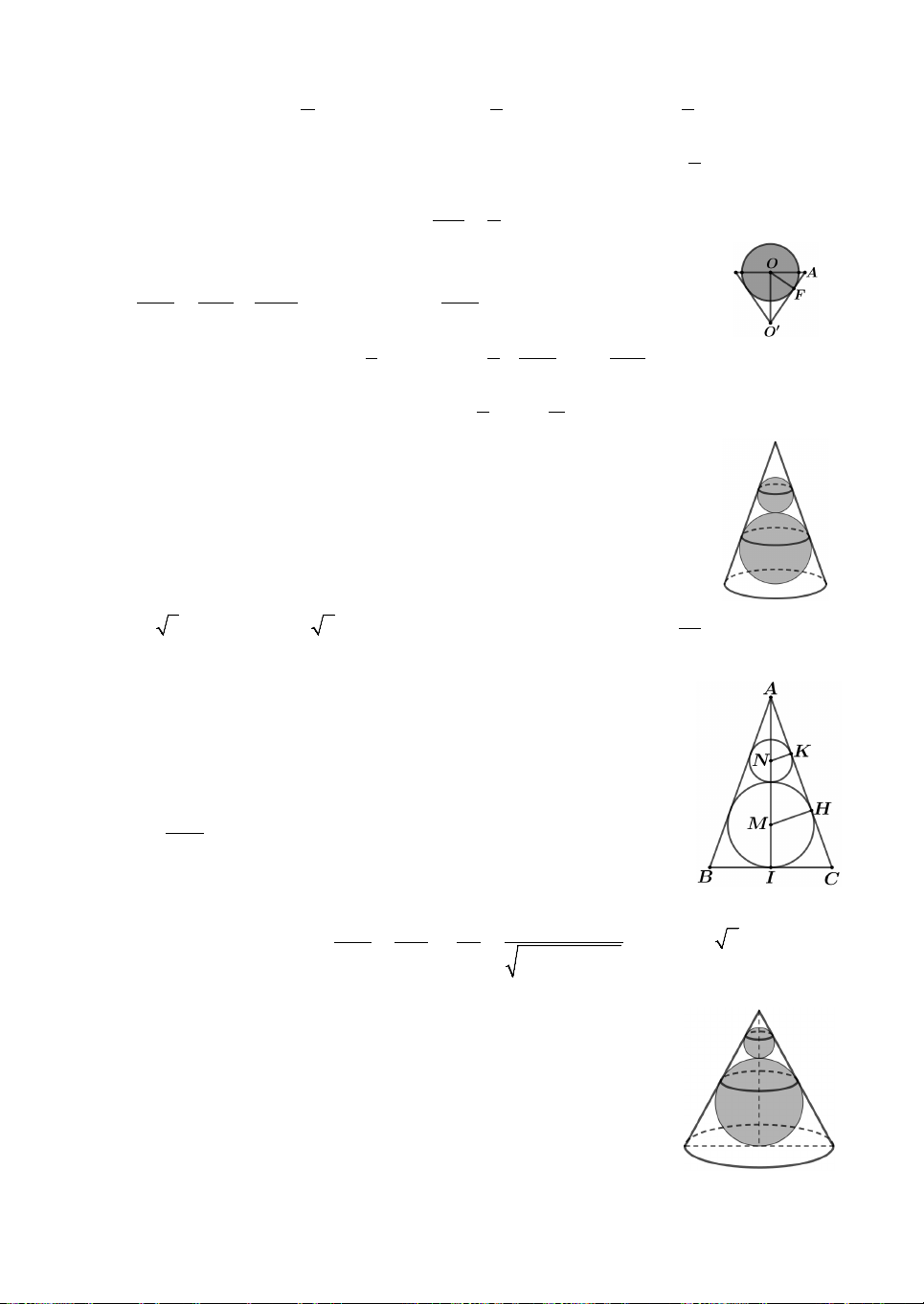
Câu 4. Có một hình nón chứa bốn quả bóng bàn bằng nhau, đường
kính mỗi quả bóng bàn là 4. Các quả bóng bàn tiếp xúc với nhau, ba
quả tiếp xúc với đáy của hình nón đồng thời bốn quả tiếp xúc với mặt
xung quanh của hình nón như hình vẽ. Chiều cao của hình nón bằng A. 4 2  2. B. 4 2 3  . C. 4 2 3   2. D. 4 2 2 3   2. 3 3 3 3
Câu 5. Một khối hộp chữ nhật có kích thước 4 cm4 cmh cm chứa
một quả cầu lớn và tám quả cầu nhỏ. Biết quả cầu lớn có bán kính
R  2 cm và quả cầu nhỏ có bán kính r  1cm ; các quả cầu tiếp xúc
nhau và tiếp xúc các mặt của hình hộp (như hình vẽ). Tìm h .
A. h  212 2 cm.
B. h  21 7 cm.
C. h  23 7 cm.
D. h  8 cm.
Câu 6. Một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba
khối nón giống nhau có thiết diện qua trục là một tam giác vuông
cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với
nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh
của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với
hai cạnh của đáy bể (tham khảo hình vẽ). Sau đó người ta đặt lên
đỉnh của ba khối nón một khối cầu có bán kính bằng 4 lần bán kính đáy của khối 3
nón. Biết khối cầu vừa đủ ngập trong nước (mặt trên của bể là tiếp diện của mặt cầu)
và lượng nước tràn ra là 337 3
cm . Thể tích lượng nước ban đầu ở trong bể xấp xỉ 3 A.  3 885,2 cm . B.  3 1106,2 cm . C.  3 1174,2 cm . D.  3 1209,2 cm . 12
Câu 7. Cho hình nón có bán kính đáy R  5a, độ dài đường sinh  13 . a Thể tích
khối cầu nội tiếp hình nón bằng 3 3 3 3 A. 40a 400a 4000a 4000a . B. . C. . D. . 9 27 27 81
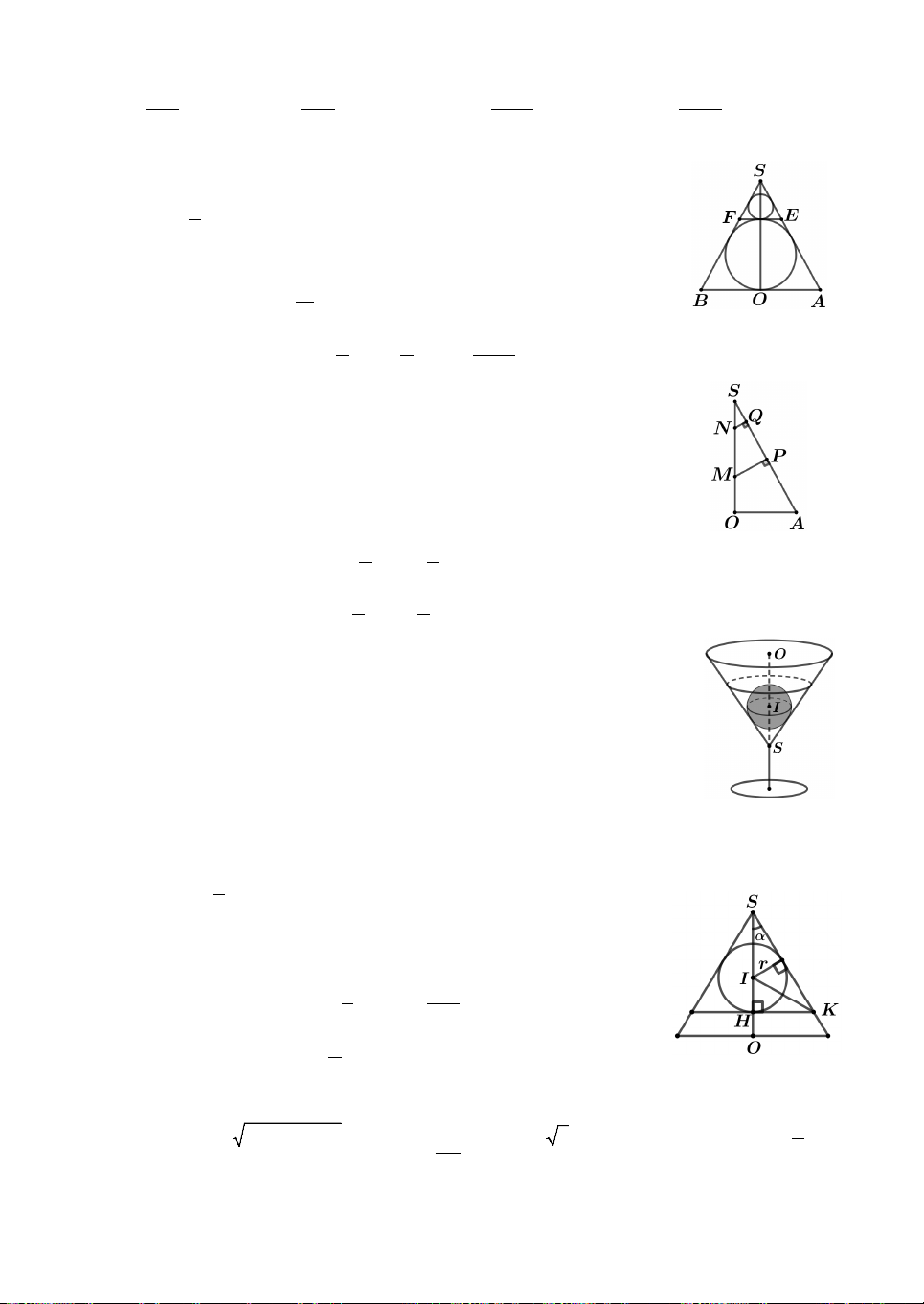
Câu 8. Một bình đựng nước dạng hình nón (không có đáy), đựng
đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng
một nửa chiều cao của bình nước và đo được thể tích tràn ra là 32 3
dm . Biết rằng khối cầu tiếp xúc với tất cả các đường sinh 3
của hình nón và toàn bộ khối cầu chìm trong nước, trong đó mặt
nước là tiết diện của khối cầu (hình vẽ bên). Thể tích nước còn lại trong bình bằng A. 16 32 40 64 3 dm . B.  3 dm . C.  3 dm . D.  3 dm . 3 3 3 3
Câu 9. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả
vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao
của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng
khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng
một nửa khối cầu chìm trong nước như hình vẽ. Thể tích nước còn lại trong ly bằng A. V. B. 1V. C. 1V. D. 1V. 3 6
Câu 10. Nguời ta đặt được vào trong một hình nón hai khối cầu có
bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với
mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và
khối cầu lớn tiếp xúc với đáy của hình nón (tham khảo hình vẽ). Bán
kính đáy của hình nón đã cho bằng A. a a 5. B. 2 2 . a C. 3 . a D. 8 . 3
Câu 11. Người ta chế tạo ra một món đồ chơi cho trẻ em theo các
công đoạn như sau: Trước tiên, chế tạo ra một hình nón tròn
xoay có góc ở đỉnh là 2 60 bằng thủy tinh cho trong suốt.
Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ
khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc
với mặt nón, quả cầu lớn tiếp xúc với cả mặt đáy của hình nón
(hình vẽ). Biết rằng chiều cao của hình nón là 9 cm. Bỏ qua bề
dày của các lớp vỏ thủy tinh, tổng thể tích của hai khối cầu bằng A. 38 40 100 112 3 cm . B.  3 cm . C.  3 cm . D.  3 cm . 3 3 3 3 13
Câu 12. Một ly nước có dạng như hình vẽ. Phần phía trên chứa
nước có dạng hình nón đỉnh S với đường kính đáy và chiều cao SO
cùng bằng 8cm. Ban đầu ly chứa lượng nước có chiều cao 4cm so
với đỉnh S. Cho vào ly nước một viên bi sắt hình cầu thì nước dâng
lên vừa phủ kín viên bi. Tính bán kính r của viên bi làm tròn đến hai chữ số thập phân.
A. r  1,23cm. B. r  1,28cm.
C. r  1,53cm.
D. r  1,78cm.
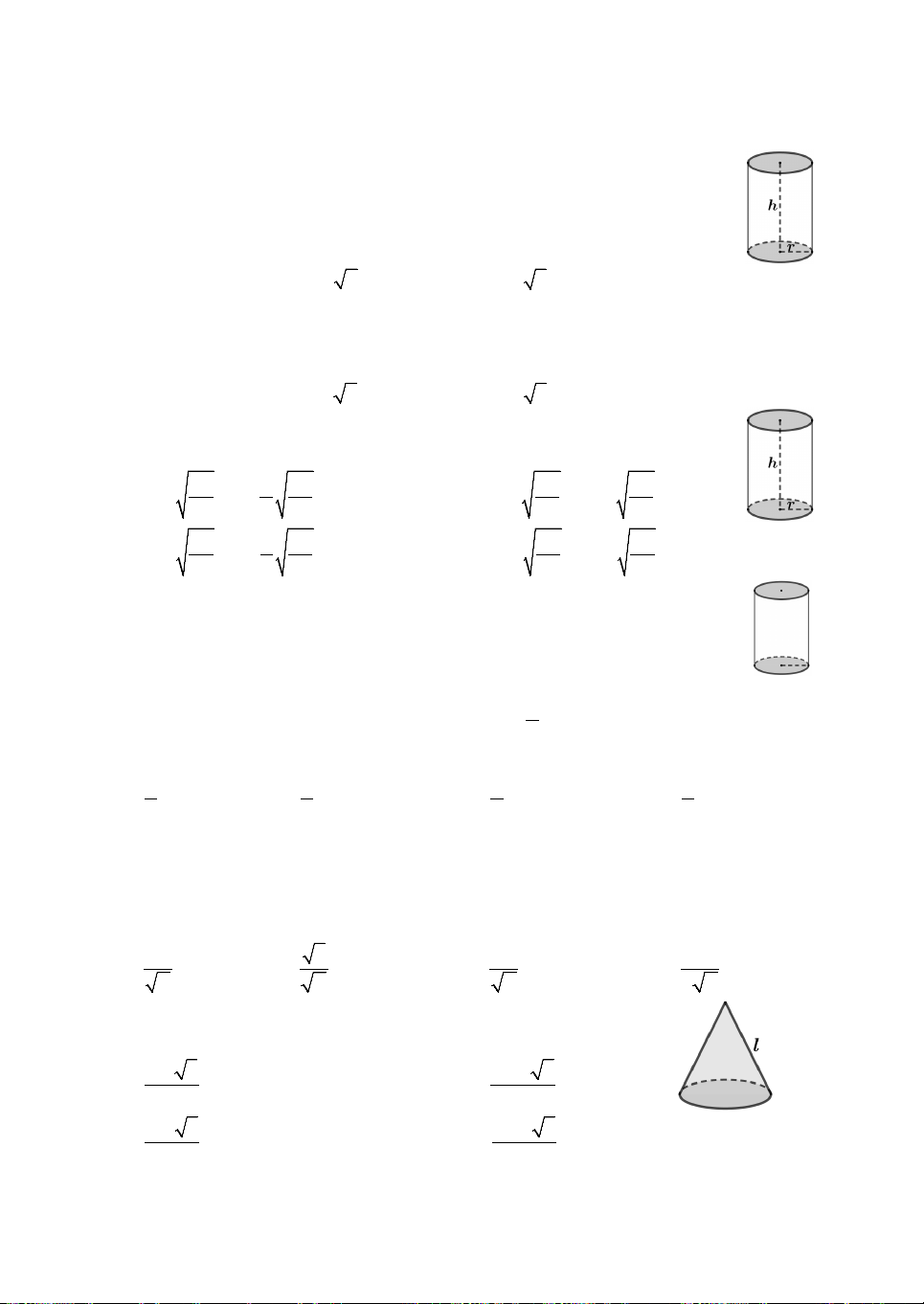
Câu 13. Một chiếc chén hình trụ có chiều cao bằng đường kính quả
bóng bàn. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài
của quả bóng có chiều cao bằng 3 chiều cao của nó. Gọi V , V lần 4 1 2
lượt là thể tích của quả bóng và chiếc chén. Khi đó
A. 3V  2V .
B. 9V  8V .
C. 16V  9V .
D. 27V  8V . 1 2 1 2 1 2 1 2
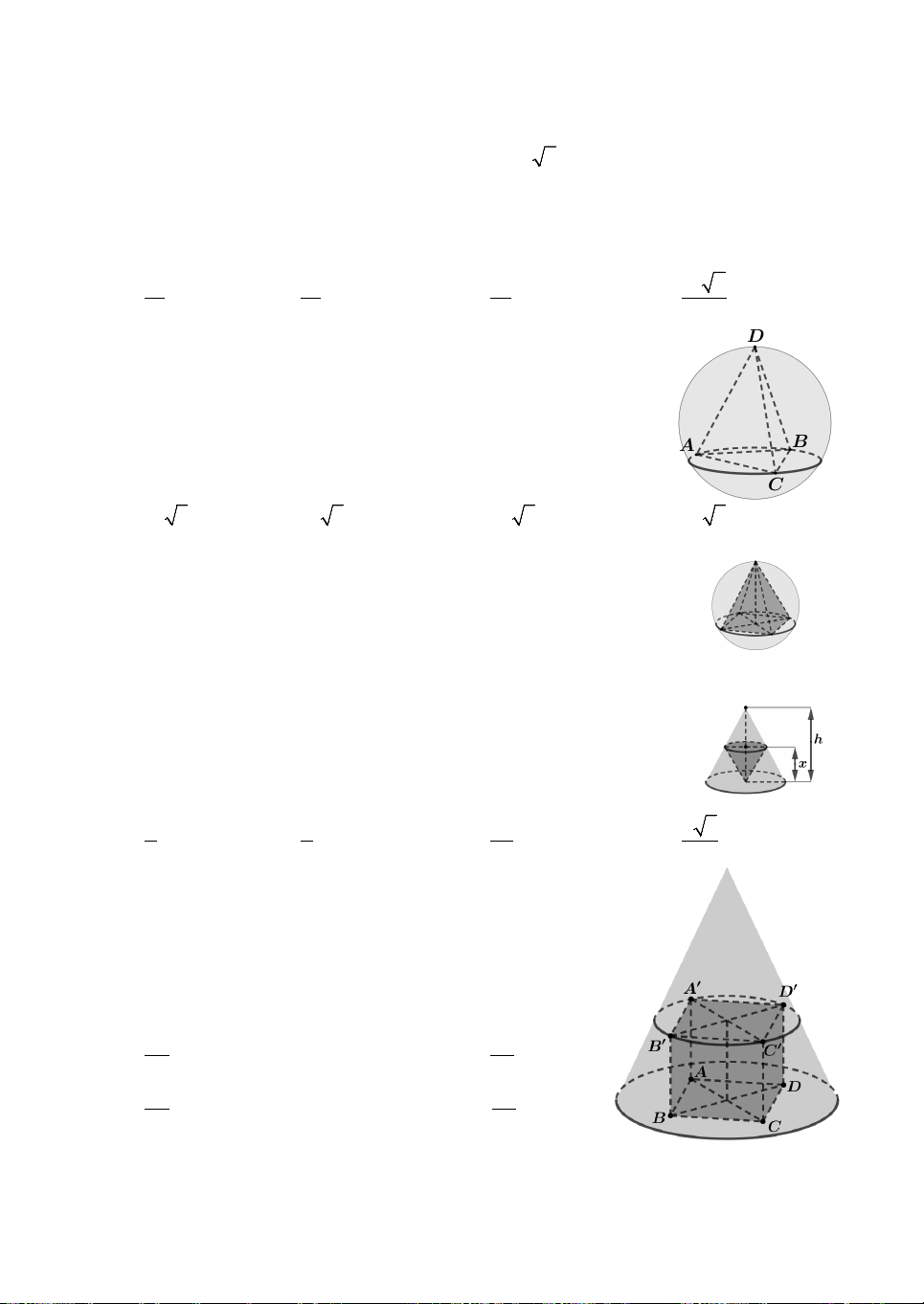
Câu 14. Một quả cầu có thể tích 256  3
cm  được đặt vào một 3
chiếc cốc có dạng hình trụ với đường kính đáy là 6 cm như hình vẽ.
Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến hàng phần trăm) A. 2,00 cm. B. 4,00 cm. C. 4,65 cm. D. 6,65 cm.
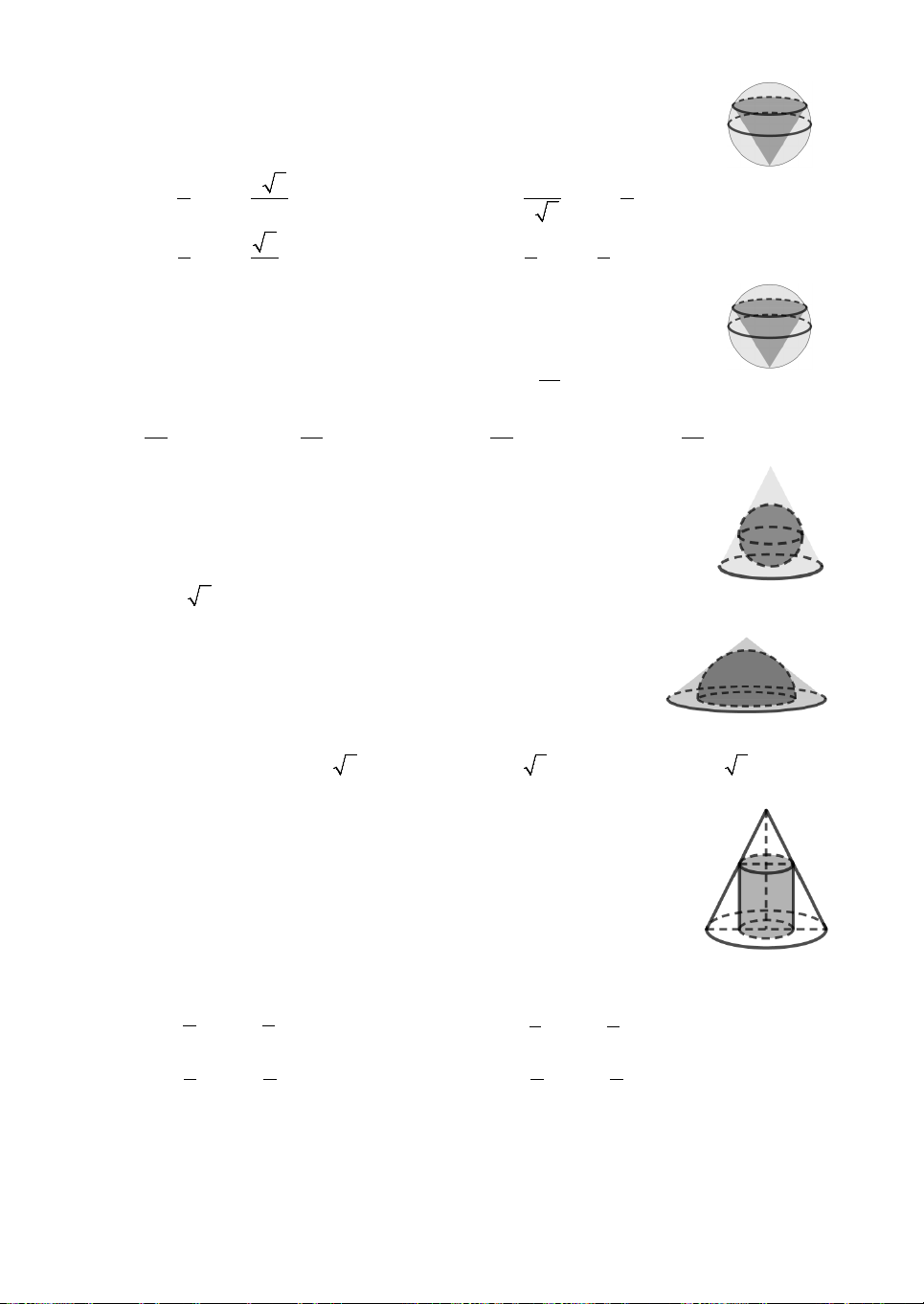
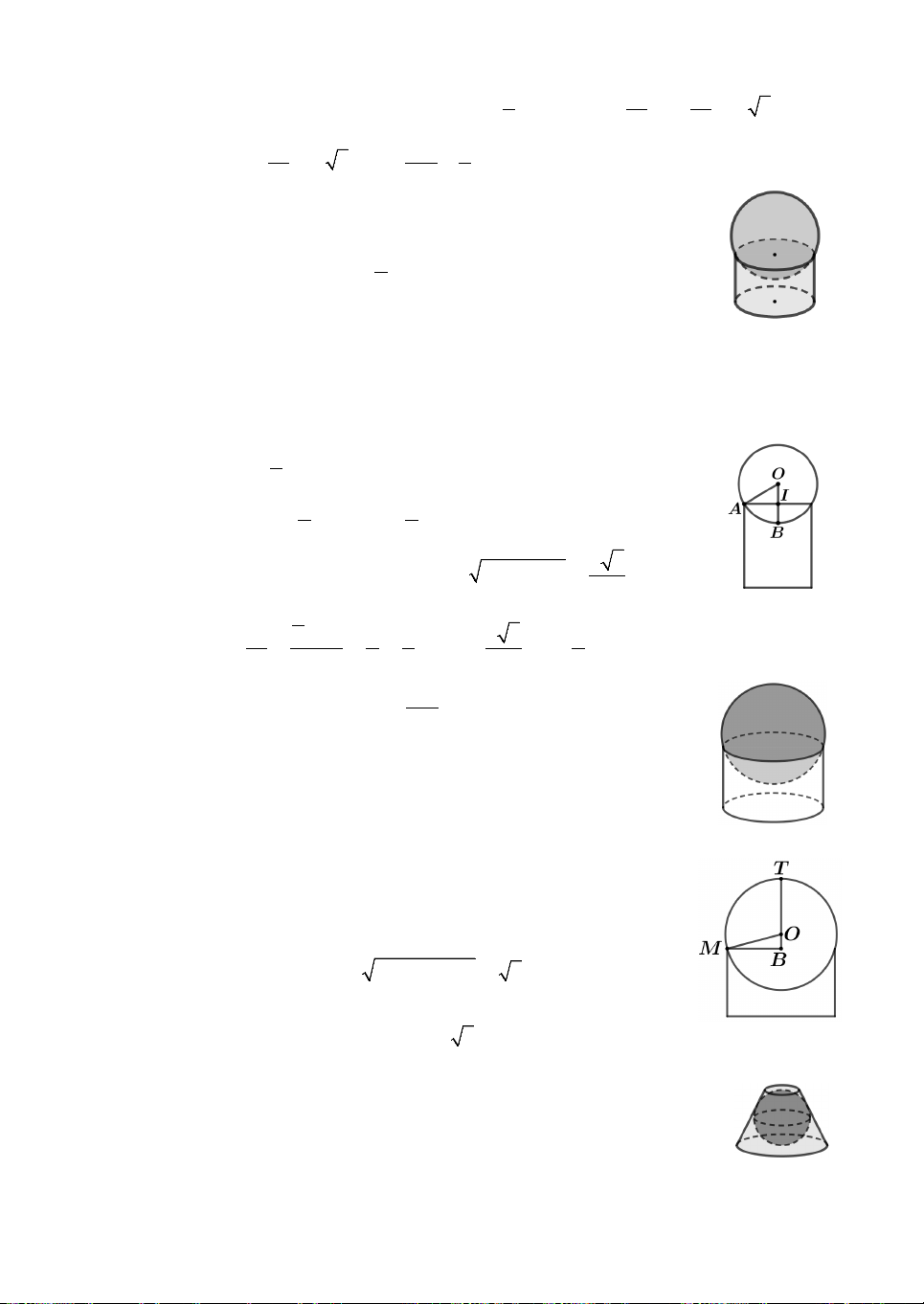
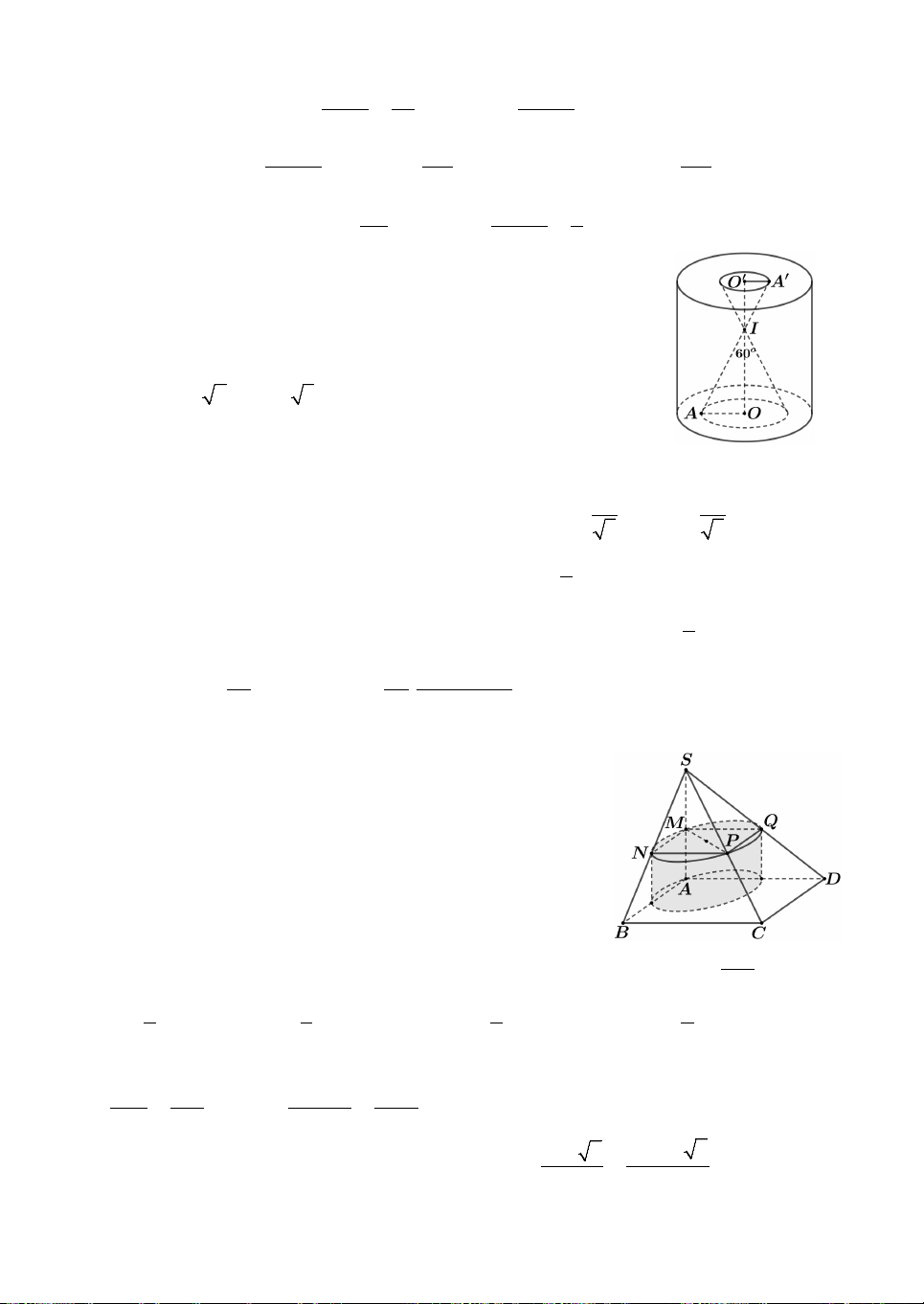
Câu 15. Một hình cầu nội tiếp trong một hình nón cụt. Hình cầu nội
tiếp trong hình nón cụt là hình cầu tiếp xúc với hai đáy của hình nón
cụt và tiếp với mặt xung quanh của hình nón cụt (tham khảo hình vẽ).
Biết rằng thể tích khối nón cụt gấp đôi thể tích của khối cầu. Tỉ lệ
giữa bán kính đáy lớn và bán kính đáy nhỏ của hình nón cụt bằng A.   3. B. 3 . C. 1 5 . D. 3 5 . 2 2 2
Phần 5. Mặt cầu ngoại tiếp khối chóp
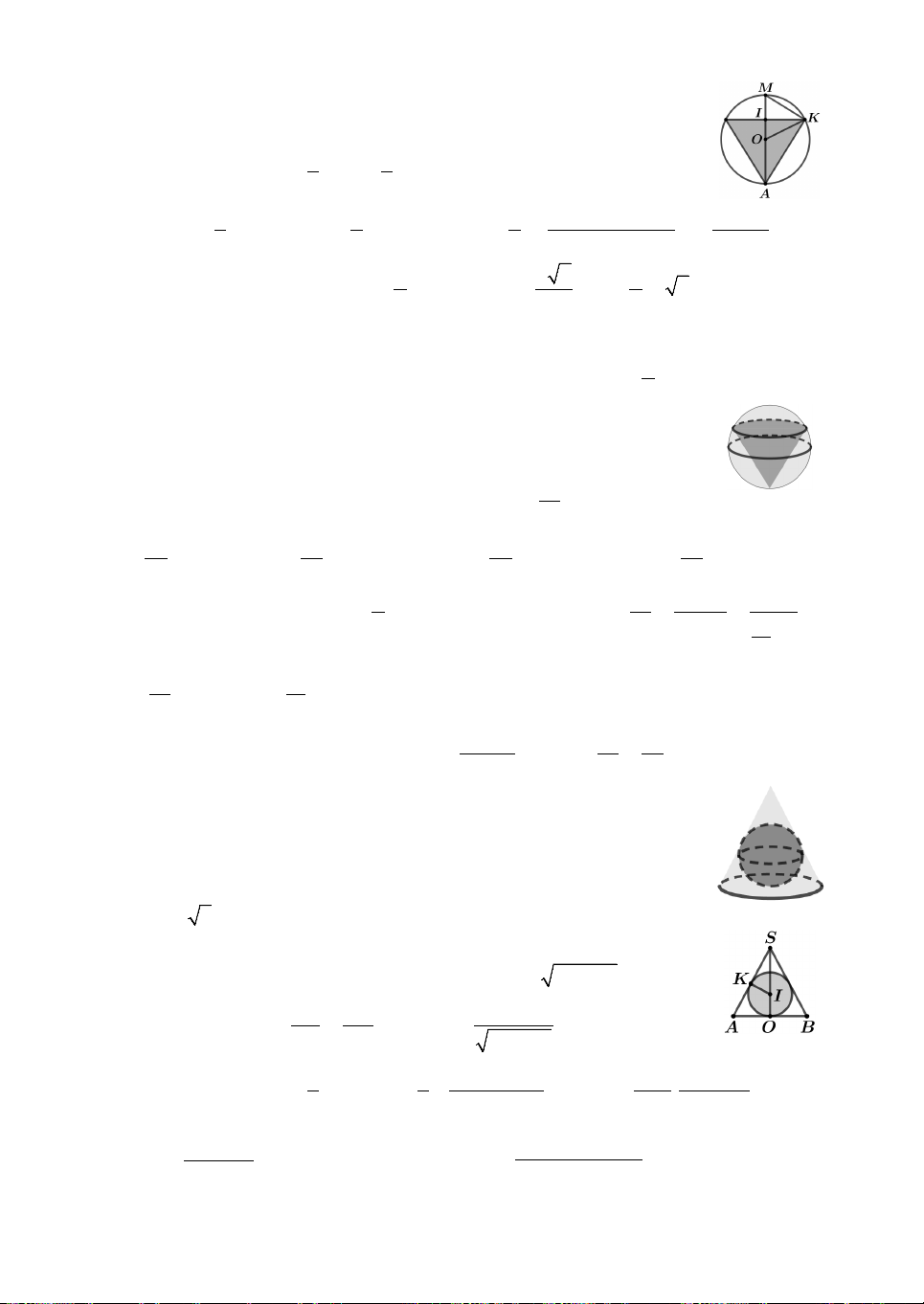
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC  . a
Cạnh bên SA vuông góc với đáy ABC. Gọi H, K lần lượt là hình chiếu vuông góc
của A lên cạnh bên SB và SC. Thể tích của khối cầu ngoại tiếp chóp . A HKCB bằng 3 3 3 A. 2 3 a a a 2a . B. . C. . D. . 2 3 6
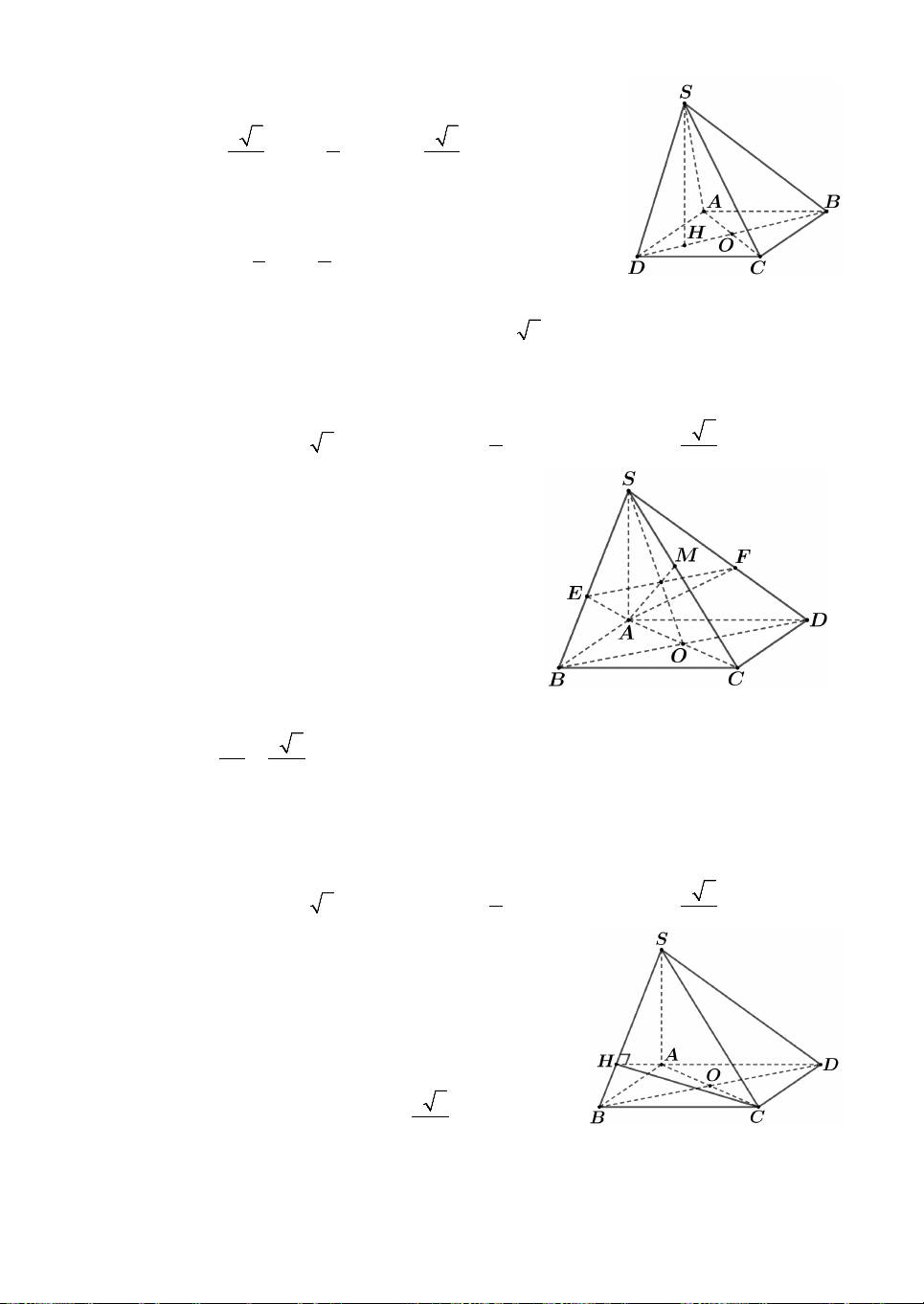
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và BD  . a Hình
chiếu vuông góc của S trên mặt phẳng đáy là trung điểm OD . Đường thẳng SD tạo
với mặt đáy một góc bằng 0
60 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. a a a . a B. . C. . D. . 2 3 4 14
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Đường
thẳng SA vuông góc với đáy ABCD và SA a 2. Gọi M là trung điểm SC, mặt
phẳng  đi qua hai điểm A và M đồng thời song song với BD cắt SB, SD lần lượt
tại E, F. Bán kính mặt cầu đi qua năm điểm S, ,
A E, M , F bằng A. a a a . B. a 2. C. . D. 2 . 2 2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Đường thẳng SA
vuông góc đáy ABCD. Gọi H là hình chiếu của A trên đường thẳng SB . Bán kính
mặt cầu ngoại tiếp tứ diện HBCD bằng A. a a a . B. a 2. C. . D. 2 . 2 2
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Tam giác SAB
vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp
hình chóp S.ABCD bằng 3 3 3 3 A. a 2a a 11 11a . B. . C. . D. . 3 3 6 162
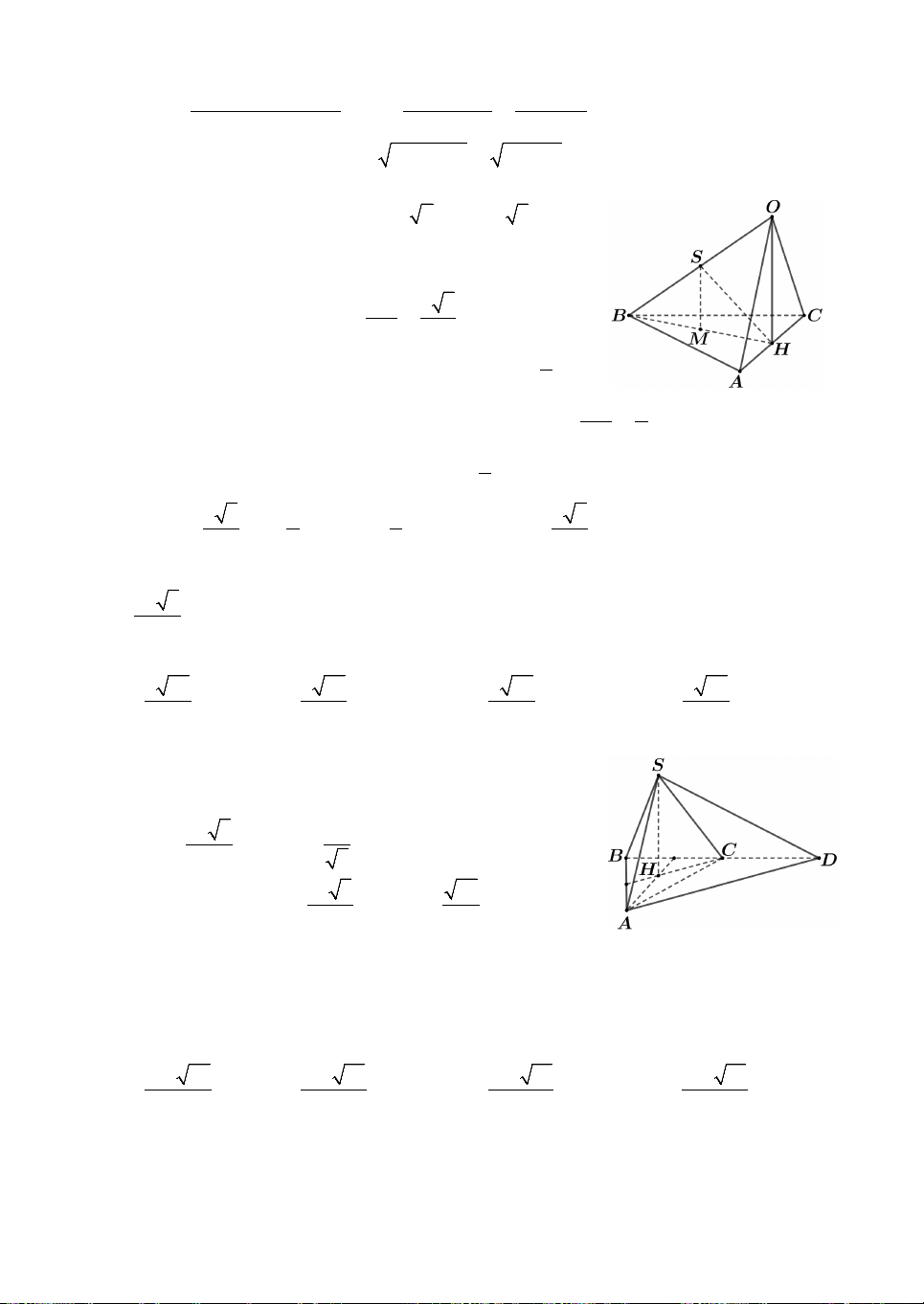
Câu 6. Cho hình chóp O.ABC có OA OB OC  , a AOB  60 ,   BOC  90 ,  
COA  120. Gọi S là trung điểm của OB. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng A. a a a a . B. 7 . C. . D. 7 . 2 2 4 4
Câu 7. Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh , a cạnh bên
bằng 2a 3 . Gọi D là điểm đối xứng của B qua C. Bán kính của mặt cầu ngoại tiếp 3
hình chóp S.ABD bằng A. a 37 a a a . B. 35 . C. 36 . D. 39 . 6 7 7 7
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với
AD DC CB  1, AB  2. Gọi O là giao điểm của AC và BD, hình chiếu vuông góc
của S xuống mặt ABCD là trung điểm của O .
A Đường thẳng SC tạo với mặt đáy
ABCD một góc bằng 60. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng A. 1759 . B. 31 61 . C. 31 51 . D. 61 61 . 54 81 162 162
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, 1
AB BC AD  .
a Cạnh bên SA a 6 và vuông góc với đáy. Gọi E là trung điểm 2
của AD. Bán kính mặt cầu ngoại tiếp chóp S.ECD bằng 15 A. 114 . a B. 114 . a C. 114 . a D. 114 . a 2 4 6 8
Câu 10. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 2 .
a Mặt bên tạo với đáy góc 0
60 . Gọi H là hình chiếu vuông góc của O trên SD. Bán
kính mặt cầu ngoại tiếp tứ diện HADC bằng A. a 21 a a a . B. 21 . C. 11 5 . D. 11 5 . 3 6 20 50
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , a SAD là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung
điểm của BC và CD. Bán kính của mặt cầu ngoại tiếp hình chóp S.CMN bằng A. a 37 a a a . B. 29 . C. 5 3 . D. 93 . 6 8 12 12
Câu 12. Cho tứ diện đều ABCD có mặt cầu nội tiếp là S và mặt cầu ngoại tiếp là 1 
S . Một hình lập phương ngoại tiếp S và nội tiếp mặt cầu S . Gọi r , r , r lần 3  2  2  1 2 3
lượt là bán kính các mặt cầu S , S , S . Khẳng định nào sau đây đúng ? 1   2   3  A. r 2 r 1 r 2 r 1 1  và 2  .
B. 1  và 2  . r 3 r r 3 r 2 3 3 2 3 2 C. r 1 r 1 r 1 r 1 1  và 2  .
D. 1  và 2  . r 3 r r 3 r 2 3 3 2 3 3 3
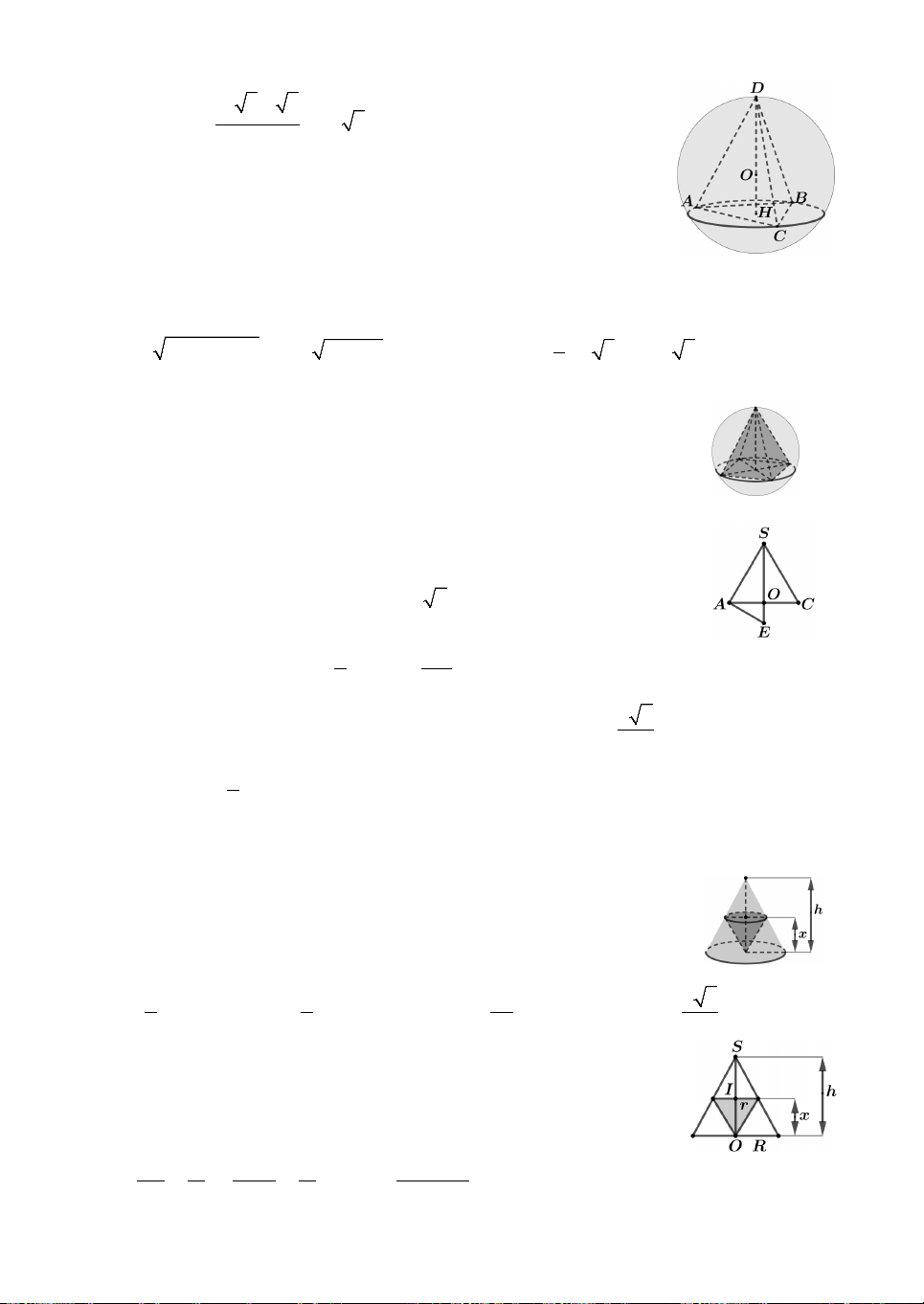
Câu 13. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2 và hình
chiếu của S lên mặt phẳng ABC là điểm H nằm trong tam giác ABC sao cho  AHB  150 ,   BHC  120 ,  
CHA  90. Biết tổng diện tích mặt cầu ngoại tiếp các hình
chóp S.HAB, S.HBC, S.HCA là 124 .
Thể tích khối chóp S.ABC bằng 3 A. 9 . B. 4 . C. 9 . D. 4. 2 3 4
Câu 14. Cho tứ diện ABCD với AB  ,
a CD b và các cạnh còn lại có độ dài bằng
nhau. Gọi M , N lần lượt là trung điểm của AB và CD và MN  .
m Biết rằng tồn tại
một mặt cầu tiếp xúc với 6 cạnh của tứ diện đã cho. Hệ thức nào sau đây đúng ? A. ab  2 m . B. ab  2 2m . C. ab  2 2 m . D. ab  2 3 2m .
Câu 15. Cho hình chóp đều S.ABC có cạnh đáy bằng .
a Gọi M , N lần lượt là trung
điểm của AB, BC và P là điểm thuộc tia đối của SC sao cho SC  3SP. Biết rằng
trong các mặt cầu đi qua ,
A M , N thì mặt cầu ngoại tiếp tứ diện AMNP có bán kính
nhỏ nhất. Thể tích của hình chóp S.ABC bằng 3 3 3 3 A. a 2 a 2 a 2 a 2 . B. . C. . D. . 16 32 48 96 16
Phần 6. Bài toán cực trị
Câu 1. Một hình trụ có thể tích V không đổi. Tìm mối quan hệ giữa
bán kính r của đáy và chiều cao h của hình trụ khi diện tích toàn
phần đạt giá trị nhỏ nhất.
A. h r.
B. h  2r.
C. h  3r.
D. h  2r.
Câu 2. Một hộp sữa hình trụ có thể tích V (không đổi) được làm từ một tấm tôn có
diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa
bán kính đáy r và đường cao h là
A. h r.
B. h  2r.
C. h  3r.
D. h  2r.
Câu 3. Trong số các hình trụ có diện tích toàn phần đều bằng S thì
bán kính r và chiều cao h của khối trụ có thể tích lớn nhất là A. S 1 S S S r  ; h  . B. r  ; h  2 . 2 2 2 2 2 C. S 1 S S S r  ; h  . D. r  ; h  2 . 6 2 6 6 6
Câu 4. Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có
thể tích V không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp
của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt
xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao
của thùng là h và bán kính đáy là r. Tính tỷ số h sao cho chi phí vật liệu sản xuất r thùng nhỏ nhất. A. h h h h  1. B.  2. C.  6. D.  9. r r r r
Câu 5. Nam muốn xây một bình chứa hình trụ có thể tích 3 72m . Đáy làm
bằng bêtông giá 100 nghìn đồng 2
/m , thành làm bằng tôn giá 90 nghìn đồng 2 /m , nắp
bằng nhôm giá 140 nghìn đồng 2
/m . Vậy đáy của hình trụ có bán kính bằng bao
nhiêu để chi phí xây dựng là thấp nhất ? A. 2  3 3 3 m. B. m. C. m. D. m. 3 3 3 3 2
Câu 6 Trong tất cả các hình nón có độ dài đường sinh bằng .
 Hình nón có thể tích lớn nhất bằng 3 3 A.  3 2 3 . B. . 9 9 3 3 C.  3 2 3 . D. . 27 27 17
Câu 7. Trong các hình nón cùng có diện tích toàn phần bằng S. Hình nón có thể tích
lớn nhất khi ( r,  lần lượt là bán kính đáy và đường sinh của hình nón) C.   r.
D.   2r.
B.   2 2r.
A.   3r.
Câu 8. Cho hình nón đỉnh S có đáy là đường tròn tâm O. Thiết diện qua trục hình
nón là một tam giác cân với cạnh đáy bằng a và có diện tích là 2 a . Gọi , A B là hai
điểm bất kỳ trên đường tròn O. Thể tích khối chóp S.OAB đạt giá trị lớn nhất bằng 3 3 3 3 A. a a a a 2 . B. . C. . D. . 2 6 12 12
Câu 9. Cho mặt cầu S bán kính R  5 cm. Mặt phẳng P
cắt mặt cầu S theo giao tuyến là đường tròn C có chu vi
bằng 8cm. Bốn điểm ,
A B, C, D thay đổi sao cho , A B, C
thuộc đường tròn C, điểm D thuộc S D  C và tam giác
ABC đều. Thể tích lớn nhất của tứ diện ABCD bằng A. 3 20 3 cm . B. 3 32 3 cm . D. 3 60 3 cm . D. 3 96 3 cm .
Câu 10. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng 9, hình chóp có thể tích lớn nhất bằng A. 484. B. 529. C. 576. D. 625.
Câu 11. Cho hình nón N có đỉnh S, chiều cao . h Một hình 1 
nón N có đỉnh là tâm của đáy N và có đáy là một thiết diện 1  2 
song song với đáy của N như hình vẽ. Khối nón N có thể 2  1 
tích lớn nhất khi chiều cao x bằng A. h h h h . B. . C. 2 . D. 3 . 2 3 3 3
Câu 12. Cho hình lập phương ABCD.AB CD   có thể tích
bằng 1. Gọi N  là một hình nón có tâm đường tròn đáy
trùng với tâm của hình vuông ABCD, đồng thời các điểm
A , B , C , D nằm trên các đường sinh của hình nón như
hình vẽ. Thể tích khối nón N  có giá trị nhỏ nhất bằng A. 2 . B. 3 . 3 4 C. 9 . D. 9 . 8 16 18
Câu 13. Trong các hình nón nội tiếp một hình cầu có bán kính
bằng R không đổi, tính chiều cao h và bán kính mặt đáy r của
hình nón có thể tích lớn nhất. A. 4 2 2 h R; . r R B. 3 3 h R; r  . R 3 3 2 2 4 C. 4 2 h R; r  . R D. 3 1 h R; . r R 3 3 2 2
Câu 14. Cho mặt cầu S có bán kính R không đổi, hình nón N
bất kì nội tiếp mặt cầu S như hình vẽ. Thể tích khối nón N  là V
V ; thể tích phần còn lại là V . Giá trị lớn nhất của 1 bằng 1 2 V2 A. 32 . B. 32 . C. 49 . D. 32 . 49 76 81 81
Câu 15. Một hạt ngọc trai hình cầu có bán kính R được bọc trong
một hộp trang sức dạng hình nón ngoại tiếp mặt cầu như hình vẽ.
Hỏi nhà sản xuất phải thiết kế hộp trang sức hình nón có chiều cao
h như thế nào để hộp quà đó có thể tích nhỏ nhất. A. h  2 2 . R B. h  3 . R C. h  4 . R D. h  5 . R
Câu 16. Cho nửa hình cầu bán kính R không đổi. Một hình nón có chiều cao ,
h bán kính đáy là r tiếp xúc với nửa hình
cầu như hình vẽ (hai đường tròn đáy là đồng tâm và cùng thuộc
một mặt phẳng). Khi diện tích xung quanh của hình nón là nhỏ
nhất, khẳng định nào sau đây đúng ?
A. h r.
B. h  2r.
C. h  3r.
D. h  2 3r.
Câu 17. Cho một hình nón có chiều cao h và bán kính của đường tròn đáy là .
R Một mặt phẳng P thay đổi song song với mặt
chứa đáy của hình nón và cắt hình nón theo một đường tròn giao
tuyến C. Dựng hình trụ H  có một đáy là đường tròn C và
đáy còn lại nằm trên mặt đáy của hình nón như hình vẽ. Khi khối
trụ H  có thể tích lớn nhất, gọi h là chiều cao
của H  và R là bán kính đáy của H . Khẳng định nào sau đây đúng ? A. 1 1 h  h; . R  R B. 1 2 h  ; . h R  R 2 2 3 3 C. 1 3 h  h; . R  R D. 3 1 h  ; . h R  R 4 4 4 4 19
Câu 18. Cho khối gỗ hình trụ có bán kính 3cm và chiều cao
6cm, đáy là hai hình tròn tâm O và O . Đục khối gỗ này
tạo ra hai khối nón có đỉnh nằm trên OO và đáy trùng với
hai đáy của khối gỗ sao cho góc ở đỉnh bằng 0 60 (như hình vẽ)
và OI x 3 2  x 3 3. Giá trị nhỏ nhất của tổng diện
tích xung quanh hai hình nón đã đục bằng A.  2 12 cm . B.  2 14 cm . C.  2 44 cm . D.  2 72 cm .
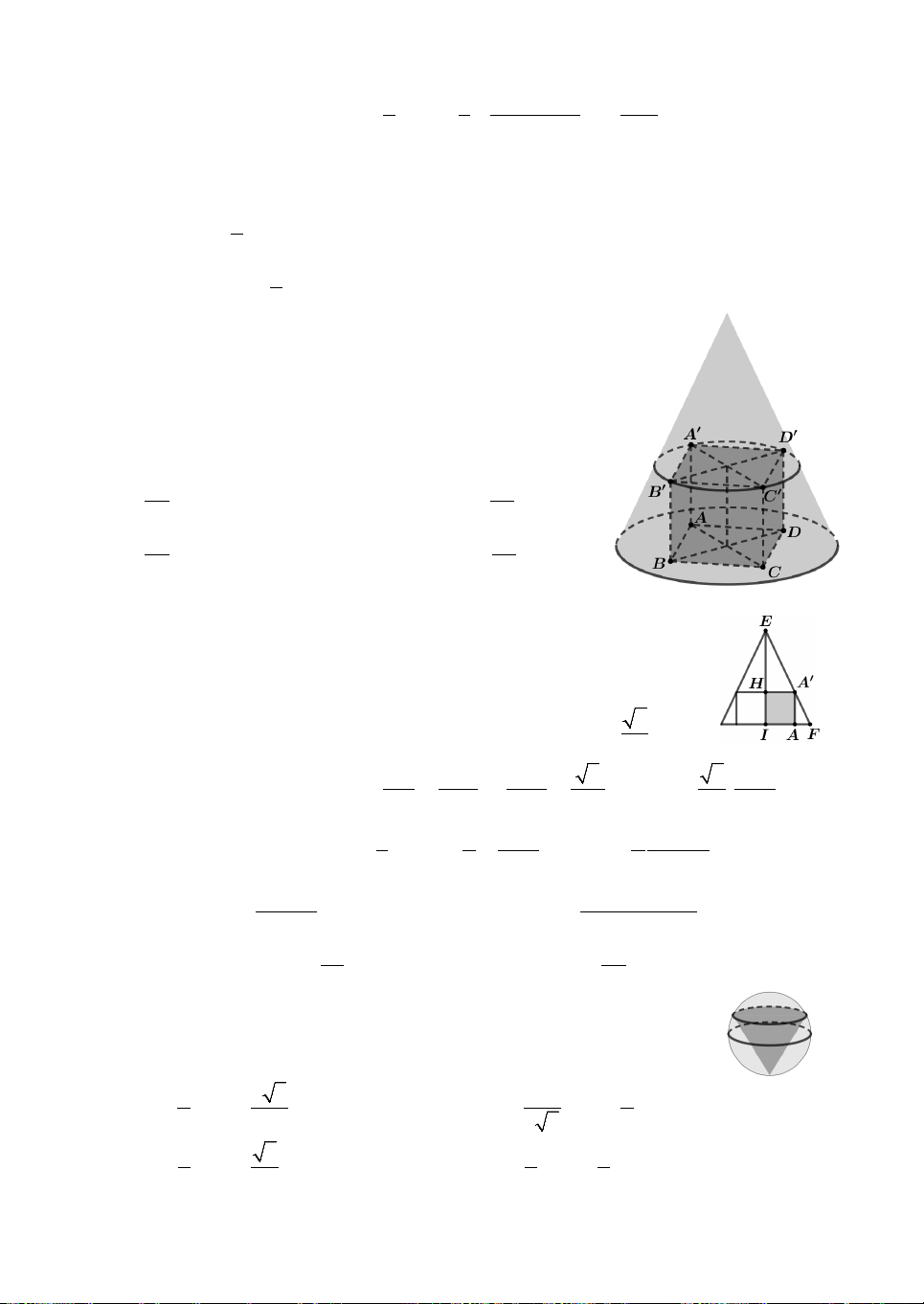
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 .
a Cạnh bên SA  4a và vuông góc với
đáy. Gọi M là một điểm trên cạnh SA (khác A và S ).
Mặt phẳng  qua M và vuông góc với SA cắt SB, SC,
SD lần lượt tại N, P, Q. Hình trụ H  có đáy là
đường tròn ngoại tiếp tứ giác MNPQ và có một đường
sinh là MA như hình vẽ. Khi khối trụ H  có thể tích lớn nhất thì tỉ số SM bằng SA A. 1 . B. 1. C. 2 . D. 3 . 2 3 3 4
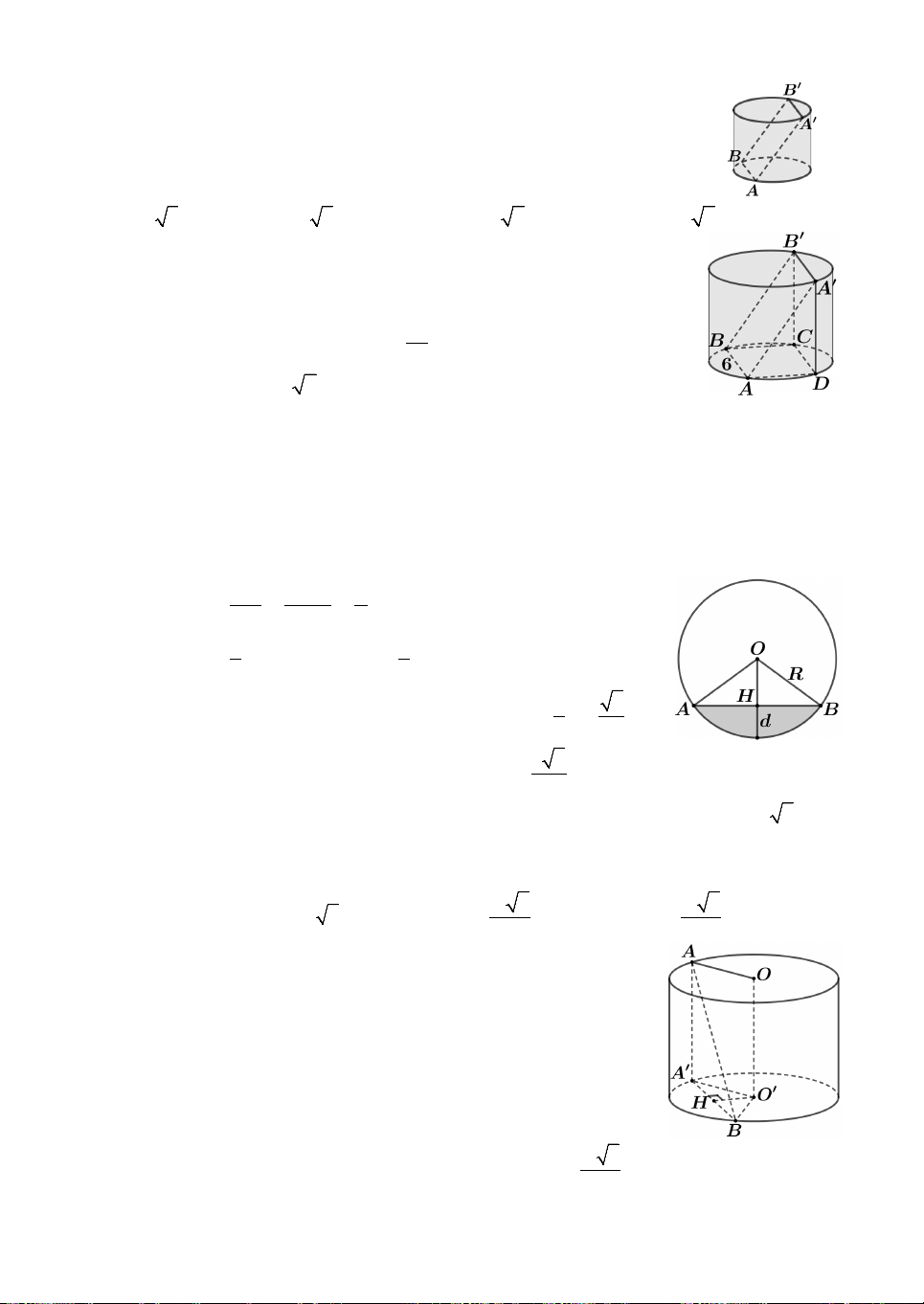
Câu 20. Cho hình trụ có đáy là hai đường tròn O;R và O ;R, chiều cao bằng
đường kính đáy. Trên đường tròn tâm O lấy điểm ,
A trên đường tròn tâm O lấy
điểm B. Thể tích của khối tứ diện OO A
B có giá trị lớn nhất bằng 3 3 3 3 A. R R 3R R . B. . C. . D. . 2 3 3 6
---------- HẾT ---------- 20
NÓN – TRỤ – CẦU Vận dụng cao
Phần 1. Thể tích và các yếu tố liên quan
Phần 2. Vật thể tròn xoay
Phần 3. Ứng dụng thực tiễn
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Phần 5. Mặt cầu ngoại tiếp khối đa diện
Phần 6. Bài toán cực trị 1
Phần 1. Thể tích và các yếu tố liên quan
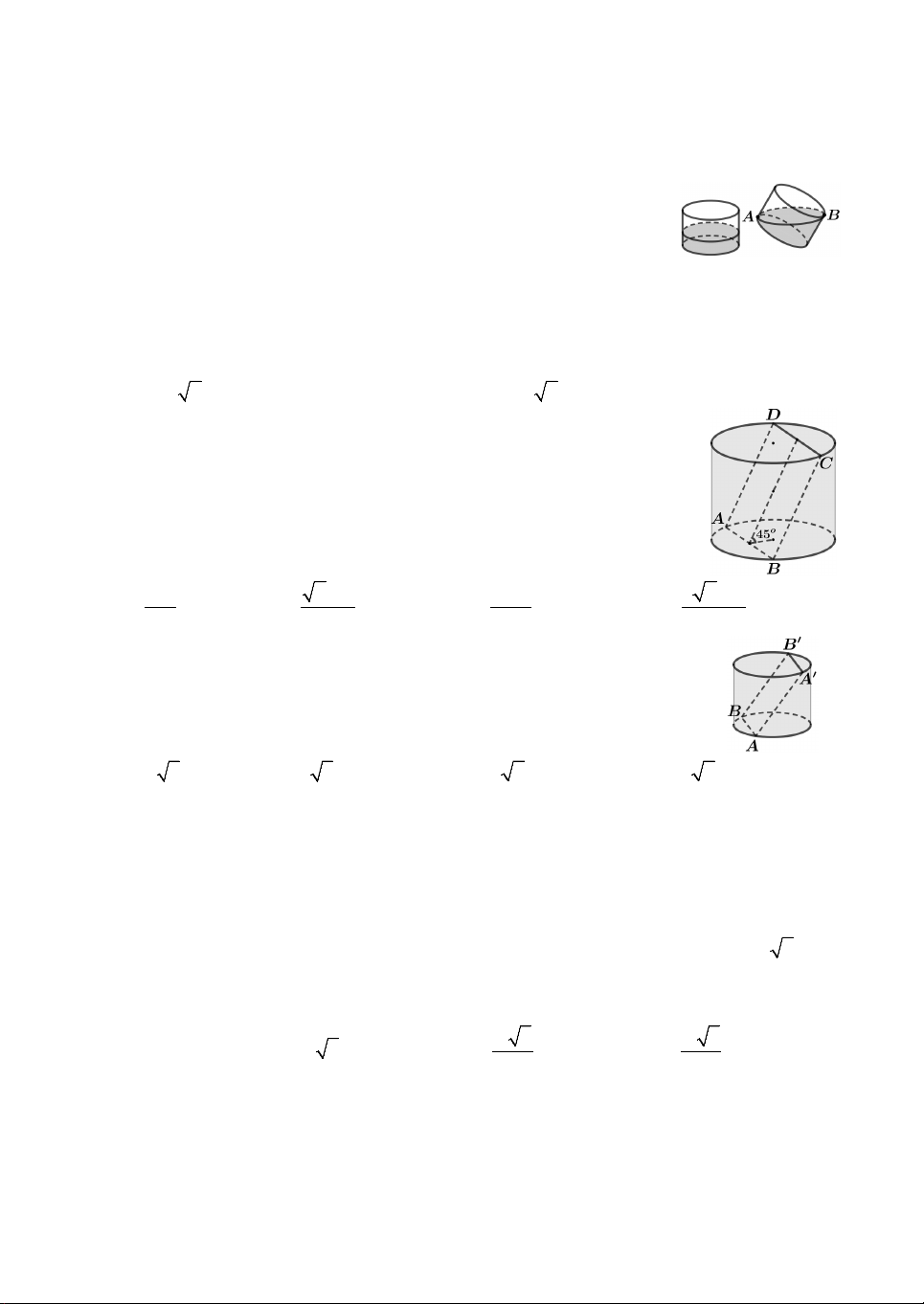
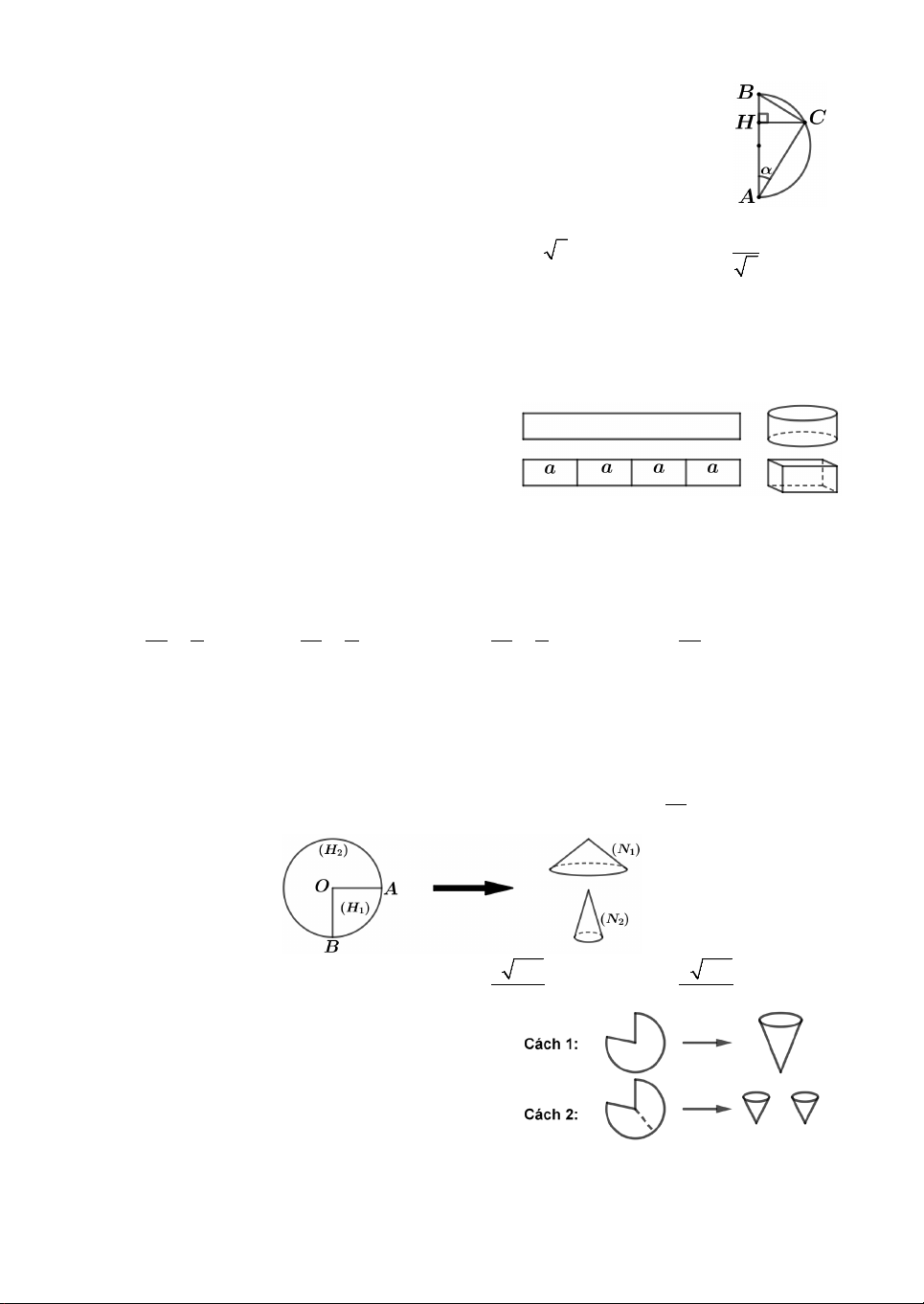
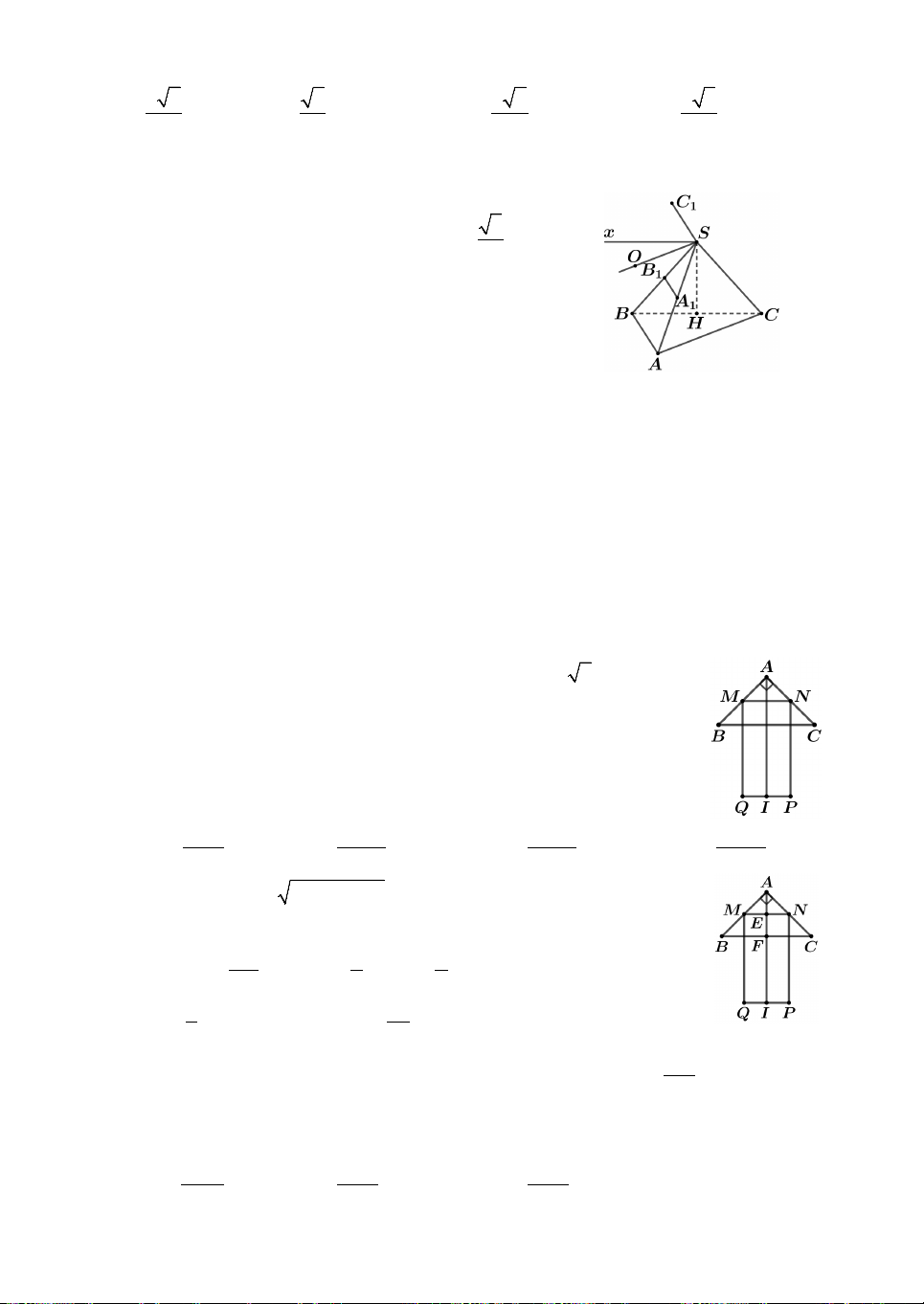
Câu 1. Một chiếc thùng hình trụ có bán kính đáy R  20, bên
trong đựng một lượng nước. Biết rằng khi nghiêng thùng sao cho
đường sinh của hình trụ tạo với mặt đáy góc 45 cho đến khi
nước lặng thì mặt nước chạm vào hai điểm A và B nằm trên hai
mặt đáy như hình vẽ bên. Thể tích của thùng đã cho bằng A. 16000 . B. 12000 . C. 8000 . D. 6000 .
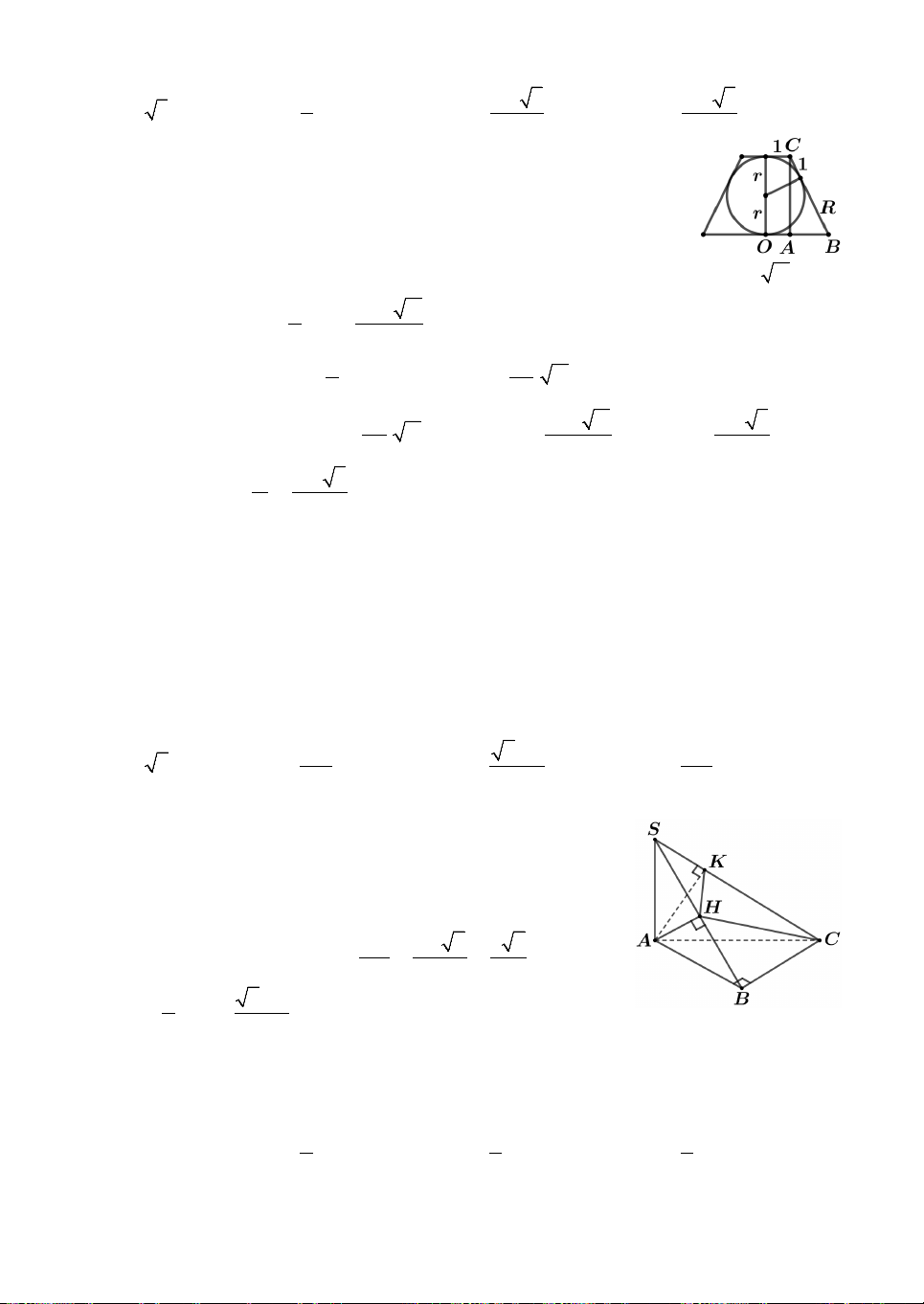
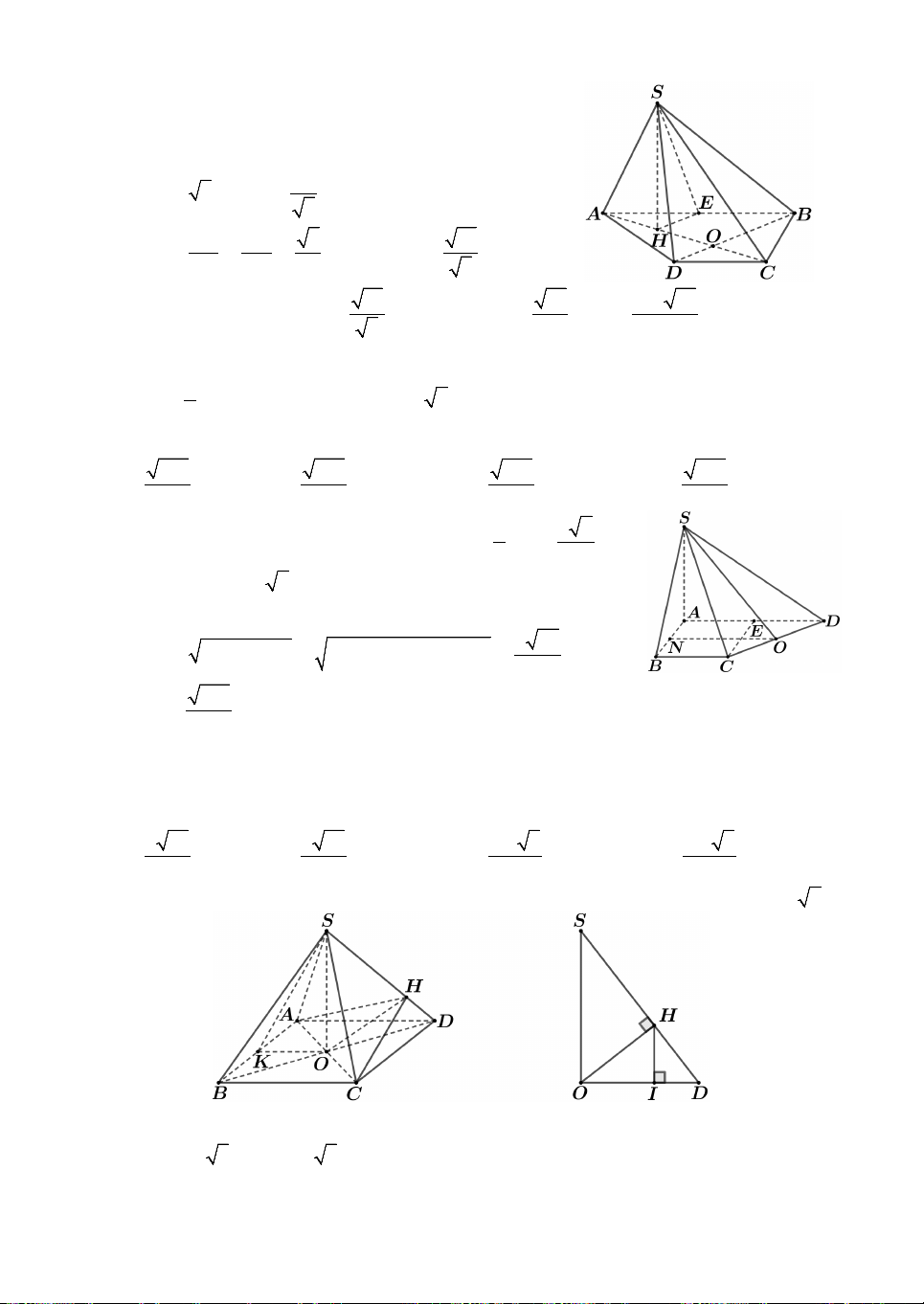
Lời giải. Xét phần mặt cắt và kí hiệu các điểm như hình vẽ. Ta có 
BAC  45 suy ra ABC
vuông cân nên BC CA  40. 2  
Vậy thể tích thùng nước AC V     .BC  16000 . Chọn A.  2 
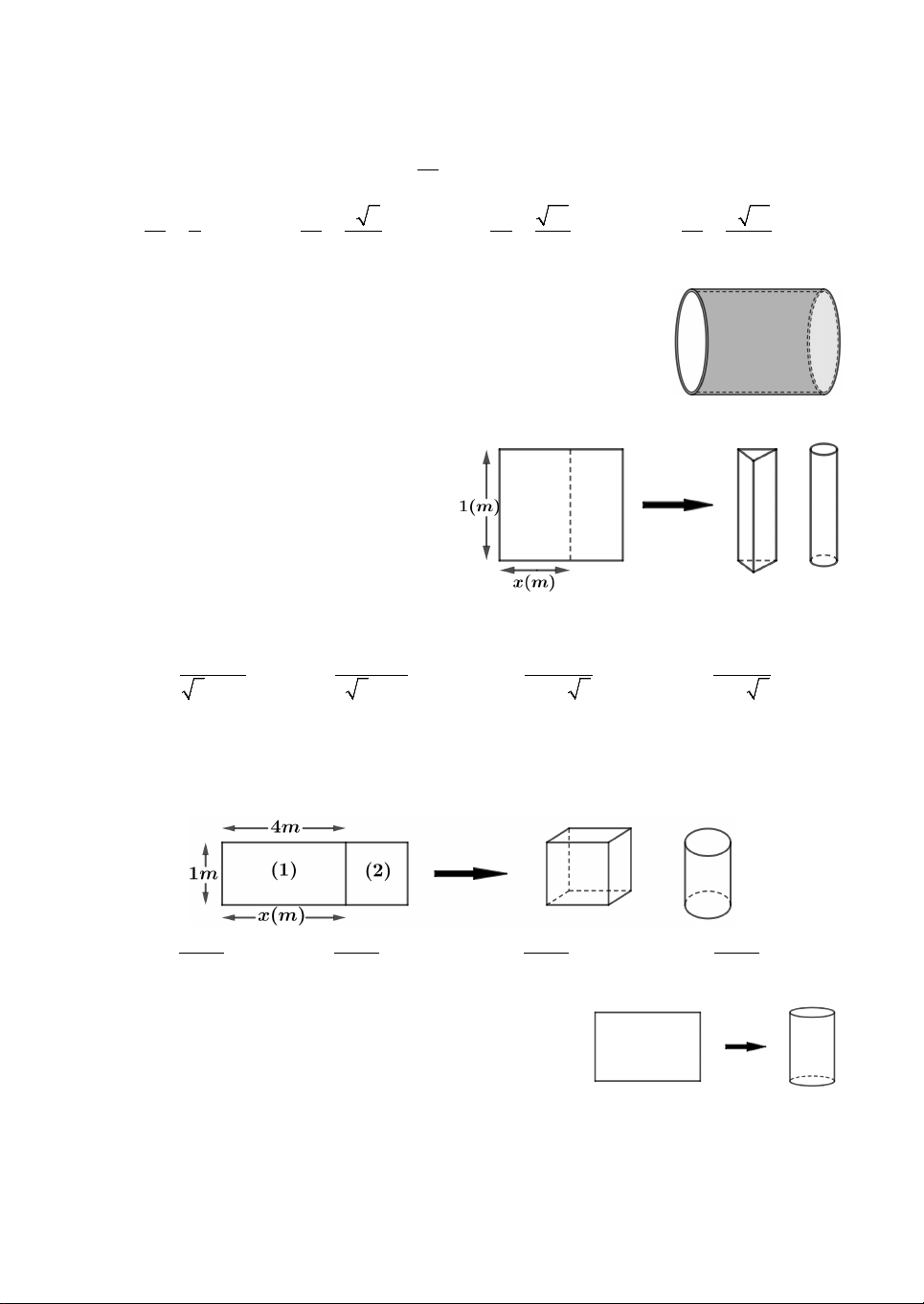
Câu 2. Cho hình lăng trụ tứ giác đều ABCD.EFGH. Tính tỉ số k giữa thể tích khối
trụ ngoại tiếp và thể tích khối trụ nội tiếp hình lăng trụ trên.
A. k  2.
B. k  2.
C. k  2 2.
D. k  4.
Lời giải. Hai khối trụ có chung đường cao nên 2 2 V R hR 1 k         2 2 V r h  r  2 với AC AB 2 R  
là bán kính đường tròn ngoại tiếp đáy; 2 2 AB r
là bán kính đường tròn nội tiếp đáy. Chọn B. 2
Câu 3. Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp ,
A B nằm trên đường tròn đáy thứ nhất của hình
trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ.
Mặt phẳng ABCD tạo với đáy hình trụ góc 45 như hình vẽ. Thể tích khối trụ bằng A. 3 a a a a . B. 3 2 . C. 3 3 . D. 3 3 2 . 16 16 16 16
Lời giải. Tam giác a
IOM vuông cân có IM  , suy ra 2 a a IO OM   OO  . 2 2 2  a OM  Tam giác cân  a OAB, có 6 
2 2  OA OB  .  4 AB a  3 Vậy 3 2 2 2 a
V R h O  A .OO  . Chọn D. 16 2
Câu 4. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không
vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song
AB, AB mà AB AB  6 cm . Biết diện tích tứ giác ABBA bằng 2
60 cm . Chiều cao của hình trụ đã cho bằng A. 4 3 cm. B. 5 3 cm. C. 6 2 cm. D. 8 2 cm.
Lời giải. Dựng đường sinh BC và A' D , suy ra tứ giác ABCD là
hình chữ nhật. Suy ra ABCD là hình bình hành và nội tiếp được
nên là hình chữ nhật. Từ đó chứng minh được ABB A   là hình chữ nhật. Do đó 60 S         AB.BB BB 10 cm ABB A 6 AB6, 2 AC R8 2   B C   6 2 cm. Chọn C.
Câu 5. Một thùng hình trụ có chiều cao h  3m, bán kính đường tròn đáy R  1m
chứa một lượng nước. Biết rằng nếu đặt thùng nằm ngang ta được chiều cao mực nước
trong thùng là d  0,5m. Hỏi thể tích lượng nước có trong thùng gần nhất với kết quả nào sau đây ? A. 3 1,75m . B. 3 1,8m . C. 3 1,85m . D. 3 1,9m .
Lời giải. Xét mặt cắt vuông góc với trục của hình trụ và kí hiệu như hình vẽ. Ta có  OH R d 1  0  0 cos HOB  
  HOB  60  AOB  120 . OB R 2 Suy ra 1 S  hình tròn đáy 1  . quat AOB 3 3
Suy ra diện phần gạch sọc bằng: 1 3 S SS    . quat AOB AOB 3 4
Vậy thể tích lượng nước trong thùng: 3 3 3
V S.h   1,84m . Chọn C. 4
Câu 6. Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R 3. Hai điểm ,
A B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 0
30 . Khoảng cách giữa AB và trục của hình trụ bằng A. R R . R B. R 3. C. 3 . D. 3 . 2 4
Lời giải. Kẻ đường sinh AA . Suy ra OO  ABA. Khi đó d O
O , AB  d OO ,   
ABA  d O  ,    ABA.  
Gọi H là trung điểm AB, ta có O  H   AB   O H
  ABA nên d O  , 
ABA O H  . OH   AA     
Tam giác vuông ABA , có 0
BA  AA tan 30  . R Suy ra tam giác R
ABO đều, có cạnh bằng R nên 3 O H   . Chọn C. 2 3
Câu 7. Cho hình trụ có hai đáy là hai hình tròn O và O, thiết diện qua trục của
hình trụ là hình vuông. Gọi ,
A B là hai điểm lần lượt nằm trên hai đường tròn O và  a
O. Biết AB  2a và khoảng cách giữa hai đường thẳng AB và OO bằng 3 . 2
Bán kính đáy của hình trụ bằng A. a 14 a a a . B. 14 . C. 2 . D. 14 . 2 3 4 4
Lời giải. Đặt OA O B   ,
R suy ra OO  2 . R
Tương tự như bài trước. Kẻ đường sinh 2 2 AA 
BA  4a 4R .
AO BO R  Xét tam giác cân a 14 AO B  , có  2 2
AB  4a 4R   R  . Chọn D.  4  a 3 OH    2
Câu 8. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng .
a Trên đường tròn tâm O lấy điểm ,
A trên đường tròn tâm O lấy điểm
B sao cho AB  2 .
a Thể tích của khối tứ diện OO AB bằng 3 3 3 3 A. 3a 3a 3a 3a . B. . C. . D. . 2 4 6 12
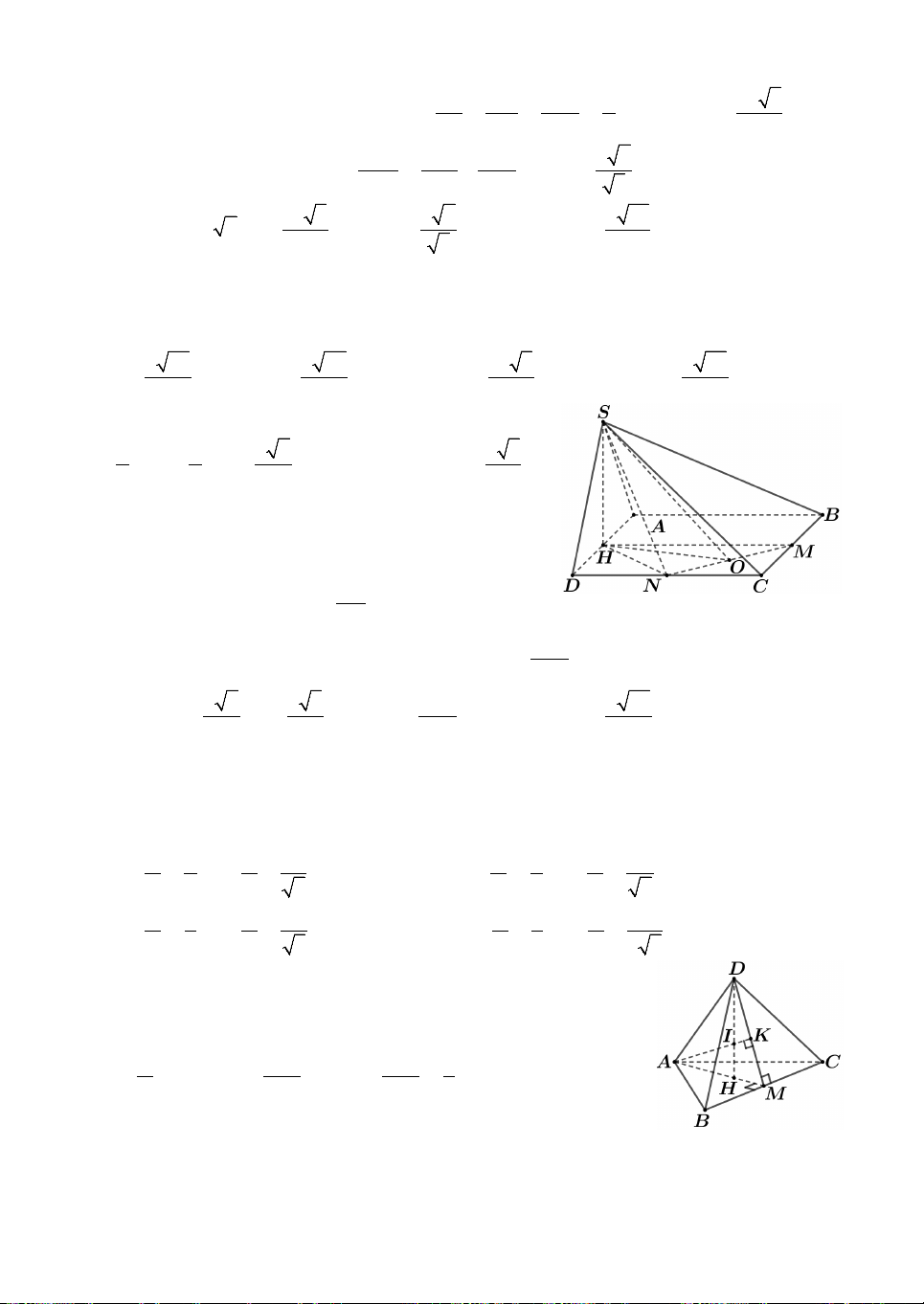
Lời giải. Kẻ đường sinh AM và BN như hình vẽ.   Ta có 1 1 2 1 V  .         V .  V .  VV . OO AB A.OO BN AON .MO B AON .MO B A. 2 2 3  3 MO B
Tương tự như bài trước. Tính được MB a 3. O  M   O B   a Xét tam giác cân a MO B  , có   O H   . MB a 3 2  3   Khi đó 1 1 a 3a V         Chọn D. V .  a 3. a . OO AB A.MO B 3 2 2 12
Câu 9. Một hình trụ có bán kính đáy R  70cm và chiều cao
h  20cm. Một hình vuông ABCD có hai cạnh AB và CD lần
lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng
ABCD không vuông góc với mặt đáy của hình trụ (tham
khảo hình vẽ). Cạnh của hình vuông ABCD có độ dài bằng A. 80cm. B. 100cm. C. 100 2cm. D. 140cm. 4
Lời giải. Dựng đường sinh AA , ta có CD   AA 
CD  AAD  CD AD. CD   AD 
Suy ra AC là đường kính đáy nên AC  2R  140cm.
Tam giác vuông AAC, có 2 2
AC AA  AC  100 2cm.
Suy ra cạnh hình vuông bằng 100cm. Chọn B.
Câu 10. Cho hình nón có đỉnh S, trục SO, bán kính , R chiều cao .
h Dây cung AB thuộc đường tròn đáy và cách O một
khoảng R như hình vẽ. Ký hiệu S , S lần lượt là diện tích 2 1 2
xung quanh của mặt nón và diện tích tam giác SAB. Biết S 10 1 
, mệnh đề nào sau đây đúng ? S2 3 3 A. 5 h  . R B. 11 h  . R
C. h   2   1 . R D. 1 h  . R 2 2 8 3
Lời giải. Đường sinh của hình nón 2 2
  SB SA R h . Khi đó 2 2
S R  R R h . 1 2 Pytago, ta được R 3 2 2 2 R
SI SO OI h  và 2 2
IA OA OI   AB R 3. 4 2 2 Khi đó 1 1 2 R
S AB.SI R 3. h  . 2 2 2 4 2 Theo đề S 10 R 3 R R 11 1 2 2 2 
 3 3.R R h  10 . . h   h  . Chọn B. S 3 3 2 4 8 2
Câu 11. Cho hình chóp tam giác đều S.ABC. Hình nón có đỉnh S
và có đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là
hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có
đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình
nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội
tiếp và hình nón ngoại tiếp hình chóp đã cho bằng A. 1 . B. 1. C. 2 . D. 1 . 2 3 3 4
Lời giải. Hai hình nón có cùng chiều cao nên tỉ số thể tích bằng tỉ số diện tích mặt
đáy. Vì tam giác ABC đều nên bán kính đường tròn ngoại tiếp bằng 2 đường cao của 3
tam giác; bán kính đường tròn nội tiếp bằng 1 đường cao của tam giác. 3 5 Suy ra r 1 V S 1 1 1     . Chọn D. R 2 V S 4 2 2
Câu 12. Cho hình nón đỉnh S có đáy là hình tròn tâm O. Dựng hai đường sinh SA
và SB, biết tam giác SAB vuông và có diện tích bằng 2
4a . Góc tạo bởi giữa trục SO
và mặt phẳng SAB bằng 0
30 . Đường cao h của hình nón bằng A. a a h a 2.
B. h a 3. C. 3 h  . D. 6 h  . 2 4
Lời giải. Gọi E là trung điểm AB.
Tam giác SAB vuông cân tại S nên AB  2SE. Ta có 1 1 2 S
 .AB.SE  4a  .2SE.SE SE  2 . a SAB 2 2
Dễ dàng xác định được: 0
30  SO,SAB    OSE.
Tam giác vuông SOE, có 
SO SE.cosOSE a 3. Chọn B.
Câu 13. Cho hình nón đỉnh S có đường cao SO. Gọi ,
A B là hai điểm thuộc đường
tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và  0 SAO  30 ,  0
SAB  60 . Độ dài đường sinh  của hình nón bằng A.   . a B.   a 2. C.   a 3. D.   2 . a
Lời giải. Gọi I là trung điểm AB, suy ra OI AB nên OI  . a Đặt SOA OA 2R
OA R  SA   . 0 cos 30 3
Tam giác SAB cân và có  0
SAB  60 nên là tam giác đều. Suy ra 1 R AI SA  . 2 3
Trong tam giác vuông OI , A ta có 2 R 3 2 2 2 2 2 a
OA OI IA R a   R  . 3 2
Suy ra   SA a 2. Chọn B.
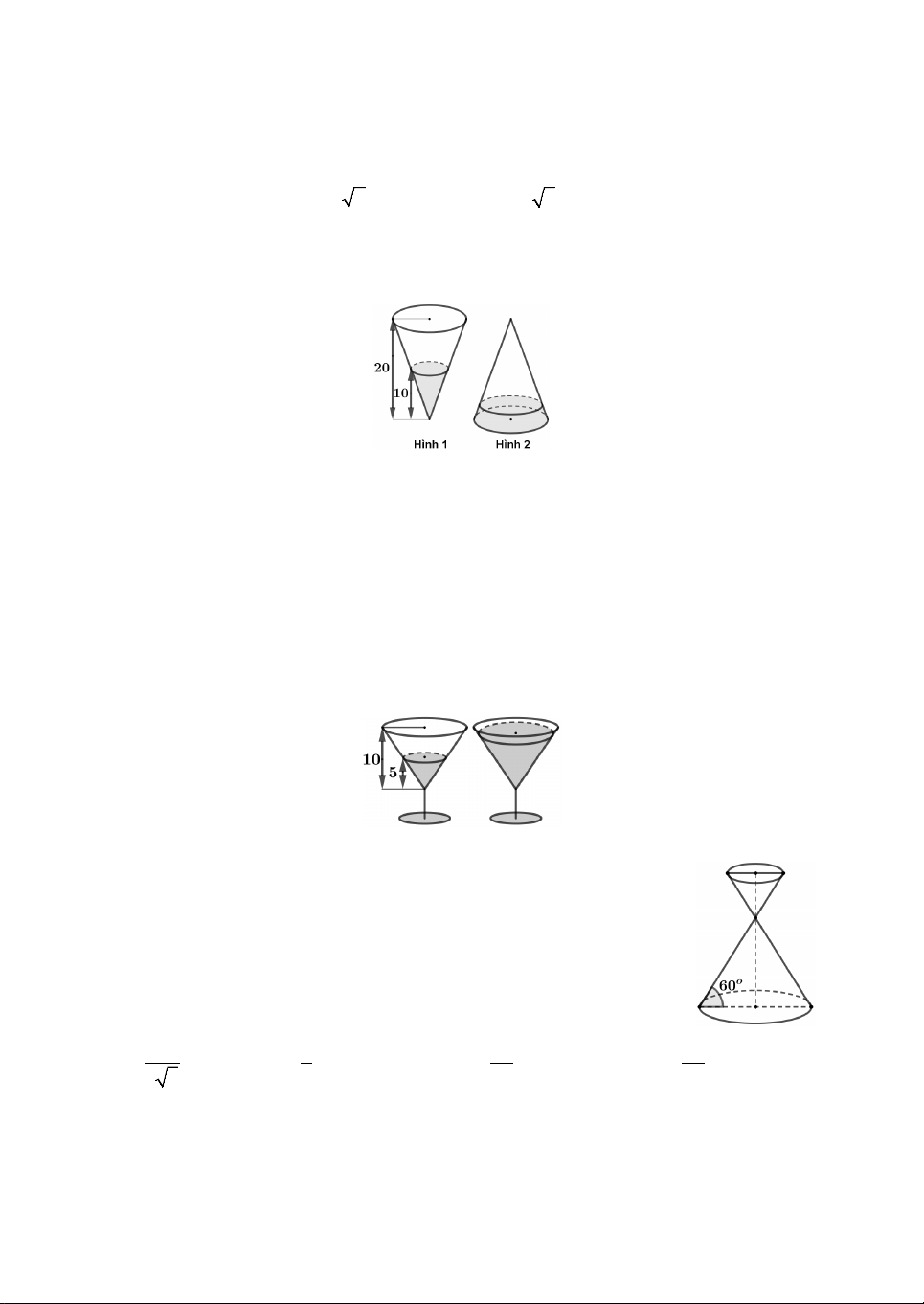
Câu 14. Một cái phễu có dạng hình nón, chiều cao của phễu là 20 cm (Hình 1). Người
ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu là 10 cm.
Nếu bịt kín miệng phễu rồi lật ngược lên (Hình 2).
Khi đó chiều cao cột nước trong phễu bằng giá trị nào sau đây ? A. 0,87 cm. B. 1,07 cm. C. 5 cm. D. 10 cm. 6
Lời giải. Xét phần mặt cắt và kí hiệu các điểm như hình vẽ.
Gọi V , V , V lần lượt là thể tích của phễu, của phần chứa 1 2  1 2 V
  HM .AH
nước, và phần không chứa nước. Ta có  3  .  1 2 V
  PN .AP 1  3 3 3 2     Suy ra V PN .AP AP 1 1 V 7 1 2                  . 2 V HM .AHAH  2 8 V 8 3 3    
Khi lật ngược phễu, ta có V AK 7 AK 7 2          3      AK  .AH  19,13cm. VAH  8  AH  8
Suy ra HK  0,87 cm. Chọn A.
Câu 15. Hai chiếc ly đựng chất lỏng giống hệt nhau, mỗi chiếc có phần chứa chất lỏng
là một khối nón có chiều cao 10 cm (mô tả như hình vẽ). Ban đầu chiếc ly thứ nhất
chứa đầy chất lỏng, chiếc ly thứ hai để rỗng. Người ta chuyển chất lỏng từ ly thứ nhất
sang ly thứ hai sao cho độ cao của cột chất lỏng trong ly thứ nhất còn 5 cm . Tính
chiều cao h của cột chất lỏng trong ly thứ hai sau khi chuyển (độ cao của cột chất
lỏng tính từ đỉnh của khối nón đến mặt chất lỏng - lượng chất lỏng coi như không hao
hụt khi chuyển. Tính gần đúng h với sai số không quá 0,01 cm ).
A. 9,09 cm. B. 9,18 cm. C. 9,56 cm. D. 9,57 cm.
Lời giải. Gọi r , r và r theo thứ tự là bán kính của chiếc ly, bán kính của khối chất 1 2 3
lỏng còn lại trong ly thứ nhất và bán kính của khối chất lỏng trong ly thứ hai (sau khi
chuyển chất lỏng từ ly thứ nhất sang ly thứ hai). Ta có r 1 r r h r h 2 1   r  và 3 1   r  . 2 r 2 2 3 r 10 10 1 1
Thể tích của khối chất lỏng được chuyển từ ly thứ nhất sang ly thứ hai là 1 V  35 2 2 r .10 r .  2 5  r .   1 1 2 1 3 12 2   Mặt khác, ta có 1 1 r h 1 2 1 2 3
V r h     h r h . 2 3 1 3 3 10  300 Từ   1 35 1 và 2, ta có 2 3 2 3 r h
r h  875  h  9,56 cm . Chọn C. 1 1   300 12 7
Câu 16. Cho một đồng hồ cát gồm 2 hình nón chung đỉnh ghép
lại, trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc
60 như hình bên. Biết rằng chiều cao của đồng hồ là 30cm và
tổng thể tích của đồng hồ là  3
1000 cm . Hỏi nếu cho đầy lượng
cát vào phần trên thì khi chảy hết xuống dưới, khi đó tỉ lệ thể
tích lượng cát chiếm chỗ và thể tích phần dưới là bao nhiêu ? A. 1 . B. 1 . C. 1 . D. 1 . 3 3 8 27 64
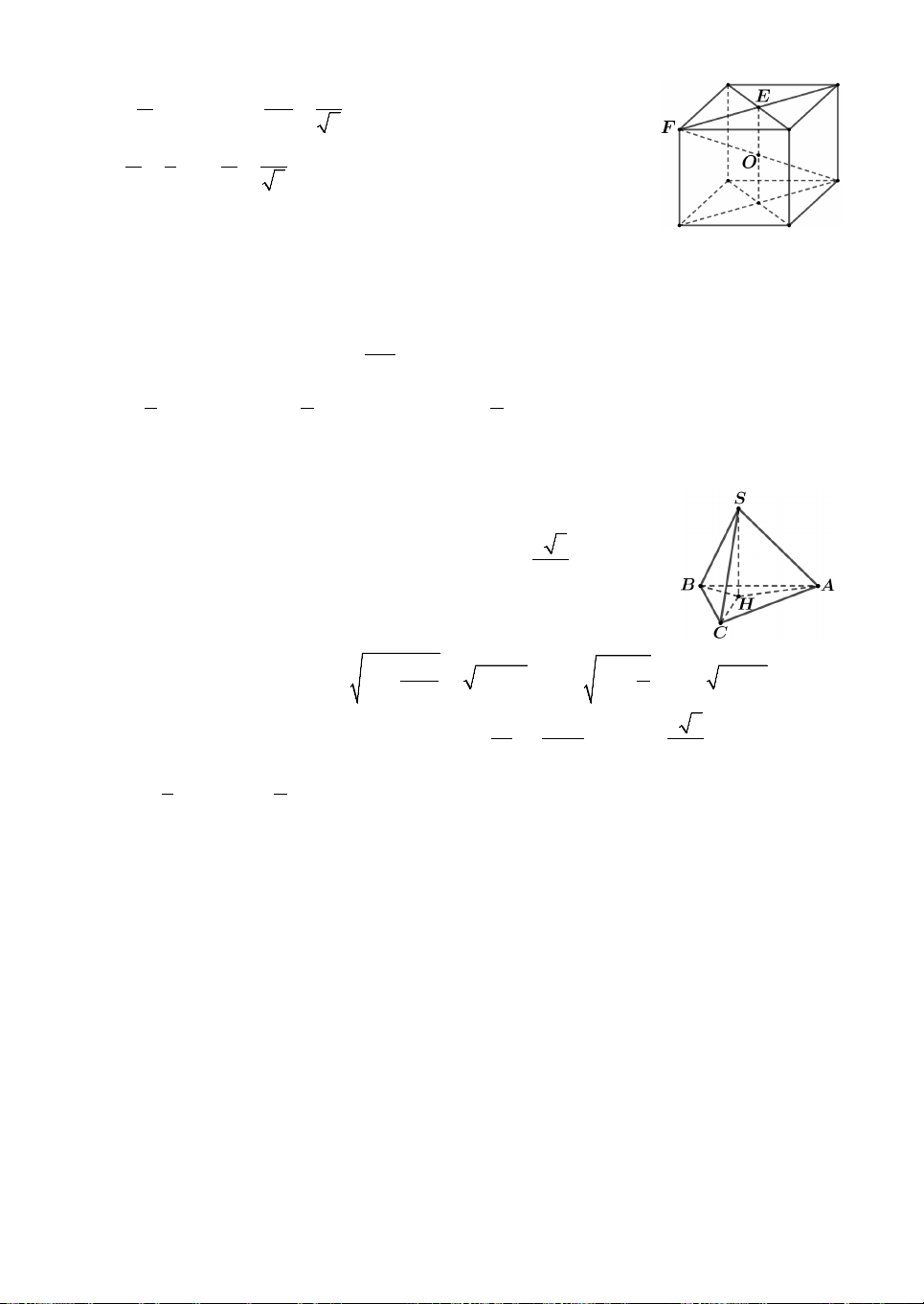
Lời giải. Gọi bán kính của hình nón lớn và nón nhỏ lần lượt là x, . y
Suy ra chiều cao của hình nón lớn và nón nhỏ lần lượt là x 3, 3. y
x 3  y 3  30 
Theo giả thiết, ta có 1 1 2 2
 x .x 3  y .y 3 1000 3 3
x y 10 3  20 3 10 3     x  , y  . 3 3
x y 1000 3 3 3  3  
Do hai hình nón đồng dạng nên tỉ số cần tính bằng y 1      .  Chọn B. x  8
Câu 17. Để tính diện tích xung quanh của một khối cầu bằng đá,
người ta thả nó vào trong một chiếc thùng hình trụ có chiều cao
h  2m, bán kính đường tròn đáy bằng R  0,5m và chứa một
lượng nước có thể tích bằng 1 thể tích khối trụ. Sau khi thả khối 8
cầu đá vào khối trụ người ta đo được mực nước trong khối trụ cao
gấp ba lần mực nước ban đầu khi chưa thả khối cầu. Hỏi diện tích
xung quanh của khối cầu gần bằng kết quả nào được cho dưới đây ? A. 2 1,5m . B. 2 1,7m . C. 2 2,6m . D. 2 3,4m .
Lời giải. Thể tích khối trụ 1 2 V V R h  .
Suy ra thể tích lượng nước 1 V    . 2 8 16
Từ giả thiết suy ra thể tích khối cầu: 4 1 3 3   3 V 2V R  2   R  . Cau Cau Cau 3 16 32
Vậy diện tích xung quanh của khối cầu là 2 2 S  4R  2,6m . Chọn C. Cau
Câu 18. Cho mặt cầu S tâm O, bán kính R  3. Mặt phẳng P
cách O một khoảng bằng 1 và cắt S theo giao tuyến là đường
tròn C có tâm H. Gọi T là giao điểm của tia HO với S, tính
thể tích V của khối nón đỉnh T , đáy là hình tròn C (như hình). A. 16 V  . B. 32 V  . C. V  16 . D. V  32 . 3 3
Lời giải. Từ giả thiết suy ra OH  1. 8
Suy ra chiều cao hình nón h TO OH  31  4.
Bán kính đường tròn đáy hình nón 2 2
r AH OA OH  2 2.
Vậy thể tích khối nón cần tính 1 1 Vr h  . 2 22 32 2 .4  . Chọn B. Non 3 3 3
Câu 19. Một bình đựng nước dạng hình nón không nắp đựng đầy
nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó.
Người ta thả vào bình đó một khối trụ và đo được thể tích nước trào ra ngoài là 16 3
dm . Biết rằng một mặt của khối trụ nằm trên mặt 9
đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của
hình nón (như hình vẽ). Tính bán kính đáy R của bình nước. A. R  2 dm. B. R  3 dm. C. R  4 dm. D. R  5 dm. Lời giải. Gọi ,
h h lần lượt là chiều cao của khối nón và khối trụ; ,
R r lần lượt là bán
kính đáy của khối nón và khối trụ. Khi đó h  3 , R h  2 . R
Xét phần mặt cắt và gọi các điểm như hình vẽ. Theo giả thiết 16 2
V r h 
. Ta sẽ chuyển V theo . R tru 9 tru h    2R  Cụ thể:  r SI h h 3R 2R 1 1 .       r R R SO h 3R 3 3 2 Khi đó R 16 V  2R  
R  2 dm. Chọn A. tru 9 9
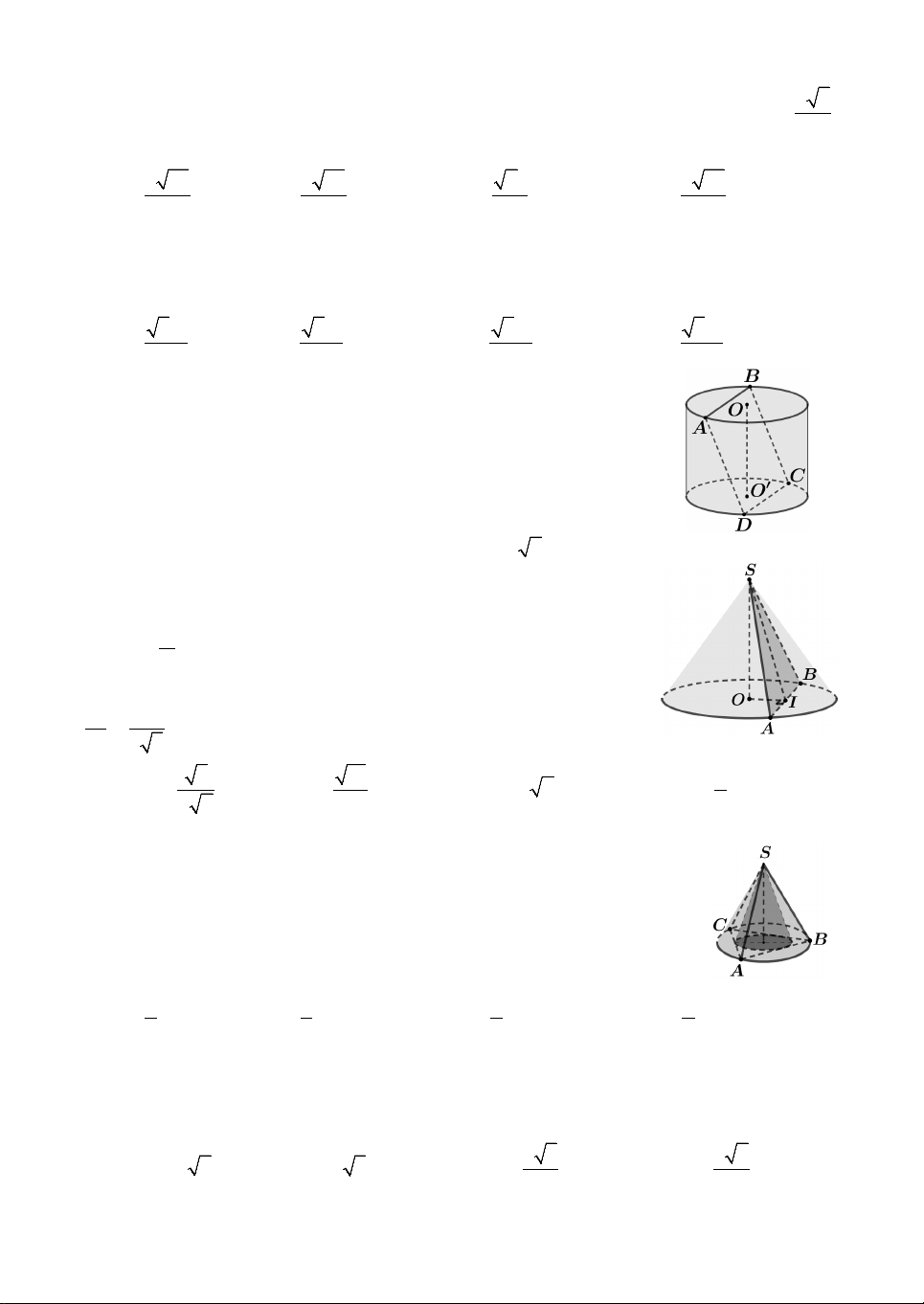
Câu 20. Xét một hình trụ nội tiếp trong hình nón như hình
bên, trong đó S là đỉnh hình nón, O là tâm đường tròn
mặt đáy. Các đoạn AB, CD lần lượt là đường kính của
đường tròn đáy của hình nón và hình trụ. Biết AC, BD cắt
nhau tại điểm M SO và tỉ số thể tích của hình trụ và
hình nón là 4 . Tỉ số SM bằng 9 SO A. 2 . B. 4 . C. 5 . D. 7 . 3 5 6 9
Lời giải. Gọi I là trung điểm DC. SI ID IM ID tOA Đặt t       . SO OA MOIO   1tSO  2 2 .
 t OA .1tSO Theo giả thiết ta có 4 2   t  . 1 2 9 3 .  OA .SO 3 Suy ra SI IM 2 SM 4      . Chọn B. SO MO 3 SO 5 9
Câu 21. Cắt một hình nón bằng một mặt phẳng song song với đáy
thì phần hình nón nằm giữa mặt phẳng và đáy gọi là hình nón
cụt. Một chiếc cốc có dạng hình nón cụt cao 9cm, bán kính của
đáy cốc và miệng cốc lần lượt là 3cm và 4cm. Hỏi chiếc cốc có thể
chứa được lượng nước tối đa là bao nhiêu trong các lựa chọn sau ? A. 250 ml. B. 348 ml. C. 349 ml. D. 350 ml. Lời giải. Gọi ,
R r, h lần lượt là bán kính mặt đáy lớn, bán kính mặt đáy nhỏ và
chiều cao của hình nón cụt. Ta thiết lập được công thức tính thể tích của khối nón cụt là 1 V  2 2
R r Rr h (lấy khối nón lớn trừ đi khối nón nhỏ). 3
Áp dụng với R  4 cm, r  3 cm,
h  9 cm. Ta được 3
V  348,7 cm  348,7 ml. Chọn B.
Câu 22. Phần không gian bên trong của chai nước ngọt có hình
dạng như hình vẽ. Biết bán kính đáy và bán kính cổ chai lần lượt
là R  5 cm, r  2 cm. Thể tích phần không gian bên trong của
chai nước ngọt (giả sử độ dày của vỏ chai không đáng kể) bằng A.  3 412 cm . B.  3 462 cm . C.  3 490 cm . D.  3 495 cm .
Lời giải. Xét phần mặt cắt và kí hiệu như hình vẽ.
Thể tích khối trụ có đường cao CD là: 2
V R .CD  400 3 cm . 1 
Thể tích khối trụ có đường cao AB là: 2
V r .AB  12 3 cm . 2 
Thể tích phần nón cụt có đường cao BC là: 1 V  2 2
R r Rr .BC  78 3 cm . 3
Vậy thể tích chai nước là: V V V V  490 3 cm . Chọn C. 1 2 3 
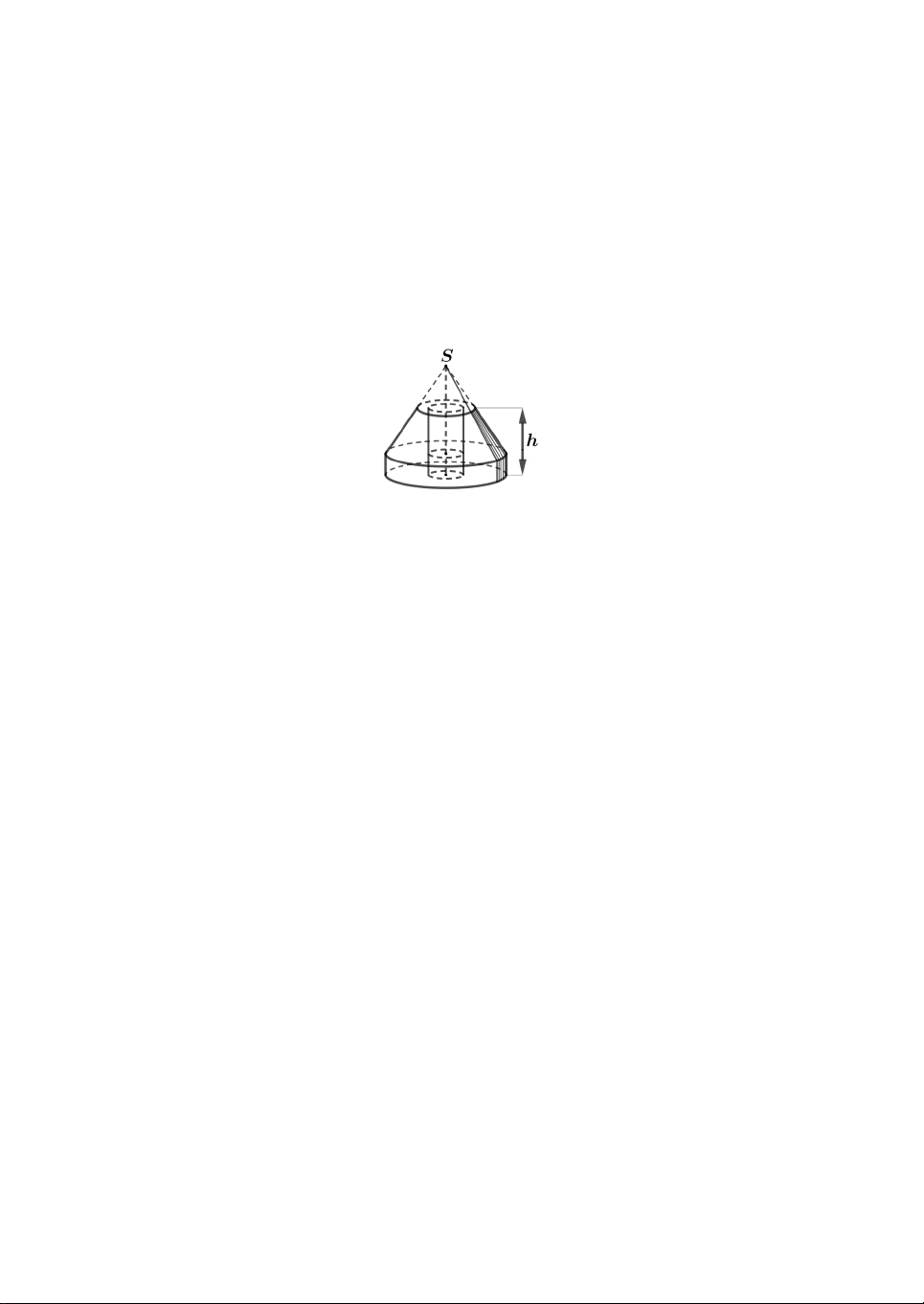
Câu 23. Để định vị một trụ điện, người ta cần đúc một khối bê
tông có chiều cao h  1,5m gồm: Phần dưới có dạng hình trụ
bán kính R  1m và có chiều cao bằng 1 ;
h Phần trên có dạng 3
hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình
nón có bán kính đáy bằng 1 R ở phía trên (người ta gọi hình đó là hình nón cụt); 2
Phần ở giữa rỗng có dạng hình trụ, bán kính đáy bằng 1 R (tham khảo hình vẽ bên). 4
Tính thể tích V của khối bê tông (làm tròn đến chữ số thập phân thứ ba). A. 3
V  2,814 m . B. 3 V  2,815m . C. 3
V  3,109 m . D. 3
V  3,403m . 10
Lời giải. Thể tích của phần dưới có dạng hình trụ: h 1,5 2 V R  . 1.   3 m . 1  3 3 2
Thể tích của phần nón cụt có R 1 R  1, r
 và chiều cao bằng 2 h  1 là 2 2 3  1 1 7 V  1   1.     3 m . 2  3  4 2 12 2  
Thể tích của phần ở giữa rỗng có dạng hình trụ: R 3 V     h    3 m . 3   4  32 Vậy thể tích cần tính 7 3 95
V V V V      3,109 3 m . Chọn C. 1 2 3  2 12 32 96
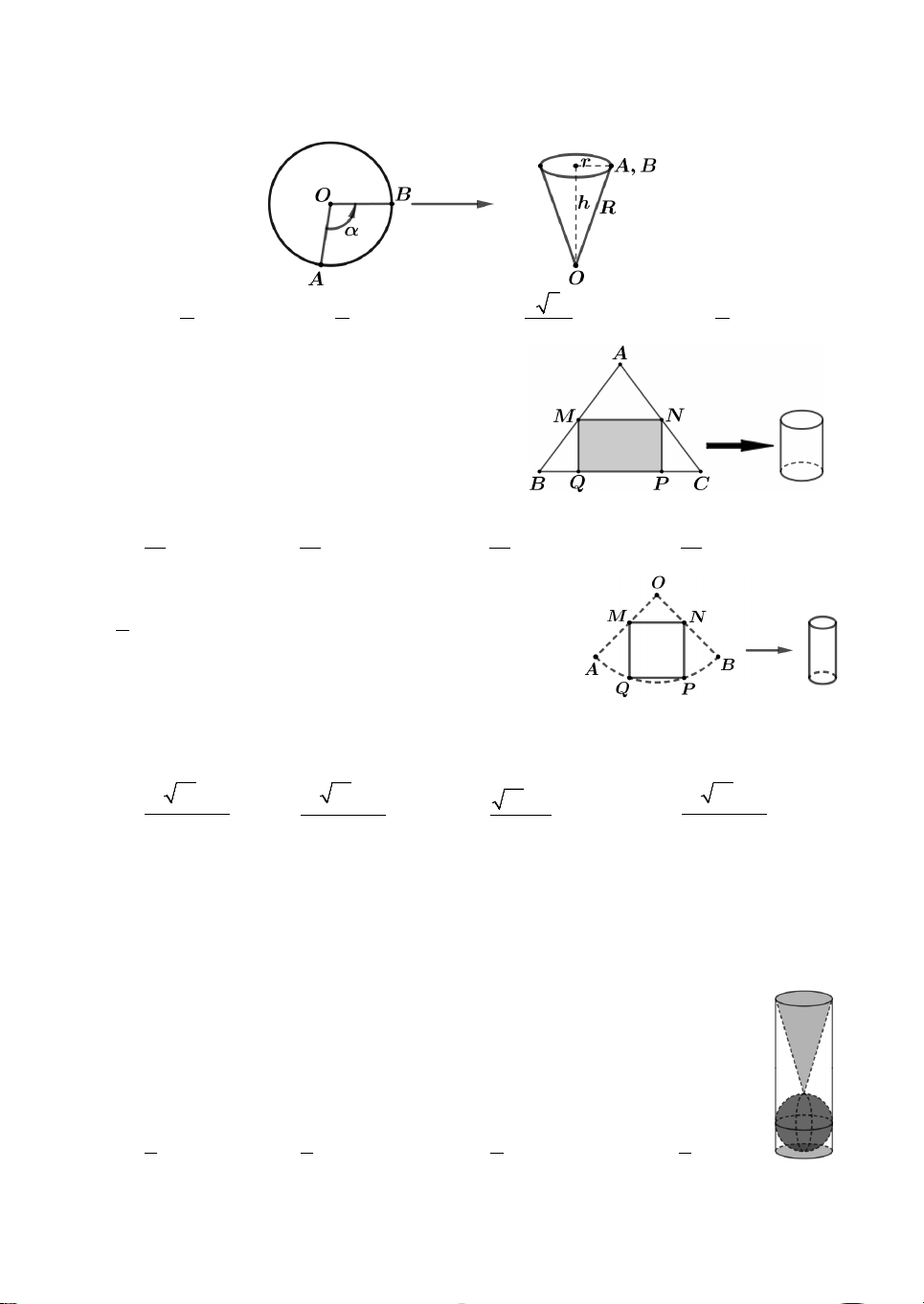
Câu 24. Trong không gian cho một hình cầu S  tâm O có bán kính R và một điểm
S cho trước sao cho SO  2R . Từ S ta kẻ các tiếp tuyến đến mặt cầu với tiếp điểm
thuộc đường tròn C . Trên mặt phẳng P chứa đường tròn C ta lấy điểm E thay 1  1 
đổi nằm ngoài mặt cầu S . Gọi N  là hình nón có đỉnh là E và đáy là đường tròn
C gồm các tiếp điểm của tiếp tuyến kẻ từ E đến mặt cầu S . Biết rằng hai đường 2 
tròn C và C luôn có cùng bán kính, khi đó quỹ tích các điểm E là một đường 2  1 
tròn, đường tròn này có bán kính R bằng A. 3R R R R . B. 15 . C. 17 . D. 15 . 2 2 2 4
Lời giải. Gọi bán kính của C , C lần lượt là r , r. 1   2  1 2
Gọi C là tâm của C và D là một điểm trên C . 1  1  Suy ra SO
D vuông tại D nên ta có CD.OS DO.DS 2 2 2 DO.DS . R OS R R  r CD    R 1 . 1 2 OS OS OS 2
Tương tự, ta tính được R r R 1 . 2 2 OE
Theo giả thiết: r r suy ra OE OS  2R 
E di động trên đường tròn giao 1 2
tuyến của mặt cầu tâm O bán kính 2R với mặt phẳng P. 2 2 Lại có: OD R R R 15 OC     R  2 OE  2 OC  2 4R   . Chọn B. OS 2 4 2
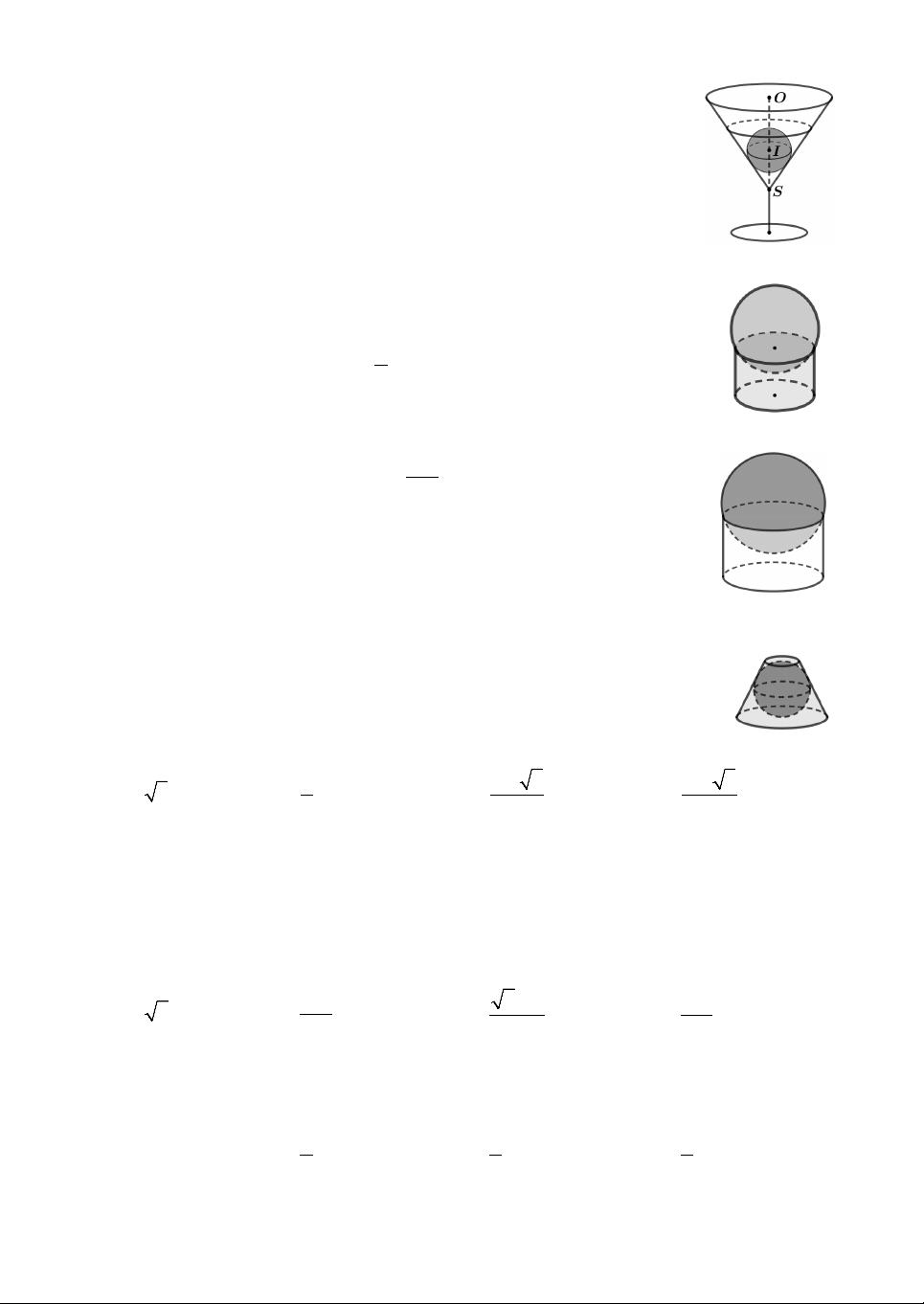
Câu 25. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại ,
A BC  2 2 và 
ACB  30. Hình chiếu của S
trên mặt phẳng đáy là trung điểm H của BC. Giả sử có mặt
cầu tâm O, bán kính bằng 1 tiếp xúc với ,
SA SB và tia đối
của SC lần lượt tại A , B , C đồng thời mặt cầu tâm O đó 1 1 1
cũng tiếp xúc với mặt phẳng ABC (tham khảo hình vẽ).
Thể tích của hình chóp S.ABC bằng 11 A. 3 2 . B. 3 . C. 2 2 . D. 2 3 . 2 3 3 3
Lời giải. Dựng  là mặt phẳng qua S và song
song với ABC. Ta chứng minh O . Khi đó 3
d S,ABC   d O  ,ABC 1.     Suy ra V  . S.ABC 3
Thật vậy: • Tam giác SBC có SH là đường cao và
cũng là đường trung tuyến nên SH là đường phân giác của góc  BSC.   1 • Hai góc  BSC và 
C SB là hai góc kề bù. 2 1 1
• Tam giác B SC cân tại S.   3 1 1 Từ   1 , 2 và  
3 , suy ra mặt phẳng phân giác của 
C SB (cũng là mặt phẳng trung 1 1
trực của B C ) đi qua S và vuông góc với SH . Mặt phẳng này trùng với mặt phẳng 1 1
 đã dựng ở trên. Vì OB OC nên suy ra O . Chọn B. 1 1
Phần 2. Vật thể tròn xoay
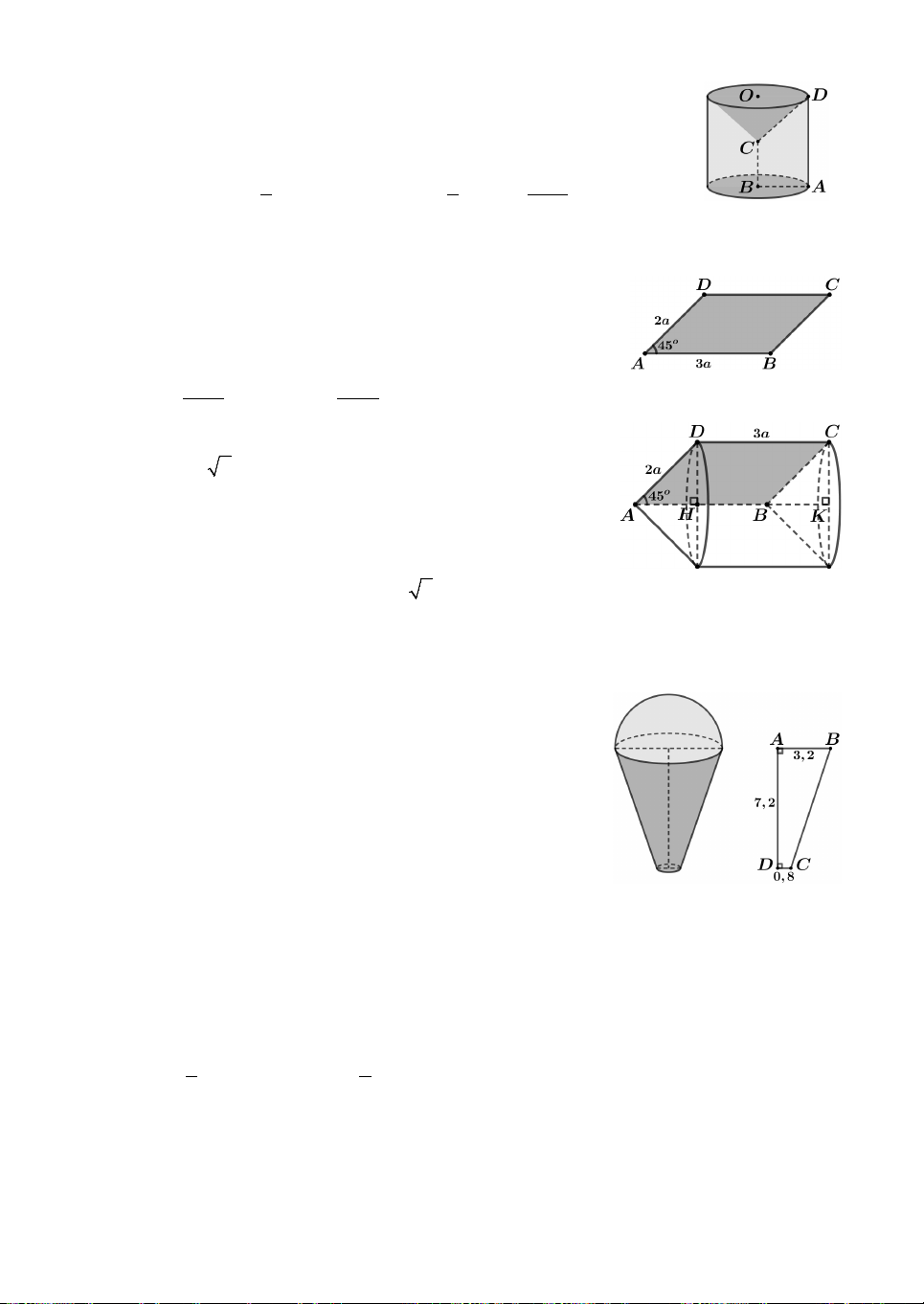
Câu 1. Cho tam giác vuông cân ABC có AB AC a 2 và hình
chữ nhật MNPQ với MQ  2MN được xếp chồng lên nhau sao cho
M , N lần lượt là trung điểm của AB, AC (như hình vẽ). Tính thể
tích V của vật thể tròn xoay khi quay mô hình trên quanh trục
AI, với I là trung điểm PQ. 3 3 3 3 A. 5a 11a 11a 17a V  . B. V  . C. V  . D. V  . 6 6 8 24 Lời giải. Ta có: 2 2
BC AB AC  2a   MN  , a MQ  2 . a
Gọi E, F lần lượt là trung điểm MN và BC. Tính được BC a 3 AF   ,
a EF   IF  . a 2 2 2 Khi đó 1 17 2 2 3
V FB .AF IQ .IF
a . Chọn D. 3 24
Câu 2. Cho hình thang AD
ABCD vuông A và B với AB BC   . a Quay hình 2
thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của
khối tròn xoay được tạo thành. 3 3 3 A. 4a 5a 7a V  . B. V  . C. V  . D. 3
V a . 3 3 3 12
Lời giải. Thể tích khối tròn xoay tạo thành bằng thể tích hình trụ
có bán kính đáy AB và đường sinh AD trừ đi phần thể tích hình
nón có bán kính đáy OD AB và đường cao OC AD BC. 3 Vậy 1 1 5 2 2 2 2 a
V AB .AD O
 D .OC a .2a a .a  . Chọn B. 3 3 3
Câu 3. Cho hình bình hành ABCD có AD  2 , a AB  3 , a
BAD  45 (như hình vẽ). Tính thể tích V của khối tròn
xoay nhận được khi quay hình bình hành ABCD quanh trục AB. 3 3 A. 5a 9a V  . B. V  . C. 3 V  5a . D. 3 V  6a . 2 2
Lời giải. Gọi H là hình chiếu vuông góc của D lên cạnh
AB DH a 2. Khối tròn xoay nhận được khi quanh
hình bình hành ABCD quanh trục AB có thể tích đúng
bằng thể tích khối trụ có đường sinh DC và bán kính đáy
DH (hai hình nón bù trừ nhau).
Vậy V DH HK DH DC a 2 2 2 3 . .
2 .3a  6a . Chọn D.
Câu 4. Một cơ sở sản xuất kem chuẩn bị làm 1000 chiếc
kem giống nhau theo đơn đặt hàng. Cốc đựng kem có
dạng hình tròn xoay được tạo thành khi quay hình thang
ABCD vuông tại A và D xung quanh trục AD (xem
hình vẽ). Chiếc cốc có bề dày không đáng kể, chiều cao
7,2 cm; đường kính miệng cốc bằng 6,4 cm; đường kính
đáy cốc bằng 1,6 cm. Kem được đổ đầy cốc và dư ra phía
ngoài một lượng có dạng nửa hình cầu, có bán kính bằng
bán kính miệng cốc. Cơ sở đó cần dùng lượng kem gần
nhất với giá trị nào trong các giá trị sau A. 3 132 dm . B. 3 170 dm . C. 3 293 dm . D. 3 954 dm .
Lời giải. Thể tích của một chiếc kem cần tính bao gồm:
• Thể tích của hình nón cụt có lớn R  3,2 cm, r  0,8 cm và h  7,2 cm.
• Thể tích của nửa khối cầu có bán kính R  3,2 cm. Suy ra 1 V h 2 2 2
R Rr r  3 3  R  170 cm . 3 3
Vậy thể tích của 1000 chiếc kem là: 3 3 3
170.10 cm  170 dm . Chọn B. 13
Câu 5. Cho tam giác SAB vuông tại , A ABS  60 ,  đường phân giác trong 
ABS cắt SA tại I. Vẽ nửa đường tròn tâm I bán kính
IA (như hình vẽ). Cho tam giác SAB và nửa đường tròn trên cùng
quay quanh SA tạo nên khối cầu và khối nón tương ứng có thể
tích là V và V . Khẳng định nào sau đây đúng ? 1 2
A. V  3V .
B. 2V  3V .
C. 4V  9V .
D. 9V  4V . 1 2 1 2 1 2 1 2  4 4 V
  IA AB tan30 3 4 3 3 3   AB 1 
Lời giải. Ta có  3 3 27 V 4 1     . Chọn D.  1 1 3 V 9 2 2 3 2 V
  AB .SA AB .AB tan 60  .  AB  2  3 3 3
Câu 6. Cho hình vuông ABCD nội tiếp đường tròn O, bán kính r;
tam giác đều MNP nội tiếp đường tròn đó và MN song song AB
(như hình vẽ). Cho mô hình trên quay quanh đường thẳng OP. Kí
hiệu V , V , V là thể tích khối tròn xoay do hình vuông, hình tròn 1 2 3
và tam giác đều tạo thành. Khẳng định nào sau đây đúng ?
A. V V V . B. V V V . C. 2
V V .V . D. 2
V V .V . 1 2 3 3 2 1 1 2 3 3 2 1
Lời giải. Gọi Q, I lần lượt là trung điểm của MN, AB. 3
Thể tích khối cầu (tạo bởi khi quay hình tròn quanh trục 4r OP ) là V  . 2 3
Ta có AC  2r  cạnh hình vuông bằng 2r nên 2 3  2  r  2 2 r
V IB .BC   . 2   r  . 1  2  2 Ta có 3
OP r PQ r  cạnh tam giác đều bằng 3r nên 2 2 3 1 1  3  r  3r 3 2 r V Q
 N .PQ   .    . 3 3 3  2  2 8 Vậy 2
V V .V . Chọn C. 1 2 3
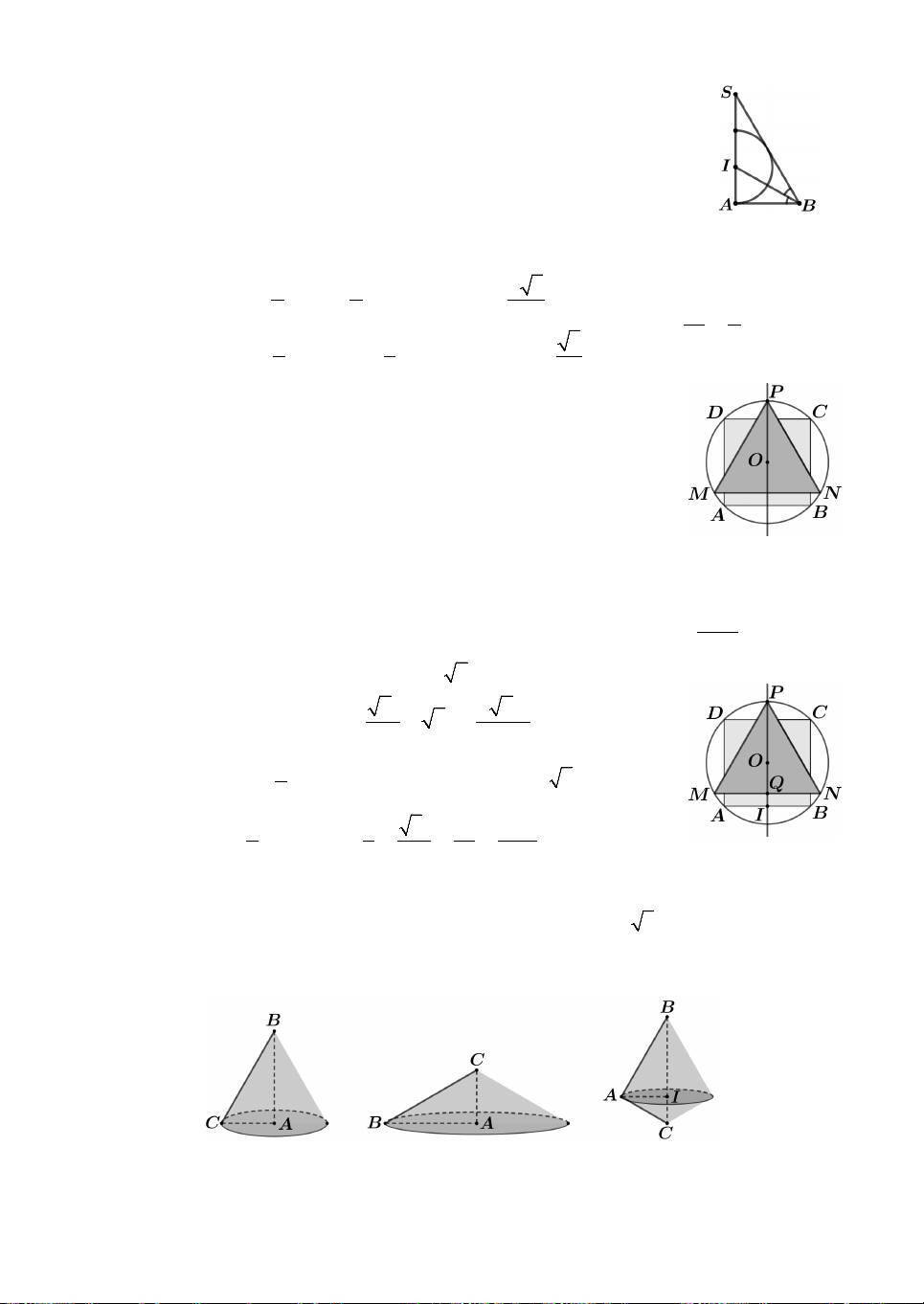
Câu 7. Cho tam giác ABC vuông tại A và có AC  ,
a AB a 3. Gọi V , V , V là thể 1 2 3
tích các khối tròn xoay sinh bởi tam giác ABC kể cả các điểm trong khi lần lượt quay
quanh các cạnh AB, AC, BC. Trong các khẳng định sau, khẳng định nào đúng ? Hình 1 Hình 2 Hình 3 14 A. 1 1 1 1 1 1 1 1 1 1 1 1   . B.   . C.   . D.   . V V V V V V 2 2 2 V V V 2 2 2 V V V 1 3 2 3 1 2 2 3 2 3 1 2
Lời giải. Khi tam giác ABC quay quanh cạch AB ta được khối nón có chiều cao 1 3
h AB a 3 và có bán kính đáy là R AC a (Hình 1) nên 2 3 V R h a . 1 1 1 1 1 3 3
Khi tam giác ABC quay quanh cạch AC ta được khối nón có chiều cao h AC a 2 và có bán kính đáy là 1
R AB a 3 (Hình 2) nên 2 3
V R h a . 2 2 2 2 3
Hạ đường cao AI của tam giác ABC . Khi quay tam giác ABC quanh cạnh BC ta
được hai khối nón sinh bởi hai tam giác ABI và ACI. Hai khối nón này có chung
đường tròn đáy có bán kính bằng độ dài đoạn AI (Hình 3). Do đó ta có 2 3 1 1 1 1 1 a 3 2 2 2  a
V AI .BI AI .CI AI BI CI  2
AI BC   2   a  . 3 3 3 3 3 3  2  2 Từ đó suy ra 1 1 1   . Chọn D. 2 2 2 V V V 3 1 2
Câu 8. Cho hình tứ diện ABCD có AD vuông góc với mặt phẳng ABC và tam giác
ABC vuông tại B. Biết BC a, AB a 3, AD  3 .
a Quay các tam giác ABC và
ABD (bao gồm cả điểm bên trong hai tam giác) xung quanh đường thẳng AB ta được
hai khối tròn xoay. Thể tích phần chung của hai khối tròn xoay bằng 3 3 3 3 A. 8a  3 3a  3 4a  3 5a  3 . B. . C. . D. . 3 16 16 16
Lời giải. Khi quay tam giác ABD quanh AB
ta được khối nón đỉnh B có đường cao , BA
đáy là đường tròn bán kính AD  3 . a Biểu
diễn các điểm như hình vẽ. Gọi I AC BE,
IH AB H AB. Phần chung của hai khối
nón khi quay tam giác ABC và tam giác
ABD quanh AB là hai khối nón có đỉnh A
và đỉnh B, có đáy là đường tròn bán kính IH. Ta có IC BC 1 IBC  ∽ IEA      IA  3IC. IA AE 3 Lại có AH IH AI 3 3.BC 3a IH BC       IH   . AB BC AC 4 4 4
Khi đó thể tích phần chung: 1 1 2 2
V IH .AH IH .BH 3 3 3 1 1 3a  3 2
IH .AH BH  2
IH .AB  . Chọn B. 3 3 16
Câu 9. Ban đầu ta có một tam giác đều cạnh bằng 3 như hình 1. Tiếp theo ta chia
mỗi cạnh của tam giác thành 3 đoạn bằng nhau, dựng một tam giác đều về phía bên 15
ngoài có một cạnh là đoạn giữa, sau đó bỏ đi đoạn giữa ta được hình 2. Khi quay hình
2 xung quanh d ta được một khối tròn xoay có thể tích bằng Hình 1 Hình 2 A. 53 . B. 5 3 . C. 5 3 . D. 9 3 . 2 3 6 8
Lời giải. Kí hiệu các điểm như hình vẽ.
Ta có thể tích khối tròn xoay tạo thành bằng 2 lần thể tích nữa trên (hình SIABK
quay quanh trục SK ). Tam giác 1 3
SIH quay quanh trục SK tạo thành khối nón có r IH  , h SH  1 2 1 2 nên 1 1 1 3 3 2 V r h  . .  . 1 1 1 3 3 4 2 24
Hình thang vuông HABK quay quanh trục HK tạo thành hình nón cụt có 3 h 193
R AH  , r BK  1, 3
h HK SH  nên V   2 2
R r Rr  . 2  2 2 3 24
Vậy thể tích khối tròn xoay tọa thành: V   5 3 2 V V  . Chọn B. 1 2  3
Câu 10. Cho nửa đường tròn đường kính AB  2R và điểm C thay
đổi trên nửa đường tròn đó, đặt 
CAB và gọi H là hình chiếu
vuông góc của C lên AB (như hình vẽ). Tìm sao cho thể tích vật
thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
A.  45.
B.  60. C. arctan 2. D. 1 arctan . 2
AC AB cos 2R cos
Lời giải. Ta có CH
  AC sin 2Rcossin. Vật thể tròn xoay tạo thành khi quay  2
AH AC cos 2R cos 
tam giác ACH quanh trục AB là một khối nón có bán kính đường tròn đáy r HC, 16 chiều cao 1 4 h AH nên 2 3 2 2 V CH .AH R .cos . cos .  2 2 2 cos  3 3
cos  cos  2 2 cos 4 32 3  3 2 2 2 3 RR .  . 3 27 81 Dấu 1 1 "  " xảy ra 2 2 2
 cos  22 cos  tan    arctan . Chọn D. 2 2
Phần 3. Ứng dụng thực tiễn
Câu 1. Bé Bách có một tấm bìa có chiều dài
20 cm; chiều rộng 1 cm. Bé muốn gấp một cái
hộp nhỏ xinh để bỏ kẹp tóc vào hộp đó tặng
quà cho mẹ ngày 20 tháng 10. Anh Siêu đã chỉ
cho bé hai cách gấp hộp. Cách thứ nhất là bé cuốn tấm bìa thành một cái hộp hình trụ
không có hai đáy có thể tích V . Cách thứ hai là bé gập tấm bìa một hình hộp chữ 1
nhật có thể tích V có các kích thước như hình vẽ. Hãy tìm tỉ số thể tích của hai hộp 2
để biết được gấp theo cách nào sẽ có thể tích lớn hơn. A. V 4 V V 1 V 1  . B. 1  . C. 1  . D. 1  4. V V 4 V 4 V 2 2 2 2
Lời giải. Chiều dài của tấm bìa là 20 cm, suy ra • 10 20  2 .  R R
( R là bán kính đường tròn đáy hình trụ).
• Theo đề bài thì hình hộp chữ nhật có đáy là hình vuông (hình vẽ) nên cạnh của hình vuông bằng 20  5. 4 2 Khi đó V S .1 S R 4 1 1 1     . Chọn A. 2 V S .1 S 5 2 2 2
Câu 2. Một tấm tôn hình tròn tâm O, bán kính R được chia thành hai hình H và 1 
H như hình vẽ. Cho biết góc 
AOB  90. Từ hình H gò tấm tôn để được hình 1  2 
nón N không đáy và từ hình H gò tấm tôn để được hình nón N không đáy. 2  2  1  Ký hiệu V
V , V lần lượt là thể tích của hình nón N ,
N . Tỉ số 1 bằng 1   2  1 2 V2 A. 2. B. 3. C. 3 105 . D. 7 105 . 5 9 17
Lời giải. Hai hình nón có độ dài đường sinh bằng nhau:     . R 1 2
Gọi r , r lần lượt là bán kính đáy của hình nón N , N . 1   2  1 2  3 3R 2
r  .2R  r  1  2 2 2 1 1 r  r 1 1 1 Ta có  4 4 V 3 3 105  . Khi đó 1   . Chọn C.  1 R V 1 5 2
 r  .2R r  2 2 2 2 r  r 2 2  4 4 2 2 2 3
Câu 3. Từ cùng một tấm kim loại dẻo hình
quạt (như hình vẽ) có kích thước bán kính
R  5 và chu vi của hình quạt là
P  810, người ta gò tấm kim loại thành
những chiếc phễu theo hai cách:
Cách 1. Gò tấm kim loại ban đầu thành mặt xung quanh của một cái phễu.
Cách 2. Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung
quanh của hai cái phễu. Gọi V là thể tích của cái phễu thứ nhất, V là tổng thể tích 1 2
của hai cái phễu ở cách thứ hai. Tỉ số V1 bằng V2 A. V 2 V 2 2 V 21 V 2 21 1  . B. 1  . C. 1  . D. 1  . V 7 V 7 V 7 V 7 2 2 2 2
Lời giải. Chu vi của hình quạt  độ dài cung 2 .
R Suy ra độ dài cung tròn   8 .
Cách 1: Chu vi đường tròn đáy của cái phễu là 8 . Ta có 1 2 2 2
2r  8r  4  h R r  3 V  . 4 .3  16 . 1 1 1 1 1 3
Cách 2: Chu vi đường tròn đáy của mỗi phễu nhỏ là 4 .   Ta có 1 8 21 2 2 2
2r  4r  2  h R r  21 V  2   . 2 . 21  . 2 2 2 2 2 3  3 Vậy V 2 21 1  . Chọn D. V 7 2
Câu 4. Để làm cống thoát nước cho một khu vực dân cư người ta
cần đúc 500 ống hình trụ có đường kính trong và chiều cao của
mỗi ống bằng 1 m, độ dày của thành ống là 10 cm. Chọn mác bê
tông là 250 (tức mỗi khối bê tông là 7 bao ximăng). Hỏi phải
chuẩn bị bao nhiêu bao ximăng để làm đủ số ống nói trên ?
A.  1110 bao. B. 1200 bao. C.  1210 bao.
D.  4 210 bao.
Lời giải. Thể tích khối trụ có bán kính đáy 9
0,6 m là: V R h 0,62 2 .1  . 1 1 25
Thể tích khối trục có bán kính đáy 1
0,5 m là: V R h 0, 2 2 5 .1  . 2 2 4 18  
Lượng bê tông cho một ống là: 9 1 11 V V V           3 m . 1 2  25 4 100
Lượng bê tông để làm 500 ống là: 11 500  55 3 m . 100
Vậy số lượng bao ximăng cần chuẩn bị là: 55 .
7  1210 bao. Chọn C.
Câu 5. Cắt một miếng tôn hình vuông
cạnh 1 m thành hai hình chữ nhật,
trong đó một hình có chiều rộng x m,
gọi miếng tôn này là miếng tôn thứ
nhất. Người ta gò miếng tôn thứ nhất
thành một lăng trụ tam giác đều, miếng còn lại gò thành một hình trụ (như hình vẽ).
Tìm x để tổng thể tích khối lăng trụ và khối trụ thu được là nhỏ nhất. A. 9 x  . B. 1 x  . C. 9 x  . D. 1 x  . 3 9 3 31 9 3  3
Lời giải. Chu vi tam giác đáy của lăng trụ là x, mà đáy của lăng trụ là tam giác đều 2
nên có diện tích bằng x 3 . 36 Gọi  x
r là bán kính đáy của hình trụ. Suy ra 1
2r  1 x r  . 2 2 2     
Tổng thể tích của hai khối: x 3 1 x 3 1      1 1 2 .1   .1        x x   f x. 36  2  36 4 2 4  
Đây là hàm bậc hai nên f x 9  f    , x 0;  1 .  Chọn A.  39
Câu 6. Một tấm tôn hình chữ nhật có chiều dài 4m, chiều rộng 1m. Một người thợ
muốn cắt tấm tôn này thành hai phần như hình vẽ. Người thợ gò phần 1 thành hình
trụ có đáy hình vuông và phần 2 thành hình trụ có đáy hình tròn. Tìm x để tổng thể
tích của hai khối trụ là nhỏ nhất. A. 4 x  . B. 8 x  . C. 16 x  . D. 16 x  .  4  4  4  4 Lời giải. Gọi  x
r là bán kính đáy của hình trụ. Suy ra 4
2r  4  x r  . 2 2 2       
Tổng thể tích của hai khối: x 4 x 1 1 2 4 2     .1       .1         
x x   f x. 4  2 16 4 19  
Đây là hàm bậc hai nên f x 16  f    , x 0;4.  Chọn C. 4  
Câu 7. Từ một tấm tôn hình chữ nhật người ta cuộn
thành một chiếc thùng hình trụ không đáy (như hình
vẽ). Biết tâm tôn có chu vi bằng 120 cm. Để chiếc thùng
có thể tích lớn nhất thì chiều dài, rộng của mảnh tôn lần lượt là
A. 35 cm; 25 cm. B. 30 cm; 30 cm. C. 40 cm; 20 cm. D. 50 cm; 10 cm.
Lời giải. Gọi chiều dài tấm tôn là x cm 0  x  60. Suy ra chiều rộng: 60 x cm.
Giả sử quấn cạnh có chiều dài là x
x  bán kính đáy r
và chiều cao h  60 x. 2x  60x
x.x. 120 2x
x x 120 2x 8000 2    3 3 2 Cosi
Khi đó V r h      3 cm . 4 8 8 . 27
Dấu "  " xảy ra  x  1202x x  40 cm. Chọn C.
Câu 8. Bạn An có một tấm bìa hình tròn như hình vẽ, An muốn biến hình tròn đó
thành một cái phễu hình nón. Khi đó An phải cắt hình quạt tròn OAB rồi dán hai bán kính O ,
A OB lại với nhau. Gọi là góc ở tâm hình quạt tròn dùng làm phễu. Tìm
để thể tích phễu là lớn nhất. A.  . B.  . C. 2 6  . D.  . 2 3 3 4
Lời giải. Thể tích của phễu 1 1 2
V r h  2 2 R h  . h 3 3 Khảo sát ta thấy R R
V đạt GTLN khi h  . Suy ra 2 r  . 3 3 Ta có
  chu vi đường tròn đáy của hình nón 2 6
R  2r  . Chọn C. AB 3
Câu 9. Có tấm bìa hình tam giác vuông cân
ABC có cạnh huyền BC bằng . a Người ta
muốn cắt tấm bìa đó thành hình chữ nhật
MNPQ rồi cuộn lại thành một hình trụ không
đáy như hình vẽ. Diện tích hình chữ nhật đó
bằng bao nhiêu để diện tích xung quanh của hình trụ là lớn nhất ? 20 2 2 2 2 A. a a a a . B. . C. . D. . 2 4 8 12
Lời giải. Kẻ đường cao AH cắt MN tại K như hình vẽ. Tam giác a
ABC vuông cân nên AH BH CH  . 2   Đặt a a
MK x 0  x   . 
Suy ra AK MK x KH   x.  2 2
Chu vi đáy hình trụ bằng 2MK  2x. 2  a
x  x 2     Do đó a  2  a
S  2x.KH  2x.  x 2  . xq 2  4 8  aMN  2x   2 Dấu aa
''  '' xảy ra  x  . Khi đó  2   S  . Chọn C. 4 MNPQa 8 KH   4
Nhận xét: Diện tích xung quanh của hình trụ chính là diện tích của hình chữ nhật.
Câu 10. Cho tấm tôn hình nón có bán kính đáy là 2
r  , độ dài đường sinh   2. Người ta cắt theo một 3
đường sinh và trải phẳng ra được một hình quạt. Gọi
M , N thứ tự là trung điểm của O , A OB.
Hỏi khi cắt hình quạt theo hình chữ nhật MNPQ (hình vẽ) và tạo thành hình trụ
(không đáy) có đường PN trùng MQ thì được khối trụ có thể tích bằng bao nhiêu ? 3 13   1 3 13   1 5 13   1 A.  . B. . C. 13 1. D. . 4 8 9 12
Lời giải. Độ dài cung 
AB bằng chu vi đáy của hình nón và bằng 2 4 2 .  . 3 3 Ta có  4   2 0     O . A AOB   .
AOB AOB
 120  ONM  30  ONP  120.  AB 3 3
Áp dụng định lí cosin trong tam giác OAB, ta được AB  2 3  MN  3.
Áp dụng định lí cosin trong tam giác   ONP, ta được 1 13 NP  . 2 Khi đó hình chữ nhât 
MNPQ được cuốn thành mặt trụ có chiều cao 13 1 h NP  , 2 3 13   1 bán kính đáy MN 3 R  
. Vậy thể tích khối trụ V  . Chọn B. 2 2 8 21
Phần 4. Các khối NÓN – TRỤ – CẦU tiếp xúc
Câu 1. Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng
3 lần đường kính của đáy; Một viên bi và một khối nón đều bằng thủy tinh.
Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước.
Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì
thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại
trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh). A. 1 . B. 2 . C. 4 . D. 5 . 2 3 9 9
Lời giải. Gọi bán kính đáy của cốc hình trụ là .
R Suy ra chiều cao của cốc nước hình
trụ là 6R; bán kính của viên bi là R; bán kính đáy hình nón là R; chiều cao của hình nón là 4 . R Thể tích khối nón là 4 4 3 V
R . Thể tích của viên bi là 3 VR . non 3 cau 3
Thể tích của cốc (thể tích lượng nước ban đầu) là 3 V  6R . 
Suy ra thể tích nước còn lại: V
V  V V V  10 3  R . Vậy 5  . Chọn D. non cau 3 V 9
Câu 2. Một cái ống nghiệm hình trụ có bán kính trong lòng ống là , R ống
nghiệm đang chứa một lượng nước có chiều cao .
h Người ta thả 3 viên bi có
cùng bán kính R vào ống nghiệm thì mực nước dâng lên vừa đủ phủ kín
viên bi cao nhất như hình vẽ. Khẳng định nào sau đây đúng? A. h  3 . R B. h  2 . R C. h  2 . R D. 3 h  3 . R
Lời giải. Gọi h là chiều cao của mực nước trong ống nghiệm sau khi thả 3 viên bi
vào ống nghiệm. Khi đó h  6 . R
Thể tích phần trụ có hai đáy là hai mặt nước là: 2 3 V  6 .
R R  6R . 1 Thể tích ba viên bi là: 4 3 3
V  3. R  4R . 2 3
Suy ra thể tích lượng nước ban đầu trong ống nghiệm là: 3 V V V   2R . 1 2 Mà 2
V hR nên ta có 2 3
hR  2R  h  2 . R Chọn B.
Câu 3. Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp
xúc nhau và tiếp xúc với mặt phẳng P. Mặt cầu S bán kính
bằng 2 tiếp xúc với ba quả bóng trên. Gọi M là điểm bất kì trên
S, MH là khoảng cách từ M đến mặt phẳng P. Giá trị lớn
nhất của MH bằng A. 30 69 123 3  . B. 3 . C. 3 . D. 52 . 2 3 4 9 22
Lời giải. Gọi tâm của ba mặt cầu bé bán kính r  1 lần lượt
là B, C, D; tâm của mặt cầu lớn bán kính R  2 là . A
Do ba mặt cầu bé tiếp xúc với nhau nên tam giác BCD đều có cạnh bằng 2.
Mặt cầu lớn tiếp xúc với ba mặt cầu bé nên tứ diện ABCD có
cạnh bên AB AC AD  3.
Khi đó khoảng cách thỏa mãn bài toán là: 69
R r d  3  . Chọn B.
A ,BCD   3
Câu 4. Có một hình nón chứa bốn quả bóng bàn bằng nhau, đường
kính mỗi quả bóng bàn là 4. Các quả bóng bàn tiếp xúc với nhau, ba
quả tiếp xúc với đáy của hình nón đồng thời bốn quả tiếp xúc với mặt
xung quanh của hình nón như hình vẽ. Chiều cao của hình nón bằng A. 4 2  2. B. 4 2 3  . C. 4 2 3   2. D. 4 2 2 3   2. 3 3 3 3 Lời giải. Gọi ,
A B, C, S lần lượt là tâm của bốn quả cầu. Khi đó khối chóp ABCD là
tứ diện đều cạnh bằng 4, gọi D là trung điểm của BC.
Xét phần mặt cắt (mặt cắt là mặt trung trực của BC ) và kí hiệu
như hình vẽ. Với M là đỉnh của hình nón; I là chân đường cao
xuất phát từ đỉnh S của tứ diện S.ABC; H, K là hình chiếu vuông
góc của S, A trên đường sinh của hình nón.
Vì S.ABC là tứ diện đều có cạnh bằng 4 nên suy ra 4 6 SI  . 3 Ta có SM AS MHS ∽ SIA     SM  2 3. SH AI
Vậy chiều cao của hình nón: 4 6
h MN SM SI IN  2 3   2. Chọn D. 3
Câu 5. Một khối hộp chữ nhật có kích thước 4 cm4 cmh cm chứa
một quả cầu lớn và tám quả cầu nhỏ. Biết quả cầu lớn có bán kính
R  2 cm và quả cầu nhỏ có bán kính r  1cm ; các quả cầu tiếp xúc
nhau và tiếp xúc các mặt của hình hộp (như hình vẽ). Tìm h .
A. h  212 2 cm.
B. h  21 7 cm.
C. h  23 7 cm.
D. h  8 cm.
Lời giải. Gọi tâm của quả cầu lớn là I, tâm của bốn quả cầu nhỏ nằm bên dưới lần lượt là ,
A B, C, D. Khi đó I.ABCD là hình chóp tứ giác đều và có độ dài các cạnh như hình vẽ bên dưới. 23
Ta có CD r r  2cm và ID R r  3cm.
Gọi O AC BD. Tính được IO  7 . Vậy h  21 7 cm. Chọn B.
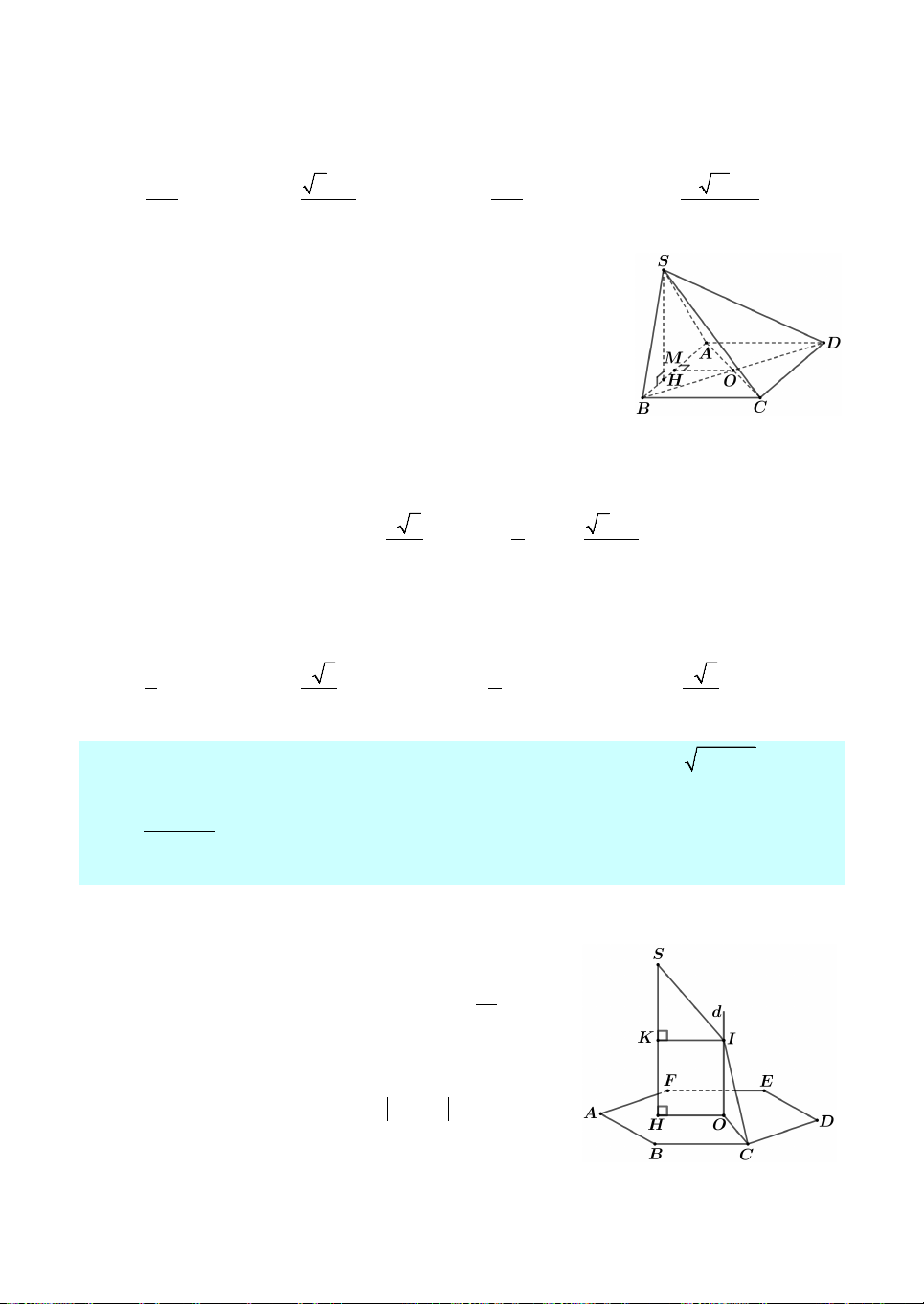
Câu 6. Một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba
khối nón giống nhau có thiết diện qua trục là một tam giác vuông
cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với
nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh
của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với
hai cạnh của đáy bể (tham khảo hình vẽ). Sau đó người ta đặt lên
đỉnh của ba khối nón một khối cầu có bán kính bằng 4 lần bán kính đáy của khối 3
nón. Biết khối cầu vừa đủ ngập trong nước (mặt trên của bể là tiếp diện của mặt cầu)
và lượng nước tràn ra là 337 3
cm . Thể tích lượng nước ban đầu ở trong bể xấp xỉ 3 A.  3 885,2 cm . B.  3 1106,2 cm . C.  3 1174,2 cm . D.  3 1209,2 cm .
Lời giải. Gọi bán kính đường tròn đáy của khối nón là r
cm, suy ra chiều cao của
khối nón là h r (do thiết diện là tam giác vuông cân) và bán kính mặt cầu là
4 r  cm. Xét mặt đáy và ký hiệu như hình vẽ. 3
Suy ra chiều dài hình chữ nhật (mặt đáy) là 4r  cm; chiều rộng
hình chữ nhật (mặt đáy) là 2r CH  2r  3r  2 3r  cm.
Mặt phẳng  qua ba đỉnh của khối nón, cắt mặt cầu theo thiết
diện là một đường tròn có bán kính bằng bán kính của đường tròn ngoại tiếp 2r 3 ABC  nên bằng
cm. Do đó khoảng cách từ tâm mặt cầu đến mặt 3 2 2     phẳng  4 2    r 3  2r
 bằng  r        . 3   3  3
Suy ra chiều cao của hình hộp chữ nhật bằng: 2r 4r r    3r. 3 3 24 3 gia thiet  
Thể tích ba khối nón và khối cầu 4 4 337 337 3 3
V   r  .
 r  r   r  3. 3 3  81 3
Thể khối hình hộp chữ nhật 3 V r    3 r      3 12 2 3 324 2 3
1209,2 cm . Chọn D.
Câu 7. Cho hình nón có bán kính đáy R  5 ,
a độ dài đường sinh   13 . a Thể tích
khối cầu nội tiếp hình nón bằng 3 3 3 3 A. 40a 400a 4000a 4000a . B. . C. . D. . 9 27 27 81
Lời giải. Ta cần tìm bán kính của mặt cầu. Xét mặt cắt qua
trục của hình nón và ký hiệu như hình vẽ.
Từ giả thiết, suy ra chiều cao của hình nón 2 2
h    R  12 . a Ta có hR S
pr với r là bán kính đường tròn nội tiếp tam SAB
giác SAB và cũng là bán kính của hình cầu nội tiếp hình nón, hR a
p là nửa chu vi tam giác SAB. Suy ra 10 r   . p 3 3 3   Thể tích khối cầu: 4 4 10a 4000 3 a
V r      . Chọn D. 3 3  3  81
Câu 8. Một bình đựng nước dạng hình nón (không có đáy), đựng
đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng
một nửa chiều cao của bình nước và đo được thể tích tràn ra là 32 3
dm . Biết rằng khối cầu tiếp xúc với tất cả các đường sinh 3
của hình nón và toàn bộ khối cầu chìm trong nước, trong đó mặt
nước là tiết diện của khối cầu (hình vẽ bên). Thể tích nước còn lại trong bình bằng A. 16 32 40 64 3 dm . B.  3 dm . C.  3 dm . D.  3 dm . 3 3 3 3
Lời giải. Xét phần thiết diện qua trục và kí hiệu các điểm như hình. Gọi 4 32
R là bán kính khối cầu. Theo đề, ta có 3 R   R  2. 3 3
Khi đó OH  4R  8. Do OI IK 6 2 OKI ∽ OHA nên     AH  2 2. 2 2 OA AH AH  8 AH
Thể tích nước còn lại trong bình: 32 32 2 .AH .OH   . Chọn B. 3 3 3
Câu 9. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả
vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao
của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng
khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng
một nửa khối cầu chìm trong nước như hình vẽ. Thể tích nước còn lại trong ly bằng 25 A. V. B. 1V. C. 1V. D. 1V. 3 6
Lời giải. Gọi bán kính mặt cầu là 4
R , suy ra thể tích khối cầu 3 VR . S  3 V
Suy ra thể tích nước tràn ra ngoài: S  2 3 V   R . 2 3
Xét phần mặt cắt qua trục hình nón và kí hiệu như hình vẽ. 2 Ta có 1 1 1 OF R 4 2 R    OA  . 2 2 2 OO 2 R OF OA OO 3 2 3
Suy ra thể tích khối nón: 1 1 4R 8 2 R V  .
 OA .OO  . .2R  . N  3 3 3 9
Vậy thể tích nước còn lại trong ly: 2 3 V V V
  R  . Chọn C.N  9 3
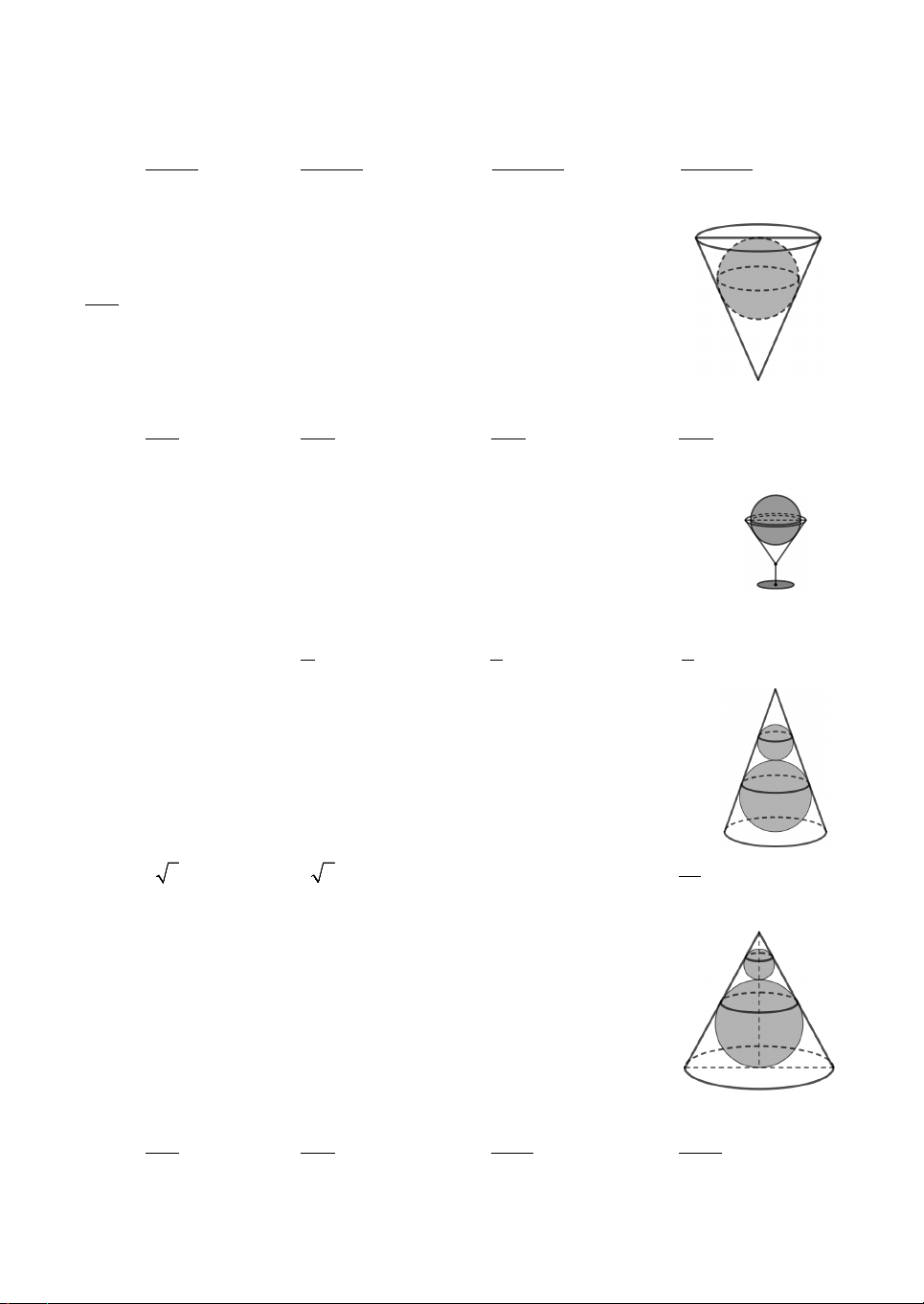
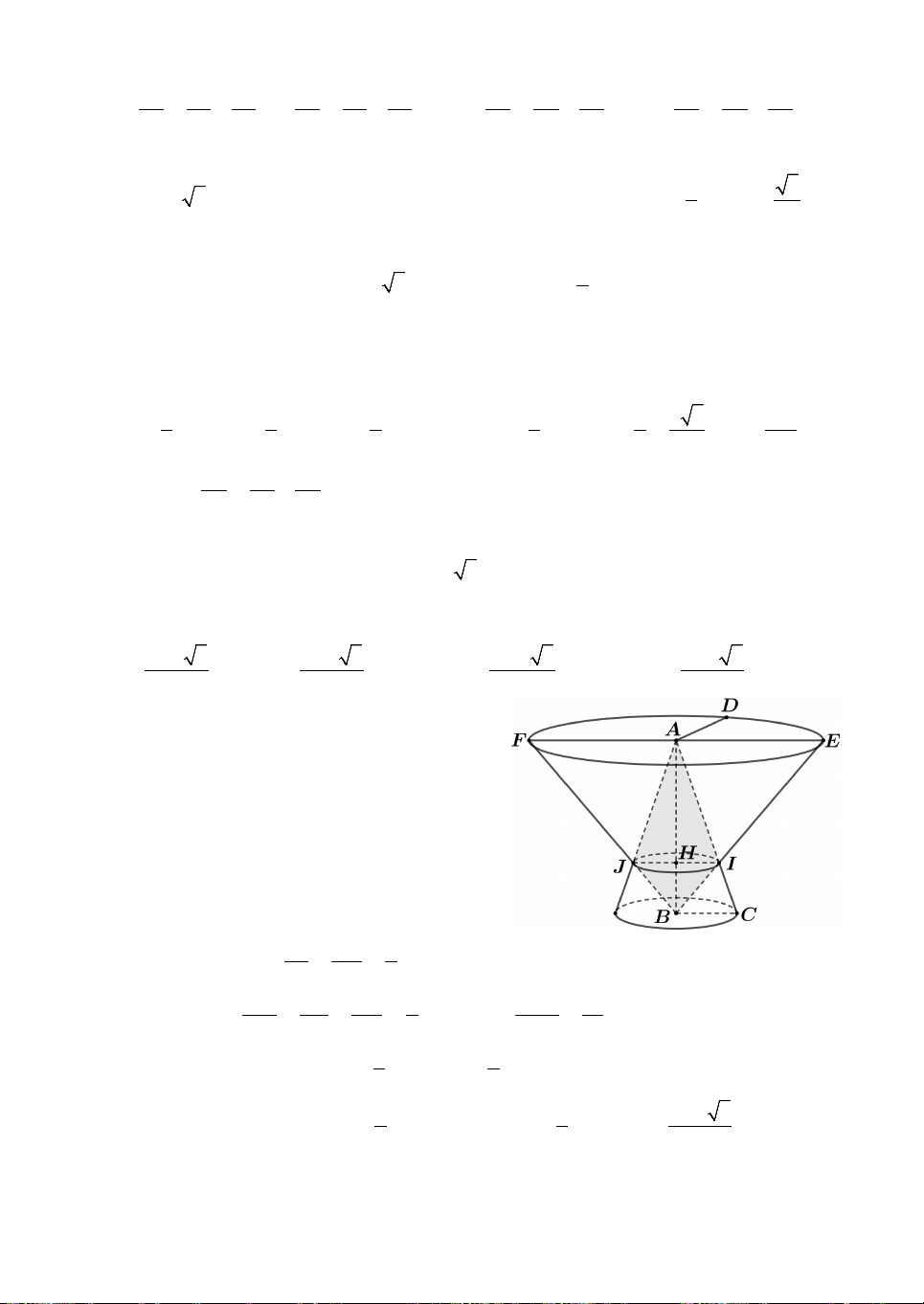
Câu 10. Nguời ta đặt được vào trong một hình nón hai khối cầu có
bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với
mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và
khối cầu lớn tiếp xúc với đáy của hình nón (tham khảo hình vẽ). Bán
kính đáy của hình nón đã cho bằng A. a a 5. B. 2 2 . a C. 3 . a D. 8 . 3
Lời giải. Xét phần thiết diện qua trục và kí hiệu các điểm như
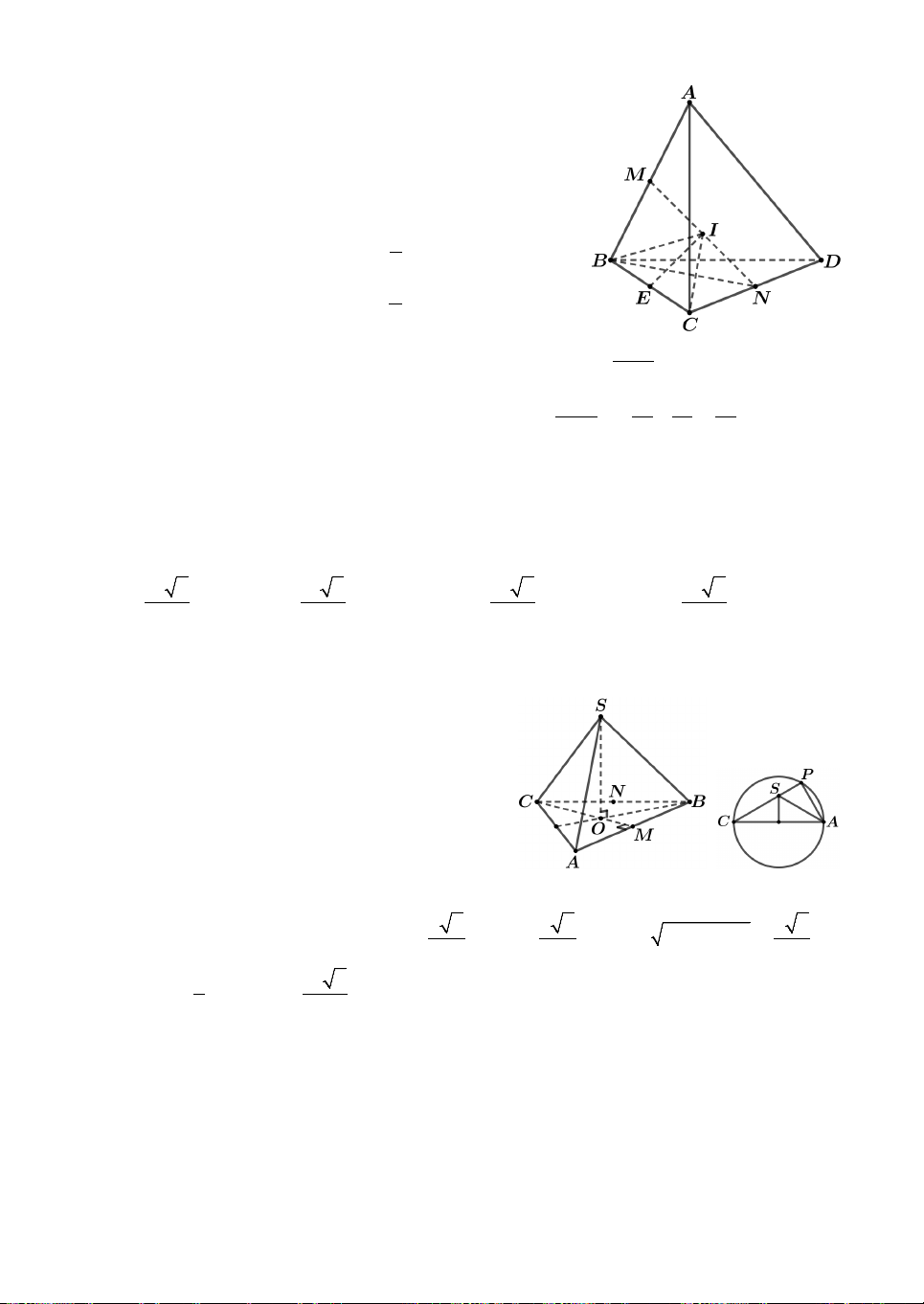
hình vẽ, trong đó A là đỉnh của hình nón và BC là đường kính
đáy của hình nón có tâm đáy là I. Gọi M ,N lần lượt là tâm của
hai khối cầu có bán kính 2 ,
a a; H , K lần lượt là điểm tiếp xúc của
AC với hai đường tròn tâm M , N. Vì MH NK
và NK MH 
NK là đường trung bình trong 2
tam giác AMH suy ra N là trung điểm AM.
Khi đó AM  2MN  6a AI  8 . a Mặt khác IC AI IC 8a AIC  ∽ AHM    
IC  2a 2. Chọn B. HM AH 2a
6a2 2a2
Câu 11. Người ta chế tạo ra một món đồ chơi cho trẻ em theo các
công đoạn như sau: Trước tiên, chế tạo ra một hình nón tròn
xoay có góc ở đỉnh là 2 60 bằng thủy tinh cho trong suốt.
Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ
khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc
với mặt nón, quả cầu lớn tiếp xúc với cả mặt đáy của hình nón
(hình vẽ). Biết rằng chiều cao của hình nón là 9 cm. Bỏ qua bề
dày của các lớp vỏ thủy tinh, tổng thể tích của hai khối cầu bằng 26 A. 38 40 100 112 3 cm . B.  3 cm . C.  3 cm . D.  3 cm . 3 3 3 3
Lời giải. Xét phần thiết diện qua trục và kí hiệu như hình vẽ. Ta có SAB
đều có chiều cao h  9 cm nên bán kính đường tròn nội tiếp h r   3. 3 Tương tự S
EF đều có chiều cao h  9 2r  3 nên có bán kính  đường tròn nội tiếp h r    1. 3
Thể tích hai khối cầu bằng: 4 4 112 3 3
r r    3 cm . Chọn D. 3 3 3
Cách 2. (Dùng khi góc ở đỉnh khác 0
60 ) Gọi N, r là tâm và bán 1
kính của quả cầu nhỏ; M , r là tâm và bán kính của quả cầu lớn. 2
Do các mặt cầu tiếp xúc với nhau và tiếp xúc với mặt nón nên
tam giác SQN vuông tại Q, tam giác SPM vuông tại P.
Hình nón tròn xoay có góc ở đỉnh là 2 60 nên  ASO  30. Ta có 1 1 0
r MP SM.sin 30  SM
SO r r  3; 2  2  2 2 2 1 1 0
r NQ SN.sin 30  SN
SO r 2r r  1. 1  1 2  1 2 2
Câu 12. Một ly nước có dạng như hình vẽ. Phần phía trên chứa
nước có dạng hình nón đỉnh S với đường kính đáy và chiều cao SO
cùng bằng 8cm. Ban đầu ly chứa lượng nước có chiều cao 4cm so
với đỉnh S. Cho vào ly nước một viên bi sắt hình cầu thì nước dâng
lên vừa phủ kín viên bi. Tính bán kính r của viên bi làm tròn đến hai chữ số thập phân.
A. r  1,23cm. B. r  1,28cm.
C. r  1,53cm.
D. r  1,78cm.
Lời giải. Đặt bằng nửa góc ở đỉnh của hình nón. Suy ra 1
tan  (do chiều cao bằng đường kính). 2
Bạn đầu lượng nước có chiều cao 4cm nên bán kính của đường
tròn giao tuyến (mặt nước với ly) bằng 4.tan  2cm. Suy ra thể
tích lượng nước ban đầu 1 16 2 V  . 2 .4  . 1 3 3
Thể tích viên bi sắt là: 4 3 V r . 2 3
Đặt SH h là chiều cao mực nước sau khi thả viên bi, ta có 2 2 IH r h
h SI IH IM SM IH h
r HK SH.tan  . IM  5 1 ; SM  2r , 2 tan 27
Suy ra thể tích ly nước sau khi thả viên bi: 1 V  .  HK .SH h  1 53 2 3 3 r . 3 12 12 Ta có:
V V V  1 53 16 4 3 3 CASIO r
r  x  1,53 cm . Chọn C. 1 2   12 3 3
Câu 13. Một chiếc chén hình trụ có chiều cao bằng đường kính quả
bóng bàn. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài
của quả bóng có chiều cao bằng 3 chiều cao của nó. Gọi V , V lần 4 1 2
lượt là thể tích của quả bóng và chiếc chén. Khi đó
A. 3V  2V .
B. 9V  8V .
C. 16V  9V .
D. 27V  8V . 1 2 1 2 1 2 1 2
Lời giải. Gọi h là chiều cao của hình trụ, r là bán kính của chén hình trụ, R là bán
kính của quả bóng. Suy ra h  2 . R
Xét phần thiết diện qua trục và kí hiệu như hình vẽ. Ta có h
OA OB R  . 2 Từ giả thiết suy ra h h IB   OI  . 4 4
Bán kính đáy của chén hình trụ là h 3 2 2
r IA OA OI  . 4 4 3 2 R 3    
Vậy tỉ số thể tích: V 3 4 h     h 3  8 1
  :       h  
9V  8V . Chọn B. 2 1 2 V r h 3 2  4  9 2
Câu 14. Một quả cầu có thể tích 256  3
cm  được đặt vào một 3
chiếc cốc có dạng hình trụ với đường kính đáy là 6 cm như hình vẽ.
Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến hàng phần trăm) A. 2,00 cm. B. 4,00 cm. C. 4,65 cm. D. 6,65 cm.
Lời giải. Từ giả thiết suy ra quả cầu có bán kính r  4 cm.
Xét phần thiết diện qua trục và kí hiệu như hình vẽ.
Khi đó OM r  4 cm; BM  3 cm.
Tam giác vuông OBM , có 2 2
OB OM MB  7 cm.
Vậy chiều cao của quả cầu nhô ra khỏi miệng cốc bằng
TB TO OB r OB  4  7 cm  6,65 cm. Chọn D.
Câu 15. Một hình cầu nội tiếp trong một hình nón cụt. Hình cầu nội
tiếp trong hình nón cụt là hình cầu tiếp xúc với hai đáy của hình nón
cụt và tiếp với mặt xung quanh của hình nón cụt (tham khảo hình vẽ).
Biết rằng thể tích khối nón cụt gấp đôi thể tích của khối cầu. Tỉ lệ
giữa bán kính đáy lớn và bán kính đáy nhỏ của hình nón cụt bằng 28 A.   3. B. 3 . C. 1 5 . D. 3 5 . 2 2 2
Lời giải. Chuẩn hóa bán kính đáy nhỏ của hình nón bằng 1. Gọi
bán kính đáy lớn của hình nón là R 1, r là bán kính của hình
cầu. Suy ra chiều cao của hình nón cụt là h  2r.
Xét mặt cắt qua trục của hình nón cụt và kí hiệu như hình vẽ.
Tam giác vuông ABC, có BC AB AC  R  2  R  2  r2 2 2 2 1 1 2  r R. Thể tích khối cầu: 4 4 3 R R V r  . 1 3 3
Thể tích khối nón cụt: V   2 2 2 R 1  . R  1 .2r  . R  2 R R 1 . 2  3 3 Theo giả thiết, ta có 2 R RV  2V  . R  8 R 3 5 2 R R   1 1    R  . 2 1 3 3 2
Vậy tỉ số cần tính: R 3  5  . Chọn D. 1 2
Phần 5. Mặt cầu ngoại tiếp khối chóp
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC  . a
Cạnh bên SA vuông góc với đáy ABC. Gọi H, K lần lượt là hình chiếu vuông góc
của A lên cạnh bên SB và SC. Thể tích của khối cầu ngoại tiếp chóp . A HKCB bằng 3 3 3 A. 2 3 a a a 2a . B. . C. . D. . 2 3 6
Lời giải. Theo giả thiết, ta có  0 ABC  90 và  0 AKC  90 .   1 AH SB Do 
AH HC. 2
AH BC do BC   SAB  Từ  
1 và 2, suy ra ba điểm B, H , K cùng nhìn xuống AC AB a AC dưới một góc 0 90 nên 2 2 R    . 2 2 2 3 Vậy 4 2 3 a V R  . Chọn C. 3 3
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và BD  . a Hình
chiếu vuông góc của S trên mặt phẳng đáy là trung điểm OD . Đường thẳng SD tạo
với mặt đáy một góc bằng 0
60 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. a a a . a B. . C. . D. . 2 3 4 29
Lời giải. Xác định được 0
60  SD,ABCD    SDH. Tính được a 3 a a SH  ; SD  và 3 SB  . 4 2 2 Ta có 2 2 2 2
SB SD a BD . Suy ra tam giác SBD vuông
tại S. Vậy các đỉnh S, ,
A C cùng nhìn xuống BD dưới một góc vuông nên 1 a
R BD  . Chọn B. 2 2
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Đường
thẳng SA vuông góc với đáy ABCD và SA a 2. Gọi M là trung điểm SC, mặt
phẳng  đi qua hai điểm A và M đồng thời song song với BD cắt SB, SD lần lượt
tại E, F. Bán kính mặt cầu đi qua năm điểm S, ,
A E, M , F bằng A. a a a . B. a 2. C. . D. 2 . 2 2
Lời giải. Dễ thấy EF BD.
Mà BD  SAC BD SC 
EF SC.   1
Tam giác SAC cân tại A 
AM SC. 2 Từ  
1 và 2, suy ra SC    SC AE. BC AB Lại có 
BC  SAB  BC AE. BC SA 
Từ đó suy ra AE  SBC AE SB.
Tương tự ta cũng có AF SD. Vậy các đỉnh E, M ,
F cùng nhìn SA dưới một góc vuông nên SA a 2 R   . Chọn D. 2 2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Đường thẳng SA
vuông góc đáy ABCD. Gọi H là hình chiếu của A trên đường thẳng SB . Bán kính
mặt cầu ngoại tiếp tứ diện HBCD bằng A. a a a . B. a 2. C. . D. 2 . 2 2
Lời giải. Gọi O AC BD. Vì ABCD là hình vuông
nên OB OD OC.   1
Dễ dàng chứng minh được AH HC nên tam giác
AHC vuông tại H và có O là trung điểm cạnh huyền
AC nên suy ra OH OC. 2 Từ   a 1 và 2, suy ra 2
R OH OB  . Chọn D. 2 30
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Tam giác SAB
vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp
hình chóp S.ABCD bằng 3 3 3 3 A. a 2a a 11 11a . B. . C. . D. . 3 3 6 162
Lời giải. Gọi O AC BD. Suy ra OA OB OC OD.   1
Gọi M là trung điểm AB, do tam giác SAB vuông tại S
nên MS MA MB.
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra
SH  ABCD. O  M AB Ta có 
OM  SAB nên OM là trục của tam giác OM SH 
SAB , suy ra OA OB OS. 2 Từ  
1 và 2, ta có OS OA OB OC OD. Vậy O là tâm mặt cầu ngoại tiếp khối 3 chóp a 4 2a
S.ABCD, bán kính 2 R OA  nên 3 V R  . Chọn B. 2 3 3
Câu 6. Cho hình chóp O.ABC có OA OB OC  , a AOB  60 ,   BOC  90 ,  
COA  120. Gọi S là trung điểm của OB. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng A. a a a a . B. 7 . C. . D. 7 . 2 2 4 4 Lời giải.
Công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp là 2 2
R x r với
r là bán kính đường tròn ngoại tiếp đa giác đáy. 2 2 SO rx
: S là đỉnh hình chóp, O là tâm đường tròn ngoại tiếp đa giác đáy, h 2h là chiều cao khối chóp.
Xét bài toán. Cho hình chóp S.ABCDEF có đường cao SH, tâm đường tròn ngoại tiếp
đáy là O. Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho.
• Qua O kẻ đường thẳng d song song với SH thì d
là trục đường tròn ngoại tiếp đáy.
• Gọi I trên d là tâm mặt cầu cần tìm, đặt OI x.  
Khi x  0 thì OI và HS cùng chiều;  
Khi x  0 thì OI và HS ngược chiều.
• Kẻ IK SH thì IK OH, SK SH x . • Ta có 2 2 2 2
IS IC IK SK OI OC    2 2 2 2 OH SH
x x OC 31 2 2 2 2 2 2 2
OH SH OC SO OC SO rx   x   . 2SH 2SH 2h
• Bán kính mặt cầu cần tìm: 2 2 2 2
R x OC x r .
Áp dụng. Tính được AB  , a BC a 2, AC a 3 nên
tam giác ABC vuông tại B.
Gọi H là trung điểm AC suy ra H là tâm đường tròn
ngoại tiếp tam giác đáy nên AC a 3 r   . 2 2 Từ giả thiết suy ra a
OH  ABC  và tính được OH  . 2 Gọi OH a
M là trung điểm BH suy ra SM  ABC  và SM   . 2 4 Trong tam giác vuông a
SMH tính được SH  . 2 Vậy ta có a 3 a a a r
, h  và SH  nên suy ra 7 R  . Chọn B. 2 4 2 2
Câu 7. Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh , a cạnh bên
bằng 2a 3 . Gọi D là điểm đối xứng của B qua C. Bán kính của mặt cầu ngoại tiếp 3
hình chóp S.ABD bằng A. a 37 a a a . B. 35 . C. 36 . D. 39 . 6 7 7 7
Lời giải. Dễ thấy C là tâm đường tròn ngoại tiếp tam
giác ABD nên r CB  .
a Tam giác vuông SHC có 2a 3 a SC  và HC  nên suy ra SH  . a 3 3 Vậy a r  ,
a h a và 2 3 SC  nên 37 R  . Chọn A. 3 6
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với
AD DC CB  1, AB  2. Gọi O là giao điểm của AC và BD, hình chiếu vuông góc
của S xuống mặt ABCD là trung điểm của O .
A Đường thẳng SC tạo với mặt đáy
ABCD một góc bằng 60. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng A. 1759 . B. 31 61 . C. 31 51 . D. 61 61 . 54 81 162 162 32
Lời giải. Gọi E là trung điểm AB. Dễ thấy ABCD là
nửa lục giác đều nội tiếp đường tròn tâm E nên
r EA  1. Tam giác ABC vuông tại C suy ra 2 SC ABCD  0 , 60
AC  3  HC
SH  2. 3 Ta có BO AC 3 SHE 13 HE    SE  . 2 3 3 3 Vậy ta có r  1, h  2 và 13 SE  nên suy ra 61 61 61 R  V  . Chọn D. 3 6 162
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, 1
AB BC AD  .
a Cạnh bên SA a 6 và vuông góc với đáy. Gọi E là trung điểm 2
của AD. Bán kính mặt cầu ngoại tiếp chóp S.ECD bằng A. 114 . a B. 114 . a C. 114 . a D. 114 . a 2 4 6 8
Lời giải. Tam giác a
ECD vuông tại E nên 1 2 r CD  . 2 2
Chiều cao h SA a 6.
Gọi N là trung điểm AB. Khi đó a 34 2 2 2
SO SA AO SA  2 2
AN NO   . 2 Suy ra 114 R  . a Chọn C. 6
Câu 10. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 2 .
a Mặt bên tạo với đáy góc 0
60 . Gọi H là hình chiếu vuông góc của O trên SD. Bán
kính mặt cầu ngoại tiếp tứ diện HADC bằng A. a 21 a a a . B. 21 . C. 11 5 . D. 11 5 . 3 6 20 50
Lời giải. Dễ thấy O là tâm đường tròn ngoại tiếp tam giác ADC nên r AO a 2.
Gọi K là trung điểm AB. Xác định được   SAB ABCD   60 ,  SKO.
Suy ra SO a 3  SD a 5. 33 2 Kẻ HI HD OD 2 a
HI OD suy ra HI  ADC . Ta có    suy ra 2 3 HI  . 2 SO SD SD 5 5 Trong tam giác vuông 1 1 1 a 6 SOD có    OH  . 2 2 2 OH SO OD 5 Vậy ta có 2a 3 a a
r a 2, h  và 6 OH  nên suy ra 21 R  . Chọn A. 5 5 3
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , a SAD là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung
điểm của BC và CD. Bán kính của mặt cầu ngoại tiếp hình chóp S.CMN bằng A. a 37 a a a . B. 29 . C. 5 3 . D. 93 . 6 8 12 12
Lời giải. Đáy là tam giác CMN vuông tại C nên 1 1 a 2 a
r MN BD  . Chiều cao 3 h SH  . 2 4 4 2
Tâm O của đường tròn ngoại tiếp tam giác CMN là trung điểm MN ;
Áp dụng công thức đường trung tuyến trong tam 2 giác 5a HMN tính được 2 HO  . 8 2 Trong tam giác vuông 11a SHO có 2 2 2
SO SH HO  . 8 2 Vậy ta có a 2 a 3 11a a r  , h  và 2 SO  nên suy ra 93 R  . Chọn D. 4 2 8 12
Câu 12. Cho tứ diện đều ABCD có mặt cầu nội tiếp là S và mặt cầu ngoại tiếp là 1 
S . Một hình lập phương ngoại tiếp S và nội tiếp mặt cầu S . Gọi r , r , r lần 3  2  2  1 2 3
lượt là bán kính các mặt cầu S , S , S . Khẳng định nào sau đây đúng ? 1   2   3  A. r 2 r 1 r 2 r 1 1  và 2  .
B. 1  và 2  . r 3 r r 3 r 2 3 3 2 3 2 C. r 1 r 1 r 1 r 1 1  và 2  .
D. 1  và 2  . r 3 r r 3 r 2 3 3 2 3 3 3
Lời giải. Tứ diện đều nên suy ra tâm mặt cầu ngoại tiếp, nội
tiếp tứ diện trùng nhau và là trọng tâm của tứ diện. Gọi các
điểm như hình vẽ, khi đó: r IK, r  . IA 1 2 AM DM Ta có r HM HM 1 1   sin IDK    . r AM DM 3 2
Mặt cầu ngoại tiếp, mặt cầu nội tiếp hình lập phương đều có
tâm là O. Gọi các điểm như hình vẽ, khi đó: r OE, r OF. 2 3 34 Ta có r OE 1 2   sin EFO   . r OF 3 3 Vậy r 1 r 1 1  và 2  . Chọn C. r 3 r 2 3 3
Câu 13. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2 và hình
chiếu của S lên mặt phẳng ABC là điểm H nằm trong tam giác ABC sao cho  AHB  150 ,   BHC  120 ,  
CHA  90. Biết tổng diện tích mặt cầu ngoại tiếp các hình
chóp S.HAB, S.HBC, S.HCA là 124 .
Thể tích khối chóp S.ABC bằng 3 A. 9 . B. 4 . C. 9 . D. 4. 2 3 4
Lời giải. Gọi r , r , r lần lượt là bán kính đường tròn ngoại tiếp 1 2 3
các tam giác HAB, HBC và HC . A
Áp dụng định lí hàm số sin, ta tìm được 2 3 r  2; r  ; 1 r  . 1 2 3 3
Gọi R , R , R lần lượt là bán kính mặt cầu ngoại tiếp các hình 1 2 3
chóp S.HAB, S.HBC và S.HC . A 2 Đặt SH 4
SH  2x  0. Suy ra 2 2 2 2 R r   x  4, R x  , R x 1. 1 1 2 3 4 3   Theo đề, ta có 19 124 2 3 2 2 2 2
4R  4R  4R  43  x       x  . 1 2 3  3  3 3 Vậy 1 4 V S
.SH  . Chọn B. 3 ABC 3
Câu 14. Cho tứ diện ABCD với AB a, CD b và các cạnh còn lại có độ dài bằng
nhau. Gọi M , N lần lượt là trung điểm của AB và CD và MN  .
m Biết rằng tồn tại
một mặt cầu tiếp xúc với 6 cạnh của tứ diện đã cho. Hệ thức nào sau đây đúng ? A. ab  2 m . B. ab  2 2m . C. ab  2 2 m . D. ab  2 3 2m .
Lời giải. Gọi I là trung điểm của MN, E là hình chiếu của I lên BC. 35
Tam giác ACD và BCD lần lượt cân tại A và B nên BN CD 
CD MN. Tương tự ta cũng có AB MN AN CD 
nên MN là đoạn vuông góc chung của AB và CD 
I là tâm của mặt cầu thỏa yêu cầu bài toán. Ta có b
IEC  INC EC CN  và 2 a
BIE  BIM BM BE  . 2
Suy ra các cạnh còn lại bằng nhau và bằng a b
BC BE EC  . 2 2 2 2    Ta có: 2 2 2 2 2 2 2 a b a b ab
m MN BN BM BC CN BM         .  Chọn B.  2  4 4 2
Câu 15. Cho hình chóp đều S.ABC có cạnh đáy bằng .
a Gọi M , N lần lượt là trung
điểm của AB, BC và P là điểm thuộc tia đối của SC sao cho SC  3SP. Biết rằng
trong các mặt cầu đi qua ,
A M , N thì mặt cầu ngoại tiếp tứ diện AMNP có bán kính
nhỏ nhất. Thể tích của hình chóp S.ABC bằng 3 3 3 3 A. a 2 a 2 a 2 a 2 . B. . C. . D. . 16 32 48 96
Lời giải. Gọi S là mặt cầu đường kính AC; S là mặt cầu đi qua , A M , N suy ra 0 
S chứa đường tròn đường kính AC.
Trong các mặt cầu chứa đường tròn đường
kính AC thì mặt cầu có bán kính nhỏ nhất
chính là mặt cầu S . 0 
Từ giả thiết suy ra P S  CP AP. 0 
Đặt SP x SC  3x. Trong APC  có 2 2 2 2 2
AP AC CP a 16x ; APS  có 2 2 2 2 2
SA AP SP a 15x . Mà a 6 a 6 a 6
SA SC nên 2 2 2 2 2
a 15x  9x x   SC
SO SC CO  . 12 4 12 3 Vậy 1 a 2 VS .SO  . Chọn C. S.ABC 3 ABC 48 36
Phần 6. Bài toán cực trị
Câu 1. Một hình trụ có thể tích V không đổi. Tìm mối quan hệ giữa
bán kính r của đáy và chiều cao h của hình trụ khi diện tích toàn
phần đạt giá trị nhỏ nhất.
A. h r.
B. h  2r.
C. h  3r.
D. h  2r. Lời giải. Ta có 2 V
V r h  h  . 2 r Diện tích toàn phần: 2 V 2 V V 2 3 2
S  2rh  2r  2  2r
  2r  3 2 V . tp r r r Dấu V "  " xảy ra 2 2 do 2   2 V r h
r rh  2r h  2r. Chọn D. r
Câu 2. Một hộp sữa hình trụ có thể tích V (không đổi) được làm từ một tấm tôn có
diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa
bán kính đáy r và đường cao h là
A. h r.
B. h  2r.
C. h  3r.
D. h  2r.
Lời giải. Tương tự như bài trên với chú ý 2
S  2rh r . Chọn A.
Câu 3. Trong số các hình trụ có diện tích toàn phần đều bằng S thì
bán kính r và chiều cao h của khối trụ có thể tích lớn nhất là A. S 1 S S S r  ; h  . B. r  ; h  2 . 2 2 2 2 2 C. S 1 S S S r  ; h  . D. r  ; h  2 . 6 2 6 6 6 2 S 2r Lời giải. Ta có 2 tp
S  2rh  2r  h  . tp 2r 2 S 2r Khi đó 1 2 2 tp
V r h r .   3 rS 2r . tp  2r 2 S
Xét hàm f r 3
rS 2r . Ta có f r 2
 6r S ; 0
f r   r  . tp   tp tp 6 S S
Lập bảng biến thiên ta thấy V tại tp r  . Suy ra tp h  2
 2r. Chọn D. max 6 6
Câu 4. Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có
thể tích V không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp
của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt
xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao
của thùng là h và bán kính đáy là r. Tính tỷ số h sao cho chi phí vật liệu sản xuất r thùng nhỏ nhất. 37 A. h h h h  1. B.  2. C.  6. D.  9. r r r r Lời giải. Ta có 2 V
V r h  h  . 2 r
Gọi t là giá tiền của một đơn vị diện tích vật liệu để làm mặt xung quanh, suy ra giá
tiền của một đơn vị diện tích vật liệu để làm mặt đáy là 3t.
Diện tích mặt xung quanh S  2r.h 
 giá tiền mặt xung quanh là T  2rht. 1 1 Diện tích hai mặt đáy 2
S  2r 
 giá tiền hai mặt đáy là 2
T  2r 3t. 2 2  
Tổng tiền hoàn thành sản phẩm: V
T T T  2t  2
rh 3r  2
 2t  3r  1 2  r    V V 3 2 2    3 2t  
3r   2t3 V .  2r 2r  4 Dấu V "  " xảy ra 2 2 do   3 V r h
r h  6r. Chọn C. 2r
Câu 5. Nam muốn xây một bình chứa hình trụ có thể tích 3 72m . Đáy làm
bằng bêtông giá 100 nghìn đồng 2
/m , thành làm bằng tôn giá 90 nghìn đồng 2 /m , nắp
bằng nhôm giá 140 nghìn đồng 2
/m . Vậy đáy của hình trụ có bán kính bằng bao
nhiêu để chi phí xây dựng là thấp nhất ? A. 2  3 3 3 m. B. m. C. m. D. m. 3 3 3 3 2 Lời giải. Ta có V 72 2
V r h  h   . 2 2 r r
Tổng chi phí xây dựng là: 72 2 2 2
P  100r  90.2rh 140r  240r  90.2r. 2 r 12960 6480 6480 2 2 3  240r   240r    6480 . r r r Dấu 6480 3 "  " xảy ra 2  240r   r  m. Chọn C. 3 r
Câu 6 Trong tất cả các hình nón có độ dài đường sinh bằng .
 Hình nón có thể tích lớn nhất bằng 3 3 A.  3 2 3 . B. . 9 9 3 3 C.  3 2 3 . D. . 27 27
Lời giải. Gọi h 0  h   là chiều cao hình nón, suy ra bán kính 2 2
r   h .
Suy ra thể tích khối nón là 1 1 1 2
V r h  2 3
h h  .  f h. 3 3 3 3    Xét hàm   2 2 3 
f h   h h trên 0;, ta được max f h  f      .   3 3 3 38 3 Vậy 2 3  V
. Dấu "  " xảy ra  h  . Chọn D. max 27 3
Câu 7. Trong các hình nón cùng có diện tích toàn phần bằng S. Hình nón có thể tích
lớn nhất khi ( r,  lần lượt là bán kính đáy và đường sinh của hình nón) C.   r.
D.   2r.
B.   2 2r.
A.   3r. 2 Lời giải. Ta có  2 S r
S r  r     . r 1 1 1 S r 1 2 2 2 2 2  2 2 Thể tích 2
V r h r
 r rr S  2 4 Sr 2r . 2 2  3 3 3  r 3
Lập bảng biến thiên cho hàm f r 2 4
Sr 2r trên 0;, ta thấy hàm số đạt giá trị lớn nhất tại S r  
   3r. Chọn D. 4
Câu 8. Cho hình nón đỉnh S có đáy là đường tròn tâm O. Thiết diện qua trục hình
nón là một tam giác cân với cạnh đáy bằng a và có diện tích là 2 a . Gọi , A B là hai
điểm bất kỳ trên đường tròn O. Thể tích khối chóp S.OAB đạt giá trị lớn nhất bằng 3 3 3 3 A. a a a a 2 . B. . C. . D. . 2 6 12 12
Lời giải. Tam giác cân 1 1 SCD, có 2 S
CD.SO a  . a SO  SO  2 . a SCD 2 2
Khối chóp S.OAB có chiều cao SO  2a không đổi nên để
thể tích lớn nhất khi và chỉ khi diện tích tam giác OAB lớn nhất. Mà 1  1 2  SO .
A OB.sin AOB r .sin AOB (với r là OAB 2 2
bán kính đường tròn mặt đáy hình nón. Do đó để S lớn OAB 3 nhất khi  a
sin AOB  1. Khi đó V  . Chọn C. max 12
Câu 9. Cho mặt cầu S bán kính R  5 cm. Mặt phẳng P
cắt mặt cầu S theo giao tuyến là đường tròn C có chu vi
bằng 8cm. Bốn điểm ,
A B, C, D thay đổi sao cho , A B, C
thuộc đường tròn C, điểm D thuộc S D  C và tam giác
ABC đều. Thể tích lớn nhất của tứ diện ABCD bằng A. 3 20 3 cm . B. 3 32 3 cm . D. 3 60 3 cm . D. 3 96 3 cm .
Lời giải. Gọi H là hình chiếu của D trên mặt phẳng P.
Đường tròn ngoại tiếp tam giác đều ABC có chu vi bằng 8cm.
Suy ra bán kính đường tròn 8 R   4 cm. 2
Suy ra cạnh của tam giác ABC bằng 4 3cm. 39 4 32 3 Suy ra 2 S   12 3 cm không đổi. ABC 4
Do đó thể tích khối tứ diện ABCD lớn nhất khi d D,ABC 
 lớn nhất  D và O
nằm cùng phía so với mặt phẳng P và D, O, H thẳng hàng  DH DO OH 2 2 1
DO OA AH  5  2516  8. Khi đó 3 V
 .12 3.8  32 3 cm . Chọn B. max 3
Câu 10. Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu
có bán kính bằng 9, hình chóp có thể tích lớn nhất bằng A. 484. B. 529. C. 576. D. 625.
Lời giải. Giả sử hình chóp tứ giác đều là S.ABCD. Xét phần mặt
cắt qua đường cao và kí hiệu như hình vẽ.
Đặt AB BC CD DA a 0  a  9 2 và SO h 0  h 18. 2 Thể tích khối chóp: 1 2 ha VAB .h  . S.ABCD 3 3 2   Tam giác a 2
SAE vuông tại A nên 2
AO SO.OE h18h     
  h18h.  2  Khi đó 2 2 V
h 18h . Xét hàm f h 2
h 18h trên 0;18, ta được f h đạt S.ABCD   3
giá trị lớn nhất tại h  12   GTLN của V bằng 576. Chọn C. S.ABCD
Câu 11. Cho hình nón N có đỉnh S, chiều cao . h Một hình 1 
nón N có đỉnh là tâm của đáy N và có đáy là một thiết diện 1  2 
song song với đáy của N như hình vẽ. Khối nón N có thể 2  1 
tích lớn nhất khi chiều cao x bằng A. h h h h . B. . C. 2 . D. 3 . 2 3 3 3
Lời giải. Xét mặt cắt qua trục hình nón và kí hiệu như hình vẽ.
Với O, I lần lượt là tâm đáy của hình nón N , N ; , R r lần 1   2 
lượt là các bán kính của hai đường tròn đáy của N , N . 1   2  SI r h x r
Rh x Ta có     r  . SO R h R h 40 1 1
R h x2 2 2
Thể tích khối nón N là: R Vr x  . .x  x h x . N 2 2  2 2 2   2  3 3 h 3h
Xét hàm f x x hx2 3 2 2
x 2hx h x trên 0;h. Ta có f x 2 2
 3x 4hx h ; x h
f x  0  
h . Lập bảng biến thiên tìm được f x đạt giá trị lớn nhất trên x   3 khoảng  h
0;h tại x  . Chọn B. 3
Câu 12. Cho hình lập phương ABCD.AB CD   có thể tích
bằng 1. Gọi N  là một hình nón có tâm đường tròn đáy
trùng với tâm của hình vuông ABCD, đồng thời các điểm
A , B , C , D nằm trên các đường sinh của hình nón như
hình vẽ. Thể tích khối nón N  có giá trị nhỏ nhất bằng A. 2 . B. 3 . 3 4 C. 9 . D. 9 . 8 16
Lời giải. Xét phần mặt cắt qua trục hình nón và kí hiệu như hình
vẽ. Với I, H lần lượt là tâm của hình vuông ABCD, AB CD   và
đỉnh A nằm trên đường sinh EF của hình nón.
Hình lập phương có thể tích bằng 1 nên 2
AA  HI  1, AH  . 2     Đặt EH A H x x
EH x x  0. Khi đó, ta có 2 2 1      FI       r. EI FI x 1 2FI 2  x  2 1 1  x 1  x 1 2  3
Thể tích khối nón N  là: V r EI   N   x   1  .     2 3 6  x  6 xx  3 1
x 2x  2 1
Xét hàm số f x
trên 0;. Ta có f x . Lập bảng biến 2 x 3 x thiên tìm được 9 f x 27 min 
tại x  2. Suy ra minV  . Chọn C. 0; 4 N  8
Câu 13. Trong các hình nón nội tiếp một hình cầu có bán kính
bằng R không đổi, tính chiều cao h và bán kính mặt đáy r của
hình nón có thể tích lớn nhất. A. 4 2 2 h R; . r R B. 3 3 h R; r  . R 3 3 2 2 4 C. 4 2 h R; r  . R D. 3 1 h R; . r R 3 3 2 2 41
Lời giải. Xét phần mặt cắt và kí hiệu các điểm như hình vẽ.
Tam giác AKM vuông tại K nên 2 2
IK AI.IM 
r h2R h. Thể tích khối nón: 1 1 2 2 V
r h h N 2Rh.   3 3 3 3      Cách 1. Ta có 1 1 1 h h 4R 2h 32 2 R
h 2R h  . h .
h 4R 2h  .      . 3 6 6  3  81 Dấu h "  " xảy ra 4
h  4R 2h h  . R Suy ra 2 2 r R và  2. 3 3 r
Cách 2. Xét hàm f h 2
h R h 3 2 2  h
  2Rh ; có f h 2  3h  4 . Rh
Lập BBT tìm được f h đạt GTLN trên khoảng 0;2R tại 4 h  . R Chọn A. 3
Câu 14. Cho mặt cầu S có bán kính R không đổi, hình nón N
bất kì nội tiếp mặt cầu S như hình vẽ. Thể tích khối nón N  là V
V ; thể tích phần còn lại là V . Giá trị lớn nhất của 1 bằng 1 2 V2 A. 32 . B. 32 . C. 49 . D. 32 . 49 76 81 81
Lời giải. Thể tích khối cầu: 4 V V 1 3
V R . Ta có 1 1 V V V      . 3 2 1 V V VV 2 1 1 V1 Suy ra V V 1 lớn nhất 
nhỏ nhất V đạt giá trị lớn nhất. V V 1 2 1 3
Như bài trên tìm được GTLN của 32R V 32 V bằng . Khi đó 1  . Chọn B. 1 81 V 76 2
Câu 15. Một hạt ngọc trai hình cầu có bán kính R được bọc trong
một hộp trang sức dạng hình nón ngoại tiếp mặt cầu như hình vẽ.
Hỏi nhà sản xuất phải thiết kế hộp trang sức hình nón có chiều cao
h như thế nào để hộp quà đó có thể tích nhỏ nhất. A. h  2 2 . R B. h  3 . R C. h  4 . R D. h  5 . R
Lời giải. Xét phần mặt cắt qua trục hình nón và kí hiệu như hình.
Đặt SI x x R
. Khi đó h SO x R và 2 2
SK x R . SK IK
RR x Ta có SKI ∽ SOA     AO  . 2 2 SO AO x R 1 1 R R x R R x 2  2  2 2 2
Thể tích khối nón: VO  A .SO  . . x R  . . N  3 3  2 2 x R    3 x R   2 R x 2 2
x Rx Rx  R Xét 2 3 f x 
trên R;. Ta có f x
; f x  0   . 2   x Rx R x  3R  42
Lập BBT tìm được f x đạt GTNN trên khoảng R; tại x  3 . R
RR x
Suy ra h SO  4R và bán kính đường tròn đáy r AO   2 . R Chọn C. 2 2 x R
Câu 16. Cho nửa hình cầu bán kính R không đổi. Một hình nón có chiều cao ,
h bán kính đáy là r tiếp xúc với nửa hình
cầu như hình vẽ (hai đường tròn đáy là đồng tâm và cùng thuộc
một mặt phẳng). Khi diện tích xung quanh của hình nón là nhỏ
nhất, khẳng định nào sau đây đúng ?
A. h r.
B. h  2r.
C. h  3r.
D. h  2 3r.
Lời giải. Xét phần mặt cắt như hình vẽ. 2 2 Ta có 1 1 1 1 1 1 2 R r       h  . 2 2 2 2 2 2 2 2 R r h h R r r R 2 2 Gọi R r  là đường sinh 2 2 2 2 
   h r   r . 2 2 r R 2 2 3 Diện tích xung quanh: R r 2 2 r
S  2r  2 .  rr  . 2 2 2 2 r R r R 3 4 2 2 Xét hàm   r 2r 3r R f r
trên R;. Ta có f r . 2 2 r R  2 2 r R  2 2 r R
Lập BBT tìm được f r đạt GTNN trên khoảng R; tại 3 r  . R 2 2 2 Khi đó 2 R r 2 h h
 3R h  3 .
R Suy ra  2 hay h  2r. Chọn B. 2 2 r R r
Câu 17. Cho một hình nón có chiều cao h và bán kính của đường tròn đáy là .
R Một mặt phẳng P thay đổi song song với mặt
chứa đáy của hình nón và cắt hình nón theo một đường tròn giao
tuyến C. Dựng hình trụ H  có một đáy là đường tròn C và
đáy còn lại nằm trên mặt đáy của hình nón như hình vẽ. Khi khối
trụ H  có thể tích lớn nhất, gọi h là chiều cao
của H  và R là bán kính đáy của H . Khẳng định nào sau đây đúng ? A. 1 1 h  h; . R  R B. 1 2 h  ; . h R  R 2 2 3 3 C. 1 3 h  h; . R  R D. 3 1 h  ; . h R  R 4 4 4 4
Lời giải. Thể tích 2 V
Rh . Ta sẽ biểu diễn h theo R để xét hàm f R. H
Xét phần mặt cắt qua trục và kí hiệu như hình vẽ. Khi đó HC  ,
R OD R và OH h . Do  AOD ∽ AHC nên có AO OD AH OH OD    AH HC AH HC 43      h h R R R    h  . h . h R R 3      3  Khi đó 2 R R 2 R VR . . hh  R    . Xét hàm   2 R f R R  trên 0;R ta H R  R  R   được R R R h
f R đạt GTLN tại 2 R   h  . h  . Chọn B. 3 R 3
Câu 18. Cho khối gỗ hình trụ có bán kính 3cm và chiều cao
6cm, đáy là hai hình tròn tâm O và O . Đục khối gỗ này
tạo ra hai khối nón có đỉnh nằm trên OO và đáy trùng với
hai đáy của khối gỗ sao cho góc ở đỉnh bằng 0 60 (như hình vẽ)
và OI x 3 2  x  3 3. Giá trị nhỏ nhất của tổng diện
tích xung quanh hai hình nón đã đục bằng A.  2 12 cm . B.  2 14 cm . C.  2 44 cm . D.  2 72 cm .  0
Lời giải. Xét tam giác vuông AIO  30 x x IO , A có   OA  và 2 IA  . IO x 3  3
Suy ra diện tích xung quanh của hình nón này: 2 2 S  x . 1 3
Tương tự, ta có diện tích xung quanh của hình nón còn lại là: 2
S 6 x2 . 2 3 2 2
2 x  6  x  2  2 Khi đó S S x  6 x      ≥ .  12   2 cm . 1 2  3   3 2
Dấu ''  '' xảy ra  x  6 x x  3cm. Chọn A.
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 .
a Cạnh bên SA  4a và vuông góc với
đáy. Gọi M là một điểm trên cạnh SA (khác A và S ).
Mặt phẳng  qua M và vuông góc với SA cắt SB, SC,
SD lần lượt tại N, P, Q. Hình trụ H  có đáy là
đường tròn ngoại tiếp tứ giác MNPQ và có một đường
sinh là MA như hình vẽ. Khi khối trụ H  có thể tích lớn nhất thì tỉ số SM bằng SA A. 1 . B. 1. C. 2 . D. 3 . 2 3 3 4
Lời giải. Chọn a  1. Đặt AM x, suy ra SM  4  x. Vì MN SM SM.AB 4  x   MN   . AB SA SA 2 MN 2 4 x 2
Chứng minh được MNPQ là hình vuông nên R   . H  2 4 44
Khi đó thể tích khối trụ: V
R AM x H   x2 2 . 4 .   8 Xét hàm 256
f x  x   x2 4
trên 0;4, ta được max f x tại 4 x  . 0;4 27 3 3   Khi đó GTLN của 32 32a SMx V bằng      và 4 2   . Chọn C.H  27  27  SA 4 3
Câu 20. Cho hình trụ có đáy là hai đường tròn O;R và O ;R, chiều cao bằng
đường kính đáy. Trên đường tròn tâm O lấy điểm ,
A trên đường tròn tâm O lấy
điểm B. Thể tích của khối tứ diện OO A
B có giá trị lớn nhất bằng 3 3 3 3 A. R R 3R R . B. . C. . D. . 2 3 3 6
Lời giải. Kẻ đường sinh AM và BN như hình vẽ.
Đặt AB x 2R x  2R 2. Ta có 1 1 2  1 V  .         V .  V .  VV . OO AB A.OO BN AON .MO B AON .MO B A. 2 2 3  3 MO B
Tam giác vuông AMB, có 2 2 2 2
MB AB AM x  4R . 2 2 Tam giác cân 8R x O MB  , tính được O H   . 2 Khi đó 1 R V       VS .   AM . x R R x OO AB A MO B O MB  2 2 4  2 2 8 . .  3 6 3
Khảo sát hàm ta được GTLN của R V bằng
đạt tại x R 6. Chọn B. OO AB 3
Cách 2. Dùng công thức nhanh 1 V     
OO .AB.d OO AB OO AB OO AB  ,   .sin , . 6 Trong đó MB
d OO , AB  O H  ;    
sinOO , AB  sin AM , AB  sin MAB  . AB 45
Document Outline

  • DE
  • DAP AN