



















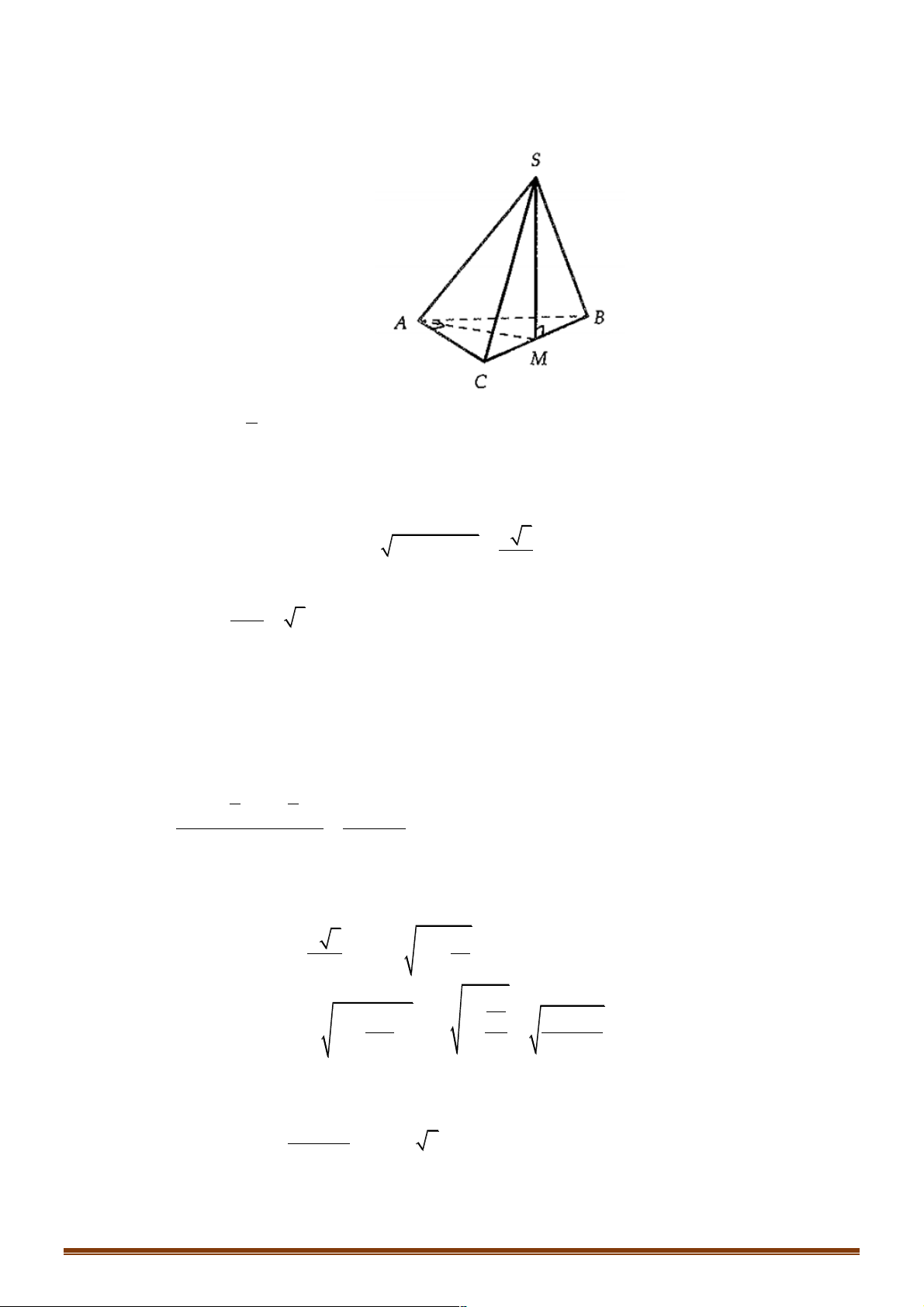

Preview text:
BÀI TẬP TRẮC NGHIỆM
VÉC TƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
VÉC TƠ TRONG KHÔNG GIAN A. LÝ THUYẾT ! ! ! Cho các véc tơ tùy ý , a ,
b c và k,l Î ! . 1. Cộng véc tơ: !!!" " !!!" " !!!" " "
Lấy điểm O tùy ý trong không gian, vẽ OA = , a AB = ,
b thì OB = a + b !!!!" !!!!" !!!"
Quy tắc ba điểm: Cho ba điểm M , N, K bất kỳ thì MN = MK + KN ! ! ! !
2. Trừ véc tơ: a - b = a + ( b - ) !!!!" !!!" !!!!"
Quy tắc ba điểm: MN = KN - KM . !!!" !!!" !!!"
Quy tắc hình bình hành: Cho hình bình hành ABCD ta có: AC = AB + AD. !!!!" !!!" !!!" !!!!"
Quy tắc hình hộp: Cho hình hộp AB . CD A¢B C ¢ D
¢ ¢ ta có AC¢ = AB + AD + AA¢. 3. Tích véc tơ: ! !
Tích của véc tơ a với một số thực k là một véc tơ. Kí hiệu là k.a !
+) Cùng hướng với a nếu k > 0 . !
+) Ngược hướng với a nếu k < 0 . ! !
+) k.a = k . a . !!!" !!!" !!"
Hệ quả: Nếu I là trung điểm của ,
A B,O tùy ý thì OA + OB = 2OI .
4. Tích vô hướng của hai véc tơ. ! ! ! ! ! ! +) Định nghĩa: .
a b = a . b .cos( , a b). ! ! ! !
+) Hệ quả: a ^ b Û . a b = 0 . !2 ! ! ! 2 +) a = . a a = a . 2 2 2 + - +) Với ba điểm AB AC BC , A B,C ta có . AB AC = . 2 Trang 1 ! ! !" !
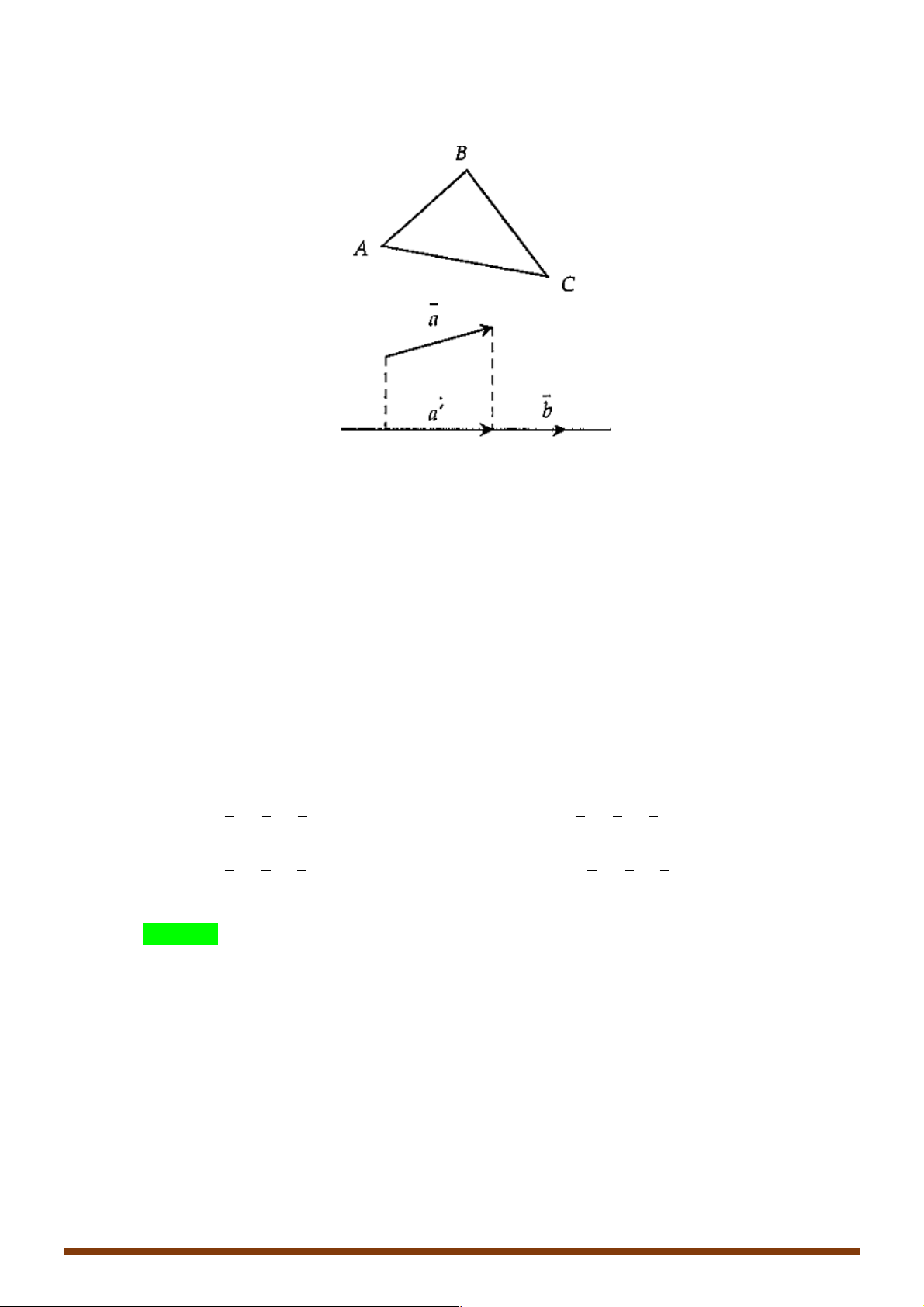
+) Quy tắc hình chiếu: Cho hai véc tơ ,
a b . Gọi a¢ là hình chiếu vuông góc của a trên đường ! ! ! "! !
thẳng chứa b thì: .
a b = a .¢b. ! ! !
5. Định nghĩa: Ba véc tơ , a ,
b c gọi là đồng phẳng nếu giá của chúng cùng song song hoặc nằm trên một mặt phẳng. 6. Các định lý: ! ! ! ! ! ! ! ! a) Cho ,
a b không cùng phương: , a ,
b c đồng phẳng Û $ ,
m nÎ" :c = ma + nb( với , m n xác định duy nhất). ! ! ! ! b) Nếu ba véc tơ , a ,
b c không đồng phẳng thì mọi véc tơ x đều được biểu diễn dưới dạng: ! ! ! !
x = ma + nb + kc với ,
m n,k xác định duy nhất.
B. CÁC DẠNG TOÁN VỀ VÉC TƠ TRONG KHÔNG GIAN.
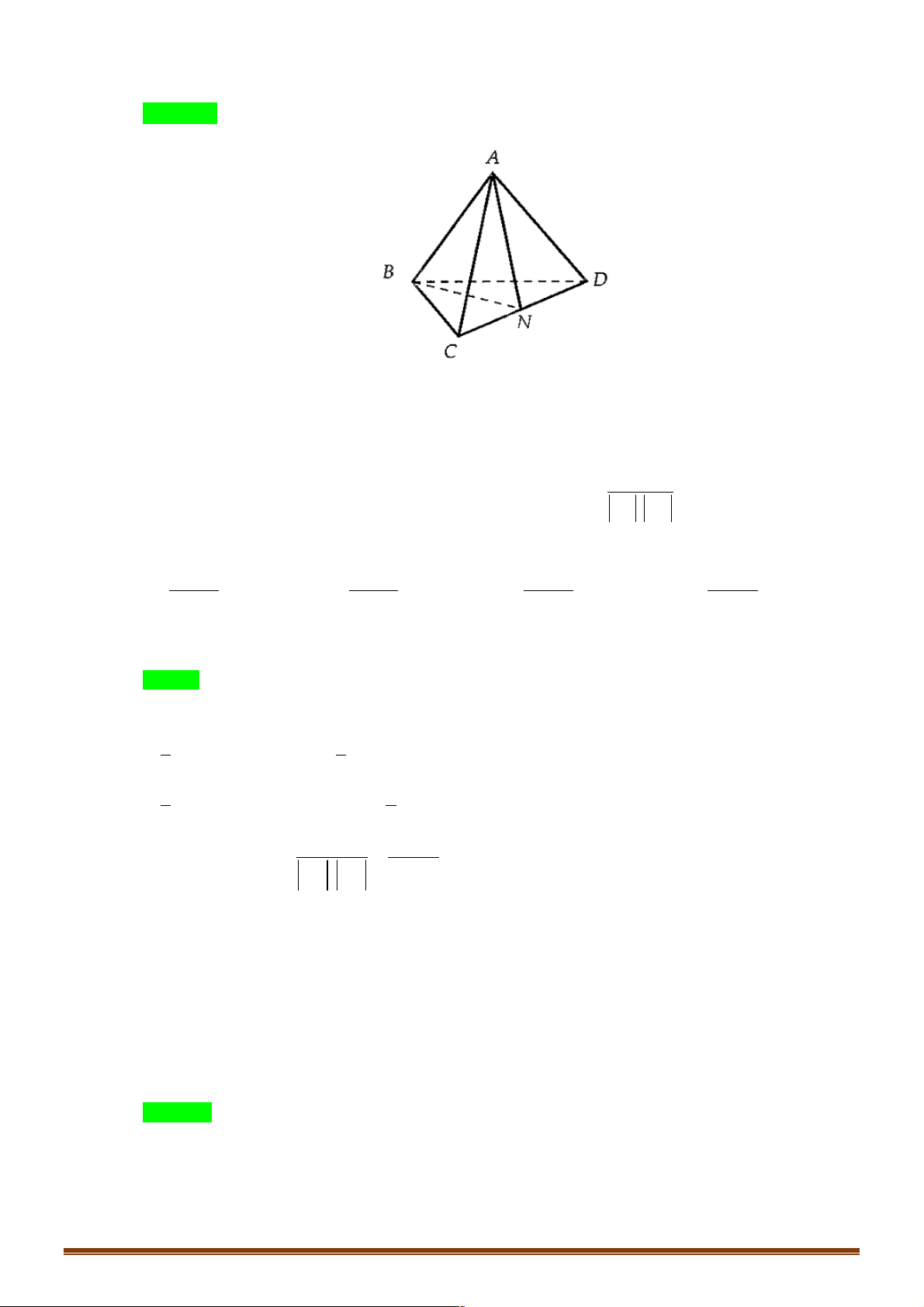
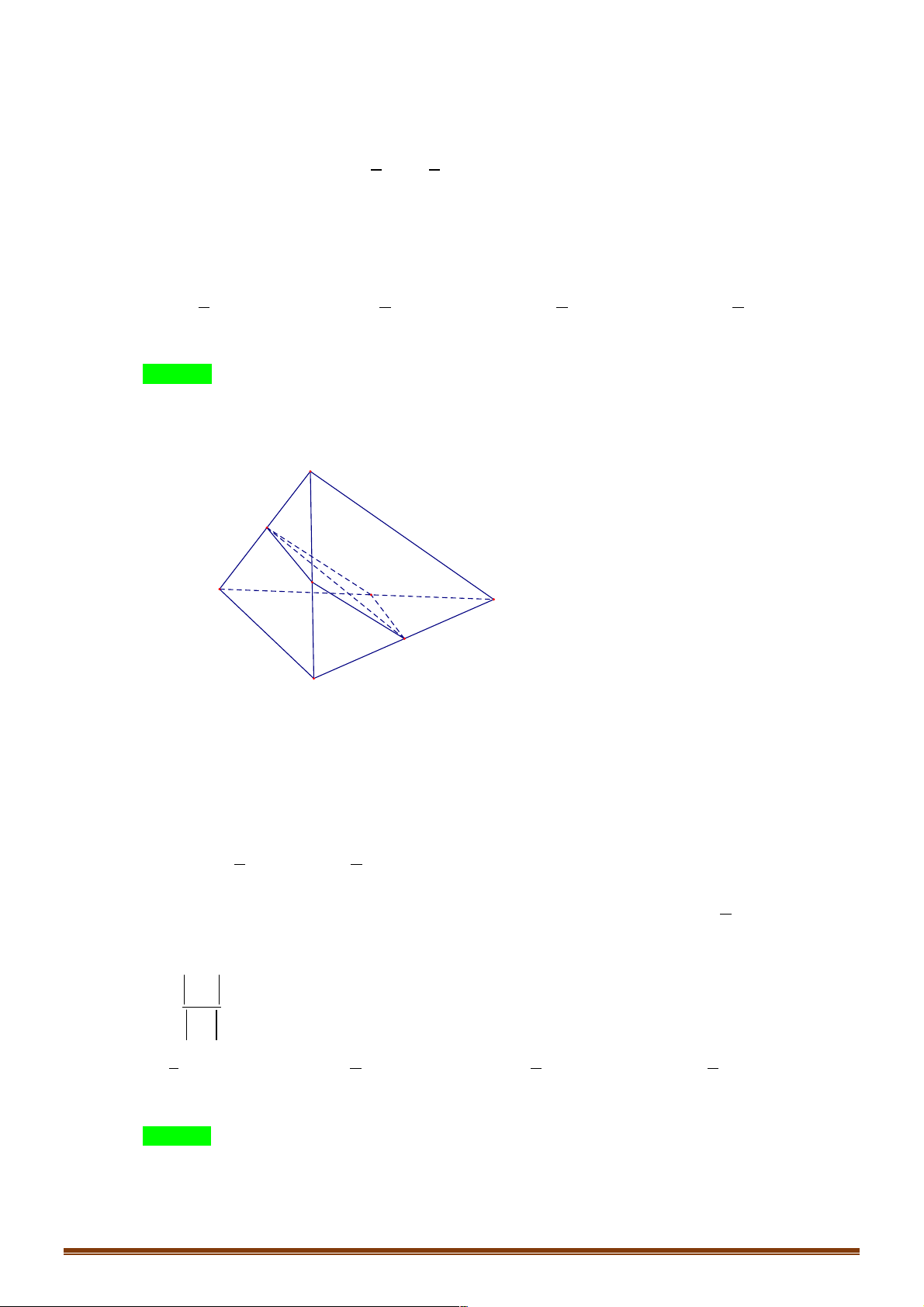
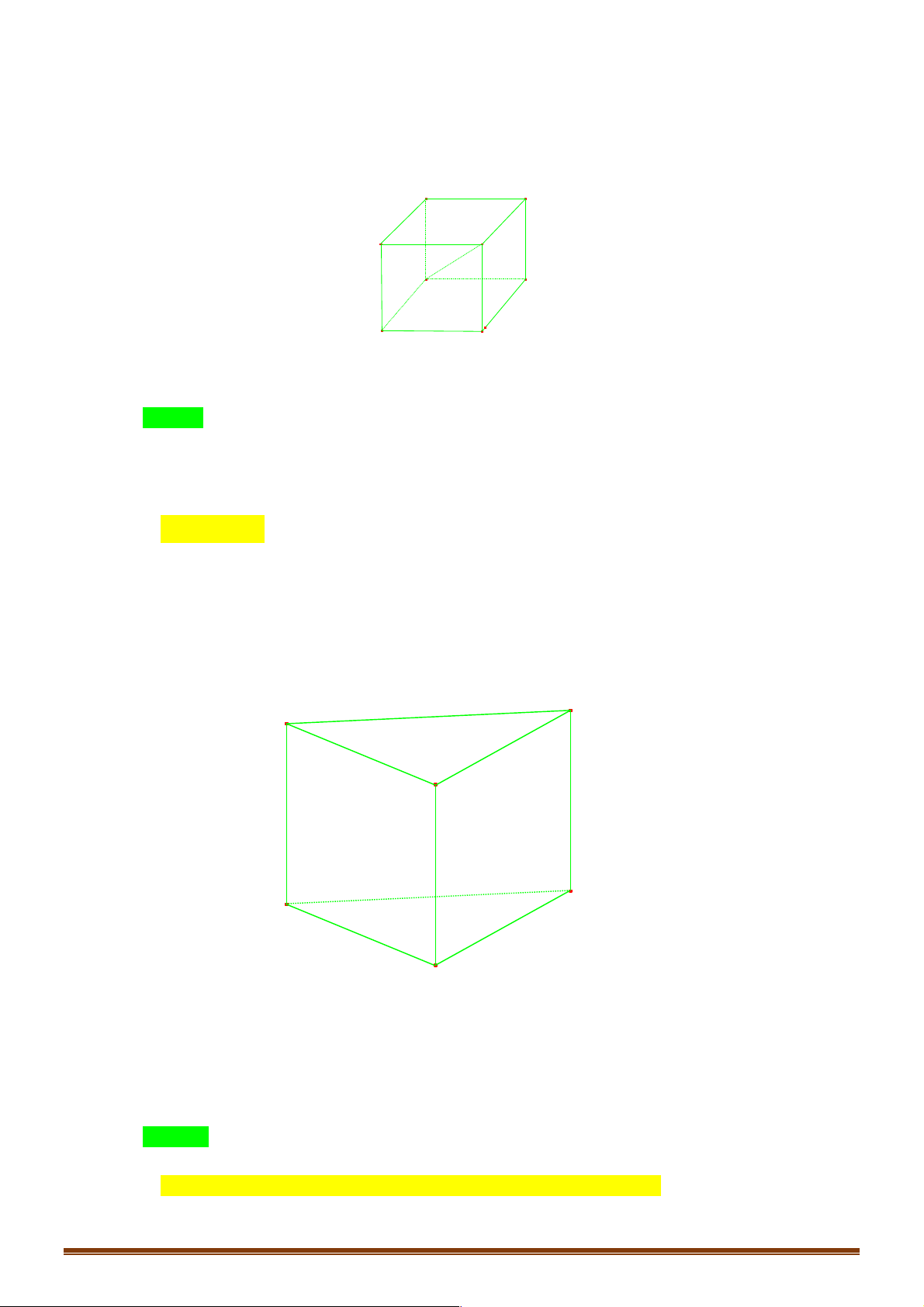
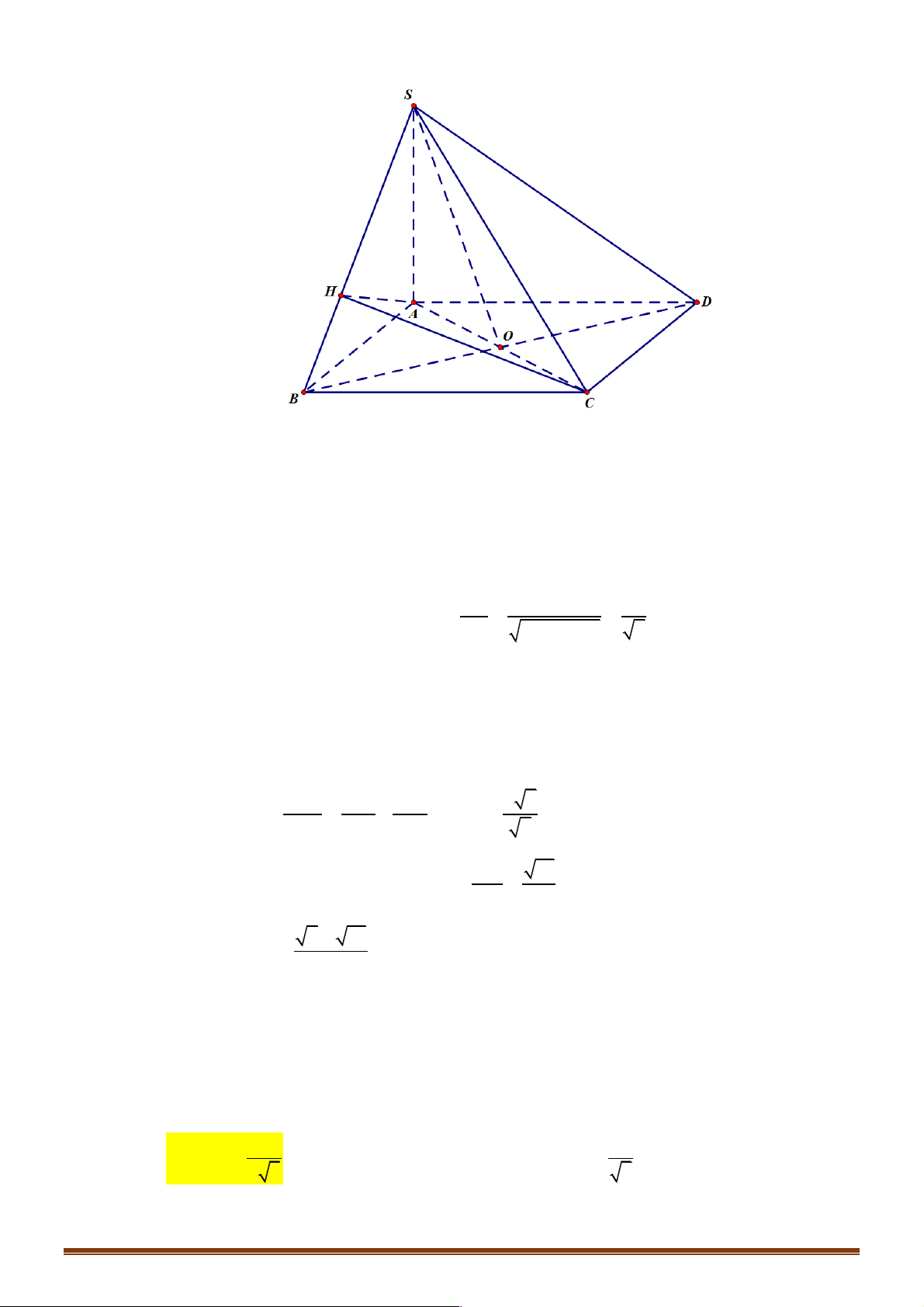
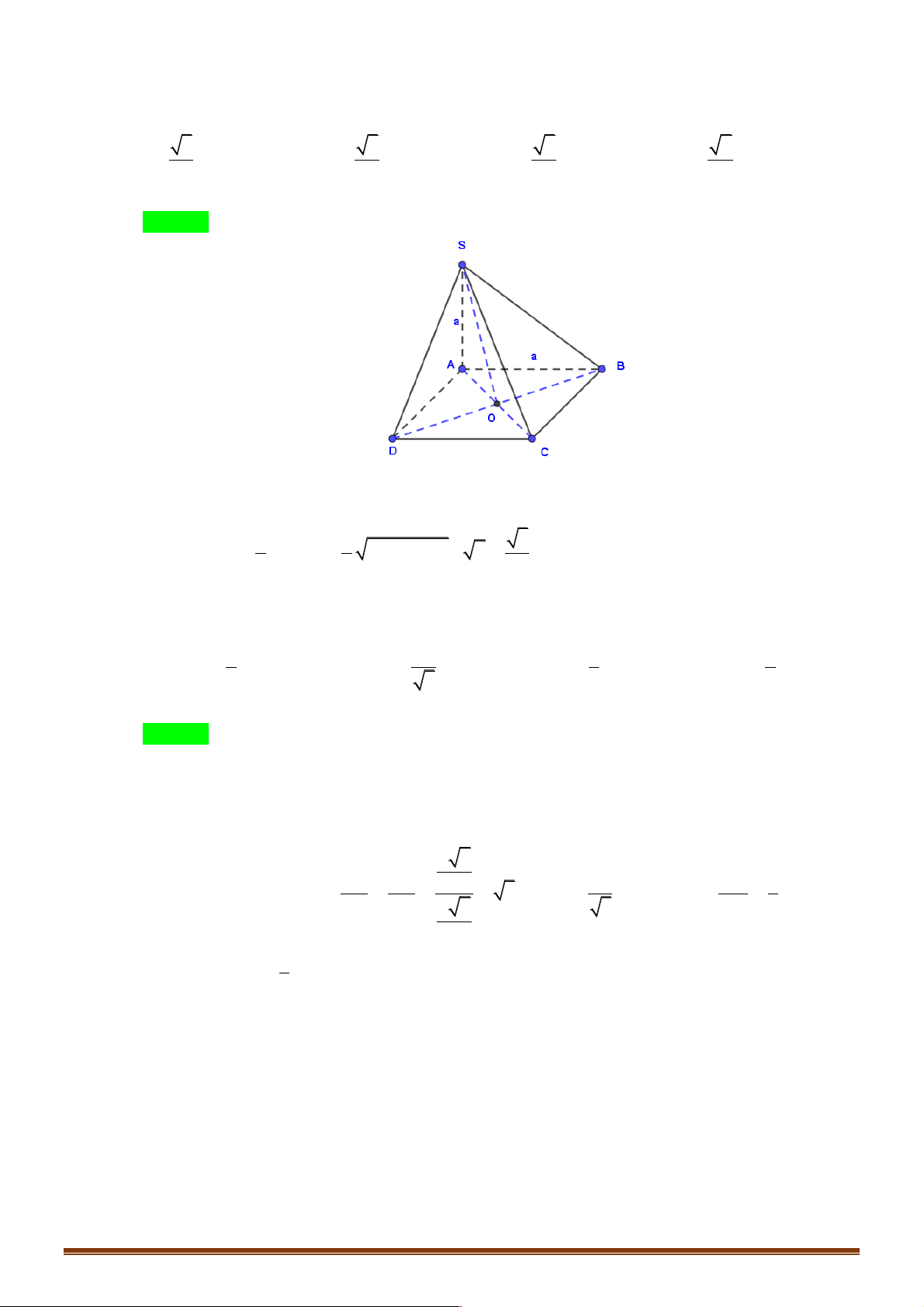
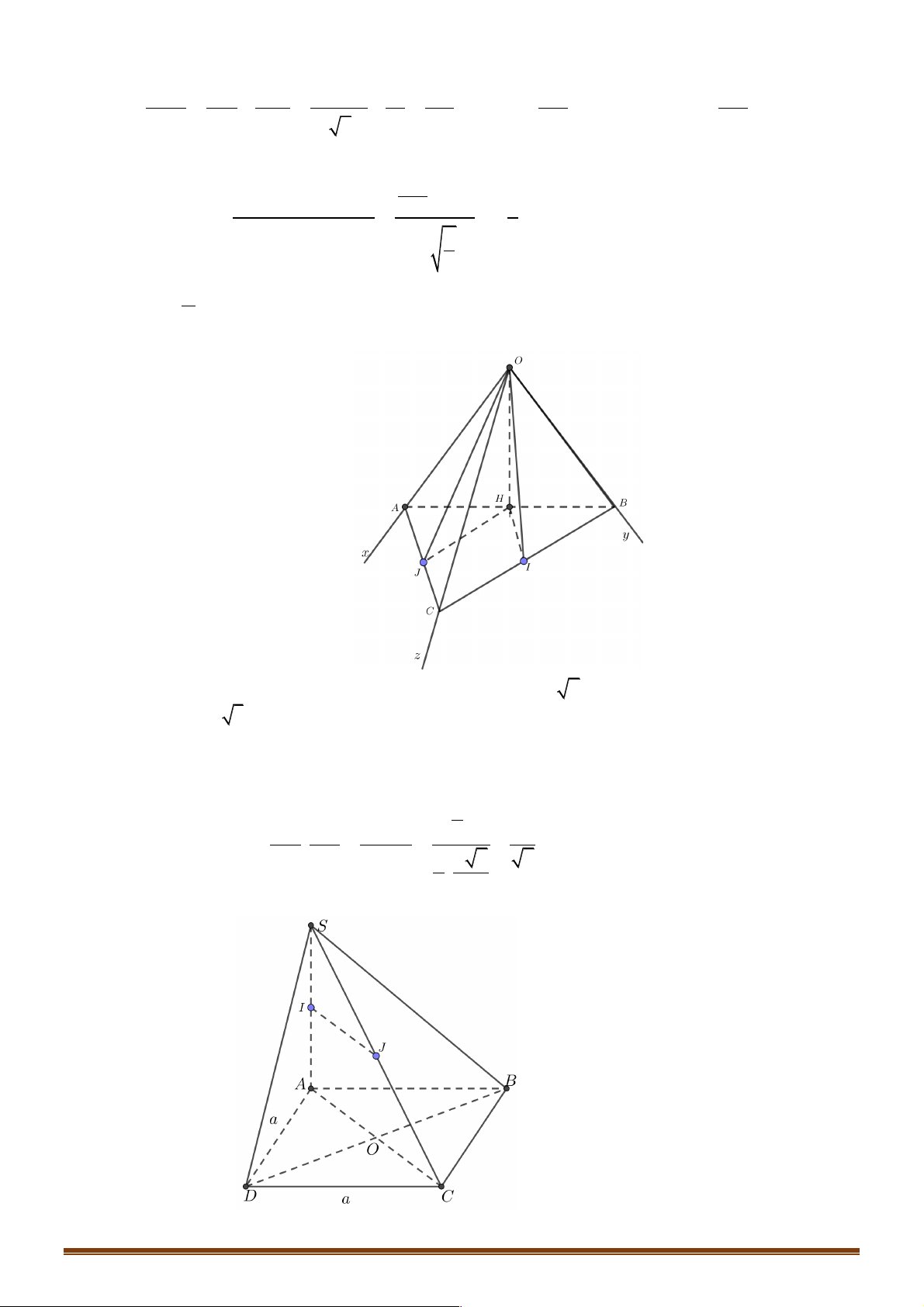
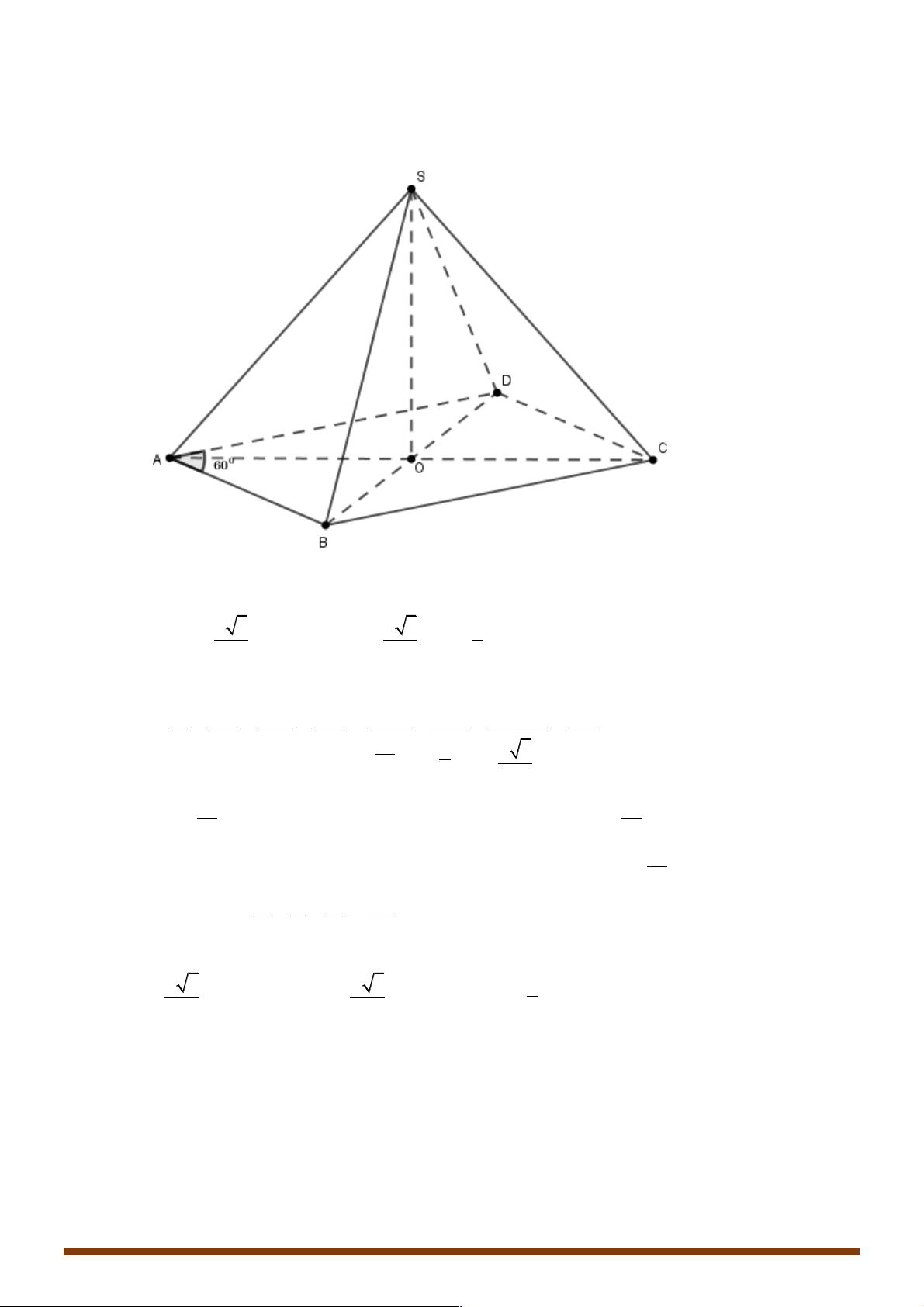
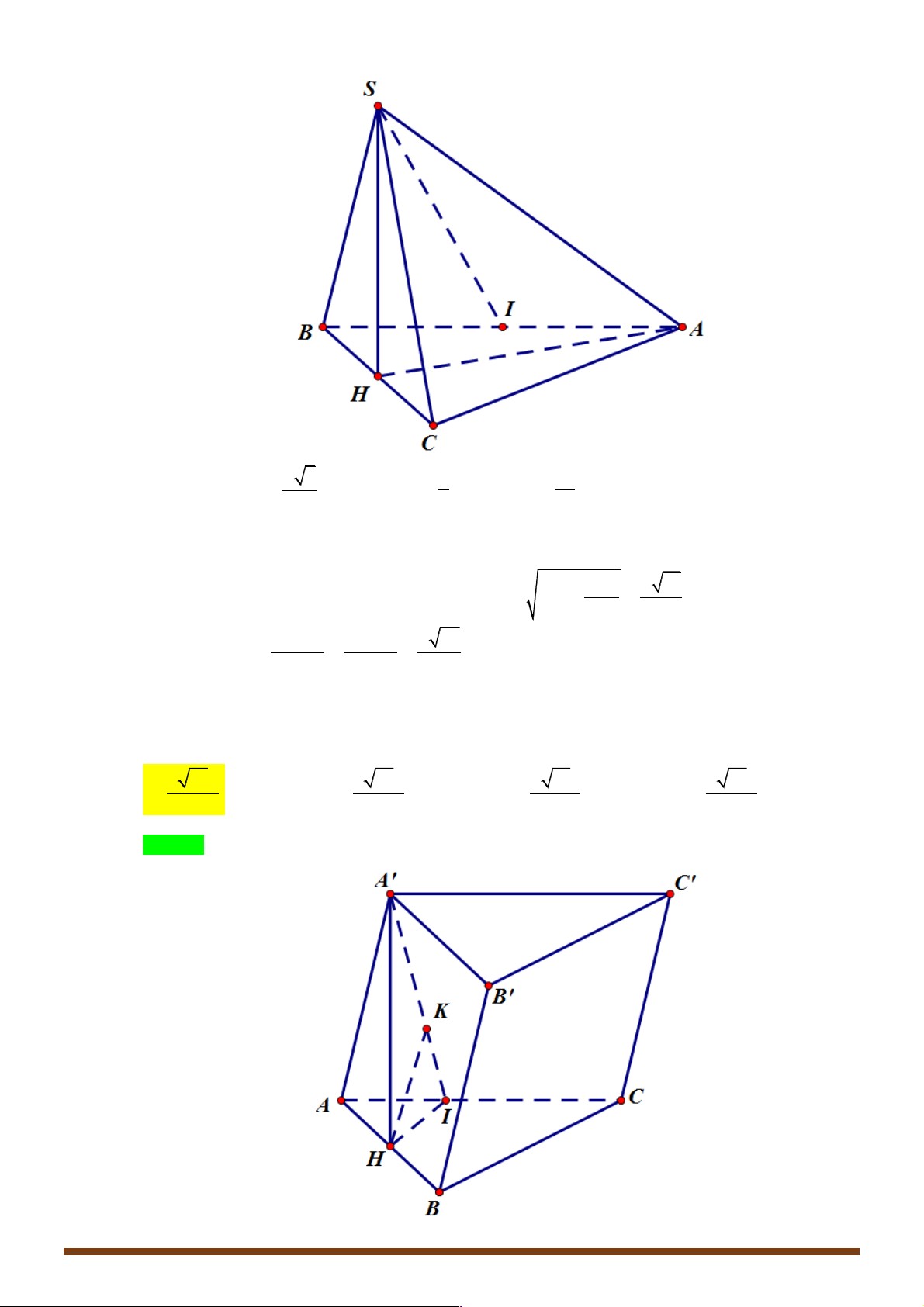
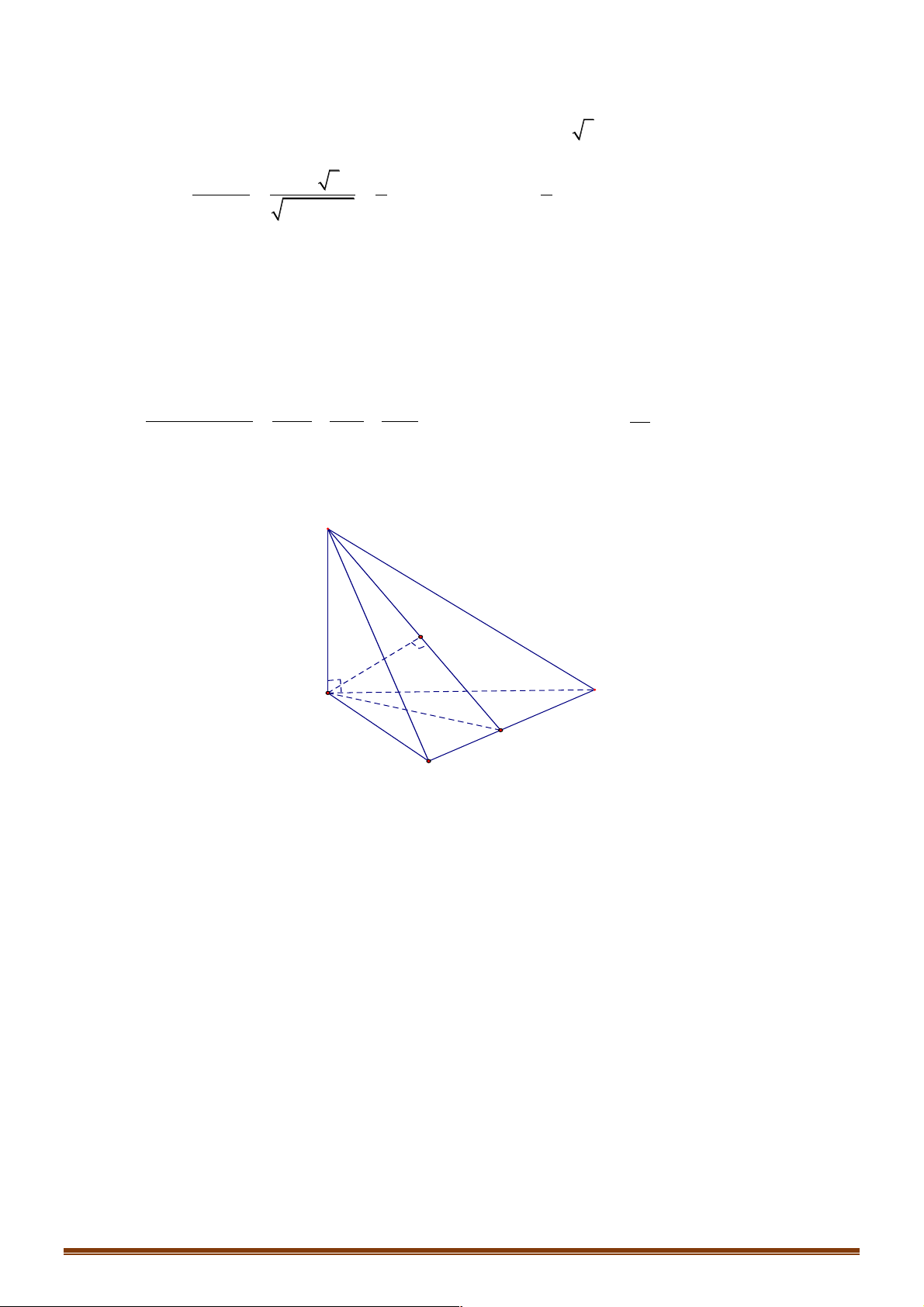
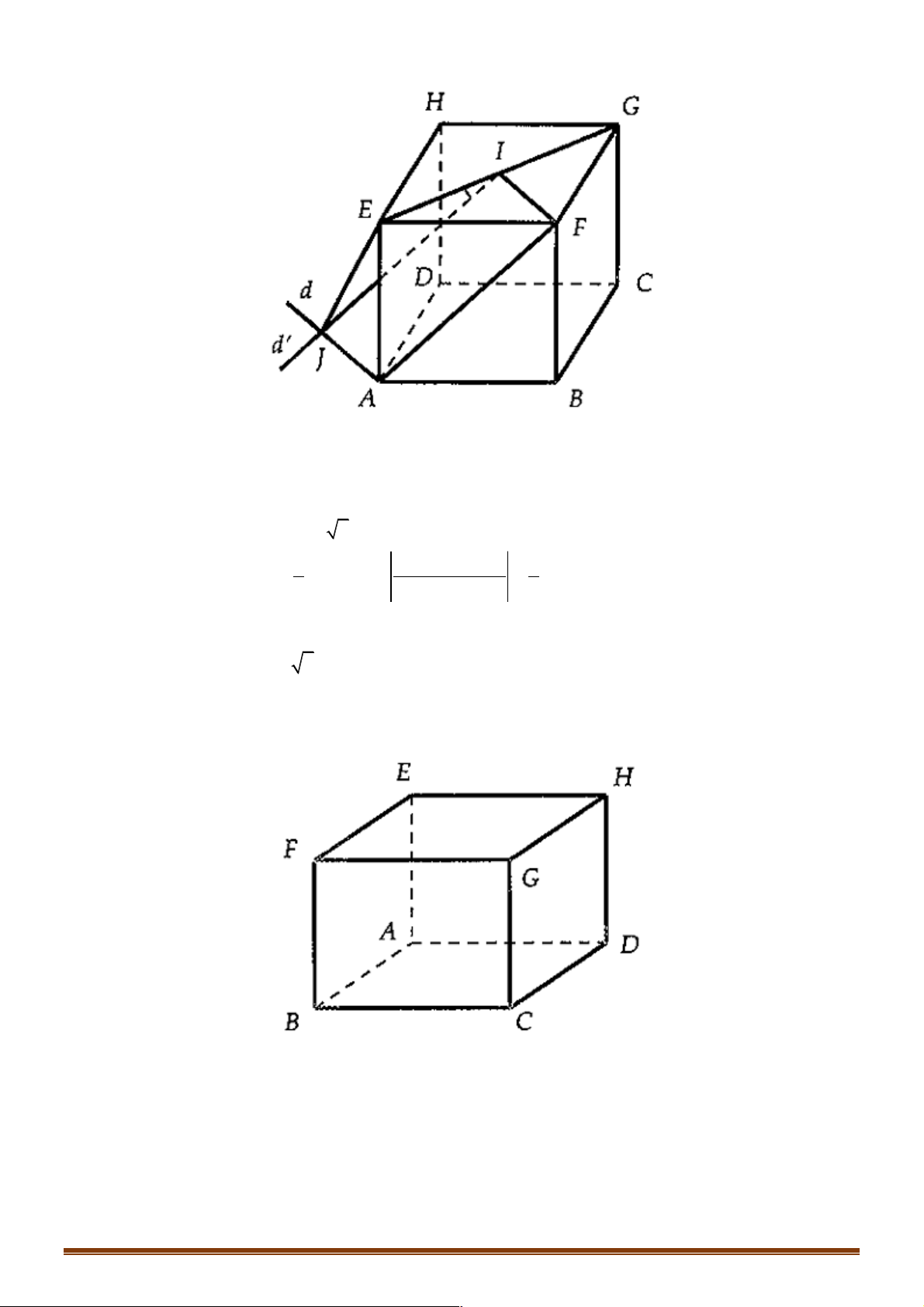
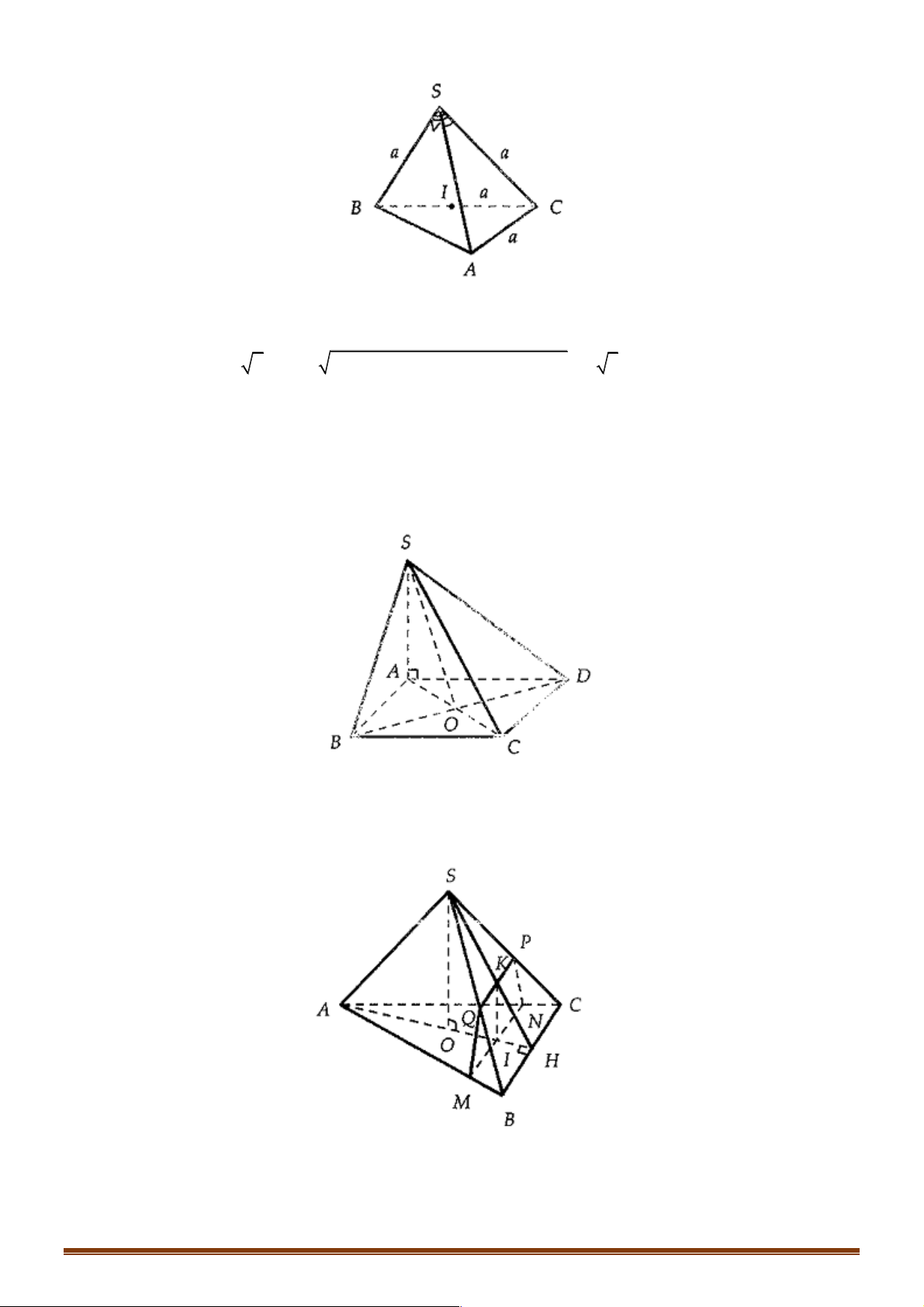
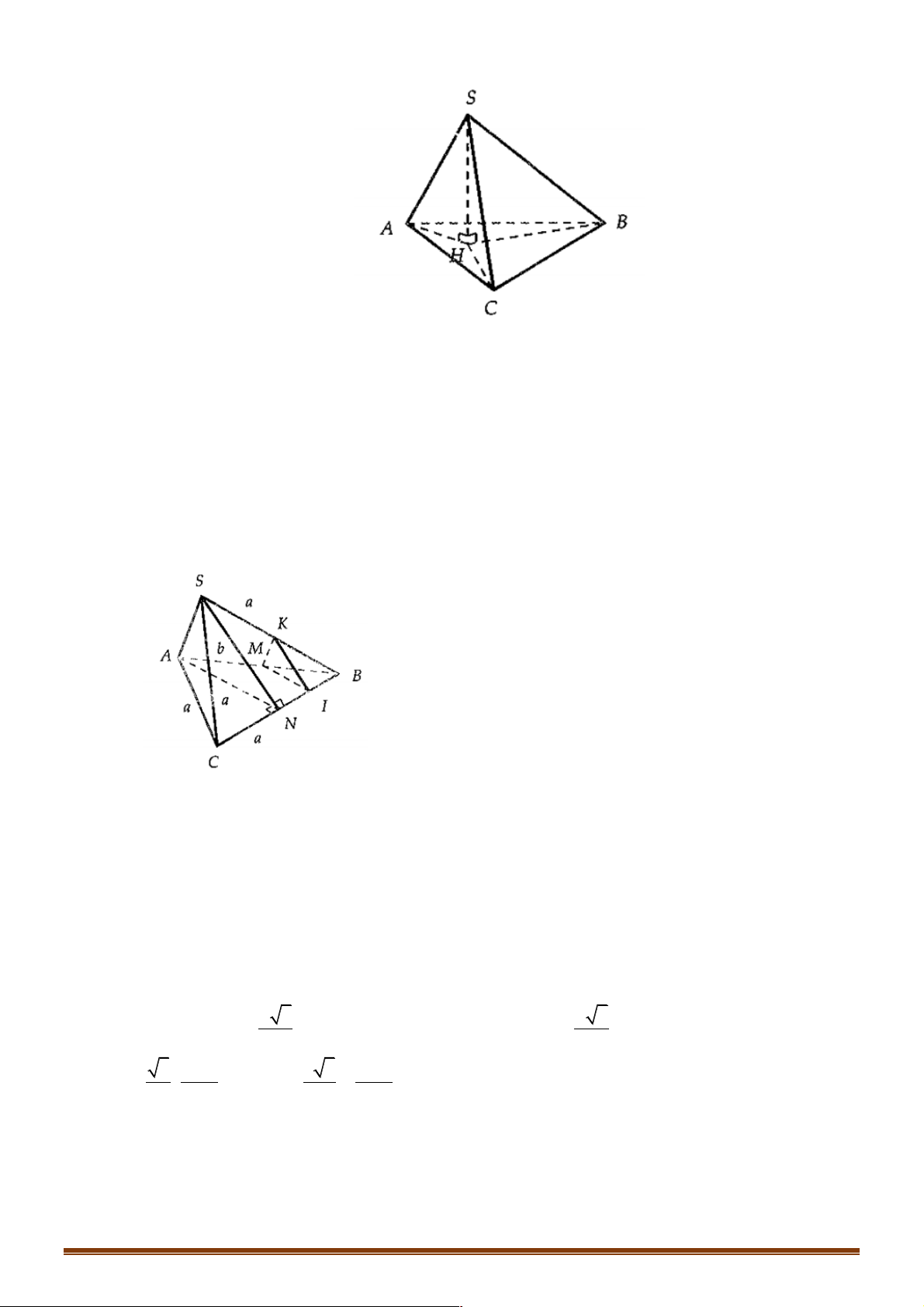
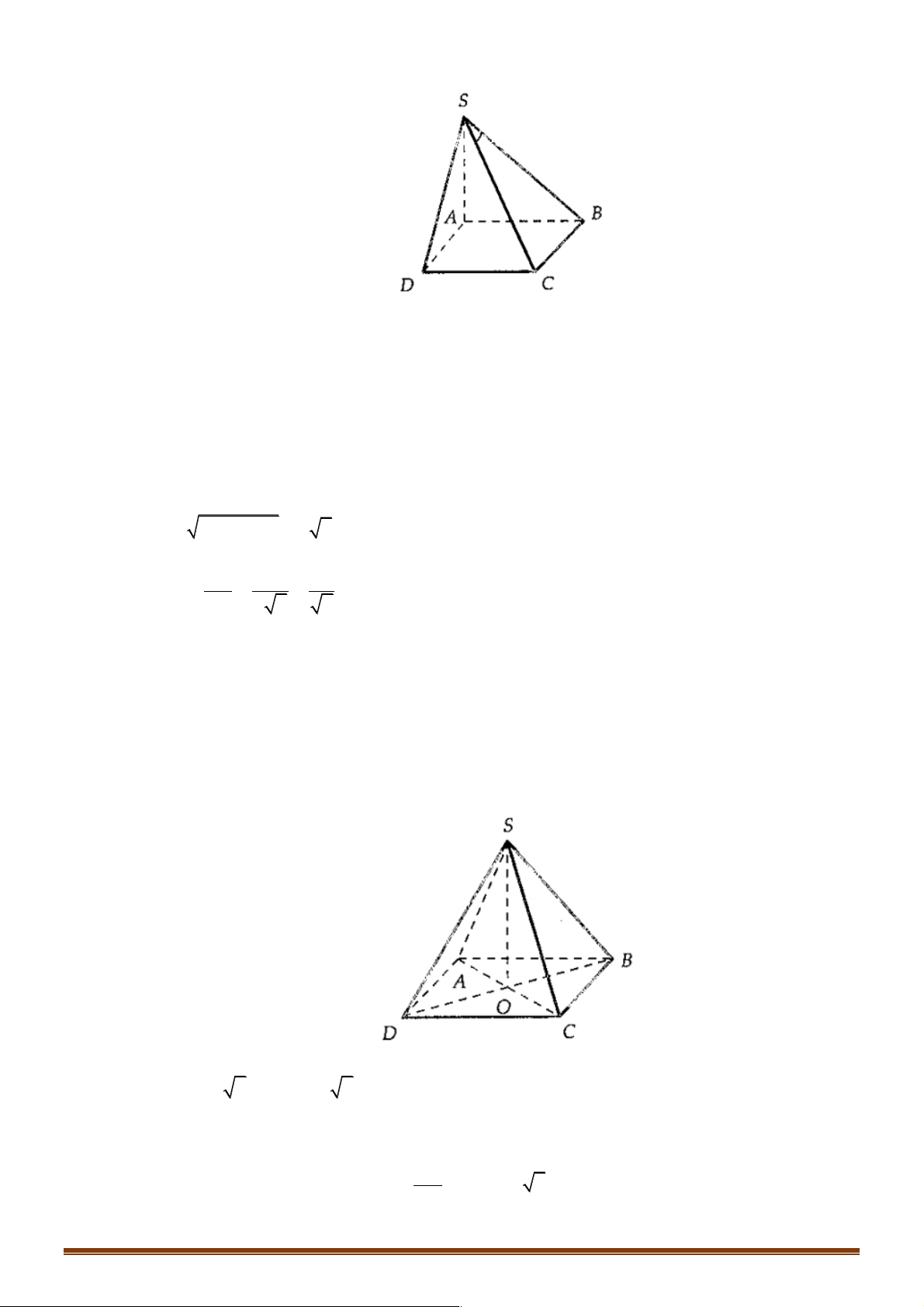
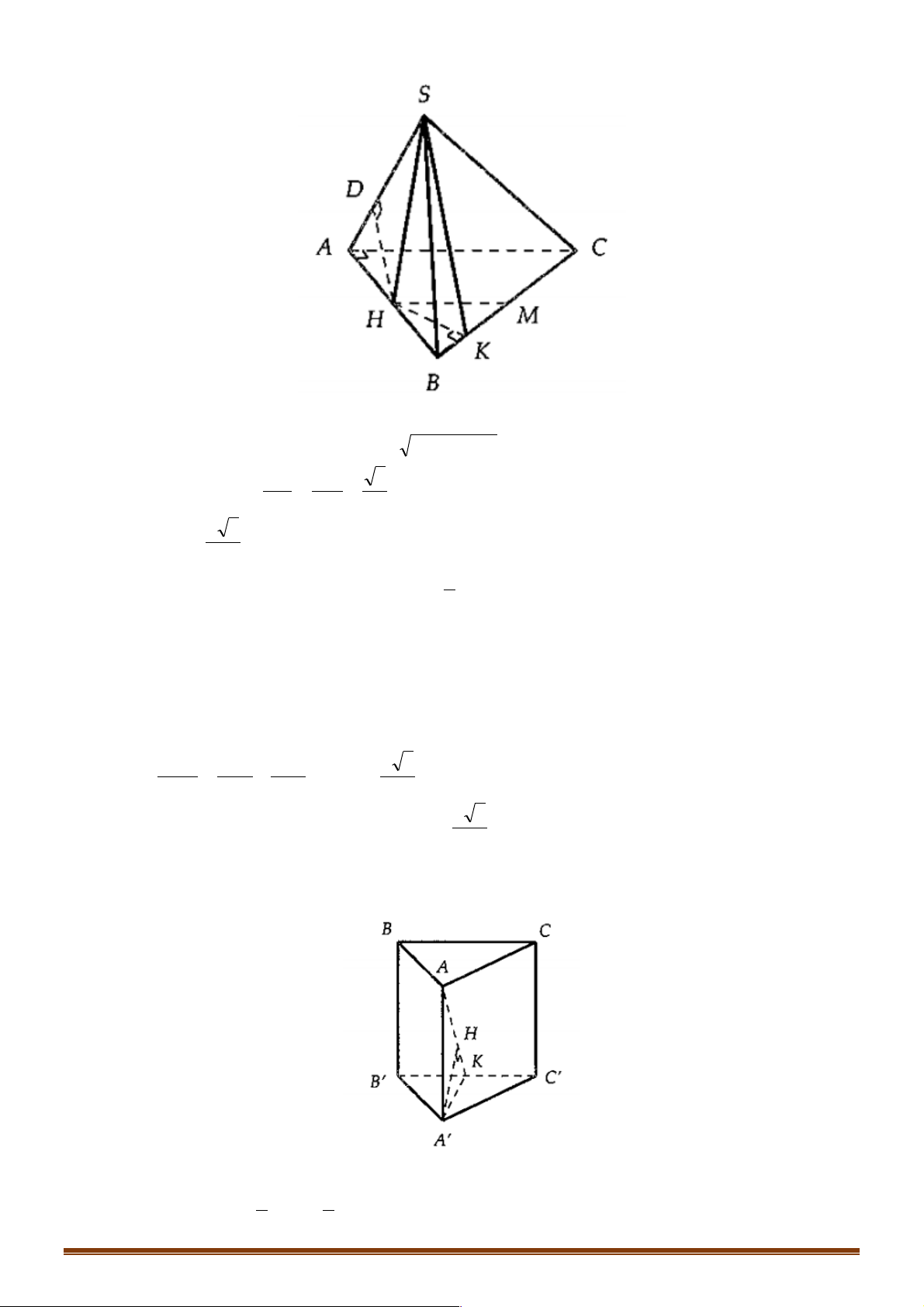
Ví dụ 1. Cho tứ diện đều ABCD , M là trung điểm của cạnh AB và G là trộng tâm cảu tam giác BCD . !!!" " !!!" " !!!" !" !!!!" !" " " Đặt AB = , b AC = ,
c AD = d . Phân tích véc tơ MG theo d, , b c . !!!!" " " !" !!!!" " " !" A. 1 1 1 1 1 1
MG = - b + c + d .
B. MG = b + c + d . 6 3 3 6 3 3 !!!!" " " !" !!!!" " " !" C. 1 1 1 1 1 1
MG = - b - c + d .
D. MG = - b - c - d . 6 3 3 6 3 3 Lời giải Đáp án A Trang 2 A M B D G C !!!!" 1 !!!" !!!!" !!!!" !!!" !!!" !!!" !!!" !!!"
MG = (MB + MC + MD) 1 1 1 =
AB + (MA + AC) 1 . + (MA+ AD) 3 3 2 3 3
1 !!!" 2 !!!" 1 !!!" 1 !!!" 1 !!!" 2 æ 1 !!!" ö 1 !!!" 1 !!!"
= AB + MA + AC + AD = AB + . - AB + AC + AD ç ÷ 6 3 3 3 6 3 è 2 ø 3 3 1 !!!" 1 !!!" 1 !!!" 1 " 1 " 1 !"
= - AB + AC + AD = - b + c + d 6 3 3 6 3 3
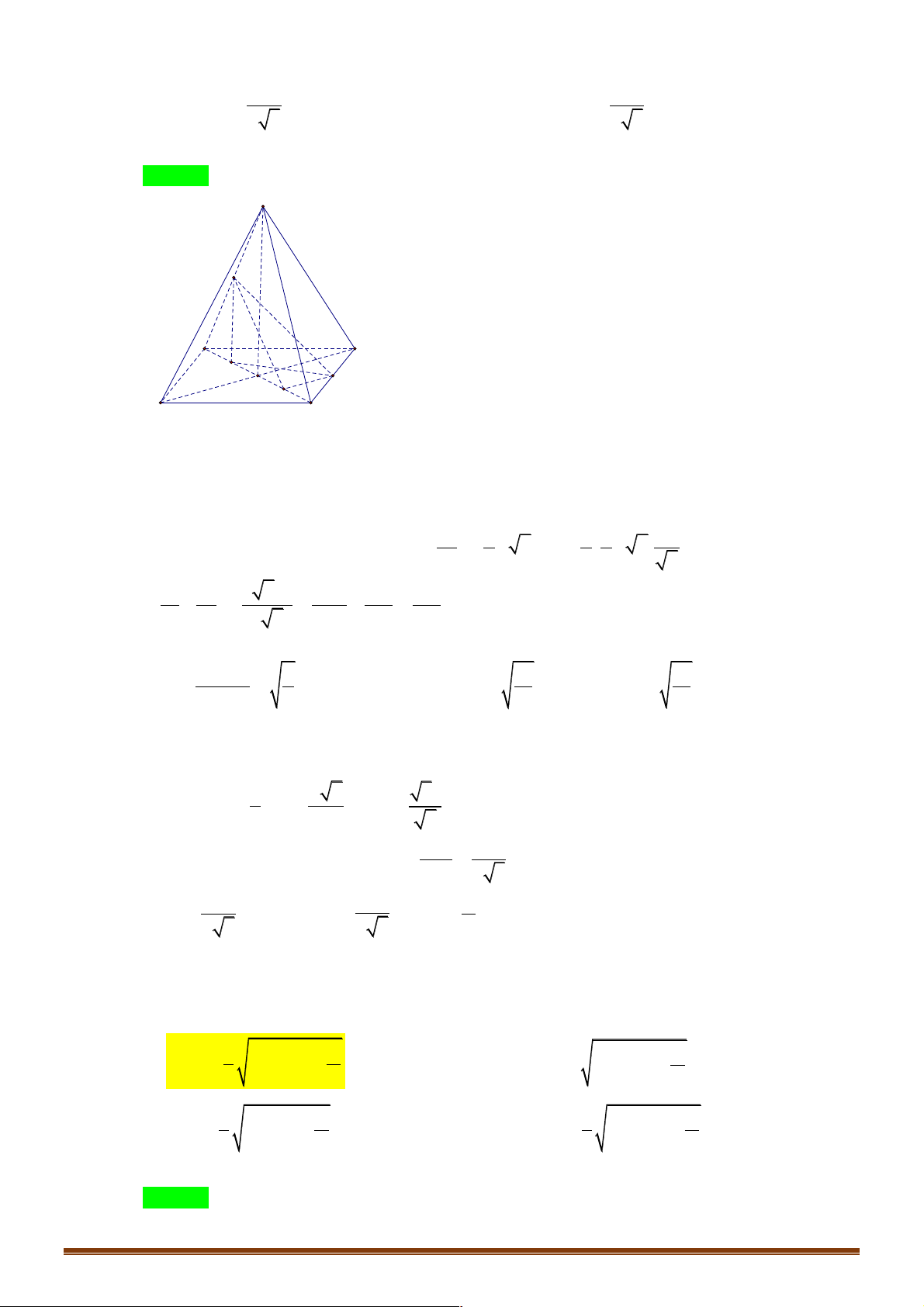
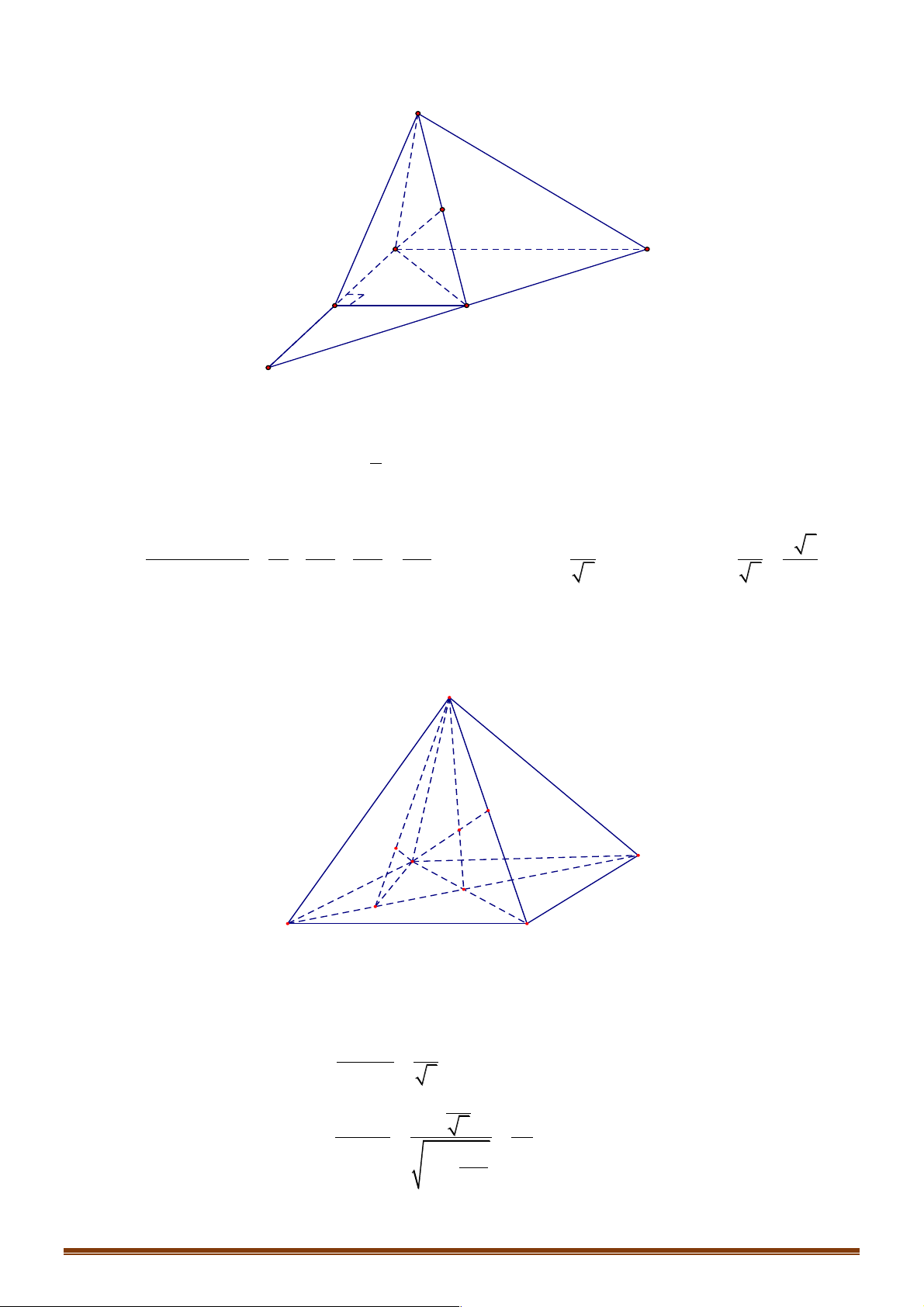
Ví dụ 2. Cho tứ diện đều ABCD , M và N theo thứ tự là trung điểm của cạnh AB và CD . Mệnh đề nào sau đây sai?. !!!" !!!" !!!" !!!" !!!!" !!!" !!!" A. 1
AC + BD = AD + BC . B. MN = ( AD + BC). 2 !!!" !!!" !!!" !!!" !!!!" !!!!" !!!!" !!!!" "
C. AC + BD + AD + BC = 4 - NM .
D. MC + MD - 4MN = 0 . Lời giải: Đáp án D A M B D N C !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
A.Đúng vì: AC + BD = (AD+ DC)+(BC +CD) = AD+ BC. !!!" !!!" !!!!" !!!!" !!!" !!!!" !!!!" !!!"
B. Đúng vì: AC + BD = (AM + MN + ND)+(BM + MN + NC) !!!!" !!!!" !!!!" !!!" !!!" !!!!"
= 2MN + (AM + BM )+(ND + NC) = 2MN !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!"
C.Đúng vì: AC + BD + AD + BC = 2AN + 2BN = 2(AN + BN) = 2 - (NA+ NB) = 4 - NM . Vậy D sai !!!" !!!"
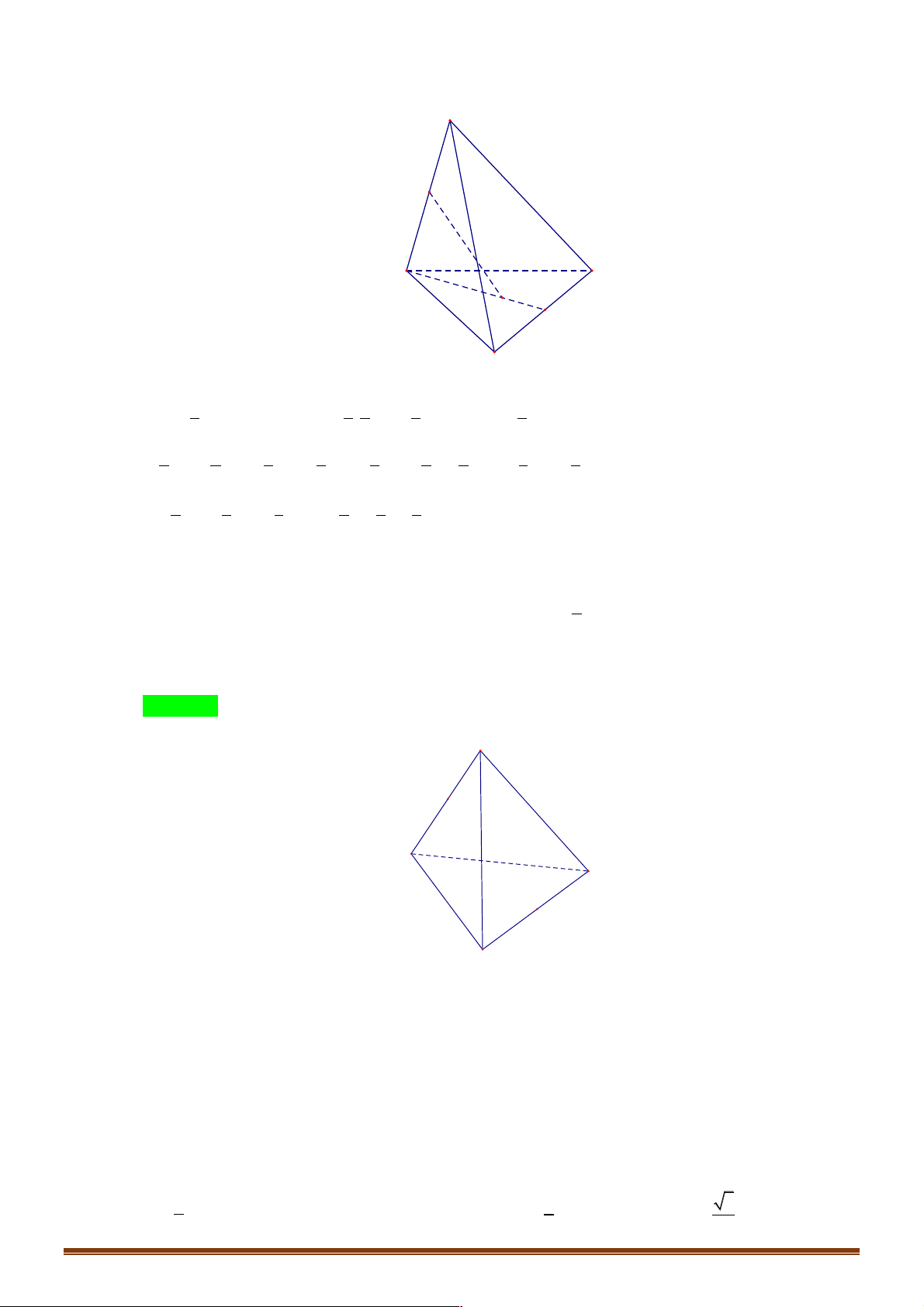
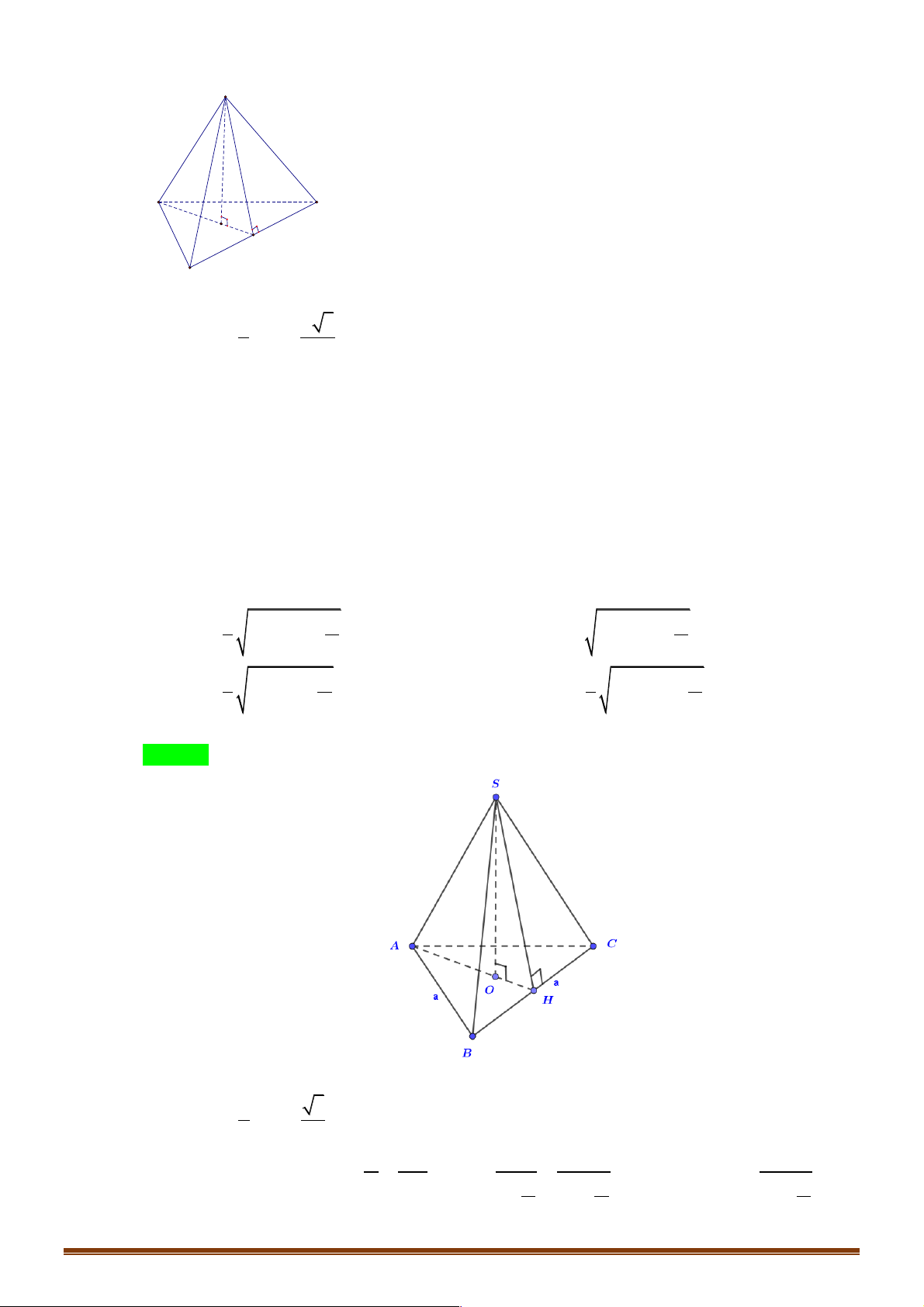
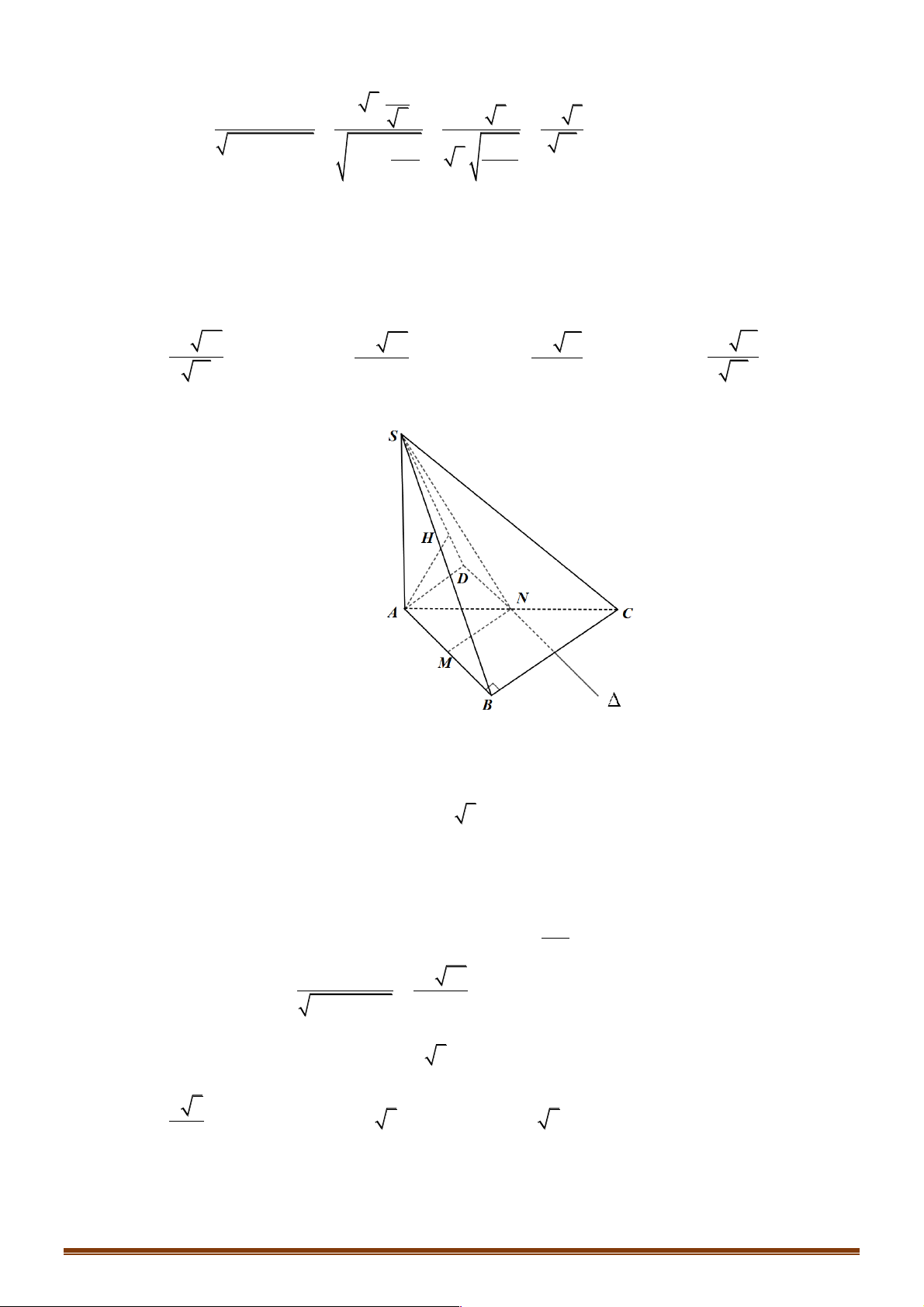
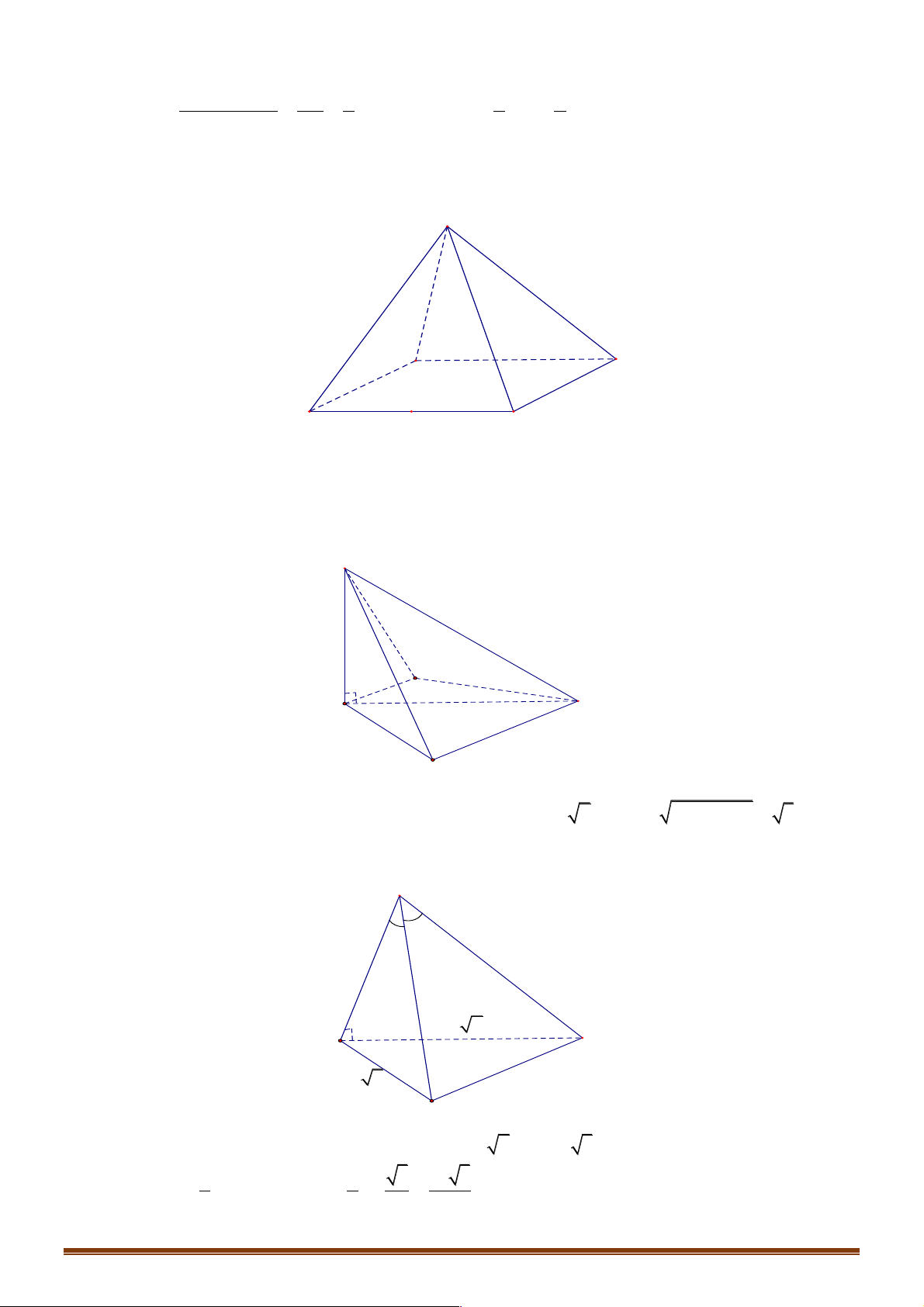
Ví dụ 3. Cho tứ diện đều ABCD có tam giác BCD đều, AD = AC . Giá tri của cos( , AB CD)là: A. 1 . B. 1 3 0 . C. - . D. . 2 2 2 Trang 3 Lời giải: Đáp án B
Gọi N là trung điểm của CD . Tam giác đều BCD nên BN ^ CD . Tam giác ACD cân tại A nên
AN ^ CD ta có: !!!" !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
AB CD = ( AN + NB) CD = AN CD + NB CD = Þ c ( AB CD) . AB CD . . . . 0 os , = !!!" !!!" = 0. AB . CD !!!" !!!"
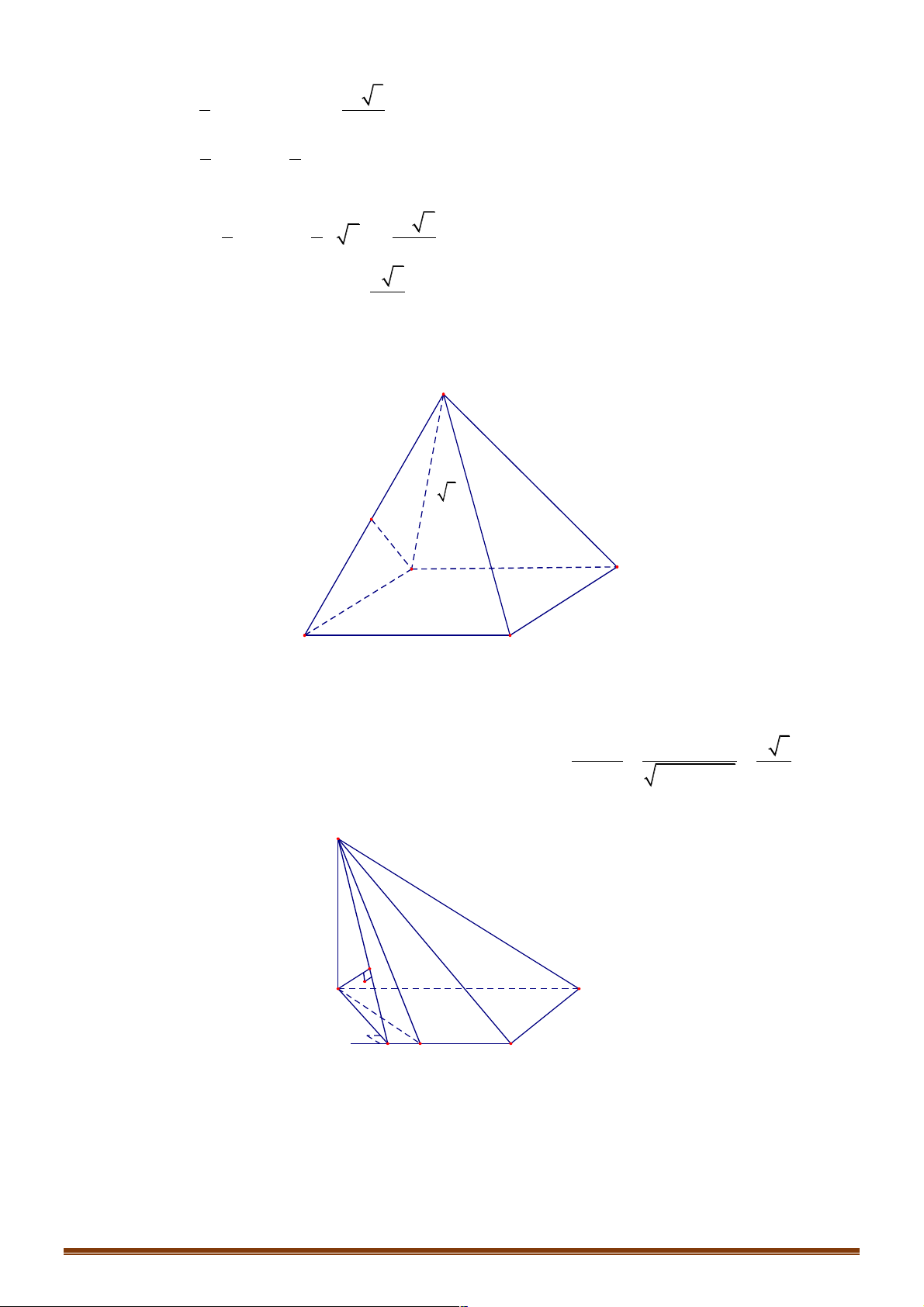
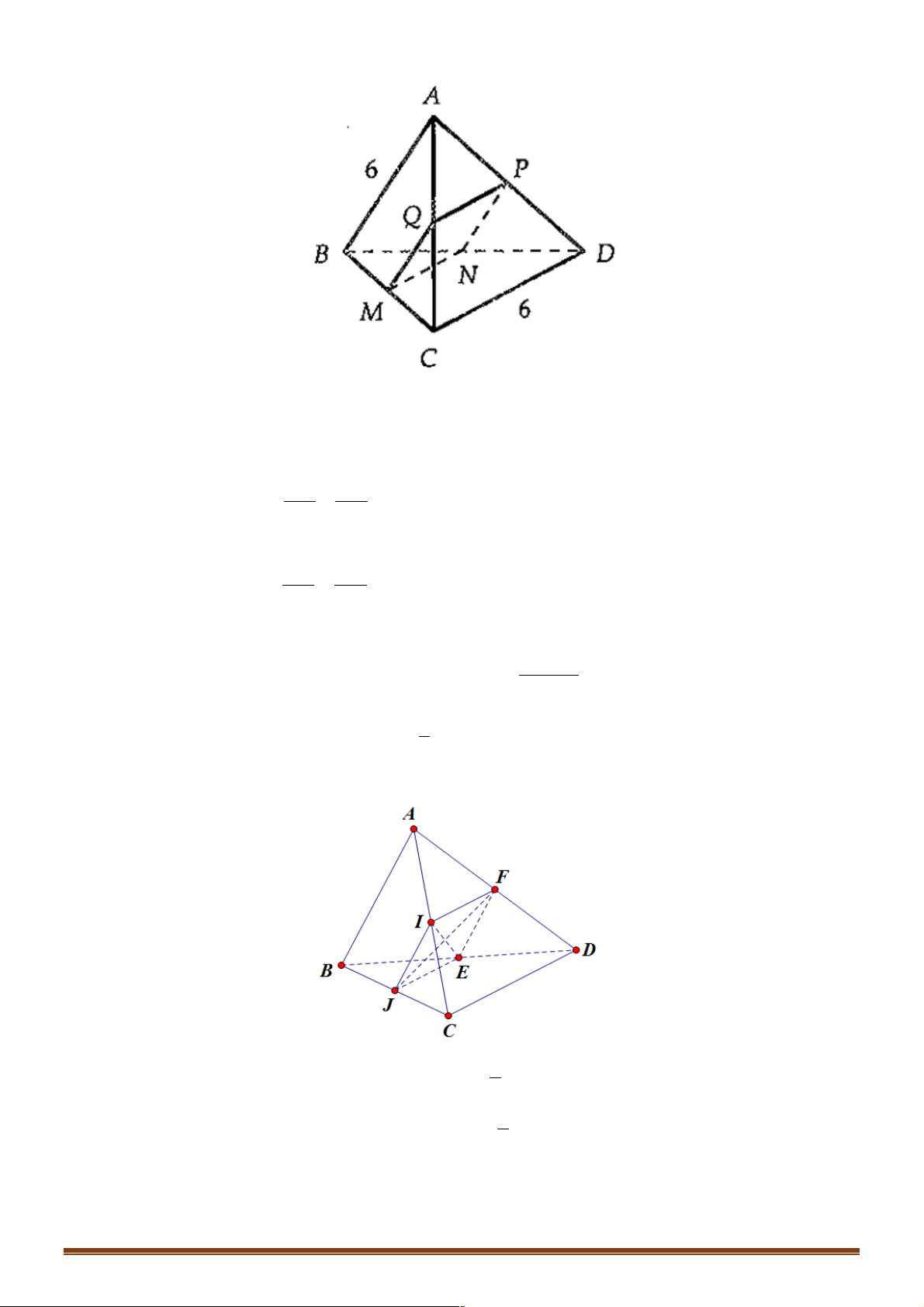
Ví dụ 4. Cho tứ diện đều ABCD có AB = CD = a;BC = AD = ;
b CA = BD = c . Giá trị của cos(BC,DA)là: 2 2 - 2 2 - 2 2 - 2 2 - A. a
c . B. b c . C. c a . D. a b . 2 b 2 a 2 b 2 c Lời giải Chọn A !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
BC.DA = BC (DC + CA) = C . B CD - C . B CA = 1 ( 1
CB2 + CD2 - BD2 ) - (CB2 + CA2 - AB2 ) 2 2 = 1 ( 1
AB2 + CD2 - BD2 - CA2 ) = (2a2 - c2 2 ) = a2 - c2 2 2 !!!" !!!" a2 - c2 a2 - c2
Vậy cos(BC, DA) = !!!" !!!" = . BC . DA b2
Ví dụ 5. Trong mặt phẳng (a ) cho tứ giác ABCD và một điểm S tùy ý. Mệnh đề nào sau đây đúng? !!!" !!!" !!!" !!!"
A. AC + BD = AB +CD. !!" !!!" !!" !!!"
B. SA+ SC = SB +CD(Với S là điểm tùy ý). !!" !!!" !!" !!!"
C. Nếu tồn tại điểm S mà SA+ SC = SB +
SD thì ABCD là hình bình hành. !!!" !!!" !!!" !!!" "
D. OA+OB +OC +OD = 0 khi và chỉ khi O là giao điểm của AC và BD. Lời giải
Đáp án C !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" "
A. Sai vì AC + BD = AB +CD Û AC - AB + DC - DB = 0 Û B º C (Vô lí)
B. Sai vì: Gọi O và O ' theo thứ tự là trung điểm của AC và BD . Ta có !!" !!!" !!!" !!" !!!" !!!" !!! !!" !!!"
SA+ SC = 2SO và SB + SD = 2SO' Û SO = SO' Û O º O' điều này không đúng nếu ABCD
không phải là hình bình hành. Trang 4
C. Đúng – Chứng minh tương tự như ý B.
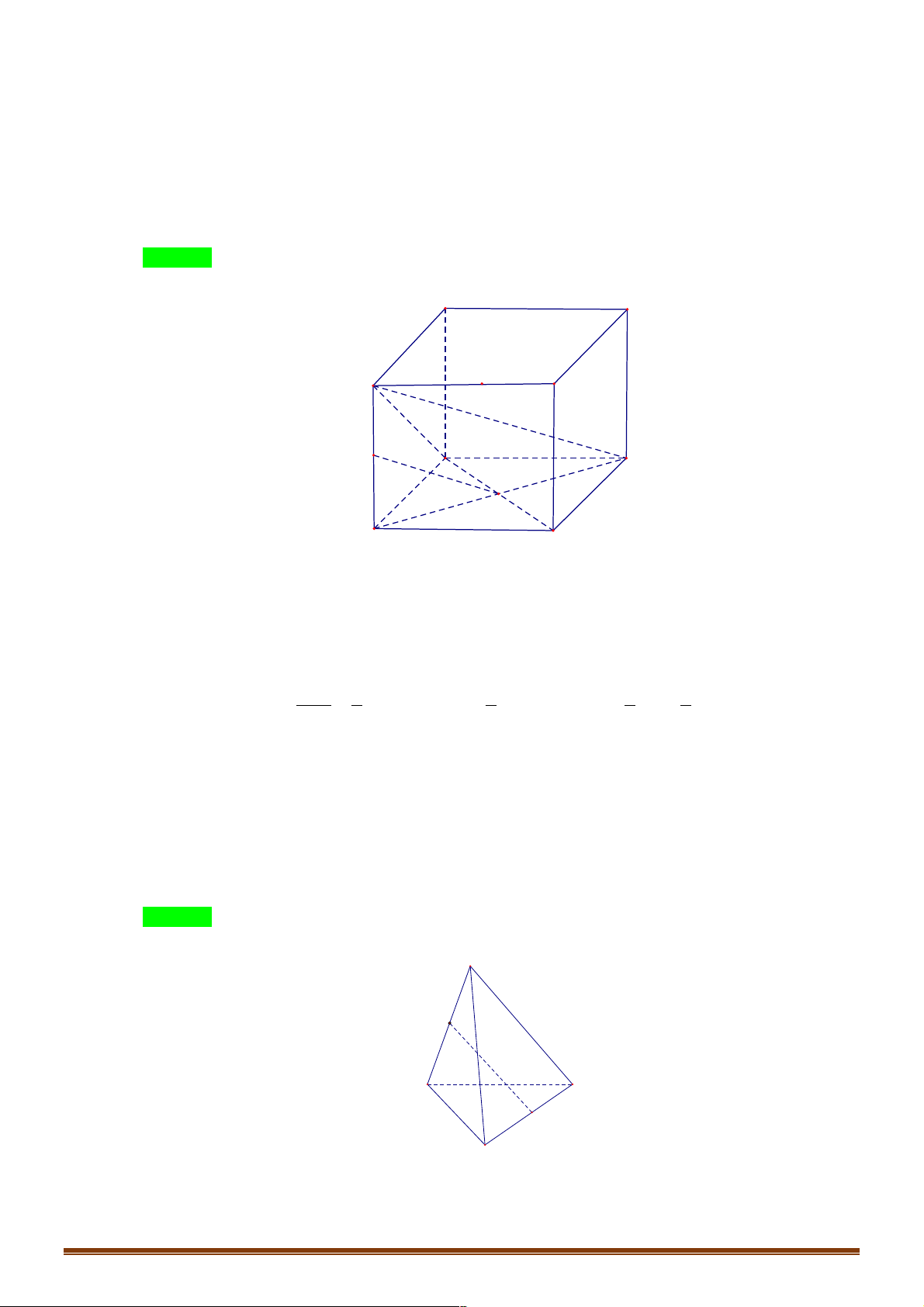
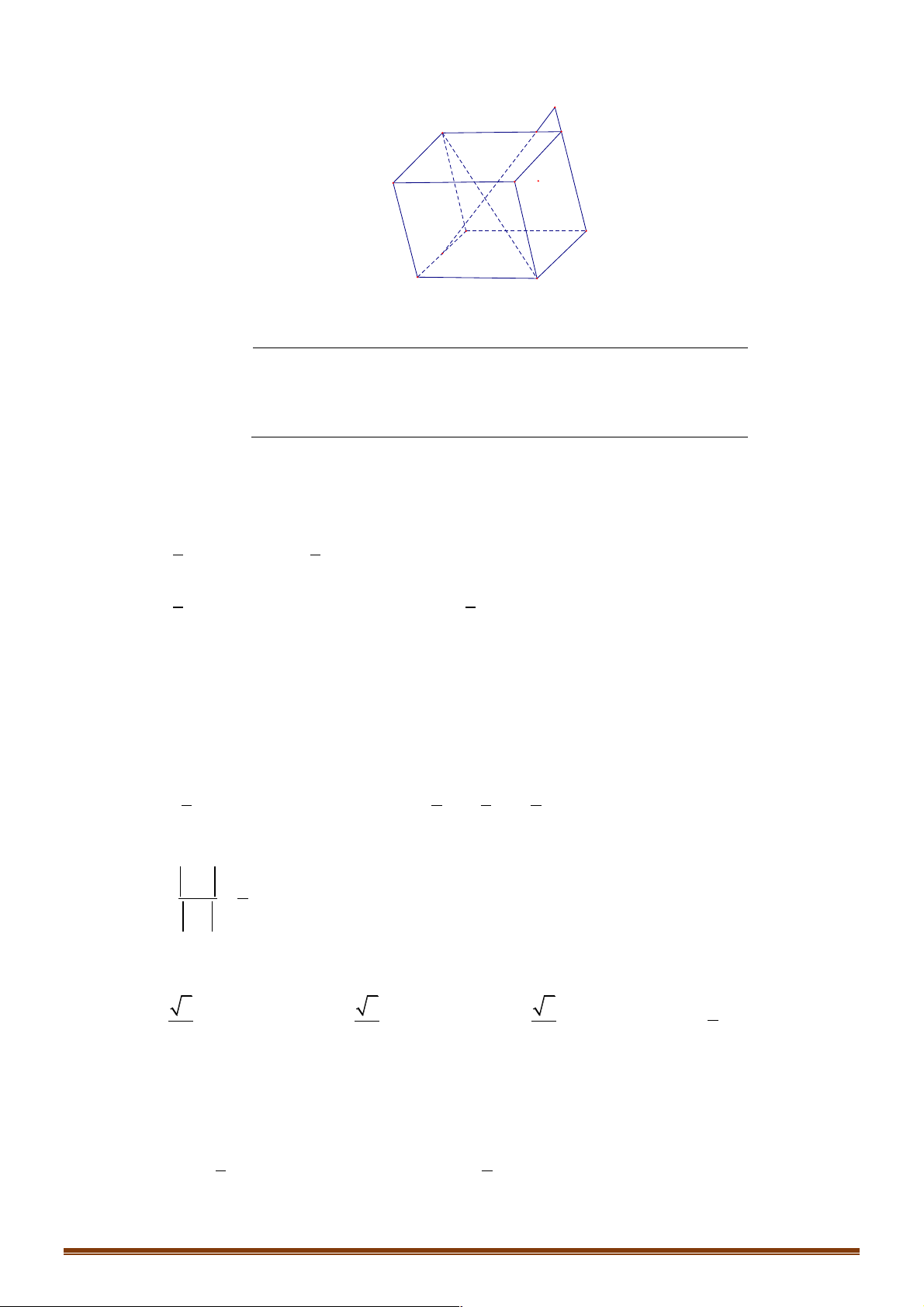
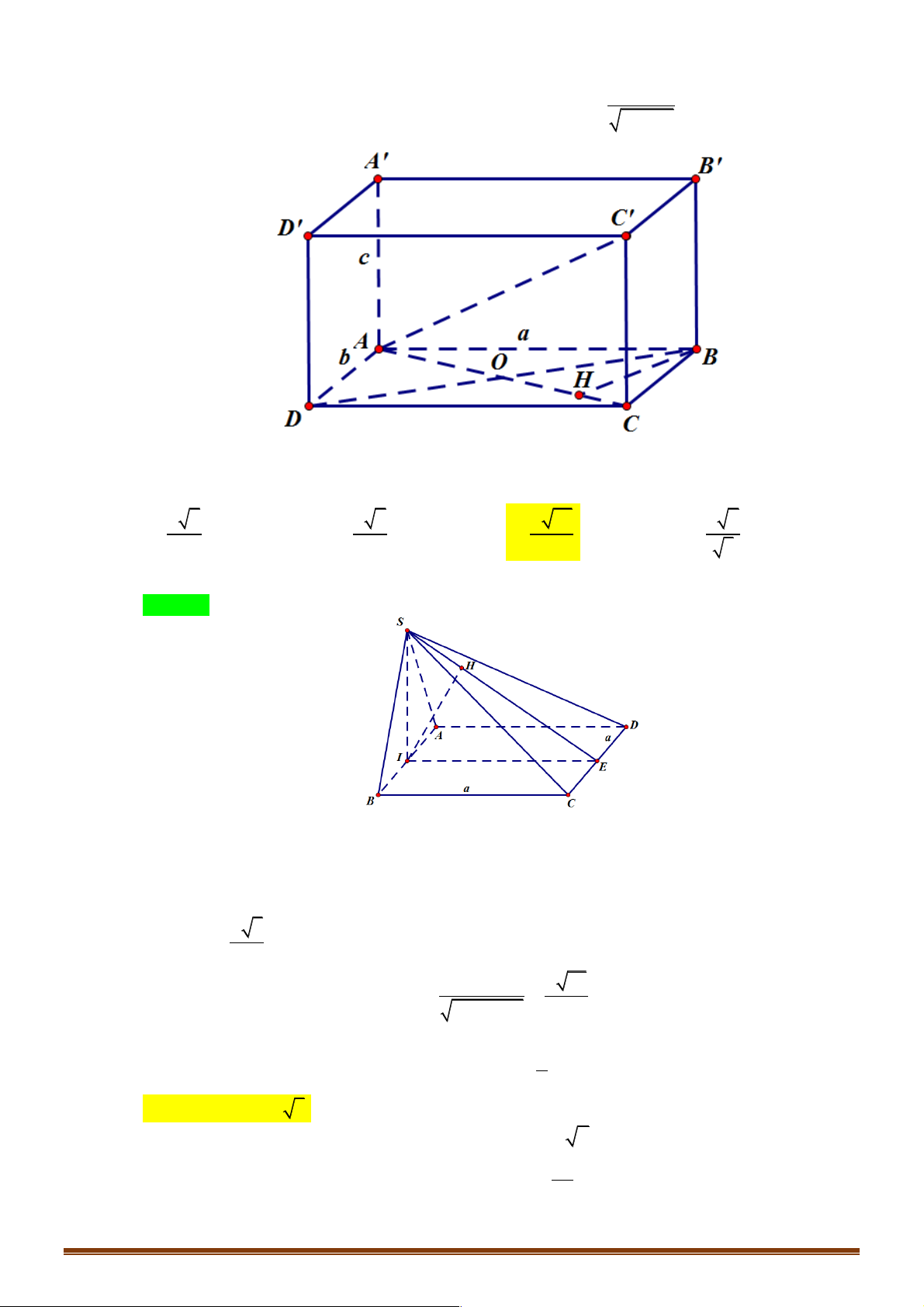
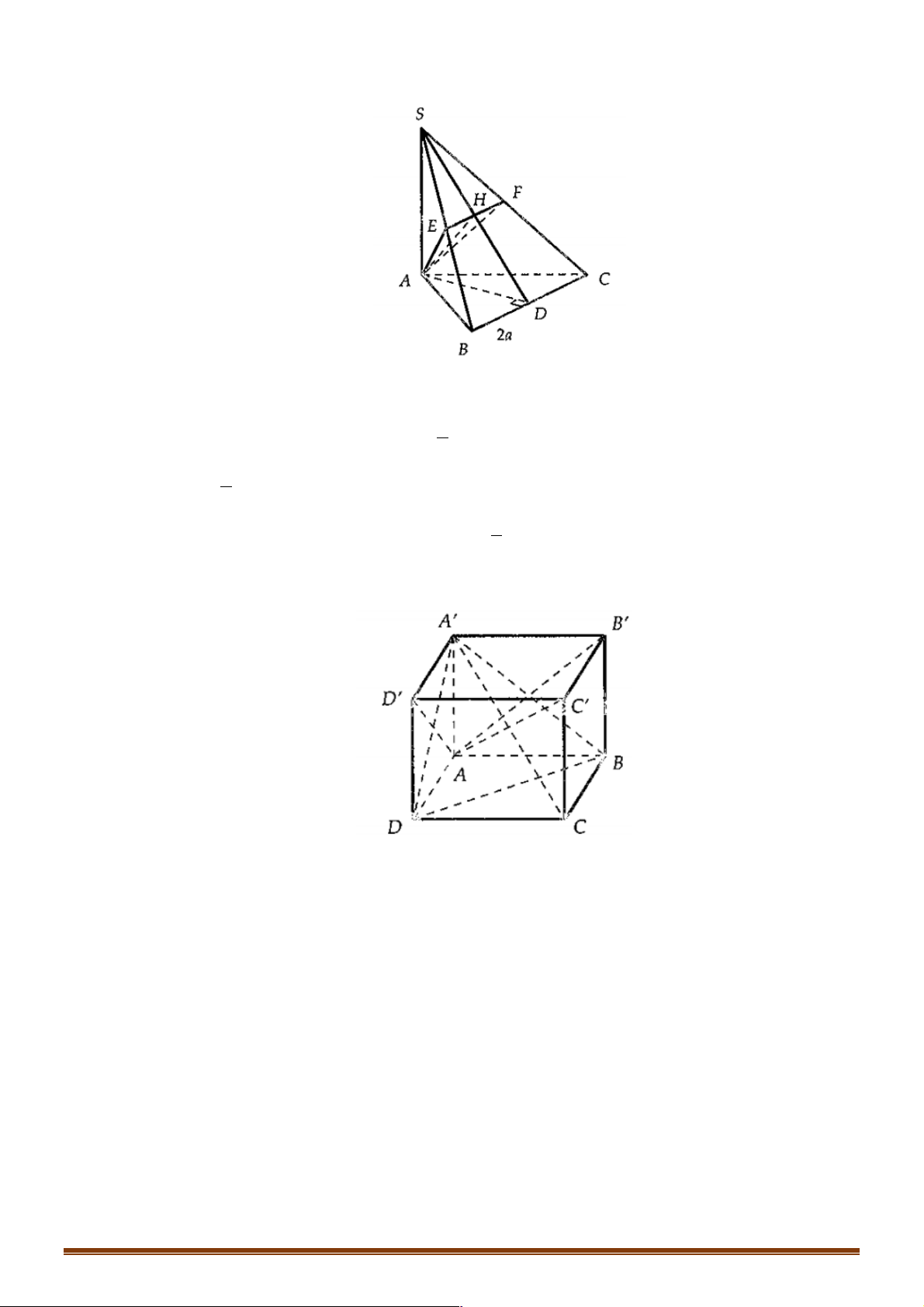
Ví dụ 6. Cho hình hộp ABC .
D A' B 'C ' D ' . Gọi M là trung điểm của AA', O là tâm của hình bình hành
ABCD . Cặp ba vecto nào sau đây đồng phẳng? !!!!" !!!" !!!!" !!!!" !!!" !!!!!"
A. MO, AB và B 'C .
B. MO, AB và A' D ' . !!!!" !!!!" !!!!" !!!!" !!!!" !!!!!"
C. MO, DC ' và B 'C .
D. MO, A' D và B'C '. Lời giải Đáp án A D' C' A' B' D M C O A B
Cách 1: Ta có MO// (CDA' B'); AB / / A' B' Þ AB// (CDA'B'), B'C ' nằm trong mặt phẳng ( !!!!" !!!" !!!"
CDA' B') nên các vecto MO, AB, BC dồng phẳng vì có giá song song hay nằm trên mặt phẳng (CDA'B'). !!!!" 1 1 !!!!!" !!!!" 1 !!!!!" !!!!!" 1 !!!" 1 !!!!"
Cách 2: Ta có MO =
= (A'B'+ B'C) = (A'B'+ B'C ') = AB + B'C. A'C 2 2 2 2 !!!!" !!!" !!!"
Vậy các vecto MO, AB, BC đồng phẳng.
Ví dụ 7. Cho tứ diện ABC .
D M và N theo thứ tự là trung điểm của AB và CD . Bộ ba vecto nào dưới đây đồng phẳng? !!!" !!!" !!!" !!!" !!!" !!!!"
A. BC, BD, . AD B. AC; ; AD MN. !!!" !!!" !!!!" !!!" !!!" !!!" C. BC; ; AD MN.
D. AC; DC; M . A Lời giải Đáp án C A M B D N C Trang 5 !!!" !!!!" !!!!" !!!"
AD = AM + MN + ND !!!" !!!!" !!!!" !!!"
BC = BM + MN + NC !!!" !!!" !!!!" !!!!" 1 !!!" 1 !!!"
Þ AD + BC = 2MN Þ MN = AD + BC 2 2 !!!" !!!" !!!!" Vậy ba vecto BC; ;
AD MN. đồng phẳng.
Ví dụ 8. Cho tứ diện ABC .
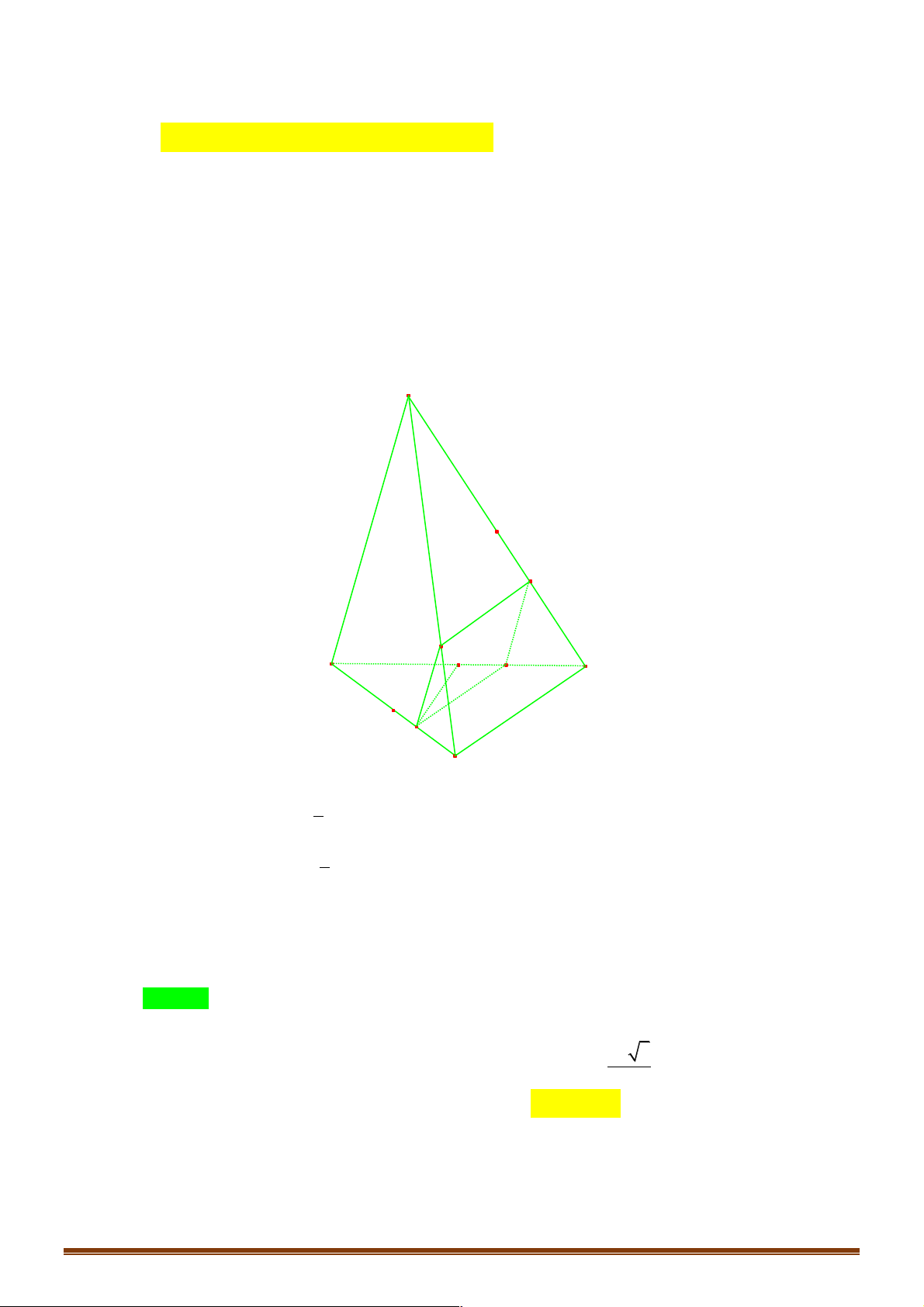
D M là điểm trên đoạn AB và MB = 2MA . N là điểm trên đường thẳng !!!" !!!" !!!!" !!!" !!!"
CD mà CN = kCD. Nếu MN, AD, BC đồng phẳng thì giá trị của k là: 2 A. k = 3 . B. k = 4 . C. k = 1 . D. k = . 3 2 3 2 Lời giải Đáp án A A M N B Q D N C
Qua M vẽ mặt phẳng (a ) song song với AD và BC .
(a)cắt AC tại P , BD tại Q và CD tại N . Ta có MP//PN//AD. !!!!" !!!" !!!"
Các vecto MN, AD, BC có giá song song hay nằm trong mặt phẳng (a ) nên đồng phẳng. !!!" 2 !!!" 2
Ta có CN = CD . Vậy k = . 3 3 !!!!" 1 !!!"
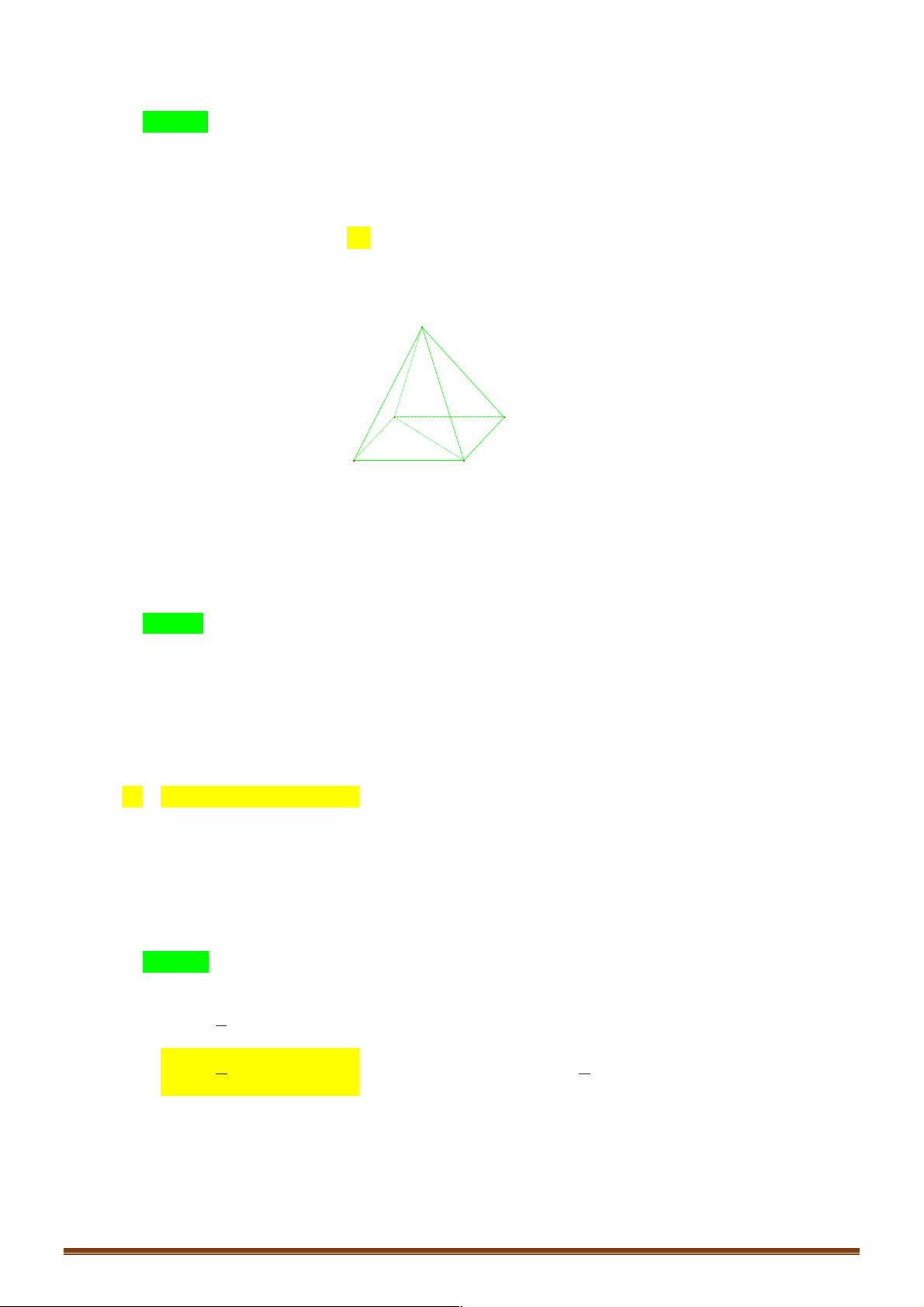
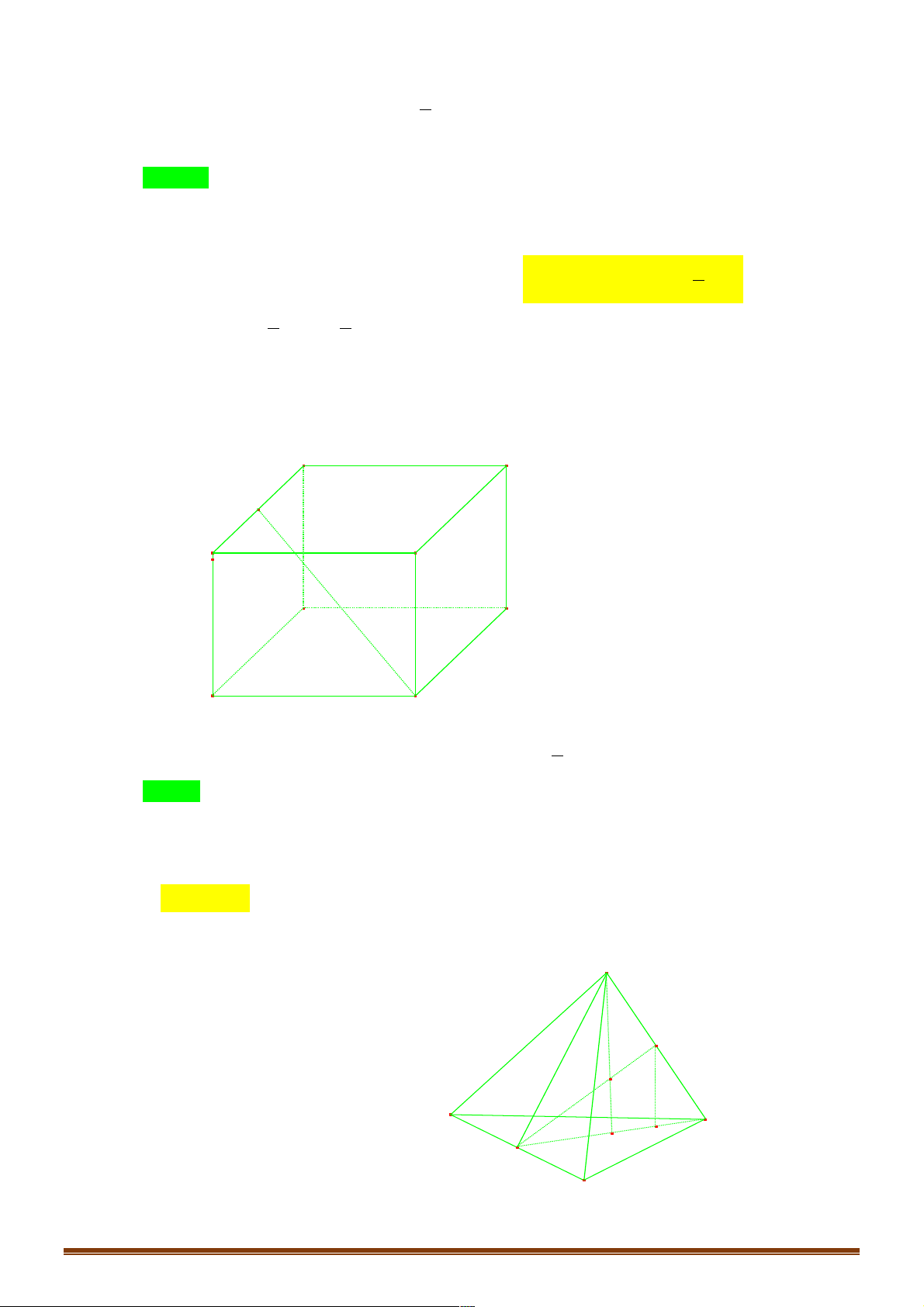
Ví dụ 9. Cho hình hộp ABC .
D A B C D . M là điểm trên cạnh AD sao cho AM = AD . N là điểm 1 1 1 1 2
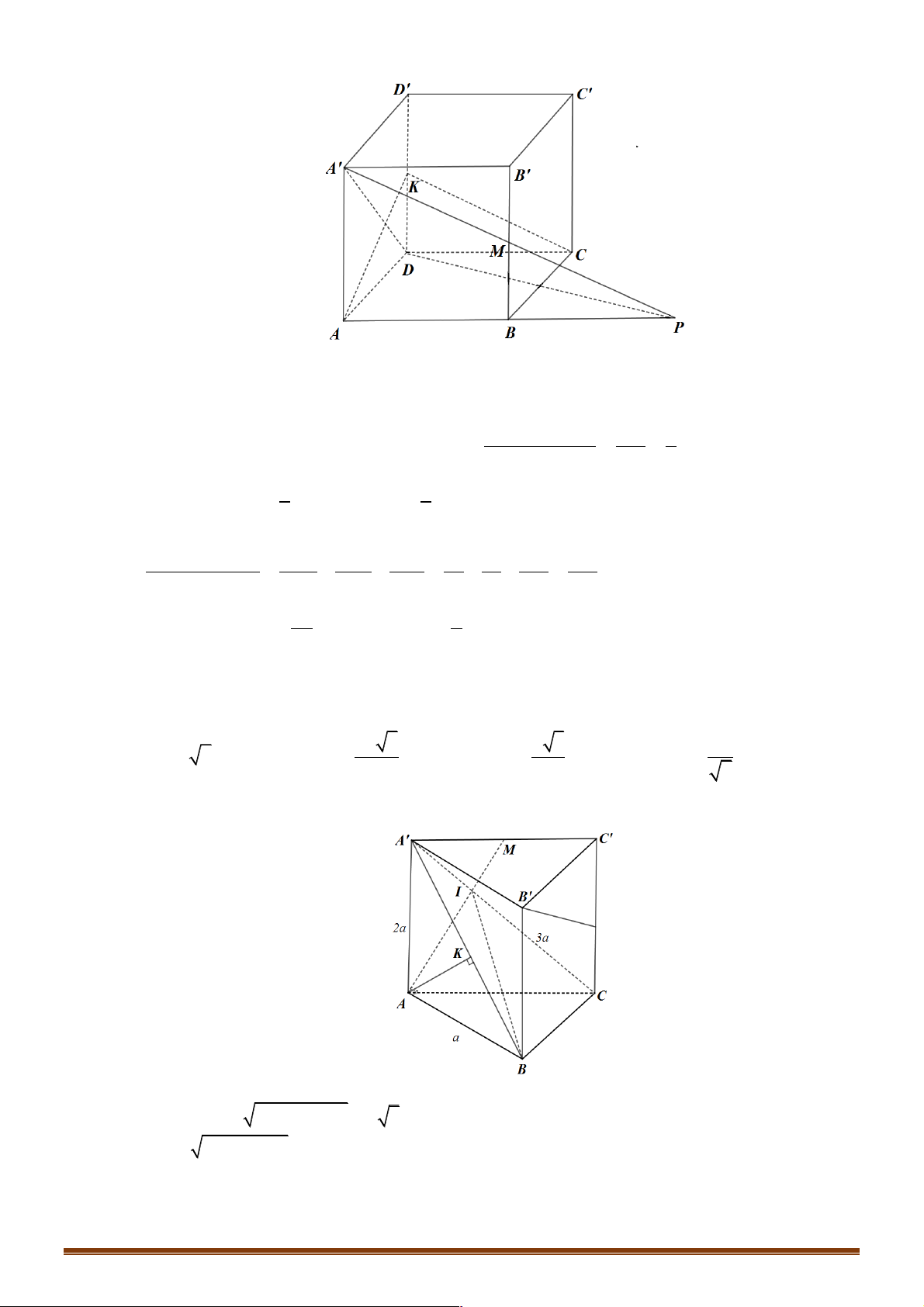
trên đường thẳng BD . P là điểm trên đường thẳng CC sao cho M , N, P thẳng hàng. 1 1 !!!!" MN Tính !!!" . NP 1 2 1 3 A. . B. . C. . D. . 3 3 2 4 Lời giải Đáp án B Trang 6 P D1 C1 A1 B1 D C M A B !!!" " !!!" " !!!" " !!!" !!!!" !!!" !!!!" " Đặt AB = , a AD = ,
b AA = c và BN = xBD ;CP = yCC = yc. 1 1 1 STUDYTIP !!!!" !!!" ! ! !
Ta biểu thi hai vecto MN, NP theo các vecto a,b, c !!!!" !!!"
Ba điểm M , N, P thẳng hàng nên MN = a.NP ( ) 1 . !!!!" !!!" !!!" !!!"
Ta có: MN = MA+ AB + BN 1 ! ! """"! 1 ! ! """! """! """!
= - b + a + xBD = - b + a + x BA + BC + BB 1 ( 1 ) 3 3 1 ! ! ! ! ! ! æ ö ! !
= - b + a + x(-a +b + c) = ( - x) 1 1 a + x - b + xc ç ÷ (2) 3 è 3 ø Ta lại có: !!!" !!!" !!!" !!!" !!!!" " " " " " " "
NP = NB + BC + CP = -xBD + b + yc = -x b - a + c + b + yc 1 ( ) !!!" " " "
Þ NP = xa + (1- x)b + ( y - x)c (3)
Thay (2), (3) vào (1) ta được: 1 ì - x = a x ïï 1 2 3 3
íx - = a (1- x) . Giải hệ ta được a = , x = , y = . 3 ï 3 5 2 ïx = a î ( y - x) !!!!" MN 2 Vậy !!!" = . NP 3
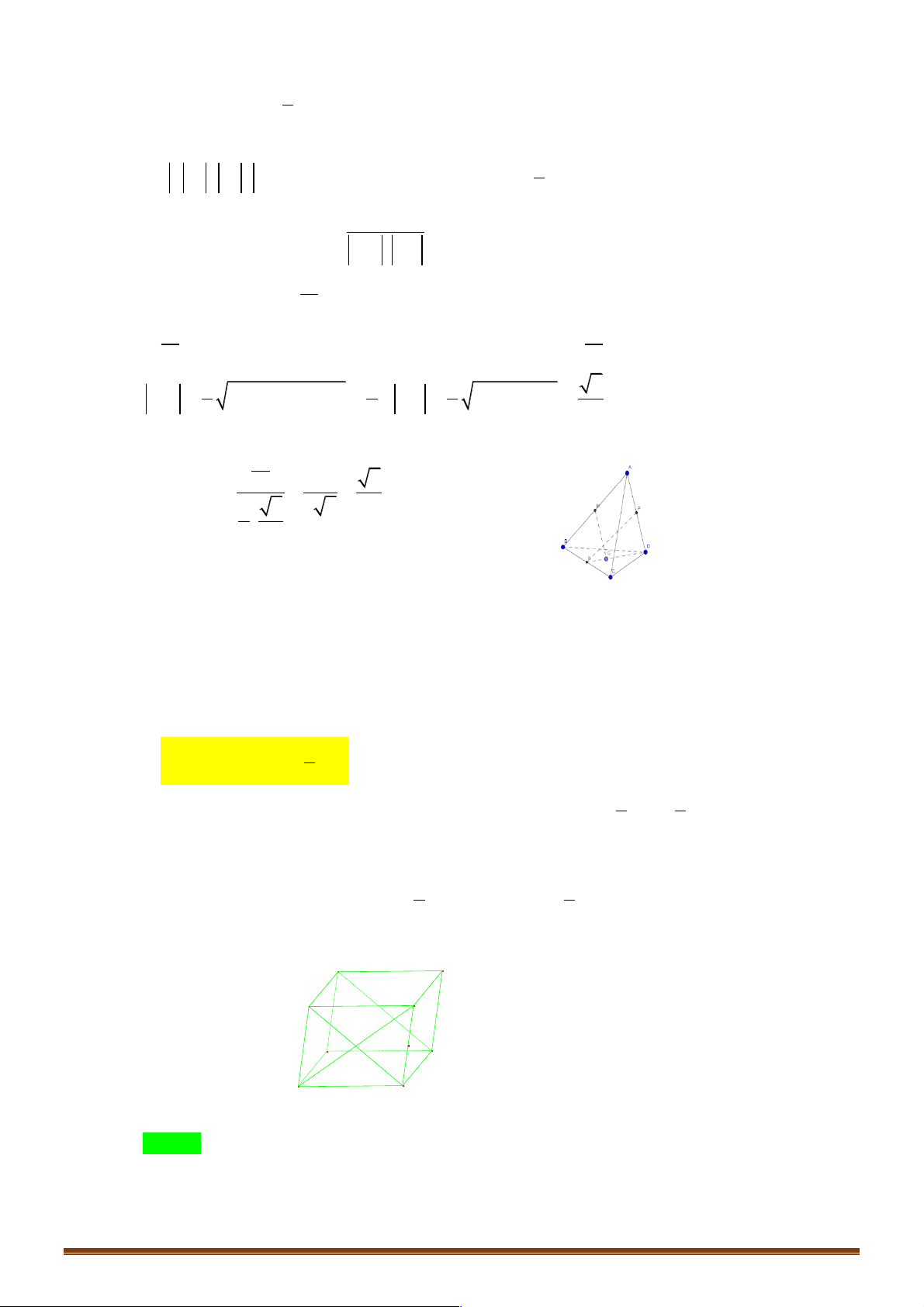
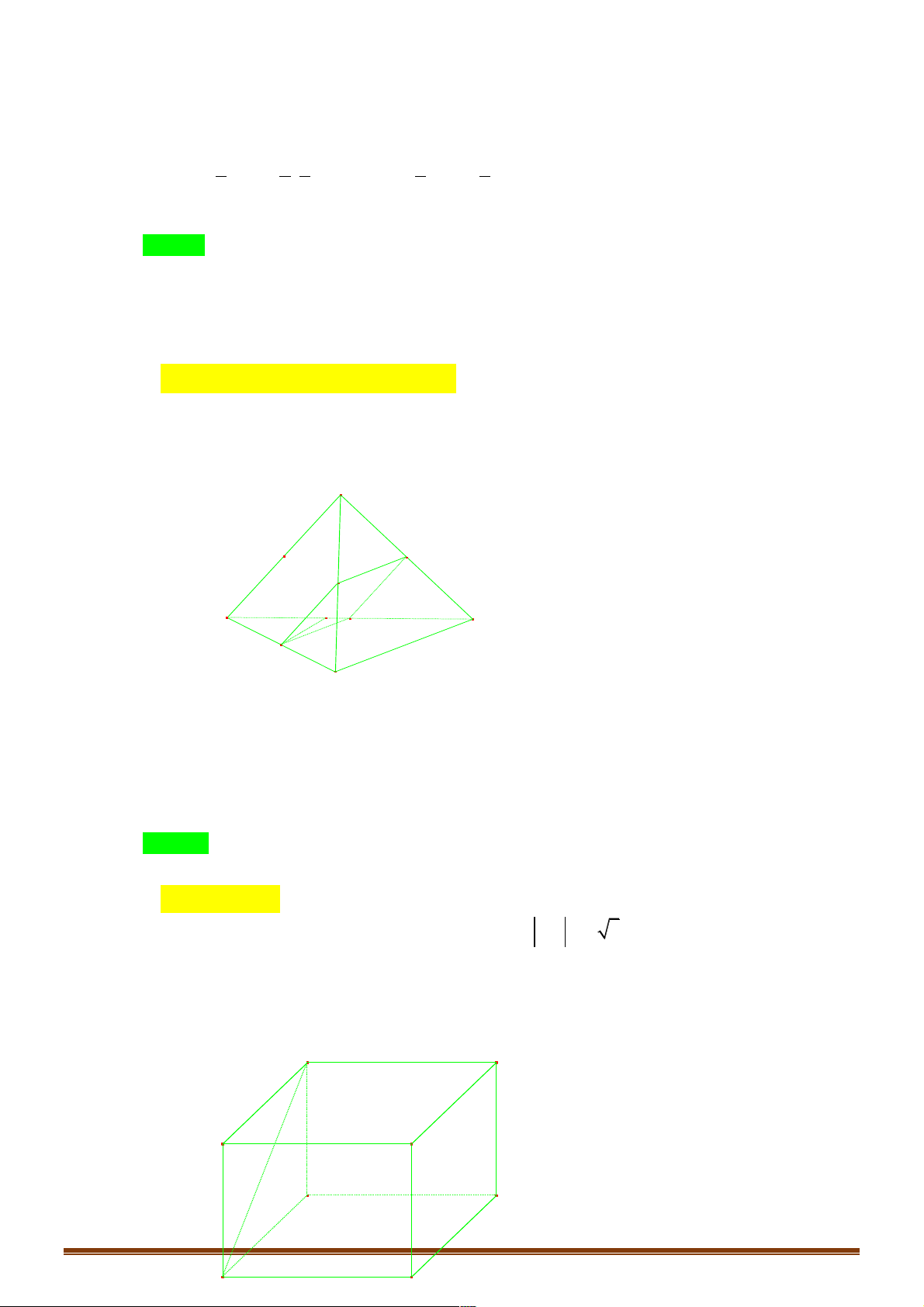
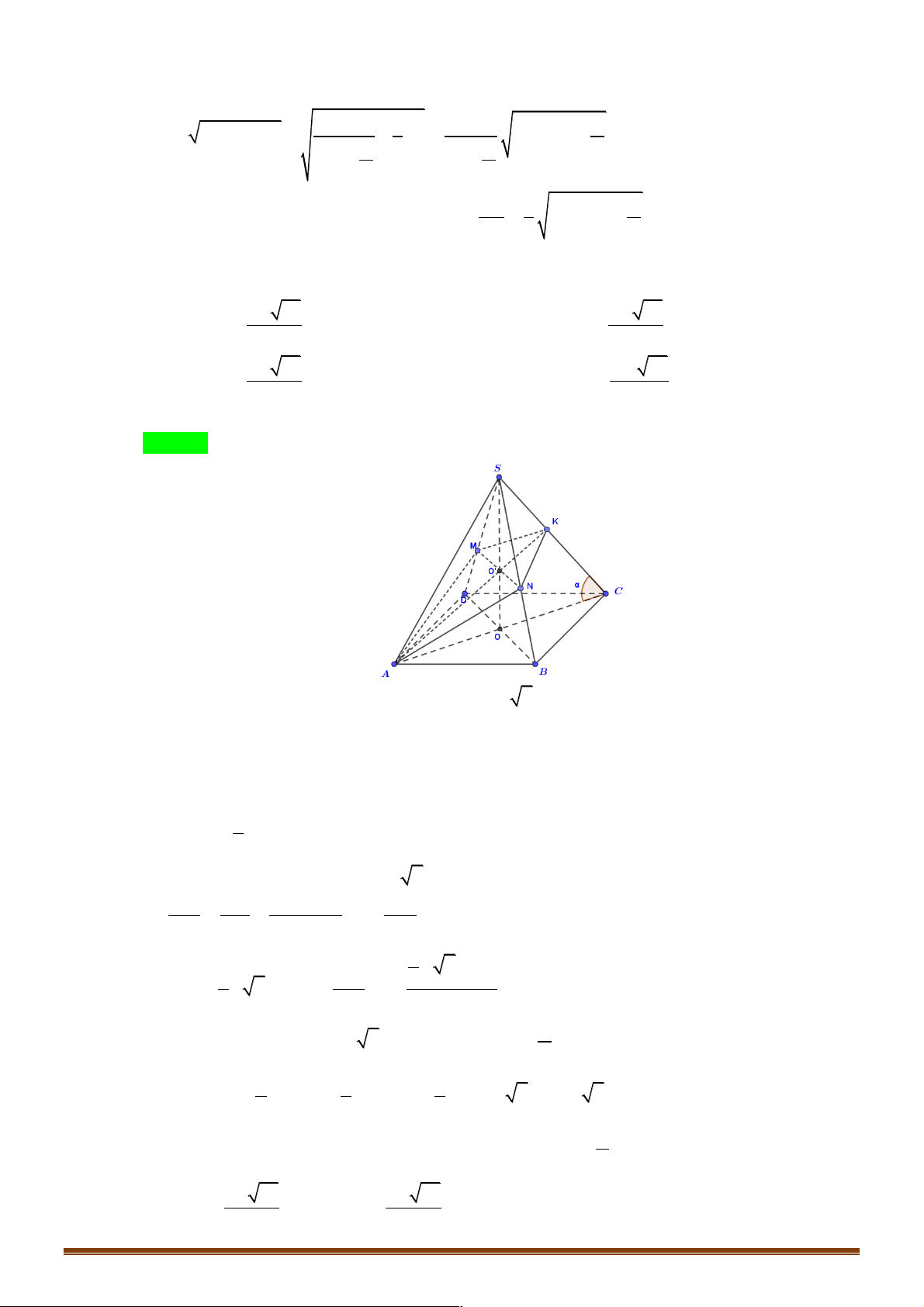
Ví dụ 10. Cho tứ diện đều ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, CB, AD và G là !!!!" !!!"
trọng tâm tam giác BCD, a là góc giữa 2 vectơ MG và NP. Khi đó cosa có giá trị là: 2 2 2 1 A. 2 B. 3 C. 6 D. 2 Đáp án: C Lời giải: !!!" !!!" !!!" Đặt AB = ; a AC = ; b AD = ; c !!!" 1 " " " !!!!" !!!" !!!!" 1 " " "
Þ AG = (a +b + c) Þ MG = AG - AM = (-a + 2b + 2c) 3 6 Trang 7 !!!" !!!" !!!" 1 " " "
PN = AN - AP = (a +b - c) 2
Không mất tính tổng quát, giả sử độ dài các cạnh của tứ diện đều bằng 1 ! ! ! ! ! ! ! ! ! Þ 1
a = b = c = 1và 0 . a b = . b c = . c a = 1.1.cos60 = 2 !!!!" !!!" !!!!" !!!" . MG PN Þ cosa = c s(
o MG, PN) = !!!!" !!!" (*) MG . PN !!!!" !!!" 1 " " " " " " Ta có: Þ . MG PN =
(-a + 2b + 2c)(a +b -c) 12 1 !2 !! !! ""!! !2 !! !! !! !2 1 =
(-a - ab + ac + 2ab + 2b - 2bc + 2ac + 2bc - 2c ) = 12 12 !!!!" 1 " " " 1 !!!" 1 " " " 2 2 2 MG =
(-a + 2b + 2c) = ; PN =
(a + b - c) = 6 2 2 2 Thay vào (*) ta được 1 1 2 12 Þ cosa == = = . (*) 1 2 3 2 6 . 2 2
C.Bài tập rèn luyện kỹ năng
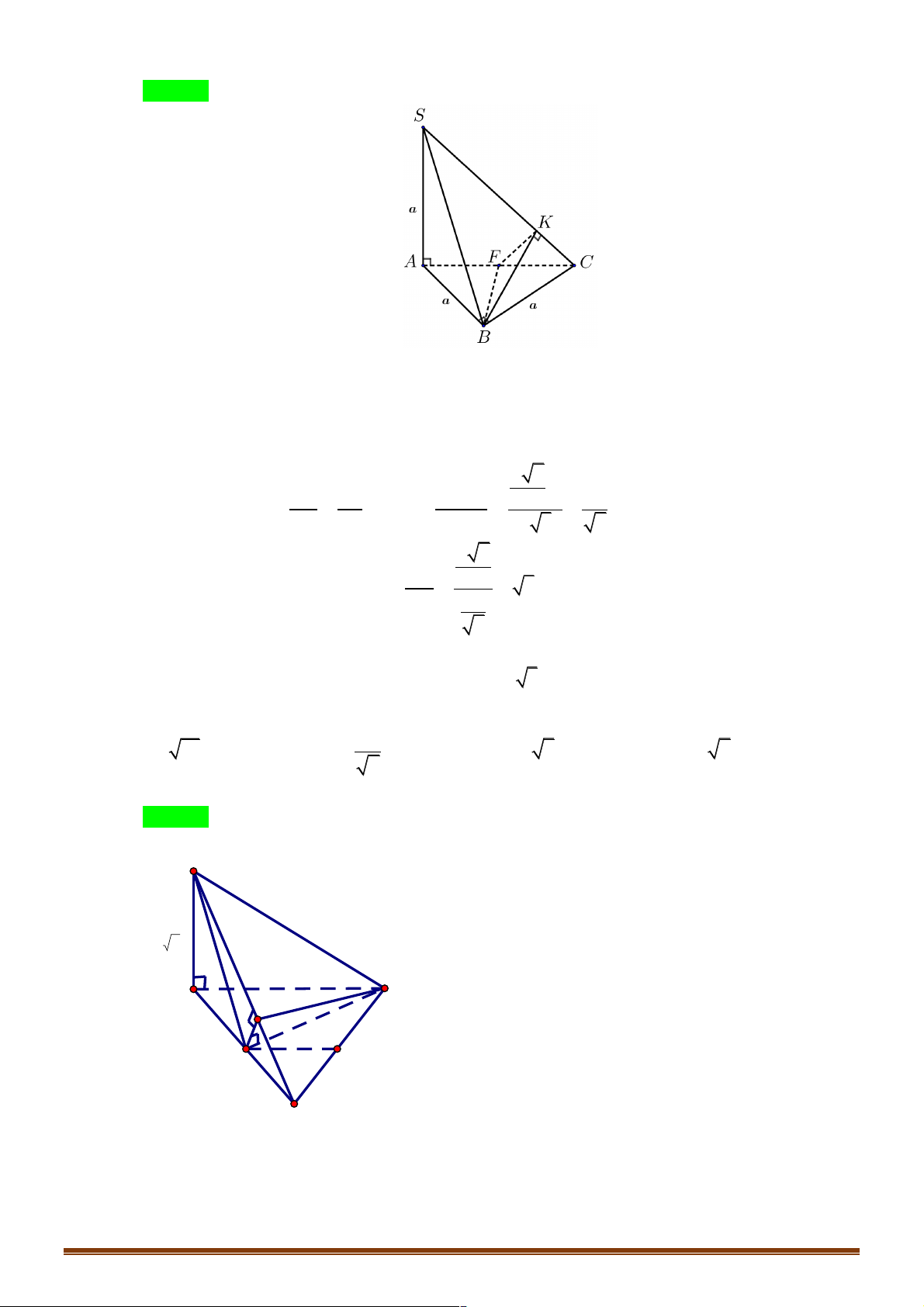
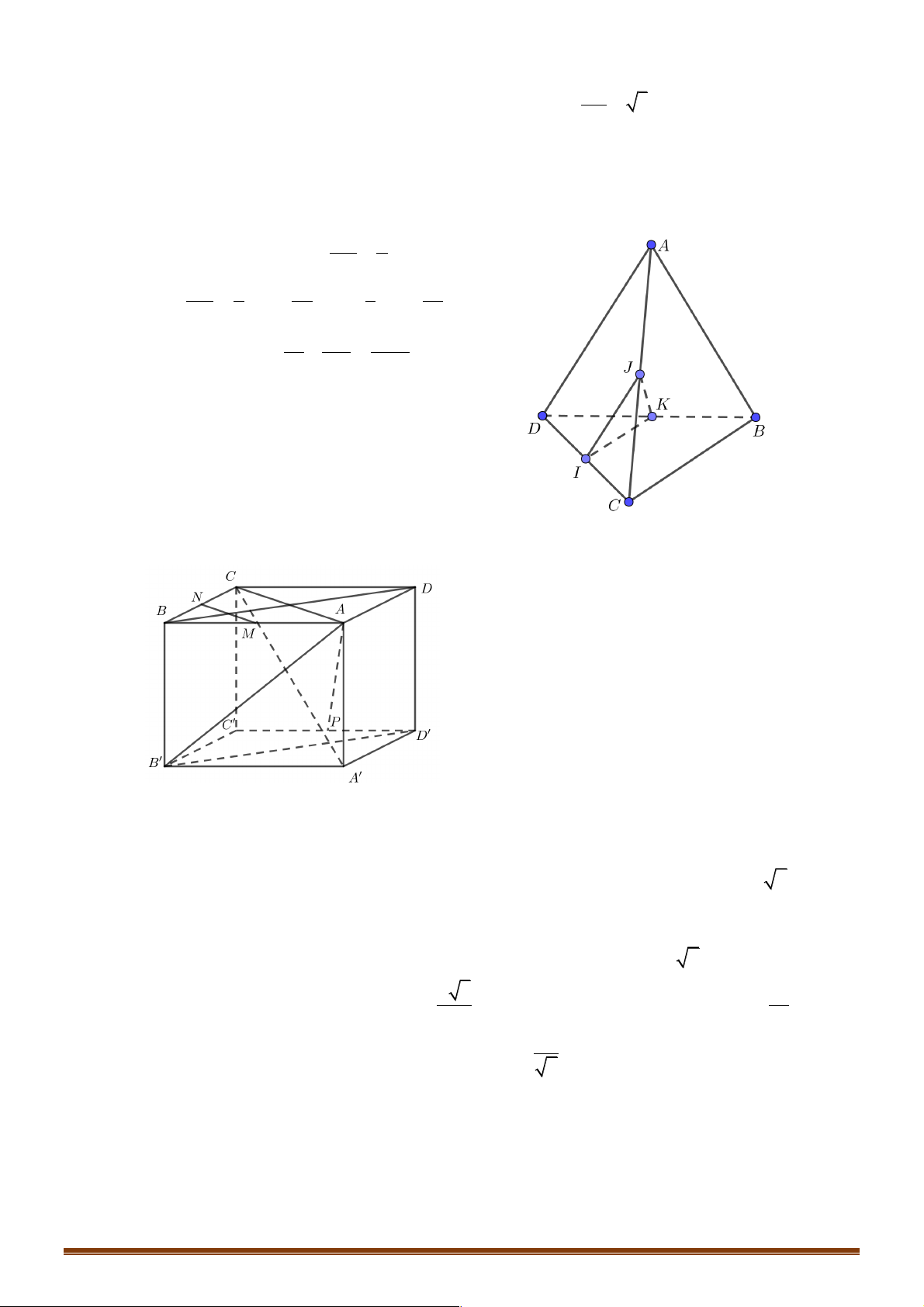
Câu 1: Cho ABC .
D A B C D là hình hộp, với K là trung điểm CC1. Tìm khẳng định đúng trong các 1 1 1 1 khẳng định sau: !!!" !!!" !!!" 1 !!!" !!!" !!!" !!!" !!!"
A. AK = AB + AD + AA
B. AK = AB + BC + AA 1 2 1 !!!" !!!" !!!" !!!" !!!" !!!" 1 !!!" 1 !!!"
C. AK = AB + AD + AA
D. AK = AB + AD + AA 1 1 2 2 Hướng dẫn giải !!!" !!!" !!!" !!!" !!!" 1 !!!" !!!" !!!" 1 !!!"
Có AK = AC + CK = (AB + AD) + AA = AB + AD + AA 1 1 2 2 A B D C K B1 A1 D1 C1 Chọn A
Câu 2: Cho hình hộp ABC .
D A B C D với M = CD Ç C D. Khi đó: 1 1 1 1 1 1 Trang 8 !!!!" 1 !!!" 1 !!!" 1 !!!" !!!!" 1 !!!" !!!" 1 !!!"
AM = AB + AD + AA
AM = AB + AD + AA 1 1 A. 2 2 2 B. 2 2 !!!!" !!!" !!!" 1 !!!" !!!!" 1 !!!" 1 !!!" !!!"
AM = AB + AD + AA
AM = AB + AD + AA C. 1 2 D. 1 2 2 Hướng dẫn giải ( hính vẽ câu 1) !!!!" !!!" !!!!" !!!" !!!!" 1 !!!" !!!!" !!!" 1 !!!" 1 !!!"
Ta có: AM = AD + DM = AD + DC = AD + (DC + DD ) = AD + AB + AA 1 1 1 2 2 2 Chọn B !!!!" !!!!" !!!!" !!!!" !!!!" !!!!"
Câu 3: Cho hình hộp ABC .
D A B C D . Khi đó: tổng 3 góc (D A ,CC ) + (C ,
B DD ) + (DC ,A ) B là: 1 1 1 1 1 1 1 1 1 1 1 A. 1800 B. 2900 C.3600 D. 3150 Hướng dẫn giải A B D C K B1 A1 D1 C1 Ta có: !!!!" !!!!" 0 (D A ,CC ) = 90 1 1 1 !!!!" !!!!" !!!!" !!!!" 0
(C B, DD ) = (C B,CC ) = 135 1 1 1 1 !!!!" !!!!" !!!!" !!!!" 0
(DC , A B) = (DC , D C) = 90 1 1 1 1 !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" 0 0 0 0
Þ (D A ,CC ) + (C ,
B DD ) + (DC ,A ) B = 90 +135 + 90 = 315 1 1 1 1 1 1 1 Chọn D !!!" !!!!" !!!!" !!!!" !!!" !!!!"
Câu 4: Cho hình lập phương ABC .
D A B C D , đặt a = (AC, DC ); b = (DA ,BB ); g = (AA ,C C) 1 1 1 1 1 1 1 1 1 Khi đó: làa + b + g : A. 3600 B. 3750 C. 3150 D. 2750 Hướng dẫn giải ( hình câu 3) !!!" !!!!" !!!" !!!!" 0
a = (AC, DC ) = (AC, AB ) = 60 1 1 !!!!" !!!!" !!!!" !!!!" 0
b = (DA ,BB ) = (DA ,A ) A = 135 1 1 1 1 !!!" !!!!" !!!" !!!" 0
g = (AA ,C C) = (AA , A ) A = 180 1 1 1 1 Trang 9 0 0 0 0
Þ a + b + g = 60 +135 +180 = 375 Chọn B !!!" !!!"
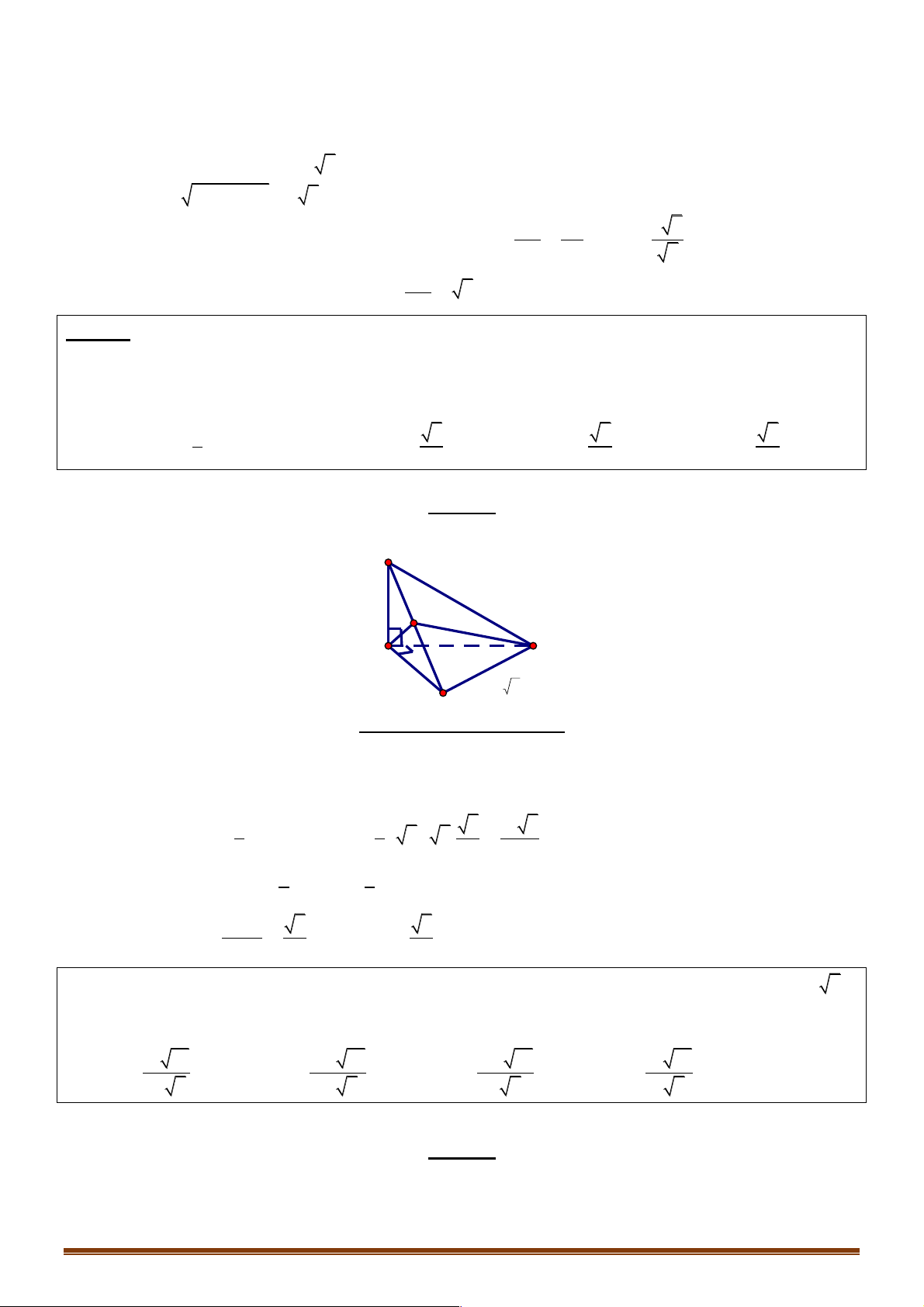
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB=6; AD=4; . AB AD =12 . Tính !!!" !!" 2 (SC. - ) SA . A. 76 B. 28 C. 52 D. 40 Hướng dẫn giải S 4 A 4 D 6 7.42 cm B C !!!" !!" !!!"2 !!!" !!!" !!!"2 !!!"2 !!!" !!!" 2 (SC. - )
SA . = AC = (AB + AD) = AB + AD + 2A . B AD 2 2 = 6 + 4 + 2( 1 - 2) = 28 Chọn B
Câu 6: Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Ba vectơ đồng phẳng là 3 vec tơ cùng nằm trong một mặt phẳng ! ! ! ! ! !
B. Ba vectơ a,b, c đồng phẳng thì có c = ma + nb, với m, n là các số duy nhất !" " " " !"
C. Ba vectơ đồng phẳng khi có d = ma + nb + pc với d là vec tơ bất kỳ
D. Cả 3 mệnh đề trên đều sai Hướng dẫn giải
-Phương án A: sai vi chỉ cần giá của chúng song song hoặc nằm trên một mặt phẳng nào đó ! !
Phương án B: Sai a, b phải không cùng phương. Phương án C sai Vậy chọn D Chọn D
Câu 7: Cho hình tứ diện ABCD, trọng tâm G. Mệnh đề nào sau đây sai? !!!" 1 !!!" !!!" !!!" !!!" !!!" !!!" "
A. OG = (OA + OB + OC)
B. GA + GB + GC = 0 4 !!!" 2 !!!" !!!" !!!" !!!" 1 !!!" !!!" !!!"
C. AG = (AB + AC + AD)
D. AG = (AB + AC + AD) 3 4 Hướng dẫn giải Trang 10 A M G B D N C
Gọi M, N lần lượt là trung điểm của AB, CD !!!!" !!!" "
Þ G là trung điểm của MN Þ GM + GN = 0 !!!" !!!" !!!" "
Û GA+ GB + GC = 0 ÞB đúng
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" Ta có:
OA + OB + OC + OD = OG + GA + OG + GB + OG + GC + OG + GD !!!" !!!" !!!" !!!" !!!" !!!"
= 4OG + (GA + GB + GC + GD) = 4OG Þ A đúng
Khi O trùng A thì D đúng vậy đáp án là C. Chọn C ! ! ! ! ! ! "! ! ! ! ! !
Câu 8: Cho ba vectơ a,b, c không đồng phẳng xét các vectơ x = 2a - ; b y = 4 - a + 2 ; b z = 3 - a - 2c
Chọn mênh đề đúng trong các mệnh đề sau: !" #
A.Hai vec tơ y, z cùng phương ! "#
B. Hai vec tơ x, y cùng phương ! "
C.Hai vec tơ x, z cùng phương ! "! #
D.Hai vec tơ x, y, z đồng phẳng Hướng dẫn giải !" " ! "! Ta thấy y = 2
- x nên x, y cùng phương. Chọn B
Câu 9: Cho hình lập phương ABC .
D A B C D , Tìm giá trị của k thích hợp để 1 1 1 1 !!!" !!!!" !!!!" !!!!"
AB + B C + DD = k AC ) 1 1 1 1 A.k=4 B. k=1 C. k=0 D. k=2 Hướng dẫn giải Trang 11 A1 B1 D1 C1 A B D C
!!!!" !!!!" !!!" !!!" !!!!" !!!!"
Có AB + B C + DD = AB + BC + CC = AC Þ k = 1 !!!" 1 1 1 1 1 Chọn B !!!!" !!!" !!!" !!!!"
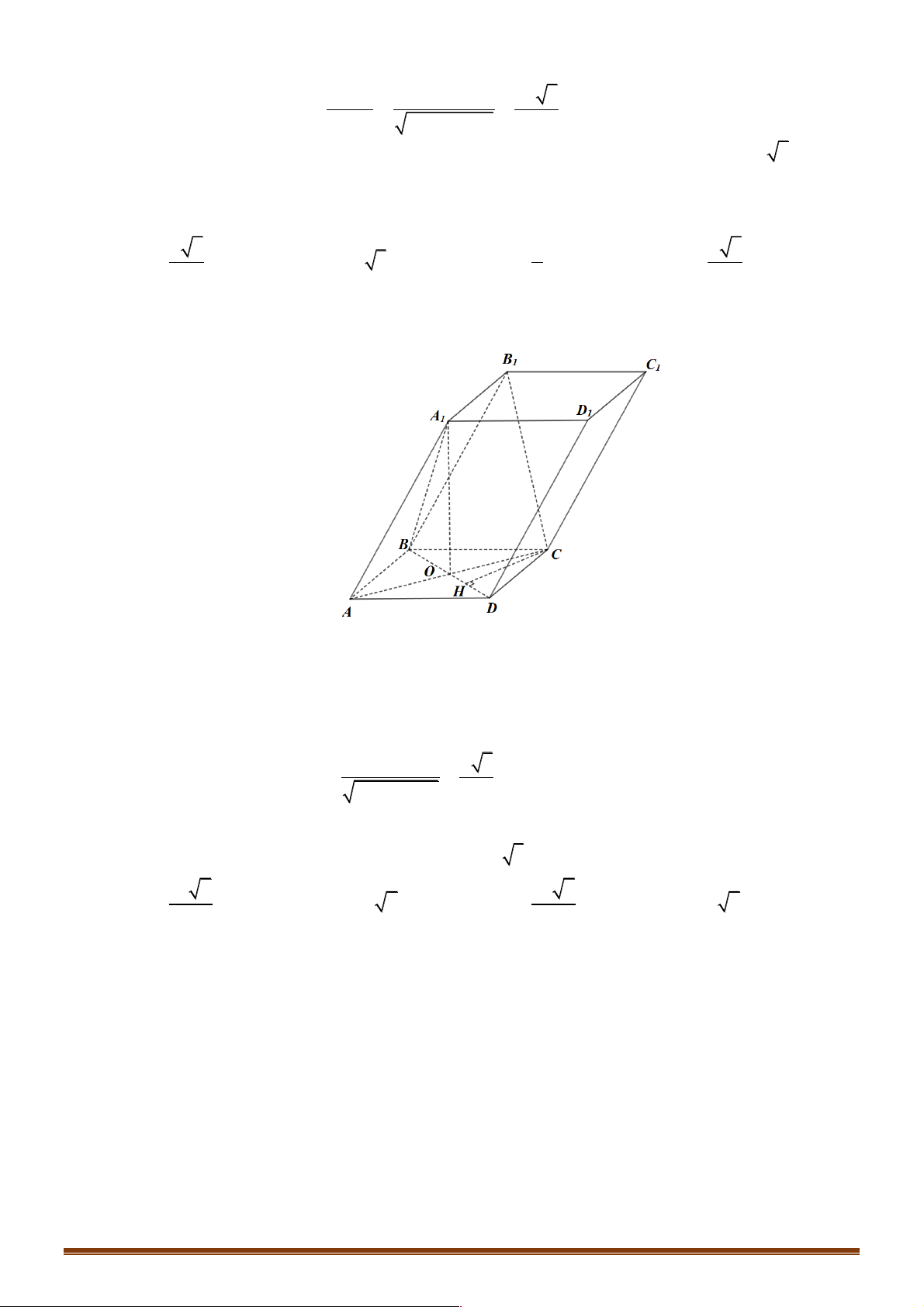
Câu 10: Cho hình lăng trụ tam giác ABC.A B C . Đặt AA = ; a AB = ; b AC = ;
c BC = d trong các 1 1 1 1 1
đẳng thức sau đẳng thức nào đúng. ! ! ! "! ! ! ! ! "!
A. a + b + c + d = 0
B. a + b + c = d ! ! "! ! ! ! !
C. b - c + d = 0
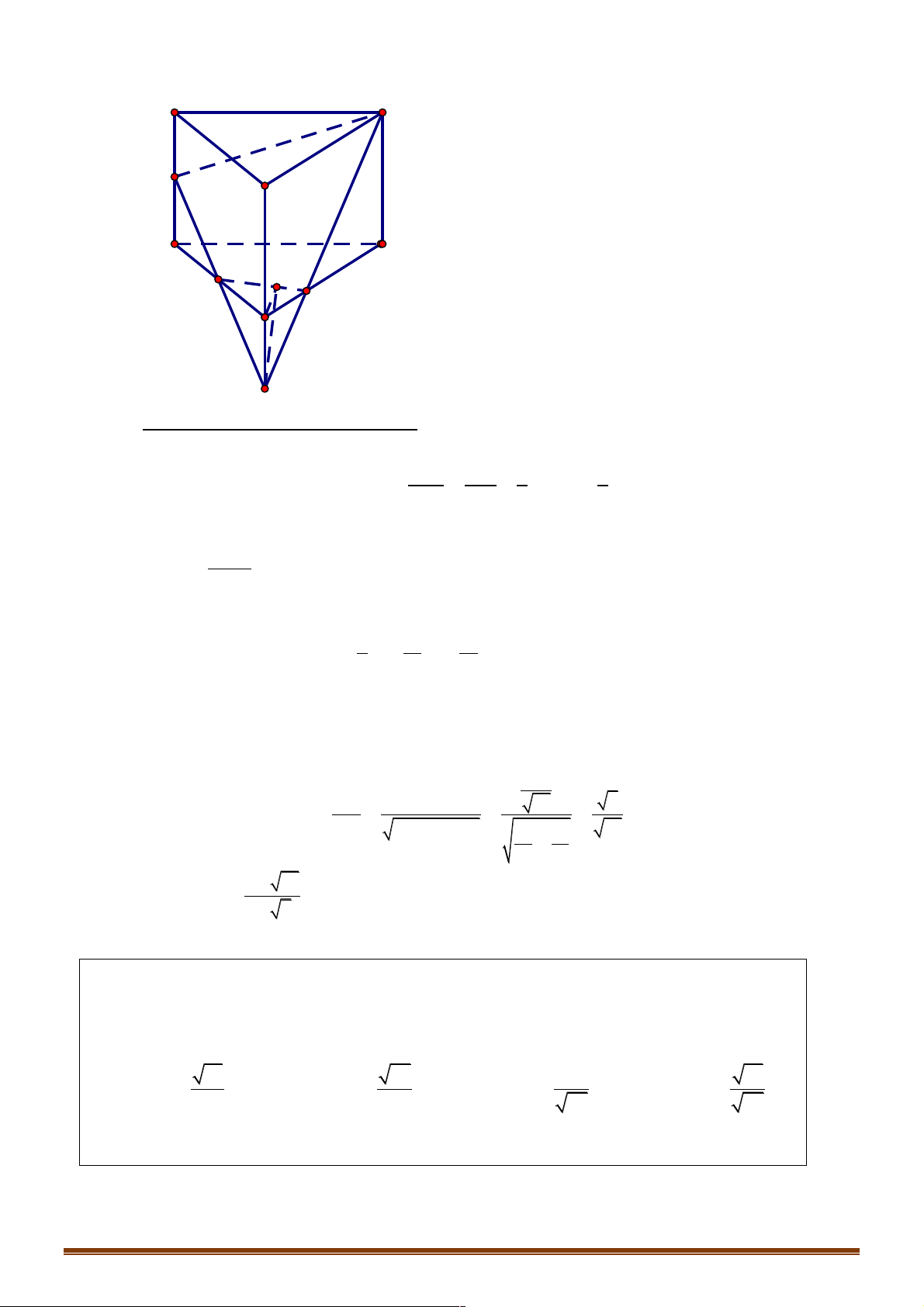
D. a = b + c Hướng dẫn giải A C A1 B1 B D1 C1 A B C1 A1 D C B1
! ! "! """! """! """! """! """! ! Ta có:
b - c + d = AB - AC + BC = CB + BC = 0 Chọn C
Câu 11: Trong các khẳng định sau đây, khẳng định nào sai?
A.Nếu giá của ba vectơ cắt nhau từng đôi một thì 3 vectơ đồng phẳng ! ! ! !
B.Nếu ba vectơ a,b, c có một vec tơ 0 thì ba vectơ đồng phẳng Trang 12 ! ! !
C.Nếu giá của ba vectơ a,b, c cùng song song với một mật phẳng thì ba vec tơ đó đồng phẳng ! ! !
D.Nếu trong ba vectơ a,b, c có ha vec tơ cùng phương thì ba vectơ đó đồng phẳng Hướng dẫn giải Chọn A
Câu 12: Cho ABC .
D A B C D là hình hộp, trong các khẳng định sau khẳng định sai: 1 1 1 1 !!!!" !!!!" !!!" !!!!" !!!" !!!!" "
A. AC + A C = 2AC
B. AC + CA + 2CC = 0 1 1 1 1 1 !!!!" !!!!" !!!" !!!" !!!" !!!!"
C. AC + A C = AA
D. CA + AC = CC 1 1 1 1 1 Hướng dẫn giải A B D C A1 B1 D1 C1
!!!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" Ta có:
AC + A C = AA AC = AA - AC Û A C = C A 1 1 1 1 1 1 1 1 1 Chọn C
Câu 13: Hãy chọn mệnh đề đúng trong các mệnh đề sau: !!!" !!!" !!!" !!!" "
A.Tứ giác ABCD là hình bình hành nếu AB + BC + CD + DA = 0 !!!" !!!"
B. Tứ giác ABCD là hình bình hành nếu AB = CD !!" !!!" !!" !!!"
C. Cho hình chóp S.ABCD, nếu có SB + SD = SA + SC thì tứ giác ABCD là hình bình hành !!!" !!!" !!!"
D.Tứ giác ABCD là hình bình hành nếu AB + AC = AD Hướng dẫn giải Chọn C
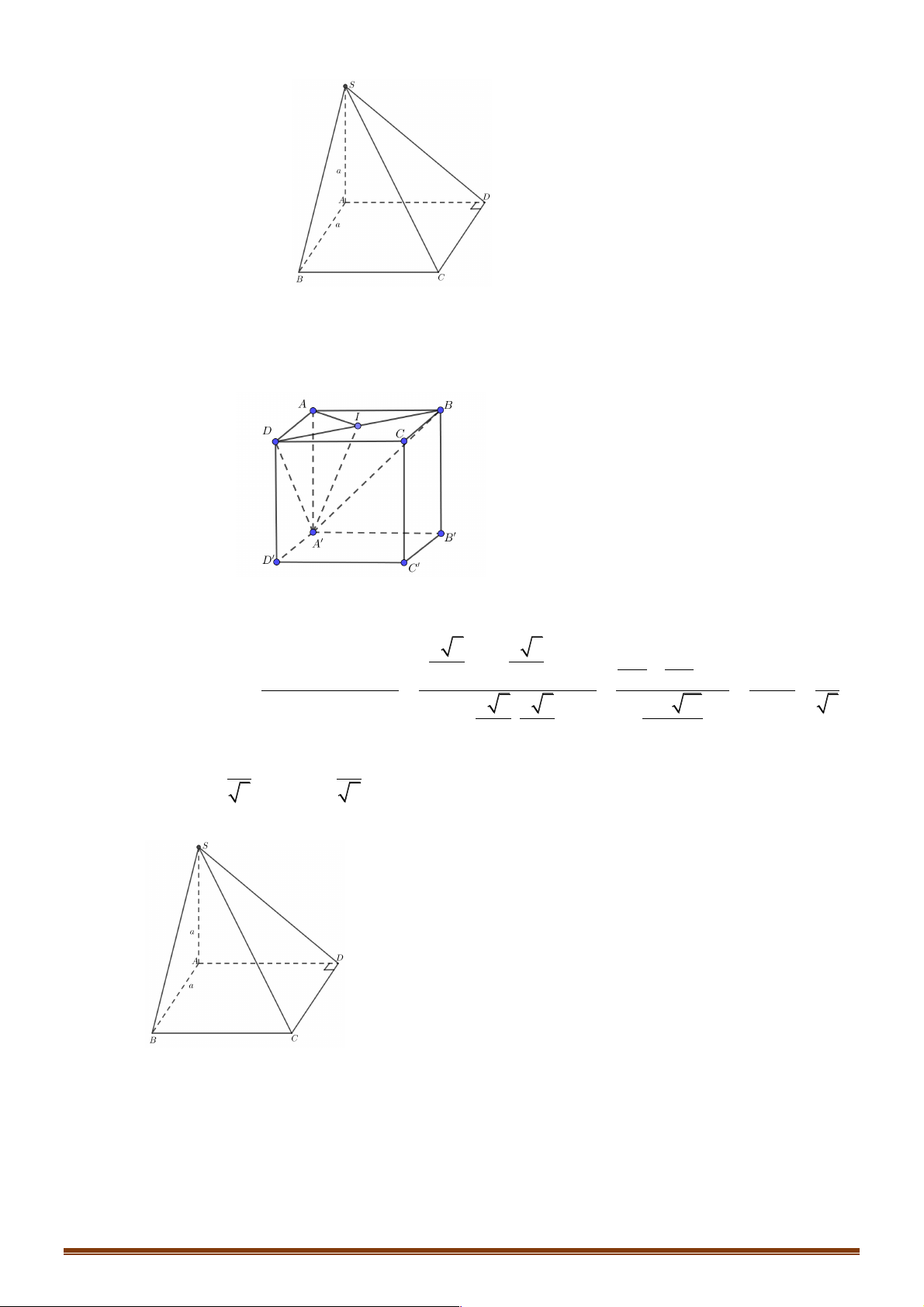
Câu 14: Cho hình hộp ' ' ' ' ABC .
D A B C D Gọi I, K lần lượt là tâm của các hình bình hành ' ' ABB A và ' '
BCC B . Khẳng định nào sau đây là sai?
A.Bốn điểm I, K, C, A đồng phẳng !!" 1 !!!" 1 !!!!" B. ' '
IK = AC = A C 2 2 !!!" !!" !!!!!"
C.Bà vec tơ BD, IK, B 'C ' không đồng phẳng !!!" !!" !!!"
D. BD + 2IK = 2BC Hướng dẫn giải Chọn C Trang 13 A B D C
Câu 15: Cho tứ diện ABCD. Trên các cạnh AC, BD lần lượt lấy M, Nsao cho AM=3MD; BN=3NC. A1
Gọi P,Q lần lượt là trung đi
B1 ểm của AD, BC. Trong các khẳng định sau, khẳng định nào sai? !!!" !!!" !!!!"
A.Các vec tơ BD, AC, MN không đồng phẳng !!!!" !!!" !!!"
B. Các vec tơ MN, DC, PQ đồng phẳng !!!" !!!" !!!"
C. Các vec tơ AB, DC, PQ đồng phẳng D1 C1 !!!" !!!" !!!!"
D. Các vec tơ AC, DC, MN đồng phẳng Hướng dẫn giải A P M E B F D Q N C
Lấy điểm E trên cạnh AC sao cho AE=3EC, lấy F trên BD sao cho BF=3FD ì 1
NE / / AB, NE = AB ïï 3 í
Þ NE / /MF, NE / /MF 1
ïMF / /AB,MF = AB ïî 3 !!!" !!!" !!!!"
Þ NEMF là hình bình hành và 3 vec tơ ,
BA DC, MN có giá song song hoặc nằm trên mặt !!!" !!!" !!!!" phẳng (MFNE) Þ ,
BA DC, MN đồng phẳng !!!" !!!" !!!!"
Þ BD, AC, MN không đồng phẳng. Chon A
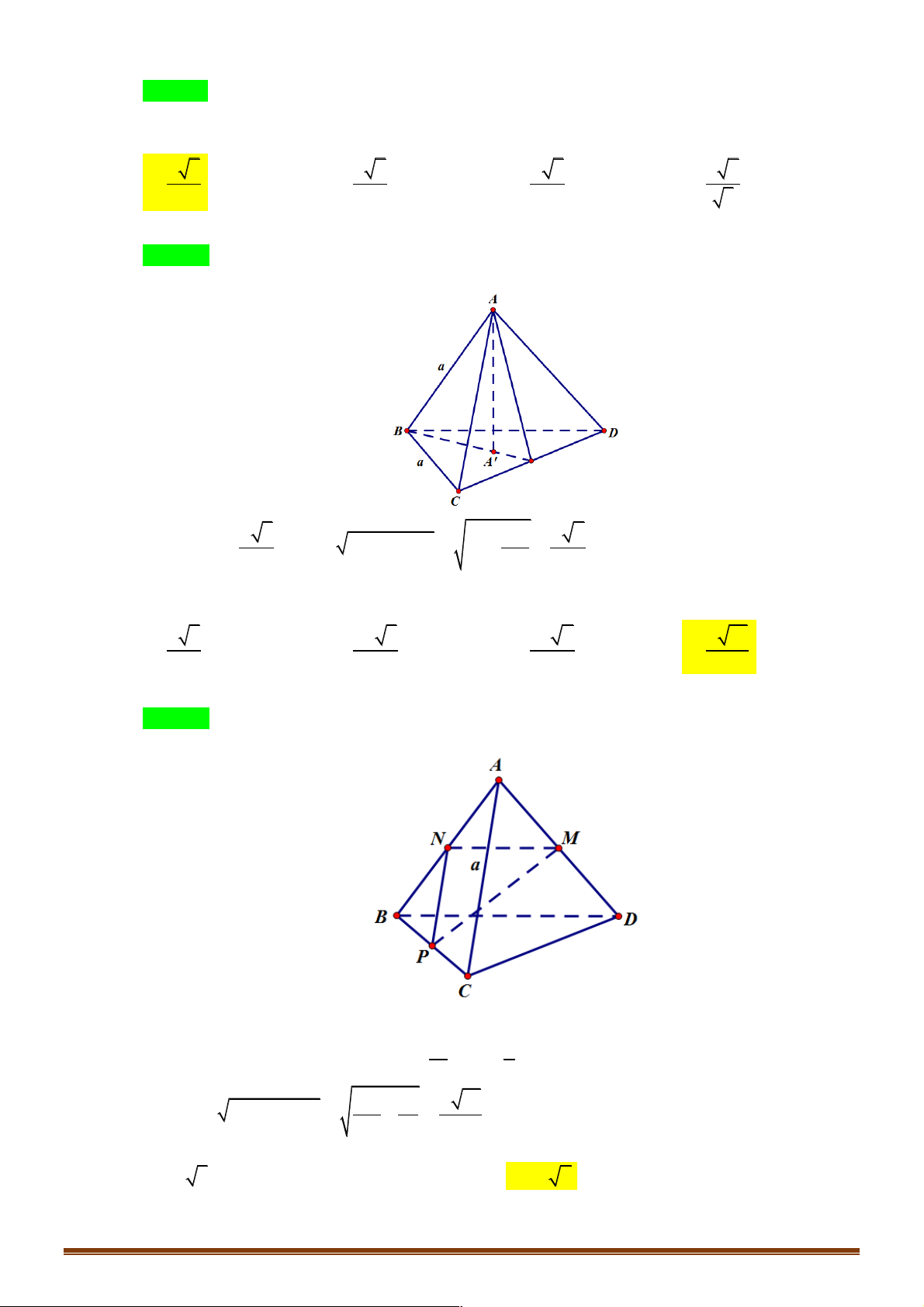
Câu 16. Cho tứ diện ABCD có các cạnh đầu bằng A. Hãy chỉ ra mệnh đề đúng trong các mệnh đề sau: !!!" !!!" !!!" !!!" " 2 !!!" !!!" a 3
A. AD + CD + BC + DA = 0 B. . AB AC = 2 !!!" !!!" !!!" !!!" !!!" !!!" C. . AC AD = . AC CD D. . AD CD = 0 Hướng dẫn giải ( sử dụng hình câu 7) Phương án A: !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" " !!!" "
AD + CD + BC + DA = (AD + D )
A + (BC + CD) = 0 + BD ¹ 0 Þ A sai Trang 14 2 !!!" !!!" a Phương án B: 0 . AB AC = . a . a c os60 = Þ B sai 2 !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" Phương án B 2
AC.AD = AC.CD Û AC(AD + DC) = 0 Û AC = 0 Þ C sai Chọn D
Câu 17: Cho hình lập phương ABC .
D A B C D . Gọi M là trung điểm của AD.Chọn khẳng định đúng: 1 1 1 1 !!!!" !!!" !!!!!" !!!!" !!!!" !!!!" !!!!!" 1 !!!!"
A. B M = B B + B A + B C A
B. C M = C C + C D + C B 1 1 1 1 1 1 1 1 1 1B 1 1 2 !!!!" !!!!" 1 !!!!!" 1 !!!!" !!!" !!!!" !!!!!" !!!!"
C. C M = C C + C D + C B
D. BB + B A + B C = 2B D 1 1 1 1 1 1 2 2 1 1 1 1 1 1 D C Hướng dẫn giải A1 B1 A aD1 B C1 a M D C A1 A B1 D1 C1 P
!!!!" !!!!!" !!!!" !!!!" !!!!!" !!!!" 1 !!!!" M Ta có
C M = C D + D D + DM = C D + C C + C B 1 1 1 1 1 1 1 1 1 2 E Chọn B B F D !!!" !!!" !!!" "
Câu 18: Cho tứ diện ABCD và điểm G thỏa GA + GB + GC = 0 ( G là trọng tâm của tứ di Q ện). G N C ọi O là
giao điểm của GA và mặt phẳng (BCD) . Trong các khẳng định sau, khẳng định nào sai? !!!" !!!" !!!" A!!!" A. GA = 2 - OG
B. GA = 4OG !!!" !!!" !!!" !!!"
C. GA = 3OG
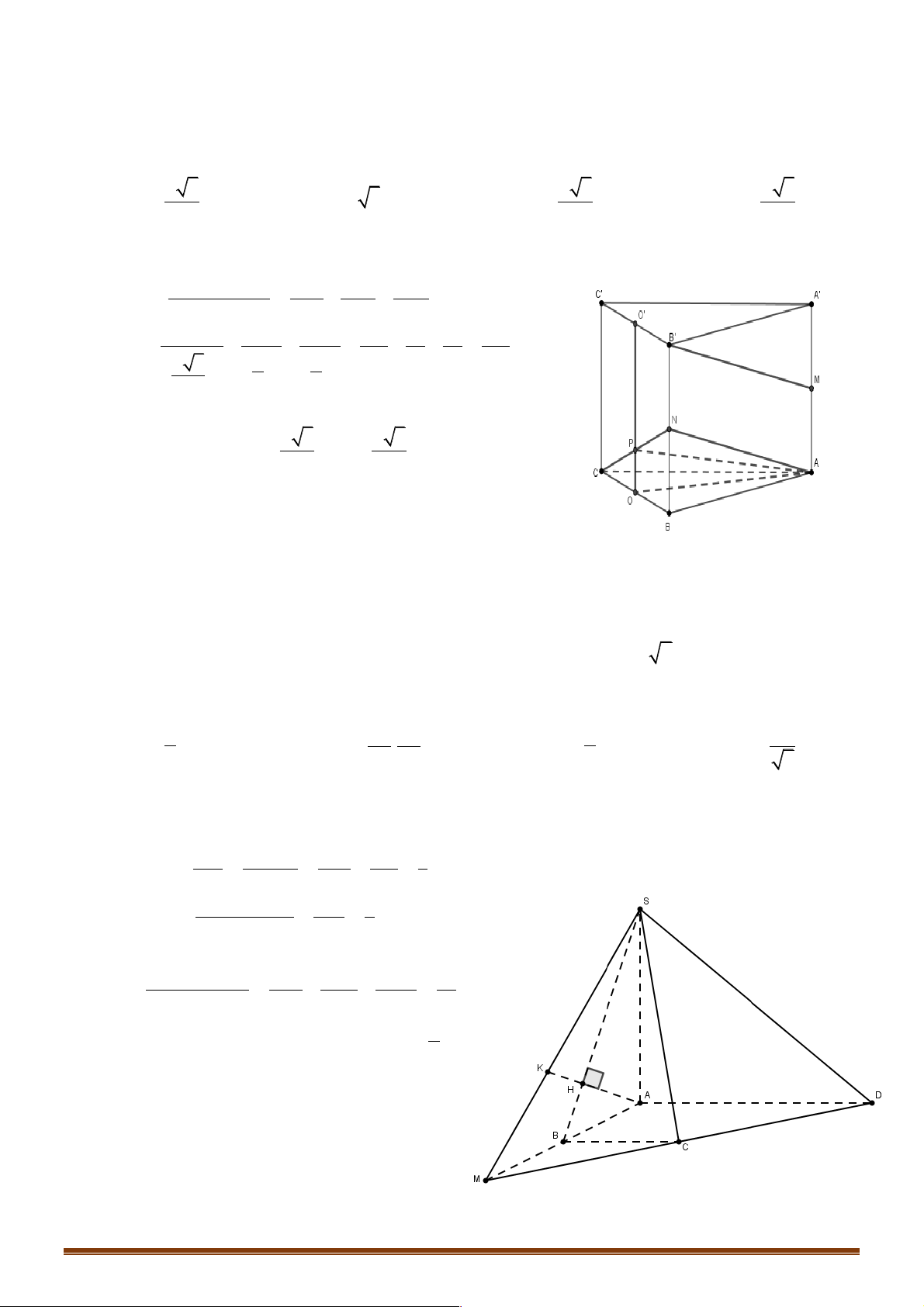
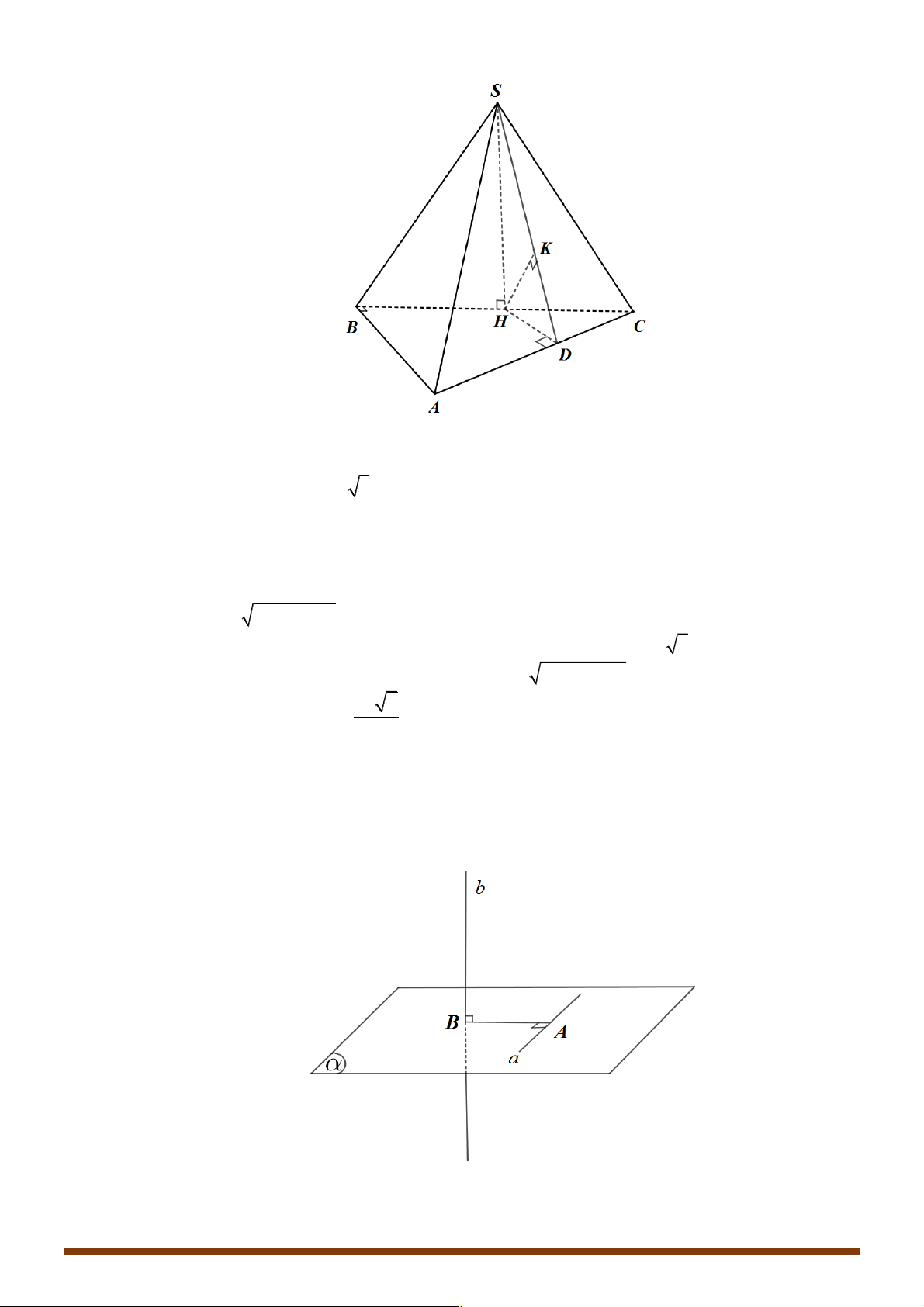
D. GA = 2OG A P M E N B F D G B Q N C D H O M C Hướng dẫn giải Trang 15 A N G B D H O M C x M A B N y A B D C A1 B1 D1 C1 A P M E B F D Q N C
Gọi M, N là trung điểm của BC, AD
Þ G là trung điểm MN. Gọi H là hình chiếu của N lên MD Þ NH là đường trung bình của AO D
D và OG là đường trung bình của MN D H A 1 1 1 1 1
Þ OG = NH = . AO Þ OG = NH = .AO 2 2 2 2 4 !!!" !!!" hay GA = 3OG N Chọn C G B
Câu 19: Cho tứ diện ABCD. Gọi M, NlaaHfn lượ
D t là trung điểm của AD, BC. Trong ccs khẳng định sau, O khẳng định nào sai? M !!!" !!!" !!!!"C
A.Các vec tơ AB, DC, MN đồng phẳng !!!!" !!!" !!!"
B. Các vec tơ MN, AB, AC không đồng phẳng !!!" !!!!" !!!!"
C. Các vec tơ AN, CM , MN đồng phẳng !!!" !!!" !!!!"
D. Các vec tơ AC, BD, MN đồng phẳng Hướng dẫn giải A M P B Q D N C
Gọi P, Q lần lượt là trung điểm AC, BD !!!" !!!" !!!!"
Þ Ba vec tơ AB, DC, MN có giá song song hoặc nằm trên mặt phẳng (MNPQ) nên 3 véc tơ !!!"
này đồng phẳng Þ A đúng !!!" !!!" !!!!"
Ba vec tơ AB, AC, MN không đồng phẳng B đúng !!!" Þ !!!" !!!!" !!!!"
Ba vec tơ AN,CM , MN có giá không thể song song với mặt phẳng nào C sai !!!" Þ Chọn C
Câu 20: Cho hình lập phương ' ' ' ' ABC .
D A B C D , có cạnh A.Hãy tìm mệnh đề sai trong các mệnh đề sau: !!!!" !!!!" !!!!" !!!!" A. 2
AD'.CC ' = a - B. 2
AD'.AB' = a !!!!" !!!!" !!!"
C. AB'.CD' = 0
D. AC = a 3 Hướng dẫn giải A a B a D C A' B' Trang 16 D' C' A P M E B F D Q N C A N G B D H O M C A M P B Q D N C A a B a D C A' B' D' C' A P M E B F D Q N C A N G B D H O !!!!" !!!!" !!!!" !!!!" !!!!" !!!!" Xết phương án A có: 0 2 M
AD '.CC ' = AD '.AA ' = AD ' . AA ' cos45 = a C Chọn A
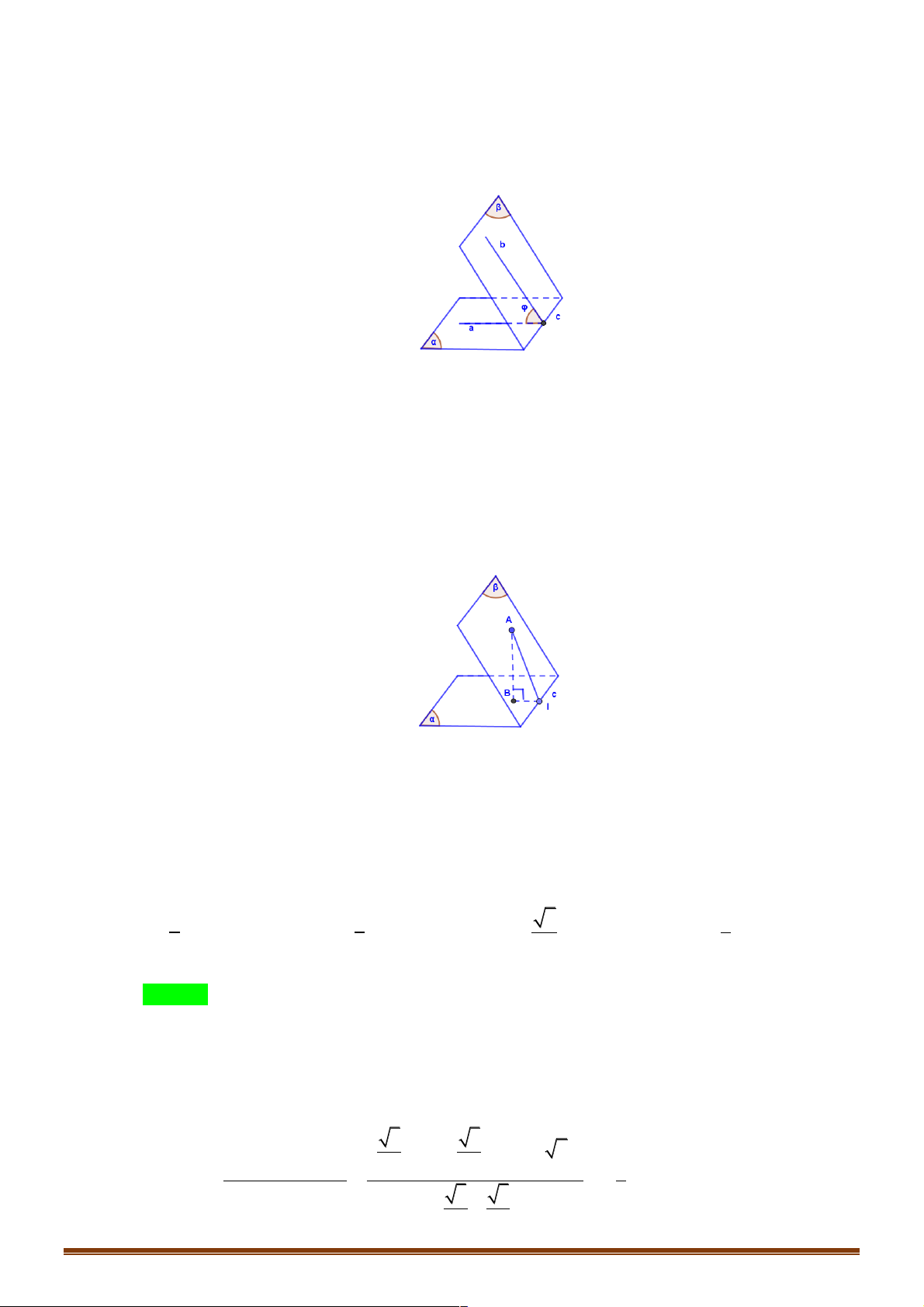
Câu 21: Trong không gian cho hai tia Ax, By chéo nhau sao cho AB vuông góc với cả hai tia đó. Các
điểm M, N lần lượt thay đổi trên Ax, By sao cho độ dài đoạn MN luôn bằng giá trị c không đổi
(c ³ AB). Gọi j là góc giữa Ax, By. Giá trị lơn nhất của AM, BN 2 2 c - AB 2 2 c - AB A. B. 2(1- os c j) 2(1+ os c j) 2 2 c + AB 2 2 c + AB C. D. 2(1- os c j) 2(1+ os c j) Hướng dẫn giải x M A B N y !!!!" !!!" !!!" !!!" Ta có: 2 2 2 2
c = MN = MN = (MA + AB + BN) 2 2 - 2 ³ c AB
AB + 2AM.BN.(1- c s
o j) Þ AM.BN. £ 2(1- os c j) 2 2 c - AB
Vậy biểu thức AM.BN đạt giá trị lớn nhất bằng 2(1- os c j) Chọn A !!!!" !!!" 2 2 2 2 2 2
= AM + AB + BN - 2AM.BN == AM + AB + BN - 2AM.BN.cosj
@Góc giữa hai đường thẳng.
Hai đường thẳng vuông góc 1. Định nghĩa: Trang 17
Góc giữa hai đường thẳng cắt nhau a và b là góc nhỏ nhất trong bốn góc mà a và b cắt nhau tạo nên.
Góc giữa hai đường thẳng cắt nhau a và b trong không gian là góc giữa hai đường thẳng a¢ và
b¢ cùng đi qua một điểm và lần lượt song song (hoặc trùng) với a và b .
Chú ý: góc giữa hai đường thẳng luôn là góc nhọn ( hoặc vuông ). 2. Phương pháp
Phương pháp 1: Sử dụng định lý hàm số cosin hoặc tỉ số lượng giác. ! !
Phương pháp 2: Sử dụng tích vô hướng: nếu u và v lần lượt là hai vecto chỉ phương ( hoặc
vecto pháp tuyến ) của hai đường thẳng a và b thì góc j của hai đường thẳng này được xác định bởi công thức ! ! ! ! j = (u v) .uv cos cos , = ! ! . u . v
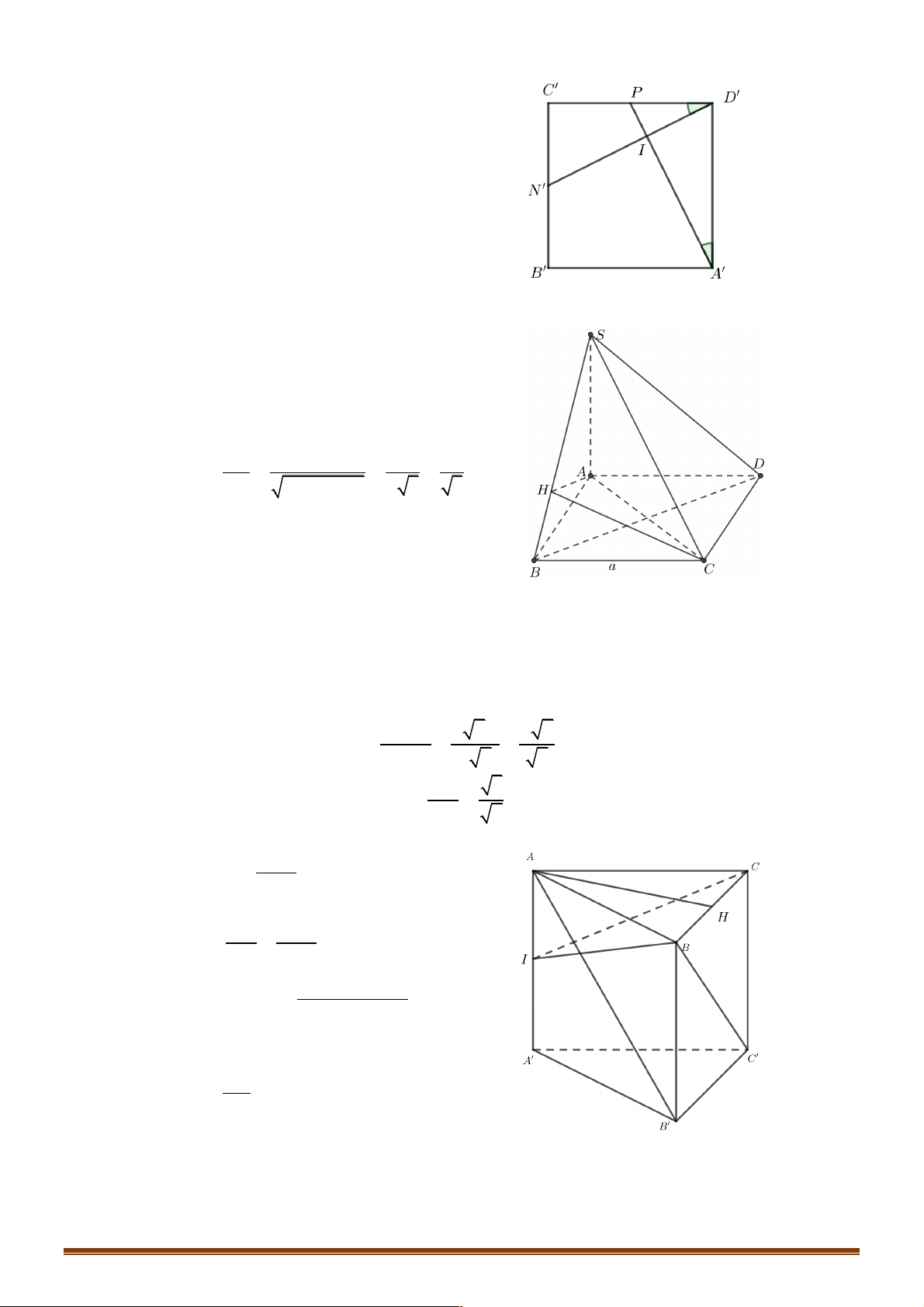
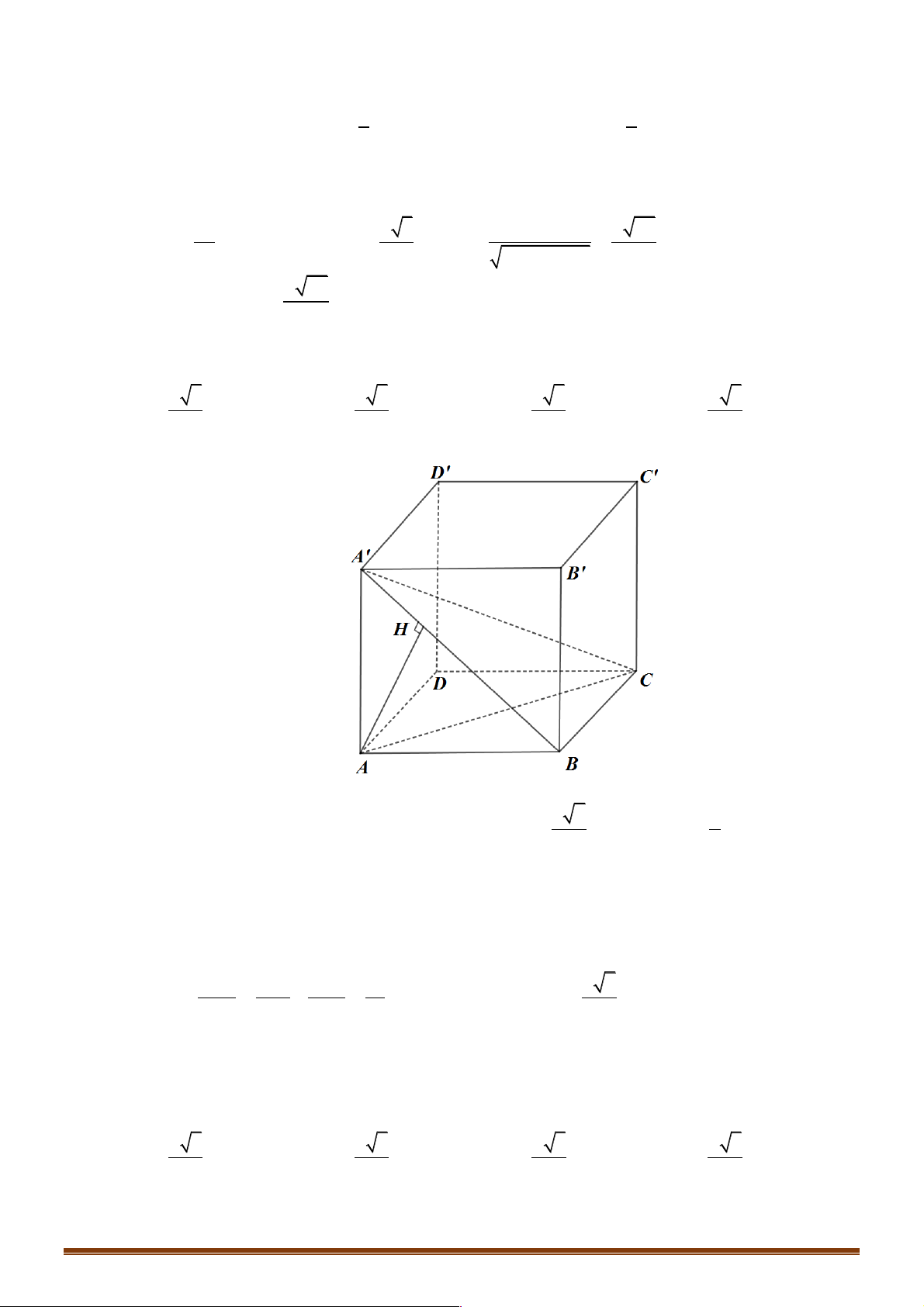
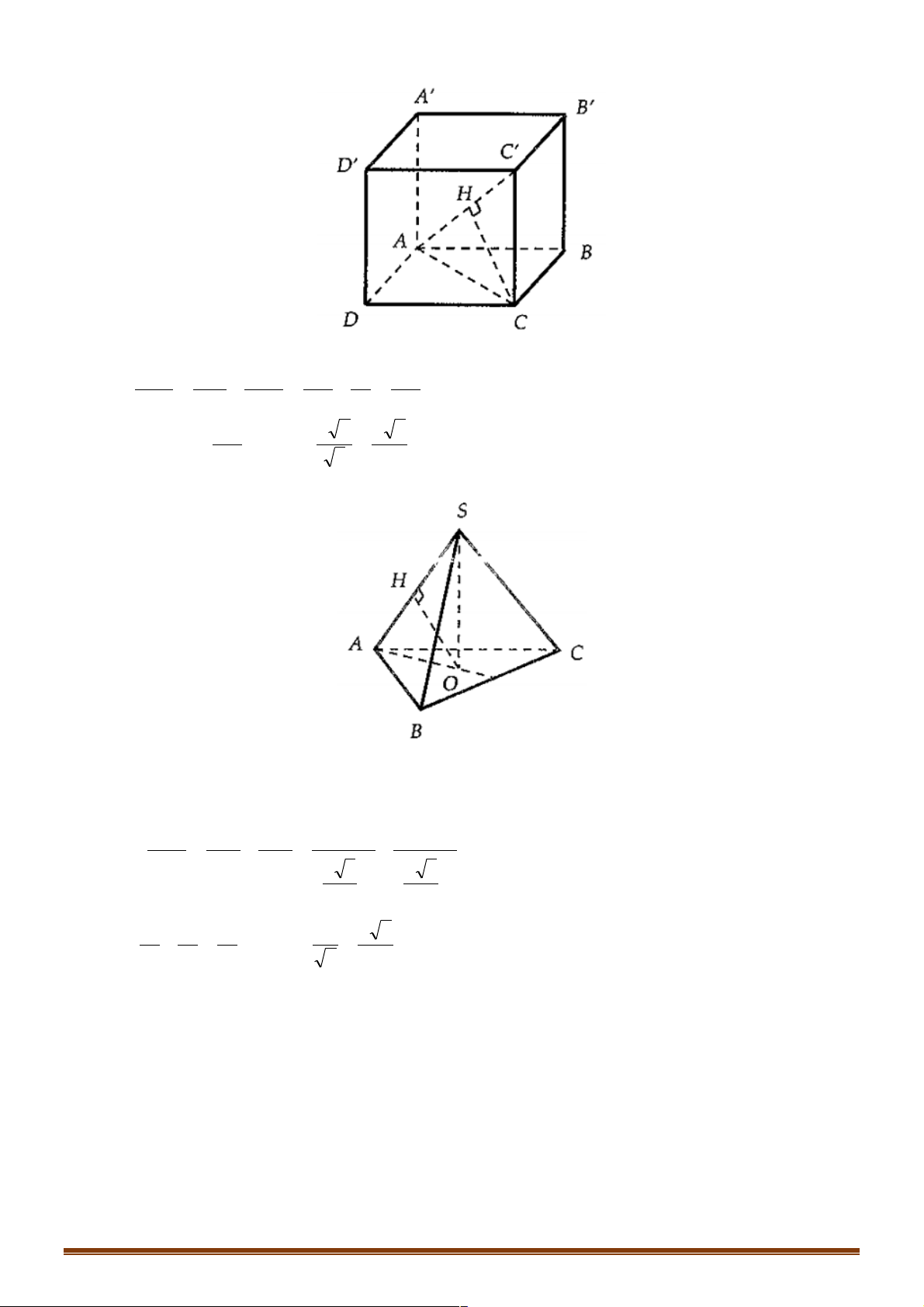
Ví dụ 1: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Gọi M , N, P lần lượt là trung điểm các cạnh AB , BC , C D
¢ ¢ . Xác định góc giữa hai đường thẳng MN và AP . A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 Đáp án A. Lời giải
Phương pháp 1: Giả sử hình lập phương có cạnh bằng a và MN //AC nên: ∑ (MN,AP) ∑
= (AC, AP). Ta tính góc ∑ PAC . Vì A D ¢D P
¢ vuông tại D¢ nên 2 æ a ö a 5 2 2 2 A P ¢ = A D ¢ ¢ + D P ¢ = a + = . ç ÷ è 2 ø 2 2 æ a 5 ö 3a AA
D ¢P vuông tại A¢ nên 2 2 2 AP = A A ¢ + A P ¢ = a + ç ÷ = . ç 2 ÷ 2 è ø 2 a a 5 CC D P
¢ vuông tại C¢ nên 2 2 2
CP = CC¢ + C P ¢ = a + = . 4 2
Ta có AC là đường chéo của hình vuông ABCD nên AC = a 2
Áp dụng định lý cosin trong tam giác ACP ta có: 2 2 2 ∑
CP = AC + AP - 2AC.A . P cosCAP ∑ 1 Þ cosCAP = 2 ∑
Þ cosCAP = 45° < 90° Trang 18 Nên ∑ (AC AP) ∑ ; = CAP = 45° hay ∑
(MN;AP)=45°. Chọn A. !!!!" !!!" !!!!" !!!" !!!!" !!!" !!!!" !!!" !!!!" !!!" MN.AP
Phương pháp 2: Ta có MN.AP = MN . AP .cos(MN, AP) Þ cos(MN, AP) = !!!!" !!!" (*) MN . AP !!!!" !!!" !!!" !!!" !!!" !!!!" !!!!"
Ta có: MN.AP = (MB + BN )( AA¢+ A D ¢ ¢ + D P ¢ )
!!!" !!!" !!!" !!!!" !!!" !!!!" !!!" !!!" !!!" !!!!" !!!" !!!!" = . MB AA¢ + . MB A D ¢ ¢+ . MB D P
¢ + BN.AA¢+ BN.A D ¢ ¢+ BN.D P ¢ 2 a a a 3a
= 0 + 0 + . + 0 + .a + 0 = ( )1 2 2 2 4 2 !!!!" !!!" a 2 3a 3 2a MN . AP = . = (2) 2 2 4 2 3a !!!!" !!!" 1 Thay ( ) 1 ,(2) vào (*) ta được: (MN AP) 4 cos , = = Þ (∑ MN, AP) 0 = 45 . 2 3 2a 2 4
Ví dụ 2. Cho tứ diện ABCD có AB = CD = 2 .
a Gọi M , N lần lượt là trung điểm BC, AD . Biết rằng
MN = a 3. Tính góc của AB và CD . A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 . Đáp án C. Lời giải
Gọi I là trung điểm của AC . Ta có IM = IN = a .
Áp dụng định lý cosin cho IM D N ta có: 2 2 2 2 2 2
IM + IN - MN
a + a - 3a 1 ∑ ∑ 0 cos MIN = = = - Þ MIN =120 . 2.IM.IN 2. . a a 2 Vì IM AB IN CD Þ (∑ AB CD) = (∑ IM IN ) 0 0 0 / / , / / , , =180 -120 = 60 . Trang 19
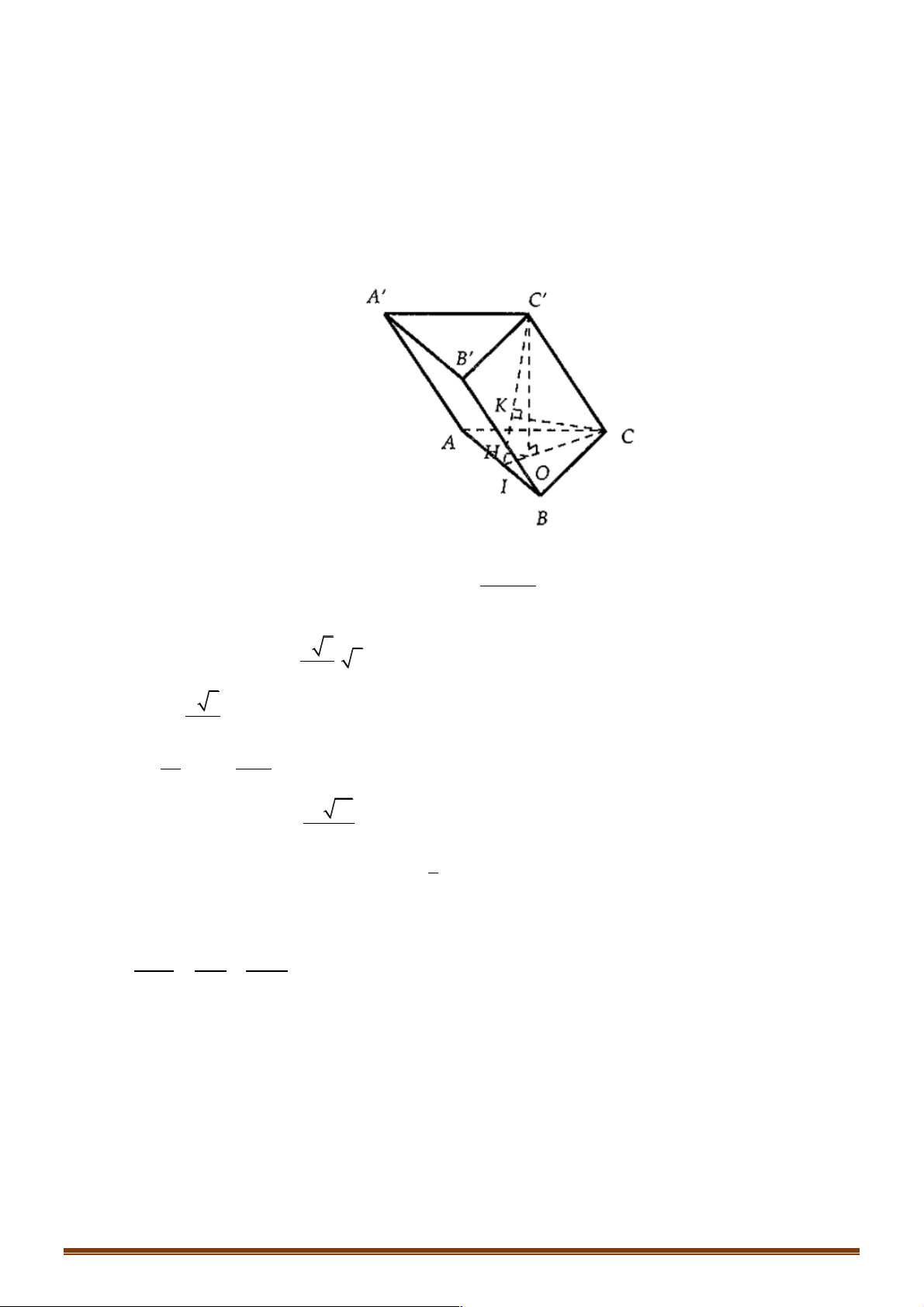
Ví dụ 3: Cho lăng trụ ABCA¢B C
¢ ¢ có độ dài cạnh bên bằng 2a , đáy ABC là tam giác vuông tại A ,
AB = a , AC = a 3 và hình chiếu vuông góc của đỉnh A¢ trên mặt phẳng ( ABC) là trung
điểm của cạnh BC . Tính cosin của góc giữa hai đường thẳng AA¢ , B C ¢ ¢. Lời giải Chọn D Phương pháp 1:
Gọi H là trung điểm của BC , j là góc giữa AA¢ và B C ¢ ¢.
Ta có AA¢ / /BB¢ và B C
¢ ¢ / /BC nên góc giữa ∑
(AA,¢BC¢¢) ∑ = (BB ,¢BC) . Ta tính góc ∑ B B ¢ H ABC D
vuông tại A nên ta có: 2 2 2 2
BC = AB + AC = a + 3a = 2a. 1 2 2 2 2
AH = BC = a Þ A H
¢ = AA¢ - AH = 4a - a = a 3. 2 Vì AH ^ ( A B ¢ C ¢ ¢) nên A D ¢B H ¢ vuông tại A¢ 2 2 2 2 B H ¢ = A H ¢ + A B
¢ ¢ = a +3a = 2a. ∑ 2 2 2 2 2 2 B B ¢ + BH - B H ¢
4a + a - 4a 1 cos B B ¢ H = = = Chọn A 2B¢ . B BH 2.2 . a a 4 Phương pháp 2: Ta có !!!" !!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!" ¢ ¢ ¢ + ¢ + ¢ j =
(AA¢ BC¢¢) AA.BC (AH HA ).BC AH.BC HA.BC AH.BC cos cos ; = !!!" !!!!" = = = 2 2 AA¢ . B C ¢ ¢ 2 . a 2a 4a 4a 1 (!!!" !!!" !!!" !!!"
AB + AC)( AC - AB) 1 ( 2 2 AC - AB ) 1 ( 2 2 3a - a ) 2 2 2 1 = = = = . 2 2 2 4a 4a 4a 4
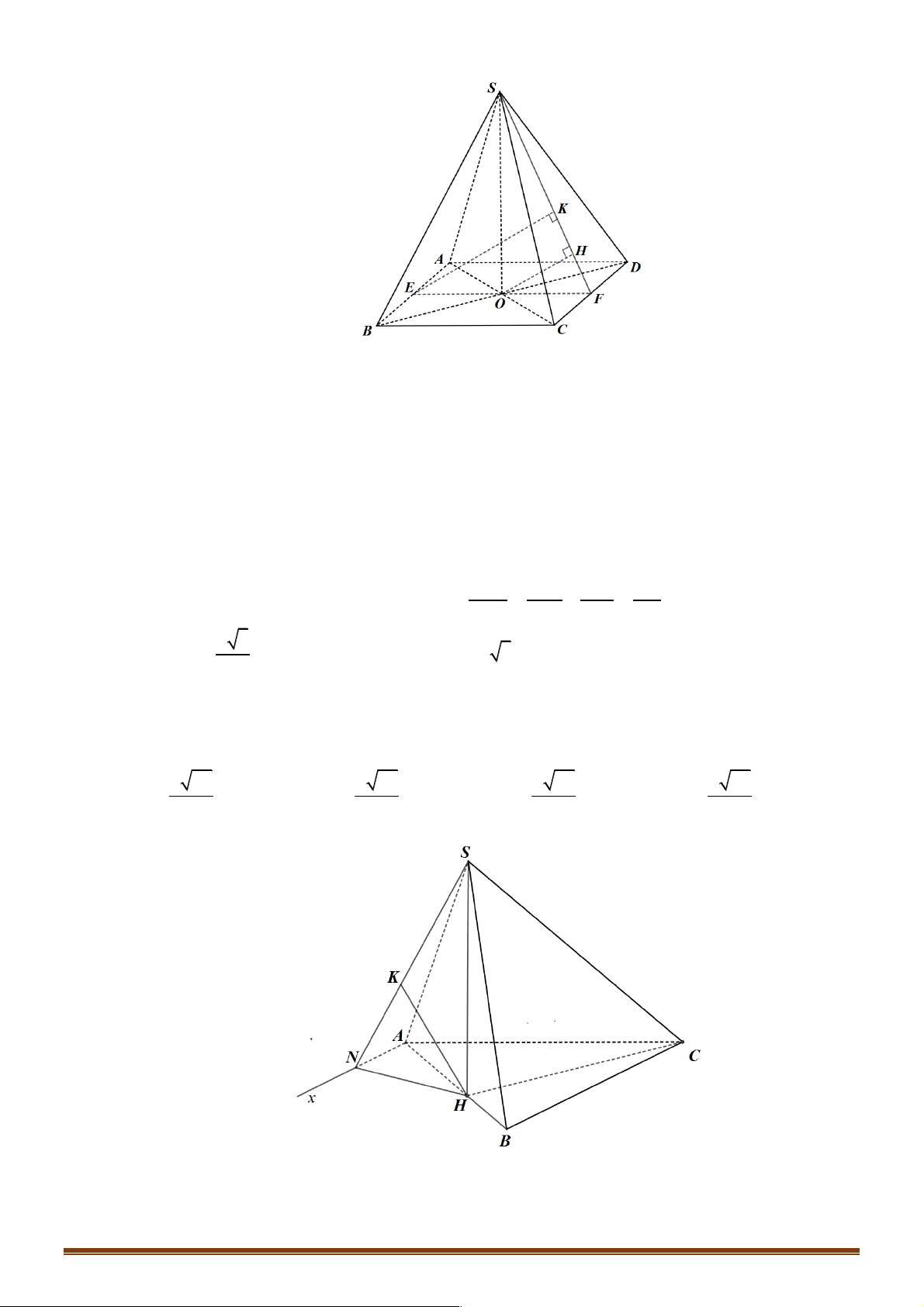
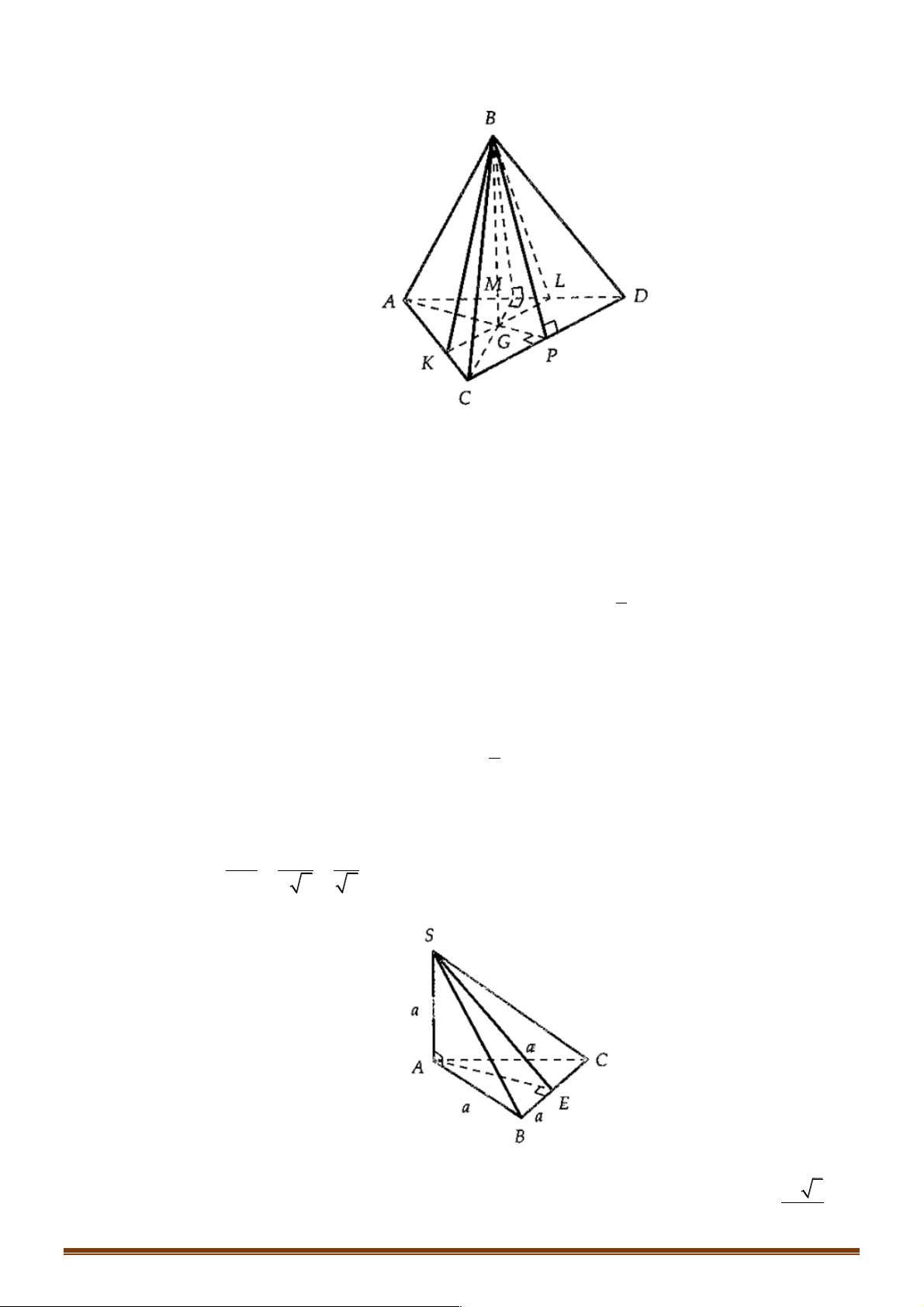
Ví dụ 11. Cho tứ diện đều ABCD cạnh a . Gọi O là tâm đường tròn ngoại tiếp BCD D . Gọi M là trung
điểm CD . Tính cosin góc của AC và BM . 3 3 3 2 A. . B. . C. . D. . 4 6 2 2 Hướng dẫn giải Chọn B
Cách 1. Gọi N là trung điểm AD ta có: MN //AC ∑ Þ ( AC;BM ) ∑
=( MN;BM ). Ta tính góc ∑ a 3
BMN . Ta có: BM = BN =
(trung tuyến tam giác đều). 2 AC a MN = = . 2 2
Áp dụng định lý cosin cho BM D N , ta được: Trang 20 ∑ 2 2 2
BM + MN - BN MN 3 cos BMN = = = > 0. 2BM.MN 2BM 6 Vậy ∑ ( AC BM) 3 cos ; = . 6 !!!" !!!!" !!!" !!!!" !!!" !!!" !!!!" AC.BM
AC. CM - CB
Cách 2. cosj = cos( AC, BM ) ( ) = !!!" !!!!" = AC . BM a 3 . a 2 2 2 2 !!!" !!!!" !!!" !!!" a a a 0 0 . a cos120 - . a . a cos120 a - +
AC.CM - AC.CB 2 4 2 3 4 = = = = = . 2 2 2 2 a 3 a 3 a 3 a 3 6 2 2 2 2
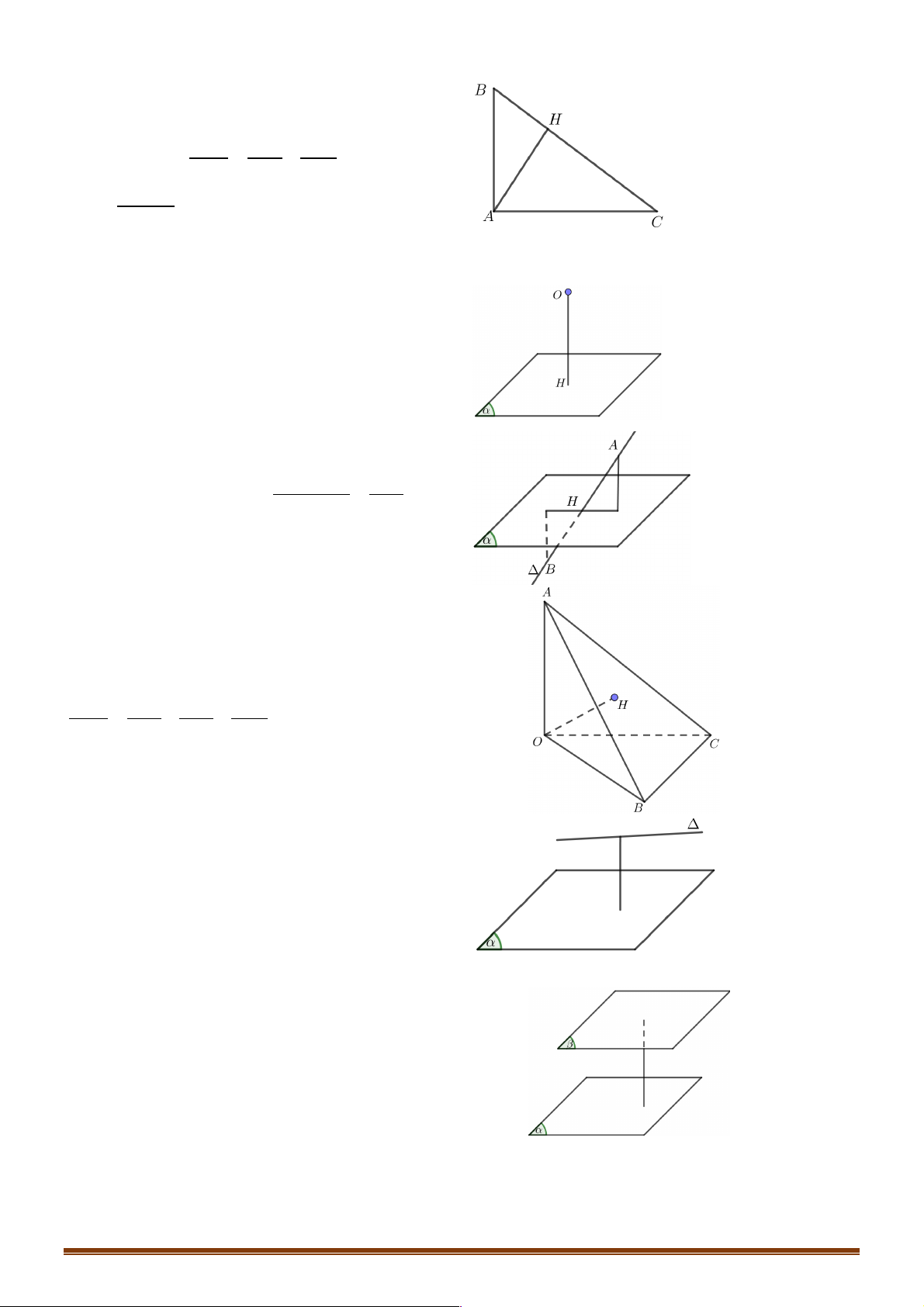
Đường thẳng vuông góc với mặt phẳng 1. Định nghĩa.
Nếu đường thẳng a ^ (P) thì góc giữa đường thẳng a và (P) bằng 0 90 .
Nếu đường thẳng a không vuông góc với (P)thì góc giữa đường thẳng a và (P) là góc giữa
a và hình chiếu a¢ của a trên (P). a a' P
2. Phương pháp tính.
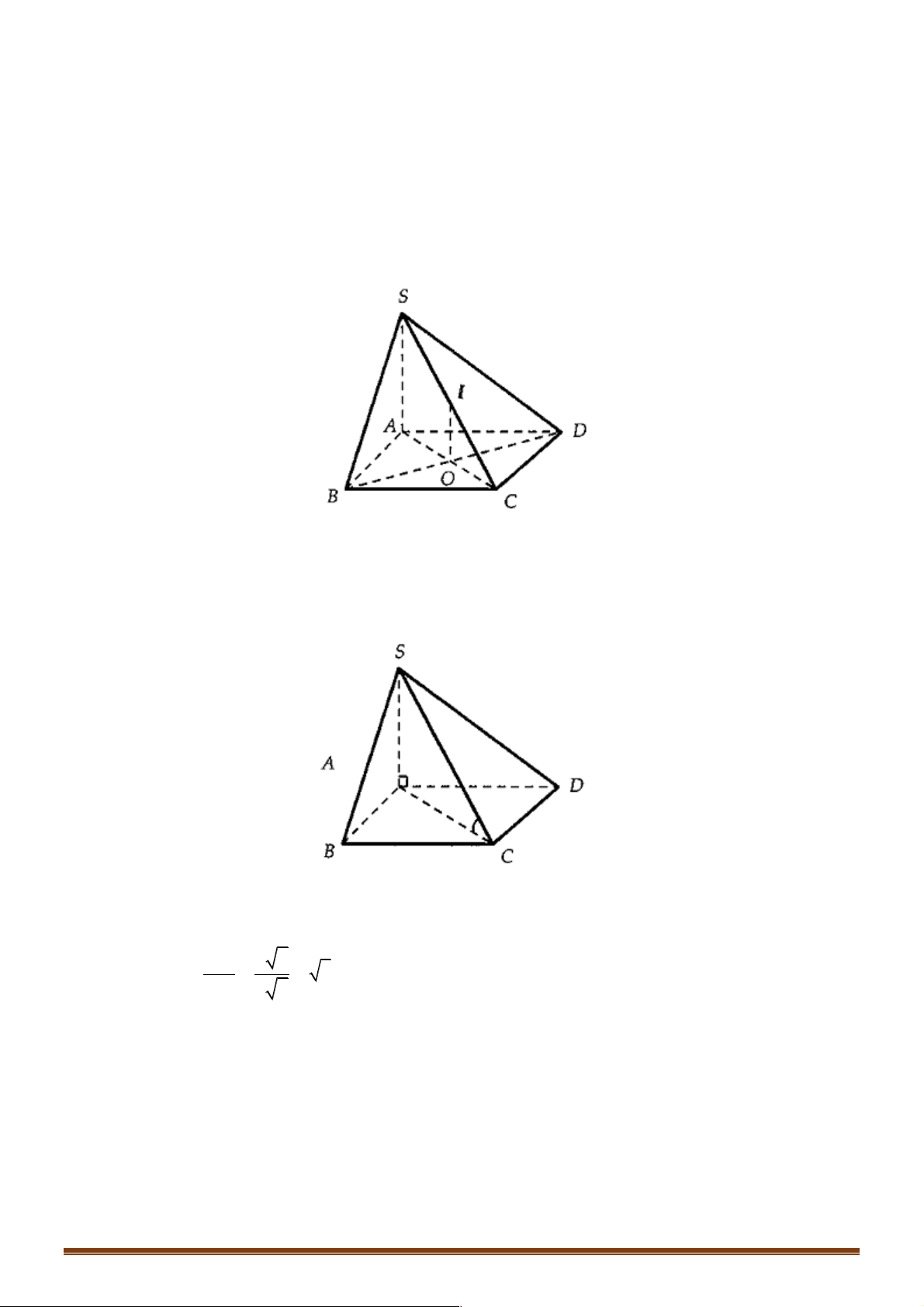
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( ABCD) và SA = a 6.
Gọi a là góc giữa SC và (SAB), b là góc giữa AC và (SBC). Giá trị tana + sin b bằng? 1+ 7 1+ 19 7 + 21 1+ 20 A. . B. . C. . D. . 7 7 7 7 Hướng dẫn giải Chọn C. Trang 21
Để xác định góc giữa SC và (SAB) ta xác định hình chiếu của SC lên mặt phẳng (SAB). Ta ìBC ^ AB
có: S là hình chiếu của S trên (SAB), B là hình chiếu của C trên (SAB) vì í . îBC ^ SA
Vậy SB là hình chiếu của SC trên (SAB) Þ (SC (SAB)) ∑ , = S B C = a . BC a 1 SB
D C vuông tại B ∑ Þ tana = tan S B C = = = . 2 2 SB SA + AB 7
Kẻ AH ^ SB tại H mà BC ^ (SAB) nên AH ^ BC .
Þ AH ^ (SBC) Þ HC là hình chiếu vuông góc của AC trên (SBC)
Þ (AC (SBC)) ∑ , = ACH = b . 1 1 1 a 6 SA D B vuông nên = + Þ AH = . 2 2 2 AH AS AB 7 AH ACH D vuông tại H ∑ 21 Þ sin b = sin ACH = = . AC 7 7 21 Vậy tana sin b + + = . 7
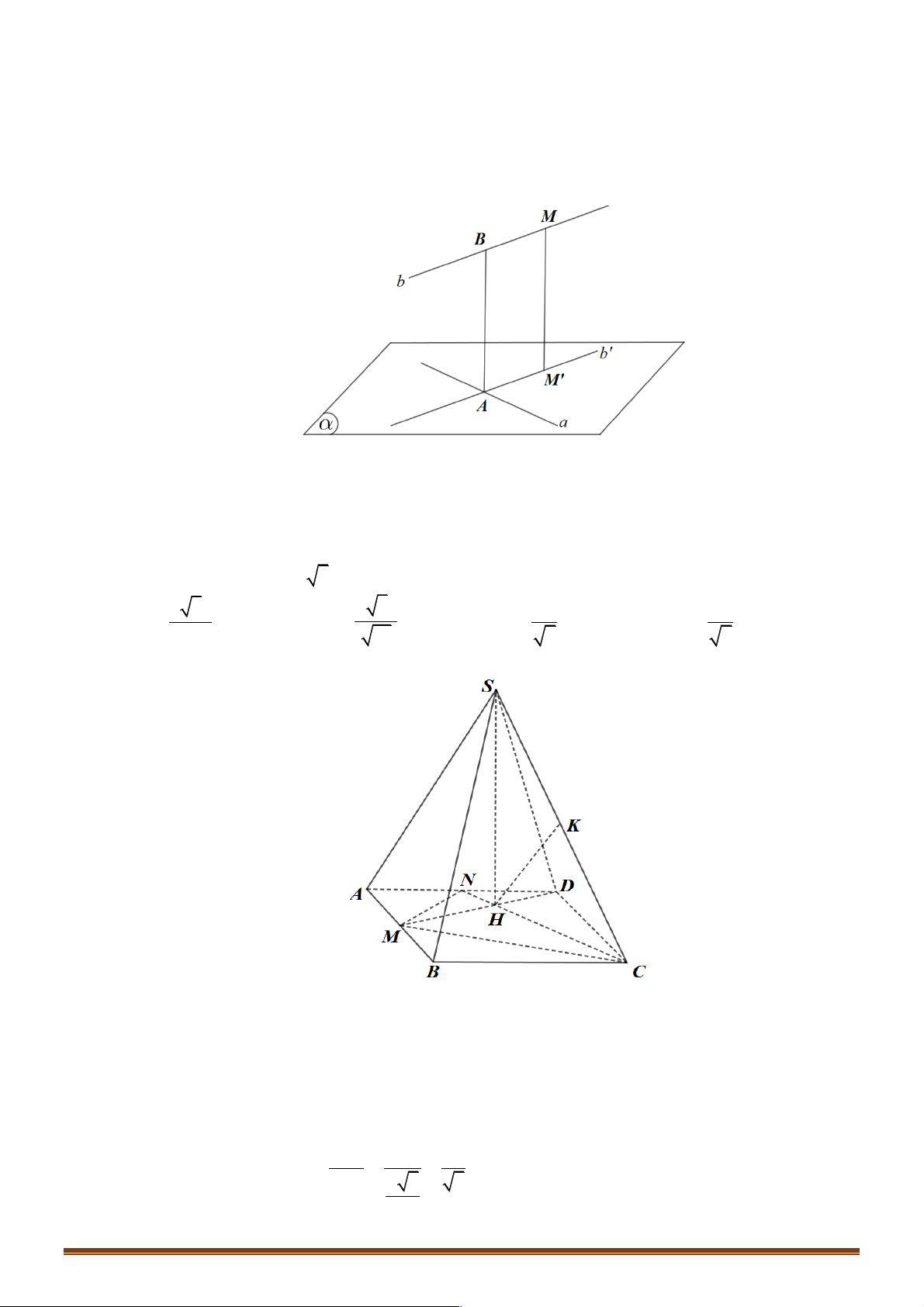
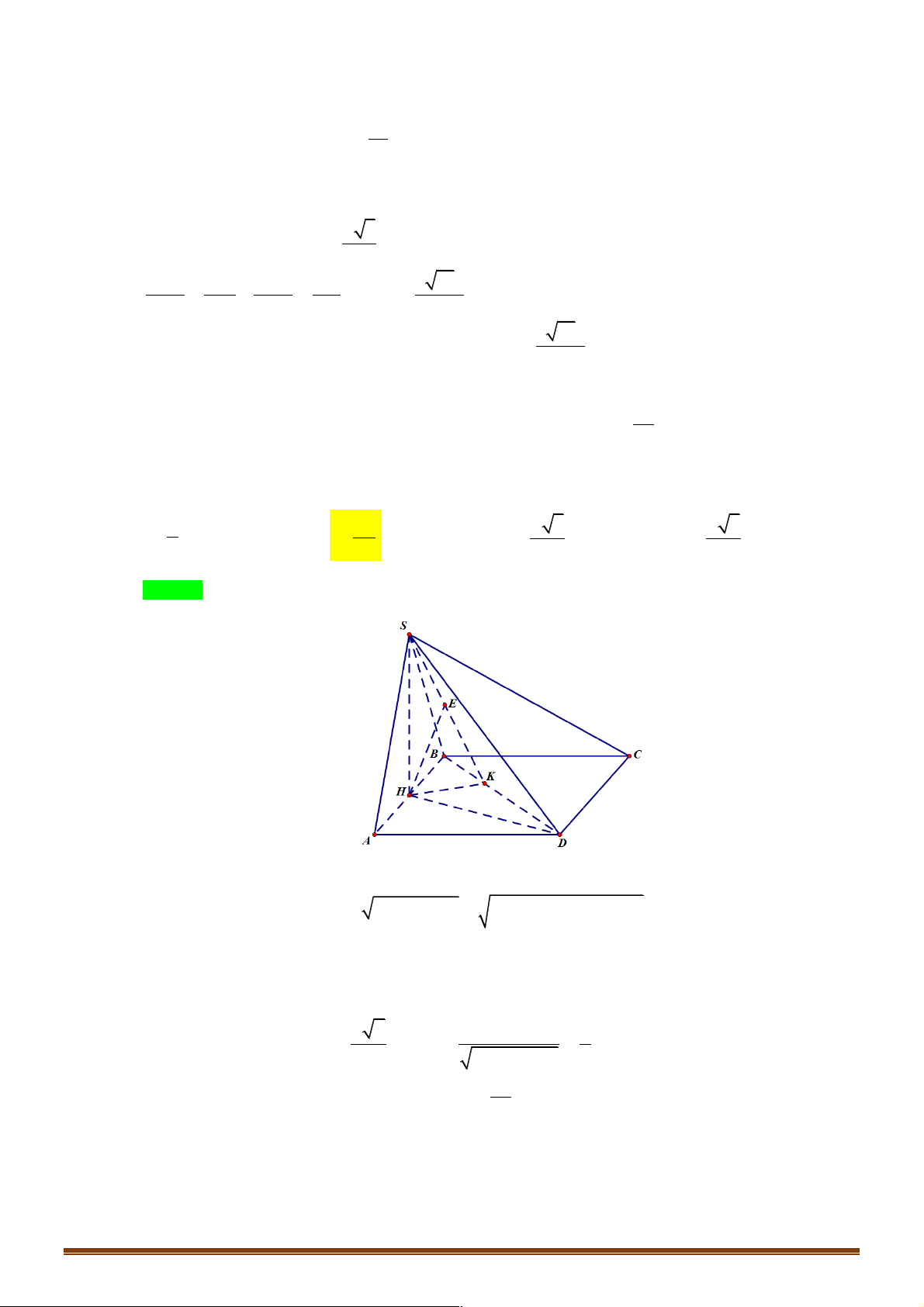
Ví dụ 2: Cho hình chóp đều S.ABCD , đáy có cạnh bằng a và có tâm O . Gọi M , N lần lượt là trung
điểm của SA , BC . Biết góc giữa MN và ( ABCD)bằng 60°. Tính góc giữa MN và (SAO .) 1 A. j = 1 arcsin . B. j = arcsin . 2 5 5 Trang 22 3 C. j = 1 arcsin . D. j = arcsin . 2 5 4 5 Lời giải Chọn A. S M A B P N O H D C
Gọi P là trung điểm của AO Þ MP là đường trung bình của SA
D O Þ MP / /SO
Þ MP ^ ( ABCD) Þ Góc giữa MN và ( ABCD) bằng góc ∑ MNP = 60 . °
Áp dụng định lý cosin cho PNC D ta có: 2 2 a æ 3 ö a 3 1 2 2 2
NP = CN + CP - 2CN. . CP cos 45° = + a 2 - 2. . a 2. ç ÷ 4 è 4 ø 2 4 2 2 2 2 2 2 2 a 9a 3 2a 11a 3a 5a = + - = - = 4 8 4 2 8 4 8
Trong tam giác vuông MNP ta có : PN 5 15 15 MN = =
.a và PM = N .t P an 60° = a Þ SO = 2MP = .a. cos 60° 2 8 2
Gọi H là trung điểm CO Þ NH / /BD Þ NH ^ AC .
Mà NH ^ SO Þ NH ^ (SAC) do đó (MN ( ∑ SAC)) ∑ , = NMH . 1 a 2 a
Ta có : HN = OB = 5 , MN = (tính trên) 2 4 2 NH Vậy trong MH D N ta có : ∑ 1 sin NMH = =
. Nên nếu gọi j là góc giữa MN và (SAO t)hì: MN 2 5 1 1 æ p ö sinj = hay j = arcsin 0 £ j £ . ç ÷ 2 5 2 5 è 2 ø
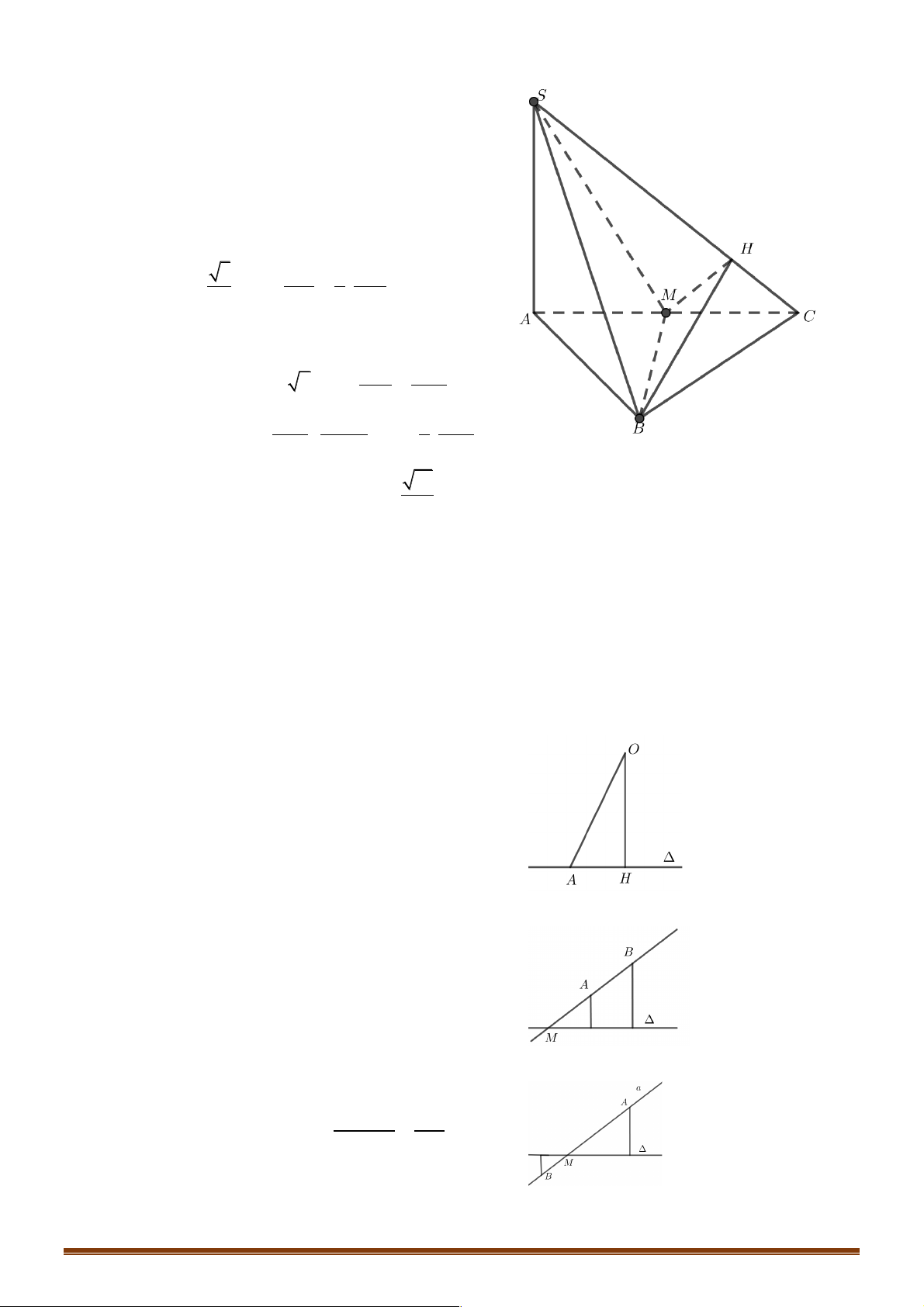
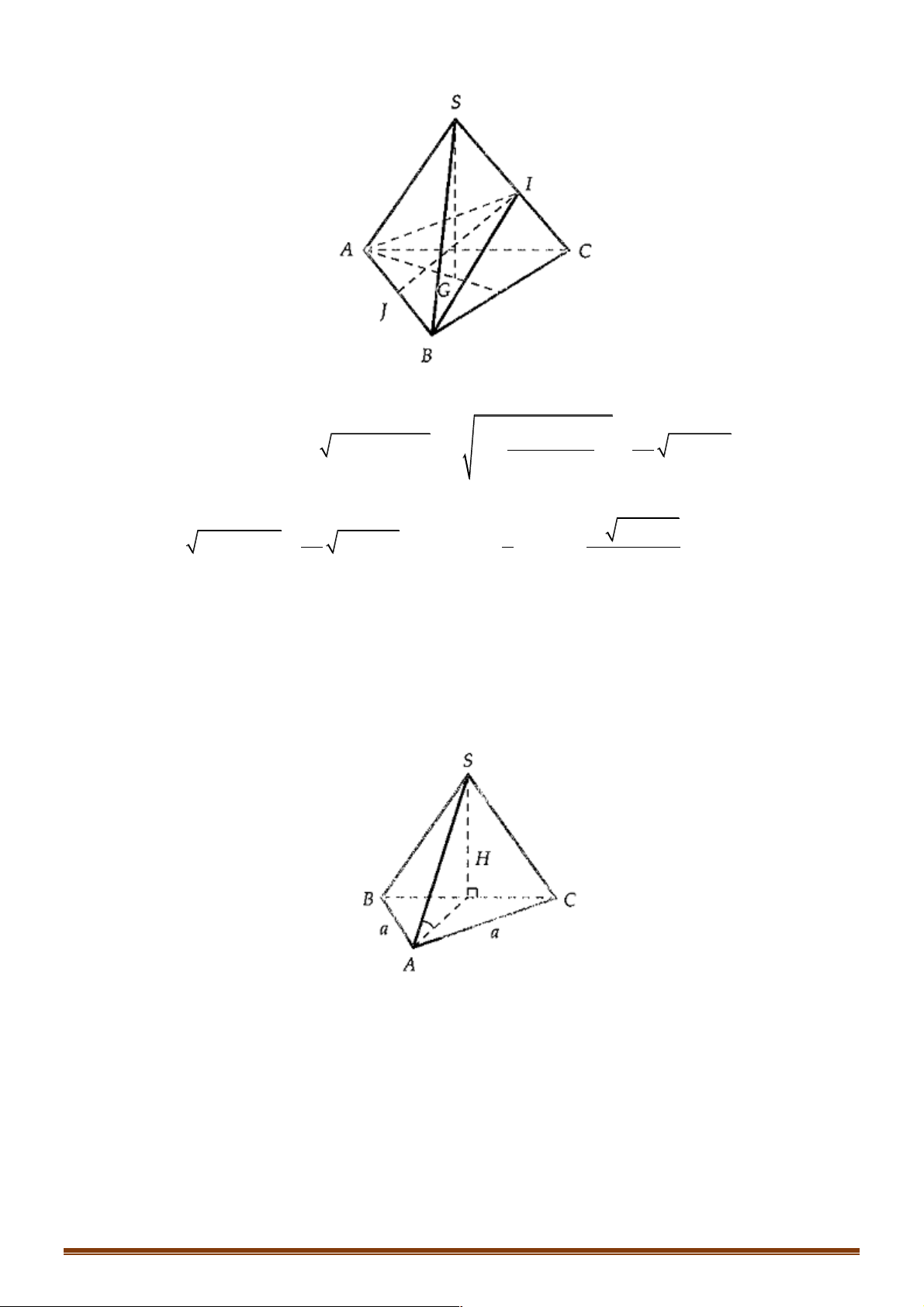
Ví dụ 3: Cho hình chóp tam giác đều S.ABC có a là độ dài cạnh đáy và ∑
CBS = a . Gọi j là góc giữa
cạnh bên với đáy. Tính sinj theo a . 1 a a A. 2 sinj = 9 -12sin . B. 2 sinj = 9 -12sin . 3 2 2 1 a 1 a C. 2 sinj = 9 - 4sin . D. 2 sinj = 9 +12sin . 3 2 3 2 Lời giải Chọn A. Trang 23 S A C a O a H B
Gọi H là trung điểm BC , O là chân đường cao hạ từ S . 2 a 3 Ta có AO = AH = , SH
D B vuông tại H nên ta có: 3 3 THIẾU PHẦN 9
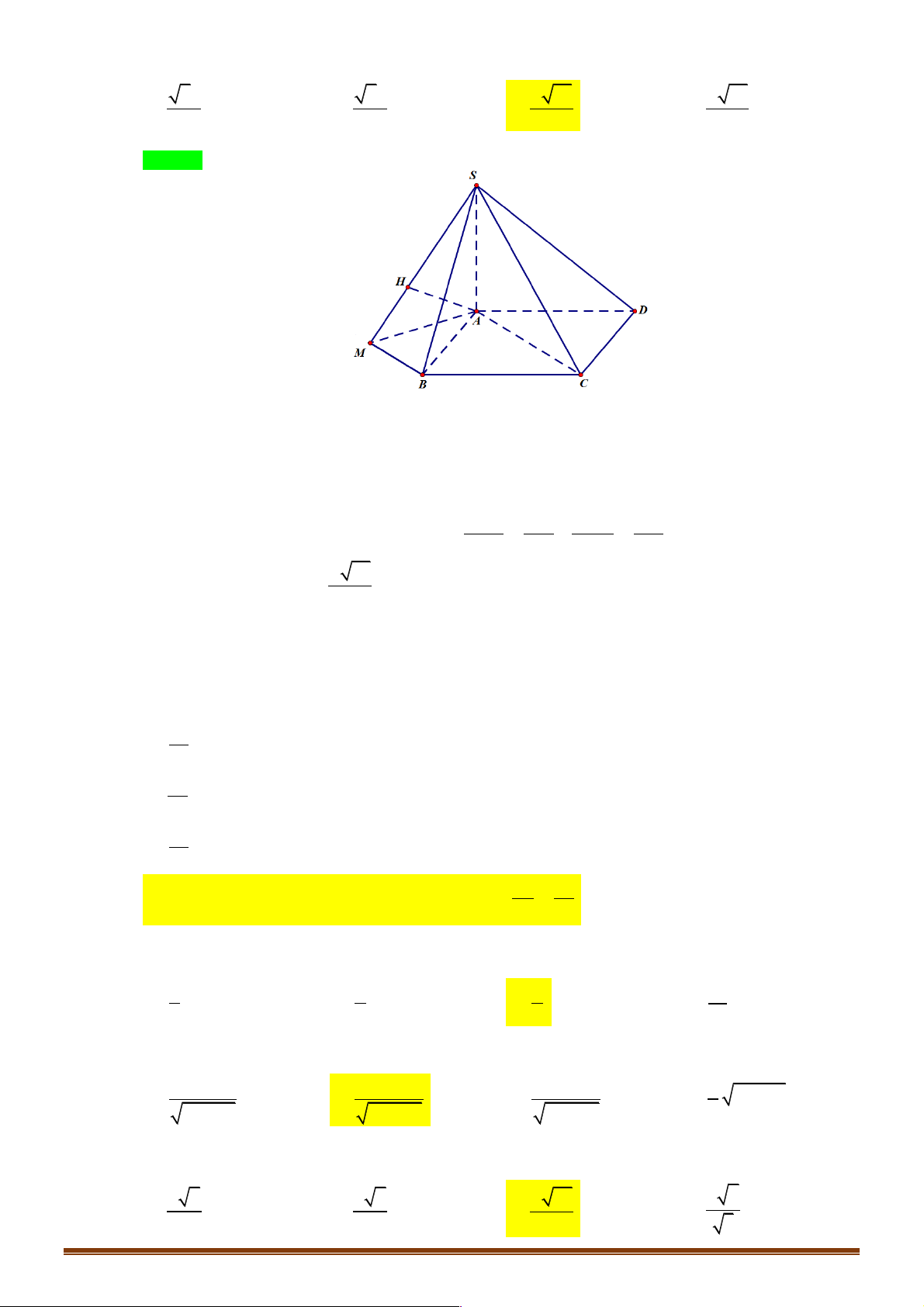
Ví dụ 12. Cho hình chóp đều S.ABC có cạnh đáy bằng a và ∑
CBS = a . Gọi j là góc giữa cạnh bên và đáy. Tính sinj theo a . 1 a a A. 2 sinj = 9 -12sin . B. 2 sinj = 9 -12sin . 3 2 2 1 a 1 a C. 2 sinj = 9 - 4sin . D. 2 sinj = 9 +12sin . 3 2 3 2 Lời giải Chọn A.
Gọi H là trung điểm BC , O là chân đường cao hạ từ S . 2 3 Ta có AO = AH = a . 3 3 a BH BH a a
!SHB vuông tại H nên: sin = Þ SB = =
Þ SA = SB = SC = . 2 SB a a a sin 2sin 2sin 2 2 2 Trang 24
Trong tam giác vuông SAO ta có: 2 a 3 a a 2 2 2 2
SO = SA - AO = - a = 9 -12sin . a a 2 9 2 4sin 6sin 2 2 SO 1 a
Góc giữa cạnh bên và đáy là ∑ 2 SAO Þ sinj = = 9 -12sin . SA 3 2
Ví dụ 13. Cho hình chóp đều S.ABCD . Thiết diện qua đỉnh A và vuông góc với cạnh bên SC có diện
tích thiết diện đó bằng nửa diện tích đáy. Gọi a là góc giữa cạnh bên và đáy. Tính a . 1 33 A. a + = 1 33 arcsin . B. a + = arcsin . 4 8 1 33 C. a - = 2 33 arcsin . D. a + = arcsin . 8 8 Lời giải Chọn B.
Đặt cạnh đáy hình vuông ABCD là a Þ AC = a 2 .
Giả sử thiết diện qua A là cắt SC , SB , SD lần lượt tại K , N , M .
Theo giả thiết SC ^ ( ANKM ) Þ MN ^ SC.
Mặt khác: BD ^ SC (vì BD ^ (SAC)) Þ MN//BD Þ MN ^ (SAC) Þ MN ^ AK 1 Þ S = AK.MN . ANKM 2 ∑
Þ SCA = a Þ AK = AC sina = a 2 sina . MN SO¢ SO - OO¢ OO¢ Þ = = =1- (vì ∑ ¢ ∑
AO O = ACK = a ; với O¢ = MN Ç AK ). BD SO SO SO 1 a 2cota 1 MN 2 2
Þ OO¢ = a 2 cota Þ =1- =1- cot a . 2 BD OC tana æ p ö Þ MN = BD( 2 - a ) = a ( 2 1 cot 2 1- cot a ) 0 £ a £ . ç ÷ è 2 ø 1 1 1 Ta có 2 S = S
Û AK.MN = a Û a 2 sina.a 2 - a = a AMKN ABCD ( 2 1 cot ) 2 2 2 2 ( æ p 2 a - ) 2 ö Û 2 2sin
1 = sina Û 4sin a - sina - 2 = 0 0 £ a £ ç ÷ è 2 ø 1+ 33 1+ 33 Þ sina = Þ a = arcsin . 8 8 Trang 25
Ví dụ 14. Cho hình chóp S.ABCD đáy là hình vuông, cạnh bên SA vuông góc với đáy, SA = AB = a .
Tính diện tích tam giác SBD theo a . 3 3 3 6 A. 2 a . B. 2 a . C. 2 a . D. 2 a . 3 4 2 2 Lời giải Chọn C. ìBD ^ AC
Gọi O = AC Ç BD ta có: í Þ BD ^ SO. îBD ^ SA 1 1 3 Khi đó 2 2 2 S = S . O BD =
SA + AO .a 2 = a . BCD 2 2 2
Ví dụ 15. Cho hình chóp S.ABCD đáy là hình vuông, cạnh bên SA vuông góc với đáy, SA = AB = a .
Tính Tính góc giữa đường thẳng SC và mặt phẳng (SBD). æ 1 ö æ 1 ö æ 1 ö æ 2 ö A. arcsin . B. arcsin . C. arcsin . D. arcsin . ç ÷ ç ÷ ç ÷ è 4 ø ç ÷ è 3 ø è 3 ø è 3 ø Lời giải Chọn C.
Gọi H là hình chiếu của C lên SO (O = AC Ç BD) (vì góc ∑
SOC tù nên H nằm ngoài SO ). CH ì ^ SO Ta có: í
Þ CH ^ (SBD) Þ SC ( ∑ ( SBD) =CSO. ) ∑ , CH î ^ BD a 6 SA SO a CH 1 Ta có: 2 ∑ S D AO ! CH D O Þ = = = 3 Þ CH = Þ sin CSO = = . SH CO a 2 3 SC 3 2 ∑ æ 1 ö Þ CSO = arcsin . ç ÷ è 3 ø
HAI MẶT PHẲNG VUÔNG GÓC. GÓC GIỮA HAI MẶT PHẲNG 1. Định nghĩa
Ø Góc giữa hai mặt phẳng (a ) và (b ) là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Ø Nếu hai mặt phẳng đó song song hoặc trùng nhau thì góc giữa chúng bằng 0 .
2. phương pháp tính góc giữa hai mặt phẳng cắt nhau Trang 26 v
Phương pháp 1: Dựng hai đường thẳng a , b lần lượt vuông góc với hai mặt phẳng (a ) và (b ).
Khi đó, góc giữa hai mặt phẳng (a ) và (b ) là (a ) ∑
( ,(b) = a,b . Tính góc ∂(a,b). ) ∂( ) v
Phương pháp 2:
Ø Xác định giao tuyến c của hai mặt phẳng (a ) và (b ).
Ø Dựng hai đường thẳng a , b lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến
c tại một điểm trên c . Khi đó: (a ) ∑ ( ,(b) = a,b . ) ∂( )
Hay ta xác định mặt phẳng phụ (g ) vuông góc với giao tuyến c mà (a )Ç(g ) = a,
(b)Ç(g ) = b. Suy ra (a) ∑ ( ,(b) = a,b . ) ∂( ) v
Phương pháp 3: (trường hợp đặc biệt)
Ø Nếu có một đoạn thẳng nối hai điểm A , B ( AÎ(a ), BÎ(b )) mà AB ^ (b ) thì qua Ahoặc B
ta dựng đường thẳng vuông góc với giao tuyến c của hai mặt phẳng tại H . Khi đó (a) ∑ ( (b) = . ) ∑ , AHB
Ví dụ 1. Cho hình chóp tứ giác đều S.ABCD cạnh đáy ABCD bằng a và SA = SB = SC = SD = a .
Tính cosin góc giauwx hai mặt phẳng (SAB) và (SAD). 1 1 3 1 A. . B. . C. . D. - . 4 3 2 3 Lời giải Chọn B. Gọi I là trung điểm SA . Do tam giác SAD và SAB đều nên ìBI ^ SA í Þ (SAB) ∑ (
,(SAD) = BI, DI . ) ∑ ( ) îDI ^ SA
Áp dụng định lý cosin cho tam giác BID ta có: 2 2 æ 3 ö æ 3 ö ç a ÷ + ç a ÷ - a 2 2 2 2 ( )2 ∑
IB + ID - BD 2 2 è ø è ø 1 cos BID = = = - . 2 . IB ID 3 3 3 2. . a a 2 2 Trang 27 Vậy (SAB) ∑ ( (SAD) = . ) 1 cos , 3
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính
AB = 2a , SA vuông góc với ( ABCD) và SA = a 3. Tính góc giữa hai mặt phẳng (SBC )và (SCD). 10 5 10 10 A. arccos . B. arccos . C. arccos . D. arccos . 5 5 10 3
Nhận xét: Theo định nghĩa góc giữa hai mặt phẳng ta đi xác định hai đường thẳng lần lượt
vuông góc với hai mặt phẳng (SBC) và (SCD). Lời giải Chọn A.
Vì ABCD là nửa lục giác đều nên AD = DC = CB = a .
Dựng đường thẳng đi qua A và vuông góc với (SCD).
Trong mặt phẳng ( ABCD) dựng AH ^ CD tại H Þ CD ^ (SAH ).
Trong mặt phẳng (SAH ) dựng AP ^ SH Þ CD ^ AP Þ AP ^ (SCD).
Dựng đường thẳng đi qua A và vuông góc với (SBC).
Trong mặt phẳng (SAC) dựng AQ ^ SC. ìBC ^ AC
Lại có AQ ^ BC vì í
Þ BC ^ (SAC) Þ BC ^ AQ. îBC ^ SA
Vậy AQ ^ (SBC).
Suy ra góc giữa hai mặt phẳng (SBC) và (SCD) là góc giữa hai đường thẳng lần lượt vuông
góc với hai mặt phẳng ấy là AP và AQ . 2 a a 3 - Ta tính góc ∑ PAQ , có 2 2 2
AH = AD - HD = a - = 4 2 1 1 1 Þ = + a 3 Þ AP = . 2 2 2 AP AS AH 5 SC a 6
Tam giác SAC vuông cân tại A Þ AQ = = . 2 2 D AP
APQ vuông tại P ∑ 10 Þ cos PAQ = = ∑ Þ PAQ = 10 arccos . AQ 5 5 Trang 28
Ví dụ 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân với BA = BC = a , SA ^ ( ABC),
SA = a . Gọi E, F lần lượt là trung điểm của các cạnh AB, AC . Tính cosin góc giữa hai mặt
phẳng (SEF ) và (SBC). 3 5 1 3 A. . B. . C. . D. . 10 10 10 2 10
Nhận xét: Giao tuyến của hai mặt phẳng (SEF ) và (SBC) là đường thẳng St đi qua S và
song song với EF và BC nên ta xác định hai đường thẳng qua S và lần lượt nằm trong hai
mặt phẳng (SEF ) và (SBC) và cùng vuông góc với St (ta đi chứng minh hai đường thẳng đó
là SE và SB ). Lời giải Chọn A. ìEF Ì (SEF ) ï
Vì íBC Ì (SBC) Þ giao tuyến của (SEF ) và (SBC) là đường thẳng qua S , song song với ïEF // BC î BC , là St . ìBC ^ AB ï (gt) í
Þ BC ^ (SAB) Þ BC ^ SB hay St ^ SB. BC ^ SA î (vì SA ^ ï (ABC))
Tương tự EF ^ (SAE) Þ EF ^ SE mà EF // St Þ St ^ SE .
Vậy SB và SE cùng đi qua S và cùng vuông góc với St nên góc giữa hai mặt phẳng (SEF )
và (SBC) bằng góc giữa hai đường thẳng SB và SE . Ta tính góc ∑ BSE. a 5 a Có 2 2
SE = SA + AE = ; 2 2
SB = SA + AB = a 2 ; BE = . 2 2
SE + SB - BE
Theo định lí cosin ta có: ∑ 2 2 2 3 cos BSE = = ∑ 3 Þ BSE = arccos . 2. . SE SB 10 10
Ví dụ 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA = a và SA ^ ( ABC),
AB = BC = a . Tính góc giữa hai mặt phẳng (SAC) và (SBC). A. 45°. B. 30° . C. 60° . D. 90° .
Nhận xét: Ta áp dụng phương pháp 3 - trường hợp đặc biệt. Lời giải Trang 29 Chọn C.
Ta có (SAC)Ç(SBC) = SC.
Gọi F là trung điểm AC Þ BF ^ (SAC).
Dựng BK ^ SC tại K Þ SC ^ (BKF ) Þ ((SAC) ∑ (SBC)) = (∑ KB KF ) ∑ , , = BKF a 2 FK SA FC.SA .a a CF D K ~ CS D A Þ = Þ FK = 2 = = . FC SC SC a 3 6 a 2 FB BFK D vuông tại F ∑ Þ tan BKF = 2 = = 3 ∑
Þ BKF = 60° = ((SAC) ∑ ,(SBC)). FK a 6
Ví dụ 5. Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính
AB = 2a , SA vuông góc với ( ABCD) và SA = a 3. Tính tan của góc giữa hai mặt phẳng
(SAD) và (SBC). 1 A. 14. B. . C. 5 . D. 7 . 7 Lời giải Chọn D. S a 3 2 a A B E D C I
Gọi J = AD« BC, ABCD là nửa lục giác đều nên AD = DC = CB = a , AI = IB = a. Ï ( ) ( ) B Ô D ^ SA SAD SBC SI Ô « = fi Ì fi BD ^ (SA )
D fi BD ^ SI . BD Ô ^ AD Ô Ó Trang 30
Vì vậy theo trường hợp đặc biệt ta chỉ cần dựng DE ^ SI với E S Œ I .
Khi đó, SI ^ (BE ) D fi (SA ) D ( ∑ (
SSBC) = EB ED = BED, (VìDBED vuông tại D ) ) ∑ ( ) ∑ , ,
DAIB đều nên BD = a 3 2 2
SI = SA + AI = a 7 DE DI a
Hai tam giác vuông SAI và DEI 3 đồng dạng nên: = fi DE = . SA SI 7 BD
DBDE vuông tại D ∑ fi tan BED = = 7 A DE
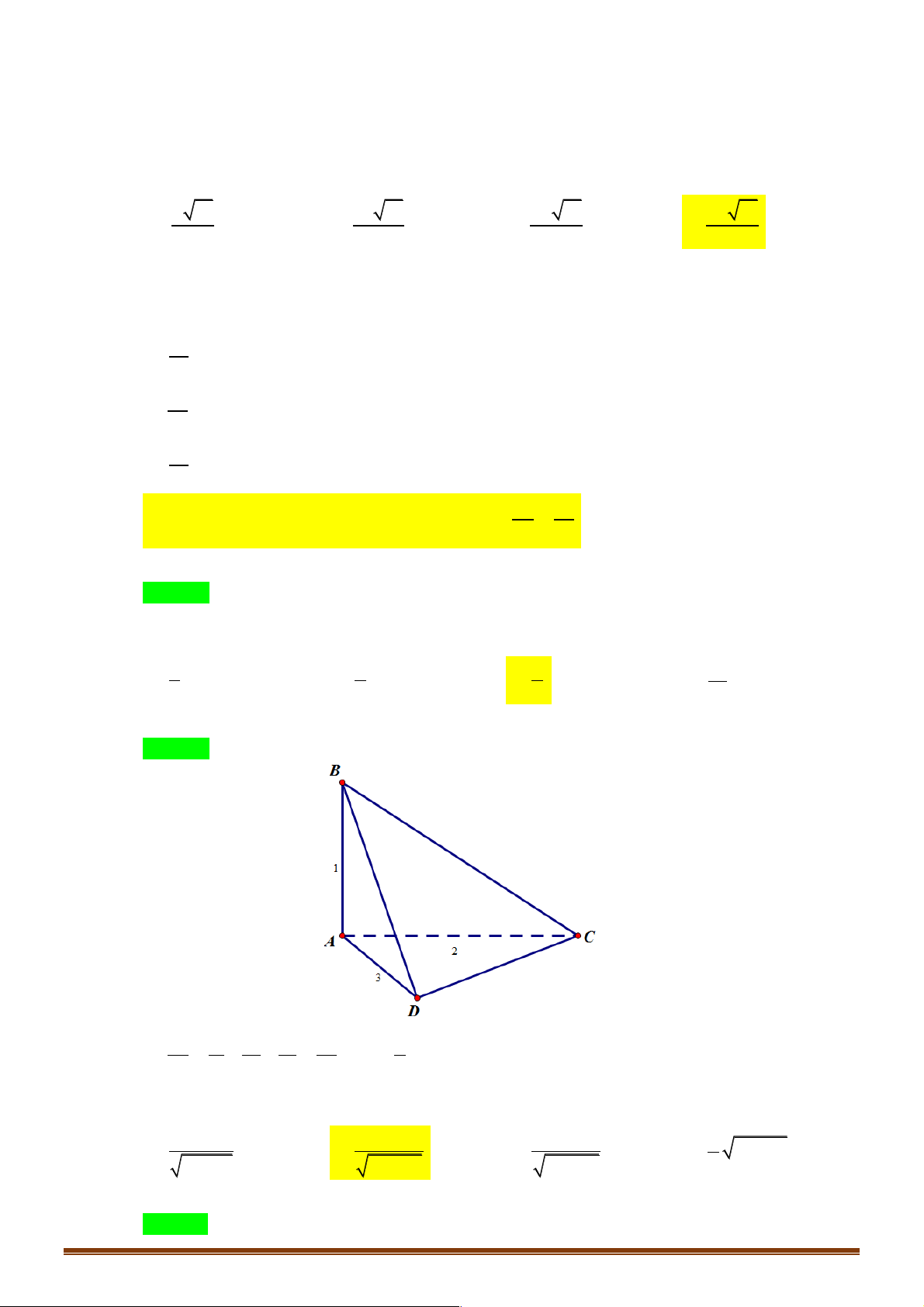
Ví dụ 6: Cho tam giác ABC vuông cân tại A có AB = a , trên đường thẳng d vuông góc với (ABC )tại
điểm A ta lấy một điểm D . Tính góc giữa hai mặt phẳng(ABC ) và(DBC , t
) rong trường hợp (DBC )là tam giác đều. 1 3 3 3 A. arccos B. arccos C. arccos D. arccos 3 3 4 6 Đáp Án: B Lời giải: D H A C a a a 2 B
Gọij là góc giữa hai mặt phẳng(ABC )và(DBC .)
Theo công thức diện tích hình chiếu của đa giác, ta có: S = S .cosj DABC DDBC 2 1 1 3 a 3 Mà: 0 S = D .
B DC.sin60 = a 2.a 2. = VDBC 2 2 2 2 1 1 Mặt khác: 2 S = A . B AC = a VABC 2 2 SVABC 3 3 fi cosj = = fi j = arccos S 3 3 VDBC
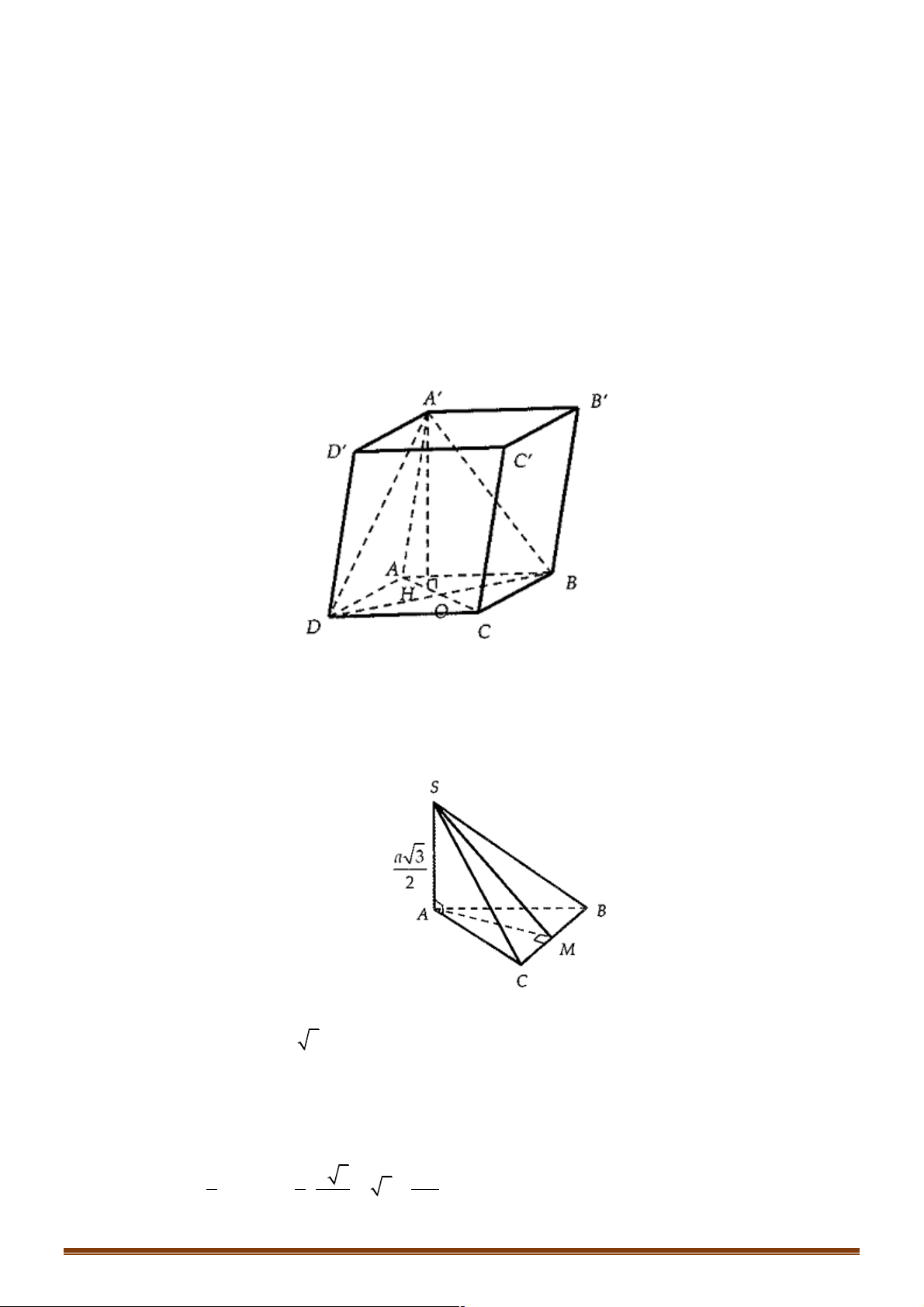
Ví Dụ 7: Cho lăng trụ đứng .
OAB O' A'B' có các đáy là các tam giác vuông cân OA = OB = a,AA' = a 2 .
Gọi M,P lần lượt là trung điểm các cạnhOA, AA'. Tính diện tích thiết diện khi cắt lăng trụ bởi (B'MP ? ) 2 a 15 2 5a 15 2 5a 15 2 a 15 A. B. C. D. 12 2 12 2 6 2 6 2 Đáp Án: C Lời giải: Trang 31 A' B' P O' A B H M Q O R
Gọi R là giao điểm của MP và OO' , Q là giao điểm của B'R với OB . OQ RO a
Thiết diện là tứ giác MPB'Q 1 , ta có: = = fi OQ = .
O'B' RO' 3 3
Tứ giác AMQB là hình chiếu vuông góc của tứ giác PMQB' trên mặt phẳng (OAB ) nên: SAMQB S = . PMQB' cosj
Với j là góc tạo bởi hai mặt phẳng(OAB ) và(MPB'Q ). 1 1 5 Ta có: 2 2 2 S = S - S = a - a = a AMQB OAB OMQ 2 12 12 Ï MQ Ô ^ OH
Hạ OH ^ MQ, ta có:Ô Ì fi MQ ^ (OHR ) MQ Ô ^ OR Ô Ó Vậy: ∑ j = OHR ( ∑ OHR nhọn) a OH OH 13 2 Ta có: ∑ cosj = cosOHR = = = = 2 2 2 2 RH OH + OR a a 15 + 13 2 2 5a 15 Vậy: S = PMQB' 12 2
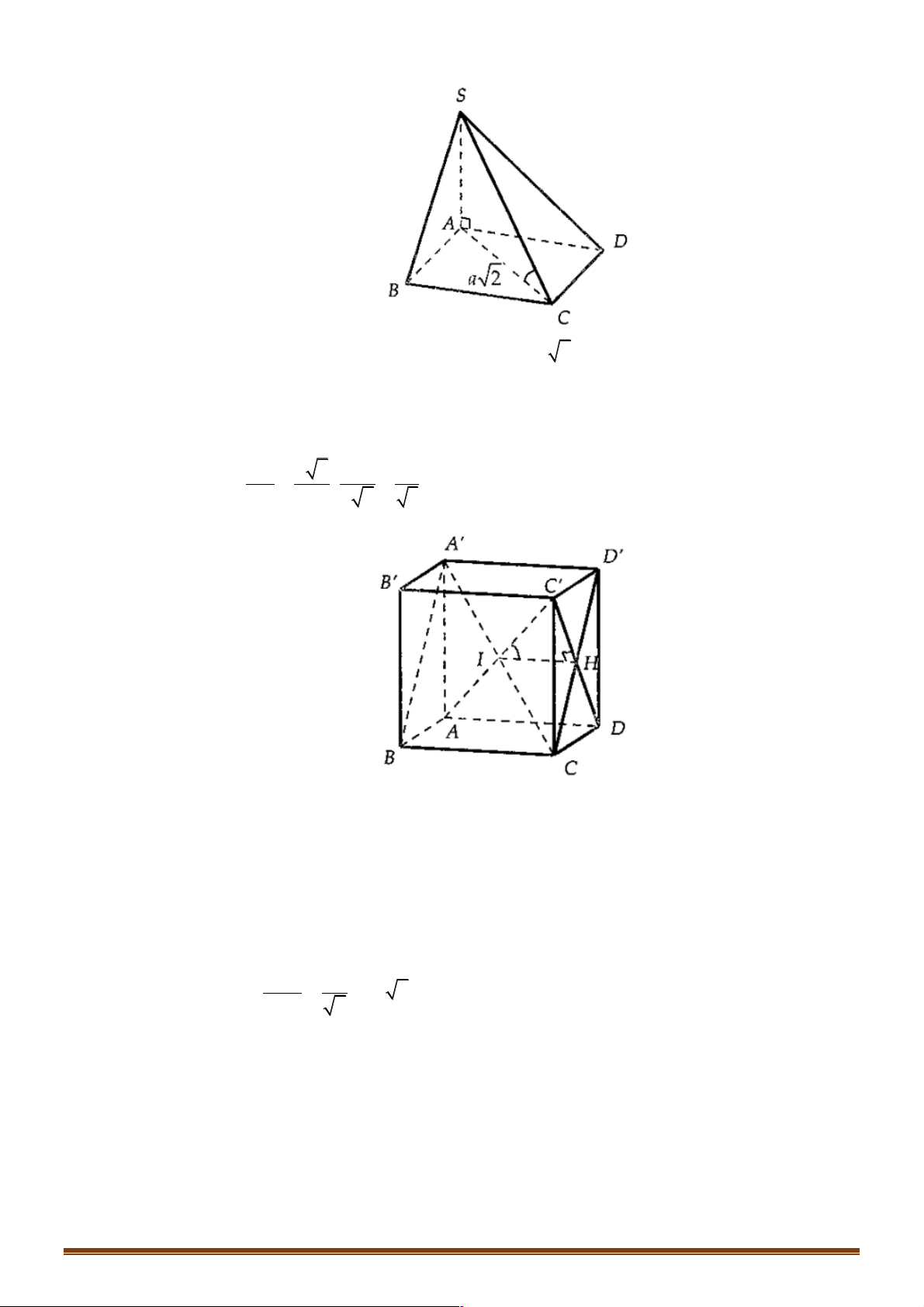
Ví dụ 8: Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là một tam giác cân với ∑
AB = AC = a BAC = 0 ,
120 , cạnh bên BB' = .a Gọi I là trung điểm CC'. Chứng minh rằng tam
giác AB'I vuông ở A. Tính cosin của góc giữa hai mặt phẳng (ABC) à
v (AB'I). 15 30 10 15 A. . B. . C. . D. . 10 10 30 30 Đáp án B. Lời giải Trang 32 B' C' a A' I B C a a A
Áp dụng định lý cosin cho DABC ta có: 2 BC = 2 a + 2 a - 2 0 a = 2 2 cos120 3a .
Áp dụng định lý Py – ta – go cho tam giác: D 2 B A B có B A = 2 ' : ' 2a . 2 2 æ 1 ö2 2 a DICA 5
có : AI = a + = . ç ÷ è 2 ø 4 2 2 a a D 2
B'C'I có B I = 2 13 : ' 3a + = . 4 4 2 2 5a 13a Ta có: 2 B' A + 2 AI = 2 2a + = = 2
B'I Þ DAB'I vuông ở . A 4 4 2 1 1 a 5 a 10 Ta có: S = AI.AB' = . .a 2 = . DAB'I 2 2 2 4 2 1 a 3 S = 2 0 a sin120 = . DABC 2 4
Gọi j là góc giữa hai mặt phẳng (ABC) à
v (AB'I). Thì ta có: 2 a 3 S ABC 4 3 30 D co j s = = = = . 2 S ABI a 10 10 10 D ' 4
BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
B. Góc giữa hai đường thẳng là góc nhọn.
C. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song
với c (hoặc b trùng với c ).
D. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c .
Câu 2. Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng
(P) khi a và b song song (hoặc a trùng với b). Trang 33
C. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng
(Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
D. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng
(P) thì a và b song song.
Câu 3. Mệnh đề nào đúng trong các mệnh đề sau?
A. Góc giữa hai mặt phẳng luôn là góc nhọn.
B. Góc giữa mặt phẳng (P) và mặt phẳng (Q)bằng góc giữa mặt phẳng (P) và mặt phẳng
(R) khi mặt phẳng (R) song song với mặt phẳng (Q) (hoặc (R) trùng với (Q)).
C. Góc giữa mặt phẳng (P) và mặt phẳng (Q)bằng góc giữa mặt phẳng (P) và mặt phẳng
(R) thì mặt phẳng (R) song song với mặt phẳng (Q).
D. Cả ba mệnh đề trên đều đúng.
Câu 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , đường thẳng SA vuông góc với mặt
phẳng đáy, SA = a . Góc giữa mặt phẳng (SCD) và mặt phẳng ( ABCD) là a . Khi đó tana
nhận giá trị nào trong các giá trị sau: 2 A. tana = . B. tana = 1 C. tana = 2 . D. tana = 3 . 2
Câu 5. Cho hình lập phương ABC . D A B ¢ C ¢ D
¢ ¢. Xét mặt phẳng ( A B
¢ D), trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa mặt phẳng ( A B
¢ D) và các mặt phẳng chứa các mặt của hình lập phương bằng nhau.
B. Góc giữa mặt phẳng ( A B
¢ D) và các mặt phẳng chứa các mặt của hình lập phương bằng nhau.
C. Góc giữa mặt phẳng ( A B
¢ D) và các mặt phẳng chứa các mặt của hình lập phương bằng a 1 mà tana = . 2
D. Cả ba mệnh đề trên đều sai.
Câu 6. Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một mặt bên vuông góc với đáy.
Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Có hai cặp mặt phẳng vuông góc nhau.
B. Có ba cặp mặt phẳng vuông góc nhau.
C. Có bốn cặp mặt phẳng vuông góc nhau.
D. Có năm cặp mặt phẳng vuông góc nhau. Trang 34 !!!" !!!!"
Câu 7. Cho hình lập phương ABC .
D EFGH , hãy xác định góc giữa cặp vectơ AB, DH ? A. 0 45 . B. 0 90 . C. 0 120 . D. 0 60 .
Câu 8. Trong không gian cho ba đường thẳng phân biệt a, ,
b c . Mệnh đề nào sau đây đúng?
A. Nếu a và b cùng vuông góc với c thì a / /b .
B. Nếu a / /b , c ^ a thì c ^ b.
C. Nếu góc giữa a và c bằng góc giữa b và c thì a / /b.
D. Nếu a và b cùng nằm trong mặt phẳng (a ) và c / / (a ) thì góc giữa a và c bằng góc giữa b và c .
Câu 9. Cho hình chóp S.ABC có ∑ ∑ ∑
SA = SB = SC, ASB = BSC = CSA. Hãy xác định góc giữa SB và AC . A. 0 60 . B. 0 120 . C. 0 45 . D. 0 90 .
Câu 10. Cho tứ diện ABCD có hai mặt ABC, ABD là các tam giác đều. Góc giữa AB và CD là A. 0 120 . B. 0 60 . C. 0 90 . D. 0 30 .
Câu 11. Cho hình hộp ABC . D A¢B C
¢ D¢ . Giả sử tam giác AB C ¢ , A D
¢ C¢ là các tam giác nhọn. Góc giữa
hai đường thẳng AC và A¢D là góc nào sau đây? B. ∑ AB C ¢ . B. ∑ DA C ¢ . C. ∑ BB C ¢ . D. ∑ DAC .
Câu 12. Trong các mện đề sau, mệnh đề nào đúng?
A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì
cũng vuông góc với đường thẳng thứ hai.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Câu 13. Cho tứ diện ABCD . Gọi I , J , K lần lượt là trung điểm của BC , CA và BD . Khi đó góc
giữa AB và CD là: A. ∑ JIK . B. ∑ ABC . C. ∑ IJK . D. ∑ JKI .
Câu 14. Cho một hình thoi ABCD cạnh a và một điểm S nằm ngoài mặt phẳng chứa hình thoi sao cho
SA = a và vuông góc với ( ABC). Tính góc giữa SD và BC A. 60! . B. 90!. C. 45! . D. arctan 2 .
Câu 15. Cho tứ diện ABCD .Gọi M , N , I lần lượt là trung điểm của BC , AD và AC . Cho AB = 2a
, CD = 2a 2 và MN = a 5. Tính góc ∑ j = (AB,CD) A. 135!. B. 60! . C. 90!. D. 45! .
Câu 16. Cho hình chóp S.ABC có SA ^ ( ABC), SA = a , ABC D
đều cạnh a . Tính góc giữa SB và (ABC) A. arctan 2 . B. 60! . C. 45! . D. 90!.
Câu 17. Cho hình chóp S.ABC có SA ^ ( ABC), SA = a, ABC D
đều cạnh a . Tính tan SC,( ∑ ( SAB) ? ) Trang 35 3 5 A. . B. . C. 1 . D. 2 . 5 3 2
Câu 18. Cho tứ diện đều ABCD cạnh a . Gọi j là góc giữa hai mặt phẳng ( ABC) và (DBC). Tính cosj ? 1 3 1 A. 3 . B. . C. . D. . 3 3 2
Câu 19. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a ; SA ^ ( ABCD) và SA = a . Tính
góc j giữa hai mặt phẳng ( ABCD) và (SBC)? p p 2p p A. . B. . C. . D. . 4 3 3 6
Câu 20. Cho hình chóp S.ABCD có cạnh đáy bằng a ; SA ^ ( ABCD) và SA = a . Tính góc j giữa hai
mặt phẳng (SBC) và (SDC)? 2p p p p A. . B. . C. . D. . 3 6 4 3
Câu 21. Cho ba tia Ox , Oy , Oz trong không gian sao cho ∑ xOy =120! , ∑ zOy = 90! , ∑ xOz = 60! Trên ba
tia ấy lần lượt lấy các điểm A , B , C sao cho OA = OB = OC = a . Gọi a , b lần lượt là góc
giữa mặt phẳng ( ABC) với mặt phẳng (OBC) và mặt phẳng (OAC) . Tính tana × tan b ? 1 3 A. . B. 2 . C. . D. 1. 2 2
Câu 22. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a ; SA ^ ( ABCD) và SA = a 3 . Tính góc
giữa hai đường thẳng SD và BC A. 60! . B. 30!. C. 45! . D. 90!.
Câu 23. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a ; SA ^ ( ABCD) và SA = a 3 . Gọi I và
J lần lượt là trung điểm của SA và SC . Tính góc giữa hai đường thẳng IJ và BD A. 90!. B. 60! 1 . C. arctan . D. 45! . 3 4
Câu 24. Cho tứ diện ABCD có CD = AB . Gọi I , J , K lần lượt là trung điểm của BC , AC , DB . 3 5
Biết IK = AB .Tính góc giữa hai đường thẳng CD và IJ 6 A. 90!. B. 60! . C. 45! . D. 30!.
Câu 25. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a . Gọi M , N lần lượt là trung điểm của AB ,
BC . Tính góc giữa hai đường thẳng MN và C D ¢ ¢ A. 90!. B. 45! . C. 60! . D. 30!.
Câu 26. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a . Tính góc giữa hai đường thẳng BD và AD¢ A. 90!. B. 45! . C. 60! . D. 30!.
Câu 27. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a . Gọi M , N , P lần lượt là trung điểm của AB , BC , C D
¢ ¢ . Tính góc giữa hai đường thẳng MN và AP A. 90!. B. 45! . C. 60! . D. 30!. Trang 36
Câu 28. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a . Gọi M , N , P lần lượt là trung điểm của AB , BC , C D
¢ ¢ . Tính góc giữa hai đường thẳng DN và A¢P A. 90!. B. 45! . C. 60! . D. 30!.
Câu 29. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ; SA ^ ( ABCD) và SA = a 6 .
Tính cosin góc tạo bởi SC và mặt phẳng (SAB). 1 1 1 3 A. . B. . C. . D. . 3 6 8 7
Câu 30. Cho hình chop S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với ( ABCD) cà
SA = a 6 . Tính sin của góc tạo bởi AC và mặt phẳng (SBC) . 1 1 1 3 A. . B. . C. . D. . 3 6 7 7
Câu 31. Cho lăng trụ đứng ABC. ’ A ’
B C’ có đáy ABC cân đỉnh ∑ ,
A ABC = a , BC ' tạo đáy góc b . Gọi
I là trung điểm của ’ AA , biết ∑ 0 BIC = 90 . Tính 2 2 tan a + tan b 1 A. . B. 2 . C. 3 . D.1 . 2
Câu 32. Cho hình chóp S.ABC có SA là đường cao và đáy là tam giác ABC vuông tại B . Cho ∑ 0 BSC = 45 , gọi ∑
ASB = a . Tìm sina để góc giữa hai mặt phẳng ( ASC) và (BSC )bằng 0 60 3 2 15 sina = 1 sina = A. sina = 2 . B. sina = . C. 9 . D. 5 . 5 2
D. HƯỚNG DẪN GIẢI Câu 1. Đáp án C.
+) Đáp án A sai vì góc giữa hai đường thẳng có thể bằng hoặc bù với góc giữa hai véc tơ chỉ phương.
+) Đáp án B sai vì có thể là góc 0 90 . Câu 2. Đáp án B.
+) Đáp án A sai vì khi đường thẳng đó vg với mặt phẳng.
+) Đáp án C, D: Vẽ hình thấy có vô số đường thẳng và mặt phẳng thỏa mãn. Câu 3. Đáp án B.
+) Đáp án A sai vì vì có thể là vg.
+) Đáp án C sai vì chẳng hạn (Q) và (R) cắt nhau, (P) là mặt phẳng phân giác. Câu 4. Đáp án B. Trang 37 CD ì ^ AD Ta có: í Þ CD ^ (SAD) ∑
Þ a = SDA. Mà !SDA vuông cân tại A nên ∑ 0 SDA = 45 . CD î ^ SA Câu 5. Đáp án A.
Đáp án B, C vì giả sử ta xác định góc giữa ( A' BD) và ( ABCD) là góc ∑
A' IA với I là trung điểm của 2 2
æ a 2 ö æ a 6 ö 2 2 2 ç ÷ + ç ÷ - a 2a 6a 2 2 2 2 + - a 2
AI + A' I - AA' 2 2 è ø è ø 4a 1 BD và ∑ 4 4 cos AIA' = = = = = 2 2 2.AI.A' I a 2 a 6 2a 12 2a 12 3 2. . 2 2 4 1 1 Þ cosa = Þ tana ¹ 3 2 Câu 6. Đáp án B.
Giả sử hình chóp đó là S.ABCD . Ta có (SAB) ^ ( ABCD);(SAB) ^ (SAD);(SAD) ^ ( ABCD) Câu 7. Đáp án B. Trang 38 (!!!" !!!!" !!!" !!!!"
AB DH ) = (DC DH ) 0 ; ; = 90 . Câu 8. Đáp án B. Câu 9. Đáp án D.
Từ giả thiết suy ra các mặt của hình chóp đều là các tam giác đều. Gọi M , N, P lần lượt là trung điểm a của ,
SA SC, BC . Giả sử cạnh hình chóp đều là a thì MN = NP = ; MP ^ SAvì !SAP cân tại P . 2 2 2 2 a a 2a 2 2 2 2 2 2 2 + -
æ a 3 ö æ a ö 3a a a 2
MN + NP - MP ∑ 4 4 4 PM = ç ÷ - = - = ;cos MNP = = ç ÷ ç ÷ 2 è ø è 2 ø 4 4 2 2.MN.NP a a 2. . 2 2 ∑ MNP = Þ (∑ SB AC) 0 cos 0 , = 90 .
Cách 2: Lấy I là trung điểm của AC ta có: AC ^ (SIB) Þ AC ^ SB. !!" !!!" !!" !!!" !!" !!" !!!" !!" !!" Cách 3: .
SB AC = SB (SC - SA) = . SB SC - . SB SA = 0 . Câu 10. Đáp án C. Trang 39
Gọi I là trung điểm của AB Þ AB ^ (IDC) Þ AB ^ CD .
Ngoài ra ta cũng có thể sử dụng tích vô hướng để giải quyết bài toán này. Câu 11. Đáp án B. Ta có: AC A C Þ (∑ AC ) = (∑ A C A D) ∑ / / ' ' ,A'D ' ', '
= DA'C ' (góc nhọn). Câu 12. Đáp án A. Câu 13. Đáp án A. Câu 14. Đáp án C. Ta có: AD BC Þ (∑ SD BC) = (∑ SD AD) ∑ 0 / / , , = ADS = 45 . Câu 15. Đáp án D. Trang 40 ì 1 IN / /C ;
D IN = CD = a 2 ïï
Theo tính chất đường trung bình trong tam giác: 2 í 1 ïIM / /A ;
B IM = AB = a ïî 2 Þj = (∑ AB CD) = (∑ ,
IM , IN ). Áp dụng định lý cosin ta có: 2 2 2
IM + IN - MN 2 2 0 cosj = = - = Þ j = 45 . 2.IM.IN 2 2 Câu 16. Đáp án C.
Ta có SA ^ ( ABC) Þ AB là hình chiếu của SB trên mặt phẳng (ABC) ∑ Þj = ASB = (∑ SD AD) 0 , = 45 . Câu 17. Đáp án A. Hình câu 16. CI ì ^ AB
Gọi I là trung điểm của AB . Ta có: í Þ CI ^ (SAB) CI î ^ SA
Þ SI là hình chiếu của SC trên mặt phẳng (SAB) ∑
Þ b = CSI = (SC ( ∑, SAB)) Trang 41 a 3 CI CI 3 2 Þ tan b = = = = . 2 2 2 SI SA + AI 5 2 æ a ö a + ç ÷ è 2 ø Câu 18. Đáp án B.
Gọi M là trung điểm CB và G là trọng tâm tam giác BCD nên ta có ^ ( ) ∑ a a a BC AGM Þj = 3 3 3 AMG. Có DM = Þ GM = ; AM = 2 6 2 a 3 GM 1 6 Þ cosj = = = . AM a 3 3 2 Câu 19. Đáp án A. Ta có giao tuyến ^ ( ) ∑ BC
SBA Þj = SBA (góc nhọn). Mà SBA D
vuông cân tại A nên 0 j = 45 Câu 20. Đáp án D. (Hình vẽ của câu 19)
Hai tam giác vuông SBC và SDC nên có chung chân đường cao M kẻ từ B và D Þ b = (∑
MB, MD). Ta đi tính góc ∑ BMD.
Trong tam giác vuông SBC ta có: Trang 42 2 1 1 1 1 1 3 2a 2 2 = + = + = Þ 2a BM = . Tương tự 2 DM = . 2 2 2 BM SB BC (a )2 2 2 a 2a 3 2 3
Áp dụng định lý cosin cho BM D D ta có: 2 4a 2 - 2a ∑ 2 2 2
MB + MD - BD 1 4 ∑ 0 0 0 0 cos BMD = =
= - Þ BMD = 120 Þ b = 180 -120 = 60 2 2. . MB MD æ ö 2 2 2.ç a ÷ 3 è ø p Hay . 3 Câu 21. Đáp án A. O
D AB đều Þ AC = a. Tam giác OBC vuông BC = a 2. Áp dụng định lý cosin cho O D AB
Þ AB = a 3 Þ ABC D có 2 2 2
AB = AC + BC Þ ABC D vuông tại C .
Gọi H là trung điểm của AB Þ H là tâm đường tròn ngoại tiếp ABC D Þ OH ^ ( ABC) ∑ ∑
Þa = OIH;b = OJH (với I, J lần lượt là trung điểm của BC và AC ). 2 æ a ö 2 OH OH OH ç ÷ è 2 ø 1 Þ tana.tan b = . = = = . HI HJ HI.HJ a a 2 2 . 2 2 Câu 22. Đáp án A. Trang 43 SA Vì ∑ 0 BC AD SAD = Þ (∑ SD BC) ∑ ∑ = SDA Þ SDA = = Þ (SD BC) 0 / / , 90 , tan 3 , = 60 . SD Câu 23. Đáp án A. (Hình vẽ như câu 22) Ta có AC (∑BD) ∑ 0 IJ / / , IJ, = AOB = 90 . Câu 24. Đáp án A. AB a
Đặt AB = a . Ta có: IJ = = . 2 2 CD 2 2a 5 5a IK = = AB = ; JK = AB = . 2 3 3 6 6 2 2 4 25 a a a a Ta có: 2 2 2 IJ + IK = + = = JK . 4 9 16 Vậy IJ
D K vuông tại I . Ta có IK CD Þ (∑ AB CD) ∑ 0 / / , = JIK = 90 . Câu 25. Đáp án B. Ta có: AB C D Þ (∑ MN C D ) = (∑ MN AB) ∑ 0 / / ' ' , ' ' , = BMN = 45 . Câu 26. Đáp án C. (Hình vẽ câu 25) Có B D BD Þ (∑ BD AD ) = (∑ B D AD ) ∑ 0 ' '/ / , ' ' ',
' = AD' B ' = 60 vì AB D
' D ' đều cạnh a 2. Câu 27. Đáp án B. (Hình vẽ câu 25) MN AC Þ (∑ MN AP) = (∑ AC AP) ∑ / / , ,
= CAP (góc nhọn). Ta có: AC = a 2. a 5 3a
Trong tam giác vuông CC ' P có CP =
. Trong tam giác vuông APA' có AP = . 2 2 1
Áp dụng định lý cosin cho C D AP ta có: ∑ cosCAP = Þ (∑ MN, AP) 0 = 45 . 2 Câu 28. Đáp án A. (Hình vẽ câu 25) Trang 44
Gọi N ' là trung điểm của B 'C '. Ta có ND N D Þ (∑ ND A P) = (∑ / / ' ' , '
N ' D ', A' P) . Có ∑ ∑
!N 'C 'D' =!PD' A' Þ C 'D' N ' = D' A'P' Mà ∑ ∑ 0
C ' D' N ' + A' D' N ' = 90 ∑ ∑ 0
Þ D' A'P + A'D' N ' = 90 ∑ 0 Þ DIA' = 90 hay (∑ DN A P) 0 , ' = 90 . Câu 29. Đáp án C.
Ta có: CB ^ (SAB) Þ SB là hình chiếu của SC
lên mặt phẳng (SAB) Þ (SC ( ∑ SAB)) = (∑ SC SB) ∑ , , = CSB . Do C
D SB vuông tại B nên: ∑ BC BC a 1 sin CSB = = = = . 2 2 SC SA + AC a 8 8 Câu 30. Đáp án D. (Hình vẽ giống câu 29)
Kẻ AH ^ SB Þ BC ^ AH Þ AH ^ (SBC) Þ AH là hình chiếu của AC lên mặt phẳng (SBC) Þ (AC ( ∑ SBC)) = (∑ AC HC ) ∑ , , = ACH . . SA AB a 6.a a 6
Tam giác SAB vuông Þ AH = = = SB a 7 7 AH Vì AH D C vuông tại ∑ 3 H Þ sin ACH = = . AC 7 Câu 31. Đáp án D. BB ' Ta có: tan b =
. !AHB vuông tại H B 'C '
( H là trung điểm của BC ) AH 2AH Þ tana = = BH BC 4( 2 2 AI + AH 2 2 ) Þ tan a + tan b = (*) 2 BC
Mà !AIH vuông tại A nên 2 2 2
AI + AH = IH . !BIC vuông tại BC 2 2 I Þ IH =
Þ BC = 4IH . Thay vào (*) 2 Ta có: 2 2 tan a + tan b =1. Câu 32. Đáp án A. Trang 45
Dựng BJ ^ SC(1), BI ^ AC Þ SA ^ BI
Þ BI ^ (SAC) Þ BI ^ SC (2) Từ ( ) 1 và (2) Þ SC ^ ( I
B J) Þ IJ ^ SC
Þ Góc giữa hai mặt phẳng ( ASC) và (BSC) là ∑ j = BJI . Do ! IJ
B vuông tại I nên ∑ 0 BJI = 60 3 1 4 1 Þ BI = BJ Þ = . (3) 2 2 2 BI 3 BJ SB D C có ∑ 0 BSC = 45 Þ S D BC vuông cân tại
B . Trong tam giác SJB vuông tại J có ∑ 1 2 0
JSB = 45 Þ SB = 2BJ Þ = 2 2 BJ BC 1 æ 1 ö 4 2 Từ (3)và (4) Þ +1 = . 2 ç 2 ÷ 2 BC è sin a ø 3 BC 15
Giải phương trình ta được sina = . 5 KHOẢNG CÁCH A. LÝ THUYẾT
I. Khoảng cách từ một điểm tới một đường thẳng
1. Cho điểm O và đường thẳng D . Hạ
OH ^ D(H Î D) . Khi đó khoảng cách từ O tới D
bằng độ dài đoạn OH . Kí hiệu là d ( , O D). 2. d ( ,
O D) £ OA ,với A là điểm bất kì thuộc D.
3. Cho hai đường thẳng a và D cắt nhau tại M . d ( , A D) MA
Trên a lấy hai điểm , A B. Khi đó: =
d (B,D) MB Trang 46 4. Cho ABC D
vuông tại A . Dựng đường cao AH ,
khi đó ta có: AH = d ( ,
A BC) và AH được tính 1 1 1 theo công thức: = + hoặc 2 2 2 AH AB AC . AB AC AH = . BC
II. Khoảng cách từ một điểm đến một mặt phẳng 1. Định nghĩa
Cho điểm O và mặt phẳng (a ). Dựng
OH ^ (a ),(H Î(a )). Khi đó khoảng cách từ O
tới (a ) bằng độ dài đoạn OH và được kí hiệu là d ( , O (a )).
2. Giả sử đường thẳng D cắt (a ) tại M . Trên D d ( , A (a )) AM lấy hai điểm , A B . Khi đó: = . d ( , B (a )) BM
3. (Tính chất tứ diện vuông)
Cho tứ diện OABC có ,
OA OB,OC đôi một vuông
góc. Gọi H là hình chiếu của O trên ( ABC).
Khi đó OH = d ( , O ( ABC)) và 1 1 1 1 = + + . 2 2 2 2 OH OA OB OC
4. Cho đường thẳng D song song với mặt phẳng
(a). Khi đó khoảng cách giữa D và (a)được định
nghĩa bằng khoảng cách từ một điểm bất kì thuộc D tới (a ).
5. Cho hai mặt phẳng (a ) và (b ) song song.
Khi đó khoảng cách giữa hai mặt phẳng (a ) và
(b ) là khoảng cách từ một điểm bất kì thuộc (a) tới (b ).
III. Khoảng cách giữa hai đường thẳng chéo nhau
1.Cho hai đường thẳng chéo nhau a và b . Khi đó tồn tại duy nhất một đường thẳng D vuông góc với cả
hai đường thẳng a và b và cắt cả hai đường thẳng Trang 47
a và b. D được gọi là đường vuông góc chung của a và b. Đoạn thẳng AB được gọi
là đoạn vuông góc chung của hai đường thẳng chéo nhau a và b.Khi đó khoảng
cách giữa hai đường thẳng a và b bằng độ dài đoạn vuông góc chung AB
2.Nếu gọi (P);(Q) là hai mặt phẳng song song với nhau và lần lượt chứa hai
thẳng a và b chéo nhau thì AB=d(A;(Q))=d(b;(P))=d(( P);(Q) Nhận xét:
-Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách
hai đường thẳng đó và mặt phẳng song song với nó chứa đường thẳng còn còn lại.
-Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai
mặt phẳng song song lần lượt chứa hai đường thẳng đó. IV.Bổ sung kiến thức
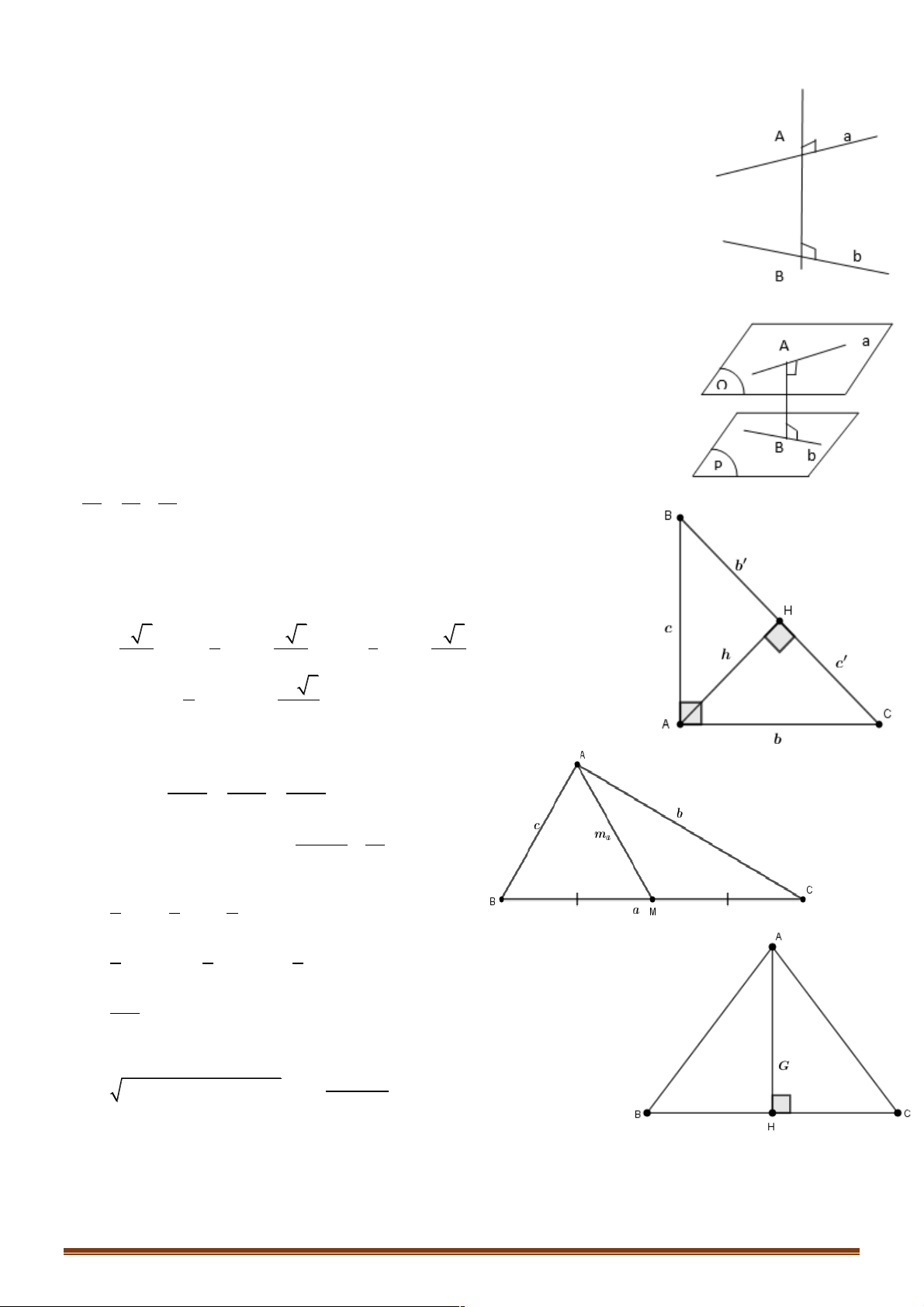
1.Hệ thức lượng trong tam giác vuông 2 2 2
+a = b + c 2 2 +b = . a b ';c = . a c ' 2 +h = b '.c' + . a h = . b c 1 1 1 + = + 2 2 2 h b c
+b = a sin B = a cosC = c tan B = c cot C
+c = a sin C = a cos B = b tan C = b cot B
2.Hệ thức lượng trong tam giác đều
-Cho tam giác đều ABC cạnh a,trung tuyến AM,trọng tâm G ta có a 3 2 a 3 1 a 3 AM = ; AG = AM = ;GM = AM = 2 3 3 3 6 2 1 a 3
-Diện tích S = AM.BC = 2 4
3.Hệ thức lượng trong tam giác thường -Định lý cosin: 2 2 2
a = b + c - 2bc cosA a b c -Định lý sin : = = = 2R sin A sin B sin C 2 2 2 b + c a -Công thức trung tuyến: 2 m = - a 2 4 -Công thức diện tích: 1 1 1
+S = ah = bh = ch 2 a 2 b 2 c 1 1 1
+S = absin C = bcsin A = acsin B 2 2 2 abc +S = 4R +S = . p r a + b + c
+S = p( p - a)( p - b)(p- c);( p = ) 2
B.Các bài toán vè khoảng cách
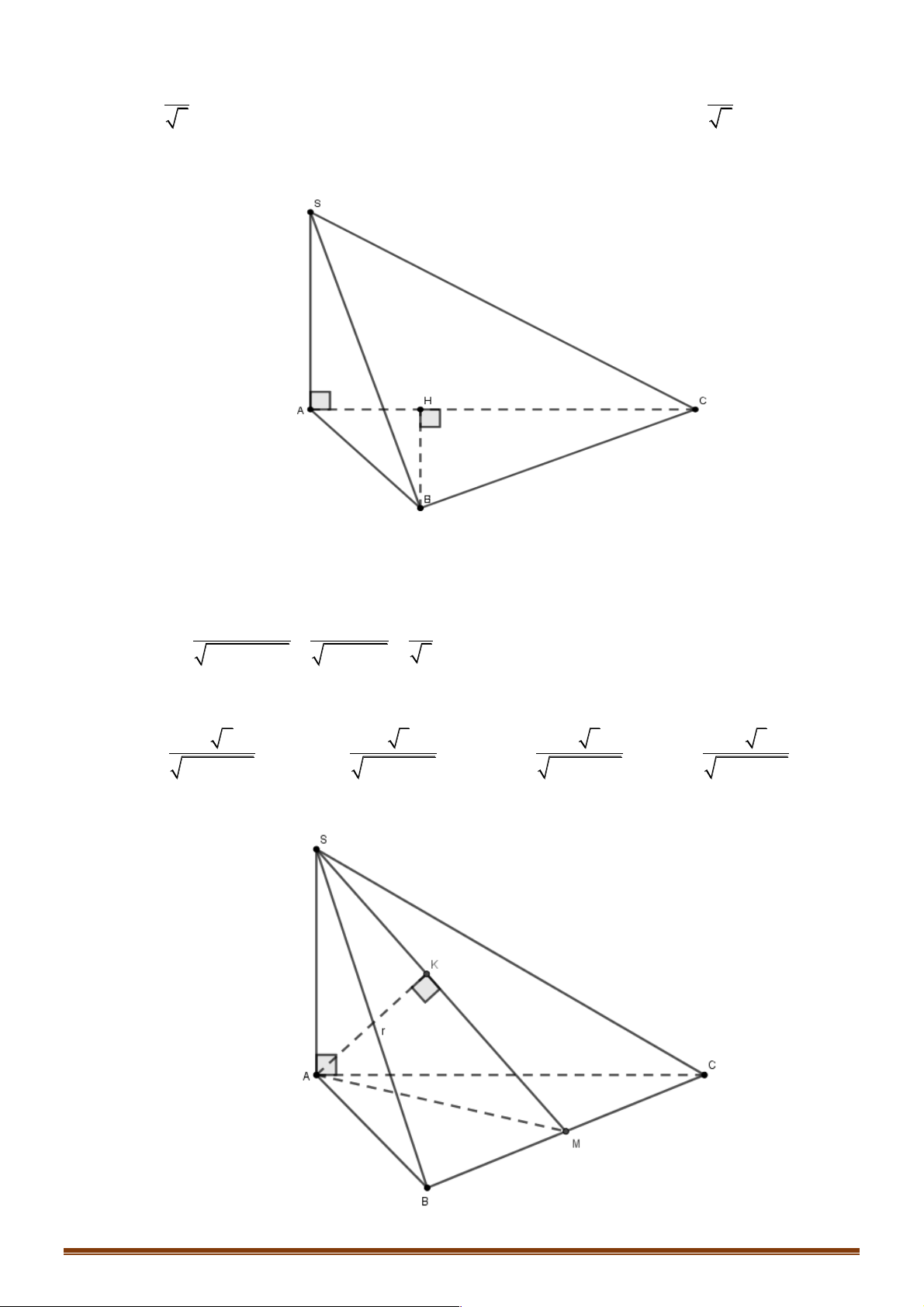
Ví dụ 1:Cho chóp S.ABC đáy là tam giác vuông tại B và AB=2BC=2a.Biết SA ^ (ABC) .Tính d( ; B ( ABC) Trang 48 2a a A. B. a C. 2a D. 5 2 Đáp án A. Lời giải
-Dựng BH ^ AC Þ BH ^ S ;( A SA ^ (ABC)) .
Vậy BH ^ (SAC) Þ BH là khoảng cách từ B đến (SAC)
theo hệ thức lượng trong tam giác vuông ta có: . BA BC 2 . a a 2a BH = = = = d( ; B (ABC)) 2 2 2 2 BA + BC 4a + a 5
Ví dụ 2:Cho hình chóp S.ABC có SA = h và
SA ^ (ABC) và tam giác ABC đều cạnh a.Tính d( ; A (SBC) ah 7 a 3 ah 3 ah 3 A. B. C. D. 2 2 3a + 4h 2 2 3a + 4h 2 2 3a + 4h 2 2 4a + 3h Đáp án:c Lời giải Trang 49
Gọi M là trung điểm của BC Þ BC ^ (SAM ) .Dựng AK ^ SM
Þ AK ^ BC;(BC ^ (SAM )) Þ AK ^ (SBC) Þ AK = d( ;( A SBC)) a 3 Có AM =
;tam giác SAM vuông tại A 2 3 a . .AS h AM 3 2 ah Þ AK = = = = d( ; A (SBC)) 2 2 2 2 AM +AS a 3 3a + 4h 2 2 ( ) + h 2
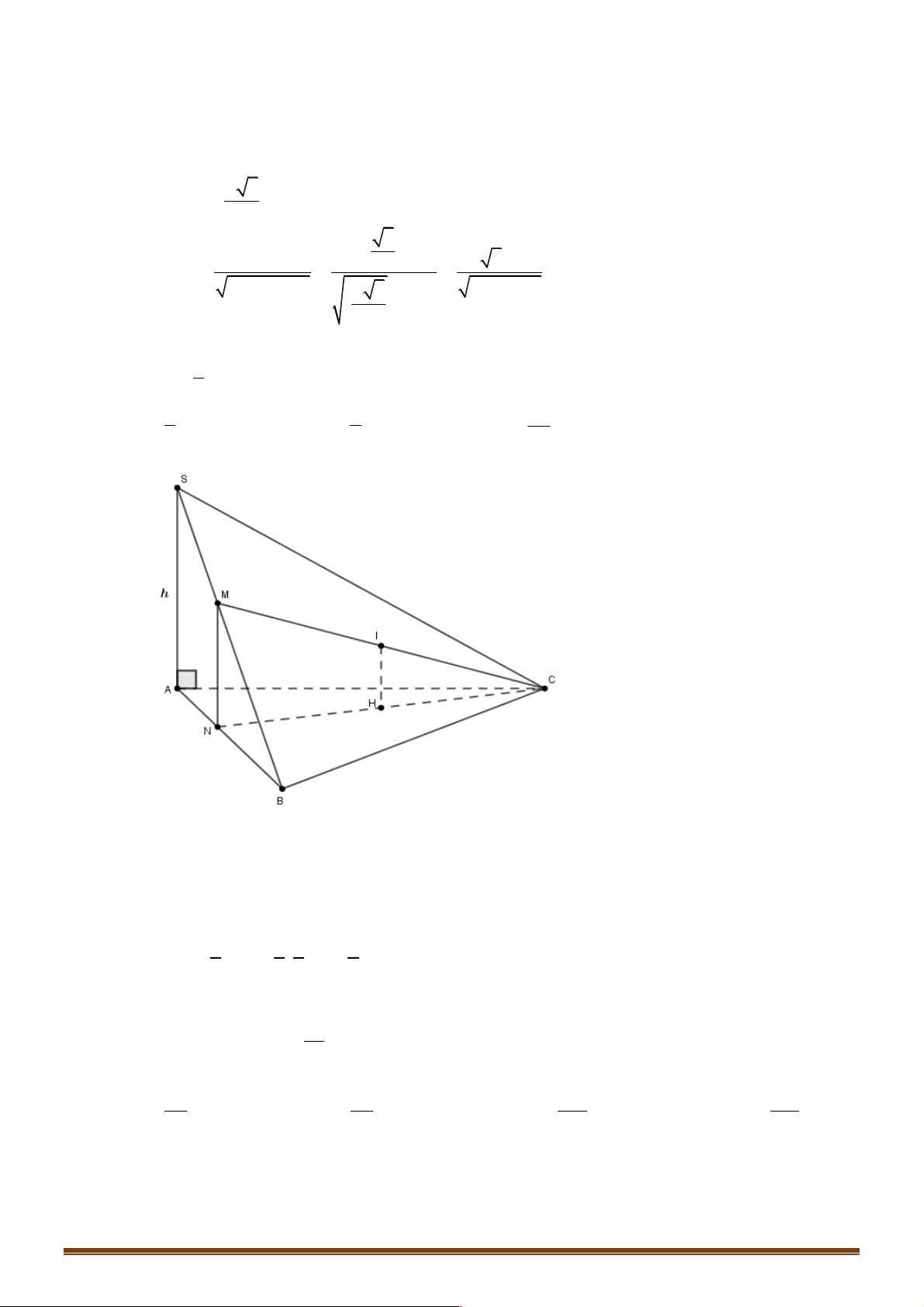
Ví dụ 3:Cho hình chóp S.ABC có SA = h và SA ^ (ABC) .Lấy điểm M Î SB sao cho 1 SM = M ;(
B M Î AB) .Gọi I là trung điểm của CM.Tính d (I;( ABC)) 2 h h 2h A. B. C. D. h 2 3 3 Đáp án B. Dựng MN / /S ,
A N Î AB Þ MN ^ (ABC)
Dựng IH ^ CN Þ IH ^ (ABC)
Þ IH = d(I;(ABC)) 1 1 2 h
Þ IH = MN = . SA = 2 2 3 3 Ù
Ví dụ 4:Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, BAD = 60! ; 3a
SO ^ (ABCD); SO =
.Đặt x = d ( ;
O (SBC)); y = d ( ;
A (SBC)); z = d ( A ; D SB). Tính 4
x + y + z 9a 3a 15a 15a A. B. C. D. 8 4 4 8 Đáp án D. Trang 50 Ù
Vì BAD = 60! Þ D BAD đều cạnh a a 3 a 3 a Þ AO = ; BD = a Þ OC = ;OB = 2 2 2
Suya ra tứ diện OSBC vuông tại O 1 1 1 1 1 1 1 64 Þ = + + = + + = 2 2 2 2 2 2 2 x SO OB OC 3a 2 æ a ö æ ö 9 ( ) a 3 a 4 ç ÷ 2 ç ÷ è ø 2 è ø 3a Þ a x = .Ta có AC = 3 2AO Þ d( ;
A (SBC)) = 2d(O;(SBC)) = = y 8 4 3a Vì AD / (
/ SBC) Þ z = d(A ;
D SB) = d(A ;
D (SBC)) = d( ; A (SBC)) = 4
3a 3a 3a 15a
Þ x + y + z = + + = 8 4 4 8
Ví dụ 5:Cho hình lập phương ABC . D ’ A ’ B C’ ’
D có cạnh bằng a .Tính d ( AC;D ’ C ) a 3 a 3 a A. B. C. D. a 3 2 3 Đáp án A. Trang 51
d ( AC;D ’
C ) = d(AC;(D ’ A ’ C ) = d( ; A (D ’ A ’ C ) = d( ’ D ;(D ’ A C ) ’
Vì AC / / (D ’ A ’ C ) nên Tứ diện ’ D ’
A DC’ vuông tại ’ D nên 1 1 1 1 1 1 1 3 = + + = + + = 2 2 2 2 2 2 2 2 d (D';(DA'C') D ' A' D ' D D 'C ' a a a a a a 3
Þ d(D';(DA'C') = =
= d(AC; DC ') 3 3
Ví dụ 6: Cho hình lăng trụ đứng ABC. ’ A ’
B C’ có đáy là tam giác vuông tại B, AB = BC = a ,cạnh bên
AA' = 2.Gọi M là trung điểm BC .Tính d ( AM; ’ B C) 2 a A. a 7 B. a 7 C. 7 D. 7 a 7 Đáp án B.
Trước hết ta đi dựng 1 mặt phẳng chứa đường này và song song với đường kia để chuyển về
khoảng cách từ 1 điểm đến mặt phẳng.Lấy E là trung điểm ’ BB
Þ ME / /CB ' Þ CB '/ /(AME)
Þ d(AM ; B 'C) = d(B'C;(AME)) = d(C;(AME)) = d(B;(AME))
Mà tứ diện BAME vuông ở B nên: 1 1 1 1 1 1 1 = + + = + + 2 2 2 2 2 2 2 d ( ; B (AME)) BM BE BA æ a ö æ a 2 ö a ç ÷ 2 ç ÷ è ø 2 è ø 4 4 1 7 = + + = 2 2 2 2 a 2a a a a Þ d( ; B (AME)) =
= d(AM; B'C) 7 Trang 52
Nhận xét:Qua 2 ví dụ trên ta luôn chuyển khoảng cách về tứ diện vuông để tính
Ví dụ 7: Cho lăng trụ đều ABC. ’ A ’
B C’ có tất cả các cạnh bằng a.Gọi M ; N lần lượt là trung điểm của ’ AA và ’.
BB Tính d = d( ’ B M ;CN) a 3 a 3 a 3 A.
B. a 3 C. D. 2 8 4
Gọi O và O’ lần lượt là trung điểm của BC và B’C’ và P = OO' Ç CN vì ’ B M / / (CAN )
Nên Tứ diện OACP vuông tại O 1 1 1 1 Þ = + + 2 2 2 2 d (O;(CAP)) OA OP OC 1 1 1 4 16 4 64 = + + = + + = 2 2 2 2 2 2 2 æ a ö æ a ö æ a ö 3a a a 3 3 a ç ÷ ç ÷ ç ÷ 2 è 4 ø è 2 ø è ø a 3 a 3 Þ d( ; O (CAP)) = Þ d = 8 4 B
Nhận xét:Ngoài việc chuyển khoảng cách giữa B’M và CN ta còn dựng thêm được tứ diện
vuông OACP và nhờ vào tính chất tứ diện vuông ta tính được khoảng cách Ù Ù
Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình thang , ABC = BAD = 90! ,
BA = BC = a, AD = 2a .Cạnh bên SA vuông góc với đáy và SA = a 2 .Gọi H là hình chiếu
vuông góc của A trên SB.Tính d (H;(SCD)) a 2a 2a a a A. B. C. D. 2 3 3 3 3 Đáp án C.
ọi M = AB ÇC ;
D K = AH Ç SM
Vì BC là đường trung bình của M
D AD Þ B là trung điểm của AM 2 BH BH.BS BA a 1 Ta có: = = =
= ÞH là trọng tâm của SA D M 2 2 2 BS BS BS 3a 3 S
d(H;(SCD)) KH 1 Từ đó = = . d( ; A (SCD)) KA 3
Tứ diện ASDM vuông tại A nên 1 1 1 1 1 = + + = 2 2 2 2 2 d (A;(SCD)) AS AD AM a a Þ d( ;
A (SCD)) = a Þ d(H;(SCD)) = 3 Trang 53
Ví dụ 9: Cho hình lập phương ABC . D ’ A ’ B C’ ’
D cạnh a .Tính khoảng cách giữa hai đường thẳng AA’ và BD’ a
A. a 2 B. a 2 C. D. a 3 2 2 2 Đáp án A.
Xét mặt phẳng (BB’D’D) chứa BD’ và song song với AA’ ìAO ^ BD Ta có í
(O là tâm hình vuông ABCD) îAO ^ BB ' AC a 2
Þ AO ^ (BB ' D ' D) Þ d(AA';BD')=AO= = 2 2
Ví dụ 10:Cho hình hộp chữ nhật ABC . D ’ A ’ B C’ ’ D có AB = ; a AD = 2a, ’
AA = a .Gọi M là điểm chia AM đoạn AD với
= 3 .Đặt x = d ( A ’; D ’
B C); y = d (M;( A ’
B C)) .Tìm .xy MD 2 3a 2 5a 2 a 2 3a A. B. C. D. 2 6 3 6 2 4 B C Đáp án C.
Ta có B 'C / /(AA ' D ' D) Þ d(B'C;AD') = B'A' = a = x
d(M ;(AB 'C)) MI AM
G I = BM Ç AC Þ = = = A’ 3 oi d( ;
B (AB 'C)) BI BC 4 3
Þ d(M;(AB'C)) = d( ;
B (AB 'C)) 4
Tứ diện BAB’C vuông tại B nên ta có 1 1 1 1 9 = + + = 2 2 2 2 2 d ( ;
B (AB 'C)) a a 4a 4a 2a 3 2a a Þ d( ;
B (AB 'C)) =
Þ d(M;(AB 'C)) = . = = y 3 4 3 2 2 a a Vậy . x y = . a = 2 2
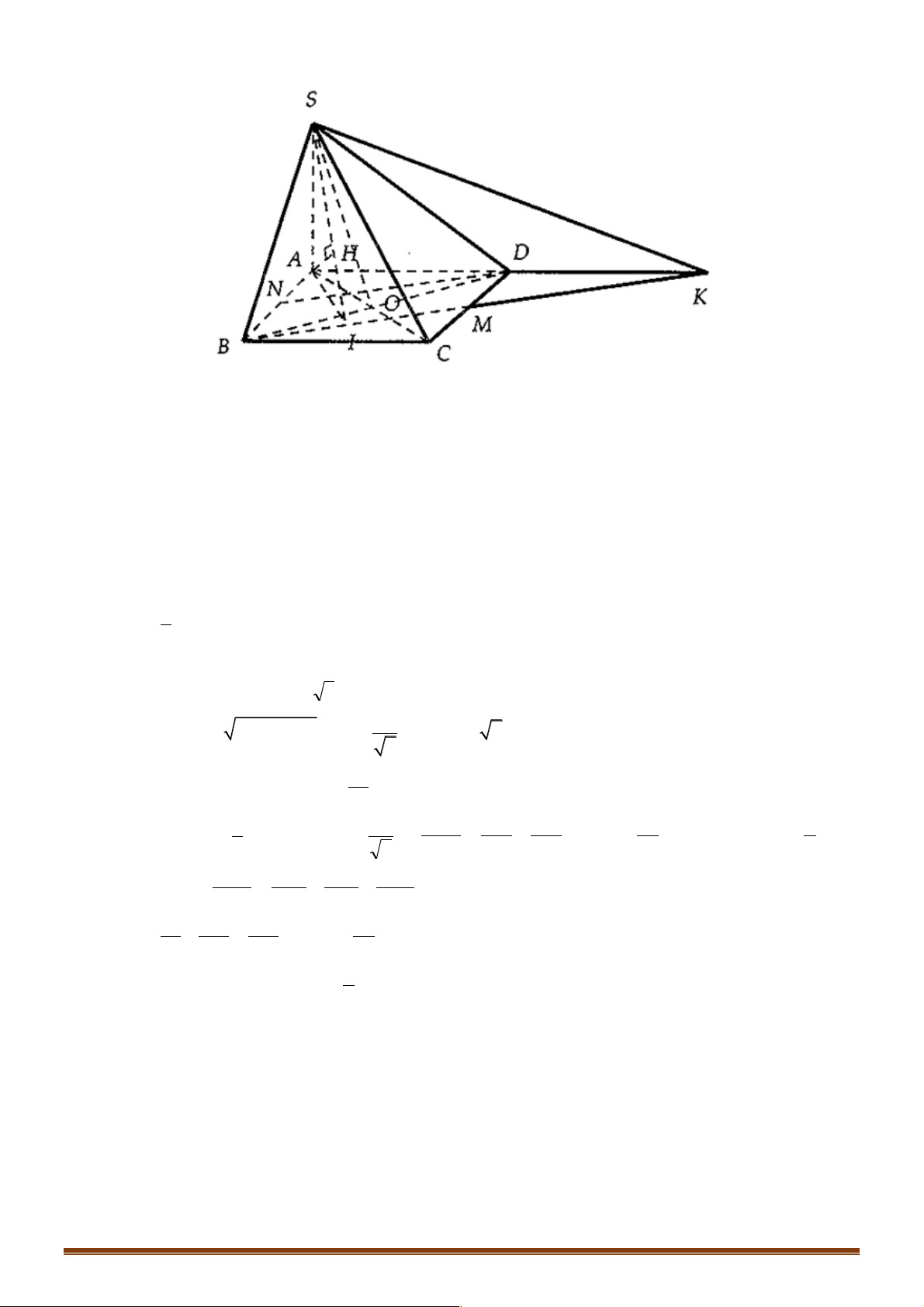
Ví dụ 16. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh bằng a. Gọi K là trung điểm DD¢. Tính
d (CK; A D ¢ ). 2a a 3a 4a A. . B. . C. . D. . 3 3 4 3 Lời giải Trang 54 Đáp án B.
Gọi M là trung điểm BB¢ .
Ta có: A¢M ! KC nên d (CK; A D
¢ ) = d (CK;(A M
¢ D)) = d (K;(A M ¢ D)).
d (K;( A M ¢ D)) NK 1
Gọi N = AK Ç A¢D , P = AB Ç A M ¢ . Khi đó = = . d ( ; A ( A M ¢ D)) NA 2 Þ d (CK A D ¢ ) 1
= d ( A ( A M ¢ D)) 1 ; ; = d ( ; A ( A D ¢ P)). 2 2
Tứ diện đều AA¢DP vuông tại A nên: 1 1 1 1 1 1 1 9 = + + = + + = 2 d ( ; A ( A D ¢ P)) 2 2 2 2 2 2 2 A A ¢ AD AP a a 4a 4a Þ ( A ( A D ¢ P)) 2a a d ; =
Þ d (CK; A D ¢ ) = . 3 3
Ví dụ 17. Cho lăng trụ đứng ABC.A¢B C
¢ ¢ có đáy ABC là tam giác vuông tại B , AB = a , AA¢ = 2a,
A¢C = 3a . Gọi M là trung điểm đoạn thẳng A¢C¢, I là giao điểm của AM và A¢C . Tính
khoảng cách từ A đến mặt phẳng (IBC). 2a 5 a 5 3a A. 2a 5 . B. . C. . D. . 5 5 5 Lời giải Đáp án B. Ta có: 2 2 AC = A C ¢ - A A ¢ = a 5 2 2
BC = AC - AB = 2a Hạ AK ^ A B ¢ (K Î A B
¢ ) vì BC ^(ABB A
¢ ¢) nên AK ^ BC Þ AK ^ (IBC). Trang 55 ¢
Þ d ( A (IBC)) 2S ¢ AA .AB 2a 5 ; AA B = AK = = = . 2 2 A¢B AA¢ + AB 5
Ví dụ 18. Cho lăng trụ ABC .
D A B C D có đáy ABCD là hình chữ nhật với AB = a , AD = a 3 . Hình 1 1 1 1
chiếu vuông góc của điểm A trên ( ABCD) trùng với giao điểm của AC BD 1 và . Tính khoảng
cách từ điểm B đến mặt phẳng ( A BD a 1 ) theo . 1 a 3 a a 3 A. . B. a 3 . C. . D. . 2 2 6 Lời giải
Gọi O là giao điểm của AC và BD. Khi đó AO ^ ABCD 1 ( ).
Ta có: B C ! A D Þ B C ! A BD 1 1 1 ( 1 )
Þ d (B ; A BD = d C; A BD 1 ( 1 )) ( ( 1 )).
Kẻ CH ^ BD thì CH ^ ( A BD 1 ) Þ d ( . CD CB a 3
B ; A BD = CH = = 1 ( 1 )) . 2 2 CD + CB 2
Ví dụ 19. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB = 3a , BC = 4a , mặt phẳng (SBC)
vuông góc với mặt phẳng ( ABC). Biết SB = 2a 3 ∑
và SBC = 30°. Tính d ( ; B (SAC)). 3a 7 6a 7 A. . B. 6a 7 . C. . D. a 7 . 14 7 Lời giải Trang 56 Đáp án C.
Kẻ SH ^ BC (H ÎBC) do (SBC) ^ ( ABC) nên SH ^ ( ABC). Ta có: SH = .s SB in30° = a 3
Kẻ HD ^ AC (DÎ AC), kẻ HK ^ SD(K ÎSD).
Khi đó HK = d (H;(SAC)) Vì BH = .
SB cos30° = 3a nên BC = 4HC Þ d ( ;
B (SAC)) = 4d (H;(SAC)) Ta có: 2 2
AC = AB + BC = 5a HC 3a SH.HD 3a 7
HC = BC - BH = a Þ HD = . AB = Þ HK = = 2 2 AC 5 SH + HD 14 a
Vậy d (B (SAC)) 6 7 ; = 4HK = . 7 * Chú ý 1:
Xác định đoạn vuông góc chung, tính khoảng cách của hai đường thẳng chéo nhau.
TH1: Giả sử hai đường thẳng a và b chéo nhau và vuông góc với nhau. Ta dựng mp (a )
chứa a và vuông góc với b tại B . Trong mặt phẳng (a ) dựng BA ^ a tại A.Khi đó độ dài
đoạn thẳng BA là khoảng cách giữa hai đường thẳng chéo nhau a và b .
TH2: Giả sử a và b là hai đường thẳng chéo nhau nhưng không vuông góc với nhau.
- Ta dựng mp (a ) chứa a và song song với b . Trang 57
- Lấy một điểm M tùy ý trên b dựng MM ¢ ^ (a ) tại M ¢.
- Từ M ¢ dựng đường thẳng b¢ ! b cắt a tại A.
- Từ A dựng AB ! MM ¢ cắt b tại B khi đó đoạn thẳng AB gọi là đoạn vuông góc chung của
hai đường thẳng chéo nhau a và b . * Chú ý 2:
Thông thường bài toán tính khoảng cách giữa hai đường thẳng chéo nhau quy về tính khoảng
cách từ một điểm tới một mặt phẳng. Như TH2 nói trên thì d ( ; a b) = d ( ;
b (a )) = d (M; a).
Ví dụ 20. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung
điểm các cạnh AB và AD ; H là giao điểm của CN và DM . Biết SH vuông góc với ABCD
mặt phẳng và SH = a 3. Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 2 3a 2 3a 2a a A. . B. . C. . D. . 19 19 5 5 Lời giải Đáp án B. Ta có: AD D M = D D CN ∑ ∑
nên ADM = DCN Þ DM ^ CN
Có DM ^ SH Þ DM ^ (SHC)
Hạ HK ^ SC tại K Þ HK là đoạn vuông góc chung của DM và SC
Do đó d (DM;SC) = HK
Trong tam giác vuông CND ta có: 2 2 CD a 2a 2
CH.CN = CD Þ CH = = = CN a 5 5 2
Mặt khác HK.SC = SH.HC Trang 58 2a a 3. 2 SH.HC 5 2a 3 2a 3 Þ HK = = = = 2 2 2 2 SH + HC 4a 19a 19 2 3a + 5. 5 5
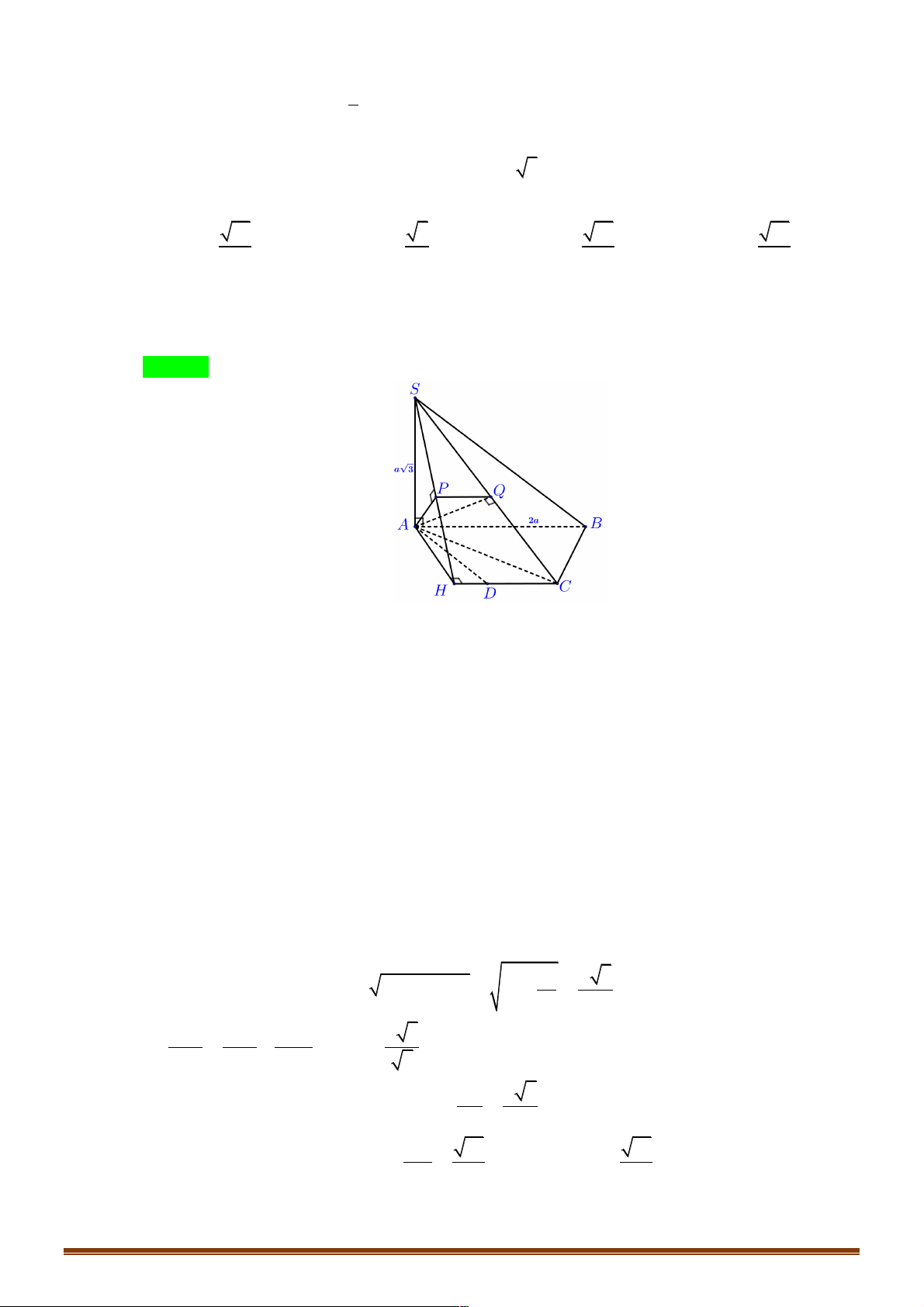
Ví dụ 21. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = BC = 2a ; hai mặt
phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng ( ABC). Gọi M là trung điểm của
AB , mặt phẳng ( ABC) đi qua SM và song song với BC cắt AC tại N . Biết góc giữa hai
mặt phẳng (SBC) và ( ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng AB và SN theo a . 2a 39 2a 39 2a 11 2a 11 A. . B. . C. . D. . 13 13 13 13 Lời giải Đáp án B.
Ta có: (SAB) và (SAC) cùng vuông góc với mặt phẳng ( ABC) nên SA ^ ( ABC). Từ
AB ^ BC Þ SB ^ BC nên ∑
SBA là góc giữa (SBC) và ( ABC). Từ đó ∑ SBA = 60°; ∑ SA = .
AB tan SBA = 2a 3
Kẻ đường thẳng D đi qua N , song song với AB .
Hạ AD ^ D (DÎD) Þ AB ! (SND) Þ d ( ; AB SN ) = d ( ;
AB (SND)) = d ( ; A (SND))
Dựng AH ^ SD tại H Þ AH ^ (SND) Þ d ( ;
A (SND)) = AH . BC
Tam giác SAD vuông tại A , có AH ^ SD và AD = = a 2 d ( AB SN ) . SA AD 2a 39 ; = AH = = . 2 2 SA + AD 13
Ví dụ 22. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = BC = 2a . Tam giác
SAC cân tại S có đường cao SO = a 3 và nằm trong mặt phẳng vuông góc với mặt phẳng
đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a . a 3 A. . B. 2a 3 . C. a 3 . D. a . 2 Lời giải Trang 59 Đáp án C.
Tam giác SAC cân tại S có SO ^ AC và (SAC) ^ ( ABC) nên SO ^ ( ABC).
Gọi D là điểm đối xứng với B qua O , khi đó ABCD là hình vuông nên AB ! CD
Þ AB ! (SCD) Þ d ( ; AB SC) = d ( ; AB (SCD))
Gọi E là trung điểm của AB Þ d ( ;
AB (SCD)) = d (E;(SCD))
Gọi F là trung điểm của CD .
Kẻ OH ^ SF (H ÎSF ) thì OH ^ (SCD) Þ d ( ,
O (SCD)) = OH .
Dựng EK ! OH (K ÎSF) Þ EK ^ (SCD) 1 1 1 4
Þ d (E;(SCD)) = EK và EK = 2OH mà = + = 2 2 2 2 OH OF OS 3a a 3 Þ OH =
Þ EK = d ( A ;
B SC ) = 2OH = a 3 2
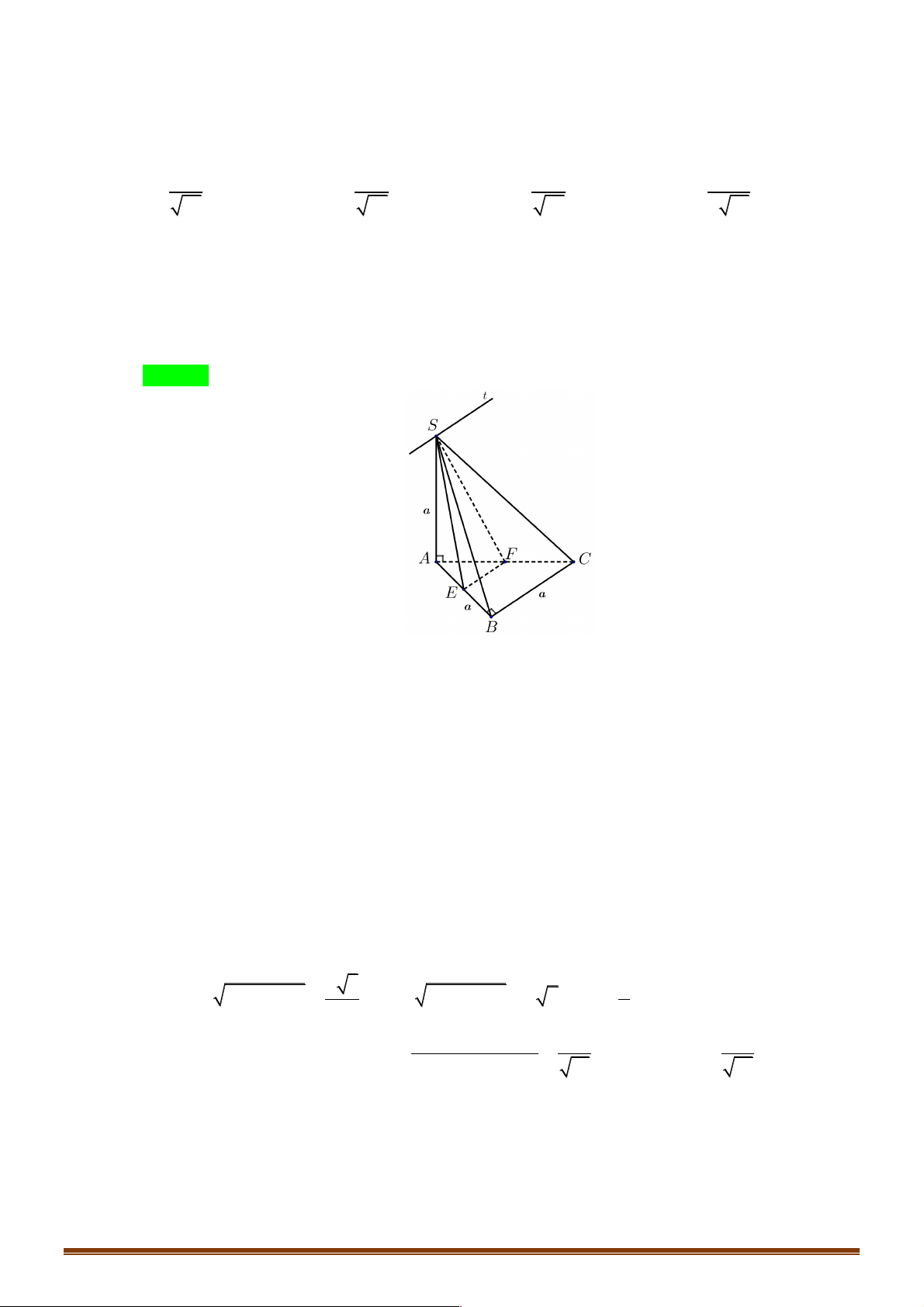
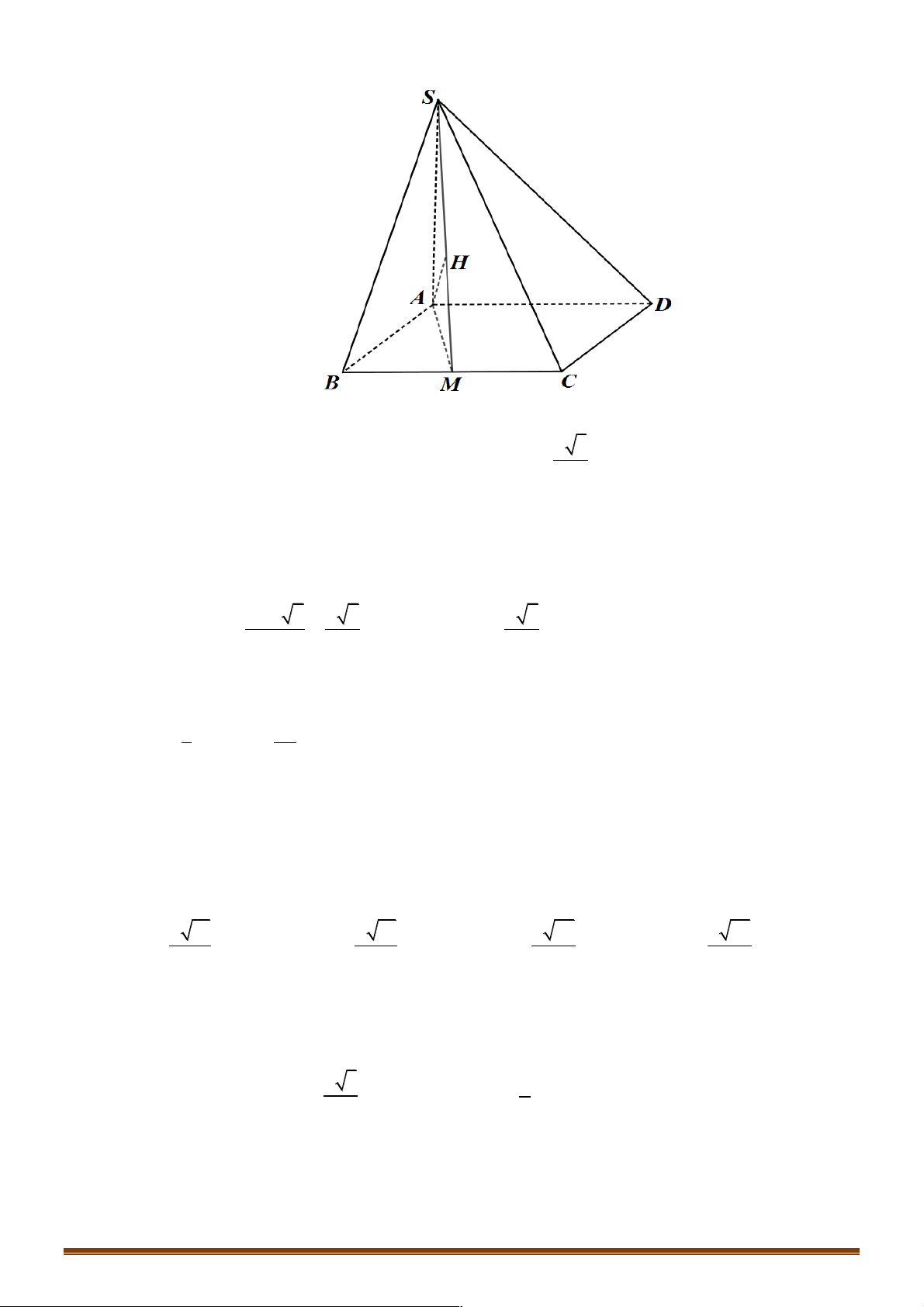
Ví dụ 23. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của S trên mặt
phẳng ( ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB . Góc giữa đường thẳng SC và
mặt phẳng ( ABC) bằng 60°. Tính khoảng cách giữa hai đường thẳng SA và BC theo a. a 42 a 42 a 42 a 42 A. . B. . C. . D. . 8 4 12 10 Lời giải Đáp án A. Ta có: ∑ SCH = (SC ( ∑ ; ABC )) = 60° Kẻ Ax ! BC . Trang 60
Gọi N và K lần lượt là hình chiếu vuông góc của H trên Ax và SN . 3 3
Ta có BC ! (SAN ) và BA = nên d (S ;
A BC) = d (B,(SAN )) = d (H,(SAN )). 2 2
Ta cũng có Ax ^ (SHN ) nên Ax ^ HK .
Do đó HK ^ (SAN ) Þ d (H,(SAN)) = HK 2a a 3 SH.HN a 42 AH =
, HN = AH.sin 60° = Þ HK = = 2 2 3 3 SH + HN 12 a Vậy d (SA BC) 42 ; = . 8
Ví dụ 24. Cho hình hộp đứng ABC . D A¢B C ¢ D
¢ ¢ có đáy là hình vuông, tam giác vuông cân A¢AC ,
A¢C = a . Tính khoảng cách từ A đến mặt phẳng (BCD¢) theo a . a 6 a 6 a 6 a 3 A. . B. . C. . D. . 3 2 6 6 Lời giải Đáp án C. a 2 a A
D ¢AC vuông cân tại A và A¢C = a nên AA¢ = AC = Þ AB = B C ¢ ¢ = . 2 2
Gọi H là chân đường cao kẻ A từ của A D ¢AB .
Do đó d (DM;SC) = HK
Ta có AH ^ A¢B và AH ^ BC nên AH ^ ( A BC ¢
) hay AH ^ (BCD¢)
Do đó AH = d ( ; A (BCD¢)). 1 1 1 6 a 6 Ta có: = + = Þ d , A BCD¢ = AH = 2 2 2 2 ( ( )) . AH AB AA¢ a 6
Ví dụ 25. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a , cạnh bên SA vuông góc với đáy, ∑
BAD =120°, M là trung điểm của cạnh BC và ∑
SMA = 45°. Tính theo a khoảng cách từ điểm
D đến mặt phẳng (SBC). a 6 a 6 a 3 a 3 A. . B. . C. . D. . 2 4 4 2 Lời giải Trang 61 Đáp án B. a Ta có: ∑ BAD =120° ∑
, ABC = 60° Þ ABC D 3 đều AM = 2
Do AD ! BC nên d ( ;
D (SBC)) = d ( ; A (SBC))
Gọi H là hình chiếu vuông góc của A trên SM .
Ta có: AM ^ BC và SA ^ BC Þ BC ^ (SAM )
Þ BC ^ AH Þ AH ^ (SBC) Þ d ( ;
A (SBC)) = AH AM. 2 a 6 a 6 Ta có: AH = =
Þ d (D,(SBC)) = . 2 4 4 STUDY TIP
Nếu ta công nhận công thức tính thể tích của khối chóp mà sau này ta học ở lớp 12 thì ta còn có
một cách khác để tính khoảng cách từ một điểm đến một mặt phẳng vì: 1 3V V = . B h Þ h = 3 B
Với B là diện tích đáy h Là chiều cao
V Là thể tích khối chóp.
Ví dụ 26. Cho hình chóp S.ABC ∑
có đáy là tam giác vuông tại A , ABC = 30°, SBC là tam giác đều cạnh
a và mặt bên SBC vuông góc với đáy. Tính theo a khoảng cách từ điểm C đến mặt phẳng (SAB). a 13 a 13 a 39 a 39 A. . B. . C. . D. . 4 13 4 13 Lời giải Đáp án D.
Gọi H là trung điểm BC Þ SH ^ BC .
Mà (SBC) ^ ( ABC) theo giao tuyến BC nên SH ^ ( ABC). a 3 a
Ta có: BC = a Þ SH =
; AC = BC.sin 30° = . 2 2 Trang 62 a 3 1 a o 3 AB = BC.cos30 = . Do đó V = SH.A . B AC = . 2 S.ABC 6 16
Tam giác ABC vuông tại A và H là trung điểm của BC nên HA = HB mà
SH ^ ( ABC) Þ SA = SB = a . 2 AB a 13
Gọi I là trung điểm của AB Þ SI ^ AB . Do đó 2 SI = SB - = . 4 4 Þ ( V V a d C;(SAB)) 3 6 39 S.ABC S.ABC = = = . S SI.AB 13 SA D B
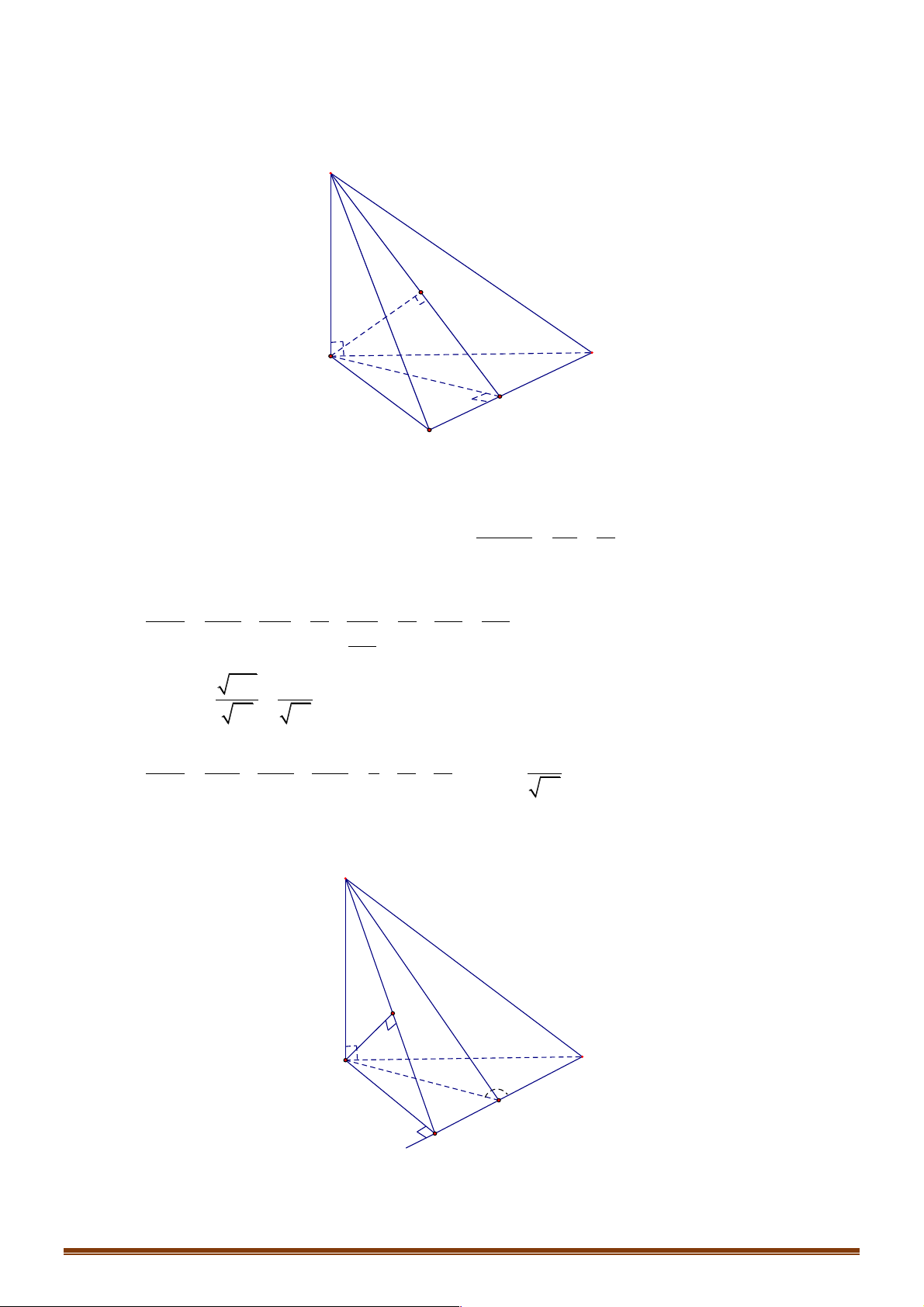
Ví dụ 27: Cho hình lăng trụ ABC.A¢B C
¢ ¢ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của A¢ trên mặt
phẳng ( ABC) là trung điểm của cạnh AB , góc giữa đường thẳng A¢C và mặt đáy bằng o 60 . Tính
theo a khoảng cách từ B đến mặt phẳng ( ACC A ¢ ¢). 3 13a 3 13a 2 13a 5 13a A. . B. . C. . D. . 13 26 13 26 Hướng dẫn giải Chọn A. Trang 63
Gọi H là trung điểm của AB Þ A H ¢ ^ (ABC) và ∑¢ = 60O A CH . Do đó ¢ ∑ 3a
A H = CH.tan A C ¢ H = . 2
Gọi I là hình chiếu vuông góc của H trên AC , K là hình chiếu vuông góc của H trên A¢I
Þ HK = d (H;(ACC A ¢ ¢)). a Ta có ∑ 3
HI = AH.sin IAH = . 4 1 1 1 52 3 13a = + = Þ HK = . 2 2 2 2 HK HI HA¢ 9a 26 a
Do đó d (B ( ACC A
¢ ¢)) = (H ( ACC A ¢ ¢)) 3 13 ; 2d ; = 2HK = . 13
STUDY TIP: Vì A H
¢ ^ ( ABC) và H là trung điểm của AB nên d ( ; B ( ACC A
¢ ¢)) = 2d(H;(ACC A ¢ ¢)). 3a
Ví dụ 28: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , D S =
. Hình chiếu vuông góc của 2
S trên mặt phẳng ( D
ABC ) là trung điểm của AB . Tính theo a khoảng cách từ A đến mặt phẳng (SBD). a 2a a 3 a 3 A. . B. . C. . D. . 3 3 2 3 Hướng dẫn giải Chọn B.
Gọi H là trung điểm của AB Þ SH ^ ( D ABC ). Do đó SH ^ D H , ta có 2 2 2 SH = S - H = S - ( 2 2 D D D AH + D H ) = a.
Gọi K là hình chiếu vuông góc của H trên BD và E là hình chiếu vuông góc của H trên SK . Ta có D B ^ HK và D B ^ SH Þ D B ^ (SHK ) Þ D B ^ HE .
Mà HE ^ SK do đó HE ^ (S D B ). a 2 S H .HK a Ta có ∑ HK = H . B sin KBH = Þ HE = = . 2 2 4 S H + HK 3
Do đó d ( A (SB )) = d (H (SB )) 2a ; D 2 ; D = 2HE = . 3 STUDY TIP: d ( ; A (S D
B )) = 2d(H;(S D B )).
Ví dụ 29: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( AB D
C ), góc giữa SC và mặt phẳng ( D ABC ) bằng o
45 . Tính theo a khoảng cách giữa hai đường thẳng SB và AC . Trang 64 5a 5a a 10 a 10 A. . B. . C. . D. . 5 2 5 2 Hướng dẫn giải Chọn B.
Kẻ đường thẳng d qua B và song song với AC . Gọi M là hình chiếu vuông góc của A trên d ; H
là hình chiếu vuông góc của A trên SM .
Ta có SA ^ BM , MA ^ BM nên AH ^ BM Þ AH ^ (SBM ).
Do đó d ( AC;SB) = d ( ;
A (SBM )) = AH . 1 1 1 5 SA
D M vuông tại A có đường cao AH nên = + = . 2 2 2 2 AH SA AM 2a a Vậy d ( AC SB) 10 ; = AH = . 5
STUDY TIP: Dựng mặt phẳng (SBM ) chứa SB và song song với AC .
C. BÀI TẬP RÈN LUYỆN KỸ NĂNG
Câu 1. Cho mặt phẳng (P) và hai điểm ,
A B không nằm trong (P). Đặt d = d ; A P 1 ( ( )) và d = d ; B P 2
( ( )). Trong các kết luận sau thì kết luận nào đúng?
A. d1 = 1 khi và chỉ khi AB// (P). d2
B. d1 ¹ 1 khi và chỉ khi đoạn thẳng AB cắt (P). d2
C. d1 ¹ 1 khi đoạn thẳng AB cắt (P). d2
D. Nếu đường thẳng IA d
AB cắt (P) tại điểm I thì 1 = . IB d2
Câu 2. Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc. Giả sử AB = ,
1 AC = 2 , AD = 3.
Khi đó khoảng cách từ A đến mặt phẳng (BCD) bằng: 7 5 6 7 A. . B. . C. . D. . 5 7 7 11
Câu 3. Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = a , AD = b, AA¢ = c. Khoảng cách giữa hai
đường thẳng BB¢ và AC¢ là: 1 A. bc . B. ab . C. bc . D. 2 2 a + b . 2 2 b + c 2 2 a + b 2 2 a + b 2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SCD). a 7 a 7 a 21 a 7 A. . B. . C. . D. . 7 21 7 3 Trang 65
Câu 5. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a . Tìm mệnh đề đúng trong các mệnh đề sau? a
A. Khoảng cách từ A đến mặt phẳng ( A B ¢ D) bằng . 3
B. Độ dài AC¢ = a 3.
C. Khoảng cách từ A đến mặt phẳng (CDD C ¢ ¢) bằng a 2. 3a
D. Khoảng cách từ A đến mặt phẳng (BCC B ¢ ¢) bằng . 2
Câu 6. Cho tứ diện đều ABCD cạnh a . Gọi A¢ là hình chiếu của A trên mặt phẳng (BCD). Độ dài cạnh AA¢ là: a 6 a 6 a 3 a 6 A. . B. . C. . D. . 3 4 2 3
Câu 7. Cho tứ diện ABCD có AC = a , BD = 3a. Gọi M , N lần lượt là trung điểm của AD và BC .
Biết AC ^ BD . Tính MN . a 6 2a 3 3a 2 a 10 A. . B. . C. . D. . 3 3 2 2
Câu 8. Cho hình lập phương ABC .
D EFGH có cạnh a . Tính tích . AB EG ? A. 2 a 3 . B. 2 a . C. 2 a 2. D. 2 2a .
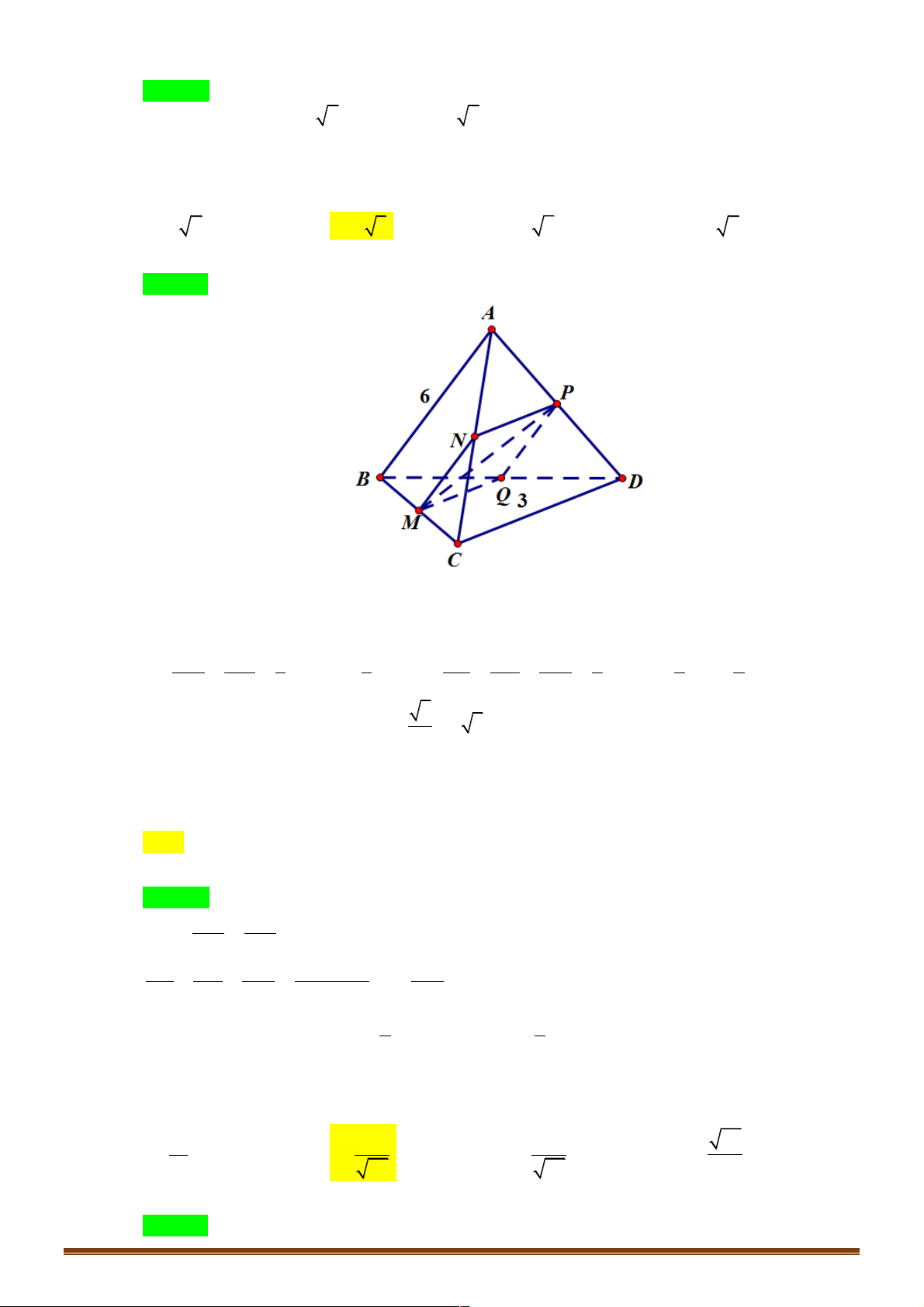
Câu 9. Cho tứ diện ABCD có AB = 6, CD = 3. Góc giữa AB và CD bằng o
60 . Điểm M nằm trên
đoạn BC sao cho BM = 2MC . Mặt phẳng (P) qua M song song với AB và CD cắt AC ,
AD và BD lần lượt tại N , P , Q . Tính diện tích MNPQ? A. 2 2 . B. 2 3 . C. 3 . D. 3 2 .
Câu 10. Cho tứ diện ABCD có AB ^ CD , AB = CD = 6; M là điểm thuộc cạnh BC sao cho
MC = xBC (0 < x < )
1 . Mặt phẳng (P) song song với AB và CD lần lượt cắt BC , AC , AD,
BD tại M , N , P , Q . Diện tích lớn nhất của tứ giác MNPQ là: A. 9 . B. 6 . C. 10 . D. 12 .
Câu 11. Cho tứ diện ABCD có DA ^ ( ABC), AC = AD = 4 , AB = 3, CD = 5. Tính khoảng cách từ
A đến mặt phẳng (BCD). 12 12 6 34 A. . B. . C. . D. . 5 34 34 3
Câu 12. Cho hình chóp S.ABC có SA ^ ( ABC), SA = 3a , AB = BC = 2a , ∑ o
ABC =120 . Tính khoảng
cách từ A đến (SBC). 3a A. a 3 a . B. 2a . C. . D. . 2 2
Câu 13. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA ^ ( ABC) và SA = a. Tính khoảng
cách từ A đến (SBC) theo a . a 3 3a a 3 3a A. . B. . C. . D. . 7 7 7 7
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = AD = a ,
CD = 2a , cạnh SD vuông góc với ( ABCD), SD = a. Tính d ( ;
A (SBC)). a 3 a 6 a 6 A. . B. a 3 . C. . D. . 3 6 3 Trang 66
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , AD = 2a , SA ^ ( ABCD),
SA = a . Tính khoảng cách từ trung điểm I của SC đến (SBD .) a 3 a a 3 2a A. . B. . C. . D. . 3 3 2 3
Câu 16. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA ^ ( ABCD), SA = a.
Tính khoảng cách giữa hai đường thẳng SB và CD . A. a . B. a 2. C. a 3 . D. 2a .
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA ^ ( ABCD), SA = a.
Gọi M là trung điểm của CD . Khoảng cách từ M đến (SAB) nhận giá trị nào sau đây? a 2 A. . B. a . C. a 2 . D. 2a . 2
Câu 18. Cho hình chóp S.ABC trong đó SA , AB , BC đôi một vuông góc và SA = AB = BC = 1. Tính độ dài SC . 3 A. 2 . B. 3 . C. 2 . D. . 2
Câu 19. Cho tứ diện ABCD có DA = DB = DC và ∑ o BCD = 60 , ∑ o ADC = 90 , ∑ o ADB =120 . Trong các mặt của tứ diện đó:
A. Tam giác ABD có diện tích lớn nhất.
B. Tam giác ACD có diện tích lớn nhất.
C. Tam giác BCD có diện tích lớn nhất. D. Tam giác C
AB có diện tích lớn nhất.
Câu 20. Cho tứ diện ABCD có hai cặp cạnh đối diện vuông góc. Cắt tứ diện đó bằng một mặt phẳng
song song với một cặp cạnh đối diện còn lại của tứ diện. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Thiết diện là hình thang.
B. Thiết diện là hình bình hành.
C. Thiết diện là hình chữ nhật.
D. Thiết diện là hình vuông.
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( ABCD), SA = a 3.
Tính khoảng cách từ A đến mặt phẳng (SBC). a a 3 3a a A. . B. . C. . D. . 2 2 2 3
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là nữa lục giác đều với đáy lớn AD = 2a
SA ^ ( ABCD) và SA = a 3 . Tính khoảng cách từ A đến (SBC). a 3 a 3 a 3 A. a . B. . C. . D. . 2 5 7
Câu 23. Cho tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau. Gọi a , b , c tương ứng là
độ dài của các cạnh OA , OB , OC . Gọi h là khoảng cách từ O đến ( ABC) thì h có giá trị là: 1 1 1 1 1 1 A. h = + + . B. h = + + . a b c 2 2 2 a b c 2 2 2 2 2 2
a b + b c + c a abc C. h = . D. h = . 2 2 2 a b c 2 2 2 2 2 2
a b + b c + c a
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , cạnh a , đường chéo AC = a , mặt
bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và (ABCD) bằng o
60 . Gọi I là trung điểm của AB . Tính khoảng cách từ I đến (SBC .) 3a 13 a 3 a 13 3a 13 A. . B. . C. . D. . 26 4 26 16 Trang 67
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = AD = 2a ,
CD = a ; góc giữa hai mặt phẳng (SBC) và ( ABCD) bằng 60o. Gọi I là trung điểm của AD,
hai mặt phẳng (SBI ) và (SCI ) cùng vuông góc với ( ABCD). Tính theo a khoảng cách từ A đến (SBC). a 15 3a 15 2a 15 2a 15 A. . B. . C. . D. . 5 10 10 5
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho mặt phẳng (P) và hai điểm ,
A B không nằm trong (P). Đặt d = d ; A P 1 ( ( )) và d = d ; B P 2
( ( )). Trong các kết luận sau thì kết luận nào đúng? d
A. 1 = 1 khi và chỉ khi AB// (P). d2 d
B. 1 ¹ 1 khi và chỉ khi đoạn thẳng AB cắt (P). d2 d
C. 1 ¹ 1 khi đoạn thẳng AB cắt (P). d2 IA d
D. Nếu đường thẳng AB cắt (P) tại điểm I thì 1 = . IB d2 Hướng dẫn giải Chọn D.
Câu 2. Cho tứ diện ABCD có AB , AC , AD đôi một vuông góc. Giả sử AB = ,
1 AC = 2 , AD = 3.
Khi đó khoảng cách từ A đến mặt phẳng (BCD) bằng: 7 5 6 7 A. . B. . C. . D. . 5 7 7 11 Hướng dẫn giải Chọn C. 1 1 1 1 49 6 Vì = + + = Þ d = . 2 2 2 2 d 1 2 3 36 7
Câu 3. Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = a , AD = b, AA¢ = c. Khoảng cách giữa hai
đường thẳng BB¢ và AC¢ là: bc ab bc 1 A. . B. . C. . D. 2 2 a + b . 2 2 b + c 2 2 a + b 2 2 a + b 2 Hướng dẫn giải Chọn B. Trang 68 ( ab
d BB ;¢ AC¢) = d (BB ;¢( ACC ' A')) = d ( ;
B ( ACC ' A')) = BH = . 2 2 a + b
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SCD). a 7 a 7 a 21 a 7 A. . B. . C. . D. . 7 21 7 3 Hướng dẫn giải Chọn C.
Gọi I là trung điểm của AB , ta có SI ^ AB và (SAB) ^ ( ABCD) Þ SI ^ ( ABCD).
Gọi E là trung điểm của CD , trong mặt phẳng (SIE) dựng IH ^ SE(H ÎSE) thì
IH ^ (SCD) Þ d (I;(SCD)) = IH . a 3 Ta có SI = , IE = a . 2
Þ d ( A (SC )) = d (I (SCD)) SI.IE a 21 ; D ; = IH = = . 2 2 SI + IE 7
Câu 5. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh a . Tìm mệnh đề đúng trong các mệnh đề sau? a
A. Khoảng cách từ A đến mặt phẳng ( A B ¢ D) bằng . 3
B. Độ dài AC¢ = a 3.
C. Khoảng cách từ A đến mặt phẳng (CDD C ¢ ¢) bằng a 2. 3a
D. Khoảng cách từ A đến mặt phẳng (BCC B ¢ ¢) bằng . 2 Hướng dẫn giải Trang 69 Chọn B.
Câu 6. Cho tứ diện đều ABCD cạnh a . Gọi A¢ là hình chiếu của A trên mặt phẳng (BCD). Độ dài cạnh AA¢ là: a 6 a 6 a 3 a 6 A. . B. . C. . D. . 3 4 2 3 Hướng dẫn giải Chọn A. a 3 2 3a a 6 Ta có BA¢ = ; 2 2 2
AA¢ = AB - BA' = a - = . 3 9 3
Câu 7. Cho tứ diện ABCD có AC = a , BD = 3a. Gọi M , N lần lượt là trung điểm của AD và BC .
Biết AC ^ BD . Tính MN . a 6 2a 3 3a 2 a 10 A. . B. . C. . D. . 3 3 2 2 Hướng dẫn giải Chọn D.
Lấy P là trung điểm của AB . Khi đó: PM //BD , PN //AC . a
Vì AC ^ BD Þ PM ^ 3a PN và PM = ; PN = . 2 2 2 2 9a a a 10 2 2
Þ MN = PM + PN = + = . 4 4 2
Câu 8. Cho hình lập phương ABC .
D EFGH có cạnh a . Tính tích . AB EG ? A. 2 a 3 . B. 2 a . C. 2 a 2. D. 2 2a . Hướng dẫn giải Trang 70 Chọn C.
Ta có AB = a , 2 EG = a 2 Þ . AB EG = a 2 .
Câu 9. Cho tứ diện ABCD có AB = 6, CD = 3. Góc giữa AB và CD bằng o
60 . Điểm M nằm trên
đoạn BC sao cho BM = 2MC . Mặt phẳng (P) qua M song song với AB và CD cắt AC ,
AD và BD lần lượt tại N , P , Q . Tính diện tích MNPQ? A. 2 2 . B. 2 3 . C. 3 . D. 3 2 . Hướng dẫn giải Chọn B.
Giao tuyến của (P) với ( ABC) là MN //AB.
Tương tự NP//MQ// D
C . Suy ra tứ giác ABCD là hình bình hành và ∑ (NM NP) o ; = 60 MN MC 1 1 NP AN BM Có = = Þ MN = AB = 2 2 2 2; = =
= Þ NP = CD = .3 = 2. AB CB 3 3 D C AC BC 3 3 3 ∑ 3 Þ S = MN. .
NP sin MNP = 2.2. = 2 3. MNPQ 2
Câu 10. Cho tứ diện ABCD có AB ^ CD , AB = CD = 6; M là điểm thuộc cạnh BC sao cho
MC = xBC (0 < x < )
1 . Mặt phẳng (P) song song với AB và CD lần lượt cắt BC , AC , AD,
BD tại M , N , P , Q . Diện tích lớn nhất của tứ giác MNPQ là: A. 9 . B. 6 . C. 10 . D. 12 . Hướng dẫn giải Chọn A. MN CM Ta có =
= x Þ MN = xAB = 6x. AB CB NP AN BM BC - CM CM = = = =1-
=1- x Þ NP = 6(1- x). D C AC BC BC BC 2 æ ö æ ö Þ S = 36x - x = - - x + x = - - x £ Þ S = MNPQ (1 ) 1 1 2 9 36 9 36 9 max 9. ç ÷ ç ÷ è 4 ø è 2 MNPQ ø
Câu 11. Cho tứ diện ABCD có DA ^ ( ABC), AC = AD = 4 , AB = 3, CD = 5. Tính khoảng cách từ A
đến mặt phẳng (BCD). 12 12 6 34 A. . B. . C. . D. . 5 34 34 3 Hướng dẫn giải Chọn B. Trang 71 D 4 H 4 A C 3 I 5 B Vì 2 2 2
AB + AC = BC nên ABC D vuông tại A .
Cách 1: Sử dụng tính chất tam giác vuông . AB AC 3.4 12
Dựng AI ^ BC Þ AI.BC = . AB AC Þ AI = = = BC 5 5
Dựng AH ^ DI Þ AH ^ (BCD) Þ AH = d ( ; A (BCD)) 1 1 1 1 1 1 25 34 = + = + = + = 2 2 2 AH AD AI 16 144 16 144 144 25 144 12 Þ AH = = . 34 34
Cách 2: Vì tứ diện ABCD vuông tại A nên áp dụng tính chất của tứ diện vuông ta có: 1 1 1 1 1 1 1 12 = + + = + + Þ AH = . 2 2 2 2 AH AB AC AD 9 16 16 34
Nhận xét: Trong 2 cách trên thì cách 2 nhanh hơn nhiều khi sử dụng tính chất tứ diện vuông. Câu 12: Đáp án D. S 3a K A C 2a 2a B H
Kẻ AH ^ BC và AK ^ SH .
Ta có: BC ^ AH và Trang 72
BC ^ SA Þ BC ^ (SAH ) Þ AK ^ (SBC) Þ AK = d ( ; A (SBC))
Trong tam giác vuông BAH ta có: AH = .s
AB in 60° = a 3 .
Trong tam giác vuông SAH ta có: AS.AH 3 . a a 3 3 AK = =
= a Þ d ( A (SBC)) 3 ; = . a 2 2 SH 9a + 3a 2 2
Nhận xét: Trong bài này ta sử dụng tính chất tam giác vuông ( SA
D H ) để tính khoảng cách d ( ;
A (SBC)) . Vậy có thể sử dụng tính chất của tứ diện vuông dduocjw không ?
Câu trả lời là được. Vì nếu lấy điểm H trên tia CB sao cho ∑ ∑ ∑ CAH = 90 ,
° CAB = ACB = 30° nên ∑
ABH = 60°, mặt khác ∑
ABH = 60° Þ ABH D
đều Þ AH = 2a , 2 2 2 2 2 2 2
AC = AB + BC - 2 .
AB BC.cos120° = 4a + 4a - 4a = 4a .
Sau đó sử dụng tính chất tứ diện vuông cho tứ diện SAHC ta có: 1 1 1 1 = + + a
. Tính được d ( A (SBC)) 3 ; = . 2 d ( ; A (SBC)) 2 2 2 AH AS AC 2 Câu 13: Đáp án A. S a A C a M a B
Gọi M là trung điểm BC. Do ABC D
đều nên AM ^ BC Þ BC ^ (SAM )
Dựng AH ^ SM Þ AH ^ (SBC) Þ AH = d ( ; A (SBC)).
Trong tam giác vuông SAM ta có:
Nhận xét: Ta cũng có thể sử dụng tính chất tứ diện vuông bằng cách sử dụng them D thuộc tia BC sao cho ∑ CAD = 90°. Câu 14: Đáp án C. Trang 73 S a H 2 a D C a A a B I
Kẻ dài AD cắt BC tại I .
Ta có: AB là đường trung bình của ID D C Þ DI = 2 . a
d ( A (SBC)) = d ( A (SIC)) 1 ; ; = d ( ; D (SIC)) 2
Áp dụng tính chất tứ diện vuông cho tứ diện SIC ta có: 1 1 1 1 6 2a a a 6 = + + = Þ d ; D SIC = Þ d ; A SBC = = . 2 2 2 2 2 ( ) ( ( )) d ( ; D (SIC)) ( ) a 4a 4a 4a 6 6 6
Nhận xét: Ta cũng có thể sử dụng tính chất tam giác vuông bằng cách dựng DH ^ (SBC) và
DH là khoảng cách cần tìm. Câu 15: Đáp án B. S I G K A B O H D C
Kẻ AH ^ BD và AK ^ SH .
Ta có BD ^ SH và BD ^ SA nên BD ^ (SAH ) Þ DB ^ AK
Ta có: AK + SH và BD ^ AK nên AK ^ (SBD) AD AB a ABD D . 2 vuông Þ AH = = BD 5 2a . a . SA AH 5 2a SA
D H vuông Þ AK = = = 2 SH 4a 3 2 a + 5
Gọi O = AC Ç BD , SO cắt AI tại G Þ G là trọng tâm SA D C Trang 74
d (I;(SBD)) GI 1 Þ = = Þ ( SBD ) 1 a d I; = AK = . d ( ; A (SBD)) ( ) GA 2 2 3 Câu 16: Đáp án A. d (S ;
B CD) = d (C ;
D (SAB)) = d (C;(SAB)) = . a S a A a B a D M C Câu 17: Đáp án B. ( Hình vẽ câu 16 )
d (M;(SAB)) = d ( ; C (SAB)) = . a Câu 18: Đáp án B. S 1 D A C 1 1 B ìSA ^ AB Ta có í Þ SA ^ ( ABCD) 2 2
Þ SA ^ AC Þ AC = 2 Þ SC = SA + AC = 3 . îSA ^ BC Câu 19: Đáp án D. D 60° a a a 2 A C a 3 a B
Gỉa sử DA = DB = DC = a Þ BC = a, AC = a 2, AB = a 3 2 1 1 3 a 3 2 S = D .
A DB sin120° = a . = ABD 2 2 2 4 Trang 75 2 1 a 3 S = D . B DC sin 60° = BCD 2 4 1 1 2 S = D . A DC = a ACD 2 2 ABC D có 2 2 2
AC + BC = AB ( cùng bằng 2 3a ) Þ ABC D vuông tại C 2 1 1 a 2 Þ S
= AC.BC = a 2.a = . ABC 2 2 2 a 2
So sánh 4 kết quả trên ta thấy
là lớn nhất nên chọn D. 2 Câu 20: Đáp án C. Câu 21: Đáp án B. S a 3 H a A D a B C ìAH ^ SB ï
Dựng AH ^ SB . Ta có: í
Þ AH ^ SBC Þ d ( ; A SBC ) = AH AH ^ BC î (vì BC ^ ï (SAB)) ( ) ( ) . SA AB . SA AB a 3
Áp dụng tính chất cho tam giác vuông SAB ta có: AH = = = . 2 2 SB SA + AB 2 Câu 22: Đáp án C. S P A D C H B
Trong mặt phẳng ( ABCD), dựng AH ^ BC t ại H Þ BC ^ (SAH )
Trong mặt phẳng (SAH ). dựng AP ^ SH Þ AP ^ (SBC)
tại P Þ d ( ;
A (SBC)) = AP Trang 76 a 3 1 1 1 a 3 Mà 2 2
AH = AB - BH = Þ = + = . 2 2 2 2 AP AS AH 5 Câu 23: Đ áp án D. 2 2 2 2 2 2 1 1 1 1
b c + c a + a b abc Ta c ó: = + + = Þ h = . 2 2 2 2 2 2 2 2 2 2 2 2 2 h a b c a b c
a b + b c + c a Câu 24: Đáp án A. S A a H D I O a B F E C Ta có: SI ^ A ,
B (SAB) ^ ( ABCD) Þ SI ^ ( ABCD)
Gọi E là trung điểm của BC , F là trung điểm của
Ta có AE ^ BC, IF / / AE Þ IF ^ BC
BC ^ IF, BC ^ SI Þ BC ^ (SBC)
Trong mặt phẳng (SIF) , dựng IH ^ SF v à H Î SF
Ta có IH ^ SF, IH ^ BC Þ IH ^ (SBC)
Do đó d (I;(SBC)) = IH . Góc giữa SC và ( ABCD) là ∑ SCI nên ∑ a 3 ∑ 3a SCI = 60 , ° CI =
Þ SI = CI.tan SCI = 2 2 a 3 AE a 3 AE = Þ IF = = 2 2 4 1 1 1 4 16 52 3a Từ đó = + = + = Þ IH = 2 2 2 2 2 2 IH IS IF 9a 3a 9a 52
Þ d (I (SBC)) 3a 3a 13 ; = IH = = 52 26
Câu 25: Đáp án D. S H A B I K D C E Trang 77 ( ì SBI ) ^ ï (ABCD) Ta có í Þ SI ^ ( ABCD) ( ï SCI î ) ^ (ABCD)
Trong mặt phẳng ( ABCD), dựng IK ^ BC, K Î BC
Trong mặt phẳng (SIK ), dựng IH ^ SK, H Î SK
Từ IH ^ (SBC) Þ d (I;(SBC)) = IB 2 2 a 3a 2 2 S = S - S - S = 3a - - a = IBC ABCD DIC ABI 2 2 2S 3a 5 2 2
BC = 2a + a = a 5 IBC Þ IK = = BC 5
Góc giữa hai mặt phẳng (SBC) và ( ABCD) là ∑ SKI . Nên ∑ ∑ 3a 15
SKI = 60° Þ SI = IK.tan SKI = 5 1 1 1 5 5 20 a Ta có: = + = + =
Þ d (I (SBC)) 3 15 ; = IH = . 2 2 2 2 2 2 IH IS IK 27a 9a 27a 10
Trong mặt phẳng ( ABCD), gọi E là giao điểm của AD và BC thì E = AI Ç(SBC). d ( ;
A (SBC)) EA 4 4 2a 15 Þ = = Þ d ( ;
A (SBC)) = d (I;(SBC)) = .
d (I;(SBC)) EI 3 3 5
Nhận xét: Sử dụng tỉ số khoảng cách ta có thể tính khoảng cách từ một điểm đến một mặt
phẳng thong qua điểm khác, quan trọng là biết xuất phát từ điểm nào trước, Từ dấu hiệu
SI ^ ( ABCD), ta chọn tính khoảng cách từ điểm I đến (SBC) sau đó dựa vào tỉ số khoảng
cách suy ra khoảng cách cần tìm.
Bài tập ôn tập chủ đề 8
Câu 1. Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD . Tìm giá trị của k !!!!" !!!" !!!"
thích hợp đẻ điền vào đẳng thức vectơ : MN = k ( AC + BD) 1 A. k = 1 . B. k = . C. k = 3. D. k = 2 . 2 3 ! ! ! ! ! !
Câu 2. Cho ba vectơ a,b, c . Điều kiện nào sau đây khẳng định a,b, c đồng phẳng? ! ! !
A.Tồn tại ba số thực ,
m n, p thoả mãn m + n + p = 0 và ma + nb + pc = 0. ! ! !
B.Tồn tại ba số thực ,
m n, p thoả mãn m + n + p ¹ 0 và ma + nb + pc = 0. ! ! !
C.Tồn tại ba số thực ,
m n, p thoả mãn ma + nb + pc = 0. ! ! !
D.Giá của a,b, c đồng quy. !!!" " !!!" " !!!" "
Câu 3. Cho lăng trụ tam giác ' ' ' ABC.A B C có '
AA = a, AB = , b AC = .
c Hãy phân tích ( biểu thị) vectơ !!!" ! ! ! '
B C qua các vectơ a,b, c. !!!" " " " !!!" " " " A. '
B C = a + b + . c B. '
B C = a + b + . c !!!" " " " !!!" " " " C. '
B C = a + b + . c D. '
B C = a + b + . c
Câu 4. Trong các mệnh đề sau đây, mệnh đề nào là đúng? !!!" 1 !!!"
A.Nếu AB = BC thì B là trung điểm của đoạn AC . 2 !!!" !!!" !!!" !!!" B.Từ AB = 3
- AC ta suy ra CB = AC. !!!" !!!" !!!"
C.Vì AB = 3AC +5ADnên bốn điểm ,
A B,C, D cùng thuộc một mặt phẳng. Trang 78 !!!" !!!" !!!" !!!"
D.Từ AB = 3AC ta suy ra BA = 3 - CA.
Câu 5. Hãy chọn mệnh đề sai trong các mệnh đề sau đây: ! ! !
A.Ba vectơ a,b, c đồng phẳng nếu có hai trong ba vectơ đó cùng phương.. ! ! ! !
B.Ba vectơ a,b, c đồng phẳng nếu có một trong ba vectơ đó bằng vectơ 0 .. ! ! ! ! ! !
C.Vectơ x = a + b + c luôn luôn đồng phẳng với hai vectơ a và b . !!!" !!!!" !!!" D.Cho hình hộp ' ' ' ' AB . CD A B C D ba vectơ ' ' ' '
AB ,C A , DA đồng phẳng.
Câu 6. Trong các kết luận sau đây, kết luận nào đúng?. !!!" !!!"
Cho hình lập phương ABC .
D EFGH có cạnh a . Ta có . AB EG bằng:. a 2 A. 2 a . B. a 2. C. a 3. D. . 2
Câu 7. Cho hình chóp S.ABCD . G ọi O là giao điểm của AC và BD . Trong các khẳng định sau, khẳng định nào sai?. !!" !!" !!!" !!!" !!!"
A.Nếu SA+ SB + 2SC + 2SD = 6SO th ì ABCD l à h ình thang. !!" !!" !!!" !!!" !!!"
B.Nếu ABCD là hình bình hành thì SA+ SB + SC + SD = 4SO . !!" !!" !!!" !!!" !!!"
C.Nếu ABCD là h ình thang thì SA+ SB + 2SC + 2SD = 6SO. !!" !!" !!!" !!!" !!!"
D.Nếu SA+ SB + SC + SD = 4SO thì ABCD là hình bình hành.
Câu 8. Trong các mệnh đề sau đây, mệnh đề nào là sai?. !!!" !!!" !!!" !!!" !!!" !!!"
A.Từ hệ thức AB = 2AC -8AD ta suy ra ba vectơ AB, AC, AD đồng phẳng. !!!!" !!!" "
B.Vì NM + NP = 0 nên N là đoạn trung điểm của đoạn MP . !!" 1 !!!" !!!"
C.Vì I là trung điểm của đoạn AB nên từ một điểm O bất kì ta có OI = (OA+OB).. 2 !!!" !!!" !!!" !!!" "
D.Vì AB + BC +CD + DA = 0 nên bốn điểm ,
A B,C, D cùng thuộc một mặt phẳng. !!!" " !!!" "
Câu 9. Cho hình hộp ' ' ' ' AB .
CD A B C D có tâm O . Đặt AB = a; BC = b . M là điểm xác định bởi !!!!" 1 " "
OM = (a -b). Khẳng định nào sau đây đúng?. 2
A. M là trung điểm của ' BB ..
B. M là tâm hình bình hành ' ' BCC B .
C. M là tâm hình bình hành ' ' ABB A.
D. M là trung điểm của ' CC . !!!" !!!!"
Câu 10. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữ cặp vectơ AB và DH ?. A. 45 . ° B. 90 . ° C.120 . ° D. 60 . °
Câu 11. Trong không gian cho hai hình vuông ABCD và ' '
ABC D có cạnh chung AB và nằm trong hai !!!" !!!!"
mặt phẳng khác nhau, lần lượt có tâm O và '
O . Hãy xác định góc giữa cặp vectơ AB và ' OO ?. A. 60 . ° B. 45 . ° C.120 . ° D. 90 . °
Câu 12. Cho hình chóp S.ABC có SA = SB = SC và ∑ ∑ ∑
ASB = BSC = CSA. Hãy xác định góc giữa cặp !!" !!!"
vectơ SB và AC ?. A. 60 . ° B.120 . ° C. 45 . ° D. 90 . °
Câu 13. Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?. A.120 . ° B. 60 . ° C. 90 . ° D. 30 . °
Câu 14. Cho hình chóp S.ABCD có tất cả các cạch đều bằng A.Gọi I và J lần lượt là trung điểm của
SC và BC.Số đo của góc (IJ,CD) bằng: A. 90 . ° B. 45 . ° C. 30 . ° D. 60 . °
Câu 15. Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Giả sử tam giác AB C
¢ và A¢DC¢ đều có 3 góc nhọn. Góc giữa
hai đường thẳng AC và A¢D là góc nào sau đây? Trang 79 A. ∑ AB C ¢ . B. ∑ DA C ¢ .¢ C. ∑ BB . D ¢ D. ∑ BDB .¢
Câu 16. Trong các mệnh đề dưới đây mệnh đề đúng là?.
A.Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì
cũng vuông góc với đường thẳng thứ hai.
B.Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
C.Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.
D.Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.
Câu 17. Cho hình chóp S.ABC có SA = SB = SC và ∑ ∑ ∑
ASB = BSC = CSA. Hãy xác định góc giữa cặp vectơ !!!" !!!" SC và AB ? A.120 . ° B. 45 . ° C. 60 . ° D. 90 . °
Câu 18. Cho hình chóp S.ABC có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a .
Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc (MN,SC) bằng: A. 45 . ° B. 30 . ° C. 90 . ° D. 60 . °
Câu 19. Cho hình lập phương ABC .
D A B C D . Chọn khẳng định sai? 1 1 1 1
A.Góc giữa AC và B D bằng 90 . ° 1 1
B.Góc giữa B D và AA bằng 60 . ° 1 1 1
C.Góc giữa AD và B C bằng 45 . ° 1
D.Góc giữa BD và AC bằng 90 . ° 1 1 !!!!" !!!!"
Câu 20. Cho hình lập phương ABC .
D A B C D có cạnh a . Gọi M là trung điểm AD . Giá trị B M.BD 1 1 1 1 1 1 là: 1 3 3 A. 2 a . B. 2 a . C. 2 a . D. 2 a . 2 4 2
Câu 21. Trong các mệnh đề sau đây, mệnh đề nào là đúng?.
A.Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường
thẳng c thì a vuông góc với c .
B.Cho ba đường thẳng a,b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d
vuông góc với a thì d song song với b hoặc c .
C.Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường
thẳng c thì a vuông góc với c .
D.Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì
c vuông góc với mọi đường thẳng nằm trong mặt phẳng ( , a b). !!!" !!!"
Câu 22. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 90 . ° B. 60 . ° C. 45 . ° D.120 . °
Câu 23. Cho tứ diện ABCD đều cạnh bằng a . Gọi M là trung điểm của CD , a là góc giữa AC và
BM . Chọn khẳng định đúng? 3 A. cosa 1 = . B. cosa 3 = . C. cosa= . D.a = 60 . ° 4 3 6 ! ! !""
Câu 24. Cho a = 3, b = 5 góc giữa a,b bằng 120 .
° Chọn khẳng định sai trong các khẳng định sau? ! ! ! ! ! ! ! !
A. a + b = 19 .
B. a - b = 7.
C. a - 2b = 139 .
D. a + 2b = 9. !!!" !!!"
Câu 25. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AF và EG ? A. 90 . ° B. 60 . ° C. 45 . ° D.120 . °
Câu 26. Trong không gian cho ba điểm ,
A B,C bất kỳ, chọn đẳng thức đúng? !!!"!!!" A. 2 2 2 2 .
AB AC = AB + AC - BC . !!!"!!!" B. 2 2 2 2 .
AB AC = AB + AC - 2BC . Trang 80 !!!"!!!" C. 2 2 2 .
AB AC = AB + AC - 2BC . !!!"!!!" D. 2 2 2 .
AB AC = AB + AC - BC . !!!" !!!"
Câu 27. Cho hình lập phương ABC .
D EFGH có cạnh bằng a . Tính . AB EG 2 a 2 A. 2 a 3 . B. 2 a . C. . D. 2 a 2 . 2
Câu 28. Cho tứ diện ABCD có AB vuông góc với CD , AB = CD = 6 . M là điểm thuộc BC sao cho MC = .
x BC (0 < x < )
1 . Mp (P) song song với AB vàCD lần lượt cắt BC, DB, AD, AC tại M , N, ,
P Q. Diện tích lớn nhất của tứ giác bằng bao nhiêu? A.9. B.11. C.10. D.8.
Câu 29. Cho tứ diện ABCD có AB = CD . Gọi I, J , E, F lần lượt là trung điểm của AC , BC , BD , DA .
Góc giữa IE và JF là: A. 30° . B. 45° . C. 60° . D. 90° .
Câu 30. Mệnh đề nào sau đây là đúng?
A. Mộtđường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D.Mộtđường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại. ! ! ! ! ! ! ! !
Câu 31. Cho hai vec tơ a, b thỏa mãn a = 4 ; b = 3; a - b = 4. Gọi a là góc giữa hai véc tơ a và b .
Chọn khẳng định đúng: 3 A. cosa = . B. a = 30° 1 . C. cosa = . D. a = 60° . 8 3 !!!" !!!" !!!" !!!" !!!" !!!"
Câu 32. Cho tứ diện ABCD . Tìm giá trị của k thích hợp thỏa mãn: . ABCD + . AC DB + . AD BC = k
A. k = 1 .
B. k = 2 .
C. k = 0 . D. k = 4 .
Câu 33. Trong không gian cho tam giác ABC . Tìm điểm M sao cho giá trị của biểu thức 2 2 2
P = MA + MB + MC đạt giá trị nhỏ nhất.
A. M là trọng tâm tam giác ABC .
B. M là tâm đường tròn ngoại tiếp tam giác ABC .
C. M là trực tâm tam giác ABC .
D. M là tâm đường tròn nội tiếp tam giác ABC . ! ! ! ! ! ! ! !
Câu 34. Cho hai vec tơ a, b thỏa mãn a = 26; b = 28; a + b = 48. Độ dài của vec tơ a -b là: A. 25 . B. 616 . C. 9 . D. 618. ! ! ! ! ! ! !" " " ! ! !
Câu 35. Cho hai vec tơ a, b thỏa mãn a = 4 ; b = 3; .
a b =10 . Xét hai véc tơ y = a - b ; x = a - 2b. Gọi ! !"
a là góc giữa hai véc tơ x và y . Chọn khẳng định đúng: 2 A. cosa = - 1 . B. cosa = 3 . C. cosa = 2 . D. cosa = . 15 15 15 15
Câu 36. Trong không gian cho tam giác ABC có diện tích S . Tìm giá trị của k thích hợp thỏa mãn: 1 !!!"2 !!!"2 !!!" !!!" S =
AB .AC - 2k ( . AB AC )2 2 1 A. k = . B. k = 1 0 . C. k = . D. k = 1 . 4 2 Trang 81
Câu 37. Trong không gian cho đường thẳng d và điểm O . Qua O có bao nhiêu đường thẳng vuông góc với d A. Vô số . B. 2 . C. 3 . D. 1.
Câu 38. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b (a > b 2). Gọi G là
trọng tâm tam giác ABC . Xét mặt phẳng (P) đi qua A và vuông góc với SC tại điểm I nằm giữa
S và C . Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là: 2 2 2 a 3b - a 2 2 2 a 3b - a A. S = . B. S = . 4b 2b 2 2 2 a 3b + a 2 2 2 a 3b + a C. S = . D. S = . 2b 4b
Câu 39. Cho tứ diện ABCD có cạnh AB , BC , BD vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng:
A. Góc giữa CD và ( ABD) là góc C Ð BD .
B. Góc giữa AC và (CBD) là góc ACB Ð .
C. Góc giữa AD và ( ABC) là góc AD Ð B .
D. Góc giữa AC và ( ABD) là góc C Ð BA .
Câu 40. Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B . Vẽ SH ^ ( ABC) ,
H Î( ABC). Khẳng định nào sau đây đúng:
A. H trùng với trung điểm của AC .
B. H là trọng tâm tam giác ABC .
C. H là trực tâm tam giác ABC .
D. H trùng với trung điểm của BC .
Câu 41. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của S lên mặt phẳng
(ABC) trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều. Tính số đo của
góc giữa SA và mặt phẳng ( ABC) . A. 30° . B. 45° . C. 60° . D. 75° .
Câu 42. Mệnh đề nào sau đây làsai?
A.Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
C. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho ) cùng vuông góc với một
đường thẳng thì song song với nhau.
D.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Câu 43. Cho hình chóp S.ABC có SA = SB = SC , BS Ð C =120° , C
Ð SA = 60° . Vẽ SH ^ ( ABC),
H Î( ABC). Khẳng định nào sau đây đúng:
A. H trùng với trung điểm của AB .
B. H là trọng tâm tam giác ABC .
C. H trùng với trung điểm của BC .
D. H trùng với trung điểm của AC .
Câu 44. Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA ^ ( ABCD). Khẳng định nào sau đây sai:
A. SA ^ BD .
B. SC ^ BD .
C. SO ^ BD .
D. AD ^ SC .
Câu 45. Cho hình chóp S.ABC có đáy là tam giác đều, O là trung điểm của đường cao AH của tam giác
ABC và SO ^ ( ABC) . Gọi I là điểm tùy ý trên OH ( không trùng với O và H ). Xét mặt phẳng
(P) đi qua I và vuông góc với OH . Thiết diện của hình chóp cắt bởi mặt phẳng (P) là:
A. Hình thang cân. B.Hình thang vuông. Trang 82
C.Hình bình hành. D.Tam giác vuông.
Câu 46. Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA ^ ( ABCD). Gọi I là trung điểm của
SC .Khẳng định nào sau đây sai:
A. IO ^ ( ABCD).
B. SC ^ BD .
C. SA = SB = SC .
D. (SAC)là mặt phẳng trung trực của BD .
Câu 47. Cho hình chóp S.ABCD có đáy là hình vuôngcạnh a , SA ^ ( ABCD) và SA = a 6 . Gọi a là góc
giữa SC và ( ABCD) . Chọn khẳng định đúng: A. a = 45° . B. a = 30° 1 . C. cosa = . D. a = 60° . 3
Câu 48. Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu H của S lên mặt phẳng ( ABC) là:
A.Trọng tâm tam giác ABC .
B. Tâm đường tròn ngoại tiếp tam giác ABC .
C. Trực tâm tam giác ABC .
D.Tâm đường tròn nội tiếp tam giác ABC .
Câu 49. Cho a, ,
b c là các đường thẳng trong không gian. Mệnh đề nào sau đây là sai?
A.Nếu a ^ b và b ^ c thì a / /b .
B. Nếu a ^ (a ) và b / / (a ) thì a ^ b .
C. Nếu a / /b và b ^ c thì a ^ c .
D.Nếu a ^ b , b ^ c và a cắt c thì b vuông góc với mặt phẳng chứa a và c .
Câu 50. Cho hình chóp S.ABC có SA ^ ( ABC)và AB ^ BC . Số các mặt của hình chóp S.ABC là tam giác vuông là A. 1. B. 2 . C. 3 . D. 4 .
Câu 51. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA ^ ( ABCD). Gọi AE; AF lần lượt là các
đường cao của tam giác SAB và SAD . Khẳng định nào sau đây đúng:
A. SC ^ ( AFB).
B. SC ^ ( AEC) .
C. SC ^ ( AED) .
D. SC ^ ( AFE) .
Câu 52. Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có đáy là hình thoi, BAD 60° Ð =
và A¢A = A¢B = A D ¢ . Gọi O là
giao điểm của AC và BD . Hình chiếu của A¢ lên mặt phẳng ( ABCD) là:
A.Trung điểm của AO .
B. Trọng tâm tam giác ABD .
C. Điểm O .
D.Trọng tâm tam giác BCD . a 3
Câu 53. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và SA ^ ( ABC), SA = . Xét mặt phẳng 2
(P) đi qua A và vuông góc với BC . Diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P) là: 2 3a 2 3a 2 3a 2 2a A. . B. . C. . D. . 8 2 4 3 a 6
Câu 54. Cho hình chóp S.ABCD có đáy là hình vuôngcạnh a , SA ^ ( ABCD) và SA = . Gọi a là góc 3
giữa SC và ( ABCD) . Chọn khẳng định đúng: Trang 83 A. a = 45° . B. a = 30° . C. a = 75° . D. a = 60° .
Câu 55. Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Gọi a là góc giữa AC¢ và ( A B
¢ CD¢). Chọn khẳng định đúng: A. a = 45° . B. a = 30° . C. tana = 2 2 . D. tana = . 3
Câu 56. Cho tứ diện SABC thỏa mãn SA = SB = SC . Gọi H là hình chiếu vuông góc của S len mặt phẳng (ABC
) . Đói với tam giác ABC ta có điểm H là A. Trực tâm.
B. Tâm đường tròn nội tiếp. C. Trọng tâm.
D. Tâm đường tròn ngoại tiếp. a 3
Câu 57. Cho tứ diện ABCD có hai mặt (ABC
) và(SBC )là hai tam giác đều cạnh a , SA = . M 2
là điểm trên AB sao cho AM = b (0 < b < a . ) (P
) là mặt phẳng qua M và vuông góc với
BC . Thiết diện của (P
) và tứ diện SABC có diện tích bằng? 2 3 3 a Ê - bˆ 2 3 a Ê - bˆ 2 3 3 a Ê - bˆ 2 3 3 a Ê - bˆ A. Á ˜ Á ˜ . B. Á ˜ Á ˜ . C. Á ˜ Á ˜ . D. Á ˜ Á ˜ . 4 Á Ë a ˜¯ 4 Á Ë a ˜¯ 16 Á Ë a ˜¯ 8 Á Ë a ˜¯
Câu 58. Cho hai đường thẳng a , b và mặt phẳng (P . Chỉ )
ra mệnh đề đúng trong các mệnh đề sau: A. Nếu a//(P
) và b ^ a thì b//(P . ) B. Nếu a//(P
) và b ^ a thì a ^ b . C. Nếu a//(P
) và b ^ a thì b ^ (P . )
D. Nếu a ^ (P
) và b ^ a thì b//(P . )
Câu 59. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a . Hình chiếu vuông
góc của S lên (ABC
) trùng với trung điểm BC . Biết SA = a . Tính số đo của góc giữa SA
và mặt phẳng (ABC . ) A. 30 . ∞ B. 45 . ∞ C. 60 . ∞ D. 75 . ∞
Câu 60. Tính chất nào sau đây không phải tính chất của hình lăng trụ đứng?
A. Các mặt bên của hình lăng trụ đứng là những hình bình hành.
B. Các mặt bên của hình lăng trụ đứng là những hình chữ nhật.
C. Các cạnh bên của hình lăng trụ đứng song song và bằng nhau.
D. Hai đáy của hình lăng trụ đứng có các cạnh đôi một song song và bằng nhau.
Câu 61. Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Cho hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này
thì cũng vuông góc với đường thẳng kia.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
C. Cho hai mặt phẳng song song, đường thẳng nào vuông góc với mặt phẳng này thì cũng
vuông góc với mặt phẳng kia.
D. Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng
vuông góc với đường thẳng kia.
Câu 62. Cho hình chóp S.ABDC có đáy ABDC là hình bình hành tâm O , AD, S ,
A AB đôi một vuông
góc , AD = 8, SA = 6. (P
) là mặt phẳng qua trung điểm của AB và vuông góc với AB . Thiết diện của (P
) và hình chóp có diện tích bằng ? A. 20. B. 16. C. 17. D. 36.
Câu 63. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là
trọng tâm tam giác ABC . Độ dài SG bằng: 2 2 9b + 3a 2 2 b - 3a 2 2 9b - 3a 2 2 b + 3a A. . B. . C. . D. . 3 3 3 3 Trang 84
Câu 64. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là
trọng tâm tam giác ABC . Xét mặt phẳng (P đi
) qua A và vuông góc với SC . Tìm hệ thức
liên hệ giữa a và b để mặt phẳng (P
) cắt SC tai điểm C nằm giữa S và C . 1 A. b > a 2 . B. b < a 2 . C. a < b 2 . D. a > b 2 .
Câu 65. Cho hình chóp S.ABCD có đáy ABCD là hình thoi thoi tâm O . Biết SA = SC , SB = SD .
Khẳng định nào sau đây đúng? A. AB ^ (SAC ). B. CD ^ AC . C. SO ^ (ABCD . ) D. CD ^ (SBD . )
Câu 66. Cho tứ diện đều cạnh a = 12 , AP là đường cao của tam giác ACD . Mặt phẳng (P ) qua B
vuông góc với AP cắt mặt phẳng (ACD
) theo đoạn giao tuyến có độ dài bằng: A. 9. B. 6. C. 8. D. 7.
Câu 67. Cho hình lập phương ABC .
D A B C D . Gọi a là góc giữa AC và mặt phẳng (ABCD . Chọ ) 1 1 1 1 1
khẳng định đúng trong các khẳng định sau: 2 A. a = 45 ∞ 1 . B. tan a = . D. tan a = . D. a = 30 . ∞ 2 3
Câu 68. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA ^ (ABC),SA= a. Gọi (P là )
mặt phẳng đi qua S và vuông góc với BC . Thiết diện của (P
) và hình chóp S.ABC có diện tích bằng?
Câu 69. Tam giác ABC có BC = 2a , đường cao AD = a 2 . Trên đường thẳng vuông góc với (ABC
) tại A , lấy điểm S sao cho SA= a 2 . Gọi E, F lần lượt là trung điểm của , SB SC .
Diện tích tam giác AEF bằng? 3 3 1 3 A. . 2 a . B. 2 a . C. 2 a . D. 2 a . 4 6 2 2
Câu 70. Cho hình lập phương ABC . D A B ¢ C ¢ D ¢ .
¢ Đường thẳng AC
¢ vuông góc với mặt phẳng nào sau đây? A.(A B ¢ D ) . B.(A D ¢ C¢ . ) C.(A C ¢ D¢ ) . D.(A B ¢ C ¢ D . )
Câu 71. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt phẳng đáy, SA = .
a Góc giữa đường thẳng SC và mặt phẳng (SAB) là a, khi đó tana nhận
giá trị nào trong các giá trị sau ? . A. tana = 2 . B. tana = 1 3 . C. tana = . D. tana = 1. 2
Câu 72. Cho hình chóp S.ABC có SA ^ ( ABC) và tam giác ABC không vuông. Gọi H , K lần lượt là
trực tâm của !ABC và !SBC . Số đo góc tạo bởi SC và (BHK ) là: A. 0 45 . B. 0 120 . C. 0 90 . D. 0 65 .
Câu 73. Cho hình vuông ABCD tâm O và cạnh bằng 2 .
a Trên đường thẳng qua O vuông góc với
(ABCD) lấy điểm S . Biết góc giữa SA và mặt phẳng (ABCD) có số đo bằng 0 45 . Tính độ dài . SO a 3 a
A. SO = a 3 .
B. SO = a 2 . C. SO = 2 . D. SO = . 2 2
Câu 74. Cho hình chóp S.ABCD trong đó ABCD là hình chữ nhật, SA ^ ( ABCD). Trong các tam
giác sau tam giác nào không phải là tam giác vuông. A.!SBC . B. !SCD . C.!SAB . D. !SBD . Trang 85
Câu 75. Cho lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều tâm O , cạnh a, hình chiếu của C '
trên mặt phẳng ( ABC) trùng với tâm của đáy. Cạnh bên CC¢ hợp với mặt phẳng ( ABC) góc 0
60 . Gọi I là trung điểm của .
AB Tính khoảng cách từ C đến IC .¢ 2a 13 3a 13 a 3 a 13 A. . B. . C. . D. . 13 13 13 13
Câu 76. Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh .
a Tính khoảng cách từ C đến AC .¢ a 6 a 3 a 6 a 3 A. . B. . C. . D. . 2 2 3 3 a
Câu 77. Cho hình chóp đều S.ABC có cạnh đáy bằng . a Gọi O 3
là tâm của đáy và SO = . Tính 3
khoảng cách từ O tới . SA a 6 a 13 a 3 a 13 A. . B. . C. . D. . 6 3 6 6
Câu 78. Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = a . Góc giữa
đường thẳng SD và mặt phẳng (SAC) bằng 0
30 , với M là trung điểm .
CD Hãy tính khoảng
cách từ D đến (SBM ). 2a 4a 5a a A. . B. . C. . D. . 3 3 3 3
Câu 79. Cho hình chóp S.ABC có đáy là tam giác vuông tại A và AB = 2a, AC = 2a 3. Hình chiếu
vuông góc của S trên mặt phẳng ( ABC) là trung điểm H của cạnh AB . Góc giữa hai mặt
phẳng (SBC) và ( ABC) bằng 0
30 . Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC). a 3 a 5 a 5 3a A. . B. . C. . D. . 5 3 5 5
Câu 80. Cho lăng trụ đứng ABC.A¢B C
¢ ¢ có đáy là tam giác cân, ! 0 AB = AC = ,
a BAC =120 . Mặt phẳng (AB C
¢ ¢) tạo với đáy góc 0
60 . Tính khoảng cách từ đường thẳng BC đến mặt phẳng ( AB C ¢ ¢) theo . a a 3 a 5 a 7 a 35 A. . B. . C. . D. . 4 14 4 21
Câu 81. Cho lăng trụ đứng ABC . D A¢B C ¢ D
¢ ¢ có đáy ABCD là hình thoi cạnh a và ∑ 0 BAD = 60 . Gọi
O,O¢ lần lượt là tâm của hai đáy, gọi S là trung điểm của OO¢ . Tính khoảng cách từ O tới
mặt phẳng (SAB) biết OO¢ = 2 . a a 3 a 3 a 3a A. . B. . C. . D. . 11 19 19 19
Câu 82. Cho hình lăng trụ .
ABC A B C có các mặt bên là các hình vuông cạnh .
a Gọi D, E, F lần lượt 1 1 1
là trung điểm các cạnh BC, AC , B C . Tính theo a khoảng cách giữa hai đường thẳng DE và 1 1 1 1 A F. 1 a 17 a 17 a a 17 A. . B. . C. . D. . 4 2 17 3 D. HƯỚNG DẪN GIẢI Câu 1. Đáp án A. Trang 86 !!!!" 1 !!!!" !!!!"
MN = (MC + MD)(quy tắc trung điểm) 2 1 !!!" !!!" !!!" !!!"
= (MA + AC + MB + BD) 2!!!" !!!" "
mà MA + MB = 0 (vì M là trung điểm AB ) !!!!" 1 !!!" !!!"
Þ MN = (AC + BD) 2 Câu 2. Đáp án B.
Theo giả thuyết m + n + p ¹ 0nên tồn tại ít nhất một số khác 0. ! ! ! ! ! n ! p !
Giả sử m ¹ 0 . Từ ma + nb + pc = 0 Þ a = - b - c m m ! ! ! a, ,
b c đồng phẳng (theo định lí về sự đồng phẳng của ba vectơ). Câu 3. Đáp án D. C' A' B' C A B !!!!" !!!" !!!!" B C ¢ = B B ¢ + B C
¢ ¢( quy tắc hình bình hành) !!!" !!!" " !!!" !!!" " " "
= -AA¢ + BC = -a + AC - AB = -a - b + c Câu 4. Đáp án C. !!!" 1 !!!"
A. Sai vì AB = - BC ÞA là trung điểm của BC. 2 B C A !!!" !!!" !!!" !!!" B. Sai vì AB = 3 - AC Þ CB = 4 - AC C B A
C. Đúng theo định lí sự đồng phẳng của 3 vectơ. !!!" !!!" !!!" !!!"
D. Sai vì AB = 3AC Þ BA = 3CA(nhân 2 vế cho -1) Câu 5. Đáp án C. Trang 87 B' C' D' A' B C A D
A. Đúng vì theo định nghĩa đồng phẳng
B. Đúng vì theo định nghĩa đồng phẳng C. Sai !!!" !!!" !!!" " "
ìDA¢ = AA¢ - AD = a - c ïï!!!" " "
D. Đúng vì íAB¢ = a + b ï!!!!" !!!" " " C A ¢ ¢ = CA = b - - c ïî !!!" !!!" !!!!" !!!" !!!" !!!!"
Þ AB¢ = DA¢ - C A ¢ ¢ Þ AB , ¢ DA , ¢ C A ¢ ¢ đồng phẳng. Câu 6. Đáp án A. F G E H B C A D !!!" !!!" !!!" !!!" !!!" !!!" !!!" .
AB EG = (EF + EH).(AE + EF + FB) !!!" !!!"
!!!" !!!" !!!!"!!!" !!!!"!!!" !!!!"!!!" 2
= EF.AE + EF + EF.FB + EH.AE + EH.EF + EH.FB !!!!"!!!" 2 2 2
= a + EH.AE = a + 0 = a Câu 7. Đáp án C S A D B C !!" !!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" "
A. Đúng vì SA + SB + 2SC + 2SD = 6SO Û OA + OB + 2OC + 2OD = 0 !!!" !!!" !!!" !!!" Vì O, ,
A C và O, B, D thẳng hàng nên đặt: OA = kOC, OB = mOD !!!" !!!" "
Þ (k + 2)OC + (m + 2)OD = 0. Trang 88 !!!" !!!" OA OB
mà OC, OD không cùng phương nên k = 2 - và m = 2 - Þ =
= 2 Þ AB / /CD. OC OD
B. Đúng. HS tự biến đổi bằng cách thêm điểm O vào vế trái.
C. Sai vì nếu ABCD là hình thang cân có 2 đáy là , AD BC thì sẽ sai.
D. Đúng. Tương tự đáp án A với k = 1 - và m = 1
- Þ O là trung điểm hai đường chéo. Câu 8. Đáp án D
A. Đúng theo định nghĩa sự đồng phẳng của ba vectơ
B. Đúng. !!!" !!!" !!" !!" !!" !!" !!" !!" "
C. Đúng vì OA + OB = OI + IA + OI + IB mà IA + IB = 0 (I là trung điểm của AB) !!!" !!!" !!"
Þ OA + OB = 2OI
D. Đúng. Tương tự đáp án A với k = 1 - và m = 1
- Þ O là trung điểm hai đường chéo.
D. Sai vì không đúng theo định nghĩa sự đồng phẳng. Câu 9: Đáp án A. !!!!" !!!" !!!" 1 !!!!" !!!!"
M là trung điểm BB¢ Þ 2.OM = OB + OB¢ = (B D
¢ + BD¢) (qt trung điểm). 2 Câu 10: Đáp án B. AB ^ AE ü ∑
ý Þ AB ^ DH Þ ( AB,DH ) = 90° . AE / /DH þ Câu 11: Đáp án D. Ta có: OO //
¢ DD¢ mà DD¢ ^ AB nên ¢ ∑
OO ^ AB Þ (OO ,¢AB) = 90°. Câu 12: Đáp án D. Ta có: SA D B = SB D C = SC
D A(c - g -c) Þ AB = BC = CA. Do đó tam giác ABC đều. Gọi G là
trọng tâm tam giác ABC . Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với ìAC ^ BG
G hay SG ^ ( ABC) . Ta có í
Þ AC ^ (SBG) Þ AC ^ SB . Vậy góc giữa cặp vectơ îAC ^ SG !!" !!!"
SB và AC bằng 90° . Câu 13: Đáp án C. Trang 89 CI ì ^ AB
Gọi I là trung điểm của AB . Vì ABC D và ABD D
là các tam giác đều nên í . Suy ra îDI ^ AB AB ^ (CID) ∑
Þ AB ^ CD Þ (AB,CD) = 90° . Câu 14: Đáp án D.
Gọi O là tâm của hình thoi ABCD . Ta có OJ / /CD . Nên góc giữa IJ và CD bằng góc giữa IJ và 1 a 1 a 1 a
OJ . Xét tam giác IOJ có: IJ = SB = ,OJ = CD = , IO = SA = . Nên tam giác OIJ đều. 2 2 2 2 2 2
Vậy góc giữa IJ và CD bằng có giữa IJ và OJ bằng góc ∑ IJO = 60°. Câu 15: Đáp án B.
Ta có: AC / / A¢C¢ nên góc giữa hai đường thẳng AC và A¢D là góc giữa hai đường thẳng A¢C¢ và
A¢D bằng góc nhọn ∑ DA C
¢ ¢ (vì tam giác A¢DC¢ đều có 3 góc nhọn). Câu 16: Đáp án A. Theo lý thuyết. Câu 17: Đáp án D. !!!" !!!" !!!" !!" !!" !!!" !!" !!!" !!"
Ta có: SC AB = SC (SB - SA) ∑ ∑ . .
= SC.SB - SC.SA = SC. .
SB cos BSC - SC. . SA cos ASC = 0. !!!" !!!"
Vì SA = SB = SC và ∑ ∑
BSC = ASC . Do đó: (SC, AB) = 90°. Câu 18: Đáp án C. Trang 90 Ta có: 2 2 2 2
AC = a 2 Þ AC = 2a = SA + SC Þ S
D AC vuông tạiS . Khi đó: !!!!" !!!" 1 !!" !!!" !!!!" !!!"
NM.SC = S .
A SC = 0 Û (NM,SC) ∑
= 90° Þ (MN,SC) = 90°. 2 Câu 19: Đáp án B.
!!!" !!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
Ta có: AA .B D = BB .BD = BB . BA + BC = BB .BA + BB .BC = 0 (BB ,BA =90° 1 ) 1 1 1 1 1 ( ) (vì và 1 1 (!!!" !!!" !!!" !!!!" BB , BC = 90°
(AA,BD =90°Þ AA,BD =90° 1 1 1 ) ∑ ( 1 1 1) 1 ) ). Do đó: . Câu 20: Đáp án A. Trang 91 Ta có: !!!!" !!!!"
!!!" !!!" !!!!" !!!" !!!" !!!!" !!!" !!!!" !!!" !!!!" !!!" a a
B M.DD = (B B + BA+ AM ).(BA+ AD + DD ) 2 2 2 2 2 = B .D
B D + BA + AM.AD = -a + a + = 1 1 1 1 1 1 2 2 . Câu 21: Đáp án C. Câu 22: Đáp án C. !!!" !!!" !!!" !!!"
Ta có: EG / / AC (Do ACGE là hình chữ nhật) Þ ( AB EG) = ( AB AC) ∑ , , = BAC = 45°. Câu 23: Đáp án C.
Gọi O là trọng tâm của BC
D D Þ AO ^ (BCD). Trên đường thẳng d qua C và song song với
BM lấy điểm N sao cho BMCN là hình chữ nhật, từ đó suy ra: ∑ (AC BM) ∑ = (AC CN) ∑ , , = ACN = a . 3 Có: CN = BM = a và 2 2 a æ 2 ö 2 2 2 2 2 2
BN = CM = ; AO = AB - BO = AB - BM = a ç ÷ 2 è 3 ø 3 2 2 2 7 5
AC + CN - AN 3 2 2 2 2 2 2
ON = BN + BO =
a ; AN = AO + ON = a Þ cosa = = 12 2 2.AC.CN 6 Câu 24: Đáp án D. ! ! 2 !2 !2 ! ! ! ! ! !
Ta có: a + b = a + b + 2 . a .
b cos(a,b) =19 Þ a +b = 19 . Câu 25: Đáp án B. Trang 92
Đặt cạnh của hình lập phương là a . Gọi I là trung điểm của EG. Qua A kẻ đường thẳng d / /FI . !!!" !!!"
Qua I kẻ đường thẳng d¢ / /FA . Suy ra d cắt d¢ tại J . Từ đó suy ra (EG AF ) ∑ , = EIJ = a . Mặt khác: IJ=AF=2EI=2FI=2AJ=a 2 2 2 2 3 EI + IJ - EJ 1 2 2 2 2
EJ = AE + AJ = a ;cosa = = Þ a = 60° 2 2.EI.IJ 2
Cách 2: Ta có: AC / /EG Þ ( AF; EG) = ( AF; AC). Mà tam giác AFC đều (vì
AF = AC = FC = a 2 ). Suy ra ∑ FAC = 60°. Câu 26: Đáp án A. !!!" !!!" 2 2 2
BC = AB + AC - AB AC (AB AC) 2 2 2. . .cos , = AB + AC - 2. . AB AC Câu 27: Đáp án B. !!!" !!!" !!!" !!!" Ta có: . AB EG = . AB AC, mặt khác !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!"
AC = AB + AD Þ AB EG = AB AC = AB AB + AD = AB + AB AD = a ( ) 2 2 . . . Câu 28: Đáp án A. Trang 93
ìMQ / /NP / / AB
Xét tứ giác MNPQ có í
Þ MNPQ là hình bình hành. Mặt khác,
îMN / /PQ / /CD
AB ^ CD Þ MQ ^ MN . Do đó, MNPQ là hình chữ nhật. MQ CM
Vì MQ / / AB nên = = x Þ MQ = .
x AB = 6x . Theo giả thiết AB CB MQ = .
x BC Þ BM = (1- x)BC . MN BM
Vì MN / /CD nên =
=1- x Þ MN = (1- x).CD = 6(1- x) . Diện tích hình chữ nhật CD BC MNPQ là: 2 æ x + - x ö S = MN PQ = - x x = x - x £ = MNPQ ( ) ( ) 1 . 6 1 .6 36. . 1 36 9 ç ÷ è 2 ø Ta có S = 1
9 khi x = 1- x Û x = . Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là MNPQ 2 trung điểm của BC . Câu 29: Đáp án D. ì 1 IJ = AB ïï 2
Tứ giác IJEF là hình bình hành. Mặt khác í
mà AB = CD nên IJ = JE . Do đó IJEF là 1 ïJE = CD ïî 2 hình thoi. Suy ra ∑ (IE,JF)=90°. Câu 30: Đáp án D.
Theo nhận xét phần 2 đường thẳng vuông góc trong SGK thì đáp án D đúng. Trang 94 Câu 31: Đáp án A. ! ! ! ! ! ! ! ! ! ! . a b 3 Ta có: (a -b)2 2 2 9 = a + b - 2 . a b Þ .
a b = . Do đó: cosa = ! ! = . 2 a . b 8 Câu 32: Đáp án C. !!!" !!!" !!!" !!!" !!!" !!!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!" Ta có: A .
B CD + AC.DB + A .
D BC = ( AC + CB).CD + AC.DB - A . D CB =
!!!" (!!!" !!!" !!!" !!!" !!!" !!!"!!!" !!!"!!!"
AC CD + DB) + CB(CD - AD) = AC.CB + . CB CA = 0. Câu 33: Đáp án A. !!!" !!!" !!!" "
Gội G là trọng tâm tam giác ABC Þ G là cố định và GA +GB +GC = 0 . !!!!" !!!" !!!!" !!!" !!!!" !!!" !!!!" !!!" !!!" !!!"
P = (MG +GA )2 +(MG +GB )2 +(MG +GC )2 2
= MG + MG (GA +GB +GC ) 2 2 2 3 2 .
+GA +GB +GC 2 2 2 2 2 2 2
= 3MG +GA +GB +GC ³GA +GB +GC . Dấu bằng xảy ra Û M ºG . Vậy 2 2 2
P =GA +GB +GC với M º G là trọng tâm tam giác ABC . min Câu 34: Đáp án B. ! ! 2 ! ! 2 ! ! !2 !2 ! ! 2 ! 2 ! 2 ! ! 2 æ ö æ ö
a -b = a -b - 2a.b = a ça +b ÷ - a +b = 2 a ç
+ b ÷ - a +b ( ) ( ) è ø è ø ! ! = ( 2 2 + ) 2 2 26
28 - 48 = 616 Þ a -b = 616 . Câu 35: Đáp án D. !" !" " " " " " " " "
Ta có: x y = (a - b )(a -b ) 2 2 . 2 = a + 2b - 3 . a b = 4 ; !" !" 2 " " 2 " 2 " 2 " " x = x
= a - 2b = a + 4 b - 4 . a b = 2 3 . ( ) ( ) ( ) ( ) !" !" " " " " " "
y = (y )2 = (a -b )2 = (a)2 + (b )2 - 2a.b = 5 !" !" x .y 4 2 cosa = !" !" = = x . y 2 3. 5 15 Câu 36: Đáp án C. 1 1 1 !!!" !!!!" !!!" !!!!"
S = AB .AC .sin A =
AB .AC sin A =
AB .AC (1- cos A ) 2 2 1 2 2 2 2 2 2 =
AB .AC - (AB .AC )2 2 2 2 2 .. Câu 27: Đáp án A. Câu 38: Đáp án A. Trang 95
Kẻ AI ^ SC Þ (AIB ) ^ SC . Thiết diện là tam giác AIB . Ta có 2 ∑ 2 2 2
æ a +b -c ö a 2 2 2
AI = AC .sin ACS = . a 1- cos ACS = . a 1- ç ÷ = 4b -a . 2ab 2b è ø
Gọi J là trung điểm của AB . Dễ thấy tam giác AIB cân tại I , suy ra IJ ^ A B và a 2 2 2 1 a 3b -a 2 2 2 2
I J = AI - AJ =
3b - a . Do đó: S = AB .IJ = . 2b 2 4b Câu 39: Đáp án B. Câu 40: Đáp án A.
+Ta có tam giác ABC vuộng tại B nên trung điểm H của AC là tâm đường tròn ngoại tiếp tam giác
ABC . Gọi d là trung trực của tam giác ABC Þd ^ (ABC ) tại H.
+ Mặt khác: SA = SB = SC nên điểm S Îd ÞSH ^ (ABC ). Câu 41: Đáp án C.
Do H là hình chiếu của S lên mặt phẳng (ABC ) nên SH ^ (ABC ). vậy AH là hình chiếu của
SH lên mp (ABC ) Þ (SA (ABC )) = (SA AH ) ∑ ; ;
= SAH . Ta có: SH ^ (ABC ) ÞSH ^ AH .Mà AB D C = S
D BC Þ SH = AH . Vậy tam giác SAH vuông cân tại ∑
H Þ SAH = 45° . Câu 42: Đáp án B.
Câu B sai vì: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì có thể cắt nhau, chéo nhau. Câu 43: Đáp án D. Trang 96
Gọi SA = SB = SC = a . Ta có: SA
! C đều Þ AC = SA = a . SA ! B vuông cân tại 2 2 2 2 2
S Þ AB = a 2;BC = SB +SC - 2SB .SC .cos BSC = a 3 Þ AC + AB = BC Þ A ! BC .
vuông tại A . Gọi I là trung điểm của BC thì I là tâm đường tròn ngoại tiếp tam giác ABC . Gọi d
là trục của tam giác ABC thì d đi qua I và d ^ (ABC ). Mặt khác: SA = SB = SC nên S Îd .
Vậy SI ^ (ABC ) nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC ). Câu 44: Đáp án D.
Ta có SA ^ (ABCD ) ÞSA ^ BD . Do tứ giác ABCD là hình thoi nên BD ^ AC , mà
SA ^ BD nên BD ^ (SAC ) hay BD ^ SC ,BD S
^ O . AD không vuông góc với SC . Câu 45: Đáp án A.
Mặt phẳng (P ) vuông góc với OH nên (P ) song song với SO . Suy ra (P )Ç(SAH ) theo giao
tuyến là đường thẳng qua I và song song với SO cắt SH tại K . Trang 97
Từ giả thiết suy ra (P ) / /BC , do đó (P )sẽ cắt (ABC),(SBC ) lần lượt là các đường thẳng qua I và K BC AB, AC,SB,SC M, N, Q, P song song với cắt lần lượt tại
. Do đó thiết diện là tứ giác MNPQ .
Ta có MN và PQ cùng song song với BC suy ra I là trung điểm của MN và K là trung điểm của
PQ , lại có tam giác ABC đều và tam giác SBC cân tại S suy ra IK vuông góc với MN và PQ
nên MNPQ là hình thang cân. Câu 46: Đáp án D.
Ta có BD ^ AC ,BD ^ SA Þ BD ^ (SAC ) Þ BD ^SC , và O là trung điểm của BD
Þ (SAC ) là mặt phẳng trung trực cyả đoạn BD . Ta có OI song song SA suy ra IO ^ (ABCD ).
Vậy SA = SB = SC là khẳng đính sai. Câu 47: Đáp án D.
Vì SA ^ (ABCD ) Þ AC là hình chiếu vuông góc của SC lên (ABCD ). Suy ra góc giữa SC và
mp (ABCD ) bằng góc giữa ∑
SC & AC Þ a = SCA . Xét tam giác SAC vuông tại A có: SA a 6 tana = = = 3 Þa = 60° . AC a 2 Câu 48: Đáp án A.
Gọi M ,N ,P lần lượt là hình chiếu của S lên các cạnh của AB ,AC ,BC . Theo định lý ba đường
vuông góc ta có M ,N ,P lần lượt là hình chiếu của H lên các cạnh AB ,AC ,BC . ∑ ∑ ∑
Þ SMH = SNH = SPH Þ SM ! H = SN ! H = SP
! H Þ HM = HN = NP
Þ H là tâm đường tròn nội tiếp của !ABC . Câu 49: Đáp án A. a ì ^ b Nếu í
thì a và c có thể trùng nhau nên đáp án A sai. b î ^ c Câu 50: Đáp án D. Trang 98
Có AB ^ BC Þ!ABC là tam giác vuông tại B. SA ì ^ AB
Ta có SA ^ (ABC ) Þ í Þ SA ! B , SA
! C là các tam giác vuông tại A . SA î ^ AC ìAB ^ BC Mặt khác í
Þ BC ^ SB Þ S
! BC là tam giác vuông tại B. SA î ^ BC
Vậy bốn mặt của tứ diện đều là tam giác vuông nên đáp án D đúng. Câu 51: Đáp án D. ìAB ^ BC ìAE ^ SB Ta có: í
Þ BC ^ (SAB ) Þ BC ^ AE . Vậy: í Þ AE ^ SC (1) SA î ^ BC îAE ^ BC
Tương tự: AF ^SC (2) . Từ (1); (2) Þ SC ^ (AEF ) . Vậy đáp án D đúng. Câu 52: Đáp án B. Vì ’ A A = ’ A B = ’
A D Þ Hình chiếu của ’
A trên ( ABCD) trùng với H là tâm đường tròn ngoại tiếp ABD D (1).
Mà tứ giác ABCD là hình thoi và ∑ 0
BAD = 60 nên ABD D là tam giác đều (2).
Từ (1) và (2) suy ra H là trọng tâm của ABD D . Câu 53. Đáp án C.
Gọi M là trung điểm của BC thì BC ^ AM (1).
Hiển nhiên AM = a 3 .
Mà SA ^ (ABC) Þ BC ^ SA (2)
Từ (1) và (2) suy ra: BC ^ (SAM ) Þ (P) º (SAM )
Khi đó, thiết diện của hình chop S.ABC được cắt bởi (P) chính là SA D M. SA D M.vuông tại A nên: 2 1 1 a 3 3 = a S S . A AM = × × a 3 = DSAM 2 2 2 4 Câu 54. Đáp án A Trang 99
Tứ giác ABCD là hình vuông cạnh a nên AC = a 2 .
SA ^ (ABCD) Þ AC là hình chiếu vuông góc của SC lên (ABCD). ∑
Þ SCA là góc giữa SC lên (ABCD).
Tam giác SAC vuông tại A nên: ∑ SA a 6 1 1 ∑ 0 tan SCA = = × = Þ SCA = 30 AC 3 a 2 3 Câu 55. Đáp án D.
ìA'C Ç AC ' = I Gọi í
îC 'D ÇCD' = H
ìC 'D ^ CD' Mà í
Þ C 'D ^ (A'BCD')
îC 'D ^ A'D'
Þ IH là hình chiếu vuông góc của AC' lên (A’BCD’) ∑
Þ C 'IH là góc giữa AC' lên (A’BCD’) C H Mà ∑ ' 1 tan C ' IH = = ×2 = 2 IH 2 Câu 56. Đáp án D. Trang 100 ìSH ^ AH ï
SH ^ (ABC) Þ íSH ^ BH ïSH ^ î CH Xét ba tam giác vuông S D HA, S D HB, S D HC có:
ìSA = SB = SC í
Þ DSHA = DSHB = DSHC îSH chung
Þ HA = HB = HC mà H Î(ABC)
Þ H là tâm đường tròn ngoại tiếp AB D C. Câu 57. Đáp án C.
Gọi N là trung điểm của BC. ìSB = SC ìBC ^ SN í Þ í Þ BC ^ (SAN) îAB = AC îBC ^ AN ìM Î(P)
Theo bài ra: BC ^ (P) Þ í î(P) / /(SAN)
Kẻ MI / / AN , MK / /SA
Þ Thiết diện của (P) và tứ diện SABC là K D MI. AB D C và SB
D C là hai tam giác đều cạnh a. a 3 Þ a 3 AN = SN =
= SA Þ DSAN là tam giác đều cạnh
Þ DKMI là tam giác đều cạnh 2 2 2 3 a - b 3 3 æ a - b ö × Þ S = × DKMI ç ÷ 2 a 16 è a ø Câu 58. Đáp án B.
Câu A: sai vì b có thể vuông góc với a .
Câu B đúng bởi: a / /(P) Þ $a 'Î(P) sao cho a '/ /a ,
b ^ (P) Þ b ^ a ' . Khi đó: a ^ b . Trang 101
Câu C và câu D sai vì: b có thể nằm trong (P). Vậy: chọn đáp án B. Câu 59. Đáp án C = = a AM BM , SB = a 2
Có SM ^ (ABC) nên AM là hình chiếu của SA lên (ABC) ∑ Þ (SA ABC ) ∑ ∑ ,( ) = ( , SA AM ) = SAM
Áp dụng định lý Pytago: 2 2 3 = - = a SM SB AM 2 Xét tam giác SAM có: ∑ SM ∑ 0 tan SAM = = 3 Þ SAM = 60 AM Câu 60. Đáp án A. Câu 61. Đáp án A.
Vì qua một đường thẳng dựng được vô số mặt phẳng. Câu 62. Đáp án D.
Thiết diện là hình thang vuông đi qua trung điểm các cạnh AB,CD,CS,SB, nên diện tích thiết diện là: æ 1 ö 1 BC + BC × ç ÷ SA è 2 ø 2 (8 + 4).6 S = = = 36 2 2 Câu 63. Đáp án C.
Theo bài ra, hình chóp SABC là hình chóp tam giác đều. Gọi H là trung điểm của BC , ta có:
SG ^ (ABC) , G Î AH . 2 a 3 a Mặt khác, ta có: 2 AH = , SH = b - 2 4 2 a 2 ∑ 2 2 æ AG ö 3 3 b - Þ = a SG .
SA sin SAG = b × 1- = b× 1- = ç ÷ 2 è SA ø b 3 Câu 64. Đáp án C.
Để C nằm giữa S và C thì ∑ 0 ASC < 90 1 ∑ 2 2 2b - Þ a cos ASC > 0 Û
> 0 Û b 2 > a 2 2b Câu 65. Đáp án C.
Do hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , SA = SC, SB = SD nên SO ^ (ABCD) Trang 102 Câu 66. Đáp án C. ìCD ^ AP Ta có: í
Þ CD ^ (APB) Þ BG ^ CD îCD ^ BP ìAD ^ CM Tương tự: í
Þ AD ^ (BCM ) Þ BG ^ AD îAD ^ BM
Suy ra: BG ^ (ACD) Þ BG ^ AP
Kẻ KL đi qua trọng tâm G của AC D
D và song song với CD Þ AP ^ KL Þ 2
(P) chính là mặt phẳng ( BKL) Þ (ACD) Ç(BKL) = KL = CD = 8 3
Có thể nói nhanh theo tính chất tứ diện đều:
Gọi G là trọng tâm Δ ACD thì G là tâm AC D
D và BG ^ (ACD).
Trong mp (ACD), kẻ qua G đường thẳng song song với CD cắt AC , AD lần lượt tại K, L .
Ta có: (BKL) ^ (ACD) , AP ^ KL Þ AP ^ (BKL) 2
Vậy: (P) º (BKL) Þ (ACD) Ç (BKL) = KL = CD = 8 3 Câu 67. Đáp án B. Ta có: ∑
(AC ,(ABCD) =CAC =a 1 ) ∑ . 1 CC a 1 1 Þ tana = = = AC a 2 2 Câu 68. Đáp án A.
Kẻ AE ^ BC, SA ^ BC Þ BC ^ (SAE) = (P) 2 a 3
Thiết diện của mặt phẳng (P) và hình chóp S.ABC là tam giác SAE có diện tích là 4 Trang 103 Câu 69. Đáp án C.
Gọi H = EF Ç SD
Do AD ^ BC, SA ^ BC Þ BC ^ (SAD) 1
Þ BC ^ AH Þ EF ^ AH Þ S = EF.AH ! AEF 2 1
Mà EF = BC = a . 2 1 Do H là trung điểm 2
SD Þ AH = a Þ S = a ! AEF 2 Câu 70. Đáp án A. Ta có:
ìA'D ^ AD' (t / c hv) ï í
ïA'D ^ C 'D'
(C ' D ' ^ (A' D ' D ) A ) î
Þ A' D ^ (AC ' D') Þ A' D ' ^ AC ' (1)
ìA' B ^ AB ' (t / c hv) ï í
ïA' B ^ B 'C '
(B 'C ' ^ (A' D ' D ) A ) î
Þ A' B ^ (AB'C ') Þ A' B ^ AC ' (2)
Từ (1),(2) Þ AC ' ^ ( A' BD) Câu 71. Đáp án C. Trang 104
Ta có: S Î(SAB) Þ S là hình chiếu của S trên (SAB) (1) ìBC ^ AB (t / c hv) ï í Þ BC ^ (SAB) ïBC ^ SA (SA ^ ( ABCD)) î
Þ B là hình chiếu của C trên (SAB) (2) Từ Þ ! (SC SAB )= ! (SC SB)= ! (1),(2) ,( ) , BSC = a
Xét tam giác SAB vuông tại A ta có: 2 2
SB = SA + AB = a 2
Xét tam giác SBC vuông tại B ta có: BC a 1 tana = = = SB a 2 2 Câu 72. Đáp án C. ìBH ^ AC (gt) ï Ta có: í ïBH ^ SA (SA ^ ( ABCD)) î
Þ BH ^ (SAC) Þ BH ^ SC Mà ^ Þ ^ Þ ! BK SC SC (BHK) (SC,(BHK))=90" Câu 73. Đáp án B.
ABCD là hình vuông cạnh 2a
Þ AC = 2a 2 Þ AO = a 2
Ta có: SO ^ ( ABCD) Þ OA là hình chiếu của SA
Vậy góc giữa SA và ( ABCD) chính là ! SAO = 45" SO
Xét tam giác SAO ta có ∑ tan SAO = Þ SO = a 2 AO Trang 105 Câu 74. Đáp án B ìAB ^ AD (t/ c hv) ï Ta có: í ïAB ^ SA (SA ^ ( ABCD)) î
Þ AB ^ (SAD) Þ AB ^ SD
Giả sử SB ^ SD Þ SD ^ (SAB) (vô lý) Hay SBD D
không thể là tam giác vuông. Câu 75. Đáp án B
Cách 1: Dựng CK ^ IC' tại K , do đó d C ( ; IC') = CK . OC'.CI Xét ICC D
' , ta có: OC'.CI = CK.IC'Þ CK = IC' Mà: a 3
OC ' = OC.tan 60° = . 3 = a 3 a 3 2 2 2 CI =
, IC ' = OI + C 'O 2 2 2 a 13a 2 = + a = 12 12 3a 13
Þ d(C; IC ') = CK = 13 1
Cách 2: Dựng OH ^ IC' , ta có OI = CI 3 Þ d C ( ; IC') = d 3 O ( ; IC') = OH 3 Sau đó dùng công thức: 1 1 1 = + 2 2 2 OH OI OC '
hay OH.IC'= OI.OC' . Suy ra OH. Câu 76. Đáp án C. Trang 106 Vì CC D
' A vuông tại C nên ta dựng CH ^ AC' thì CH là khoảng cách từ C đến AC' . 1 1 1 1 1 3 = + = + = 2 2 CH CA CC'2 2 2 2 a a 2 2 a 2 2 a a a 2 2 6 Þ CH = Þ CH = = 3 3 3 Câu 77. Đáp án A.
Do SABC là hình chóp đều nên SO ^ (ABC) Þ SAO D
vuông tại O , dựng OH ^ SA Câu 78. Đáp án D. 1 1 1 1 1 Þ = + = + 2 2 2 2 2 OH OA OS æ a 3 ö æ a 3 ö çç 3 ÷÷ çç 3 ÷÷ è ø è ø 3 3 6 a a 6 = + = Þ OH = = 2 2 2 a a a 6 6 Trang 107 Cách 1:
Gọi I là hình chiếu của A trên BM
H là hình chiếu của A trên SI ì AH ^ SI Þ í Þ AH ^ (SBM) îAH ^ BM Þ AH = d( ; A (SBM ))
Gọi N là trung điểm của AB
Þ DN song song BM Þ d( ;
D (SBM )) = d(N;(SBM )) 1 = d( ; A (SBM )) 2
Mặt khác ta có hình chiếu vuông góc của DS lên (SAC)là SO Þ ˆO S D = ° 30 .
Đặt DO = x Þ SO = x 3(O = AC Ç BD) . a Từ 2 2
SO = AO + SA Þ x =
Þ BD = a 2 Þ ABCD là hình vuông cạnh a 2 2 a Þ S = S - 2S = ABM ABCD BCM 2 1 2a 1 1 1 2a a Mà S
= AI.BM Þ AI = Þ = + Þ AH = Þ d( ; D (SBM )) = . ABM 2 5 2 2 2 AH AI SA 3 3 1 1 1 1 Cách 2: = + + 2 2 2 2 AH AB AS AK 2 1 9 2a = + = Þ AH = 2 a 4 2 a 4 2 a 3 a Þ d( ;
D (SBM )) = 2AH = . 3 Câu 79. Đáp án C Trang 108
Trong mặt phẳng (ABC) dựng HK ^ BC tại K Þ BC ^ (SKH ).
Từ giả thiết ta có ˆK H S = 30 ,
° BC = AB2 + AC2 = 4a AC HK 3 Ta có sin ABC = = = BC HB 2 a 3 Þ HK = . 2 a Trong SHK D
ta có SH = HK.tan SKH = 2
Do M là trung điểm cạnh BC nên MH song song AC Þ MH song song (SAC)
Þ d(M;(SAC)) = d(H;(SAC)) .
Trong mặt phẳng (SAB) kẻ DH ^ SA tại D ta có: AC ^ (SA )
B Þ AC ^ DH Þ DH ^ (SAC) 1 1 1 a 5 Þ = + Þ HD = 2 2 2 DH HA HS 5 a 5
Vậy d(M ;(SAC)) = d(H;(SAC)) = HD = 5
Câu 80. Câu 80: Đáp án A.
Theo giả thiết mặt phẳng (AB'C') tạo với ( ' A B'C') góc ° 60 nên ˆ ' A K A = ° 60 . 1 a Ta có ' A K = ' A C'= 2 2 Trang 109 a 3 Þ ' AA = ' A K.tan 60° = 2 d( ;
B (AB'C')) = d ( '
A ;(AB'C')) Dựng ' A H ^ AK Þ '
A H ^ (AB'C') Þ d( '
A ;(AB'C')) = ' A H. a 3 Tính ' A H =
= d(BC;(AB'C')). 4 Câu 81. Đáp án B. ì AB = AD Theo giả thiết í Þ DBADđều cạnh î ˆ a D A B = 60°
Þ OA ^ OB và OO'^ (ABCD) ÞTứ diện OSAB vuông tại O có a a 3 OB = ;OA = ;OS = a 2 2 1 1 1 1 Þ = + + 2 d ( ; O (SAB)) 2 2 2 OA OB OS 1 1 1 4 4 1 = + + = + + 2 2 2 æ a ö æ a ö a 3 2 2 2 3 a a a ç ÷ çç 2 ÷÷ è 2 ø è ø 19 a 3 = Þ d( ; O (SA )) B = . 3 2 a 19 Câu 82. Đáp án C.
Gọi K là trung điểm C F . 1 Trang 110 Do A
D B C đều nên A F ^ B C 1 1 1 1 1 1
Þ EK ^ B C và EK song song A F 1 1 1
ÞA F song song (DEK) 1 Dựng
FH ^ DK Þ d(DE; A F) = d(A F;(DEK)) = FH 1 1
(vì FH ^ (DEK ))
Trong tam giác vuông DFK ta có: 1 1 1 1 1 1 16 17 = + = + = + = 2 2 2 2 2 2 2 2 FH FD FK a æ a ö a a a ç ÷ è 4 ø a Þ FH = . 17 Trang 111




