

















































Preview text:
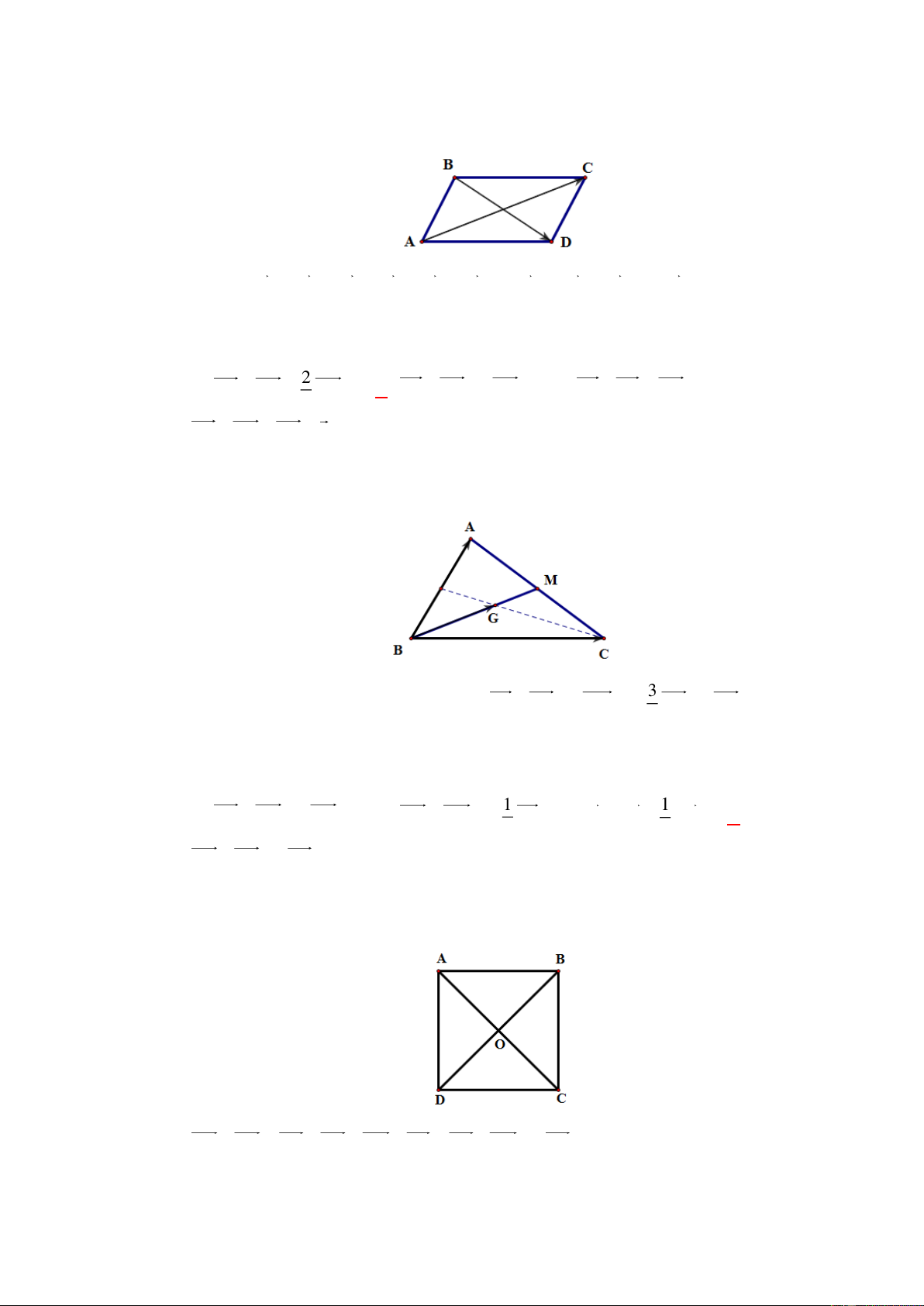
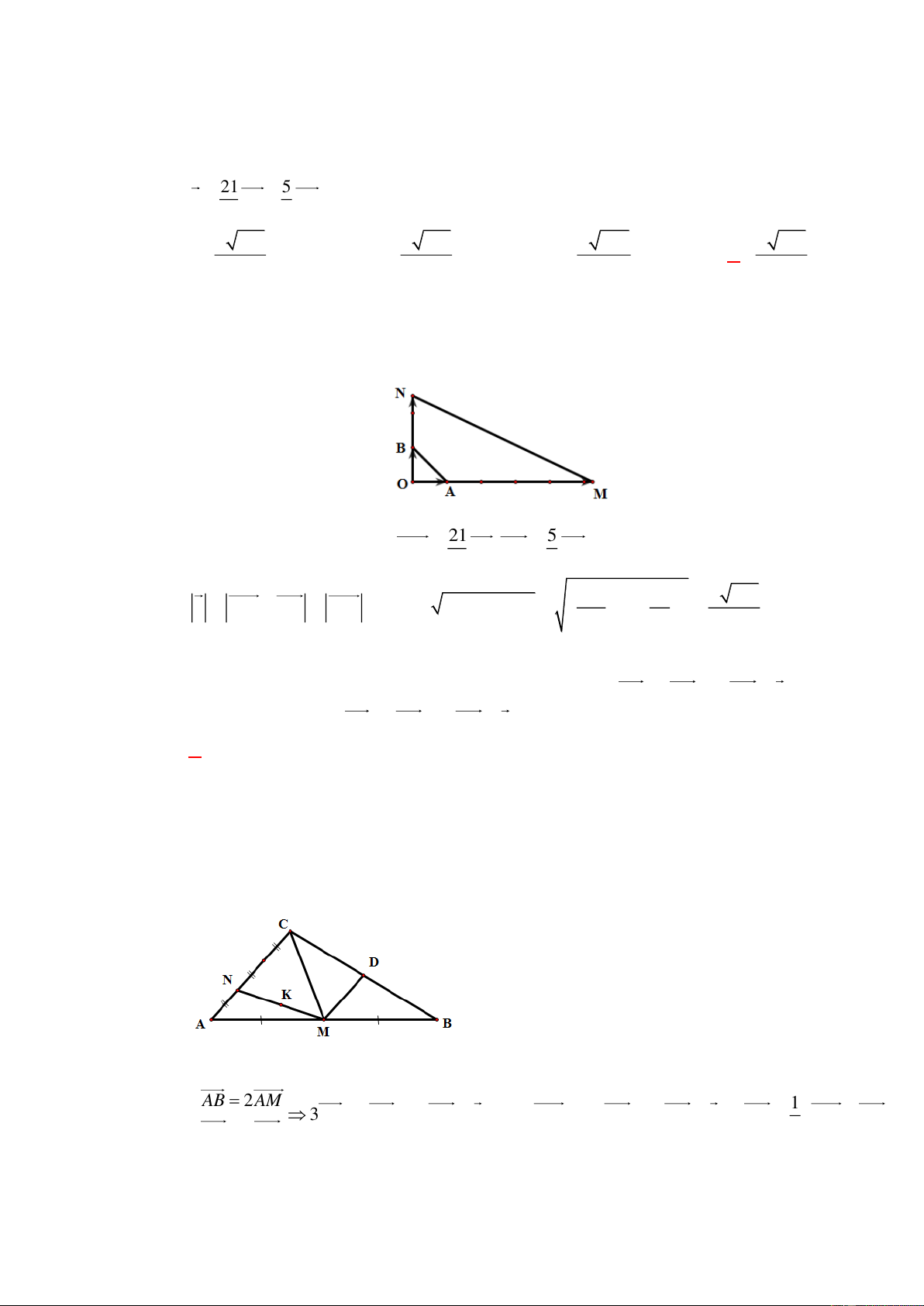
Câu 1: [0H1-1-1]Cho lục giác đều ABCDEF tâm O . Số các vectơ bằng OC có điểm đầu và
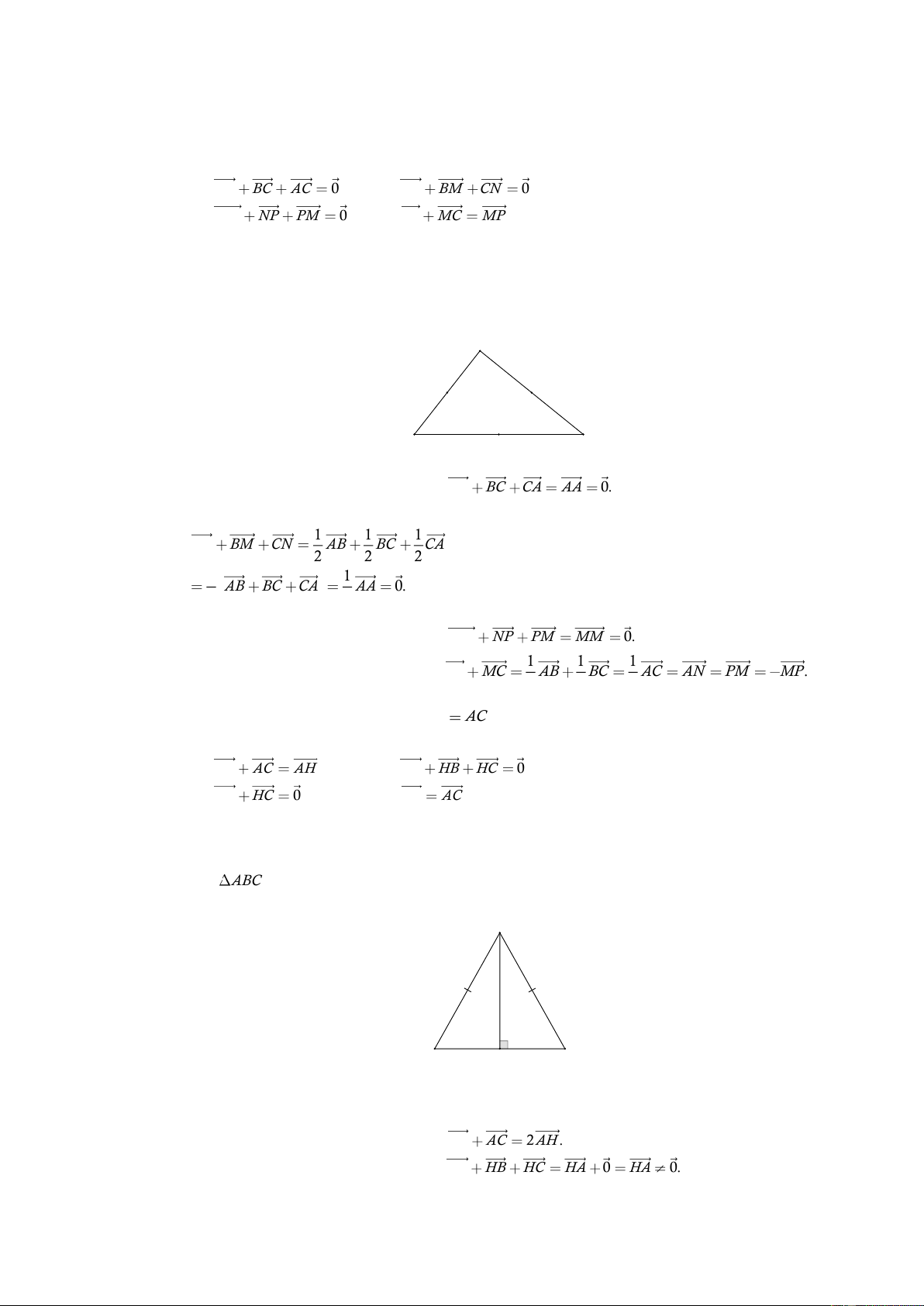
điểm cuối là các đỉnh của lục giác là A. 2 . B. 3 . C. 4 . D. 6 . Lời giải Chọn A C B D A O E F
Đó là các vectơ: AB, ED .
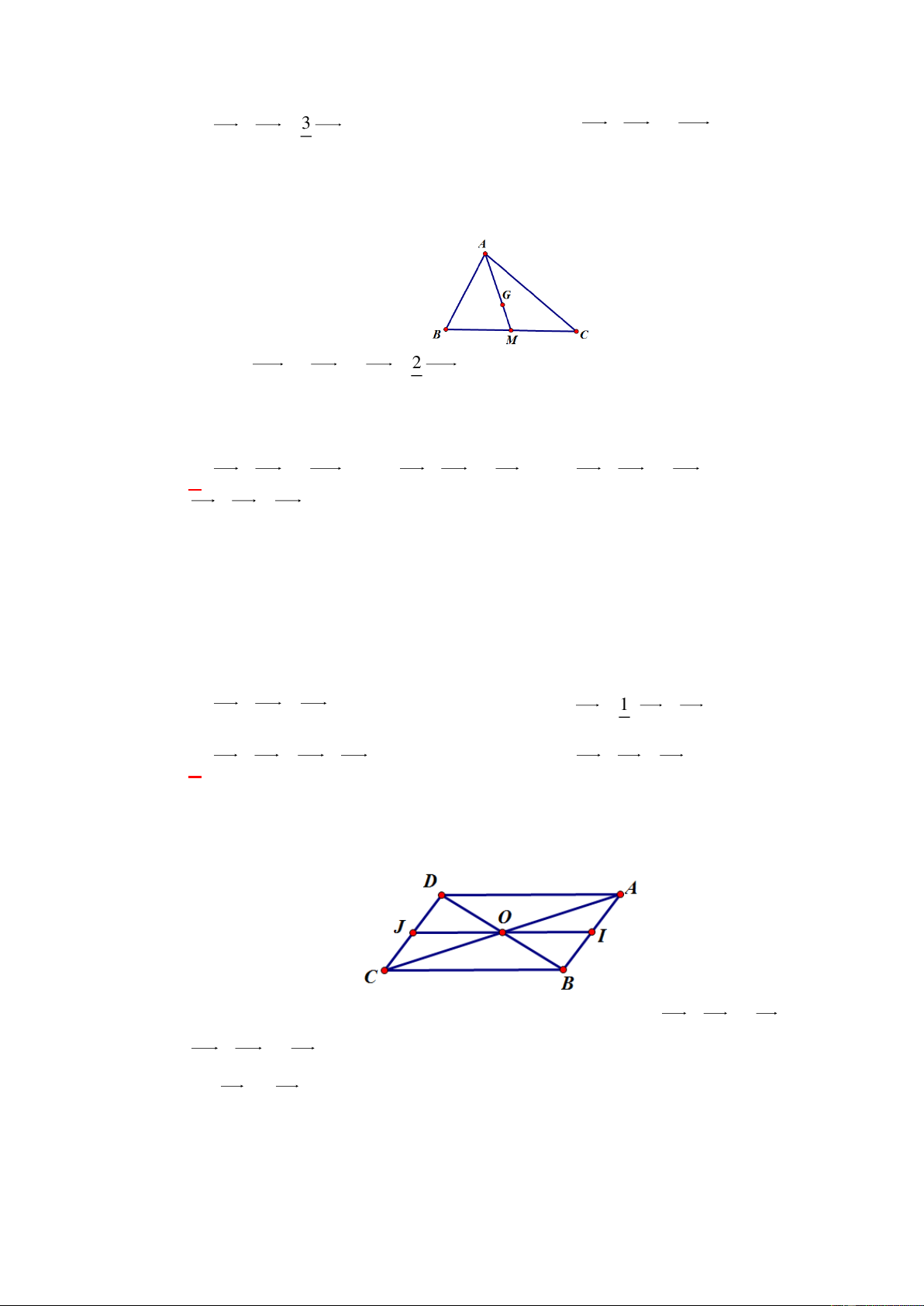
Câu 2: [0H1-1-1] Cho tam giác ABC . Gọi M , N lần lượt là trung điểm của các cạnh
AB, AC . Hỏi cặp véctơ nào sau đây cùng hướng?
A. AB và MB .
B. MN và CB .
C. MA và MB .
D. AN và CA . Lời giải Chọn A A M N B C
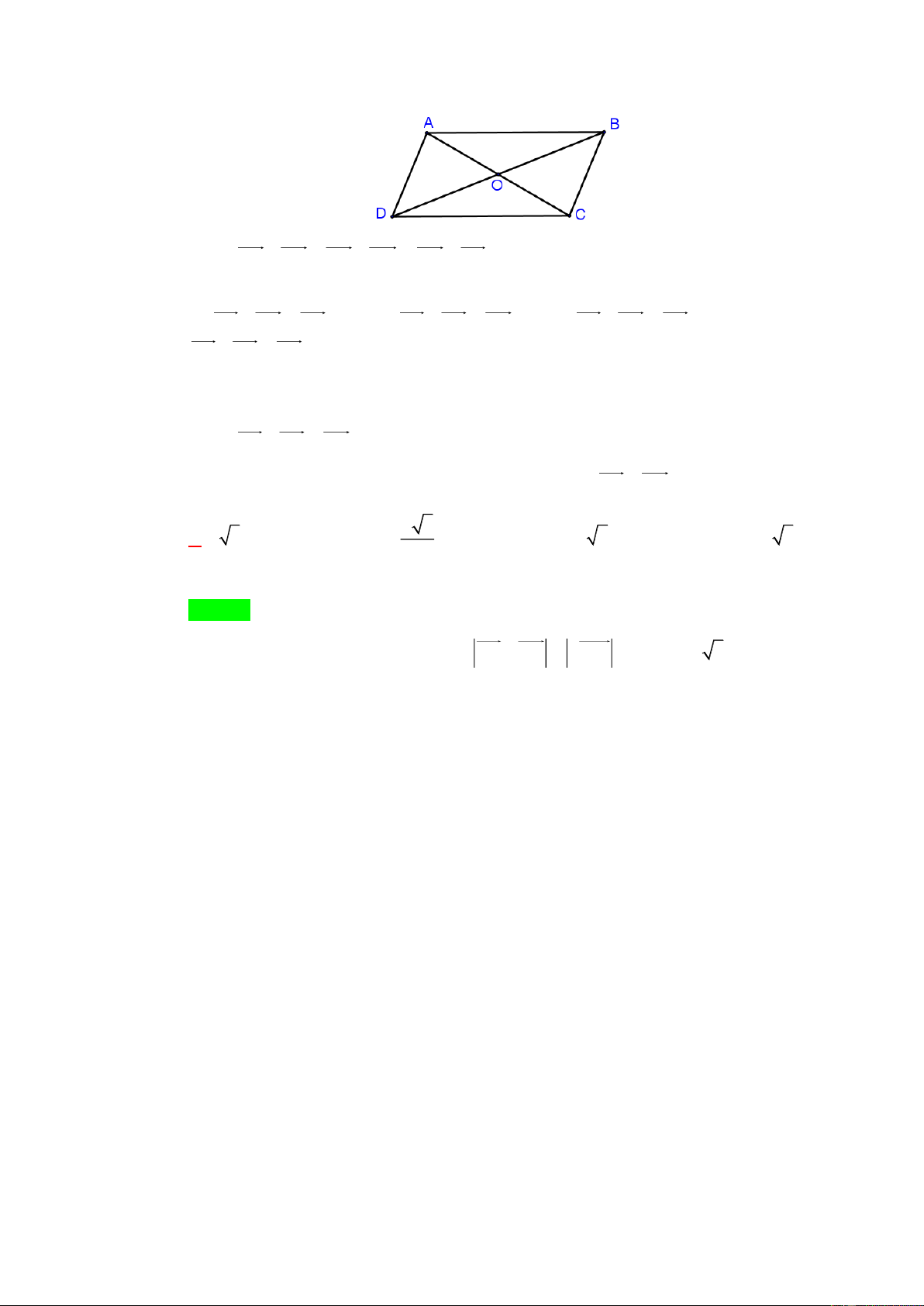
Câu 3: [0H1-1-1] Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành
ABCD . Đẳng thức nào sau đây là đẳng thức sai?
A. OB DO .
B. AB DC .
C. OA OC . D.
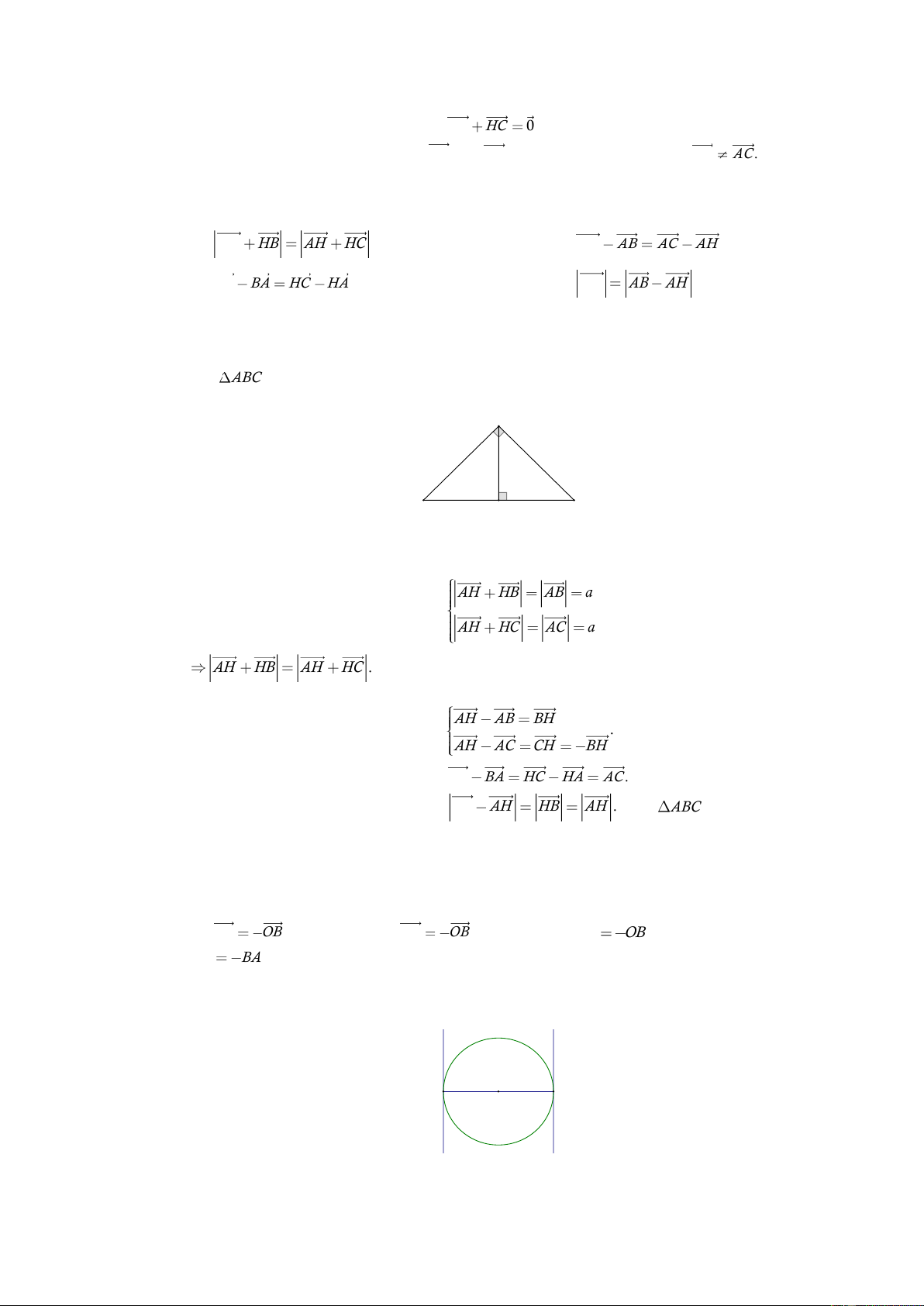
CB DA. Lời giải Chọn C A B O D C
OA và OC là hai vectơ đối nhau.
Câu 4: [0H1-1-1] Gọi M là trung điểm của đoạn AB . Khẳng định nào sau đây là khẳng định sai? 1
A. MA MB 0 . B. MA AB .
C. MA MB . D. 2
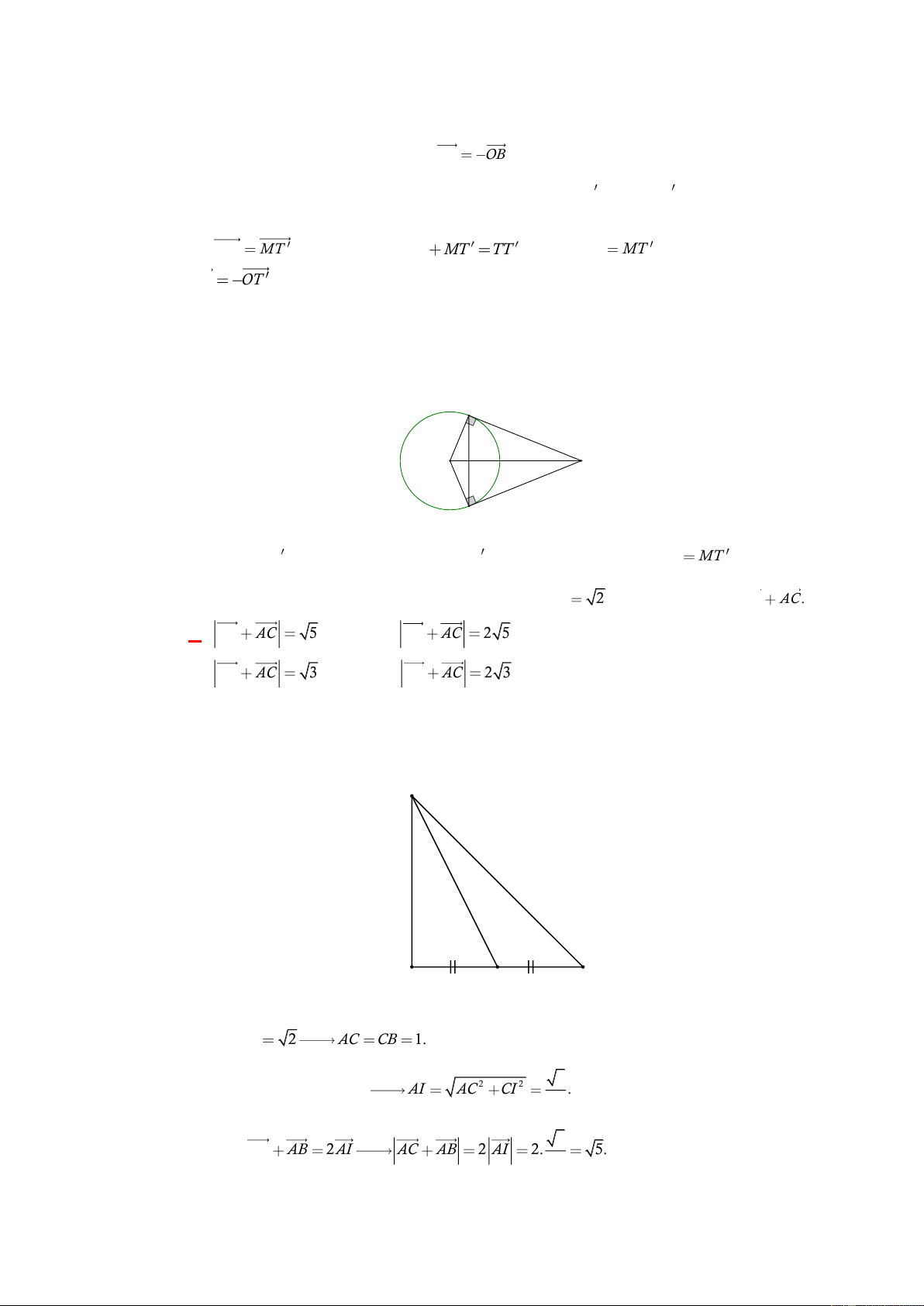
AB 2MB . Lời giải Chọn C
M là trung điểm AB thì MA MB .
Câu 5: [0H1-1-1] Cho ba điểm M , N , P thẳng hàng, trong đó điểm N nằm giữa hai điểm
M và P . Khi đó các cặp vectơ nào sau đây cùng hướng?
A. MN và PN .
B. MN và MP .
C. MP và PN .
D. NM và NP . Lời giải Chọn B
Câu 6: [0H1-1-1] Cho tam giác ABC , có thể xác định được bao nhiêu vectơ (khác vectơ
không) có điểm đầu và điểm cuối là các đỉnh ,
A B, C . A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn D Có 6 vectơ là A , B B ,
A AC, C ,
A BC, CB .
Câu 7: [0H1-1-1] Cho hai điểm phân biệt A và B , số vectơ khác vectơ - không có thể xác
định được từ 2 điểm trên là: A. 4 . B. 3 . C. 2 . D. 1 . Lời giải Chọn C
Ta có hai vectơ đó là AB và BA .
Câu 8: [0H1-1-1] Cho trước véc-tơ MN 0 thì số véctơ cùng phương với véc-tơ đã cho là A. 1. B. 2 . C. 3 . D. Vô số. Lời giải Chọn C
Có vô số véc-tơ cùng phương với một véc-tơ cho trước.
Câu 9: [0H1-1-1] Hai véc-tơ được gọi là bằng nhau khi và chỉ khi:
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
C. Chúng trùng với một trong các cặp cạnh của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau. Lời giải Chọn D
Hai véc-tơ được gọi là bằng nhau khi và chỉ khi chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 10: [0H1-1-1] Chọn câu dưới đây để mệnh đề sau là mệnh đề đúng: Nếu có AB AC thì
A. tam giác ABC là tam giác cân.
B. tam giác ABC là tam giác đều.
C. A là trung điểm của đoạn BC .
D. điểm B trùng với điểm C . Lời giải Chọn D AB AC ,
A B, C là ba điểm thằng hàng và B, C nằm cùng phía so với A ;.
mà AB AC nên B C .
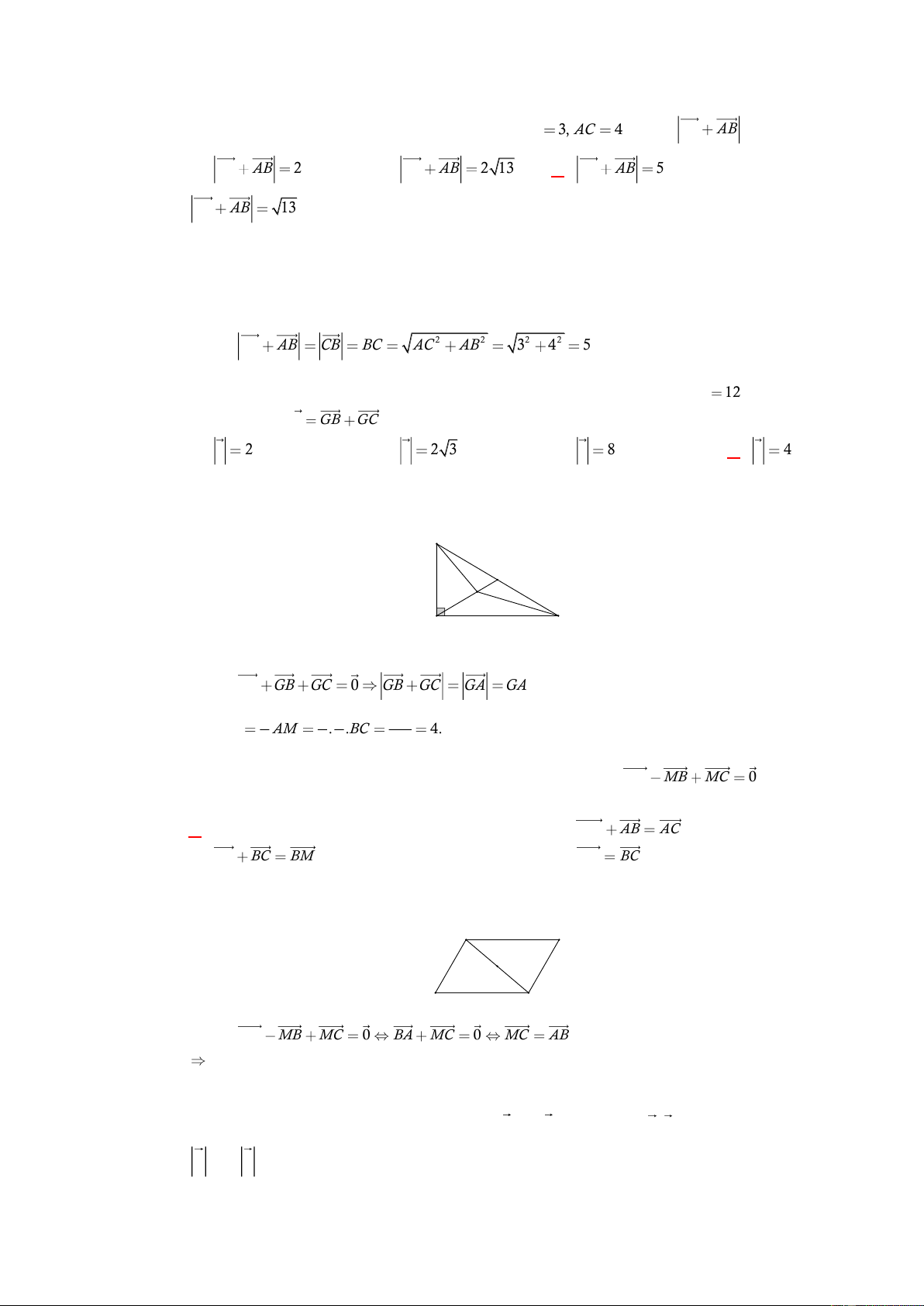
Câu 11: [0H1-1-1] Cho hình chữ nhật ABCD có AB 3cm, BC 5cm . Độ dài của véctơ AC là: A. 4 . B. 6 . C. 8 . D. 13 . Lời giải Chọn D 2 2 2 AC
AB AD 25 144 13 .
Câu 12: [0H1-1-1] Cho tam giác MNP vuông tại M và MN 3cm, MP 4cm . Khi đó độ
dài của véctơ NP là A. 3 cm. B. 4 cm. C. 5 cm. D. 6 cm. Lời giải Chọn C 2 2
NP MN MP 5 .
Câu 13: [0H1-1-1] Cho hình chữ nhật ABCD có AB 3cm , AD 4cm . Tính AC ? A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn C Ta có 2 2 AC
AB AD 9 16 5.
Câu 14: [0H1-1-1] Trong hệ trục ;
O i; j , mệnh đề nào sau đây sai ? 2 A. i . i B. i 1.
C. i j . D. . i j 0. Lời giải Chọn A
Vì i và j lần lượt là hai vectơ đơn vị trong hệ trục ;
O i; j ta có: + i j . i j 0.
+ i j 1.
Mặt khác : Tích của hai vectơ là một số.
Do đó các mệnh đề B, C, D là mệnh đề đúng và mệnh đề A là mệnh đề sai.
Câu 1: [0H1-1-2] Vectơ có điểm đầu là D , điểm cuối là E được kí hiệu là: A. DE . B. DE . C. ED . D. DE . Lời giải Chọn D
Câu 2: [0H1-1-2] Cho tam giác ABC , có thể xác định được bao nhiêu vectơ khác vectơ không
có điểm đầu và điểm cuối là các đỉnh , A , B C ? A. 3 . B. 6 . C. 4 . D. 9 . Lời giải Chọn B
Đó là các vectơ: AB, ,
BA BC, CB, C , A AC. .
Câu 3: [0H1-1-2]Cho tứ giác ABCD . Có bao nhiêu vectơ khác vectơ không có điểm đầu và
cuối là các đỉnh của tứ giác? A. 4 . B. 6 . C. 8 . D. 12 . Lời giải Chọn D
Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt. Do đó có 12 cách
chọn 2 điểm trong 4 điểm của tứ giác (có tính thứ tự các điểm) nên có thể lập được 12 vectơ.
Câu 4: [0H1-1-2]Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Lời giải Chọn A
Vì Vectơ - không cùng phương với mọi vectơ.
Câu 5: [0H1-1-2]Cho ba điểm ,
A B, C phân biệt. Khi đó:
A. Điều kiện cần và đủ để ,
A B, C thẳng hàng là AB cùng phương với AC .
B. Điều kiện đủ để ,
A B, C thẳng hàng là với mọi M , MA cùng phương với AB .
C. Điều kiện cần để ,
A B, C thẳng hàng là với mọi M , MA cùng phương với AB .
D. Điều kiện cần để ,
A B, C thẳng hàng là AB AC Lời giải Chọn A
Câu 6: [0H1-1-2]Gọi M, N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều
ABC . Hỏi cặp vectơ nào sau đây cùng hướng?
A. MN và CB .
B. AB và MB .
C. MA và MB . D. AN và CA . Lời giải Chọn B
Câu 7: [0H1-1-2]Cho lục giác đều ABCDEF tâm O . Số các vectơ khác vectơ không, cùng
phương với OC có điểm đầu và điểm cuối là các đỉnh của lục giác là: A. 4 . B. 6 . C. 7 . D. 9 . Lời giải Chọn B C B D A O E F
Đó là các vectơ: AB, ,
BA DE, ED, FC, CF .
Câu 8: [0H1-1-2]Với DE (khác vectơ không) thì độ dài đoạn ED được gọi là
A. Phương của ED .
B. Hướng của ED .
C. Giá của ED .
D. Độ dài của ED . Lời giải Chọn D
Câu 9: [0H1-1-2]Mệnh đề nào sau đây sai? A. AA 0 .
B. 0 cùng hướng với mọi vectơ. C. AB 0 .
D. 0 cùng phương với mọi vectơ. Lời giải Chọn C
Vì có thể xảy ra trường hợp AB 0 A B. .
Câu 10: [0H1-1-2]Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau. Lời giải Chọn D
Câu 11: [0H1-1-2] Gọi C là trung điểm của đoạn thẳng AB . Khẳng định nào sau đây là đúng? A. CA CB .
B. AB và AC cùng phương.
C. AB và CB ngược hướng. D. AB BC . Lời giải Chọn B
Câu 12: [0H1-1-2]Cho tứ giác ABCD . Điều kiện nào là điều kiện cần và đủ để AB CD ?
A. ABCD là vuông.
B. ABDC là hình bình hành.
C. AD và BC có cùng trung điểm. D. AB D C . Lời giải Chọn B Ta có: AB CD AB CD
ABDC là hình bình hành. AB CD AB CD
Mặt khác, ABDC là hình bình hành AB CD . AB CD
Do đó, điều kiện cần và đủ để AB CD là ABDC là hình bình hành.
Câu 13: [0H1-1-2]Từ mệnh đề AB CD , ta suy ra
A. AB cùng hướng CD . B. AB cùng phương CD . C. AB CD .
D. ABCD là hình bình hành.
Hỏi khẳng định nào là sai? Lời giải Chọn D
Phải suy ra ABDC là hình bình hành.
Câu 14: [0H1-1-2]Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD . Đẳng
thức nào sau đây sai? A. AB DC . B. OB DO . C. OA OC . D. CB DA . Lời giải Chọn C
Câu 15: [0H1-1-2]Cho hình vuông ABCD . Khẳng định nào sau đây là đúng? A. AC BD . B. AB CD . C. AB BC .
D. AB, AC cùng hướng. Lời giải Chọn C Vì AB BC AB BC . .
Câu 16: [0H1-1-2]Gọi O là giao điểm của hai đường chéo hình chữ nhật ABCD . Mệnh đề nào sau đây đúng? A. OA OC .
B. OB và OD cùng hướng.
C. AC và BD cùng hướng. D. AC BD Lời giải Chọn D
Câu 17: [0H1-1-2]Cho tam giác ABC đều cạnh a . Gọi M là trung điểm BC . Khẳng định nào sau đây đúng? a 3 A. MB MC . B. AM . C. AM a . D. 2 a 3 AM . 2 Lời giải Chọn D
Câu 18: [0H1-1-2]Cho AB
0 và một điểm C . Có bao nhiêu điểm D thỏa mãn AB CD ? A. 0 . B. 1 . C. 2 . D. Vô số. Lời giải Chọn D
Lời giải. Ta có AB CD AB
CD . Suy ra tập hợp các điểm D thỏa yêu cầu bài
toán là đường tròn tâm C, bán kính AB .
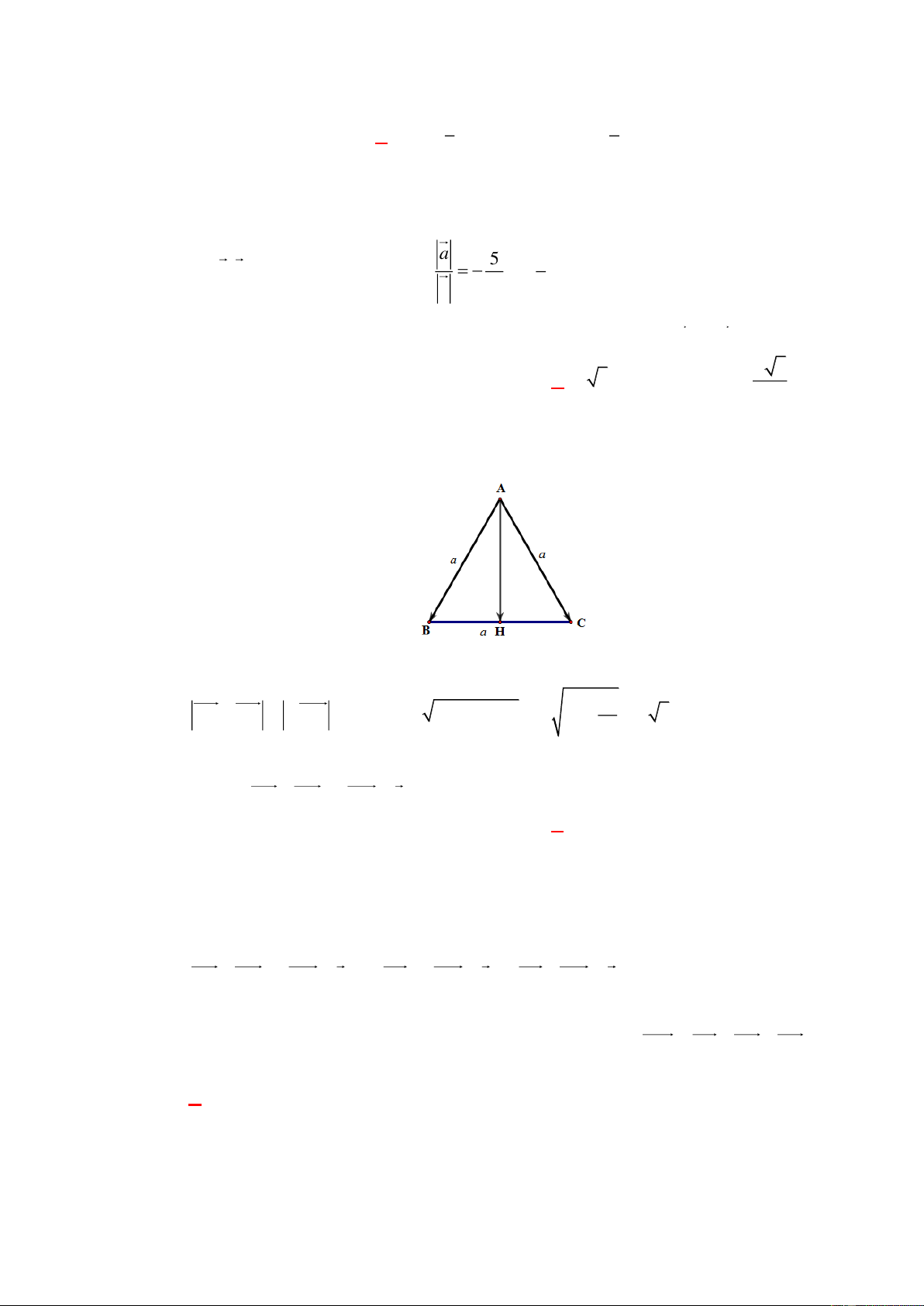
Câu 19: [0H1-1-2] Cho tam giác đều ABC với đường cao AH . Đẳng thức nào sau đây đúng? 3
A. HB HC .
B. AC 2 HC . C. AH HC . D. 2
AB AC . Lời giải Chọn B A B H C
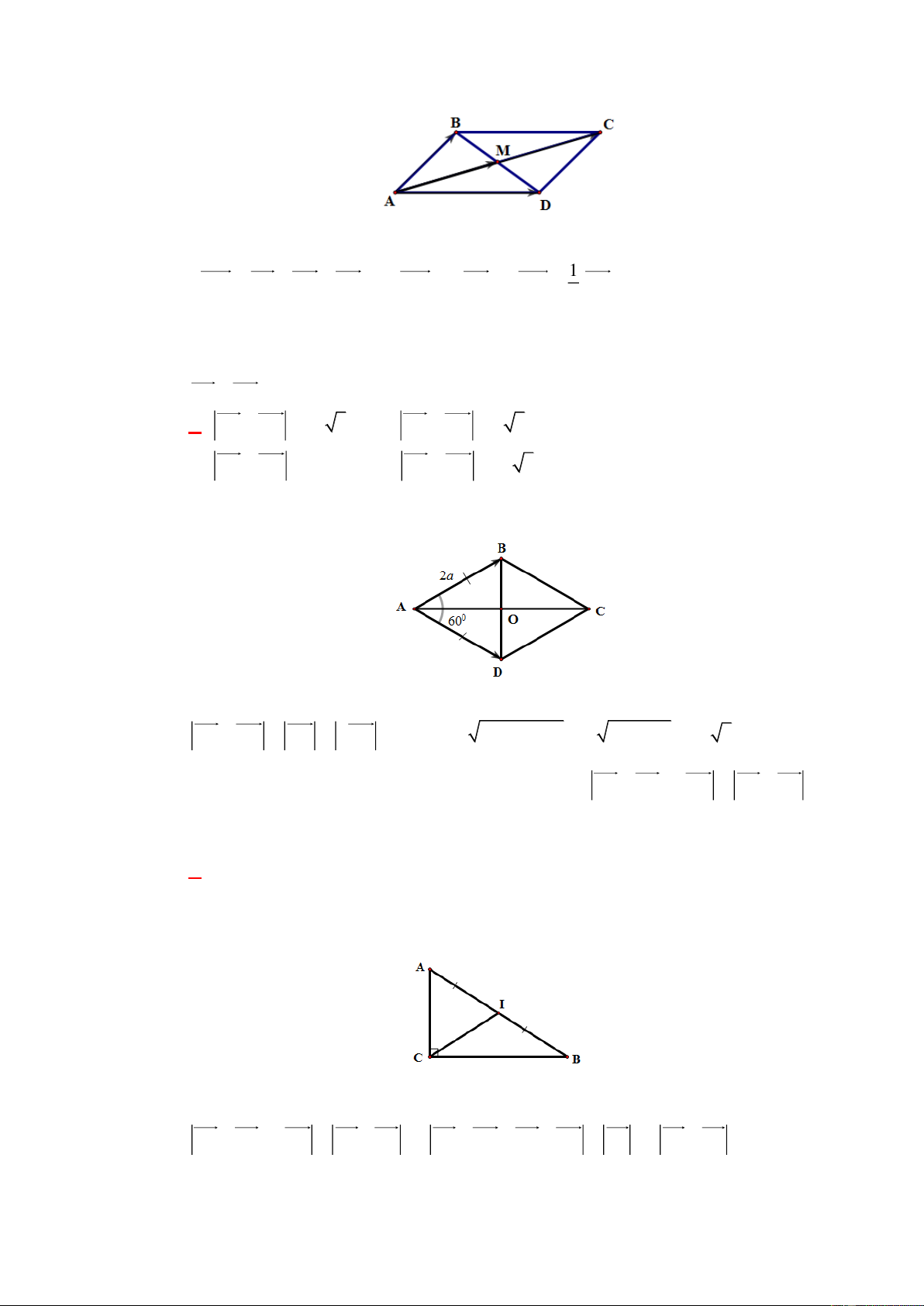
Câu 20: [0H1-1-2] Cho hình thoi ABCD tâm O , cạnh bằng a và góc A bằng 60 . Kết
luận nào sau đây đúng? a 3 A. OA .
B. OA a .
C. OA OB . D. 2 a 2 OA . 2 Lời giải Chọn A D C a O a A B a 3
Ta có: OA OA
(vì tam giác ABD là tam giác đều) 2
Câu 21: [0H1-1-2] Cho hai vectơ khác vectơ - không, không cùng phương. Có bao nhiêu
vectơ khác 0 cùng phương với cả hai vectơ đó? A. 2 . B. 1. C. không có. D. vô số. Lời giải Chọn C
Giả sử tồn tại một vec-tơ c cùng phương với cả hai véc-tơ a, b . Lúc đó tồn tại các
số thực h và k sao cho c ha và c kb . Từ đó suy ra k
ha kb a b . h
Suy ra hai véc-tơ a và b cùng phương. (mâu thuẫn). Chọn C
Câu 22: [0H1-1-2] Cho tam giác ABC đều cạnh bằng 1, trọng tâm G . Độ dài vectơ AG bằng: 3 3 3 3 A. . B. . C. . D. . 2 3 4 6 Lời giải Chọn B 2 2 3 3
Ta có: AG AG AM
. (với M là trung điểm của BC ). 3 3 2 3
Câu 23: [0H1-1-2] Cho tam giác ABC , trọng tâm G . Kết luận nào sau đây đúng?
A. GA GB GC .
B. GA GB GC 0 .
C. GC GA GB . D. Không xác định được
GA GB GC . Lời giải Chọn B
Ta có: GA GB GC 0 (tính chất trọng tâm).
Câu 24: [0H1-1-2] Phát biểu nào sau đây là đúng?
A. Hai véc-tơ không bằng nhau thì có độ dài không bằng nhau.
B. Hiệu của hai véc-tơ có độ dài bằng nhau là véc-tơ – không.
C. Tổng của hai véc-tơ khác véc-tơ – không là một vé-ctơ khác véc-tơ – không.
D. Hai véc-tơ cùng phương với 1 véctơ 0 thì hai véc-tơ đó cùng phương với nhau. Lời giải Chọn D
+) Hai véc-tơ có cùng độ dài nhưng không cùng phương thì không bằng nhau. A sai.
+) Xét tam giác ABC đều. Lúc đó: hai véc-tơ A ,
B AC có độ dài bằng nhau.
Nhưng AB AC CB 0 B sai.
+) Cho hai điểm A và B phân biệt. Lúc đó các véc-tơ A ,
B BA là những véc-tơ
khác 0 . Nhưng AB BA 0 C sai.
+) Khẳng định D đúng.
Câu 25: [0H1-1-2] Cho tứ giác ABCD có AD BC . Mệnh đề nào trong các mệnh đề sau là sai?
A. Tứ giác ABCD là hình bình hành.
B. DA BC .
C. AC BD .
D. AB DC . Lời giải Chọn C
AC và BD là hai đường chéo của tứ giác ABCD nên hai vectơ AC, BD không
cùng phương vì vậy không thể bằng nhau.
Câu 26: [0H1-1-2] Cho hình bình hành ABCD . Số vectơ khác 0 , cùng phương với vectơ
AB và có điểm đầu, điểm cuối là đỉnh của hình bình hành ABCD là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Các vectơ cùng phường với AB mà thỏa mãn điều kiện đầu bài là: ,
BA CD , DC .
Câu 27: [0H1-1-2] Cho lục giác đều ABCDEF tâm O . Số vectơ khác 0 , có điểm đầu điểm
cuối là đỉnh của lục giác hoặc tâm O và cùng phương với vectơ OC là A. 3 . B. 4 . C. 8 . D. 9 . Lời giải Chọn D A B O F C E D Các vectơ thỏa mãn là: , CO ,
FO OF, FC, CF, AB, , BA , ED DE .
Câu 28: [0H1-1-2] Cho hình chữ nhật ABCD . Véctơ nào dưới đây có độ dài lớn nhất? A. AB . B. AD .
C. BC BA . D. 0 . Lời giải Chọn C
Vì BC BA AC mà AC là đường chéo của hình chữ nhật nên dài nhất (so với các cạnh).
Câu 29: [0H1-1-2] Cho hình chữ nhật ABCD . Tìm đẳng thức đúng trong các đẳng thức dưới đây.
A. AB CD .
B. AC BD .
C. AD BC . D. BC DA . Lời giải Chọn C
Theo tính chất hình chữ nhật ta có AD BC và AD , BC cùng hướng. Vậy AD BC .
Câu 30: [0H1-1-2] Cho ba điểm phân biệt ,
A B, C . Đẳng thức nào sau đây là đúng?
A. CA BA BC .
B. AB AC BC .
C. AB CA CB . D.
AB BC CA. Lời giải Chọn C
Áp dụng quy tắc ba điểm ta có AB CA CA AB CB .
Câu 31: [0H1-1-2] Cho hai điểm phân biệt ,
A B . Điều kiện để điểm I là trung điểm AB là
A. IA IB .
B. IA IB .
C. IA IB . D. AI BI . Lời giải Chọn C
Vì I là trung điểm AB nên ta có IA IB 0 IA IB .
Câu 32: [0H1-1-2] Cho 3 điểm ,
A B, C phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là A. M
, MA MB MC 0 . B. M
, MA MC MB .
C. AC AB BC . D. k
,k 0: AB k AC . Lời giải Chọn D
Lý thuyết: Điều kiện cần và đủ để ba điểm ,
A B, C phân biệt thẳng hàng là k
,k 0: AB k AC .
Câu 33: [0H1-1-2] Cho tứ giác ABCD . Số các véctơ khác véctơ-không có điểm đầu và điểm
cuối là đỉnh của tứ giác là A. 4 . B. 6 . C. 8 . D. 12 . Lời giải Chọn D
Từ mỗi đỉnh ta có một điểm đầu và ba đỉnh còn lại là ba điểm cuối, vậy tạo nên ba
véctơ. Với bốn đỉnh như vậy ta có tất cả 4.3 12 véctơ.
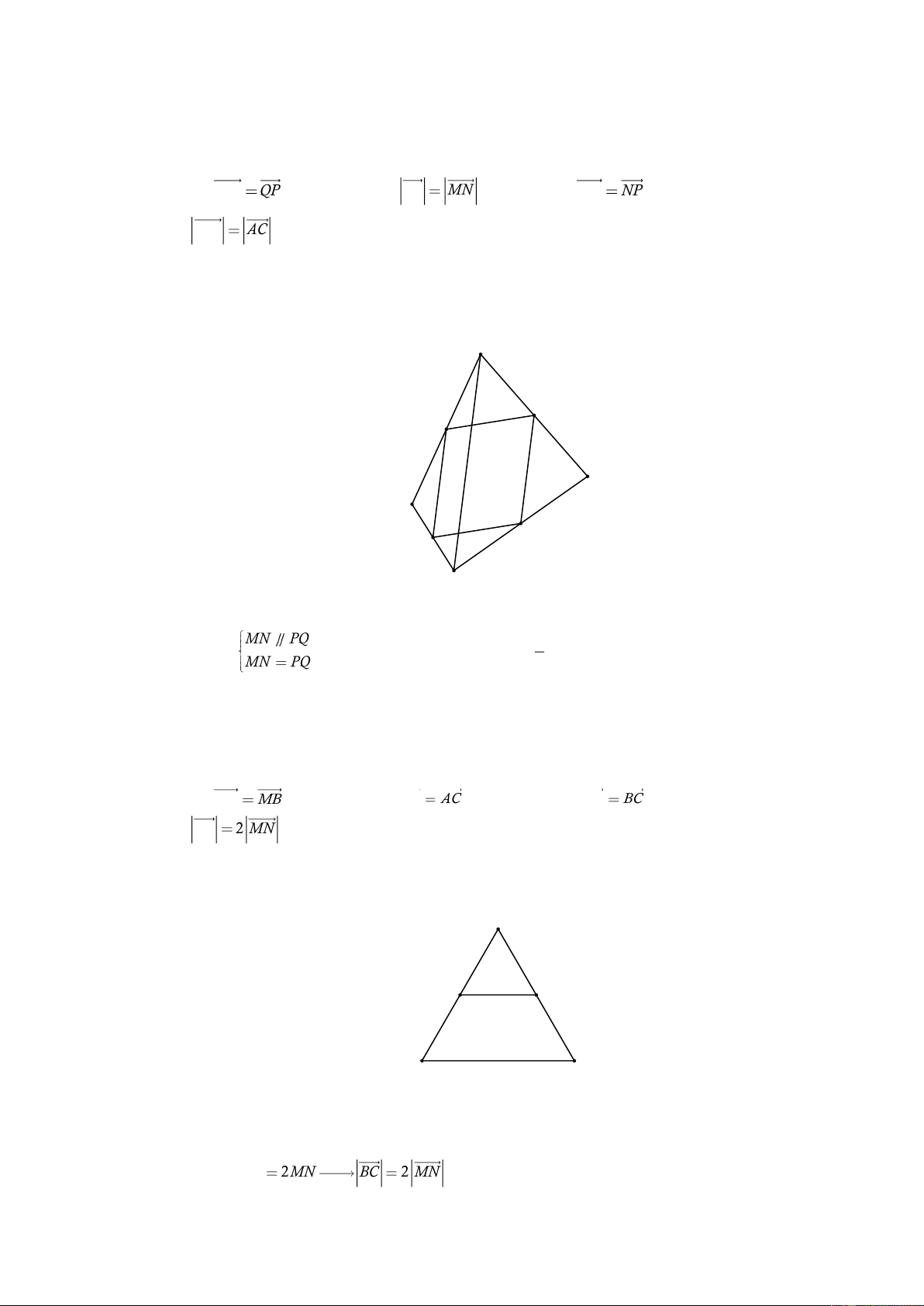
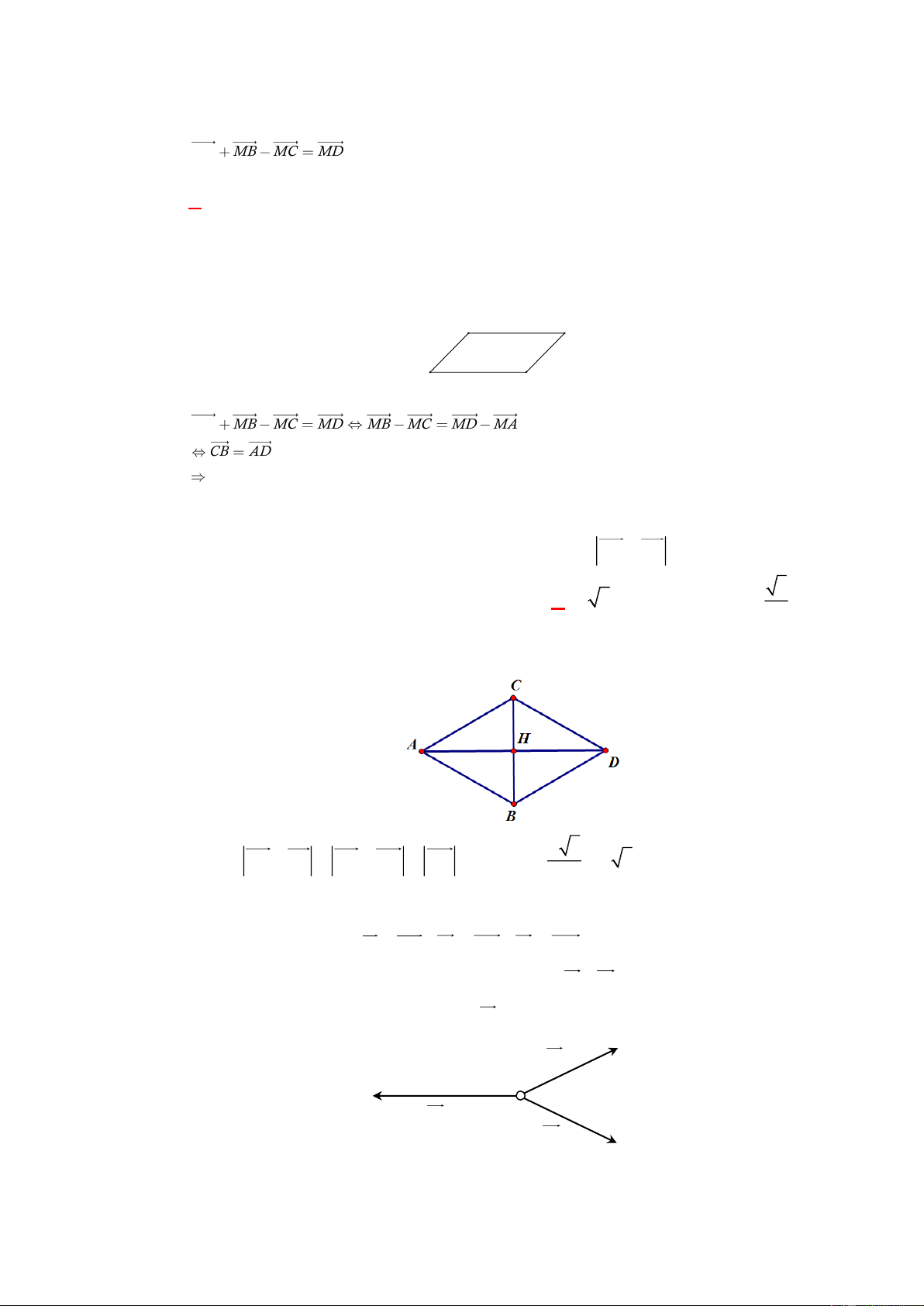
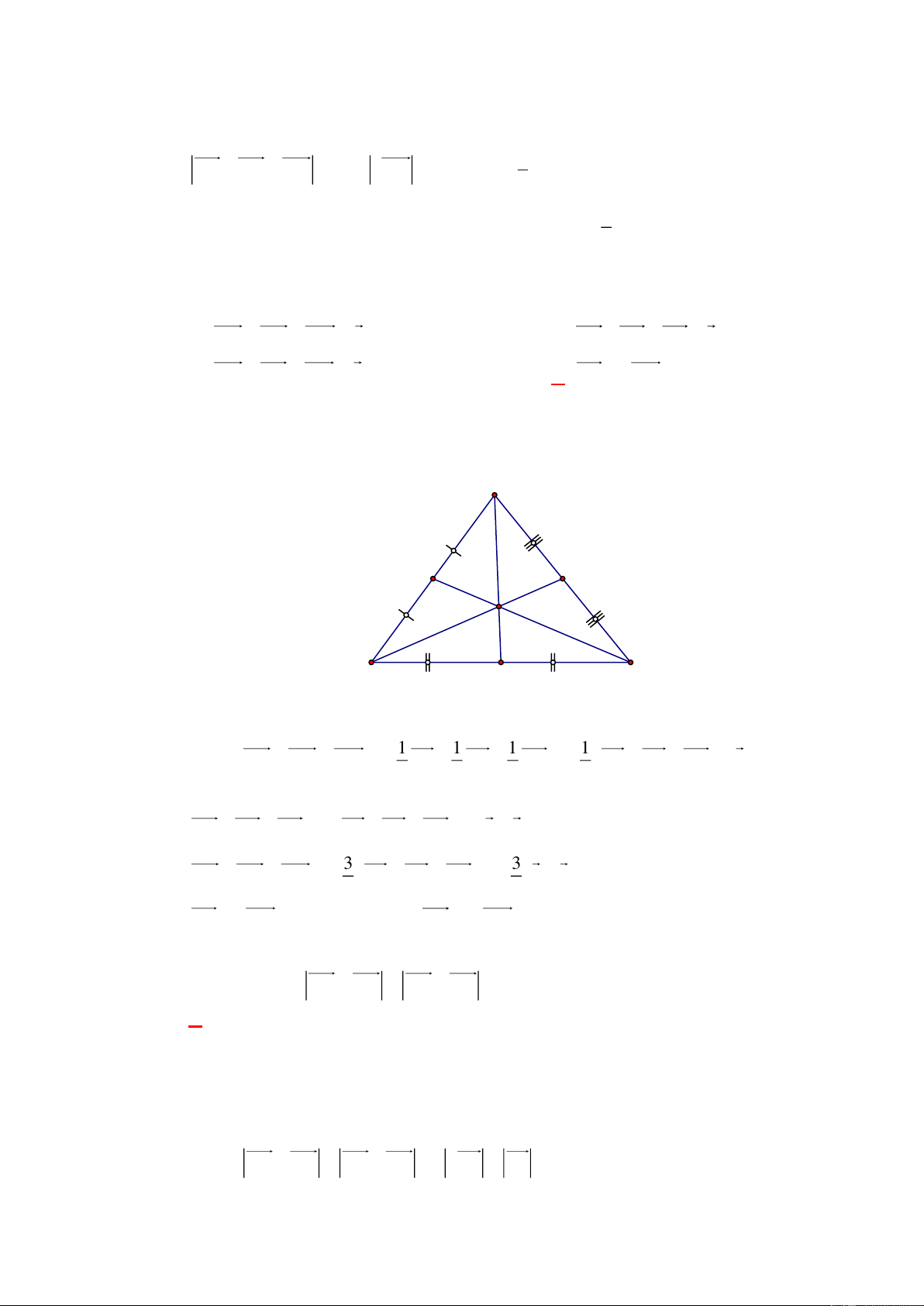
Câu 1: [0H1-1-3]Cho tứ giác ABC .
D Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, .
DA Khẳng định nào sau đây là sai? A. MN QP . B. QP MN . C. MQ NP . D. MN AC . Lời giải Chọn D A M Q B D N P C MN PQ 1 Ta có
(do cùng song song và bằng AC ). MN PQ 2
Do đó MNPQ là hình bình hành.
Câu 2: [0H1-1-3]Gọi M, N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều
ABC . Đẳng thức nào sau đây đúng? A. MA MB . B. AB AC . C. MN BC . D. BC 2 MN . Lời giải. A M N B C
Ta có MN là đường trung bình của tam giác ABC . Do đó BC 2MN BC 2 MN . Chọn D
Câu 3: [0H1-1-3]Cho hình thoi ABCD cạnh a và BAD
60 . Đẳng thức nào sau đây đúng? A. AB AD . B. BD a . C. BD AC . D. BC DA . Lời giải Chọn B Lời giải. B A C D
Từ giả thiết suy ra tam giác ABD đều cạnh a nên BD a BD . a
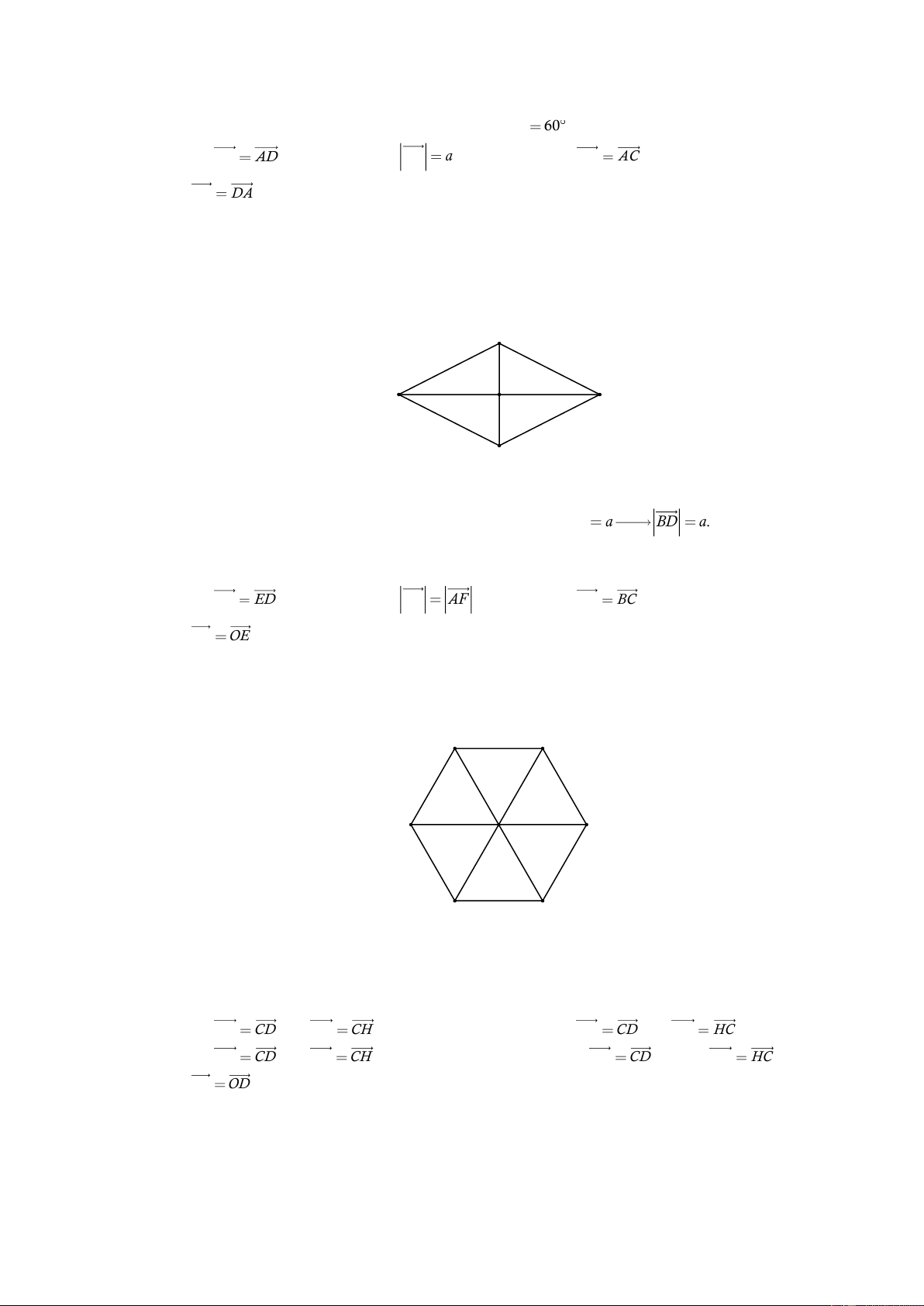
Câu 4: [0H1-1-3]Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào sau đây là sai? A. AB ED . B. AB AF . C. OD BC . D. OB OE . Lời giải Chọn D C B D A O E F .
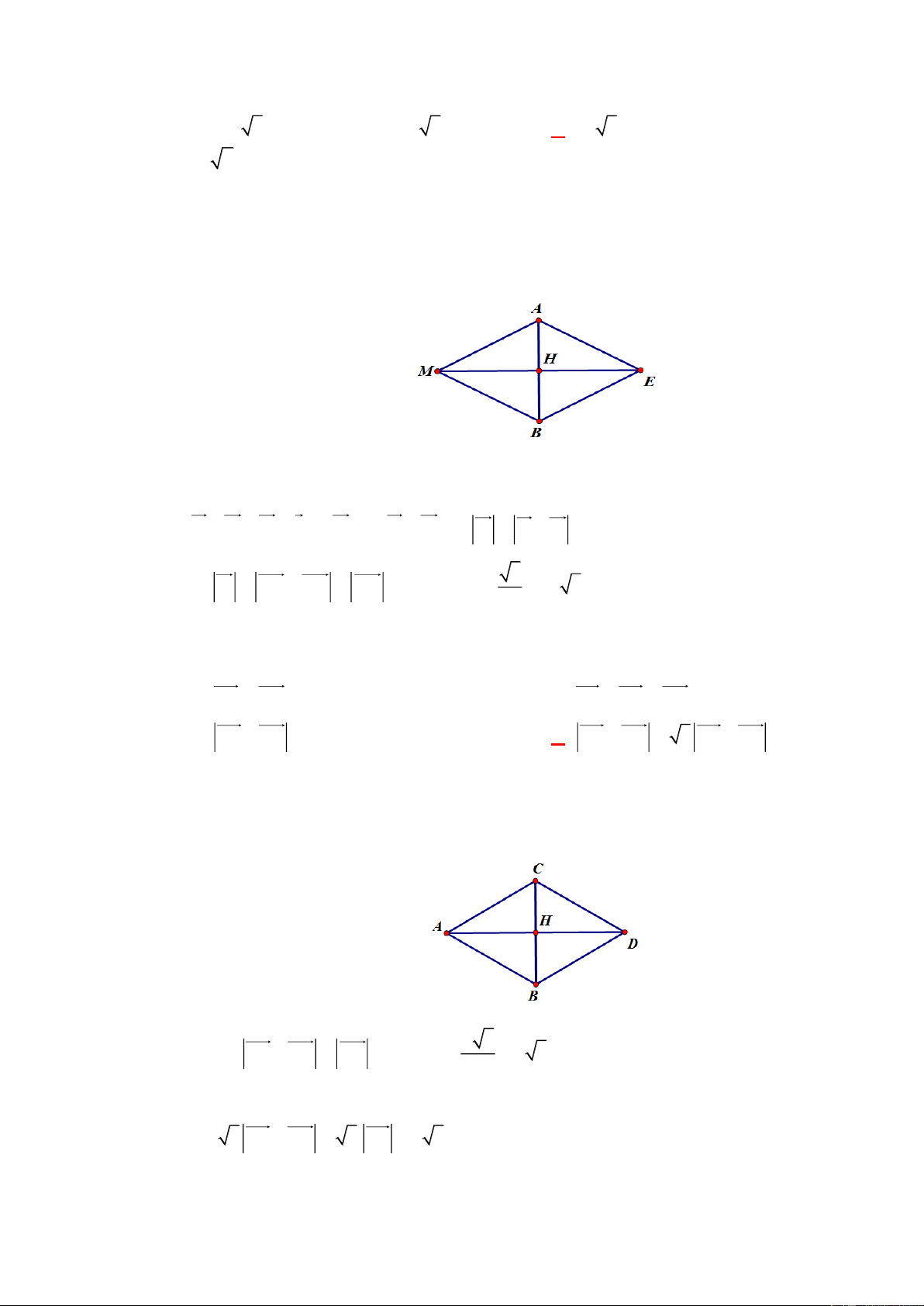
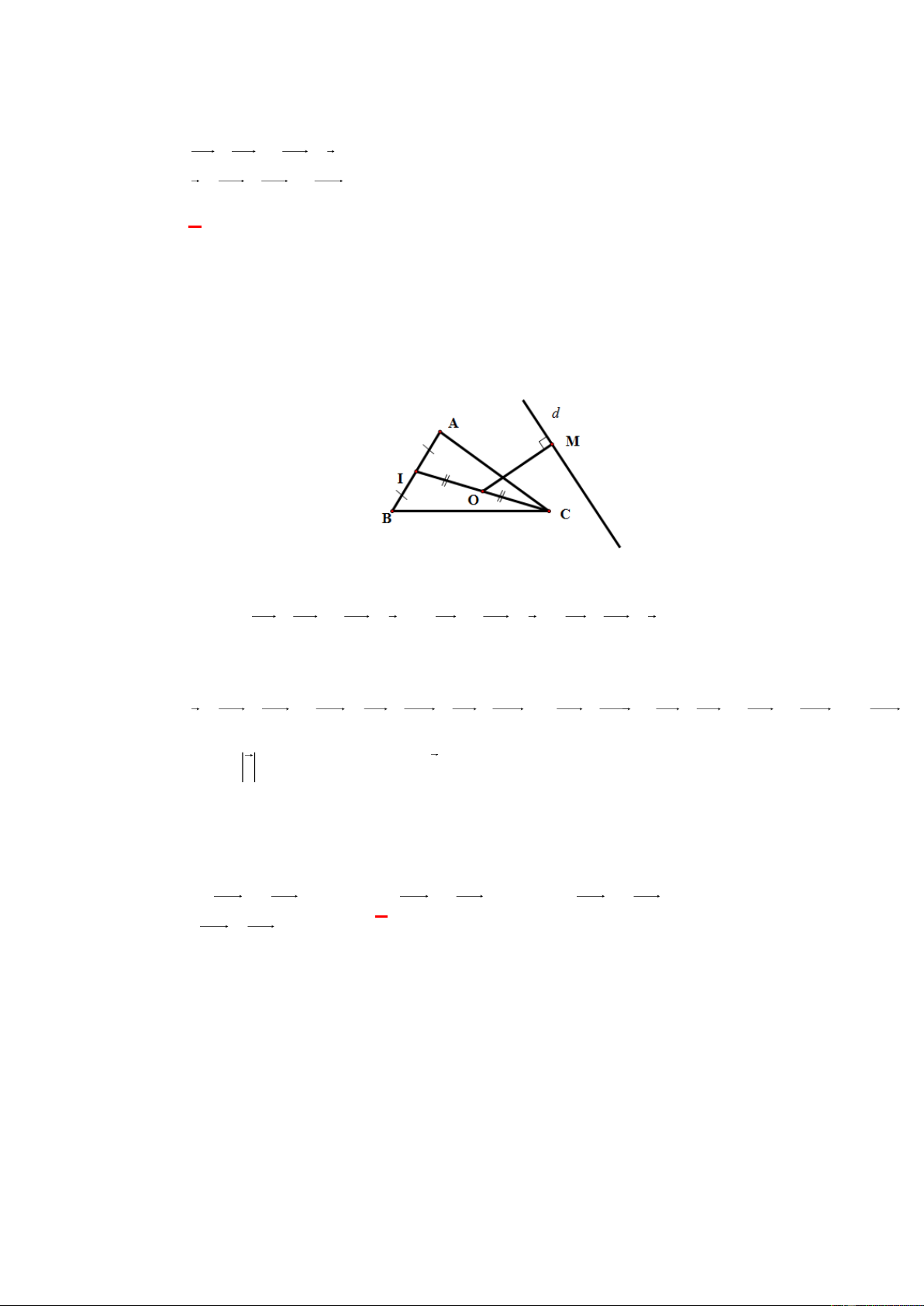
Câu 5: [0H1-1-3]Cho tam giác ABC có trực tâm H . Gọi D là điểm đối xứng với B qua tâm
O của đường tròn ngoại tiếp tam giác ABC . Khẳng định nào sau đây là đúng? A. HA CD và AD CH . B. HA CD và AD HC . C. HA CD và AC CH . D. HA CD và AD HC và OB OD . Lời giải Chọn B A D H O B C Ta có AH BC và DC
BC (do góc DCB chắn nửa đường tròn). Suy ra AH DC.
Tương tự ta cũng có CH AD.
Suy ra tứ giác ADCH là hình bình hành. Do đó HA CD và AD HC .
Câu 6: [0H1-1-3]Cho AB
0 và một điểm C , có bao nhiêu điểm D thỏa mãn AB CD. A. 1 . B. 2 . C. 0 . D. Vô số. Lời giải Chọn A
Câu 1: [0H1-2-1] Cho ba điểm ,
A B, C phân biệt. Đẳng thức nào sau đây là đẳng thức sai
A. AB BC AC .
B. CA AB BC .
C. BA AC BC . D.
AB AC CB . Lời giải Chọn B
CA AB CB .
Câu 2: [0H1-2-1] Cho hình bình hành ABCD với I là giao điểm của 2 đường chéo.
Khẳng định nào sau đây là khẳng định sai?
A. IA IC 0 .
B. AB DC .
C. AC BD .
D. AB AD AC . Lời giải Chọn C A B I D C
AC và BD không cùng phương nên AC BD sai.
Câu 3: [0H1-2-1] Cho tam giác ABC đều có độ dài cạnh bằng a . Độ dài AB BC bằng 3 A. a . B. 2a . C. a 3 . D. a . 2 Lời giải Chọn A
Ta có: AB BC AC AC a .
Câu 4: [0H1-2-1] Cho tam giác ABC , trọng tâm là G . Phát biểu nào là đúng?
A. AB BC AC .
B. GA GB GC 0 .
C. AB BC AC .
D. GA GB GC 0 . Lời giải Chọn D
Ta có: GA GB GC 0 0 .
Câu 5: [0H1-2-1] Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB .
A. OA OB .
B. OA OB .
C. AO BO . D.
OA OB 0 . Lời giải Chọn D
Câu 6: [0H1-2-1] Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng?
A. AB AD CA.
B. AB BC CA .
C. BA AD AC . D.
BC BA BD . Lời giải Chọn D
Ta có: AB AD AC CA A sai.
AB BC AC CA B sai.
BA AD BD AC C sai.
BC BA BD (quy tắc hình bình hành) D đúng.
Câu 7: [0H1-2-1] Cho tam giác ABC vuông tại A có AB 3; BC 5 . Tính AB BC ? A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B 2 2
AB BC AC AC
BC AB 4 .
Câu 8: [0H1-2-1] Cho tam giác ABC đều có độ dài cạnh bằng a . Khi đó, AB BC bằng : 3 A. a . B. 2a . C. a 3 . D. a . 2 Lời giải Chọn A
Ta có AB BC BC nên AB BC a .
Câu 1: [0H1-2-2]Khẳng định nào sau đây đúng? A. AB AC BC . B. MP NM NP . C. CA BA CB . D. AA BB AB . Lời giải Chọn B
Lời giải. Xét các đáp án:
Đáp án. A. Ta có AB AC AD
BC (với D là điểm thỏa mãn ABDC là hình bình hành). Vậy A sai.
Đáp án. B. Ta có MP NM NM MP NP . Vậy B đúng.
Đáp án. C. Ta có CA BA AC AB AD
CB (với D là điểm thỏa mãn
ABDC là hình bình hành). Vậy C sai.
Đáp án. D. Ta có AA BB 0 0 0 AB . Vậy D sai.
Câu 2: [0H1-2-2]Cho a và b là các vectơ khác 0 với a là vectơ đối của b . Khẳng định nào sau đây sai?
A. Hai vectơ a, b cùng phương.
B. Hai vectơ a, b ngược hướng.
C. Hai vectơ a, b cùng độ dài.
D. Hai vectơ a, b chung điểm đầu. Lời giải Chọn D Ta có a
b . Do đó, a và b cùng phương, cùng độ dài và ngược hướng nhau.
Câu 3: [0H1-2-2]Cho ba điểm phân biệt , A ,
B C . Đẳng thức nào sau đây đúng? A. CA BA BC . B. AB AC BC . C. AB CA CB . D. AB BC CA . Lời giải Chọn C Xét các đáp án: Đáp án. A. Ta có CA BA CA AB CB BC . Vậy A sai. Đáp án. B. Ta có AB AC AD
BC (với D là điểm thỏa mãn
ABDC là hình bình hành). Vậy B sai. Đáp án. C. Ta có AB CA CA AB CB . Vậy C đúng.
Câu 4: [0H1-2-2]Cho AB
CD . Khẳng định nào sau đây đúng?
A. AB và CD cùng hướng.
B. AB và CD cùng độ dài.
B. ABCD là hình bình hành. D. AB DC 0 . Lời giải Chọn B Ta có AB CD DC . Do đó:
AB và CD ngược hướng.
AB và CD cùng độ dài.
ABCD là hình bình hành nếu AB và CD không cùng giá. AB CD 0.
Câu 5: [0H1-2-2]Tính tổng MN PQ RN NP QR . A. MR . B. MN . C. PR . D. MP . Lời giải Chọn B Ta có MN PQ RN NP QR MN NP PQ QR RN MN .
Câu 6: [0H1-2-2]Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là: A. IA IB . B. IA IB . C. IA IB . D. AI BI . Lời giải Chọn C
Câu 7: [0H1-2-2]Điều kiện nào là điều kiện cần và đủ để I là trung điểm của đoạn thẳng AB ? A. IA IB . B. IA IB 0 . C. IA IB 0 . D. IA IB . Lời giải Chọn B
Điều kiện cần và đủ để I là trung điểm của đoạn thẳng AB là IA IB IA IB 0 .
Câu 8: [0H1-2-2]Cho ABC cân ở A , đường cao AH . Khẳng định nào sau đây sai? A. AB AC . B. HC HB . C. AB AC . D. BC 2HC . Lời giải Chọn A A B H C
ABC cân ở A , đường cao AH . Do đó, H là trung điểm BC . Ta có: AB AC AB AC HC HB
H là trung điểm BC . BC 2HC
Câu 9: [0H1-2-2]Gọi O là tâm hình bình hành ABCD . Đẳng thức nào sau đây sai? A. OA OB CD . B. OB OC OD OA . C. AB AD DB . D. BC BA DC DA . Lời giải Chọn B Xét các đáp án: A B O D C Đáp án. A. Ta có OA OB BA CD . Vậy A đúng. OB OC CB AD Đáp án. B. Ta có . Vậy B sai. OD OA AD Đáp án. C. Ta có AB AD DB. Vậy C đúng. BC BA AC Đáp án. D. Ta có . Vậy D đúng. DC DA AC
Câu 10: [0H1-2-2]Gọi O là tâm hình vuông ABCD . Tính OB OC . A. BC . B. DA . C. OD OA . D. AB Lời giải Chọn B Ta có OB OC CB DA .
Câu 11: [0H1-2-2]Cộng các vectơ có cùng độ dài 5 và cùng giá. Khẳng định nào sau đây đúng?
A. Cộng 5 vectơ ta được kết quả là 0 .
B. Cộng 4 vectơ đôi một ngược hướng ta được kết quả là 0 .
C. Cộng 121 vectơ ta được kết quả là 0 .
D. Cộng 25 vectơ ta được vectơ có độ dài là 0 . Lời giải Chọn B
Cộng số chẵn các vectơ ngược hướng cùng độ dài ta được vectơ 0 .
Câu 12: [0H1-2-2]Cho bốn điểm , A ,
B C, D . Mệnh đề nào sau đây đúng? A. AB CD
AD CB . B. AB BC CD DA . C. AB BC CD
DA . D. AB AD CD CB . Lời giải Chọn A Ta có AB CD AD DB CB BD AD CB .
Câu 13: [0H1-2-2]Gọi O là tâm của hình vuông ABCD . Vectơ nào trong các vectơ dưới đây bằng CA ? A. BC AB . B. OA OC . C. BA DA . D. DC CB . Lời giải Chọn C Xét các đáp án: A B O D C Đáp án. A. Ta có BC AB AB BC AC . CA Đáp án. B. Ta có OA OC OC OA AC . CA Đáp án. C. Ta có BA DA AD AB AC C . A Đáp án. D. Ta có DC CB DC BC CD CB C . A
Câu 14: [0H1-2-2]Cho tam giác ABC có M thỏa mãn điều kiện MA MB MC 0 . Xác định vị trí điểm M.
A. M là điểm thứ tư của hình bình hành ACBM .
B. M là trung điểm của đoạn thẳng AB .
C. M trùng C .
D. M là trọng tâm tam giác ABC . Lời giải Chọn D
Gọi G là trọng tâm tam giác ABC . Ta có GA GB GC 0 M G .
Câu 15: [0H1-2-2] Cho bốn điểm ,
A B, C, D phân biệt. Khi đó, AB DC BC AD bằng véctơ nào sau đây? A. 0 . B. BD . C. AC . D. 2DC . Lời giải Chọn A
Ta có: AB DC BC AD AB BC AD DC AC AC 0 .
Câu 16: [0H1-2-2] Cho tam giác ABC . Gọi M , N , P lần lượt là trung điểm các cạnh
AB, AC, BC . Hỏi MP NP bằng véctơ nào? A. AM . B. PB . C. AP . D. MN . Lời giải Chọn C A M N B C P
MP NP AN NP AP .
Câu 17: [0H1-2-2] Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới
đây là đẳng thức sai?
A. OA OC OE 0 .
B. BC FE AD .
C. OA OB OC EB . D. AB CD FE 0 . Lời giải Chọn D A B O F C E D
Ta có: AB CD FE AB BO AO 2AO 0 .
Câu 18: [0H1-2-2] Cho hình vuông ABCD cạnh a . Tính AB AC AD ? A. 2a 2 . B. 3a . C. a 2 . D. 2a . Lời giải Chọn A A a B D C
Ta có: AB AC AD AB AD AC 2AC 2AC 2a 2 .
Câu 19: [0H1-2-2] Cho ABC
vuông tại A và AB 3 , AC 4 . Véctơ CB AB có độ dài bằng A. 13 . B. 2 13 . C. 2 3 . D. 3 . Lời giải Chọn B B A C M
Gọi M là trung điểm AC . Ta có : 2 2 2 2
CB AB BA BC 2BM 2BM 2 AB AM 2 3 2 2 13 .
Câu 20: [0H1-2-2] Cho hình vuông ABCD có cạnh bằng a . Khi đó AB AD bằng: a 2 A. a 2 . B. . C. 2a . D. a . 2 Lời giải Chọn A A a B D C
Ta có: AB AD AC a 2 .
Câu 21: [0H1-2-2] Cho hình vuông ABCD có cạnh bằng a . Khi đó AB AC bằng: a 5 a 3 a 3 A. . B. . C. . D. a 5 . 2 2 3 Lời giải Chọn D A a B M D C
Gọi M là trung điểm BC . 2 a Ta có: 2 2 2
AB AC 2AM 2AM 2 AB BM 2 a a 5 . 2
Câu 22: [0H1-2-2] Cho hình chữ nhật ABCD biết AB 4a và AD 3a thì độ dài
AB AD bằng A. 7a . B. 6a .
C. 2a 3 . D. 5a . Lời giải Chọn D A a B D C 2 2
Ta có: AB AD AC AC 4a 3a 5a .
Câu 23: [0H1-2-2] Cho hình chữ nhật ABCD , gọi O là giao điểm của AC và BD , phát biểu nào là đúng?
A. OA OB OC OD .
B. AC BD .
C. OA OB OC OD 0 .
D. AC AD AB . Lời giải Chọn D
Ta có AC AD DC AB .
Câu 24: [0H1-2-2] Cho 4 điểm bất kỳ ,
A B, C, O . Đẳng thức nào sau đây là đúng?
A. OA CA CO .
B. BC AC AB 0 . C. BA OB OA. D.
OA OB BA. Lời giải Chọn B
Ta có: BC AC AB BC (AC AB) BC BC 0 .
Câu 25: [0H1-2-2] Cho hình bình hành ABCD , giao điểm của hai đường chéo là O . Tìm
mệnh đề sai trong các mệnh đề sau:
A. CO OB BA .
B. AB BC DB .
C. DA DB OD OC .
D. DA DB DC 0 . Lời giải Chọn D
Ta có: DA DB DC DA DC DB DB DB 2DB 0 .
Câu 26: [0H1-2-2] Cho hình bình hành ABCD tâm O . Khi đó OC OD bằng
A. OC OB . B. AB .
C. OA OB . D. CD . Lời giải Chọn A
Ta có OC OD OC DO OC OB .
Câu 27: [0H1-2-2] Cho tam giác ABC , khẳng định nào sau là đúng?
A. AB AC BC .
B. AB BC AC .
C. AB AC BC . D.
AB BC AC . Lời giải Chọn B
Ta có AB BC AC .
Câu 28: [0H1-2-2] Cho tam giác đều ABC cạnh a . Độ dài của AB AC là a 3 A. a 3 . B. . C. a 6 . D. 2a 3 . 3 Lời giải Chọn A
Gọi M là trung điểm của BC , ta có: AB AC 2AM 2AM a 3 .
Câu 1: [0H1-2-3]Cho tam giác ABC đều cạnh a . Mệnh đề nào sau đây đúng? A. AB BC CA . B. CA AB . C. AB BC CA a . D. CA BC . Lời giải Chọn C
Độ dài các cạnh của tam giác là a thì độ dài các vectơ AB BC CA a .
Câu 2: [0H1-2-3]Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây đúng? A. OA OC OE 0 . B. BC FE AD . C. OA OC OB EB . D. AB CD EF 0 Lời giải Chọn C A B O F C E D
Ta có OABC là hình bình hành. OA OC OB OA OC OB 2OB.
O là trung điểm của EB EB 2OB. OA OC OB EB 2OB.
Câu 3: [0H1-2-3] Cho O là tâm hình bình hành ABCD . Hỏi vectơ AO
DO bằng vectơ nào? A. BA . B. BC . C. DC . D. AC . Lời giải Chọn B Ta có AO DO OD OA AD BC . A B O D C .
Câu 4: [0H1-2-3] Cho hình bình hành ABCD và tâm O của nó. Đẳng thức nào sau đây sai? A. OA OB OC OD 0 . B. AC AB AD . C. BA BC DA DC . D. AB CD AB CB . Lời giải Chọn D
Xét các đáp án: A B O D C
Đáp án. A. Ta có OA OB OC OD OA OC OB OD 0.
Đáp án. B. Ta có AB AD AC (quy tắc hình bình hành). BA BC BD BD
Đáp án. C. Ta có . DA DC DB BD
Đáp án. D. Do CD CB AB CD AB CB .
Câu 5: [0H1-2-3] Gọi O là tâm hình bình hành ABCD ; hai điểm E, F lần lượt là trung điểm A ,
B BC . Đẳng thức nào sau đây sai? A. DO EB EO . B. OC EB EO . C. OA OC OD OE OF 0 . D. BE BF DO 0 . Lời giải Chọn D A E B F O D C
Ta có OF, OE lần lượt là đường trung bình của tam giác BCD và ABC .
BEOF là hình bình hành. BE BF BO BE BF DO BO DO OD OB BD.
Câu 6: [0H1-2-3]Cho hình bình hành ABC .
D Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây đúng? A. GA GC GD BD . B. GA GC GD CD . C. GA GC GD O . D. GA GD GC CD . Lời giải Chọn A B C G A D
Vì G là trọng tâm của tam giác ABC nên GA GB GC O. Do đó GA GC GD GA GC GB BC CD GA GB GC BC CD BC CD BD .
Câu 7: [0H1-2-3]Cho hình chữ nhật ABCD . Khẳng định nào sau đây đúng? A. AC BD . B. AB AC AD 0 . C. AB AD AB AD . D. BC BD AC AB Lời giải Chọn C A B D C Ta có AB AD DB BD; AB AD AC AC. Mà BD AC AB AD AB AD
Câu 8: [0H1-2-3]Cho hình thoi ABCD có AC 2 , a BD a . Tính AC BD . A. AC BD 3a . B. AC BD a 3 . C. AC BD a 5 . D. AC BD 5a . Lời giải Chọn C B A C O M D Gọi O AC BD .
Gọi M là trung điểm của CD AC BD 2 OC OD 2 2OM 4OM 2 1 a 2 2 2 4. CD 2 OD OC 2 a a 5. 2 4
Câu 9: [0H1-2-3]Cho hình vuông ABCD cạnh a . Tính AB DA . A. AB DA 0 . B. AB DA a . C. AB DA a 2 . D. AB DA 2a . Lời giải Chọn C Ta có AB DA AB AD AC AC a 2.
Câu 10: [0H1-2-3]Cho hình vuông ABCD cạnh a , tâm O . Tính OB OC . a A. OB OC a . B. OB OC a 2 . C. OB OC . D. 2 a 2 OB OC . 2 Lời giải Chọn A A B M O D C
Gọi M là trung điểm của BC . OB OC 2 OM 2OM AB . a
Câu 11: [0H1-2-3]Cho tam giác ABC. Tập hợp các điểm M thỏa mãn MB MC BM BA là?
A. đường thẳng AB .
B. trung trực đoạn BC .
C. đường tròn tâm ,
A bán kính BC .
D. đường thẳng qua A và song song với BC . Lời giải Chọn C Ta có MB MC BM BA CB AM AM BC Mà , A , B C cố định
Tập hợp điểm M là đường tròn tâm A , bán kính BC .
Câu 12: [0H1-2-3]Cho hình bình hành ABCD . Tập hợp các điểm M thỏa mãn MA MB MC MD là?
A. một đường tròn.
B. một đường thẳng. C. tập rỗng.
D. một đoạn thẳng. Lời giải Chọn C A B D C MA MB MC MD MB MC MD MA CB AD sai
Không có điểm M thỏa mãn.
Câu 13: [0H1-2-3] Cho tam giác đều ABC có cạnh a . Giá trị AB CA bằng bao nhiêu? 3 A. 2a . B. a . C. a 3 . D. a . 2 Lời giải Chọn C a 3
Ta có: AB CA AB AC AD 2AH 2. a 3 2
(với ABDC là hình bình hành tâm H ).
Câu 14: [0H1-2-3] Cho ba lực F MA , F MB , F MC cùng tác động vào một vật tại 1 2 3
điểm M và vật đứng yên. Cho biết cường độ của F , F đều bằng 50N và góc 1 2
AMB 60 . Khi đó cường độ lực của F là 3 A F1 C M F3 F2 B
A. 100 3N .
B. 25 3N .
C. 50 3N . D. 50 2N . Lời giải Chọn C
Ta có tam giác MAB đều. Do vật đứng yên nên ta có:
F F F 0 F (F F ) F F F 1 2 3 3 1 2 3 1 2 3
F MA MB ME 2MH 2.50 50 3 3 2
(với MAEB là hình bình hành tâm H ).
Câu 15: [0H1-2-3] Cho tam giác đều ABC cạnh a , trọng tâm là G . Phát biểu nào là đúng?
A. AB AC .
B. GA GB GC .
C. AB AC 2a .
D. AB AC 3 AB AC . Lời giải Chọn D a 3
Ta có: AB AC AD 2AH 2. a 3 2
(với ABDC là hình bình hành tâm H )
Và 3 AB AC 3. CB a 3 . Vậy D đúng.
Câu 16: [0H1-2-3] Cho tam giác ABC . Để điểm M thoả mãn điều kiện
MA MB MC 0 thì M phải thỏa mãn mệnh đề nào?
A. M là điểm sao cho tứ giác ABMC là hình bình hành.
B. M là trọng tâm tam giác ABC .
C. M là điểm sao cho tứ giác BAMC là hình bình hành.
D. M thuộc trung trực của AB . Lời giải. Chọn C
Ta có: MA MB MC 0 BA MC 0
MC BA MC AB .
Câu 17: [0H1-2-3] Cho ba lực F M ,
A F M ,
B F MC cùng tác động vào một vật tại 1 2 3
điểm M và vật đứng yên. Cho biết cường độ của F , F đều bằng 100N và 1 2
AMB 60 . Khi đó cường độ lực của F là 3 A F1 M C F3 F2 B A. 50 2N . B. 50 3N . C. 25 3N . D. 100 3N . Lời giải Chọn D
Dựng hình bình hành MAEB, khi đó ME MA MB A F1 M E C F3 F2 B
Do AM BM và AMB 60 nên M AB đều
Để vật M đứng yên thì MA MB MC 0 MC ME AM 3
F MC ME 2.
AM 3 100 3 N . 3 2
Câu 1: [0H1-3-2]Cho hình vuông ABCD . Khẳng định nào sau đây đúng? A. AB BC . B. AB CD . C. AC BD . D. AD CB . Lời giải Chọn D A B C D AB DC ABCD là hình vuông . AD BC CB AD CB
Câu 2: [0H1-3-2]Mệnh đề nào sau đây sai?
A. Nếu M là trung điểm đoạn thẳng AB thì MA MB 0 .
B. Nếu G là trọng tâm tam giác ABC thì GA GB GC 0 .
C. Nếu ABCD là hình bình hành thì CB CD CA .
D. Nếu ba điểm phân biệt , A ,
B C nằm tùy ý trên một đường thẳng thì AB BC AC . Lời giải Chọn D
Vời ba điểm phân biệt , A ,
B C năm trên một đường thẳng, AB BC AC khi B
nằm giữa A và C .
Câu 3: [0H1-3-2]Cho tam giác ABC , với M là trung điểm BC . Mệnh đề nào sau đây đúng? A. AM MB BA 0 . B. MA MB AB . C. MA MB MC . D. AB AC AM . Lời giải Chọn A Xét các đáp án: A N B M C Đáp án. A. Ta có AM MB BA
0 (theo quy tắc ba điểm). Đáp án B,. C. Ta có MA MB
2MN (với điểm N là trung điểm của AB ). Đáp án. D. Ta có AB AC 2AM .
Câu 4: [0H1-3-2]Cho ba điểm , A ,
B C . Mệnh đề nào sau đây đúng? A. AB BC AC . B. AB BC CA 0 . C. AB BC CA BC . D. AB CA BC . Lời giải Chọn D
Đáp án A chỉ đúng khi 3 điểm , A ,
B C thẳng hàng và B nằm giữa ,
A C . Đáp án B
đúng theo quy tắc ba điểm.
Câu 5: [0H1-3-2]Cho M, N, P lần lượt là trung điểm các cạnh A ,
B BC, CA của tam giác ABC. Hỏi vectơ MP
NP bằng vectơ nào? A. AP . B. PB . C. MN . D. MB NB . Lời giải Chọn B A P M C B N Ta có NP BM MP NP MP BM BP.
Câu 6: [0H1-3-2]Cho tam giác ABC đều cạnh a . Khi đó AB AC bằng: a 3 A. AB AC a 3 . B. AB AC . 2 C. AB AC 2a .
D. Một đáp án khác. Lời giải Chọn A A B H C
Gọi H là trung điểm của BC AH BC. BC 3 a 3 Suy ra AH . 2 2 a 3 Ta lại có AB AC 2AH 2. a 3 . 2
Câu 7: [0H1-3-2]Cho tam giác vuông cân ABC tại A có AB a . Tính AB AC . a 2 A. AB AC a 2 . B. AB AC . 2 C. AB AC 2a . D. AB AC a . Lời giải Chọn A B D A C
Gọi D là điểm thỏa mãn tứ giác ABDC là hình vuông. AB AC AD AD a 2.
Câu 8: [0H1-3-2]Tam giác ABC có AB AC , a ABC
120 . Tính độ dài vectơ tổng AB AC . A. AB AC a 3 . B. AB AC a . a C. AB AC . D. AB AC 2a . 2 Lời giải Chọn B A B C D
Gọi D là điểm thỏa mãn tứ giác ABDC là hình thoi. Ta có AB AC AD A . D
ABDC là hình thoi có 0 ABC 120
ABD và ADC là hai tam giác đều AD AB . a
Câu 9: [0H1-3-2]Cho tam giác ABC đều cạnh a , H là trung điểm của BC . Tính CA HC . a 3a 2 3a A. CA HC . B. CA HC . C. CA HC . D. 2 2 3 a 7 CA HC . 2 Lời giải Chọn D D A B H C
Gọi D là điểm thỏa mãn tứ giác ACHD là hình bình hành.
AHBD là hình chữ nhật. CA HC CA CH CD C . D 2 3a a 7 Ta có: 2 2 2 2 2 CD BD BC AH BC a . 4 2
Câu 10: [0H1-3-2]Cho tam giác ABC và điểm M thỏa mãn MB MC
AB . Tìm vị trí điểm M.
A. M là trung điểm của AC .
B. M là trung điểm của AB .
C. M là trung điểm của BC .
D. M là điểm thứ tư của hình bình hành ABCM . Lời giải Chọn A A M B C I
Gọi I là trung điểm của BC. MB MC 2MI AB 2MI
M là trung điểm AC.
Câu 11: [0H1-3-2] Cho ba điểm phân biệt ,
A B, C . Nếu AB 3
AC thì đẳng thức nào dưới đây đúng? A. BC 4 AC . B. BC 2 AC .
C. BC 2AC . D. BC 4AC . Lời giải Chọn D .
Câu 12: [0H1-3-2] Cho ba điểm ,
A B, C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:
A. AB AC . B. k
0: AB k.AC .
C. AC AB BC .
D. MA MB 3MC, điểm M . Lời giải Chọn B Ba điểm ,
A B, C thẳng hàng khi và chỉ khi có số k khác 0 để AB k AC . Câu 13: [0H1-3-2] Cho ABC
. Đặt a BC,b AC . Các cặp vectơ nào sau đây cùng phương?
A. 2a b, a 2b .
B. a 2b, 2a b .
C. 5a b, 1
0a 2b . D.
a b, a b . Lời giải Chọn C Ta có: 1
0a 2b 2
.(5a b) 5a b và 1
0a 2b cùng phương.
Câu 14: [0H1-3-2] Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 3a 2b
và (x 1)a 4b cùng phương. Khi đó giá trị của x là: A. 7 . B. 7 . C. 5 . D. 6 . Lời giải Chọn A
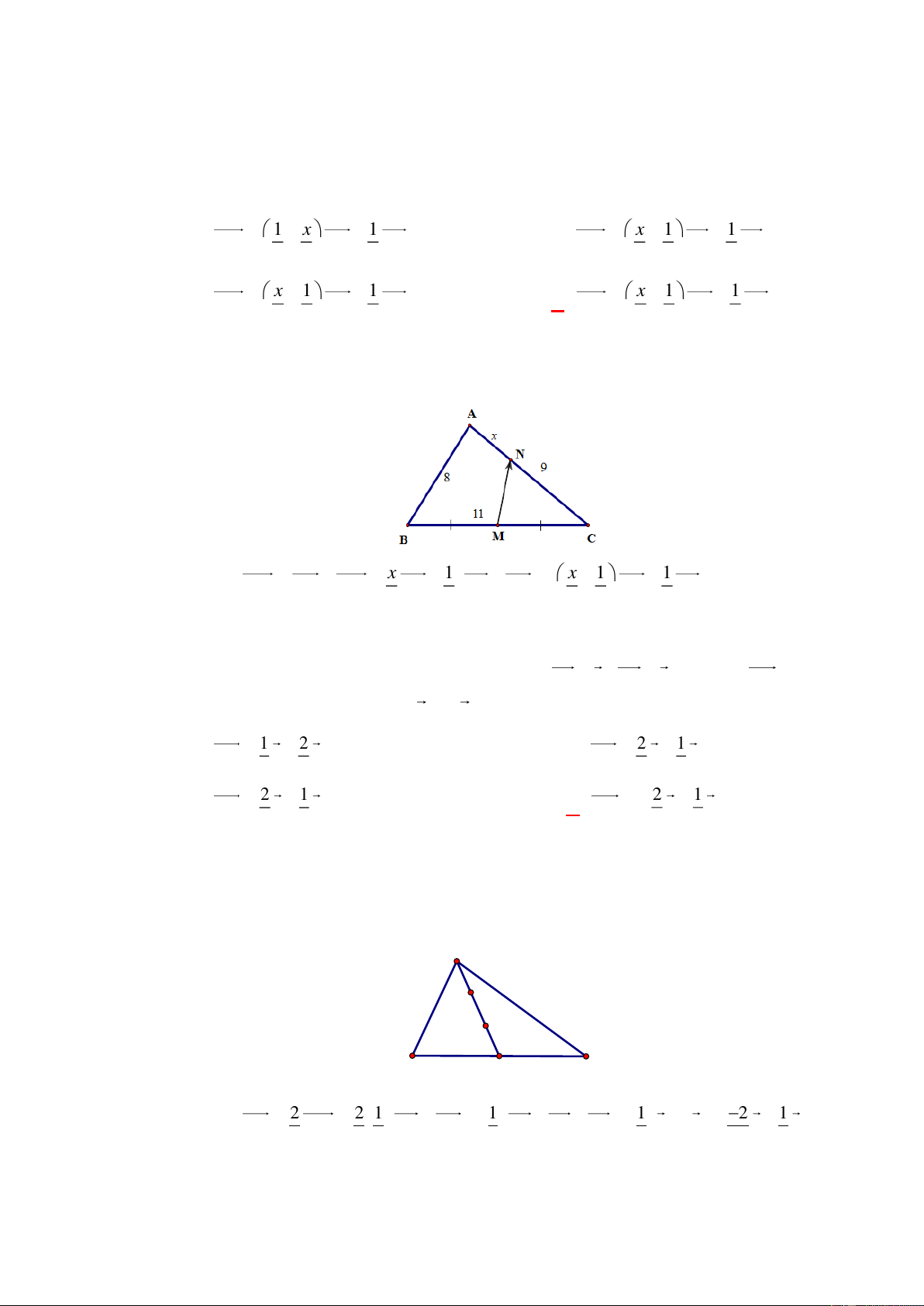
Điều kiện để hai vec tơ 3a 2b và (x 1)a 4b cùng phương là: x 1 4 x 7 . 3 2
Câu 15: [0H1-3-2] Cho ngũ giác ABCDE . Gọi M , N , P, Q lần lượt là trung điểm các cạnh
AB, BC, CD, DE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng
định nào sau đây đúng? 1 1 1 A. IJ AE . B. IJ AE . C. IJ AE . D. 2 3 4 1 IJ AE . 5 Lời giải Chọn C
Ta có: 2IJ IQ IN IM MQ IP PN MQ PN
MQ MA AE EQ 1 1
2MQ AE BD MQ
AEBD, PN BD 2 MQ MB BD DQ 2 1 1 1 1 Suy ra: 2IJ
AE BD BD AE IJ AE. 2 2 2 4
Câu 16: [0H1-3-2] Cho I là trung điểm của đoạn thẳng AB . Với điểm M bất kỳ, ta luôn có:
A. MA MB MI .
B. MA MB 2MI . C. MA MB 3MI . D. 1 MA MB MI . 2 Lời giải Chọn B
Áp dụng tính chất trung điểm của đoạn thẳng: Với điểm M bất kỳ, ta luôn có
MA MB 2MI .
Câu 17: [0H1-3-2] Cho G là trọng tâm của tam giác ABC . Với mọi điểm M , ta luôn có:
A. MA MB MC MG .
B. MA MB MC 2MG .
C. MA MB MC 3MG .
D. MA MB MC 4MG . Lời giải Chọn C
Áp dụng tính chất trọng tâm của tam giác: Với mọi điểm M , ta luôn có
MA MB MC 3MG .
Câu 18: [0H1-3-2] Cho ABC
có G là trọng tâm, I là trung điểm BC . Đẳng thức nào đúng? 1
A. GA 2GI .
B. IG IA .
C. GB GC 2GI . D. 3
GB GC GA . Lời giải
Áp dụng tính chất trung điểm của đoạn thẳng, ta có: GB GC 2GI .
Câu 19: [0H1-3-2] Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC
. Trong các mệnh đề sau, tìm mệnh đề sai?
A. AB 2 AM .
B. AC 2CN . C. BC 2 NM . D. 1 CN AC . 2 Lời giải Chọn B
Ta thấy AC và CN ngược hướng nên AC 2CN là sai. 1
Câu 20: [0H1-3-2] Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho MA AB 5
. Trong các khẳng định sau, khẳng định nào sai ? 1 1 A. AM AB . B. MA MB .
C. MB 4MA . D. 5 4 4 MB AB . 5 Lời giải Chọn D 4
Ta thấy MB và AB cùng hướng nên MB AB là sai. 5
Câu 21: [0H1-3-2] Cho hình bình hành ABCD . Đẳng thức nào đúng?
A. AC BD 2BC .
B. AC BC AB .
C. AC BD 2CD . D.
AC AD CD . Lời giải Chọn A
Ta có: AC BD AB BC BC CD 2BC (AB C ) D 2BC .
Câu 22: [0H1-3-2] Cho G là trọng tâm của tam giác ABC . Trong các mệnh đề sau, tìm mệnh đề đúng? 2
A. AB AC AG .
B. BA BC 3BG .
C. CA CB CG . D. 3
AB AC BC 0 . Lời giải Chọn B
Gọi M là trung điểm của AC . Khi đó: 3
BA BC 2BM 2. BG 3BG . 2
Câu 23: [0H1-3-2] Cho hình vuông ABCD có tâm là O . Trong các mệnh đề sau, tìm mệnh đề sai? 1 1
A. AB AD 2AO .
B. AD DO CA . C. OA OB CB . D. 2 2
AC DB 4AB . Lời giải Chọn D
AC DB AB BC DC CB AB DC 2AB .
Câu 24: [0H1-3-2] Cho ba điểm phân biệt ,
A B, C . Nếu AB 3
AC thì đẳng thức nào dưới đây đúng? A. BC 4 AC . B. BC 2 AC .
C. BC 2AC . D. BC 4AC . Lời giải Chọn D
Từ đẳng thức: AB 3
AC suy ra ba điểm ,
A B, C thẳng hàng; AB và AC ngược
hướng; AB 3AC nên BC 4AC .
Câu 25: [0H1-3-2] Cho tam giác ABC có trọng tâm G . Gọi các điểm D, E, F lần lượt là
trung điểm của các cạnh BC,CA và AB . Trong các khẳng định sau, khẳng định nào đúng ? 1 1 1 1 A. AG AE AF . B. AG AE AF . 2 2 3 3 3 3 2 2 C. AG AE AF . D. AG AE AF . 2 2 3 3 Lời giải Chọn D 2 2 1 1 2 2 Ta có: AG AD
. AB AC 2AF 2AE AE AF 3 3 2 3 3 3
Câu 26: [0H1-3-2] Cho a 0 và điểm O . Gọi M , N lần lượt là hai điểm thỏa mãn OM 3a và ON 4 a. Khi đó:
A. MN 7a B. MN 5 a C. MN 7 a D. MN 5 a Lời giải Chọn C
Ta có: MN ON OM 4
a 3a 7 a .
Câu 27: [0H1-3-2] Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M
sao cho MB 3MC . Khi đó đẳng thức nào sau đây đúng ? 1 3 A. AM AB AC
B. AM 2AB AC 2 2 1
C. AM AB AC D. AM ( AB AC) 2 Lời giải Chọn A
Gọi I là trung điểm của BC . Khi đó C là trung điểm của MI . Ta có: 1 1 3
AM AI 2 AC AM AI 2 AC
( AB AC) 2 AC AB AC . 2 2 2
Câu 28: [0H1-3-2] Cho tứ giác ABCD . Gọi M , N lần lượt là trung điểm của AB và CD .
Khi đó AC BD bằng: A. MN B. 2MN C. 3MN D. 2 MN Lời giải Chọn B
MN MA AC CN Ta có:
MN MB BD DN
2MN AC BD .
Câu 29: [0H1-3-2] Cho hình bình hành ABCD tâm O và điểm M bất kì. Khẳng định nào sau đây đúng ?
A. MA MB MC MD MO
B. MA MB MC MD 2MO
C. MA MB MC MD 3MO
D. MA MB MC MD 4MO Lời giải Chọn D
Ta có: MA MB MC MD (MA MC) (MB M )
D 2MO 2MO 4MO
Câu 30: [0H1-3-2] Trên đường thẳng MN lấy điểm P sao cho MN 3
MP. Hình vẽ nào
sau đây xác định đúng vị trí điểm P ? A. B. M P N N M P C. D. N M P M P N Lời giải Chọn C MN 3
MP MN 3MP MN và MP ngược hướng.
Câu 31: [0H1-3-2] Cho tam giác ABC có trọng tâm G và trung tuyến AM . Khẳng định
nào sau đây là sai?
A. GA 2GM 0 .
B. GA GB GC 0 . C. AM 2 MG .
D. AG BG CG 0 Lời giải Chọn C A G B C M AM 3 MG .
Câu 32: [0H1-3-2] Cho tam giác ABC có trọng tâm G và M là trung điểm của BC . Đẳng
thức vectơ nào sau đây đúng?
A. 2AM 3AG .
B. AM 2AG . 3
C. AB AC AG .
D. AB AC 2GM . 2 Lời giải. Chọn A 2
Ta có: 2 AM 3AG AG AM (đúng) 3
Câu 33: [0H1-3-2] Cho tam giác ABC , gọi M là trung điểm của BC và G là trọng tâm
của tam giác ABC . Câu nào sau đây đúng?
A. GB GC 2GM .
B. GB GC 2GA .
C. AB AC 2AG . D.
GA GB GC . Lời giải Chọn A
Do M là trung điểm của BC nên A là đáp án đúng.
Câu 34: [0H1-3-2] Cho hình bình hành ABCD có O là giao điểm của AC và BD .Tìm câu sai? 1
A. AB AD AC . B. OA
(BA CB) . 2
C. OA OB OC OD .
D. OB OA DA . Lời giải Chọn C
Gọi I , J lần lượt là trung điểm của AB, CD ta có: OA OB 2OI và
OC OD 2OJ
Mà OI và OJ không bằng nhau nên C sai.
Câu 35: [0H1-3-2] Phát biểu nào là sai?
A. Nếu AB AC thì AB AC .
B. AB CD thì ,
A B, C, D thẳng hàng.
C. Nếu 3AB 7AC 0 thì ,
A B, C thẳng hàng. D. AB CD DC BA . Lời giải Chọn B
AB CD thì có thể lập thành hình bình hành ABDC .
A đúng vì hai vectơ bằng nhau thì có độ dài bằng nhau. C đúng vì 7
3AB 7 AC 0 AB
AC nên AB , AC cùng phương nên , A B, C 3 thẳng hàng.
D đúng vì AB CD DC BA AB BA DC CD 0 0 .
Câu 36: [0H1-3-2] Biết rằng hai vectơ a và b không cùng phương nhưng hai vectơ
2a 3b và a (x 1)b cùng phương. Khi đó giá trị của x là 1 3 1 3 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn C 1 x 1 1 Từ giả thiết, ta có x 2 3 . 2
Câu 37: [0H1-3-2] Hãy chọn kết quả đúng khi phân tích vectơ AM theo hai véctơ AB và
AC của tam giác ABC với trung tuyến AM .
A. AM AB AC .
B. AM 2AB 3AC . 1 1 C. AM
AB AC. D. AM
AB AC. 2 3 Lời giải Chọn C 1
Theo quy tắc trung điểm: AB AC 2AM AM
AB AC. 2
Câu 38: [0H1-3-2] Cho tam giác ABC có trọng tâm G . Biểu diễn vectơ AG qua hai vectơ A , B AC là: 1 1 A. AG
AB AC. B. AG
AB AC. 3 6 1 1 C. AG
AB AC. D. AG AB AC. 6 3 Lời giải Chọn A A G B I C
Gọi I là trung điểm của BC . 2 2 1 1 Ta có: AG AI
AB AC AB AC . 3 3 2 3 1
Câu 39: [0H1-3-2] Cho tam giác ABC , E là điểm trên đoạn BC sao cho BE BC . 4
Hãy chọn đẳng thức đúng: 1 1
A. AE 3AB 4AC . B. AE AB AC . 3 5 3 1 1 1 C. AE AB AC . D. AE AB AC . 4 4 4 4 Lời giải Chọn C 1 Ta có: BE
BC ; BE và BC cùng hướng 4 1 1 3 1 BE
BC AE AB
AC AB AE AB AC . 4 4 4 4
Câu 40: [0H1-3-2] Cho tam giác ABC . Gọi M là điểm nằm trên đoạn AB sao cho
AM 3MB . Chọn khẳng định đúng. 1 3 7 3 A. CM CA CB . B. CM CA CB . 4 4 4 4 1 3 1 3 C. CM CA CB . D. CM CA CB . 2 4 4 4 Lời giải Chọn A BM AM
Áp dụng cách phân tích vectơ 1 3 CM CA CB CA CB . BA AB 4 4
Câu 41: [0H1-3-2] Nếu I là trung điểm đoạn thẳng AB và IA k AB thì giá trị của k bằng 1 1 A. 1. B. . C. . D. 2 . 2 2 Lời giải Chọn C 1 1 Ta có IA
AB và IA , AB ngược hướng. Vậy IA AB . 2 2
Câu 42: [0H1-3-2] Cho tứ giác ABCD . Gọi G và G lần lượt là trọng tâm ABC và B CD
. Chọn khẳng định đúng. 1 1 A. GG AD . B. GG AD .
C. GG 0 . D. 3 3 GG AD . Lời giải Chọn B
GB GC GD 3.GG
1 (do G là trọng tâm tam giác BCD ).
Mà GB GC GA 0 GB GC G
A 2 (do G là trọng tâm tam giác ABC ). Vậy kết hợp
1 và 2 ta được: 3.GG GD GA 1 AD GG AD . 3
Câu 43: [0H1-3-2] Cho tam giác ABC có G là trọng tâm, I là trung điểm của đoạn thẳng BC
. Đẳng thức nào sau đây đúng? 1
A. GA 2GI . B. IG IA .
C. GB GC 2GI . D. 3
GB GC GA . Lời giải Chọn C
Vì I là trung điểm BC nên ta có GB GC 2GI .
Câu 44: [0H1-3-2] Cho hình bình hành ABCD , với giao điểm hai đường chéo là I . Khi đó:
A. AI BI AB .
B. AI AC 0 .
C. IA IB IC ID 0 .
D. AC 2AI . Lời giải Chọn D
Ta có AC 2AI .
Câu 45: [0H1-3-2] Cho tam giác ABC , có AM là trung tuyến. I là trung điểm của AM . Ta có:
A. 2IA IB IC 0 .
B. IA IB IC 0.
C. 2IA IB IC 4IA.
D. IB IC IA . Lời giải Chọn A
Ta có 2IA IB IC 2IA 2IM 2IA IM 2.0 0 .
Câu 1: [0H1-3-3]Cho tam giác ABC , với M, N, P lần lượt là trung điểm của BC, C , A AB .
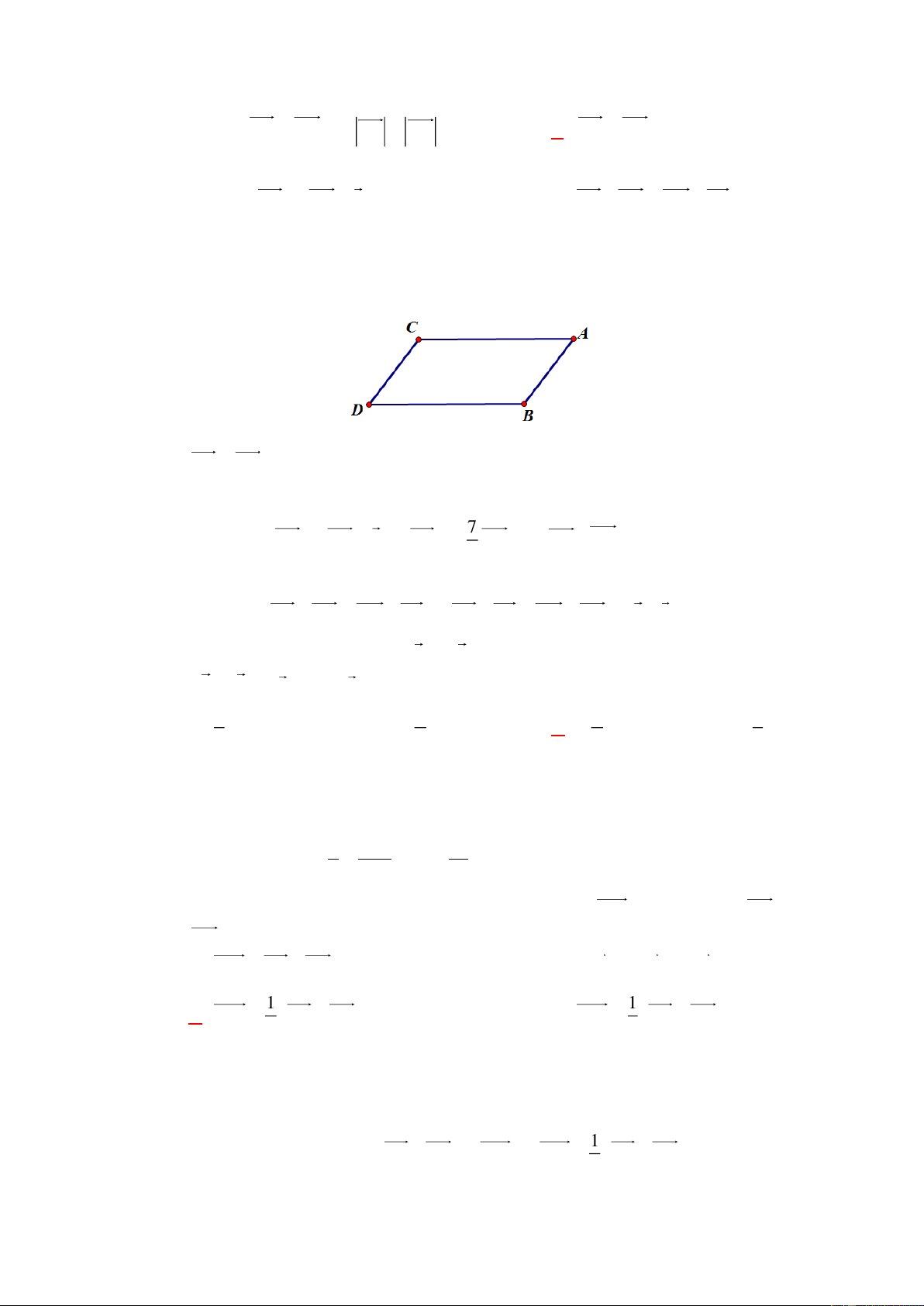
Khẳng định nào sau đây sai? A. AB BC AC 0 . B. AP BM CN 0 . C. MN NP PM 0 . D. PB MC MP . Lời giải Chọn D Xét các đáp án: A N P B M C Đáp án. A. Ta có AB BC CA AA 0. Đáp án. B. Ta có 1 1 1 AP BM CN AB BC CA 2 2 2 1 1 AB BC CA AA 0. 2 2 Đáp án. C. Ta có MN NP PM MM 0. 1 1 1 Đáp án. D. Ta có PB MC AB BC AC AN PM MP. 2 2 2
Câu 2: [0H1-3-3]Cho tam giác ABC có AB
AC và đường cao AH . Đẳng thức nào sau đây đúng? A. AB AC AH . B. HA HB HC 0 . C. HB HC 0 . D. AB AC . Lời giải Chọn C
Do ABC cân tại A , AH là đường cao nên H là trung điểm BC . A B H C Xét các đáp án: Đáp án. A. Ta có AB AC 2AH. Đáp án. B. Ta có HA HB HC HA 0 HA 0. Đáp án. C. Ta có HB HC
0 ( H là trung điểm BC ). Đáp án.
D. Do AB và AC không cùng hướng nên AB AC.
Câu 3: [0H1-3-3]Cho tam giác ABC vuông cân đỉnh A , đường cao AH . Khẳng định nào sau đây sai? A. AH HB AH HC . B. AH AB AC AH . C. BC BA HC HA . D. AH AB AH . Lời giải Chọn B
Do ABC cân tại A , AH là đường cao nên H là trung điểm BC . A B H C Xét các đáp án: AH HB AB a Đáp án. A. Ta có AH HC AC a AH HB AH HC . AH AB BH Đáp án. B. Ta có . AH AC CH BH Đáp án. C. Ta có BC BA HC HA AC. Đáp án. D. Ta có AB AH HB
AH . (do ABC vuông cân tại A ).
Câu 4: [0H1-3-3]Cho đường tròn O và hai tiếp tuyến song song với nhau tiếp xúc với O tại
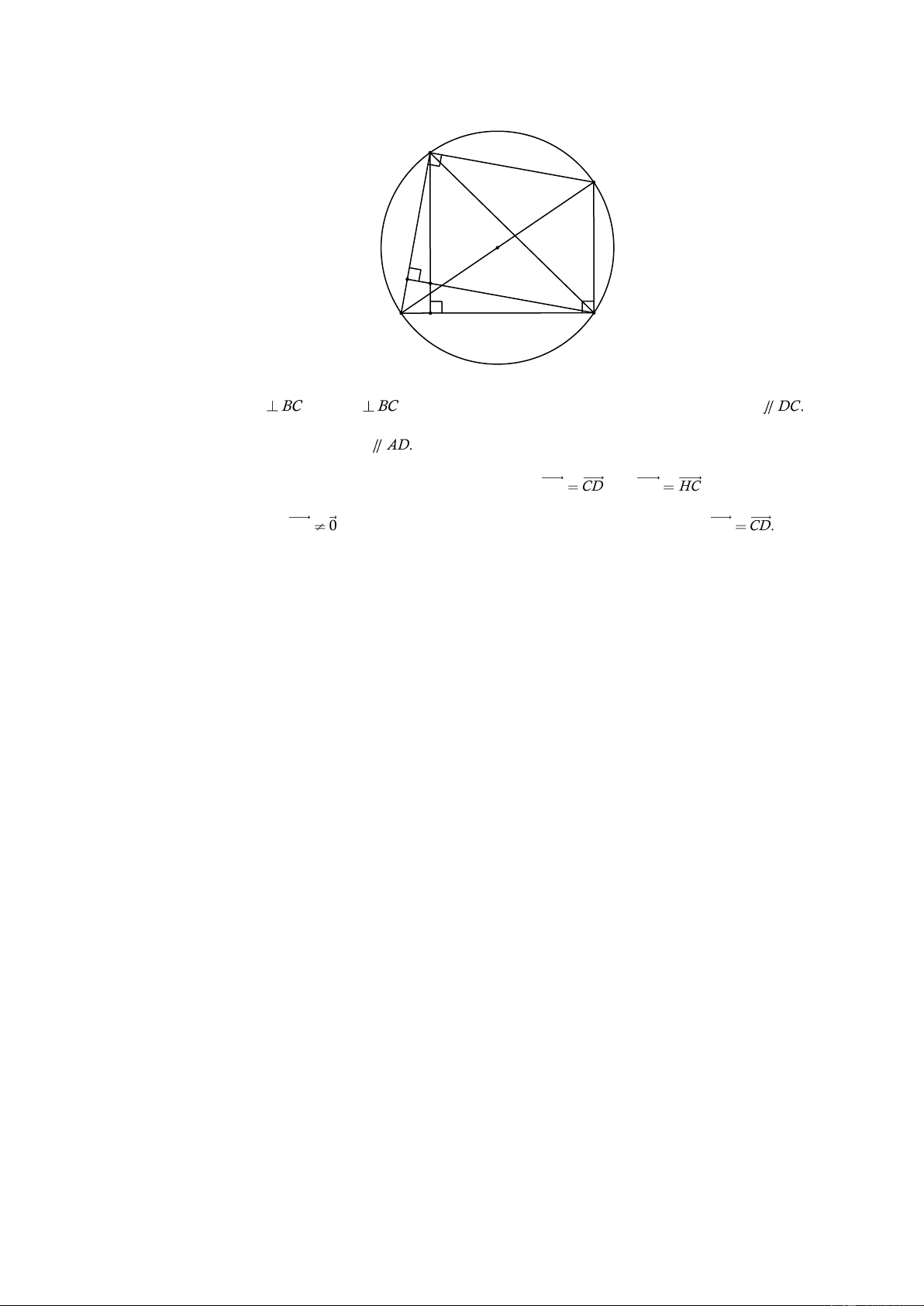
hai điểm A và B . Mệnh đề nào sau đây đúng? A. OA OB . B. AB OB . C. OA OB . D. AB BA . Lời giải Chọn A B A O
Do hai tiếp tuyến song song và ,
A B là hai tiếp điểm nên AB là đường kính. Do đó
O là trung điểm của AB . Suy ra OA OB .
Câu 5: [0H1-3-3]Cho đường tròn O và hai tiếp tuyến MT , MT (T và T là hai tiếp điểm).
Khẳng định nào sau đây đúng? A. MT MT . B. MT MT TT . C. MT MT . D. OT OT . Lời giải Chọn C T O M T'
Do MT , MT là hai tiếp tuyến (T và T là hai tiếp điểm) nên MT MT .
Câu 6: [0H1-3-3]Cho tam giác ABC vuông cân đỉnh C , AB
2 . Tính độ dài của AB AC. A. AB AC 5 . B. AB AC 2 5 . C. AB AC 3 . D. AB AC 2 3 . Lời giải Chọn A A C I B Ta có AB 2 AC CB 1. 5
Gọi I là trung điểm 2 2 BC AI AC CI . 2 Khi đó 5 AC AB 2AI AC AB 2 AI 2. 5. Chọn A 2
Câu 7: [0H1-3-3]Cho tam giác ABC vuông tại A có AB 3, AC 4 . Tính CA AB . A. CA AB 2 . B. CA AB 2 13 . C. CA AB 5 . D. CA AB 13 . Lời giải Chọn C
Gọi D là điểm thỏa mãn tứ giác ABDC là hình chữ nhật. Ta có 2 2 2 2 CA AB CB BC AC AB 3 4 5 .
Câu 8: [0H1-3-3]Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12 . Tính độ dài của vectơ v GB GC . A. v 2 . B. v 2 3 . C. v 8 . D. v 4 . Lời giải Chọn D B M G A C
Gọi M là trung điểm của BC. Ta có GA GB GC 0 GB GC GA GA 2 2 1 BC Mà GA AM . .BC 4. 3 3 2 3
Câu 9: [0H1-3-3]Cho tam giác ABC và điểm M thỏa mãn điều kiện MA MB MC 0 . Mệnh
đề nào sau đây sai?
A. MABC là hình bình hành. B. AM AB AC . C. BA BC BM . D. MA BC . Lời giải Chọn A A M B C Ta có MA MB MC 0 BA MC 0 MC AB
MABC là hình bình hành.
Câu 10: [0H1-3-3] Tìm giá trị của m sao cho a mb , biết rằng a,b ngược hướng và
a 5, b 15 1 1 A. m 3 . B. m . C. m . D. m 3 . 3 3 Lời giải Chọn B a 5 1
Do a,b ngược hướng nên m . b 15 3
Câu 11: [0H1-3-3] Cho tam giác ABC đều có cạnh bằng a . Độ dài của AB AC bằng: a 3 A. 2a . B. a . C. a 3 . D. . 2 Lời giải Chọn C
Gọi H là trung điểm của BC . Khi đó: 2 a 2 2 2
AB AC 2.AH 2.AH 2. AB BH 2. a a 3 . 4
Câu 12: [0H1-3-3] Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn
hệ thức MA MB 2MC 0 .
A. M là trung điểm của BC .
B. M là trung điểm của IC .
C. M là trung điểm của IA .
D. M là điểm trên cạnh IC sao
cho IM 2MC . Lời giải Chọn B
MA MB 2MC 0 2MI 2MC 0 MI MC 0 M là trung điểm của IC .
Câu 13: [0H1-3-3] Cho hình bình hành ABCD , điểm M thõa mãn 4AM AB AD AC .
Khi đó điểm M là:
A. Trung diểm của AC . B. Điểm C .
C. Trung điểm của AB . D. Trung điểm của AD . Lời giải Chọn A
Theo quy tắc hình bình hành, ta có: 1
4 AM AB AD AC 4 AM 2.AC AM
.AC M là trung điểm của 2 AC .
Câu 14: [0H1-3-3] Cho hình thoi ABCD tâm O , cạnh 2a . Góc 0
BAD 60 . Tính độ dài vectơ AB AD .
A. AB AD 2a 3 . B. AB AD a 3 .
C. AB AD 3a .
D. AB AD 3a 3 . Lời giải Chọn A
Tam giác ABD cân tại A và có góc 0
BAD 60 nên ABD đều 2 2 2 2
AB AD AC 2AO 2.AO 2. AB BO 2. 4a a 2a 3 .
Câu 15: [0H1-3-3] Cho tam giác ABC có điểm O thỏa mãn: OA OB 2OC OA OB .
Khẳng định nào sau đây là đúng?
A. Tam giác ABC đều. B. Tam giác ABC cân tại C .
C. Tam giác ABC vuông tại C .
D. Tam giác ABC cân tại B . Lời giải Chọn C
Gọi I là trung điểm của AB . Ta có:
OA OB 2OC OA OB OA OC OB OC BA CA CB AB 1
2.CI AB 2CI AB CI AB Tam giác ABC vuông tại C . 2
Câu 16: [0H1-3-3] Cho tam giác ABC , có bao nhiêu điểm M thoả mãn: MA MB MC 1 A. 0. B. 1. C. 2. D. vô số. Lời giải Chọn D
Gọi G là trọng tâm của tam giác ABC 1
Ta có MA MB MC 3MG 3MG 1 MG 3
Tập hợp các điểm M thỏa mãn MA MB MC 1 là đường tròn tâm G bán 1 kính R . 3
Câu 17: [0H1-3-3] Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vectơ
v MA MB 2MC . Hãy xác định vị trí của điểm D sao cho CD v .
A. D là điểm thứ tư của hình bình hành ABCD .
B. D là điểm thứ tư của hình bình hành ACBD .
C. D là trọng tâm của tam giác ABC .
D. D là trực tâm của tam giác ABC . Lời giải Chọn B
Ta có: v MA MB 2MC MA MC MB MC CA CB 2CI (Với I là
trung điểm của AB )
Vậy vectơ v không phụ thuộc vào vị trú điểm M . Khi đó: CD v 2CI I là
trung điểm của CD
Vậy D D là điểm thứ tư của hình bình hành ACBD .
Câu 18: [0H1-3-3] Cho tam giác ABC . Gọi M là trung điểm của BC và N là trung điểm
AM . Đường thẳng BN cắt AC tại P . Khi đó AC xCP thì giá trị của x là: 4 2 3 5 A. . B. . C. . D. . 3 3 2 3 Lời giải Chọn C
Kẻ MK / / BP (K AC) . Do M là trung điểm của BC nên suy ra K là trung điểm của CP
Vì MK / /BP MK / /NP mà N là trung điểm của AM nên suy ra P là trung điểm của AK Do đó: 3 3
AP PK KC . Vậy AC CP x . 2 2
Câu 19: [0H1-3-3] Cho tam giác ABC . Hai điểm M , N được xác định bởi các hệ thức
BC MA 0 , AB NA 3AC 0 . Trong các khẳng định sau, khẳng định nào đúng?
A. MN AC .
B. MN / / AC .
C. M nằm trên đường thẳng AC .
D. Hai đường thẳng MN và AC trùng nhau. Lời giải Chọn B
Ta có: BC MA 0 AM BC M là điểm thứ tư của hình bình hành ABCM
nên M AC (1)
Cộng vế theo vế hai đẳng thức BC MA 0 , AB NA 3AC 0 , ta được:
BC MA AB NA 3AC 0
(MA AN) (AB BC) 3AC 0 MN AC 3AC MN 2AC MN
cùng phương với AC (2)
Từ (1) và (2) suy ra MN / / AC .
Câu 20: [0H1-3-3] Cho tam giác OAB vuông cân tạ O với OA OB a . Độ dài của véc tơ 21 5 u OA OB là: 4 2 a 140 a 321 a 520 a 541 A. . B. . C. . D. 4 4 4 4 . Lời giải Chọn D 21 5
Dựng điểm M , N sao cho: OM O , A ON OB . Khi đó: 4 2 2 2 21a 5a a 541 2 2
u OM ON NM MN OM ON . 4 2 4
Câu 21: [0H1-3-3] Cho tam giác ABC . Gọi M là trung điểm của AB và N thuộc cạnh AC
sao cho NC 2NA. Hãy xác định điểm K thỏa mãn: 3AB 2AC 12AK 0 và
điểm D thỏa mãn: 3AB 4AC 12KD 0 .
A. K là trung điểm của MN và D là trung điểm của BC .
B. K là trung điểm của BC và D là trung điểm của MN .
C. K là trung điểm của MN và D là trung điểm của AB .
D. K là trung điểm của MN và D là trung điểm của AC . Lời giải Chọn A Ta có: AB 2AM 1
3AB 2AC 12AK 0 3.2AM 2.3AN 12AK 0 AK AM AN 2 AC 3AN
Suy ra K là trung điểm của MN Ta có:
3AB 4AC 12KD 0 3AB 4AC 12 AD AK 0 3AB 4AC 12AK 12AD 1
12AD 3AB 4AC 3AB 2AC 12AD 6AB 6AC AD AB AC 2
Suy ra D là trung điểm của BC .
Câu 22: [0H1-3-3] Cho G và G' lần lượt là trọng tâm của tam giác ABC và A' B'C ' . Khi
đó tổng AA' BB' CC ' bằng: A. GG '. B. 3GG ' . C. 2GG ' . D. 4GG ' . Lời giải Chọn B
AA' BB ' CC ' (AG GG ' G ' A') (BG GG ' G ' B ') (CG GG ' G 'C ')
3GG' (AG BG C )
G (G ' A' G ' B ' G 'C ') 3GG ' 0 0 .
Câu 23: [0H1-3-3] Cho tứ giác ABCD . Gọi G là trọng tâm của tam giác ABD , I là điểm
trên GC sao cho IC 3IG . Với mọi điểm M ta luôn có MA MB MC MD bằng: A. 2MI B. 3MI C. 4MI D. 5MI Lời giải Chọn C
Ta có: 3IG IC .
Do G là trọng tâm của tam giác ABD nên
IA IB ID 3IG IA IB ID IC IA IB IC ID 0 Khi đó:
MA MB MC MD MI IA MI IB MI IC MI ID
4MI (IA IB IC I )
D 4MI 0 4MI
Câu 24: [0H1-3-3] Cho tam giác ABC biết AB 8, AC 9, BC 11. Gọi M là trung điểm
BC và N là điểm trên đoạn AC sao cho AN x (0 x 9) . Hệ thức nào sau đây đúng ? 1 x 1 x 1 1 A. MN AC AB B. MN CA BA 2 9 2 9 2 2 x 1 1 x 1 1 C. MN AC AB D. MN AC AB 9 2 2 9 2 2 Lời giải Chọn D x 1 x 1 1
Ta có: MN AN AM AC (AB AC) AC AB . 9 2 9 2 2
Câu 25: [0H1-3-3] Cho ABC
với G là trọng tâm. Đặt CA
a ,CB b . Khi đó, AG
được biểu diễn theo hai vectơ a và b là 1 2 2 1 A. AG a b . B. AG a b . 3 3 3 3 2 1 2 1 C. AG a b . D. AG a b . 3 3 3 3 Lời giải Chọn D A G B C M 2 2 1 1 1 2 1 Ta có: AG AM
. AB AC CB CA CA b 2a a b . 3 3 2 3 3 3 3
Câu 26: [0H1-3-3] Cho tam giác ABC và I thỏa IA 3IB . Đẳng thức nào sau đây là đẳng thức đúng? 1
A. CI CA 3CB . B. CI 3CBCA. 2 1 C. CI CA3CB.
D. CI 3CB CA . 2 Lời giải Chọn B B A C I 3 3 3 1
Ta có: CI AI AC AB AC
CBCACA CB CA. 2 2 2 2
Câu 27: [0H1-3-3] Gọi AM là trung tuyến của tam giác ABC , I là trung điểm của AM .
Đẳng thức nào sau đây đúng?
A. 2IA IB IC 0 .
B. IA IB IC 0 .
C. IA IB IC 0 .
D. IA IB IC 0. Lời giải Chọn A
Ta có: IB IC 2IM nên 2IA IB IC 2(IA IM ) 0 .
Câu 28: [0H1-3-3] Cho tam giác ABC , có bao nhiêu điểm M thỏa MA MB MC 5? A. 1. B. 2. C. vô số.
D. Không có điểm nào. Lời giải Chọn C
Gọi G là trọng tâm tam giác ABC , ta có: 5
MA MB MC 5 3MG 5 MG 3 5
Vậy quỹ tích điểm M là đường tròn tâm G , bán kính . 3
Câu 29: [0H1-3-3] Cho tam giác ABC , có trọng tâm G . Gọi A , B , C lần lượt là trung 1 1 1
điểm của BC, C ,
A AB . Chọn khẳng định sai?
A. GA GB GC 0 .
B. AG BG CG 0 . 1 1 1
C. AA BB CC 0 .
D. GC 2GC . 1 1 1 1 Lời giải Chọn D A C B 1 1 G B A C 1
Ta xét tính đúng sai của từng mệnh đề: 1 1 1 1
Ta có: GA GB GC GA GB GC
GA GB GC 0 A 1 1 1 2 2 2 2 đúng.
AG BG CG GA GB GC 0
0 B đúng. 3 3
AA BB CC
GA GB GC
0 0 C đúng. 1 1 1 2 2
GC 2GC là biểu thức sai vì GC và GC là hai vectơ ngược hướng. 1 1
Câu 30: [0H1-3-3] Cho hai điểm cố định ,
A B ; gọi I là trung điểm AB . Tập hợp các
điểm M thoả: MA MB MA MB là
A. Đường tròn đường kính AB .
B. Trung trực của AB .
C. Đường tròn tâm I , bán kính AB .
D. Nửa đường tròn đường kính AB . Lời giải Chọn A
Ta có: MA MB MA MB 2MI BA 2MI AB .
Vậy tập hợp các điểm M là đường tròn đường kính AB .
Câu 31: [0H1-3-3] Gọi M , N lần lượt là trung điểm của các cạnh AB và CD của tứ giác
ABCD . Mệnh đề nào sau đây đúng ?
A. AC BD BC AD 4MN .
B. 4MN BC AD .
C. 4MN AC BD .
D. MN AC BD BC AD . Lời giải Chọn A
Ta có: AC BD BC AD
AM MN NCBM MN NDBM MN NCAM MN ND
2 AM BM 2NC ND 4MN 4MN . 0 0
Câu 1: [0H1-3-4] Cho tam giác ABC và đường thẳng d . Gọi O là điểm thỏa mãn hệ thức
OA OB 2OC 0. Tìm điểm M trên đường thẳng d sao cho vectơ
v MA MB 2MC có độ dài nhỏ nhất.
A. Điểm M là hình chiếu vuông góc của O trên d .
B. Điểm M là hình chiếu vuông góc của A trên d .
C. Điểm M là hình chiếu vuông góc của B trên d .
D. Điểm M là giao điểm của AB và d . Lời giải Chọn A
Gọi I là trung điểm của AB .
Khi đó: OA OB 2OC 0 2OI 2OC 0 OI OC 0 O là trung điểm của IC Ta có:
v MA MB 2MC OA OM OB OM 2(OC OM ) OA OB 2OC 4OM 4 OM
Do đó v 4OM . Độ dài vectơ v nhỏ nhất khi và chỉ khi 4OM nhỏ nhất hay M
là hình chiếu vuong góc của O trên d .
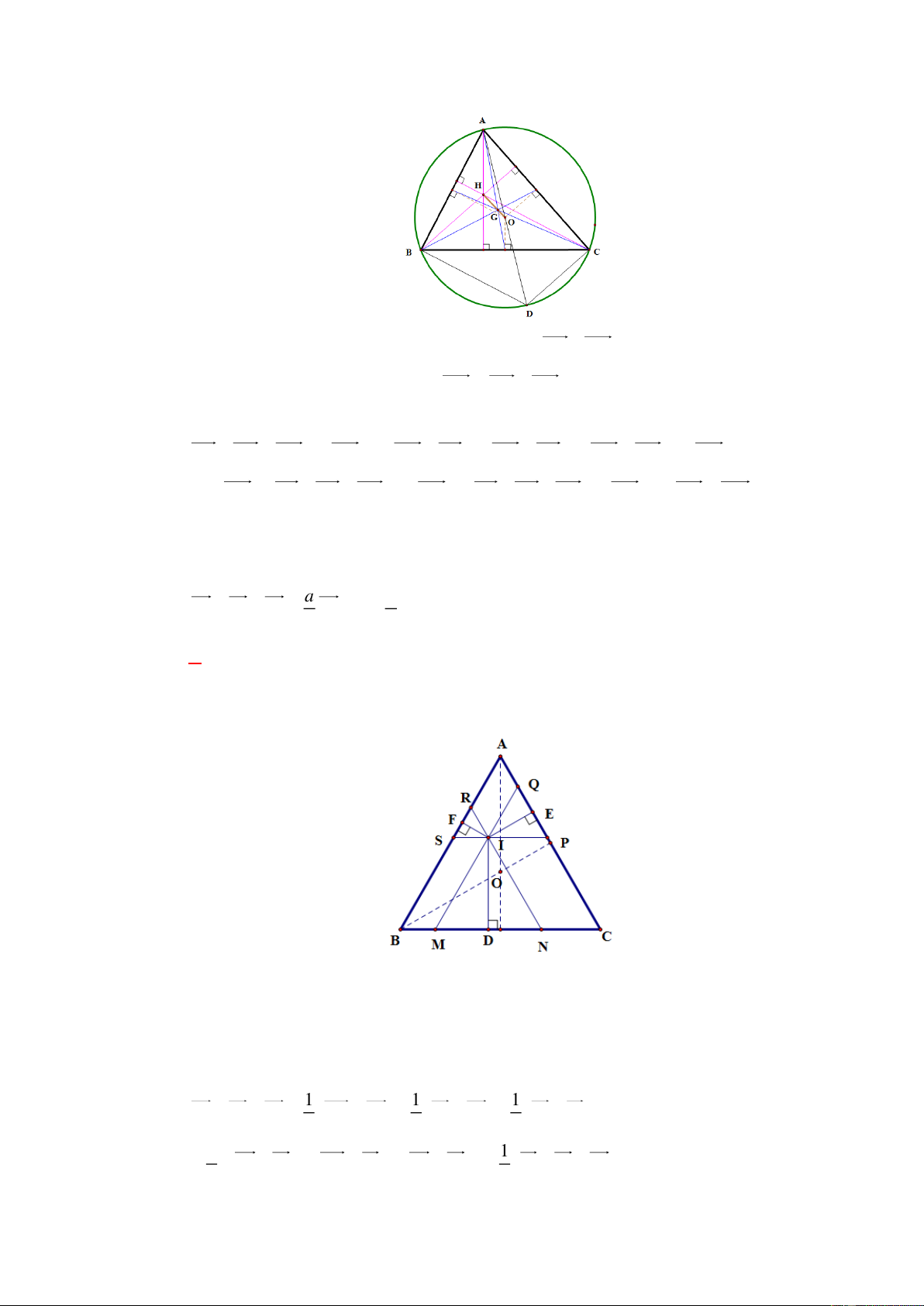
Câu 2: [0H1-3-4] Cho tam giác ABC nội tiếp trong đường tròn tâm O . Gọi H là trực tâm
của tam giác. Trong các khẳng định sau, khẳng định nào đúng ?
A. OH 4OG
B. OH 3OG
C. OH 2OG D. 3OH OG Lời giải Chọn B
Gọi D là điểm đối xứng với A qua O . Ta có: HA HD 2HO(1)
Vì HBDC là hình bình hành nên HD HB HC (2) Từ (1), (2) suy ra:
HA HB HC 2HO (HO O )
A (HO O )
B (HO OC) 2HO
3HO (OAOB OC) 2HO OAOB OC HO 3OG OH .
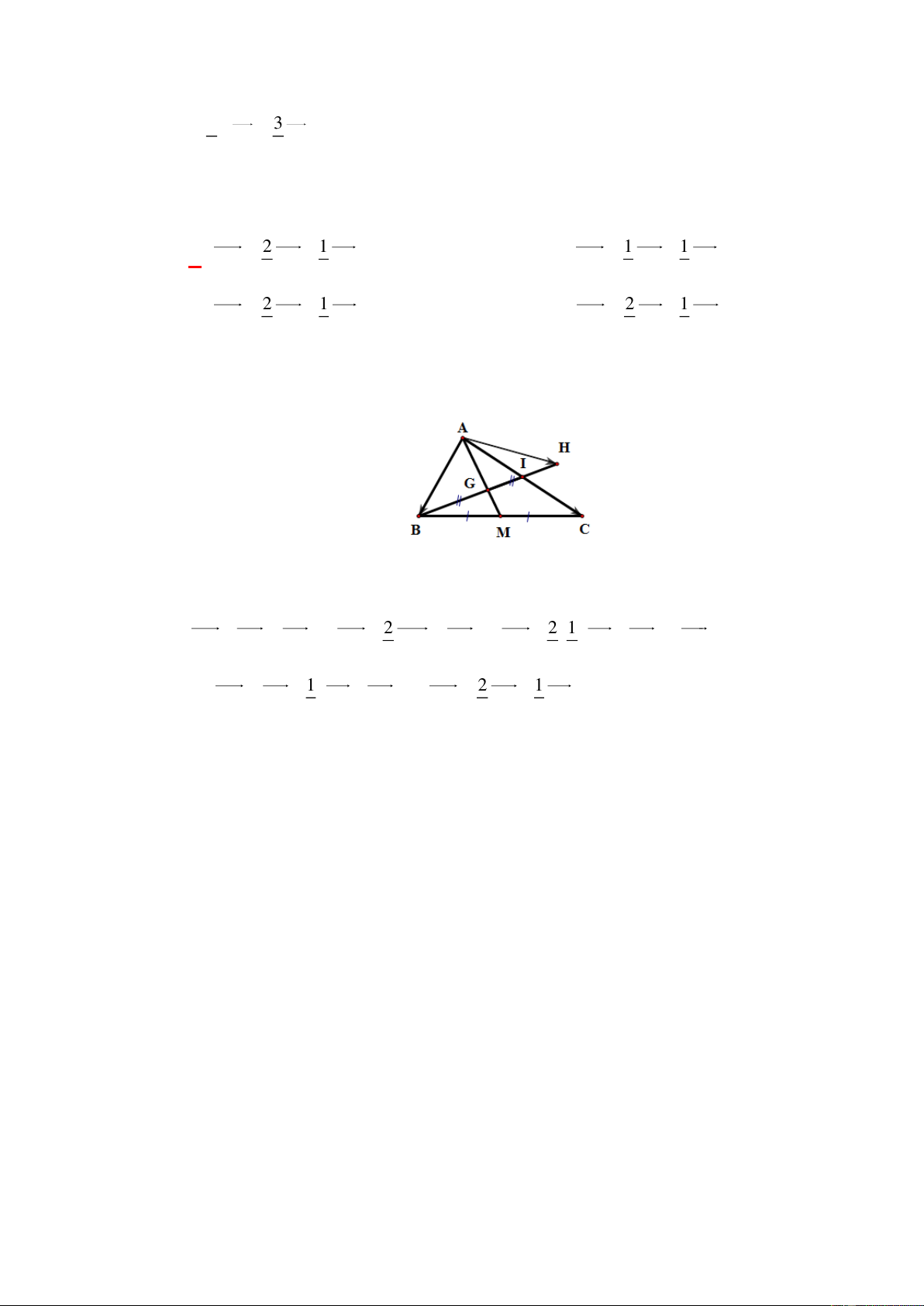
Câu 3: [0H1-3-4] Cho tam giác đều ABC có tâm O . Gọi I là một điểm tùy ý bên trong tam
giác ABC . Hạ ID, IE, IF tương ứng vuông góc với BC, C , A AB . Giả sử a a
ID IE IF IO (với
là phân số tối giản). Khi đó a b bằng: b b A. 5 B. 4 C. 6 D. 7 Lời giải Chọn A
Qua điểm I dựng các đoạn MQ / / AB, PS / /BC, NR / /CA. Vì ABC là tam giác
đều nên các tam giác IMN, IPQ, IRS cũng là tam giác đều. Suy ra D, E, F lần lượt
là trung điểm của MN, PQ, RS . Khi đó: 1 1 1
ID IE IF (IM IN ) (IP IQ) (IR IS ) 2 2 2 1 1
(IQ IR) (IM IS) (IN IP) (IA IB IC) 2 2 1 3
.3IO IO a 3,b 2 . Do đó: a b 5. 2 2
Câu 4: [0H1-3-4] Cho tam giác ABC . Gọi G là trọng tâm và H là điểm đối xứng với B
qua G . Trong các khẳng định sau, khẳng định nào đúng ? 2 1 1 1 A. AH AC AB B. AH AC AB 3 3 3 3 2 1 2 1 C. AH AC AB D. AH AB AC 3 3 3 3 Lời giải Chọn A
Gọi M , I lần lượt là trung điểm của BC và AC .
Ta thấy AHCG là hình bình hành nên 2 2 1
AH AG AC AH
AM AC AH
. AB AC AC 3 3 2 1
AH AC AB AC 2 1
AH AC AB 3 3 3
Câu 1: [0H1-5-1] Trên trục tọa độ ; O e , các điểm ,
A B và C có tọa độ lần lượt là 1 ;2 và
3 . Tìm giá trị của AB 2AC . A. 11. B. 1. C. 7 . D. 11 . Lời giải Chọn A AB 2
1 3, AC 3
1 4 AB 2AC 3 2.4 11 . 1
Câu 2: [0H1-5-1] Cho tam giác ABC với A 3 ;6 ; B9; 1 0 và G ;0 là trọng tâm. Tọa 3 độ C là :
A. C 5; 4 .
B. C 5; 4 . C. C 5 ;4. D. C 5 ; 4. Lời giải. Chọn C
x x x 3x
x 3x x x C G A B Ta có : A B C G C 5 ;4 .
y y y 3y
y 3y y y C G A B A B C G a 1; 2 b 3; 4 Câu 3: [0H1-5-1] Cho và
với c 4a b thì tọa độ của c là:
A. c 1; 4 .
B. c 4; 1 .
C. c 1; 4 . D. c 1 ; 4 . Lời giải. Chọn C
Ta có: c 4a 2b 4 1; 2 3; 4 1; 4 .
Câu 4: [0H1-5-1] Trong mặt phẳng tọa độ Oxy cho A5;3 , B 7;8 . Tìm tọa độ của véctơ AB A. 15;10 . B. 2;5 . C. 2;6 . D. 2 ; 5 . Lời giải. Chọn B
Ta có : AB 2;5 .
Câu 5: [0H1-5-1] Trong mặt phẳng tọa độ Oxy cho A3;5 , B 1; 2 . Tìm tọa độ trung điểm
I của đoạn thẳng AB . 7
A. I 4;7 . B. I 2 ;3. C. I 2; . D. 2 7 I 2; . 2 Lời giải. Chọn C x x A B x I 2 7 Ta có : I 2; . y y 2 A B y I 2
Câu 6: [0H1-5-1] Trong hệ trục ,
O i, j , tọa độ của i j là A. 0; 1 . B. 1 ;1 . C. 1; 1 . D. 1 ;1 . Lời giải. Chọn C i 1;0 Ta có :
i j 1; . j 1 0;1 a 3; 4 b1;2 Câu 7: [0H1-5-1] Cho ,
. Tọa độ của véctơ a 2b là A. 4 ;6 . B. 4; 6 . C. 1;0 . D. 0; 1 . Lời giải. Chọn C a 3; 4 b 1
;2 2b 2 ;4
a 2b 1;0 .
a 4;10 b 2, x
Câu 8: [0H1-5-1] Cho hai vectơ ,
. Hai vectơ a , b cùng phương nếu A. x 4 . B. x 5. C. x 6 D. x 7 . Lời giải. Chọn B Để x
hai vectơ a , b cùng phương 2 x 5. 4 10
A3;5 B1;2 C 2;0
Câu 9: [0H1-5-1] Trong mặt phẳng tọa độ Oxy cho , và . Tìm tọa độ
trọng tâm G của tam giác ABC 7
A. G 3, 7 .
B. G 6;3 . C. G 3, D. 3 7 G 2; . 3 Lời giải. Chọn D
x x x 3x Để 7
G là trọng tâm tam giác ABC A B C G G 2; .
y y y 3y 3 A B C G
Câu 10: [0H1-5-1] Trong mặt phẳng tọa độ Oxy cho A2; 3
, B4;7 . Tọa độ trung điểm I
của đoạn thẳng AB là: A. I 6; 4
B. I 2;10 .
C. I 3; 2 . D. I 8; 2 1 . Lời giải. Chọn C x x A B x I 2 Ta có : I 3; 2 . y y A B y I 2
a 2;7 b 3;5 Câu 11: [0H1-5-1] Cho ,
. Tọa độ của véctơ a b là. A. 5; 2 . B. 1 ;2 . C. 5 ; 2 . D. 5; 2 . Lời giải. Chọn A
Ta có: a b 2;7 3;5 5; 2 .
Câu 12: [0H1-5-1] Trong mặt phẳng toạ độ Oxy cho hai điểm A1; 4 và B 3;5 . Khi đó:
A. AB 2; 1 .
B. BA 1; 2 .
C. AB 2; 1 . D. AB 4;9 . Lời giải. Chọn C
Ta có : AB 2; 1 . A5; 2 B0;3
Câu 13: [0H1-5-1] Trong mặt phẳng toạ độ Oxy Oxy, cho ba điểm , , C 5 ;
1 . Khi đó trọng tâm ABC là: A. G 0;1 1 .
B. G 1; 1 .
C. G 10;0 . D. G 0;0 . Lời giải. Chọn D
x x x 3x Ta có : A B C G
G 0;0.
y y y 3y A B C G
B 3;2 C 5; 4
Câu 14: [0H1-5-1] Cho hai điểm ,
. Toạ độ trung điểm M của BC là
A. M –8;3 .
B. M 4;3 .
C. M 2; 2 . D. M 2; –2 . Lời giải. Chọn B x x C B x M 2 Ta có : M 4;3 . y y C B y M 2
Câu 15: [0H1-5-1] Cho tam giác ABC có tọa độ ba đỉnh lần lượt là A2;3 , B 5; 4 , C 2; 2
. Tọa độ trọng tâm G của tam giác có tọa độ là A. 3;3 B. 2; 2 C. 1 ;1 D. 4; 4 . Lời giải. Chọn A
x x x 3x Ta có : A B C G
G3;3 .
y y y 3y A B C G
Câu 16: [0H1-5-1] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có tọa độ ba đỉnh lần
lượt là A2; 3, B5; 4, C 1 ;
1 . Tọa độ trọng tâm G của tam giác có tọa độ là: A. 3; 3. B. 2; 2 . C. 1; 1 . D. 4; 4 . Lời giải Chọn B
x x x A B C x G Để 3
G là trọng tâm tam giác ABC G 2;2 .
y y y A B C y G 3
Câu 17: [0H1-5-1] Trong mặt phẳng tọa độ Oxy , cho a 2; 1 , b 3; 2
và c 2a 3b .
Tọa độ của vectơ c là A. 13; 4. B. 13; 4 . C. 13 ; 4 . D. 1 3; 4. Lời giải Chọn A
Ta có: c 2a 3b 2 2 ;1 33; 2 13; 4 .
Câu 18: [0H1-5-1] Trong mặt phẳng tọa độ Oxy , tọa độ i là
A. i 0; 0 .
B. i 0; 1 .
C. i 1; 0 . D. i 1; 1 . Lời giải Chọn C
Câu 19: [0H1-5-1] Trong mặt phẳng tọa độ Oxy , cho a 1; 2,b 3; 4 . Tọa độ c 4a b là A. c 1 ; 4 .
B. c 4; 1 .
C. c 1; 4 . D. c 1; 4 . Lời giải Chọn C
Ta có: c 4a 2b 4 1; 2 3; 4 1; 4 .
Câu 20: [0H1-5-1]Trong mặt phẳng Oxy cho A 5; 2
, B 10;8. Tọa độ vectơ AB là:
A. AB 15;10 .
B. AB 2; 4 .
C. AB 5;10 . D. AB 50;16 . Lời giải Chọn C A 5; 2
, B 10;8 AB 5;10 .
Câu 21: [0H1-5-1]Trong mặt phẳng Oxy cho tam giác ABC có
A 3;5, B 1;2,C 5;2 . Trọng tâm G của tam giác ABC có tọa độ là: A. 3 ;4. B. 4;0 . C. 2;3. D. 3;3 . Lời giải Chọn D
Ta có G x ; y
là trọng tâm tam giác ABC nên: G G
x x x 3 1 5 A B C x 3 G 3 3 G 3;3 .
y y y 5 2 2 A B C y 3 G 3 3
Câu 22: [0H1-5-1]Trong mặt phẳng Oxy cho a 1
;3 , b 5;7. Tọa độ vectơ 3a 2b là: A. 6; 1 9 . B. 13; 2 9 . C. 6 ;10. D. 1 3;23 . Lời giải Chọn D a 1 ;3 3 a 3 ;9 3a 2b 1 3;23 . b 5; 7 2b 10; 1 4
Câu 23: [0H1-5-1] Trong hệ trục tọa độ ; O ;
i j tọa độ i j là: A. 0; 1 . B. (1; 1) C. ( 1 ; 1) D. (1; 1) Lời giải Chọn D
Ta có i 1; 0, j 0;
1 i j 1; 1
Câu 24: [0H1-5-1] Cho a 3; 4, b 1; 2 Tìm tọa độ của a . b A. 4 ; 6
B. 2; 2
C. 4; 6 D. 3 ; 8 Lời giải Chọn B
Ta có a b 3
1 ; 4 2 2; 2 .
Câu 25: [0H1-5-1] Cho a 1; 2 , b 5; 7 Tìm tọa độ của a . b
A. 6; 9
B. 4; 5 C. 6 ; 9 D. 5 ; 14 . Lời giải Chọn C
Ta có a b 1 5; 2 7 6 ; 9.
Câu 26: [0H1-5-1] Trong hệ tọa độ Oxy, cho A5; 2 , B 10; 8 Tìm tọa độ của vectơ AB ?
A. 15; 10 . B. 2; 4 . C. 5; 6 . D. 50; 16. Lời giải Chọn C
Ta có AB 5; 6 .
Câu 27: [0H1-5-1] Trong hệ tọa độ Oxy, cho A2; 3 , B 4; 7 . Tìm tọa độ trung điểm
I của đoạn thẳng AB A. 6; 4 .
B. 2; 10 . C. 3; 2 . D. 8; 2 1 . Lời giải Chọn C 2 4 3 7 Ta có I ; 3; 2 . 2 2
Câu 28: [0H1-5-1] Trong hệ tọa độ Oxy, cho tam giác ABC có A3; 5 , B 1; 2 ,
C 5; 2 . Tìm tọa độ trọng tâm G của tam giác ABC ? A. 3 ; 4. B. 4; 0 . C. 2; 3 . D. 3; 3 . Lời giải Chọn D
31 5 5 2 2
Ta có tọa độ G ; 3; 3. 3 3
Câu 29: [0H1-5-1] Cho A4; 0 , B 2; – 3 , C 9; 6 . Tọa độ trọng tâm G của tam giác ABC là: A. 3; 5 . B. 5; 1 . C. 15; 9 . D. 9; 15 . Lời giải Chọn B
Trọng tâm G của tam giác ABC có toạ độ thoả mãn:
x x x 4 2 9 A B C x x G G x 5 3 3 G G 5; 1 .
y y y 3 6 y 1 A B C G y y G 3 G 3
Câu 30: [0H1-5-1] Hai vectơ nào có toạ độ sau đây là cùng phương?
A. 1; 0 và 0; 1 . B. 2; 1 và 2; –
1 . C. –1;0 và 1;0 . D. 3; –2 và 6; 4 . Lời giải Chọn C
Ta có: i 1; 0 và i 1; 0 cùng phương.
Câu 31: [0H1-5-1] Tìm tọa độ vectơ u biết u b 0 , b 2; –3 . A. 2; –3 . B. –2; –3 .
C. –2;3 . D. 2; 3 . Lời giải Chọn C
Ta có u b 0 u b 2; 3 .
Câu 32: [0H1-5-1] Cho hai vectơ a 1; 4 ; b 6;15 . Tìm tọa độ vectơ u biết u a b A. 7;19 . B. –7;19 . C. 7; –19 . D. –7;–19. Lời giải Chọn B
Ta có u a b u b a 7;19 .
Câu 33: [0H1-5-1] Cho a 2i 3 j và b i
2 j . Tìm tọa độ của c a b .
A. c 1 ; 1 .
B. c 3 ; 5 . C. c 3 ; 5 . D. c 2 ; 7 . Lời giải Chọn B
c a b 2i 3 j i
2 j 3i 5 j c 3 ; 5 .
Câu 34: [0H1-5-1] Cho a 2i 3 j , b m j i . Nếu a, b cùng phương thì: 2 A. m 6 .
B. m 6 . C. m . D. 3 3 m . 2 Lời giải Chọn D m
a 2 ; 3 và b 1 ; m cùng phương 1 3 m 2 3 . 2
Câu 35: [0H1-5-1] Cho a 1; 5 , b 2;
1 . Tính c 3a 2b .
A. c 7; 13 .
B. c 1; 17 . C. c 1 ; 17. D. c 1; 16 . Lời giải Chọn B a 1; 5 3 a 3; 15 Ta có
c 3a 2b 1 ; 17. b 2 ; 1 2b 4 ; 2
Câu 36: [0H1-5-1] Trong mặt phẳng Oxy cho A4; 2, B 1; 5
. Tìm trọng tâm G của tam giác OAB . 5 5 A. G ; 1 . B. G ; 2 .
C. G 1;3 . D. 3 3 5 1 G ; . 3 3 Lời giải Chọn A
x x x 0 4 1 5 O A B x G 3 3 3 5 G ; 0 .
y y y 0 2 5 3 O A B y 1 G 3 3
A3; 2 B 5 ;4 1 Câu 1: [0H1-5-2] Cho , và C ; 0
. Ta có AB nAC thì giá trị n là: 3 A. n 3. B. n 3 . C. n 2 D. n 4 . Lời giải. Chọn A 8 Ta có : AB 8
;6 , AC ;2
AB 3AC . 3 A 5 ;6 B 4 ; 1 C 4;3
Câu 2: [0H1-5-2] Cho tam giác ABC với , và
. Tìm D để ABCD là hình bình hành:
A. D 3;10 . B. D 3; 1 0 . C. D 3 ;10 . D. D 3 ; 1 0 . Lời giải. Chọn A Gọi D ,
x y là điểm cần tìm Ta có : AB 1; 7
, DC 4 ; x 3 y 4 x 1
Để ABCD là hình bình hành AB DC D 3;10 . 3 y 7 A 2 ;0 B0; 1 C 4; 4
Câu 3: [0H1-5-2] Cho hình bình hành ABCD có ; , . Toạ độ đỉnh D là:
A. D 2;3 .
B. D 6;3 . C. D 6;5 D. D 2;5 . Lời giải. Chọn D Gọi D ,
x y là điểm cần tìm
Ta có : AB 2; 1 , DC 4 ; x 4 y 4 x 2
Để ABCD là hình bình hành AB DC D 2;5 . 4 y 1
Câu 4: [0H1-5-2] Cho tam giác. ABC . Gọi M , N , P lần lượt là trung điểm BC , CA , AB .
Biết A1;3 , B 3
;3, C 8;0 . Giá trị của x x x bằng: M N P A. 2 . B. 3 . C. 1. D. 6 . Lời giải. Chọn D 5
Ta có : M là trung điểm BC x M 2 9
N là trung điểm AC x N 2
P là trung điểm AB x 1 P 5 9
x x x 1 6 M N P 2 2 A1; 1 B 1 ;2 C 0 ;1
Câu 5: [0H1-5-2] Cho hình bình hành ABCD . Biết , , . Tọa độ điểm D là: A. 2;0 . B. 2 ;0 C. 2 ;2 . D. 2; 2 Lời giải. Chọn A Gọi D ,
x y là điểm cần tìm Ta có : AB 2 ;1 , DC ;1 x y x 2
Để ABCD là hình bình hành AB DC D 2;0 . 1 y 1
A2;5 B1;7 C 1;5 D 0;9
Câu 6: [0H1-5-2] Cho bốn điểm , , ,
. Ba điểm nào sau đây thẳng hàng: A. , A B, C . B. , A C, D .
C. B, C, D . D. , A B, D . Lời giải. Chọn D
Ta có: AB 1; 2 , AC 1
;0 , AD 2;4 AD 2AB ,
A B, D thẳng hàng.
Câu 7: [0H1-5-2]Trong mặt phẳng Oxy cho 3 điểm A 1
;3, B 2;0,C 6;2 . Tìm
tọa độ D sao cho ABCD là hình bình hành. A. 9; 1 . B. 3;5 . C. 5;3 . D. 1 ;9. Lời giải Chọn B
ABCD là hình bình hành khi AB DC .
Ta có AB 3; 3, DC 6 ;
x 2 y , D ; x y . 6 x 3 x 3
Nên AB DC D3;5. 2 y 3 y 5
Câu 8: [0H1-5-2] Khẳng định nào sau đây là đúng? A. a 5 ; 0, b 4 ; 0 cùng hướng.
B. c 7; 3 là vectơ đối của d ; 7 3 .
C. u 4; 2, v 8; 3 cùng phương.
D. a 6; 3, b 2; 1 ngược hướng. Lời giải Chọn A 5 5
Ta có a 5; 0 4
; 0 b a, b cùng hướng. 4 4
Câu 9: [0H1-5-2] Cho u 3; 2, v 1; 6. Chọn khẳng định đúng?
A. u v và a 4; 4 ngược hướng.
B. u, v cùng phương.
C. u v và c k.a . h b cùng hướng. D. 2u ,
v v cùng phương. Lời giải Chọn C
Ta có u v 4; 4 và u v 2; 8 4 4 Xét tỉ số a 4; 4 u v và
không cùng phương. Loại A 4 4 3 2 Xét tỉ số
u, v không cùng phương. Loại B 1 6 2 8 Xét tỉ số
3 0 và b 6; 24 cùng hướng. 6 24 u v
Câu 10: [0H1-5-2] Cho u 2i j và v i xj . Xác định x sao cho u và v cùng phương. 1 1 A. x 1 . B. x . C. x . D. x 2 . 2 4 Lời giải Chọn B u
2i j u 2; 1 Ta có
v i xj v x . 1;
Để u và v cùng phương thì 1
v k.u x . 2
Câu 11: [0H1-5-2] Cho a 5
; 0 , b 4; x Tìm x để hai vectơ a, b cùng phương. A. x 5.
B. x 4.
C. x 0. D. x 1. Lời giải Chọn C
Câu 12: [0H1-5-2] Cho a ;
x 2 , b 5; 1 , c ;
x 7 . Tìm x biết c 2a 3b . A. x 15.
B. x 3.
C. x 15. D. x 5. Lời giải Chọn C x x Ta có ; x 7 2 ; x 2 3 5 2 15 ; 1 x 15 7 2.2 3.1
Câu 13: [0H1-5-2] Cho a 2; 4 , b 5; 3 . Tìm tọa độ của u 2a b
A. u 7; 7 .
B. u 9; 11
C. u 9; 5 . D. u 1 ; 5 . Lời giải Chọn B
Ta có u 2 2; 4 5 ; 3 9; 11 .
Câu 14: [0H1-5-2] Cho ba vectơ a 2;
1 , b 3; 4 , c 7; 2 . Giá trị của k, h để
c k.a . h b là:
A. k 2, 5; h 1 ,3.
B. k 4, 6; h 5 ,1.
C. k 4, 4; h 0, 6.
D. k 3, 4; h 0, 2. Lời giải Chọn C
k.a 2k; k
7 2k 3h k 4,4 Ta có
c k a h b . . h b 3 ; h 4h . .
2 k 4h h 0 ,6
Câu 15: [0H1-5-2] Trong hệ tọa độ Oxy, cho hình bình hành OABC, C O .
x Khẳng định nào sau đây đúng?
A. AB có tung độ khác 0. B. ,
A B có tung độ khác nhau.
C. C có hoành độ khác 0.
D. x x x 0. A C B Lời giải Chọn C
Ta có OABC là hình bình hành AB OC x ; 0 . C
Câu 16: [0H1-5-2] Trong hệ tọa độ Oxy, cho bốn điểm A 5 ; 2, B 5
; 3 , C 3; 3 ,
D 3; 2 . Khẳng định nào sau đây đúng? A. A ,
B CD cùng hướng.
B. ABCD là hình chữ nhật. C. I 1 ;1 là trung điểm . AC
D. OA OB O . C Lời giải Chọn B
Ta có AB 0; 5 , DC 0; 5 , AD 8; 0 . A .
B AD 0 AB AD 1
AB DC ABCD là hình bình hành 2
1 2 ABCD là hình chữ nhật.
Câu 17: [0H1-5-2] Trong hệ tọa độ Oxy, cho bốn điểm A3; 2 , B 7; 1 , C 0; 1 , D 8
; 5 . Khẳng định nào sau đây đúng? A. A ,
B CD là hai vectơ đối nhau. B. A ,
B CD ngược hướng. C. A ,
B CD cùng hướng. D. ,
A B, C, D thẳng hàng. Lời giải Chọn B
Ta có AB 4; 3 , CD 8 ; 6 2 AB A ,
B CD ngược hướng.
Câu 18: [0H1-5-2] Trong hệ tọa độ Oxy, cho A 1
; 5 , B5; 5 , C 1 ; 1 1 . Khẳng định nào sau đây đúng? A. ,
A B, C thẳng hàng. B. A ,
B AC cùng phương. C. A ,
B AC không cùng phương. D. A ,
B AC cùng hướng. Lời giải Chọn C
Ta có AB 6; 0 , AC 0; 6 A ,
B AC không cùng phương.
Câu 19: [0H1-5-2] Trong hệ tọa độ Oxy, cho ba điểm A 1 ;
1 , B 1; 3 , C 2 ; 0.
Khẳng định nào sau đây sai?
A. AB 2A . C B. ,
A B, C thẳng hàng. 2 C. BA BC.
D. BA 2CA 0. 3 Lời giải Chọn A
Ta có AB 2; 2 , AC 1 ; 1 và AB 2 A . C
Câu 20: [0H1-5-2] Trong hệ tọa độ Oxy, cho ba điểm A1; 3 , B 1 ; 2 , C 2 ; 1 . Tìm
tọa độ của vectơ AB AC ? A. 5 ; 3. B. 1; 1 . C. 1 ; 2 . D. 4; 0 . Lời giải Chọn B
Ta có AB AC CB 1; 1 .
Câu 21: [0H1-5-2] Trong hệ tọa độ Oxy, cho bốn điểm A1;
1 , B 2;
1 , C 4; 3 ,
D 3; 5 . Khẳng định nào sau đây đúng? 5
A. Tứ giác ABCD là hình bình hành. B. G 2;
là trọng tâm tam 3 giác BC . D
C. AB C . D
D. AC, AD cùng phương. Lời giải Chọn A
Ta có AB 1; 2, DC 1; 2 Tứ giác ABCD là hình bình hành.
Câu 22: [0H1-5-2] Trong hệ tọa độ Oxy, cho M 3; 4 Gọi M , M lần lượt là hình chiếu 1 2
vuông góc của M trên Ox, .
Oy Khẳng định nào đúng? A. OM 3.
B. OM 4. 1 2
C. OM OM 3 ; 4 .
D. OM OM 3; 4 . 1 2 1 2 Lời giải Chọn D
Ta có M 3; 0 , M 0; 4 2 1 A. Sai vì OM 3. 1 B. Sai vì OM 4. 2
C. Sai vì OM OM M M 3; 4 . 1 2 2 1
Câu 23: [0H1-5-2] Trong hệ tọa độ Oxy, cho hình vuông ABCD có gốc O làm tâm hình
vuông và các cạnh của nó song song với các trục tọa độ. Khẳng định nào đúng?
A. OA OB A . B
B. OA O ,
B DC cùng hướng.
C. x x , y y .
D. x x , y y . A C A C B C B C Lời giải Chọn A
Ta có OA OB CO OB CB A .
B (do OA CO ).
Câu 24: [0H1-5-2] Trong hệ tọa độ Oxy, cho ba điểm A2;
1 , B 0; 3 , C 3; 1 . Tìm
tọa độ điểm D để ABCD là hình bình hành. A. 5; 5 .
B. 5; 2 .
C. 5; 4 . D. 1 ; 4. Lời giải Chọn A A B D C Gọi D ;
x y, ABCD là hình bình hành AD BC x 2; y 1 3; 4 x 2 3 x 5 y 1 4 y 5
Vậy D 5; 5 .
Câu 25: [0H1-5-2] Trong hệ tọa độ Oxy, cho ba điểm A1;
1 , B 3; 2, C 6; 5 . Tìm tọa
độ điểm D để ABCD là hình bình hành. A. 4; 3 . B. 3; 4 . C. 4; 4 . D. 8; 6 . Lời giải Chọn C Gọi D ;
x y , ABCD là hình bình hành AD BC x 1; y 1 3; 3 . x 1 3 x 4 y 1 3 y 4
Vậy D 4; 4 .
Câu 26: [0H1-5-2] Cho ba điểm M , N , K thỏa MN k MP . Tìm k để N là trung điểm MP? 1 A. . B. 1. C. 2. D. 2. 2 Lời giải Chọn A 1
Ta có N là trung điểm MP MN . MP 2
Câu 27: [0H1-5-2] Trong hệ tọa độ Oxy, cho tam giác ABC có B 9; 7, C 11; 1 . Gọi
M , N lần lượt là trung điểm của AB, AC. Tìm tọa độ vectơ MN ?
A. 2; 8 .
B. 1; 4 .
C. 10; 6 . D. 5; 3 . Lời giải Chọn B A N M C B 1 1 Ta có MN BC
2; 8 1; 4. 2 2
Câu 28: [0H1-5-2] Trong hệ tọa độ Oxy, cho tam giác ABC có
M 2; 3, N 0; 4, P 1
; 6 lần lượt là trung điểm của các cạnh BC,C , A AB .
Tìm tọa độ đỉnh A ? A. 1; 5 . B. 3 ; 1 . C. 2 ; 7 . D. 1; 10 . Lời giải Chọn B A N P C M B Gọi A ;
x y . Ta có PA MN x 1; y 6 2; 7 . x 1 2 x 3 . Vậy A 3 ; 1 .. y 6 7 y 1
Câu 29: [0H1-5-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A6; 1 , B 3 ; 5 và trọng tâm G 1 ;
1 . Tìm tọa độ đỉnh C ?
A. 6; 3 . B. 6 ; 3 . C. 6 ; 3. D. 3 ; 6 . Lời giải Chọn C
6 3 x 1 x 6 Gọi C ;
x y . Ta có 3
G là trọng tâm 1 5 y y 3 1 3 Vậy C 6 ; 3.
Câu 30: [0H1-5-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A1; 1 , B 2 ; 2, C 7
; 7 . Khẳng định nào sau đây đúng?
A. G 2; 2 là trọng tâm tam giác . ABC
B. B ở giữa hai điểm A và C.
C. A ở giữa hai điểm B và C. D. A ,
B AC cùng hướng. Lời giải Chọn C Ta có AB 3
; 3, AC 6; 6 và AC 2 AB
Vậy A ở giữa hai điểm B và C.
Câu 31: [0H1-5-2] Trong hệ tọa độ Oxy, cho tam giác ABC có A 2
; 2, B3; 5 và
trọng tâm là gốc O . Tìm tọa độ đỉnh C ? A. 1 ; 7.
B. 2; 2 . C. 3 ; 5. D. 1; 7 . Lời giải Chọn A 2 3 x 0 x 1 3 Gọi C ;
x y . Ta có O là trọng tâm 2 5 y y 7 0 3 Vậy C 1 ; 7.
Câu 32: [0H1-5-2] Trong hệ tọa độ Oxy, cho A2; 5, B 1;
1 , C 3; 3 . Tìm tọa độ đỉểm
E sao cho AE 3AB 2AC
A. 3; 3 . B. 3 ; 3 . C. 3 ; 3 . D. 2 ; 3. Lời giải Chọn C Gọi E ;
x y .
Ta có AE 3AB 2AC AE AB 2 AB AC BE 2CB x y x 1 4 x 3 1; 1 2 2; 2 y 1 4 y 3 Vậy E 3 ; 3 .
Câu 33: [0H1-5-2] Cho 3 điểm A–4;0 , B –5;0, C 3;0 . Tìm điểm M trên trục Ox sao
cho MA MB MC 0 . A. –2;0 .
B. 2; 0 . C. –4;0 .
D. –5;0 . Lời giải Chọn A 4 5 3
Ta có M Ox nên M x; 0 . Do MA MB MC 0 nên x 2 . 3
Câu 34: [0H1-5-2] Cho 3 vectơ a 5; 3 ; b 4; 2 ; c 2; 0 . Hãy phân tích vectơ c theo
2 vectơ a và b .
A. c 2a 3b . B. c 2 a 3b .
C. c a b . D.
c a 2b . Lời giải Chọn B 5
m 4n 2 m 2
Giả sử c ma nb , ta có: .
3m 2n 0 n 3
Câu 35: [0H1-5-2] Cho hai điểm M –2; 2 , N 1;
1 . Tìm tọa độ điểm P trên Ox sao cho 3
điểm M, N, P thẳng hàng.
A. P 0; 4 .
B. P 0; –4 .
C. P –4;0 . D. P 4; 0 . Lời giải Chọn D
Do P Ox nên P x;0 , mà MP x 2; 2 ; MN 3; 1 x 2 2
Do M, N, P thẳng hàng nên x 4 3 . 1
Câu 36: [0H1-5-2] Trong mặt phẳng Oxy , cho ba vectơ a (1; 2),b ( 3 ;1),c ( 4 ;2) . Biết
u 3a 2b 4c . Chọn khẳng định đúng.
A. u cùng phương với i .
B. u không cùng phương với i .
C. u cùng phương với j .
D. u vuông góc với i . Lời giải Chọn B x 3.1 2.( 3 ) 4.( 4 ) 1 9 Gọi u ( ; x y) . Ta có u ( 1 9;16) .
y 3.2 2.1 4.2 16
Câu 37: [0H1-5-2] Cho hình bình hành ABCD biết ( A 2
;0), B(2;5),C(6;2) . Tọa độ điểm D là A. D(2; 3) . B. D(2;3) . C. D( 2 ; 3 ) . D. D(2; 3) . Lời giải Chọn A
Gọi D(x; y) . Ta có AD (x 2; y), BC (4; 3 ) x 2 4 x 2
AD BC D(2; 3 ). y 3 y 3
Câu 38: [0H1-5-2] Cho ABC với (
A 2; 2) , B(3;3) , C(4;1) . Tìm toạ độ đỉnh D sao cho
ABCD là hình bình hành. A. D(5; 2) . B. D(5; 2) . C. D(5; 2) . D. D(3; 0) . Lời giải Chọn D
Gọi D(x; y) . Ta có AD (x 2; y 2), BC (1; 2 ) x 2 1 x 3
AD BC D(3; 0) . y 2 2 y 0
Câu 39: [0H1-5-2] Cho bốn điểm ( A 1; 1
), B(2;4),C( 2 ; 7
), D(3;3) . Ba điểm nào trong bốn
điểm đã cho thẳng hàng? A. , A B, C . B. , A B, D .
C. B, C, D . D. , A C, D . Lời giải Chọn D 3
AB (1;5), AC ( 3 ; 6)
, AD (2;4) AC AD ,
A C, D thẳng hàng. 2
Câu 40: [0H1-5-2] Trong mặt phẳng Oxy , cho ABC với (
A 2; 2), B(3;3), C(4;1) . Tìm toạ độ
đỉnh D sao cho ABCD là hình bình hành. A. D(5; 2) . B. D(5; 2) . C. D(5; 2) . D. D(3; 0) . Lời giải Chọn D
Gọi D(x; y) . Ta có AD (x 2; y 2), BC (1; 2 ) x 2 1 x 3
AD BC ( D 3;0) . y 2 2 y 0
Câu 41: [0H1-5-2] Trong hệ trục O,i, j cho 2 vectơ a 3 ; 2 , b i
5 j . Mệnh đề nào sau đây sai ?
A. a 3i 2 j . B. b 1; 5 .
C. a b 2 ; 7 . D.
a b 2 ; 3 . Lời giải Chọn D
a 3 ; 2, b 1
; 5 a b 4 ; 3 .
Câu 42: [0H1-5-2] Cho u 2i 3 j , v 5
i j . Gọi X ;Y là tọa độ của w 2u 3v thì tích XY bằng: A. 57 . B. 57 . C. 63 . D. 63 . Lời giải Chọn A
w 2u 3v 22i 3 j 3 5
i j 19i 3j . X 19, Y 3 XY 57 .
Câu 43: [0H1-5-2] Cho A0 ; 2 , B 3 ;
1 . Tìm tọa độ giao điểm M của AB với trục x O x. 1 A. M 2 ; 0 .
B. M 2 ; 0 . C. M ; 0 . D. 2 M 0 ; 2 . Lời giải Chọn A
M x ; 0 x O
x AM x ; 2 ; AB 3 ; 3. x ,
A B, M thẳng hàng A , B AM cùng phương 2 x 2 . 3 3 Vậy, M 2 ; 0 .
Câu 44: [0H1-5-2] Cho u 2x 1; 3 , v 1 ; x 2 . Có hai giá trị x , x của x để u cùng 1 2
phương với v . Tính x .x . 1 2 5 5 5 5 A. . B. . C. . D. . 3 3 2 3 Lời giải Chọn C x
u, v cùng phương 2 1 3 x ) 1 x (với 2 2 5
x x 2 2 1
2 3 2x 3x 5 0 . Vậy x .x . 1 2 2
Câu 45: [0H1-5-2] Cho ba điểm A0 ; 1 , B 0 ; 2
,C 3 ; 0 . Vẽ hình bình hành ABDC .
Tìm tọa độ điểm D . A. D 3 ; 3 . B. D 3 ; 3 .
C. D 3 ; 3 . D. D 3 ; 3 . Lời giải Chọn B x 3 0 x 3 D D
ABDC là hình bình hành CD AB . Vậy y 0 3 y 3 D D D 3 ; 3 .
Câu 46: [0H1-5-2] Hai vectơ nào sau đây không cùng phương: 6 10
A. a 3 ; 5 và b ; . B. c và 4 c . 7 7 5
C. i 1 ; 0 và m ; 0 .
D. m 3 ; 0 và 2
n 0 ; 3 . Lời giải Chọn D
m 3 ; 0 và n 0 ; 3 . Ta có: a b a b 3 3 0 3 0 1 2 2 1
Vậy m và n không cùng phương.
Câu 47: [0H1-5-2] Các điểm và các vectơ sau đây cho trong hệ trục O ;i, j (giả thiết , m ,
n p , q là những số thực khác 0 ). Mệnh đề nào sau đây sai ?
A. a m ; 0 a // i .
B. b 0 ; n b // j .
C. Điểm An ; p x O
x n 0 .
D. A0 ; p, B q ; p thì AB // x Ox . Lời giải Chọn C
An ; p x O
x p 0 .
Câu 48: [0H1-5-2] Cho ba điểm A2 ; 4
, B6 ; 0,C m ; 4 . Định m để , A B, C thẳng hàng ?
A. m 10 . B. m 6 .
C. m 2 . D. m 10 . Lời giải Chọn A
AB 4 ; 4 ; AC m 2 ; 8. m ,
A B, C thẳng hàng A , B AC cùng phương 2 8 m 10 . 4 4
Câu 49: [0H1-5-2] Cho hai điểm A x ; y , B x ; y
. Tọa độ của điểm M mà A A B B
MA k MB k 1 là: x k.x x x x k.x A B x A B x A B x M 1 k M 1 k M 1 k A. . B. . C. . D. y k.y y y y k.y A B y A B y A B y M 1 k M 1 k M 1 k x k.x A B x M 1 k . y k.y A B y M 1 k Lời giải Chọn C x k.x
x x k x x A B x M A M B M 1 k
MA k MB .
y y k y y y k y A M B M . A B y M 1 k
Câu 50: [0H1-5-2] Cho hai điểm M 1 ; 6 và N 6 ; 3 . Tìm điểm P mà PM 2PN .
A. P 11; 0 .
B. P 6; 5 .
C. P 2; 4 . D. P 0; 1 1 . Lời giải Chọn A 1 2.6 x 11 P 1 2
PM 2PN P11 ; 0 . 6 2.3 y 0 P 1 2
Câu 51: [0H1-5-2] Cho 3 điểm A3; 5 , B 6; 4 , C 5; 7 . Tìm tọa độ điểm D biết CD AB . A. D 4 ; 2 .
B. D 8; 6 .
C. D 4; 3 . D. D 6; 8 . Lời giải Chọn B Ta có
x x x x
x x x x 5 6 3 8 D C B A D C B A
CD AB D8; 6.
y y y y
y y y y 7 4 5 6 D C B A D C B A
Câu 52: [0H1-5-2] Trong mặt phẳng Oxy cho A1;3, B 4;9 . Tìm điểm C đối xứng của A qua B .
A. C 7;15 .
B. C 6;14 .
C. C 5;12 . D. C 15;7 . Lời giải Chọn A
C đối xứng của với A qua B B là trung điểm của AC .
2x x x
x 2x x x 2.4 1 7
Câu 53: Tọa độ của B là B A C C B A C C 7; 15
2 y y y
y 2 y y y 2.9 3 15 B A C C B A C
. [0H1-5-2] Ba điểm nào sau đây không thẳng hàng ? A. M 2 ;4, N 2 ;7, P 2 ;2. B. M 2
;4, N 5;4, P7;4.
C. M 3;5, N 2 ;5, P 2 ;7. D. M 5; 5 , N 7; 7 , P 2 ;2. Lời giải Chọn C C. MN 5
; 0, MP 5; 2 MN , MP không cùng phương
M , N , P không thẳng hàng.
Câu 54: [0H1-5-2] Cho 2 điểm A 2 ; 3
, B4;7. Tìm điểm M y O
y thẳng hàng với A và B . 4 1 A. M ;0 . B. M ;0 .
C. M 1;0 . D. 3 3 1 M ; 0 . 3 Lời giải Chọn B M y O
y M 0; m . AM 2; m 3; AB 6; 10 . Để 2 m 3 1
A , B , M thẳng hàng thì
3m 3 10 m . 6 10 3
Câu 55: [0H1-5-2] Trong mặt phẳng Oxy cho A 2 ;
m m, B 2 ;
m m. Với giá trị nào của
m thì đường thẳng AB đi qua O ? A. m 3 . B. m 5 . C. m .. D. Không có m . Lời giải Chọn C Ta có OA 2 ;
m m , OB 2 ;
m m . Đường thẳng AB đi qua O khi OA , OB cùng phương
Mặt khác ta thấy OA 2 ;
m m 2 ; m m O B, m
nên AB đi qua O , m .
Câu 56: [0H1-5-2] Trong hệ tọa độ Oxy, cho 4 điểm A3;0, B 4; 3 ,C 8; 1 , D 2 ; 1 . Ba
điểm nào trong bốn điểm đã cho thẳng hàng ?
A. B, C, D . B. ,
A B, C . C. ,
A B, D . D. ,
A C, D . Lời giải Chọn D
Ta có AC 5; 1 ; AD 5 ;
1 AC AD . Vậy ba điểm ,
A C, D thẳng hàng.
Câu 1: [0H1-5-3] Trong hệ tọa độ Oxy, cho bốn điểm A2; 1 , B 2; 1 , C 2 ; 3, D 2 ;
1 . Xét ba mệnh đề:
I ABCD là hình thoi.
II ABCD là hình bình hành.
III AC cắt BD tại M 0; 1 . Chọn khẳng định đúng
A. Chỉ I đúng.
B. Chỉ II đúng.
C. Chỉ II và III đúng.
D. Cả ba đều đúng. Lời giải Chọn C Ta có 0; 2,
0; 2 ABDC AB DC
ABCD là hình bình hành.
Trung điểm AC là 0;
1 III đúng. AC 4
; 4, BD 4
; 0 AC.BD 16 0 AC, BD không vuông góc nhau.
Câu 2: [0H1-5-3] Trong hệ tọa độ Oxy, cho A1; 2, B 2
; 3 . Tìm tọa độ đỉểm I sao
cho IA 2IB 0 2 8 A. 1; 2 . B. 1; . C. 1 ; . D. 5 3 2; 2. Lời giải Chọn C Gọi I ;
x y . Ta có IA 2IB 0 1 ;
x 2 y 2 2 ;
x 3 y 0; 0 x 1 1
x 4 2x 0 8
2 y 6 2y 0 y 3 8 Vậy I 1 ; . 3
Câu 3: [0H1-5-3] Trong hệ tọa độ Oxy , cho hai điểm A2; 3, B 3; 4 . Tìm tọa độ điểm
M trên trục hoành sao cho ,
A B, M thẳng hàng. 5 1
A. M 1; 0.
B. M 4; 0 . C. M ; . D. 3 3 17 M ; 0 . 7 Lời giải Chọn D
Điểm M Ox M ; m 0 .
Ta có AB 1; 7 và AM m 2; 3 . Để m 2 3 17 ,
A B, M thẳng hàng m . 1 7 7
Document Outline
- 1-1.pdf
- Lời giải
- Chọn A
- 1-2.pdf
- Lời giải
- Chọn D
- Lời giải
- Chọn B
- Lời giải
- Chọn D
- Lời giải
- Chọn A
- Lời giải
- Chọn A
- Lời giải
- Chọn B
- Lời giải
- Chọn B
- Lời giải
- Chọn D
- Lời giải
- Chọn C
- Lời giải
- Chọn D
- Lời giải
- Chọn B
- Lời giải
- Chọn B
- Lời giải
- Chọn D
- Lời giải
- Chọn C
- Lời giải
- Chọn C
- Lời giải
- Chọn D
- Lời giải
- Chọn D
- Lời giải
- Chọn D
- 1-3.pdf
- Lời giải
- Chọn D
- Lời giải.
- Do đó Chọn D
- Lời giải
- Chọn B
- Lời giải.
- Từ giả thiết suy ra tam giác đều cạnh nên
- Lời giải
- Chọn D
- Lời giải
- Chọn B
- Lời giải
- Chọn A
- 2-1.pdf
- 2-2.pdf
- Lời giải
- Chọn B
- Lời giải. Xét các đáp án:
- Lời giải
- Chọn D
- Lời giải
- Chọn C
- Lời giải
- Chọn B
- Lời giải
- Chọn B
- Lời giải
- Chọn C
- Lời giải
- Chọn B
- Lời giải
- Chọn A
- Lời giải
- Chọn B
- Lời giải
- Chọn B
- Lời giải
- Chọn B
- Lời giải
- Chọn A
- Lời giải
- Chọn C
- Lời giải
- Chọn D
- 2-3.pdf
- Lời giải
- Chọn C
- Lời giải
- Chọn C
- Lời giải
- Chọn B
- Lời giải
- Chọn D
- Lời giải
- Chọn D
- Ta có lần lượt là đường trung bình của tam giác và .
- là hình bình hành.
- Lời giải
- Chọn A
- Lời giải
- Chọn C
- Lời giải
- Chọn C
- Gọi .
- Gọi là trung điểm của
- Lời giải
- Chọn C
- Lời giải
- Chọn A
- Gọi là trung điểm của .
- Lời giải
- Chọn C
- Lời giải
- Chọn C
- sai
- Không có điểm thỏa mãn.
- 3-2.pdf
- Lời giải
- Chọn D
- Lời giải
- Chọn D
- Lời giải
- Chọn A
- Lời giải
- Chọn D
- Lời giải
- Chọn B
- Ta có
- Lời giải
- Chọn A
- Gọi là trung điểm của
- Suy ra
- Lời giải
- Chọn A
- Gọi là điểm thỏa mãn tứ giác là hình vuông.
- Lời giải
- Chọn B
- Gọi là điểm thỏa mãn tứ giác là hình thoi.
- Ta có
- là hình thoi có
- và là hai tam giác đều
- Lời giải
- Chọn D
- Gọi là điểm thỏa mãn tứ giác là hình bình hành.
- là hình chữ nhật.
- Ta có:
- Lời giải
- Chọn A
- Gọi là trung điểm của
- là trung điểm
- 3-3.pdf
- Lời giải
- Chọn D
- Lời giải
- Chọn C
- Lời giải
- Chọn B
- ( Đáp án. A. Ta có
- Lời giải
- Chọn A
- Lời giải
- Chọn C
- Lời giải
- Chọn A
- Lời giải
- Chọn C
- Lời giải
- Chọn D
- Gọi là trung điểm của
- Ta có
- Mà
- Lời giải
- Chọn A
- Ta có
- là hình bình hành.
- 3-4.pdf
- 5-1.pdf
- 5-2.pdf
- 5-3.pdf




