Bài tập vận dụng cao vectơ, tích vô hướng của hai vectơ và ứng dụng

Tài liệu gồm 144 trang tuyển chọn các bài tập vận dụng cao có lời giải chi tiết chuyên đề vectơ, tích vô hướng của hai vectơ và ứng dụng trong chương trình Hình học 10 chương 1 – 2.

Các bài toán trong tài liệu được phân dạng thành 6 vấn đề:
+ Vấn đề 1: Biểu diễn véctơ.
+ Vấn đề 2: Ba điểm thẳng hàng.
+ Vấn đề 3: Quỹ tích.
+ Vấn đề 4: Tỉ lệ.
+ Vấn đề 5: Min – Max.
+ Vấn đề 6: Tích vô hướng.

Chủ đề:

Chương 4: Vectơ (KNTT) 49 tài liệu

Môn:

Toán 10 2.8 K tài liệu

Thông tin:
170 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bài tập vận dụng cao vectơ, tích vô hướng của hai vectơ và ứng dụng

Tài liệu gồm 144 trang tuyển chọn các bài tập vận dụng cao có lời giải chi tiết chuyên đề vectơ, tích vô hướng của hai vectơ và ứng dụng trong chương trình Hình học 10 chương 1 – 2.

Các bài toán trong tài liệu được phân dạng thành 6 vấn đề:
+ Vấn đề 1: Biểu diễn véctơ.
+ Vấn đề 2: Ba điểm thẳng hàng.
+ Vấn đề 3: Quỹ tích.
+ Vấn đề 4: Tỉ lệ.
+ Vấn đề 5: Min – Max.
+ Vấn đề 6: Tích vô hướng.

97 49 lượt tải Tải xuống

Chủ đề: Chương 4: Vectơ (KNTT) 49 tài liệu

Môn: Toán 10 2.8 K tài liệu

Thông tin:

170 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
1
CÁC PHẦN CHÍNH CỦA CHUYÊN ĐỀ
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG
VẤN ĐỀ 3. QUỸ TÍCH
VẤN ĐỀ 4. TỈ LỆ
VẤN ĐỀ 5. MIN,MAX
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
Phần I: Đề Bài
Trang: VĐ1-P1; VĐ2-P12; VĐ3-P14; VĐ4-P17; VĐ5-P20; VĐ6-P28
Phần II: Hướng Dẫn Giải
Trang: VĐ1-P35; VĐ2-P74; VĐ3-P88; VĐ4-P99; VĐ5-P110; VĐ6-P149
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
Email: daytoan2018@gmail.com
Câu 1: Cho tam giác ABC biết 3, 4, 6AB BC AC ,
I
là tâm đường tròn nội tiếp tam giác
ABC
.Gọi
, ,x y z
là các số thực dương thỏa mãn
. . . 0x IA y IB z IC
.Tính
x y z
P
y z x
A.
3
4
P
. B.
41
12
P
. C.
23
12
P
. D.
2
3
P
.
Họ và tên tác giả: Vũ Ngọc Thành Tên FB: Vũ Ngọc Thành
Câu 2: Cho hình bình hành
ABCD
. Gọi
I
là trung điểm của
CD
,
G
là trọng tâm tam giác
BCI
. Đặt
,a AB b AD
. Hãy tìm đẳng thức đúng trong các đẳng thức sau?
A.
5 2
6 3
AG a b
. B.
5
6
AG a b
.
C.
5
6
AG a b
. D.
4 2
3 3
AG a b
.
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet, Email:
tiethanh.78@gmail.com
Câu 3: Cho tam giác
ABC
với các cạnh
AB c BC a CA b , ,
. Gọi I là tâm đường tròn nội tiếp
tam giác ABC. Đẳng thức nào sau đây đúng.
A.
aIA bIB cIC 0
  
B.
0bIA cIB aIC
  
C.
0cIA bIB aIC
  
D.
0cIA aIB bIC
  
Họ và tên: Dương Bảo Trâm Facebook: Bảo Trâm, Email: ilovemath.ddt@gmail.com
Câu 4: Cho hình thang cân ABCD có CD là đáy lớn,
0
30ADC
. Biết DA = a, DC = b, hãy biểu
diễn
DB
theo hai vectơ
DA
và
DC

.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
2
A.
.DB DA DC
B.
3
.
b a
DB DA DC
b
C.
.
b a
DB DA DC
b
D.
.DB bDA aDC
Họ tên: Đỗ Thị Hồng Anh, Đ/c mail: honganh161079@gmail.com
Email: kimduyenhtk@gmail.com, FB: Kim Duyên Nguyễn.
Câu 5: Cho hình bình hành
ABCD
,
M
là điểm thỏa mãn
5 2 0AM CA
 
. Trên các cạnh
AB
,
BC
lần lượt lấy các điểm
,P Q
sao cho
MP BC MQ AB/ / , / /
. Gọi
N
là giao điểm của
AQ
và
CP
. Giá trị của tổng
AN
AQ
CN
CP
bằng:
A.
21
19
B.
24
19
C.
23
19
D.
25
19
Họ và tên tác giả: Phạm Thị Ngọc Tên FB: Giang Thao
Email: thuangiaoyen@gmail.com
Câu 6: Cho tứ giác ABCD, M là điểm tùy ý. K là điểm cố định thỏa mãn đẳng thức
MA MB MC 3MD xMK
. Tìm x:
A. 2. B. 6. C. 5. D. 4.
Email: kimduyenhtk@gmail.com, FB: Kim Duyên Nguyễn.
Câu 7: Cho tam giác
ABC
, trên cạnh
AC
lấy điểm
M
, trên cạnh
BC
lấy điểm
N
sao cho
3AM MC
,
2NC NB
. Gọi
O
là giao điểm của
AN
và
BM
. Tính diện tích tam giác
ABC
biết diện tích tam giác
OBN
bằng 1.
A.
24
. B.
20
. C.
30
. D.
45
Họ và tên: Nguyễn Thanh Hoài, Email: ngthhoai1705@gmail.com
Câu 8: Cho tam giác
ABC
, gọi
I
là điểm trên
BC
kéo dài sao cho
3IB IC
. Gọi
,J K
lần lượt là
những điểm trên cạnh
,AC AB
sao cho
2 ; 3JA JC KB KA
. Khi đó
. .BC m AI n JK
. Tính
tổng
P m n
?
A.
34P
. B.
34P
. C.
14P
. D.
14P
.
Họ và tên tác giả: Trần Ngọc Uyên Tên FB: Tran Ngoc Uyen, Email:
ngocuyen203@gmail.com
Câu 9: Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho
1 1
,
3 2
AM AB DN DC
. Gọi I và J là các điểm thỏa mãn
,BI mBC AJ nAI

.
Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu?
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
3
A.
1
3
B.
3
C.
2
3
D.
1
(Họ và tên tác giả: Phạm Văn Huấn, Tên FB: Pham Van Huan)
Câu 10: Cho tam giác ABC, trên cạnh AB lấ
y
điểm M, trên cạnh BC lấ
y
N sao cho AM=3MB,
NC=2BN. Gọi I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam
giác ICN bằng 2.
A.
3
2
B.
33
2
C.
11
D.
9
11
Họ và tên: Hứa Nguyễn Tường Vy, Email: namlongkontum@gmail.com, FB: nguyennga
Câu 11: Cho ∆ABC có trọng tâm G và hai điểm M, N thỏa mãn:
,
2 0
NA NB
.
Chọn mệnh đề đúng.
A.
4
NG GM
. B.
5
NG GM
. C.
6
NG GM
. D.
7
NG GM
.
(Họ và tên tác giả: Trần Công Sơn, Tên FB: Trần Công Sơn)
Câu 12: (Đẳng thức vec tơ) Cho tam giác
ABC
. Gọi A', B',C' là các điểm xác định bởi
2018 ' 2019 ' 0
A B A C
,
2018 ' 2019 ' 0
B C B A
,
2018 ' 2019 ' 0
C A C B
. Khi đó,
mệnh đề nào sau đây đúng?
A.
ABC
và
' ' 'A B C
có cùng trọng tâm.
B.
' ' ' ABC A B C
.
C.
' ' ' ABC A B C
.
D.
ABC
và
' ' 'A B C
có cùng trực tâm.
(Email): tranminhthao2011@gmail.com
Câu 13: ( tính độ dài vec tơ) Cho tam giác đều
ABC
cạnh
a
. Gọi điểm
M
là trung điểm
BC
. Tính độ
dài của vec tơ
1
2
2
 
AB AC
A.
21
3
a
. B.
21
2
a
. C.
21
4
a
. D.
21
7
a
.
Câu 14: Cho
ABC có M là trung điểm của BC, H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm
x
để
HA HB HC xHO
 
.
A.
x
.2
B.
x
2
. C.
x
.1
D.
x
3
.
Họ và tên: Trần Quốc An, Email: tranquocan1980@gmail.com, Facebook: Tran Quoc An
Câu 15: Cho tam giác
ABC
có đường trung tuyến
CM
vuông góc với phân giác trong
AL
. Giả sử
ngoài ra còn có
CM kAL
. Biết
2
2
cos
a bk
A
c dk
. Tính
a b c d
A.
18
. B.
5
. C.
26
. D.
17
.
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1)
Câu 16: Cho tam giác
ABC
. Gọi
, ,M N P
là các điểm lần lượt thỏa mãn
MA MB
3 0
 
,
AN AC
1
3
 
,
2 3 0
PB PC
Gọi
K
là giao điểm của
AP
và
MN
. Trong các mệnh đề sau, mệnh đề nào
đúng?
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
4
A.
KA KP 4 5 0
 
. B.
KA KP 3 2 0

.
C.
KA KP 0
 
. D. KA KP
 
.
Họ và tên: Phạm Thanh My, Email: phamthanhmy@gmail.com, Facebook: Pham Thanh
My
Câu 17: Cho hình thang
( / / )ABCD AB CD
có hai đường chéo vuông góc với nhau. Biết
20 . AB CD cm
Tìm .
AC BD
A.
40 .cm
. B.
20 .cm
. C.
30 .cm
. D.
10 .cm
.
Họ và tên tác giả: Nguyễn Thị Yến Tên FB: Nguyễn Yến, Email: ntyen.c3lqd@gmail.com
Câu 18: Cho tam giác
ABC
có
3; 4AB AC
.Gọi
AD
là đường phân giác trong của góc
A
.Biết
AD m AB nAC

.Khi đó tổng m n có giá trị là:
A.
1
B.
1
C.
1
7
D.
1
7
Họ và tên tác giả:Lê Thanh Lâm, Mail:quyphucvn@gmail.com Fb:Thanh Lâm Lê
Câu 19: Cho tam giác
ABC
bất kỳ, gọi
, ,M N P
lần lượt là trung điểm các cạnh
, ,AB BC CA
.
, 'H H
lần lượt là trực tâm các tam giác
,ABC MNP
. Khẳng định nào đúng trong các khẳng định sau?
A.
3 'HA HB HC HH
. B.
2 'HA HB HC HH
.
C.
0HA HB HC
. D.
3 'HM HN HP HH
.
Câu 20: Cho tam giác đều ABC tâm O. M là một điểm bất kì bên trong tam giác. Gọi D, E, F lần lượt là
hình chiếu của M lên BC, CA, AB. Với giá trị nào của k ta có hệ thức:

MD ME MF kMO
A.
1
2
k
. B.
1k
. C.
3
2
k
. D.
2k
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa
Câu 21: Một giá đỡ hình tam được gắn vào tường (như hình vẽ). Tam giác ABC vuông cân tại B.
Người ta treo vào điểm A một vật nặng 10N. Tính độ lớn của các lực tác động vào tường tại B
và C? (Bỏ qua khối lượng của giá đỡ)
A.
10 2 , 10
B C
F N F N
B.
10 , 10 2
B C
F N F
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
5
C.
10
B C
F F N
D.
10 , 10 2
B C
F N F
Họ và tên: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng,Email:
thanhdungtoan6@gmail.com
Câu 22: Cho ba điểm
A
,
B
,
C
thuộc đường tròn tâm
O
, thỏa mãn
0
OA OC OB
. Tính góc
AOB
?
A.
0
120
AOB
. B.
0
90
AOB
. C.
0
150
AOB
. D.
0
30
AOB
.
Họ và tên: Trần Gia Chuân, Tên facebook: Trần Gia Chuân
Câu 23: Cho tam giác
ABC
. Điểm
M
trên cạnh
BC
thỏa mãn
. .AM AB AC
1 2
3 3
 
, khẳng định nào
sau đây là khẳng định đúng?
A.
2
MB MC
. B.
2
MB MC
. C.
2
MC MB
. D.
3
MC MB
.
Họ và tên: Trần Gia Chuân, Tên facebook: Trần Gia Chuân
âu 24. Cho tam giác đều
ABC
nội tiếp đường tròn tâm
,O
M
là một điểm tùy ý nằm bên
trong tam giác đã cho; gọi
'; '; 'A B C
theo thứ tự là hình chiếu vuông góc của
M
lên các cạnh
;BC CA
và
AB
. Khi đó ta có đẳng thức vectơ
' ' ' , . 0,
   
k
k M A MB MC l MO k l
l
là
phân số tối giản. Tính
2 2
2 .k l
.
A.
2 2
2 1
k l
. B.
2 2
2 1
k l
. C.
2 2
2 14
k l
. D.
2 2
2 5
k l
.
Họ và tên tác giả: Cao Văn Tùng Tên FB: Cao Tung
Câu 24: Cho hình vuông ABCD, E,F thõa mãn
1 1
;
3 2
BE BC CF CD
;
AE BF I
Ta có
AI k AB l AD
. Khi đó tỉ số k,l thõa mãn cặp nào sau:
A.
3 2
;
5 5
k l
B.
6 2
;
5 5
k l
C.
5 3
;
6 6
k l
D.
6 1
;
5 3
k l
Họ tên: Nguyễn Thị Trang, Fb: Trang Nguyen
Câu 25: Cho tam giác
ABC
, trên cạnh
AC
lấy điểm
M
, trên cạnh
BC
lấy điểm
N
sao cho:
3
AM MC
,
2
NC NB
, gọi
O
là giao điểm của
AN
và
BM
.Tính diện tích
ABC
biết diện
tích
OBN
bằng 1.
A.
10
. B.
20
. C.
25
. D.
30
.
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Câu 26: Cho tam giác
ABC
có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng
định đúng?
A.
4HA HB HC HO
   
. B.
2HA HB HC HO
  
.
C.
2
3
HA HB HC HO
   
. D.
3HA HB HC HO
   
.
Họ và tên: Nguyễn Văn Quân Tên FB: Quân Nguyễn, Email: Quanvan09@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
6
Câu 27: Cho tam giác
ABC
có
D
là trung điểm của
BC
,
O
là một điểm trên đoạn
AD
sao cho
4
AO OD
. Gọi
E CO AB
,
F BO AC
,
M AD EF
. Khẳng định nào sau
đây đúng?
A.
1
7
MO AD

B.
2
15
MO AD
 
C.
1
8
MO AD

D.
2
7
EM BC
 
Họ và tên tác giả: Nguyễn Đặng, Tên facebook: NT AG
Câu 28: Cho hình thang
ABCD
có
//AB CD
. Gọi
,M N
lần lượt là trung điểm của
,AC BD
. Kẻ
( )NH AD H AD
và
( )ME BC E BC
. Gọi
I ME NH
, kẻ
( )IK DC K DC
.
Khi đó trong tam giác
MNK
hệ thức nào sau đây đúng?
A.
. . . 0
MK IN NK IM MN IK
B.
.tan .tan .tan 0
IN N IM M IK K
C.
.cot .cot .cot 0
IN N IM M IK K
D.
IM IN IK
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát,Email:
nguyenvantoannbk@gmail.com
Câu 29: Cho
ABC
, điểm
M
thuộc cạnh
BC
sao cho
2018. 2019.
ABM ACM
S S
. Đẳng thức nào sau
đây sai?
A.
2018. 4037.
ABC ACM
S S
. B.
2018. 2019. 0
BM CM
.
C.
4037
.
2018
BC BM
D.
2019
.
4037
ABM ABC
S S
.
Câu 30: Cho tam giác
ABC
.
M
là điểm nằm trên cạnh
BC
sao cho
3
ABC AMC
S S
. Một đường thẳng
cắt các cạnh
, ,AB AM AC
lần lượt tại
, ,B M C
phân biệt. Biết rằng
2 .
AB AC AM
k
AB AC AM
.
Tìm số
k
.
A.
1
k
. B.
2
k
. C.
3
k
. D.
2
3
.
(Tác giả: Nguyễn Văn Phùng,Gmail: nvpmaster0808@gmail.com)
Câu 31: Cho
n
điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là
1 2
, ,...,
n
A A A
. Bạn Bình kí hiệu
chúng là
1 2
, ,...,
n
B B B
(
1
n
A B
). Vectơ tổng
1 1 2 2
...
n n
A B A B A B

bằng
A.
0
. B.
1
n
A A
. C.
1
n
B B
. D.
1
n
A B
.
(Sưu tầm, Tên FB: Trung Nguyễn Chí)
Câu 32: Trong đường tròn (O) với hai dây cung AB và CD cắt nhau tại M. Qua trung điểm S của BD kẻ
SM cắt AC tại K sao cho
AK
a
CK
.Tính:
2
2
AM
CM
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
7
A. 2a B.
2
a
C.
2
1
a
D. a
Câu 33: Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn:
2 1
,
3 4
BD BC AE AC
.
Điểm K trên AD sao cho 3 điểm B, K,E thẳng hàng. Xác định tỷ số
AK
AD
A.
1
2
B.
1
3
C.
1
4
D.
1
5
Câu 34: Cho tam giác ABC vuông tại C, có
,AC b BC a
, D là chân đường cao kẻ từ C.
Khẳng định nào sau đây là đúng?
A.
2 2
2 2 2 2
a b
CD CA CB
a b a b
. B.
2 2
2 2 2 2
a b
CD CA CB
a b a b
.
C.
2 2
2 2 2 2
a b
CD AC BC
a b a b
D.
2 2
2 2 2 2
a b
CD AC BC
a b a b
.
Facebook: Lê Văn Kỳ, Email: lethithuy@thpthv.vn
Câu 35:
Cho tam giác ABC có trọng tâm G. Gọi I là điểm xác định bởi
5 7 0.IA IB IC
Gọi E là
giao điểm của AI và BG. Tính tỷ số
.
EA
EI
A. 2. B.
1
.
2
C. 3. D.
1
.
3
(Họ tên tác giả: Nguyễn Thị Thu Huyền. Tên FB: Thu Huyen Nguyen)
Câu 36: Cho 2 tia Ox, Oy vuông góc. Trên tia Ox lấy các điểm A,B sao cho OA = OB = 1. C là điểm
thuộc đoạn OA, N là một điểm thuộc đoạn OB và dựng hình vuông OCMN. Trên đoạn CM lấy
điểm Q và dựng hình vuông ACQP. Gọi S là giao điểm của AM và PN. Giả sử
OAkOC
,
AMxAS
, NPyNS ,
1;
2
1
k
Khi x + y =
10
13
thì k =
b
a
, với
ba,
và a, b nguyên tố cùng nhau thì a.b bằng
A. 7 B. 4 C. 5 D.
12
Email: nghiepbt3@gmail.com, FB: Ngô Quang Nghiệp
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
8
Câu 37: Cho tam giác
ABC
. Giả sử điểm
M
nằm trên cạnh
BC
thỏa các tam giác
,
MAB MAC
lần
lượt có diện tích là
1 2
,S S
. Khẳng định nào sau đây đúng?
A.
1 2 2 1
.S S AM S AB S AC
B.
1 2 1 2
.S S AM S AB S AC
C.
2 1 2 1
.S S AM S AB S AC
D.
2 1 1 2
.S S AM S AB S AC
Họ Tên: Lê Duy Tên FB: Duy Lê Email: Duyleag@gmail.com
Câu 38: Cho tam giác ABC có có M là trung điểm của BC,
1
2
AI MI
. Điểm K thuộc cạnh AC sao
cho B,I,K thẳng hàng. Khi đó
m
KA CK
n
. Tính
25 6 2019S m n
A.
2019
S
. B.
2068
S
. C.
2018
S
. D.
2020
S
.
Họ và tên tác giả: Nguyễn Đức Duẩn Tên FB: Duan Nguyen Duc, Email:
Duanquy@gmail.com
Câu 39: Cho tam giác ABC có trọng tâm G, lấy các điểm I, J sao cho
IA 2IB
và
3JA 2JC 0
và thỏa
mãn đẳng thức
IJ kIG
. Giá trị của biểu thức
2 2 500
P (25k 36)(k k 1)
là:
A.
P 1235
B.
P 0
C.
5
P
6
D.
6
P
5
Họ và tên: Nguyễn Quang Huy, Fb: Nguyễn Quang Huy, Email: boigiabao98@gmail.com
Câu 40: Cho tam giác
ABC
. M là điểm nằm trên cạnh BC sao cho
ABC AMC
S S 3
. Một đường thẳng
cắt các cạnh
AB AM AC, ,
lần lượt tại
B M C', ', '
phân biệt. Biết
' ' '
AB AC AM
m n
AB AC AM
.
Tính
m n
.
A. 2. B. 5. C. 3. D. 4.
(Họ và tên tác giả: Nguyễn Thị Trà My, Tên FB: Nguyễn My)
Câu 41: Cho tam giác
ABC
có
D
là trung điểm của
BC
,
O
là một điểm trên đoạn
AD
sao cho
4
AO OD
. Gọi
E CO AB
,
F BO AC
,
M AD EF
. Khẳng định nào sau
đây đúng?
A.
1
7
MO AD

B.
2
15
MO AD
 
C.
1
8
MO AD

D.
2
7
EM BC
 
Họ và tên tác giả: Nguyễn Đặng, Tên facebook: NT AG
Câu 42: Cho hình thang
ABCD
có
//AB CD
. Gọi
,M N
lần lượt là trung điểm của
,AC BD
. Kẻ
( )NH AD H AD
và
( )ME BC E BC
. Gọi
I ME NH
, kẻ
( )IK DC K DC
.
Khi đó trong tam giác
MNK
hệ thức nào sau đây đúng?
A.
. . . 0
MK IN NK IM MN IK
B.
.tan .tan .tan 0
IN N IM M IK K
C.
.cot .cot .cot 0
IN N IM M IK K
D.
IM IN IK
Câu 43: Cho hình bình hành
ABCD
. Gọi
I
là trung điểm của
CD
,
G
là trọng tâm tam giác
BCI
. Đặt
,
a AB b AD
 
. Hãy tìm đẳng thức đúng trong các đẳng thức sau?
A.
5 2
6 3
AG a b
. B.
5
6
AG a b
.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
9
C.
5
6
AG a b
. D.
4 2
3 3
AG a b
.
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet, Email:
tiethanh.78@gmail.com
Câu 44: Một đường thẳng cắt các cạnh
, DA DC
và đường chéo
DB
của hình bình hành
ABCD
lần
lượt tại các điểm
, E F
và
.M
Biết
. ,DE m DA

.DF n DC
( , 0).
m n
Khẳng định đúng là:
A.
.
m n
DM DB
m n

. B.
m
DM DB
m n

.
C.
n
DM DB
m n

. D.
.m n
DM DB
m n

.
(Email): locleduc10@gmail.com
(Họ và tên tác giả: Lê Đức Lộc, Tên FB: Lê Đức Lộc)
Câu 45:
Hình thang cân ABCD có độ dài đường cao
; / / , 3; 2;
AH a AB CD AB a AD a AB DC
AC cắt BH tại I.
Biết
; ; ; ;
x y z
AI AC x y z m N
m
.
Tính tổng
T x y z m
A. 20 B. 18 C. 17 D. 21
Họ và tên tác giả: Nguyễn Thị Phương Thu FB: Buisonca Bui
Câu 46: Cho hình thang ABCD với O là giao điểm của hai đường chéo AC và BD. Qua O vẽ đường
thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên AD và BC theo thứ tự
tại M và N. Với
AB a
,
D
C b
, khi đó
MN
bằng:
A.
a. .AB b DC
a b
. B.
. .b AB a DC
a b
. C.
a. .AB b DC
a b
. D.
. .b AB a DC
a b
.
Họ và tên: Nguyễn Thanh Tâm Tên FB: Tâm Nguyễn
Câu 47: Cho tam giác
ABC
đều tâm
O
; điểm
M
thuộc miền trong tam giác
OBC
;
D
,
E
,
F
lần lượt
là hình chiếu vuông góc của
M
trên
BC
,
CA
,
AB
. Khẳng định nào sau đây đúng?
A.
1
2
MD ME MF MO
. B.
MD ME MF MO
   
.
C.
3
MD ME MF MO

. D.
3
2
MD ME MF MO
.
Phan Minh Tâm
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG
Email: phunghang10ph5s@gmail.com
Câu 48: Cho hình bình hành
ABCD
có các điểm
, ,M I N
lần lượt thuộc các cạnh
, ,AB BC CD
sao cho
1 1
, ,
3 2
AM AB BI kBC CN CD
. Gọi
G
là trọng tâm tam giác
BMN
. Xác định
k
để
AI
đi
qua
G
.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
10
A.
1
3
. B.
9
13
. C.
6
11
. D.
12
13
.
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng
Câu 49: Cho tam giác
ABC
. Gọi M là điểm thuộc cạnh AB, N là điểm thuộc cạnh AC sao cho
AM AB AN AC
1 3
,
3 4
. Gọi O là giao điểm của CM và BN. Trên đường thẳng BC lấy E.
Đặt
BE xBC
 
.
Tìm x để A, O, E thẳng hàng.
Chọn C
A.
2
3
B.
8
9
C.
9
13
D.
8
11
Ý tưởng: Cho tam giác
ABC
,
I
là trung điểm của
BC
. Gọi
, , P Q R
là các điểm xác
định bởi:
, ,
AP pAB AQ q AI AR r AC

với
0
pqr
.
Chứng minh rằng:
, , P Q R
thẳng hàng khi và chỉ khi
2 1 1
q p r
.
Họ và tên: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng, Email:
thanhdungtoan6@gmail.com
Câu 50: Cho tam giác
ABC
. Gọi
I
là trung điểm
BC
;
P
là điểm đối xứng với
A
qua
B
;
R
là điểm
trên cạnh
AC
sao cho
2
5
AR AC
. Khi đó đường thẳng
AR
đi qua điểm nào trong các điểm
sau đây?
A. Trọng tâm tam giác
ABC
. B. Trọng tâm tam giác
ABI
.
C. Trung điểm
AI
. D. Trung điểm
BI
.
(có thể phát triển P, J, G, M, R thẳng hàng với J – có lẽ là trung điểm BH, còn M chia
AI theo tỷ số tính được)
Câu 51: Cho
ABC
có
H
là trung điểm của
AB
và
: 2
G AC GC AG
. Gọi
F
là giao điểm của
CH
và
BG
. Tìm điểm
I
trên
BC
sao cho
, ,I F A
thẳng hàng
A.
2 .

IC IB
B.
2 .

IB IC
C.
.IB IC
D.
3 .

IC IB
Câu 52: Cho tam giác ABC. I là trung điểm của BC. Gọi M, N, P lần lượt là các điểm xác định bởi
; ;
AM mAB AN nAI AP pAC

, với
0
mnp
. Tìm điều kiện của
, ,m n p
để M, N, P thẳng
hàng.
A.
mp mn np
B.
2
mp mn np
C.
2
np mn mp
D.
2
mn mp np
Họ và tên tác giả: Hoàng Thị Trà FB: Hoàng Trà
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
11
Câu 53: Cho tam giác ABC. Gọi G là trọng tâm của tam giác, I là trung điểm của BC, M và N là các
điểm được xác định bởi
1
2
3 4 0
CN BC
MA MB
. Gọi P là giao điểm của AC và MN. Tính tỉ số diện
tích tam giác ANP và tam giác CNP.
A. 3 B.
7
2
C. 4 D. 2
Câu 54: Cho tam giác
ABC
. Gọi
,D E
lần lượt là các điểm thỏa mãn:
2
;
3
BD BC
1
AC
4
AE
. Điểm
K
trên
AD
thỏa mãn
a
b
AK AD
(với
a
b
là phân số tối giản) sao cho 3 điểm
, ,B K E
thẳng
hàng. Tính
2 2
P a b
.
A.
10
P
. B.
13
P
. C.
29
P
. D.
5
P
.
Câu 55: Cho tam giác ABC, I là điểm thỏa mãn:
2 4 0
IA IB IC
K là điểm thỏa mãn:
2 3 0
KA KB KC
P là điểm thỏa mãn:
0
PA mPB nPC
Có bao nhiêu cặp
, , , , , 10;10
m n m n Z m n
sao cho
, ,I K P
thẳng hàng.
A. 2 B. 3 C.
4
D. 5
Email: themhaitotoanyp1@gmail.com, (Fb: Lưu Thêm)
Câu 56: Cho tam giác
ABC
,
M
và
N
là hai điểm thỏa mãn:
2
BM BC AB

,
CN x AC BC
. Xác
định
x
để
A
,
M
,
N
thẳng hàng.
A.
3.
B.
1
.
3
C.
2.
D.
1
.
2
Email : boyhanam@gmail.com
Câu 57: Cho tam giác
ABC
có
G
là trọng tâm,
I
là trung điểm
AG
, lấy
K
thuộc cạnh
AC
sao cho
. Nếu thẳng hàng thì giá trị của nằm trong khoảng?
A. B. C. D.
(Họ tên: Nguyễn Thu Hương. Tên FB: Thu Hương)
Câu 58: Cho tam giác , là điểm thuộc cạnh sao cho , thuộc sao cho
, là điểm thuộc . Biết rằng ba điểm thẳng hàng khi .
Khẳng định nào sau đây là đúng?
A. . B. . C. . D. .
Họ và tên: Trần Văn Luật, Email: Tvluatc3tt@gmail.com, FB: Trần Luật
Họ và tên: Hoàng Thị Kim Liên
AK kAC
B, I, K
k
1
0;
6
1
0;
2
1 1
;
5 3
1
;1
5
ABC
M
AC
2.MA MC
N
BM
3
NB NM
P
BC
, ,A N P
PB kPC
5
3;
2
k
5
; 1
2
k
1
1;
2
1
;0
2
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
12
Câu 59: Cho tam giác . Gọi lần lượt nằm trên đường thẳng sao cho
, . Tính tích để thẳng hàng?
A. . B. . C. . D. .
Email: lientiencl@gmail.com, Facebook: Kim Liên
Câu 60: Cho hình bình hành ABCD gọi M là trung điểm của cạnh CD, N là điểm thuộc cạnh AD sao cho
. Gọi G là trọng tâm của tam giác BMN, đường thẳng AG cắt BC tại K. Khi đó
( là tối giản). Tính
A. . B. . C. . D. .
( Tên FB: Phùng Hằng )
Câu 61: Cho hình thang có đáy , , . , lần lượt là các điểm thuộc cạnh
và sao cho , . Gọi là giao điểm của và ; là
giao điểm của và ; Khi đó , với là phân số tối giản. Khi đó
bằng
A. . B. . C. . D. .
Họ tên: Bùi Thị Lợi Facebook: LoiBui
Câu 62: Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = 3MC, NC
= 2BN. Gọi I là giao điểm của AN và BN. Tính diện tích tam giác ABC biết diện tích tam giác
ABN bằng 4.
A. . B. . C. . D. .
Họ và tên tác giả: Vũ Thị Hằng Tên FB: Đạt Lâm Huy
Câu 63: Cho tam giác ABC M thuộc cạnh AC sao cho , N thuộc BM sao cho
, P thuộc BC sao cho . Tìm giá trị k để ba điểm A, N, P thẳng hàng.
A. . B. . C. . D. .
Họ và tên: Nguyễn Khắc Sâm Facebook: Nguyễn Khắc Sâm
VẤN ĐỀ 3. QUỸ TÍCH
Câu 64: Cho tam giác với là điểm thoả mãn , gọi là điểm thuộc
và thoả mãn . Xác định để thẳng hàng.
A. . B. . C. . D.
Nguyễn Văn Dũng Fb: Nguyễn Văn Dũng, Email: dungtoanc3hbt@gmail.com
Câu 65: Cho hình vuông tâm cạnh . Biết rằng tập hợp các điểm thỏa mãn
là một đường tròn có bán kính . Khẳng định nào sau đây
đúng?
ABC
M,
N,
P
BC,
CA,
AB
MB mMC
 
,NC nNA
 
PA k PB
 
mnk
M,
N,
P
1
1
2
2
1
3
AN AD
m
BK BC
n
m
n
S m n
16
S
17
S
18
S
19
S
ABCD
AB
CD
2
CD AB
M
N
AD
BC
5
AM MD
3 2
BN NC
P
AC
MN
Q
BD
MN
PM QN a
PN QM b
a
b
a b
386
385
287
288
110
ABC
S
115
ABC
S
125
ABC
S
120
ABC
S
MCMA .2
NMNB .3 PCkPB .
k
1
2
k
2
k
1
2
k
2
ABC
J
2 5 3 0JA JB JC

E
AB
AE kAB
k
, ,C E J
2; 1
k
1;0
k
0;1
k
1;2
k
ABCD
O
1
M
2 2 2 2
2 2 9
MA MB MC MD
R
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
13
A. . B. . C. . D. .
(Sưu tầm: Lê Hồ Quang Minh – FB: Lê Minh)
Câu 66: Cho tam giác . Tập hợp những điểm thỏa mãn:
là:
A. Đường thẳng đi qua B. Đường thẳng qua và
C. Đường tròn D. Một điểm duy nhất.
(Họ và tên tác giả: Cấn Việt Hưng, Tên FB: Viet Hung)
Câu 67: Cho tam giác ABC có hai đỉnh B, C cố định với . Gọi H là trực tâm của tam giác
ABC và M là trung điểm của đoạn BC. Nếu đỉnh A thay đổi nhưng luôn thỏa
thì điểm A luôn thuộc một đường tròn cố định có bán kính bằng
A. . B. . C. . D. .
(Họ và tên tác giả: Ngô Lê Tạo, Tên FB: Ngô Lê Tạo)
Câu 68: Cho hai điểm và cố định. Tìm giá trị để tập hợp điểm thỏa mãn điều kiện
là một đường tròn.
A. . B. . C. . D. .
Câu 69: Cho tam giác vuông tại . Tìm tập hợp sao cho .
A. Đường thẳng. B. Đường tròn. C. Đoạn thẳng. D. Một điểm.
PHẠM THANH LIÊM FB: Liêm Phạm, Email: Phamthanhliem1@gmail.com
Câu 70: Cho tam giác vuông cân tại có . Gọi là tập hợp các điểm trong mặt
phẳng thỏa mãn hệ thức: . Gọi là trung điểm của . Kết luận nào
sau đây đúng?
A. là đường thẳng trung trực của đoạn thẳng .
B. là đoạn thẳng .
C. là đường tròn cố định bán kính .
D. là đường tròn tâm bán kính
(Họ và tên tác giả: Trịnh Văn Thạch, FB: www.facebook.com/thachtv.tc3)
Câu 71: Cho tam giác đều cạnh . Tập hợp các điểm thỏa mãn đẳng thức
nằm trên một đường tròn có bán kính là:
A. . B. . C. . D. .
Câu 72: Cho . Tìm tập hợp các điểm sao cho: .
A. Tập hợp các điểm là một đường tròn.
0;1
R
1; 2
R
1 3
;
2 2
R
3
;2
2
R
ABC
M
4 2
MA MB MC MA MB MC
A
B
C
2BC a
2 2
. 4MA MH MA a
2a
3a
2a
a
A
B
0
k
M
2 2
MA MB k
2
2
3
k AB
2
2
3
k AB
2
2
3
k AB
2
2
3
k AB
ABC
A
M
2 2 2
MB MC MA
ABC
A
5AB cm
( )S
M
. . 25
MAMB MA MC
I
BC
( )S
AI
( )S
AI
( )S
5 10
4
R
( )S
I
5 2
4
R
ABC
a
M
2
2 2 2
5
4
2
a
MA MB MC
C
3
a
4
a
3
2
a
6
a
ABC
M
3 2 2
MA MB MC MA MB MC

M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
14
B. Tập hợp của các điểm là một đường thẳng.
C. Tập hợp các điểm là tập rỗng.
D. Tập hợp các điểm chỉ là một điểm trùng với .
Câu 73: Cho tam giác đều cạnh . Tập hợp các điểm thỏa mãn đẳng thức
nằm trên một đường tròn có bán kính là:
A. . B. . C. . D. .
Họ và tên tác giả: Vũ Thị Nga Tên FB: Linh Nga,Email: linhnga.tvb@gmail.com
Câu 74: Cho đều, có cạnh bằng a. Khi đó tập hợp những điểm sao cho
là:
A. Đường tròn có bán kính .
B. Đường tròn có bán kính .
C. Đường tròn có bán kính .
D. Đường tròn có bán kính .
Câu 75: Cho tìm tập hợp điểm :
Họ và tên tác giả: Tô Quốc An Tên FB: Tô Quốc An, Email: antq4949@gmail.com
Câu 76: Cho tam giác đều cạnh bằng . Biết rằng tập hợp các điểm thỏa mãn đẳng thức
là đường tròn cố định có bán kính bằng:
A. . B. . C. . D. .
(Họ tên: Lê Thị Bích Hải, Tên face: Bich Hai Le)
Câu 77: Cho tam giác có là trọng tâm . Tìm tập hợp điểm thỏa mãn
.
A. Đường tròn đường kính . B. Đường trung trực đoạn thẳng .
C. Đường tròn đường kính . D. Đường trung trực đoạn thẳng .
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông)
Câu 78: Cho đoạn thẳng . Biết rằng tập hợp điểm thỏa mãn là
một đường tròn có bán kính . Tìm giá trị của .
A. . B. . C. . D. .
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông)
M
M
M
A
ABC
a
M
2
2 2 2
5
4
2
a
MA MB MC
C
3
a
4
a
3
2
a
6
a
ABC
M
2
. . .
6
a
MA MB MB MC MC MA

3
a
R
2
a
R
2
3
a
R
3
9
a
R
ABC
M
2
.MB MC AM
ABC
3
M
2 3 4
MA MB MC MB MA
    
1
1
3
3
2
1
2
ABC
G
M
2 2 2
3
MA MB MC BC MA MC MG CB AC
AB
AB
AC
AC
5
AB
M
2 2
3 .MA MB MA MB

R
R
5
2
R
5
2
R
3
2
R
3
2
R
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
15
Câu 79: Cho tam giác , có bao nhiêu điểm thỏa ?
A. . B. .
C. vô số. D. Không có điểm nào.
Họ và tên: Võ Khánh Huyền Vân Fb: Vân Võ, Email: huyenvanqt050185@gmail.com
.
VẤN ĐỀ 4. TỈ LỆ
Câu 80: Cho có ; . Phân giác trong của góc cắt trung tuyến tại
. Tính .
A. . B. . C. . D.
Họ và Tên: Trần Quốc Đại, Email: quocdai1987@gmail.com
Câu 81: [Đề thi olympic 30/4 TPHCM khối không chuyên lần 2 ] Cho gọi điểm nằm trên
cạnh sao cho , là trung điểm của . Một đường thẳng bất kì qua và cắt
các cạnh lần lượt tại . Tình tỉ số
A. . B. .
C. . D.
Họ và Tên: Trần Quốc Đại, Email: quocdai1987@gmail.com
Câu 82: Cho tam giác . Trên cạnh lấy điểm sao cho . Trên cạnh lấy điểm
sao cho . Gọi là trung điểm của . Tia cắt tại . Tỉ số có
giá trị là:
A. . B. . C. . D. .
Họ và tên tác giả: Đỗ Văn Đức Tên FB: Đỗ Văn Đức
Câu 83: (Bài toán tổng quát của bài toán 1). Cho tam giác . Gọi là điểm chia theo tỉ số .
Trên các tia và lấy các điểm . cắt tại . Đặt , . Tỷ
số có giá trị bằng
A. . B. . C. . D. .
Câu 84: (Hệ quả hay dùng của bài toán 2). Cho tam giác . Gọi là trung điểm của BC. Trên các
tia và lấy các điểm . cắt tại . Đặt , . Tỷ số có
giá trị bằng
ABC
M
5
MA MB MC
1
2
ABC
3
AB
4
AC
AD
BAC
BM
I
AD
AI
3
2
AD
AI
10
7
AD
AI
29
20
AD
AI
7
5
AD
AI
ABC
D
BC
2
BD BC
E
AD
E
;AB AC
,M N
2
AB AC
AM AN
2 6
AB AC
AM AN
2 5
AB AC
AM AN
28
2
5
AB AC
AM AN
29
2
5
AB AC
AM AN
ABC
AB
D
2AD DB
AC
E
3CE EA
M
DE
AM
BC
N
BN
CN
1
4
3
8
1
2
2
7
ABC
I
BC
k
AB
AC
,M N
AI
MN
P
AB
b
AM
AC
c
AN
AI
AP
1
b kc
k
1
b kc
k
1
c kb
k
1
c kb
k
ABC
I
AB
AC
,M N
AI
MN
P
AB
b
AM
AC
c
AN
AI
AP
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
16
A. . B. . C. . D. .
Câu 85: Cho tam giác . Gọi lần lượt là các các điểm thỏa mãn .
Điểm trên đoạn thẳng sao cho ba điểm thẳng hàng. Tìm tỉ số .
A. . B. . C. . D. .
Tên: Nam Phương Tên FB: Nam Phương, Email:nguyentrietphuong@gmail.com
Câu 86: Cho tứ giác có hai đường chéo cắt nhau tại thỏa mãn .
Qua trung điểm của dựng đường thẳng cắt tại . Tính tỉ số .
A. . B. . C. . D. .
Email: haivanxinh99@gmail.com Face Hải Vân
Câu 87: Cho tam giác và điểm thỏa mãn . Đường thẳng cắt
đường thẳng tại . Giá trị của tỉ số là:
A. B. C. D.
(Họ và tên tác giả: Ngô Ngọc Hà, Tên FB: Ngô Ngọc Hà)
Câu 88: Cho tam giác . Điểm chia trung tuyến theo tỷ số kể từ đỉnh.
Đường thẳng chia diện tích tam giác theo tỷ số , giá trị của bằng?
A.
B. C.
D.
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
Câu 89: Cho tam giác với là trung điểm . Lấy các điểm thỏa mãn ,
. Gọi là giao điểm của và . Đặt . Hỏi
A. . B. . C. . D. .
Họ và tên: Tăng Lâm Tường Vinh, Facebook: tanglamtuong.vinh
Câu 90: Cho tam giác . Trên cạnh lấy điểm D, trên cạnh BC lấy E, F sao cho ;
;
. Đường thẳng chia đoạn theo tỷ số . Giá trị của bằng?
A.
B. C.
D.
bc
2
b c
2 2
2
b c
2
bc
b c
ABC
,D E
2 1
,
3 4
BD BC AE AC
K
AD
, ,B K E
AD
AK
1
3
AD
AK
3
AD
AK
2
3
AD
AK
3
2
AD
AK
ABCD
O
3 , 4OC OA OD OB
M
AB
MO
CD
N
CN
ND
3
4
1
4
2
3
1
3
ABC
I
23 8 2018 0
IA IB IC
AI
BC
J
JB
JC
23
8
2018
23
2018
8
8
23
ABC
K
AD
3:1
BK
ABC
ABF
BCF
S
k
S
k
5
8
k
3
8
k
3
5
k
3
2
k
ABC
K
BC
M N,
AM AB
3
4
 
AN AC
1
3
 
I
MN
AK
MI xMN AI yAK
,
   
x
y
3
2
4
3
1
5
3
ABC
AB
3
2
AD
DB
1
3
BE
EC
4
1
BF
FC
AE
DF
KD
k
KF
k
3
11
k
11
3
k
3
14
k
11
14
k
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
17
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
Câu 91: Cho tam giác . Kéo dài một đoạn , gọi là trung điểm của . Vẽ hình
bình hành . Đường thẳng cắt tại . Tính tỉ số ?
A. . B. . C. . D. .
Câu 92: Họ và tên: Hoàng Ngọc Lâm,Email: hoangngoclammath1112@gmail.com
Câu 93: Cho tam giác có , . Phân giác trong của góc cắt trung tuyến
tại . Tính tỉ số .
A. . B. . C. . D. .
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Câu 94: Cho hình bình hành , là điểm bất kì trên đoạn , đường thẳng cắt cạnh
tại và đường thẳng tại sao cho . Tỷ số bằng
A. . B. . C. . D. .
Họ và tên: Nguyễn Văn Toản Tên FB: Dấu Vết Hát,Email: nguyenvantoannbk@gmail.com
Câu 95: Cho hai tam giác và ; gọi lần lượt là trọng tâm các tam giác
. Gọi lần lượt là trọng tâm các tam giác ,
. Tính tỉ số ta được kết quả :
A. B. C. D.
Họ và Tên : Nguyễn Văn Mạnh FB : Nguyễn Văn Mạnh, Email :
manhluonghl4@gmail.com
VẤN ĐỀ 5. MIN,MAX
Câu 96: Cho đều cạnh bằng 3, là điểm thuộc đường tròn ngoại tiếp . Đặt
. Gọi lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của . Khi đó,
giá trị biểu thức là:
A. . B. . C. . D. .
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng
Câu 97: Cho và 3 số dương x, y, z thay đổi có tổng bình phương: , . Giá
trị lớn nhất của là:
A. . B. . C. . D. .
Họ và tên tác giả: Trần Văn Ngờ Tên FB: Tran Van Ngo Tth, Email:
vanngodhqn@gmail.com
ABC
AB
BE AB
F
AC
EAFG
AG
BC
K
KB
KC
1
4
3
8
1
5
2
7
ABC
3
AB
4
AC
AD
BAC
BM
I
AD
AI
13
8
11
6
10
7
10
5
ABCD
O
AC
BO
CD
E
AD
F
2
EF BO
AF
AD
1 5
2
2
1 2
5
2
ABC
A B C
1 1 1
2 2 2
, ,A B C
BCA CAB ABC
1 1 1
, ,
G G G
1 2
, ,
ABC A B C
1 1 1
,
A B C
2 2 2
GG
GG
1
2
1
3
1
2
3
2
ABC
M
ABC
2 2 2
P MA MB MC
,a b
P
4
T a b
3
6
9
12
ABC
2 2 2 2
x y z k
k R
cos cos cosB
P xy C yz A zx
2
k
2
2
k
3
k
2
3
k
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
18
Câu 98: Cho hai điểm và , thỏa mãn : . Khi thay đổi tìm giá
trị nhỏ nhất của biểu thức ?
A. . B. . C. . D. .
( Họ và tên tác giả : Đặng Mơ- Tư Duy Mở )
Câu 99: Cho tứ giác , M là điểm tùy ý và các điểm I, J, K cố định sao cho đẳng thức thỏa mãn
với mọi điểm M: Giá trị của k là
A. k = 3 B. k = 4 C. k = 5 D. k = 6
Câu 100: Cho tam giác ABC vuông tại A. Gọi là góc giữa hai đường trung tuyến BD và CK. Giá
trị nhỏ nhất của bằng
A. B. C. D.
Câu 101: Cho hai điểm cố định G và là trọng tâm của tam giác ABC và tam giác Giá trị
nhỏ nhất của biểu thức bằng
A. B. C. D.
Họ và tên: Nguyễn Đức Hoạch – email: nguyenhoach95@gmail.com
Câu 102: Cho hình thang có . Với
mỗi điểm di động trên cạnh ta xác định điểm sao cho . Tìm
độ dài nhỏ nhất của .
A. . B. . C. . D. .
Mail: nguyennga82nvc@gmail.com, FB: Nguyễn Nga Nvc
Câu 103: Cho tam giác ABC vuông ở A; BC = 2; CA = b; AB = c và điểm M di động
Biểu thức F= đạt giá trị lớn nhất bằng
A. 4 B. 12 C. 16 D. 24
Nguyễn Văn Công- Trường THPT Kinh Môn II, Gmail: nguyencongkm2@gmail.com
Câu 104: Cho đều có cạnh bằng . Gọi là đường thẳng qua và song song , điểm di
động trên . Tìm giá trị nhỏ nhất của .
A. . B. . C. . D. .
Họ và tên tác giả: Vũ Viên Tên FB: Vũ Viên, Email: tieplen@gmail.com
, ( ;6)A B I
( ;3)M I
60
AIB
, ,A B M
2
P MA MB
9
3 2 6
3 13
6 3
ABCD
3 .
 
MA MB MC MD k MK
cos
4
5
5
4
4
3
3
4
'G
' ' '.A B C
' ' 'P AA BB CC
'GG
3 'GG
2 'GG
1
'
3
GG
1 1 1 1
A B C D
0
1 1 1 1 1 1 1 1 1 1 1 1 1 1
// , 3 , 2 , 60
A B C D A B a C D a D A B C B A
1
G
1 1
A B
1
F
1 1 1 1 1 1
G F G C G D
  
1 1
G F

2a
3a
3 3
2
a
3
2
a
2 2 2 2 2
8MA b MB c MC
ABC
2a
d
A
BC
M
d
2
MA MB MC

2 3a
3a
3
4
a
3
2
a
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
19
Câu 105: Trong mặt phẳng cho tam giác ABC và một điểm M bất kỳ. Đặt . Tìm
giá trị nhỏ nhất của biểu thức .
A. . B. . C. . D. .
Họ và tên tác giả: Phạm Khắc Thành, Email: phamkhacthanhkt@gmail.com
Câu 106: Cho tam giác ABC có trung tuyến . Tìm giá trị nhỏ nhất của
A. . B. . C. . D.
Mail: thuytrangmn@gmail.com
Câu 107: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto
có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê, Email: hongle.ad@gmail.com
Câu 108: Cho tam giác là tam giác đều cạnh bằng , là điểm di động trên đường thẳng .
Khi đó, giá trị nhỏ nhất của biểu thức là:
A. B. C. D.
Họ và tên: Ngô Gia Khánh, Địa chỉ mail: ngkhanh4283@gmail.com
Câu 109: Cho và có các trọng tâm G và cố định và . Khi đó giá trị nhỏ nhất
của là:
A. . B. . C. . D. .
(Họ và tên tác giả: Phạm văn Tài, Tên FB: TaiPhamVan)
Câu 110: Cho tam giác với các cạnh ; . Gọi là đường phân giác
trong của góc . Biết biểu thị vectơ . Tính .
A. . B. . C. . D. .
Mail: thongbui1987@gmail.com
Câu 111: Cho có ; . Phân giác trong của góc cắt trung tuyến tại
. Biết , với và tối giãn. Tính .
A. . B. . C. . D. .
Câu 112: Cho tứ giác có và cùng vuông góc với , , , . Gọi
là một điểm thuộc cạnh . Biết , giá trị lớn nhất của là
A. . B. . C. . D. .
, ,
a BC b CA c AB
MA MB MC
T
a b c
3 3
3
3
3
3
2
' 'AA CC
' , '
A BC C AB
cos .B
4
5
2
5
1
1
2
aMA bMB cMC
ABC
a
M
AC
3
T MA MB MC MA MB MC
     
2 3
.
3
a
MinT
2 3.MinT a
3.MinT a
5 3
.
2
a
MinT
ABC
' ' 'A B C
'G
'GG a
AA' ' 'T BB CC
T a
2T a
3T a
4T a
ABC
,
AB x AC y
0
x y
AD
A
AD mAB nAC
S m n
2
S
0
S
1
S
2
S
ABC
3
AB
4
AC
AD
BAC
BM
I
AD a
AI b
,
a b
a
b
2 S a b
10
S
14
S
24
S
27
S
ABCD
AD
BC
AB
8
AB
AD a
BC b
E
CD
90
AEB
T ab
4
16
8
64
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
20
Họ và tên tác giả: Lê Hồng Phi Tên FB: Lê Hồng Phi, Email: lehongphivts@gmail.com
Câu 113: Cho tứ giác có và cùng vuông góc với , , , . Cho
là số thực dương thuộc và điểm thỏa mãn . Tìm hệ thức liên hệ
giữa , , , để góc ?
A. . B. .
C. . D. .
Câu 114: Cho tam giác có trọng tâm , qua dựng đường thẳng cắt cách cạnh , lần lượt
tại , . Đặt , , gọi , lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của
. Tính .
A. . B. . C. . D. .
(Họ và tên tác giả: Hoàng Thị Thanh Nhàn, Tên FB: Hoàng Nhàn)
Câu 115: Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho .
Điểm M di động trên BC sao cho . Tìm x sao cho đạt giá trị nhỏ nhất.
A. B. C. D.
Họ và tên: Nguyễn Thị Thu, Email: thutoan83@gmail.com, Facebook: Nguyễn Thị Thu
Câu 116: Cho tam giác ABC đều cạnh , là đường thẳng qua B và tạo với AB một góc
. Tìm giá trị nhỏ nhất của ?
A. B. C. D.
(Tác giả: Hoàng Thị Thúy - Facebook: Cỏ ba lá )
Câu 117: Cho tam giác đều cạnh nội tiếp đường tròn và điểm thay đổi trên . Gọi ,
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính .
A. . B. . C. . D. .
Câu 118: Cho lục giác đều cạnh . Trên đường chéo , lấy hai điểm , sao cho
. Độ dài đạt giá trị nhỏ nhất khi bằng bao nhiêu?
A. . B. . C. . D. .
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1)
Câu 119: Cho hình chữ nhật có , . và lần lượt là trung điểm và .
là điểm thỏa mãn và lớn nhất. Tính .
ABCD
AD
BC
AB
AB h
AD a
BC b
k
0;1
E
1 0
kEC k ED
a
b
h
k
90
AEB
1 1
k b ka h k k
1 1
kb k a hk k
1 1
kb k a h k k
1 1
k b ka hk k
G
G
d
AB
AC
M
N
AM
x
AB
AN
y
AC
m
M
T x y
m M
10
3
17
6
11
6
5
2
1
BH HC
3

BM xBC
MA GC
4
.
5
5
.
4
5
.
6
6
.
5
2 3
d
0
60
C
3
A MA MB MC
3
5
12
5
4
5
2
ABC
1
( )O
M
O
s
i
MA MB MC
  
s i
3
s i
4 3
3
s i
5 3
3
s i
2 3
s i
ABCDEF
a
AC
CE
M
N
AM CN
k
AC CE
0 1
k
2 2
BM BN
k
1
2
1
4
2
3
3
4
ABCD
AD a
AB b
O
I
DB
DO
N
2 2 2
NA NC AB AD AD
   
NB
NB
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
21
A. B. C. D. .
Câu 120: Cho tam giác ABC, Điểm M thuộc đường tròn ngoại tiếp
tam giác ABC. Giá trị nhỏ nhất của biểu thức là
A. . B. . C. . D. .
Phuongthao.nguyenmaths@gmail.com
Câu 121: Cho tam giác có là trọng tâm. Gọi là chân đường cao hạ từ sao cho
. Điểm di động nằm trên sao cho . Tìm sao cho độ dài của
vectơ đạt giá trị nhỏ nhất.
A. . B. . C. . D.
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Câu 122: Cho hình thang ABCD có đáy CD gấp đôi đáy AB. Lấy một điểm E sao cho và
đồng thời thỏa mãn . Giá trị nhỏ nhất của góc nằm trong khoảng nào dưới đây?
A. . B. . C. . D. .
Họ tên tác giả: Đoàn Phú Như, Tên fb: Như Đoàn, Email: doanphunhu@gmail.com
Câu 123: Cho hình thang ABCD có , , góc tạo bởi hai véc tơ và
bằng . Khi đó giá trị của bằng:
A. . B. . C. . D. .
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Câu 124: Cho hình thang ABCD có , . Giá trị của biểu thức
bằng:
A. . B. . C. . D. .
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Câu 125: Cho tam giác có và đã biết. Biểu thức đạt
giá trị nhỏ nhất bằng với mọi giá trị thực . Giá trị của nằm trong khoảng
nào dưới đây?
2 2
2 3
2
a a b
2 2
2
a a b
2 2
2 3
4
a a b
2 2
2
4
a a b
3( ), 4( ), 5( ).AB cm BC cm CA cm
2 2 2
P MB MC MA
0
5 97
5
2
5 97
5
2
5 97
5
4
ABC
G
H
A
1
3
BH HC
M
BC
BM xBC
x
MA GC
4
.
5
5
.
6
6
.
5
5
.
4
3 2
BC DE

CA CE
ABC
(95 ;100 )
(100 ;106 )
(106 ;115 )
(115 ;120 )
2
AB DC

8, 6
AC BD
AC

BD
120
( )AD BC
13 2 5
2
14 4 7
3
15 2 10
4
6 4 3
2
AB DC

9, 6
AC BD
2 2
( )BC AD
15
80
3
12
14
ABC
60
BAC
,AB AC
.
P k MA MB MC
( )AB AC
0
k k
0
k
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
22
A. . B. . C. . D. .
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Câu 126: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto
có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê
Câu 127: Cho tam giác đều cạnh a và điểm M thay đổi. Giá trị nhỏ nhất của biểu thức
là:
A. B. C. D.
Họ và tên: Nguyễn Thị Tuyết Lê FB: Nguyen Tuyet Le
Câu 128: Cho tam giác có hai đường trung tuyến kẻ từ và vuông góc với nhau. Tính giá trị
nhỏ nhất của .
A. . B. . C. . D. .
Họ và tên tác giả: Đặng Văn Tâm Tên FB: Đặng Văn Tâm, Email: dvtam0189@gmail.com
Câu 129: Cho đoạn thẳng có độ dài bằng Một điểm di động sao cho .
Gọi là hình chiếu của lên . Tính độ dài lớn nhất của ?
A. B. C. D.
Họ và tên: Phương Xuân Trịnh Tên FB:: Phương Xuân Trịnh, Email:
phuongtrinhlt1@gmail.com
Câu 130: Cho tam giác vuông tại . Gọi là góc giữa hai trung tuyến và . Giá trị nhỏ
nhất của là:.
A. . B. . C. . D. .
Câu 131: Cho có trọng tâm G. Gọi H là chân đường cao kẻ từ A sao cho . Điểm M di
động trên BC sao cho . Tìm x sao cho độ dài vecto đạt giá trị nhỏ nhất.
A. . B. . C. . D. .
( Họ và tên tác giả: Nguyễn Văn Phu, Tên FB Nguyễn Văn Phu)
Câu 132: Cho đoạn thẳng có độ dài bằng Một điểm di động sao cho .
Gọi là hình chiếu của lên . Tính độ dài lớn nhất của ?
(0;1)
3
( ;2)
2
3
(1; )
2
(2;3)
aMA bMB cMC
ABC
2 2 2
2 3 4
P MA MB MC
2
14a
2
14a
2
26
3
a
2
26
3
a
ABC
B
C
cos A
1
2
2
3
3
4
4
5
AB
.a
M
MA MB MA MB
H
M
AB
MH
.
2
a
3
.
2
a
.a
2 .a
ABC
A
BD
CK
cos
1
2
4
5
2
3
3
4
ABC
1
3
CH HB
.CM x CB
MA GB
8
5
5
6
6
5
5
8
AB
.a
M
MA MB MA MB
H
M
AB
MH
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
23
A. B. C. D.
Câu 133: Cho và là hai phân giác trong của tam giác . Biết , và .
Khi đó bằng:
A. . B. . C. . D. .
Họ và tên: Nguyễn Thị Thanh Thảo Tên FB: Nguyễn Thanh Thảo
Câu 134: : Cho đoạn thẳng có độ dài bằng Một điểm di động sao cho
. Gọi là hình chiếu của lên . Tính độ dài lớn nhất của ?
A. B. C. D.
Câu 135: Một miếng gỗ có hình tam giác có diện tích là điểm , lần lượt thỏa mãn ;
. Cắt miếng gỗ theo một đường thẳng qua , đường thẳng này đi qua lần
lượt trên các cạnh . Khi đó diện tích miếng gỗ chứa điểm thuộc đoạn:
A. . B. . C. . D.
Họ và tên tác giả: Hoàng Tiến Đông, Tên FB: tiendongpt, Email: dongpt@c3phuctho.edu.vn
Câu 136: Cho tam giác có bán kính đường tròn ngoại tiếp . Tìm giá trị lớn nhất của
.
A. 1. B. 2. C. 3. D. 4
Đỗ Công Dũng, Email: congdung812@gmail.com
Câu 137: Cho tam giác đều cạnh Gọi là điểm nằm trên cạnh Tính giá trị nhỏ nhất của
biểu thức theo
A. . B. . C. . D. .
Câu 138: Cho hình bình hành ABCD, M thuộc đường chéo AC, (M không trùng với các đỉnh A, C)
Trên các đường thẳng AB, BC, lấy các điểm P và Q sao cho MP // BC, MQ // AB. Gọi N là
giao hai đường thẳng AQ và CP. Giả sử . Tìm giá trị lớn nhất của m + n
A. B. C. D. 2
Email: themhaitotoanyp1@gmail.com, (Fb: Lưu Thêm)
Câu 139: : Cho tam giác có là trọng tâm. Gọi là chân đường cao hạ từ
sao cho
. Điểm di động nằm trên sao cho . Tìm sao cho độ dài của
vectơ đạt giá trị nhỏ nhất.
A. B.
C. D.
.
2
a
3
.
2
a
.a
2 .a
AD
BE
ABC
4AB
5
BC
6
CA

DE
5 3
9 5

CA CB
3 5
5 9

CA CB
9 3
5 5

CA CB
3 9
5 5

CA CB
AB
.a
M

MA MB MA MB
H
M
AB
MH
.
2
a
3
.
2
a
.a
2 .a
S
I
O
0
IB IC
0
OA OI
O
,M N
,AB AC
A
;
4 3
S S
;
3 2
S S
3
;
8 2
S S
3
;
4 8
S S
ABC
2R
2 2 2
BC AB AC
ABC
.a
M
.AB
2
MA MB MC
.a
3
4
a
3
2
a
3
8
a
2 3
3
a
DCnDAmDN
3
4
4
3
2
1
ABC
G
H
A
1
3

BH HC
M
BC

BM xBC
x
 
MA GC
4
.
5
5
.
6
6
.
5
5
.
4
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
24
Họ và tên: Lê Thị Lan FB: Lê Lan, Email: lelanqx2@gmail.com
Câu 140: Cho tam giác ABC có nội tiếp đường tròn tâm O, bán kính R. M là
điểm thuộc đường tròn (O). Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức . Khi đó giá trị của bằng
A. . B. .
C. . D. .
Tác giả: Nguyễn Văn Hưng Facebook: Nguyễn Hưng
Câu 141: Cho tam giác đều nội tiếp đường tròn tâm ,bán kính , là một điểm bất kì trên
đường tròn. Giá trị lớn nhất của biểu thức là
A. . B. . C. . D. .
Họ và tên: Nguyễn Xuân Giao Tên FB: giaonguyen, Email: giaohh2@gmail.com
Câu 142: Cho tam giác . Tìm giá trị nhỏ nhất của biểu thức
A. . B. . C. . D. .
Họ và tên: Đồng Anh Tú Facebook: Anh Tú
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
Câu 143: Cho tam giác đều cạnh . Tính
A. B. C. D.
Họ và tên: Nguyễn Văn Nho Facebook: Nguyễn Văn Nho
Câu 144: Cho tam giác có là trung tuyến, là trọng tâm. Một đường thẳng qua cắt các
cạnh lần lượt tại . Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Email: ngvnho93@gmail.com
Câu 145: Cho các véc tơ thỏa mãn và . Tính
.
A. . B. .
C. . D. .
Tác giả: Quang Phi
, ,
BC a AC b AB c
,N n
2 2 2
P MA MB MC
N n
2
12R
2 2 2 2
4R 9R
a b c
2 2 2 2
2R 9R
a b c
2 2 2 2
8R 9R
a b c
ABC
O
R
M
2 2 2
2 3
S MA MB MC
2
21
R
2
21
R
2
2 21
R
2
2 21
R
ABC
3 cos 2 2cos2 2 3 cos 2P A B C
P
4
min
P
3 1
2
min
P
2 3 3
min
P
5
min
ABC
a
. . .AB BC BC CA CA AB
2
3
2
a
2
3
2
a
2
3
2
a
2
3
2
a
ABC
AD
G
G
,AB AC
,M N
1 2
. . .
2 3
AM AN AN MB AM NC
    
. . .AM AN AN MB AM NC
2
. ( . . )
3
AM AN AN MB AM NC
    
3
. ( . . )
2
AM AN AN MB AM NC
    
, ,a b c
, ,
a a b b c c
3 0
a b c
2 2 2
3
2
c a b
2 2 2
3
2
a c b
2 2 2
3
2
b a c
2 2 2
3
2
c a b
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
25
Câu 146: Cho tam giác ABC vuông tại A có BC = 2a, M là điểm trên đoạn BC sao cho MB = 2MC. Biết
rằng . Độ dài cạnh AC là:
A. B. C. D.
Họ và tên: Đoàn Thị Hường, Email: ngochuongdoan.6@gmail.com, Fb: Đoàn Thị Hường
Câu 147: Cho tam giác có .Dựng điểm M sao cho
. Đặt .Tính
A. . B. . C. . D. .
Họ tên: Đào Hữu Nguyên FB: Đào Hữu Nguyên, Mail: huunguyen1979@gmail.com
Câu 148: Cho tam giác ABC vuông tại A. Quỹ tích điểm M thỏa mãn là
A. Đường thẳng AC. B. Đường thẳng AB.
C. Đường thẳng BC. D. Đường trung trực cạnh BC.
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon
Câu 149: Cho tam giác đều cạnh , . Lấy các điểm , , lần lượt trên các cạnh
, , sao cho , , . Tìm để .
A. . B. .
C. . D.
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon
Câu 150: Cho tam giác vuông cân tại . Gọi là trung điểm và là điểm di động trên
đường thẳng . Khi đạt giá trị nhỏ nhất, hãy tính tỉ số .
A. . B. . C. . D. .
(Họ và tên tác giả: Nguyễn Đức Lợi, Tên FB: Nguyễn Đức Lợi)
Câu 151: Cho có trọng tâm , là chân đường cao kẻ từ sao cho . Điểm di
động trên sao cho . Tìm sao cho nhỏ nhất.
A. B. C. D.
Họ tên: Vũ Thị Chuyền FB: Vũ Thị Chuyền
Câu 152: Cho tam giác ABC, nhọn, không cân và nội tiếp đường tròn . Gọi G và M lần lượt là
trọng tâm tam giác ABC và trung điểm cạnh BC. Cho đường thẳng OG vuông góc với đường
thẳng OM tính giá trị biểu thức
theo R.
A. 8R
2
. B. 10R
2
. C. 12R
2
. D. 14R
2
.
2
.
AM BC a

33
3
a
AC
3AC a
3
3
a
AC
5AC a
ABC
0
90 , 1, 2
BAC AB AC
, 3
AM BC AM
. .AM x AB y AC

2 2
?T x y
153
20
T
151
20
T
157
20
T
159
20
x
2
. .
MB MC MA BC MA
ABC
3a
0
a
M
N
P
BC
CA
AB
BM a
2CN a
AP x
0 3x a
x
AM PN
3
5
a
x
4
5
a
x
5
a
x
2
5
a
x
ABC
B
M
AB
I
MC
2
IM AC
AC
AI
1
AC
AI
2
AC
AI
2
AC
AI
3
2
AC
AI
ABC
G
H
A
1
3
BH HC

M
BC
BM xBC
x
MA GC

6
5
5
4
4
5
5
6
;O R
2 2 2
2
AC AB BC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
26
Lời giải
Họ và tên: Nguyễn Thị Trăng Fb: Trăng Nguyễn
Câu 153: Cho tam giác MNP có MN=4,MP=8, = Lấy điểm E trên tia MP và đặt .Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP.
A. k= . B. k= . C. k= . D. k= .
Họ và tên tác giả: Phạm Hồng Quang Tên FB: Quang Phạm
Câu 154: Đẳng thức đúng với mọi điểm M. Khi đó tứ giác ABCD là hình gì.
A. Hình thang vuông. B. Hình chữ nhật.
C. Hình thoi. D. Tứ giác có hai đường chéo vuông góc.
Lời giải
(Họ và tên tác giả: Phạm Trung Khuê, Tên FB: Khoi Pham)
Câu 155: Cho hình vuông cạnh . Gọi lần lượt thuộc các đoạn thẳng và sao cho
, và . Khi đó thuộc khoảng nào dưới đây?
A. . B. . C. . D. .
Họ và tên: Nguyễn Đắc Giáp Facebook: dacgiap
Câu 156: Cho hai vector thỏa mãn đồng thời các điều kiện , vector
vuông góc với . Tính cosin của góc tạo bởi hai vector và .
A. . B. . C. . D. .
Họ và tên tác giả: Ngô Nguyễn Quốc Mẫn Tên FB: Ngonguyen Quocman
Câu 157: Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh . Tìm
giá trị biểu thức:
A. B. C. D.
Câu 158: Cho hình vuông ABCD. M, N lần lượt nằm trên hai cạnh BC và CD sao cho
Gọi E là điểm thỏa mãn Khi Tính giá trị biểu thức .
A. B. C. D.
Họ và tên: Lê Thái Bình, Email: lebinhle80@gmail.com, Facebook: Lê Thái Bình
Câu 159: Cho hình vuông ABCD, điểm M nằm trên đoạn thẳng AC sao cho . Gọi N là trung
điểm CD. Tam giác BMN là
A. Tam giác đều. B. Tam giác cân.
M
0
60
ME kMP
2
3
2
5
1
3
1
2
. .
MA AD MB BC
ABCD
a
,M N
BC
AC
1
3
BM MC
CN k AN
AM DN
k
3;5
5; 3
4; 2
2;4
,a b
2 7, 2
a b a b
(3 )a b
( )a b
a
b
1
3
2
4
1
3
2
4
; ;
BC a CA b AB c
2 2 2
. . .
OA OB OC
K
b c c a a b
1
2
K
1
3
K
1K
1
4
K
1
.
3
CM CN
CB CD
.AE kAN
.BE AM
T k k
2
1
13
16
7
9
8
9
5
16
4
AC
AM
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
27
C. Tam giác Vuông. D. Tam giác vuông cân
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa
Câu 160: Cho tam giác . Gọi là trực tâm và là tâm đường tròn ngoại tiếp của tam giác .
Đặt , , . Tìm hệ thức liên hệ giữa , , sao cho vuông góc với
trung tuyến vẽ từ đỉnh của tam giác .
A. . B. . C. . D. .
(Email): luongthanh80tm@gmail.com
Câu 161: Cho tam giác có là trung tuyến, là trọng tâm. Một đường thẳng qua cắt các
cạnh lần lượt tại . Khẳng định nào sau đây đúng?
A.
B.
C.
D.
(Sưu tầm, Họ và tên: Nguyễn Lương Thành, Tên FB: luongthanh.nguyen.7)
Câu 162: Cho hình chữ nhật ABCD có cạnh AB=2 và AD=4.Gọi M là trung điểm của cạnh AB và N là
điểm trên cạnh AD sao cho ,CM vuông góc với BN.Khi đó k thuộc vào khoảng nào
sau đây
A. B. C. D.
Họ và tên:Phan Thông, Email:quocthong1182@gmail.com, Facebook:Quocthongphan
Câu 163: Cho tam giác MNP có MN=4,MP=8, = Lấy điểm E trên tia MP và đặt .Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP.
A. k= . B. k= . C. k= . D. k= .
Câu 164: Họ và tên: Phạm Hồng Quang Tên FB: Quang Phạm, Email:
phamhongquangltv@gmail.com
Câu 165: Cho tam giác có . là trung điểm của , là chân đường
phân giác trong góc . Tính
A. . B. .
C. . D.
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Câu 166: Cho tam giác ABC có AB = c, AC = b và Các điểm M, N được xác định bởi
và . Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với
nhau.
ABC
H
O
ABC
BC a
CA b
AB c
a
b
c
OH
A
ABC
2 2 2
2
a b c
2 2 2
2
b a c
2 2 2
2
c a b
2 2 2
2 2b a c
ABC
AD
G
G
,AB AC
,M N
1 2
. . .
2 3
AM AN AN MB AM NC
    
. . .AM AN AN MB AM NC
2
. ( . . )
3
AM AN AN MB AM NC
    
3
. ( . . )
2
AM AN AN MB AM NC
    
AN k AD
1
0;
16
1 1
;
16 20
1 1
;
20 9
1 1
;
9 6
M
0
60
ME kMP
2
3
2
5
1
3
1
2
ABC
, ,
BC a CA b AB c
M
BC
D
A
2
AD
2
2
4c
AD p p a
b c
2
2
4bc
AD p a
b c
2
2
4bc
AD p p a
b c
2
2
4bc
AD p p a
b c
0
60 .
BAC
2
MC MB
 
2NB NA
 
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
28
A. . B. .
C. . D. .
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Câu 167: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi I là trung điểm của AC và M là điểm thỏa
mãn . Biết rằng OM vuông góc với BI và . Tính góc
.
A. . B. C. . D. .
Họ tên: Trần Ngọc Tên FB: Ngọc Trần, Email: soantailieutoanhoc2018@gmail.com
Câu 168: Cho hình thang vuông ABCD, đường cao AD = h, đáy AB = a, đáy CD = b. Gọi M là trung
điểm của BC. Hệ thức giữa a, b, h để là
A. . B. C. . D. .
Họ và tên tác giả: Đào Trung Kiên (st) Tên FB: kienyenthe, Email: kienyenthe@gmail.com
Câu 169: Cho tam giác đều ABC cạnh bằng a. Gọi M, N là các điểm thỏa mãn ,
. Gọi I là giao điểm của AM và CN. Tính diện tích của tam giác IBC theo a?
A. . B. . C. . D. .
Họ và tên: Vũ Huỳnh Đức, Email: vutoanpvd@gmail.com, Facebook: vuhuynhduc2017
Câu 170: Cho tam giác đều và các điểm thỏa mãn , ,
. Tìm để vuông góc với .
A.
B.
C. D.
Họ và tên: Huỳnh Thanh Tịnh Tên FB: huynhthanhtinh, Email:
huynhthanhtinhspt@gmail.com
Câu 171: : Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh . Tìm
giá trị biểu thức:
A. B. C. D.
Người sưu tầm: Tăng Duy Hùng. FB: Hùng Tăng
Câu 172: Cho hai véc tơ và thỏa mãn các điều kiện Đặt và
Tìm tất cả các giá trị của sao cho
A. B. C. D.
Họ và tên: Nguyễn Thị Huệ, FB: Nguyễn Thị Huệ, Gmail: nguyenthihue1611@gmail.com
2 2
6 4 5 0
c b bc
2 2
4 5 6 0
c b bc
2 2
6 5 4 0
c b bc
2 2
4 6 5 0
c b bc
2 2
OM OA OB OC

2
3 .AC BC BA
ABC
30
45
60
120
DAM B
2 2
0
a h ab
2 2
0
h a ab
2 2
0
h b ab
2 2
0
b h ab
1
3
 
BM BC
1
3
 
AN AB
2
3
7
IBC
a
S
2
7
7
IBC
a
S
2
2 7
7
IBC
a
S
2
2 3
7
IBC
a
S
ABC
, ,M N P
BM k BC
2
3
CN CA
4
15
AP AB
k
AM
PN
1
3
k
1
2
k
3
4
k
; ;
BC a CA b AB c
2 2 2
. . .
OA OB OC
K
b c c a a b
1
2
K
1
3
K
1K
1
4
K
a
b
1
1,
2
a b
2 15.
a b
u a b
2 , .
v ka b k
k
0
, 60 .
u v
3 5
4 .
2
k
3 5
4 .
2
k
17
5 .
2
k
17
5 .
2
k
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
29
Câu 173: Cho tứ giác , hai điểm thỏa mãn và
Tính theo để
A. . B. . C. . D. .
Họ và tên tác giả: Lê Thị Nguyệt Tên FB: NguyệtLê, Email: Lenguyet150682@gmail.com
Câu 174: Cho tam giác có Gọi là điểm thuộc cạnh sao cho
và là điểm thuộc sao cho ( ). Biết
( là phân số tối giản, a,b là các số nguyên) sao cho đường thẳng vuông góc với đường
thẳng
Tính giá trị biểu thức .
A. B. C. D.
Họ và tên tác giả: Trần Thanh Hà Tên FB: Hatran, Email: tranthanhha484@gmail.com
Câu 175: Cho tam giác ABC có AB = c, AC = b và Các điểm M, N được xác định bởi
và . Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với
nhau.
A. B.
C. D.
Họ và tên tác giả: Đỗ Thế Nhất Tên FB: Đỗ Thế Nhất, Email: nhatks@gmail.com
Câu 176: Cho hình chữ nhật ABCD có AB= a, AD=2a. Gọi M là trung điểm AB, N là điểm trên cạnh
AD sao cho . Tìm k để CM
BN.
A. k=7,9 B. k=8 C. k=8,1 D. k=7.8
Câu 177: Cho hình bình hành có đường chéo lớn là . Gọi lần lượt là hình chiếu vuông
góc của trên . Biểu thức nào sau đây là đúng.
A. . B. .
C. . D. .
Họ và tên tác giả: Nguyễn Ngọc Duy Tên FB: Ngọc Duy, Email:
nguyenngocduyakgl@gmail.com
Câu 178: Cho hình thang vuông , đường cao , cạnh đáy . Tìm hệ thức
giữa để vuông góc trung tuyến của tam giác .
A. . B. .
C. . D.
Email: thuy.tranthithanhdb@gmail.com
ABCD
,M N
2 0;2 0
MB MA NC ND
.
AD
x
BC
cos
cos
DBC
ADB
x
.MN BD
2
x
2
x
3
x
3x
ABC
6; 7; 5.
AB BC CA
M
AB
2AM MB
N
AC
AN k AC
k
a
k
b
a
b
CM
.BN
2018 2019 5
T a b
2017.
T
2020.
T
2030.
T
2030.
T
0
60 .BAC
2MC MB
2NB NA
2 2
6 5 4 0
c b bc
2 2
6 5 0
c b bc
2 2
4 6 5 0
c b bc
2 2
4 6 5 0
c b bc
AD kAN
 
ABCD
AC
,E F
C
,AB AD
2
. .
AB AH AD AF AC
2
. .
AB AE AD AF AC
2
. .
AB AE AD AH AC
. . .AB AE AD AF AC AH
ABCD
AD h
,
AB a CD b
, ,a b h
BD
AM
ABC
2
h a a b
2
h a b a
h h b a a b h
2
2
h a a b
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
30
Câu 179: Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R), M là điểm chính giữa cung BC (
cung BC không chứa điểm A). Chọn đẳng thức đúng trong các đẳng thức sau:
A. B.
C. D.
Họ và tên tác giả: Nguyễn Quang Nam Tên FB: Quang Nam, Email:
quangnam68@gmail.com
Câu 180: Cho tam giác có . là trung điểm của , là chân đường
phân giác trong góc . Tính
A. B.
C. D.
Họ Tên: Lương Thị Hương Liễu Tên FB: Hương Liễu Lương, Email:
lieuluong.290983@gmail.com
Câu 181: Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt
Nam có một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc như
hình vẽ dưới đây. Trên các đường thẳng và người ta để hai vật nặng cùng trọng lượng.
Buộc hai vật thể với nhau bằng một thanh cứng sao cho mỗi vật đều có thể chuyển
động được trên hai đường ray. Nối hai vật bằng một sợi giây vòng qua một cột có gốc tại .
Người tham dự cuộc thi sẽ đứng tại vị trí điểm để kéo vật thể chuyển động trên . Người
thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc . Hãy dùng kiến thức toán
học để tính toán vị trí xa nhất mà người tham dự cuộc thi có thể đạt được.
A. . B. . C. . D. .
Họ và tên: Phạm Thành Trung Tên FB: Phạm Thành Trung, Email:
trungthuong2009@gmail.com
Câu 182: Cho tam giác ABC có AB= c,BC=a,CA=b. Trung tuyến CM vuông góc với phân giác trong AL
và . Tính .
.sin .sinMA MB C MC B
.cos .cosMA MB C MC B
.sin .sinMA MB B MC C
.cos .cosMA MB B MC C
ABC
, ,BC a CA b AB c
M
BC
D
A
2
AD
2
4
2
c
AD p p a
b c
2
2
4bc
AD p a
b c
2
2
4bc
AD p p a
b c
2
2
4bc
AD p p a
b c
0
30
Ox
Oy
1AB m
O
B
Oy
O
O
B
A
1m
2m
3m
2m
3
2
CM
AL
cos A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
31
A. B. C. D.
Câu 183: Cho hình chữ nhật ABCD có . Điểm M thuộc cạnh AD và N là trung điểm BC
sao cho . Phân số tối giản có bằng bao nhiêu
A. 29. B. 18. C. 16. D. 27.
(Họ và tên tác giả: Trần Văn Đoàn, Tên FB: Trần Văn Đoàn)
Câu 184: Cho tam giác có ; , . Gọi là trung điểm của và là
chân đường phân giác trong góc của tam giác . Biết rằng trung tuyến vuông góc
với phân giác trong . Khi đó đẳng thức nào sau đây đúng?
A. . B. . C. . D. .
Họ và tên: Nguyễn Thị Thỏa Tên FB: Nguyễn Thị Thỏa, Email:
phamquynhanhbaby56@gmail.com
Câu 185: Cho tam giác ABC đều nội tiếp (O;R). M là điểm bất kì trên cung nhỏ . Khi đó
A. B.
C. D.
CÁC PHẦN CHÍNH CỦA CHUYÊN ĐỀ
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG
VẤN ĐỀ 3. QUỸ TÍCH
VẤN ĐỀ 4. TỈ LỆ
VẤN ĐỀ 5. MIN,MAX
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
Phần II: Hướng Dẫn Giải
Trang: VĐ1-P35; VĐ2-P74; VĐ3-P88; VĐ4-P99; VĐ5-P110; VĐ6-P149
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
Email: daytoan2018@gmail.com
Câu 186: Cho tam giác ABC biết
3, 4, 6AB BC AC
,
I
là tâm đường tròn nội tiếp tam giác
ABC
.Gọi
, ,x y z
là các số thực dương thỏa mãn
. . . 0
x IA y IB z IC
.Tính
x y z
P
y z x
A.
3
4
P
. B.
41
12
P
. C.
23
12
P
. D.
2
3
P
.
Lời giải
Họ và tên tác giả: Vũ Ngọc Thành Tên FB: Vũ Ngọc Thành
Chọn B
2
cos
2
A
5 1
cos
4
A
3
cos
2
A
1
cos
2
A
1; 3
AB CD
MN BD
m BN
n NC
m n
ABC
AB c
BC a
CA b
M
AB
D
A
ABC
CM
AD
2b c
2c b
a b c
c a b
BC
MA MB MC
MA MB MC
MA MB MC
2
MA MB MC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
32
Dựng hình bình hành
BDIE
như hình vẽ. Khi đó
IE ID
IB IE ID IA IC
IA IC

Theo tính chất đường phân giác trong tam giác:
IE MB BC
IA MA AC
,
ID BN AB
IC NC AC
Suy ra
BC AB
IB IA IC
AC AC
.
Từ
. . . 0
x IA y IB z IC
suy ra
. .
x z
IB IA IC
y y

.
Do
,IA IC
là hai véc tơ không cùng phương suy ra
4 , 6 , 3x t y t z t
với
0t
.
Vậy
41
12
x y z
P
y z x
.
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet
Email: tiethanh.78@gmail.com
Câu 187: Cho hình bình hành
ABCD
. Gọi
I
là trung điểm của
CD
,
G
là trọng tâm tam giác
BCI
. Đặt
,
a AB b AD
. Hãy tìm đẳng thức đúng trong các đẳng thức sau?
A.
5 2
6 3
AG a b
. B.
5
6
AG a b
.
C.
5
6
AG a b
. D.
4 2
3 3
AG a b
.
Lời giải
Chọn A
N
M
E
D
I
A
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
33
*
I
là trung điểm của
CD
nên:
1 1 1
2 2 2
AI AC AD AB AD

.
*
G
là trọng tâm tam giác
BCI
nên:
1 1 1
3 3 3
AG AB AC AI
, thay
AC AB AD
và
1
2
AI AB AD
ta được
1 1 1 1 5 2
3 3 3 2 6 3
AG AB AB AD AB AD AB AD

.
Họ và tên: Dương Bảo Trâm Facebook: Bảo Trâm
Email: ilovemath.ddt@gmail.com
Câu 188: Cho tam giác
ABC
với các cạnh
AB c BC a CA b , ,
. Gọi I là tâm đường tròn nội tiếp
tam giác ABC. Đẳng thức nào sau đây đúng.
A.
aIA bIB cIC 0
  
B.
0bIA cIB aIC
  
C.
0cIA bIB aIC
  
D.
0cIA aIB bIC
  
Lời giải
Chọn A
Qua C dựng đường thẳng song song với AI cắt BI tai B’;song song với BI cắt AI tại A’
Ta có
IC IA IB ' '
  
(*)
Theo định lý Talet và tính chất đường phân giác
trong ta có:
' ( )
'
IB BA c b
IB IB
IB CA b c
1
1
1
 
Tương tự:
a
IA IA
c
' (2)
 
Từ (1) và (2) thay vào (*) ta có:
I
A
B
C
B
'
C'
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
34
a b
IC IA IB aIA bIB cIC
c c
0
     
Họ tên: Đỗ Thị Hồng Anh
Đ/c mail: honganh161079@gmail.com
Câu 189: Cho hình thang cân ABCD có CD là đáy lớn,
0
30ADC
. Biết DA = a, DC = b, hãy biểu
diễn
DB
theo hai vectơ
DA
và
DC

.
A.
.DB DA DC
B.
3
.
b a
DB DA DC
b
C.
.
b a
DB DA DC
b
D.
.DB bDA aDC
Lời giải
Kẻ BE // AD, E nằm trên cạnh CD. Ta có:
2 3
DE DE
DB DA DE DA DC DA DC
DC DC
DC KC b a
DA DC DA DC
DC b
.
Vậy đáp án đúng là câu B.
Email: kimduyenhtk@gmail.com
FB: Kim Duyên Nguyễn.
Câu 190: Cho hình bình hành
ABCD
,
M
là điểm thỏa mãn
5 2 0AM CA
 
. Trên các cạnh
AB
,
BC
lần lượt lấy các điểm
,P Q
sao cho
MP BC MQ AB/ / , / /
. Gọi
N
là giao điểm của
AQ
và
CP
. Giá trị của tổng
AN
AQ
CN
CP
bằng:
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
35
A.
21
19
B.
24
19
C.
23
19
D.
25
19
Lời giải
Đặt
AN xAQ CN yCP ,
   
Vì
2
/ / , / /
5
BQ AP AM
MQ AB MP BC
BC AB AC
Ta có:
2 2 2 3
( )
5 5 5 2
AQ AB BQ AB BC AB AC AB AC AP
         
Nên
2 3
(1)
5 2
AN xAQ xAC xAP
   
Do
, ,N C P
thẳng hàng nên
2 3 10
1
5 2 19
x x x
Mặt khác
( ) (1 ) (2)
CN yCP AN AC y AP AC AN y AC yAP
        
Từ (1) và (2) suy ra
3 15
2 19
y x
. Do đó
25
19
AN CN
x y
AQ CP
. Đáp án D
Họ và tên tác giả: Phạm Thị Ngọc Tên FB: Giang Thao
Email: thuangiaoyen@gmail.com
Câu 191: Cho tứ giác ABCD, M là điểm tùy ý. K là điểm cố định thỏa mãn đẳng thức
MA MB MC 3MD xMK
. Tìm x:
A. 2. B. 6. C. 5. D. 4.
Lời giải
Chọn B
Vì đẳng thức
MA MB MC 3MD xMK
(1) thỏa mãn với mọi M nên nó đúng khi M
trùng với K. Khi đó ta có:
KA KB KC 3KD xKK 0
(2).
Gọi G là trọng tâm
ABC
, ta có
KA KB KC 3KG
(3).
Thay (3) vào (2) ta được
3KG 3KD 0 KG KD 0
, suy ra K là trung điểm của GD.
Từ (1) ta có:
N
A
D
C
B
Q
M
P
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
36
MK KA MK KB MK KCKB 3MK 3KD (KA KB KC 3KD) 6MK 6MK
Vậy
6MK xMK
suy ra x = 6.
Họ và tên: Nguyễn Thanh Hoài
Email: ngthhoai1705@gmail.com
Facebook: https://www.facebook.com/hoaihappy
Câu 192: Cho tam giác
ABC
, trên cạnh
AC
lấy điểm
M
, trên cạnh
BC
lấy điểm
N
sao cho
3AM MC
,
2NC NB
. Gọi
O
là giao điểm của
AN
và
BM
. Tính diện tích tam giác
ABC
biết diện tích tam giác
OBN
bằng 1.
A.
24
. B.
20
. C.
30
. D.
45
Lời giải
Chọn C
Ta có:
1
BO xBA x BN
  
và
1
AO yAM y AB
  
.
1 1
AB yAM x y AB x BN
   
1 0
x y AB yAM x BN
  
(1)
Đặt
,CB a CA b
 
ta được
3 1
; ;
4 3
AB a b AM b BN a
  
Thay vào (1) và thu gọn ta được:
1 3
3 4
x
x y a x y b a yb
Suy ra
1 1
3 10
3 2
4 5
x
x y x
y x y y
. Với
1
10
x
ta được
1 1
1
10 10
BO BA BN
 
1
10
BO BN BA BN
   
1
10
NO NA
 
10
NA
NO
Vì
1 10 30
ONB NAB ABC
S S S
.
O
B
A
C
N
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
37
Họ và tên tác giả: Trần Ngọc Uyên Tên FB: Tran Ngoc Uyen
Email: ngocuyen203@gmail.com
Câu 193: Cho tam giác
ABC
, gọi
I
là điểm trên
BC
kéo dài sao cho
3IB IC
. Gọi
,J K
lần lượt là
những điểm trên cạnh
,AC AB
sao cho
2 ; 3JA JC KB KA
. Khi đó
. .BC m AI n JK
. Tính
tổng
P m n
?
A.
34
P
. B.
34
P
. C.
14P
. D.
14P
.
Lời giải
Chọn B
Ta có:
3 3 3 1
2 2 2 2
AI AB BI AB BC AB AC AB AC AB
(1)
1 2
4 3
JK AK AJ AB AC

(2)
Từ (1) và (2) ta có hệ phương trình
3 1
6 12
2 2
2 1
16 36
3 4
AI AC AB
AC AI JK
AB AI JK
JK AC AB

Ta có:
10 24 10; 24 34
BC AC AB AI JK m n m n
 
. Chọn đáp án
B.
Email: huanpv@dtdecopark.edu.vn
Câu 194: Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho
1 1
,
3 2
AM AB DN DC
. Gọi I và J là các điểm thỏa mãn
,
BI mBC AJ nAI

.
Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu?
A.
1
3
B.
3
C.
2
3
D.
1
(Họ và tên tác giả: Phạm Văn Huấn, Tên FB: Pham Van Huan)
Lời giải
Chọn A
J là trọng tâm tam giác BMN khi và chỉ khi
3AB AM AN AJ
 
(9)
Ta có
M
N
C
A
B
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
38
*
1
3
AM AB
*
1 1 1
2 2 2
AN DN DA DC DC CA AC DC AC AB
*
AJ nAI n AB BI n AB mBC n AB m AC AB
(1 )
n m AB mnAC
Nên thay vào (9) ta có
1 1
3 (1 ) 3
3 2
AB AB AC AB n m AB mnAC
5
3 (1 ) 1 3 0
6
n m AB mn AC
5
3 (1 ) 0
1
6
3
1 3 0
n m
mn
mn
Họ và tên: Hứa Nguyễn Tường Vy
Email: namlongkontum@gmail.com FB: nguyennga
Câu 195: Cho tam giác ABC, trên cạnh AB lấ
y
điểm M, trên cạnh BC lấ
y
N sao cho AM=3MB,
NC=2BN. Gọi I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam
giác ICN bằng 2.
A.
3
2
B.
33
2
C.
11
D.
9
11
Lời giải
Chọn đáp án B
Đặt
;
BC a BA c

.
Suy ra
3 2
; ;
4 3
AC a c AM c CN a
Do A, I, N thẳng hàng nên
(1 )
CI xCA x CN
Và M, I, C thẳng hàng nên
(1 )
AI y AC y AM

Mặt khác
(1 ) ( (1 ) )AC AI CI y AC y AM xCA x CN

3 1 1 4
0
3 4
y x y x
a c
I
N
C
B
A
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
39
Mà
;a c
không cùng phương suy ra
3 1
2
0
3
11
3
1 4
0
11
4
y x
x
y x
y
Với
2 2 9 2
11 11 11 11
x CI CA CN NI NA

Hay
2 2
11
11 11
NCI
NCA
NCA
S
NI
S
NA S
Mà
3 33
2 2
ABC
ABC
ANC
S
BC
S
S NC
congsondienan@gmail.com
Câu 196: Cho ∆ABC có trọng tâm G và hai điểm M, N thỏa mãn:
,
2 0
NA NB
.
Chọn mệnh đề đúng.
A.
4
NG GM
. B.
5
NG GM
. C.
6
NG GM
. D.
7
NG GM
.
(Họ và tên tác giả: Trần Công Sơn, Tên FB: Trần Công Sơn)
Lời giải
Chọn B
.
Gọi E là trung điểm BC. M, N là các điểm như hình vẽ.
Ta có:
2 2 1 5 1
2 . 2
3 3 2 3 3
     
NG AG AN AE AB AB AC AB AB AC
.
2 2 2 2 1 1 1
.
5 3 5 3 2 3 15
    
GM AM AG AC AE AC AB AC AB AC
.
Nên
5 1 1 1
5 5
3 3 3 15
NG AB AC AB AC GM
.
Vậy
5
NG GM
.
(Email): tranminhthao2011@gmail.com
M
G
E
N
A
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
40
Câu 197: (Đẳng thức vec tơ) Cho tam giác
ABC
. Gọi A', B',C' là các điểm xác định bởi
2018 ' 2019 ' 0
A B A C
,
2018 ' 2019 ' 0

B C B A
,
2018 ' 2019 ' 0

C A C B
. Khi đó,
mệnh đề nào sau đây đúng?
A.
ABC
và
' ' 'A B C
có cùng trọng tâm.
B.
' ' ' ABC A B C
.
C.
' ' ' ABC A B C
.
D.
ABC
và
' ' 'A B C
có cùng trực tâm.
Lời giải
Chọn A
Ta có
2018 ' 2019 ' 0
A B A C
2018 ' 2019 ' 0
A A AB A A AC
4037 ' 2018 2019 0
A A AB AC
(1)
Tương tự ta có
4037 ' 2018 2019 0 ; 4037 ' 2018 2019 0

B B BC BA C C CA CB
Cộng vế với vế lại ta được
4023 ' ' ' 0 ' ' ' 0
AA BB CC BA AC CB AA BB CC
.
Vậy
ABC
và
' ' 'A B C
có cùng trọng tâm
Câu 198: ( tính độ dài vec tơ) Cho tam giác đều
ABC
cạnh
a
. Gọi điểm
M
là trung điểm
BC
. Tính độ
dài của vec tơ
1
2
2
AB AC
A.
21
3
a
. B.
21
2
a
. C.
21
4
a
. D.
21
7
a
.
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
41
Chọn B
Gọi
N
là trung điểm
AB
,
Q
là điểm đối xứng của
A
qua
C
và
P
là đỉnh của hình bình hành
AQPN
.
Khi đó ta có
1
, 2
2
AB AN AC AQ
suy ra theo quy tắc hình bình hành ta có
1
2
2
 
AB AC AN AQ AP
Gọi
L
là hình chiếu của
A
lên
PN
Vì
0
/ / 60
MN AC ANL MNB CAB
Xét tam giác vuông
ANL
ta có
0
3
sin .sin sin 60
2 4
AL a a
ANL AL AN ANL
AN
0
cos .cos cos60
2 4
NL a a
ANL NL AN ANL
AN
Ta lại có
9
2
4 4
a a
AQ PN PL PN NL AQ NL a
Áp dụng định lí Pitago trong tam giác
ALP
ta có
2 2 2
2 2 2
3 81 21 21
16 16 4 2
a a a a
AP AL PL AP
Vậy
1 21
2
2 2
a
AB AC AP
Họ và tên: Trần Quốc An
Email: tranquocan1980@gmail.com
Facebook: Tran Quoc An
Câu 199: Cho
ABC có M là trung điểm của BC, H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm
x
để
HA HB HC xHO
  
.
A.
x
.2
B.
x
2
. C.
x
.1
D.
x
3
.
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
42
Chọn A
Gọi
'A
là điểm đối xứng với A qua O, ta có:
'
' (1)
A B AB
CH A B
CH AB
Tương tự ta chứng minh được
' (2)
BH A C
Từ (1),(2) suy ra tứ giác BHCA’ là hình bình hành.
Do đó M là trung điểm của
'HA
.
Ta có:
2 'HB HC HM HA
' 2 2.HA HB HC HA HA HO x

buiduynam1993@gmail.com
Câu 200: Cho tam giác
ABC
có đường trung tuyến
CM
vuông góc với phân giác trong
AL
. Giả sử
ngoài ra còn có
CM kAL
. Biết
2
2
cos
a bk
A
c dk
. Tính
a b c d
A.
18
. B.
5
. C.
26
. D.
17
.
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1)
Lời giải
Chọn A
H
O
C
B
A
A'
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
43
Ta có
ACM
cân tại
A
1
2
AC AM AB
2c b
với
b AC
,
c AB
.
Theo đề bài
AL
là phân giác trong của góc
A
nên:
2
3
b c
AL AB AC AM AC
c b c b
 
.
2 2 2 2 2
4 4
2 . 2 2 cos
9 9
AL AM AC AM AC b b A
2
8
1 cos
9
b A
.
Lai có
2 2 2
2 .AC AM AC AM CM
2 2 2 2 2
2 cos 2 2 1 cosb A b CM CM b A
.
Từ
2 2 2
8
2 1 cos . 1 cos
9
CM kAL b A k b A
2
9 1 cos 4 1 cosA k A
2
2
9 4
cos
9 4
k
A
k
.
Vậy
18a b c d
.
Họ và tên: Phạm Thanh My
Email: phamthanhmy@gmail.com
Facebook: Pham Thanh My
Câu 201: Cho tam giác
ABC
. Gọi
, ,M N P
là các điểm lần lượt thỏa mãn
MA MB 3 0
 
,
AN AC
1
3
 
,
2 3 0PB PC
Gọi
K
là giao điểm của
AP
và
MN
. Trong các mệnh đề sau, mệnh đề nào
đúng?
A.
KA KP 4 5 0
 
. B.
KA KP 3 2 0

.
C.
KA KP 0
 
. D. KA KP
 
.
Lời giải
Chọn C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
44
Gọi
I
là giao điểm của
MN
và
BC
.
Áp dụng định lý Menelaus ta có
. . 1
IB NC MA
IC NA MB
1
6
IB IC
mà
2 3 0
PB PC

P
là
trung điểm
IC
.
Áp dụng định lý Menelaus ta có
. . 1
KA IP MB
KP IB MA
1 0
KA
KA KB
KP
Câu 202: Cho hình thang
( / / )ABCD AB CD
có hai đường chéo vuông góc với nhau. Biết
Tìm
.
AC BD
A.
40 .cm
. B.
20 .cm
. C.
30 .cm
. D.
10 .cm
.
Lời giải
Chọn B
Họ và tên tác giả: Nguyễn Thị Yến Tên FB: Nguyễn Yến
Email: ntyen.c3lqd@gmail.com
I
K
P
M
N
C
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
45
20 .
AC BD BE BD BF DE cm
Họ và tên tác giả:Lê Thanh Lâm
Mail:quyphucvn@gmail.com Fb:Thanh Lâm Lê
Câu 203: Cho tam giác
ABC
có
3; 4
AB AC
.Gọi
AD
là đường phân giác trong của góc
A
.Biết
AD m AB n AC
  
.Khi đó tổng
m n
có giá trị là:
A.
1
B.
1
C.
1
7
D.
1
7
Lời giải
Chọn A
Theo tính chất đường phân giác trong của góc
A
trong tam giác
ABC
ta có:
3
3 4 3( ) 4( )
4
DB AB
DC DB AC AD AB AD
DC AC
4 3
7 4 3
7 7
AD AB AC AD AB AC
.Ta có
4 3
;
7 7
m n
.Vậy tổng
1m n
. Chọn A
Câu 204: Cho tam giác
ABC
bất kỳ, gọi
, ,M N P
lần lượt là trung điểm các cạnh
, ,AB BC CA
.
, 'H H
lần lượt là trực tâm các tam giác
,
ABC MNP
. Khẳng định nào đúng trong các khẳng định sau?
A.
3 'HA HB HC HH
. B.
2 'HA HB HC HH
.
F
E
D
C
B
A
B
C
D
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
46
C.
0
HA HB HC
. D.
3 'HM HN HP HH
.
Lời giải
Chọn B
'H
là trực tâm tam giác
MNP
nên
'H
là tâm đường tròn ngoại tiếp tam giác
ABC
.
Gọi
AD
là đường kính của đường tròn ngoại tiếp tam giác
ABC
nên
BHCD
là hình bình hành
suy ra
2 'HA HB HC HA HD HH
.
Mail: kimlinhlqd@gmail.com
Câu 205: Cho tam giác đều ABC tâm O. M là một điểm bất kì bên trong tam giác. Gọi D, E, F lần lượt là
hình chiếu của M lên BC, CA, AB. Với giá trị nào của k ta có hệ thức:
 
MD ME MF kMO
A.
1
2
k
. B.
1
k
. C.
3
2
k
. D.
2
k
Lời giải
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa
Chọn C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
47
Gọi hình chiếu của M lên cạnh BC là D. Ta có
3
. '
' 2
a a a
S MD S S
MD AA AO
S AA S S
.
a MBC
S S
Tương tự cho các đánh giá khác.
Do đó:
3
=
2
a b c
MD ME MF S AO S BO S CO
S
3
2
a b c
S MO MA S MO MB S MO MC
S
3 3 3
.
2 2 2
a b c a b c
S S S MO S MA S MB S MC MO
S S
Cách Khác: Qua M kẻ các đường thẳng song song với các cạnh BC, CA, AB
Họ và tên tác giả: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng
Email: thanhdungtoan6@gmail.com
Câu 206: Một giá đỡ hình tam được gắn vào tường (như hình vẽ). Tam giác ABC vuông cân tại B.
Người ta treo vào điểm A một vật nặng 10N. Tính độ lớn của các lực tác động vào tường tại B
và C? (Bỏ qua khối lượng của giá đỡ)
A.
10 2 , 10
B C
F N F N
B.
10 , 10 2
B C
F N F
C. 10
B C
F F N
D.
10 , 10 2
B C
F N F
Lời giải
Đáp án: B
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
48
Hệ chất điểm cân bằng nên
0 10
B C
F F P F P F P N
Tam giác ABC vuông cân tại B suy ra
10
2 2 10 2
B B
C C
F F F P N
F F F P N
Email: giachuan85@gmail.com
Câu 207: Cho ba điểm
A
,
B
,
C
thuộc đường tròn tâm
O
, thỏa mãn
0OA OC OB
. Tính góc
AOB
?
A.
0
120AOB . B.
0
90AOB . C.
0
150AOB . D.
0
30AOB .
Lời giải
Họ và tên: Trần Gia Chuân Tên facebook: Trần Gia Chuân
Chọn A
Do
0OA OC OB
nên
O
là trọng tâm tam giác
ABC
.
Mà
O
là tâm đường tròn ngoại tiếp tam giác nên tam giác ABC đều. Vậy góc
0
120AOB
Email: giachuan85@gmail.com
Câu 208: Cho tam giác
ABC
. Điểm
M
trên cạnh
BC
thỏa mãn
. .AM AB AC
1 2
3 3
 
, khẳng định nào
sau đây là khẳng định đúng?
A.
2MB MC
. B.
2MB MC
. C.
2MC MB
. D.
3MC MB
.
Lời giải
Họ và tên: Trần Gia Chuân Tên facebook: Trần Gia Chuân
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
49
Chọn B
Cách 1: Giả sử
.BM k BC
khi đó
Ta có
.
.
. .
AM AB BM
AB k BC
AB k AC AB
k AB k AC
1


Mà
. .AM AB AC k
1 2 2
3 3 3
 
suy ra
. .BM BC MB MC 3 2 2
Cách 2:
. . . . . .
. .
.
AM AB AC AM MB AM MC
MB MC
MB MC
MB MC
1 2 1 1 2 2
3 3 3 3 3 3
1 2
0
3 3
2 0
2
 
Email: cvtung.lg2@bacgiang.edu.vn
Câu 209: Cho tam giác đều
ABC
nội tiếp đường tròn tâm
,O
M
là một điểm tùy ý nằm bên trong tam
giác đã cho; gọi
'; '; 'A B C
theo thứ tự là hình chiếu vuông góc của
M
lên các cạnh
;BC CA
và
AB
. Khi đó ta có đẳng thức vectơ
' ' ' , . 0,
   
k
k M A MB MC l MO k l
l
là phân số tối
giản. Tính
2 2
2 .k l
.
A.
2 2
2 1
k l
. B.
2 2
2 1
k l
. C.
2 2
2 14
k l
. D.
2 2
2 5
k l
.
Lời giải
Họ và tên tác giả: Cao Văn Tùng Tên FB: Cao Tung
Chọn B
Từ M kẻ các đường thẳng song song với các cạnh
; ;BC CA AB
và các đường thẳng này cắt các
cạnh của tam giác
ABC
tại các điểm
1 2 1 2 1 2
, , , , ,A A B B C C
như hình trên.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
50
Xét tam giác
1 2
MA A
do tam giác
ABC
đều và tính chất của góc đồng vị nên góc
0
1 2 2 1
60
MA A MA A
suy ra tam giác
1 2
MA A
đều và
'A
là trung điểm của
1 2
A A
từ đó ta có:
1 2
1
'
2

MA MA MA
Chứng minh tương tự ta có
1 2 1 2
1 1
' ; '
2 2
 
MB MB MB MC MC MC
.
Suy ra
1 2 2 2 1 1
1
' ' '
2
  
MA MB MC MA MC MA MB MB MC
, mặt khác các tứ giác
1 1 1 2 2 2
; ;
AB MC BA MC CA MB
là hình bình hành nên
1 3
' ' '
2 2
   
MA MB MC MA MB MC MO
2 ' ' ' 3
MA MB MC MO
.
Vậy
2 2
2; 3 2 1
k l k l
.
Email: trang145@gmail.com
Câu 210: Cho hình vuông ABCD, E,F thõa mãn
1 1
;
3 2
BE BC CF CD
;
AE BF I
Ta có
AI k AB l AD
. Khi đó tỉ số k,l thõa mãn cặp nào sau:
A.
3 2
;
5 5
k l
B.
6 2
;
5 5
k l
C.
5 3
;
6 6
k l
D.
6 1
;
5 3
k l
Lời giải
Họ tên: Nguyễn Thị Trang Fb: Trang Nguyen
Chọn B
Kẻ EK//AB
1 1
3 6
EK EI EK
CF AI AB
Ta có:
6 6 6 1 6 2
( ) ( ) )
5 5 5 3 5 5
AI AE AB BE AB BC AB BC
Câu 211: Cho tam giác
ABC
, trên cạnh
AC
lấy điểm
M
, trên cạnh
BC
lấy điểm
N
sao cho:
3
AM MC
,
2
NC NB
, gọi
O
là giao điểm của
AN
và
BM
.Tính diện tích
ABC
biết diện
tích
OBN
bằng 1.
A.
10
. B.
20
. C.
25
. D.
30
.
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
A
B
C
D
F
E
I
K
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
51
Lời giải
Chọn D
BO xBA x BN
Vì
, ,A O N
thẳng hàng nên:
Tương tự:
1
AO yAM y AB
( 1) ( 1)
AB AM AB BN
y x y x
hay
0
( ) ( 1)
AB AM BN
x y y x
(1)
Đặt
CB
a
,
CA
b
.
Ta có:
3 1
4 3
; ;
AB a b AM b BN a
Thay vào (1) ta có:
3 1
0
4 3
x y a b yb x y a
1 3
3 4
x y
x y a x y b a b
Từ đó ta có:
1
1
10
3
2
3
5
4
x
x
x y
y
y x y
Với
1
10
x
1 1
10 10
(1 )
BO BA BN
10
1
BO BN BA BN
hay
10
1
NO NA
10
NA
NO
.
Vì
1 10 30
ONB NAB ABC
S S S
.
Họ và tên: Nguyễn Văn Quân Tên FB: Quân Nguyễn
Email: Quanvan09@gmail.com
Câu 212: Cho tam giác
ABC
có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng
định đúng?
A.
4HA HB HC HO
   
. B.
2HA HB HC HO
   
.
C.
2
3
HA HB HC HO
   
. D.
3HA HB HC HO
   
.
Lời giải
O
N
M
C
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
52
Dễ thấy:
2HA HB HC HO
  
nếu tam giác
ABC
vuông.
Nếu tam giác
ABC
không vuông gọi D là điểm đối xứng của A qua O. Khi đó:
/ /BH DC
(vì cùng vuông góc với AC).
/ /BD CH
(vì cùng vuông góc với AB).
Suy ra
BDCH
là hình bình hành, do đó theo quy tắc hình bình hành thì
HB HC HD
  
(1).
Mặt khác vì O là trung điểm của AD nên
2HA HD HO
  
(2).
Từ (1) và (2) suy ra.
2HA HB HC HO
  
.
Tên facebook: NT AG
Câu 213: Cho tam giác
ABC
có
D
là trung điểm của
BC
,
O
là một điểm trên đoạn
AD
sao cho
4
AO OD
. Gọi
E CO AB
,
F BO AC
,
M AD EF
. Khẳng định nào sau
đây đúng?
A.
1
7
MO AD

B.
2
15
MO AD
 
C.
1
8
MO AD

D.
2
7
EM BC

Lời giải
Họ và tên tác giả: Nguyễn Đặng
Chọn B
M
F
E
D
A
B
C
O
H
O
A
B
C
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
53
Đặt:
AB xAE
,
AC y AF
,
( , )
x y
.
Theo bài ra ta có
4 2 2 2 2 2
5 5 5 5 5 5
AO AD AB AC x AE AC AB y AF
    
Do
, ,O B F
thẳng hàng nên
2 2 3
1
5 5 2
y y
Do
, ,C O E
thẳng hàng nên
2 2 3
1
5 5 2
x x
Từ đó:
3
2
AB AC AD
AE AF AM
, lại có
4 2
5 15
AO AD MO AD
 
Câu 214: Cho hình thang
ABCD
có
//AB CD
. Gọi
,M N
lần lượt là trung điểm của
,AC BD
. Kẻ
( )NH AD H AD
và
( )ME BC E BC
. Gọi
I ME NH
, kẻ
( )IK DC K DC
.
Khi đó trong tam giác
MNK
hệ thức nào sau đây đúng?
A.
. . . 0
MK IN NK IM MN IK
B.
.tan .tan .tan 0
IN N IM M IK K
C.
.cot .cot .cot 0
IN N IM M IK K
D.
IM IN IK
Lời giải
Chọn B
Ta chứng minh
ID IC
Kẻ
,
AF BC BJ AD
. Tứ giác
ABFJ
nội tiếp
180
180
O
O
ABF AJF
DCB AJF
Khi đó
DCFJ
là tứ giác nội tiếp.
,
NH ME
là các đường trung bình của các tam giác
,
DBJ CAF
,IH IE
là các đường trung trực của
,DJ CF
nên
IJ IF ID IC
. Vậy
ID IC KD KC
//
//
NH BC NK ME NK MI
MK AD MK HN MK NI
Từ đó suy ra
I
là trực tâm tam giác
MNK
. Nên đáp án đúng là B
J
F
K
I
E
H
M
N
A
B
D
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
54
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Email: nguyenvantoannbk@gmail.com
Câu 215: Cho
ABC
, điểm
M
thuộc cạnh
BC
sao cho 2018. 2019.
ABM ACM
S S . Đẳng thức nào sau
đây sai?
A.
2018. 4037.
ABC ACM
S S
. B.
2018. 2019. 0
BM CM
.
C.
4037
.
2018
BC BM
D.
2019
.
4037
ABM ABC
S S
.
Lời giải
Chọn C
Kẻ đường cao
AH
của
ABC
.
Ta có
2019 4037
2018 2018
ABC ABM ACM ACM ACM ACM
S S S S S S
, suy ra A đúng.
Tương tự D cũng đúng.
Từ giả thiết ta có
1
. .
2019 2019
2
1
2018 2018
. .
2
ABM
ACM
AH BM
S BM
BM CM
S CM
AH CM
, suy ra B đúng.
(C sai vì
4037
.
2019
BC BM
).
(Tác giả: Nguyễn Văn Phùng,Gmail: nvpmaster0808@gmail.com)
Câu 216: Cho tam giác
ABC
.
M
là điểm nằm trên cạnh
BC
sao cho 3
ABC AMC
S S
. Một đường thẳng
cắt các cạnh
, ,AB AM AC
lần lượt tại
, ,B M C
phân biệt. Biết rằng
2 .
AB AC AM
k
AB AC AM
.
Tìm số
k
.
A.
1
k
. B.
2
k
. C.
3
k
. D.
2
3
.
(Tác giả: Nguyễn Văn Phùng,Gmail: nvpmaster0808@gmail.com)
Lời giải
Chọn C
C'
B'
M'
A
B
C
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
55
Ta có
2
3 3
3
ABC AMC
S S BC MC BM BC
Đặt
' ; '= ; '
AB xAB AC yAC AM zAM
Ta có
' ' ' '
B M AM AB z AM xAB
   
2
3
2 2
3 3 3
z
z AB BM xAB z x AB BC
z z z
z x AB AC AB x AB AC
Lại có:
' ' ' '
B C AC AB yAC xAB
Mặt khác
' 'B M
,
' 'B C
cùng phương nên
2
3 1 2
3 3
z z
x
x y z x y
Hay
2 3
' ' '
AB AC AM
AB AC AM
.
Từ đó suy ra
3
k
.
nguyenchitrung12@gmail.com
Câu 217: Cho
n
điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là
1 2
, ,...,
n
A A A
. Bạn Bình kí hiệu
chúng là
1 2
, ,...,
n
B B B
(
1
n
A B
). Vectơ tổng
1 1 2 2
...
n n
A B A B A B
 
bằng
A.
0
. B.
1
n
A A
. C.
1
n
B B
. D.
1
n
A B
.
(Sưu tầm, Tên FB: Trung Nguyễn Chí)
Lời giải
Chọn A
Lấy điểm
O
bất kì. Khi đó
1 1 2 2 1 2 1 2
... ... ...
n n n n
A B A B A B A O A O A O OB OB OB
        
Vì
1 2 1 2
, ,..., , ,...,
n n
B B B A A A
nên
1 2 1 2
... ...
n n
OB OB OB OA OA OA
Do đó
1 1 2 2 1 1 2 2
... ... 0
n n n n
A B A B A B A O OA A O OA A O OA
        
.
Câu 218: Trong đường tròn (O) với hai dây cung AB và CD cắt nhau tại M. Qua trung điểm S của BD kẻ
SM cắt AC tại K sao cho
AK
a
CK
.Tính:
2
2
AM
CM
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
56
A. 2a B.
2
a
C.
2
1
a
D. a
Lời giải
0
AK
a
CK
Ta có:
1
. .
1 1
a
MK MA MC
a a
(1)
Do
,MK MS
cùng phương nên:
( )
2
l
MK lMS MB MD
Mặt khác
2
2
2 2
. . 0
(2)
2 2
b
MB MA
MA
MA MB MC MD b
b
MD MC
MC
bl bl
MK MA MC
MA MC
Từ (1) và (2) suy ra
2
2
2
2
1
1 2
1 2
bl
MA
a MA
a
a bl
MC
a MC
Câu 219: Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn:
2 1
,
3 4
BD BC AE AC
.
Điểm K trên AD sao cho 3 điểm B, K,E thẳng hàng. Xác định tỷ số
AK
AD
A.
1
2
B.
1
3
C.
1
4
D.
1
5
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
57
Ba điểm K, B, E thẳng hàng khi và chỉ khi tồn tại
sao cho:
(1 )AK AB AE
(1)
Đặt
1 2
( )
3 3
AK xAD x AB AC
1 2 2
( )
3 3 3 3
x x
AK x AB AC AB AC
(2)
Áp dụng hệ quả 5 thì từ (1) và (2) ta có:
1
3 3
1 2 1
(1 )
4 3 9
x
x
x
Vậy
1
3
AK AD
1
3
AK
AD
Facebook: Lê Văn Kỳ
Email: lethithuy@thpthv.vn
Câu 220: Cho tam giác ABC vuông tại C, có
,AC b BC a
, D là chân đường cao kẻ từ C.
Khẳng định nào sau đây là đúng?
A.
2 2
2 2 2 2
a b
CD CA CB
a b a b
. B.
2 2
2 2 2 2
a b
CD CA CB
a b a b
.
C.
2 2
2 2 2 2
a b
CD AC BC
a b a b
D.
2 2
2 2 2 2
a b
CD AC BC
a b a b
.
Lời giải
Chọn A
K
B
C
A
E
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
58
Ta có
2 2 2 2
2
2 2 2 2 2
.
CB BD CB a a
BC BD BA BD BD BA
BA BA BA a b a b
.
Lại có:
2
2 2
a
BA CA CB BD CA CB
a b
   
.
Vậy
2 2 2
2 2 2 2 2 2
a a b
CD CB BD CB CA CB CA CB
a b a b a b
       
Email: huyenbla81@gmail.com
Câu 221:
Cho tam giác ABC có trọng tâm G. Gọi I là điểm xác định bởi
5 7 0.
IA IB IC
Gọi E là
giao điểm của AI và BG. Tính tỷ số
.
EA
EI
A. 2. B.
1
.
2
C. 3. D.
1
.
3
(Họ tên tác giả: Nguyễn Thị Thu Huyền. Tên FB: Thu Huyen Nguyen)
Lời giải
Chọn B
Vì G là trọng tâm của tam giác ABC nên ta có:
3 .IA IB IC IG

G
A
B
C
E
I
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
59
Mà:
5 7 0.
IA IB IC
Vậy ta có:
6 6 3IA IB IG
2
BA IG
/ /
2
IG AB
IG AB
(hình vẽ)
1
.
2
EA AB
EI IG
Email: nghiepbt3@gmail.com
Câu 222: Cho 2 tia Ox, Oy vuông góc. Trên tia Ox lấy các điểm A,B sao cho OA = OB = 1. C là điểm
thuộc đoạn OA, N là một điểm thuộc đoạn OB và dựng hình vuông OCMN. Trên đoạn CM lấy
điểm Q và dựng hình vuông ACQP. Gọi S là giao điểm của AM và PN. Giả sử
OAkOC
,
AMxAS
,
NPyNS
,
1;
2
1
k
Khi x + y =
10
13
thì k =
b
a
, với
ba,
và a, b nguyên tố cùng nhau thì a.b bằng
A. 7 B. 4 C. 5 D.
12
Lời giải
FB: Ngô Quang Nghiệp
Ta có:
OMxOAxOAOMxOAAMxOAASOAOS 1
OBxkOAxkOAxONOCxOAx 11
OBxkOAkxx 1
, (1).
Mặt khác:
OBykAPyOAyOBkONOPyOBkNPyOBkNSONOS
OBkyOAyOByk 11
, (vì AP = CA = 1 - k nên
OBkAP 1
)
OBkyykOAy 2
, (2).
Từ (1) và (2), ta có
kyykkx
ykxx
2
1
122
122
1
2
2
2
kk
k
y
kk
k
x
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
60
Ta có:
4
1
4
3
10
13
122122
1
10
13
2
2
2
k
k
kk
k
kk
k
yx
Đối chiếu điều kiện, ta chọn
4
3
k
. ĐÁP ÁN D.
Họ Tên: Lê Duy Tên FB: Duy Lê Email: Duyleag@gmail.com
Câu 223: Cho tam giác
ABC
. Giả sử điểm
M
nằm trên cạnh
BC
thỏa các tam giác
,
MAB MAC
lần
lượt có diện tích là
1 2
,S S
. Khẳng định nào sau đây đúng?
A.
1 2 2 1
.S S AM S AB S AC

B.
1 2 1 2
.S S AM S AB S AC
C.
2 1 2 1
.S S AM S AB S AC

D.
2 1 1 2
.S S AM S AB S AC
Lời giải
Chọn A
Gọi
,
h d A BC
.
Ta có
1
2
1
, .
2
1
, .
2
d A BC BM
S
BM
S CM
d A BC CM
1
2 1
2
S
BM MC S BA AM S MA AC
S

2 1 2 1
S S AM S AB S AC
Họ và tên tác giả: Nguyễn Đức Duẩn Tên FB: Duan Nguyen Duc
Email: Duanquy@gmail.com
Câu 224: Cho tam giác ABC có có M là trung điểm của BC,
1
2
AI MI
. Điểm K thuộc cạnh AC sao
cho B,I,K thẳng hàng. Khi đó
m
KA CK
n
. Tính
25 6 2019S m n
A.
2019
S
. B.
2068
S
. C.
2018
S
. D.
2020
S
.
Lời giải
Chọn B
S
2
S
1
A
B
C
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
61
Ta có
1
( )
2
AM AB AC
.
Gọi điểm
K
thuộc cạnh AC sao cho
.AK x AC
.
Ta có
.BK AB x AC
và
1 1 1 5 1
.
3 6 6 6 6
BI AB AM AB AB AC AB AC
   
Để B,I,K thẳng hàng thì
1 1
5 1
5
6 6
x
x
1
1
4
4
m
KA CK
n
Vậy
25.1 6.4 2019 2068S
Họ và tên: Nguyễn Quang Huy Fb: Nguyễn Quang Huy
Email: boigiabao98@gmail.com
Câu 225: Cho tam giác ABC có trọng tâm G, lấy các điểm I, J sao cho
IA 2IB
và
3JA 2JC 0
và thỏa
mãn đẳng thức
IJ kIG
. Giá trị của biểu thức
2 2 500
P (25k 36)(k k 1)
là:
A.
P 1235
B.
P 0
C.
5
P
6
D.
6
P
5
Lời giải
Thật vậy nếu ta gọi M là trung điểm của BC ta có:
2 2 1 1 5
IG AG AI AM 2AB . (AB AC) 2AB AC AB
5 3 2 3 3
 
Mặt khác ta lại có
2 6 1 5 6
IJ AJ AI AC 2AB ( AC AB) IG
5 5 3 3 5

Do đó
6
k
5
Nhận thấy
2
36
25k 36 25. 36 36 36 0
25
do đó
P 0
.vậy chọn B
(Email): nguyenmy181@gmail.com
Câu 226: Cho tam giác
ABC
. M là điểm nằm trên cạnh BC sao cho
ABC AMC
S S 3
. Một đường thẳng
cắt các cạnh
AB AM AC, ,
lần lượt tại
B M C', ', '
phân biệt. Biết
' ' '
AB AC AM
m n
AB AC AM
.
Tính
m n
.
A. 2. B. 5. C. 3. D. 4.
Lời giải
A
B
C
I
K
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
62
Ta có
ABC AMC
S S BC MC BM BC
2
3 3
3
 
Đặt
AB xAB AC yAC AM zAM ' ; '= ; '
     
Ta có
B M AM AB zAM xAB ' ' ' '
    
z
z AB BM xAB z x AB BC
z z z
z x AB AC AB x AB AC
2
3
2 2
3 3 3
    
    
B C AC AB yAC xAB ' ' ' '
    
Mặt khác
B M' '

,
B C' '

cùng phương nên
z z
x
x y z x y
2
3 1 2
3 3
Hay
AB AC AM
AB AC AM
2 3
' ' '
(Họ và tên tác giả: Nguyễn Thị Trà My, Tên FB: Nguyễn My)
Họ và tên tác giả: Nguyễn Đặng
Tên facebook: NT AG
Câu 227: Cho tam giác
ABC
có
D
là trung điểm của
BC
,
O
là một điểm trên đoạn
AD
sao cho
4
AO OD
. Gọi
E CO AB
,
F BO AC
,
M AD EF
. Khẳng định nào sau
đây đúng?
A.
1
7
MO AD

B.
2
15
MO AD
 
C.
1
8
MO AD

D.
2
7
EM BC

Lời giải
Chọn B
Đặt:
AB xAE
,
AC yAF
,
( , )
x y
.
M
F
E
D
A
B
C
O
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
63
Theo bài ra ta có
4 2 2 2 2 2
5 5 5 5 5 5
AO AD AB AC x AE AC AB y AF
   
Do
, ,O B F
thẳng hàng nên
2 2 3
1
5 5 2
y y
Do
, ,C O E
thẳng hàng nên
2 2 3
1
5 5 2
x x
Từ đó:
3
2
AB AC AD
AE AF AM
, lại có
4 2
5 15
AO AD MO AD
 
Câu 228: Cho hình thang
ABCD
có
//AB CD
. Gọi
,M N
lần lượt là trung điểm của
,AC BD
. Kẻ
( )NH AD H AD
và
( )ME BC E BC
. Gọi
I ME NH
, kẻ
( )IK DC K DC
.
Khi đó trong tam giác
MNK
hệ thức nào sau đây đúng?
A.
. . . 0
MK IN NK IM MN IK
B.
.tan .tan .tan 0
IN N IM M IK K
C.
.cot .cot .cot 0
IN N IM M IK K
D.
IM IN IK
Lời giải
Chọn B
Ta chứng minh
ID IC
Kẻ
,
AF BC BJ AD
. Tứ giác
ABFJ
nội tiếp
180
180
O
O
ABF AJF
DCB AJF
Khi đó
DCFJ
là tứ giác nội tiếp.
,
NH ME
là các đường trung bình của các tam giác
,
DBJ CAF
,IH IE
là các đường trung trực của
,DJ CF
nên
IJ IF ID IC
. Vậy
ID IC KD KC
//
//
NH BC NK ME NK MI
MK AD MK HN MK NI
Từ đó suy ra
I
là trực tâm tam giác
MNK
. Nên đáp án đúng là B
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet
Email: tiethanh.78@gmail.com
J
F
K
I
E
H
M
N
A
B
D
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
64
Câu 229: Cho hình bình hành
ABCD
. Gọi
I
là trung điểm của
CD
,
G
là trọng tâm tam giác
BCI
. Đặt
,a AB b AD

. Hãy tìm đẳng thức đúng trong các đẳng thức sau?
A.
5 2
6 3
AG a b
. B.
5
6
AG a b
.
C.
5
6
AG a b
. D.
4 2
3 3
AG a b
.
Lời giải
Chọn A
*
I
là trung điểm của
CD
nên:
1 1 1
2 2 2
AI AC AD AB AD
.
*
G
là trọng tâm tam giác
BCI
nên:
1 1 1
3 3 3
AG AB AC AI
, thay
AC AB AD
và
1
2
AI AB AD
 
ta được
1 1 1 1 5 2
3 3 3 2 6 3
AG AB AB AD AB AD AB AD
.
(Email): locleduc10@gmail.com
Câu 230: Một đường thẳng cắt các cạnh
, DA DC
và đường chéo
DB
của hình bình hành
ABCD
lần
lượt tại các điểm
, E F
và
.M
Biết
. ,DE m DA
.DF n DC
( , 0).m n
Khẳng định đúng là:
A.
.
m n
DM DB
m n
 
. B.
m
DM DB
m n
 
.
C.
n
DM DB
m n
 
. D.
.m n
DM DB
m n

.
Lời giải
Chọn D
Đặt
. ; .DM x DB EM yFM
  
Khi đó:
( )EM DM DE x m DA xDC
 
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
65
( )
FM DM DF xDA x n DC
  
Ta có:
( ) ( ) .EM yFM x m DA xDC xyDA y x n DC
 
Do
; DA DC
không cùng phương nên
( )
x m xy
x y x n
Giải hệ được
m
y
n
và
.
mn
x
m n
Vậy
.m n
DM DB
m n

(Họ và tên tác giả: Lê Đức Lộc, Tên FB: Lê Đức Lộc)
Email: phuogthu081980@gmail.com
Câu 231:
Hình thang cân ABCD có độ dài đường cao
; / / , 3; 2;
AH a AB CD AB a AD a AB DC
AC cắt BH tại I.
Biết
; ; ; ;
x y z
AI AC x y z m N
m
.
Tính tổng
T x y z m
A. 20 B. 18 C. 17 D. 21
Lời giải
Họ và tên tác giả: Nguyễn Thị Phương Thu FB: Buisonca Bui
) 1
3 1
) . .
3
)
AI AB BI AB kHB AB k AB AH k AB k AH
HC
AC AH HC AH AB AH AB
AB
I AC AI mAC
Mà
;AH AB
không cùng phương
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
66
3 1
1
6 3 6 3
3
11 11
6 1 3 11 21
k m
m AI AC
k m
T
tambc3vl@gmail.com
Câu 232: Cho hình thang ABCD với O là giao điểm của hai đường chéo AC và BD. Qua O vẽ đường
thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên AD và BC theo thứ tự
tại M và N. Với
AB a
,
D
C b
, khi đó
MN
bằng:
A.
a. .AB b DC
a b
. B.
. .b AB a DC
a b
. C.
a. .AB b DC
a b
. D.
. .b AB a DC
a b
.
Lời giải
Họ và tên: Nguyễn Thanh Tâm Tên FB: Tâm Nguyễn
Chọn B
Do
/ / / / DMN AB C
nên:
D OD
MA NB OA OB AB a
M NC OC DC b
.
Do đó
.
a
MA MD
b
;
.
a
NB NC
b
, nên:
.
1
a
OA OD
b
OM
a
b
;
.
1
a
OB OC
b
ON
a
b
Có:
. .
. .
1 1
a a
OB OA OC OD AB DC
b AB a DC
b b
MN ON OM
a a
a b
b b

Câu 233: Cho tam giác
ABC
đều tâm
O
; điểm
M
thuộc miền trong tam giác
OBC
;
D
,
E
,
F
lần lượt
là hình chiếu vuông góc của
M
trên
BC
,
CA
,
AB
. Khẳng định nào sau đây đúng?
A.
1
2
MD ME MF MO
. B.
MD ME MF MO
   
.
C.
3
MD ME MF MO
 
. D.
3
2
MD ME MF MO
.
Lời giải.
Phan Minh Tâm
Chọn D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
67
Từ
M
kẻ đường thẳng
Mx AC
cắt
AB
,
BC
tại
H
,
K
;
Từ
M
kẻ đường thẳng
My AB
cắt
BC
,
CA
tại
P
,
Q
;
Từ
M
kẻ đường thẳng
Mz BC
cắt
AB
,
AC
tại
R
,
S
;
Suy ra
HMR
,
PMK
,
QMS
là các tam giác đều nên
MD
,
ME
,
MF
là các đường cao
đồng thời cũng là đường trung tuyến. Khi đó
1
2
MD MP MK
;
1
2
ME MS MQ
;
1
2
MF MH MR

.
Ta được
1
2
MD ME MF MQ MH MP MR MS MK
 
.
Hay
1 1
2 2
MD ME MF MA MB MC MO OA MO OB MO OC
  
.
Mặt khác ta có tam giác
ABC
đều nên tâm
O
cũng là trọng tâm tam giác
ABC
nên
0
OA OB OC

;
Vậy
3
2
MD ME MF MO
.
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG
Email: phunghang10ph5s@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
68
Câu 234: Cho hình bình hành
ABCD
có các điểm
, ,M I N
lần lượt thuộc các cạnh
, ,AB BC CD
sao cho
1 1
, ,
3 2
AM AB BI kBC CN CD
. Gọi
G
là trọng tâm tam giác
BMN
. Xác định
k
để
AI
đi
qua
G
.
A.
1
3
. B.
9
13
. C.
6
11
. D.
12
13
.
Lời giải
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng
Chọn C
Gọi
E
là trung điểm của
MB
. Khi đó:
AM ME EB
Ta có:
1
3
EG EN
1
3
EA AG EA AN
2 1 2 2 1 4 1 1 5 1
.
3 3 3 3 3 9 3 2 18 3

AG AE AN AG AB AC CN AB AC AB AB AC
Do
BI kBC
và điểm
I
nằm trên đoạn
BC
nên
BI kBC
1

BA AI k BA AC AI k AB k AC
Do
AI
đi qua
G
nên
, ,A I G
thẳng hàng
1 18 6
1 3
5 1
5 11
18 3
k k
k k k
.
Câu 235: Cho tam giác
ABC
. Gọi M là điểm thuộc cạnh AB, N là điểm thuộc cạnh AC sao cho
AM AB AN AC
1 3
,
3 4
. Gọi O là giao điểm của CM và BN. Trên đường thẳng BC lấy E.
Đặt
BE xBC
 
.
Tìm x để A, O, E thẳng hàng.
Chọn C
A.
2
3
B.
8
9
C.
9
13
D.
8
11
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
69
Ta có:
AO AB AC
1 1
9 4
  
AE x AB xAC (1 )
  
A, E, O thẳng hàng
AE kAO
 
k k
x AB xAC AB AC k x
36 9
(1 ) ;
9 4 13 13
   
Vậy
x
9
13
là giá trị cần tìm.
Họ và tên tác giả: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng
Email: thanhdungtoan6@gmail.com
Ý tưởng: Cho tam giác
ABC
,
I
là trung điểm của
BC
. Gọi
, , P Q R
là các điểm xác
định bởi:
, ,
AP p AB AQ q AI AR r AC

với
0
pqr
.
Chứng minh rằng:
, , P Q R
thẳng hàng khi và chỉ khi
2 1 1
q p r
.
Chứng minh
Ta có
1 2
2 2 2
q p q
PQ AQ AP qAI pAB q AB AC pAB AB AC
PR AR AP r AC pAB


Do đó,
, , P Q R
thẳng hàng khi và chỉ khi tồn tại số thực
m
sao cho
PQ mPR

2 2 2 2
0
2 2 2 2
q p q q p mp q mr
AB AC m r AC pAB AB AC
2 2
0
2
2
0
2
q p mp
q mr
(vì
,
AB AC

không cùng phương)
1
2 1 1
2
1
2 2
2
q
m
q q
p
p r q p r
q
m
r
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
70
Câu 236: Cho tam giác
ABC
. Gọi
I
là trung điểm
BC
;
P
là điểm đối xứng với
A
qua
B
;
R
là điểm
trên cạnh
AC
sao cho
2
5
AR AC
. Khi đó đường thẳng
AR
đi qua điểm nào trong các điểm
sau đây?
A. Trọng tâm tam giác
ABC
. B. Trọng tâm tam giác
ABI
.
C. Trung điểm
AI
. D. Trung điểm
BI
.
Lời giải
Đáp án: B
Theo đề bài,
2 2
2 2
5 5
AP AB p
AR AC r

Gọi
G
là trọng tâm tam giác
ABI
, ta được
2 2
3 3
AG AH q

Ta có
1 1 1 1 2
3
5
2
2
p r q
suy ra P, G, R thẳng hàng.
(có thể phát triển P, J, G, M, R thẳng hàng với J – có lẽ là trung điểm BH, còn M chia
AI theo tỷ số tính được)
Câu 237: Cho
ABC
có
H
là trung điểm của
AB
và
: 2
G AC GC AG
. Gọi
F
là giao điểm của
CH
và
BG
. Tìm điểm
I
trên
BC
sao cho
, ,I F A
thẳng hàng
A.
2 .

IC IB
B.
2 .

IB IC
C.
.IB IC
D.
3 .

IC IB
Lời giải
J
M
R
G
H
I
B
A
C
P
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
71
Gọi
D
là đỉnh thứ tư của hình bình hành
ABCD
và
E
là trung điểm của
.AD
Khi đó, ta có:
1
4

FH FC
Vận dụng định lý
Menelauyt
trong
HBC
có
, ,A F I
thẳng hàng
1
. . 1 . . 4 1
2
1
2
AH IB FC IB
AB IC FH IC
IB
IC
Vậy 2 .
 
IC IB
Họ và tên tác giả: Hoàng Thị Trà FB: Hoàng Trà
Câu 238: Cho tam giác ABC. I là trung điểm của BC. Gọi M, N, P lần lượt là các điểm xác định bởi
; ;AM mAB AN nAI AP p AC

, với
0mnp
. Tìm điều kiện của
, ,m n p
để M, N, P thẳng
hàng.
A.
mp mn np
B.
2mp mn np
C.
2np mn mp
D.
2mn mp np
Lời giải
Ta có
MP AP AM pAC mAB
MN AN AM nAI mAB


. Mà
1
( )
2
AI AB AC

( ) ( )
2 2 2
n n n
MN AB AC mAB m AB AC
 
Do
0mnp
nên M, N, Q thẳng hàng khi và chỉ khi
2 2
2
n n
m
mp mn np
m p
Chọn đáp án B.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
72
Nhận xét: Với bài toán trên thì việc cụ thể hóa bộ ba số m,n,p sao cho thỏa mãn điều kiện trên
ta đều ra được bài toán chứng minh ba điểm thẳng hàng. Kết quả trên chúng ta có thể vận dụng
vào để giải nhanh bài toán sau:
Câu 239: Cho tam giác ABC. Gọi G là trọng tâm của tam giác, I là trung điểm của BC, M và N là các
điểm được xác định bởi
1
2
3 4 0
CN BC
MA MB
. Gọi P là giao điểm của AC và MN. Tính tỉ số diện
tích tam giác ANP và tam giác CNP.
A. 3 B.
7
2
C. 4 D. 2
Lời giải.
Ta có
ANP
CNP
S
PA
S PC
. Yêu cầu bài toán dẫn đến tìm tỉ số
PA
PC
.
Ta dễ dàng chứng minh được M, N, G thẳng hàng.
Ta có
1
2 2( )
2
2 3 3 4
2 3 4 3 4 ( 3 4 0)
2 7
CN BC CN GC GB GN GN GC GB
GN GC GB GA GB
GN GA GB MA MB vi MA MB
GN GM

 
Vậy G, M, N thẳng hàng. Mặt khác MN cắt AC tại P, nên M, G, P thẳng hàng.
Áp dụng kết quả G, M, P thẳng hàng theo câu 1 vào ta có
4
7
AM mAB m

2
3
AG nAI n
,
.AP p AC

Khi đó
4 4 2 2 4
2 2. . . .
7 7 3 3 5
mp mn np p p p
, khi
đó
4
PA
PB
. Vậy
4
ANP
CNP
S
S
Câu 240: Cho tam giác
ABC
. Gọi
,D E
lần lượt là các điểm thỏa mãn:
2
;
3
BD BC
1
AC
4
AE
. Điểm
K
trên
AD
thỏa mãn
a
b
AK AD
(với
a
b
là phân số tối giản) sao cho 3 điểm
, ,B K E
thẳng
hàng. Tính
2 2
P a b
.
A.
10
P
. B.
13
P
. C.
29
P
. D.
5
P
.
Lời giải
Chọn A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
73
Vì
1 1 3
(1)
4 4 4
AE AC BE BC BA
Giả sử
. . (1 )AK x AD BK x BD x BA

Mà
2
3
BD BC
nên
2
. (1 )
3
x
AK x AD BK BD x BA
Vì
, ,B K E
thẳng hàng (
B E
)nên có m sao cho
BK mBE
Do đó có:
3 2
(1 )
4 4 3
m m x
BC BA BC x BA
Hay
2 3
1 0
4 3 4
m x m
BC x BA
Do
;BC BA
không cùng phương nên
2 3
0;1 0
4 3 4
m x m
x
Từ đó suy ra
1 8
;
3 9
x m
Vậy
1
3
AK AD
Email: themhaitotoanyp1@gmail.com
Câu 241: Cho tam giác ABC, I là điểm thỏa mãn:
2 4 0
IA IB IC
K là điểm thỏa mãn:
2 3 0
KA KB KC
P là điểm thỏa mãn:
0
PA mPB nPC
Có bao nhiêu cặp
, , , , , 10;10
m n m n Z m n
sao cho
, ,I K P
thẳng hàng.
A. 2 B. 3 C.
4
D. 5
Lời giải
Ta có
PCnPBmPA
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
74
Có:
2 4 0
IA IB IC
042 PIPCPIPBPIPA
PCPBPAPI 425
PCnPBmPI 42125
Có:
2 3 0 2 3 0 6 2 3KA KB KC PA PK PB PK PC PK PK PA PB PC
6 2 3
PK m PB n PC
I,K,P thẳng hàng khi và chỉ khi
PKPI 6,5
cùng phương
1152422312
nmnmnm
Do
, , , , , 10;10
m n m n Z m n
nên
, 8; 1 , 3, 1 , 2,3 , 5,7
m n
(Fb: Lưu Thêm)
Email : boyhanam@gmail.com
Bài em sưu tầm ạ !
Câu 242: Cho tam giác
ABC
,
M
và
N
là hai điểm thỏa mãn:
2
BM BC AB
 
,
CN xAC BC
 
. Xác
định
x
để
A
,
M
,
N
thẳng hàng.
A.
3.
B.
1
.
3
C.
2.
D.
1
.
2
Lời giải
Chọn D
Ta có
2 2
. 1
BM BC AB AM BC AB AM AC BC
CN xAC BC CA AN xAC BC AN x AC BC


Để
, , A M N
thẳng hàng thì
0
k
sao cho
AM k AN

Hay
1
1
2
1 2
1 2 1
2
k
x k
x AC BC k AC BC
k
x

Huonghungc3@gmail.com
Câu 243: Cho tam giác
ABC
có
G
là trọng tâm,
I
là trung điểm
AG
, lấy
K
thuộc cạnh
AC
sao cho
AK kAC
. Nếu
B, I, K
thẳng hàng thì giá trị của
k
nằm trong khoảng?
A.
1
0;
6
B.
1
0;
2
C.
1 1
;
5 3
D.
1
;1
5
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
75
Lời giải
(Họ tên: Nguyễn Thu Hương. Tên FB: Thu Hương)
Chọn B
Không giảm tính tổng quát: giả sử tam giác
ABC
có:
A(0;0);B 6;0 ;C 0;6
thì
G 2;2 ; I 1;1
Gọi
K 0;m
Khi đó:
IB 5; 1 ;KB 6; m
 
. Để
B, I, K
thẳng hàng:
6
5m 6 m
5
suy ra
1
k
5
Họ và tên: Trần Văn Luật
Email: Tvluatc3tt@gmail.com
FB: Trần Luật
Câu 244: Cho tam giác
ABC
,
M
là điểm thuộc cạnh
AC
sao cho
2.MA MC
,
N
thuộc
BM
sao cho
3
NB NM
,
P
là điểm thuộc
BC
. Biết rằng ba điểm
, ,A N P
thẳng hàng khi
PB kPC
.
Khẳng định nào sau đây là đúng?
A.
5
3;
2
k
. B.
5
; 1
2
k
. C.
1
1;
2
. D.
1
;0
2
.
Lời giải
Chọn B
N
O
B
C
G
K
I
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
76
Ta có
1 1
3 3 3 4
4 2
NB NM AB AN AM AN AB AM AN AN AB AC
.
Do
P
là điểm thuộc
BC
nên
PB k PC AB AP k AC AP

1
AB k AC k AP
1
1 1
k
AP AB AC
k k
.
Ba điểm
, ,A N P
thẳng hàng khi và chỉ khi
1
2
1 4
4
1
3
1 2
h
k
k
AP hAN
h
h
k
.
Vậy
2
k
.
Họ và tên: Hoàng Thị Kim Liên
Email: lientiencl@gmail.com
Facebook: Kim Liên
Câu 245: Cho tam giác
ABC
. Gọi
M,
N,
P
lần lượt nằm trên đường thẳng
BC,
CA,
AB
sao cho
MB mMC
 
,
,NC nNA
 
PA k PB
 
. Tính tích
mnk
để
M,
N,
P
thẳng hàng?
A.
1
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn A
Ta có :
1
1
1 1 1
; ; ( ) ;
m n
MB BC BP AB BC m MC CN AC
m k n
       
1 1
1 1 1
n
MN AB AC
m m n
  
P
N
M
A
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
77
1
1 1 1
m m
MP AB AC
m k m
  
Để
M, N,
P
thẳng hàng thì ta có :
Câu 246:
m 1 m
1 m 1 k 1 m
mnk 1
1 1 n
1 m 1 m 1 n
(Email): thuhangnvx@gmail.com
Câu 247: Cho hình bình hành ABCD gọi M là trung điểm của cạnh CD, N là điểm thuộc cạnh AD sao cho
1
3
AN AD
. Gọi G là trọng tâm của tam giác BMN, đường thẳng AG cắt BC tại K. Khi đó
m
BK BC
n

(
m
n
là tối giản). Tính
S m n
A.
16S
. B.
17S
. C.
18S
. D.
19S
.
Lời giải
( Tên FB: Phùng Hằng )
Chọn B
Ta có
1 1
2
2 2
1 1 5 1
3
3 2 6 2
AG AE AF AN AM AG AB
AG AN AM AB AD AD AC AB AD AC AB
 
 
5 1 4 3
6 2 3 2
AD AB AD AB AD AB
 
1 4
2 9
AG AB AD
.
Đặt
.BK x BC AK AB BK AB xBC AB xAD
 
.
Do A,G,K thẳng hàng thì
2
4
8
2 9
9
k
k k
AK k AG AB xAD AB AD
x

Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
78
Suy ra
8
9
m
n
Vậy
17
S
Email: builoiyka@gmail.com
Câu 248: Cho hình thang
ABCD
có đáy
AB
,
CD
,
2
CD AB
.
M
,
N
lần lượt là các điểm thuộc cạnh
AD
và
BC
sao cho
5
AM MD
,
3 2
BN NC
. Gọi
P
là giao điểm của
AC
và
MN
;
Q
là
giao điểm của
BD
và
MN
; Khi đó
PM QN a
PN QM b
, với
a
b
là phân số tối giản. Khi đó
a b
bằng
A.
386
. B.
385
. C.
287
. D.
288
.
Lời giải
Họ tên: Bùi Thị Lợi Facebook: LoiBui
Chọn A
Gọi
E
là giao điểm của
AD
và
BC
. Ta có A, lần lượt là trung điểm của
EC
,
ED
.
Giả sử
PM xPN
 
;
QN yQM
.
Ta có
1
EM xEN
EP
x
11 7
6 10
1
x
EA EC
x
11 7
6 1 10 1
x
EA EC
x x
Do
, ,P A C
thẳng hàng nên
11 7
1
6 1 10 1
x
x x
55 21 30 30x x
25
9
x
.
Vậy
25
9
PM
PN
.
Ta có
1
EN yEM
EQ
y
7 11
5 12
1
y
y
7 11
5 1 12 1
y
EB ED
y y
Do
, ,Q B D
thẳng hàng nên
7 11
1
5 1 12 1
y
y y
84 55 60 60y y
24
5
y
.
P
Q
N
M
A
B
D
C
E
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
79
Vậy
24
5
QN
QM
.
Suy ra
341
341; 45 386
45
PM QN
a b a b
PN QM
.
Cách 2:
Áp dụng định lý Menelaus cho tam giác
AMN
với ba điểm thẳng hàng là
, ,A P C
, ta có
. . 1
PM CN AE
PN CE AM
3 6 25
. . 1
10 5 9
PM PM
PN PN
.
Áp dụng định lý Menelaus cho tam giác
EMN
với ba điểm thẳng hàng là
, ,B Q D
, ta có
. . 1
QN DM BE
QM DE BN
1 5 24
. . 1
12 2 5
QN QN
QM QM
.
Vậy
341
341; 45 386
45
PM QN
a b a b
PN QM
.
Email: datltt09@gmail.com
Câu 249: Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = 3MC, NC
= 2BN. Gọi I là giao điểm của AN và BN. Tính diện tích tam giác ABC biết diện tích tam giác
ABN bằng 4.
A.
110
ABC
S
. B.
115
ABC
S
. C.
125
ABC
S
. D.
120
ABC
S
.
Lời giải
Họ và tên tác giả: Vũ Thị Hằng Tên FB: Đạt Lâm Huy
Chọn D
Giả sử
AI k AN
ta có
1 (1)
3
BI BA k BN k BA
k
BI k BA BC
Tương tự
4 3 3 (2)
AM AC BM BA BC
 
Vì B,I,M thẳng hàng nên từ(1) và(2) ta có
1 9
3
1 3 10
k
k
k
Suy ra
10 40
ABN BNI
S S
3 120
ABC ABN
S S
(Có thể dùng định lý Menelauyt để tính tỷ số)
Email: samnk.thptnhưthanh@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
80
Câu 250: Cho tam giác ABC M thuộc cạnh AC sao cho
MCMA .2
, N thuộc BM sao cho
NMNB .3
, P thuộc BC sao cho
PCkPB .
. Tìm giá trị k để ba điểm A, N, P thẳng hàng.
A.
k
1
2
. B.
k
2
. C.
k
1
2
. D.
k
2
.
Lời giải
Họ và tên: Nguyễn Khắc Sâm Facebook: Nguyễn Khắc Sâm
Chọn B
Ta có:
1.
2
1
4
1
.4.3.3.3
ACABAN
ANAMABANAMANABNMNB
)1(1.. kAPkACkABAPACkAPABPCkPB
2
11
1
AC
k
k
AB
k
AP
Ba điểm A, N, P thẳng hàng khi và chỉ khi:
21
41
1
.
h
k
k
h
k
ANhAP
2
k
.
VẤN ĐỀ 3. QUỸ TÍCH
Nguyễn Văn Dũng Fb: Nguyễn Văn Dũng
Email: dungtoanc3hbt@gmail.com
Câu 251: Cho tam giác
ABC
với
J
là điểm thoả mãn
2 5 3 0JA JB JC
, gọi
E
là điểm thuộc
AB
và thoả mãn
AE kAB
. Xác định
k
để
, ,C E J
thẳng hàng.
A.
2; 1
k
. B.
1;0
k
. C.
0;1
k
. D.
1;2
k
Lời giải
A
B
C
M
P
N
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
81
Ta có
 
2 5 3 0 2 2 5 5 3 0 7 3 2 5 0JA JB JC JE EA JE EB JC JE JC EA EB
Để
, ,C E J
thẳng hàng thì
5 5
2 5 0 7 5 0
7 7
EA EB EA AB AE AB k
.
Chọn C
Leminh0310@gmail.com
Câu 252: Cho hình vuông
ABCD
tâm
O
cạnh
1
. Biết rằng tập hợp các điểm
M
thỏa mãn
2 2 2 2
2 2 9
MA MB MC MD
là một đường tròn có bán kính
R
. Khẳng định nào sau đây
đúng?
A.
0;1
R
. B.
1; 2
R
. C.
1 3
;
2 2
R
. D.
3
;2
2
R
.
(Sưu tầm: Lê Hồ Quang Minh – FB: Lê Minh)
Lời giải
Chọn C
Vì
ABCD
là hình vuông tâm
O
nên ta có:
0
0
OA OC
OB OD
Theo giải thiết:
2 2 2 2
2 2 9
MA MB MC MD
2 2 2 2
2 2 9
MO OA MO OB MO OC MO OD

2 2 2 2 2
0
6 2 2 2 2 2 9
MO OA OB OC OD MO OA OC OB OD

2
6 3 9 1
MO MO
.
Vậy tập hợp các điểm
M
là đường tròn tâm
O
bán kính
1R
.
Email: thuyhung8587@gmail.com
Câu 253: Cho tam giác
ABC
. Tập hợp những điểm
M
thỏa mãn:
O
D
C
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
82
4 2
MA MB MC MA MB MC
là:
A. Đường thẳng đi qua
A
B. Đường thẳng qua
B
và
C
C. Đường tròn D. Một điểm duy nhất.
Lời giải
4 2
MA MB MC MA MB MC
3 2 2
MA MB MC MA MA MI
, (
I
: là trung điểm
BC
)
3 2
MG MA MA MI
, (
G
: trọng tâm
ABC
)
1
6 2
3
MJ IA MJ IA
,(
J
là trung điểm của
AG
)
1
2
JM AG
(không đổi). Vậy tập hợp điểm
M
là đường tròn tâm
J
, bán kính
2
AG
R
.
Chọn đáp án C.
(Họ và tên tác giả: Cấn Việt Hưng, Tên FB: Viet Hung)
ngoletao@gmail.com
Câu 254: Cho tam giác ABC có hai đỉnh B, C cố định với
2BC a
. Gọi H là trực tâm của tam giác
ABC và M là trung điểm của đoạn BC. Nếu đỉnh A thay đổi nhưng luôn thỏa
2 2
. 4MA MH MA a
thì điểm A luôn thuộc một đường tròn cố định có bán kính bằng
A.
2a
. B.
3a
. C.
2a
. D.
a
.
(Họ và tên tác giả: Ngô Lê Tạo, Tên FB: Ngô Lê Tạo)
Lời giải
Chọn B
Ta có
A
B
C
H
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
83
1
.
4
MA MH BA CA BH CH

.
1
. .
4
BA BH CA CH
(do
,
BA CH CA BH
1
. .
4
BA BH CA CH
(định lý chiếu vectơ)
2
1
4
BC
Suy ra
2 2 2 2 2
1
. 4 .4 4 3
4
MA MH MA a a MA a AM a
.
Câu 255: Cho hai điểm
A
và
B
cố định. Tìm giá trị
0
k
để tập hợp điểm
M
thỏa mãn điều kiện
2 2
MA MB k
là một đường tròn.
A.
2
2
3
k AB
. B.
2
2
3
k AB
. C.
2
2
3
k AB
. D.
2
2
3
k AB
.
Lời giải
Chọn D
Gọi
E
là điểm thỏa mãn:
2 0
EA EB
ta có
2 0
EA EB
ta có:
2 2
2 2
MA MB k ME EA ME EB k
2 2 2
3 2 *
ME k EA EB
Mà
2
2 0
3
EA EB EA AB
;
1
3
EB AB
nên
2 2
2
* 3
3
ME k AB
2 2
1 2
3 3
ME k AB
Nếu
2
2
3
k AB
: Quỹ tích điểm
M
là rỗng.
Nếu
2
2
3
k AB
: Quỹ tích điểm
M
là điểm
E
.
Nếu
2
2
3
k AB
: Quỹ tích điểm
M
là đường tròn tâm
E
bán kính
2
1 2
3 3
R k AB
.
PHẠM THANH LIÊM FB: Liêm Phạm
Email: Phamthanhliem1@gmail.com
Câu 256: Cho tam giác vuông
ABC
tại
A
. Tìm tập hợp
M
sao cho
2 2 2
MB MC MA
.
A. Đường thẳng. B. Đường tròn. C. Đoạn thẳng. D. Một điểm.
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
84
Chọn D
2 2 2 2 2 2
0
MB MC MA MB MC MA
. Gọi
E
là điểm được xác định bởi
0
EB EC EA
. ( E là điểm thứ tư của hình bình hành
ABEC
).
Ta có:
2 2 2
2 2 2
MB MC MA ME EB ME EC ME EA
2 2 2 2
ME EB EC EA
2
2 2 2
ME EB EC EB EC
2 2
2 . 2 .ME EB EC ME AB AC
2
ME
. Vậy
2
0
ME
.
Nên tập hợp điểm
M
là điểm
E
.
( Cách chứng minh trên phục vụ cho cả tam giác
ABC
là tam giác thường và khi đó các tập
hợp điểm là khác nhau )
Email: thachtv.tc3@nghean.edu.vn
Câu 257: Cho tam giác
ABC
vuông cân tại
A
có
5AB cm
. Gọi
( )S
là tập hợp các điểm
M
trong mặt
phẳng thỏa mãn hệ thức:
. . 25
MA MB MA MC
. Gọi
I
là trung điểm của
BC
. Kết luận nào
sau đây đúng?
A.
( )S
là đường thẳng trung trực của đoạn thẳng
AI
.
B.
( )S
là đoạn thẳng
AI
.
C.
( )S
là đường tròn cố định bán kính
5 10
4
R
.
D.
( )S
là đường tròn tâm
I
bán kính
5 2
4
R
(Họ và tên tác giả: Trịnh Văn Thạch, FB: www.facebook.com/thachtv.tc3)
Lời giải
Chọn C
Từ giả thiết:
2 2 2 2 2 2
5 2 1 1
. . 25
2 2 2
MA MB MA MC MA MB AB MA MC AC
2 2 2 2 2 2
2 50 50 2 100
MA MB MC MA MB MC
Gọi
D
là điểm thỏa mãn
2 0 2 2 0 0
DA DB DC DA DI DA DI
C
A
B
I
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
85
D
là trung điểm của đoạn thẳng
AI
Ta có
2 2 2 2 2 2 2
2 4 2
MA MB MC MD DA DB DC
Và
1 1 5 2
2 4 4
DA AI BC
,
2 2
2 2
5 2 5 2 125
2 4 8
DB DC IB ID
.
Suy ra
2 2
2 2 2 2 2 2 2 2 2
5 2 125 75
2 4 2 4 2. 2. 4
4 8 2
MA MB MC MD DA DB DC MD MD
Ta có kết quả:
2 2
75 125
4 100
2 8
MD MD
Như vậy
( )S
là đường tròn tâm
D
bán kính
5 10
4
R
.
Câu 258: Cho tam giác đều
ABC
cạnh
a
. Tập hợp các điểm
M
thỏa mãn đẳng thức
2
2 2 2
5
4
2
a
MA MB MC
nằm trên một đường tròn
C
có bán kính là:
A.
3
a
. B.
4
a
. C.
3
2
a
. D.
6
a
.
Lời giải
Chọn D
Gọi
M
lần lượt là trung điểm của
BC
.
Gọi
I
là điểm thỏa mãn điều kiện:
4 0
IA IB IC
Khi đó, ta có:
4 0
IA IB IC
4 2 0
IA IM
3 0
IA AM
1
3
AI AM

.
Suy ra:
3
6
a
IA
;
2 2
21
6
a
IB IC IM BM
.
Ta lại có:
2
2 2 2
5
4
2
a
MA MB MC
2
2 2 2
5
4
2
a
MA MB MC

2
2 2 2
5
4
2
a
MI IA MI IB MI IC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
86
2
2 2 2 2
5
6 2 4 4
2
a
MI MI IA IB IC IA IB IC
6
a
MI .
Vậy tập hợp điểm
M
là đường tròn tâm
I
bán kính
6
a
R .
Câu 259: Cho
ABC
. Tìm tập hợp các điểm
M
sao cho: 3 2 2MA MB MC MA MB MC

.
A. Tập hợp các điểm
M
là một đường tròn.
B. Tập hợp của các điểm
M
là một đường thẳng.
C. Tập hợp các điểm
M
là tập rỗng.
D. Tập hợp các điểm
M
chỉ là một điểm trùng với
A
.
Lời giải
Chọn A
Gọi
I
là điểm thỏa mãn
3 2 0IA IB IC
.
3 2 2MA MB MC MA MB MC
2 3 2MI IA IB IC BA CA
1
.
Gọi
N
là trung điểm
BC
. Ta được:
1 2 2MI AN IM AN
.
I
,
A
,
N
cố định nên tập hợp các điểm
M
là đường tròn tâm
I
, bán kính
AN
.
Câu 260: Cho tam giác đều
ABC
cạnh
a
. Tập hợp các điểm
M
thỏa mãn đẳng thức
2
2 2 2
5
4
2
a
MA MB MC nằm trên một đường tròn
C
có bán kính là:
A.
3
a
. B.
4
a
. C.
3
2
a
. D.
6
a
.
Lời giải
Chọn D
Gọi
M
lần lượt là trung điểm của
BC
.
Gọi
I
là điểm thỏa mãn điều kiện:
4 0IA IB IC
Khi đó, ta có:
4 0IA IB IC
A
A
N
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
87
4 2 0
IA IM
3 0
IA AM
1
3
AI AM
.
Suy ra:
3
6
a
IA
;
2 2
21
6
a
IB IC IM BM
.
Ta lại có:
2
2 2 2
5
4
2
a
MA MB MC
2
2 2 2
5
4
2
a
MA MB MC

2
2 2 2
5
4
2
a
MI IA MI IB MI IC

2
2 2 2 2
5
6 2 4 4
2
a
MI MI IA IB IC IA IB IC
6
a
MI
.
Vậy tập hợp điểm
M
là đường tròn tâm
I
bán kính
6
a
R
.
Họ và tên tác giả: Vũ Thị Nga Tên FB: Linh Nga
Email: linhnga.tvb@gmail.com
Câu 261: Cho
ABC
đều, có cạnh bằng a. Khi đó tập hợp những điểm
M
sao cho
2
. . .
6
a
MA MB MB MC MC MA

là:
A. Đường tròn có bán kính
3
a
R
.
B. Đường tròn có bán kính
2
a
R
.
C. Đường tròn có bán kính
2
3
a
R
.
D. Đường tròn có bán kính
3
9
a
R
.
Lời giải
Chọn C
Gọi
G
là trọng tâm
ABC
. Suy ra
G
là tâm đường tròn ngoại tiếp
ABC
và
G
cố định.
Ta có
3
MA MB MC MG
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
88
2 2
2 2 2 2
9
2 . . . 9
MA MB MC MG
MA MB MC MA MB MB MC MC MA MG
Mà
2 2 2
2 2 2
MA MB MC MA MB MC
2 2 2
2 2 2 2
2 2 2 2
2 2
2
2
2 2
3 2. .
3 2. .0
3 3
2 3
3 3 .
3 2
3
MG GA MG GB MG GC
MG GA GB GC MG GA GB GC
MG GA GB GC MG
MG GA
a
MG
MG a

 
Ta có
2 2 2
3 2 . . . 9
MG a MA MB MB MC MC MA MG
2
2
2 2
2
2
2
. . . 3
2
3
6 2
2
9
a
MA MB MB MC MC MA MG
a a
MG
a
MG

Vậy tập hợp điểm M là đường tròn tâm
G
bán kính
2
3
a
R
.
Họ và tên tác giả: Tô Quốc An Tên FB: Tô Quốc An
Email: antq4949@gmail.com
Câu 262: Cho
ABC
tìm tập hợp điểm
M
:
2
.MB MC AM

Lời giải
Gọi
I
là trung điểm của
BC
, ta có:
2 2
. .
MB MC AM MI IB MI IC MA
2
2 2 2 2
. .
4
BC
MI IC IB MI IC IB MA MI MA IC IB
 
2 2
(*)
4 4
BC BC
MI MA MI MA AI MI MA
Gọi
O
là trung điểm của
AI
, suy ra:
2MI MA MO

Suy ra:
2 2 2
* 2 . 4 . .
4 4 16
BC BC BC
AI MO OI MO OI OM
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
89
Trên tia đối của tia
OI
lấy điểm
H
sao cho
2
.
16
BC
OI OH
hay
2
.
16
BC
OI OH
, suy ra
điểm
H
xác định duy nhất.
Dựng đường thẳng
đi qua
H
và vuông góc với
OI
, khi đó với mọi điểm
M
nằm trên
ta có:
2
. . . . .
16
BC
OI OM OI OH HM OI OH OI HM OI OH
.
Vậy tập hợp điểm
M
là đường thẳng
Email: Bichhai1975@gmail.com
Câu 263: Cho tam giác đều
ABC
cạnh bằng
3
. Biết rằng tập hợp các điểm
M
thỏa mãn đẳng thức
2 3 4
MA MB MC MB MA
    
là đường tròn cố định có bán kính bằng:
A.
1
. B.
1
3
. C.
3
2
. D.
1
2
.
(Họ tên: Lê Thị Bích Hải, Tên face: Bich Hai Le)
Lời giải
Họ tên: Lê Thị Bích Hải. Tên face: Bich Hai Le
Chọn B
Gọi
G
là trọng tâm của tam giác
.ABC
Ta có
2 3 4 2 3 4 .MA MB MC MI IA MI IB MI IC
  
Chọn điểm
I
sao cho
2 3 4 0
IA IB IC
3 0.
IA IB IC IC IA

Mà
G
là trọng tâm của tam giác
ABC
3 .IA IB IC IG
Khi đó
9 0 9 0 9 .
IG IC IA IG AI IC IG CA
Do đó
2 3 4 9 2 3 4 9 .MA MB MC MB MA MI IA IB IC AB MI AB

Vì
I
là điểm cố định thỏa mãn
nên tập hợp các điểm
M
cần tìm là đường tròn tâm
,I
bán
kính
1
.
9 3
AB
r
thongqna@gmail.com
Câu 264: Cho tam giác
ABC
có là trọng tâm
G
. Tìm tập hợp điểm
M
thỏa mãn
2 2 2
3
MA MB MC BC MA MC MG CB AC
.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
90
A. Đường tròn đường kính
AB
. B. Đường trung trực đoạn thẳng
AB
.
C. Đường tròn đường kính
AC
. D. Đường trung trực đoạn thẳng
AC
.
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông)
Lời giải
Chọn A
Ta có
MA MB MC BC

MA CB BC
MA
.
Gọi điểm
I
là trung điểm cạnh
AC
.
Ta có
3MA MC MG

2 3MI MG
2 3
MB BI MB BG
2
2 3.
3
MB BI BI

MB
.
Do đó
2 2 2
3
MA MB MC BC MA MC MG CB AC
2
2
2
MA MB AB
2 2 2
MA MB AB
.
Từ đó suy ra tam giác
MAB
vuông tại
M
hay tập hợp các điểm
M
là đường tròn đường kính
AB
.
Câu 265: Cho đoạn thẳng
5
AB
. Biết rằng tập hợp điểm
M
thỏa mãn
2 2
3 .MA MB MA MB
là
một đường tròn có bán kính
R
. Tìm giá trị của
R
.
A.
5
2
R
. B.
5
2
R
. C.
3
2
R
. D.
3
2
R
.
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông)
Lời giải
Chọn A
Ta có
2 2
3 .MA MB MA MB
2 2
2 . .MA MB MA MB MA MB
2
.MA MB MA MB
2
.AB MA MB
.
Gọi điểm
I
là trung điểm cạnh
AB
.
Ta có
2
.AB MA MB
2
.
AB MI IA MI IB
2
.
AB MI IA MI IA
2 2 2
AB MI IB
2 2 2
MI AB IB
2 2
5
4
MI AB
5 5 5
. 5
2 2 2
MI AB
.
Vậy tập hợp điểm
M
thỏa mãn
2 2
3 .MA MB MA MB
là đường tròn tâm
I
có bán kính
5
2
R
.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
91
Họ và tên: Võ Khánh Huyền Vân Fb: Vân Võ
Email: huyenvanqt050185@gmail.com
Câu 266: Cho tam giác
ABC
, có bao nhiêu điểm
M
thỏa 5
MA MB MC ?
A.
1
. B.
2
.
C. vô số. D. Không có điểm nào.
Lời giải.
Chọn C
Gọi
G
là trọng tâm của tam giác
ABC
, ta có
3
  
MA MB MC MG
.
Thay vào ta được:
5
5 3 5
3
 
MA MB MC MG MG
, hay tập hợp các điểm M là
đường tròn có tâm là trọng tâm của tam giác
ABC
và bán kính bằng
5
3
.
VẤN ĐỀ 4. TỈ LỆ
Họ và Tên: Trần Quốc Đại
Email: quocdai1987@gmail.com
Facebook: https://www.facebook.com/tqd1671987
Câu 267: Cho
ABC
có
3AB
;
4AC
. Phân giác trong
AD
của góc
BAC
cắt trung tuyến
BM
tại
I
. Tính
AD
AI
.
A.
3
2
AD
AI
. B.
10
7
AD
AI
. C.
29
20
AD
AI
. D.
7
5
AD
AI
Lời giải
Chọn B
* Phân tích
,AD AI

theo các vectơ
,AB AC

.
Ta có:
3
2
IB AB
IM AM
2 3 0IB IM

2 3 5 1AB AM AI

.
3
4
DB AB
DC AC
4 3 0DB DC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
92
4 3 7 2
AB AC AD

.
Lấy
2 2. 1
suy ra:
3 6 7 10AC AM AD AI
 
7 10 0
AD AI

7 10AD AI
10
7
AD
AI
.
Câu 268: [Đề thi olympic 30/4 TPHCM khối không chuyên lần 2 ] Cho
ABC
gọi điểm
D
nằm trên
cạnh
BC
sao cho
2
BD BC
,
E
là trung điểm của
AD
. Một đường thẳng bất kì qua
E
và cắt
các cạnh
;AB AC
lần lượt tại
,M N
. Tình tỉ số
2
AB AC
AM AN
A.
2 6
AB AC
AM AN
. B.
2 5
AB AC
AM AN
.
C.
28
2
5
AB AC
AM AN
. D.
29
2
5
AB AC
AM AN
Lời giải
Chọn A
Do
M
nằm trên cạnh
AB
nên ta có
. ( 1)
AB k AM k
Do
N
nằm trên cạnh
AC
nên ta có
AC l AN l
Ta có
2 2 2 3
DB DC AB AD AC AD AB AC AD
Suy ra
. 2 . 6. 2 6
k AM l AN AE k AE ME l AE EN AE

Suy ra
2 6 2
k l AE kEM lEN
Do hai vecto
AE
và
MN

không cùng phương nên suy ra
2 6 0 2 6 2 6
AB AC
k l k l
AM AN
Họ và tên tác giả: Đỗ Văn Đức Tên FB: Đỗ Văn Đức
Email: hoctoancunganhduc@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
93
Câu 269: Cho tam giác
ABC
. Trên cạnh
AB
lấy điểm
D
sao cho
2AD DB
. Trên cạnh
AC
lấy điểm
E
sao cho
3CE EA
. Gọi
M
là trung điểm của
DE
. Tia
AM
cắt
BC
tại
N
. Tỉ số
BN
CN
có
giá trị là:
A.
1
4
. B.
3
8
. C.
1
2
. D.
2
7
.
Lời giải
Chọn B
Giả sử
N
chia
BC
theo tỉ số
x
. Ta có:
1
1 1 1

AB xAC x
AN AB AC
x x x
(1).
Lại có:
1 1 2 1 1 1
2 2 3 4 3 8
  
AM AD AE AB AC AB AC
(2).
Vì
AM
và
AN
là 2 vectơ cùng phương nên
3 8 3
1 1 8
x
x
x x
.
Do đó
3 3
8 8
NB
NB NC
NC
.
Câu 270: (Bài toán tổng quát của bài toán 1). Cho tam giác
ABC
. Gọi
I
là điểm chia
BC
theo tỉ số
k
.
Trên các tia
AB
và
AC
lấy các điểm
,M N
.
AI
cắt
MN
tại
P
. Đặt
AB
b
AM
,
AC
c
AN
. Tỷ
số
AI
AP
có giá trị bằng
A.
1
b kc
k
. B.
1
b kc
k
. C.
1
c kb
k
. D.
1
c kb
k
.
Lời giải
Chọn B
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
94
Giả sử P chia MN theo tỉ số x. Ta có
1

AM xAN
AP
x
1
. .
1 1
AB x AC
x b x c
.
Lại có:
1 1 1
AB k AC AB k
AI AC
k k k
(1).
Vì
AP
và
AI
đồng phương nên
1
1
1 1
x k
k
b x kc x
1
x
b kc
c
x k
b
.
Do đó
1

k
AP AB AC
b kc b kc
(2).
Từ
(1)
và
(2)
, ta có
1
AI b kc
AP k
.
Câu 271: (Hệ quả hay dùng của bài toán 2). Cho tam giác
ABC
. Gọi
I
là trung điểm của BC. Trên các
tia
AB
và
AC
lấy các điểm
,M N
.
AI
cắt
MN
tại
P
. Đặt
AB
b
AM
,
AC
c
AN
. Tỷ số
AI
AP
có
giá trị bằng
A.
bc
. B.
2
b c
. C.
2 2
2
b c
. D.
2
bc
b c
.
Lời giải
Chọn B
I
là trung điểm của
BC
nên I chia BC theo tỷ số
1
k
. Áp dụng kết quả ở bài 2, ta có:
1
1 1 2
b c
AI b c
AP
.
Tên: Nam Phương Tên FB: Nam Phương
Email:nguyentrietphuong@gmail.com
Câu 272: Cho tam giác
ABC
. Gọi
,D E
lần lượt là các các điểm thỏa mãn
2 1
,
3 4
BD BC AE AC
.
Điểm
K
trên đoạn thẳng
AD
sao cho ba điểm
, ,B K E
thẳng hàng. Tìm tỉ số
AD
AK
.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
95
A.
1
3
AD
AK
. B.
3
AD
AK
. C.
2
3
AD
AK
. D.
3
2
AD
AK
.
Lời giải
Chọn B
Vì
1
4
AE AC
nên
1 3
4 4
BE BC BA
Giả sử
(1 )
2
(1 )
2
3
3
AK xAD BK xBD x BA
x
BK BC x BA
BD BC
Do
, ,B K E
thẳng hàng ta có:
8
2
0
9
4 3
1
3
1 0
3
4
m x
m
mBK BE
m
x
x
Vậy
3
AD
AK
Email: haivanxinh99@gmail.com Face Hải Vân
Câu 273: Cho tứ giác
ABCD
có hai đường chéo cắt nhau tại
O
thỏa mãn
3 , 4OC OA OD OB

.
Qua trung điểm
M
của
AB
dựng đường thẳng
MO
cắt
CD
tại
N
. Tính tỉ số
CN
ND
.
A.
3
4
. B.
1
4
. C.
2
3
. D.
1
3
.
Lời giải
Chọn A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
96
Ta có
3 , 4OC OA OD OB

Đặt
, 0
CN
k k
ND
, ta có
CN k ND CO ON k NO OD

1
1 1
k
ON CO OD
k k
3 4
1 1
k
ON OA OB
k k
Vì
,
OM ON

cùng phương nên có số thực
k
sao cho
2
k
ON kOM ON OA OB
 
Suy ra
3
6 8 3
4
1 1 4
1
k
k
k
k k k k
k
.
(Email): hatoanlgm@gmail.com
Câu 274: Cho tam giác
ABC
và điểm
I
thỏa mãn
23 8 2018 0
IA IB IC
. Đường thẳng
AI
cắt đường
thẳng
BC
tại
J
. Giá trị của tỉ số
JB
JC
là:
A.
23
8
B.
2018
23
C.
2018
8
D.
8
23
Lời giải
Chọn C
(Họ và tên tác giả: Ngô Ngọc Hà, Tên FB: Ngô Ngọc Hà)
Giả sử
1
JB k JC k
1
1 1
k
AJ AB AC
k k

.
Từ giả thiết suy ra:
23 8 2018 0
AI AB AI AC AI

8 2018
2049 2049
AI AB AC
.
Do
, ,A I J
thẳng hàng nên
,AI AJ
cùng phương
N
M
o
A
B
C
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
97
1
2018
1 1
8 2018
8
2049 2049
k
k k
k
.
Gmail: Binh.thpthauloc2@gmail.com
Câu 275: Cho tam giác
ABC
. Điểm
K
chia trung tuyến
AD
theo tỷ số
3:1
kể từ đỉnh.
Đường thẳng
BK
chia diện tích tam giác
ABC
theo tỷ số
ABF
BCF
S
k
S
, giá trị của
k
bằng?
A.
5
8
k
B.
3
8
k
C.
3
5
k
D.
3
2
k
Lời giải
Đáp án D
Do
D
là trung điểm của
BC
thiết:
1
( ) 1
2
AD AB AC
Gọi F là giao điểm của BK và AC.
Mà
; ;A F C
thẳng hàng:
2
AF mAC
; ;B K F
thẳng hàng:
1 3
AK nAF n AB
; ;A K D
thẳng hàng và
1
3
KD
KA
3
4
4
AK AD
Từ
2 ; 3
suy ra:
. . 1 5
AK n m AC n AB
Từ
1 ; 4
suy ra:
3 3
6
8 8
AK AC AB
Do hai véctơ
;AB AC
không cùng phương nên từ
5 ; 6
ta có:
3 5
.
8 8
3 3
1
8 5
m n n
n m
Do đó:
3 3
5 2
FA
AF AC
FC
Vậy
3
2
ABF
BCF
S FA
k
S FC
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
K
F
D
B
A
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
98
Họ và tên: Tăng Lâm Tường Vinh
Email: tanglamtuongvinh@gmail.com
Facebook: tanglamtuong.vinh
Câu 276: Cho tam giác
ABC
với
K
là trung điểm
BC
. Lấy các điểm
M N,
thỏa mãn
AM AB
3
4

,
AN AC
1
3
 
. Gọi
I
là giao điểm của
MN
và
AK
. Đặt MI xMN AI y AK ,
   
. Hỏi
x
y
A.
3
2
. B.
4
3
. C.
1
. D.
5
3
.
Lời giải
Chọn A
Ta có
MN AN AM AC AB
1 3
3 4
   
x x x x
MI xMN AI AM x AC AB AI AC AB AM AC AB
1 3 3 3 3
3 4 3 4 3 4
           
y y
AC AB
AI y AK y AB AC
2 2 2
 
   
Mà
AC AB,
 
là 2 vector không cùng phương nên ta có
y
x
x
x
y
y
x
y
93 3
13
4 2
3
2
6
13
3 2
Gmail: Binh.thpthauloc2@gmail.com
Câu 277: Cho tam giác
ABC
. Trên cạnh
AB
lấy điểm D, trên cạnh BC lấy E, F sao cho
3
2
AD
DB
;
1
3
BE
EC
;
4
1
BF
FC
. Đường thẳng
AE
chia đoạn
DF
theo tỷ số
KD
k
KF
. Giá trị của
k
bằng?
A.
3
11
k
B.
11
3
k
C.
3
14
k
D.
11
14
k
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
99
Lời giải
Đáp án A
Theo giả thiết:
3 3
1
2 5
AD
AD AB
DB
1 3 1
2
3 4 4
BE
AE AB AC
EC
4 1 4
3
1 5 5
BF
AF AB AC
FC
Mà
; ;A K E
thẳng hàng:
4
AK mAE
; ;D K F
thẳng hàng:
1 5
AK nAF n AD
Từ
2 ; 4
suy ra:
3 1
6
4 4
AK mAB mAC
Từ
1 ; 3 ; 5
suy ra:
1 4 3
1
5 5 5
AK n AB AC n AB
3 2 4
7
5 5 5
n n
AK AB AC
Do hai véctơ
;AB AC
không cùng phương nên từ
6 ; 7
ta có:
3 3 2
4 5 5
4
4 5
m n
m n
1 2 4 3
5 15 5 14
n n
n
Vậy
3 11 3
14 14 11
KD
AK AB AC k
KF
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
Họ và tên: Hoàng Ngọc Lâm
Email: hoangngoclammath1112@gmail.com
Facebook: Hoàng Ngọc Lâm
Câu 278: Cho tam giác
ABC
. Kéo dài
AB
một đoạn
BE AB
, gọi
F
là trung điểm của
AC
. Vẽ hình
bình hành
EAFG
. Đường thẳng
AG
cắt
BC
tại
K
. Tính tỉ số
KB
KC
?
A.
1
4
. B.
3
8
. C.
1
5
. D.
2
7
.
Lời giải
Chọn A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
100
Để xác định giao điểm
K
của
AG
và
BC
, ta tính
AG
theo
AB
và
AC
.
Ta có:
1
2
2
AG AE AF AB AC
.
AG
cắt
BC
tại điểm
K
mà
1
2 0
2
KB KC
.
Suy ra
1
4
KB
KC
.
Câu 279: Cho tam giác
ABC
có
3AB
,
4AC
. Phân giác trong
AD
của góc
BAC
cắt trung tuyến
BM
tại
I
. Tính tỉ số
AD
AI
.
A.
13
8
. B.
11
6
. C.
10
7
. D.
10
5
.
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Lời giải
Chọn C
Theo tính chất đường phân giác ta có
3
2 3 0
2
IB AB
IB IM
IM AM
Và
3
4 3 0
4
DB AB
DB DC
DC AC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
101
Vậy ta có
2 3 0
4 3 0
IB IM
DB DC
2 3 5
4 3 7
AB AM AI
AB AC AD


4 6 10
4 3 7
AB AM AI
AB AC AD
Suy ra
3 6 7 10AC AM AD AI
7 10 0
AD AI
10
7
AD
AI
.
Hoặc ta có thể giải như sau:
Ta có
3 3 3
4 4 4
BD AB
BD DC BC BD
DC AC
7 3
D
4 4
B BC
3
D
7
B BC
Ta lại có
3 3
7 7
AD AB BD AB BC AB AC AB
4 3
7 7
AB AC
.
Theo tính chất phân giác, ta lại có
3
2
BI AB
IM AM
3
2
BI IM
2 3BI IM
2 3
BA AI IA AM

3
5 2 3 2
2
AI AB AM AB AC
2 3 7 4 3 7
5 10 10 7 7 10
AI AB AC AB AC AD

Vậy
10
7
AD
AI
.
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Email: nguyenvantoannbk@gmail.com Nhờ thầy cô góp ý!
Câu 280: Cho hình bình hành
ABCD
,
O
là điểm bất kì trên đoạn
AC
, đường thẳng
BO
cắt cạnh
CD
tại
E
và đường thẳng
AD
tại
F
sao cho
2
EF BO
. Tỷ số
AF
AD
bằng
A.
1 5
2
. B.
2
. C.
1 2
. D.
5
2
.
Lời giải
Chọn C
E
F
C
D
A
B
O
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
102
Đặt:
AF xAD
1
x
và
AO y AC
0 1
y
.
Theo định lý talet:
1 1DE DF DE DF x x
DE AB
CE BC DC AF x x
.
Ta có:
1
BO BA y AC y AB yAD
;
1
1
x
EF DF DE x AD AB
x
 
.
Theo đề bài:
1 2
1 2
2
1
2
2 1
2
x y
x
EF BO
x
y
y
x
 
.
Họ và Tên : Nguyễn Văn Mạnh FB : Nguyễn Văn Mạnh
Email : manhluonghl4@gmail.com
Câu 281: Cho hai tam giác
ABC
và
A B C
1 1 1
; gọi
2 2 2
, ,A B C
lần lượt là trọng tâm các tam giác
BCA CAB ABC
1 1 1
, ,
. Gọi
G G G
1 2
, ,
lần lượt là trọng tâm các tam giác
ABC A B C
1 1 1
,
,
A B C
2 2 2
. Tính tỉ số
GG
GG
1
2
ta được kết quả :
A.
1
3
B.
1
2
C.
3
D.
2
Lời giải
Chọn C
Vì
,G G
1
là trọng tâm tam giác
ABC A B C
1 1 1
,
suy ra
GG GA GB GC
1 1 1 1
3
   
1 1 1 1 1 1 1 1
3 3GG GA GB GC AA BB CC GG AA BB CC
          
Tương tự
,G G
2
là trọng tâm tam giác
ABC A B C
2 2 2
,
suy ra
GG GA GB GC
2 2 2 2
3
   
GG AA BB CC
2 2 2 2
3
   
Mặt khác
AA BB CC AA BB CC A A B B C C
2 2 2 1 1 1 1 2 1 2 1 2
        
Mà
2 2 2
, ,A B C
lần lượt là trọng tâm các tam giác
BCA CAB ABC
1 1 1
, ,
Suy ra
A A B B C C A B AC B C B A C A C B
1 2 1 2 1 2 1 1 1 1 1 1
3
        
A A AB A A AC B B BC B B BA C C CA C C CB
AA BB CC
1 1 1 1 1 1
1 1 1
2
           
  
Do đó
AA BB CC AA BB CC AA BB CC
2 2 2 1 1 1 1 1 1
2
3
        
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
103
AA BB CC
1 1 1
1
3
  
. Vậy
GG
GG GG
GG
1
2 1
2
1
3
3
 
.
VẤN ĐỀ 5. MIN,MAX
Email: phunghang10ph5s@gmail.com
Câu 282: Cho
ABC
đều cạnh bằng 3,
M
là điểm thuộc đường tròn ngoại tiếp
ABC
. Đặt
2 2 2
P MA MB MC
. Gọi
,a b
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
. Khi đó,
giá trị biểu thức
4T a b
là:
A.
3
. B.
6
. C.
9
. D.
12
.
Lời giải
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng
Chọn B.
Gọi
,O R
lần lượt là tâm và bán kính của đường tròn ngoại tiếp
ABC
. Ta có:
2 2 2
2 2 2
2 2 2 2
2 2
2 2 2
2. .
2 2. . ' 2 2 .2
2 4. . 2 4 .cos ;
P MA MB MC
MO OA MO OB MO OC
MO MO OA OB OC OA OB OC
R MO OA OA R MO OA
R OM OA R R OM OA
     
   
    
   
2
min
6P R
khi và chỉ khi
cos ; 1OM OA M
 
trùng
A
2
2
max
P R
khi và chỉ khi
cos ; 1OM OA M
 
trùng
'A
là điểm đối xứng của
A
qua
O
2 2 2
4 4.2 6 2T a b R R R
ABC
đều cạnh bằng 3
2
3 2 6R T R
.
Họ và tên tác giả: Trần Văn Ngờ Tên FB: Tran Van Ngo Tth
Email: vanngodhqn@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
104
Câu 283: Cho
ABC
và 3 số dương x, y, z thay đổi có tổng bình phương:
2 2 2 2
x y z k
,
k R
. Giá
trị lớn nhất của
cos cos cosB
P xy C yz A zx
là:
A.
2
k
. B.
2
2
k
. C.
3
k
. D.
2
3
k
.
Lời giải
Chọn B.
Đặt 3 vectơ
BX
,
CY
,
AZ

tương ứng là
x
,
y
,
z
như hình vẽ.
Ta có:
2
0
x y z
2 2 2
2 2 2 0
x y z xy yz xz
2 0 0 0
2 cos 180 2 cos 180 2 cos 180 0
k xy C yz A xz B
2
2
2 cos 2 cosA 2 zxcosB 0 xycosC yzcosA zxcosB
2
k
k xy C yz
Vậy Max
2
2
k
P
Câu 284: Cho hai điểm
, ( ;6)A B I
và
( ;3)M I
, thỏa mãn :
60
AIB
. Khi
, ,A B M
thay đổi tìm giá
trị nhỏ nhất của biểu thức
2
P MA MB
?
A.
9
. B.
3 2 6
. C.
3 13
. D.
6 3
.
( Họ và tên tác giả : Đặng Mơ- Tư Duy Mở )
Lời giải
Bổ đề : Cho hai véc tơ
u
và
v
khác véc tơ
0
, ta luôn có :
| | | |
| | | . . |
| | | |
v u
u v u v
u v
Chứng minh : Bình phương vô hướng vế phải ta được :
2 2 2
2 2 2
| | | | | | | | | | | |
| . . | . . 2. . . . 2.
| | | | | | | | | | | |
v u v u v u
u v u v u v v u u v u v
u v u v u v
Từ đó suy ra :
| | | |
| . . | | |
| | | |
v u
u v u v
u v
(đpcm).
Áp dụng vào bài toán cân bằng hệ số : Chúng ta có thể ghi nhớ công thức để áp dụng nhanh
vào các bài toán cân bằng hệ số đối với đường tròn và mặt cầu như sau :
Ta có :
2 | | 2| |P MA MB IA IM IB IM

và
6, 3
IA IB IM
Trong đó :
1 1
| | | . . | | 2 | 2 | |
2 4
IA IM
IA IM IM IA IM IA IM IA
IM IA
Suy ra :
1 1 1
2| | 2| | 2 | | | 2 |
4 4 2
P IM IA IB IM IM IA IB IM IB IA
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
105
Có :
2
2 2 2 2
1 1 1 1 1
| 2 | 4 2 . .cos60 4.6 .6 2.6.6. 117 | 2 | 3 13
2 4 4 2 2
IB IA IB IA IA IB IB IA
Suy ra giá trị nhỏ nhất của biểu thức
P
là
min
3 13
P
chọn đáp án C.
Câu 285: Cho tứ giác
ABCD
, M là điểm tùy ý và các điểm I, J, K cố định sao cho đẳng thức thỏa mãn
với mọi điểm M:
3 .

MA MB MC MD kMK
Giá trị của k là
A. k = 3 B. k = 4 C. k = 5 D. k = 6
Lời giải
Chọn D
Vì
3MA MB MC MD kMK
 
thỏa mãn với mọi M.
Do đó, đẳng thức cũng đúng với
M K
Tức là:
3 0KA KB KC KD k KK
Gọi G là trọng tâm
3ABC KA KB KC KG

3 3 0KG KD K
 
là trung điểm GD.
Mặt khác:
3MA MB MC MD

( ) ( ) ( ) 3( )MK KA MK KB MK KC MK KD
    
( 3 ) 6
6
KA KB KC KD MK
MK

6k
Câu 286: Cho tam giác ABC vuông tại A. Gọi
là góc giữa hai đường trung tuyến BD và CK. Giá
trị nhỏ nhất của
cos
bằng
A.
4
5
B.
5
4
C.
4
3
D.
3
4
Lời giải
Chọn A
Ta có:
1 1
( ). ( )
.
2 2
cos
. .
BA BC CA CB
BD CK
BD CK BD CK
2
. ( ) )
. . . . )
4. . 4. .
BACA BC CA BA BC
BACA BACB BC CA BC CB
BD CK BD CK


Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
106
2
2
2
4. . 2. .
BC
BC
BD CK BD CK
(Vì tam giác ABC vuông tại A nên
. 0)
BACA
Mặt khác,
2 2 2 2 2 2
2 2
2. .
2 4 2 4
Cauchy
AB BC AC AC BC AB
BD CK BD CK
2 2 2 2
2 2
5
4 4 4
AB AC BC BC
BC BC
Suy ra,
2
2
4
cos
5
5
4
BC
BC
Dấu “=” xảy ra khi và chỉ khi BD = CK hay
ABC vuông cân tại A
Câu 287: Cho hai điểm cố định G và
'G
là trọng tâm của tam giác ABC và tam giác
' ' '.A B C
Giá trị
nhỏ nhất của biểu thức
' ' 'P AA BB CC
bằng
A.
'GG
B.
3 'GG
C.
2 'GG
D.
1
'
3
GG
Lời giải
Chọn B
Do G và
'G
là trọng tâm
, ' ' 'ABC A B C
nên
0GA GB GC
và
' ' ' ' ' ' 0.G A G B G C
 
Ta có:
' ' ' ( ' ' ') ( ' ' ') ( ' ' ')AA BB CC AG GG G A BG GG G B CG GG G C
3 ' ( ) ( ' ' ' ' ' ')GG GA GB GC G A G B G C
  
3 'GG
Mặt khác,
' ' ' ' ' ' ' ' 'P AA BB CC AA BB CC AA BB CC

3 ' 3 'GG GG
Dấu “=” xảy ra khi và chỉ khi
', ', 'AA BB CC

cùng hướng
Họ và tên: Nguyễn Đức Hoạch – email: nguyenhoach95@gmail.com
Mail: nguyennga82nvc@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
107
FB: Nguyễn Nga Nvc
Câu 288: Cho hình thang
1 1 1 1
A B C D
có
0
1 1 1 1 1 1 1 1 1 1 1 1 1 1
// , 3 , 2 , 60A B C D A B a C D a D A B C B A
. Với
mỗi điểm
1
G
di động trên cạnh
1 1
A B
ta xác định điểm
1
F
sao cho
1 1 1 1 1 1
G F G C G D
  
. Tìm
độ dài nhỏ nhất của
1 1
G F

.
A.
2a
. B. 3a . C.
3 3
2
a
. D.
3
2
a
.
Lời giải
Chọn B
Gọi
1 1 1 1
Z A B C D , từ giả thiết suy ra tam giác
1 1
ZA B đều cạnh
3a
. Gọi
1 1
,H I lần lượt là
trung điểm của
1 1 1 1
,A B C D , suy ra
1 1
,H I cố định và
1 1 1
1 3
3 2
a
H I ZH
Từ giả thiết ta có tứ giác
1 1 1 1
G D F C là hình bình hành, nên
1 1 1 1 1 1
2 2 3G F G I H I a
.
Vậy độ dài nhỏ nhất của
1 1
G F

bằng
3a
.
Nguyễn Văn Công- Trường THPT Kinh Môn II
Gmail: nguyencongkm2@gmail.com
Câu 289: Cho tam giác ABC vuông ở A; BC = 2; CA = b; AB = c và điểm M di động
Biểu thức F=
2 2 2 2 2
8MA b MB c MC
đạt giá trị lớn nhất bằng
J
1
I
1
Z
A
1
B
1
F
1
C
1
D
1
G
1
E
1
H
1
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
108
A. 4 B. 12 C. 16 D. 24
Lời giải
Xét điểm I thỏa mãn:
2 2
8IA b IB c IC 0
(1)
( Dựng đường cao AH, dựng I sao cho A là trung điểm IH; I thỏa (1))
Bình phương hai vế của (1) chú ý rằng
2 2 2
2 2 2
2 2 2
2IA.IB IA IB AB ;
2IB.IC IB IC BC
2IC.IA IC IA AC
rồi biến đổi ta được kết quả
2 2 2 2 2 2 2
8.IA b .IB c .IC 3b c
.
2 2 2
2 2 2 2 2 2 2
2 2 2 2 2
2 2 2 2 2 2 2 2 2
2
2 2
2 2
F 8MA b MB c MC 8MA b MB c MC
8(MI IA) b (MI IB) c (MI IC)
4MI 8.IA b IB c IC 4MI 3b c
b c
3b c 3 12
2
Họ và tên tác giả: Vũ Viên Tên FB: Vũ Viên
Email: tieplen@gmail.com
Câu 290: Cho
ABC
đều có cạnh bằng
2a
. Gọi
d
là đường thẳng qua
A
và song song
BC
, điểm
M
di
động trên
d
. Tìm giá trị nhỏ nhất của 2MA MB MC
.
A.
2 3a
. B.
3a
. C.
3
4
a
. D.
3
2
a
.
Lời giải
Chọn B.
Xét điểm I
sao cho:
2 0IA IB IC
2 0IA IA AB IC
2 2 0IA AB AC
2 0IA AB CB
A
B
C
K
I
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
109
2
BA BC
IA BK
(với
K
là trung điểm
AC
).
I
là điểm thứ 4 của hình bình hành
AIBK
.
Ta có:
2
MA MB MC
2
MI IA MI IB MI IC
2 2 2 2MI IA IB IC MI MI
.
M d
Min đạt được khi
LM d
. Khi đó:
60 60 30 30
MAI MAB IAB ABK
2 2
2 2 sin 30 2. sin 30 2sin 30 (2 ) 3IM IA BK a a a
.
Họ và tên tác giả: Phạm Khắc Thành
Email: phamkhacthanhkt@gmail.com
Câu 291: Trong mặt phẳng cho tam giác ABC và một điểm M bất kỳ. Đặt
, ,
a BC b CA c AB
. Tìm
giá trị nhỏ nhất của biểu thức
MA MB MC
T
a b c
.
A.
3 3
. B.
3
. C.
3
3
. D.
3
2
.
Lời giải
Chọn B.
Theo công thức độ dài đường trung tuyến ta có:
2 2 2
2 2 2 2 2 2 2 2 2
4 2 2 4 3 4 3
2 3
a a a a
b c a
m b c a b c a m a am am
Gọi G là trọng tâm của tam giác ABC khi đó:
2
2 2 2
2 2 2 2 2 2
. . 3 3 3 3
. .
2
.
.
3
2 3
MA MAGA MAGA
MG GA GA MG GA GA
b c a
a a GA b c a b c a
Từ đó suy ra:
2 2 2
2 2 2
3 3
.
MA MB MC
MG GA GB GC GA GB GC
a b c b c a
Lại có
0
GA GB GC
và
2 2 2 2 2 2
1
3
GA GB GC a b c
Do đó
2 2 2
2 2 2
3 3 1
0 3
3
MA MB MC
a b c
a b c b c a
. Đẳng thức xảy ra khi tam
giác ABC đều đồng thời M trùng với trọng tâm của tam giác ABC.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
110
Mail: thuytrangmn@gmail.com
Chủ đề: Vectơ.
Câu 292: Cho tam giác ABC có trung tuyến
' 'AA CC
' , '
A BC C AB
. Tìm giá trị nhỏ nhất của
cos .B
A.
4
5
. B.
2
5
. C.
1
. D.
1
2
Lời giải:
Chọn. A.
Đặt
BC a
,
BA c
ta có:
1
'
2
AA a c

và
1
'
2
CC c a

Do
' 'AA CC
nên
1 1
0
2 2
a c c a
2 2
2 2
2 2 4
.
5 5 5
ac a c a c a c
+ Nếu
0
ac
thì
cos 1
B
+ Nếu
0
ac
thì
. 4
cos
. 5
a c
B
a c
. Dấu đẳng thức xảy ra khi
a c
Vậy giá trị nhỏ nhất của cosB là
4
5
, đạt dược khi tam giác ABC cân tại
.B
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê
Email: hongle.ad@gmail.com
Câu 293: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto
aMA bMB cMC
có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Lời giải
A
A’
C
C’
B
G
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
111
Chọn B.
Gọi I là tâm đường tròn nội tiếp của tam giác ABC
Theo tính chất phân giác trong:
.
DB AB c c
DB DC
DC AC b b
, mà hai vecto
DC
,
DB
ngược
hướng nên ta có
0 0
c
DB DC bDB cDC b IB ID c IC ID
b
hay
0
bIB cIC b c ID
(*)
Mặt khác
DB c DB c ac
DB
DC b BC b c b c
c b c
IA BA b c
aIA b c ID
ID BD ac a
Mà
,IA ID
ngược hướng nên
aIA b c ID
Thay vào (*) ta có
0
bIB cIC aIA
Vậy độ dài của
aMA bMB cMC
nhỏ nhất bằng 0 khi M trùng I
Họ và tên: Ngô Gia Khánh
Địa chỉ mail: ngkhanh4283@gmail.com
Câu 294: Cho tam giác
ABC
là tam giác đều cạnh bằng
a
,
M
là điểm di động trên đường thẳng
AC
.
Khi đó, giá trị nhỏ nhất của biểu thức
3
T MA MB MC MA MB MC
     
là:
A.
2 3
.
3
a
MinT
B.
2 3.MinT a
C.
3.MinT a
D.
5 3
.
2
a
MinT
Lời giải
+, Gọi G là trọng tâm tam giác
ABC
, ta có:
.MA MB MC MG
   
+, Dựng hình bình hành
ABCD
, ta được:
A
B
C
D
I
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
112
BA CD MA MB MC BA MC CD MC MD
         
+, Khi đó
3 3 3
T MA MB MC MA MB MC MG MD GD
     
( Vì G,D nằm khác phía với đường thẳng AC)
Dấu bằng xảy ra khi M là giao điểm của GD và đường thẳng AC hay M là trung điểm của AC
+ Nhận xét
4 4 3 2 3
.
3 3 2 3
a a
GD BM
Vậy
2 3.MinT a
.
Email: vntip3@gmail.com
Câu 295: Cho
ABC
và
' ' 'A B C
có các trọng tâm G và
'G
cố định và
'GG a
. Khi đó giá trị nhỏ nhất
của
AA' ' 'T BB CC
là:
A.
T a
. B.
2T a
. C.
3T a
. D.
4T a
.
Lời giải
Chọn C.
Ta có:
AA' ' '
AG ' G'A ' BG ' G'B' CG ' G'C'
3 '
T BB CC
GG GG GG
GG
 
 
Vậy
AA' ' '
AA' ' ' AA' ' ' 3 ' 3 ' 3
T BB CC
BB CC BB CC GG GG a
Giâ trị nhỏ nhất của T là 3a khi
AA ', ', 'BB CC

cùng phương.
(Họ và tên tác giả: Phạm văn Tài, Tên FB: TaiPhamVan)
Mail: thongbui1987@gmail.com
Câu 296: Cho tam giác
ABC
với các cạnh
,
AB x AC y
;
0
x y
. Gọi
AD
là đường phân giác
trong của góc
A
. Biết biểu thị vectơ
AD mAB nAC
. Tính
S m n
.
A.
2
S
. B.
0
S
. C.
1
S
. D.
2
S
.
Lời giải
Chọn C.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
113
Theo tính chất đường phân giác trong của tam giác ta có
DB AB x
DC AC y
DB x
y
DC
điểm
D
chia đoạn thẳng
BC
theo tỉ số
x
k
y
Nên ta có:
1
x
AB AC
y x
y
AD AB AC
x
x y x y
y
1
y x
m n
x y
.
Câu 297: Cho
ABC
có
3
AB
;
4
AC
. Phân giác trong
AD
của góc
BAC
cắt trung tuyến
BM
tại
I
. Biết
AD a
AI b
, với
,
a b
và
a
b
tối giãn. Tính
2 S a b
.
A.
10
S
. B.
14
S
. C.
24
S
. D.
27
S
.
Lời giải:
Chọn C.
Ta có:
3
2
IB AB
IM AM
2 3 0
IB IM
2 3 5 1
AB AM AI
.
3
4
DB AB
DC AC
4 3 0
DB DC
4 3 7 2
AB AC AD
.
Từ
1
và
2
ta có hệ
2 3 5
4 3 7
AB AM AI
AB AC AD
4 6 10
4 3 7
AB AM AI
AB AC AD
y
x
A
C
B
D
I
M
B
C
A
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
114
6 3 10 7
AM AC AI AD
7 10AD AI
7 10 AD AI
10
7
AD
AI
10, 7 10 2.7 24
a b S
Họ và tên tác giả: Lê Hồng Phi Tên FB: Lê Hồng Phi
Email: lehongphivts@gmail.com
Câu 298: Cho tứ giác
ABCD
có
AD
và
BC
cùng vuông góc với
AB
,
8
AB
,
AD a
,
BC b
. Gọi
E
là một điểm thuộc cạnh
CD
. Biết
90
AEB
, giá trị lớn nhất của
T ab
là
A.
4
. B.
16
. C.
8
. D.
64
.
Lời giải
Chọn B.
Vì
E
là một điểm thuộc cạnh
CD
nên tồn tại
0;1
k
sao cho
1 0
k EC k ED
.
Khi đó,
1
kBC k BD BE

và
1
k AC k AD AE

.
Suy ra
2
2
2
2
2
2 2 2 2
. . 1 . 1 . 1 .
1 1 1
1 1 8 1
BE AE k BC AC k k BC AD k k BD AC k BD AD
k BC AB BC k k ab k k BA AD AB BC k BA AD AD
k b k k ab k k ab k a
kb

2
1 64 1 .k a k k
Do
1
90 . 0 1 8 1 8
1
k k
AEB BE AE kb k a k k b a
k k
.
Theo bất đẳng thức Cô-si ta có
1
8 2 16
1
k k
b a ab ab
k k
.
Đẳng thức xảy ra chẳng hạn khi
4
a b
và
0,5
k
.
Vậy
max 16
T
.
Câu 299: Cho tứ giác
ABCD
có
AD
và
BC
cùng vuông góc với
AB
,
AB h
,
AD a
,
BC b
. Cho
k
là số thực dương thuộc
0;1
và điểm
E
thỏa mãn
1 0
k EC k ED
. Tìm hệ thức liên hệ
giữa
a
,
b
,
h
,
k
để góc
90
AEB
?
A.
1 1
k b ka h k k
. B.
1 1
kb k a hk k
.
C.
1 1
kb k a h k k
. D.
1 1
k b ka hk k
.
Lời giải
Chọn C.
Từ
1 0
kEC k ED
suy ra
8
a
b
E
A
D
B
C
h
a
b
E
A
D
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
115
1
k BC k BD BE
và
1
k AC k AD AE

.
Khi đó,
2
2
2
2
2
2 2 2 2
. . 1 . 1 . 1 .
1 1 1
1 1 1
BE AE k BC AC k k BC AD k k BD AC k BD AD
k BC AB BC k k ab k k BA AD AB BC k BA AD AD
k b k k ab k k h ab k a
kb

2
2
1 1 .k a k k h
Do
90
AEB
nên
. 0 1 1
BE AE kb k a h k k
.
Vậy hệ thức liên hệ giữa
a
,
b
,
h
,
k
để góc
90
AEB
là
1 1
kb k a h k k
.
Câu 300: Cho tam giác có trọng tâm
G
, qua
G
dựng đường thẳng
d
cắt cách cạnh
AB
,
AC
lần lượt
tại
M
,
N
. Đặt
AM
x
AB
,
AN
y
AC
, gọi
m
,
M
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của
T x y
. Tính
m M
.
A.
10
3
. B.
17
6
. C.
11
6
. D.
5
2
.
(Họ và tên tác giả: Hoàng Thị Thanh Nhàn, Tên FB: Hoàng Nhàn)
Lời giải
Chọn B
Ta có
AM xAB
,
AN y AC
,
1 1
3 3
AG AB AC
.
MN AN AM
xAB y AC

.
1 1
3 3
MG x AB AC
.
d
M
G
D
A
B
C
N
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
116
Do
M
,
N
,
G
thẳng hàng nên
MG kMN
1
3
1
3
x kx
ky
1
1
3
1
3
k x
ky
1
1
3
1
3
k
x
k
y
1 1
3
x y
.
3 1
x
y
x
.
Do
M
,
N
lần lượt nằm trên các cạnh
AB
,
AC
nên
1
, 1
2
x y
.
1 1 2
3
x y
xy
4
9
xy
4
3
3
T x y xy
Đẳng thức xảy ra khi và chỉ khi
2
3
x y
.
giá trị nhỏ nhất
4
3
m
.
Ta có
1
;1
2
x
2 1 1 0
x x
2
2 3 1 0
x x
2
2 3 1x x
2
2
1
3 1
x
x
2
3 3
3 1 2
x
x
.
Đẳng thức xảy ra khi và chỉ khi
1
2
1
x
x
Ta có
2
3 3
3
3 1 2
x
T x y xy
x
giá trị lớn nhất là
3
2
M
.
Vậy
4 3 17
3 2 6
m M
.
Họ và tên: Nguyễn Thị Thu
Email: thutoan83@gmail.com
Facebook: Nguyễn Thị Thu
Câu 301: Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho
1
BH HC
3

.
Điểm M di động trên BC sao cho
BM xBC
. Tìm x sao cho
MA GC
đạt giá trị nhỏ nhất.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
117
A.
4
.
5
B.
5
.
4
C.
5
.
6
D.
6
.
5
Lời giải
Chọn B.
Dựng hình bình hành AGCE. Ta có
MA GC MA AE ME ME FE

.
Do đó
MA GC
nhỏ nhất khi
M F
.
Gọi P là trung điểm của AC; Q, F lần lượt là hình chiếu vuông góc của P, E trên BC.
Ta có
BPQ
và
BEF
đồng dạng nên
BQ BP 3
BF BE 4
hay
4
BF BQ
3

.
Có PQ là đường trung bình của
AHC
nên Q là trung điểm của HC hay
1
HQ HC
2
 
.
1 1 5 5 3 5
BQ BH HQ HC HC HC . BC BC
3 2 6 6 4 8
    
.
Do đó
4 5
BF BQ BC
3 6
 
. Vậy
5
x
6
.
gmail: hoangthuyvinhuni@gmail.com
Câu 302: Cho tam giác ABC đều cạnh
2 3
,
d
là đường thẳng qua B và tạo với AB một góc
0
60
C
. Tìm giá trị nhỏ nhất của
3
A MA MB MC

?
A.
3
5
B.
12
5
C.
4
5
D.
2
Hướng dẫn giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
118
Gọi E là trung điểm AB.
Gọi I là điểm thỏa mãn:
3 0
IA IB IC
2 3 0
IE IC
I
nằm giữa đoạn EC và
3
5
EI EC
Ta có:
3
MA MB MC
2 3 3MI IA IB MI IC
5MI
Vậy
5
A MI
min
M là hình chiếu của I trên đường thẳng d.
Đường thẳng d qua B và tạo với AB 1 góc
0
60
nên d song song AC và cắt EC tại K.
. .KEB CEA g c g
nên
E
là trung điêm KC
3 3
2 3. 3
2 2
EC a
3 9
.3
5 5
EI
9 24
3
5 5
KI
EKB MKI
EB KB
MI KI
. 12
5
EB KI
MI
KB
(Tác giả: Hoàng Thị Thúy - Facebook: Cỏ ba lá )
Câu 303: Cho tam giác
ABC
đều cạnh
1
nội tiếp đường tròn
( )O
và điểm
M
thay đổi trên
O
. Gọi
s
,
i
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
MA MB MC
 
. Tính
s i
.
A.
3
s i
. B.
4 3
3
s i
. C.
5 3
3
s i
. D.
2 3
s i
.
Lời giải
d
E
K
A
B
C
I
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
119
Dựng hình bình hành
DBCA
. Ta có
.MA MB MC MD DA MD DB MD DC MD MD
    
Gọi
E
là giao điểm khác
C
của
DC
với
( )O
. Áp dụng bất đẳng thức tam giác ta có
MD DO OM DO OE DE
và
MD DO OM DO OC DC
Dấu bằng xảy ra lần lượt khi
M
trùng
E
và
M
trùng
C
.
Vậy
3 1 4 3
2 2 2 2
2 3
3
s i DE DC DC CE DC DC OC
.
buiduynam1993@gmail.com
Câu 304: Cho lục giác đều
ABCDEF
cạnh
a
. Trên đường chéo
AC
,
CE
lấy hai điểm
M
,
N
sao cho
AM CN
k
AC CE
0 1k
. Độ dài
2 2
BM BN
đạt giá trị nhỏ nhất khi
k
bằng bao nhiêu?
A.
1
2
. B.
1
4
. C.
2
3
. D.
3
4
.
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1)
Lời giải
Chọn B.
Ta có
BM BA AM
 
mà
AM
k AM k AC
AC
k BC BA
.
Vậy
BM BA k BC BA
1BM k BC k BA
.
Lại có
BN BC CN
mà
2
CN
k CN kCE k CF FE k BA BC
CE

.
Vậy
1 2BN k BC k BA

.
Khi đó
2 2
2 2
1 1 2BM BN k BC k BA k BC k BA
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
120
2 2
2 2 2 2 2 2
1 2 1 . 1 4 4 1 .k BC k BA k k BC BA k BC k BA k k BC BA
.
Mà
2 2 2
BC BA a
và
2 2 2 2
.
2 2
BC BA AC a
BC BA
.
Vậy
2 2 2 2
6 3 2BM BN a k k
0 1k
.
2 2 2 2
0 1
min min 6 3 2
k
BM BN a k k
.
Xét
2
6 3 2f k k k
0 1k
, ta có
0 1
1 13
min
4 8
k
f k f
.
Vậy
2
2 2
13
min
8
a
BM BN khi
1
4
k
.
Câu 305: Cho hình chữ nhật
ABCD
có
AD a
,
AB b
.
O
và
I
lần lượt là trung điểm
DB
và
DO
.
N
là điểm thỏa mãn
2 2 2NA NC AB AD AD
 
và
NB
lớn nhất. Tính
NB
.
A.
2 2
2 3
2
a a b
B.
2 2
2
a a b
C.
2 2
2 3
4
a a b
D.
2 2
2
4
a a b
.
Lời giải
2 2 4 4 4 4NA NC AB AD NO BD NO OI NI
Suy ra
2 2
AD a
NI
Để
NB
lớn nhất thì
N
là giao điểm của đường tròn tâm
I
bán kính
2
a
với
BD
(
N
và
B
khác phía so với
I
).
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
121
Do đó
2 2
2 2
3 2 3
2 4 4
a a a b
NB NI IB a b
Họ tên tác giả: Đoàn Phú Như Tên fb: Như Đoàn
Email: doanphunhu@gmail.com
Câu 306: Cho tam giác ABC,
3( ), 4( ), 5( ).AB cm BC cm CA cm
Điểm M thuộc đường tròn ngoại tiếp
tam giác ABC. Giá trị nhỏ nhất của biểu thức
2 2 2
P MB MC MA
là
A.
0
. B.
5 97
5
2
. C.
5 97
5
2
. D.
5 97
5
4
.
Lời giải:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC thì O là trung điểm AC.
Gọi D đỉnh thứ tư của hình bình hành ABDC thì
0
DB DC DA
Ta có
2 2 2
2 2 2
2 2 2
P MB MC MA MB MC MA MD DB MD DC MD DA

2 2 2 2 2 2 2 2 2
2 18
P MD DB DC DA MD DB DC DA MD DB DC DA MD
Do đó P nhỏ nhất khi và chỉ khi DM nhỏ nhất.
Vì M thuộc đường tròn ngoại tiếp tam giác ABC nên DM nhỏ nhất khi và chỉ khi O,M,D theo
thứ tự thẳng hàng.
Ta có
2
2 2 2
1 1 1
.
2 2 4
OD OC CD AC AB OD AC AB AC AB AC AB

2
25 3 97 97 5
9 5.3.
4 5 4 2 2
OD MD OD OM
Vậy
2
97 5 5 97
18 5
2 2 2
MinP
.
Chọn đáp án B
Phuongthao.nguyenmaths@gmail.com
M
D
C
O
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
122
Câu 307: Cho tam giác
ABC
có
G
là trọng tâm. Gọi
H
là chân đường cao hạ từ
A
sao cho
1
3
BH HC
. Điểm
M
di động nằm trên
BC
sao cho
BM xBC
. Tìm
x
sao cho độ dài của
vectơ
MA GC
đạt giá trị nhỏ nhất.
A.
4
.
5
. B.
5
.
6
. C.
6
.
5
. D.
5
.
4
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Lời giải
Chọn B.
Dựng hình bình hành
AGCE
. Ta có
MA GC MA AE ME
.
Kẻ
EF BC
F BC
. Khi đó
MA GC ME ME EF

.
Do đó
MA GC
nhỏ nhất khi
M F
.
Gọi
P
là trung điểm
AC
,
Q
là hình chiếu vuông góc của
P
lên
BC
Q BC
.
Khi đó
P
là trung điểm
GE
nên
3
4
BP BE
.
Ta có
BPQ
và
BEF
đồng dạng nên
3
4
BQ BP
BF BE
hay
4
3
BF BQ
.
Mặt khác,
1
3
BH HC
.
PQ
là đường trung bình
AHC
nên
Q
là trung điểm
HC
hay
1
2
HQ HC
.
Suy ra
1 1 5 5 3 5
. .
3 2 6 6 4 8
BQ BH HQ HC HC HC BC BC
Do đó
4 5
3 6
BF BQ BC
.
Câu 308: Cho hình thang ABCD có đáy CD gấp đôi đáy AB. Lấy một điểm E sao cho
3 2
BC DE
 
và
đồng thời thỏa mãn
CA CE
. Giá trị nhỏ nhất của góc
ABC
nằm trong khoảng nào dưới đây?
A.
(95 ;100 )
. B.
(100 ;106 )
. C.
(106 ;115 )
. D.
(115 ;120 )
.
Lời giải:
Q
F
E
G
P
B
C
H
A
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
123
Gọi
ABC
. Ta có:
2 2 2
2 . .cos
AC AB BC AC AB BC AB BC

(1)
Lại có:
2 2 2 2
3 9
2 4 6 . .cos
2 4
CE CD DE AB BC CE AC AB BC AB BC
(2)
Lấy (2) – (1) vế theo vế ta được :
2 2
5 3 5 3 5 15
0 3 8 . .cos cos 2. .
4 8 32 8 32 8
AB BC AB BC
AB BC AB BC
BC AB BC AB
Suy ra:
118,96
GTNN
của
nằm trong khoảng
(115 ;120 )
chọn đáp án D.
Câu 309: Cho hình thang ABCD có
2
AB DC
,
8, 6
AC BD
, góc tạo bởi hai véc tơ
AC
và
BD
bằng
120
. Khi đó giá trị của
( )AD BC
bằng:
A.
13 2 5
2
. B.
14 4 7
3
. C.
15 2 10
4
. D.
6 4 3
.
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Lời giải:
Ta có:
AC AB BC
  
và
BD BC CD
 
. Suy ra:
2 (2 ) 3 3
AC BD AB CD BC BC

Bình phương vô hướng hai vế ta được:
2 2 2 2 2
14
9 4 4 . .cos120 4.8 6 4.8.6.cos120
3
BC AC BD AC BD BC
B
C
A
D
E
B
C
A
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
124
Tương tự ta có:
Ta có:
AC AD DC
và
BD BA AD
. Suy ra:
2 (2 ) 3 3
AC BD BA BC AD AD
Bình phương vô hướng hai vế ta được:
2 2 2 2 2
4 7
9 4 4 . .cos120 8 4.6 4.8.6.cos120
3
AD AC BD AC BD AD
Suy ra:
14 4 7
( )
3
AD BC
chọn đáp án B.
Câu 310: Cho hình thang ABCD có
2
AB DC

,
9, 6
AC BD
. Giá trị của biểu thức
2 2
( )BC AD
bằng:
A.
15
. B.
80
3
. C.
12
. D.
14
.
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Lời giải:
Ta có:
AC AB BC
  
và
BD BC CD
 
. Suy ra:
2 (2 ) 3 3
AC BD AB CD BC BC

Bình phương vô hướng hai vế ta được:
2 2 2
9 4 4 .BC AC BD AC BD
 
(1)
Tương tự ta có:
Ta có:
AC AD DC
và
BD BA AD
. Suy ra:
2 (2 ) 3 3
AC BD BA BC AD AD
Bình phương vô hướng hai vế ta được:
2 2 2
9 4 4 .AD AC BD AC BD

(2)
Lấy (1) trừ đi (2) vế theo vế, ta được :
2 2 2 2
2 2
9 6
15
3 3
AC BD
BC AD
Chọn đáp án
A.
Suy ra:
14 4 7
( )
3
AD BC
chọn đáp án B.
B
C
A
D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
125
Câu 311: Cho tam giác
ABC
có
60
BAC
và
,AB AC
đã biết. Biểu thức
.
P k MA MB MC
đạt giá
trị nhỏ nhất bằng
( )AB AC
với mọi giá trị thực
0
k k
. Giá trị của
0
k
nằm trong khoảng nào
dưới đây?
A.
(0;1)
. B.
3
( ;2)
2
. C.
3
(1; )
2
. D.
(2;3)
.
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Lời giải:
Ta có:
| |.| | . | | .
| |
v
u v u v u u
v
và:
. | | .| |u v u v
. Áp dụng vào bài này, ta có :
. . . . . ( ). ( ).
AB AC AB AC
P k MA MB MC k MA MB MC k MA MA AB MA AC
AB AC AB AC
. ( ) . .| |
AB AC AB AC
P k MA AB AC MA k MA AB AC MA
AB AC AB AC
 
| |
AB AC
P MA k AB AC
AB AC

. Giả thiết cho biết:
| |
AB AC
P MA k AB AC AB AC
AB AC
Suy ra:
| | 0 | |
AB AC AB AC
k k
AB AC AB AC

Sử dụng bình phương vô hướng để tính:
2 2
2
| | 2 . 1 1 2.cos60 3
AB AC AB AC AB AC
AB AC AB AC AB AC
Suy ra:
0
| | 3
AB AC
k k
AB AC
. Vậy ta chọn đáp án B.
Email: hongle.ad@gmail.com
Câu 312: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto
aMA bMB cMC
có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Lời giải
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê
Chọn B.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
126
Gọi I là tâm đường tròn nội tiếp của tam giác ABC
Theo tính chất phân giác trong:
.
DB AB c c
DB DC
DC AC b b
, mà hai vecto
DC
,
DB
ngược
hướng nên ta có
0 0
c
DB DC bDB cDC b IB ID c IC ID
b
hay
0
bIB cIC b c ID
(*)
Mặt khác
DB c DB c ac
DB
DC b BC b c b c
c b c
IA BA b c
aIA b c ID
ID BD ac a
Mà
,IA ID
ngược hướng nên
aIA b c ID
Thay vào (*) ta có
0
bIB cIC aIA
Vậy độ dài của
aMA bMB cMC
nhỏ nhất bằng 0 khi M trùng I
Email: nguyentuyetle77@gmail.com
Câu 313: Cho tam giác
ABC
đều cạnh a và điểm M thay đổi. Giá trị nhỏ nhất của biểu thức
2 2 2
2 3 4
P MA MB MC
là:
A.
2
14a
B.
2
14a
C.
2
26
3
a
D.
2
26
3
a
Lời giải
Họ và tên: Nguyễn Thị Tuyết Lê FB: Nguyen Tuyet Le
Gọi G là trọng tâm tam giác
ABC
. Ta có:
2 2
2( ) 3( ) 4( )P MG GA MG GB MG GC
  
=
2
2 (2 3 4 )MG MG GA GB GC
2
2 (2 2 2 6 )MG MG GA GB GC GB GC

A
B
C
D
I
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
127
2 2
2 ( 5 )
MG MG CB GC GC

2 2 2
2 ( 5 ) ( 5 ) 42
MG MG CB GC CB GC GC
(Vì
2
2 2 2 2
( 5 ) 10 . 25 43. 43
3
a
CB GC CB CB GC GC GC

)
2 2 2 2
( 5 ) 42 42 14p MG CB GC GC GC a
 
.
Dấu “=”xẩy ra
5
MG GC CB
.
Vậy min
2
14P a
khi M là điểm thỏa mãn
5
MG GC CB
Họ và tên tác giả: Đặng Văn Tâm Tên FB: Đặng Văn Tâm
Email: dvtam0189@gmail.com
Câu 314: Cho tam giác
ABC
có hai đường trung tuyến kẻ từ
B
và
C
vuông góc với nhau. Tính giá trị
nhỏ nhất của
cos A
.
A.
1
2
. B.
2
3
. C.
3
4
. D.
4
5
.
Lời giải
Chọn D
Gọi
,M N
lần lượt là trung điểm của
, .AC AB
Ta có:
; .BM AM AB CN AN AC
Theo giả thiết
BM CN
nên ta có
0
CB NM
hay
.
0AM AB AN AC A
AC AM AN AM AC AN AB
B
    
Mà
1
2
AM AC

và
1
2
AN AB
nên suy ra
2 2 2 2
1 1 2
.
4 2 5
AC AB AC AB AA C AB AC AB ACB
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
128
Áp dụng định nghĩa tích vô hướng, kết hợp Bất đẳng thức Cosi ta có
2 2 22
.
2
cos cos
.
2 2 . 4
.
. 5 . 5
;
5
AB AB AC
A AB AC
AB AC AB AC
AC AB AC
AB AC
Dấu
" "
xảy ra khi
AB AC
hay tam giác
ABC
cân tại
.A
Vậy
4
min cos .
5
A
Họ và tên: Cấn Việt Hưng
Email: thuyhung8587@gmail.com
FB: Viet Hung
Câu 315: Cho đoạn thẳng
AB
có độ dài bằng
.a
Một điểm
M
di động sao cho

MA MB MA MB .
Gọi
H
là hình chiếu của
M
lên
AB
. Tính độ dài lớn nhất của
MH
?
A.
.
2
a
B.
3
.
2
a
C.
.a
D.
2 .a
Lời giải:
Chọn A.
Gọi
N
là đỉnh thứ 4 của hình bình hành
MANB
. Khi đó
MA MB MN
.
Ta có MA MB MA MB MN BA
 
hay
MN AB
.
Suy ra
MANB
là hình chữ nhật nên
90
o
AMB .
Do đó
M
nằm trên đường tròn tâm
O
đường kính
AB
.
MH
lớn nhất khi
H
trùng với tâm
O
hay
max .
2 2
AB a
MH MO
Họ và tên tác giả: Phương Xuân Trịnh Tên FB:: Phương Xuân Trịnh
Email: phuongtrinhlt1@gmail.com
Câu 316: Cho tam giác
ABC
vuông tại
A
. Gọi
là góc giữa hai trung tuyến
BD
và
CK
. Giá trị nhỏ
nhất của
cos
là:.
A.
1
2
. B.
4
5
. C.
2
3
. D.
3
4
.
Lời giải
Chọn B.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
129
Ta có:
. . .BD CK AD AB AK AC AD AC AK AB
(do
AB AC
)
2 2 2
1 1
2 2
AB AC BC
.
Mặt khác:
2 2 2 2 2 2
2 2
2 2 2 2
2 .
4
BA BC AC CA CB AB
BD CK BD CK
2 2 2 2
4 5
4 4
AB AC BC BC
.
Do đó:
2 2
2
.
4 4
cos
. 2 . 5 5
BD CK
BC BC
BD CK BD CK BC
.
4
cos
5
BD CK ABC
vuông cân tại
A
.
Vậy
4
min cos
5
.
vanphu.mc@gmail.com
Câu 317: Cho
ABC
có trọng tâm G. Gọi H là chân đường cao kẻ từ A sao cho
1
3
CH HB
. Điểm M di
động trên BC sao cho
.CM x CB
. Tìm x sao cho độ dài vecto
MA GB
đạt giá trị nhỏ nhất.
A.
8
5
. B.
5
6
. C.
6
5
. D.
5
8
.
Lời giải
Chọn B.
D
K
A
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
130
Dựng hình bình hành AGBE. Ta có
MA GB MA AE ME
MA GB ME ME EF
min
MA GB EF M F
.
Gọi
P
là trung điểm của
AB
. Khi đó
P
cũng là trung điểm của
GE
và
3
4
CP CE
Gọi
Q
là hình chiếu vuông góc của
P
trên BC.
Ta có
CPQ
và
CEF
đồng dạng nên
3 4
4 3
CQ CP
CF CQ
CF CE
.
Mặt khác
PQ
là đường trung bình của
AHB
nên
1
2
HQ HB
. Theo giả thiết
1
3
CH HB
Suy ra
1 1 5
3 2 6
CQ CH HQ HB HB HB

Từ giả thiết
3
4
HB CB
. Do đó
5 5 3 5 4 4 5 5
. .
6 6 4 8 3 3 8 6
CQ HB CB CB CF CQ CB CB
 
( Họ và tên tác giả: Nguyễn Văn Phu, Tên FB Nguyễn Văn Phu)
Họ và tên tác giả: Trần Tuyết Mai Tên FB: Mai Mai
Email: maimai1.hn@gmail.com
Câu 318: Cho đoạn thẳng
AB
có độ dài bằng
.a
Một điểm
M
di động sao cho

MA MB MA MB
.
Gọi
H
là hình chiếu của
M
lên
AB
. Tính độ dài lớn nhất của
MH
?
A.
.
2
a
B.
3
.
2
a
C.
.a
D.
2 .a
Lời giải
Chọn A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
131
Gọi
O
là trung điểm của
AB
. Khi đó
2MA MB MO
.
Ta có 2MA MB MA MB MO BA
hay
1
2
MO AB
Suy ra
MAB
vuông tại
M
nên
90
o
AMB
. Do đó
M
nằm trên đường tròn tâm
O
đường kính
AB
.
MH
lớn nhất khi
H
trùng với tâm
O
hay
max .
2 2
AB a
MH MO
Họ và tên tác giả: Nguyễn Thị Thanh Thảo Tên FB: Nguyễn Thanh Thảo
Email: nghianguyennhan78@gmail.com
Câu 319: Cho
AD
và
BE
là hai phân giác trong của tam giác
ABC
. Biết
4AB
,
5BC
và
6CA
.
Khi đó

DE
bằng:
A.
5 3
9 5

CA CB
. B.
3 5
5 9

CA CB
. C.
9 3
5 5

CA CB
. D.
3 9
5 5

CA CB
.
Lời giải
Chọn A.
AD
là phân giác trong của tam giác
ABC
nên
6 6
4 6 4
CD AC CD
DB AB CD DB
6 3
10 5

CD
CD CB
CB
.
Tương tự:
5 5
9 9
 
CE
CE CA
CA
.
Vậy
5 3
9 5
  
DE CE CD CA CB
.
Câu 320: : Cho đoạn thẳng
AB
có độ dài bằng
.a
Một điểm
M
di động sao cho
MA MB MA MB
. Gọi
H
là hình chiếu của
M
lên
AB
. Tính độ dài lớn nhất của
MH
?
A
O
B
M
H
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
132
A.
.
2
a
B.
3
.
2
a
C.
.a
D.
2 .a
Lời giải
Chọn A.
Gọi
N
là đỉnh thứ 4 của hình bình hành
MANB
. Khi đó
MA MB MN
.
Ta có
 
MA MB MA MB MN BA hay
MN AB
.
Suy ra
MANB
là hình chữ nhật nên
90
o
AMB
.
Do đó
M
nằm trên đường tròn tâm
O
đường kính
AB
.
MH
lớn nhất khi
H
trùng với tâm
O
hay
max .
2 2
AB a
MH MO
Họ và tên tác giả: Hoàng Tiến Đông Tên FB: tiendongpt
Email: dongpt@c3phuctho.edu.vn
Câu 321: Một miếng gỗ có hình tam giác có diện tích là
S
điểm
I
,
O
lần lượt thỏa mãn
0IB IC
;
0OA OI
. Cắt miếng gỗ theo một đường thẳng qua
O
, đường thẳng này đi qua
,M N
lần
lượt trên các cạnh
,AB AC
. Khi đó diện tích miếng gỗ chứa điểm
A
thuộc đoạn:
A.
;
4 3
S S
. B.
;
3 2
S S
. C.
3
;
8 2
S S
. D.
3
;
4 8
S S
Lời giải
Chọn A
Từ
O
kẻ
//M N BC
, suy ra:
O
là trung điểm
M N
.
Ta có:
. . 1
NN MA OM
NA MM ON
1
, 0
2
NN MM
x x
NA MA
.
N'
M'
N
O
I
A
B
C
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
133
1
1
NN xNA AN AN xNA NA AN
x
.
1
1
MM xMA M A MA xMA MA M A
x
.
Ta có:
2
. 1
.
4. .
4 1
AMN
ABC
S
AM AN AM AN
S AB AC AM AN
x
.
Xét hàm số:
2
4 1
f x x
trên
1
0;
2
. suy ra:
3 4
4 3
AMN
S S
f x S
.
Đỗ Công Dũng
Email: congdung812@gmail.com
Câu 322: Cho tam giác
ABC
có bán kính đường tròn ngoại tiếp
2R
. Tìm giá trị lớn nhất của
2 2 2
BC AB AC
.
A. 1. B. 2. C. 3. D. 4
Giải
Chọn D
Gọi O là tâm của đường tròn ngoại tiếp tam giác
ABC
. Dựng hình bình hành
ABMC
Ta có
OA OM MA
2 2 2
2
OA OM MA OM MA
1
Tương tự ta có:
2 2 2
2
OB OM MB OM MB
2
2 2 2
2
OC OM MC OM MC

3
Lấy
2 3 – 1
từng vế ta có:
2 2 2 2 2
2
R OM MB MC MA OM MB MC MA
   
( do tứ giác
ABMC
là hình bình
hành nên
MB MC MA
)
Khi đó
2 2 2 2 2
R OM MB MC MA
2 2 2 2
4
OM MB MC MI
2 2 2
2 2 2
4
2 4
AB AC BC
OM MB MC
2 2 2 2 2 2
2
OM MB MC AB AC BC
mà
MB AC
,
MC AB
I
M
O
C
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
134
nên
2 2 2 2 2
R OM AB AC BC
2 2 2 2 2
BC AB AC R OM
2
4R
Vậy giá trị lớn nhất của
2 2 2
BC AB AC
là
4
.
Đẳng thức xảy ra
M O
2 2
3AB AC R BC R
. Áp dụng định lý cosin trong tam
giác ABC có
0
120
BAC
. Hay là tam giác
ABC
cân tại
A
và có
0
120
BAC
.
Họ và tên tác giả: Nguyễn Tân Quang Tên FB: Nguyễn Tân Quang
Email: quangmath@gmail.com
Câu 323: Cho tam giác đều
ABC
cạnh
.a
Gọi
M
là điểm nằm trên cạnh
.AB
Tính giá trị nhỏ nhất của
biểu thức
2
MA MB MC

theo
.a
A.
3
4
a
. B.
3
2
a
. C.
3
8
a
. D.
2 3
3
a
.
Lời giải
Chọn B.
Ta có
2 2 2 2 4 4 ,MA MB MC MA MC MB MN MB MI MI

trong đó
,N I
lần lượt là trung điểm của
, .AC BN
Do đó
I
cố định.
Kẽ
IH
vuông góc với
.AB
Ta có
.MI HI
Tính được
0
3 3
.sin 30 .
2 8
a a
BN IH BI
Email: themhaitotoanyp1@gmail.com
Câu 324: Cho hình bình hành ABCD, M thuộc đường chéo AC, (M không trùng với các đỉnh A, C)
Trên các đường thẳng AB, BC, lấy các điểm P và Q sao cho MP // BC, MQ // AB. Gọi N là
giao hai đường thẳng AQ và CP. Giả sử
DCnDAmDN
. Tìm giá trị lớn nhất của m + n
A.
3
4
B.
4
3
C.
2
1
D. 2
Lời giải
H
I
N
C
B
A
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
135
Đặt
k
AC
AM
k
BC
BQ
và
k
AB
BP
1
,
1;0k
Có
BQABxDAAQxDAANDADN
DAkxDCxDA
DCxDAkx 1
, (1)
Mặt khác
BPCByDCCPyDCCNDCDN
DCkyDAyDC 1
DCyykDAy 1
, (2)
Từ (1) và (2), ta có
1
1
1
1
1
2
2
kk
k
y
kk
k
x
xyky
kxy
Do đó
DC
kk
k
DA
kk
k
DN
11
1
22
1;0,
3
4
4
3
2
1
1
1
1
22
k
k
kk
nm
3
4
max nm
, đạt được khi k =
2
1
hay M là trung điểm AC.
(Fb: Lưu Thêm)
Họ và tên: Lê Thị Lan FB: Lê Lan
Email: lelanqx2@gmail.com
Câu 325: : Cho tam giác
ABC
có
G
là trọng tâm. Gọi
H
là chân đường cao hạ từ
A
sao cho
1
3
BH HC
. Điểm
M
di động nằm trên
BC
sao cho
BM xBC
. Tìm
x
sao cho độ dài của
vectơ
 
MA GC
đạt giá trị nhỏ nhất.
A.
4
.
5
B.
5
.
6
C.
6
.
5
D.
5
.
4
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
136
Chọn B.
Dựng hình bình hành
AGCE
. Ta có
  
MA GC MA AE ME
.
Kẻ
EF BC
F BC
. Khi đó
MA GC ME ME EF .
Do đó
MA GC nhỏ nhất khi
M F
.
Gọi
P
là trung điểm
AC
,
Q
là hình chiếu vuông góc của
P
lên
BC
Q BC
.
Khi đó
P
là trung điểm
GE
nên
3
4
BP BE
.
Ta có
BPQ
và
BEF
đồng dạng nên
3
4
BQ BP
BF BE
hay
4
3
BF BQ
.
Mặt khác,
1
3

BH HC
.
PQ
là đường trung bình
AHC
nên
Q
là trung điểm
HC
hay
1
2
 
HQ HC
.
Suy ra
1 1 5 5 3 5
. .
3 2 6 6 4 8
BQ BH HQ HC HC HC BC BC
Do đó
4 5
3 6
BF BQ BC
.
Tác giả: Nguyễn Văn Hưng Facebook: Nguyễn Hưng
Câu 326: Cho tam giác ABC có
, ,BC a AC b AB c
nội tiếp đường tròn tâm O, bán kính R. M là
điểm thuộc đường tròn (O). Gọi
,N n
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức
2 2 2
P MA MB MC
. Khi đó giá trị của
N n
bằng
A.
2
12R . B.
2 2 2 2
4R 9R a b c
.
C.
2 2 2 2
2R 9R a b c
. D.
2 2 2 2
8R 9R a b c
.
Lời giải
Chọn B.
Ta có:
2 2 2
P MO OA MO OB MO OC
2 2
6R 2 . 6R 2 . .cosMO OA OB OC MO OA OB OC
2
6R 2 . .cosR OA OB OC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
137
Vậy:
`
2 2
6R 2 . 6R 2 .
R OA OB OC P R OA OB OC
4R.
N n OA OB OC

Mà:
2
2
3R 2
OA OB OC OAOB OBOC OAOC

2 2 2
2
( )
3R 2.
2
OA OB OA OB
2 2 2 2
9R
a b c
2 2 2 2
4R. 9R
N n a b c
Họ và tên tác giả: Nguyễn Xuân Giao Tên FB: giaonguyen
Email: giaohh2@gmail.com
Câu 327: Cho tam giác đều
ABC
nội tiếp đường tròn tâm
O
,bán kính
R
,
M
là một điểm bất kì trên
đường tròn. Giá trị lớn nhất của biểu thức
2 2 2
2 3
S MA MB MC
là
A.
2
21
R
. B.
2
21
R
. C.
2
2 21
R
. D.
2
2 21
R
.
Lời giải
Chọn C.
Ta có
2 2 2
2 2 2
2 3 2 3
 
S MA MB MC MO OA MO OB MO OC
2 2 3 2 2 3 .cos
S MO OA OB OC MO OA OB OC
2 2 .cos

S R CA CB
Trong đó
, 2
MO CA CB
Do tam giác
ABC
đều nội tiếp đường tròn bán kính
R
nên có cạnh là
3R
2
2 2
2 0 2
2 4 . 4 15 4. . .cos60 21
CA CB CA CACB CB R CACB R
2 21

CA CB R
2
2 21.cos
S R
2
2 21
S R
Dấu bằng xảy ra khi
cos 1
, 2
MO CA CB
cùng chiều.
Vậy
2
2 21
MaxS R
Email: anhtu82t@gmail.com
Câu 328: Cho tam giác
ABC
. Tìm giá trị nhỏ nhất của biểu thức
3 cos2 2cos 2 2 3 cos2P A B C
A.
P
4
min
. B.
P
3 1
2
min
. C.
P
2 3 3
min
. D.
P
5
min
.
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
138
Họ và tên: Đồng Anh Tú Facebook: Anh Tú
Chọn A
Gọi
O R,
lần lượt là tâm và bán kính đường tròn ngoại tiếp tam giác
ABC
Ta có:
2
(2 3 ) 0
OA OB OC

2 2 2
4 3 4 . 4 3 . 2 3 . 0
OA OB OC OAOC OAOB OB OC
2
8 4 . .cos 2 4 3 . .cos 2 2 3 . .cos2 0
R OAOC B OAOB C OB OC A
2 2 2 2
8 4 cos 2 4 3 cos2 2 3 cos2 0
R R B R C R A
3 cos 2 2cos2 2 3 cos 2 4
A B C
. Dấu bằng xẫy ra khi
0 0 0
45 , 60 , 75
A B C
.
Vậy
P
4
min
.
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
Email: ngvnho93@gmail.com
Câu 329: Cho tam giác đều
ABC
cạnh
a
. Tính
. . .AB BC BC CA CA AB
A.
2
3
2
a
B.
2
3
2
a
C.
2
3
2
a
D.
2
3
2
a
Lời giải
Họ và tên: Nguyễn Văn Nho Facebook: Nguyễn Văn Nho
Chọn A
Cách 1
Nhận xét: Với mọi điểm M bất kỳ, ta luôn có
2
2 2 2
2 .AB AM MB AM MB AM MB

2 2 2
1
.
2
AM MB AB AM MB

Do đó
2
2 2 2
2
2 2 2
2
2 2 2
1
.
2 2
1
.
2 2
1
.
2 2
a
AB BC AC AB BC
a
BC CA BA BC CA
a
CA AB CB CA AB
2
3
. . .
2
a
AB BC BC CA CA AB

.
Cách 2
Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Do tam giác ABC đều nên
, , BM CP AN

lần lượt là các hình chiếu của
, , BC CA AB
lên các cạnh BA, CB, AB.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
139
Áp dụng công thức chiếu, ta có
2
2
2
. . . . .
2 2
. . . . .
2 2
. . . . .
2 2
a a
AB BC AB BM AB MB AB MB a
a a
BC CA BC CP BC PC BC PC a
a a
CA AB CA AN CA NA CA NA a

Cộng vế theo vế ta được
2
3
. . .
2
a
AB BC BC CA CA AB
.
Cách 3. Vì tam giác ABC đều nên
0
, , , 120
AB BC BC CA CA AB
.
Do đó
2
2
2
1
. . .cos , . .
2 2
1
. . .cos , . .
2 2
1
. . .cos , . .
2 2
a
AB BC AB BC AB BC a a
a
BC CA BC CA BC CA a a
a
CA AB CA AB CA AB a a
2
3
. . .
2
a
AB BC BC CA CA AB
Câu 330: Cho tam giác
ABC
có
AD
là trung tuyến,
G
là trọng tâm. Một đường thẳng qua
G
cắt các
cạnh
,AB AC
lần lượt tại
,M N
. Khẳng định nào sau đây đúng?
A.
1 2
. . .
2 3
AM AN AN MB AM NC
    
B.
. . .AM AN AN MB AM NC
C.
2
. ( . . )
3
AM AN AN MB AM NC
    
D.
3
. ( . . )
2
AM AN AN MB AM NC
    
Lời giải
Chọn B
P
N
M
B
A
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
140
Trước hết ta chứng minh
1(1)
BM CN
AM AN
Thật vậy, kẻ
//
//
BP MN
CQ MN
BM PG
AM AG
CN QG
AN AG
Do đó
(1) 1 ( ) ( )
PG QG
PG QG AG GD PD GD DQ AG
AG AG
2
GD AG
( luôn đúng)
Vậy ta có
1
BM CN
AM AN
. . .
. . .
cos cos cos
BM AN CN AM AM AN
AN MB AM NC AM AN
A A A
. . .AM AN AN MB AM NC
( Do
cos 0
A
)
Câu 331: Cho các véc tơ
, ,a b c
thỏa mãn
, ,
a a b b c c
và
3 0
a b c
. Tính
.
A.
2 2 2
3
2
c a b
. B.
2 2 2
3
2
a c b
.
C.
2 2 2
3
2
b a c
. D.
2 2 2
3
2
c a b
.
Lời giải
Tác giả: Quang Phi
Chọn A
Ta có
2
2
3 0 3 9a b c a b c a b c
2 2 2
2. . 9a b a b c
2 2 2
9
.
2
c a b
a b
Q
P
N
G
D
A
B
C
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
141
Tương tự ta có
2
2 2 2 2
3 3 9 6. .
b c a b c a b c b c a
2 2 2
9
.
6
a b c
b c
.
Và ta lại có
2
2
3 3
a c b a c b
2 2 2
2 2 2
9
9 6. . .
6
b a c
a c a c b a c
.
Suy ra
2 2 2 2 2 2 2 2 2 2 2 2
9 9 9 3
2 6 6 2
c a b a b c b a c c a b
A
.
Họ và tên: Đoàn Thị Hường
Email: ngochuongdoan.6@gmail.com Fb: Đoàn Thị Hường
Câu 332: Cho tam giác ABC vuông tại A có BC = 2a, M là điểm trên đoạn BC sao cho MB = 2MC. Biết
rằng
2
.
AM BC a
 
. Độ dài cạnh AC là:
A.
33
3
a
AC
B.
3AC a
C.
3
3
a
AC
D.
5AC a
Bài giải
Từ giả thiết M là điểm trên đoạn BC sao cho MB = 2MC nên ta có
1
3
BM BC
Đặt AB = x; AC = y ta có
2 2 2
4x y a
(1) (Tam giác ABC vuông tại A)
Mặt khác từ
1 1 2 1
( )
3 3 3 3
AM AB BM AB BC AB AC AB AB AC
Nên có
2 2
2 1
. ( )( )
3 3
AM BC a AB AC AC AB a
2 2
2
1 2
3 3
AC AB a
( Do
. 0
AB AC
)
2 2 2
1 2
3 3
y x a
(2)
Từ (1) và (2) ta có
33
3
a
y
Chọn đáp án A
Họ tên: Đào Hữu Nguyên FB: Đào Hữu Nguyên
Mail: huunguyen1979@gmail.com
Câu 333: Cho tam giác
ABC
có
0
90 , 1, 2
BAC AB AC
.Dựng điểm M sao cho
, 3
AM BC AM
. Đặt
. .AM x AB y AC

.Tính
2 2
?T x y
A.
153
20
T
. B.
151
20
T
. C.
157
20
T
. D.
159
20
x
.
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
142
Chọn A
Từ
2 2 2 2 2 2 2
. . 9 4AM x AB y AC AM x AB y AC x y
Và
. . . . . 0 . ( ) . ( ) 9 4AM BC x AB BC y AC BC x AB AC AB y AC AC AB x y

Ta có hệ:
2
2 2
144
4 9
20
4 0
4
x
x y
x y
x y
. Suy ra
2 2
153
20
T x y
.
Email: truongthanhha9083@gmail.com
Câu 334: Cho tam giác ABC vuông tại A. Quỹ tích điểm M thỏa mãn
2
. .
MB MC MA BC MA
là
A. Đường thẳng AC. B. Đường thẳng AB.
C. Đường thẳng BC. D. Đường trung trực cạnh BC.
Lời giải
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon
Chọn B
Yêu cầu bài toán trở thành
2
2 2
( ).( ) .
( ) . .
( ) ( ) (*)
MA AB MA AC MA BC MA
MA MA AB AC AB AC MA BC MA
MA AB AC MA AB AC

 
Gọi E là đỉnh thứ tư của hình chữ nhật ABEC. Hệ thức (*) trở thành
. .
( ) 0
( ) 0
. 0
MA AE MA BC
MA AE BC
MA AE AC
MACE MA AC



Vậy điểm M thuộc đường thẳng AB.
Câu 335: Cho tam giác đều
ABC
cạnh
3a
,
0
a
. Lấy các điểm
M
,
N
,
P
lần lượt trên các cạnh
BC
,
CA
,
AB
sao cho
BM a
,
2CN a
,
AP x
0 3x a
. Tìm
x
để
AM PN
.
A.
3
5
a
x
. B.
4
5
a
x
.
C.
5
a
x
. D.
2
5
a
x
Lời giải
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon
Chọn B
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
143
Ta có
1
3
AM AB BM AB BC

1 2 1
3 3 3
AM AB AC AB AB AC
.
Ta có
1
3 3
x
PN AN AP AC AB
a
.
Để
AM PN
thì
2 1 1
. 0 0
3 3 3 3
x
AM PN AB AC AC AB
a
  
2 2
2 2 1
. . 0
9 9 9 9
x x
AB AC AB AC AB AC
a a
.
2 2
2 2 1
. .cos60 3 3 . .cos 60 0
9 9 9 9
x x
AB AC a a AB AC
a a
2 2
2 1 2 1 1
3 3 9 9 3 3 0
9 2 9 9 9 2
x x
a a a a a a
a a
.
2
5 4
2 0
2 5
a
a ax x
. Vậy
4
5
a
x
thì
AM PN
.
Nguyenducloi qv2@gmail.com
Câu 336: Cho tam giác
ABC
vuông cân tại
B
. Gọi
M
là trung điểm
AB
và
I
là điểm di động trên
đường thẳng
MC
. Khi 2IM AC
đạt giá trị nhỏ nhất, hãy tính tỉ số
AC
AI
.
A.
1
AC
AI
. B.
2
AC
AI
. C.
2
AC
AI
. D.
3
2
AC
AI
.
(Họ và tên tác giả: Nguyễn Đức Lợi, Tên FB: Nguyễn Đức Lợi)
Lời giải
Chọn B
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
144
Gọi
N
là trung điểm
BC
.
Có 2 2 .IM AC IA IB IC IA IB IC IN
  
Do đó
2IM AC
đạt giá trị nhỏ nhất khi và chỉ khi
I
là hình chiếu vuông góc của
N
trên
MC
.
Dựng hình vuông
ABCD
. Gọi
P
là trung điểm
CD
và
H
là giao điểm của
AP
với
DN
.
Dễ dàng chứng minh được
DN CM I DN
.
Lại có tứ giác
AMCP
là hình bình hành, suy ra
/ /AP CM
.
Do đó
AP DI
và
H
là trung điểm
.DI
Suy ra tam giác
AID
cân tại
.A
Vậy
2.
AC AC
AI AD
Email: buivuongphung@gmail.com
Câu 337: Cho
ABC
có trọng tâm
G
,
H
là chân đường cao kẻ từ
A
sao cho
1
3
BH HC

. Điểm
M
di
động trên
BC
sao cho
BM xBC
. Tìm
x
sao cho MA GC

nhỏ nhất.
A.
6
5
B.
5
4
C.
4
5
D.
5
6
Lời giải
Họ tên: Vũ Thị Chuyền FB: Vũ Thị Chuyền
Chọn D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
145
Gọi
I
là trung điểm cạnh
BC
.
2
3
2
3
2 1 2
.
3 4 3
5 2
6 3
MA GC MC CG GA GC MC IA
BC BM IH HA
BC xBC CB HA
x BC HA



Suy ra
2
2
2 2 2
5 4 4
6 9 9
MA GC x BC HA HA
Dấu “=” xảy ra khi
5
6
x
.
Email: nguyenthitrangtnh@gmail.com
Câu 338: Cho tam giác ABC, nhọn, không cân và nội tiếp đường tròn
;O R
. Gọi G và M lần lượt là
trọng tâm tam giác ABC và trung điểm cạnh BC. Cho đường thẳng OG vuông góc với đường
thẳng OM tính giá trị biểu thức
2 2 2
2
AC AB BC
theo R.
A. 8R
2
. B. 10R
2
. C. 12R
2
. D. 14R
2
.
Lời giải
Họ và tên: Nguyễn Thị Trăng Fb: Trăng Nguyễn
Áp dụng quy tắc trọng tâm và quy tắc trung điểm ta có:
,
3 2
OA OB OC OB OC
OG OM
  
 
. Khi đó
. 0 0
OG OM OG OM OA OB OC OB OC
2
. . 2 . 2 0
OAOB OAOC OB OC R
2 2 2 2 2 2 2
1 1
2 2 2 2 0
2 2
R AB R AC R BC R
G
C
M
I
H
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
146
(chú ý
2
2 2
.
2
a b a b
a b
)
2 2 2 2
2 12AB AC BC R
Email: phamhongquangltv@gmail.com
Câu 339: Cho tam giác MNP có MN=4,MP=8,
M
=
0
60
Lấy điểm E trên tia MP và đặt
ME kMP
.Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP.
A. k=
2
3
. B. k=
2
5
. C. k=
1
3
. D. k=
1
2
.
Lời giải
Họ và tên tác giả: Phạm Hồng Quang Tên FB: Quang Phạm
Chọn B
Ta có:
 
NE NM ME kMP MN
1
MF (MP MN)
2
NE
MF
(MP MN)
.(
kMP MN
)=0
.


2
2
MN.(MP MN) MN.MP MN 16 16 2
k
64 16 5
MP.(MP MN)
MN.MP MP
.
(Email): Khueninhbinh2004@gmail.com
Câu 340: Đẳng thức
. .
MA AD MB BC
đúng với mọi điểm M. Khi đó tứ giác ABCD là hình gì.
A. Hình thang vuông. B. Hình chữ nhật.
C. Hình thoi. D. Tứ giác có hai đường chéo vuông góc.
Lời giải
(Họ và tên tác giả: Phạm Trung Khuê, Tên FB: Khoi Pham)
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
147
Chọn B
Đẳng thức
. .
MA AD MB BC
đúng với mọi điểm M
Cho M trùng với
,A B
ta được
. 0
. 0

AB BC AB BC
AB AD
BA AD
Cho M trùng với C ta được
. . . .

CA AD CB BC CB BA AD CA AB BC
. .
CB AD CA BC
(vì
. . 0
BA AD AB BC
)
. . 0 . 0 . 0
CB AD CACB CB AD CA CB CD CB CD
Vậy tứ giác ABCD là hình chữ nhật.
Email: dacgiap@gmail.com
Câu 341: Cho hình vuông
ABCD
cạnh
a
. Gọi
,M N
lần lượt thuộc các đoạn thẳng
BC
và
AC
sao cho
1
3
BM MC
,
CN k AN
và
AM DN
. Khi đó
k
thuộc khoảng nào dưới đây?
A.
3;5
. B.
5; 3
. C.
4; 2
. D.
2;4
.
Lời giải
Họ và tên: Nguyễn Đắc Giáp Facebook: dacgiap
Chọn B
Ta có:
1
4
AM AB BM AB BC
;
Từ
CN k AN
và
N
nằm giữa hai điểm
,A C
nên suy ra
0
k
và
1 1
1 1
AN AC AB AD
k k
1
1
DN DA AN DA AB AD
k
1 1
. 0 0
4 1
AM DN AM DN AB BC DA AB AD
k
   
N
M
D
A
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
148
2
1 1 1
. . . . . 0
1 4 4 1
AB DA AB AB AD BC DA BC AB BC AD
k k
2 2
5
0 4
4 1 4
a a
k
k
.
Email: nnqman235@gmail.com
Câu 342: Cho hai vector
,a b
thỏa mãn đồng thời các điều kiện
2 7, 2
a b a b
, vector
(3 )a b
vuông góc với
( )a b
. Tính cosin của góc tạo bởi hai vector
a
và
b
.
A.
1
3
. B.
2
4
. C.
1
3
. D.
2
4
.
Lời giải
Họ và tên tác giả: Ngô Nguyễn Quốc Mẫn Tên FB: Ngonguyen Quocman
Chọn B
Ta có
2 2 2
2 2 2
2 2
2 7
4 4 . 7 1
2 2 . 4 2
1
3 2 . 0
(3 ).( ) 0
.
2
a b
a b a b a
a b a b a b b
a b a b
a b a b
a b
.
Suy ra
. 2
cos( ; )
4
.
a b
a b
a b
.
Câu 343: Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh
; ;
BC a CA b AB c
. Tìm
giá trị biểu thức:
2 2 2
. . .
OA OB OC
K
b c c a a b
A.
1
2
K
B.
1
3
K
C.
1K
D.
1
4
K
Lời giải
Áp dụng tính chất đường phân giác vào các phân giác
, ,OA OB OC
ta luôn có:
. . . 0
a OA b OB c OC
. Từ đó
2
. . . 0
a OA b OB c OC
2 2 2 2 2 2
2. . . 2 . . . 2. . . . 0
a OA b OB c OC a bOAOB b c OBOC c a OC OA
Vì
2
2 2 2 2
2. .
OA OB BA OA OB c OAOB OA OB c
Tương tự ta có:
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
149
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
0a OA b OB c OC ab OA OB c bc OB OC a ca OC OA b
2 2 2
2 2 2
1
a b c aOA bOB cOC abc a b c
OA OB OC
bc ac ab
Chọn đáp án C.
1K
Họ và tên: Lê Thái Bình
Email: lebinhle80@gmail.com
Facebook: Lê Thái Bình
Câu 344: Cho hình vuông ABCD. M, N lần lượt nằm trên hai cạnh BC và CD sao cho
1
.
3
CM CN
CB CD
Gọi E là điểm thỏa mãn
.AE kAN
Khi
.BE AM
Tính giá trị biểu thức
T k k
2
1
.
A.
13
16
B.
7
9
C.
8
9
D.
5
16
Lời giải.
Đặt
;AB a AD b
.
Ta có
2 2 3
3 3
BE BA AE BA kAN BA k AD DN
k
a k b a a kb
và
2
.
3
AM AB BM a b

Khi đó

2 3 2 3
. 0 0 .
3 3 4
k
BE AM BE AM k k
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
150
Câu 345: Cho hình vuông ABCD, điểm M nằm trên đoạn thẳng AC sao cho
4
AC
AM
. Gọi N là trung
điểm CD. Tam giác BMN là
A. Tam giác đều. B. Tam giác cân.
C. Tam giác Vuông. D. Tam giác vuông cân
Lời giải
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa
Chọn D
Đặt
,
AD a AB b
.
Khi đó:
1
3
4

MB a b
1 1
( );
4 4 2
1 1
(3 )
4 4
b
AM AC a b AN AD DN a
MN AC a b
Ta có:
1
. ( 3 )(3 )
16
 
MB MN a b a b
2 2
1
( 3 3 8 . ) 0 1
16
a b a b MB MN
2 2 2 2
2
1 1 5
( 3 ) ( 9 6 . )
16 16 8

MB a b a b a b a
2 2 2 2
2
1 1 5
(3 ) (9 6 . )
16 16 8

MN a b a b a b a
Suy ra
2
MB MN
Vậy MB vuông góc với MN và MB =MN, tam giác BMN vuông cân tại đỉnh M
(Email): luongthanh80tm@gmail.com
Câu 346: Cho tam giác
ABC
. Gọi
H
là trực tâm và
O
là tâm đường tròn ngoại tiếp của tam giác
ABC
.
Đặt
BC a
,
CA b
,
AB c
. Tìm hệ thức liên hệ giữa
a
,
b
,
c
sao cho
OH
vuông góc với
trung tuyến vẽ từ đỉnh
A
của tam giác
ABC
.
A.
2 2 2
2
a b c
. B.
2 2 2
2
b a c
. C.
2 2 2
2
c a b
. D.
2 2 2
2 2b a c
.
Lời giải
Chọn A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
151
Gọi
AD
là đường kính của đường tròn ngoại tiếp tam giác
ABC
.
Chứng minh được tứ giác
BHCD
là hình bình hành.
Nên
HB HC HD
  
Ta có
O
là trung điểm của đoạn
AD
nên
2
HA HD HO
  
Suy ra
2
HA HB HC HO
Ta có:
2
OB OC OM AH
 
; tương tự
;
OA OC BH OA OB CH
OA OB OC OH
 
Gọi
M
,
N
,
P
lần lượt là trung điểm của các cạnh
BC
,
CA
và
AB
.
. 0
( ).( ) 0
OH AM OH AM
OA OB OC AB AC
(3 ).( ) 0
OA AB AC AB AC
2
3 .( ) ( ) 0
OA AB AC AB AC
2 2
3 . 3 . 2 . 0
OA AB OA AC AB AB AC AC
   
2 2
3 . 3 . 2 . 0
AB AP AC AN AB AB AC AC

2 2
2 2
3 3
2 . 0
2 2
c b
c AB AC b
Lại có:
2
2 2 2 2
( ) 2 .a BC AC AB b c AB AC
2 2 2
2 .
AB AC b c a
 
Suy ra:
2 2 2
2
a b c
.
N
P
D
M
H
O
B
C
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
152
(Sưu tầm, Họ và tên: Nguyễn Lương Thành, Tên FB: luongthanh.nguyen.7)
Câu 347: Cho tam giác
ABC
có
AD
là trung tuyến,
G
là trọng tâm. Một đường thẳng qua
G
cắt các
cạnh
,AB AC
lần lượt tại
,M N
. Khẳng định nào sau đây đúng?
A.
1 2
. . .
2 3
AM AN AN MB AM NC
    
B.
. . .AM AN AN MB AM NC
C.
2
. ( . . )
3
AM AN AN MB AM NC
    
D.
3
. ( . . )
2
AM AN AN MB AM NC
    
Lời giải
Chọn B
Trước hết ta chứng minh
1(1)
BM CN
AM AN
Thật vậy, kẻ
//
//
BP MN
CQ MN
BM PG
AM AG
CN QG
AN AG
Do đó
(1) 1 ( ) ( )
PG QG
PG QG AG GD PD GD DQ AG
AG AG
2
GD AG
( luôn đúng)
Vậy ta có
1
BM CN
AM AN
. . .
. . .
cos cos cos
BM AN CN AM AM AN
AN MB AM NC AM AN
A A A
. . .AM AN AN MB AM NC
( Do
cos 0
A
)
Họ và tên:Phan Thông
Email:quocthong1182@gmail.com
Q
P
N
G
D
A
B
C
M
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
153
Facebook:Quocthongphan
Câu 348: Cho hình chữ nhật ABCD có cạnh AB=2 và AD=4.Gọi M là trung điểm của cạnh AB và N là
điểm trên cạnh AD sao cho
AN k AD
,CM vuông góc với BN.Khi đó k thuộc vào khoảng nào
sau đây
A.
1
0;
16
B.
1 1
;
16 20
C.
1 1
;
20 9
D.
1 1
;
9 6
Giải: Đặt
AB a
,
AD b
Ta có
1 1
2 2
CM CB BM AD AB b a
BN BA AN AB k AD a kb
Theo giả thiết ta có
. 0
CM BN
1 1 1
. 0 16 .4 0
2 2 8
b a a kb k k
Họ và tên tác giả: Phạm Hồng Quang Tên FB: Quang Phạm
Email: phamhongquangltv@gmail.com
Câu 349: Cho tam giác MNP có MN=4,MP=8,
M
=
0
60
Lấy điểm E trên tia MP và đặt
ME kMP
.Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP.
A. k=
2
3
. B. k=
2
5
. C. k=
1
3
. D. k=
1
2
.
Lời giải
Chọn B
Ta có:
 
NE NM ME kMP MN

1
MF (MP MN)
2
NE
MF
(MP MN)
.(
kMP MN
)=0
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
154
.


2
2
MN.(MP MN) MN.MP MN 16 16 2
k
64 16 5
MP.(MP MN)
MN.MP MP
.
Câu 350: Cho tam giác
ABC
có
, ,
BC a CA b AB c
.
M
là trung điểm của
BC
,
D
là chân đường
phân giác trong góc
A
. Tính
2
AD
A.
2
2
4c
AD p p a
b c
. B.
2
2
4bc
AD p a
b c
.
C.
2
2
4bc
AD p p a
b c
. D.
2
2
4bc
AD p p a
b c
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Lời giải
Chọn D
Vì
M
là trung điểm của
BC
nên
1
2
AM AB AC
 
Suy ra
2
2 2 2
1 1
2
4 4
AM AB AC AB ABAC AC

Ta lại có
2 2 2
1
.
2
AB AC c b a
nên
2 2 2
2
2 2 2 2 2
2
1 1
2.
4 2 4
b c a
AM c c b a b
Theo tính chất đường phân giác thì
BD AB c
DC AC b
Suy ra
BD b
BD DC DC
DC c
(*)
Mặt khác
BD AD AB
và
DC AC AD
thay vào (*) ta được
2 2
2
2
2
2
2 2 2 2 2 2 2
2
2
2
1
2 .
2
b
AD AB AC AD b c AD bAB cAC
c
b c AD bAB bcABAC cAC
b c AD b c bc c b a c b
bc
AD b c a b c a
b c
Hay
2
2
4bc
AD p p a
b c
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
155
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Email: nguyenvantoannbk@gmail.com Bài ở mức độ VD, nhờ thầy cô góp ý!
Câu 351: Cho tam giác ABC có AB = c, AC = b và
0
60 .
BAC
Các điểm M, N được xác định bởi
2
MC MB
 
và
2NB NA
 
. Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với
nhau.
A.
2 2
6 4 5 0
c b bc
. B.
2 2
4 5 6 0
c b bc
.
C.
2 2
6 5 4 0
c b bc
. D.
2 2
4 6 5 0
c b bc
.
Lời giải
Chọn D
Ta có:
2 2( ) 3 2
MC MB AC AM AB AM AM AB AC
        
.
Tương tự ta cũng có:
3 2
CN CA CB
  
.
Vậy:
0
(2 )(2 ) 0
AM CN AM CN
AB AC CA CB
 
   
2 2
(2 )( 3 ) 0 2 3 5 . 0
AB AC AB AC AB AC AB AC
     
.
2 2 2 2
5
2 3 0 4 6 5 0
2
bc
c b c b bc
.
Họ tên: Trần Ngọc Tên FB: Ngọc Trần
Email: soantailieutoanhoc2018@gmail.com
Câu 352: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi I là trung điểm của AC và M là điểm thỏa
mãn
2 2
OM OA OB OC

. Biết rằng OM vuông góc với BI và
2
3 .AC BC BA
. Tính góc
ABC
.
A.
30
. B.
45
C.
60
. D.
120
.
Lời giải
Chọn C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
156
Ta có
2 . =0 2 2 0
OM BI OM BI OA OB OC BA BC
2
5 2 2 0 5 . +5 . 2 0
OB BA BC OB BA OB BC BA BC
Gọi
,H K
tương ứng là trung điểm của đoạn
,AB BC
Khi đó
2
5 . +5 . 2 0
OB BA OB BC BA BC
2
5 . 5 . 2 0
OH HB BA OK KB BC BA BC
2 2 2 2
5 5
2 2 2.2 . 0
2 2
BC BC BA BC BA BC

2 2 2 2 2 2 2 2
1 1 3
0 .
2 2 4
BA BC AB BC AC AC AB BC
Do đó
2 2
2 2 2
2
4
3
cos
2
2 .
3
AC AC
BA BC AC
ABC
BA BC
AC
. Suy ra
60
ABC
.
Họ và tên tác giả: Đào Trung Kiên (st) Tên FB: kienyenthe
Email: kienyenthe@gmail.com
Câu 353: Cho hình thang vuông ABCD, đường cao AD = h, đáy AB = a, đáy CD = b. Gọi M là trung
điểm của BC. Hệ thức giữa a, b, h để
DAM B
là
A.
2 2
0
a h ab
. B.
2 2
0
h a ab
C.
2 2
0
h b ab
. D.
2 2
0
b h ab
.
Lời giải
Chọn B
M
K
H
I
O
A
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
157
Ta có
2 2
2 2
D 2 . D 0
0
0
. 0
0
AM B AM B
AB AC BD
AB AD DC AD AB
AB AD DC AB
h a ab
Họ và tên: Vũ Huỳnh Đức
Email: vutoanpvd@gmail.com
Facebook: vuhuynhduc2017
Câu 354: Cho tam giác đều ABC cạnh bằng a. Gọi M, N là các điểm thỏa mãn
1
3
 
BM BC ,
1
3
 
AN AB . Gọi I là giao điểm của AM và CN. Tính diện tích của tam giác IBC theo a?
A.
2
3
7
IBC
a
S
. B.
2
7
7
IBC
a
S
. C.
2
2 7
7
IBC
a
S
. D.
2
2 3
7
IBC
a
S
.
Lời giải
Chọn A
2
x+y=1 3 x+y=1
3
     
, : , ,
x
I CN x y BI x BN y BC BI BN y BC
và do I AM nên từ
2
3
3
  
x
BI BA y BC ta cũng có
2
3 1
3
.
x
y
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
158
x+y=1
6 1 4 1
x= y=
2
7 7 7 7
3 1
3
  
,
BI BA BC
x
y
-
Từ giả thiết ta có
2 1
CN=
3 3
  
CA CB
2 1 4 1
CN
3 3 7 7
8 4 2 1
0
21 21 21 21
     
       
. .
. . . .
BI CA CB BA BC
BA CA BA CB BC CA BC CB
BIC
vuông tại I.
2
2 2
4 1 4 1 21
7 7 7 7 49
    
BI BA BC BI BA BC a
2 2 2 2 2 2
2 7
21 28
49 49 7
IC BC BI a a a IC a
Vậy
2
3
1
2 7
.
IBC
a
S BI IC
.
Họ và tên tác giả: Huỳnh Thanh Tịnh Tên FB: huynhthanhtinh
Email: huynhthanhtinhspt@gmail.com
Câu 355: Cho tam giác đều
ABC
và các điểm
, ,M N P
thỏa mãn
BM k BC
,
2
3
CN CA
,
4
15
AP AB
. Tìm
k
để
AM
vuông góc với
PN
.
A.
1
3
k
B.
1
2
k
C. D.
3
4
k
Lời giải
Chọn A
I
M
N
C
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
159
( )

BM kBC AM AB k AC AB
(1 )

AM k AB k AC
+)
PN AN AP
4 1
15 3
AB AC
.
Để
AM
vuông góc với
PN
thì
. 0

AM PN
4 1
(1 ) 0
15 3

k AB k AC AB AC
2 2
0
4(1 ) 1 4
( ) 0
15 3 3 15
4(1 ) 1 4
( )cos60 0
15 3 3 15
1
3
k k k k
AB AC AB AC
k k k k
k
Email: duyhung2501@gmail.com
Câu 356: : Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh
; ;BC a CA b AB c
. Tìm
giá trị biểu thức:
2 2 2
. . .
OA OB OC
K
b c c a a b
A.
1
2
K
B.
1
3
K
C.
1K
D.
1
4
K
Lời giải
Chọn C
Áp dụng tính chất đường phân giác vào các phân giác
, ,OA OB OC
ta luôn có:
. . . 0a OA b OB c OC
. Từ đó
2
. . . 0a OA b OB c OC
2 2 2 2 2 2
2. . . 2 . . . 2. . . . 0a OA b OB c OC a bOAOB b c OB OC c a OC OA
Vì
2
2 2 2 2
2. .OA OB BA OA OB c OAOB OA OB c
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
160
Tương tự ta có:
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
0
a OA b OB c OC ab OA OB c bc OB OC a ca OC OA b
2 2 2
2 2 2
1
a b c aOA bOB cOC abc a b c
OA OB OC
bc ac ab
Chọn đáp án C.
1K
Người sưu tầm: Tăng Duy Hùng. FB: Hùng Tăng
Họ và tên: Nguyễn Thị Huệ FB: Nguyễn Thị Huệ
Gmail: nguyenthihue1611@gmail.com
Câu 357: Cho hai véc tơ
a
và
b
thỏa mãn các điều kiện
1
1,
2
a b
2 15.
a b
Đặt
u a b
và
2 , .
v ka b k
Tìm tất cả các giá trị của
k
sao cho
0
, 60 .
u v
A.
3 5
4 .
2
k
B.
3 5
4 .
2
k
C.
17
5 .
2
k
D.
17
5 .
2
k
Lời giải. Chọn A
Từ giả thiết
2
1
2 15 2 15 .
2
a b a b a b
.
9
. 2 3
2
u v a b ka b k
,
2 2
2
6, 4 2 4
u u v v k k
0
2
9
3
1 3 5
2
, 60 4 .
2 2
6. 4 2 4
k
u v k
k k
Họ và tên tác giả: Lê Thị Nguyệt Tên FB: NguyệtLê
Email: Lenguyet150682@gmail.com
Câu 358: Cho tứ giác
ABCD
, hai điểm
,M N
thỏa mãn
2 0;2 0
MB MA NC ND
và
.
AD
x
BC
Tính
cos
cos
DBC
ADB
theo
x
để
.MN BD
A.
2
x
. B.
2
x
. C.
3
x
. D.
3x
.
Lời giải
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
161
Phân tích: Ta thấy
. 0;
; ; ;
MN BD MN BD
DBC BD BC ADC AD BD


nên cần phân tích
MN
theo
AD
và
BC
.
Giải. Ta có biểu diễn
2 2 2 1
3 3 3 3
2 1 2 1
3 3 3 3
MN MA AN BA AN BN NA AN BN AN
BC CN AD DN BC AD
  
Vậy
2 1
3 3
MN BC AD
  
. Do đó
2 . 0 2 .cos .cos 0MN BD BC AD BD BC DBC AD ADB

.
Suy ra
cos
.
2 2
cos
DBC AD x
BC
ADB
Đáp án B.
Họ và tên tác giả: Trần Thanh Hà Tên FB: Hatran
Email: tranthanhha484@gmail.com
Câu 359: Cho tam giác
ABC
có
6; 7; 5.AB BC CA
Gọi
M
là điểm thuộc cạnh
AB
sao cho
2AM MB
và
N
là điểm thuộc
AC
sao cho
AN k AC
(
k
). Biết
a
k
b
(
a
b
là phân số tối giản, a,b là các số nguyên) sao cho đường thẳng
CM
vuông góc với đường
thẳng
.BN
Tính giá trị biểu thức
2018 2019 5T a b
.
A.
2017.T
B.
2020.T
C.
2030.T
D.
2030.T
Lời giải
Chọn B
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
162
2
3
CM AM AC AB AC

.
BN AN AB k AC AB
.
Suy ra:
2 2
2 2 2
( )( )
3 3 3
k
CM BN AB AC k AC AB ABAC AB k AC AB AC
   
2 2 2
2
2
. 6
2
6
7
AB AC BC
AB AC CB AB AC
BN CM k
Theo giả thiết, ta có:
6; 7 2018.6 2019.7 5 2020.
a b T
Họ và tên tác giả: Đỗ Thế Nhất Tên FB: Đỗ Thế Nhất
Email: nhatks@gmail.com
Câu 360: Cho tam giác ABC có AB = c, AC = b và
0
60 .BAC
Các điểm M, N được xác định bởi
2MC MB
và
2NB NA
. Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với
nhau.
A.
2 2
6 5 4 0
c b bc
B.
2 2
6 5 0
c b bc
C.
2 2
4 6 5 0
c b bc
D.
2 2
4 6 5 0
c b bc
Lời giải
Chọn C
Ta có:
2 2( ) 3 2
MC MB AC AM AB AM AM AB AC
  
Tương tự ta cũng có:
3 2
CN CA CB
Vậy:
0 (2 )(2 ) 0
AM CN AM CN AB AC CA CB

(2 )( 3 ) 0
AB AC AB AC

2 2
2 3 5 . 0
AB AC AB AC
2 2
5
2 3 0
2
bc
c b
2 2
4 6 5 0
c b bc
Câu 361: Cho hình chữ nhật ABCD có AB= a, AD=2a. Gọi M là trung điểm AB, N là điểm trên cạnh
AD sao cho
AD kAN
 
. Tìm k để CM
BN.
A. k=7,9 B. k=8 C. k=8,1 D. k=7.8
Lời giải
Chọn B
giải: Ta có
1
2
CM CB BM AD AB
    
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
163
1
BN BA AN AB AD
k
    
Để CMBN thì
. 0CM BN
 
Mà
2 2
2 2
2
2
1 1
.
2
1 1 1
. .
2 2
1 1 1 1
2
2 2
CM BN AD AB AB AD
k
AD AB AD AB AB AD
k k
AD AB a a
k k
     
     
 
2
2
1 1
. 0 2 0
2
4 1
0 8
2
CM BN a a
k
k
k
 
Vậy
8k
thì
CM BN
Họ và tên tác giả: Nguyễn Ngọc Duy Tên FB: Ngọc Duy
Email: nguyenngocduyakgl@gmail.com
Câu 362: Cho hình bình hành
ABCD
có đường chéo lớn là
AC
. Gọi
,E F
lần lượt là hình chiếu vuông
góc của
C
trên
,AB AD
. Biểu thức nào sau đây là đúng.
A.
2
. .
AB AH AD AF AC
. B.
2
. .
AB AE AD AF AC
.
C.
2
. .
AB AE AD AH AC
. D.
. . .AB AE AD AF AC AH
.
Lời giải
Chọn B
Vì
,E F
lần lượt là hình chiếu vuông góc của
C
trên
,AB AD
nên ta có:
. .
AB AE AC AB
. .
AD AF AC AD
Suy ra:
2
. .
 
AB AE AD AF AC AB AD AC
(*)
Do
AC
là đường chéo lớn nên
0
90
ABC
và
B
nằm
giữa hai điểm
,A E
. Suy ra
. .
AB AE AB AE
Tương tự ta có:
D
nằm giữa hai điểm
,A F
. Suy ra
. .
AD AF AD AF
Vậy đẳng thức (*) trở thành:
2
. .
AB AE AD AF AC
.
Email: thuy.tranthithanhdb@gmail.com
A
C
B
D
H
E
F
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
164
Câu 363: Cho hình thang vuông
ABCD
, đường cao
AD h
, cạnh đáy
,
AB a CD b
. Tìm hệ thức
giữa
, ,a b h
để
BD
vuông góc trung tuyến
AM
của tam giác
ABC
.
A.
2
h a a b
. B.
2
h a b a
.
C.
h h b a a b h
. D.
2
2
h a a b
Lời giải
Chọn A
Thay
1
.
2
AM AB AC
, ta có:
. 0 . 0 . . 0
AM BD AM BD AB AC BD AB BD AC BD
        
(1)
mà
2
2
. .
AB BD AB AD AB AB a
và
2
2
. .
AC BD AD DC AD AB AD DC AB h ab
nên:
2
1
h a a b
.
Họ và tên tác giả: Nguyễn Quang Nam Tên FB: Quang Nam
Email: quangnam68@gmail.com
Câu 364: Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R), M là điểm chính giữa cung BC (
cung BC không chứa điểm A). Chọn đẳng thức đúng trong các đẳng thức sau:
A.
.sin .sinMA MB C MC B
B.
.cos .cosMA MB C MC B
C.
.sin .sinMA MB B MC C
D.
.cos .cosMA MB B MC C
Lời giải:
Chọn C
Ta có
2
2 . 2 . 2sin . . sin . (1)
MA MA
MO MA MA MO MA A MO A MA
MA MA

Tương tự
2sin . . sin . (2)
MB
B MO B MB
MB
,
2sin . . sin . (3)
MC
C MO C MC
MC
Từ (1), (2) và (3):
h
b
a
M
A
D
B
C
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
165
sinA. sin . sin .
2 ( sin . sin . sin . )
2 .0 0
MA B MB C MC
MA MB MC
MO A B C
MA MB MC
MO
Ta sẽ chứng minh
sin . sin . sin . 0
MA MB MC
A B C
MA MB MC
(*)
Thật vậy,
1 1 1
(*) . .sin . . .sinB. . .sinC. 0
2 2 2
MB MC A MA MA MC MB MB MA MC
0
a b c
S MA S MB S MC
( đúng)
( với
, ,
a b c
S S S
lần lượt là diện tích các tam giác MBC, MAC, MAB)
Vậy
.sin .sin .sin 0
MA A MB B MC C
.sin .sin .sinMA A MB B MC C
(*)
Theo bài ra:
0
sin sin 90 1
A
thay vào (*):
.sin .sinMA MB B MC C
Họ Tên: Lương Thị Hương Liễu Tên FB: Hương Liễu Lương
Email: lieuluong.290983@gmail.com
Câu 365: Cho tam giác
ABC
có
, ,BC a CA b AB c
.
M
là trung điểm của
BC
,
D
là chân đường
phân giác trong góc
A
. Tính
2
AD
A.
2
4
2
c
AD p p a
b c
B.
2
2
4bc
AD p a
b c
C.
2
2
4bc
AD p p a
b c
D.
2
2
4bc
AD p p a
b c
Lời giải
Chọn D
* Vì M là trung điểm của BC nên
1
2
AM AB AC
O
A
B
C
M
M
A
B
C
D
Hình 2.3
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
166
Suy ra
2
2 2 2
1 1
2
4 4
AM AB AC AB ABAC AC
  
Ta có
2
2 2
1
.
2
AB AC AB AC AB AC
2 2 2
1
2
AB AC CB
2 2 2
1
2
c b a
nên
2 2 2
2
2 2 2 2 2
2
1 1
2.
4 2 4
b c a
AM c c b a b
* Theo tính chất đường phân giác thì
BD AB c
DC AC b
Suy ra
BD c
BD DC DC
DC b
(*)
Mặt khác
BD AD AB
và
DC AC AD
thay vào (*) ta được
2 2
2
2
2
2
2 2 2 2 2 2 2
2
2
2
1
2 .
2
c
AD AB AC AD b c AD bAB cAC
b
b c AD bAB bcABAC cAC
b c AD b c bc c b a c b
bc
AD b c a b c a
b c

Hay
2
2
4bc
AD p p a
b c
Họ và tên tác giả: Phạm Thành Trung Tên FB: Phạm Thành Trung
Email: trungthuong2009@gmail.com
Câu 366: Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt
Nam có một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc
0
30
như
hình vẽ dưới đây. Trên các đường thẳng
Ox
và
Oy
người ta để hai vật nặng cùng trọng lượng.
Buộc hai vật thể với nhau bằng một thanh cứng
1AB m
sao cho mỗi vật đều có thể chuyển
động được trên hai đường ray. Nối hai vật bằng một sợi giây vòng qua một cột có gốc tại
O
.
Người tham dự cuộc thi sẽ đứng tại vị trí điểm
B
để kéo vật thể chuyển động trên
Oy
. Người
thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc
O
. Hãy dùng kiến thức toán
học để tính toán vị trí xa nhất mà người tham dự cuộc thi có thể đạt được.
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
167
A.
1m
. B.
2m
. C.
3m
. D.
2m
.
Lời giải
Chọn B
+ Đặt
; ( , 0)
OB x OA y x y
. Khi đó theo định lý cosin ta có:
2 2 2 0 2 2
2 cos30 3AB x y xy x y xy
Do đó ta có hệ thức:
2 2
3 1x y xy
Xét phương trình bậc hai:
2 2
3 1 0
y xy x
Phương trình có nghiệm
y
khi
2 2
3 4( 1) 0 0 2
x x x
Vậy học vị trí xa nhất mà học sinh có thể đạt được cách
O
một khoảng là
2m
Câu 367: Cho tam giác ABC có AB= c,BC=a,CA=b. Trung tuyến CM vuông góc với phân giác trong AL
và
3
2
CM
AL
. Tính
cos A
.
A.
2
cos
2
A
B.
5 1
cos
4
A
C.
3
cos
2
A
D.
1
cos
2
A
Lời giải
Chọn D
Ta có:
b c
AL AB AC
b c b c

2
2 2
CA CB AB AC
CM
Theo giả thiết:
. 0
AL CM AL CM
2 2 2 2
2 0 cos 2 cos 2 0
2 1 cos 0 2 ( cos 1)
bAB cAC AB AC bc bc A cb A cb
c b A c b do A

Khi đó:
2 2 2 2 2
2
2 4 2
b a c a b
CM
O
B
A
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
168
2
2 2 2 2 2
1 1 2
2 . 9
9 9 9
AL AB AC AB AC AB AC b a
  
2 2 2
2 2
2 2 2
3 9 3
. 3
2 4 9 4
CM CM a b
a b
AL AL b a
2 2 2 2 2
2
5 1
cos
2 4 2
b c a b a
A
bc b
doantv.toan@gmail.com
Câu 368: Cho hình chữ nhật ABCD có
1; 3AB CD
. Điểm M thuộc cạnh AD và N là trung điểm BC
sao cho
MN BD
. Phân số tối giản
m BN
n NC
có m n bằng bao nhiêu
A. 29. B. 18. C. 16. D. 27.
(Họ và tên tác giả: Trần Văn Đoàn, Tên FB: Trần Văn Đoàn)
Lời giải
Chọn B
Ta có
( )BD BA BC
m BN BN m m
BN BC k BC
n NC BC m n m n
1
2
MN MA AB BN k BC AB
 
. 0BD MN
nên
1 11 11
1 9 0 11, 7
2 18 11 7
k k m n
Họ và tên tác giả: Nguyễn Thị Thỏa Tên FB: Nguyễn Thị Thỏa
Email: phamquynhanhbaby56@gmail.com
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
169
Câu 369: Cho tam giác
ABC
có
AB c
;
BC a
,
CA b
. Gọi
M
là trung điểm của
AB
và
D
là
chân đường phân giác trong góc
A
của tam giác
ABC
. Biết rằng trung tuyến
CM
vuông góc
với phân giác trong
AD
. Khi đó đẳng thức nào sau đây đúng?
A.
2b c
. B.
2c b
. C.
a b c
. D.
c a b
.
Lời giải
Chọn B
Ta có
D
là chân đường phân giác trong góc
A
nên
DB AB c
DC AC b
và
DB
,
DC
ngược hướng suy ra
. . 0
c
DB DC b DB c DC
b
 
Ta có:
b c
AD AB AC
b c b c
.
Vì
CM
là trung tuyến nên
2
2 2
CA CB AB AC
CM
.
Theo giả thiết:
. 0
AL CM AL CM
2 0
bAB cAC AB AC
 
2 2 2 2
cos 2 cos 2 0
bc bc A cb A cb
2 1 cos 0 2 ( cos 1)
c b A c b do A
Vậy
2c b
.
Câu 370: Cho tam giác ABC đều nội tiếp (O;R). M là điểm bất kì trên cung nhỏ
BC
. Khi đó
A.
MA MB MC
B.
MA MB MC
C.
MA MB MC
D.
2
MA MB MC
Lời giải
Chọn A
Ta có
2 2 2 2 2
2
( ) 2 .
2. . 0 2. . 0
R OA OM MA R MA OM OA
MA
MA OM MA MA OM
MA
Tương tự
2. . 0
MB
MB OM
MB
2. . 0
MC
MC OM
MC
Suy ra
2 ( ) 0
MA MB MC
MA MB MC OM
MA MB MC
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com
170
Vì
; ;
MA MB MC
MA MB MC
 
là các véc tơ đơn vị và đôi một tạo với nhau một góc 120
0
nên
0
MA MB MC
MA MB MC
, do đó
0
MA MB MC
| 1/170

Tài liệu khác của Toán 10

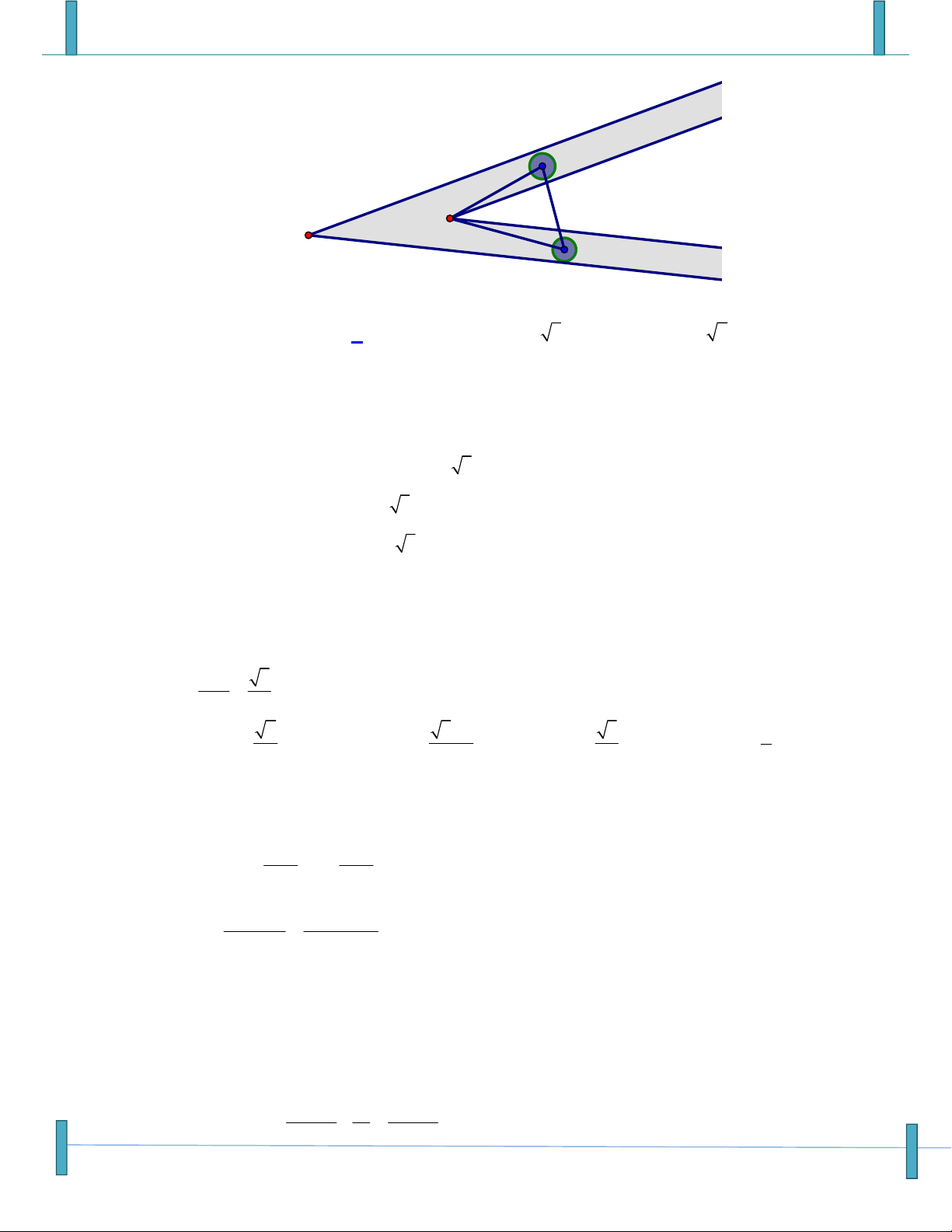
Preview text:

Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
CÁC PHẦN CHÍNH CỦA CHUYÊN ĐỀ
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG VẤN ĐỀ 3. QUỸ TÍCH VẤN ĐỀ 4. TỈ LỆ VẤN ĐỀ 5. MIN,MAX
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG Phần I: Đề Bài
Trang: VĐ1-P1; VĐ2-P12; VĐ3-P14; VĐ4-P17; VĐ5-P20; VĐ6-P28
Phần II: Hướng Dẫn Giải
Trang: VĐ1-P35; VĐ2-P74; VĐ3-P88; VĐ4-P99; VĐ5-P110; VĐ6-P149
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
Email: daytoan2018@gmail.com Câu 1:
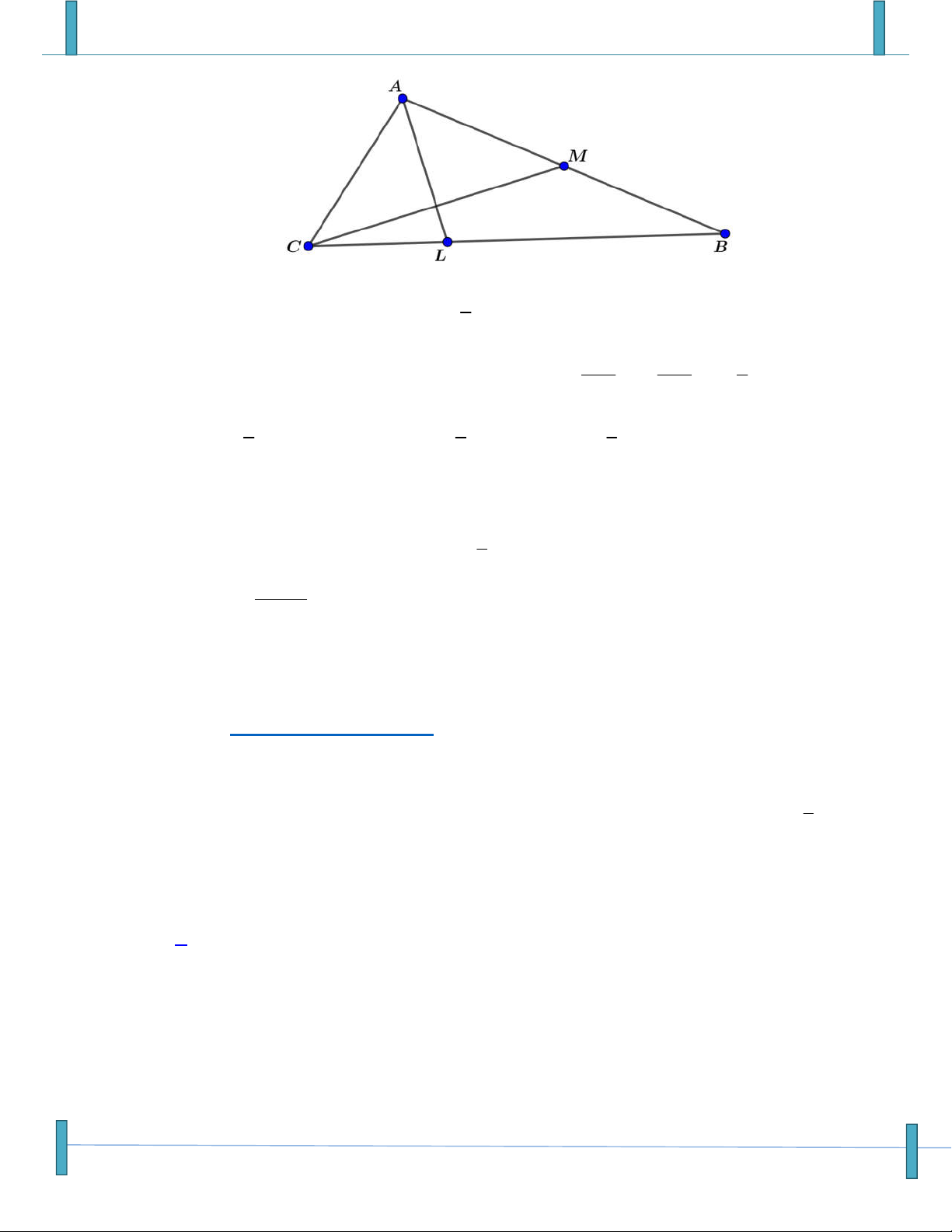
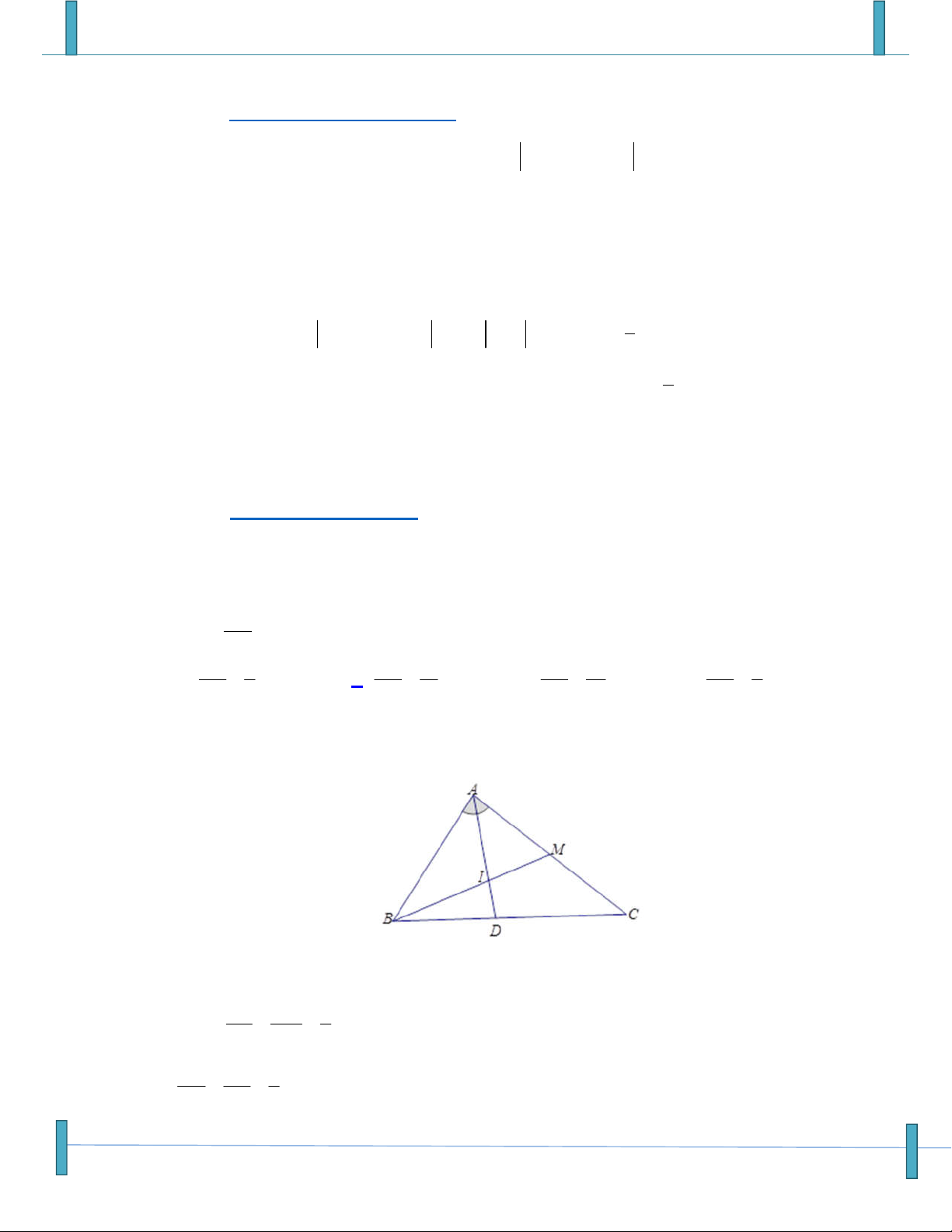
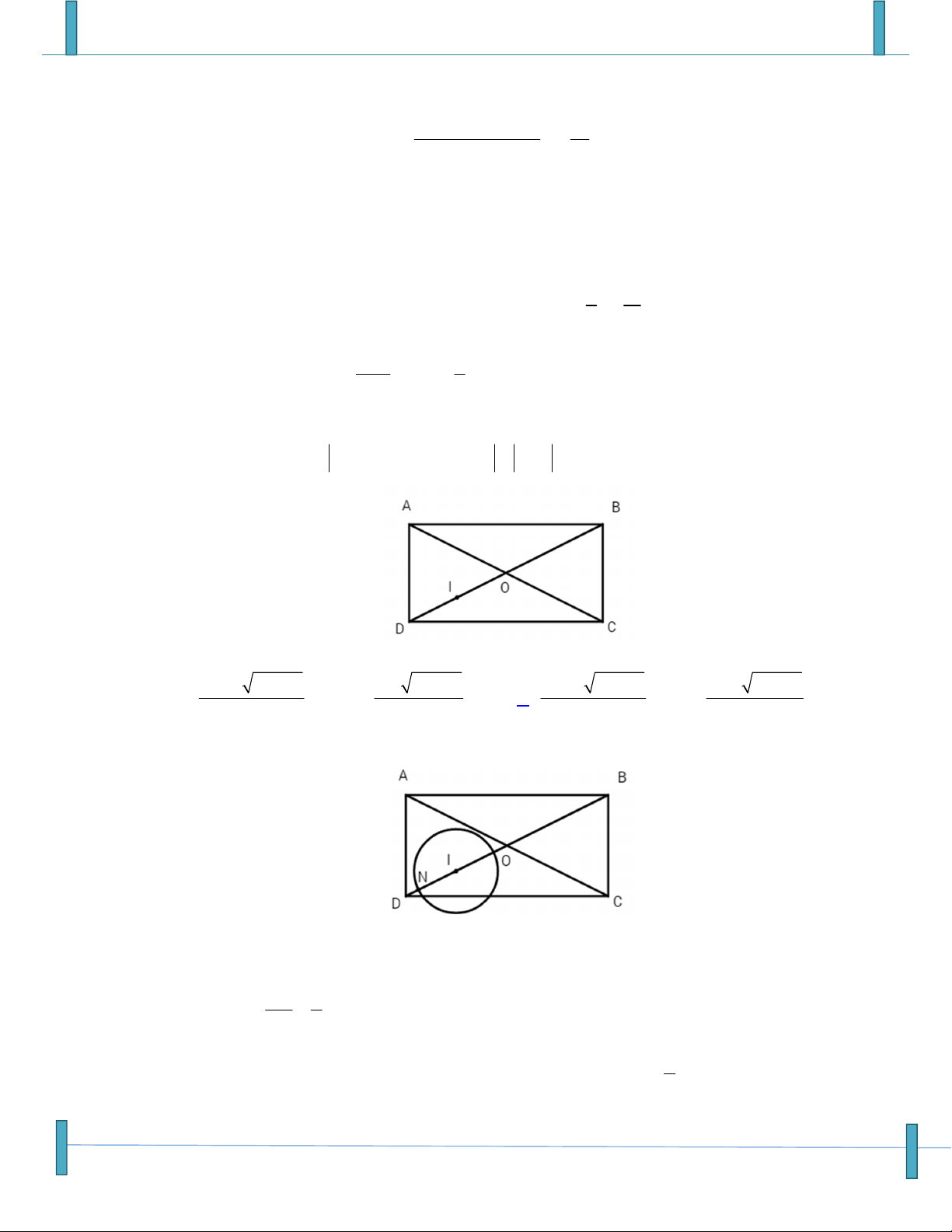
Cho tam giác ABC biết AB  3, BC  4, AC  6 , I là tâm đường tròn nội tiếp tam giác ABC     x y z
.Gọi x, y, z là các số thực dương thỏa mãn x.IA y.IB  .
z IC  0 .Tính P    y z x 3 41 23 2 A. P  . B. P  . C. P  . D. P  . 4 12 12 3
Họ và tên tác giả: Vũ Ngọc Thành Tên FB: Vũ Ngọc Thành Câu 2:
Cho hình bình hành ABCD . Gọi I là trung điểm của CD , G là trọng tâm tam giác BCI . Đặt    
a AB, b AD . Hãy tìm đẳng thức đúng trong các đẳng thức sau?  5  2   5   A. AG a b . B. AG a b . 6 3 6   5   4  2 
C. AG a b . D. AG a b . 6 3 3
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet, Email:
tiethanh.78@gmail.com Câu 3:
Cho tam giác ABC với các cạnh AB c, BC a, CA b . Gọi I là tâm đường tròn nội tiếp
tam giác ABC. Đẳng thức nào sau đây đúng.        
A. aIA bIB cIC  0
B. bIA cIB aIC  0        
C. cIA bIB aIC  0
D. cIA aIB bIC  0
Họ và tên: Dương Bảo Trâm Facebook: Bảo Trâm, Email: ilovemath.ddt@gmail.com  0 Câu 4:
Cho hình thang cân ABCD có CD là đáy lớn, ADC  30 . Biết DA = a, DC = b, hãy biểu   
diễn DB theo hai vectơ DA và DC .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 1
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
  
  b a 3 
A. DB DA DC.
B. DB DA DC. b
  b a    
C. DB DA DC.
D. DB bDA a DC. b
Họ tên: Đỗ Thị Hồng Anh, Đ/c mail: honganh161079@gmail.com
Email: kimduyenhtk@gmail.com, FB: Kim Duyên Nguyễn.    Câu 5:
Cho hình bình hành ABCD , M là điểm thỏa mãn 5AM  2CA  0 . Trên các cạnh AB , BC
lần lượt lấy các điểm P, Q sao cho MP / B
/ C, MQ / A
/ B . Gọi N là giao điểm của AQ và AN CN
CP . Giá trị của tổng  bằng: AQ CP 21 24 23 25 A. B. C. D. 19 19 19 19
Họ và tên tác giả: Phạm Thị Ngọc Tên FB: Giang Thao
Email: thuangiaoyen@gmail.com Câu 6:
Cho tứ giác ABCD, M là điểm tùy ý. K là điểm cố định thỏa mãn đẳng thức
    
MA  MB  MC  3MD  xMK . Tìm x: A. 2. B. 6. C. 5. D. 4.
Email: kimduyenhtk@gmail.com, FB: Kim Duyên Nguyễn. Câu 7:
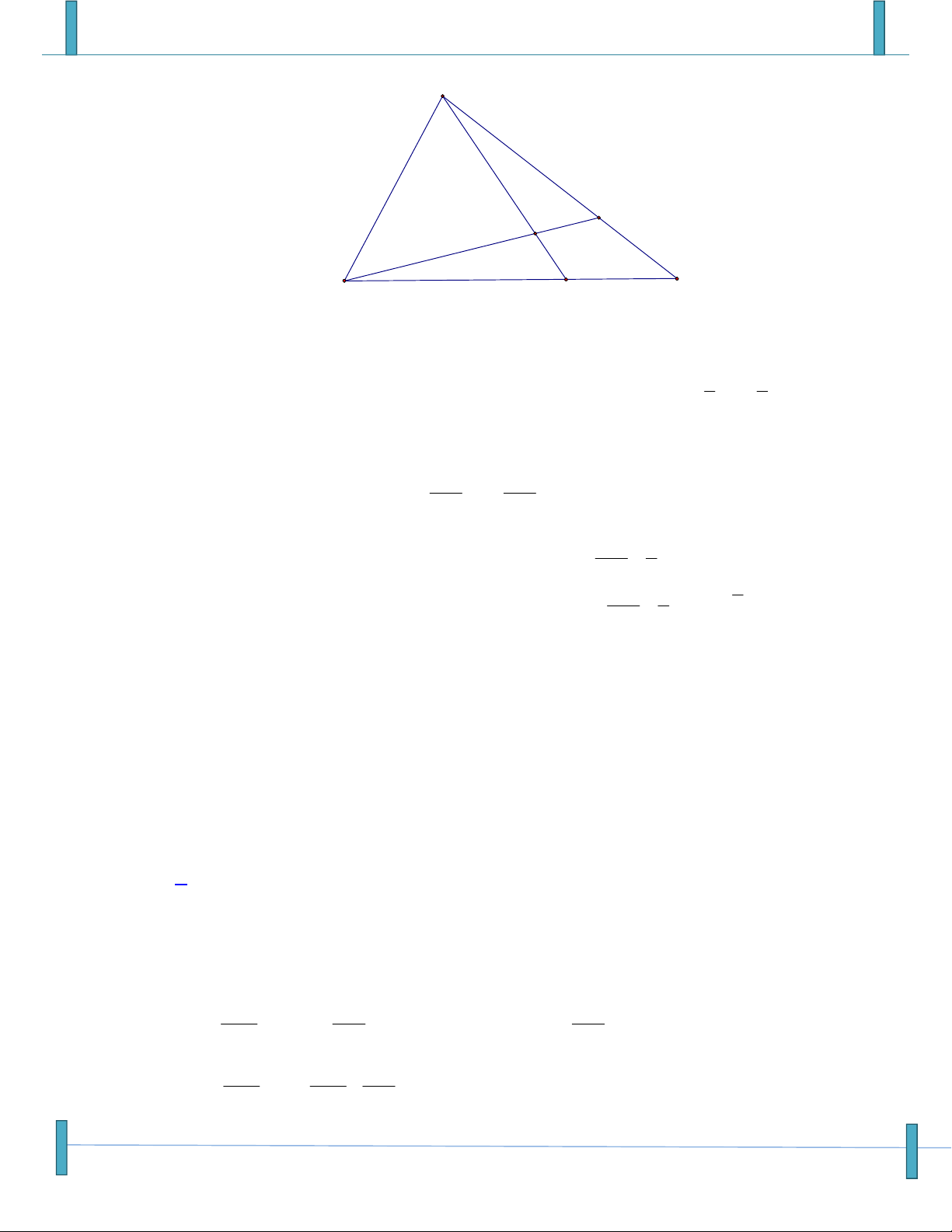
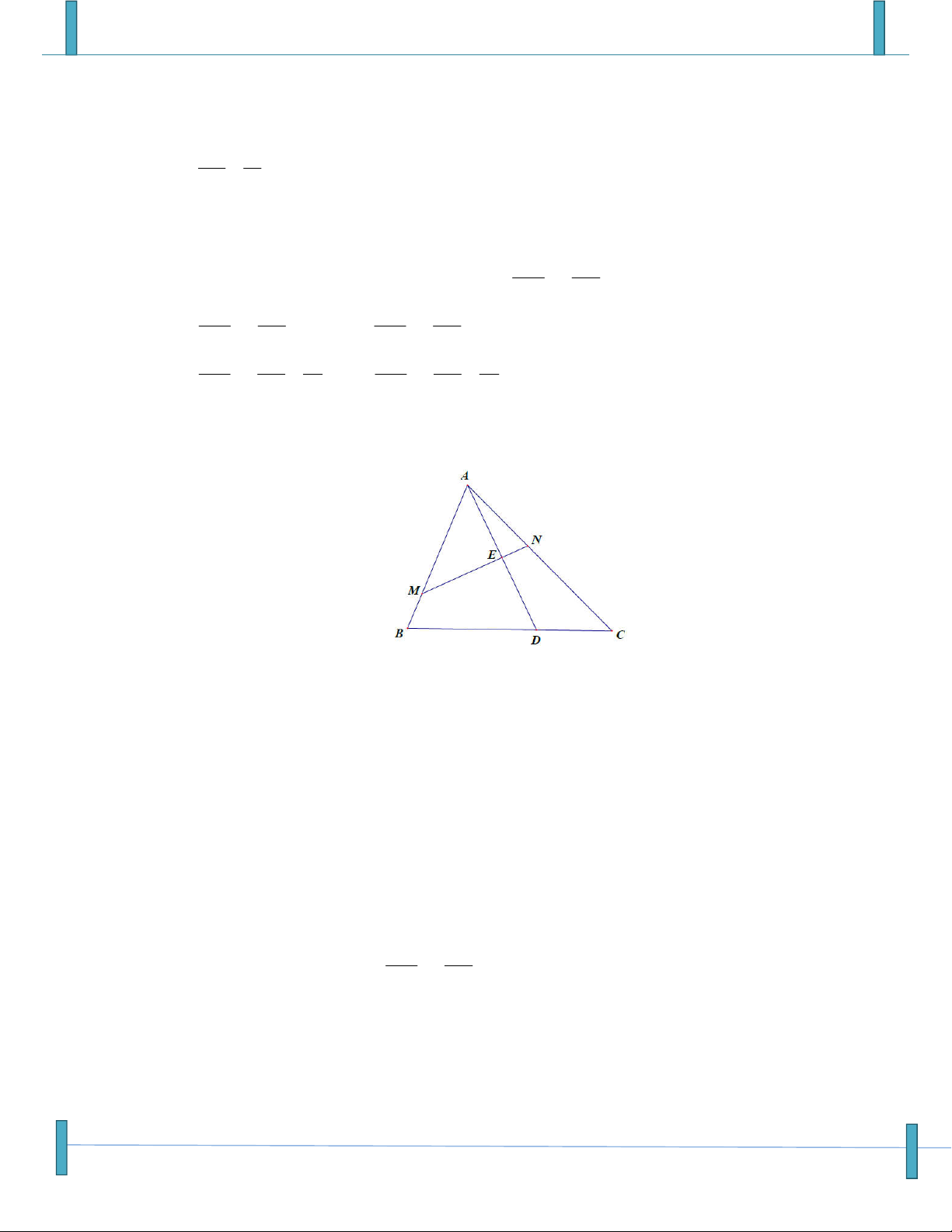
Cho tam giác ABC , trên cạnh AC lấy điểm M , trên cạnh BC lấy điểm N sao cho
AM  3MC , NC  2NB . Gọi O là giao điểm của AN và BM . Tính diện tích tam giác
ABC biết diện tích tam giác OBN bằng 1. A. 24 . B. 20 . C. 30 . D. 45
Họ và tên: Nguyễn Thanh Hoài, Email: ngthhoai1705@gmail.com Câu 8:
Cho tam giác ABC , gọi I là điểm trên BC kéo dài sao cho IB  3IC . Gọi J , K lần lượt là   
những điểm trên cạnh AC, AB sao cho JA  2JC; KB  3KA . Khi đó BC  . m AI  . n JK . Tính
tổng P m n ?
A. P  34 . B. P  3  4 .
C. P  14 . D. P  14 .
Họ và tên tác giả: Trần Ngọc Uyên Tên FB: Tran Ngoc Uyen, Email: ngocuyen203@gmail.com Câu 9:
Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho
 1   1      AM AB, DN
DC . Gọi I và J là các điểm thỏa mãn BI mBC, AJ n AI . 3 2
Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu?
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 2
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 2 A. B. 3 C. D. 1 3 3
(Họ và tên tác giả: Phạm Văn Huấn, Tên FB: Pham Van Huan)
Câu 10: Cho tam giác ABC, trên cạnh AB lấ y điểm M, trên cạnh BC lấ y N sao cho AM=3MB,
NC=2BN. Gọi I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam giác ICN bằng 2. 3 33 9 A. B. C. 11 D. 2 2 11
Họ và tên: Hứa Nguyễn Tường Vy, Email: namlongkontum@gmail.com, FB: nguyennga 
    
Câu 11: Cho ∆ABC có trọng tâm G và hai điểm M, N thỏa mãn: 3MA  2CM  0 , NA  2NB  0 . Chọn mệnh đề đúng.        
A. NG  4GM .
B. NG  5GM .
C. NG  6GM .
D. NG  7GM .
(Họ và tên tác giả: Trần Công Sơn, Tên FB: Trần Công Sơn)
Câu 12: (Đẳng thức vec tơ) Cho tam giác ABC . Gọi A', B',C' là các điểm xác định bởi         
2018A' B  2019 A'C  0 , 2018B 'C  2019B ' A  0 , 2018C ' A  2019C ' B  0 . Khi đó,
mệnh đề nào sau đây đúng?
A. ABC và A' B 'C ' có cùng trọng tâm.
B. ABC  A' B 'C '.
C. ABC  A' B 'C '.
D. ABC và A' B 'C ' có cùng trực tâm.
(Email): tranminhthao2011@gmail.com
Câu 13: ( tính độ dài vec tơ) Cho tam giác đều ABC cạnh a . Gọi điểm M là trung điểm BC . Tính độ 1   dài của vec tơ AB  2 AC 2 a 21 a 21 a 21 a 21 A. . B. . C. . D. . 3 2 4 7
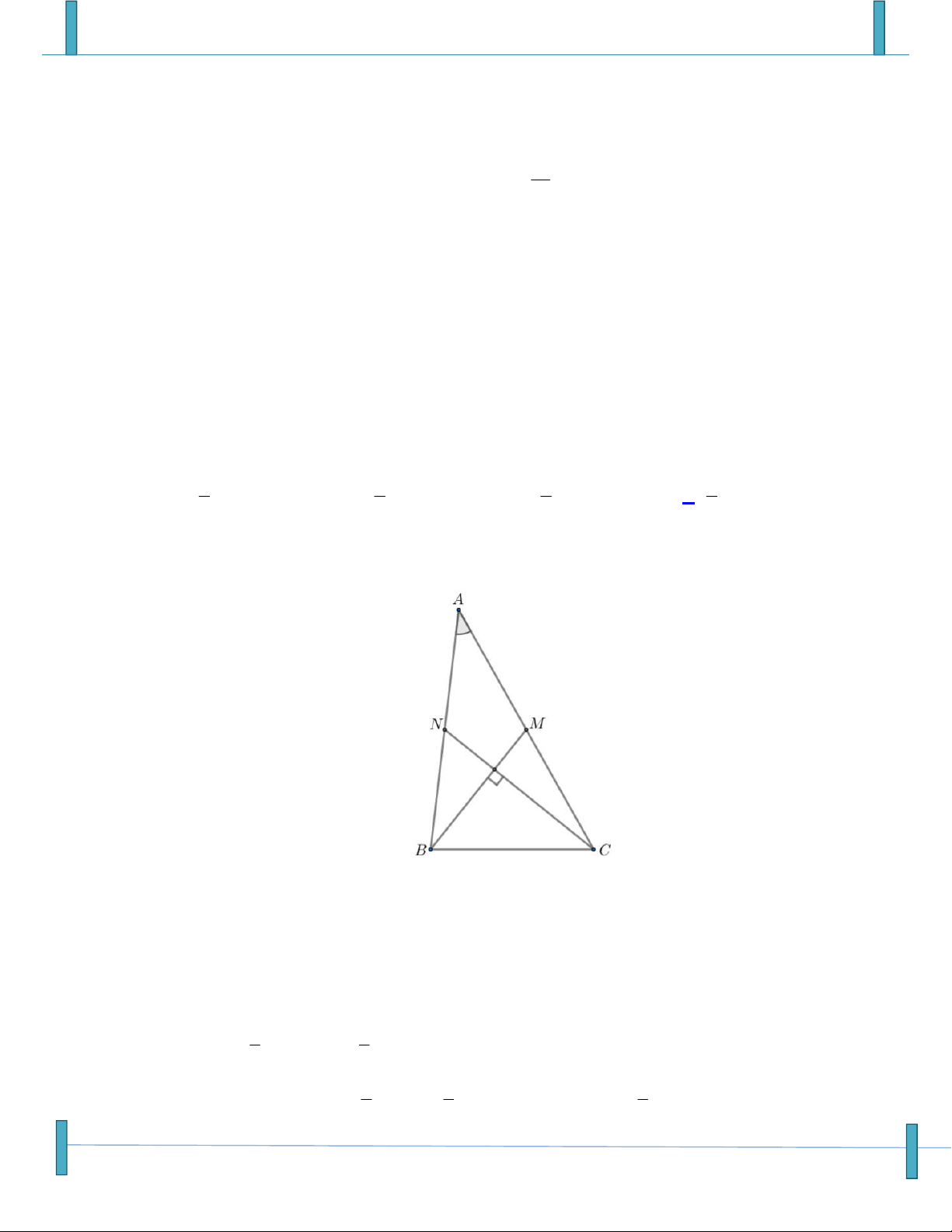
Câu 14: Cho ABC có M là trung điểm của BC, H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm x
   
để HA HB HC xHO .
A. x . 2
B. x  2 .
C. x . 1
D. x  3 .
Họ và tên: Trần Quốc An, Email: tranquocan1980@gmail.com, Facebook: Tran Quoc An
Câu 15: Cho tam giác ABC có đường trung tuyến CM vuông góc với phân giác trong AL . Giả sử 2 a bk
ngoài ra còn có CM kAL . Biết cos A
. Tính a b c d 2 c dk A. 18 . B. 5 . C. 26 . D. 17 .
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1)      1
Câu 16: Cho tam giác ABC . Gọi M , N , P là các điểm lần lượt thỏa mãn MA  3MB  0 , AN AC , 3   
2PB  3PC  0 Gọi K là giao điểm của AP và MN . Trong các mệnh đề sau, mệnh đề nào đúng?
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 3
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New      
A. 4KA  5KP  0 .
B. 3KA  2KP  0 .     
C. KA KP  0 .
D. KA KP .
Họ và tên: Phạm Thanh My, Email: phamthanhmy@gmail.com, Facebook: Pham Thanh My
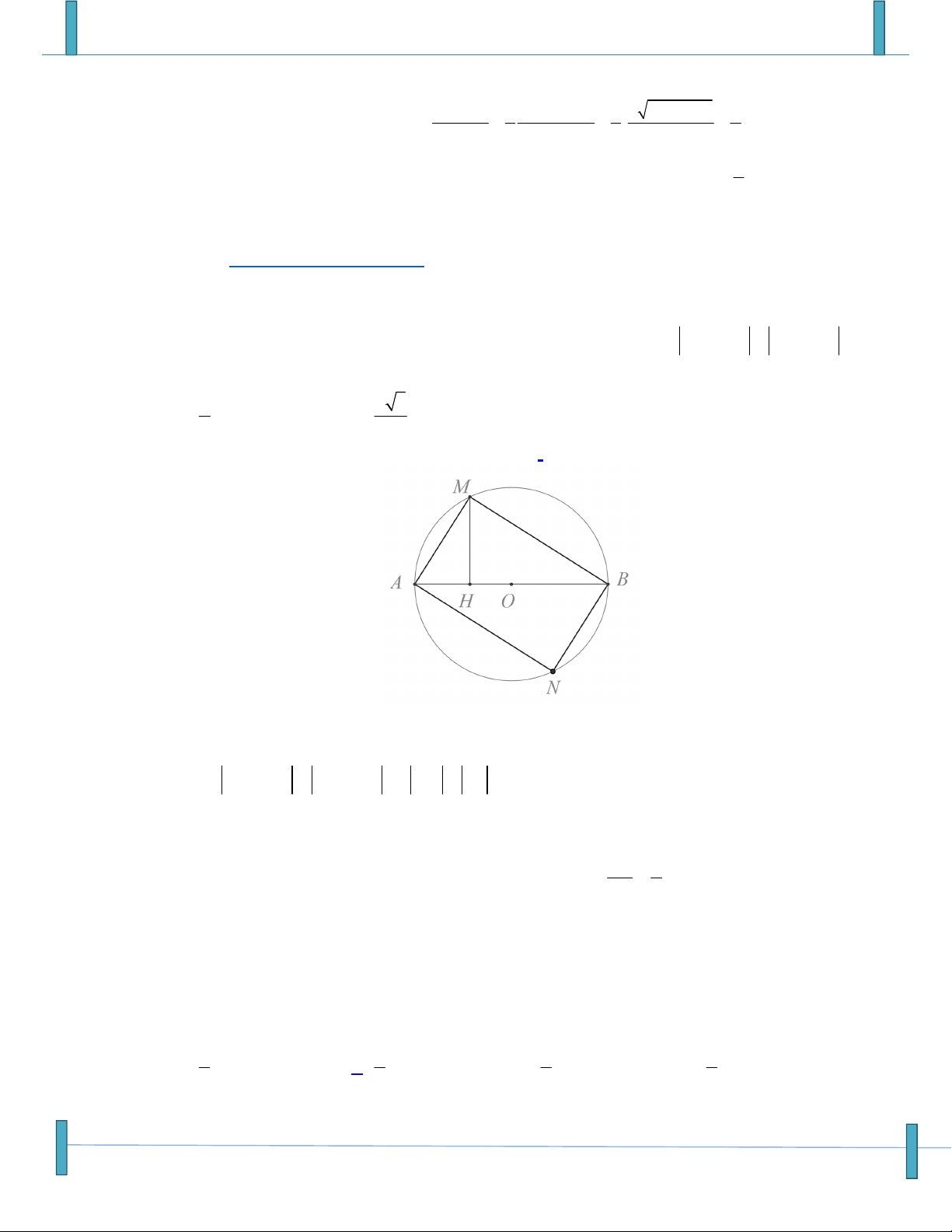
Câu 17: Cho hình thang ABCD ( AB / /CD) có hai đường chéo vuông góc với nhau. Biết  
AB CD  20c .
m Tìm AC BD . A. 40c . m . B. 20c . m . C. 30c . m . D. 10c . m .
Họ và tên tác giả: Nguyễn Thị Yến Tên FB: Nguyễn Yến, Email: ntyen.c3lqd@gmail.com
Câu 18: Cho tam giác ABC có AB  3; AC  4 .Gọi AD là đường phân giác trong của góc A .Biết   
AD m AB n AC .Khi đó tổng m n có giá trị là: 1 1 A. 1 B. 1 C. D.  7 7
Họ và tên tác giả:Lê Thanh Lâm, Mail:quyphucvn@gmail.com Fb:Thanh Lâm Lê
Câu 19: Cho tam giác ABC bất kỳ, gọi M , N , P lần lượt là trung điểm các cạnh AB, BC, CA . H , H '
lần lượt là trực tâm các tam giác ABC, MNP . Khẳng định nào đúng trong các khẳng định sau?
   
   
A. HA HB HC  3HH ' .
B. HA HB HC  2HH ' .
   
   
C. HA HB HC  0 . D. HM HN HP  3HH ' .
Câu 20: Cho tam giác đều ABC tâm O. M là một điểm bất kì bên trong tam giác. Gọi D, E, F lần lượt là
hình chiếu của M lên BC, CA, AB. Với giá trị nào của k ta có hệ thức:
   
MD ME MF k MO 1 3 A. k  . B. k  1. C. k  . D. k  2 2 2
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa
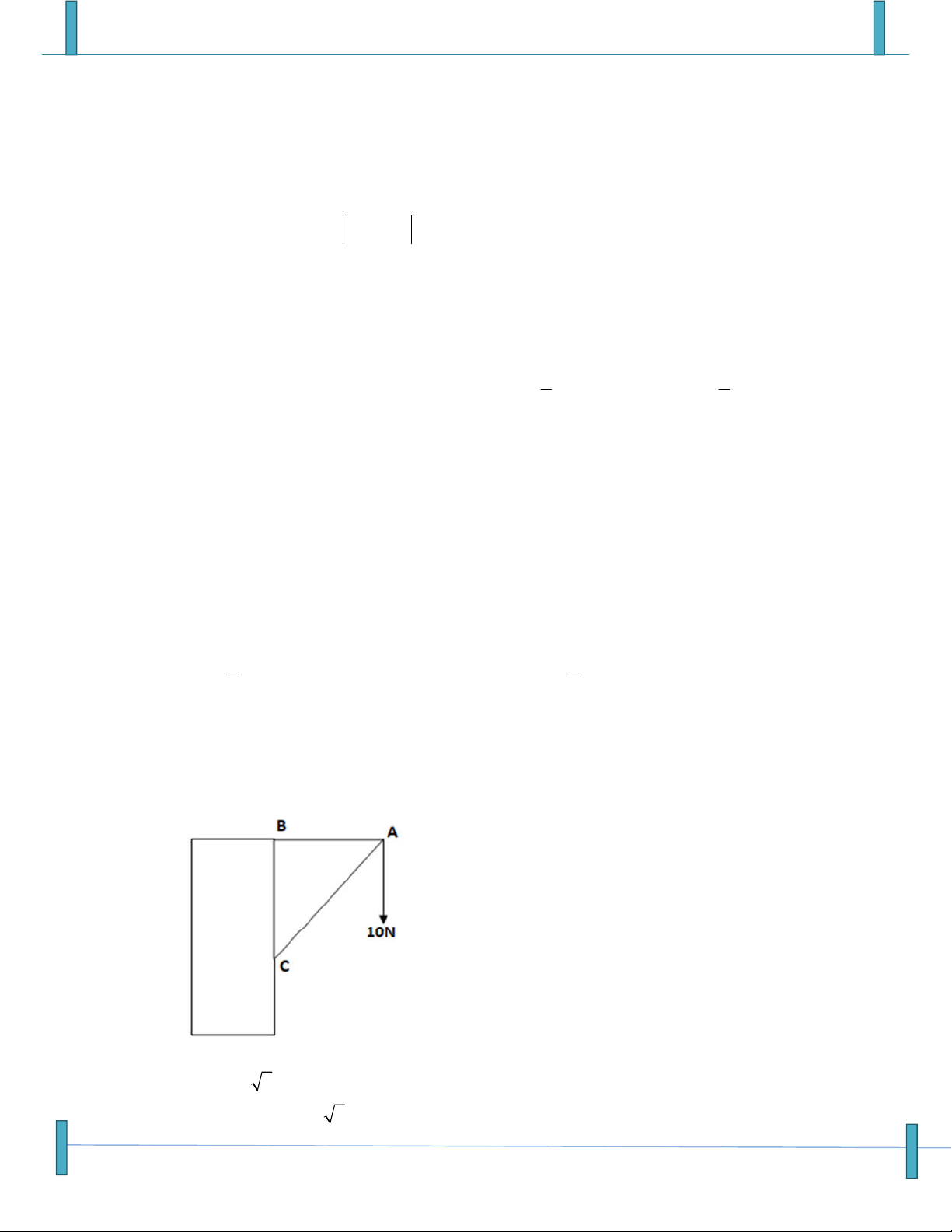
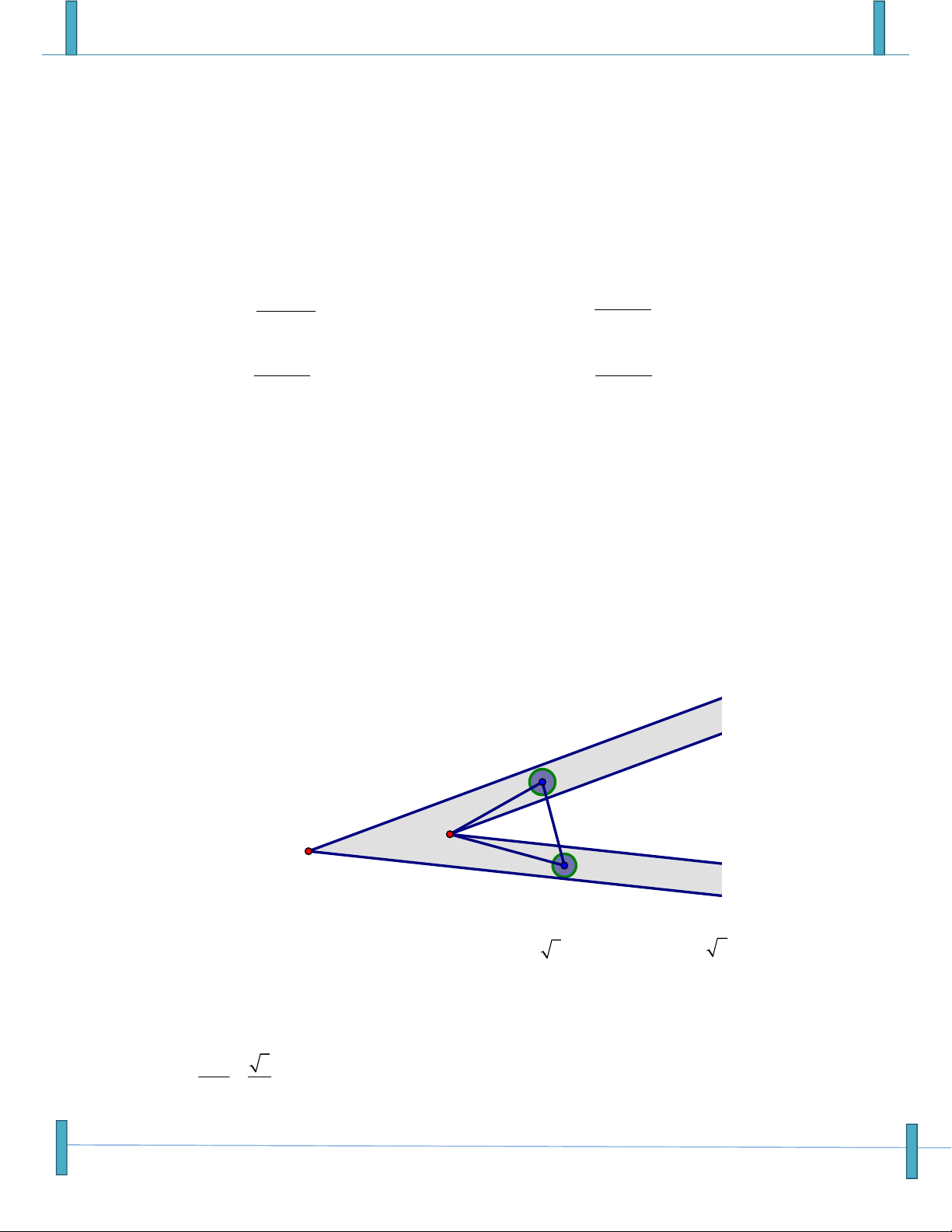
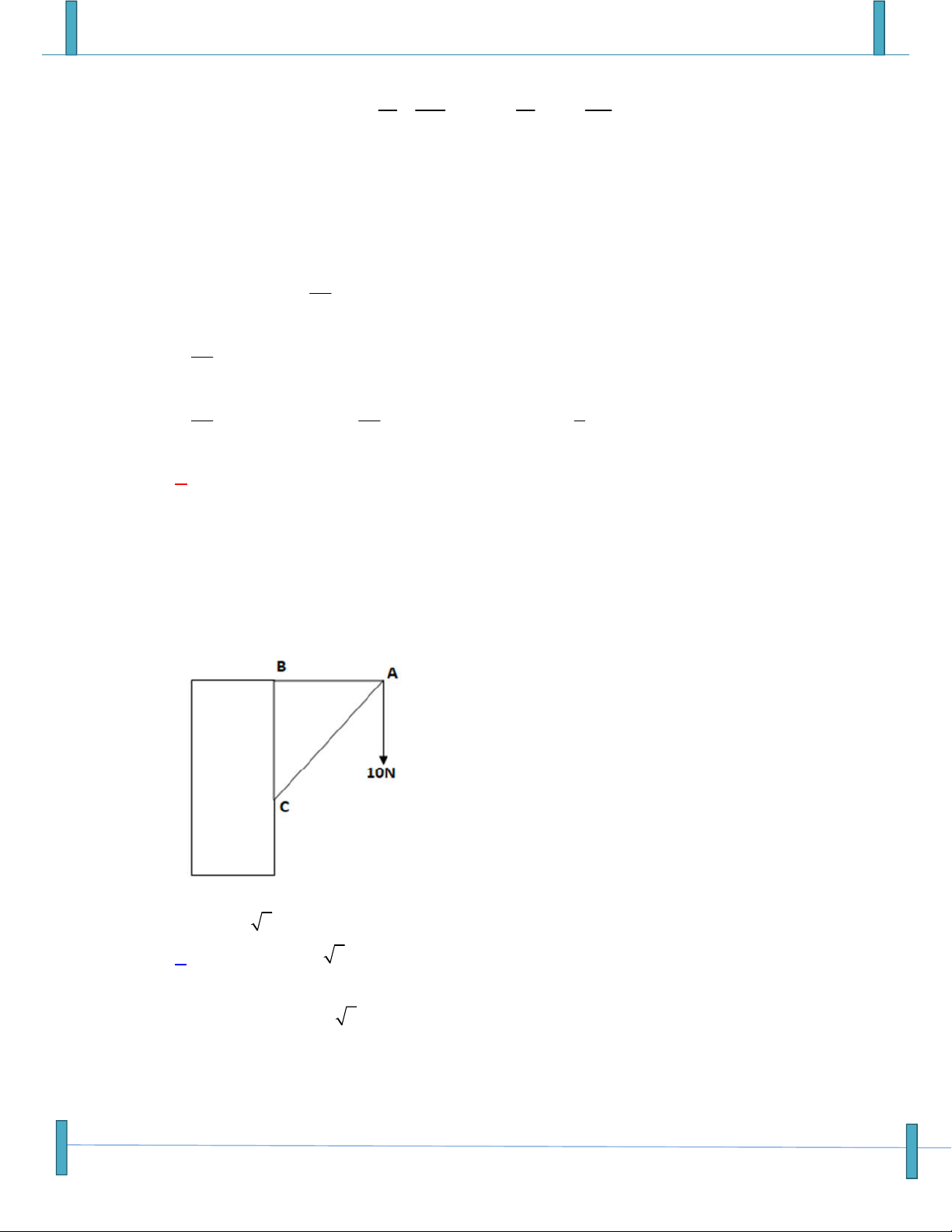
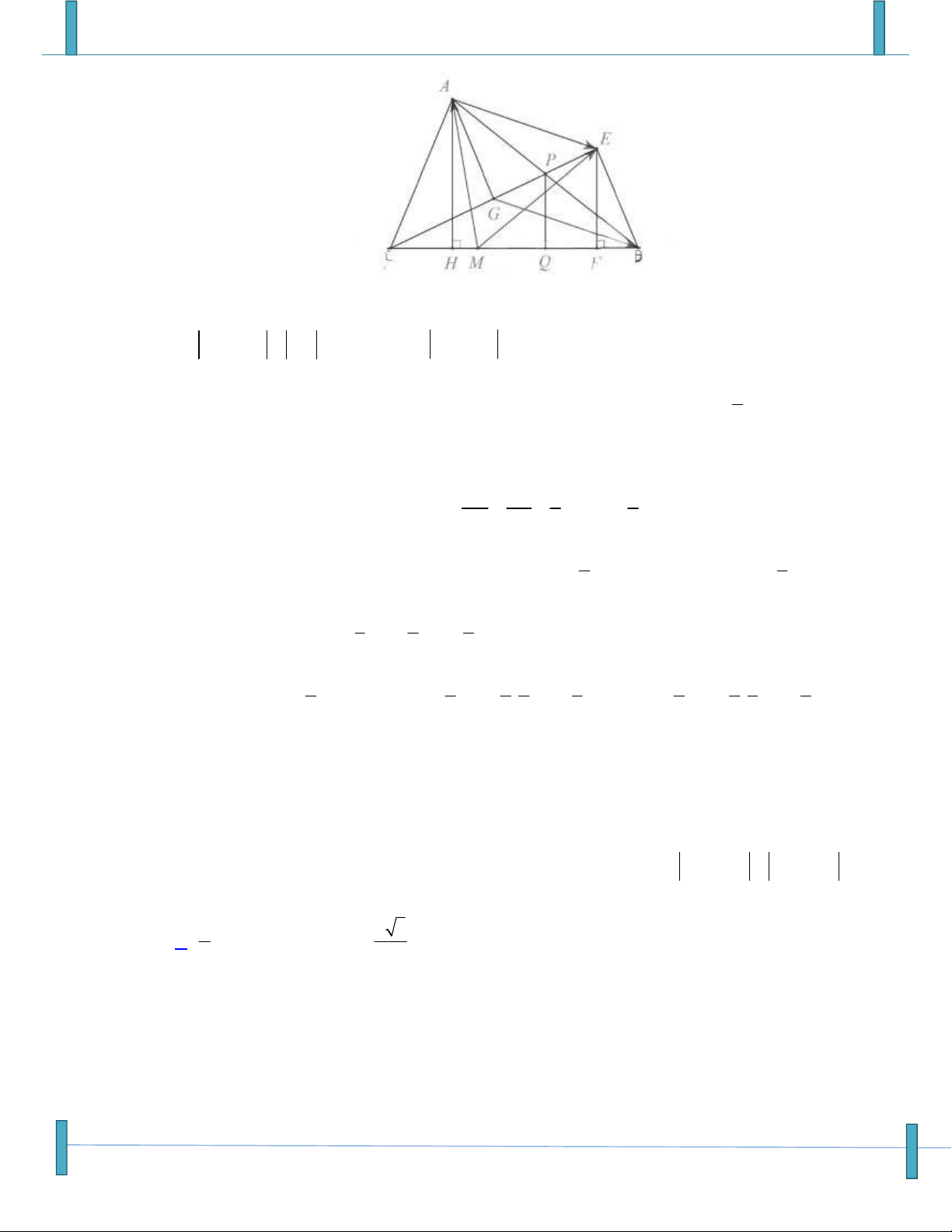
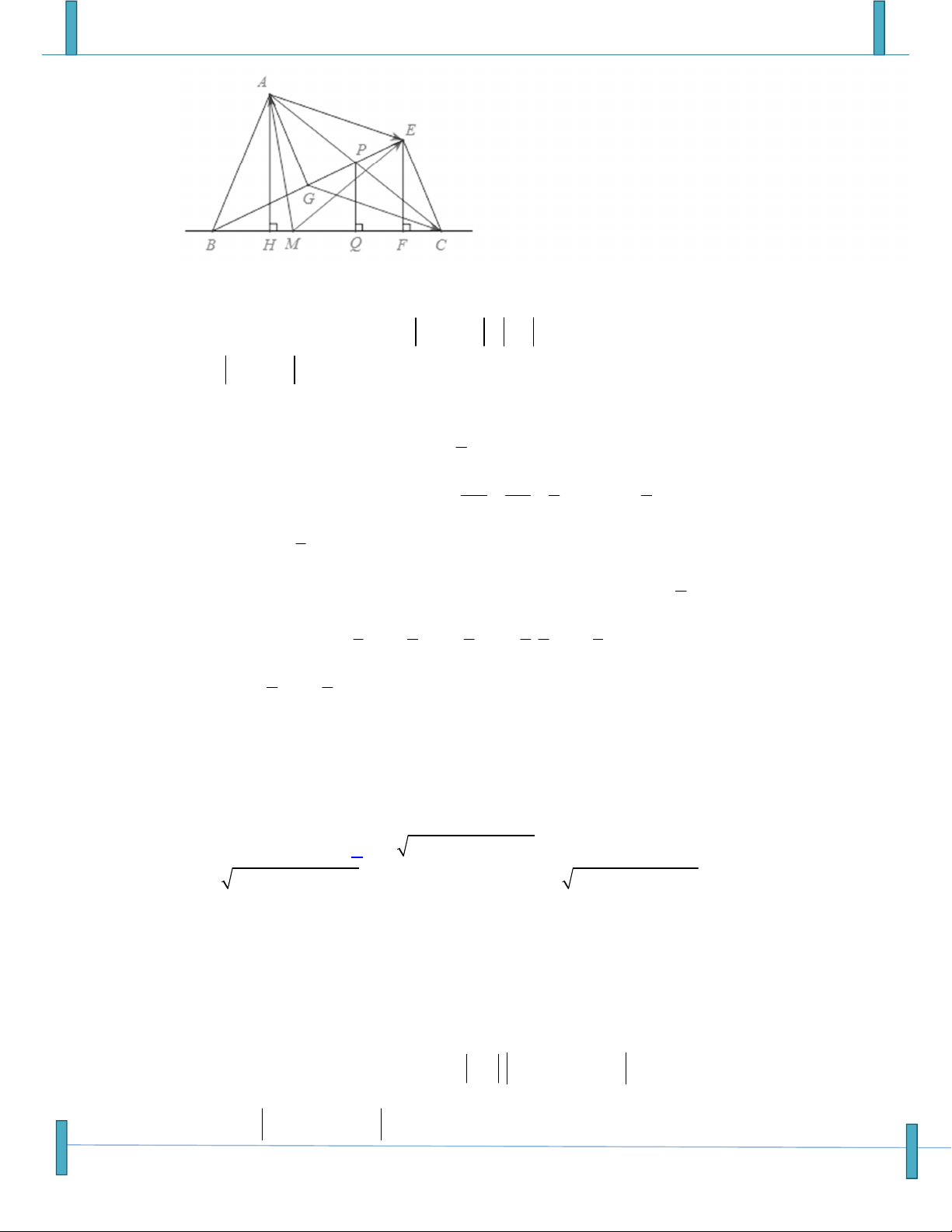
Câu 21: Một giá đỡ hình tam được gắn vào tường (như hình vẽ). Tam giác ABC vuông cân tại B.
Người ta treo vào điểm A một vật nặng 10N. Tính độ lớn của các lực tác động vào tường tại B
và C? (Bỏ qua khối lượng của giá đỡ)
A. F  10 2N, F  10N B C
B. F  10N, F  10 2 B C
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 4
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
C. F F  10N B C
D. F  10N, F  1  0 2 B C Họ và tên: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng,Email:
thanhdungtoan6@gmail.com
    
Câu 22: Cho ba điểm A , B , C thuộc đường tròn tâm O , thỏa mãn OA OC OB  0 . Tính góc AOB ?     A. 0 AOB  120 . B. 0 AOB  90 . C. 0 AOB  150 . D. 0 AOB  30 .
Họ và tên: Trần Gia Chuân, Tên facebook: Trần Gia Chuân  1  2 
Câu 23: Cho tam giác ABC . Điểm M trên cạnh BC thỏa mãn AM  .AB
.AC , khẳng định nào 3 3
sau đây là khẳng định đúng?    
A. MB  2MC .
B. MB  2MC .
C. MC  2MB . D. MC  3  MB .
Họ và tên: Trần Gia Chuân, Tên facebook: Trần Gia Chuân
âu 24. Cho tam giác đều ABC nội tiếp đường tròn tâm O , M là một điểm tùy ý nằm bên
trong tam giác đã cho; gọi A '; B '; C ' theo thứ tự là hình chiếu vuông góc của M lên các cạnh     k
B C ; C A và AB . Khi đó ta có đẳng thức vectơ k M A '  MB '  MC '   l MO , k.l  0, là l
phân số tối giản. Tính 2 2 2 k l . . A. 2 2
2k l  1. B. 2 2
2k l  1. C. 2 2
2k l  14 . D. 2 2
2k l  5 .
Họ và tên tác giả: Cao Văn Tùng Tên FB: Cao Tung
 1   1 
Câu 24: Cho hình vuông ABCD, E,F thõa mãn BE BC;CF  
CD ; AE BF I 3 2   
Ta có AI k AB l AD . Khi đó tỉ số k,l thõa mãn cặp nào sau: 3 2 6 2 5 3 6 1 A. k  ;l B. k  ;l C. k  ;l
D. k   ;l  5 5 5 5 6 6 5 3
Họ tên: Nguyễn Thị Trang, Fb: Trang Nguyen
Câu 25: Cho tam giác ABC , trên cạnh AC lấy điểm M , trên cạnh BC lấy điểm N sao cho:
AM  3MC , NC  2NB , gọi O là giao điểm của AN và BM .Tính diện tích ABC biết diện tích OBN bằng 1. A. 10 . B. 20 . C. 25 . D. 30 .
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
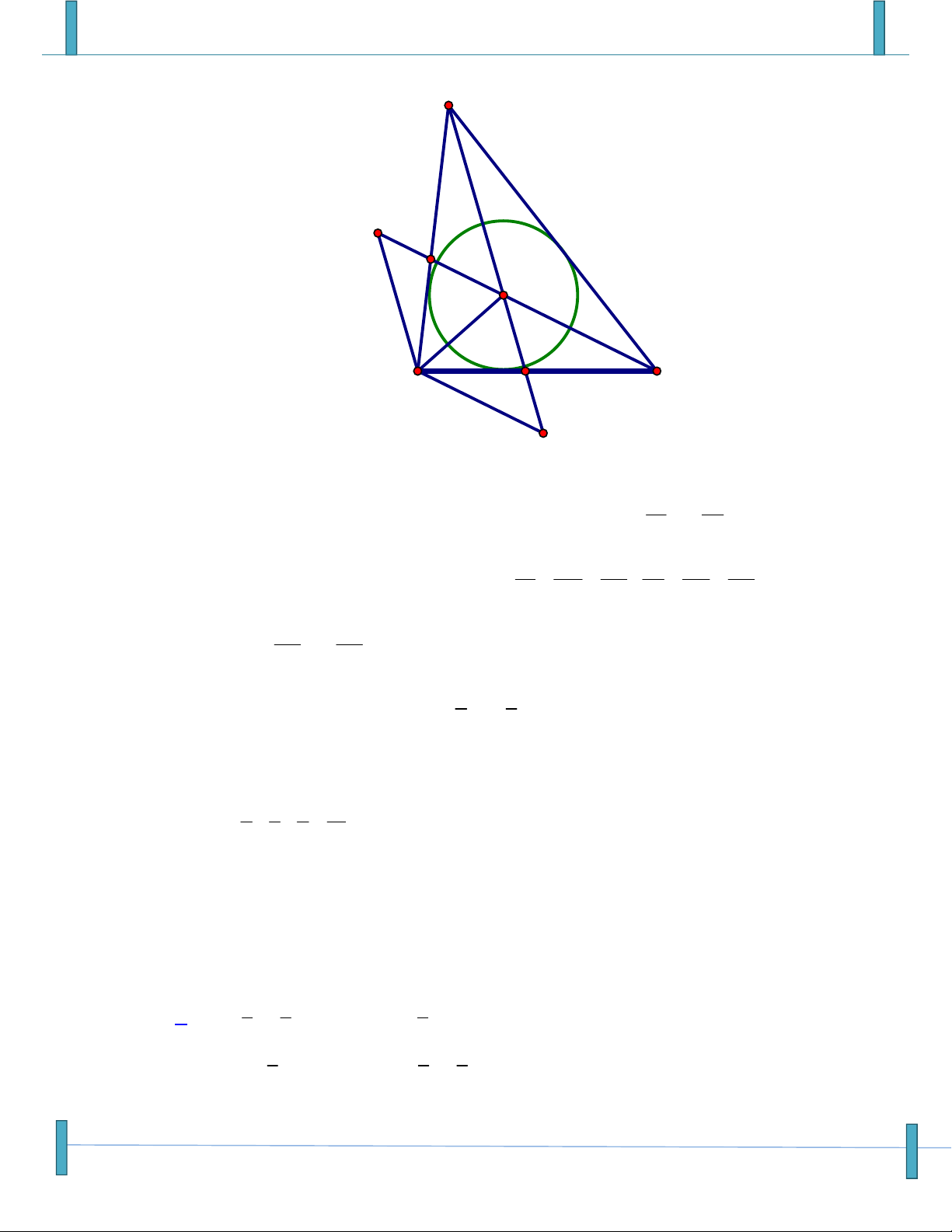
Câu 26: Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng định đúng?        
A. HA HB HC  4HO .
B. HA HB HC  2HO .    2     
C. HA HB HC HO .
D. HA HB HC  3HO . 3
Họ và tên: Nguyễn Văn Quân Tên FB: Quân Nguyễn, Email: Quanvan09@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 5
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
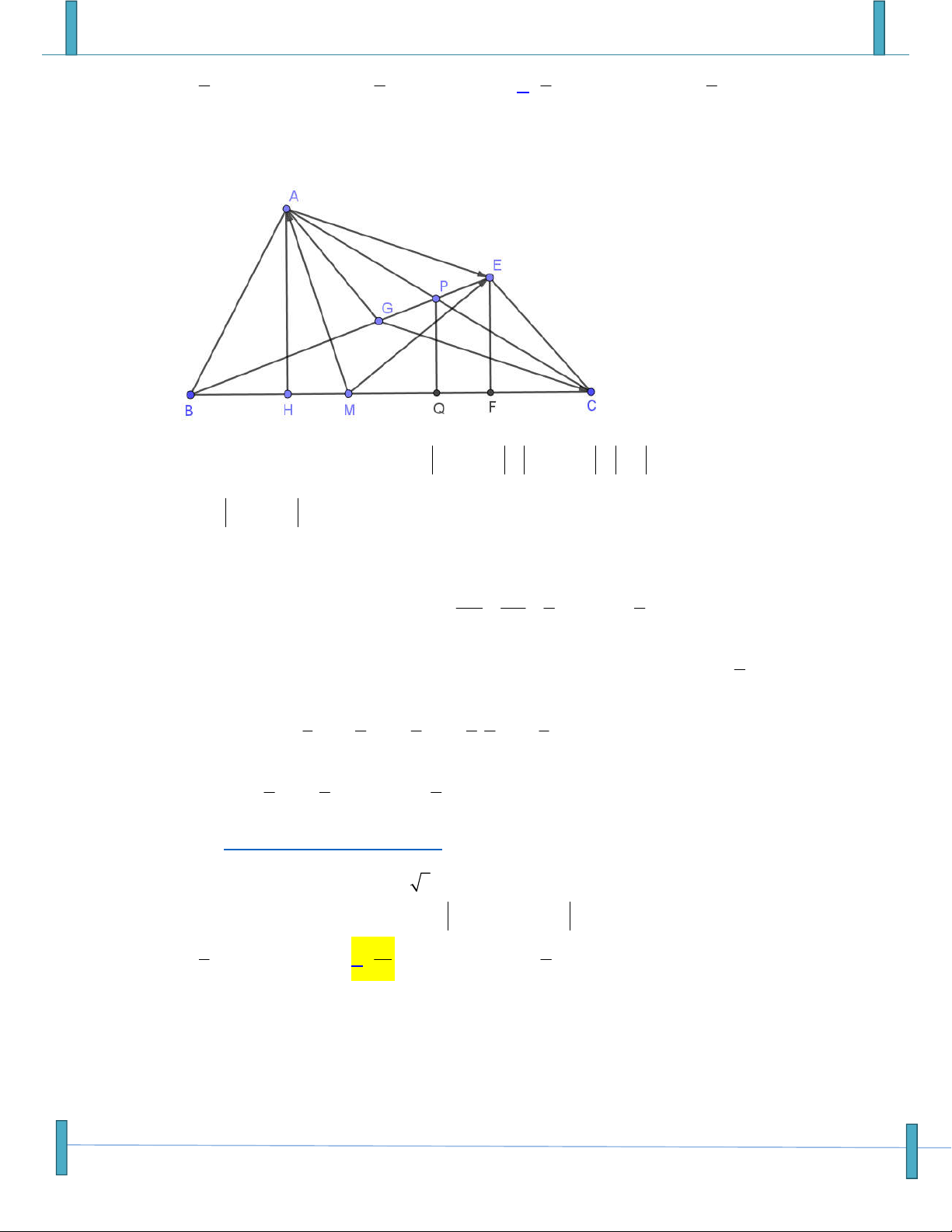
Câu 27: Cho tam giác ABC có D là trung điểm của BC , O là một điểm trên đoạn AD sao cho
AO  4OD . Gọi  
E CO AB , F  BO AC , M  AD EF . Khẳng định nào sau đây đúng?  1   2   1   2  A. MO AD B. MO AD C. MO AD D. EM BC 7 15 8 7
Họ và tên tác giả: Nguyễn Đặng, Tên facebook: NT AG
Câu 28: Cho hình thang ABCD có AB //CD . Gọi M , N lần lượt là trung điểm của AC, BD . Kẻ
NH AD (H AD) và ME BC (E BC) . Gọi I  ME NH , kẻ IK DC (K DC) .
Khi đó trong tam giác MNK hệ thức nào sau đây đúng?        
A. MK.IN NK.IM MN.IK  0
B. IN.tan N IM . tan M IK.tan K  0    
   
C. IN.cot N IM .cot M IK.cot K  0
D. IM IN IK  0
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát,Email:
nguyenvantoannbk@gmail.com
Câu 29: Cho ABC , điểm M thuộc cạnh BC sao cho 2018.S  2019.S . Đẳng thức nào sau ABMACM đây sai?    A. 2018.S  4037.S .
B. 2018.BM  2019.CM  0 . ABCACM  4037  2019 C. BC  .BM D. S  .S . 2018 ABM 4037 ABC
Câu 30: Cho tam giác ABC . M là điểm nằm trên cạnh BC sao cho S  3S . Một đường thẳng ABC AMC AB AC AM cắt các cạnh A ,
B AM , AC lần lượt tại B ,
M ,C phân biệt. Biết rằng  2  k. . ABACAM  Tìm số k . 2 A. k  1 . B. k  2 . C. k  3 . D. . 3
(Tác giả: Nguyễn Văn Phùng,Gmail: nvpmaster0808@gmail.com)
Câu 31: Cho n điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là A , A ,..., A . Bạn Bình kí hiệu 1 2 n
  
chúng là B , B ,..., B
A  B ). Vectơ tổng A B A B  ...  A B bằng 1 2 n ( 1 n 1 1 2 2 n n     A. 0 . B. A A . C. B B . D. A B . 1 n 1 n 1 n
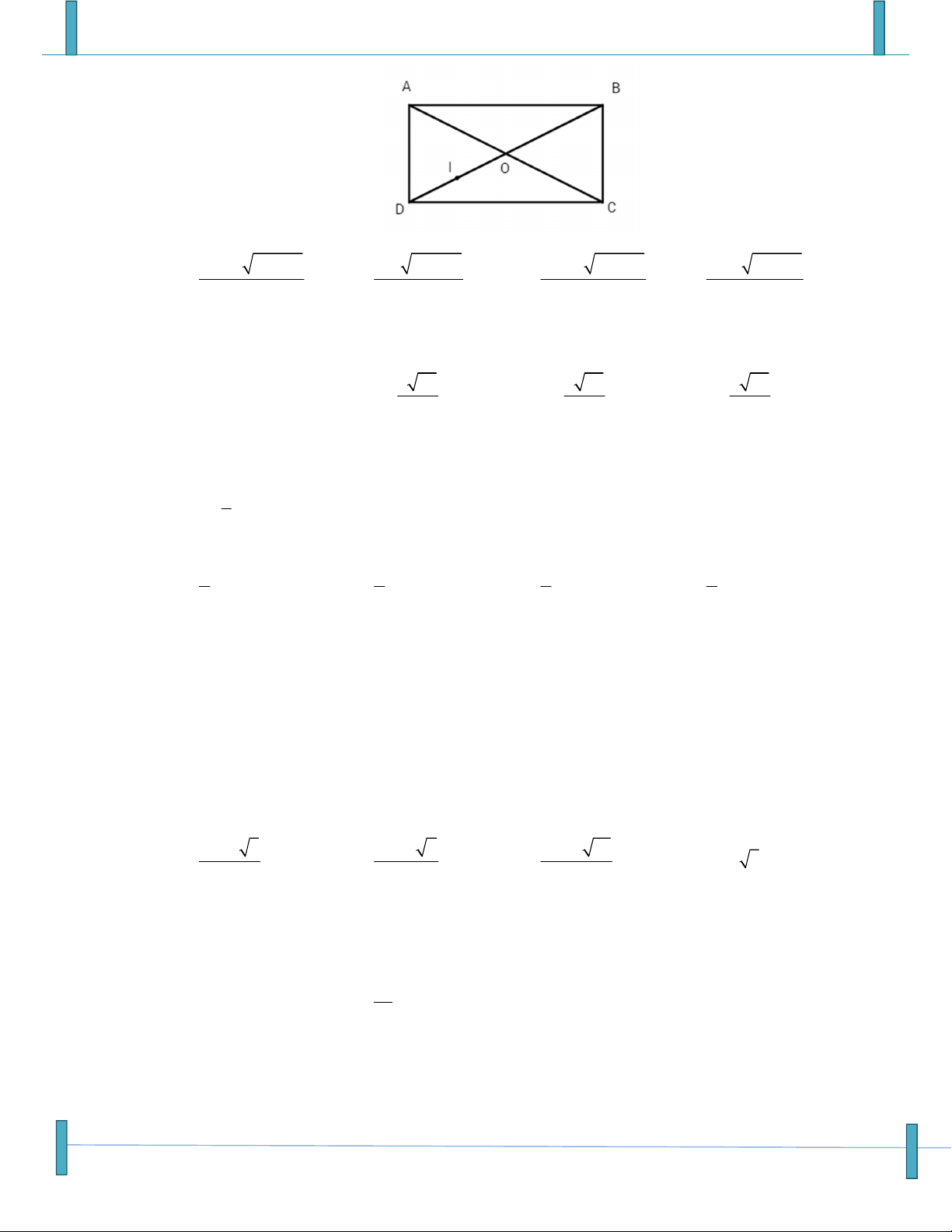
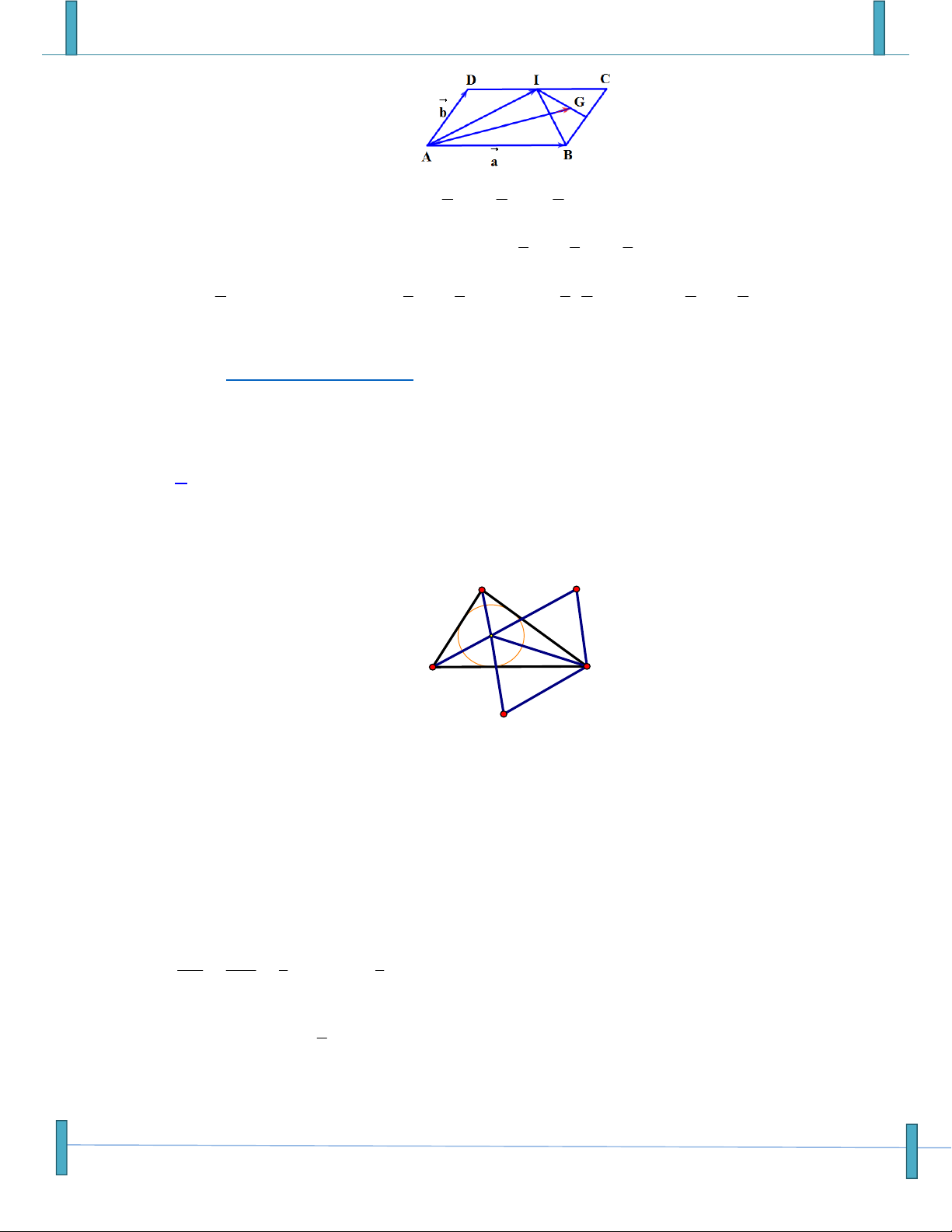
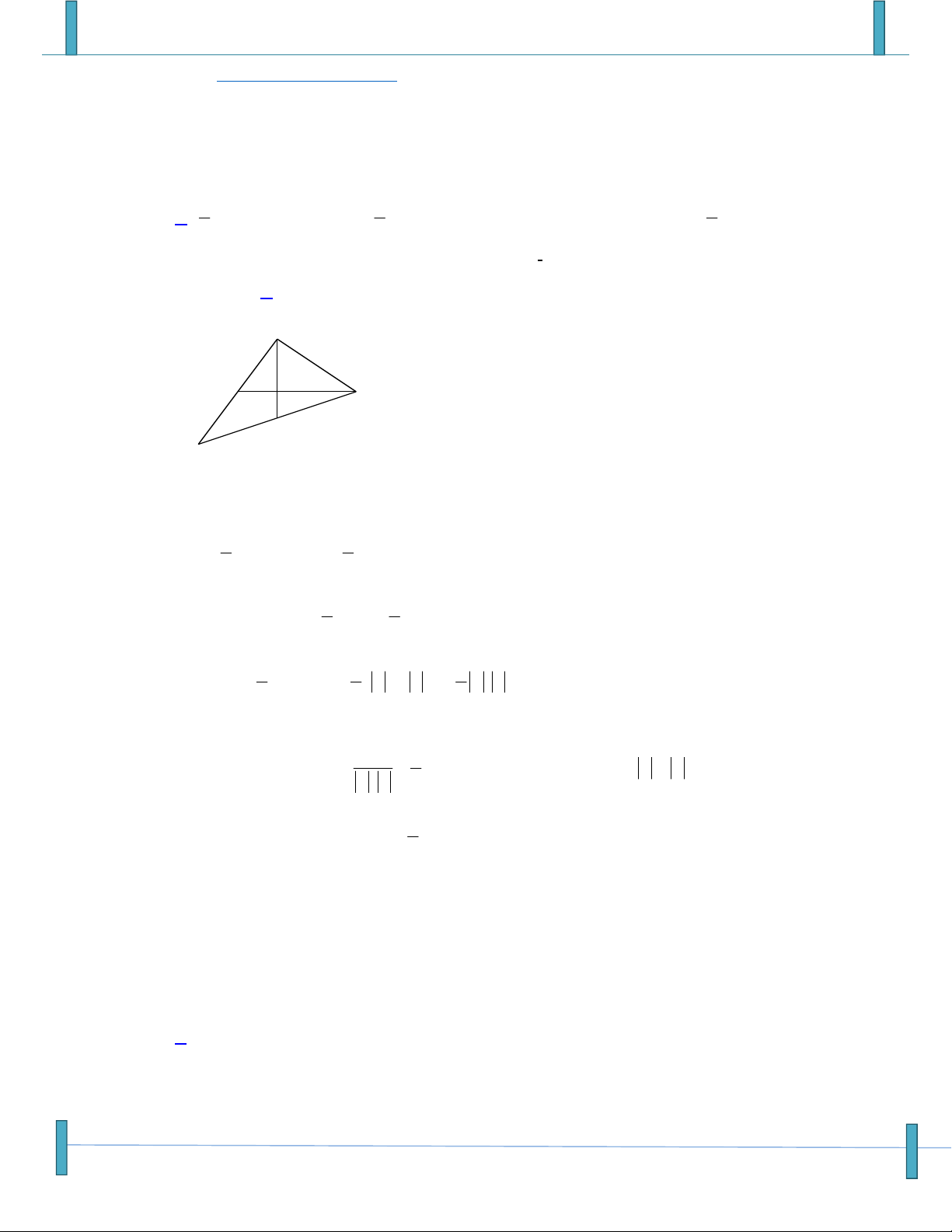
(Sưu tầm, Tên FB: Trung Nguyễn Chí)
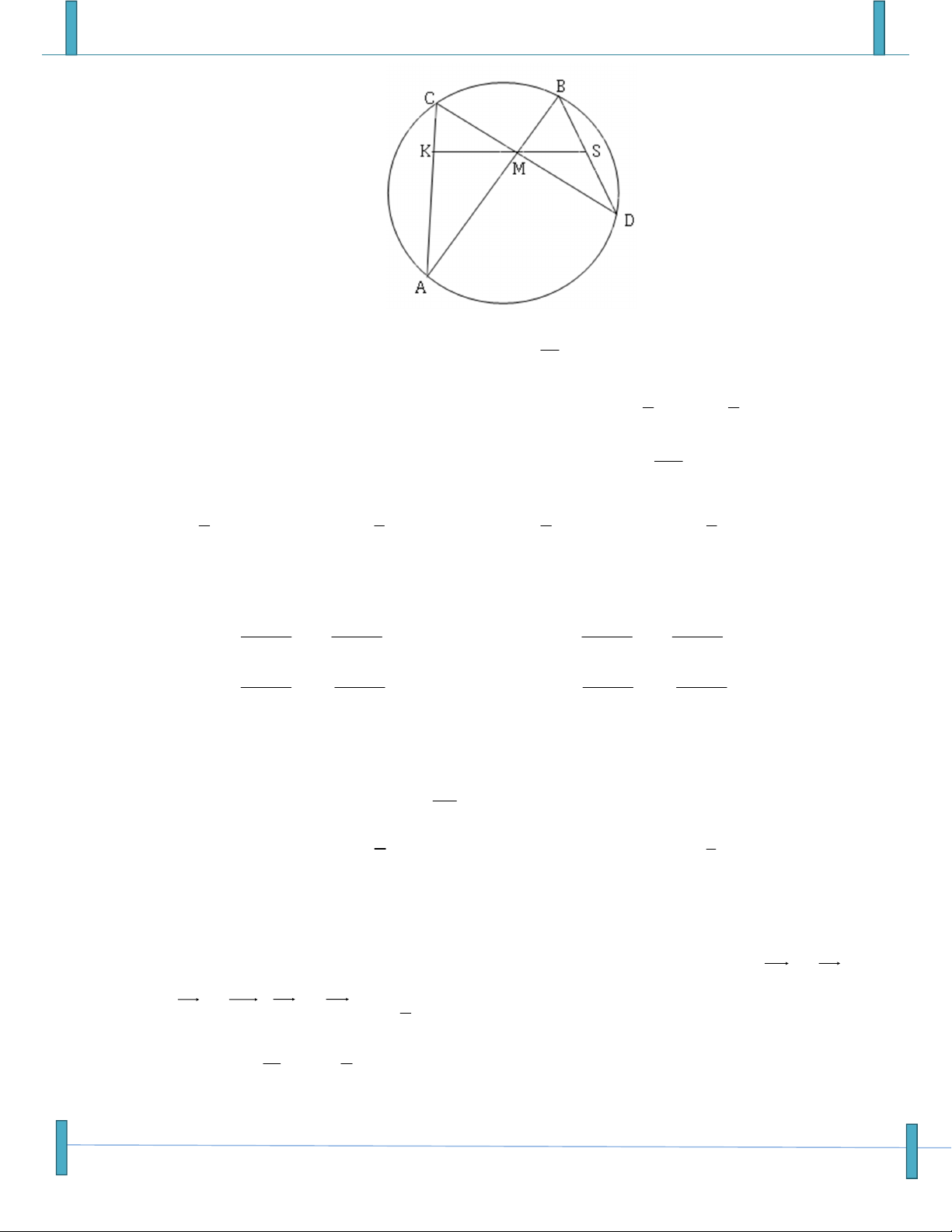
Câu 32: Trong đường tròn (O) với hai dây cung AB và CD cắt nhau tại M. Qua trung điểm S của BD kẻ AK 2 AM SM cắt AC tại K sao cho  a .Tính: CK 2 CM
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 6
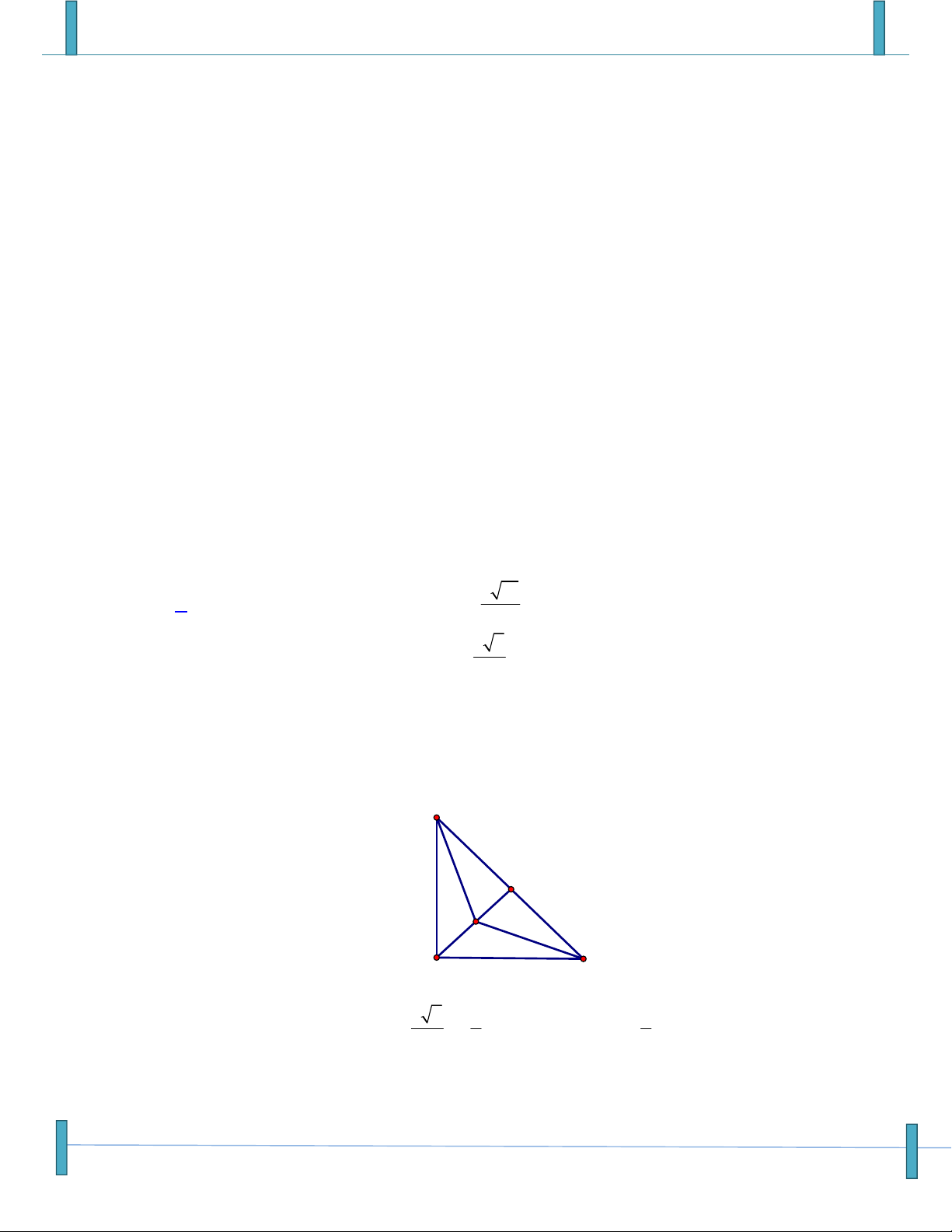
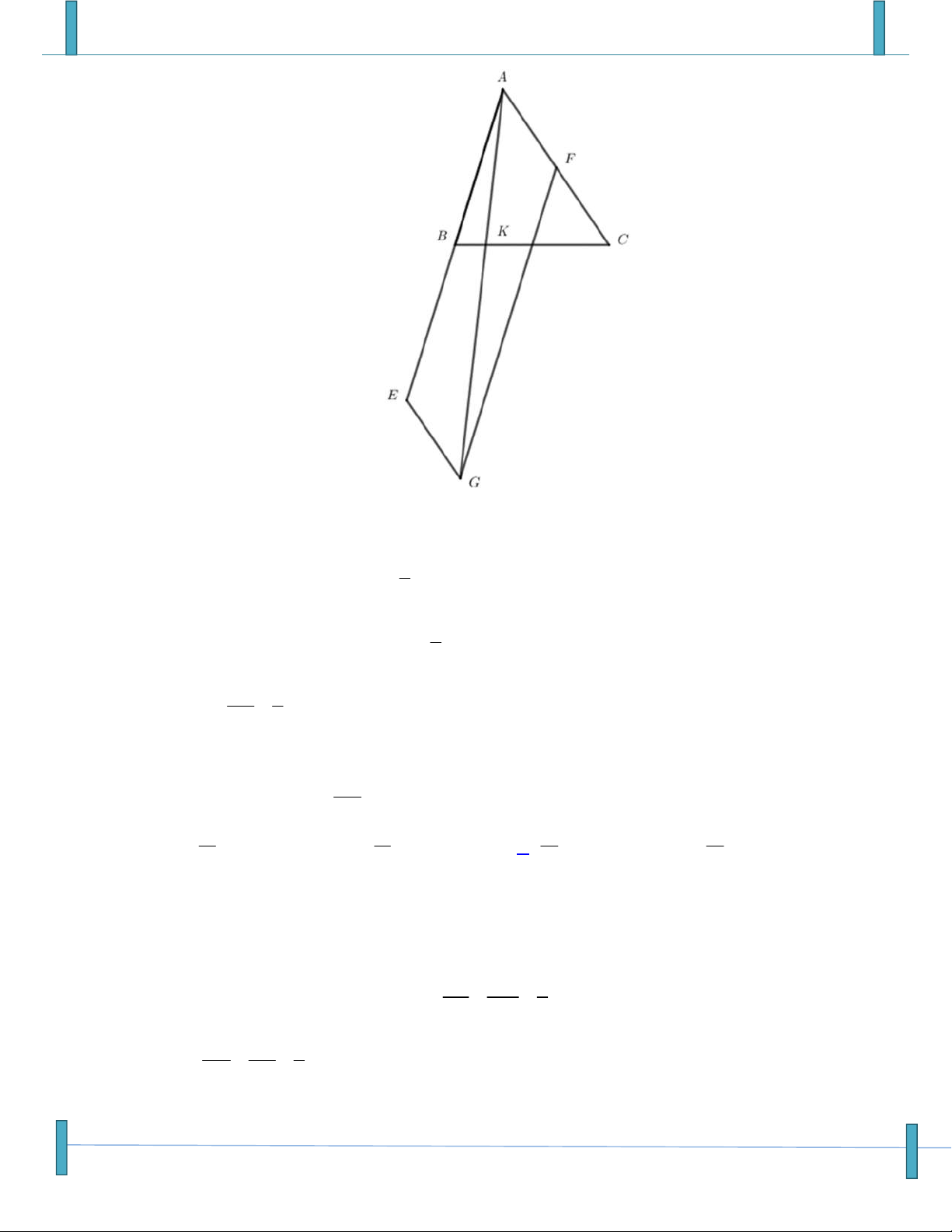
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 A. 2a B. 2 a C. D. a 2 a
 2   1 
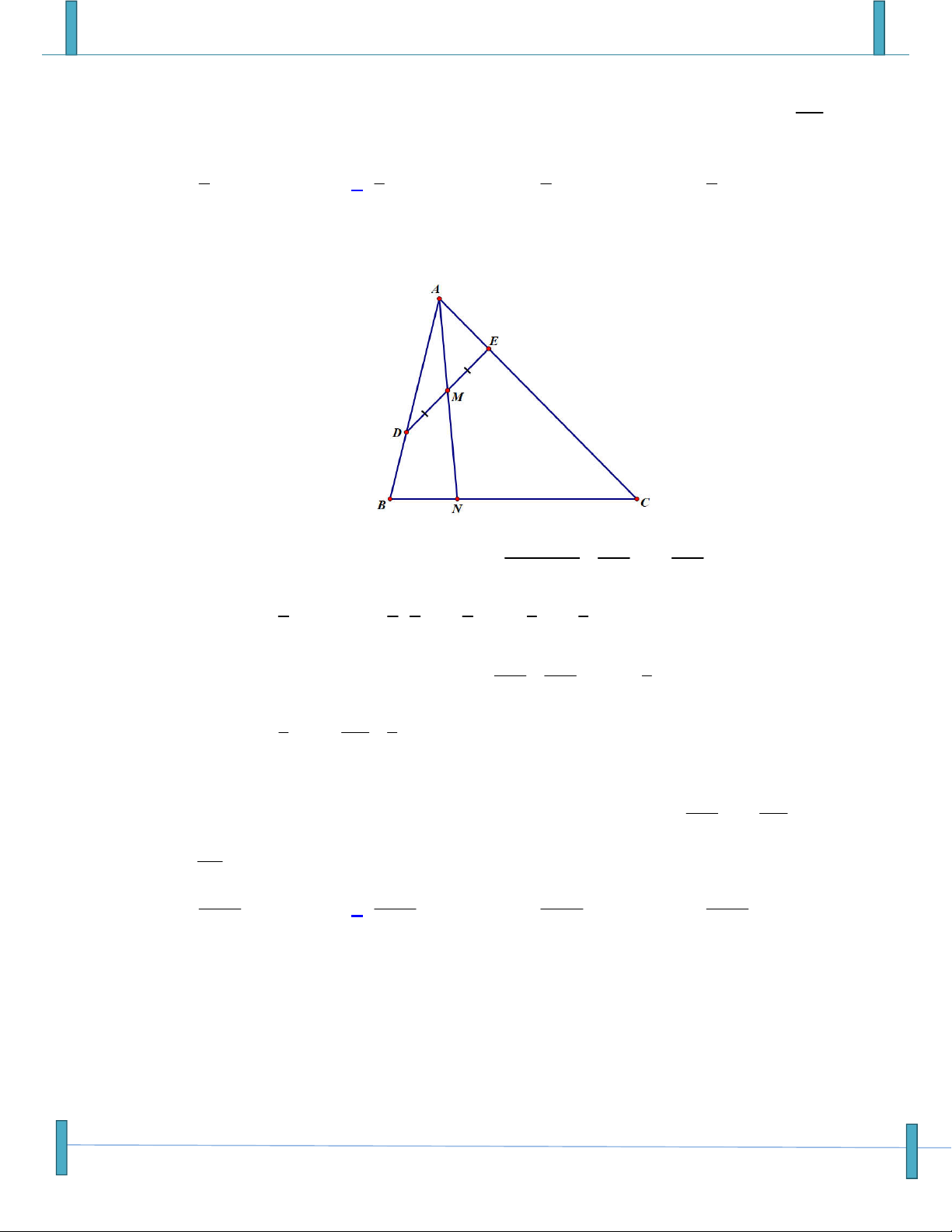
Câu 33: Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn: BD BC, AE AC . 3 4  AK
Điểm K trên AD sao cho 3 điểm B, K,E thẳng hàng. Xác định tỷ số  AD 1 1 1 1 A. B. C. D. 2 3 4 5
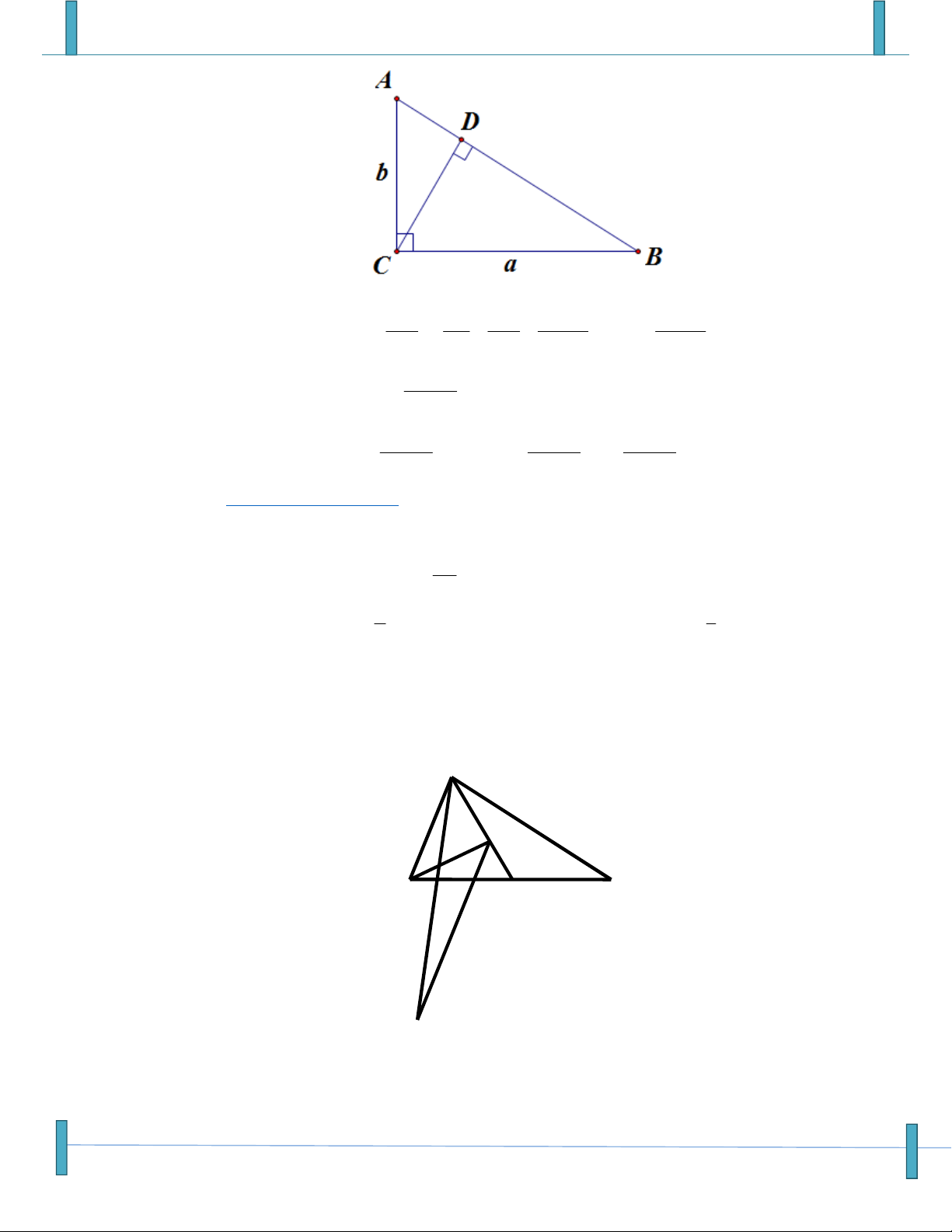
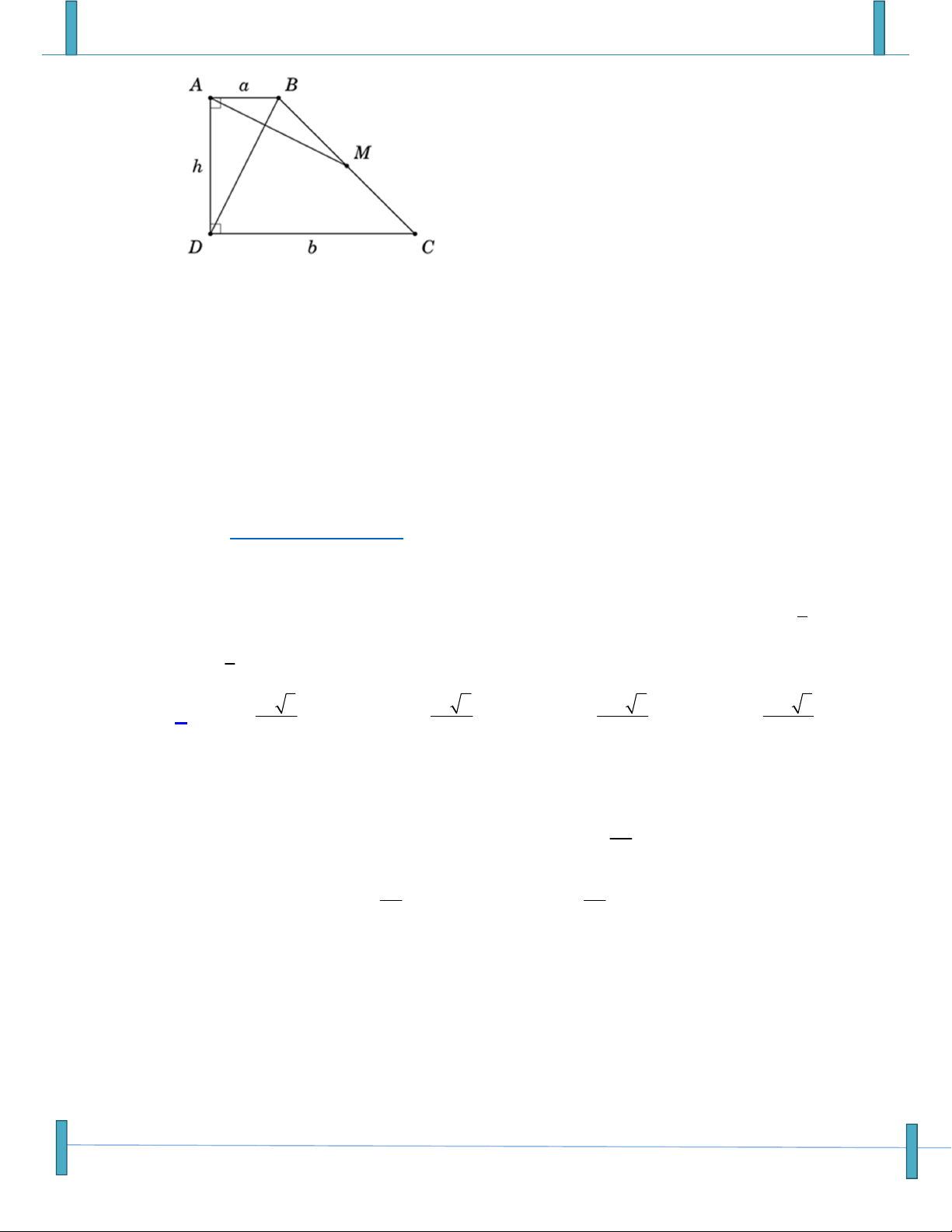
Câu 34: Cho tam giác ABC vuông tại C, có AC b, BC a , D là chân đường cao kẻ từ C.
Khẳng định nào sau đây là đúng? 2 2  a  b  2 2  a  b  A. CD CA CB . B. CD CA CB . 2 2 2 2 a b a b 2 2 2 2 a b a b 2 2  a  b  2 2  a  b  C. CD AC BC D. CD AC BC . 2 2 2 2 a b a b 2 2 2 2 a b a b
Facebook: Lê Văn Kỳ, Email: lethithuy@thpthv.vn    
Câu 35: Cho tam giác ABC có trọng tâm G. Gọi I là điểm xác định bởi 5IA  7IB IC  0. Gọi E là EA
giao điểm của AI và BG. Tính tỷ số . EI 1 1 A. 2. B. . . 2 C. 3. D. 3
(Họ tên tác giả: Nguyễn Thị Thu Huyền. Tên FB: Thu Huyen Nguyen)
Câu 36: Cho 2 tia Ox, Oy vuông góc. Trên tia Ox lấy các điểm A,B sao cho OA = OB = 1. C là điểm
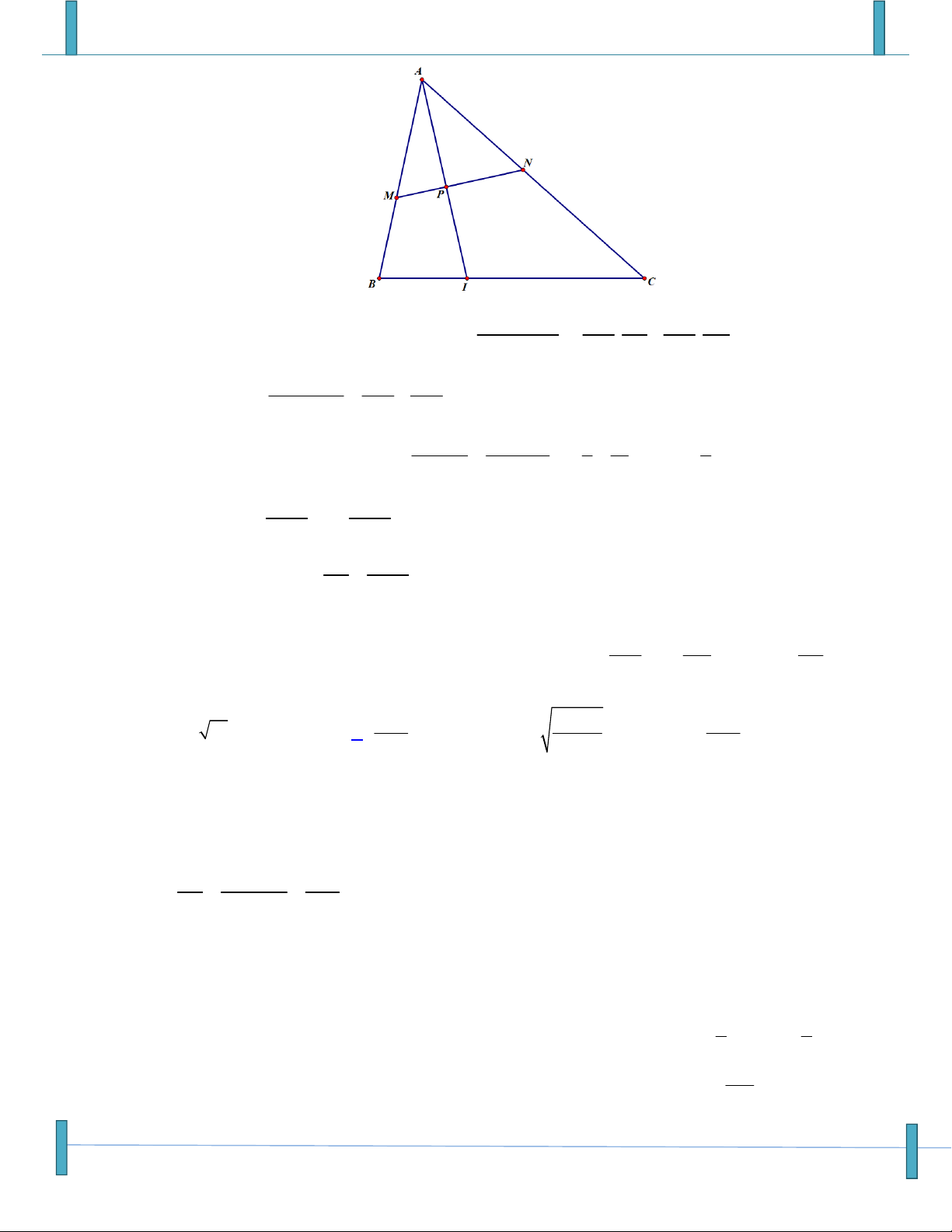
thuộc đoạn OA, N là một điểm thuộc đoạn OB và dựng hình vuông OCMN. Trên đoạn CM lấy
điểm Q và dựng hình vuông ACQP. Gọi S là giao điểm của AM và PN. Giả sử OC kOA ,  1 
AS x AM , NS y NP , k   1 ;   2  13 a Khi x + y = thì k =
, với a,b   và a, b nguyên tố cùng nhau thì a.b bằng 10 b A. 7 B. 4 C. 5 D. 12
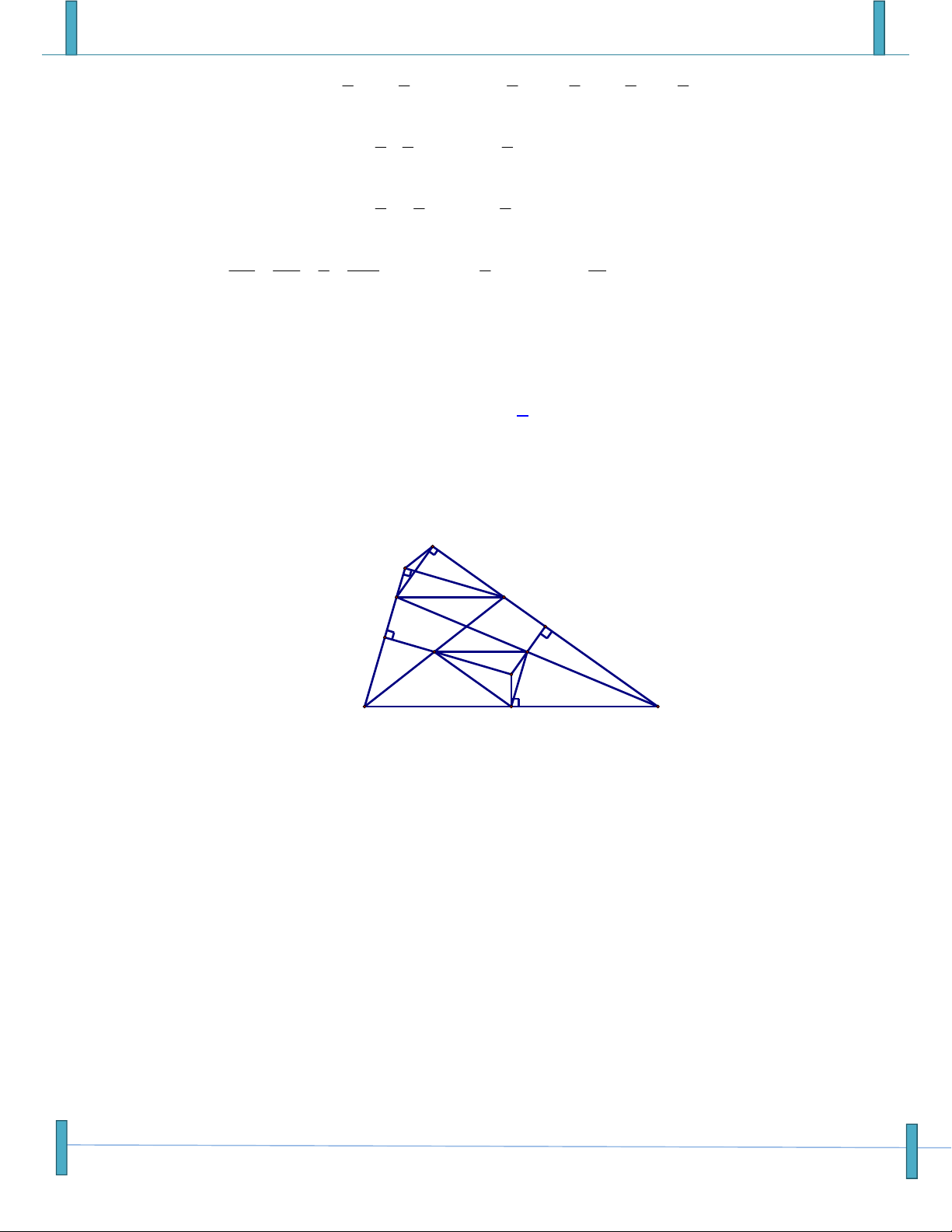
Email: nghiepbt3@gmail.com, FB: Ngô Quang Nghiệp
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 7
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 37: Cho tam giác ABC . Giả sử điểm M nằm trên cạnh BC thỏa các tam giác MA , B MAC lần
lượt có diện tích là S , S . Khẳng định nào sau đây đúng? 1 2      
A. S S AM S AB S AC.
B. S S AM S AB S AC. 1 2  1 2  2 1 1 2      
C. S S AM S AB S AC.
D. S S AM S AB S AC. 2 1  2 1  2 1 1 2
Họ Tên: Lê Duy Tên FB: Duy Lê Email: Duyleag@gmail.com  1  
Câu 38: Cho tam giác ABC có có M là trung điểm của BC, AI
MI . Điểm K thuộc cạnh AC sao 2  m 
cho B,I,K thẳng hàng. Khi đó KA
CK . Tính S  25m  6n  2019 n
A. S  2019 . B. S  2068 .
C. S  2018 . D. S  2020 .
Họ và tên tác giả: Nguyễn Đức Duẩn Tên FB: Duan Nguyen Duc, Email: Duanquy@gmail.com     
Câu 39: Cho tam giác ABC có trọng tâm G, lấy các điểm I, J sao cho IA  2IB và 3JA  2JC  0 và thỏa  
mãn đẳng thức IJ  kIG . Giá trị của biểu thức 2 2 500
P  (25k  36)(k  k 1) là: 5 6 A. P  1235 B. P  0 C. P  D. P  6 5
Họ và tên: Nguyễn Quang Huy, Fb: Nguyễn Quang Huy, Email: boigiabao98@gmail.com
Câu 40: Cho tam giác ABC . M là điểm nằm trên cạnh BC sao cho SS 3 . Một đường thẳng ABC AMC AB AC AM
cắt các cạnh AB, AM, AC lần lượt tại B ',M ',C ' phân biệt. Biết  mn . AB ' AC ' AM ' Tính m n . A. 2. B. 5. C. 3. D. 4.
(Họ và tên tác giả: Nguyễn Thị Trà My, Tên FB: Nguyễn My)
Câu 41: Cho tam giác ABC có D là trung điểm của BC , O là một điểm trên đoạn AD sao cho
AO  4OD . Gọi  
E CO AB , F  BO AC , M  AD EF . Khẳng định nào sau đây đúng?  1   2   1   2  A. MO AD B. MO AD C. MO AD D. EM BC 7 15 8 7
Họ và tên tác giả: Nguyễn Đặng, Tên facebook: NT AG
Câu 42: Cho hình thang ABCD có AB//CD . Gọi M , N lần lượt là trung điểm của AC, BD . Kẻ
NH AD (H AD) và ME BC (E BC ) . Gọi I  ME NH , kẻ IK DC (K DC) .
Khi đó trong tam giác MNK hệ thức nào sau đây đúng?        
A. MK.IN NK.IM MN.IK  0
B. IN. tan N IM .tan M IK. tan K  0    
   
C. IN.cot N IM .cot M IK.cot K  0
D. IM IN IK  0
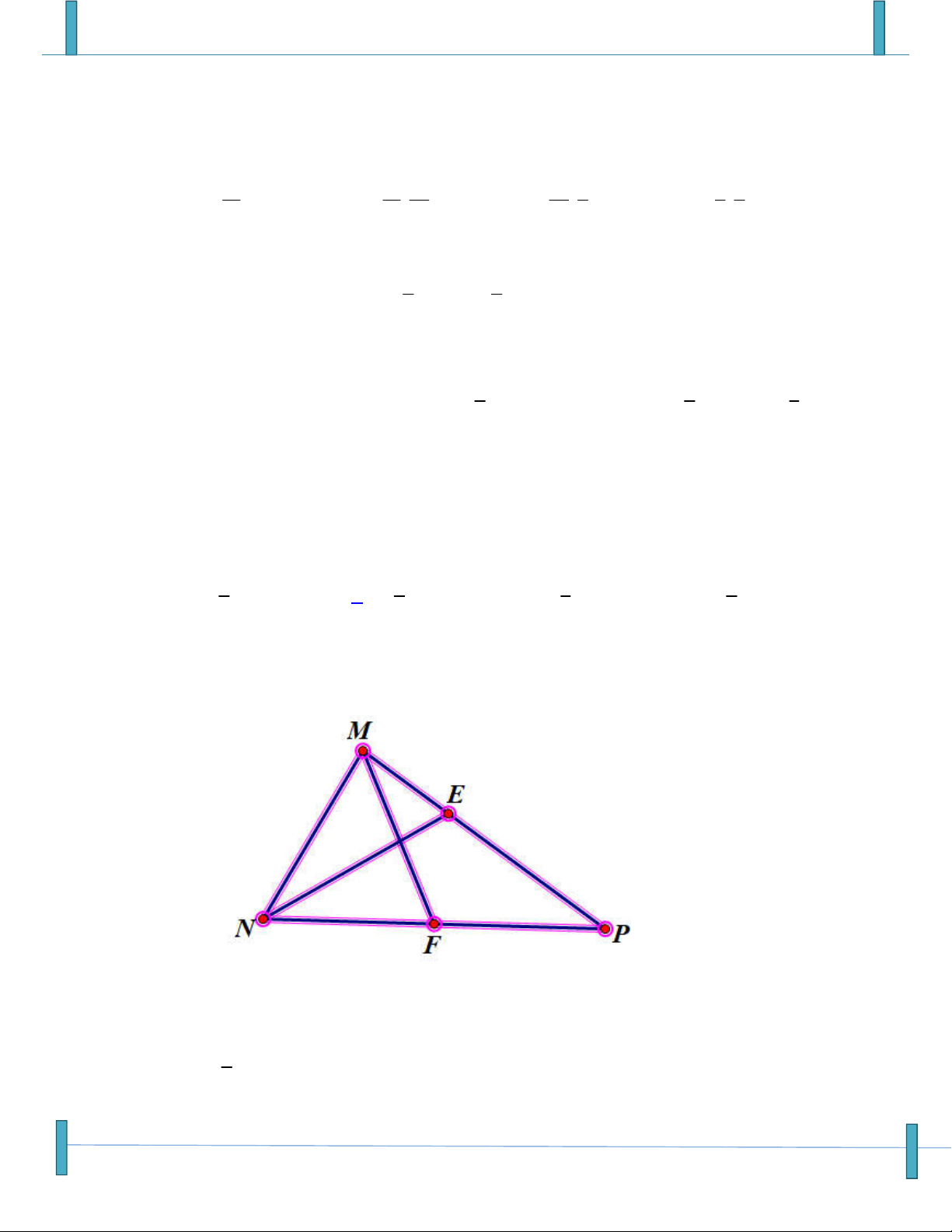
Câu 43: Cho hình bình hành ABCD . Gọi I là trung điểm của CD , G là trọng tâm tam giác BCI . Đặt    
a AB, b AD . Hãy tìm đẳng thức đúng trong các đẳng thức sau?  5  2   5   A. AG a b . B. AG a b . 6 3 6
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 8
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New   5   4  2 
C. AG a b . D. AG a b . 6 3 3
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet, Email: tiethanh.78@gmail.com
Câu 44: Một đường thẳng cắt các cạnh D ,
A DC và đường chéo DB của hình bình hành ABCD lần    
lượt tại các điểm E, F và M . Biết DE  . m D , A DF  .
n DC (m, n  0). Khẳng định đúng là: 
m n   m  A. DM DB . B. DM DB . . m n m n  n   . m n  C. DM DB . D. DM DB . m n m n
(Email): locleduc10@gmail.com
(Họ và tên tác giả: Lê Đức Lộc, Tên FB: Lê Đức Lộc)
Câu 45: Hình thang cân ABCD có độ dài đường cao AH  ; a AB / /C ,
D AB a 3; AD a 2; AB DC 
x y z 
AC cắt BH tại I. Biết AI AC; ; x ;
y z; m N . m
Tính tổng T x y z m A. 20 B. 18 C. 17 D. 21
Họ và tên tác giả: Nguyễn Thị Phương Thu FB: Buisonca Bui
Câu 46: Cho hình thang ABCD với O là giao điểm của hai đường chéo AC và BD. Qua O vẽ đường
thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên AD và BC theo thứ tự 
tại M và N. Với AB a , D C
b , khi đó MN bằng:         a .AB  . b DC . b AB  . a DC a .AB  . b DC . b AB  . a DC A. . B. . C. . D. . a b a b a b a b
Họ và tên: Nguyễn Thanh Tâm Tên FB: Tâm Nguyễn
Câu 47: Cho tam giác ABC đều tâm O ; điểm M thuộc miền trong tam giác OBC ; D , E , F lần lượt
là hình chiếu vuông góc của M trên BC , CA , AB . Khẳng định nào sau đây đúng?
   1 
   
A. MD ME MF MO .
B. MD ME MF MO . 2
   
   3 
C. MD ME MF  3MO .
D. MD ME MF MO . 2 Phan Minh Tâm
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG
Email: phunghang10ph5s@gmail.com
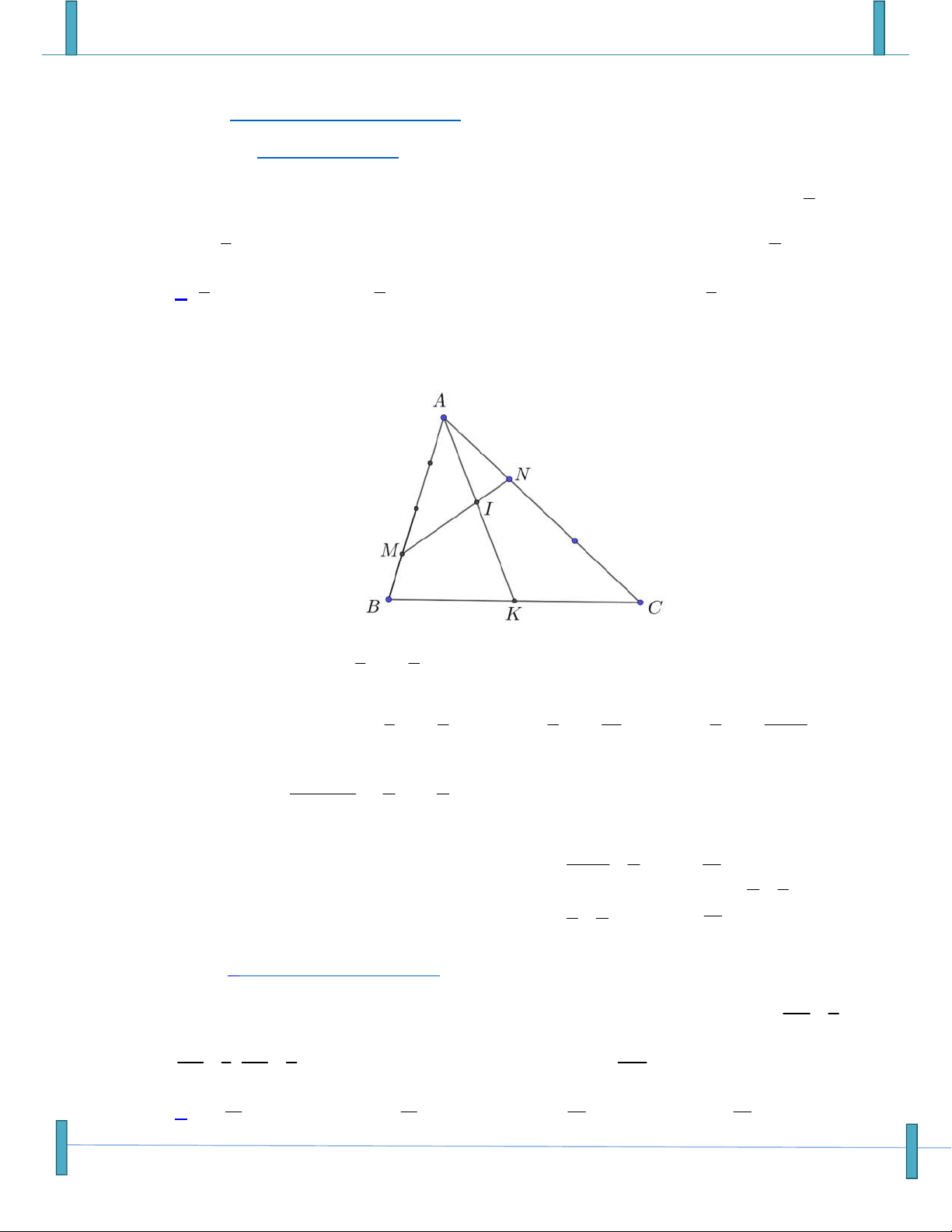
Câu 48: Cho hình bình hành ABCD có các điểm M , I , N lần lượt thuộc các cạnh AB, BC, CD sao cho 1 1 AM
AB, BI kBC, CN
CD . Gọi G là trọng tâm tam giác BMN . Xác định k để AI đi 3 2 qua G .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 9
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 9 6 12 A. . B. . C. . D. . 3 13 11 13
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng
Câu 49: Cho tam giác ABC . Gọi M là điểm thuộc cạnh AB, N là điểm thuộc cạnh AC sao cho 1 3
AM AB, A
N AC . Gọi O là giao điểm của CM và BN. Trên đường thẳng BC lấy E. 3 4  
Đặt BE xBC .
Tìm x để A, O, E thẳng hàng. Chọn C 2 8 9 8 A. B. C. D. 3 9 13 11
Ý tưởng: Cho tam giác ABC , I là trung điểm của BC . Gọi P, Q, R là các điểm xác định bởi:      
AP p AB, AQ q AI , AR r AC với pqr  0 . 2 1 1
Chứng minh rằng: P, Q, R thẳng hàng khi và chỉ khi   . q p r
Họ và tên: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng, Email:
thanhdungtoan6@gmail.com
Câu 50: Cho tam giác ABC . Gọi I là trung điểm BC ; P là điểm đối xứng với A qua B ; R là điểm 2
trên cạnh AC sao cho AR
AC . Khi đó đường thẳng AR đi qua điểm nào trong các điểm 5 sau đây?
A. Trọng tâm tam giác ABC .
B. Trọng tâm tam giác ABI .
C. Trung điểm AI .
D. Trung điểm BI .
(có thể phát triển P, J, G, M, R thẳng hàng với J – có lẽ là trung điểm BH, còn M chia
AI theo tỷ số tính được)
Câu 51: Cho ABC có H là trung điểm của AB và G AC : GC  2AG . Gọi F là giao điểm của CH
và BG . Tìm điểm I trên BC sao cho I , F , A thẳng hàng       A. IC  2  I . B
B. IB  2IC.
C. IB I . C D. IC  3  I . B
Câu 52: Cho tam giác ABC. I là trung điểm của BC. Gọi M, N, P lần lượt là các điểm xác định bởi      
AM m AB; AN n AI; AP p AC , với mnp  0 . Tìm điều kiện của m, n, p để M, N, P thẳng hàng.
A. mp mn np
B. 2mp mn np
C. 2np mn mp
D. 2mn mp np
Họ và tên tác giả: Hoàng Thị Trà FB: Hoàng Trà
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 10
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 53: Cho tam giác ABC. Gọi G là trọng tâm của tam giác, I là trung điểm của BC, M và N là các  1  CN BC
điểm được xác định bởi  2 
  . Gọi P là giao điểm của AC và MN. Tính tỉ số diện 3
MA  4MB  0 
tích tam giác ANP và tam giác CNP. 7 A. 3 B. C. 4 D. 2 2
 2   1  BD BC; AE  AC
Câu 54: Cho tam giác ABC . Gọi ,
D E lần lượt là các điểm thỏa mãn: 3 4 . Điểm
 a  a AK AD
K trên AD thỏa mãn b
(với b là phân số tối giản) sao cho 3 điểm , B K, E thẳng hàng. Tính 2 2
P a b . A. P  10 . B. P  13 . C. P  29 . D. P  5 .    
Câu 55: Cho tam giác ABC, I là điểm thỏa mãn: 2IA IB  4IC  0    
K là điểm thỏa mãn: KA  2KB  3KC  0    
P là điểm thỏa mãn: PA mPB nPC  0 Có bao nhiêu cặp  , m n, , m n Z, , m n   1
 0;10 sao cho I, K, P thẳng hàng. A. 2 B. 3 C. 4 D. 5
Email: themhaitotoanyp1@gmail.com, (Fb: Lưu Thêm)      
Câu 56: Cho tam giác ABC , M và N là hai điểm thỏa mãn: BM BC  2 AB , CN x AC BC . Xác
định x để A, M , N thẳng hàng. 1 1 A. 3. B.  . C. 2. D.  . 3 2
Email : boyhanam@gmail.com
Câu 57: Cho tam giác ABC có G là trọng tâm, I là trung điểm AG , lấy K thuộc cạnh AC sao cho  
AK  kAC . Nếu B, I, K thẳng hàng thì giá trị của k nằm trong khoảng?  1   1   1 1   1  A. 0; B. 0; C. ; D. ;1        6     2   5 3   5 
(Họ tên: Nguyễn Thu Hương. Tên FB: Thu Hương)  
Câu 58: Cho tam giác ABC , M là điểm thuộc cạnh AC sao cho MA  2
 .MC , N thuộc BM sao cho     NB  3
NM , P là điểm thuộc BC . Biết rằng ba điểm ,
A N , P thẳng hàng khi PB k PC .
Khẳng định nào sau đây là đúng?  5   5   1   1  A. k  3  ;  . B. k   ; 1  . C. 1;  . D.  ; 0 .          2   2   2   2 
Họ và tên: Trần Văn Luật, Email: Tvluatc3tt@gmail.com, FB: Trần Luật
Họ và tên: Hoàng Thị Kim Liên
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 11
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 59: Cho tam giác ABC . Gọi M, N, P lần lượt nằm trên đường thẳng BC, CA, AB sao cho      
MB mMC , NC nN ,
A PA k PB . Tính tích mnk để M, N, P thẳng hàng? A. 1 . B. 1 . C. 2 . D. 2 .
Email: lientiencl@gmail.com, Facebook: Kim Liên
Câu 60: Cho hình bình hành ABCD gọi M là trung điểm của cạnh CD, N là điểm thuộc cạnh AD sao cho 1 AN
AD . Gọi G là trọng tâm của tam giác BMN, đường thẳng AG cắt BC tại K. Khi đó 3  m  m BK BC (
là tối giản). Tính S m n n n
A. S  16 . B. S  17 .
C. S  18 . D. S  19 .
( Tên FB: Phùng Hằng )
Câu 61: Cho hình thang ABCD có đáy AB , CD , CD  2AB . M , N lần lượt là các điểm thuộc cạnh
AD và BC sao cho AM  5MD , 3BN  2NC . Gọi P là giao điểm của AC và MN ; Q là PM QN a a
giao điểm của BD và MN ; Khi đó   , với
là phân số tối giản. Khi đó a b PN QM b b bằng A. 386 . B. 385 . C. 287 . D. 288 .
Họ tên: Bùi Thị Lợi Facebook: LoiBui
Câu 62: Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = 3MC, NC
= 2BN. Gọi I là giao điểm của AN và BN. Tính diện tích tam giác ABC biết diện tích tam giác ABN bằng 4. A. S  110 . B. S  115 . C. S  125 . D. S  120 . ABC ABC ABC ABC
Họ và tên tác giả: Vũ Thị Hằng Tên FB: Đạt Lâm Huy
Câu 63: Cho tam giác ABC M thuộc cạnh AC sao cho MA   M . 2
C , N thuộc BM sao cho NB  . 3
NM , P thuộc BC sao cho PB k.PC . Tìm giá trị k để ba điểm A, N, P thẳng hàng. 1 1 A. k .
B. k  2 . C. k   .
D. k  2 . 2 2
Họ và tên: Nguyễn Khắc Sâm Facebook: Nguyễn Khắc Sâm
VẤN ĐỀ 3. QUỸ TÍCH    
Câu 64: Cho tam giác ABC với J là điểm thoả mãn 2JA  5JB  3JC  0 , gọi E là điểm thuộc  
AB và thoả mãn AE kAB . Xác định k để C, E, J thẳng hàng.
A. k  2;  1 .
B. k  1;0 .
C. k  0;  1 .
D. k  1;2
Nguyễn Văn Dũng Fb: Nguyễn Văn Dũng, Email: dungtoanc3hbt@gmail.com
Câu 65: Cho hình vuông ABCD tâm O cạnh 1 . Biết rằng tập hợp các điểm M thỏa mãn 2 2 2 2
2MA MB  2MC MD  9 là một đường tròn có bán kính R . Khẳng định nào sau đây đúng?
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 12
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  1 3   3 
A. R  0;  1 .
B. R  1; 2 . C. R  ; . D. R  ; 2 .      2 2   2 
(Sưu tầm: Lê Hồ Quang Minh – FB: Lê Minh)
Câu 66: Cho tam giác ABC . Tập hợp những điểm M thỏa mãn:
  
  
4MA MB MC  2MA MB MC là:
A. Đường thẳng đi qua A
B. Đường thẳng qua B và C C. Đường tròn
D. Một điểm duy nhất.
(Họ và tên tác giả: Cấn Việt Hưng, Tên FB: Viet Hung)
Câu 67: Cho tam giác ABC có hai đỉnh B, C cố định với BC  2a . Gọi H là trực tâm của tam giác
ABC và M là trung điểm của đoạn BC. Nếu đỉnh A thay đổi nhưng luôn thỏa   2 2 M .
A MH MA  4a thì điểm A luôn thuộc một đường tròn cố định có bán kính bằng A. 2a . B. a 3 . C. a 2 . D. a .
(Họ và tên tác giả: Ngô Lê Tạo, Tên FB: Ngô Lê Tạo)
Câu 68: Cho hai điểm A và B cố định. Tìm giá trị k  0 để tập hợp điểm M thỏa mãn điều kiện 2 2
MA MB k là một đường tròn. 2 2 2 2 A. 2 k AB . B. 2 k AB . C. 2 k AB . D. 2 k AB . 3 3 3 3
Câu 69: Cho tam giác vuông ABC tại A . Tìm tập hợp M sao cho 2 2 2
MB MC MA . A. Đường thẳng. B. Đường tròn. C. Đoạn thẳng. D. Một điểm.
PHẠM THANH LIÊM FB: Liêm Phạm, Email: Phamthanhliem1@gmail.com
Câu 70: Cho tam giác ABC vuông cân tại A có AB  5cm . Gọi (S ) là tập hợp các điểm M trong mặt
   
phẳng thỏa mãn hệ thức: M . A MB M .
A MC  25 . Gọi I là trung điểm của BC . Kết luận nào
sau đây đúng?
A. (S ) là đường thẳng trung trực của đoạn thẳng AI .
B. (S ) là đoạn thẳng AI . 5 10
C. (S ) là đường tròn cố định bán kính R  . 4 5 2
D. (S ) là đường tròn tâm I bán kính R  4
(Họ và tên tác giả: Trịnh Văn Thạch, FB: www.facebook.com/thachtv.tc3)
Câu 71: Cho tam giác đều ABC cạnh a . Tập hợp các điểm M thỏa mãn đẳng thức 2 5a 2 2 2
4MA MB MC
nằm trên một đường tròn C  có bán kính là: 2 a a a 3 a A. . B. . C. . D. . 3 4 2 6   
   Câu 72: Cho A
BC . Tìm tập hợp các điểm M sao cho: MA  3MB  2MC  2MA MB MC .
A. Tập hợp các điểm M là một đường tròn.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 13
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
B. Tập hợp của các điểm M là một đường thẳng.
C. Tập hợp các điểm M là tập rỗng.
D. Tập hợp các điểm M chỉ là một điểm trùng với A.
Câu 73: Cho tam giác đều ABC cạnh a . Tập hợp các điểm M thỏa mãn đẳng thức 2 5a 2 2 2
4MA MB MC
nằm trên một đường tròn C  có bán kính là: 2 a a a 3 a A. . B. . C. . D. . 3 4 2 6
Họ và tên tác giả: Vũ Thị Nga Tên FB: Linh Nga,Email: linhnga.tvb@gmail.com
Câu 74: Cho ABC đều, có cạnh bằng a. Khi đó tập hợp những điểm M sao cho 2
      a . MA MB  .
MB MC MC.MA  là: 6 a
A. Đường tròn có bán kính R  . 3 a
B. Đường tròn có bán kính R  . 2 a 2
C. Đường tròn có bán kính R  . 3 a 3
D. Đường tròn có bán kính R  . 9  
Câu 75: Cho ABC tìm tập hợp điểm M 2 : . MB MC AM
Họ và tên tác giả: Tô Quốc An Tên FB: Tô Quốc An, Email: antq4949@gmail.com
Câu 76: Cho tam giác đều ABC cạnh bằng 3 . Biết rằng tập hợp các điểm M thỏa mãn đẳng thức     
2MA 3MB  4MC MB MA là đường tròn cố định có bán kính bằng: 1 3 1 A. 1. B. . C. . D. . 3 2 2
(Họ tên: Lê Thị Bích Hải, Tên face: Bich Hai Le)
Câu 77: Cho tam giác ABC có là trọng tâm G . Tìm tập hợp điểm M thỏa mãn
        
MAMB MC BC2 MAMC MG2  CB AC2 3 .
A. Đường tròn đường kính AB .
B. Đường trung trực đoạn thẳng AB .
C. Đường tròn đường kính AC .
D. Đường trung trực đoạn thẳng AC .
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông)  
Câu 78: Cho đoạn thẳng AB  5 . Biết rằng tập hợp điểm M thỏa mãn 2 2 MA MB  3 . MA MB là
một đường tròn có bán kính R . Tìm giá trị của R . 5 5 3 3 A. R  . B. R  . C. R  . D. R  . 2 2 2 2
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông)
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 14
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
  
Câu 79: Cho tam giác ABC , có bao nhiêu điểm M thỏa MA MB MC  5 ? A. 1. B. 2 . C. vô số.
D. Không có điểm nào.
Họ và tên: Võ Khánh Huyền Vân Fb: Vân Võ, Email: huyenvanqt050185@gmail.com .
VẤN ĐỀ 4. TỈ LỆ
Câu 80: Cho  ABC có AB  3 ; AC  4 . Phân giác trong AD của góc BAC cắt trung tuyến BM tại AD I . Tính . AI AD 3 AD 10 AD 29 AD 7 A.  . B.  . C.  . D. AI 2 AI 7 AI 20 AI 5
Họ và Tên: Trần Quốc Đại, Email: quocdai1987@gmail.com
Câu 81: [Đề thi olympic 30/4 TPHCM khối không chuyên lần 2 ] Cho  ABC gọi điểm D nằm trên
cạnh BC sao cho BD  2BC , E là trung điểm của AD . Một đường thẳng bất kì qua E và cắt AB AC các cạnh A ;
B AC lần lượt tại M , N . Tình tỉ số  2 AM AN AB AC AB AC A.  2  6 . B.  2  5 . AM AN AM AN AB AC 28 AB AC 29 C.  2  . D.  2  AM AN 5 AM AN 5
Họ và Tên: Trần Quốc Đại, Email: quocdai1987@gmail.com
Câu 82: Cho tam giác ABC . Trên cạnh AB lấy điểm D sao cho AD  2DB . Trên cạnh AC lấy điểm BN
E sao cho CE  3EA . Gọi M là trung điểm của DE . Tia AM cắt BC tại N . Tỉ số có CN giá trị là: 1 3 1 2 A. . B. . C. . D. . 4 8 2 7
Họ và tên tác giả: Đỗ Văn Đức Tên FB: Đỗ Văn Đức
Câu 83: (Bài toán tổng quát của bài toán 1). Cho tam giác ABC . Gọi I là điểm chia BC theo tỉ số k . AB AC
Trên các tia AB và AC lấy các điểm M , N . AI cắt MN tại P . Đặt  b ,  c . Tỷ AM AN AI số có giá trị bằng AP b kc b kc c kb c kb A. . B. . C. . D. . 1 k 1 k 1 k 1 k
Câu 84: (Hệ quả hay dùng của bài toán 2). Cho tam giác ABC . Gọi I là trung điểm của BC. Trên các AB AC AI
tia AB và AC lấy các điểm M , N . AI cắt MN tại P . Đặt  b ,  c . Tỷ số có AM AN AP giá trị bằng
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 15
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New b c 2 2 b c 2bc A. bc . B. . C. . D. . 2 2 b c
 2   1 
Câu 85: Cho tam giác ABC . Gọi D, E lần lượt là các các điểm thỏa mãn BD BC, AE AC . 3 4 AD
Điểm K trên đoạn thẳng AD sao cho ba điểm B, K , E thẳng hàng. Tìm tỉ số . AK AD 1 AD AD 2 AD 3 A.  . B.  3 . C.  . D.  . AK 3 AK AK 3 AK 2
Tên: Nam Phương Tên FB: Nam Phương, Email:nguyentrietphuong@gmail.com    
Câu 86: Cho tứ giác ABCD có hai đường chéo cắt nhau tại O thỏa mãn OC  3O ,
A OD  4OB . CN
Qua trung điểm M của AB dựng đường thẳng MO cắt CD tại N . Tính tỉ số . ND 3 1 2 1 A. . B. . C. . D. . 4 4 3 3
Email: haivanxinh99@gmail.com Face Hải Vân    
Câu 87: Cho tam giác ABC và điểm I thỏa mãn 23IA  8IB  2018IC  0 . Đường thẳng AI cắt JB
đường thẳng BC tại J . Giá trị của tỉ số là: JC 23 2018 2018 8 A. B. C. D. 8 23 8 23
(Họ và tên tác giả: Ngô Ngọc Hà, Tên FB: Ngô Ngọc Hà)
Câu 88: Cho tam giác ABC . Điểm K chia trung tuyến AD theo tỷ số 3 :1 kể từ đỉnh. S
Đường thẳng BK chia diện tích tam giác ABC theo tỷ số ABF k
, giá trị của k bằng? SBCF 5 3 3 3 A. k B. k C. k D. k  8 8 5 2
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)  
Câu 89: Cho tam giác ABC với K là trung điểm BC . Lấy các điểm M , N thỏa mãn 3 AM AB , 4       1 x AN
AC . Gọi I là giao điểm của MN và AK . Đặt MI xMN , AI y AK . Hỏi 3 y A. 3 . B. 4 . C. 1. D. 5 . 2 3 3
Họ và tên: Tăng Lâm Tường Vinh, Facebook: tanglamtuong.vinh AD 3
Câu 90: Cho tam giác ABC . Trên cạnh AB lấy điểm D, trên cạnh BC lấy E, F sao cho  ; DB 2 BE 1 BF 4 KD  
. Đường thẳng AE chia đoạn DF theo tỷ số
k . Giá trị của k bằng? ; EC 3 FC 1 KF 3 11 3 11 A. k B. k C. k D. k  11 3 14 14
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 16
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
Câu 91: Cho tam giác ABC . Kéo dài AB một đoạn BE AB , gọi F là trung điểm của AC . Vẽ hình KB
bình hành EAFG . Đường thẳng AG cắt BC tại K . Tính tỉ số ? KC 1 3 1 2 A. . B. . C. . D. . 4 8 5 7
Câu 92: Họ và tên: Hoàng Ngọc Lâm,Email: hoangngoclammath1112@gmail.com
Câu 93: Cho tam giác ABC có AB  3 , AC  4 . Phân giác trong AD của góc BAC cắt trung tuyến AD
BM tại I . Tính tỉ số . AI 13 11 10 10 A. . B. . C. . D. . 8 6 7 5
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Câu 94: Cho hình bình hành ABCD , O là điểm bất kì trên đoạn AC , đường thẳng BO cắt cạnh CD AF
tại E và đường thẳng AD tại F sao cho EF  2BO . Tỷ số bằng AD 1 5 5 A. . B. 2 . C. 1 2 . D. . 2 2
Họ và tên: Nguyễn Văn Toản Tên FB: Dấu Vết Hát,Email: nguyenvantoannbk@gmail.com
Câu 95: Cho hai tam giác ABC và A B C ; gọi A , B ,C lần lượt là trọng tâm các tam giác 1 1 1 2 2 2
BCA , CAB , ABC . Gọi G,G ,G lần lượt là trọng tâm các tam giác ABC, A B C , 1 1 1 1 2 1 1 1 GG
A B C . Tính tỉ số 1 ta được kết quả : 2 2 2 GG2 1 1 A. B. C. 3 D. 2 3 2
Họ và Tên : Nguyễn Văn Mạnh FB : Nguyễn Văn Mạnh, Email :
manhluonghl4@gmail.com VẤN ĐỀ 5. MIN,MAX Câu 96: Cho A
BC đều cạnh bằng 3, M là điểm thuộc đường tròn ngoại tiếp ABC . Đặt 2 2 2
P MA MB MC . Gọi a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P . Khi đó,
giá trị biểu thức T  4a b là: A. 3 . B. 6 . C. 9 . D. 12 .
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng Câu 97: Cho A
BC và 3 số dương x, y, z thay đổi có tổng bình phương: 2 2 2 2
x y z k , k R . Giá
trị lớn nhất của P xy cos C yz cos A zx cosB là: k 2 k k 2 k A. . B. . C. . D. . 2 2 3 3
Họ và tên tác giả: Trần Văn Ngờ Tên FB: Tran Van Ngo Tth, Email:
vanngodhqn@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 17
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 98: Cho hai điểm ,
A B (I;6) và M (I;3) , thỏa mãn : AIB  60 . Khi A, B , M thay đổi tìm giá
trị nhỏ nhất của biểu thức P MA  2MB ? A. 9 . B. 3  2 6 . C. 3 13 . D. 6  3 .
( Họ và tên tác giả : Đặng Mơ- Tư Duy Mở )
Câu 99: Cho tứ giác ABCD , M là điểm tùy ý và các điểm I, J, K cố định sao cho đẳng thức thỏa mãn
    
với mọi điểm M: MA MB MC  3MD k MK. Giá trị của k là A. k = 3 B. k = 4 C. k = 5 D. k = 6
Câu 100: Cho tam giác ABC vuông tại
A. Gọi  là góc giữa hai đường trung tuyến BD và CK. Giá
trị nhỏ nhất của cos bằng 4 5 4 3 A. B. C. D. 5 4 3 4
Câu 101: Cho hai điểm cố định G và G ' là trọng tâm của tam giác ABC và tam giác A' B 'C '. Giá trị
nhỏ nhất của biểu thức P AA' BB ' CC ' bằng 1 A. GG '
B. 3GG '
C. 2GG ' D. GG ' 3
Họ và tên: Nguyễn Đức Hoạch – email: nguyenhoach95@gmail.com  
Câu 102: Cho hình thang A B C D có 0
A B / /C D , A B  3a,C D  2a, D A B C B A  60 . Với 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1   
mỗi điểm G di động trên cạnh A B ta xác định điểm F sao cho G F G C G D . Tìm 1 1 1 1 1 1 1 1 1 1 
độ dài nhỏ nhất của G F . 1 1 3a 3 3a A. 2a . B. a 3 . C. . D. . 2 2
Mail: nguyennga82nvc@gmail.com, FB: Nguyễn Nga Nvc
Câu 103: Cho tam giác ABC vuông ở A; BC = 2; CA = b; AB = c và điểm M di động Biểu thức F= 2 2 2 2 2 8
 MA  b MB  c MC đạt giá trị lớn nhất bằng A. 4 B. 12 C. 16 D. 24
Nguyễn Văn Công- Trường THPT Kinh Môn II, Gmail: nguyencongkm2@gmail.com
Câu 104: Cho ABC đều có cạnh bằng 2a . Gọi d là đường thẳng qua A và song song BC , điểm M di   
động trên d . Tìm giá trị nhỏ nhất của MA  2MB MC . a 3 a 3
A. 2a 3 . B. a 3 . C. . D. . 4 2
Họ và tên tác giả: Vũ Viên Tên FB: Vũ Viên, Email: tieplen@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 18
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 105: Trong mặt phẳng cho tam giác ABC và một điểm M bất kỳ. Đặt a BC, b C ,
A c AB . Tìm MA MB MC
giá trị nhỏ nhất của biểu thức T    . a b c 3 3 A. 3 3 . B. 3 . C. . D. . 3 2
Họ và tên tác giả: Phạm Khắc Thành, Email: phamkhacthanhkt@gmail.com
Câu 106: Cho tam giác ABC có trung tuyến A ' A C ' C  ' A BC, '
C AB . Tìm giá trị nhỏ nhất của cos . B 4 2 1 A. . B. . C. 1. D. 5 5 2
Mail: thuytrangmn@gmail.com
Câu 107: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto   
aMA bMB cMC có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê, Email: hongle.ad@gmail.com
Câu 108: Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC .      
Khi đó, giá trị nhỏ nhất của biểu thức T MA MB MC  3 MA MB MC là: 2a 3 5a 3 A. MinT  .
B. MinT  2a 3.
C. MinT a 3. D. MinT  . 3 2
Họ và tên: Ngô Gia Khánh, Địa chỉ mail: ngkhanh4283@gmail.com Câu 109: Cho ABC và A
 ' B 'C ' có các trọng tâm G và G ' cố định và GG '  a . Khi đó giá trị nhỏ nhất
của T  AA ' BB ' CC ' là:
A. T a .
B. T  2a .
C. T  3a .
D. T  4a .
(Họ và tên tác giả: Phạm văn Tài, Tên FB: TaiPhamVan)
Câu 110: Cho tam giác ABC với các cạnh AB  ,
x AC y ;  x y  0 . Gọi AD là đường phân giác   
trong của góc A . Biết biểu thị vectơ AD mAB n AC . Tính S m n . A. S  2 . B. S  0 . C. S  1 . D. S  2 .
Mail: thongbui1987@gmail.com
Câu 111: Cho ABC có AB  3 ; AC  4 . Phân giác trong AD của góc BAC cắt trung tuyến BM tại I AD a a . Biết 
, với a, b   và
tối giãn. Tính S a  2b . AI b b
A. S  10 .
B. S  14 .
C. S  24 .
D. S  27 .
Câu 112: Cho tứ giác ABCD có AD và BC cùng vuông góc với AB , AB  8 , AD a , BC b . Gọi
E là một điểm thuộc cạnh CD . Biết 
AEB  90 , giá trị lớn nhất của T ab là A. 4 . B. 16 . C. 8 . D. 64 .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 19
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên tác giả: Lê Hồng Phi Tên FB: Lê Hồng Phi, Email: lehongphivts@gmail.com
Câu 113: Cho tứ giác ABCD có AD và BC cùng vuông góc với AB , AB h , AD a , BC b . Cho   
k là số thực dương thuộc 0 
;1 và điểm E thỏa mãn k EC  1 k ED  0 . Tìm hệ thức liên hệ
giữa a , b , h , k để góc  AEB  90 ?
A. 1 k b ka h k 1 k  .
B. kb  1 k a hk 1 k  .
C. kb  1 k a h k 1 k  .
D. 1 k b ka hk 1 k  .
Câu 114: Cho tam giác có trọng tâm G , qua G dựng đường thẳng d cắt cách cạnh AB , AC lần lượt AM AN
tại M , N . Đặt  x ,
y , gọi m , M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của AB AC
T x y . Tính m M . 10 17 11 5 A. . B. . C. . D. . 3 6 6 2
(Họ và tên tác giả: Hoàng Thị Thanh Nhàn, Tên FB: Hoàng Nhàn)  1 
Câu 115: Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho BH  HC . 3    
Điểm M di động trên BC sao cho BM  xBC . Tìm x sao cho MA  GC đạt giá trị nhỏ nhất. 4 5 5 6 A. . B. . C. . D. . 5 4 6 5
Họ và tên: Nguyễn Thị Thu, Email: thutoan83@gmail.com, Facebook: Nguyễn Thị Thu
Câu 116: Cho tam giác ABC đều cạnh 2 3 , d là đường thẳng qua B và tạo với AB một góc 0 60   
C  . Tìm giá trị nhỏ nhất của A MA MB  3MC ? 3 12 4 A. B. C. D. 2 5 5 5
(Tác giả: Hoàng Thị Thúy - Facebook: Cỏ ba lá )
Câu 117: Cho tam giác ABC đều cạnh 1 nội tiếp đường tròn ( )
O và điểm M thay đổi trên O . Gọi s , i
  
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức MA MB MC . Tính s i . 4 3 5 3
A. s i  3 .
B. s i  .
C. s i  .
D. s i  2 3 . 3 3
Câu 118: Cho lục giác đều ABCDEF cạnh a . Trên đường chéo AC , CE lấy hai điểm M , N sao cho AM CN
k 0  k   1 . Độ dài 2 2
BM BN đạt giá trị nhỏ nhất khi k bằng bao nhiêu? AC CE 1 1 2 3 A. . B. . C. . D. . 2 4 3 4
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1)
Câu 119: Cho hình chữ nhật ABCD có AD a , AB b . O và I lần lượt là trung điểm DB và DO . 
   
N là điểm thỏa mãn 2NA  2NC AB AD  2 AD và NB lớn nhất. Tính NB .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 20
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 2
2a  3 a b 2 2
a a b 2 2
2a  3 a b 2 2
2a a b A. B. C. D. . 2 2 4 4
Câu 120: Cho tam giác ABC, AB  3(cm), BC  4(cm), CA  5(cm). Điểm M thuộc đường tròn ngoại tiếp
tam giác ABC. Giá trị nhỏ nhất của biểu thức 2 2 2
P MB MC MA là 5 97 5 97 5 97 A. 0 . B. 5  . C. 5  . D. 5  . 2 2 4
Phuongthao.nguyenmaths@gmail.com
Câu 121: Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho  1    BH
HC . Điểm M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của 3  
vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . . B. . . C. . . D. . 5 6 5 4
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)  
Câu 122: Cho hình thang ABCD có đáy CD gấp đôi đáy AB. Lấy một điểm E sao cho 3BC  2DE và
đồng thời thỏa mãn CA CE . Giá trị nhỏ nhất của góc 
ABC nằm trong khoảng nào dưới đây? A. (95;100 ) . B. (100;106 ) . C. (106;115 ) . D. (115;120 ) .
Họ tên tác giả: Đoàn Phú Như, Tên fb: Như Đoàn, Email: doanphunhu@gmail.com    
Câu 123: Cho hình thang ABCD có 2 AB DC , AC  8, BD  6 , góc tạo bởi hai véc tơ AC và BD
bằng 120 . Khi đó giá trị của (AD BC) bằng: 13  2 5 14  4 7 15  2 10 A. . B. . C. . D. 6  4 3 . 2 3 4
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )  
Câu 124: Cho hình thang ABCD có 2 AB DC , AC  9, BD  6 . Giá trị của biểu thức 2 2 (BC AD ) bằng: 80 A. 15 . B. . C. 12 . D. 14 . 3
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Câu 125: Cho tam giác ABC có BAC  60 và A ,
B AC đã biết. Biểu thức P k.MA MB MC đạt
giá trị nhỏ nhất bằng (AB AC) với mọi giá trị thực k k . Giá trị của k nằm trong khoảng 0 0 nào dưới đây?
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 21
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 3 3 A. (0;1) . B. ( ; 2) . C. (1; ) . D. (2;3) . 2 2
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái )
Câu 126: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto   
aMA bMB cMC có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê
Câu 127: Cho tam giác ABC đều cạnh a và điểm M thay đổi. Giá trị nhỏ nhất của biểu thức 2 2 2
P  2MA  3MB  4MC là: 2 26a 2 26a A. 2 14a B. 2 14a C. D. 3 3
Họ và tên: Nguyễn Thị Tuyết Lê FB: Nguyen Tuyet Le
Câu 128: Cho tam giác ABC có hai đường trung tuyến kẻ từ B và C vuông góc với nhau. Tính giá trị
nhỏ nhất của cos A . 1 2 3 4 A. . B. . C. . D. . 2 3 4 5
Họ và tên tác giả: Đặng Văn Tâm Tên FB: Đặng Văn Tâm, Email: dvtam0189@gmail.com    
Câu 129: Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB .
Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2 . a 2 2
Họ và tên: Phương Xuân Trịnh Tên FB:: Phương Xuân Trịnh, Email:
phuongtrinhlt1@gmail.com
Câu 130: Cho tam giác ABC vuông tại A . Gọi  là góc giữa hai trung tuyến BD và CK . Giá trị nhỏ nhất của cos là:. 1 4 2 3 A. . B. . C. . D. . 2 5 3 4  1  Câu 131: Cho A
BC có trọng tâm G. Gọi H là chân đường cao kẻ từ A sao cho CH HB . Điểm M di 3    
động trên BC sao cho CM  .
x CB . Tìm x sao cho độ dài vecto MA GB đạt giá trị nhỏ nhất. 8 5 6 5 A. . B. . C. . D. . 5 6 5 8
( Họ và tên tác giả: Nguyễn Văn Phu, Tên FB Nguyễn Văn Phu)    
Câu 132: Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB .
Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ?
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 22
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New a a 3 A. . B. . C. a. D. 2a. 2 2
Câu 133: Cho AD và BE là hai phân giác trong của tam giác ABC . Biết AB  4 , BC  5 và CA  6 .  Khi đó DE bằng: 5  3  3  5  9  3  3  9  A. CA CB .
B. CA CB .
C. CA CB .
D. CA CB . 9 5 5 9 5 5 5 5
Họ và tên: Nguyễn Thị Thanh Thảo Tên FB: Nguyễn Thanh Thảo
Câu 134: : Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho    
MA MB MA MB . Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2 . a 2 2   
Câu 135: Một miếng gỗ có hình tam giác có diện tích là S điểm I , O lần lượt thỏa mãn IB IC  0 ;   
OA OI  0 . Cắt miếng gỗ theo một đường thẳng qua O , đường thẳng này đi qua M , N lần
lượt trên các cạnh AB, AC . Khi đó diện tích miếng gỗ chứa điểm A thuộc đoạn: S S   S S   3S S   S 3S A. ; . B. ; . C. ; . D. ;  4 3           3 2   8 2   4 8 
Họ và tên tác giả: Hoàng Tiến Đông, Tên FB: tiendongpt, Email: dongpt@c3phuctho.edu.vn
Câu 136: Cho tam giác ABC có bán kính đường tròn ngoại tiếp R  2 . Tìm giá trị lớn nhất của 2 2 2
BC AB AC . A. 1. B. 2. C. 3. D. 4
Đỗ Công Dũng, Email: congdung812@gmail.com
Câu 137: Cho tam giác đều ABC cạnh .
a Gọi M là điểm nằm trên cạnh A .
B Tính giá trị nhỏ nhất của   
biểu thức MA  2MB MC theo . a a 3 a 3 a 3 2a 3 A. . B. . C. . D. . 4 2 8 3
Câu 138: Cho hình bình hành ABCD, M thuộc đường chéo AC, (M không trùng với các đỉnh A, C)
Trên các đường thẳng AB, BC, lấy các điểm P và Q sao cho MP // BC, MQ // AB. Gọi N là
giao hai đường thẳng AQ và CP. Giả sử DN mDA nDC . Tìm giá trị lớn nhất của m + n 4 3 1 A. B. C. D. 2 3 4 2
Email: themhaitotoanyp1@gmail.com, (Fb: Lưu Thêm)
Câu 139: : Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho  1    BH
HC . Điểm M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của 3  
vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . B. . C. . D. . 5 6 5 4
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 23
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên: Lê Thị Lan FB: Lê Lan, Email: lelanqx2@gmail.com
Câu 140: Cho tam giác ABC có BC  , a AC  ,
b AB c nội tiếp đường tròn tâm O, bán kính R. M là
điểm thuộc đường tròn (O). Gọi N, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2 2
P MA MB MC . Khi đó giá trị của N n bằng A. 2 12R . B. 2 2 2 2
4R 9R  a b c . C. 2 2 2 2
2R 9R  a b c . D. 2 2 2 2
8R 9R  a b c .
Tác giả: Nguyễn Văn Hưng Facebook: Nguyễn Hưng
Câu 141: Cho tam giác đều ABC nội tiếp đường tròn tâm O ,bán kính R , M là một điểm bất kì trên
đường tròn. Giá trị lớn nhất của biểu thức 2 2 2
S MA  2MB  3MC là A. 2 R 21 . B. 2 R 21 . C. 2 2R 21 . D. 2 2  R 21 .
Họ và tên: Nguyễn Xuân Giao Tên FB: giaonguyen, Email: giaohh2@gmail.com
Câu 142: Cho tam giác ABC . Tìm giá trị nhỏ nhất của biểu thức P  3 cos 2 A  2 cos 2B  2 3 cos 2C 3 1 A. P  4 . B. . C. 2 3 3 . D. . min Pmin P    2 min P  5 min
Họ và tên: Đồng Anh Tú Facebook: Anh Tú
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
     
Câu 143: Cho tam giác đều ABC cạnh a . Tính A .
B BC BC.CA C . A AB 2 3a 2 3a 2 a 3 2 a 3 A. B. C. D.  2 2 2 2
Họ và tên: Nguyễn Văn Nho Facebook: Nguyễn Văn Nho
Câu 144: Cho tam giác ABC có AD là trung tuyến, G là trọng tâm. Một đường thẳng qua G cắt các
cạnh AB, AC lần lượt tại M , N . Khẳng định nào sau đây đúng?   1   2  
A. AM .AN AN.MB AM .NC 2 3
     
B. AM .AN AN.MB AM .NC   2    
C. AM .AN
( AN.MB AM .NC) 3   3    
D. AM .AN
( AN.MB AM .NC) 2
Email: ngvnho93@gmail.com          
Câu 145: Cho các véc tơ a , b , c thỏa mãn
a a , b b , c c và a b  3c  0 . Tính       A  . a b  . b c  . c a . 2 2 2
3c a b 2 2 2
3a c b A. . B. . 2 2 2 2 2
3b a c 2 2 2
3c a b C. . D. . 2 2
Tác giả: Quang Phi
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 24
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 146: Cho tam giác ABC vuông tại A có BC = 2a, M là điểm trên đoạn BC sao cho MB = 2MC. Biết   rằng 2
AM .BC a . Độ dài cạnh AC là: a 33 a 3 A. AC
B. AC a 3 C. AC
D. AC a 5 3 3
Họ và tên: Đoàn Thị Hường, Email: ngochuongdoan.6@gmail.com, Fb: Đoàn Thị Hường Câu 147: Cho tam giác ABCcó 0
BAC  90 , AB  1, AC  2 .Dựng điểm M sao cho   
AM BC , AM  3. Đặt AM  . x AB  . y AC .Tính 2 2
T x y ? 153 151 157 159 A. T . B. T . C. T . D. x . 20 20 20 20
Họ tên: Đào Hữu Nguyên FB: Đào Hữu Nguyên, Mail: huunguyen1979@gmail.com
   
Câu 148: Cho tam giác ABC vuông tại
A. Quỹ tích điểm M thỏa mãn 2 M . B MC M .
A BC MA là
A. Đường thẳng AC.
B. Đường thẳng AB.
C. Đường thẳng BC.
D. Đường trung trực cạnh BC.
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon
Câu 149: Cho tam giác đều ABC cạnh 3a , a  0 . Lấy các điểm M , N , P lần lượt trên các cạnh
BC , CA , AB sao cho BM a , CN  2a , AP x 0  x  3a . Tìm x để AM PN . 3a 4a A. x  . B. x  . 5 5 a 2a C. x  . D. x  5 5
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon
Câu 150: Cho tam giác ABC vuông cân tại B . Gọi M là trung điểm AB và I là điểm di động trên   AC
đường thẳng MC . Khi 2IM AC đạt giá trị nhỏ nhất, hãy tính tỉ số . AI AC AC AC AC 3 A.  1 . B.  2 . C.  2 . D.  . AI AI AI AI 2
(Họ và tên tác giả: Nguyễn Đức Lợi, Tên FB: Nguyễn Đức Lợi)  1  Câu 151: Cho A
BC có trọng tâm G , H là chân đường cao kẻ từ A sao cho BH
HC . Điểm M di 3    
động trên BC sao cho BM xBC . Tìm x sao cho MA GC nhỏ nhất. 6 5 4 5 A. B. C. D. 5 4 5 6
Họ tên: Vũ Thị Chuyền FB: Vũ Thị Chuyền
Câu 152: Cho tam giác ABC, nhọn, không cân và nội tiếp đường tròn  ;
O R . Gọi G và M lần lượt là
trọng tâm tam giác ABC và trung điểm cạnh BC. Cho đường thẳng OG vuông góc với đường
thẳng OM tính giá trị biểu thức 2 2 2
AC AB  2BC theo R. A. 8R2. B. 10R2. C. 12R2. D. 14R2.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 25
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Lời giải
Họ và tên: Nguyễn Thị Trăng Fb: Trăng Nguyễn   
Câu 153: Cho tam giác MNP có MN=4,MP=8, M 0
= 60 Lấy điểm E trên tia MP và đặt ME  kMP .Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP. 2 2 1 1 A. k= . B. k= . C. k= . D. k= . 3 5 3 2
Họ và tên tác giả: Phạm Hồng Quang Tên FB: Quang Phạm
   
Câu 154: Đẳng thức M . A AD M .
B BC đúng với mọi điểm M. Khi đó tứ giác ABCD là hình gì.
A. Hình thang vuông. B. Hình chữ nhật. C. Hình thoi.
D. Tứ giác có hai đường chéo vuông góc. Lời giải
(Họ và tên tác giả: Phạm Trung Khuê, Tên FB: Khoi Pham)
Câu 155: Cho hình vuông ABCD cạnh a . Gọi M , N lần lượt thuộc các đoạn thẳng BC và AC sao cho  1    BM
MC , CN k AN và AM DN . Khi đó k thuộc khoảng nào dưới đây? 3 A. 3;5 . B.  5  ; 3   . C. 4; 2 . D. 2; 4 .
Họ và tên: Nguyễn Đắc Giáp Facebook: dacgiap        
Câu 156: Cho hai vector a, b thỏa mãn đồng thời các điều kiện a  2b  7, a b  2 , vector (3a b)    
vuông góc với (a b) . Tính cosin của góc tạo bởi hai vector a và b . 1 2 1 2 A.  . B. . C. . D.  . 3 4 3 4
Họ và tên tác giả: Ngô Nguyễn Quốc Mẫn Tên FB: Ngonguyen Quocman
Câu 157: Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh BC a;CA  ;
b AB c . Tìm 2 2 2 OA OB OC
giá trị biểu thức: K    . b c . c a . a b 1 1 1 A. K B. K C. K  1 D. K  2 3 4 CM CN 1
Câu 158: Cho hình vuông ABCD. M, N lần lượt nằm trên hai cạnh BC và CD sao cho   . CB CD 3  
Gọi E là điểm thỏa mãn AE kAN . Khi BE AM . Tính giá trị biểu thức T k 2  k  1. 13 7 8 5 A. B. C. D. 16 9 9 16
Họ và tên: Lê Thái Bình, Email: lebinhle80@gmail.com, Facebook: Lê Thái Bình AC
Câu 159: Cho hình vuông ABCD, điểm M nằm trên đoạn thẳng AC sao cho AM  . Gọi N là trung 4
điểm CD. Tam giác BMN là A. Tam giác đều. B. Tam giác cân.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 26
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New C. Tam giác Vuông.
D. Tam giác vuông cân
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa
Câu 160: Cho tam giác ABC . Gọi H là trực tâm và O là tâm đường tròn ngoại tiếp của tam giác ABC .
Đặt BC a , CA b , AB c . Tìm hệ thức liên hệ giữa a , b , c sao cho OH vuông góc với
trung tuyến vẽ từ đỉnh A của tam giác ABC . A. 2 2 2
2a b c . B. 2 2 2
2b a c . C. 2 2 2
2c a b . D. 2 2 2
b  2a  2c .
(Email): luongthanh80tm@gmail.com
Câu 161: Cho tam giác ABC có AD là trung tuyến, G là trọng tâm. Một đường thẳng qua G cắt các
cạnh AB, AC lần lượt tại M , N . Khẳng định nào sau đây đúng?   1   2  
A. AM .AN AN.MB AM .NC 2 3
     
B. AM .AN AN.MB AM .NC   2    
C. AM .AN
( AN.MB AM .NC) 3   3    
D. AM .AN
( AN.MB AM .NC) 2
(Sưu tầm, Họ và tên: Nguyễn Lương Thành, Tên FB: luongthanh.nguyen.7)
Câu 162: Cho hình chữ nhật ABCD có cạnh AB=2 và AD=4.Gọi M là trung điểm của cạnh AB và N là  
điểm trên cạnh AD sao cho AN k AD ,CM vuông góc với BN.Khi đó k thuộc vào khoảng nào sau đây  1   1 1   1 1   1 1  A. 0; B. ; C. ; D. ;          16   16 20   20 9   9 6 
Họ và tên:Phan Thông, Email:quocthong1182@gmail.com, Facebook:Quocthongphan   
Câu 163: Cho tam giác MNP có MN=4,MP=8, M 0
= 60 Lấy điểm E trên tia MP và đặt ME  kMP .Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP. 2 2 1 1 A. k= . B. k= . C. k= . D. k= . 3 5 3 2 Câu 164: Họ và tên: Phạm Hồng Quang Tên FB: Quang Phạm, Email:
phamhongquangltv@gmail.com
Câu 165: Cho tam giác ABC có BC a, CA b, AB c . M là trung điểm của BC , D là chân đường 2
phân giác trong góc A . Tính AD   2 4c 2 4bc A. AD p p a AD p a 2   2   . B. . b c b c   2 4bc 2 4bc C. AD p p a AD p p a 2   2   . D. b c b c
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Câu 166: Cho tam giác ABC có AB = c, AC = b và 0
BAC  60 . Các điểm M, N được xác định bởi     MC  2
MB và NB  2
NA . Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với nhau.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 27
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A. 2 2
6c  4b  5bc  0 . B. 2 2
4c  5b  6bc  0 . C. 2 2
6c  5b  4bc  0 . D. 2 2
4c  6b  5bc  0 .
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Câu 167: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi I là trung điểm của AC và M là điểm thỏa    
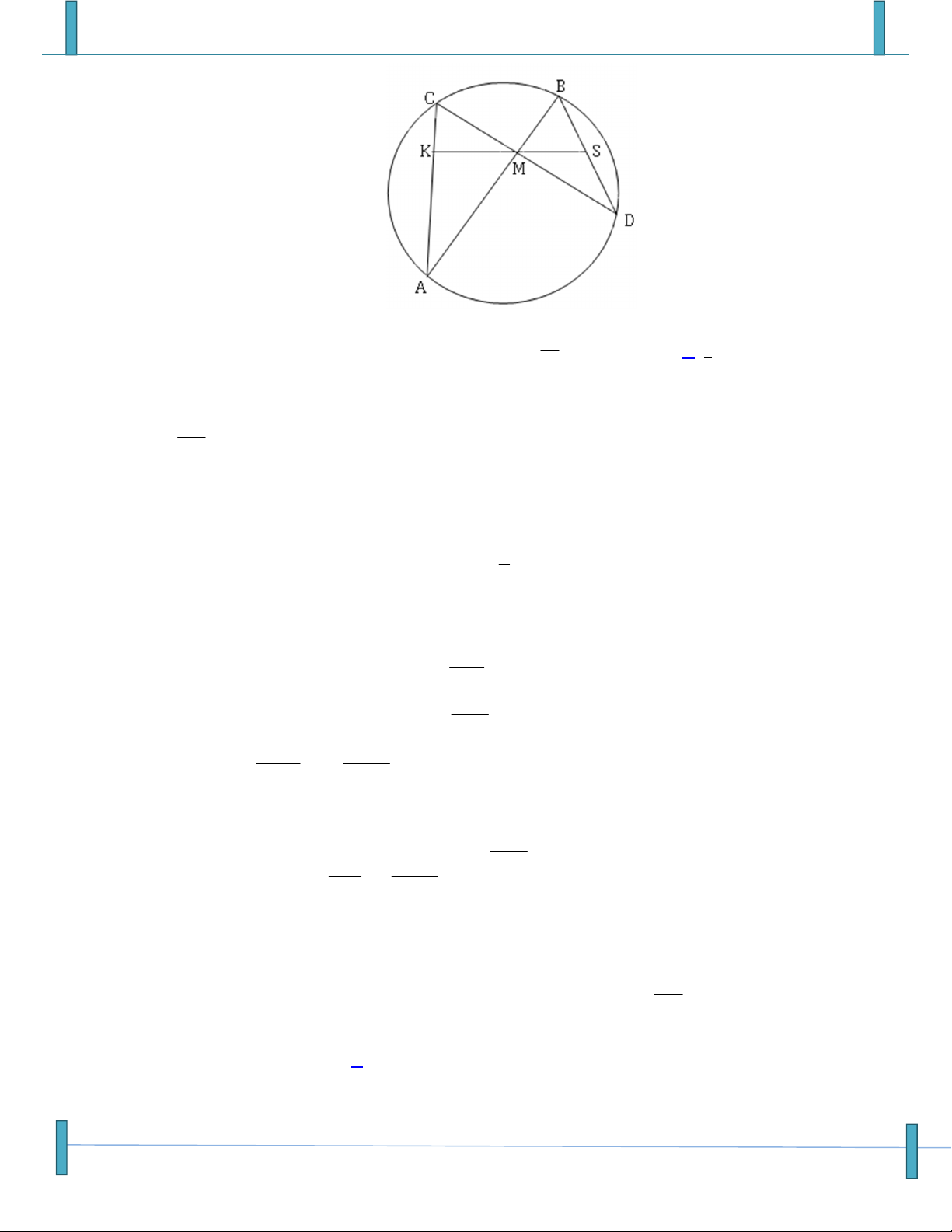
mãn OM  2OA OB  2OC . Biết rằng OM vuông góc với BI và 2 AC  3B . C BA . Tính góc  ABC . A. 30 . B. 45 C. 60 . D. 120 .
Họ tên: Trần Ngọc Tên FB: Ngọc Trần, Email: soantailieutoanhoc2018@gmail.com
Câu 168: Cho hình thang vuông ABCD, đường cao AD = h, đáy AB = a, đáy CD = b. Gọi M là trung
điểm của BC. Hệ thức giữa a, b, h để AM BD là A. 2 2
a h ab  0 . B. 2 2
h a ab  0 C. 2 2
h b ab  0 . D. 2 2
b h ab  0 .
Họ và tên tác giả: Đào Trung Kiên (st) Tên FB: kienyenthe, Email: kienyenthe@gmail.com   1
Câu 169: Cho tam giác đều ABC cạnh bằng a. Gọi M, N là các điểm thỏa mãn BM BC , 3   1 A N
AB . Gọi I là giao điểm của AM và CN. Tính diện tích của tam giác IBC theo a? 3 2 a 3 2 a 7 2 2a 7 2 2a 3 A. S. B. S. C. S. D. S. IBC 7 IBC 7 IBC 7 IBC 7
Họ và tên: Vũ Huỳnh Đức, Email: vutoanpvd@gmail.com, Facebook: vuhuynhduc2017    2 
Câu 170: Cho tam giác đều ABC và các điểm M , N , P thỏa mãn BM k BC , CN CA , 3  4  AP
AB . Tìm k để AM vuông góc với PN . 15 1 1 3 A. k B. k C. D. k 3 2 4
Họ và tên: Huỳnh Thanh Tịnh Tên FB: huynhthanhtinh, Email:
huynhthanhtinhspt@gmail.com
Câu 171: : Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh BC a;CA  ;
b AB c . Tìm 2 2 2 OA OB OC
giá trị biểu thức: K    . b c . c a . a b 1 1 1 A. K B. K C. K  1 D. K  2 3 4
Người sưu tầm: Tăng Duy Hùng. FB: Hùng Tăng    1      
Câu 172: Cho hai véc tơ a và b thỏa mãn các điều kiện a
b  1, a  2b  15. Đặt u a b và 2     
v  2k a b, k  .
 Tìm tất cả các giá trị của k sao cho u v    0 , 60 . 3 5 3 5 17 17 A. k  4  . B. k  4  . C. k  5  . D. k  5  . 2 2 2 2
Họ và tên: Nguyễn Thị Huệ, FB: Nguyễn Thị Huệ, Gmail: nguyenthihue1611@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 28
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
      AD
Câu 173: Cho tứ giác ABCD , hai điểm M , N thỏa mãn 2MB MA  0; 2NC ND  0 và  . x BC  cosDBC Tính
theo x để MN B . D  cos ADB x x x A. . B.  . C. . D. x 3 . 2 2 3
Họ và tên tác giả: Lê Thị Nguyệt Tên FB: NguyệtLê, Email: Lenguyet150682@gmail.com
Câu 174: Cho tam giác ABC có AB  6; BC  7;CA  5. Gọi M là điểm thuộc cạnh AB sao cho  
AM  2MB và N là điểm thuộc AC sao cho AN k AC ( k   a ). Biết k   b a (
là phân số tối giản, a,b là các số nguyên) sao cho đường thẳng CM vuông góc với đường b thẳng BN.
Tính giá trị biểu thức T  2018a  2019b  5 .
A. T  2017. B. T  2  020.
C. T  2030. D. T  2  030.
Họ và tên tác giả: Trần Thanh Hà Tên FB: Hatran, Email: tranthanhha484@gmail.com  0
Câu 175: Cho tam giác ABC có AB = c, AC = b và BAC  60 . Các điểm M, N được xác định bởi     MC  2
MB và NB  2
NA . Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với nhau. A. 2 2
6c  5b  4bc  0 B. 2 2
c  6b  5bc  0 2 2 2 2
C. 4c  6b  5bc  0 D. 4c  6b  5bc  0
Họ và tên tác giả: Đỗ Thế Nhất Tên FB: Đỗ Thế Nhất, Email: nhatks@gmail.com
Câu 176: Cho hình chữ nhật ABCD có AB= a, AD=2a. Gọi M là trung điểm AB, N là điểm trên cạnh  
AD sao cho AD  kAN . Tìm k để CM  BN. A. k=7,9 B. k=8 C. k=8,1 D. k=7.8
Câu 177: Cho hình bình hành ABCD có đường chéo lớn là AC . Gọi E, F lần lượt là hình chiếu vuông
góc của C trên AB, AD . Biểu thức nào sau đây là đúng. A. 2 AB.AH  .
AD AF AC . B. 2 . AB AE  . AD AF AC . C. 2 AB.AE  .
AD AH AC . D. A . B AE A .
D AF AC.AH .
Họ và tên tác giả: Nguyễn Ngọc Duy Tên FB: Ngọc Duy, Email:
nguyenngocduyakgl@gmail.com
Câu 178: Cho hình thang vuông ABCD , đường cao AD h , cạnh đáy AB a, CD b . Tìm hệ thức
giữa a, b, h để BD vuông góc trung tuyến AM của tam giác ABC . A. 2
h a a b . B. 2
h a b a .
C. h h b  a a b h . D. 2
2h a a b
Email: thuy.tranthithanhdb@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 29
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 179: Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R), M là điểm chính giữa cung BC (
cung BC không chứa điểm A). Chọn đẳng thức đúng trong các đẳng thức sau:
A. MA M .
B sin C MC.sin B
B. MA M .
B cos C MC.cos B
C. MA M .
B sin B MC.sin C
D. MA M .
B cos B MC.cosC
Họ và tên tác giả: Nguyễn Quang Nam Tên FB: Quang Nam, Email: quangnam68@gmail.com
Câu 180: Cho tam giác ABC có BC a, CA b, AB c . M là trung điểm của BC , D là chân đường   2
phân giác trong góc A . Tính AD 2  4c 2 4bc A. AD
p p a B. AD  p a 2 b c2 b c   2 4bc 2 4bc C. AD
pp a D. AD
pp a  2 b c2 b c
Họ Tên: Lương Thị Hương Liễu Tên FB: Hương Liễu Lương, Email:
lieuluong.290983@gmail.com
Câu 181: Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt
Nam có một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc 0 30 như
hình vẽ dưới đây. Trên các đường thẳng Ox và Oy người ta để hai vật nặng cùng trọng lượng.
Buộc hai vật thể với nhau bằng một thanh cứng AB  1m sao cho mỗi vật đều có thể chuyển
động được trên hai đường ray. Nối hai vật bằng một sợi giây vòng qua một cột có gốc tại O .
Người tham dự cuộc thi sẽ đứng tại vị trí điểm B để kéo vật thể chuyển động trên Oy . Người
thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc O . Hãy dùng kiến thức toán
học để tính toán vị trí xa nhất mà người tham dự cuộc thi có thể đạt được. A O B A. 1m . B. 2m . C. 3m . D. 2m .
Họ và tên: Phạm Thành Trung Tên FB: Phạm Thành Trung, Email:
trungthuong2009@gmail.com
Câu 182: Cho tam giác ABC có AB= c,BC=a,CA=b. Trung tuyến CM vuông góc với phân giác trong AL CM 3 và  . Tính cos A . AL 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 30
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 5 1 3 1 A. cos A B. cos A C. cos A D. cos A 2 4 2 2
Câu 183: Cho hình chữ nhật ABCD có AB  1;CD  3 . Điểm M thuộc cạnh AD và N là trung điểm BC m BN
sao cho MN BD . Phân số tối giản 
có m n bằng bao nhiêu n NC A. 29. B. 18. C. 16. D. 27.
(Họ và tên tác giả: Trần Văn Đoàn, Tên FB: Trần Văn Đoàn)
Câu 184: Cho tam giác ABC có AB c ; BC a , CA b . Gọi M là trung điểm của AB và D là
chân đường phân giác trong góc A của tam giác ABC . Biết rằng trung tuyến CM vuông góc
với phân giác trong AD . Khi đó đẳng thức nào sau đây đúng?
A. b  2c .
B. c  2b .
C. a b c .
D. c a b .
Họ và tên: Nguyễn Thị Thỏa Tên FB: Nguyễn Thị Thỏa, Email:
phamquynhanhbaby56@gmail.com
Câu 185: Cho tam giác ABC đều nội tiếp (O;R). M là điểm bất kì trên cung nhỏ BC . Khi đó
A. MA MB MC
B. MA MB MC
C. MA MB MC
D. MA  2MB MC
CÁC PHẦN CHÍNH CỦA CHUYÊN ĐỀ
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG VẤN ĐỀ 3. QUỸ TÍCH VẤN ĐỀ 4. TỈ LỆ VẤN ĐỀ 5. MIN,MAX
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
Phần II: Hướng Dẫn Giải
Trang: VĐ1-P35; VĐ2-P74; VĐ3-P88; VĐ4-P99; VĐ5-P110; VĐ6-P149
VẤN ĐỀ 1. BIỂU DIỄN VÉC TƠ
Email: daytoan2018@gmail.com
Câu 186: Cho tam giác ABC biết AB  3, BC  4, AC  6 , I là tâm đường tròn nội tiếp tam giác ABC     x y z
.Gọi x, y, z là các số thực dương thỏa mãn x.IA  . y IB  .
z IC  0 .Tính P    y z x 3 41 23 2 A. P  . B. P  . C. P  . D. P  . 4 12 12 3 Lời giải
Họ và tên tác giả: Vũ Ngọc Thành Tên FB: Vũ Ngọc Thành Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 31
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A D M I B N C E    IE  ID 
Dựng hình bình hành BDIE như hình vẽ. Khi đó IB IE ID   IA IC IA IC IE MB BC ID BN AB
Theo tính chất đường phân giác trong tam giác:   ,   IA MA AC IC NC AC  BC  AB  Suy ra IB   IA IC . AC AC      x  z  Từ x.IA  . y IB  .
z IC  0 suy ra IB   .IA  .IC . y y  
Do IA, IC là hai véc tơ không cùng phương suy ra x  4t, y  6t, z  3t với t  0 . x y z 41 Vậy P     . y z x 12
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet
Email: tiethanh.78@gmail.com
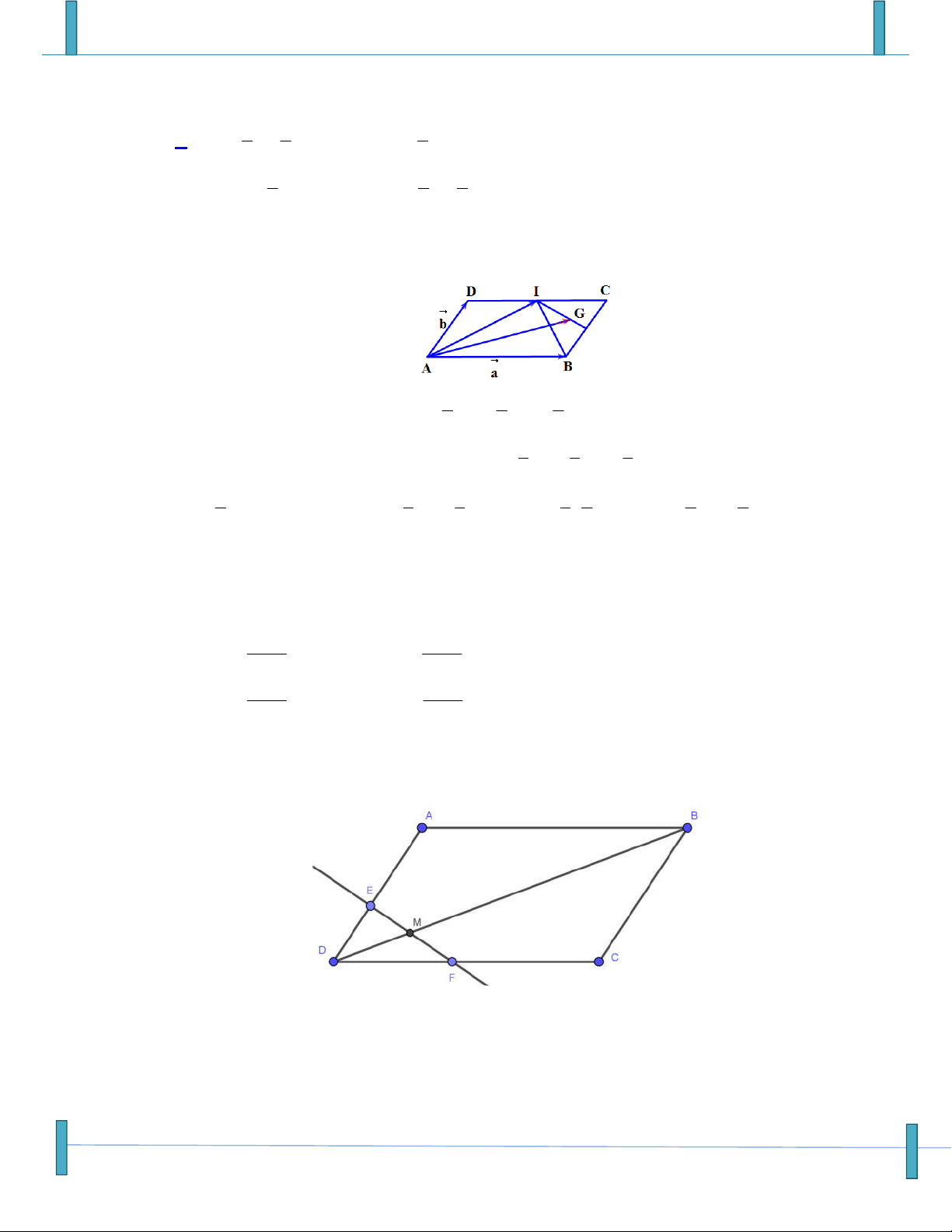
Câu 187: Cho hình bình hành ABCD . Gọi I là trung điểm của CD , G là trọng tâm tam giác BCI . Đặt    
a AB, b AD . Hãy tìm đẳng thức đúng trong các đẳng thức sau?  5  2   5   A. AG a b . B. AG a b . 6 3 6   5   4  2 
C. AG a b . D. AG a b . 6 3 3 Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 32
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  1  1  1  
* I là trung điểm của CD nên: AI AC AD AB AD . 2 2 2
 1  1  1 
  
* G là trọng tâm tam giác BCI nên: AG AB AC
AI , thay AC AB AD và 3 3 3  1  
 1  1   1  1    5  2  AI
AB AD ta được AG
AB   AB AD  AB AD AB AD   . 2 3 3 3  2  6 3
Họ và tên: Dương Bảo Trâm Facebook: Bảo Trâm
Email: ilovemath.ddt@gmail.com
Câu 188: Cho tam giác ABC với các cạnh AB c, BC a, CA b . Gọi I là tâm đường tròn nội tiếp
tam giác ABC. Đẳng thức nào sau đây đúng.        
A. aIA bIB cIC  0
B. bIA cIB aIC  0        
C. cIA bIB aIC  0
D. cIA aIB bIC  0 Lời giải A B' I B C C' Chọn A
Qua C dựng đường thẳng song song với AI cắt BI tai B’;song song với BI cắt AI tại A’   
Ta có IC IA'  IB ' (*)
Theo định lý Talet và tính chất đường phân giác trong ta có: IB BA c  b  
1   IB '   IB ( ) 1 IB ' CA1 b c  a 
Tương tự: IA '   IA (2) c
Từ (1) và (2) thay vào (*) ta có:
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 33
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  a  b     
IC   IA IB aIA bIB cIC  0 c c
Họ tên: Đỗ Thị Hồng Anh
Đ/c mail: honganh161079@gmail.com  0
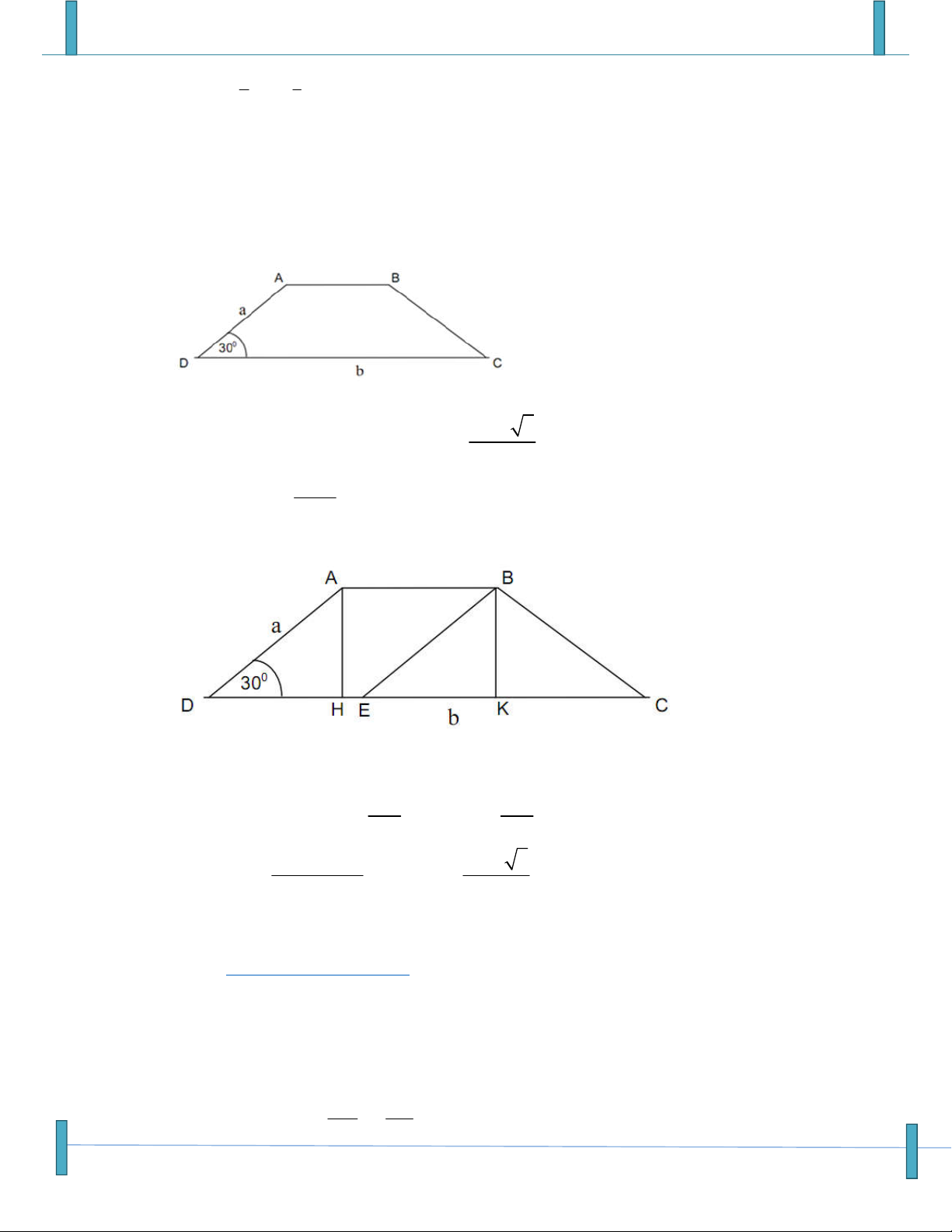
Câu 189: Cho hình thang cân ABCD có CD là đáy lớn, ADC  30 . Biết DA = a, DC = b, hãy biểu   
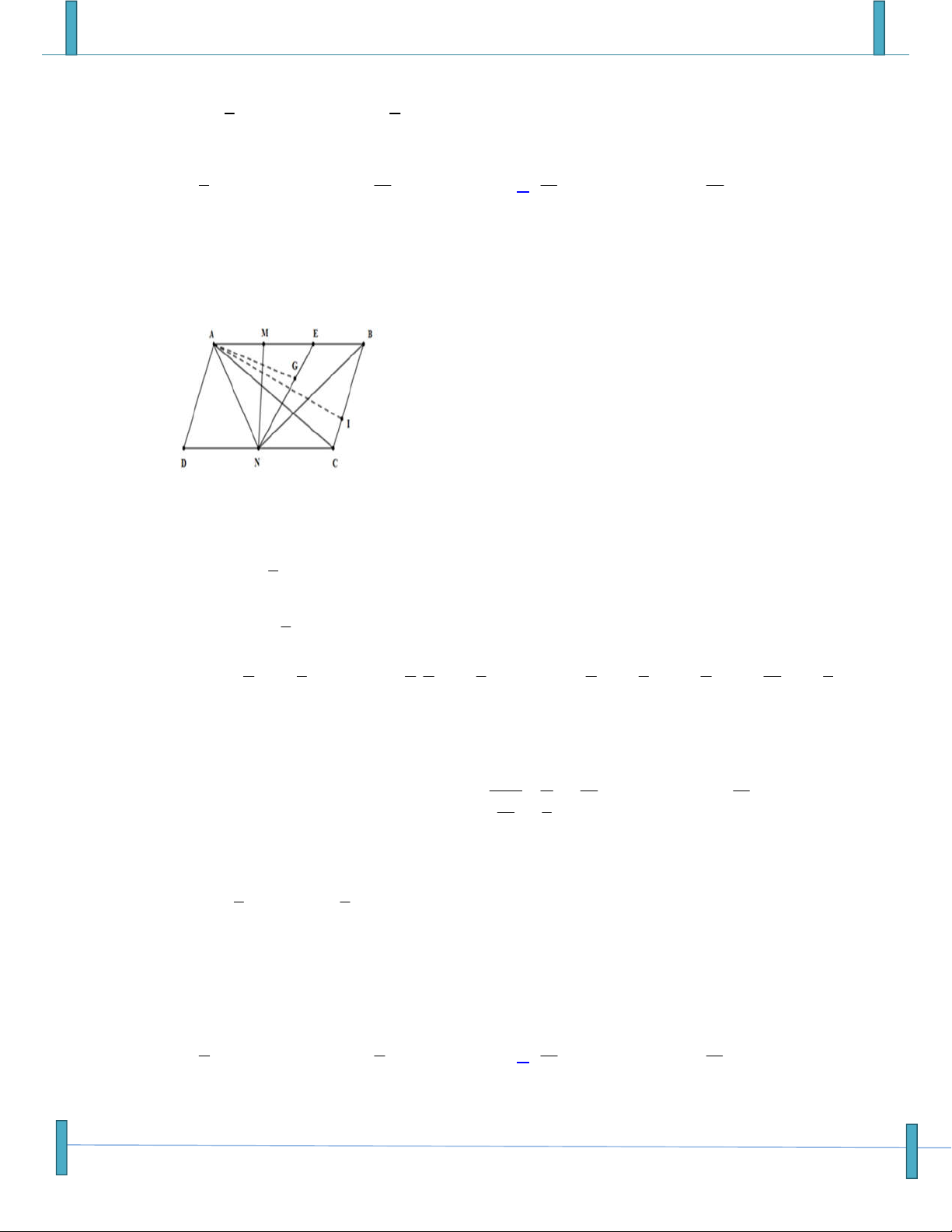
diễn DB theo hai vectơ DA và DC .
  
  b a 3 
A. DB DA DC. B. DB DA DC. b
  b a    
C. DB DA DC.
D. DB bDA a DC. b Lời giải
Kẻ BE // AD, E nằm trên cạnh CD. Ta có:
    DE   DE 
DB DA DE DA DC DA DC DC DC
 DC  2KC   b a 3  .  DA DC DA DC DC b
Vậy đáp án đúng là câu B. Email: kimduyenhtk@gmail.com FB: Kim Duyên Nguyễn.   
Câu 190: Cho hình bình hành ABCD , M là điểm thỏa mãn 5AM  2CA  0 . Trên các cạnh AB , BC
lần lượt lấy các điểm P, Q sao cho MP / B
/ C, MQ / A
/ B . Gọi N là giao điểm của AQ và AN CN
CP . Giá trị của tổng  bằng: AQ CP
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 34
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 21 24 23 25 A. B. C. D. 19 19 19 19 Lời giải A P B N Q M D C    
Đặt AN xAQ , C N yCP BQ AP AM 2 Vì MQ / /A , B MP / /BC     BC AB AC 5     2   2   2  3 
Ta có: AQ AB BQ AB
BC AB  (AC AB)  AC AP 5 5 5 2   2  3 
Nên AN xAQ xAC xAP (1) 5 2 2 3 10
Do N , C, P thẳng hàng nên x
x  1  x  5 2 19         
Mặt khác CN yCP AN AC y(AP AC )  AN  (1  y)AC yAP (2) 3 15 AN CN 25
Từ (1) và (2) suy ra y x  . Do đó   x y  . Đáp án D 2 19 AQ CP 19
Họ và tên tác giả: Phạm Thị Ngọc Tên FB: Giang Thao
Email: thuangiaoyen@gmail.com
Câu 191: Cho tứ giác ABCD, M là điểm tùy ý. K là điểm cố định thỏa mãn đẳng thức
    
MA  MB  MC  3MD  xMK . Tìm x: A. 2. B. 6. C. 5. D. 4. Lời giải Chọn B
    
Vì đẳng thức MA  MB  MC  3MD  xMK (1) thỏa mãn với mọi M nên nó đúng khi M
     
trùng với K. Khi đó ta có: KA  KB  KC  3KD  xKK  0 (2).
   
Gọi G là trọng tâm ABC , ta có KA  KB  KC  3KG (3).      
Thay (3) vào (2) ta được 3KG  3KD  0  KG  KD  0 , suy ra K là trung điểm của GD. Từ (1) ta có:
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 35
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
       
     
MK  KA  MK  KB  MK  KCKB  3MK  3KD  (KA  KB  KC  3KD)  6MK  6MK  
Vậy 6MK  xMK suy ra x = 6.
Họ và tên: Nguyễn Thanh Hoài
Email: ngthhoai1705@gmail.com
Facebook: https://www.facebook.com/hoaihappy
Câu 192: Cho tam giác ABC , trên cạnh AC lấy điểm M , trên cạnh BC lấy điểm N sao cho
AM  3MC , NC  2NB . Gọi O là giao điểm của AN và BM . Tính diện tích tam giác
ABC biết diện tích tam giác OBN bằng 1. A. 24 . B. 20 . C. 30 . D. 45 Lời giải C M N O A B Chọn C      
Ta có: BO xBA  1  xBN và AO yAM  1  yAB .        
AB yAM  x y  
1 AB  x  
1 BN  x yAB yAM  x   1 BN  0 (1)         3   1 
Đặt CB a,CA b ta được AB a b ;AM   b ;BN   a 4 3  x    
Thay vào (1) và thu gọn ta được: x ya  x y 1 3 b a yb 3 4  x  1  1 x  y x              1 1 1   Suy ra 3  10    . Với x  ta được BO BA  1   BN  3  2 10 10  10 y    x y y       4  5   1    1  NA
BO BN
BABN  NO NA  10 10 10 NO Vì S  1  S  10  S  30 . ONB NAB ABC
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 36
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên tác giả: Trần Ngọc Uyên Tên FB: Tran Ngoc Uyen
Email: ngocuyen203@gmail.com
Câu 193: Cho tam giác ABC , gọi I là điểm trên BC kéo dài sao cho IB  3IC . Gọi J , K lần lượt là   
những điểm trên cạnh AC, AB sao cho JA  2JC; KB  3KA . Khi đó BC  . m AI  . n JK . Tính
tổng P m n ?
A. P  34 . B. P  3  4 .
C. P  14 . D. P  14 . Lời giải Chọn B
    3   3   3  1 
Ta có: AI AB BI AB BC AB
AC AB  AC AB (1) 2 2 2 2
   1  2 
JK AK AJ AB AC (2) 4 3  3  1  AI AC AB      
AC  6 AI 12 2 2 JK
Từ (1) và (2) ta có hệ phương trình       2  1  
AB  16 AI  36JK JK   AC AB    3 4
    
Ta có: BC AC AB  10 AI  24JK m  10; n  24  m n  34 . Chọn đáp án B.
Email: huanpv@dtdecopark.edu.vn
Câu 194: Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho
 1   1      AM A , B DN
DC . Gọi I và J là các điểm thỏa mãn BI mBC, AJ n AI . 3 2
Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu? 1 2 A. B. 3 C. D. 1 3 3
(Họ và tên tác giả: Phạm Văn Huấn, Tên FB: Pham Van Huan) Lời giải Chọn A D N C A M B
   
J là trọng tâm tam giác BMN khi và chỉ khi AB AM AN  3AJ (9) Ta có
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 37
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  1  * AM AB 3
   1   
 1   1 
* AN DN DA
DC  DC CA  AC DC AC AB 2 2 2            * AJ n AI
n AB BI nAB mBCn AB mAC AB        
n(1 m) AB mn AC  
 1   1   
Nên thay vào (9) ta có AB AB AC AB  3n(1 )
m AB  3mn AC 3 2     5  5 
  3n(1 m)  0 1   3n(1 ) m
AB  1 3mnAC  0   6  mn   6    3 1   3mn  0 
Họ và tên: Hứa Nguyễn Tường Vy
Email: namlongkontum@gmail.com FB: nguyennga
Câu 195: Cho tam giác ABC, trên cạnh AB lấ y điểm M, trên cạnh BC lấ y N sao cho AM=3MB,
NC=2BN. Gọi I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam giác ICN bằng 2. 3 33 9 A. B. C. 11 D. 2 2 11 Lời giải Chọn đáp án B A M I C B N    
Đặt BC a; BA c .     3   2 
Suy ra AC a c ; AM   ; c CN   a 4 3   
Do A, I, N thẳng hàng nên CI xCA  (1 x) CN   
Và M, I, C thẳng hàng nên AI y AC  (1 y) AM       
Mặt khác AC AI CI y AC  (1 y) AM  (xCA  (1 x) CN )
3y x 1 
1 y  4x    a c  0 3 4
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 38
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 3y x 1  2    0 x   3    11 Mà ;
a c không cùng phương suy ra    1 y  4x 3   0  y    4   11 2  2  9   2  Với x   CI CA CN NI NA 11 11 11 11 NI 2 S 2 Hay NCI     S  11 NA 11 S 11 NCA NCA S BC 3 33 Mà ABC    SS NC 2 ABC 2 ANC
congsondienan@gmail.com 
    
Câu 196: Cho ∆ABC có trọng tâm G và hai điểm M, N thỏa mãn: 3MA  2CM  0 , NA  2NB  0 . Chọn mệnh đề đúng.        
A. NG  4GM .
B. NG  5GM .
C. NG  6GM .
D. NG  7GM .
(Họ và tên tác giả: Trần Công Sơn, Tên FB: Trần Công Sơn) Lời giải Chọn B A M G B C E N .
Gọi E là trung điểm BC. M, N là các điểm như hình vẽ.    2   2 1    5  1 
Ta có: NG AG AN AE  2 AB
.  AB AC   2AB   AB AC . 3 3 2 3 3    2  2  2  2 1    
GM AM AG AC AE AC   AB AC 1 1 .    AB AC . 5 3 5 3 2 3 15  5  1   1  1    Nên NG   AB AC  5  AB AC  5   GM . 3 3  3 15   
Vậy NG  5GM .
(Email): tranminhthao2011@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 39
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 197: (Đẳng thức vec tơ) Cho tam giác ABC . Gọi A', B',C' là các điểm xác định bởi         
2018A' B  2019A'C  0 , 2018B 'C  2019B ' A  0 , 2018C ' A  2019C ' B  0 . Khi đó,
mệnh đề nào sau đây đúng?
A. ABC và A' B 'C ' có cùng trọng tâm.
B. ABC  A' B 'C ' .
C. ABC  A' B 'C '.
D. ABC và A' B 'C ' có cùng trực tâm. Lời giải Chọn A   
Ta có 2018A' B  2019 A'C  0     
 2018 A' A AB  2019 A' A AC  0    
 4037 A' A  2018AB  2019 AC  0 (1)        
Tương tự ta có 4037B ' B  2018BC  2019BA  0 ; 4037C 'C  2018CA  2019CB  0
Cộng vế với vế lại ta được
  
   
   
4023 AA'  BB'  CC '  BA AC CB  0  AA'  BB'  CC '  0 .
Vậy ABC và A' B 'C ' có cùng trọng tâm
Câu 198: ( tính độ dài vec tơ) Cho tam giác đều ABC cạnh a . Gọi điểm M là trung điểm BC . Tính độ 1   dài của vec tơ AB  2 AC 2 a 21 a 21 a 21 a 21 A. . B. . C. . D. . 3 2 4 7 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 40
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn B
Gọi N là trung điểm AB , Q là điểm đối xứng của A qua C và P là đỉnh của hình bình hành AQPN . 1     Khi đó ta có
AB AN , 2 AC AQ suy ra theo quy tắc hình bình hành ta có 2 1 
   
AB  2 AC AN AQ AP 2
Gọi L là hình chiếu của A lên PN    Vì 0
MN / / AC ANL MNB CAB  60  ALa a 3
Xét tam giác vuông ANL ta có 0 sin ANL
AL AN.sin ANL  sin 60  AN 2 4  NLa a 0 cos ANL
NL AN.cos ANL  cos 60  AN 2 4 a 9a
Ta lại có AQ PN PL PN NL AQ NL  2a   4 4
Áp dụng định lí Pitago trong tam giác ALP ta có 2 2 2 3a 81a 21a a 21 2 2 2
AP AL PL     AP  16 16 4 2 1   a 21 Vậy
AB  2AC AP  2 2
Họ và tên: Trần Quốc An
Email: tranquocan1980@gmail.com Facebook: Tran Quoc An
Câu 199: Cho ABC có M là trung điểm của BC, H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm x
   
để HA HB HC xHO .
A. x . 2
B. x  2 .
C. x . 1
D. x  3 . Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 41
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A H O C B M A' Chọn A
Gọi A' là điểm đối xứng với A qua O, ta có:
A' B AB
  CH A' B (1) CH AB
Tương tự ta chứng minh được BH A'C (2)
Từ (1),(2) suy ra tứ giác BHCA’ là hình bình hành.
Do đó M là trung điểm của HA ' .  
 
Ta có: HB HC  2HM HA'
     
HA HB HC HA HA'  2HO x  2. buiduynam1993@gmail.com
Câu 200: Cho tam giác ABC có đường trung tuyến CM vuông góc với phân giác trong AL . Giả sử 2 a bk
ngoài ra còn có CM kAL . Biết cos A
. Tính a b c d 2 c dk A. 18 . B. 5 . C. 26 . D. 17 .
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1) Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 42
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 Ta có A
CM cân tại A AC AM
AB c  2b với b AC , c AB . 2  b  c  2  
Theo đề bài AL là phân giác trong của góc A nên: AL AB AC
AM AC . c b c b 3 4   4 8 2  AL   2 2
AM AC  2 AM .AC    2 2
2b  2b cos A 2 
b 1 cos A . 9 9 9   Lai có 2 2 2
2AC.AM AC AM CM 2 2 2 2 2
 2b cos A  2b CM CM  2b 1 cos A . 8 Từ 2
CM kAL  2b 1 cos A 2 2
k . b 1 cos A    A 2 9 1 cos
 4k 1 cos A 9 2 9  4k  cos A  . 2 9  4k
Vậy a b c d  18 .
Họ và tên: Phạm Thanh My
Email: phamthanhmy@gmail.com
Facebook: Pham Thanh My      1
Câu 201: Cho tam giác ABC . Gọi M , N , P là các điểm lần lượt thỏa mãn MA  3MB  0 , AN AC , 3   
2PB  3PC  0 Gọi K là giao điểm của AP và MN . Trong các mệnh đề sau, mệnh đề nào đúng?      
A. 4KA  5KP  0 .
B. 3KA  2KP  0 .     
C. KA KP  0 .
D. KA KP . Lời giải Chọn C
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 43
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A N K M I P C B
Gọi I là giao điểm của MN và BC . IB NC MA     1 
Áp dụng định lý Menelaus ta có . .  1  IB
IC mà 2PB  3PC  0 P là IC NA MB 6 trung điểm IC . KA IP MB
Áp dụng định lý Menelaus ta có . .  1 KP IB MA KA      1
  KA KB  0 KP
Câu 202: Cho hình thang ABCD ( AB / /CD) có hai đường chéo vuông góc với nhau. Biết  
AB CD  20c .
m Tìm AC BD . A. 40c . m . B. 20c . m . C. 30c . m . D. 10c . m . Lời giải Chọn B
Họ và tên tác giả: Nguyễn Thị Yến Tên FB: Nguyễn Yến
Email: ntyen.c3lqd@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 44
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A B D C E F     
AC BD BE BD BF DE  20c . m
Họ và tên tác giả:Lê Thanh Lâm
Mail:quyphucvn@gmail.com Fb:Thanh Lâm Lê
Câu 203: Cho tam giác ABC có AB  3; AC  4 .Gọi AD là đường phân giác trong của góc A .Biết   
AD m AB n AC .Khi đó tổng m n có giá trị là: 1 1 A. 1 B. 1 C. D.  7 7 Lời giải A Chọn A B C D
Theo tính chất đường phân giác trong của góc A trong tam giác ABC ta có: DB AB 3         3DC  4
DB  3( AC AD)  4
 ( AB AD) DC AC 4     4  3  4 3
 7 AD  4AB  3AC AD AB AC .Ta có m  ; n
.Vậy tổng m n  1. Chọn A 7 7 7 7
Câu 204: Cho tam giác ABC bất kỳ, gọi M , N , P lần lượt là trung điểm các cạnh AB, BC, CA . H , H '
lần lượt là trực tâm các tam giác ABC, MNP . Khẳng định nào đúng trong các khẳng định sau?
   
   
A. HA HB HC  3HH ' .
B. HA HB HC  2HH '.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 45
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
   
   
C. HA HB HC  0 . D. HM HN HP  3HH ' . Lời giải Chọn B
H ' là trực tâm tam giác MNP nên H ' là tâm đường tròn ngoại tiếp tam giác ABC .
Gọi AD là đường kính của đường tròn ngoại tiếp tam giác ABC nên BHCD là hình bình hành
     
suy ra HA HB HC HA HD  2HH ' .
Mail: kimlinhlqd@gmail.com
Câu 205: Cho tam giác đều ABC tâm O. M là một điểm bất kì bên trong tam giác. Gọi D, E, F lần lượt là
hình chiếu của M lên BC, CA, AB. Với giá trị nào của k ta có hệ thức:
   
MD ME MF k MO 1 3 A. k  . B. k  1. C. k  . D. k  2 2 2 Lời giải
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa Chọn C
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 46
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Gọi hình chiếu của M lên cạnh BC là D. Ta có   S MD S 3  S a
MD a .AA'  a AO . S AA' S 2S S S a MBC
Tương tự cho các đánh giá khác. Do đó:
   3   
MD ME MF
S AO S BO S CO a b c = 2S 3    
  
S MO MA S MO MB S MO MC a     b     c    2S 3  3    3  
S S S MO S MA S MB S MC MO a b c  .     a b c   2S 2S 2
Cách Khác: Qua M kẻ các đường thẳng song song với các cạnh BC, CA, AB
Họ và tên tác giả: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng
Email: thanhdungtoan6@gmail.com
Câu 206: Một giá đỡ hình tam được gắn vào tường (như hình vẽ). Tam giác ABC vuông cân tại B.
Người ta treo vào điểm A một vật nặng 10N. Tính độ lớn của các lực tác động vào tường tại B
và C? (Bỏ qua khối lượng của giá đỡ)
A. F  10 2N, F  10N B C
B. F  10N, F  10 2 B C
C. F F  10N B C
D. F  10N, F  1  0 2 B C Lời giải Đáp án: B
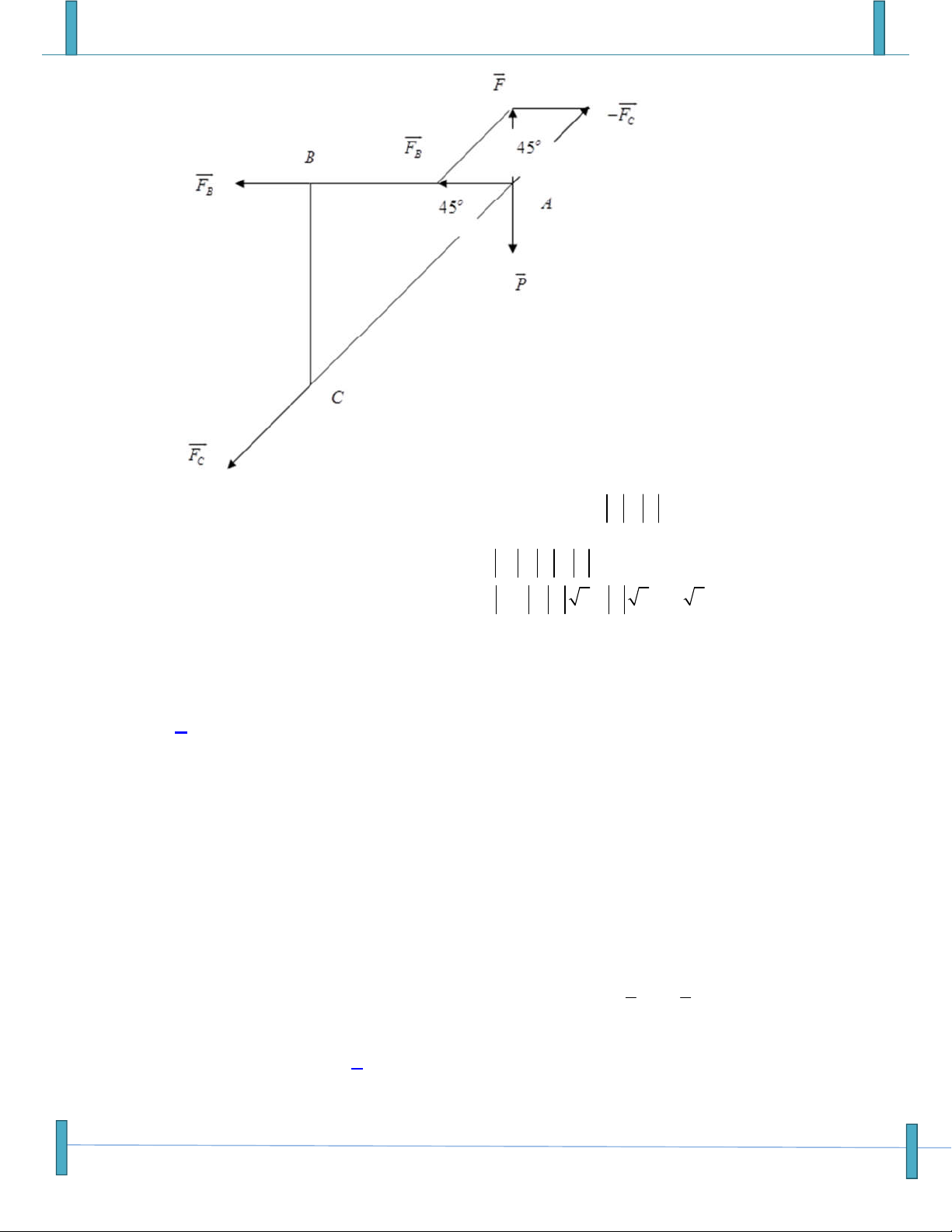
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 47
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New        
Hệ chất điểm cân bằng nên F  F   P  0  F  P F P 10N B C   
F F F P  10N B B
Tam giác ABC vuông cân tại B suy ra    
F  F F 2  P 2  10 2N C C
Email: giachuan85@gmail.com
    
Câu 207: Cho ba điểm A , B , C thuộc đường tròn tâm O , thỏa mãn OA OC OB  0 . Tính góc AOB ?     A. 0 AOB  120 . B. 0 AOB  90 . C. 0 AOB  150 . D. 0 AOB  30 . Lời giải
Họ và tên: Trần Gia Chuân Tên facebook: Trần Gia Chuân Chọn A
  
Do OA OC OB  0 nên O là trọng tâm tam giác ABC .
Mà O là tâm đường tròn ngoại tiếp tam giác nên tam giác ABC đều. Vậy góc  0 AOB  120
Email: giachuan85@gmail.com  1  2 
Câu 208: Cho tam giác ABC . Điểm M trên cạnh BC thỏa mãn AM  .AB
.AC , khẳng định nào 3 3
sau đây là khẳng định đúng?    
A. MB  2MC .
B. MB  2MC .
C. MC  2MB . D. MC  3  MB . Lời giải
Họ và tên: Trần Gia Chuân Tên facebook: Trần Gia Chuân
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 48
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn B  
Cách 1: Giả sử BM k.BC khi đó Ta có
  
AM AB BM  
AB k.BC   
AB k. AC AB  
 1  k .AB k.AC  1  2  2   Mà AM  .AB  .AC k  suy ra . 3 BM  .
2 BC MB  2MC 3 3 3 Cách 2:  1  2 
1  1  2  2  AM  .AB  .AC
.AM  .MB  .AM  .MC 3 3 3 3 3 3
1  2   
.MB  .MC  0 3 3   
MB  2.MC  0  MB  2MC
Email: cvtung.lg2@bacgiang.edu.vn
Câu 209: Cho tam giác đều ABC nội tiếp đường tròn tâm O , M là một điểm tùy ý nằm bên trong tam
giác đã cho; gọi A '; B ';C ' theo thứ tự là hình chiếu vuông góc của M lên các cạnh BC ; C A và     k
AB . Khi đó ta có đẳng thức vectơ k M A '  MB '  MC '   l MO , k.l  0, là phân số tối l giản. Tính 2 2 2 k l . . A. 2 2
2k l  1. B. 2 2
2k l  1. C. 2 2
2k l  14 . D. 2 2
2k l  5 . Lời giải
Họ và tên tác giả: Cao Văn Tùng Tên FB: Cao Tung Chọn B
Từ M kẻ các đường thẳng song song với các cạnh BC;C ;
A AB và các đường thẳng này cắt các
cạnh của tam giác ABC tại các điểm A , A , B , B , C ,C như hình trên. 1 2 1 2 1 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 49
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Xét tam giác MA A do tam giác ABC đều và tính chất của góc đồng vị nên góc 1 2   0
MA A MA A  60 suy ra tam giác MA A đều và A ' là trung điểm của A A từ đó ta có: 1 2 2 1 1 2 1 2  1   MA ' 
MA MA 1 2  2  1 
  1  
Chứng minh tương tự ta có MB ' 
MB MB ;MC '  MC MC . 1 2   1 2  2 2
   1 
    
Suy ra MA '  MB '  MC ' 
MA MC MA MB MB MC , mặt khác các tứ giác 1 2 2 2 1 1  2
AB MC ; BA MC ;CA MB là hình bình hành nên 1 1 1 2 2 2
   1    
   
MA MB MC
MAMB MC 3 ' ' ' 
MO  2MA'  MB '  MC '   3MO . 2 2 Vậy 2 2
k  2;l  3  2k l  1  . Email: trang145@gmail.com
 1   1 
Câu 210: Cho hình vuông ABCD, E,F thõa mãn BE BC;CF  
CD ; AE BF I 3 2   
Ta có AI k AB l AD . Khi đó tỉ số k,l thõa mãn cặp nào sau: 3 2 6 2 5 3 6 1 A. k  ;l B. k  ;l C. k  ;l
D. k   ;l  5 5 5 5 6 6 5 3 Lời giải
Họ tên: Nguyễn Thị Trang Fb: Trang Nguyen Chọn B A B E K I D C F EK 1 EI EK 1 Kẻ EK//AB      CF 3 AI AB 6  6  6   6  1  6  2  Ta có: AI AE  ( AB BE)  ( AB BC)  AB BC) 5 5 5 3 5 5
Câu 211: Cho tam giác ABC , trên cạnh AC lấy điểm M , trên cạnh BC lấy điểm N sao cho:
AM  3MC , NC  2NB , gọi O là giao điểm của AN và BM .Tính diện tích ABC biết diện tích OBN bằng 1. A. 10 . B. 20 . C. 25 . D. 30 .
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo)
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 50
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Lời giải Chọn D A    Vì ,
A O, N thẳng hàng nên:
BO xBA    x BN   
Tương tự: AO y AM  1 yAB M O    
AB y AM  (x y 1)AB  (x 1)BN B N C    
hay (x y)AB y AM  (x 1)BN  0 (1)    
Đặt CB a , CA b .     3   1 
Ta có: AB a  ; b AM   ; b BN   a 4 3   3   1   
Thay vào (1) ta có:  x ya b  yb   x y  a  0   4  3    x 1  3y
  x ya   x yb a b 3 4  x 1  1 x y x    3   10 Từ đó ta có:    3 2
y x yy    4   5 1  1  1  Với x   BO BA  (1 )BN 10 10 10   1    1  NA
BO BN
BABN  hay NO NA 10 . 10 10 NO Vì S  1  S  10  S  30 . ONB NAB ABC
Họ và tên: Nguyễn Văn Quân Tên FB: Quân Nguyễn
Email: Quanvan09@gmail.com
Câu 212: Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng định đúng?        
A. HA HB HC  4HO .
B. HA HB HC  2HO .    2     
C. HA HB HC HO .
D. HA HB HC  3HO . 3 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 51
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A H O B C D    
Dễ thấy: HA HB HC  2HO nếu tam giác ABC vuông.
Nếu tam giác ABC không vuông gọi D là điểm đối xứng của A qua O. Khi đó:
BH / /DC (vì cùng vuông góc với AC).
BD / /CH (vì cùng vuông góc với AB).   
Suy ra BDCH là hình bình hành, do đó theo quy tắc hình bình hành thì HB HC HD (1).   
Mặt khác vì O là trung điểm của AD nên HA HD  2HO (2).    
Từ (1) và (2) suy ra. HA HB HC  2HO .
Tên facebook: NT AG
Câu 213: Cho tam giác ABC có D là trung điểm của BC , O là một điểm trên đoạn AD sao cho
AO  4OD . Gọi  
E CO AB , F  BO AC , M  AD EF . Khẳng định nào sau đây đúng?  1   2   1   2  A. MO AD B. MO AD C. MO AD D. EM BC 7 15 8 7 Lời giải
Họ và tên tác giả: Nguyễn Đặng Chọn B A E M F O B C D
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 52
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    
Đặt: AB x AE , AC y AF , (x, y  ) .  4  2   2  2  2  2 
Theo bài ra ta có AO AD
AB AC  xAE AC AB yAF 5 5 5 5 5 5 2 2 3
Do O, B, F thẳng hàng nên 
y  1  y  5 5 2 2 2 3
Do C, O, E thẳng hàng nên x   1  x  5 5 2 AB AC 3 AD 4  2  Từ đó:    , lại có AO AD MO AD AE AF 2 AM 5 15
Câu 214: Cho hình thang ABCD có AB //CD . Gọi M , N lần lượt là trung điểm của AC, BD . Kẻ
NH AD (H AD) và ME BC (E BC) . Gọi I  ME NH , kẻ IK DC (K DC) .
Khi đó trong tam giác MNK hệ thức nào sau đây đúng?        
A. MK.IN NK.IM MN.IK  0
B. IN.tan N IM . tan M IK.tan K  0    
   
C. IN.cot N IM .cot M IK.cot K  0
D. IM IN IK  0 Lời giải Chọn B F J A B E H N M I D K C
Ta chứng minh ID IC  
ABF AJF  180O
Kẻ AF BC, BJ AD . Tứ giác ABFJ nội tiếp  
DCB AJF  180O
Khi đó  DCFJ là tứ giác nội tiếp.
NH , ME là các đường trung bình của các tam giác DBJ , CAF
IH , IE là các đường trung trực của DJ , CF nên IJ IF ID IC . Vậy NH //BCNK MENK MI
ID IC KD KC       MK //AD MK HN MK NI   
Từ đó suy ra I là trực tâm tam giác MNK . Nên đáp án đúng là B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 53
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Email: nguyenvantoannbk@gmail.com
Câu 215: Cho ABC , điểm M thuộc cạnh BC sao cho 2018.S  2019.S . Đẳng thức nào sau ABMACM đây sai?    A. 2018.S  4037.S .
B. 2018.BM  2019.CM  0 . ABCACM  4037  2019 C. BC  .BM D. S  .S . 2018 ABM 4037 ABC Lời giải Chọn C
Kẻ đường cao AH của ABC . 2019 4037 Ta có SSSSSS , suy ra A đúng. ABCABMACM 2018 ACMACM 2018 ACM
Tương tự D cũng đúng. 1 .AH.BM S BM 2019  2019 
Từ giả thiết ta có ABM 2     BM  
CM , suy ra B đúng. S 1 CM 2018 2018 ACM .AH .CM 2  4037 
(C sai vì BC  .BM ). 2019
(Tác giả: Nguyễn Văn Phùng,Gmail: nvpmaster0808@gmail.com)
Câu 216: Cho tam giác ABC . M là điểm nằm trên cạnh BC sao cho S  3S . Một đường thẳng ABC AMC AB AC AM cắt các cạnh A ,
B AM , AC lần lượt tại B ,
M ,C phân biệt. Biết rằng  2  k. . ABACAM  Tìm số k . 2 A. k  1 . B. k  2 . C. k  3 . D. . 3
(Tác giả: Nguyễn Văn Phùng,Gmail: nvpmaster0808@gmail.com) Lời giải Chọn C A C' M' B' C B M
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 54
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  2  Ta có S  3S
BC  3MC BM BC ABC AMC 3   
  
Đặt AB '  x AB ; AC '=y AC ; AM '  z AM
    
Ta có B ' M '  AM '  AB '  z AM x AB          2z z AB
BM x AB   z xAB BC 3
 2z    z   2z 
  z xAB
AC AB   x AB AC   3  3  3
    
Lại có: B 'C '  AC '  AB '  y AC x AB z 2z
   x 3 1 2
Mặt khác B ' M ' , B 'C ' cùng phương nên 3 3     x y z x y AB AC AM Hay  2  3 . AB ' AC ' AM '
Từ đó suy ra k  3 .
nguyenchitrung12@gmail.com
Câu 217: Cho n điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là A , A ,..., A . Bạn Bình kí hiệu 1 2 n
  
chúng là B , B ,..., B
A  B ). Vectơ tổng A B A B  ...  A B bằng 1 2 n ( 1 n 1 1 2 2 n n     A. 0 . B. A A . C. B B . D. A B . 1 n 1 n 1 n
(Sưu tầm, Tên FB: Trung Nguyễn Chí) Lời giải Chọn A
Lấy điểm O bất kì. Khi đó
        
A B A B  ...  A B A O A O  ...  A O OB OB  ...  OB 1 1 2 2 n n  1 2 n   1 2 n
Vì B , B ,..., B A , A ,..., A nên 1 2 n   1 2 n   
   
OB OB  ...  OB OA OA  ...  OA 1 2 n 1 2 n
    
 
  
Do đó A B A B  ...  A B A O OA A O OA  ...  A O OA  0 . 1 1 2 2 n n  1 1   2 2   n n
Câu 218: Trong đường tròn (O) với hai dây cung AB và CD cắt nhau tại M. Qua trung điểm S của BD kẻ AK 2 AM SM cắt AC tại K sao cho  a .Tính: CK 2 CM
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 55
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 A. 2a B. 2 a C. D. a 2 a Lời giải AK a  0 CK  1  a  Ta có: MK  .MA  .MC (1) 1 a 1 a     l  
Do MK , MS cùng phương nên: MK lMS  (MB MD) 2 Mặt khác  b  MB   MA  2  MA M .
A MB MC.MD b  0   b  MD   MC 2   MC  bl  bl   MK   MA MC(2) 2 2 2MA 2MC  1 bl   2  2 1   a 2MA MA Từ (1) và (2) suy ra   a  2 a bl MC    2 1    a 2MC
 2   1 
Câu 219: Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn: BD BC, AE AC . 3 4  AK
Điểm K trên AD sao cho 3 điểm B, K,E thẳng hàng. Xác định tỷ số  AD 1 1 1 1 A. B. C. D. 2 3 4 5 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 56
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A E K B C D
Ba điểm K, B, E thẳng hàng khi và chỉ khi tồn tại  sao cho:   
AK   AB  (1  ) AE (1)   1  2 
Đặt AK x AD x( AB AC) 3 3  1  2  x  2x 
AK x( AB AC)  AB AC (2) 3 3 3 3
Áp dụng hệ quả 5 thì từ (1) và (2) ta có:  x  1   x   3    3    1 2x 1  (1  )        4 3   9   1  AK 1 Vậy AK
AD    3 AD 3
Facebook: Lê Văn Kỳ
Email: lethithuy@thpthv.vn
Câu 220: Cho tam giác ABC vuông tại C, có AC b, BC a , D là chân đường cao kẻ từ C.
Khẳng định nào sau đây là đúng? 2 2  a  b  2 2  a  b  A. CD CA CB . B. CD CA CB . 2 2 2 2 a b a b 2 2 2 2 a b a b 2 2  a  b  2 2  a  b  C. CD AC BC D. CD AC BC . 2 2 2 2 a b a b 2 2 2 2 a b a b Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 57
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 2 2 2 CB BD CB a  a  Ta có 2 BC B . D BA BD      BD BA . 2 2 2 2 2 BA BA BA a b a b 2     a  
Lại có: BA CA CB BD CA CB . 2 2   a b 2 2 2     a   a  b 
Vậy CD CB BD CB CA CB CA CB 2 2   2 2 2 2 a b a b a b Email: huyenbla81@gmail.com    
Câu 221: Cho tam giác ABC có trọng tâm G. Gọi I là điểm xác định bởi 5IA  7IB IC  0. Gọi E là EA
giao điểm của AI và BG. Tính tỷ số . EI 1 1 A. 2. B. . . 2 C. 3. D. 3
(Họ tên tác giả: Nguyễn Thị Thu Huyền. Tên FB: Thu Huyen Nguyen) Lời giải Chọn B A G E B C I
Vì G là trọng tâm của tam giác ABC nên ta có:    
IA IB IC  3IG.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 58
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    
Mà: 5IA  7IB IC  0.   
Vậy ta có: 6IA  6IB  3IG    2BA IG IG / / AB
 IG  2AB (hình vẽ)  EA AB 1    . EI IG 2
Email: nghiepbt3@gmail.com
Câu 222: Cho 2 tia Ox, Oy vuông góc. Trên tia Ox lấy các điểm A,B sao cho OA = OB = 1. C là điểm
thuộc đoạn OA, N là một điểm thuộc đoạn OB và dựng hình vuông OCMN. Trên đoạn CM lấy
điểm Q và dựng hình vuông ACQP. Gọi S là giao điểm của AM và PN. Giả sử OC kOA ,  1 
AS x AM , NS y NP , k   1 ;   2  13 a Khi x + y = thì k =
, với a,b   và a, b nguyên tố cùng nhau thì a.b bằng 10 b A. 7 B. 4 C. 5 D. 12 Lời giải
FB: Ngô Quang Nghiệp
Ta có: OS OA AS OA x AM OA xOM OA  1 xOA xOM
 1  xOA xOC ON   1  xOA xkOA xkOB
 1  x kxOA xkOB , (1).
Mặt khác: OS ON NS kOB y NP kOB yOP ON   kOB yOA y AP ykOB
k1  yOB yOA y1  k OB , (vì AP = CA = 1 - k nên AP  1  k OB )
yOA  k y  2kyOB , (2).  1  k x
1  x kx y   2 2 k  2k  1 Từ (1) và (2), ta có    2
kx k y  2kyk y    2 2 k  2k  1
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 59
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  3 k 2   13 1  k k 13 4
Ta có: x y       10 2 2 k  2k  1 2 2 k  2k  1 10  1 k   4 3
Đối chiếu điều kiện, ta chọn k  . ĐÁP ÁN D. 4
Họ Tên: Lê Duy Tên FB: Duy Lê Email: Duyleag@gmail.com
Câu 223: Cho tam giác ABC . Giả sử điểm M nằm trên cạnh BC thỏa các tam giác MA , B MAC lần
lượt có diện tích là S , S . Khẳng định nào sau đây đúng? 1 2      
A. S S AM S AB S AC.
B. S S AM S AB S AC. 1 2  1 2  2 1 1 2      
C. S S AM S AB S AC.
D. S S AM S AB S AC. 2 1  2 1  2 1 1 2 Lời giải Chọn A A S1 S2 B C M
Gọi h d  , A BC  . 1 d  , A BC .BM S BM Ta có 1 2   S 1 CM 2 d  , A BC .CM 2  S      1  BM MC S
BA AM S MA AC 2   1   S2   
 S S AM S AB S AC 2 1  2 1
Họ và tên tác giả: Nguyễn Đức Duẩn Tên FB: Duan Nguyen Duc
Email: Duanquy@gmail.com  1  
Câu 224: Cho tam giác ABC có có M là trung điểm của BC, AI
MI . Điểm K thuộc cạnh AC sao 2  m 
cho B,I,K thẳng hàng. Khi đó KA
CK . Tính S  25m  6n  2019 n
A. S  2019 . B. S  2068 .
C. S  2018 . D. S  2020 . Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 60
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A K I  1   C B M Ta có AM  ( AB AC) . 2  
Gọi điểm K thuộc cạnh AC sao cho AK  . x AC .      1 
 1  1  5  1 
Ta có BK   AB  .
x AC và BI   AB  .AM   AB AB AC AB AC 3 6 6 6 6 1  x 1  1  m  1
Để B,I,K thẳng hàng thì   x   KA CK  5  1  5 4 n  4  6 6
Vậy S  25.1 6.4  2019  2068
Họ và tên: Nguyễn Quang Huy Fb: Nguyễn Quang Huy Email: boigiabao98@gmail.com     
Câu 225: Cho tam giác ABC có trọng tâm G, lấy các điểm I, J sao cho IA  2IB và 3JA  2JC  0 và thỏa  
mãn đẳng thức IJ  kIG . Giá trị của biểu thức 2 2 500
P  (25k  36)(k  k 1) là: 5 6 A. P  1235 B. P  0 C. P  D. P  6 5 Lời giải
Thật vậy nếu ta gọi M là trung điểm của BC ta có:    2   2 1    1  5  IG  AG  AI  AM  2AB  . (AB  AC)  2AB  AC  AB 5 3 2 3 3    2   6 1  5  6 
Mặt khác ta lại có IJ  AJ  AI  AC  2AB  ( AC  AB)  IG 5 5 3 3 5 6 Do đó k  5 36 Nhận thấy 2 25k  36  25.
 36  36  36  0 do đó P  0 .vậy chọn B 25
(Email): nguyenmy181@gmail.com
Câu 226: Cho tam giác ABC . M là điểm nằm trên cạnh BC sao cho SS 3 . Một đường thẳng ABC AMC AB AC AM
cắt các cạnh AB, AM, AC lần lượt tại B ',M ',C ' phân biệt. Biết  mn . AB ' AC ' AM ' Tính m n . A. 2. B. 5. C. 3. D. 4. Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 61
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  2  Ta có SS 3  BC MC 3  BM BC ABC AMC 3      
Đặt AB '  xAB ; AC '=yAC ; AM '  zAM     
Ta có B ' M '  AM '  AB '  zAM x AB     2          z z AB BM xAB z x AB BC 3        z 2   z z 2 z x AB AC AB     
   x AB AC   3  3  3     
B 'C '  AC '  AB '  yAC xAB z z 2
   x 3 1 2 3 3
Mặt khác B ' M ' , B 'C ' cùng phương nên     xy z x y AB AC AM Hay  2  3 AB ' AC ' AM '
(Họ và tên tác giả: Nguyễn Thị Trà My, Tên FB: Nguyễn My)
Họ và tên tác giả: Nguyễn Đặng
Tên facebook: NT AG
Câu 227: Cho tam giác ABC có D là trung điểm của BC , O là một điểm trên đoạn AD sao cho
AO  4OD . Gọi  
E CO AB , F  BO AC , M  AD EF . Khẳng định nào sau đây đúng?  1   2   1   2  A. MO AD B. MO AD C. MO AD D. EM BC 7 15 8 7 Lời giải Chọn B A E M F O B C D    
Đặt: AB x AE , AC y AF , (x, y  ) .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 62
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  4  2   2  2  2  2 
Theo bài ra ta có AO AD
AB AC  xAE AC AB yAF 5 5 5 5 5 5 2 2 3
Do O, B, F thẳng hàng nên 
y  1  y  5 5 2 2 2 3
Do C, O, E thẳng hàng nên x   1  x  5 5 2 AB AC 3 AD 4  2  Từ đó:    , lại có AO AD MO AD AE AF 2 AM 5 15
Câu 228: Cho hình thang ABCD có AB//CD . Gọi M , N lần lượt là trung điểm của AC, BD . Kẻ
NH AD (H AD) và ME BC (E BC) . Gọi I  ME NH , kẻ IK DC (K DC) .
Khi đó trong tam giác MNK hệ thức nào sau đây đúng?        
A. MK.IN NK.IM MN.IK  0
B. IN. tan N IM .tan M IK. tan K  0    
   
C. IN.cot N IM .cot M IK.cot K  0
D. IM IN IK  0 Lời giải Chọn B F J A B E H N M I D K C
Ta chứng minh ID IC  
ABF AJF  180O
Kẻ AF BC, BJ AD . Tứ giác ABFJ nội tiếp  
DCB AJF  180O
Khi đó  DCFJ là tứ giác nội tiếp.
NH , ME là các đường trung bình của các tam giác DBJ , CAF
IH , IE là các đường trung trực của DJ , CF nên IJ IF ID IC . Vậy NH //BCNK MENK MI
ID IC KD KC       MK //AD MK HN MK NI   
Từ đó suy ra I là trực tâm tam giác MNK . Nên đáp án đúng là B
Họ và tên tác giả: Nguyễn Thi Tiết Hạnh Tên FB: Hạnhtiettiet
Email: tiethanh.78@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 63
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 229: Cho hình bình hành ABCD . Gọi I là trung điểm của CD , G là trọng tâm tam giác BCI . Đặt    
a AB, b AD . Hãy tìm đẳng thức đúng trong các đẳng thức sau?  5  2   5   A. AG a b . B. AG a b . 6 3 6   5   4  2 
C. AG a b . D. AG a b . 6 3 3 Lời giải Chọn A  1  1  1  
* I là trung điểm của CD nên: AI AC AD AB AD . 2 2 2
 1  1  1 
  
* G là trọng tâm tam giác BCI nên: AG AB AC
AI , thay AC AB AD và 3 3 3  1  
 1  1   1  1    5  2  AI
AB AD ta được AG
AB   AB AD  AB AD AB AD   . 2 3 3 3  2  6 3
(Email): locleduc10@gmail.com
Câu 230: Một đường thẳng cắt các cạnh D ,
A DC và đường chéo DB của hình bình hành ABCD lần    
lượt tại các điểm E, F và M . Biết DE  . m D , A DF  .
n DC (m, n  0). Khẳng định đúng là: 
m n   m  A. DM DB . B. DM DB . . m n m n  n   . m n  C. DM DB . D. DM DB . m n m n Lời giải Chọn D     Đặt DM  .
x DB; EM y FM . Khi đó:
    
EM DM DE  (x m)DA xDC
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 64
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
    
FM DM DF xDA  (x n)DC Ta có:      
EM y FM  (x m)DA xDC xy DA y(x n)DC.  
x m xy Do ;
DA DC không cùng phương nên 
x y(x  ) nm mn
Giải hệ được y   và x  . n m n  . m n  Vậy DM DB m n
(Họ và tên tác giả: Lê Đức Lộc, Tên FB: Lê Đức Lộc)
Email: phuogthu081980@gmail.com
Câu 231: Hình thang cân ABCD có độ dài đường cao AH  ; a AB / /C ,
D AB a 3; AD a 2; AB DC 
x y z 
AC cắt BH tại I. Biết AI AC; ; x ;
y z; m N . m
Tính tổng T x y z m A. 20 B. 18 C. 17 D. 21 Lời giải
Họ và tên tác giả: Nguyễn Thị Phương Thu FB: Buisonca Bui
         
) AI AB BI AB k HB AB k AB AH   1 k AB k AH
    HC   3 1 
) AC AH HC AH  .AB AH A . B AB 3  
)I AC AI mAC  
Mà AH; AB không cùng phương
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 65
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  3 1 k 1  m 6  3  6  3    3  m   AI AC 11 11  k  m
T  6 1 3 11  21 tambc3vl@gmail.com
Câu 232: Cho hình thang ABCD với O là giao điểm của hai đường chéo AC và BD. Qua O vẽ đường
thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên AD và BC theo thứ tự 
tại M và N. Với AB a , D C
b , khi đó MN bằng:         a .AB  . b DC . b AB  . a DC a .AB  . b DC . b AB  . a DC A. . B. . C. . D. . a b a b a b a b Lời giải
Họ và tên: Nguyễn Thanh Tâm Tên FB: Tâm Nguyễn Chọn B MA NB OA OB AB a
Do MN / / AB / / D C nên:      . MD NC OC OD DC b  a 
Do đó MA   .MD ; b  a 
NB   .NC , nên: b
 a 
 a  OA  .OD  OB  .OC  b OM  ; b ON a a 1 1 b b
  a  
 a    OB OA  .
  
OC ODAB  .DC . b AB  . a DC Có: b b
MN ON OM    a a a b 1 1 b b
Câu 233: Cho tam giác ABC đều tâm O ; điểm M thuộc miền trong tam giác OBC ; D , E , F lần lượt
là hình chiếu vuông góc của M trên BC , CA , AB . Khẳng định nào sau đây đúng?
   1 
   
A. MD ME MF MO .
B. MD ME MF MO . 2
   
   3 
C. MD ME MF  3MO .
D. MD ME MF MO . 2 Lời giải. Phan Minh Tâm Chọn D
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 66
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Từ M kẻ đường thẳng Mx AC cắt AB , BC tại H , K ;
Từ M kẻ đường thẳng My AB cắt BC , CA tại P , Q ;
Từ M kẻ đường thẳng Mz BC cắt AB , AC tại R , S ;
Suy ra HMR , PMK , Q
MS là các tam giác đều nên MD , ME , MF là các đường cao
đồng thời cũng là đường trung tuyến. Khi đó  1   MD
MP MK ; 2  1   ME
MS MQ; 2  1   MF
MH MR. 2
   1 
    
Ta được MD ME MF
MQ MH MP MR MS MK . 2
   1    1 
    
Hay MD ME MF
MAMB MC  MO OAMO OB MO OC . 2 2
Mặt khác ta có tam giác ABC đều nên tâm O cũng là trọng tâm tam giác ABC nên
   
OA OB OC  0 ;
   3 
Vậy MD ME MF MO . 2
VẤN ĐỀ 2. BA ĐIỂM THẲNG HÀNG
Email: phunghang10ph5s@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 67
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 234: Cho hình bình hành ABCD có các điểm M , I , N lần lượt thuộc các cạnh AB, BC, CD sao cho 1 1 AM
AB, BI kBC, CN
CD . Gọi G là trọng tâm tam giác BMN . Xác định k để AI đi 3 2 qua G . 1 9 6 12 A. . B. . C. . D. . 3 13 11 13 Lời giải
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng Chọn C
Gọi E là trung điểm của MB . Khi đó:
AM ME EB  1  Ta có: EG EN 3
  1  
EA AG
EAAN 3  2  1   2 2  1         AG AE AN AG
AB   AC CN  4 1  1  5 1 .  AB AC AB AB    AC 3 3 3 3 3 9 3  2  18 3  
Do BI kBC và điểm I nằm trên đoạn BC nên BI k BC       
BA AI k BA AC  AI  1 k AB k AC 1  k k 18 6
Do AI đi qua G nên ,
A I , G thẳng hàng   
1 k   3k k  . 5 1 5 11 18 3
Câu 235: Cho tam giác ABC . Gọi M là điểm thuộc cạnh AB, N là điểm thuộc cạnh AC sao cho 1 3
AM AB, A
N AC . Gọi O là giao điểm của CM và BN. Trên đường thẳng BC lấy E. 3 4  
Đặt BE xBC .
Tìm x để A, O, E thẳng hàng. Chọn C 2 8 9 8 A. B. C. D. 3 9 13 11 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 68
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  1  1  Ta có: AO
AB AC 9 4   
AE  (1  x A ) B xAC  
A, E, O thẳng hàng  AE kAO   k  k  36 9  (1  x A
) B xAC AB AC k  ; x  9 4 13 13 9 Vậy x  là giá trị cần tìm. 13
Họ và tên tác giả: Nguyễn Thanh Dũng Tên FB: Nguyễn Thanh Dũng
Email: thanhdungtoan6@gmail.com
Ý tưởng: Cho tam giác ABC , I là trung điểm của BC . Gọi P, Q, R là các điểm xác định bởi:      
AP p AB, AQ q AI , AR r AC với pqr  0 . 2 1 1
Chứng minh rằng: P, Q, R thẳng hàng khi và chỉ khi   . q p r Chứng minh Ta có      1               q  2 p q PQ AQ AP q AI p AB q AB AC p AB AB AC  2 2 2
    
PR AR AP r AC p AB   
Do đó, P, Q, R thẳng hàng khi và chỉ khi tồn tại số thực m sao cho PQ mPR
q  2 p  q            
q  2 p  2mp q  2mr AB AC m r AC p AB AB AC  0 2 2 2 2
q  2 p  2mp  0     2  
(vì AB, AC không cùng phương) q  2mr   0   2  q m  1   2 p q q 2 1 1    1     q 2 p 2r q p rm    2r
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 69
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 236: Cho tam giác ABC . Gọi I là trung điểm BC ; P là điểm đối xứng với A qua B ; R là điểm 2
trên cạnh AC sao cho AR
AC . Khi đó đường thẳng AR đi qua điểm nào trong các điểm 5 sau đây?
A. Trọng tâm tam giác ABC .
B. Trọng tâm tam giác ABI .
C. Trung điểm AI .
D. Trung điểm BI . Lời giải Đáp án: B A R M G B C J H I P  
AP  2AB p  2 
Theo đề bài,  2   2  AR AC r     5   5   2   2 
Gọi G là trọng tâm tam giác ABI , ta được AG AH q    3  3  1 1 1 1 2 Ta có     3 
suy ra P, G, R thẳng hàng. p r 2 5 q 2
(có thể phát triển P, J, G, M, R thẳng hàng với J – có lẽ là trung điểm BH, còn M chia
AI theo tỷ số tính được)
Câu 237: Cho ABC có H là trung điểm của AB và G AC : GC  2AG . Gọi F là giao điểm của CH
và BG . Tìm điểm I trên BC sao cho I , F , A thẳng hàng       A. IC  2  I . B
B. IB  2IC.
C. IB I . C D. IC  3  I . B Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 70
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Gọi D là đỉnh thứ tư của hình bình hành ABCD và E là trung điểm của A . D Khi đó, ta có:  1  FH   FC 4
Vận dụng định lý Menelauyt trong HBC có ,
A F , I thẳng hàng AH IB FC 1 IB  . .  1  . . 4    1 AB IC FH 2 IC IB 1    IC 2   Vậy IC  2  . IB
Họ và tên tác giả: Hoàng Thị Trà FB: Hoàng Trà
Câu 238: Cho tam giác ABC. I là trung điểm của BC. Gọi M, N, P lần lượt là các điểm xác định bởi      
AM m AB; AN n AI; AP p AC , với mnp  0 . Tìm điều kiện của m, n, p để M, N, P thẳng hàng.
A. mp mn np
B. 2mp mn np
C. 2np mn mp
D. 2mn mp np Lời giải
    
MP AP AM p AC m AB  1  
Ta có    
 . Mà AI  (AB AC)
MN AN AM n AI m AB 2  n    n
 n  MN
( AB AC)  m AB  (  m) AB AC 2 2 2 n nm
Do mnp  0 nên M, N, Q thẳng hàng khi và chỉ khi 2 2 
 2mp mn np m p Chọn đáp án B.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 71
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Nhận xét: Với bài toán trên thì việc cụ thể hóa bộ ba số m,n,p sao cho thỏa mãn điều kiện trên
ta đều ra được bài toán chứng minh ba điểm thẳng hàng. Kết quả trên chúng ta có thể vận dụng
vào để giải nhanh bài toán sau:
Câu 239: Cho tam giác ABC. Gọi G là trọng tâm của tam giác, I là trung điểm của BC, M và N là các  1  CN BC
điểm được xác định bởi  2 
  . Gọi P là giao điểm của AC và MN. Tính tỉ số diện 3
MA  4MB  0 
tích tam giác ANP và tam giác CNP. 7 A. 3 B. C. 4 D. 2 2 Lời giải. S PA PA Ta có ANP
. Yêu cầu bài toán dẫn đến tìm tỉ số . S PC PC CNP
Ta dễ dàng chứng minh được M, N, G thẳng hàng.  1 
       CN
BC  2CN GC GB  2(GN GN )  GC GB 2     
Ta có  2GN  3GC GB  3  GA  4GB          2GN  3
GA  4GB  3MA  4MB(vi3MA  4MB  0)    2GN  7GM
Vậy G, M, N thẳng hàng. Mặt khác MN cắt AC tại P, nên M, G, P thẳng hàng.   4
Áp dụng kết quả G, M, P thẳng hàng theo câu 1 vào ta có AM m AB m  7   2   4 4 2 2 4
AG n AI n
, AP p AC. Khi đó 2mp mn np  2. . p  .  . p p  , khi 3 7 7 3 3 5 PA S đó
 4 . Vậy ANP  4 PB SCNP
 2   1  BD BC; AE  AC
Câu 240: Cho tam giác ABC . Gọi ,
D E lần lượt là các điểm thỏa mãn: 3 4 . Điểm
 a  a AK AD
K trên AD thỏa mãn b
(với b là phân số tối giản) sao cho 3 điểm , B K, E thẳng hàng. Tính 2 2
P a b . A. P  10 . B. P  13 . C. P  29 . D. P  5 . Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 72
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  1 
 1  3  Vì AE AC BE BC B ( A 1) 4 4 4      Giả sử AK  .
x AD BK  .
x BD  (1 x)BA  2   
 2x   Mà BD
BC nên AK  . x AD BK
BD  (1 x)BA 3 3   Vì ,
B K, E thẳng hàng ( B E )nên có m sao cho BK mBE m  3m  2x   Do đó có: BC BA
BC  (1 x)BA 4 4 3  m 2x    3m    Hay 
BC  1 x BA  0      4 3   4   
Do BC; BA không cùng phương nên m 2x 3m 1 8   0;1 x
 0 Từ đó suy ra x  ; m  4 3 4 3 9  1  Vậy AK AD 3
Email: themhaitotoanyp1@gmail.com    
Câu 241: Cho tam giác ABC, I là điểm thỏa mãn: 2IA IB  4IC  0    
K là điểm thỏa mãn: KA  2KB  3KC  0    
P là điểm thỏa mãn: PA mPB nPC  0 Có bao nhiêu cặp  , m n, , m n Z, , m n   1
 0;10 sao cho I, K, P thẳng hàng. A. 2 B. 3 C. 4 D. 5 Lời giải
Ta có PA  mPB nPC
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 73
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    
Có: 2IA IB  4IC  0  2PA PI  PB PI  4PC PI   0
 5PI  2PA PB  4PC
 5PI   2m  
1 PB   2n  4PC Có:               
KA  2KB  3KC  0  PA PK   2PB PK   3PC PK   0  6PK PA  2PB  3PC   
 6PK  m  2 PB  n  3 PC
I,K,P thẳng hàng khi và chỉ khi 5PI 6 , PK cùng phương  2m   1 n  
3  m  22n  4  2m  5n  11 Do  , m n, , m n Z , , m n   1  0;10 nên  , m n    8  ;   1 , 3  ,   1 , 2,3,5, 7
(Fb: Lưu Thêm)
Email : boyhanam@gmail.com
Bài em sưu tầm ạ !      
Câu 242: Cho tam giác ABC , M và N là hai điểm thỏa mãn: BM BC  2 AB , CN x AC BC . Xác
định x để A, M , N thẳng hàng. 1 1 A. 3. B.  . C. 2. D.  . 3 2 Lời giải Chọn D Ta có         
BM BC  2 AB AM BC AB AM   AC  2BC          
CN x AC BC.  CA AN x AC BC AN   x   1 AC BC   Để ,
A M , N thẳng hàng thì k
  0 sao cho AM k AN  1  k     
x 1  k   2 Hay  x  
1 AC BC k AC  2BC      1  2k 1   x    2 Huonghungc3@gmail.com
Câu 243: Cho tam giác ABC có G là trọng tâm, I là trung điểm AG , lấy K thuộc cạnh AC sao cho  
AK  kAC . Nếu B, I, K thẳng hàng thì giá trị của k nằm trong khoảng?  1   1   1 1   1  A. 0;  B. 0;   C. ;   D. ;1   6     2   5 3   5 
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 74
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Lời giải
(Họ tên: Nguyễn Thu Hương. Tên FB: Thu Hương) C N G K O B Chọn B
Không giảm tính tổng quát: giả sử tam giác ABC có: A(0; 0); B6;  0 ;C0;  6 thì G2;  2 ; I1;  1   I 6
Gọi K0;m Khi đó: IB5;  1 ;KB6; m
 . Để B, I,K thẳng hàng:5m  6  m  5 1 suy ra k  5
Họ và tên: Trần Văn Luật Email: Tvluatc3tt@gmail.com FB: Trần Luật  
Câu 244: Cho tam giác ABC , M là điểm thuộc cạnh AC sao cho MA  2
 .MC , N thuộc BM sao cho     NB  3
NM , P là điểm thuộc BC . Biết rằng ba điểm ,
A N , P thẳng hàng khi PB k PC .
Khẳng định nào sau đây là đúng?  5   5   1   1  A. k  3  ;    . B. k   ; 1    . C. 1;    . D.  ; 0   .  2   2   2   2  Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 75
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A M N B C P Ta có            
NB   NM AB AN    AM AN  1 1 3 3
AB  3AM  4AN AN AB AC . 4 2       Do P là điểm thuộc BC nên
PB k PC AB AP k AC AP     1  k 
AB k AC  1 k AP AP AB AC . k 1 1 k  1 h  k  2   1    k 4  Ba điểm ,
A N , P thẳng hàng khi và chỉ khi AP h AN     4 . 1 h h       3   1 k 2 Vậy k  2  .
Họ và tên: Hoàng Thị Kim Liên
Email: lientiencl@gmail.com Facebook: Kim Liên
Câu 245: Cho tam giác ABC . Gọi M, N, P lần lượt nằm trên đường thẳng BC, CA, AB sao cho      
MB mMC , NC nN ,
A PA k PB . Tính tích mnk để M, N, P thẳng hàng? A. 1 . B. 1  . C. 2 . D. 2  . Lời giải Chọn A Ta có :         m 1  ;;( 1 ) ;n MB BC BP AB BC m MC CN AC 1 m k 1 1 n    1   1 n MN AB     AC 1 m  1 m 1 n
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 76
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New     m 1   m MP    AB AC  1 m 1 k  1 m
Để M, N, P thẳng hàng thì ta có : m 1 m  1 m 1 k 1 m Câu 246:   mnk  1 1  1 n  1 m 1 m 1 n
(Email): thuhangnvx@gmail.com
Câu 247: Cho hình bình hành ABCD gọi M là trung điểm của cạnh CD, N là điểm thuộc cạnh AD sao cho 1 AN
AD . Gọi G là trọng tâm của tam giác BMN, đường thẳng AG cắt BC tại K. Khi đó 3  m  m BK BC (
là tối giản). Tính S m n n n
A. S  16 . B. S  17 .
C. S  18 . D. S  19 . Lời giải
( Tên FB: Phùng Hằng ) Chọn B Ta có    1    
AG AE AF
AN AM  1 2  AG AB 2 2 
   1  1      
AG AN AM AB AD  AD AC 5 1 3  AB AD AC AB 3 2 6 2 5  1       AD  AB AD 4 3  AB AD AB 6 2 3 2  1  4   AG AB AD . 2 9  
       Đặt BK  .
x BC AK AB BK AB xBC AB x AD . k  2     k  4k  
Do A,G,K thẳng hàng thì AK k AG AB x AD AB AD   8 2 9 x    9
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 77
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New m 8 Suy ra  n 9 Vậy S  17
Email: builoiyka@gmail.com
Câu 248: Cho hình thang ABCD có đáy AB , CD , CD  2 AB . M , N lần lượt là các điểm thuộc cạnh
AD và BC sao cho AM  5MD , 3BN  2NC . Gọi P là giao điểm của AC và MN ; Q là PM QN a a
giao điểm của BD và MN ; Khi đó   , với
là phân số tối giản. Khi đó a b PN QM b b bằng A. 386 . B. 385 . C. 287 . D. 288 . Lời giải
Họ tên: Bùi Thị Lợi Facebook: LoiBui Chọn A E A B N P M Q D C
Gọi E là giao điểm của AD và BC . Ta có A, lần lượt là trung điểm của EC , ED .    
Giả sử PM xPN ; QN yQM .     11 7x  EA EC EM xEN 11  7x  Ta có EP  6 10   EA EC 1 x 1 x 61 x 101 x 11 7x 25 Do P, ,
A C thẳng hàng nên 
 1  55  21x  30  30x x   .
61 x 101 x 9 PM 25 Vậy  . PN 9  
7  11y   EB ED EN yEM 7  11y  Ta có EQ  5 12   EB ED 1 y 1 y 51 y 121 y 7 11y 24
Do Q, B, D thẳng hàng nên 
 1  84  55 y  60  60 y y   .
51 y 121 y 5
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 78
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New QN 24 Vậy  . QM 5 PM QN 341 Suy ra  
a  341;b  45  a b  386 . PN QM 45 Cách 2:
Áp dụng định lý Menelaus cho tam giác AMN với ba điểm thẳng hàng là , A P, C , ta có PM CN AE PM 3 6 PM 25 . .  1  . .  1   . PN CE AM PN 10 5 PN 9
Áp dụng định lý Menelaus cho tam giác EMN với ba điểm thẳng hàng là B, Q, D , ta có QN DM BE QN 1 5 QN 24 . .  1  . .  1   . QM DE BN QM 12 2 QM 5 PM QN 341 Vậy  
a  341;b  45  a b  386 . PN QM 45
Email: datltt09@gmail.com
Câu 249: Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = 3MC, NC
= 2BN. Gọi I là giao điểm của AN và BN. Tính diện tích tam giác ABC biết diện tích tam giác ABN bằng 4. A. S  110 . B. S  115 . C. S  125 . D. S  120 . ABC ABC ABC ABC Lời giải
Họ và tên tác giả: Vũ Thị Hằng Tên FB: Đạt Lâm Huy Chọn D  
Giả sử AI k AN ta có    
BI BA k BN k BA 
 k 
BI  1 k BA BC(1) 3     
Tương tự 4 AM  3AC BM BA  3BC(2) k 1 k 9
Vì B,I,M thẳng hàng nên từ(1) và(2) ta có 3   k  1 3 10 Suy ra S  10S  40 ABN BNI S  3S  120 ABC ABN
(Có thể dùng định lý Menelauyt để tính tỷ số)
Email: samnk.thptnhưthanh@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 79
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 250: Cho tam giác ABC M thuộc cạnh AC sao cho MA   M . 2
C , N thuộc BM sao cho NB  . 3
NM , P thuộc BC sao cho PB k.PC . Tìm giá trị k để ba điểm A, N, P thẳng hàng. 1 1 A. k .
B. k  2 . C. k   .
D. k  2 . 2 2 Lời giải
Họ và tên: Nguyễn Khắc Sâm Facebook: Nguyễn Khắc Sâm Chọn B A M N B C P Ta có: NB  3
 .NM AB AN   .
3 AM AN  AB  . 3 AM  . 4 AN 1 1  AN AB  .AC   1 4 2
PB k.PC AB AP kAC AP AB k.AC  1 kAP (k  ) 1 1 kAP AB AC 2 1  k 1  k
Ba điểm A, N, P thẳng hàng khi và chỉ khi:  1 h   1 k 4 AP  . h AN    k  2  .  k h     1  k 2
VẤN ĐỀ 3. QUỸ TÍCH
Nguyễn Văn Dũng Fb: Nguyễn Văn Dũng
Email: dungtoanc3hbt@gmail.com    
Câu 251: Cho tam giác ABC với J là điểm thoả mãn 2JA  5JB  3JC  0 , gọi E là điểm thuộc  
AB và thoả mãn AE kAB . Xác định k để C, E, J thẳng hàng.
A. k  2;  1 .
B. k  1;0 .
C. k  0;  1 .
D. k  1;2 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 80
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Ta có               
2JA  5JB  3JC  0  2JE  2EA  5JE  5EB  3JC  0  7JE  3JC  2EA  5EB  0         5 5
Để C , E, J thẳng hàng thì 2EA  5EB  0  7EA  5AB  0  AE AB k  . 7 7 Chọn C Leminh0310@gmail.com
Câu 252: Cho hình vuông ABCD tâm O cạnh 1 . Biết rằng tập hợp các điểm M thỏa mãn 2 2 2 2
2MA MB  2MC MD  9 là một đường tròn có bán kính R . Khẳng định nào sau đây đúng?  1 3   3 
A. R  0;  1 .
B. R  1; 2 . C. R  ;   . D. R  ; 2   .  2 2   2 
(Sưu tầm: Lê Hồ Quang Minh – FB: Lê Minh) Lời giải Chọn C A D O C B    OA    OC  0
Vì ABCD là hình vuông tâm O nên ta có:    OB   OD  0  Theo giải thiết: 2 2 2 2
2MA MB  2MC MD  9        
 MO OA2  MO OB2  MO OC 2  MO OD2 2 2  9  
   2 2 2 2 2
 6MO  2OA OB  2OC OD  2MO 2OA  2OC OB OD  9
  0 2
 6MO 3  9  MO  1 .
Vậy tập hợp các điểm M là đường tròn tâm O bán kính R  1 .
Email: thuyhung8587@gmail.com
Câu 253: Cho tam giác ABC . Tập hợp những điểm M thỏa mãn:
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 81
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
  
  
4MA MB MC  2MA MB MC là:
A. Đường thẳng đi qua A
B. Đường thẳng qua B và C C. Đường tròn
D. Một điểm duy nhất. Lời giải
  
  
4MA MB MC  2MA MB MC
     
MA MB MC  3MA  2MA  2MI , ( I : là trung điểm BC )    
 3MG MA  2 MA MI , (G : trọng tâm ABC )   1
 6 MJ  2 IA MJ
IA ,( J là trung điểm của AG ) 3 1 AGJM
AG (không đổi). Vậy tập hợp điểm M là đường tròn tâm J , bán kính R  . 2 2 Chọn đáp án C.
(Họ và tên tác giả: Cấn Việt Hưng, Tên FB: Viet Hung) ngoletao@gmail.com
Câu 254: Cho tam giác ABC có hai đỉnh B, C cố định với BC  2a . Gọi H là trực tâm của tam giác
ABC và M là trung điểm của đoạn BC. Nếu đỉnh A thay đổi nhưng luôn thỏa   2 2 M .
A MH MA  4a thì điểm A luôn thuộc một đường tròn cố định có bán kính bằng A. 2a . B. a 3 . C. a 2 . D. a .
(Họ và tên tác giả: Ngô Lê Tạo, Tên FB: Ngô Lê Tạo) Lời giải Chọn B A H B C M Ta có
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 82
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New   1 
   . MA MH
BACABH CH  . 4 1       . BA BH C .
A CH  (do BA CH ,CA BH 4 1       . BA BH C .
A CH  (định lý chiếu vectơ) 4 1 2  BC 4 Suy ra   1 2 2 2 2 2 .
MA MH MA  4a
.4a MA  4a AM a 3 . 4
Câu 255: Cho hai điểm A và B cố định. Tìm giá trị k  0 để tập hợp điểm M thỏa mãn điều kiện 2 2
MA MB k là một đường tròn. 2 2 2 2 A. 2 k AB . B. 2 k AB . C. 2 k AB . D. 2 k AB . 3 3 3 3 Lời giải Chọn D   
Gọi E là điểm thỏa mãn: EA  2EB  0 ta có   
EA  2EB  0 ta có:          2   2 2 2 MA MB k ME EA ME EBk 2 2 2
 3ME k EA  2EB * 2 1 2
Mà EA  2EB  0  EA AB ; EB AB nên * 2 2
 3ME k AB 3 3 3 1  2 2 2   ME k AB   3  3  2 Nếu 2 k
AB : Quỹ tích điểm M là rỗng. 3 2 Nếu 2 k
AB : Quỹ tích điểm M là điểm E . 3 2 1  2  Nếu 2 k
AB : Quỹ tích điểm M là đường tròn tâm E bán kính 2 R k AB   . 3 3  3 
PHẠM THANH LIÊM FB: Liêm Phạm
Email: Phamthanhliem1@gmail.com 2 2 2
Câu 256: Cho tam giác vuông ABC tại A . Tìm tập hợp M sao cho MB MC MA . A. Đường thẳng. B. Đường tròn. C. Đoạn thẳng. D. Một điểm. Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 83
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn D 2 2 2 2 2 2
MB MC MA MB MC MA  0 . Gọi E là điểm được xác định bởi
  
EB EC EA  0 . ( E là điểm thứ tư của hình bình hành ABEC ).       2 2 2 Ta có: 2 2 2
MB MC MA  ME EB  ME EC  ME EA 2 2 2 2
ME EB EC EA             2 2 2 2 ME EB EC EB EC 2 2  ME  2E .
B EC ME  2A . B AC 2  ME . Vậy 2 ME  0 .
Nên tập hợp điểm M là điểm E .
( Cách chứng minh trên phục vụ cho cả tam giác ABC là tam giác thường và khi đó các tập
hợp điểm là khác nhau )
Email: thachtv.tc3@nghean.edu.vn
Câu 257: Cho tam giác ABC vuông cân tại A có AB  5cm . Gọi (S ) là tập hợp các điểm M trong mặt
   
phẳng thỏa mãn hệ thức: M . A MB M .
A MC  25 . Gọi I là trung điểm của BC . Kết luận nào
sau đây đúng?
A. (S ) là đường thẳng trung trực của đoạn thẳng AI .
B. (S ) là đoạn thẳng AI . 5 10
C. (S ) là đường tròn cố định bán kính R  . 4 5 2
D. (S ) là đường tròn tâm I bán kính R  4
(Họ và tên tác giả: Trịnh Văn Thạch, FB: www.facebook.com/thachtv.tc3) Lời giải Chọn C C I D A B
    5 2 1 1 Từ giả thiết: M . A MB  . MA MC    2 2 2
MA MB AB    2 2 2
MA MC AC   25 2 2 2 2 2 2 2 2 2
 2MA MB MC  50  50  2MA MB MC  100
         
Gọi D là điểm thỏa mãn 2DA DB DC  0  2DA  2DI  0  DA DI  0
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 84
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
D là trung điểm của đoạn thẳng AI Ta có 2 2 2 2 2 2 2
2MA MB MC  4MD  2DA DB DC 2 2 1 1 5 2  5 2   5 2  125 Và DA AI BC  , 2 2 DB DC
IB ID        . 2 4 4  2   4  8     Suy ra 2 2  5 2   125  75 2 2 2 2 2 2 2 2 2
2MA MB MC  4MD  2DA DB DC  4MD  2.   2.   4MD   4   8  2     75 125 Ta có kết quả: 2 2 4MD   100  MD  2 8 5 10
Như vậy (S ) là đường tròn tâm D bán kính R  . 4
Câu 258: Cho tam giác đều ABC cạnh a . Tập hợp các điểm M thỏa mãn đẳng thức 2 5a 2 2 2
4MA MB MC
nằm trên một đường tròn C  có bán kính là: 2 a a a 3 a A. . B. . C. . D. . 3 4 2 6 Lời giải Chọn D
Gọi M lần lượt là trung điểm của BC .
   
Gọi I là điểm thỏa mãn điều kiện: 4IA IB IC  0
   
Khi đó, ta có: 4IA IB IC  0        1 
 4IA  2IM  0  3IA AM  0  AI AM . 3 a 3 a 21 Suy ra: IA  ; 2 2 IB IC IM BM  . 6 6 2 5a Ta lại có: 2 2 2
4MA MB MC  2 2    2 2 2 5a
 4MA MB MC  2 2      
 MI IA2  MI IB2  MI IC2 5a 4  2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 85
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2
    5a 2
 6MI  2MI 4IA IB IC 2 2 2
 4IA IB IC  2 aMI  . 6 a
Vậy tập hợp điểm M là đường tròn tâm I bán kính R  . 6   
   Câu 259: Cho A
BC . Tìm tập hợp các điểm M sao cho: MA  3MB  2MC  2MA MB MC .
A. Tập hợp các điểm M là một đường tròn.
B. Tập hợp của các điểm M là một đường thẳng.
C. Tập hợp các điểm M là tập rỗng.
D. Tập hợp các điểm M chỉ là một điểm trùng với A . Lời giải Chọn A A A N C    
Gọi I là điểm thỏa mãn IA  3IB  2IC  0 .   
        
MA  3MB  2MC  2MA MB MC  2MI IA  3IB  2IC BA CA   1 .  
Gọi N là trung điểm BC . Ta được:  
1  2 MI  2  AN IM AN .
I , A , N cố định nên tập hợp các điểm M là đường tròn tâm I , bán kính AN .
Câu 260: Cho tam giác đều ABC cạnh a . Tập hợp các điểm M thỏa mãn đẳng thức 2 5a 2 2 2
4MA MB MC
nằm trên một đường tròn C  có bán kính là: 2 a a a 3 a A. . B. . C. . D. . 3 4 2 6 Lời giải Chọn D
Gọi M lần lượt là trung điểm của BC .
   
Gọi I là điểm thỏa mãn điều kiện: 4IA IB IC  0
   
Khi đó, ta có: 4IA IB IC  0
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 86
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New        1 
 4IA  2IM  0  3IA AM  0  AI AM . 3 a 3 a 21 Suy ra: IA  ; 2 2 IB IC IM BM  . 6 6 2 5a Ta lại có: 2 2 2
4MA MB MC  2 2    2 2 2 5a
 4MA MB MC  2 2      
 MI IA2  MI IB2  MI IC2 5a 4  2 2
    5a 2
 6MI  2MI 4IA IB IC 2 2 2
 4IA IB IC  2 aMI  . 6 a
Vậy tập hợp điểm M là đường tròn tâm I bán kính R  . 6
Họ và tên tác giả: Vũ Thị Nga Tên FB: Linh Nga
Email: linhnga.tvb@gmail.com
Câu 261: Cho ABC đều, có cạnh bằng a. Khi đó tập hợp những điểm M sao cho 2
      a . MA MB  .
MB MC MC.MA  là: 6 a
A. Đường tròn có bán kính R  . 3 a
B. Đường tròn có bán kính R  . 2 a 2
C. Đường tròn có bán kính R  . 3 a 3
D. Đường tròn có bán kính R  . 9 Lời giải Chọn C
Gọi G là trọng tâm ABC . Suy ra G là tâm đường tròn ngoại tiếp ABC và G cố định.
   
Ta có MA MB MC  3MG
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 87
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
   
 MA MB MC2  9MG2
      2 2 2
MA MB MC  2 . MA MB M .
B MC MC.MA 2  9MG    2 2 2 Mà 2 2 2
MA MB MC MA MB MC      
 MG GA2  MG GB2  MG GC2
    2 2 2 2
 3MG GA GB GC  2.M .
G GA GB GC  2 2 2 2
 3MG GA GB GC  2.M . G 0 2 2  3MG  3GA 2  2 a 3  2  3MG  3 .   3 2    2 2  3MG a
      Ta có 2 2
MG a  MA MB MB MC MC MA 2 3 2 . . .  9MG 2
        a . MA MB  .
MB MC MC.MA 2  3MG  2 2 2 a a 2    3MG 6 2 2 2a 2  MG  9 a 2
Vậy tập hợp điểm M là đường tròn tâm G bán kính R  . 3
Họ và tên tác giả: Tô Quốc An Tên FB: Tô Quốc An
Email: antq4949@gmail.com   2 Câu 262: Cho AB
C tìm tập hợp điểm M : . MB MC AM Lời giải      
Gọi I là trung điểm của BC , ta có: 2
MB MC AM  MI IB MI IC 2 . .  MA 2
      BC 2
MI IC IB MI IC IB 2 2 2 .
MA MI MA  IC.IB  4 2 2
   
         BC      BC MI MA MI MA AI MI MA  (*) 4 4   
Gọi O là trung điểm của AI , suy ra: MI MA  2MO 2 2 2   BC   BC   BC Suy ra:   *  2AI.MO   4OI.MO
OI.OM   4 4 16
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 88
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 BC 2   BC
Trên tia đối của tia OI lấy điểm H sao cho OI.OH
hay OI.OH   , suy ra 16 16
điểm H xác định duy nhất.
Dựng đường thẳng  đi qua H và vuông góc với OI , khi đó với mọi điểm M nằm trên  ta có: 2
    
      BC
OI.OM OI.OH HM   OI.OH OI.HM OI.OH   . 16
Vậy tập hợp điểm M là đường thẳng 
Email: Bichhai1975@gmail.com
Câu 263: Cho tam giác đều ABC cạnh bằng 3 . Biết rằng tập hợp các điểm M thỏa mãn đẳng thức     
2MA  3MB  4MC MB MA là đường tròn cố định có bán kính bằng: 1 3 1 A. 1. B. . C. . D. . 3 2 2
(Họ tên: Lê Thị Bích Hải, Tên face: Bich Hai Le) Lời giải
Họ tên: Lê Thị Bích Hải. Tên face: Bich Hai Le Chọn B
Gọi G là trọng tâm của tam giác ABC.         
Ta có 2MA  3MB  4MC  2 MI IA  3MI IB  4MI IC.          
Chọn điểm I sao cho 2IA  3IB  4IC  0  3IA IB IC  IC IA  0.    
Mà G là trọng tâm của tam giác ABC IA IB IC  3 . IG
   
     
Khi đó 9 IG IC IA  0  9 IG AI IC  0  9 IG CA .          
Do đó 2MA  3MB  4MC MB MA  9MI  2IA  3IB  4IC AB  9MI A . B
Vì I là điểm cố định thỏa mãn  nên tập hợp các điểm M cần tìm là đường tròn tâm I , bán AB 1 kính r   . 9 3 thongqna@gmail.com
Câu 264: Cho tam giác ABC có là trọng tâm G . Tìm tập hợp điểm M thỏa mãn
        
MAMB MC BC2 MAMC MG2  CB AC2 3 .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 89
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
A. Đường tròn đường kính AB .
B. Đường trung trực đoạn thẳng AB .
C. Đường tròn đường kính AC .
D. Đường trung trực đoạn thẳng AC .
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông) Lời giải Chọn A
       
Ta có MA MB MC BC MA CB BC MA .
Gọi điểm I là trung điểm cạnh AC .         
Ta có MA MC  3MG  2MI  3MG  2MB BI   3MB BG   2  
 MB  2BI  3. BI  MB . 3
         2 2 2
Do đó MA MB MC BC  MA MC  3MG  CB AC   2    2 2 MA MBAB 2 2 2
MA MB AB .
Từ đó suy ra tam giác MAB vuông tại M hay tập hợp các điểm M là đường tròn đường kính AB .  
Câu 265: Cho đoạn thẳng AB  5 . Biết rằng tập hợp điểm M thỏa mãn 2 2
MA MB  3M . A MB là
một đường tròn có bán kính R . Tìm giá trị của R . 5 5 3 3 A. R  . B. R  . C. R  . D. R  . 2 2 2 2
(Họ và tên tác giả: Trần Văn Thông, Tên FB: Trần Thông) Lời giải Chọn A  
    Ta có 2 2
MA MB  3M . A MB 2 2
MA MB  2 . MA MB M . A MB      
 MA MB2  M . A MB 2  AB M . A MB .
Gọi điểm I là trung điểm cạnh AB .           Ta có 2 AB M . A MB 2
AB  MI IA.MI IB 2
AB  MI IA.MI IA 2 2 2 5
AB MI IB 2 2 2
MI AB IB 2 2  MI AB 4 5 5 5  MI AB  . 5  . 2 2 2  
Vậy tập hợp điểm M thỏa mãn 2 2
MA MB  3M .
A MB là đường tròn tâm I có bán kính 5 R  . 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 90
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên: Võ Khánh Huyền Vân Fb: Vân Võ
Email: huyenvanqt050185@gmail.com
  
Câu 266: Cho tam giác ABC , có bao nhiêu điểm M thỏa MA MB MC  5 ? A. 1. B. 2 . C. vô số.
D. Không có điểm nào. Lời giải. Chọn C
   
Gọi G là trọng tâm của tam giác ABC , ta có MA MB MC  3MG .
    5
Thay vào ta được: MA MB MC  5  3MG  5  MG
, hay tập hợp các điểm M là 3 5
đường tròn có tâm là trọng tâm của tam giác ABC và bán kính bằng . 3
VẤN ĐỀ 4. TỈ LỆ
Họ và Tên: Trần Quốc Đại
Email: quocdai1987@gmail.com
Facebook: https://www.facebook.com/tqd1671987
Câu 267: Cho  ABC có AB  3 ; AC  4 . Phân giác trong AD của góc BAC cắt trung tuyến BM tại I AD . Tính . AI AD 3 AD 10 AD 29 AD 7 A.  . B.  . C.  . D. AI 2 AI 7 AI 20 AI 5 Lời giải Chọn B    
* Phân tích AD, AI theo các vectơ AB, AC . IB AB 3       Ta có:  
 2IB  3IM  0  2 AB  3AM  5AI   1 . IM AM 2 DB AB 3     
 4DB  3DC  0 DC AC 4
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 91
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New   
 4 AB  3AC  7 AD 2 .        Lấy 2  2. 
1  suy ra: 3AC  6 AM  7 AD 10 AI  7 AD 10 AI  0  7 AD  10AI AD 10   . AI 7
Câu 268: [Đề thi olympic 30/4 TPHCM khối không chuyên lần 2 ] Cho ABC gọi điểm D nằm trên
cạnh BC sao cho BD  2BC , E là trung điểm của AD . Một đường thẳng bất kì qua E và cắt AB AC các cạnh A ;
B AC lần lượt tại M , N . Tình tỉ số  2 AM AN AB AC AB AC A.  2  6 . B.  2  5 . AM AN AM AN AB AC 28 AB AC 29 C.  2  . D.  2  AM AN 5 AM AN 5 Lời giải Chọn A  
Do M nằm trên cạnh AB nên ta có AB k.AM (k  1)  
Do N nằm trên cạnh AC nên ta có AC l AN l   1         
Ta có DB  2DC AB AD  2
  AC AD  AB  2AC  3AD        
Suy ra k.AM  2l.AN  6.AE k AE ME  2l AE EN   6AE   
Suy ra k  2l  6 AE  k EM  2l EN  
Do hai vecto AE và MN không cùng phương nên suy ra AB AC
k  2l  6  0  k  2l  6   2  6 AM AN
Họ và tên tác giả: Đỗ Văn Đức Tên FB: Đỗ Văn Đức
Email: hoctoancunganhduc@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 92
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 269: Cho tam giác ABC . Trên cạnh AB lấy điểm D sao cho AD  2DB . Trên cạnh AC lấy điểm BN
E sao cho CE  3EA . Gọi M là trung điểm của DE . Tia AM cắt BC tại N . Tỉ số có CN giá trị là: 1 3 1 2 A. . B. . C. . D. . 4 8 2 7 Lời giải Chọn B     1   AB x AC x
Giả sử N chia BC theo tỉ số x . Ta có: AN   AB AC (1). 1 x 1 x x 1  1   1  2  1   1  1  Lại có: AM
AD AE  AB AC AB    AC (2). 2 2  3 4  3 8   3 8x 3
Vì AM và AN là 2 vectơ cùng phương nên   x   . 1 x x 1 8  3  NB 3
Do đó NB   NC   . 8 NC 8
Câu 270: (Bài toán tổng quát của bài toán 1). Cho tam giác ABC . Gọi I là điểm chia BC theo tỉ số k . AB AC
Trên các tia AB và AC lấy các điểm M , N . AI cắt MN tại P . Đặt  b ,  c . Tỷ AM AN AI số có giá trị bằng AP b kc b kc c kb c kb A. . B. . C. . D. . 1 k 1 k 1 k 1 k Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 93
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New      AM x AN 1 AB x AC
Giả sử P chia MN theo tỉ số x. Ta có AP   .  . . 1 x 1 x b x 1 c       AB k AC AB k Lại có: AI    AC (1). 1 k 1 k k 1   1 k x k   1 1 x c
Vì AP và AI đồng phương nên     x k . b 1 xkc x   1 b kc b  1   k Do đó AP AB AC (2). b kc b kc AI b kc Từ (1) và (2) , ta có  . AP 1 k
Câu 271: (Hệ quả hay dùng của bài toán 2). Cho tam giác ABC . Gọi I là trung điểm của BC. Trên các AB AC AI
tia AB và AC lấy các điểm M , N . AI cắt MN tại P . Đặt  b ,  c . Tỷ số có AM AN AP giá trị bằng b c 2 2 b c 2bc A. bc . B. . C. . D. . 2 2 b c Lời giải Chọn B
I là trung điểm của BC nên I chia BC theo tỷ số k  1
 . Áp dụng kết quả ở bài 2, ta có: AI b    1 c b c   . AP 1   1 2
Tên: Nam Phương Tên FB: Nam Phương
Email:nguyentrietphuong@gmail.com
 2   1 
Câu 272: Cho tam giác ABC . Gọi D, E lần lượt là các các điểm thỏa mãn BD BC, AE AC . 3 4 AD
Điểm K trên đoạn thẳng AD sao cho ba điểm B, K , E thẳng hàng. Tìm tỉ số . AK
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 94
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New AD 1 AD AD 2 AD 3 A.  . B.  3 . C.  . D.  . AK 3 AK AK 3 AK 2 Lời giải Chọn B  1 
 1  3  Vì AE AC nên BE BC BA 4 4 4     
AK x AD BK xBD  (1 x)BA   2x   Giả sử    BK BC  (1 x) 2 BA BD BC 3   3  m 2x  8   0 m      4 3   9
Do B, K , E thẳng hàng ta có: mBK BE     3m 1 1   x   0 x    4   3 AD Vậy  3 AK
Email: haivanxinh99@gmail.com Face Hải Vân    
Câu 273: Cho tứ giác ABCD có hai đường chéo cắt nhau tại O thỏa mãn OC  3 ,
OA OD  4OB . CN
Qua trung điểm M của AB dựng đường thẳng MO cắt CD tại N . Tính tỉ số . ND 3 1 2 1 A. . B. . C. . D. . 4 4 3 3 Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 95
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New D A M o B N C     Ta có OC  3 ,
OA OD  4OB CN       Đặt
k, k  0 , ta có CN k ND CO ON k NO ODND  1  k   3  4k   ON CO
OD ON   OA OB 1 k k 1 1 k k 1      k  
Vì OM , ON cùng phương nên có số thực k sao cho ON kOM ON  OAOB 2  3 6 8k k  3 Suy ra      4  k  . k 1 k k k   1  4 k  1  
(Email): hatoanlgm@gmail.com    
Câu 274: Cho tam giác ABC và điểm I thỏa mãn 23IA  8IB  2018IC  0 . Đường thẳng AI cắt đường JB
thẳng BC tại J . Giá trị của tỉ số là: JC 23 2018 2018 8 A. B. C. D. 8 23 8 23 Lời giải Chọn C
(Họ và tên tác giả: Ngô Ngọc Hà, Tên FB: Ngô Ngọc Hà)    1  k 
Giả sử JB k JC k   1  AJ AB AC . 1  k 1  k Từ giả thiết suy ra:        8  2018 
23AI  8 AB AI   2018 AC AI   0  AI AB AC . 2049 2049   Do ,
A I , J thẳng hàng nên AI , AJ cùng phương
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 96
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 k  2018 1 k 1 k    k   . 8 2018 8 2049 2049
Gmail: Binh.thpthauloc2@gmail.com
Câu 275: Cho tam giác ABC . Điểm K chia trung tuyến AD theo tỷ số 3 :1 kể từ đỉnh. S
Đường thẳng BK chia diện tích tam giác ABC theo tỷ số ABF k
, giá trị của k bằng? SBCF 5 3 3 3 A. k B. k C. k D. k  8 8 5 2 Lời giải Đáp án D A F K B D C
 1  
Do D là trung điểm của BC thiết: AD  ( AB AC)   1 2
Gọi F là giao điểm của BK và AC.   Mà ;
A F ;C thẳng hàng: AF mAC
2 B; K; F thẳng hàng:   
AK nAF  1 nAB 3 KD 1  3  ;
A K; D thẳng hàng và   AK AD 4 KA 3 4   
Từ 2;3 suy ra: AK  . n .
m AC  1 nAB 5
 3  3  Từ  
1 ;4 suy ra: AK AC AB 6 8 8  3  5   . m n n   8    8
Do hai véctơ AB; AC không cùng phương nên từ 5;6 ta có:    3 3 1  n    m    8   5  3  F A 3 Do đó: AF AC   5 FC 2 S FA 3 Vậy ABF k    S FC 2 BCF
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 97
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên: Tăng Lâm Tường Vinh
Email: tanglamtuongvinh@gmail.com
Facebook: tanglamtuong.vinh   3
Câu 276: Cho tam giác ABC với K là trung điểm BC . Lấy các điểm M , N thỏa mãn AM AB , 4       1 AN
AC . Gọi I là giao điểm của MN và AK . Đặt MI xMN , AI y AK . Hỏi x 3 y 3 4 5 A. . B. . C. 1. D. . 2 3 3 Lời giải Chọn A      Ta có 1 3
MN AN AM AC AB 3 4              1 3  x 3x x 3  3x
MI xMN AI AM x AC AB   AI AC AB AM AC AB  3 4  3 4 3 4        AC AB   y y
AI y AK yAB AC    2  2 2 3  3x y  9    x     4 2  13
Mà AC , AB là 2 vector không cùng phương nên ta có x 3      y  2 x y  6  y     3 2  13
Gmail: Binh.thpthauloc2@gmail.com AD 3
Câu 277: Cho tam giác ABC . Trên cạnh AB lấy điểm D, trên cạnh BC lấy E, F sao cho  ; DB 2 BE 1 BF 4 KD  
. Đường thẳng AE chia đoạn DF theo tỷ số
k . Giá trị của k bằng? EC 3 ; FC 1 KF 3 11 3 11 A. k B. k C. k D. k  11 3 14 14
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 98
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Lời giải Đáp án A AD 3  3  BE 1
 3  1  Theo giả thiết:   AD AB   1   AE AB AC 2 DB 2 5 EC 3 4 4 BF 4
 1  4    AF AB AC 3 FC 1 5 5   Mà ;
A K; E thẳng hàng: AK mAE 4 ;
D K; F thẳng hàng:   
AK nAF  1 nAD 5
 3  1 
Từ 2;4 suy ra: AK mAB mAC 6 4 4     1 4  3 Từ   1 ;  3 ; 
5 suy ra: AK n AB
AC  1 nAB 5 5    5     3 2n  4nAK   AB AC   7  5 5  5 3m 3 2n       4 5 5 Do hai véctơ A ;
B AC không cùng phương nên từ 6;7 ta có:  m 4n     4 5 1 2n 4n 3     n  5 15 5 14  3  11  KD 3 Vậy AK AB AC   k  14 14 KF 11
(Họ tên: Phạm Văn Bình, tên FB: Phạm văn Bình)
Họ và tên: Hoàng Ngọc Lâm
Email: hoangngoclammath1112@gmail.com Facebook: Hoàng Ngọc Lâm
Câu 278: Cho tam giác ABC . Kéo dài AB một đoạn BE AB , gọi F là trung điểm của AC . Vẽ hình KB
bình hành EAFG . Đường thẳng AG cắt BC tại K . Tính tỉ số ? KC 1 3 1 2 A. . B. . C. . D. . 4 8 5 7 Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 99
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New   
Để xác định giao điểm K của AG và BC , ta tính AG theo AB và AC .
    1 
Ta có: AG AE AF  2AB AC . 2
 1  
AG cắt BC tại điểm K mà 2KB KC  0 . 2 KB 1 Suy ra  . KC 4
Câu 279: Cho tam giác ABC có AB  3 , AC  4 . Phân giác trong AD của góc BAC cắt trung tuyến AD
BM tại I . Tính tỉ số . AI 13 11 10 10 A. . B. . C. . D. . 8 6 7 5
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo) Lời giải Chọn C IB AB 3   
Theo tính chất đường phân giác ta có  
 2IB  3IM  0 IM AM 2 DB AB 3    Và  
 4DB  3DC  0 DC AC 4
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 100
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New          
2IB  3IM  0 
2 AB  3AM  5AI
4AB  6 AM  10 AI Vậy ta có  
     
     
4DB  3DC  0 
4 AB  3AC  7 AD
4AB  3AC  7 AD         AD 10
Suy ra 3AC  6AM  7 AD 10AI  7 AD 10AI  0   . AI 7
Hoặc ta có thể giải như sau: BD AB 3 3 3 7 3  3  Ta có    BD DC
BC BD  D BBC  D BBC DC AC 4 4 4 4 4 7
    3   3   4  3 
Ta lại có AD AB BD AB
BC AB   AC AB  AB AC . 7 7 7 7 BI AB 3  3   
Theo tính chất phân giác, ta lại có    BI
IM  2BI  3IM IM AM 2 2         3 
 2 BA AI   3IA AM   5AI  2AB  3AM  2AB AC 2  2  3  7  4  3   7   AI AB AC AB AC AD   5 10 10  7 7  10 AD 10 Vậy  . AI 7
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Email: nguyenvantoannbk@gmail.com Nhờ thầy cô góp ý!
Câu 280: Cho hình bình hành ABCD , O là điểm bất kì trên đoạn AC , đường thẳng BO cắt cạnh CD AF
tại E và đường thẳng AD tại F sao cho EF  2BO . Tỷ số bằng AD 1 5 5 A. . B. 2 . C. 1 2 . D. . 2 2 Lời giải Chọn C A B O D C E F
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 101
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    
Đặt: AF x AD x  
1 và AO y AC 0  y   1 . DE DF DE DF x 1  x 1  Theo định lý talet:        DE AB . CE BC DC AF x x    
   
 x 1 
Ta có: BO BA y AC   y  
1 AB y AD ; EF DF DE   x   1 AD AB . x
x 1  2 yx  1 2    
Theo đề bài: EF  2BO   1   x    .   y   2 2 1   y   x  2
Họ và Tên : Nguyễn Văn Mạnh FB : Nguyễn Văn Mạnh
Email : manhluonghl4@gmail.com A B C A ,B ,C
Câu 281: Cho hai tam giác ABC và 1 1 1 ; gọi 2 2
2 lần lượt là trọng tâm các tam giác BCA , C AB , A BC G,G ,G ABC, A B C 1 1 1 . Gọi 1
2 lần lượt là trọng tâm các tam giác 1 1 1 , A B C GG 2 2 2 . Tính tỉ số 1 ta được kết quả : GG2 1 1 A. B. C. 3 D. 2 3 2 Lời giải Chọn C     Vì G, G , 3 1  1  1 
1 là trọng tâm tam giác ABC A B C suy ra GG GA GB GC 1 1 1 1           
 3GG GA GB GC AA BB CC  3GG AA BB CC 1 1 1 1 1 1 1 1    
Tương tự G, G , 3   
2 là trọng tâm tam giác ABC A B C suy ra GG GA GB GC 2 2 2 2 2 2 2      G
3 G AA BB CC 2 2 2 2         
Mặt khác AA2  BB2 CC2  AA1  BB1 CC1   A A 1 2  B B 1 2 C C 1 2 
Mà A , B ,C lần lượt là trọng tâm các tam giác BCA , CAB , ABC 2 2 2 1 1 1          Suy ra 3A A 1 2  B B 1 2 C C 1 2   A B 1  AC 1  B C 1  B A 1 C A 1 C B 1            
A A AB A A AC B B BC B B BA C C CA C C CB 1 1 1 1 1 1   
 2AA1  BB1 CC1     2      
Do đó AA2  BB2 CC2 
AA1 BB1 CC1 AA1 BB1 CC1 3
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 102
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1     1  GG
 AA BB CC GG GG  1 3 2 1  1 1 1  . Vậy . 3 3 GG2 VẤN ĐỀ 5. MIN,MAX
Email: phunghang10ph5s@gmail.com Câu 282: Cho A
BC đều cạnh bằng 3, M là điểm thuộc đường tròn ngoại tiếp ABC . Đặt 2 2 2
P MA MB MC . Gọi a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P . Khi đó,
giá trị biểu thức T  4a b là: A. 3 . B. 6 . C. 9 . D. 12 . Lời giải
Họ và tên tác giả: Phùng Hằng Tên FB: Phùng Hằng Chọn B.
Gọi O, R lần lượt là tâm và bán kính của đường tròn ngoại tiếp ABC . Ta có: 2 2 2
P MA MB MC        MO 2
OA MO OB2 MO OC2
    2  M
O  2.MO .OAOBOC 2 2 2
OA OB OC
     2  2
R  2.MO .OAOA  2 '  2  R  2M . O 2OA     2 2 2  2
R 4.OM .OA  2R 4R .cosOM;  OA   2 P
 6R khi và chỉ khi cosOM;O
A  1  M trùng A min   2 P
 2R khi và chỉ khi cosOM;O A  1
  M trùng A' là điểm đối xứng của A qua O max 2
T a b R  2  R  2 4 4.2 6  2R A
BC đều cạnh bằng 3 2
R  3  T  2R  6 .
Họ và tên tác giả: Trần Văn Ngờ Tên FB: Tran Van Ngo Tth
Email: vanngodhqn@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 103
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Câu 283: Cho A
BC và 3 số dương x, y, z thay đổi có tổng bình phương: 2 2 2 2
x y z k , k R . Giá
trị lớn nhất của P xy cos C yz cos A zx cosB là: k 2 k k 2 k A. . B. . C. . D. . 2 2 3 3 Lời giải Chọn B.
     
Đặt 3 vectơ BX , CY , AZ tương ứng là x , y , z như hình vẽ.      
Ta có:  x y z2  0 2 2 2
x y z  2x y  2 y z  2x z  0 2  k xy
0  C   yz
0  A  xz  0 2 cos 180 2 cos 180 2 cos 180  B  0 2 k 2
k  2xy cos C  2 yz cosA 2 zxcosB  0  xycosC yzcosA zxcosB  2 2 k Vậy Max P  2
Câu 284: Cho hai điểm ,
A B (I;6) và M (I;3) , thỏa mãn : 
AIB  60 . Khi A, B, M thay đổi tìm giá
trị nhỏ nhất của biểu thức P MA  2MB ? A. 9 . B. 3  2 6 . C. 3 13 . D. 6  3 .
( Họ và tên tác giả : Đặng Mơ- Tư Duy Mở ) Lời giải        | v |  | u | 
Bổ đề : Cho hai véc tơ u và v khác véc tơ 0 , ta luôn có : | u v | |  .u   .v | | u | | v |
Chứng minh : Bình phương vô hướng vế phải ta được :       2 2 2  v  u    v    u   v  u       
 u   v     u     v  
 u  v  v 2 u 2  u v  u v 2 | | | | | | | | | | | | | . . | . . 2. . . . 2. | u | | v | | u | | v | | u | | v |         | v |  | u |   
Từ đó suy ra : |  .u   .v | | u v | (đpcm). | u | | v |
Áp dụng vào bài toán cân bằng hệ số : Chúng ta có thể ghi nhớ công thức để áp dụng nhanh
vào các bài toán cân bằng hệ số đối với đường tròn và mặt cầu như sau :    
Ta có : P MA  2MB | IA IM |  2| IB IM | và IA IB  6, IM  3   IA  IM   1   1 
Trong đó : | IA IM |  | .IM
.IA |  | 2IM
IA |  2 | IM IA | IM IA 2 4  1   
 1     1 
Suy ra : P  2| IM
IA |  2| IB IM | 2 | IM
IA IB IM | | 2IB IA | 4 4 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 104
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Có : 2   1   1    1 1 1 2 2 2 2 | 2IB IA |  4IB IA  2 . IA .
IB cos 60  4.6  .6  2.6.6.  117 |  2IB IA | 3 13    2  4 4 2 2
Suy ra giá trị nhỏ nhất của biểu thức P là P
 3 13  chọn đáp án C. min
Câu 285: Cho tứ giác ABCD , M là điểm tùy ý và các điểm I, J, K cố định sao cho đẳng thức thỏa mãn
    
với mọi điểm M: MA MB MC  3MD k MK . Giá trị của k là A. k = 3 B. k = 4 C. k = 5 D. k = 6 Lời giải Chọn D
    
Vì MA MB MC  3MD k MK thỏa mãn với mọi M.
Do đó, đẳng thức cũng đúng với M K
     
Tức là: KA KB KC  3KD k KK  0
   
Gọi G là trọng tâm ABC KA KB KC  3KG   
 3KG  3KD  0  K là trung điểm GD. Mặt khác:
           
MA MB MC  3MD  (MK K )
A  (MK KB)  (MK KC)  3(MK KD)
    
 (KA KB KC  3KD)  6MK   6MKk  6
Câu 286: Cho tam giác ABC vuông tại
A. Gọi  là góc giữa hai đường trung tuyến BD và CK. Giá
trị nhỏ nhất của cos bằng 4 5 4 3 A. B. C. D. 5 4 3 4 Lời giải Chọn A 1 
 1    
(BA BC). (CA CB) . BD CK 2 2 Ta có: cos   . BD CK . BD CK
       
     2 .
BA CA BC(CA  ) BA BC ) . BA CA  .
BA CB BC.CA BC.CB)   4. . BD CK 4. . BD CK
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 105
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 2  BC 2 BC    
(Vì tam giác ABC vuông tại A nên . BA CA  0) 4. . BD CK 2. . BD CK Mặt khác, 2 2 2 2 2 2 CauchyAB BC AC   AC BC AB  2 2 2. .
BD CK BD CK         2 4 2 4     2 2 2 2 AB AC BC 5BC 2 2  BC   BC   4 4 4 2 BC 4 Suy ra, cos   2 5BC 5 4
Dấu “=” xảy ra khi và chỉ khi BD = CK hay ABC vuông cân tại A
Câu 287: Cho hai điểm cố định G và G ' là trọng tâm của tam giác ABC và tam giác A' B 'C '. Giá trị
nhỏ nhất của biểu thức P AA' BB ' CC ' bằng 1 A. GG '
B. 3GG '
C. 2GG ' D. GG ' 3 Lời giải Chọn B
    Do G
và G ' là trọng tâm ABC  , A
 ' B 'C ' nên GA GB GC  0 và
   
G ' A'  G ' B '  G 'C '  0. Ta có:
  
  
  
  
AA'  BB'  CC'  (AG GG'  G' A')  (BG GG'  G'B')  (CG GG'  G'C') 
  
  
 3GG '  (GA GB GC)  (G ' A'  G ' B '  G 'C ')   3GG '   
  
Mặt khác, P AA' BB ' CC '  AA'  BB '  CC '  AA'  BB '  CC ' 
 3 GG '  3GG '
  
Dấu “=” xảy ra khi và chỉ khi AA', BB ', CC ' cùng hướng
Họ và tên: Nguyễn Đức Hoạch – email: nguyenhoach95@gmail.com
Mail: nguyennga82nvc@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 106
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New FB: Nguyễn Nga Nvc A B C D   0
A B / /C D , A B  3a,C D  2 ,
a D A B C B A  60
Câu 288: Cho hình thang 1 1 1 1 có 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . Với    G A B F
G F G C G D
mỗi điểm 1 di động trên cạnh 1 1 ta xác định điểm 1 sao cho 1 1 1 1 1 1 . Tìm  G F
độ dài nhỏ nhất của 1 1 . 3a 3 3a A. 2a . B. a 3 . C. . D. . 2 2 Lời giải Chọn B Z J F 1 1 E1 C1 D1 I1 A1 B1 G1H1
Gọi Z A B C D , từ giả thiết suy ra tam giác ZA B đều cạnh 3a . Gọi H , I lần lượt là 1 1 1 1 1 1 1 1 1 a 3
trung điểm của A B ,C D , suy ra H , I cố định và H I ZH  1 1 1 1 1 1 1 1 1 3 2
Từ giả thiết ta có tứ giác G D F C là hình bình hành, nên G F  2G I  2H I a 3 . 1 1 1 1 1 1 1 1 1 1 
Vậy độ dài nhỏ nhất của G F bằng a 3 . 1 1
Nguyễn Văn Công- Trường THPT Kinh Môn II
Gmail: nguyencongkm2@gmail.com
Câu 289: Cho tam giác ABC vuông ở A; BC = 2; CA = b; AB = c và điểm M di động Biểu thức F= 2 2 2 2 2 8
 MA  b MB  c MC đạt giá trị lớn nhất bằng
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 107
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A. 4 B. 12 C. 16 D. 24 Lời giải     Xét điểm I thỏa mãn: 2 2 8
 IA  b IB  c IC  0 (1)
( Dựng đường cao AH, dựng I sao cho A là trung điểm IH; I thỏa (1))
Bình phương hai vế của (1) chú ý rằng   2 2 2 2IA.IB  IA  IB  AB ;   2 2 2 2IB.IC  IB  IC  BC   2 2 2 2IC.IA  IC  IA  AC
rồi biến đổi ta được kết quả 2 2 2 2 2 2 2 8.
 IA  b .IB  c .IC  3b c .    2 2 2 2 2 2 2 2 2 2 F  8  MA  b MB  c MC  8  MA  b MB  c MC       2 2 2 2 2  8
 (MI  IA)  b (MI  IB)  c (MI  IC) 2 2 2 2 2 2 2 2 2  4M 
I  8.IA  b IB  c IC  4  MI  3b c 2 2 2  b  c  2 2  3b c  3  12   2  
Họ và tên tác giả: Vũ Viên Tên FB: Vũ Viên
Email: tieplen@gmail.com
Câu 290: Cho ABC đều có cạnh bằng 2a . Gọi d là đường thẳng qua A và song song BC , điểm M di   
động trên d . Tìm giá trị nhỏ nhất của MA  2MB MC . a 3 a 3
A. 2a 3 . B. a 3 . C. . D. . 4 2 Lời giải M A I K B C Chọn B.         
Xét điểm I sao cho: IA  2IB IC  0  IA  2IA AB  IC  0    
   
 2IA  2AB AC  0  2IA AB CB  0
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 108
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    BA BC   IA
BK (với K là trung điểm AC ). 2
I là điểm thứ 4 của hình bình hành AIBK .         
Ta có: MA  2MB MC  MI IA  2MI IB MI IC     
2MI  IA  2IB IC  2MI  2MI .
M d  Min đạt được khi LM d . Khi đó:    
MAI MAB IAB  60  ABK  60  30  30 2 2
2IM  2IA  sin 30  2.BK  sin 30  2 sin 30  (2a)  a a 3 .
Họ và tên tác giả: Phạm Khắc Thành
Email: phamkhacthanhkt@gmail.com
Câu 291: Trong mặt phẳng cho tam giác ABC và một điểm M bất kỳ. Đặt a BC, b C ,
A c AB . Tìm MA MB MC
giá trị nhỏ nhất của biểu thức T    . a b c 3 3 A. 3 3 . B. 3 . C. . D. . 3 2 Lời giải Chọn B.
Theo công thức độ dài đường trung tuyến ta có: 2 2 2
b c a 2 m b ca
b c am a am am a  2 2  2  2 2 2  2 2 4 2 2 4 3 4 3 a a a 2 3
Gọi G là trọng tâm của tam giác ABC khi đó:   MA . MA GA . MA GA 3 3
        MG GA 3 3 .GA   2
MG.GA GA 2 2 2 2 2 2 2 2 2  a . a GA
2 b c a
b c a
b c a . 3 2 3 Từ đó suy ra: MA MB MC 3 3
   
MG.GA GB GC 2 2 2 GA GB GC          2 2 2 a b c b c a    
    1
Lại có GA GB GC  0 và 2 2 2
GA GB GC   2 2 2
a b c  3 MA MB MC 3 3  1  Do đó    0    2 2 2
a b c
 3 . Đẳng thức xảy ra khi tam 2 2 2  a b c b c a 3     
giác ABC đều đồng thời M trùng với trọng tâm của tam giác ABC.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 109
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Mail: thuytrangmn@gmail.com Chủ đề: Vectơ.
Câu 292: Cho tam giác ABC có trung tuyến A ' A C ' C  '
A BC,C' AB . Tìm giá trị nhỏ nhất của cos . B 4 2 1 A. . B. . C. 1. D. 5 5 2 Lời giải: Chọn. A. A C’ G C A’ B    
Đặt BC a , BA c ta có:  1    1   AA' 
a c và CC'  c a 2 2  1    1    Do A ' A C ' C nên a c c a  0      2   2   2        ac  a c  2   2 2 4 2 2
a c   a . c 5 5 5 
+ Nếu ac  0 thì cosB  1    a.c 4  
+ Nếu ac  0 thì cosB     . Dấu đẳng thức xảy ra khi a c a . c 5 4
Vậy giá trị nhỏ nhất của cosB là
, đạt dược khi tam giác ABC cân tại . B 5
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê
Email: hongle.ad@gmail.com
Câu 293: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto   
aMA bMB cMC có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC. Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 110
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn B. A I B D C
Gọi I là tâm đường tròn nội tiếp của tam giác ABC DB AB c c  
Theo tính chất phân giác trong:    DB
.DC , mà hai vecto DC , DB ngược DC AC b b  c         
hướng nên ta có DB  
DC bDB cDC  0  b IB ID  cIC ID  0 b    
hay bIB cIC  b cID  0 (*) DB c DB c ac Mặt khác     DB DC b BC b c b c IA BA
c b cb c   
aIA  b cID ID BD ac a     Mà ,
IA ID ngược hướng nên aIA   b cID    
Thay vào (*) ta có bIB cIC aIA  0   
Vậy độ dài của aMA bMB cMC nhỏ nhất bằng 0 khi M trùng I
Họ và tên: Ngô Gia Khánh
Địa chỉ mail: ngkhanh4283@gmail.com
Câu 294: Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC .      
Khi đó, giá trị nhỏ nhất của biểu thức T MA MB MC  3 MA MB MC là: 2a 3 5a 3 A. MinT  .
B. MinT  2a 3.
C. MinT a 3. D. MinT  . 3 2 Lời giải    
+, Gọi G là trọng tâm tam giác ABC , ta có: MA MB MC MG.
+, Dựng hình bình hành ABCD , ta được:
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 111
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New          
BA CD MA MB MC BA MC CD MC MD      
+, Khi đó T MA MB MC  3 MA MB MC  3MG MD  3GD
( Vì G,D nằm khác phía với đường thẳng AC)
Dấu bằng xảy ra khi M là giao điểm của GD và đường thẳng AC hay M là trung điểm của AC 4 4 a 3 2a 3 + Nhận xét GD BM   . 3 3 2 3
Vậy MinT  2a 3. .
Email: vntip3@gmail.com Câu 295: Cho ABC và A
 ' B 'C ' có các trọng tâm G và G ' cố định và GG '  a . Khi đó giá trị nhỏ nhất
của T  AA ' BB ' CC ' là:
A. T a .
B. T  2a .
C. T  3a .
D. T  4a . Lời giải Chọn C. Ta có:
  
T  AA '  BB '  CC '
      
 
 AG  GG '  G'A '  BG  GG '  G'B '  CG  GG '  G'C '   3GG ' Vậy
T  AA ' BB ' CC '   
   
 AA '  BB '  CC '  AA '  BB '  CC '  3 GG '  3GG '  3a
  
Giâ trị nhỏ nhất của T là 3a khi AA ', BB ', CC ' cùng phương.
(Họ và tên tác giả: Phạm văn Tài, Tên FB: TaiPhamVan)
Mail: thongbui1987@gmail.com
Câu 296: Cho tam giác ABC với các cạnh AB  ,
x AC y ;  x y  0 . Gọi AD là đường phân giác   
trong của góc A . Biết biểu thị vectơ AD m AB n AC . Tính S m n . A. S  2 . B. S  0 . C. S  1 . D. S  2 . Lời giải Chọn C.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 112
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A x y B C D
Theo tính chất đường phân giác trong của tam giác ta có  DB AB x DB x x      
 điểm D chia đoạn thẳng BC theo tỉ số k   DC AC y DC y y   x AB   AC   y y x y x Nên ta có: AD   AB
AC m n   1. x x y x y x y 1 y
Câu 297: Cho ABC có AB  3 ; AC  4 . Phân giác trong AD của góc BAC cắt trung tuyến BM tại I AD a a . Biết 
, với a, b   và
tối giãn. Tính S a  2b . AI b b
A. S  10 .
B. S  14 .
C. S  24 .
D. S  27 . Lời giải: Chọn C. A M I B C D IB AB 3       Ta có:  
 2IB  3IM  0  2 AB  3AM  5AI   1 . IM AM 2 DB AB 3        
 4DB  3DC  0  4 AB  3AC  7 AD 2 . DC AC 4       
2 AB  3AM  5AI
4 AB  6 AM  10 AI Từ  
1 và 2 ta có hệ   
     
4 AB  3AC  7  AD
4 AB  3AC  7 AD
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 113
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New       AD 10
 6AM  3AC  10AI  7 AD  7 AD  10AI  7 AD  10 AI   AI 7
a  10,b  7  S  10  2.7  24
Họ và tên tác giả: Lê Hồng Phi Tên FB: Lê Hồng Phi
Email: lehongphivts@gmail.com
Câu 298: Cho tứ giác ABCD có AD và BC cùng vuông góc với AB , AB  8 , AD a , BC b . Gọi 
E là một điểm thuộc cạnh CD . Biết AEB  90 , giá trị lớn nhất của T ab là A. 4 . B. 16 . C. 8 . D. 64 . Lời giải B b C Chọn B.
Vì E là một điểm thuộc cạnh CD nên tồn tại k  0;  1 sao cho    8 E
k EC  1 k ED  0 .      
Khi đó, k BC  1 k BD BE và k AC  1 k AD AE . A D Suy ra a          
BE.AE k BC.AC k 1 k BC.AD k 1 k  .
BD AC  1 k 2 2 . BD AD
  
   
  
k BC AB BC  k 1 k ab k 1 k BA AD AB BC  1 k 2 2
BAADAD
k b k 1 k ab k 1 k  8 
ab  1 k 2 2 2 2 2 a 2
 kb  1 k a  64k 1 k .    k 1 k
Do AEB  90  BE.AE  0  kb  1 k a  8 k 1 k   b a  8 . 1 k k k 1 k
Theo bất đẳng thức Cô-si ta có 8  b
a  2 ab ab  16 . 1 k k
Đẳng thức xảy ra chẳng hạn khi a b  4 và k  0,5 . Vậy max T  16 .
Câu 299: Cho tứ giác ABCD có AD và BC cùng vuông góc với AB , AB h , AD a , BC b . Cho   
k là số thực dương thuộc 0 
;1 và điểm E thỏa mãn k EC  1 k ED  0 . Tìm hệ thức liên hệ 
giữa a , b , h , k để góc AEB  90 ?
A. 1 k b ka h k 1 k  .
B. kb  1 k a hk 1 k  .
C. kb  1 k a h k 1 k  .
D. 1 k b ka hk 1 k  . Lời giải B b C Chọn C.   
Từ k EC  1 k ED  0 suy ra h E
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 114 A a D
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New      
k BC  1 k BD BE và k AC  1 k AD AE . Khi đó,          
BE.AE k BC.AC k 1 k BC.AD k 1 k  .
BD AC  1 k 2 2 . BD AD
  
   
  
k BC AB BC  k 1 k ab k 1 k BA AD AB BC  1 k 2 2
BAADAD
k b k 1 k ab k 1 k h ab  1 k 2 2 2 2 2 a 2
 kb    k a  k   k  2 1 1 h .   Do 
AEB  90 nên BE.AE  0  kb  1 k a h k 1 k  .
Vậy hệ thức liên hệ giữa a , b , h , k để góc 
AEB  90 là kb  1 k a h k 1 k  .
Câu 300: Cho tam giác có trọng tâm G , qua G dựng đường thẳng d cắt cách cạnh AB , AC lần lượt AM AN
tại M , N . Đặt  x ,
y , gọi m , M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của AB AC
T x y . Tính m M . 10 17 11 5 A. . B. . C. . D. . 3 6 6 2
(Họ và tên tác giả: Hoàng Thị Thanh Nhàn, Tên FB: Hoàng Nhàn) Lời giải Chọn B A N d M G C D B   
  1  1 
Ta có AM x AB , AN y AC , AG AB AC . 3 3
    
MN AN AM  x AB y AC .   1   1  MG   x AB AC   .  3  3
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 115
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1 1  1    x  kx  1 k
 1 k x   3  3 3x
Do M , N , G thẳng hàng nên MG k MN       1 1  1  ky   ky   k  3  3 3y  1 1    3 . x y xy  . 3x 1 1
Do M , N lần lượt nằm trên các cạnh AB , AC nên  x, y  1. 2 1 1 2 4 4 3     xy
T x y  3xy x y xy 9 3 2
Đẳng thức xảy ra khi và chỉ khi x y  . 3 4
 giá trị nhỏ nhất m  . 3  1  2 2x Ta có x  ;1   2x   1  x   1  0 2
 2x  3x 1  0 2
 2x  3x 1   1 2    3x 1 2 3x 3   . 3x 1 2  1 x
Đẳng thức xảy ra khi và chỉ khi  2 x 1  2 3x 3
Ta có T x y  3xy   3x 1 2 3
 giá trị lớn nhất là M  . 2 4 3 17
Vậy m M    . 3 2 6
Họ và tên: Nguyễn Thị Thu
Email: thutoan83@gmail.com
Facebook: Nguyễn Thị Thu  1 
Câu 301: Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho BH  HC . 3    
Điểm M di động trên BC sao cho BM  xBC . Tìm x sao cho MA  GC đạt giá trị nhỏ nhất.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 116
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 4 5 5 6 A. . B. . C. . D. . 5 4 6 5 Lời giải Chọn B.     
Dựng hình bình hành AGCE. Ta có MA  GC  MA  AE  ME  ME  FE .  
Do đó MA  GC nhỏ nhất khi M  F .
Gọi P là trung điểm của AC; Q, F lần lượt là hình chiếu vuông góc của P, E trên BC. BQ BP 3  4 
Ta có BPQ và BEF đồng dạng nên   hay BF  BQ . BF BE 4 3  1 
Có PQ là đường trung bình của A
 HC nên Q là trung điểm của HC hay HQ  HC . 2    1  1  5  5 3  5  BQ  BH  HQ  HC  HC  HC  . BC  BC . 3 2 6 6 4 8  4  5  5 Do đó BF  BQ  BC . Vậy x  . 3 6 6
gmail: hoangthuyvinhuni@gmail.com
Câu 302: Cho tam giác ABC đều cạnh 2 3 , d là đường thẳng qua B và tạo với AB một góc 0 60   
C . Tìm giá trị nhỏ nhất của A MA MB  3MC ? 3 12 4 A. B. C. D. 2 5 5 5 Hướng dẫn giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 117
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A K E I B C M d
Gọi E là trung điểm AB.       
Gọi I là điểm thỏa mãn: IA IB  3IC  0  2IE  3IC  0 3
I nằm giữa đoạn EC và EI EC 5   
     
Ta có: MA MB  3MC  2MI IA IB  3MI  3IC  5MI 
Vậy A  5MI min  M là hình chiếu của I trên đường thẳng d.
Đường thẳng d qua B và tạo với AB 1 góc 0
60 nên d song song AC và cắt EC tại K.  KEB CEAg. .
c g  nên E là trung điêm KC 3 3 3 9 EC a  2 3.  3  EI  .3  2 2 5 5 9 24 KI   3  5 5 EB KB EB.KI 12
EKB  MKI    MI   MI KI KB 5
(Tác giả: Hoàng Thị Thúy - Facebook: Cỏ ba lá )
Câu 303: Cho tam giác ABC đều cạnh 1 nội tiếp đường tròn ( )
O và điểm M thay đổi trên O . Gọi s , i
  
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức MA MB MC . Tính s i . 4 3 5 3
A. s i  3 .
B. s i  .
C. s i  .
D. s i  2 3 . 3 3 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 118
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Dựng hình bình hành DBCA . Ta có
  
      
MA MB MC MD DA MD DB MD DC MD M . D
Gọi E là giao điểm khác C của DC với (O) . Áp dụng bất đẳng thức tam giác ta có
MD DO OM DO OE DE và MD DO OM DO OC DC
Dấu bằng xảy ra lần lượt khi M trùng E và M trùng C . 3 1 4 3
Vậy s i DE DC DC CE DC  2DC  2OC  2   2   . 2 3 3 buiduynam1993@gmail.com
Câu 304: Cho lục giác đều ABCDEF cạnh a . Trên đường chéo AC , CE lấy hai điểm M , N sao cho AM CN
k 0  k   1 . Độ dài 2 2
BM BN đạt giá trị nhỏ nhất khi k bằng bao nhiêu? AC CE 1 1 2 3 A. . B. . C. . D. . 2 4 3 4
(Bùi Duy Nam sưu tầm. FB: Bùi Duy Nam https://www.facebook.com/duynam.bui.1) Lời giải Chọn B.
   AM    
Ta có BM BA AM mà
k AM k AC k BC BA . AC       
Vậy BM BA k BC BA  BM k BC  1 k BA .
   CN      
Lại có BN BC CN mà
k CN kCE k CF FE  k 2BA BC  . CE   
Vậy BN  k  
1 BC  2k BA .     2 2 Khi đó 2 2
BM BN  k BC  1 k BA  k  
1 BC  2k BA    
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 119
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    
k BC    k 2 BA k   k BC BA  k  2 2 2 2 2 2 2 1 2 1 .
1 BC  4k BA  4k k   1 BC.BA . 2 2 2 2  
BC BA AC a Mà 2 2 2
BC BA a và BC.BA    . 2 2 Vậy 2 2 2
BM BN a  2
6k  3k  2 0  k   1 .  min  2 2 BM BN  2  a min  2
6k  3k  2 . 0k 1   1  13 Xét f k  2
 6k  3k  2 0  k  
1 , ta có min f k   f    . 0k 1   4  8 2 13a 1 Vậy min  2 2
BM BN   khi k  . 8 4
Câu 305: Cho hình chữ nhật ABCD có AD a , AB b . O và I lần lượt là trung điểm DB và DO . 
   
N là điểm thỏa mãn 2NA  2NC AB AD  2AD và NB lớn nhất. Tính NB . 2 2
2a  3 a b 2 2
a a b 2 2
2a  3 a b 2 2
2a a b A. B. C. D. . 2 2 4 4 Lời giải 
       
2NA  2NC AB AD  4NO BD  4NO  4OI  4NI AD a Suy ra NI   2 2 a
Để NB lớn nhất thì N là giao điểm của đường tròn tâm I bán kính
với BD ( N và B 2
khác phía so với I ).
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 120
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 2 a 3
2a  3 a b Do đó 2 2
NB NI IB   a b 2 4 4
Họ tên tác giả: Đoàn Phú Như Tên fb: Như Đoàn Email: doanphunhu@gmail.com
Câu 306: Cho tam giác ABC, AB  3(cm), BC  4(cm), CA  5(cm). Điểm M thuộc đường tròn ngoại tiếp
tam giác ABC. Giá trị nhỏ nhất của biểu thức 2 2 2
P MB MC MA là 5 97 5 97 5 97 A. 0 . B. 5  . C. 5  . D. 5  . 2 2 4 Lời giải: B D M A C O
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC thì O là trung điểm AC.
   
Gọi D đỉnh thứ tư của hình bình hành ABDC thì DB DC DA  0 Ta có          2 2 2 2 2 2
P MB MC MA MB MC MA  MD DB2  MD DC2  MD DA2
    2 2 2 2
P MD DB DC DA MD DB DC DA 2 2 2 2 2 2
MD DB DC DA MD 18
Do đó P nhỏ nhất khi và chỉ khi DM nhỏ nhất.
Vì M thuộc đường tròn ngoại tiếp tam giác ABC nên DM nhỏ nhất khi và chỉ khi O,M,D theo thứ tự thẳng hàng. 2
   1    1    1   Ta có 2 2 2
OD OC CD
AC AB OD AC AB
AC AB AC.AB   2  2  4 25 3 97 97 5 2 OD   9  5.3. 
MD OD OM   4 5 4 2 2 2  97 5  5 97 Vậy MinP     18  5  .  2 2  2   Chọn đáp án B
Phuongthao.nguyenmaths@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 121
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 307: Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho  1    BH
HC . Điểm M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của 3  
vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . . B. . . C. . . D. . 5 6 5 4
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo) Lời giải Chọn B. A E P G B H M Q F C
    
Dựng hình bình hành AGCE . Ta có MA GC MA AE ME .   
Kẻ EF BC F BC  . Khi đó MA GC ME ME EF .  
Do đó MA GC nhỏ nhất khi M F .
Gọi P là trung điểm AC , Q là hình chiếu vuông góc của P lên BC Q BC  . 3
Khi đó P là trung điểm GE nên BP BE . 4 BQ BP 3  4  Ta có BPQ
và BEF đồng dạng nên   hay BF BQ . BF BE 4 3  1  Mặt khác, BH HC . 3  1 
PQ là đường trung bình AHC
nên Q là trung điểm HC hay HQ HC . 2
   1  1  5  5 3  5 
Suy ra BQ BH HQ HC HC HC  . BC BC. 3 2 6 6 4 8
 4  5  Do đó BF BQ BC . 3 6  
Câu 308: Cho hình thang ABCD có đáy CD gấp đôi đáy AB. Lấy một điểm E sao cho 3BC  2DE và
đồng thời thỏa mãn CA CE . Giá trị nhỏ nhất của góc 
ABC nằm trong khoảng nào dưới đây? A. (95;100 ) . B. (100;106 ) . C. (106;115 ) . D. (115;120 ) . Lời giải:
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 122
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A B D C E    Gọi    ABC . Ta có: 2 2 2
AC AB BC AC AB BC  2 A . B BC.cos (1)
    3  9 Lại có: 2 2 2 2
CE CD DE  2  AB
BC CE AC  4AB BC  6A . B BC.cos (2) 2 4
Lấy (2) – (1) vế theo vế ta được : 5  3AB 5BC  3AB 5BC 15 2 2 0  3AB BC  8A .
B BC.cos  cos     2  . .     4  8BC 32AB  8BC 32AB 8
Suy ra:   118, 96  GTNN của  nằm trong khoảng (115;120 )  chọn đáp án D.    
Câu 309: Cho hình thang ABCD có 2 AB DC , AC  8, BD  6 , góc tạo bởi hai véc tơ AC và BD
bằng 120 . Khi đó giá trị của (AD BC) bằng: 13  2 5 14  4 7 15  2 10 A. . B. . C. . D. 6  4 3 . 2 3 4
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái ) Lời giải: A B C D            
Ta có: AC AB BC và BD BC CD . Suy ra: 2 AC BD  (2AB CD)  3BC  3BC
Bình phương vô hướng hai vế ta được:   14 2 2 2 2 2
9BC  4AC BD  4AC.B .
D cos120  4.8  6  4.8.6.cos120  BC  3
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 123
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Tương tự ta có:
  
        
Ta có: AC AD DC và BD BA AD . Suy ra: AC  2BD  (2BA BC)  3AD  3AD
Bình phương vô hướng hai vế ta được:   4 7 2 2 2 2 2
9 AD AC  4BD  4 AC. .
BD cos120  8  4.6  4.8.6.cos120  AD  3 14  4 7
Suy ra: ( AD BC) 
chọn đáp án B. 3  
Câu 310: Cho hình thang ABCD có 2 AB DC , AC  9, BD  6 . Giá trị của biểu thức 2 2 (BC AD ) bằng: 80 A. 15 . B. . C. 12. D. 14. 3
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái ) Lời giải: A B C D            
Ta có: AC AB BC và BD BC CD . Suy ra: 2 AC BD  (2AB CD)  3BC  3BC
Bình phương vô hướng hai vế ta được:   2 2 2
9BC  4 AC BD  4 AC.BD (1) Tương tự ta có:
  
        
Ta có: AC AD DC và BD BA AD . Suy ra: AC  2BD  (2BA BC)  3AD  3AD
Bình phương vô hướng hai vế ta được:   2 2 2
9 AD AC  4BD  4 AC.BD (2) 2 2 2 2 AC BD 9  6
Lấy (1) trừ đi (2) vế theo vế, ta được : 2 2 BC AD  
 15  Chọn đáp án 3 3 A. 14  4 7
Suy ra: ( AD BC) 
chọn đáp án B. 3
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 124
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 311: Cho tam giác ABC có 
BAC  60 và A ,
B AC đã biết. Biểu thức P k.MA MB MC đạt giá
trị nhỏ nhất bằng ( AB AC) với mọi giá trị thực k k . Giá trị của k nằm trong khoảng nào 0 0 dưới đây? 3 3 A. (0;1) . B. ( ; 2) . C. (1; ) . D. (2;3) . 2 2
(Tác giả: Thầy Nguyễn Đăng Ái, FB: Nguyễn Đăng Ái ) Lời giải:        v    
Ta có: | u | .| v | u .v |
u | u .  và: u .v   | u | .| v | . Áp dụng vào bài này, ta có : | v|    
 AB  AC
  AB
  AC
P k.MA MB MC k.MA  . MBMC.
k.MA  (MA AB).  (MA AC). AB AC AB AC      AB AC AB AC
P k.MA AB AC  ( MA
)  k.MA AB AC  . MA |  | AB AC AB AC    AB AC  
P MAk  | 
|  AB AC . Giả thiết cho biết: AB AC      AB AC
P MAk  | 
|  AB AC AB AC AB AC        AB AC AB AC Suy ra:  k  |  |  0  k |  | AB AC AB AC   Sử dụng bình phương vô hướng để tính:       2 2 AB ACAB   AC AB AC 2 |  |         2 .  11 2.cos 60  3 AB AC AB AC AB AC       AB AC Suy ra: k | 
|  3  k . Vậy ta chọn đáp án B. 0 AB AC
Email: hongle.ad@gmail.com
Câu 312: Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto   
aMA bMB cMC có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC. Lời giải
Họ và tên tác giả: Vũ Thị Hồng Lê Tên FB: Hồng Lê Chọn B.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 125
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A I B D C
Gọi I là tâm đường tròn nội tiếp của tam giác ABC DB AB c c  
Theo tính chất phân giác trong:    DB
.DC , mà hai vecto DC , DB ngược DC AC b b  c         
hướng nên ta có DB  
DC bDB cDC  0  b IB ID  cIC ID  0 b    
hay bIB cIC  b cID  0 (*) DB c DB c ac Mặt khác     DB DC b BC b c b c IA BA
c b cb c   
aIA  b cID ID BD ac a     Mà ,
IA ID ngược hướng nên aIA   b cID    
Thay vào (*) ta có bIB cIC aIA  0   
Vậy độ dài của aMA bMB cMC nhỏ nhất bằng 0 khi M trùng I
Email: nguyentuyetle77@gmail.com
Câu 313: Cho tam giác ABC đều cạnh a và điểm M thay đổi. Giá trị nhỏ nhất của biểu thức 2 2 2
P  2MA  3MB  4MC là: 2 26a 2 26a A. 2 14a B. 2 14a C. D. 3 3 Lời giải
Họ và tên: Nguyễn Thị Tuyết Lê FB: Nguyen Tuyet Le      
Gọi G là trọng tâm tam giác ABC . Ta có: 2 2
P  2(MG G ) A
 3(MG GB)  4(MG GC)     = 2
MG  2MG(2GA  3GB  4GC)       2
MG  2MG(2GA  2GB  2GC GB  6GC)
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 126
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    2 2
MG  2MG(CB  5GC)  GC      2 2 2
MG  2MG(CB  5GC)  (CB  5GC)  42GC 2     a (Vì 2 2 2 2
(CB  5GC)  CB 10 .
CB GC  25GC  43.  43GC ) 3    2 2 2 2
p  (MG CB  5GC)  42GC  42GC  14a .   
Dấu “=”xẩy ra  MG  5GC CB .    Vậy min 2
P  14a khi M là điểm thỏa mãn MG  5GC CB
Họ và tên tác giả: Đặng Văn Tâm Tên FB: Đặng Văn Tâm
Email: dvtam0189@gmail.com
Câu 314: Cho tam giác ABC có hai đường trung tuyến kẻ từ B và C vuông góc với nhau. Tính giá trị
nhỏ nhất của cos A . 1 2 3 4 A. . B. . C. . D. . 2 3 4 5 Lời giải Chọn D
Gọi M , N lần lượt là trung điểm của AC, AB. Ta có:
     
BM AM AB; CN AN AC.    
Theo giả thiết BM CN nên ta có BM CN  0 hay          
         
AM ABAN AC   0  AB AC  AM AN AM AC AN AB.  1   1  Mà AM AC và AN AB nên suy ra 2 2   1   1  
AB AC   AB AC   2 2 2
AB AC   AB AC   2 2 AB AC . 4 2 5
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 127
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Áp dụng định nghĩa tích vô hướng, kết hợp Bất đẳng thức Cosi ta có     2 2 2 2         AB AC AB AC AB AC A AB; AC  2 2 2 . 4 cos cos    .  . AB.AC 5 AB.AC 5 AB.AC 5 4
Dấu "  " xảy ra khi AB AC hay tam giác ABC cân tại .
A Vậy min cos A  . 5
Họ và tên: Cấn Việt Hưng
Email: thuyhung8587@gmail.com FB: Viet Hung    
Câu 315: Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB .
Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2 . a 2 2 Lời giải: Chọn A.   
Gọi N là đỉnh thứ 4 của hình bình hành MANB . Khi đó MA MB MN .      
Ta có MA MB MA MB MN BA hay MN AB .
Suy ra MANB là hình chữ nhật nên   90o AMB .
Do đó M nằm trên đường tròn tâm O đường kính AB . AB a
MH lớn nhất khi H trùng với tâm O hay max MH MO   . 2 2
Họ và tên tác giả: Phương Xuân Trịnh Tên FB:: Phương Xuân Trịnh
Email: phuongtrinhlt1@gmail.com
Câu 316: Cho tam giác ABC vuông tại A . Gọi  là góc giữa hai trung tuyến BD và CK . Giá trị nhỏ nhất của cos là:. 1 4 2 3 A. . B. . C. . D. . 2 5 3 4 Lời giải Chọn B.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 128
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A D K C B Ta có:  
   
   
BD .CK   AD AB  AK AC   AD .AC AK .AB (do AB AC ) 1    1 2 2 AB AC  2   BC . 2 2 Mặt khác:  2 2 2
2BA  2BC AC    2 2 2
2CA  2CB AB 2 2  2B .
D CK BD CK  4 2 2 2 2
AB AC  4BC 5BC   . 4 4 Do đó:   2 2 BD .CK BC 4BC 4 cos     . 2 B . D CK 2 . BD CK 5BC 5 4 cos 
BD CK  ABC vuông cân tại A . 5 4
Vậy min cos   . 5 vanphu.mc@gmail.com  1  Câu 317: Cho A
BC có trọng tâm G. Gọi H là chân đường cao kẻ từ A sao cho CH HB . Điểm M di 3    
động trên BC sao cho CM  .
x CB . Tìm x sao cho độ dài vecto MA GB đạt giá trị nhỏ nhất. 8 5 6 5 A. . B. . C. . D. . 5 6 5 8 Lời giải Chọn B.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 129
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
    
Dựng hình bình hành AGBE. Ta có MA GB MA AE ME     
MA GB ME ME EF MA GB
EF M F . min 3
Gọi P là trung điểm của AB . Khi đó P cũng là trung điểm của GE và CP CE 4
Gọi Q là hình chiếu vuông góc của P trên BC. CQ CP 3  4 
Ta có CPQ và CEF đồng dạng nên    CF CQ . CF CE 4 3  1   1 
Mặt khác PQ là đường trung bình của AHB nên HQ
HB . Theo giả thiết CH HB 2 3
   1  1  5 
Suy ra CQ CH HQ HB HB HB 3 2 6  3   5  5 3  5   4  4 5  5 
Từ giả thiết HB
CB . Do đó CQ HB  . CB CB CF CQ  . CB CB 4 6 6 4 8 3 3 8 6
( Họ và tên tác giả: Nguyễn Văn Phu, Tên FB Nguyễn Văn Phu)
Họ và tên tác giả: Trần Tuyết Mai Tên FB: Mai Mai
Email: maimai1.hn@gmail.com    
Câu 318: Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB .
Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2 . a 2 2 Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 130
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New M A B H O   
Gọi O là trung điểm của AB . Khi đó MA MB  2MO .       1
Ta có MA MB MA MB  2 MO BA hay MO AB Suy ra M
AB vuông tại M 2  nên  90o AMB
. Do đó M nằm trên đường tròn tâm O đường kính AB . AB a
MH lớn nhất khi H trùng với tâm O hay max MH MO   . 2 2
Họ và tên tác giả: Nguyễn Thị Thanh Thảo Tên FB: Nguyễn Thanh Thảo
Email: nghianguyennhan78@gmail.com
Câu 319: Cho AD và BE là hai phân giác trong của tam giác ABC . Biết AB  4 , BC  5 và CA  6 .  Khi đó DE bằng: 5  3  3  5  9  3  3  9 
A. CA CB . B. CA CB . C. CA CB . D. CA CB . 9 5 5 9 5 5 5 5 Lời giải Chọn A. CD AC 6 CD 6
AD là phân giác trong của tam giác ABC nên     DB AB 4 CD DB 6  4 6  3  CD    CD CB . CB 10 5 5  5  CE Tương tự:   CE CA . CA 9 9    5  3 
Vậy DE CE CD CA CB . 9 5    
Câu 320: : Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB
. Gọi H là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ?
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 131
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New a a 3 A. . B. . C. a. D. 2 . a 2 2 Lời giải Chọn A.   
Gọi N là đỉnh thứ 4 của hình bình hành MANB . Khi đó MA MB MN .      
Ta có MA MB MA MB MN BA hay MN AB . 
Suy ra MANB là hình chữ nhật nên  90o AMB .
Do đó M nằm trên đường tròn tâm O đường kính AB . AB a
MH lớn nhất khi H trùng với tâm O hay max MH MO   . 2 2
Họ và tên tác giả: Hoàng Tiến Đông Tên FB: tiendongpt
Email: dongpt@c3phuctho.edu.vn   
Câu 321: Một miếng gỗ có hình tam giác có diện tích là S điểm I , O lần lượt thỏa mãn IB IC  0 ;   
OA OI  0 . Cắt miếng gỗ theo một đường thẳng qua O , đường thẳng này đi qua M , N lần
lượt trên các cạnh AB, AC . Khi đó diện tích miếng gỗ chứa điểm A thuộc đoạn: S S   S S   3S S   S 3S A. ;  . B. ; . C. ; . D. ; 4 3           3 2   8 2   4 8  Lời giải Chọn A A M M' N' O N B I C Từ O kẻ M N
 //BC , suy ra: O là trung điểm M N   . NN MA OM NN MM   1  Ta có: . .  1  
x, 0  x    . NA MM ONNA MA  2 
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 132
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1
NN   xNA AN AN   xNA NA AN  . 1 x 1
MM   xMA M A
  MA xMA MA M A  . 1 x S AM AN AM .AN 1 Ta có: AMN  .   . S AB AC 4.AM .AN  x ABC 4 2 1   1  S S
Xét hàm số: f x   2 4 1 x  trên 0; 
. suy ra: 3  f x  4   S  . 2  AMN   4 3 Đỗ Công Dũng Email: congdung812@gmail.com
Câu 322: Cho tam giác ABC có bán kính đường tròn ngoại tiếp R  2 . Tìm giá trị lớn nhất của 2 2 2
BC AB AC . A. 1. B. 2. C. 3. D. 4 Giải Chọn D A O C I B M
Gọi O là tâm của đường tròn ngoại tiếp tam giác ABC . Dựng hình bình hành ABMC
   
Ta có OA OM MA 2 2 2
OA OM MA  2OM MA 1  Tương tự ta có: 2 2 2
OB OM MB  2OM MB 2  2 2 2
OC OM MC  2OM MC 3
Lấy 2  3 –   1 từng vế ta có:
    2 2 2 2 2
R OM MB MC MA  2OM MB MC MA ( do tứ giác ABMC là hình bình
  
hành nên MB MC MA ) Khi đó 2 2 2 2 2
R OM MB MC MA 2 2 2 2
OM MB MC  4MI 2 2 2  AB AC BC  2 2 2
OM MB MC  4    2 4   2 2 2
OM MB MC   2 2 2
2 AB AC BC  mà MB AC , MC AB
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 133
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New nên 2 2 2 2 2
R OM AB AC BC 2 2 2 2 2
BC AB AC R OM 2  R  4
Vậy giá trị lớn nhất của 2 2 2
BC AB AC là 4 .
Đẳng thức xảy ra  M O 2 2
AB AC R BC  3R . Áp dụng định lý cosin trong tam giác ABC có  0
BAC  120 . Hay là tam giác ABC cân tại A và có  0 BAC  120 .
Họ và tên tác giả: Nguyễn Tân Quang Tên FB: Nguyễn Tân Quang
Email: quangmath@gmail.com
Câu 323: Cho tam giác đều ABC cạnh .
a Gọi M là điểm nằm trên cạnh A .
B Tính giá trị nhỏ nhất của   
biểu thức MA  2MB MC theo . a a 3 a 3 a 3 2a 3 A. . B. . C. . D. . 4 2 8 3 Lời giải Chọn B.         
Ta có MA  2MB MC  MA MC  2MB  2MN  2MB  4 MI  4MI,
trong đó N , I lần lượt là trung điểm của AC, BN. Do đó I cố định. A M N H I B C
Kẽ IH vuông góc với A .
B Ta có MI HI. a 3 a 3 Tính được 0 BN
IH BI.sin 30  . 2 8
Email: themhaitotoanyp1@gmail.com
Câu 324: Cho hình bình hành ABCD, M thuộc đường chéo AC, (M không trùng với các đỉnh A, C)
Trên các đường thẳng AB, BC, lấy các điểm P và Q sao cho MP // BC, MQ // AB. Gọi N là
giao hai đường thẳng AQ và CP. Giả sử DN mDA nDC . Tìm giá trị lớn nhất của m + n 4 3 1 A. B. C. D. 2 3 4 2 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 134
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New AM BQ BP Đặt  k   k và
 1  k , k    1 ; 0 AC BC AB
Có DN DA AN DA x AQ DA xAB BQ
DA xDC kxDA  1  kxDA xDC , (1)
Mặt khác DN DC CN DC yCP DC yCB BP
DC yDA yk  
1 DC yDA  1  yk yDC , (2)  k x
y  1  kx   2 k k  1 Từ (1) và (2), ta có   
1  ky y x  1  k y    2 k k  1 1  k k Do đó DN DA DC k 2  k  1 k 2  k  1 1 1 4  m n    , k    1 ; 0 2 k k  1 2  1  3 3  k     2  4 1  m n 4 max  , đạt được khi k =
hay M là trung điểm AC. 3 2
(Fb: Lưu Thêm)
Họ và tên: Lê Thị Lan FB: Lê Lan
Email: lelanqx2@gmail.com
Câu 325: : Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho  1    BH
HC . Điểm M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của 3  
vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . B. . C. . D. . 5 6 5 4 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 135
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn B.     
Dựng hình bình hành AGCE . Ta có MA GC MA AE ME .   
Kẻ EF BC F BC . Khi đó MA GC ME ME EF .  
Do đó MA GC nhỏ nhất khi M F .
Gọi P là trung điểm AC , Q là hình chiếu vuông góc của P lên BC Q BC . 3
Khi đó P là trung điểm GE nên BP BE . 4 BQ BP 3  4 
Ta có BPQ và BEF đồng dạng nên   hay BF BQ . BF BE 4 3  1  Mặt khác, BH HC . 3  1 
PQ là đường trung bình AHC nên Q là trung điểm HC hay HQ HC . 2
   1  1  5  5 3  5 
Suy ra BQ BH HQ HC HC HC  . BC BC. 3 2 6 6 4 8  4  5  Do đó BF BQ BC . 3 6
Tác giả: Nguyễn Văn Hưng Facebook: Nguyễn Hưng
Câu 326: Cho tam giác ABC có BC a, AC  ,
b AB c nội tiếp đường tròn tâm O, bán kính R. M là
điểm thuộc đường tròn (O). Gọi N, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2 2
P MA MB MC . Khi đó giá trị của N n bằng A. 2 12R . B. 2 2 2 2
4R 9R  a b c . C. 2 2 2 2
2R 9R  a b c . D. 2 2 2 2
8R 9R  a b c . Lời giải Chọn B. Ta có:          2   2   2 P MO OA MO OB MO OC
    
   2 
MO OAOB OC 2 6R 2 .
 6R  2 MO . OA OB OC .cos
   2  6R  2 .
R OA OB OC .cos
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 136
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Vậy:
  
   `
2  R OAOB OC 2 6R 2 .  P  6R  2 .
R OA OB OC
  
N n  4R. OA OB OC
  
   2 Mà: 2
OA OB OC  3R  2 OAOB OBOC OAOC    2 2 2
OA OB  (OA OB) 2  3R  2. 2 2 2 2
 9R  a b c 2 2 2 2 2
N n  4R. 9R  a b c
Họ và tên tác giả: Nguyễn Xuân Giao Tên FB: giaonguyen
Email: giaohh2@gmail.com
Câu 327: Cho tam giác đều ABC nội tiếp đường tròn tâm O ,bán kính R , M là một điểm bất kì trên
đường tròn. Giá trị lớn nhất của biểu thức 2 2 2
S MA  2MB  3MC là A. 2 R 21 . B. 2 R 21 . C. 2 2R 21 . D. 2 2  R 21 . Lời giải Chọn C.          2 2 2 2 2 2
Ta có S MA  2MB  3MC  MO OA  2MO OB  3MO OC        
S  2MO OA  2OB  3OC  2 MO OA  2OB  3OC .cos  
S  2R CA  2CB .cos   
Trong đó   MO,CA  2CB
Do tam giác ABC đều nội tiếp đường tròn bán kính R nên có cạnh là R 3         CACB2 2 2 2 0 2 2  CA  4C .
A CB  4CB  15R  4.C . A .
CB cos 60  21R CA  2CB R 21 2 S  2R 21.cos 2  S  2R 21   
Dấu bằng xảy ra khi cos  1  MO, CA  2CB cùng chiều. Vậy 2 MaxS  2R 21
Email: anhtu82t@gmail.com
Câu 328: Cho tam giác ABC . Tìm giá trị nhỏ nhất của biểu thức P  3 cos 2 A  2 cos 2B  2 3 cos 2C 3 1 A. P  4 2 3 3 min . B. Pmin . C. P    2 min . D. P  5 min . Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 137
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên: Đồng Anh Tú Facebook: Anh Tú Chọn A
Gọi O, R lần lượt là tâm và bán kính đường tròn ngoại tiếp tam giác ABC    Ta có: 2
(2OA  3OB OC)  0       2 2 2
 4OA  3OB OC  4 . OA OC  4 3O . A OB  2 3O . B OC  0 2  8R  4 .
OA OC.cos 2B  4 3O . A .
OB cos 2C  2 3O .
B OC.cos 2 A  0 2 2 2 2
 8R  4R cos 2B  4 3R cos 2C  2 3R cos 2A  0  0  0 
 3 cos 2 A  2 cos 2B  2 3 cos 2C  4
 . Dấu bằng xẫy ra khi 0
A  45 , B  60 ,C  75 . Vậy P  4 min .
VẤN ĐỀ 6 TÍCH VÔ HƯỚNG
Email: ngvnho93@gmail.com
     
Câu 329: Cho tam giác đều ABC cạnh a . Tính A .
B BC BC.CA C . A AB 2 3a 2 3a 2 a 3 2 a 3 A. B. C. D.  2 2 2 2 Lời giải
Họ và tên: Nguyễn Văn Nho Facebook: Nguyễn Văn Nho Chọn A Cách 1    
Nhận xét: Với mọi điểm M bất kỳ, ta luôn có AB   AM MB2 2 2 2
AM MB  2AM .MB   1  AM .MB   2 2 2
AB AM MB  2 2   1 a A . B BC   2 2 2
AC AB BC     2 2  2   1 a 2
      3a
Do đó BC.CA   2 2 2
BA BC CA     .
AB BC BC.CA  . CA AB   . 2 2  2 2   1 a C . A AB   2 2 2
CB CA AB     2 2  Cách 2
Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Do tam giác ABC đều nên
  
  
BM , CP, AN lần lượt là các hình chiếu của BC, C ,
A AB lên các cạnh BA, CB, AB.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 138
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Áp dụng công thức chiếu, ta có 2       a a . AB BC  .
AB BM   A . B MB   . AB MB   . a   A  2 2  2       a a
BC.CA BC.CP  BC.PC  BC.PC   . a   2 2 M N  2       a a . CA AB  . CA AN   . CA NA   . CA NA   . a    2 2  B C P 2
      3a
Cộng vế theo vế ta được A .
B BC BC.CA  . CA AB   . 2      
Cách 3. Vì tam giác ABC đều nên  AB BC  BC CA  CA AB 0 , , ,  120 . 2       B BC AB BC   AB BC 1 a A . . .cos ,  . a . a       2  2  2       1  a
Do đó BC.CA BC. .
CA cos BC,CA  . a . a       2  2  2       CAAB CA ABCA AB 1 a . . .cos ,  . a . a         2  2 2
      3aA .
B BC BC.CA  . CA AB   2
Câu 330: Cho tam giác ABC có AD là trung tuyến, G là trọng tâm. Một đường thẳng qua G cắt các
cạnh AB, AC lần lượt tại M , N . Khẳng định nào sau đây đúng?   1   2  
A. AM .AN AN.MB AM .NC 2 3
     
B. AM .AN AN.MB AM .NC   2    
C. AM .AN
( AN.MB AM .NC) 3   3    
D. AM .AN
( AN.MB AM .NC) 2 Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 139
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A N G M PD B C Q BM CN
Trước hết ta chứng minh   1(1) AM ANBM PG  BP//MN   AM AG Thật vậy, kẻ    CQ//MNCN QG     AN AG PG QG Do đó (1)  
 1  PG QG AG  (GD PD)  (GD DQ)  AG AG AG
 2GD AG ( luôn đúng) BM CN Vậy ta có   1 AM AN
BM .AN CN.AM AM .AN
      AN.MB AM .NC AM .AN    cos A cos A cos A
     
AM .AN AN.MB AM .NC ( Do cos A  0 )          
Câu 331: Cho các véc tơ a , b , c thỏa mãn a a , b b , c c và a b  3c  0 . Tính       A  . a b  . b c  . c a . 2 2 2
3c a b 2 2 2
3a c b A. . B. . 2 2 2 2 2
3b a c 2 2 2
3c a b C. . D. . 2 2 Lời giải Tác giả: Quang Phi Chọn A          
Ta có a b c
a b   c  a b2 2 3 0 3  9c      2 2 2   2 2 2
9c a b
a b  2. . a b  9c  . a b 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 140
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New            2 2 2  
a b  9c
Tương tự ta có b c  a  b c2 2 2 2 2 3 3
a b  9c  6. . b c a  . b c  . 6       2 2 2        2 2 2
b a  9c
Và ta lại có a c b
  a c2 2 3 3
b a  9c  6. . a c b  . a c  . 6 2 2 2 2 2 2 2 2 2 2 2 2
9c a b
a b  9c
b a  9c
3c a b Suy ra A     . 2 6 6 2
Họ và tên: Đoàn Thị Hường
Email: ngochuongdoan.6@gmail.com Fb: Đoàn Thị Hường
Câu 332: Cho tam giác ABC vuông tại A có BC = 2a, M là điểm trên đoạn BC sao cho MB = 2MC. Biết   rằng 2
AM .BC a . Độ dài cạnh AC là: a 33 a 3 A. AC
B. AC a 3 C. AC
D. AC a 5 3 3 Bài giải  1 
Từ giả thiết M là điểm trên đoạn BC sao cho MB = 2MC nên ta có BM BC 3 Đặt AB = x; AC = y ta có 2 2 2
x y  4a (1) (Tam giác ABC vuông tại A)
    1   1   2  1 
Mặt khác từ AM AB BM AB
BC AB  ( AC AB)  AB AC 3 3 3 3   2  1    Nên có 2 2
AM .BC a  ( AB
AC)( AC AB)  a 3 3     2 2 1 2 2  AC
AB a ( Do A . B AC  0 ) 3 3 1 2 2 2 2  y x a (2) 3 3 a 33
Từ (1) và (2) ta có y  Chọn đáp án A 3
Họ tên: Đào Hữu Nguyên FB: Đào Hữu Nguyên
Mail: huunguyen1979@gmail.com  0
Câu 333: Cho tam giác ABC có BAC  90 , AB  1, AC  2 .Dựng điểm M sao cho AM BC , AM  3    2 2
. Đặt AM  . x AB  .
y AC .Tính T x y ? 153 151 157 159 A. T . B. T . C. T . D. x . 20 20 20 20 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 141
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn A    Từ 2 2 2 2 2 2 2 AM  .
x AB y.AC AM x AB y AC  9  x  4 y      
  
   Và AM .BC  . x A . B BC  .
y AC.BC  0  .
x AB( AC AB)  .
y AC( AC AB)  9  x  4 y  144 2 2 2
x  4y  9 x  153 2 2 Ta có hệ:   
20 . Suy ra T x y  .
x  4y  0   20 x  4 y
Email: truongthanhha9083@gmail.com
   
Câu 334: Cho tam giác ABC vuông tại
A. Quỹ tích điểm M thỏa mãn 2 M . B MC M .
A BC MA là
A. Đường thẳng AC.
B. Đường thẳng AB.
C. Đường thẳng BC.
D. Đường trung trực cạnh BC. Lời giải
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon Chọn B
Yêu cầu bài toán trở thành
      2
(MA AB).(MA AC)  . MA BC MA
  
    2 2  MA  (
MA AB AC)  . AB AC  . MA BC MA
  
    (
MA AB AC)  (
MA AB AC) (*)
Gọi E là đỉnh thứ tư của hình chữ nhật ABEC. Hệ thức (*) trở thành
   M . A AE M . A BC
    M (
A AE BC)  0
    M (
A AE AC)  0    M .
A CE  0  MA AC
Vậy điểm M thuộc đường thẳng AB.
Câu 335: Cho tam giác đều ABC cạnh 3a , a  0 . Lấy các điểm M , N , P lần lượt trên các cạnh
BC , CA , AB sao cho BM a , CN  2a , AP x 0  x  3a . Tìm x để AM PN . 3a 4a A. x  . B. x  . 5 5 a 2a C. x  . D. x  5 5 Lời giải
Họ và tên tác giả: Nguyễn Bá Trường Tên FB: thanhphobuon Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 142
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
    1 
Ta có AM AB BM AB BC 3
  1    
AM AB   AC AB 2 1  AB AC . 3 3 3
   1  x 
Ta có PN AN AP AC AB . 3 3a    2 
1    1  x  
Để AM PN thì AM .PN  0  AB AC AC AB  0      3 3   3 3a        2 2 2 2x 1 x  . AB AC AB AC  . AB AC  0 . 9 9a 9 9a 2 2x 1 xA . B AC.cos 60 
3a2  3a2  A . B AC.cos 60  0 9 9a 9 9a 2 1 2x 1 x 1 2 2 
 3a  3a    9a  9a
 3a  3a   0 . 9 2 9a 9 9a 2 5 4a 4a 2  2a
ax  0  x  . Vậy x
thì AM PN . 2 5 5
Nguyenducloi qv2@gmail.com
Câu 336: Cho tam giác ABC vuông cân tại B . Gọi M là trung điểm AB và I là điểm di động trên   AC
đường thẳng MC . Khi 2IM AC đạt giá trị nhỏ nhất, hãy tính tỉ số . AI AC AC AC AC 3 A.  1. B.  2 . C.  2 . D.  . AI AI AI AI 2
(Họ và tên tác giả: Nguyễn Đức Lợi, Tên FB: Nguyễn Đức Lợi) Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 143
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Gọi N là trung điểm BC .  
     
Có 2IM AC IA IB IC IA IB IC  2IN.  
Do đó 2IM AC đạt giá trị nhỏ nhất khi và chỉ khi I là hình chiếu vuông góc của N trên MC .
Dựng hình vuông ABCD . Gọi P là trung điểm CD và H là giao điểm của AP với DN .
Dễ dàng chứng minh được DN CM I DN .
Lại có tứ giác AMCP là hình bình hành, suy ra AP / /CM .
Do đó AP DI và H là trung điểm DI. Suy ra tam giác AID cân tại . A AC AC Vậy   2. AI AD
Email: buivuongphung@gmail.com  1  Câu 337: Cho A
BC có trọng tâm G , H là chân đường cao kẻ từ A sao cho BH
HC . Điểm M di 3    
động trên BC sao cho BM xBC . Tìm x sao cho MA GC nhỏ nhất. 6 5 4 5 A. B. C. D. 5 4 5 6 Lời giải
Họ tên: Vũ Thị Chuyền FB: Vũ Thị Chuyền Chọn D
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 144
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A G B H I M C
Gọi I là trung điểm cạnh BC .
       2 
MA GC MC CG GA GC MC IA 3
  2  
BC BM  IH HA 3   2 1  2 
BC xBC  . CB HA 3 4 3  5   2    x BC HA    6  3 2
  2  5  4 4 Suy ra 2 2 2 MA GC   x BC HA HA    6  9 9 5
Dấu “=” xảy ra khi x  . 6
Email: nguyenthitrangtnh@gmail.com
Câu 338: Cho tam giác ABC, nhọn, không cân và nội tiếp đường tròn  ;
O R . Gọi G và M lần lượt là
trọng tâm tam giác ABC và trung điểm cạnh BC. Cho đường thẳng OG vuông góc với đường
thẳng OM tính giá trị biểu thức 2 2 2
AC AB  2BC theo R. A. 8R2. B. 10R2. C. 12R2. D. 14R2. Lời giải
Họ và tên: Nguyễn Thị Trăng Fb: Trăng Nguyễn
Áp dụng quy tắc trọng tâm và quy tắc trung điểm ta có:
     
OA OB OC  OB OC OG  , OM  . Khi đó 3 2  
    
OG OM OG.OM  0  OA OB OCOB OC  0
      2  O . A OB O . A OC  2O .
B OC  2R  0 1   1 2 2
2R AB    2 2 2R AC  2 2 2
 2R BC  2R  0 2 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 145
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New     2 2  
a b  a b2 (chú ý . a b  ) 2 2 2 2 2
AB AC  2BC  12R
Email: phamhongquangltv@gmail.com   
Câu 339: Cho tam giác MNP có MN=4,MP=8, M = 0
60 Lấy điểm E trên tia MP và đặt ME  kMP .Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP. 2 2 1 1 A. k= . B. k= . C. k= . D. k= . 3 5 3 2 Lời giải
Họ và tên tác giả: Phạm Hồng Quang Tên FB: Quang Phạm Chọn B
    
Ta có: NE  NM  ME  kMP  MN    1 MF  (MP  MN) 2    
NE  MF  (MP  MN) .( kMP  MN )=0
  
  2 MN.(MP  MN) MN.MP  MN 16 16 2
 . k       
   . MP.(MP  2 MN) 64 16 5 MN.MP  MP
(Email): Khueninhbinh2004@gmail.com
   
Câu 340: Đẳng thức M . A AD M .
B BC đúng với mọi điểm M. Khi đó tứ giác ABCD là hình gì.
A. Hình thang vuông. B. Hình chữ nhật. C. Hình thoi.
D. Tứ giác có hai đường chéo vuông góc. Lời giải
(Họ và tên tác giả: Phạm Trung Khuê, Tên FB: Khoi Pham)
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 146
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Chọn B
    Đẳng thức M . A AD M .
B BC đúng với mọi điểm M     . AB BC  0  AB BC Cho M trùng với ,
A B ta được      . 0 AB     AD BA AD
Cho M trùng với C ta được
   
  
   . CA AD  .
CB BC  CB BA.AD  CA AB.BC
   
     C . B AD C . A BC (vì B . A AD A . B BC  0 )
   
      . CB AD  . CA CB  0  .
CB AD CA  0  .
CB CD  0  CB CD
Vậy tứ giác ABCD là hình chữ nhật.
Email: dacgiap@gmail.com
Câu 341: Cho hình vuông ABCD cạnh a . Gọi M , N lần lượt thuộc các đoạn thẳng BC và AC sao cho    1  BM
MC , CN k AN và AM DN . Khi đó k thuộc khoảng nào dưới đây? 3 A. 3;5 . B.  5  ; 3   . C. 4; 2 . D. 2; 4 . Lời giải
Họ và tên: Nguyễn Đắc Giáp Facebook: dacgiap Chọn B A D N B M C
    1 
Ta có: AM AB BM AB BC ; 4   Từ CN k AN và N nằm giữa hai điểm , A C nên suy ra k  0 và  1  1   AN AC
AB AD 1 k 1 k
    1  
DN DA AN DA  AB AD 1 k    
1    1   
AM DN AM .DN  0  AB BC DA    
AB AD  0   4   1 k
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 147
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New       
     AB DA   2 1
AB AB AD 1 1 . .  BC.DA
BC.AB BC.AD  0 1 k 4 41 k  2 2 5a a    0  k  4 . 4 1 k  4
Email: nnqman235@gmail.com        
Câu 342: Cho hai vector a, b thỏa mãn đồng thời các điều kiện a  2b  7, a b  2 , vector (3a b)    
vuông góc với (a b) . Tính cosin của góc tạo bởi hai vector a và b . 1 2 1 2 A.  . B. . C. . D.  . 3 4 3 4 Lời giải
Họ và tên tác giả: Ngô Nguyễn Quốc Mẫn Tên FB: Ngonguyen Quocman Chọn B        2 2  2
a  2b  7
a  4b  4 . a b  7 a  1           2 2    2
Ta có  a b  2
 a b  2 . a b  4  b   2 .           2 2   1
(3a b).(a b)  0 3a b  2 . a b  0   . a b     2     . a b 2 Suy ra cos( ; a b)     . a . b 4
Câu 343: Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh BC a;CA  ;
b AB c . Tìm 2 2 2 OA OB OC
giá trị biểu thức: K    . b c . c a . a b 1 1 1 A. K B. K C. K  1 D. K  2 3 4 Lời giải
Áp dụng tính chất đường phân giác vào các phân giác O ,
A OB, OC ta luôn có:    . a OA  . b OB  . c OC  0 . Từ đó   
a OAbOB c OC2 . . .  0       2 2 2 2 2 2
a OA b OB c OC  2. . a bO . A OB  2 . b . c O . B OC  2. . c . a O . C OA  0
      
Vì OA OB BA  OA OB2 2 2 2 2  c  2.O .
A OB OA OB c Tương tự ta có:
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 148
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 2 2 2 2 2 2
a OA b OB c OC ab  2 2 2
OA OB c   bc  2 2 2
OB OC a   ca  2 2 2
OC OA b  0
 a b c 2 2 2
aOA bOB cOC   abc a b c 2 2 2 OA OB OC     1 bc ac ab Chọn đáp án C. K  1
Họ và tên: Lê Thái Bình
Email: lebinhle80@gmail.com
Facebook: Lê Thái Bình CM CN 1
Câu 344: Cho hình vuông ABCD. M, N lần lượt nằm trên hai cạnh BC và CD sao cho   . CB CD 3  
Gọi E là điểm thỏa mãn AE kAN . Khi BE AM . Tính giá trị biểu thức T k 2  k  1. 13 7 8 5 A. B. C. D. 16 9 9 16 Lời giải.
   
Đặt AB a; AD b . Ta có        
BE BA AE BA kAN BA k AD DN         2 2k  3
 a k b a a    kb  3  3     2 
và AM AB BM a  . b 3   2k  3 2 3
Khi đó BE AM BE.AM  0  
k  0  k  . 3 3 4
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 149
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New AC
Câu 345: Cho hình vuông ABCD, điểm M nằm trên đoạn thẳng AC sao cho AM  . Gọi N là trung 4
điểm CD. Tam giác BMN là A. Tam giác đều. B. Tam giác cân. C. Tam giác Vuông.
D. Tam giác vuông cân Lời giải
Huỳnh Kim Linh GV Trường THPT Chuyên Lê Quý Đôn Khánh Hòa Chọn D    
Đặt AD a, AB b .  1   Khi đó: MB
a  3b 4   1  1  
    b AM AC  (a b);
AN AD DN a  4 4 2  1  1    MN AC  (3a b) 4 4   1    
Ta có: MB.MN
(a  3b)(3a b) 16     2 2 1 
(3a  3b  8a.b)  0  MB MN   1 16         2 2 2 2 1 1 5 2 MB
(a  3b) 
(a  9b  6a.b)  a 16 16 8         2 2 2 2 1 1 5 2 MN  (3a b) 
(9a b  6 . a b)  a 16 16 8 Suy ra MB MN 2
Vậy MB vuông góc với MN và MB =MN, tam giác BMN vuông cân tại đỉnh M
(Email): luongthanh80tm@gmail.com
Câu 346: Cho tam giác ABC . Gọi H là trực tâm và O là tâm đường tròn ngoại tiếp của tam giác ABC .
Đặt BC a , CA b , AB c . Tìm hệ thức liên hệ giữa a , b , c sao cho OH vuông góc với
trung tuyến vẽ từ đỉnh A của tam giác ABC . A. 2 2 2
2a b c . B. 2 2 2
2b a c . C. 2 2 2
2c a b . D. 2 2 2
b  2a  2c . Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 150
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A N P O H B M C D
Gọi AD là đường kính của đường tròn ngoại tiếp tam giác ABC .
Chứng minh được tứ giác BHCD là hình bình hành.   
Nên HB HC HD   
Ta có O là trung điểm của đoạn AD nên HA HD  2HO
   
Suy ra HA HB HC  2HO    
     
Ta có: OB OC  2OM AH ; tương tự OA OC BH;OA OB CH
   
OA OB OC OH
Gọi M , N , P lần lượt là trung điểm của các cạnh BC , CA và AB .  
OH AM OH.AM  0
    
 (OA OB OC).( AB AC)  0
    
 (3OA AB AC).(AB AC)  0
     2  3O .(
A AB AC)  (AB AC)  0  
  
   2 2  3O . A AB  3O .
A AC AB  2 A .
B AC AC  0   2 2  3A .
B AP  3AC.AN AB  2 A .
B AC AC  0 2 2 3c 3b   2 2     c  2 A . B AC b  0 2 2      2 Lại có: 2 2 2 2
a BC  ( AC AB)  b c  2A . B AC   2 2 2
 2 AB.AC b c a Suy ra: 2 2 2
2a b c .
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 151
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
(Sưu tầm, Họ và tên: Nguyễn Lương Thành, Tên FB: luongthanh.nguyen.7)
Câu 347: Cho tam giác ABC có AD là trung tuyến, G là trọng tâm. Một đường thẳng qua G cắt các
cạnh AB, AC lần lượt tại M , N . Khẳng định nào sau đây đúng?   1   2  
A. AM .AN AN.MB AM .NC 2 3
     
B. AM .AN AN.MB AM .NC   2    
C. AM .AN
( AN.MB AM .NC) 3   3    
D. AM .AN
( AN.MB AM .NC) 2 Lời giải Chọn B A N G M PD B C Q BM CN
Trước hết ta chứng minh   1(1) AM ANBM PG  BP//MN   AM AG Thật vậy, kẻ    CQ//MNCN QG     AN AG PG QG Do đó (1)  
 1  PG QG AG  (GD PD)  (GD DQ)  AG AG AG
 2GD AG ( luôn đúng) BM CN Vậy ta có   1 AM AN
BM .AN CN.AM AM .AN
      AN.MB AM .NC AM .AN    cos A cos A cos A
     
AM .AN AN.MB AM .NC ( Do cos A  0 ) Họ và tên:Phan Thông Email:quocthong1182@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 152
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Facebook:Quocthongphan
Câu 348: Cho hình chữ nhật ABCD có cạnh AB=2 và AD=4.Gọi M là trung điểm của cạnh AB và N là  
điểm trên cạnh AD sao cho AN k AD ,CM vuông góc với BN.Khi đó k thuộc vào khoảng nào sau đây  1   1 1   1 1   1 1  A. 0;   B. ;   C. ;   D. ;    16   16 20   20 9   9 6 
   
Giải: Đặt AB a , AD b
    1   1 
Ta có CM CB BM   AD AB b   a 2 2
      
BN BA AN   AB k AD  a kb     1     1 1
Theo giả thiết ta có CM .BN  0  b  
a .a kb  0  16  k  .4  0  k     2  2 8
Họ và tên tác giả: Phạm Hồng Quang Tên FB: Quang Phạm
Email: phamhongquangltv@gmail.com   
Câu 349: Cho tam giác MNP có MN=4,MP=8, M = 0
60 Lấy điểm E trên tia MP và đặt ME  kMP .Tìm
k để NE vuông góc với trung tuyến MF của tam giác MNP. 2 2 1 1 A. k= . B. k= . C. k= . D. k= . 3 5 3 2 Lời giải Chọn B
    
Ta có: NE  NM  ME  kMP  MN    1 MF  (MP  MN) 2    
NE  MF  (MP  MN) .( kMP  MN )=0
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 153
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
  
  2 MN.(MP  MN) MN.MP  MN 16 16 2
 . k       
   . MP.(MP  2 MN) 64 16 5 MN.MP  MP
Câu 350: Cho tam giác ABC có BC a, CA  ,
b AB c . M là trung điểm của BC , D là chân đường 2
phân giác trong góc A . Tính AD   2 4c 2 4bc A. AD p p a . B. AD p a . 2   2   b c b c   2 4bc 2 4bc C. AD p p a . D. AD
p p a 2   2   b c b c
(Họ và tên tác giả: Nguyễn Thị Phương Thảo, Tên FB: Nguyễn Thị Phương Thảo) Lời giải Chọn D  1  
Vì M là trung điểm của BC nên AM
AB AC 2    
  2 2 2 2 1 1 Suy ra AM
AB AC  AB  2ABAC AC  4 4   1 Ta lại có . AB AC   2 2 2
c b a  nên 2  2 1  1 b ca 2 2 2 2   2 2  2 2 2 AM
c  2. c b a   b    4  2  4 BD AB c
Theo tính chất đường phân giác thì   DC AC b  BD  b  Suy ra BD DC DC (*) DC c
  
  
Mặt khác BD AD AB và DC AC AD thay vào (*) ta được
  b      AD AB
AC AD  b cAD bAB cAC c     2 2 2
 b c2 AD  bAB  2bcABAC  cAC  2 1
 b c2 2 2
AD b c  2 . bc  2 2 2
c b a  2 2  c b 2 2 bcAD
b c a b c a 2    b c 2 4bc Hay AD p p a 2   b c
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 154
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Họ và tên tác giả: Nguyễn Văn Toản Tên FB: Dấu Vết Hát
Email: nguyenvantoannbk@gmail.com Bài ở mức độ VD, nhờ thầy cô góp ý!
Câu 351: Cho tam giác ABC có AB = c, AC = b và  0
BAC  60 . Các điểm M, N được xác định bởi     MC  2
MB và NB  2
NA. Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với nhau. A. 2 2
6c  4b  5bc  0 . B. 2 2
4c  5b  6bc  0 . C. 2 2
6c  5b  4bc  0 . D. 2 2
4c  6b  5bc  0 . Lời giải Chọn D          Ta có: MC  2
MB AC AM  2
 (ABAM )  3AM  2AB AC .   
Tương tự ta cũng có: 3CN  2CA CB . Vậy:  
AM CN AM CN  0    
 (2AB AC)(2CACB)  0        2 2
(2AB AC)( AB 3AC)  0  2AB 3AC 5A . B AC  0 . 5bc  2 2 2 2 2c 3b
 0  4c 6b 5bc  0 . 2
Họ tên: Trần Ngọc Tên FB: Ngọc Trần
Email: soantailieutoanhoc2018@gmail.com
Câu 352: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi I là trung điểm của AC và M là điểm thỏa    
mãn OM  2OA OB  2OC . Biết rằng OM vuông góc với BI và 2 AC  3B . C BA . Tính góc  ABC . A. 30 . B. 45 C. 60 . D. 120 . Lời giải Chọn C
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 155
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A M H I B O K C    
  
Ta có OM BI  2OM.BI =0  2OAOB  2OCBABC  0         
  OB BA BC   OB BA OB BC  BA BC2 5 2 2 0 5 . +5 . 2  0
Gọi H, K tương ứng là trung điểm của đoạn A , B BC       Khi đó OB BA
OB BC  BABC2 5 . +5 . 2  0 
  
    
OH HBBA OK KBBC  BABC2 5 . 5 . 2  0 5 5   2 2 2 2   BC
BC  2BA  2BC  2.2B . A BC  0 2 2 1 1 3 2 2   BA BC   2 2 2
AB BC AC  2  0  AC   2 2 AB BC . 2 2 4 4 2 2 2 2 2 AC AC
BA BC AC Do đó  3 cos ABC   . Suy ra  ABC  60 . 2B . A BC 2 2 AC 3
Họ và tên tác giả: Đào Trung Kiên (st) Tên FB: kienyenthe
Email: kienyenthe@gmail.com
Câu 353: Cho hình thang vuông ABCD, đường cao AD = h, đáy AB = a, đáy CD = b. Gọi M là trung
điểm của BC. Hệ thức giữa a, b, h để AM BD là A. 2 2
a h ab  0 . B. 2 2
h a ab  0 C. 2 2
h b ab  0 . D. 2 2
b h ab  0 . Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 156
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Ta có   AM  D B
 2 AM .BD  0
  
  AB ACBD  0
    
  AB AD DC AD AB  0   2 2
  AB AD DC.AB  0 2 2
h a ab  0
Họ và tên: Vũ Huỳnh Đức
Email: vutoanpvd@gmail.com
Facebook: vuhuynhduc2017   1
Câu 354: Cho tam giác đều ABC cạnh bằng a. Gọi M, N là các điểm thỏa mãn BM BC , 3   1 A N
AB . Gọi I là giao điểm của AM và CN. Tính diện tích của tam giác IBC theo a? 3 2 a 3 2 a 7 2 2a 7 2 2a 3 A. S. B. S. C. S. D. S. IBC 7 IBC 7 IBC 7 IBC 7 Lời giải Chọn A       2     ,   :   , x+y=1   x I CN x y BI x BN y BC BI
BN  3y BC , x+y=1 3    2 2
và do I A M nên từ  x BI
BA  3y BC ta cũng có x  3y  1. 3 3
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 157
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A N I B M C x+y=1     6 1 4 1   x= , y=  BI BA BC - 2x   y  7 7 7 7 3 1  3    2 1
Từ giả thiết ta có CN= CA CB 3 3        2 1   4 1 
 CN.BI   CA CB .BA BC   3 3   7 7          8 4 2 1  BA .CA BA .CB BC .CA BC .CB  0 21 21 21 21
 BIC vuông tại I.      2 4 1 2  4 1  21
BI BA BC BI  2  BA BC   a 7 7  7 7  49 2 21 28 IC  2 BC  2 BI  2 a  2 a  2 2 7 a IC a 49 49 7 2 1 a 3 Vậy SBI .IC  . IBC 2 7
Họ và tên tác giả: Huỳnh Thanh Tịnh Tên FB: huynhthanhtinh
Email: huynhthanhtinhspt@gmail.com    2 
Câu 355: Cho tam giác đều ABC và các điểm M , N , P thỏa mãn BM k BC , CN CA , 3  4  AP
AB . Tìm k để AM vuông góc với PN . 15 1 1 3 A. k B. k C. D. k 3 2 4 Lời giải Chọn A
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 158
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New         
BM k BC AM AB k( AC AB)  AM  (1  k ) AB k AC
   4  1 
+) PN AN AP   AB AC . 15 3  
Để AM vuông góc với PN thì AM .PN  0      4 1 
 (1  k) AB k AC   AB AC  0      15 3  4(  1  ) 1  4   k k k k 2 2  AB AC  (  ) AB AC  0 15 3 3 15 4(  1  k) k 1  k 4k 0    (  )c os60  0 15 3 3 15 1  k  3 Email: duyhung2501@gmail.com
Câu 356: : Giả sử O là tâm đường tròn nội tiếp tam giác ABC với các cạnh BC a;CA  ;
b AB c . Tìm 2 2 2 OA OB OC
giá trị biểu thức: K    . b c . c a . a b 1 1 1 A. K B. K C. K  1 D. K  2 3 4 Lời giải Chọn C
Áp dụng tính chất đường phân giác vào các phân giác O ,
A OB, OC ta luôn có:    . a OA  . b OB  . c OC  0 . Từ đó   
a OAbOB c OC2 . . .  0       2 2 2 2 2 2
a OA b OB c OC  2. . a bO . A OB  2 . b . c O . B OC  2. . c . a OC.OA  0
      
Vì OA OB BA  OA OB2 2 2 2 2  c  2.O .
A OB OA OB c
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 159
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New Tương tự ta có: 2 2 2 2 2 2
a OA b OB c OC ab  2 2 2
OA OB c   bc  2 2 2
OB OC a   ca  2 2 2
OC OA b  0
 a b c 2 2 2
aOA bOB cOC   abc a b c 2 2 2 OA OB OC     1 bc ac ab Chọn đáp án C. K  1
Người sưu tầm: Tăng Duy Hùng. FB: Hùng Tăng
Họ và tên: Nguyễn Thị Huệ FB: Nguyễn Thị Huệ
Gmail: nguyenthihue1611@gmail.com       1   
Câu 357: Cho hai véc tơ a và b thỏa mãn các điều kiện a
b  1, a  2b  15. Đặt u a b và 2     
v  2k a b, k  .
 Tìm tất cả các giá trị của k sao cho u v 0 ,  60 . 3 5 3 5 17 17 A. k  4  . B. k  4  . C. k  5  . D. k  5  . 2 2 2 2 Lời giải. Chọn A      
Từ giả thiết a b
 a b2 1 2 15 2  15  . a b  . 2           2 2
u v  a b ka b 9 . 2  3k  , 2
u u  6, v v  4k  2k  4 2 9 3k    u v 1 3 5 0 2 ,  60    k  4  . 2 2 2
6. 4k  2k  4
Họ và tên tác giả: Lê Thị Nguyệt Tên FB: NguyệtLê
Email: Lenguyet150682@gmail.com
      AD
Câu 358: Cho tứ giác ABCD , hai điểm M , N thỏa mãn 2MB MA  0; 2NC ND  0 và  . x Tính BC  cosDBC MN BD  theo x để . cos ADB x x x A. . B.  . C. . D. x 3 . 2 2 3 Lời giải
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 160
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  
MN BD MN.BD  0;   Phân tích: Ta thấy     
nên cần phân tích MN theo AD và DBC   ; BD BC  
; ADC   A ; D BD  BC .
Giải. Ta có biểu diễn
   2   2     
MN MA AN BA AN  BN NA 2 1  AN BN AN 3 3 3 3 2       
BC CN  1
  AD DN  2 1  BC AD 3 3 3 3  2  1  Vậy MN BC AD . Do đó 3 3
  
MN BD   BC AD   2
.BD  0  2BC.c osDBC A .
D c os ADB  0 .  cosDBC AD x Suy ra      . Đáp án B. cos ADB 2BC 2
Họ và tên tác giả: Trần Thanh Hà Tên FB: Hatran
Email: tranthanhha484@gmail.com
Câu 359: Cho tam giác ABC có AB  6; BC  7;CA  5. Gọi M là điểm thuộc cạnh AB sao cho   a
AM  2MB và N là điểm thuộc AC sao cho AN k AC ( k   ). Biết k   b a (
là phân số tối giản, a,b là các số nguyên) sao cho đường thẳng CM vuông góc với đường b thẳng BN.
Tính giá trị biểu thức T  2018a  2019b  5 .
A. T  2017. B. T  2  020.
C. T  2030. D. T  2  030. Lời giải Chọn B
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 161
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    2  
CM AM AC AB AC . 3
    
BN AN AB k AC AB .          2 2 2 2k 2 Suy ra: CM BN
( AB AC)(k AC AB)  AB AC
AB k AC AB AC 3 3 3      2 2 2   2 2
AB AC BC AB ACCB  . AB AC   6 2 6
BN CM k   7
Theo giả thiết, ta có: a  6; b  7  T  2018.6  2019.7  5  2020.
Họ và tên tác giả: Đỗ Thế Nhất Tên FB: Đỗ Thế Nhất
Email: nhatks@gmail.com  0
Câu 360: Cho tam giác ABC có AB = c, AC = b và BAC  60 . Các điểm M, N được xác định bởi     MC  2
MB và NB  2
NA . Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với nhau. A. 2 2
6c  5b  4bc  0 B. 2 2
c  6b  5bc  0 C. 2 2
4c  6b  5bc  0 D. 2 2
4c  6b  5bc  0 Lời giải Chọn C         
Ta có: MC  2MB AC AM  2( AB AM )  3AM  2 AB AC   
Tương tự ta cũng có: 3CN  2CA CB      
Vậy: AM CN AM CN  0  (2 AB AC)(2CA CB)  0
     
 (2 AB AC)( AB  3AC)  0  2 2
2AB  3AC  5A . B AC  0 bc  2 2 5 2c  3b   0  2 2
4c  6b  5bc  0 2
Câu 361: Cho hình chữ nhật ABCD có AB= a, AD=2a. Gọi M là trung điểm AB, N là điểm trên cạnh  
AD sao cho AD  kAN . Tìm k để CM  BN. A. k=7,9 B. k=8 C. k=8,1 D. k=7.8 Lời giải Chọn B     1 
giải: Ta có CM CB BM AD AB 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 162
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New     1 
BN BA AN AB   AD k  
Để CMBN thì CM.BN  0    
1      1 
CM.BN   AD   AB   AB   AD  2   k    2 2 1 1 1  
Mà  AD.AB AD AB AB.AD k 2 2k 2 2 1 1 1
  AD AB   2a2 1 2  a k 2 k 2   1
CM.BN  0   2a2 1 2  a  0 k 2 4 1
    0  k  8 k 2
Vậy k  8 thì CM BN
Họ và tên tác giả: Nguyễn Ngọc Duy Tên FB: Ngọc Duy
Email: nguyenngocduyakgl@gmail.com
Câu 362: Cho hình bình hành ABCD có đường chéo lớn là AC . Gọi E, F lần lượt là hình chiếu vuông
góc của C trên AB, AD . Biểu thức nào sau đây là đúng. A. 2 AB.AH  .
AD AF AC . B. 2 . AB AE  . AD AF AC . C. 2 . AB AE  .
AD AH AC . D. A . B AE A .
D AF AC.AH . Lời giải Chọn B
Vì E, F lần lượt là hình chiếu vuông góc của C trên F
AB, AD nên ta có:
    A .
B AE AC.AB C D
    A .
D AF AC.AD H
       
Suy ra: AB AE AD AF AC AB AD 2 . .  AC (*) A B E
Do AC là đường chéo lớn nên  0
ABC  90 và B nằm   giữa hai điểm , A E . Suy ra A . B AE A . B AE  
Tương tự ta có: D nằm giữa hai điểm , A F . Suy ra A . D AF A . D AF
Vậy đẳng thức (*) trở thành: 2 . AB AE  . AD AF AC .
Email: thuy.tranthithanhdb@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 163
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 363: Cho hình thang vuông ABCD , đường cao AD h , cạnh đáy AB a, CD b . Tìm hệ thức
giữa a, b, h để BD vuông góc trung tuyến AM của tam giác ABC . A. 2
h a a b . B. 2
h a b a .
C. h h b  a a b h . D. 2
2h a a bLời giải Chọn A a A B h M D C b  1   Thay AM
. AB AC , ta có: 2    
  
   
AM BD AM .BD  0   AB AC .BD  0  AB.BD AC.BD  0 (1)
     
mà AB BD AB AD AB 2 2 . .
  AB  a  
      
và AC BD   AD DC AD AB 2 2 .
AD DC.AB h ab nên:   2
1  h a a b .
Họ và tên tác giả: Nguyễn Quang Nam Tên FB: Quang Nam
Email: quangnam68@gmail.com
Câu 364: Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R), M là điểm chính giữa cung BC (
cung BC không chứa điểm A). Chọn đẳng thức đúng trong các đẳng thức sau:
A. MA M .
B sin C MC.sin B
B. MA M .
B cos C MC.cos B
C. MA M .
B sin B MC.sin C
D. MA M .
B cos B M . C cos C Lời giải: Chọn C      MA  MA Ta có 2 2 .
MO MA MA  2 . MOMA  2 sin . A . MO  sin . A MA (1) MA MA    MB  MC Tương tự 2 sin . B . MO  sin .
B MB (2) , 2 sin C. . MO
 sin C.MC (3) MB MC Từ (1), (2) và (3):
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 164
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New  sinA.MA  sin .
B MB  sin C.MC      MA MB MC  2MO( sin . A  sin . B  sin C. )  MA MB MC    2M . O 0  0 A O B C M    MA MB MC  Ta sẽ chứng minh  sin . A  sin . B  sin C.  0 (*) MA MB MC 1  1  1   Thật vậy, (*)   . MB MC.sin . A MA M . A MC.sinB.MB  . MB .
MA sinC.MC  0 2 2 2    
 S MA S MB S MC  0 ( đúng) a b c
( với S , S , S lần lượt là diện tích các tam giác MBC, MAC, MAB) a b c Vậy M .
A sin A M .
B sin B MC.sin C  0  M .
A sin A M .
B sin B M . C sin C (*) Theo bài ra: 0
sin A  sin 90  1 thay vào (*): MA M .
B sin B M . C sin C
Họ Tên: Lương Thị Hương Liễu Tên FB: Hương Liễu Lương
Email: lieuluong.290983@gmail.com
Câu 365: Cho tam giác ABC có BC a, CA b, AB c . M là trung điểm của BC , D là chân đường   2
phân giác trong góc A . Tính AD 2  4c 2 4bc A. AD
p p a B. AD  p a 2 b c2 b c   2 4bc 2 4bc C. AD
pp a D. AD
pp a  2 b c2 b cLời giải Chọn D  1   A
* Vì M là trung điểm của BC nên AM  AB AC 2 B C D M
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com Hình 2.3 165
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New    
  2 2 2 1 1   Suy ra AM
AB AC2  AB  2ABAC   AC  4 4         2 2 1   Ta có A . B AC AB AC   ABAC2 2    1 2 2 2 1 
AB AC CB    2 2 2
c b a  nên 2   2  2 1  1 b ca 2 2 2 2   2 2  2 2 2 AM
c  2. c b a   b    4  2  4 BD AB c
* Theo tính chất đường phân giác thì   DC AC b  BD  c  Suy ra BD DC DC (*) DC b
     
Mặt khác BD AD AB và DC AC AD thay vào (*) ta được  
c     
AD AB  AC AD  b cAD bAB cAC b     2 2 2 2
 b cAD  bAB  2bcABAC  cAC  2 2
 b c 2 2 1
AD b c  2 . bc  2 2 2
c b a  2 2  c b 2 2 bcAD
b c ab c a b c2 2 4bc Hay AD
pp a b c2
Họ và tên tác giả: Phạm Thành Trung Tên FB: Phạm Thành Trung
Email: trungthuong2009@gmail.com
Câu 366: Trong cuộc thi giải trí toán học tổ chức nhân dịp hoạt động chào mừng Ngày nhà giáo Việt
Nam có một trò chơi như sau: Người ta thiết kế hai đường ray tạo với nhau một góc 0 30 như
hình vẽ dưới đây. Trên các đường thẳng Ox và Oy người ta để hai vật nặng cùng trọng lượng.
Buộc hai vật thể với nhau bằng một thanh cứng AB  1m sao cho mỗi vật đều có thể chuyển
động được trên hai đường ray. Nối hai vật bằng một sợi giây vòng qua một cột có gốc tại O .
Người tham dự cuộc thi sẽ đứng tại vị trí điểm B để kéo vật thể chuyển động trên Oy . Người
thắng cuộc sẽ là người kéo được vật thể ra xa nhất so với điểm gốc O . Hãy dùng kiến thức toán
học để tính toán vị trí xa nhất mà người tham dự cuộc thi có thể đạt được.
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 166
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New A O B A. 1m . B. 2m . C. 3m . D. 2m . Lời giải Chọn B + Đặt OB  ;
x OA y(x, y  0) . Khi đó theo định lý cosin ta có: 2 2 2 0 2 2
AB x y  2xy cos 30  x y  3xy Do đó ta có hệ thức: 2 2
x y  3xy  1
Xét phương trình bậc hai: 2 2
y  3xy x 1  0
Phương trình có nghiệm y khi 2 2
  3x  4(x 1)  0  0  x  2
Vậy học vị trí xa nhất mà học sinh có thể đạt được cách O một khoảng là 2m
Câu 367: Cho tam giác ABC có AB= c,BC=a,CA=b. Trung tuyến CM vuông góc với phân giác trong AL CM 3 và  . Tính cos A . AL 2 2 5 1 3 1 A. cos A B. cos A C. cos A D. cos A 2 4 2 2 Lời giải Chọn D  b  c  Ta có: AL AB AC b c b c      CA CB AB  2AC CM   2 2  
Theo giả thiết: AL CM A . L CM  0    
 bAB cAC AB AC 2 2 2 2 2
 0  bc bc cos A  2cb cos A  2cb  0
 c  2b1 cos A  0  c  2b (do cos A  1  ) 2 2 2 2 2 b a c a b Khi đó: 2 CM    2 4 2
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 167
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New 1     AL
AB AC2 1 2 2   2 2
AB AC  2 A . B AC    2 2 9b a  9 9 9 2 2 2 CM 3 CM 9 a b 3 2 2    .   a  3b 2 2 2 AL 2 AL 4 9b a 4 2 2 2 2 2
b c a 5b a 1 cos A    2 2bc 4b 2 doantv.toan@gmail.com
Câu 368: Cho hình chữ nhật ABCD có AB  1;CD  3 . Điểm M thuộc cạnh AD và N là trung điểm BC m BN
sao cho MN BD . Phân số tối giản 
có m n bằng bao nhiêu n NC A. 29. B. 18. C. 16. D. 27.
(Họ và tên tác giả: Trần Văn Đoàn, Tên FB: Trần Văn Đoàn) Lời giải Chọn B   
Ta có BD  (BA BC) m BN BN m  m       BN BC k BC n NC BC m n m n
       1 
MN MA AB BN k BC AB    2     1  11 11 B .
D MN  0 nên 1 9 k   0  k  
m  11, n  7    2  18 11 7
Họ và tên tác giả: Nguyễn Thị Thỏa Tên FB: Nguyễn Thị Thỏa
Email: phamquynhanhbaby56@gmail.com
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 168
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
Câu 369: Cho tam giác ABC có AB c ; BC a , CA b . Gọi M là trung điểm của AB và D là
chân đường phân giác trong góc A của tam giác ABC . Biết rằng trung tuyến CM vuông góc
với phân giác trong AD . Khi đó đẳng thức nào sau đây đúng?
A. b  2c .
B. c  2b .
C. a b c .
D. c a b . Lời giải Chọn B DB AB c
Ta có D là chân đường phân giác trong góc A nên   DC AC b    c    
và DB , DC ngược hướng suy ra DB   DC  . b DB  . c DC  0 b  b  c  Ta có: AD AB AC . b c b c    
 CA CB AB  2AC
Vì CM là trung tuyến nên CM   . 2 2  
Theo giả thiết: AL CM A . L CM  0    
 bAB cAC AB  2AC  0 2 2 2 2
bc bc cos A  2cb cos A  2cb  0
 c  2b1 cos A  0  c  2b (do cos A  1  )
Vậy c  2b .
Câu 370: Cho tam giác ABC đều nội tiếp (O;R). M là điểm bất kì trên cung nhỏ  BC . Khi đó
A. MA MB MC
B. MA MB MC
C. MA MB MC
D. MA  2MB MC Lời giải Chọn A     2 2 2 2 2
R OA  (OM M ) A
R MA  2OM .OA  Ta có    MA 2
MA  2.OM .MA  0  MA  2.OM .  0 MA Tương tự   MB MB  2.OM .  0 MB   MC MC  2.OM .  0 MC     MA MB MC
Suy ra MA MB MC  2OM (   )  0 MA MB MC
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 169
Sản phẩm chuyên đề lớp 10 của tập thể các thầy cô Group: Strong Team TOÁN VD–VDC-New
   MA MB MC Vì  ; ;
là các véc tơ đơn vị và đôi một tạo với nhau một góc 1200 nên MA MB MC    MA MB MC    
 0 , do đó MA MB MC  0 MA MB MC
Véc tơ- Tích Vô Hướng – Chú ý: Sản phẩm chưa qua phản biện, mọi góp ý xin gửi email: Strongvdc@gmail.com 170