Bài tập về các nguyên mẫu cổ điển - Cơ sở vật lí | Đại học Sư Phạm Hà Nội
Bài tập về các nguyên mẫu cổ điển - Cơ sở vật lí | Đại học Sư Phạm Hà Nội giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống
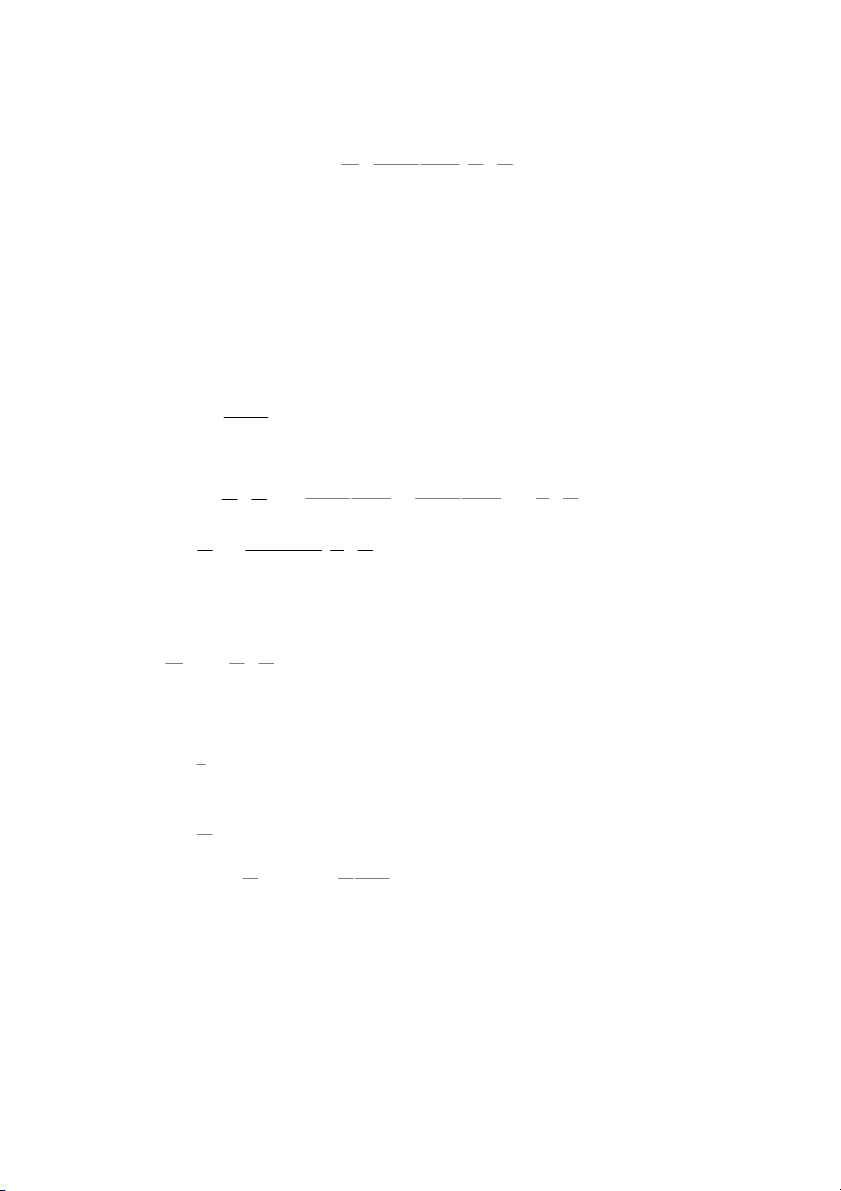
Preview text:
Chương I Các m u nguyên t ẫ ử cổ i đ ển
CÁC MẪU NGUYÊN TỬ CỔ ĐIỂN PHẦN 1 ĐỀ BÀI
5.1)Dựa vào mẫu Thomson, tính bán kính nguyên tử Hydro và bước sóng ánh
sáng do nó phát ra nếu biết năng lượng Ion hóa của nguyên tử là E eV 6 . 13 .
5.2)Một hạt có động năng 0.27MeV bị tán xạ bởi một lá vàng dưới một góc o
60 . Tìm giá trị tương ứng của tham số ngắm. Biết số thứ tự của vàng là Z=79.
5.3)Với một khoảng cách cực tiểu bằng bao nhiêu, khi một hạt có động năng T 50 . 0
MeV (khi va chạm trực diện) đến gần:
a)Một hạt nhân nguyên tử chì nặng đứng nghỉ;
b)Một hạt nhân Li7 nhẹ, tự do ban đầu đứng nghỉ?
5.4)Một hạt có động năng T 50 . 0
MeV bị tán xạ dưới góc o 90 trong
trường Coulomb của một hạt nhân nguyên tử thủy ngân đứng yên. Tìm:
a)Bán kính cong nhỏ nhất của quỹ đạo của hạt;
b)Khoảng cách cực tiểu mà hạt lại gần hạt nhân.
5.5)Một proton có động năng T và tham số ngắm b , bị tán xạ trong trường
Coulomb của một hạt nhân nguyên tử vàng đứng yên. Tìm xung truyền cho hạt nhân này do sự tán xạ.
5.6)Một hạt có động năng T bị tán xạ bởi một giếng thế năng hình cầu có bán
kính R và độ sâu U 0, tức là trường mà trong đó thế năng của hạt có dạng: , 0 r R U
U ,0r R
Trong đó r là khoảng cách từ tâm của giếng. Tìm sự liên hệ giữa tham số ngắm
b của hạt và góc mà hạt lệch khỏi phương chuyển động ban đầu.
5.7)Người ta chiếu một dòng song song các hạt có bán kính r , vào một quả cầu
đứng yên có bán kính R . Giả thử sự va chạm của hạt với quả cầu là đàn hồi, tìm:
a)Góc lệch của hạt phụ thuộc vào tham số ngắm b của nó;
b)Phần hạt tỉ đối, tán xạ trong khoảng từ đến d ;
c)Xác suất tán xạ hạt ở bán cầu trước ( 2 ).
5.8)Một chùm hạt hẹp có động năng T 1
.0MeV đập vuông góc lên một lá Platin dày 0 . 1
m . Quan sát các hạt tán xạ theo góc o
60 với phương của chum tới
bằng một máy đếm có lỗ vào hình tròn có diện tích 2
1cm ; lỗ đặt cách khu vực 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển
tán xạ của lá một khoảng cm 10
. Phần các hạt đập vào lỗ của máy đếm bằng bao nhiêu?
5.9)Một chùm hạt hẹp có động năng T 5 . 0
MeV và cường độ 5 I 0 . 5 10
hạt/s đập vuông góc lên một lá vàng. Tìm bề dày của lá, nếu cách khu vực tán xạ một khoảng r cm 15 và dưới một góc o 60
với phương của chùm tới mật
độ dòng hạt tán xạ là 2 j 40 p / scm .
5.10)Một chùm hạt hẹp đập vuông góc lên một lá bạc.Sau lá bạc đặt một máy
đếm ghi các hạt tán xạ ứng với công thức Rutherford. Khi thay lá bạc bằng một
lá Platin có cùng diện tích khối lượng, thì số hạt ghi được trong một đơn vị thời gian tăng lên 52 . 1
lần. Tìm số thứ tự của Platin, giả sử rằng đã biết số
thứ tự của bạc và trọng lượng của cả hai nguyên tố.
5.11)Một chùm hạt hẹp có động năng T 0
.5MeV đập vuông góc lên một lá 3
vàng có mật độ khối lượng trên một đơn vị diện tích là d 5 .
1 mg / cm cường độ 5
chùm hạt này là I 0 . 5 10 0
hạt/s. Tìm số hạt ; bị tán xạ bởi lá vàng sau 3 0
phút trong các khoảng góc: a) o o 59 61 ; b)Trên 0 60 .
5.12)Một chùm hẹp các proton có vận tốc v 6 106
m / s đập vuông góc lên một
lá bạc có độ dày d 0 . 1
m tìm xác suất tán xạ của các hạt proton ở bán cầu sau ( o 90 ).
5.13)Một chùm hạt hẹp có động năng T 5 . 0
MeV đập vuông góc lên một lá vàng, chứa 19 n 1 . 1 10
hạt nhân /cm2. Tìm số tỉ đối các hạt tán xạ dưới góc o 0 20 .
5.14)Tìm tiết diện hiệu dụng của hạt nhân nguyên tử Urani ứng với sự tán xạ o
các hạt có động năng T 5 . 1
MeV trong khoảng các góc lớn hơn 0 60 .
5.15)Tiết diện hiệu dụng của hạt nhân nguyên tử vàng ứng với sự tán xạ các hạt
đơn năng lượng trong khoảng các góc từ o 90 đến o 180 bằng 50 . 0 kilobac. Xác định:
a)Năng lượng của các hạt ; d
b)Tiết diện vi phân của sự tán xạ: d (kilobac/steradian) ứng với góc tán xạ o 60 . 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển
5.16)Theo điện động lực học cổ điển, một electron chuyển động với gia tốc w
sẽ mất một năng lượng do bức xạ theo quy luật: 2 dE 2e 2 w 3 dt 3c
Trong đó e là điện tích của electron, c là vận tốc ánh sáng. Xác định khoảng
thời gian mà sau đó năng lượng của electron thực hiện một dao động gần điều hòa với tần số 5 1015
(rad / s) giảm 10 lần.
5.17)Dùng công thức ở bài tập trên, xác định khoảng thời gian, trong đó
electron chuyển động trong nguyên tử Hydro theo một quỹ đạo tròn có bán kính r 50
pm có thể rơi vào hạt nhân. Để đơn giản giả thử rằng vector gia tốc w
luôn hướng vào tâm nguyên tử.
5.18) Trong phổ của Hydro nguyên tử người ta biết bước sóng của ba vạch
thuộc cùng một dãy là: 97 2 . 6nm , 10 . 2 5 n 8 m , và 12 .
1 57nm . Tìm bước sóng của
những vạch khác trong phổ trên mà có thể đoán trước được chúng nhờ ba vạch này.
5.19)Một hạt có khối lượng m chuyển động theo một quỹ đạo tròn trong một 1 2
U (r) kr
trường thế đối xứng xuyên tâm 2
. Bằng điều kiện lượng tử của Bohr,
hãy tìm các bán kính có thể có của các quỹ đạo và các mức năng lượng của hạt này.
5.20)Đối với nguyên tử Hydro và Ion He+ hãy tính:
a)Bán kính quỹ đạo Bohr thứ nhất và vận tốc của electron trên quỹ đạo đó;
b)Động năng và năng lượng liên kết của electron ở trạng thái cơ bản;
c)Thế Ion hóa, thế kích thích thứ nhất và bước sóng của vạch cộng hưởng ( n 2 n 1 ).
5.21)Tính vận tốc góc của electron trên quỹ đạo Bohr thứ hai của Ion He+.
5.22)Đối với các hệ tương tự Hydro, tìm momen từ n ứng với chuyển động
của electron trên quỹ đạo thứ n cũng như tỉ số giữa momen từ với momen cơ n
Mn . Tính momen từ của một electron trên quỹ đạo Bohr thứ nhất.
5.23)Tính toán và vẽ thang các bước sóng, các khoảng phổ trong đó có chứa
dãy Lyman, Balmer và Pashen đối với Hydro nguyên tử. Tách ra miền phổ khả kiến trên thang này.
5.24)Tính đối với Hydro nguyên tử:
a)Các bước sóng của ba vạch đầu tiên của dãy Balmer; 3
Chương I Các m u nguyên t ẫ ử cổ i đ ển
b)Năng suất phân giải cực tiểu của máy quang phổ, trong đó có thể phân
giải hai mươi vạch đầu tiên của dãy Balme.
5.25)Một bức xạ của Hydro nguyên tử đập vuông góc lên một cách tử nhiễu xạ có bề rộng l 6 . 6
mm. Trong phổ quan sát được, dưới một góc nhiễu xạ nào
đó, vạch thứ 48 của dãy Balme xuất hiện tại giới hạn phân giải (theo tiêu chuẩn Rayleigh). Tìm góc này.
5.26)Phổ tương tự Hydro phụ thuộc yếu tố nào, nếu bước sóng của nó ngắn hơn
bước bốn lần bước sóng của phổ Hydro nguyên tử.
5.27)Hydro nguyên tử sẽ pất ra bao nhiêu vạch phổ, khi người ta kích thích nó
lên mức năng lượng thứ n ?
5.28)Tìm số lượng tử n ứng với trạng thái kích thích của Ion He+, nếu khi dịch
chuyển về trạng thái cơ bản, Ion này phát ra liên tiếp hai photon với các bước sóng 108 5
. nm và 30.4nm .
5.29)Tính hằng số Rydberg (ra cm-1), nếu biết rằng đối với các Ion He+ hiệu số
các bước sóng giữa các vạch đầu của dãy Balme và dãy Lyman bằng 133 7 . nm .
5.30) Ở Ion tương tự Hydro nào thì hiệu số các bước sóng của các vạch đầu dãy
Balmer và dãy Lyman bằng 5 9. n 3 m.
5.31)Tìm bước sóng của vạch đầu của của dãy phổ của các Ion He+, trong đó
khoảng cách về tần số giữa vạch cuối và vạch đầu là 18 . 5 1015 rad / s .
5.32)Năng lượng liên kết của electron trong nguyên tử He bằng E 6 . 24 eV 0 .
Tìm năng lượng cần thiết để bứt cả hai electron ra khỏi nguyên tử này.
5.33)Nguyên tử Hydro phải chuyển động với động năng cự tiểu bằng bao nhiêu,
để khi va chạm trực diện không đàn hồi với nguyên tử Hydro khác đang đứng
nghỉ thì một trong các nguyên tử đó có thể phát ra một photon? Trước khi va
chạm cả hai nguyên tử đều ở trạng thái cơ bản.
5.34)Một nguyên tử Hydro đứng nghỉ phát ra một photon ứng với vạch đầu của
dãy Lyman. Nguyên tử đã có vận tốc bằng bao nhiêu?
5.35)Trong các điều kiện của bài toán trên, tính năng lượng của photon được
phát ra khác với năng lượng của sự dịch chuyển tương ứng trong nguyên tử là bao nhiêu phần trăm? 4
Chương I Các m u nguyên t ẫ ử cổ i đ ển
5.36)Một Ion He+ đứng nghỉ phát ra một photon ứng với vạch đầu tiên của dãy
Lyman. Photon này đã bứt một quang electron khỏi một nguyên tử Hydro đứng
nghỉ đang ở trạng thái cơ bản. Tính vận tốc của quang electron.
5.37)Bằng cách tính toán sự chuyển động của hạt nhân nguyên tử Hydro, tìm
biểu thức đối với năng lượng liên kết của electron ở trạng thái cơ bản và hằng
số Rydberg. Năng lượng liên kết và hằng số Rydberg thu được khi không kể đến
chuyển động của hạt nhân sẽ khác giá trị chính xác tương ứng của các đại lượng này bao nhiêu phần trăm?
5.38)Đối với các nguyên tử Hydro nhẹ và nặng, H và D, tìm hiệu số:
a) Năng lượng liên kết của các electron của chúng ở trạng thái cơ bản;
b)Bước sóng của vạch đầu tiên của dãy Lyman.
5.39)Tính khoảng cách giữa các hạt của một hệ ở tạng thái cơ bản, ứng với
năng lượng liên kết và bước sóng của vạch đầu tiên của dãy Lyman. Khảo sát các hệ sau:
a)Nguyên tử meson Hydro có hạt nhân là một proton (trong nguyên tử Hydro
meson thay cho electron, meson chuyển động, có cùng điện tích nhưng khối
lượng lớn hơn 207 lần).
b)Pozitroni có cấu tạo gồm một electron và một positron chuyển động xung quanh một khối tâm chung. 5
Chương I Các m u nguyên t ẫ ử cổ i đ ển PHẦN 2 LỜI GIẢI
5.1) a)Theo mẫu nguyên tử Thompson thì điện tích dương e phân bố đều trong
hình cầu bán kính R nên ta có lực của điện tích dương tác dụng lên electron: 1 e2 ,r R 4 r2 F 0 2 1 e r ,r R 4 R3 0 W Mà F gradW Fdr hay 1 e2
C ,r R 4 r 1 W 0 2 2
1 1 e r C2,r R 2 4 R3 0
Do điều kiện liên tục của W tại r R và do W 0 ở vô cùng nên: C 0 1 3 e2 C 2 2 4 R 0 Cuối cùng ta được: 1 e2 , r R 4 r W 0 2 2 2
1 1 e r 3 e ,r R 2 4 R3 2 4 R 0 0
Dễ thấy W là hàm đồng biến của W r do đó ta có: min W r 0 , tức là: 6
Chương I Các m u nguyên t ẫ ử cổ i đ ển 3 e 2 W E min ion 2 4 R 0 3 e 2 R 16 nm 2 4 E 0 ion
b)Tần số chuyển động của electron trên quỹ đạo bán kính r : 2 e 1 2 e m r 2 4 r 4 0r mr 0 c 2 c
Bước sóng mà nguyên tử Hydro phát ra: f Cuối cùng ta được: 2 c 3 40mr e Thay số ta có: 24 . 0 m .
5.2)Từ công thức liên hệ giữa tham số ngắm và góc tán xạ: a 1 2 zZe 0 b cot g cot g 2 2 8 E 2 0 0 Thay số ta được: b 73 . 0 pm . 2
5.3)Năng lượng nghỉ của hạt , m c 2000 MeV , 0 4MeV vì vậy ta có thể áp
dụng các công thức phi tương đối tính trong bài toán này.
Ta có thể hình dung quá trình va chạm như sau: Hai hạt nhân lúc đầu tiến lại
gần nhau (do hạt chuyển động lại gần hạt nhân bia) tương tác (đẩy) với nhau
cuối cùng là đi ra xa nhau. Do đó hai hạt nhân sẽ gần nhau nhất khi chúng đứng
yên tương đối so với nhau, vì vậy ta sẽ áp dụng các công thức của bài toán va chạm mềm.
Theo định luật bảo toàn xung lượng ta có:
m v (m m )v 0 X
mX là khối lượng hạt nhân bia. 7
Chương I Các m u nguyên t ẫ ử cổ i đ ển
Vì va chạm là trực diện (xuyên tâm) nên v và v0 cùng phương. Chiếu lên phương của 0 v ta được m v ( m m ) m 0 v v X 0 v m m X (1)
Theo định luật bảo toàn năng lượng ta có: 2 1 2 1 2 1 2
m v ( m m ) Ze 0 v 2 2 X 40 dmin (2)
Thế (1) vào (2) ta được: 2 mX 2 m m v X 2 Ze 0 T m m m m d X X 0 min m m Ze2 d X min m 2 T X 0 Thay số ta được: m 0
a) Trường hợp 1 X là Pb ta có thể coi m d min 5 , 0 9 Pb khi đó pm
b) Trường hợp 2 X là Li d min , 0 034 pm
5.4 Khi khoảng cách giữa hạt và bia là cực tiểu thì vận tốc của hạt là nhỏ nhất
nhưng lực hướng tâm (lực Coulomb là lớn nhất do đó bán kính cong của quỹ
đạp lúc này là nhỏ nhất: 0 a 2 0 a 2 r b ( )
Khoảng cách cực tiểu: min 2 2 a r 0 1 ( 1 cot 2 g ) Hay min 2 2 1 2 zZe 1 2 zZe 2 r 1 ( ) E0 min 8 E 4 r 1 0 0 sin 0 min 1 2 sin 2 (*) Ta lại có 8
Chương I Các m u nguyên t ẫ ử cổ i đ ển 2 2 mv zZe E 0 2 40rmin 2 2 2 2 mv zZe ( 2 zZe E ) / zZe 2 0 min 2 min 4 0 min r 4 0rmin 4 0 min r Kết hợp với (*) ta có 2E 2E 4 0 0 2 0 ( 2 E ) / ( ) 0 min 2 1 1 1 1 zZe sin sin 2 2 2 zZe 1 ( sin 1 )( sin ) 2 2 2 zZe cot min g 2 8E 0 0 2 8E sin 0 0 2 2 zZe cot min g Vậy 8E 2 0 0
5.5 Xung lượng mà proton truyền cho hạt nhân vàng:
P P P 0 P 2P sin 0 2 1 1 P sin 2 2 8 E b 0 0 2 1 cot g 1 ( ) 2 2 zZe 0 P P 2 0 0 mE 2mE0 P 2 8 E b 0 0 2 1 ( ) 2 zZe Proton có z 1 nên 2 0 2 mE P 8 E b 0 0 2 1 ( ) 2 Ze 9
Chương I Các m u nguyên t ẫ ử cổ i đ ển
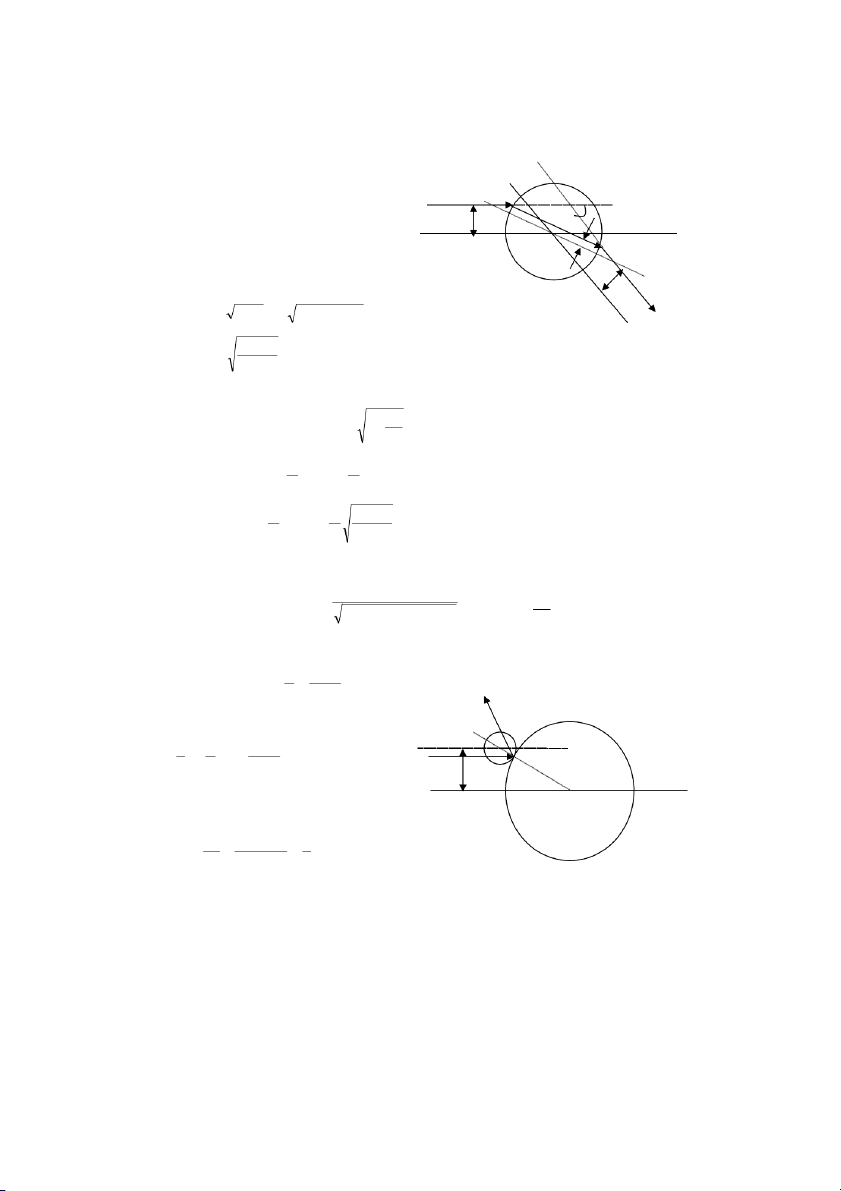
5.6 Lưu ý rằng trong trường hợp của
bài toán, hạt chỉ chịu tác dụng lực khi
r R lực này rất lớn làm thay đổi
xung lượng của hạt mặc dù thời gian b
tương tác bằng không. Ta coi rằng .O
tương tác là tương tác xuyên tâm khi
đó momen xung lượng của hạt được bảo toàn (Hình vẽ): b
b 2 mT 2 ( m T U ) 0 T U b 0 Hay T
Đường đi của hạt giống hệt đường đi U n 0 1
của tia sáng có chiết suất T ( 2 sin b ar arcsin ) R R (arcsi 2 n b arcsin b T ) Hay R R T U 0 Dễ nhận thấy: Rnsin( / ) 2 b U 1 2
n 2n cos( / ) 2 n 0 1 với T b cos 5.7 a) Dễ thấy 2 R r
b) Từ công thức trên ta có: 1 1 . sin d db 2 2 R r , b R
Số hạt tỉ đối trong khoảng từ . đến d dn 2 |bdb | 1 sin d n b2 2 , 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển
c) Xác suất phát hiện hạt trong
phần mặt cầu phía trước: 2 1 1 w sin d 2 2 0 .
5.8.Xác xuất phát hiện hạt 2 nd S a ndS 1 2 2 4 P ( ) 0 z Z e 2 2 R R 4 (4 )2 16sin 0 16 2 E 0 sin4 2 2
n là mật độ hạt nhân trên bia. Thay số ta được 5 P 3 . 3 10
5.9) Từ biểu thức xác suất ở trên ta có: Mật độ dòng hạt tán xạ Ind 1 2 2 4 z Z e j 2 R (4 )2 0 16 2 E sin4 0 2 , Ta có: 2 2 E2 4 16 sin (4 ) R 0 d 0 2 j In z2 Z2 e4 . Thay số ta được: d 5 . 1 m .
5.10) từ công thức xác định mật độ dòng tán xạ: IN 1 2 2 4 z Z e j 2 R (4 )2 0 16 20 E sin4 2 Ta có: 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển 2 j N Z Pt Pt Pt 2 j N Z Ag Ag Ag
Số thứ tự của Platin NAg Z Z Pt Ag NPt
Vì hai tấm có cùng khối lượng nên N A Ag Pt N A Pt Ag Cuối cùng ta có: APt Z Z Pt Ag AAg Thay số ta được: Z 78 Pt d
nA nd 5.11) Ta có: A
Thế vào biểu thức xác định mật độ dòng tán xạ ta được: Id 1 2 2 4 z Z e j 2 AR (4 )2 0 16 2 E sin4 0 2
Do đó ta có: Số hạt tán xạ trên diện tích S trong khoảng thời gian Id S 1 2 2 4 z Z e N 2 AR ( 4 )2 2 4 0 16E sin 0 2
Mặt khác ta lại có: Công thức tính diện tích đới cầu: 2 2 dS 2 Rdh
2 R sind 4 R sin cos d 2 2 Cuối cùng ta được: 2 2 4 cot I z Z e g d 1 N 2 d A ( 4 )2 2 2 0 4E sin 0 2 (*) 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển a) Thay số ta được: 6 N 6 . 1 10
b) Tích phân biểu thức (*) trên từ ta được: 2 2 4 2 z Z e cotg d 1 2 N I A ( 4 2) E2 0 4 0 .
5.12) Từ công thức xác suất tán xạ: ndS 1 2 2 4 P ( ) z Z e 2 R (4 )2 0 16 2 E sin 4 0 2 ,
Kết hợp với công thức tính diện tích đới cầu trên Ta có: 2 2 4 z Z e cot g nd 1 P 2 ( ) d R2 (4 )2 2 2 0 4E sin 0 2 ,
Cuối cùng ta có xác suất tán xạ của electron ở bán cầu sau: Pbh P()d 2 . 2 mv E
Tích phân biểu thức trên (chú ý là 0 2 ) ta được: 2 2 4 nd z Z e P bh 2 2 2 (4 ) (mv ) 0 . Thay số ta được: P . 0 006 bh
5.13) Tương tự như bài trên chỉ khác là cận lấy tích phân từ o 0 20 tuy nhiên
việc làm này sẽ làm tích phân tính xác suất bị phân kì. Ta chỉ cần áp dụng một thủ thuật đơn giản: 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển 2 2 4 2 z Z e cot g nd 2 P 1 P 1 2 2 (4 ) 4E 0 0 Thay số ta được: P 6 . 0
5.14) Từ công thức tính khoảng ngắm: 1 2 zZe b cot g 8 E 2 0 0
Ta có: Tiết diện hiệu dụng của hạt nhân Uran z Z e 2 1 2 2 4 b cot 2 g (4 )2 4 2 E 2 0 0 Thay số ta được 21 2 73 . 0 10 cm
5.15) a)Áp dụng kết quả của bài 5.14 1 2 2 4 z Z e cot 2 g (4 )2 0 4 2 E0 2 (5-14-1) cot g 1 Do đó (ở đây o 90 do đó 2 ): 1 2 zZe E cot 0 g (4 0 ) 2 2 Thay số ta được: E 9 . 0 MeV 0
b)Tiết diện vi phân của sự tán xạ: 2 2 4 cos 1 z Z e 2 d (4 )2 4 2 0 0 E sin3 d 1 2 2 4 z Z e 1 d 2 d d 2 sin (4 )2 E 0 4 20 4 sin4 d 2 Chú ý (5-14-1) ta có: 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển d d 4 sin4 2 d . 0 kba 64 c /sr
Thay số ta được: d
5.16) Vì electron dao động gần điều hòa nên năng lượng của electron là 1 2 2
E m A 2
Với A là biên độ dao động:
Kết hợp với công thức mà đầu bài đã cho ta có: dE 2e2w2 2 2 4 dE e dt dt E c3 3 E E mc 3 3
Tích phân hai vế ta được: e 2 2 2 ln t m2 3 c3 Hay 3 3 mc t ln 2e 2 2 (5.16.1) Thay số ta được: t 15 ns .
5-17) Vận tốc góc của electron thỏa mãn hệ thức: 1 e2 2 m r 4 r2 0 2 2 1 e 3 Do đó: 40 mr
Electron sẽ rơi vào hạt nhân nếu của nó giảm khoảng 2 lần
Thế vào (5.16.1) ta được: 2 3 3
t (4 ) m c r 0 4 4e 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển Thay số ta được: t 13 ps .
hc E E n k
5.18) Từ công thức: nk Ta có: hc 1 1
E E (E E ) (E E ) hc ( ) n m n k m k nm nk mk nk mk nm Hay: mk nk
Nếu biết hai bước sóng của phổ ta sẽ đoán được bước sóng thứ ba của phổ. Từ
đó ta có thể đoán được ba bước sóng khác của phổ: 1 88 . 1 m . 0 657m 2 . 0 487m 3 .
5.19) Năng lượng của electron 1 2 1 2 E mv kr 2 2 (5-19-1)
Đây là biểu thức năng lượng của chuyển động dao động điều hòa với tần số k góc: m
Vì quỹ đạo của electron là đường tròn, và do sự tương ứng giữa chuyển động
dao động điều hòa và chuyển động tròn đều nên: v r
Theo điều kiện lượng tử hóa của Born ta có p d nh 2
2mr nh n n r Do vậy: n m
Thế vào (5-19-1) ta được: 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển E n n .
5.20)a) Từ điều kiện lượng tử hóa của Born ta có: pdq nh
mvr d mvr nh m r n 2 2 n n n n Do: 2 2 2 2 2 1 Ze n 1 Ze m r 2 m r n n 2 4 r n n 3 mr 4 r 0 n 2 n 0 n
Bán kính quỹ đạo Bohr thứ n : 2 2 4 n r n 0 2 mZe (5.20.1)
Vận tốc của electron trên quỹ đạo thứ n: n v r n n n mrn Hay 1 Ze2 v n 4 n 0
b) Động năng và năng lượng liên kết của electron ở quỹ đạo thứ n : 1 Ze2 2 4 1 mZ e T T n 4 r 2 n 2 2 2 (4 ) 2n 0 n hay 0 1 Ze2 2 4 1 mZ e E E n 4 r 2 n 2 2 2 (4 ) 2 n 0 n hay 0 c) Thế Ion hóa: 2 4 1 mZ e 2 3 1 mZ e E V 2 2 (4 ) 2 2 2 (4 ) 2 0 Thế ion hóa 0
Thế kích thích thứ nhất: 1 2 4 mZ e 1 1 1 2 3 mZ e 1 1
E E E V 21 ( ) 21 2 1 ( ) (4 ) 2 2 2 12 22 (4 )2 2 2 12 22 0 0
Bước sóng của vạch cộng hưởng tương ứng: 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển hc 21 E21
Thay số vào các biểu thức trên ta sẽ thu được kết quả ghi trong bảng dưới đây: r ( ) v 10 ( 6 T ( ) E ( ) V (V ) V ( ) ( ) 1 m / s) 1 pm 1 eV 21 eV 12 V 12 nm H 52.9 2.18 13.6 -13.6 13.6 10.2 121.5 He+ 26.5 4.36 54.5 -54.5 54.5 40.8 30.4
5.21) Áp dụng bài 5.20, v 2 4 1 mZ e n n r n 2 3 (4 ) n n 3 0 Thay số ta được 07 . 2 1016 2 (rad / s)
5.22) Momen từ quỹ đạo của electron chuyển động trên quỹ đạo thứ n : 2 I S ef r n n n n n , (5.22.1)
fn là tần số chuyển động của electron trên quỹ đạo thứ n . Tiếp tục biến đổi (5.22.1) ta được: n 2 1 2 e r e r n 2 n 2 n n .
Sử dụng các biểu thức của r
n và n ở các bài tập trên ta có: 2 4 2 2 1 1 mZ e n 2 n e (4 ) 2 3 3 0 2 2 (4 ) 0 n mZe . 1 e n n Hay n B 2 m 2 Momen cơ L P m r n n n n
Tỉ số giữa momen từ quỹ đạo và momen cơ: e n L 2m n . 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển
Trên quỹ đạo Bohr thứ nhất ta có: 1 B .
5.23) Từ quy luật quang phổ của nguyên tử Hydro: 4 1 1 me 1 1 2 3 2 2 (4 ) 4 c n n ik 0 i
Khoảng bước sóng của các ánh sáng trong dãy Lyman 2 4 3 2 (4 ) c n 1 n 0 4 2 me n 1 3 3 2 4 c 2 16 (4 ) (4 ) c 0 4 1 n 0 4 me 3me
Khoảng bước sóng của các ánh sáng trong dãy Balmer 4 3 2 c 4 2 (4 ) n n 2 0 4 2 me n 4 3 3 2 16 c 2 144 (4 ) (4 ) c 0 4 n2 0 4 me 5me
Khoảng bước sóng của các ánh sáng trong dãy Pashen 4 3 2 c 9 2 ( 4 ) n n 3 0 4 2 me n 9 3 3 2 36 c 2 574 (4 ) ( 4 ) c 0 4 2 n 0 4 me 7me
Thay số vào các biểu thức trên ta thấy trong quang phổ của Hydro có bốn vạch
sáng nằm trong vùng khả kiến. Đó là bốn vạch đầu tiên trong dãy Balme, các
vạch này có màu lần lượt là: đỏ lam, chàm, tím.
5.24) a) Áp dụng các công thức của bài trên ta có bước sóng của ba vạch đầu của dãy Balme: 657, 478 và 434nm
b) Các vạch trong cùng một dãy có bậc càng cao thì càng sít nhau, do đó nếu
máy quang phổ phân giải được vạch thứ 19 và vạch thứ 20 thì nó sẽ phân giải
được cả hai mươi vạch. Năng suất phân giải cực tiểu: 1
Chương I Các m u nguyên t ẫ ử cổ i đ ển 2 22 2 2 19 22 2 3 5 . 1 10 2 2 22 23 min 19 20 2 2 2 2 22 2 23 2 .
5.25)Theo tiêu chuẩn Rayleigh ta có: Giới hạn phân giải của cách tử: l sin (*) Mặt khác ta lại có: 1 1 1 1 R R n 2 2 2 n 2 2 1 1 2 1 R 2
2 n 2 2 n 2 3 n 2 hay R Thế vào (*) ta được:
n 2 Rl sin 2 n 2 Từ đó ta có: n 2 3 sin Rl 2
Ở giới hạn phân giải ta có n 2 3 sin Rl 2 Thay số ta được: 0 60 .
5.26) Từ biểu thức xác định bước sóng của phổ phát xạ: 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển 2 4 1 1 mZ e 1 1 2 3 2 2 (4 ) 4 c n n ik 0 i k
Vì vậy nếu bước sóng của nó ngắn hơn bước sóng của Hydro bốn lần thì điện
tích hạt nhân lớn gấp hai lần điện tích hạt nhân của Hydro tức là Z 2 . Đây
chính là trường hợp Ion He .
5.27) Ở mức lượng tử n electron có thể chuyển xuống n 1 mức lượng tử nhỏ
hơn n . Nếu electron chưa chuyển về mức cơ bản mà vẫn còn ở mức k thì nó lại
có thể chuyển xuống k 1 mức khác… Mặt khác cứ mỗi lần chuyển mức
nguyên tử lại bức xạ photon. Do đó số vạch phổ mà nguyên tử Hydro phát ra:
N n 1 n 2 ... 3 2 1 n( ) 1 N n Hay 2
5.28) Năng lượng của
He ở mức lượng tử đã cho: 2 4 2 4 hc hc 1 mZ e 1 mZ e 1 1 E hc n 1 E 2 2 2 2 2 (4 ) 2n (4 ) 2 1 2 0 0 1 2 1 4 2 3 4 c 1 1 1 0 2 2 4 Hay n mZ e 1 2
Thay số ta được: n 5 .
5.29) Từ biểu thức xác định bước sóng trong phổ phát xạ của Ion He 1 1 2 1 RZ 2 2 n n ik i k Ta có: Vạch đầu của dãy Lyman 4 2 21 RZ 3
Vạch đầu của dãy Balmer 36 2 RZ 32 5 88 2 88 1 RZ R Do đó 15 15 Z 2 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển Thay số ta được 5 1 R . 1 097 10 cm
5.30) Tương tự bài trên ta có: 88 1 88 1 R Z 15 Z 2 15 R Thay số ta được: Z 3 Ion đã cho là Li
5.31) Khoảng giữa vạch đầu và vạch cuối: 1 2 1 1 1 2 1 c 2 cRZ 2 2 2
n n (n ) 1 2 2 (n ) 1 2 cRZ 2 n 1 cR Z
Từ đó ta có bước sóng của vạch đầu tiên: 1 1 1 2 RZ 2 2 2 2 cRZ cR Z 1 Cuối cùng ta được: 2 2c 2cR 2cR Z 1 / 2Z 1 Thay số ta được 41 . 0 m
5.32)Để tách electron thứ nhất cần cung cấp một năng lượng bằng E0 . Sau khi
mất một electron nguyên tử trở thành Ion đồng dạng Hydro, vì vậy năng lượng
cơ bản mới của electron còn lại là: 1 mZ 2e4 E 2 2 0 2 4 cZ R 2 2
Do đó để bứt tiếp electron thứ hai cần cung cấp tiếp một lượng năng lượng bằng 0
E. Do đó năng lượng cần thiết để bứt cả hai electron ra khỏi nguyên tử Heli là: E E 2 c Z 2 R 0 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển
5.33) Nguyên tử Hydro sẽ phát xạ ra một photon nếu sự mất mát động năng do
va chạm lớn hơn hoặc bằng hiệu hai mức năng lượng của hai mức lượng tử nào
đó. Do đó động năng cực tiểu của nguyên tử Hydro thỏa mãn đầu bài ứng với
trường hợp bức xạ ra một photon ứng với trường hợp xảy ra sự chuyển mức lượng tử 1 và 2.
Giả sử vận tốc ban đầu của nguyên tử Hydro là v0 , vận tốc của hệ sau va chạm
là V . Theo định luật bảo toàn xung lượng ta có: v0
V 2 Độ mất mát năng lượng do va chạm không đàn hồi
Phần động năng bị mất: 1 1 1 2 2 2 T m v
(2m )V m v H 0 H H 0 2 2 4 T0 T Hay 2 1 1 T 2T (
2 E E ) 2 2 c R 0 min 2 1 2 2 1 2 Hay: T 3 c R 0 min Thay số được: T 0 min eV 5 . 20
5.34) Vì khối lượng của photon (khối lượng tương đối tính) rất bé nên động
năng giật lùi của electron là rất nhỏ so với năng lượng photon phát xạ. Vì vậy ta
có thể coi gàn đúng là không có sự thay đổi bước sóng của photon do sự giật lùi của nguyên tử. Xung lượng của photon: h p 2
Theo định luật bảo toàn momen xung lượng ta có: p p 0 H
p m v p 2 v 2 H H Do đó: m H
Bước sóng vạch đầu dãy Lyman: 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển 1 1 1 3 R R 12 22 4
Thế vào biểu thức vận tốc ta được: 3 R v 2 mH
Thay số ta được v 3 m 25 . / s
5.35) Độ sai khác về năng lượng của photon do ảnh hưởng của sự giật lùi: 9 2 2R2 9 2 2R2 8 8 3 2 E m m R 1 H H 2 9 R 2 2 E m v E 2 c 3 c 4 m c H 2 8 H m R H 2 E 3 R Vậy: E 4 m c H Thay số ta được: E 55 . 0 10 6 % E
5.36) Năng lượng của photon bức xạ từ Ion He+ được dùng vào hai việc: Ion
hóa nguyên tử Hydro và truyền cho electron một động năng T
E E E T 2 1 E ,
1 E2 tương ứng là năng lượng của electron ở các mức lượng tử 1 và 2 của Ion He+,
E là năng lượng Ion hóa của nguyên tử Hydro.
Áp dụng công thức tính năng lượng của các mức lượng tử của các Ion đồng dạng Hydro ta có: 2 1 1 1 2 2 cRZ 2 cR mv 2 2 1 2 2 cR 3 2 Z v 2 1 m 4
Thay số ta được v 1 . 3 106 m / s .
5.37) Do ảnh hưởng của sự chuyển động của hạt nhân nguyên tử nên ta phải sử
dụng khối lượng hiệu dụng thay cho khối lượng thực tế m của electron. 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển mM m M
Biểu thức năng lượng liên kết: 2 4 1 Z e E 2 2 (4 ) 2 0 Hằng số Rydberg: 4 1 e R 4 2 3 4 c 0
Ta thấy sự sai lệch của năng lượng liên kết và hằng số Rydberg đều do sự thay
khối lượng thành khối lượng rút gọn mà ra. Cả hai đại lượng này đều tỉ lệ với
khối lượng rút gọn nên sai số của hai đại lượng này trùng với sai số của khối lượng: m m m . 0 055% E R m m m M M
5.38) Như ta đã biết ở trên sai lệch về năng lượng liên kết hay, hằng số Ryberg
là do chuyển động của hạt nhân hay do việc thay khối lượng bằng khối lượng
hiệu dụng mà ra. Do đó sai lệch về bước sóng hay năng lượng liên kết được tính như sau:
-)Sai số về năng lượng liên kết: 1 2 4 Z e 2 4 1 Z e
E E E D H ( 4 2 2 ) 2 (4 2 2 ) 2 0 0 1 mZ e 2 4 M M E D H 2 2 (4 ) 2 0 M D m M m H 1 mZ e
2 4 mM M D H E 2 2 (4 ) 2 M M 0 H D m E E 7 . 3 meV MD -)Sai số về bước sóng: 3 1 3 2 4 R 4 4 R R 4 2 2 4 3 R R 3 R 3 2
Chương I Các m u nguyên t ẫ ử cổ i đ ển 4 M M D H R
3 M m M m D H Cuối cùng ta có: m 8 33 pm H D M 9 H
5.39) Bài này giải hoàn toàn tương tự hai bài trên, chú ý phải thay khối lượng
bằng khối lượng rút gọn. 2 2 n r 4 n 0 2 Ze 2 4 1 Z e E 2 2 (4 ) 2 0 4 1 e R 4 4 c 0 2 3
Đối với nguyên tử meson Hydro: mM 207 207m M Đối với pozitroni: m 2
Áp dụng các công thức của bài trên ta được: r( ) ( ) 0 E (eV ) 1 pm 21 nm Meson 0.258 0.65 2530 Hydro Pozitroni 106 0.243 6.8 2