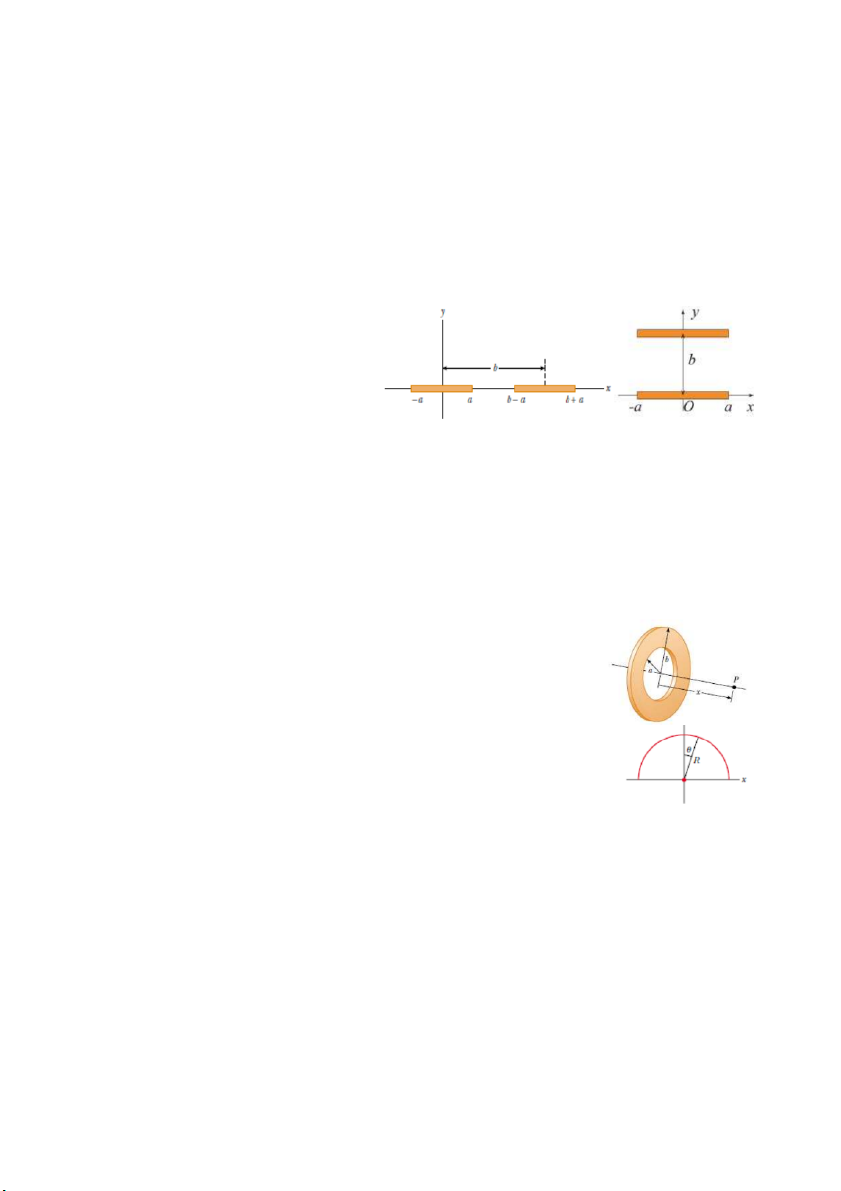
Preview text:
LỰC TĨNH ĐIỆN – ĐIỆN TRƯỜNG
Bài 1. Khoảng cách trung bình giữa electron và proton trong nguyên tử hydro là r -11 o = 5,3.10 m. Electron xem
như chuyển động tròn đều xung quanh hạt nhân.
a. Tính độ lớn lực tương tác tĩnh điện trung bình giữa electron và hạt nhân và so sánh với lực hấp dẫn trung bình giữa chúng.
b. Tính vận tốc của electron trên quỹ đạo và tần số quay quanh hạt nhân.
Bài 2. Hai quả cầu nhỏ không dẫn điện được treo ở đầu của hai sợi dây có cùng chiều dài l = 20 cm, hai sợi
dây được gắn vào một điểm cố định.
a. Sau khi truyền cho các quả cầu điện tích giống nhau qo = 4.10-8 C thì chúng đẩy nhau và góc tạo bởi
giữa hai sợi dây với nhau là 10o Tính khối lượng .
mỗi quả cầu cho trường hợp hai quả cầu có cùng khối lượng.
b. Đem nhúng cả hai quả cầu trong câu (a) vào dầu hỏa có khối lương riêng D 3 d = 0,8 g/cm thì thấy
góc giữa hai sợi dây vẫn không đổi như khi hệ ở trong không khí. Tính khối lượng riêng Dc của các quả cầu.
c. Tính khối lượng các quả cầu trong trường hợp sau khi truyền cho các quả cầu điện tích giống nhau
qo = 4.10-8 C thì chúng đẩy nhau và góc tạo bởi giữa hai sợi dây với phương thẳng đứng lần lượt là 5o và 10o.
Bài 3. Hai điện tích điểm tự do q1 và = +q
q2 = +4q đặt cách nhau một khoảng L.
a. Giữ q1 và q2 cố định, tìm vị trí, độ lớn và dấu của điện tích thứ ba q3 để q3 nằm cân bằng.
b. Nếu q1 và q2 không gắn cố định, tìm vị trí, độ lớn và dấu của q3 để cả hệ nằm ở trạng thái cân bằng.
Bài 4. Đặt hai điện tích điểm Q vào hai đỉnh đối diện của một hình vuông, ở hai đỉnh còn lại đặt hai điện tích
q. Nếu lực tác dụng lên điện tích Q bằng không, tính Q theo q. Có thể chọn q để lực tĩnh điện tổng hợp tác
dụng lên mỗi điện tích bằng không không? Tại sao?
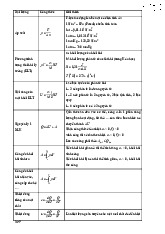
Bài 5. Hai quả cầu nhỏ cùng khối lượng m, được tích điện lần lượt q1 và q2 và nối với nhau bằng một lò xo
nhẹ (có thể bỏ qua khối lượng) cách điện có chiều dài tự nhiên lo và độ cứng k. Mỗi quả cầu được nối vào một
đầu của một sợi dây chỉ, cách điện, mảnh nhẹ và không dãn có chiều dài 2L. Cho điểm điểm giữa O của sợi
dây chuyển động theo phương thẳng đứng với gia tốc 𝑎, xác định chiều dài của lò xo trong các trường hợp sau: 1. q1 = q2 = q;
a. 𝑎 hướng lên trên, b. 𝑎 = 0,
c. 𝑎 hướng xuống dưới. 2. q1 = -q 2 = q;
a. 𝑎 hướng lên trên, b. 𝑎 = 0,
c. 𝑎 hướng xuống dưới. 1
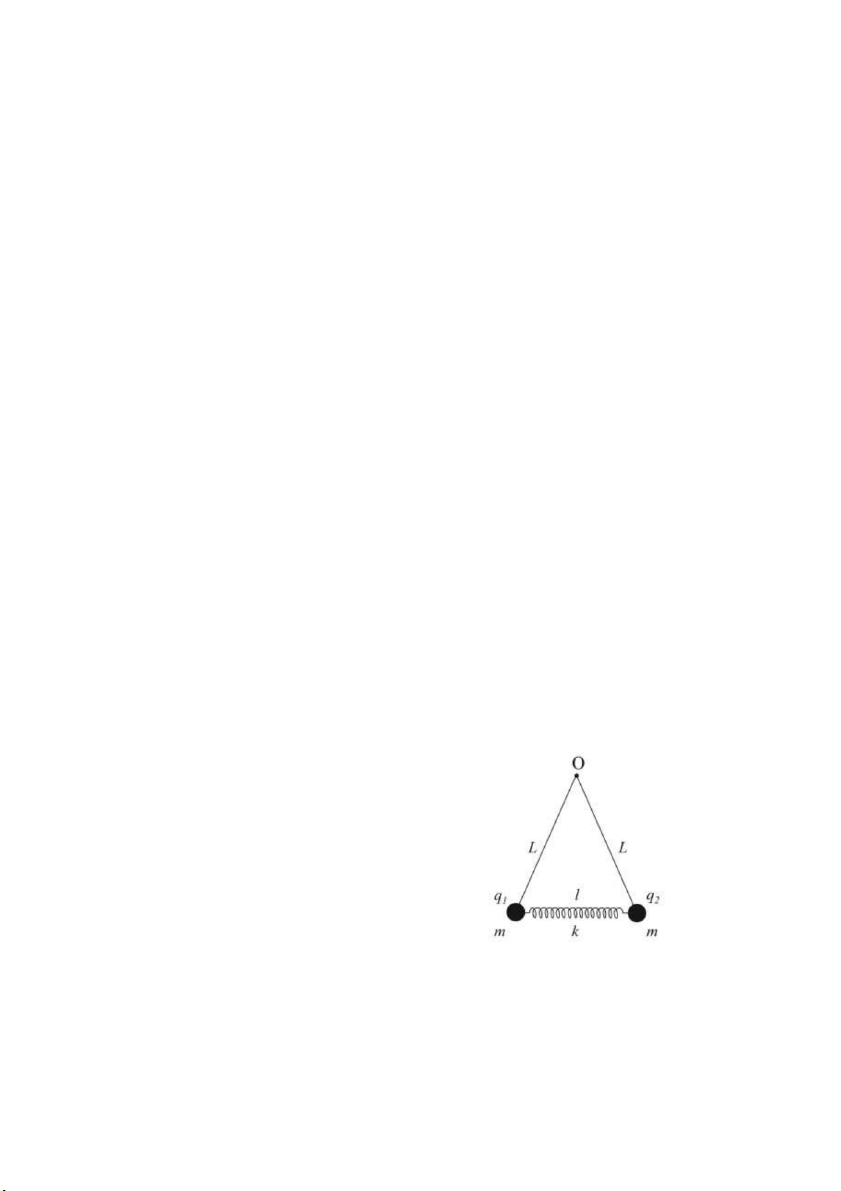
Bài 7. Một điện trường đều có độ lớn 2.103 V/m, hướng lên trên được
thiết lập bởi hai bản nằm ngang có chiều dài L = 10 cm và cách nhau một
khoảng d = 2 cm bằng cách tích điện dương cho bản dưới và điện âm cho d
bản trên. Một electron được bắn vào giữa hai bản từ mép trái của bản dưới
với vận tốc ban đầu có độ lớn 6.106 m/s theo phương hợp với bản dưới L
một góc 45o. Electron có đập vào một trong hai bản không? Nếu có thì bản nào và cách mép trái bao xa theo phương ngang?
Bài 8. Giữa hai mặt phẳng kim loại song song rộng vô hạn (kích thước của chúng lớn hơn rất nhiều so với
khoảng cách giữa hai bản) cách nhau một khoảng d = 1 cm đặt nằm ngang, có một hạt bụi mang điện khối
lượng m = 5.10-11 g. Biết rằng khi không có điện trường, do lực cản của không khí hạt bụi rơi với vận tốc
không đổi bằng v1 và khi hiệu điện thế giữa hai bản mặt là 600 V thì hạt bụi rơi chậm đi với vận tốc không
đổi v2 bằng một nửa của v1. Cho rằng lực cản của không khí tỉ lệ thuận với vận tốc của vật.
a. Tìm điện tích của hạt bụi.
b. Bây giờ đặt hai mặt phẳng đó thẳng đứng cách nhau d1 = 2 cm vàn ban đầu hạt bụi đứng yên tại vị trí
cách đều hai mặt phẳng. Nối hai mặt phẳng đó vào nguồn điện có hiệu điện thế 100 V. Do lực cả cản
của không khí, hạt bụi rơi đều theo phương thẳng đứng với vận tốc không đổi 2 cm/s. Hỏi sau bao lâu
hạt bụi rơi vào một trong hai mặt phẳng kim loại đó. Lấy g = 10 m/s2.
Bài 9. Cho một tứ cực điện như hình vẽ, nó gồm hai lưỡng cực điện với
momen lưỡng cực điện bằng nhau về độ lớn nhưng ngược chiều nhau.
Chứng minh rằng giá trị của cường độ điện trường tại các điểm P nằm trên
trục Ox và Oy như hình vẽ cách tâm lần lượt là x, y (x, y a) là: 3Q 3Q E và E x 4 4 x y 4 8 y o o với 2 Q 2
qd là momen tứ cực điện của hệ điện tích. n n n 1 (cho biết 1 1 2 n . ..... nếu 1) 2
Bài 10. Một sợi dây dài vô hạn tích điện đều với mật độ điện dài (C/m). Xác định cường độ điện trường tại
một điểm cách sợi dây 1 khoảng a.
Bài 11. Một mặt phẳng rộng vô hạn tích điện đều với mật độ điện mặt (C/m2). Xác định cường độ điện
trường tại một điểm cách mặt phẳng 1 khoảng h. Nhận xét về đặc điểm của điện trường do mặt phẳng này gây ra.
Bài 12. Một tấm rộng vô hạn bề dày h được giới hạn bởi 2 bề mặt phẳng, tích điện đều với mật độ (C/m3) .
a. Xác định cường độ điện trường tại những điểm bên trong và bên ngoài tấm cách một trong hai bề mặt một khoảng x.
b. Người ta khoét một hốc rỗng hình cầu có đường kính h trùng với bề dày của tấm. Hãy tính cường độ
điện trường tại một điểm bên trong hốc rỗng cách tâm của hốc rỗng 1 khoảng r với r h/2. 2
Bài 13. Một mặt cầu bán kính R tích điện đều với mật độ điện mặt (C/m2). Xác định cường độ điện trường
tại một điểm cách tâm quả cầu một khoảng trong hai trường hợp 𝑟 < 𝑅 và 𝑟 ≥ 𝑅.
Bài 14. Một quả cầu bán kính R tích điện đều với mật độ điện kh i
ố là (C/m3). Xác định cường độ điện trường
tại một điểm cách tâm của quả cầu m t kho ộ
ảng r trong hai trường hợp 𝑟 < 𝑅 và 𝑟 ≥ 𝑅.
Bài 15. Một không gian vô hạn mang điện với mật độ điện tích phụ thuộc vào khoảng cách từ gốc tọa độ đến
điểm đang xét r có dạng = o/r trong đó o là hằng số. Tính cường độ điện trường tại điểm đang xét, loại bỏ
các điểm ở gần gốc tọa độ.
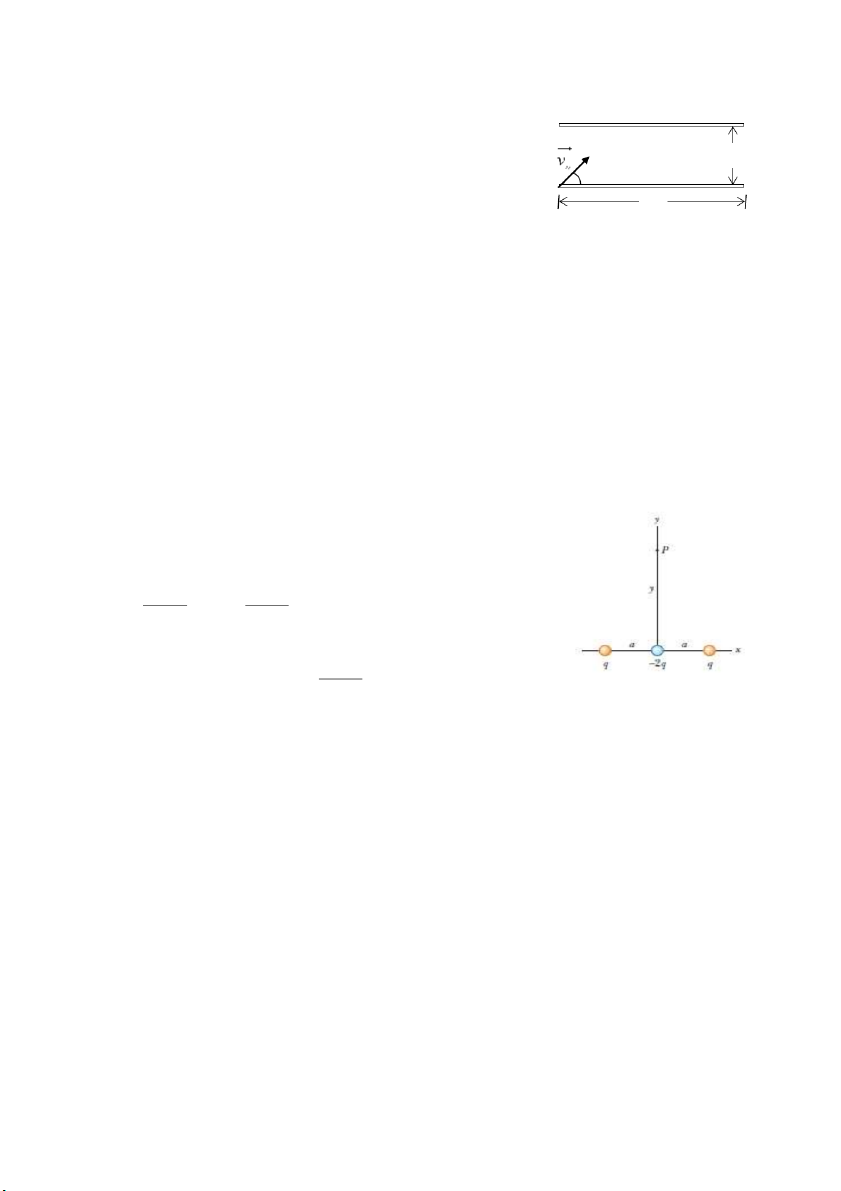
Bài 16. Hai đoạn dây thẳng mảnh không dẫn điện chiều dài 2a cùng tích một lượng điện tích Q phân bố đều
trên dây được bố trí trong hai trường hợp
như hình vẽ. Tính lực tĩnh điện do một đoạn
dây tác dụng lên đoạn dây còn lại.
Bài 17. Trong chân không, một hệ gồm một
vòng dây tròn mảnh bán kính R tích điện đều với điện tích q (q >
0) và một sợi dây thẳng rất dài tích điện đều với mật độ điện dài ( > 0) trong đó sợi dây được đặt dọc theo
trục đối xứng đi qua tâm của vòng dây và vuông góc với mặt phẳng vòng dây. Biết rằng một đầu của sợi dây
thẳng dài trùng với tâm của vòng dây. Xác định lực tương tác giữa vòng dây và sợi dây thẳng dài.
Bài 17. Một vòng tròn mảnh bán kính R tích điện tích q được phân bố đều trên vòng tròn. Xác định vectơ
cường độ điện trường tạo ra bởi vòng tròn tại điểm M nằm trên trục của đường tròn cách tâm một khoảng d.
Bài 18. Xác định vec tơ cường độ điện trường tạo ra bởi một đĩa tròn bán kính R, tích điện đều với mật độ
điện mặt (C/m2) tại điểm M nằm trên trục của đĩa và cách tâm đĩa một khoảng h.
Bài 19. Một bản rất mỏng có hình dạng vành khăn có bán kính trong là a và bán
kính ngoài là b. Một điện tích q phân bố đều trên bản. Tính cường độ điện trường
tại điểm P trên trục của bản cách tâm bản một khoảng x như hình vẽ.
Bài 20. Một đoạn dây mảnh được uốn thành nửa hình tròn bán kính R = 60 cm. Tích
điện cho đoạn dây với tổng điện tích trên đoạn dây 12 C
với mật độ điện dài được
phân bố theo hàm co
s . Tính lực tác dụng lên điện tích điểm q = 3 C đặt tại 0 tâm của hình tròn.
Bài 21. Một chiếc nhẫn không dẫn điện bán kính R được tích điện với mật độ điện dài: = 0cos với là
góc phương vị, 0 là hằng số. Tính cường độ điện trường tại: a. Tâm của chiếc nhẫn.
b. Tại một điểm trên trục đi qua tâm và vuông góc với mặt chiếc nhẫn, cách tâm của chiếc nhẫn một khoảng
x. Xét trường hợp x , có nhận xét gì về kết quả này? 3
Bài 22. Một đầu dây mảnh dài l = 10 cm tích điện đều với mật độ B A
điện tích dài = 10-8 C/m. xác định cường độ điện trường:
a. Tại một điểm A cách đầu dây dẫn 10 cm.
b. Tại điểm B trên đường trung trực của dây và cách dây 10 cm.
c. Tại điểm C nằm trên trục dây cách đầu dây gần nhất một l C đoạn 10 cm.
Bài 23. Một quả cầu bán kính R được tích điện với phân bố mật độ điện tích tại các điểm cách tâm quả cầu r một khoảng r là 1
trong đó là hằng số. Cho rằng hằng số điện môi ở bên trong và môi trường 0 o R
bên ngoài quả cầu là đồng nhất. Tính:
a. Cường độ điện trường và điện thế tại một điểm ở bên trong và bên ngoài quả cầu cách tâm quả cầu 1 khoảng r.
b. Tìm vị trí và cường độ điện trường tại điểm có cường độ điện trường đạt giá trị cực đại.
Bài 24. Bên trong một quả cầu mang điện với mật độ điện khối không đổi ,
có một hốc hình cầu không có
điện tích. Tâm của hốc cách tâm của quả cầu một khoảng a. Tìm vectơ cường độ điện trường E ở trong hốc.
Biết hằng số điện môi ở trong hốc là = 1. Xét trường hợp a = 0. 4