CHƯƠNG 1 –
ĐIỆN TRƯỜNG TĨNH 1. Mở đầu
2. Định luật Coulomb 3. Điện trường 4. Định lý Gauss 5. Điện thế
6. Cường độ điện trường và điện thế 1 1. Mở đầu Điện tích
) Thuộc tính tự nhiên của những hạt cơ bản có kích thước rất nhỏ (không thể
nhìn thấy bằng mắt thường) tạo lên liên kết về điện trong nguyên tử. Nguyên tử Proton (p): ) điện tích (+)
Phần tử cơ sở cấu tạo vật chất:
ª Trạng thái bình thường: trung hòa điện ⇒ số e và p bằng nhau, Neutron: ª Không
p gắn cố định trong hạt nhân nguyên điện tích
tử, e có thể dễ dàng di chuyển ⇒ dễ tạo ra Electron (e) - điện tử:
sự mất cân bằng điện tích giữa 2 vật trung điện tích (-)
hòa điện khi được cho tiếp xúc với nhau ⇒ tạo ra i-ôn Điện tích điểm
) Điện tích có kích thước không đáng kể so với khoảng cách giữa điện tích
và 1 điểm trong không gian nằm trong vùng ảnh hưởng của nó. 2 1. Mở đầu
Điện tích nguyên tố
) Điện tích của một electron (hoặc một proton) có giá trị là là 1,6 . 10-19 C,
được qui ước làm giá trị một đơn vi điện tích. Hạt cơ bản Khối lượng Điện tích Electron 9,11.10-31 kg -1,60.10-19 C (-e) Proton 1,672.10-27 kg +1,60.10-19 C (+p) Neutron 1,674.10-27 kg 0
Điện tích của vật thể tích điện
) Đại lượng vô hướng được xác định bằng một số nguyên (kết quả sự
chênh lệch số các proton và electron) lần điện tích nguyên tố trong vật thể,
tức là Q = e.(N -N ) = n.e p e 3 1. Mở đầu Phân loại
Điện tích dương (+) và điện tích âm (-) + + Khác d Cùng dấu: đẩy nhau ấu: hút nhau 4 1. Mở đầu Truyền điện tĩnh Cảm ứng Dẫn điện Ma sát (tiếp xúc) (điện hưởng)
Bảo toàn điện tích
Điện tích không tự sinh ra hay mất đi mà chỉ dịch chuyển bên trong một vật
hoặc từ vật này sang vật khác 5 1. Mở đầu
Phân loại vật liệu theo khả năng truyền điện của điện tích
) Vật liệu dẫn điện: Điện tích có thể chuyển động tự do trong toàn bộ thể tích vật (kim loại)
) Vật liệu cách điện – điện môi: Điện tích định xứ cố định tại những miền
nào đó, và không thể di chuyển tự do trong vật liệu (cao su, chất dẻo, gỗ, giấy, không khí khô …)
) Vật liệu bán dẫn: Điện tích cũng định xứ cố định tại những miền nào đó,
nhưng có thể di chuyển tự do trong vật liệu dưới tác động của nhiệt độ, ánh
sáng hoặc điện trường ngoài (silicon, germanium…). 6
2. Định luật Coulomb
(Định luật về tương tác tĩnh điện) Dây xoắn → Charles-Augustin de Coulomb Cân xoắn Coulomb
Nguyên lý xác định tương tác tĩnh
điện bằng cân xoắn Coulomb 7
2. Định luật Coulomb
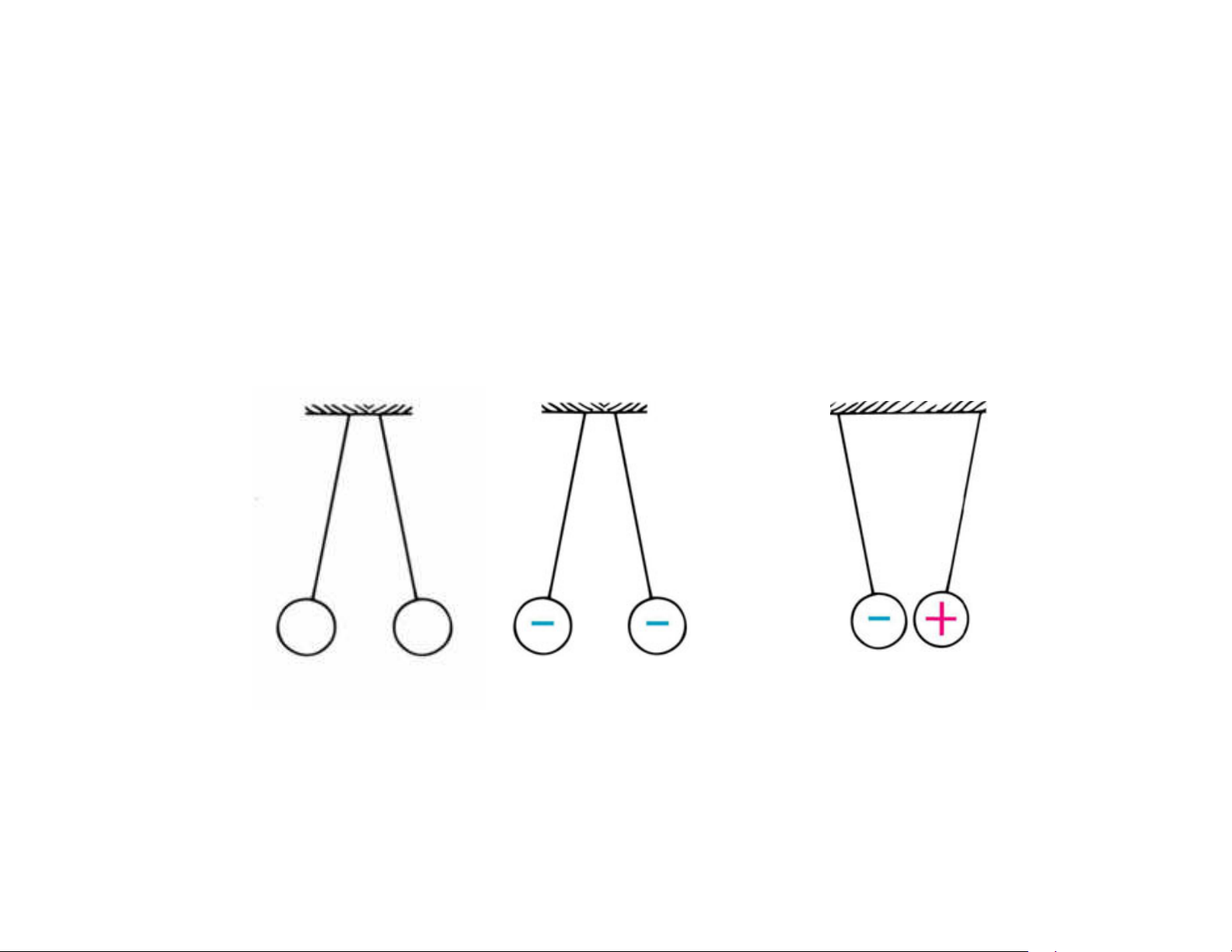
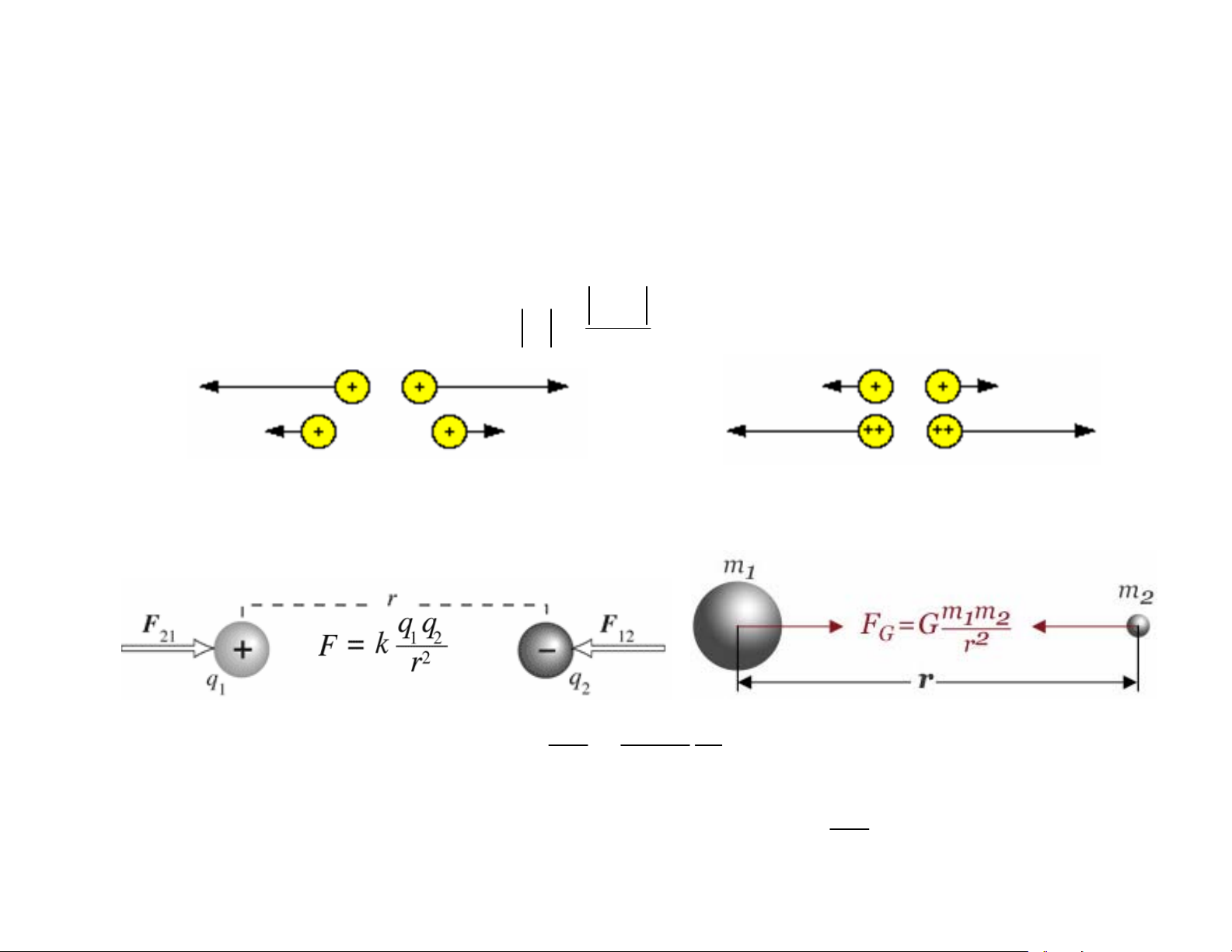
Lực tương tác giữa 2 điện tích điểm
) Lực tương tác tĩnh điện giữa 2 điện tích q , q 1 2
đặt trong chân không, có phương nằm trên
đường thẳng nối 2 điện tích, có chiều phụ thuộc
vào dấu 2 điện tích, có độ lớn tỉ lệ thuận tích số
q , q và tỉ lệ nghịch với bình phương khoảng 1 2 cách giữa chúng. q q r r 1 2 F = k q q r
Tổng quát: F = k 1 2 2 r r 2 r 2 1 1 Nm 9
Hệ số tỉ lệ: k = Trong chân không: k = = 10 . 9 2 4πεε 4πε C 0 0 2 − C 12 Vói: ε = 8 85 , .10 0 2 N m . 8
2. Định luật Coulomb Đặc điểm
) Lực Coulomb phụ thuộc khoảng cách và độ lớn các điện tích q q 1 2 F = 2 r
Gấp đôi khoảng cách, lực giảm 1/4
Gấp đôi điện tích, lực tăng 4 lần
) Lực Coulomb và lực hấp dẫn F q q k e 1 2 = F m m G G 1 2 F
ª Đ/v electron: q = 1,6.10-19 C, m = 9,31.10-31 kg ⇒ e 42 = 17 , 4 10 . F 9 G
2. Định luật Coulomb
Nguyên lý chồng chất r r r
) Điện tích q chịu tác dụng của các lực F , F ,..., F gây b 1 2 n
ởi hệ đ/tích q , q ,..., q 0 1 2 n r
ª Tương tác tổng cộng của hệ điện r q q F 1 F 0 2 1 tích lên q : 0 n r r r r r r
F=F + F + ... + F = F 1 2 n ∑ F i 3 i=1
ª Vật bất kỳ (vòng tròn) mang điện
tích q tác dụng lên điện tích điểm q0
⇒ có thể chia nhỏ q thành các điện q q 2 3
tích vô cùng nhỏ dq sao cho dq được
coi là điện tích điểm ⇒ xác đinh lực Σ Fi
tổng hợp của các điện tích dq lên q . 0
ª 2 quả cầu đồng chất phân bố điện q0
tích đều ⇒ coi như 2 đ/tích điểm có r
vị trí tại tâm 2 quả cầu và r là
khoảng cách tính từ tâm của chúng. dq 10 3. Điện trường “Trường”
) Không gian mà một đại lượng vật lý được xác định tại mỗi điểm trong đó.
ª Đại lượng vector ⇒ trường vector
ª Đại lượng vô hướng ⇒ trường vô hướng
Khái niệm điện trường ) Thuyết tác dụng xa:
ª Tương tác giữa các điện tích điểm được truyền đi tức thời (v ~ ∞)
ª Tương tác được thực hiện không có sự tham gia của vật chất trung gian
ª Khi chỉ có 1 điện tích ⇒ tính chất vật lý của khoảng không gian bao quanh bị biến đổi.
Tồn tại vận động phi vật chất ⇒ trái với triết học duy vật biện chứng ⇒ Không phù hợp! 11 3. Điện trường
Khái niệm điện trường ) Thuyết tác dụng gần:
ª Tương tác giữa các điện tích điểm được truyền đi không tức thời (v hữu hạn)
ª Tương tác được thực hiện thông qua sự tham gia của vật chất trung gian
ª Khi chỉ có 1 điện tích ⇒ tạo ra điện trường xung quanh ⇒ giữ vai trò truyền tương tác.
Phù hợp với triết học duy vật biện chứng ⇒ được khoa học công nhận!
) Đ/nghĩa: Điện trường là khoảng không gian bao quanh các điện tích, thông
qua đó tương tác (lực) tĩnh điện được xác định.
ª Điện trường là trường vector. 12 3. Điện trường
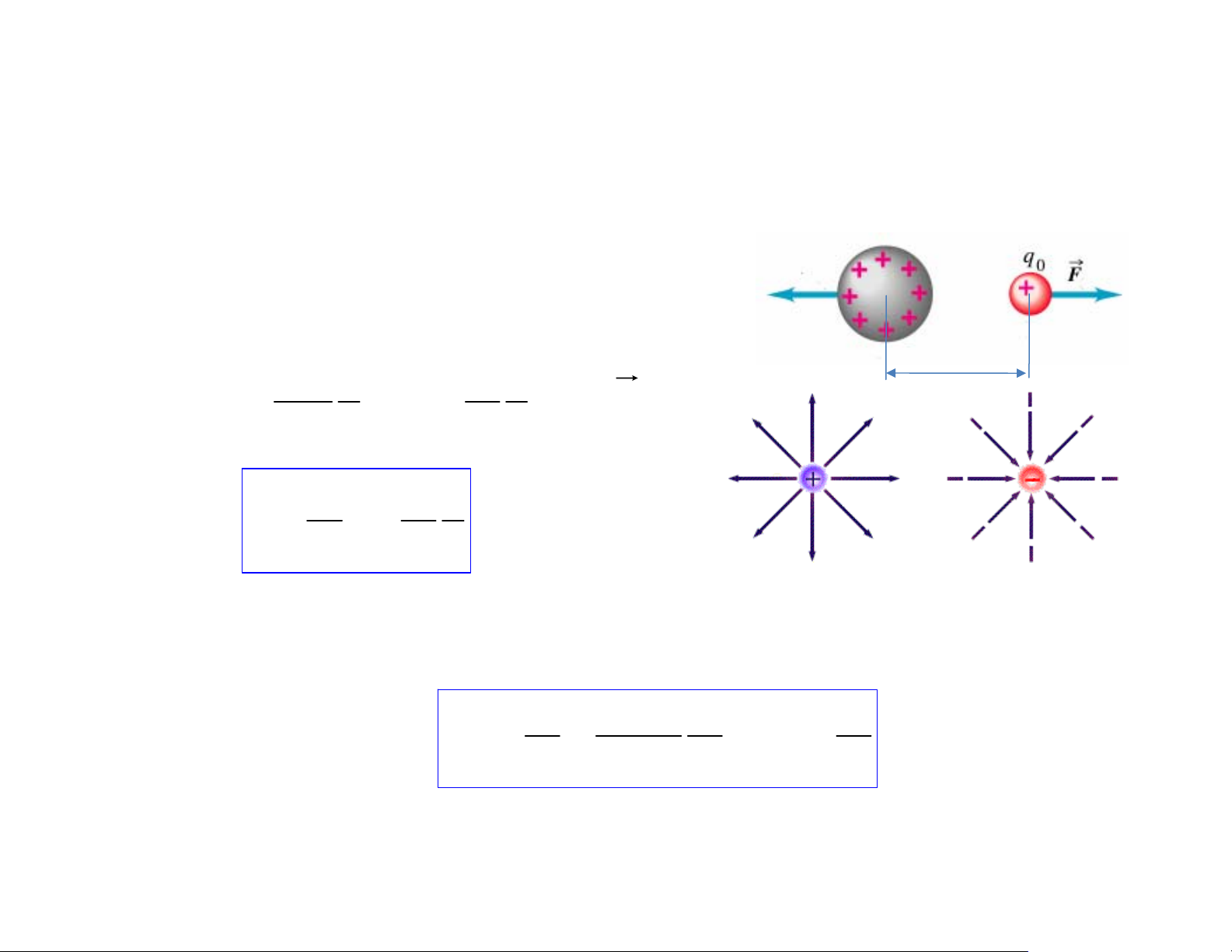
Vector cường độ điện trường Q Điện tích thử
) Xét điện tích q đặt trong điện trường của Q 0 ª Lực Coulomb r r r r Qq r ⎛ Q r ⎞ F = k 0 = q ⎜k ⎟ = q .E r 2 r 0 ⎝ r2 r 0 ⎠ r r ⇒ r F Q r E = = k q r 2 r 0
ª Cường độ điện trường tại 1 điểm nào đó là đại lượng vật lý có độ lớn
bằng độ lớn của lực điện trường tác dụng lên 1 đơn vị điện tích +1 đặt tại điểm đó Q 1 Q Q 9 E = k = = 9.10 2 2 2 r 4πεε r r 0
) Đơn vị: N/C hoặc V/m 13 3. Điện trường
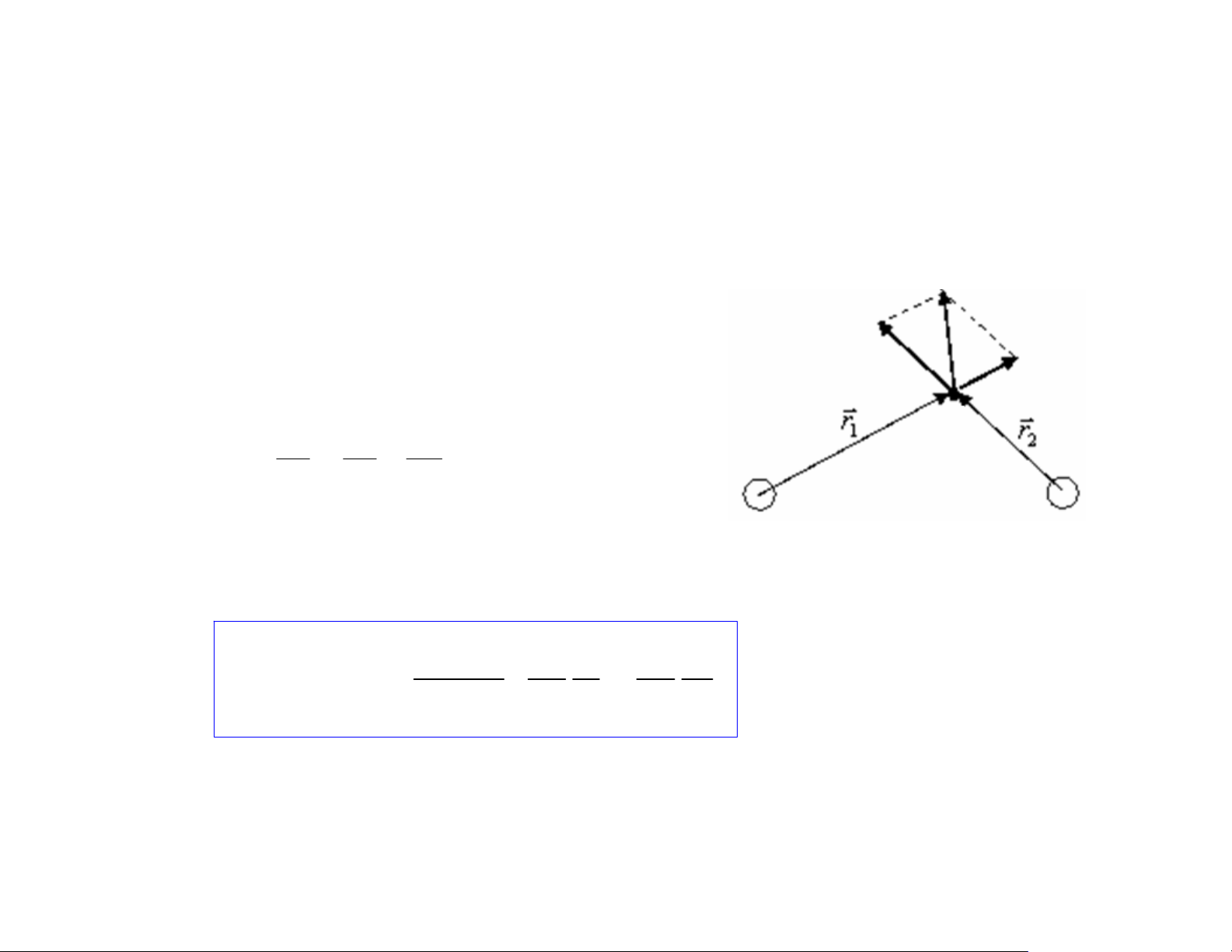
Nguyên lý chồng chập điện trường r r
) Xét q , q tác dụng lực F , F lên q (đặt tại P): 1 2 1 2 0 r r r r F r r
ª có: F = F + F F F 1 r P 1 2 2 r E r r r 1 E q 2 F F F 0 r 1 2 ⇒ = + E q q q 0 0 0 q q2 1
ª Điện trường gây bởi q và q : 1 2 r r r r r 1 ⎛ q r q r ⎞
E =E + E = 1 2 ⎜⎜ 1 1 + 2 2 2 2 ⎟⎟ 4πεε r r r r 0 ⎝ 1 1 2 2 ⎠ 14 3. Điện trường
Nguyên lý chồng chập điện trường
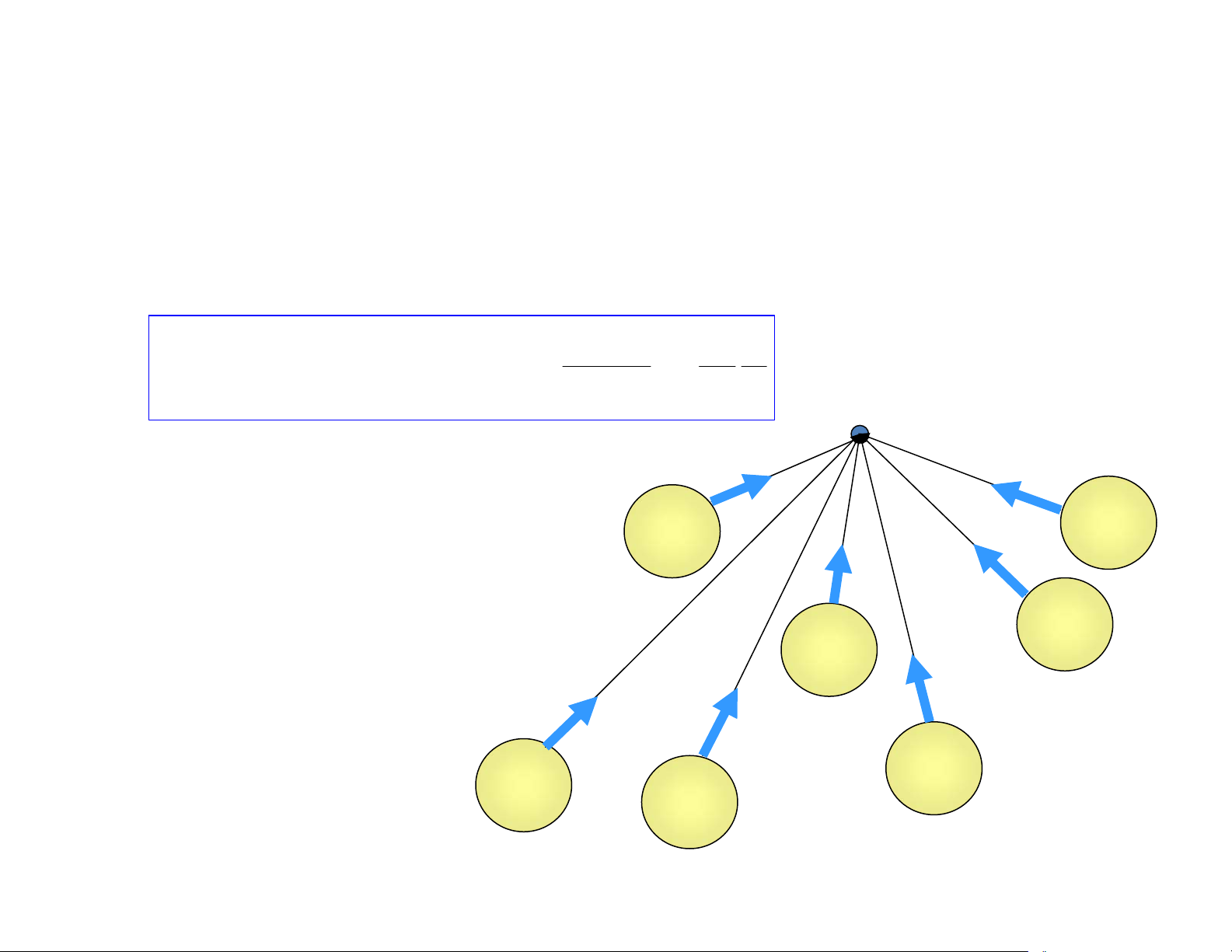
) Điện trường gây bởi n điện tích điểm tại vị trí bất kỳ: r n n r r r r r 1
E =E + E + ... + E = q r E 1 2 n ∑ =i ∑ i i 2 4πεε 1 0 1 r r i= i= i i P
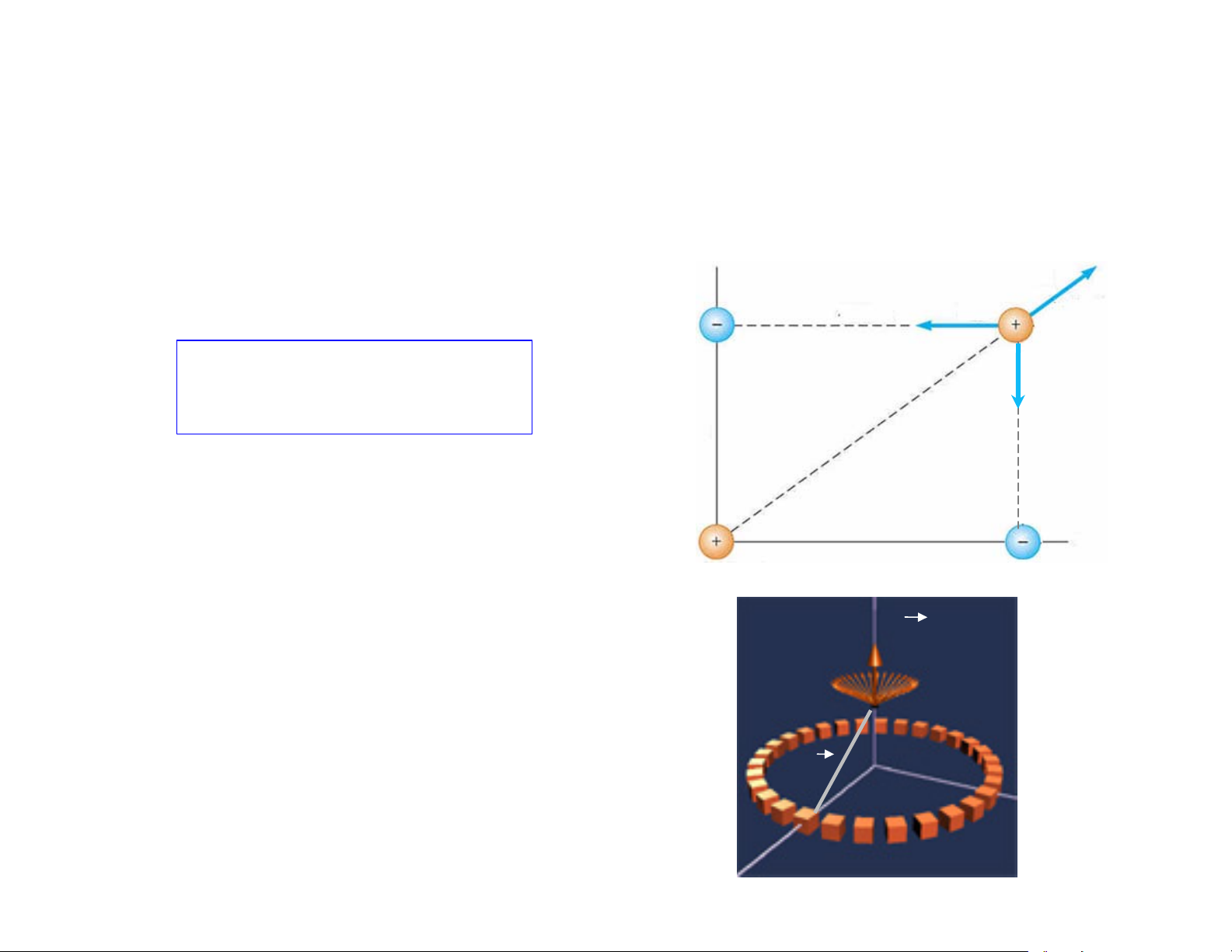
ª Vector cường độ điện trường
gây bởi một hệ điện tích tại bất kỳ
điểm nào trong trường là tổng các
vector cường độ điện trường gây + -
bởi từng điện tích tại điểm đó. + - + - + 15 3. Điện trường
Nguyên lý chồng chập điện trường
) Điện trường gây bởi vật mang điện có điện tích phân bố liên tục:
ª Chia vật thành vô số các phần tử vô cùng
nhỏ mang điện tích dq ⇔ điện tích điểm. Σ Ei
ª Điện trường gây bởi dq tại 1 điểm cách dq đoạn r: P 9 r r r 9.10 dq r dE = ε r 2 r dq
ª Điện trường tổng hợp gây bởi toàn bộ vật mang
điện tại 1 điểm trong không gian của điện trường: 9 r r r 9.10 E = ∫dE = ∫ dq r ε r 2 r toàn bô vât toàn bô vât 16 3. Điện trường
Nguyên lý chồng chập điện trường
) Điện trường gây bởi vật mang điện có điện tích phân bố liên tục
ª Dây tích điện có độ dài l r 9 r Đ 9.10 dl r
/tích của vi phân độ dài: dq = λdl ⇒ E = ∫ λ ε 2 r r
(λ: mật độ điện dài = điện tích/đơn vị độ dài) (l )
ª Mặt tích điện có diện tích S r Đ 9 r
/tích của vi phân diện tích: dq = σdS
⇒ E = 9.10 ∫ σdS r ε 2 r r
(σ: mật độ điện mặt = điện tích/đơn vị diện tích) (l )
ª Khối tích điện có thể tích V Đ r
/tích của vi phân thể tích: dq = ρdV 9 r
⇒ E = 9.10 ∫ ρdV r ε 2 r r
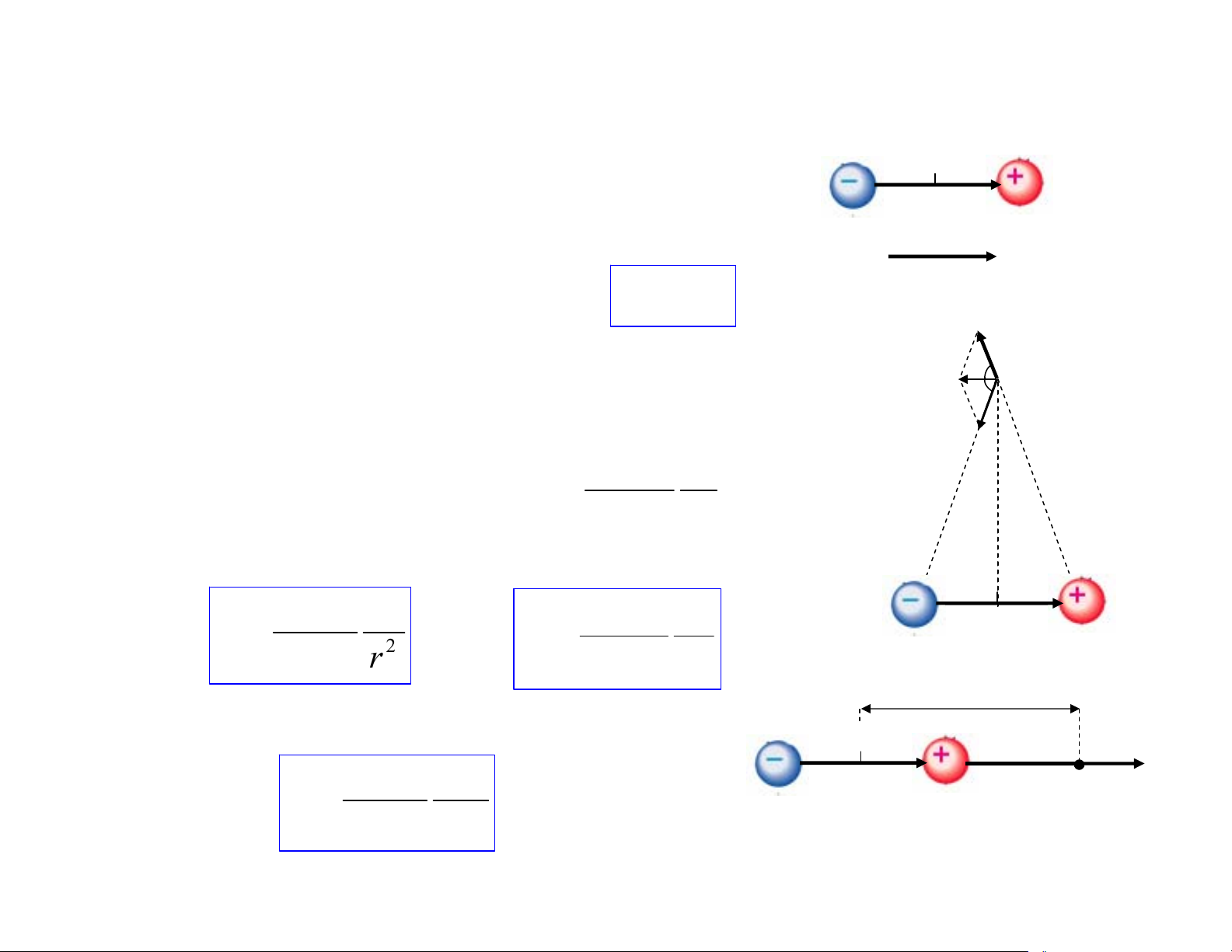
(ρ : mật độ điện khối = đ/tích/đơn vị thể tích) (l ) 17 3. Điện trường r 0 Lưỡng cực điện d ) - q +q
Hệ 2 điện tích điểm trái dấu có độ lớn bằngr r
nhau cách nhau một khoảng d (rất nhỏ) r p p = qd e r E Đ 2
iện trường gây bởi lưỡng cực điện r α E α M r
ª Tại điểm nằm trên đường trung trực (r >> d) E1 r r r 1 q
Có: E =E + E với: E = E = r r r 1 2 1 2 1 2 2 4πεε r 0
hay: E = E .cosα + E .cosα = 2E .cosα ; (cosα = d/2r ) 1 2 1 1 r 0 1 qd r r 1 p ⇒ E = hay: E e = d 2 - q +q 3 - q d + 4πεε r πεε 0 4 r 0 r r
ª Tại điểm nằm trên trục lưỡng cực (r >> d) 0 r r r E 1 2 p Có: E e = - q d +q N 3 4πεε r 0 18 3. Điện trường
Điện trường gây bởi dây dẫn thẳng dài vô hạn
) Dây: độ dài 2l, điện tích Q, mật độ điện tích dài λ.
ª Vi phân độ dài dy, có điện tích: l l Q dQ = dy = λdy l 2
ª Điện trường tại P gây bởi dQ: r r r E d = E d + E d x y +l E = E = x dy dE x ∫ λ = x ∫ π 4 εε 3/ 2 2 2
0 −l (x + y ) -l -l λ 2 x l λ dy l λ = = = ∫ x << l ⇒ E 2πεε x 3/ 2 2 2 4πεε + πεε + 0 0 0 (x y ) 2 x x l 0 ( 2 2)1/2 Q x >> l ⇒ E = 2 4πεε x 0 19 3. Điện trường
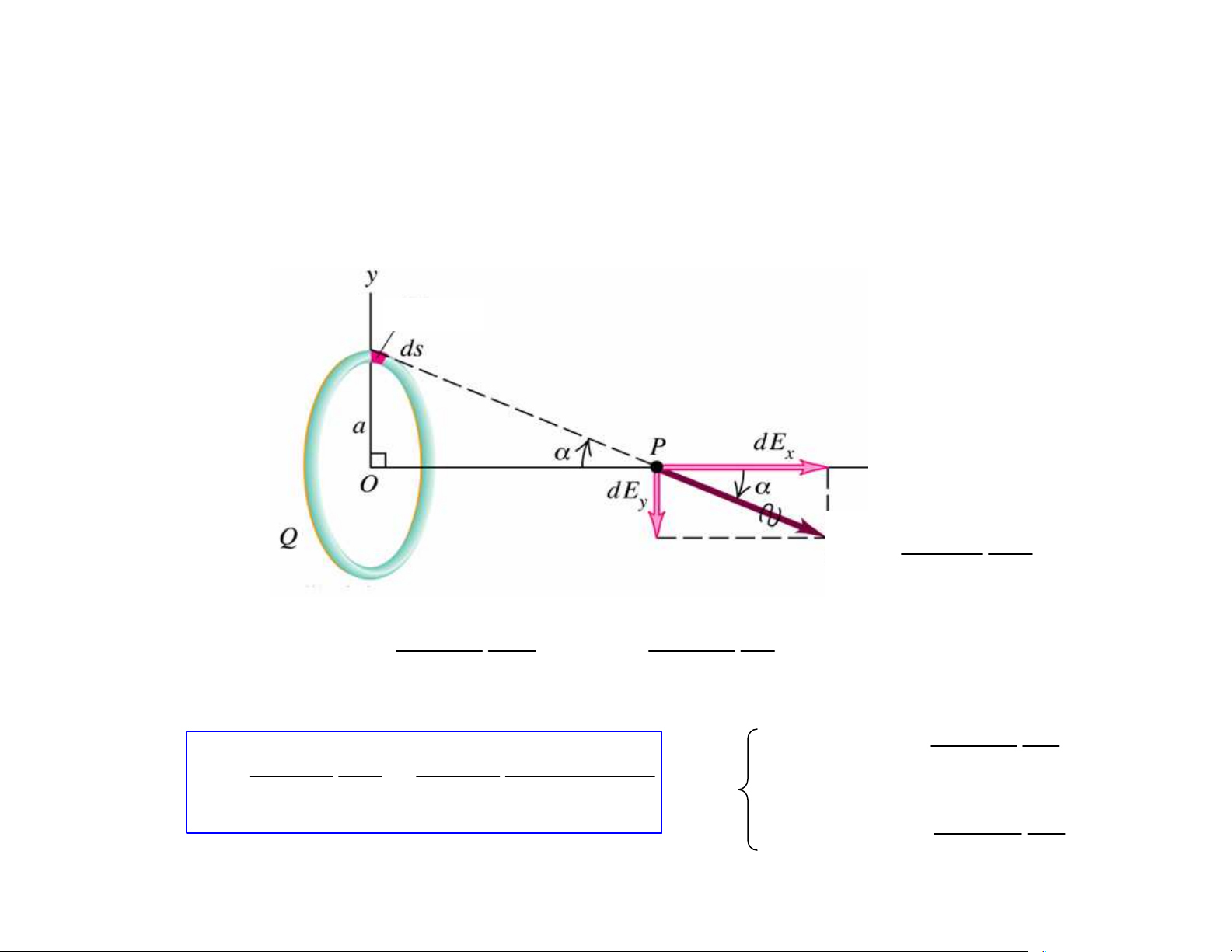
Điện trường gây bởi vòng dây tròn tích điện đều
) Dây tròn: bán kính a, mật độ điện tích dài λ, điện tích Q. dQ dQ = = λ λ dsds r x 1 dQ dE = 2 4πεε r 0 2πR 1 E = E = dQ x cos ds x ∫ λ α = 2 3 ∫ 4πεε r 4πεε r vòng tròn 0 0 0 1 Q 1 Qx 1 Qx x << a: E = 3 E = = 4πεε a 3 ⇒ 0 4πεε r 4πεε + 0 0 ( 2 2 x a )3/2 1 Q x >> a: E = 2 4πεε r 20 0