Bài tập về nhà học phần Fluid Mechanics Lab | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
When a viscous fluid flows past a thin sharp-edged plate, a thin sharp-edged plate, a thin layer adjacent to the plate surface develops in which the velocity, u, changed rapidly from zero to the approach velocity, U, in a small distance, δ. This layer is called a boundary layer. The thickness of this layer increases with the distance x along the plate as shown in figure 3. Assume that u = U y/ δ; and δ = 3.5 √ ϑ x/U , where ϑ is kinetic viscosity of the fluid. Determine an expression for the force (drag) that would be developed on one side of the plate of length l and width b. Express your answer in terms of l, b, ϑ, and ρ, where ρ is the fluid density. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đón xem.
Môn: Fluid Mechanics Lab
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Preview text:
FM Assignment 1 Problem 1
The density of oxygen contained in a tank is 2.0 kg/m3 when the temperature is
Determine the gage pressure of the gas if the atmospheric pressure is 97 kPa. Problem 2
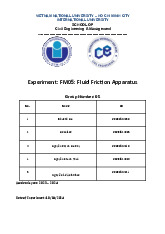
Crude oil having a viscosity of
9.52 x 10-4 lb.s/ft2 is contained between parallel plates. The
bottom plate is fixed and the upper plate moves when a force P is
applied (see the figure 1). If the
distance between the two plate is
0.1 in., what value of P is required to translate the plate with a
velocity of 3 ft/s? the effective are of upper plate is 200 in2.
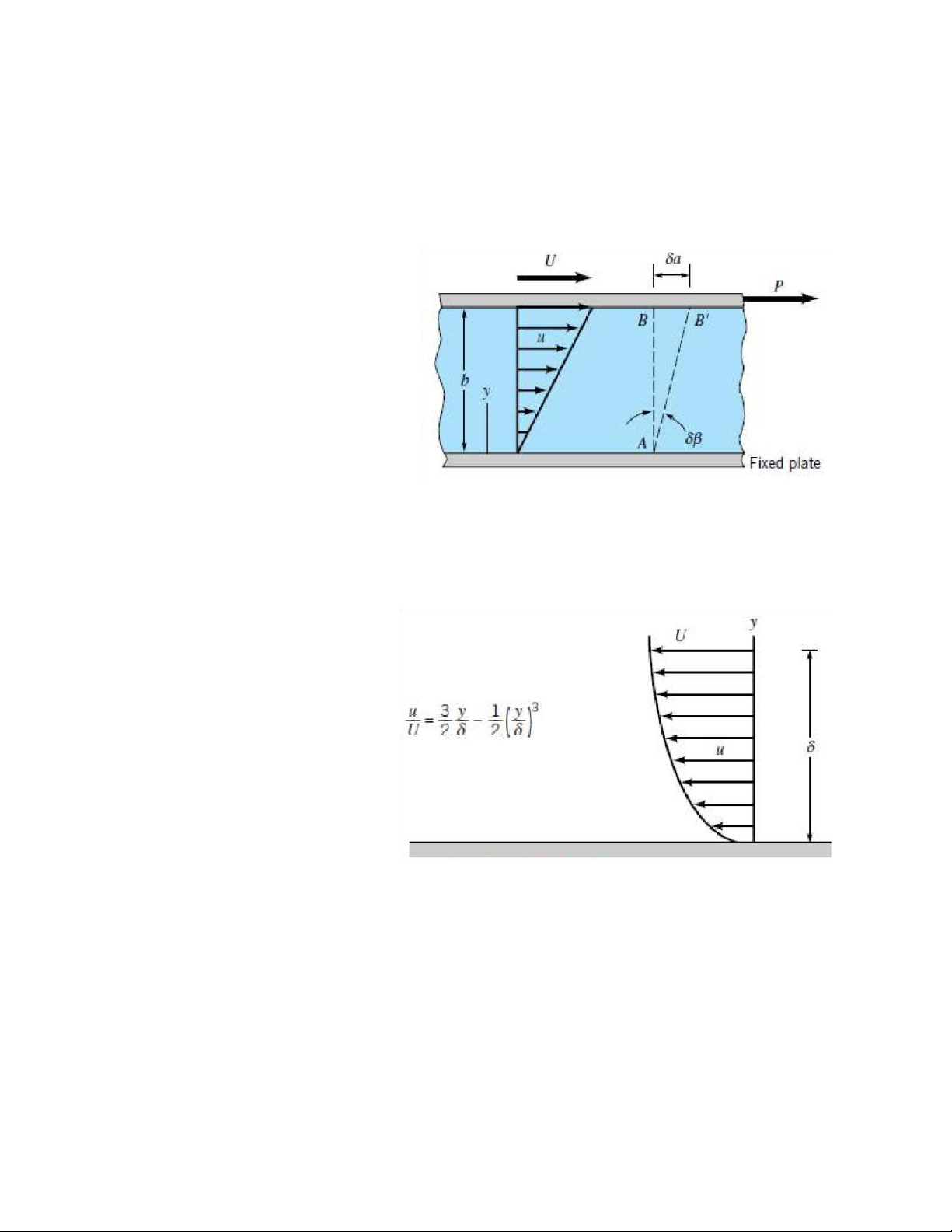
The figure 1: Problem 2 Problem 3 A Newtonian fluid having a
specific gravity of 0.92 and a kinematic viscosity of 4x10-4
m2/s flows past affixed surface.
Due to the no-slip condition, the
velocity at the fixed surface is
zero, and the velocity profile
near the surface is showed in the figure 2. Determine the
magnitude and the direction of
the shearing stress developed on
the plate. Express your answer The figure 2: Problem 3 in term of U
and δ expressed in units of meters per second and meters, respectively. Problem 4
When a viscous fluid flows past a thin sharp-edged plate, a thin sharp-edged plate, a thin
layer adjacent to the plate surface develops in which the velocity, u, changed rapidly
from zero to the approach velocity, U, in a small distance, δ. This layer is called a
boundary layer. The thickness of this layer increases with the distance x along the plate
as shown in figure 3. Assume that u = U y/ δ; and δ = 3.5 √
ϑx/U , where ϑ is kinetic
viscosity of the fluid. Determine an expression for the force (drag) that would be
developed on one side of the plate of length l and width b. Express your answer in terms
of l, b, ϑ, and ρ, where ρ is the fluid density. Problem 5
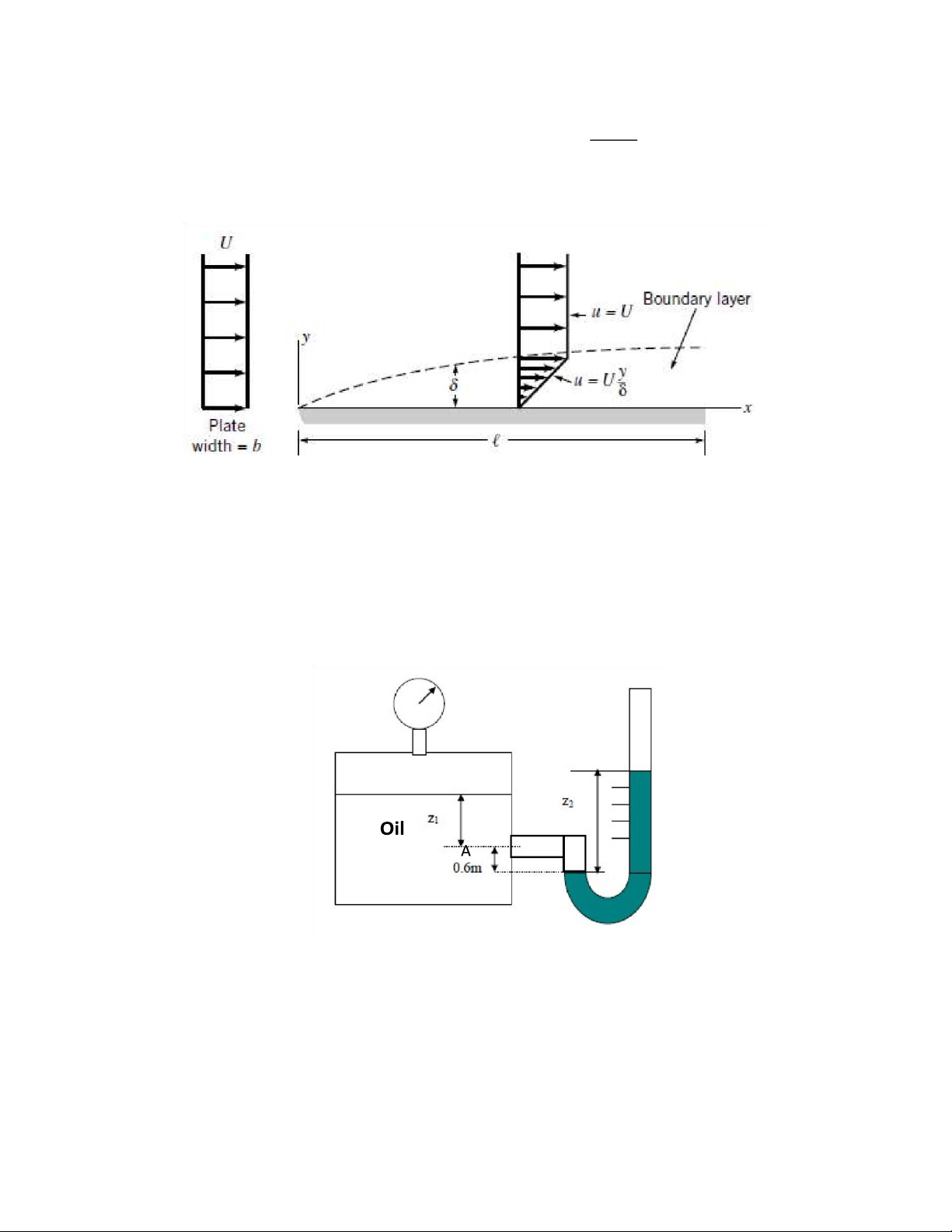
A U-tube manometer is connected to a closed tank, showed in the figure below,
containing oil having a density of 860 kg/m3, the pressure of the air above the oil being
3500Pa. If the pressure at point A in the oil is 14000Pa and the manometer fluid has a RD
of 3, determine: (1) the depth of oil, Z1; (2) the differential reading, Z2 on the manometer. Problem 6
Determine the elevation Mercury
difference, h, between the water
levels in the tank A and tank B
shown in the figure. It is give that
pressure at free surface of these tanks is considerable, and difference of the pressure between tank A and tank B is 100mm Hg. Problem 7
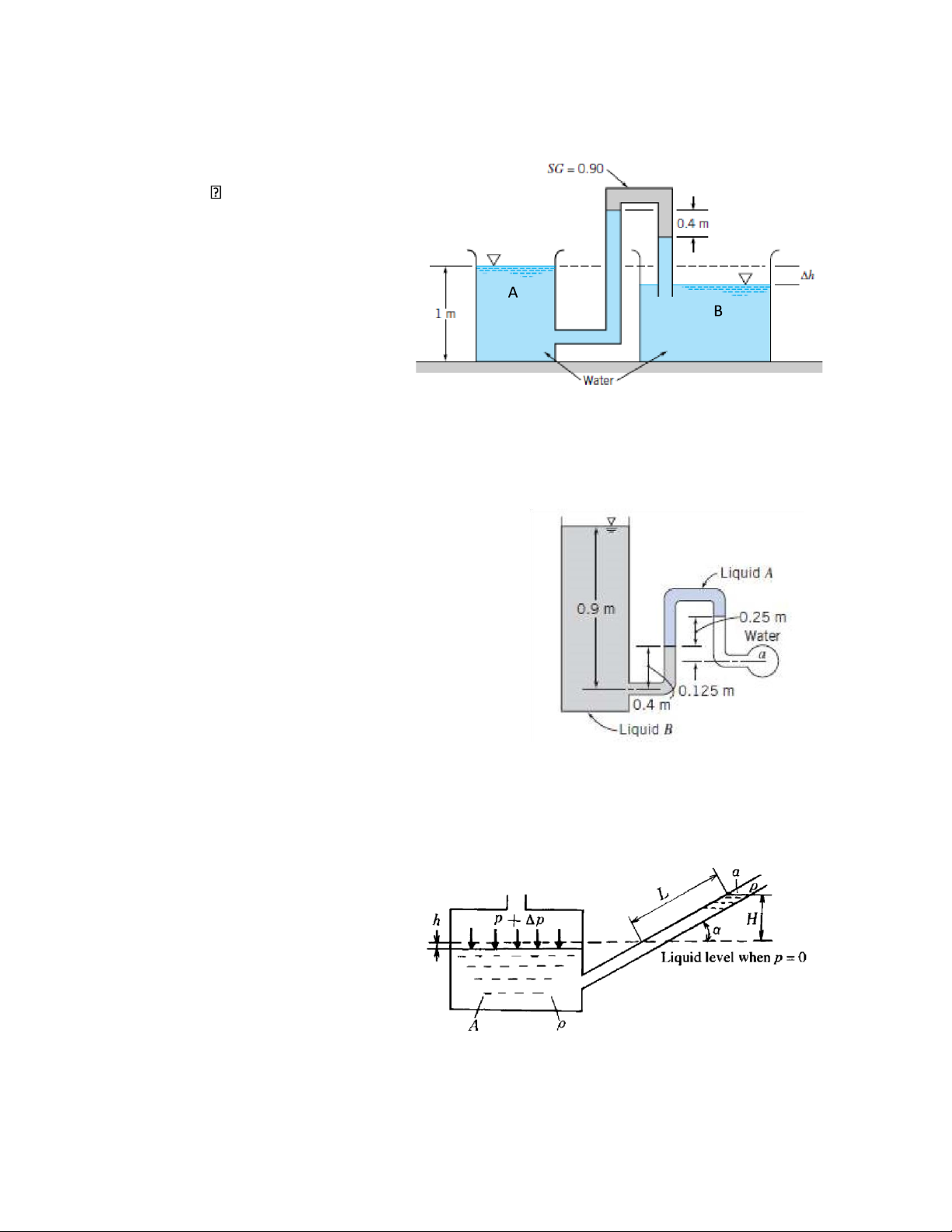
A reservoir manometer is showed in the figure.
Determine the gage pressure in kPa at point a if
liquid A has SG = 1.20 and liquid B has SG =
0.75. The liquid surrounding point a is water,
and the tank on the left is open to the atmosphere Problem 8
On the inclined manometer in the
adjacent figure, whenever h
changes by 1 mm, how high (in mm) is H?
(Sectional area A = 100a, α = 30o.)