







Preview text:
ĐỀ 1 (đề của k20 nên bỏ phần xấp xỉ, nhưng k21 vẫn phải học phần này nhé :v)
PHẦN I: (Trắc nghiệm - 12 câu, 6 điểm)
1. Một lô hàng có 6 sản phẩm trong đó có 3 tốt. Bạn Duyên mua 2 sản phẩm. Tính đúng (không xấp xỉ) xác
suất để 2 sản phẩm đó là sản phẩm tốt. A. 0.5 B. 0.36 C. 0.2 D. 0.72
Bài này tính đúng, nên c n ầ nh n ậ diện nó là d n ạ g gì. Đây là d n ạ g c ơ b n ả , ki u ể t ổ h p ợ ch n ỉ h h p ợ c p ấ 3: Có 6, 3 t t ố , 3 h ư không gian m u ẫ là: C2= 2 15, s ố cách ch n ọ ra 2 t t ố t ừ 3 t t
ố là C =3 đáp s ố là 3/15 6 3 = 1/5 = 0.2
2. Tại một cửa hàng tiện lợi, theo thống kê cho biết: 30% các khách hàng mua cà phê; 50% khách hàng mua bánh
ngọt và nếu khách hàng đã mua cà phê thì 60% khách hàng sẽ mua kèm bánh ngọt. Quan sát ngẫu nhiên một
khách hàng, tính đúng (không xấp xỉ) xác suất để khách hàng đó mua cà phê và bánh ngọt: A. 0.30 B. 0.09 C. 0.15 D. 0.18 Đ t ặ C, B l n ầ l t ượ là bi n
ế cố chỉ ng đó mua cà phê, bánh ng t ọ . Theo đ
ề ta có: P(B) = 0.5, P(C) = 0.3; P(B|C) = 0.6. Ta c n
ầ tìm P(CB) (xác suất để khách hàng đó mua cà phê VÀ bánh ngọt) Nhìn th y ấ có d n ạ g công th c ứ nhân
P(CB) = P(C)P(B|C)=0.3x0.6 = 0.18
3. Xác suất học sinh của một trường phổ thông thi đậu đại học là 0.88. Nếu lấy ngẫu nhiên 12 học sinh từ
trường đó. Tính xấp xỉ (quy tròn đến 4 chữ số lẻ thập phân) xác suất để có đúng 3 học sinh không thi đậu đại học là: A. 0.2157 B. 0.3529 C. 0.2647 D. 0.1203 Giải:
Bài này dạng toán xấp xỉ (chương 3 á), nhưng dạng xấp xỉ được lược bỏ khỏi đề cương ôn thi, nên không làm cũng được nhe.
Mình giải cho bạn nào cần tham khảo thôi.
Đặt p là xác suất thi rớt ĐH: p = 1-0.88 = 0.12
Khi đó ta có mô hình: Chọn người đầu tiên
xs rớt là 0.12, chọn người thứ 2 xs rớt = 0.12… Có dạng
Bernouli, Do đó, nếu đặt X là số người rớt,
X ~B(12, 0.12) Tuy nhiên, người ta yêu cầu tính xấp xỉ nên lật
sách ta thấy có thể xấp xỉ nhị thức bởi Poisson, Chuẩn. Tuy nhiên, phân phối nhị thức là phân phối rời rạc, nên
em ưu tiên tính bằng Poisson sẽ dễ tính hơn. Ta có, X~B(12,0.12)
X~P(12x0.12) hay X~P(1.44). 3
Ta cần tính P(X = 3) = 1.44 e−1.44=0.1179. Đáp án bị sai á :sss (Đáp án trong sách họ tính theo kiểu chính xác). 3!
Tính đúng: P ( X= 3 3 9
3 )=C 0.12 × 0.88 = 0.1203 12
4. Tỷ lệ sản phẩm ra lò bị khuyết tật tại một xí nghiệp sản xuất là 10%. Người ta dùng một thiết bị tự động
kiểm tra chất lượng loại sản phẩm đó. Thiết bị đó có khả năng phát hiện đúng sản phẩm có khuyết tật với xác
suất 85% và phát hiện đúng sản phẩm không bị khuyết tật với xác suất 95%. Chọn ngẫu nhiên 1 sản phẩm cho
thiết bị tự động kiểm tra thì thấy kết luận là có khuyết tật. Tính đúng (không xấp xỉ) xác suất để thực chất sản
phẩm đó không bị khuyết tật.
A. 0.346, B. 0.045, C. 0.13, D. 0.085 Giải:
Đọc đề ta thấy, nó có dạng sơ đồ cây:
Từ đây ta có P(báo là hư) = Tổng 2 nhánh màu đỏ (có đuôi báo hư) = 0.1*0.85+0.05*0.9=0.13
Tuy nhiên đề yêu cầu tìm P(Tốt|báo là hư). Ta có
P(Tốt và báo là hư ) 0.9 × 0.05
P ( Tốt|báo là hư )= = Nhánhđỏ dưới = =0.346 P(báo là hư )
Tổng 2 nhánh đỏ 0.13
5. Một doanh nghiệp đã nhận được 10 hồ sơ ứng viên là sinh viên vừa tốt nghiệp UEL tham gia phỏng vấn
tuyển dụng. Biết rằng trong số 10 ứng viên đó có: 2 ứng viên loại giỏi, 3 ứng viên loại khá và 5 ứng viên loại
trung bình. Xác suất loại giỏi, loại khá và loại trung bình được tuyển dụng lần lượt là 0.7, 0.6 và 0.5. Chọn ngẫu
nhiên một ứng viên. Tính đúng (không xấp xỉ xác suất để ứng viên này được tuyển dụng). A. 0.57 B. 0.43 C. 0.18 D. 0.82 Giải:
Bài này cũng tương tự bài trên, vẽ sơ đồ cây ra là giải ra:
Xác suất sv này được tuyển chọn:
P(chọn) = P(khá)P(chọn|khá)+P(trung bình)P(chọn|trung bình)+P(giỏi)P(chọn|giỏi) =0.3*0.6+0.5*0.5+0.2*0.7=0.57
6. Lợi nhuận (đơn vị %) trong môt năm khi đầu tư vào hai ngành là biến ngẫu nhiên hai chiều (X, Y) với bảng phân phối: Y 0 10 20 X -5 0.05 0.1 0.15 15 0.1 0.25 0.05 30 0.1 0.15 0.05
Một người chọn đầu tư cả hai ngành với 40% vào X và 60% vào Y. Tính lợi nhuận trung bình của phương án đầu tư này. A. 10.25 B. 11.4 C. 12.25 D. Một đáp số khác Giải:
Đề cho cần tính lợi nhuận trung bình
liên tưởng đến kỳ vọng. Tức là ta cần tính E(0.4X+0.6Y) Ta có E(0.4X+0.6Y)=0.4E(x) + 0.6E(Y) =
0.4 × (−5 ×0.3+15 × 0.4 +30 0.3 ×
)+0.6 ×(0 ×0.25 10 0.5 0.25 + × +20 × )=11.4
7. Tuổi thọ X của sản phẩm mũi khoan (đơn vị tính: 1000 giờ) là một đại lượng ngẫu nhiên liên tục, với hàm
mật độ xác suất được cho theo công thức:
f (x)=¿Trong đó: k là tham số thực.
Tính đúng (không xấp xỉ) tuổi thọ trung bình (tức là kỳ vọng) (đơn vị tính là giờ) của sản phẩm mũi khoan đó. A. 750 B. 1000 C. 3000 D. 0.75 Giải:
Bài này từng giải ở lớp rồi. Đầu tiên, tính k: ∞ 1
∫ f =1→∫ k x2=1→k=3 −∞ 0
Từ đây ta tính ra được ∞ 1
E ( X ) =∫ 3 x2× x d x=∫3 x3 d x=0.75tức là 750 giờ. −∞ 0
8. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau: X 0 1 4 6 P 0.125 0.5 0.125 a
Trong đó, a là hằng số thích hợp. Phương sai của (2X) là: A. 5.25 B. 11.5 C. 21 D. Một đáp số khác Giải:
Tinhs a: a = 1-0.125-0.5-0.125=0.25
Tính Var ( X )=E(X2 )−[ E (X )]2=5.25
Chú ý công thức: Var(2X) = 22Var(X) = 4Var(X) = 5.25*4=21
9. Cho vectơ ngẫu nhiên 2 chiều (X, Y) với bảng phân phối xác suất đồng thời như sau: Y 1 2 3 X 0 0.1 0.3 0.15 2 0.2 0.15 0.1
Xét các mệnh đề dưới đây: (1)
EX = 0.45, EY = 1.95 và E(XY) = 0.8775 (2) X, Y độc lập. (3) Cov(X, Y) = 0.0775.
Đếm số khẳng định đúng: A. 0 B. 1 C. 2 D. 3 Giải
Đối với các dạng bảng hai chiều, bước đầu tiên là tìm các phân phối xác suất biên: P(X=xi) Y 1 2 3 X 0 0.1 0.3 0.15 0.55 2 0.2 0.15 0.1 0.45 P(Y=yj) 0.3 0.45 0.25 1
Sau đó, tính E(X), E(Y) dựa trên xs biên:
E ( X ) =0 ×0.55+2 ×0.45=0.9
E ( Y )=1 × 0.3+ 2× 0.45+3 ×0.25=1.95
Tính E(XY) tụi em lấy từng phần tử trong bảng nhân với vị trí ở hàng và cột tương ứng: 1 P(X=xi) Y 2 3 X 0 0.1 0.3 0.15 0.55
E ( XY )=0× 0.1 ×1+0.3 ×0 × 2+ 0.15× 0 × 2 0.2 0.15 0.1 0.45 P(Y=yj) 0.3 0.45 0.25 1 Do đó, câu 1 sai.
Để xét tính độc lập của XY, thường mình sẽ xét xem E(XY) có bằng E(X)E(Y) không, nếu nó không bằng
nhau tức là X, Y của em không độc lập.
Ta có E ( XY )=1.6 ≠ 0.9 ×1.95=E( X ) E(Y )
Do đó X, Y không độc lập. Ý 2 sai.
Để tính Cov(X, Y) ta lấy E(XY)-E(X)E(Y) = 1.6-0.9x1.95=-0.155 Do đó câu 3 cũng sai
10. Một lô hàng có 20 sản phẩm trong đó có 6 phế phẩm và 14 chính phẩm. Chọn ngẫu nhiên đồng thời 5 sản
phẩm để kiểm tra chất lượng. Gọi C là số phế phẩm trong số 5 sản phẩm đã kiểm tra.
Xét các khẳng định dưới đây. (1)
C có phân phối siêu bội kiểu H (20, 14, 5). (2) E(C) = 3.5. (3) Var(C) = 63/76.
Đếm số khẳng định sai: A. 2 B. 3 C. 0 D. 1 Giải
Ta có Lô hàng có 20sp, trong đó 6 phế phẩm lấy ra 5 sản phẩm, tính xác suất số phế phẩm lấy ra.
Nếu 1 bài toán có dạng kiểu này (Có N sản phẩm, trong đó có m sản phẩm có tính chất T, lấy ra n sản phẩm)
thì đây là phân phối siêu bội nhe. Có thể phân biệt nó với nhị thức bằng cách xét xem có cho yếu tố xác suất
không đổi (kiểu: xác suất bắn trung bia, xs khoanh trắc nghiệm…) , nếu có thì là nhị thức, còn không thường là
siêu bội (thường siêu bội sẽ cho số lượng).
Đặt C là số phế phẩm C ~H(20, 6, 5) câu 1 sai 6
E(C) = (lật sách ta có) = np = m n =5× =1.5 N 20 N−n 6 6 20 5 − 63
Var(C) = lật sách ta có = npq =5× ×(1− )× = câu 3 đúng N−1 20 20 20−1 76
11. Một trạm điện thoại trung bình nhận được 15 cuộc gọi trong 1 phút. Tính xấp xỉ (quy tròn đến 4 chữ số lẻ
thập phân) xác suất để trạm nhận được đúng 16 cuộc gọi trong 1 phút là: A. 0.0960 B. 0.1462 C. 0.0963 D. 0.0624 Giải:
Như đã nói, dạng xấp xỉ năm nay không thi, nên bài này tụi em có thể bỏ qua nha.
Còn nếu giải, thì đây là dạng xấp xỉ phân phối Poisson bởi phân phối chuẩn. Tụi em xem ví dụ trong sách rồi làm tương tự nhé :D
12. Xác suất có bệnh hen suyễn của những người chờ khám bệnh tại 1 bệnh viện là 12%. Khám lần lượt 20
người này, xác suất có ít hơn 2 người bị bệnh hen suyễn là: A. 0.7109 B. 0.3891 C. 0.2891 D. 0.6109 Giải:
Nhận định bài này như sau:
Chọn lần lượt từng người trong số 20 người, người thứ nhất
xs hen suyễn là 0.12, người thứ 2 cũng có xác suất hen là 0.12….
Xác suất không đổi theo từng người, do đó nó sẽ có dạng nhị thức.
Đặt X là số người bị hen suyễn trong số 20 ng đó. Khi đó X~B(20, 0.12). Ta cần tìm P(X<2)
Ta có: P ( X < 0 0 20 1 1 19
2 )=P ( X =0) + P(X =1 )=C 0.12 ×0.88 +C × 0.12 ×0.88 =0.2891 20 20
PHẦN II: (Tự luận - 2 câu, 4 điểm)
1. Tuổi thọ của một loại lốp ô tô tuân theo phân phối chuẩn với trung bình 34.000 km và độ lệch chuẩn 4.000 km. Tính:
a. (0.5đ) Xác suất để một lốp có tuổi thọ lớn hơn 40.000km?
b. (1đ) Xác suất để một lốp có tuổi thọ từ 30.000 km đến 35.000 km? Giải:
Nhận định, bài này là bài toán tính các xác suất của phân phối chuẩn. (Ở đâu mà cho trung bình/kỳ vọng và độ
lệch chuẩn/phương sai, thì đó là phân phối chuẩn). Dạng này QUAN TRỌNG nha.
Đặt X là số km của xe ô tô đi được. Theo đề ta có X~N(34000, 40002).
Lưu ý, tham số trong phân phối chuẩn sẽ là N ( μ,σ2), trong đó, σ là độ lệch chuẩn, σ 2 là phương sai, nên
tuỳ theo đề cho là phương sai hay độ lệch chuẩn mà điền tham số vào cho thích hợp. Giả sử đề bài này
mà cho phương sai bằng 4000, thì tụi em phải ghi là N (34000 , (20√ 10)2).
Trở lại bài toán, ở đây câu a người ta cần tính P(X>40000).
Quy trình giải bài toán liên quan phân phối chuẩn như sau:
Xem thử nó có phải là chuẩn tắc N(0, 12) hay chưa, nếu không chuẩn tắc thì đưa về chuẩn tắc => tra bảng
Ta có, phân phối kia chưa chuẩn tắc, nên sẽ đưa về chuẩn tắc.
P ( X > 40000)=1−P (X ≤ 40000) ( Đưa về lệchbên trái cho dễ trabảng ) 40000 34000 −
¿ 1−P (X−μ ≤ )=1−ϕ(1.5) σ 4000
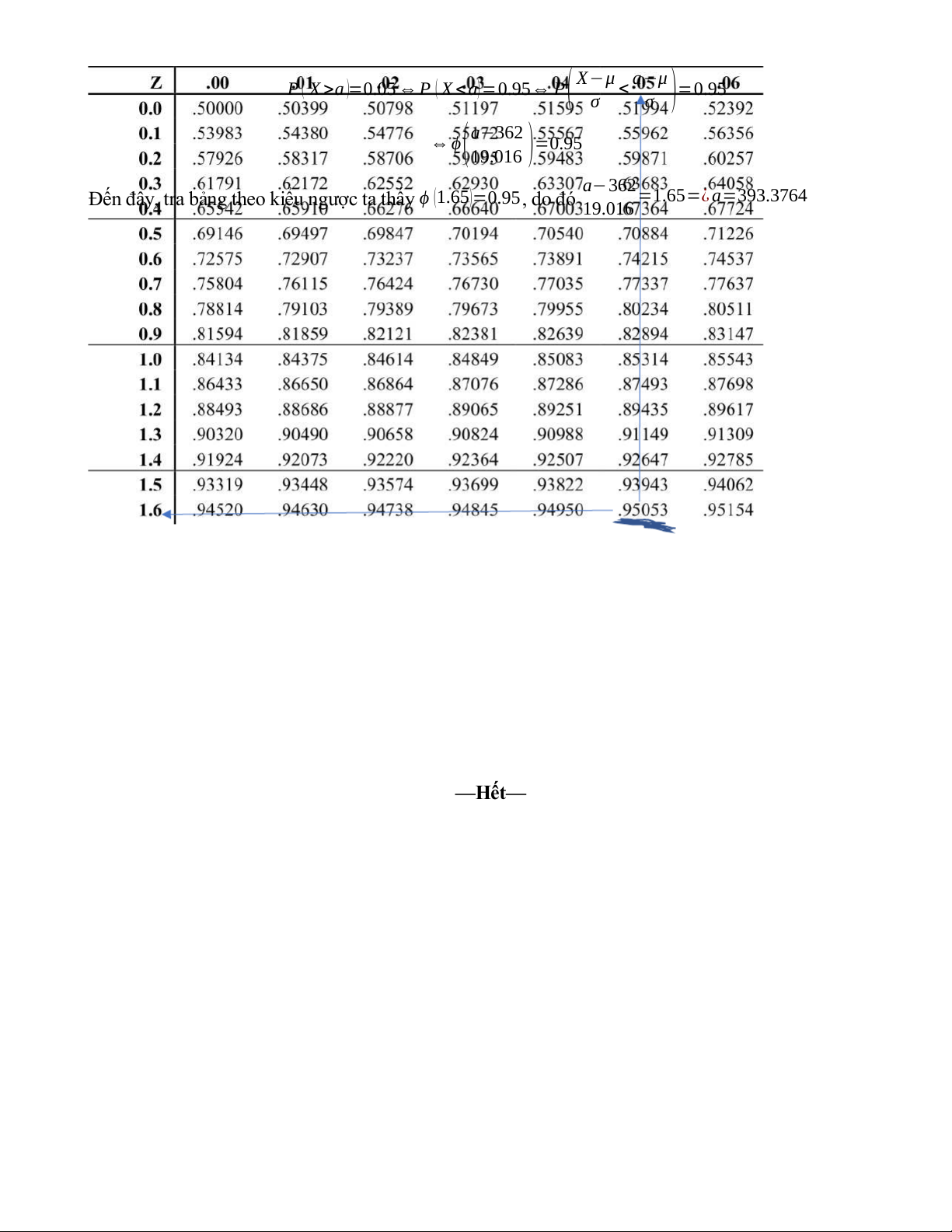
Đến đây, tra bảng (bảng phân phối Gauss ở trong sách) ta thấy: ϕ (1.5)=0.93319 do đó, xác suất cần tìm là 1- 0.93319 = 0.06681 Câu b:
Ta cần tính P(30000 ≤ X ≤35000) . Ta cũng đưa về phân phối chuẩn tắc cho dễ. X −μ 35000 34000 − P ( 30000 35000 ≤ X ≤ )=P( 30000 34000 − ≤ ≤ ) 4000 σ 4000 ¿ X −μ P(−1≤ ≤ 0.25) σ
¿ ϕ (0.25)−ϕ (−1) ¿ 0.59871 0.15866 0.44 − =
Hình: Cách tra bảng phân phối chuẩn của ϕ(1.5)
2. Một công ty cung cấp nước đã cung cấp cho khoảng 1.4 triệu người sử dụng thông qua hơn 362000 tài
khoản. Tất cả các tài khoản được đo và thanh toán hàng tháng. Xác suất một tài khoản có lỗi trong một tháng là
0.001 và các tài khoản có thể được coi là độc lập với nhau.
a. (0.5đ) Số tài khoản có lỗi trung bình và sự biến động (độ lệch chuẩn) của số tài khoản có lỗi mỗi tháng là bao nhiêu?
Câu này mình chỉ cần xác định bài toán tuân theo phân phối nhị thức. Đặt X là số tài khoản bị lỗi, khi đó ta
có X~B(362000, 0.001) (cái 1.4 triệu ng kia cho vào để làm nhiễu thôi)
Suy ra số tài khoản có lỗi trung bình là:
E ( X ) =np=362000 0.001 × =362 Sự biến động là:
σ (X )= √Var( X )=√npq= √362000 0.001 0.999 19.016 × × =
b. (1đ) Tính xác suất có ít hơn 350 lỗi trong một tháng, nếu xấp xỉ dữ liệu thông qua phân phối chuẩn.
Bài này là xấp xỉ nhị thức bởi chuẩn, năm nay không thi dạng xấp xỉ nên tụi em bỏ qua cũng được nha. Nếu
muốn đọc thêm cho biết thì đọc tiếp. (Đọc thêm sẽ vững hơn về phân phối chuẩn)
Theo đề ta có X B (362000 , 0.001)=¿>X N (np , npq) hay X N ( 2 362 , 19.016 ) Do đó: 350 362 −
P ( X <350) =P ( X−μ< )=ϕ(−0.63)=0.26435 σ 19.016
c. (1đ) Tìm số tài khoản lỗi sao cho xác suất số lỗi vượt quá giá trị này là 0.05, nếu xấp xỉ dữ liệu thông qua phân phối chuẩn.
Đây là dạng toán ngược, thường sẽ xuất hiện ở các bài khó nhé.
Ta cần tìm số tài khoản lỗi a sao cho P(X>a)=0.05 Tương tự ta cũng có:
P ( X >a )=0.05 ⇔ P ( X < a)=0.95⇔ P (X−μ <a−μ )=0.95 σ σ
⇔ ϕ (a−362 )=0.95 19.016 a−362
Đến đây, tra bảng theo kiểu ngược ta thấy ϕ (1.65)=0.95, do đó =1.65=¿ a=393.3764 19.016 —Hết—



