Bài tập Xác suất thống kê 1 | Đại học Kiến trúc Hà Nội

Bài tập chương 1
Bài 1: Phát hành 100 vé số, trong đó có 5 vé trúng thưởng. Một người mua 3 vé. Tính xác
suất để có đúng 1 vé trúng thưởng ? -
Sử dụng công thức Bernoulli:
+ Xác suất chọn đúng 1 vé trúng thưởng trong 100 vé là: p=5/100=0,05 => q=0,95.
 Xác suất có đúng 1 vé trúng thưởng trong 3 vé là :
P3(1;0.05)= 3.0,051.0,952= 13,5375(%).
Bài 2: Có thể xem xác suất sinh con trai là bao nhiêu nếu theo dõi 88.200 trẻ sơ sinh trong
một Quốc gia thấy có 45.600 bé trai ? -
Xác suât sinh con trai của QG đó xấp xỉ : P=45.600/88.200 = 0,517
Bài 3: Hai người X, Y thỏa thuận gặp nhau ở một địa điểm hẹn trước. Mỗi người đến đó độc
lập với nhau tại một thời điểm ngẫu nhiên từ 8 đến 9 giờ và quy ước người nào thì chờ 20
phút, nếu người kia không đến thì sẽ bỏ đi. Tìm xác suất để hai người gặp nhau ? -
Gọi A là biến cố 2 người đó gặp nhau. -
Gọi x là số phút tại thời điểm người X tới điểm hẹn (0 ≤ x ≤ 60) -
Gọi y là số phút tại thời người Y đến điểm hẹn: (0 ≤ y ≤ 60). -
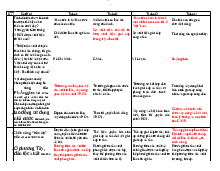
Nếu ta biểu diễn số phút tại thời điểm 2 người gặp nhau là điểm có tọa độ (x,y) nằm
trong hình vuông có cạnh bằng 60, đơn vị là phút. Y=x-20 D Y=x+20 -
Như vậy số phút lúc đến của cả hai người được biểu diễn bằng một điểm có tọa độ (x,
y) nằm trong hình vuông có cạnh là 60 (ta lấy phút làmđơn vị). Đó chính là miền D.
 D = {(x,y): 0 ≤x ≤ 60; 0 ≤ y ≤ 60}
 Để hai người gặp nhau thì số phút lúc đến x, y của mỗi người phải thỏa mãn điều kiện:  | X-Y | ≤ 20.  hay X-20 ≤ Y ≤ X+20.
 Như vậy các điểm (x, y) thích hợp cho việc gặp nhau là các điểm nằm trong phần A
có gạch chéo nằm giữa hai đường thẳng y = x – 20 và y = x + 20 (như hình vẽ).
 Theo công thức xác suất hình học: P(A)= (602-502)/602=5/9.
Bài 4: Một phòng điều trị có 3 bệnh nhân nặng cùng nhập viện một lúc. Gọi A1, A2, A3
là các sự kiện các sự kiện các bệnh nhân tương ứng cần cấp cứu trong vòng 1 giờ. Xác
suất để mỗi bệnh nhân cần cấp cứu trong vòng 1 giờ tương ứng là 0,7; 0,8; 0,9. Tính xác suất để:
a. Cả 3 bệnh nhân cần cấp cứu trong vòng 1 giờ.
b. Có ít nhất 1 bệnh nhân cần cấp cứu trong vòng 1 giờ.
c. Có ít nhất 1 bệnh nhân cần cấp cứu trong vòng 1 giờ.
d. Có đúng 2 bệnh nhân cần cấp cứu trong vòng 1 giờ. Trả lời:
a. Vì A1, A2, A3 xảy ra độc lập.
 P(A1A2A3)= PA1.PA2.PA3=0,7.0,8.0,9=0,504
b. Gọi B là biến cố: “ Có ít nhất 1 bệnh nhân cần cấp cứu trong vòng 1 giờ.”
 B’ : “Không có bệnh nhân nào cần cấp cứu trong vòng 1 giờ.”
P(B’)= P(A1’).P(A2’).P(A3’) = 0,3 . 0,2 . 0,1 = 0,006
 P(B) = 1 – P(B’) = 1 – 0,006 = 0,994 c. Trùng câu b.
d. C: “Có đúng 2 bệnh nhân cần cấp cứu trong vòng 1 giờ”.
P(C) = P(A1’).P(A2).P(A3) + P(A1).P(A2’).P(A3) + P(A1).P(A2).P(A3’)
= 0,3.0,8.0,9 + 0,7.0,2.0,9 + 0,7.0,8.0,1 = 0,398
Bài 6: Điều tra sở thích xem tivi của các cặp vợ chồng trẻ trong một vùng, ta có các kết
quả sau: 0,5 các cô vợ thích xem phim Hàn quốc, tỉ lệ này ở các ông chồng là 0,3. Song
nếu thấy vợ thích xem thì xác suất để các ông chồng thích xem cùng là 0,4. Gặp ngẫu
nhiên một cặp vợ chồng. Tính xác suất để:
a. Hai người cùng thích xem.
b. Ít nhất một người thích xem.
c. Cả hai người đều không thích xem.
d. Nếu thấy chồng thích xem thì vợ cũng xem.
e. Vợ không xem nhưng chồng vẫn xem. Trả lời: -
Gọi A là biến cố: “ Vợ thích xem Phim Hàn Quốc.” -
Gọi B là biến cố: “ Chồng thích xem Phim Hàn Quốc.”
a. Xác suất hai người cùng thích xem :
P(AB) = P(A | B). P(B)= 0,4 . 0,3 = 0,12.
b. Xác suất có ít nhất 1 người thích xem: P=1−P( ´ AB)=1−0,5.0,7=0,65
c. Xác suất cả 2 người không thích xem: P ( ´
AB)=P ( ´A ) . P ( ´B)=0,5.0,7=0,35
d. Xác suất chồng thích xem thì vợ cũng thích xem: P 0,4.0,5 P
( B|A ). P( A ) ( A|B)= = =66,67 % P (B ) 0,3
e. Xác suất vợ không xem nhưng chồng vẫn xem:
P (B )−P( B|A ). P( A) 0,3 P −0,4.0,5 (B| ´A )= = P( ´A) 0,5
Bài 7: Tỉ lệ cha mắt đen và con mắt đen là 0,05; cha mắt đen và con mắt xanh là 0,079;
cha mắt xanh và con mắt đen là 0,089; cha mắt xanh và con mắt xanh là 0,782.
a. Tìm khả năng con mắt xanh biết rằng cha mắt xanh.
b. Tìm khả năng con mắt không đen biết rằng cha mắt đen. Trả lời: 0,782 782 a. P= = ≈ 89,78 % 0,782+0,089 871 0,079 79 b. P= = ≈61,24 % 0,079+0,05 129
Bài 8: Trong điều trị bệnh lao có hiện tượng kháng thuốc. Gọi A là hiện tượng “kháng
INH của vi khuẩn lao”, B là hiện tượng “kháng PAS của vi khuẩn lao” và C là hiện tượng
“kháng Streptomycin của vi khuẩn lao”. Qua theo dõi ta biết khả năng kháng INH của vi
khuẩn lao là 0,2, nghĩa là P(A)=0,2. Tương tự, P(B)=0,4 và P(C)=0,3. Việc kháng các loại
thuốc khác nhau là độc lập với nhau. Nếu phối hợp cả 3 loại thuốc trên thì khả năng khỏi bệnh là bao nhiêu ? Trả lời: -
Khả năng khỏi bệnh chính là xác suất xảy ra biến cố: “có ít nhất 1 hiện tượng không
kháng thuốc của vi khuẩn Lao”.  P ( ´
ABC )=1−P ( ABC)=1−0,2.0,4 .0,3=0,976.
Bài 9: Trong một trạm cấp cứu bỏng có 80% bệnh nhân bỏng do nóng, 20% bệnh nhân
bỏng do hóa chất. Loại bỏng do nóng có 30% bị biến chứng, loại bỏng do hóa chất có 50% bị biến chứng.
a. Từ tập hồ sơ bệnh nhân, người ta chọn ngẫu nhiên ra một bệnh án. Tìm xác suất để
gặp một bệnh án của bệnh nhân bị biến chứng.
b. Rút ngẫu nhiên được một bệnh án của bệnh nhân bị biến chứng. Tìm xác suất để bệnh
án đó là của bệnh nhân bị biến chứng do bỏng nóng gây ra. Trả lời: -
Gọi A là biến cố: “bị biến chứng” -
Gọi H1 là biến cố : ‘ bỏng do nóng’. -
Gọi H2 là biến cố: “ bỏng do hóa chất”. - Ta có:
P ( H 1)=0.8 ;P ( H 2)=0,2P ( A|H 1 )=0,3=¿ P ( ´A|H 1)=0,7
P ( A|H 2)=0,5=¿ P ( ´A|H 2)=0,5
a. Theo công thức xác suất đầy đủ:
P ( A )=P ( H 1) . P( A|H 1)+P ( H 2) . P ( A|H 2)=0,8.0,3+0,2.0,5=0,34 b. Theo công thức Bayes:
Xác suất để bệnh án đó là của bệnh nhân bị biến chứng do bỏng nóng gây ra: P 0,3.0 .8 12 P
( A|H 1) . P ( H 1) ( H 1|A )= = = ≈ 70,59 % P ( A ) 0,34 17
Bài 10:Tỉ lệ người nghiện thuốc lá là 30%, biết rằng tỉ lệ người bị viêm họng trong số
người nghiện thuốc lá là 60%; còn tỉ lệ người bị viêm họng trong số người không hút thuốc lá là 40%.
a. Chọn ngẫu nhiên một người, biết rằng người đó viêm họng. Tính xác suất để
người đó nghiện thuốc lá.
b. Nếu người đó không bị viêm họng, tính xác suất để người đó nghiện thuốc lá . Trả lời: -
Gọi A là biến cố: “bị viêm họng”. -
Gọi B là biến cố : ‘ nghiện thuốc lá’  ´B là bi n ế cố: không nghi n ệ thu c ố lá .  Ta có :
P (B )=0.3=¿ P ( ´B)=0.7P ( A|B)=0,6 ; P ( A|´B)=0,4
a. Xác suất người đó bị viêm họng là :
P ( A )=P (B ). P ( A|B )+ P( ´B) . P ( A|´B )=0,3.0,6+0,7.0,4=0,46
 Xác suất người đó nghiện thuốc lá là : P 0,6.0,3 9 P
( A|B ). P( B) (B|A )= = = ≈ 39,13 % P ( A) 0,46 23
b. Xác suất người đó không bị viêm họng :
P ( ´A )=1−P ( A )=1−0,46=0,54
Xác suất người đó không bị viêm họng nếu biết là người đó không nghiện thuốc lá là :
P ( ´A∨B)=1−P ( A|B)=1−0,6=0,4
 Xác suất người đó nghiện thuốc lá nếu biết người đó không bị viêm họng là :
P ( ´A|B) . P (B ) 0,4.0,3 2
P (B| ´A )= = = ≈ 22% P( ´A ) 0,54 9
Bài 11 : Một người đến khám vì ho ra máu, nguyên nhân có thể là lao phổi 40%, K
phổi 30%, dãn phế quản 20%, còn lại là do bệnh khác. Cho bệnh nhân làm xét nghiệm
T, kết quả xét nghiệm là dương tính. Biết rằng khả năng xét nghiệm T cho kết quả
dương tính đối với lao phổi là 80%, K phổi là 40%, dãn phế quản là 20% và bệnh
khác là 10%. Tính khả năng người này bị lao phổi ?
Bài 12 : Trong một vùng dân cư có tỉ lệ nam : nữ là 9: 11, một nạn dịch truyền nhiễm
xuất hiện trong vùng với khả năng mắc bệnh ở nam giới là 6% và ở nữ giới là 2%.
a. Khả năng gặp một người trong vùng bị mắc bệnh là bao nhiêu ?
b. Chọn ngẫu nhiên một người trong vùng thì gặp phải người mắc bệnh. Xét xem
khả năng người được chọn đó là nam giới cao hơn hay nữ giới cao hơn. Trả lời : -
Gọi A là biến cố : ‘‘Mắc bệnh truyền nhiễm’’. -
Gọi B là biến cố : ‘‘ Người bắt gặp là nam’’.  ´B là biến c ố : Ngư i ờ bắt g p ặ là nữ .
a. Ta có : P ( A|B)=0,06 ; P ( A|´B)=0,02 9 P (B )=
=0,45 ; P ( ´B)=1−P (B)=0,55 20
 Xác suất bắt gặp một người mắc bệnh truyền nhiễm trong vùng là :
P ( A )=P ( A|B) . P (B )+ P( A|´B ). P ( ´B )=0,06.0,45+0,02.0,55=0,038=3,8 %
b. Xác suất người đó là nam khi biết đã mắc bệnh truyền nhiễm là : P 0,06.0,45 27 P
( A|B ). P( B) (B|A )= = = ≈ 71.05 % P ( A) 0,038 38
Xác suất người đó là nữ khi biết đã mắc bệnh truyền nhiễm là : 27 11
P ( ´B|A )=1−P( B|A )=1− = ≈ 28,95 % 38 38
 Khả năng người đó là nam cao hơn là nữ.
Bài 13 : Ta biết rằng một cặp sinh đôi có thể là sinh đôi thật (do một trứng sinh ra),
trong trường hợp đó chúng cùng giới hoặc có thể là giả sinh đôi (do hai trứng sinh ra),
trong trường hợp này xác suất để chúng cùng giới là 0,5. Ta giả thiết rằng đã biết xác
suất của một cặp sinh đôi là sinh đôi thật trong một họ nào đó là p.
a. Tìm xác suất để một cặp sinh đôi là sinh đôi thật biết rằng chúng cùng giới.
b. Tìm xác suất để một cặp sinh đôi là sinh đôi giả biết rằng chúng khác giới. Trả lời : -
Gọi A là biến cố : « Cặp sinh đôi là sinh đôi thật ».  ´A là bi n ế c : ố C p
ặ sinh ⁡đôi là giả sinh ⁡đôi -
Gọi B là biến cố : « Cặp sinh đôi là cùng giới ».
 ´Blà biếncố :Cặp sinh đôi là khác giới a. Ta có :
P ( A )= p ; P ( ´A )=1−p ; P ( B|A )=1=¿ P( ´B|A )=0 ; P (B| ´A )=0,5=¿ P ( ´B| ´A )=0,5
 P (B )=P (B|A ). P ( A )+ P( B|´A ). P ( ´A )=1. p+0,5. (1− p)=0,5.(1+ p)
 Xác suất để một cặp sinh đôi là sinh đôi thật biết rằng chúng cùng giới là : P 1. p 2 p P
( B|A ). P( A ) ( A|B)= = = P (B ) 0,5. (1+p ) 1+ p b. Ta có :
P ( ´B )=1−P ( B)=1−0,5 (1+ p )=0,5. (1− p)
 Xác suất để một cặp sinh đôi là sinh đôi giả biết rằng chúng khác giới là :
P ( ´B| ´A ) . P ( ´A) 0,5. P (1− p) ( ´A|´B)= = =1=100 % P ( ´B) 0,5. (1− p)
Bài 14 : Có hai chuồng thỏ thí nghiệm : chuồng 1 có 12 thỏ trắng và 3 thỏ nâu ;
chuồng 2 có 16 thỏ trắng và 4 thỏ nâu. Tình cờ một con thỏ từ chuồng 2 nhảy sang
chuồng 1. Từ chuồng 1, người ta bắt ngẫu nhiên một con. Tính xác suất để thỏ bắt được là thỏ trắng ? Trả lời : -
Gọi A là biến cố : « Bắt được thỏ trắng từ chuồng 1 sau khi 1 con thỏ từ chuồng 2 nhảy sang ». -
Gọi B là biến cố : « Con thỏ nhảy sang là con thỏ màu trắng ».
 ´Blà biếncố : Conthỏ nhảy sanglàcon thỏ màunâu . 16 4 Ta có : P (B )=
= =0,8; P ( ´B)=1−0,8=0,2. 16 +4 5 12 13 12 12 P +1 ( A|B)= =
; P ( A|´B )= = . 12+1+3 16 12+3+1 16
 Xác suất bắt được thỏ trắng từ chuồng 1 sau khi 1 con thỏ nhảy từ chuồng 2 sang chuồng 1 là : 13 12
P ( A )=P ( A|B) . P (B )+ P( A|´B ). P ( ´B )= .0,8+ .0,2=0,8. 16 16
Bài 16 : Có 2 bình thí nghiệm đựng các hạt đậu trắng và đen : Bình I có 2 trắng và 3
đen ; bình II có 3 trắng và 2 đen.
a. Từ mỗi bình lấy ra 1 hạt. Tính xác suất để lấy được 2 hạt cùng màu.
b. Từ mỗi bình lấy ra một hạt đậu, sau đó lấy ra một hạt. Tính xác suất để chọn được hạt trắng.
c. Chọn ngẫu nhiên một bình, rồi từ đó lấy ra 2 hạt đậu. Tính xác suất để lấy được 2
hạt đậu trắng. Cho biết xác suất lựa chọn từng bình là 2/5 và 3/5. Trả lời :
a. Gọi A là biến cố : « Lấy được hạt màu trắng ở bình I ».
Gọi B là biến cố : « Lấy được hạt màu trắng ở bình II ».
 P ( A )=0,4 ;P ( B)=0,6=¿ P ( ´A )=0,6 ; P( ´B)=0,4
 Xác suất để lấy được hai hạt cùng màu là :
P=P ( AB)+P ( ´
AB)=P ( A) . P ( B)+P ( ´A ) . P ( ´B)=0,4.0,6+0,6.0,4=0,48
b. Xác suất để chọn được hạt đậu trắng là :
P= 0,4.0,6+0,5.0,4.0,4+0,5.0,6.0,6 = 0,24+0,08+0,18=0,5.
c. Gọi C là biến cố : « Chọn được bình I ».
Gọi D là biến cố : « Chọn được bình II ».
Gọi E là biến cố : « Lấy được đồng thời 2 hạt đậu trắng». C2 1 C2 3 2 3  P ( E 2 3 ∨C )= =
; P ( E∨D )= =
; P (C )= ; P ( D)= C2 10 C2 10 5 5 5 5
 Xác suất để lấy được 2 hạt đậu trắng là : 1 2 3 3 11
P ( E)=P ( E|C ). P (C)+P ( E|D) . P ( D)= . + . = =0,22 10 5 10 5 50
Bài 17 : Theo dõi kết quả điều tra về bệnh lao, tỉ lệ người bị lao ở một vùng nọ là
0,001. Tìm xác suất để khi khám cho 10 người : a. Không ai bị lao. b. Có 5 người bị lao.
c. Ít nhất 1 người bị lao.
d. Tìm số người không bị lao có khả năng nhất. Trả lời : Ta có : -
Xác suất một người không bị lao trong vùng đó : q=0,999 -
Xác suất một người bị lao trong vùng đó : p=0,001
 Quá trình điều tra tuân theo quá trình bernoulli
 Áp dụng công thức Bernoulli, ta có :
a. Xác suất khám cho 10 người không ai bị lao : P k 0
n ( k ; p )=C n . pk . qn−k =P 10 ( 0 ; 0,001)=C 10 . 0,0010 .0,999 10 ≈ 0,99
b. Xác suất có 5 người bị lao : P 5
10 ( 5 ; 0,001)= C10 . 0,0015 . 0,9995 ≈ 2,507. 10−3
c. Xác suất có ít nhất 1 người bị lao : 1 0
−P10 (0 ; 0,001)=1−C10. 0,0010 . 0,99910≈ 9,95. 10−3
d. Vì (n+1).p = 10,989 (số thập phân) => k0=10.
 Số người không bị lao có khả năng nhất trong quá trình khám cho 10 người là : 10 người.
Bài 18 : Một bác sỹ có tiếng về chữa một loại bệnh với xác suất chữa khỏi bệnh là 0,8.
Có người nói rằng cứ 5 người đến chữa thì chắc chắn có 4 người khỏi bệnh. Điều đó
có đúng không ? Tại sao ? Trả lời : -
Ta có thể xem việc chữa bệnh cho 5 người là một dãy các phép thử độc lập. Nếu gọi
A là biến cố chữa khỏi bệnh cho 1 người thì P ( A )=0,8=¿ P ( ´A )=0,2
 Xác suất cứ 5 người đến chữa có 4 người chắc chắn khỏi bệnh là : P 4
5 ( 4 ; 0,8 )=C5 . 0,8 4 .0,21 =0,4096 <100 %
 Kết luận trên là SAI.
Bài 19 : Một lô thuốc đóng chai có tỷ lệ phế phẩm là 5%. Lấy ngẫu nhiên 10 chai.
Tìm xác suất để trong số chai thuốc lấy ra : a. Có đúng 4 phế phẩm.
b. Có ít nhất 8 phế phẩm. Trả lời : -
Ta có thể xem việc lấy ngẫu nhiên 10 chai là 1 dãy các phép thử độc lập.
 Gọi A là biến cố : « Lấy được chai thuốc phế phẩm ».
 P ( A )=0,05 ; P ( ´A )=0,95
 Xác suất của quá trình tuân theo quá trình Bernoulli.
a. Xác suất có đúng 4 phế phẩm trong số 10 chai thuốc là : P 4
10 ( 4 ; 0,05 ) =C10 .0,05 4 .0,95 6 ≈ 9,65. 10− 4
b. Xác suất có ít nhất 8 phế phẩm :
P10(8 ;0,05 )+P10(9 ;0,05)+P10 (10 ;0,05 )≈ 1,605.10−9
Bài 20 : Biết tỉ lệ mắc bệnh A ở một địa phương là 2%. Để điều tra tình hình mắc
bệnh, người ta sử dụng một phản ứng mà nếu người bị bệnh thì kết quả luôn luôn
dương tính, nếu người không bị bệnh thì phản ứng có thể dương tính với xác suất 2%.
a. Tính xác suất phản ứng dương tính.
b. Tính tỉ lệ người mắc bệnh, người không mắc bệnh trong nhóm người có phản ứng dương tính. Trả lời : -
Gọi A là biến cố : « mắc bệnh A ». -
Gọi T là biến cố : « dương tính với bệnh A ».
 P ( A )=0,02=¿ P( ´A )=0,98 ; P (T|A )=1 ;P (T|´A )=0,02
a. Xác suất phản ứng dương tính (% những người có kết quả xét nghiệm dương tính với bệnh A) :
P (T )=P (T|A ) . P ( A)+P (T|´A ) . P ( ´A )=1.0,02+0,02.0,98=0,0396
b. Tỉ lệ người mắc bệnh trong nhóm người có kết quả xét nghiệm dương tính : P 1.0,02 50 P
(T|A ) . P ( A ) ( A|T )= = = ≈ 50,51 % P(T ) 0,0396 99
Tỉ lệ người không mắc bệnh trong nhóm người có kết quả xét nghiệm dương tính :
P(T|´A) . P( ´A ) 0,02 . 0,98 49
P ( ´A|T )= = = ≈ 49,49 % P (T ) 0,0396 99
Bài 21 : Một người ốm bị nghi là mắc một trong hai bệnh A và B. Thống kê tình
hình mắc bệnh trong nhiều năm cho thấy xác suất mắc bệnh A cao gấp đôi xác
suất mắc bệnh B. Bệnh viện cho bệnh nhân tiến hành hai xét nghiệm T1 và T2 một
cách độc lập. Biết rằng đối với bệnh , độ nhạy của xét nghiệm T1 là 0,9 và của xét
nghiệm T2 là 0,8. Đối với bệnh B, xét nghiệm T1 cho kết quả dương tính với xác
suất 0,05 và xét nghiệm T2 cho kết quả dương tính là 0,1. Giả sử kết quả của cả
hai xét nghiệm T1, T2 của bệnh nhân đều dương tính. Hãy đánh giá khả năng mắc bênh A của bệnh nhân. Trả lời : -
Gọi A là biến cố : « bệnh nhân mắc bệnh A ». -
Gọi B là biến cố : « bệnh nhân mắc bệnh B ». -
Gọi T1 là biến cố : « xét nghiệm T1 cho kết quả dương tính ». -
Gọi T2 là biến cố : « xét nghiệm T2 cho kết quả dương tính ».  2 1
P ( A )= =¿ P (B )= ; P 3 3
( T1|A)=0,9 ; P(T 2|A)=0,8P (T1|B)=0,05 ;P (T 2|B )=0,1
 Xác suất xét nghiệm T1 cho kết quả dương tính là : 2 1 37
P (T1)=P( T1|A). P( A )+P (T 1|B ).P (B )=0,9. +0,05. = 3 3 60
Xác suất xét nghiệm T2 cho kết quả dương tính là : 2 1 17
P (T2)=P( T2|A). P ( A )+ P(T 2|B).P (B )=0,8. +0,1. = 3 3 30 -
Vì xét nghiệm T1 và T2 độc lập với nhau  P (T T 1
2|A )= P (T 1|A ). P (T 2|A )=0,9 . 0,8= 0,72 P (T T 1
2|B )=0,05 . 0,1=0,005 2 1 289  P (T T T T ≈ 0,4817 1 2 )= P ( T 1
2|A ) . P ( A )+ P (T 1
2|B ) . P ( B )=0,72. +0,005. = 3 3 600
 Khả năng mắc bệnh A của bệnh nhân trên là : 2 P 0,72 . (T T 3 288 P 1
2|A ) . P ( A ) ( A|T T ≈ 99,65 % 1 2 )= = = P (T T 289 289 1 2 ) 600
Bài 22 : Có 4 bệnh nhân cần được tiếp máu, trong đó 1 người có nhóm máu O, 1
người nhóm máu A, 1 người có nhóm máu B, 1 người có nhóm máu AB. Trong số
những người hiến máu : 33% có nhóm máu O, 38% có nhóm máu A, 20% có nhóm
máu B, 9% nhóm máu AB. Biết rằng người có nhóm máu AB có thể nhận máu của
một người thuộc bất kì nhóm máu nào. Người có nhóm máu O, A, B chỉ có thể nhận
máu của người có cùng nhóm máu với mình hoặc nhóm máu O. Chọn ngẫu nhiên một
bệnh nhân trong số các bệnh nhân nói trên và chọn ngẫu nhiên một người hiến máu.
Tính khả năng sự truyền máu thực hiện được. Trả lời : -
Gọi A là biến cố : « Chọn được bệnh nhân nhóm máu A ». -
Gọi B là biến cố : « Chọn được bệnh nhân nhóm máu B ». -
Gọi C là biến cố : « Chọn được bệnh nhân nhóm máu O ». -
Gọi D là biến cố : « Chọn được bệnh nhân nhóm máu AB ».
 Gọi A’ là biến cố : « Chọn được người hiến máu nhóm máu A ».
Gọi B’ là biến cố : « Chọn được người hiến máu nhóm máu B ».
Gọi C’ là biến cố : « Chọn được người hiến máu nhóm máu O ».
Gọi D’ là biến cố : « Chọn được người hiến máu nhóm máu AB ».
 P ( A )=P (B )=P (C)=P ( D)=0,25
P ( A' )=0,38 ; P ( B' )=0,2 ; P( C' )=0,33; P ( D' )=0,09
 Xác suất sự truyền máu thực hiện được là :
P ( A ) .[ P ( A' )+P (C')]+P ( B) .[ P (B' )+P( C' )]+P (C) . P (C')+P( D)
¿ 0,25. (0,38+0,33)+0,25. (0,2+0,33)+0,25.0,33+0,25=0,6425
Bài 23 : Một người có 4 chỗ câu cá với xác suất lựa chọn lân lượt là 0,3 ; 0,4 ; 0,2 ;
0,1. Xác suất để thả câu thì câu được một con cá ở mỗi chỗ là 0,55 ; 0,45 ; 0,75 ; 0,9.
Người đó chọn ngẫu nhiên một chỗ câu cá và thả câu 5 lần thì câu được một con cá.
Hỏi khả năng anh ta đã câu được ở chỗ nào ? Trả lời : -
Gọi A, B, C, D là 4 chỗ câu cá với xác suất được chọn lần lượt là 0,3 ; 0,4 ; 0,2 ; 0,1. -
Gọi A là biến cố : « người đó chọn vị trí A để câu cá ». -
Gọi B là biến cố : « người đó chọn vị trí B để câu cá ». -
Gọi C là biến cố : « người đó chọn vị trí C để câu cá ». -
Gọi D là biến cố : « người đó chọn vị trí D để câu cá ».
 P ( A )=0,3 ; P (B )=0,4 ; P (C )=0,2 ;P ( D)=0,1 -
Ta có thể xem việc thả câu 5 lần và bắt được 1 con cá của người đó là dãy các phép
thử độc lập => tuân theo quá trình bernoulli => áp dụng công thức bernoulli :
 Xác suất thả câu 5 lần và bắt được 1 con cá của người đó ở vị trí A là :
P ( A ) . P 1
5 ( 1 ; 0,55 )=0,3 .C 5 .0,55 1 . 0,454 ≈ 0,034
Xác suất thả câu 5 lần và bắt được 1 con cá của người đó ở vị trí B là : P (B ). P 1
5 ( 1 ; 0,45 )= 0,4 . C 5 . 0,45 1 . 0,554 ≈ 0,082
Xác suất thả câu 5 lần và bắt được 1 con cá của người đó ở vị trí C là : P (C) . P 1
5 ( 1 ; 0,75 )=0,2 . C5 . 0,751 . 0,254 ≈ 0,00293
Xác suất thả câu 5 lần và bắt được 1 con cá của người đó ở vị trí D là : P ( D). P 1
5 (1 ; 0,9) =0,1. C 5 . 0,91 . 0,14=0,000045
 Khả năng người đó đã câu cá ở vị trí B (0,082 > 0,034 > 0,00293 > 0,000045).
Bài 24 : Một người ốm vào bệnh viện, bác sỹ chẩn đoán sơ bộ người này có thể bị
mắc bệnh A với xác suất 70%, mắc bệnh B với xác suất 30%. Để có thêm thông tin
chẩn đoán , bác sỹ đã cho tiến hành xét nghiệm sinh hóa. Sau 3 lần xét nghiệm thấy
có 1 lần dương tính, biết rằng khả năng dương tính của mỗi lần xét nghiệm đối với
bệnh A là 10%, đối với bệnh B là 30%. Hãy cho biết nên chẩn đoán bệnh nhân mắc bệnh nào. Trả lời : -
Gọi A là biến cố : « người đó mắc bệnh A ».
 ´A làbiến cố :người đó m c ắ b n ệ h B .
 P ( A )=0,7=¿ P ( ´A )=0,3 -
Gọi T là biến cố : « dương tính với bệnh ».
 P (T|A ) 1 1
=C3 .0,1 .0,92=0,243 ; P (T| ´A)=C3 .0,3 .0,72=0,441
 P (T )=P (T|A ) . P ( A)+P (T|´A ) . P ( ´A )=0,243 .0,7+0,441.0,3=0,3024
P (T|A ) . P ( A ) 0,243.0,7 9
 P ( A|T )= = = =0,5625 P(T ) 0,3024 16
P(T|´A) . P( ´A ) 0,441.0,3 7
 P ( ´A|T )= = = =0,4375 P (T ) 0,3024 16
 Bệnh nhân có thể mắc bệnh A.
Bài 25 : Trong một kho rượu số lượng chai rượu loại A và loại B là bằng nhau. Người
ta lấy ngẫu nhiên một chai rượu trong kho và đưa cho 4 người sành rượu nếm thử để
xác định xem đây là rượu loại nào. Giả sử mỗi người có khả năng đoán đúng là 80%.
Có 3 người kết luận chai rượu thuộc loại A và một người kết luận chai rượu thuộc loại
B. Vậy chai rượu được chọn thuộc loại A với xác suất bằng bao nhiêu ? Trả lời : -
Gọi A là biến cố : « Chai rượu là loại A ». -
Gọi B là biến cố : « Chai rượu là loại B ». -
Gọi F là biến cố : « có 3 người kết luận chai rượu thuộc loại A và 1 người kết luận loại B ».
 P ( A )=0,5 ; P ( F|A )=P ( X=3 ) v i ớ X làsố ngư i ờ kết lu n
ậ đúng khi biết chai rượuđã ch n ọ ra làlo i ạ A
Ta có : X B (4 ;0,8 ) P ( X 3
=3 )=C4 .0,83.0,2=0,4096=P ( F|A )
 P (B )=0,5 ; P( F|B)=P (Y =1) v i ớ Y là số ngư i ờ k t ế lu n ậ đúng khi bi t ế chairư u ợ đã ch n ọ ralà lo i ạ B
Ta có : Y B ( 4 ;0,2) P (Y 1
=1)=C 4 .0,8 . 0,23=0,0256=P( F|B )
 P (F )=P ( F|A ) . P ( A )+P (F|B) . P ( B)=0,4096 . 0,5+0,0256 . 0,5=0,2176
 Xác suất chai rượu được chọn thuộc loại A là : P 0,4096 .0,5 16 P
( F|A ). P ( A ) ( A|F )= = = ≈ 94,12 % P ( F ) 0,2176 17
Bài 26 : Tại một bệnh viện, trung bình 1000 người thì có 100 người mắc bệnh B. Để
chẩn đoán xác định bệnh B, người ta làm một phản ứng miễn dịch, với người không
bị bệnh thì phản ứng dương tính là 10%. Làm phản ứng miễn dịch cho một bệnh nhân
thì thấy kết quả phản ứng dương tính, khả năng người này thuộc nhóm có bệnh là
50%. Xác định độ nhạy, độ đặc hiệu của phản ứng miễn dịch ? Trả lời : -
Gọi B là biến cố : « mắc bệnh B của bệnh nhân ngẫu nhiên trong bệnh viện trên ». 100 P (B )=
=0,1=¿ P ( ´B )=0,9 1000
Ta có : P (T+¿¿ ´B )=0,1 ; P¿ P ¿  P 0,5 (T +¿¿ B) .0,1
= P(T+¿¿ B).0,1+0,1.0,9
Giải phương trình 1 ẩn => P (T+¿¿B )=0,9
Ta có : P (T+¿¿ ´B )+P (T−¿¿ ´B)=1=¿ P (T−¿¿ ´B )=1−P (T +¿¿ ´B)=1−0,1=0,9  Kết luận :
Độ nhạy của phản ứng miễn dịch : P (T+¿¿B )=0,9
Độ đặc hiệu của phản ứng miễn dịch : P (T−¿¿ ´B)=0,9
Bài 27 : Một nghiên cứu về bệnh ung thư vú đã phẫu thuật cho thấy tỉ lệ sống quá 5
năm là 60%, tỉ lệ có hạch là 30%. Số ca sống quá 5 năm và có hạch chỉ bằng nửa số
ca không sống quá 5 năm và không có hạch. Tính khả năng một người bị ung thư vú,
không có hạch sau khi phẫu thuật sống quá 5 năm ? Trả lời : -
Đặt x là tỉ lệ số ca sống quá 5 năm và có hạch sau khi phẫu thuật ung thư vú.
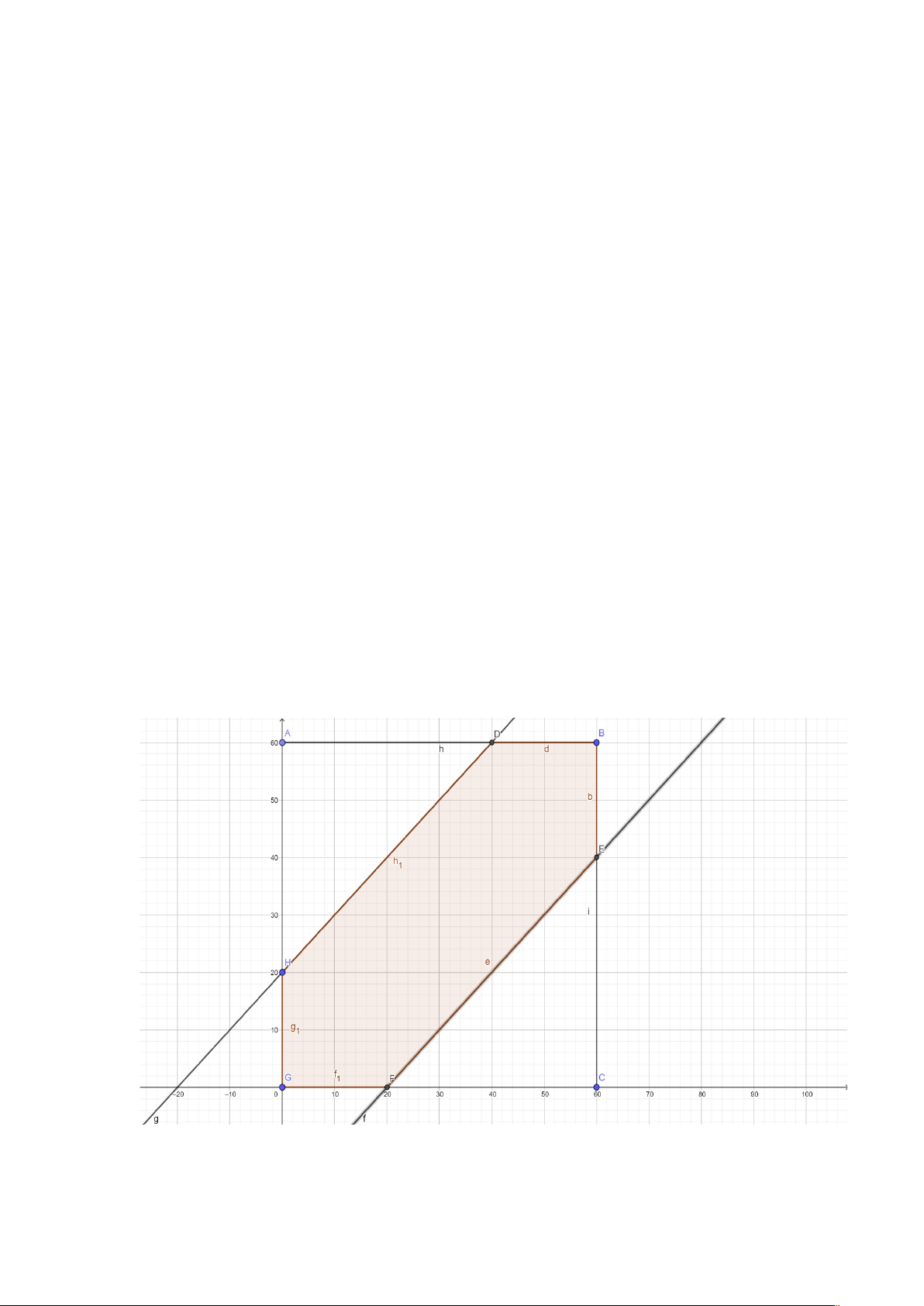
 Bảng thống kê tỉ lệ như sau : Tỉ lệ sống quá 5 Tỉ lệ sống không Tổng
năm sau phẩu thuật quá 5 năm sau phẫu thuật Tỉ lệ có hạch sau x 0,4-2x 0,3 phẫu thuật Tỉ lệ không có hạch 0,6-x 2x 0,7 sau phẫu thuật Tổng 0,6 0,4
Giải phương trình : x + 0,4 – 2x = 0,3 => x = 0,1.
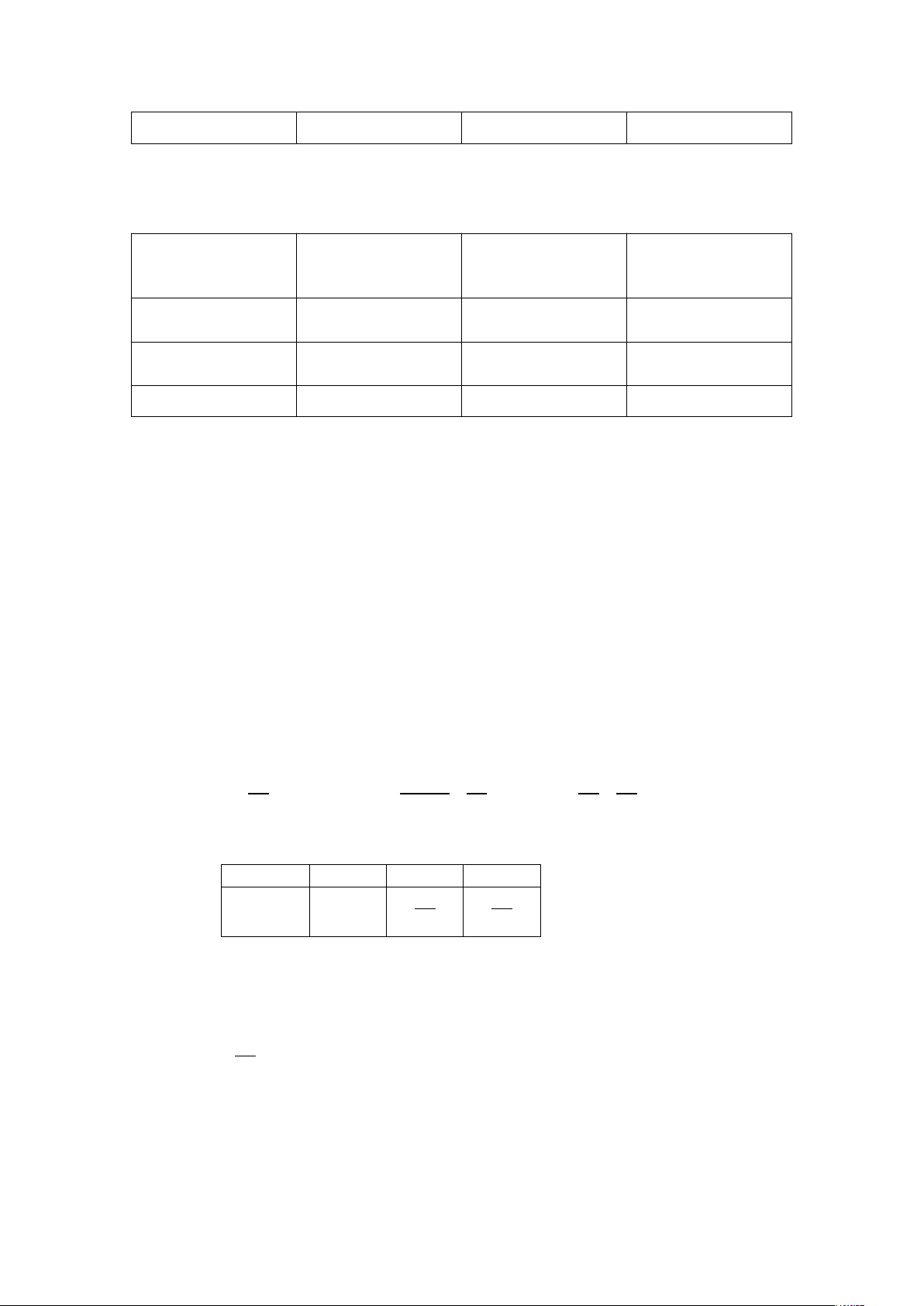
 Bảng thống kê tỉ lệ với giá trị thực : Tỉ lệ sống quá 5 Tỉ lệ sống không Tổng
năm sau phẩu thuật quá 5 năm sau phẫu thuật Tỉ lệ có hạch sau 0,1 0,2 0,3 phẫu thuật Tỉ lệ không có hạch 0,5 0,2 0,7 sau phẫu thuật Tổng 0,6 0,4
 Khả năng một người bị ung thư vú, không có hạch sau khi phẫu thuật sống quá 5 năm : 50%. Bài tập chương 2
Bài 1 : Trong một hộp thuốc có 6 lọ, trong đó có 2 lọ đã quá hạn sử dụng. Lấy ngẫu nhiên
2 lọ. Gọi X là số thuốc quá hạn sử dụng được lấy ra.
a. Lập bảng phân phối xác suất của X.
b. Viết biểu thức hàm phân phối xác suất của X.
c. Tính kỳ vọng EX , E (6 X −2) và phương sai VarX , Var (3 X −5) . Trả lời :
a. X là biến ngẫu nhiên rời rạc có tập giá trị là {0 ; 1 ; 2}. C2 C1. C1 8 C2 1 P 4 2 4 2 ( X=0)= =0,4 ; P ( X=1)= = ; P ( X=2 )= = C2 C2 15 C2 15 6 6 6
Bảng phân phối xác suất của X là : X 0 1 2 P 0,4 8 1 15 15
b. Hàm phân phối xác suất của X :
FX ( x)={ 0n uếx≤0 0,4 n u ế 0<x ≤ 1 14 n u ế 1<x ≤2 15 1 n u ế x>2 c. Kỳ vọng EX : 2 EX=∑ x p i i= 3 i=1 2
Kỳ vọng E (6 X −2)=6. EX+ E (−2)=6. −2=2 3 Phương sai : 2 4 4 16 VarX 2 2
=E( X −EX ) =E X2−( EX )2=∑ xi . pi−(2 = − = i 3 ) 5 9 45 =1 16
Var (3 X−5 )=9. VarX=9. =3,2 45
Bài 2 : Một nhóm có 10 người gồm 6 nam và 4 nữ. Chọn ngẫu nhiên ra 3 người và gọi
X là số nữ trong nhóm. Lập bảng phân phối xác suất của X và tínhEX ,VarX , modX , medX Trả lời : X 0 1 2 3 P 1 1 3 1 6 2 10 30
Tính : EX=∑ x p i i=1,2 i=1
VarX =E X2−( EX )2=2−1,22=0,56 ;modX =1 ;medX=1
Bài 13 : Xác suất bị mắc bệnh T của mỗi người ở một vùng dân cư là 0,001. Chọn
ngẫu nhiên 1000 người dân ở vùng này. Gọi X là số người bị mắc bệnh T.
a. Tính kỳ vọng và phương sai của X.
b. Tính xác suất để có ít nhất 3 người bị mắc bệnh T. Trả lời :
a. X B (1000 ;0,001)  Kỳ vọng : EX=1
 Phương sai : VarX =1000.0,001 . 0,999=0,999
b. Trường hợp này n rất lớn(n=1000),p rất bé(p=0,001) và λ=np=1000.0,001=1
nên có thể vận dụng công thức xấp xỉ Poisson.
 Xác suất để có ít nhất 3 người bị mắc bệnh T là : λ1 λ2
P ( X ≥3 )=1−P ( X =0)−P ( X =1)−P ( X=2)≈ 1−e−λ ( λ0 + +
0! 1 ! 2 !)≈ 0,0803
Bài 14 : Gọi X là số người tới trạm điện thoại trung tâm của một vùng trong vòng 5
phút. Giả sử X có phân phối Poisson với λ=3 , bi t
ế e−3≈ 0,05
a. Nói rằng trong 5 phút có 3 người tới trạm điện thoại đúng không ?
b. Tính xác suất để trong 5 phút có không quá 3 người tới trạm ; có từ 2 đến 5 người
tới trạm ; có trên 5 người tới trạm. Trả lời :
a. Trong 5 phút số người trung bình tới trạm là : EX=λ=3
 Kết luận trên là đúng. b. X
ác suất để trong 5 phút có không quá 3 người tới trạm là :
P ( X ≤3 )=P ( X=0 )+P ( X =1)+P ( X=2)+P ( X =3)
λ1 λ2 λ3 9 27
¿ e− λ .( λ0 + + + +
0 ! 1 ! 2 ! 3! )=0,05.(1+3+ 2 6 )=0,65 X
ác suất có từ 2 đến 5 người tới trạm là :
P (3≤ X ≤ 5)=P ( X =3)+P ( X=4)+P ( X =5) λ4 λ5
¿ e−λ .( λ3 + + )=0,05.(4,5+3,375+2,025)=0,495
3! 4 ! 5 ! X
ác suất có trên 5 người tới trạm là :
P ( X >5)=1−P ( X ≤5)=1−( P ( X =0)+P ( X=1)+P ( X =2)+ P( X=3)+P ( X =4 )+P ( X=5))
λ1 λ2 λ3 λ4 λ5
¿ 1−e−λ( λ0 + + + + +
0 ! 1! 2 ! 3 ! 4 ! 5 !)
¿ 1−0,05 (1+3+ 4,5+4,5+ 3,375+ 2,025)=0,08
Bài 15 : Cho biến ngẫu nhiên X có phân phối chuẩn μ=1,5; σ=1,2. Tính xác
suất sao cho trong 3 phép thử độc lập có ít nhất một lần X lấy giá trị trong khoảng (1, 2). Trả lời : -
Xác suất X nhận giá trị trong khoảng (1, 2) là :
P (1< X <2)=Φ (2−μ
σ )−Φ( 1−μ σ )=Φ ( 5 12 )−Φ (−5
12 )=2. Φ (0,42)−1=0,3256
 Xác suất X nhận giá trị ngoài khoảng (1, 2) là :
1−P (1<X <2)=1−0,3256=0,6744
 Xác suất sao cho trong 3 phép thử độc lập có ít nhất một lần X lấy giá trị trong khoảng (1, 2) là :
P=1−0,67443 ≈ 0,6933
Bài 16 : Chiều cao nam giới khi trưởng thành ở một vùng dân cư là biến ngẫu nhiên
có phân phối chuẩn với μ=160 cm, σ =6 cm. Một thanh niên bị coi là lùn nếu có chiều cao dưới 155cm.
a. Tìm tỉ lệ thanh niên bị lùn của vùng đó.
b. Tìm xác suất để lấy ngẫu nhiên 4 người có ít nhất 1 người không bị lùn. Trả lời :
a. Gọi X là chiều cao của thanh niên trưởng thành ở vùng đó.
 X N (160;36 ).
 Tỷ lệ thanh niên bị lùn ở vùng đó là xác suất để lấy ngẫu nhiên 1 người thì người đó
có kích thước nhỏ hơn 155 cm. Ta có:
P (0<X <155 )=Φ(155−160 6 )−Φ(0−160 6
)=Φ(−56)−Φ(−160 6 )¿ 0,2033−0=0,2033
b. Gọi A là biến cố : « lấy ngẫu nhiên 4 người thì có 4 người bị lùn ».  ´A : l y ng ấ u ẫ nhiên 4 ng i ườ có ít nhất 1 ng i ườ không b l ị ùn .
 Xác suất lấy ngẫu nhiên 4 người có 4 người lùn là : P ( A ) 4 0 =P . 0,20334 .
4 ( 4 ; 0,2033 )=C 4
(1−0,2033) =0,20334 ≈ 1,708.10−3
Xác suất lấy ngẫu nhiên 4 người có ít nhất 1 người không bị lùn là :
P ( ´A )=1−P ( A )=1−0,20334 ≈ 0,9983
Bài 17 : Chỉ số thông minh IQ của trẻ em lứa tuổi 12 – 15 ở một vùng dân cư là biến
ngẫu nhiên phân phối chuẩn. Biết rằng tỉ lệ trẻ có IQ trên 85 là 84% và tỉ lệ trẻ có IQ dưới 106 là 65%.
a. Hãy tính IQ trung bình của trẻ lứa tuổi 12-15 của vùng dân cư này.
b. Tính xác suất để khi gặp ngẫu nhiên 1000 trẻ của vùng này thì có từ 620 đến 680 trẻ có IQ thấp hơn 106. Trả lời :
a. Gọi X là chỉ số thông minh IQ của trẻ em lứa tuổi 12 – 15 ở một vùng dân cư có
phân phối chuẩn N (μ ;σ2).
 Theo dữ kiện cho trước, ta có :
P ( X >85)=0,84=¿ P( X ≤ 85)=1−0,84=0,16 85−μ
¿>Φ (85−μ
=−0,99≤¿−0,99 σ + μ=85(¿) σ )=0,16≤¿ σ 106 P − μ
( X <106)=0,65 ≤> Φ(106−μ = 0,39 σ )=0,65≤¿ σ
≤>0,39 σ +μ=106 ¿
Từ (*) và(**) ta có hệ phương trình :
{−0,99σ+μ=85≤¿ 0,39 σ { σ≈15,22 + μ=106 μ ≈100,07
 IQ trung bình của trẻ lứa tuổi 12 – 15 của vùng dân cư này là : EX=μ ≈ 100,07
b. Gọi X là số trẻ có chỉ số IQ thấp hơn 106 trong 1000 trẻ của vùng này được khảo
sát ngẫu nhiên thì X B (n , p) với n=1000 , p=0,65. Do n khá lớn và p không quá
bé nên có thể xem X xấp xỉ phân phối chuẩn N ( μ ;σ2) với :
μ=np=650 và σ2=npq=227,5
Vận dụng công thức xấp xỉ :
P (620<X <680 )≈ Φ (680−μ σ )−Φ(620−μ σ
)=Φ(1,99)−Φ(−1,99)=0,9767−0,0233≈0,9534
Bài 18 : Cho biết trọng lượng X (mg) viên thuốc của lô thuốc sản xuất tại một xí nghiệp dược
phẩm là một biến ngẫu nhiên có phân phối chuẩn với
μ=250,5(mg) và σ2=18,49
a. Hãy tìm mức trọng lượng x0 sao cho có 25% các viên thuốc có trọng lượng cao hơn x0 .
b. Hãy tìm mức trọng lượng x0 lớn nhất sao cho ít nhất có 65% các viên thuốc có trọng
lượng nặng hơn x0.
c. Hãy xác định tỉ lệ các viên thuốc của lô thuốc có trọng lượng thuộc khoảng μ ± 0,25 σ Trả lời :
a. Ta có : P (X >x0)=0,25P ( X ≤ x0)=0,75Φ(x0−μ )=0,75 σ x ≤ 0 − μ > =0,675=¿ x σ 0 =253,4025
b. Ta có x0 lớn nhất thỏa mãn điều kiện : P ( X >x0)=0,65 (vì khi tăng xác suất tìm được
viên thuốc có trọng lượng lớn hơnx0 lên thì x0 sẽ giảm) x  P 0− μ
( X ≤ x0)=0,35≤¿Φ ( x0−μ)=0,35≤¿ =−0,385=¿ x σ σ 0=248,8445
c. Xác định tỉ lệ các viên thuốc của lô thuốc có trọng lượng thuộc khoảng μ ± 0,25 σ là :
P (μ−0,25 σ < X <μ+0,25 σ )=1−P ( X ≤ μ−0,25 σ )−P ( X ≥ μ+0,25 σ )
¿ 1−Φ (μ−0,25σ−μ σ
)−(1−Φ(μ+0,25σ−μ σ
) =Φ(0,25)−Φ(−0,25) ¿ 0,5987−0,4013=0,1974
Bài 19 : Giả thiết rằng tuổi thọ của dân cư ở một nước là biến ngẫu nhiên có hàm mật độ xác suất : 2 p ( x) n u ế x ∈ ={A.x2(100−x) [ 0 ; 100] 0 n u
ế x ∉ [0 ;100 ]
a. Xác định A và tính tuổi thọ trung bình của dân cư nước đó.
b. Khả năng trong 10 người dân có ít nhất 2 người có tuổi thọ từ 60 đến 70 tuổi là bao nhiêu ? Trả lời :
a. Vì p ( x) là hàm mật độ xác suất nên ta có : +∞ 100 1 2
=∫ p ( x) dx= A . ∫ x2(100−x) dx −∞ 0 ¿> A=3. 10−9
Tuổi thọ trung bình của dân cư nước đó là : +∞ 100 EX 2
=∫ x . p (x )=∫ x .3 .10−9. x2(100−x ) dx=50 −∞ 0
b. Xác suất 1 người có tuổi thọ từ 60 đến 70 tuổi là : 70 P (60 2
< X <70 )=3.10−9∫ x2(100−x) dx=0,15436 60
Gọi B là biến cố : « trong 10 người có ít nhất 2 người có tuổi thọ từ 60 đến 70 tuổi ».
P (B )=1−P10 (0;0,15436)−P10 (1;0,15436 )≈ 1−0,187−0,341=0,472
Bài 20 : Tại một bệnh viện khu vực có 5000 người đến làm xét nghiệm máu tìm
ký sinh trùng sốt rét. Tỉ lệ mắc bệnh sốt rét ở địa phương đó theo thống kê là 10%.
Tại bệnh viện có thể làm xét nghiệm máu theo 2 phương pháp :
Phương pháp 1 : Xét nghiệm từng người một ;
Phương pháp 2 : lấy máu của 10 người trộn lẫn làm một xét nghiệm. Nếu kết
quả xét nghiệm là âm tính (vô trùng) thì trong 10 người không có ai mắc bệnh.
Nếu kết quả xét nghiệm là dương tính (có trùng) thì trong 10 người ít nhất có 1
người mắc bệnh. Lúc đó phải làm thêm 10 xét nghiệm lẻ để phát hiện các con bệnh cụ thể.
Hãy xét xem xét nghiệm theo phương pháp nào là có lợi hơn, tại sao ? Trả lời :