Bài thu hoạch | Môn Tối ưu hóa - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58794847
Một công ty cần thực hiện một dự án lắp đặt hệ thống nhà xưởng
bao gồm các công việc với các yêu cầu nêu ra trong bảng sau. Trong
đó, a là thời gian ước tính hoàn thành công việc một cách lạc quan, m
là thời gian ước tính hoàn thành công việc trong điệu kiện bình thường,
b là thời gian ước tính hoàn thành công việc một cách bi quan. Công Thời gian cần (ngày) Thứ tự tiến hành việc a m b Bắt đầu ngay Bắt đầu ngay A 2 3 4 Bắt đầu ngay B 2 2,5 3,5 Sau A hoành thành C 1,5 2,5 7 Sau B, C, D hoàn thành D 6 6,5 10 Sau A hoàn thành E 4 6 8 Sau B, C, D hoàn thành F 6 7,5 10 Sau C hoàn thành G 2,5 3,5 5,5 Sau C hoàn thành H 1,5 2 2,5 Sau E, F, G, H hoàn thành I 3 5,5 6 Sau E, F hoàn thành J 3 3,5 7 Sau E, F hoàn thành K 6 6,5 10 Sau B, D, H hoàn thành L 3,5 5,5 6 Sau J, K, M hoàn thành M 4 5 6 Sau B, D, H hoàn thành N 5 6 7 O 2 2,5 3
a)Hãy tính kỳ vọng và phương sai cho các đại lượng ngẫu nhiên biểu
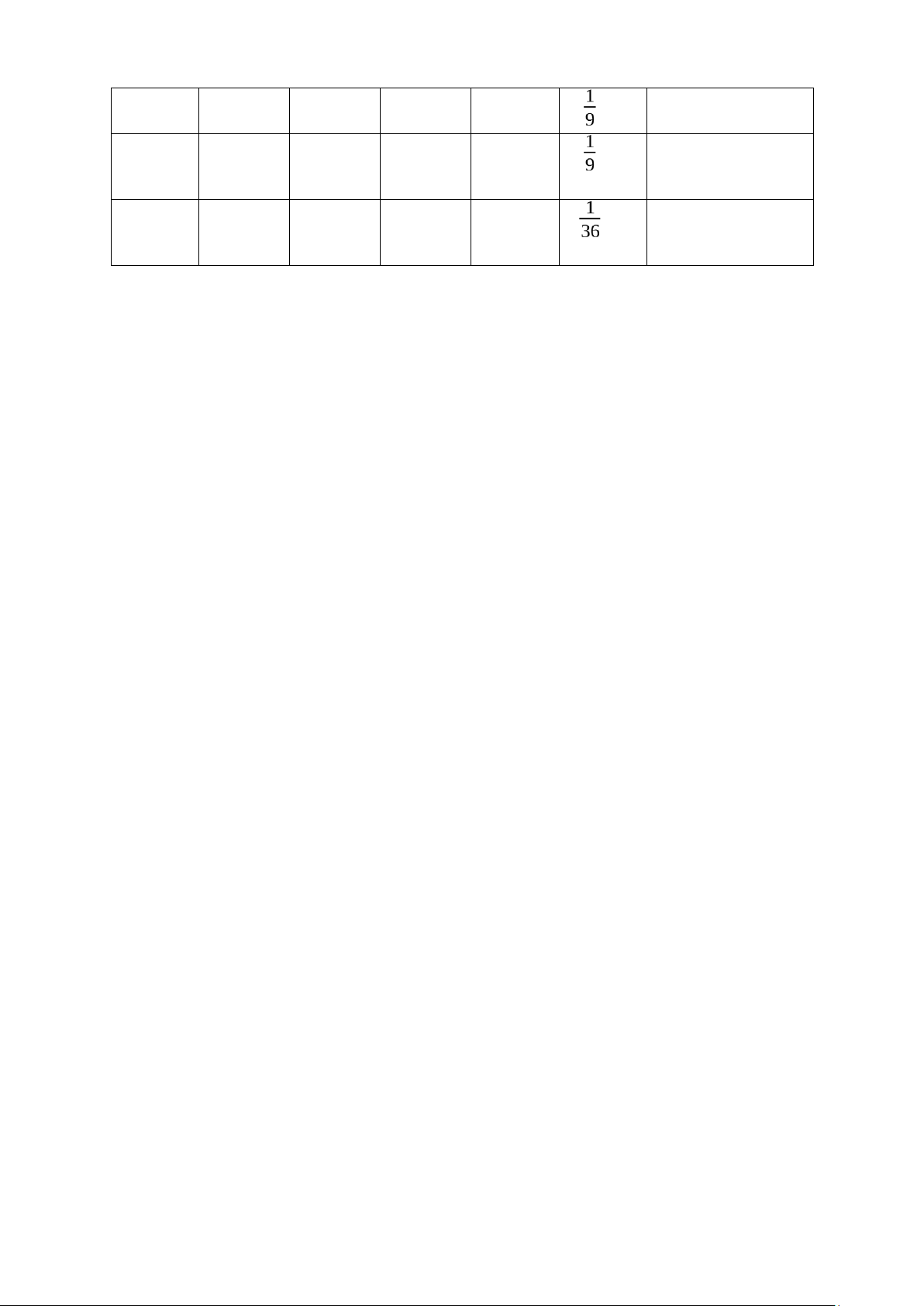
thị thời gian hoàn thành công việc. Khi tính kỳ vọng làm tròn số phần thập phân như sau: Khoản g (0; 0,125] (0,125; 0,25] (0,25; 0,375] (0,375,0,5] (0,5; 0,625] (0,625; 0,75] (0,75; 0,875] (0,875,1) Làm tròn thành 0,125 0,25 0,375 0,5 0.625 0,75 0,875 1
b)Lập sơ đồ PERT, xác định đường găng, ước tính thời gian trung bình
để hoàn thành dự án. Tính xác suất để toàn bộ dự án được hoàn lOMoAR cPSD| 58794847
thành với thời gian không quá 30 ngày (bỏ qua sai số do việc làm
tròn số). Lập bảng chỉ tiêu thời gian cho các công việc. Dựng sơ đồ
PERT ngang với điều kiện công việc H và I không thể thực hiện
trong cùng một thời điểm. Dựng sơ đồ PERT ngang với điều kiện
nguồn lực của công ty không thể thực hiện 4 công việc cùng một thời điểm.
c)Giả sử chi phí để rút ngắn thời gian hoàn thành mỗi công việc theo
quy luật C =4αk−5 k
( là hệ số tỷ lệ được cho trong bảng, Ck là chi
phí rút ngắn ngày thứ k ứng với mỗi công việc và có đơn vị tính là triệu đồng) C. A B C D E F G H I J K L M N O việc Hệ số 10 9 7 13 9 8 7 9 8 10 9 8 9 10 11
Hãy rút ngắn thời gian trung bình hoàn thành dự án không quá 25
ngày với chi phí thấp nhất và tính chi phí tăng thêm đó. Lập bảng chỉ
tiêu thời gian cho các công việc và dựng sơ đồ PERT ngang đối với
kế hoạch sau khi rút ngắn thời gian trung bình hoàn thành dự án không quá 25 ngày. d)
Dự án đang thực hiện theo kế hoạch đã lập ở (c) thì vào đầu ngày
5 có một sự cố xảy ra làm toàn bộ công việc của công ty phải ngưng
thực hiện 01 ngày. Hãy điều chỉnh kế hoạch sao cho thời gian trung
bình hoàn thành dự án không quá 25 ngày với chi phí thấp nhất. e)
Trình bày chi tiết mỗi kế hoạch ở (c) và (d) trên 1 trang giấy A3
biết: Dự án bắt đầu sáng thứ hai ngày 03/07/2023, mỗi tuần làm việc
5 ngày (thứ hai đến thứ sáu), sáng từ 8 giờ đến 12 giờ và chiều từ
13 giờ đến 17 giờ.(phần này giáo viên sẽ hướng dẫn chi tiết)
Phần II (3,5 điểm)
Tìm hiểu cách sử dụng một trong các phần mềm Excel, Maple,
Matlab,…để giải bài toán quy hoạch tuyến tính, bài toán vận tải. Trình
bày cách giải, nhập số liệu, giải và in kết quả đối với các bài toán (đối
với bài 3, bài 4 phải lập mô hình toán học) sau: Baøi 1 Giải bài toán quy hoạch tuyến tính lOMoAR cPSD| 58794847
(1) f (x)=6 x1+14 x2+36x3+23x4 max x1
+2x2 +2x3 +4x4 ¿−8 x2 ¿−5 x1 +4x3 +3x4 ¿2 (2)−3x1
+4x2 −18x3 −10x4 ¿4
(3) x1≥0 , x2 tùy ý, x3≤0 , x4≤0 Bài 2 Minimizing Cost
A manufacturer has two assembly plants, plant A and plant B, and
two distribution outlets, outlet I and outlet II. Plant A can assemble 5000
units of a product in a year and plant B can assemble 4000 units of the
same product in a year. Outlet I must have 3000 units per year and outlet
II must have 5000 units per year. The table shows the costs of
transportation from each plant to each outlet. Find the shipping
schedule that will produce the minimum cost. What is the minimum cost? Baøi 3
AMCHEM Chemical Company produces three products: A, B, and C.
Each product requires labor to produce it, and production of each
product creates pollutants.Bylawthe firm is not allowed to produce
more than the following pollutants per day: 210 pounds of sulfur
dioxide, 300 pounds of carbon monoxide, 160 pounds of hydrogen
sulfide, and 60 pounds of benzene. The total number of person-hours of
labor available per day is 6000. In addition, the total output per day of
products A and B combined cannot be more than the output of product
C. Each pound of product A generates a profit of $7, each pound of B
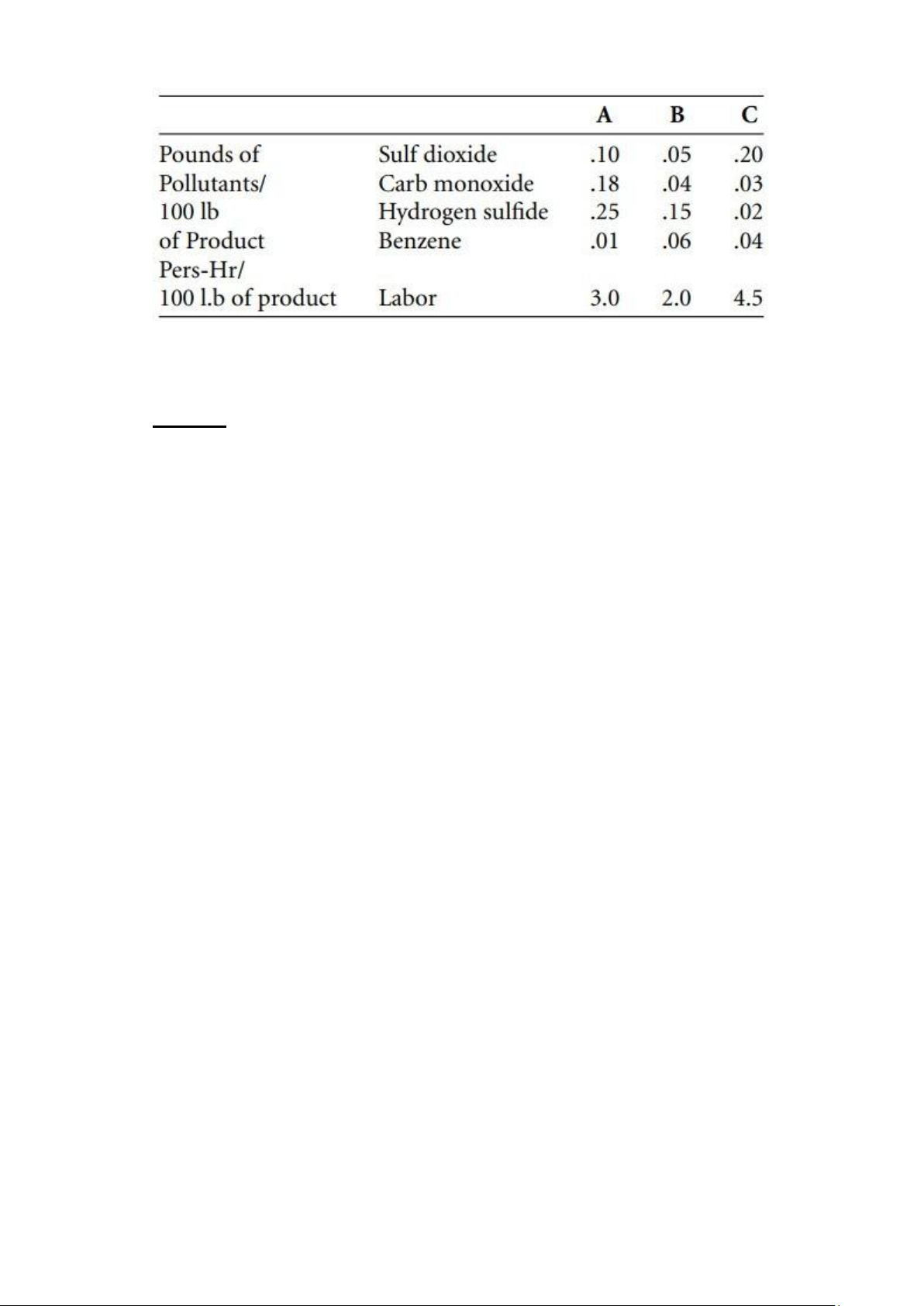
generates $9, and each pound of C generates $6. Pollutant and labor
rates per hundred pounds of product are given here. lOMoAR cPSD| 58794847
a. Formulate this problem as a linear program to maximize daily profit.
b. Solve the problem using a computer. Bài 4 lOMoAR cPSD| 58794847
…………………………………………………………………………………
………………………………………………
Phần III (1,5 điểm)
CUỘC ĐỜI CỦA BẠN như thế nào là TỐI ƯU?
3.1) CUỘC ĐỜI CỦA BẠN như thế nào là TỐI ƯU?
Nếu bạn có được một đời Bình an-Hạnh phúc-Cân bằng-Viên mãn
là tối ưu chưa? Hay bạn cần phải Giàu sang-Thành đạt có đầy đủ Của
cải vật chất và Địa vị xã hội thì mới tối ưu? Hay bạn chỉ cần một cuộc
sống đạt ở mức cơ bản về vật chất-không mất nhiều thời gian công sức
học tập làm việc phục vụ cho nhu cầu vật chất- dành thời gian và nguồn
lực đời người để tạo dựng một đời sống thật khỏe mạnh về thể chất,
phong phú về tinh thần, thăng hoa tâm thức,…? Hãy suy ngẫm về tính
tương đối&tính tuyệt đối của hệ thống các giá trị trong cộng đồng, xã
hội, đời sống, nhân sinh,… lOMoAR cPSD| 58794847
3.2) Bạn có những thiết kế/quy hoạch dài hạn, trung hạn, ngắn hạn
như thế nào và ước tính cách thực hiện ra sao để được một cuộc đời tối
ưu hoặc gần tối ưu? (khi quy hoạch/thiết kế cần chú ý đến các giới hạn
về mặt sinh học của chính bản thân bạn, các ràng buộc mối quan hệ của
bạn với gia đình, cộng đồng, các điều kiện tự nhiên-xã hội,…..)
Hãy nêu trả lời cơ bản ngắn gọn các câu hỏi trên trong một hoặc
vài trang giấy. Mỗi người có điều kiện, hoàn cảnh, trải nghiệm, nhân
sinh quan, thế giới quan,… khác nhau có thể trả lời khác nhau nhưng
phù hợp cho cùng một câu hỏi (nếu người trả lời yêu cầu giữ bí mật các
thông tin rieâng tư có trong câu trả lời thì giáo viên sẽ tuyệt đối thực hiện). ***
Caùc bạn SINH VIÊN thân mến,
Ñaây laø caâu hoûi môû về vấn đề quá rộng và còn rất nhiều bất
định nên không thể có câu trả lời xác định. Trong câu hỏi ẩn chứa nhiều
điều không tường minh. Tuy nhiên, giáo viên mong muốn hỏi để học
từ các bạn sinh viên và để các bạn sinh viên thực sự áp dụng những
kiến thức và kỹ năng đã học được vào trong công việc và cuộc sống để
thành công và hạnh phúc hơn. Khi trả lời các câu hỏi này sẽ giúp người
trả lời hiểu rõ hơn bản chất và ý nghĩa cuộc sống, có các hoạch định/thiết
kế và thực hiện các kế hoạch tương lai tốt hơn nhờ đó tăng khả năng
thành công, thích ứng tốt hơn và vững vàng hơn với các khó khăn và
biến động trong đời sống xã hội, từ đó giúp bạn có được một đời sống
sáng tạo-phong phú-biến đổi tiến triển-đầy thú vị- cân bằng-viên mãn.
Giáo viên tin vaø uûng hoä quan ñieåm: “Ngöôøi hoïc thaät nhieàu
kieán thöùc maø khoâng bieát öùng duïng gì cho cuoäc soáng ñöôïc
haïnh phuùc thì gioáng nhö con löøa thoà saùch”.
Chúc Bạn và Gia đình KHỎE MẠNH-BÌNH AN-HẠNH PHÚC! Ngô Hữu Tâm
……………………………………………………………………
……………………………
Có thể tìm trên Internet (nên làm theo cách này) hay tham khảo các tài liệu sau: lOMoAR cPSD| 58794847 [1]
Nguyễn Đình Tê, EXCELL XP quyển 2, nhà xuất bản Lao động Xã hội – 2007. [2]
Trần Trí Dũng, EXCELL Solver cho kỹ sư, NXB Khoa học Kỹ thuật – 2005.
[3]Phạm Minh Hoàng, MAPLE &các bài toán ứng dụng, NXB
Khoa học Kỹ thuật–2005.
[4] Phạm Trí Cao, Tối Ưu hóa Ứng dụng, NXB Lao động Xã hội - 2014.
Một số yêu cầu đối với bài thu hoạch:
Bài làm được đánh máy trên giấy A4, các hình vẽ thì vẽ bằng tay
hay vẽ bằng máy cũng được miễn sao đạt yêu cầu rõ ràng chính
xác. (kỹ năng vẽ bằng máy hiện chưa cần nên vẽ tay thì tốt hơn)
Ghi đầy đủ họ tên, mã số sinh viên các thành viên trong nhóm và
ít nhất một số điện thoại để liên lạc khi cần. Tự nhận xét và đánh
giá nhóm của các bạn.
Thời gian nộp bài: Từ 27/4/2023 đến 4/5/2023. Nộp lại đề bài này
chung với bài làm– Đề bài ghép chung ngay trước phần bài làm
(không nhận bài nộp mà không có đề). Mục tiêu đánh giá
Phần I Sử dụng sơ đồ PERT-CPM để: Lập kế hoạch cho dự án có
thời gian ngẫu nhiên và biết cách sử dụng thời gian dữ trữ các công việc
không găng để điều chỉnh tối ưu kế hoạch sao cho thuận tiện trong việc
thực hiện và quản lý (câu a&b). Điều chỉnh tối ưu hóa về mặt tài chính
với quy định thời gian cho trước (câu c). Khắc phục sự cố dự án sao cho
tối ưu hóa về mặt tài chính với thời gian quy định cho trước (câu d).
Biết cách lập kế hoạch ngắn gọn chi tiết triển khai thực hiện kế hoạch
dự án với thời gian thực (câu e).
Phần II Nhận dạng được bài toán thực tế dưới dạng ngôn ngữ
thông thường (tiếng Việt hoặc tiếng Anh), lập được mô hình toán học,
sử dụng máy tính và phần mềm thích hợp để giải tìm lời giải tối ưu rồi
suy ra kết quả bài toán thực tế.
Phần III Hoạch định cuộc đời bạn phù hợp nhất/tốt nhất với các
điều kiện/ràng buộc của chính bạn, luôn vững vàng và an lạc trước vạn
biến/vô thường của cuộc đời. lOMoAR cPSD| 58794847 Hết lOMoAR cPSD| 58794847 Bài Làm PHẦN I:
Câu 1: a) Kỳ vọng và phương sai cho các đại lượng ngẫu nhiên biểu thị
thời gian hoàn thành công việc a+4m+b b−a 2 2 E(T)= 6 , Var(T)=( 6 ) =σ Công a m b E(T) V(T) Thứ tự việc (ngày) (ngày) (ngày) tiến hành A 2 3 4 3 Bắt đầu ngay B 2 2,5 3,5 2,625 Bắt đầu ngay C 1,5 2,5 7 3,125 Bắt đầu ngay D 6 6,5 10 7 Sau A hoành thành E 4 6 8 6 Sau B,C,D F 6 7,5 10 7,75 Sau A hoành thành G 2,5 3,5 5,5 3,75 Sau E,F,G,H H 1,5 2 2,5 2 Sau C I 3 5,5 6 5,125 Sau C J 3 3,5 7 4 Sau E,F,G,H K 6 6,5 10 7 Sau E,F L 3,5 5,5 6 5,25 Sau E,F lOMoAR cPSD| 58794847 M 4 5 6 5 Sau B,D,H N 5 6 7 6 Sau J,K,M O 2 2,5 3 2,5 Sau B,D,H
Dựa vào bảng trên ta vẽ sơ đồ Pert 1: lOMoAR cPSD| 58794847 Câu b)
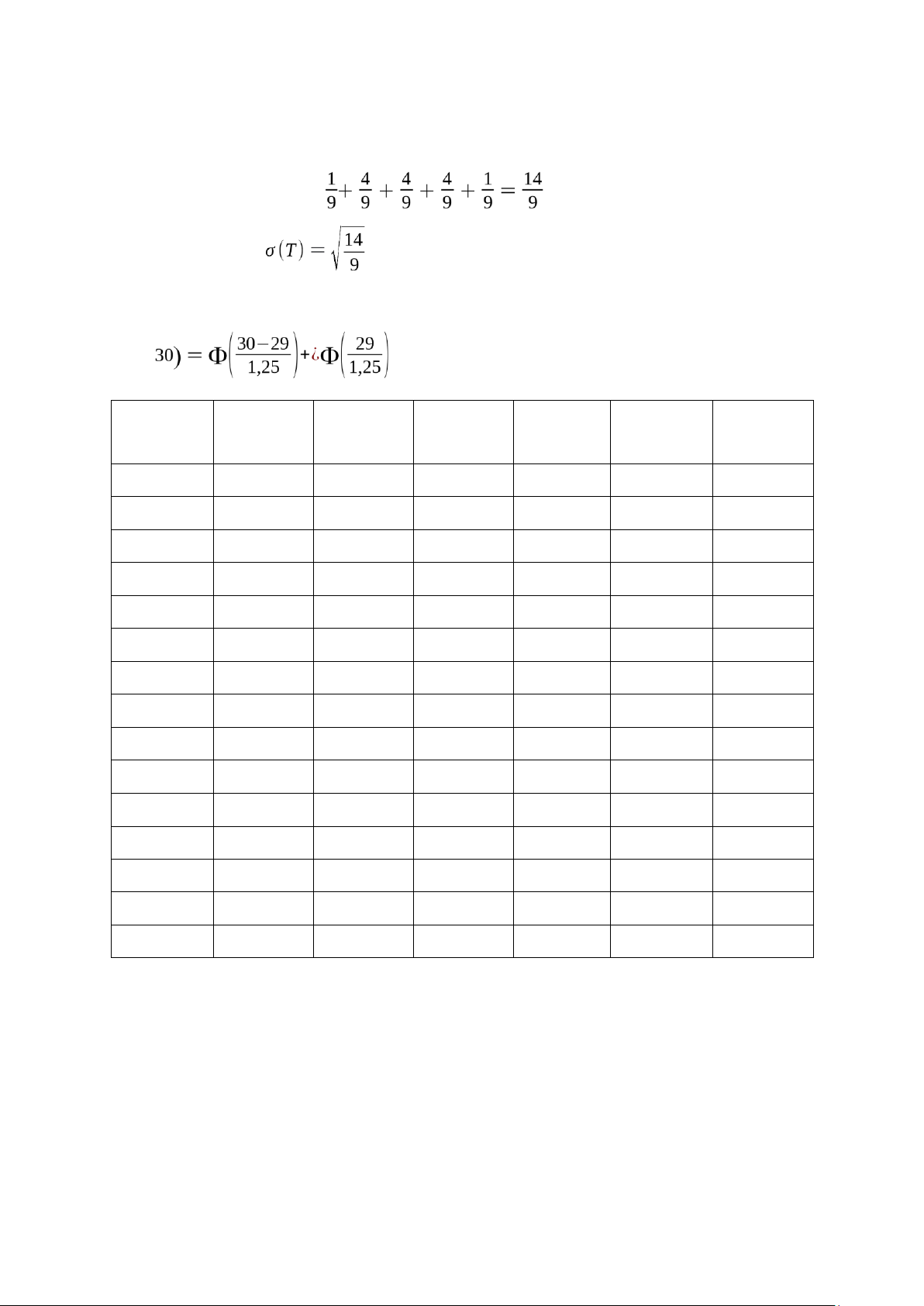
Thời gian trung bình hoàn thành dự án E(T) = 29 Phương sai: Var(T) = Độ lệch chuẩn: = 1,25
Xác suất dự án hoành thành trong thời gian không quá 30 ngày: P(T≤
= 0,288 + 0,5 = 0,788 = 78,88% Công t t t t d d Việc ksij hsij kmij hmij cij dlij A(1;2) 0 3 0 3 0 0 B(1;4) 0 2,625 7,375 10 7,375 7,375 C(1;3) 0 3,125 6,875 10 6,875 0 D(2;4) 3 10 3 10 0 0 E(4;5) 10 16 10 16 0 0 F(2;5) 3 10,75 8,25 16 5,25 5,25 G(4;7) 10 13,75 15,25 19 5,25 2,25 H(3;6) 3,125 5,125 16 18 12,875 0 I(3;9) 3,125 8,375 23,75 29 20,625 13,75 J(7;8) 16 20 19 23 3 0 K(5;8) 16 23 16 23 0 0 L(5;9) 16 21,25 23,75 29 7,75 7,75 M(6;8) 10 15 18 23 8 0 N(8;9) 23 29 23 29 0 0 O(6;9) 10 12,5 26,5 29 16,5 8,5
Với điều kiện công việc H và I không thể thực hiện cùng một thời
điểm và 4 công việc không thể thực hiện cùng một lúc. Dựa vào bảng
trên ta vẽ được sơ đồ Pert ngang 1: Câu c)
Theo đề bài ta có bảng chi phí cho việc rút ngắn thời gian hoàn
thành từng công việc găng như bảng sau ( đơn vị: Triệu đồng/ngày ) lOMoAR cPSD| 58794847 Công việc
Chi phí rút ngắn ngày thứ nhất
Chi phí rút ngắn ngày thứ hai A 35 75 D 47 99 E 31 67 K 31 67 N 35 75
Để rút ngắn thời gian trung bình hoàn thành dự án không quá 25
ngày với chi phí thấp nhất ta nên tiến hành như sau: -
Công việc trên đường găng có chi phí thấp nhất là E ( 31
triệu/ngày ) và K( 31 triệu/ngày). Ta rút E xuống còn 5 ngày ( rút 1
ngày ). Tính lại tất cả chỉ tiêu trên đỉnh ta được sơ đồ pert 2. -
Công việc trên đường găng có chi phí thấp nhất là K( 31
triệu/ngày ). Ta rút K xuống còn 6 ngày (rút 1 ngày). Tính lại tất cả chỉ
tiêu trên đỉnh ta được sơ đồ pert 3. -
Công việc trên đường găng có chi phí thấp nhất là A ( 35
triệu/ngày ) và N ( 35 triệu/ngày ). Ta rút A xuống còn 2 ngày ( rút 1
ngày ). Tính lại tất cả chỉ tiêu trên đỉnh ta được sơ đồ pert 4. -
Công việc trên đường găng có chi phí thấp nhất là N( 35
triệu/ngày ). Ta rút N xuống còn 5 ngày ( rút 1 ngày ). Tính lại tất cả
chỉ tiêu trên đỉnh ta được sơ đồ pert 5.
=> Vậy chi phí tăng thêm là: 31 + 31 + 35 + 35 = 132 triệu
Ta có bảng chỉ tiêu thời gian cho các công việc mới như sau: Công việc tijks tijhs tijkm tijhm dijc dijđe lOMoAR cPSD| 58794847 A (1;3) 0 2 0 2 0 0 B (1;4) 0 2.625 6.375 9 6.375 6.375 C (1;2) 0 3.125 5.875 9 5.875 0 D (3;4) 2 9 2 9 0 0 E (4;5) 9 14 9 14 0 0 F (3;5) 2 9.75 6.25 14 4.25 4.25 G (4;7) 9 12.75 12.25 16 3.25 1.25 H (2;6) 3.125 5.125 13 15 9.875 0 I (2;9) 3.125 8.25 19.875 25 16.75 10.875 J (7;8) 14 18 16 20 2 0 K (5;8) 14 20 14 20 0 0 M (6;8) 9 14 15 20 6 0 N (8;9) 20 25 20 25 0 0 O (6;9) 9 11.5 22.5 25 13.5 7.5 L (5;9) 14 19.25 19.75 25 5.75 5.75
Dựa vào bảng trên ta có sơ đồ pert ngang 2:
Câu d) Dự án đang thực hiện theo kế hoạch như câu c) thì bị sự cố vào
đầu ngày thứ 5 làm gián đoạn 1 ngày, ảnh hưởng đến các công việc D,
F, H, I. Nên ta điều chỉnh bằng cách tăng thêm 1 ngày làm việc cho các công việc này Ta được sơ đồ pert 6
Vì phải đảm bảo thời gian trung bình hoàn thành dự án không
quá 25 ngày, ta rút D xuống còn 7 ngày ( rút 1 ngày ). Tính lại tất
cả các chỉ tiêu trên đỉnh ta được sơ đồ pert 7 Lập bảng chỉ tiêu thời gian mới: Công việc tijks tijhs tijkm tijhm dijc lOMoAR cPSD| 58794847 A (1;3) 0 2 0 2 0 B (1;4) 0 2.625 7.375 10 7.375 C (1;2) 0 3.125 6.875 10 6.875 D (3;4) 2 10 2 10 0 E (4;5) 10 14 10 14 0 F (3;5) 2 10.75 5.25 14 3.25 G (4;7) 10 13.75 12.25 16 2.25 H (2;6) 3.125 6.125 12 15 8.875 I (2;9) 3.125 9.125 18.875 25 15.75 J (7;8) 14 18 16 20 2 K (5;8) 14 20 14 20 0 L (5;9) 14 19.25 19.75 25 5.75 M (6;8) 10 15 15 20 5 N (8;9) 20 25 20 25 0 O (6;9) 10 12.5 22.5 25 12.5
Ta được sơ đồ pert ngang 3 PHẦN II Câu 1:
Đặt x2=x5-x6 với x5 >= 0 và x6 >= 0
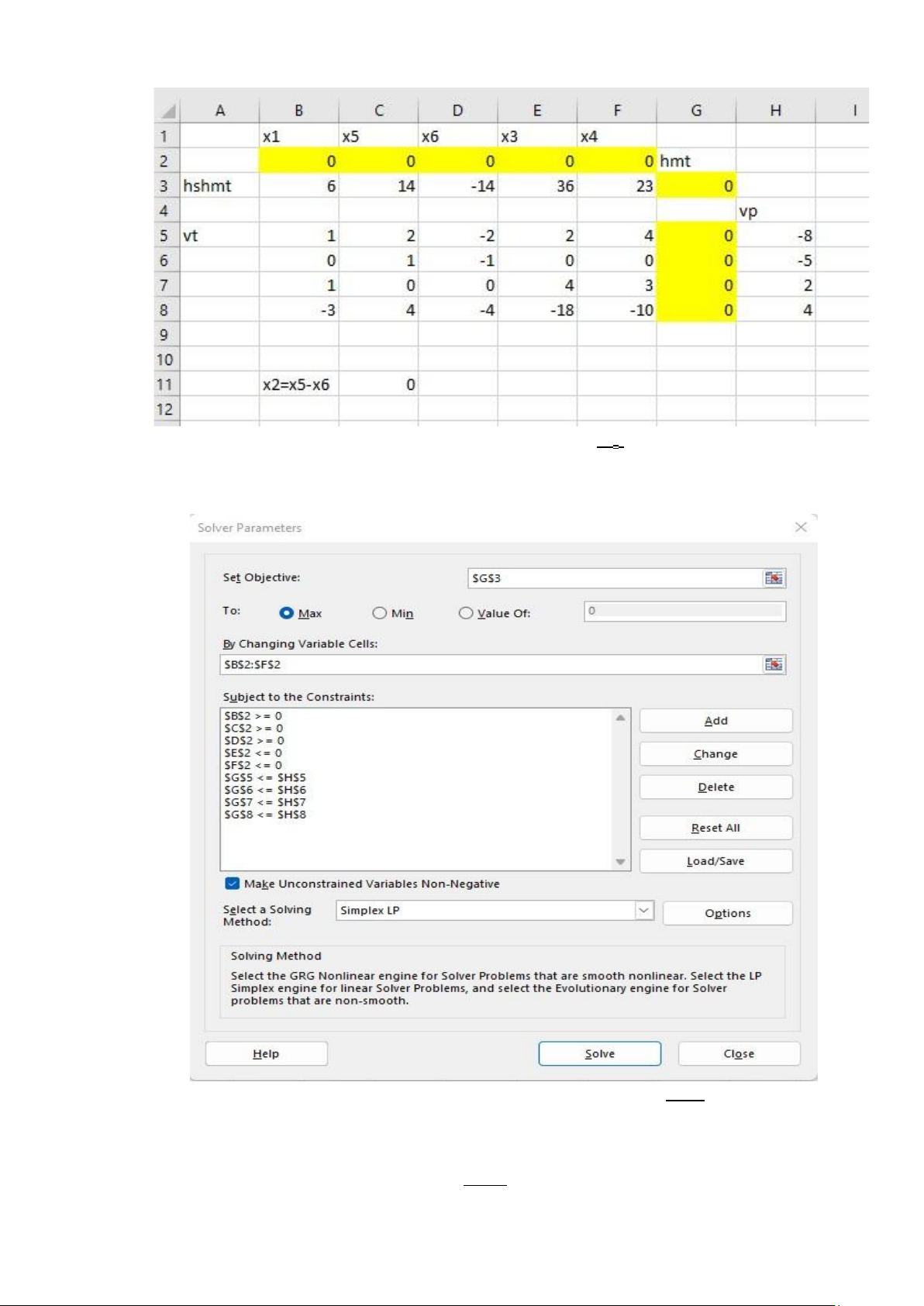
Tiếp đó ta nhập các dữ liệu vào bảng Excel thì được như sau: lOMoAR cPSD| 58794847
Trên thanh công cụ của Excel, bấm chọn Data Solver, ta có được bảng tính như sau:
Ô set objective là ô tính kết quả của hàm mục tiêu Bấm chọn ô $G$3
Vì hàm mục tiêu tiến đến Max Chọn ô Max lOMoAR cPSD| 58794847
Tiếp theo, tại ô By Changing Variable Cells là những ô chứa x thay
đổi, nên ta chọn hàng phương án Chọn ô $B$2:$F$2
Biểu diễn ràng buộc tại ô Subject to the Constraints. Chọn Add sau
đó nhập ràng buộc như sau: $B$2 >= 0 $C$2 >= 0 $D$2 >= 0 $E$2 <= 0 $F$2 <= 0 $G$5 <= $H$5 $G$6 <= $H$6 $G$7 <= $H$7 $G$8 <= $H$8
Sau đó tại mục Select a Solving Method Chọn ô Simplex LP
để giải bài toán tương ứng với thuật toán đơn hình
Cuối cùng ta nhấn Solver để giải thì được kết quả như sau: lOMoAR cPSD| 58794847
Vậy bài toán đã cho có phương án tối ưu (x1,x2,x3,x4)=(2,-5,0,0) và Fmax= -58 Câu 2:
Từ dữ liệu đề bài, ta tổng quát được số liệu của bài toán qua bảng sau:
Gọi x11, x12 là số sản phẩm nhà máy A cần phân phối cho các cửa hàng 1, 2 lOMoAR cPSD| 58794847
Gọi x21, x22 là số sản phẩm nhà máy B cần phân phối cho các cửa hàng 1, 2
Khi đó ta có hàm mục tiêu f=4x11+5x12+5x21+6x22 min
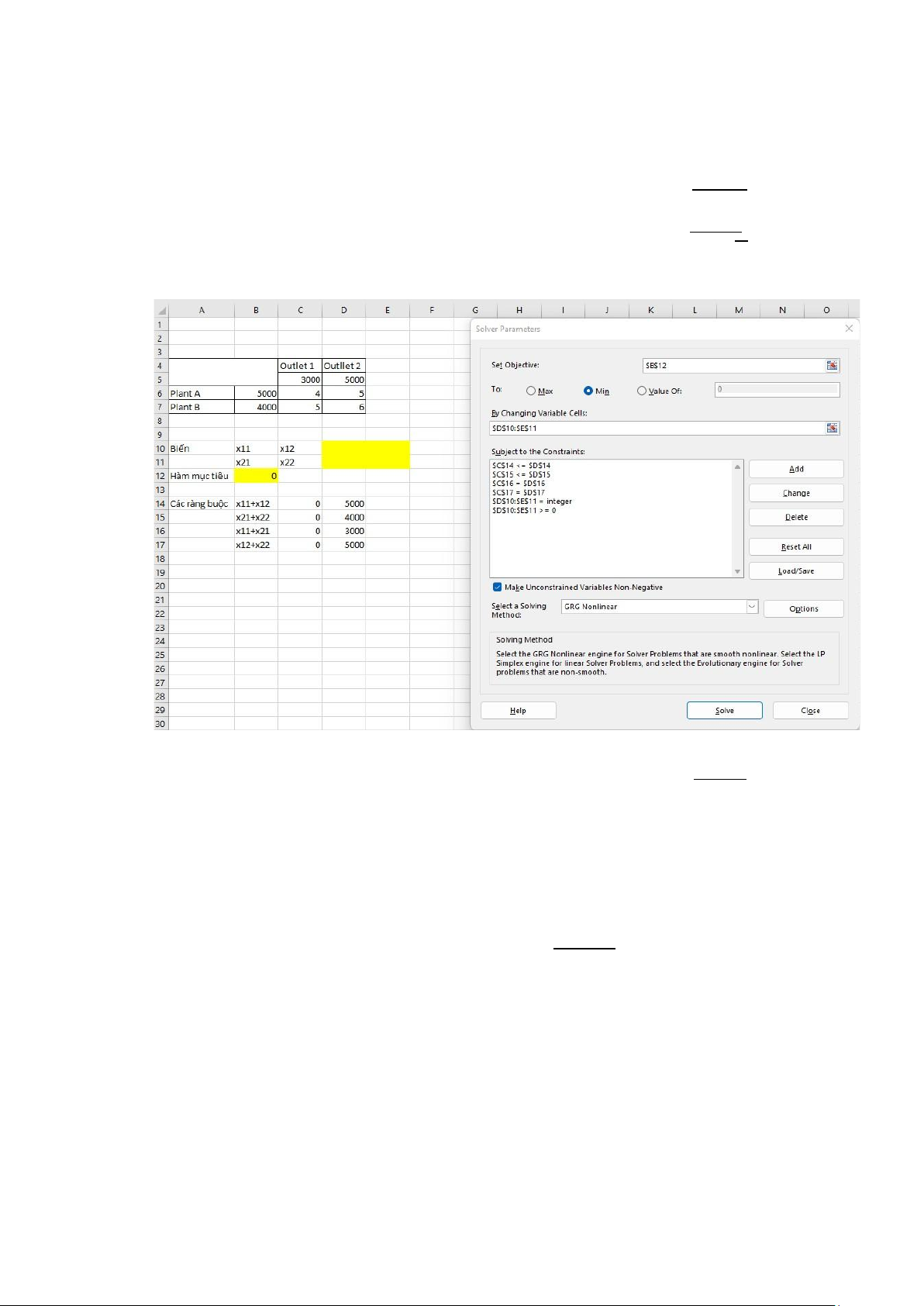
Ta đưa các dữ liệu cần thiết vào Excel và chọn Data Solver thì được như hình sau
Ô Set Objective là là ô tính kết quả của hàm mục tiêu Bấm chọn $B$12
Vì để chi phí vận chuyển là thấp nhất nên ta chọn ô Min
Tiếp theo, tại ô By Changing Variable Cells là những ô chứa các
giá trị thay đổi, nên ta chọn hàng phương án $D$10:$E$11
Biểu diễn ràng buộc tại ô Subject to the Constraints. Chọn Add sau
đó nhập ràng buộc như sau: $C$14 <= $D$14 $C$15 <= $D$15 $C$16 = $D$16 $C$17 = $D$17 lOMoAR cPSD| 58794847 $D$10:$E$11 >= 0 $D$10:$E$11 = integer
Sau đó tại mục Select a Solving Method Chọn ô GRG
Nonlinear để giải bài toán
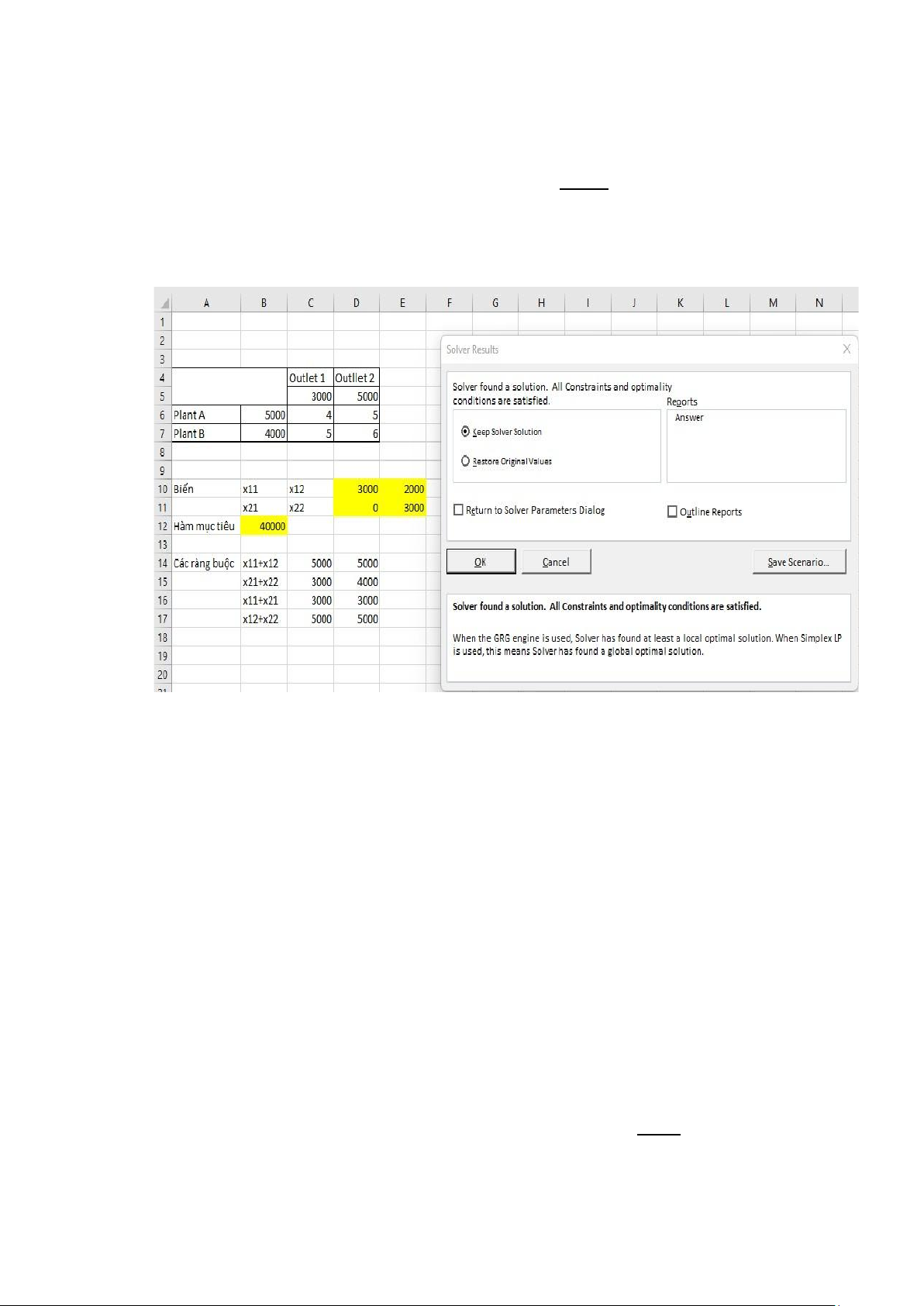
Cuối cùng ta nhấn Solver để giải thì được kết quả như sau:
Vậy ta có thể kết luận được để có thể giảm thiểu chi phí vận chuyển
thì công ty A sẽ phải phân phối 3000 sản phẩm đến cho cửa hàng 1,
2000 sản phẩm đến cho cửa hàng 2. Công ty B sẽ phân phối
3000 sản phẩm đến cho cửa hàng 2
Chi phí tối thiểu khi đó là 40000$ Câu 3
Gọi x1, x2, x3 lần lượt là khối lượng 3 sản phẩm A, B, C mà công ty
hóa học sản xuất trong 1 ngày
Tổng lợi nhuận lớn nhất: fmax= 7x1 + 9x2 + 6x3 max
Lượng chất lưu huỳnh dioxit thải ra khi sản xuất 3 chất A, B, C : lOMoAR cPSD| 58794847
0,1x1 + 0,05x2 + 0,2x3 ≤ 210 (pounds)
Lượng khí cacbonic thải ra khi sản xuất 3 sản phẩm A, B, C:
0,18x1 + 0,04x2 + 0,03x3 ≤ 300 (pounds)
Lượng hydro sunfua thải ra khi sản xuất 3 sản phẩm A, B, C:
0,25x1 + 0,15x2 + 0,02x3 ≤ 160 (pounds) Lượng
benzen thải ra khi sản xuất 3 sản phẩm A, B, C:
0,01x1 + 0,06x2 + 0,04x3≤ 60 (pounds)
Lượng giờ nhân công nhà máy dùng để sản xuất 3 sản phẩm A, B, C:
3x1 + 2x2 + 4,5x3 ≤6000 (giờ )
Tổng sản lượng chất A, B sản xuất ra trong 1 ngày không lớn hơn sản lượng chất C: x1 + x2 – x3 ≤ 0
Lượng sản phẩm được sản xuất ra phải không âm: x1≥0, x2 ≥0 ,x3 ≥0 Tóm lại: (1)
F(x)= 7x1 + 9x2 + 6x3 max 0,1x1 + 0,05x2 + 0,2x3 ≤ 210
0,18x1 + 0,04x2 + 0,03x3 ≤ 300 (2)
0,25x1 + 0,15x2 + 0,02x3 ≤ 160 0,01x1 + 0,06x2 + 0,04x3≤ 60 3x1 + 2x2 + 4,5x3 ≤6000 x1 + x2 – x3 ≤ 0 (3) x1≥0, x2 ≥0 ,x3 ≥0
Lập dữ liệu cho bài toán trong excel như hình: