Mô hình hóa và tối ưu hóa trong công nghệ hóa học và thực phẩm | Môn Tối ưu hóa - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58794847 Nguyễn Tấn Dũng
MÔ HÌNH HÓA VÀ TỐI ƯU HÓA
TRONG CÔNG NGHỆ HÓA HỌC VÀ THỰC PHẨM
NHÀ XUẤT BẢN ĐẠI HỌC QUỐC GIA TP HCM, 2017 lOMoAR cPSD| 58794847 lOMoAR cPSD| 58794847 Chương 1
ĐẠI LƯỢNG NGẪU NHIÊN VÀ ĐÁNH GIÁ SAI
SỐ ĐO LƯỜNG CÁC THÔNG SỐ KỸ THUẬT
1.1. MỘT SỐ KHÁI NIỆM CHUNG 1.1.1. Định nghĩa
Đại lượng ngẫu nhiên là đại lượng biến đổi biểu thị giá trị kết quả của một
phép thử ngẫu nhiên [1].
Như vậy, các đại lượng, các thông số kỹ thuật xác định từ thực nghiệm
cũng có thể được xem là các đại lượng ngẫu nhiên.
1.1.2. Các thông số cơ bản và sai số phép đo của đại lượng ngẫu
nhiên hay các thông số kỹ thuật
1.1.2.1. Một số khái niệm cơ bản
Để xác định sự sai lệch trong các phép đo các thông số kỹ thuật, người ta
thường sử dụng hai đại lượng cơ bản, đó là sai số tuyệt đối và sai số tương đối.
▪ Sai số tuyệt đối
Khi quan sát một đại lượng ngẫu nhiên nào đó cần quan tâm, nếu giá trị
chân thực của nó là a, kết quả quan sát xác định được là X thì sai số phép
đo đó, hay gọi là sai số tuyệt đối, được xác định theo biểu thức: s x = X = X−a (1.1)
▪ Sai số tương đối
Trong thực nghiệm đôi khi cũng cần đến đại lượng sai số tương đối để
biểu diễn sự chính xác trong phép đo lường thực nghiệm, sai số tương đối
được xác định theo biểu thức sau [1]: X X −a =x = (1.2) X X
1.1.2.2. Sai số trong đo lường
Sai số trong đo lường được chia làm 3 loại cơ bản [1]: lOMoAR cPSD| 58794847 ▪
Sai số thô: do vi phạm các điều kiện cơ bản của phép đo,
kết quả quan sát rất khác biệt so với các lần đo khác. Sai số thô sẽ được
loại bỏ dựa vào tiêu chuẩn Cochran. ▪
Sai số hệ thống: giá trị quan sát không khác biệt, không
thay đổi trong toàn bộ loại đo hoặc thay đổi theo một quy luật xác định.
Để phát hiện cần phải có những nghiên cứu đặc biệt, nhưng khi phát hiện
được chúng sẽ loại bỏ một cách dễ dàng bằng cách đưa vào hệ số hiệu chỉnh thích hợp. ▪
Sai số ngẫu nhiên: giá trị sai số s = X sau khi loại bỏ sai
số thô và sai số hệ thống thì sai số còn lại gọi là sai số ngẫu nhiên.
1.1.2.3. Kỳ vọng toán học
Giá trị thực của đại lượng ngẫu nhiên cần quan sát gọi là kỳ vọng toán học, ký hiệu [1]: X = a ± X (1.3) M[X] = a; M[ X] = 0 (1.4)
1.1.2.4. Định luật cộng sai số
Đối với các đại lượng ngẫu nhiên độc lập, tính cộng thể hiện ở những
phương sai chứ không phải ở sai số bình phương trung bình. Nếu X1, X2,
…, Xn là những đại lượng ngẫu nhiên độc lập; a1, a2, …, an là lOMoAR cPSD| 58794847
những đại lượng không ngẫu nhiên và [1]:
Z = a1X1 + a2X2 + … + anXn (1.5)
Thì phương sai s2Z của đại lượng Z được xác định:
s = a .s2Z12 2x1 2 x+a .s2 22+...+a .s2 2n xn (1.6) n Xi
Nếu a1= a2 = … = an = 1/n thì Z = i 1= = X n (1.7) n s2xi
2 2 s2x1+s2x2n+...+s2xn = i 1=n2 s = s = Tương tự ta cũng có: 2 Z X (1.8) n n s2xi s2xi 2 s =2Xi 1= thì s =s =2 2 i 1= 2 = sZ Nếu (1.9) n Z X n n
Trường hợp các đại lượng X1, X2, …, Xn có kết quả đo n lần độc lập
của cùng một đại lượng ngẫu nhiên X thì: s2x (1.10) s2x1 x2=s2
=...=s2xn = =s2x s2x khi đó s =2X n
1.1.2.5. Ước lượng toán học
Ước lượng toán học của các đại lượng ngẫu nhiên xi (i = 1 n) được định
nghĩa là giá trị trung bình của các đại lượng ngẫu nhiên đó [1]. n x lOMoAR cPSD| 58794847 x = 1 + + +x2 ... xn = i 1= xi (1.11) n n
Với: n là số lần thí nghiệm để xác định giá trị xi (i = 1 n) của chúng, xi
là giá trị được xác định ở lần thí nghiệm hay đo thứ i.
1.1.2.6. Phương sai
a) Thiết lập phương trình tính phương sai
Trong lĩnh vực Quá trình và thiết bị công nghệ hóa học – thực phẩm
có rất nhiều đối tượng trong đó có các đại lượng cần xác định nhưng chưa
biết trước quy luật thay đổi của chúng bởi các yếu tố đầu vào, hoặc không
thể thiết lập được mô hình toán để xác định các đại lượng đó. Vấn đề đặt
ra ở đây là làm thế nào để xác định được mối quan hệ giữa đại lượng cần
xác định y với các yếu tố đầu vào xi (i = 1 → n) [1]: y = f(x1, x2, …, xn) + (1.12)
= y– f(x1, x2, …, xn) = y– f(xi) (1.13)
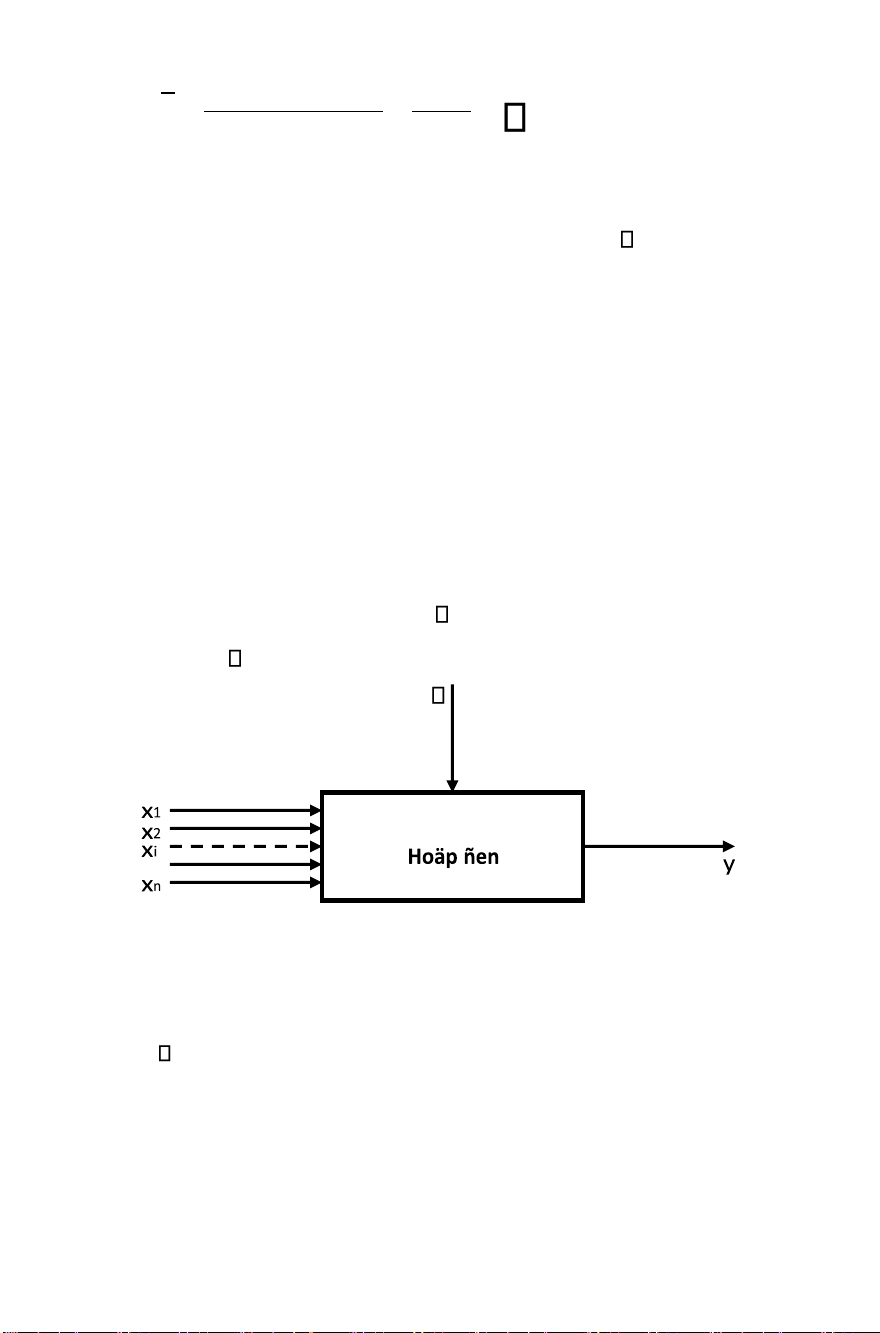
Hình 1.1. Mô hình hộp đen trong nghiên cứu thực nghiệm
xi: biến đầu vào (điều khiển được),
y: thông số đầu ra bị điều khiển bởi biến đầu vào,
: biến ngẫu nhiên (nhiễu) không điều khiển được. lOMoAR cPSD| 58794847
Như vậy, thể hiện sai số của phép đo, khi cho các thông số đầu vào xi sẽ
xác định được giá trị đầu ra là y = f(xi) với (i = 1 → n). Một điều mong muốn ở đây [1]: D[ ] = 2( ); M[ ] = 0 (1.14)
▪ Biến nhiễu này được đánh giá qua các giá trị phương sai
s2 = 2 và kỳ vọng toán học (hay còn gọi là ước lượng toán học) mx = x
của hàm phân phối chuẩn.
▪ Nếu gọi phương sai của các biến đầu vào X = xi (i = 1 → n) là
s2 = 2 và ước lượng toán học là mx = x thì hàm phân phối của đại lượng
ngẫu nhiên X tuân theo định luật chuẩn: f(x) = 1 2 exp - x -m2σ ) 2x 2 (1.15) 2πσ
Khi ấy, xác suất xảy ra đồng thời của n sự kiện độc lập X = xi (i = 1 → n) bằng:
P(x, mx, 2) = f(x1).f(x2)…f(xn). n = 1 ) n exp - 212 n x -mix 2 εn (1.16) 2πσ ) 2 σ i=1
Hàm hợp lý là: L(x, mx, 2) = ln Pn = ε n n 1 n 2 =- 2ln2 - ) 2 - 2 x -mi x (1.17) π 2lnσ 2σ i=1 lOMoAR cPSD| 58794847
Thay mx và 2 bằng x và s2 sẽ được: L(x, x , s - 2) = ln εP n n =- 2ln2π 2lnsn - n 2 21s2 i=1 x - x ) i 2 (1.18)
Thực ra sự kiện với xác suất P đã được thực hiện. Tất nhiên hy vọng rằng:
ngay phép thử đầu tiên sự kiện thực hiện được sẽ có xác suất cực đại (giá
trị đại lượng khảo sát gần đúng nhất, sai số tối thiểu). Có nghĩa là: Lx = 0 sL2 = 0 2L và 2L 2 0 (1.19) 0 x ) 2 s2 L 2 n x = 2s 2
i=1 xi − x)=0 2L 2n Hay
x2 =− 2s2 0 (ñuùng) L 1 1 n 2 2 =− 2s2
n− s2 i=1 xi − x) = 0 s (1.20) lOMoAR cPSD| 58794847 2L 1 n 1 n 2 s ) ) 2 = s2 2
2 − s2 i=1 xi − x) 0 (ñuùng) 2
Vì 1/s2 ≠ 0, từ đây sẽ xác định được ước lượng toán học, phương sai của
sự kiện độc lập. Kỳ vọng toán học hay ước lượng toán học: n 1 n ) i=1 x -x =0i x= n i=1 xi (1.21)
Phương sai được xác định: ) )
n- s12 i=1n x -xi 2 =0 s =2 1 n x -xi 2 (1.22) n i=1
Trong thực nghiệm ước lượng cuối cùng có phần chệch, để nhận n
được ước lượng không chệch thì lấy công thức (1.21) nhân với , như n -1
vậy phương sai được tính theo công thức [1, 27, 28, 29]: n 2 n 2 ) ) x -xi x -xi s =2 i=1 = i=1 (1.23) n - 1 f
Với: f = n -1 gọi là bậc tự do, n là số thí nghiệm.. lOMoAR cPSD| 58794847
b) Độ lệch bình phương trung bình n n 2 x-x x-x 2 i=1 2 i ) i i=1 ) s = s= n - 1 = f (1.24)
Nhận xét: Phương sai đặc trưng cho độ chính xác của phép đo.
c) Các loại phương sai
Trong phương pháp xây dựng mô hình toán thực nghiệm mô tả cho đối
tượng công nghệ thường sử dụng các loại phương sai tái hiện, phương sai
dư và phương sai tương thích để kiểm định mô hình toán. Các loại phương
sai này được định nghĩa như sau.
▪ Phương sai tái hiện
Giả sử tại một chế độ thí nghiệm nào đó (chẳng hạn cùng một áp
suất, nhiệt độ, độ pH, nồng độ, thể tích, …., hay thời gian), ta thực hiện n
thí nghiệm để xác định đại lượng mẫu cần quan tâm, đặt tên cho nó là yj
(j = 1 n). Các thí nghiệm và giá trị yj được mô tả như ở Bảng 1.1 [1, 2, 3, 27]
Bảng 1.1. Các thí nghiệm song song N (số thí nghiệm) 1 2
3 …….. j ….. n - 2 n - 1 n yj (đại lượng cần y quan tâm) 1 y2 y3 ……..yj ….. yn-2 yn-1 yn
Thí nghiệm song song là các thí nghiệm ở cùng một chế độ thí
nghiệm nhưng lập lại n lần, trong trường hợp này ta xác định phương sai tái hiện như sau: 1 n
Ước lượng toán học: y= n j=1 yj (1.25) n 2 n 2
y -i y) yj -y)
Phương sai tái hiện: s = 2 j =1 th = j=1 (1.26) n - 1 f2 lOMoAR cPSD| 58794847
Với: f2 = n – 1 gọi là bậc tự do, n là số thí nghiệm.
Tổng độ lệch bình phương giữa yj & y cũng được xác định: n 2 Sth = y yj - ) (1.27) j=1
Ví dụ 1.1: Người ta tiến hành một quá trình trích ly hợp chất
polyphenol từ lá cây bằng dung môi etanol ở nhiệt độ 370C, tỷ lệ giữa khối
lượng lá cây và dung môi là 1 kg : 4 lít, thời gian trích ly là 6h. Để xác
định hiệu suất của quá trình trích ly cần phải thực hiện n = 9 thí nghiệm
song song nhau, kết quả xác định được ở Bảng 1.2 như sau [1, 27, 28]:
Bảng 1.2. Kết quả xác định hiệu suất trích ly Thí nghiệm 1 2 3 4 5 6 7 8 9
Hiệu suất yj (%) 0,97 0,98 0,95 0,99 0,93 0,97 0,96 0,88 0,94
Hãy xác định phương sai tái hiện và độ chính xác của phép đo. Giải:
Từ số liệu Bảng 1.2, ta xác định ước lượng toán học như sau: 1 n y= n j=1 yj = 0,952222
Bảng 1.3. Kết quả tính toán tổng độ lệch bình phương Thí 1 2 3 4 5 6 7 8 9 nghiệm Hiệu
suất yj 0,97 0,98 0,95 0,99 0,93 0,97 0,96 0,88 0,94 (%)
0,000 0,000 4,94E 0,001 0,000 0,000 6,05E 0,005 0,000
y yj - )2 316 772 -06 427 494 316 -05 216 149
Từ Bảng 3.1, ta xác định được phương sai tái hiện: n 2 n 2 lOMoAR cPSD| 58794847 2 j =1 y -i y)
j=1 yj -y) 0,008756 0,001094 s =th = = = n - 1 f2 9−1
Độ chính xác của phép đo:
1 - s = 1 - s =2 1 – 0,033 = 0,967 = 96,7%
▪ Phương sai dư
Giả sử một đối tượng công nghệ nào đó muốn sử dụng mô hình
toán yM = f(x1, x2, …, xk) ứng dụng vào sản xuất như không biết chúng có
phù hợp hay không? Vì thế, mô hình toán này cần phải sử dụng phương
sai dư để kiểm định tính tương thích trước khi ứng dụng, muốn vậy phải
làm thực nghiệm để kiểm chứng. Giả sử ta thực hiện n thí nghiệm ở n chế
độ khác nhau (x1, x2, …, xk)1, (x1, x2, …, xk)2, …., (x1, x2, …, xk)N để xác
định giá trị yjE (j = 1 N). Các thí nghiệm và giá trị yjE được mô tả như ở Bảng 1.4.
Bảng 1.4. Các thí nghiệm ở các chế độ khác nhau N (số thí nghiệm) 1 2 3 …… j ….. N - 2 N - 1 N yM (xác định bằng mô hình
y1M y2M y3M …yjM ….. y(N-2)M y(N-1)M yNM toán) yE (xác định bằng y thực nghiệm) 1 y2
y3 …yjE ….. y(N-2)E y(N-1)E yNE
Trong trường hợp này, ta xác định phương sai dư như sau [1]: N 2 N 2 y ) ) jM - y jE y jM - y jE
Phương sai tái hiện: s2dư = j = 1 = j = 1 (1.28) N −l f1
Với: f1 = N – l gọi là bậc tự do.
N là số thí nghiệm, l là số hệ số có trong mô hình toán hay là số hệ
số có ý nghĩa trong mô hình toán yM = f(x1, x2, …, xk). lOMoAR cPSD| 58794847
Tổng độ lệch bình phương giữa yjM & yjE cũng được xác định: N 2 S ) du = y jM - y jE (1.29) j=1
Ví dụ 1.2: Mô hình toán mô tả độ tổn thất gluxit của sản phẩm sữa
ong chúa sấy thăng hoa là:
yM = f(x1, x2, x3) = 1,978 + 0,225x1 + 0,228x2 + 0,263x3 + 0,144x2x3 + 0,239x 2 2 2 1 + 0,162x2 + 0,169x3 (1.30)
Với x1 (Z1) là nhiệt độ môi trường sấy thăng hoa; x2 (Z2) là áp suất
môi trường sấy thăng hoa; x3 (Z3) là thời gian sấy thăng hoa. Để kiểm
chứng mô hình toán này người ta thực hiện n = 18 thí nghiệm, kết quả đã
xác định được độ tổn thất gluxit của sản phẩm sữa ong chúa sấy thăng hoa
yE như ở Bảng 1.5. Hãy xác định phương sai dư giữa số liệu mô hình toán
và số liệu thực nghiệm [2, 3, 4, 5, 6]
Bảng 1.5. Kết quả thực nghiệm xác định độ tổn thất gluxit của sản
phẩm sữa ong chúa sấy thăng hoa
Giá trị của các hàm Số Biến thực Biến mã hóa mục tiêu
TN Z1 Z2 Z3 x1 x2 x3 yE
yM (yE – yM)2 1 30 0,758 22 +1 +1 +1 3,25 3,44 0,0357 2 20 0,758 22 -1 +1 +1 2,92 2,93 0,0001 3 30 0,137 22 +1 -1 +1 2,66 2,69 0,0011 4 20 0,137 22 -1 -1 +1 2,12 2,18 0,0037
Giá trị của các hàm Số Biến thực Biến mã hóa mục tiêu
TN Z1 Z2 Z3 x1 x2 x3
yE yM (yE – yM)2 5 30 0,758 18 +1 +1 -1 2,58 2,62 0,0016 6 20 0,758 18 -1 +1 -1 1,97 2,11 0,0207 7 30 0,137 18 +1 -1 -1 2,35 2,46 0,0105 8 20 0,137 18 -1 -1 -1 1,97 1,95 0,0006 9 32,07 0,447 20 +1,414 0 0 3,02 2,82 0,0409 10 17,93 0,447 20 -1,414 0 0 2,17 2,10 0,0063 11 25 0,886 20 0 +1,414 0 2,84 2,62 0,0464 12 25 0,008 20 0 -1,414 0 2,05 1,98 0,0045 lOMoAR cPSD| 58794847 13 25 0,447 22,828 0 0 +1,414 2,84 2,69 0,0231 14 25 0,447 17,172 0 0 -1,414 2,07 1,94 0,0164 15 25 0,447 20 0 0 0 1,87 1,98 0,0122 16 25 0,447 20 0 0 0 2,00 1,98 0,0003 17 25 0,447 20 0 0 0 1,82 1,98 0,0261 18 25 0,447 20 0 0 0 1,94 1,98 0,0011 Tổng 0,2513 Giải:
Thay x1, x2, x3 (tương đương với Z1, Z2, Z3) từ Bảng 1.5 vào mô hình toán
(1.30) sẽ xác định được yM, tất cả ghi vào cột yM của Bảng 1.5, sau đó tiến
hành thực nghiệm ở các chế độ Z1, Z2, Z3 khác nhau (tương đương với x1,
x2, x3) sẽ xác định được yE, tất cả ghi vào cột yE của Bảng 1.5. Tính toán
(yE – yM)2, tính xong ghi vào cột (yE – yM)2 của Bảng 1.5.
Số hệ số trong mô hình toán (1.30) là: l = 8
Số thí nghiệm là: N = 18
Vậy phương sai dư trong trường hợp này được xác định như sau: N 2 N 2 ) ) 2 =
j = 1 y jM - y jE
= j = 1 y jM - y jE = 0,25 31 = 0,02513 s dư N −l f1 18−8
▪ Phương sai tương thích
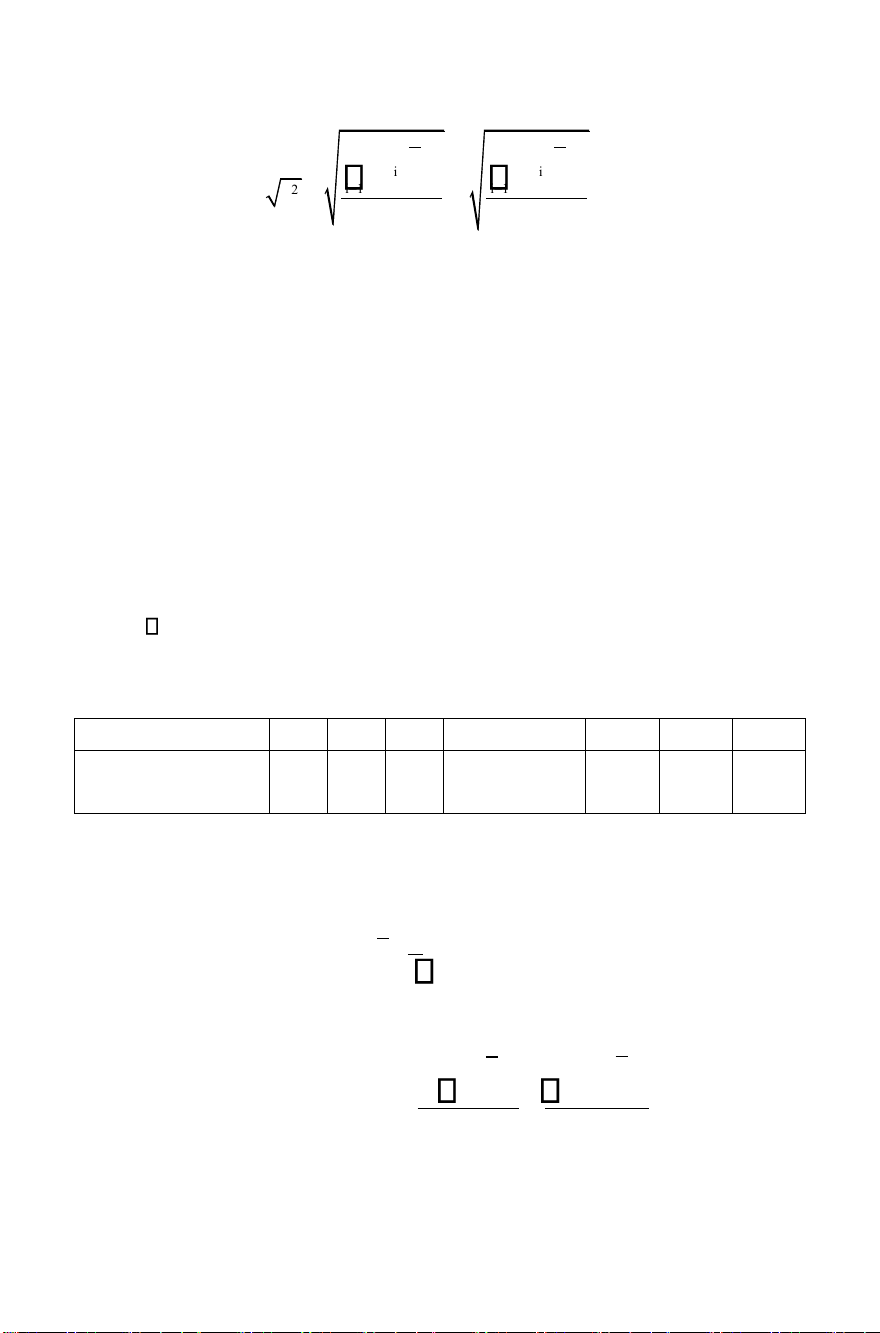
Được xác định theo biểu thức sau [1]: s =tt2 Sdu −Sth (1.31) f
Với: f = f1 – f2 = (N – l) – (n – 1): gọi là bậc tự do.
Ví dụ 1.3: Cũng với bài toán như ví dụ 1.2, hãy xác định phương
sai tương thích của chúng. Giải: lOMoAR cPSD| 58794847 N 2
Từ Bảng 1.5 sẽ xác định được: S ) dư =
y jM - y jE = 0,2513 j = 1
Từ Bảng 1.5 ta thấy các thí nghiệm 15, 16, 17, 18 là các thí nghiệm
thực hiện ở một chế độ song song nhau. Vì thế, ta có thể xác định Sth như sau: n yjE 1= Ta có n = 4, y = j = =1,9058 E n 4 n 2 )
Vậy: Sth = y yjE - E = 0,019 j=1
f = f1 – f2 = (N – l) – (n – 1) = (18 – 8) – (4 – 1) = 7
Phương sai tương thích được xác định như sau:
s =tt2 Sdu −Sth = 0,2513−0,019 =0,03318 f 7
1.1.2.7. Đoạn tin cậy và xác suất tin cậy
Trong nghiên cứu thực nghiệm, khi số lượng mẫu thực nghiệm có hạn thì
cần phải đánh giá mức độ chính xác và độ vững bền của ước lượng, lúc đó
người ta thường dùng giá trị trung bình thay cho kỳ vọng
toán học. Có nghĩa x m− x [1, 27, 28, 29].
Khi nghiên cứu về kỹ thuật công nghệ thì các chỉ tiêu về chất lượng sản
phẩm, về kinh tế kỹ thuật không vượt ra ngoài những biên xác định nào
đó. Việc xác định giá trị của các biên ấy bằng số liệu thực nghiệm rất khó
khăn khi người làm thí nghiệm chỉ thực hiện được một ít thí nghiệm. Để
tránh được vấn đề này thường người ta dùng toán học thống kê. lOMoAR cPSD| 58794847
Cho xác suất đủ lớn cho sự kiện với xác suất có thể xem là chắc chắn
và tìm giá trị = f( ) = thỏa mãn: P(|x m− x | ) = (1.32)
Khi đó: gọi là xác suất tin cậy, trong kỹ thuật thường chọn xác suất tin
cậy = 1 – p = 0,90 (p = 0,1) hoặc = 1 – p = 0,95 (p = 0,05), p gọi là mức ý nghĩa.
Vì: |x m− x | = |m xx −| nên − mx − x + Hay: x − mx + x (1.33)
Các điểm x ' = −x ;x ' = +x là những điểm biên của đoạn tin cậy,
càng lớn thì càng lớn.
Với đại lượng ngẫu nhiên luôn có hàm phân phối chuẩn: P(|x m− x | ) = = 2. x (1.34) x Với: là hàm Laplace; = n x; x ; n là số lượng mẫu. 2 Đặt: k = = = k x; k ) (1.35) x lOMoAR cPSD| 58794847 x Vậy: = = k x k n (1.36) x xk − Từ (1.33) suy ra: m x k n x + x (1.37) n
Kỳ vọng toán học mx biên thiên trong đoạn −k n n x x ; x + k x
, đoạn này gọi là đoạn tin cậy. Khi n tăng thì xác suất tin cậy tăng.
1.2. KIỂM ĐỊNH GIẢ THIẾT THỐNG KÊ
Kiểm định giả thiết thống kê là kiểm tra sự tương thích giữa mô hình toán
yM = f(x1, x2, …, xk) xây dựng từ các số liệu thực nghiệm so với số liệu
thực nghiệm có phù hợp hay không? Nếu phù hợp thì mô hình toán mới
có thể mô tả đối tượng công nghệ cần nghiên cứu, từ đó cho chúng ta biết
hay dự đoán được quy luật biến đổi của quá trình công nghệ xảy ra bên
trong đối tượng nghiên cứu. Nếu không phù hợp thì cần phải chọn lại dạng
mô hình toán dự định mô tả cho đối tượng nghiên cứu, xây dựng lại từ đầu
từ số liệu thực nghiệm để tìm kiếm mô hình cho phù hợp [1, 2, 3, 7, 8, 9].
Để kiểm định sự tương thích mô hình toán yM = f(x1, x2, …, xk) so với số
liệu thực nghiệm, người ta thường sử dụng tiêu chuẩn Fisher như sau: F=SSdu2 2tt 2th hay F=SS2th (1.38)
Nếu F < F1-p(f1, f2) thì yM = f(x1, x2, …, xk) tương thích với số liệu
thực nghiệm [1, 11, 12, 27].
Nếu F > F1-p(f1, f2) thì yM = f(x1, x2, …, xk) không tương thích với số liệu
thực nghiệm [1, 11, 12, 27]. lOMoAR cPSD| 58794847
Với: (1 – p) là xác suất tin cập hay độ tin cậy, f1, f2 là bậc tự do.
1.3. CƠ SỞ KHOA HỌC ĐÁNH GIÁ SAI SỐ TRONG ĐO LƯỜNG
1.2.1. Sai số phép đo trực tiếp
Trong trường hợp này, các đại lượng cần xác định được đo trực
tiếp và sai số của chúng được xác định theo công thức (1.1) [1, 11, 12, 27].
1.2.2. Sai số phép đo gián tiếp
Là đại lượng cần xác định z lại phụ thuộc các đại lượng quan sát x1, x2,
…, xn theo một quy luật đã biết [1, 11, 12, 27]:
z = f(x1, x2, x3, …, xn) (1.39)
Từ phương trình (1.39) khai triển thành chuỗi Taylor tại điểm kỳ vọng
toán học: z = f(xm1, xm2, …, xmn) + xf1 (x1 −1!xm1) + k 2 =
xk1kf (x1 −k!xm1)k + f (x2 −xm2) +
xkk2f (x2 −k!xm2)k + x2 1! k 2= f (xn −xmn) +
kf (xn −xmn)k (1.40) xn 1! k 2= xkn k!
Vì xm1, xm2, …, xmn là kỳ vọng toán học (giá trị chuẩn) của các đại lượng quan sát x ,x ,...,x
1, x2, …, xn, và az = f(xm1 m2
mn) là kỳ vọng toán học (giá trị
chuẩn) của đại lượng z, do đó: x1 −x ) ) )
m1 , x2 −xm2 , ..., x n−xmn chính
là các sai số trực tiếp phép đo của các đại lượng quan sát x1, x2, …, xn,
thực tế khi thực hiện phép đo trực tiếp của các đại lượng quan sát để tính
cho đại lượng quan sát gián tiếp, các hãng chế tạo thiết bị đo làm ra các lOMoAR cPSD| 58794847
thiết bị đo có sai số rất nhỏ, có nghĩa: điểm quan sát đo lường được giá trị
lân cận giá trị chuẩn, do đó sai số tương đối rất bé.
Từ (1.40) chuyển vế rồi bình phương hai vế sẽ được [27, 29]: 2 f (x1 −xm1) n k z -f x m1, xm2, , xmn ) = x1 1! + k 2 = x1kf (x1 −k!xm1)k + xf2 (x2 −1!xm2) + k 2 n= xkk2f (x2 −k!xm2)k + f (xn −xmn) + n kf (xn −xmn)k 2 xn 1! k 2= xkn k! (1.41) k n k 2 n k f 1 x i x − mi 2 2 + k x k! x i i r k 1 x x s2z =i 1 = xf j mi − mj i (xi (1 .42) r! x − j x mi )2 + i 1k 2= = xi x j x − mj 1 , 0 xj 1 , = x j lOMoAR cPSD| 58794847 2i,j 1 n= k,r 2 = x k rf ik kf xrj r k!1 xi −xix i j) (k r) xi xj − Theo (1.42) thì:0 = xmi xi xi xi (i =j 2,3,...,n) kxi 2 → 0, kxi rxj → 0, (k = 2,3,...,n) . Suy ra: k! k! r!
Mặt khác: f(x1, x2, x3, …, xn) là một đại lượng quan sát nên nó là k kf
một hàm liên tục (thông thường f là hàm đa thức) nên đạo hàm xi xik k 2
luôn tồn tại hữu hạn (nếu xi 5% = 5.10-2 → xi 1,25.10−8 k!
(k = 2,3,...,n) , với sai số như vậy thì khó có máy móc thiết bị nào phát
hiện được. Vì vậy, chuỗi số (1.42) sẽ hội tụ về giá trị: 2 n f 2 (1.43)