Đáp án đề thi cuối kì năm 2024-2025 | Môn Tối ưu hóa - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ HỌC KỲ 1
THÀNH PHỐ HỒ CHÍ MINH KHOA KINH NĂM HỌC 2024-2025 TẾ Môn: TỐI ƯU HOÁ
Ngành Quản lý công nghiệp
Mã môn học: MAOP230706
Đề số/Mã đề: 02 Đề thi có 02 trang.
------------------------- Thời gian: 60 phút.
Được phép sử dụng tài liệu Câu 1 (4 điểm): Cho bài toán gốc:
( ):P f x( ) =10x1 −5x +2x2 3 → Max Các ràng buộc: 2x +14x + 2x 1 2 3 0 x - 7x - x 1 2 3 1 16x - 2x 1 3
10 x1 0,x2 ,x3 0
a) Lập bài toán đối ngẫu (D) tương ứng của (P).
b) Sử dụng thuật toán đơn hình để giải bài toán đối ngẫu (D), tìm phương án tối ưu.
c) Sử dụng định lý độ lệch bù yếu để tìm phương án tối ưu của bài toán gốc (P). Câu 2 (3 điểm):
Công ty cổ phần Nông nghiệp Quốc tế Hoàng Anh Gia Lai đang sở hữu 3 miếng đất nông
nghiệp có diện tích đất ở Lâm Đồng, Đắk Nông, Bình Phước lần lượt là 45 ha, 35 ha và 40 ha. Công
ty dự định nhập các giống cây trồng, với số lượng hạt giống này, quỹ đất cần thiết được sử dụng để
trồng trọt bao gồm: Mít: 42 ha, Sầu riêng: 26 ha, Xoài: 37 ha.
Năng suất khi sử dụng đất của HTX để trồng các loại cây ăn quả này được cho trong bảng sau: (ĐVT: tạ/ha) Mít Sầu riêng Xoài Lâm Đồng 36 29 45 Đắk Nông 57 65 90 Bình Phước 54 79 72
Theo tình hình hiện tại, công ty mong muốn được sử dụng hết diện tích đất ở Lâm Đồng cho việc trồng
trọt, và lô đất ở Bình Phước không phù hợp để trồng sầu riêng. lOMoAR cPSD| 58794847
Hãy xác định kế hoạch trồng trọt tối ưu để tối đa hoá năng suất cho Công ty cổ phần Nông nghiệp
Quốc tế Hoàng Anh Gia Lai? Câu 3 (3 điểm):
Xưởng Mây nhận một đơn hàng xuất khẩu 100 túi mây tre. 3 tổ sản xuất A,B,C sẽ tham gia
quá trình sản xuất cho sản phẩm này. Cụ thể, tổ A có 1 công nhân, tổ B có 3 công nhân, tổ C có 2
công nhân. Theo kế hoạch sản xuất, hàng ngày các công nhân sẽ tiến hành đan thân túi, đáy túi và
quai xách. Sau đó, liên kết các chi tiết theo cấu trúc 1 thân, 1 đáy, 2 quai xách để tạo thành thành phẩm.
Năng suất sản xuất trong 1 ngày của các công nhân được cho trong bảng sau: Thân Đáy Quai xách (1) (1) (2)
Tổ A : 1 công nhân 3 2 6
Tổ B : 3 công nhân 2 3 2
Tổ C : 2 công nhân 7 4 12
a) Hỏi phải phân công thời gian sản xuất của các tổ sản xuất như thế nào để số túi mây tre sản xuất
trong 1 ngày là nhiều nhất? Ước tính thời gian trung bình để hoàn thành hợp đồng ? (2,5 điểm)
b) Hỏi phải phân công trình tự sản xuất Thân, Đáy, Quai xách cho các tổ sản xuất như thế nào để
hoàn thành hợp đồng sớm nhất? (0,5 điểm)
Ở bài toán SXĐB, SV trình bày kết quả ở dạng số, lấy 2 chữ số thập phân sau dấu phẩy, KHÔNG
trình bày ở dạng phân số.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Chuẩn đầu ra của học phần (về kiến thức) Nội dung kiểm tra
[CĐR 1.2]: Sử dụng một số phương pháp để giải bài toán Câu 1
quy hoạch tuyến tính
[CĐR 2.1]: Sử dụng thuật toán thế vị để giải bài toán vận Câu 2 tải
[CĐR 3.1]: Sử dụng thuật toán nhân tử để giải bài toán sản Câu 3 xuất đồng bộ Ngày tháng năm 2024 Thông qua bộ môn
(ký và ghi rõ họ tên) lOMoAR cPSD| 58794847 Đáp án Câu 1 (4 điểm):
a. Lập bài toán đối ngẫu (D) tương ứng của (P).
(D): g y( ) = +y2 10y3 → Min 2y +y + 16y 1 2 3 10 1 điểm 14y - 7y 1 2 -5 2y - y - 2y 1 2 3 2 y y1, 2, y3 0
b. Sử dụng thuật toán đơn hình để giải bài toán đối ngẫu (D), tìm phương án tối ưu.
Đưa bài toán về dạng chuẩn: Các ràng buộc chính 2y +y + 16y +y = 1 2 3 4 10 -14y + 7y +y 1 2 5 =5 0.25 điểm
2y - y - 2y -y1 2 3 6 +y7=2
y y1, 2, y3, y4, y5, y6, y7 0
Ẩn phụ: y y y4, 5, 6 Ẩn giả: y7 0.5 điểm Hàm mục tiêu
(D): g(y) = 𝑦2 + 10𝑦3 + 𝑀𝑦7 → 𝑀𝑖𝑛 lOMoAR cPSD| 58794847 1 điểm ci yi bi Y1 Y2 Y3 Y4 Y5 Y6 𝝀𝒊 0 1 10 0 0 0 0 Y4 10 2 1 16 1 0 0 5 0 Y5 5 -14 7 0 0 1 0 - M Y7 2 2 -1 -2 0 0 -1 1 g(y) 2M 2M -M -2M 0 0 -M -1 -10 0 Y4 8 0 2 18 1 0 1 - 0 Y5 19 0 0 -14 0 1 -7 - 0 Y1 1 1 -1/2 -1 0 0 -1/2 - g(y) 0 0 -1 -10 0 0 0 Kết luận:
Điều kiện tối ưu: ∆𝑗≤ 0∀𝑗 nên PATU của BT dạng chuẩn là y* = (1,0,0,8,19,0,0); g(y*)=0
0.25 điểm Vì y7 = 0 là ẩn giả nên phương án tối ưu: y* = (1,0,0)
Giá trị tối ưu: g(y*) = 0
c. Sử dụng định lý độ lệch bù yếu để tìm phương án tối ưu của bài toán gốc (P).
𝑦1 = 1 ⇒ 2𝑥1 + 14𝑥2+2𝑥3 = 0
2𝑦1 + 𝑦2 + 16𝑦3 = 2 < 10 ⇒ 𝑥1 = 0 14𝑦1 − 1 điểm
7𝑦2 = 14 > −5 ⇒ 𝑥2 = 0 𝑥1 = 0  {𝑥2 = 0 𝑥3 = 0 f(x*) = 0 Câu 2 (3 điểm):
Giả sử diện tích đất ở Lâm Đồng, Đắk Nông, Bình Phước lần lượt là A1:45 ha, A2: 35 ha
và A3:40 ha. Quỹ đất cần thiết được sử dụng để trồng trọt bao gồm: B1:42 ha, B2:26 ha, B3:37 ha. lOMoAR cPSD| 58794847 A1 + A2 + A3 = 120 (ha) B1 + B2 + B3 = 105 (ha) 0.5 điểm
=> Thêm trạm thu giả B4 = 15 (ha)
Vì công ty mong muốn được sử dụng hết diện tích đất ở Lâm Đồng cho việc trồng trọt, và
lô đất ở Bình Phước không phù hợp để trồng sầu riêng nên: c14 = - M; c32 = - M (M >0, rất lớn). 1 điểm
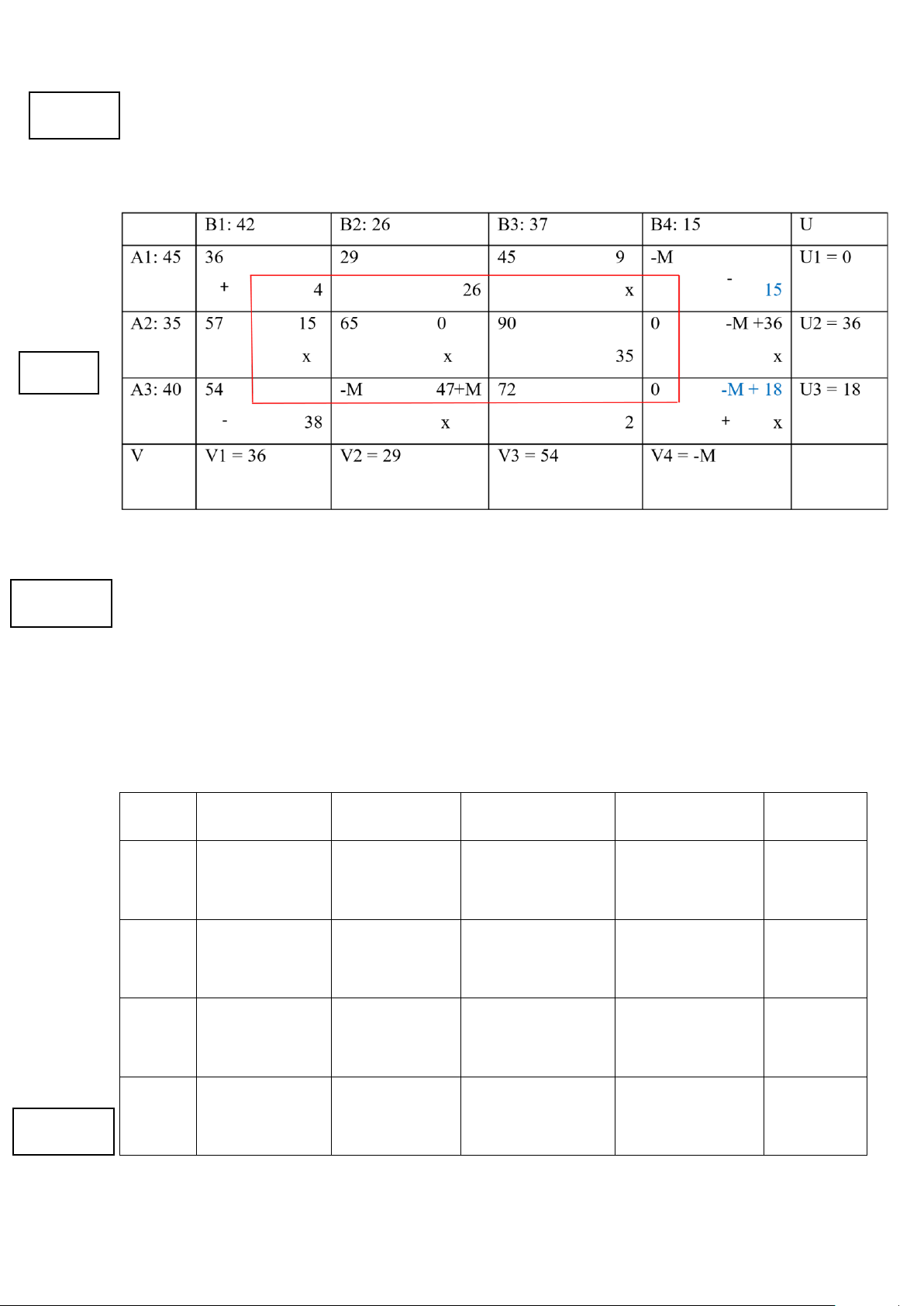
Tồn tại ∆ ij ≤ 0, => PA trên chưa phải là PATƯ của bài toán Ô đưa vào (3;4) 0.25 điểm Ô đưa ra (1;4) d=15 B1: 42 B2: 26 B3: 37 B4: 15 U A1: 45 36 29 45 9 x -M -18+M U1 = 0 19 26 A2: 35 57 15 65 0 x 90 0 18 U2 = 36 x x 35 A3: 40 54 -M 47+M 72 0 U3 = 18 23 x 15 2 V V1 = 36 V2 = 29 V3 = 54 V4 = -18 0.75 điểm
∆ ij ≥ 0 với mọi ô ij, => PA trên là PATƯ của bài toán lOMoAR cPSD| 58794847 19 26 0 0
0.25 điểm X* = ( 0 0 35 0 ), f(x*) = 5974 (tạ) 23 0 2 15
X14 = 0, X32 = 0 là ô cấm nên BTBĐ có PATƯ là: 19 26 0 0.25 điểm X* = ( 0 0 35) , f(x*) = 5974 (tạ) 23 0 2 Câu 3 (3 điểm):  Cách 1:
Ma trận năng suất ước lượng: 0.25 điểm Thân Đáy Quai xách (1) (1) (1)
Tổ A : 1 công nhân 3 2 3
Tổ B : 1 công nhân 6 9 3
Tổ C : 1 công nhân 14 8 12 Bước 1:
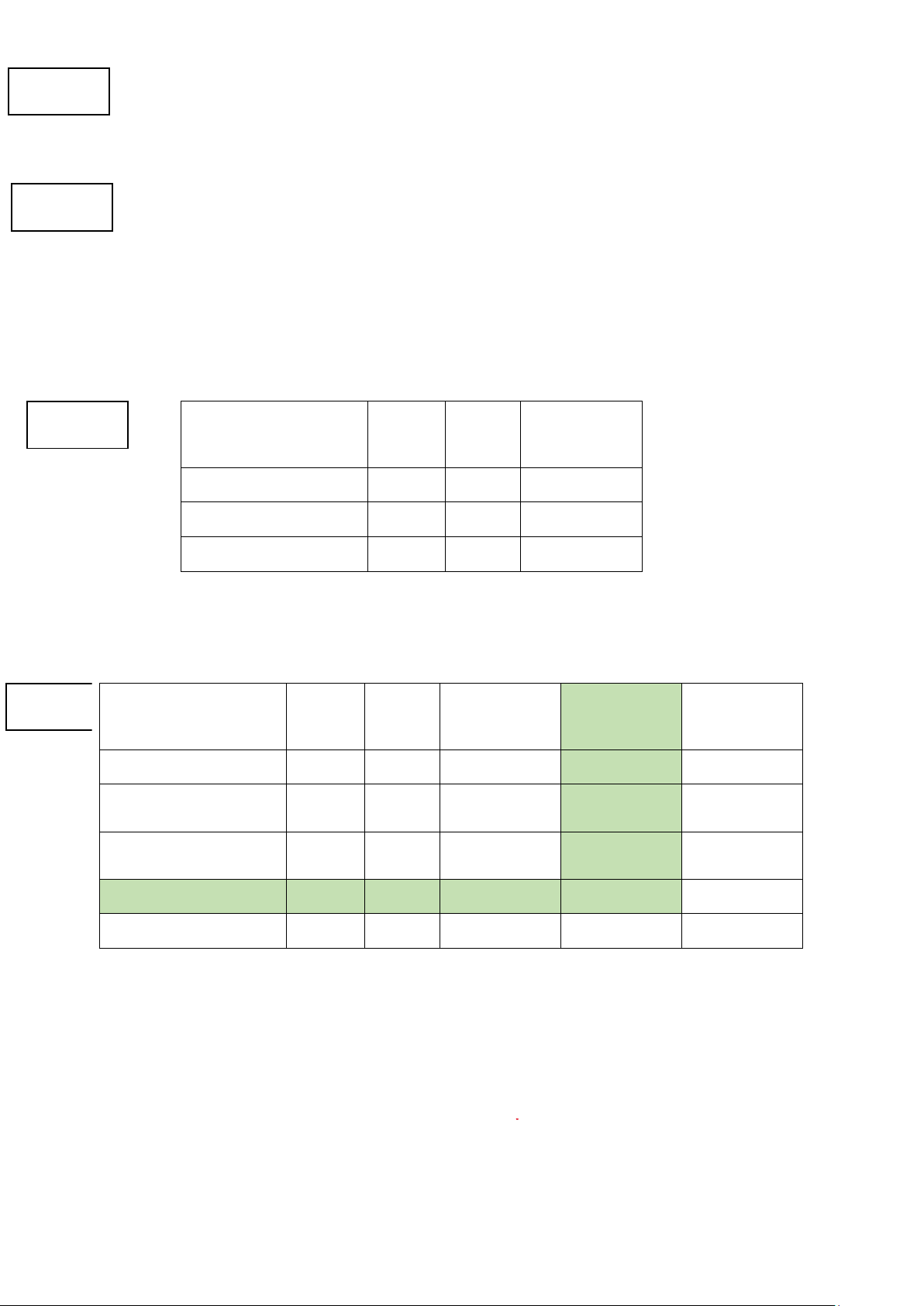
Hệ thống nhân tử và ô chọn: Thân Đáy Quai xách ui 0.5 điểm (1) (1) (1)
Tổ A : 1 công nhân 3 2 3 * 3,51 + Tổ B : 1 công 6 9 * 3 15,75 - nhân Tổ C : 1 công 14 * 8 * 12 * 14 + nhân vj 1 1,75 1,17 + - + Z=8,49
Hệ phương trình giải đúng ( SV phải trình bày hệ phương trình để giải) Ma trận phương án lOMoAR cPSD| 58794847 0 0 1 0 1 0 0,61 -0,07 0,46 0.25 điểm  Ô đi ra: (3,2) 0.25 điểm
Lamda: 2,63 => Ô đi vào: (2,1) Thân Đáy Quai xách ui 0.5 điểm (1) (1) (1)
Tổ A : 1 công nhân 3 2 3 * 9,19 Tổ B : 1 công 6 * 9 * 3 15,75 nhân Tổ C : 1 công 14 * 8 12 * 36,75 nhân vj 2,63 1,75 3,06 Z = 8,29 0.25 điểm
Hệ phương trình giải đúng suy ra Ma trận phương án 0 0 1 0.5 điểm 0,08 0,92 0 0,56 0 0,44
a. Phương án tối ưu của bài toán 0 0 1 0,08 0,92 0 0,56 0 0,44 0.25 điểm
Thời gian trung bình để hoàn thành hợp đồng: 100/8,29 = 12,06 ngày
b. Phân công trình tự sản xuất: 0.25 điểm
Tổ 1 sản xuất quai xách trong 12,06 ngày.
Tổ 2 sản xuất đế trong 11,1 ngày, sau đó sản xuất thân trong 0,96 ngày.
Tổ 3 sản xuất quai 5,31 ngày, sau đó sản xuất thân trong 6,75 ngày.  Cách 2: lOMoAR cPSD| 58794847 Thân Đáy Quai xách ui 1.5 điểm (1) (1) (1)
Tổ A : 1 công nhân 3 2 3 * 3.51 Tổ B : 1 công 6 * 9 * 3 6 nhân Tổ C : 1 công 14 * 8 12 * 14 nhân vj 1 0.67 1.17 Z = 8,28 0.5 điểm
Hệ phương trình giải đúng suy ra Ma trận phương án 0 0 1 0.5 điểm 0,08 0 0,92 0,56 0 0,44
a. Phương án tối ưu của bài toán 0 0 1 0,08 0,92 0 0.25 điểm 0,56 0 0,44 Thời gian
trung bình để hoàn thành hợp đồng: 100/8,29 = 12,06 ngày
b. Phân công trình tự sản xuất: 0.25 điểm
Tổ 1 sản xuất quai xách trong 12,06 ngày.
Tổ 2 sản xuất đế trong 11,1 ngày, sau đó sản xuất thân trong 0,96 ngày.
Tổ 3 sản xuất quai 5,31 ngày, sau đó sản xuất thân trong 6,75 ngày.