-
Thông tin
-
Hỏi đáp
Bài toán đếm Toán rời rạc- Công nghệ thông tin | Đại học Mở Hà Nội
Dạng tổng quát nhất của bài toán đếm có thể phát biểu ngắn gọn như sau: Cho một tập rời rạc A; tìm bản số |A| của tập A, tức là hãy đếm xem Acó bao nhiêu phần tử. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Công nghệ thông tin (Mở HN) 16 tài liệu
Đại học Mở Hà Nội 405 tài liệu
Bài toán đếm Toán rời rạc- Công nghệ thông tin | Đại học Mở Hà Nội
Dạng tổng quát nhất của bài toán đếm có thể phát biểu ngắn gọn như sau: Cho một tập rời rạc A; tìm bản số |A| của tập A, tức là hãy đếm xem Acó bao nhiêu phần tử. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn: Công nghệ thông tin (Mở HN) 16 tài liệu
Trường: Đại học Mở Hà Nội 405 tài liệu
Thông tin:
Tác giả:
Preview text:
TOÁN RỜI RẠC – Lý thuyết
Chương 2. BÀI TOÁN ĐẾM
2.1. PHÁT BIỂU BÀI TOÁN
Dạng tổng quát nhất của bài toán đếm có thể phát biểu ngắn gọn như
sau: Cho một tập rời rạc A; tìm bản số |A| của tập A, tức là hãy đếm xem A
có bao nhiêu phần tử.
Khi đếm các phần tử của A phải đảm bảo nghiêm ngặt 2 nguyên tắc:
Một là: Không bỏ sót, nghĩa là phần tử nào cũng được đếm.
Hai là: Không trùng lặp, nghĩa là không có phần tử nào được đếm quá một lần.
Phương pháp tổng quát để giải bài toán đếm có thể diễn giải như sau:
Giả sử A là tập cần đếm, N = {1, 2, 3, ..., n} là tập n số nguyên dương đầu
tiên. Nếu lập được sự tương ứng đơn trị hai chiều giữa các phần tử của A
và các phần tử của N; nghĩa là tìm được một song ánh f f : A Nthì | A | = n
Tuy nhiên có rất nhiều cách cho tập A khác nhau nên phương pháp nêu
trên chỉ có ý nghĩa như một định hướng tổng quát, còn trên thực tế thì
người ta phải căn cứ vào hình thái cụ thể của tập A mà tìm ra một giải pháp thích hợp.
Hãy xét một vài ví dụ dưới đây để thấy rõ điều đó
Thí dụ 1.
Cho A = {x}: x là các số nguyên, dương, 100 và x2 − 1 chia hết cho 24. Tìm |A|.
Thí dụ 2.
Cho A = {x}: x là các con số hàng nghìn mà các chữ số của nó tạo
thành một dãy tăng (thí dụ 1348, 2569, …). Về mặt hình thức thì trong hai
thí dụ trên đều là tìm các con số thỏa mãn những điều kiện nhất định;
nhưng trong thí dụ 2 thì mỗi con số lại là một cấu hình tổ hợp gồm 4 chữ số
chọn trong 9 chữ số và xếp theo một thứ tự nhất định. Việc đếm các cấu
hình tổ hợp như vậy nói chung là phức tạp hơn.
Thí dụ 3.
Một người vượt cầu thang có 13 bậc, lúc thì bước 1 bậc, lúc thì bước 2
bậc, lúc thì bước 3 bậc một bước. Hỏi có bao nhiêu cách vượt cầu thang
như thế, tập A ở đây là tập các cách vượt cầu thang, có ý nghĩa như là tập
TOÁN RỜI RẠC – Lý thuyết
các “giải pháp” cho một vấn đề đặt ra, phức tạp hơn nhiều so với các thí dụ trước.
Thí dụ 4.
Có bao nhiêu lần lặp trong đoạn chương trình C++ dưới đây: int n1 = 5, n2 = 10, S = 0;
for (int i = 1; i = n1; i + +) S + +;
for (int i = 1; i = n2; i + +) S + +;
Số lần lặp ở đây tương ứng với số phép toán để thực hiện đoạn chương
trình nói trên. Mở rộng thí dụ này, vấn đề đặt ra có thể là: Tìm số phép toán
của chương trình thực hiện một thuật toán nào đó; con số này đặc trưng cho
độ phức tạp của thuật toán.
Thí dụ 5.
Một loài khuẩn sinh trưởng theo nguyên tắc sau đây: khi đủ a ngày tuổi
(a nguyên dương) thì nó bắt đầu sinh sản, mỗi ngày một lứa, mỗi lứa sinh
được b khuẩn con (b nguyên dương). Tại thời điểm t = 0, số khuẩn là n0
con đều là mới sinh ra. Tìm số khuẩn n tại thời điểm T T a (T nguyên
dương) với giả thiết trong khoảng thời gian t [0, T] không có con khuẩn
nào bị chết. A ở đây là tập các con khuẩn trong quá trình sinh trưởng của nó.
Qua các thí dụ trên ta thấy tập A có rất nhiều hình thái khác nhau, do đó
phương pháp đếm các phần tử của A cũng có một đa dạng tương ứng.
Mỗi phương pháp đếm là một thuật toán, nên trước tiên ta tìm hiểu
những khái niệm cơ bản về thuật toán.
2.2. KHÁI NIỆM THUẬT TOÁN
2.2.1. Định nghĩa
Thuật toán giải một bài toán nào đó, có thể hiểu một cách trực quan là
một dãy hữu hạn các bước chỉ rõ những thao tác toán học phải thực hiện
trên các đối tượng để thu được lời giải của bài toán.
Thuật toán có các đặc trưng sau:
a) Tính hữu hạn, còn gọi là tính dừng của thuật toán.
b) Tính chính xác. Tại mỗi bước các thao tác toán học phải được chỉ ra 1
cách chính xác, không cần tư duy, chỉ cần thực hiện một cách máy móc.
Đó cũng là cách đưa tư duy toán học vào máy tính.
TOÁN RỜI RẠC – Lý thuyết
c) Tính đơn trị. Các kết quả trung gian của các bước của thuật toán phải
xác định một cách đơn trị, chỉ phụ thuộc vào input (đầu vào) và kết quả của bước trước.
d) Tính phổ dụng. Thuật toán có thể giải được bất kỳ bài toán nào trong
lớp bài toán bài toán đã cho.
e) Tính tối ưu. Khi xây dựng thuật toán cần chú ý đến việc bảo đảm điều
kiện tốt nhất cho quá trình thực hiện, bao gồm việc sắp xếp các input,
output, bố trí chặt chẽ các thao tác để giảm thiểu phép toán và do đó
giảm đến mức thấp nhất thời gian thực hiện thuật toán.
2.2.2. Biểu diễn thuật toán
Có 3 cách biểu diễn thuật toán, mỗi cách đều có ưu nhược điểm nhất
định nên tùy theo từng trường hợp ta lựa chọn sao cho thích hợp.
a) Biểu diễn bằng ngôn ngữ tự nhiên, liệt kê các bước của thuật toán. Thí dụ.
Giải phương trình bậc 2: ax2 + bx + c = 0 với a, b, c là các số thực và a 0
Bước 1: Đưa vào input a, b, c
Bước 2: Tính biệt số = b2 − 4ac Bước 3: Xét dấu
Nếu 0 chuyển sang bước 4.
Ngược lại chuyển sang bước 5. Bước 4: Tính nghiệm −b + −b − x = ; x = 1 2a 2 2a
(Output) đưa ra thông báo nghiệm của phương trình là x và x , 1 2 chuyển sang bước 6.
Bước 5: (Output) đưa ra thông báo phương trình vô nghiệm. Bước 6: Kết thúc.
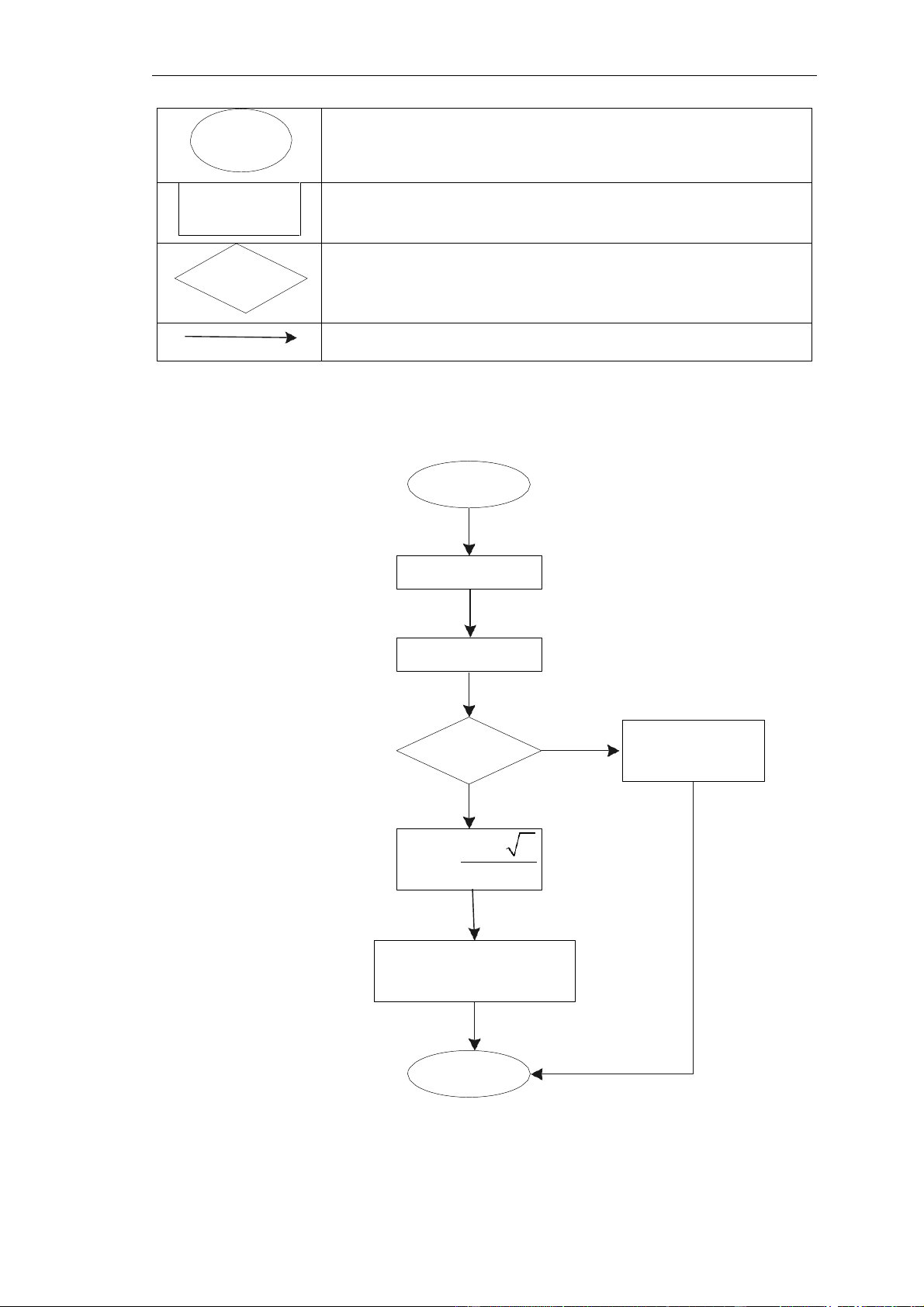
b) Biểu diễn bằng sơ đồ khối.
Phương pháp này sử dụng các biểu trưng hình học quy ước để diễn đạt
các bước và thao tác cần thực hiện trong thuật toán. Ta quy ước có các khối sau:
TOÁN RỜI RẠC – Lý thuyết
Nút khởi đầu hoặc kết thúc
Nút thao tác, ghi câu lệnh cần thực hiện
Nút điều kiện, ghi rõ điều kiện cần kiểm tra trong quá trình tính toán
Cung, dùng để chỉ đường đi của thuật toán Thí dụ.
Sơ đồ khối mô tả thuật toán giải phương trình bậc hai: ax2 + bx + c = 0 như sau Bắt đầu Input a, b, c = b2 − 4ac sai Thông báo PT 0 vô nghiệm đúng −b x = 1, 2 2a Thông báo pt có 2 nghiệm là x1 và x2 Kết thúc
Ưu điểm của phương pháp này là có tính phổ dụng cao, khắc phục được
tính đa nghĩa và hàng rào ngôn ngữ, rất tiện lợi trong chuyên ngành toán và tin học.
TOÁN RỜI RẠC – Lý thuyết
2.2.3. Phương pháp quy nạp
Quy nạp toán học là một phương pháp hữu hiệu để chứng minh một
mệnh đề toán học đúng với mọi số tự nhiên n. Để thực hiện điều đó ta phải
tiến hành các bước sau:
Bước 1: Chứng minh mệnh đề đúng với n = 1.
Bước 2: Giả sử mệnh đề đã đúng với n, ta chứng minh mệnh đề đúng với (n + 1)
Thí dụ 1. Chứng minh rằng n N* n(n + 1)(2n + 1) 12 + 22 + ... + n2 = 6 1(1 + 1)(2 + 1)
Bước 1: Với n = 1 ta có 12 =
. Vậy công thức đúng với n = 1 6
Bước 2: Giả sử công thức trên đúng với n, tức là ta có n(n + 1)(2n + 1) 12 + 22 + ... + n2 = 6
Ta phải chứng minh công thức đúng với (n + 1), nghĩa là: (n + 1)(n + 2)(2n + 3)
12 + 22 + ... + n2 + (n + 1)2 = 6 = n(n + 1)(2n + 1) +
Ta có vế trái 12 + 22 + ... + n2 + (n + 1)2 = (n + 1)2 6 = (n + 1)(n + 2)(2n + 3) =vế phải. 6
Vậy công thức được chứng minh.
Thí dụ 2.Tìm tổng S = 1.2 + 2.3 + ... + n(n + 1) 2.3.4 Ta thấy 1.2 + 2.3 = 8 = 3 3.4.5 1.2 + 2.3 + 3.4 = 20 = 3 n(n + 1)(n + 2)
Vậy có thể dự đoán 1.2 + 2.3 + ... + n(n + 1) = 3
Vấn đề đặt ra là dự đoán này có đúng không. Ta kiểm tra sự đúng đắn này
bằng phương pháp quy nạp: 1.2.3
Bước 1: Với n = 1 ta có 1.2 =
. Vậy công thức đúng với n = 1 3
TOÁN RỜI RẠC – Lý thuyết
Bước 2: Giả sử công thức trên đúng với n, ta phải chứng minh công thức
đúng với (n + 1), nghĩa là: (n + 1)(n + 2)(n + 3)
1.2 + 2.3 + ... + n(n + 1) + (n + 1)(n + 2) = 3
Ta có vế trái = 1.2 + 2.3 + ... + n(n + 1) + (n + 1)(n + 2) = n(n + 1)(n + 2) + (n + 1)(n + 2) 3 = (n + 1)(n + 2)(n + 3) =vế phải. 3
Vậy dự đoán trên là đúng. Tuy nhiên cần thấy rằng quy nạp toán học
không phải là phương pháp duy nhất để giải quyết lớp các bài toán như vậy
(xem lời giải bài tập 2.1, ý d) chương 2)
2.2.4. Phương pháp đệ quy
Đệ quy là khái niệm rất hay gặp trong toán học cũng như trong lập trình,
nó cho phép ta mô tả một cách ngắn gọn và sáng sủa các đối tượng cũng
như các quá trình liên quan đến dãy số tự nhiên.
Như vậy đệ quy là một phương pháp xác định các đối tượng thỏa mãn
một tính chất nào đó; nó bao gồm các quy tắc, trong đó một số quy tắc để
xác định các đối tượng ban đầu và quy tắc còn lại dùng để xác định các đối
tượng tiếp theo nhờ các đối tượng ban đầu đã được xác định. Thí dụ.
Cho dãy số a , a , a , ..., a , ... có tính chất sau: 0 1 2 n a = 0, a = 1và a = a + a ; 0 1 n n −1 n −2 n 2.
Đó chính là dãy Fibonacci mà n 2 ta có thể tìm được số Fibonacci
thứ n nếu biết số Fibonacci thứ (n − 1) và thứ (n − 2). Bằng quy nạp toán
học hoặc bằng cách giải phương trình truy hồi tuyến tính cấp 2 hệ số hằng
ta có thể chứng minh rằng n 0 ta có: 1 1 + 5 n 1 1 − 5 n a = 5 − n 2 5 2
Tuy nhiên ta có thể tính a trực tiếp như sau: n
Trước hết hãy tìm cặp số , sao cho a − a = (a − a ) n n −1 n −1 n −2 Suy ra a = ( + )a − . a n n −1 n −2 Từ điều kiện a = a + a ta suy ra n n −1 n −2 + = 1 và . = −1
TOÁN RỜI RẠC – Lý thuyết
Khi đó và là nghiệm của phương trình x2 − x − 1 = 0; do đó có thể chọn 1 + 5 1 − 5 = và = 2 2 Đặt q = a thì sẽ có q = .q với n 2 và q = 1 n n − .an −1 n n −1 1
Từ đó suy ra q = n −1 n
Vậy ta có a − .a = n −1 hay n a = .a + n−1 n −1 n n −1 Từ đây suy ra a = .a + 2 1 (1) a = .a + 2 (2) 3 2 a = .a + 3 (3) 4 3 ……………… a = .a + n −2 (n − 2) n −1 n −2 a = .a + n−1 (n − 1) n n −1
Nhân 2 vế của đẳng thức thứ k với n −1−k ; (k = 1, 2, 3, ..., n − 1) rồi cộng vế với vế ta có: n − n (vì a = n −1
+ n −2 + n −32 + + n −2 + n −1 = a = 1) .a n 1 ... . − 1 1 + 5 1 − 5 Ta thấy = ; =
nên − = 5 và ta có: 2 2 1 1 + 5 n 1 1 − 5 n a = 5 − n 2 5 2 Điều phải chứng minh.
2.3. CÁC TỔ HỢP KHÔNG LẶP
2.3.1. Chỉnh hợp
Định nghĩa. Chỉnh hợp chập k của n phần tử là một nhóm gồm k phần
tử lấy trong n phần tử đã cho và sắp xếp theo một thứ tự nhất định. Ở đây
mỗi phần tử chỉ được lấy một lần (không lặp). Thí dụ.
Cho X = {0, 1, 2, 3, 4, 5} gồm 6 phần tử.
TOÁN RỜI RẠC – Lý thuyết
Các nhóm dưới đây 123, 213, 402, 305, … đều là các chỉnh hợp chập 3
của 6 phần tử. Hai chỉnh hợp 123 và 213 có các phần tử như nhau nhưng khác nhau về thứ tự.
Như vậy hai chỉnh hợp là khác nhau nếu chúng có ít nhất một phần tử
khác nhau hoặc thứ tự các phần tử khác nhau. Để xây dựng một chỉnh hợp
ta xây dựng dần từ thành phần đầu tiên. Thành phần đầu tiên có n cách
chọn, thành phần thứ hai chỉ có (n − 1) khả năng chọn, …, thành phần thứ
k chỉ có (n − k + 1) khả năng chọn.
Nếu ký hiệu số chỉnh hợp chập k của n phần tử là Ak thì ta có: n k
A = n.(n − 1). ... .(n − k + 1) (1) n Thí dụ.
Từ các phần tử của X đã cho ở trên, có thể lập được bao nhiêu con số
hàng trăm mà các chữ số là khác nhau?
Ta thấy ngay S = A3 − A2 = 6.5.4 − 5.4 = 120 − 20 = 100 số. 6 5
Ở đây, A2 chính là số các chỉnh hợp chập 3 có số 0 đứng ở phía trước; con 5
số này không phải con số hàng trăm.
2.3.2. Hoán vị
Định nghĩa. Hoán vị của n phần tử là một cách sắp xếp thứ tự n phần tử
đó. Ký hiệu số hoán vị là P thì n
P = An = n.(n − 1) ..... 2.1 = n! (2) n n
Thí dụ. Có 5 người dàn hàng ngang chụp ảnh, hỏi có bao nhiêu kiểu ảnh khác nhau?
Mỗi kiểu ảnh là một hoán vị, vậy số kiểu ảnh là: P5 = 5! = 120
2.3.3. Tổ hợp
Định nghĩa. Tổ hợp chập k của n phần tử là một nhóm gồm k phần tử
lấy trong n phần tử đã cho (không kể thứ tự).
Nếu ký hiệu Ck là số tổ hợp chập k của n phần tử thì dễ dàng thấy rằng: n Ak k k k
n.(n − 1). ... .(n − k + 1) C .P (3) n k =An Cn = n = P k! k
Nếu chú ý rằng C k là số nguyên thì ta có nhận xét thú vị sau đây: Tích n
của k số tự nhiên liên tiếp nhau luôn chia hết cho tích của k số tự nhiên đầu tiên (k!).
TOÁN RỜI RẠC – Lý thuyết
Thí dụ 1.
Có 10 người thi đấu bóng bàn vòng tròn, hỏi có bao nhiêu trận đấu?
Cứ 2 người tạo nên 1 trận đấu, mỗi trận đấu là một tổ hợp chập 2 của 10. Vậy số trận đấu là: 10.9 2 = = 45trận C 10 1.2
Thí dụ 2.
Có bao nhiêu dãy nhị phân độ dài 10 có đúng 3 số 1 (và 7 số 0).
Mỗi dãy nhị phân như thế tương ứng với việc chọn 3 vị trí trong 10 vị trí để
gán số 1 tức là tương ứng với một tổ hợp chập 3 của 10 phần tử.
Vậy số dãy nhị phân cần tìm là: 3 C = 10.9.8 = 120 10 1.2.3
Các số tổ hợp Ck rất hay gặp trong toán rời rạc, ta thường gọi là hệ số tổ n
hợp. Dưới đây là một số công thức đáng nhớ: k C = n! (4) n k!.(n − k)! Ck = Cn −k (5) n n Ck = Ck −1 + Ck ; (n k 0) (6) n n −1 n −1
Chứng minh các công thức (4), (5), (6) rất đơn giản, xin dành cho độc giả.
Để có thể áp dụng công thức (4) và (5) cho mọi k n ta quy ước: C0 = Cn = 1và 0! = 1 n n Chú ý:
- Công thức (5) giúp ta tính toán nhanh hơn. Thay cho tính Ck ta sẽ tính n Cn −knếu n n − k k
Thí dụ.Tính C8 ; ta thấy 10 − 8 = 2 8 nên ta tính 10 C8 = C2 = 10.9 = 45 10 10 1.2
- Công thức (6) với quy ước 0
C = 1 cho phép ta tính tất cả các hệ số tổ hợp n chỉ bằng phép cộng.
Các hệ số này được tính và viết theo quy tắc sau: Các dòng tương ứng
với n = 0, 1, 2, ...; các cột tương ứng với k = 0, 1, 2, ... và ta có bảng tam
giác dưới đây gọi là tam giác Pascal
TOÁN RỜI RẠC – Lý thuyết 0 C 0 0 C C 1 1 1 0 C C 1 C 2 2 2 2 0 C C 1 C 2 C 3 3 3 3 3 …. .... .... …. …. 0 3 C C 1 C 2 …. n −1 C C C n n n n n n n
Dòng hệ số tổ hợp cuối cùng: C0, C1 , C2, …, Cn −1, Cn là các hệ số trong n n n n n
khai triển nhị thức Newton: n (x + y)n = Ck.xk yn −k n k = 0
Cho y = 1 ta có công thức: n (x + 1)n = C k.x k (7) n k = 0
Từ hệ thức này ta suy ra một số công thức sau đây: - Cho x = 1 thì sẽ có: C0 + C1 + C2 + ... + Cn = 2n (8) n n n n - Cho x = −1 thì sẽ có:
C0 − C1 + C2 − C3 ... + (−1)n Cn = 0 n n n n n Từ đó suy ra
C0 + C2 + ... = C1 + C3 + ... = 2n − 1 (9) n n n n
- Đạo hàm theo x hai vế của (7) rồi thay x = 1 sẽ có:
C1 + 2C2 + ... + nCn = n2n −1 (10) n n n
2.4. CÁC TỔ HỢP CÓ LẶP
2.4.1. Chỉnh hợp lặp
Định nghĩa. Chỉnh hợp lặp chập k của n phần tử là một nhóm gồm k
phần tử lấy trong n phần tử đã cho và sắp xếp theo một thứ tự nhất định;
các phần tử có thể lấy lặp.
Thí dụ 1.
Với X = {0, 1, 2, 3, 4, 5} các chỉnh hợp lặp chập 3 có thể là 123, 213, 211, 111, …
TOÁN RỜI RẠC – Lý thuyết
Nếu ký hiệu L k là số chỉnh hợp lặp chập k của n phần tử thì dễ dàng n
thấy rằng mỗi thành phần của nó đều có n cách lựa chọn nên ta có công thức: k L = nk (11) n
Chú ý rằng trong chỉnh hợp lặp số k không bị giới hạn bởi điều kiện
k n mà trái lại k có thể lấy giá trị lớn hơn n. Chẳng hạn như với 3 chữ số
1, 2, 3 ta vẫn có thể lập được các con số hàng triệu gồm 7 chữ số: 1 222 333; 2 221 111; …
Thí dụ 2.
Từ các chữ số thuộc X = {0, 1, 2, 3, 4, 5} có thể lập được bao nhiêu con số hàng trăm?
Mỗi con số hàng trăm là một chỉnh hợp lặp chập 3 của 6 chữ số đã cho,
loại trừ các chỉnh hợp lặp có số 0 đứng trước.
Do đó ta có số các con số hàng trăm là:
s = L3 − L2 = 63 − 62 = 180số 6 6
2.4.2. Hoán vị lặp.
Ta hãy xét 2 nhóm gồm 5 chữ cái: THANG và NHANH
Nếu ta hoán vị 5 chữ cái trong nhóm THANG thì sẽ được P5 = 5! = 120
hoán vị khác nhau. Nhưng khi hoán vị các chữ cái trong nhóm NHANH thì
sẽ không được 120 hoán vị khác nhau; vì khi ta đổi vị trí 2 chữ N với nhau
hoặc 2 chữ H với nhau thì sẽ không tạo ra một hoán vị mới.
Trong các hoán vị này, chữ N lặp 2 lần, chữ H lặp 2 lần, ta gọi đó là các
hoán vị lặp. Số hoán vị lặp trong trường hợp này dễ dàng tính được là: 120 = 30 2.2
Bây giờ ta xét trường hợp tổng quát:
Cho k phần tử khác nhau; ta ký hiệu P(n , n , ..., n ) là số hoán vị của k 1 2 k
phần tử trên, trong đó phần tử thứ nhất lặp n lần, phần tử thứ hai lặp n 1 2
lần, …, phần tử thứ k lặp n lần. k
Ta dễ dàng chứng minh được công thức sau đây: (n + n + ... + n )! P(n , n , ..., n ) = 1 2 k (12) 1 2 k n ! n ! ... n ! 1 2 k
TOÁN RỜI RẠC – Lý thuyết Thí dụ.
Hoán vị các chữ cái trong tên của dòng sông MISSISIPI, ta thấy ở đây
chỉ có 4 chữ cái M, P, S, I trong đó M và P không lặp, S lặp 3 lần, I lặp 4
lần. Vậy số hoán vị là: (1 + 1 + 3 + 4)! 9! P(1, 1, 3, 4) = = = 2520 1!1! 3!4! 3!4!
Nếu ta đặt n = n + n + ... + n thì sẽ có định lý sau đây: 1 2 k
Định lý 1.
Ký hiệu C (n , n , ..., n ) là số cách chia n phần tử khác nhau thành k n 1 2 k
nhóm với số các phần tử tương ứng là n 1, n2, ..., n . Nếu n n k i j i j thì
C (n , n , ..., n ) = P(n , n , ..., n ). n 1 2 k 1 2 k Chứng minh.
Không mất tính tổng quát ta chỉ cần chứng minh cho trường hợp k = 3.
Thật vậy, ta có Cn1 là số cách chọn n n
1 phần tử trong n phần tử. Tương ứng
với mỗi cách chọn n1 phần tử cho nhóm thứ nhất, ta còn lại
n − n = n + n phần tử; do đó có Cn2
cách chọn n phần tử cho 1 2 3 n + 2 2 n3 nhóm thứ hai.
Đương nhiên sau khi chọn n2 phần tử cho nhóm thứ hai thì sẽ còn lại
n3 phần tử của nhóm thứ ba. Vậy số cách chia ấy là: C (n , n , n ) = Cn1 .Cn2 = n! (n + n )! (n + n + n )! . 2 3 = 1 2 3 n 1 2 3 n n2 + n3 n !(n − n )! n !n ! n !n !n ! 1 1 2 3 1 2 3
Với chú ý rằng n = n1 + n2 + n3 thì ta có:
C (n , n , n ) = P(n , n , n ) n 1 2 3 1 2 3 Điều phải chứng minh.
Thí dụ 1.
Có bao nhiêu cách chia bộ bài tú lơ khơ 52 quân thành 4 phần tương
ứng với số quân là 10, 12, 14, 16.
Vì số quân của các phần khác nhau nên C52 (10, 12, 14, 16) = 52! 10!12!14!16! Giả thiết n n i
j i j là để cho các nhóm được tạo thành không có sự trùng lặp. Nếu n = n 1
2 = ... = ni (i k) tức là có i nhóm có số phần tử
bằng nhau thì công thức tính sẽ là:
TOÁN RỜI RẠC – Lý thuyết P(n , n , ..., n )
C (n , n , ..., n , n , ..., n ) = 1 2 k n 1 2 i i +1 k i!
Nghĩa là số cách chia nhóm sẽ giảm đi i! lần.
Thí dụ 2.
Chia 4 đối tượng a, b, c, d thành 2 nhóm, mỗi nhóm gồm 2 đối tượng thì chỉ có 3 cách (a, b) và (c, d) (a, c) và (b, d) (a, d) và (b, c)
Chú ý rằng nếu lấy ra 2 đối tượng từ 4 đối tượng thì có C2 = 6 cách, 4
nhưng chia thành 2 nhóm, mỗi nhóm 2 đối tượng thì lại chỉ có: P(2, 2) 4! 24 C (2, 2) = = = = 3 cách như trên. 4 2! 2!. 2!2! 8
Thí dụ 3.
Có bao nhiêu cách chia bộ bài tú lơ khơ 52 quân thành 4 phần bằng nhau?
Khi đó mỗi phần có 13 quân nên: P(13, 13, 13, 13) C (13, 13, 13, 13) = = 52! 52 4! 4!. (13!)4
2.4.3. Tổ hợp lặp
Định nghĩa.Tổ hợp lặp chập k của n phần tử là một nhóm gồm k phần
tử lấy (có thể lặp) trong n phần tử đã cho. Giống như trong chỉnh hợp lặp,
số k có thể lớn hơn n.
Thí dụ 1.
Hai quả cam, ba quả quýt, bốn quả chanh có thể coi như tổ hợp lặp chập
9 của 3 phần tử ; trong đó cam lặp 2 lần, quýt lặp 3 lần, chanh lặp 4 lần.
Ta ký hiệu số tổ hợp lặp chập k của n phần tử là R k và tìm công thức n cho Rk. n
Ta gán cho mỗi phần tử trong n phần tử đã cho một số nguyên dương
khác nhau từ 1 đến n. Khi đó mỗi tổ hợp chập k không lặp của n phần tử
tương ứng với 1 dãy số tăng a1a2...a trong đó: k 1 a 1 a2 ... a n, (k n) k
Và mỗi tổ hợp lặp chập k của n phần tử tương ứng với 1 dãy số không
giảm a a ...a trong đó 1 a a ... a n và không nhất thiết 1 2 k 1 2 k k n.
Ta thiết lập sự tương ứng giữa dãy a với như 1a2...a dãy b sau: k 1b2...bk
TOÁN RỜI RẠC – Lý thuyết b = a 1 1 b = a + 1 2 2 b = a + 2 3 3 ………….. b = a + (k − 1) k k
Khi đó ta có 1 b b ... b n + k − 1 1 2 k
Mỗi dãy b b ...b như vậy tương ứng với một tổ hợp (không lặp) chập k 1 2 k
của ( n + k − 1) phần tử. Vậy Rk Ck n n + k − 1
Ngược lại với mỗi tổ hợp không lặp chập k của ( n + k − 1) phần tử
(tương ứng với 1 dãy tăng b b ...b : b 1, b 1 2 k 1
k n + k − 1) ta có thể tìm
được một tổ hợp lặp chập k của n phần tử (tương ứng với dãy không giảm a a ...a : a 1, a 1 2 k 1 k n), nghĩa là: Ck Rk n + k − 1 n Từ đó suy ra Ck = Rk n + k − 1 n
Thí dụ 2.
Có bao nhiêu cách chia 10 chiếc kẹo cho 5 em bé?
Mỗi cách chia là một tổ hợp lặp chập 10 của 5 phần tử, vậy số cách chia là: 14.13.12.11 R10 = C10 = C10 = C4 = = 1001cách. 5 5 +10 −1 14 14 4!
Thí dụ 3. Phương trình x + x + x 1 2 + x3 4 = 8; x
0 và nguyên ( i = 1, 4) có bao i nhiêu nghiệm?
Mỗi nghiệm là một tổ hợp lặp chập 8 của 4 phần tử, vậy số nghiệm là: 11.10.9 R8 = C8 = C8 = C3 = = 165 nghiệm. 4 4 +8 −1 11 11 3!
2.5. CÁC NGUYÊN LÝ ĐẾM
Mỗi bài toán đếm có một cấu trúc khác nhau nên chúng ta cần phải lựa
chọn phương pháp đếm phù hợp với cấu trúc của bài toán đó. Một số
phương pháp đếm có tính chất tổng quát cho một lớp bài toán, ta gọi nó là
nguyên lý đếm. Dưới đây là các nguyên lý quan trọng.
TOÁN RỜI RẠC – Lý thuyết
2.5.1. Nguyên lý cộng
Nếu A , A , ..., A là một phân hoạch của A, nghĩa là 1 2 n
A = A A ... A và A A = , i j thì 1 2 n i j n | A | = | A | (14) j j=1
Thí dụ 1.
X = {x , x , ..., x }; A = P(X)là tập lũy thừa của X. Tìm |A|. 1 2 n
Ta biết rằng P(X) là tập mọi tập con có thể có của X kể cả tập rỗng và
bản thân tập X. Ta ký hiệu A là tập mọi tập con gồm k phần tử của X; k
k = 0, 1, 2, ..., n. Trong đó A là tập rỗng. Ta thấy 0
A = P(X) = A A A ... A và A A = , i j 0 1 2 n i j
Áp dụng nguyên lý cộng thì sẽ có: n | A | = | A | k k = 0 n
Vì |A | = Ck nên ta có |A | = k C = 2 n k n n k = 0
Thí dụ 2.
Hỏi giá trị của S sẽ là bao nhiêu sau khi đoạn chương trình C++ dưới đây được thực hiện? int n = 5; n = 10; n = 15; 1 2 3 S = 0;
for ( int i = 1; i = n1; i + +) S + +;
for ( int i = 1; i = n2; i + +) S + +;
for ( int i = 1; i = n3; i + +) S + +;
Ta thấy rằng đầu tiên giá trị của S được gán bằng 0 và có 3 vòng lặp for
độc lập. Sau mỗi lần lặp của mỗi vòng giá trị của S tăng lên 1 đơn vị. Vòng
for thứ nhất lặp 5 lần, vòng for thứ hai lặp 10 lần, vòng for thứ ba lặp 15
lần. Vậy sau 3 lần lặp giá trị của S sẽ là: 5 + 10 + 15 = 30.
2.5.2. Nguyên lý nhân
Nếu A là tích Descarte: A = E1 E2 ... E thì n
| A | = | E | | E | ... | E | (15) 1 2 n
Trường hợp đặc biệt: A = En thì |A | = |E |n
TOÁN RỜI RẠC – Lý thuyết
Thí dụ 1.
Mỗi biển số ô tô được ghi bởi 1 bộ gồm 2 chữ cái có thể lặp trong 26
chữ cái tiếng Anh và một bộ 4 chữ số có thể lặp. Hỏi có bao nhiêu biển số khác nhau?
Ký hiệu E1 là tập các bộ 2 chữ cái có thể lặp trong 26 chữ cái, ta có |E | = L2 = 262 = 676 1 26
Ký hiệu E là tập các bộ 4 chữ số có thể lặp thì |E | = L4 = 104 2 2 10
Ký hiệu E là tập các biển số ô tô thì A = E1 E2. Do đó
|A | = |E | |E | = 676.104 1 2
Thí dụ 2.
Có bao nhiêu xâu nhị phân có độ dài 10?
Ký hiệu E = {0, 1}; A là tập các xâu nhị phân có độ dài 10 thì A = E10. Vậy |A | = 210 = 1024.
Thí dụ 3.
Giá trị của S sẽ là bao nhiêu sau khi đoạn chương trình C++ dưới đây được thực hiện? Int n = 5; n = 15; 1 2 = 10; n3 S = 0;
for ( int i = 1; i = n1; i + +)
for ( int i = 1; i = n2; i + +)
for ( int i = 1; i = n3; i + +) S + +;
Đầu tiên giá trị của S được gán bằng 0 và vòng lặp for lồng nhau. Sau
mỗi lần lặp của vòng for, giá trị của S tăng lên 1 đơn vị. Vòng for thứ nhất
lặp 5 lần, vòng for thứ hai lặp 10 lần, vòng for thứ ba lặp 15 lần.
Vậy sau 3 lần vòng lặp for lồng nhau, giá trị của S sẽ là: S = 5.10.15 = 750.
2.5.3. Nguyên lý loại trừ Nếu A B thì |A | = | B| − | B \ A | (16)
Ta gọi đó là nguyên lý loại trừ Thí dụ.
Có 8 nam và 10 nữ; có bao nhiêu cách chọn ra 6 người có cả nam và nữ?
- Nếu muốn áp dụng nguyên lý cộng ta làm như sau:
TOÁN RỜI RẠC – Lý thuyết
Ký hiệu A là tập các nhóm 6 người có cả nam và nữ; trong đó có i nam i (1 i 5) thì ta có:
A = A A A A A và A A = , i j 1 2 3 4 5 i j
Vậy |A | = | A | + | A | + | A | + | A | + | A | 1 2 3 4 5
Nhưng khi tính | A | ta phải áp dụng nguyên lý nhân. i |A | = Ci .C6−i; (1 i 5) i 8 10
Vậy |A | = C1.C5 + C2.C4 + C3.C3 + C4.C2 + C5.C1 8 10 8 10 8 10 8 10 8 10
- Nếu áp dụng nguyên lý loại trừ ta làm như sau:
Tổng số nam và nữ là: 8 + 10 = 18; có thể tạo ra 6 C các nhóm gồm 6 18
người. Nếu loại bỏ số các nhóm chỉ có nam hoặc chỉ có nữ thì sẽ được số
các nhóm có cả nam và nữ.
Số nhóm chỉ có nam là C 6 8
Số nhóm chỉ có nữ là C 6 10
Vậy số nhóm cần tìm là: |A | = C6 − (C6 + C6 ) = 18272 18 8 10
2.5.4. Nguyên lý bù trừ
Nguyên lý bù trừ giải quyết bài toán đếm số phần tử của một phủ của A,
nghĩa là: A = A A ... A mà không có điều kiện 1 2 n
A A = , i j nên không thể áp dụng nguyên lý cộng. i j Dễ dàng thấy rằng:
- Với n = 2thì A = A A . Ta dễ dàng chứng minh được 1 2
|A | = | A | + | A | − | A A | 1 2 1 2
Các phần tử x A A được đếm 2 lần, một lần tính trong A 1 2 1 và một
lần tính trong A2, vậy phải trừ đi 1 lần.
- Với n = 3thì A = A A A ; công thức đếm sẽ là: 1 2 3
| A | = (| A |+ | A |+| A |) −(| A A |+| A A |+| A A |) +| A A A | 1 2 3 1 2 2 3 3 1 1 2 3
Ý nghĩa của công thức này là: Các phần tử thuộc giao của 2 tập được
đếm 2 lần phải trừ đi một lần. Các phần tử x A A A 1 2 3 được tính 3
lần trong | A |, | A |, | A | và bị trừ đi 3 lần trong giao của các 2 tập 1 2 3
| A A |, | A A |, | A A |; như vậy coi như chưa được đếm. Vậy 1 2 2 3 3 1
phải bù vào | A A A | 1 2 3
Trường hợp tổng quát: Nếu A = A1 A2 ... A thì n
TOÁN RỜI RẠC – Lý thuyết
|A | = N − N + N − ... + (−1)n N (17) 1 2 3 n n Trong đó N = | A | 1 i i =1 N = | A A | 2 i j i j N = 3 | A A A | i j k i j k …………………… N = | A A ... A | n 1 2 n
Công thức (17) được gọi là nguyên lý bù trừ.
Thí dụ 1.
Trong một lớp học, mỗi sinh viên đều biết ít nhất một ngoại ngữ. Có 30
sinh viên biết tiếng Anh, 31 sinh viên biết tiếng Pháp, 32 sinh viên biết
tiếng Nga, 15 sinh viên biết tiếng Anh và Pháp, 16 sinh viên biết tiếng Pháp
và Nga, 17 sinh viên biết tiếng Nga và Anh, 5 sinh viên biết cả 3 ngoại ngữ.
Hỏi cả lớp có bao nhiêu sinh viên?
Theo nguyên lý bù trừ ta có: N = N − N nên 1 2 + N3
N = (30 + 31 + 32) − (15 + 16 + 17) + 5 = 50sinh viên.
Thí dụ 2.
Có bao nhiêu số nguyên dương, 1000 chia hết cho 2, 3 hoặc 5. Ký hiệu A , A , A 2 3
5 là tập các số tương ứng chia hết cho 2, 3, 5 và A = A A A . 2 3 5 Theo nguyên lý bù trừ: |A | = N − N + N 1 2 3
Trong đó N = | A | + | A | + | A | 1 2 3 5
N = | A A | + | A A | + | A A | 2 2 3 2 5 3 5 N = | A A A | 3 2 3 5 1000 Ta có: | A | =
= 500 trong đó [x] là phần nguyên của x. 2 2 1000 | A | = = 333; 3 3 1000 | A | = = 200; 5 5
N1 = 500 + 333 + 200 = 1033
TOÁN RỜI RẠC – Lý thuyết 1000 | A A | = = 166; 2 3 6 1000 | A A | = = 100; 2 5 10 1000 |A A | = = 66; 3 5 15 N2 = 166 + 100 + 66 = 332 1000 N = | A A A | = = 33. 3 2 3 5 30
Vậy |A | = 1033 − 332 + 33 = 734.
Thí dụ 3.Tìm số mất thứ tự.
Bỏ n bức thư vào n phong bì ghi sẵn địa chỉ. Tìm xác suất để không một
bức thư nào đúng địa chỉ.
Số cách bỏ thư là n!, số cách bỏ thư không bức thư nào đúng địa chỉ là Dn
D thì xác suất cần tìm là: P = n n!
D là số mất thứ tự. D được tính theo nguyên lý bù trừ n n
D = N − N + N − ... + (−1)n N n 1 2 n Trong đó N = n!
N là số cách bỏ thư có ít nhất k lá thư đúng địa chỉ. k
Dễ dàng thấy rằng N = Ck.(n − k)!. Trong đó k C là số cách chọn k k n n
bức thư để bỏ đúng địa chỉ, còn (n − k) bức thư còn lại ta bỏ một cách tùy
ý, nghĩa là có (n − k)! cách. Trong (n − k)! cách bỏ thư này vẫn có những n!
thư đúng địa chỉ nên N = Ck.(n − k)! =
là số cách bỏ thư để có ít nhất k n k! k thư đúng địa chỉ. Thay vào đó ta có: n! n! n n! n (−1)k D = n! − + − ... + (−1) = (18) n n!. 1! 2! n! k! k = 0 Vậy xác suất là: 1 1 1 P = 1 − + − ... + (−1)n 1! 2! n! 1 1 Điều
lý thú là khi cho n → thì P → e−1 = e 3
TOÁN RỜI RẠC – Lý thuyết
Số mất thứ tự D tăng rất nhanh. Sau đây là một vài giá trị của D n n n 1 2 3 4 5 6 7 8 9 10 Dn 0 1 2 9
44 265 1854 14833 133496 1334961
Thí dụ 4.Bài toán xếp chỗ của Lucas.
Có bao nhiêu cách xếp chỗ cho n cặp vợ chồng vào 2n chiếc ghế quanh
bàn tròn sao cho nam nữ xen kẽ nhau và không có cặp vợ chồng nào ngồi cạnh nhau?
- Trước tiên xếp chỗ cho các ông chồng: có 2.n! cách xếp.
Ký hiệu U là số cách xếp cần tìm và V là số cách xếp chỗ cho các bà n n
vợ tương ứng với một cách xếp chỗ cho các ông chồng thì U = 2.n!.V n n
- Vấn đề còn lại là tìm V : n
Đánh số các ông chồng (đã xếp chỗ) từ 1 đến n, và các bà vợ (chưa được
xếp chỗ) cũng được đánh số như các ông chồng: nghĩa là bà i là vợ ông i;
sau đó đánh số các ghế còn trống theo nguyên tắc ghế số i ở giữa ông i và
ông i + 1 và được thực hiện theo nguyên tắc vòng tròn, nghĩa là n + 1 = 1.
Mỗi cách xếp chỗ cho các bà được biểu diễn bằng một phép thế f trên tập
{1, 2, …, n} với quy ước f (i) = j nghĩa là ghế i được xếp cho bà j. Phép
thế này phải thỏa mãn điều kiện
f (i) ivà f (i) i + 1 (*)
Như vậy V là tổng số tất cả các phép thế thỏa mãn điều kiện (*), ta gọi n là một phân bố.
Xét tập mọi phép thế f của {1, 2, …, n}. Trên tập này gọi P là tính chất i
f (i) = i và Q là tính chất = Q thì theo nguyên lý bù i f (i) = i + 1. Đặt Pn +i i trừ ta có: = V n! − N n 1 + N2 − ...
Trong đó N là tổng số tất cả các phép thế thỏa mãn k tính chất lấy từ k (2n) tính chất đang xét.
Vì không thể xảy ra đồng thời thỏa mãn P và Q hoặc P và Q nên i i i +1 i
trong các cách lấy ra k tính chất từ (2n) tính chất đang xét, cần thêm điều
kiện: các P và Q hoặc P và
không được đồng thời có mặt. Gọi số i i i +1 Qi
cách này là g(2n, k) với (k n).
Với mỗi cách lấy ra k tính chất như vậy ta có (n − k)! phép thế thỏa
mãn chúng nên N = g(2n, k).(n − k)!. k