Bài toán GTLN – GTNN biểu thức mũ – lôgarit nhiều biến số

Tài liệu gồm 36 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán GTLN – GTNN biểu thức mũ – lôgarit nhiều biến số

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

36 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
BÀI TOÁN GTLN - GTNN BIỂU THỨC MŨ – LOGARIT HAI BIẾN SỐ
PHƯƠNG PHÁP
Cách 1: Đánh giá, áp dụng BDT cơ bản đã biết như BĐT Côsi và BĐT Bunhiacopxki.
Cách 2: Áp dụng phương pháp hàm số, hàm đặc trưng.
Thông thường ta thực hiện theo các bước sau :
Biến đổi các số hạng chứa trong biểu thức về cùng một đại lượng giống nhau.
Đưa vào một biến mới
t
, bằng cách đặt
t
bằng đại lượng đã được biến đổi như trên.
Xét hàm số
(
)
ft
theo biến
t
. Khi đó ta hình thành đượ
c bài toán tương đương sau: Tìm giá
trị lớn nhất, giá trị nhỏ nhất của hàm số
(
)
ft
với
.
tD∈
Lúc này ta sử dụng đạo hàm để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
(
)
ft
với
.
tD∈
Chú ý : Ta chứng minh được:
•
Nếu hàm số
( )
y fx=
luôn đồng biến (hoặc luôn nghịch biến) và liên tục trên
D
mà phương
trình
( )
fx k=
có nghiệm thì nghiệm đó là nghiệm duy nhất trên
D
.
•
Nếu hàm số
( )
y fx=
luôn đồng biến (hoặc luôn nghịch biến) và hàm số
( )
y gx=
luôn nghịch
biến (hoặc luôn đồng biến) và liên tục trên
D
mà phương trình
có nghiệm thì
nghiệm đó là nghiệm duy nhất trên
D
.
•
Nếu hàm số
()y fx
=
luôn đồng biến (hoặc luôn nghịch biến) và liên tục trên
D
thì
() ()
fx fy>
nếu
xy>
(hoặc
)xy<
.
Cách 3: Áp dụng hình học giải tích.
Câu 1. Xét các số thực dương
x
và
y
thỏa mãn
12
ln 3 1.
x
xy
xy

−
= +−

+

Giá
trị nhỏ nhất của biểu thức
12
()gx
xxy
= +
+
bằng
A.
1
8
. B.
8
. C.
1
4
. D.
4
.
Lời giải
Chọn B
Điều kiện
1
0.
2
x<<
Ta có từ giả thiết:
( ) ( ) ( ) ( )
12
ln 3 1 ln 1 2 1 2 ln (1)
x
xy x x xy xy
xy

−
= + −⇔ − + − = + + +

+

.
Xét hàm số
( )
lnft t t= +
trên khoảng
( )
0; +∞
. Ta có
( )
1
10ft
t
′
=+>
với mọi
0
t >
Do đó hàm số
( )
ft
luôn đồng biến trên khoảng
( )
0; +∞
.
Vậy (1)
12 13xxy y x⇔− = + ⇔ =−
Ta có
( )
( )
( )
2
2
2
1 2 1 41 1
() 0
12 2 4
2
x
gx gx gx x
x xx x
xx
−
′′
=+= ⇒= ⇒=⇔=
−−
−
.
Khi đó ta có BBT
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Vậy GTNN của
()gx
là
8
khi
11
,
44
xy= =
.
Câu 2. Cho hai số thực dương
,ab
thỏa mãn hệ thức:
( )
222
2log log log 6a b ab−≤ +
. Tìm giá trị lớn nhất của biểu thức
2
22
22
ab b
P
a ab b
−
=
−+
.
A.
2
3
Max
P =
. B.
0
Max
P =
. C.
1
2
Max
P =
. D.
2
5
Max
P =
.
Lời giải
Chọn C
Ta có:
( )
( )
2 22 2
222 2 2
2log log log 6 log log 6 6a b a b a ab b a ab b− ≤ + ⇔ ≤ + ⇔≤+
2
60 3 2
aa a
bb b

⇔ − − ≤ ⇔− ≤ ≤


. Do
,ab
dương nên
02
a
b
<≤
.
Đặt
,0 2
a
tt
b
= <≤
. Khi đó:
2
2 22
1
2 2 22
ab b t
P
a ab b t t
−−
= =
− + −+
Xét hàm số
( )
2
1
22
t
ft
tt
−
=
−+
với
02t<≤
. Ta có:
( )
( )
(
]
2
2
2
2
0, 0; 2
22
tt
ft t
tt
−+
′
= ≥ ∀∈
−+
.
Suy ra
( )
( )
1
2
2
ft f
≤=
với
(
]
0; 2t∀∈
. Do đó
(
]
(
)
0;2
1
2
Max f t =
khi
2t =
. Vậy
1
2
Max
P =
.
Câu 3. Cho hai số thực dương
,xy
thỏa mãn
22 4
xy
+=
. Tìm giá trị lớn nhất
max
P
của biểu thức
( )( )
22
22 9P x y y x xy= + ++
.
A.
max
27
2
P
=
. B.
max
18
P =
. C.
max
27P =
. D.
max
12P =
.
Lời giải
Chọn B
Ta có
4 2 2 22 4 2 2
x y xy xy
xy
++
= + ≥ ⇔≥ ⇔+≤
. Suy ra
2
1
2
xy
xy
+

≤=


.
Khi đó
( )( ) ( )
2 2 3 3 22
2 2 9 2 4 10
P x y y x xy x y x y xy= + ++ = + + +
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
( ) ( )
(
)
22
2 3 2 10P x y x y xy xy xy

= + +− + +

( ) ( )
22 22
4 4 3 4 10 16 2 2 1 18
xy x y xy x y xy xy≤−++=++ −≤
. Vậy
max
18P =
khi
1xy= =
.
Câu 4. Cho hai số thực
,0ab>
thỏa mãn
( ) ( )
22
log 2 1 log 3 1 6 0ab++ +−≥
. Giá trị nhỏ nhất của biểu
thức
23ab+
là.
A.
12
. B.
14
. C.
16
. D.
8
.
Lời giải
Chọn B
Ta có
( ) ( )
22
log 2 1 log 3 1 6 0ab++ +−≥
( )( )
2
log 2 1 3 1 6ab⇔ + +≥


( )( )
2 1 3 1 64
ab
⇔ + +≥
.
Áp dụng bất đẳng thức Cô-si cho hai số dương
21a +
và
31b +
, ta được
( ) ( ) ( )( )
2 1 3 1 2 2 1 3 1 2 64 16a b ab++ +≥ + +≥ =
2 3 2 16ab⇔ + +≥
2 3 14ab⇔+≥
Dấu
""
=
xảy ra khi
3
2 13 1
2
a b ab+= +⇔ =
. Vậy
( )
min 2 3 14ab+=
khi
77
;
23
ab= =
.
Câu 5. Trong các nghiệm
( )
;xy
thỏa mãn bất phương trình
( )
22
2
log 2 1
xy
xy
+
+≥
. Khi đó giá trị lớn nhất của biểu thức
2T xy= +
là
A.
9
4
B.
9
C.
9
2
D.
9
8
Lời giải
Chọn C
- Trường hợp 1:
22
21xy+>
Bất phương trình
( )
22
22
2
log 2 1 2x 2
xy
xy yx y
+
+ ≥⇔ + ≥ +
22
2x 2 1yx y⇒ +≥ + >
Áp dụng bất đẳng thức Bunyakovsky, ta có
( )
( )
2
2
2 22
1
2 2 2x
2
xy y


+ + ≥+





( )
2
22
2 2x
2
9
y
xy
+
⇒+ ≥
( )
( )
2
2 2x
99
2 2 2 0 2 1;
9 22
y
xy xy xy xy
+

⇒+≥ ⇔ + +−≤⇒+∈


Giá trị lớn nhất của
9
2
2
T xy= +=
. Dấu bằng xảy ra khi
1
2;
2
xy= =
- Trường hợp 2:
22
0 21xy<+ <
Bất phương trình
( )
22
22
2
9
log 2 1 2x 2 1
2
xy
xy yx y
+
+ ≥⇔ + ≤ + <<
.
Vậy giá trị lớn nhất của
9
2
2
T xy
= +=
.
Câu 6. Xét các số nguyên dương
, ab
sao cho phương trình
2
ln ln 5 0a xb x+ +=
có hai nghiệm phân
biệt
12
, xx
và phương trình
2
5log log 0xb xa+ +=
có hai nghiệm phân biệt
34
, xx
thỏa mãn
12 34
xx xx>
. Tìm giá trị nhỏ nhất của
23S ab= +
A.
min
33S =
. B.
min
30S =
. C.
min
17S =
. D.
min
25S =
.
Lời giải
Chọn B
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Điều kiện để hai phương trình
2
ln ln 5 0a xb x+ +=
và
2
5log log 0xb xa+ +=
có hai nghiệm
phân biệt là:
2
20 0ba−>
.
Theo giả thiết ta có
( )
(
)
1 2 12
12
5
3 4 34
34
ln ln ln
log log log
10
55
b
a
b
bb
x x xx
xx e
aa
bb
x x xx
xx
−
−

+=− =−

=

⇒⇒


+=− =−
=


.
Mà
5
12 34
10
bb
a
xx xx e
−−
> ⇒>
nên suy ra
ln10
5
bb
a
− >−
5
3
ln10
aa⇒> ⇒≥
.
Theo điều kiện có
22
20 0 20 60 8
ba b a b
− >⇒ > ≥ ⇒≥
.
Từ đó suy ra
min
2 3 30 30S ab S=+≥⇒ =
khi và chỉ khi
3
8
a
b
=
=
.
Câu 7. Cho các số thực
1
, 1.
3
ab>>
Khi biểu thức
( )
42
3
log log 9 81
ab
b aa+ −+
đạt giá trị nhỏ nhất thì tổng
ab
+
bằng
A.
3
92+
. B.
2
39+
. C.
3 32+
. D.
2 92
+
.
Lời giải
Chọn B
Ta có
3 1, 1ab>>
nên
3
log 0,log 3 0.
ab
ba
>>
Theo bất đẳng thức Cauchy ta được
(
) ( )
42 22
3 33
log log 9 81 log log 18 9 log 2log 3 2 2.
ab ab a b
b aa b aa b a
+ −+≥ + − = + ≥
Dấu “
=
” xảy ra khi và chỉ khi
4
2
3
3 1, 1
3
81 .
9
log 2log 3
ab
ab
a
a
b
ba
>>
=
= ⇔

=
=
Vậy
2
39.ab+=+
Câu 8. Cho các số thực
,xy
thỏa mãn
( )
2 22
2 222
5 16.4 5 16 .7
xy xy yx− − −+
+ ≤+
và
2
1.
2
x
y≥+
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
10 6 26
.
225
xy
P
xy
++
=
++
Khi đó, giá trị của biểu thức
TMm= +
bằng
A.
10T =
. B.
21
2
T
=
. C.
19
2
T =
. D.
15T =
.
Lời giải
Chọn C
Đặt
2
2.tx y= −
Ta có
( )
( )
22
22
22
54 54
5 16.4 5 4 .7 1 .
77
tt
t tt
tt
+
−
+
++
+ ≤+ ⇔ ≤
Xét hàm số
( )
54 1 4
5
7 77
uu
u
u
fu
+
 
= = +
 
 
ta có
( )
1144
5 ln ln 0,
7777
uu
fu u
 
′
= + < ∀∈
 
 
Suy ra hàm số
( )
fu
luôn nghịch biến trên
.
Khi đó
( ) ( ) ( )
1 2 2 2 2 2.ft f t t t t⇔ + ≤ ⇔+ ≥ ⇔≤
Mặt khác
2
2
1 2 2 2.
2
x
y xy t≥ +⇔ − ≥ ⇔≥
Suy ra
2
2
2.
2
x
ty
−
=⇔=
Thay vào
P
ta được
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
( )
(
) (
)
2
2
2
3 10 20
3 2 5 20 3 0 2 .
23
xx
P Px Px P
xx
++
= ⇔− + − +− =
++
Khi
3,P ≠
vì
P
xác định nên phương trình
( )
2
có nghiệm.
Khi đó
( )
( )
( )
2
2
0 5 3 20 3 0 2 19 35 0
P P P PP
′
∆≥⇔ − − − − ≥⇔− + − ≥
5
7.
2
P⇔≤≤
Vậy
5 19
7.
22
TMm= + = +=
Câu 9. Xét các số thực dương
,xy
thỏa
( )
( )
2
22
2
42
2021 0.
2
xy
xy
x
−+
++
−≥
+
Tìm giá trị nhỏ nhất của biểu thức
2 4.P yx= −
A.
2021
. B.
2020
. C.
1
2
. D.
2
.
Lời giải
Chọn D
Từ giả thiết, ta suy ra
( )
( )
( )
( )
( )
2
22
2
2021
22
42 42
2021 2 2 log 1 .
22
xy
xy xy
xy
xx
−+
++ ++
≥ ⇔ −+ ≥
++
Đặt
(
)
2
2
2
42
2
2 44
a xy
ba x y
bx x x
= ++
⇒−= −+
=+ =++
thì
( )
1
trở thành
( ) (
)
2021 2021 2021 2021
2 log log log 2 log 2 2 .ba a b a a b b⇒−≥−⇔+≥+
Xét hàm số
(
)
2021
log 2ft t t
= +
trên
(
)
0;
+∞
ta có
( )
1
2 0, 0
ln 2021
ft t
t
′
= + > ∀>
Suy ra hàm số
( )
ft
luôn đồng biến trên khoảng
( )
0; .+∞
Khi đó
( ) ( ) ( ) ( )
2
2
2 4 2 2 2.fa fb a b x y x y x⇔ ≥ ⇔≥⇔ ++≥ + ⇔ ≥ +
Thay vào
,P
ta được
( )
2
2
2 4 4 2 1 2 2.Px x x≥ − += − +≥
Vậy
min
2
P =
khi và chỉ khi
1, 3.xy= =
Câu 10. Cho hai số thực dương
, xy
thỏa mãn
(
)
ln
ln
ln5
2
2 .5 2
xy
xy
+


+

=
. Giá trị nhỏ nhất của biểu thức
( 1) ln ( 1) lnPx xy y=+ ++
với
13
22
x≤≤
và
13
22
y≤≤
là
m
, khi đó
m
thuộc khoảng nào sau
đây
A.
1
;0
2
m

∈−


. B.
( )
0;1m ∈
. C.
( )
1; 2m ∈
. D.
( )
2; 4m ∈
.
Lời giải
Chọn A
Ta có:
ln
ln( ) ln 5 ln( ) ln 2 ln( ) ln 5 ln( ) ln( ) ln5 ln 2
2
2 .5 2 2 .5 2 2 .5 2 .2
xy
xy xy xy xy xy
+


++−+++

=⇔ =⇔=
ln( ) ln10
10 2
xy+
⇔=
( )
ln10 ln( ) ln10.log2
ln( ) log 2 ln( ) ln10.log 2
xy
xy xy e e
+
⇔ += ⇔ += ⇔ =
log 2
10 2xy xy⇔+= ⇔+=
. Do đó
( ) ( ) ( )
( 1) ln ( 1)ln 1 ln 3 ln 2Px xy y x x x x=+ ++ =+ +− −
.
Xét hàm số
( ) ( 1)ln (3 )ln(2 )fx x x x x=+ +− −
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có:
1 3 22
( ) ln ln(2 ) ln
2 2 (2 )
x xx x
fx x x
x x xx x
+− −
′
= + − −− = +
− −−
.
Lại có:
( )
( )
( )
( )
( )
2
2
2 22
22
41
2 2 2 4 4 13
. 0, ;
22
2
22
x
xx x
fx x
x
x
xx xx
−−
− −+

′′
= − = < ∀∈


−
−−
Do đó
(
)
0fx
′
=
có nhiều nhất một nghiệm trên
13
;
22



.
Mà
1x
=
là một nghiệm của pt
( )
0fx
′
=
nên phương trình
( )
0fx
′
=
có nghiệm duy nhất là
1x =
. Từ đó ta có bảng biến thiên như sau:
Dựa vào BBT, ta suy ra
( )
13
;
22
1 3 3 15 3 1
min min ln ln ;0
2 2 2222 2
P fx f f



 
= = = = + ∈−
 
 
.
Câu 11. Xét các số thực không âm
x
và
y
thỏa mãn
34
3 .3 4
xy
xy
+−
+≥
. Giá trị nhỏ nhất của biểu thức
22
54Px y x y
=+++
bằng
A.
43
8
. B.
33
4
. C.
49
8
. D.
57
8
.
Lời giải
Chọn A
Ta có
( )
34 34 3 4
3 .3 4 3 .3 4 3 .3 4 3
xy xy y x
xy y x y x
+− +− −
+ ≥⇔ ≥−⇔ ≥ −
( )
*
Xét hàm số
( )
.3
t
ft t=
,
0
t∀≥
, ta có
(
) ( )
3 1 ln 3 0
t
ft t
′
=+>
,
(
)
0t ft∀≥ ⇒
đồng biến trên
[
)
0; +∞
.
( ) ( ) ( )
* 3 4 , , 0 3 4 43, , 0f y f x xy y x x y xy⇔ ≥ − ∀ ≥⇔ ≥−⇔≥− ∀ ≥
Xét biểu thức
( ) ( )
2
22 2
5 4 43 543 4Px y x y P y y y y=+++⇒≥− ++ − +
2
43
10 35 36
8
Py y⇔≥ − + ≥
Vậy
43
min
8
P =
khi và chỉ khi
( )
7
57
;;
4
44
43
y
xy
xy
=

⇔=−


= −
Câu 12. Cho 2 số thực dương
,xy
thỏa mãn phương trình sau:
( )
3
11
22
11
22 2
2 3.4 4 3.2
xy
xy
xy y x
xye
+−
−−
+−
+=
+
++
.
Biết rằng, giá trị của
34
xy+
được viết dưới dạng
m
n
với m,n là các số nguyên dương và
m
n
là
phân số tối giản. Hỏi
T mn= +
có giá trị là bao nhiêu?
A.
149
. B.
147
. C.
160
. D.
151
.
Lời giải
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Chọn D
Biến đổi giả thiết ta được:
(
)
3
3
11
2 2 22 22
1 1 22 22
22 2
2 3.4 4 3.2 2 3.2 2 3.2
xy xy xy
xy
xy
xyyx xy yx
xye
xye
+−
+−
−−
−− + +
+ = ⇔ + =−−
+
++ + +
Đặt
2 ,2
xy
ab= =
thì theo bất đẳng thức AM – GM ta có:
(
)
(
)
( )
( )
( )
( )
(
)
2
2 2 12 3
;
3 2 3 42
33 3
2
2 2 12 3
;
3 2 3 42
33 3
22
3
42
22
3 3 33
ab
a a ab b b a
ab a b a b ab
ab ab ab
ab
b b ab a a b
baba ba ab
ba ba ba
ab ab
ab ab ab
ab
ab ab ab ab
+
+
≤ + ≤+ ⇒ ≤+
++ + +
++ +
+
+
≤ + ≤+ ⇒ ≤+
++ + +
++ +
++
+ ++
⇒+≤+=⇔+≤
+
+ + ++
Suy ra
22 22
22 22
2
33
2 3.2 2 3.2
xy xy
xy yx
ab ab
ab ab
+ + ++
+ =+≤
++
++
Mặt khác theo một bất đẳng thức phụ quen thuộc ta có:
( )
33
3 3312
xy xy
xye xy e
+− +−
+− = +− − +≤−=
Vậy
2VT VP≥≥
. Dấu “=” xảy ra khi và chỉ khi
22
3
2
30
xy
xy
xy
=
⇔==
+−=
Khi đó
34
135
151
16
m
x y T mn
n
+ = = ⇒ = +=
.
Câu 13. Cho hai số thực
,xy
thỏa mãn
(
)
33
12
2
2
11 1
log log 2 log
62 3
yx
+ +≥
. Tìm giá trị nhỏ nhất của
biểu thức
(
)
3
24
22
1
1
2
xx y
xy
P xy y
e
++−
+

= − + +−


A.
min 0
P =
. B.
min 1
P
=
. C.
min 2P =
. D.
min
Pe=
.
Lời giải
Chọn B
Điều kiện
3
0
(*)
2
y
x
>
>−
; Với
,xy
thuộc (*) và thỏa mãn
( ) ( )
33 3
1 2 22 2
2
2
11 1
log log 2 log log log 2 log 3
62 3
y x yx
+ +≥ ⇔ − +≥−
( ) ( )
33
222 2 2
log log 3 log 2 log 3 log 2y x yx⇔+≥+⇔≥+
( )
33
3 2 3 3 2 (**)yx yx x x⇔≥+⇔ −≥−+
Xét hàm số
3
() 3 2fx x x=−+
xác định và liên tục trên
( )
3
2;− +∞
Có
( )
22
'( ) 3 3 3 1fx x x= −= −
. Với
2
1
'( ) 0 1 0
1
x
fx x
x
=
= ⇔ −= ⇔
= −
Và
33
( 1) 4; (1) 0; ( 2 ) 3 2 0f ff−= = − = >
Bảng biến thiên
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Do đó
( )
3
2;
min ( ) (1) 0fx f
− +∞
= =
nên suy ra
(
)
30 0
yx yx− ≥⇔−≥
Mà
(
)
( )
3
3
24
22 22
42
1
11
22
xx y
yx x
xy xy
P xy y e xy y
e
++−
− −−
++

= − + +−= − + +−


( )
( )
( )
( )
( )
( )
( )
3
22
32
22
yx y x
yx
yx yx
e yx e yx
−+ − +
−
−−
= − −−≥ − −−
Xét hàm số (*)
2
1
()
2
t
gt e t t
=−−
xác định và liên tục trên
[
)
0; +∞
Do đó
'( ) 1
t
gt e t= −−
xác định và liên tục trên
[
)
0;
+∞
Và
[
)
0
''( ) 1 1 0, 0;
t
gt e e t= − ≥ − = ∀ ∈ +∞
.
Do đó hàm số
( )
'gt
đồng biến trên
[
)
0;
+∞
. Tức là
0
0 '( ) '(0) 0 1 0,t gt g e≥ ⇒ ≥ = −−=
Do đó hàm số
( )
gt
đồng biến trên
[
)
0; +∞
. Tức là
0
0 ( ) (0) 0 0 1t gt g e
≥⇒ ≥ = −−=
Suy ra
[
)
0;
min ( ) (0) 1gt g
+∞
= =
Dấu
""=
xảy ra khi và chỉ khi
33
0
00
1
1
3 2 3 20
2
xy
xy xy
xy
x
yx x x
x
= >
=>=>

⇔ ⇔ ⇔==
=

= + − +=

= −
.
Câu 14. : Cho các số thực
,xy
thỏa mãn
22 2
2 2 21
( 1) 0
x y xy xy y
e e x xy y e
+ ++
+ − + −− =
. Gọi
,Mm
lần lượt
là GTLN, GTNN của biểu thức
1
1
P
xy
=
+
. Tính
Mm−
.
A.
1Mm−=
. B.
2Mm−=
. C.
1
2
Mm
−=
. D.
3Mm−=
.
Lời giải
Chọn A
Ta có
22 2
2 2 21
( 1) 0
x y xy xy y
e e x xy y e
+ ++
+ − + −− =
22 2
2 2 21
( 1) 0
x y xy y
e x xy y e
+− +
⇔ + − + −− =
22 2
2 2 21 2
21
x xy y y
e x xy y e y
−+ +
⇔ + − + = ++
(1)
Xét hàm
() ,
t
f t e tt=+∈
. Ta có
() 1 0
t
ft e t
′
= + > ∀∈
nên
()ft
đồng biến trên
.
Do đó (1)
22 222222
( 2 ) (1 ) 2 1 1f x xy y f y x xy y y x xy y⇔ −+ = + ⇔−+ =+⇔−+=
Khi đó
( )
( )
2
2
1
1 33
x y xy xy
x y xy xy
=− +≥
= + − ≥−
suy ra
1
1
3
xy
−
≥≥
.
Do đó
1 11
1
11 1
1
3
P
xy
≤= ≤
++
−
1 13
21 2
P
xy
⇔≤= ≤
+
. Vậy
1Mm−=
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Câu 15. Cho các số thực
x
,
y
thỏa mãn
( )
2 22
2 222
5 16.4 5 16 .7
xy xy yx− − −+
+=+
. Gọi
M
và
m
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
10 6 26
225
P
xy
xy
++
=
++
. Tính
TMm= +
.
A.
21
2
T
=
. B.
10T
=
. C.
15T =
. D.
19
2
T =
.
Lời giải
Chọn D
Đặt
2
2
tx y= −
, khi đó giả thiết tương đương với
( )
22
2
22
54 54
5 16.4 5 16 .7 .(1)
77
tt
t tt
tt
+
−
+
++
+=+ ⇔ =
Xét hàm số
( )
14
5
77
uu
fu
 
= +
 
 
trên
. Ta có:
( )
1144
5 ln ln 0
7777
uu
fu
 
′
= +<
 
 
,
t∀∈
Suy ra
( )
fu
là hàm số nghịch biến trên
.
Do đó
( ) ( )
22
(1) 2 2 2 2 2 2 2 2 2ft f t t t t x y y x⇔ + = ⇔+ = ⇔= ⇔ − = ⇔ = −
Khi đó
2
2
310 6 26
322
10 20
25
xx
P
xy x
xy
x
++
=
+
+
+
=
+++
Ta có
( )
2
2
2
5
4 22 10
0
1
23
2
x
xx
P
x
xx
= −
−− −
′
= = ⇔
= −
++
. Bảng biến thiên như sau:
Từ BBT, ta suy ra
7M =
,
5
2
m =
. Vậy
5 19
7
22
Mm+=+=
.
Câu 16. Cho
,ab
là hai số thực thay đổi thỏa
12
ab
<≤≤
, biết giá trị nhỏ nhất của biểu thức
( )
22
2.log 4 4 log
b
a
a
aP bb
= +−+
là
3
3mn+
với
,mn
là số nguyên dương. Tính
S mn= +
.
A.
S9=
. B.
18S =
. C.
54S =
. D.
15
S =
.
Lời giải
Chọn D
Ta có:
( )
( )
2
2
10
1 2 1 40
40
b
b bb
b
−>
<≤⇒ ⇒ − − ≤
−≤
32 2 3
4 40 4 4bb b b b b⇒ − − +≤⇒ + −≥
mà
1a
>
nên
( )
23
log 4 4 log
aa
bb b+−≥
Do đó
( )
2
23
1
2.log log l6 og
log 1
a
ab a
a
ba b
b
P = ++
−
≥
Đặt
log
a
tb=
, từ điều kiện
12
1
1
ab
t
b
a
<≤≤
⇒>
≠
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
Khi đó
(
)
( ) ( )
( )
3
22
11
6. 3. 1 3 1 6 3 9 6
11
P
tt t
tt
+ = −+ −+ +≥
−
≥ +
−
Dấu “=” xảy ra khi
( )
( )
( )
3
3
2
1 11
31 1 1
33
1
t tt
t
− = ⇔ − = ⇔=+
−
. Vậy
6; 9mn= =
.
Câu 17. Cho hai số thực
,ab
thay đổi thỏa mãn
02 1ba< <<
. Giá trị nhỏ nhất của biểu thức
( )
25
3 2 12
2
2
log .log log 4 log
bb b
a
a
b
S a ba b
a
= + −+
bằng
m
. Khẳng định đúng là:
A.
( )
0;1m ∈
. B.
( )
1; 2m ∈
. C.
( )
2;3m ∈
. D.
(
)
3; 5m ∈
.
Lời giải
Chọn C
Ta có:
( ) ( )
( )
25
3 2 12 2 2
22
2 2 24
2
2 12 1
log .log log 4 log log .log log 4
25 log
12 1
log log .log log 4
25 log
bb b a b b
a
a
aa
b a bb
a
a
b
S a ba b b a ba
ab
a b a ab a
b
= +−+ = + +−
=−+ + + −
Ta có:
(
)
2
4 2 2 24 2
02 1 2 0 4 4 0 4 4b a a b a ab b ab a b< < <⇒ − ≥ ⇒ − + ≥ ⇔ − ≤
Mà mặt khác
1
02 1 0 1
2
ba b< < <⇒ < < <
nên suy ra
(
) (
)
24 2
log 4 log 4
bb
ab a b
−≥
Từ đó ta có:
( )
2 22 2
22
22
22
3
2 2 22
2
2
12 1 2 12 1
log log .log log 4 2log log .log
25 log 25 log
log log
1 1 12 1 1 12
log 3 . . log
log log log 25 log log log 25
log
3
log
babbbab
aa
aa
bb
aa
aa
b b a b ba
a a aa
b
a
b
a
b
Sabab ba
b ab
aa
bb
b b b b bb
a
b

=−++ + ≥ ++




= ++ + ≥ +



=
( )
2
3
3
3
1 12 1 12
. log 3 log
log 25 25
log
3 12 3 12 12.3 12
log 2 . log 2
log 25 log 25 25 5
aa
a
a
aa
aa
bb
b
b
bb
bb
+= +

=+≥ ==
Như vậy giá trị nhỏ nhất của biểu thức
S
bằng
12
5
với
( )
12
2;3
5
m = ∈
Câu 18. Cho 2 số thực
,xy
thỏa mãn phương trình sau:
( )( )( ) ( )
3
23
12 12 12 12
xyxyxy x++ −
+ + +=+
.
Đặt
( )
22
2
2
2
2
4
xy
y
Pe x x y
+
= ++ −−
. Hỏi mệnh đề nào sau đây đúng?
A.
1Pe= −
. B.
Pe=
. C.
2
max
Pe=
. D.
2Pe= −
.
Lời giải
Chọn B
Một bất đẳng thức mà ta hay gặp:
( )( )( )
(
)
3
3
111 1a b c abc+ + + ≥+
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
Có bổ đề sau: Cho các số thực dương
,,,,,, ,,abcx yzmn p
khi đó ta luôn có:
( )( )( )
( )
3
3333 33 33 3
a b c x y z m n p axm byn czp++ ++ ++ ≥ + +
Chứng minh: Theo bất đẳng thức
AM GM−
ta có:
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
3 33
333 33 3 3 33
333 33 3 33 3
333
333 33 3 3 33
333 33 3 33 3
3 33
333 33 3 3 33
333 33 3 33 3
3
..
3
..
3
..
a m x axm
abc mn p x yz
abc mn p mn p
b n y bny
abc mn p x yz
abc mn p mn p
c p z cpz
abc mn p x yz
abc mn p mn p
+ +≥
++ ++ ++
++ ++ ++
+ +≥
++ ++ ++
++ ++ ++
+ +≥
++ ++ ++
++ ++ ++
Cộng 3 bất đẳng thức trên có điều phải chứng minh.
Quay lại bài khi đó phương trình trở thành:
( )( )( )
( )
3
3
111 1a b c abc+ + + ≥+
Theo bất đẳng thức Holder, ta có
(
) (
)
33
33
33
33
11
1
22
cyc
a abc


+ + ≥+





∏
Với bài toán này nếu đặt
23
3
2 ,2 ,2 2
xy x y x y x
a b c abc
++ −
= = =⇒=
, đây chính là dạng trên.
Dấu
""=
xảy ra khi và chỉ khi
23
22 2 0
xyxyxy
xy
++ −
= = ⇔==
. Vậy khi đó
Pe=
.
Câu 19. Cho 2 số thực
,
ab
không âm thỏa mãn
( ) ( )
2
log 0;1ab ∈
đồng
thời
( ) ( )
22
1
log 1 log
22
22
2
log 1 log 1
21
ab
ab ab
ab
ab ab
−+
−
−
+− = +
+
. Biết rằng
4 10
ab
được viết dưới dạng
mn
với a,b là các số nguyên dương. Hỏi có tất cả bao nhiêu bộ số
( )
;
mn
như vậy?
A.
( )
0;1m ∈
. B.
( )
1; 2m ∈
. C.
( )
2;3m ∈
. D.
( )
3; 5m ∈
.
Lời giải
Chọn C
Bất đẳng thức Jensen và tính chất của hàm lồi
Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
và n điểm tùy ý nên
[ ]
;ab
. Ta có
• Nếu
( )
'' 0fx>
thì
( )
12
1
...
n
n
i
i
xx x
f x nf
n
=
+ ++

≥


∑
• Nếu
( )
'' 0fx<
thì
( )
12
1
...
n
n
i
i
xx x
f x nf
n
=
+ ++

≤


∑
Ngoài ra cần chú ý thêm
• Nếu hàm số
( )
fx
có
( )
[
]
'' 0, ;f x x ab> ∀∈
thì
( )
fx
làm hàm lồi trên
[ ]
;ab
• Nếu hàm số
( )
fx
có
( )
[ ]
'' 0, ;f x x ab< ∀∈
thì
(
)
fx
làm hàm lõm trên
[ ]
;ab
Trước tiên ta sẽ đặt
22
log ,1 log 1
ab x ab y x y= − =⇒+=
.
Vế trái viết lại là
xy
xy+
.
Ta có bất đẳng thức
( ) ( )
( )
*
22
fx fy
xy
f
+
+

≥


- Bất đẳng thức Jensen
Thật vậy ta có thể giả thiết
01ab<<<
và viết bất đẳng thức dưới dạng
( ) ( )
0
22
xy xy
f fx fy f
+  +
 
−−− ≤
 

 

NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
Vế trái của bất đẳng thức này có dạng
( )
( )
(
)
( )
' ' ''
22 2
yx yx yx
ff f
α β γαβ
−− −
−=−
Trong đó
,
2
xy
xy
α β αγβ
+
<< < < <<
.
Vì
( )
ln lnfx x x=
(
) ( )( ) ( ) ( ) ( ) (
)
2
1
' 1 ln '' 1 ln 0, 0;1
f x fx x f x fx x x
x

⇒ = + ⇒ = + + > ∀∈


Suy ra
(
)
( )
'' 0
2
yx
f
γαβ
−
−<
. Vậy bất đẳng thức
( )
*
đúng. Khi đó áp dụng ta có
( ) ( ) ( )
1
1
1 12 2
2
x
xyx
x y x x fx f x f
−

+ = +− = + − ≥ =


Theo bất đẳng thức AM – GM ta có
1
22
22
2 2.2
11 2
21
22
ab ab
ab
ab
−+ −
−
−
+ ≤+ =
+
.
Vậy
VT VP≥
. Dấu “=” xảy ra khi
4 10
4
2 128 2 32 4 8 8 2x y xy==⇒====
Câu 20. Cho 2 số thực
,1
xy
>
thỏa mãn điều kiện:
( )
22 2
9
1 log 3 2log 3 3 log 3 log 2
2
x
y y xy++ − =
.
Đặt
22
P x xy y
=++
. Hỏi mệnh đề nào sau đây đúng?
A.
[ ]
11;12P ∈
. B.
[ ]
12;13P ∈
. C.
[ ]
10;11P ∈
. D.
min
10P =
.
Lời giải
Chọn C
Ý tưởng ở bài này là sẽ kiếm một điều kiện ràng buộc giữa x,y rồi sau đó chỉ ra giả thiết chỉ nhận
duy nhất 1 bộ nghiệm. Dưới đây là cách giải quyết của bài toán trên
Biến đổi giả thiết ta được:
(
)
22 2
9
1 log 3 2log 3 3 log 3 log 2
2
x
y y xy
++ − =
2 22 2 22
89
log log log 3 2log 3 log log
32
x x y yx
xy
⇔+ + =
Ta nhận thấy rằng
22 2
8
log log 3 log 3
3
xy
xy
++ =
.
Để đơn giản ta đặt
2
2
2
log
log 3
8
log
3
xa
yb
c
xy
=
=
=
. Lúc này ta có 2 giả thiết
3
9
2
2
abc
a ab abc
++=
++ =
.
Thế
3b ac=−−
vào giả thiết dưới ta được:
( )
( )
22
9
21 2 54 0
2
ca cc a
+ + − − +=
Coi vế trái là tam thức bậc 2 theo biến
a
với
c
là tham số ta có:
(
)
( ) (
)
( )
2
2
22
2 5 4 18 2 1 2 1 4 2cc c c cc∆= − − − + = − − −
Chú ý với điều kiện
,1
xy>
ta sẽ có
,, 0abc>
. Mặt khác
33abc c++=⇒<
Suy ra
0∆≤
, điều này đồng nghĩa
0VT ≥
Dấu “=” xảy ra khi và chỉ khi
2
2
2
33
log
22
22
1 log 3 1
2
1
81
3
log
2
32
ax
x
by
y
c
xy
= =
=

=⇒=⇔

=


=
=
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Từ đây suy ra
[ ]
76 12 2
10;11
9
P
+
= ∈
.
Câu 21. Cho hàm số
( ) ( )( )( )( )
1234y fx x x x x m= =+ + + ++
. Khi đó, giá
trị
m
để giá trị cực tiểu của hàm số
( )
fx
bằng với giá trị nhỏ nhất của biểu thức
(
) ( )
log 3 2 log 3 2
ab
Pb a= ++ +
với
(
]
, 1; 2ab∀∈
nằm trong khoảng nào sau đây
A.
[
]
3; 4
. B.
[ ]
5; 6
. C.
[ ]
7;8
. D.
[ ]
9;10
.
Lời giải
Chọn C
Cách 1: Ta có:
( )
(
)
( )
(
)
3
4
3
4
3
4
3
4
31
log 3 2 log 4 2 log 4 log log 2
3 2 2 42
44
31
3 2 2 42
log 3 2 log 4 2 log 4 log log 2
44
b b bbb
a a aaa
aa a
a aaa a
b bbb b
bb b
+≥ = + +
+=+++≥

⇒

+=+++≥

+≥ = + +
Suy ra:
( ) ( ) ( )
( ) ( )
31
log 3 2 log 3 2 log 4 log 4 log log log 2 log 2
44
a b ab ba ba
b a ab++ +≥ + + + + +
( ) ( )
22 22
31
log 4 log 4 2 log .log log 2 log 2
44
ba
ab
≥++ + +
(do
(
]
, 1; 2ab∀∈
)
6=
. Suy ra
min
6P =
khi và chỉ khi
2ab= =
Từ đó ta cũng suy ra:
(
)(
)
( )( ) (
)
( )
( )( )
(
)( )
( )( ) (
)
min
2
22 2 2 2
6 1234 1423
54 56 551 551 55 1
Pxxxx mxxxx m
xx xx mxx xx mxx m
==+++++=+++++
= ++ +++= ++− ++++= ++ +−
Do phương trình
2
5 50xx
+ +=
có hai nghiệm
(
]
1; 2∉
) nên ta cũng suy ra
( )
2
2
5 5 1 1 16 7Px x m m m m= + + +−≥−⇒−=⇔=
. Như vậy
Cách 2: Nhìn vào biểu thức
P
trên ta dự đoán được điểm rơi
2ab= =
Ta có:
( ) (
) (
)( )
(
)
(
)( )
(
)
22
22
log 3 2 log 3 2 log 2 1 log 2 1
ab a b
P b a b bb a aa= ++ +≥ +− + + +− +
Xét hàm số
( ) ( )( )
2
21y fx x x= =−+
với
(
]
1; 2x∀∈
có
( )
0fx≥
(
]
1; 2
x∀∈
(
) ( ) ( )
( )
2
0 1, 0 2 1 0
ft t f t xx
′ ′′
= ⇔= <⇒ − + >
Từ đó ta suy ra
( )( )
( )
( )
( )
( )
(
) ( )
22
2 2 33
log 2 1 log 2 1 log log
a b ab
P b bb a aa b a≥ +− + + +− + ≥ +
( )
11
3 log log 3 log 3.2 log . 6
log log
ab a a
aa
ba b b
bb

= += + ≥ =


Suy ra
min
6P =
khi và chỉ khi
2ab= =
--Khúc sau làm tương tự như cách 1 đã trình bày--
Câu 22. Lần lượt cho hai số thực dương
,xy
thỏa mãn phương trình sau đây:
( )
22
2
22
33
log 6 2
3
xy
x y xy x y
x y xy

+
=++− ++

+++

. Gọi giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
232
1
xy
P
xy
++
=
++
lần lượt là
M
và
m
. Giá trị của biểu thức
( )
Mm+
bằng
A.
60
13
. B.
12
. C.
26
5
. D.
40
13
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Lời giải
Chọn A
Ta có:
( )
22
2
22
33
log 6 2
3
xy
x y xy x y
x y xy

+
=++− ++

+++

( )
(
)
( )
( )
( )
( )
( )
( )
( )
22
2
22
22
2
22
22 22
22
33
1 log 6 3
3
6
log 6 3
3
log 3 3 log 6 6
xy
x y xy x y
x y xy
xy
x y xy x y
x y xy
x y xy x y xy x y x y

+
⇔+ = + + − + +

+++

+

⇔ =++− ++

+++

++++ +++= + + +
Xét hàm đặc trưng
( ) ( )
2
1
log 1 0 0
ln 2
y ft t t f t t
t
′
= = + ⇒ = + > ∀>
.
Suy ra hàm số
( )
ft
đồng biến trên
( ) ( )
22
0; 3 6x y xy x y+∞ ⇒ + + + = +
Đặt:
( ) ( ) ( )( ) ( ) ( )
22
36 6
x ab
ab ab abab ab ab
y ab
= +
⇒+ +− ++ −+= ++ −
= −
( )
2
22
3 2 93ab⇔ − +==
. Đặt:
3 cos 2
3sin
at
bt
= +
=
Suy ra biểu thức
( ) ( )
( ) ( )
( )
( )
( )
5 3 cos 2 3sin 2
232
232 5 2
1 1 21
2 3 cos 2 1
5 3 cos 3sin 12
2 3 5 3 cos 3sin 12 5
2 3 cos 5
tt
ab ab
x y ab
P
x y ab ab a
t
tt
P tt P
t
+− +
++ −+
+ + −+
= = = =
++ + + − + +
++
−+
= ⇔ − +=−
+
Điều kiện có nghiệm
(
)
(
)
2
2
30 2 30 30 2 30
2 3 5 3 9 12 5
13 13
P PP
−+
− +≥ − ⇔ ≤ ≤
Như vậy suy ra:
max
min
30 2 30
60
13
13
30 2 30
13
PM
Mm
Pm
+
= =
⇒ +=
−
= =
Câu 23. Cho hai số thực dương, tính giá trị lớn nhất của biểu thức sau đây:
( )
3 3 log
2022 16 10 24 12.10
x xy
P yy
+
= − +− +
A.
2046
. B.
2048
. C.
2050
. D.
2038
.
Lời giải
Chọn A
Ta có:
( ) ( )
33 log 33
2022 16 10 24 12.10 2022 16 10 24 12 .10
x xy x x
P yy yyy
+
= − +− + = − +− +
Áp dụng bất đẳng thức Cosi ta có:
( ) ( )
( )
2
2
22
2. 2 .10 2 10 4 10
xxx
yy y≤+ =+
Dấu bằng xảy ra khi và chỉ khi:
2 10
x
y =
Suy ra:
( )
( )
( ) ( ) ( ) ( )
33
33 22 3 2 3 2
2022 16 10 24 3.2. 2 .10
2022 16 10 24 3 4 10 2022 4 4 3 6 10 3.10
xx
x x xx
P y yy
y y y yyy
= − +− +
≤ − + − + + = + − + + +− +
Khảo sát các hàm số sau:
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
( ) (
)
( )
( )
( )
32
32
4 3 6 0;
10 3.10 0;
xx
fy y y y y
gx x
= − + + ∀ ∈ +∞
= − + ∀ ∈ +∞
ta có:
(
)
( )
( )
(
)
( ) ( )
3 2 32
15
10 3.10 3 2 4
xx
fy f
g x t t ht h
≤=
⇒
=− + =−+ = ≤ =
Dấu bằng xảy ra khi:
1
log log 2
y
xt
=
= =
Suy ra:
(
)
(
)
(
) (
)
32 3 2
2022 4 4 3 6 10 3.10
2022 4 2018 4.5 4 2046
xx
P yyy
f y gx
= + − + + +− +
≤ + + ≤ + +=
Như vậy
max
2046P =
khi và chỉ khi
log 2
10 2
1
22
x
x
y
y
=
=
⇔

=
=
Câu 24. Cho 2 số thực x,y thay đổi thỏa mãn
( )
12 2 3xy x y
+ += − + +
.
Giá trị lớn nhất của biểu thức
( )
( )
4 7 22
3 12 3
xy xy
S xy x y
+− −−
= + ++ − +
là
a
b
với a,b là các số
nguyên dương và
a
b
tối giản. Tính
P ab= +
A.
8P =
. B.
141P =
. C.
148P
=
. D.
151P =
.
Lời giải
Chọn A
Đây chính là đề thi THPT Quốc Gia 2016 đã được biến tấu để trở thành 1 câu hỏi trắc nghiệm
Từ giả thiết ta có
( )
( ) ( )
2
2
1 4 2 3 4 12 2 3xy x y xy x y++ = −+ + = +++ − +
Áp dụng bất đẳng thức AM – GM cho 2 số thực không âm ta có:
( ) ( )
2
2 2 3 1 18 1 1 7x y xy xy xy xy− +≤++⇒ ++ ≤ ++ ⇒−≤+≤
Mặt khác ta lại có:
( )
( )
( )
2
33 7
1 4 12 2 3 4 1
11
xy xy
xy xy x y xy
xy xy
+≥ ≤+≤

++ = +++ − + ≥ ++ ⇒ ⇒

+ ≤− + =−

Nếu
2
2 30
9746
1
3
243
1
x
xy
xy S
y
xy
=
− +=
+ =−⇒ ⇔ ⇒ =−

= −
+=−
Nếu
37xy≤+≤
. Đặt
[ ]
( )
3; 7t x yt=+∈
Xét hàm số
( ) ( )
[ ]
( )
47
3 1 .2 3; 7
tt
ft t t
−−
= ++ ∈
( ) ( )
( ) ( )
( )
( )
( )
[ ]
47 7
42 7 7 7
42 2 7
' 3 ln 3 2 1 2 ln 2
'' 3 ln 3 2 ln 2 ln 2 2 1 2 ln 2
3 ln 3 1 ln 2 2 ln 2 2 0 3;7
tt t
t t tt
tt
ft t
ft t
tt
−− −
−− − −
−−
⇒ = + −+
⇒ = − − −+
= + + − > ∀∈
Vì
( ) ( )
' 3 0, ' 7 0ff<>
nên tồn tại số
( )
3; 7a ∈
sao cho
( )
'0fa=
. Suy ra
( )
ft
nghịch biến
trên
( )
3; a
và đồng biến trên
( )
;7a
. Mặt khác
( ) ( ) ( ) (
)
[ ]
193 193
3 ; 7 35 3 3; 7
33
f f ft f t= = ⇒ ≤ = ∀∈
Ta sẽ đi chứng minh
22
5xy+≥
với
3, 2xy x+≥ ≥
. Nhận thấy rằng khi:
+
[ ]
( )( )
22 22 2
2;3 3 0 69 2 692 2 155
x y x yxx xy xx x x∈ ⇒ ≥−≥⇒ ≥ − +⇒ + ≥ − += − − +≥
+
22
39x xy>⇒ + >
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
Vậy
22
5
xy
+≥
148
148
151
3
3
a
a
S ab
b
b
=
⇒ ≤ = ⇒ ⇒+=
=
.
Câu 25. Cho các số thực
,ab
thỏa mãn
0ab
>>
và
( ) ( )
23
log logab ab−= +
Khi biểu thức
( )
( )
22
22 3 2
log log 2log 2logP a b ab a b= + + +− +
đạt giá trị lớn nhất, giá trị
ab
−
thuộc khoảng
nào sau đây?
A.
( )
3;4
. B.
( )
5;6
. C.
( )
4;5
. D.
(2;3)
.
Lời giải
Chọn D
Đặt:
22
22
22
94
02 24
2
0 3 2 9 94
4
tt
tt
t t tt
ab
ab a abb
a b a ab b
ab
+
+=

<−= − + =

⇔⇒

<+= + + = −


=
(
)
( )
( ) (
)
22
23 2
2 2 2 22
22
log 2 log 2log
9 4 9 4 9 4 36 16
log 2 2log log log 4 log
42
94 94
tt tt tt t t
t
tt tt
P ab a b a b
t
= + +− +
− +− −
= +− = + =
++
Đặt
( )
22
2
9
1
36 16 1
4
21
99
94
21
44
t
tt
tt
tt
k
S
kk

−

−−

= = =
++
 
+
++
 
 
với
9
4
t
k

=


P
đạt giá trị lớn nhất khi và chỉ khi
S
đạt giá trị lớn nhất.
Giả sử
S
có giá trị lớn nhất. Suy ra phương trình
( )
2
2 1 10Sk S k S+ − + +=
có nghiệm.
( )
( )
2
21 4 10S SS
⇒∆= − − + ≥
1
8
S⇔≤
.
Suy ra
S
đạt GTLN bằng
1
8
khi
9
4
9
3 3 log 3
4
t
kt

=⇒ =⇔=


.
Do đó
P
đạt GTLN bằng
2
1
log 3
8
= −
khi
9
4
log 3t =
.
Khi đó
( )
9
4
log 3
29
4
l 6og log 3 2 2,5ab t ab−= ≈= ⇔−=
.
Câu 26. Cho hai số thực
x
và
y
thỏa mãn:
2 24xy x y+= ++ −
. Khi ấy,
giá trị nhỏ nhất của biểu thức
22
2
6
ln 2
xy
P x y xy
+
= +++
tương ứng là:
A.
4
28.
ln 2
−
B.
2
4.
ln 2
−
C.
8
6.
ln 2
+
D.
4
.
ln 2
Lời giải
Chọn A
ĐK:
2
2
x
y
≥−
≥
Ta có:
( )
( )
2
2
2 24 2 24xy x y xy x y+= ++ −⇒ + = ++ −
( ) ( )( )
( ) ( ) ( )
22
22 22 4 0 11xy xyy x y xy xy xy xy+ =++−+ + − ≥+⇒ + − + ≥⇒+≥
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
Áp dụng BĐT Bunhiacôpki ta có:
( )
( )
( ) ( ) ( ) ( )
2
22
2 2 4 3 3 0 0 32xy x y xy xy xy xy+ = ++ − ≤ + ⇒ + − + ≤→≤+≤
Từ
( ) ( )
1&2 1 3xy⇒≤ + ≤
Lại có:
( )( ) ( )
2
2 20 2 4
2
x
x y xy x y
y
≥−
⇒ + + ≥ ⇒ ≥− + −
≥
( )
(
)
(
) ( )
22
22
4 8 16 4 8 16
ln 2 ln 2
xy xy
xy xy P xy xy xy xy
++
⇒ ≥− +−⇒= ++ + ≥ ++ − +−
Đặt
( )
13uxy u
=+ ≤≤
khi đó:
2
2
8 16
ln 2
u
P uu≥ +−−
( )
( ) ( )
2
2
8 16 1 3 ; 2 2 8 0 2
ln 2
u
u
fu u u u f u u u
′
= + − − ≤≤ = + −=⇒ =
Ta có BBT hàm số
( )
fu
như sau:
Từ BBt suy ra:
4
28 2
ln 2
Pt≥ − ⇔=
. Vậy GTNN của
2
4
28
4
ln 2
x
P
y
= −
= −⇔
=
.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
BÀI TOÁN GTLN - GTNN BIỂU THỨC MŨ – LOGARIT NHIỀU BIẾN SỐ
Câu 1. Cho
,,xyz
lần lượt là các số thực dương và thỏa mãn hệ phương trình sau
(
)
( ) ( )
33
3log 3 3log 27 log 81 0
x x xy
y z yz
= = >
. Khi biểu thức
54
P xyz=
đạt giá trị nhỏ nhất thì
giá trị của
1000P
nằm trong khoảng nào ?
A.
( )
18;20
. B.
( )
20;22
. C.
( )
22;24
. D.
( )
24;26
.
Lời giải
Chọn B
Ta có hệ phương trình sau:
(
) (
)
( )
33
3log 3 3log 27 log 81 0 (*)
x x xy
y z yz
= = ≠
Từ phương trình (*), ta có:
( ) ( )
( )
33
3log 3 3log 27 log 81 0
x x xy
y z yz k
= = = >
Đặt:
( )
( )
( )
( )
( )
( )
33
33
3
3
1
3
3
3log 3
1
3log 27 3 27 3
27
log 81
3 81 (*)
kk
x
kk
x
k
xy
x yy x
yk
zk x zz x
yz k
xy yz
= →=
=
=⇒ = →=


=
=
Thay nghiệm
,yz
theo
x
vào
( )
32
3 3 3 33
3
1 11
(*) 3 81 . 3 3 .
3 3 27
kk
k k k kk
k
xx x x x x
+

⇒ = ⇔=


( )
( )
( )
( )
( )
( )
2
2
23
1
31 31
3
1
32 1
11
3 33 3 3 3 1
3
79
31
3
1
33
3
3. 3 3 3 3
1
33
27
kk
k
kk
kk
kk k k k k
k
kk
k
kk
k
k
yx
x xx x x x
zx
−−
−
++
+
+
++
+
−−
+
= = =
⇔ = ⇔ = ⇔ = ⇔ =⇒= ⇒
= =
Thế các nghiệm
,,xyz
theo
k
vào biểu thức cần tính, suy ra:
( )
( ) ( ) ( )
( )
2 22
4
5
2 3 7 9 5 8 12 7 9 15 6
1
31 31 131 31 31
54
1
3 . 3 .3 3 3
k kk k kk k k
k k kk k k
k
P xyz
−− −− + −− − −
−+
+ + ++ + +
+


= = = =





Khi
( )
2
min
min
15 6
31
kk
P
k

−−
⇔


+

. Xét hàm
( )
( )
2
15 6
0
31
kk
y fk k
k
−−
= = ∀>
+
( )
( )
2
2
1 10
29
0 0 1 10
91
1 10
k
kk
fk k
k
k
=−+
−−
′
= ⇔ = ⇔ ⇒ =−+
+
=−−
Dễ dàng suy ra
(
)
( )
2 10 17
3
min
2 10 17
min 1 10 1000 1000.3 20.052698
3
fk f P
−
−
= −+ = ⇒ = ≈
Câu 2. Cho các số thực không âm
,,abc
thỏa mãn
2484
abc
++=
. Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
23Sa b c=++
. Giá trị của biểu thức
4 log
M
M
m+
bằng
A.
2809
500
. B.
281
50
. C.
4096
729
. D.
14
25
.
Lời giải
Chọn C
Đặt
222
log , 2 log , 3 loga xb yc z= = =
. Ta có
( )
2
logS xyz
=
.
3
3
2
44
4 3 3log
33
x y z xyz xyz S
 
=++≥ ⇒ ≤ ⇔ ≤
 
 
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 2 TÀI LIỆU ÔN THU THPT QUỐC GIA
2
44
3log ,
33
MaxS M khi x y z

= = = = =


Gọi
(
)
4
min , , 1
3
zxyzz= ⇒≤ ≤
.
Do
(
)(
)
1 1 0 13x y xy x y z
− − ≥⇒ ≥++=−
( )
32xyz z z⇒ ≥ −≥
(vì
4
1;
3
z

∈


Suy ra
1S ≥
, do đó
min 1mS= =
khi
1, 2xz y
= = =
2
2
4
3log
3
4
3log
3
4096
4 log 4 log 1
729
M
M
m






+=+ =
.
Câu 3. Cho ba số thực thay đổi
,, 1
abc>
thỏa mãn
6abc++=
. Gọi
12
,xx
là
hai nghiệm của phương trình
(
)
( )
2
log 2 log 3log log 2022 0
a a aa
x b cx−+ + − =
. Khi đó giá trị lớn
nhất của
12
xx
là
A.
2022−
. B.
216
. C.
2
12 6log 3+
. D.
108
.
Lời giải
Chọn C
Do phương trình
( ) ( )
2
log 2 log 3log log 2022 0
a a aa
x b cx−+ + − =
có hai nghiệm
12
,xx
nên ta suy
ta hệ thức Viét như sau:
( ) ( ) ( )
1 2 12
log log log 2 log 3log
a a a aa
x x xx b c+ = =++
2 log 3log
23
12
aa
bc
x x a a bc
++
= =
Ta lại có tiếp
23
6
6
6 6 ..... 6
2 2 3 3 3 2 2 3 3 3 108
a a c c c aa ccc abc
abc b b=++= + ++++ ≥ =
Suy ra
23
12
108x x a bc= ≤
. Như vậy giá trị lớn nhất của
12
xx
là
108
Câu 4. Cho ba số thực không âm
,,xyz
thỏa mãn
222
2356
xyz
++=
. Giá trị
lớn nhất của biểu thức
34Tx y z
=++
nằm trong khoảng nào sau đây
A.
( )
4;5
. B.
( )
5; 6
. C.
( )
6;7
. D.
( )
7;8
.
Lời giải
Chọn C
Ta có:
2 2 2 222 222
3
6 2 3 5 3 2 .3 .5 2 .3 .5 8
x y z xyz xyz
=++≥ ⇒ ≤
Loga cơ số 2 cho hai vế ta có:
( )
222
22 2
2 22
log 2 .3 .5 3 log 3 log 5 3
xyz
xy z≤⇔ + + ≤
Áp dụng bất đẳng thức Bunyakovsky, ta có:
( )
2
2
2
22
22
34
3 4 1. log 3 log 5
log 3 log 5
T xyz x y z

=++ = + +



( )
(
)
(
)
( )
( )
( )
22 2
22
22
2 22 2
35 22 35
35
9 16
1 . log 3 log 5
log 3 log 5
1 9log 2 16log 2 . log 3 log 5 3. 1 9log 2 16log 2
3 1 9log 2 16log 2 6,38 6;7
xy z
T xy z
T

≤+ + + +


⇒≤++ + + =++
⇒≤ + + ≈ ∈
Câu 5. Cho ba số thực
,,
abc
nhận những giá trị dương lớn hơn
1
. Khi đó giá trị
nhỏ nhất của biểu thức
( )
( )
( )
( )
( )
3
2 22
34
34 34
3
log 4 9
2log 2 3 log 3
ab
ab ab
T a bc
a bc
+
++

= ++ +

++−
là:
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Chọn D
Ta có:
( )
( )
( )
(
)
(
)
( )
( )
( )
( )
( )
( )
( )
(
)
2
3
2 22
34
34 34
3
2 22
34
2
34
3
2 22
34
23
3
3
log 4 9
2log 2 3 log 3
3
log 4 9
23
log
3
log 4 9 3log 3 4
ab
ab ab
ab
ab
ab
a bc
T a bc
a bc
a bc
a bc
a b c ab
+
++
+
+
+
++

= ++ +

++−

= ++ +

++

= ++ + +

Theo Bunhia, ta có:
( )
(
)
( )
(
)
( )
2
2
2 22 2 22
23
1114 9 2 3 4 9
3
a bc
a bc abc a bc
++
++ ++≥ ++⇔ ++≥
Suy ra:
( )
( )
( )
( )
2
3
2
34
23
3
23
log 3log 3 4
3
ab
a bc
a bc
T ab
+
++

++
≥ ++



. Đặt
(
)
( )
2
34
23
log
3
ab
a bc
t
+
++
=
Khi ấy,
33 3
4
3 1 1 1 111
4 ... 4Tx x x
x x x x xxx
≥ += +++≥ =
.Vậy
min
4T =
Câu 6. Cho ba số thực
[ ]
, , 1; 4xyz∈
và đồng thời thỏa điều kiện
16xyz
=
. Giá
trị lớn nhất của biểu thức
( )
222
2 2 2 3 log log logT xyz x y z=++− + +
tương ứng là:
A.
3
. B.
6
. C.
6 33+
. D.
4 26+
.
Lời giải
Chọn D
Đầu tiên, ta khảo sát hàm số
( )
4
3log 1fx x x=−−
trên đoạn
[ ]
1; 4
như sau:
Có:
( )
33
10
ln 4 ln 4
fx x
x
′
=− =⇔=
. Ta có tiếp:
( ) (
)
4
33 3
1 4 0; 3log 1 0,51
ln 4 ln 4 ln 4
ff f
 
= = = − − ≈−
 
 
Suy ra
( )
[ ]
4
3 log 1 0, 1; 4fx x x x= − −≤ ∀∈
và dấu bằng xảy ra khi
1
4
x
x
=
=
Tương tự như thế ta cũng thu được
[ ]
[ ]
4
4
3 log 1 0, 1; 4
3 log 1 0, 1; 4
yy y
zz z
− −≤ ∀∈
− − ≤ ∀∈
Suy ra
( ) ( )
( )
222 444
2 2 2 3 log log log 2 3 log log log
Txyz xyzxyz xyz=++− ++ =++− ++
( )
( ) (
)
(
)
(
)
444
2 3log 1 3log 1 3log 1 3 2. 0 3 6x xy yz z= − −+ − −+ − −+ ≤ + =
. Vậy
max
6T =
Câu 7. Cho ba số thực
[ ]
, , 1; 3xyz∈
và đồng thời thỏa điều kiện
9xyz =
. Giá
trị lớn nhất của biểu thức
( )
( )
2 22
333
2 log log log
T x y z x xy yz z
= ++ − + +
tương ứng là:
A.
33
. B.
7
. C.
8 33+
. D.
9
.
Lời giải
Chọn B
Đầu tiên, ta có:
( ) ( )
( )
2
33
2 1 log 1 1 2log 1x x x xx x− + += + − −
Xét hàm số sau:
( )
[ ]
3
2 log 1 1; 3y fx x x x= = − − ∀∈
Có:
( )
22
10
ln 3 ln 3
fx x
x
′
=− =⇔=
.
Ta có tiếp:
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 4 TÀI LIỆU ÔN THU THPT QUỐC GIA
( ) ( )
3
22 2
1 3 0; 2log 1 0,27
ln 3 ln 3 ln 3
ff f
 
= = = − − ≈−
 
 
Suy ra
( )
[ ]
3
2 log 1 0 1; 3y fx x x x= = − −≤ ∀∈
Và ta cũng suy ra được
( )
(
)(
)
[ ]
2
33
2 1 log 1 1 2log 1 0 1;3x x x xx x x
− + + = + − − ≤ ∀∈
[ ]
2
33
2 log 2log 1 1;3xxx x x⇒ − ≤ + ∀∈
Tương tự, ta cũng dễ dàng chứng minh được:
[ ]
[ ]
2
33
2
33
2 log 2log 1 1;3
2 log 2log 1 1;3
yyy y y
zzz z z
− ≤ + ∀∈
− ≤ + ∀∈
Suy ra:
(
)
( )
2 22
333
2 log log logT x y z x xy yz z= ++ − + +
( ) ( ) ( )
( ) ( ) ( ) ( )
( )
222
3 33
3 3 3 333
33
2 log 2 log 2 log
2log 1 2log 1 2log 1 2 log log log 3
2log 3 2 log 9 3 7
x x xy y yz z z
x y z xyz
xyz
=− +− +−
≤ ++ ++ += + + +
= += +=
Vậy
max
7
T =
Câu 8. Cho ba số thực
1a >
,
1b >
,
1c >
. Biết rằng tồn tại số thực dương
1x ≠
thỏa mãn hệ thức
9
log log
ba
xx
ab=
. Khi đó, biểu thức
( )
2
log ( ) log
cb
T ab a bc= +
đạt giá trị
nhỏ nhất tương ứng bằng
A.
11
. B.
7
. C.
8
. D.
5
.
Lời giải
Chọn A
Với ba số thực
1a >
,
1b >
,
1c >
, ta có:
( )
log
log log .log log log
b
b ab a b
a
c ca c a
aa a c= = =
.
Do tồn tại số thực
0x
>
,
1x ≠
thỏa mãn hệ thức
9
log log
ba
xx
ab=
nên áp dụng tính chất trên ta
được:
9
log log
ba
xx
ab=
log 9log
ba
ab
xx⇔=
log 9 log
ba
ab⇔=
log 3
b
a⇔=
.
Do đó,
( )
22
log ( ) log log ( )
.log 1 loglog
cb c
b b b
bT ab a bc ab a c++ += = +
( )
log 1 2. log 1 lol gog
c bbb
a acb= ++ ++
l4log og 7
c b
b c+= +
.
Vì
1a >
,
1b >
,
1c >
nên
log 0
c
b >
,
log 0
b
c >
.
Theo bất đẳng thức Cauchy, ta có:
4log 2 4loglog .l 4og
ccbb
ccbb≥=+
.
Suy ra
11T ≥
. Đẳng thức xảy ra khi
2
3
4log
log 3
log
bc
b
c
cb
a
a
b
b
=
⇔

=
=
=
.
Vậy giá trị nhỏ nhất của biểu thức
T
bằng
11
.
Câu 9. Cho
1
, , ;1
4
abc

∈


. Tìm giá trị nhỏ nhất của biểu thức sau:
111
log log log
444
abc
Pb c a

= −+ −+ −


A.
6
. B.
7
. C.
8
. D.
5
.
Lời giải
Chọn A
Ta có:
( )
2
22 2
1 1 1 11
0 log log , ;1
2 4 4 44
yy
x xx x x x x y
 
− = − + ≥ ⇔ ≥ − ⇒ ≤ − ∀∈
 

 
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
Suy ra
(
)
11
2log log , ;1
44
yy
x xy

≤ − ∀∈



Từ đó ta suy ra
11
log 2log , ;1
44
11
log 2log , ;1
44
11
log 2log , ;1
44
aa
bb
cc
b b ab
c c bc
a a ca

−≥ ∀∈




−≥ ∀∈




−≥ ∀∈



Suy ra
( )
3
111
log log log
444
2 log log log 2.3 log .log .log 6
abc
a b c abc
Pb c a
b c a bca

= −+ −+ −


≥ ++ = =
Vậy
min
6P =
Câu 10. Cho
[ ]
, , 0;1abc
∈
thỏa
333
222
log log log 1
abc
++≤
. Khi đó, biếu thức
( )
333
222
3 log log log
abc
Tabc a b c=++− + +
đạt giá trị lớn nhất là:
A.
4
. B.
7
. C.
8
. D.
5
.
Lời giải
Chọn A
Ta xét hàm:
( )
[ ]
2
log 1 1; 2y fx x x x
= = − + ∀∈
có
( )
11
10
ln 2 ln 2
fx x
x
′
= −= ⇔ =
. Ta lại có:
( ) ( )
2
1 11
1 2 0; log 1 0
ln 2 ln 2 ln 2
ff f
 
= = = − +>
 
 
Suy ra
( )
[ ] [ ]
22
log 1 0 1; 2 log 1 1; 2y fx x x x a a a= = − +≥ ∀∈ ⇒ ≥ − ∀∈
Đặt:
2
3 3 3 3 33
222
2
2
log
log log log 1
log
1; 1; 1
log
xa
abcxyz
yb
ax by cz
zc
=
+ + =++≤
= ⇒

≤+ ≤+ ≤+
=
Ta có:
( )
( ) ( ) ( ) ( ) ( ) ( )
333
222
3 33
3 33
3 log log log
1 1 13 1 1 1
313 4
abc
Tabc a b c
x y z xx yy zz
xyz
=++− + +

≤ + + + + + − ++ ++ +



= + + +≤+ =
Suy ra
max
1T
=
khi và chỉ khi
( ) ( )
; ; 1;1; 2abc =
và các hoán vị
Câu 11. Cho
,,xyz
lần lượt là các số nguyên dương thỏa mãn hệ thức sau đây
( ) ( ) ( )
22 2
22 2
log 2 log 2 3 log 3 3xy yz xz+ + ++ +=
. Khi đó biểu thức
632
xyz
T
=++
có giá trị
nhỏ nhất là:
A.
1
8
. B.
8
. C.
1
16
. D.
1
32
.
Lời giải
Chọn A
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 6 TÀI LIỆU ÔN THU THPT QUỐC GIA
Áp dụng bất đẳng thức Svac-Xo (hay gọi là cộng mẫu):
( )
2
2 22
xyz
xyz
a b c abc
++
++≥
++
, ta có:
( ) ( ) ( )
( )
( ) ( )
( ) ( ) ( )
( )( )( )
( )( )( )
22 2
22 2
22 2
22 2
2
22 2
2
log 2 log 2 3 log 3
3 log 2 log 2 3 log 3
111
log 2 log 2 3 log 3
3 log 2 2 3 3 3
111
1
223 3 8
8
xy yz xz
xy yz xz
xy yz xz
x y y zx z
x y y zx z
+ ++
= + + ++ += + +
+ + ++ +


≥ ⇒− ≤ + + + ≤


++
⇒≤ + + + ≤
Mặt khác:
( )( )( )
( )
( )
33
2233 8 23
223 3
27 27
xy yzzx xyz
x y y zx z
+++++ ++
+ + +≤ =
Nên ta suy ra
( )
( )
(
)(
)
(
)
33
8 23 8 23
11
223 3
27 8 27 8
xyz xyz
x y y zx z
++ ++
≥ + + + ≥⇔ ≥
( )
3
3
27 3 3
23 23
64 4 4
xyz xyz

⇒++ ≥ = ⇒++≥


Suy ra
( )
2 3 1 13 1
. 23 .
63266 648
xyz x y z
T xyz
++
=++= = + + ≥ =
. Vậy
min
1
8
T =
Câu 12. Cho các số thực
,,abc
lớn hơn 1 thỏa
( )
2
8
log 1 4abc ab
c
=+−
. Khi ấy, giá trị nhỏ nhất của biểu
thức
236
222
111
log 2 log 2 log 2
236
abc
T = ++
bằng
A.
1
2
. B.
1
4
. C.
6
2
. D.
3
2
.
Lời giải
Chọn A
Đầu tiên, ta có:
( ) ( ) ( )
2 22
8 88
log 1 4 log 4 4 logabc ab ab ab
c cc

=+− ⇔ + = +


Xét hàm số
(
) (
) (
)
2
1
log , 1 0,
ln 2
y ft t t f t t R ft
t
′
= = + = + > ∀∈ ⇒
đồng biến trên
R
( )
222
88
4 4 2 log log log 1f ab f ab abc a b c
cc

⇒ = ⇔=⇔=⇒ + + =


Đặt
2 22
log ; log ; log 1x ay bz c x y z
= = = ⇒++=
Ta có:
236
23 6
222
22 2
1 1 1 1 1 11 1 1
log 2 log 2 log 2 . .
2 3 6 2 log 2 3 log 2 6 log 2
abc
T
ab c
= ++= + +
22 2
1 1 1 11 1
2 4log 3 9log 6 36log 2 4 3 9 6 36a b c xy z
= + + =++
+ + + +++
1 2 4 1 3 9 1 6 36 2 4 3 9 6 36
2 4 16 3 9 36 6 36 144 16 36 144
1 2 4 1 3 9 1 6 36 2 4 3 9 6 36
2 . 2. . 2. .
2 4 16 3 9 36 6 36 144 16 36 144
1 1 1 2 4 3 9 6 36
2 3 6 16 36 144
x y z xy z
xy z
x y z xy z
xy z
xy z

+ + + +++

=++++ + −++


+++


+ + + +++

≥ + + − ++

+++

+++
=++− + +
3 31 1
4 4 442
xyz++
=− =−=
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Vậy
min
1
2
T =
khi và chỉ khi
( )
( )
36
111
; ; ; ; 2; 2; 2
236
x y z abc===⇒=
Câu 13. Cho các số thực
,,xyz
thỏa
4916234
xy z xyz
++ =++
. Khi ấy, giá trị lớn nhất của biểu thức
111
234
xyz
T
+++
=++
bằng
A.
9 87
2
+
. B.
1
4
. C.
7 87
2
+
. D.
3 87
2
+
.
Lời giải
Chọn A
Đầu tiên, ta có:
4916234
xy z xyz
++ =++
222
222
11 11 11 3
2 2.2 . 3 2.3 . 4 2.4 .
24 24 24 4
1 1 13
234
2 2 24
xx xx xx
xxx
 
⇔ − ++ − ++ − +=
 
 
 
⇔−+−+−=
 
 
Khi đó, ta suy ra
( ) ( )
111
222
222 222
3
4
2
9
1 1 19
2 3 4 22 33 44
2 2 22
1 1 1 93 9
34.2 3 4 234
2222
8
2
7
24
xyz x x x
xxx
T
+++
=

= + + = −+ −+ −+



 
≤ ++ − + − + − += ++ +=

 
 


+

Vậy
max
9 87
2
T
+
=
Câu 14. Cho các số thực
,,xyz
. Tính giá trị nhỏ nhất của biểu thức sau:
222
3 2011 3 2011 3 2011
xy z yz x zx y
P
+− +− +−
=+ ++ ++
A.
4
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn A
Áp dụng bất đẳng thức Bunyakovsky, ta có:
( ) ( )
( )
( )
222
222
222
222
222
2
222
2
222
222
222
3 2011 3 2011 3 2011
3 2011 3 2011 3 2011
3 3 3 2011 2011 2011
27 2011 2011 2011
xy z yz x zx y
xy z yz x zx y
xy z yz x zx y
xy z yz x zx y
P
+− +− +−
+− +− +−
+− +− +−
+− +− +−
=+ ++ ++
  
=+ ++ ++
  
 
+
+

≥ ++ +



= ++
+
2
2
222
3
222
27 3 2011 2 .011 1. 201
xy z yz x zx y+− +− +−


≥+


2
222
3
222
27 3 2011 6
xy z yz x zx y+− +− +−
++


=+=


. Vậy
min
6P =
Câu 15. Cho các số thực dương thỏa mãn
222
222
5log 16log 27 log 1ab c++ =
.
Khi đó giá trị lớn nhất của biểu thức
22 22 22
log .log log .log log .logS ab bc ca=++
bằng
A.
1
12
. B.
1
6
. C.
1
9
. D.
1
8
.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 8 TÀI LIỆU ÔN THU THPT QUỐC GIA
Lời giải
Chọn A
Cách 1:
Đặt:
2
2 2 2 222
222
2
22 22 22
2
log
5log 16log 27log 5 16 27 1
log
log .log log .log log .log
log
xa
a b cx y z
yb
S a b b c c a xy yz zx
zc
=
+ + =++=
= ⇒

= + + =++
=
Mặt khác:
(
)
(
) (
)
22222 22 22
1 5 16 27 3 12 2 18 4 9
xyzxy xz yz=++ =+ ++ ++
( ) ( )
2 2 2 2 22
2 3 .12 2 2 .18 24 .9 12 12 1x y x z y z xy yz zx xy yz zx≥ + + = ++ ⇒ ++ ≤
Nên suy ra
1
12
S xy yz zx
=++≤
. Vậy
max
1
12
S =
.
Cách 2:
Đặt:
2 2 2 2 22
2
222
2
22 22 22
2
log
5log 16log 27log 5 4 3 1
2log
log .log log .log log .log
3log
263
xa
a b cx y z
yb
xy yz zx
S ab bc ca
zc
=
+ + =++=

= ⇒

= + + =++

=
Suy ra
63 2S xy yz zx= ++
Ta có:
( )
( )
2 22 2 22
1543 112 543 23 2x y z S x y z xy yz zx=++⇔−= ++ − ++
( ) ( )
( )
(
) ( ) ( )
22 2
2 22 2 2 2
363 2 242 3 2 0x xy y y yz z x xz z x y y z z x
=−++−++−+=−+−+−≥
Suy ra
1
1 12 0
12
SS− ≥⇒ ≤
Vậy
max
1
12
S =
.
Câu 16. Cho các số thực
,,abc
lớn hơn 1 thỏa mãn
( )
2 22
log 1 log log log 2
bc
a bc≥−
. Tìm giá trị nhỏ nhất của biểu thức sau:
2 22
2 22
10log 10log log
S a bc
=++
A.
4
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn A
Biến đổi giả thiết ta được
( )
2 22
log 1 log log log 2
bc
a bc
≥−
( )
2 2 2 22 22 22 22
log . log log 1 log log log log log log log log 1a b c bc ab ac bc⇔ +≥−⇔++≥
Đặt
2
2
2
log
log
log
xa
yb
zc
=
=
=
. Tiếp theo, ta cần tìm giá trị nhỏ nhất của
2 22
10 10S x yz
=++
Bây giờ ta cần tìm số
k
dương sao cho
( )
2 22
10 10 2x y z k xy yz xz+ +≥ ++
( ) ( )
( )
2 22 2 22 2 22
10 10 2x y z k x y z k x y z k xy yz xz⇔ + ++ ++ ≥ ++ + ++
( ) ( ) ( ) ( )
( )
2 22
22
2 22
10 10 1
1 11
10 10 1
x yz
k x k y k z kx y z kx y z
kkk
⇔ + + + + + ≥ ++ ⇔ + + ≥ ++
+++
Sử dụng bất đẳng thức Cauchy – Schwarz dạng cộng mẫu ta có
( )
2
2 22
1 1 1 1 11
10 10 1 10 10 1
xyz
x yz
k k kkkk
++
+ +≥
++
+ + ++++
Đến đây sử dụng được giả thiết ta sẽ chọn
k
sao cho
1
2
1 11
10 10 1
kk
kkk
=⇔=
++
+++
Như vậy suy ra
( ) ( )
2 22
10 10 2.2 4x y z xy yz xz xy yz xz
+ +≥ ++ = ++
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Mà mặt khác
22 22 22
log log log log log log 1a b a c b c xy yz zx
+ + =++≥
Nên suy ra
( )
2 22
10 10 4 4.1 4x y z xy yz xz+ +≥ ++ = =
. Vậy
min
4S
=
Câu 17. Cho 3 số thực dương a,b,c thỏa mãn
log log log log 3log log 1ab bc ca
++ =
. Biết giá trị nhỏ nhất của biểu thức
222
log log logP abc=++
là
mn
p
−+
với
,,mn p
lần lượt là các số nguyên dương và
m
p
là
phân số tối giản. Tính
mn p++
?
A.
64
. B.
16
. C.
102
. D.
22
.
Lời giải
Chọn D
Lưu ý: Với bài toán này nếu đặt
( ) ( )
log ;log ;log , , 3 1a b c x y z xy yz xz→ ⇒++ =
thì ta sẽ
không thể áp dụng phương pháp làm của bài trên, khi đó ta sẽ cần phải nghĩ ra cách đặt khác.
Cách 1:
Đặt
( )
( )
log ;log ;log , , 3 1a b c ix jy kz ijxy jkyz kixz→ ⇒+ + =
Tìm
,,i jk
sao cho thỏa mãn
3
3
j
ij kj ki i k= = ⇒= =
. (Cân bằng hệ số)
Chọn
31j ik=⇒= =
Khi đó ta được
( ) ( )
1
log ;log ;log ,3 , 3 3 3 1
3
a b c x y z xy yz xz xy yz xz→ ⇒ + + =⇒++=
Khi đó ta có được đánh giá như sau:
(
)
(
)
(
)
(
)
( )
( ) ( ) ( )
2 2 2 2 22
2 22 2 22 2 22
2
2 22
log log log 9 2
92
191
a b c x y z k xy yz xz
x y z k x y z k xy yz xz k x y z
kxk ykzkxyz
+ + =+ +≥ ++
⇔+ ++ ++ ≥ ++ + ++
⇔+ ++ ++ ≥ ++
Mặt khác ta có:
( ) ( ) ( )
( )
2
222
2 22
191
1 1 1 111
1 9 1 191
xyz
xyz
kxk ykz
kk kkkk
++
+ ++ ++ = + + ≥
++
++ ++++
Đến đây sử dụng được giả thiết ta sẽ chọn
k
sao cho
1 9 3 17
111
4
191
kk
kk k
−+
=⇔=
++
++ +
Mặt khác ta có:
1
3
xy yz xz++=
nên suy ra
2 22
1 9 3 17 3 17
9 2. .
34 2
Px y z

−+ −+
=+ +≥ =



Vậy
min
3 17
2
P
−+
=
Cách 2:
Chú ý rằng ở giả thiết và yêu cầu của bài toán vai trò của 2 biến
,ac
là như nhau nên dấu
""=
sẽ xảy ra tại
ac=
, đây chính là điểm rơi mấu chốt của bài toán trên. Khi đó ta có:
( )
( )
22
2 22 2 2
2
2
3 2 2 32 2 0
321
P xy
P x xy x y P x Pyx y
x xy
= +
⇒ + = +⇔ − + −=
+=
( )
2
3 2 2 10
xx
PP
yy
 
⇔ − + −=
 
 
. Sử dụng điều kiện có nghiệm của phương trình bậc 2 theo
ẩn
x
y



, ta có:
2
3 17
2
3 20
3 17
2
P
PP
P
−+
≥
′
∆= + − ≥ ⇔
−−
≤
Vậy
min
3 17
2
S
−+
=
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 10 TÀI LIỆU ÔN THU THPT QUỐC GIA
Câu 18. Cho các số thực dương
,,
xyz
khi biểu thức
( )
( ) ( )
22 2 2
log 10 7 15 2log 2 2log
xy yz zx
P x y z x y z xyz
zxy

= + + − + + + ++ −


đạt giá trị nhỏ
nhất thì giá trị
xyz
gần với giá trị nào nhất trong các giá trị sau
A.
4
. B.
7
. C.
5
. D.
6
.
Lời giải
Chọn D
Cách 1:
Viết lại
( )
(
)
( )
2 2 2 2 2 2 22 22
log 10 7 15 2log 2
P x y z x y y z z x xyz x y z
= + + − + + + ++
(
)
( )
(
)
(
)
2
22 2 2 22 2 2
log 10 7 15 2log log 10 7 15 4log
x y z xy yz zx x y z xy yz zx
= + + − ++ = + + − ++
Ta cần chỉ ra
( )
22 2
10 7 15x y z m xy yz zx+ + ≥ ++
để đưa
P
về một biến ta biến đổi như
sau:
( )
222
20 14 30 2x y z m xy yz zx+ + ≥ ++
( )
(
) ( )
( )
2 2 2 2 22
20 14 30 2 2 2
m x m y m z m x y z xy yz zx⇔+ ++ ++ ≥ +++++
( )
2
2 22
111 1
20 14 30
xyz
xyz
mmm m
++
⇔ ++≥
+++
.
Mặt khác theo bất đẳng thức Svac-Xo (hay còn gọi là cộng mẫu) thì:
( )
2
2 22
1 1 1 111
20 14 30 20 14 30
++
++≥
++
+ + + +++
xyz
xyz
m m m mmm
Đến đây ta chỉ việc chọn m thỏa mãn
1 1 11
10
20 14 30
m
m m mm
+ + =⇔=
+++
.
Vậy ta được
( )
22 2
10 7 15 10
x y z xy yz zx+ + ≥ ++
dấu bằng xảy ra khi và chỉ khi
15 12 20
111
30 24 40
==⇔==
xyz
xyz
Cách 2:
Ngoài ra ta cũng có thể dùng phương pháp cân bằng hệ số trong bất đẳng thức CAUCHY để
chứng minh
22
22
22
25
4 10
4
15 20
10
43
25
3 10
3
x y xy
x z xz
y z yz
+≥
+≥
+≥
cộng các vế ta được
(
)
22 2
10 7 15 10x y z xy yz zx+ + ≥ ++
.
Từ đó ta có
( )
( )
( ) ( )
( )
2
2
log 10 4log log 1 0P xy yz zx xy yz zx xy yz zx≥ ++ − ++ = ++ − ≥
Dấu bằng xảy ra
3
53
;
15 600 10
6
44
16 47 47
10
y xz x
xyz x
xy yz zx
= =
⇔= = ≈
++=
.
Câu 19. Cho biểu thức sau:
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
( )
( ) ( )
2
2
2 4 64 22 42
12 5 4
log log log 2
3
a
a
a
zy
P xy y x y x z x y z
+−
= + + ++ +
.
Với
1a >
,
1y ≥
thì
P
đạt giá trị nhỏ nhất bằng
b
khi
0
aa
=
và
( ) ( )
1 11
;; ; ;xyz x y z=
hoặc
( ) ( )
2 22
;; ; ;xyz x y z=
. Hãy tính
( )
22
0 1 11 2 2 2
21 22 8S a b xyz x y z=−+ +
.
A.
42−
. B.
37−
. C.
42
. D.
44
.
Lời giải
Chọn D
Có
2
0
4
1
xy
y
z
y
>
≥
≥
;
64 22 42 64 22 42 42 1684 42
4
2 44
xy xz xyz xy xz xyz xyz x yz xyz++ =++ + ≥ =
Khi đó:
( )
( ) ( )
2
2 2 42
54
log log log 4 4
3
aa
a
zy
P xy y x y z
−
≥ + + ++
( ) (
)
( )
( )
2
2
2
2
54
log 4log 4 log 4
3
54
log 2 log 4 0
3
aa
a
a
a
zy
P xy xy z
zy
P xy z
−
≥ + ++ +
−
≥ ++ + ≥
Suy ra
min
0P =
khi
(
)
2
2
6 4 22
1
2
log 2
11
1
1
22
4
4
11
4
1
11
1
44
2
a
a
a
xy
xy
xx
z
z
yy
yz
y
zz
xy xz
x
=
=
= −

= = −

=
=

⇔⇔


=∨=−


=
= ±



= =

=
= ±

.
( )
22
0 1 11 2 2 2
11
21 22 8 21.2 22.0 8 44
88
S a b xyz x yz

= − + + = − + +=


.
Câu 20. Cho
,,abc
là ba số thực dương đôi một phân biệt. Có bao nhiêu bộ
( )
;;abc
thỏa mãn
2 22 22 2
;;
b ac ba c
a bb cc a
+ ++ ++ +
≤≤≤
.
A.
1
. B.
3
. C.
6
. D.
0
.
Lời giải
Chọn D
Ta có
,,
abc∀
thỏa mãn
1abc
++=
thì
..
..
bca
cab
a b c ab bc ca
a b c ab bc ca
≤++
≤++
( ) ( ) ( )
( ) ( ) ( )
2
222
2
222
. . 1
. . 2
bca
cab
a b c abc ab bc ca
a b c abc ab bc ca
+++
+++
≤ ++
⇔
≤ ++
Cộng vế với vế của (1) và (2) ta được
( ) ( )
2
222 222
.. .. 2
bca cab
a b c a b c abc ab bc ca
+++ +++
+ ≤ ++
(*)
Mà
2 22 22 2
;;
a bb c c a
b ac ba c
+ ++ ++ +
≥≥≥
nên từ (*) suy ra
( )
( )
( )
2
2
222
2 ..
bca
abc ab bc ca a b c
+++
++ ≥
( )
222
2 ..
bca
abc ab bc ac a b c
+++
⇒ ++ ≥
( )
( ) ( ) ( )
111
2 .. 1 1 1
bca
ab bc ac a b c b a c b a c
+++
⇔ ++ ≥ ≥+ ++ ++
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 12 TÀI LIỆU ÔN THU THPT QUỐC GIA
( )
(
)
2 ab bc ac ab bc ca a b c⇔ ++ ≥ ++ +++
( )
( )
21ab bc ac ab bc ca⇔ ++ ≥ ++ +
( )
(
)
2
2 10ab bc ac ab bc ca⇔ ++ − ++ +≤
2
11
0
2
2
ab bc ac

⇔ + + − +≤


(vô lý)
Vậy suy ra không có bộ
( )
;;abc
nào thỏa mãn
Câu 21. Hỏi có tất cả bao nhiêu bộ số thực
( )
;;abc
với
[ ]
, , 0;1abc∈
, thỏa mãn
2
abc++=
và đồng
thời làm cho biểu thức
22
44 2 2
3 16 3 8 4 6 2
a a bb c
T a b ab
−−
= + ++ + − −
đạt giá trị lớn nhất ?
A.
4
. B.
18
. C.
6
. D.
6
.
Lời giải
Chọn A
Để làm được câu hỏi trên, ta cần áp dụng bất đẳng thức:
( )
11
x
a ax≤+ −
với
[ ]
0;1x∀∈
và dấu
bằng xảy ra tại
0
1
x
x
=
=
. Khi đó ta suy ra:
-
( )
2
44 2
3 1 24 4
aa
aa
−
≤+ −
⇒
Dấu bằng xảy ra tại
2
2
0
44 0
1
44 1
1
2
a
aa
a
aa
a
=
−=
⇔=
−=
=
-
(
)
22
44 2
16 2 1 4 4
bb b b
bb
−−
≤ ≤+ − ⇒
Dấu bằng xảy ra tại
2
2
0
44 0
1
44 1
1
2
b
bb
b
bb
b
=
−=
=
⇔
−=
=
-
3 12
c
c≤+ ⇒
Dấu bằng xảy ra tại
0
1
c
c
=
=
Suy ra
22
44 2 2
3 16 3 8 4 6 2
a a bb c
T a b ab
−−
= + ++ + − −
( ) ( )
( )
( )
2 2 22
124 4 1 4 4 12 8 4 6 2
2 3 2.2 3 7
aa bb c a b ab
abc

≤+ − ++ − ++ + + − −

= ++ += +=
Như vậy dấu bằng xảy ra khi và chỉ khi:
00
0
1; 1;
1
11
22
ab
c
ab
c
ab


= =
=

= =

=

= =


,
cùng với
2
abc++=
ta thu được các bộ số
( ) ( ) ( ) ( )
11
; ; 1;1;0 ; 0;1;1 ; 1;0;1 ; ; ;1
22
abc


=




tức có
tất cả 4 bộ số thực
( )
;;
abc
thỏa mãn
Câu 22. Xét các số
,, 1abc>
thỏa mãn
log 2log 3log 8
a bc
bca++=
. Khi đó giá trị lớn nhất của biểu
thức
2log 3log 12log
ac b
cb a++
nằm trong khoảng nào ?
A.
( )
15;20
. B.
( )
25;30
. C.
( )
20;25
. D.
( )
30;35
Lời giải
Chọn D
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Đầu tiên, ta đặt:
log
log 2log 3log 2 3 8
log
log .log .log 1
log
a
a bc
b
abc
c
xb
b c ax y z
yc
b c a xyz
za
=
+ + =++=
= ⇒

= =
=
Ta lại có:
log log .log
log log .log
log log .log
a ab
c ca
b bc
c b c xy
b a b xz
a c a yz
= =
= = ⇒
= =
Tìm giá trị lớn nhất của
2 3 12P xy zx yz= ++
Suy ra
2 3 12 12 3 2 12 2 3
1
P P xy zx yz y z
P
xyz xyz x y z x yz
++ +
= = = = ++= +
Do
( )
238238
12 8 12
8
1
1
1
xyz yz x
x
P xx
xx
xyz yz
x
x
++=→+=−
−
⇒= + = + −
=→=
(*)
Ta lại có:
( )
66
8 2 3 2 2 .3 2 2 8 0 5 21 6
Cauchy
x y z x yz x x x
xx
=+ + ≥+ =+ ⇒+ −≤⇔− ≤≤

Suy ra ta khảo sát hàm số (*)
( ) ( )
12
8 5 21;6yfx xxx
x

= = + − ∀∈ −

Đạo hàm + Lập bảng biến thiên, ta dễ dàng suy ra
( )
( )
( )
max
5 21;6
max 5 21 9 5 21 30;35P fx f

−

= =−=+∈
Vậy
9 5 21
max
P = +
khi và chỉ khi
5 21
5 21
3 21
23
4
238
3 21
6
x
x
yz y
xyz
z
= −
= −
+
= ⇔=


++=
+
=
Câu 23. Cho các số thực
[
]
, , 0;1xyz
∈
. Biết rằng giá trị nhỏ nhất của biểu thức
(
)(
)
2222 2 2
xyz x y z
P
−−−
= ++ + +
được viết dưới dạng
m
n
với m,n là các số nguyên không âm
và
m
n
là phân số tối giản. Hỏi
mn+
có giá trị bằng bao nhiêu?
A.
86
. B.
87
. C.
88
. D.
89
Lời giải
Chọn D
Đặt
( )
( )( )
2 ;2 ;2 , , 1 , , 2
xyz
abc abc→ ≤≤
.
Ta có
( )( )
2
1 2 1 20 3a aa a
a
≤≤⇒ − − ≤⇔+ ≤
. Chứng minh tương tự
22
3, 3bc
bc
+≤ +≤
Cộng 3 bất đẳng thức trên vế theo vế ta được
( ) ( )
111 111 81 111
9 2 22 ( )
8
abc abc abc
abc abc abc
  
≥ ++ + + + ≥ ++ + + ⇒ ≥ ++ + +
  
  
Vậy giá trị lớn nhất của P là
max
81
8
P =
tức
81 8 89mn+= +=
Từ đó, ta có tổng quát cho dạng này như sau:
Cho n số
12
; ;...; [ ; ], 1
n
x x x ab c∈>
. Khi đó ta luôn có
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 14 TÀI LIỆU ÔN THU THPT QUỐC GIA
(
)( )
( )
12 1 2
2
.... ....
4
nn
ab
xx
xx x x
ab
nc c
cc cc c c
c
−
−−
+

+

+ ++ + ++ ≤
Câu 24. Cho a,b,c,d là các số thực dương có tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức sau:
( )( )
2 2 22 2 2 2 2
11P a b ab c d cd
=+++ ++ +
A.
2
. B.
17
4ln
16
. C.
4
17
16



. D.
17
ln
16
Lời giải
Chọn C
Từ giả thiết ta có:
( )
( ) ( ) ( )
2 2 22 2 2 2 2 2 2
1 1 1 ln ln 1P a b ab c d cd a P a=+ + + + + + = +⇒ = +
∑
∏
Ta có đánh giá sau
(
)
2
ln 1
t mt n+≥ +
, để tìm được hai số m,n ta sẽ sử dụng tới bất đẳng thức
tiếp tuyến, đây là một phương pháp rất hay để chứng minh các bất đẳng thức đối xứng với các
biến độc lập nhau.
Cơ sở của phương pháp
• Nếu đường thẳng
y ax b= +
là tiếp tuyến của đồ thị hàm số
( )
y fx=
tại điểm
( )
00
;Ax y
, A không phải điểm uốn thì khi đó tồn tại một khoảng D chứa
0
x
sao cho
( )
f x ax b≥+
hoặc
( )
f x ax b
≤+
. Đẳng thức xảy ra khi
0
xx
=
• Nếu đường thẳng
y ax b= +
là tiếp tuyến của đồ thị hàm số
( )
y fx=
tại điểm
( )
00
;Ax y
thì ta luôn phân tích được
(
)
(
) (
)
( )
0
,2
k
f x ax b x x g x k
− +=− ≥
Sau đây ta áp dụng lý thuyết trên vào bài toán trên. Chú ý ta có
( )
2
ln 1a +
∑
là một biểu thức
đối xứng theo bốn biến a,b,c,d đồng thời giả thiết cũng là đối xứng nên ta sẽ dự đoán dấu
""=
xảy ra khi
1
4
abcd= = = =
.
Quay lại bất đẳng thức phụ mà ta đang đi tìm hệ số
( )
2
ln 1t mt n+≥ +
, ta sẽ tìm
,mn
sao cho
hai đồ thị hàm số
( )
2
ln 1 ,y t y mt n= +=+
tiếp xúc nhau tại điểm có hoành độ
1
4
t =
ta được
8
17
2 17
ln
17 16
m
n
=
=−+
.
Vậy ta có bất đẳng thức phụ là
( )
2
8 2 17
ln 1 ln
17 17 16
tt+≥ − +
, dễ thấy bất đẳng thức này luôn
đúng, khi đó áp dụng vào bài toán ta có:
( )
4
2
1
8 2 17 8 8 17 17 17
ln ln 1 4 ln 4ln 4ln
17 17 16 17 17 16 16 16
Pa a P
=

= +≥ + − + = − + = ⇒≥


∑∑
Câu 25. Cho các số thực
. Biết giá trị lớn nhất của biểu thức
( )
3
1
444
4
abc
S abc= + + − ++
là
m
n
với m,n là các số nguyên dương và
m
n
là phân số tối giản.
Tính
2Pm n= +
A.
257P =
. B.
258P =
. C.
17P =
. D.
18P =
Lời giải
Chọn D
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
Với dạng toán này ta sẽ xét tới bất đẳng thức phụ
[ ]
4 , 2;3
t
mt n t
≤ + ∀∈
Thay
2, 3tt= =
ta được hệ phương trình
16 2 48
64 3 80
mn m
mn n
=+=

⇒

=+=−

Giờ ta cần chỉ ra bất đẳng thức
4 48 80
t
t≤−
đúng với mọi
[ ]
2;3
t ∈
là bài toán sẽ được giải
quyết. Ta xét
( )
( )
( )
4
48
4 48 80 ' 4 ln 4 48; ' 0 log
ln 4
tt
ft t ft ft t= − + ⇒ = − = ⇔=
.
Nhận thấy rằng
( ) ( )
4
48
2 3 0; log 0
ln 4
ff f

= = <


nên bất đẳng thức luôn đúng.
Dấu
""=
xảy ra khi và chỉ khi
{ }
2;3t
∈
. Khi đó ta được
( ) ( )
( )
3
3
3
1
4 4 4 48 240 48 240 16
4 44
abc
abc
t
S abc abc t
++
= + + − ++ ≤ ++ − − =− + − ≤
Như vậy
max
16S
=
khi
2t =
với
t abc
=++
2 16 2.1 18mn⇒+ = + =
Câu 26. Cho bốn số thực dương
,,,abcd
lớn hơn
1
thay đổi thoả mãn
2021abcd
+++ =
. Gọi
12
,xx
là hai nghiệm của phương trình
( )
(
) ( )
2020
log . log 1 2 log 3log 5log .log log 0
a b a a abb
x x b c dxa
−+ + + − =
. Tìm giá trị biểu thức
235
Sa b c d
=+++
khi
12
.xx
đạt giá trị lớn nhất.
A.
8084
11
S =
. B.
22231
4
S =
. C.
78819
4
S =
. D.
78819
11
S =
.
Lời giải
Chọn D
Ta có
( ) ( ) ( )
2020
log . log 1 2 log 3log 5log .log log 0
a b a a abb
x x b c dxa−+ + + − =
( ) ( )
2
2020
log . log 1 2log 3log 5log .log log 0
ab a a abb
bx b c d x a⇔ −+ + + − =
(1).
Đặt
log
b
xt=
, phương trình (1) có dạng:
( ) ( )
( )
2 2020
log 1 2log 3log 5log log 0
a aaa b
bt b c dt a⇔ −+ + + − =
(2).
Từ phương trình (2) ta có
(
)
2
2020
1 2log 3log 5log 4.log .log
a a a ab
b c d ba∆= + + + +
( )
2
1 2log 3log 5log 4.2020 0
aaa
bcd=+++ +>
.
Suy ra phương trình (2) luôn có hai nghiệm phân biệt . Từ đó ta có hệ thức Vi-ét như sau:
Đặt
(
)
11
1 2 12
22
log
1 2log 3log 5log
log .
log
log
b
aaa
b
b
a
tx
bcd
t t xx
tx
b
=
+++
⇒+= =
=
( ) ( )
12
log . log . 1 2log 3log 5log log 2 3log 5log
b b aaa b bb
xx a b c d a c d⇔ = + + + = ++ +
( )
( )
23 5 23 5 2 3 5
12 12
log . log . 2 .3 .5 . . . . . . . . . .
2233355555
bb
bbcccddddd
x x ab c d x x ab c d a

⇔ = ⇔= =


Ta có
11
235
12
. 2 .3 .5 . . . . . . . . . . 337500
2233355555 11
bbcccddddd a b c d
xx a
+++

= ≤


(BĐT Cosi)
11
12
2021
. 337500.
11
xx

⇔≤


. Vậy biểu thức
12
xx
đạt giá trị lớn nhất bằng
11
2021
337500.
11



khi
và chỉ khi
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 16 TÀI LIỆU ÔN THU THPT QUỐC GIA
235
2021
bcd
a
abcd
= = =
+++ =
2021
11
2021
2.
78819
11
235
2021
11
3.
11
2021
5.
11
a
b
abcd
c
d
=
=
⇔ ⇒+ + + =
=
=
.
Câu 27. Lần lượt cho hai số thực dương
,,abc
thỏa mãn phương trình sau
đây:
( ) ( ) ( )
2
222
log 2 2 2
1
abc
aabbcc
abc
++

= −+ −+ −

+++

. Gọi giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức
2
1
a bc
P
abc
++
=
+++
lần lượt là
M
và
m
. Giá trị của biểu thức
( )
3mM+
bằng
A.
16 2 6
5
+
. B.
86
5
+
. C.
26
5
. D.
16 2 6
5
−
.
Lời giải
Chọn A
Điều kiện:
222
00
1
abc
abc
abc
++
>⇒++>
+++
Ta có:
( ) ( ) ( )
2
222
log 2 2 2
1
abc
aabbcc
abc
++

= −+ −+ −

+++

(
)
(
) (
)
(
)
( )
( )
(
)
2
222
222
2
222
222 222
22
1 log 2 2 2 1
1
222
log 2 2 2 1
1
log 2 2 2 2 2 2 log 1 1
abc
aabbcc
abc
abc
a ab bc c
abc
abc abc abc abc
++

⇔+ = −+ −+ −+

+++

++

⇔ =− +−+−+

+++

⇔ ++ + ++ = ++++ +++
Xét hàm đặc trưng
( ) ( )
2
1
log 1 0 0
ln 2
y ft t t f t t
t
′
= = +⇒ = + > ∀>
.
Suy ra hàm số
( )
ft
đồng biến trên
(
)
222
0; 2 2 2 1 0abcabc
+∞ ⇒ + + = + + + >
( )
(
) ( )
222
1 1 12
abc⇒−+−+−=
Ta có:
( )
2
12
1
a bc
P Pabc a bc
abc
++
= ⇒ +++ =+ +
+++
( )( ) (
)( ) ( )( )
1 1 2 1 1 1 44Pa P b Pc P
⇔ − −+ − −+ − −=−
Suy ra
( ) ( )( ) ( )( ) ( )( )
( )
2
2
44 1 1 2 1 1 1P Pa P b Pc− ≤ − −+ − −+ − −
( ) ( ) ( ) ( )
( )
( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
2 2 2 2 222
2
2 2 22
2
44 1 2 1 1 1 1
46 46
44 2 1 2 1 5 8 20
55
PPP Pabc
P P P P PP P
=
⇒− ≤ −+− +− −+−+−
−+
⇔− ≤ −+− +− ⇔ −+≤⇔ ≤≤

max
min
46
4 6 4 6 16 2 6
5
3 3.
5 55
46
5
PM
mM
Pm
+
= =
− ++
⇒ ⇒+ = + =
−
= =
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
Câu 28. Cho
,,xyz
là các số thực dương với
[ ]
, , 1; 2xyz∈
. Tìm giá trị lớn
nhất của biểu thức
22 2 2 22
222
log .log log .log log .log
Px y z
yzx
=++
A. 1. B.
2
3
. C.
3
. D.
4
3
.
Lời giải
Chọn A
Ta có:
( ) (
)
( )
22 2 2 22
2 2 2 22 2
222
log .log log .log log .log
log 1 log log 1 log log 1 log
Px y z
yzx
x yy zz x
=++
= −+ −+ −
Đặt:
2
2
2
log
log (1 ) (1 ) (1 )
log
ax
b yPabbcca
cz
=
= ⇒= −+ −+ −
=
Xét tam giác đều
ABC
cạnh bằng
1
,trên các cạnh
,,AB BC CA
lần lượt lấy các điểm
,,MNP
,với
a MA
b PC
c BN
=
=
=
,khi đó ta có bất đẳng thức :
AMP NCP MBN ABC
SSS S
∆∆∆ ∆
++ ≤
000
1 11 3
(1 ). sin 60 (1 ) sin 60 (1 ) sin 60
2 22 4
(1 ) (1 ) (1 ) 1
ab bc ca
abbcca
⇔ − +− +− ≤
⇔ −+ −+ −≤
Vậy
max
1P =
. Dấu “=” xảy ra khi
1
0
01
a
b
c
=
=
≤≤
và các hoán vị của nó.
Câu 29. Cho ba số thực
,,xyz
thỏa:
+=
2 2 222
2log log log .log .logz y xyz
. Giá trị nhỏ nhất của biểu
thức
=++
222
3log 4log 5log
xyz
P
yz xz xy
có dạng
mn
. Tính giá trị của biểu thức
+2018 2019mn
A. 14129. B. 16147. C. 10092. D. 16149.
Lời giải
c
a
b
A
B
C
M
N
P
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 18 TÀI LIỆU ÔN THU THPT QUỐC GIA
Chọn A
Đặt:
2 22
222
2
2
2 22 222 22 2
2
345
3log 4log 5log
log log log
log
345
log
log log log log log log log log log
log
345
xyz
P
yz xz xy
yz xz xy
xyz
ax
by
yzx xzy xyz
cz
bca acb abc
= + + =++
=

= ⇒= + +

+− +− +−

=
=++
+− +− +−
+= ⇔
2 2 222
2log log log .log .logz y xyz
+= ⇔ + =
2 42 2c b abc c b abc
Áp dụng BĐT
+≥
+
11 4
m n mn
Dấu “=” xảy ra khi
=
mn
.
Ta có:
=++
+− +− +−
345
P
bca acb abc

=++ + + +

+− +− +− +− +− +−

+
≥ + + =++= += += +≥ =
11 11 11
23
4 4 4 2462 4 62 6 6 6
2. 3. 2 2 2 . 4 3
222
P
bca acb bca abc acb abc
b c abc
aa
c b a c b a bc a bc a a a
Dấu “=” xảy ra khi:
= =
⇔===
=
3
6
2
abc
abc
a
a
Suy ra:
==⇒ +=4; 3 2018 2019 14129
mn m n
Câu 30. Cho hai các số thực a, b, c, d, e dương thỏa mãn
1000abcde+++ +=
và
0
0
0
0
0
abcd e
abcde
abcde
abcde
abcd e
−+− +>
+−+−>
−++− +>
−++ −>
−+−+ +>
Tìm giá trị lớn nhất của biểu thức
(
)
bd
M ac
+
= +
A.
499
499
. B.
500
500
. C.
499
500
. D.
500
499
.
Lời giải
Chọn A
Đặt
abcd e h
abcde k
abcdel
abcde m
abcd e n
−+− +=
+−+−=
−++− +=
−++ −=
−+−+ +=
ta thấy rằng
1000hknml abcde+ + + += +++ +=
và đồng thời
2 ,2 ,2 ,2 ,2ahkbklclmd mnenh=+ =+=+ =+ =+
. Từ đó suy ra
, ,, ,hklmn
đều là các số
chẵn.
Bên cạnh đó ta suy ra được
( ) ( ) ( )
11 1
1000 , 1000
22 2
ac hklm nbd h+ = + ++ = − + = −
.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 19
Để
( )
bd
M ac
+
= +
đạt giá trị lớn nhất thì
n
và
h
có giá trị nhỏ nhất, mà
,
nh
chia hết cho 2 nên
499
2 max 499
hn M
==⇒=
.
Đẳng thức xảy ra khi
(
)
9974 2
2,4,...,2
1,496
22
996
kt
lt
t
lm t
klm
= −
=
=
+=+
++ =
.
_______________ TOANMATH.com _______________
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
BÀI TOÁN GTLN - GTNN BIỂU THỨC MŨ – LOGARIT HAI BIẾN SỐ PHƯƠNG PHÁP
Cách 1: Đánh giá, áp dụng BDT cơ bản đã biết như BĐT Côsi và BĐT Bunhiacopxki.
Cách 2: Áp dụng phương pháp hàm số, hàm đặc trưng.
Thông thường ta thực hiện theo các bước sau :
Biến đổi các số hạng chứa trong biểu thức về cùng một đại lượng giống nhau.
Đưa vào một biến mới t , bằng cách đặt t bằng đại lượng đã được biến đổi như trên.
Xét hàm số f (t) theo biến t . Khi đó ta hình thành được bài toán tương đương sau: Tìm giá
trị lớn nhất, giá trị nhỏ nhất của hàm số f (t) với t ∈ . D
Lúc này ta sử dụng đạo hàm để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (t) với t ∈ . D
Chú ý : Ta chứng minh được:
• Nếu hàm số y = f ( x) luôn đồng biến (hoặc luôn nghịch biến) và liên tục trên D mà phương
trình f (x) = k có nghiệm thì nghiệm đó là nghiệm duy nhất trên D .
• Nếu hàm số y = f ( x) luôn đồng biến (hoặc luôn nghịch biến) và hàm số y = g ( x) luôn nghịch
biến (hoặc luôn đồng biến) và liên tục trên D mà phương trình f (x) = g (x) có nghiệm thì
nghiệm đó là nghiệm duy nhất trên D .
• Nếu hàm số y = f (x) luôn đồng biến (hoặc luôn nghịch biến) và liên tục trên D thì
f (x) > f (y) nếu x > y (hoặc x < y) .
Cách 3: Áp dụng hình học giải tích.  − 
Câu 1. Xét các số thực dương x
x và y thỏa mãn 1 2 ln = 3x + y −   1.Giá  x + y
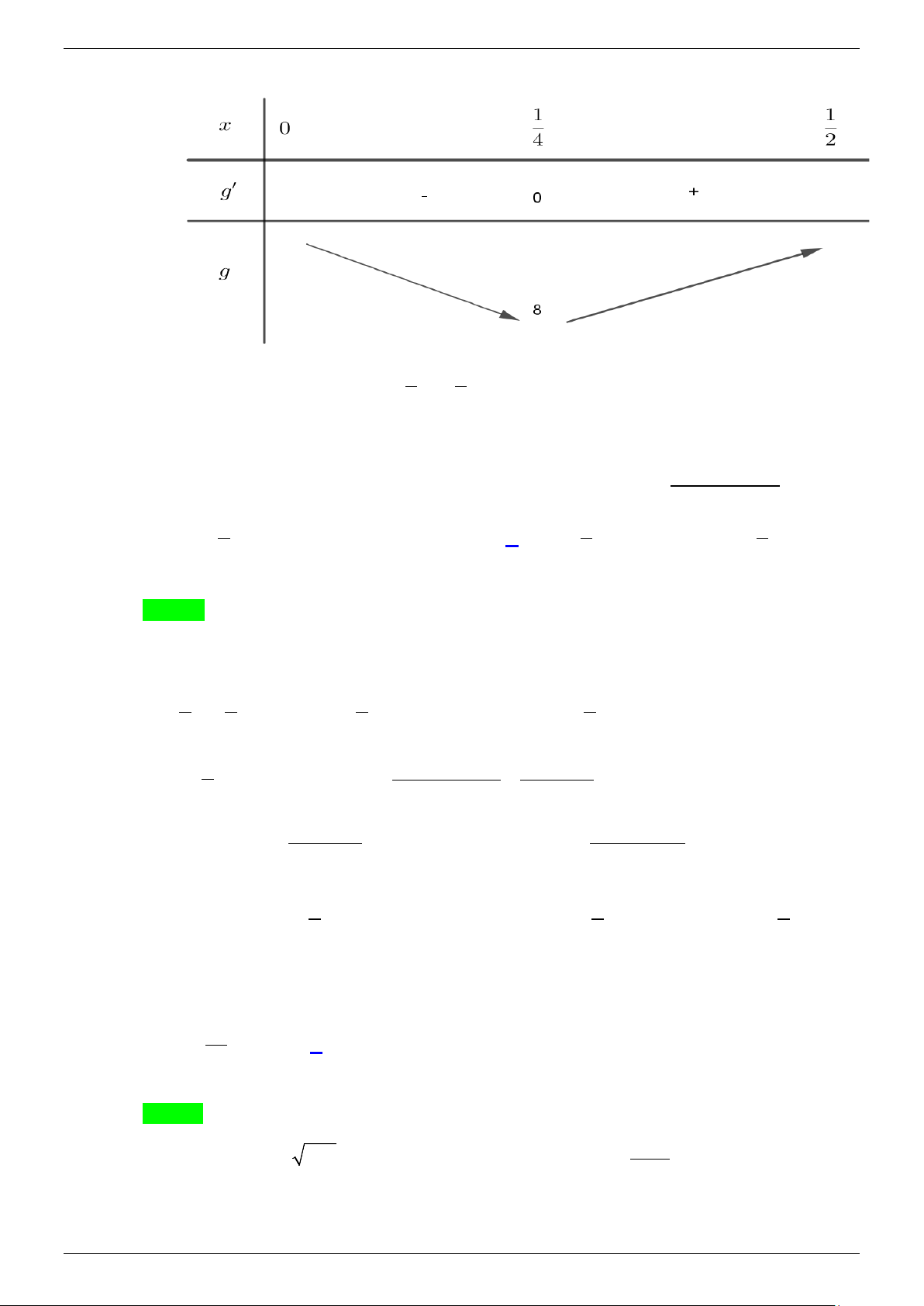
trị nhỏ nhất của biểu thức 1 2 g(x) = + bằng x x + y A. 1 . B. 8 . C. 1 . D. 4 . 8 4 Lời giải Chọn B Điều kiện 1 0 < x < . 2  −  Ta có từ giả thiết: 1 2 ln
x = 3x+ y −1⇔ ln(1−2x)+(1−2x) = ln(x+ y)+(x+   y) (1) .  x + y
Xét hàm số f (t) = ln t + t trên khoảng (0;+∞). Ta có f ′(t) 1
= +1 > 0 với mọi t > 0 t
Do đó hàm số f (t) luôn đồng biến trên khoảng (0;+∞).
Vậy (1) ⇔ 1− 2x = x + y ⇔ y =1− 3x 1 2 1 4x −1 1 Ta có g(x) = + = ⇒ g′ x =
⇒ g′ x = 0 ⇔ x = . 2 ( ) 2 ( )
x 1− 2x x − 2x ( 2 x − 2x ) 4 Khi đó ta có BBT
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Vậy GTNN của g(x) là 8 khi 1 1 x = , y = . 4 4
Câu 2. Cho hai số thực dương a,b thỏa mãn hệ thức: 2 ab − b
2log a − log b ≤ log a + 6b . Tìm giá trị lớn nhất của biểu thức P = . 2 2 2 ( ) 2 2
a − 2ab + 2b A. 2 P = . B. P = P = P = Max 0. C. 1 . D. 2 . Max 3 Max 2 Max 5 Lời giải Chọn C
Ta có: 2log a − log b ≤ log (a + 6b) 2 ⇔ log a ≤ log ( 2 ab + 6b ) 2 2
⇔ a ≤ ab + 6b 2 2 2 2 2 2  a a ⇔ − − 6 ≤ 0 ⇔ 3 a − ≤ ≤ a  
2. Do a,b dương nên 0 < ≤ 2.  b b b b a 2 − −
Đặt t = ,0 < t ≤ 2 . Khi đó: ab b t 1 P = = b 2 2 2
a − 2ab + 2b t − 2t + 2 t − 2 − +
Xét hàm số f (t) 1 =
với 0 < t ≤ 2 . Ta có: ′( ) t 2t f t = ≥ 0, t ∀ ∈ 0;2 . 2 ( ] 2 t − 2t + 2 ( 2t −2t +2)
Suy ra f (t) ≤ f ( ) 1 2 = với 1 t
∀ ∈(0;2]. Do đó Max f (t) = khi t = 2. Vậy 1 P = . 2 (0;2] 2 Max 2
Câu 3. Cho hai số thực dương x, y thỏa mãn 2x 2y +
= 4 . Tìm giá trị lớn nhất Pmax của biểu thức P = ( 2 x + y)( 2 2
2y + x) + 9xy . A. 27 P = . B. P =18 . C. P = 27 . D. P =12 . max 2 max max max Lời giải Chọn B 2  x y
Ta có 4 = 2x + 2y ≥ 2 2x+y ⇔ 4 ≥ 2x+y ⇔ x + y ≤ 2 . Suy ra xy +  ≤ =   1.  2  Khi đó P = ( 2 x + y)( 2
y + x) + xy = ( 3 3 x + y ) 2 2 2 2 9 2 + 4x y +10xy . Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
P = (x + y) (x + y)2 − xy + ( xy)2 2 3 2 +10xy   ≤ ( − xy) 2 2 2 2 4 4 3
+ 4x y +10xy =16 + 2x y + 2xy (xy − ) 1 ≤18. Vậy P =18 x = y = max khi 1.
Câu 4. Cho hai số thực a,b > 0 thỏa mãn log 2a +1 + log 3b +1 − 6 ≥ 0. Giá trị nhỏ nhất của biểu 2 ( ) 2 ( )
thức 2a + 3b là. A. 12. B. 14. C. 16. D. 8 . Lời giải Chọn B
Ta có log 2a +1 + log 3b +1 − 6 ≥ 0 ⇔ log  2a +1 3b +1  ≥ 6 ⇔ + + ≥ . 2 ( )( ) 2a 1 3b 1 64 2 ( ) 2 ( )  ( )( )
Áp dụng bất đẳng thức Cô-si cho hai số dương 2a +1 và 3b +1, ta được (2a + ) 1 + (3b + ) 1 ≥ 2 (2a + ) 1 (3b + )
1 ≥ 2 64 =16 ⇔ 2a + 3b + 2 ≥16 ⇔ 2a + 3b ≥14 Dấu " = " xảy ra khi 3
2a +1 = 3b +1 ⇔ a = b . Vậy min (2a + 3b) =14 khi 7 7 a = ;b = . 2 2 3
Câu 5. Trong các nghiệm (x; y) thỏa mãn bất phương trình log
2x + y ≥1. Khi đó giá trị lớn nhất của biểu thức T = 2x + y là 2 2 ( ) x +2 y A. 9 B. 9 C. 9 D. 9 4 2 8 Lời giải Chọn C - Trường hợp 1: 2 2 x + 2y >1 Bất phương trình 2 2 log
2x + y ≥1 ⇔ 2x + y ≥ x + 2y 2 2
⇒ 2x + y ≥ x + 2y >1 2 2 ( ) x +2 y
Áp dụng bất đẳng thức Bunyakovsky, ta có 2   2 2x + y 2 2 ( )2 2  1  2  +    ( 2 2
x + 2y ) ≥ (2x + y)2  ⇒ x + 2y ≥ 2      9 ( + y)2 2 2x x y ( x y) 9   9 2 2  2x y  0 2x y 1;  ⇒ + ≥ ⇔ + + − ≤ ⇒ + ∈ 9 2 2     Giá trị lớn nhất của 9
T = 2x + y = . Dấu bằng xảy ra khi 1 x = 2; y = 2 2 - Trường hợp 2: 2 2
0 < x + 2y <1 Bất phương trình 2 2 9 log
2x + y ≥1 ⇔ 2x + y ≤ x + 2y <1< . 2 2 ( ) x +2 y 2
Vậy giá trị lớn nhất của 9
T = 2x + y = . 2
Câu 6. Xét các số nguyên dương a, b sao cho phương trình 2
a ln x + bln x + 5 = 0 có hai nghiệm phân biệt x , x x + b x + a = x , x 1 2 và phương trình 2 5log log
0 có hai nghiệm phân biệt 3 4 thỏa mãn x x > x x = + 1 2
3 4 . Tìm giá trị nhỏ nhất của S 2a 3b A. S = 33 S = 30 S =17 S = 25 min . B. min . C. min . D. min . Lời giải Chọn B
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Điều kiện để hai phương trình 2
a ln x + bln x + 5 = 0 và 2
5log x + blog x + a = 0 có hai nghiệm phân biệt là: 2
b − 20a > 0 . ln x +ln b x  = − ln b b x x = −  −  1 2 (  1 2 ) aaax x = e Theo giả thiết ta có 1 2  ⇒  ⇒  . b log x log b x log(x x ) b −  + = − = − 5 3 4 3 4 x x =    10 3 4 5  5 b b b b Mà − 5 a 5
x x > x x ⇒ e− >10 nên suy ra − > − ln10 ⇒ a > ⇒ a ≥ 3. 1 2 3 4 a 5 ln10 Theo điều kiện có 2 2
b − 20a > 0 ⇒ b > 20a ≥ 60 ⇒ b ≥ 8. a = 3
Từ đó suy ra S = 2a + 3b ≥ 30 ⇒ S = 30 min khi và chỉ khi . b   = 8
Câu 7. Cho các số thực 1
a > ,b >1. Khi biểu thức 3 log b + a − a +
đạt giá trị nhỏ nhất thì tổng + bằng a logb ( 4 2 9 81 3 ) a b A. 3 9 + 2 . B. 2 3+ 9 . C. 3+ 3 2 . D. 2 + 9 2 . Lời giải Chọn B
Ta có 3a >1,b >1 nên log b > a > a 0,logb 3 0. 3
Theo bất đẳng thức Cauchy ta được log b + a − a + ≥ b + a − a = b + a ≥ a logb ( 4 2 9 ) 81 log a logb ( 2 2 18 9 log a 2logb 3 2 2. 3 3 ) 3 3
a >1,b >1  a = 3
Dấu “ = ” xảy ra khi và chỉ khi 4 a = 81 ⇔  . Vậy 2 a + b = 3+ 9 . 2  b  = 9 log b = aa 2logb 3 3 2
Câu 8. Cho các số thực x, y thỏa mãn 2 x − y x + ≤ ( 2 x − y + ) 2 2 2 2 y−x +2 5 16.4 5 16 .7 và
≥ y +1. Gọi M và m 2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 10x + 6y + 26 P =
. Khi đó, giá trị của biểu thức T = M + m bằng 2x + 2y + 5
A. T =10 . B. 21 T = . C. 19 T = .
D. T =15 . 2 2 Lời giải Chọn C Đặt 2
t = x − 2 .y t+2 2t + + Ta có t + ≤ ( 2t + ) 2−t 5 4 5 4 5 16.4 5 4 .7 ⇔ ≤ 1 . t+2 2t ( ) 7 7 u u u + u u
Xét hàm số f (u) 5 4  1   4 5  = = + ta có f ′(u)  1  1  4  4
= 5  ln +   ln < 0, u ∀ ∈  7u  7   7       7  7  7  7
Suy ra hàm số f (u) luôn nghịch biến trên .  Khi đó ( )
1 ⇔ f (t + 2) ≤ f (2t) ⇔ t + 2 ≥ 2t ⇔ t ≤ 2. 2 2 Mặt khác x 2
≥ y +1 ⇔ x − 2y ≥ 2 ⇔ t ≥ 2. Suy ra x 2 t 2 y − = ⇔ =
. Thay vào P ta được 2 2 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2 3x +10x + 20 P = ⇔ (3− P) 2
x + 2 5 − P x + 20 − 3P = 0 2 . 2 ( ) ( ) x + 2x + 3
Khi P ≠ 3, vì P xác định nên phương trình (2) có nghiệm.
Khi đó ∆′ ≥ ⇔ ( − P)2 − ( − P)( − P) 2 0 5 3 20 3 ≥ 0 ⇔ 2
− P +19P − 35 ≥ 0 5 ⇔ ≤ P ≤ 7. Vậy 5 19
T = M + m = + 7 = . 2 2 2 2 + + Câu 9. x − y+ 4x y 2
Xét các số thực dương x, y thỏa 2( 2) 2021 − ≥ 0. (
Tìm giá trị nhỏ nhất của biểu thức x + 2)2
P = 2y − 4 .x A. 2021. B. 2020 . C. 1 . D. 2 . 2 Lời giải Chọn D 2 x − y+ 4x + y + 2 4x + y + 2 Từ giả thiết, ta suy ra 2( 2) 2021 ≥
⇔ 2 x − y + 2 ≥ log 1 . 2 ( 2 ) 2021 2 ( ) (x + 2) (x + 2)
a = 4x + y + 2  Đặt 2  thì ( ) 1 trở thành  =  (
⇒ b − a = x − y + b x + 2) 2 2 2 = x + 4x + 4
⇒ 2(b − a) ≥ log a − log b ⇔ log a + 2a ≥ log b + 2b 2 . 2021 2021 2021 2021 ( )
Xét hàm số f (t) = log t + 2t trên (0;+∞) ta có f ′(t) 1 = + 2 > 0, t ∀ > 0 2021 t ln 2021
Suy ra hàm số f (t) luôn đồng biến trên khoảng (0;+∞).
Khi đó ( ) ⇔ f (a) ≥ f (b) ⇔ a ≥ b ⇔ x + y + ≥ (x + )2 2 2 4 2
2 ⇔ y ≥ x + 2.
Thay vào P, ta được 2
P ≥ 2x − 4x + 4 = 2(x − )2 1 + 2 ≥ 2. Vậy P = 2 = = min
khi và chỉ khi x 1, y 3.  + ln x y
Câu 10. Cho hai số thực dương x, y thỏa mãn  2  ln(x+   y) ln5 2 .5
= 2 . Giá trị nhỏ nhất của biểu thức
P = (x +1)ln x + (y +1)ln y với 1 3 ≤ x ≤ và 1 3
≤ y ≤ là m , khi đó m thuộc khoảng nào sau 2 2 2 2 đây A. 1 m  ;0 ∈ −  . B. m∈(0; ) 1 .
C. m∈(1;2). D. m∈(2;4). 2    Lời giải Chọn A  + ln x y
Ta có:  2  ln(x+y) ln5
ln(x+ y)−ln 2 ln(x+ y) ln5
ln(x+ y) ln(x+ y) ln5 ln 2 2 .5 = 2 ⇔ 2 .5 = 2 ⇔ 2 .5 = 2 .2 ln(x+ y) ln10 ⇔ 10 = 2 ⇔ + = ( ln10) ln( + ) ln10.log2 ln( ) log 2 ⇔ ln( + ) = ln10.log 2 x y x y x y ⇔ e = e log2 ⇔ x + y =10
⇔ x + y = 2. Do đó P = (x +1)ln x + (y +1)ln y = (x + )
1 ln x + (3− x)ln (2 − x) .
Xét hàm số f (x) = (x +1)ln x + (3− x)ln(2 − x)
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
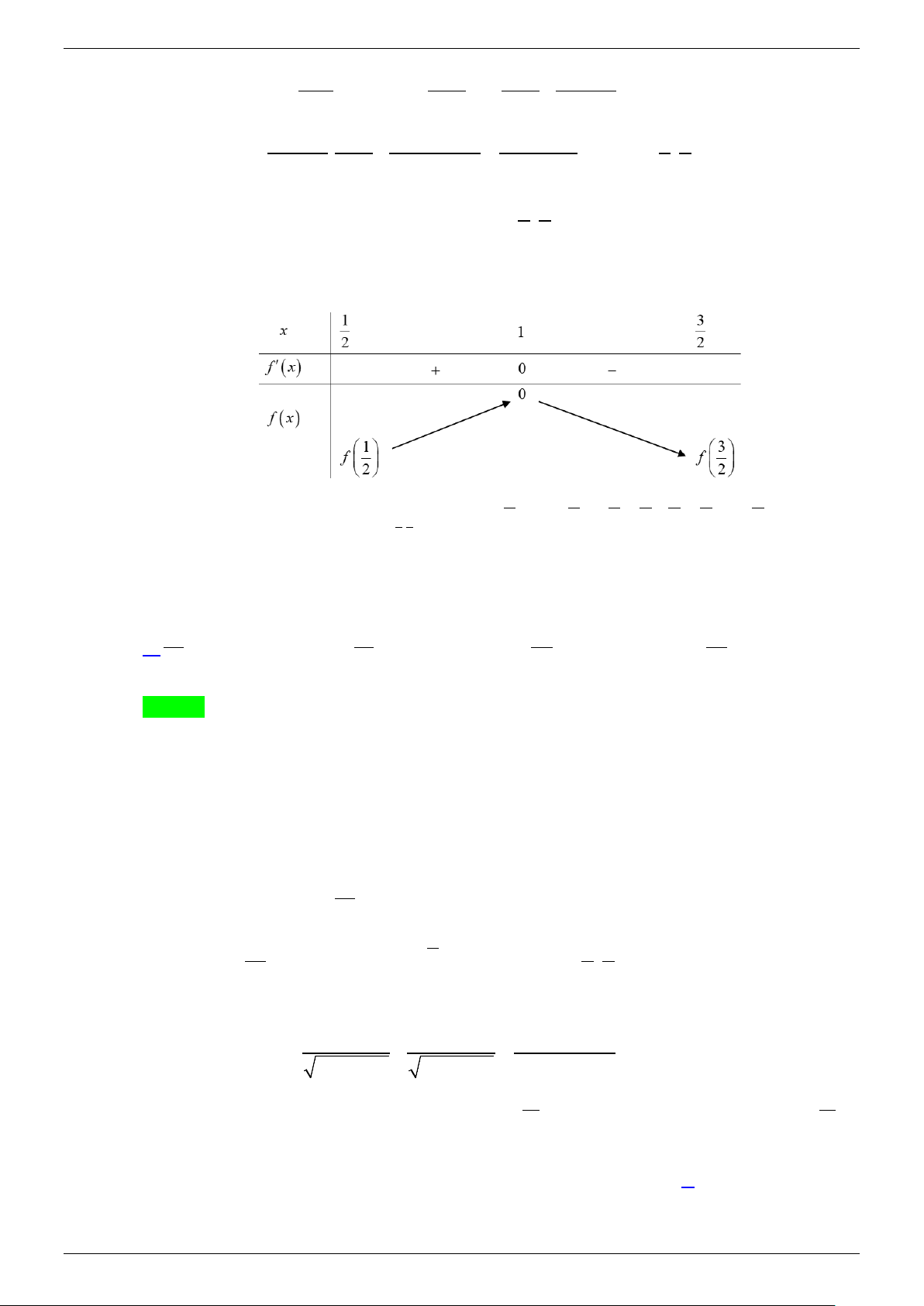
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC + − − Ta có: x 1 3 x x 2 2 (′ ) = ln + − ln(2 − ) − = ln x f x x x + . x 2 − x
2 − x x(2 − x) 2
2 − x 2x − 4x + 4 4 − (x − )2 2 1 Lại có: f (x) 1 3 . 0, x ;  ′′ = − = < ∀ ∈ (2− x)2 x (   2x − x )2 (2x− x )2 2 2 2 2 1 3 Do đó f ′(x) 
= 0 có nhiều nhất một nghiệm trên ;  . 2 2  
Mà x =1 là một nghiệm của pt f ′(x) = 0 nên phương trình f ′(x) = 0 có nghiệm duy nhất là
x =1. Từ đó ta có bảng biến thiên như sau:  1   3  3 1 5 3  1
Dựa vào BBT, ta suy ra min P min f (x) f f ln ln ;0 = = = = + ∈ −       . 1 3 ;   2   2  2 2 2 2  2  2 2  
Câu 11. Xét các số thực không âm x và y thỏa mãn x 3y 4 x 3 .3 y + − +
≥ 4 . Giá trị nhỏ nhất của biểu thức 2 2
P = x + y + 5x + 4y bằng A. 43 . B. 33 . C. 49 . D. 57 . 8 4 8 8 Lời giải Chọn A Ta có x+3 y−4 x+3 y−4 3 y + ≥ ⇔ ≥ − ⇔ ≥ ( − ) 4 3 .3 4 3 .3 4 3 .3 4 3 −x x y y x y x (*)
Xét hàm số ( ) = .3t f t t , t ∀ ≥ 0 , ta có ′( ) = 3t f t
(1+t ln3) > 0 , t
∀ ≥ 0 ⇒ f (t) đồng biến trên [0;+∞) .
(*) ⇔ f (3y) ≥ f (4− x), x
∀ , y ≥ 0 ⇔ 3y ≥ 4 − x ⇔ x ≥ 4 − 3y , x ∀ , y ≥ 0 Xét biểu thức 2 2
P = x + y + x + y ⇒ P ≥ ( − y)2 2 5 4 4 3
+ y + 5(4 −3y) + 4y 2 43
⇔ P ≥10y − 35y + 36 ≥ 8  7 y = Vậy 43 min P = khi và chỉ khi    4 ⇔ (x y) 5 7 ; = −  ; 8   4 4  x = 4 − 3y
Câu 12. Cho 2 số thực dương x, y thỏa mãn phương trình sau: x y 3 1 1
x + y − e + − + = . 2x y y 2 2 + 3.4 4 + 3.2 x 2( x 1− y 1 2 + 2 − )
Biết rằng, giá trị của 3 4
x + y được viết dưới dạng m với m,n là các số nguyên dương và m là n n
phân số tối giản. Hỏi T = m + n có giá trị là bao nhiêu? A. 149. B. 147 . C. 160. D. 151. Lời giải Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Chọn D
Biến đổi giả thiết ta được: x+ y−3 1 1
x − y − e 2x + 2y 2x + 2y x+ y−3 + = ⇔ +
= x − y − e 2x y y 2 2 + 3.4 4 + 3.2 x 2( x 1− y 1 2 + 2 − ) 2x 2 y 2 y 2 2 + 3.2 2 + 3.2 x Đặt 2x = ,2y a
= b thì theo bất đẳng thức AM – GM ta có:  2 2 2 1 2 ( a + + b a a a b b b ) 3  ≤ + ; a ≤ + ⇒ ≤ +
 a + 3b a + b a + 3b a + 3b 2 a + 3b a + 3b 4 2(a + b)   + 2 2 2 1 2 ( a + b b b a b a a ) 3  ≤ + ; b ≤ + ⇒ ≤ +
 b + 3a b + a b + 3a b + 3a 2 b + 3a b + 3a 4 2(a + b)
2( a + b) 2( a + b) 3 a + b a + b a + b ⇒ + ≤ + = ⇔ + ≤ a + 3b a + 3b (a +b) 4 2 2 2 a + 3b a + 3b x y x y Suy ra 2 + 2 2 + 2 a + b a + b + = + ≤ 2 2x 2 y 2 y 2 2 + 3.2 2 + 3.2 x a + 3b a + 3b
Mặt khác theo một bất đẳng thức phụ quen thuộc ta có: x+ y−3
x + y − e
= (x + y − ) x+y−3 3 − e + 3 ≤ 3−1 = 2 x y  =
Vậy VT ≥ 2 ≥ VP . Dấu “=” xảy ra khi và chỉ khi 2 2 3  ⇔ x = y =
x + y − 3 = 0 2 Khi đó 3 4 135 m x + y = =
⇒ T = m + n =151. 16 n
Câu 13. Cho hai số thực x, y thỏa mãn 1 3 1 1 log y + log x + 2 ≥ log
. Tìm giá trị nhỏ nhất của 2 ( 3 1 ) 2 6 2 3 2 3
x +x+2−4 y 2 2 biểu thức  1  x + y P = − + x( y + ) 1 −   y e  2 A. min P = 0 . B. min P =1. C. min P = 2.
D. min P = e . Lời giải Chọn B y > 0 Điều kiện 
(*) ; Với x, y thuộc (*) và thỏa mãn 3 x > − 2 1 3 1 1 log y + log x + 2 ≥ log
⇔ log y − log x + 2 ≥ −log 3 2 ( 3 ) ( 3 1 2 2 2 ) 2 6 2 3 2
⇔ log y + log 3 ≥ log ( 3
x + 2) ⇔log 3y ≥ log ( 3x + 2 2 2 2 2 2 ) 3
⇔ y ≥ x + ⇔ ( y − x) 3 3 2 3
≥ x − 3x + 2 (**) Xét hàm số 3
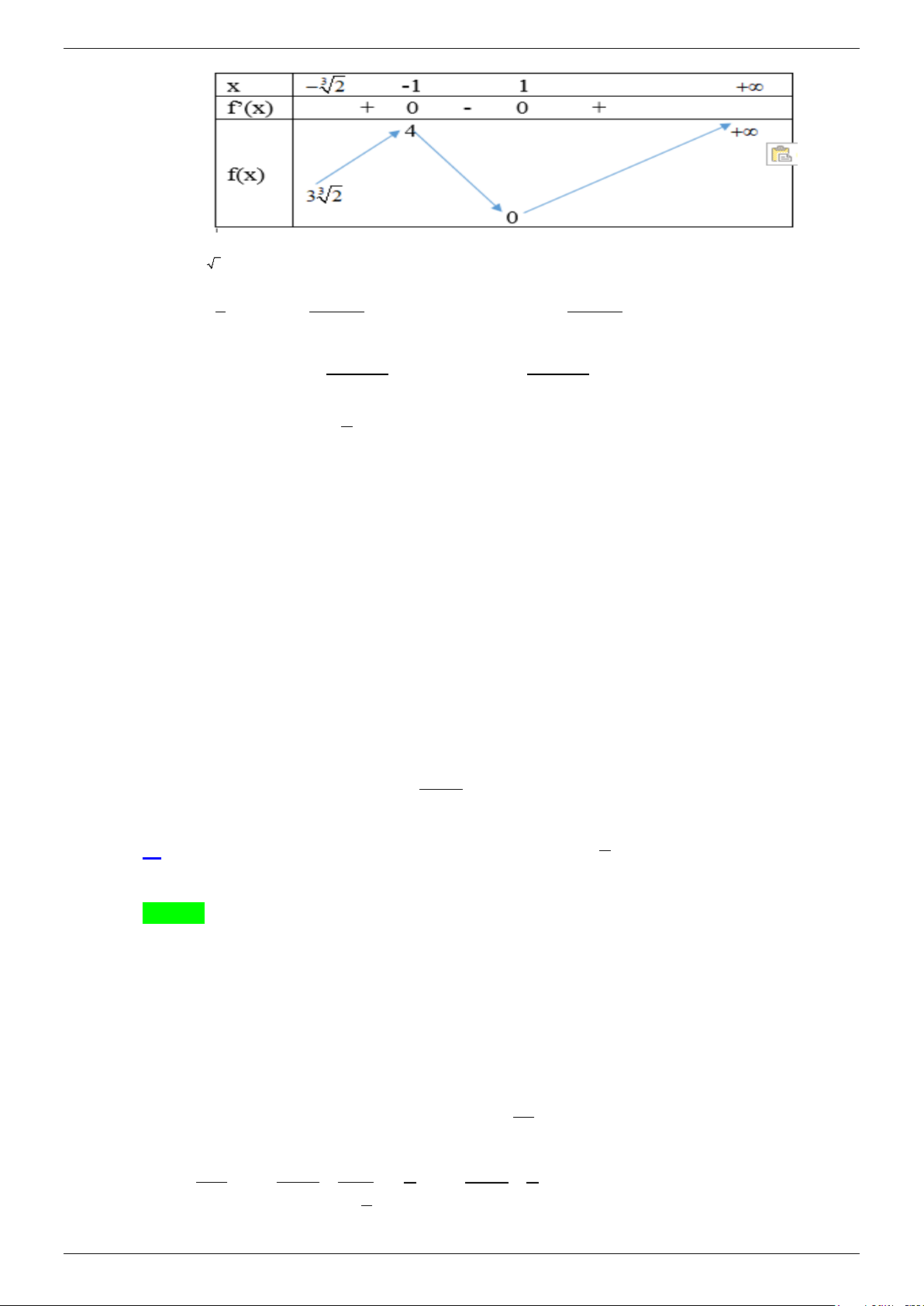
f (x) = x − 3x + 2 xác định và liên tục trên ( 3 − 2;+∞) x =1 Có 2
f x = x − = ( 2 '( ) 3 3 3 x − ) 1 . Với 2
f '(x) = 0 ⇔ x −1 = 0 ⇔  x = 1 − Và 3 3 f ( 1)
− = 4; f (1) = 0; f (− 2) = 3 2 > 0 Bảng biến thiên
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Do đó min f (x) = f (1) = 0 nên suy ra 3( y − x) ≥ 0 ⇔ y − x ≥ 0 ( 3− 2;+∞) 3
x +x+2−4 y 2 2 2 2 Mà  1  x + y = − + ( + ) 3
4 y−x −x−2 + 1 x y P x y − y = e − + x( y + ) 1 −   y e  2 2 2 2 3 − + − + y − x − − y x
( y x) 3y (x 2) ( ) = e − − ( y − x) ( y x) ( ) ≥ e − − ( y − x) 2 2 Xét hàm số (*) t 1 2
g(t) = e − t − t xác định và liên tục trên [0;+∞) 2 Do đó '( ) t
g t = e − t −1 xác định và liên tục trên [0;+∞) Và t 0
g '(t) = e −1≥ e −1 = 0, t ∀ ∈[0;+∞) .
Do đó hàm số g '(t) đồng biến trên [0;+∞) . Tức là 0
t ≥ 0 ⇒ g '(t) ≥ g '(0) = e − 0 −1 = 0,
Do đó hàm số g (t) đồng biến trên [0;+∞) . Tức là 0
t ≥ 0 ⇒ g(t) ≥ g(0) = e − 0 − 0 =1
Suy ra min g(t) = g(0) =1 [0;+∞) x = y > 0 x = y > 0 x = y > 0
Dấu " = " xảy ra khi và chỉ khi   ⇔  ⇔ x =1
⇔ x = y =1. 3 3 3  y = x + 2
x − 3x + 2 = 0  x = 2 −
Câu 14. : Cho các số thực x, y thỏa mãn 2 2 2 x +2 y xy 2 2 1 + ( − + −1) +xy+ y e e x xy y − e
= 0 . Gọi M ,m lần lượt
là GTLN, GTNN của biểu thức 1 P =
. Tính M − m . 1+ xy
A. M − m =1.
B. M − m = 2 . C. 1
M − m = .
D. M − m = 3. 2 Lời giải Chọn A Ta có 2 2 2 x +2 y xy 2 2 1 + ( − + −1) +xy+ y e e x xy y − e = 0 2 2 2
x +2 y −xy 2 2 1 ⇔ + ( − + −1) + y e x xy y − e = 0 2 2 2
x −xy+2 y 2 2 1+ y 2 ⇔ e
+ x − xy + 2y = e +1+ y (1) Xét hàm ( ) t
f t = e + t,t ∈ . Ta có (′ ) t
f t = e +1 > 0 t
∀ ∈  nên f (t) đồng biến trên  . Do đó (1) 2 2 2 2 2 2 2 2
⇔ f (x − xy + 2y ) = f (1+ y ) ⇔ x − xy + 2y =1+ y ⇔ x − xy + y =1 1
 = (x − y)2 + xy ≥  xy Khi đó  suy ra 1 1 xy − ≥ ≥ . 1  = 
(x + y)2 −3xy ≥ 3 − xy 3 1 1 1 Do đó ≤ P = ≤ 1 1 3 ⇔ ≤ P =
≤ . Vậy M − m =1 1+1 1+ xy 1 1− 2 1+ xy 2 3 Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Câu 15. Cho các số thực x , y thỏa mãn 2 x − y + = ( 2 x − y + ) 2 2 2 2 y−x +2 5 16.4 5 16 .7
. Gọi M và m lần lượt là + +
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 10 6 26 P x y =
. Tính T = M + m . 2x + 2y + 5 A. 21 T = .
B. T =10 .
C. T =15 . D. 19 T = . 2 2 Lời giải Chọn D Đặt 2
t = x − 2y , khi đó giả thiết tương đương với + = ( + ) t+2 2t t t 2−t 5 + 4 5 + 4 5 16.4 5 16 .7 ⇔ = .(1) t+2 2 7 7 t u u u u
Xét hàm số f (u)  1   4 5  = +     
trên  . Ta có: f ′(u) 1 1 4 4 = 5 ln + ln <     0, t ∀ ∈  7   7       7  7  7  7
Suy ra f (u) là hàm số nghịch biến trên  .
Do đó ⇔ f (t + ) = f ( t) 2 2 (1) 2
2 ⇔ t + 2 = 2t ⇔ t = 2 ⇔ x − 2y = 2 ⇔ 2y = x − 2 2 Khi đó
10x + 6y + 26 3x +10x + 20 P = = 2 2x + 2y + 5 x + 2x + 3 x = 5 − 2 Ta có 4
− x − 22x −10 P′  = ( = ⇔
. Bảng biến thiên như sau: x + 2x + 3) 0 2 1 2 x = −  2
Từ BBT, ta suy ra M = 7 , 5 m = . Vậy 5 19 M + m = 7 + = . 2 2 2
Câu 16. Cho a,b là hai số thực thay đổi thỏa 1< a ≤ b ≤ 2 , biết giá trị nhỏ nhất của biểu thức P = b + b − + a là 3 m + 3 n với ,
m n là số nguyên dương. Tính S = m + n . a ( 2 ) 2 2.log 4 4 logb a A. S = 9 . B. S =18 . C. S = 54 .
D. S =15 . Lời giải Chọn D b  −1 > 0
Ta có: 1< b ≤ 2 ⇒  ⇒ (b − ) 1 ( 2 b − 4 ≤ 0 2 ) b  − 4 ≤ 0 3 2 2 3
⇒ b − b − 4b + 4 ≤ 0 ⇒ b + 4b − 4 ≥ b mà a >1 nên b + b − ≥ b a ( 2 ) 3 log 4 4 loga 1 Do đó 3 2 P ≥ 2.log b + a = b + a logb 6loga a (log b − a )2 1 1
 < a ≤ b ≤ 2 Đặt t = log b  b ⇒ t >1 a , từ điều kiện . ≠  1 a
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 1 1
Khi đó P ≥ 6.t +
= 3. t −1 + 3 t −1 + + 6 ≥ 3 9 + 6 2 ( ) ( ) 3 (t − )1 (t − )2 1 1 1 1
Dấu “=” xảy ra khi 3(t − ) 1 =
⇔ t −1 = ⇔ t =1+
. Vậy m = 6;n = 9. 2 ( )3 3 (t − )1 3 3
Câu 17. Cho hai số thực a,b thay đổi thỏa mãn 0 < 2b < a <1. Giá trị nhỏ nhất của biểu thức 3 2 = log b S a + b − a + b b .logb logb 4 log
bằng m . Khẳng định đúng là: 2 ( 2 ) 12 25 a a a A. m∈(0; ) 1 . B. m∈(1;2) . C. m∈(2;3) . D. m∈(3;5) . Lời giải Chọn C  Ta có: 3 2b 12 1 S = log a + b − a + b = b + a + b − a b .logb logb 4 log log a a .log b logb 4 2 ( 2 ) 12 2 2 25 2 ( ) a 25 log b a a a 2 12 1 2 = −log a + b + a + a b − a b loga .log b logb ( 2 4 4 2 ) 25 log b a a
Ta có: < b < a < ⇒ (a − b)2 4 2 2 2 4 2 0 2 1 2
≥ 0 ⇒ a − 4a b + 4b ≥ 0 ⇔ 4a b − a ≤ 4b 1
Mà mặt khác 0 < 2b < a <1⇒ 0 < b < <1 nên suy ra a b − a ≥ b b ( 2 4 ) b ( 2 log 4 log 4 ) 2 Từ đó ta có: 2 12 1 2 log  b S a b a b  = − + + + ≥ + b +   a b loga .log b logb ( 2 4 ) 2 12 1 2 2logb loga .log 2 2 25 log ba  25 log b b a a a a 2 2  log a a b log 2 2  1 1  12 1 1 b a a 12 = + + + log b ≥ + b   a 33 . . log log b b b b b bb log b loga 25 log  b log b loga 25 a 2 2 2 2  a aa a  log a 2  2b = 3   1 12 1 12 a 3  . + log b = + ba 3 log log b 3 3 log b   a 25 log b 25 a 2b ( a )  a  3 12 3 12 12.3 12 = + log b ≥ b = = a 2 . loga 2 log b b a 25 loga 25 25 5 12 12
Như vậy giá trị nhỏ nhất của biểu thức S bằng với m = ∈(2;3) 5 5
Câu 18. Cho 2 số thực x, y thỏa mãn phương trình sau: ( x+y + )( x+ y + )( x− y + ) = ( x + )3 2 3 1 2 1 2 1 2 1 2 . 2 Đặt 2 2 x + y 2 y P = e + x +
− (x − 2y)2 . Hỏi mệnh đề nào sau đây đúng? 4
A. P = e −1.
B. P = e . C. 2 P = e .
D. P = e − 2 . max Lời giải Chọn B
Một bất đẳng thức mà ta hay gặp: ( + a)( + b)( + c) ≥ ( + abc)3 3 1 1 1 1 Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Có bổ đề sau: Cho các số thực dương a,b,c, x, y, z, ,
m n, p khi đó ta luôn có: ( 3 3 3 + + )( 3 3 3 + + )( 3 3 3 a b c x y z
m + n + p ) ≥ (axm + byn + czp)3
Chứng minh: Theo bất đẳng thức AM − GM ta có: 3 3 3 a m x 3axm + + ≥ 3 3 3 3 3 3 3 3 3 a + b + c m + n + p x + y + z ( 3 3 3
a + b + c ).( 3 3 3
m + n + p ).( 3 3 3
m + n + p ) 3 3 3 b n y 3bny + + ≥ 3 3 3 3 3 3 3 3 3 a + b + c m + n + p x + y + z ( 3 3 3
a + b + c ).( 3 3 3
m + n + p ).( 3 3 3
m + n + p ) 3 3 3 c p z 3cpz + + ≥ 3 3 3 3 3 3 3 3 3 a + b + c m + n + p x + y + z ( 3 3 3
a + b + c ).( 3 3 3
m + n + p ).( 3 3 3
m + n + p )
Cộng 3 bất đẳng thức trên có điều phải chứng minh.
Quay lại bài khi đó phương trình trở thành: ( + a)( + b)( + c) ≥ ( + abc)3 3 1 1 1 1 3 3  3  3
Theo bất đẳng thức Holder, ta có  1   1  ∏ + +     (3 a)  ≥( 3 1+ abc 3 3 ) cyc  2   2   
Với bài toán này nếu đặt x+y x+2 y x−3y 3 2 = ,2 = ,2 = ⇒ = 2x a b c abc
, đây chính là dạng trên.
Dấu " = " xảy ra khi và chỉ khi x+y x+2 y x−3 2 = 2
= 2 y ⇔ x = y = 0 . Vậy khi đó P = e .
Câu 19. Cho 2 số thực a,b không âm thỏa mãn log ab ∈ 0;1 đồng 2 ( ) ( ) a−b 1 + thời ( ab − ab 2 log ab + 1− log ab = 1+ . Biết rằng 4 10
a b được viết dưới dạng 2 )log2 ( 2 )1 log2 2a−2 2 b +1
m n với a,b là các số nguyên dương. Hỏi có tất cả bao nhiêu bộ số ( ; m n) như vậy? A. m∈(0; ) 1 . B. m∈(1;2) . C. m∈(2;3) . D. m∈(3;5) . Lời giải Chọn C
Bất đẳng thức Jensen và tính chất của hàm lồi
Cho hàm số f (x) liên tục trên đoạn [a;b] và n điểm tùy ý nên [ ; a b]. Ta có n
x + x +...+ x
• Nếu f ''(x) > 0 thì ∑ f (x ) 1 2 n nf  ≥ i   i 1 =  nn
x + x +...+ x
• Nếu f ''(x) < 0 thì ∑ f (x ) 1 2 n nf  ≤ i   i 1 =  n  Ngoài ra cần chú ý thêm
• Nếu hàm số f (x) có f ''(x) > 0, x
∀ ∈[a;b] thì f (x) làm hàm lồi trên [a;b]
• Nếu hàm số f (x) có f ''(x) < 0, x
∀ ∈[a;b] thì f (x) làm hàm lõm trên [a;b]
Trước tiên ta sẽ đặt log ab = x,1− log ab = y ⇒ x + y =1 2 2 .
Vế trái viết lại là x y x + y .
f (x) + f ( y)  + Ta có bất đẳng thức x y f  ≥ 
(*) - Bất đẳng thức Jensen 2  2 
Thật vậy ta có thể giả thiết 0 < a < b <1 và viết bất đẳng thức dưới dạng
  x + y  −  ( )  −   ( )  x + y f f x f y − f  ≤     0   2     2 
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Vế trái của bất đẳng thức này có dạng − − −
'(α ) y x − '(β ) y x = ''(γ )(α − β ) y x f f f 2 2 2 Trong đó x + y x < α <
< β < y,α < γ < β . 2
Vì ln f (x) = xln x
f (x) f (x)( x)
f (x) f (x)( x)2 1 ' 1 ln ' 1 ln  ⇒ = + ⇒ = + + > 0, x ∀ ∈   (0; )1  x  Suy ra ''( )( ) y x f γ α β − −
< 0 . Vậy bất đẳng thức (*) đúng. Khi đó áp dụng ta có 2 x y x x y
x ( x)1−x f (x) f ( x)  1 1 1 2 f  + = + − = + − ≥ =   2  2  a−b 1 + a−b
Theo bất đẳng thức AM – GM ta có 2 2.2 1+ ≤ 1+ = 2 . 2a−2b 2a−2 2 +1 2 2 b
Vậy VT ≥ VP . Dấu “=” xảy ra khi 4 4 10
x = y = 2 ⇒ x y = 128 = 2 32 = 4 8 = 8 2
Câu 20. Cho 2 số thực x, y >1 thỏa mãn điều kiện: 9
1+ log 3y + 2log 3y 3− log 3xy = log 2 . 2 2 ( 2 ) 2 x Đặt 2 2
P = x + xy + y . Hỏi mệnh đề nào sau đây đúng?
A. P ∈[11;12] . B. P ∈[12; ] 13 . C. P ∈[10; ] 11 . D. P =10 min . Lời giải Chọn C
Ý tưởng ở bài này là sẽ kiếm một điều kiện ràng buộc giữa x,y rồi sau đó chỉ ra giả thiết chỉ nhận
duy nhất 1 bộ nghiệm. Dưới đây là cách giải quyết của bài toán trên
Biến đổi giả thiết ta được: 9
1+ log 3y + 2log 3y 3− log 3xy = log 2 2 2 ( 2 ) 2 x 8 9
⇔ log x + log x log 3y + 2log 3y log x log = 2 2 2 2 2 2 3xy 2 Ta nhận thấy rằng 8
log x + log 3y + log = 3 . 2 2 2 3xy  log x = a 2 
a + b + c = 3
Để đơn giản ta đặt  
log 3y = b . Lúc này ta có 2 giả thiết . 2  9 
a + ab + 2abc = 8 log = c  2 2  3xy
Thế b = 3− a − c vào giả thiết dưới ta được: ( c + ) 2 a + ( 2 c − c − ) 9 2 1 2 5 4 a + = 0 2
Coi vế trái là tam thức bậc 2 theo biến a với c là tham số ta có: ∆ = ( 2
c − c − )2 − ( c + ) = ( c − )2 ( 2 2 5 4 18 2 1
2 1 c − 4c − 2)
Chú ý với điều kiện x, y >1 ta sẽ có a,b,c > 0 . Mặt khác a + b + c = 3 ⇒ c < 3
Suy ra ∆ ≤ 0 , điều này đồng nghĩa VT ≥ 0  3  3 a =  log x = 2 2 2 x =   2 2
Dấu “=” xảy ra khi và chỉ khi b  1  log 3y 1  = ⇒ = ⇔ 2  2  1   = 8 1 y  3 c = log = 2  2  3xy 2 Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Từ đây suy ra 76 12 2 P + = ∈[10; ] 11 . 9
Câu 21. Cho hàm số y = f (x) = (x + )
1 (x + 2)(x + 3)(x + 4) + m . Khi đó, giá
trị m để giá trị cực tiểu của hàm số f (x) bằng với giá trị nhỏ nhất của biểu thức P = log b + + a + với a
∀ ,b∈(1;2]nằm trong khoảng nào sau đây a (3 2) logb (3 2) A. [3;4]. B. [5;6]. C. [7;8]. D. [9;10]. Lời giải Chọn C Cách 1: Ta có:  3 1 4 3 log a + ≥ a = + a +  + = + + + ≥  b (3 2) logb a a a a a  ( 4 3
4 2 ) logb 4 logb logb 2 3 2 2 4 2 4 4  ⇒  4 3
 b + = b + b + b + ≥ bb + ≥ b = + b + a ( ) a  ( 4 3) 3 1 3 2 2 4 2 log 3 2 log 4 2 loga 4 loga loga 2  4 4 Suy ra: b + + a + ≥ + + a + b + + a ( ) b ( ) ( a b ) 3 ( b a ) 1 log 3 2 log 3 2 log 4 log 4 log log (logb 2 loga 2) 4 4 ≥ ( 3 1 log 4 + log 4 + 2 log a b + + (do a ∀ ,b∈(1;2]) b .loga log 2 log 2 2 2 ) ( 2 2 ) 4 4 = 6 . Suy ra P = 6 = = min
khi và chỉ khi a b 2 Từ đó ta cũng suy ra:
6 = P = x +1 x + 2 x + 3 x + 4 + m = x +1 x + 4 x + 2 x + 3 + m min ( )( )( )( ) ( )( )( )( )
= (x + 5x + 4)(x + 5x + 6) + m = (x + 5x + 5− ) 1 (x + 5x + 5+ )
1 + m = (x + 5x + 5)2 2 2 2 2 2 + m −1 Do phương trình 2
x + 5x + 5 = 0 có hai nghiệm ∉(1;2]) nên ta cũng suy ra
P = (x + x + )2 2 5
5 + m −1≥ m −1⇒ m −1 = 6 ⇔ m = 7 . Như vậy m = 7∈[7;8]
Cách 2: Nhìn vào biểu thức P trên ta dự đoán được điểm rơi a = b = 2 Ta có: P = b + + a + ≥ b + − b b + + a + − a a + a ( ) b ( ) a ( 2 ( )( )2 ) b ( 2 log 3 2 log 3 2 log 2 1 log (2 )( )2 1 )
Xét hàm số y = f (x) = ( − x)(x + )2 2 1 với x
∀ ∈(1;2] có f (x) ≥ 0 x ∀ ∈(1;2]
f ′(t) = ⇔ t =
f ′′(t) < ⇒ ( − x)(x + )2 0 1, 0 2 1 > 0
Từ đó ta suy ra P ≥ b + − b b + + a + − a a + ≥ b + a a ( 2 ( )( )2 ) b ( 2 ( )( )2 ) a ( 3 ) b ( 3 log 2 1 log 2 1 log log ) (   = b + a =  b +  ≥ b = a b ) 1 1 3 log log 3 loga 3.2 loga . 6  log b b a loga Suy ra P = 6 = = min
khi và chỉ khi a b 2
--Khúc sau làm tương tự như cách 1 đã trình bày--
Câu 22. Lần lượt cho hai số thực dương x, y thỏa mãn phương trình sau đây:  +  3x 3y 2 2 log
= x + y + xy − 6 x + y +  
2. Gọi giá trị lớn nhất và giá trị nhỏ nhất của 2 2 2 ( )
x + y + xy + 3  + + biểu thức 2x 3y 2 P =
lần lượt là M và m . Giá trị của biểu thức (M + m) bằng x + y +1 A. 60 . B. 12. C. 26 . D. 40 . 13 5 13
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Lời giải Chọn A  +  Ta có: 3x 3y 2 2 log
= x + y + xy − 6 x + y +   2 2 2 2 ( )
x + y + xy + 3   3x + 3y  2 2 ⇔ 1+ log
= x + y + xy − 6 x + y +   3 2 2 2 ( )
x + y + xy + 3   6(x + y)  2 2 ⇔ log 
 = x + y + xy − 6 x + y + 3 2 2 2 ( )
x + y + xy +  3  log ( 2 2
x + y + xy + 3) + ( 2 2
x + y + xy + 3 = log 6 x + y + 6 x + y 2 ) 2 ( ( )) ( ( ))
Xét hàm đặc trưng y = f (t) 1
= log t + t ⇒ f ′ t = +1 > 0 t ∀ > 0 . 2 ( ) tln2
Suy ra hàm số f (t) đồng biến trên ( +∞) 2 2 0;
⇒ x + y + xy + 3 = 6(x + y)
x = a + b Đặt: 
⇒ (a + b)2 + (a − b)2 + (a + b)(a − b) + 3 = 6(a + b) + 6(a − b)
y = a − b  ⇔ (a − )2 2 2 3 2 + b = 9 = 3 a = t + . Đặt: 3 cos 2  b  = 3sin t Suy ra biểu thức
2x + 3y + 2 2(a + b) + 3(a − b) + 2 − + 5 5a b 2
( 3cost +2)−3sint +2 P = = = = x + y +1
(a +b)+(a −b)+1 2a +1 2( 3cost + 2)+1
5 3 cost − 3sin t +12 =
⇔ (2 3P −5 3)cost +3sint =12−5P 2 3 cost + 5 2 − + Điều kiện có nghiệm ( P −
) + ≥( − P)2 30 2 30 30 2 30 2 3 5 3 9 12 5 ⇔ ≤ P ≤ 13 13  30 + 2 30 P = M = max Như vậy suy ra:  13 60  ⇒ M + m =  30 − 2 30 13 P = m = min  13
Câu 23. Cho hai số thực dương, tính giá trị lớn nhất của biểu thức sau đây: ( 3 3x ) x log 2022 16 10 24 12.10 y P y y + = − + − + A. 2046 . B. 2048 . C. 2050 . D. 2038 . Lời giải Chọn A Ta có: = − ( 3 3x + − ) x+log y + = − ( 3 3 2022 16 10 24 12.10
2022 16 +10 x − 24 ) +12 .10x P y y y y y
Áp dụng bất đẳng thức Cosi ta có: ( ) x ≤ ( )2 + ( x )2 2 2 2. 2 .10 2 10 = 4 +10 x y y y
Dấu bằng xảy ra khi và chỉ khi: 2 10x y = Suy ra: P = 2022 − ( 3 3
16y +10 x − 24y) + 3.2.(2y).10x ≤ 2022 − ( 3 3
16y +10 x − 24y) + 3( 2 2
4y +10 x ) = 2022 + 4( 3 2 4
− y + 3y + 6y) + ( 3x 2 10 − + 3.10 x )
Khảo sát các hàm số sau: Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDCf ( y) 3 2 = 4
− y + 3y + 6y y ∀ ∈(0;+∞)  ta có: g ( x) =  ( 3x 2 10 − + 3.10 x ) x ∀ ∈(0;+∞)
f ( y) ≤ f ( ) 1 = 5  y =1 
⇒ Dấu bằng xảy ra khi:  g (x) =  ( 3x 2 10 − + 3.10 x ) 3 2 = t
− + 3t = h(t) ≤ h(2) =  4
x = log t = log 2 Suy ra: = + ( 3 2 − + + )+( 3x 2 2022 4 4 3 6 10 − + 3.10 x P y y y )
≤ 2022 + 4 f ( y) + g (x) ≤ 2018 + 4.5 + 4 = 2046 10x  = 2 x = log 2
Như vậy P = 2046 khi và chỉ khi  ⇔ max  2y = 2  y = 1
Câu 24. Cho 2 số thực x,y thay đổi thỏa mãn x + y +1 = 2( x − 2 + y +3). a
Giá trị lớn nhất của biểu thức x+ y−4 =
+ ( + + ) 7−x−y S x y − ( 2 2 3 1 2
3 x + y ) là với a,b là các số b a
nguyên dương và tối giản. Tính P = a + b b A. P = 8. B. P =141. C. P =148. D. P =151. Lời giải Chọn A
Đây chính là đề thi THPT Quốc Gia 2016 đã được biến tấu để trở thành 1 câu hỏi trắc nghiệm 2
Từ giả thiết ta có (x + y + )2
1 = 4( x − 2 + y +3) = 4(x + y +1+ 2 x − 2 y +3)
Áp dụng bất đẳng thức AM – GM cho 2 số thực không âm ta có: x −
y + ≤ x + y + ⇒ (x + y + )2 2 2 3 1
1 ≤ 8(x + y + ) 1 ⇒ 1
− ≤ x + y ≤ 7 Mặt khác ta lại có: (  + ≥  ≤ + ≤
x + y + )2 = (x + y + + x − y + ) ≥ (x + y + ) x y 3 3 x y 7 1 4 1 2 2 3 4 1 ⇒ ⇒  x y 1  + ≤ − x + y = 1 −
 x − 2 y + 3 = 0 x = 2 Nếu 9746 x + y = 1 − ⇒  ⇔  ⇒ S = − x + y = 1 − y = 3 − 243
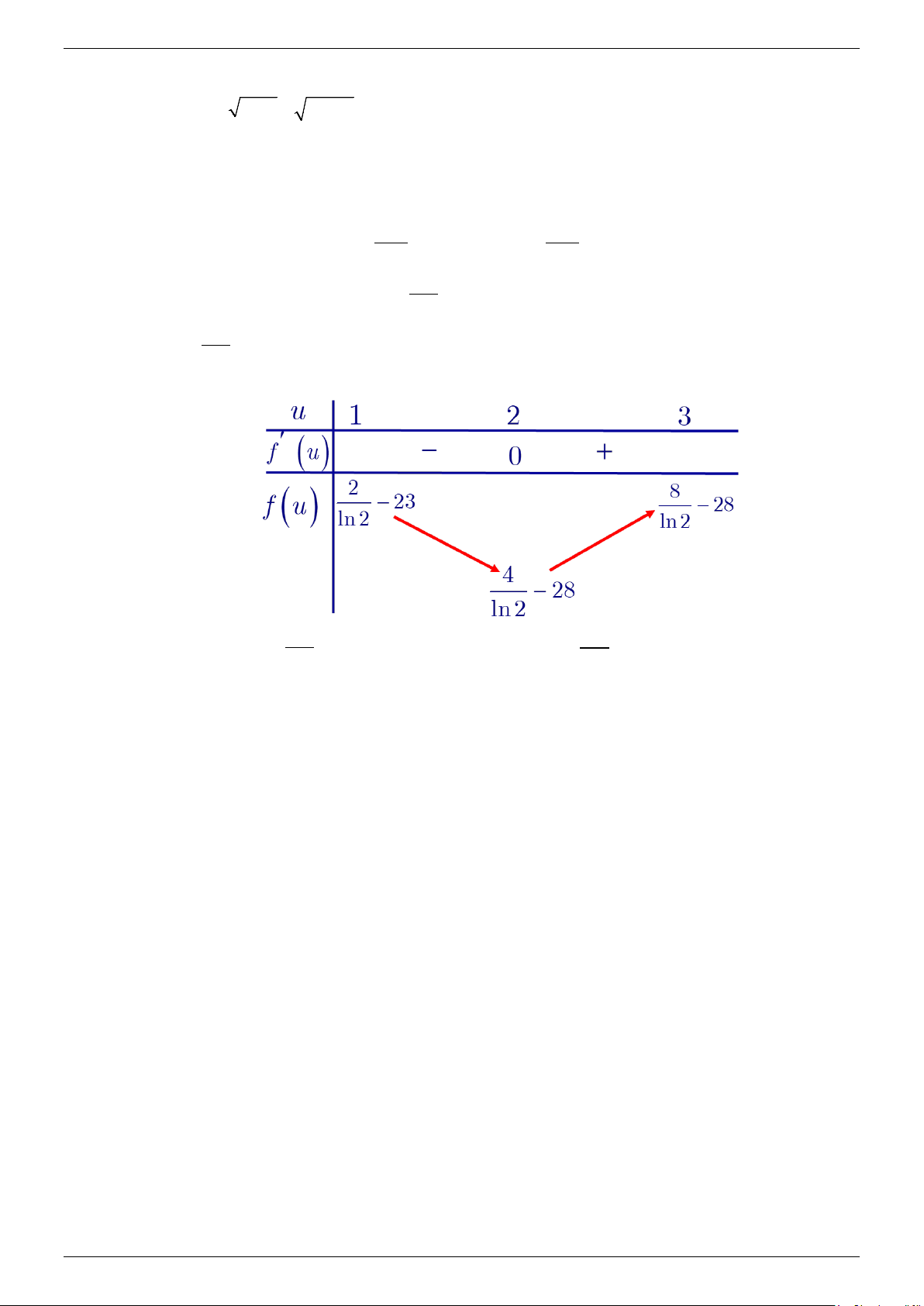
Nếu 3 ≤ x + y ≤ 7 . Đặt t = x + y (t ∈[3;7]) Xét hàm số ( ) t−4 = + ( + ) 7 3 1 .2 −t f t t (t∈[3;7]) ⇒ f '(t) t−4 7
= 3 ln 3+ 2 −t − (t + ) 7 1 2 −t ln 2 ⇒ f ' (t) t−4 2 7
= 3 ln 3− 2 −t ln 2 − ln 2( 7
2 −t − (t + ) 7 1 2 −t ln 2) t−4 2 = 3 ln 3+ ( t + ) 2 1 ln 2 − 2ln 2) 7 2 −t > 0 t ∀ ∈[3;7]
Vì f '(3) < 0, f '(7) > 0 nên tồn tại số a ∈(3;7) sao cho f '(a) = 0. Suy ra f (t) nghịch biến
trên (3;a) và đồng biến trên ( ;7 a ) . Mặt khác f ( ) 193 =
f ( ) = ⇒ f (t) ≤ f ( ) 193 3 ; 7 35 3 = t ∀ ∈[3;7] 3 3 Ta sẽ đi chứng minh 2 2
x + y ≥ 5 với x + y ≥ 3, x ≥ 2 . Nhận thấy rằng khi: + x ∈[ ] 2 2 2 2 2
2;3 ⇒ y ≥ 3− x ≥ 0 ⇒ y ≥ x − 6x + 9 ⇒ x + y ≥ 2x − 6x + 9 = 2(x − 2)(x − ) 1 + 5 ≥ 5 + 2 2
x > 3 ⇒ x + y > 9
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 148 aa =148 Vậy 2 2
x + y ≥ 5 ⇒ S ≤ = ⇒  ⇒ a + b =151. 3 b b  = 3
Câu 25. Cho các số thực a,b thỏa mãn a > b > 0 và log a − b = log a + b Khi biểu thức 2 ( ) 3 ( )
P = log a + log b + 2log (a + b) − 2log ( 2 2
a + b đạt giá trị lớn nhất, giá trị − thuộc khoảng 2 2 3 2 ) a b nào sau đây? A. (3;4) . B. (5;6) . C. (4;5) . D. (2;3) . Lời giải Chọn D t t  2 2 9 + 4 t 2 2 0 < − = 2  − 2 + = 4t a + b a b a ab b =  Đặt:  2  ⇔  ⇒  t 2 2
0 < a + b = 3
a + 2ab + b = 9t  9t − 4t ab =  4
P = log ab + 2log (a + b) − 2log ( 2 2 a + b 2 3 2 ) 9t − 4t 9t + 4t 9t − 4t t 36t −16t = log + 2t − 2log = log + log 4 = log 2 2 2 4 2 (9t +4t )2 2 2 (9t + 4t )2  9 t − t t   1 −   − t Đặt 36 16 4 k 1 S = ( = = với 9 k   =   9t + 4t )2 2t t 2  9   9  k + 2k +1  4  + 2 +     1  4   4 
P đạt giá trị lớn nhất khi và chỉ khi S đạt giá trị lớn nhất.
Giả sử S có giá trị lớn nhất. Suy ra phương trình 2 Sk + (2S − )
1 k + S +1 = 0 có nghiệm. ⇒ ∆ = ( S − )2 2 1 − 4S (S + ) 1 ≥ 0 1 ⇔ S ≤ . 8 t
Suy ra S đạt GTLN bằng 1 khi  9 k 3  = ⇒ = 3 ⇔ t =   log 3. 8 9  4  4
Do đó P đạt GTLN bằng 1 log = 3 − khi t = log 3 . 2 8 9 4 log 3
Khi đó log a − b = t = log 3 ⇔ a − b = 2 ≈ 2,56 . 2 ( ) 9 4 9 4
Câu 26. Cho hai số thực x và y thỏa mãn: x + y = x + 2 + 2y − 4 . Khi ấy, x+ y
giá trị nhỏ nhất của biểu thức 2 2 2 P =
+ x + y + 6xy tương ứng là: ln 2 A. 4 − 28. B. 2 − 4. C. 8 + 6. D. 4 . ln 2 ln 2 ln 2 ln 2 Lời giải Chọn A x ≥ 2 − ĐK:  y ≥ 2
Ta có: x + y = x + +
y − ⇒ (x + y) = ( x + + y − )2 2 2 2 4 2 2 4
(x + y)2 = x + y + y − + (x + )( y − ) ≥ x + y ⇒ (x + y)2 2 2 2 2 4
− (x + y) ≥ 0 ⇒ x + y ≥1( ) 1 Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Áp dụng BĐT Bunhiacôpki ta có:
(x + y) = ( x+ + y − )2 2
≤ (x + y) ⇒ (x + y)2 2 2 4 3
− 3(x + y) ≤ 0 → 0 ≤ x + y ≤ 3(2) Từ ( )
1 & (2) ⇒1≤ x + y ≤ 3 x ≥ 2 − Lại có: 
⇒ (x + 2)( y + 2) ≥ 0 ⇒ xy ≥ 2
− (x + y) − 4 y ≥ 2 x+ y x+ y
⇒ xy ≥ − (x + y) 2 − ⇒ P = + (x + y)2 2 4 8 16 + 4xy ≥
+ (x + y)2 −8(x + y) −16 ln 2 ln 2 u Đặt u 2
= x + y (1≤ u ≤ 3) khi đó: 2 P ≥
+ u −8u −16 ln 2 u ( ) 2 2 = +
− 8 −16(1≤ ≤ 3); ′( ) = 2u f u u u u f u
+ 2u −8 = 0 ⇒ u = 2 ln 2
Ta có BBT hàm số f (u) như sau: 4 x = 2 − Từ BBt suy ra: 4 P ≥
− 28 ⇔ t = 2 . Vậy GTNN của P = − 28 ⇔ . ln 2 ln 2  y = 4
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
BÀI TOÁN GTLN - GTNN BIỂU THỨC MŨ – LOGARIT NHIỀU BIẾN SỐ
Câu 1. Cho x, y, z lần lượt là các số thực dương và thỏa mãn hệ phương trình sau 3log y = z =
yz > . Khi biểu thức 5 4
P = x y z đạt giá trị nhỏ nhất thì x (3 ) 3log x 27 log xy 81 0 3 ( ) 3 ( )
giá trị của 1000P nằm trong khoảng nào ? A. (18;20) . B. (20;22) . C. (22;24) . D. (24;26) . Lời giải Chọn B
Ta có hệ phương trình sau: 3log y = z = yz ≠ x (3 ) 3log x 27 log xy 81 0 (*) 3 ( ) 3 ( )
Từ phương trình (*), ta có: 3log y = z = yz = k > x (3 ) 3log x 27 log xy 81 0 3 ( ) 3 ( ) k  1 k 3 3
x = 3y → y = x 3  log y = k x (3 ) 3   k k Đặt: 3  log z k
= ⇒  x = z → z = x x ( 27 ) (3 ) 1 3 27 (3 )3 3 27 log 81yz k  =  3 ( ) (  3xy)k xy = 81yz (*)   k +3 k k k k k 2k k      
Thay nghiệm y, z theo x vào 1 1 1 3 3
(*) ⇒ 3x x  = 81 x . (3x) 3 3 3 3 ⇔  x  = 3 .x  3   3  27   k 2 − k −3  1 k ( − k+ ) 1 3 1 ( 3 k + ) 1 3 2  = = = + + y x k k k k k k k k k 3 3 3 2 ( )1 k+ k+  k+ 3 3 3 3 3 3 ⇔ x = 3 .x ⇔ x = 3 ⇔ (x ) 1 1 3 3 1 1
= 3 ⇔ x = 3 ⇒ x = 3 ⇒  2 k −7k−9  1 z = ( k 3x) ( 3 k+ ) 1 3 =  3  27
Thế các nghiệm x, y, z theo k vào biểu thức cần tính, suy ra: 4 2 2 2 5 2 − k−3 k −7k−9 5 8k 12 + k −7k−9 k 15 − k−6 1     − + 5 4 (3k+ )1 (3k+ )1 k 1 + (3k+ )1 (3k+ )1 (3k+ + )1 k 1
P = x y z = 3  .3  .3 = 3 = 3       2
k −15k − 6  2 k −15k − 6 Khi P ⇔ y = f k = k ∀ > 0 min    . Xét hàm ( ) 3(k ) 1  +   3(k + ) 1 min 2 − −  = − + f ′(k ) k 2k 9 k 1 10 = 0 ⇔ = 0 ⇔  ⇒ k = 1 − + 10 9(k + )2 1 k = 1 − − 10 2 10 17 − −
Dễ dàng suy ra min f (k ) = f ( 1 − + 10) 2 10 17 3 = ⇒1000P =1000.3 ≈ 20.052698 min 3
Câu 2. Cho các số thực không âm a, ,
b c thỏa mãn 2a 4b 8c + +
= 4 . Gọi M ,m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S = a + 2b + 3c . Giá trị của biểu thức
4M + log m bằng M A. 2809 . B. 281 . C. 4096 . D. 14 . 500 50 729 25 Lời giải Chọn C
Đặt a = log x, 2b = log y, 3c = log z . Ta có S = log xyz . 2 ( ) 2 2 2 3  4   4  3
4 = x + y + z ≥ 3 xyz ⇒ xyz ≤ ⇔ S ≤   3log 2 3  3    
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC  4  4
MaxS = M = 3log  , khi x = y = z = 2  3  3 Gọi z = (x y z) 4
min , , ⇒1≤ z ≤ . 3 Do (x − ) 1 ( y − )
1 ≥ 0 ⇒ xy ≥ x + y +1 = 3− z ⇒ xyz ≥ z(3− z) ≥ 2 (vì  4 z 1;  ∈  3  
Suy ra S ≥1, do đó m = min S =1 khi x = z =1, y = 2  4 3log  2 M  3   4096 4 + log m = + = . M 4 log 1  4 3log  2  729  3 
Câu 3. Cho ba số thực thay đổi a,b,c >1 thỏa mãn a + b + c = 6 . Gọi x , x là 1 2
hai nghiệm của phương trình ( x − + b + c x − = a )2 log
(2 loga 3loga )loga 2022 0. Khi đó giá trị lớn nhất của x x là 1 2 A. 2022 − . B. 216 . C. 12 + 6log 3 . D. 108. 2 Lời giải Chọn C Do phương trình ( x − + b + c x − = a )2 log
(2 loga 3loga )loga 2022 0 có hai nghiệm x ,x nên ta suy 1 2
ta hệ thức Viét như sau: (log x + x = x x = + b + c a loga loga 2 loga 3log 1 ) ( 2 ) ( 1 2 ) a 2+loga b+3loga c 2 3 x x = a = a bc 1 2 2 3 Ta lại có tiếp a a c c c a a c c c a bc = + + = + + + + + ≥ 6 6 6 a b c b 6 . . . b . . = 6 2 2 3 3 3 2 2 3 3 3 108 Suy ra 2 3
x x = a bc ≤108 . Như vậy giá trị lớn nhất của x x là 1 2 108 1 2
Câu 4. Cho ba số thực không âm x, y, z thỏa mãn 2 2 2 2x 3y 5z + + = 6 . Giá trị
lớn nhất của biểu thức T = x + 3y + 4z nằm trong khoảng nào sau đây A. (4;5) . B. (5;6). C. (6;7) . D. (7;8). Lời giải Chọn C Ta có: 2 2 2 2 2 2 2 2 2 x y z 3 6 2 3 5
3 2x .3y .5z
2x .3y .5z = + + ≥ ⇒ ≤ 8
Loga cơ số 2 cho hai vế ta có: log ( 2 2 2
2x .3y .5z ) 2 2 2
≤ 3 ⇔ x + y log 3+ z log 5 ≤ 3 2 2 2
Áp dụng bất đẳng thức Bunyakovsky, ta có: 2   2
T = (x + y + z)2 3 4 3 4 = 1.x + y log 3 + z log 5  2 2  log 3 log 5   2 2   9 16  ≤ 1+ + .( 2 2 2
x + y log 3+ z log 5 2 2 )  log 3 log 5 2 2  2
⇒ T ≤ (1+ 9log 2 +16log 2).( 2 2 2
x + y log 3+ z log 5 = 3. 1+ 9log 2 +16log 2 3 5 2 2 ) ( 3 5 )
⇒ T ≤ 3(1+ 9log 2 +16log 2 ≈ 6,38∈ 6;7 3 5 ) ( )
Câu 5. Cho ba số thực a,b,c nhận những giá trị dương lớn hơn 1. Khi đó giá trị 3 3
nhỏ nhất của biểu thức T = log + +  + là: + a b cab ( 2 2 2 4 9 3 4 ) ( )  2log + + − + 2a 3b c log + 3 3ab 4 ( ) ( ) (3ab 4) A. 1. B. 2 . C. 3. D. 4 . Lời giải Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Chọn D Ta có: 3 T = log + +  + + 4a 9b c  3ab 4 ( ) 3 2 2 2 ( )  2log + + − + 2a 3b c log + 3 3ab 4 ( ) ( ) (3ab 4) 3 = log + +  + + 4a 9b c  3ab 4 ( ) 3 2 2 2 ( ) 
(2a +3b + c)2 log(3ab+4) 3 = log + +  + + + 4a 9b c 3log 3ab 4  3ab 4 ( ) 3 2 2 2 2 ( ) ( )  (2a+3b+c) 3 Theo Bunhia, ta có: ( a + b + c 1+1+ ) 1 ( 2 3 2 2 2
4a + 9b + c ) ≥ (2a + 3b + c) ⇔ ( 2 2 2
4a + 9b + c ) ( )2 2 ≥ 3 
(2a +3b + c) 3 2 
(2a +3b + c)2 Suy ra:T ≥ log  + + . Đặt t = log + 3log 3ab 4 2 3ab 4 ( ) ( ) (2a+3b+c)  3  (3ab+4)   3 3 Khi ấy, 3 3 3 1 1 1 3 1 1 1 ≥ + = + + + ≥ 4 T x x
4 x . . . = 4 .Vậy T = 4 x x x x x x x min
Câu 6. Cho ba số thực x, y, z ∈[1;4] và đồng thời thỏa điều kiện xyz =16 . Giá
trị lớn nhất của biểu thức T = 2x + 2y + 2z − 3(log x + log y + log z tương ứng là: 2 2 2 ) A. 3. B. 6 . C. 6 + 3 3 . D. 4 + 2 6 . Lời giải Chọn D
Đầu tiên, ta khảo sát hàm số f (x) = x −3log x −1 trên đoạn [1;4] như sau: 4 Có: f ′(x) 3 3 =1− = 0 ⇔ x = . Ta có tiếp: xln 4 ln 4 f ( ) f ( ) 3 3  3 1 4 0; f   3log  = = = − −1 ≈ 0 −     ,51 4  ln 4  ln 4  ln 4  x =1
Suy ra f (x) = x − 3log x −1≤ 0, x
∀ ∈ 1;4 và dấu bằng xảy ra khi 4 [ ]  x = 4
y − 3log y −1≤ 0, y ∀ ∈  1;4 4 [ ]
Tương tự như thế ta cũng thu được 
z − 3log z −1 ≤ 0, z ∀ ∈ 1;4  4 [ ]
Suy ra T = 2x + 2y + 2z − 3(log x + log y + log z = 2 x + y + z − 3 log x + log y + log z 2 2 2 ) ( ( 4 4 4 ))
= 2((x −3log x −1 + y −3log y −1 + z −3log z −1 + 3 ≤ 2. 0 + 3 = 6. Vậy T = 6 4 ) ( 4 ) ( 4 ) ) ( ) max
Câu 7. Cho ba số thực x, y, z ∈[1; ]
3 và đồng thời thỏa điều kiện xyz = 9 . Giá
trị lớn nhất của biểu thức T = ( 2 2 2
x + y + z ) − 2(xlog x + ylog y + z log z tương ứng là: 3 3 3 ) A. 3 3 . B. 7 . C. 8 + 3 3 . D. 9. Lời giải Chọn B Đầu tiên, ta có: 2 x − 2(x + )
1 log x +1 = x +1 x − 2log x −1 3 ( )( 3 )
Xét hàm số sau: y = f (x) = x − 2log x −1 x ∀ ∈ 1;3 3 [ ] Có: f ′(x) 2 2 =1− = 0 ⇔ x = . xln 3 ln 3 Ta có tiếp:
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC f ( ) f ( ) 2 2  2 1 3 0; f   2log  = = = − −1 ≈ 0 −     ,27 3  ln 3  ln 3  ln 3 
Suy ra y = f (x) = x − 2log x −1≤ 0 x ∀ ∈ 1;3 3 [ ] Và ta cũng suy ra được 2 x − 2(x + )
1 log x +1 = x +1 x − 2log x −1 ≤ 0 x ∀ ∈ 1;3 3 ( )( 3 ) [ ] 2
⇒ x − 2x log x ≤ 2log x +1 x ∀ ∈ 1;3 3 3 [ ] 2
y − 2y log y ≤ 2log y +1 y ∀ ∈  1;3 3 3 [ ]
Tương tự, ta cũng dễ dàng chứng minh được:  2
z − 2z log z ≤ 2log z +1 z ∀ ∈ 1;3  3 3 [ ] Suy ra: T = ( 2 2 2
x + y + z ) − 2(xlog x + ylog y + z log z 3 3 3 ) = ( 2
x − 2x log x) + ( 2
y − 2y log y) + ( 2
z − 2z log z 3 3 3 )
≤ (2log x +1 + 2log y +1 + 2log z +1 = 2 log x + log y + log z + 3 3 ) ( 3 ) ( 3 ) ( 3 3 3 )
= 2log xyz + 3 = 2log 9 + 3 = 7 3 ( ) 3 Vậy T = 7 max
Câu 8. Cho ba số thực a >1, b >1, c >1. Biết rằng tồn tại số thực dương
x ≠ 1 thỏa mãn hệ thức 9 logb x loga x a = b
. Khi đó, biểu thức T = ab + a bc c b ( 2 log ( ) log ) đạt giá trị
nhỏ nhất tương ứng bằng A. 11. B. 7 . C. 8. D. 5. Lời giải Chọn A
Với ba số thực a >1, b >1, c >1, ta có: c c a = = ( c )log log log .log log b a b a b a logb a a a a = c .
Do tồn tại số thực x > 0 , x ≠ 1 thỏa mãn hệ thức 9 logb x loga x a = b
nên áp dụng tính chất trên ta được: 9 logb x loga x a = b logb a 9loga b ⇔ x = x ⇔ log a = b ⇔ log a = . b 3 b 9loga Do đó, T = ab + a bc = b ab + a + + c c b ( 2 ) 2 log ( ) log
logc .logb( ) logb 1 logb = log b a + + a + + c = b + c + c .(logb )1 2logb 1 logb 4log . c logb 7
Vì a >1, b >1, c >1 nên log b > , log c > . b 0 c 0
Theo bất đẳng thức Cauchy, ta có: 4log b + c ≥ b c = . c logb 2 4logc .logb 4 2 4log b = c  = c log c b
Suy ra T ≥11. Đẳng thức xảy ra khi b  ⇔  . 3 log a = b 3 a = b
Vậy giá trị nhỏ nhất của biểu thức T bằng 11. Câu 9. Cho 1
a,b,c  ;1 ∈ 
. Tìm giá trị nhỏ nhất của biểu thức sau: 4     1   1   1 P log b  c   a  = − + − + − a logb log 4 4 c 4        A. 6 . B. 7 . C. 8. D. 5. Lời giải Chọn A 2 Ta có:  1  2 1 2 1 x x x x x x   x   y   − = − + ≥ ⇔ ≥ − ⇒ ≤ − ∀ ∈   y ( 2 ) 1 1 0 log logy , ;1 2 4 4 4  4        Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Suy ra x   x   y   ≤ − ∀ ∈ y ( ) 1 1 2log logy , ;1 4  4        1  1 log bb a b  − ≥ ∀ ∈ a 2loga , ;1 4 4        Từ đó ta suy ra  1  1 log cc b c  − ≥ ∀ ∈ b 2logb , ;1 4 4         1  1 log aa c a  − ≥ ∀ ∈ c 2logc , ;1  4 4      Suy ra  1   1   1 P log b  c   a  = − + − + − a logb log 4 4 c 4        ≥ 2(log b + c + a = b c a = a logb logc ) 3
2.3 loga .logb .logc 6 Vậy P = 6 min Câu 10. Cho
a,b,c∈[0; ] 1 thỏa 3 3 3
log a + log b + log c ≤1. Khi đó, biếu thức 2 2 2 3 3 3 = +
+ − 3(log a + log b + log c T a b c a b
c đạt giá trị lớn nhất là: 2 2 2 ) A. 4 . B. 7 . C. 8. D. 5. Lời giải Chọn A
Ta xét hàm: y = f (x) = log x − x +1 x ∀ ∈ 1;2 có 2 [ ] f ′(x) 1 1 = −1 = 0 ⇔ x = . Ta lại có: x ln 2 ln 2 f ( ) = f ( ) 1  1  1 1 2 = 0; f   = log − +1 >     0 2  ln 2   ln 2  ln 2 Suy ra
y = f (x) = log x − x +1≥ 0 x
∀ ∈ 1;2 ⇒ log a ≥ a −1 a ∀ ∈ 1;2 2 [ ] 2 [ ] x = log a 2 3 3 3 3 3 3 
log a + log b + log c = x + y + z ≤1 Đặt: 2 2 2 y = log b ⇒ 2  
a ≤ x +1;b ≤ y +1;c ≤ z +1 z =  log c 2 Ta có: 3 3 3 =
+ + − 3(log a + log b + log c T a b c a b c 2 2 2 ) ≤ (x + )3 1 + ( y + )3 1 + (z + )3
1  − 3x(x + ) 1 + y ( y + ) 1 + z (z + ) 1      3 3 3
= x + y + z + 3 ≤1+ 3 = 4
Suy ra T =1 khi và chỉ khi ( ; a ;
b c) = (1;1;2) và các hoán vị max
Câu 11. Cho x, y, z lần lượt là các số nguyên dương thỏa mãn hệ thức sau đây 2 log (x + 2y) 2 + log (2y + 3z) 2 + log
x + 3z = 3. Khi đó biểu thức x y z T = + + có giá trị 2 2 2 ( ) 6 3 2 nhỏ nhất là: A. 1 . B. 8 . C. 1 . D. 1 . 8 16 32 Lời giải Chọn A
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC x y z ( + + )2 2 2 2 x y z
Áp dụng bất đẳng thức Svac-Xo (hay gọi là cộng mẫu): + + ≥ , ta có: a b c a + b + c 2 2 2 log x + 2y log 2y + 3z log x + 3z 2 3 = log (x + 2y) 2 + log (2y + 3z) 2 + log x + 3z = + + 2 2 2 ( ) 2 ( ) 2 ( ) 2 ( ) 1 1 1
log (x + 2y) + log (2y + 3z) + log (x + 3z) 2   2 2 2  ≥ ⇒ 3
− ≤ log  x + 2y 2y + 3z x + 3z  ≤ 3 2 ( )( )( ) 1 1 1  + + 1
⇒ ≤ (x + 2y)(2y + 3z)(x + 3z) ≤ 8 8 3 3
x + 2y + 2y + 3z + 3z + x
8 x + 2y + 3z
Mặt khác: (x + 2y)(2y + 3z)(x + 3z) ( ) ( ) ≤ = 27 27
(x + y + z)3 3 8 2 3 1
8 x + 2y + 3z Nên ta suy ra
≥ (x + y)( y + z)(x + z) ( ) 1 2 2 3 3 ≥ ⇔ ≥ 27 8 27 8 3
⇒ (x + y + z)3 27  3  3 2 3 ≥ = ⇒  
x + 2y + 3z ≥ 64  4  4 Suy ra
x y z x + 2y + 3z 1 T = + + = =
(x + y + z) 1 3 1 . 2 3 ≥ . = . Vậy 1 T = 6 3 2 6 6 6 4 8 min 8
Câu 12. Cho các số thực a,b,c lớn hơn 1 thỏa 8
log abc =1+ − 4ab . Khi ấy, giá trị nhỏ nhất của biểu 2 ( ) c thức 1 1 1
T = log 2 + log 2 + log 2 bằng 2 3 6 2a 2b 2 2 3 6 c A. 1 . B. 1 . C. 6 2 . D. 3 . 2 4 2 Lời giải Chọn A Đầu tiên, ta có: 8  8   8 log abc 1 4ab log 4ab 4ab log  = + − ⇔ + = + 2 ( ) 2 ( ) ( ) 2 c
c   c     
Xét hàm số y = f (t) 1
= log t + t, f ′ t = +1 > 0, t
∀ ∈ R ⇒ f t đồng biến trên R 2 ( ) ( ) t ln 2 ⇒ f ( ab)  8  8 4 = f
⇔ 4ab = ⇔ abc = 2 ⇒ log a + log b + log c =   1 2 2 2  c c
Đặt x = log a; y = log ;
b z = log c ⇒ x + y + z =1 2 2 2 Ta có: 1 1 1 1 1 1 1 1 1
T = log 2 + log 2 + log 2 = . + + . 2 3 6 2a 2b 2c 2 3 6 2 3 6 2 log 2a 3 log 2b 6 log 2c 2 2 2 1 1 1 1 1 1 = + + = + +
2 + 4log a 3+ 9log b 6 + 36log c 2 + 4x 3+ 9y 6 + 36z 2 2 2  1 2 + 4x   1 3+ 9y   1
6 + 36z   2 + 4x 3+ 9y 6 + 36z  = + + + + + − + +   2 4x 16     3 9y 36     6 36z 144     16 36 144  + + +  1 2 + 4x 1 3+ 9y 1
6 + 36z  2 + 4x 3+ 9y 6 + 36 2 . 2. . 2. . z  ≥ + + − + + 2 4x 16 3 9y 36 6 36z 144  16 36 144  + + +  
1 1 1  2 + 4x 3+ 9y 6 + 36z  + + = + + − + + 3 x y z 3 1 1 = − = − = 2 3 6    16 36 144  4 4 4 4 2 Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Vậy 1 T = khi và chỉ khi 1 1 1
x = ; y = ; z = ⇒ ( ; a ; b c) = ( 3 6 2; 2; 2) min 2 2 3 6
Câu 13. Cho các số thực x, y, z thỏa 4x 9y 16z 2x 3y 4z + + = +
+ . Khi ấy, giá trị lớn nhất của biểu thức x 1 + y 1 + z 1 T 2 3 4 + = + + bằng A. 9 + 87 . B. 1 . C. 7 + 87 . D. 3+ 87 . 2 4 2 2 Lời giải Chọn A
Đầu tiên, ta có: 4x 9y 16z 2x 3y 4z + + = + +  2x x 1 1   2x x 1 1   2x x 1 1  3 ⇔ 2 − 2.2 . + +  3 − 2.3 . + +   4 − 2.4 . + =  2 4 2 4 2 4        4 2 2 2  x 1   x 1   x 1  3 ⇔ 2 − +  3 − +   4 − =  2 2 2        4 Khi đó, ta suy ra x 1 + y 1 + z 1 +  x 1   x 1   x 1  9 T = 2 + 3 + 4 = 2 2 − +  33 − +  4 4 − +  2 2 2        2 + ≤ (   2 + 3 + 4 ) 2 2 2 2 2 2
x 1   x 1   x 1  9 3 .2 − +  3 − +   4 −   + = ( 2 2 2 2 + 3 + 4 ) 9 9 87 + =  2   2   2    2 4 2 2 
 =34 Vậy 9 87 T + = max 2
Câu 14. Cho các số thực x, y, z . Tính giá trị nhỏ nhất của biểu thức sau: x y 2z y z 2x z x 2 3 2011 3 2011 3 2011 y P + − + − + − = + + + + + A. 4 . B. 5. C. 6 . D. 7 . Lời giải Chọn A
Áp dụng bất đẳng thức Bunyakovsky, ta có: x+ y−2z y+z−2x z+x−2 P = 3+ 2011 + 3+ 2011 + 3+ 2011 y ( x+ y− z y+z− x z+x− y       = 3) 2 + 2011  + ( 3) 2 + 2011  + ( 3) 2 2 2 2 2 2 2 2 2 2 + 2011        ( x+ y− z y+z− x z+x− y   ≥ 3 + 3 + 3) 2 2 2 2 2 2 2 2 + 2011 + 2011 + 2011    2 x+ y−2z y+z−2x z+x−2 y  2 x+ y−2z y+z−2x z+x−  2 y  3 2 2 2 = 27 + 2011 + 2011 + 2011 2 2 2  ≥ 27 + 3 2011 .2011 .2011        2 
x+ y−2z y+z−2x z+x−2 y  3 + + 2 2 2 = 27 + 3 2011  = 6 .   Vậy P = 6 min  
Câu 15. Cho các số thực dương thỏa mãn 2 2 2
5log a +16log b + 27log c =1. 2 2 2
Khi đó giá trị lớn nhất của biểu thức S = log . a log b + log . b log c + log . c log a bằng 2 2 2 2 2 2 A. 1 . B. 1 . C. 1 . D. 1 . 12 6 9 8
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Lời giải Chọn A Cách 1: x = log a 2 2 2 2 2 2 2  5
 log a +16log b + 27log c = 5x +16y + 27z =1 Đặt: 2 2 2 y = log b ⇒ 2   S = log . a log b + log . b log c + log .
c log a = xy + yz +  zx 2 2 2 2 2 2 z =  log c 2 Mặt khác: 2 2 2
= x + y + z = ( 2 2 x + y ) + ( 2 2 x + z ) + ( 2 2 1 5 16 27 3 12 2 18 4y + 9z ) 2 2 2 2 2 2
≥ 2 3x .12y + 2 2x .18z + 24 y .9z =12(xy + yz + zx) ⇒12(xy + yz + zx) ≤1 Nên suy ra 1
S = xy + yz + zx ≤ . Vậy 1 S = . 12 max 12 Cách 2: 2 2 2 2 2 2 x = log a 2 5
 log a +16log b + 27log c = 5x + 4y + 3z =1 2 2 2
Đặt: y 2log b  = ⇒ 2
 = log .log +log .log +log .log xy yz zx S a b b c c a = + +   2 2 2 2 2 2 z = 3log c 2  2 6 3
Suy ra 6S = 3xy + yz + 2zx Ta có: 2 2 2
= x + y + z ⇔ − S = ( 2 2 2 1 5 4 3 1 12
5x + 4y + 3z ) − 2(3xy + yz + 2zx) = ( 2 2
x − xy + y ) + ( 2 2
y − yz + z ) + ( 2 2 3 6 3 2
2x − 4xz + 2z ) = 3(x − y)2 + ( y − z)2 + 2(z − x)2 ≥ 0 Suy ra 1
1−12S ≥ 0 ⇒ S ≤ Vậy 1 S = . 12 max 12
Câu 16. Cho các số thực a,b,c lớn hơn 1 thỏa mãn
log a ≥ 1− log blog c log
. Tìm giá trị nhỏ nhất của biểu thức sau: bc 2 2 ( 2 2 ) 2 2 2
S =10log a +10log b + log c 2 2 2 A. 4 . B. 5. C. 6 . D. 7 . Lời giải Chọn A
Biến đổi giả thiết ta được log a ≥ 1− log blog c log bc 2 2 ( 2 2 ) ⇔ log .
a log b + log c ≥1− log blog c ⇔ log a log b + log a log c + log blog c ≥1 2 ( 2 2 ) 2 2 2 2 2 2 2 2 x = log a 2
Đặt y = log b . Tiếp theo, ta cần tìm giá trị nhỏ nhất của 2 2 2
S =10x +10y + z 2 z =  log c 2
Bây giờ ta cần tìm số k dương sao cho 2 2 2
10x +10y + z ≥ 2k (xy + yz + xz) 2 2 2
⇔ x + y + z + k ( 2 2 2
x + y + z ) ≥ k ( 2 2 2 10 10
x + y + z ) + 2k (xy + yz + xz) 2 2 2
⇔ ( + ) 2 + ( + ) 2 + ( + ) 2 10 10 1 ≥ ( + + )2 x y z k x k y k z k x y z ⇔ + +
≥ k (x + y + z)2 1 1 1
k +10 k +10 k +1
Sử dụng bất đẳng thức Cauchy – Schwarz dạng cộng mẫu ta có x y z
(x + y + z)2 2 2 2 + + ≥ 1 1 1 1 1 1 + +
k +10 k +10 k +1 k +10 k +10 k +1
Đến đây sử dụng được giả thiết ta sẽ chọn k sao cho 1 = k ⇔ k = 2 1 1 1 + +
k +10 k +10 k +1 Như vậy suy ra 2 2 2
10x +10y + z ≥ 2.2(xy + yz + xz) = 4(xy + yz + xz) Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Mà mặt khác log a log b + log a log c + log blog c = xy + yz + zx ≥1 2 2 2 2 2 2 Nên suy ra 2 2 2
10x +10y + z ≥ 4(xy + yz + xz) = 4.1 = 4. Vậy S = 4 min
Câu 17. Cho 3 số thực dương a,b,c thỏa mãn
log a logb + logblog c + 3log c log a =1. Biết giá trị nhỏ nhất của biểu thức − + 2 2 2
P = log a + log b + log c là m
n với ,m ,n p lần lượt là các số nguyên dương và m là p p
phân số tối giản. Tính m + n + p ? A. 64 . B. 16. C. 102. D. 22 . Lời giải Chọn D
Lưu ý: Với bài toán này nếu đặt (log a;log ;
b log c) → (x, y, z) ⇒ xy + yz + 3xz =1 thì ta sẽ
không thể áp dụng phương pháp làm của bài trên, khi đó ta sẽ cần phải nghĩ ra cách đặt khác. Cách 1: Đặt (log a;log ;
b log c) → (ix, jy,kz) ⇒ ijxy + jkyz + 3kixz =1
Tìm i, j,k sao cho thỏa mãn = = 3 j ij kj
ki ⇒ i = k = . (Cân bằng hệ số) 3
Chọn j = 3 ⇒ i = k =1 Khi đó ta được ( a b c) → (x y z) 1 log ;log ;log
,3 , ⇒ 3xy + 3yz + 3xz =1⇒ xy + yz + xz = 3
Khi đó ta có được đánh giá như sau: 2 2 2 2 2 2
log a + log b + log c = x + 9y + z ≥ 2k (xy + yz + xz) 2 2 2
⇔ x + 9y + z + k ( 2 2 2
x + y + z ) ≥ 2k (xy + yz + xz) + k ( 2 2 2
x + y + z ) ⇔ (k + ) 2 1 x + (k + 9) 2 y + (k + ) 2
1 z ≥ k (x + y + z)2 x y z x + y + z
Mặt khác ta có: (k + ) x + (k + ) y + (k + ) ( )2 2 2 2 2 2 2 1 9 1 z = + + ≥ 1 1 1 1 1 1 + +
k +1 k + 9 k +1 k +1 k + 9 k +1
Đến đây sử dụng được giả thiết ta sẽ chọn k sao cho 1 9 − + 3 17 = ⇔ = 1 1 1 k k 4 + +
k +1 k + 9 k +1  − +  Mặt khác ta có: 1 xy − +
+ yz + xz = nên suy ra 2 2 2 1 9 3 17 3 17
P = x + 9y + z ≥ 2. .  = 3 3  4  2   Vậy 3 17 P − + = min 2 Cách 2:
Chú ý rằng ở giả thiết và yêu cầu của bài toán vai trò của 2 biến a,c là như nhau nên dấu
" = " sẽ xảy ra tại a = c , đây chính là điểm rơi mấu chốt của bài toán trên. Khi đó ta có: 2 2
P = 2x + y  ⇒ P( 2 3x + 2xy) 2 2
= 2x + y ⇔ (3P − 2) 2 2
x + 2Pyx − y = 0 2 3
 x + 2xy =1 2 (     ⇔ 3 − 2) x + 2 x P P −1 =    
0 . Sử dụng điều kiện có nghiệm của phương trình bậc 2 theo  y   y   3 − + 17   P ≥ ẩn x 2 3 17  , ta có: 2
∆′ = P + 3P − 2 ≥ 0 ⇔  Vậy S − + = y     3 − − 17 min 2 P ≤  2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Câu 18. Cho các số thực dương x, y, z khi biểu thức  xy yz zx  2 P = ( 2 2 2
log 10x + 7y +15z ) − 2log + +
+ 2(x + y + z) − 
 2log ( xyz) đạt giá trị nhỏ  z x y
nhất thì giá trị xyz gần với giá trị nào nhất trong các giá trị sau A. 4 . B. 7 . C. 5. D. 6 . Lời giải Chọn D Cách 1:  Viết lại 2 P = ( 2 2 2
x + y + z ) − ( 2 2 2 2 2 2 log 10 7 15
2log x y + y z + z x + 2xyz (x + y + z)) 2 = ( 2 2 2
x + y + z ) −
(xy + yz + zx)2 2 = ( 2 2 2 log 10 7 15 2log
log 10x + 7y +15z ) − 4log(xy + yz + zx)  Ta cần chỉ ra 2 2 2
10x + 7y +15z ≥ m(xy + yz + zx) để đưa P về một biến ta biến đổi như sau: 2 2 2
20x +14y + 30z ≥ 2m(xy + yz + zx) ⇔ ( + m) 2 x + ( + m) 2 y + ( + m) 2 z ≥ m( 2 2 2 20 14 30
x + y + z + 2xy + 2yz + 2zx) x y z
(x + y + z)2 2 2 2 ⇔ + + ≥ . 1 1 1 1
20 + m 14 + m 30 + m m
Mặt khác theo bất đẳng thức Svac-Xo (hay còn gọi là cộng mẫu) thì: x y z
(x + y + z)2 2 2 2 + + ≥ 1 1 1 1 1 1 + +
20 + m 14 + m 30 + m 20 + m 14 + m 30 + m
Đến đây ta chỉ việc chọn m thỏa mãn 1 1 1 1 + + = ⇔ m =10 .
20 + m 14 + m 30 + m m Vậy ta được 2 2 2
10x + 7y +15z ≥ 10(xy + yz + zx) dấu bằng xảy ra khi và chỉ khi
x = y = z ⇔15x =12y = 20 1 1 1 z 30 24 40 Cách 2:
Ngoài ra ta cũng có thể dùng phương pháp cân bằng hệ số trong bất đẳng thức CAUCHY để chứng minh 25 2 2 x 4y 10xy  + ≥ 4   15 2 20 2 x z 10xz + ≥ cộng các vế ta được 2 2 2
10x + 7y +15z ≥ 10(xy + yz + zx) . 4 3   2 25 2 3y z 10yz  + ≥ 3  Từ đó ta có P ≥
( (xy + yz + zx)) −
(xy + yz + zx) = ( (xy + yz + zx) − )2 2 log 10 4log log 1 ≥ 0  5 3 y = ; x z = x Dấu bằng xảy ra 15 3 600 10  4 4 ⇔ xyz = x = ≈ 6 . 16 47 47
xy + yz + zx =10
Câu 19. Cho biểu thức sau: Trang 10
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC 2 + − 2 z y P = xy + y +
x y + x z + x y z + a ( ) 4 6 4 2 2 4 2 12 5 4 log log log 2 . 2 a ( ) ( ) a 3
Với a >1, y ≥1 thì P đạt giá trị nhỏ nhất bằng b khi a = a và ( ;
x y; z) = (x ; y ; z hoặc 1 1 1 ) 0 ( ;
x y; z) = (x ; y ; z . Hãy tính 2 2
S = 21a − 22b + 8 x y z + x y z . 0 ( 1 1 1 2 2 2 ) 2 2 2 ) A. 42 − . B. 37 − . C. 42 . D. 44 . Lời giải Chọn D xy > 0  2 Có  yz ≥ ; 6 4 2 2 4 2 6 4 2 2 4 2 4 2 4 16 8 4 4 2
x y + x z + 2x y z = x y + x z + x y z + x y z ≥ 4 x y z = 4x y z 4  y ≥1  z − y Khi đó: P ≥ xy + y + x y z + + a ( ) a ( ) ( ) 2 2 2 4 2 5 4 log log log 4 4 a 3 2 − 2 z y P ≥ xy + xy + + z + a ( ) ( ) 5 4 log 4log 4 log a a 4 3 ≥ ( 2 ( ) z − y P xy + + z + ≥ a )2 5 4 log 2 loga 4 0 3  1 a = axy = = −  a ( ) 2 2 log 2 xy     1  1  1  1 x = xz = − =  =   Suy ra P = 0 khi z 2 2  ⇔  ⇔ . min 4 4    2 
y = 1 ∨ y = 1 y = 4z y = 1 − ±    1  1 6 4 2 2 x y = x z  1 z = z x = = ±   4  4  2 2 2  1 1 S 21a 22b 8 x y z x y z 21.2 22.0 8  = − + + = − + + =   44 . 0 ( 1 1 1 2 2 2 )  8 8 
Câu 20. Cho a,b,c là ba số thực dương đôi một phân biệt. Có bao nhiêu bộ ( ; a ; b c) thỏa mãn b+2 a+2 c+2 b+2 a+2 c+2
a ≤ b ;b ≤ c ;c ≤ a . A. 1.
B. 3 . C. 6 . D. 0 . Lời giải Chọn D b a . c b . a
c ≤ ab + bc + ca Ta có a
∀ ,b,c thỏa mãn a + b + c =1 thì  c a . a b . b
c ≤ ab + bc + ca b+2 c+2 a+2
a .b .c ≤ (abc)2 (ab +bc +  ca) ( ) 1 ⇔  c+2 a+2 b+2
a .b .c ≤ 
(abc)2 (ab +bc + ca) (2)
Cộng vế với vế của (1) và (2) ta được b+2 c+2 a+2 c+2 a+2 b+2
a .b .c + a .b .c
≤ 2(abc)2 (ab + bc + ca) (*) Mà a+2 b+2 b+2 c+2 c+2 a+2 b ≥ a ;c
≥ b ;a ≥ c nên từ (*) suy ra
(abc)2 (ab +bc + ca) ≥ ( b+2 c+2 a+2 2
a .b .c )2 ⇒ abc (ab + bc + ac) b+2 c+2 a+2 2
≥ a .b .c
(ab bc ac) b 1+ c 1+ a 1 2 a .b .c + ⇔ + + ≥ ≥ (b + ) 1 a + (c + ) 1 b + (a + ) 1 c
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
⇔ 2(ab + bc + ac) ≥ (ab + bc + ca) + a + b + c ⇔ 2(ab + bc + ac) ≥ (ab + bc + ca) +1 2
⇔ ( ab +bc + ac)2 − 2(ab +bc + ca) +1≤ 0  1  1 ⇔
ab + bc + ac − + ≤   0 (vô lý)  2  2
Vậy suy ra không có bộ ( ; a ; b c) nào thỏa mãn
Câu 21. Hỏi có tất cả bao nhiêu bộ số thực ( ; a ;
b c) với a,b,c∈[0; ]
1 , thỏa mãn a + b + c = 2 và đồng thời làm cho biểu thức 2 2 4a−4a b−b c 2 2 T = 3 +16
+ 3 + 8a + 4b − 6a − 2b đạt giá trị lớn nhất ? A. 4 .
B. 18. C. 6 . D. 6 . Lời giải Chọn A
Để làm được câu hỏi trên, ta cần áp dụng bất đẳng thức: x a ≤1+ (a − ) 1 x với x ∀ ∈[0; ] 1 và dấu x = 0 bằng xảy ra tại  . Khi đó ta suy ra: x = 1  a = 0 2 4a − 4a = 0  - 2 4a−4a ≤ + ( 2 3
1 2 4a − 4a ) ⇒Dấu bằng xảy ra tại  ⇔ a =1 2 4a − 4a =1  1 a =  2 b = 0 2 4b 4b 0   − = - 2 2 b  ⇔  = −b 4b−4b ≤ ≤ + ( 2 16 2
1 4b − 4b ) ⇒ Dấu bằng xảy ra tại b 1 2 4b − 4b =1  1 b =  2 c = 0
- 3c ≤1+ 2c ⇒ Dấu bằng xảy ra tại  c =1 Suy ra 2 2 4a−4a b−b c 2 2 T = 3 +16
+ 3 + 8a + 4b − 6a − 2b ≤  +  ( 2
a − a ) +  +   ( 2
b − b ) + ( + c) 2 2 1 2 4 4 1 4 4
1 2 + 8a + 4b − 6a − 2b
= 2(a + b + c) + 3 = 2.2 + 3 = 7  
a = 0 b = 0   c = 0
Như vậy dấu bằng xảy ra khi và chỉ khi: a =1 ;b =1 ; , c = 1  1  1 a = b =  2  2   
cùng với a + b + c = 2 ta thu được các bộ số (a b c) = (  ) ( ) ( ) 1 1 ; ;
1;1;0 ; 0;1;1 ; 1;0;1 ; ; ;1 tức có   2 2  
tất cả 4 bộ số thực ( ; a ; b c) thỏa mãn
Câu 22. Xét các số a,b,c >1 thỏa mãn log b + c +
a = . Khi đó giá trị lớn nhất của biểu a 2logb 3logc 8 thức 2log c + b +
a nằm trong khoảng nào ? a 3logc 12logb A. (15;20) .
B. (25;30) . C.(20;25) . D. (30;35) Lời giải Chọn D Trang 12
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDCx = log b a  log b + c +
a = x + y + z = a 2logb 3logc 2 3 8
Đầu tiên, ta đặt: y = log c ⇒ b log b c a = xyz =  
a .logb .logc 1 z =  log a c log c = b c = xy a loga .logb
Ta lại có: log b = a
b = xz ⇒ Tìm giá trị lớn nhất của P = 2xy + 3zx +12yz c logc .loga log a = c a =  yz b logb .logc + + + Suy ra P P
2xy 3zx 12yz 12 3 2 12 2y 3z P = = = = + + = + 1 xyz xyz x y z x yz
x + 2y + 3z = 8 → 2y + 3z = 8 − x Do  12 8 − x 12  1 ⇒ P = + =
+ x(8 − x) (*)
xyz = 1 → yz = x 1 xx x
Ta lại có: = x + ( y + z) 6 6 8 2 3 ≥ x + 2 2 .3 y z = x + 2 ⇒ x + 2
− 8 ≤ 0 ⇔ 5 − 21 ≤ x ≤ 6  x x Cauchy
Suy ra ta khảo sát hàm số (*) y = f (x) 12 = + x(8 − x) x ∀ ∈ 5 − 21;6 x  
Đạo hàm + Lập bảng biến thiên, ta dễ dàng suy ra
P = max f x = f 5 − 21 = 9 + 5 21∈ 30;35 max ( ) ( ) ( ) 5− 21;6    x = 5 − 21 x = 5− 21    + Vậy P 3 21 = +
khi và chỉ khi 2y = 3z ⇔ y = max 9 5 21 4
x 2y 3z 8  + + =   3+ 21 z =  6
Câu 23. Cho các số thực x, y, z ∈[0; ]
1 . Biết rằng giá trị nhỏ nhất của biểu thức
(2x 2y 2z)(2 x 2 y 2 z P − − − = + + + + ) m
được viết dưới dạng với m,n là các số nguyên không âm n m
và là phân số tối giản. Hỏi m + n có giá trị bằng bao nhiêu? n A. 86 .
B. 87 . C.88 . D. 89 Lời giải Chọn D
Đặt (2x;2y;2z ) → (a,b,c)(1≤ a,b,c ≤ 2) .
Ta có ≤ a ≤ ⇒ (a − )(a − ) 2 1 2 1
2 ≤ 0 ⇔ a + ≤ 3. Chứng minh tương tự 2 2
b + ≤ 3,c + ≤ 3 a b c
Cộng 3 bất đẳng thức trên vế theo vế ta được
(a b c)  1 1 1  (a b c) 1 1 1  81  1 1 1 9 2 2 2   (a b c)  ≥ + + + + + ≥ + + + + ⇒ ≥ + + + +  a b c a b c 8  a b c       
Vậy giá trị lớn nhất của P là 81 P = tức + = + = max m n 81 8 89 8
Từ đó, ta có tổng quát cho dạng này như sau:
Cho n số x ; x ;...; x ∈ a b c > . Khi đó ta luôn có n [ ; ], 1 1 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC 2 a b ( n c + c x x c + c +....   n x + c )( −x − x
c + c +.... − nx + c ) ( ) 1 2 1 2 ≤ 4 a+b c
Câu 24. Cho a,b,c,d là các số thực dương có tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức sau: P = ( 2 2 2 2
+ a + b + a b )( 2 2 2 2 1
1+ c + d + c d ) 4 A. 2 . B. 17 4ln
. C.17  . D. 17 ln 16 16    16 Lời giải Chọn C
Từ giả thiết ta có: P = ( 2 2 2 2
+ a + b + a b )( 2 2 2 2
+ c + d + c d ) = ∏( 2
a + ) ⇒ P = ∑ ( 2 1 1 1 ln ln a + ) 1 Ta có đánh giá sau ( 2 ln t + )
1 ≥ mt + n , để tìm được hai số m,n ta sẽ sử dụng tới bất đẳng thức
tiếp tuyến, đây là một phương pháp rất hay để chứng minh các bất đẳng thức đối xứng với các biến độc lập nhau.
Cơ sở của phương pháp
• Nếu đường thẳng y = ax + b là tiếp tuyến của đồ thị hàm số y = f (x) tại điểm
A(x ; y , A không phải điểm uốn thì khi đó tồn tại một khoảng D chứa x sao cho 0 0 ) 0
f (x) ≥ ax + b hoặc f (x) ≤ ax + b . Đẳng thức xảy ra khi x = x 0
• Nếu đường thẳng y = ax + b là tiếp tuyến của đồ thị hàm số y = f (x) tại điểm
A(x ; y thì ta luôn phân tích được ( ) − ( + ) = ( k f x ax b x − x g x ,k ≥ 2 0 ) ( ) 0 0 )
Sau đây ta áp dụng lý thuyết trên vào bài toán trên. Chú ý ta có ∑ ( 2 ln a + ) 1 là một biểu thức
đối xứng theo bốn biến a,b,c,d đồng thời giả thiết cũng là đối xứng nên ta sẽ dự đoán dấu " = " xảy ra khi 1
a = b = c = d = . 4
Quay lại bất đẳng thức phụ mà ta đang đi tìm hệ số ( 2 ln t + )
1 ≥ mt + n , ta sẽ tìm , m n sao cho
hai đồ thị hàm số y = ( 2 ln t + )
1 , y = mt + n tiếp xúc nhau tại điểm có hoành độ 1 t = ta được 4  8 m =  17  . 2 17 n = − + ln  17 16
Vậy ta có bất đẳng thức phụ là ( 2t + ) 8 2 17 ln 1 ≥ t − + ln
, dễ thấy bất đẳng thức này luôn 17 17 16
đúng, khi đó áp dụng vào bài toán ta có: P ∑ (a ) 4 2 8  2 17  8 8 17 17 17 ln ln 1 ∑a 4 ln  4ln 4ln P  = + ≥ + − + = − + = ⇒ ≥ 17  17 16 17 17 16 16 16      1 =
Câu 25. Cho các số thực a,b,c∈[2; ]
3 . Biết giá trị lớn nhất của biểu thức a b c 1
S = 4 + 4 + 4 − (a + b + c)3 m m
là với m,n là các số nguyên dương và là phân số tối giản. 4 n n
Tính P = m + 2n A. P = 257 .
B. P = 258 . C. P =17 . D. P =18 Lời giải Chọn D Trang 14
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Với dạng toán này ta sẽ xét tới bất đẳng thức phụ 4t ≤ mt + , n t ∀ ∈[2; ] 3 16  = 2m + nm = 48
Thay t = 2,t = 3 ta được hệ phương trình  ⇒ 64 3m n  = + n = 80 −
Giờ ta cần chỉ ra bất đẳng thức 4t ≤ 48t −80 đúng với mọi t ∈[2; ]
3 là bài toán sẽ được giải quyết. Ta xét ( ) t = − + ⇒ ( ) t f t t f t = − f (t) 48 4 48 80 ' 4 ln 4 48; ' = 0 ⇔ t = log . 4 ln 4 48
Nhận thấy rằng f (2) f (3) 0; f log  = = < 
 0 nên bất đẳng thức luôn đúng. 4  ln 4 
Dấu " = " xảy ra khi và chỉ khi t ∈{2; } 3 . Khi đó ta được a + b + c a b c 1
= 4 + 4 + 4 − ( + + ) ≤ 48( + + ) ( )3 3 3 − − 240 t S a b c a b c
= − + 48t − 240 ≤16 4 4 4 Như vậy S
= 16 khi t = 2 với t = a + b + c ⇒ m + 2n =16 + 2.1 =18 max
Câu 26. Cho bốn số thực dương a,b,c,d lớn hơn 1 thay đổi thoả mãn
a + b + c + d = 2021. Gọi x , x là hai nghiệm của phương trình 1 2 ( x x − + b + c + d x − a
= . Tìm giá trị biểu thức a ) ( b ) ( a a a ) 2020 log . log 1 2log 3log 5log .logb logb 0
S = a + 2b + 3c + 5d khi x .x đạt giá trị lớn nhất. 1 2 A. 8084 S = . B. 22231 S = . C. 78819 S = . D. 78819 S = . 11 4 4 11 Lời giải Chọn D Ta có ( x x − + b + c + d x − a = a ) ( b ) ( a a a ) 2020 log . log 1 2log 3log 5log .logb logb 0 ⇔ b x − + b + c + d x − a = a ( b )2 ( a a a ) 2020 log . log 1 2log 3log 5log .logb logb 0 (1).
Đặt log x = t , phương trình (1) có dạng: b ⇔ ( b t − + b + c + d t − a = a ) 2 ( a a a ) ( 2020 log 1 2log 3log 5log logb ) 0 (2).
Từ phương trình (2) ta có ∆ = ( + b + c + d + b a a a a )2 2020 1 2log 3log 5log 4.loga .logb = ( + b + c + d + > a a a )2 1 2log 3log 5log 4.2020 0 .
Suy ra phương trình (2) luôn có hai nghiệm phân biệt . Từ đó ta có hệ thức Vi-ét như sau: t  = log x Đặt 1 b 1 1+ 2log b + c + d a 3loga 5log 
⇒ t + t = log x x = b . a 1 2 ( 1 2) t =  log x b b log 2 2 a ⇔ log x x = a + b + c + d = a + + c + d b ( . logb . 1 2loga 3loga 5loga logb 2 3logb 5log 1 2 ) ( ) b log  b b c c c d d d d d x x ab c d x x ab c da  ⇔ = ⇔ = = b ( . ) logb ( 2 3 5 ) 2 3 5 2 3 5 . 2 .3 .5 . . . . . . . . . . 1 2 1 2 2 2 3 3 3 5 5 5 5 5    11
b b c c c d d d d d   a b c d Ta có 2 3 5 x .x 2 .3 .5  .a + + + . . . . . . . . .  337500  = ≤ (BĐT Cosi) 1 2 2 2 3 3 3 5 5 5 5 5  11      11  2021 11 x .x 337500.  ⇔ ≤
. Vậy biểu thức x x đạt giá trị lớn nhất bằng  2021 337500.  khi 1 2  11      1 2  11  và chỉ khi
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC  2021 a =  11   b c d  2021 b = 2. a = = =  11 78819  2 3 5 ⇔ 
⇒ a + 2b + 3c + 5d = .  2021 11
a + b + c + d = 2021 c = 3.  11  2021 d = 5.  11
Câu 27. Lần lượt cho hai số thực dương a,b,c thỏa mãn phương trình sau  a + b + c đây: log
 = a a−2 +b b−2 +c c−  
2 . Gọi giá trị lớn nhất và giá trị nhỏ 2 2 2 2 ( ) ( ) ( )
a + b + c +1 a + b + c nhất của biểu thức 2 P =
lần lượt là M và m . Giá trị của biểu thức (m + 3M ) bằng
a + b + c +1 + − A. 16 + 2 6 . B. 8 6 . C. 26 . D. 16 2 6 . 5 5 5 5 Lời giải Chọn A a + b + c Điều kiện:
> 0 ⇒ a + b + c > 0 2 2 2
a + b + c +1  a + b + c Ta có: log
 = a a−2 +b b−2 +c c−   2 2 2 2 2 ( ) ( ) ( )
a + b + c +1  + + 1 log a b c  ⇔ +
= a a − 2 + b b − 2 + c c − 2 +   1 2 2 2 2 ( ) ( ) ( )
a + b + c +1
 2a + 2b + 2c  2 2 2 ⇔ log
= a − 2a + b − 2b + c − 2c +   1 2 2 2 2
a + b + c +1
⇔ log (2a + 2b + 2c) + (2a + 2b + 2c) = log ( 2 2 2
a + b + c + ) 1 + ( 2 2 2
a + b + c +1 2 2 )
Xét hàm đặc trưng y = f (t) 1
= log t + t ⇒ f ′ t = +1 > 0 t ∀ > 0 . 2 ( ) tln2
Suy ra hàm số f (t) đồng biến trên ( +∞) 2 2 2 0;
⇒ 2a + 2b + 2c = a + b + c +1 > 0
⇒ (a − )2 + (b − )2 + (c − )2 1 1 1 = 2 a + b + c Ta có: 2 P =
⇒ P(a + b + c + )
1 = a + 2b + c
a + b + c +1 ⇔ (P − ) 1 (a − )
1 + (P − 2)(b − ) 1 + (P − ) 1 (c − ) 1 = 4 − 4P Suy ra ( − P)2 4 4 ≤ ((P − ) 1 (a − )
1 + (P − 2)(b − ) 1 + (P − ) 1 (c − ) 1 )2
⇒ (4 − 4P)2 ≤ ( P − )2
1 + (P − 2)2 + (P − )2 1 )( a − )2 1 + (b − )2 1 + (c − )2 1 )
  =2
⇔ ( − P)2 ≤ ( P − )2 +(P − )2 +(P − )2 ) 2 4 − 6 4 + 6 4 4 2 1 2 1
⇔ 5P −8P + 2 ≤ 0 ⇔ ≤ P ≤ 5 5  4 + 6 P = M = max  5 4 − 6 4 + 6 16 + 2 6 ⇒  ⇒ m + 3M = + 3. =  4 − 6 5 5 5 P = m = min  5 Trang 16
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Câu 28. Cho x, y, z là các số thực dương với x, y, z ∈[1;2]. Tìm giá trị lớn nhất của biểu thức 2 2 2 P = log . x log + log . y log + log z.log 2 2 2 2 2 2 y z x A. 1. B. 2 . C. 3. D. 4 . 3 3 Lời giải Chọn A Ta có: 2 2 2 P = log . x log + log . y log + log z.log 2 2 2 2 2 2 y z x
= log x 1− log y + log y 1− log z + log z 1− log x 2 ( 2 ) 2 ( 2 ) 2 ( 2 ) a = log x 2 Đặt: b
 = log y ⇒ P = a(1− b) + b(1− c) + c(1− a) 2 c =  log z 2 A a P M b c B C N
Xét tam giác đều ABC cạnh bằng 1,trên các cạnh AB, BC,CA lần lượt lấy các điểm M , N, Pa = MA ,với b
 = PC ,khi đó ta có bất đẳng thức : S + + ≤ ∆ S∆ S∆ S AMP NCP MBN ABC ∆ c =  BN 1 0 1 0 1 0 3
⇔ a(1− b).sin 60 + b(1− c)sin 60 + c(1− a)sin 60 ≤ 2 2 2 4
⇔ a(1− b) + b(1− c) + c(1− a) ≤1 a = 1
Vậy P =1. Dấu “=” xảy ra khi b   = 0
và các hoán vị của nó. max 0 ≤ c ≤  1
Câu 29. Cho ba số thực x, y, z thỏa: 2log z + log y = log x.log y.log z. Giá trị nhỏ nhất của biểu 2 2 2 2 2 x y z thức P = 3log + 4 log + 5log
có dạng m n . Tính giá trị của biểu thức 2 2 2 yz xz xy 2018m + 2019n A. 14129. B. 16147. C. 10092. D. 16149. Lời giải
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Chọn A x y z 3 4 5 P = 3log + 4log + 5log = + +  2 2 2 yz xz xy
log yz log xz log xy 2 2 2  = log  x y z a x 2    3 4 5 Đặt: b  = log y ⇒ = + + 2
log y + log z − log x log x + log z − log y log x + log y − log z   2 2 2 2 2 2 2 2 2 c =  log z 2  3 4 5 = + +
b + c − a a + c − b a + b −  c 
2 log z + log y = log x.log y.log z ⇔ 2c + b = abc ⇔ 4c + 2b = 2abc 2 2 2 2 2 1 1 4 Áp dụng BĐT + ≥
Dấu “=” xảy ra khi m = n . m n m + n 3 4 5 Ta có: P = + +
b + c − a a + c − b a + b − c 1 1  1 1   1 1  P = + + 2 + + 3 +    
b + c − a a + c − b
b + c − a a + b − c
a + c − b a + b − c  4 4 4
2 4 6 2b + 4c 6 2abc 6 6 6 ≥ + 2. + 3. = + + = + = + = 2a + ≥ 2 2 . a = 4 3 2c 2b 2a c b a bc a bc a a a
a = b = c
Dấu “=” xảy ra khi: 
6 ⇔ a = b = c = 3 2a =  a
Suy ra: m = 4;n = 3 ⇒ 2018m + 2019n = 14129
Câu 30. Cho hai các số thực a, b, c, d, e dương thỏa mãn
a + b + c + d + e =1000 và
a − b + c − d + e > 0
a +b−c + d −e > 0
−a+b+c−d +e>0
a −b + c + d −e > 0  −
a + b − c + d + e > 0
Tìm giá trị lớn nhất của biểu thức ( )b d M a c + = + A. 499 499 . B. 500 500 . C. 499 500 . D. 500 499 . Lời giải Chọn A
a − b + c − d + e = h
a +b−c + d −e = k
Đặt −a + b + c − d + e = l ta thấy rằng h + k + n + m + l = a + b + c + d + e =1000 và đồng thời
a −b + c + d −e = m  −
a + b − c + d + e = n
2a = h + k,2b = k + l,2c = l + ,2
m d = m + n,2e = n + h . Từ đó suy ra h,k,l, ,
m n đều là các số chẵn.
Bên cạnh đó ta suy ra được 1
a + c = (h + k + l + m) 1 = ( − n) 1 1000
,b + d = (1000 − h). 2 2 2 Trang 18
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Để ( )b d M a c + = +
đạt giá trị lớn nhất thì n và h có giá trị nhỏ nhất, mà ,
n h chia hết cho 2 nên 499
h = n = 2 ⇒ max M = 499 .
k = 9974 − 2t l   = 2, 4,..., 2t
Đẳng thức xảy ra khi  (t =1,496).
l + m = 2 + 2t
k +l + m = 996
_______________ TOANMATH.com _______________
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 19
Document Outline

  • Dạng-1-Bài-toán-max-min-biểu-thức-2-ẩn-PB3
  • Dạng-2-Max-min-mũ-loga-hàm-nhiều-biến-(3-biến-trở-lên)-PB3