














Preview text:
CHỦ ĐỀ 6: BÀI TOÁN KHOẢNG CÁCH
Vấn đề 1: KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG
Dạng 1: Khoảng cách từ một điểm trên mặt phẳng đáy tới mặt phẳng chứa đường cao
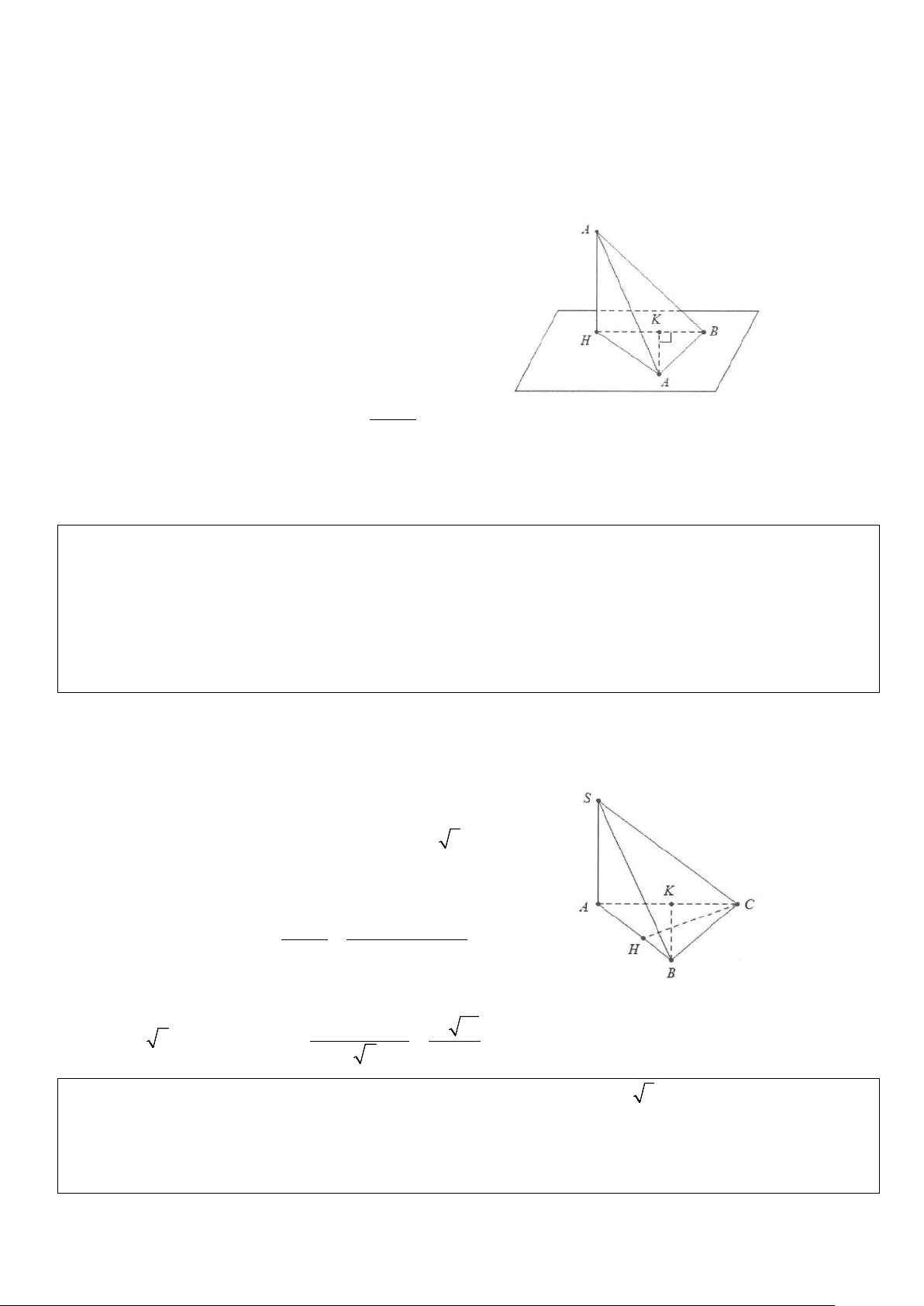
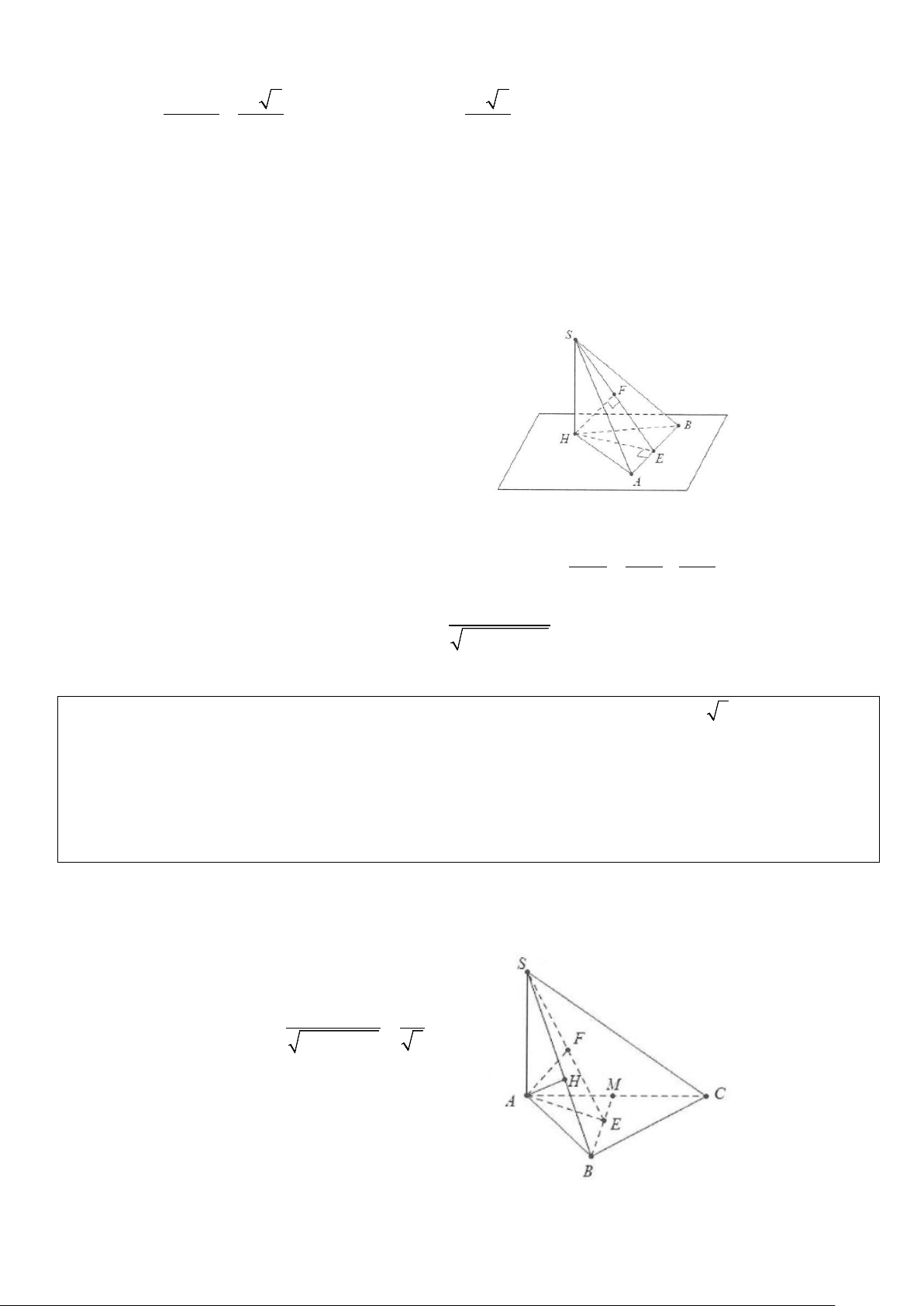
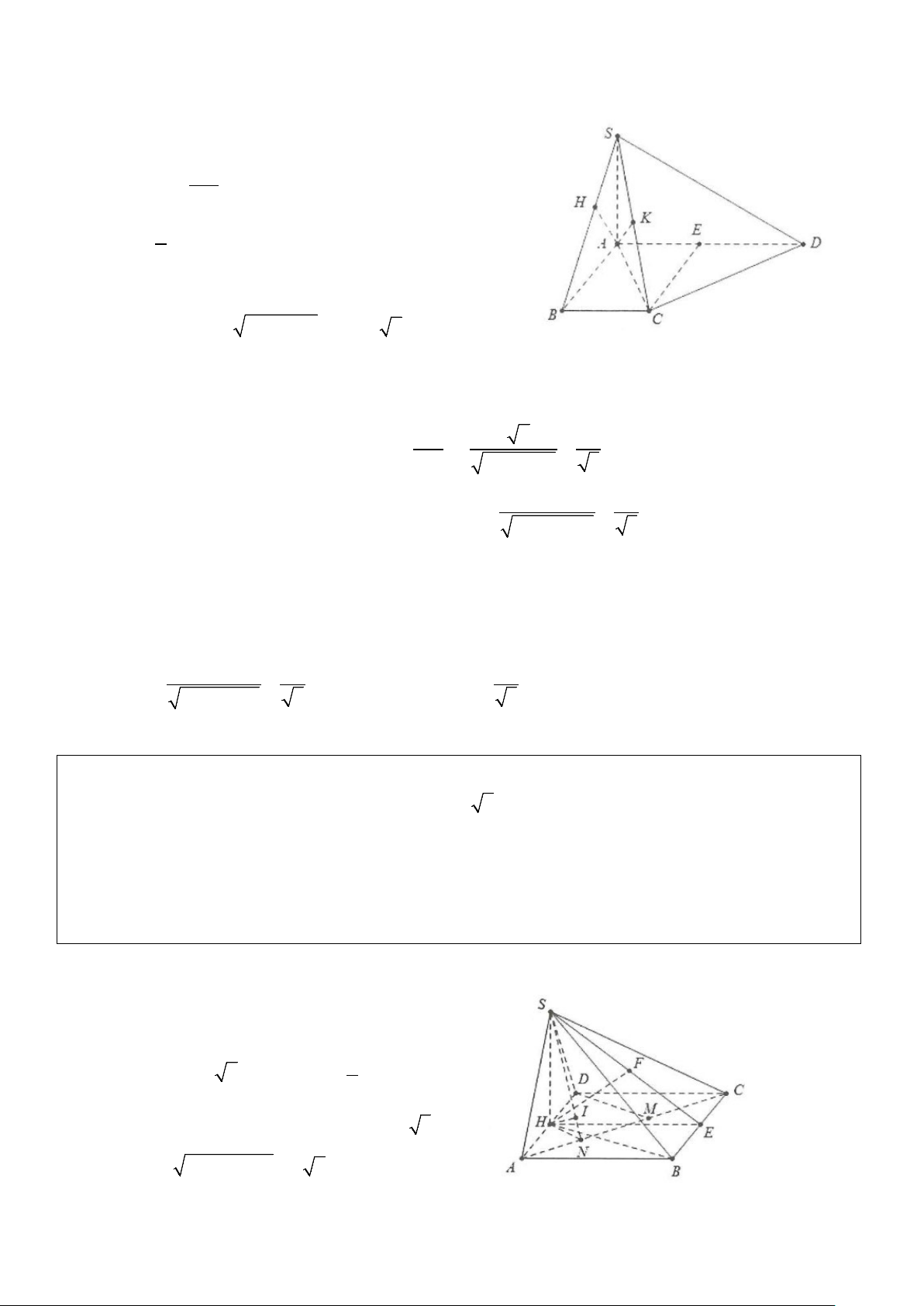
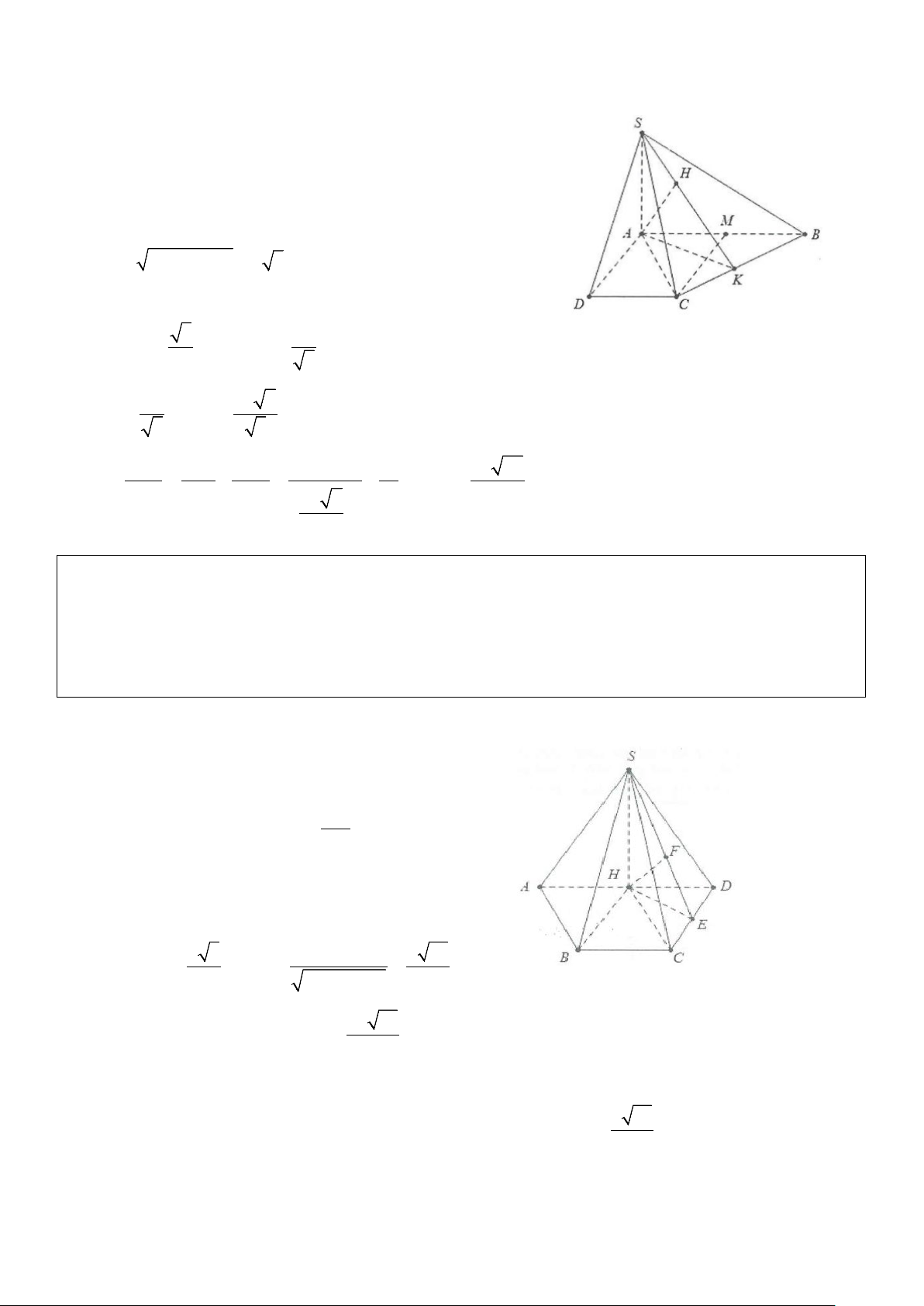
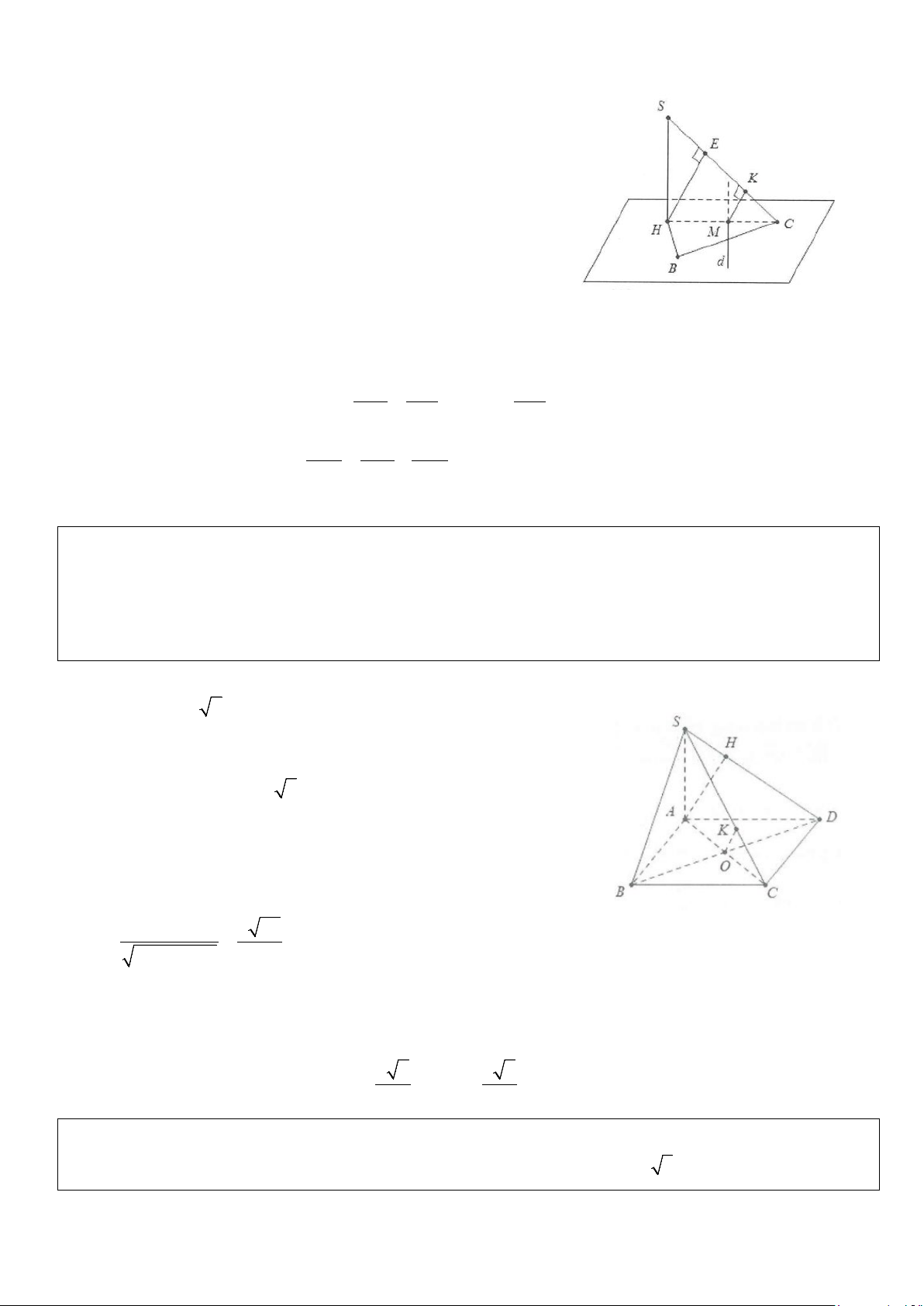
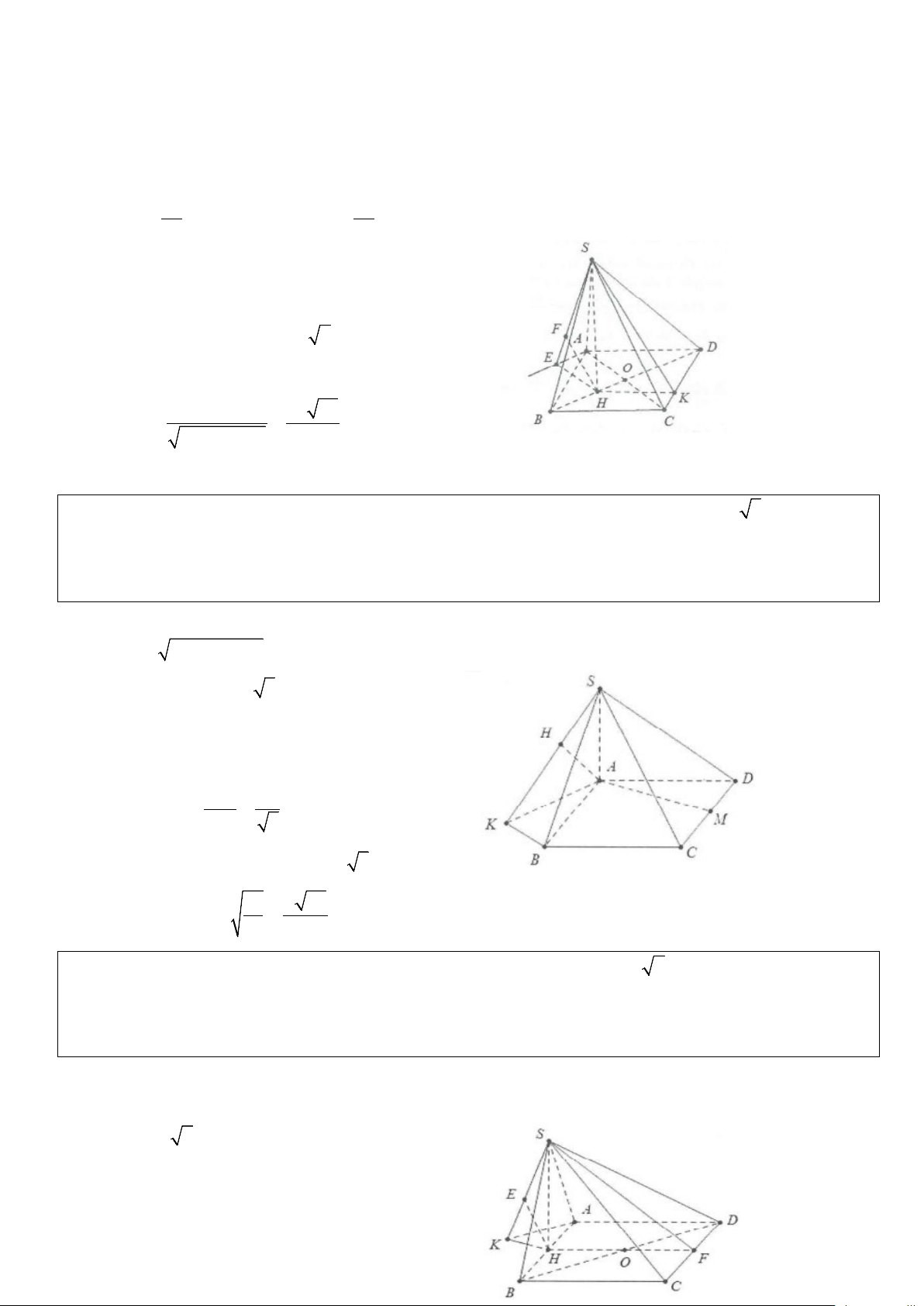
Xét bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ
điểm A bất kì đến mặt bên (SHB).
Kẻ AH ⊥ HB ta có: AK ⊥ HB ⇒ AK ⊥ (SHB) AK ⊥ SH Suy ra d ( ;
A (SHB)) = AK .
Cách tính: Ta có: d ( A (SHB)) 2 ; SAHB = AK = HB = =
ABsin ABK AH.sin AHK .
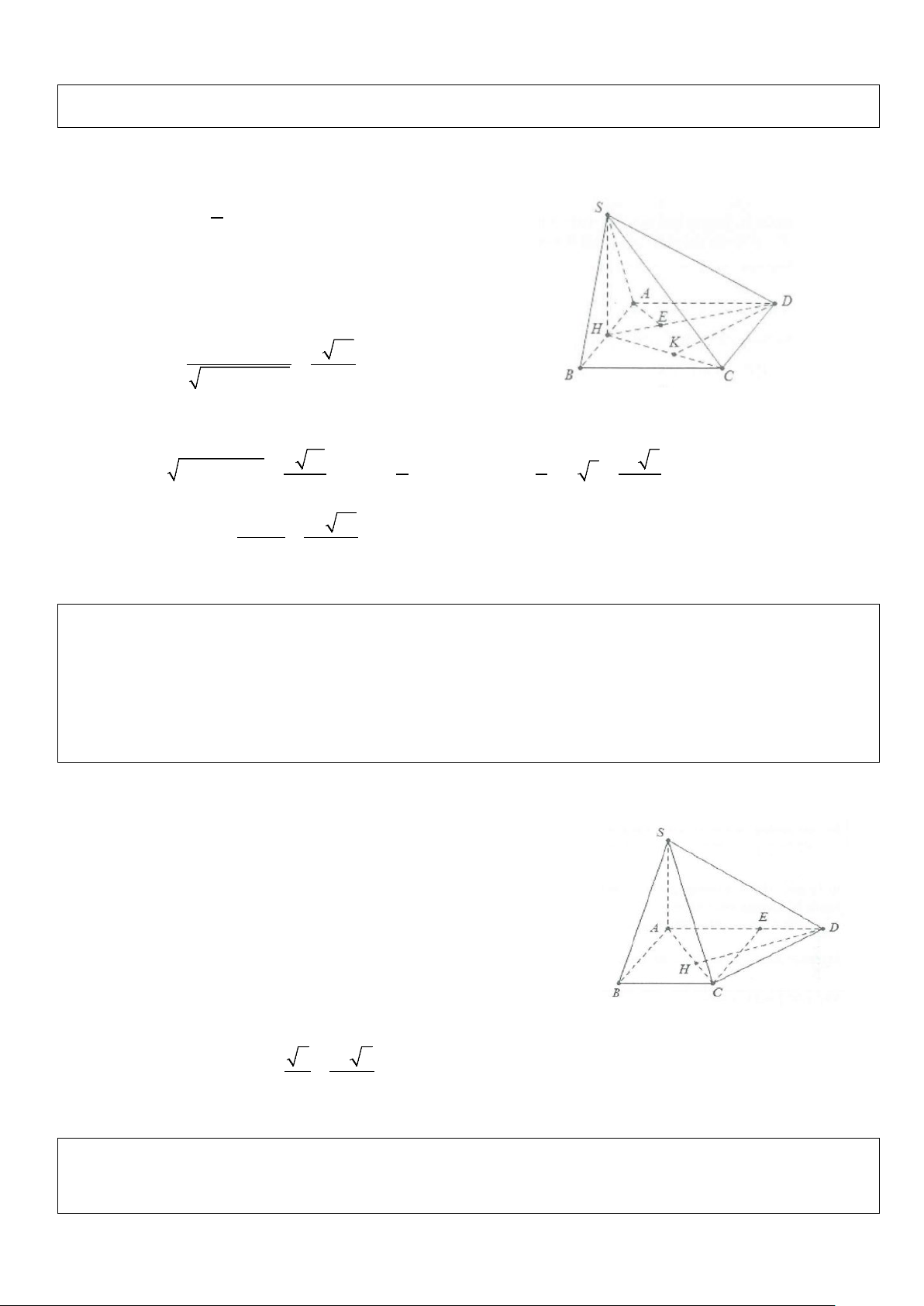
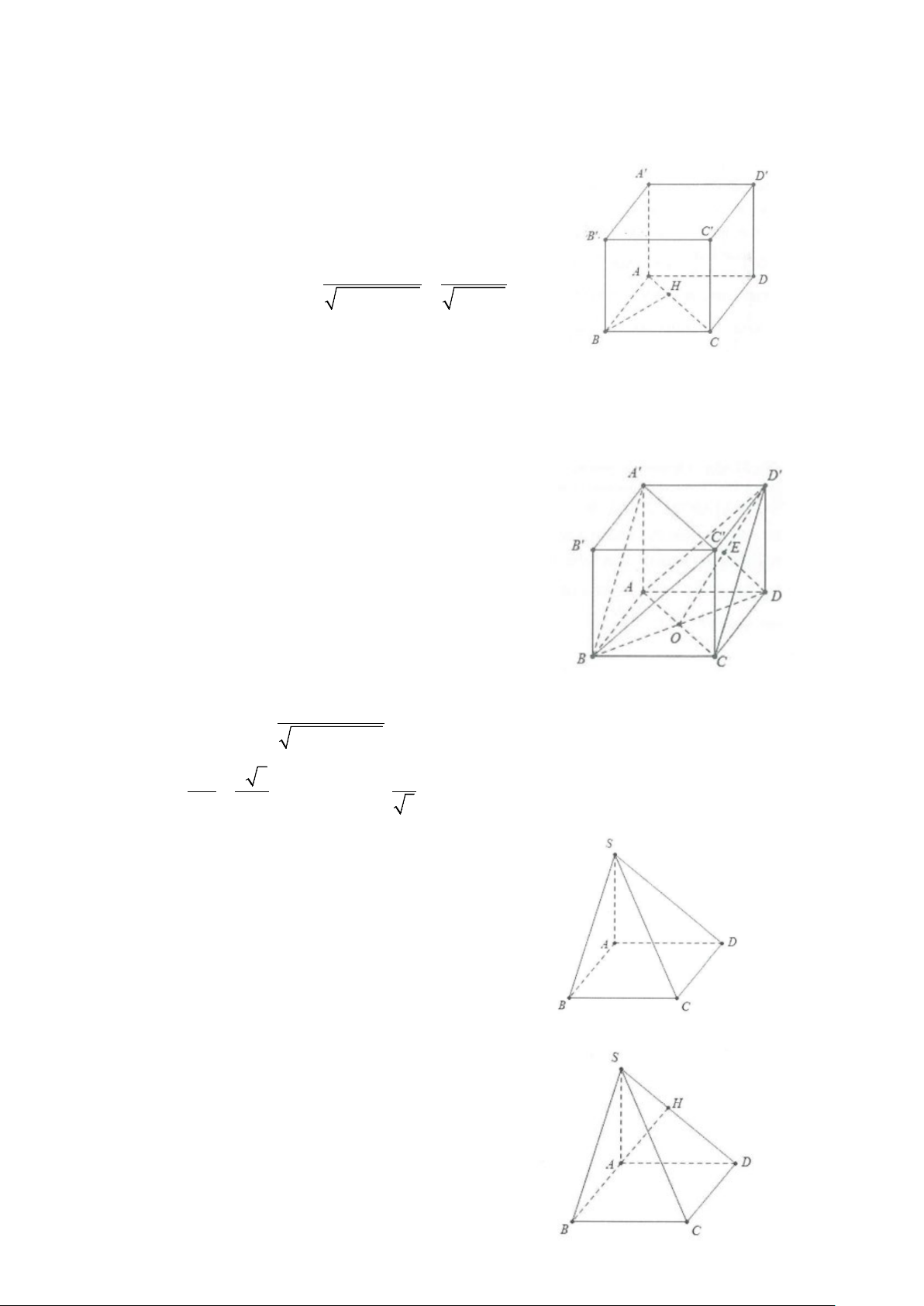
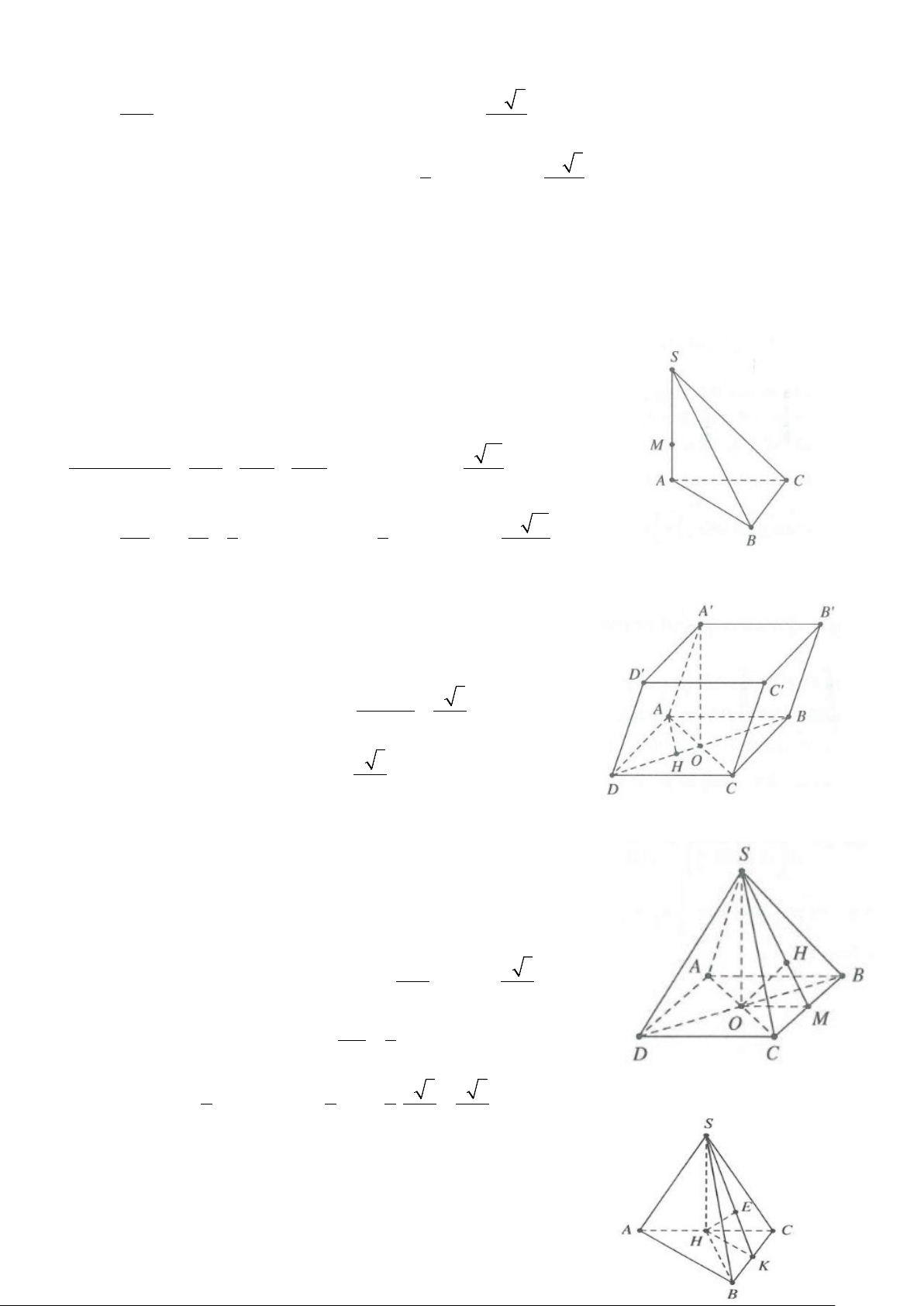
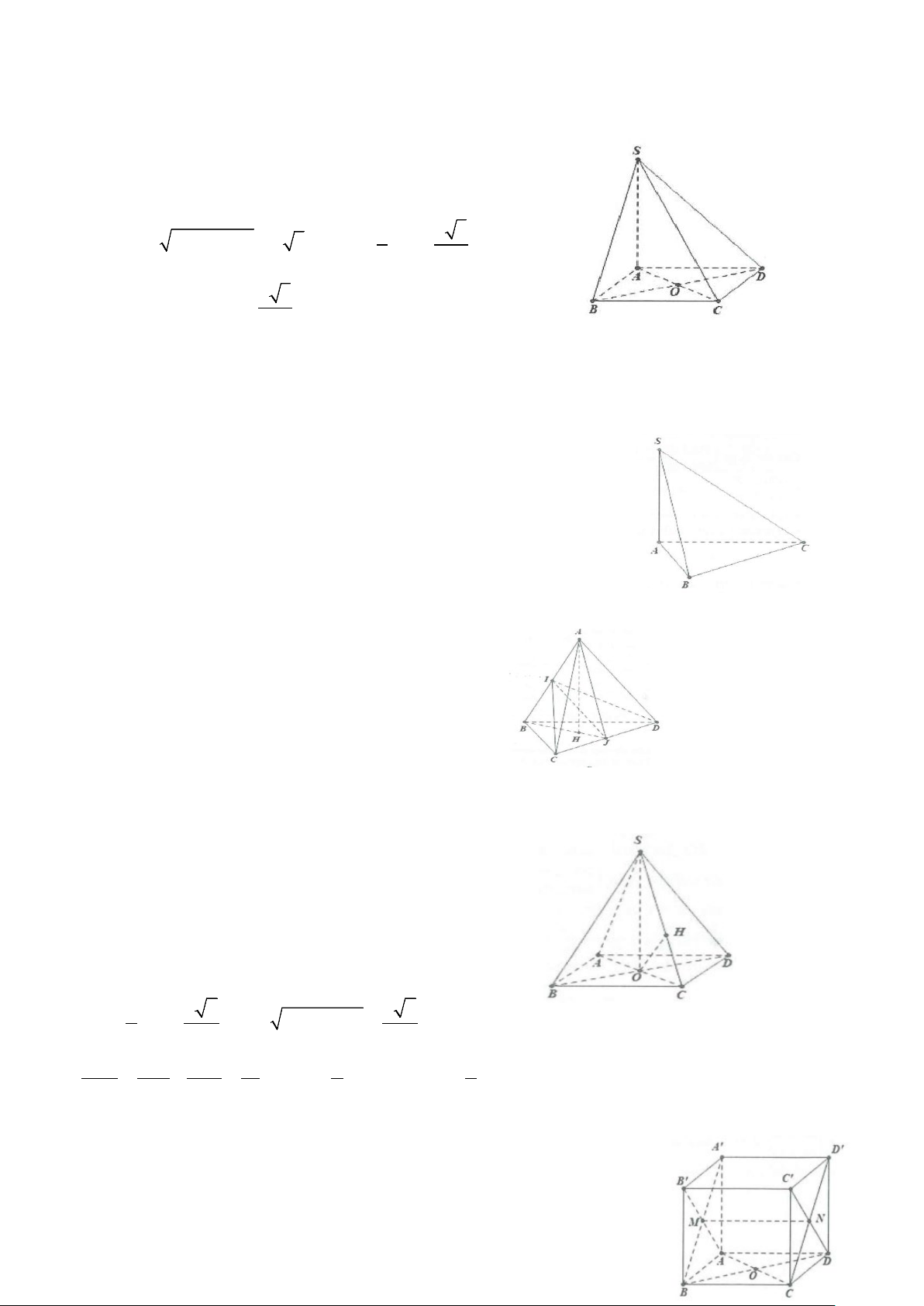
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC có = =
AB 3a, BC 2a, ABC = 60° . Biết SA ⊥ ( ABC) .
a) Tính khoảng cách từ C đến mặt phẳng (SAB) .
b) Tính khoảng cách từ B đến mặt phẳng (SAC). Lời giải CH ⊥ AB
a) Dựng CH ⊥ AB ta có: ⇒ CH ⊥ (SAB) CH ⊥ SA Do đó
d (C (SAB)) = = ;
CH CBsin ABH = 2asin 60° = a 3 .
b) Dựng CK ⊥ AC ⇒ CK ⊥ (SAC) .
Ta có: d (B (SAC)) 2S A . B BC sin ; ABC ABC = CH = = AC AC Trong đó 2 2 2 = + − AC AB BC 2B . A BC cos B ⇒ AC = a
⇒ d (B (SAC)) 3 .2 a . a sin 60° 3a 21 7 ; = = . a 7 7
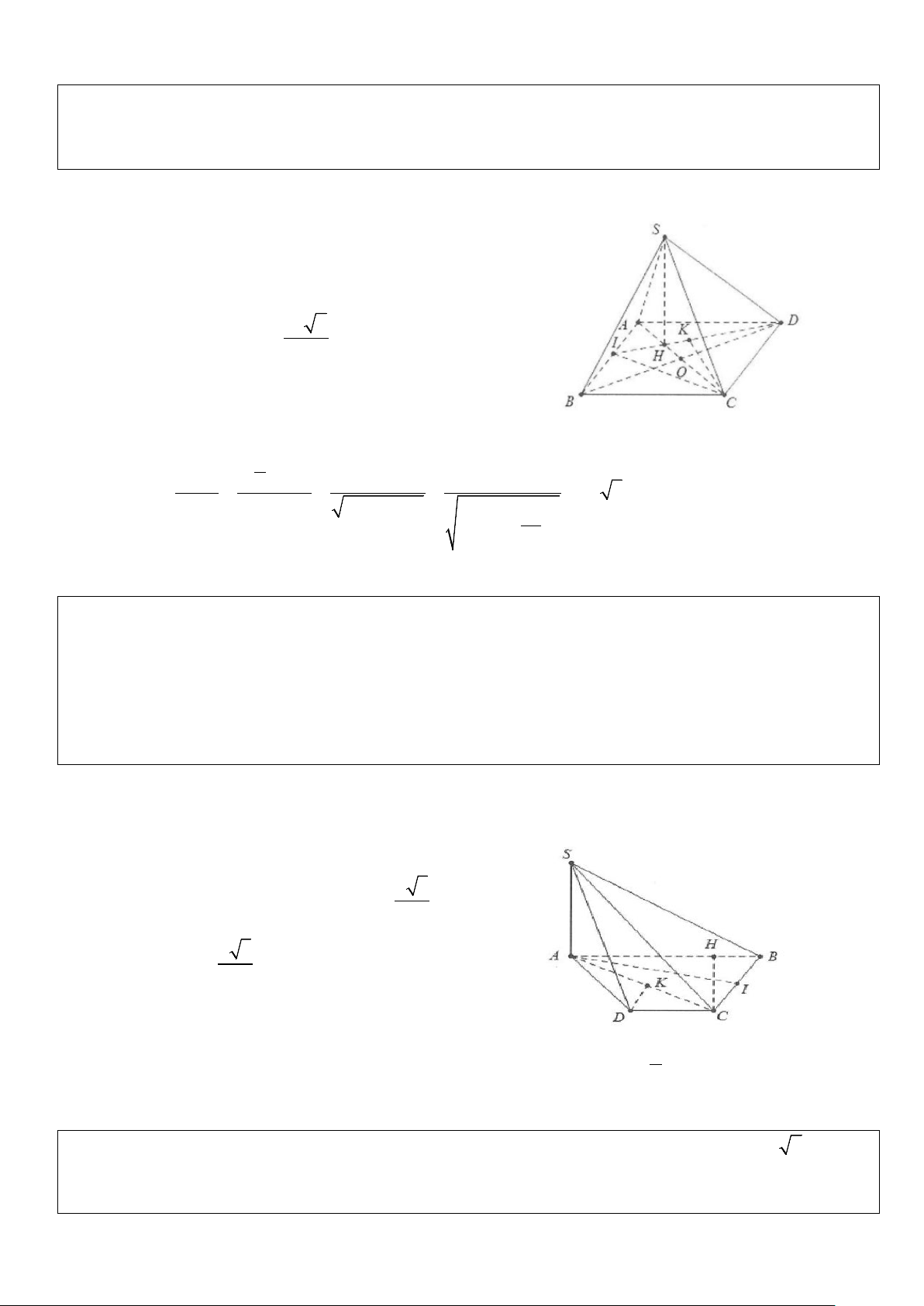
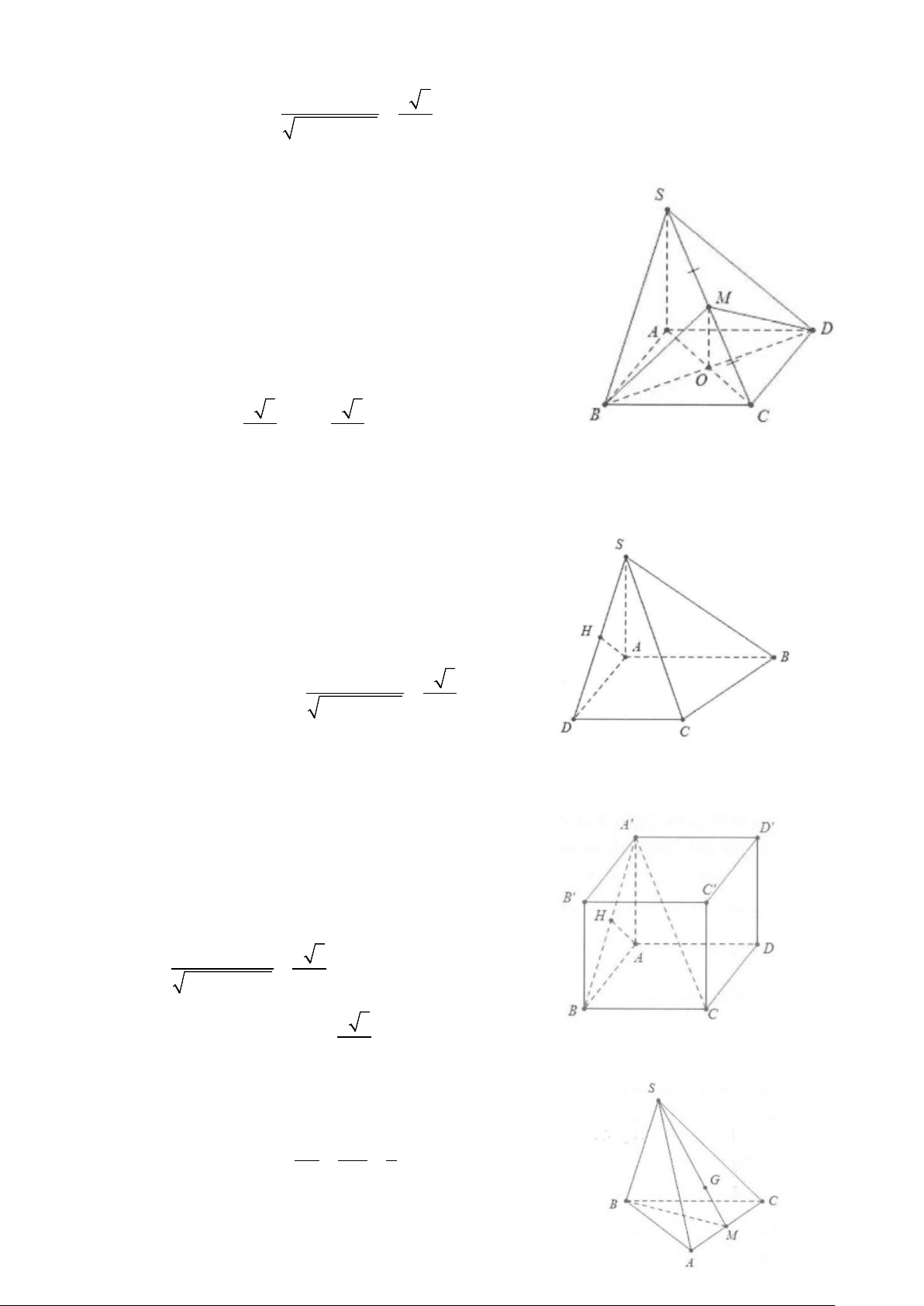
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật với B = a, AD = a 3 . Tam giác SAB cân tại S và
thuộc mặt phẳng vuông góc với đáy. Gọi H là trung tâm của AB.
a) Tính khoảng cách từ A đến mặt phẳng (SHD) .
b) Tính khoảng cách từ D đến mặt phẳng (SHC) . Lời giải
a) Do tam giác SAB cân tại S nên SH ⊥ AB . Ta có: a HA = HD = . 2
Mặt khác (SAB) ⊥ ( ABCD) ⇒ SH ⊥ ( ABCD) .
Dựng AE ⊥ DH ⇒ AE ⊥ (SHD) ⇒ d ( ;
A (SHD)) = AE . Mặt khác AH.AD a 39 AE = = . 2 2 AH + AD 13
b) Dựng DK ⊥ CH ⇒ d ( ;
D (SHC)) = DK . 2 Ta có: 2 2 a 13
CH = HB + BC = , 1 a S
= CD d H CD = a a = . HCD ( ) 1 3 . ; . . 3 2 2 2 2
Do đó d ( (SHC)) 2S a HCD 2 39 D; = = . CH 13
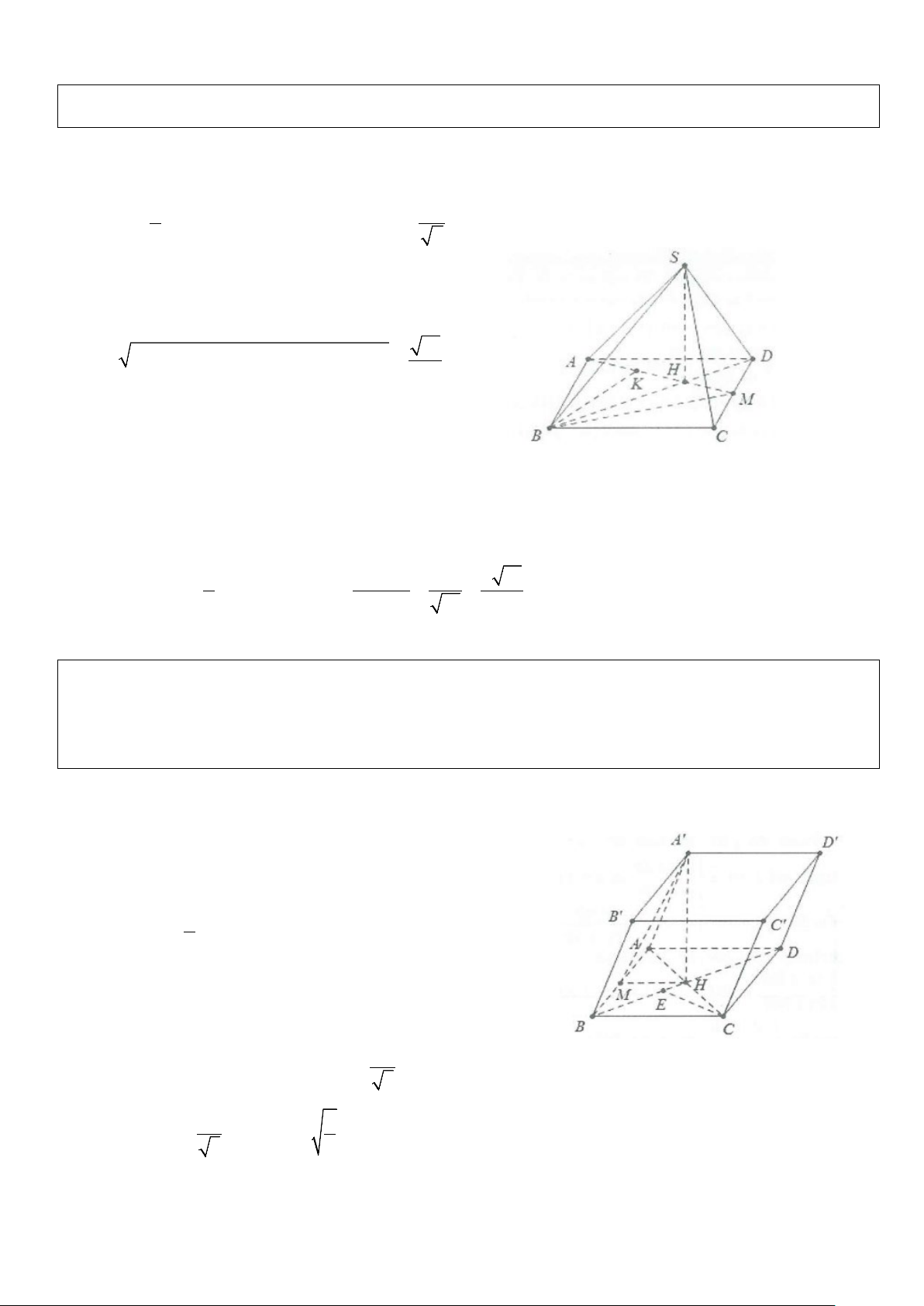
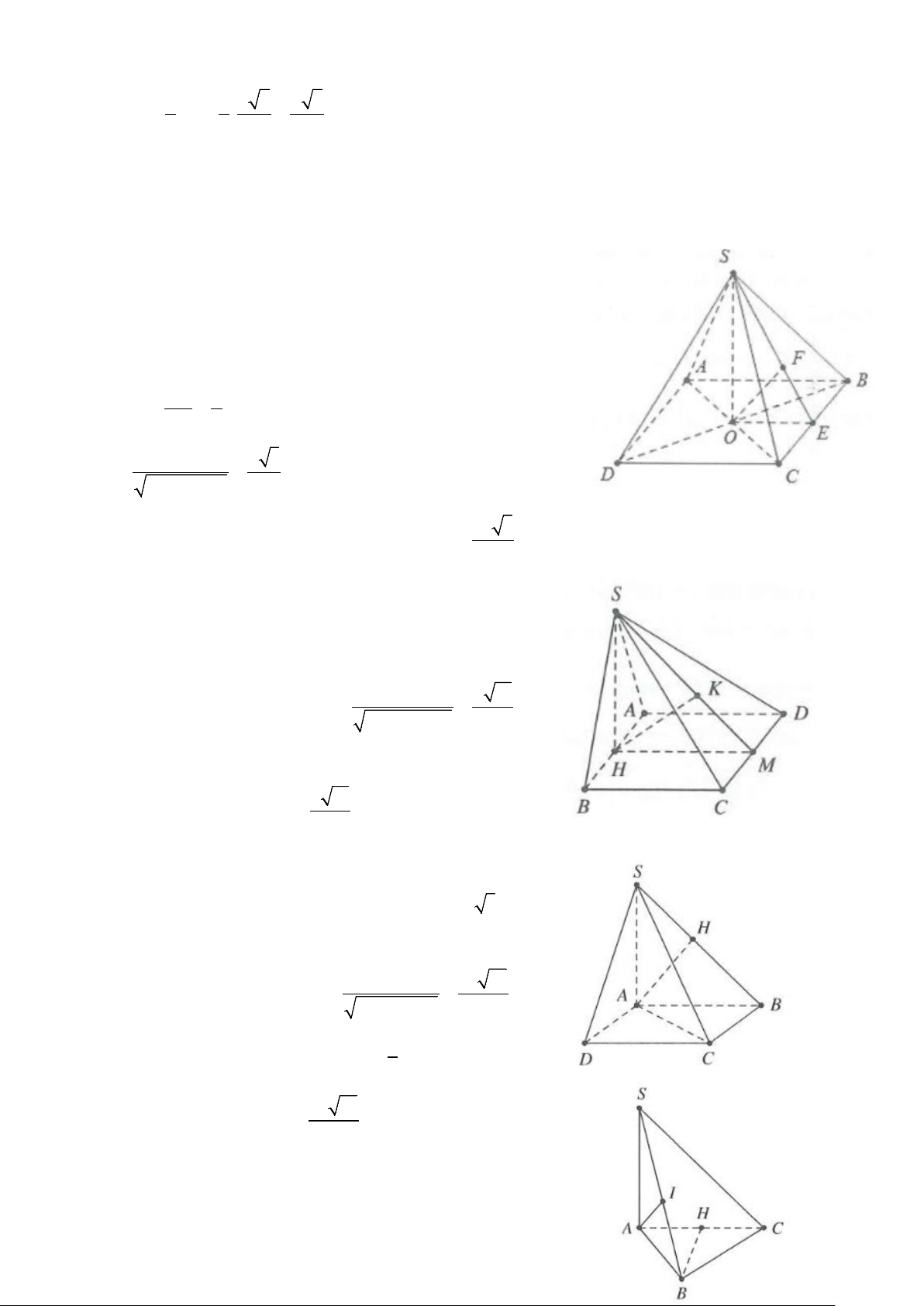
Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD = 3a , AB = BC = 2a . Biết
SA ⊥ ( ABCD) .
a) Tính khoảng cách từ C đến mặt phẳng (SAD).
b) Tính khoảng cách từ D đến mặt phẳng (SAC). Lời giải
a) Dựng CE ⊥ AD ⇒ CE ⊥ (SAD) .
Khi đó d (C;(SAD)) = CE , do ABCE là hình vuông cạnh 2a nên
CE = AE = 2a ⇒ d (C;(SAD)) = 2a .
b) Dựng DH ⊥ AC ⇒ DH ⊥ (SAC). Khi đó d ( ;
D (SAC)) = DH .
Ta có: ABCE là hình vuông nên CAD = 45°. Do đó 2 3a 2 DH = ADsin 45° = 3 . a = . 2 2
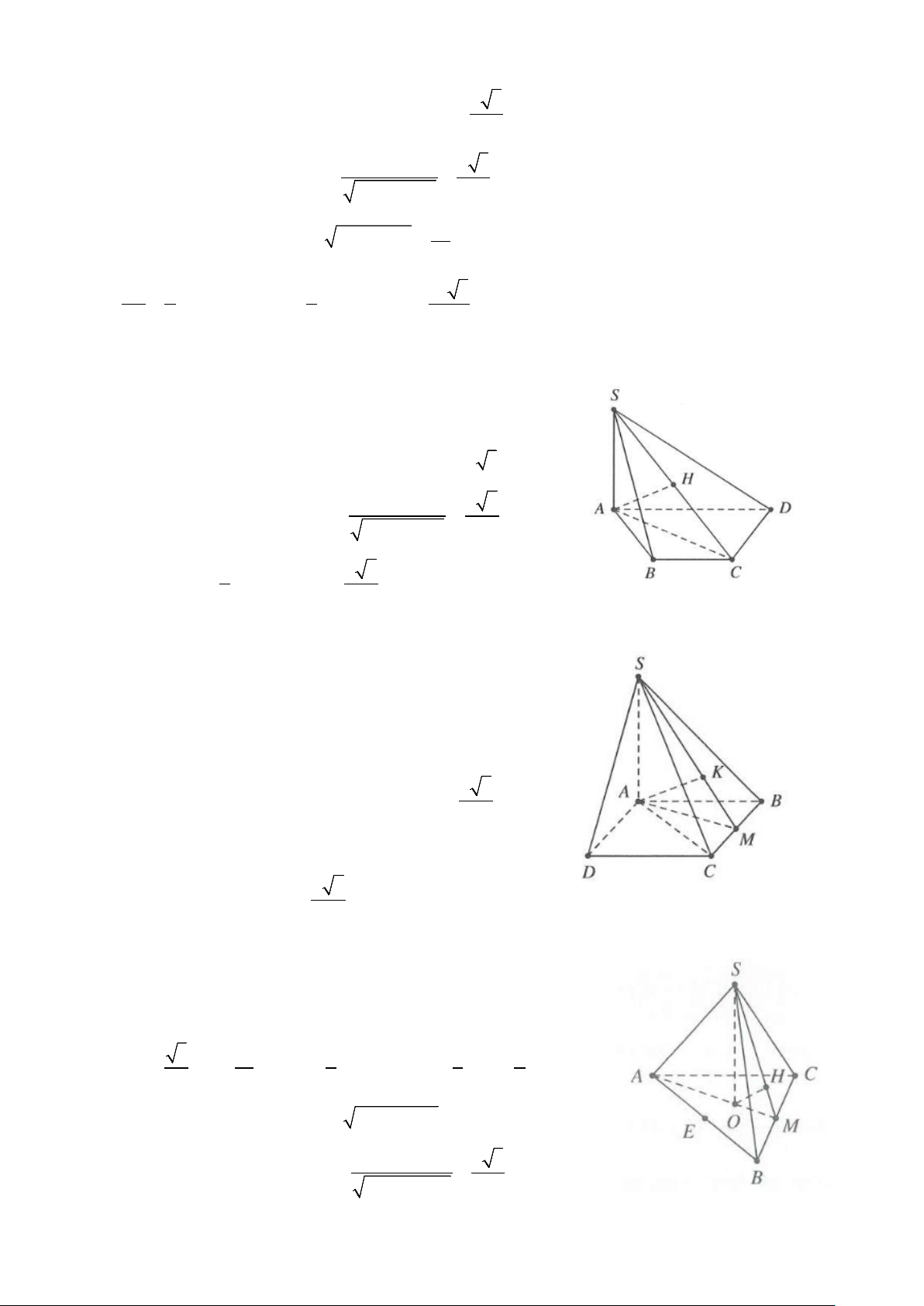
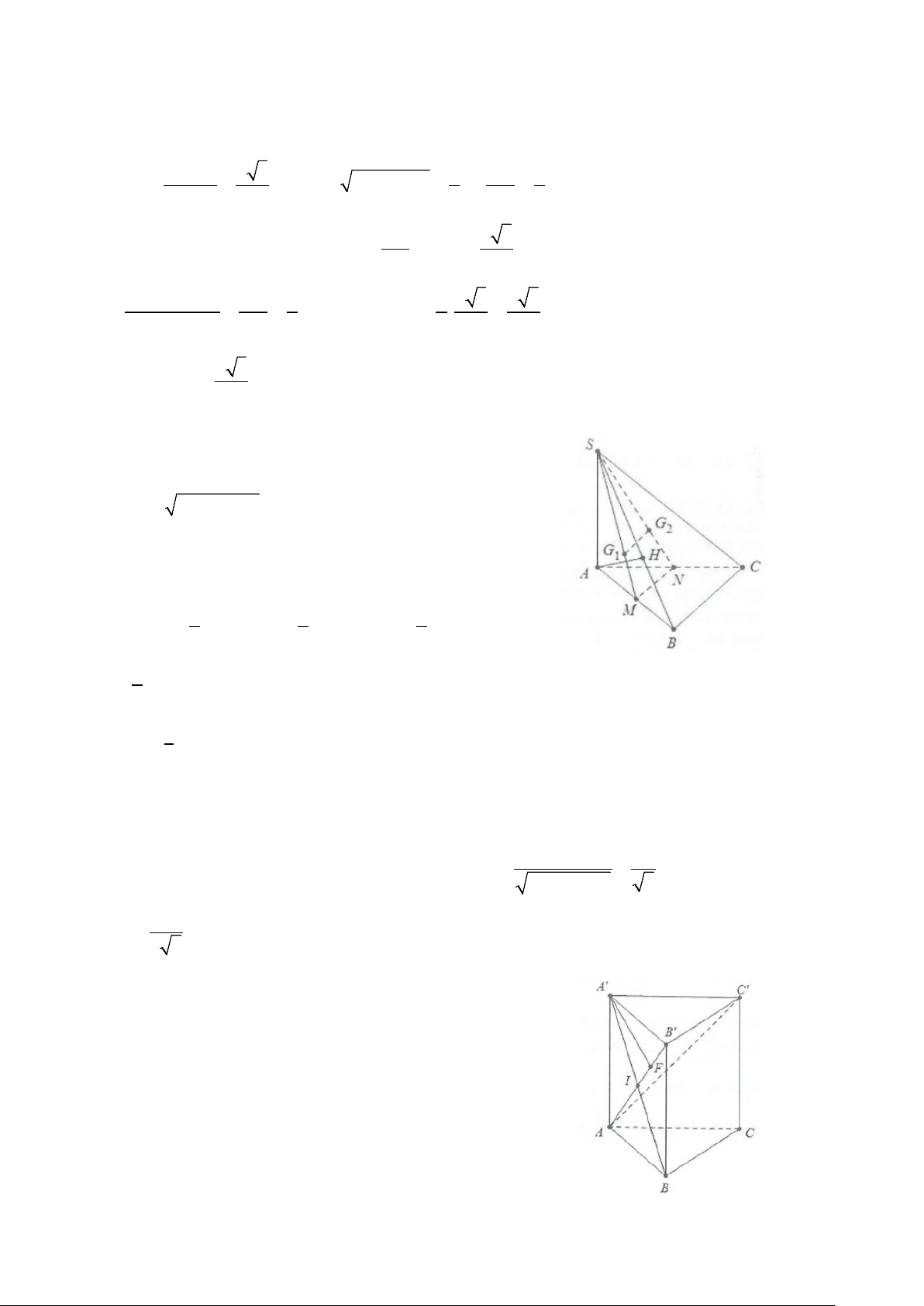
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 5a . Hình chiếu vuông góc của đỉnh S
trên mặt phẳng ( ABCD) trùng với trọng tâm H của tam giác ABD.
a) Tính khoảng cách từ B đến mặt phẳng (SAC).
b) Tính khoảng cách từ C đến mặt phẳng (SHD) . Lời giải
a) Do H là trọng tâm tam giác ABD ⇒ H ∈ AC .
Gọi O là tâm của hình vuông ABCD ⇒ BO ⊥ AC .
Mặt khác BO ⊥ SH ⇒ BO ⊥ (SAC)
Khi đó d (B (SAC)) 5a 2 ; = BO = . 2
b) Dựng CK ⊥ HD ⇒ CK ⊥ (SHD) ⇒ d (C;(SHD)) = CK .
Gọi I là trung điểm của AB thì H = DI ∩ AO . 1 2. S 2 2 ABCD Khi đó: 2S a a ICD 2 25 25 CK = = = = = 2a 5 . 2 2 2 DI DI DA + AI 2 5 25 a a + 2
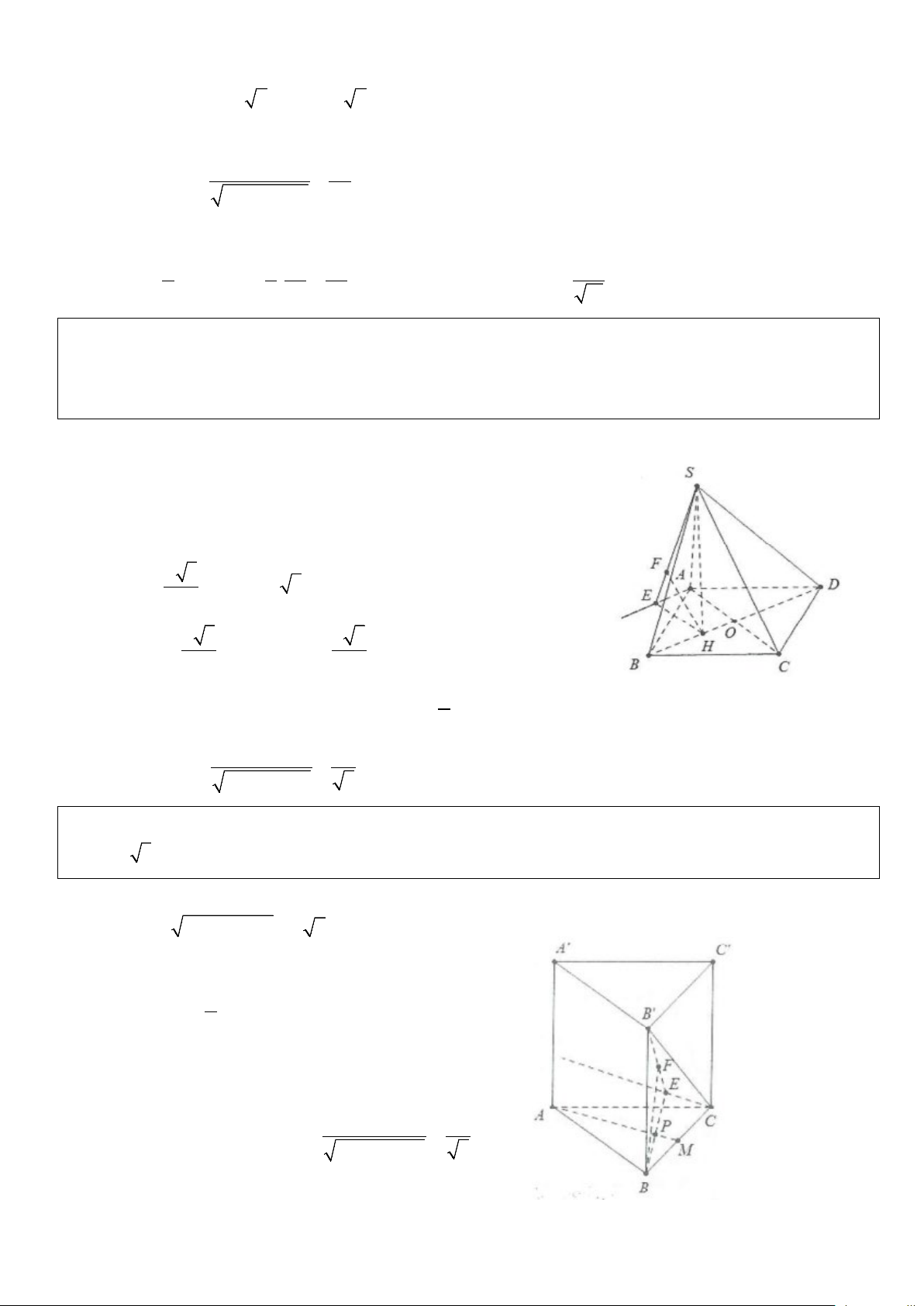
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD nửa lục giác đều cạnh a , với AB = 2a . Biết SA ⊥ ( ABCD)
và mặt phẳng (SBC) tạo với đáy một góc 60°.
a) Tính khoảng cách từ C đến mặt phẳng (SAB) .
b) Tính khoảng cách từ D đến mặt phẳng (SAC). Lời giải
a) Tứ giác ABCD là nửa lục giác đều cạnh a nên nó nội tiếp đường tròn đường kính AB = 2a .
Dựng CH ⊥ AB ⇒ CH ⊥ (SAB) ⇒ d (C;(SAB)) = CH . Mặt khác a 3
ABC = 60° ⇒ CH = BC sin 60° = . 2
Vậy d (C (SAB)) a 3 ; = . 2
b) Dựng DK ⊥ AC ⇒ DK ⊥ (SAC) ⇒ d ( ;
D (SAC)) = DK . Do = ° = ° ⇒ = ° ⇒ = 120 , 90 30 sin = sin 30 a DCB ACB ACD DK CD DCK a ° = . 2
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có diện tích bằng 2, AB = 2, BC = 2 .
Gọi M là trung điểm của CD, hai mặt phẳng (SBD) và (SAM ) cùng vuông góc với đáy. Tính khoảng cách
từ B đến mặt phẳng (SAM ). Lời giải Ta có S = S = = ⇒ = = . ∆ S∆ S∆ S ABCD 2 ABC 2 MAB 2 ABC M ∆ AB 1 1 ⇒ = = ⇒ 1 S = . ∆ AB BC ABC ABC ABC . . .sin 1 sin 2 2 Do đó = ° ⇒ ABC 45 ADM = 45°.
Áp dụng định lý Cosin trong tam giác ADM, ta có: 2 2 = + − 10 AM AD DM 2.A . D DM.cosADM = 2
Gọi H là giao điểm của AM và BD ⇒ SH ⊥ ( ABCD) .
Kẻ BK vuông góc với AM, K ∈ AM ⇒ BK ⊥ AM ( ) 1 .
Ta có (SAM ) ∩(SBD) = SH ⇒ SH ⊥ ( ABCD) ⇒ SH ⊥ BK (2) . Từ ( )
1 ,(2) ⇒ BK ⊥ (SAM ) ⇒ d ( ;
B (SAM )) = BK . Mặt khác 1 2.S MA ∆ B 4 2 10 S = ⇒ = = = . ∆ BK AM BK MAB . . 2 AM 10 5
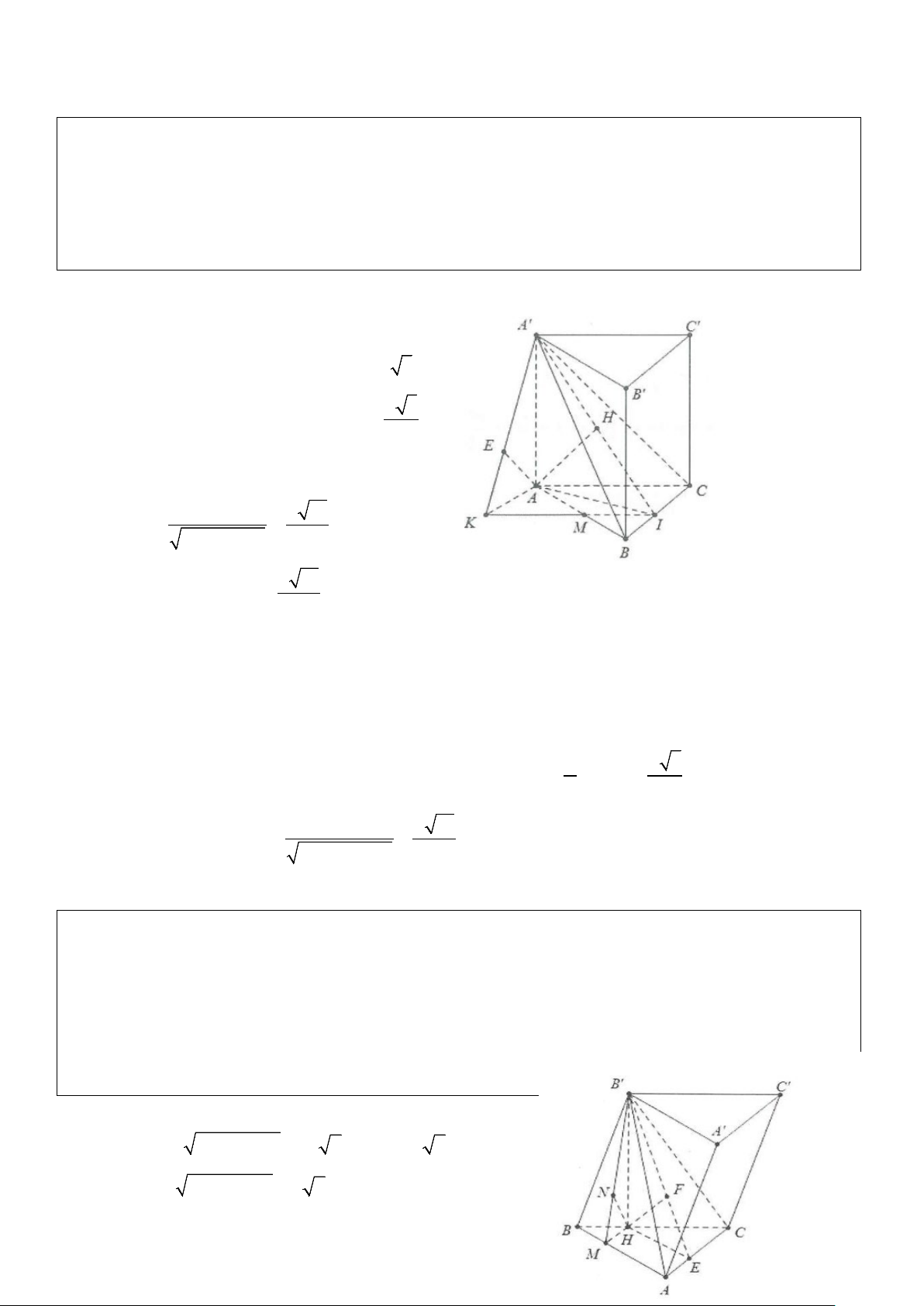
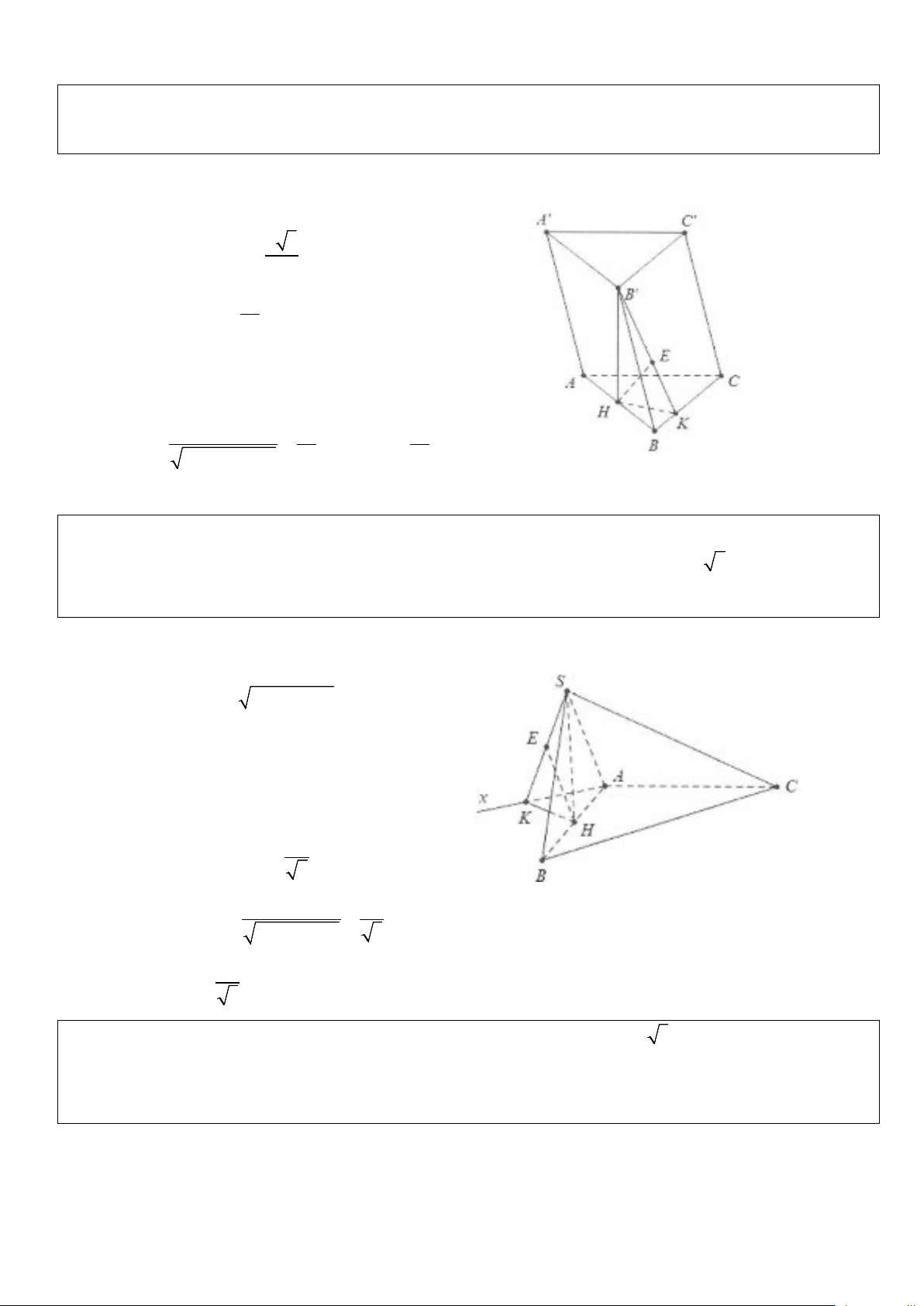
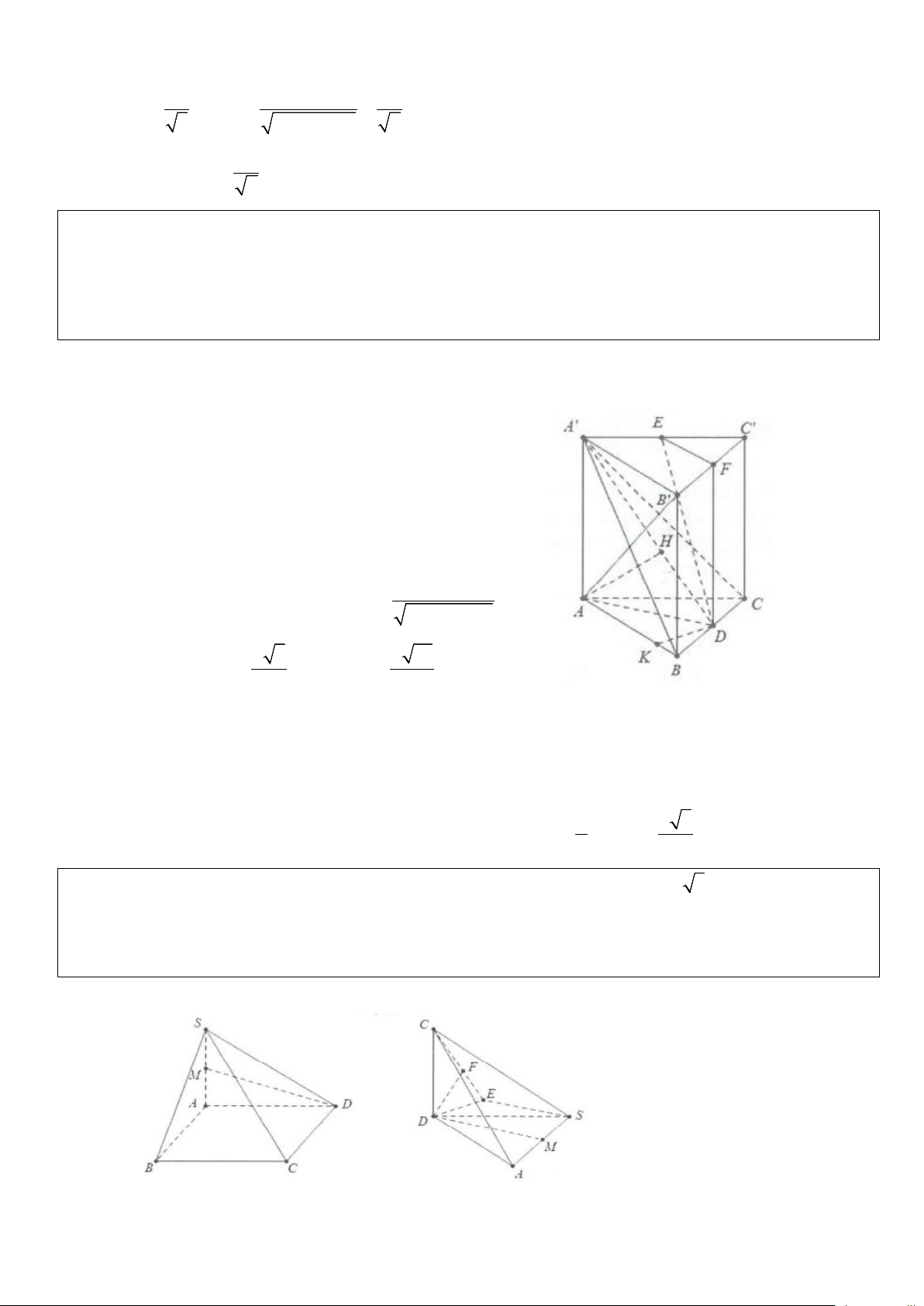
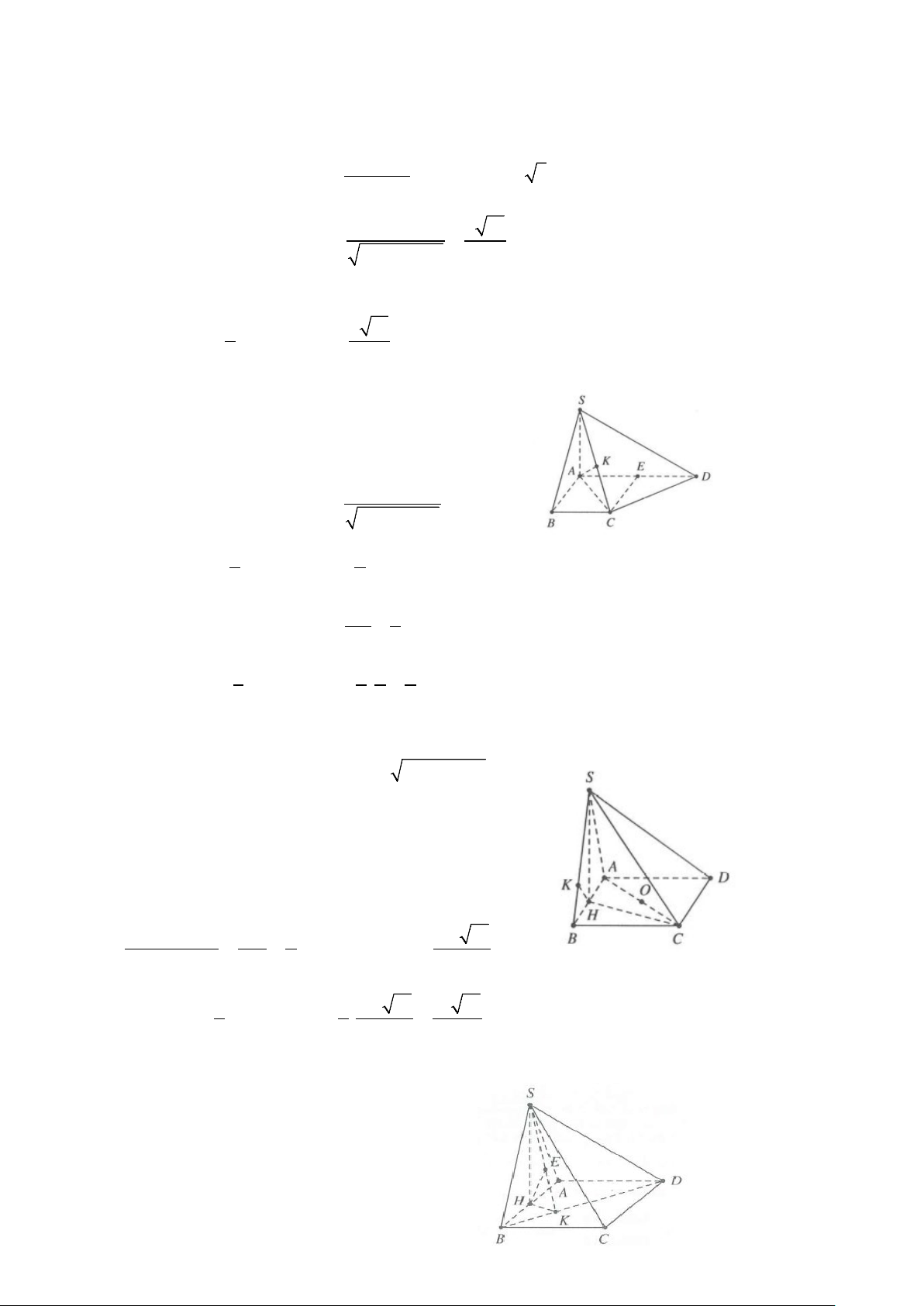
Ví dụ 7: Cho hình lăng trụ ABC .
D A' B 'C ' D ' có đáy là hình chữ nhật ABCD có hai đường chéo
AC = BD = 2a . Tam giác A’BD vuông cân tại A’ và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng
( A' AB) tạo với đáy một góc 60°. Tính khoảng cách d (B';(A'BD)). Lời giải
Gọi H là tâm hình chữ nhật ABCD
⇒ HA = HC ⇒ A' H ⊥ BD (Do A
∆ ' BD cân tại A’).
Do ( A'BD) ⊥ ( ABCD) ⇒ A'H ⊥ ( ABCD) . Ta có: 1
A'H = BD = a (trong tam giác vuông đường trung 2
tuyến ứng cạnh huyền bằng nửa cạnh ấy).
Dựng HM ⊥ AB ⇒ AB ⊥ ( A HM ) ⇒ ' A'MH = 60° +) Khi đó: tan 60° = ' a HM A H ⇒ HM = 3 2a 2 ⇒ AD = 2HM = ⇒ AB = 2a 3 3
Do: A'D / /B 'C ⇒ B 'C / / ( A'BD) ⇒ d (B';( A'BD)) = d (C;( A'BD)) . Ta có: . CD CB 2a 2 CE = =
. Vậy d (B ( A BD)) 2a 2 '; ' = . BD 3 3
Dạng 2: Khoảng cách từ chân đường cao đến mặt phẳng bên.
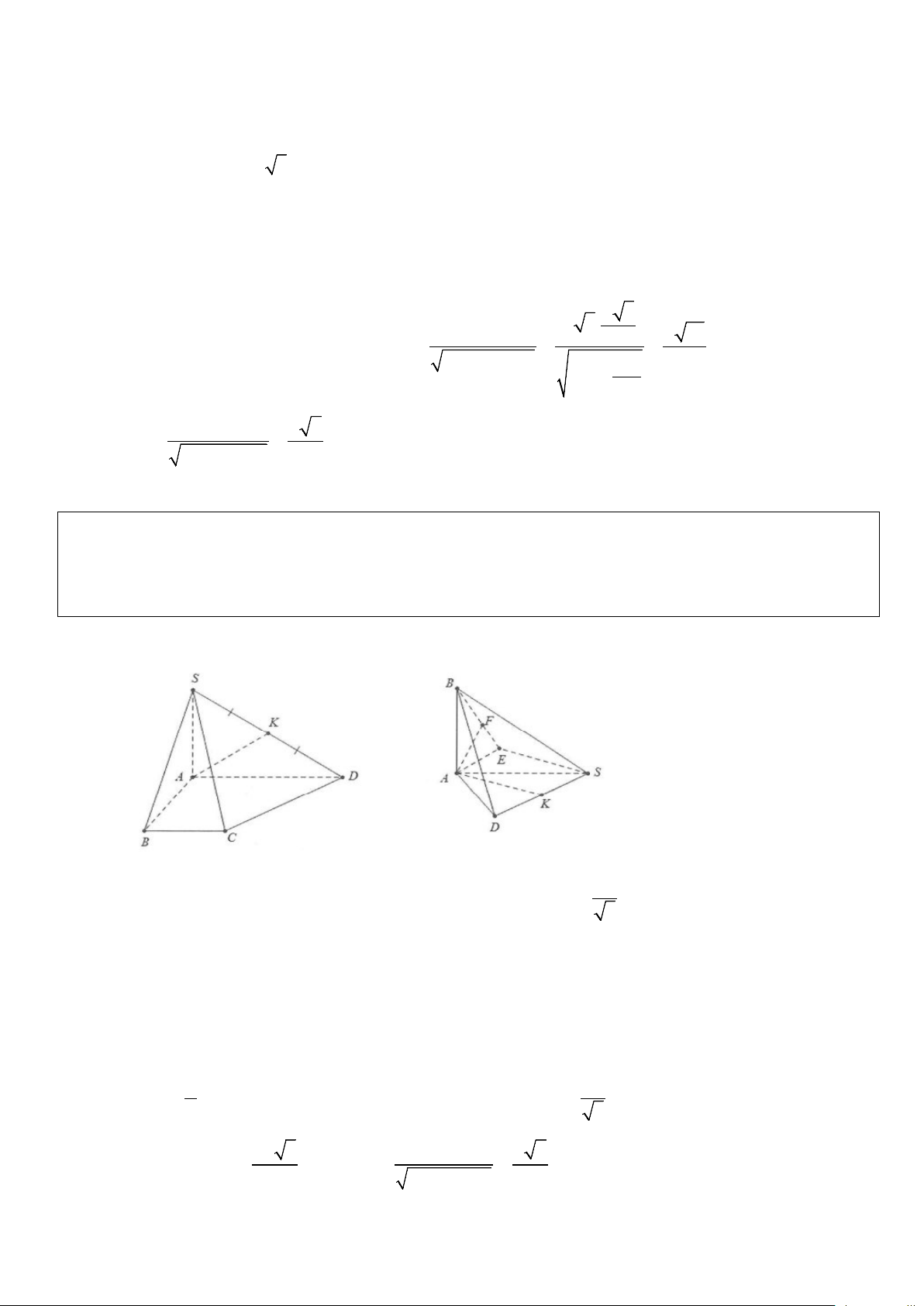
Xét bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ
điểm H đến mặt bên (SAB) .
Dựng HE ⊥ AB,(E ∈ AB) ta có: AB ⊥ SH ⇒ AB ⊥ (SHE) ( ) 1 . AB ⊥ HE
Dựng HF ⊥ SE,(F ∈ SE) . Từ ( ) 1 HF ⊥ AB
Do đó HF ⊥ (SAB) ⇒ d (H;(SAB)) = HF .
Cách tính: Xét tam giác SHE vuông tại H có đường cao HF ta có: 1 1 1 = + 2 2 2 HF HE SH Hay HE.SH HF = . 2 2 HE + SH
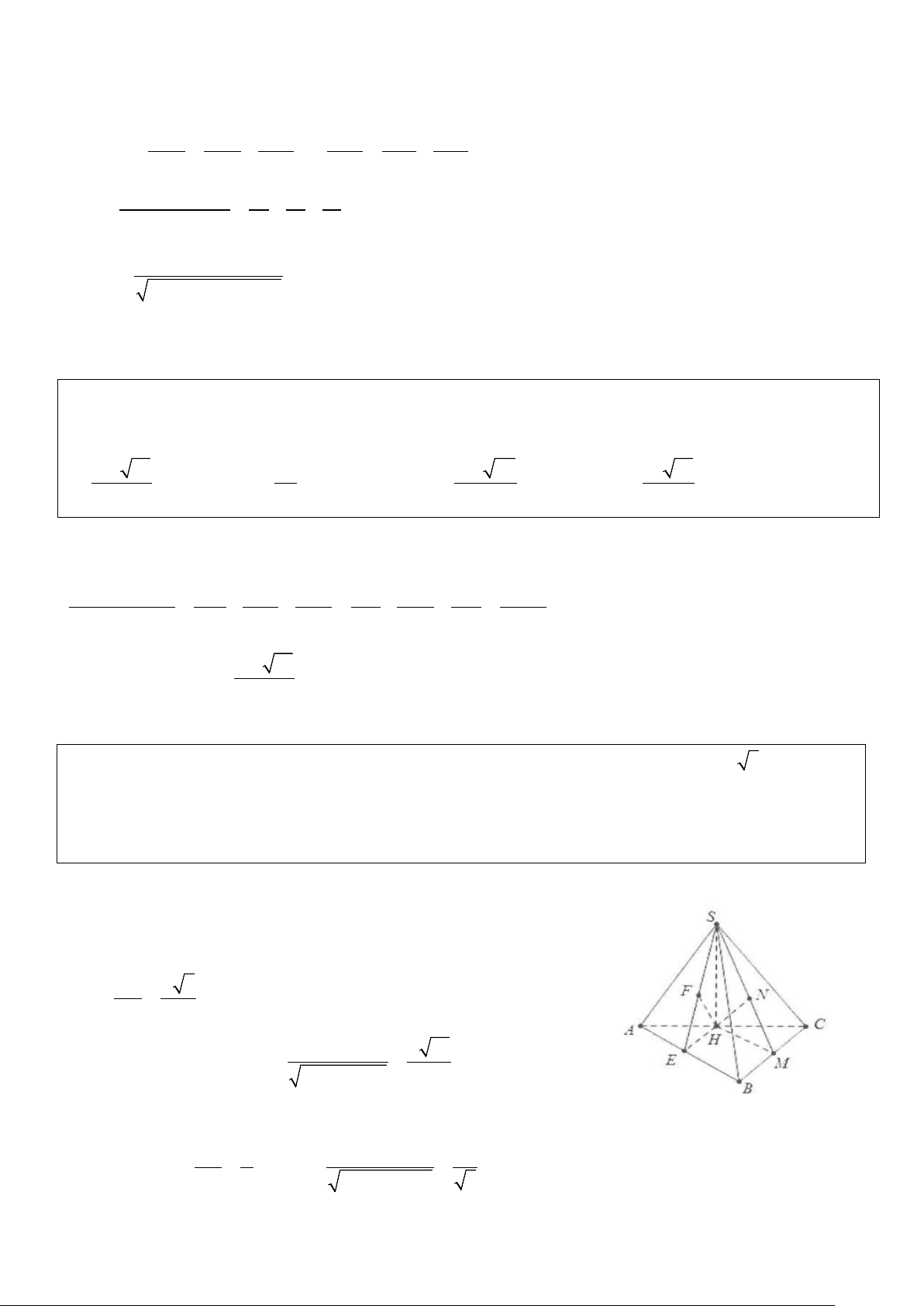
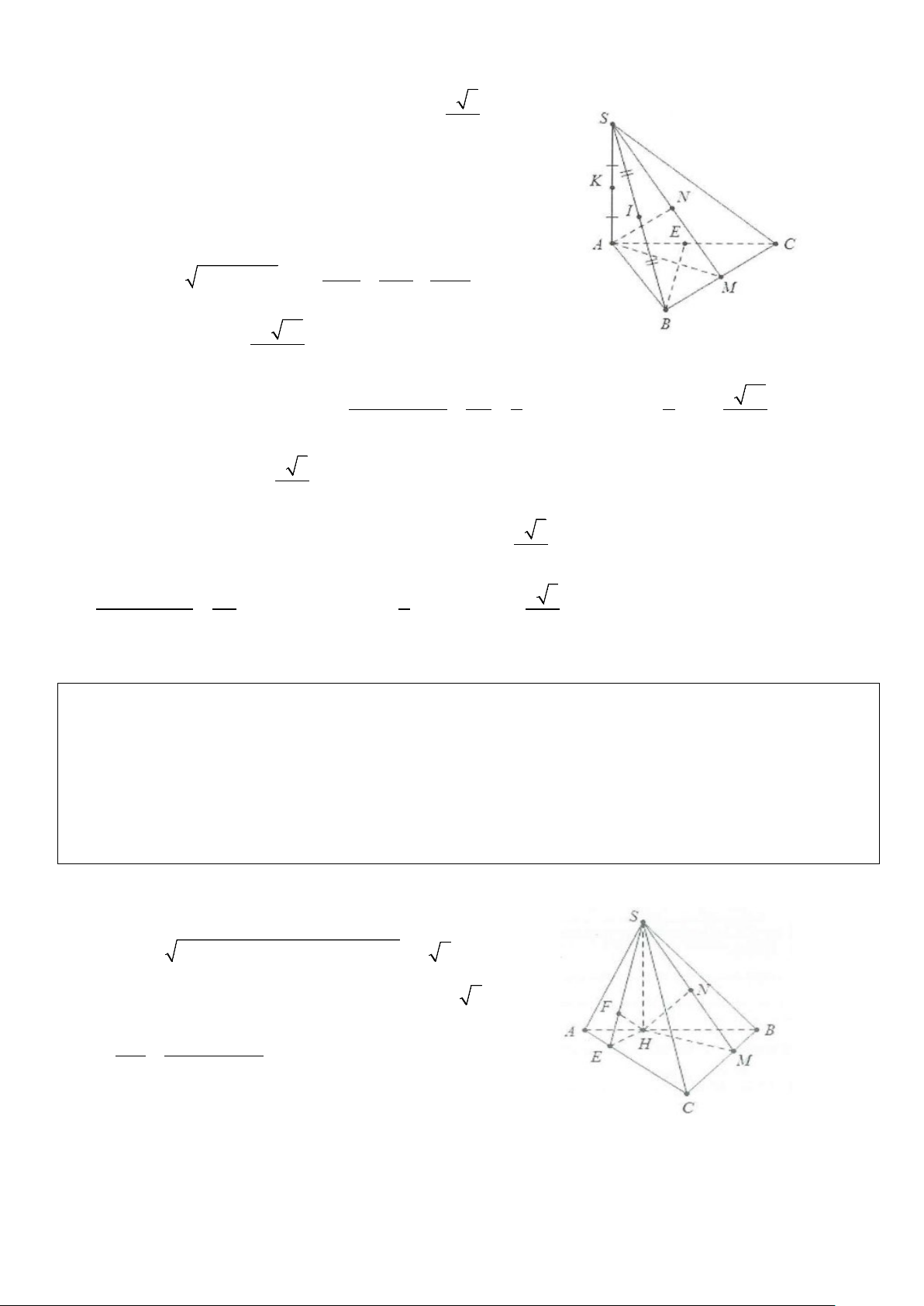
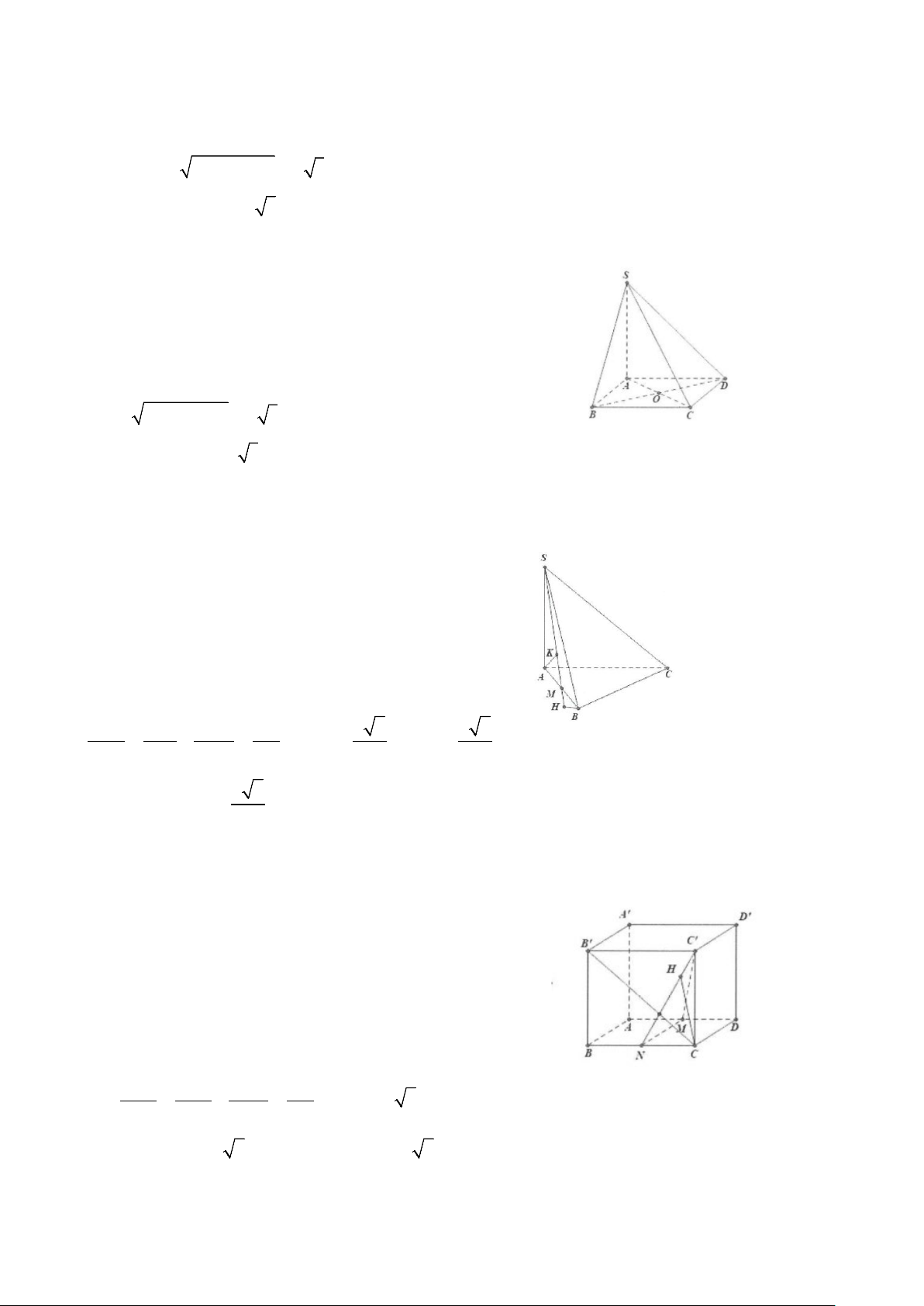
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB = a, BC = a 3 . Biết SA = 2a và SA ⊥ ( ABC) .
a) Tính khoảng cách từ A đến mặt phẳng (SBC).
b) Gọi M là trung điểm của AC. Tính khoảng cách từ A đến mặt phẳng (SBM ). Lời giải
a) Ta có : AB ⊥ BC , mặt khác BC ⊥ SA ⇒ BC ⊥ (SAB) . AH ⊥ SB
Dựng AH ⊥ SB ⇒ ⇒ AH ⊥ (SBC) . AH ⊥ BC Khi đó ( ( )) S . A AB 2 ; a d A SBC = AH = = . 2 2 SA + AB 5
b) Dựng AE ⊥ BM , AF ⊥ SE ta có: AE ⊥ BM
⇒ BM ⊥ (SAE) ⇒ BM ⊥ AF. AE ⊥ BM AF ⊥ SE Khi đó: ⇒ AF ⊥ (SBM) . AF ⊥ BM Ta có: 2 2
AB = a, AC = AB + AC = 2a . Do BM là đường trung tuyến ứng với cạnh huyền nên 1
BM = AC = AM = AB = a ⇒ A
∆ BM đều cạnh a a 3 ⇒ AE = . 2 2
Khi đó d ( A (SBM )) AE.SA 2a 57 ; = = . 2 2 AE + SA 19
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA ⊥ ( ABC) . Đường thẳng SB tạo với đáy một góc 60°.
a) Tính khoảng cách từ A đến mặt phẳng (SBC).
b) Tính khoảng cách từ A đến mặt phẳng (SCM ) , với M là trung điểm của cạnh AB. Lời giải
a) Do SA ⊥ ( ABC) ⇒ (SB ( ABC)) = ; SBA = 60° .
Do đó SA = AB tan 60° = 2a 3 .
Dựng AE ⊥ BC, A
∆ BC đều nên AB 3 = a 3 . 2 BC ⊥ SA
Dựng AF ⊥ SE , mặt khác ⇒ BC ⊥ AF. BC ⊥ AE
⇒ AF ⊥ (SBC) ⇒ d ( A (SBC)) S . A AE 2a 21 ; = AF = = . 2 2 SA + AE 7
b) Do M là trung điểm của AB nên CM ⊥ AB .
Mặt khác CM ⊥ SA ⇒ CM ⊥ (SAM) . Dựng AH ⊥ SM ⇒ AH ⊥ (SMC) . Khi đó ( ( )) S . A AM 2 ; a d A SMC = = . 2 2 SA + AM 5
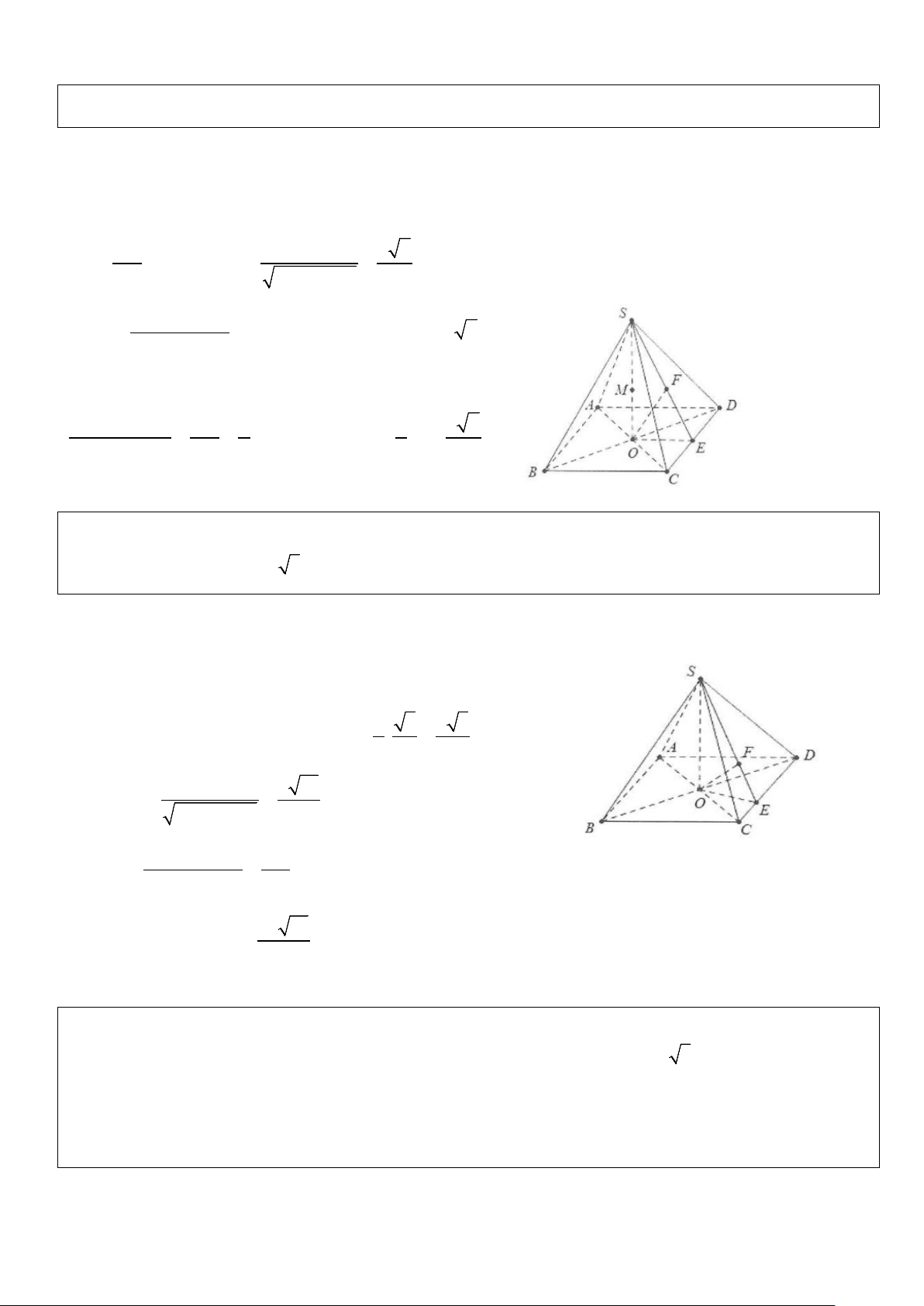
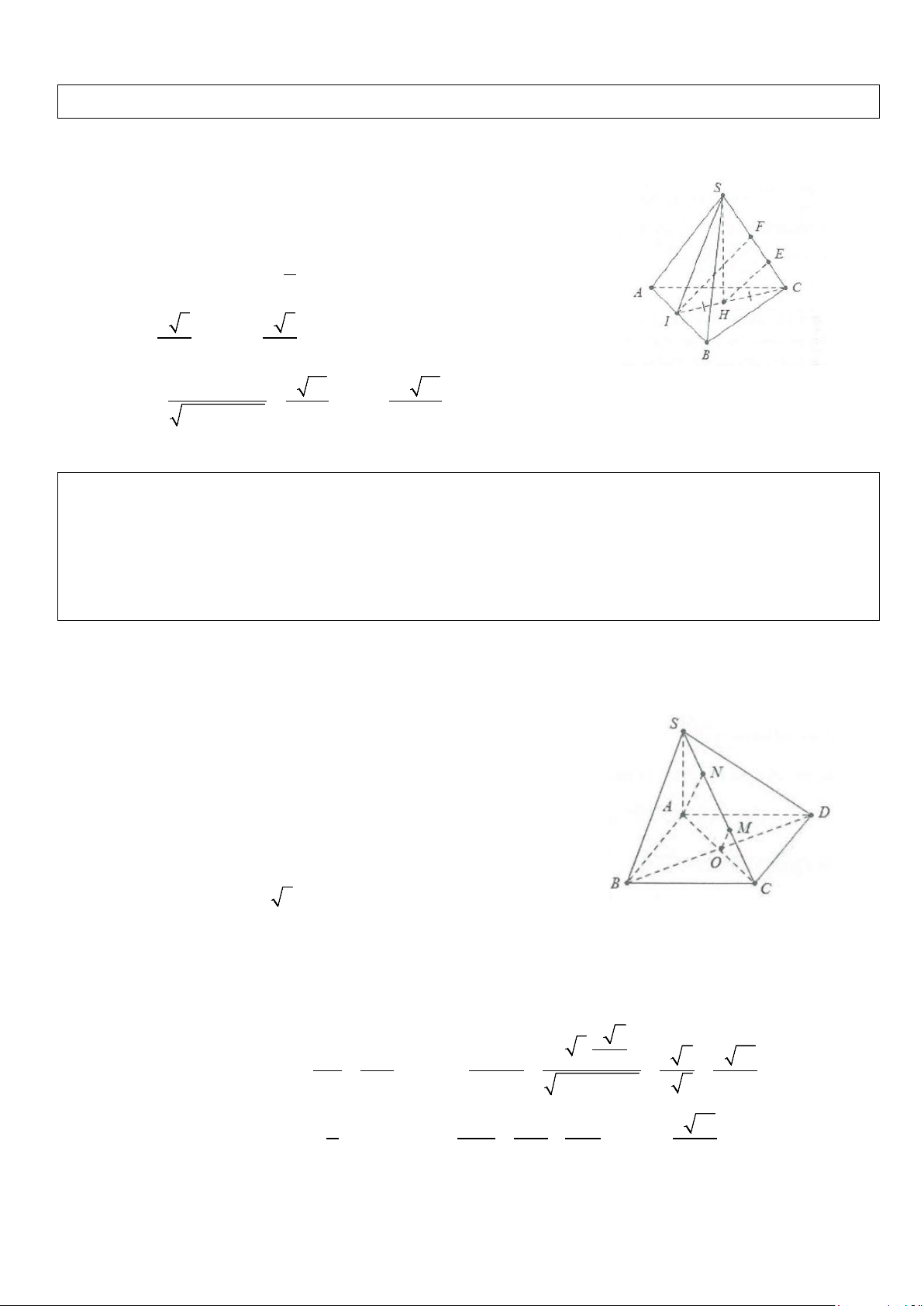
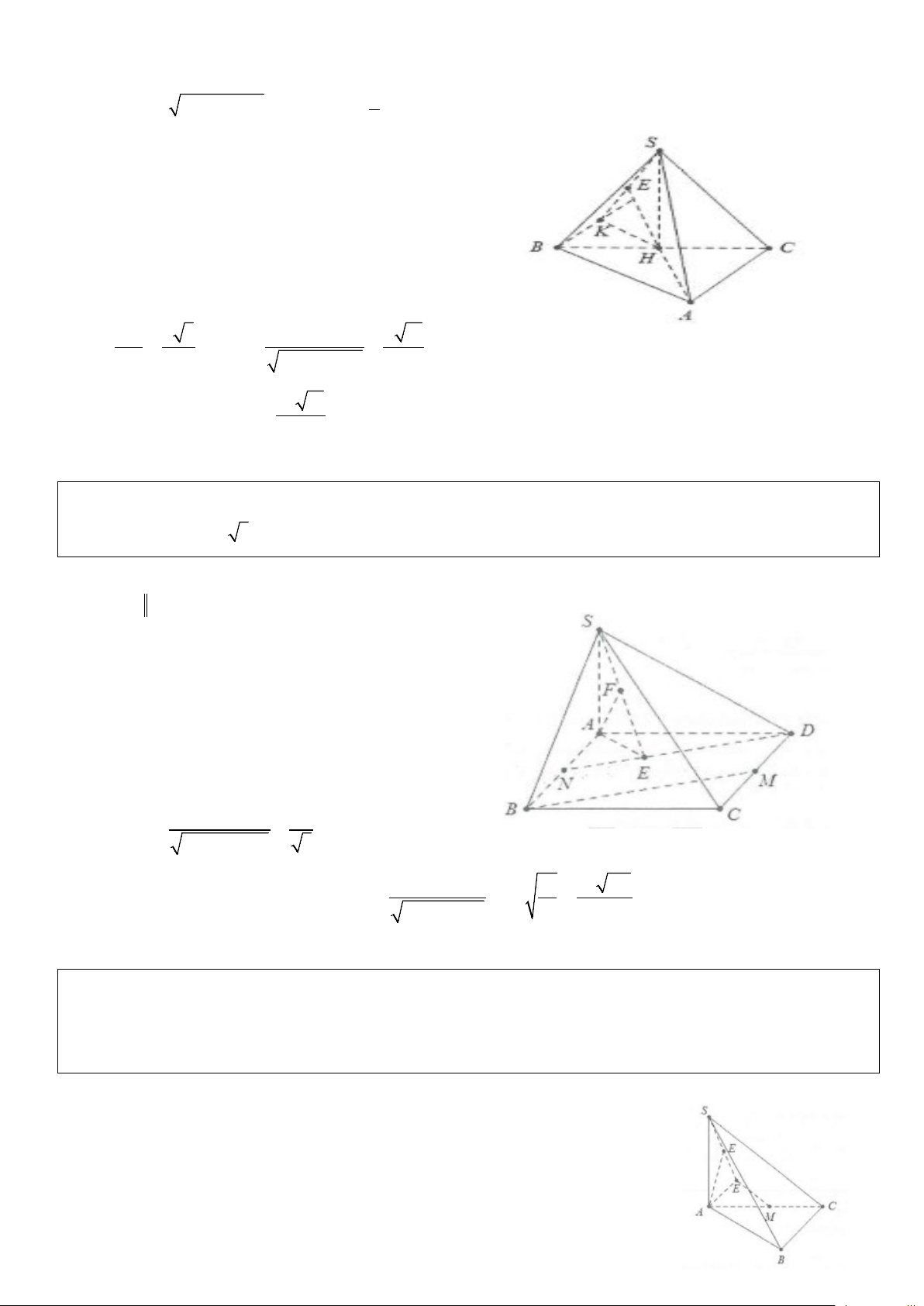
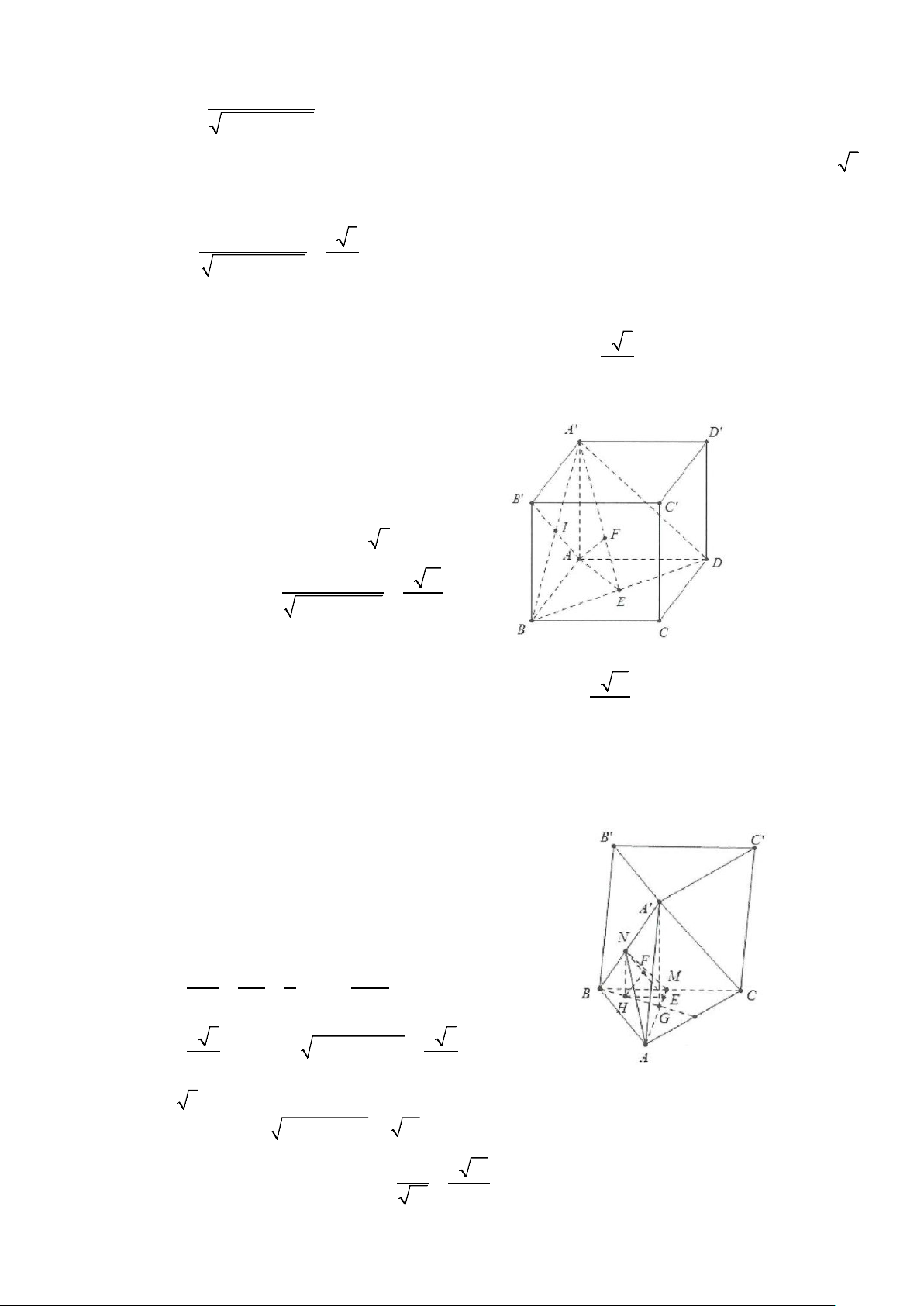
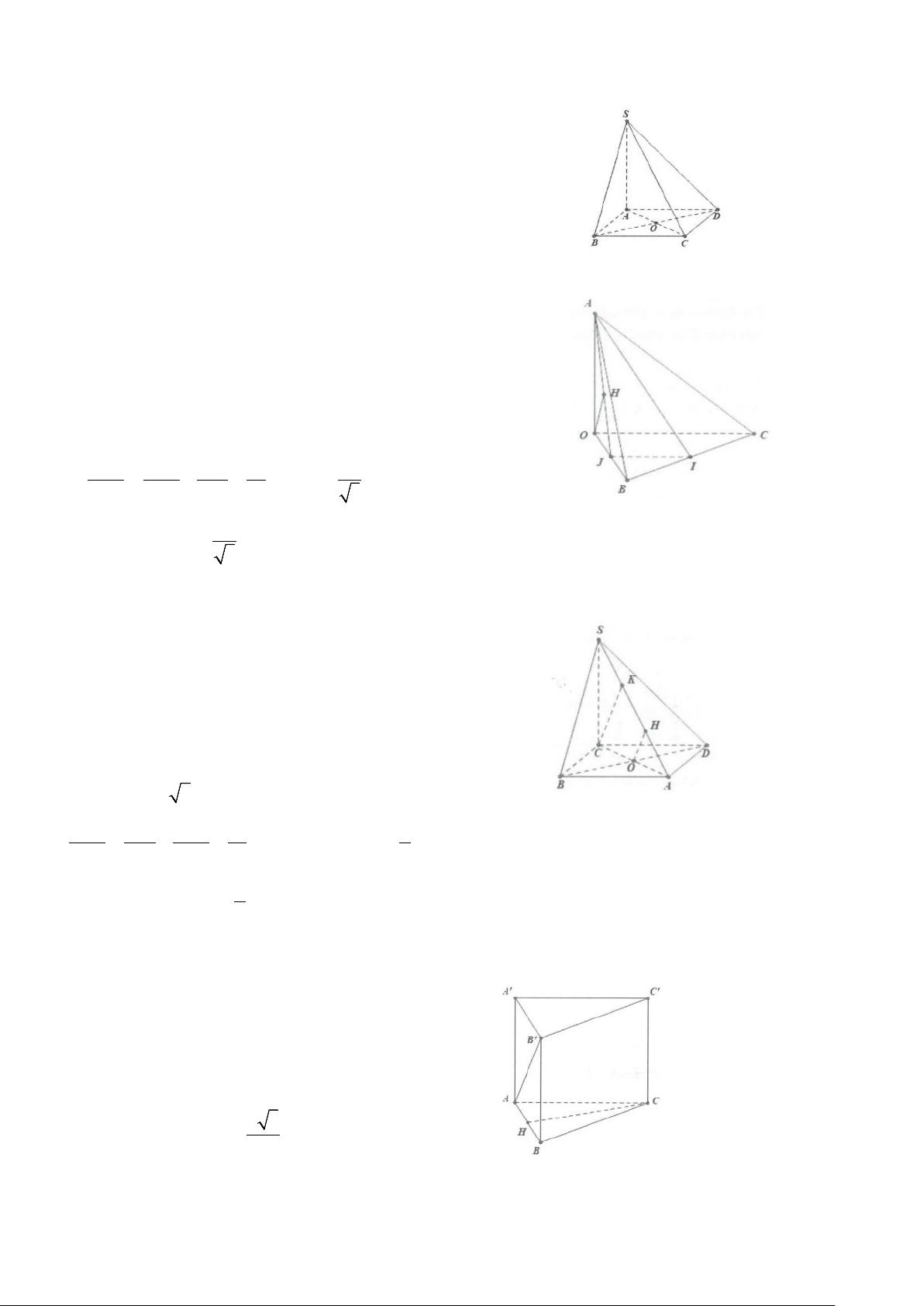
Ví dụ 3: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết OA = a,OB = , b OC = c .
Tính khoảng cách d từ O đến mặt phẳng ( ABC). Lời giải OC ⊥ OA Do
⇒ OC ⊥ (OAB) ⇒ AB ⊥ OC . OC ⊥ OB
Dựng OE ⊥ AB,OF ⊥ CE suy ra OF ⊥ BC .
Khi đó OF ⊥ ( ABC) ⇒ d ( ;
O ( ABC)) = OF . Mặt khác: 1 1 1 = + và 1 1 1 = + 2 2 2 OF OC OE 2 2 2 OE OA OB Do đó 1 1 1 1 = + + 2 d ( ; O ( ABC)) 2 2 2 a b c Vậy abc d = . 2 2 2 2 2 2
a b + b c + c a
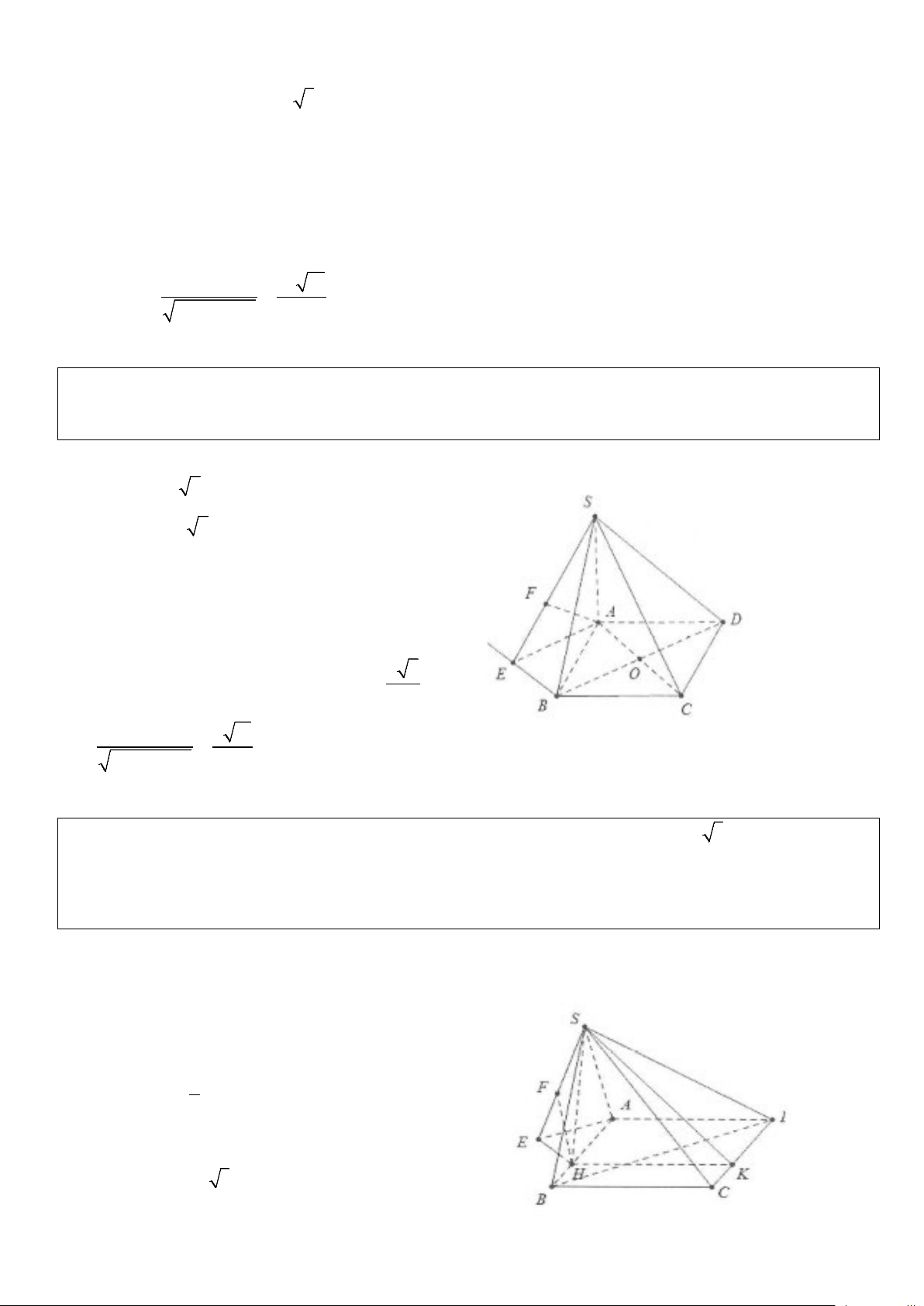
Ví dụ 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt
phẳng đáy. Cho biết SB = 3a, AB = 4a, BC = 2a . Tính khoảng cách từ B đến mặt phẳng (SAC). A. 12a 61 B. 4a C. 12a 29 D. 3a 14 61 5 29 14 Lời giải
Ta có: BS, BA, BC đôi một vuông góc với nhau nên ta có: 1 1 1 1 1 1 1 61 = + + = + + = 2 d ( ; B (SAC)) 2 2 2 2 2 2 2 SB AB AC 9a 16a 4a 144a
Do đó d (B (SAC)) 12a 61 ; = . Chọn A. 61
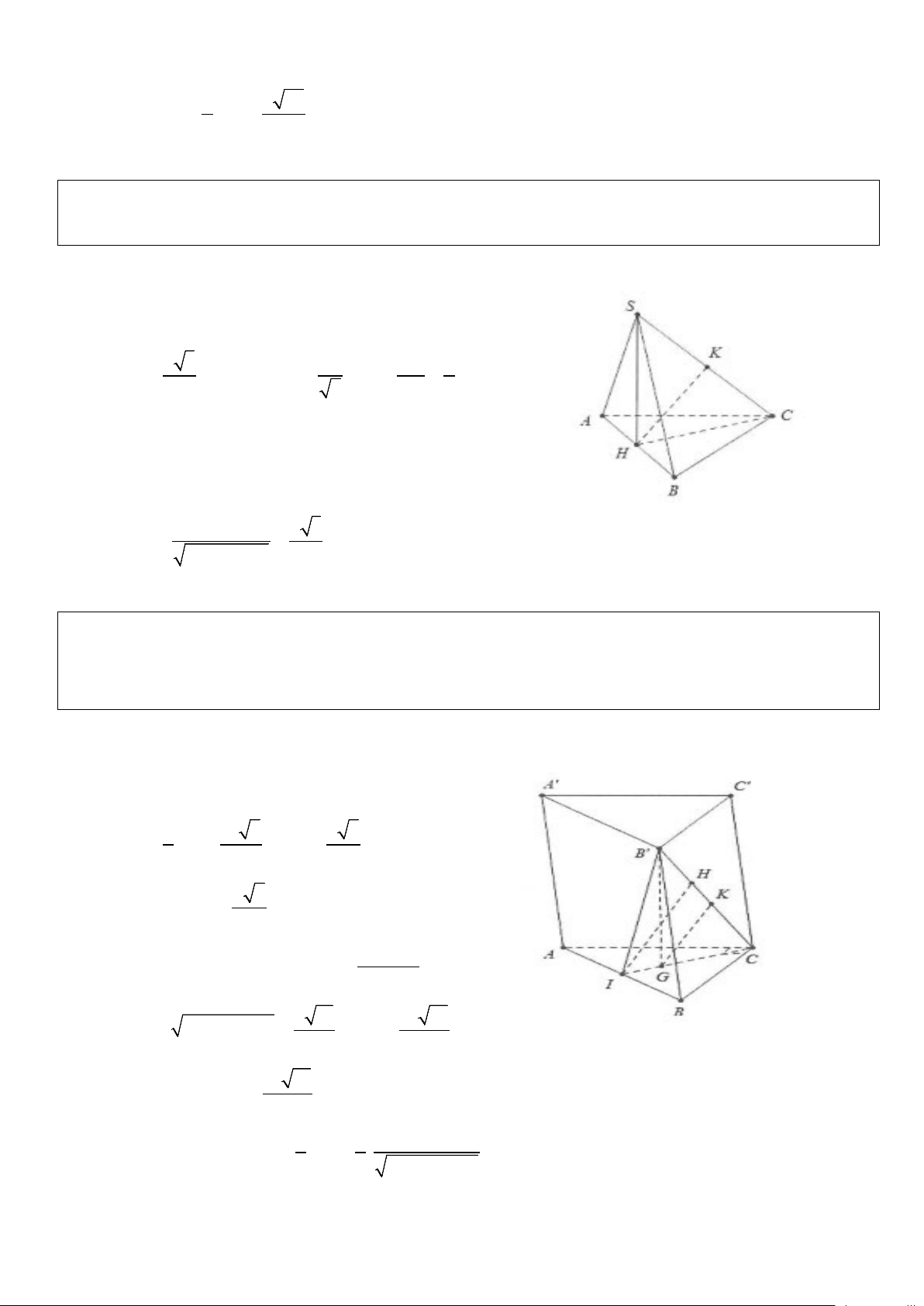
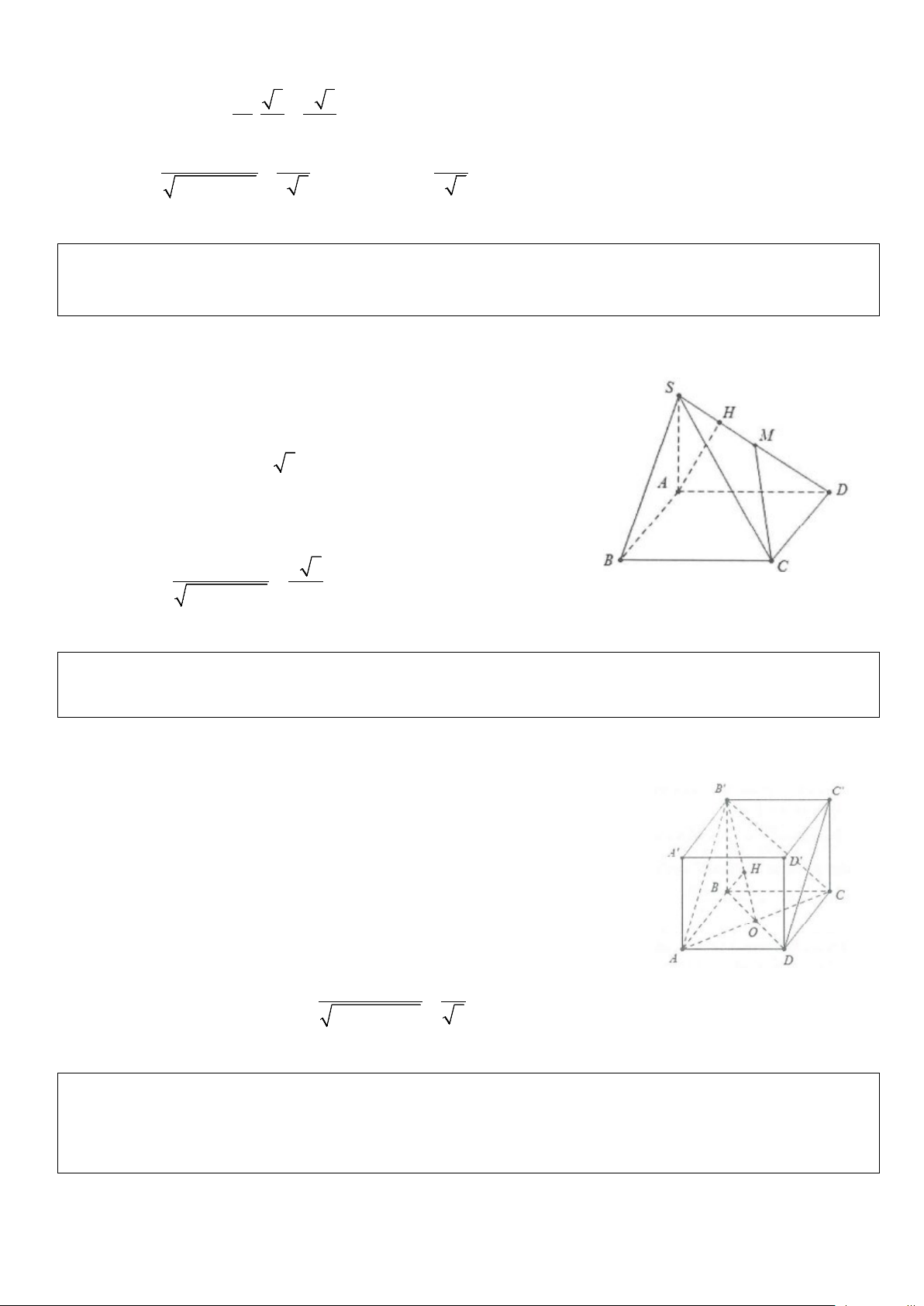
Ví dụ 5: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và AB = a, BC = a 3 . Hình chiếu
vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm H của cạnh AC. Biết SH = a , tính khoảng cách
từ H đến các mặt phẳng (SAB) và (SAC). Lời giải
Dựng HE ⊥ AB và HF ⊥ SE thì ta có d (H;(SAB)) = HF .
Mặt khác HE là đường trung bình trong tam giác ABC nên BC a 3 HE = = . 2 2
Khi đó d (H (SAB)) HE.SH a 21 ; = HF = = . 2 2 HE + SH 7
Tương tự dựng HM ⊥ BC, HN ⊥ SM ⇒ d (H;(SBC)) = HN Mặt khác AB a SH.HM a HM = = ⇒ HN = = . 2 2 2 2 SH + HM 5
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, AD = 2a , SA vuông góc với
đáy và SA = a .
a) Tính khoảng cách từ A đến mặt phẳng (SCD) và (SBC).
b) Tính khoảng cách từ A đến mặt phẳng (SBD). Lời giải BC ⊥ SA
a) Dựng AN ⊥ SB . Do ⇒ BC ⊥ AN . BC ⊥ AB ⊥ ( ) ⇒ ( ( )) . ; SA AB AN SBC d A SBC = AN = 2 2 SA + AB
Vậy ( A (SBC)) a 2 ; = . 2 Tương tự ( ( )) S . A AD 2 ; a d A SCD = AM = = . 2 2 SA + AD 5
b) Dựng AE ⊥ BD,AF ⊥ SE .
Ta chứng minh được d ( ;
A (SBD)) = d = AF Vì 1 1 1 1 2a
AS ⊥ AB ⊥ AD ⇒ = + + ⇒ d = . 2 2 2 2 d AB AD SA 3
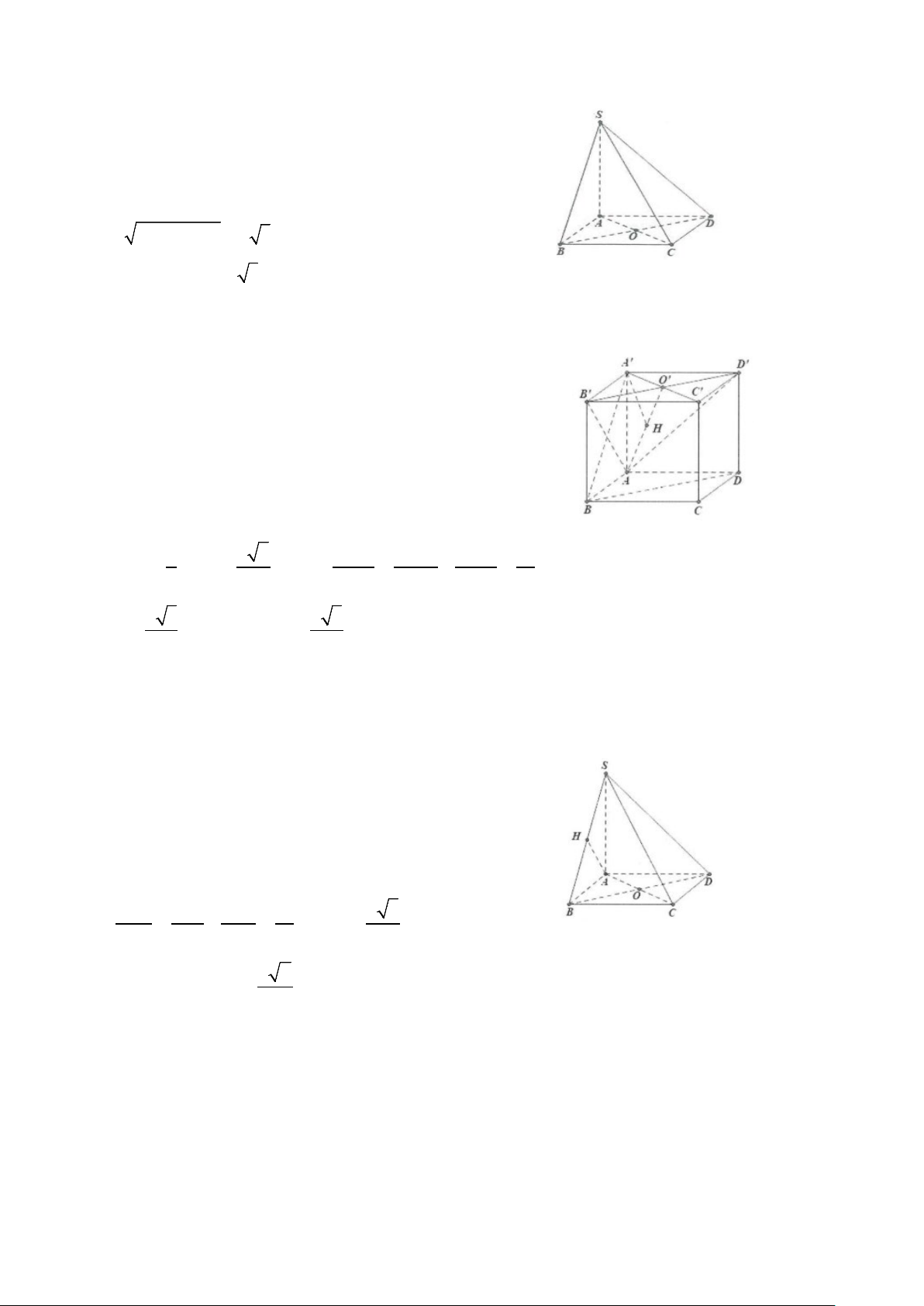
Ví dụ 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a . Hình chiếu vuông góc của đỉnh S lên
mặt đáy trùng với trung điểm H của AB. Biết SD = 3a .
a) Tính khoảng cách từ H đến mặt phẳng (SCD) .
b) Tính khoảng cách từ điểm H đến mặt phẳng (SBD). Lời giải a) Ta có: 2 2
HD = AH + AD = a 5 Mặt khác 2 2
SH = SD − DH = 2a .
Dựng HM ⊥ CD, HN ⊥ SM ⇒ d (H;(SCD)) = HN .
Do AHMD là hình chữ nhật nên AD = HM = 2a . Khi đó ( ( )) SH. ; HM d H SCD = = a 2 . 2 2 SH + HM
b) Dựng HE ⊥ B ;
D HF ⊥ SE khi đó d (H;(SBD)) = HF Ta có: OA a 2
AC = 2a 2 ⇒ OA = a 2 ⇒ HE = = 2 2 Do đó 1 1 1 2a 2 = + ⇒ = ⇒ ; a HF d H SBD = HF = . 2 2 2 ( ( )) HF SH HE 3 3
Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi có tam giác ABC đều cạnh a . Gọi H là trung
điểm của AB. Biết SH vuông góc với mặt đáy, mặt phẳng (SCD) tạo với đáy một góc 60°. Tính
a) Khoảng cách từ H đến mặt phẳng (SCD) .
b) Khoảng cách từ H đến mặt phẳng (SBC). Lời giải a) Do A
∆ BC đều nên CH ⊥ AB ⇒ CH ⊥ CD
CH ⊥ (SHC) ⇒ a 3 SCH = 60 ,°CH = . 2 Ta có: 3 = tan 60 a SH CH ° = . 2 a 3
HK ⊥ BC, HK =
; HF ⊥ SK ⇒ HF ⊥ (SBC) 4 Mặt khác: HK.SH 42a HF = = . 2 2 HK + SH 14
Khi đó d (H (SBC)) a 42 ; = 14
b) Dựng HE ⊥ SC ta có: HE ⊥ (SCD) . Ta có: HC.SH 3a = = ⇒ ( ( )) 3 ; a HE d H SCD = HE = . 2 2 HC + SH 4 4
Ví dụ 9: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AD AB = BC = . Mặt 2
phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết SA = 2a và đường thẳng SD tạo với mặt
phẳng (SAC) một góc 30° . tính
a) Khoảng cách từ A đến mặt phẳng (SCD) .
b) Khoảng cách từ A đến mặt phẳng (SBC). Lời giải (
SAB) ⊥ ( ABCD) a) Do
⇒ SA ⊥ ( ABCD) ( . SAD ) ⊥ ( ABCD) Đặt AD AB = BC =
= x , gọi E là trung điểm của AC ta có: 2 1
CE = AB = AD ⇒ A
∆ CD vuông tại C (tính chất trung 2
tuyến ứng cạnh huyền trong tam giác vuông). +) Khi đó ta có: 2 2
SC = 2x + 4a ,CD = x 2 . C D ⊥ SA +) Mặt khác:
⇒ CD ⊥ (SAC). C D ⊥ AC Do đó ( ; SD (SAC)) = DC x 2 1 2 2
DSC = 30° ⇒ tan 30° = ⇒ =
⇔ 4x = 4a ⇔ x = a . 2 2 SC 2x + 4a 3 Dựng ⊥ ⇒ ⊥ ( ) ⇒ ( ( )) S . A AC 2 ; a AK SC AK SCD d A SCD = AK = = . 2 2 SA + AC 3 BC ⊥ SA
b) Dựng AH ⊥ SB , ta có: ⇒ BC ⊥ AH . BC ⊥ AB
Mặt khác: AH ⊥ SB ⇒ AH ⊥ (SBC) . Do đó A . B SA 2a = = ⇒ ( ( )) 2 ; a AH d A SBC = AH = . 2 2 AB + SA 5 5
Ví dụ 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tam giác SAD là tam giác vuông cân tại
S và thuộc mặt phẳng vuông góc với đáy. Biết SA = a 2 và SB tạo với đáy một góc 30° . Gọi H là trung
điểm của AD. Tính các khoảng cách sau:
a) d (H;(SBC))
b) d (H;(SAC)) Lời giải
a) Gọi H là trung điểm của AD ta có: SH ⊥ AD
Lại có: (SAD) ⊥ ( ABCD) ⇒ SH ⊥ ( ABCD) . Mặt khác: 1
AD = SA 2 = 2a ⇒ SH = AD = a . 2
SBH = 30° ⇒ HB tan 30° = SH = a ⇒ HB = a 3 Khi đó: 2 2
AB = HB − AH = a 2 HE ⊥ BC Dựng
ta có: BC ⊥ HF từ đó suy ra HF ⊥ (SBC) ⇒ d (H;(SBC)) = HF . HE ⊥ SE Ta có: 1 1 1 a 6 = + ⇒ HF = = d H; SBC . 2 2 2 ( ( )) HF SH HE 3
b) Dựng HN ⊥ AC ⇒ AC ⊥ (SHN ) , dựng HI ⊥ SN ⇒ HI ⊥ (SAC) Dựng 2a 2 a HN.SH a
DM ⊥ AC ⇒ DM = ⇒ HN = ⇒ HI = = . 2 2 6 3 HN + SH 2 Do đó ( ;( )) a d H SAC = HI = 2
Ví dụ 11: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân ( AD / /BC) có
AB = BC = CD = a, AD = 2a , SA vuông góc với đáy. Biết mặt phẳng (SCD) tạo với mặt phẳng
( ABCD) một góc 60°. Tính cách các khoảng cách sau: a) d ( ; A (SCD)) b) d ( ; A (SBC)) Lời giải
a) Gọi O là trung điểm của cạnh AD ta có tứ giác ABCO là hình bình hành 1
⇒ AB = CO = a = AD do đó
ACD = 90° ⇒ AC ⊥ CD 2
mà SA ⊥ CD nên (SAC) ⊥ ⇒ CD SCA = 60° . +) Ta có: 2 2
AC = AD − CD = a 3 suy ra SA = AC tan 60° = 3a
+) Dựng AE ⊥ SC, AE ⊥ CD ⇒ AE ⊥ (SCD) .
+) Khi đó d (B SCD) = d (O SCD) 1 ; ; = d ( ; A (SCD)) . 2 +) Ta có: S . A AC 3a = = ⇒ ( ( )) 3 ; a AE d A SCD = AE = . 2 2 SA + AC 2 2
b) Dựng AK ⊥ BC, AH ⊥ SK ⇒ AH ⊥ (SBC) +) Ta có: d ( ;
A (SBC)) = AH . +) Mặt khác: = ( ) AC.CD a 3 AK.SA 3 ; a AK d C AD = = ⇒ AH = = 2 2 2 2 AC + CD 2 SA + AK 13 Do đó ( ( )) 3 ; a d A SBC = AH = . 13
Ví dụ 12: Cho hình lăng trụ đứng ABC.A'B 'C 'có đáy là tam giác đều cạnh a , gọi I là trung điểm cạnh
BC, đường thẳng A’C tạo với đáy một góc 60°.
a) Tính khoảng cách từ A đến mặt phẳng ( A'BC) .
b) Tính khoảng cách từ A đến mặt phẳng (α ) chứa A’I và song song với AC. Lời giải
a) Do AA ⊥ ( ABC) ⇒ ( A ( ABC)) = ' 'C; A'CA. Ta có:
A'CA = 60° ⇒ AA' = AC tan 60° = a 3
Dựng AI ⊥ BC ⇒ BC ⊥ ( A' AI ) và a 3 AI = 2
Dựng AH ⊥ A'I ⇒ d ( ;
A ( A'BC)) = AH Ta có: AI.AA' a 15 AH = = 2 2 AI + AA' 5
Vậy d ( A ( A BC)) a 15 ; ' = AH = 5
b) Dựng Ix / / AC ⇒ (α ) ≡ ( A'Ix) Khi đó: d ( ; A (α )) = d ( ;
A ( A'Ix)), Ix cắt AB tại trung điểm M và AB.
Dựng AK ⊥ Ix, AE ⊥ A'K Do ⇒ = IM / / AC AMK MAC = 60° suy ra = a a 3
AK AM sin AMK = sin 60° = 2 4
Ta có: d ( A ( A IK )) AK.A' A a 51 ; ' = AE = = 2 2 AK + A' A 17
Ví dụ 13: Cho hình lăng trụ ABC.A'B 'C 'có đáy là tam giác vuông cân tại A với AB = AC = 3a . Hình
chiếu vuông góc của B’ lên mặt đáy là điểm H thuộc BC sao cho HC = 2HB . Biết cạnh bên của lăng trụ bằng 2a .
a) Tính khoảng cách từ H đến mặt phẳng (B' AC) .
b) Tính khoảng cách từ H đến mặt phẳng (BAA'B') . Lời giải a) Ta có: 2 2
BC = AB + AC = 3a 2 ⇒ HB = a 2 Lại có 2 2
B 'H = BB ' − HB = a 2
Dựng HE ⊥ AC, HF ⊥ B 'E ⇒ HF ⊥ (B' AC)
Áp dụng định lý Talet trong tam giác BAC ta có: HE CH 2 HE.B 'H 2 = = ⇒ = 2 a HE a ⇒ HF = = 2 2 AB BC 3 HE + B 'H 3 Do có: ( ( )) 2 ; ' a d H B AC = HF = 3
b) Dựng HM ⊥ AB, HN ⊥ B 'M
Khi đó d (H;(B'BA)) = HN . Ta có: AC HB '.HM a 6 HM = = a ⇒ HN = = . 2 2 3 HB ' + HM 3
Dạng 3: Khoảng cách từ một điểm bất kỳ đến mặt bên.
Nếu AB / / (α ) thì ta có d ( ; A (α )) = d ( ; B (α )) . d ( ; A (α )) AI
Nếu AB cắt (α ) tại I thì ta có: = (định lý Talet). d ( ; B (α )) BI
Xét bài toán: Tính khoảng cách từ điểm C bất kỳ đến mặt phẳng bên (SAB).
Nếu CH / / (SAB) ⇒ d (C;(SAB)) = d (H;(SAB)).
d (C; SAB ) Nếu ∩ ( ) ( ) CI CH SAB = I ⇒ =
d (H (SAB)) . ; HI
Quay trở về bài toán tính khoảng cách từ chân đường cao H đến mặt phẳng bên.
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB = a, BC = 2a . Tam giác SAC cân tại
S và thuộc mặt phẳng vuông góc với đáy. Biết 3a SB = , tính: 2
a) Khoảng cách từ điểm C đến mặt phẳng (SAB).
b) Khoảng cách từ A đến mặt phẳng (SBC) . Lời giải
a) Gọi H là trung điểm của AC⇒ SH ⊥ AC
Mặt khác (SAC) ⊥ ( ABC) ⇒ SH ⊥ ( ABC) 2 2 Ta có: AC AB BC a 5 BH + = = =
(trong tam giác vuông thì trung 2 2 2
tuyến ứng với cạnh huyền bằng nửa cạnh ấy). Do đó 2 2
SH = SB − BH = a
Dựng HE ⊥ AB, HF ⊥ SE khi đó HF ⊥ (SAB)
Do vậy d (H;(SCD)) = HF . Lại có BC HE = = a 2 Mặt khác 1 1 1 SH.HE a 2 = + ⇒ HF = = 2 2 2 2 2 HF HE SH SH + HE 2 d(C;(SAB)) Lại có CA = = ⇒ = = . d( 2 d(C; SAB ) 2d(H; SAB ) H;(SAB)) ( ) ( ) a 2 HA
b) Dựng HM ⊥ BC,HN ⊥ SM ⇒ d(H;(SBC)) = HN . Trong đó AB a SH.HM a HM = = ⇒ HN = = 2 2 2 2 SH + HM 5 d(A;(SBC)) Lại có AC 2a = = ⇒ = = = . d( 2 d(A; SBC ) 2d(H; SBC ) H;(SBC)) ( ) ( ) 2HN HC 5
Ví dụ 2: Cho hình chóp S.ABC có SA ⊥ (ABC) , đáy là tam giác đều cạnh a. Biết SB = a 5 .
a) Tính khoảng cách từ trung điểm K của SA đến mặt phẳng (SBC) .
b) Tính khoảng cách từ trung điểm I của SB đến mặt phẳng (SAC) . Lời giải a) Dựng a 3
AM ⊥ BC ⇒ AM = ACsinC = a sin 60° = 2 BC ⊥ SA Dựng AN ⊥ SM . Do ⇒ BC ⊥ AN BC ⊥ AM
Lại có AN ⊥ SM ⇒ AN ⊥ (SBC) Mặt khác 2 2 1 1 1 SA = SB − AB = 2a, = + 2 2 2 AN SA AM ⇒ ( ( )) 2a 57 d A; SBC = AN = 19 d(K;(SBC))
Do K là trung điểm của SA nên ta có KS 1 1 a 57 = = ⇒ = = . d( d(K; SBC ) A;(SBC)) ( ) AN AS 2 2 19 b) Dựng a 3 BE ⊥ AC ⇒ BE = 2 Mặt khác ⊥ ⇒ ⊥ ( ) ⇒ ( ( )) a 3 BE SA BE SAC d B; SAC = BE = 2 d(B;(SAC)) Do BS 1 a 3 = = ⇒ = = . d( 2 d(I; SAC ) d(B; SAC ) I;(SAC)) ( ) ( ) IS 2 4
Ví dụ 3: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 3a, hình chiếu vuông góc của đỉnh S trên mặt
phẳng đáy và điểm H thuộc cạnh AB sao cho HB=2HA. Biết SC tạo với đáy một góc 45°. Tính các khoảng cách sau: a) d(B;(SAC)) b) d(I;(SBC)) Lời giải
a) Tam giác ABC đều nên HAC = 60°. Ta có: 2 2
HC = AH + AC − 2AH.ACcos60° = a 7 Mặt khác ( ( )) = SC; ABC SCH = 45° ⇒ SH = HC = a 7 BA d(B;(SAC)) Ta có: = HA d(H;(SAC)) ⇒ d(B;(SAC)) = 3d(H;(SAC))
Dựng HE ⊥ AC,HF ⊥ SE ⇒ HF ⊥ (SAC) Ta có: a 3 HE = HAsin 60° = a sin 60° = 2 HE.SH a 651 ⇒ = = ⇒ ( ( )) 3a 651 HF d B; SAC = 3HF = 2 2 SH + HE 31 31 d(A;(SBC)) b) Ta có: AB 3 3 = = ⇒ = d( d(A; SBC ) d(H; SBC ) H;(SBC)) ( ) ( ) HB 2 2
Dựng HM ⊥ BC,HN ⊥ SM ⇒ d(H;(SBC)) = HN Mặt khác SH.HM a 210
HM = HBsin 60° = 2a sin 60° = a 3 ⇒ HN = = 2 2 SH + HM 10 Do đó ( ( )) 3 3a 210 d A; SBC = HN = . 2 20
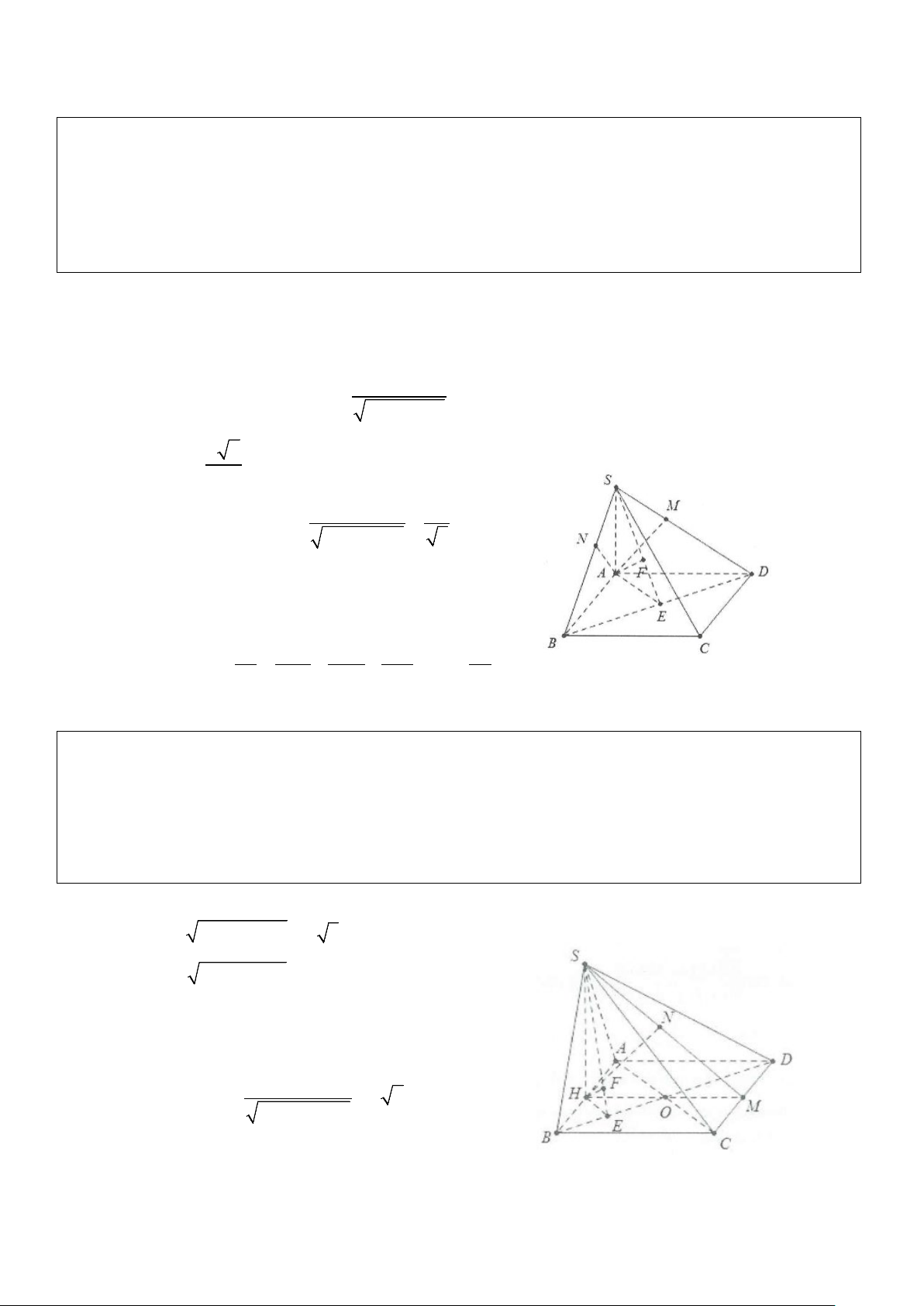
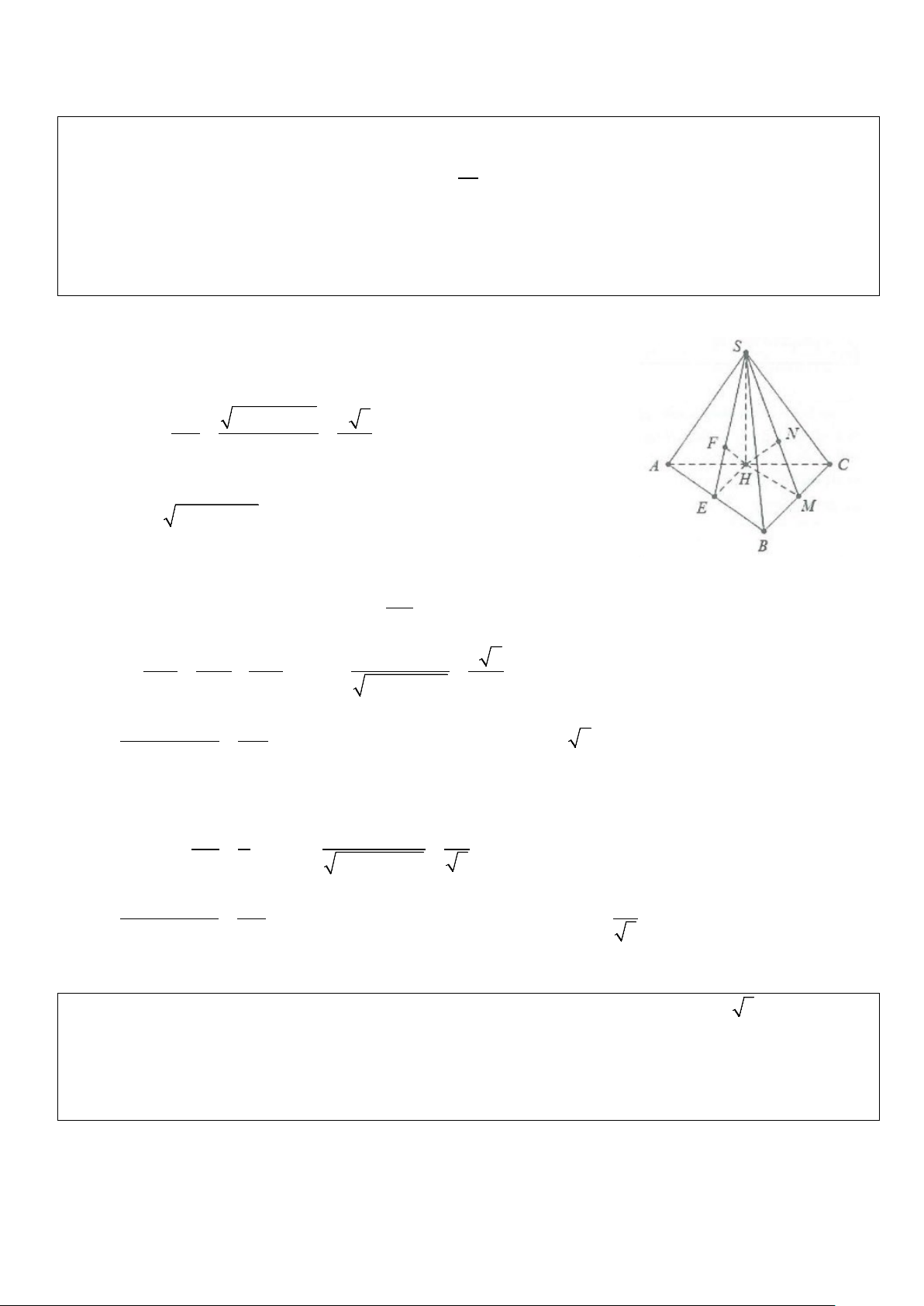
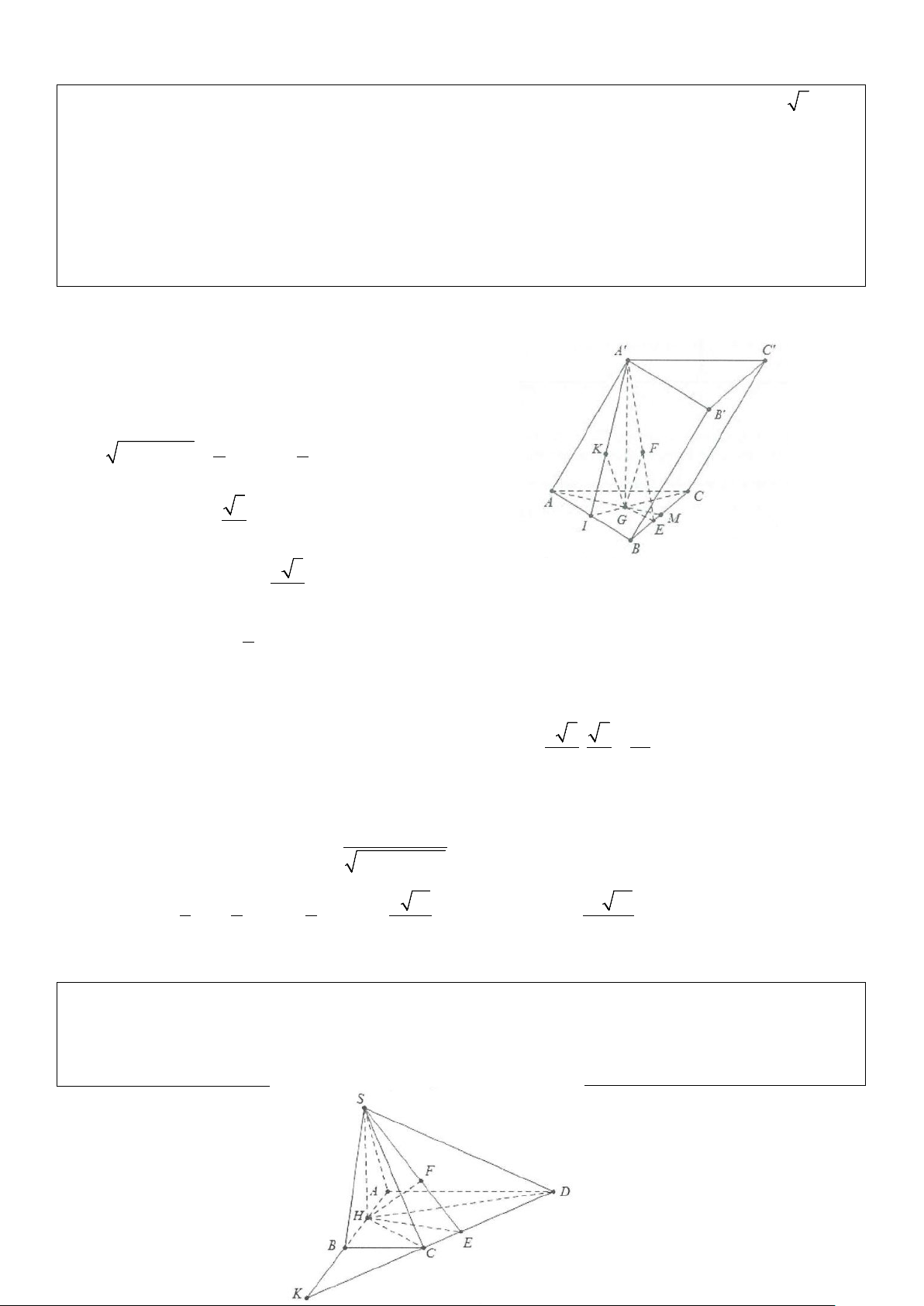
Ví dụ 4: Cho hình chóp tam giác đều S.ABC có đáy là tam giác đều cạnh. Cạnh bên tạo với đáy góc 60°.
Tính khoảng cách từ A đến mặt phẳng (SBC) . Lời giải
Gọi G là trọng tâm tam giác ABC ⇒ SG ⊥ (ABC)
Gọi M là trung điểm của BC ⇒ BC ⊥ GM , lại có: BC ⊥ SG suy ra BC ⊥ (SGM) . GE ⊥ SM Dựng GE ⊥ SM ⇒ ⇒ GE ⊥ (SBC) GE ⊥ BC Do đó d(G;(SBC)) = GE trong đó 1 1 a 3 a 3 2 a 3 GM = AM = . = ,GA = AM = 3 3 2 6 3 3 Do ⊥ ⇒ ( ( )) = SG (ABC) SA; ABC SAG = 60° a 3 ⇒ SG = GA tan 60° = tan 60° = a 3 d(A;(SBC)) Do đó SG.GM a GE = = , mặt khác AM = = 3 2 2 SG + GM 13 d(G;(SBC)) GM Vậy ( ( )) = ( ( )) 3a d A; SBC 3d G; SBC = . 13
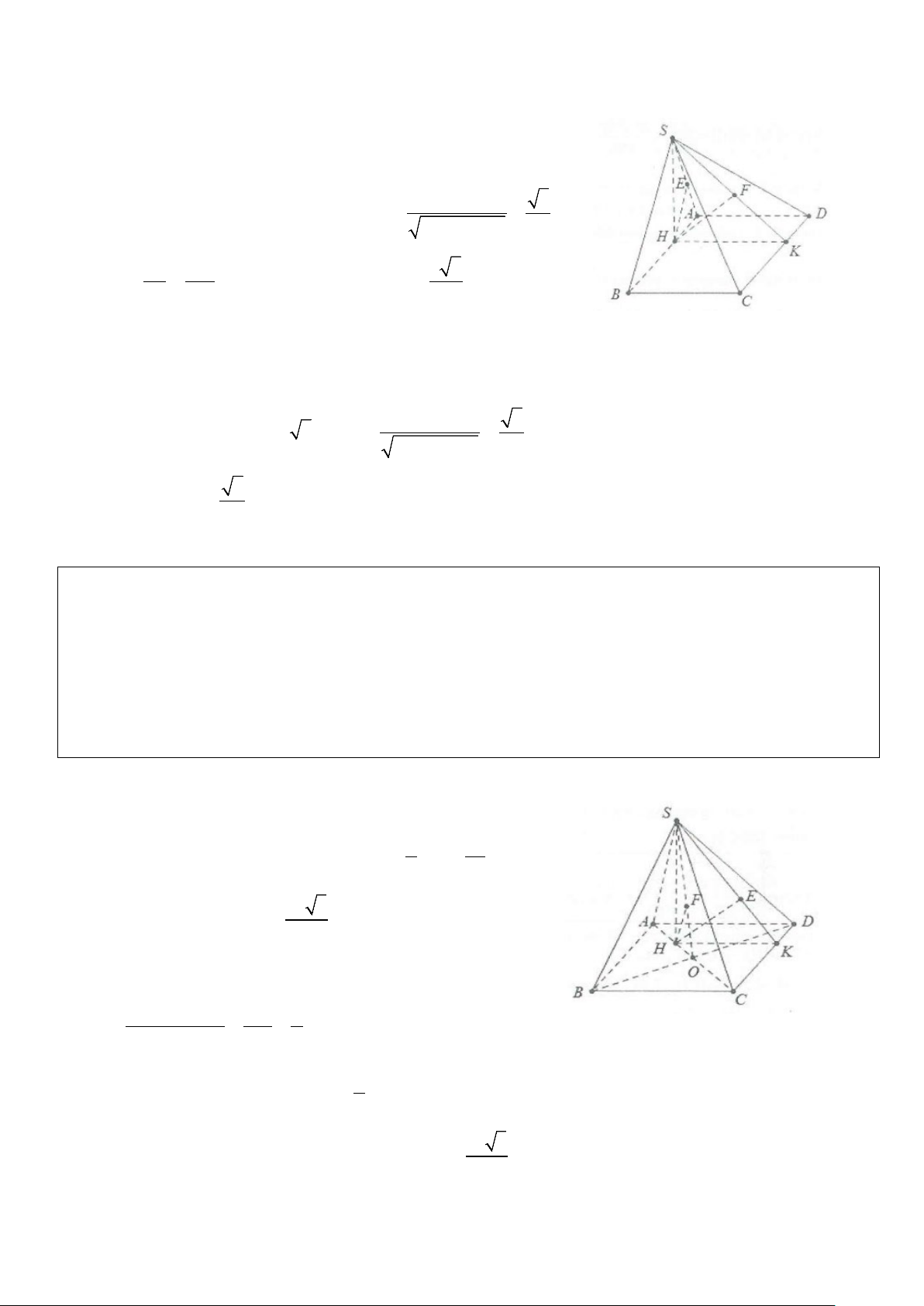
Ví dụ 5: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO=a
a) Tính khoảng cách từ A đến mặt phẳng(SCD) .
b) Tính khoảng cách từ trung điểm của SO đến mặt phẳng (SCD) . Lời giải
a) Dựng OE ⊥ SE,OF ⊥ SE ⇒ d(O;(SCD))=OF Mặt khác AD SO.OE a 2 OE = = a ⇒ d =OF= = 0 2 2 2 SO + OE 2 d(A;(SCD)) Lại có: = ⇒ = = d( 2 d(A; SCD ) O;(SCD)) ( ) 2d a 2 o
b) Gọi M là trung điểm của SO thì d(M;(SCD)) MS 1 1 a 2 = = ⇒ = = d( d(M; SCD ) O;(SCD)) ( ) do OS 2 2 4
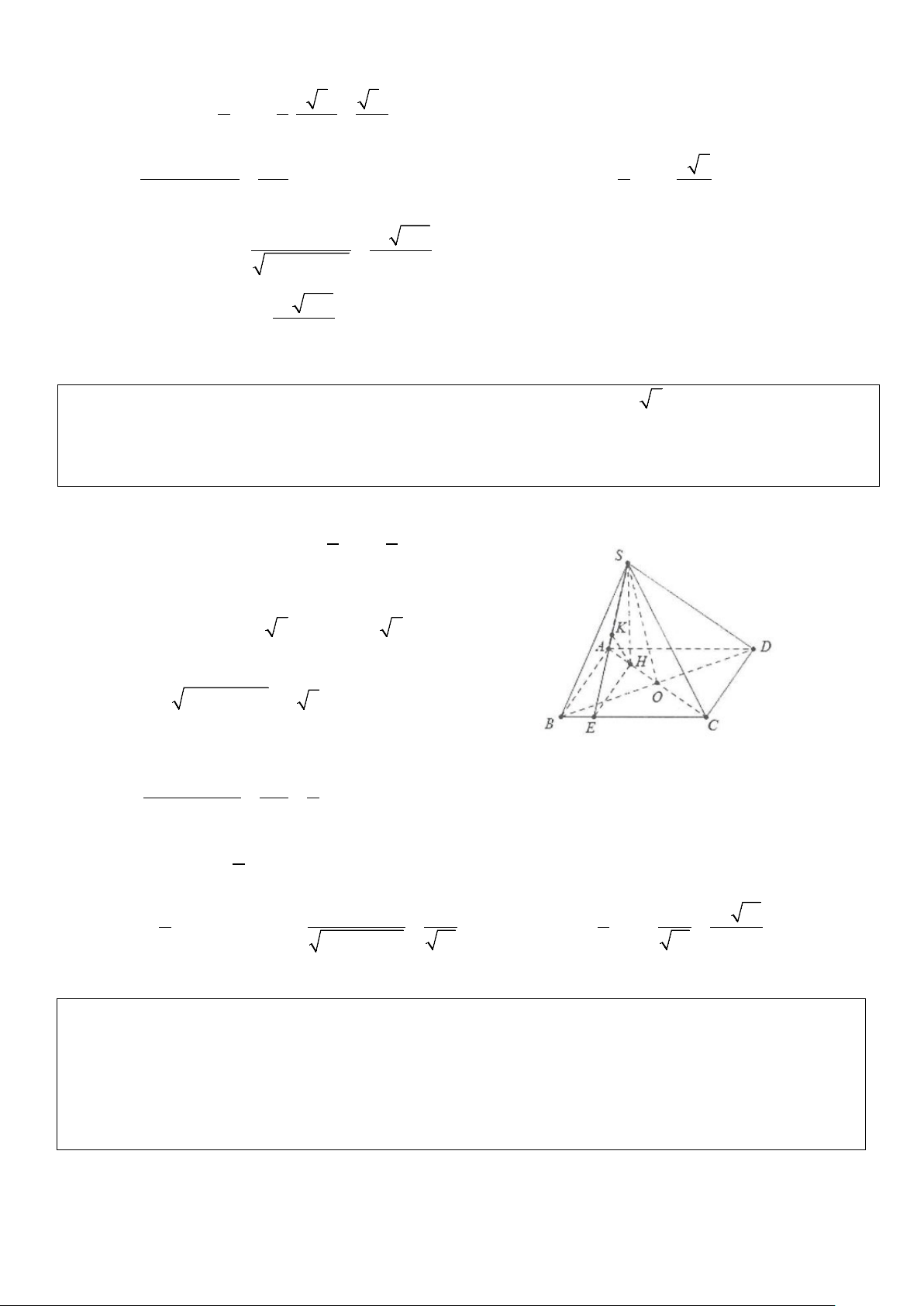
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, biết BAD =120° và
SO ⊥ (ABCD). Biết SO = a 3 , tính khoảng cách từ A đến mặt phẳng (SCD) . Lời giải
Dựng OE ⊥ CD,OF ⊥ SE ⇒ d(O;(SCD))=OF Do = ° ⇒ BAD 120 CAD = 60° ⇒ C
∆ AD là tam giác đều cạnh a Khi đó a 3 a 3
OCE = 60° ⇒ OE = OCsin 60° = . = 2 2 4 Do đó SO.OE a 51 OF = = = d(O;(SCD)) 2 2 SO + OE 17 d(A;(SCD)) Mặt khác AC = = d(O;(SCD)) 2 OC ⇒ ( ( )) 2a 51 d A; SCD = 2OF = 17
Ví dụ 7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3AD = 3. Hình chiếu vuông góc của
đỉnh S lên mặt phẳng (ABCD) là điểm H∈AB sao cho HB = 2HA . Biết SH = 3
a) Tính khoảng cách từ B đến mặt phẳng (SAD).
b) Tính khoảng cách từ A đến mặt phẳng (SCD) . Lời giải a) AB = 3 ⇒ HA =1 AD ⊥ SH Dựng HE ⊥ SA . Ta có: ⇒ AD ⊥ HE AD ⊥ AB Khi đó ⊥ ( ) ⇒ ( ( )) HA.SH 3 HE SAD d H; SAD = HE = = 2 2 HA + SH 2 Mặt khác d BA 3 3 B = = 3 ⇒ d(B;(SAD)) = 3d = H d HA 2 H
b) Do AH / /CD ⇒ AH / / (SCD) ⇒ d(A;(SCD)) = d(H;(SCD))
Dựng HK ⊥ CD,HF ⊥ SK ⇒ d(H;(SCD))=HF Mặt khác SH.HK 3 HK = AD =1,SH = 3 ⇒ HF = = 2 2 SH + HK 2 Vậy ( ( )) 3 d A; SCD = 2
Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, hình chiếu của đỉnh S trên
mặt phẳng đáy trùng với trung điểm của cạnh OA. Biết góc giữa mặt phẳng (SCD) và đáy bằng 60°. Tính khoảng cách: a) d(B;(SCD)) b) d(A;(SBD)) Lời giải
a) Dựng HK ⊥ CD ⇒ CD ⊥ (SHK) (( ) ( )) = SCD ; SHK SKH = 60°. Ta có: 3 3a HK = AD = 4 4 Mặt khác 3a 3 SH = HK tan 60° = 4
Ta có: AB / /CD ⇒ AB / / (SCD) d(A;(SCD)) Lại có: AC 4 = = d(H;(SCD)) HC 3 Do đó: ( ( )) = ( ( )) 4 d B; SCD d A; SCD = d(H;(SCD)) 3 Dựng ⊥ ⇒ = 3a 3 HE SK HE HK sin HKE = HK sin 60° = 8 Vậy ( ( )) 4 4 3 3a 3a d B; SCD = HE = . = 3 3 8 2 d(A;(SBD)) b) Ta có: AO 1 a 2 = = ⇒ = = = d( 2 d(A; SBD ) 2d(H; SBD ) H;(SBD)) ( ) ( ) ,HO AC HO 4 4 Dựng HO.SH 3a 696 HF ⊥ SO ⇒ HF = = 2 2 HO + SH 232 Vậy d(A;(SBD)) 3a 696 = 2HF = 232
Ví dụ 9: Cho hình chóp S.ABCD có đáy hình vuông ABCD tâm O, SA = 2a 2 . Hình chiếu vuông góc của
S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh OA, biết tam giác SBD vuông tại S. Tính khoảng
cách từ điểm D đến mặt phẳng (SBC) Lời giải
Ta có ∆SBD vuông tại S nên 1 1 SO = BD = AC 2 2 ⇒ S
AC vuông tại S ta có: 2 2 SA = HA.AC = 4HA 2 2
⇔ 8a = 4HA ⇔ HA = a 2 ⇔ AC = 4a 2 ⇒ AB = AC = 4a Khi đó: 2 2 SH = SA − HA = a 6
Do AD / /BC ⇒ d(D;(SBC)) = d(A;(SBC)) d(A;(SBC)) Mặt khác AC 4 = = d(H;(SBC)) HC 3 Do đó ( ( )) 4
d D; SBC = d(H;(SBC)) . Dựng HE ⊥ BC,HK ⊥ SE ⇒ HK ⊥ (SBC) . 3 Ta có 3 HE.SH 6a = = ⇒ = = ⇒ ( ( )) 4 8a 4a 10 HE AB 3a HK d D; SBC = HK = = 2 2 4 HE + SH 10 3 10 5
Ví dụ 10: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB là đáy lớn và tam
giác ABC là tam giác đều. Các mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy, cạnh bên SC = 2a
và khoảng cách từ C đến mặt phẳng (SAB) bằng a. Tính khoảng cách từ điểm A đến mặt phẳng (SBC). Lời giải ( SAB) ⊥ (ABC) Ta có: ( ) ⊥ ( ) ⇒ SA ⊥ (ABC) SAC ABC
Gọi M là trung điểm của AB suy ra CM ⊥ AB ⇒ CM ⊥ (SAB) Do đó d(C;(SAB)) = CM = a 2 2 ⇒ SM = SC − CM = a 3
Gọi K là trung điểm của BC nên AK = CM = a Lại có 3 2a CM = AB ⇒ AB = 2 3 a 2a 6 ⇒ AM = ⇒ SA =
. Kẻ AH ⊥ SK,H ∈SK nên AH ⊥ (SBC) ⇒ d(A;(SBC)) = AH 3 3 Khi đó 1 1 1 1 1 2a 22 = + = + ⇒ AH = 2 2 2 2 2 AH SA AK a 11 2a 6 3
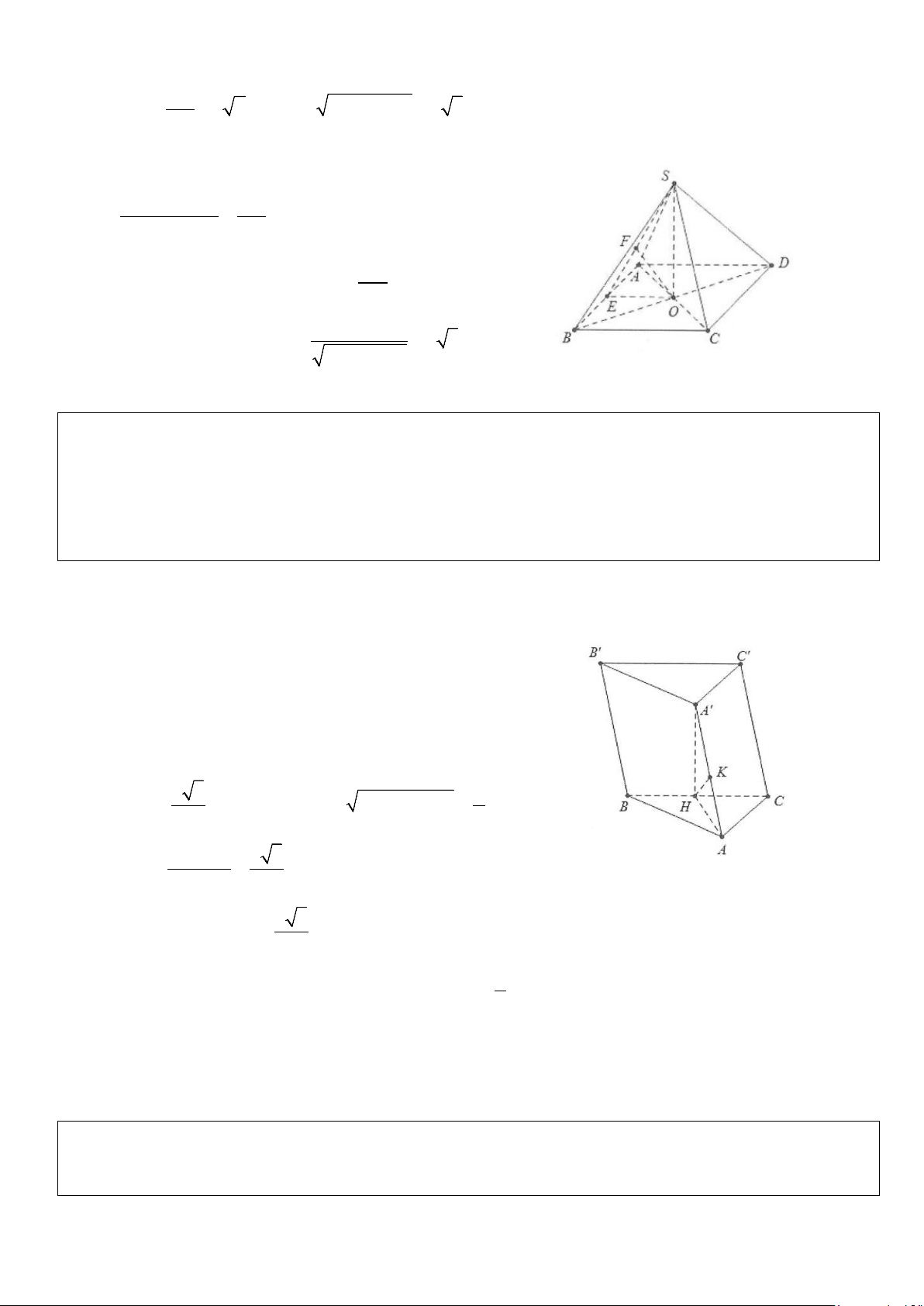
Ví dụ 11: Cho hình chóp S.ABCD có đáy là lục giác đều cạnh a. Tam giác SAD vuông cân tại S và thuộc
mặt phẳng vuông góc với đáy (ABCD) .
a) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
b) Tính khoảng cách từ điểm B đến mặt phẳng (SCD). Lời giải
a) Gọi H là trung điểm của AD ⇒ SH ⊥ AD
Mặt khác (SAD) ⊥ (ABCD) ⇒ SH ⊥ (ABCD) S
∆ AD vuông cân tại S nên AD SH = = a 4
Dễ thấy HC=AB=a ⇒ HC ∆ D đều cạnh a
Dựng HE ⊥ CD,HF ⊥ SE ⇒ d(H;(SCD))=HF Mặt khác a 3 SH.HE a 21 HE = ⇒ HF = = 2 2 2 SH + HE 7 Do D=2HD⇒ ( ( )) 2a 21 d A; SCD = 2HF = 7
b) Dễ thấy HDCB là hình thoi cạnh a Do đó ⇒ ( ) ⇒ ( ( )) = ( ( )) a 21 BH / /CD BD / / SCD d B; SCD d H; SCD = HF = 7
Ví dụ 12: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân AC = BC = a,AB = a 3 , hình
chiếu vuông góc của A’ lên mặt phẳng đáy trùng với trọng tâm G của tam giác ABC. Biết mặt phẳng
(B'C'CB) tạo với đáy một góc 60°. Tính các khoảng cách: a) d(A;(A'BC)) . b) d(C;(ABB'A')) . Lời giải
a) Gọi I là trung tâm của AB ta có: CI ⊥ AB
Dựng GE ⊥ BC ⇒ (A'EG) ⊥ BC Ta có:
A 'EG = 60° ⇒ GA ' = GE tan 60° 2 2 a a CI = BC − IB = ⇒ CG = 2 3 Mặt khác: 3 = ⇒ sin ICB ICB = 60° 2 Khi đó: a 3 GE = CG sin 60° = 6 a ⇒ A 'G = GE tan 60° = 2
Dựng GF ⊥ A 'E ta có: GF ⊥ (A'BC) ⇒ d(G;(A'BC))=GF Ta có: ( ( )) = ( ( )) a 3 3 3a d A; A 'BC
3d G; A 'BC = 3GF = 3GEsin 60° = 3 . = 6 2 4
b) Do CI = 3GI ⇒ d(C;(B'AB)) = 3d(G;(B'AB)) Dựng ⊥ ⇒ ( ( )) GI.A 'G GK A 'I d G; A 'AB = 2 2 GI + A 'G Trong đó 1 a a a 10 = = = ⇒ = ⇒ ( ( )) 3a 10 GI CI ,A 'G GK d C; A 'AB = 3 6 2 20 20
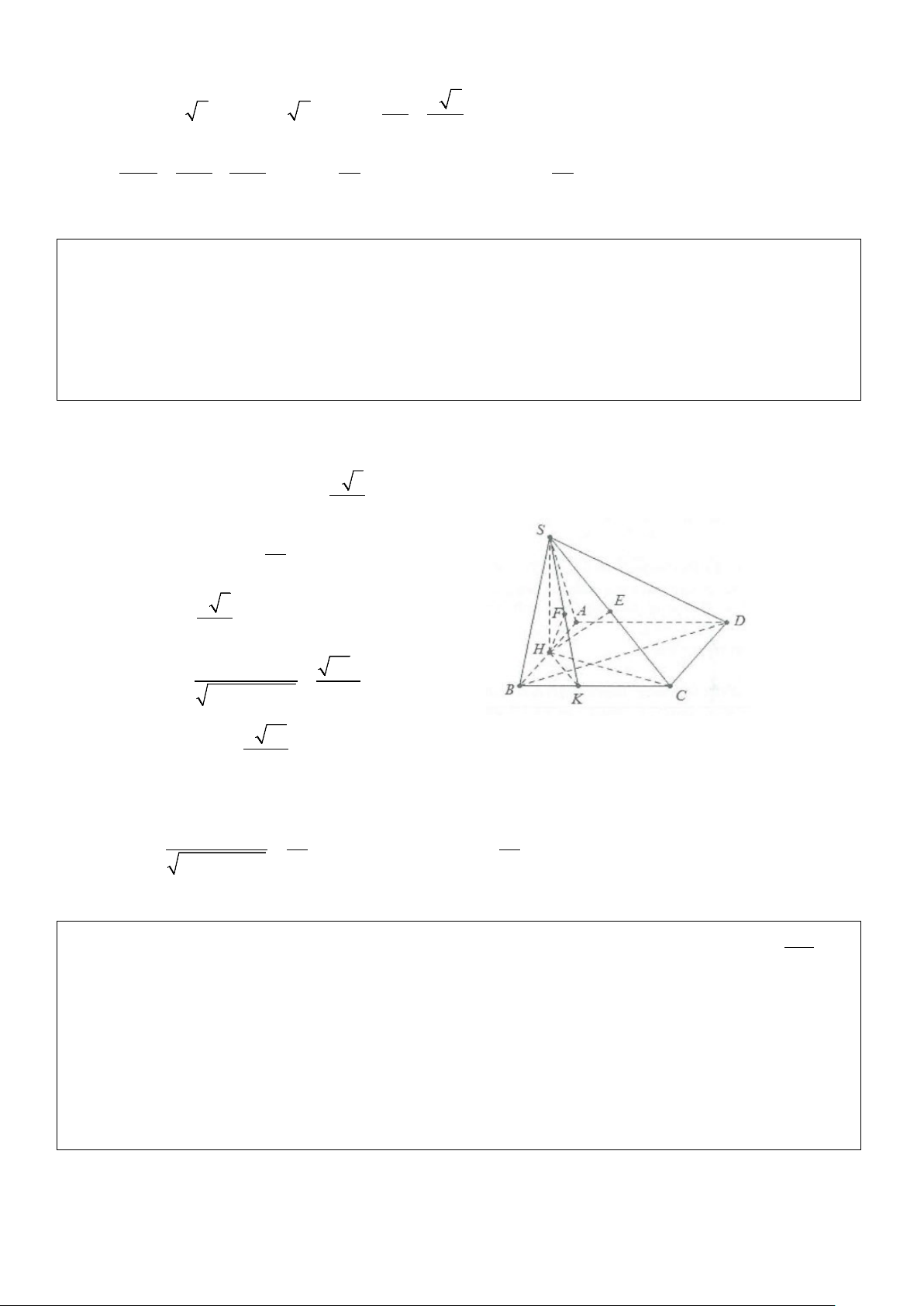
Ví dụ 13: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = AD = 2a,BC = a ,
tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD), biết cạnh bên SD = 3a , tính khoảng
cách từ A đến mặt phẳng SCD Lời giải
Gọi H là trung điểm của AB ta có: SH ⊥ AB mặt khác (ABC) ⊥ (ABCD) ⇒ SH ⊥ (ABCD) Ta có: 2 2
HD = AH + AD = a 5 . Khi đó: 2 2 SH = SD − HD = 2a Gọi KB BC 1 4 K = AB∩ CD ⇒ = = ⇒ AK = HK KA AD 2 3 Ta có: ( ( )) 4 = ( ( )) 4 d A; SCD
d H; SCD = HF. Dựng HE ⊥ CD,HF ⊥ SE ⇒ HF ⊥ (SCD) 3 3 2 2 Ta có: 2
CD = AB + (AD − BC)2 = a 5 ; 2 3a 3a S = S − S − S = 3a − = HCD ABCD HBC HAD 2 2 2 Do vậy 2S 3a 3a SH.HE 6a 8a HCD HE = = = ⇒ HF = = ⇒ d(A;SCD) = . 2 2 CD a 5 5 SH + HE 29 9
Ví dụ 14: Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều cạnh a, AD=2a, tam giác SAB cân tại
S và nằm trong mặt phẳng vuông góc với đáy, cạnh bên SD tạo với đáy một góc ϕ thỏa mãn 1 tan ϕ =
. Tính khoảng cách từ A đến mặt phẳng SCD. 13 Lời giải
Gọi H là trung điểm của AB ta có: SH ⊥ AB
Mặt khác (SAB) ⊥ (ABCD) ⇒ SH ⊥ (ABCD) Ta có: = + − 2 2 2 2 2 a 2 2 13a HD AH AD 2AD.AH.cos HAD = + 4a − 2a .cos60° = 4 4 a 13 ⇒ HD = 2 Ta có: a SDH = ϕ ⇒ SH = HD tan ϕ = 2 Gọi AF 4 F = AB∩ CD ⇒ AF = 2AB ⇒ = HF 3 Do đó: ( ( )) 4 = ( ( )) 4 d A; SCD d H; SCD = HK 3 3 Mặt khác 3a 3 3a 3 HE = HFsin 60° = . = 2 2 4 HE.SH 3a 93 ⇒ = = ⇒ ( ( )) 4 2a 93 HK d A; SCD = HK = 2 2 SH + HE 62 3 61
Dạng 4: Khoảng cách giữa đường thẳng và mặt phẳng song song. Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa đường thẳng và mặt phẳng song song
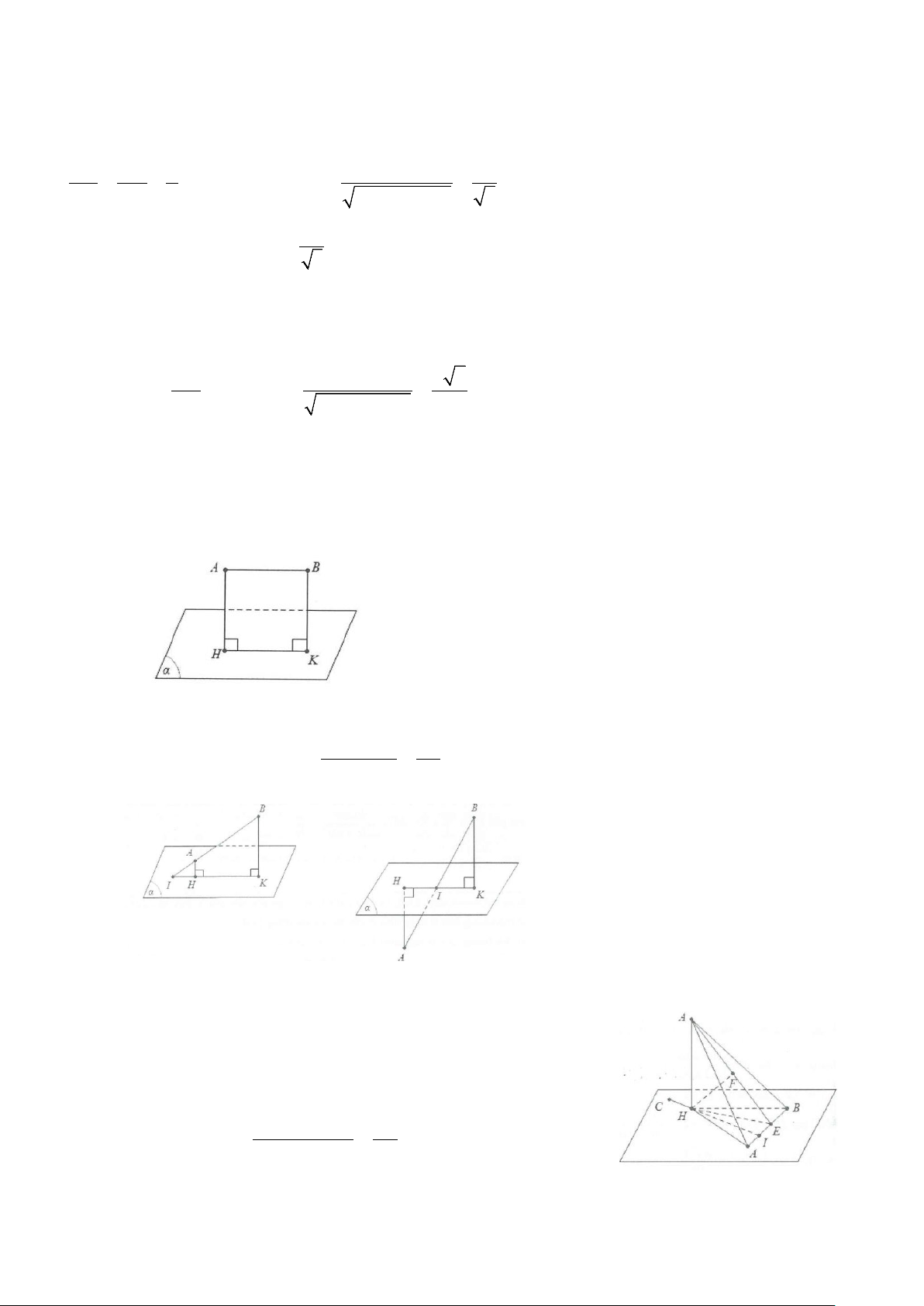
Khoảng cách giữa đường thẳng a và mặt phẳng (α) song song với nhau là khoảng cách từ một điểm M
bất kì thuộc đường a đến mặt thẳng (α) .
d(a;(α)) = d(M;(α)) = MH(M∈(α)).
Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng kia.
d((α);(β)) = d(a;(β)) = d(A;(β)) = AH(a ⊂ (α),A∈a)
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt bên SBC vuông góc với đáy ABC, Gọi
M, N, P lần lượt là trung điểm của AB, SA, AC. Tính khoảng cách giữa hai mặt phẳng (MNP) và (SBC) . Lời giải MP / /BC Do ⇒ (MNP) ⊥ (SBC) MN / /SB
Dựng SH ⊥ BC(H∈BC). Mặt khác (SBC) ⊥ (ABC) Do đó SH ⊥ (ABC)
Gọi M là trung điểm của BC⇒ AM ⊥ BC
Gọi K = AE ∩ MP ⇒ KE ⊥ BC
Mặt khác KE ⊥ SH ⇒ KE ⊥ (SBC) Suy ra (( ) ( )) = ( ( )) AE a 3 d MNP ; SBC d K; SBC = KE = = 2 4
Ví dụ 2: Cho hình chóp tứ giác đều S.ABC có cạnh đáy băng 2a và cạnh bên đều bằng a 5 . Tính khoảng
cách giữa đường thẳng CD và mặt phẳng (SAB). Lời giải
Gọi O là tâm của đáy ABCD⇒ SO ⊥ (ABCD) Ta có: AC OA = = a 2 2 2 ⇒ SO = SA − OA = a 3 2
Mặt khác d(CD;(SAB)) = d(D;(SAB)) d(D;(SAB)) Ta có: DB = = d(O;(SAB)) 2 OB
Dựng OE ⊥ AB,OF ⊥ SE ta có: AD OE = = a 2 Khi đó: ( ( )) SO.OE d D; SAB = 2OF = 2. = a 3 2 2 SO + OE
Ví dụ 3: Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh bên và cạnh đáy bằng a. Hình chiếu vuông góc
của A’ trên (ABC) trùng với trung điểm của BC.
a) Tính khoảng cách từ AA’ đến các mặt bên (BCC'B')
b) Tính khoảng cách giữa hai mặt đáy của lăng trụ. Lời giải
a) Gọi H là trung điểm của BC ta có: A 'H ⊥ BC Do AB ∆
C đều nên AH ⊥ BC ⇒ BC ⊥ (A'HA) HK ⊥ BB' Dựng HK ⊥ AA ' thì ⇒ KH ⊥ (BCC'B') KH ⊥ BC
Do đó d(AA';(BCC'B')) = d(K;(BCC'B')) = KH Lại có: a 3 2 2 a AH =
,AA ' = a ⇒ A'H = A 'A − AH = 2 2 Suy ra AA'.AH a 3 HK = = AA' 4 Do đó ( ( )) a 3 d AA '; BCC'B' = . 4 b) Ta có: (( ) ( )) = ( ( )) a d ABC ; A 'B'C' d A '; ABC = A 'H = 2
Ví dụ 4: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung
điểm của AD, DC và A’D’. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC') . Lời giải
Ta có: MN / /AC, NP / / A A ' ⇒ (MNP) / / (ACC'A')
Gọi O là tâm hình vuông ABCD và I = DO ∩ MN IO ⊥ AC Ta có: ⇒ IO ⊥ (ACC'A ') IO ⊥ AA '
Do đó d((MNP);(ACC'A')) = d(I;(ACC'A')) = IO Lại có: OD BD a 2 IO = = = 2 4 4
Vấn đề 2: KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
Đường vuông góc chung và đoạn vuông góc chung hai đường chéo nhau.
- Đường thẳng ∆ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy được
gọi là đường vuông góc chung của a và b.
- Đường thẳng vuông góc chung ∆ cắt hai đường thẳng chéo nhau a và b lần lượt tại M và N thì độ dài
đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
Cách xác định đoạn vuông góc chung của 2 đường chéo nhau.
Cho 2 đường thẳng chéo nhau a và b. Gọi (β) là mặt phẳng chứa b và
song song với a, a’ là hình chiếu vuông góc của a trên (β) .
Vì a / / (β) nên a / /a ' . Gọi N = a '∩ b và (α) là mặt phẳng chứa a và
a’. Dựng đường thẳng ∆ qua N và vuông góc chung và MN là đoạn
vuông góc chung của a và b. Nhận xét:
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến
mặt phẳng song song với nó và chứa đường thẳng còn lại
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song với nó
và chứa đường thẳng còn lại.
Dạng 1: Khoảng cách giữa hai đường thẳng chéo nhau và vuông góc với nhau.
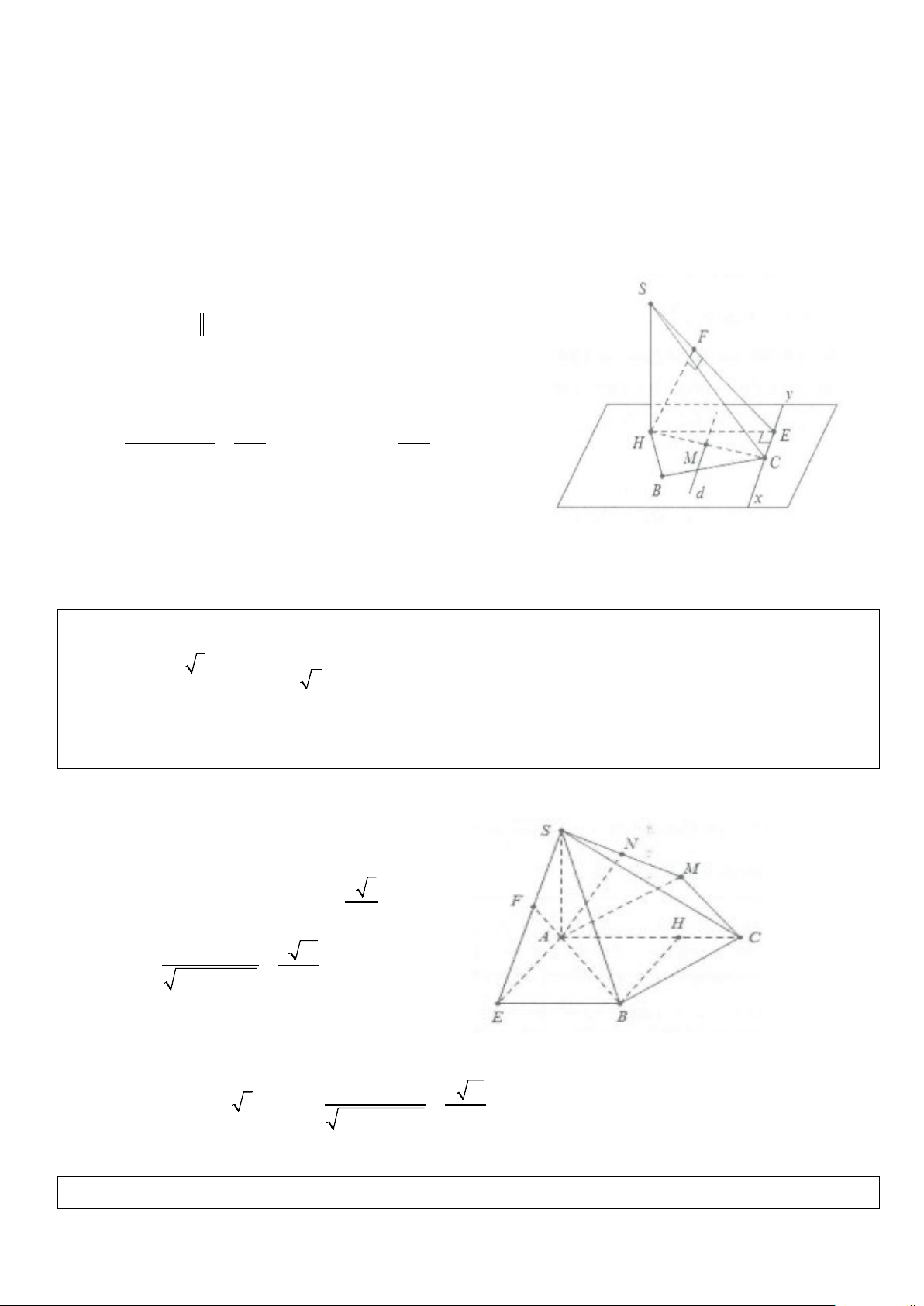
Phương pháp giải: Dựng đường vuông góc chung. Khảo sát khối
chóp đỉnh S có đường cao SH, yêu cầu tính khoảng cách giữa 2
đường chéo nhau d (thuộc mặt đáy) và đường thẳng SC thuộc bên
khối chóp trong trường hợp d ⊥ SC.
Dựng hình: Hình chiếu vuông góc của SC trên mặt phẳng đáy là HC SC ⊥ d Mặt khác: ⇒ d ⊥ (SHC) SH ⊥ d
Gọi M = d ∩ HC, dựng MK ⊥ SC khi đó MK là đoạn vuông góc chung của AC và SC
Cách tính: Dựng HE ⊥ SC khi đó MK MC MC = ⇒ MK = .HE HE HC HC
Xét tam giác vuông SHC ta có: 1 1 1 = + ⇒ HE = MK = d d;SC 2 2 2 ( ) HE SH HC
Ví dụ 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ⊥ (ABCD) . Biết rằng SC tạo với mặt đáy một góc 60°
a) Tính khoảng cách giữa 2 đường thẳng AB và SD
b) Tính khoảng cách giữa BD và SC. Lời giải
a) Ta có: AC = a 2 . Do SA ⊥ (ABCD) và SC tạo với đáy góc 60° nên SCA = 60°
Khi đó SA = AC tan 60° = a 6 AB ⊥ AD Do ⇒ AB ⊥ (SAD) AB ⊥ SA
Dựng AH ⊥ SD suy ra AH là đoạn vuông góc chung của AB và SD Ta có: SA.AB a 42 = 2 2 SA + AB 7
b) Ta có: BD ⊥ SC tại O và BD ⊥ SA ⇒ BD ⊥ (SAC)
Dựng OK ⊥ SC ⇒ OK ⊥ BD nên OK là đoạn vuông góc chung của BD và SC Do đó ( ) = = a 2 a 6 d BD;SC OK OCsin OCK = sin 60° = 2 4
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, gọi I là trung điểm của AB. Hình chiếu vuông
góc của S trên mặt đáy là trung điểm CI. Biết chiều cao của khối chóp là h = a 3 . Tính khoảng cách d giữa
đường thẳng AB và SC. Lời giải CI ⊥ AB a) Ta có: ⇒ AB ⊥ (SIC) S H ⊥ AB
Dựng IF ⊥ SC khi đó IF là đoạn vuông góc chung của AB và SC. Dựng HE ⊥ SC ta có: 1 HE = IF 2 Lại có a 3 a 3 CI = ⇒ CH = 2 4 Khi đó SH.HC a 51 2a 51 HE = = ⇒ IF = 2 2 SH + HC 17 17
Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD cạnh a và SA ⊥ (ABCD) . Biết mặt
phẳng (SBC) tạo với đáy một góc 60°
a) Tính khoảng cách giữa 2 đường thẳng SB và CD.
b) Tính khoảng cách giữa 2 đường thẳng BD và SC. Lời giải BC ⊥ AB a) Do:
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB ⇒ BC là đoạn vuông BC ⊥ SA góc chung của SB và CD. Ta có: d(SB;CD) = BC = a c) Mặt khác BC ⊥ (SAB) Do đó (( ) ( )) = SBC ; ABCD SBA = 60° Suy ra SA = ABtan 60° = a 3 BD ⊥ AC
Gọi O là tâm hình vuông ABCD ta có ⇒ BD ⊥ (SAC) BD ⊥ SA
Dựng OM ⊥ SC khi đó OM là đường vuông góc chung của BD và SC a 2 a 3. Ta có CA ∆ S CM ∆ O(g − g) SC SA SA.OC 2 a 6 a 30 ⇒ = ⇒ OM = = = = 2 2 CO MO SC SA + AC 2 5 10 Cách 2: Dựng 1
AN ⊥ SC ⇒ OM = AN . Mặt khác 1 1 1 a 30 = + ⇒ AN = 2 2 2 2 AN SA AC 5 Khi đó 1 a 30 d = OM = AN = 2 10
Ví dụ 4: Cho chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác SBC là tam giác đều cạnh a và
thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách d giữa 2 đường thẳng SA và BC. Lời giải
Gọi H là trung điểm của BC khi đó SH ⊥ BC
Mặt khác (SBC) ⊥ (ABC) do đó SH ⊥ (ABC) Ta có: a SH = 3 và a BC a AB = AC = ;AH = = 2 2 2 2 BC ⊥ AH Do
⇒ BC ⊥ (SHA) . Dựng HK ⊥ SA khi đó BC ⊥ SH
HK là đoạn vuông góc chung của BC và SA. Lại có: SH.AH a HK = = 3 SH2 + HA2 4
Ví dụ 5: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân AB = BC = 3a, hình chiếu vuông góc
của B’ lên mặt phẳng đáy trùng với trọng tâm tam giác ABC, mặt phẳng (ABB’A’) tạo với mặt phẳng (ABC)
một góc 60°. Tính khoảng cách giữa 2 đường thẳng AB và B’C. Lời giải
Dựng CI ⊥ AB ⇒ I là trung điểm của AB.
Ta có: (B'GI) ⊥ AB ⇒ B'IG = 60 Lại có: 1 a 3 2 a CI = AB = ⇒ GI = 2 2 2 2 a ⇒ B'G = GI tan = 6 60 2 Dựng B'G.CI
IH ⊥ B'C ⇒ d(AB;B'C) = IH = B'C Ta có: 2 2 a 14 a B'C = B'G + GC = ⇒ IH = 3 42 2 14 Do đó a d(AB;B'C) = IH = 3 42 14 Hoặc dựng : 3 3 B'G.GC GK / /IH ⇒ IH = GK = . 2 2 B'G2 + GC2
Dạng 2: Tính khoảng cách giữa hai đường thẳng chéo nhau không vuông góc.
Phương pháp giải : Dựng đường thẳng chứa a và song song với b (hoặc đường thẳng chứa b và song song
với a) để tính khoảng cách giữa hai đường thẳng chéo nhau.
Khảo sát khối chóp đỉnh S có đường cao SH, yêu cầu tính khoảng cách giữa 2 đường thẳng chéo nhau d
(thuộc mặt đáy) và đường thẳng SC thuộc mặt bên của khối chóp trong trường hợp d không vuông góc với SC.
Dựng hình: Tìm giao điểm C của cạnh bên SC và mặt đáy
(giao điểm của cạnh thuộc mặt bên và mặt đáy). Từ C ta dựng đường thẳng xCy d
Khi đó d(d;SC) = d(d;(Sxy))
Gọi M = d ∩ HC ⇒ d = d(M;(Sxy)) Ta có : d(M;(Sxy)) MC MC = ⇒ d(M;(Sxy)) = .d(H;(Sxy)) d(H;(Sxy)) HC HC
Chú ý: Để tính d(d;(Sxy)) ta có thể lấy bất kỳ điểm nào
thuộc d (không nhất thiết là điểm M) sao cho việc quy đổi
khoảng cách cần tìm về khoảng cách từ chân đường cao H đến mặt phẳng (Sxy) dễ dàng nhất.
Ví dụ 1: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có
AB = a, BC = a 3. Biết a SA = 2
a) Tính khoảng cách giữa hai đường thẳng SB và AC
b) Tính khoảng cách giữa hai đường thẳng SC và AB. Lời giải
a) Dựng Bx / /AC,AE ⊥ Bx ⇒ (SAE) ⊥ Bx
Dựng AF ⊥ SE ⇒ d(AC;SB) = AF Dựng BH ⊥ AC dễ thấy a AE = BH = 3 2 Ta có: AE.SA a AF = = 30 SA2 + AE2 10
b) Dựng Cy/ /AB ⇒ d(AB,SC) = d(AB,(SCy))
Dựng AM ⊥ Cy,AN ⊥ SM ⇒ d(AB;(SCy)) = AN Lại có : AM.SA a AM = BC = a ⇒ AN = = 21 3 SA2 + AM2 27
Ví dụ 2: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu vuông góc của B’ lên
mặt phẳng đáy trùng với trung điểm H của cạnh AB, góc giữa mặt phẳng (BCC’B’) và mặt phẳng đáy bằng
60. Tính khoảng cách giữa 2 đường thẳng AA’ và BC. Lời giải
Dựng HK ⊥ BC ⇒ BC ⊥ (B'HK) ⇒ B'KH = 60 Ta có : a HK = HBsin = 3 60 4 a ⇒ B'H = HK tan = 3 60 4
Do AA '/ / BB' ⇒ d(AA ';BC) = d(AA ';(B'C'C)) d(A;(B'C'CB)) = d 2 (H;(B'C'CB)) = H 2 E Ta có : HK.B'H a HE = = 3 . Do đó a d = 3 B'H2 + HK2 8 4
Ví dụ 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = AC = 2a, hình chiếu vuông
góc của đỉnh S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB, biết SA = a 2. Tính khoảng cách
d giữa 2 đường thẳng SA và BC. Lời giải
Gọi H là trung điểm của cạnh AB. Khi đó
SH ⊥ (ABC) và SH = SA2 − HA2 = a
Dựng Ax / /BC ⇒ d(SA;BC) = d(B;(SAx))
Dựng HK ⊥ Ax ⇒ (SHK) ⊥ Ax
Dựng HE ⊥ SK ⇒ d(B;(SAx)) = d 2 (H;(SAx)) Ta có : a HK = AHsin HAK = 2 SH.HK a ⇒ d(H;(SAx)) = HE = = SH2 + HK2 3 Do đó a d(SA;BC) = 2 3
Ví dụ 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a 3, AC = a, tam giác SBC là
tam giác vuông cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính khoảng cách d
giữa hai đường thẳng SB và AC. Lời giải
Gọi H là trung điểm của BC. Ta có SH ⊥ BC
Mặt khác (SBC) ⊥ (ABC) ⇒ SH ⊥ (ABC)
Ta có : BC = AB2 + AC2 = a ⇒ SH = 1 2 BC = a 2
Dựng Bx / /AC ⇒ d(AC;SB) = d(AC;(SBx)) = d(C;(SBx)) = d
Dựng : HK ⊥ Bx,HE ⊥ SK ⇒ HE ⊥ (SBx) d(C;(SBx)) = d 2 (H;(SBx)) = H 2 E Ta có : AB a 3 SH.HK a HK = = ⇒ HE = = 21 2 2 SH2 + HK2 7 Do đó : a d = d(H;(SBK)) = 2 21 2 7
Ví dụ 5: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA ⊥ (ABCD) . Gọi M là trung điểm của
cạnh CD, biết SA = a 5. Tính khoảng cách giữa hai đường thẳng SD và BM Lời giải
Dựng DN BM ⇒ N là trung điểm của AB.
Khi đó d(SD;BM) = d(BM;(SDN)) = d(B;(SDN)) = d(A;(SDN))
Dựng AE ⊥ DN ⇒ DN ⊥ (SAE) , dựng AF ⊥ SE AF ⊥ SE Khi đó ⇒ AF ⊥ (SDN) AF ⊥ DN Ta có : AN.AD a AE = = 2 AN2 + AD2 5 Do vậy AE.SA 5 a d(B;(SDN)) = d(A;(SDN)) = AF = = a. = 2 145 2 AE2 + SA2 29 29
Ví dụ 6: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = BC = 2a và SA ⊥ (ABC) . Gọi M
là trung điểm của AC. Biết góc giữa 2 mặt phẳng (SBC) và (ABC) bằng 60. Tính khoảng cách d giữa 2
đường thẳng AB và SM theo a. Lời giải AB ⊥ BC Ta có :
⇒ BC ⊥ (SAB) ⇒ SBA là góc giữa 2 mặt phẳng (SBC) và BC ⊥ SA (ABC) Ta có : SA = ABtanSBA = a 2 3. Dựng Mx//AB
Khi đó d(AB;SM) = d(AB;(SMx)) = d(A;(SMx))
Dựng AE ⊥ Mx;AF ⊥ SE khi đó d(A;(SMx)) = AF
Do AE//BC nên EAM = ACB = 45 Suy ra AE = AMcos45 = a Do đó SA.AE a AF = = 2 39 = d SA2 + AE2 13
Ví dụ 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) , đường thẳng SC tạo với đáy
góc 45 . Tính khoảng cách giữa 2 đường thẳng SB và AC Lời giải AC = a ; 2 SCA = Ta có : (SC;(ABCD) = 45 ⇒ SA = AC = a 2
Dựng Bx / /AC ⇒ d(AC;SB) = d(AC;SBx)
Dựng AE ⊥ Bx,AF ⊥ SE ⇒ d = AF
Ta có : BE / /AC ⇒ BE ⊥ BD dễ dàng suy ra
OEBO là hình chữ nhật suy ra a AE = OB = 2 2 AE.SA a d = = 10 AE2 + SA2 5
Ví dụ 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = a, BC = a 3. Hình chiếu vuông
góc H của đỉnh S lên mặt phẳng (ABCD) là điểm H thỏa mãn HA = HB 2
. Góc giữa mặt phẳng (SCD) và
mặt phẳng (ABCD) bằng 60. Tính khoảng cách giữa 2 đường thẳng SA và BD. Lời giải
Dựng HK ⊥ CD ⇒ SKH = 60
Ta có : SH = HK.tan 60 = BC.tan 60 = a 3
Dựng Ax / /BD ⇒ d(SA;BD) = d(BD;(SAx)) = d(B;(SAx)) = 3d(H;(SAx)) 2
Dựng HE ⊥ Ax,HF ⊥ SE ⇒ d(H;(SAx)) = HF
Ta có : tan ABD = 3⇒ HAE = ABD = 60 a 2 3 a ⇒ HE = HA.sin = . = 3 60 3 2 3 Do đó SH.HE a 3 a HF = = ⇒ d(SA;BD) = 9 SH2 + HE2 2 7 4 7
Ví dụ 9: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) . Biết mặt phẳng (SBC) tạo
với đáy một góc 60 và M là trung điểm của SD. Tính khoảng cách d giữa 2 đường thẳng AB và CM. Lời giải BC ⊥ AB Ta có: ⇒ ⊥ ⇒ BC (SAB)
SBA là góc giữa 2 mặt phẳng BC ⊥ SA (SBC) và (ABC) Ta có: =
SA AB tan SBA = a 3
Do AB//CM do đó d(AB;CM) = d(AB;(CMD))
Dựng AH ⊥ SD khi đó d(A;(SCD)) = AH Lại có: SA.AD a 3 AH = = = d(A ; B CM ) 2 2 SA + AD 2
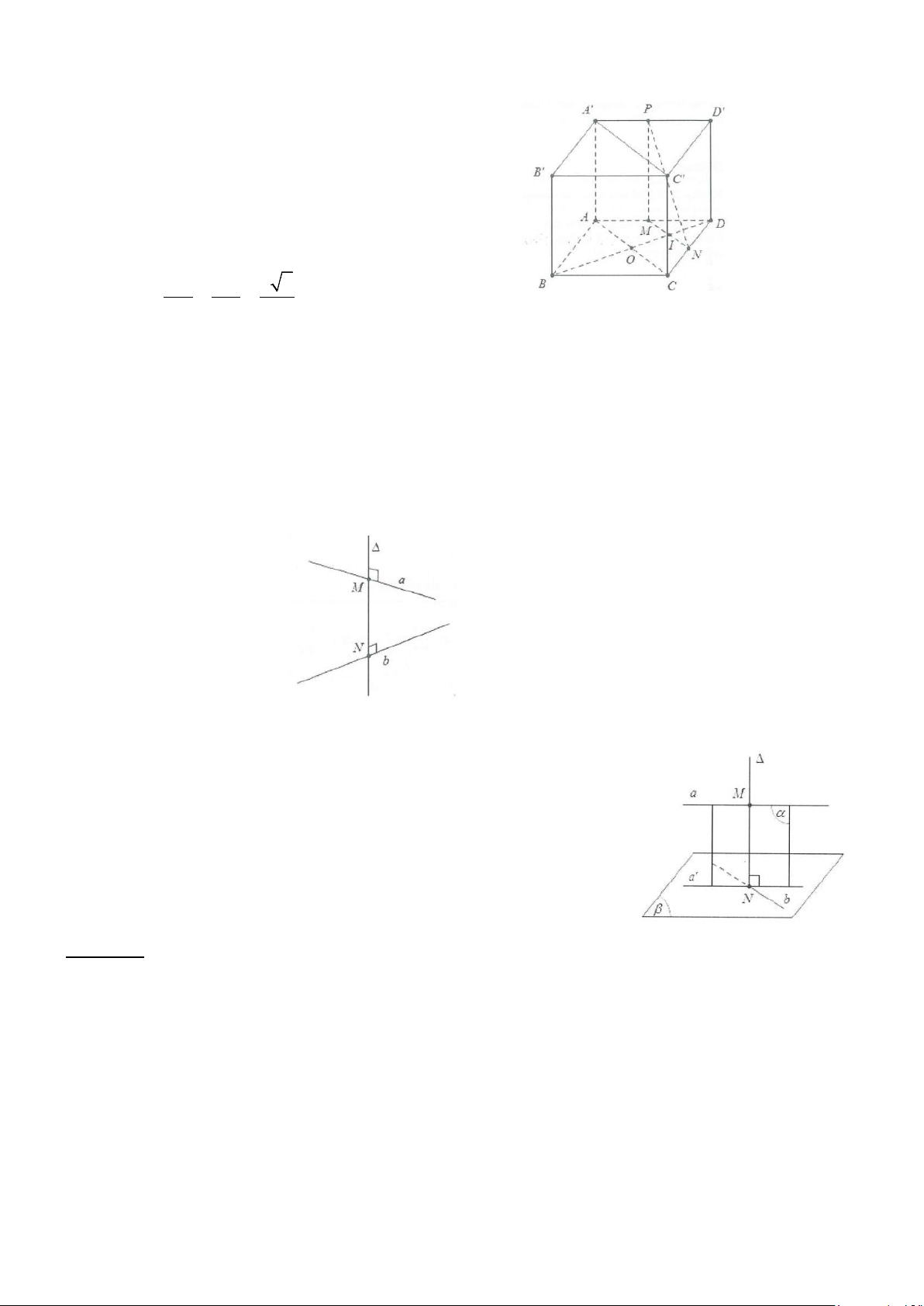
Ví dụ 10: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính d là khoảng cách giữa 2 đường
thẳng AC và C’D. Lời giải
Dễ thấy AB’//C’D do đó
d(AC;C’D) = d(C’D;(ACB’))
Khi đó d = d(D;(B’AC)). Mặt khác OB = OD (với O là tâm hình vuông ABCD)
Khi đó d(D;(B’AC)) = d(B;(B’AC)) BD ⊥ AC Do
⇒ AC ⊥ (BB 'O) , dựng BH ⊥ B 'O AC ⊥ BB ' Suy ra B . O BB ' ⊥ ( ' ) a H
B AC ⇒ h = BH = = 2 2 BO + BB ' 3
Ví dụ 11: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S trên
mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt phẳng (SCD) và mặt
phẳng đáy bằng 45 . Tính khoảng cách giữa 2 đường thẳng SA và BD. Lời giải
Dựng HK ⊥ CD ⇒ CD ⊥ (SHK)do vậy = (S ;
CD ABCD) SKH = 45
Ta có: ∆ HKD vuông cân tại K do vậy 3a 3 = = ⇒ = tan 45 a HK KD SH HK = 2 2
Dựng Ax / /BD ta có: d(S ;
A BD) = d(B ;
D (SAx)) = d(H;(SAx))
Dựng HE ⊥ Ax ⇒ HE = OA = a 2
Dựng HF ⊥ SE ⇒ HF ⊥ (SAx) Ta có: SH.HE 3a 34 HF = = = d(S ; A BD) 2 2 SH + HE 17
Ví dụ 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2a, AD = a 3 , cạnh bên SA
vuông góc với đáy, gọi M là trung điểm của cạnh CD. Biết SM tạo với mặt phẳng (ABCD) một góc 60 ,
tính khoảng cách d giữa 2 đường thẳng AM và SB. Lời giải Ta có: 2 2
M = AD + DM = 2a
⇒ SA = AM tan 60 = 2a 3
Dựng Bx / / AM ⇒ d(AM ;SB) = d( ; A SBx)
Dựng AK ⊥ Bx, AH ⊥ SK Ta có: MD 1 = = ⇒ tan MAB MAD = 30 AD 3 ⇒
BAK = 30 ⇒ AK = ABcos30 = a 3 12 a 60 d( ;
A (SBx)) = AH = a = 5 5
Ví dụ 13: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AD = a 2 , hình chiếu vuông góc của
đỉnh S xuống mặt đáy là trung điểm của AB, biết tam giác SCD là tam giác vuông tại S và nằm trong mặt
phẳng tạo với đáy một góc 45 . Tính khoảng cách d giữa 2 đường thẳng SA và BD. Lời giải
Gọi H là trung điểm của AB. Dựng HF ⊥ CD khi đó
HF = AD = a 2 Ta có: ⊥ ⇒ CD (SHF) SFH = 45
⇒ SH = HF tan 45 = a 2;SF = HF 2 = 2a
Do tam giác SCD vuông cân nên CD = 2SF = 4a Suy ra A . B AD 4 ( ; ) a d A BD = = 2 2 AB + AD 3
Dựng Ax / / B D, HK ⊥ Ax, HE ⊥ SK Ta có 1 1 4a 2 = ( ; ) = . a HK d A BD = . Do vậy 4 ( ; ) = 2 a d SA BD HE = 2 2 3 3 11
Ví dụ 14: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, hình chiếu vuông góc của đỉnh
S lên mặt phẳng đáy trùng với trọng tâm H của tam giác đều ABC, biết mặt phẳng (SCD) tạo với mặt phẳng
(ABCD) một góc 60 . Tính khoảng cách giữa 2 đường thẳng SA và BD. Lời giải
Ta có ∆ ABC đều cạnh a nên H là trực tâm của tam giác ABC
⇒ CH ⊥ AB ⇒ CH ⊥ BC ⇒ ⊥ ⇒ CD (SHC) SCH = 60 Ta có: a 3 OB = ⇒ BD = a 3 2 a 3 ⇒ HB = HC = . Khi đó a 3 SH = .tan 60 = a 2 2 Dựng Ax//BD,HE ⊥ Ax, a
HF ⊥ SE ⇒ HE = OA = 2 HE. ( ; ) SH a d SA BD = HF = = 2 2 HE + SH 5
Ví dụ 15: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông có AB = BC = a,
A’B = a 3 . Gọi M là trung điểm cạnh BC. Tính theo a khoảng cách giữa hai đường thẳng AM và B’C. Lời giải Ta có: 2 2
AA ' = A'B − AB = a 2
Dựng Cx / / AM khi đó d(AM ; B 'C) = d(AM ;(B 'Cx)) 1
= d(M ;(B 'Cx)) = d( ;
B (B 'Cx)) 2 BE ⊥ Cx Dựng
⇒ BF ⊥ (B 'Cx) ⇒ d(B;(B'Cx)) = BF
BF ⊥ B ' E
Lại có BE = 2BP , trong đó AB. BP BM a = = 2 2 AB + BM 5 Suy ra 2a BE.BB ' 2 BE a = ⇒ BF = = 2 2 5 BE + BE 7 Do đó ( ; ' ) a d AM B C = 7
Ví dụ 16: Cho hình lăng trụ ABC.A’B’C’ có các mặt bên đều là hình vuông cạnh a. Gọi D, E lần lượt là
trung điểm của BC, A’C’. Tính khoảng cách giữa các cặp đường thẳng.
a) B’C’ và A’B
b) DE và AB’ Lời giải
a) Do lăng trụ ABC.A’B’C’ có các mặt bên đều là hình vuông cạnh a. Nên ABC.A’B’C’ là lăng trụ đứng
với hai đáy là tam giác đều cạnh a.
Ta có: B 'C '/ /BC ⇒ B 'C '/ /(A'BC)
⇒ d(B'C';A'B) = d(B'C';(A'BC)) = d(B';(A'BC))
Gọi I = A'B∩ AB ' ⇒ I là trung điểm của AB’
Khi đó d(B ';(A'BC)) = d( ;
A (A'BC)) Dựng AA'.AD
AH ⊥ A'D ⇒ d(A';(A'BC)) = AH = 2 2 AA' + AD Trong đó a 3 a 21 AA' = ; a AD = ⇒ d = AH = 2 7 EF / / A'B'
b) Gọi F là trung điểm của B’C’ ⇒
⇒ (EFD)//(A'B'BA) ⇒ DE//(A'B'BA)
FD / /B ' B
Khi đó d(DE;AB') = d(DE;(A'B'BA)) = d(D;(A'B'BA)) Dựng ⊥ ∈ ⇒ = = a a 3 DK AB(K AB)
d(D;(A'B'BA)) DK DBsin DBK = sin 60 = 2 4
Ví dụ 17: Cho hình chóp S.ABCD có đáy là hình chữ nhật có AB = a, AD = a 3 , SA ⊥ (ABCD) . Mặt
phẳng (SBC) tạo với đáy một góc 60 . Gọi M là trung điểm của SA. Tính khoảng cách giữa hai đường
thẳng SC và DM Lời giải BC ⊥ SA Ta có: ⇒ ⊥ ⇒ = BC (SB ) A
(SBC);(ABC)) SDB = 60 BC ⊥ AB
Do đó SA = AB tan 30 = a 3
Để tính d(SC;DM) ta đổi về đỉnh của hình chóp C.DAS có CD ⊥ (SAD)
Dựng Sx / / DM ⇒ d(DM;SC) = d(DM;(CSx)) = d(D;(CSx))
Dựng DE ⊥ Sx,DF ⊥ CE ⇒ d( ;
D (SCx)) = DF a 3 a 3. Do A . D AM 2 a 15
SE / /DM ⇒ DE = d(S; DM ) = d( ; A DM ) = = = 2 2 2 AD + AM 3a 5 2 3a + 4 Suy ra DE.CD a 6 DF = =
= d(SC; DM ) 2 2 CD + DE 4
Ví dụ 18: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, SA ⊥ (ABCD) . Biết AD = 2a, AB
= BC = a và SD tạo với đáy một góc 30 . Gọi K là trung điểm của SD. Tính khoảng cách giữa hai đường
thẳng SB và AK. Lời giải Do ⊥ ⇒ = 2 ( ) ( ;( )) = 30 ⇒ = tan 30 a SA ABCD SD ABCD SDA SA AD = 3 BA ⊥ AD Ta có:
⇒ BA ⊥ (SAD) ta cắt khối chóp B.SAD có đường cao BA. BA ⊥ SA
Dựng Sx / / AK ⇒ d(S ;
B AK) = d(AK;(SBx))
Dựng AE ⊥ Sx,AF ⊥ BE ⇒ d(AK;(SBx)) = d( ; A (SBx)) = AF Do 1
AK = SK = SD và = −
ASK 90 ADS = 60 ⇒ a
SAK đều cạnh 2 2 3 Do đó SA 3 A . B AE a 2
AE = d(S; AK) = = a ⇒ AF = = 2 2 2 AB + AE 2 Vậy a 2 d(S ; B AK) = 2
BÀI TẬP TỰ LUYỆN
Câu 1: Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau và AB = a, AC = b, AD = c . Gọi d là
khoảng cách từ A đến mặt phẳng (BCD) . Đẳng thức nào dưới đây đúng? A. 1 1 1 1 = + + B. 2 2 2 2
d = a + b + c C. 2 1 1 1 d = + +
D. d = abc 2 2 2 2 d a b c 2 2 2 a b c
Câu 2: Cho tam giác ABC vuông tại A. Gọi d là khoảng cách từ A đến đường thẳng chứa cạnh BC. Đẳng
thức nào dưới đây đúng? 2 2 A. A . B AC + d + = B. AB AC d = C. 2 2
d = AB + AC D. AB AC d = 2 2 AB + AC 2 2 AB .AC A . B AC
Câu 3: Cho đường thẳng MN song song với mặt phẳng (α ) . Gọi d ,d lần lượt là khoảng cách từ M và N 1 2
đến (α ) . Khẳng định nào sau đây đúng?
A. d = d B. 1 d = d
C. d = 2d
D. d = d = 0 1 2 1 2 2 1 2 1 2
Câu 4: Cho hai mặt phẳng (α ),(β ) song song với nhau. Lấy hai điểm M, N lần lượt nằm trên (α ) và (β )
sao cho đường thẳng MN không vuông góc với (α ) . Khẳng định nào sau đây sai?
A. d (M ,(β )) = d (N,(α ))
B. d (M ,(β )) = d ((α ),(β ))
C. d (N,(α )) = d ((α ),(β ))
D. d ((α ),(β )) = MN
Câu 5: Cho tứ diện ABCD. Gọi d là khoảng cách từ D đến mặt phẳng ( ABC). Mệnh đề nào dưới đây sai?
A. d=DG với G là trọng tâm tam giác ABC.
B. d=DH với H là hình chiếu vuông góc của D lên mặt phẳng ( ABC).
C. d=DI với I là tâm đường tròn ngoại tiếp tam giác ABC
D. d=DN trong đó N là trung điểm AM (với M là trung điểm đoạn BC)
Câu 6: Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau và AB=2, AC=3, AD=4. Tính
khoảng cách từ A đến mặt phẳng (BCD) A. 12 61 d = B. 144 d = C. 61 d = D. d = 61 61 61 12
Câu 7: Khoảng cách lớn nhất giữa hai đỉnh của một hình lập phương cạnh a là bao nhiêu? A. a 3 B. a 2 C. 2a
D. d = a 5
Câu 8: Cho mặt phẳng (α ) và đường thẳng MN cắt (α ) tại điểm I. Biết rằng 3MI = 2MN . Gọi d ,d lần 1 2
lượt là khoảng cách từ M và N đến (α ) . Tính tỉ số d1 d2 A. d 2 d 3 d 1 d 1 = B. 1 = C. 1 = D. 1 = 2 d 3 d 2 d 3 d 2 2 2 2
Câu 9: Cho mặt phẳng (α ) và đường thẳng MN cắt (α ) tại điểm I. Biết rằng 4IN = 3IM . Gọi d ,d lần 1 2
lượt là khoảng cách từ M và N đến (α ) . Tính tỉ số d1 d2 A. d 4 d 3 d 1 d 1 = B. 1 = C. 1 = D. 1 = 4 d 3 d 4 d 4 d 2 2 2 2
Câu 10: Cho hình lăng trụ đều ABC.A'B 'C '. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, M là trung
điểm CC’ và d là khoảng cách từ A đến mặt phẳng ( A'BC) . Mệnh đề nào dưới đây sai?
A. d = d (B',( A'BC))
B. d = 2.d (M ,( A'BC))
C. d = 3.d (O,( A'BC)) D. 1
d = d (O,( A'BC)) 3
Câu 11: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có ba kích thước AB = a, AD = b, AA'=c . Tính khoảng
cách d từ điểm A đến mặt phẳng (DA'C '). A. abc d = B. abc d =
(ab)2 +(bc)2 +(ac)2 2 2 2 a + b + c C. bc d = D. abc d = 2 2 b + c
ab + bc + ac
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với đáy và SA = h . Tính
khoảng cách từ A đến mặt phẳng (SBC) theo a và h ? A. ah 3 d = B. ah 3 d = C. ah d = D. ah 5 d = 2 2 4a + 3h 2 2 3a + 4h 2 2 a + h 2 2 a + h
Câu 13: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Khoảng cách từ A đến đường thẳng CC’ là A. a B. a 2 C. a 3 D. a 2
Câu 14: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Khoảng cách từ A đến đường thẳng B’D’ là A. a 6 B. a C. a 3 D. a 2 2 2
Câu 15: Cho hình chóp tam giác đều S.ABC có SA = a 7, AB = 3a . Khoảng cách từ S đến mặt phẳng ( ABC) bằng A. a B. 2a C. a 20 D. a 10 3
Câu 16: Cho hình chóp S.ABCD có đường cao SC, đáy là hình chữ nhật. Gọi H là trung điểm của SB.
Khoảng cách từ A đến mặt phẳng (SBC) là đoạn thẳng A. AS B. AB C. AC D. AH
Câu 17: Cho hình chóp S.ABCD có đường cao SC = 2a , đáy là hình chữ nhật có AB = a 2, AD = a . Gọi K
là trung điểm của SA. Khoảng cách từ A đến mặt phẳng ( ABCD) bằng A. a B. 2a C. a 2 D. a 3
Câu 18: Cho hai đường thẳng ∆ ,∆ chéo nhau, đường thẳng ∆ bất kì cắt ∆ tại M và cắt ∆ tại N. Khẳng 1 2 3 1 2
định nào dưới đây luôn đúng?
A. d(∆ ,∆ ≤ MN
B. d(∆ ,∆ > MN 1 2 ) 1 2 )
C. d(M ,∆ = d N,∆
D. d(∆ ,∆ = MN 1 2 ) 2 ) ( 1 )
Câu 19: Cho hai đường thẳng ∆ ,∆ chéo nhau, mặt phẳng (β ) chứa ∆ và song song với ∆ , mặt phẳng 1 2 2 1
(α ) chứa ∆ và song song với ∆ . Khẳng định nào dưới đây sai? 1 2
A. d(∆ ,∆ = d ∆ , β
B. d(∆ , β = d ∆ , α 1 ( )) ( 2 ( )) 1 2 ) ( 1 ( ))
C. d(∆ ,∆ < d α , β
D. d((α ),(β )) ≤ MN, M ∀ ∈ ∆ , N ∈∆ 1 2 ) (( ) ( )) 1 2
Câu 20: Cho đường thẳng ∆ và mặt phẳng (α ) song song với nhau. Mặt phẳng (β ) chứa ∆ , vuông góc 1 1
với (α ) và cắt (α ) theo giao tuyến là ∆ . Khi đó khẳng định nào dưới đây đúng? 2
A. d(∆ ,∆ = d ∆ , α B. d(∆ ,∆ 1 2 ) ( 1 ( )) 1 2 ) ( 1 ( ))
C. d(M ,∆ >d M , α , M ∀ ∈ ∆
D. d(∆ , α = MN, M ∀ ∈ ∆ , N ∈∆ 1 ( )) 2 ) ( ( )) 1 1 2
Câu 21: Cho đường thẳng ∆ song song với mặt phẳng (α ) . Gọi d là khoảng cách từ ∆ đến (α ) . Mệnh đề nào sau đây sai?
A. d bằng khoảng cách từ điểm bất kì trên ∆ đến (α ) .
B. d bằng khoảng cách từ điểm bất kì trên (α ) đến ∆ .
C. d bằng khoảng cách từ mặt phẳng (β ) đến (α ) với (β )là mặt phẳng chứa ∆ và song song với (α ) .
D. d bằng khoảng cách giữa ∆ và hình chiếu vuông góc của ∆ lên (α ) .
Câu 22: Cho hai đường thẳng chéo nhau ∆ ,∆ . Gọi d là khoảng cách giữa ∆ ,∆ . Mệnh đề nào sau đây 1 2 1 2 sai?
A. d bằng độ dài đoạn vuông góc chung của ∆ ,∆ . 1 2
B. d bằng khoảng cách giữa ∆ và (β ) là mặt phẳng chứa ∆ và song song với ∆ . 1 2 1
C. d bằng khoảng cách giữa ∆ và (α ) là mặt phẳng chứa ∆ và song song với ∆ . 2 1 2
D. d bằng độ dài đoạn thẳng MM’ với điểm M bất kì thuộc ∆ và M’ là hình chiếu vuông góc của M lên ∆ . 1 2
Câu 23: Cho hai mặt phẳng (α ) và (β ) song song với nhau. Gọi d là khoảng cách giữa (α ) và (β ). Mệnh đề nào sau đây sai?
A. d bằng khoảng cách từ một điểm bất kì thuộc (α ) đến (β ).
B. d bằng khoảng cách giữa một đường thẳng bất kì nằm trong (β ) đến (α ) .
C. d bằng khoảng cách giữa một đường thẳng ∆ bất kì nằm trong (α ) đến hình chiếu vuông góc của ∆ lên (β ).
D. d bằng khoảng cách giữa hai đường thẳng bất kì ∆ và ∆ lần lượt nằm trong (α ) và (β ). 1 2
Câu 24: Cho hình hộp ABC .
D A' B 'C ' D ' . Khẳng định nào sau đây sai? A. d( ,
A (CDD'C ')) = d(B,(CDD'C '))
B. d(( ABCD),( A'B'C 'D')) = d(B,( A'B'C 'D'))
C. d(( ABCD),( A'B'C 'D')) = d(( ABB' A'),(CDC 'D'))
D. d(( ABCD),( A'B'C 'D')) = d(AC,( A'B'C 'D'))
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Khẳng định nào sau đây sai?
A. d(B,(SCD)) = d(A,(SCD))
B. d(C,(SAB)) = d(D,(SAB))
C. d(C,(SBD)) = d(A,(SBD))
D. d(B,(SCD)) = d(BC,(SAD))
Câu 26: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Tính d( AB',(CDD'C '))
A. d( AB',(CDD'C ')) = a B. d( B',( ' ')) a A CDD C = 2 C. d( B',( ' ')) a A CDD C =
D. d( AB',(CDD'C ')) = a 2 3
Câu 27: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB = a,BC = b,CC' = c . Khẳng định nào sau đây sai?
A. d(( ABCD),( A'B'C 'D')) = c B. d( ',( 'A')) ab BB ACC = 2 a + b
C. d( AB',(CDD'C ')) = b
D. d(BB',( ACC 'A')) = a 2
Câu 28: Cho hình lập phương ABC .
D A' B 'C ' D ' có AB = a . Tính khoảng cách h giữa hai mặt phẳng
(BA'C ') và ( ACD'). A. a h = B. a h = C. a 2 h =
D. h = a 3 3 2
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) . Tính d(CD,(SAB)) .
A. d(CD,(SAB)) = a
B. d(CD,(SAB)) = a 2 C. ( (SAB)) a 2 d CD, =
D. d(CD,(SAB)) = 2a 2
Câu 30: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ⊥ ( ABCD) và SA = a . Tính d( AB,(SCD)).
A. d( AB,(SCD)) = a
B. d( AB,(SCD)) = a 2
C. ( AB (SCD)) a 2 d , =
D. d( AB,(SCD)) = 2a 2
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình thoi,
ABC =120° và SA ⊥ ( ABCD) . Gọi M là trung
điểm của SC. Tính d(SA,(BMD)).
A. d(SA,(BMD)) = a
B. d(SA,(BMD)) = a 3 C. ( (BMD)) a 3 d SA, =
D. d(SA,(BMD)) = a 2 2
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết SA = a 3, AD = a và
SA vuông góc với đáy. Tính theo a khoảng cách từ B đến (SCD) . A. a 3 B. a C. a 3 D. 2a 2 2 4
Câu 33: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh a . Tính theo a khoảng cách từ điểm D đến mặt
phẳng ( A'BC) . A. a 2 B. a C. a 2 D. a 2 2
Câu 34: Cho hình chóp S.ABC, gọi M là trung điểm của AC và G là trọng tâm tam giác SAC. Biết khoảng
cách từ điểm M đến mặt phẳng (SBC) bằng a 6 . Tính theo a khoảng cách từ điểm G đến mặt phẳng 6 (SBC). A. a 6 B. a 6 C. a 6 D. a 6 18 9 3 6
Câu 35: Cho hình chóp đều S.ABCD có O là tâm của đáy. Biết cạnh đáy và đường cao bằng nhau và bằng
a . Tính theo a khoảng cách từ điểm D đến mặt phẳng (SBC). A. a 5 B. a 5 C. 2a 5 D. a 5 10 5 5 2
Câu 36: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Tính theo a khoảng cách từ điểm A đến mặt phẳng (SCD) . A. a 3 B. a 21 C. 2a 21 D. 2a 3 7 7 7 7
Câu 37: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a,AD = a 3 , hai mặt phẳng (SAB) và
(SAD) cùng vuông góc với mặt phẳng đáy. Góc giữa cạnh SC và mặt phẳng đáy bằng 60°. Gọi G là trọng
tâm tam giác ABC. Tính theo a khoảng cách từ điểm G đến mặt phẳng (SBC). A. 2a 39 B. 2a 39 C. 6a 39 D. a 39 13 39 13 13
Câu 38: Cho hình chóp S.ABC có SA = a 3 và SA vuông góc với mặt phẳng đáy, tam giác ABC đều cạnh
a . Vẽ AI vuông góc với SB. Tính theo a khoảng cách từ điểm I đến mặt phẳng (SAC) . A. a 3 B. a 3 C. 3a 3 D. 3a 3 8 4 8 4
Câu 39: Cho hình chóp S.ABCD có hai mặt phẳng (SAB),(SAC) cùng vuông góc với mặt phẳng đáy và đáy
ABCD là nửa lục giác đều. Biết SA = a 3 và AB = BC = CD = a . Tính theo a khoảng cách từ điểm B đến mặt phẳng (SCD) . A. a 6 B. a 6 C. a 6 D. a 6 2 4 8
Câu 40: Cho hình chóp S.ABCD có đáy là hình thoi cạnh a 2 , cạnh bên SA vuông góc vói mặt phẳng đáy,
BAD =120° , góc giữa mặt phẳng (SBC) và đáy bằng 30° . Tính theo a khoảng cách từ điểm B đến mặt phẳng (SBC). A. 3a 2 B. a 3 C. 3a D. a 6 4 4 2 4
Câu 41: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 và cạnh bên bằng a 2 . Gọi E là trung
điểm của AB. Tính theo a khoảng cách từ điểm E đến mặt phẳng (SBC). A. a 5 B. 3a 5 C. 3a 5 D. 2a 5 5 5 10 5
Câu 42: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Tam giác ABC vuông tại A có
AB = a,AC = a 3 . Góc giữa SB và mặt phẳng (SAC) bằng 45°. Lấy điểm M trên cạnh SA sao cho a
AM = . Tính theo a khoảng cách từ điểm M đến mặt phẳng (SBC) . 3 A. 2a 21 B. a 21 C. 2a 21 D. a 21 21 7 7 21
Câu 43: Cho hình lăng trụ ABC .
D A' B 'C ' D ' có đáy ABCD là hình chữ nhật, AB = a và AD = a 3 . Hình
chiếu vuông góc của điểm A’ lên mặt phẳng ( ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách
từ B’ đến mặt phẳng ( A'BD) theo a . A. a 2 B. 2 C. a 3 D. a 3 2 2
Câu 44: Cho hình chóp đều S.ABCD cạnh đáy bằng a , góc giữa mặt bên và mặt đáy bằng 60°. Gọi G là
trọng tâm của tam giác ABD. Tính theo a khoảng cách từ điểm G đến mặt phẳng (SBC). A. a B. a 3 C. a 3 D. a 3 3 6 6
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a ,
ACB = 30° . Mặt bên SAC là
tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi G là trung điểm của SA. Tính theo a khoảng
cách từ điểm G đến mặt phẳng (SBC). A. a 3 B. 2a 39 C. a 39 D. a 3 4 13 13 2
Câu 46: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, BA = BC = a, AD = 2a . Cạnh bên
SA vuông góc với đáy và SA = a 2 . Gọi H là hình chiếu vuông góc của A trên cạnh SB. Tính khoảng cách
từ điểm H đến mặt phẳng (SCD) theo a . A. a B. a C. a D. a 2 4 3
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 4 a . Hình chiếu của S trên mặt phẳng
( ABCD) là điểm H thuộc AB sao cho HB = 3HA. Góc giữa cạnh bên SC và đáy bằng 45°. Tính theo a
khoảng cách từ O đến mặt phẳng (SBC), với O là tâm của hình vuông ABCD. A. 5a 34 B. 5a 34 C. 5a 34 D. 5a 17 17 34 2
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a . Mặt phẳng bên SAB vuông góc
với mặt phẳng đáy và SA = a, SB = a 3 . Góc giữa mặt phẳng (SBD) và đáy bằng 60°. Tính theo a khoảng
cách từ điểm C đến mặt phẳng (SBD). A. a 3 B. a 3 C. 3a D. a 3 4 4
Câu 49: Cho hình chóp S.ABC, đáy ABC là tam giác vuông tại B với AB = a, BC = 3,SA ⊥ ( ABC) và SC
tạo với ( ABC) một góc 45°. Gọi G ,G lần lượt là trọng tâm của tam giác SAB và SAC. Tính 1 2
d (G G , SBC . 1 2 ( ))
A. d (G G , SBC = a 5 B. ( 4 , a d G G SBC = 1 2 ( )) 1 2 ( )) 3 5 C. ( 2 , a d G G SBC = D. ( 6 , a d G G SBC = 1 2 ( )) 1 2 ( )) 3 5 5
Câu 50: Cho hình lăng trụ đứng ABC.A'B 'C có đáy ABC là tam giác vuông tại B, BC = a 3 , AB ' = 2a và
đường thẳng AB’ tạo với mặt phẳng đáy một góc 60°. Tính d(BC,( AB'C ')). A. d(BC,( ' ')) a AB C =
B. d(BC,( AB'C ')) = a 3 2 C. ( ( AB C )) a 3 d BC, ' ' = D. ( ( AB C )) a 3 d BC, ' ' = 2 4
Câu 51: Cho hình lăng trụ đứng ABC .
D A'B 'C 'D' có đáy ABCD là hình thoi cạnh a , ABC =120°, đường
thẳng A’B tạo với mặt phẳng đáy một góc 60°. Tính d(B'D',( A'BD)) .
A. d(B'D',( A'BD)) = a 15 B. d(B'D',( ' )) a A BD = 5
C. d(B'D',( A'BD)) = a 3 D. ( ( A BD)) a 15 d B'D', ' = 5
Câu 52: Cho hình lăng trụ ABC.A'B 'C có đáy ABC là tam giác đều cạnh a và AA' = A'B = A'C = a . Gọi
M, N lần lượt là trung điểm của BC và A’B. Tính d( A'C,( AMN )) . A. ( ( AMN )) a 22 d A'C, = B. d(A'C,( )) a AMN = 11 11
C. d(A'C,( AMN )) = a 22 D. ( ( AMN )) a 2 d A'C, = 3
Câu 53: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a và SA vuông góc với đáy. Tính khoảng
cách d giữa hai đường thẳng SA và BD. A. a d =
B. d = a
C. d = a 2 D. a 2 d = 2 2
Câu 54: Cho hình chóp S.ABC có SA, AB, BC đôi một vuông góc, tam giác ABC cân và có AC = a 2 . Tính
khoảng cách d giữa hai đường thẳng SA và BC.
A. d = a 2
B. d = a C. a 2 d =
D. d = 2a 2
Câu 55: Cho tứ diện đều ABCD có I, J lần lượt là trung điểm các cạnh AB, CD. Khoảng cách giữa hai đường
thẳng AB, CD bằng độ dài của đoạn thẳng nào dưới đây? A. AI B. IJ C. AB D. AJ
Câu 56: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Tính khoảng cách d giữa hai đường
thẳng BD và SC. A. a d = B. a d = C. a 2 d =
D. d = a 2 4 2 2
Câu 57: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB=AA' = a, AC = 2a . Tính khoảng cách d giữa hai
đường thẳng AB’ và CD’.
A. d = a 3
B. d = a 5 C. a 3 d = D. a 3 d = 3 2
Câu 58: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình chữ nhật với AC = 2a và BC = a .
Tính d (SD, BC) . A. ( ) 2 , a d SD BC =
B. d (SD BC) a 3 , = C. ( ) 3 , a d SD BC =
D. d (SD, BC) = a 3 3 2 4
Câu 59: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a , cạnh bên SA vuông góc với
đáy và SA = a 2 . Gọi M là trung điểm của AB. Tính khoảng cách d giữa hai đường thẳng SM và BC. A. a 2 d = B. a d = C. a 3 d = D. a 3 d = 3 2 3 2
Câu 60: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AA' = 2a, AD = 4a . Gọi M là trung điểm của AD.
Tính khoảng cách d giữa hai đường thẳng A’B’ và C’M.
A. d = 3a
B. d = 2a 2
C. d = a 2
D. d = 2a
Câu 61: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt phẳng
đáy và SA = a . Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau? A. a B. a 2 C. a 3 D. 2a
Câu 62: Cho tứ diện OABC, trong đó OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC = a . Gọi
I là trung điểm BC. Khoảng cách giữa hai đường thẳng AI và OC nhận giá trị nào trong các giá trị sau? A. a B. a C. a 3 D. a 5 2 2
Câu 63: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. cạnh bằng a và BAC = 60° . Biết a 6 SC =
và vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BD nhận giá trị nào trong các 2 giá trị sau? A. a B. a 6 C. a 3 D. a 3 2 4 3 4
Câu 64: Cho hình lăng trụ đứng ABC.A'B 'C ' có tất cả các cạnh đều bằng a . Tính khoảng cách d giữa hai
đường thẳng AB’ và CC’. A. 2a d = B. a 3 d = C. 3a d =
D. d = a 3 3 2 4
Câu 65: Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình chữ nhật với AC = a 5 và
BC = a 2 . Tính khoảng cách d giữa hai đường thẳng SD và BC. A. 2a d = B. a 3 d = C. 3a d =
D. d = a 3 3 2 4
Câu 66: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Tính khoảng cách d giữa hai đường thẳng AD’ và BD. A. a 3 d = B. a 3 d =
C. d = a 3 D. 2a d = 2 3 3
Câu 67: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy ( ABCD) và SA = a . Tính khoảng cách d giữa hai đường thẳng SB và AD. A. a 2 d = B. a 3 d = C. a 2 d =
D. d = a 3 2 2
LỜI GIẢI BÀI TẬP TỰ LUYỆN BC ⊥ AH
Câu 1: Kẻ AH ⊥ BC,AK ⊥ DH ta có
⇒ BC ⊥ (HAD) ⇒ BC ⊥ AK BC ⊥ DA
Mà AK ⊥ DH ⇒ AK ⊥ (BCD) . Ta có 1 = 1 + 1 = 1 + 1 + 1 AK2 AH2 AD2 AB2 AC2 AD2 Do đó 1 1 1 1 = + + . Chọn A. 2 2 2 2 d a b c 2 2 Câu 2: Ta có 1 1 1 2 AB .AC AB.AC = + ⇔ d = ⇔ d = . Chọn A. d2 AB2 AC2 AB2 + AC2 AB2 + AC2
Câu 3: Do MN // (α) nên d1 = d2. Chọn A.
Câu 4: Khẳng định sai là d((α),( )) β = MN . Chọn D.
Câu 5: Khoảng cách từ D đến mặt phẳng (ABC) là khoảng cách từ D đến tâm đường tròn ngoại tiếp tam giác
ABC. Mà tam giác ABC đều nên trọng tâm cũng là tâm đường tròn ngoại tiếp. Do đó A, B, C đúng. Chọn D. Câu 6: 1
= 1 + 1 + 1 = 1 + 1 + 1 = 61 ⇒ d(A,(BCD)) = 12 61 d(A,(BCD))2 AB2 AC2 AD2 2 2 2 2 3 4 144 61 Chọn A.
Câu 7: Khoảng cách lớn nhất giữa 2 đỉnh chính là đường chéo là a 3. Chọn A.
Câu 8: Ta có 3MI = 2MN ⇔ 3MI = 2(IN − IM) ⇔ IM + 2IN = 0. Ta có d1 IM = = 2. Chọn D. d2 IN Câu 9: Ta có d 4 1 IM = = . Chọn A. d 3 2 IN
Câu 10: Gọi N là trung điểm của BC d(A,(A 'BC)) NA = = 3⇒ d(A,(A 'BC)) = d 3 (O,(A 'BC)) d(O,(A 'BC)) NO
Do đó đáp án D sai. Chọn D.
Câu 11: Ta có d(A,(DA’C’) = d(D’,(DA’C’))
Kẻ D'E ⊥ A 'C',D'F' ⊥ DE A 'C' ⊥ DD' Ta có
⇒ A 'C' ⊥ (DD'E) ⇒ A 'C' ⊥ D'F A 'C' ⊥ D'E
Mà D'F ⊥ DE ⇒ D'F ⊥ (DA'C') Ta có 1 = 1 + 1 = 1 + 1 + 1
D'F2 DD'2 D'E2 DD'2 D'A'2 D'C'2 1 1 1 a b 2 2 + b c 2 2 + c a 2 2 abc = + + = ⇒ D'F = a2 b2 c2 a b 2 c 2 2 a b 2 2 + b c 2 2 + c a 2 2 Chọn A.
Câu 12: Kẻ AE ⊥ BC,AF ⊥ SE BC ⊥ AE Ta có
⇒ BC ⊥ (SAE) ⇒ BC ⊥ AF BC ⊥ SA
Mà AF ⊥ SE ⇒ AF ⊥ (SBC) . Ta có a AE = 3 2 1 1 1 1 1 a2 3 + h2 4 ah = + = + = ⇒ AF = 3 AF2 SA2 AE2 h2 a2 3 a 3 h 2 2 a2 3 + h2 4 4 Chọn B.
Câu 13: Ta có d(A,CC') = AC = a 2. Chọn B.
Câu 14: Gọi O là trung điểm của A’C’ và B’D’ B'D' ⊥ A 'C' Ta có
⇒ B'D' ⊥ (AA 'C') ⇒ B'D' ⊥ AO B'D' ⊥ AA ' a 2 2 2 2 2 a
d(A,B'D') = AO = AA ' + A 'O = a + 6 = 2 2 Chọn A.
Câu 15: Gọi H là tâm đường tròn ngoại tiếp ∆ABC
⇒ SH ⊥ (ABC) . Gọi M là trung điểm của BC Ta có 2 2 a AH = AM = . 3 3 = a 3 3 3 2 d(S,(ABC)) 2 2
= SH = SA2 − AH2 = (a 7) −(a ) 3 = a 2 Chọn B. AB ⊥ BC Câu 16:
⇒ AB ⊥ (SBC) ⇒ d(A,(SBC)) = AB AB ⊥ SC Chọn B.
Câu 17: Ta có d(K,(ABCD)) = 1d(S,(ABCD)) = 1SC = a . Chọn A. 2 2
Câu 18: Có vô số các đường thẳng cắt ∆1 tại M và cắt ∆2 tại N
Ta có d(∆1,∆2) ≤ MN, dấu bằng xảy ra ⇔ MN là đoạn vuông góc chung của ∆1 và ∆2. Chọn A.
Câu 19: Theo giả thiết bài toán ta có: d(∆ ,( ))
β = d(∆ ,(α)) = d(∆ ,∆ ) = d((α),( )) β 1 2 1 2 Mặt khác : d((α),( )) β ≤ MN, M ∀ ∈ ∆ , N ∈∆ 1 2
Do vậy khẳng định C là sai. Chọn C.
Câu 20: Do ∆ / /(α , mặt phẳng ( )
β chứa ∆ và cắt (α) theo giao tuyến là ∆ ⇒ ∆ 1 / /∆ 1 ) 1 2 2
Mặt phẳng (∆ ;∆ ) ≡ ( )
β ⊥ (α nên d(∆ ,∆ ) = d(∆ ,(α . Chọn A. 1 2 1 )) 1 2 )
Câu 21: Do ∆ song song với mặt phẳng (α) nên khoảng cách từ ∆ đến (α) bằng khoảng cách từ một điểm
bất kì trên ∆ đến (α) . Bằng khoảng cách từ mặt phẳng ( ) β đến (α) với ( )
β là mặt phẳng chứa ∆ và song
song với (α) và cũng bằng khoảng cách từ mặt phẳng ( ) β đến (α) với ( )
β là mặt phẳng chứa ∆ và song song với (α) .
Các khẳng định đúng là A, C và D. Khẳng định B sai. Chọn B.
Câu 22: Các khẳng định đúng là A, B và C.
Khẳng định sai là D. Chọn D.
Câu 23: d bằng khoảng cách giữa một đường thẳng ∆ bất kì nằm trong (α) đến hình chiếu vuông góc của ∆ lên ( )
β suy ra khẳng định C đúng và D sai. Chọn D.
Câu 24: Ta có AB / /CD ⇒ AB / /(CDD'C') : nên
d(A,(CDD'C')) = d(B,(CDD'C')) → A đúng Do (ABCD) / /(A 'B'C'D') nên
d((ABCD),(A 'B'C'D')) = d(B,(A 'B'C'D')) và
d((ABCD),(A 'B'C'D')) = d(AC,(A 'B'C'D')) → B,D đều đúng.
Khẳng định sai là C. Chọn C.
Câu 25: Ta có: AB / /CD ⇒ AB / /(SCD)
⇒ d(A,(SCD)) = d(B,(SCD)) ⇒ A đúng
Tương tự CD / /(SAB) ⇒ d(C,(SAB)) = d(D,(SAB))
Do AC∩ BD tại O và OA = OC
⇒ d(A;(SBD)) = d(C;(SBD)) suy ra B và C đúng.
Khẳng định sai là D. Chọn D.
Câu 26: Dễ thấy AB'/ /C'D ⇒ AB'/ /(CDD'C') nên
d(AB',(CDD'C')) = d(A;(CDD'C')) = d
Mặt khác ABCD.A’B’C’D’ là hình lập phương nên
AD ⊥ (CDD'C') ⇒ d = AD = a .Chọn A.
Câu 27: Ta có d((ABCD),(A'B'C'D')) = AA' = CC' = c
d(BB',(ACC'A ')) = d(B;(ACC'A')
Dựng BH ⊥ AC, mặt khác BH ⊥ AA ' ⇒ BH ⊥ (ACC'A') Khi đó AB.BC ab d(BB',(ACC'A ')) = BH = = BA2 + BC2 a2 + b2
Dễ thấy AB'/ /C'D ⇒ AB'/ /(CDD'C') nên
d(AB',(CDD'C')) = d(A;(CDD'C')) = AD = BC = b
Khẳng định sai là D. Chọn D. A 'B'/ /CD'
Câu 28: Dễ thấy ⇒ (BA 'C') / /(ACD') BC'/ /AD'
Do đó d((BA 'C');(ACD')) = d(B;(ACD'))
Mặt khác BD cắt AC tại trung điểm O của BD suy ra
d((BA 'C');(ACD')) = d(B;(ACD')) AC ⊥ DO
Dựng DE ⊥ D'O, mặt khác ⇒ AC ⊥ DE AC ⊥ DD' Do đó DE ⊥ (D'AC) DO.DD' ⇒ d = d(D;(D'AC) = DE = DO2 + DD'2 Trong đó DB a 2 a DO = = ;DD' = a ⇒ d = . Chọn A. 2 2 3
Câu 29: Ta có: SA ⊥ (ABCD) ⇒ SA ⊥ AD
Mặt khác AD ⊥ AB ⇒ SA ⊥ (SAB)
Do CD / /(SAB) ⇒ d(CD,(SAB)) = d(D;(SAB)) = DA = a Chọn A.
Câu 30: Do AB / /CD ⇒ AB / /(SCD)
Khi đó d(AB,(SCD)) = d(A;(SCD))
Dựng AH ⊥ SD, ta có SA ⊥ (ABCD) ⇒ SA ⊥ CD CD ⊥ SA Do
⇒ CD ⊥ (SAH) ⇒ CD ⊥ AH CD ⊥ AD
Lại có AH ⊥ SD ⇒ AH ⊥ (SCD) Suy ra SA.AD a d(A : (SCD)) = AH = = 2 SA2 + AD2 2 Chọn C.
Câu 31: Gọi O là tâm của hình thoi ABCD thì OA = OC suy ra
OM là đường trung bình trong ∆SAC ⇒OM//SA
⇒ OM ⊥ (ABCD) ⇒ OM ⊥ OA
Do ABCD là hình thoi nên OA ⊥ BD ⇒ OA ⊥ (MBD)
Khi đó d(SA;(MBD)) = d(A;(MBD)) = AO
Mặt khác: ABC = 120 ⇒ BAD = 60 ⇒ AB D đều cạnh a Nên a 3 a AO = ABsin = ⇒ d = 3 60 . Chọn C. 2 2
Câu 32: Do AB / / CD ⇒ AB/ /(SCD)
Suy ra d(B;(SCD)) = d(A;(SCD)) = d CD ⊥ SA Ta có: ⇒ CD ⊥ (SAD) CD ⊥ AD
Dựng AH ⊥ SD ⇒ AH ⊥ (SCD) Khi đó SA.AD a d = d(A;(SBC)) = AH = = 3 SA2 + AD2 2 Chọn A.
Câu 33: Do AD / / BC ⇒ AD/ /(A'BC)
Suy ra d(B;(A'BC)) = d(A;(A'BC))
Dựng AH ⊥ A 'B, lại có BC ⊥ (A'AB) ⇒ BC ⊥ AH
Do đó AH ⊥ (A 'BC) ⇒ d(A;(A'BC)) = AH Lại có: AA '.AB a AH = = 2 AA '2+ AB2 2 Vậy a d(D;(A'BC)) = d(A;(A'BC)) = 2 . Chọn C 2
Câu 34: Ta có: G là trọng tâm tam giác SAC ⇒ SG = 3MG Mặt khác d MS M MG ∩ (SBC) = S ⇒ = = 3 d GS 2 G Suy ra . 2 2 a 6 a d = d = . = 6 Chọn B. G M 3 3 6 9
Câu 35: Do S.ABCD là hình chóp đều có O là tâm của đáy nên đáy
là hình vuông tâm O và SO ⊥ (ABCD)
Dựng OE ⊥ BC , mặt khác SO ⊥ BC ⇒ BC ⊥ (SOE)
Dựng OF ⊥ SE ⇒ OF ⊥ (SBC) ⇒ d(O;(SBC)) = OF Ta có: AB a OE = = ;SO = AB = a 2 2 SO.OE a ⇒ OF = = 5 SO2 + OE2 5 Mặt khác a
DB = OB ⇒ d(D;(SBC)) = d(O;(SBC)) = 2 5 2 2 . Chọn C. 5
Câu 36: Gọi H, M lần lượt là trung điểm của AB, CD
Ta có SH ⊥ AB ⇒ SH ⊥ (ABCD),HM ⊥ CD ⇒ CD ⊥ (SHM)
Kẻ HK ⊥ SM(K ∈SM) mà HK ⊥ CD ⇒ HK ⊥ (SCD)
Tam giác SHM vuông tại H, có SH.HM a HK = = 21 SH2 + HM2 7
Mặt khác AB / /CD ⇒ AB / /(SCD) ⇒ [ ] = [ ] a d d;(SCD) d H;(SCD) = 21. Chọn B. 7 SC;(ABCD) = Câu 37: Ta có ( ) (SC;AC) = SCA = 60
Tam giác SAC vuông tại A, có SA = AC.tanSCA = a 2 3
Kẻ AH ⊥ SB(H ∈SB) mà BC ⊥ (SAB) ⇒ AH ⊥ (SBC)
Tam giác SAB vuông tại A, có SA.AB a AH = = 2 39 SA2 + AB2 13
Vì G là trọng tâm A
BC ⇒ d[G;(SBC)] = 1d[A;(SBC)] 3
Vậy khoảng cách cần tìm là a d = 2 39 . Chọn B. 39
Câu 38: Gọi H là trung điểm AC ⇒ BH ⊥ AC Mà ⊥ ⇒ ⊥ ⇒ [ ] a SA BH BH (SAC) d B;(SAC) = BH = 3 2
Tam giác SAB vuông tại A, có SA.AB a AI = = 3 SA2 + AB2 2
Tam giác SAI vuông tại I, có 2 2 a SI = SA − AI = 3 2 Suy ra IS = 3 → [ ] = 3 [ ] a d I;(SAC) d B;(SBC) = 3 3 SB 4 4 8 Chọn C.
Câu 39: ABCD là nửa lục giác đều ⇒ ABC = 120;AC ⊥ CD
Kẻ AH ⊥ SC(H ∈SC) mà CD ⊥ AH ⇒ AH ⊥ (SCD)
Tam giác ABC có AB = BC = a;ABC = 120 ⇒ AC = a 3
Tam giác SAC vuông tại A, có SA.AC a AH = = 6 SA2 + AC2 2 Vậy. [ ] = 1 [ ] a d B;(SCD) d A;(SCD) = 6 . Chọn C. 2 4
Câu 40: Ta có BAD = 120 ⇒ ABC = 60 ⇒ AB C đều
Gọi M là trung điểm BC ⇒ AM ⊥ BC ⇒ BC ⊥ (SAM) (SBC);(ABCD) = Suy ra ( ) (SM;AM) = SMA = 30
Kẻ AK ⊥ SM(K ∈SM) mà BC ⊥ AK ⇒ AK ⊥ (SBC)
Tam giác AKM vuông tại K, có a AK = AM.sin = 6 30 4
Lại có AD / /BC ⇒ AD / /(SBC) ⇒ [ ] = [ ] a d D;(SBC) d A;(SBC) = 6 . Chọn D. 4
Câu 41: Gọi O là trọng tâm ∆ABC, M là trung điểm BC
Suy ra SO ⊥ (ABC),OM ⊥ BC ⇒ BC ⊥ (SMO)
Kẻ OH ⊥ SM(H ∈SM) mà BC ⊥ OH ⇒ OH ⊥ (SBC) Ta có 3 a 3 2 1 a AM = AB = → OA = AM = a;OM = AM = 2 2 3 3 2
Tam giác SAO vuông tại O, có SO = SA2 − OA2 = a
Tam giác SMO vuông tại O, có SO.OM a OH = = 5 SO2 + OM2 2 Lại có AM = ⇒ [ ] = [ ] a d A;(SBC) d O;(SBC) = OH = 3 5 3 3 3 OM 5
Mặt khác E là trung điểm AB → [ ] = 1 [ ] a d E;(SBC) d A;(SBC) = 3 5 2 10 Chọn C. S A ⊥ AB ⇒ AB ⊥ (SAC) ⇒ ( Câu 42: SB;(SAC)) = BSA = 45 AC ⊥ AB
Suy ra tam giác SAB vuông cân tại A → SA = AB = a
Xét hình chóp S.ABC, ta được 1 1 1 1 21 2 [ ] = + + ⇒ 2 2 2 [ ] a d A;(SBC) = d A;(SBC) SA AB AC 7 Lại có SA a = 2 = 3⇒ [ ] = 2 [ ] a a : d M;(SBC) d A;(SBC) = 2 21 MS 3 2 3 21 Chọn A.
Câu 43: Kẻ AH ⊥ BD(H∈BD) mà A'O ⊥ BD
⇒ AH ⊥ (A 'BD) ⇒ d[A;(A'BD)] = AH
Tam giác ABD vuông tại A, có AB.AD a AH = = 3 BD 2 Vậy [ ] = [ ] a d A;(A 'BD) d B';(A 'BD) = 3 . Chọn D. 2
Câu 44: Gọi O là tâm hình vuông ABCD, M là trung điểm BC
Suy ra SO ⊥ (ABCD),OM ⊥ BC ⇒ BC ⊥ (SMO) (SBC);(ABCD) = Khi đó (SM;OM) = SMO = 60
Kẻ OH ⊥ SM(H ∈SM) → OH ⊥ (SBC)
Tam giác OHM vuông tại H, có OH a sin HMO = ⇒ OH = 3 OM 4
Vì G là trọng tâm tam giác ABC GC → = 4 OC 3 ⇒ [ ] = 4 [ ] 4 4 a 3 a d G;(SBC) d O;(SBC) = OH = . = 3 . Chọn B. 3 3 3 4 3
Câu 45: Gọi H, K lần lượt là trung điểm AC, BC
Ta có SH ⊥ AC ⇒ SH ⊥ (ABC) và HK / /AB ⇒ HK ⊥ BC BC ⊥ HE
Kẻ HE ⊥ SK(E ∈SK) ⇒ ⇒ HE ⊥ (SBC) S K ⊥ HE
Tam giác ABC vuông tại B, có = AB AC = 2a ⇒ SH = a 3 cosBAC
Tam giác SHK vuông tại H, có SH.HK a HE = = 39 SH2 + HK2 13
Lại có G là trung điểm SA, H là trung điểm AC = [ ] = 1 [ ] a HK d G;(SBC) d A;(SBC) = 39 .Chọn C. 2 13
Câu 46: Gọi E là trung điểm AD ⇒ABCE là hình vuông
⇒ AC ⊥ CD mà SA ⊥ CD ⇒ CD ⊥ (SAC)
Kẻ AK ⊥ SC(K ∈SC) ⇒ AK ⊥ (SCD)
Tam giác SAC vuông tại A, có SA.AC AK = = a SA2 + AC2 Do đó [ ] = 1 [ ] a d B;(SCD) d A;(SCD) = 2 2
Mà H là hình chiếu của A trên HS SB ⇒ = 2 SB 3 Suy ra [ ] = 2 [ ] 2 a a d H;(SCD)
d B;(SCD) = . = . Chọn C. 3 3 2 3
Câu 47: Kẻ HK ⊥ SB(K ∈SB) ⇒ HK ⊥ (SBC)
Vì HB = HA ⇒ HA = a,HB = a ⇒ HC = BH2 + BC2 3 3 = a 5 SC;(ABCD) = Ta có
(SC;HC) = SCH = 45 ⇒ SH = HC = a 5
Tam giác SBH vuông tại B, có SC;(ABCD) =
(SC;HC) = SCH = 45 ⇒ SH = HC = a 5 d[H;(SBC)] Khi đó BH 3 a = = ⇒ = 10 34 d[A;(SBC)] d[A;(SBC)] AB 4 17 Vậy [ ] = 1 [ ] 1 a 10 34 a d O;(SBC) d A;(SBC) = . = 5 34 2 2 17 17 Chọn B.
Câu 48: Kẻ SH ⊥ AB(H∈AB) → SH ⊥ (ABCD)
Kẻ HK ⊥ BD(K ∈BD) ⇒ BD ⊥ (SBD) (SBD);(ABCD) = Do đó (SK;HK) = SKH = 60
Kẻ HE ⊥ SK(E ∈SK) ⇒ HE ⊥ (SBD) Ta có SA2+ SB2 = AB2 ⇒ SA Bvuông tại S Suy ra SA.SB a 3 2 2 3 BH SH = = ⇒ BH = SB −SH = ⇒ = 3 AB 2 2 AB 4
Tam giác SHE vuông tại E, có HE a sin HSK = ⇒ HE = 3 SH 4 d[H;(SBD)] Khi đó AB 4 4 a 3 a 3 [ ] = = ⇒ d[A;(SBD)] = . = d A;(SBD) BH 3 3 4 3 Vậy [ ] a d C;(SBD) = 3. Chọn A. 3
Câu 49: Do SA ⊥ (ABC) và SC tạo với (ABC) một góc 45° nên SCA = 45 Ta có: AC = AB2 + BC2 = a 2 ⇒ SA = AC tan 45 = a 2
Gọi M, N lần lượt là trung điểm của AB và AC thì
G G / /MN / /BC ⇒ d(G G ;(SBC)) = d(G ;(SBC)) = 1 2 1 2 1 d Mặt khác G S = 2 2 mà MB = 1AB 1 MS ⇒ d = d G1 M 3 3 2 ⇒ d = 1d(A;(SBC)) M 2 Suy ra d = 1d(A;(SBC)) G1 3 BC ⊥ AB Dựng AH ⊥ SB , do
⇒ BC ⊥ (SAB) ⇒ BC ⊥ AH BC ⊥ SA Mặt khác SA.AB 2a
AH ⊥ SB ⇒ AH ⊥ (SBC) ⇒ d(A;(SBC)) = AH = = 2 2 SA + AB 5 Suy ra 2a d = . Chọn C. 3 5
Câu 50: Ta có: A’B cắt AB’ tại trung điểm I của mỗi đường
Do đó d(BC,(AB'C')) = d(B;(AB'C')) = d(A ';(AB'C')) = d B'C' ⊥ A 'B'
Dựng A 'F ⊥ AB' ta có: B'C' ⊥ AA ' A'F ⊥ AB'
⇒ B'C' ⊥ (A 'B'A). Lại có ⇒ A 'F ⊥ (AB'C') A'F ⊥ BC Khi đó: AB'.AA ' d = A 'F = AB'2+ AA '2
Trong đó AB’ tạo với mặt phẳng đáy một góc 60° nên A'BA = 60 ⇒ AA' = A'Bsin 60 = a 2 sin 60 = a 3
Mặt khác AB = AB'cos60 = a Suy ra AB'.AA ' a d = A 'F = = 3 . Chọn C. AB'2+ AA '2 2
Câu 51: Dựng AE ⊥ BD;AF ⊥ A'E
Do ABC = 120 ⇒ BAD = 60 ⇒ AB D là tam giác đều cạnh a a ⇒ AE = 3 2 BD ⊥ AE Do
⇒ BD ⊥ (A 'AE) ⇒ BD ⊥ AF BD ⊥ AA '
Mặt khác AF ⊥ A 'E ⇒ AF ⊥ (A 'BD)
Do A’B tạo với mặt phẳng đáy một góc 60°
⇒ A 'BA = 60 ⇒ A 'A = ABtan 60 = a 3 Khi đó AA '.AE a d(A;(A 'BD) = AF = = 15 AA '2+ AE2 5
Do B'D / /BD ⇒ d(B'D';(A'BD)) = d(B';(A'BD)) = d
Mà A 'B∩ AB' = I là trung điểm của AB’ a ⇒ d = d(A;(A 'BD)) = AF = 15. Chọn D. 5
Câu 52: Dễ thấy A’.ABC là hình chóp tam giác đều nên hình chiếu của A’ xuống mặt đáy trùng với trọng
tâm tam giác ABC. MN là đường trung bình trong tam giác BA’C nên MN//A’C.
Khi đó d(A'C,(AMN)) = d(A';(AMN)) = d(B;(AMN) = d
Gọi H là hình chiếu của N trên mặt phẳng (ABC)
⇒ NH/ / A'G' ⇒ H là trung điểm của BG.
Dựng HE ⊥ AM;HF ⊥ NE ⇒ d(H;(AMN)) = HF Mặt khác BM BC a A 'G HE = = = , NH = 2 4 4 2 Trong đó a 3 2 2 a BG = ⇒ A 'G = A 'B − BG = 6 3 3 Do đó a 6 NH.NE a NH = ⇒ HF = = 6 NH2 + NE2 22 Suy đó a 2 a d = d(B;(AMN)) = d(H;(AMN)) = = 22 2 . Chọn A. 22 11
Câu 53: Gọi O là giao điểm của AC và BD OA ⊥ SA Ta có
⇒ OA là đoạn vuông góc chung của SA và BD OA ⊥ BD Ta có 2 2 1 a AC = AB + BC = a ⇒ OA = AC = 2 2 2 2 Ta có a d(SA,BD) = OA = 2 . Chọn D. 2 AB ⊥ SA Câu 54: Ta có
⇒ AB là đoạn vuông góc chung của SA và BC AB ⊥ BC
Ta có AB ⊥ BC và ∆ABC cân nên ∆ABC vuông cân tại B. Do đó AB = BC = a
Ta có d(SA,BC) = AB = a. Chọn B.
Câu 55: Ta có JA = JB ⇒ IJ ⊥ AB
Ta có IC = ID ⇒ IJ ⊥ CD
Do đó IJ là đoạn vuông góc chung của AB và CD
Do đó d(AB,CD)=IJ. Chọn B.
Câu 56: Gọi O là giao điểm của AC và BD ⇒ SO ⊥ (ABCD) Kẻ OH ⊥ SC BD ⊥ AC
⇒ BD ⊥ (SAC) ⇒ BD ⊥ OH BD ⊥ SO OH ⊥ SC
⇒ OH là đoạn vuông góc chung của BD và SC OH ⊥ BD 1 a 2 a 2 2 2 OC = AC = ,SO = SC − OC = 2 2 2 1 1 1 4 a a = + = ⇒ OH = ⇒ d(BD,SC) = OH2 OS2 OC2 a3 2 2 Chọn B.
Câu 57: Gọi M là giao điểm của AB’ và A’B, N là giao điểm của CD’ và C’D MN ⊥ AB'
⇒ MN là đoạn vuông góc chung của AB’ và CD’ MN ⊥ CD'
MN = BC = AC2 − AB2 = a 3
d(AB',CD ') = MN = a 3. Chọn A. CD ⊥ AD Câu 58: Ta có
⇒ CD ⊥ (SAD) ⇒ CD ⊥ SD CD ⊥ SA CD ⊥ SD
⇒ CDlà đoạn vuông góc chung của SD và BC CD ⊥ BC CD = AC2 − AD2 = a 3
d(SD, BC) = CD = a 3. Chọn D.
Câu 59: Kẻ BH ⊥ SM,AK ⊥ SM ⇒ BH = AK BC ⊥ AB
⇒ BC ⊥ (SAB) ⇒ BC ⊥ BH BC ⊥ SA BH ⊥ BC
⇒ BH là đoạn vuông góc của BC và SM BH ⊥ SM 1 1 1 9 2 2 a a = + = ⇒ AK = ⇒ BH = AK2 SA2 AM2 a2 2 3 3 a d(BC,SM) = BH = 2 . Chọn A. 3
Câu 60: Gọi N là trung điểm của BC
Ta có A 'B'/ /MN ⇒ d(A 'B',C'M) = d(A 'B',(C'MN)) = d(B',(B'MN)) = d 2 (C,(B'MN)) MN ⊥ BC Kẻ CH ⊥ C'N ⇒
⇒ MN ⊥ (BCC') ⇒ MN ⊥ HC MN ⊥ CC'
Mà HC ⊥ C'N ⇒ HC ⊥ (C'MN)
Lại có 1 = 1 + 1 = 1 ⇒ HC = a 2 HC2 NC2 CC'2 a2 2
⇒ d(C,(B'MN)) = a 2 ⇒ d(A 'B',C'M) = a 2 2. Chọn B. BC ⊥ AB Câu 61: Ta có
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB BC ⊥ SA BC ⊥ SB
⇒ BC là đoạn vuông góc chung của SB và CD BC ⊥ CD
d(SB,CD) = BC = a . Chọn A.
Câu 62: Gọi J là trung điểm của OB ⇒ IJ//OC, kẻ OH ⊥ AJ
IJ / /OC ⇒ d(AI,OC) = d(OC,(AIJ)) = d(O,(AIJ)) IJ ⊥ OB
⇒ IJ ⊥ (OAB) ⇒ IJ ⊥ OH IJ ⊥ OA
Mà OH ⊥ AJ ⇒ OH ⊥ (AIJ) 1 1 1 5 a = + = ⇒ OH = OH2 OA2 OJ2 a2 5 Do đó a d(AI,OC) = . Chọn B. 5
Câu 63: Kẻ OH ⊥ SA,CK ⊥ SA BD ⊥ AC
⇒ BD ⊥ (SAC) ⇒ BD ⊥ OH BD ⊥ SA OH ⊥ SA
⇒ OH là đoạn vuông góc chung của SA và BD OH ⊥ BD Ta có AC = a 3 1 1 1 1 a = + = ⇒ CK = a ⇒ OH = CK2 CS2 CA2 a2 2 a
⇒ d(SA,BD) = OH = . Chọn A. 2
Câu 64: Ta có AA'//CC' ⇒ d(AB',CC')
=d(CC',(ABB'A'))=d(C,(ABB'A')) CH ⊥ AB Kẻ CH ⊥ AB ta có ⇒ CH ⊥ (ABB'A') CH ⊥ AA ' Ta có a d(AB',CC')=CH= 3 . Chọn A. 2 CD ⊥ AD Câu 65: Ta có
⇒ CD ⊥ (SAD) ⇒ CD ⊥ SD CH ⊥ SA CD ⊥ SD
⇒ CDlà đoạn vuông góc chung của SD và BC CD ⊥ BC CD= AC2 − AD2 = a 3
d(SD, BC) = CD = a 3. Chọn D.
Câu 66: Ta có BD / /B'D' ⇒ d(AD',BD) = d(BD,(AB'D'))
= d(B,(AB'D')) = d(A',(AB'D'))
Gọi O’ là giao điểm của A’C’ và B’D’, kẻ A'H ⊥ O'A B'D' ⊥ A 'O' Ta có
⇒ B'D' ⊥ (AA 'O) ⇒ B'D' ⊥ O'A B'D' ⊥ AA '
Mà A 'H ⊥ AO' ⇒ A 'H ⊥ (AB'D') Ta có 1 a A'O' = A 'C' = 2 . Ta có 1 = 1 + 1 = 3 2 2 A 'H2 A 'O'2 AA '2 a2 a 3 a ⇒ A 'H = ⇒ d(AD',BD) = 3 . Chọn B. 3 3 Câu 67: Kẻ AH ⊥ SB AD ⊥ AB
⇒ AD ⊥ (SAB) ⇒ AD ⊥ AH AD ⊥ SA AH ⊥ SB
⇒ AH là đoạn vuông góc chung của SB và AD AH ⊥ AD Ta có 1 1 1 2 a = + = ⇒ AH = 2 AH2 AS2 AB2 a2 2 Ta có a 2 d(SB,AD) = AH = . Chọn C. 2
Document Outline
- ITMTTL~1
- IIBITP~1
- IIILIG~1




