



























Preview text:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
MIN-MAX LIÊN QUAN HÀM MŨ, HÀM LÔ-GA-RÍT (NHIỀU BIẾN)
DẠNG 1: ÁP DỤNG ĐÁNH GIÁ, ÁP DỤNG BĐT.
DẠNG 2: ÁP DỤNG PHÁP HÀM SỐ, HÀM ĐẶC TRƯNG. + ÁP DỤNG HÀM SỐ
+ ÁP DỤNG HÀM ĐẶC TRƯNG
DẠNG 3: ÁP DỤNG HÌNH HỌC GIẢI TÍCH.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
DẠNG 1: ÁP DỤNG ĐÁNH GIÁ, ÁP DỤNG BĐT.
Câu 1: Xét các số thức , , , thỏa mãn > 1, > 1và = = √ . Giá trị nhỏ nhất của biểu thức =
+ 3 thuộc tập hợp nào dưới đây? A. (0; 1). B. 2; , ; 2 . C. ; 2 . D. ; 3 . Lời giải Chọn B 1 = √ = (1 + ) = = √ ⇒ 3 1 = √ = (1 + ) 3 1 4 1 4 1 5 ⇒ = + 3 = (1 + ) + 1 + = + + ≥ + 2 ∈ 2; 3 3 3 3 3 2
Câu 2: Cho hai số thực , đều lớn hơn 1. Giá trị nhỏ nhất của biểu thức = + bằng √ A. . B. . C. . D. Lời giải Chọn B Ta có = + = ( ) + √ √ = 1 + + ( + 1) = + + . Đặt = . Do , > 1 nên > 0. Khi đó = + + ≥ 2 .
+ = (Áp dụng BĐT Cauchy cho hai số dương và ). = = ± Dấu " = " xảy ra ⇔ ⇔ ⇒ = . > 0 > 0 Vậy = tại = ⇔ = √ .
Câu 3: Với , , là các số thực lớn hơn 1, đặt = ( ) , = ( ) , = ( ). Tìm giá trị
nhỏ nhất của biếu thức = + + 4 . A. 6. B. 12. C. 10. D. 16. Lời giải Chọn C Ta có = + ; = + ; = + . Khi đó = + + 4 = + + + + 4 + 4 . = + + + + + . Vì , , > 1 ⇒ > 0; > 0; > 0 nên = + + + + + ≥ 2.2 + 2.2 + 2.1 = 10. = 2 = = Vậy = 10 ⇔ = 1 ⇔ = ⇔ . = = 2 =
Câu 4: Xét các số thực dương , , , thỏa mãn > 1, > 1 và = = √
. Giá trị nhỏ nhất của biểu thức =
+ 2 thuộc tập hợp nào dưới đây? A. (1; 2). B. (2; . C. (3; 4). D. ( ; 3 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn D = √ = (1 + ) Ta có = = √ ⇔ ⇔ . = √ = (1 + ) = + 2 = + + 1 + = + + . Đặt = > 0 ⇒ = + + ( > 0). = + + ≥ 2 . + = √2 + ∈ ( ; 3 . =
Dấu bằng xảy ra khi và chỉ khi ⇔ = √2. > 0 Vậy = √2 + ∈ ; 3 .
Câu 5: Cho , là các số thực thỏa ( +
) ≤ 1. Khi 3 + đạt giá trị lớn nhất, thì giá trị = là A. = 1. B. = . C. = 3. D. = . Lời giải Chọn C Xét trường hợp 3 + > 1. log x y
x y x y (1). x y 2 2 2 2 1 3 3 Đặt = 3 + ⇒ = − 3 . (1) ⇔ + ( − 3 ) − ≤ 0 2 2
10x 6Px P P 0 (2). Δ = 9 − 10( − 2) = − + 10
Nếu Δ < 0 thì (2) vô nghiệm. Do đó Δ ≥ 0 ⇔ 0 ≤ ≤ 10. Vậy . Khi đó (2) ⇔ = = 3 ⇒ = 1 ⇒ = = 3.
Câu 6: Cho các số thực ; thỏa mãn + 4 + 12
= 4. Giá trị lớn nhất của biểu thức = ( − 2 ) là A. = 3 2. B. = 1 2. C. = 12. D. = 16. Lời giải Chọn B Điều kiện ≠ 2 . Từ + 4 + 12 = 4suy ra: Nếu = 0 thì = 4 ⇒ = 2 Nếu ≠ 0ta có: =
( − 2 ) ⇔ 4( − 2 ) = 4. 2 4. 2 4. ( − 2 ) 4 2 − 1 ⇒ = = 4 + 4 + 12 2 + 2 2 + 3 Đặt = , ∈ ℝ, 2 = ⇔ 2 ( + 2 + 3) = 4 − 8 + 4 ⇔ (2 − 4)
+ 2(2 + 4) + 3. 2 − 4 = 0Xét với ( ≠ 2)
Để phương trình có nghiệm:
≥ 0 ⇔ (2 + 4) − (2 − 4)(3. 2 − 4) ≥ 0
⇔ −2(2 ) + 24. 2 ≥ 0 ⇔ 0 ≤ 2 ≤ 12 ⇒ ≤ 1 2 Vậy = 1 2. = −2 = −4
Dấu đẳng thức xảy ra khi = ⇒ . = + 4 + 12 = 4
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 7: Cho , là các số thực dương, thỏa mãn log x log y log 3x y
. Tìm giá trị nhỏ nhất 1 1 1 2 2 2 2 P của biểu thức = 4 + . min A. √5 B. √5 C. √5 D. √5 . Lời giải: Chọn A
log x log y log 2 3x y 2 2
xy 3x y x( y 3) y .Từ đây, , là các số thực dương nên ta 1 1 1 2 2 2 suy ra > 3 và ≥ = + 3 + Do đó, ≥ 4 + 3 + + = 5( − 3) + + 27 ≥ 12√5 + 27.
Dấu bằng xảy ra khi = 3 + √ , = 6 + √ . Câu 8: Cho = √ với > 1, > 1 và = + 16
. Tìm sao cho đạt giá trị nhỏ nhất. A. = . B. = 4. C. = 1. D. = 2. Lời giải Chọn C Theo giả thiết ta có = ( ) = (1 + ) ⇒ = 3 − 1. Suy ra = + ⇔ = (3 − 1) + ⇔ = (3 − 1) + + . Vì > 1, > 1 nên = 3 − 1 > 0.
Áp dụng bất đẳng thức Cosi cho ba số dương ta có: ⇔ = (3 − 1) + + ≥ 3. (3 − 1) . ⇔ ≥ 12. ( ) Dấu bằng xảy ra khi (3 − 1) = ⇔ = 1.
Câu 9: Xét các số thực dương , , , thỏa mãn > 1, > 1 và = = . Biết giá trị nhỏ nhất của biểu thức = + 3 + 2 có dạng
+ √14 (với , là các số tự nhiên), tính = + . A. 48 B. 34 C. 30. D. 38. Lời giải Chọn D 2 = ( ) 2 = 4 + 4 Theo bài ra ta có: = = ⇔ = ⇔ ⇔ = = ( ) = 4 + 4 = 2(1 + ) ⇔ = 4(1 + ) Do đó: = + 3 + 2 = 8(1 + )(1 + ) + 6(1 + ) + 8(1 + ) = 16 + 8 + 8 + 6 + 6 + 8 + 8 = 30 + 14 + 16 Đặt = . Vì , > 1 nên > 1 = 0. Khi đó = 30 + 14 + ≥ 30 + 2 14 . = 30 + 8√14. √
Vậy đạt giá trị nhỏ nhất là 30 + 8√14 khi 14 = ⇒ = √ hay = .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 = 30 Ta có: ⇒ = + = 38 = 8 .
Câu 10: Trong các nghiệm ( ; ) thỏa mãn bất phương trình
( + 2 ) ≥ 1, tìm giá trị lớn nhất của biểu thức = + 2 . A. . B. . C. . D. 1. Lời giải Chọn B Nếu 0 < 3 + 2
< 1 thì từ giả thiết
( + 2 ) ≥ 1 ta suy ra + 2 ≤ 1. Nếu 3 + 2 > 1 thì khi đó ta có: ( + 2 ) ≥ 1 ⇔ + 2 ≥ 3 + 2 ⇔ 3 − + 2 − 2 ≤ 0 ⇔ √3 − + √2 − ≤ . √ √ Ta viết lại = + 2 = √3 − + √2 √2 − + √ √ √
Theo bất đẳng thức Cauchy – Schwartz thì 1 1 1 1 1 1 √3 − + √2 √2 − ≤ + √2 . √3 − + √2 − √3 2√3 √2 √3 2√3 √2 ≤ . = .
Do đó ≤ + = . Dấu “=” xảy ra khi ( ; ) = ; 1 . Vậy đạt được khi ( ; ) = ; 1 .
Câu 11: Xét các số thực , thỏa mãn ( − 1) +
( − 1) = 1. Khi biểu thức = 2 + 3 đạt
giá trị nhỏ nhất thì 3 − 2 =
+ √3 với , ∈ ℚ. Tính = . A. = 9. B. = . C. = . D. = 7. Lời giải Chọn C − 1 > 0 > 1 Điều kiện: ⇔ − 1 > 0 > 1. Khi đó: ( − 1) +
( − 1) = 1 ⇔ ( − 1)( − 1) = 2 ⇔ − 1 = ⇔ = + 1. Suy ra: = 2 + 3 = 2 + + 3 = 2( − 1) + + 5.
Cách 1: Dùng bất đẳng thức
Áp dụng bất đẳng thức Côsi, ta có: 2( − 1) + ≥ 2 2( − 1). ⇒ 2( − 1) + ≥ 4√3 ⇒ ≥ 4√3 + 5. = 1 + √3( )
Dấu “=” xảy ra ⇔ 2( − 1) =
⇔ ( − 1) = 3 ⇔ | − 1| = √3 ⇔ . = 1 − √3( ) ⇒ = + 1 = √ . √
Do đó: 3 − 2 = 3 1 + √3 − 2 √ = 1 + √3 ⇒ = 1; = ⇒ = = .
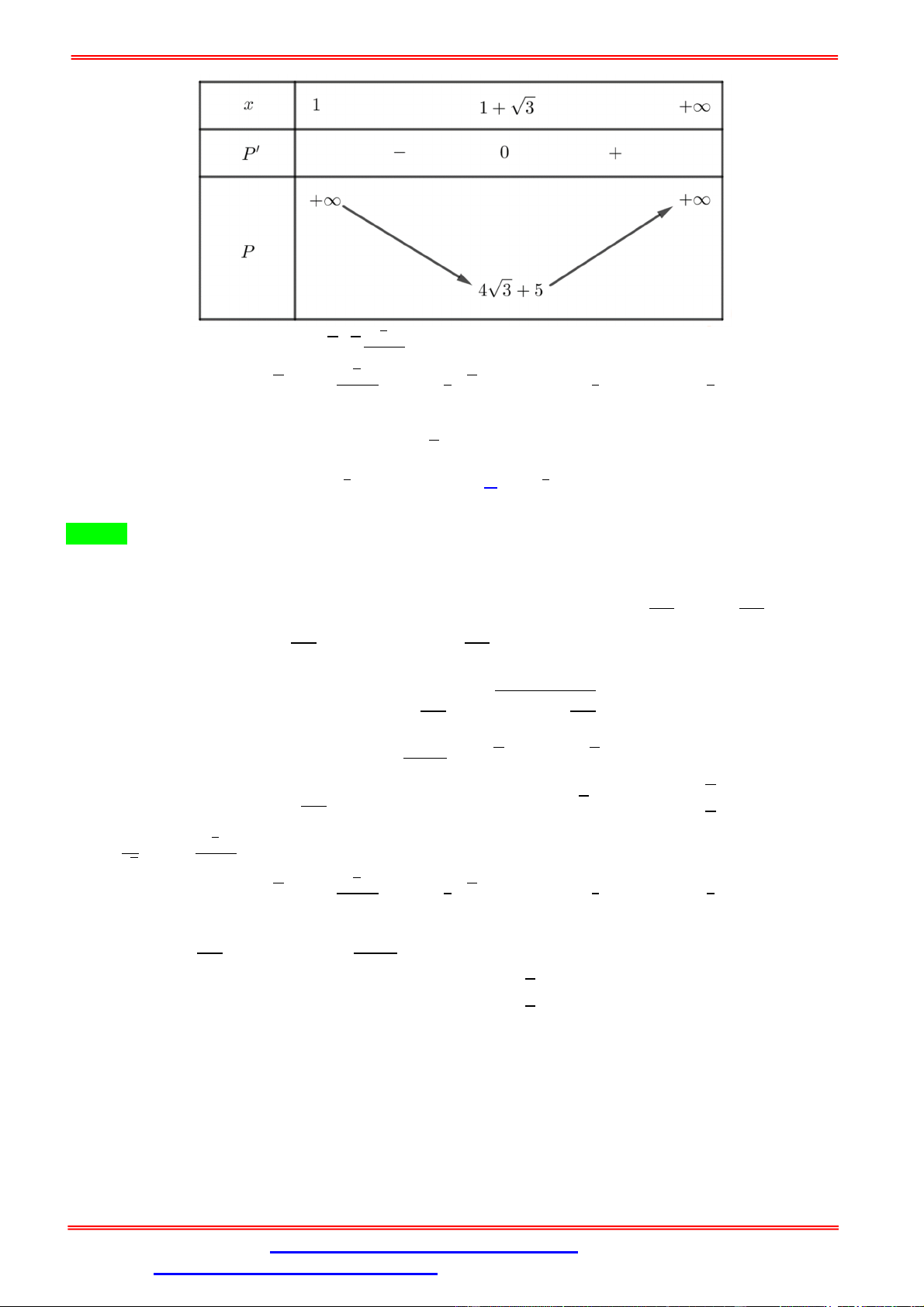
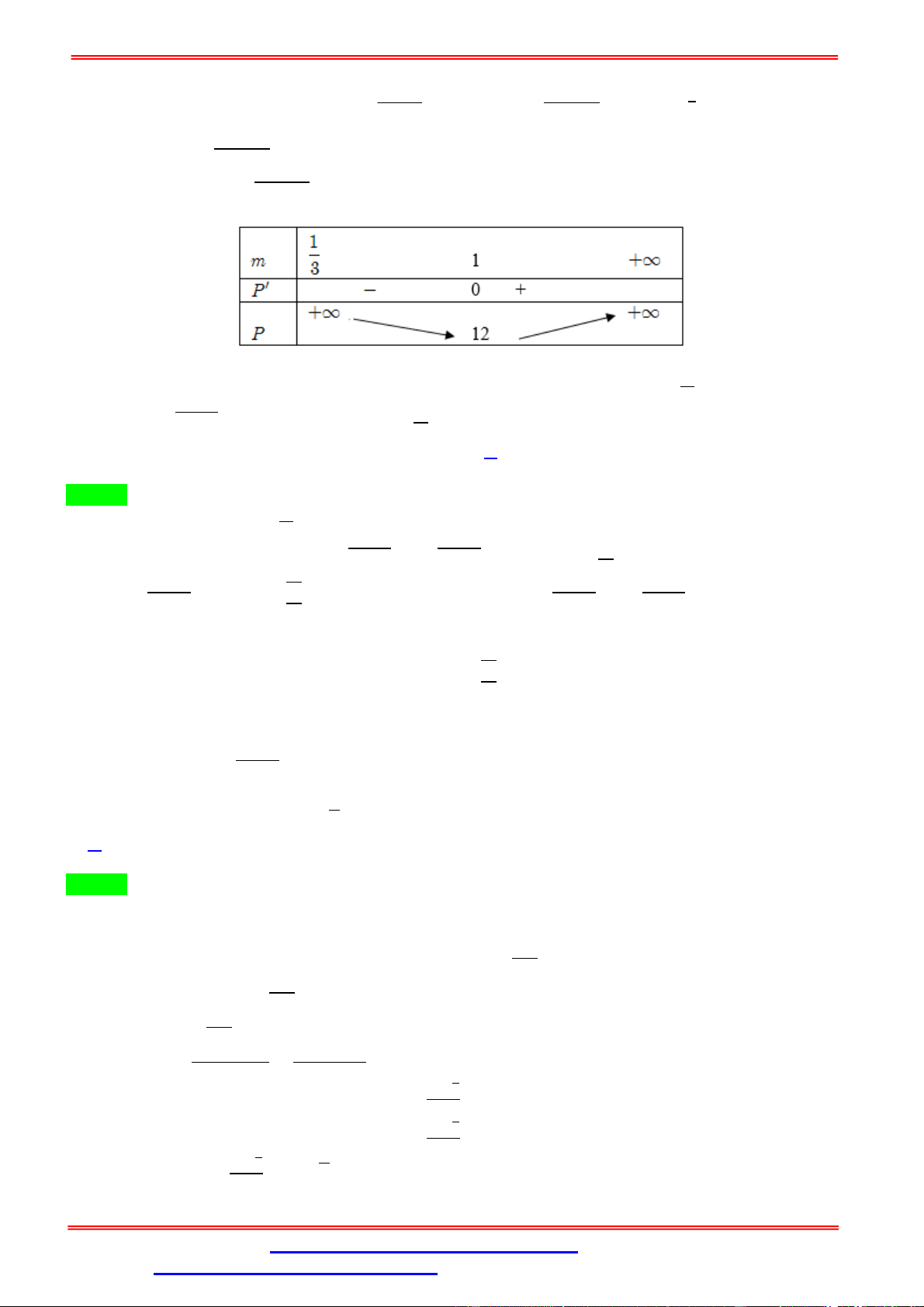
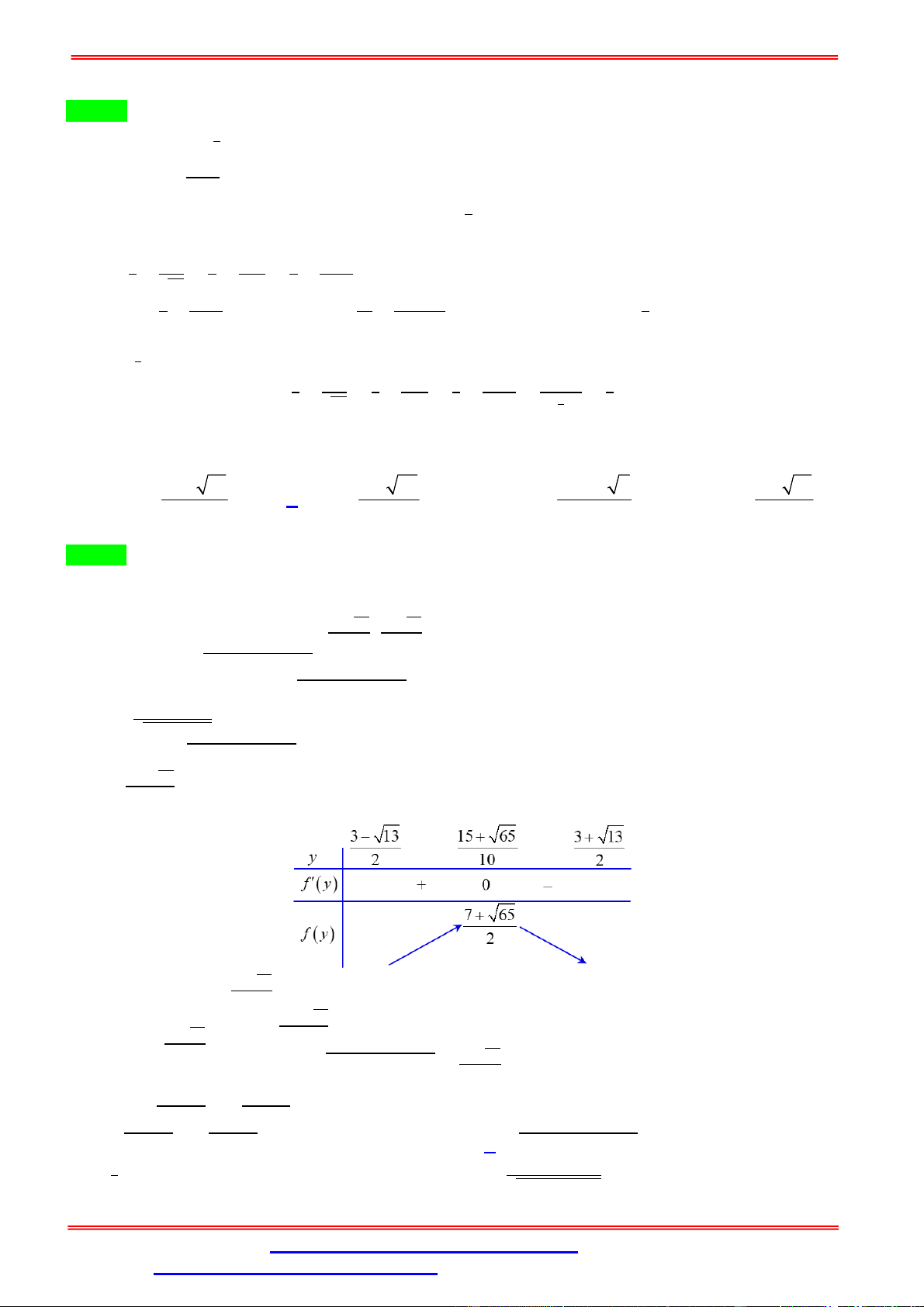
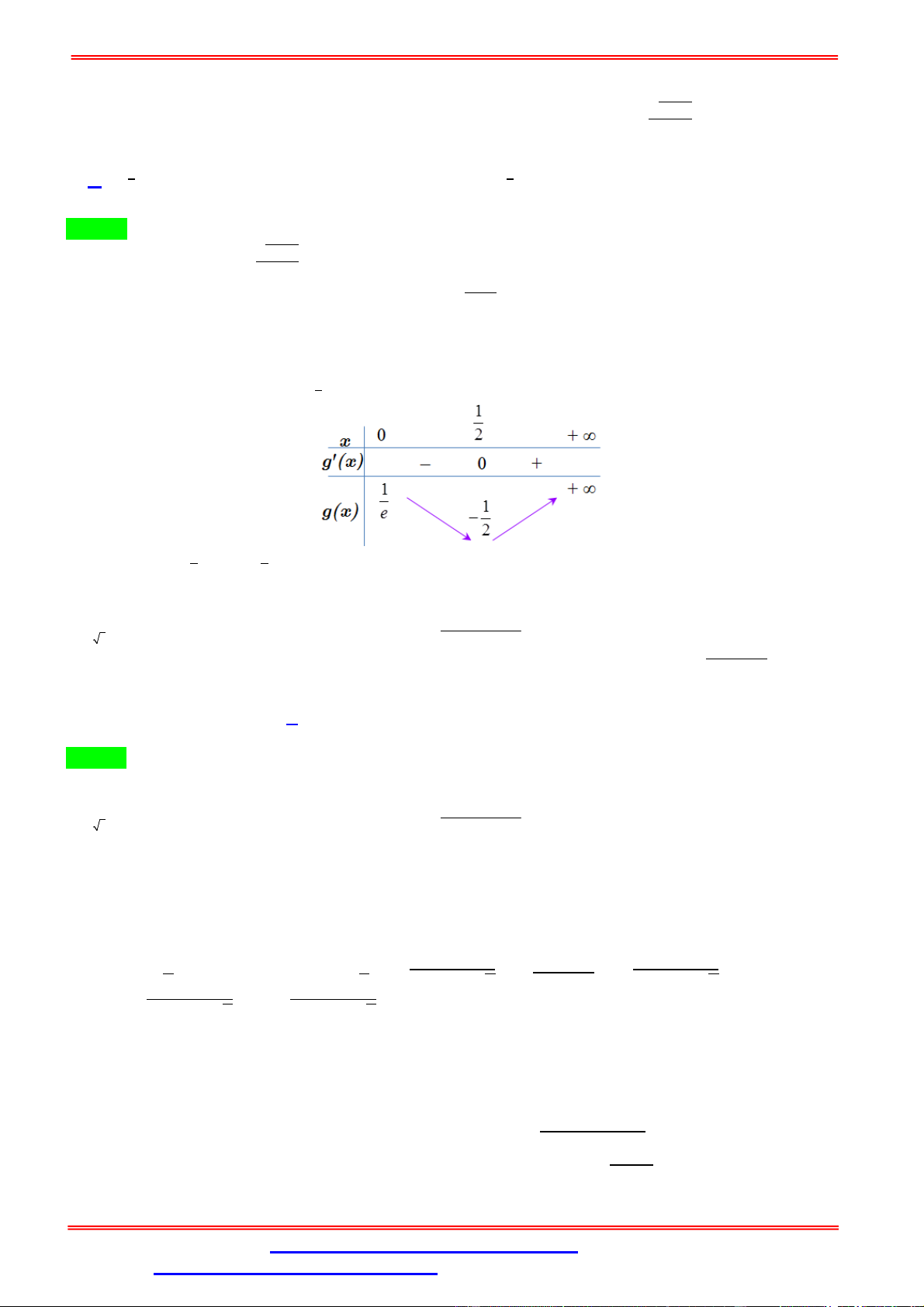
Cách 2: Dùng bảng biến thiên Ta có: = 2 + + 3 ⇒ ′ = 2 − ( ) = 1 + √3( ) ′ = 0 ⇔ = 1 − √3( ) Bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dựa vào bảng biến thiên, ta có: √3√3 √ .
Do đó: 3 − 2 = 3 1 + √3 − 2 √ = 1 + √3 ⇒ = 1; = ⇒ = = .
Câu 12: Xét các số thực , thỏa mãn ( − 1) +
( − 1) = 1. Khi biểu thức = 2 + 3 đạt
giá trị nhỏ nhất thì 3 − 2 = + √3với , ∈ ℚ. Tính = ? A. = 9. B. = . C. = . D. = 7. Lời giải Chọn C − 1 > 0 > 1 Điều kiện: ⇔ − 1 > 0 > 1 Khi đó: ( − 1) +
( − 1) = 1 ⇔ ( − 1)( − 1) = 2 ⇔ − 1 = ⇔ = + 1 Suy ra: = 2 + 3 = 2 + + 3 = 2( − 1) + + 5
Cách 1: Dùng bất đẳng thức
Áp dụng bất đẳng thức Côsi, ta có: 2( − 1) + ≥ 2 2( − 1). 6 ⇒ 2( − 1) + ≥ 4√3 ⇒ ≥ 4√3 + 5 − 1 = 1 + √3( )
Dấu “=” xảy ra ⇔ 2( − 1) =
⇔ ( − 1) = 3 ⇔ | − 1| = √3 ⇔ = 1 − √3( ) ⇒ = + 1 = √ . √
Do đó: 3 − 2 = 3 1 + √3 − 2 √ = 1 + √3 ⇒ = 1; = ⇒ = = .
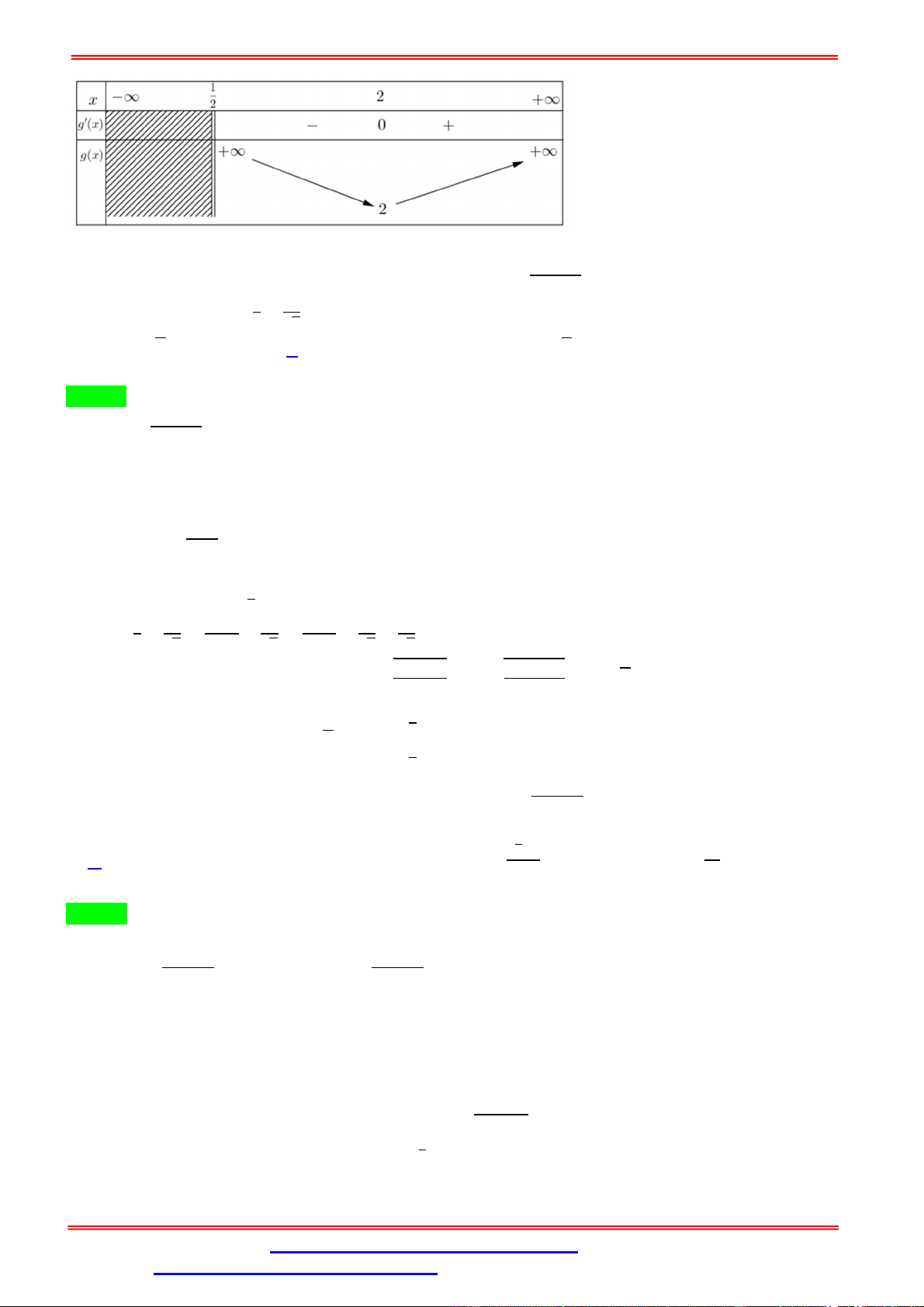
Cách 2: Dùng bảng biến thiên Ta có: = 2 + + 3 ⇒ ' = 2 − ( ) = 1 + √3( ) ' = 0 ⇔ = 1 − √3( ) Bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dựa vào bảng biến thiên, ta có: √3√3 √ .
Do đó: 3 − 2 = 3 1 + √3 − 2 √ = 1 + √3 ⇒ = 1; = ⇒ = = .
Câu 13: Cho , , là các số thực dương thỏa mãn 64 + 64 + 64 = 3. 4
. Giá trị lớn nhất của biểu thức = + + + 1515 A. 2020. B. 2019. C. 2021. D. 2018. Lời giải Chọn A
Áp dụng hệ quả của bất đẳng thức côsi cho 4 số dương ta có: 1 1 1 1 1 1 1 2 1 ( + 2 + 2 + 3 ) + + + ≥ 16 ⇔ ≤ + + 2 2 3 + 2 + 2 + 3 16 2 3 1 1 1 1 1 1 2 1 1 ( + + 2 + 3 ) + + + ≥ 16 ⇔ ≤ + + 2 3 + + 2 + 3 16 2 3 1 1 1 1 1 1 1 1 2 ( + 2 + 3 + 3 ) + + + ≥ 16 ⇔ ≤ + + 2 3 3 + 2 + 3 + 3 16 2 3 Từ đó suy ra = + + + 1515 ≤ + + + 1515
Từ giả thiết ta lại có 3. 4 = 64 + 64 + 64 ≥ 3 64 . 64 . 64 = 3. 4 Suy ra 4 ≤ 4 ⇔ + + ≤ 2020 Vậy ≤ + + + 1515 ≤ + 1515 = 2020 = =
Dấu bằng xảy ra khi và chỉ khi ⇔ = ; = ; = . + + = 2020
Câu 14: Xét các số thực dương , , , , , thỏa mãn > 1, > 1, > 1 và = = = √ .
Giá trị nhỏ nhất của biểu thức = +
+ + thuộc tập hợp nào dưới đây? A. 10; 13). B. 7; 10). C. 3; 5). D. 5; 7). Lời giải Chọn D Từ giả thiết ta có 1 1 1
x 1 log b log c , y 1 log a log c, z 1 log b log a . Khi đó ta có 2 a a 2 b b 2 c c
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
2P 4 log b log a log c log a log c log b . a b a c b c
Vì > 1, > 1, > 1 nên log b 0 , log c 0 , log a 0 , log a 0 , log b 0 , log c 0 . a b c b c a
Áp dụng bất đẳng thức Cô Si ta được
log b log a 2 log .
b log a hay log b log a 2 . a b a b a b
Tương tự log c log a 2 và log c log b 2 . a c b c Do đó 2
≥ 10 hay ≥ 5. Dấu " = " xảy ra khi và chỉ khi = = .
Vậy giá trị nhỏ nhất P 5 . min
Câu 15: Cho hai số thực dương , thỏa mãn ( + + 2) = 1 + + . Giá trị nhỏ nhất của biểu thức
= với , ∈ ℕ, ( , ) = 1. Hỏi + bằng bao nhiêu. A. 2. B. 9. C. 12. D. 13 Lời giải Chọn D Ta có ( + + 2) = 1 + + ⇔ = − − ⇔ = (
). Gọi > 0là giá trị nhỏ nhất của
khi đó là số dương nhỏ nhất để hệ + = có nghiệm. = + = ( ) − 2 = ( + ) = ( + 2) Ta có ⇔ ⇔ = + = + = Từ ( + ) = ( + 2) ⇒ ( + 2) ≥ 4 ⇒ ≥ 2.
Đặt t x y 0 + = ⇔ + (2 − 3 ) + 6 + 3 = 0 (*). Ta đi tìm ≥ 2để (*) có nghiệm dương ⇔ = 9 − 24 − 20 ≥ 0 ⇔ ≥ . Do đó ≥ , dấu “=” xảy ra khi + = 4 ⇒ ( ; ) = (1;3). = 3 Vậy + = 13.
Câu 16: Cho các số thực dương và thỏa mãn 4 + 9. 3 = 4 + 9 . 7 . Tìm giá trị nhỏ nhất của biểu thức = . A. = 9. B. = √ . C. = 1 + 9√2. D. = √ . Lời giải Chọn A Từ giả thiết ta đặt = − 2 , ∈ ℝ. Phương trình 4 + 9. 3 = 4 + 9 . 7 trở thành 4 + 9. 3 = (4 + 9 ). ⇔ 4(7 − 49) + 9 9. − 49 = 0.
Nhận thấy = 2là nghiệm phương trình.
Ta chứng minh = 2là nghiệm duy nhất của phương trình. Xét > 2: 7 > 49và 9.
> 49nên vế trái phương trình luôn dương, nên phương trình vô nghiệm. Xét < 2: 7 < 49và 9.
< 49nên vế trái phương trình luôn âm, nên phương trình vô nghiệm.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Vậy = − 2 = 2 ⇔ = thay vào = = 16 16 x 1 2 . x 1 9 x x
. Dấu bằng đạt được khi = ⇒ = 4.
Câu 17: Xét các số thực dương , , , thỏa mãn > 1, > 1và = = . Biết giá trị nhỏ nhất của biểu thức = 3 + 2 + có dạng
+ √30 (với , là các số tự nhiên), tính = + A. 34 B. 36. C. 52. D. 48 Lời giải Chọn C 2 = ( ) 2 = 6 + 6 Theo bài ra ta có: = = ⇔ = ⇔ ⇔ = 3 = ( ) 3 = 6 + 6 = 3(1 + ) ⇔ = 2(1 + ) Do đó: = 3 + 2 + = 18(1 + )(1 + ) + 6(1 + ) + 2(1 + ) = 18 + 18 + 18 + 18 + 6 + 6 + 2 + 2 = 44 + 24 + 20 Đặt = . Vì , > 1nên > 1 = 0. Khi đó = 44 + 24 + ≥ 44 + 2 24 . = 44 + 8√30. √
Vậy đạt giá trị nhỏ nhất là 44 + 8√30khi 24 = ⇒ = √ hay = . = 44 Ta có: ⇒ = + = 52 = 8
Câu 18: Cho hai số thực ; ; thỏa mãn hệ thức + ≤ 3 +
+ . Giá trị nhỏ nhất của biểu thức = + + 2 − 22 bằng? A. −19. B. 12. C. −15. D. 8. Lời giải Chọn A
Chúng ta nắm bắt được dạng thì sẽ có cách giải như sau: = + 2 + = 0 = 2 − 2 + ≤ 3 + + ⇔ + ≤ + + 2 ⇔ ⇔ = 2 − − 2 = 0 = −5 + 4
Thế vào biểu thức , ta được: =
+ (2 − 2) + 2(−5 + 4) − 22 = 55
− 110 + 36 = 55( − 1) − 19 ≥ −19
Vậy giá trị nhỏ nhất của là: = −19.
Câu 19: Cho hai số thực dương , lớn hơn 1 và biết phương trình .
= 1 có nghiệm thực. Biết 4
giá trị nhỏ nhất của biểu thức P log ab có dạng với
, là số tự nhiên và là a log b a
phân số tối giản. Khi đó + 2 bằng A. 34. B. 21. C. 23. D. 10. Lời giải Chọn C
Phương trình tương đương với 2
x x 2
2 log b 0 x x log b 2 log b 0 . a a a
Điều kiện để phương trình có nghiệm là: b b log b 8 ( ) > 0. a 2 log 8log 0 a a
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 4
Khi đó P log b 1 = ( ) = + + 1 ≥ ( ) = (8) = = . a log b ; ) a Vậy + 2 = 23.
Câu 20: Cho các số thực , thỏa mãn điều kiện 0 < <
< 1. Tìm giá trị nhỏ nhất của biểu thức = ( ) + 8 − 1. A. 6. B. 8. C. 3√2. D. 7. Lời giải Chọn D Ta có: = = . ( ) ( ( ) 3 − 2) ≥ 0 ⇒ 9 − 12 + 4 ≥ 0 ⇒ ≤ ⇒ ≥ = 2 . Do đó: ≥ 2 + − 1 ⇒ ≥ ( − 1) + ( − 1) + + 1. ( ) ( ) Mà 0 < < < 1 ⇒ > = 1 ⇒ − 1 > 0.
Áp dụng BĐT Cô-si ta có: ( − 1) + ( − 1) + ≥ 6 ⇒ ≥ 7. ( ) 3 − 2 = 0 = = Dấu " = " xảy ra ⇔ − 1 = ⇔ ⇔ . ( ) = 3 = Vậy = 7.
Câu 21: Cho số thực ,
> 1 thỏa mãn điều kiện +
= 2020 . Tìm giá trị lớn nhất của biểu thức = + ? 1 A. 2020 log 2018 log 2019 . B. log 2018 log 2019 . 2019 2018 2019 2018 2020 2020 C. . D. 2020 log 2018 2020 log 2019 . 2019 2018 log 2018 log 2019 2019 2018 Lời giải Chọn A Ta có: P log a log b log 2018. log a log 2019 log b . 2019 2018 2019 2018 2018 2019
Áp dụng bất đẳng thức Bunhiacopsky, ta có: P log 2018. log a log 2019 log b 2 2 2019 2018 2018 2019 log 2018 log 2019log a log b log 2018 log 2019 2 2020 2019 2018 2018 2019 2019 2018 P 2020 log 2018 log 2019 . 2019 2018 log a log b 2018 2019
Đẳng thức xảy ra khi và chỉ khi log 2018 log 2019 2019 2018 2 log a log b 20 0 2 2018 2019 log 2019 log a log 2018 log b 2018 2018 2019 2019 2 log a log b 2020 2018 2019 ⇔ & = = (với = 2019)
Vậy tồn tại , > 1 để đẳng thức xảy ra nên max P 2020 log 2018 log 2019 . 2019 2018
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Câu 22: Cho > 0, > 0 thỏa mãn log a b a b . Giá trị của + a b 2 2 16 1 log 4 5 1 2 4 5 1 8ab 1 2 bằng A. . B. 6. C. . D. 9. Lời giải Chọn A Ta có: 16 + + 1 ≥ 2√16 + 1 = 8 + 1 do đó: log a b a b a b 2 2 16 1 log 4 5 1 4 5 1 8ab 1 log 8ab 1 log 4a 5b 1 4a5b 1 8ab 1 1 log 8ab 1 4a5b 1 log 8ab 1 4a5b 1 1 2 log 8ab 1 . 2 4a5b 1 log 8ab 1 4a5b 1
Dấu " = " xảy ra khi và chỉ khi: 3 16 = 4 = ⇔ ⇔ = 8 + 1 = 4 + 5 + 1 2 + 1 = 6 + 1 4 = 3 Vậy + 2 = . Câu 23: Cho , , > 0; , , > 1 và = = = √
. Giá trị lớn nhất của biểu thức = + −
thuộc khoảng nào dưới đây? A. (10; 15). B. ; . C. −10; 10). D. [15; 20]. Lời giải Chọn D Ta có: = = = √ 1 ⇒ = = = 2 1 ⎧ = 2 ⎪1 ⇒ = 2 ⎨ ⎪1 ⎩ = 2 Do đó: + + = 2( + + ) = 2 = 2 Suy ra: + = 2 − Ta có: = + − = 16 2 − − = 32 − − ( > 0). Mặc khác, + = + + ≥ 3 . . = 12. Dấu “=” xảy ra ⇔ = 2.
Vậy giá trị lớn nhất của biểu thức là 32 − 12 = 20 tại = 2.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
DẠNG 2: ÁP DỤNG PHÁP HÀM SỐ, HÀM ĐẶC TRƯNG. ÁP DỤNG HÀM SỐ
Câu 24: Cho , là các số thực dương thỏa mãn > 1 và √ ≤
< . Giá trị nhỏ nhất của biểu thức = + 2 √ bằng A. 6. B. 7. C. 5. D. 4. Lời giải Chọn C Đặt = , vì > 1 và √ ≤ < nên ≤ < 1. Ta có = + 2 = + − 4 = ( ) √ . Xét hàm số ( ) =
+ − 4 trên nửa khoảng ; 1 , ta có ( ) ( )( ) = − = ;
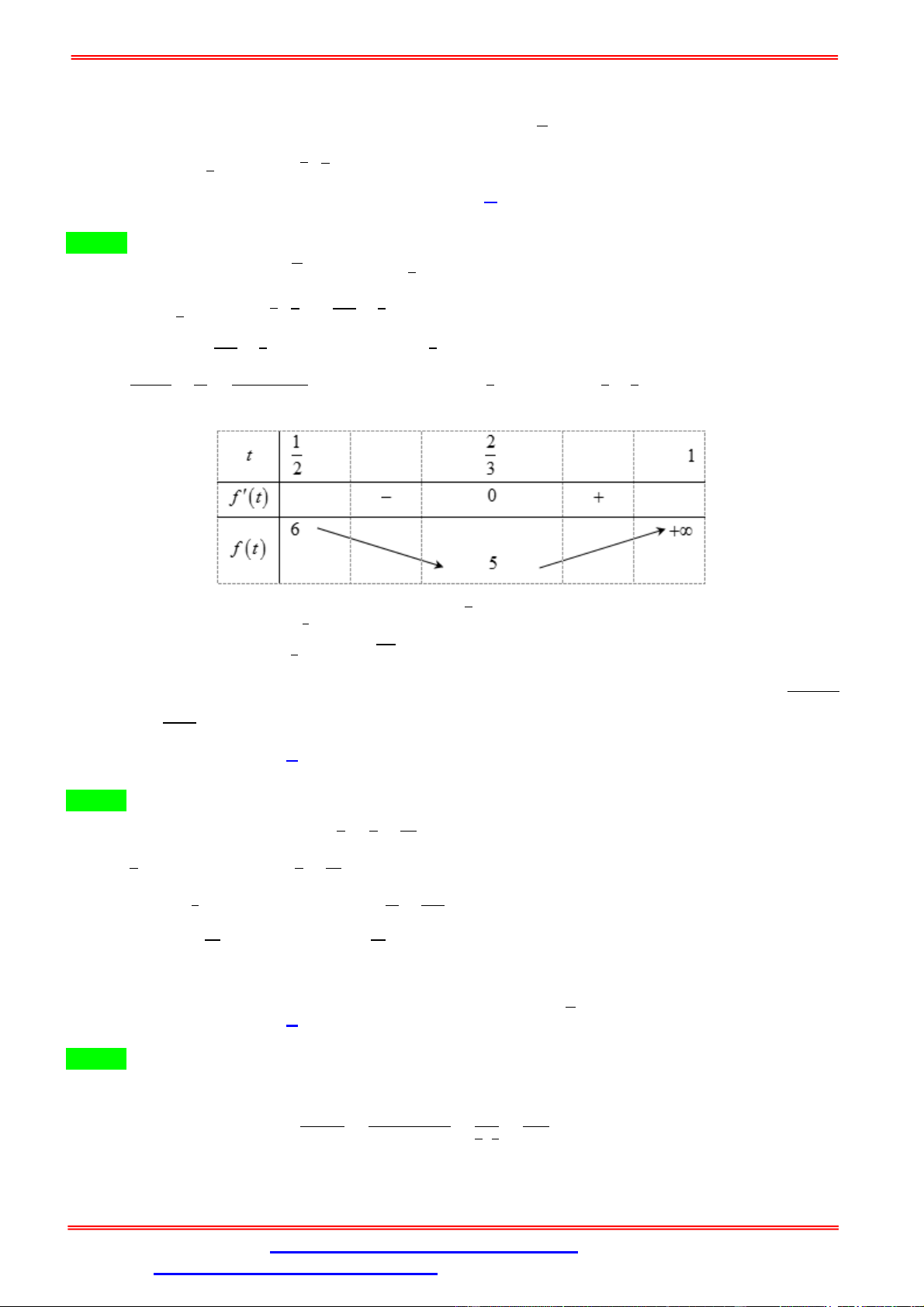
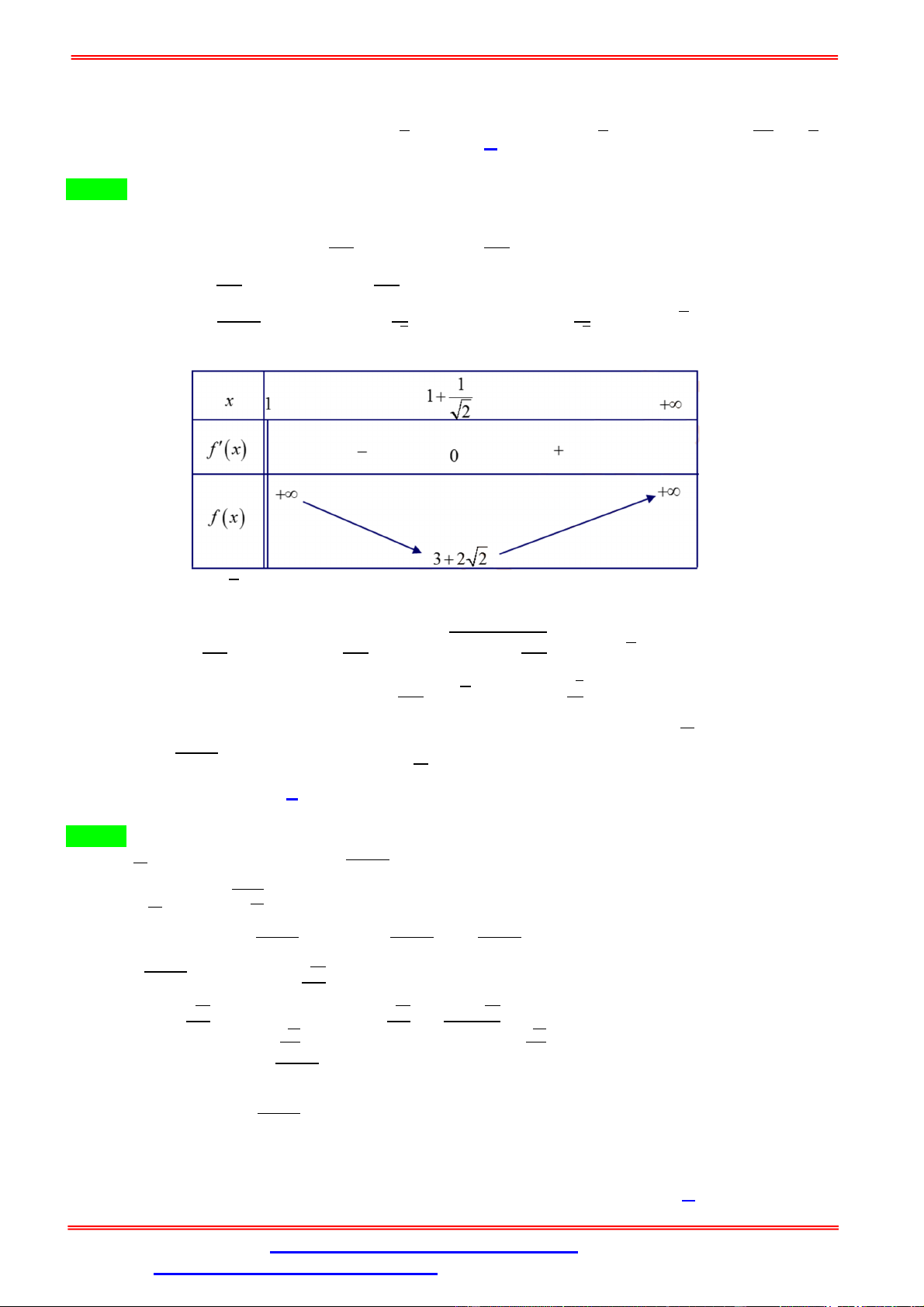
( ) = 0 ⇔ = 2 ∉ ; 1 hoặc = ∈ ; 1 . ( ) .( ) Bảng biến thiên:
Dựa vào bảng biến thiên, ta có ( ) = 5 khi = . ; Vậy = 5 khi = ⇔ = √ . ( )
Câu 25: Cho , là các số thực dương thỏa mãn
≤ 4 − 1. Giá trị nhỏ nhất của = + là +
. Giá trị của tích . là A. 45. B. 81. C. 115. D. 108. Lời giải Chọn B Từ giả thiết, ta có ≤ 4 − 1 nên ≤ − . Đặt = , ta có 0 < ≤ 4 (vì − ≤ 4, ∀ > 0). Ta có = 12 + + ( + 2); ( ) = − +
< 0, với mọi 0 < ≤ 4. Do đó (4) = + 6. Suy ra = , = 6 nên . = 81.
Câu 26: Cho các số thực , , khác 0 thỏa mãn 3 = 5 = 15
. Hỏi giá trị nhỏ nhất của biểu thức = + + − 4( + + ) là? A. −3 − 3. B. −4. C. −2 − √3. D. −2 − 5. Lời giải Chọn B Đặt = 3 = 5 = 15 ; > 0. = Suy ra = ⇒ − = = = = ⇔ + + = 0. − = Ta có = + + − 4( + + ) = ( + + ) − 2( + + ) − 4( + + ). ⇒ = ( +
+ ) − 4( + + ) = [( + + ) − 2] − 4 ≥ −4.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 + + = 2 ⇒ . + + = 0
Câu 27: Xét các số thực , sao cho > 1, √ ≤ < . Biểu thức = + 2 √ đạt giá trị nhỏ nhất khi A. = . B. = . C. = . D. = . Lời giải Chọn A
Do > 1 mà > suy ra > 1. Ta có √ ≤ < ⇔ log √ ≤ log < log ⇔ ≤ log < 1. Theo bài ra = + 2 ⇔ = + 2 √ √ ⇔ = + 4 . Đặt = log suy ra ∈ ; 1 ta được = + 4 với ∈ ; 1 . = − cho = 0 ⇒ = 4(1 − ) ( ) ⇔ 3
− 8 + 4 = 0 ⇔ = (thỏa mãn) hoặc = 2(loại)
Dựa vào bảng biến thiên giá trị nhỏ nhất = 5 khi = ⇔ = ⇔ = .
Cho , là các số thực thỏa mãn 1 < <
. Tìm giá trị nhỏ nhất của biểu thức = ( − 1) + 8 √ . √ A. 18. B. 9. C. 27. D. 30 Lời giải Chọn C √ Ta có = = . = = √ . √ √ Suy ra = 2 − 1 + 8 √ . √ Đặt = 2 , do 1 < < ⇔ 1 < < ⇒ > 2.
Ta có hàm số ( ) = ( − 1) + 8. với > 2. ( ) ( )( ) = 1 = ; ′( ) = 0 ⇒ . ( ) = 4
Lập bảng biến thiên trên (2; +∞) ta được
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Vậy giá trị nhỏ nhất của biểu thức = ( − 1) + 8 √ là 27 đạt được khi = 4 ⇔ √ 2 = 4 ⇔ = ⇔ = .
Câu 28: Cho , là hai số thực dương thỏa mãn = 3 + 4 và
∈ [4; 2 ]. Gọi , lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của biểu thức = 4 + . Tính tổng = + . A. = . B. = . C. = . D. = . Lời giải Chọn B = − Ta có = 3 + 4 ⇔ −
= 3 ( + ) ⇔ ( + )( − 4 ) = 0 ⇔ = 4
Vì , dương nên = 4 , ta thay vào ta được 3 4 3 + 2 3 = 4 + = + = + 4 4 − 1 4 2 Đặt
= vì ∈ [4; 2 ] nên ∈ [2; 32] Xét hàm số ( ) = + −3 3 ( ) = −1 ( ) = + ⇒ ( ) = 0 ⇔ ( − 1) 4 = 3 Ta có bảng biến thiên Vậy = ; = ⇒ = + = .
Câu 29: Cho m 3 log
ab với > 1, > 1 và 2
P log b 16 log a . Tìm sao cho đạt giá trị a a b nhỏ nhất. A. = . B. = 4. C. = 1. D. = 2. Lời giải Chọn C 1 1 Ta có: m log ab ab b . a 3
loga 1 loga 3 3
3m 1 log b log b 3m 1. a a Do > 1,
> 1nên log b log 1 0 ⇒ > . a a
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 16 16
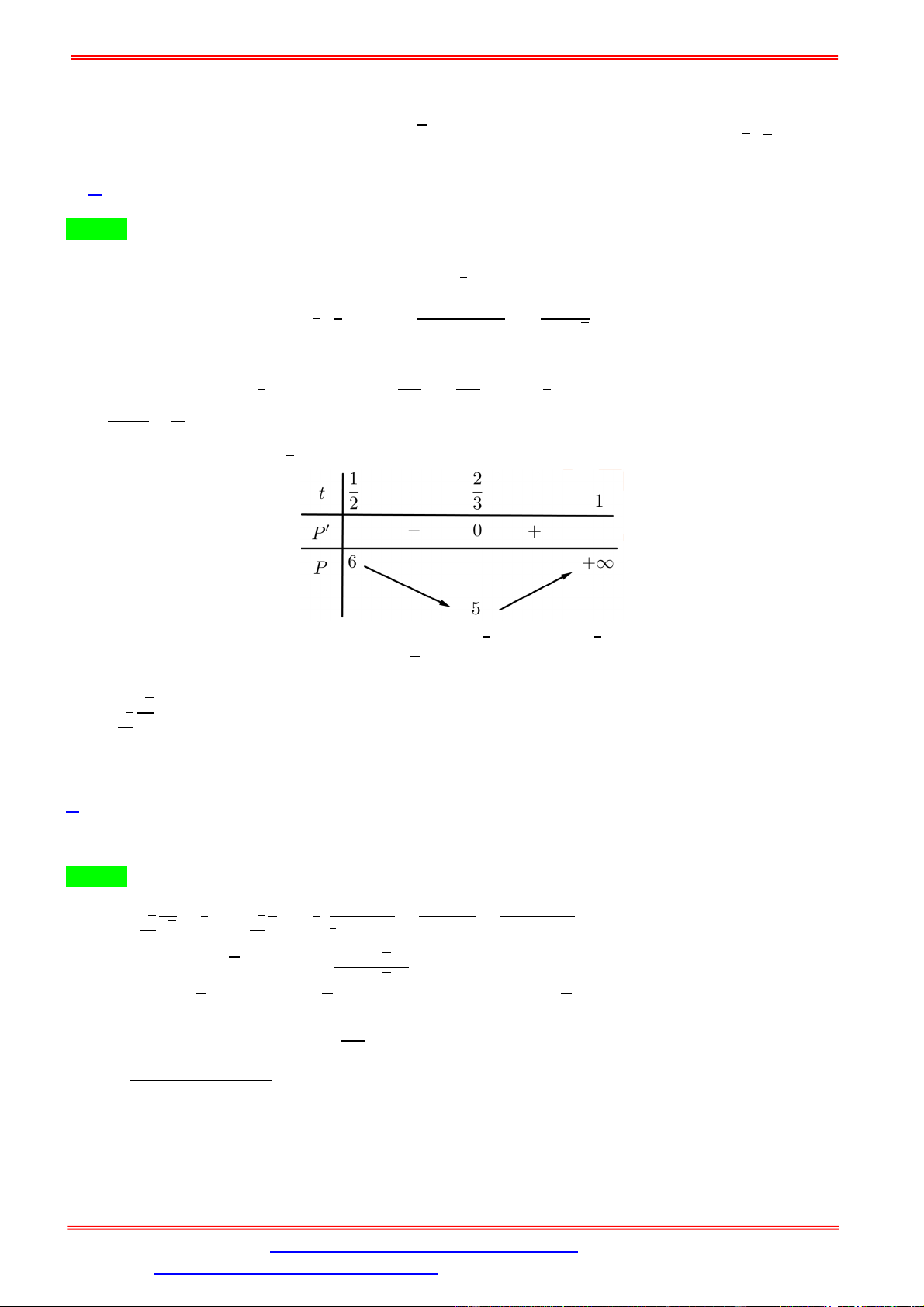
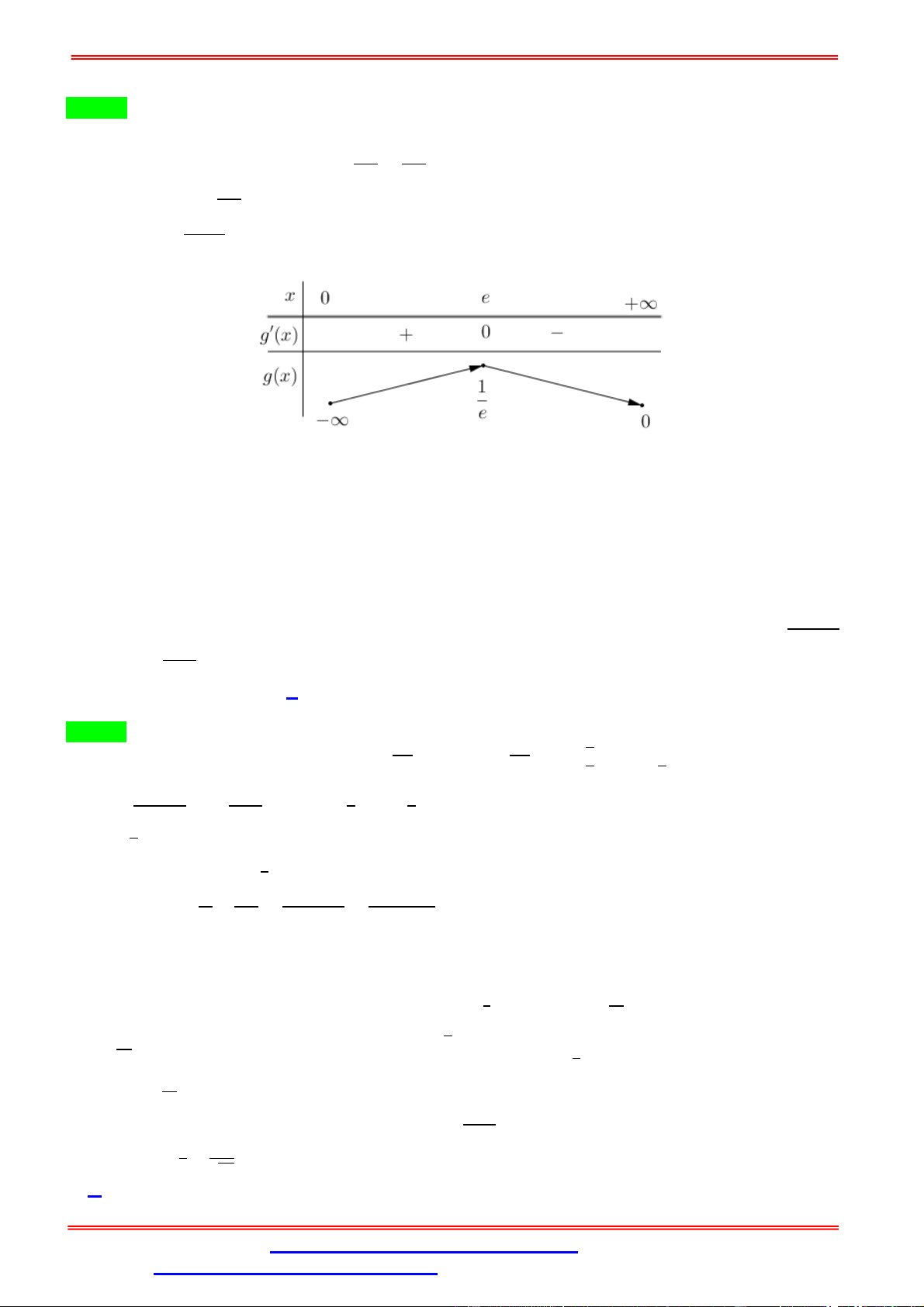
Ta có: P log b 16 log a log b m , với ∈ ; +∞ . a b a 3 2 2 2 1 log b 3m 1 a = 6(3 − 1) − . ( ) = 0 ⇔ 6(3 − 1) − = 0 ⇔ (3 − 1) = 8 ⇔ 3 − 1 = 2 ⇔ = 1. ( ) Bảng biến thiên
Vậy min P 12 m 1.
Câu 30: Tính giá trị của biểu thức = + − + 1 biết rằng 4 = 14 − ( − 2)
+ 1 với ≠ 0 và −1 ≤ ≤ . A. = 1. B. = 4. C. = 2. D. = 3. Lời giải Chọn C
Ta có biểu thức vế trái: 4 ≥ 4 = 4. (1)
Xét biểu thức ( ) = 14 − ( + 1) + 1 + 3 + 1 với −1 ≤ ≤ . Đặt = + 1 ⇒ ∈ 0; suy ra ( ) = 14 − ( + 1) + 1 + 3 + 1 = ( ) = − + 3 + 14
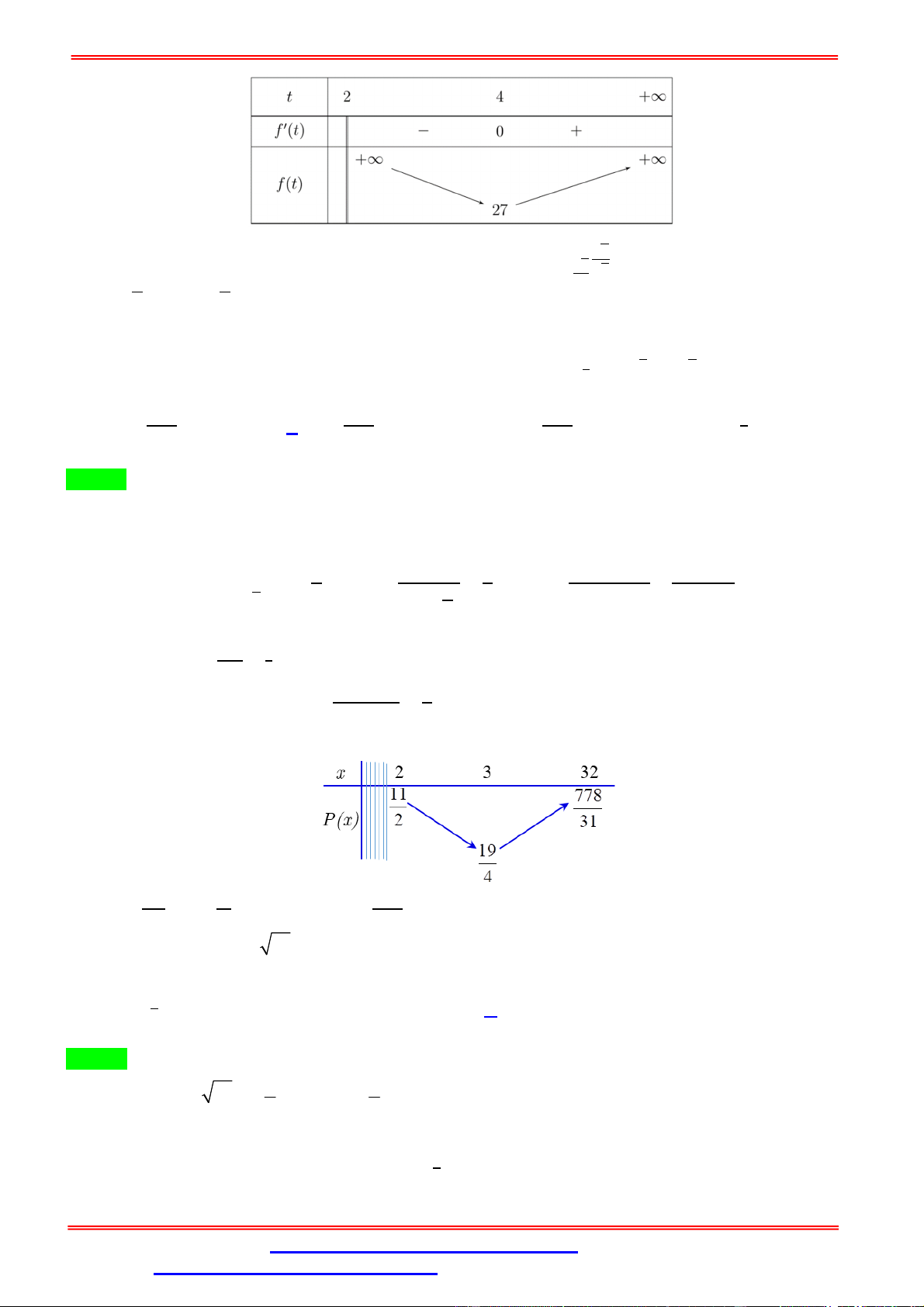
Khảo sát hàm số ( ) = − + 3 + 14trên đoạn 0;
ta được kết quả: ( ) ≤ 16. ⇒ ( ) ≤ 1 6 = 4(2) = 1 Từ (1) và (2) ta có: ⇒ = 1, = 0 ⇒ = 1 + 1 = 2. + 1 = 1
Câu 31: Cho , là số thực dương thỏa mãn + (7 ) ≥ (
+ 7 ). Giá trị nhỏ nhất của
= 4 + 7 có dạng √ + , trong đó , , là số tự nhiên và > 1. Xác định: + + A. + + = 13. B. + + = 12. C. + + = 11. D. + + = 10 Lời giải Chọn A Từ + (7 ) ≥ ( + 7 ) ⇔ 7 ≥ + 7 . Nhận xét: Nếu 0 < ≤ 1 thì 7 ≥ 7 ≥ + 7 ⇔ 0 ≥ (vô lý) Xét > 1 thì 7 ≥ + 7 ⇔ 7 ( − 1) ≥ ⇔ 7 ≥ . Vậy = 4 + 7 ≥ 4 + . Xét: ( ) = 4 + trên (1; +∞). Có ( ) = 4 + ( ) = ( ) ( ) = √ (loai) Xét ( ) = 0 ⇔ 5 − 10 + 4 = 0 ⇔ . = √ (nhan) Vậy ( ) = √ = 2√5 + 6. ( ; )
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 32: Cho , là các số thực dương thoả mãn + ≥ (
+ ). Tìm giá trị nhỏ nhất của = + . A. = 6. B. = 2 + 3√2. C. = 3 + 2√2. D. = √17 + √3. Lời giải Chọn C Ta có + ≥ ( + ) ⇔ ≥ ( + ) ⇔ ≥ + ⇔ ( − 1) ≥ > 0
Mà > 0, > 0nên > 1và ≥ . Suy ra + ≥ + . Xét hàm số ( ) = + = 2 + 1 + , > 1. Ta có: ( ) = 2 − = 0 ⇔ = 1 + (Do > 1)⇒ 1 + = 3 + 2√2. ( ) √ √ Bảng biến thiên Vậy = 3 + 2√2.
Chú ý: Ta có tìm minh của ( )như sau: ( ) = 2 + 1 + = 2( − 1) + + 3 ≥ 2 2( − 1) + 3 = 2√2 + 3.
Đẳng thức xảy ra khi và chỉ khi 2( − 1) = = √2 ⇔ = 1 + √ .
Câu 33: Tính giá trị của biểu thức = + − + 1 biết rằng 4 = 14 − ( − 2) + 1 với ≠ 0 và −1 ≤ ≤ . A. = 4. B. = 2. C. = 1. D. = 3. Lời giải Chọn B Xét 4 = 14 − ( − 2) + 1 . . Ta có 4 ≥ 4
= 4, dấu bằng xảy ra khi và chỉ khi = ±1,. Mặt khác 14 − ( − 2) + 1 = 14 + 3 + 1 − + 1 . Đặt =
+ 1 ta có 0 ≤ ≤ √ . Xét hàm số ( ) = −
+ 3 + 14. Ta tìm GTLN – GTNN của hàm số trên đoạn 0; √ được ( ) = √ = √ ; ( ) = (1) = 16. ;√ ;√ Suy ra 14 − ( − 2) + 1 ≤ 1 6 = 4,. = ±1 = ±1 Từ và suy ra ta có ⇔ = + 1 = 1 = 0 . Thay vào = 2.
Câu 34: Xét các số thực , thỏa mãn > 0và + − 3 = . (1 − 2 .
). Giá trị lớn nhất của biểu thức =
+ thuộc tập hợp nào dưới đây? A. (1; 2). B. 2; 4). C. −3; 0). D. 0; 3).
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn D Xét phương trình + − 3 = . (1 − 2 . ) Đặt = ( > 0)ta có: + − 3 = (1 − 2 ) ⇔ 3 + = ( + ) ≥ 4( ) ⇔ − ≤ ≤ 1. Lại do , > 0 ⇒ 0 < ≤ 1 ⇒ 0 < . ≤ 1 ⇔ + ≤ 0nên ≤ 0. = = 1
Dấu bằng xảy ra khi và chỉ khi = 1 ⇔ = = 1hay = 0 , > 0 Vậy 0; 3) .
Câu 35: Gọi là tập các cặp số thực ( , ) sao cho ∈ [−1; 1] và ( − ) − 2017 = ( − ) − 2017 +
. Biết rằng giá trị lớn nhất của biểu thức = ( + 1) − 2018 với
( , ) ∈ đạt được tại ( ;
). Mệnh đề nào sau đây đúng ? A. ∈ (−1; 0). B. = −1. C. = 1. D. ∈ 0; 1). Lời giải Chọn A Điều kiện − > 0 Ta có ( − ) − 2017 = ( − ) − 2017 + ⇔ ( − ) ( − ) − 2017( − ) = ⇔ ( − ) − 2017 − = 0 (*) Xét hàm ( ) = − 2017 − , có ( ) = + > 0 với ∀ > 0
Do đó ( ) đồng biến trên khoảng (0; +∞),
suy ra (∗) ⇔ ( − ) = 0 = ( ) ⇔ − = ⇔ = − Khi đó = (1 + − ) − 2018 = ( ) g x (2019 + 2018 − 2018 ) − 4036
g x (2018.2020 + 2018 − 2018 ) − 4036 ≤ (2018.2020 + 2018 − 2018
) − 4036 < 0 với ∀ ∈ [−1; 1] Nên
( ) nghịch biến trên đoạn [−1; 1], mà (−1) = + 2018 > 0, (0) = 2019 − 2018 < 0 nên tồn tại ∈ (−1; 0) sao cho ( ) = 0 và khi đó ( ) = ( ) [ ; ] Vậy lớn nhất tại ∈ (−1; 0).
Câu 36: Cho , thỏa mãn ( + ) +
( − ) ≥ 1. Tìm giá trị nhỏ nhất của biểu thức = 2 − . √ A. √3 . B. C. . D. . Lời giải Chọn A + > 0 > 0 Theo giả thiết: ( + ) + ( − ) ≥ 1 ⇔ − > 0 ⇒ ≥ + 4 − ≥ 4 Ta có: = 2 − ≥ 2 + 4 − . Xét hàm số: ( ) = 2 + 4 − có 2 2 − + 4 ( ) = − 1 = + 4 + 4
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 ≥ 0 ( ) = 0 ⇔ 2 − + 4 = 0 ⇔ ⇔ = √ . = BBT: = √ = √ Từ BBT suy ra = 2 −
≥ ( ) ≥ 2√3, dấu " = "xảy ra khi ⇔ . = + 4 = √ = √ Vậy √3 khi . = √
Câu 37: Cho hai số thực , thỏa mãn 0 ≤ ≤ , 0 ≤ ≤ và
(11 − 2 − ) = 2 + 4 − 1. Xét biểu thức = 16 − 2 (3 + 2) −
+ 5. Gọi , lần lượt là giá trị nhỏ nhất và giá trị
lớn nhất của . Khi đó giá trị của = (4 + ) bằng bao nhiêu? A. 16. B. 18. C. 17. D. 19. Lời giải Chọn A Ta có
(11 − 2 − ) = 2 + 4 − 1 ⇔ 2(2 + ) − 11 − (2 + ) − 1 = 0 Đặt = 2 + , 0 <
< 11. Phương trình trở thành: 2 − (11 − ) − 1 = 0. (1) Xét hàm số ( ) = 2 −
(11 − ) − 1 trên khoảng (0; 11). Có = 2 +
> 0, ∀ ∈ (0; 11). Do đó hàm số ( ) luôn đồng biến.
Dễ thấy (1) có nghiệm = 1. Do đó = 1 là nghiệm duy nhất của (1). ( ) Suy ra 2 = 1 − . Khi đó = 16 − (1 − )(3 + 2) − + 5 = 4 − 5 + 2 + 3. Xét hàm số ( ) = 4 − 5 + 2 + 3 trên 0; , có ( ) = 12
− 10 + 2 > 0, ∀ ∈ 0; . Do đó, ( ) = (0) = 3, ( ) = (1) = 4. ; ; Suy ra = 3, = 4. Vậy = 4.3 + 4 = 16.
Câu 38: Xét các số thực dương , thỏa mãn + ≤ ( +
). Tìm giá trị nhỏ nhất của biểu thức = + 3 . √ A. . B. . C. . D. . Lời giải Chọn B Với , > 0, ta có:
log x log y log 2
x y log . x y log 2 x y 2 1
xy x y 1 1 1 1 2 2 2 2 2 ⇔ ≤ − ⇔
≤ ( − 1). Suy ra: − 1 > 0.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Từ ≤ ( − 1) ⇒ ≥ , với > 1. Khi đó: = + 3 ≥ + 3 = 4 + 1 + , với > 1.
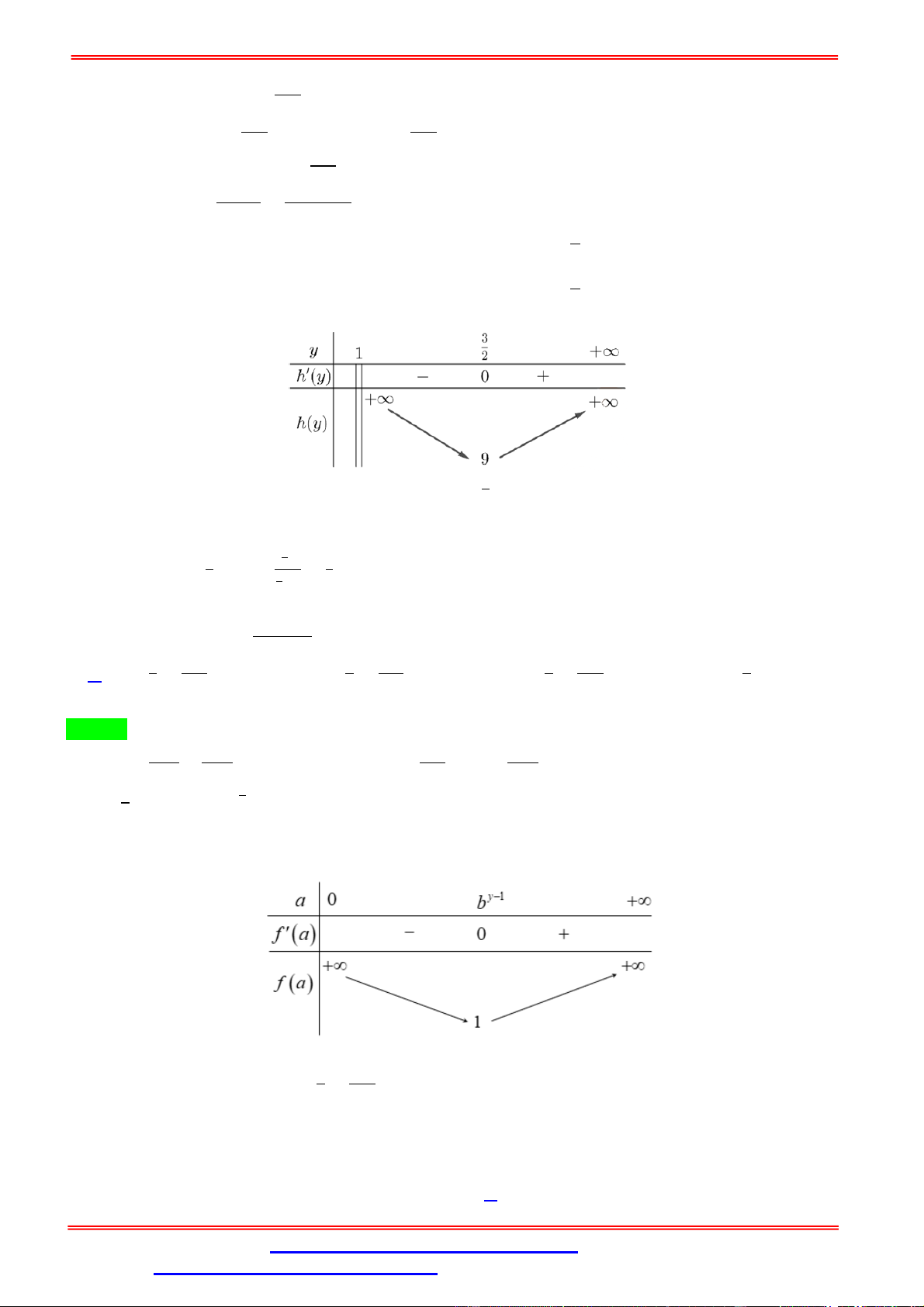
Xét hàm số: ℎ( ) = 4 + 1 + trên khoảng (1; +∞). Ta có: ℎ ( ) = 4 − = ; ( ) ( ) 3 = ℎ ( ) = 0 ⇔ 4 − 8 + 3 = 0 ⇔ 2 1 = ∉ (1; +∞) 2 Bảng biến thiên:
Dựa vào bảng biến thiên ta có: ℎ( ) = 9 khi = . ( ; ) Suy ra: ≥ ℎ( ) = 9. ( ; ) Vậy khi = và = = .
Câu 39: Cho các số thực , , , thỏa mãn điều kiện > 1, > 1, > 0, > 0, + = . Biết rằng biểu thức =
đạt giá trị nhỏ nhất khi =
. Khẳng định nào sau đây đúng ? A. + = . B. + = . C. + = . D. + = . Lời giải Chọn A Ta có = + = ( ), suy ra ( ) = − = 0 ⇔ = ⇔ . = . ⇔ = ⇔ = ⇔ = ( ) = 1, ( ) = +∞, ( ) = +∞ → → Ta có BBT Từ BBT⇒ = 1, đạt được khi = . Do đó = 1, = − 1 ⇒ + = .
Câu 40: Với hai số thực , bất kỳ, ta kí hiệu : ( ; )( ) = | − | + | − | + | − 2| + | − 3|. Biết
rằng luôn tồn tại duy nhất số thực để ( ; )( ) = ( ; )(
) với mọi số thực , thỏa ∈ℝ mãn = và 0 < < . Số bằng A. 2 − 1. B. 2,5. C. . D. 2 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn C
Trước tiên ta xét , thỏa mãn = và 0 < < . Ta có: = ⇔ = ⇔ = . Xét hàm số ( ) = trên (0; +∞). Ta có: ′( ) = ; ′( ) = 0 ⇔ = . Bảng biến thiên Do 0 <
< và ( ) = ( ) nên ta có 0 < < < .
Khi đó ( ; )( ) = | − | + | − | + | − 2| + | − 3|
= (| − | + | − |) + (| − 2| + |3 − |) ≥ | − + − | + | − 2 + 3 − | = − + 1 Mặt khác do < < và 2 < < 3 nên ta có: ( ; )( ) = |
− | + | − | + | − 2| + | − 3| = − + − + − 2 + 3 − = − + 1. Vậy = . ( )
Câu 41: Cho , là các số thực dương thỏa mãn
≤ 4 − 1. Giá trị nhỏ nhất của = + là +
. Giá trị của tích . là A. 45. B. 81. C. 108. D. 115. Lời giải Chọn B Ta có: ≤ 4 − 1 ⇔ 4 ≥ + 1 ≥ 2 ⇒ 4 ≥ 2 nên: ≤ 2 ⇔ ≤ 4. ( ) Xét = + = 12 + 6. + + 2 . Đặt = , 0 < ≤ 4. Suy ra: = ( ) = 12 + + ( + 2). ( ) Ta có: ( ) = − + = = . .( ) .( ) Với 0 <
≤ 4 thì −3 < − 3 ≤ 1 ⇒ 0 ≤ ( − 3) < 9 nên ( − 3) − 21 < 0, ∀ ∈ 0; 4. Do đó: ( ) < 0.
Hàm số ( ) nghịch biến trên (0; 4].
Suy ra: ( ) ≥ (4), ∀ ∈ 0; 4. Hay ≥ (4) = 12 + + 6 ⇔ ≥ + 6. = 4 = 2 Vậy 6
. Dấu bằng xảy ra khi và chỉ khi ⇔ = 1 = Khi đó: = ; = 6 nên = 81.
Câu 42: Xét các số thực dương , thỏa mãn = 3 +
− 1. Tìm giá trị nhỏ nhất của = + . √ A. . B. . C. . D. .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn A Điều kiện 0 < < . Từ giả thiết = 3 + − 1 ⇔ (1 − 2 ) + (1 − 2 ) = ( + ) + ( + ) (1) Xét hàm số ( ) =
+ trên (0; +∞) có ( ) = + 1 > 0, ∀ > 0 do đó hàm ( ) đơn điệu. Vậy (1) ⇔ 1 − 2 = + ⇔ 3 + = 1 (2) Có = + ≥ + = + √ Đặt ( ) = + , ta có ( ) = − + suy ra ( ) = 0 ⇔ = . ( ) Do đó ( ) = 8. Vậy . ;
Bổ sung: có thể đánh giá = + ≥ + = + ≥ = √
Câu 43: Xét các số thực , thỏa mãn 2 2
x y 1 và
(2 + 3 ) ≥ 1. Giá trị lớn nhất P
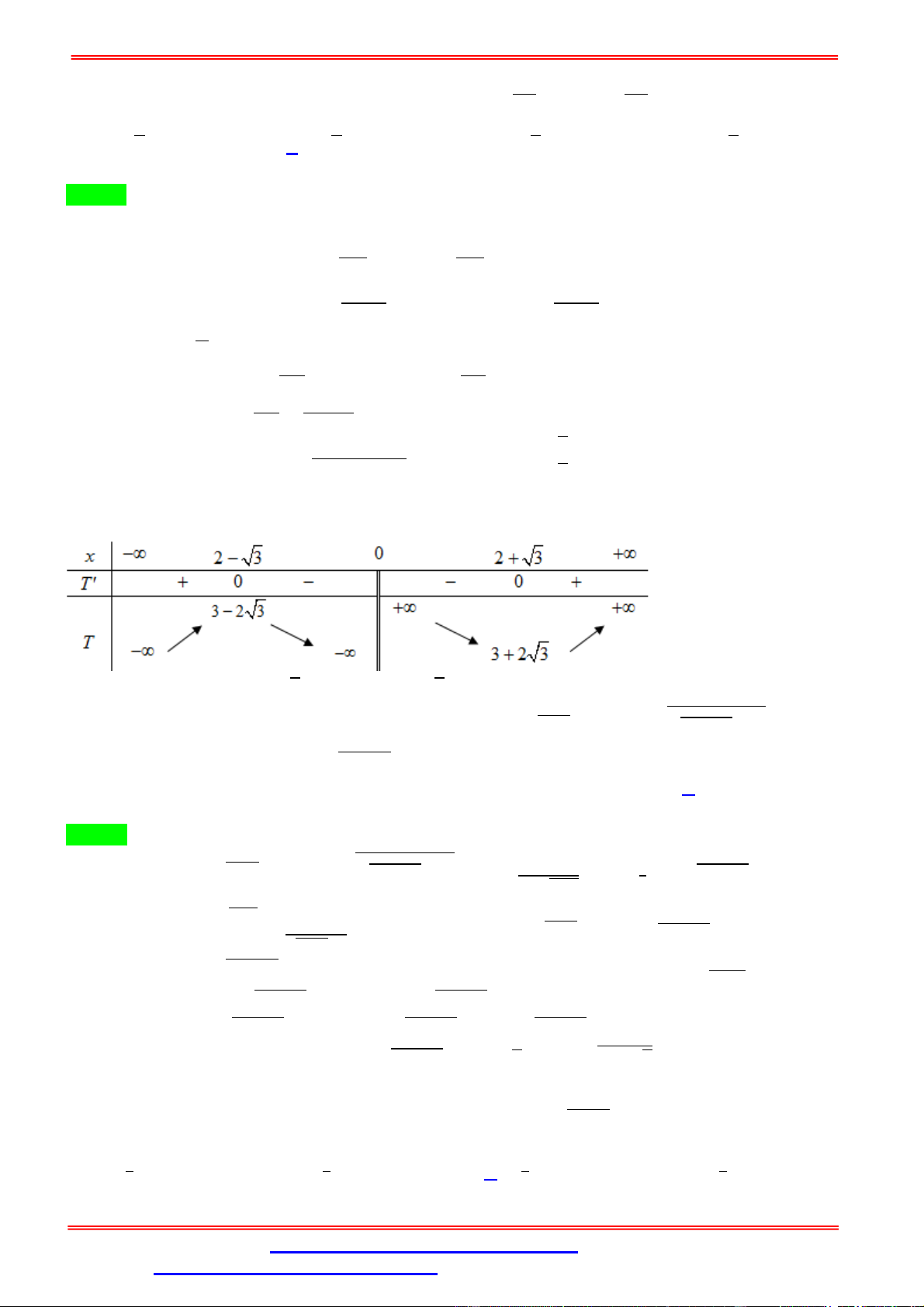
của biểu thức P 2x y bằng max 19 19 7 65 1110 2 7 10 A. P . B. P . C. P . D. P . max 2 max 2 max 3 max 2 Lời giải Chọn B Ta có: (2 + 3 ) ≥ 1 ⇔ 2 + 3 ≥ + ⇔ − 2 + − 3 ≤ 0. = 1 − ( − 3 ) = − + 3 + 1. Để tồn tại , thì ≥ 0 ⇔ ∈ √ ; √ . Khi đó = 1 ± − + 3 + 1. Ta có: = 2 + ≤ 2 1 + − + 3 + 1 + = ( ). ( ) = + 1. ( ) = 0 ⇔ − + 3 + 1 = 2 − 3 ⇔ − + 3 + 1 = 4 − 12 + 9, = 16. ⇔ = √ . Bảng biến thiên. Do đó = + 2 ≤ √ = √ Vậy = √ khi (thỏa mãn điều kiện 2 2 x y 1 ) = 1 + − + 3 + 1 = √
Câu 44: Cho hai số thực , thỏa mãn +
= 1. Giá trị lớn nhất của biểu thức = + bằng A. 3 + 2. B. 3 + 2. C. ( 3 + 2). D. .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn B
Biến đổi yêu cầu của bài toán ta được: = + = + = + . Xét hàm số ( ) = √ + 3 . √1 − ⇒ ( ) = − . √ √ Ta có ( ) = 0 ⇔ √1 − = 3 √ ⇔ 1 − = . 3 ⇔ = . ⇒ ( ) ≥ = 3 + 2 ⇒ = 3 + 2.
Câu 45: Cho , là các số dương thỏa mãn + 1 + − 10 + 9 ≤ 0. Gọi , lần
lượt là giá trị lớn nhất, giá trị nhỏ nhất của = . Tính = 10 − . A. = 60. B. = 94. C. = 104. D. = 50. Lời giải Chọn B + 5 + 1 + − 10 + 9 ≤ 0 + 10 + ⇔ ( + 5 ) − ( + 10 + ) + 2 + 2( + 5 ) − ( + 10 + ) ≤ 0 ⇔ (2 + 10 ) + 2( + 5 ) ≤ ( + 10 + ) + ( + 10 + ) ⇔ 2 + 10 ≤ + 10 + vi) ⇔ − 10 + 9 ≤ 0 ⇔ − 10 + 9 ≤ 0 ⇔ 1 ≤ ≤ 9 + + 9 + + 9 = = + + 1
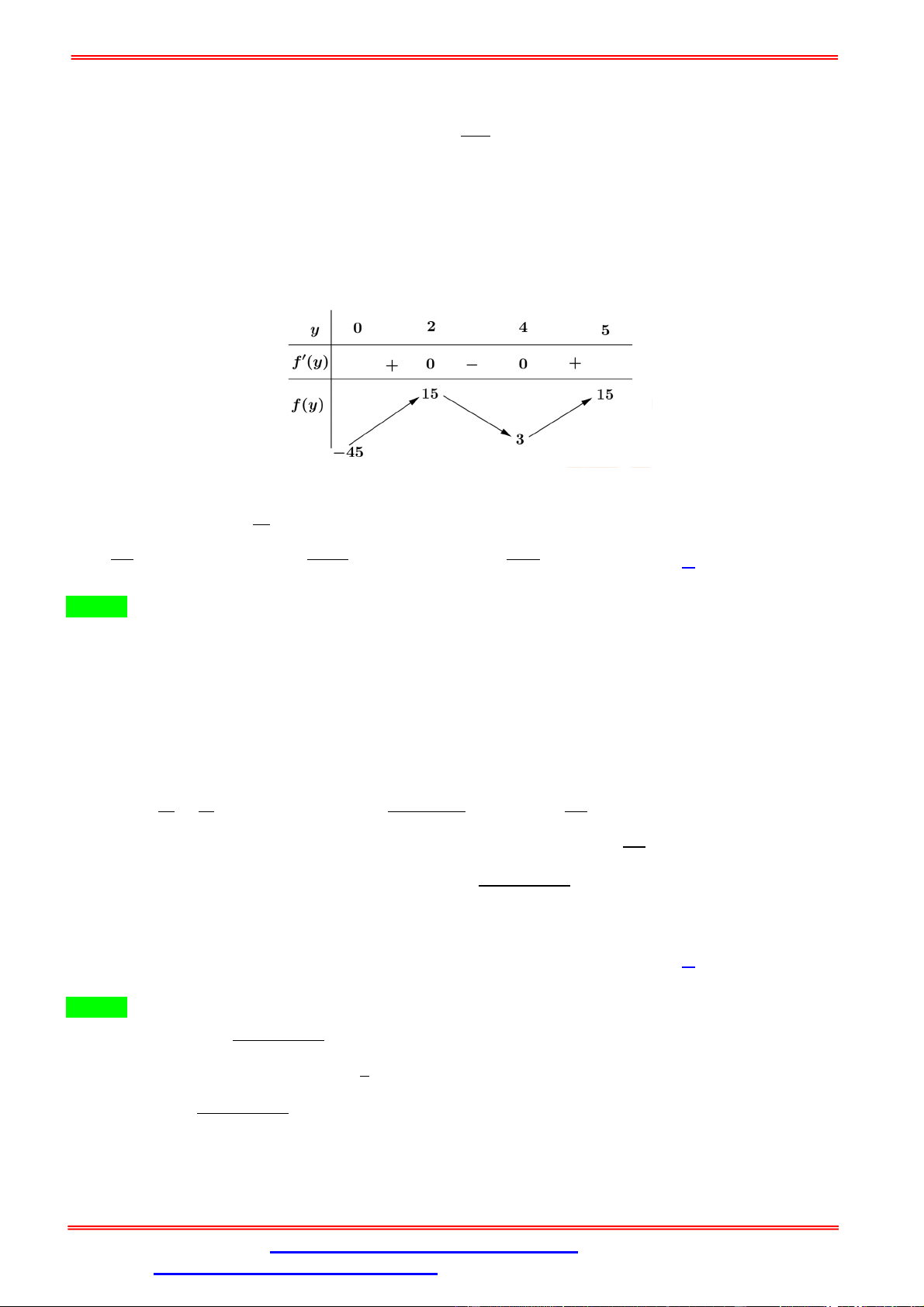
Đặt = , điều kiện: 1 ≤ ≤ 9 ( ) = −4 = ; ( ) = ; ( ) = 0 ⇔ ( ) = 2 (1) = ; (2) = 5 ; (9) = Nên = , = 5. Vậy = 10 − = 94.
ÁP DỤNG HÀM ĐẶC TRƯNG
Câu 46: Cho hai số thực dương , thay đổi thỏa mãn đẳng thức ( − 1). 2 = ( + ). 2 . Tìm giá trị nhỏ nhất của . A. . B. . C. . D. √3 . Lời giải Chọn B Ta có ( − 1)2 = ( + )2 ⇔ (2 − 1 − 1)2 = ( + )2 (1)
Xét hàm ( ) = ( − 1). 2 với ≥ 1.
Khi đó ( ) = 2 + ( − 1). 2 . 2 > 0 với ∀ ≥ 1. Từ (1) ⇔ 2 − 1 = + + 1 ⇔ = 2 − 2 − 4 = 2 = = 0 ⇔ 2 − 2 − 4 = 0 ⇔ (2 − 1) = −1
Loại = −1 vì điều kiện của nên (2) = 2.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 47: Cho các số thực , thỏa mãn 0 ≤ , ≤ 1và + ( + 1)( + 1) − 2 = 0
Tìm giá trị nhỏ nhất của với = 2 + . A. 2. B. 1. C. . D. 0. Lời giải Chọn B
+ ( + 1)( + 1) − 2 = 0 log
x y x y log 1 xy 1 xy (1). 3 3 Xét hàm số ( ) = + với > 0, ta có ( ) = + 1 > 0∀ > 0 . 1 x 2
⇒ ( )luôn đồng biến với ∀ > 0 (1) ⇔ + = 1 − y 1 (2). x 1 x 1 Thế (2)vào ta được = 2 + Với 0 ≤ ≤ 1 = 0 ∉ [0; 1] = 2 − ; = 0 ⇔ . (0) = 1; (1) = 2. ( ) = −2 ∉ [0; 1]
Vậy giá trị nhỏ nhất của là 1 đạt được khi = 0; = 1.
Câu 48: Cho , là hai số thực dương thỏa mãn =
+ 3 − 4. Tìm giá trị nhỏ nhất của biểu thức = + A. . B. . C. . D. 1. Lời giải Chọn B 4 + 2 + 5 = + 3 − 4 ⇔ (4 + 2 + 5) − 5 ( + ) + = 5( + ) − (4 + 2 + 5) ⇔ (4 + 2 + 5) + (4 + 2 + 5) = 5 ( + ) + 5( + )(*) Hàm số ( ) = + ( > 0) có '( ) = + 1 > 0
( ) đồng biến nên (*)⇔ (4 + 2 + 5) =
5( + ) ⇔ 4 + 2 + 5 = 5( + ). 4 + 2 + 5 = 5( + ) ⇔ = 5 − 3 = + ⇒ = (5 − 3 ) + = 10 − 30 + 25 = 10 − + ≥ . Vậy GTNN = .
Câu 49: Cho 2 số thực dương , thỏa mãn [( + 1)( + 1)]
= 9 − ( − 1)( + 1). Giá trị nhỏ nhất của biểu thức = + 2 là A. . B. . C. √3 . D. √2 . Lời giải Chọn D Ta có [( + 1)( + 1)] = 9 − ( − 1)( + 1) ⇔ ( + 1)[ ( + 1) + ( + 1)] + ( − 1)( + 1) = 9. ⇔ ( + 1)[ ( + 1) + ( + 1) + − 1] = 9 9 ⇔ ( + 1) + − 1 = − ( + 1) + 1 ⇔ ( + 1) + + 1 − 2 = − 2 + (*). Xét hàm số ( ) = + − 2 với > 0 có ( ) =
+ 1 > 0 với mọi > 0 nên hàm số ( )
luôn đồng biến và liên tục trên (0; +∞).
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Từ (*) suy ra + 1 = ⇔ = − 1 = , do > 0 nên ∈ (0; 8). Vậy = + 2 = + 2 = 2 − 1 + = 2( + 1) + − 3 ≥ −3 + 6√2. Vậy √2 khi 2( + 1) = ⇔ = − 1. √
Câu 50: Cho các số thực dương x, y thỏa mãn: 3 + 2 + ( + 1) = + + 2 + 5.
Tìm giá trị nhỏ nhất của biểu thức = 3 + 2 . A. √6 . B. √2 . C. √2 . D. √2 . Lời giải Chọn B Ta có: 3 + 2 + ( + 1) = + + 2 + 5 3 − + − 5 = 3 − + 2 − (∗) Xét hàm số ( ) = 3 − + có ( ) = 3 . 3 − . + 1 > 0, ∀
suy ra hàm số ( ) luôn đồng biến. Từ (*) ta có ( − 5) = (2 − ) ⇔ − 5 = 2 − ⇔ = Suy ra = + 2 = 2( + 1) + 4( + 1) + 9 9 ⇔ = = 2( + 1) + 4 + ≥ 4 + 6√2. + 1 + 1 ( )
Câu 51: Cho hai số thức , thỏa mãn 16. 2 =
. Tính giá trị lớn nhất của biểu thức = + A. . B. C. D. 1 Lời giải Chọn C
Từ giải thiết suy ra 1 − 2 > 0. Theo bài ra: 8(1 − 2 ) 8(1 − 2 ) 16 . 2 = ⇔ ( + 2 ) = + 2 16 8(1 − 2 ) ⇔ 2 ( + 2 ) = ⇔ 2 ( + 2 ) = 2 (2 − 4 )(1) 2
Xét hàm số ( ) = . 2 với ∈ = (0; +∞)
Do hàm số liên tục trên và có ( ) = 2 + . 2 .
> 0, ∀ ∈ suy ra hàm số đồng biến trên . Khi đó (1) ⇔ + 2 = 2 − 4
⇔ (1 + 4 ) = 2 − 2 suy ra 2 − 2 > 0 ⇔ < 1. Ta có = + = (1 + 4 ) = (2 − 2 ) = (1 − ) ≤ = = Vậy = xảy ra khi . =
Câu 52: Cho hai số dương , thỏa mãn = 3
− 2 − 1. Tìm giá trị lớn nhất của biểu thức = 2
− 18 + 72 − 45 trên nửa khoảng 0; 5. A. 2020. B. 20. C. 15. D. 30. Lời giải Chọn C Ta có: + = 3 − 2 − 1 3 + 3 + ⇔ ( + ) − (3 + 3 + ) = 3 − 2 − 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 ⇔ ( + ) + 2 + 1 = (3 + 3 + ) + 3 ⇔ (3 + 3 ) + 3 + 3 = (3 + 3 + ) + 3 + 3 + Hàm đặc trưng ( ) = + ∀ > 0 ⇒ ( ) = + 1 > 0∀ > 0
⇒ Hàm số đồng biến trên khoảng (0; +∞) Do đó: 3 + 3 = 3 + 3 + ⇔ 2 = 3 Thay vào ta có: = ( ) = 3 − 27 + 72 − 45 ( ) = 9 − 54 + 72 = 2 ( ) = 0 ⇔ = 4 Ta có bảng biến thiên:
Dựa vào bảng biến thiên ta có giá trị lớn nhất của P là 15
Câu 53: Cho hai số thực dương , thỏa mãn 6. 3 + + 1 = 3 +
( + 3 ). Giá trị nhỏ nhất của biểu thức = bằng . A. . B. . C. . D. 3 Lời giải Chọn D Đặt = ( + 3 ) ⇔ 3 = + 3 ⇔ 3 = 3 − 3
Khi đó phương trình 6. 3 + + 1 = 3 + ( + 3 ) trở thành: 3 + + 1 = 3 − 3 + ⇔ 3. 3 + + 1 = 3 + ⇔ 3 + + 1 = 3 + (1) Xét hàm số: ( ) = 3 + trên khoảng (0; +∞) Ta có: ( ) = 3 .
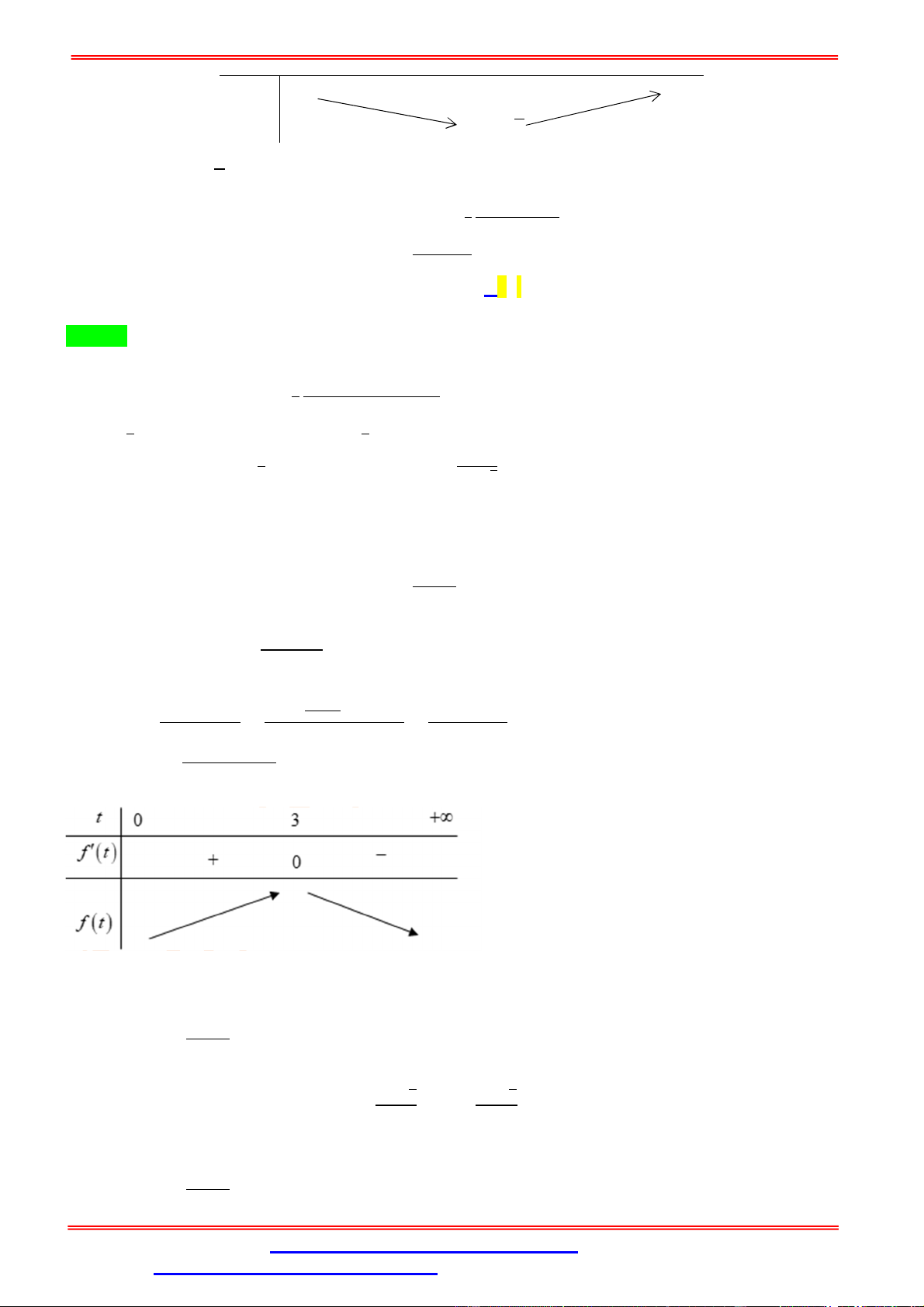
3 + 1 > 0, ∀ ∈ (0; +∞) suy ra hàm số luôn đồng biến Do (1) suy ra ( + 1) = ( ) ⇔ + 1 = ⇔ + 1 = ( + 3 ) ⇔ 3 − 3 = ⇔ = 2. 3 Khi đó = = = ( )có ⇒ ( ) = . = 0 ⇔ = .
Lập bảng biến thiên của hàm số trên khoảng (0; +∞) suy ra = = 3. ( ; )
Câu 54: Cho hai số thực , thỏa mãn hệ thức log , = 4 + 4 − − − 2 . Gọi và
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
= 3 + 4 + 12. Giá trị biểu thức ( + 2 ) tương ứng bằng A. 28. B. 26. C. 29. D. 27. Lời giải Chọn D
Điều kiện xác định: > 0 ⇔ + 4 − 2 + 10 > 0.(*)
Ta sẽ đưa phương trình về dạng log = − ⇔. . ⇔ = (với > 1) Giả thiết log , = 4 + 4 − − − 2 ⇔ log( + 4 − 2 + 10) − log(2 + + 6) = (2 + + 6) − ( + 4 − 2 + 10). ⇔ log( + 4 − 2 + 10) + ( + 4 − 2 + 10) = log(2 + + 6) + (2 + + 6) (1)
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Xét hàm số đồng biến ( ) = log + vì ′( ) = + 1 > 0 ∀t > 0. Từ (1) suy ra ( + 4 − 2 + 10) = (2 + + 6) ⇔ + 4 − 2 + 10 = 2 + + 6 ⇔ ( − 2) + ( + 1) = 9 (2)
Xét biểu thức: = 3 + 4 + 12 = 3( − 2) + 4( + 1) + 14
Theo BĐT buhia, ta có 3( − 2) + 4( + 1)
≤ (3 + 4 )(( − 2) + ( + 1) ) = 225
⇔ |3( − 2) + 4( + 1)| ≤ 15 ⇔ −|3( ≤ −2) + 4( + 1)| ≤ 3( − 2) + 4( + 1) ≤ |3( ≤ −2) +
4( + 1)| ⇔ −15 ≤ 3( − 2) + 4( + 1) ≤ 15 ⇔ −1 ≤
= 3( − 2) + 4( + 1) + 14 ≤ 29
Suy ra giá trị nhỏ nhất của là: = 9; = −1 ⇒ ( + 2 ) = 27.
Câu 55: Cho , , là các số thực thỏa mãn
= ( − 2) + ( − 2) + ( − 2). Tìm
giá trị lớn nhất của Cho ; là các số thực dương thỏa mãn điều kiện 5 + + + 1 = + 3
+ ( − 4). Tìm giá trị nhỏ nhất của biểu thức = + . A. 3. B. 5 + 2√5. C. 3 − 2√5. D. 1 + √5. Lời giải Chọn B Ta có 5 + + + 1 = + 3 + ( − 4) 5 − 3 + + 4 = 5 − 3 + − 1(1). Xét hàm số ( ) = 5 − 3 + trên ℝ. Vì ( ) = 5 . 5 + 3 .
3 + 1 > 0; ∀ ∈ ℝnên hàm số ( )đồng biến trên (2). Từ (1)và (2)ta có + 4 =
− 1(3). Dễ thấy = 4không thỏa mãn (3). Với ≠ 4, (3) ⇔ =
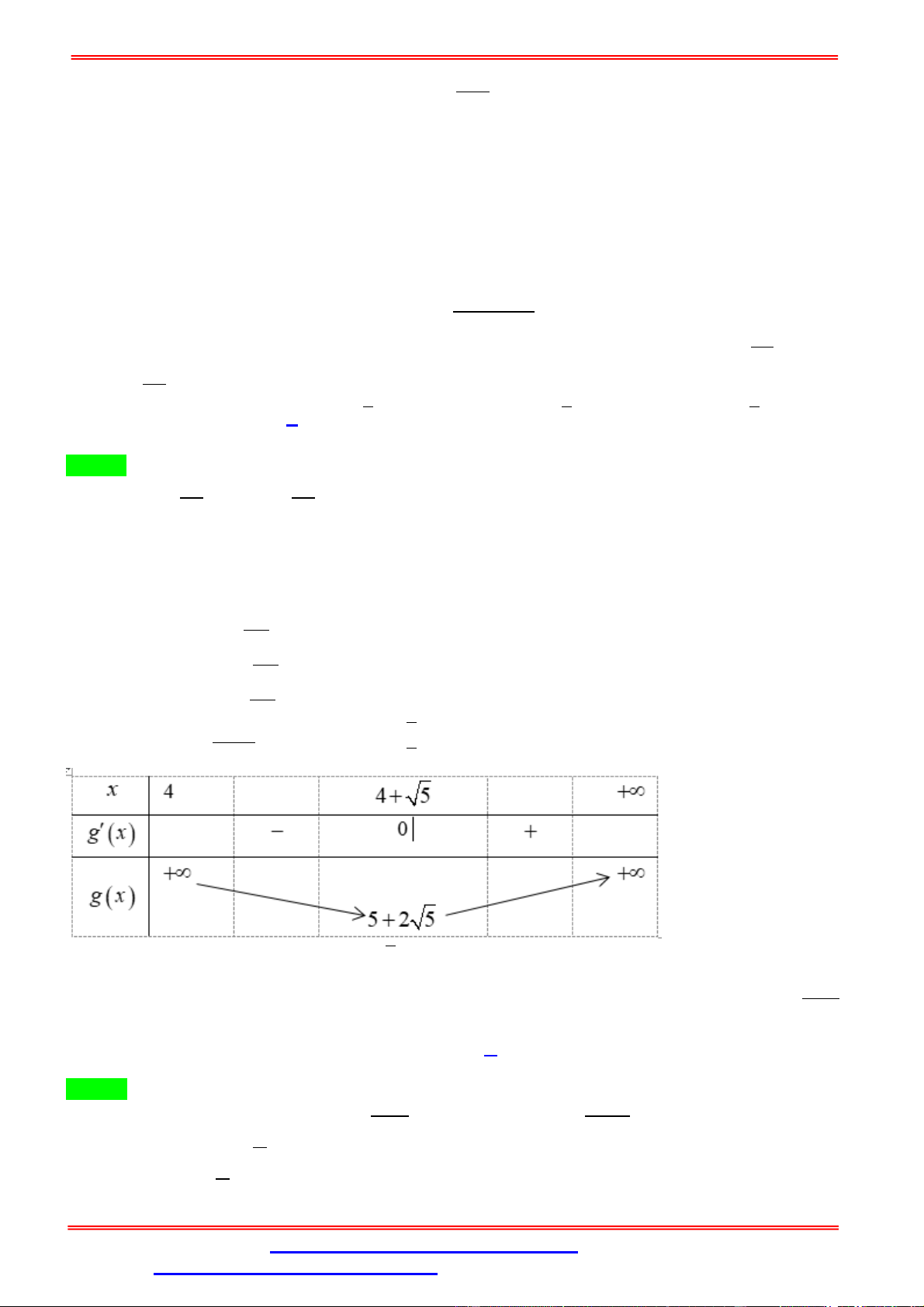
kết hợp điều kiện > 0suy ra > 4. Do đó = + = + . Xét hàm số ( ) = + trên (4; +∞). = 4 + √5 Ta có ( ) = 1 − = 0 ⇔ . ( ) = 4 − √5
Dựa vào bảng biến thiên ta có ( )√5 . ( ; ∞)
Câu 56: Cho các số thực , với ≥ 0 thỏa mãn + + ( + 1) + 1 = + −
3 . Gọi là giá trị nhỏ nhất của biểu thức =
+ 2 + 1. Mệnh đề nào sau đây là đúng? A. ∈ (2; 3). B. ∈ (−1; 0). C. ∈ (0; 1). D. ∈ (1; 2). Lời giải Chọn C
Đẳng thức đã cho tương đương − + + 3 = − + (− − 1) (∗). Xét hàm số ( ) = − + với ∈ ℝ. Ta có ( ) = + + 1 ⇒
( ) > 0 với ∀ ∈ ℝ. Suy ra hàm số ( ) đồng biến trên ℝ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Khi đó (∗) được viết lại thành ( + 3 ) = (− − 1) ⇔ + 3 = −
− 1 ⇔ ( + 3) = − − 1 ⇔ = . Thay =
vào biểu thức ta được = + 2 + 1 = + 2 − 1 + 1 = + − 1 = + 3 + − 4.
Đặt + 3 = . Vì ≥ 0 nên ≥ 3. Ta có Côsi = + − 4 = + + − 4 ≥ 2 . + . − 4= . Do đó với = 3 thì = suy ra = ∈ (0; 1).
Câu 57: Cho hai số thực dương ,
thay đổi thỏa mãn đẳng thức ( − 1). 2 = ( + ). 2 .Tìm giá trị nhỏ nhất của . A. . B. . C. . D. √3 . Lời giải Chọn B Ta có ( − 1)2 = ( + )2 ⇔ (2 − 1 − 1)2 = ( + )2 (1)
Xét hàm ( ) = ( − 1). 2 với ≥ 1.
Khi đó ( ) = 2 + ( − 1). 2 . 2 > 0với ∀ ≥ 1. Từ (1) ⇔ 2 − 1 = + + 1 ⇔ = 2 − 2 − 4 = 2 = = 0 ⇔ 2 − 2 − 4 = 0 ⇔ (2 − 1) = −1
Loại = −1vì điều kiện của nên (2) = 2.
Câu 58: Cho các số dương , thỏa mãn
+ 3 + 2 ≤ 4. Giá trị nhỏ nhất của biểu thức = 6 + 2 + + bằng √ √ A. . B. 11√3. C. . D. 19. Lời giải Chọn D > 0 ĐK: ⇔ + > 1 , > 0 Ta có: + − 1 + 3 + 2 ≤ 4 2 + 3 ⇔ (
( + − 1) + 1) + 5( + − 1) ≤ (2 + 3 ) + 2 + 3 ⇔
[5( + − 1)] + 5( + − 1) ≤ (2 + 3 ) + 2 + 3 (∗) Xét hàm số ( ) = ( ) + trên (0; +∞) ta có 1 ( ) = + 1 > 0, ∀ ∈ (0; +∞). 5 ⇒ Hàm số ( ) =
( ) + đồng biến trên (0; +∞).
(∗) ⇔ 5( + − 1) ≤ 2 + 3 ⇔ 3 + 2 ≤ 5 Mặt khác, ta có: 4 9 = 6 + 2 + + 4 9 = 9 + + 4 +
− (3 + 2 ) ≥ 2.6 + 2.6 − 5 = 19
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 ⎧9 = =
⇒ GTNN của = 19, dấu “ = ” xảy ra ⇔ ⇔ ( ) 4 = ⎨ = ⎩3 + 2 = 5
Câu 59: Cho các số thực , với ≥ 0 thỏa mãn 5 + 5 + ( + 1) + 1 = 5 + −
3 . Gọi là giá trị nhỏ nhất của biểu thức =
+ 2 + 1. Mệnh đề nào sau đây là đúng? A. ∈ (0; 1). B. ∈ (1; 2). C. ∈ (2; 3). D. ∈ (−1; 0). Lời giải Chọn A Ta có: 5 + 5 + ( + 1) + 1 = 5 + − 3 ⇔ 5 − 5 + + 3 = 5 − 5 − − 1. Xét hàm số ( ) = 5 − 5 + có ( ) = 5 5 + 5 5 + 1 > 0, ∀ ∈ ℝ.
Do đó hàm số ( ) đồng biến trên ℝ ⇒ ( + 3 ) = (− − 1) ⇔ + 3 = − − 1 ⇔ (3 + ) = − − 1 ⇔ = (do ≥ 0 nên + 3 ≠ 0) ⇔ + 2 + 1 = + + 1 = . Xét hàm số ( ) = với ≥ 0 có ( ) = > 0, ∀ ≥ 0. ( )
Do đó: ( ) ≥ (0) = , ∀ ≥ 0 hay + 2 + 1 ≥ , ∀ ≥ 0. Vậy = ∈ (0; 1). Câu 60: Cho ,
∈ (0; 2) thỏa mãn ( − 3)( + 8) = (
− 11). Giá trị lớn nhất của = √ + 1 + bằng A. √1 + 3 − 2. B. 2√ 3 − 2. C. 1 + √ 3 − 2. D. 1 + √ 2. Lời giải Chọn B Điều kiện: ≥ 1, ≥ . Ta có : ( − 3)( + 8) = ( − 11) ⇔ + 5 − 24 = − 11 ⇔ − 11 − (
+ 5 − 24) = 0, có = (2 + 5) > 0, ∀ ≥ 1. ( ) = = + 8 = Do đó ⇔ ⇔ ⇔ . ( ) = = 3 − = +) Do = > > 2 nên loại = . +) Với = , 1 ≤ < 2: Cách 1: Khi đó, ta được: = √ + (3 − ) trên 1; 2). Ta có = − √ ( ) ( ) 1 1 = 0 ⇔ − = 0 2 √ 2(3 − ) (3 − ) ⇔ (3 − ) (3 − ) − √ = 0 ⇔ (3 − ) (3 − ) = √ Xét hàm ( ) = √ trên 1; +∞), có ( ) = √ + > 0, ∀ ∈ (1; +∞). √
Khi đó ⇔ (3 − ) = ( ) ⇔ 3 − = ⇔ = . Bảng biến thiên:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Từ đó max = 2√ 3 − 2 tại = , = . Cách 2: Khi đó, ta được: = √ + (3 − ) trên 1; 2). ⇒ = √ + (3 − ) ≤ 2( + (3 − )) = 2 [ (3 − )] ≤ 2 = 4( 3 − 2), ∀ ∈ 1; 2) √ = (3 − ) Dấu “=” xảy ra khi = 3 − ⇔ = . ∈ 1; 2) Vậy Từ đó max = 2√ 3 − 2 tại = , = .
Câu 61: Cho hai số thực ; thỏa mãn: ( + 8 + 16) + [(5 − )(1 + )] = √ 2 + (2 + 8) .
Gọi là tập các giá trị nguyên của tham số
để giá trị lớn nhất của biểu thức = + −
không vượt quá 10. Hỏi có bao nhiêu tập con khác rỗng. A. 16385. B. 2047. C. 32. D. 16383. Lời giải Chọn D −1 < < 5 ĐKXĐ: ≠ −4 . Ta có: ( + 8 + 16) + [(5 − )(1 + )] = 2 + (2 + 8) √ ⇔ ( + 4) + [(5 − )(1 + )] = 2{ [(5 − )(1 + )] − 3} + [ 4 + ( + 4) ] ⇔ 2 ( + 4) + [(5 − )(1 + )] = 2 [(5 − )(1 + )] + ( + 4) 2 2
⇔ 2log y 4 log y 4
2log 5 x 1 x log 5 x 1 x 3 2 3 2 (∗) Xét hàm số: ( ) = 2 − trên (0; +∞) Ta có: ′( ) = − = > 0 . . . .
⇒ ( ) đồng biến trên (0; +∞). (∗) ⇔ (( + 4) ) = (5 − )(1 + ) ( + 4) = (5 − )(1 + ) ( − 2) + ( + 4) = 9 = 2 + 3 Đặt: = −4 + 3 = + − = (2 + 3 ) + (−4 + 3 ) − = √29 + 12 − 24 −
Ta có: 29 − 12√5 ≤ 29 + 12 − 24 ≤ 29 + 12√5
⇒ −3 + 2√5 ≤ √29 + 12 − 24 ≤ 3 + 2√5 ⇒ −3 + 2√5 − ≤ √29 + 12 − 24 − ≤ 3 + 2√5 −
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 −3 + 2√5 − 3 + 2√5 − [ −3 + 2√5 − ≤ 10 3 + 2√5 − ≤ 10 −10 ≤ −3 + 2√5 − ≤ 10 −13 + 2√5 ≤ ≤ 7 + 2√5 ⇔ −7 + 2√5 ≤ ≤ 7 + 2√5. −10 ≤ 3 + 2√5 − ≤ 10 −7 + 2√5 ≤ ≤ 13 + 2√5 Vì ∈ ℤ ⇒ ∈ {−2; −1; . .10; 11}.
Do đó số phần tử của là: 14
⇒Số tập con khác rỗng của là 2 − 1 = 16383.
Câu 62: Cho hai số thực , thỏa mãn 0 ≤ ,
≤ 1 trong đó , không đồng thời bằng 0 hoặc 1 và
+ ( + 1). ( + 1) − 2 = 0. Tìm giá trị nhỏ nhất của với = 2 + A. 2. B. 1. C. . D. 0. Lời giải Chọn B
Từ điều kiện đề bài và > 0; 1 − ≠ 0 ⇒ + > 0; 1 − > 0khi đó + + ( + 1). ( + 1) − 2 = 0 ⇔ ( + ) + ( + ) = (1 − ) + (1 − )(1) 1 − Xét hàm số ( ) = + ( > 0) có ( ) = + 1 > 0∀ > 0 .
⇒ ( ) là hàm số đồng biến trên khoảng (0; +∞). Vậy phương trình (1) ⇔ + = 1 − ⇒ = ⇒ = 2 + = 0 Xét hàm số ( ) = 2 + với ∈ [0; 1]có ( ) = 2 + cho ( ) = 0 ⇔ ( ) = −2 (0) = 1; (1) = 2 ⇒ ( ) = 1 ⇒Chọn B [ ; ]
Câu 63: Cho ; là các số thực dương thỏa mãn điều kiện 5 + + + 1 = + 3 +
( − 4). Tìm giá trị nhỏ nhất của biểu thức = + . A. 3. B. 5 + 2√5. C. 3 − 2√5. D. 1 + √5. Lời giải Chọn B Ta có 5 + + + 1 = + 3 + ( − 4) ⇔ 5 − 3 + + 4 = 5 − 3 + − 1(1). Xét hàm số ( ) = 5 − 3 + trên ℝ. Vì ( ) = 5 . 5 + 3 .
3 + 1 > 0; ∀ ∈ ℝ nên hàm số ( ) đồng biến trên ℝ (2). Từ (1) và (2) ta có + 4 =
− 1(3). Dễ thấy = 4 không thỏa mãn (3). Với ≠ 4, (3) ⇔ =
kết hợp điều kiện > 0 suy ra > 4. Do đó = + = + . Xét hàm số ( ) = + trên (4; +∞). = 4 + √5 Ta có ( ) = 1 − = 0 ⇔ . ( ) = 4 − √5 4 4 + √5 +∞ ( ) – 0 +
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 +∞ +∞ ( ) 5 + 2√5
Dựa vào bảng biến thiê n ta có ( )√5 . ( ; )
Câu 64: Xét các số thực dương , thỏa mãn = ( − 3) + ( − 3) + . Tìm giá √ trị lớn nhất của biểu thức = . A. 3. B. 2. C. 1. D. 4. Lời giải Chọn C Ta có: + = ( − 3) + ( − 3) + √ + + + 2 ⇔ 3 ( + ) + 3( + ) = ( + + + 2) + + + + 2. √ √ Xét hàm số ( ) = + , > 0 có ( ) =
+ 1 > 0, ∀ > 0. Vậy hàm số ( ) luôn đồng √ √
biến và liên tục trên khoảng (0; +∞). Do đó: 3( + ) = ( + + + 2) ⇔ 3( + ) = + + + 2 (1) Cách 1: Từ (1) ⇔ = ( + ) − 3( + ) + 2. Ta có = + − = ( + 1) − ≤ −
Đẳng thức xảy ra khi và chỉ khi = + 1. ( ) Do đó từ (1), suy ra: ≤ − ( + ) + 3( + ) − 2. Đặt = + , > 0. ( ) ( ) Suy ra: = ≤ = = ( ). ( ) Ta có: ( ) = = 0 ⇔ = 3 (nhận) ( ) Bảng biến thiên = + 1 = 2 Dựa vào BBT, ta có =
( ) = (3) = 1 khi và chỉ khi ⇔ ( ; ) + = 3 = 1. Cách 2: (Trắc nghiệm) Ta có: = 2 + .
Trong (1) coi là ẩn, là tham số. Ta có + ( − 3) +
− 3 + 2 = 0 có nghiệm khi = ( − 3) − 4( − 3 + 2) ≥ 0 ⇔ √ ≤ ≤ √ < 3 nên − 11 < 0 Vậy
< 2 nên trong 4phương án thì khi đó = 2, = 1. Cách 3: (Trắc nghiệm) Ta có: = 3 − < 3 với , > 0.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 + Nếu = 2 thì = 2 ⇔
= 11. Thay vào (1) ta được: + 3 + 90 = 0 (vô lý). + Nếu = 1 thì = 1 ⇔ 2 + = 5 ⇔
= 5 − 2 . Thay vào (1), ta được: 3( + 5 − 2 ) =
+ (5 − 2 ) + (5 − 2 ) + 2 ⇔ 3 − 12 + 12 = 0 ⇔ = 2 ⇒ = 1. Vậy .
Câu 65: Cho các số thực dương và thỏa mãn 4 + 9. 3 = 4 + 9 . 7 . Tìm giá trị
nhỏ nhất của biểu thức = . A. = 9. B. = √ . C. = 1 + 9√2. D. Hàm số không có giá trị nhỏ nhất. Lời giải Chọn A Từ giả thiết ta đặt = − 2 , ∈ ℝ. Phương trình 4 + 9. 3 = 4 + 9 . 7 trở thành 4 + 9. 3 = (4 + 9 ). ⇔ 4(7 − 49) + 9 9. − 49 = 0.
Nhận thấy = 2 là nghiệm phương trình.
Ta chứng minh = 2 là nghiệm duy nhất của phương trình.
Xét > 2: 7 > 49 và 9.
> 49 nên vế trái phương trình luôn dương, nên phương trình vô nghiệm.
Xét < 2: 7 < 49 và 9.
< 49 nên vế trái phương trình luôn âm, nên phương trình vô nghiệm. Vậy = − 2 = 2 ⇔ = thay vào = = 16 16 x 1 2 . x
1 9 . Dấu bằng đạt được khi = ⇒ = 4. x x .
Câu 66: Cho hai số thực , thay đổi thỏa mãn đẳng thức + ( − 1). 2 = 0. Tìm giá trị
lớn nhất của , biết rằng > 1. A. = − . B. = −3. C. = 1. D. = 0. Lời giải Chọn B . Ta có: + ( − 1). 2 = 0 ⇔ . 2 = ( + − − 1). 2 (∗).
Xét hàm số ( ) = . 2 trên 0; +∞). Ta có ( ) = 2 + . 2 2 > 0∀ ≥ 0.
Vậy hàm số ( ) = . 2 đồng biến trên 0; +∞). Suy ra: (∗) ⇔ ( ) = ( + − − 1) ⇔ + − − 1 = ⇒ = do > 1. ( )( ) = 0 Ta có: = = ; = 0 ⇔ . ( ) ( ) = 2 Bảng biến thiên:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Từ bảng biến thiên suy ra: = −3.
Câu 67: Cho hai số thực , không âm thỏa mãn + 2 − + 1 =
. Giá trị nhỏ nhất của biểu thức = + 4 − 2 + 1 là A. − . B. 1. C. . D. −1. Lời giải Chọn A + 2 − + 1 = ⇔ 2( + 1) + (2( + 1) ) = (2 + 1) + (2 + 1). Xét hàm số ( ) = + , ( > 0); ( ) = 1 + > 0, ∀ > 0 .
Suy ra 2( + 1) = 2 + 1 ⇒ 2 = 2( + 1) − 1. = + 4 − 2 + 1 = + 4 − 2( + 1) + 1 + 1 = + 2 − 4 = ( ). ( ) = 2
+ 4 − 4 là hàm số đồng biến trên nửa khoảng 0; +∞) nên ( ) = 0 có tối đa 1
nghiệm, nhẩm được nghiệm = nên nghiệm đó là duy nhất. Vậy = − tại = .
Câu 68: Cho hai số thực , thỏa mãn 2 y y 5 4x x log 8
16 log 5 x1 x 2 log
log 2 y 82 2 . 2 3 2 3 3
Gọi là tập các giá trị nguyên của tham số để giá trị lớn nhất của biểu thức = + − không
vượt quá 10. Hỏi có bao nhiêu tập con không phải là tập rỗng? A. 2047. B. 16383. C. 16384. D. 32. Lời giải Chọn B ĐK: −1 < < 5, ≠ −4. Ta có: 2 y y 5 4x x log 8
16 log 5 x1 x 2 log
log 2 y 82 2 . 2 3 2 3 3 2 log 2
y 8y 16 2log 2
5 4x x log 2
y 8y 16 log 2 5 4x x 3 3 2 2 log 4 1 .log 2
y 8y 16 log 4 1 .log 2 5 4x x 3 2 3 2 ⇔ + 8 + 16 = 5 + 4 −
(vì hàm f t log 4 1 .log t đồng biến trên (0; +∞)). 3 2 ⇒ ( + + 11) = (4 − 8 ) ≤ 80( + ) ⇒ ( + ) − 58( + ) + 121 ≤ 0 ⇒ 29 − 12√5 ≤ +
≤ 29 + 12√5 ⇒ 29 − 12√5 ≤ + ≤ 29 + 12√5. Đặt =
29 − 12√5, = 29 + 12√5, ta có: = {| − |, | − |}. [ ; ] | − | ≤ 10 − 10 ≤ ≤ + 10 Do đó, ≤ 10 ⇔ ⇔ ⇒ − 10 ≤ ≤ + 10. [ ; ] | − | ≤ 10 − 10 ≤ ≤ + 10 Vì
∈ ℤnên = {−2; −1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11}.
Câu 69: Cho các số thực , , thỏa mãn điều kiện = ( − 2) + ( − 2) +
( − 2). Tổng giá trị lớn nhất và nhỏ nhất của biểu thức = bằng?
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 A. − . B. . C. − . D. . Lời giải Chọn B Ta có: + +
= ( − 2) + ( − 2) + ( − 2) 2 + 2 + 2 + 1 ⇔ ( + + ) + 2( + + ) = (2 + 2 + 2 + 1) + ( + + ) ⇔ 2 ( + + ) + 4( + + ) = 2 (2 + 2 + 2 + 1) + 2( + + ) ⇔ ( + + ) + 4( + + ) + 1 = (2 + 2 + 2 + 1) + ( + + ) + 1 ⇔ 4 ( + + ) + 4( + + ) = (2 + 2 + 2 + 1) + (2 + 2 + 2 + 1) Xét hàm số: ( ) = + ( > 0).
Hàm số luôn đồng biến trên tập xác định. Suy ra: 4( + + ) = (2 + 2 + 2 + 1) ⇒ 4( + + ) = 2 + 2 + 2 + 1 1 ⇔ + + − 2 − 2 − 2 + = 0( ) 2 (1; 1; 1) Ta có mặt cầu: ( ): = √ Ta có: =
⇔ ( − 1) + ( − 1) + ( + 1) = 0( )
Để mặt phẳng ( ) và mặt cầu ( ) có điểm chung: [ | | ; ( )] ≤ ⇔ ≤ √ . ( ) ( ) ⇔ 3 − 2 − 13 ≤ 0. ⇔ √ ≤ ≤ √ .
Tổng giá trị lớn nhất và nhỏ nhất của biểu thức = bằng .
Câu 70: Cho hai số thực dương , thay đổi thỏa mãn đẳng thức: (2 − 1)4 = ( + + 1)2
. Tìm giá trị nhỏ nhất của . A. . B. √3 . C. . D. . Lời giải Chọn D
Do , là số thực dương đẳng thức (2 − 1)4 = ( + + 1)2 . Suy ra 2 − 1 > 0. Khi đó ta có (2 − 1) + (2 − 1) = ( + + 1) + ( + + 1) (1) Xét hàm số ( ) =
+ . Hàm số này đồng biến trên (0; +∞). Nên từ (1) ta được (2 − 1) = ( + + 1) ⇔ 2 − 2 = + ⇔ (2 − 1) = + 2 Do > 0,
+ 2 > 0 nên 2 − 1 > 0 ⇔ > Suy ra = . Xét hàm số ( ) = trên ; +∞ . Bảng biến thiên ( )
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Dựa vào bảng biến thiên suy ra tại = 2.
Câu 71: Cho ; là các số thực dương thỏa mãn =
+ 2 . Tìm giá trị nhỏ nhất của biểu thức = + . √ A. 3 + √3. B. 4. C. 3 + 2√3. D. 6. Lời giải Chọn B Ta có = + 2 ⇔ (2 + + 1) − ( + ) = + 2 ⇔ (2 + + 1) = (3 + 3 ) + + 2 − 1 ⇔ (2 + + 1) + 2 + + 1 = (3 + 3 ) + 3 + 3 (*) Xét hàm số ( ) = + với > 0. Khi đó ( ) =
+ 1 > 0, ∀ > 0, suy ra hàm số ( ) liên tục và đồng biến trên (0; +∞). Do đó (∗) ⇔ 2 + + 1 = 3 + 3 ⇔ + 2 = 1 ⇔ = 1 − 2 . Vì , > 0 ⇒ 0 < < . Xét = + = + = + + √ √ √ √
Áp dụng bất đẳng thức Cô si ta có ≥ 3. = 3. ≥ 3. √8 = 6. ( ) ( ) = 1 − 2 =
Dấu " = " xảy ra ⇔ 1 − 2 = ⇔ . 2 = 1 − 2 = ( )
Câu 72: Cho hai số thực dương và thỏa mãn 4 . 2 =
. Giá trị lớn nhất của biểu thức = + 2 bằng √ A. 1. B. 3. C. . D. . Lời giải Chọn A
Từ giả thiết suy ra 1 − > 0. ( ) ( ) 4 . 2 = ⇔ ( + ). 2 = ⇔ ( + ). 2 = (2 − 2 ). 2 (1).
Xét hàm số ( ) = . 2 với ∈ (0; +∞) =
. Dễ thấy hàm số ( )liên tục trên và ( ) = 2 + . 2 .
2 > 0, ∀ ∈ suy ra ( )là hàm số đồng biến trên . (1) ⇔ + = 2 − 2
⇒ (1 + 2 ) = 2 − (2). Từ (2), suy ra 2 − > 0 ⇒ < 2. ( ) Ta được = + 2 = (1 + 2 ) = (2 − ). ( )
Theo bất đẳng thức Cô – si, ta được = (2 − ) ≤ = 1. = Vậy
= 1, đạt được khi và chỉ khi . = 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 73: Cho , là các số thực dương thỏa mãn 5 + + + 1 = + 3 + ( − 2). Tìm
giá trị nhỏ nhất của biểu thức = + . A. √2 . B. √3 . C. √5 . D. √2 . Lời giải Chọn B Theo đề ra ta có 3 5 5 + + + 1 = + 3 + ( − 2) 3 5 1 1 ⇔ 5 − + + 2 = 5 − + − 1 3 3 Xét ( ) = 5 − + .⇒ ( ) = 5 5 + 3 3 + 1 > 0 ⇒ + 2 = − 1 ⇒ = .Do > 0, > 0 ⇒ > 0 ⇒ > 2 Ta có: = + = + = − 4 + 1 = 2 + √3 ∈ (2; +∞) = = 0 ⇔ ( − 2) = 2 − √3 ∉ (2; +∞) Bảng biến thiên
Chỉnh lại bbt cho em,chỉ xét với > 2nhé,kết quả không thay đổi.
Từ bảng biến thiên ta thấy √3 tại = 2 + √3.
Câu 74: Cho hai số thực , dương thỏa mãn hệ thức 3 log + log + 1 − = 0. Khi biểu thức = − − +
+ 1 đạt giá trị nhỏ nhất thì biểu thức = ( − 1) + 2 bằng A. 9. B. 1. C. 5. D. 4. Lời giải Chọn D Từ giả thiết: 3 log + log + 1 − = 0 ⇔ log + log + 1 − = 0 ⇔ 2. 3 log + 3 log = 0 ⇔ 3 log = 3 log + + 1 . ⇔ ( ) = +
+ 1 . Với hàm số: ( ) = 3 log ; ′( ) = 3 . log . ln3 + 3 . > 0 . Suy ra ( ) = + + 1 ⇔ = +
+ 1. Thế vào biểu thức ta được: = − − + + 1 = − + + 1 − + + 1 =
− 2 = ( − 1) − 1 ≥ −1.
Dấu ′′ = ′′ xảy ra khi = 1 ⇒ = + + 1 = 1 + √2 ⇒ = 1 + √2 Suy ra: = ( − 1) + 2 = 4.
Câu 75: Xét các số thực dương , thoả mãn 2018 = . Giá trị nhỏ nhất của biểu ( ) thức = 2 − 3 bằng A. . B. . C. . D. .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Lời giải Chọn C Ta có: 2 + 2018 = ( + 1) ⇒ 2( − + 1) = (2 + ) − ( + 2 + 1) ⇔ ( + 2 + 1) + 2( + 2 + 1) = (2 + ) + 2(2 + )(∗). Xét hàm: ( ) = + 2 , > 0. Suy ra: ( ) = + 2 > 0, ∀ > 0.
Do đó hàm ( ) đồng biến trên khoảng (0; +∞). Mà (∗) ⇔ ( + 2 + 1) = (2 + ) ⇔ + 2 + 1 = 2 + ⇔ = + 1. Khi đó: = 2 − 3 = 2 − 3 + 2 = 2 − + ≥ . Kết luận: khi = .
Câu 76: Cho hai số thực dương , thỏa mãn + ( + ) ≥
(6 − ) + 6 . Giá trị nhỏ nhất của biểu thức = 3 + 2 + + bằng A. . B. 19. C. . D. 8 + 6√2. Lời giải Chọn B > 0 Điều kiện: 0 < < 6. Từ giả thiết ta có: + ( + ) ≥ (6 − ) + 6 ⇔ + ≥ [ (6 − )] + (6 − ) (*) Xét hàm số ( ) =
+ với > 0, Ta có ′( ) =
+ 1 > 0, ∀ > 0 nên hàm số ( ) = +
đồng biến trên khoảng (0; +∞). Do đó (∗) ⇔ ( ) ≥ [ (6 − )] ⇔ ≥ (6 − ) ⇔ ≥ 6 − ⇔ + ≥ 6(∗∗) (do > 0)
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức (∗∗), ta có: = 3 + 2 + + = ( + ) + + + + ≥ . 6 + 2 . + 2 . = 19. + = 6 ⎧ = = 2
Đẳng thức xảy ra khi và chỉ khi ⇔ ⎨
= 4. Vậy giá trị nhỏ nhất của bằng 19. ⎩ =
Câu 77: Xét các số thực , y ( ≥ 0)thỏa mãn 2018 + 2018 + + 1 = 2018 + − ( + 3).
Gọi là giá trị nhỏ nhất của biểu thức =
+ 2 . Mệnh đề nào sau đây đúng ? A. ∈ (0; 1). B. ∈ (1; 2). C. ∈ (2; 3). D. ∈ (−1; 0). Lời giải Chọn D Ta có 2018 + 2018 + + 1 = 2018 + − ( + 3) ⇔ 2018 − 2018 + + 3 = 2018 − 2018 − − 1
f x 3y f xy 1 (1)
Xét hàm số ( ) = 2018 − 2018 + , với ∈ ℝta có
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 ( ) = 2018 2 018 + 2018
2 018 + 1 > 0, ∀ ∈ ℝ.
Do đó ( )đồng biến trên ℝnên (1) ⇔ + 3 = − − 1 ( ) ⇔ ( + 3) = − − 1 ⇒ = − ⇒ = − . ( ) Xét hàm số ( ) = − , với ∈ 0; +∞)có ( ) = 1 − = > 0, ∀ ∈ (0; +∞). ( ) ( )
Do đó ( )đồng biến trên 0; +∞) ⇒ ( ) ≥ (0) = − . Dấu “=” xảy ra ⇔ = 0 ⇒ = − . Câu 78: Cho 0 ≤ ; ≤ 1 thỏa mãn 2017 = . Gọi
, lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của biểu thức = (4 + 3 )(4 + 3 ) + 25 . Khi đó + bằng bao nhiêu? A. . B. . C. . D. . Lời giải Chọn B Ta có 2017 = ⇔ = ( ) ⇔ 2017 [(1 − ) + 2018] = 2017 ( + 2018) Xét hàm số ( ) = 2017 ( + 2018), với 0 ≤ ≤ 1. ⇒ ( ) = ( + 2018). 2017 . 2 017 + 2 . 2017 = 2017 [( + 2018). 2 017 + 2 ] > 0
⇒ Hàm số ( ) đồng biến trên 0 ≤ ≤ 1 ⇒ 1 − = ⇔ = 1 − Cách 1: Theo giả thiết = (4 + 3 )(4 + 3 ) + 25 = [4
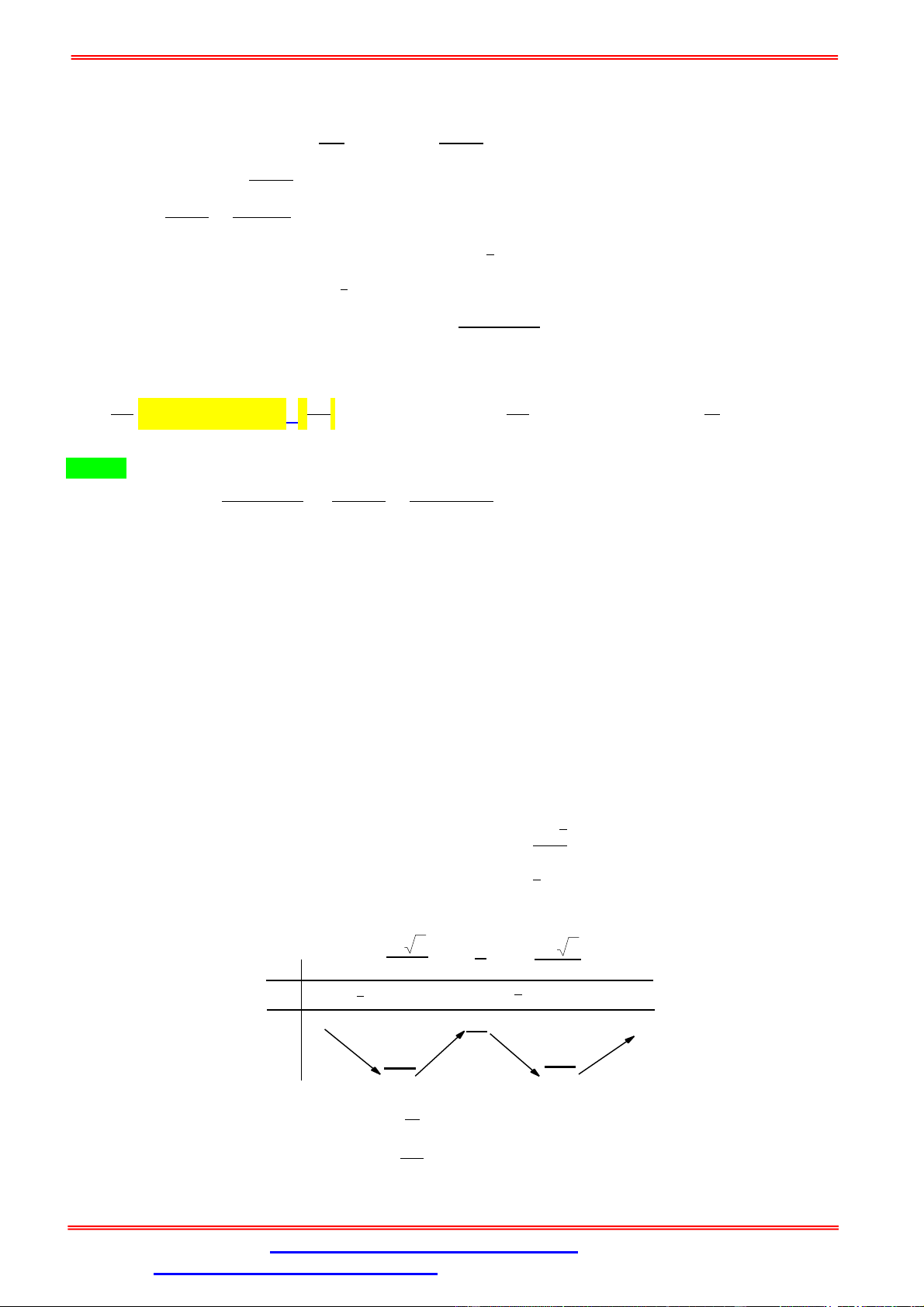
+ 3(1 − )]. [4(1 − ) + 3 ] + 25 (1 − ) = (4 − 3 + 3)(4 − 5 + 4) + 25 (1 − ) = 16 − 20 + 16 − 12 + 15 − 12 + 12 − 15 + 12 + 25 − 25 = 16 − 32 + 18 − 2 + 12 Xét hàm số ( ) = 16 − 32 + 18 − 2 + 12, với 0 ≤ ≤ 1. = ±√ ⇒ ( ) = 64 − 96 + 36 − 2. Cho ( ) = 0 ⇔ = Bảng biến thiên 2- 3 1 2+ 3 x 0 4 2 4 1 y' 0 + 0 0 + 12 25 12 y 2 191 191 16 16 = ( ) = [ ; ]
Từ bảng biến thiên, ta có . = ( ) = [ ; ]
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Vậy + = + = . Cách 2: Từ 0 ≤ ; ≤ 1và + = 1 suy ra 0 ≤ ≤ = . Viết lại = 16 + 12( + ) + 34 = 16 + 12[( + ) − 3 ( + )] + 34 = 16 − 2 + 12 Đặt = , ∈ 0; thì = ( ) = 16 − 2 + 12.
Khảo sát hàm ( ) ta được ( ) = = , max ( ) = = . ∈ ; ∈ ; Vậy + = + =
Cho các số thực , thỏa mãn log
= ( − 2) + ( − 2) + ( − 2). Câu 79:
Giá trị lớn nhất của biểu thức = bằng √ √ √ √ A. . B. . C. . D. . Lời giải Chọn D Điều kiện: > 0 ⇔ + + > 0 (∗).
Ta biến đổi hệ thức ban đầu ⇔ log
= ( − 2) + ( − 2) + ( − 2) + + ⇔ 1 + log = + + + 1 − 2 − 2 − 2 + + + 1 2 + 2 + 2 ⇔ log = + + + 1 − (2 + 2 + 2 ) + + + 1 ⇔ log (2 + 2 + 2 ) − log ( + + + 1) = + + + 1 − (2 + 2 + 2 )
⇔ log (2 + 2 + 2 ) + (2 + 2 + 2 ) = log ( + + + 1) + ( + + + 1) (1) Xét hàm số ( ) = log + , > 0 ⇒ ′( ) =
+ 1 > 0, ∀ > 0 ⇒ ( ) tăng trên (0 ; +∞). Từ (1) ⇔ (2 + 2 + 2 ) = ( + + + 1) ⇔ 2 + 2 + 2 = + + + 1
Suy ra: ( − 1) + ( − 1) + ( − 1) = 2 (∗∗)
Dễ thấy điều kiện (∗) được thỏa mãn ở hệ thức: 2 + 2 + 2 = + + + 1 > 0 Ta có: =
⇔ ( − 1) + ( − 2) + ( − 1) = −
⇔ ( − 1)( − 1) + ( − 2)( − 1) + ( − 1)( − 1) = 4 − 4
⇒ (4 − 4 ) = [( − 1)( − 1) + ( − 2)( − 1) + ( − 1)( − 1)] Áp dụng BĐT Bunhiacopxki:
⇒ (4 − 4 ) ≤ [( − 1) + ( − 2) + ( − 1) ][( − 1) + ( − 1) + ( − 1) ] 4 − √6 4 + √6
⇒ (4 − 4 ) ≤ 2[( − 1) + ( − 2) + ( − 1) ] ⇔ 5 − 8 + 2 ≤ 0 ⇔ ≤ ≤ 5 5
Suy ra giá trị lớn nhất của là = √ .
Câu 80: Cho hai số thực , thỏa mãn hệ thức log = 5 + 2 − 5
+ 1. Giá trị nhỏ nhất của biểu thức = − 10
+ 4 + 2019 tương ứng bằng A. 2019. B. 2010. C. 2011. D. 1990. Lời giải Chọn D
Điều kiện xác định: > 0.(*) Ta có log = 5 + 2 − 5 + 1 ⇔ log = (5 + 7 + 1) − (5 + 5 )
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 ⇔ 1 + log = (5 + 7 + 12) − 5( + + 2). ⇔ log = (5 + 7 + 12) − (5 + 5 + 10). ⇔ log (5
+ 5 + 10) − log (5 + 7 + 12) = (5 + 7 + 12) − (5 + 5 + 10). ⇔ log (5
+ 5 + 10) + (5 + 7 + 12) = log (5 + 7 + 12) + (5 + 5 + 10). ⇔ (5 + 5 + 10) = (5 + 7 + 12) ⇔ 5 + 5 + 10 = 5 + 7 + 12. Suy ra 5 − 2 = 5 + 2 ⇒ = − 2(5 − 2 ) + 2019 = − 2(5 + 2) + 2019 = ( − 5) + 1990 Khi = 5 ⇒ =
⇒ thỏa mãn điều kiện (*).
Suy ra giá trị nhỏ nhất của là: = 1990. Câu 81: Cho , > 0 thỏa 2019 −
= 0. Tìm giá trị nhỏ nhất P của = 2 − 4 . ( ) min A. 2018. B. 2019. C. . D. 2. Lời giải Chọn D Ta có: 2019 − = 0 ⇔ 2019 ( ) = ( ) ( ) ⇔ 2019 ( ) . ( + 2) = 2019 ( ). (4 + + 2)(∗). = ( + 2) Đặt ( , > 0) = 4 + + 2 Khi đó: (∗) ⇔ 2019 . = 2019 . ⇔ ( ) = ( )
với ( ) = 2019 . , ( > 0) ⇒ ′( ) = 2019 . 2 2 019. + 2019 > 0, ∀ > 0 Do đó: ( ) = ( ) ⇔ = ⇔ ( + 2) = 4 + + 2 ⇔ = + 2. ⇒ = 2 − 4 = 2
− 4 + 4 = 2( − 1) + 2 ≥ 2. Vậy . ( )
Câu 82: Cho , là các số dương thỏa mãn
≤ 4 − 1. Giá trị nhỏ nhất của: = + là + . Giá trị của tích là A. = 18. B. = 81. C. = 28. D. = 82. Lời giải Chọn B Với > 0, > 0 ta có ≤ 4 − 1 ⇔ < − + ⇔ < − − 2.2. + 4 + 4 ⇔ < 4 − − 2 ⇒ ≤ 4. Vậy 0 < ≤ 4. ( ) = + = 12 + 6. + + 2 . Đặt = ⇒ 0 < ≤ 4. ( ) = 12 + 6 + ( + 2) ⇒ ( ) = − + = . ( ) = 3 − √21( ) ( ) = 0 ⇔ − 6 − 12 = 0 ⇔ = 3 + √21( ) Lập bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Vậy . = 81.
Câu 83: Cho hai số thực dương , thỏa mãn 2 log + 2 log + 1 − = 0. Giá trị lớn nhất của = 3 − − 3 tương ứng bằng A. . B. 3. C. . D. . Lời giải Chọn D
Ta đổi biến giả thiết như sau: 2. 2 log 2 log + 2 log + 1 − = 0 ⇔ 2 + 1 − + 1 + = −2 log + 1 + 1 ⇔ 2. 2 log = −2 . 2 log ⇔ 2. 2 log = 2 . 2 log + 1 + + 1 + ⇔ 2 log = 2 log + + 1 ⇔ ( ) = + + 1 ⇔ = + + 1 (Với hàm ( ) = 2 log ⇒ ′( ) = 2 log . ln2 + 2 .
> 0 với ∀ > 0. Suy ra hàm đặc trưng đang
xét là đơn điệu tăng). Thay = + + 1 vào biểu thức: = 3 + + 1 − − 3 = − + 3 + 1 = − + 1 − ≤ .
Dấu ′′ = ′′ xảy ra khi + 1 − = 0 ⇔ = ± √ ⇒ = √ ; = √
Suy ra giá trị lớn nhất của biểu thức là: = .
Câu 84: Xét các số thực , thỏa mãn > 0 và + − 3 = . (1 − 2 .
). Giá trị lớn nhất của biểu thức
= ln + thuộc tập hợp nào dưới đây? A. (1; 2). B. [2; 4). C. [−3; 0). D. [0; 3). Lời giải Chọn D Xét phương trình + − 3 = . (1 − 2 . ) Đặt = ( > 0) ta có: + − 3 = (1 − 2 ) ⇔ 3 + = ( + ) ≥ 4( ) ⇔ − ≤ ≤ 1. Lại do , > 0 ⇒ 0 < ≤ 1 ⇒ 0 < . ≤ 1 ⇔ ln + ≤ 0 nên ≤ 0. = = 1
Dấu bằng xảy ra khi và chỉ khi = 1 ⇔ = = 1 hay = 0 , > 0 Vậy = 0 ∈ [0; 3).
Câu 85: Cho hai số thực , lớn hơn 1 và thỏa mãn . ( ) ≥ . (
) . Tìm giá trị nhỏ nhất của biểu thức = + .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 √ √ √ A. . B. 2√2. C. . D. . Lời giải Chọn C Với , > 1, ta có . ( ) ≥ . ( ) ⇔ . ( ) ≥ . ( ) ⇔ + ≥ + ⇔ + ≥ + (1). Xét hàm số ( ) = − + 1 − trên 1; +∞), có ′( ) = − > 0, ∀ ≥ 1.
Hàm số ( ) đồng biến trên 1; +∞) nên ( ) > (1) = 1 > 0, ∀ > 1. Xét hàm số ( ) =
+ trên (1; +∞), có ′( ) = ( ) > 0, ∀ > 1, nên ( ) đồng biến trên (1; +∞). Với ,
> 1 thì (1) ⇔ ( ) ≥ ( ) ⇔ ≥ . Đặt = . Do ≥ > 1 nên ≥ 1. Ta có = ℎ( ) = + . Nhận thấy ℎ′( ) = , nên
ℎ′( ) = 0 khi = √2, ℎ′( ) < 0 khi 1 ≤
< √2, ℎ′( ) > 0 khi > √2. Dẫn tới = ℎ( ) ≥ ℎ √2 =
√ , ∀ ≥ 1, đẳng thức xảy ra khi = √2. Vậy =
√ , đạt được khi = √ và > 1.
Câu 86: Cho hai số thực dương , thỏa mãn hệ thức: 2 − ≤ ( + 6 ). Tìm giá trị 2 ab b lớn nhất
của biểu thức P . 2 2
a 2ab 2b 1 A. = . B. = 0. C. P . D. = . Max 2 Lời giải Chọn C Ta có: 2 − ≤ ( + 6 ) ⇔ ≤ ( + 6 ) ⇔ ≤ + 6 ⇔ − − 6 ≤ 0 ⇔ −3 ≤ ≤ 2. Do , dương nên 0 < ≤ 2. Đặt = , 0 < ≤ 2. 2 ab b t 1 Khi đó: P 2 2 2
a 2ab 2b t 2t 2 Xét hàm số ( ) = với 0 < ≤ 2. Ta có: ( ) = ≥ 0, ∀ ∈ 0; 2. ( ) Suy ra ( ) ≤ (2) = . Vậy ( ) = khi = 2. ; 1 Do đó P . Max 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
DẠNG 3: ÁP DỤNG HÌNH HỌC GIẢI TÍCH.
Câu 87: Cho hai số thực , thỏa mãn đồng thời các điều kiện + ≤ 4 và log (2 + 2 + 3
− 4) ≥ 1. Gọi là tập chứa tất cả các giá trị nguyên của tham số để tồn tại một cặp số
thực ( ; ) thỏa mãn bài toán. Số phần tử của tập là: A. 2. B. 1. C. 3. D. 0. Lời giải Chọn B Miền điều kiện +
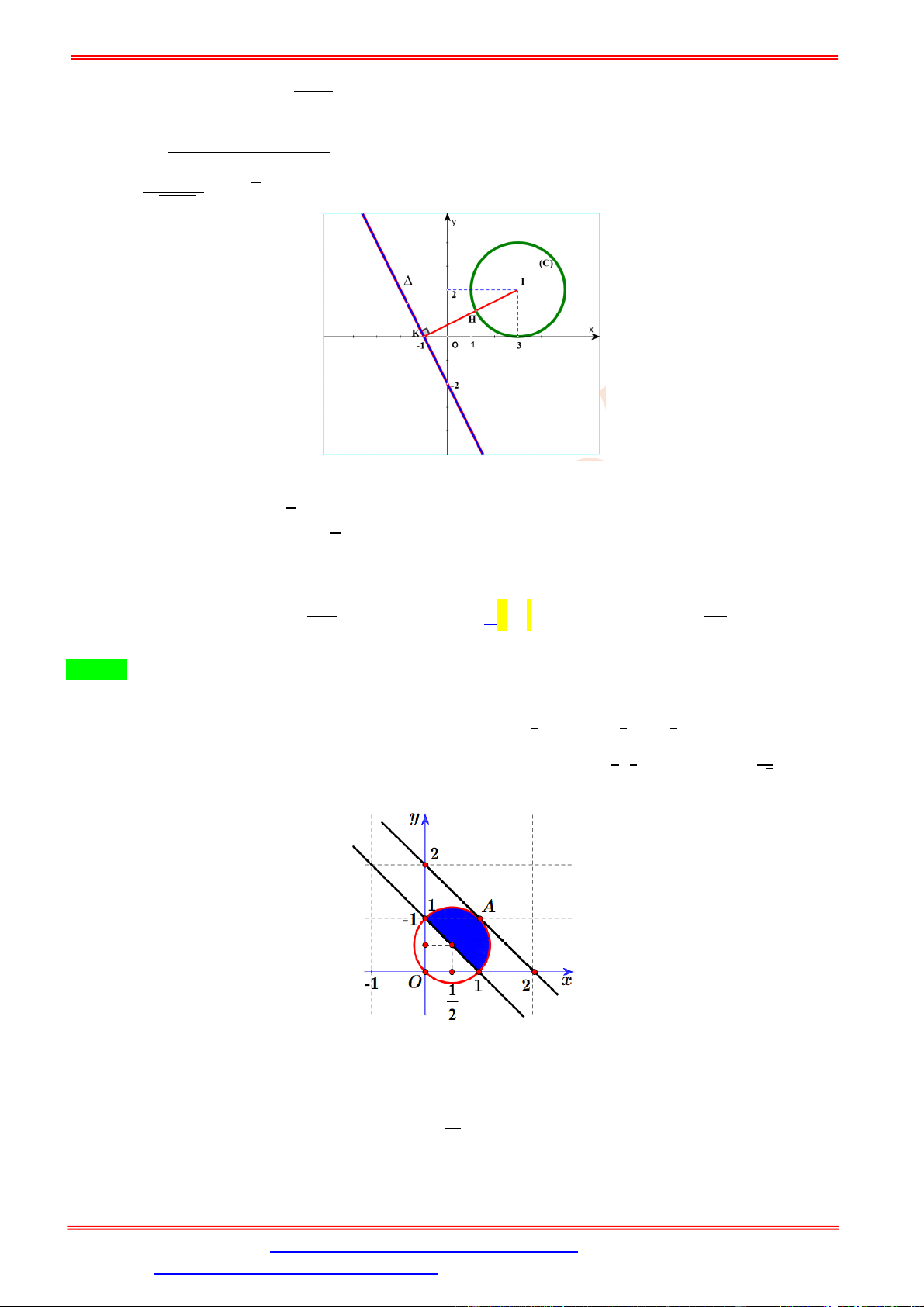
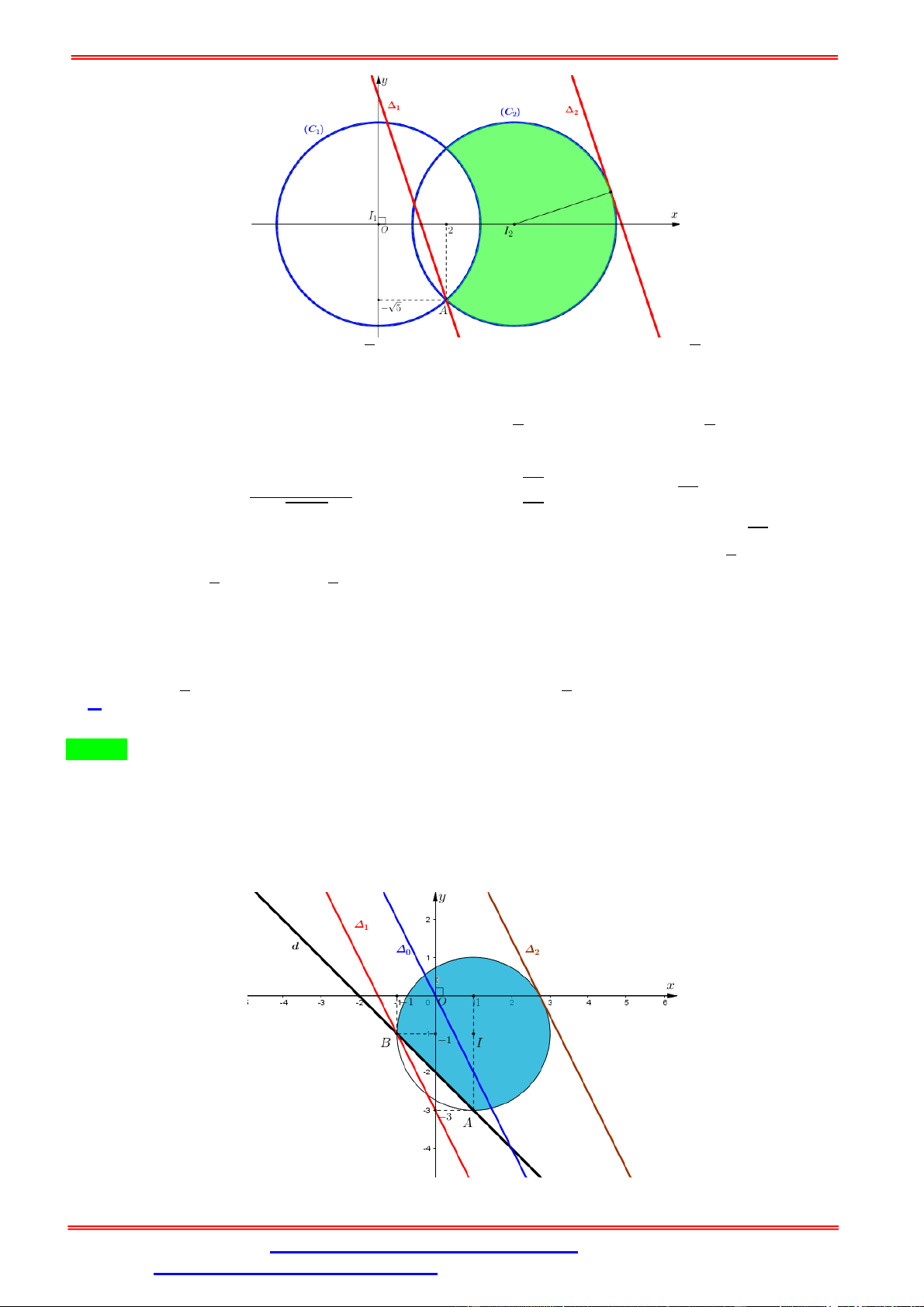
≤ 4 là miền nằm trong hình tròn ( ) tâm là gốc toạn độ (0; 0) bán kính =
2 kể cả đường tròn ( ) như hình vẽ. Từ giả thiết: log (2 + 2 + 3 − 4) ≥ 1 ⇔ 2 + 2 + 3 − 4 ≥ + + 1 ⇔ ( − 1) + ( − ) ≤ + 3 − 4 Nằm trong hình tròn ( ) tâm (1; ) bán kính = √ + 3 − 4 ( ≤ −`4 ; ≥ 1) kể cả đường tròn ( ) như hình vẽ.
Để tồn tại một cặp số thực ( ; ) thỏa mãn đềtoán thì xảy ra hai trường hợp sau: (C1) (C1) I O O I (C2) (C2)
Trường hợp 1: Đường tròn ( ) có
= 0 coi như chỉ là một điểm và điểm này sẽ nằm trong hoặc trên ( )
Ta có điều kiện tương ứng: = 0 = √ + 3 − 4 = 0 = 1; = −4 ⇔ ⇔ ⇔ = 1 ≤ = 2 (thỏa mãn) (1) = √1 + ≤ = 2 | | ≤ √3
Trường hợp 2: Đường tròn (
) tiếp xúc ngoài với đường tròn ( ).
Ta có điều kiện tương ứng: = + ⇔ 1 + = 2 + + 3 − 4 ⇔ + 1 = 4 + + 3 − 4 + 4 + 3 − 4 ⇔ 1 − 3 = 4 + 3 − 4 1 1 ≤ ⇔ 3 ⇔ < 3 (1 − 3 ) = 16 + 48 − 64 7 + 54 − 65 = 0 ⎧ ≤ ⎪ ⇔ = √ ⇔ = √ , ( ∈ ℤ) (loại) ⎨ ⎪ ⎩ = √
Câu 88: Cho hai số thực , thỏa mãn = ( − 3) + ( − 3) + . Tìm giá trị lớn √ nhất của biểu thức = . √ √ √ √ A. . B. . C. . D. . Lời giải Chọn D • Ta có: = ( − 3) + ( − 3) + √
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 ⇔ ( + ) − ( + + + 2) + 3 = + + + 2 − 3( + ) √ √ √ ⇔ + + + 2 + ( + + + 2) = 3( + ) + 3 ( + ). √ √ ⇔ + + + 2 = 3( + ). ⇔ + + + − + − 3 + + = 1. ⇔ + − 3 + + + √ − √ = 1. ⇔ + − + √ − √ = 1 (*) = + − = − + 1 Đặt: ⇒ √ = √ − √ = + 1 √ ⇒ (*) trở thành: 2 2
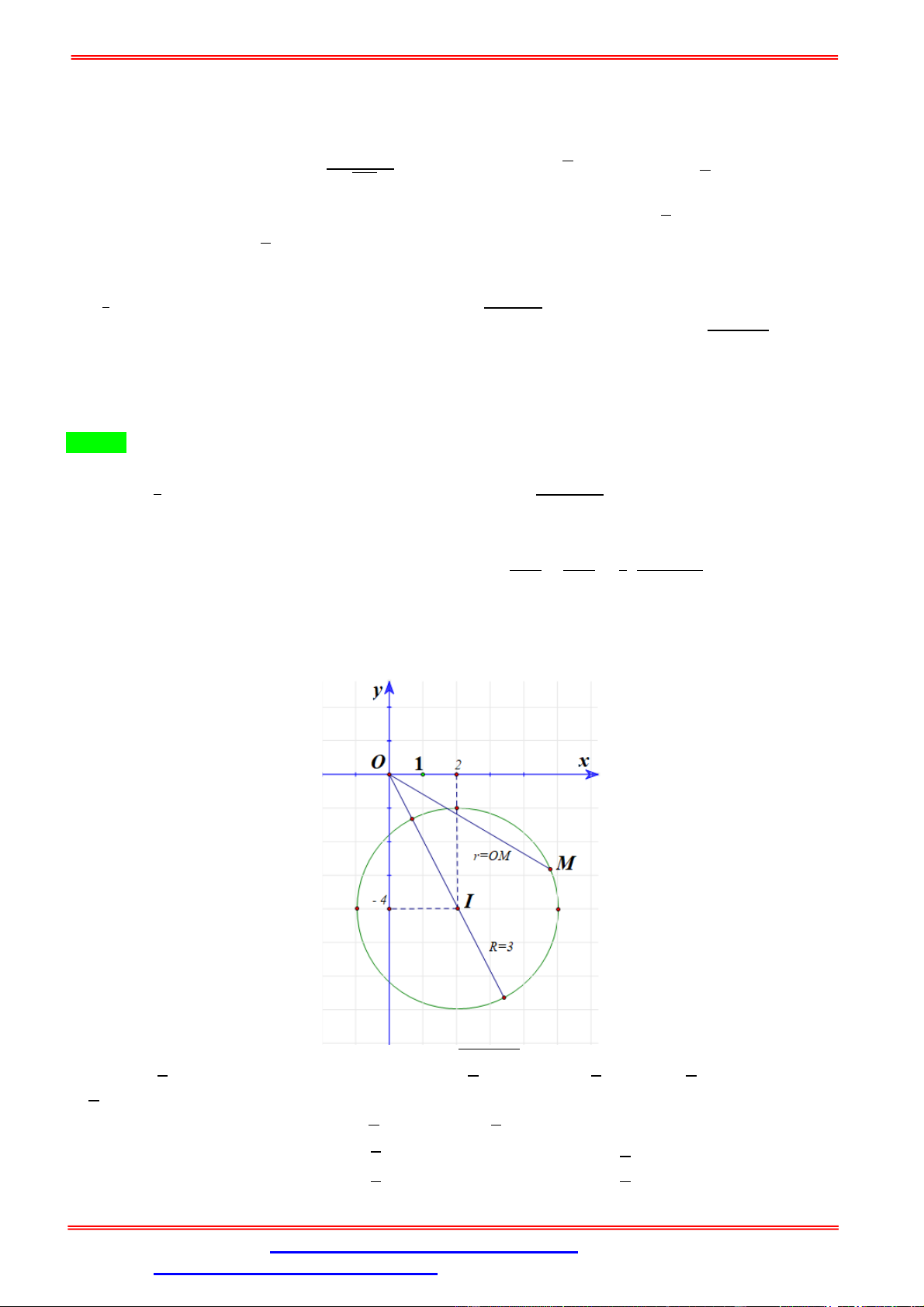
a b 1 ( ) là đường tròn tâm (0; 0), bán kính = 1. • = ⇒ ( + + 6) = + 2 + 3. ⇒ + + 8 = + √3 + 6. √ ⇒ ( − 1) + + 8 − 6 = 0 ( ). √
• Điều kiện để đường tròn ( ) và đường thẳng có giao điểm là: ( | | ; ) ≤ 1 ⇔ ≤ 1. ( ) ( ) ( ) ⇔ |8 − 6| ≤ ( − 1) + . ⇔ − 92 + 32 ≤ 0. ⇔ √ ≤ ≤ √ . ⇒ √ .
Câu 89: Cho hai số thực , thỏa điều kiện log (2 + + 1) ≥ 1, +
≤ 6. Gọi giá trị lớn nhất
và giá trị nhỏ nhất của biểu thức
= 2 + lần lượt là và . Giá trị của biểu thức = + bằng: A. 7. B. 5. C. 8. D. 11. Lời giải Chọn D
Đây là dạng toán max-min trên miền điển hình. log (2 + + 1) ≥ 1 2 + + 1 ≥ − 2 + 3 ≥ − 4 + 2 Từ giả thiết suy ra: ⇔ ⇔ + ≤ 6 ≤ 6 − ≤ 6 −
Chúng ta dể dàng phác họa nhanh được miền như trên hình vẽ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
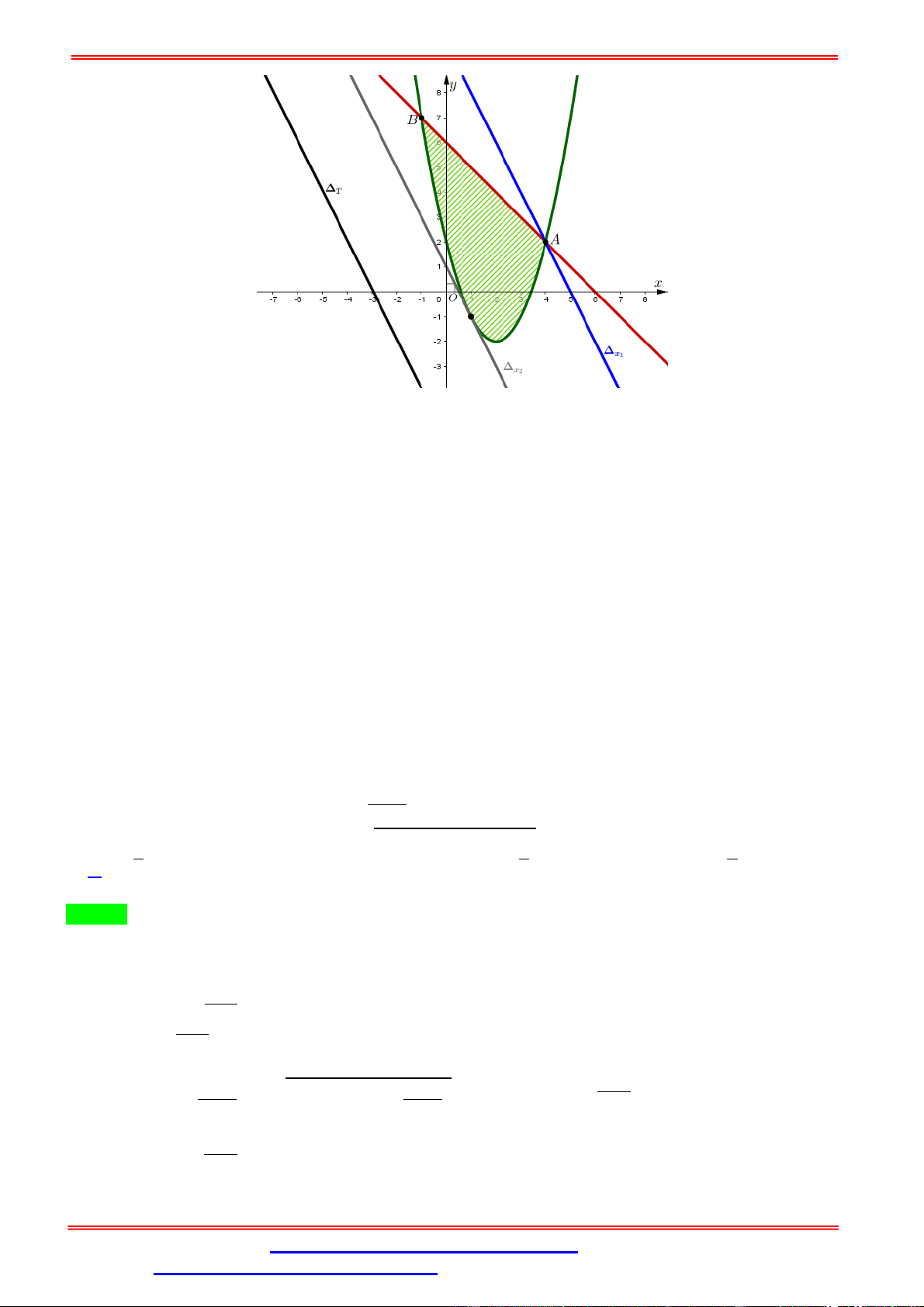
Ta xác định rõ được hai giao điểm của hai đường cong tạo nên miền là: = − 4 + 2 = −1; = 7 ⇒ (−1; 7) ⇔ = 6 − = 4; = 2 ⇒ (4; 2)
Tiếp đó ta xử lý tới biểu thức max-min: = 2 + ⇔
= −2 + ; đây là một họ đường thẳng song
song với nhau ta gọi họ đường thẳng Δ .
Trong đó mỗi cặp ( ; ) thỏa mãn điều kiện bài tọa đã cho sẽ ứng với một điểm ( ; ) ∈
Điều kiện là đường thẳng Δ phải cắt miền (có ít nhất một điểm chung với miền ).
Bằng trực quan trên đồ thị, ta có thể xác định được trường hợp đường thẳng Δ đi qua điểm ứng với giá trị . Thõa mản: = −2 + ⇔ 2 = −2.4 + ⇒ = 10.
Đường thẳng Δ tiếp xúc với đường parabol ( ) tại hoành độ < 2 ứng với giá trị . Thỏa mãn
phương trình có nghiệm kép: = −2 + = − 4 + 2 ⇔ − 2 + 2 − = 0 ⇔ = 1
Các giá trị phải nằm trong đoạn: 1 = ≤ ≤ = 10 = 10 = Suy ra: ⇒ = + = 11. = 1 =
Câu 90: Cho các số thực , , , sao cho 2 +
< 0 và thỏa mãn điều kiện ( + + 9) = 1 + (3 + 2 ) 9 . 3 . 3 + [(2 + + 2) + 1] = 81
Tìm giá trị nhỏ nhất của biểu thức = ( − ) + ( − ) . A. 2√5 − 2. B. 2. C. √5 − 2. D. 2√5. Lời giải Chọn A Ta có: ( + + 9) = 1 + (3 + 2 ) ⇔ ( + + 9) = [2(3 + 2 )] ⇔ +
+ 9 = 6 + 4 ⇔ ( − 3) + ( − 2) = 4.
Gọi ( ; ), suy ra thuộc đường tròn ( ) có tâm (3; 2), bán kính = 2. Lại có 9 . 3 . 3 + [(2 + + 2) + 1] = 81 ⇔ 3 ( ) + [(2 + + 2) + 1] = 81, (1) Với ∀ , thỏa mãn 2 + < 0, ta có: +) −(2 + ) + ≥ 2 [−(2 + )]. = 4 ⇒ 3 ( ) ≥ 81 +) [(2 + + 2) + 1] ≥ 1 = 0. Suy ra 3 ( ) + [(2 + + 2) + 1] ≥ 81
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 −(2 + ) = Do đó (1) ⇔ ⇔ 2 + + 2 = 0. 2 + + 2 = 0
Gọi ( ; ), suy ra thuộc đường thẳng có phương trình 2 + + 2 = 0. Ta có: = ( − ) + ( − ) = . ( | , ) = .
| = 2√5 > 2 ⇒ đường thẳng không cắt đường tròn ( ). √ Do đó
ngắn nhất khi là hình chiếu của điểm trên đường thẳng và điểm là giao điểm của đoạn thẳng với đường tròn ( ). Lúc đó = − = 2√5 − 2.
Vậy giá trị nhỏ nhất của bằng 2√5 − 2.
Câu 91: Cho các số thực dương , thỏa mãn ( )( +
) ≤ 1. Giá trị lớn nhất của biểu thức
= 48( + ) − 156( + ) + 133( + ) + 4 là A. 29. B. . C. 30. D. . Lời giải Chọn C + > 1 + > 1 TH1: ( )( + ) ≤ 1 ⇔ ⇔ (1). + ≤ + − + − ≤ (∗)
Tập nghiệm của BPT (*) là tọa độ tất cả các điểm thuộc hình tròn tâm ; bán kính = . √
Miền nghiệm của hệ (1) là phần tô màu như hình vẽ. Đặt = + ⇒ 1 < ≤ 2 Khi đó ( ) = 48 − 156 + 133 + 4 = ( ) = 144 − 312 + 133; ( ) = 0 ⇔ = Bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 Do đó, ( ) = 30 ⇒ = 2 ⇒ + = 2. 0 < + < 1 0 < + < 1 TH2: ( )( + ) ≤ 1 ⇔ ⇔ (2). + ≥ + − + − ≥
(2) không thỏa điều kiện > 0, > 0.
Câu 92: Cho hai số thực , thỏa mãn điều kiện log ( + − 1) ≤ 1, ≥ 0,
≥ 0. Gọi giá trị lớn nhất
và giá trị nhỏ nhất của biểu thức = +
− 6 − 4 + 1 lần lượt là và . Giá trị của biểu thức = + bằng: A. 12. B. 104. C. 20. D. 48. Lời giải Chọn B
Đây là bài toán max-min trên miền điển hình. + − 1 > 0 > 1 −
Từ giả thiết ta suy ra: log ( + − 1) ≤ 1 ⇔ ⇔ + = 1 ≤ 2 ≤ 3 −
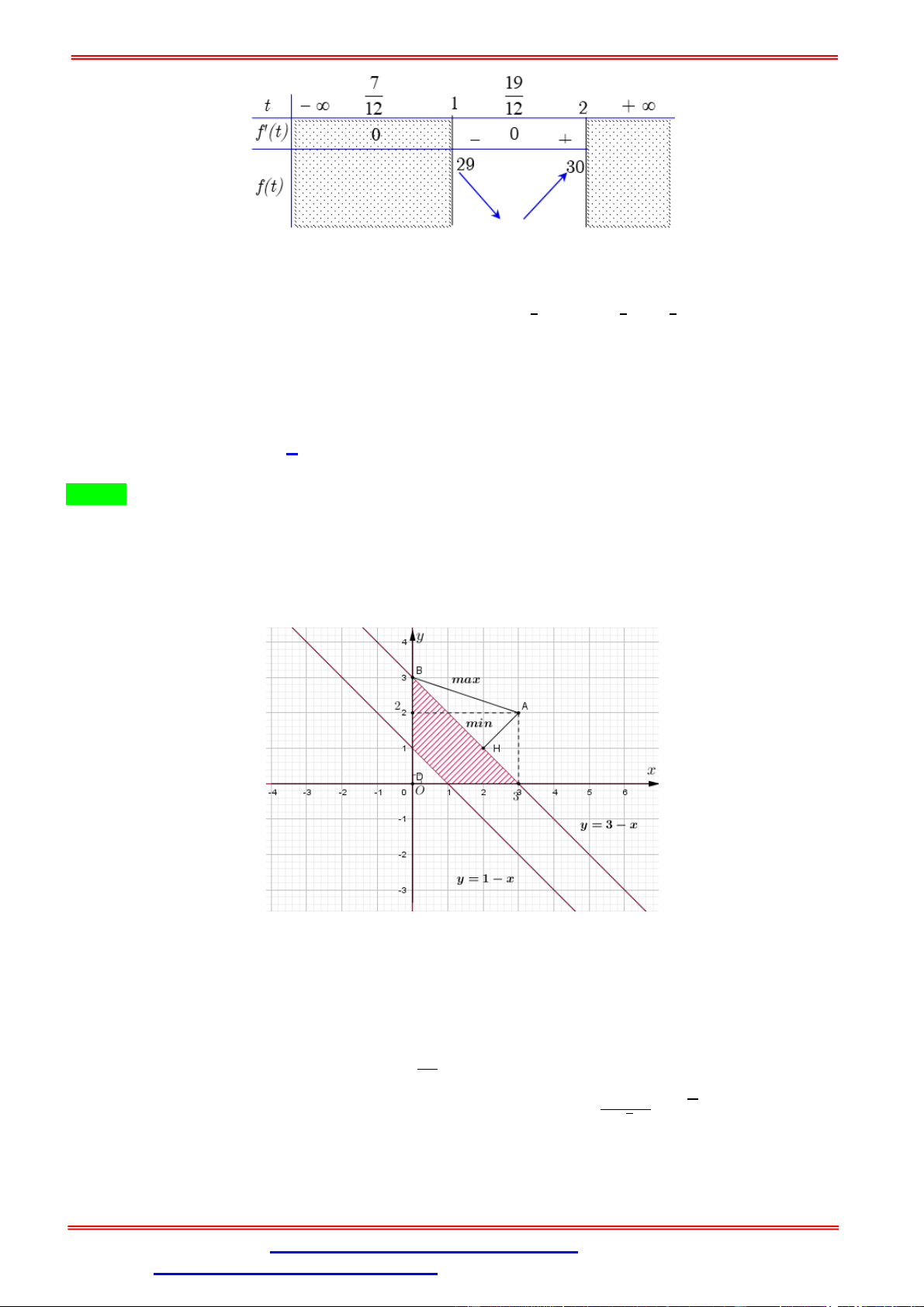
Chúng ta có miền như sau: = { ≥ 0; ≥ 0; > 1 − ; ≤ 3 − }.
Chúng ta dễ dàng phác họa nhanh được miền như trên hình vẽ.
Mô tả qua về miền như sau: là phần gạch chéo bao gồm tất cả các đường biên chỉ bỏ đi phần đường
biên màu đỏ ứng với đường thẳng = 1 −
Tiêp đó ta xử lý tới biểu thức max-min: = +
− 6 − 4 + 1 = ( − 3) + ( − 2) − 12
Trong đó mỗi cặp ( ; ) thỏa mãn điều kiện bài toán đã cho sẽ ứng với một điểm ( ; ) ∈
Nếu ta gọi điểm (3; 2) ⇒ = − 12.
Đến đây ta chỉ việc đi tìm giá trị nhỏ nhất và lớn nhất của khoảng cách . = = √10
Dễ thấy trực quan hình vẽ: = = ( ; ( + − 3 = 0)) = | | = √2 √ = − 12 = −2 = Suy ra: ⇒ = + = 104. = − 12 = −10 =
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Câu 93: Cho hai số thực , thỏa mãn đồng thời các điều kiện + = 9 và log (2 − 2 +
− 1) ≥ 1. Gọi là tập chứa tất cả các giá trị thực của tham số để tồn tại duy nhất một cặp
số thực ( ; ) thỏa mãn bài toán. Tổng giá trị tất cả các phần tử của tập nằm trong khoản nào cho ở dưới đây? A. (4; 5). B. (1; 2). C. (2; 3). D. (3; 4). Lời giải Chọn D + = 9 + = 9 Miền điều kiện ⇔ log (2 − 2 + − 1) ≥ 1 2 − 2 + − 1 ≥ + + 2 + = 9 ( ) ⇔ có duy nhất 1 nghiệm. ( − 1) + ( + 1) ≤ − 1 ( )
( ) là đường tròn có tâm là gốc toạn độ (0; 0) bán kính = 3.
( ) là miền trong đường tròn và đường tròn tâm (1 ; −1), = √ − 1 ( > 1).
Để tồn tại một cặp số thực ( ; ) thỏa mãn đề toán thì xảy ra hai trường hợp sau:
Trường hợp 1: Đường tròn ( ) có
= 0 coi như chỉ là một điểm (1 ; −1) và điểm (1 ; −1) này sẽ nằm trong hoặc trên ( )
Ta có điều kiện tương ứng: = 0 = − 1 = 0 = 1 ⇔ ⇔ ⇔ = 1. ≤ = 3 = 1 + (−1) ≤ = 3 √2 ≤ √3 (C1) (C1) I O O I (C2) (C2)
Trường hợp 2: Đường tròn (
) tiếp xúc ngoài với đường tròn ( ).
Ta có điều kiện tương ứng: = + ⇔ 1 + (−1) = 3 + √ − 1 ⇔ √ − 1 = 3 − √2 ⇔ − 1 = 11 − 6√2 ⇔ = 12 − 6√2 (thỏa mãn > 1) Vậy tìm được: = 12 − 6√2, = 1. Suy ra + = 13 − 6√2 ≈ 4,5.
Câu 94: Cho hai số thực và thõa mãn các điều kiện + ≥ 9 và log ( (8 + 8 − 7 ) − 7
) ≥ 2. Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu thức = 3 + lần lượt là và .
Khi đó giá trị của biểu thức + 3 √2 bằng: A. 12 + 18√2. B. 24. C. 6√10. D. 10 − 2√3 Lời giải Chọn A Từ log ( (8 + 8 − 7 ) − 7 ) ≥ 2 ⇔ ( + )(8 − 7) ≥ ( + ) ⇔ ( − 4) + ≤ 9 + ≥ 9 Như vậy và thỏa mãn:
. Đây là miền giới hạn bởi bên trong đường tròn ( − 4) + ≤ 9 ( ): ( − 4) +
= 9 và bên ngoài đường tròn ( ): + ≥ 9
Hai đường tròn cùng bán kính =
= 3 và tâm (0; 0) và tâm (4; 0) như hình vẽ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Giao điểm của hai đường tròn là 2; ±√5 . Cụ thể điểm như hình vẽ, có 2; −√5
Xét họ đường thẳng Δ song song với nhau: 3 + − = 0
Để thỏa mãn bài toán thì họ đường thẳng này phải cắt miền .
Ứng với vị trí đường thẳng Δ đi qua điểm , ta có: 3.2 − √5 − = 0 → = 6 − √5
Ứng với vị trí đường thẳng Δ tiếp xúc với ( ) ta có: ( ; Δ ) = |3.4 + 0 − | ⇔ = 3 ↔ = 12 − 3√10 ⇒ = 12 + 3√10 √9 + 1 = 12 + 3√10 = = = 12 + 3√10
Suy ra: giá trị lớn nhất và giá trị nhỏ nhất của tương ứng là: = = = 6 − √5 Suy ra: + 3 √2 = 12 + 18√2.
Câu 95: Cho hai số thực và thõa mãn đồng thời các điều kiện: + + 2 ≥ 0 và log (2 −
2 + 3) ≥ 1. Giá trị nhỏ nhất và lớn nhất của biểu thức = 2 + lần lượt là và . Giá trị của biểu thức = + bằng: A. −2 + 2√5. B. 2. C. 4 − 2√3. D. 4 Lời giải Chọn A Từ giả thiết log
(2 − 2 + 3) ≥ 1 ⇔ 2 − 2 + 3 ≥ +
+ 1 ⇔ ( − 1) + ( + 1) ≤ 4
Như vậy, điểm ( ; ) nằm trong miền giới hạn bởi: = {( − 1) + ( + 1) ≤ 4; + + 2 ≥ 0}
Miền được xác định như hình vẽ:
Biểu thức được biến đổi về dạng họ đường thẳng: : 2 + − = 0 Khi
= 0 thì đường thẳng đi qua gốc tọa độ và tương ứng là: Δ : 2 + = 0, như hình vẽ.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020
Ứng với vị trí: Δ : 2 + −
= 0; đi qua điểm (−1; −1); suy ra: 2(−1) + (−1) − = 0 ⇔ = −3 Suy ra: ở vị trí Δ : 2 + − = 0 (thì
> 0). Ở vị trí này đường thẳng Δ tiếp xúc với đường tròn ( | ; Δ ) = . | = 2 ( ), nên ta có: ⇔ √ ⇔ = 1 ± 2√5 ⇔ = 1 + 2√5 > 0 > 0 > 0
Từ đó suy ra giá trị lớn nhất và giá trị nhỏ nhất của biểu thức là: = 1 + 2√5 = ; = −3 = . Suy ra: + = −2 + 2√5.
Câu 96: Cho hai số thực , thỏa mãn: ( + 8 + 16) + (5 − ) (1 + ) = 2 + (2 + 8) . √
Gọi là tập các giá trị nguyên của tham số để giá trị lớn nhất của biểu thức = + −
không vượt quá 10. Hỏi có bao nhiêu tập con không phải là tập rỗng? A. 2047. B. 16383. C. 16384. D. 32. Lời giải Chọn B
Điều kiện: ≠ −4; −1 < < 5. Ta có: ( + 8 + 16) + (5 − ) (1 + ) = 2 + (2 + 8) (1) √ ⇔ 2 ( + 4) + (− + 4 + 5) = 2[ (− + 4 + 5) − 1] + [4( + 4) ] ⇔ 2 ( + 4) − ( + 4) = 2 (− + 4 + 5) − (− + 4 + 5) (2). Xét hàm số ( ) = 2 −
, > 0, ta có: ′( ) = − = . > 0, ∀ > 0 . ⇒ Hàm số ( ) đồng biến với
> 0, suy ra: (2) ⇔ ( + 4) = − + 4 + 5 ⇔ ( − 2) + ( + 4) = 9
⇒ Tập hợp các cặp số ( ; ) thỏa mãn (1) là đường tròn ( )tâm là (2; −4) và bán kính = 3 bỏ bớt 2
điểm (−1; −4), (5; −4).
Gọi ( ; ) là điểm thuộc đường tròn ( ) ⇒ = +
là khoảng cách từ đến gốc . Vì
= 2√5 > 3 nên nằm ngoài ( ) và ta có: 2√5 − 3 ≤
≤ 2√5 + 3 ⇔ 2√5 − 3 − ≤ − ≤ 2√5 + 3 − ⇒ Với = | − |, = 2√5 − 3 − , 2√5 + 3 − 2√5 − 3 − ≤ 10 −10 ≤ 2 ⇒ √5 − 3 − ≤ 10
Để thỏa mãn bài toán ta phải có: ⇔ 2√5 + 3 − ≤ 10 −10 ≤ 2√5 + 3 − ≤ 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn thi TN THPT 2020 2 ⇔ √5 − 13 ≤
≤ 2√5 + 7 ⇔ 2√5 − 7 ≤ ≤ 2√5 + 7. 2√5 − 7 ≤ ≤ 13 + 2√5
Ta có: 2√5 − 7 ≈ −2,5; 2√5 + 7 ≈ 11,5 ⇒
∈ {−2; −1; 0; . ; 11} ⇒ Tập có 14 phần tử ⇒ Số tập con
khác rỗng của tập là: 2 − 1 = 16383.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông




