Bài toán tối đa hóa lợi nhuận
 Ta có, doanh thu bằng giá bán sản phẩm nhân với sản lượng.
 Lại có, chi phí sản xuất bao gồm chi phí thuê mướn nhân công và chi phí thuê vốn (giả định là hãng
đi vay để đầu tư mua máy móc và nguyên vật liệu). Chi phí thuê mướn nhân công lại bằng tiền công
nhân với số lượng lao động. Còn chi phí thuê vốn bằng lãi suất nhân với số tiền đi vay.
Từ đó, công thức tính lợi nhuận là: Π=p×F(L,K)-(wL+rK)
Trong vế phải của công thức trên, nhóm số bị trừ chính là doanh thu, còn nhóm số trừ chính là tổng chi phí.
Tối đa hóa lợi nhuận chính là giải bài toán tính vi phân cả hai vế của công thức nói trên lần lượn theo L
và K, đồng thời cho đạo hàm của Π theo L và K bằng 0. Kết quả
Kết quả giải bài toán nói trên là MR=MC=P* Tối thiểu hóa chi phí
Tối thiểu hóa chi phí là hành vi của người sản xuất tìm một kết hợp tối ưu lượng của các yếu tố sản
xuất sao cho với mức chi phí thấp nhất để đạt được một mức sản lượng mục tiêu đã xác định sẵn. Kinh
tế học vi mô phân tích hành vi tối thiểu hóa chi phí của người sản xuất bằng mô hình dưới đây. Giả thiết
 Để cho đơn giản, giả định nhà sản xuất chỉ sử dụng hai yếu tố sản xuất là lao động và vốn.
 Giá của lao động là w, còn giá của vốn là r. Hai mức giá w và r là cố định.
 Lượng lao động được sử dụng là L, và lượng vốn được sử dụng là K.
 Chi phí để sản xuất là C và chỉ bao gồm chi phí cho hai loại yếu tố sản xuất nói trên. C = wL + rK =
f(w, L, r, K). Hàm số này được gọi là hàm chi phí.
 Sản lượng mục tiêu là Y cố định. Y = f(L,K) Mô hình C = minK,L wL + rK với Y = f(L,K)
Tổ hợp L* và K* cho phép tối thiểu hóa chi phí để đạt được một sản lượng xác định trước.
Giải bài toán tối ưu hóa có ràng buộc trên cho ra kết quả là tỷ lệ biên thay thế kỹ thuật giữa hai yếu
tố sản xuất đúng bằng tỷ lệ giữa mức giá của hai yếu tố đó. Trên cơ sở đó, tính ra L* và K* là các mức đầu vào tối ưu. Minh họa bằng hình
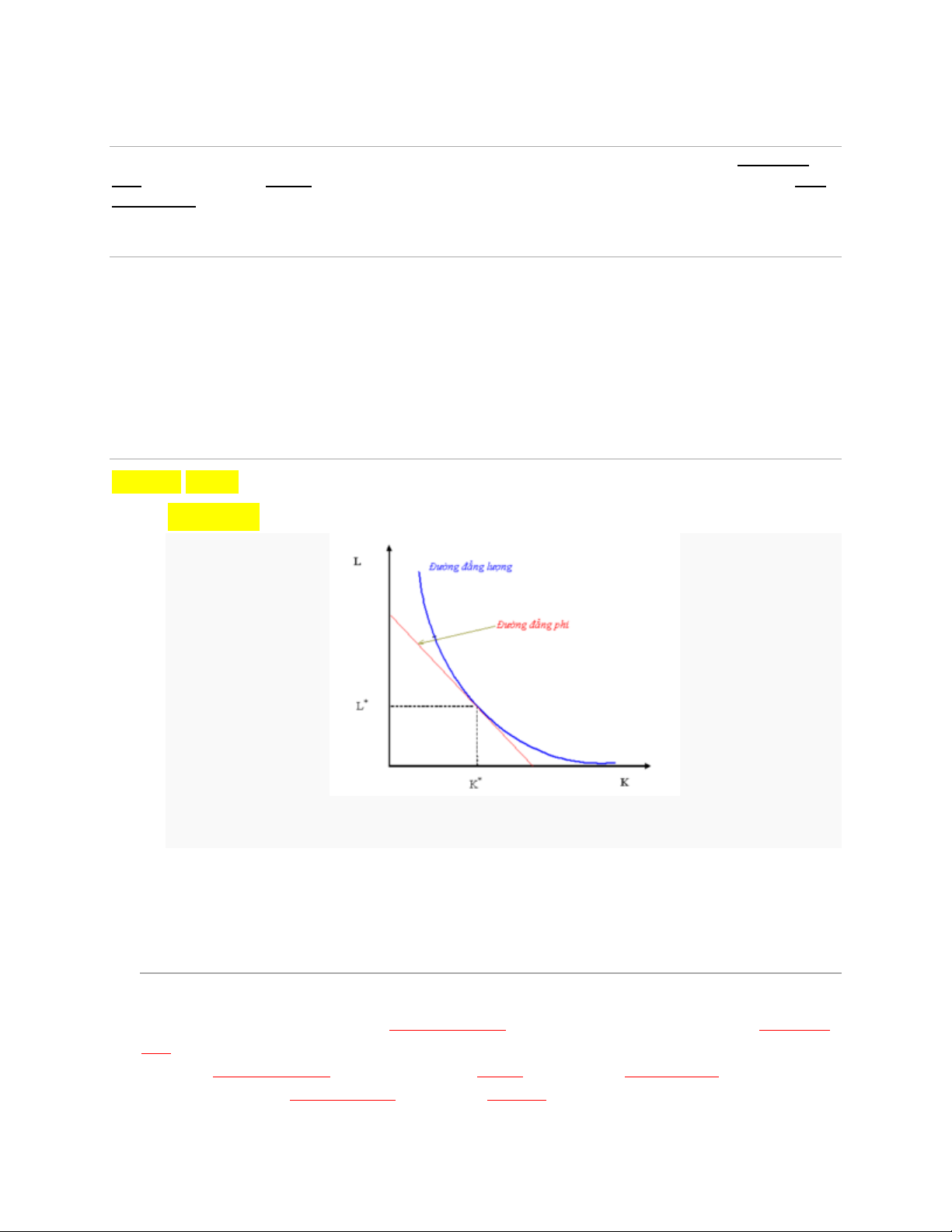
Khi minh họa bằng hình vẽ, lời giải tối ưu của bài toán trên chính là tiếp điểm của đường đẳng
lượng (Đường đẳng lượng, trong kinh tế học vi mô, là tập hợp các kết hợp giữa những yếu tố sản
xuất (đầu vào) để đạt được cùng một mức sản lượng (đầu ra)) và đường đẳng phí (Đường đẳng
phí, trong kinh tế học vi mô, là tập hợp các mức chi phí không đổi mà doanh nghiệp bị ràng buộc khi
tìm cách kết hợp các yếu tố sản xuất(đầu vào) để sản xuất ra mức sản lượng lớn nhất.) Độ dốc của
đường đẳng lượng bằng tỷ lệ biên thay thế kỹ thuật, còn độ dốc của đường đẳng phí bằng tỷ lệ giữa
mức giá của hai yếu tố sản xuất. Tối thiểu hóa chi tiêu
Bách khoa toàn thư mở Wikipedia
Tối thiểu hóa chi tiêu là hành vi của người tiêu dùng lựa chọn một tổ hợp hàng hóa để có thể đạt được một
mức thỏa dụng xác định trước với mức chi thấp nhất. Đây là bài toán ngược lại với bài toán tối đa hóa thỏa dụng. Giả thiết
Giả định một chủ thể kinh tế muốn tiêu dùng 2 mặt hàng và mức thỏa dụng mà 2 mặt hàng đó đem lại
được ký hiệu bằng U(X,Y). Người tiêu dùng đã xác định sẵn một mức thỏa dụng mà mình muốn có, ký hiệu là Ū.
Lượng của mỗi mặt hàng mà người tiêu dùng này có nhu cầu được ký hiệu bằng X và Y.
Mức giá của mỗi mặt hàng này được ký hiệu là PX và PY.
Chi phí E cho tiêu dùng, vì thế là: E = PX.X + PY.Y
Kinh tế học gọi quan hệ trên là hàm chi tiêu. Thành lập mô hình
Mô hình này được biểu diễn bằng toán học thành bài toán tối ưu hóa có ràng buộc: Min PX.X + PY với U(X,Y) = Ū Hàm ý
Giải bài toán này với định lý Kuhn-Tucker sẽ cho đáp số là lượng cầu cụ thể X* và Y* và các lượng
cầu này phụ thuộc vào PX, PY và Ū. Viết kiểu toán học là: X* = X(P ,Ū) X,PY Y* = Y(P ,Ū) X,PY
Hàm số biểu diễn quan hệ phụ thuộc của lượng cầu vào mức giá hàng hóa và mức thỏa dụng gọi là hàm cầu Hicks.
Có thể thấy bài toán tối thiểu hóa chi tiêu và bài toán tối đa hóa thỏa dụng cùng là những mô hình
về hành vi tối ưu hóa của người tiêu dùng. Cách tiếp cận hành vi của người tiêu dùng qua hai cách
ngược nhau như trên được kinh tế học vi mô gọi là cách tiếp cận song đối. Hàm cầu Hicks
Bách khoa toàn thư mở Wikipedia
Hàm cầu Hicks (còn gọi là hàm cầu bù đắp, hàm cầu thỏa dụng cố định) là hàm số cho biết với mỗi
mức giá cả hàng hóa và một mức thỏa dụng xác định trước thì người tiêu dùng tối thiểu hóa chi tiêu sẽ
có lượng cầu về tổ hợp hàng hóa bằng bao nhiêu.
Biểu diễn dạng công thức toán, hàm cầu Hicks sẽ là: X = h(P,Ū)
trong đó X là lượng cầu, P là mức giá cả, Ū là mức thỏa dụng cố định.
Điểm khác biệt giữa hàm cầu Hicks và hàm cầu Marshall chính là hàm cầu Hicks lấy mức thỏa dụng là cố
định trong khi hàm cầu Marshall lấy thu nhập là cố định. Hàm cầu Hicks có thể lập ra qua việc giải bài toán
tối thiểu hóa chi tiêu. Còn hàm cầu Marshall có thể lập ra qua việc giải bài toán tối đa hóa thỏa dụng.
Sự thay đổi của lượng cầu Hicks theo sự thay đổi của mức giá thể hiện qua đường cầu Hicks, ∂X/∂P = ∂h(P,Ū)/∂P. Tối đa hóa thỏa dụng
Bách khoa toàn thư mở Wikipedia
Tối đa hóa thỏa dụng là hành vi của người tiêu dùng điển hình. Người tiêu dùng khi đối mặt với một chế ước
ngân sách của bản thân, sẽ tìm cách chọn một tổ hợp hàng tiêu dùng tối ưu sao cho mức thỏa dụng mà tổ hợp
này đem lại cho mình là lớn nhất.
Nếu minh họa bằng đồ thị, tổ hợp cho phép đạt mức thỏa dụng tối đa là tổ hợp hàng hóa tại tiếp điểm
của đường bàng quan và đường ngân sách. Tại đó, tỷ lệ giữa mức thỏa dụng biên của hai hàng hóa (hay
chính là tỷ lệ thay thế biên của hàng tiêu dùng) bằng tỷ lệ giữa hai mức giá của các hàng hóa. Điều này gọi
là điều kiện tối đa hóa thỏa dụng.
Về mặt toán học, hành vi tối đa hóa thỏa dụng được diễn đạt bằng bài toán sau: u = max U(X,Y) với PX.X + PY.Y = M trong đó:
 u = U(X,Y) là hàm thỏa dụng.
 X và Y là lượng của lần lượt 2 hàng hóa được tiêu dùng;
 PX và PY là giá cả của lần lượt 2 hàng hóa;
 U(X,Y) là mức thỏa dụng do tiêu dùng 2 hàng hóa đem lại.
 M là thu nhập có thể sử dụng của người tiêu dùng.
Giải bài toán tối ưu hóa có điều kiện này bằng định lý Kuhn-Tucker sẽ cho ra lời giải.
Một cách giải tắt bài toán tối đa hóa thỏa dụng nói trên là trước tiên giả định bài toán có lời giải bên trong.
Khi đó áp dụng điều kiện tối đa hóa thỏa dụng, tức là MUX/MUY = PX/PY (MU là ký hiệu của thỏa dụng
biên), từ đó tìm ra lời giải. Nếu không ra lời giải, nghĩa là bài toán có giải pháp góc, lúc đó tìm xem khi X
bằng 0 hay khi Y bằng 0 thì mức thỏa dụng lớn hơn mà tìm ra lời giải.
Đáp số của bài toán tối đa hóa thỏa dụng là lượng cầu cụ thể đối với mỗi hàng hóa, X* = X(PX,M) và Y* = Y(P ,M). Đây chính là Y hàm cầu Marshall.
Có thể thấy bài toán tối đa hóa thỏa dụng và bài toán tối thiểu hóa chi tiêu cùng là những mô hình về hành
vi tối ưu hóa của người tiêu dùng. Cách tiếp cận hành vi của người tiêu dùng qua hai cách ngược nhau
như trên được kinh tế học vi mô gọi là cách tiếp cận song đối. Hàm cầu Marshall
Bách khoa toàn thư mở Wikipedia
Hàm cầu Marshall (còn gọi là hàm cầu Walras) là hàm số biểu diễn quan hệ phụ thuộc của lượng cầu về
một mặt hàng vào giá cả của mặt hàng đó và của các mặt hàng khác trong tổ hợp hàng mà người mua phải
chọn lựa để tối đa hóa thỏa dụng, và vào thu nhập của người mua.
Hàm cầu Marshall có thể tìm ra thông qua việc giải bài toán tối đa hóa thỏa dụng.
Về mặt công thức toán, hàm cầu Marshall có thể được biểu diễn như sau: X = X(PX,PY,M)
trong đó X là lượng cầu về một mặt hàng, PX giá của mặt hàng đó, PY là giá của các mặt hàng khác, và M
là thu nhập của người mua. Giá cả của các mặt hàng khác và thu nhập được xem là biến ngoại sinh.
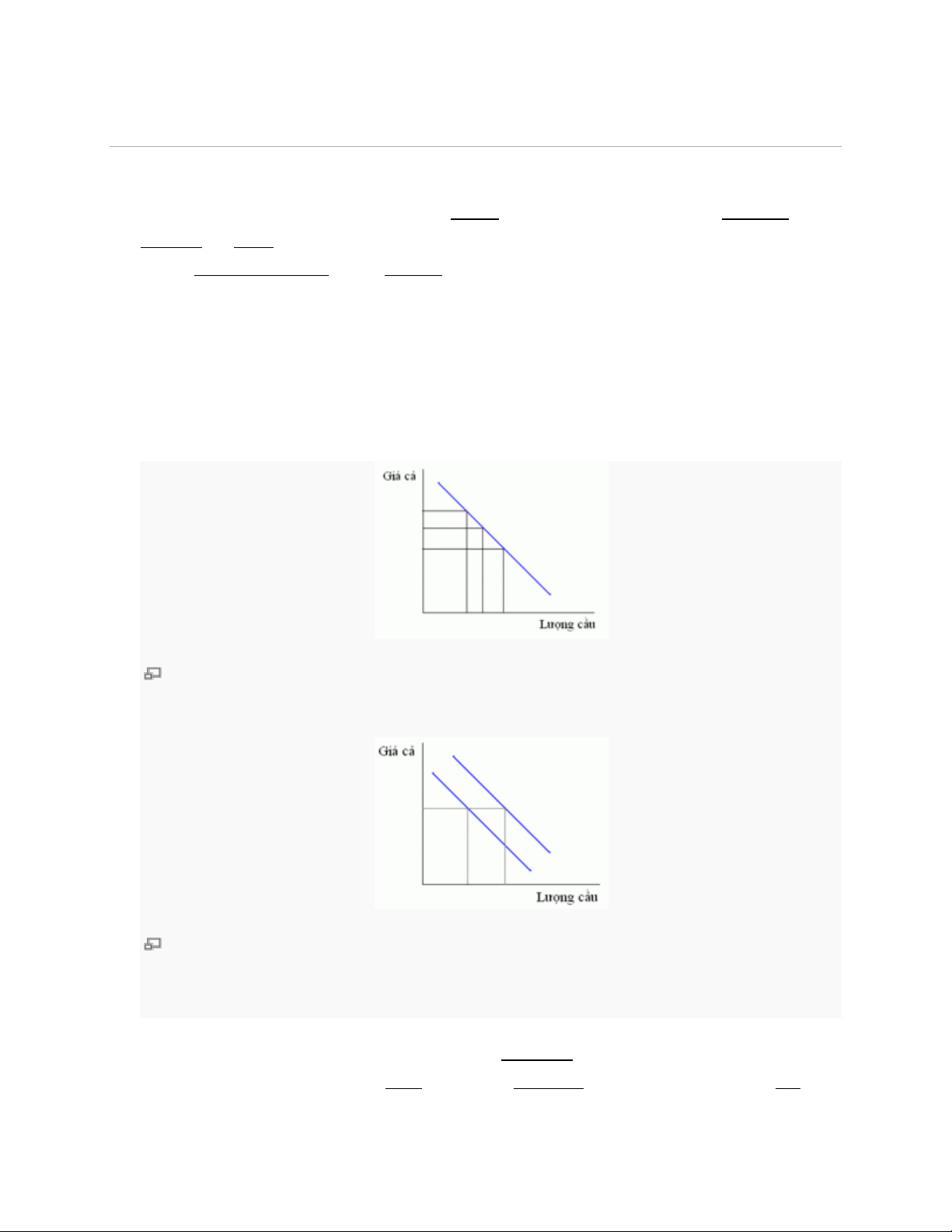
Đường cong nhu cầu dốc xuống. Giá cả tăng, lượng cầu giảm. Đây là sự dịch chuyển dọc theo đường cầu
Khi mức giá của bản thân mặt hàng đang xem xét không đổi, các yếu tố khác (giá hàng khác, thu nhập) thay
đổi, cả đường cầu sẽ dịch chuyển khiến lượng cầu thay đổi.
Khi biểu diễn hàm cầu Marshall bằng hình vẽ, các nhà kinh tế học sử dụng đường cầu Marshall. Đây là
một đường dốc xuống phía phải trên đồ thị hai chiều mà trục hoành là tập hợp các lượng cầu và trục
tung là tập hợp các mức giá của bản thân mặt hàng đó. Ở đây giả định mặt hàng đang xem xét là hàng hóa thông thường.
Khi giá mặt hàng tăng lên, lượng cầu giảm đi; như có thể thấy qua sự dịch chuyển dọc theo đường cầu.
Khi thu nhập của người mua tăng lên, người ta tiêu dùng nhiều hơn; đường cầu dịch chuyển hẳn sang
phải và lượng cầu tăng lên đối với mỗi mức giá. Khi giá cả của mặt hàng khác tăng lên, đường cầu cũng
sẽ dịch chuyển, song dịch sang hướng nào còn phụ thuộc vào việc mặt hàng khác đó là hàng bổ
sung hay hàng thay thế cho mặt hàng đang xem xét. Nếu là hàng bổ sung, thì đường cầu dịch sang trái,
lượng cầu giảm đi đối với mỗi mức giá của mặt hàng đang xem xét. Còn nếu là hàng thay thế, thì đường
cầu dịch sang phải, lượng cầu tăng lên với mỗi mức giá của mặt hàng đang xem xét.