











Preview text:
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
CHỦ ĐỀ: HÀM SỐ ĐƠN ĐIỆU
VẬN DỤNG – VẬN DỤNG CAO DẠNG 1
1.1. XÉT TÍNH ĐƠN ĐIỆU BẰNG BBT – ĐỒ THỊ
NỘI DUNG CẦN NẮM VỮNG Bài t
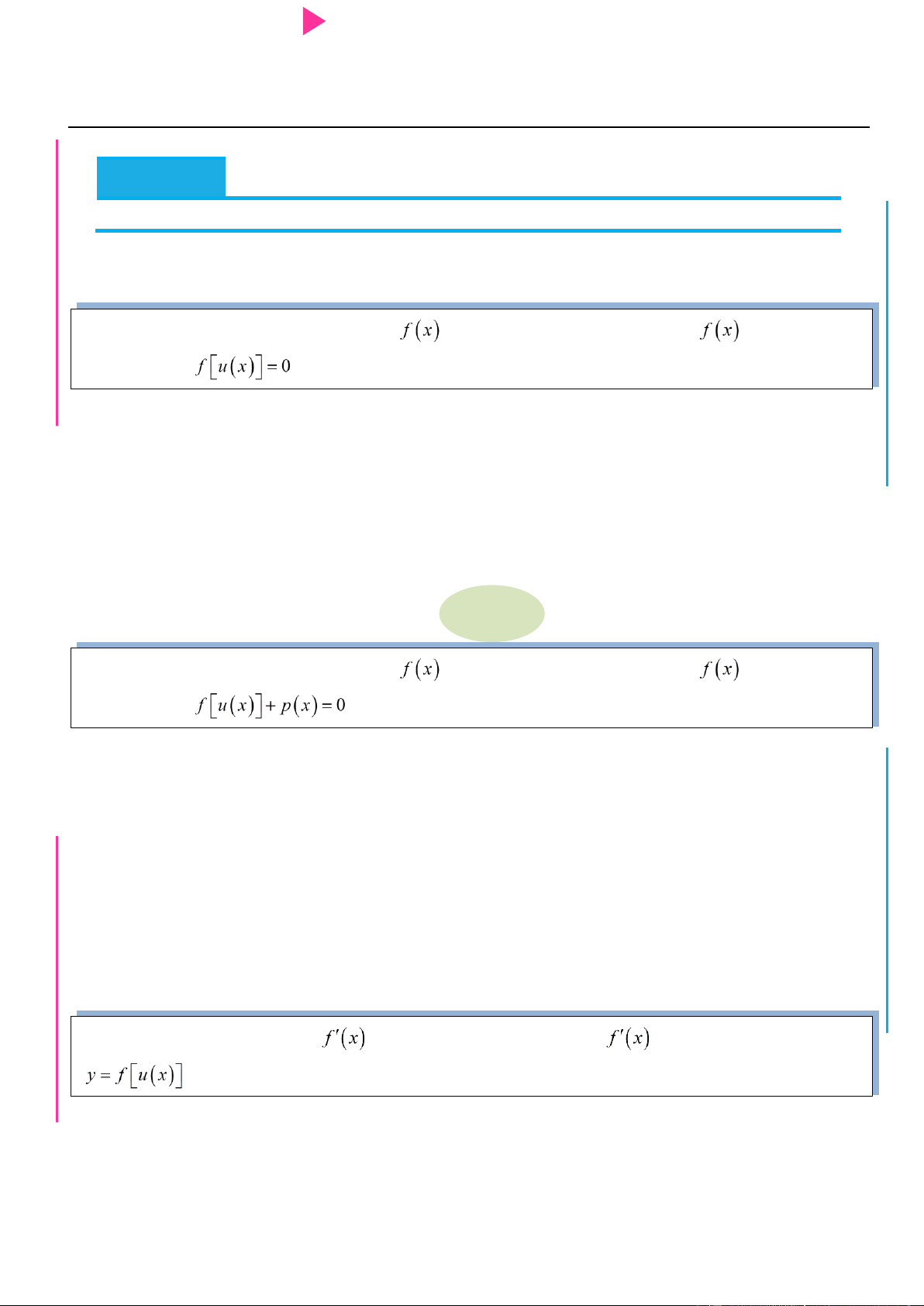
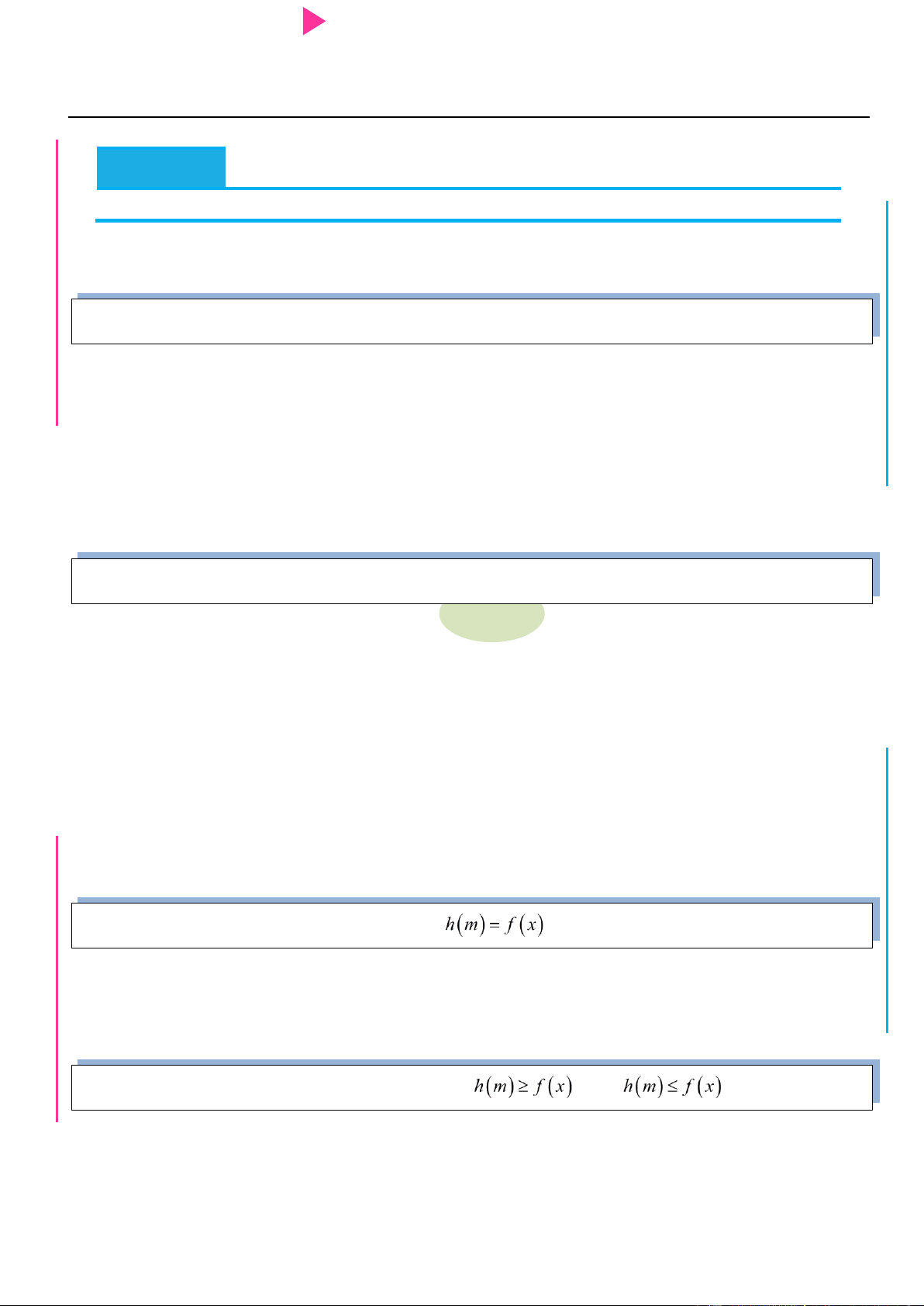
oán bổ trợ 1: Cho đồ thị hàm số
hoặc bảng biến thiên hàm số . Tìm nghiệm phƣơng trình . Phương pháp : I
+ Dựa vào đồ thị (hoặc BBT) của hàm số f x để tìm các nghiệm x x của phƣơng Ơ i
trình f x 0. M D Ầ
+ Khi đó phƣơng trình f u
x 0 u
x x . Giải các phƣơng trình ux x ta tìm i i Đ NH
đƣợc các nghiệm của phƣơng trình f u x 0 Ị . Đ
Nhận xét : Đôi khi chỉ tìm ra được các nghiệm gần đúng x hoặc chỉ tìm ra được số nghiệm của i G THPT
phương trình f u x 0 . N.C.Đ NG CÔN Ờ N Ễ Bài t
oán bổ trợ 2: Cho đồ thị hàm số
hoặc bảng biến thiên hàm số . Tìm nghiệm Y TRƢ phƣơng trình . GU N N Phương pháp :
+ Đặt t u x , biểu diễn p x φt . ÁO VIÊ GI
+ Biến đổi phƣơng trình f u
x p
x 0 f t φt
+ Dựa vào đồ thị (hoặc BBT) của hàm số f x để tìm các nghiệm x x từ phƣơng i
trình f x φ x.
+ Khi đó phƣơng trình f u
x p
x 0 t ux x . Giải các phƣơng trình i
u x x ta tìm đƣợc các nghiệm của phƣơng trình f u x 0 i .
Nhận xét : Bài toán bổ trợ 1 là trường hợp đặc biệt của bài toán bổ trợ 2.
Bài toán 1: Cho đồ thị hàm số
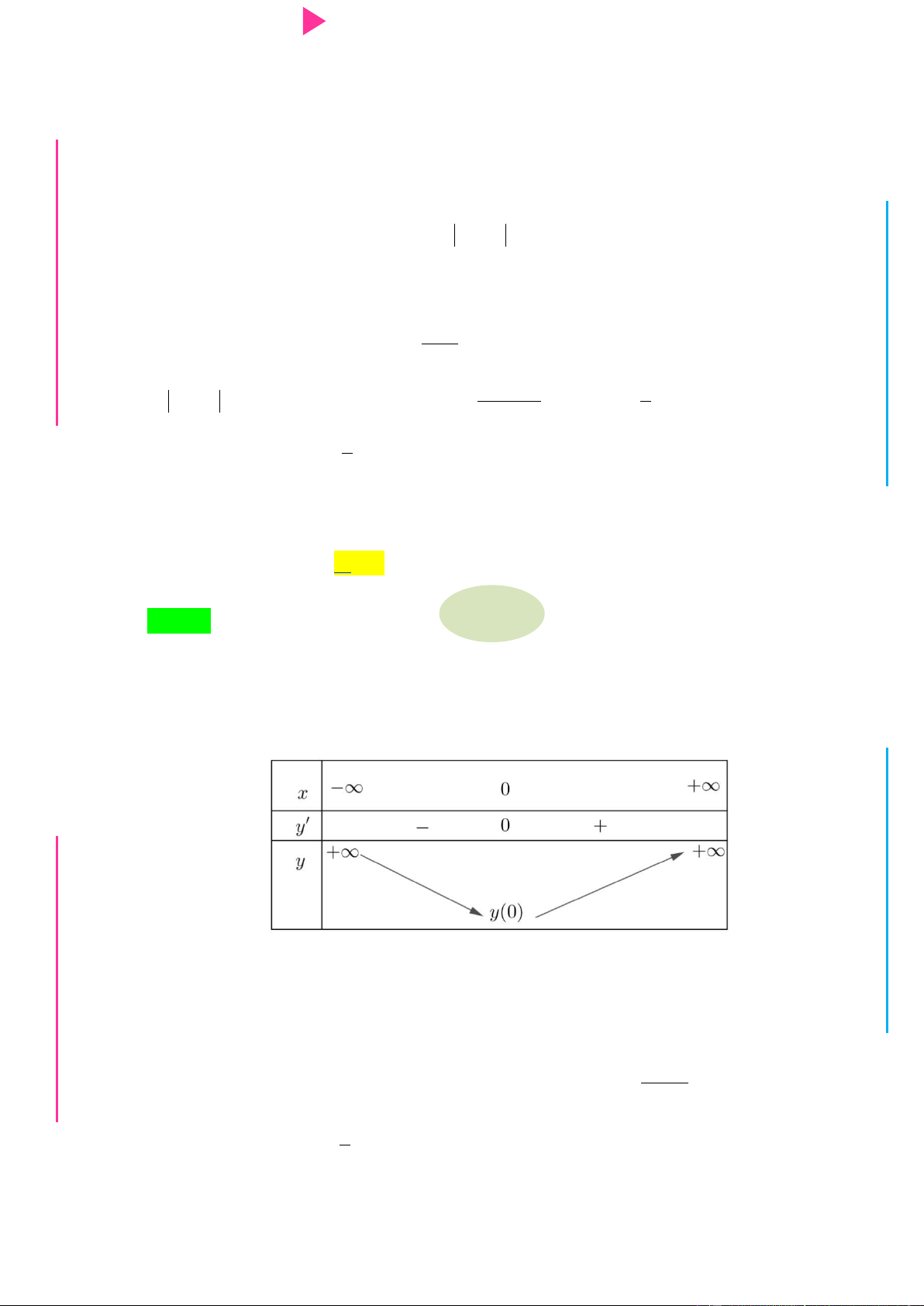
hoặc bảng biến thiên hàm số
. Xét tính đơn điệu hàm số . Phương pháp :
u 'x 0
+ Xác định y u x. f u
x . Cho y ' 0 f 'u
x 0
(Dựa vào bài toán toán bổ trợ 1 để tìm các nghiệm phƣơng trình y ' 0 ).
NGUYỄN CÔNG ĐỊNH | 1
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
+ Lập bảng xét dấu của y .
+ Từ đó kết luận đƣợc về khoảng đồng biến, nghịch biến của hàm số y f u
x và có
thể phát triển bài toán thành tìm số cực đại, cực tiểu của hàm số.
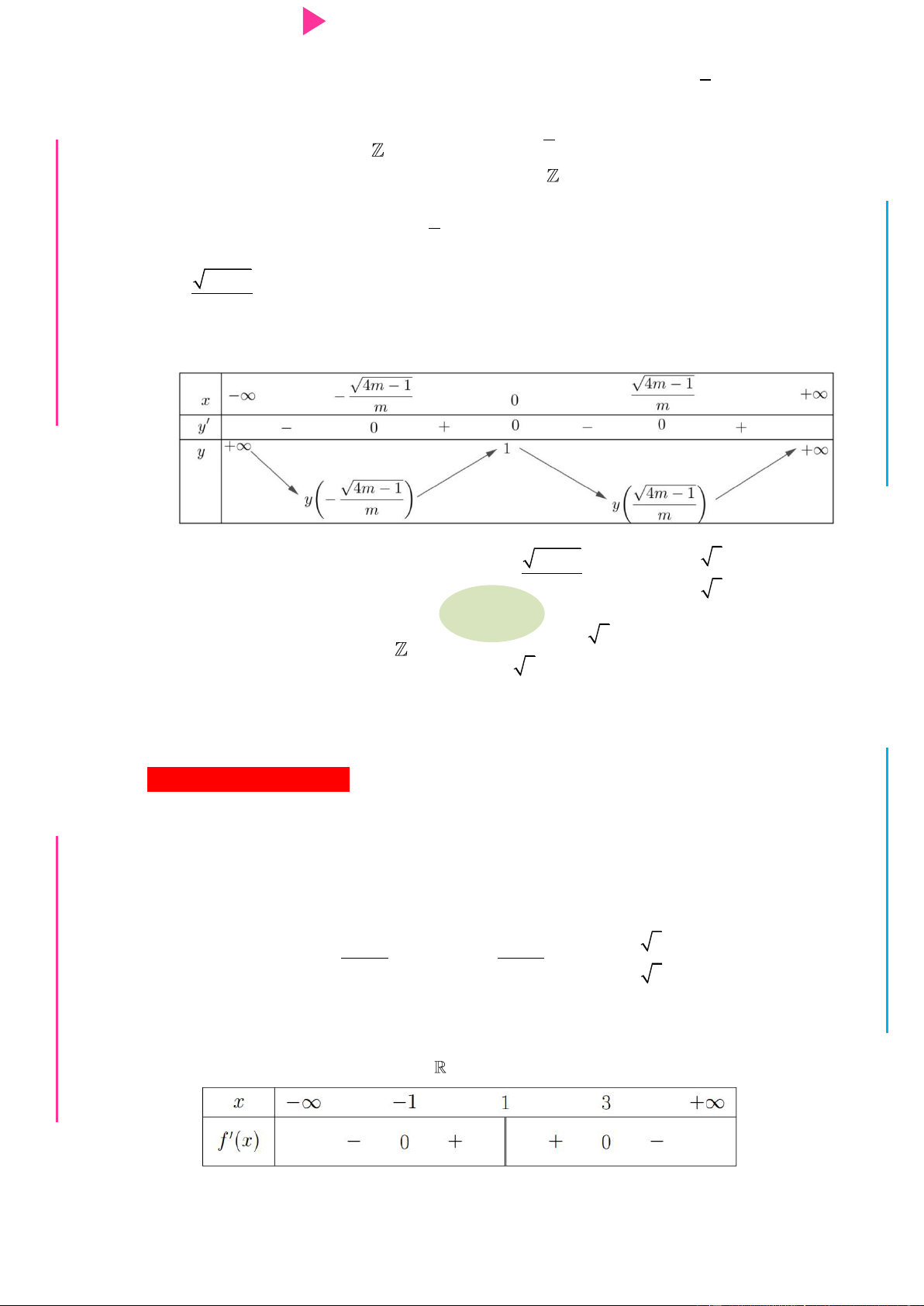
Bài toán 2: Cho đồ thị hàm số
hoặc bảng biến thiên hàm số
. Xét tính đơn điệu hàm số . Phương pháp :
u 'x 0
+ Xác định y ' u ' x f ' u
x p '
x. Cho y' 0 p x f ' u x ' u
x , u'x 0 '
(Dựa vào bài toán toán bổ trợ 2 để tìm các nghiệm phƣơng trình y ' 0 ).
+ Lập bảng xét dấu của y . I Ơ
+ Từ đó kết luận đƣợc về khoảng đồng biến, nghịch biến của hàm số và có thể phát
triển bài toán thành tìm số cực đại, cực tiểu của hàm số. M D Ầ Đ BÀI TẬP NHỊ Đ Câu 1.
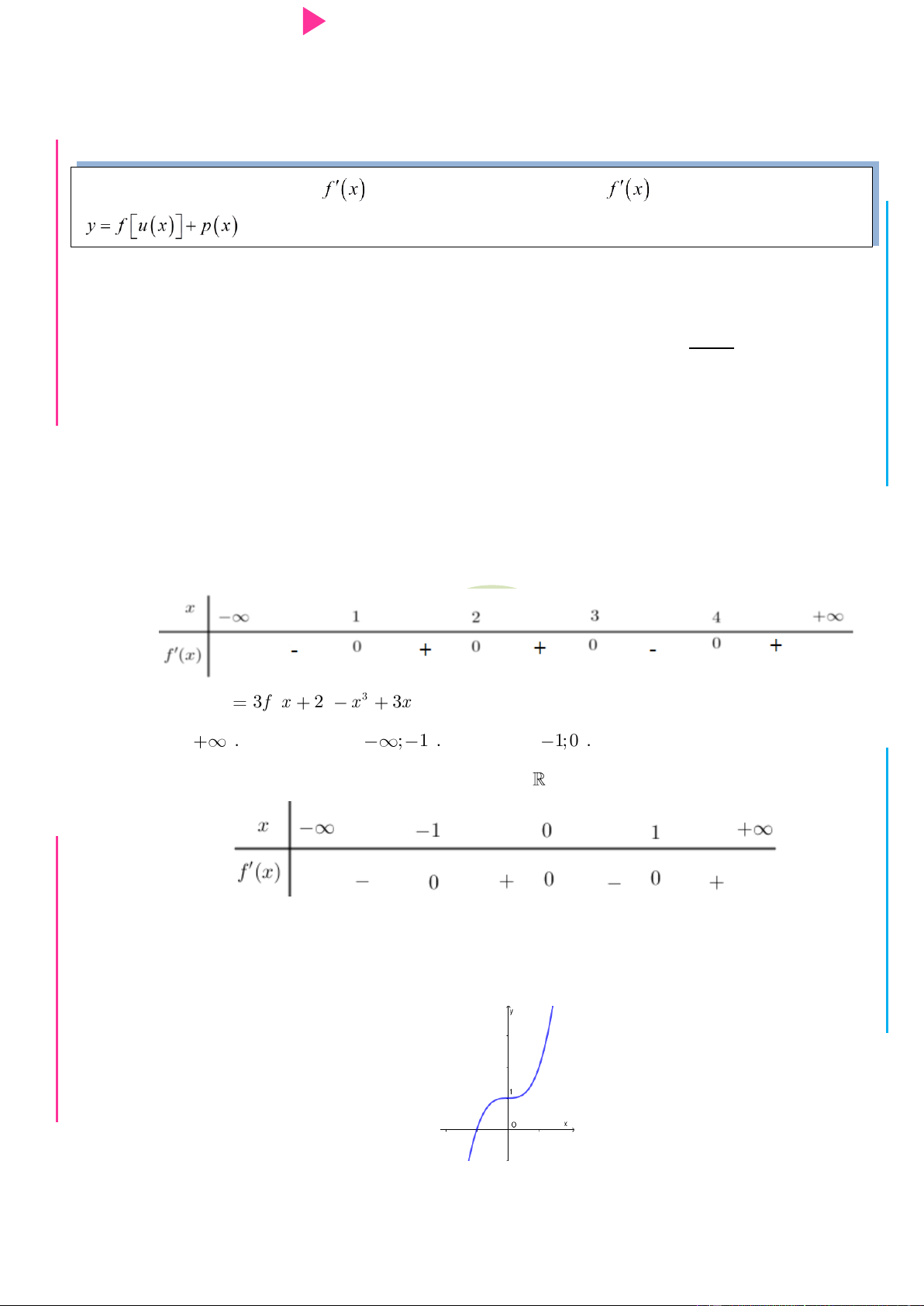
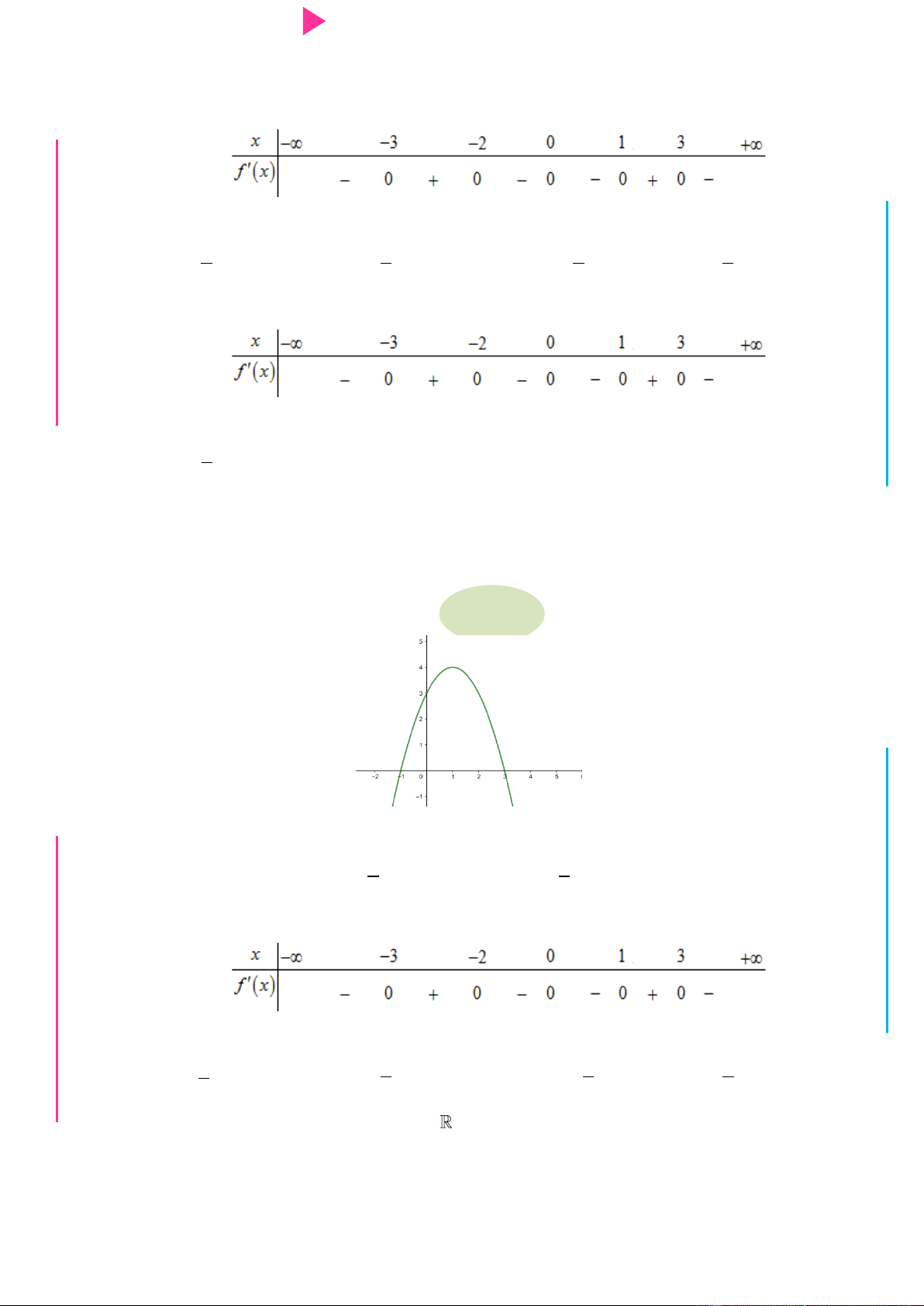
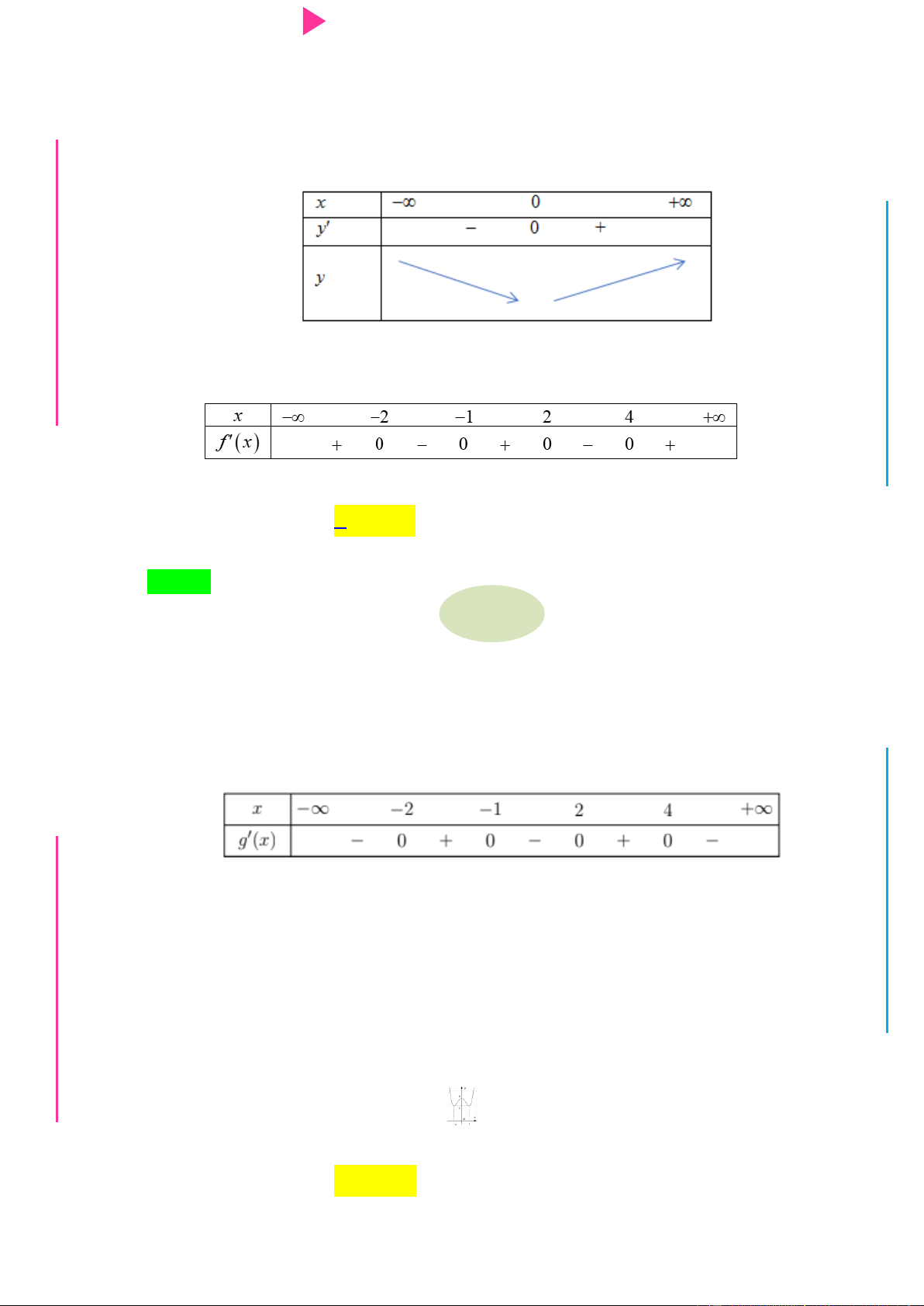
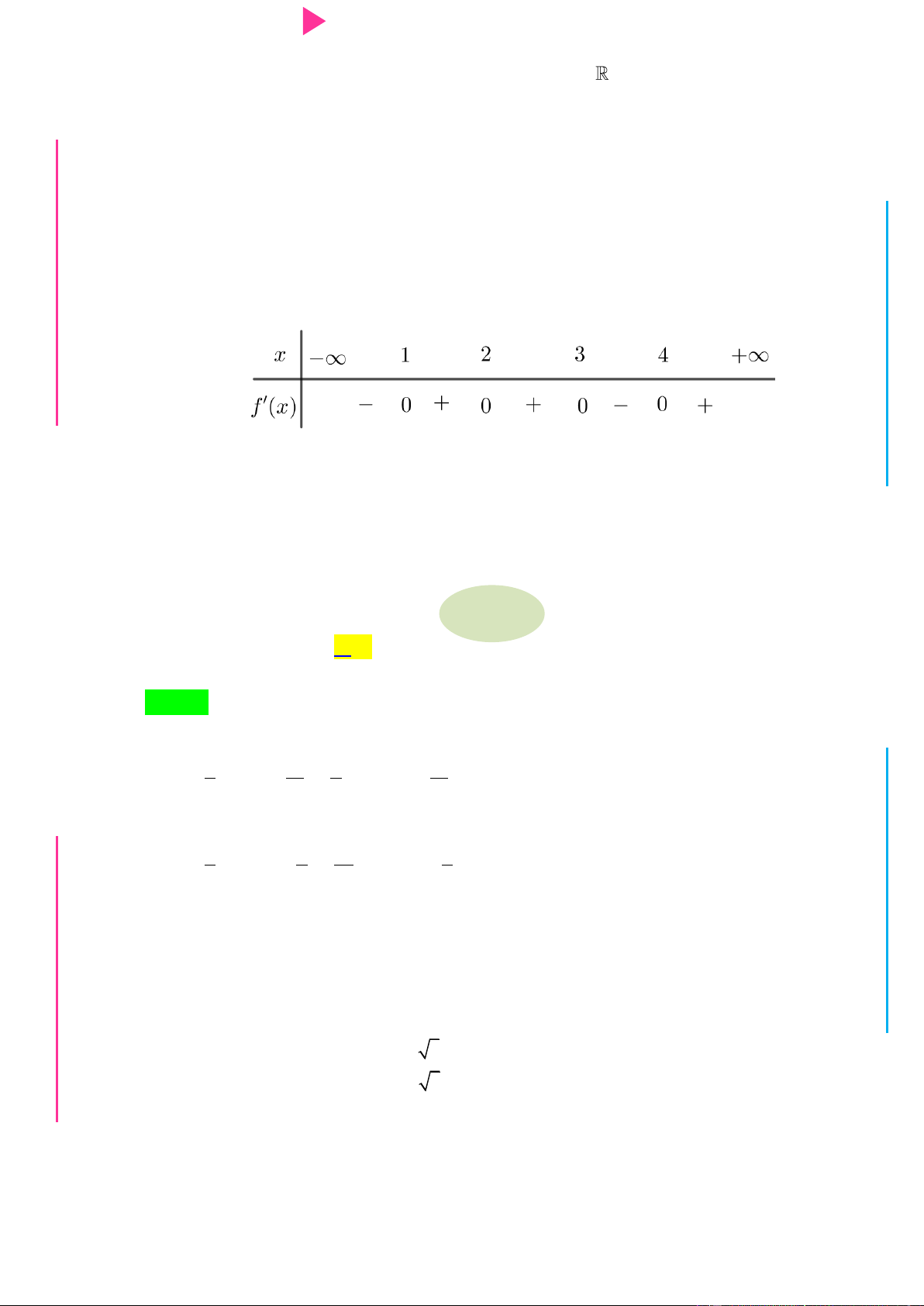
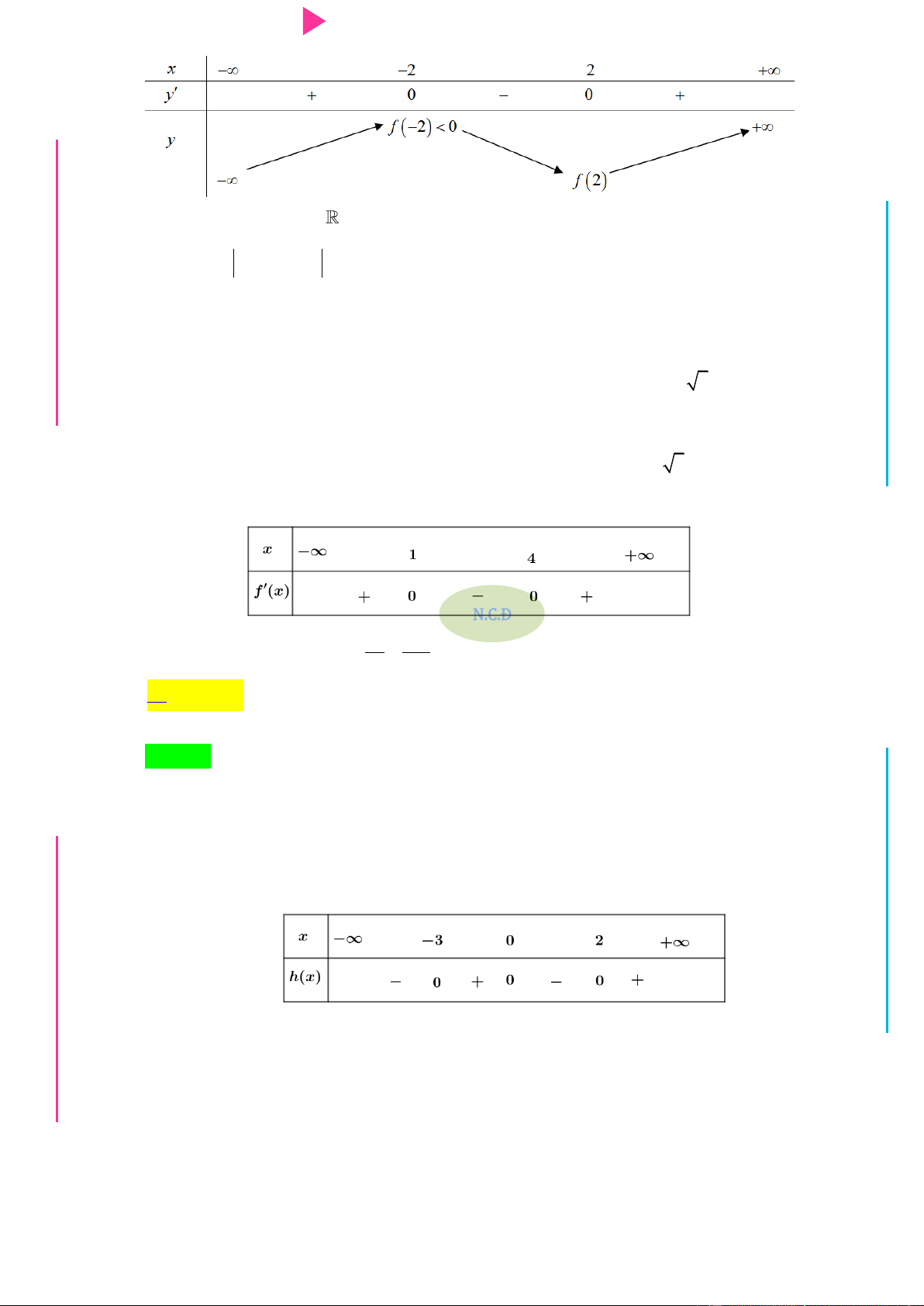
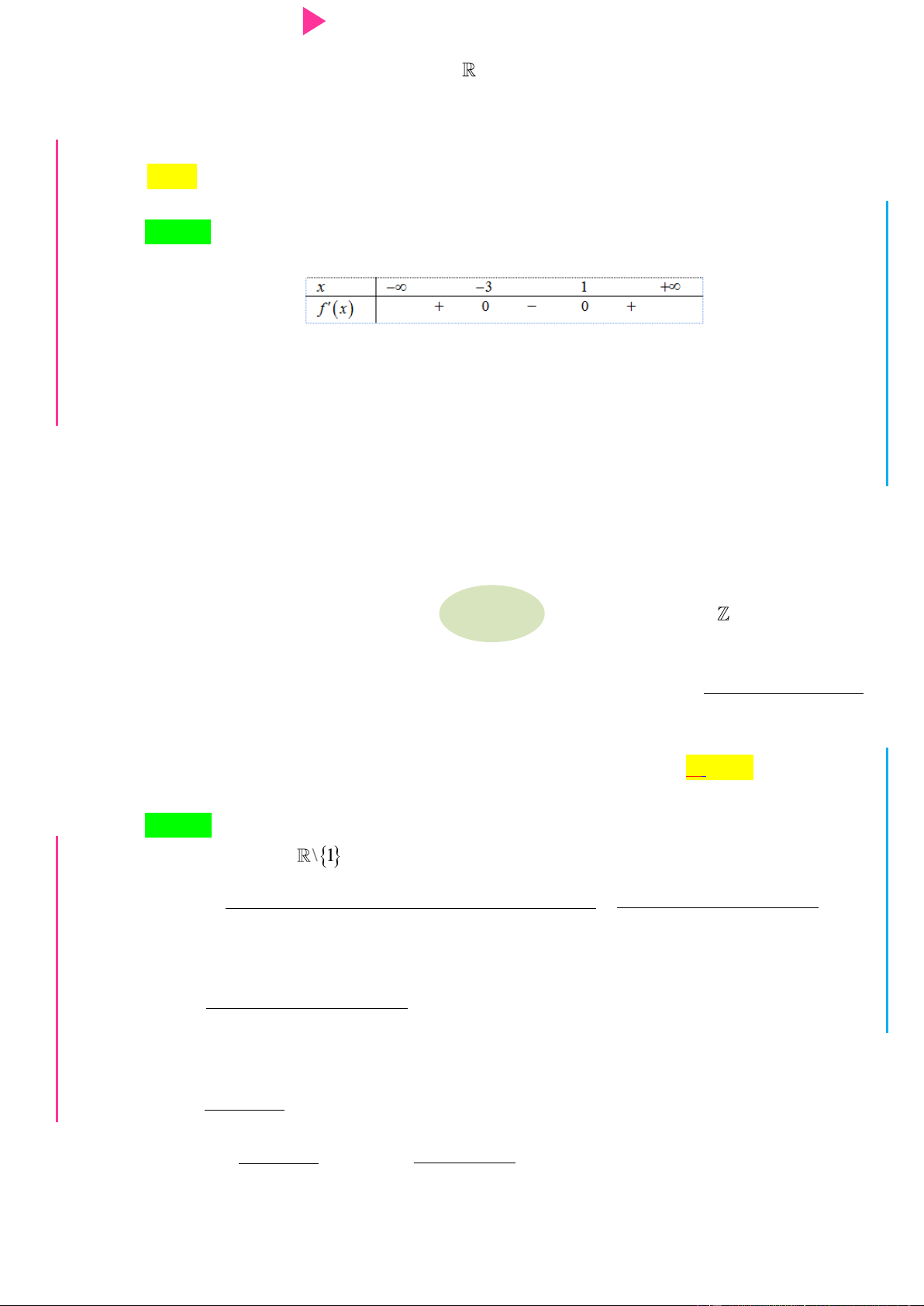
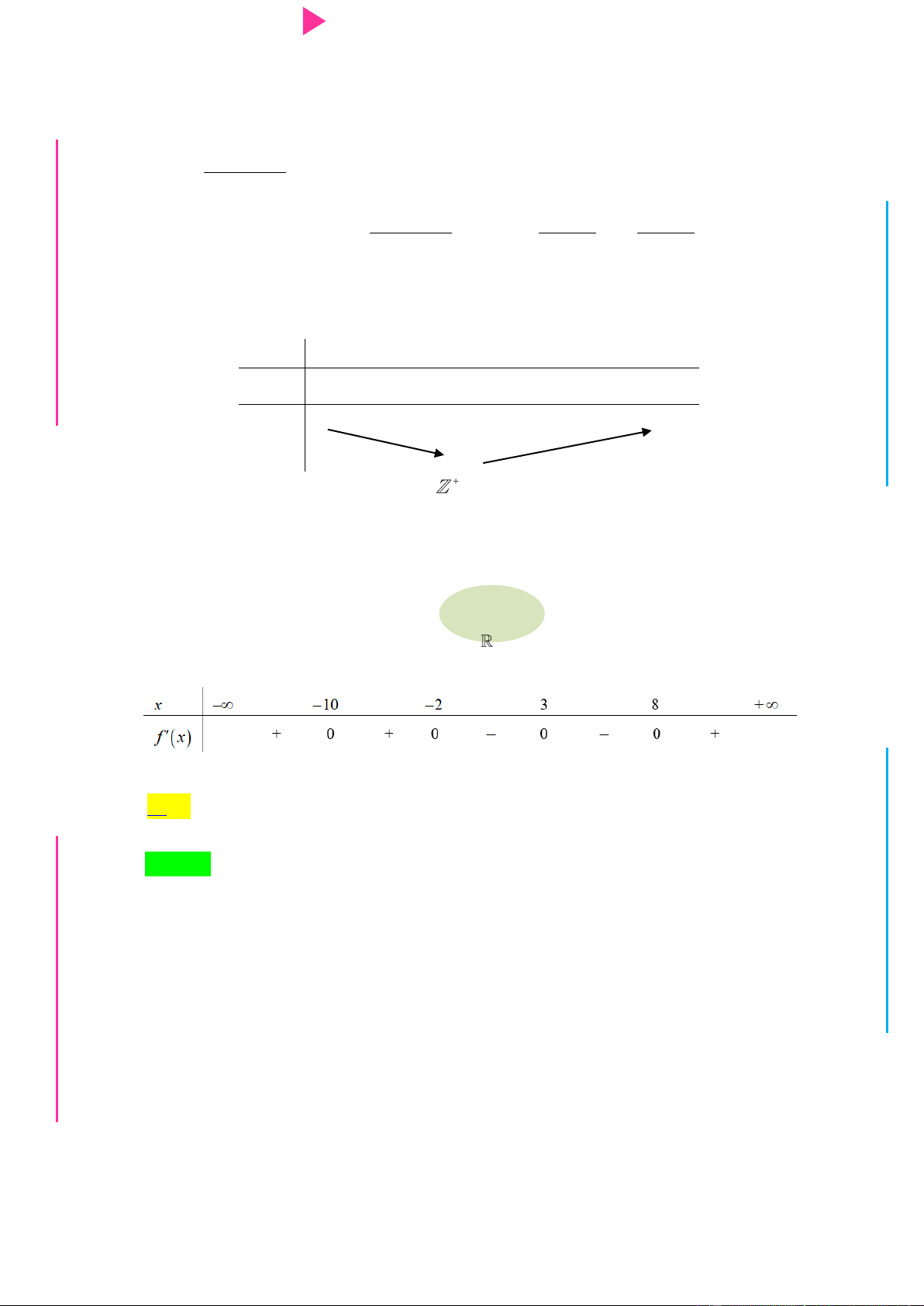
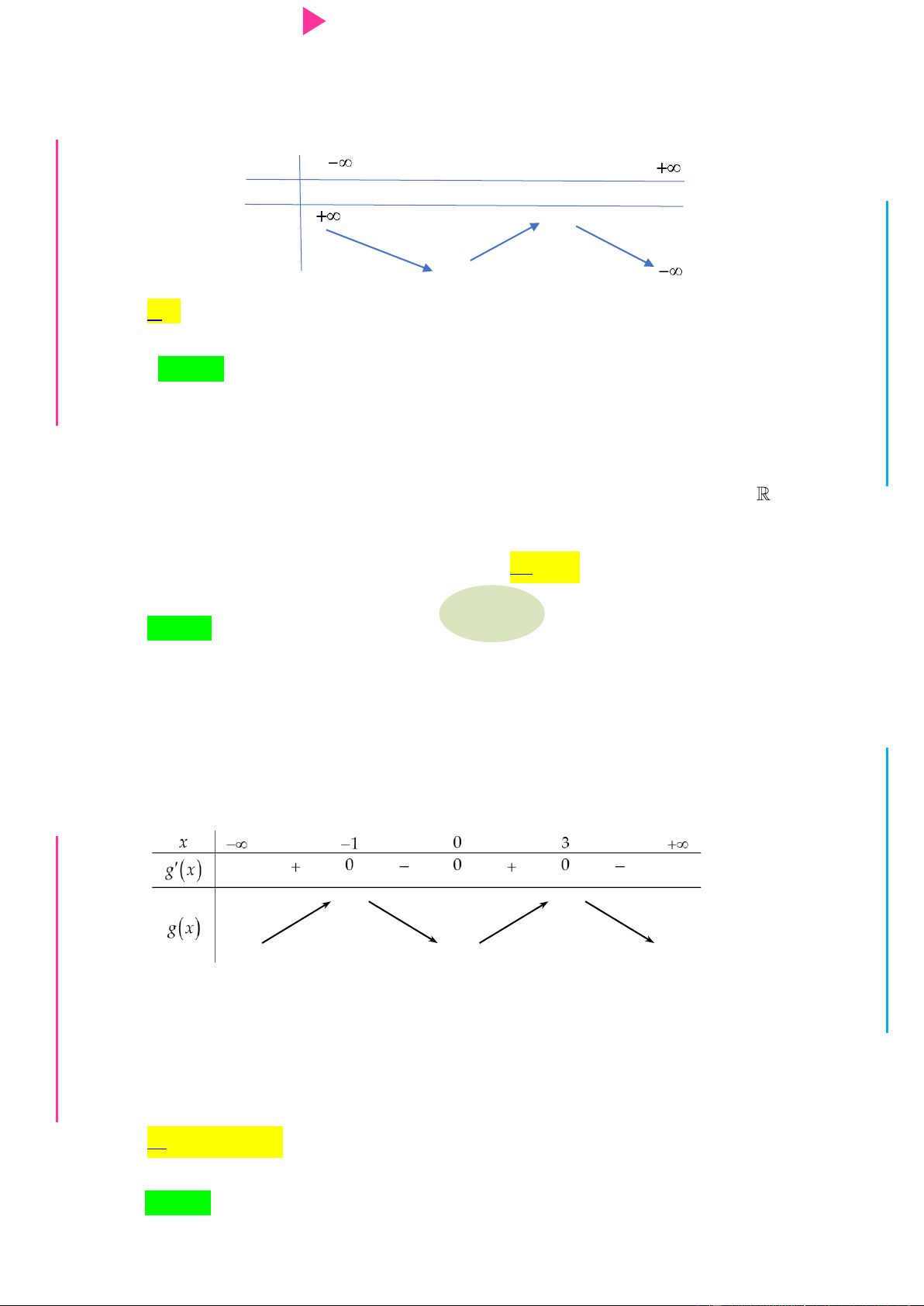
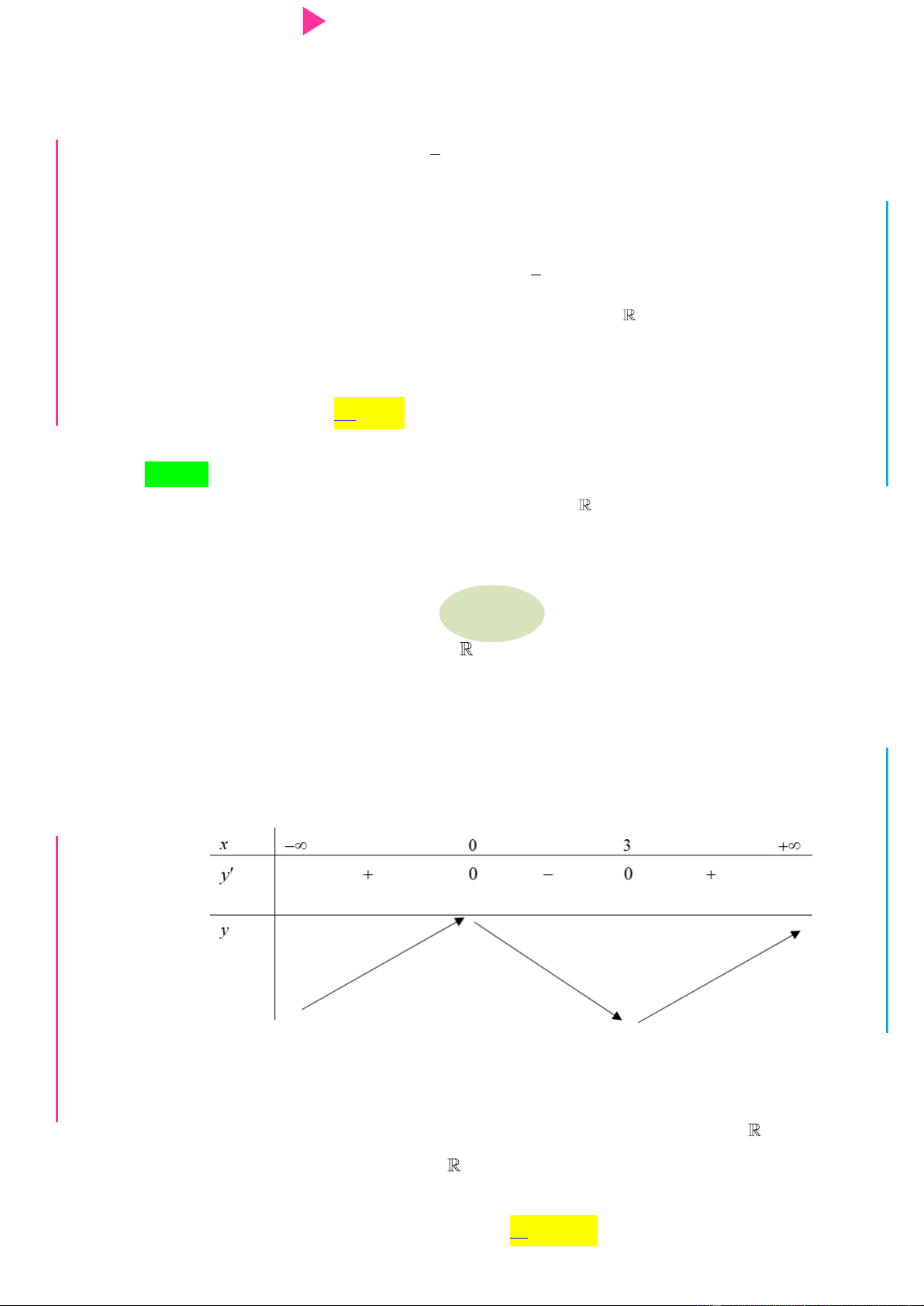
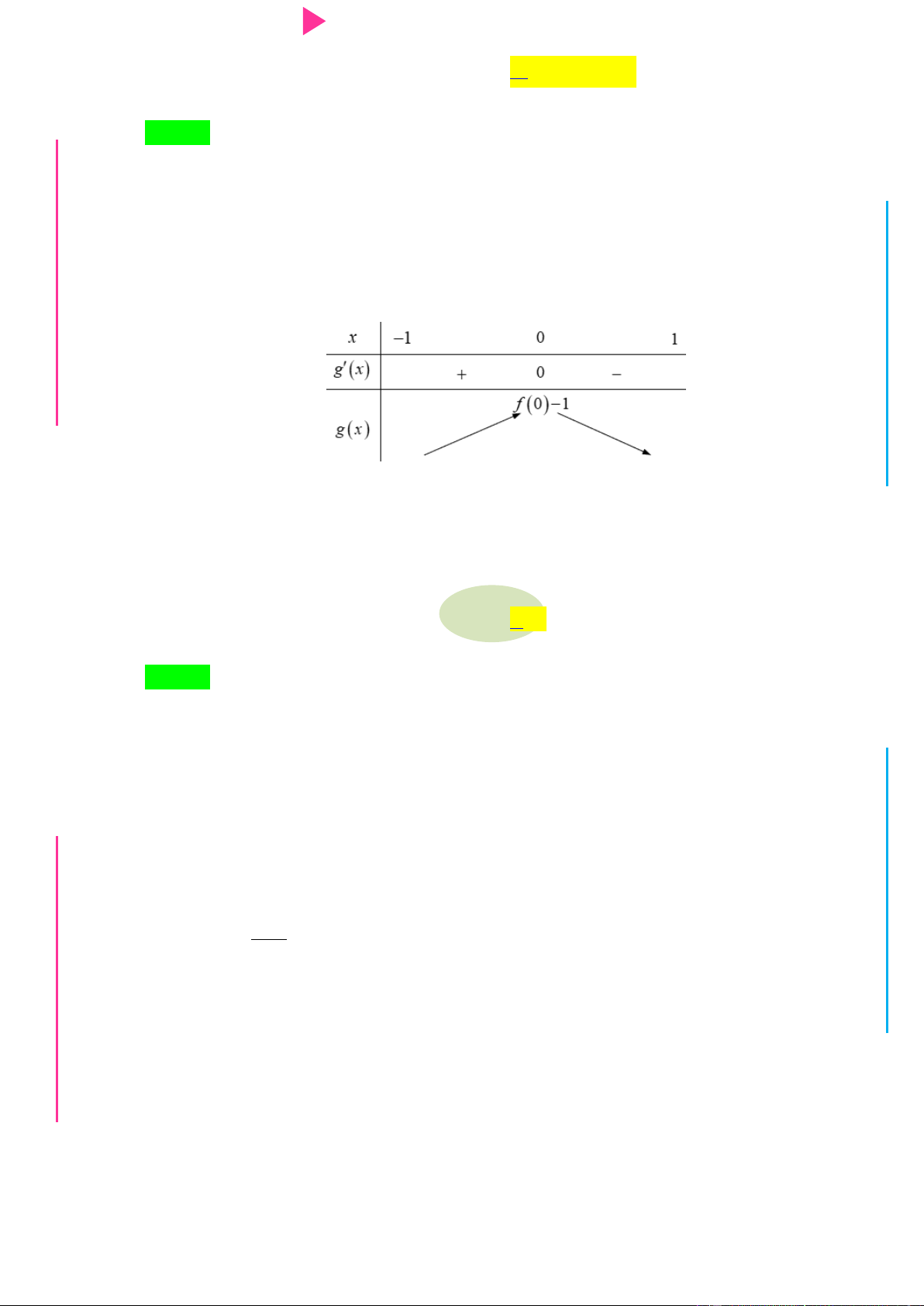
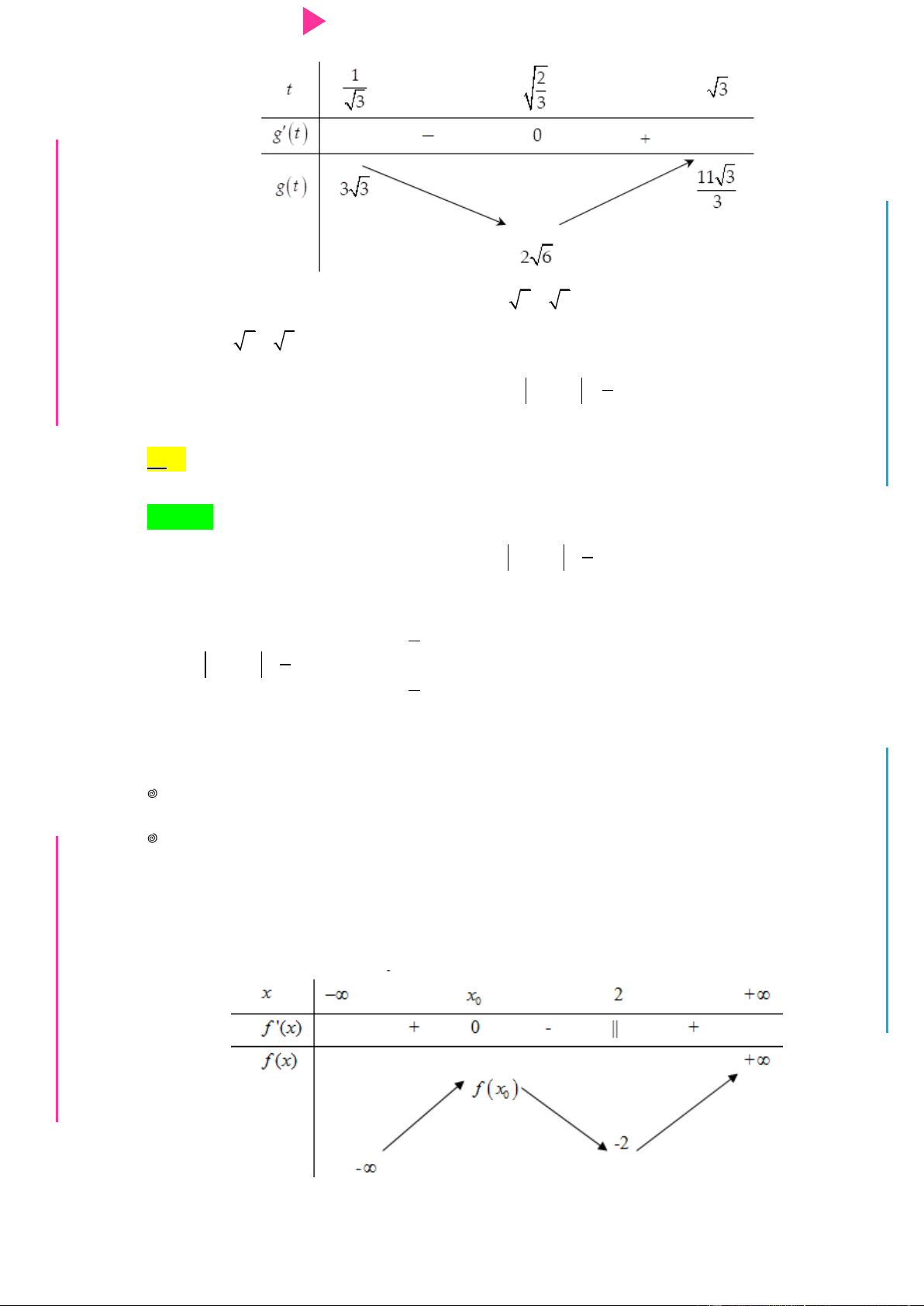
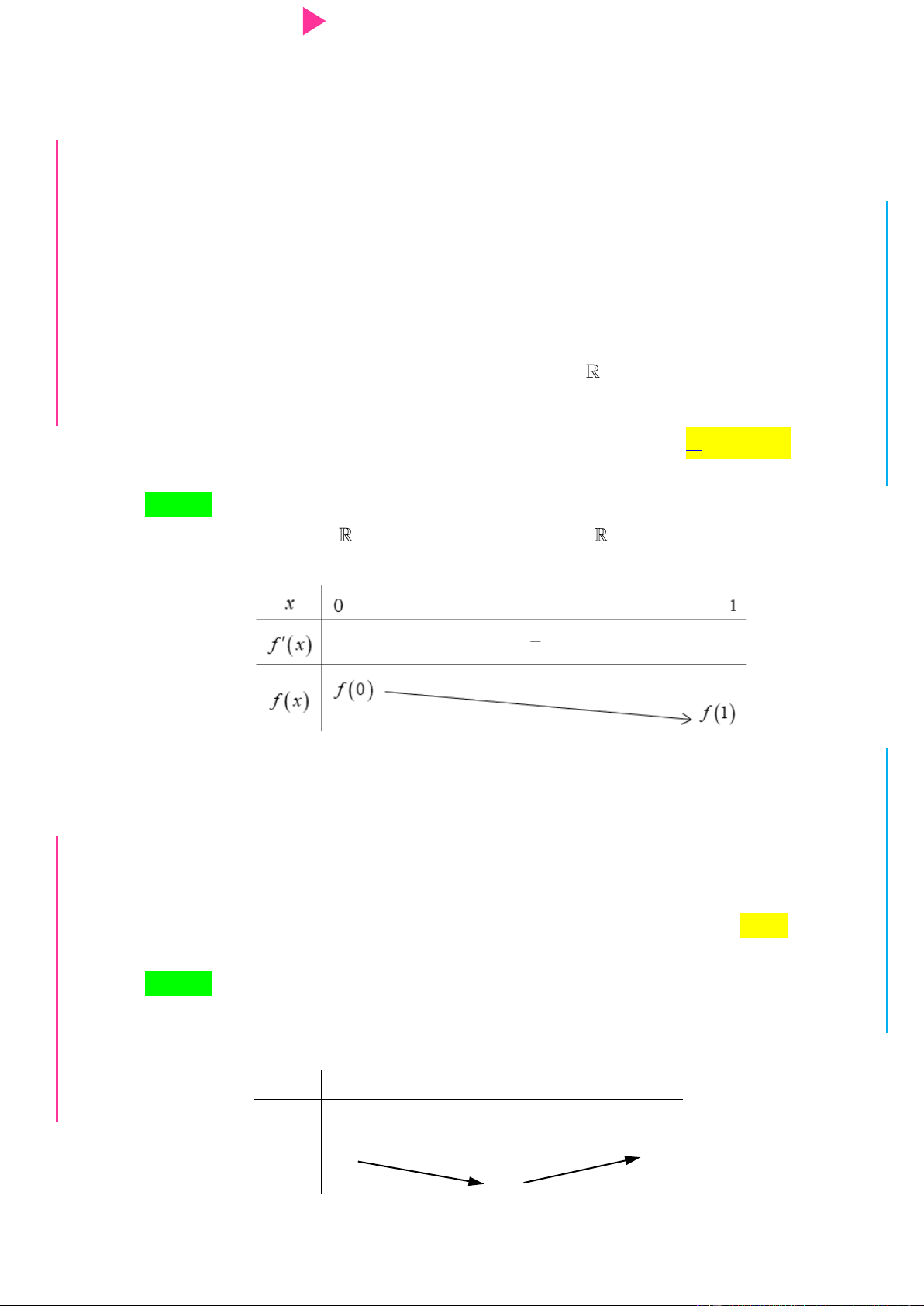
Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ Hàm số 3 y 3f x 2 x
3x đồng biến trên khoảng nào dƣới đây? GU N N A. 1; . B. ; 1 . C. 1; 0 . D. 0;2 . Câu 2.
Cho hàm số y f x xác định và liên tục trên , có đạo hàm f x thỏa mãn ÁO VIÊ GI
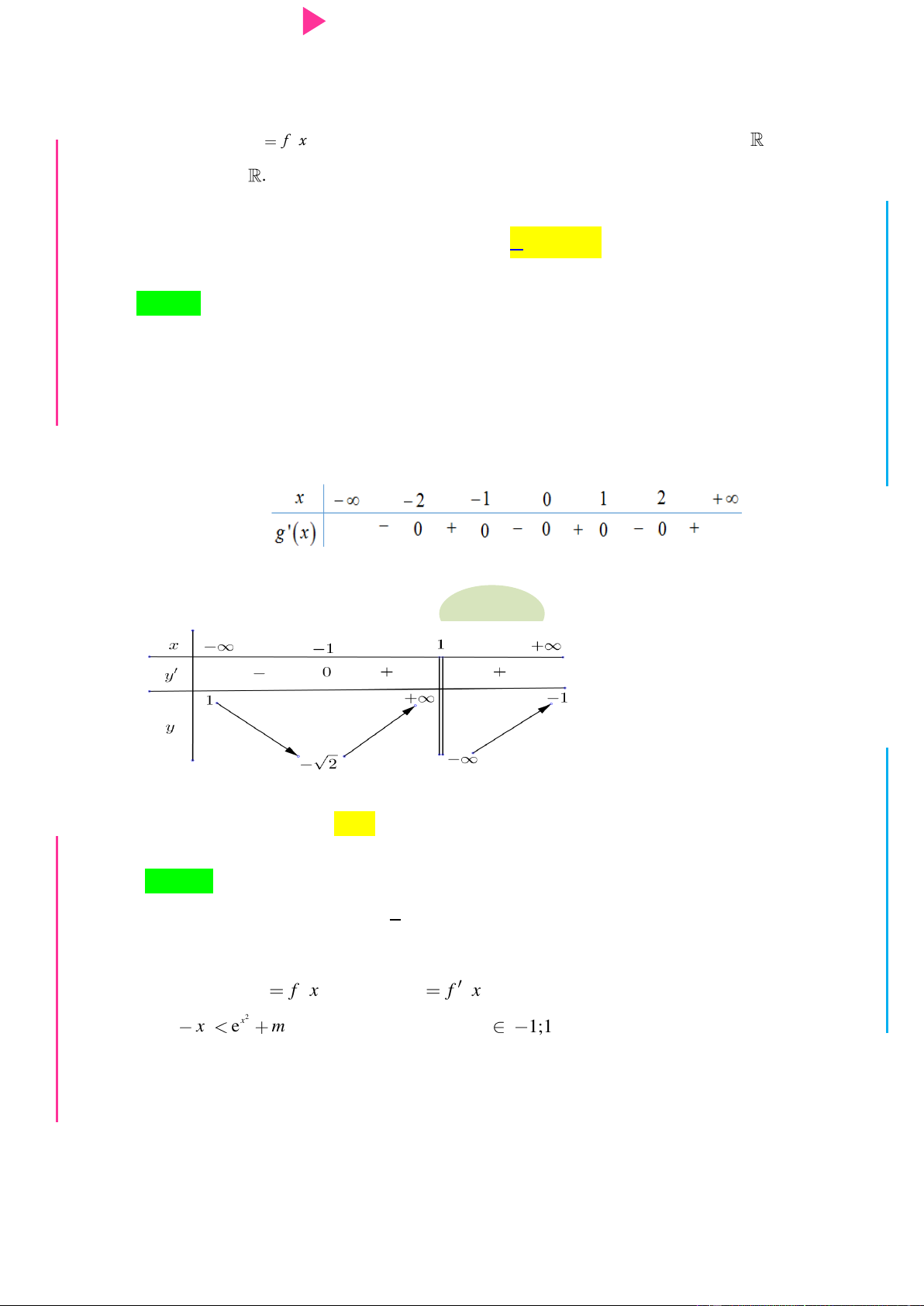
Hàm số y f 1 x nghịch biến trên khoảng nào dƣới đây A. 1 ; 1 . B. 2 ;0 . C. 1 ;3 . D. 1; . Câu 3.
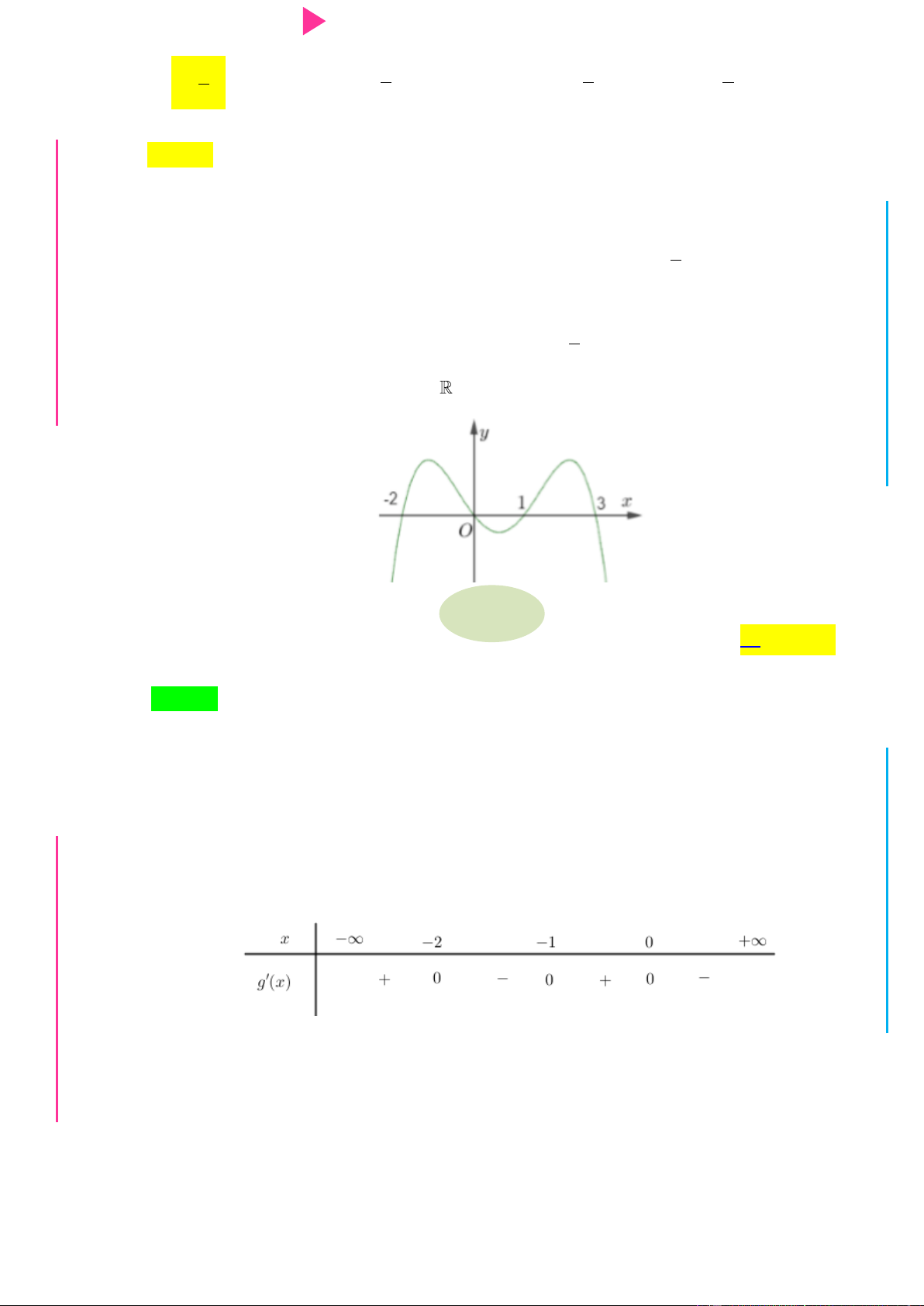
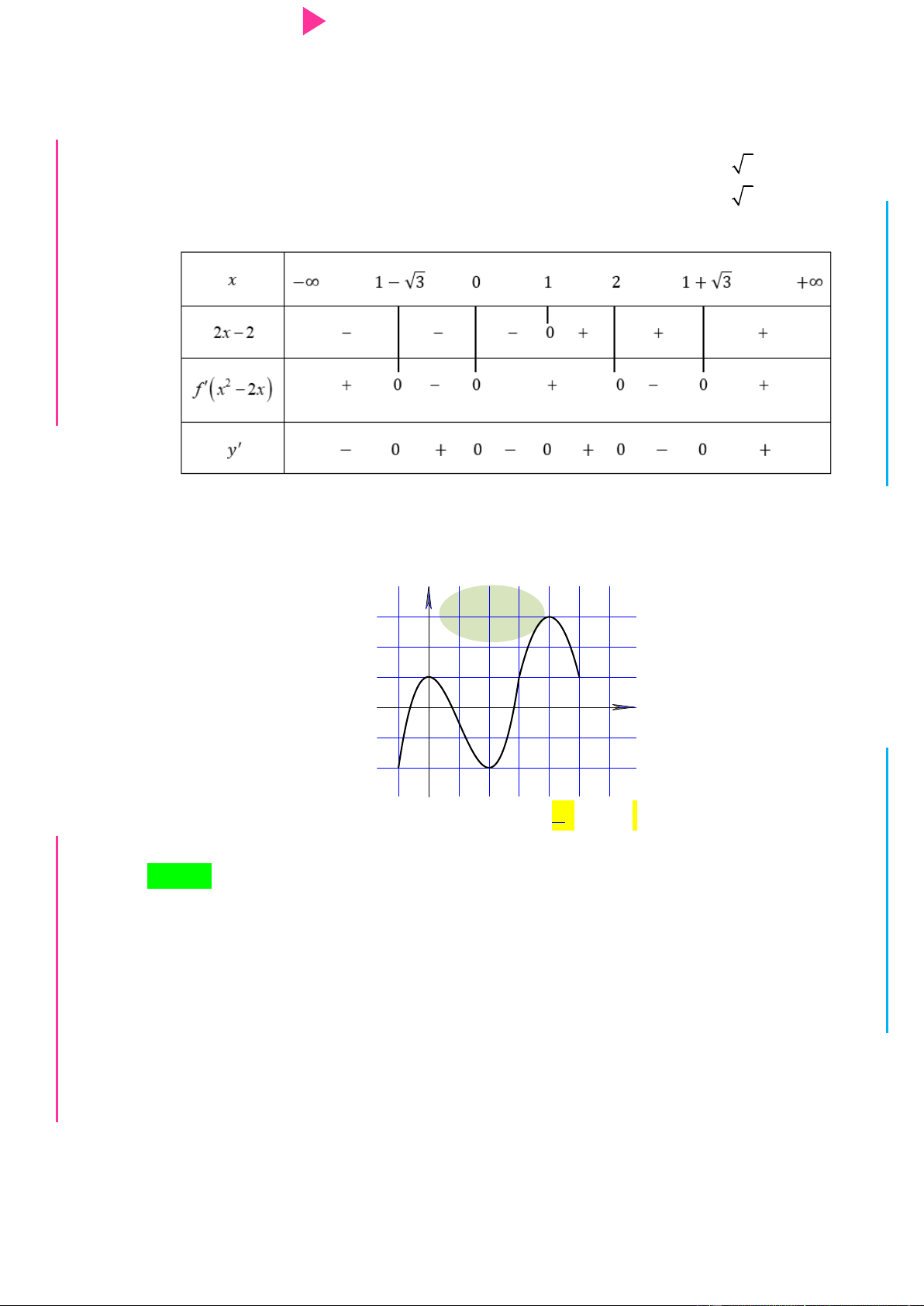
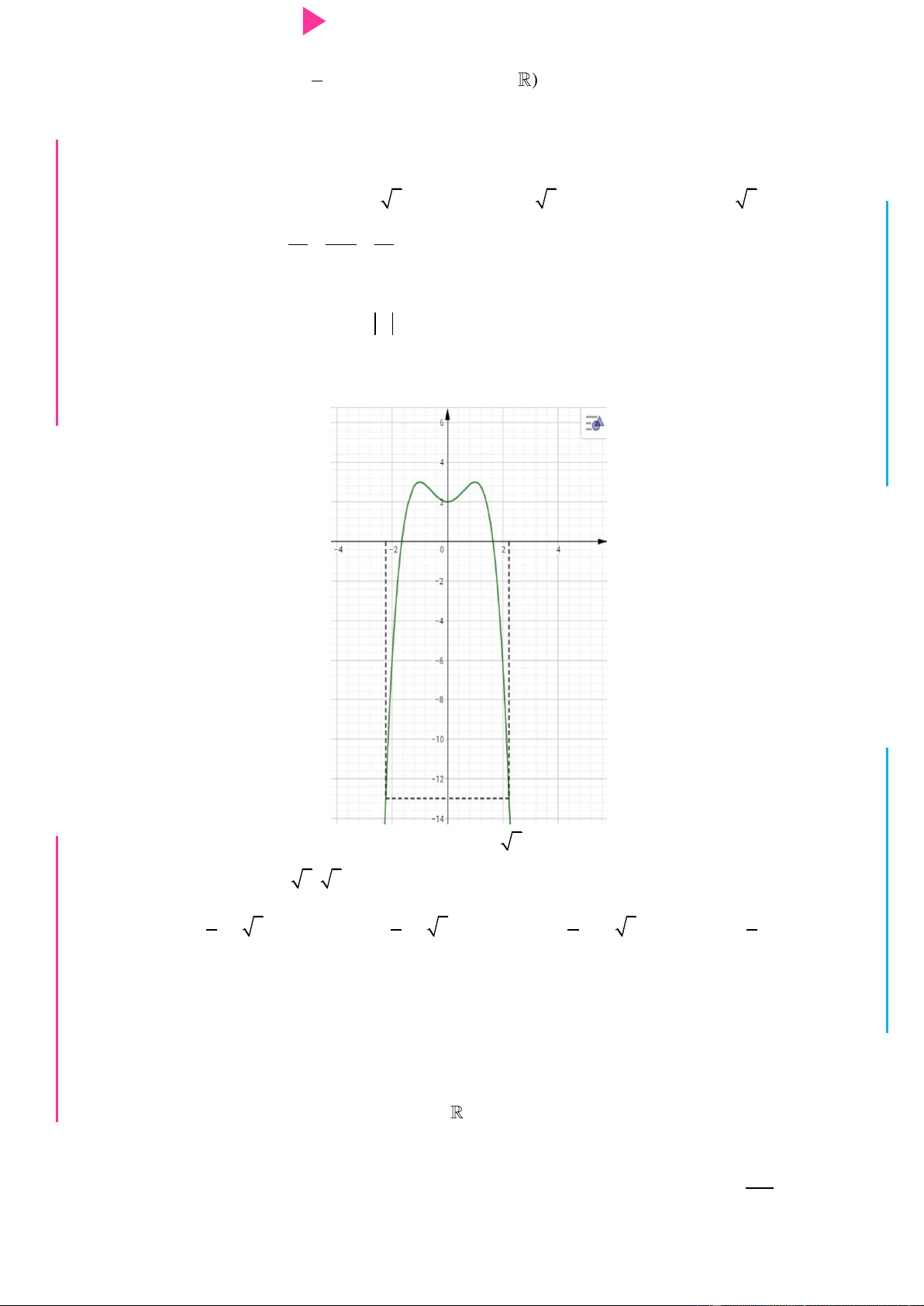
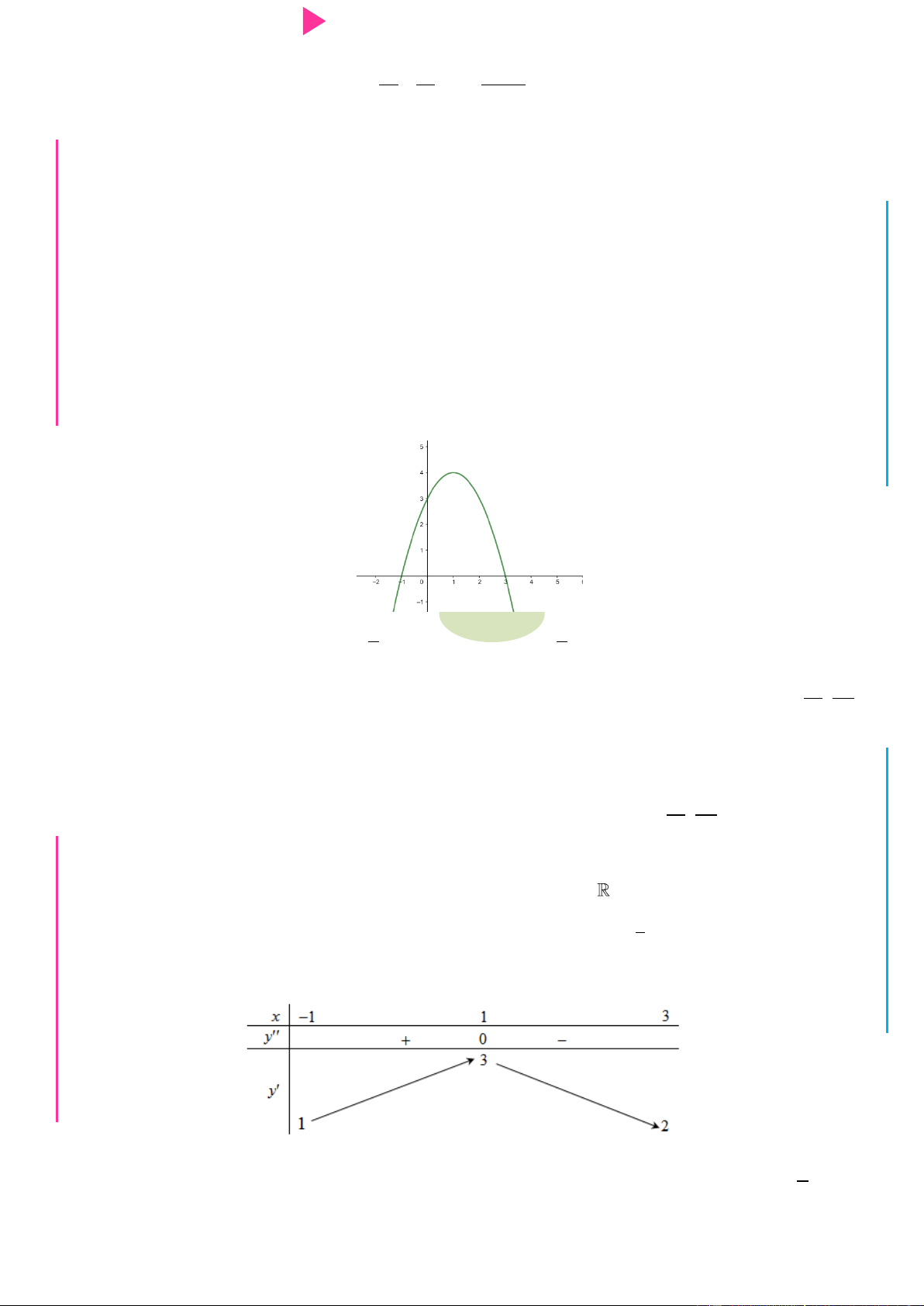
Cho hàm số y f x có đồ thị hàm số f x nhƣ hình vẽ Hàm số 2 2 x y f x e
nghịch biến trên khoảng nào cho dƣới đây? A. 2 ;0 . B. 0; . C. ; . D. 1 ; 1 .
NGUYỄN CÔNG ĐỊNH | 2
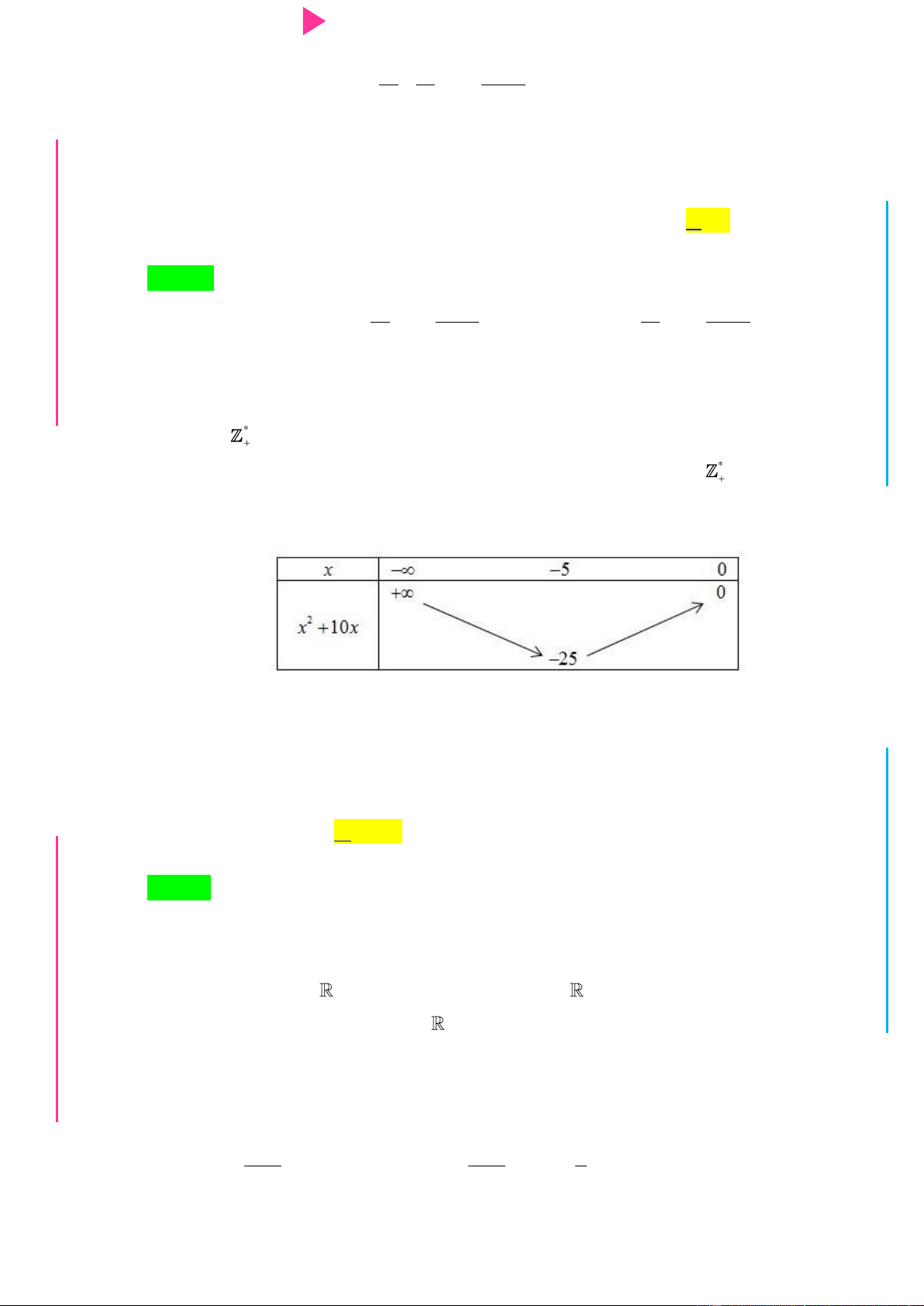
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Câu 4.
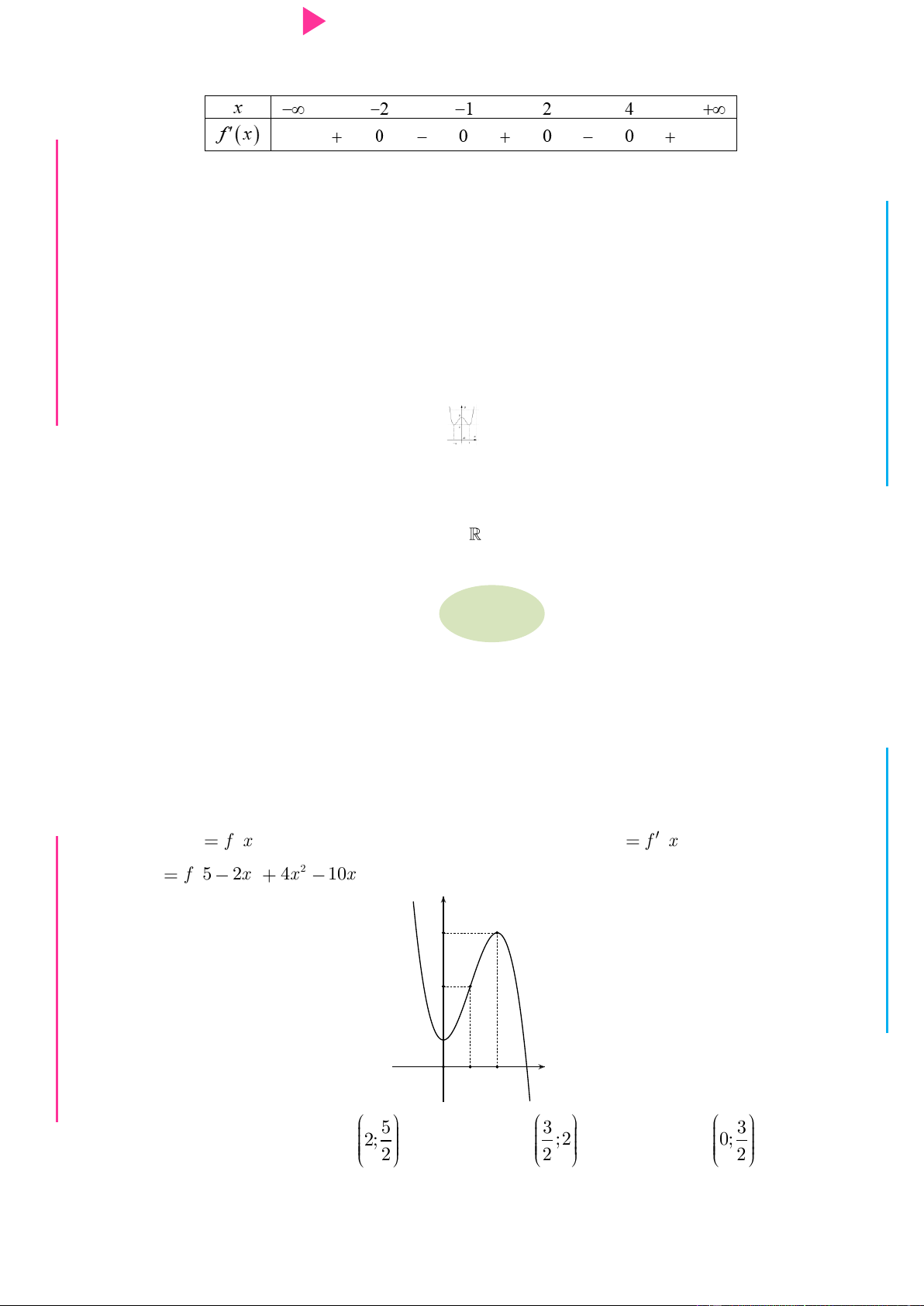
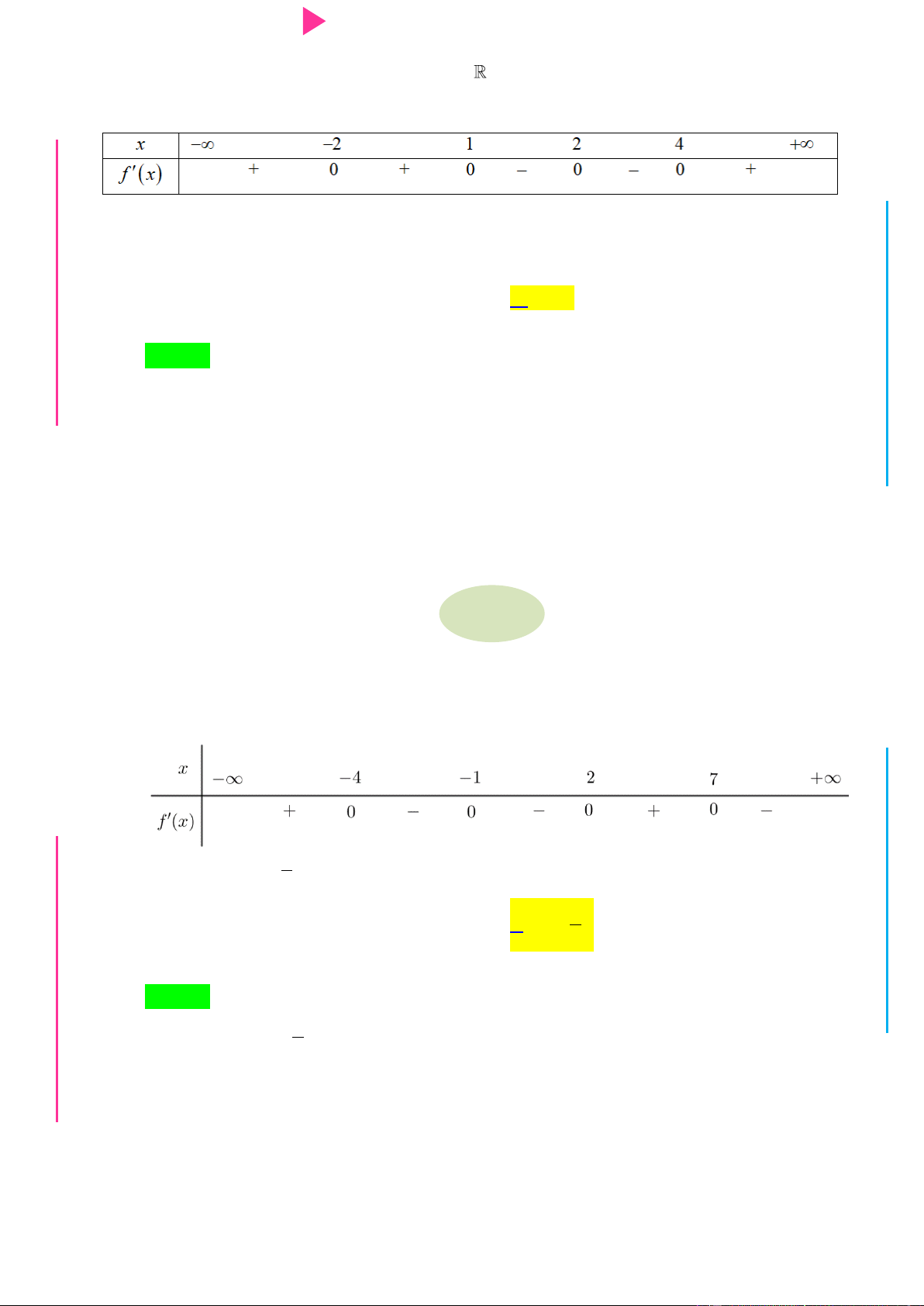
Cho hàm số y f x có bảng xét dấu của đạo hàm nhƣ sau Hàm số y 2
f x 2019 nghịch biến trên khoảng nào trong các khoảng dƣới đây? A. 4 ;2 . B. 1 ;2 . C. 2 ; 1 . D. 2; 4 . Câu 5.
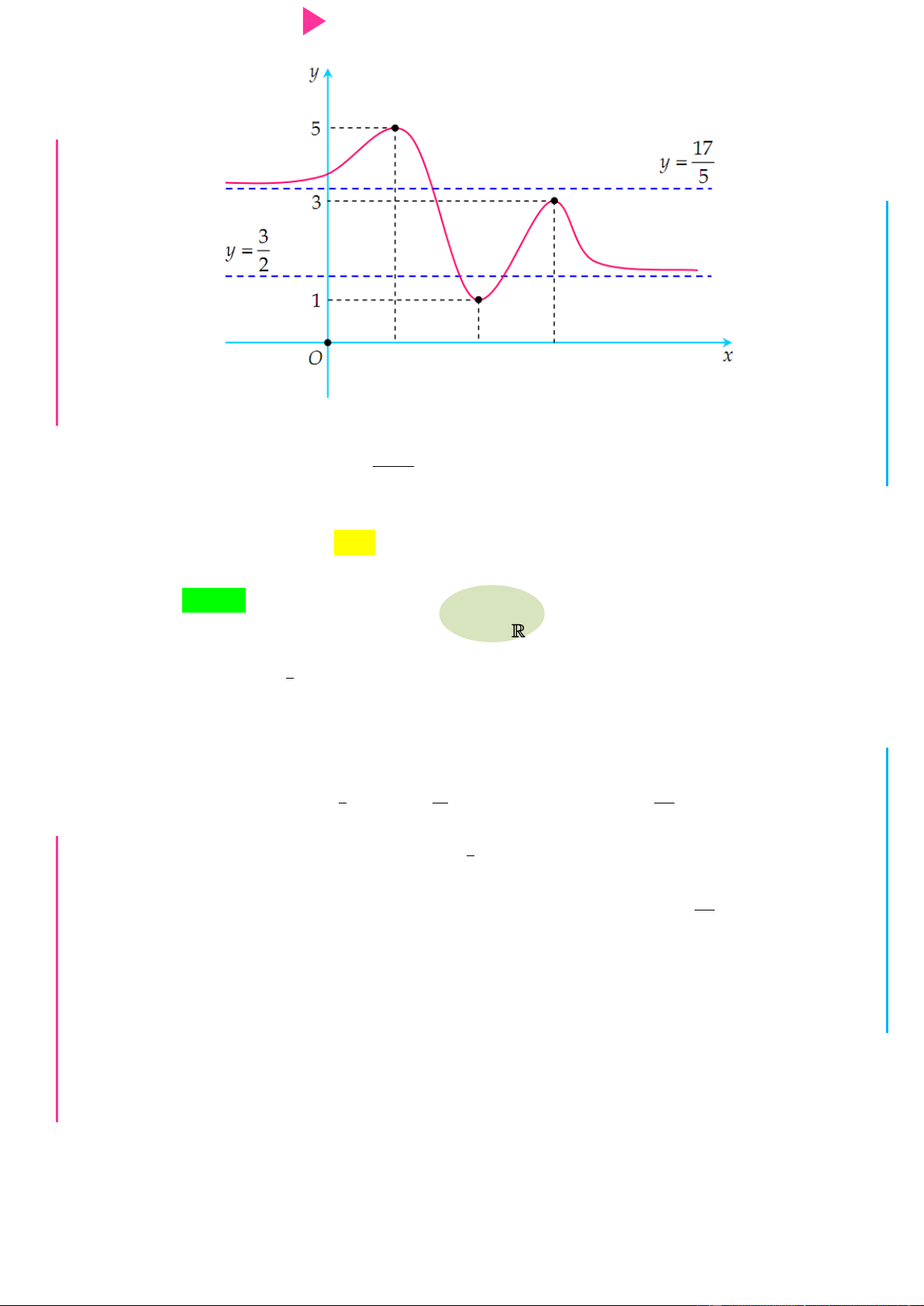
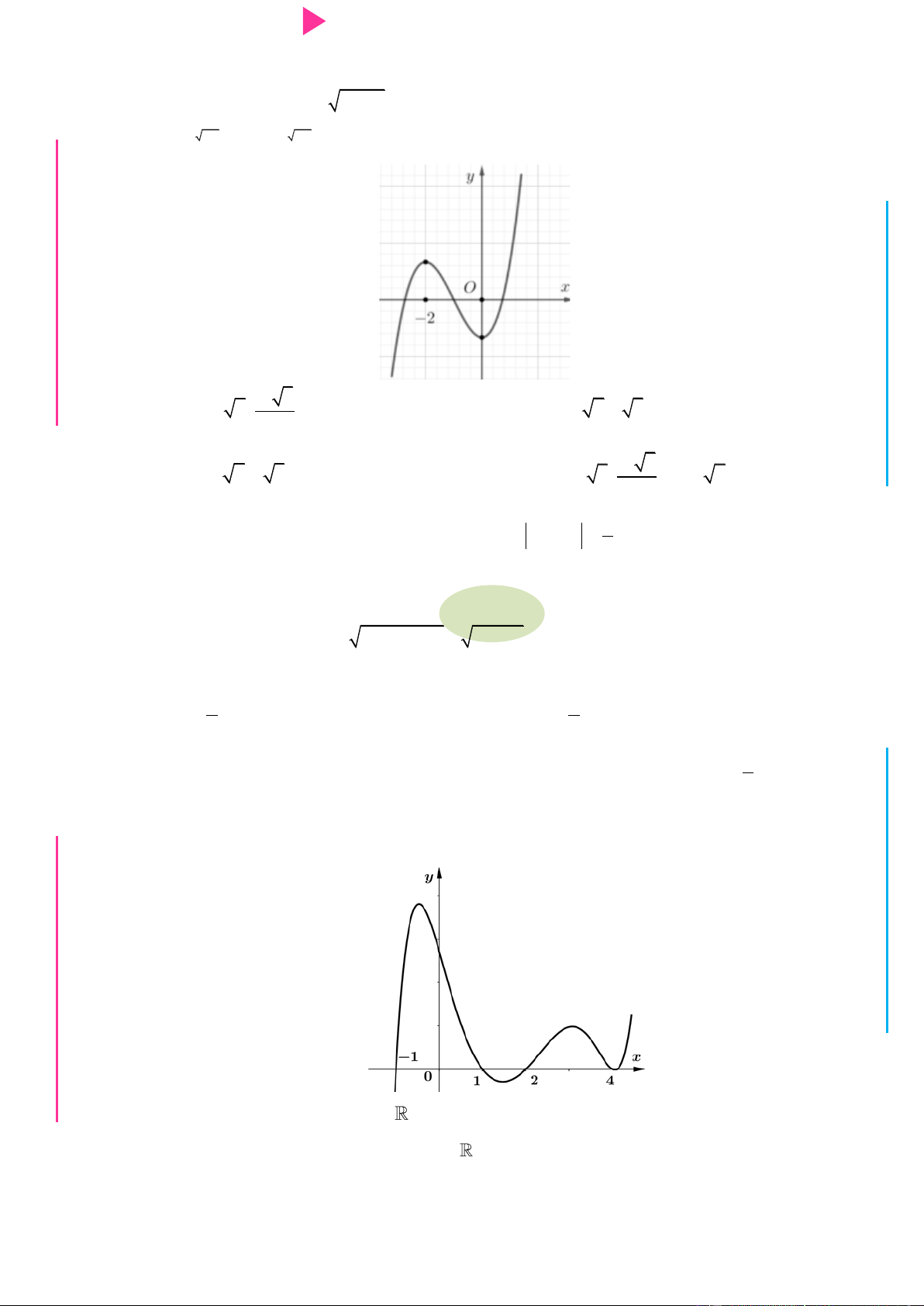
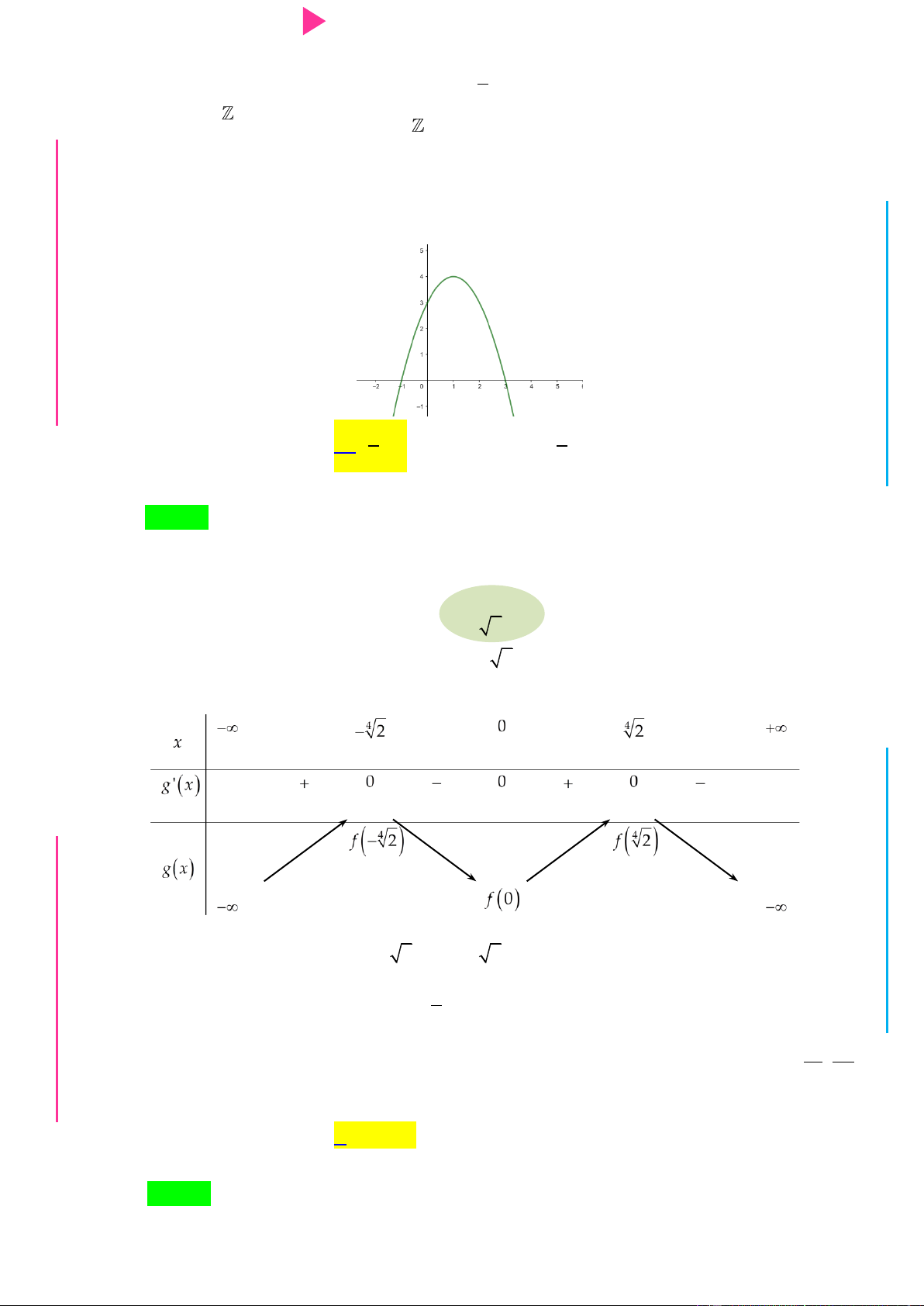
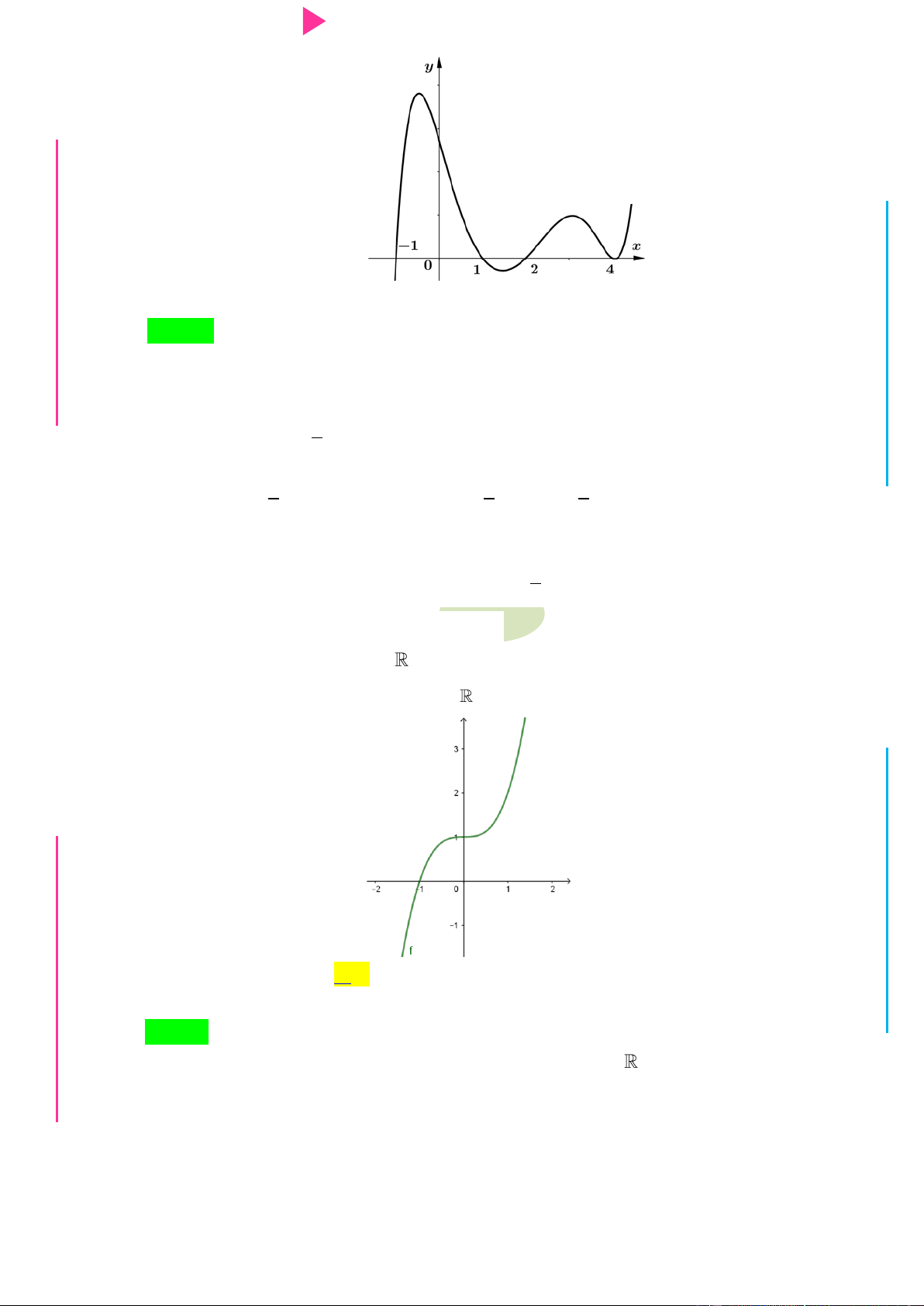
Cho hàm số f x có đồ thị nhƣ hình dƣới đây I Ơ
Hàm số g x ln f x đồng biến trên khoảng nào dƣới đây? M D A. ;0 .
B. 1; . C. 1 ; 1 . D. 0; . Ầ
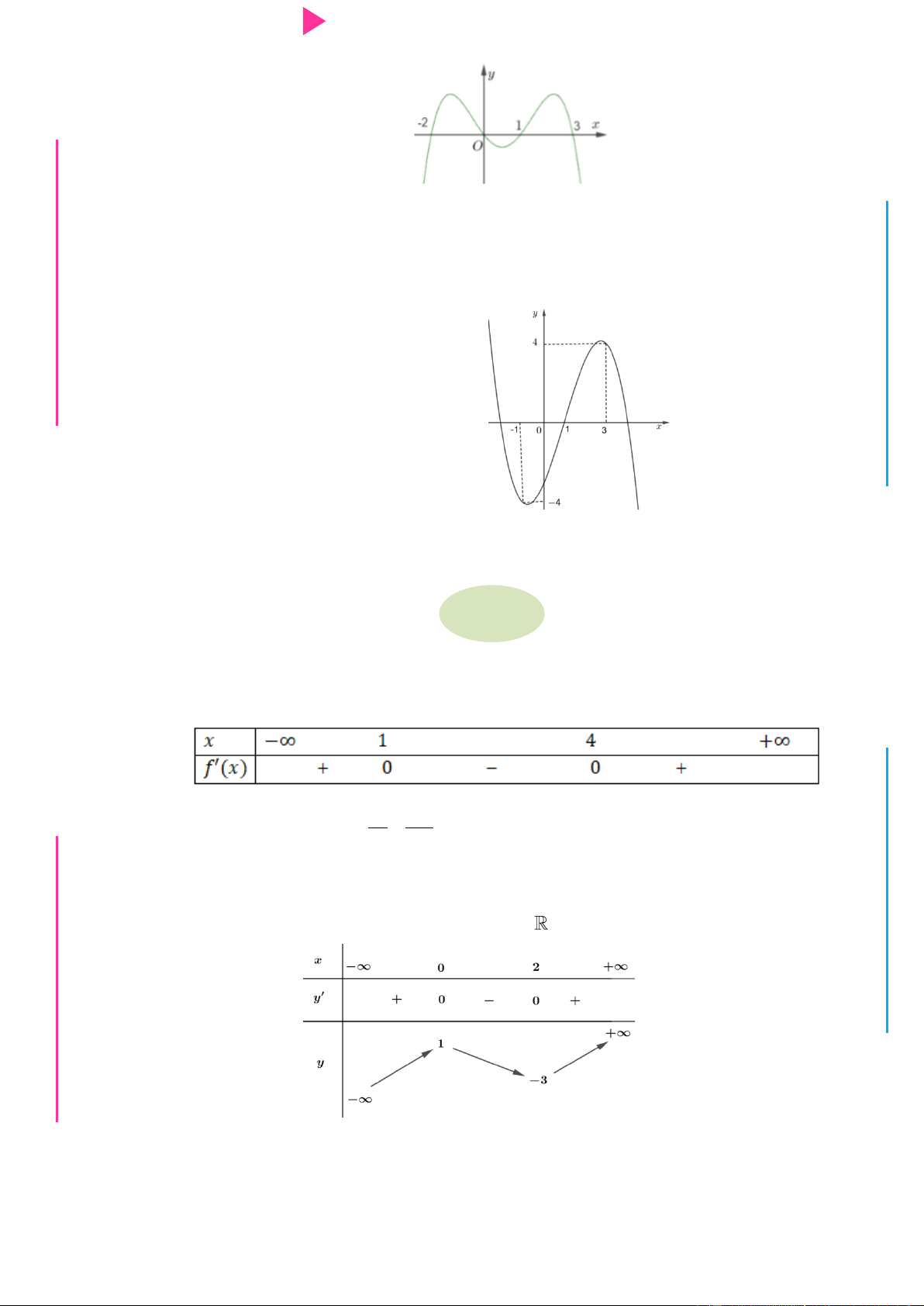
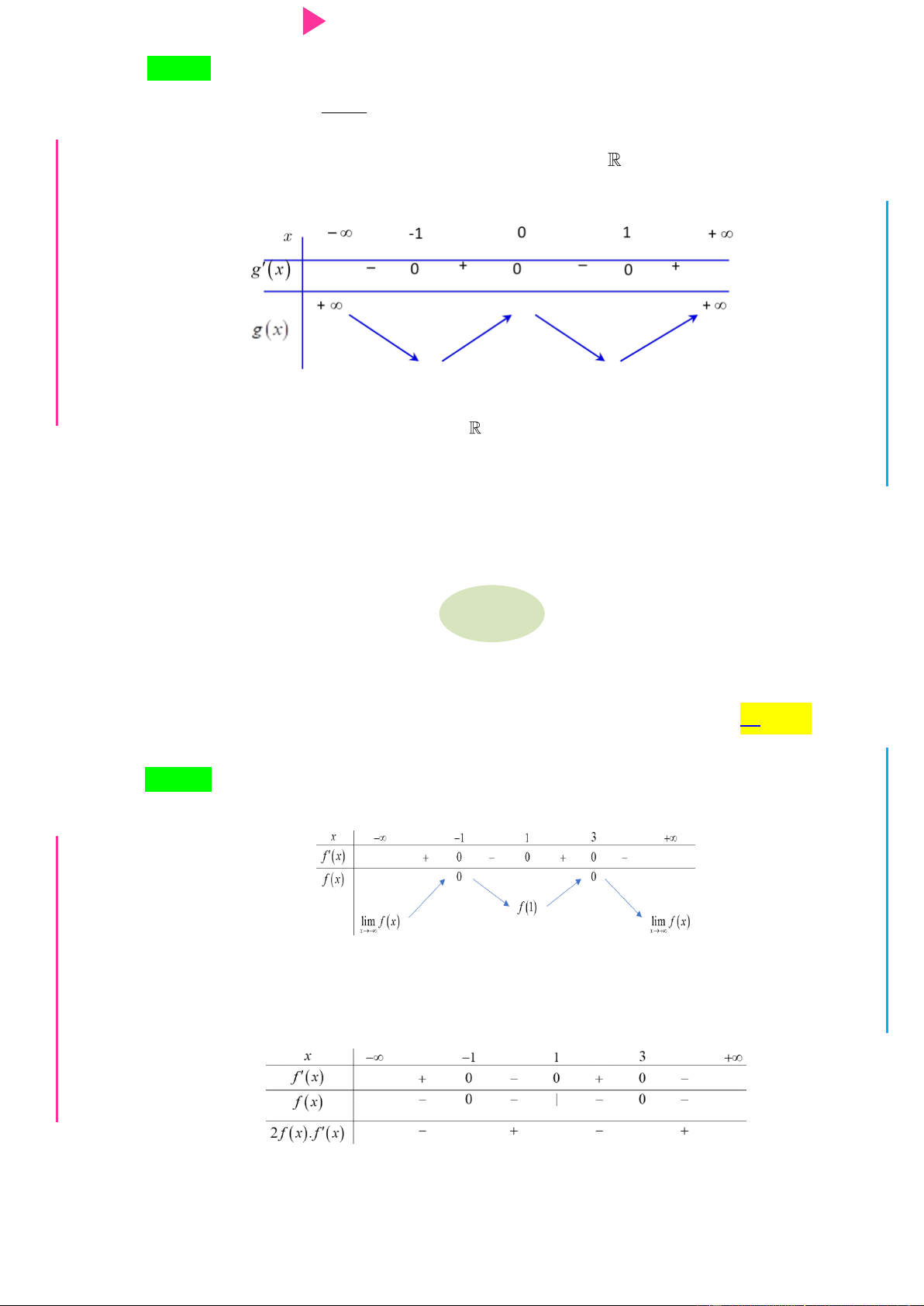
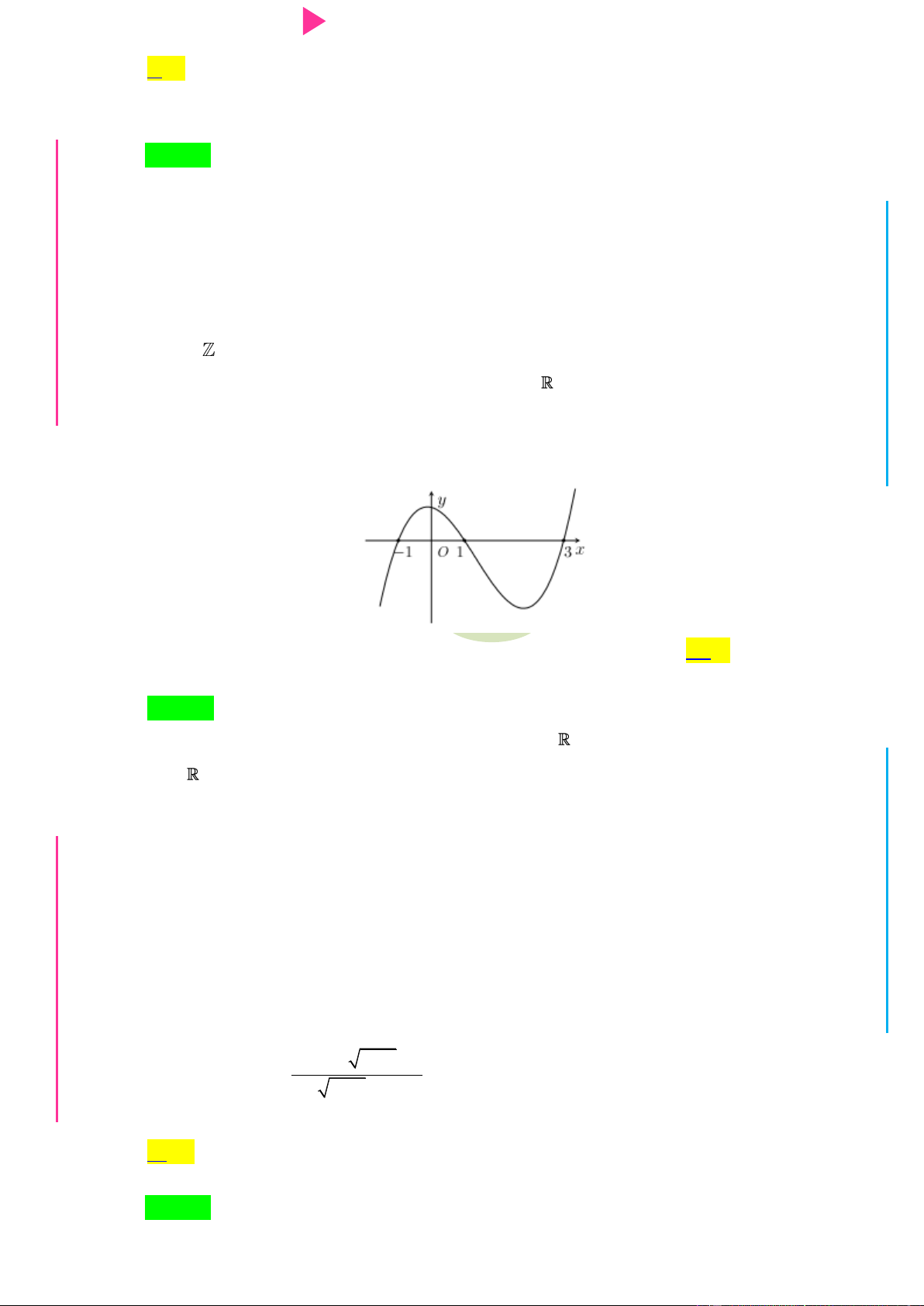
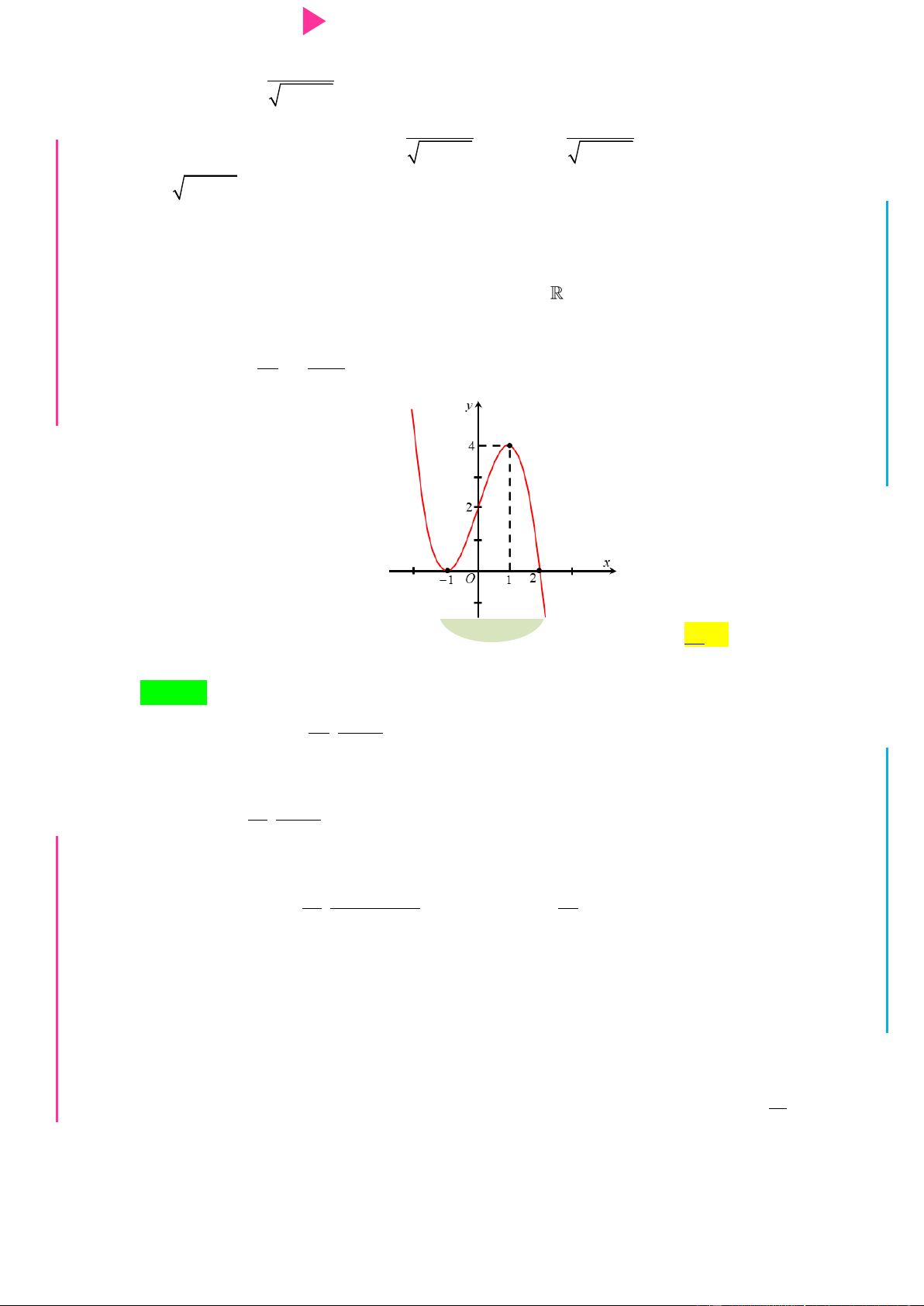
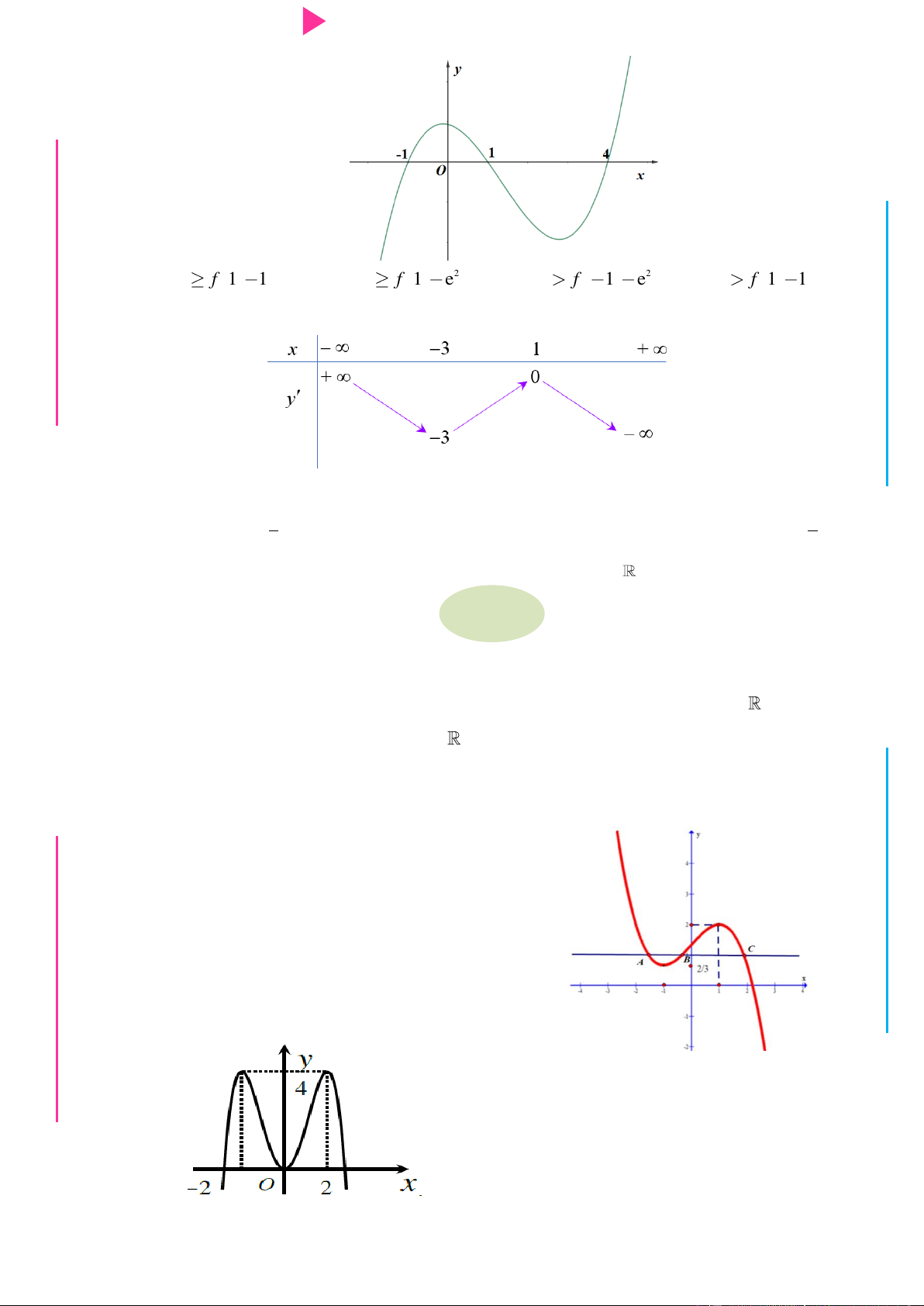
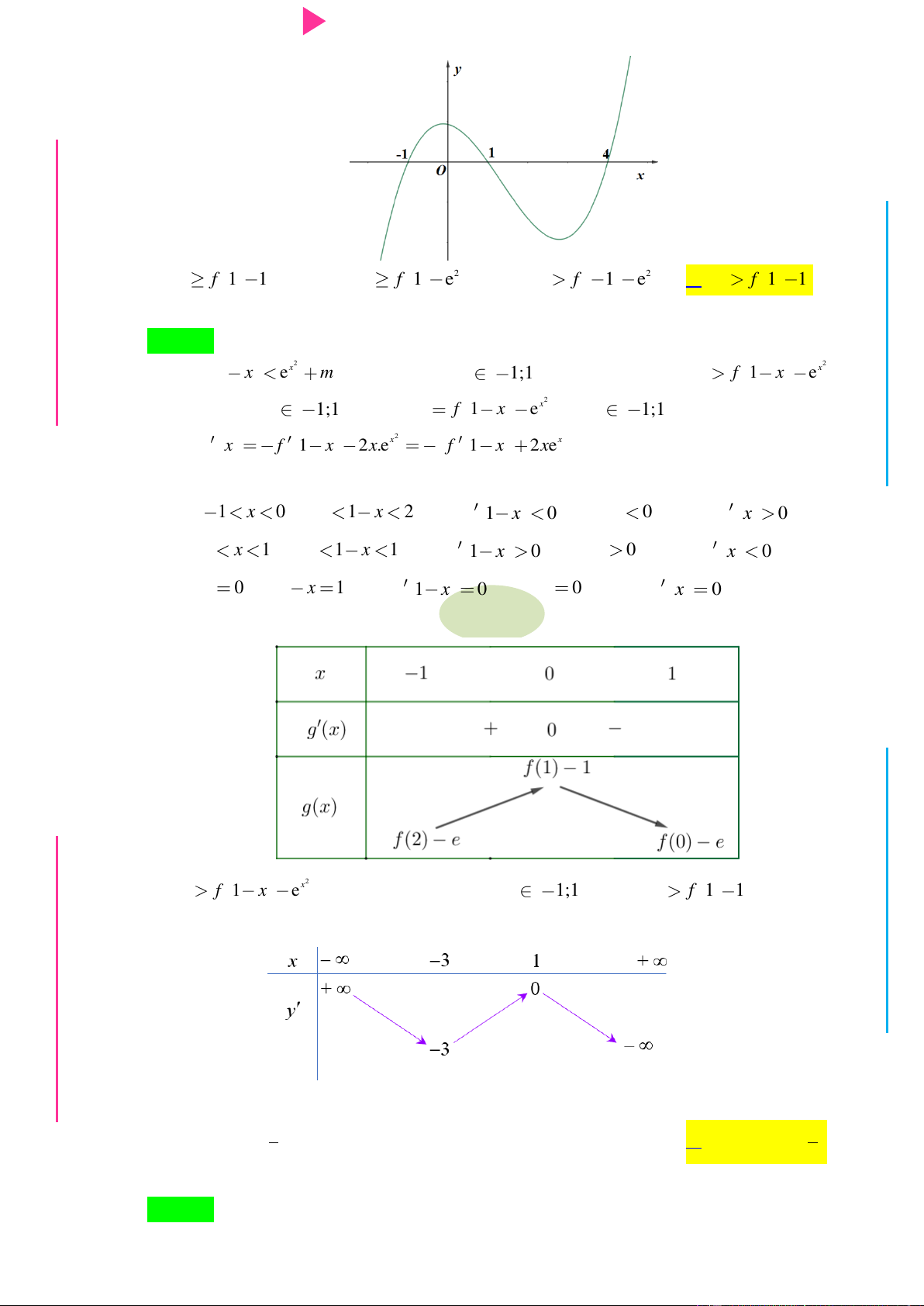
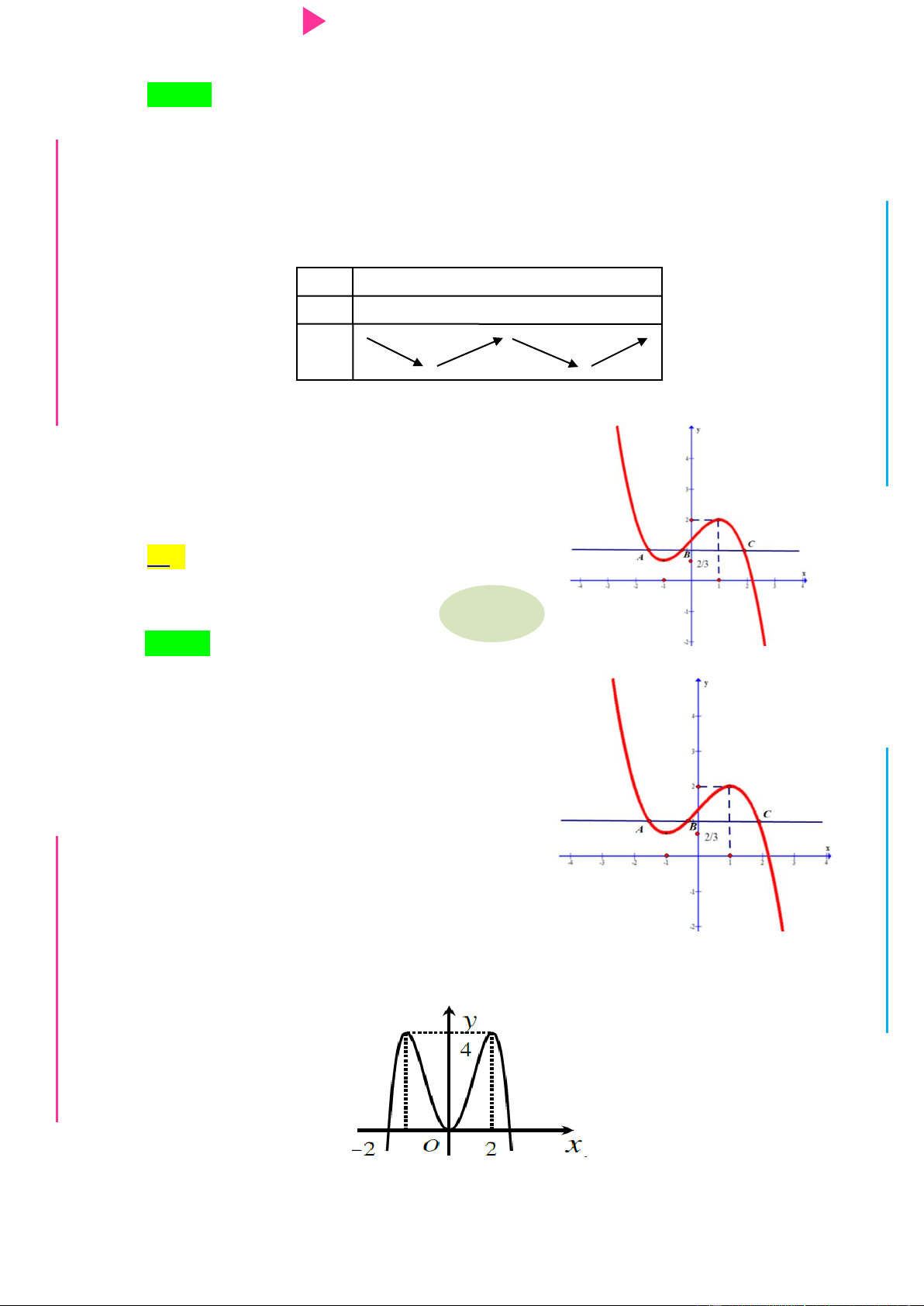
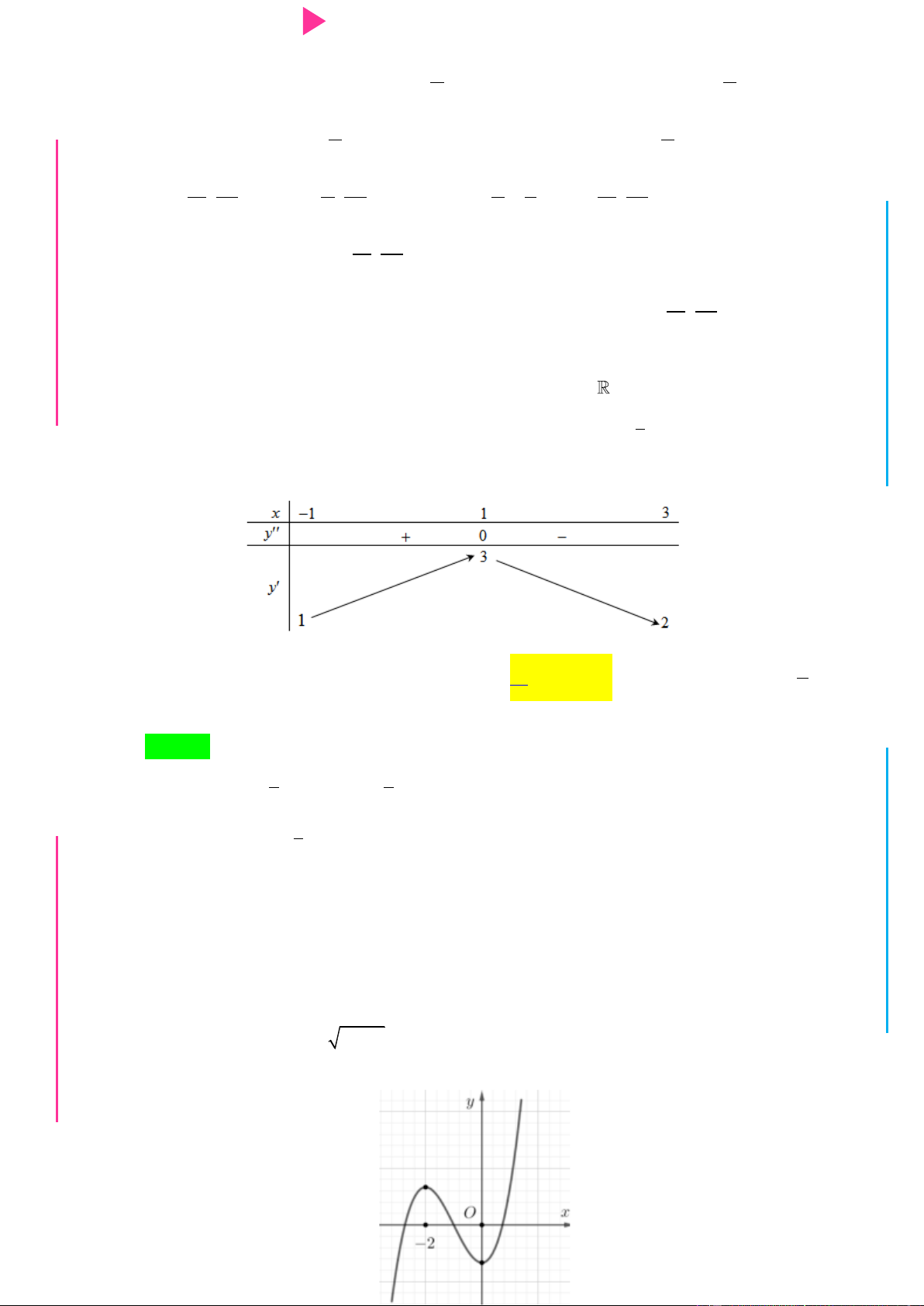
Đ Câu 6. Cho hàm số y f x có đạo hàm trên , thỏa mãn f 1 f
3 0 và đồ thị của hàm NHỊ Đ
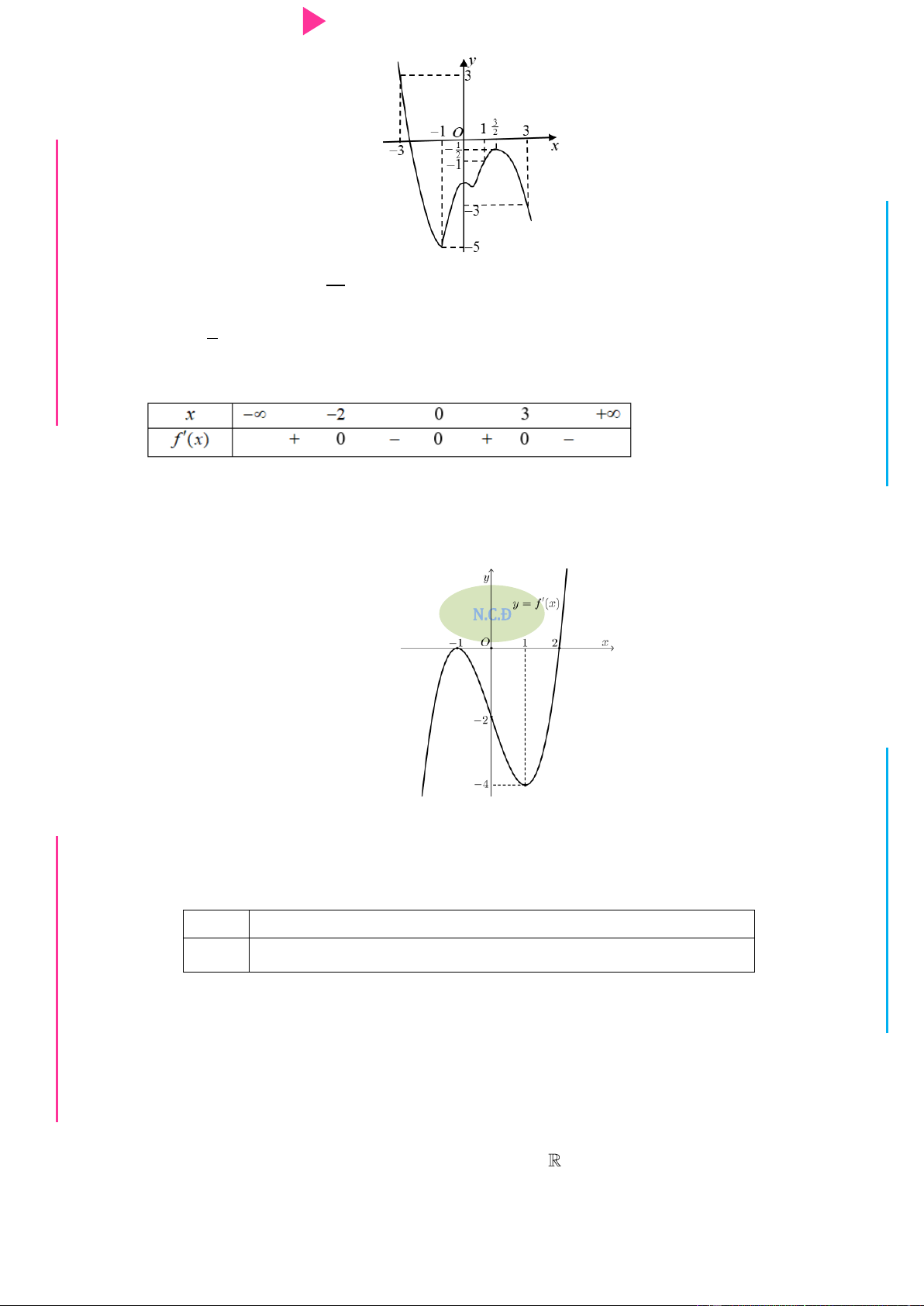
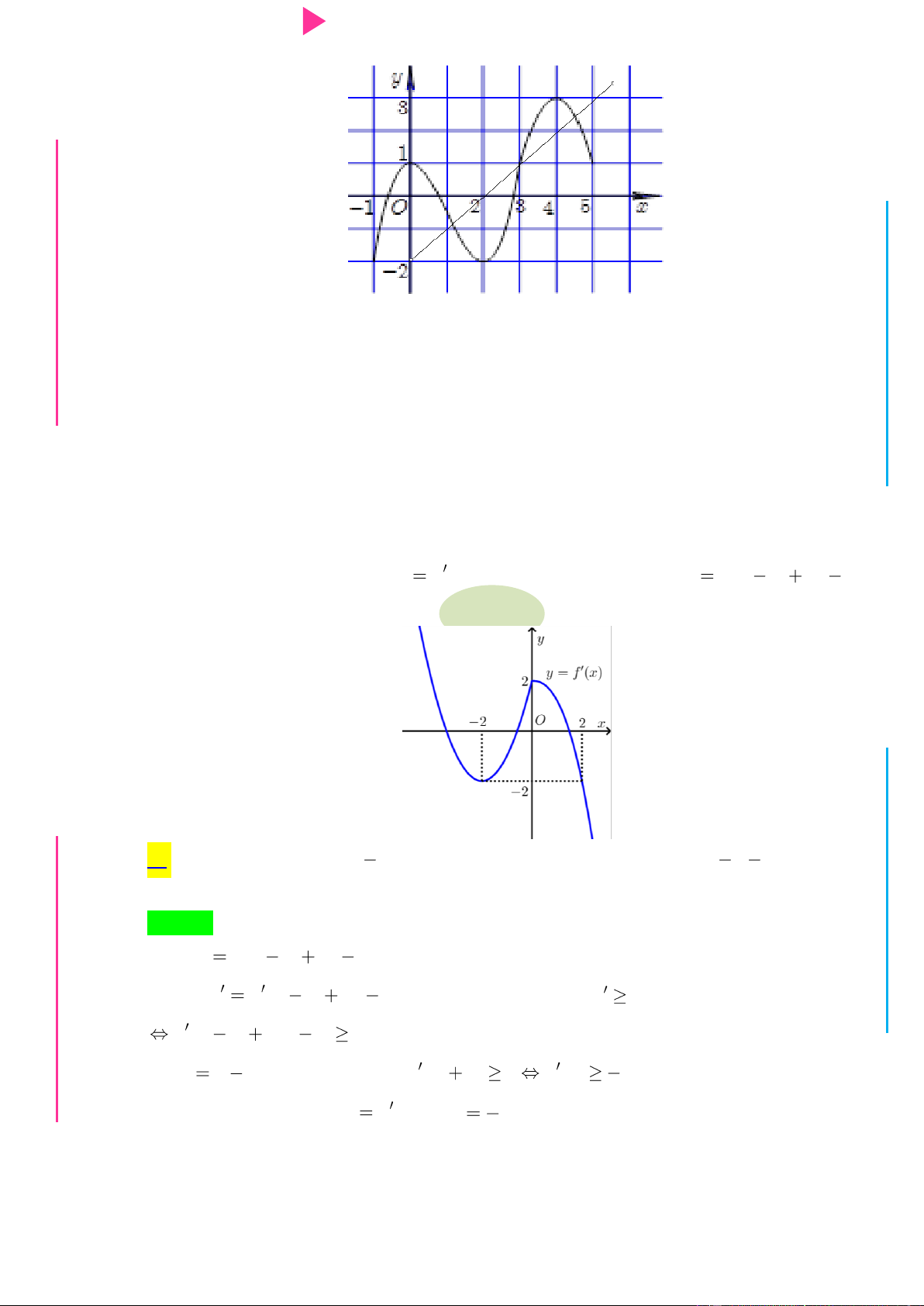
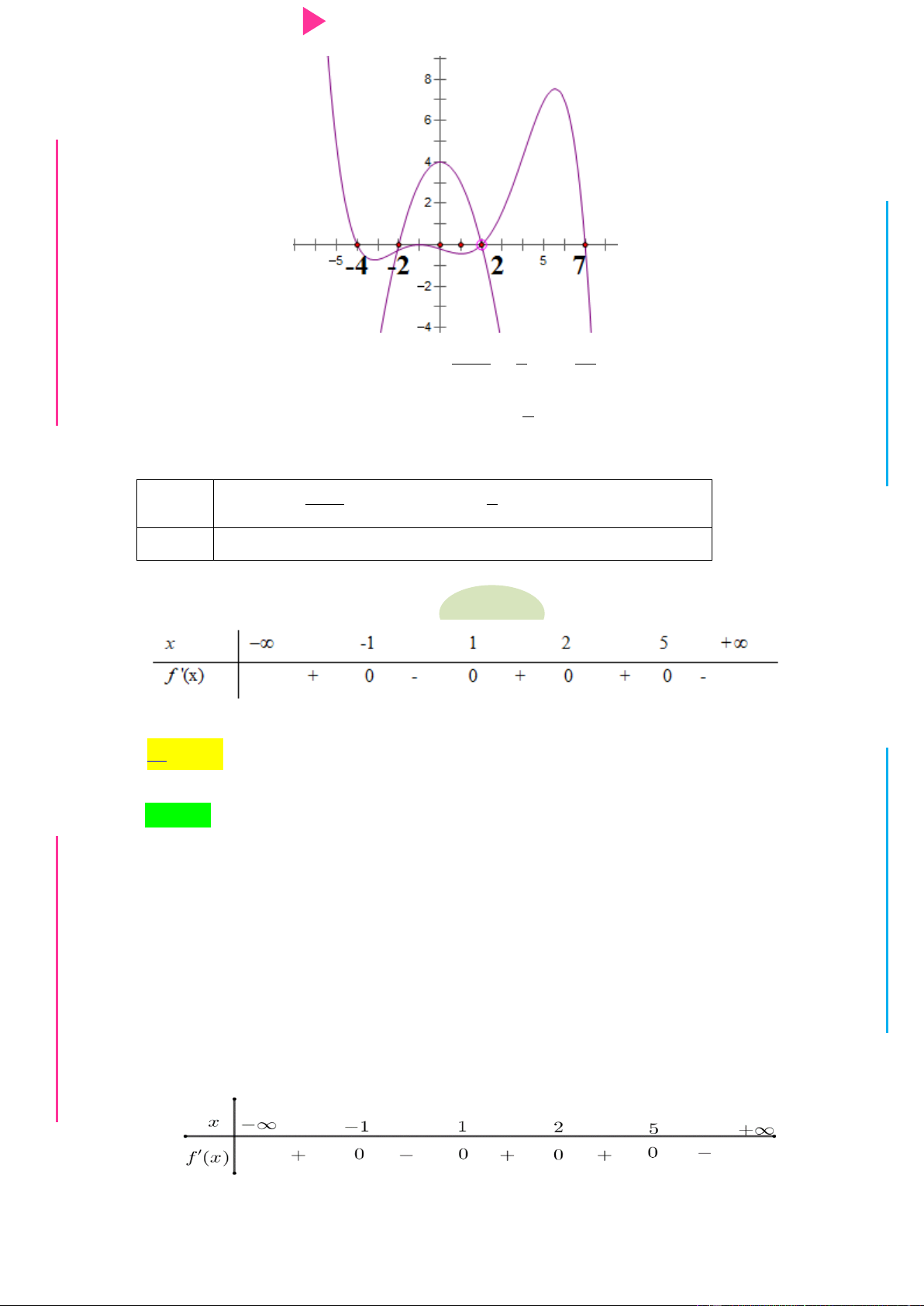
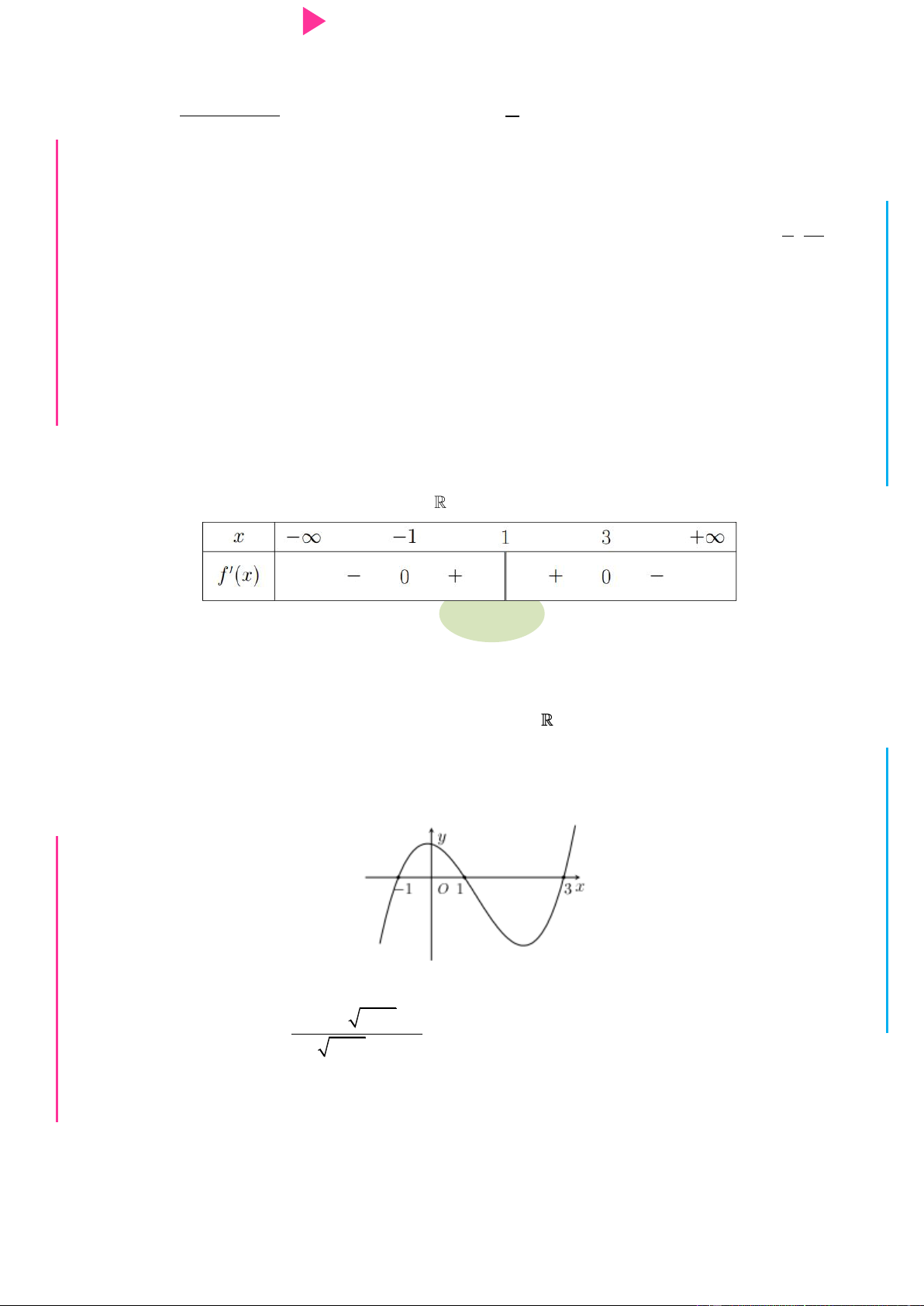
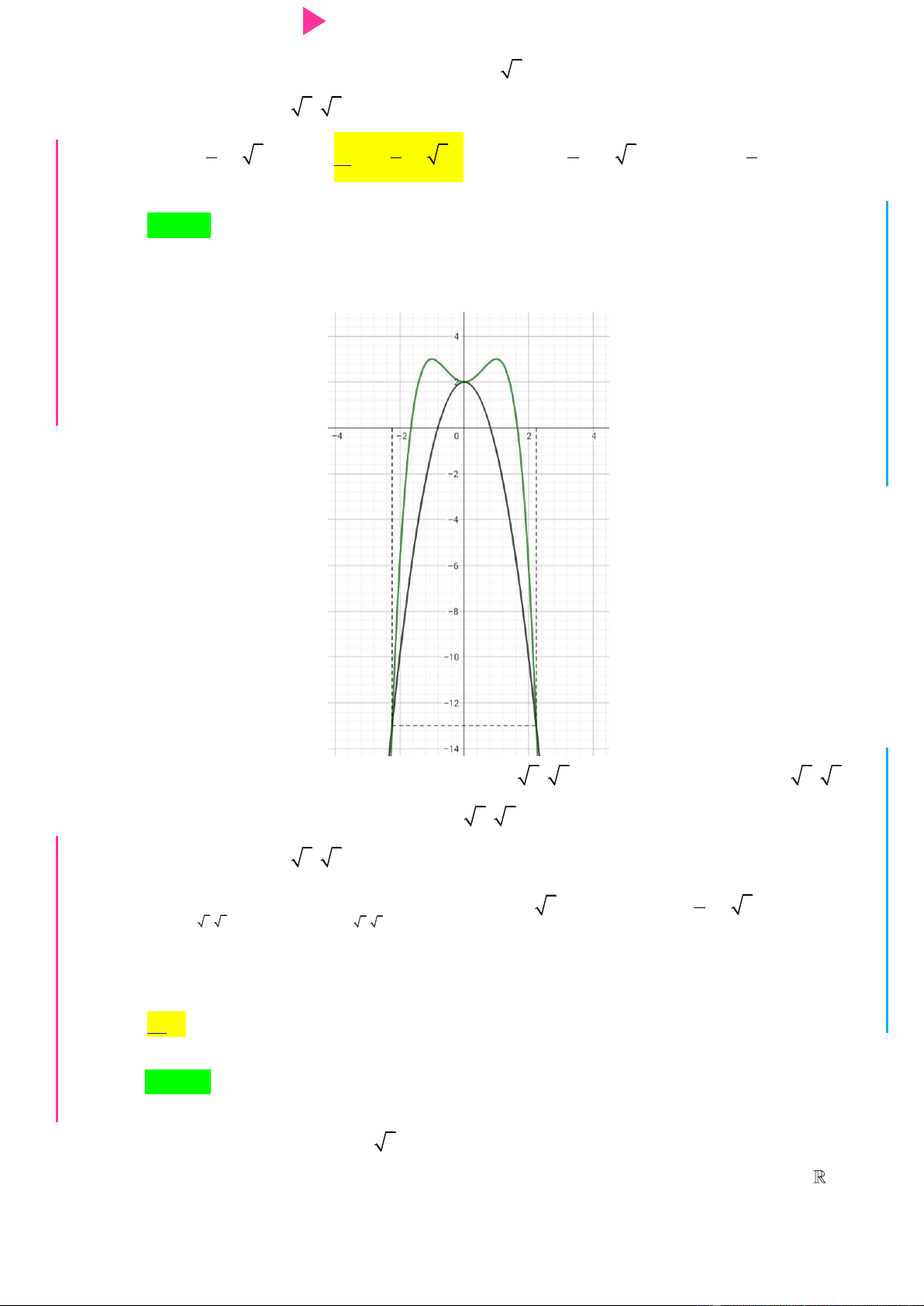
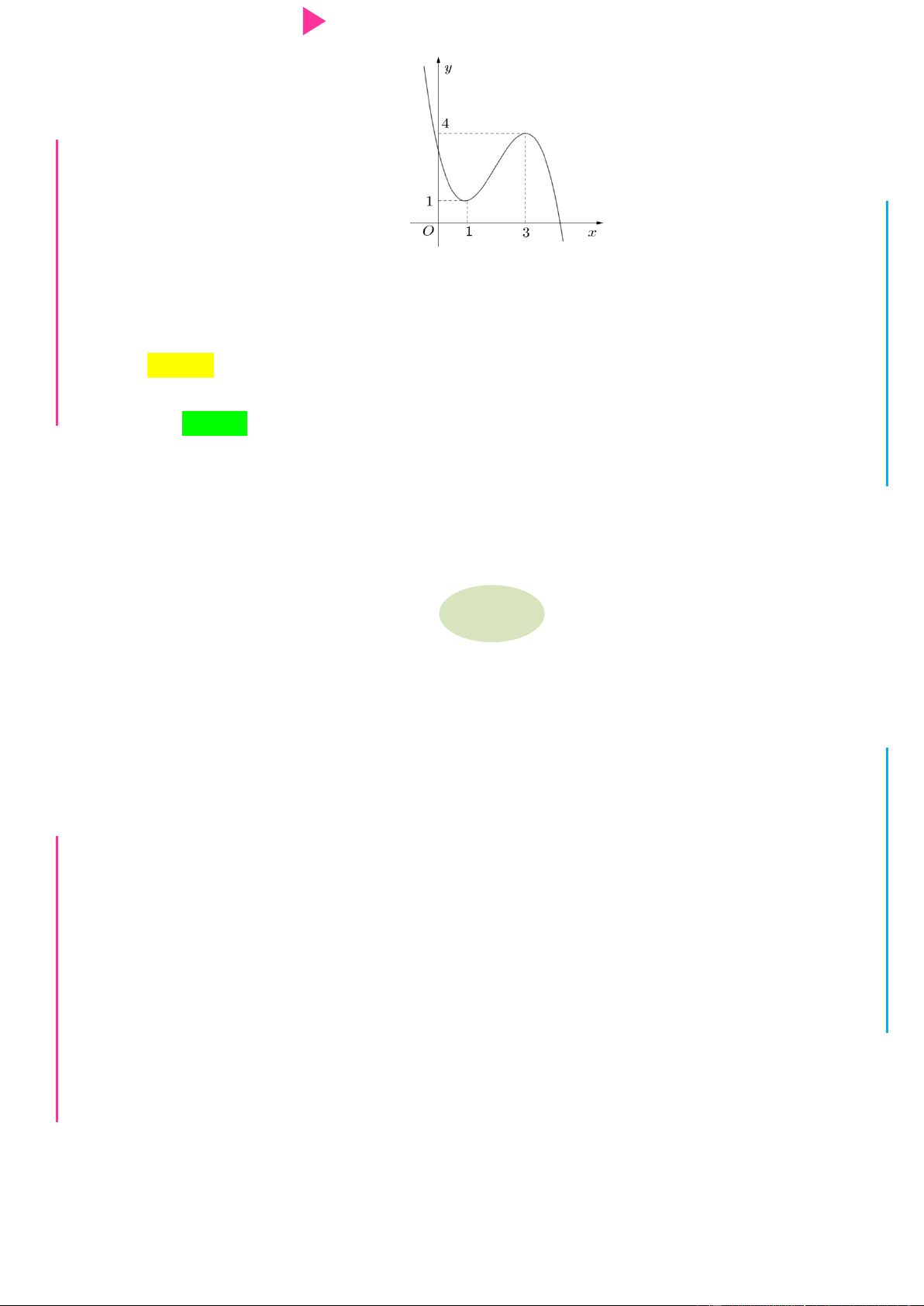
số y f x có dạng nhƣ hình dƣới đây. Hàm số 2 y f x
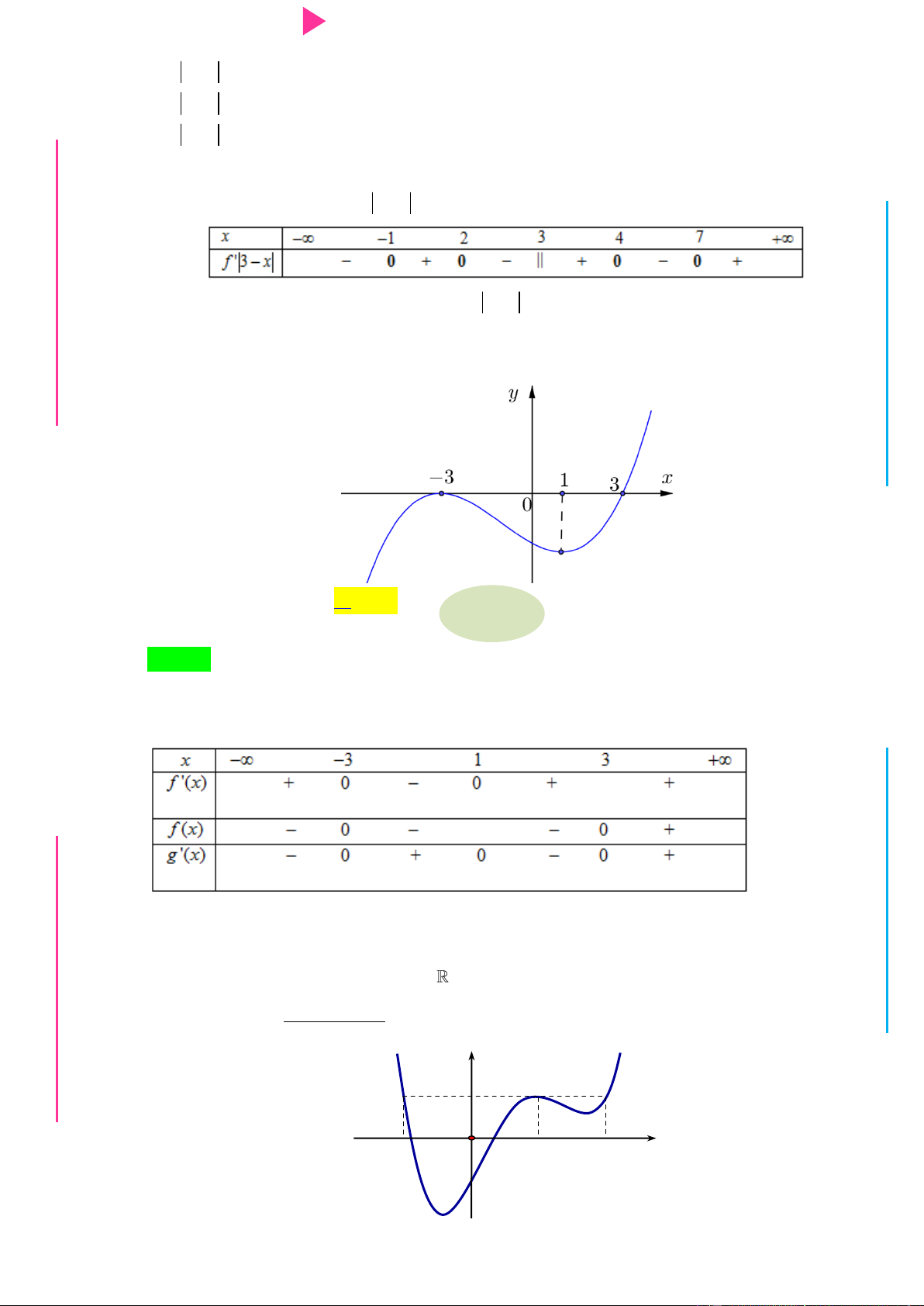
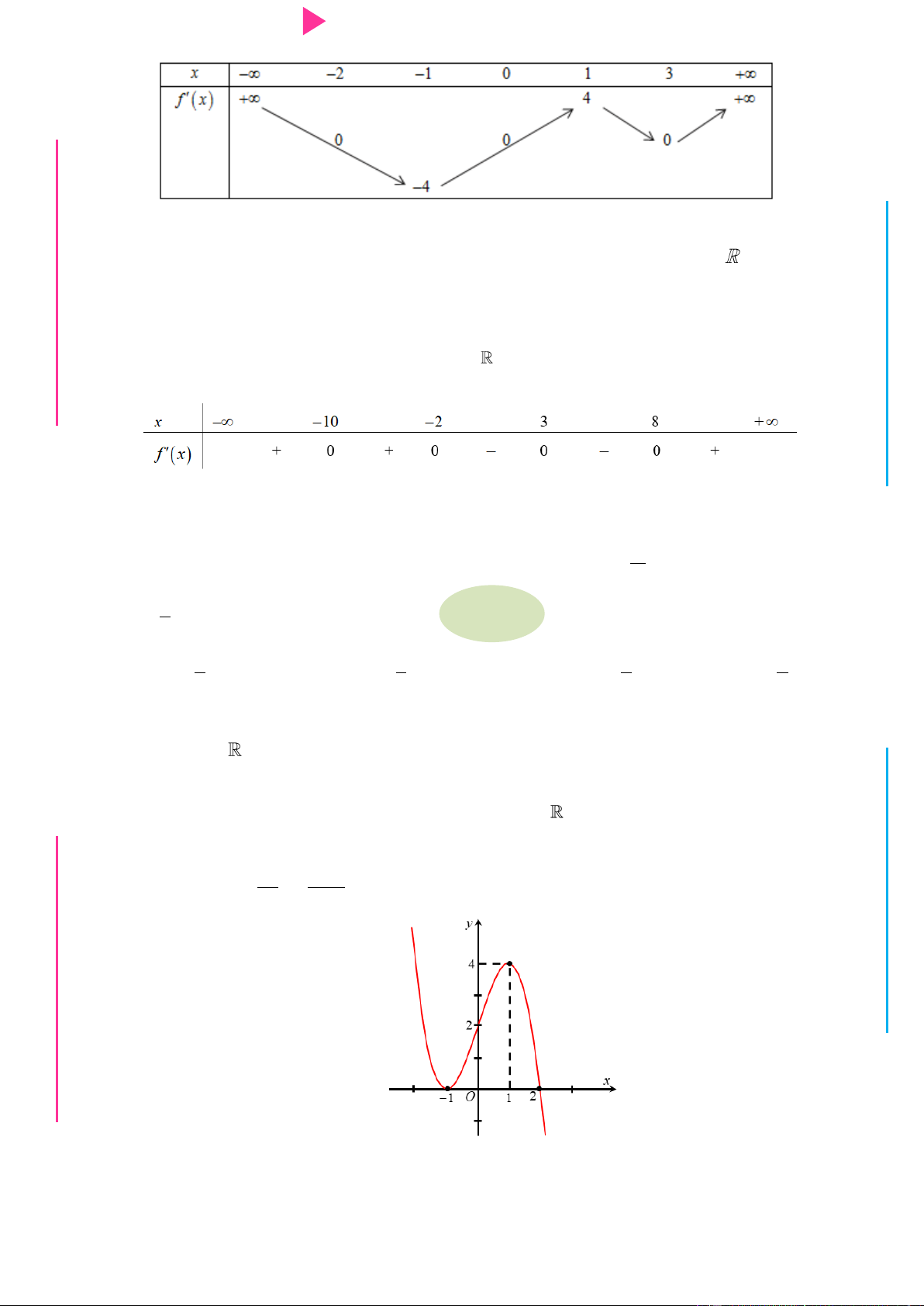
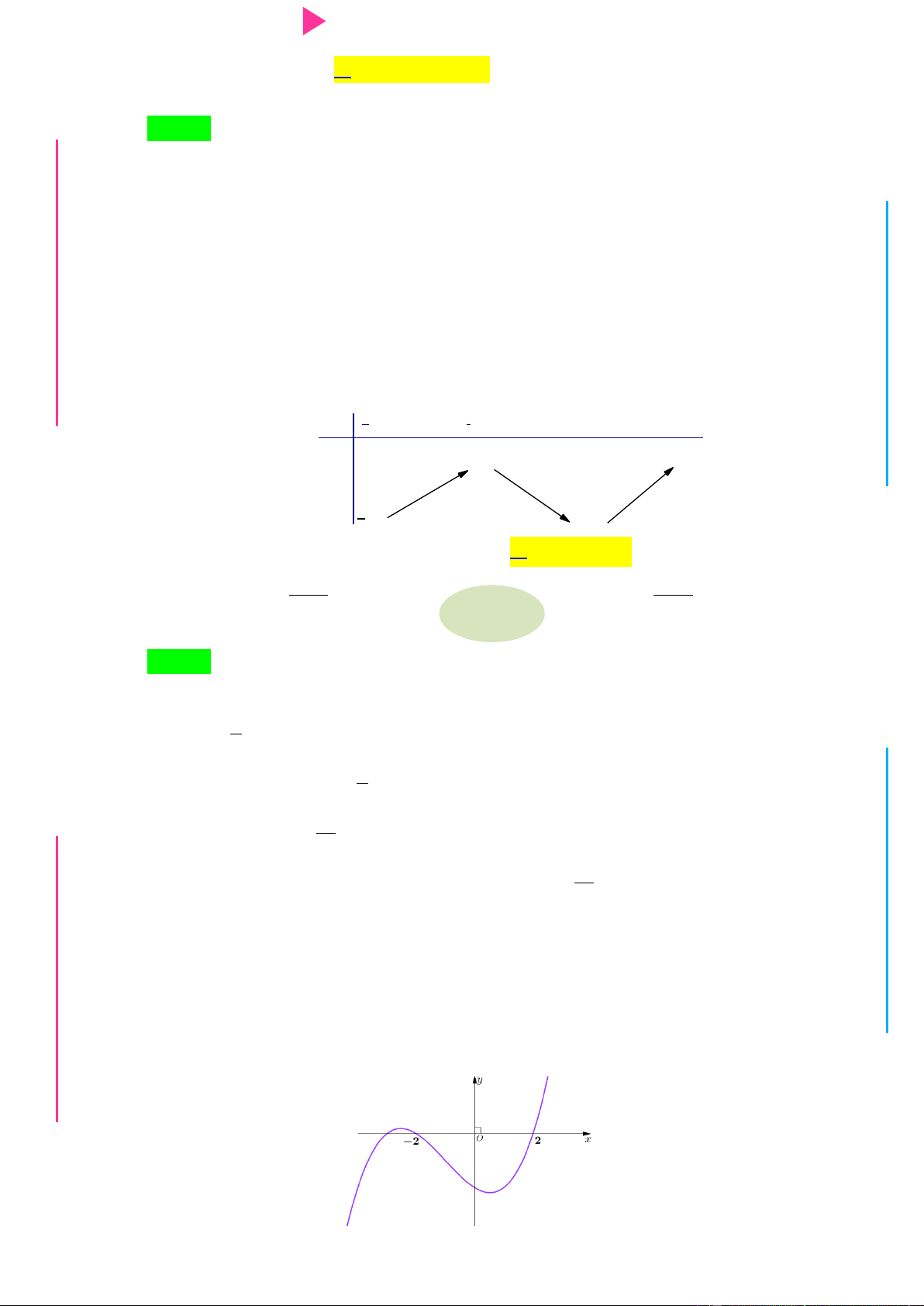
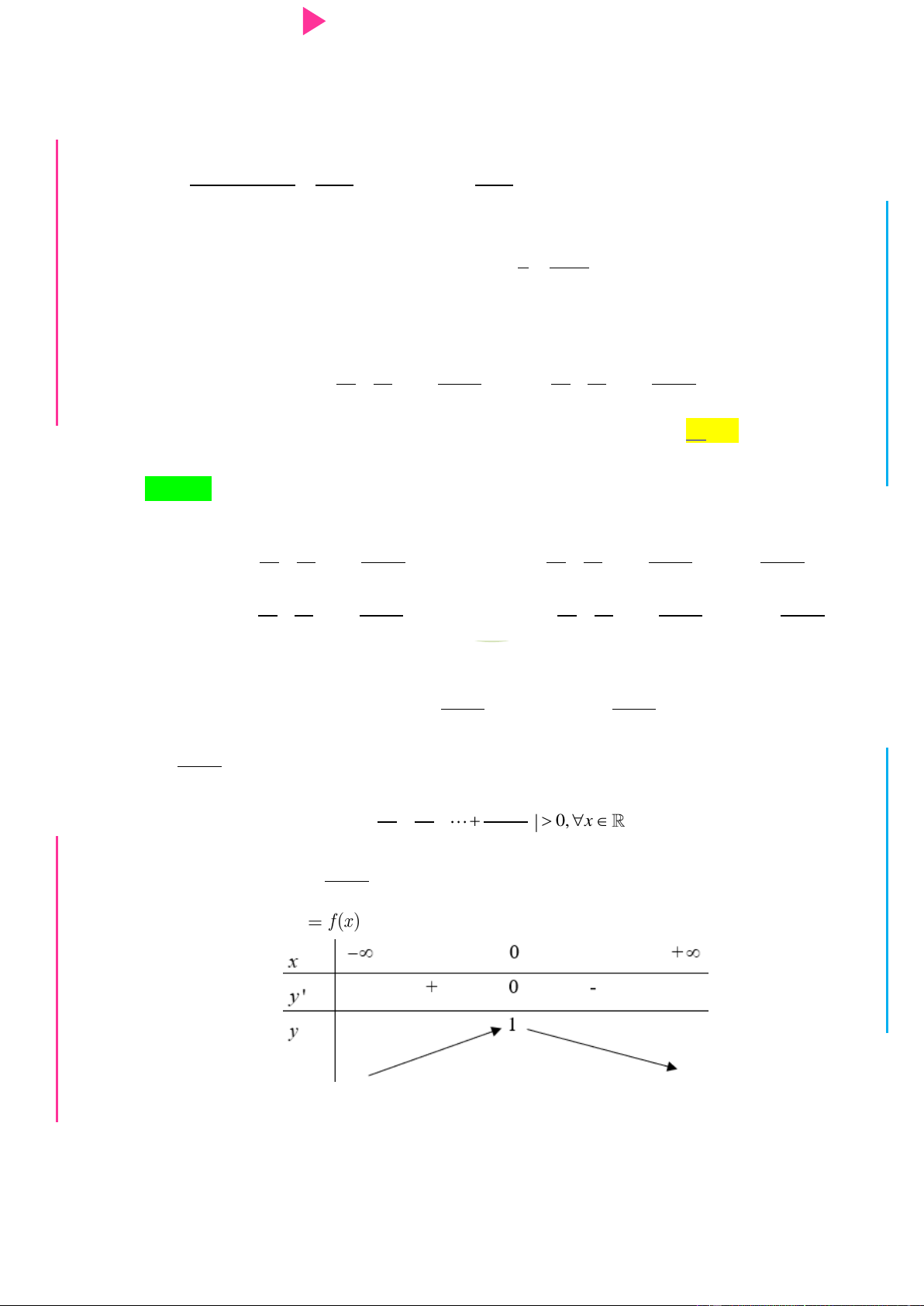
nghịch biến trên khoảng G THPT nào trong các khoảng sau? N.C.Đ NG y 4 CÔN Ờ 3 N Ễ 2 Y TRƢ f(x)=-X^3+3X^2+X-3 1 x -3 -2 -1 1 2 3 GU N -1 N -2 -3 -4 ÁO VIÊ A. 2 ;2 . B. 0; 4 . C. 2 ; 1 . D. 1;2 .
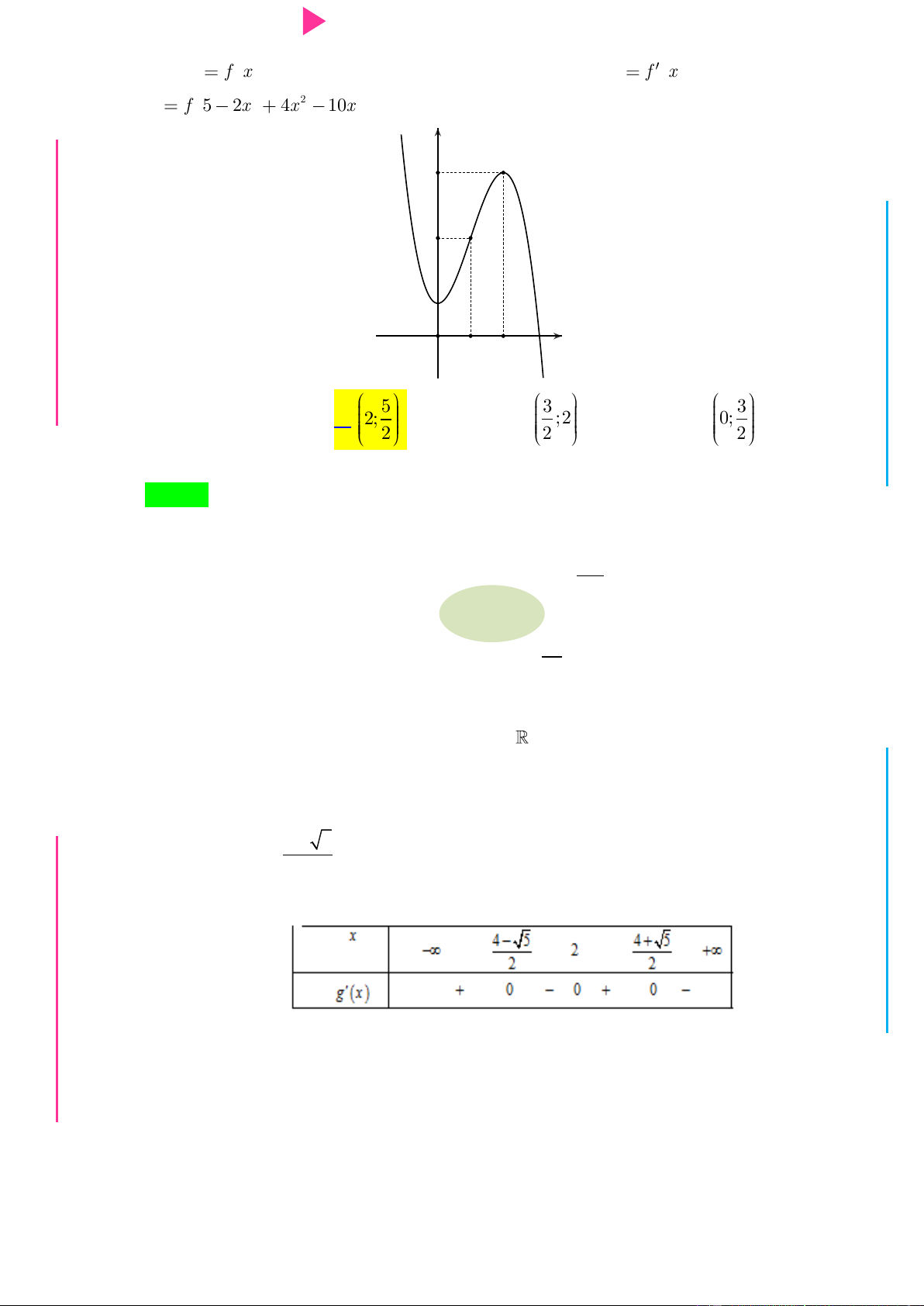
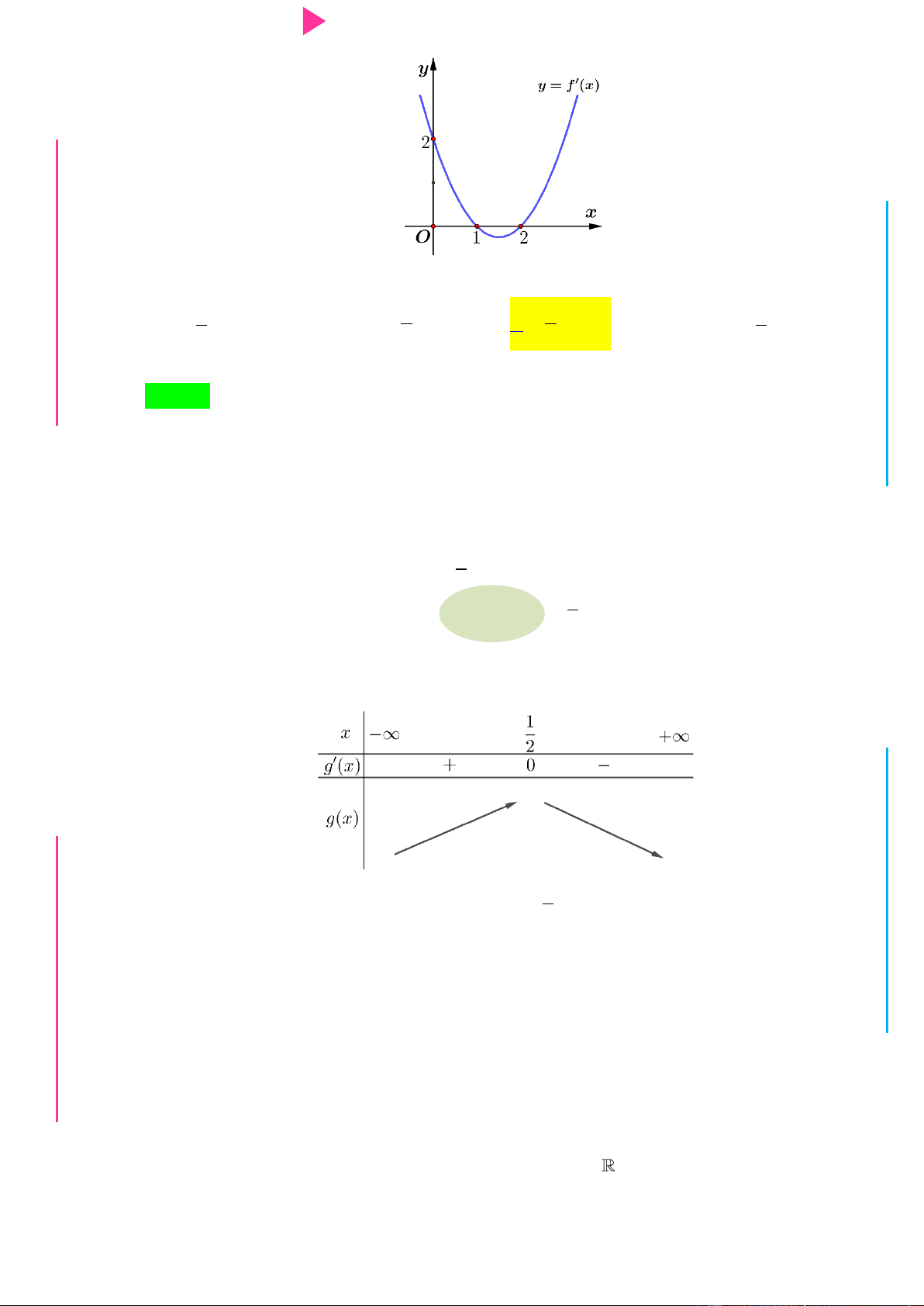
GI Câu 7. Cho y f x là hàm đa thức bậc 4, có đồ thị hàm số y f x nhƣ hình vẽ. Hàm số 2 y f 5 2x 4x
10x đồng biến trong khoảng nào trong các khoảng sau đây? y 5 3 1 O 1 2 x 5 3 3 A. 3; 4 . B. 2; . C. ;2 . D. 0; . 2 2 2 Câu 8.
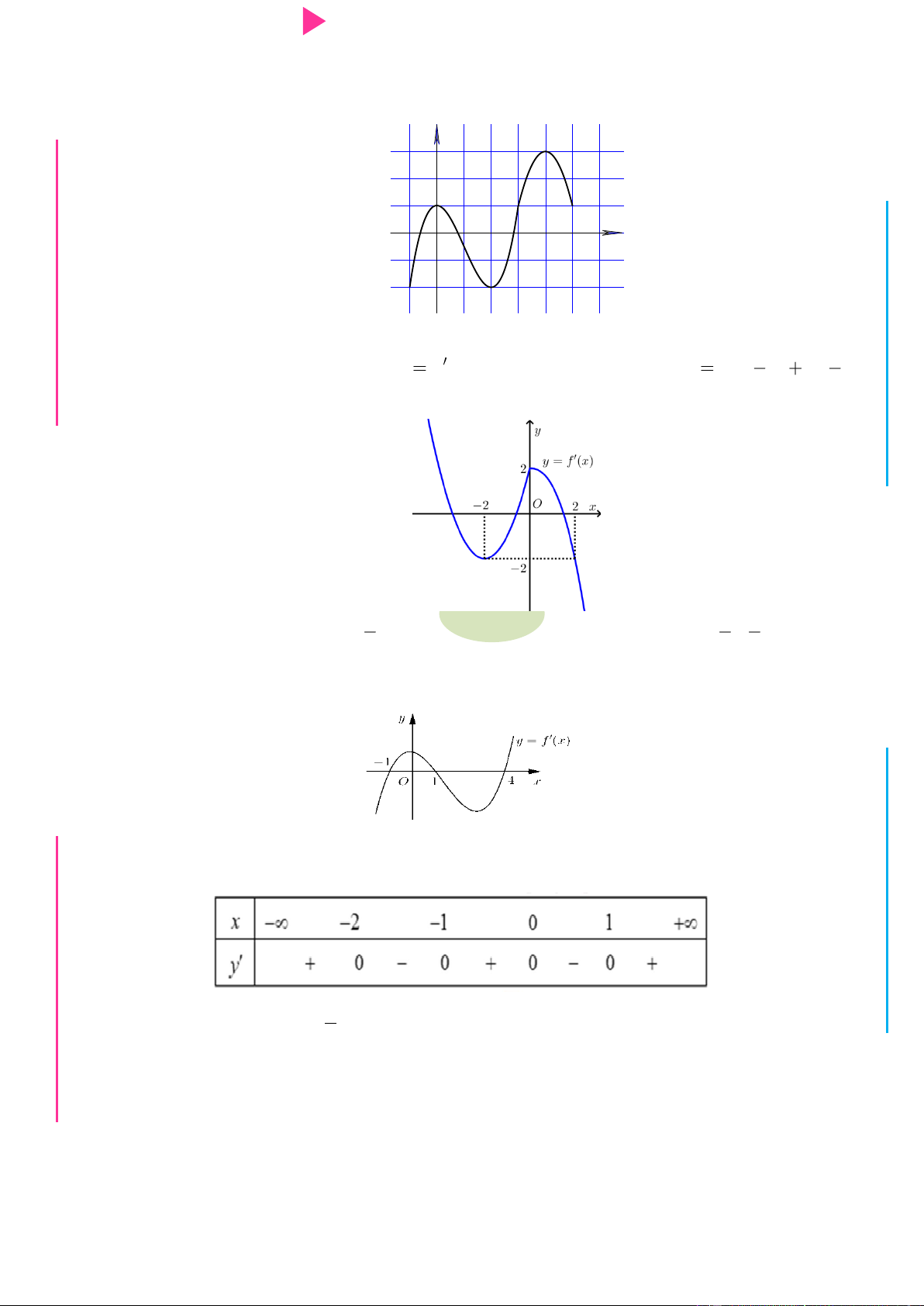
Cho hàm số bậc bốn y f x có đồ thị hàm số y f x nhƣ hình vẽ bên. Hàm số
g x f 2 x x
1 đồng biến trên khoảng
NGUYỄN CÔNG ĐỊNH | 3
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 1 A. 0 ;1 . B. 2 ; 1 . C. 2; . D. ; 2 . 2 Câu 9.
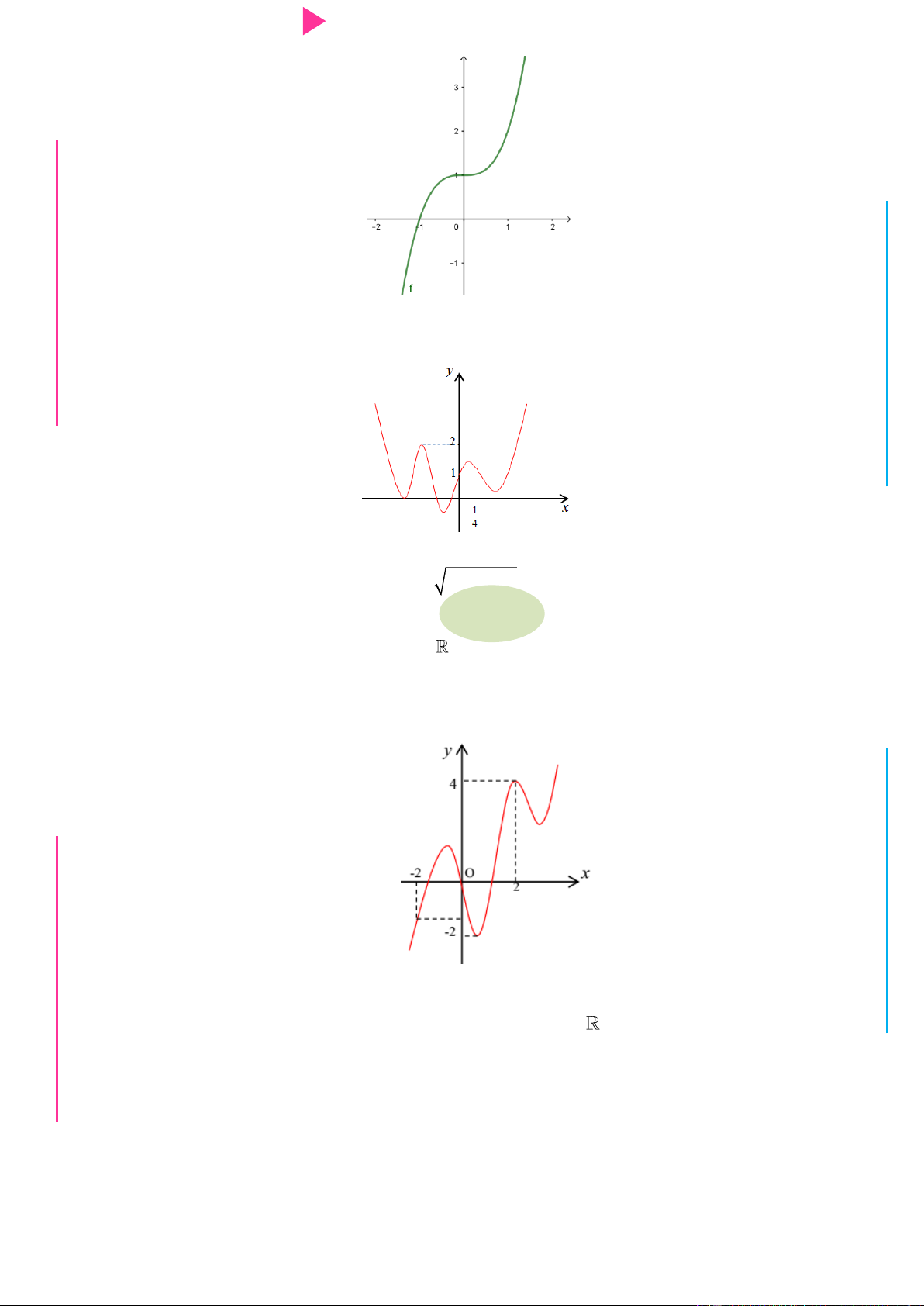
Cho hàm số f (x) , đồ thị hàm số y f (
x) nhƣ hình vẽ dƣới đây. I Ơ M D
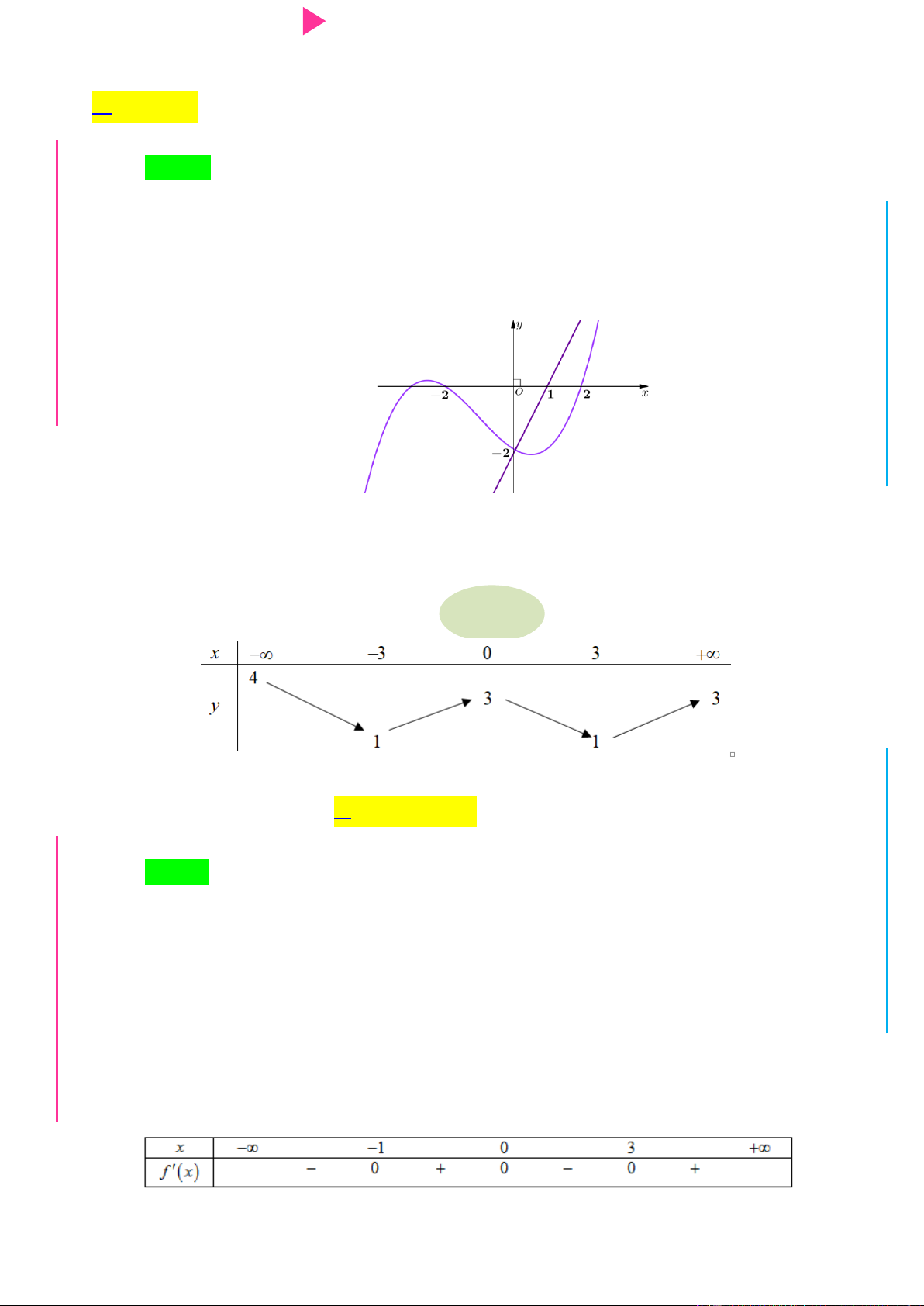
Hàm số y f 3 x đồng biến trên khoảng nào dƣới đây ? Ầ Đ NH A. 4;6 . B. 1;2 . C. ; 1. D. 2;3. Ị Đ Câu 10. Cho hàm số 3 2
f (x) ax bx cx d có đồ thị nhƣ hình vẽ. Hàm số 2
g(x) [ f (x)] G THPT
nghịch biến trên khoảng nào dƣới đây?N .C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ A. ( ; 3) . B. (1;3) . C. (3; ) . D. ( 3 ;1) .
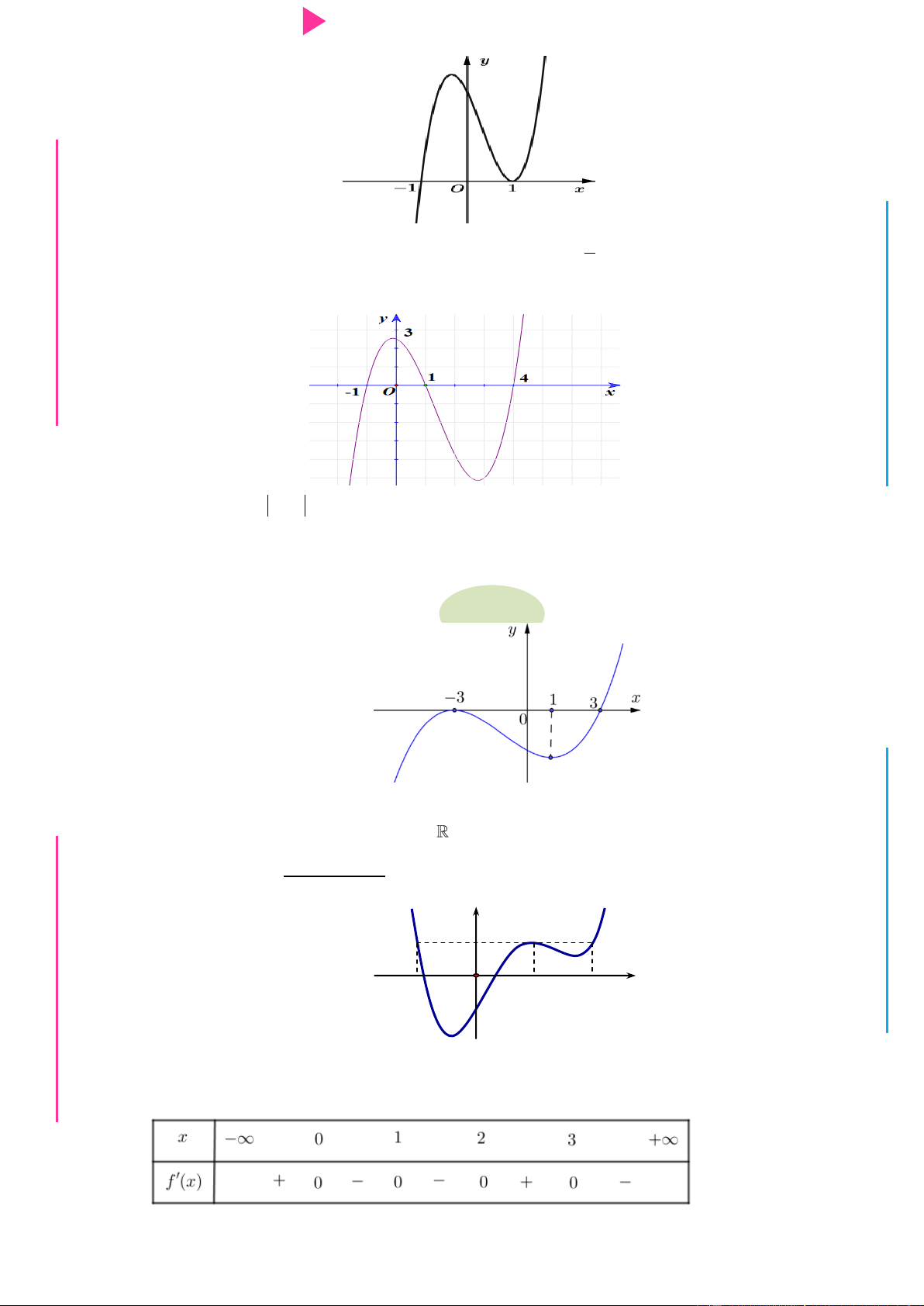
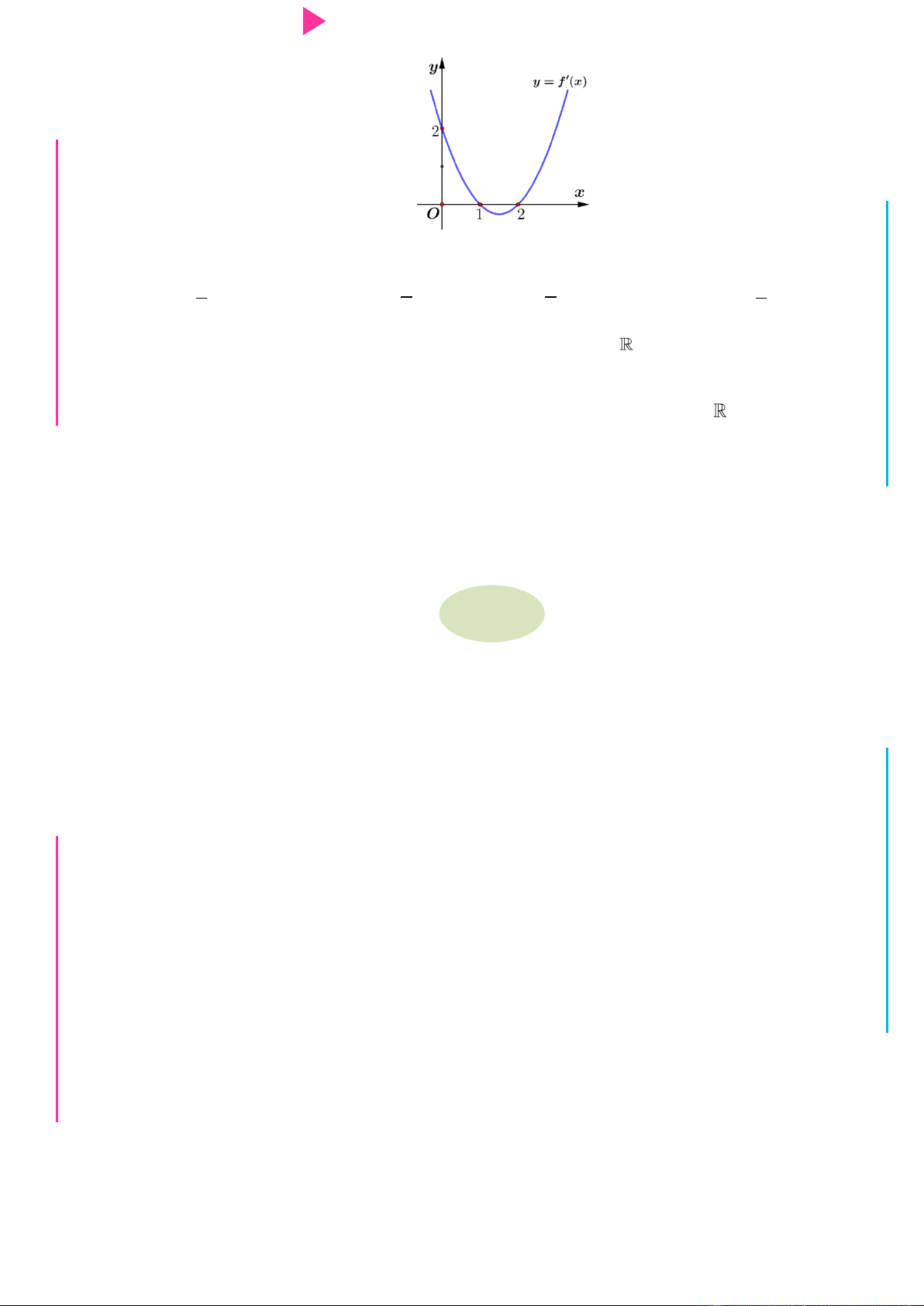
GI Câu 11. Cho hàm số y f x liên tục trên . Hàm số y f x có đồ thị nhƣ hình vẽ. Hàm số
2019 2018x g x f x 1
đồng biến trên khoảng nào dƣới đây? 2018 y 1 1 O 1 2 x 1 A. 2 ; 3 . B. 0 ; 1 . C. -1 ; 0 . D. 1 ; 2 .
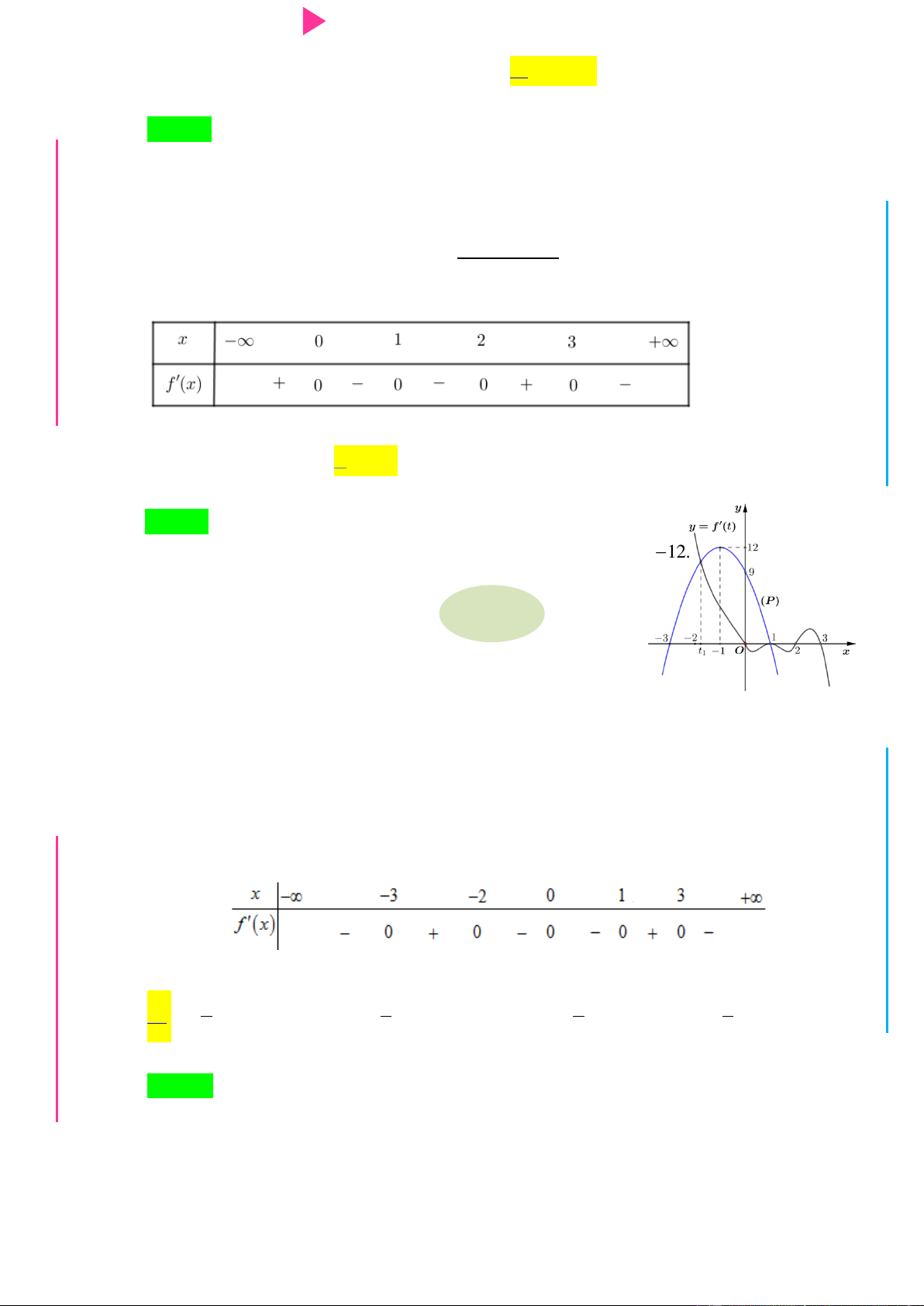
Câu 12. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau:
Hàm số y f x 3
1 x 12x 2019 nghịch biến trên khoảng nào dƣới đây?
NGUYỄN CÔNG ĐỊNH | 4
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 1; . B. 1; 2 C. ;1 . D. 3;4 .
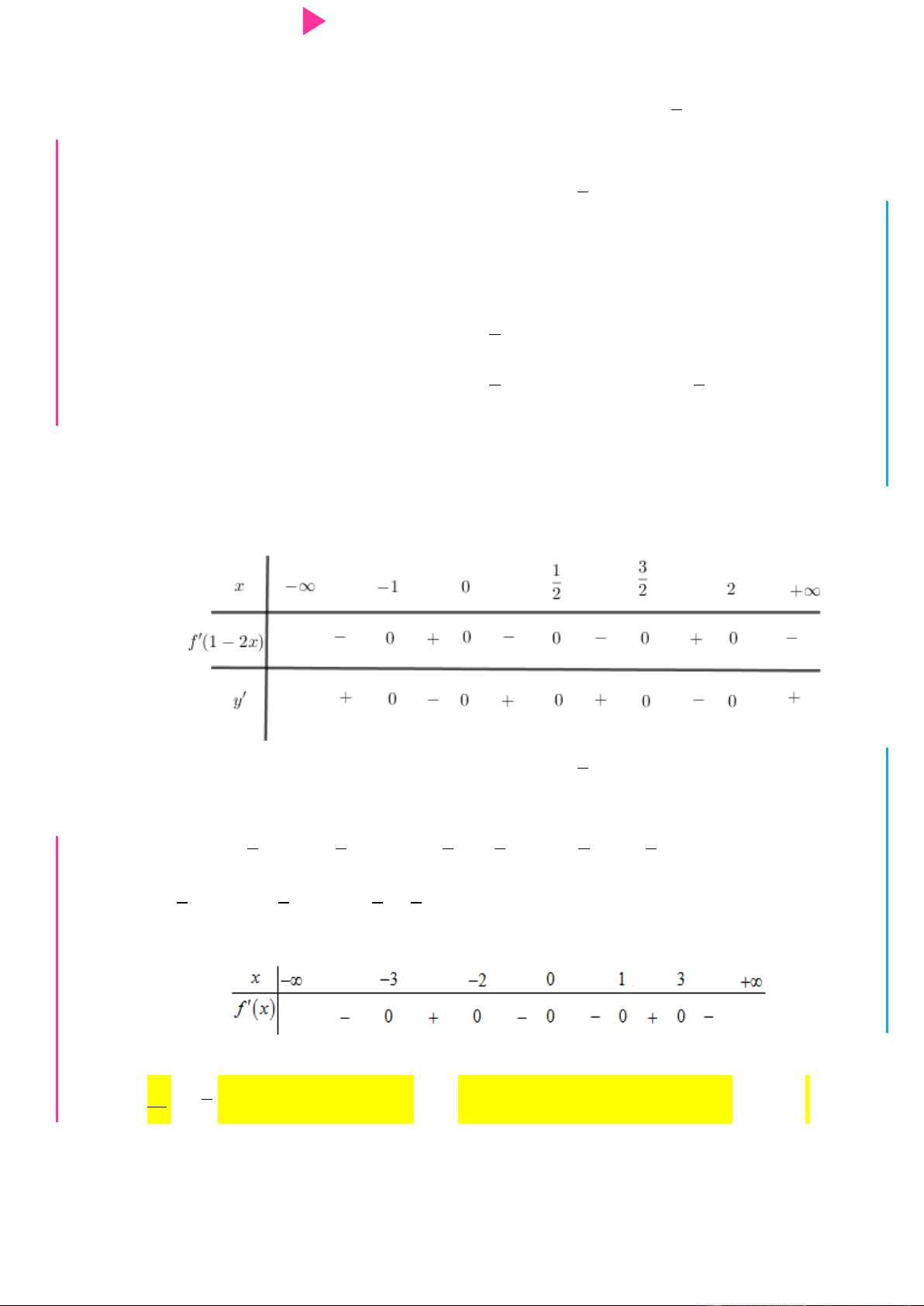
Câu 13. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ hình bên dƣới
Hàm số y f 1 2x đồng biến trên khoảng 3 1 1 3 A. 0; . B. ;1 . C. 2; . D. ;3 . 2 2 2 2
Câu 14. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ hình bên dƣới
và hàm số g x f 1 2x . Chọn khẳng định sai trong các khẳng định sau I Ơ 1 A. x
là một điểm cực đại và x 0 là một điểm cực tiểu của hàm số y g x . 2 M D
y g x 2 2 Ầ B. Hàm số
có điểm cực đại và điểm cực tiểu. Đ NH C. Hàm số y
g x đạt cực tiểu tại x 0 và x 2 . Ị Đ
D. x 1 là một điểm cực đại và x 2 là một điểm cực tiểu của hàm số y g x . G
THPT Câu 15. Cho hàm số y f x. Đồ thị hàm số yN.C.Đf x đƣợc cho nhƣ hình vẽ sau NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
Hàm số g x f 4 2x
1 đồng biến trên khoảng nào sau đây? 1 3 A. ; 1 . B. ;1 . C. 1; .
D. 2; . 2 2
Câu 16. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ hình bên dƣới
Hàm số y f 1 2x đồng biến trên khoảng 3 1 1 3 A. 0; . B. ;1 . C. 2; . D. ;3 . 2 2 2 2
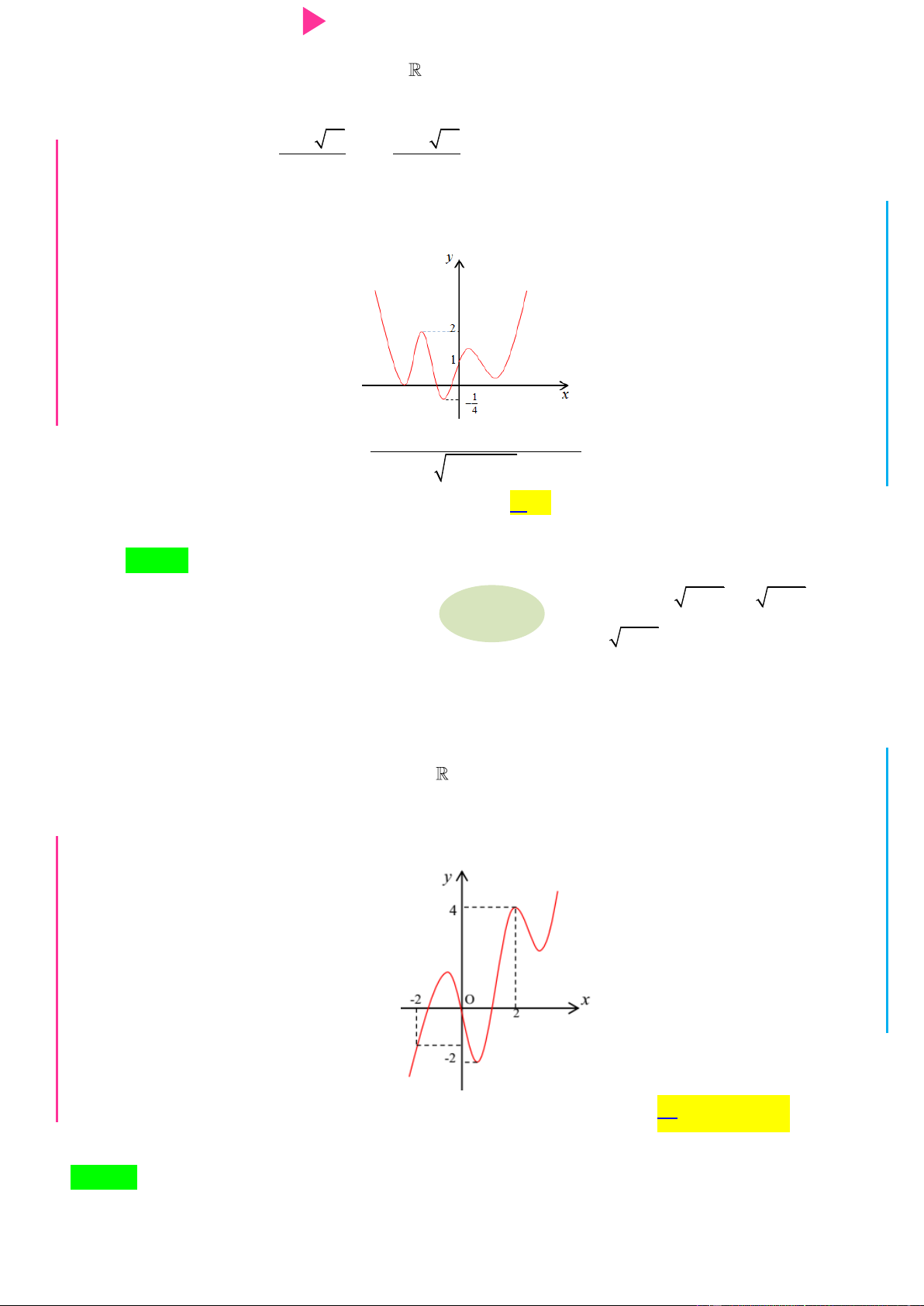
Câu 17. Cho hàm số y f x liên tục trên và có đồ thị nhƣ hình vẽ sau
NGUYỄN CÔNG ĐỊNH | 5
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Hàm số y f 2
x 2x 3 nghịch biến trên khoảng nào dƣới đây ? A. ; 1 . B. 1; . C. 2 ;0 . D. 2 ; 1 .
Câu 18. Cho hàm số y f (x) liên tục trên R và có đồ thị hàm số y f (
x) nhƣ hình vẽ dƣới. I Ơ M D Ầ Đ Hàm số 2
y f (x) x 2x nghịch biến trên khoảng NHỊ A. ( 1 ;2) . B. (1;3) . C. (0;1) . D. ( ; 0). Đ 2 2 G
THPT Câu 19. Cho hàm số y f x có đạo hàm f x x
1 x x 2 . Hỏi hàm số N.C.Đ 2 NG
g x f x x đồng biến trên khoảng nào trong các khoảng sau? CÔN Ờ N A. 1 ; 1 . B. 0; 2 . C. ; 1 . D. 2; . Ễ Y
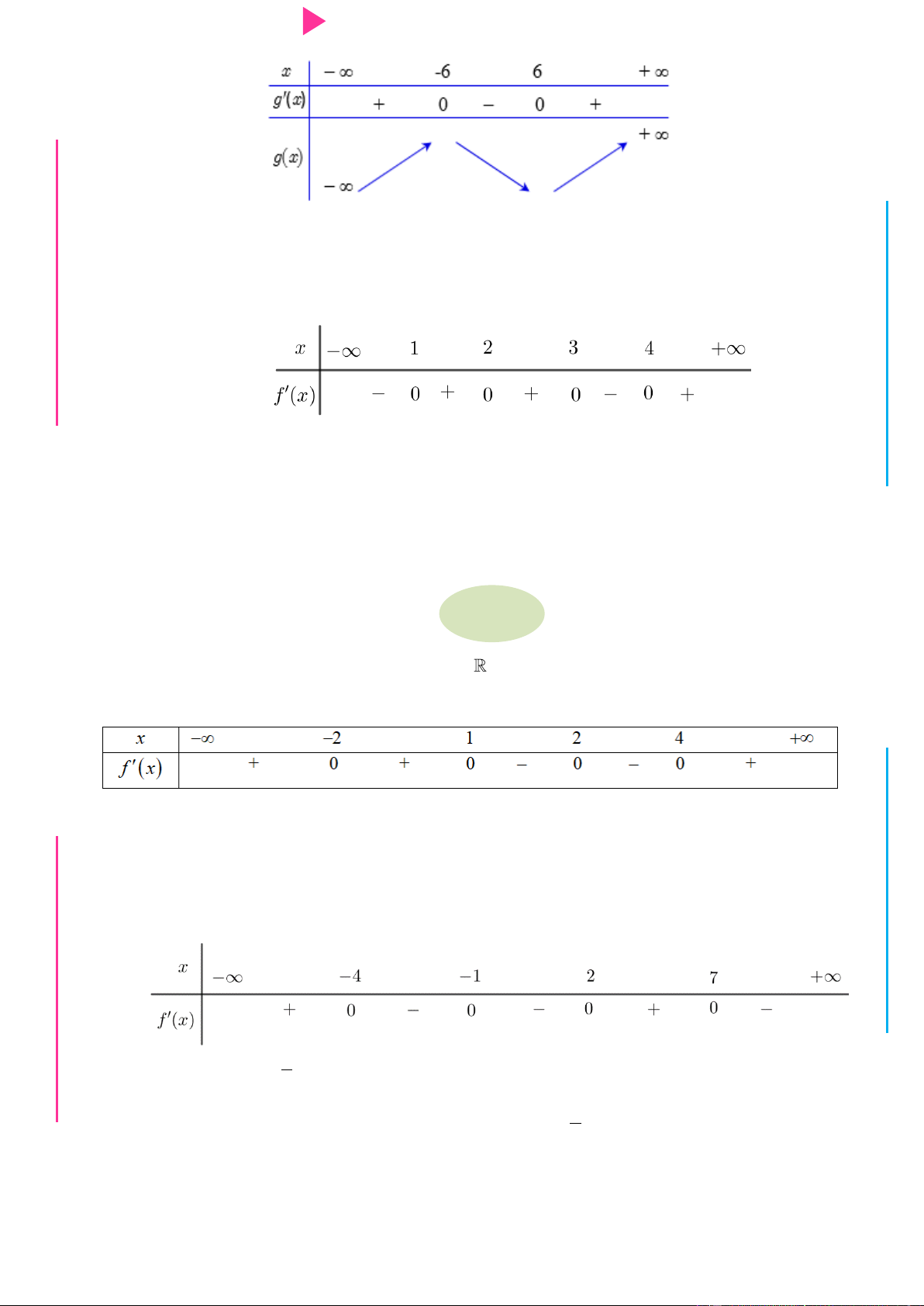
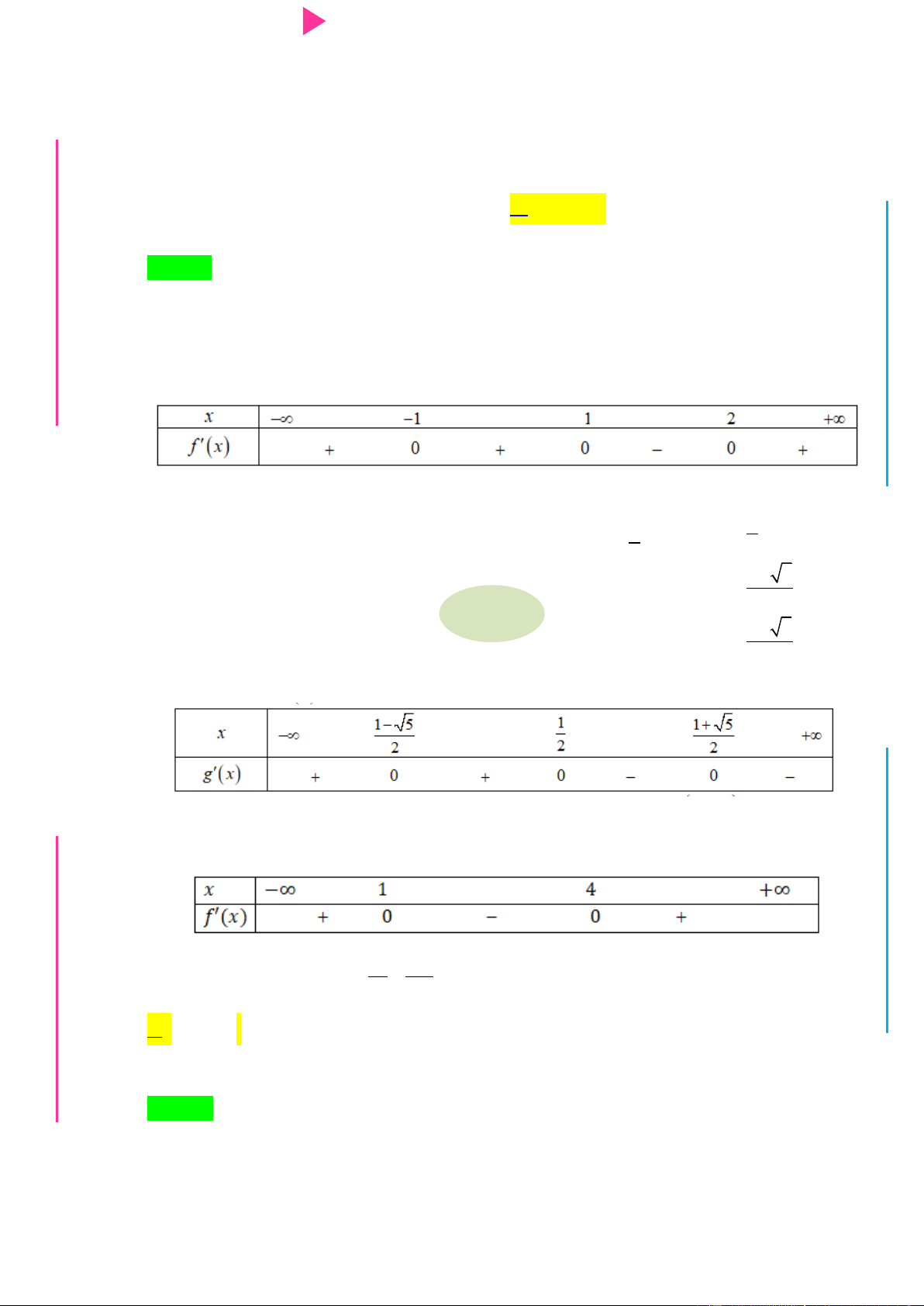
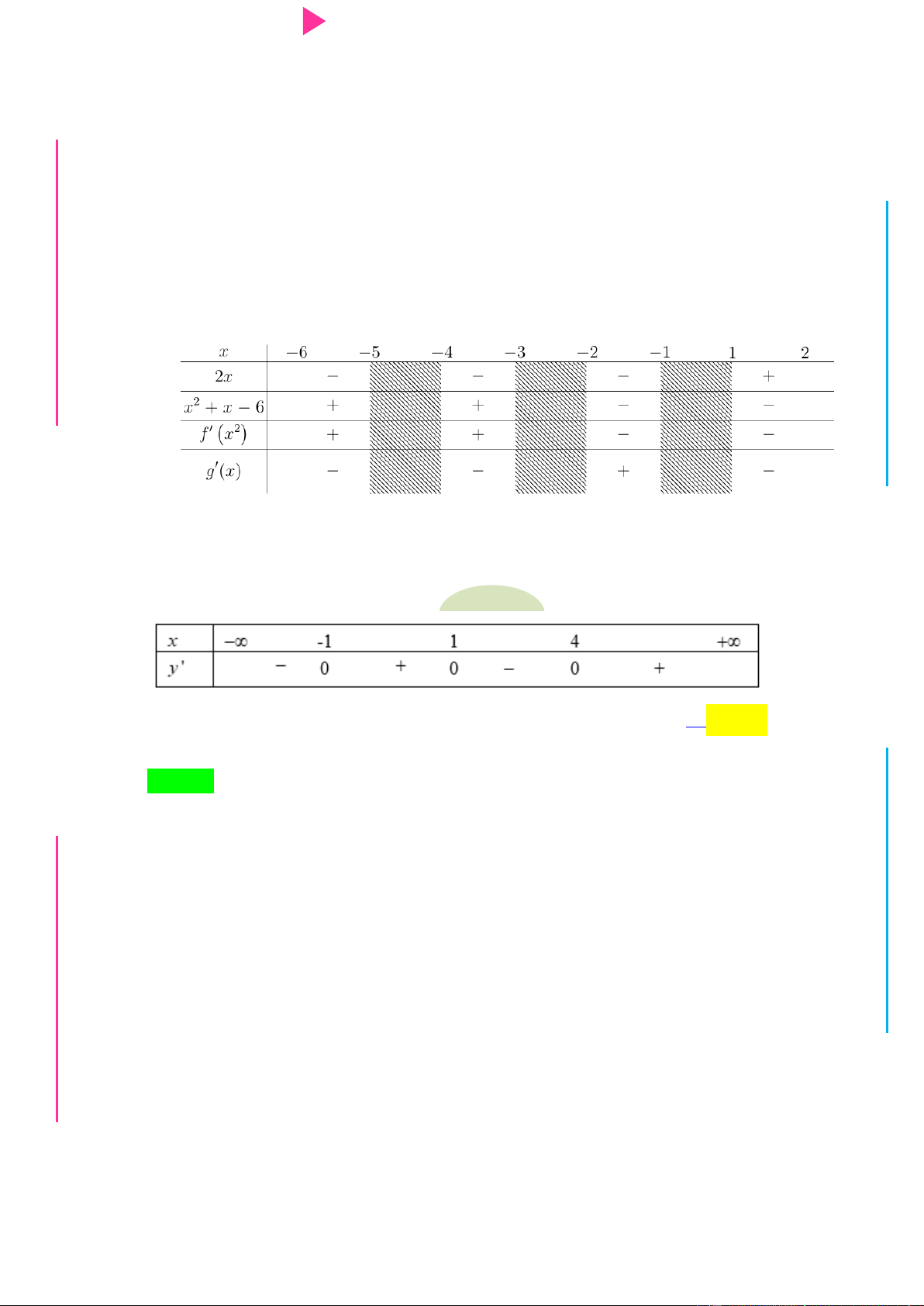
TRƢ Câu 20. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: GU N N ÁO VIÊ GI x 2x
Hàm số y g x f x 4 3 2 2
6x đồng biến trên khoảng nào dƣới đây? 2 3 A. 2 ; 1 . B. 1; 2 . C. 4 ; 3 . D. 6 ;5 .
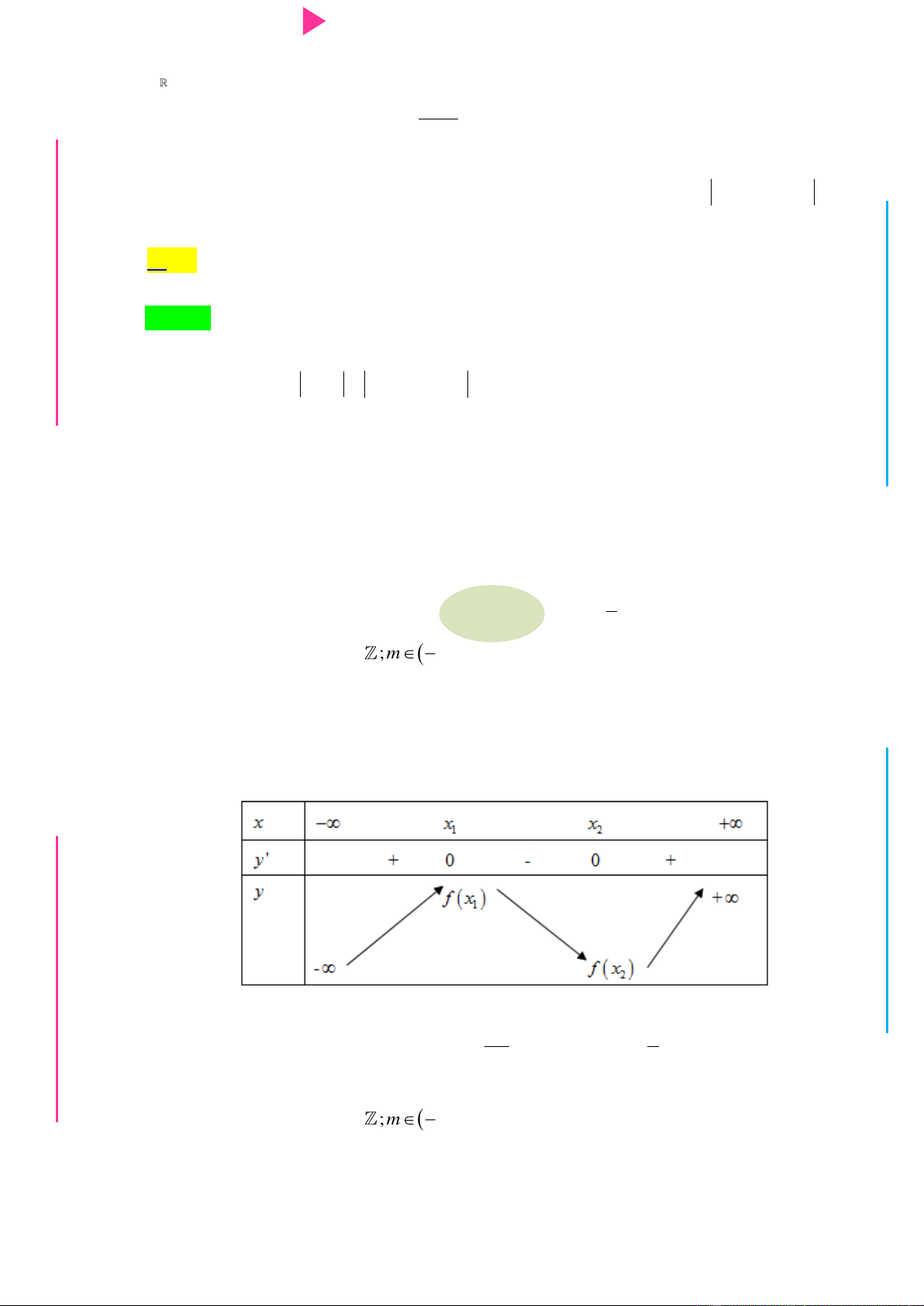
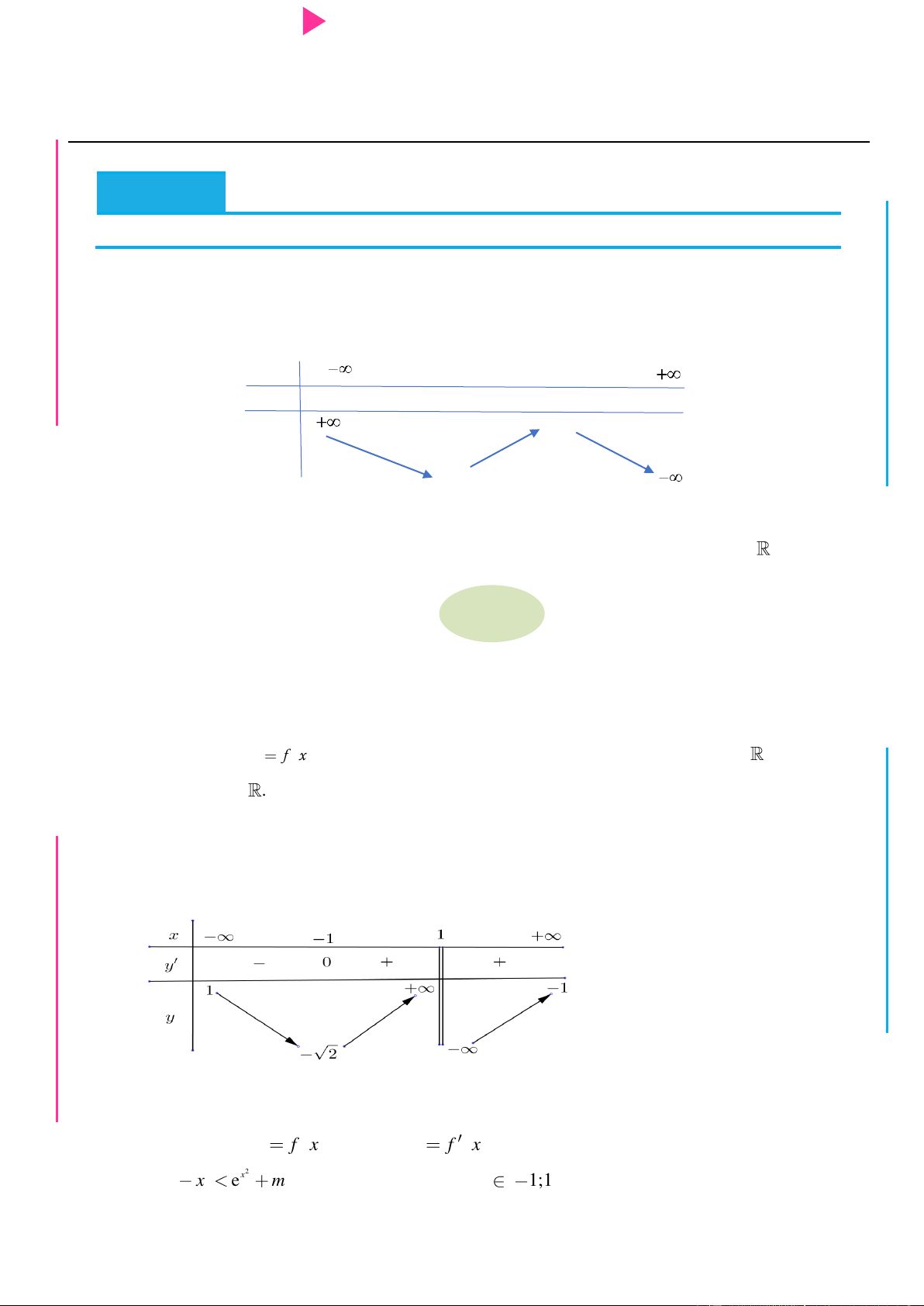
Câu 21. Cho hàm số y f x có đạo hàm liên tục trên và có bảng biến thiên nhƣ sau:
Hàm số y f 2
x 2x nghịch biến trên khoảng nào dƣới đây ? A. ;0 . B. 0 ;1 . C. 2; . D. 1;2 .
NGUYỄN CÔNG ĐỊNH | 6
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
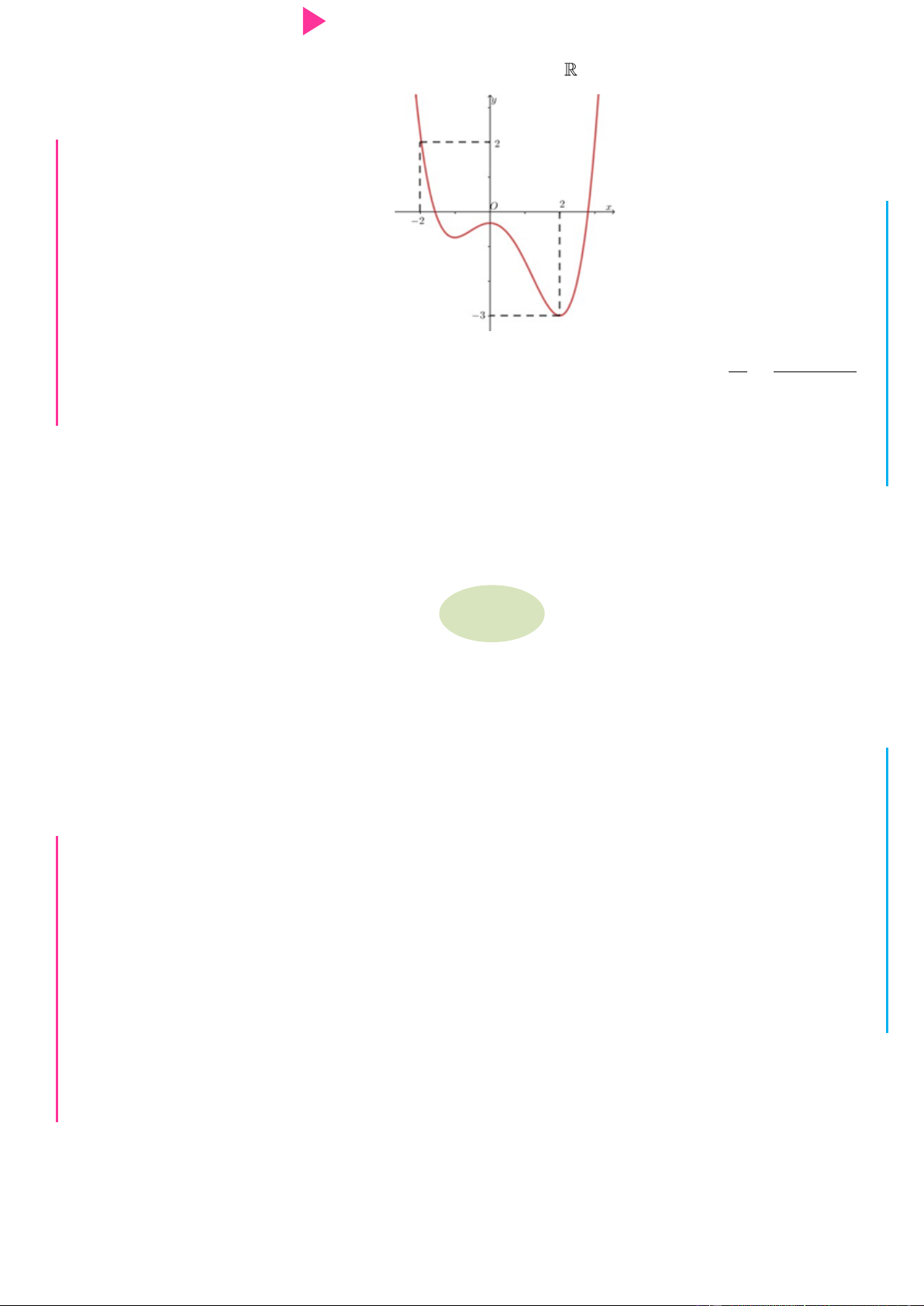
Câu 22. Cho hàm số y f x có đồ thị của hàm số y f x đƣợc cho nhƣ hình bên. Hàm số
y f x 2 2 2
x nghịch biến trên khoảng y 3 1 1 O 2 3 4 5 x 2 A. 3 ; 2 . B. 2 ; 1 . C. 1 ; 0 . D. 0; 2 .
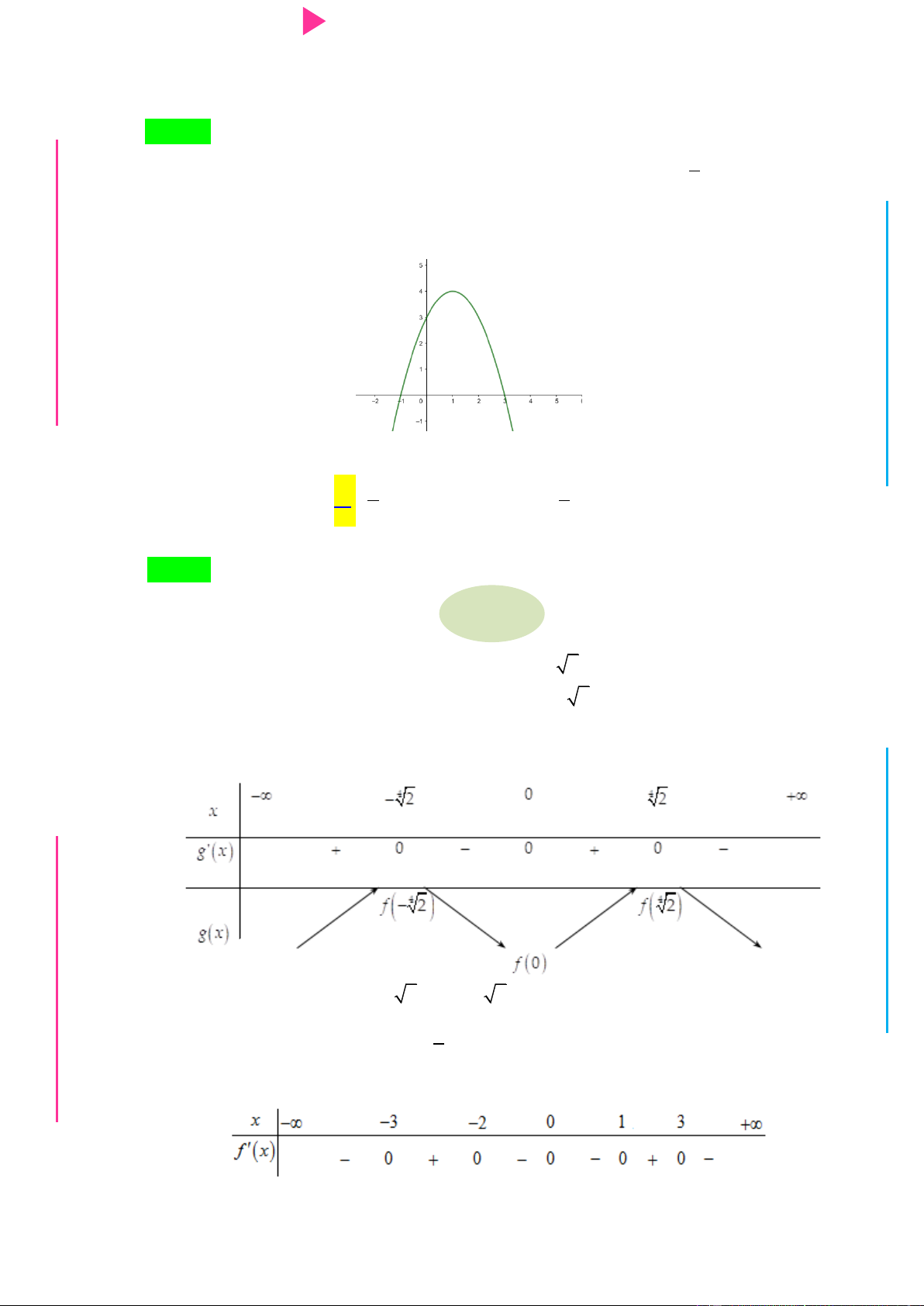
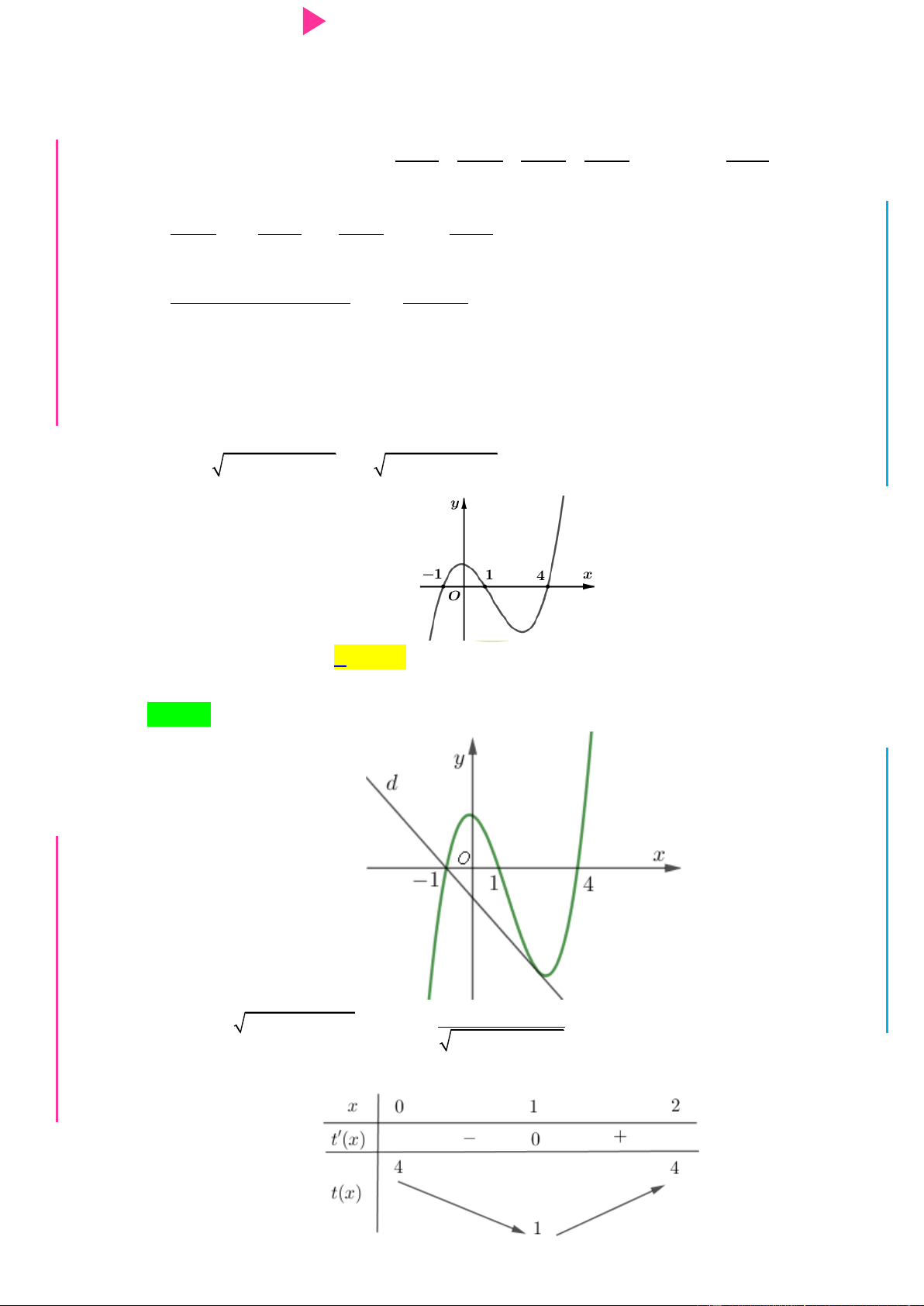
Câu 23. Cho f x mà đồ thị hàm số y
f x nhƣ hình bên. Hàm số 2 y f x 1 x 2x đồng biến trên khoảng I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG A. 1;2 . B. 1;0 . C. 0;1 . D. 2; 1 . CÔN Ờ N
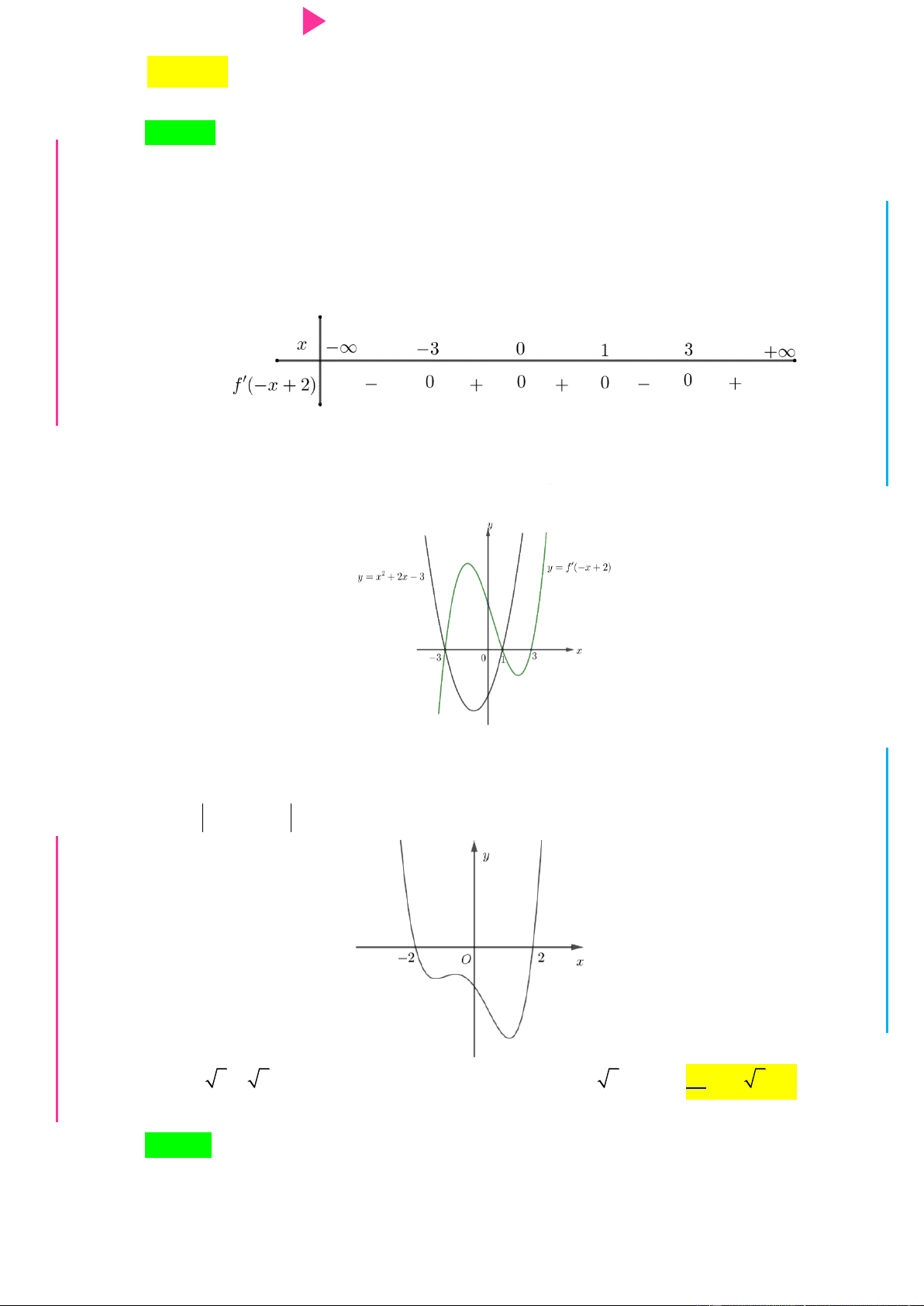
Câu 24. Cho hàm số y=f(x) có đồ thị y=f ‘(x) nhƣ hình vẽ bên. Hỏi hàm số y=f(3-2x)+2019 nghịch ỄY TRƢ
biến trên khoảng nào sau đây? GU N N ÁO VIÊ GI A. 1;2 . B. 2; . C. ;1 . D. 1 ; 1 .
Câu 25. Cho hàm số y f x có bảng xét dấu đạo hàm nhƣ sau 1
Gọi g x 2 f 1 x 4 3 2
x x x 5 . Khẳng định nào sau đây đúng ? 4
A. Hàm số g x đống biến trên khoảng ; 2 .
B. Hàm số g x đồng biến trên khoảng 1 ;0 .
C. Hàm số g x đồng biến trên khoảng 0; 1 .
D. Hàm số g x nghịch biến trên khoảng 1; .
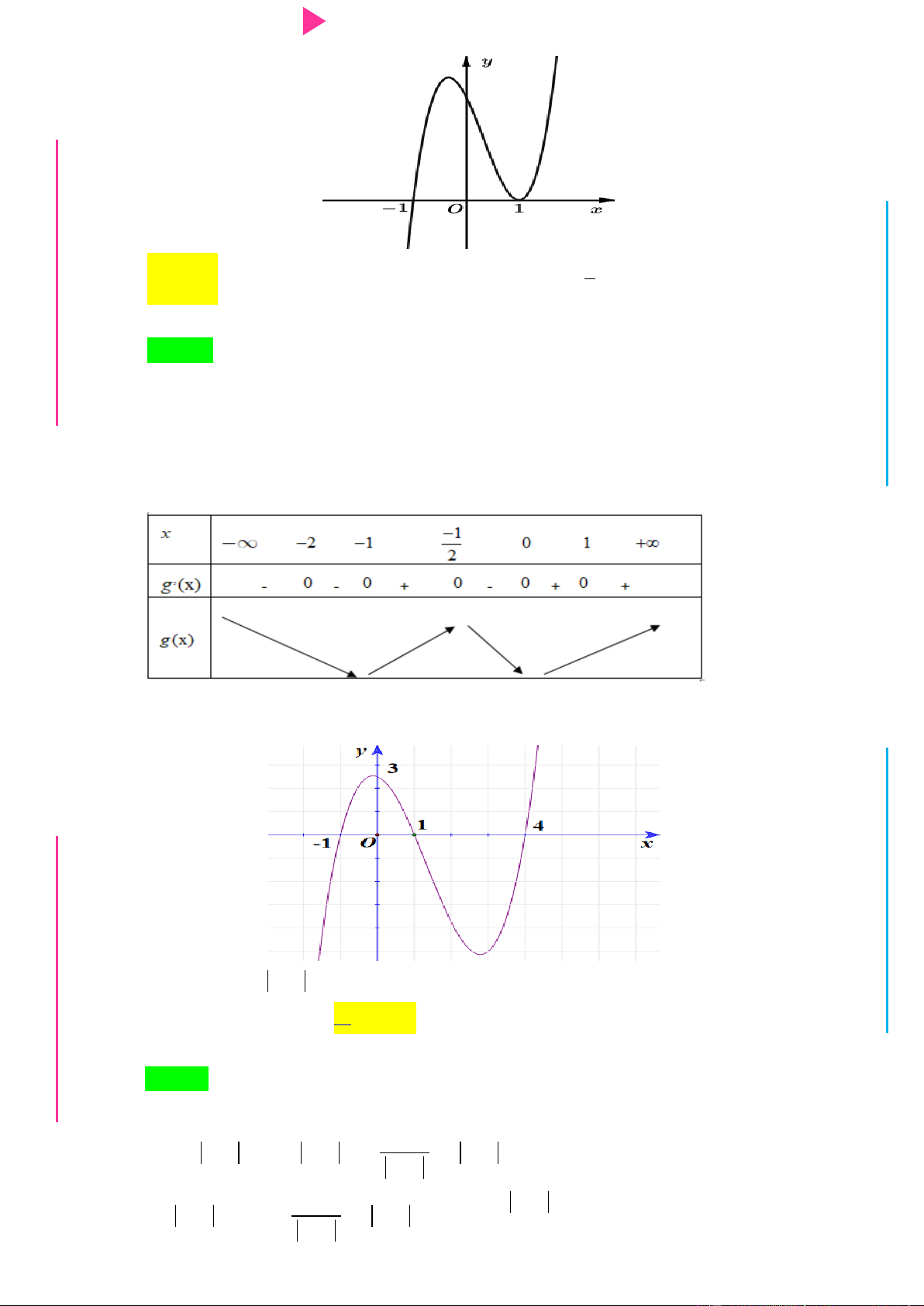
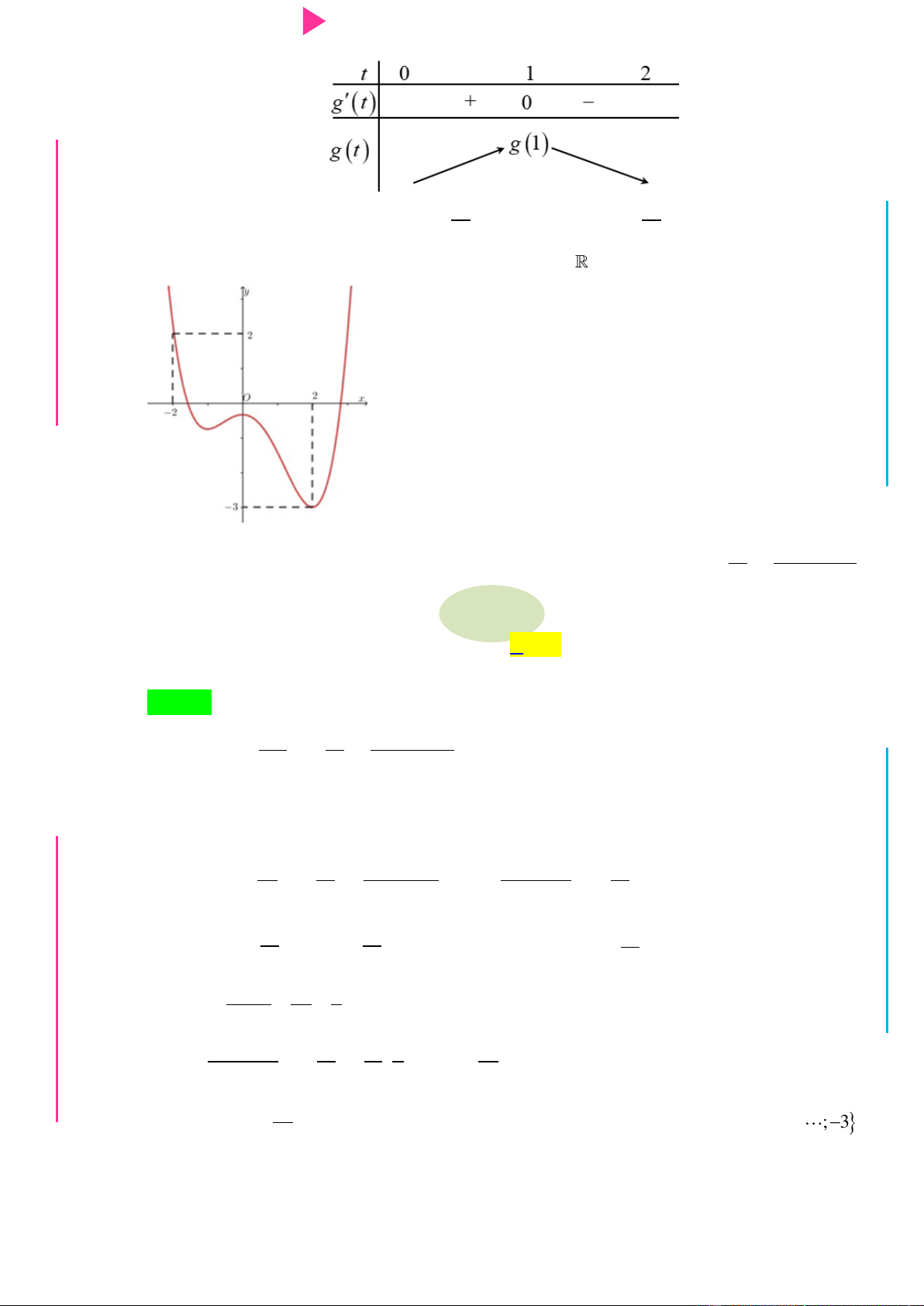
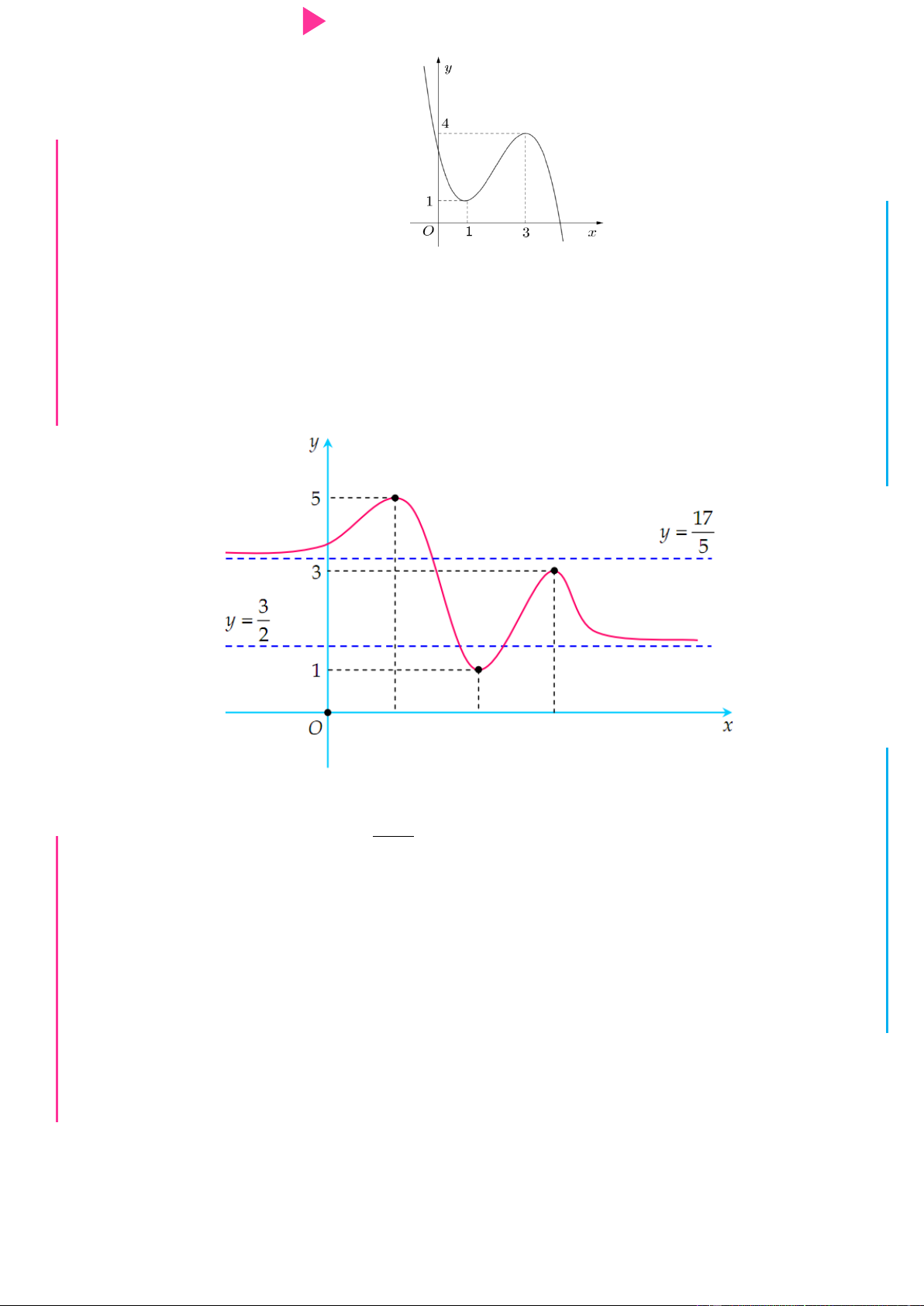
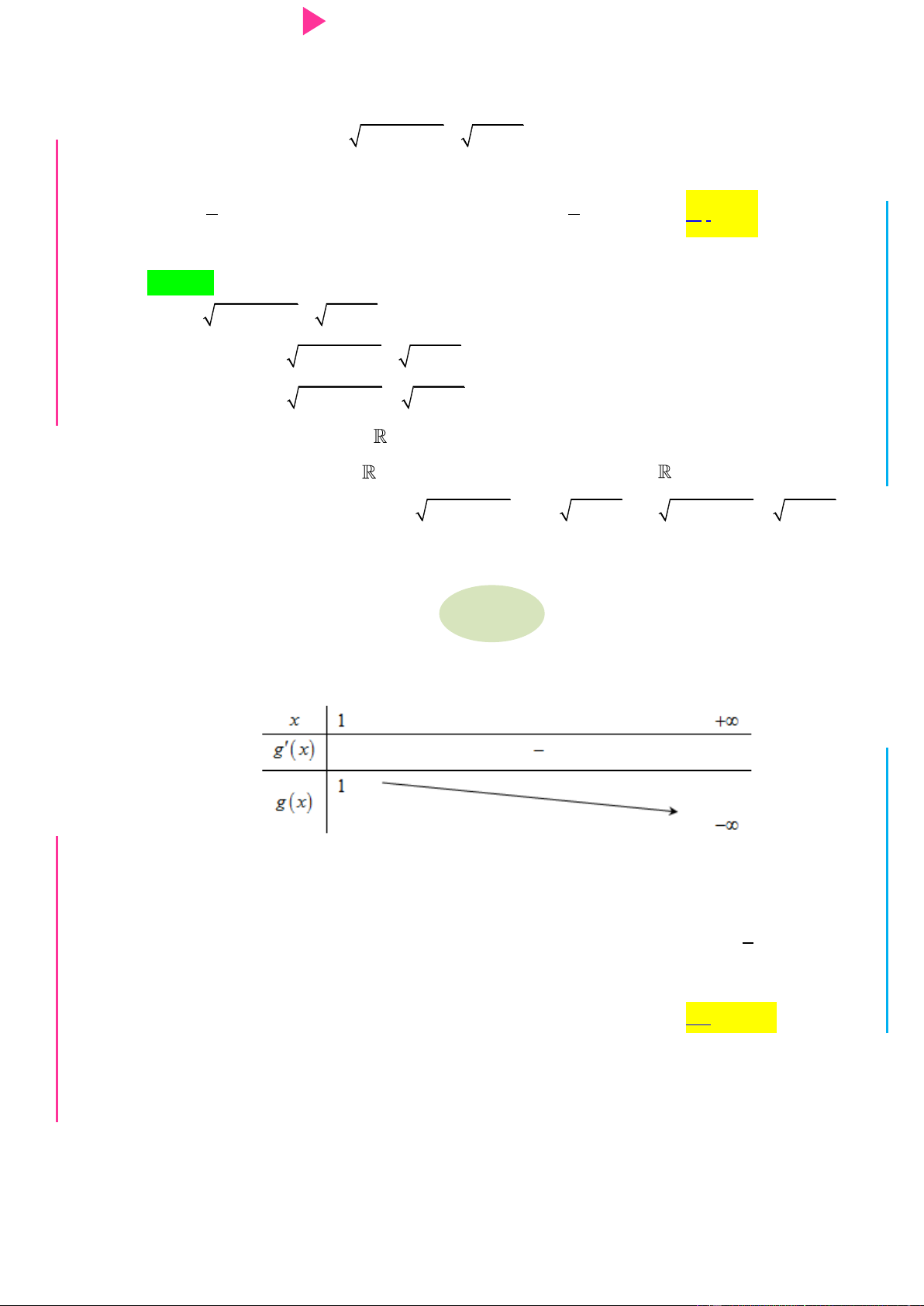
Câu 26. Cho hàm số f x 3 2
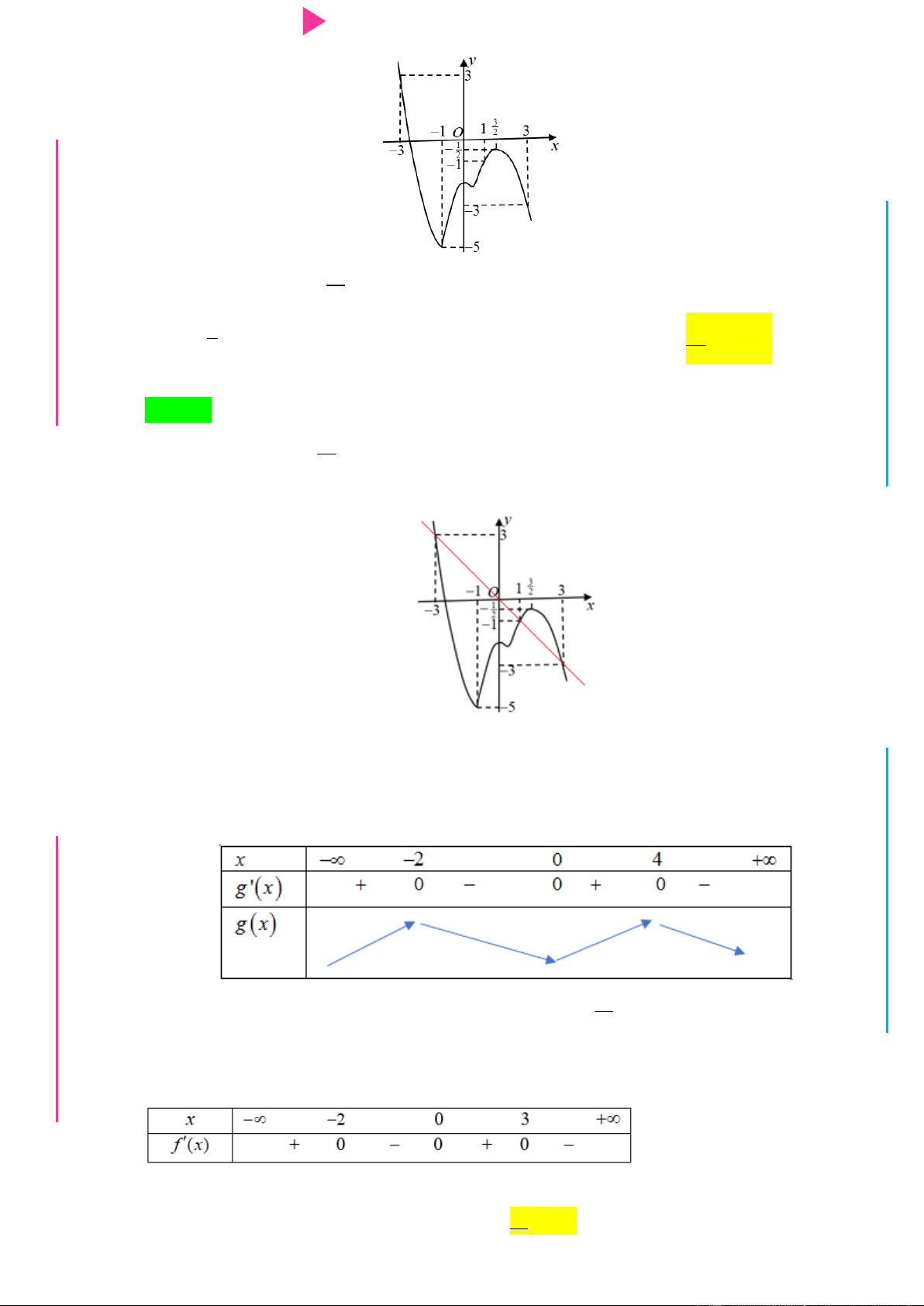
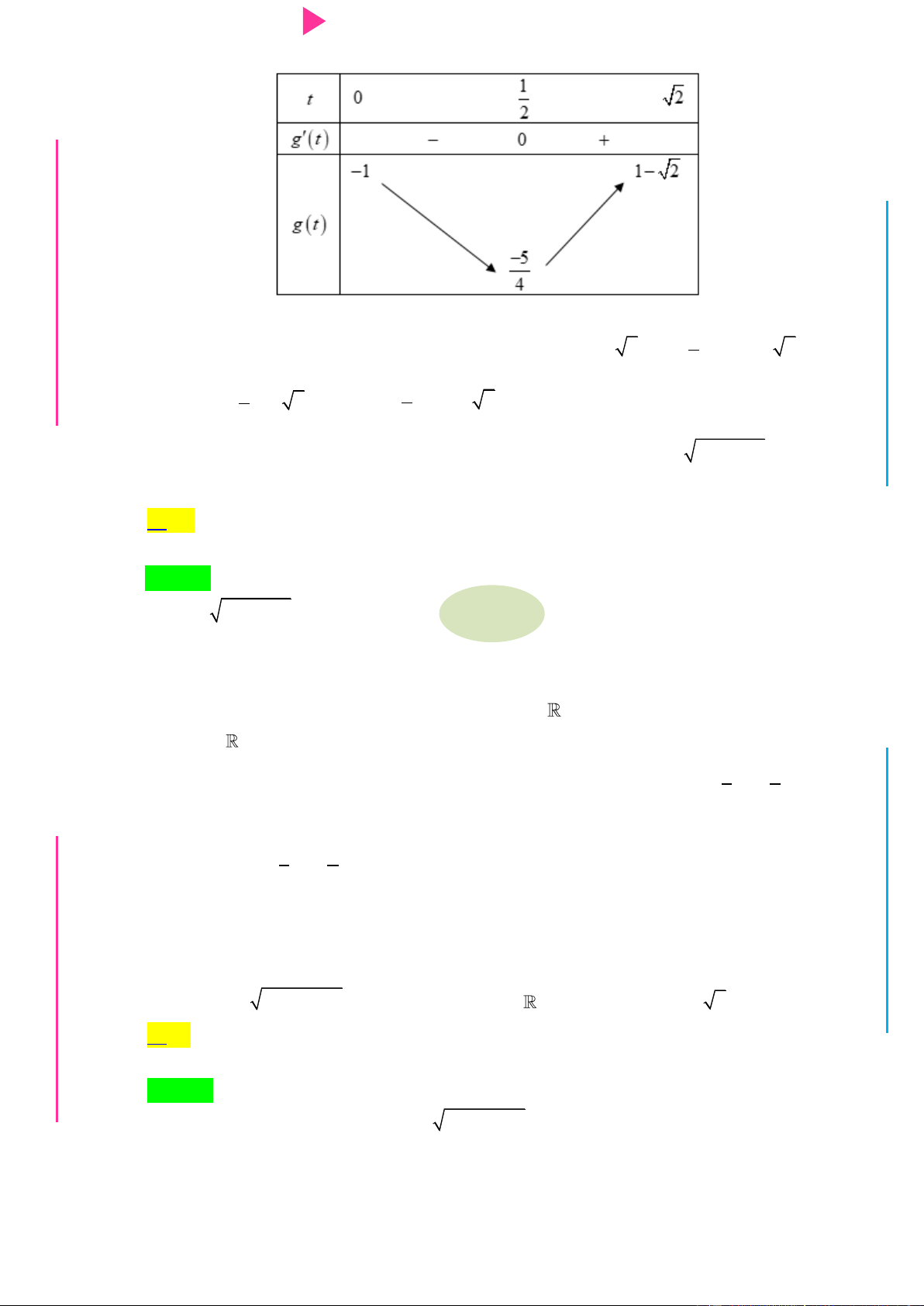
x 3x 5x 3 và hàm số g x có bảng biến thiên nhƣ sau
NGUYỄN CÔNG ĐỊNH | 7
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
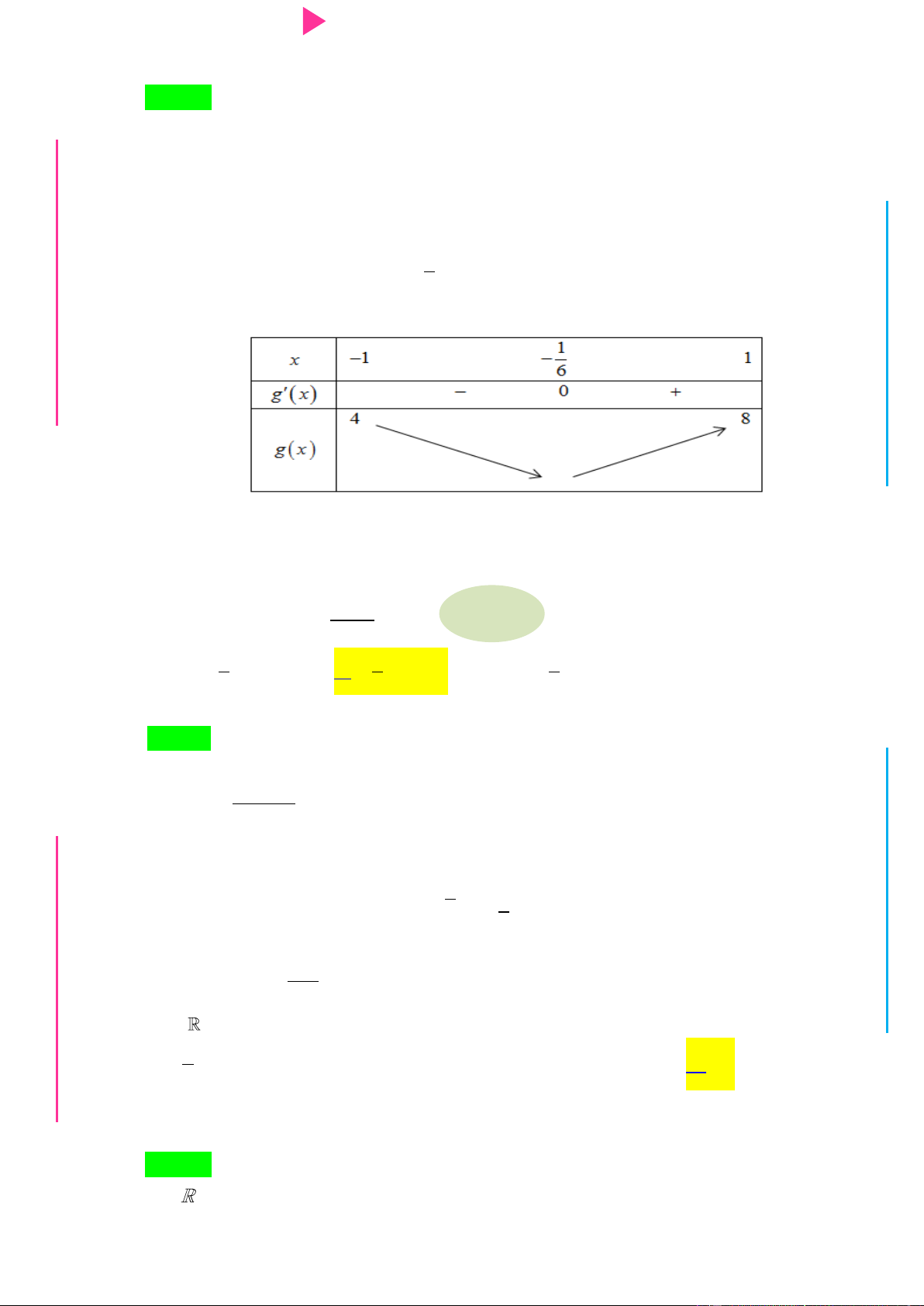
Hàm số y g f x nghịch biến trên khoảng A. 1 ; 1 . B. 0;2 . C. 2 ;0 . D. 0;4 .
Câu 27 . Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau I
Đặt g x f 2 x x 3 2 2
2 x 3x 6x . Ơ Xét các khẳng định M D
1) Hàm số g x đồng biến trên khoảng 2;3. Ầ Đ
2) Hàm số g x nghịch biến trên khoảng 0 ;1 . NHỊ Đ
3) Hàm số g x đồng biến trên khoảng 4; . G THPT
Số khẳng định đúng trong các khẳng đ N ị .C nh .Đ t rên là NG A. 0 . B. 1. C. 2 . D. 3 . CÔN Ờ N
Câu 28. Cho hàm số y f x có đạo hàm trên và có bảng xét dấu của đạo hàm nhƣ hình vẽ ỄY TRƢ sau: GU N N ÁO VIÊ GI
Có bao nhiêu số nguyên m 0;2020 để hàm số 2 g x
f x x m nghịch biến trên khoảng 1 ;0? A. 2018. B. 2017. C. 2016. D. 2015.
Câu 29. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau 2
Hàm số y f 2x 3 1
x 8x 2019 nghịch biến trên khoảng nào dƣới đây? 3 1 A. 1; . B. ; 2 . C. 1 ; . D. 1 ;7 . 2
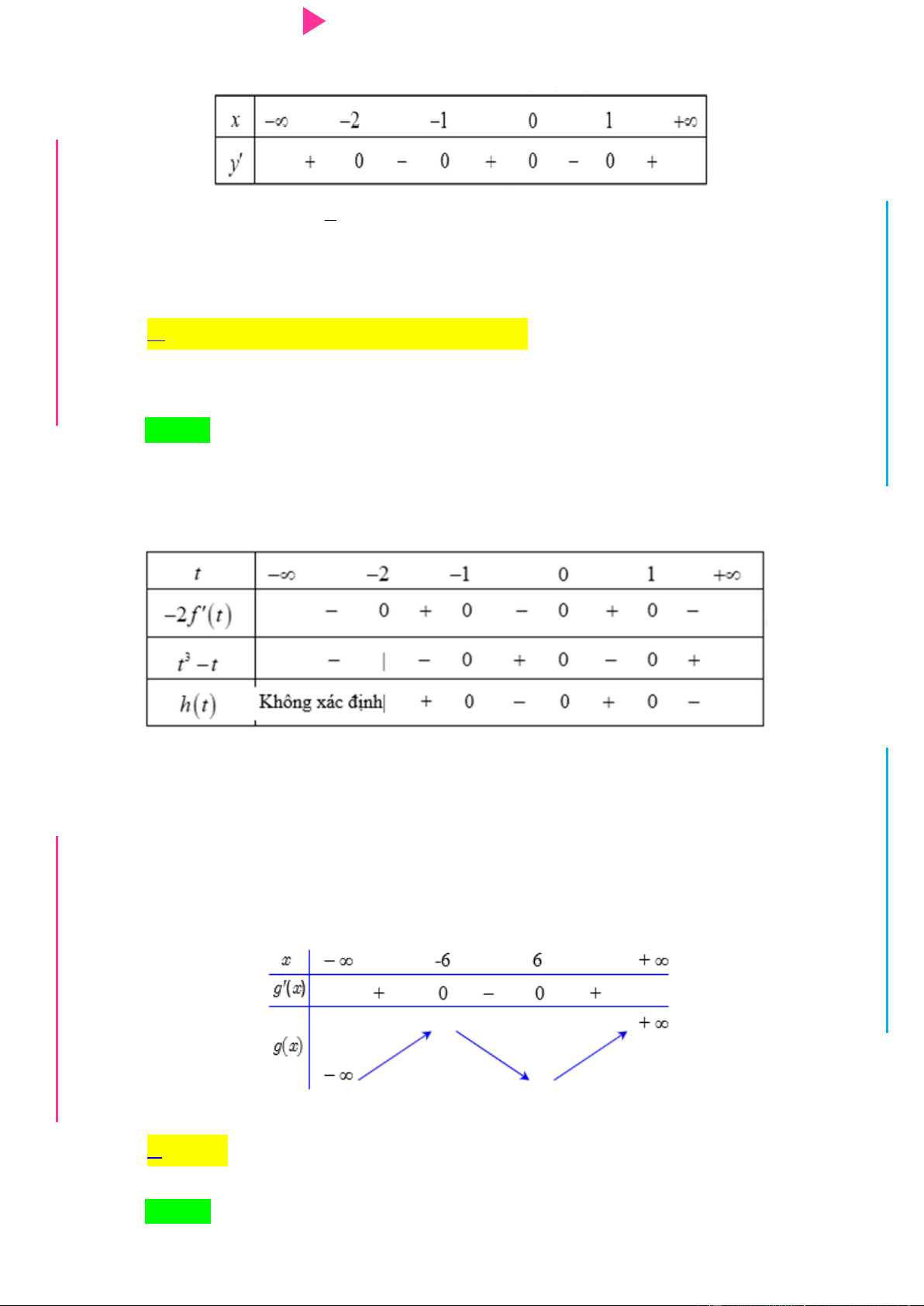
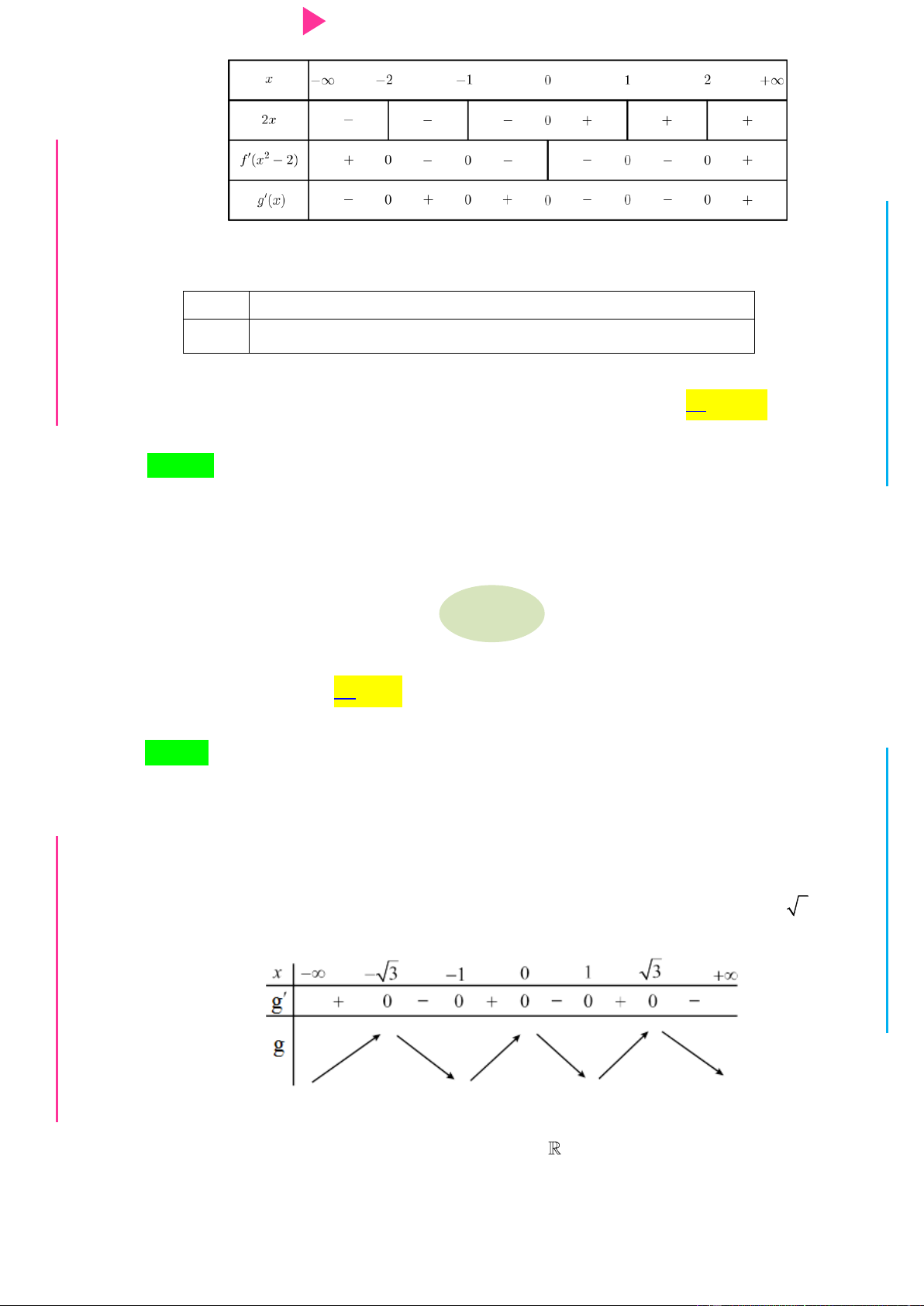
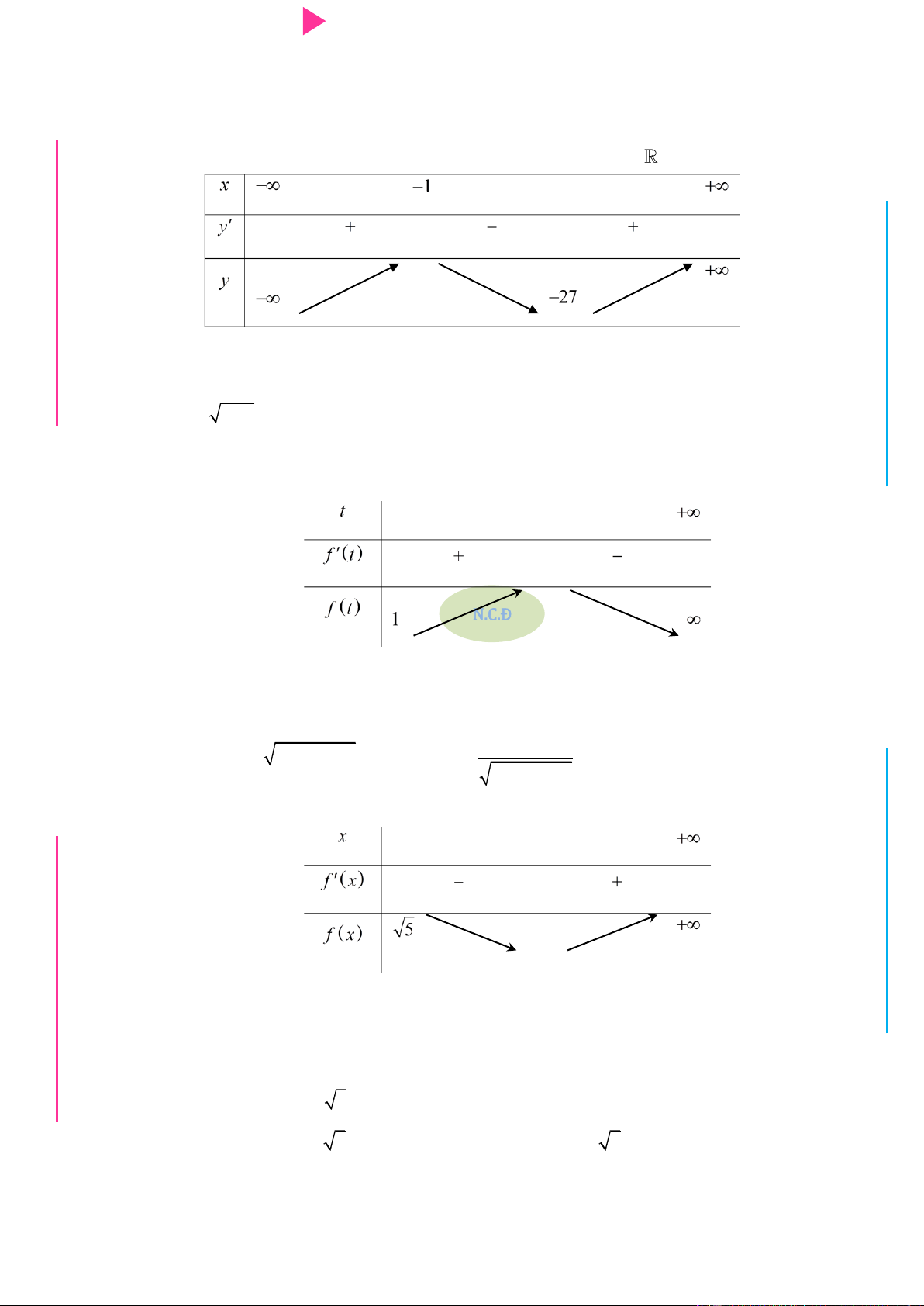
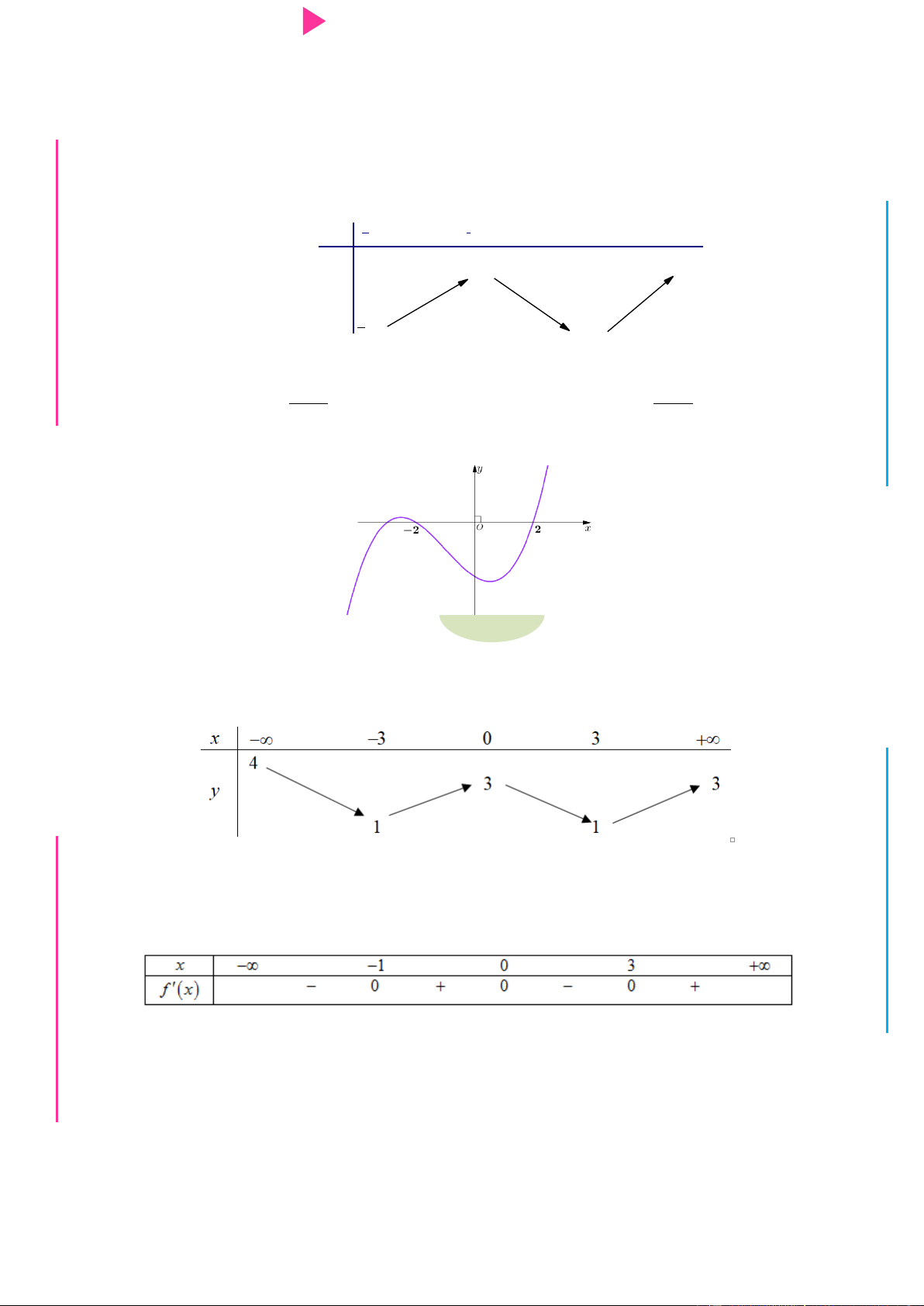
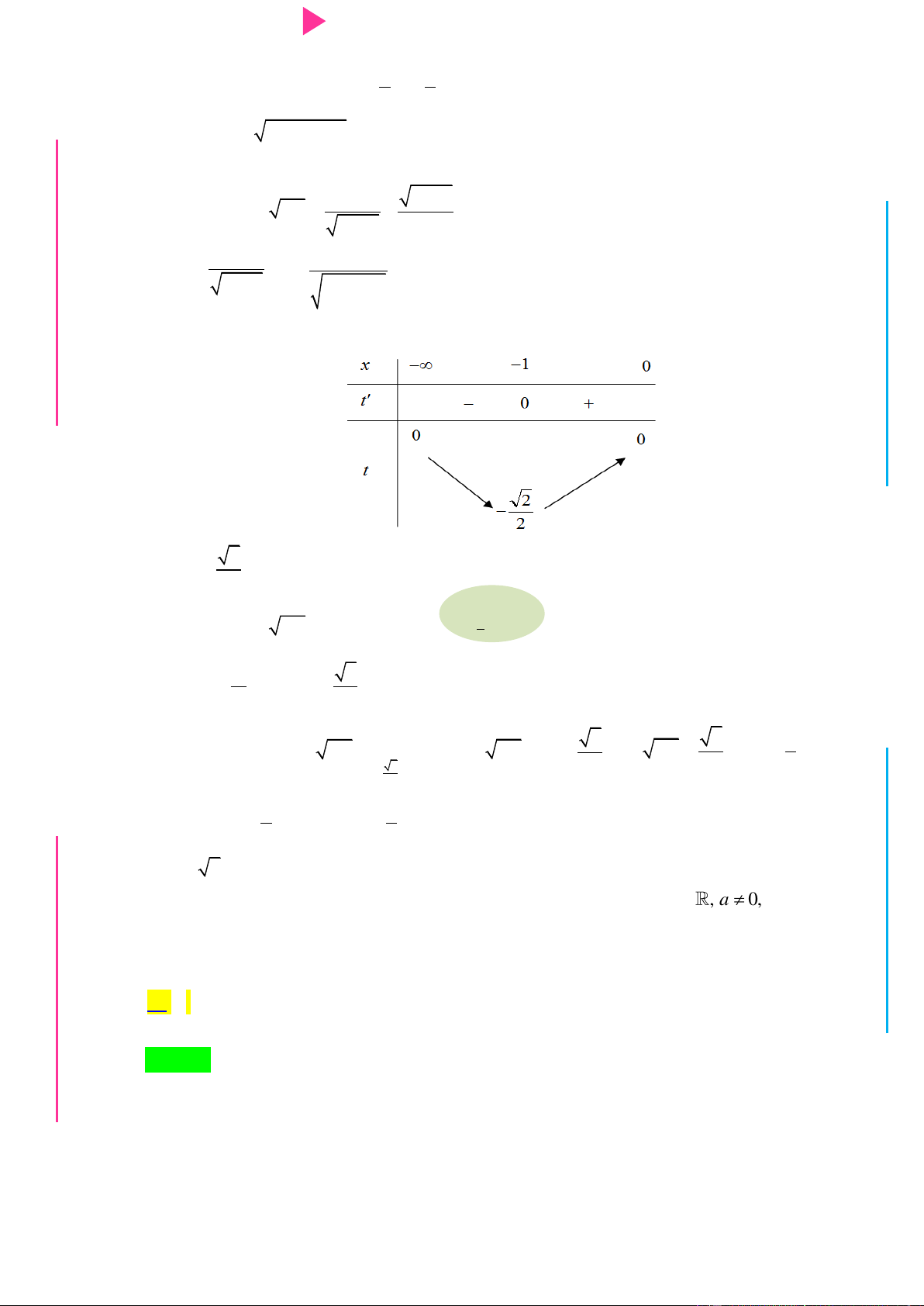
Câu 30. Cho hàm số y f (x) có bảng xét dấu của đạo hàm f '(x) nhƣ sau
NGUYỄN CÔNG ĐỊNH | 8
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Hàm số 3 2
y 3 f (x 2) x 3x 9x 1 nghịch biến trên khoảng nào sau đây? A. 2 ; 1 . B. 2; . C. 0;2 .
D. ; 2 .
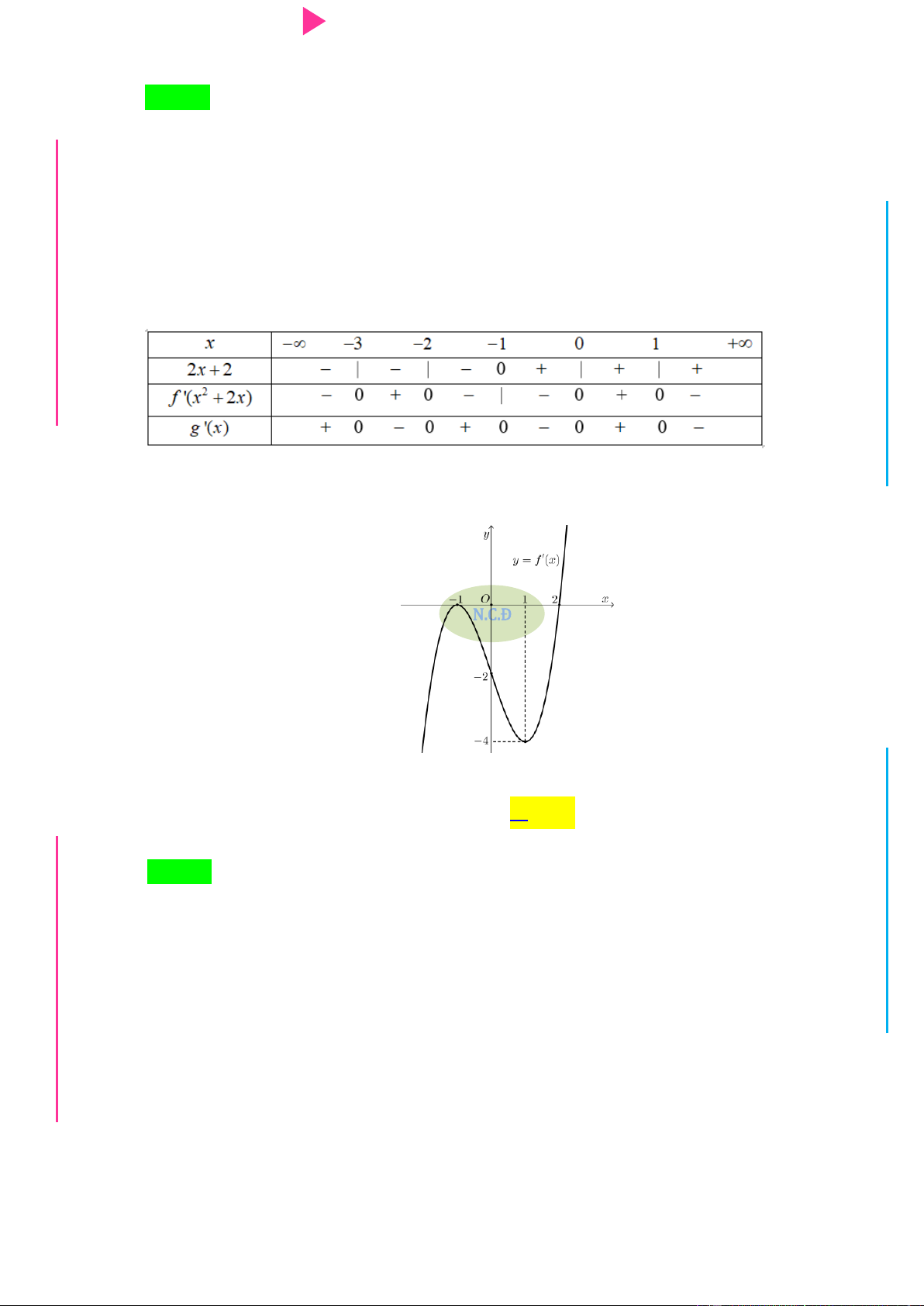
Câu 31. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ sau
Hàm số y f x 3 2 3
2 x 3x 9x nghịch biến trên khoảng nào dƣới đây A. 2 ; 1 . B. ; 2 . C. 0; 2 . D. 2; .
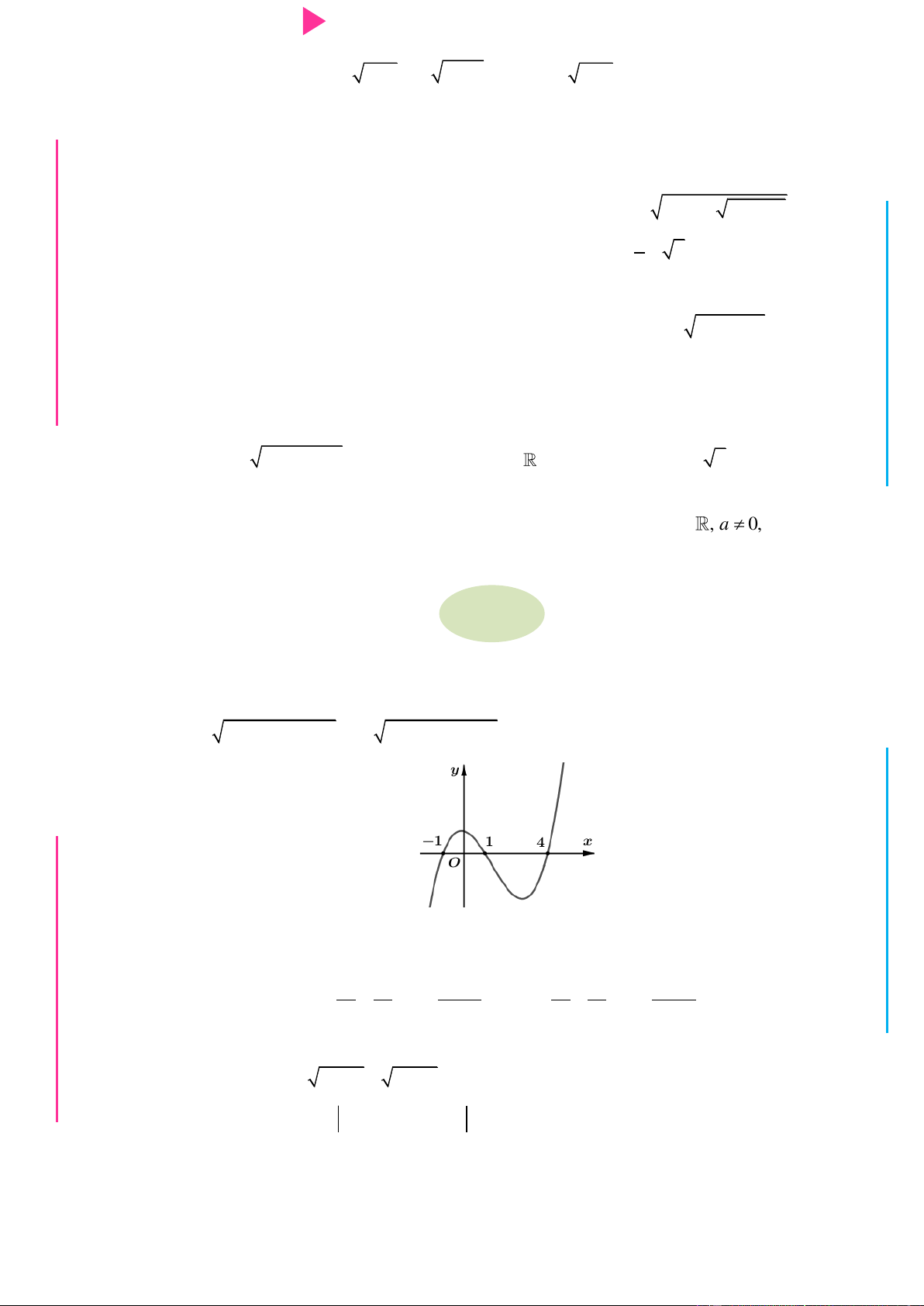
I Câu 32. Cho hàm số y f x có đồ thị hàm số y f x nhƣ hình vẽ bên. Biết f 2 0, hàm Ơ số y f 2018 1 x
đồng biến trên khoảng nào dƣới đây? M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ 2018 2018 2018 2018 Y TRƢ A. 3; 3 . B. 1 ;. C. ; 3 . D. 3; 0 . GU
N Câu 33. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ sau: N ÁO VIÊ GI x 2x
Hàm số y g x f x 4 3 2 2
6x đồng biến trên khoảng nào dƣới đây? 2 3 A. 2 ; 1 . B. 1;2 . C. 6 ;5. D. 4 ;3 .
Câu 34. Cho hàm số y f x có bảng xét dấu đạo hàm nhƣ hình bên. Hàm số
3 f 2x 1 f 2x y e 3
đồng biến trên khoảng nào dƣới đây.
A 1; B. ; 2 . C. 1 ;3 . D. 2 ; 1 .
Câu 35. Cho hàm số y f x có đồ thị hàm số y f ' x nhƣ hình vẽ
NGUYỄN CÔNG ĐỊNH | 9
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x
Hàm số y f x 2 1
x nghịch biến trên khoảng 2 3 A. 1 ; . B. 1;3 . C. 3 ; 1 . D. 2 ;0 . 2
Câu 36. Cho hàm số y f (x) có bảng xét dấu đạo hàm nhƣ sau I Ơ
Hàm số y f 2
x 2x đồng biến trên khoảng nào dƣới đây ? M D Ầ A. (1; ) . B. ( 3 ; 2 ) . C. (0;1) . D. ( 2 ;0) . Đ NH Ị
Câu 37. Cho hàm số y
f x có đồ thị f x nhƣ hình vẽ sau Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
Hàm số g x f 2
x 2 nghịch biến trên khoảng nào dƣới đây? A. 1;3 3 ; 4; . B. 1 . C. 0 ;1 . D. .
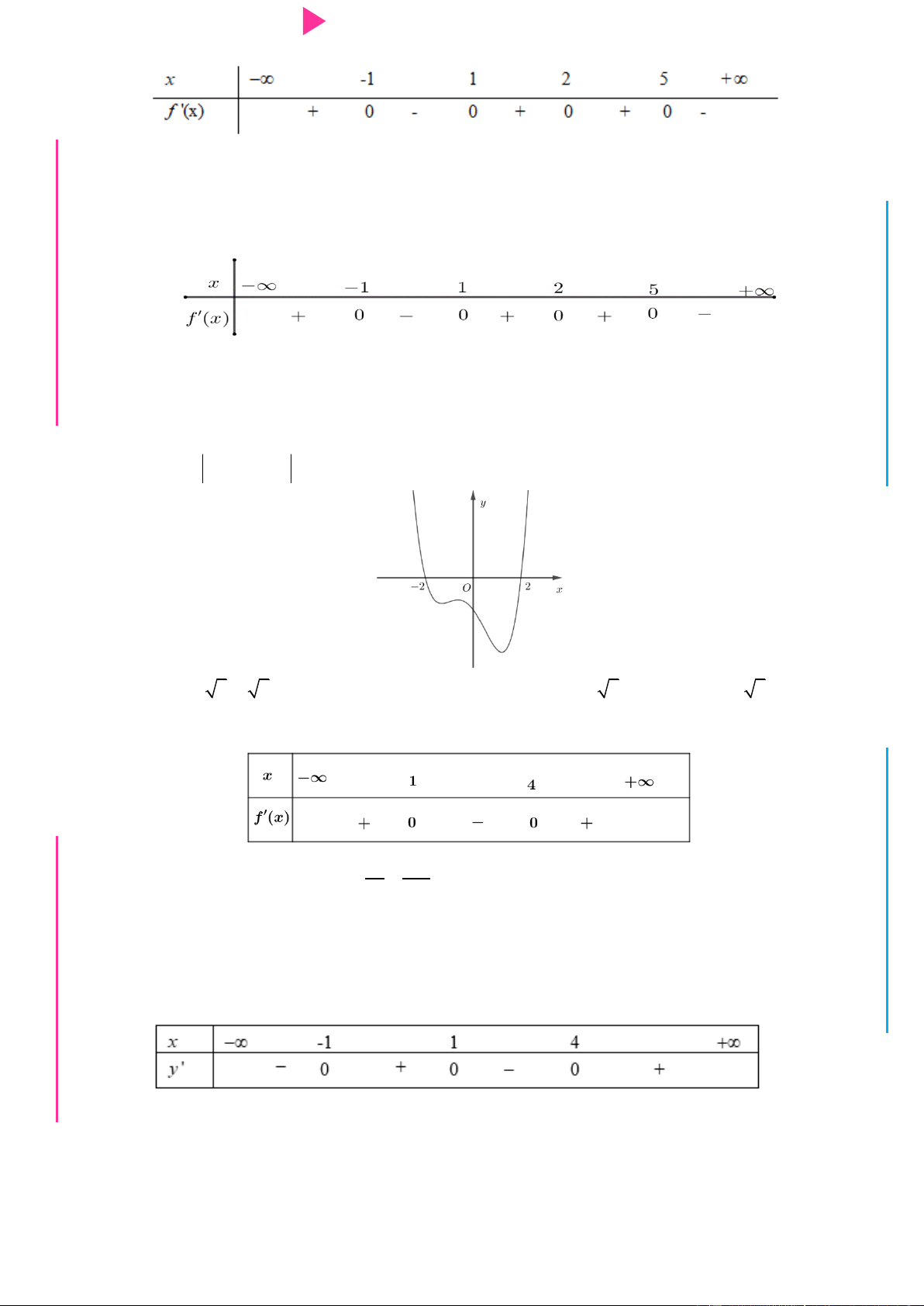
Câu 38. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: x 1 1 2 5 f x 0 0 0 0
Cho hàm số y f x 3 3
3 x 12x nghịch biến trên khoảng nào sau đây? A. ; 1 B. 1 ;0 C. 0;2 D. 2;
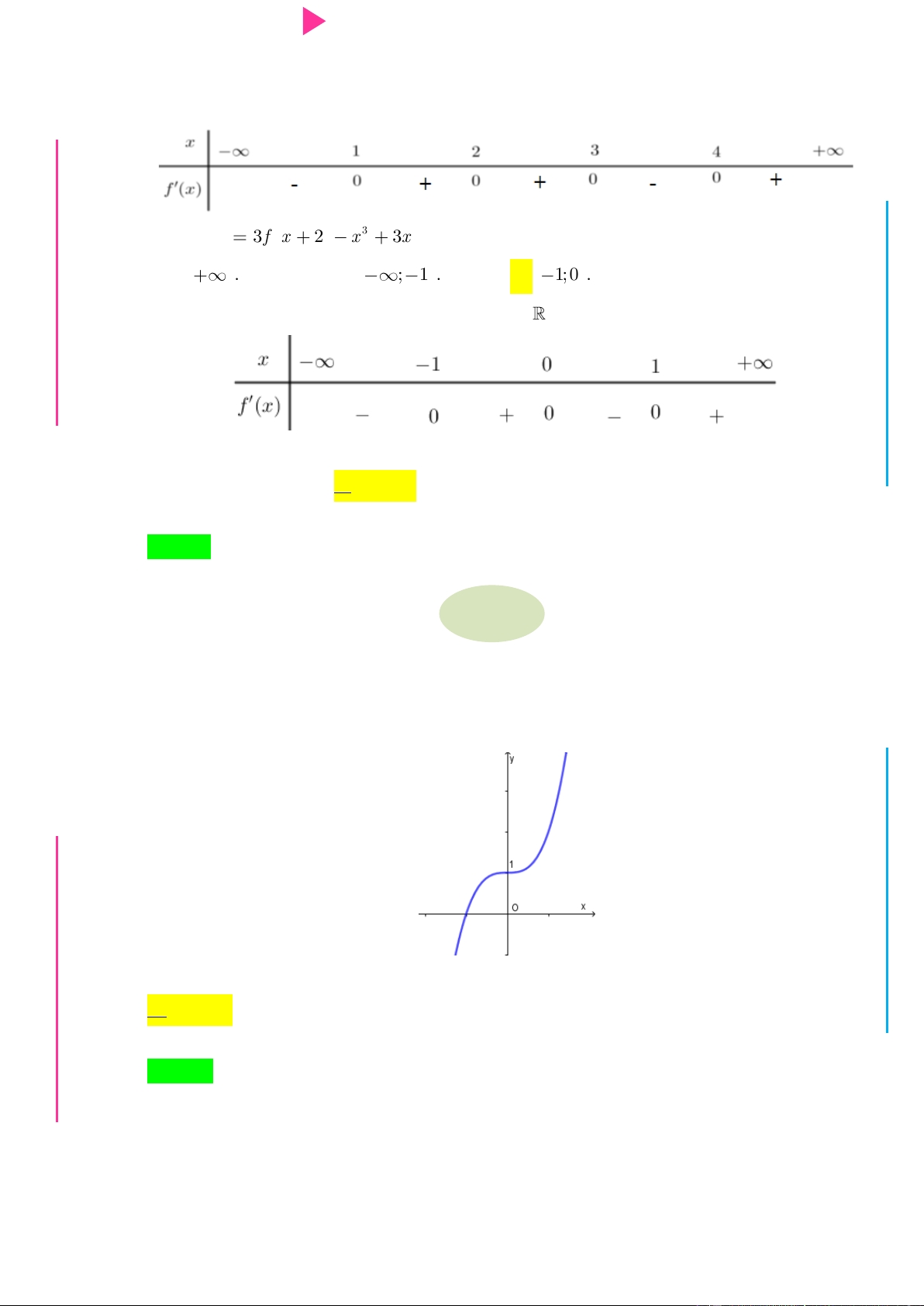
Câu 39. Cho hàm số y f x có đạo hàm f x 2 '
x 2x . Hàm số g x f 2 x 1 nghịch
biến trên khoảng nào sau đây? A. 1; . B. 0 ;1 . C. ; 1 . D. 1 ;0 .
Câu 40. Cho hàm số y f x có đạo hàm f x trên
. Hình vẽ bên là đồ thị của hàm số
y f x .
NGUYỄN CÔNG ĐỊNH | 10
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Hàm số 2 g x
f x x nghịch biến trên khoảng nào trong các khoảng dƣới đây? 3 3 1 1 A. ; . B. ; . C. ; . D. ; . 2 2 2 2
Câu 41. Cho hàm số y f x có đạo hàm f x 3 x 2 2x , x
. Hàm số y f 2 x đồng biến trên khoảng A. 2; . B. ;2 . C. 4;2 . D. . I
Ơ Câu 42. Cho hàm số y f x nghịch biến x ;
a b . Hàm số y f 2 x đồng biến trên M D khoảng Ầ A. 2 ; b 2 a.
B. ;2 a . C. ; a b. D. 2 ; b . Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
NGUYỄN CÔNG ĐỊNH | 11
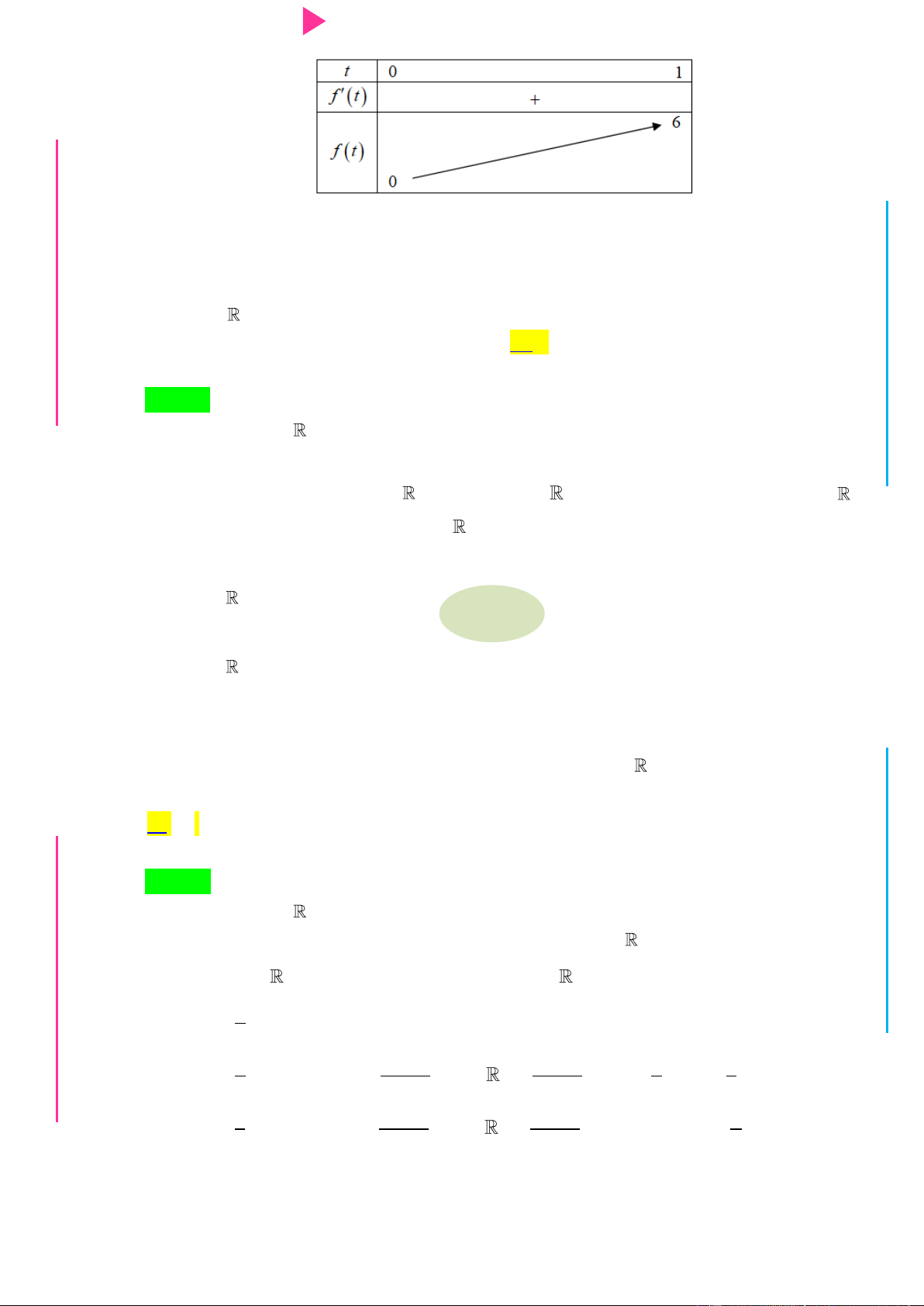
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA HƢỚNG DẪN GIẢI Câu 1.
Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: Hàm số 3 y 3f x 2 x
3x đồng biến trên khoảng nào dƣới đây? A. 1; . B. ; 1 . C. 1; 0 . D. 0;2 . Câu 2.
Cho hàm số y f x xác định và liên tục trên , có đạo hàm f x thỏa mãn I Ơ
Hàm số y f 1 x nghịch biến trên khoảng nào dƣới đây A. 1 ; 1 . B. 2 ;0 . C. 1 ;3 . D. 1; . M D Ầ Lời giải Đ NHỊ Chọn B Đ
y f 1 x y f 1 x . G THPT N.C.Đ 1 x 1 NG Hàm số y
f 1 x nghịch biến f 1 x 0 f 1 x 0 CÔN 1 1 x 0 Ờ N Ễ x 0 Y
. Vậy hàm số y f 1 x có nghịch biến trên khoảng 2 ;0 . TRƢ 1 x 2 GU N N Câu 3. Cho hàm số y
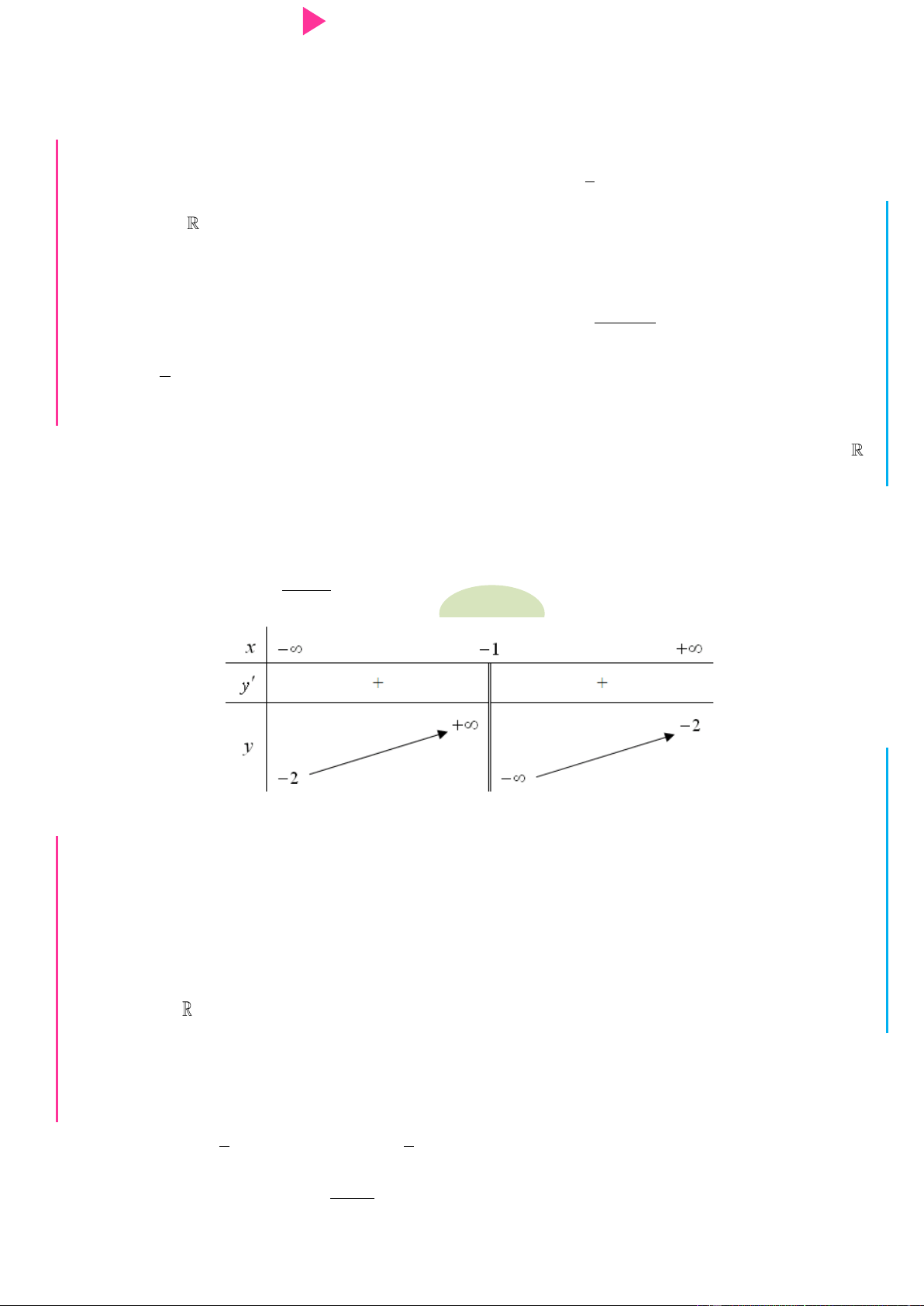
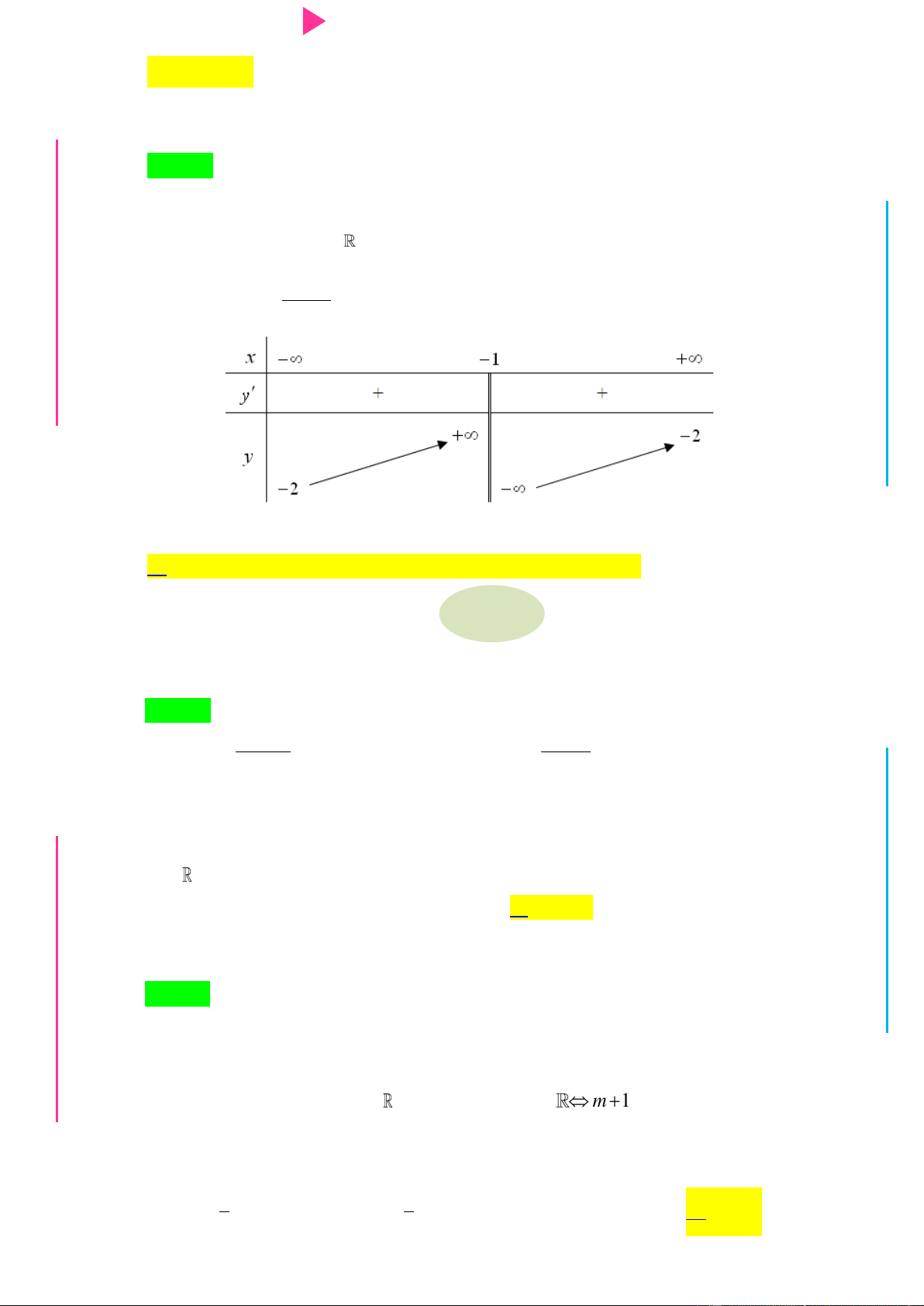
f x có đồ thị hàm số f x nhƣ hình vẽ ÁO VIÊ GI Hàm số 2 2 x y f x e
nghịch biến trên khoảng nào cho dƣới đây? A. 2 ;0 . B. 0; . C. ; . D. 1 ; 1 . Lời giải Chọn A 2 2 x y f x e
2 2 2 x y f x e 2 2 x f x e
f x 1, x 0
f 2x 1, x 0
Từ đồ thị ta thấy f x 1, x 0 f 2x 1, x 0 f
x 1, x 0 f
2x 1, x 0
NGUYỄN CÔNG ĐỊNH | 12
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x e 1, x 0 f x x e 0, x 0 Mà x
e 1, x 0
Suy ra f x x
e 0, x 0 x e 1, x 0
f x x e 0, x 0
Từ đó ta có bảng biến thiên
Vậy hàm số nghịch biến trong khoảng ;0 Câu 4.
Cho hàm số y f x có bảng xét dấu của đạo hàm nhƣ sau I Ơ Hàm số y 2
f x 2019 nghịch biến trên khoảng nào trong các khoảng dƣới đây? M D Ầ 4 ;2 1 ;2 2 ; 1 2; 4 Đ A. . B. . C. . D. . NHỊ Lời giải Đ Chọn B G THPT
Xét y g x 2
f x 2019 . N.C.Đ NG CÔN Ờ x 2 N Ễ x 1 Y g x 2
f x 2019 2 f x TRƢ Ta có , g x 0 . x 2 GU N x 4 N
Dựa vào bảng xét dấu của f x , ta có bảng xét dấu của g x : ÁO VIÊ GI
Dựa vào bảng xét dấu, ta thấy hàm số y g x nghịch biến trên khoảng 1 ;2 . Câu 5.
Cho hàm số f x có đồ thị nhƣ hình dƣới đây
Hàm số g x ln f x đồng biến trên khoảng nào dƣới đây? A. ;0 .
B. 1; . C. 1 ; 1 . D. 0; . Lời giải
NGUYỄN CÔNG ĐỊNH | 13
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Chọn B f x
g x ln
f x . f x
Từ đồ thị hàm số y f x ta thấy f x 0 với mọi x . Vì vậy dấu của g x là dấu
của f x . Ta có bảng biến thiên của hàm số g x
Vậy hàm số g x ln f x đồng biến trên khoảng 1; .
I Câu 6. Cho hàm số y
f x có đạo hàm trên , thỏa mãn f 1 f 3 0 và đồ thị của hàm Ơ
số y f x có dạng nhƣ hình dƣới đây. Hàm số 2 y f x
nghịch biến trên khoảng M D nào trong các khoảng sau? Ầ Đ y 4 NHỊ 3 Đ 2 G THPT f(x)=-X^3+3X^2+X-3 1 x -3 -2 -1 N.C.Đ 1 2 3 NG -1 CÔN Ờ -2 N -3 Ễ -4 Y TRƢ GU N A. 2 ;2 . B. 0; 4 . C. 2 ; 1 . D. 1;2 . N Lời giải Chọn D ÁO VIÊ GI
Từ đồ thị và giả thiết, ta có bảng biến thiên của y f x :
y f x2 2 f x. f x. 2
Ta có bảng xét dấu của y f x :
Ta đƣợc hàm số 2 y f x
nghịch biến trên 1;2 .
NGUYỄN CÔNG ĐỊNH | 14
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Câu 7. Cho y
f x là hàm đa thức bậc 4 , có đồ thị hàm số y
f x nhƣ hình vẽ. Hàm số 2 y f 5 2x 4x
10x đồng biến trong khoảng nào trong các khoảng sau đây? y 5 3 1 O 1 2 x 5 3 3 A. 3; 4 . B. 2; . C. ;2 . D. 0; . I 2 2 2 Ơ Lời giải M D Chọn B Ầ Đ
Từ đồ thị của y f x ta suy ra y f x có hai điểm cực trị A0; 1 , B 2;5 . NHỊ 3 ax Đ
Ta có f x ax x 2
2 ax 2ax , do đó y f x 2
ax b 1 . G THPT 3 N.C.Đ b 1 NG b 1 CÔN
Thay tọa độ các điểm , A B vào 1 ta đƣợc hệ: . Ờ 8a a 3 N 4a b 5 Ễ 3 Y TRƢ
Vậy f x 3 2
x 3x 1. GU N N
Đặt g x f x 2 5 2
4x 10x hàm có TXĐ .
Đạo hàm g x f
x x 3 2 2 5 2 4 5
4 4x 24x 43x 22 , ÁO VIÊ GI x 2
g x 0 4 5 x 2
Ta có bảng xét dấu của g x
Từ BBT ta chọn đáp án B. Câu 8.
Cho hàm số bậc bốn y f x có đồ thị hàm số y f x nhƣ hình vẽ bên. Hàm số
g x f 2 x x
1 đồng biến trên khoảng
NGUYỄN CÔNG ĐỊNH | 15
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 1 A. 0 ;1 . B. 2 ; 1 . C. 2; . D. ; 2 . 2 Lời giải Chọn A
Dựa vào đồ thị ta có: f x a x x 2 1 1 với a 0
g x 2x
1 f x x
1 a 2x
1 x x x x 22 2 2 2 I Ơ
ax2x 1 x 1 x 2 1 x 22 M D Bảng biến thiên Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ
Dựa vào bảng biến thiên chọn A . GU N Câu 9.
Cho hàm số f (x) , đồ thị hàm số y f (
x) nhƣ hình vẽ dƣới đây. N ÁO VIÊ GI
Hàm số y f 3 x đồng biến trên khoảng nào dƣới đây ? A. 4;6 . B. 1 ;2 . C. ; 1 . D. 2;3. Lời giải Chọn B Ta có: x y
f 3 x f 3 x 3
f 3 x (x 3) 3 x f x f x 3 x 3 0
f 3 x 3 0 0 3 x 3 x 0
NGUYỄN CÔNG ĐỊNH | 16
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
3 x 1L x 1
3 x 1 N x 7
3 x 4N x 2 x L x 4 3
Ta có bảng xét dấu của f 3 x :
Từ bảng xét dấu ta thây hàm số y f 3 x đồng biến trên khoảng 1 ;2. Câu 10. Cho hàm số 3 2
f (x) ax bx cx d có đồ thị nhƣ hình vẽ. Hàm số 2
g(x) [ f (x)]
nghịch biến trên khoảng nào dƣới đây? I Ơ M D Ầ Đ NHỊ Đ G THPT A. ( ; 3) . B. (1;3) . C. (3; ) . D. ( 3 ;1) . N.C.Đ NG Lời giải CÔN Ờ N Chọn B Ễ Y TRƢ
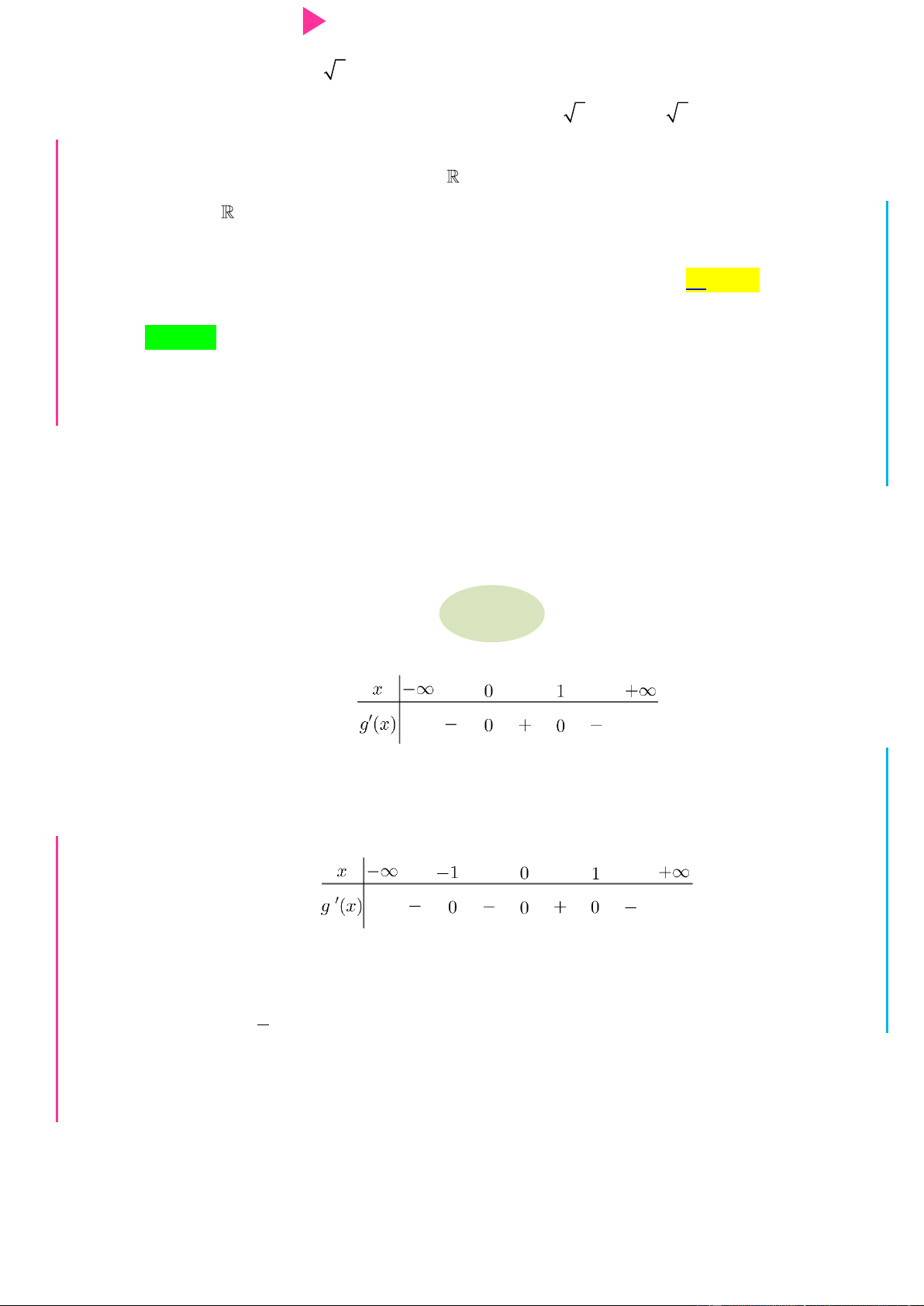
f x 0
g '(x) 2 f '(x). f (x) g '(x) 0 , ta có bảng xét dấu GU N f x 0 N ÁO VIÊ GI
Dựa vào bảng biến thiên, hàm số g(x) nghịch biến trên khoảng ( ; 3 ) và (1;3) . => Chọn B.
Câu 11. Cho hàm số y f x liên tục trên . Hàm số y f x có đồ thị nhƣ hình vẽ. Hàm số
2019 2018x g x f x 1
đồng biến trên khoảng nào dƣới đây? 2018 y 1 1 O 1 2 x 1
NGUYỄN CÔNG ĐỊNH | 17
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 2 ; 3 . B. 0 ; 1 . C. -1 ; 0 . D. 1 ; 2 . Lời giải Chọn C
Ta có g x f x 1 1. x 1 1 x 0
g x 0 f x
1 1 0 f x 1 1 . x 1 2 x 3 x
Từ đó suy ra hàm số g x f x 2019 2018 1
đồng biến trên khoảng -1 ; 0 . 2018
Câu 12. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: I Hàm số y f x 3 1 x 12x
2019 nghịch biến trên khoảng nào dƣới đây? Ơ A. 1; . B. 1; 2 C. ;1 . D. 3;4 . M D Lời giải Ầ Đ
Chọn B NHỊ
Đặt g x f x 3
1 x 12x 2019, ta có x f x 2 g' ' 1 3x 12. Đ G
Đặt t x 1 x t 1 THPT 2 N2.C .Đ g ' x
f 't 3t 6t 9
f 't 3t 6t 9 . NG CÔN Ờ x f
t t t N
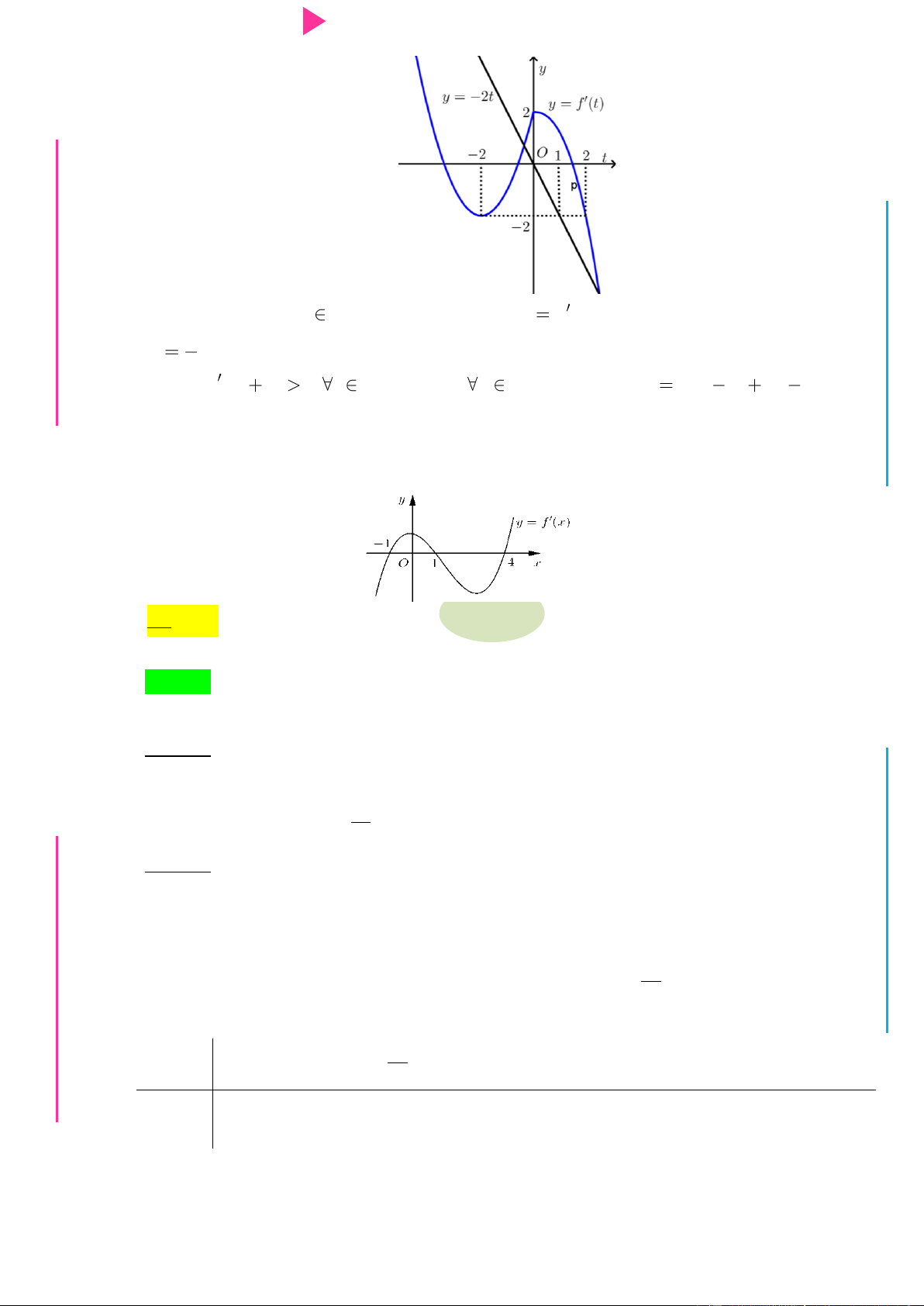
Hàm số nghịch biến khi 2 g' 0 ' 3 6 9 (1). Ễ Y TRƢ
Dựa vào đồ thị của hàm f 't và parabol(P): 2 y 3t 6t 9 GU N (Hình bên) ta có: N
1 t t 1 3 t 1 3 x 11 2 x 2 1 g x ÁO VIÊ nghịch biến trên (-2;2) GI
g x nghịch biến trên (1; 2).
Câu 13. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ hình bên dƣới
Hàm số y f 1 2x đồng biến trên khoảng 3 1 1 3 A. 0; . B. ;1 . C. 2; . D. ;3 . 2 2 2 2 Lời giải Chọn A Ta có: y 2
f 1 2x Cách 1:
NGUYỄN CÔNG ĐỊNH | 18
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x 2 1 2x 3 3 y 2
f 1 2x 0 f 1 2x 0 2
1 2x 1 0 x 2 1 2x 3 x 1 3
hàm số đồng biến trên mỗi khoảng ; 1 , 0; và 2; . 2 Cách 2:
Từ bảng xét dấu f x ta có x 2 1 2x 3 3 x 1 2x 2 2 1 1 y 2
f 1 2x 0 1
2x 0 x ( trong đó nghiệm x là nghiệm bội 2 2 1 2x 1 x 0 I 1 2x 3 Ơ x 1 M D Ầ chẵn) Đ
Bảng xét dấu y nhƣ sau : NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N 3
hàm số đồng biến trên mỗi khoảng ; 1 , 0; và 3; . 2 ÁO VIÊ GI
Cách 3( Trắc nghiệm ) 1 3 1 1 1 1 Ta có : y 2 f 0 , mà ;1 và 2;
nên loại đáp án B và C. 4 2 4 2 4 2 7 5 7 3 y 2 f 0 , mà ;3 nên loại đáp án D. 4 2 4 2
Câu 14. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ hình bên dƣới
và hàm số g x f 1 2x . Chọn khẳng định sai trong các khẳng định sau 1 A. x
là một điểm cực đại và x 0 là một điểm cực tiểu của hàm số y g x . 2
B. Hàm số y g x có 2 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số y g x đạt cực tiểu tại x 0 và x 2 .
NGUYỄN CÔNG ĐỊNH | 19
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
D. x 1 là một điểm cực đại và x 2 là một điểm cực tiểu của hàm số y g x . Lời giải Chọn A
Theo cách 2 của câu 34 kết luận hàm số có 2 cực đại là x 3 1 , x và 2 điểm cực tiểu 2
là x 0 , x 2 nên chỉ có đáp án A sai.
Câu 15. Cho hàm số y f x . Đồ thị hàm số y f x đƣợc cho nhƣ hình vẽ sau I Ơ
Hàm số g x f 4 2x
1 đồng biến trên khoảng nào sau đây? M D 1 3 A. ; 1 . B. ;1 . C. 1; .
D. 2; . Ầ 2 2 Đ NH Lời giải Ị Đ Chọn B G THPT
Ta có g x 3 x f 4 8 2x 1 N.C.Đ NG x 0 x 0 CÔN Ờ 3 x 0 N
g x 0 4 4 2x 1 1 x 2 . Ễ f ' 4 2x 1 0 Y TRƢ 4 4 2x 1 3 x 2 GU N
(Trong đó x 0 là nghiệm bội lẻ (bội 7)). N
Dựa vào đồ thị hàm số f x và dấu của g x , ta có BBT nhƣ sau: ÁO VIÊ GI
g x đồng biến trên 4 ; 2 và 4 0; 2 . 1
Vậy g x đồng biến trên khoảng ;1 . 2
Câu 16. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ hình bên dƣới
Hàm số y f 1 2x đồng biến trên khoảng
NGUYỄN CÔNG ĐỊNH | 20
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 3 1 1 3 A. 0; . B. ;1 . C. 2; . D. ;3 . 2 2 2 2 Lời giải Chọn A Ta có: y 2
f 1 2x 0 f 1 2x 0 x 2 1 2x 3 3
Từ bảng xét dấu ta có f 1 2x 0 2 1 2x 1 0 x 2 1 2x 3 x 1 3
Từ đây ta suy ra hàm số đổng biến trên khoảng 0; 2
Câu 17. Cho hàm số y f x liên tục trên và có đồ thị nhƣ hình vẽ sau I Ơ M D Ầ Đ NHỊ Đ G THPT
Hàm số y f 2
x 2x 3 nghịch biến trên khoảng nào dƣới đây ? N.C.Đ NG CÔN A. ; 1. B. 1; . C. 2;0 . D. 2; 1. Ờ N Ễ Lời giải Y TRƢ Chọn D GU N
Đặt g x f 2
x 2x 3 g x x f 2 2 1
x 2x 3 . N
Do x x x 2 2 2 3 1
2 2 và đồ thị hàm số y f x ta có: ÁO VIÊ x 1 GI x 1 0 x 1
g x 0 x 0 . f 2
x 2x 3 0 2
x 2x 3 3 x 2
Ta có bảng xét dấu g x nhƣ sau
Suy ra hàm số y f 2
x 2x 3 nghịch biến trên mỗi khoảng 2 ; 1 và 0; nên chọn D.
Câu 18. Cho hàm số y f (x) liên tục trên R và có đồ thị hàm số y f (
x) nhƣ hình vẽ dƣới.
NGUYỄN CÔNG ĐỊNH | 21
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Hàm số 2
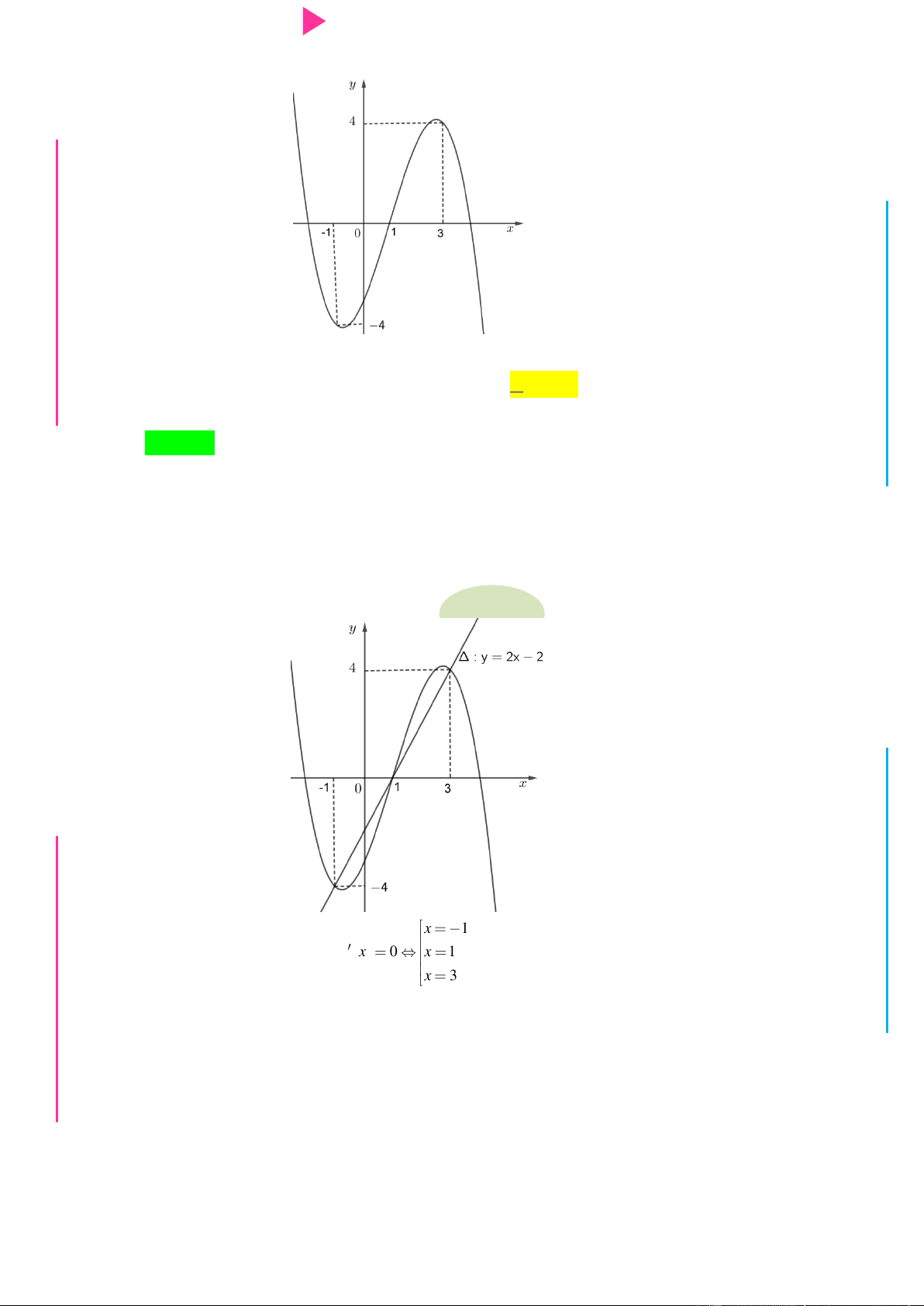
y f (x) x 2x nghịch biến trên khoảng A. ( 1 ;2) . B. (1;3) . C. (0;1) . D. ( ; 0). Lời giải I Ơ Chọn C. Đặt 2
y g(x) f (x) x 2x . M D Ầ Ta có: 2 g (x) ( f (x) x 2x)
f (x) 2x 2 . Đ
g (x) 0 f (x) 2x 2. NHỊ Đ
Số nghiệm của phƣơng trình g (
x) 0 chính bằng số giao điểm của đồ thị hàm số f (x) G THPT
và đƣờng thẳng () : y 2x 2 (nhƣ nhình vẽ dƣới). N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI x 1
Dựa vào đồ thị ta thấy g x 0 x 1 x 3 Dấu của g (
x) trên khoảng ( ;
a b) đƣợc xác định nhƣ sau: Nếu trên khoảng ( ;
a b) đồ thị hàm f (
x) nằm hoàn toàn phía trên đƣờng thẳng
() : y 2x 2 thì g ( x) 0 x ( ; a b) . Nếu trên khoảng ( ;
a b) đồ thị hàm f (
x) nằm hoàn toàn phía dƣới đƣờng thẳng
() : y 2x 2 thì g ( x) 0 x ( ; a b) .
Dựa vào đồ thị ta thấy trên ( 1
;1) đồ thị hàm f (x) nằm hoàn toàn phía dƣới đƣờng
thẳng () : y 2x 2 nên g ( x) 0 x ( 1 ;1) .
NGUYỄN CÔNG ĐỊNH | 22
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Do đó hàm số 2
y f (x) x 2x nghịch biến trên ( 1 ;1) mà (0;1) ( 1 ;1) nên hàm số nghịch biến trên (0;1) .
Câu 19. Cho hàm số y f x 2 2 có đạo hàm
f x x
1 x x 2 . Hỏi hàm số 2 g x
f x x đồng biến trên khoảng nào trong các khoảng sau? A. 1 ; 1 . B. 0; 2 . C. ; 1 . D. 2; . Lời giải Chọn C x 1 2 x 1 0
f x 0 2 x 2 1
x x 2 0 x 1 . 2
x x 2 0 x 2
Bảng xét dấu f x I Ơ 2 M D
Ta có g x 1 2x f x x . Ầ Đ 1 1 x NH x 2 Ị 2 Đ 1 2x 0 2 1 5 2
x x 1 G g x 0
1 2x f x x 0 x THPT . f 2
x x 0 2 N.C.Đ 2 x x 1 NG 1 5 2 CÔN x Ờ x x 2 N 2 Ễ Y
Bảng xét dấu g x TRƢ GU N N ÁO VIÊ 2 GI
Từ bảng xét dấu suy ra hàm số g x f x x đồng biến trên khoảng ; 1 .
Câu 20. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: x 2x
Hàm số y g x f x 4 3 2 2
6x đồng biến trên khoảng nào dƣới đây? 2 3 A. 2 ; 1 . B. 1; 2 . C. 4 ; 3 . D. 6 ;5 . Lời giải Chọn A Cách 1: Giải nhanh
Ta có: y x f 2 x 3 2 2 .
2x 2x 12x
NGUYỄN CÔNG ĐỊNH | 23
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA + Chọn x 5 ,5 6 ; 5
y f 825 5, 5 11 30, 25 0 4
vì theo BBT 30, 25 4 f 30, 25 0 1
1f 30,25 0 nên loại bỏ đáp án D.
+ Tƣơng tự chọn x 4
,5 ta đều đƣợc y' 4
,5 0 nên loại bỏ đáp án C.
+ Chọn x 1,5 ta đều đƣợc y f 27 ' 1, 5 3 2, 25 0 4
vì theo BBT 1 2, 25 4 f 2, 25 0 3 f 2, 25 0 nên loại bỏ đáp án B. Cách 2: Tự luận
Ta có y x f 2 x 3 2
x x x x f 2 x 2 2 . 2 2 12 2
x x 6 f 2
x 0 x 1; 2 I Ơ Mặt khác: 2
x x 6 0 x 2 x 3 M D Ta có bảng xét dấu: Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ (kxđ: không xác định) GU N
y g x 2 ; 1 2; N Vậy hàm số
đồng biến trên khoảng và .
Câu 21. Cho hàm số y f x có đạo hàm liên tục trên và có bảng biến thiên nhƣ sau: ÁO VIÊ GI
Hàm số y f 2
x 2x nghịch biến trên khoảng nào dƣới đây ? A. ;0 . B. 0 ;1 . C. 2; . D. 1;2 . Lời giải Chọn B
NGUYỄN CÔNG ĐỊNH | 24
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x 1 x 1 x 0 x y
2x 2 f 2 2 0 2
x 2x 0 2
x 2x 0 x 2 f 2
x 2x 0 2
x 2x 2 x 1 3 x 1 3
Lập bảng xét dấu y I Ơ M D
Dựa vào bảng xét dấu hàm số nghịch biến trên 0 ;1 . Ầ
Đ Câu 22. Cho hàm số y f x có đồ thị của hàm số y f x đƣợc cho nhƣ hình bên. Hàm số NHỊĐ
y f x 2 2 2
x nghịch biến trên khoảng G THPT y N.C.Đ 3 NG CÔN Ờ N 1 Ễ Y TRƢ GU N 1 O 2 3 4 5 x N 2 ÁO VIÊ GI A. 3 ; 2 . B. 2 ; 1 . C. 1 ; 0 . D. 0; 2 . Lời giải Chọn C Cách 1: Giải nhanh
Ta có : y 2 f 2 x 2 . x + Chọn x 2 ,1 3 ; 2 y 2 , 1 2 f 4, 1 4, 2 0
vì theo đồ thị f 4,
1 3 2 f 4,
1 4, 2 0 .Nên đáp án A sai. + Chọn x 1 ,9 2 ; 1 y 1
,9 2 f 3,9 3,8 0
vì theo đồ thị f 3,9 3 2 f 3,9 3,8 0 .Nên đáp án B sai.
+ Chọn x 1,50;2 y1,5 2 f 0,5 3 0
vì theo đồ thị f 0,5 0 2 f 0,5 3 0 .Nên đáp án D sai.
Cách 2: Giải tự luận
NGUYỄN CÔNG ĐỊNH | 25
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Ta có y f x 2 2 2
x y 2 x 2 f 2 x 2x
y 2 f 2 x 2x y 0 f 2 x x 0 f 2 x 2 x 2 .
Dựa vào đồ thị ta thấy đƣờng thẳng y x 2 cắt đồ thị y f x tại hai điểm có hoành I 1 x 2 Ơ
độ nguyên liên tiếp là 1
và cũng từ đồ thị ta thấy f x x 2 trên miền x 3 2 M D
2 x 3 nên f 2 x 2 x 2 trên miền 2 2 x 3 1 x 0 . Ầ Đ
Vậy hàm số nghịch biến trên khoảng 1 ; 0 . NHỊ Đ
Câu 23. Cho f x mà đồ thị hàm số y
f x nhƣ hình bên. Hàm số 2 y f x 1 x 2x G THPT đồng biến trên khoảng N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI A. 1;2 . B. 1;0 . C. 0;1 . D. 2; 1 . Lời giải Chọn A Ta có 2 y f x 1 x 2x Khi đó y f x 1 2x
2 . Hàm số đồng biến khi y 0 f x 1 2 x 1 0 1 Đặt t x
1 thì 1 trở thành: f t 2t 0 f t 2t .
Quan sát đồ thị hàm số y f t và y
2t trên cùng một hệ trục tọa độ nhƣ hình vẽ.
NGUYỄN CÔNG ĐỊNH | 26
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Khi đó ta thấy với t
0;1 thì đồ thị hàm số y
f t luôn nằm trên đƣờng thẳng y 2t . Suy ra f t 2t 0, t 0;1 . Do đó x 1;2 thì hàm số 2 y f x 1 x 2x đồng biến. I
Ơ Câu 24. Cho hàm số y=f(x) có đồ thị y=f ‘(x) nhƣ hình vẽ bên. Hỏi hàm số y=f(3-2x)+2019 nghịch
biến trên khoảng nào sau đây? M D Ầ Đ NHỊ Đ G THPT N.C.Đ A. 1;2 . B. 2; . C. ;1 . D. 1 ; 1 . NG CÔN Ờ Lời giải N Ễ Y Chọn A TRƢ
Đặt g x f 3 2x 2019 g x 2f3 2x . GU N N
Cách 1 : Hàm số nghịch biến khi gx 2
f3 2x 0 f3 2x 0 1 x 2 ÁO VIÊ 1 3 2x 1 1 . Chọn đáp án A GI 3 2x 4 x 2
Cách 2 : Lập bảng xét dấu 3 2x 1 x 2 gx 2f
3 2x 0 f 3 2x 0 3 2x 1 x 1 3 2x 4 1 x 2 Bảng xét dấu x 1 1 2 2 g'(x) - 0 + 0 - 0 +
Lƣu ý : cách xác đinh dấu của g’(x). Ta lấy 32;,g 3 2 .f3 2. 3 2 f 3 0
(vì theo đồ thị thì f’(-3) nằm dƣới trục Ox nên f 3 0)
Dựa vào bảng xét dấu, ta chọn đáp án A.
NGUYỄN CÔNG ĐỊNH | 27
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
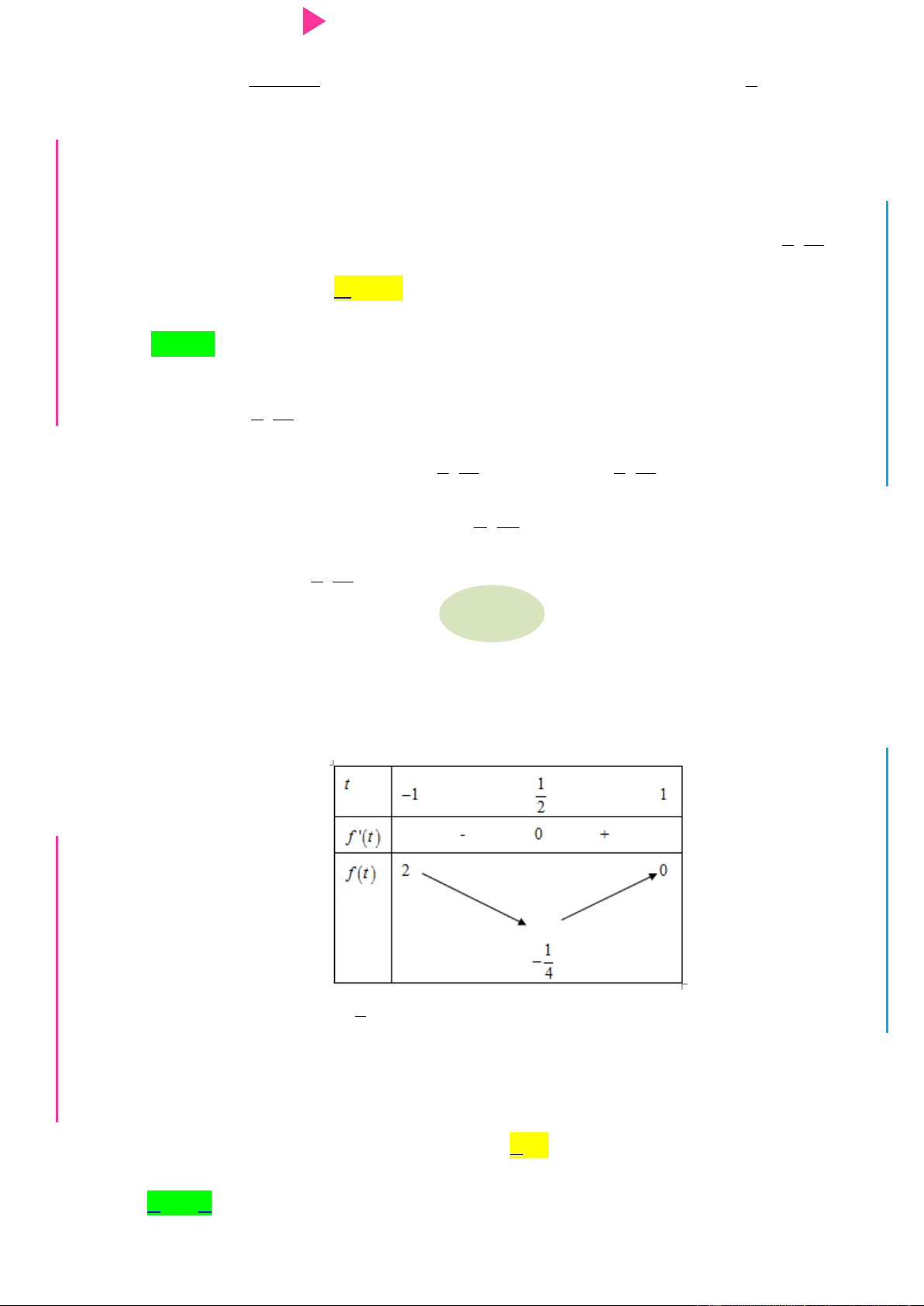
Câu 25. Cho hàm số y f x có bảng xét dấu đạo hàm nhƣ sau 1
Gọi g x 2 f 1 x 4 3 2
x x x 5 . Khẳng định nào sau đây đúng ? 4
A. Hàm số g x đống biến trên khoảng ; 2 .
B. Hàm số g x đồng biến trên khoảng 1 ;0 .
C. Hàm số g x đồng biến trên khoảng 0; 1 .
D. Hàm số g x nghịch biến trên khoảng 1; . Lời giải I Chọn C Ơ
Xét g x f x x x x f x x3 3 2 2 1 3 2 2 1 1 1 x M D
Đặt 1 x t , khi đó g x trở thành ht f t 3 2 t t Ầ Đ Bảng xét dấu NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N
Từ bảng xét dấu ta suy ra ht nhận giá trị dƣơng trên các khoảng 2 ; 1 và 0; 1
,nhận giá trị âm trên các khoảng 1
;0 và 1; . ÁO VIÊ GI
hàm số gx nhận giá trị dƣơng trên 2;3 và 0;
1 ,nhận giá trị âm trên 1;2 và ;0
Vậy hàm số đồng biến trên khoảng 0; 1 .
Câu 26. Cho hàm số f x 3 2
x 3x 5x 3 và hàm số g x có bảng biến thiên nhƣ sau
Hàm số y g f x nghịch biến trên khoảng A. 1 ; 1 . B. 0;2 . C. 2 ;0 . D. 0;4 . Lời giải Chọn A
NGUYỄN CÔNG ĐỊNH | 28
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Ta có f x 2
3x 6x 5; f x x 2 3 1 2 0, x . y g
f x g
f x.f x. 3 2
x 3x 5x 9 0
y 0 g f x 0 6
f x 6 3 2
x 3x 5x 3 0 x 1
2x 4x 9 0 1 x 1. x 1
2x 2x 3 0
Câu 27 . Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau I 2 3 2 Ơ
Đặt g x f x 2x 2 x 3x 6x. Xét các khẳng định M D Ầ
1) Hàm số g x đồng biến trên khoảng 2;3. Đ NHỊ
2) Hàm số g x nghịch biến trên khoảng 0 ;1 . Đ g x 4; G
3) Hàm số đồng biến trên khoảng . THPT N.C.Đ
Số khẳng định đúng trong các khẳng định trên là NG CÔN Ờ A. 0 . B. 1. C. 2 . D. 3 . N Ễ Lời giải Y TRƢ Chọn B GU N 2 2 N
Ta có: g x 2x 2 f x 2x 2 3x 6x 6 . 5 13 9 13 Do g 3. f 0 vì f 0
(dựa vào bảng dấu của f x ), do đó hàm số ÁO VIÊ 2 4 4 4 GI
g x không thể đồng biến trên khoảng 2;3. Vậy mệnh đề 1) là sai. 1 5 33 5 Do g 1 . f 0 vì f 0
(dựa vào bảng dấu của f x ), do đó hàm 2 4 4 4
số g x không thể đồng biến trên khoảng 0
;1 . Vậy mệnh đề 2) là sai.
Với x 4; E , ta thấy:
x x x 2 2 f 2 2 2 1 1 10
x 2x 2 0 và 2x 2 0 nên
x f 2 2 2 .
x 2x 2 0, x 4; (a); x 1 3 Dễ thấy 2 2
3x 6x 6 0
3x 6x 6 0, x 4; (b). x 1 3
Cộng theo vế của (a) và (b) suy ra
g x x f 2 x x 2 2 2 2
2 3x 6x 6 0, x 4; .
Vậy g x đồng biến trên khoảng 4; . Do đó 3) là mệnh đề đúng.
NGUYỄN CÔNG ĐỊNH | 29
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 28. Cho hàm số y f x có đạo hàm trên và có bảng xét dấu của đạo hàm nhƣ hình vẽ sau:
Có bao nhiêu số nguyên m 0;2020 để hàm số 2 g x
f x x m nghịch biến trên khoảng 1 ;0? A. 2018. B. 2017. C. 2016. D. 2015. Lời giải Chọn C Hàm số 2 g x
f x x m nghịch biến trên khoảng 1 ;0
gx x f 2 2 1 .
x x m 0 x 1;0 I Ơ f 2
x x m 0 x
1;0 (do 2x 1 0 x 1 ;0 ) M D 2 2
x x m 1
m 1 x x Ầ x 1;0 x 1; 0 Đ 2 2
x x m 4
m 4 x x NHỊ 2 Đ
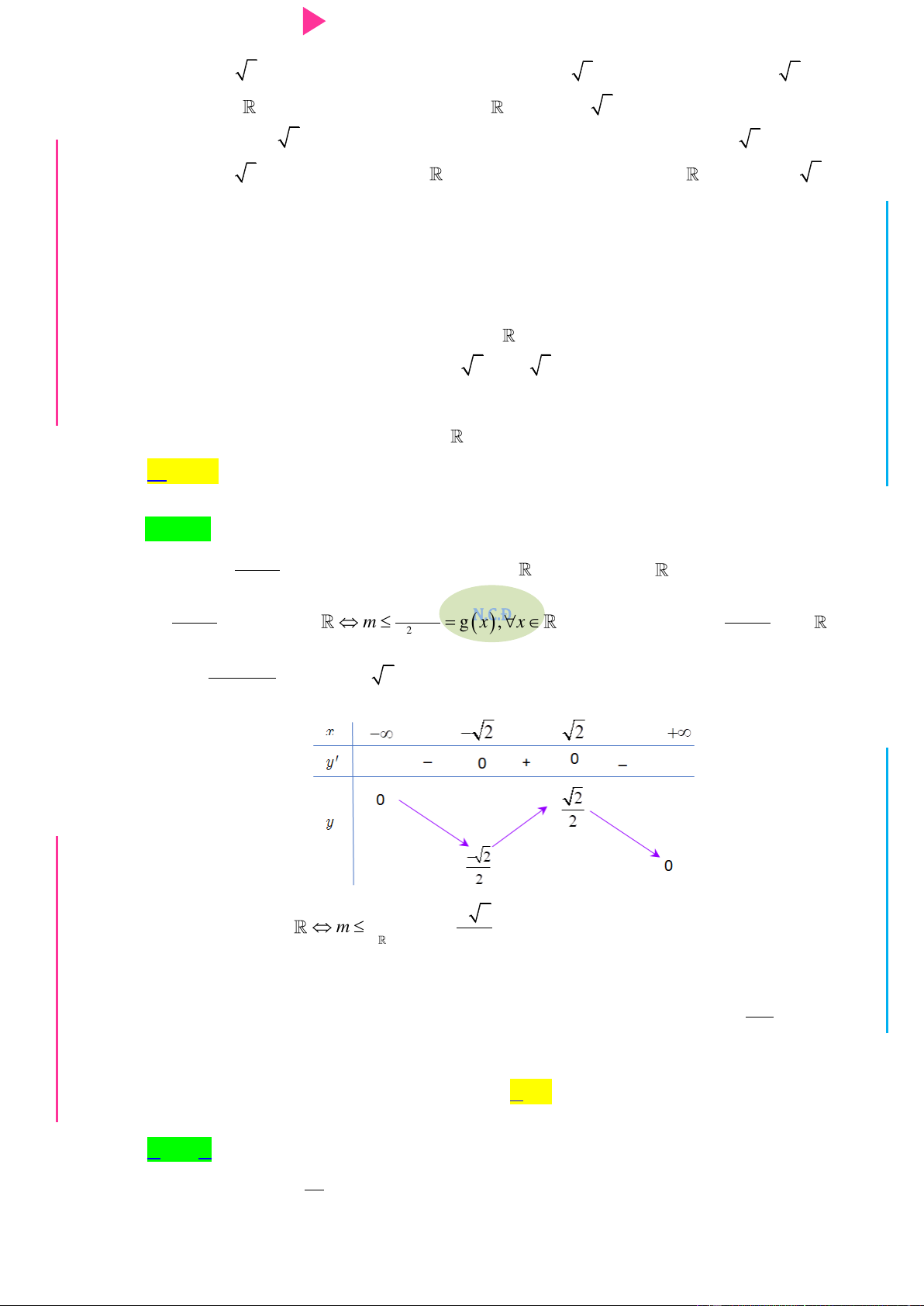
m 1 min h x x x h 1 2 1 ; 0 m 1 G THPT m max hx 2
x x h N.C.Đ m 4 4 0 0 1 ; 0 NG CÔN Ờ N
Kết hợp điều kiện m 0;2020 , suy ra: m 4;2020 . Ễ Y TRƢ
Vậy có 2016 giá trị m nguyên thỏa đề. GU
N Câu 29. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau N ÁO VIÊ GI 2
Hàm số y f 2x 3 1
x 8x 2019 nghịch biến trên khoảng nào dƣới đây? 3 1 A. 1; . B. ; 2 . C. 1 ; . D. 1 ;7 . 2 Lời giải Chọn C
g x f 2x 2 3 1
x 8x 2019 . 3
g x f x 2 2 2
1 2x 8 .
g x f x 2 0 ' 2 1 4 x 1 .
Hàm số f 2x
1 có bảng xét dấu nhƣ hàm số f x nên ta có:
NGUYỄN CÔNG ĐỊNH | 30
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x 1 5 3 1 x x
2x 1 x 4 x 2 1 1 2 2 2 1 . 2x 1 2 1 x I 2 Ơ
Bảng xét dấu của g x nhƣ sau: M D x x 1 1 1 1 Ầ 2 2 Đ NH
g x
0 0 Ị Đ G
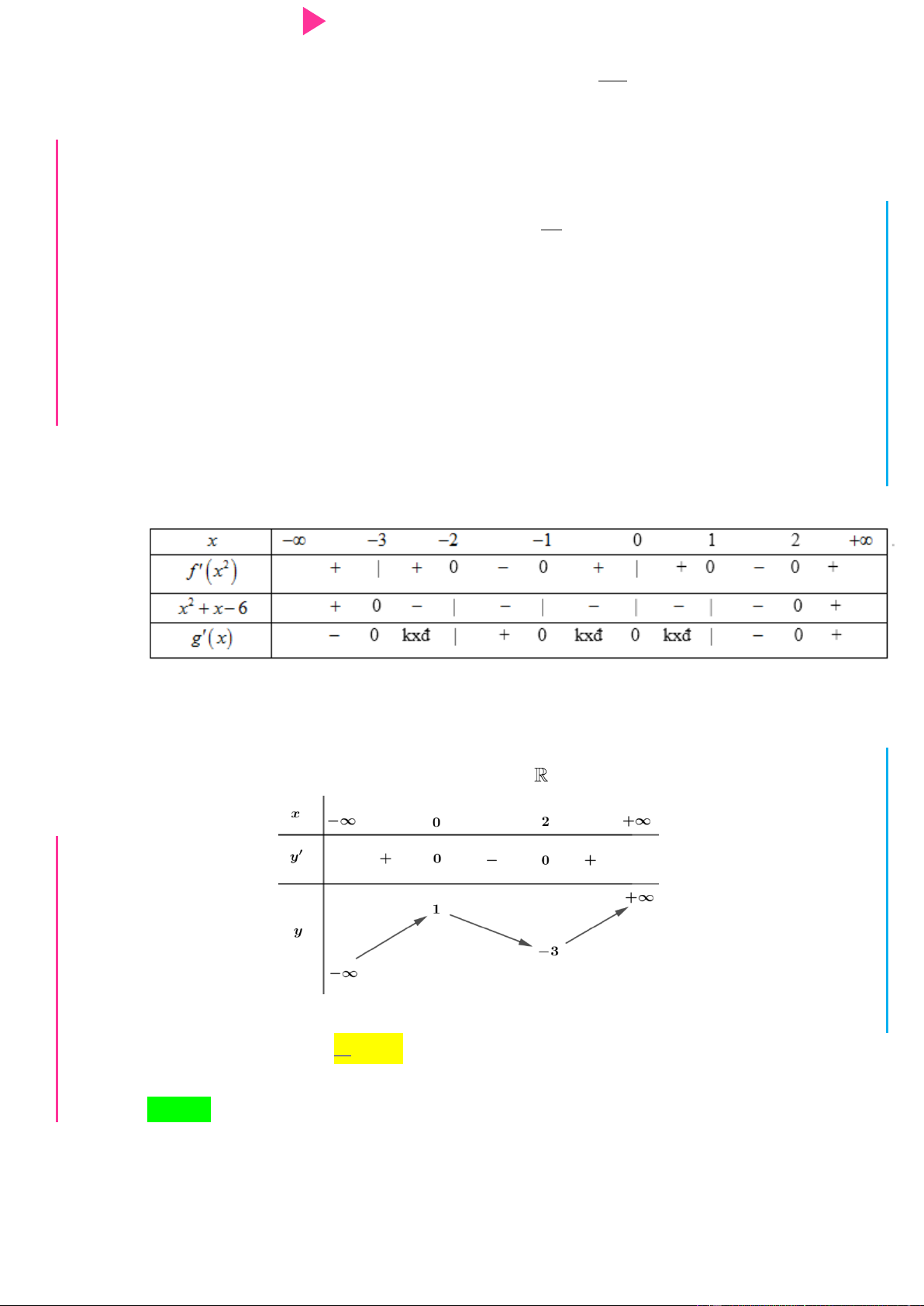
THPT Câu 30. Cho hàm số y f (x) có bảng xét dấu của đạo hàm f '(x) nhƣ sau N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N Hàm số 3 2
y 3 f (x 2) x 3x 9x 1 nghịch biến trên khoảng nào sau đây? N A. 2 ; 1 . B. 2; . C. 0;2 .
D. ; 2 . ÁO VIÊ Lời giải GI Chọn A Ta có 2
y ' 3x 6x 9 3 f '(2 x).
Hàm số y nghịch biến khi 2
y ' 0 x 2x 3 f '(2 x). Bất phƣơng trình này không
thể giải trực tiếp ta sẽ tìm điều kiện để 2
x 2x 3 0 3 x 1 2
x 2x 3 0 2 x 1 x 3 3 x 1.
f '(2 x) 0 1
2 x 5 3 x 1
Đối chiếu các đáp án chọn A.
Câu 31. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ sau
Hàm số y f x 3 2 3
2 x 3x 9x nghịch biến trên khoảng nào dƣới đây
NGUYỄN CÔNG ĐỊNH | 31
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 2 ; 1 . B. ; 2 . C. 0; 2 . D. 2; . Lời giải Chọn A.
Theo đề bài: y f x 3 2
x x x f x 2 ' 3 2 3 9 3
2 3x 6x 9 .
Để hàm số nghịch biến y f x 2 0 3
2 3x 6x 9 0
f x 2
2 x 2x 3
Từ BXD f x ta có BXD của f x 2 nhƣ sau: I
Từ BXD trên, ta có hình dạng đồ thị của hàm số y f x 2 và 2
y x 2x 3 đƣợc Ơ
vẽ trên cùng hệ trục tọa độ nhƣ hình vẽ. M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N
Dựa vào đồ thị ta có hàm số nghịch biến trên 3 ; 1 .
Câu 32. Cho hàm số y f x có đồ thị hàm số y f x nhƣ hình vẽ bên. Biết f 2 0, hàm ÁO VIÊ GI số y f 2018 1 x
đồng biến trên khoảng nào dƣới đây? A. 2018 2018 3; 3 . B. 1 ;. C. 2018 ; 3 . D. 2018 3; 0 . Lời giải Chọn D
Dựa vào đƣờng thẳng hàm số y f x và f 2
0, ta có bảng biến thiên của hàm số
y f x nhƣ sau
NGUYỄN CÔNG ĐỊNH | 32
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Ta có 2018 1 x 1 x
mà max f x f 2 0 f 2018 1 x 0 ;2
Do đó y f 2018 1 x f 2018 1 x 2017 y x f 2018 2018 1 x .
Hàm số đồng biến y 0 2017 x f 2018 2018 1 x 0 .
Trƣờng hợp 1. Với x 0 x 2018 x 1 loai
y 0 f 1 x 2018 1 2 2018 0 2018 x 3 (vì x 0 ). 2018 1 x 2 2018 x 3 I
Trƣờng hợp 2. Với x 0 Ơ y f 2018 x 2018 0 1
0 2 1 x 2 2018 1 x 3 2018 3 x 0 .
M D Câu 33. Cho hàm số f x có bảng xét dấu đạo hàm nhƣ sau: Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN x 2x Ờ
Hàm số y g x f x 4 3 2 2
6x đồng biến trên khoảng nào dƣới đây? N 2 3 Ễ Y TRƢ A. 2 ; 1 . B. 1;2 . C. 6 ;5. D. 4 ;3 . GU N Lời giải N Chọn A ÁO VIÊ Cách 1: GI
Ta có y g x xf 2 x 3 2 2
2x 2x 12x . Đặt h x 3 2
2x 2x 12x .
Bảng xét dấu h x :
Đối với dạng toán này ta thay từng phƣơng án vào để tìm ra khoảng đồng biến của g x . 2
x 1;4 f 2x 0 2xf 2x 0 Với x 2 ; 1 x 0 . h x h x 0 0 xf 2 x 3 2 2
2x 2x 12x 0 gx 0 . Vậy g x đồng biến trong khoảng 2 ; 1 .
NGUYỄN CÔNG ĐỊNH | 33
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2
x 1;4 f 2x 0 2xf 2x 0
Với x 1; 2 x 0 . h x h x 0 0 xf 2 x 3 2 2
2x 2x 12x 0 gx 0. Vậy g x nghịch biến trong khoảng 1;2.
Kết quả tƣơng tự với x 6
;5 và x 4 ;3 . Cách 2:
Ta có g x x f 2 x 2 2
x x 6 .
Bảng xét dấu của g x trên các khoảng 6 ;5, 4 ;3 , 2 ; 1 , 1; 2 I Ơ M D Ầ 2 ;1 Đ
Từ bảng xét dấu ta chọn hàm số đồng biến trên khoảng NHỊ
Câu 34. Cho hàm số y f x có bảng xét dấu đạo hàm nhƣ hình bên. Hàm số Đ
3 f 2x 1 f 2x G THPT y e 3
đồng biến trên khoảng nào dƣới đây. N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N
A 1; B. ; 2 . C. 1 ;3 . D. 2 ; 1 . N Lời giải Chọn D ÁO VIÊ GI x
Từ bảng đạo hàm ta thấy f x 1 ' 0 1 x 4
3 f 2x 1 f 2x y e 3 y ' 3
. f '2 x 3 f 2 x 1 .e
f '2 x f 2 x .3 .ln 3 ' '
y f 2 x 3 f 2 x 1 f 2 x .3.e 3 .ln 3
Để hàm số đồng biến thì y ' f '2 x 3 f 2 x 1 f 2 x .3.e 3 .ln 3 0
3 f 2x 1 f 2x
f '2 x 0 (Vì 3.e 3 .ln 3 0 )
f x 2 x 1 x 3 ' 2 0 1 2 x 4 2 x 1 x 2 ; 1 .
Câu 35. Cho hàm số y f x có đồ thị hàm số y f ' x nhƣ hình vẽ
NGUYỄN CÔNG ĐỊNH | 34
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x
Hàm số y f x 2 1
x nghịch biến trên khoảng 2 3 A. 1 ; . B. 1;3 . C. 3 ; 1 . D. 2 ;0 . 2 Lời giải Chọn D I x Ơ
Đặt g x f x 2 1
x . Ta có g 'x f '1 x (1 x) . 2 M D
g ' x 0 f '1 x 1 x (*) Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N 1 x 3 x 4
Dựa vào đồ thị ta có (*) 1 x 1 x 0 . ÁO VIÊ 1 x 3 x 2 GI
Bảng biến thiên của hàm số y g x : x
Từ bảng biến thiên suy ra hàm số y g x f x 2 1
x nghịch biến trên mỗi 2 khoảng 2
;0 và 4; .
Câu 36. Cho hàm số y f (x) có bảng xét dấu đạo hàm nhƣ sau
Hàm số y f 2
x 2x đồng biến trên khoảng nào dƣới đây ? A. (1; ) . B. ( 3 ; 2 ) . C. (0;1) . D. ( 2 ;0) .
NGUYỄN CÔNG ĐỊNH | 35
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Lời giải Chọn C
Đặt g x f 2 ( )
x 2x . Ta có g x f 2 ( )
x 2x.(2x 2) . x 1 x 1 x 0 2 x 2x 2 g ( x) 0 x 2 . 2 x 2x 0 x 1 2
x 2x 3 x 3 Bảng xét dấu g ( x) I Ơ
Dựa vào bảng xét dấu của g (
x) suy ra hàm số g x f 2 ( )
x 2x đồng biến trên (0;1) . M D y f x f x
Ầ Câu 37. Cho hàm số
có đồ thị nhƣ hình vẽ sau Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N
Hàm số g x f 2
x 2 nghịch biến trên khoảng nào dƣới đây? ÁO VIÊ 1;3 3 ; 4; GI A. . B. 1 . C. 0 ;1 . D. . Lời giải Chọn C
g x f 2
x 2 2
x f 2 2 .
x 2 x f 2 2 . x 2 . x 0 x 0 g x 2x 0 0 .
x x f x 2 2 2 1 1 2 0 2 x 2 2 x 2 f x 2 2 x 2 2
0 x 2 2 , f 2 x 2
2 0 x 2 2 2 x 2 . x 2
Bảng xét dấu của g x :
NGUYỄN CÔNG ĐỊNH | 36
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Vậy g x nghịch biến trên khoảng 0 ;1 .
Câu 38. Cho hàm số f x có bảng xét dấu của đạo hàm nhƣ sau: x 1 1 2 5 f x 0 0 0 0
Cho hàm số y f x 3 3
3 x 12x nghịch biến trên khoảng nào sau đây? A. ; 1 B. 1 ;0 C. 0;2 D. 2; I Lời giải Ơ Chọn D M D Đặt 3
t x 3 khi đó y t 3 f t t 3 12t 3 Ta có Ầ Đ
yt f t t 2 3 3 3
12 3 f t t 1 t 5 NHỊ Đ
Dựa vào bảng biến thiên ta có t 5 thì f t 0; t 1t 5 0 nên G THPT
hàm số nghịch biến với t 5 hay x 2 . N.C.Đ 2
NG Câu 39. Cho hàm số y
f x có đạo hàm f x 2 ' x
2x . Hàm số g x f x 1 nghịch CÔN Ờ N
biến trên khoảng nào sau đây? Ễ Y TRƢ A. 1; . B. 0 ;1 . C. ; 1 . D. 1 ;0 . GU N
Lời giải N Chọn B x ÁO VIÊ
Ta có: f x 0 0 . GI x 2 x 0 x 0 x 0
Ta có: g x x f 2 2 . x
1 g x 0 . f x 2 x 1 0 x 1 2 1 0 2 x 1 2 x 3 Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy hàm số nghịch biến trên 0 ;1 .
Câu 40. Cho hàm số y f x có đạo hàm f x trên
. Hình vẽ bên là đồ thị của hàm số
y f x .
NGUYỄN CÔNG ĐỊNH | 37
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Hàm số 2 g x
f x x nghịch biến trên khoảng nào trong các khoảng dƣới đây? 3 3 1 1 A. ; . B. ; . C. ; . D. ; . 2 2 2 2 Lời giải Chọn C I Cách 1: Ơ x
Từ đồ thị ta thấy: f x 1 0 . x 2 M D Ầ
Ta có: g x f 2
x x 2
x x f 2
x x x f 2 . 1 2 . x x ; Đ NHỊ 1 Đ x 2 G THPT 1 2x 0 g x 1 0
x x N. C1.Đ . f
x x 2 x 2 0 2 NG 2 CÔN x x 2 Ờ N Ễ Y TRƢ Bảng biến thiên GU N N ÁO VIÊ GI 1
Vậy hàm số y g x nghịch biến trên khoảng ; . 2 Cách 2:
Ta có: g x f 2
x x 2
x x f 2
x x x f 2 . 1 2 . x x .
Hàm số y g x nghịch biến trên khoảng a; b
g x 0, x
a; b và g x 0 chỉ tại hữu hạn điểm thuộc khoảng a; b .
Chọn x 0 ta có: g 0 1 2.0. f 0 f 0 0 .
Suy ra loại các đáp án A , B , D . Vậy chọn đáp án C . 3 2
Câu 41. Cho hàm số y f x có đạo hàm f x x 2x , x
. Hàm số y f 2 x đồng biến trên khoảng
NGUYỄN CÔNG ĐỊNH | 38
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 2; . B. ;2 . C. 4;2 . D. . Lời giải Chọn A 4 3 3 2 x 2x
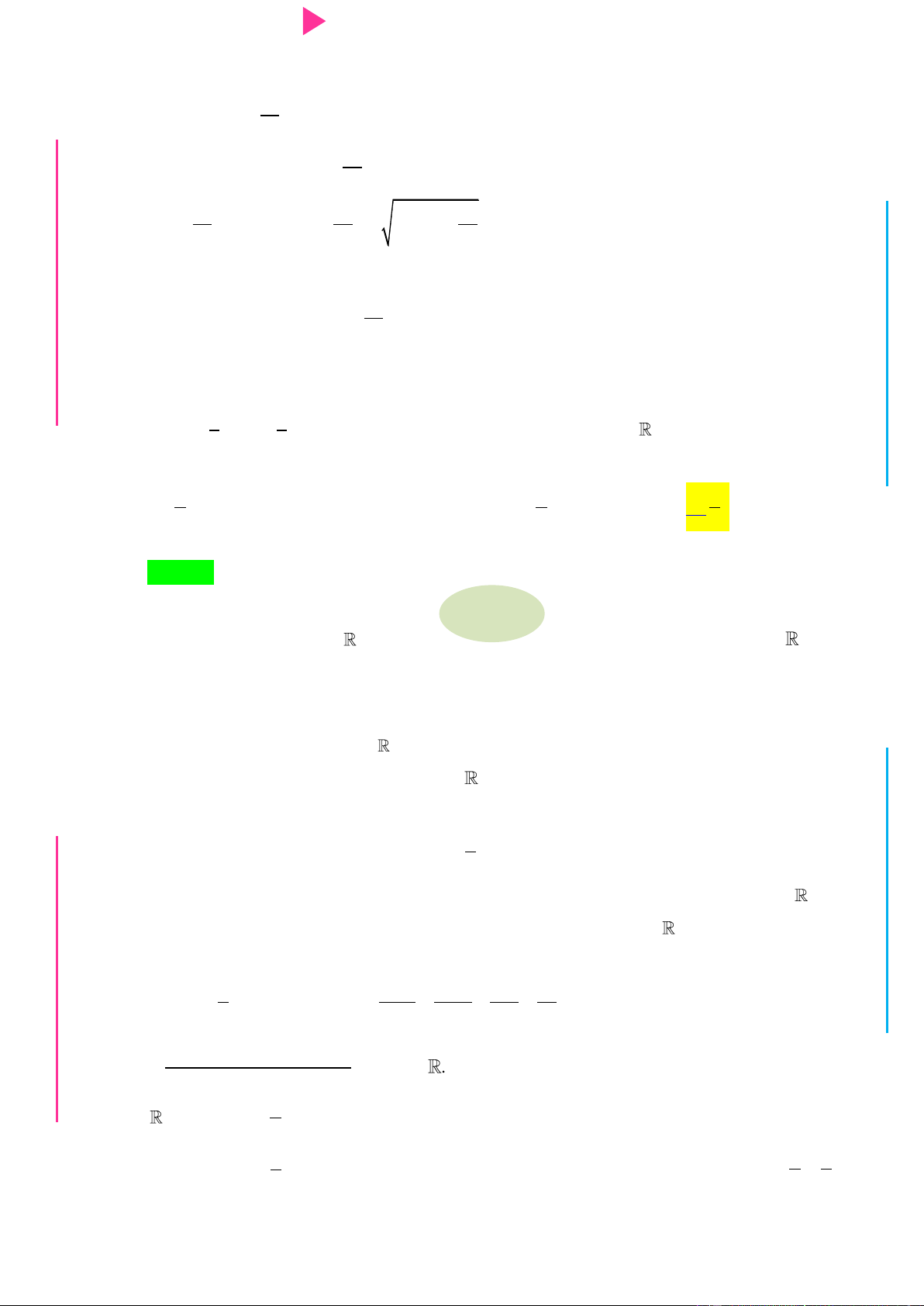
+ Ta có f x x 2x suy ra f x f
xdx 3x 2 2x dx C 4 3 4 x 3 2 2 2 x
+ Suy ra y g x f 2 x C 4 3
2 x4 22 x3 3 2
+ Tính g ' x f 2 x =
C = 2 x 22 x 2 2 x x 4 3
+ Hàm số đồng biến suy ra g ' x 0 x 0. Chọn A..
Câu 42. Cho hàm số y f x nghịch biến x ;
a b . Hàm số y f 2 x đồng biến trên I Ơ khoảng
2 ;b2a ;2a ;ab 2 ;b M D A. . B. . C. . D. . Ầ Đ Lời giải NHỊ Chọn A Đ
+ Vì hàm số y f x nghịch biến x ;
a b nên f x 0; x ; a b . G THPT N.C.Đ
+ Xét y g x f 2 x có
g x f 2 x NG CÔN Ờ N
+ Hàm số y f 2 x đồng biến thì
g x 0 f 2 x 0 f 2 x 0 Ễ Y TRƢ
Suy ra a 2 x b 2 b x 2 a . Chọn A. GU N N ÁO VIÊ GI
NGUYỄN CÔNG ĐỊNH | 39
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
CHỦ ĐỀ: ĐƠN ĐIỆU
VẬN DỤNG – VẬN DỤNG CAO DẠNG 2
BÀI TOÁN CHỨA THAM SỐ
KIẾN THỨC CẦN NẮM VỮNG
Kiến th ức bổ sung 1: Biện luận nghiệm bất phƣơng trình chứa tham số .
m f x x ;
a b m max f x. a;b I
m f x x ;
a b m min f x. Ơ a;b
m f x có nghiệm trên ;
a b m min f x. M D a;b Ầ
m f x có nghiệm trên ;
a b m max f x. Đ a;b NHỊ Đ
Kiến thức bổ sung 2: So sánh 2 nghiệm của tam thức với số thực G THPT N.C.Đ NG CÔN a f α Ờ x α x . 0. 1 2 N Ễ 0 Y TRƢ
x x α S 2α . 1 2 GU N N . a f α 0 0 ÁO VIÊ
α x x S 2α . 1 2 GI .af α 0
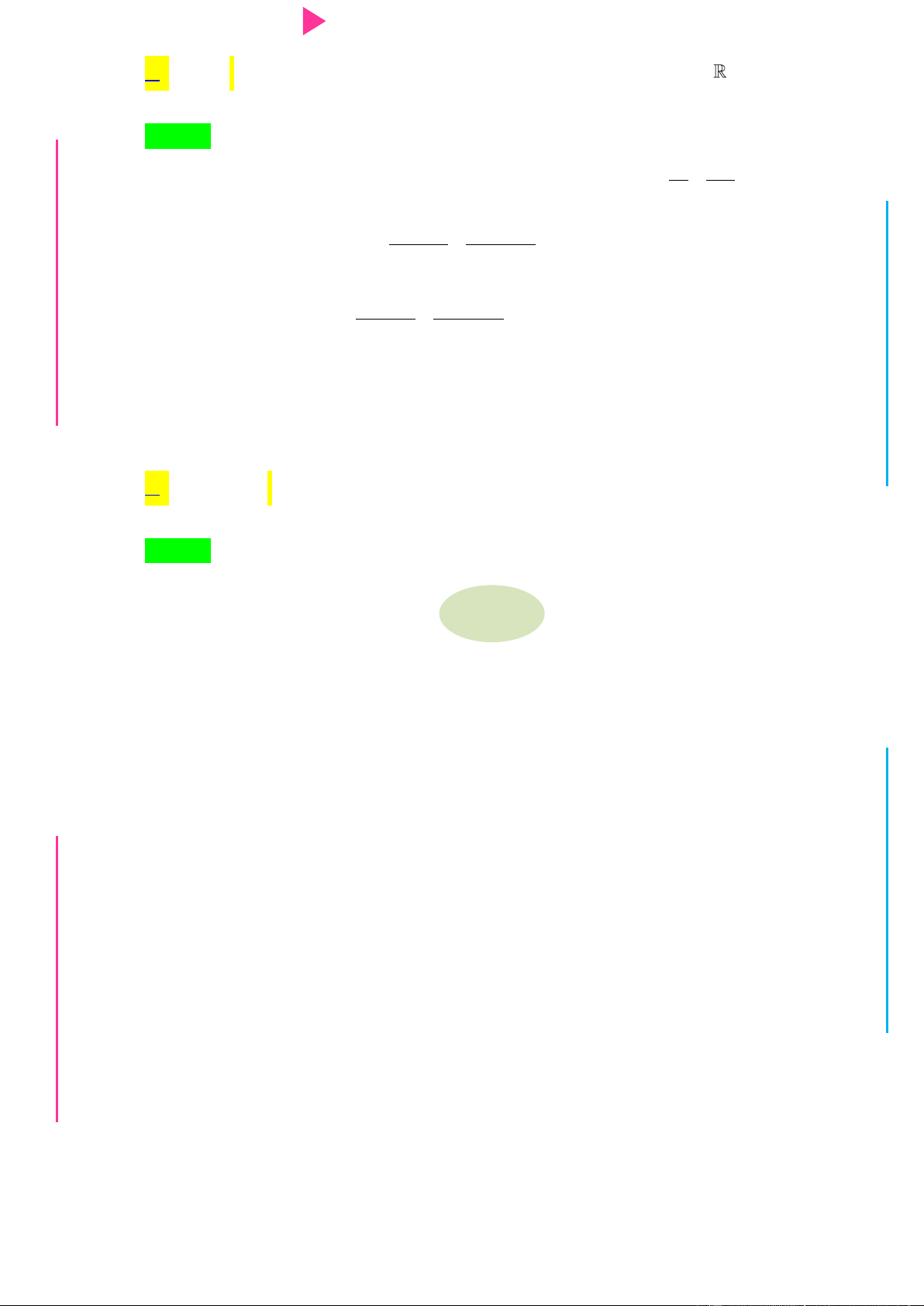
Bài toán 1: Tìm tham số m để hàm số bậc ba đơn điệu trên . Phương pháp : + Tính 2
y ' 3ax 2bx c là tam thức bậc 2 có biệt thức . a 0
+ Để hàm số đồng biến trên R 0 a a
+ Để hàm số nghịch biến trên R 0
Bài toán 2: Tìm tham số m để hàm số bậc ba đơn điệu trên . Phương pháp : + Tính 2
y ' 3ax 2bx c là tam thức bậc 2 chứa tham số m.
NGUYỄN CÔNG ĐỊNH | 40
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
+ Hàm số đồng biến trên ;
a b y ' f , x m 0 x ;
a b (hoặc hàm số nghịch biến trên ;
a b y ' f , x m 0 x ; a b ).
Cách 1: ( f ,
x m bậc nhất đối với m, hoặc f ,
x m không có nghiệm ‚chẵn‛)
+ Biến đổi bpt f , x m 0 x ;
a b g x hm x ;
a b hoặc g x hm x a;b .
+ Tìm GTLN, GTNN của y g x trên ; a b.
(Sử dụng kiến thức bổ sung 1 để kết luận tập nghiệm bất phƣơng trình).
Cách 2: (tham số m trong f ,
x m có chứa bậc 1 và bậc 2, hoặc f ,
x m có nghiệm ‚chẵn‛)
+ Tìm các nghiệm của tam thức bậc hai, lập bảng xét dấu.
+ Gọi S là tập hợp có dấu ‚thuận lợi‛. Yêu cầu bài toán xảy ra khi ;
a b S. Sau đó sử
dụng kiến thức bổ sung 2 giải quyết bài toán.
Nhận xét: Nên xét cụ thể trường hợp a 0 nếu hệ số a có chứa tham số. I Ơ
Bài toán 3: Tìm tham số m để hàm số trùng phƣơng đơn điệu trên . M D
Ầ Phương pháp : Đ NH x 0 Ị Đ + Tính 3
y ' 4ax 2b ; x y ' 0 b . 2 G x THPT 2a N.C.Đ NG
+ Lập bảng xét dấu y’, giả sử có S là tập ‚thuận lợi‛. CÔN Ờ N
+ Yêu cầu của bài toán thỏa mãn khi ;
a b S. Sau đó sử dụng kiến thức bổ sung 2 giải ỄY TRƢ quyết bài toán. GU N
Nhận xét: Nên xét cụ thể trường hợp a 0 nếu hệ số a có chứa tham số. N
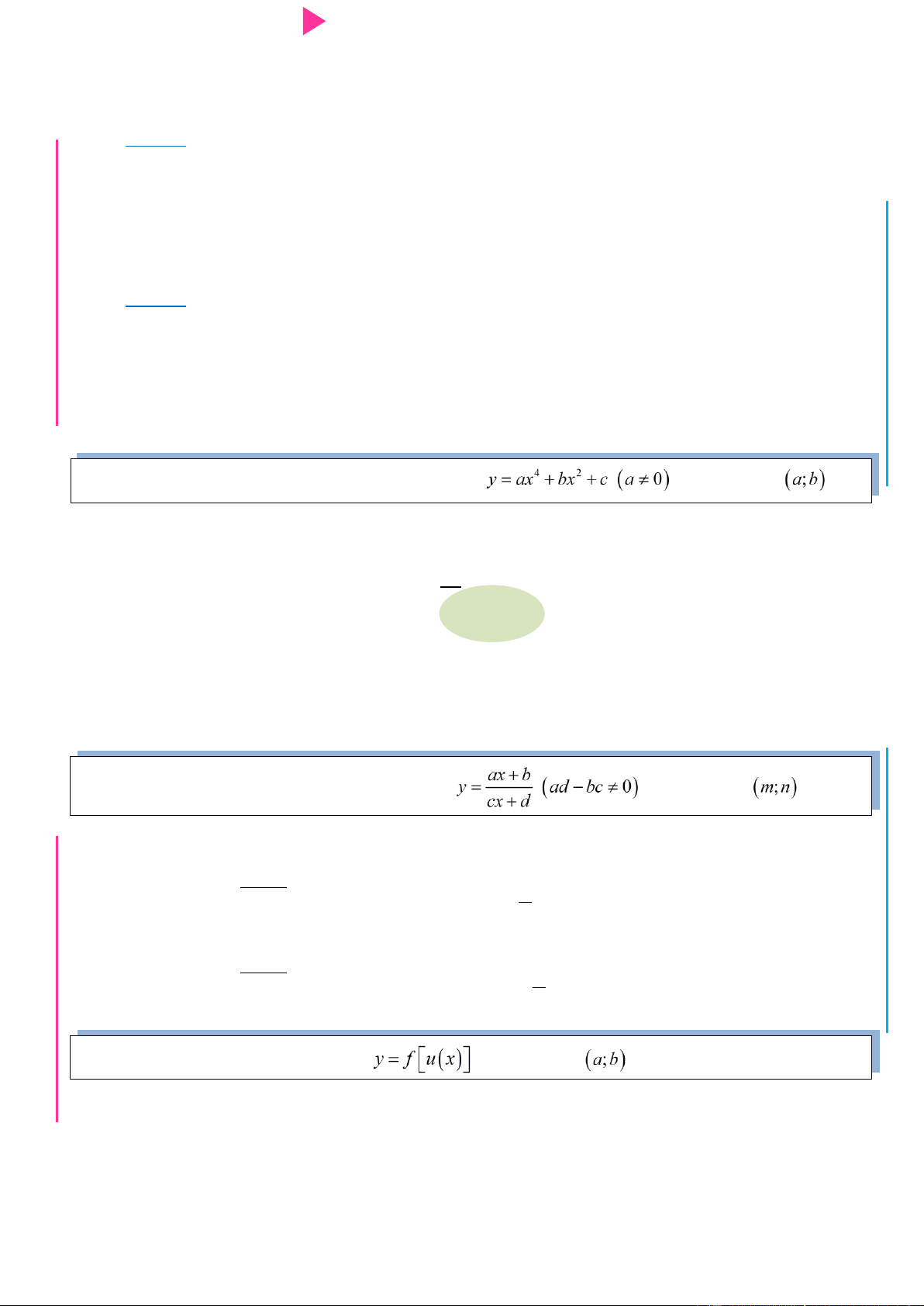
ÁO VIÊ Bài toán 4: Tìm tham số m để hàm số phân thức đơn điệu trên .
GI Phương pháp :
ad bc 0 ax b + Hàm số y đồng biến trên ; m n d . cx d ; m n c
ad bc 0 ax b + Hàm số y nghịch biến trên ; m n d . cx d ; m n c
Bài toán 5: Tìm tham số m để hàm số đơn điệu trên . Phương pháp :
Đặt t u x hàm số trờ thành y f t . Trƣờng hợp này cần chú ý 3 vấn đề sau:
1. Tìm miền xác định của t u x cho chính xác.
2. Nếu t u x đồng biến trên thì f u x
và f t cùng tính chất đồng biến hoặc nghịch biến.
NGUYỄN CÔNG ĐỊNH | 41
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
3. Nếu t u x nghịch biến trên thì f u x
và f t ngƣợc tính chất, nghĩa là f u x
đồng biến thì f t nghịch biến và ngƣợc lại. BÀI TẬP 1 Câu 1.
Tìm tất cả các giá trị của tham số m để hàm số y 2 m 2m 3 2
x mx 3x đồng biến 3 trên . m 0 m 0 A. m 0 . B. . C. .
D. 1 m 3 . m 3 m 3 mx 2 Câu 2.
Số giá trị nguyên của tham số thực m để hàm số y
nghịch biến trên khoảng 2x m 1 ; là 2 A. 4 . B. 3 . C. 5 . D. 2 . I
Ơ Câu 3. Tập tất cả các giá trị của tham số m để hàm số 3 2
y x 3mx 3x 1 đồng biến trên là: M D Ầ A. m 1 ; 1 . B. m ; 1 1; . Đ NH C. m ; 1 1; . D. m 1 ; 1 . Ị Đ mx 4 G
THPT Câu 4. Cho hàm số y
(với m là tham số thực) có bảng biến thiên dƣới đây x 1 N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
Mệnh đề nào dƣới đây đúng?
A. Với m 2 hàm số đồng biến trên từng khoảng xác định.
B. Với m 9 hàm số đồng biến trên từng khoảng xác định.
C. Với m 3 hàm số đồng biến trên từng khoảng xác định.
D. Với m 6 hàm số đồng biến trên từng khoảng xác định.
Câu 5. Tìm tất cả các giá trị của tham số m để hàm số f x m 1 sinx m 1 x nghịch biến trên .
A. m 1 . B. m 1. C. m 1.
D. Không tồn tại m .
Câu 6. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y 2x x mx 2m 1 nghịch biến trên đoạn 1 ;1 . 1 1 A. m . B. m . C. m 8 . D. m 8 . 6 6 2x 1
Câu 7. Tìm m để hàm số y
nghịch biến trên khoảng 1; ? x m
NGUYỄN CÔNG ĐỊNH | 42
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 1 1 1 A. m .
B. m 1.
C. m 1. D. m 1. 2 2 2 3 mx Câu 8. Cho hàm số 2 y
x 2x 1 .
m Tập hợp các giá trị của m để hàm số nghịch biến 3 trên là 1 A. ; . B. 0 . C. ;0 . D. . 2 3 x Câu 9. Cho hàm số y m 2 x 2 1
m 2m x 1 với m là tham số. Có tất cả bao nhiêu 3
giá trị nguyên của m để hàm số đã cho nghịch biến trên khoảng 2;3? A. 2. B. 1. C. 3. D. Vô số.
Câu 10. Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng 1 000;1000 để hàm số 3
y x m 2 2 3 2
1 x 6mm
1 x 1 đồng biến trên khoảng 2; ? I Ơ A. 999 . B. 1001. C. 1998 . D. 998 . x 2
M D Câu 11. Cho hàm số y . Tìm các giá trị thực của tham số m để hàm số đồng biến trên Ầ x m Đ 0; 3 . NHỊ Đ A. m 3 .
B. 0 m 2 .
C. 2 m 3 . D. m 0 . G
THPT Câu 12. Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2
y x 6x mx 1 đồng N.C.Đ NG
biến trên khoảng 0; . CÔN Ờ N A. 3; . B. 48; . C. 36;. D. 12; . Ễ Y
TRƢ Câu 13. Cho hàm số 3
y x m 2 1 2
x 2 m x m 2 . Giá trị của tham số m để hàm số đồng GU N N b b
biến trên 0; là ;
với là phân số tối giản. Khi đó T 2a b bằng a a ÁO VIÊ A. 19. B. 14. C. 13. D. 17.
GI Câu 14. Có bao nhiêu giá trị nguyên của m để hàm số 3 2 y (x ) m 8(x ) m 16 nghịch biến trên khoảng 1 ;2?
A. 2. B. 5. C. 4. D. 3.
Câu 15. Có bao nhiêu số nguyên m ( 2 0;20) để hàm số 3
y x 3mx 1 đơn điệu trên khoảng (1;2)? A. 37 . B. 16 . C. 35 . D. 21 .
Câu 16. Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2 3
y x 3mx 3x 6m đồng
biến trên khoảng 0; là: A. ;1 . B. ;2 . C. ;0 . D.2; .
Câu 17. Tất cả giá trị của tham số thực m sao cho hàm số 3 2
y x 2mx m
1 x 1 nghịch biến trên khoảng 0;2 là 11 11
A. m 2 . B. m . C. m .
D. m 2 . 9 9
NGUYỄN CÔNG ĐỊNH | 43
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 18. Tìm tất cả các giá trị của tham số m sao cho hàm số 4
y x m 2 2
1 x 3m 2 đồng
biến trên khoảng 2;5 . A. m 1. B. m 5. C. m 5. D. m 1.
Câu 19. Cho hàm số f x có đạo hàm trên
là f x x 1 x 3 . Có bao nhiêu giá trị
nguyên của tham số m thuộc đoạn 1
0;20 để hàm số y f 2
x 3x m đồng biến trên khoảng 0;2 ? A.18 . B.17 . C.16 . D. 20 . m 2
1 x 2mx 6m
Câu 20. Số các giá trị nguyên của tham số m 2 019;201 9 để hàm số y x 1
đồng biến trên khoảng 4; ? A. 2034 . B. 2018 . C. 2025 . D. 2021.
I Câu 21. Có bao nhiêu giá trị nguyên của tham số m để hàm số 2
y x m x 2 đồng biến trên Ơ ? M D A. 1. B. 2 . C. 4 . D. 3 . Ầ 2x m
Đ Câu 22. Hàm số y
đồng biến trên khoảng 0; khi và chỉ khi? 2 NH x 1 Ị Đ A. m 0 . B. m 0 . C. m 2 . D. m 2 . G THPT 2 cos x 1
Câu 23. Tất cả các giá trị của m để hàm số y N.C.Đ
đồng biến trên khoảng là NG cos x 0; m 2 CÔN Ờ N Ễ A. m 1 1. B. m 1 . C. m . D. m 1. Y 2 2 TRƢ GU
N Câu 24. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2019;2019 để hàm số N 3 2
y sin x 3cos x msin x 1 đồng biến trên đoạn 0; . 2 ÁO VIÊ A. 2028.
B. 2018.C. 2020 . D. 2019 .
GI Câu 25. Gọi S là tập hợp các số thực m thỏa mãn hàm số 4 3
y mx x m 2
1 x 9x 5 đồng biến trên
. Số phần tử của S là A. 3 B. 2 . C. 1. D. 0 .
Câu 26. Cho hàm số y 2m
1 x 3m 2cos x . Gọi X là tập hợp tất cả các giá trị nguyên của
tham số thực m sao cho hàm số đã cho nghịch biến trên
. Tổng giá trị hai phần tử
nhỏ nhất và lớn nhất của X bằng A. 4 . B. 5 . C. 3 . D. 0 . 2 x x 1
Câu 27. Tập hợp tất cả các giá trị thực của tham số m để hàm số y x đồng biến trên m khoảng ; 3 là 8 8 8 8 A. ; . B. 3; . C. ; . D. ; . 5 5 5 5
NGUYỄN CÔNG ĐỊNH | 44
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 28. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 1 9;19 để hàm số
tan x 3m 3 y
đồng biến trên khoảng 0; . tan x m 4 A. 17. B. 10. C. 11. D. 9. Câu 29. Cho hàm số 3 2 y 2
sin x 3sin x 62m
1 sin x 2019. Có tất cả bao nhiêu giá trị của π 3π
tham số m thuộc khoảng 2
016;2019 để hàm số nghịch biến trên khoảng ; ? 2 2 A. 2019 . B. 2017 . C. 2021. D. 2018 .
Câu 30. Có bao nhiêu giá trị nguyên âm của tham số thực m để hàm số 3 2
y x 3x m
1 x 2m 3 đồng biến trên đoạn có độ dài lớn hơn 1? A. 0 . B. 3 . C. 1. D. 2 .
Câu 31. Có bao nhiêu giá trị nguyên của m 1 0;10 để hàm số 2 4
y m x m 2 2 4 1 x 1 I
đồng biến trên khoảng 1; . Ơ A. 7 . B. 16 . C. 15. D. 6 .
M D Câu 32. Cho hàm số y f x liên tục trên và có bảng xét dấu đạo hàm nhƣ sau Ầ Đ NHỊ Đ G THPT N.C.Đ
Có bao nhiêu giá trị nguyên của tham số m để hàm số g x f x m đồng biến trên NG CÔN Ờ N khoảng 0 ;2 . Ễ Y TRƢ A. 3. B. 4. C. 2. D. 1. GU
N Câu 33. Cho hàm số y f x có đạo hàm liên tục trên . Biết hàm số y f x có đồ thị nhƣ N
hình vẽ. Gọi S là tập hợp các giá trị nguyên m 5 ;
5 để hàm số g x f x m ÁO VIÊ
nghịch biến trên khoảng 1;2 . Hỏi S có bao nhiêu phần tử? GI A. 4 . B. 3 . C. 6 . D. 5 .
4m 6 x 3
Câu 34. Cho hàm số y
. Có bao nhiêu giá trị nguyên của m trong khoảng 6 x m 1
0;10 sao cho hàm số đồng biến trên khoảng 8 ;5? A. 14. B. 13. C. 12. D. 15.
NGUYỄN CÔNG ĐỊNH | 45
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 1
Câu 35. Cho hàm số f x 3 2
x ax bx c (a,b,c ) thỏa mãn f 0 f
1 f 2 . Tổng giá 6
trị lớn nhất và giá trị nhỏ nhất của c để hàm số g x f f 2
x 2 nghịch biến trên khoảng 0 ;1 là A. 1. B. 1 3. C. 3. D. 1 3. 4 3 2 x mx x
Câu 36. Cho hàm số y
mx 2019 ( m là tham số). Gọi S là tập hợp tất cả các 4 3 2
giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng 6; . Tính
số phần tử của S biết rằng m 2020 . A. 4041 . B. 2027 . C. 2026 . D. 2015 .
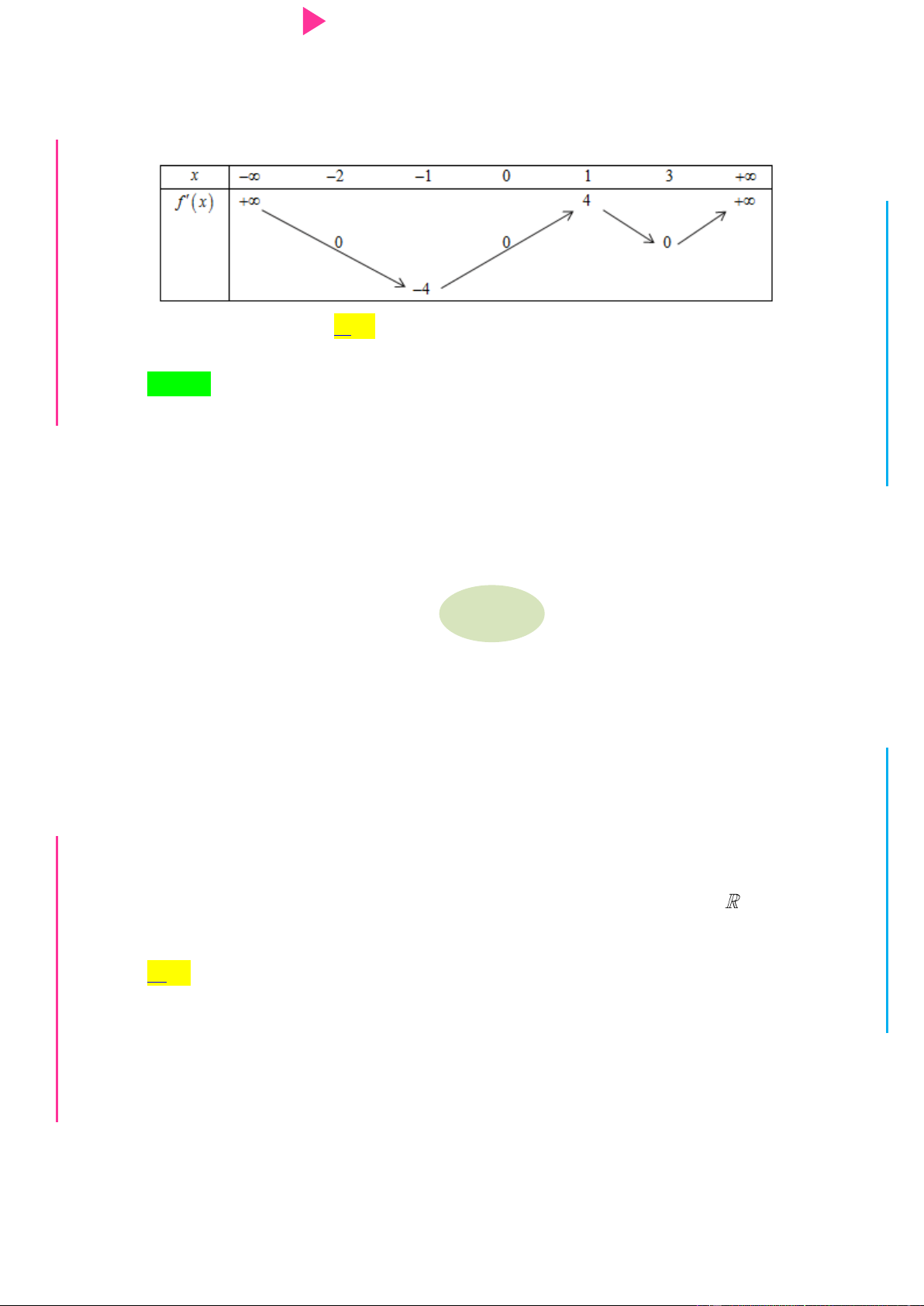
Câu 37. Hàm số y f x có đồ thị hàm số y f x nhƣ hình vẽ: I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
Xét hàm số g x f x 3 2
2x 4x 3m 6 5 với m là số thực. Điều kiện cần và đủ để
g x 0 , x 5; 5 là 2 2 2 2 A. m f 5 B. m f 5 . C. m f 5 . D. m f 0 . 3 3 3 3
Câu 38. Có bbao nhiêu số thực m để hàm số y 3 m m 4 2 3 2 3
x m x mx x 1 đồng biến trên
khoảng ; . A. 3 . B. 1. C. Vô số. D. 2 .
Câu 39. Có bao nhiêu gia trị nguyên của tham số m trong đoạn 2
019;2019 để hàm số y 2
ln x 2 mx 1 đồng biến trên ? A. 2019 . B. 2020 . C. 4038 . D. 1009. 1
Câu 40 Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 3
y x mx đồng biến 5 5x
trên khoảng 0; ?
NGUYỄN CÔNG ĐỊNH | 46
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 12 . B. 0 . C. 4 . D. 3 .
Câu 41. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 1 1 f x 2 5 3 2
m x mx 10x 2
m m 20 x đồng biến trên . Tổng giá trị của tất cả 5 3
các phần tử thuộc S bằng 3 5 1 A. . B. 2 . C. D. . 2 2 2 Câu 42. Cho hàm số 3 2 f x x 3mx 3 2m 1 x
1. Với giá trị nào của m thì f x 6x 0 với mọi x 2? 1 1 A. m .
B. m . C. m 1. D. m 0. 2 2 Câu 43. Cho hàm số 3 2 f x x 2m 1 x 2 m x
2 . Với giá trị nào của tham số m thì f x 0 với mọi x 1? I 7 5 Ơ
A. m ; B. m ; 3 4 M D 7 5 7 5 Ầ C. m ; D. m ; 1 1; . Đ 3 4 3 4 NHỊ
Câu 44. Tìm tất cả các giá trị của tham số m để hàm số y m x m 2 2 2019 2018 cos x Đ G THPT nghịch biến trên ? N.C.Đ 4037 NG A. m 1. B. m . C. m 1. D. m 1. CÔN Ờ 3 N Ễ
Câu 45. Có bao nhiêu số nguyên m thuộc khoảng 1 0;10 để hàm số 3
y 2x 2mx 3 đồng Y TRƢ biến trên 1; ? GU N N A. 12 . B. 8 . C. 11. D. 7 .
Câu 46. Cho hàm số y f x liên tục trên và có đạo hàm f x 2
x x 2 2
x 6x m với ÁO VIÊ GI mọi x
. Có bao nhiêu số nguyên m thuộc đoạn 2
019;2019 để hàm số
g x f 1 x nghịch biến trên khoảng ; 1 ? A. 2012 . B. 2009 . C. 2011. D. 2010 .
Câu 47. Cho hàm số y f x có đạo hàm f x 2
x x 2 ' 2
x mx 5 với x . Số giá trị
nguyên âm của m để hàm số g x f 2
x x 2 đồng biến trên khoảng 1; là A. 3 . B. 4 . C. 5 . D. 7 . Câu 48. Cho hàm số 3
y f x liên tục trên
và có đạo hàm f x x x 2 1
x 4x m với
mọi x . Có bao nhiêu số nguyên m thuộc đoạn 2
019;2019 để hàm số
g x f 1 x nghịch biến trên khoảng ;0 ? A. 2020 . B. 2014 . C. 2019 . D. 2016 .
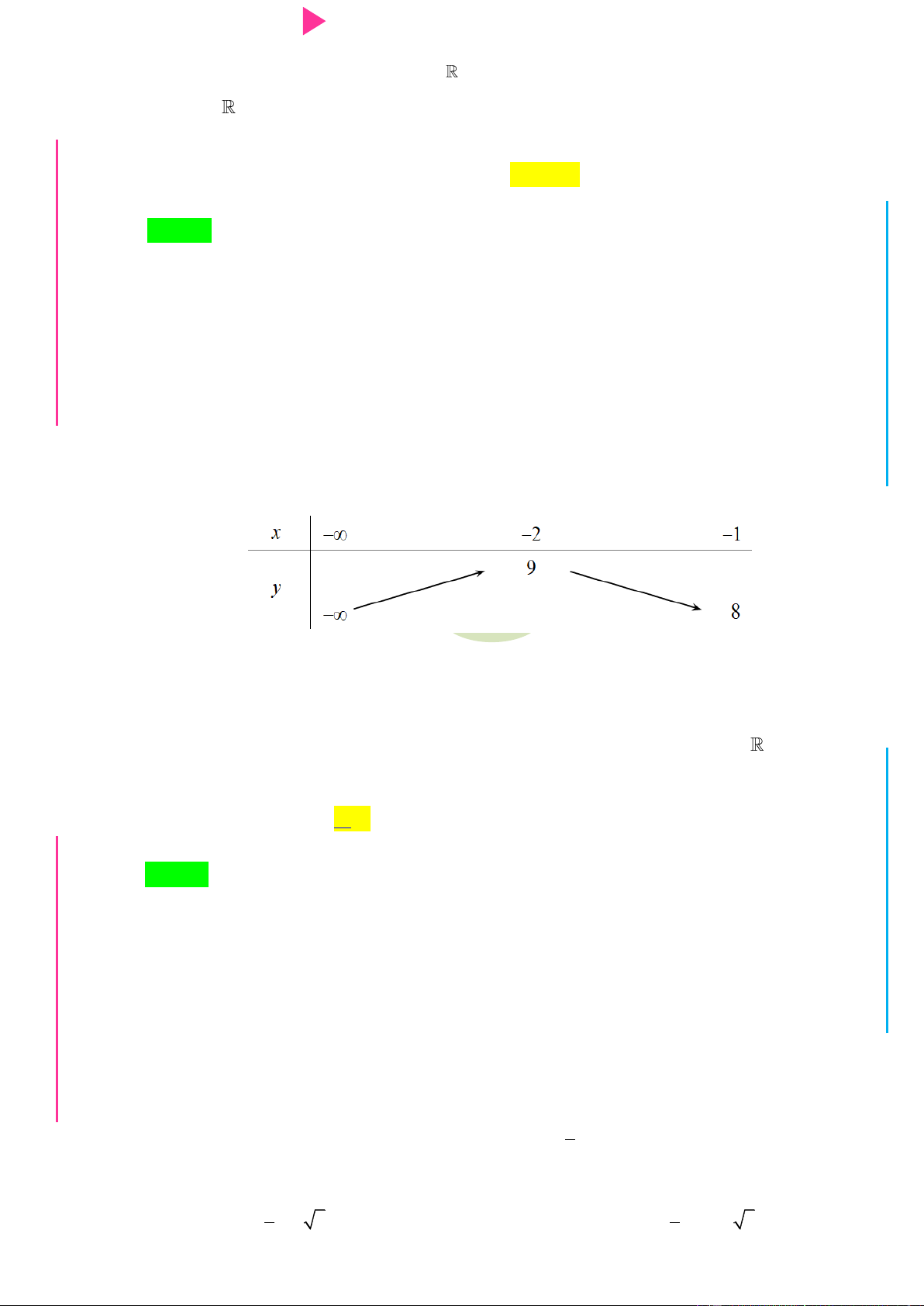
Câu 49. Cho hàm số f x có bảng biến thiên của hàm số y f x nhƣ hình vẽ bên. Có bao
nhiêu giá trị nguyên của tham số m 1
0;10 để hàm số y f x 3 3
1 x 3mx đồng biến trên khoảng 2 ; 1 ?
NGUYỄN CÔNG ĐỊNH | 47
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 8 . B. 6 . C. 7 . D. 5 . 4
Câu 50. Giá trị y f x có đạo hàm f x x x 2 1
x mx 9 với mọi x . Có bao nhiêu
số nguyên dƣơng m để hàm số g x f 3 x đồng biến trên khoảng 3; ? A. 6 . B. 5 . C. 7 . D. 8 .
Câu 51. Cho hàm số y f (x) có đạo hàm trên
và bảng xét dấu của đạo hàm nhƣ hình vẽ bên. I Ơ 2 M D
Có bao nhiêu số nguyên m để hàm số y f x 4x
m nghịch biến trên khoảng 1; 1 ? Ầ Đ A. 3 . B. 1. C. 0 . D. 2 . NHỊ m
Câu 52. Tập các giá trị thực của tham số m để hàm số y ln(3x 1)
2 đồng biến trên khoảng Đ x G THPT 1 ; . N.C.Đ NG 2 CÔN Ờ N 7 1 4 2 Ễ A. ; . B. ; . C. ; . D. ; . Y 3 3 3 9 TRƢ GU
N Câu 53. Có tất cả bao nhiêu cặp số nguyên ;
a b để hàm số f x x . a sin x .
b cos x đồng N biến trên . A. 5 . B. 6 . C. 4 . D. 3 . ÁO VIÊ
GI Câu 54. Cho hàm số y
f x có đạo hàm liên tục trên
và có đồ thị hàm số y f x nhƣ
hình vẽ bên. Có bao nhiêu giá trị nguyên dƣơng của tham số m để hàm số
20 2 x y f x 1 ln
nghịch biến trên khoảng 1 ; 1 ? m 2 x A. 3 . B. 6 . C. 4 . D. 5 .
NGUYỄN CÔNG ĐỊNH | 48
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 55. Cho hàm số y f x xác định và liên tục trên , có đồ thị f x nhƣ hình vẽ. mx x 2 2 3 4
Có bao nhiêu giá trị nguyên âm của m 2
0;20 để hàm số g x f 4 20
đồng biến trên khoảng 0; . I Ơ A. 6 . B. 7 . C. 17 . D. 18 . M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
NGUYỄN CÔNG ĐỊNH | 49
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA HƢỚNG DẪN GIẢI 1 Câu 1.
Tìm tất cả các giá trị của tham số m để hàm số y 2 m 2m 3 2
x mx 3x đồng biến 3 trên . m 0 m 0 A. m 0 . B. . C. .
D. 1 m 3 . m 3 m 3 Lời giải Chọn C Ta có: y 2 m m 2 2
x 2mx 3 . m TH1: 2
m 2m 0 0 . m 2
Với m 0 , y 3 y 0, x
. Do đó, m 0 thỏa mãn hàm số đồng biến trên .
Với m 2 , y 4x 3 . Do đó, m 2 không thỏa mãn hàm số đồng biến trên . I Ơ m TH2: 2
m 2m 0 0 . m 2 M D 2 Ầ
m 2m 0 Đ
Hàm số đồng biến trên 2 2 NH m 3
m 2m 0 Ị Đ m 2 G THPT 2
m 2m 0 m 0 m N.C.Đ 3 . NG 2 m 0 CÔN
2m 6m 0 m 3 Ờ N m 0 Ễ Y TRƢ m 0 Vậy
thỏa mãn yêu cầu bài toán. GU N m 3 N mx 2 Câu 2.
Số giá trị nguyên của tham số thực m để hàm số y
nghịch biến trên khoảng 2x m ÁO VIÊ 1 GI ; là 2 A. 4 . B. 3 . C. 5 . D. 2 . Lời giải Chọn B mx 2 m m Hàm số y có tập xác định là D ; ; 2x m 2 2 2 m 4 m Ta có: y x . 2x m , 2 2 2 m 4 0 1 2 m 2
Hàm số nghịch biến trên khoảng ; 2 m 1 mà m 1 2 m 1 2 2 m nên m 1 ;0; 1 . Câu 3.
Tập tất cả các giá trị của tham số m để hàm số 3 2
y x 3mx 3x 1 đồng biến trên là:
NGUYỄN CÔNG ĐỊNH | 50
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. m 1 ; 1 . B. m ; 1 1; . C. m ; 1 1; . D. m 1 ; 1 . Lời giải Chọn A 2
y 3x 6mx 3 . 3 0
Hàm số đồng biến trên
y 0 x R 2
m m 1 ; 9 9 0 1 . 3 m2 9 0 mx 4
Câu 4. Cho hàm số y
(với m là tham số thực) có bảng biến thiên dƣới đây x 1 I Ơ M D Ầ Đ
Mệnh đề nào dƣới đây đúng? NHỊ Đ
A. Với m 2 hàm số đồng biến trên từng khoảng xác định. G THPT
B. Với m 9 hàm số đồng biến trên từng khoảng xác định. N.C.Đ NG
C. Với m 3 hàm số đồng biến trên từng khoảng xác định. CÔN Ờ
D. Với m 6 hàm số đồng biến trên từng khoảng xác định. N Ễ Y Lời giải TRƢ Chọn A GU N N m 4 mx 4 Ta có: y ' . Mà lim y lim m . x 0 m 4 2 1 x x x 1 ÁO VIÊ
Từ bảng biến thiên ta có lim y 2
. Do đó: m 2 . GI x
Câu 5. Tìm tất cả các giá trị của tham số m để hàm số f x m 1 sinx m 1 x nghịch biến trên .
A. m 1 . B. m 1. C. m 1.
D. Không tồn tại m . Lời giải Chọn C Khi m 1
: f x 0 nên không thỏa YCBT. Suy ra loại , A C . Khi m 1:
f ' x m 1 cosx + 1
Để hàm số nghịch biến trên thì f ' x 0 x
m 1 0 m 1 .
Câu 6. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y 2x x mx 2m 1 nghịch biến trên đoạn 1 ;1 . 1 1 A. m . B. m . C. m 8 . D. m 8 . 6 6
NGUYỄN CÔNG ĐỊNH | 51
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Lời giải Chọn D Ta có: 2
y 6x 2x m .
Hàm số nghịch biến trên đoạn 1
;1 khi và chỉ khi y 0, x 1 ;1 . 2
6x 2x m 0, x 1 ; 1 2
6x 2x , m x 1 ; 1 .
Xét hàm g x 2
6x 2x trên đoạn 1 ;1 .
g x 12x 2 ; g x 1 0 x . 6 Bảng biến thiên: I Ơ M D Ầ Để 2 6x 2x , m x 1 ;
1 thì đồ thị của hàm g x nằm phía dƣới đƣờng thẳng y m Đ NHỊ . Đ
Từ bảng biến thiên ta có m 8 . G THPT 2x 1 N.C.Đ
Câu 7. Tìm m để hàm số y
nghịch biến trên khoảng 1; ? NG x m CÔN Ờ N 1 1 1 Ễ A. m .
B. m 1.
C. m 1. D. m 1. Y 2 2 2 TRƢ Lời giải GU N N Chọn B
Điều kiện: x m . ÁO VIÊ 2 m 1 Ta có y . GI x m2
Để hàm số nghịch biến trên khoảng 1; thì 1 y 0 2 m 1 0 m 1 . m m 1; 2 1 m 1 2 m 1 x 3 mx Câu 8. Cho hàm số 2 x y
x 2x 1 .
m Tập hợp các giá trị của m để hàm số nghịch biến 3 trên là 1 A. ; . B. 0 . C. ;0 . D. . 2 Lời giải Chọn D D 2
y ' mx 2x 2.
NGUYỄN CÔNG ĐỊNH | 52
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA TH1: m 0 Ta có: y ' 2
x 2.Hàm số nghịch biến khi y ' 0 x 1 3 mx Hàm số 2 y
x 2x 1 m nghịch biến trên 1;. 3
Vậy m 0 không thỏa mãn yêu cầu bài toán. TH2: m 0 3 mx Hàm số 2 y
x 2x 1 m nghịch biến trên 3 2
y ' mx 2x 2 0 x . m 0 m 0
1 không có giá trị nào của m thỏa mãn.
' 1 2m 0 m 2
Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán. I 3 Ơ x Câu 9. Cho hàm số y m 2 x 2 1
m 2m x 1 với m là tham số. Có tất cả bao nhiêu 3 M D
giá trị nguyên của m để hàm số đã cho nghịch biến trên khoảng 2;3? Ầ Đ A. 2. B. 1. C. 3. D. Vô số. NHỊ Đ Lời giải G THPT Chọn A 3 N.C.Đ NG x 2 2
y f (x)
m 1 x m 2m x 1 CÔN Ta có : Ờ 3 N Ễ 2
y x m 2 ' 2
1 x m 2m Y TRƢ GU N x m 2
y x m 2 ' 0 2
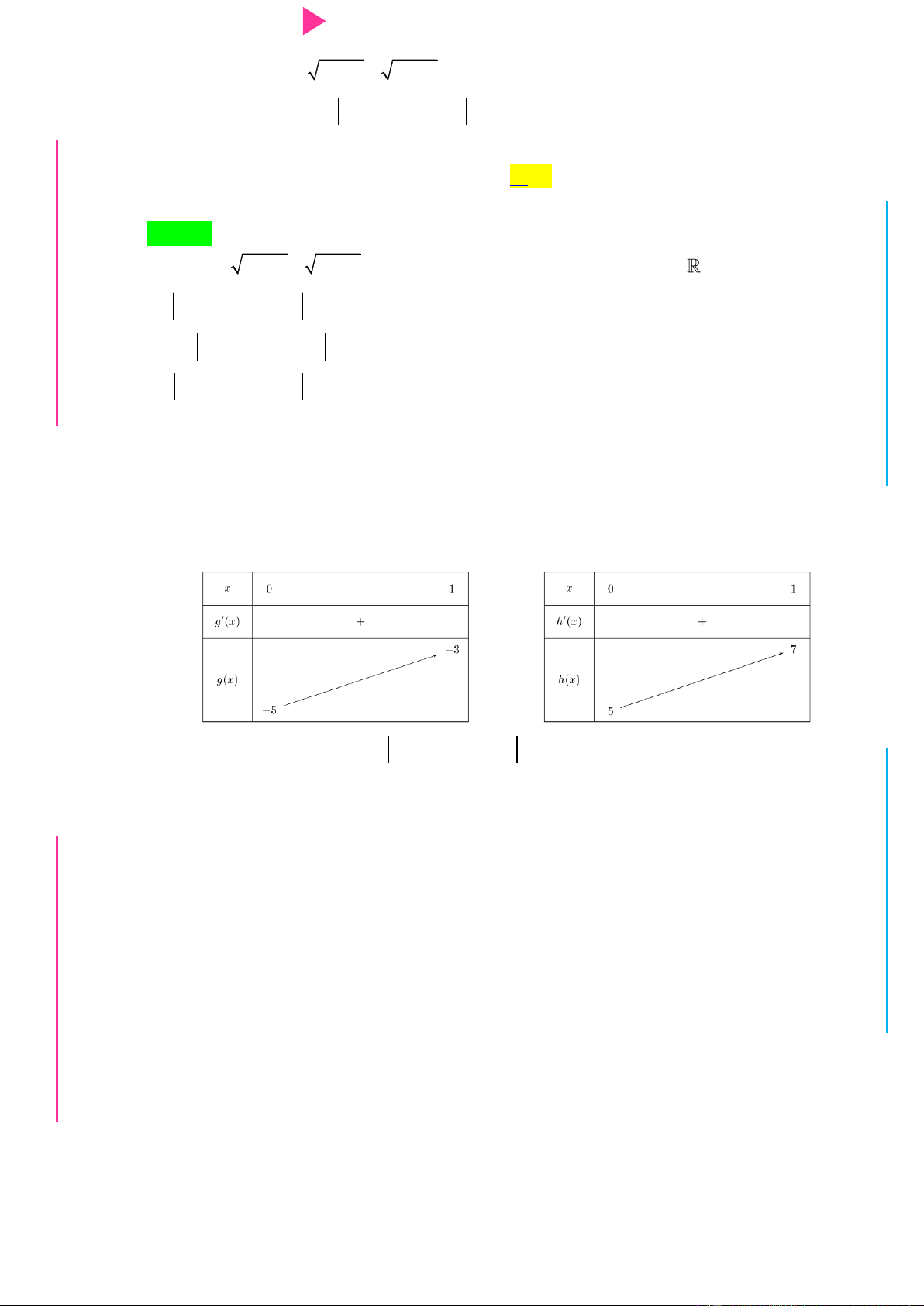
1 x m 2m 0 N x m 2 Ta có bảng biến thiên: ÁO VIÊ GI
Dựa vào bảng biến thiên trên để hàm số đã cho nghịch biến trên khoảng 2;3 ta có
m 2 3 m 2 tức là : 1 m 2 . Vậy có 2 giá trị nguyên của m thỏa mãn. Chọn A.
Câu 10. Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng 1 000;1000 để hàm số 3
y x m 2 2 3 2
1 x 6mm
1 x 1 đồng biến trên khoảng 2; ? A. 999 . B. 1001. C. 1998 . D. 998 . Lời giải Chọn B 3
y x m 2 2 3 2
1 x 6mm 1 x 1.
Tập xác định D . Hàm số có 2
y 6x 62m
1 x 6mm 1 .
NGUYỄN CÔNG ĐỊNH | 53
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2
y 0 6x 62m
1 x 6mm 1 0 . x m 2
x 2m
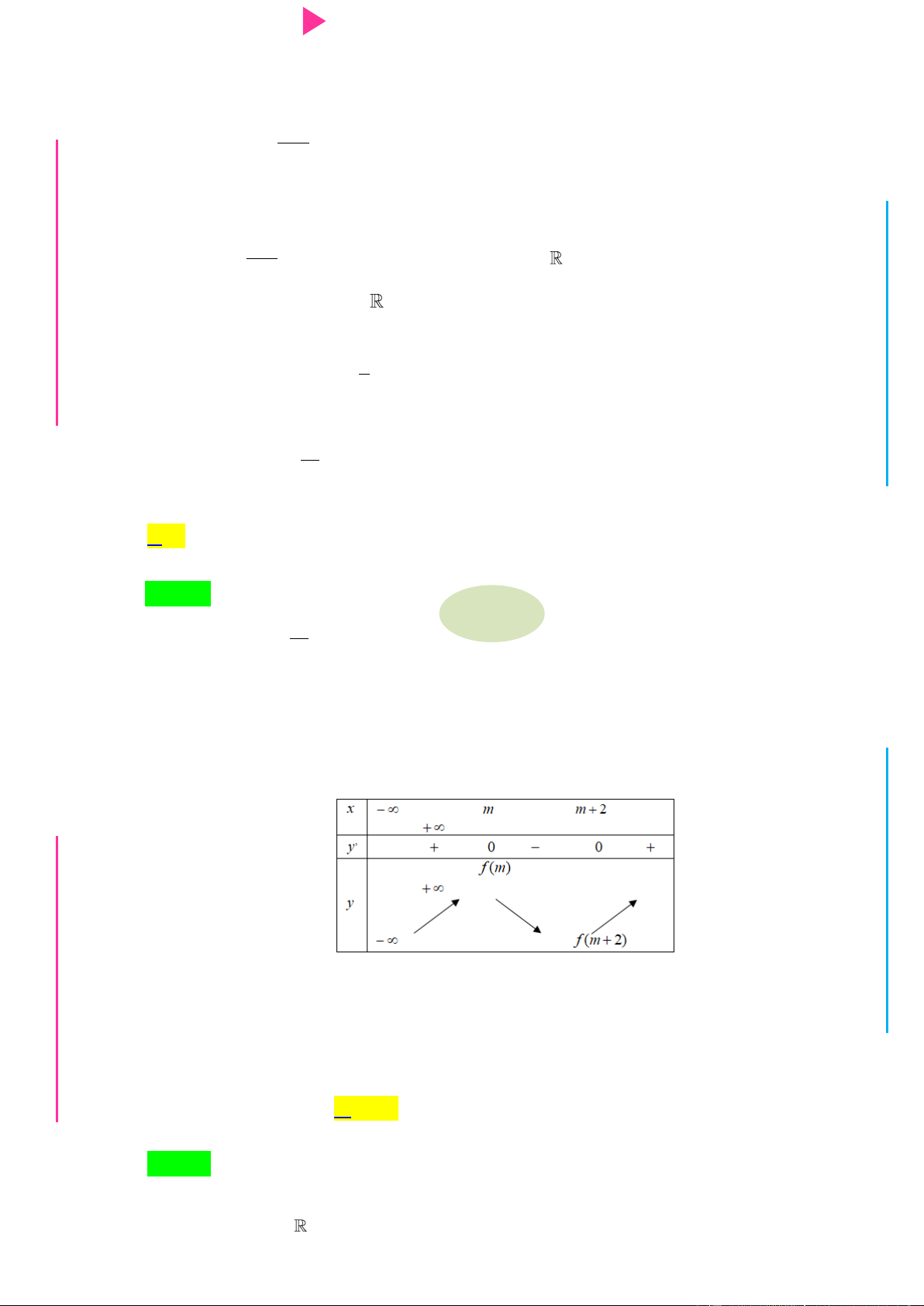
1 x mm 1 0 . x m 1 Ta có bảng biến thiên: x ∞ m m+1 + ∞ y' + 0 0 + + ∞ y ∞
Từ bảng biến thiên ta có hàm số đồng biến trên ;m và m 1; . Suy ra hàm số
đồng biến trên 2; khi 2; m 1; m 1 2 m 1. I
Mà m là số nguyên thuộc khoảng 1
000;1000 m 9 99 ; 998 ; ... ; 1 . Ơ
Có tất cả 1001 giá trị nguyên của tham số m thỏa mãn bài toán. M D x 2
Câu 11. Cho hàm số y Ầ x
. Tìm các giá trị thực của tham số m để hàm số đồng biến trên m Đ NH 0; 3 . Ị Đ A. m 3 .
B. 0 m 2 .
C. 2 m 3 . D. m 0 . G THPT N. LC ờ.Đ i giải NG CÔN Chọn D Ờ N m 2 Ễ Ta có y Y TRƢ x m2 GU N m 2 N
Hàm số đồng biến trên 0;
3 y 0 , x0; 3 , x 0; 3 x m 0 2 ÁO VIÊ m 2 m 2 0 GI Hay
m 3 m 0 . m 0; 3 m 0
Câu 12. Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2
y x 6x mx 1 đồng
biến trên khoảng 0; . A. 3; . B. 48; . C. 36;. D. 12; . Lời giải Chọn D Ta có: 2
y 3x 12x m .
Để hàm số đồng biến trên khoảng 0; thì 2
y 3x 12x m 0 , x 0; . Suy ra 2
m 3x 12x , x 0; . Xét g x 2 3
x 12x trên 0;.
g x 6x 12 .
g x 0 6
x 12 0 x 2. Bảng biến thiên:
NGUYỄN CÔNG ĐỊNH | 54
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x 0 2 g x 0 12 g x 0
Do đó: max g x 12 m max g x 12 . 0; 0; Câu 13. Cho hàm số 3
y x m 2 1 2
x 2 m x m 2 . Giá trị của tham số m để hàm số đồng b b
biến trên 0; là ;
với là phân số tối giản. Khi đó T 2a b bằng a a A. 19. B. 14. C. 13. D. 17. Lời giải Chọn C I 3 2 Ơ
Xét hàm số hàm số y x 1 2m x 2 m x m 2 .
Tập xác định: D . M D 2 Ầ
Ta có: y 3x 21 2m x 2 m . Đ NH
Hàm số đồng biến trên 0; khi và chỉ khi y 0, x
0; và y 0 chỉ tại hữu Ị Đ
hạn điểm trên 0; 2
3x 21 2m x 2 m 0, x 0; G THPT 2 3x 2x 2 N.C.Đ NG m , x 0; . CÔN Ờ 4x 1 N Ễ x x Xét g x 2 3 2 2 trên 0; . Y TRƢ 4x 1 GU N x 1 2 N 12x 6x 6
Ta có g x ; g x 0 1 . 4x 2 1 x 2 ÁO VIÊ x x GI
Bảng biến thiên của hàm số g x 2 3 2 2 trên 0; . 4x 1 5
Dựa vào bảng biến thiên ta thấy g x , x 0; . 4 5 5
Do đó m g x, x
0; m hay m ; . 4 4
Suy ra: a 4 , b 5 nên T 2a b 13 .
Câu 14. Có bao nhiêu giá trị nguyên của m để hàm số 3 2 y (x ) m 8(x ) m 16 nghịch biến trên khoảng 1 ;2?
NGUYỄN CÔNG ĐỊNH | 55
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 2. B. 5. C. 4. D. 3. Lời giải Chọn D Ta có: 2 2 2 2
y ' 3x 6mx 3m 16x 16m 3x (6m 16)x 3m 16 . m x m Có y ' 0 16
nên suy ra đồ thị hàm số nghịch biến trong khoảng x m 3 16 ; m m . 3
mà theo yêu cầu đề bài hàm số nghịch biến trên khoảng 1 ;2 nên 16 16 m 2 10 ( 1 ;2) ; m m 3 1 m m1;2; 3 . 3 3 m 1 I Ơ
Vậy có 3 giá trị nguyên của m thỏa yêu cầu bài toán.
Câu 15. Có bao nhiêu số nguyên m ( 2 0;20) để hàm số 3
y x 3mx 1 đơn điệu trên khoảng M D Ầ (1;2)? Đ A. 37 . B. 16 . C. 35 . D. 21 . NHỊ Đ Lời giải G THPT Chọn A N.C.Đ NG Ta có: 2 y 3x 3m . CÔN Ờ N
+ Nếu 3m 0 m 0
1 , khi đó hàm số đồng biến trên
nên hàm số đơn điệu tăng Ễ Y TRƢ
trên khoảng 1;2 .Suy ra: m 0 thỏa mãn yêu cầu bài toán. GU N
+ Nếu m 0 thì hàm số đồng biến trên các khoảng ;
m và m; và hàm số N
nghịch biến trên khoảng m; m . ÁO VIÊ GI
* TH1: Hàm số đơn điệu tăng trên khoảng 1;2 khi m 1 0 m 12 .
* TH 2 :Hàm số đơn điệu giảm trên khoảng 1;2 khi 2 m m 43 .
Kết hợp điều kiện
1 ,2,3 suy ra: m 1 hoặc m 4 . 2 0 m 1
Đối chiếu điều kiện: m ( 2 0;20) suy ra: 4 m 20
Do m là số nguyên nên m 1 9; 1 8;...; 1 ;0;1;4;...;1 9 ( 37 giá trị nguyên)
Câu 16. Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2 3
y x 3mx 3x 6m đồng
biến trên khoảng 0; là: A. ;1 . B. ;2 . C. ;0 . D.2; . Lời giải Chọn A Ta có: 2
y ' 3x 6mx 3 .
Để hàm số đồng biến trên khoảng 0; thì y ' 0, x 0;.
NGUYỄN CÔNG ĐỊNH | 56
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Tức là: 2
y ' 3x 6mx 3 0 ; x 0; . 2 x 1 m ; x 0; 2x 2 x 1 m Min 0; 2x x
Đặt f x 2 1 . 2x 2 x 1
Ta có: f ' x
; f ' x 0 x 1 N x 1 L . 2 2x 2 x 1 Lập BBT ta thấy Min f 1 1.
0; 2x
Vậy m 1 hay m ;1 . 3 2
I Câu 17. Tất cả giá trị của tham số thực m sao cho hàm số y x 2mx m 1 x 1 nghịch biến Ơ trên khoảng 0;2 là M D 11 11
A. m 2 . B. m . C. m .
D. m 2 . Ầ 9 9 Đ NH Lời giải Ị Đ Chọn C G THPT Cách 1: N.C.Đ NG Xét phƣơng trình 2
y 3x 4mx m 1 0 . CÔN Ờ N 2 Ễ
2m2 3m 3 39 2
1 4m 3m 3 2m 0, m Y . TRƢ 4 16 GU N 2 N 2m 4m 3m 3
Vậy y 0 luôn có 2 nghiệm phân biệt x , 1 3 2 ÁO VIÊ
2m 4m 3m 3 x . 2 GI 3 Bảng biến thiên: 2
2m 4m 3m 3 0 1 x 0 3
Để hàm số nghịch biến trên 1 0; 2 I : . 2 x 2 2
2m 4m 3m 3 2 2 3 m 0 m 0 2 1
4m 3m 3 2m m 0
m 0 m R . 2 2
4m 3m3 4m m 1
NGUYỄN CÔNG ĐỊNH | 57
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA m 3 6 2m 0 m 2 3 11 2
4m 3m 3 6 2m 6 2m 0 m 11 9 2 2
4m 3m3 3624m 4m m 9 . m R Vậy I 11 11 m . m 9 9 Cách 2: 2
y 3x 4mx m 1 .
Hàm số nghịch biến trên 0;2 y 0, x 0;2 . x y 0, x
0;2 3x 4mx m 1 0, x 0;2 2 3 1 2 m , x 0;2 4x . 1 I Ơ 2 3x 1
m max f x , trong đó f x , x 0; 2 0;2 4x . 1 M D 2 Ầ 1 13 12 x Đ 2 12x 6x 4 4 4 NH
Ta có: f x 0, x 0;2 . 2 2 Ị 4x 1 4x 1 Đ G THPT
f x đồng biến trên khoảng 0;2 N.C.Đ NG 3.2 1 11 CÔN
max f (x) f 2 2 Ờ N 0;2 4.2 1 9 Ễ Y 11 TRƢ Vậy m . 9 GU N 4 2 N
Câu 18. Tìm tất cả các giá trị của tham số m sao cho hàm số y x 2m
1 x 3m 2 đồng
biến trên khoảng 2;5 . ÁO VIÊ A. m 1. B. m C. m D. m 1. GI 5. 5. Lời giải Chọn B Hàm số 4 2
y x 2(m 1)x 3m 2 đồng biến trên khoảng (2;5)
y ' 0 với x 2;5 3
4x 4m
1 x 0 với x 2;5 x 2 4
x m 1 0 với x 2;5 2
x m 1 0 với x 2;5 2
x 1 m với x 2;5 Xét 2
g(x) x 1 g '(x) 2x 1 0 với x 2;5
min g(x) g(2) 5 m . 2; 5
NGUYỄN CÔNG ĐỊNH | 58
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 19. Cho hàm số f x có đạo hàm trên
là f x x 1 x 3 . Có bao nhiêu giá trị
nguyên của tham số m thuộc đoạn 1
0;20 để hàm số y f 2
x 3x m đồng biến trên khoảng 0;2 ? A.18 . B.17 . C.16 . D. 20 . Lời giải Chọn A Bảng biến thiên
Ta có: y x f 2 2 3
x 3x m .
Vì 2x 3 0,x 0;2 . Do đó , để hàm số y f 2
x 3x m đồng biến trên khoảng 0;2 I Ơ thì f 2
x 3x m 0, x 0;2 (*) . M D Đặt 2 t x 3x
m . Vì x 0;2 t m;10 m . Ầ Đ
(*) trở thành : f t 0, t m;10 m . NHỊ 13 m 20 Đ 10 m 3 m 13 f x 10 m 1 G
Dựa vào bảng xét dấu của ta có : THPT 1 m m 1 N.C.Đ m NG CÔN Ờ m 1 0; 9 ;..; 1 ;3;4;..;20} . N Ễ m 2
1 x 2mx 6m Y
TRƢ Câu 20. Số các giá trị nguyên của tham số m 2 019;201 9 để hàm số y x 1 GU N N
đồng biến trên khoảng 4; ? A. 2034 . B. 2018 . C. 2025 . D. 2021. ÁO VIÊ Lời giải GI Chọn D
Tập xác định: D \ 1 . 2m 1 x 2m x 1 m 2
1 x 2mx 6m m 2
1 x 2 m 1 x 4m Ta có y . 2 x 2 1 x 1
Hàm số đã cho đồng biến trên khoảng 4; m 2
1 x 2 m 1 x 4m y . x 0, x 4 2 1 m 2
1 x 2m
1 x 4m 0, x 4 2 x x 2 2
4 m x 2x 0, x 4 . 2 x 2x m , x 4 (Do 2
x 2x 4 0 với mọi x 4) * 2 x 2x 4 x 2x 8x 8
Đặt g x 2
có g x 0, x 4. 2 x 2x 4
x 2x42 2 Bảng biến thiên:
NGUYỄN CÔNG ĐỊNH | 59
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Từ bảng biến thiên suy ra * m 1 .
Mà m ; m 2
019;2019 m 1 ;0;...;201 9
Có 2021 giá trị của m thỏa mãn.
Câu 21. Có bao nhiêu giá trị nguyên của tham số m để hàm số 2
y x m x 2 đồng biến trên ? A. 1. B. 2 . C. 4 . D. 3 . I Lời giải Ơ Chọn D 2 M D x x 2 mx y 1 m . Ầ 2 2 Đ x 2 x 2 NHỊ
Hàm số đồng biến trên
y 0, x 2
x 2 mx 0, x Đ G THPT N.C.Đ 2 0 , x 0 NG 2 CÔN Ờ x 2 m , x 0 * N x Ễ Y TRƢ 2 x 2 m , x 0 GU N x N x 2 Xét g x 2 2
có g x 0, x 0 x 2 2 ÁO VIÊ x x 2 GI 0 + + m 1
Do đó, từ * suy ra 1 m 1. m 1
Có 3 giá trị nguyên của m thỏa mãn là 1 ;0;1. 2x m
Câu 22. Hàm số y
đồng biến trên khoảng 0; khi và chỉ khi? 2 x 1 A. m 0 . B. m 0 . C. m 2 . D. m 2 . Lời giải Chọn A
NGUYỄN CÔNG ĐỊNH | 60
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 mx
Ta có: y ' 0, x 0 0, x 0 x 3 2 1
2 mx 0, x 0 2 m , x 0 m 0. x Ta chọn đáp án A. 2 cos x 1
Câu 23. Tất cả các giá trị của m để hàm số y
đồng biến trên khoảng là cos x 0; m 2 A. m 1 1. B. m 1 . C. m . D. m 1. 2 2 Lời giải Chọn D t 0; 1 y cos x I
Đặt cos x t . Ta có x 0; . Vì hàm số
nghịch biến trên khoảng 2 Ơ 0;
nên yêu cầu bài toán tƣơng đƣơng với tìm tất cả các giá trị của m để hàm số M D 2 Ầ Đ 2 m 1 f t 2t 1
nghịch biến trên khoảng 0 ;1 y 0 , t 0; 1 NHỊ t m t m2 Đ G 1 THPT m 2m 1 0 2 N.C.Đ NG m 1 . CÔN m 0; m 0 Ờ 1 N m 1 Ễ Y
TRƢ Câu 24. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2
019;2019 để hàm số GU N N 3 2
y sin x 3cos x msin x 1 đồng biến trên đoạn 0; . 2 ÁO VIÊ A. 2028.
B. 2018.C. 2020 . D. 2019 . GI Lời giải Chọn D 3 2
y sin x 3cos x msin x 1 3 2
y sin x 3sin x msin x 4 . y 2 '
3sin x 6 sin x mcos x .
Hàm số đồng biến trên đoạn 0;
khi và chỉ khi hàm số liên tục trên 0; và hàm 2 2 π số đồng biến trên 0; 2 π π y ' 0 x 0; 2
3sin x 6sin x m 0 x 0; 2 2 π 2
3sin x 6sin x m x 0; 1 . 2 π
Đặt t sin x, x 0; t 0 ;1 . 2
Xét hàm số f t 2
3t 6t trên 0
;1 ta có bảng biến thiên sau
NGUYỄN CÔNG ĐỊNH | 61
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Dựa vào bảng biến thiên ta có
1 xảy ra khi và chỉ khi m 0 .
Suy ra có 2019 giá trị nguyên của m thuộc khoảng 2
019;2019 thỏa mãn đề bài.
Câu 25. Gọi S là tập hợp các số thực m thỏa mãn hàm số 4 3
y mx x m 2
1 x 9x 5 đồng biến trên
. Số phần tử của S là A. 3 B. 2 . C. 1. D. 0 . Lời giải Chọn C I
Tập xác định D Ơ 3 2
y 4mx 3x 2m 1 x 9 M D
Hàm số đã cho đồng biến trên
y 0 , x
và y 0 tại hữu hạn điểm trên . Ầ Đ TH1: m 0 , 2
y 3x 2x 9 0 , x
, Suy ra m 0 thỏa mãn. NHỊ
TH2: m 0 , ta có lim y . Suy ra hàm số 4 3
y mx x m 2
1 x 9x 5 không đồng Đ x G THPT biến trên . N.C.Đ 4 3 2 NG
TH3: m 0 , ta có lim y . Suy ra hàm số y mx x m
1 x 9x 5 không đồng x CÔN Ờ N biến trên . Ễ Y TRƢ Vậy S
0 , số phần tử của S là 1. GU N N
Câu 26. Cho hàm số y 2m
1x 3m 2cos x . Gọi X là tập hợp tất cả các giá trị nguyên của
tham số thực m sao cho hàm số đã cho nghịch biến trên
. Tổng giá trị hai phần tử ÁO VIÊ
nhỏ nhất và lớn nhất của X bằng GI A. 4 . B. 5 . C. 3 . D. 0 . Lời giải Chọn A
Tập xác định D
y 2m 1 3m 2sin x . Hàm số đã cho nghịch biến trên
y 0, x
2m 1 3m 2sin x 0 , x (*) 2
Nếu m thì (*) không thỏa. 3 2 m m 2 1 Nếu m 1 2 thì (*) sin x , x 1 2
1 m . 3 3m 2 3m 2 3 5 2 m m 2 Nếu m 1 2 thì (*) sin x , x 1 2 1
3 m . 3 3m 2 3m 2 3 Ta có X 3 ; 2 ; 1 . Vậy 3 1 4 .
NGUYỄN CÔNG ĐỊNH | 62
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 x x 1
Câu 27. Tập hợp tất cả các giá trị thực của tham số m để hàm số y x đồng biến trên m khoảng ; 3 là 8 8 8 8 A. ; . B. 3; . C. ; . D. ; . 5 5 5 5 Lời giải Chọn D 2
x 2mx m 1 Ta có y . x m2
Hàm số xác định trên khoảng ; 3 m ; 3 m 3
Khi đó để hàm số đồng biến trên khoảng ;
3 thì y 0 x ; 3 . 2
x 2mx m 1 0 x ; 3 2
x 1 m2x 1 với x ; 3 . I 2 x 1 Ơ m x ;3 . 2x với 1 2 M D x 2x 2x 2
Đặt g x 2 1 g x 0 với x ; 3 . Ầ 2x ta có 1 2x 2 1 Đ NHỊ BBT Đ G THPT x ∞ 3 N.C.Đ NG g'(x) + CÔN Ờ N Ễ 8 Y TRƢ g(x) - 5 GU N N ∞ 8
Vậy m ( Thỏa mãn điều kiện m 3 ). ÁO VIÊ 5
GI Câu 28. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 1 9;19 để hàm số
tan x 3m 3 y
đồng biến trên khoảng 0; . tan x m 4 A. 17. B. 10. C. 11. D. 9. Lời giải Chọn A.
Đặt t tan x , khi x trong 0;
thì t tăng trong 0; 1 . 4 t 3m 3
Do đó hàm số ban đầu đồng biến trên khoảng 0; khi hàm số y 4 t m
đồng biến trên khoảng 0; 1 . t 3m 3 Xét hàm số y có: t m 2m 3 y ' t m2
NGUYỄN CÔNG ĐỊNH | 63
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA t 3m 3 2m 3 0 3 Hàm số y
đồng biến trên khoảng 0 ;1 khi m t m m 0; 1 2 Trong khoảng 1
9;19 có 17 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán! Câu 29. Cho hàm số 3 2 y 2
sin x 3sin x 62m
1 sin x 2019. Có tất cả bao nhiêu giá trị của π 3π
tham số m thuộc khoảng 2
016;2019 để hàm số nghịch biến trên khoảng ; ? 2 2 A. 2019 . B. 2017 . C. 2021. D. 2018 . Lời giải Chọn B 2 y ' 6
sin x 6sin x 62m 1 cosx π 3π Ta có x ; : cos x 0 I 2 2 Ơ π 3π π 3π
Hàm số nghịch biến trên khoảng ; y ' 0 x ; M D 2 2 2 2 Ầ 3 Đ 2 6
sin x 6sin x 62m 1 0 x ; 1 NH 2 2 Ị Đ π 3π
Đặt t s inx, x ; t 1 ;1 G THPT 2 2 N.C.Đ NG
Điều kiện (1) trở thành tìm m thỏa mãn CÔN Ờ 2 6
t 6t 62m 1 0 t 1 ;1 N Ễ 2
2m 1 t t t 1 ;1 Y TRƢ 2 GU N
Xét hàm số nghịch biến trên khoảng f t t t,t 1; 1 . N Ta có bảng biến thiên ÁO VIÊ GI 3
Ycbt 2m 1 2 m
mà m thuộc khoảng 2
016;2019 nên có 2017 giá trị thỏa 2 mãn.
Câu 30. Có bao nhiêu giá trị nguyên âm của tham số thực m để hàm số 3 2
y x 3x m
1 x 2m 3 đồng biến trên đoạn có độ dài lớn hơn 1? A. 0 . B. 3 . C. 1. D. 2 . Lời giải Chọn C
NGUYỄN CÔNG ĐỊNH | 64
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Ta có: 3 2
y x x m 2 3
1 x 2m 3 y 3
x 6x m 1.
Nếu 0 thì hàm số luôn nghịch biến. y '
Nếu 0 thì hàm số đồng biến trên x ; x với x , x x x là hai nghiệm của 1 2 1 2 1 2 y '
phƣơng trình y ' 0 .
Do vậy, hàm số đồng biến trên đoạn có độ dài lớn hơn 1 khi và chỉ khi phƣơng trình
y ' 0 có hai nghiệm x , x thoả mãn x x 1. 1 2 1 2
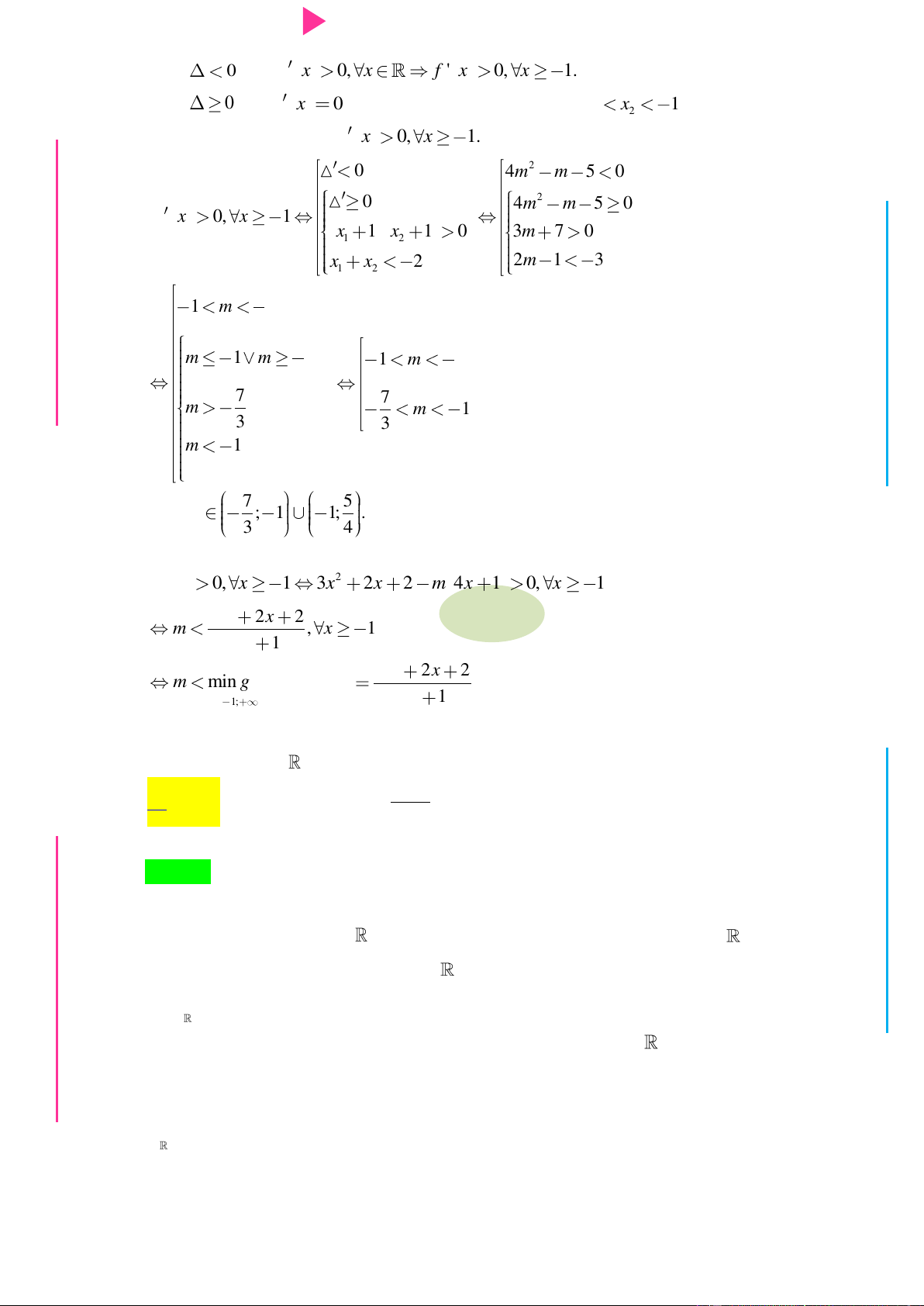
+) 0 9 3 m 1 0 m 2 (1) y ' x x 2 1 2
+) Theo định lý Viet ta có: m 1 x x 1 2 3 2 4 m 1 5
+) x x 1 x x 4x x 1 4 1 m (2) 1 2 1 2 1 2 3 4 I 5 Ơ
Từ (1) và (2) ta có m mà m nguyên âm do đó m 1. 4
M D Câu 31. Có bao nhiêu giá trị nguyên của m 1 0;10 để hàm số 2 4
y m x m 2 2 4 1 x 1 Ầ Đ
đồng biến trên khoảng 1; . NHỊ Đ A. 7 . B. 16 . C. 15. D. 6 . G THPT Lời giải N.C.Đ Chọn B NG CÔN Ờ Ta có: 2 4 2 2 3
y m x 2(4m 1)x 1 y 4m x 4(4m 1)x . N Ễ Y TRƢ
+ TH1: Nếu m 0 thì y 4x . GU N BBT: N ÁO VIÊ GI
Hàm số đã cho đồng biến trên khoảng (0;) .
Suy ra hàm số đồng biến trên khoảng (1; ) . Nhận m 0 . x 0 + TH2: Nếu m 0 thì 2 2
y 0 m x 4m 1 0 4m 1 . 2 x 1 2 m 1
* Nếu 4m 1 0 m thì phƣơng trình
1 vô nghiệm hoặc có nghiệm kép x 0 . 4 Ta có 2
a m 0, m
0 khi đó hàm số đã cho đồng biến trên khoảng (0;) .
NGUYỄN CÔNG ĐỊNH | 65
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 1
Suy ra hàm số đồng biến trên khoảng (1; ) . Nhận các giá trị m . 4 1 10 m Mà ta có m 1
0;10, m khi đó
4 nên có 9 giá trị của m thỏa mãn.
m 0, m 1
* Nếu 4m 1 0 m
thì y 0 có ba nghiệm phân biệt là x 0 và 4 4m 1 x . m BBT: I Ơ M D Ầ Đ NHỊ 4m 1 m 2 3 Đ
Để hàm số đồng biến trên khoảng (1; ) thì 1 . G m THPT m 2 3 N.C.Đ NG 10 m 2 3 CÔN Ờ
Kết hợp với m 1
0;10, m , ta có:
do m nguyên nên có 16 giá N
2 3 m 10 Ễ Y TRƢ
trị của m thỏa mãn. GU N N
Vậy có 16 giá trị m để hàm số đồng biến trên khoảng 1; . Bổ sung cách 2 nhƣ sau: ÁO VIÊ
Hàm số đồng biến trên 1; 2 3
y 4m x 44m 1 x 0, x
1 và y 0 có nghiệm GI
hữu hạn trên 1; . 2 2
m x 4m 1 0, x 1 (*)
+ Với m 0 : * 1 0, x
1 luôn đúng nên ta nhận m 0 . 4m 1 4m 1 m
+ Với m 0 : * 2 x , x 1 1 2 3 . 2 m 2 m m 2 3
Tổng hợp các điều kiện và trƣờng hợp ta có: m 9 , 8 ,...,0,4,5,..., 9 . Vậy có 16 giá trị m .
Câu 32. Cho hàm số y f x liên tục trên
và có bảng xét dấu đạo hàm nhƣ sau
Có bao nhiêu giá trị nguyên của tham số m để hàm số g x f x m đồng biến trên khoảng 0 ;2 .
NGUYỄN CÔNG ĐỊNH | 66
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 3. B. 4. C. 2. D. 1. Lời giải Chọn A
Từ giả thiết suy ra hàm số y f x đồng biến trên các khoảng 1 ; 1 , 1;3 và liên tục
tại x 1 nên đồng biến trên 1 ;3.
Ta có g x f x m và x 0;2 x mm;m 2 . m
g x đồng biến trên khoảng 0 ;2 m m 1 ; 2 1;3 1 m 1. 2 m 3
Vì m nên m có 3 giá trị là m 1
;m 0;m 1.
Câu 33. Cho hàm số y f x có đạo hàm liên tục trên . Biết hàm số y f x có đồ thị nhƣ
hình vẽ. Gọi S là tập hợp các giá trị nguyên m 5 ;
5 để hàm số g x f x m I Ơ
nghịch biến trên khoảng 1;2 . Hỏi S có bao nhiêu phần tử? M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ A. 4 . B. 3 . C. 6 . D. 5 . N Ễ Lời giải Y TRƢ Chọn D GU N N
Ta có g x f x m . Vì y f x liên tục trên nên g x f x m cũng liên tục
trên . Căn cứ vào đồ thị hàm số y f x ta thấy ÁO VIÊ
x m
x m GI
g x 0 f x m 1 1 0 . 1
x m 3 1
m x 3 m
Hàm số g x f x m nghịch biến trên khoảng 1;2 2 1 m m 3 3 m 2 . 0 m 1 1 m 1
Mà m là số nguyên thuộc đoạn 5 ;
5 nên ta có S 5 ; 4 ; 3 ;0; 1 .
Vậy S có 5 phần tử.
4m 6 x 3
Câu 34. Cho hàm số y
. Có bao nhiêu giá trị nguyên của m trong khoảng 6 x m 1
0;10 sao cho hàm số đồng biến trên khoảng 8 ;5? A. 14. B. 13. C. 12. D. 15. Lời giải Chọn A
NGUYỄN CÔNG ĐỊNH | 67
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 4 m t 3
Đặt t 6 x , t 0 khi đó ta có hàm số y f t t . m 2
m 4m 3
Ta có f t . t m2
Hàm số y 6 x nghịch biến trên khoảng ;6 nên với 8
x 5 thì 1 t 14 .
4m 6 x 3 Hàm số y
đồng biến trên khoảng 8
;5 khi và chỉ khi hàm số 6 x m
f t 4 mt 3
1; 14 f t 0,t 1; 14 t
nghịch biến trên khoảng m m 1 2 m 3
m 4m 3 0 m 3 1 m 1. m 1; 14 m 1 m 14 I m 14 Ơ
Mà m nguyên thuộc khoảng 1
0;10 nên m 9 ; 8 ; 7 ; 6 ; 5 ; 4 ; 1 ;0;4;5;6;7;8; 9 . M D
Vậy có 14 giá trị nguyên của m thoả mãn bài toán. Ầ 1
Đ Câu 35. Cho hàm số f x 3 2
x ax bx c (a,b,c ) thỏa mãn f 0 f
1 f 2 . Tổng giá NH 6 Ị Đ
trị lớn nhất và giá trị nhỏ nhất của c để hàm số g x f f 2
x 2 nghịch biến trên G THPT khoảng 0 ;1 là N.C.Đ NG CÔN Ờ A. 1. B. 1 3. C. 3. D. 1 3. N Ễ Lời giải Y TRƢ Chọn A GU N N
f 0 c 1 ÁO VIÊ Ta có : f
1 a b c . 6 GI f 4
2 4a 2b c 3 1 1 a b a
Theo giả thiết f (0) f (1) f (2) 6 2 . 4 1 4a 2b b 3 3 1 1 1
Suy ra : f x 3 2
x x x c . 6 2 3
Hàm số g x nghịch biến trên 0
;1 khi g x xf 2
x f f 2 ' 2 ' 2 ' x 2 0 , x 0; 1 . 1 1
Ta có: f ' x 2
x x f x 3 3 ' 0 1 x 1 . 2 3 3 3 2x 0 Ta thấy x 0; 1 thì . f ' 2 x 2 0 Suy ra x 0;
1 , g x f f 2 ' 0 ' x 2 0
NGUYỄN CÔNG ĐỊNH | 68
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Xét 2
0 x 1 2 x 2 3 , vì f ' x 0 , x
2;3 nên f x đồng biến trên 2;3.
Do đó : f f 2 2
x 2 f 3 . 3 3 Suy ra 1
f 2 f 3 1 . 3 3 f 3 2 1 3 3 3 1 c . 3 3 f 3 3 1 3
Vậy min c max c 1. 4 3 2 x mx x
Câu 36. Cho hàm số y
mx 2019 ( m là tham số). Gọi S là tập hợp tất cả các 4 3 2
giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng 6; . Tính
số phần tử của S biết rằng m 2020 . I Ơ A. 4041 . B. 2027 . C. 2026 . D. 2015 . Lời giải M D Ầ Chọn B Đ NH
Hàm số đã cho đồng biến trên khoảng 6; khi và chỉ khi y 0, x 6; . Ị Đ 3 2 3
y x mx x m x m 2 x 1 x 0, x 6; . G THPT 3 x x N.C.Đ NG m x, x 6; 2 CÔN . Ờ x 1 N Ễ
Đặt f x x thì m f x, x
6; m min f x, x 6; . Y TRƢ m 6 . GU N N
Mà m 2020 nên m 2 020; 2019;...,
6 , có 2027 phần tử. Ta chọn B.
Câu 37. Hàm số y f x có đồ thị hàm số y f x nhƣ hình vẽ: ÁO VIÊ GI
NGUYỄN CÔNG ĐỊNH | 69
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Xét hàm số g x f x 3 2
2x 4x 3m 6 5 với m là số thực. Điều kiện cần và đủ để
g x 0 , x 5; 5 là 2 2 2 2 A. m f 5 B. m f 5 . C. m f 5 . D. m f 0 . 3 3 3 3 Lời giải Chọn B
Ta có g x f x 2 2 6x 4 .
g x f x 2 0 3
x 2 hx . I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N
Dựa vào đồ thị rõ ràng f x h x , x 5; 5
. Suy ra g x 0, x 5; 5 . ÁO VIÊ GI
Do đó, g x đồng biến với mọi x 5; 5 . Khi đó,
g x 0 , x 5; 5 2
Max g x 0 Max g x g
5 2 f 5 3m 0 m f 5 . x 5; 5 x 5; 5 3
Câu 38. Có bbao nhiêu số thực m để hàm số y 3 m m 4 2 3 2 3
x m x mx x 1 đồng biến trên
khoảng ; . A. 3 . B. 1. C. Vô số. D. 2 . Lời giải Chọn A m 0 TH1: 3
m 3m 0 . m 3
+) Với m 0 thì hàm số đã cho trở thành y x 1, hàm số này đồng biến trên nên m 0 thỏa mãn.
NGUYỄN CÔNG ĐỊNH | 70
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
+) Với m 3 thì hàm số đã cho trở thành 3 2
y 3x 3x x 1 có 2
y 9x 2 3x 1 0 ,
với mọi x nên hàm số đồng biến trên
. Vậy m 3 thỏa mãn.
+) Với m 3 thì hàm số đã cho trở thành 3 2
y 3x 3x x 1 có 2
y 9x 2 3x 1 0 , với mọi x
nên hàm số đồng biến trên
. Vậy m 3 thỏa mãn. TH2: 3
m 3m 0 . Ta có: y 3 m m 3 2 2 4 3
x 3m x 2mx 1. Nhận thấy, với 3
m 3m 0 thì y là hàm số bậc ba nên phƣơng trình y 0 có ít nhất 1
nghiệm và y đổi dấu khi qua nghiệm đó.
Suy ra hàm số đã cho không đơn điệu trên .
Vậy có 3 giá trị của m thỏa mãn là 0 ; 3 và 3 .
Câu 39. Có bao nhiêu gia trị nguyên của tham số m trong đoạn 2
019;2019 để hàm số I y 2
ln x 2 mx 1 đồng biến trên ? Ơ A. 2019 . B. 2020 . C. 4038 . D. 1009. M D Lời giải Ầ Đ Chọn A NHỊ 2x Đ Ta có: y m y x 2 x
. Hàm số đồng biến trên 0, 2 G THPT 2x 2x N.C.Đ 2x m 0, x m g x , x g x 2 2 NG x 2 x . Xét hàm số 2 2 x trên . 2 CÔN Ờ N 2 4 2x Ễ g x
0 x 2 . Bảng biến thiên: 2 Y TRƢ 2x 2 GU N N ÁO VIÊ GI
Do m g x x m g x 2 , min . Vì m 2 019;201
9 nên các giá trị m thỏa 2 mãn là m 2 019; 2 018,..., 2 ;
1 . Vậy có 2019 giá trị m thỏa mãn. 1
Câu 40 Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 3
y x mx đồng biến 5 5x
trên khoảng 0; ? A. 12 . B. 0 . C. 4 . D. 3 . Lời giải Chọn C 1 Ta có 2
y 3x m , x 0; . 6 x
NGUYỄN CÔNG ĐỊNH | 71
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Hàm số đồng biến trên khoảng 0; y 0, x 0; 1 2
m 3x , x 0; 6 x 1 Xét hàm số 2
g(x) 3x
với x (0; ) . Ta có 6 x 1 1 1 2 2 2 2 2 2 2 4 3x
x x x
4 x .x .x .
4 , dấu bằng xảy ra khi x 1 nên 6 6 6 x x x
Min g(x) 4 . (0;) 1 Mặt khác, ta có 2 m 3x , x
0; m Min g(x) m 4 m 4 . 6 (0; ) x
Vậy có 4 giá trị nguyên âm của m là 1; 2; 3; 4 thỏa mãn yêu cầu bài toán.
Câu 41. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 1 1 2 5 3 2 2 I
f x m x mx 10x m m 20 x đồng biến trên . Tổng giá trị của tất cả Ơ 5 3
các phần tử thuộc S bằng M D 3 5 1 Ầ A. . B. 2 . C. D. . Đ 2 2 2 NH Lời giải Ị Đ Chọn D G THPT
Ta có f x 2 4 2
m x mx x 2 20
m m 20 . N.C.Đ NG 2 4 2 2 CÔN
Hàm số đồng biến trên
f x m x mx 20x m m 20 0, x (*). Ờ N 2 3 2 2 2 2 Ễ Ta có f
1 0 nên f x x
1 m x m x
m mxm m20 x 1g(x) Y . TRƢ
Nếu x 1 không phải là nghiệm của g(x) thì f x đổi dấu khi x đi qua 1 , suy ra GU N N
f x không đồng biến trên .
Do đó điều kiện cần để f x 0, x
là g 1 0 ÁO VIÊ GI m 2 g 2 1 0 4m 2m 20 0 5 . m 2 Với m 2
f x x 3 2
1 4x 4x 6x 14 x 2 1 2
4x 8x 14 0, x .
và f x 0 x 1
, do đó f (x) đồng biến trên . Suy ra m 2 thoả mãn. x x x Với m
f x x 3 2 5 25 25 15 65 1 2 4 4 4 4 x 2 2 1
25x 50x 65 , 0 x
. và f x 0 x 1
, do đó f (x) đồng biến trên 4 5 . Suy ra m thoả mãn. 2 5 5 1 Từ đó S 2;
, suy ra tổng giá trị của tất cả các phần tử thuộc S bằng 2 . 2 2 2
NGUYỄN CÔNG ĐỊNH | 72
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Câu 42. Cho hàm số 3 2 f x x 3mx 3 2m 1 x
1. Với giá trị nào của m thì f x 6x 0 với mọi x 2? 1 1 A. m .
B. m . C. m 1. D. m 0. 2 2 Lời giải Chọn B Ta có: 2 f x 3x 6mx 3 2m 1 , x Cách 1: 2 f x 6x 0, x 2 3x 6mx 3 2m 1 6x 0, x 2 2 x 2 m 1 x 2m 1 0, x 2 0 2 m 2 0 0 2 m 2 0 1 m . I x 2 x 2 0 2m 1 0 2 1 2 Ơ x x 4 2 m 1 4 1 2 M D
Với x ; x là hai nghiệm của phƣơng trình 2 x 2 m 1 x 2m 1 0 1 2 Ầ Đ Lƣu ý: NHỊ Đặt 2 g x x 2 m 1 x 2m
1 . Ta có g x là một tam thức bậc hai có hệ số a 0 Đ G Nếu 0 thì g x 0, x g x 0, x 2 THPT N.C.Đ Nếu 0 và g x
0 có hai nghiệm x ; x sao cho x x
2 thì theo định lí dấu tam NG 1 2 1 2 CÔN Ờ
thức bậc hai ta có g x 0, x 2. N Ễ Y Cách 2. TRƢ 2 f x 6x 0, x 2 3x 6mx 3 2m 1 6x 0, x 2 GU N N 2 x 2m x 1 2x 1 0, x 2 2 x 2x 1 2 x 2x 1 ÁO VIÊ m , x 2 m
min g x với g(x) 2(x 1) 2 x 1 GI 2; 2 x 2x 3 1 Vì g x 0, x 2 nên min g x g 2 . 2 2 x 1 2; 2 1 Vậy m . 2 Câu 43. Cho hàm số 3 2 f x x 2m 1 x 2 m x
2 . Với giá trị nào của tham số m thì f x 0 với mọi x 1? 7 5
A. m ; B. m ; 3 4 7 5 7 5 C. m ; D. m ; 1 1; . 3 4 3 4 Lời giải Chọn D Ta có: 2 f x 3x 2 2m 1 x 2 , m x f
x là một tam thức bậc hai có hệ số a 0
NGUYỄN CÔNG ĐỊNH | 73
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Nếu 0 thì f x 0, x f ' x 0, x 1. Nếu 0 và f x
0 có hai nghiệm x ; x sao cho x x 1 thì theo định lí dấu 1 2 1 2
tam thức bậc hai ta có f x 0, x 1. 0 2 4m m 5 0 0 2 4m m 5 0 f x 0, x 1 x 1 x 1 0 3m 7 0 1 2 x x 2 2m 1 3 1 2 5 1 m 4 5 5 m 1 m 1 m 4 4 . 7 7 m m 1 3 3 I Ơ m 1 M D 7 5 Ầ Vậy m ; 1 1; . Đ 3 4 NHỊ
Sai lầm của học sinh dùng cách hàm số: Đ 2 f ' x 0, x 1 3x 2x 2 m 4x 1 0, x 1 G THPT 2 3x 2x 2 N.C.Đ NG m , x 1 CÔN Ờ 4x 1 N 2 Ễ 3x 2x 2 m
min g x với g x . Y TRƢ 1; 4x 1 GU
N Câu 44. Tìm tất cả các giá trị của tham số m để hàm số y m x m 2 2 2019 2018 cos x N nghịch biến trên ? ÁO VIÊ 4037 A. m 1. B. m . C. m 1. D. m 1. GI 3 Lời giải Chọn A
Ta có y 2m 2019 2018 msin 2x .
Hàm số nghịch biến trên
y 2m 2019 2018 msin 2x 0, x .
2018 msin 2x 2019 2 , m x
max g(x) 2019 2m
1 , Với g(x) 2018 msin 2 x .
Trƣờng hợp 1: 2018 m 0 m 2018 thì y 2017 0, x
. Suy ra m 2018 không là giá trị cần tìm.
Trƣờng hợp 2: 2018 m 0 m 2018 .
max g(x) 2018 m .
1 2018 m 2019 2m m 1 (thỏa mãn).
Trƣờng hợp 3: 2018 m 0 m 2018 .
NGUYỄN CÔNG ĐỊNH | 74
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
max g(x) m 2018 . 4037
1 m 2018 2019 2m m (loại). 3
Kết luận: m 1 là giá trị cần tìm.
Câu 45. Có bao nhiêu số nguyên m thuộc khoảng 1 0;10 để hàm số 3
y 2x 2mx 3 đồng biến trên 1; ? A. 12 . B. 8 . C. 11. D. 7 . Lời giải Chọn A
Xét hàm số: f x 3
2x 2mx 3 có: f x 2 '
6x 2m ; 12m
Đồ thị hàm số y f x 3
2x 2mx 3 đƣợc suy ra từ đồ thị hàm số y f x C bằng cách: I Ơ
- Giữ nguyên phần đồ thị C nằm trên Ox .
- Lấy đối xứng phần đồ thị C nằm dƣới Ox qua Ox và bỏ phần đồ thị C nằm dƣới M D Ầ Ox . Đ
+ Trƣờng hợp 1: 0 m 0 . Suy ra f x 0, x 1; . NHỊ Đ m 0 m 0 m 0 G THPT
Vậy yêu cầu bài toán . f 5 m 0 1 0 5 N .C2.Đ m 0 m NG 2 CÔN Ờ
Kết hợp với điều kiện m ;m 1 0;10 ta đƣợc N Ễ Y m 9
;8; 7; 6;5; 4;3; 2; 1;0 TRƢ
. Ta có 10 giá trị của m thoả mãn yêu cầu bài GU N toán (1) N
+ Trƣờng hợp 2: 0 m 0 . Suy ra f ' x 0 có 2 nghiệm phân biệt x , x x x 1 2 1 2 Ta có bảng biến thiên: ÁO VIÊ GI m 0 m 0 2m 5
Vậy yêu cầu bài toán x x 1
1 0 0 m . 1 2 f 6 2 1 0 5 2m 0
Kết hợp với điều kiện m ;m 1
0;10 ta đƣợc m1;
2 . Ta có 2 giá trị của m thoả
mãn yêu cầu bài toán (2).
Từ (1) và (2) suy ra: có tất cả có 12 giá trị của m thoả mãn yêu cầu bài toán.
NGUYỄN CÔNG ĐỊNH | 75
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 46. Cho hàm số y f x liên tục trên và có đạo hàm f x 2
x x 2 2
x 6x m với mọi x
. Có bao nhiêu số nguyên m thuộc đoạn 2
019;2019 để hàm số
g x f 1 x nghịch biến trên khoảng ; 1 ? A. 2012 . B. 2009 . C. 2011. D. 2010 . Lời giải Chọn C
g x f x x2 x x2 1 1 1 1
61 x m
x 2 x 2 1
1 x 4x m 5 .
Hàm số g x nghịch biến trên khoảng ; 1
gx 0, x 1
, (dấu " " xảy ra tại hữu hạn điểm). Với x 1 thì x 2 1
0 và x 1 0 nên 2
x 4x m 5 0, x 1 I 2
m x x x Ơ 4 5, 1. Xét hàm số 2
y x 4x 5
;1 , ta có bảng biến thiên: M D trên khoảng Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ
Từ bảng biến thiên suy ra m 9 . N Ễ
Kết hợp với m thuộc đoạn 2
019;2019 và m nguyên nên m9;10;11;...;201 9 . Y TRƢ GU N
Vậy có 2011 số nguyên m thỏa mãn đề bài. N
Câu 47. Cho hàm số y f x có đạo hàm f x 2
x x 2 ' 2
x mx 5 với x . Số giá trị
nguyên âm của m để hàm số g x f 2
x x 2 đồng biến trên khoảng 1; là ÁO VIÊ GI A. 3 . B. 4 . C. 5 . D. 7 . Lời giải Chọn B
Ta có g x x f 2 ' 2
1 . ' x x 2 .
Để hàm số g x đồng biến trên khoảng 1;
g x x
f 2 ' 0 1;
' x x 2 0 x 1;
x x 2 x x x x 2 2 2 2 m 2 2 2
x x 2 5 0 x 1;
x x 2 2 m 2 2
x x 2 5 0 1 x 1; . Đặt 2
t x x 2 , x 1; t 0 . 5 Khi đó 1 trở thành 2
t mt 5 0 t
0; t m 2 t 0; t Để
1 nghiệm đúng với mọi x 1; 2 nghiệm đúng với mọi t 0; . 5
Ta có h t 5
t 2 5 với t
0;. Dấu bằng xảy ra khi t t 5 . t t
NGUYỄN CÔNG ĐỊNH | 76
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Suy ra Min ht 2 5 . t 0;
Vậy 2 nghiệm đúng với mọi t 0; m 2 5 m 2 5 .
KL: Số giá trị nguyên âm của m là 4 . Câu 48. Cho hàm số 3
y f x liên tục trên
và có đạo hàm f x x x 2 1
x 4x m với
mọi x . Có bao nhiêu số nguyên m thuộc đoạn 2
019;2019 để hàm số
g x f 1 x nghịch biến trên khoảng ;0 ? A. 2020 . B. 2014 . C. 2019 . D. 2016 . Lời giải Chọn D
Ta có: g x f 1 x 3
g x 1 x . f 1 x (
x x 1 x2 1). 1 1 1
41 x m I Ơ gx 3
x x 2
1 x 2x m 3 M D x 0 Ầ
Cho g x 0 x 1 Đ NH 2 Ị x 2x m 3 0 1 Đ Phƣơng trình
1 có 4 m G THPT N.C .Đ
Trường hợp 1: Nếu 4 m 0 m 4 thì phƣơng trình 1 vô nghiệm; NG CÔN Ờ 2
x 2x m 3 0, x N ta có bảng xét dấu: Ễ Y TRƢ GU N N
Suy ra hàm số g x nghịch biến trên khoảng ;0 nên m 4 thỏa mãn ycbt. ÁO VIÊ
Trường hợp 2: Nếu m 4 thì phƣơng trình
1 có nghiệm kép x 1 . GI
Khi đó g x x x x 2 3 1 1 , ta có bảng xét dấu:
Suy ra hàm số g x nghịch biến trên khoảng ;0 nên m 4 thỏa mãn ycbt.
Trường hợp 3: Nếu m 4 thì phƣơng trình
1 có 2 nghiệm phân biệt x , x x x 1 2 1 2 b
Mà x x
2 nên tồn tại ít nhất 1 nghiệm x thuộc khoảng ;0 1 2 a 1
Khi đó g x sẽ đổi dấu khi qua điểm x nên hàm số không thể nghịch biến trên 1
khoảng ;0. Suy ra m 4 không thỏa mãn ycbt.
Kết hợp 3 trƣờng hợp ta đƣợc: m 4 .
Do m là số nguyên thuộc đoạn 2
019;2019 nên m4;5;6; ... ;201 9
Vậy có 2016 số nguyên m thỏa mãn.
NGUYỄN CÔNG ĐỊNH | 77
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 49. Cho hàm số f x có bảng biến thiên của hàm số y f x nhƣ hình vẽ bên. Có bao
nhiêu giá trị nguyên của tham số m 1
0;10 để hàm số y f x 3 3
1 x 3mx đồng biến trên khoảng 2 ; 1 ? A. 8 . B. 6 . C. 7 . D. 5 . Lời giải Chọn B
Để hàm số y f x 3 3
1 x 3mx đồng biến biến trên khoảng 2 ; 1 I Ơ
y 0, x 2 ; 1
f x 2 3 3
1 3x 3m 0, x 2 ; 1 M D Ầ
m f x 2 3 1 x , x 2 ; 1 (*) Đ NH 2 Ị
Đặt k x f 3x 1 , 2
h x x và g x f 3x
1 x k x h x Đ G
Ta có min h x h0 0 THPT 2 ; 1 N.C.Đ NG
Từ bảng biến thiên suy ra: min f x f 1 4 . CÔN 2; 1 Ờ N
x x Ễ
Do đó ta có: min f 3x 1 f 1 4 khi 3 1 1 0 2 ; 1 Y TRƢ
min k x k 0 4 GU N 2 ; 1 N
Do đó min g x g 0 k 0 h0 0 4 4 2 ; 1 ÁO VIÊ
Từ (*) ta có m f x 2 3 1 x , x 2 ;
1 m min g x m 4 2 ; 1 GI Mà m 1
0;10 m 9 ,..., 4
Vậy có tất cả 6 số nguyên thoả mãn. 4
Câu 50. Giá trị y f x có đạo hàm f x x x 2 1
x mx 9 với mọi x . Có bao nhiêu
số nguyên dƣơng m để hàm số g x f 3 x đồng biến trên khoảng 3; ? A. 6 . B. 5 . C. 7 . D. 8 . Lời giải Chọn A
Ta có: g x 3 x f 3 x f 3 x .
Hàm số g x f 3 x đồng biến trên khoảng 3; khi và chỉ khi
g x 0, x
3; hay f 3 x 0, x
3; .( Dấu bằng chỉ xảy ra tại hữu hạn
điểm thuộc 3; )
f x x x4 x2 3 3 2 3
m3 x 9 0, x 3;
NGUYỄN CÔNG ĐỊNH | 78
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
x x4 x2 3 2 3
m3 x 9 0, x 3; x2 3
m3 x 9 0, x 3; x 2 9 3 m , x 3; x . 3 x 2 9 x 6x
m min h x với h x 2 9 3
hx 1 . 2 2 3; x 3 x 3 x 3
x 03;
h x 0
. Ta có bảng biến thiên: x 6 3; x 3 6
h x – 0 I
h x Ơ 6 M D m
min h x h6 6 . Ta có
m 1;2;3;4;5; 6 . Ầ 3; m 6 Đ NH Ị
Vậy có 6 số nguyên dƣơng m để hàm số g x
f 3 x đồng biến trên khoảng 3; . Đ G THPT N.C.Đ NG CÔN y f x
Ờ Câu 51. Cho hàm số ( ) có đạo hàm trên
và bảng xét dấu của đạo hàm nhƣ hình vẽ NỄ bên. Y TRƢ GU N N
Có bao nhiêu số nguyên m để hàm số y f 2
x 4x m nghịch biến trên khoảng 1 ; 1 ? ÁO VIÊ A. 3 . B. 1. C. 0 . D. 2 . GI Lời giải Chọn A Xét hàm số 2
y f (x 4x ) m .
Ta có: y x f 2 2 4
x 4x m .
Để hàm số nghịch biến trên khoảng 1 ;
1 y x f 2 2 4
x 4x m 0, x 1; 1
(chú ý rằng 2x 4 0, x 1 ; 1 ) f 2
x 4x m 0, x 2 1;1 2
x 4x m 8, x 1;1 2 m max g(x) g( 1) 1
m g(x) x 4x 2 , x 1 1; 1 ;1 m1;2; 3 2
m h(x) x 4x 8
m min h(x) h(1) 3 1 ; 1 (do hàm số 2
y x 4x c có y 2
x 4 0, x 1 ; 1 ).
NGUYỄN CÔNG ĐỊNH | 79
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA m
Câu 52. Tập các giá trị thực của tham số m để hàm số y ln(3x 1)
2 đồng biến trên khoảng x 1 ; . 2 7 1 4 2 A. ; . B. ; . C. ; . D. ; . 3 3 3 9 Lời giải Chọn C m 1
Xét hàm số y ln(3x 1) 2 trên khoảng ; . x 2 3 m Ta có y ' . 2 3x 1 x 1 3 m 1
Hàm số đồng biến trên khoảng ; y ' 0, x ; . 2 2 3x 1 x 2 I Ơ 2 3x 1 2 3x m , x ; m max . 1 3x 2 1 1 3x M D ; 2 Ầ 2 Đ 3x 1
Xét hàm số f (x) , x ; . NHỊ 1 3x 2 Đ 1 G THPT x 0 ; 3x(2 3x) 2 N.C.Đ Ta có f (x) 0 . NG 2 (1 3x) 2 1 CÔN Ờ x ; N 3 2 Ễ Y TRƢ 1 3 2 4 4 4 Ta có f ; f
; lim f (x) max f (x) . Vậy m . GU N x 1 2 2 3 3 ; 3 3 N 2
Câu 53. Có tất cả bao nhiêu cặp số nguyên ;
a b để hàm số f x x . a sin x .
b cos x đồng ÁO VIÊ biến trên . GI A. 5 . B. 6 . C. 4 . D. 3 . Lời giải Chọn C
Để hàm số đồng biến trên R thì điều kiện là f ' x 0, x . Ta có
f ' x 1 a cos x bsin x
f ' x 0 1 a cos x bsin x 0
a cos x bsin x 1
TH1: a 0, b 0.TM a 0 TH 2 : b 0 a b 1
1 a cos x b sin x 0 cos x sin x 2 2 2 2 2 2 a b a b a b a b : sin; cos 2 2 2 2 a b a b
NGUYỄN CÔNG ĐỊNH | 80
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 1 sin x 2 2 a b f x x R x 1 1 ' 0, sin , x R 1 2 2 2 2 a b a b 2 2 2 2
a b 1 a b 1 Do a, b nguyên nên ; a b 1 ;0,0; 1
Vậy theo cả hai trƣờng hợp ta có tất cả 5 bộ giá trị ; a b
Câu 54. Cho hàm số y f x có đạo hàm liên tục trên
và có đồ thị hàm số y f x nhƣ
hình vẽ bên. Có bao nhiêu giá trị nguyên dƣơng của tham số m để hàm số
20 2 x y f x 1 ln
nghịch biến trên khoảng 1 ; 1 ? m 2 x I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG A. 3 . B. 6 . C. 4 . D. 5 . CÔN Ờ N Lời giải Ễ Y TRƢ Chọn D GU N 20 4 N Ta có y f x 1 . . 2 m 4 x
Hàm số nghịch biến trên khoảng 1 ;
1 khi y 0, x 1 ; 1 ÁO VIÊ 80 1 GI
f x 1 . 0, x 1 ;1 2 m 4 . x
Đặt t x 1 khi đó x 1 ;
1 suy ra t 0;2 . 80 1 80
Từ ta có f t . t
f t .3 t t 1 , t 0;2 1 . m
3 t t 0, 0;2 1 m
Dựa vào đồ thị hàm số 2
y f x thì ta có f x x 1 x 2 .
Suy ra ta có f t t 2 1 t 2 .
Xét hàm số g t t 2
1 t 23 t t 1 , t 0;2 . t 1 2 13
gt t 2 2 1 5
t 18t 13 ; gt 0 t 2 1 5
t 18t 13 0 t . 5 t 1 Bảng xét dấu
NGUYỄN CÔNG ĐỊNH | 81
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 80
Dựa vào bảng xét dấu và từ 1 ta có
max g t 80 g 1 16 m 5 . 0;2 m m
Câu 55. Cho hàm số y f x xác định và liên tục trên
, có đồ thị f x nhƣ hình vẽ. I Ơ M D Ầ Đ NH mx x 2 2 3 4 Ị
Có bao nhiêu giá trị nguyên âm của m 2
0;20 để hàm số g x f Đ 4 20 G THPT
đồng biến trên khoảng 0; . N.C.Đ NG CÔN Ờ A. 6 . B. 7 . C. 17 . D. 18 . N Ễ Lời giải Y TRƢ Chọn C GU N 2 2 3 N mx x x x 4 3
Ta có g x f . 4 4 5 ÁO VIÊ
Hàm số g x đồng biến trên 0; khi và chỉ khi g x 0, x
0; ( gx 0 GI
chỉ tại hữu hạn điểm). Điều này tƣơng đƣơng với m x x 2 3 x 4 3 3 15x x f m f x . 4 4 5 4 , 0; 2 x 4 4 3 3 x x 3 x Với x 0 thì
0 f 3. Đẳng thức xảy ra khi 3
2 x 8 x 2 . 4 4 4 x x 1 Ta có 0 , x 0 x . 2 x . Đẳng thức xảy ra khi 2 4 4x 4 3 15x x 15 1 45 Suy ra
f
. Đẳng thức xảy ra khi x 2 . 4 3 2 x 4 4 4 4 16 45 Nhƣ thế, m
. Kết hợp với m nguyên âm và m 2
0;20 thì m 1 9; 1 8; ; 3 . 16
Vậy có 17 số nguyên âm của m 2
0;20 để hàm số g x đồng biến trên 0;.
NGUYỄN CÔNG ĐỊNH | 82
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
CHỦ ĐỀ: HÀM SỐ ĐƠN ĐIỆU
VẬN DỤNG – VẬN DỤNG CAO DẠNG 3.1
BIỆN LUẬN SỐ NGHIỆM PHƢƠNG TRÌNH, BẤT PHƢƠNG TRÌNH
KIẾN THỨC CẦN NẮM VỮNG
Kiến th ức quan trọng 1: Dùng tính đơn điệu để giải phƣơng trình.
Phương pháp :
Phƣơng trình : f x c có nhiều nhất một nghiệm nếu f x đơn điệu trên toàn bộ tập xác định. I Ơ
Phƣơng trình : f x g x có nhiều nhất một nghiệm nếu hai hàm số f x, g x có
M D tính đơn điệu trái ngƣợc nhau. Ầ
Phƣơng trình : f u
x f v
x u
x vx nếu f đơn điệu trên miền xác định. Đ NHỊ Đ
Kiến th ức quan trọng 2: Dùng tính đơn điệu để giải bất phƣơng trình. G THPT N.C.Đ
Phương pháp : NG CÔN Ờ
Bất phƣơng trình : f x c f x x x nếu f x đồng biến trên toàn bộ tập xác 0 0 N Ễ Y
định và f x c f x x
x nếu f x nghịch biến trên toàn bộ tập xác định 0 TRƢ 0 GU N
Bất phƣơng trình : f x g x và số x thỏa f x g x : 0 0 0 N
+ Có nghiệm x x nếu f x đồng biến và g x nghịch biến. 0 ÁO VIÊ
+ Có nghiệm x x nếu f x nghịch biến và g x đồng biến. 0 GI
Bất phƣơng trình : f u
x f v
x u
x vx nếu f đồng biến trên miền xác
định và f u
x f v
x u
x vx nếu f nghịch biến trên miền xác định. Bài toá
n 1: Biện luận số nghiệm phƣơng trình . Phương pháp :
+ Tìm miền giá trị của hàm số f x là ; a b.
+ Phƣơng trình có nghiệm khi a hm . b Bài t
oán 2: Biện luận số nghiệm bất phƣơng trình hoặc . Phương pháp :
m f x x ;
a b m max f x. a;b
m f x x ;
a b m min f x. a;b
NGUYỄN CÔNG ĐỊNH | 83
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
m f x có nghiệm trên ;
a b m min f x. a;b
m f x có nghiệm trên ;
a b m max f x. a;b Bài t
oán 3: Tìm tham số m để phƣơng trình có nghiệm Phương pháp :
+ Giả sử f x liên tục trên ;
a b và f a f b.
+ Phƣơng trình có nghiệm x ;
a b thì f a hm f b. BÀI TẬP Câu 1.
Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình 3 2
x 3x 9x m 0 có đúng 1 nghiệm? A. 27 m 5.
B. m 5 hoặc m 27 . I C. m 27 hoặc m 5 . D. 5 m 27 .
Ơ Câu 2. Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình 2 x 1 x m có M D nghiệm thực? Ầ Đ A. m 2 . B. m 2 . C. m 3 . D. m 3 . NHỊ Câu 3.
Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình Đ 2 2
x 4x 5 m 4x x có đúng 2 nghiệm dƣơng? G THPT
A. 1 m 3 . B. 3
m 5 . N.C.Đ
C. 5 m 3 .
D. 3 m 3 . NG CÔN
Ờ Câu 4. Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phƣơng trình: N 2 2 Ễ
x 3x 2 0 cũng là nghiệm của bất phƣơng trình mx m
1 x m 1 0 ? Y TRƢ 4 4 GU N A. m 1. B. m . C. m . D. m 1. N 7 7 Câu 5.
Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình: ÁO VIÊ 2 2
log x log x 1 2m 1 0 có ít nhất một nghiệm trên đoạn 3 1 ;3 3 3 ? GI A. 1 m 3.
B. 0 m 2 .
C. 0 m 3 . D. 1 m 2 . Câu 6.
Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình 2
x mx 2 2x 1 có hai nghiệm thực? 7 3 9 A. m . B. m . C. m . D. m . 2 2 2 Câu 7.
Tìm tất cả các giá trị thực của tham số m sao cho phƣơng trình 4 2
3 x 1 m x 1 2 x 1 có hai nghiệm thực? 1 1 1 1 A. m 1. B. 1 m . C. 2 m .
D. 0 m . 3 4 3 3 Câu 8.
Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình 2 1
(1 2x)(3 x) m 2x 5x 3 nghiệm đúng với mọi x ;3 ? 2 A. m 1. B. m 0 . C. m 1. D. m 0 . Câu 9.
Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình
NGUYỄN CÔNG ĐỊNH | 84
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
3 1 x 3 x 2 (1 x)(3 x) m nghiệm đúng với mọi x [ 1;3] ? A. m 6 . B. m 6 .
C. m 6 2 4 .
D. m 6 2 4 .
Câu 10. Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình 2 2
3 x 6 x 18 3x x m m 1 nghiệm đúng x 3 ,6 ? A. m 1.
B. 1 m 0 .
C. 0 m 2 .
D. m 1 hoặc m 2 .
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình x m
m x 2 .4 1 .2
m 1 0 nghiệm đúng x ? A. m 3 . B. m 1.
C. 1 m 4 . D. m 0 . 1
Câu 12. Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình: 3
x 3mx 2 3 x nghiệm đúng x 1 ? I 2 2 3 1 3 Ơ A. m . B. m . C. m .
D. m . 3 3 2 3 2 2 2 2
M D Câu 13. Tìm giá trị lớn nhất của tham số m sao cho bất phƣơng trình cos x sin x cos 2 3 .3 x m có Ầ Đ nghiệm? NHỊ A. m 4 . B. m 8 . C. m 12 . D. m 16 . Đ G
Câu 14. Bất phƣơng trình 3 2 2x 3x 6x 16 4 x
2 3 có tập nghiệm là ; a b . Hỏi tổng THPT N.C.Đ
a b có giá trị là bao nhiêu? NG CÔN Ờ A. 2 . B. 4. C. 5. D. 3. N Ễ Câu 15.
x x x x x x ; a b Y Bất phƣơng trình 2 2 2 3 6 11 3 1 có tập nghiệm . Hỏi TRƢ GU N
hiệu b a có giá trị là bao nhiêu? N A. 1. B. 2. C. 3. D. 1.
Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình: ÁO VIÊ m 2 2
1 x 1 x 2 4 2 2 GI 2 1 x 1 x 1 x có nghiệm.
A. m 2 1.
B. 2 1 m 1. C. m 1. D. m 1.
Câu 17. Tìm các giá trị của tham số m để phƣơng trình sau có đúng hai nghiệm thực phân biệt 4 4
2x 2x 2 6 x 2 6 x , m m A. 4
2 6 2 6 m 3 2 6 B. 4
2 6 3 6 m 3 2 8 C. 4
6 2 6 m 3 2 6 D. 4
6 2 6 m 3 2 6
Câu 18: Cho hàm số 3 2 y
f x ax bx cx d với a, ,
b c, d; a 0 là các số thực, có đồ thị nhƣ hình bên.
NGUYỄN CÔNG ĐỊNH | 85
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Có bao nhiêu số nguyên m thuộc khoảng ( 2 019;2019) để hàm số g x f 3 2 ( )
x 3x m
nghịch trên khoảng 2; ? A. 2012 B. 2013 C. 4028 D. 4026
Câu 19: Cho hàm số f x có đồ thị nhƣ hình vẽ I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ
Giá trị nguyên nhỏ nhất của tham số m để phƣơng trình GI 3 f x 2
2 f x7 f x5 f x 1 e ln
m có nghiệm là f x A. 3 . B. 4 . C. 5 . D. 6 .
NGUYỄN CÔNG ĐỊNH | 86
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA HƢỚNG DẪN GIẢI Câu 1. Chọn C. 3 2
(1) m x 3x 9x f (x) . Bảng biến thiên của f (x) trên . 3 0 0 5
Từ đó suy ra pt có đúng 1 nghiệm khi m 27 hoặc m 5 Câu 2. Chọn B.
Đặt t x 1,t 0 . Phƣơng trình thành: 2 2
2t t 1 m m t 2t 1 I
f t t t t f Ơ Xét hàm số 2 ( ) 2 1, 0; (t) 2 t 2
Bảng biến thiên của f t : M D Ầ 0 1 Đ NHỊ 0 Đ G THPT 2 N.C.Đ NG CÔN Ờ N Ễ Y TRƢ
Từ đó suy ra phƣơng trình có nghiệm khi m 2 . GU N Câu 3. Chọn B N x 2 Đặt 2
t f (x)
x 4x 5 . Ta có f ( x) . f (
x) 0 x 2 2 x 4x 5 ÁO VIÊ
Xét x 0 ta có bảng biến thiên GI 0 2 0 1
Khi đó phƣơng trình đã cho trở thành 2 2
m t t 5 t t 5 m 0 (1).
Nếu phƣơng trình (1) có nghiệm t ,t thì t t 1
. (1) có nhiều nhất 1 nghiệm t 1. 1 2 1 2
Vậy phƣơng trình đã cho có đúng 2 nghiệm dƣơng khi và chỉ khi phƣơng trình (1) có
đúng 1 nghiệm t 1; 5 . Đặt 2
g(t) t t 5 . Ta đi tìm m để phƣơng trình g(t) m có
đúng 1 nghiệm t 1; 5 . Ta có g (t) 2t 1 0,t 1; 5 . Bảng biến thiên:
NGUYỄN CÔNG ĐỊNH | 87
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Từ bảng biến thiên suy ra 3
m 5 là các giá trị cần tìm. Câu 4. Chọn C. Bất phƣơng trình 2
x 3x 2 0 1 x 2 . x 2 Bất phƣơng trình 2
mx m
1 x m 1 0 2
m(x x 1) x 2 m 2 x x 1 x 2 2 x 4x 1
Xét hàm số f (x)
với 1 x 2 . Có f ( x) 0,x [1;2] 2 x x 1 2 2 x x I ( 1) Ơ
Yêu cầu bài toán m 4
max f (x) m [1;2] 7 M D Ầ Câu 5. Chọn B. Đ NH Đặt 2 t
log x 1 . Điều kiện: t 1. 3 Ị Đ Phƣơng trình thành: 2
t t 2m 2 0 (*) . Khi 3 x 1
;3 t [1;2] G THPT 2 N.C.Đ t t 2 NG
(*) f (t)
m . Bảng biến thiên : CÔN Ờ 2 N Ễ 2 Y TRƢ GU N N 2 ÁO VIÊ 0 GI
Từ bảng biến thiên ta có : 0 m 2 Câu 6. Chọn C 1
Điều kiện: x 2 Phƣơng trình 2
x mx 2 2x 1 2
3x 4x 1 mx (*) 2 3x 4x 1
Vì x 0 không là nghiệm nên (*) m x 2 3x 4x 1 2 3x 1 1 Xét f (x) . Ta có f ( x) 0 x ; x 0 x 2 x 2 Bảng biến thiên
NGUYỄN CÔNG ĐỊNH | 88
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 0 + + 9
Từ bảng biến thiên ta có để phƣơng trình có hai nghiệm thì m . 2 Câu 7. Chọn D.
Điều kiện : x 1 4 2 x 1 x 1 x 1 x 1 Pt 3 m 2 4 3 m 2 2 I 4 x 1 (x 1) x 1 x 1 Ơ x 1 4 t
x ta có 0 t 1 . Thay vào phƣơng trình ta đƣợc 2
m 2t 3t f (t) M D x với 1 1 Ầ Đ 1 Ta có: f (
t) 2 6t ta có: f (t) 0 t NH 3 Ị Đ Bảng biến thiên: G THPT N.C.Đ 0 1 NG CÔN Ờ N Ễ 0 Y TRƢ GU N N 0 ÁO VIÊ 1 GI
Từ bảng biến thiên ta có để phƣơng trình có hai nghiệm khi 0 m 3 Câu 8. Chọn D. 1 7 2
Đặt t (1 2x)(3 x) khi x ;3 t 0; 2 4
Thay vào bất phƣơng trình ta đƣợc 2
f (t) t t m Bảng biến thiên 0
Từ bảng biến thiên ta có : m 0 Câu 9. Chọn D.
NGUYỄN CÔNG ĐỊNH | 89
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Đặt 2 2
t 1 x 3 x t 4 2 (1 ) x (3 ) x 2 (1 ) x (3 ) x t 4
Với x [ 1;3] t [2;2 2] . Thay vào bất phƣơng trình ta đƣợc: 2 m t 3t 4 3 Xét hàm số 2
f (t) t 3t 4; f ( t) 2
t 3 ; f (t) 0 t 2 2 - 6
Từ bảng biến thiên ta có m 6 2 4 thỏa đề bài Câu 10. Chọn D. 2
Đặt t 3 x 6 x 0 2
t 3 x 6 x 9 2 3 x6 x I Ơ 2
9 t 9 2 3 x6 x 9 3 x 6 x 18 2
x x x x 1 18 3 3 6 2 t 9 M D ;t 3 ;3 2 2 Ầ Đ Xét f t 1 2 9
t t ; f t 1t 0; t 3
;3 2 max f t f 3 3 NH 2 2 3 ;3 2 Ị Đ
ycbt max f t 2 2
3 m m 1 m m 2 0 m 1 hoặc m 2 G THPT 3;3 2 N.C.Đ Câu 11. Chọn B NG CÔN Ờ Đặt 2 x t 0 thì x m
m x 2 .4 1 .2
m 1 0, đúng x N Ễ 2
m t m t m t m 2 . 4 1 . 1 0, 0 t 4t 1 4t 1, t 0 Y TRƢ g t 4t 1 GU N , m t 0 2 t 4t . 1 N 2 Ta có 4t 2t g t
nên g t nghịch biến trên 0; t 4t 0 2 2 ÁO VIÊ 1 GI
ycbt max g t g 0 1 m t 0 Câu 12. Chọn A. Bpt 3 1 2 1 2
3mx x 2, x
1 3m x
f x, x 1. 3 4 x x x
Ta có f x 4 2 4 2 4 2 2 2x 2 2x
0 suy ra f x tăng. 5 2 x x 5x 2 2 x x
Ycbt f x m x
f x f 2 3 , 1 min 1 2 3m m x 1 3 Câu 13. Chọn A. 2 2 cos x cos x 2 1 (1) 3 m . Đặt 2 t cos , x 0 t 1 3 9 t t t t 2 1 2 1 (1) trở thành 3 m
(2). Đặt f (t) 3 . 3 9 3 9
Ta có (1) có nghiệm (2) có nghiệm t [0;1] m Max f (t) m 4 t [ 0;1] Câu 14. Chọn C
NGUYỄN CÔNG ĐỊNH | 90
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Điều kiện: 2 x 4 . Xét 3 2 f (x)
2x 3x 6x 16 4 x trên đoạn 2 ;4. 3 2 x x 1 1 Có f ( x) 0, x 2 ;4 . 3 2
2x 3x 6x 16 2 4 x
Do đó hàm số đồng biến trên 2
;4, bpt f (x) f (1) 2 3 x 1.
So với điều kiện, tập nghiệm của bpt là S [1; 4] a b 5. Câu 15. Chọn A. Điều kiện: 2 2
1 x 3 ; bpt x 1 2
x 1 3 x 2 3 x t 1 Xét 2
f (t) t 2 t với t 0 . Có f '(t) 0, t 0 . 2 2 t 2 2 t
Do đó hàm số đồng biến trên [0; ) . (1) f (x 1) f (3 x) x 1 3 x 2
So với điều kiện, bpt có tập nghiệm là S (2;3].
I Câu 16. Tìm tất cả các giá trị thực của tham số m sao cho bất phƣơng trình: Ơ m 2 2 x x 4 2 2 1 1
2 2 1 x 1 x 1 x có nghiệm. M D Ầ
A. m 2 1.
B. 2 1 m 1. C. m 1. D. m 1. Đ NH Ị Đ Lời giải G THPT ĐK: x 1; 1 . N.C.Đ NG CÔN Ờ Đặt 2 2 t 1 x
1 x . Với x 1;
1 , ta xác định ĐK của t nhƣ sau: N Ễ Y Xét hàm số 2 2 t 1 x
1 x với x 1; 1 . TRƢ GU N Ta có: N x 2 2
1 x 1 x x x t '
, cho t ' 0 x 0 ÁO VIÊ 2 2 4 1 x 1 x 1 x GI Ta có t 1
2,t 0 0,t 1 2
Vậy với x 1;
1 thì t 0; 2 Từ 2 2 4 2
t 1 x 1 x 2 1 x 2 t . t t 2
Khi đó pt đã cho tƣơng đƣơng với: mt 2 2 2 t t 2 t 2 2 t t 2
Bài toán trở thành tìm m để phƣơng trình m t . t có nghiệm 0; 2 2 t t
Xét hàm số f t 2 2 t . t với 0; 2 2 2 t 4t
Ta có: f 't t t 2 0, 0; 2 2
Suy ra: max f t f 0 1, min f t f 2 2 1 . t 0; 2 t 0; 2
NGUYỄN CÔNG ĐỊNH | 91
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Bây giờ yêu cầu bài toán xảy ra khi: min f t m max f t 2 1 m 1 t 0; 2 t 0; 2
Vậy với 2 1 m 1 thảo yêu cầu bài toán. Chọn B.
Câu 17. Tìm các giá trị của tham số m để phƣơng trình sau có đúng hai nghiệm thực phân biệt 4 4
2x 2x 2 6 x 2 6 x , m m A. 4
2 6 2 6 m 3 2 6 B. 4
2 6 3 6 m 3 2 8 C. 4
6 2 6 m 3 2 6 D. 4
6 2 6 m 3 2 6 Lời giải ĐK: 0 x 6
Đặt vế trái của phƣơng trình là f x, x 0;6 . Ta có: I 1 1 1 1 Ơ f ' x 3 2x 3 4 4 6 2 2 2 6 x x x M D Ầ Đ 1 1 1 1 1 , x 0;6 NH 3 3 Ị 2 4 4 2x 6 2 6 x x x Đ G THPT Đăt: N.C.Đ NG CÔN 1 1 1 1 Ờ u x ,v(x) , x 0;6 N 3 3 4 4 2x 6 x Ễ 2x 6 x Y TRƢ
Ta thấy u 2 v2 0, x 0;6 f '2 0 . Hơn nữa u x,v x cùng dƣơng trên GU N N
khoảng (0;2) và cùng âm trên khoảng (2;6). BBT ÁO VIÊ x 0 2 6 GI f ' x || + 0 − || 3 2 6 f x 4 2 6 2 6 4 12 2 3 Vậy với 4
2 6 2 6 m 3 2 6 thỏa mãn yêu cầu đề bài. Chọn A.
Câu 20: Cho hàm số 3 2 y
f x ax bx cx d với a, ,
b c, d; a 0 là các số thực, có đồ thị nhƣ hình bên.
NGUYỄN CÔNG ĐỊNH | 92
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Có bao nhiêu số nguyên m thuộc khoảng ( 2 019;2019) để hàm số g x f 3 2 ( )
x 3x m
nghịch trên khoảng 2; ? A. 2012 B. 2013 C. 4028 D. 4026 Lời giải: Chọn A I Ơ Ta có 2 3 g (
x) (3x 6x) f (x 3x ) m .
Với mọi x (2; ) ta có 2
3x 6x 0 nên để hàm số g x f 3 2 ( )
x 3x m nghịch biến M D Ầ Đ trên NHỊ khoảng 2; 3 2 f (
x 3x ) m 0, x (2; ) . Đ y f x G
Dựa vào đồ thị ta có hàm số
( ) nghịch biến trên các khoảng ( ;1) và (3; ) THPT N.C.Đ nên NG CÔN Ờ f (
x) 0 với x ; 1 3; . N Ễ 3 2
x 3x m 1, x (2;) Y TRƢ Do đó: 3 2 f (
x 3x ) m 0, x (2; ) 3 2
x 3x m 3, x (2;) GU N N 3 2
m x 3x 1, x (2;) 3 2
m x 3x 3, x (2;) ÁO VIÊ GI Nhận thấy 3 2
lim (x 3x 1) nên trƣờng hợp 3 2
m x 3x 1, x (2;) không x xảy ra. Trƣờng hợp: 3 2
m x 3x 3, x (2; ) . Ta có hàm số 3 2 (
h x) x 3x 3 liên tục trên 2; và 2 h ( x) 3
x 6x 0, x (2; )
nên h(x) nghịch biến trên 2; suy ra
max h(x) h(2) . Do đó 3 2
m x 3x 3, x (2; )
m max h(x) h(2) m 7 . 2; 2;
Do m nguyên thuộc khoảng ( 2
019;2019) nên m7;8;9;...;201 8 .
Vậy có 2012 số nguyên m thỏa mãn yêu cầu bài toán.
Câu 21: Cho hàm số f x có đồ thị nhƣ hình vẽ
NGUYỄN CÔNG ĐỊNH | 93
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Giá trị nguyên nhỏ nhất của tham số m để phƣơng trình I Ơ 3 f x 2
2 f x7 f x5 f x 1 e ln
m có nghiệm là f x M D Ầ Đ NH A. 3 . B. 4 . C. 5 . D. 6 . Ị Đ Lời giải G THPT Chọn B N.C.Đ NG
Quan sát đồ thị ta thấy 1 f x 5,x , đặt t f x giả thiết trở thành CÔN Ờ N 3 2
t t t 1 2 7 5 Ễ e ln t m . Y TRƢ t 3 2 GU N
Xét hàm: g t t 2t 7t 5, t 1; 5 N gt 2
3t 4t 7 0t 1 g
1 g t g 5 1 g t 145 . ÁO VIÊ 1 1 26
Mặt khác h t t , ht 1
0t 1;5 2 h t . 2 GI t t 5
t t t 1
Do đó hàm u t 3 2 2 7 5 e ln t
đồng biến trên đoạn 1; 5 . t 26
Suy ra: Phƣơng trình đã cho có nghiệm 145
e ln 2 m e ln . 5
Vậy giá trị nguyên nhỏ nhất của m là 4 .
NGUYỄN CÔNG ĐỊNH | 94
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
CHỦ ĐỀ: HÀM SỐ ĐƠN ĐIỆU
VẬN DỤNG – VẬN DỤNG CAO DẠNG 3.2
BIỆN LUẬN SỐ NGHIỆM PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH Câu 1.
Cho hàm số y f (x) có bảng biến thiên nhƣ hình vẽ dƣới. Số nghiệm của phƣơng trình 2
f (x ) 4 là: x 0 4 y’ - 0 + 0 - I y 5 Ơ 1 M D Ầ A. 4 B. 6 C. 2 D. 8 Đ NH 2 Ị Câu 2. Cho hàm số y
f (x) có đạo hàm f ' x 3 x x 1 2x , x . Hàm số Đ G g x f x 2 x
1 đồng biến trên khoảng nào trong các khoảng dƣới đây? THPT N.C.Đ A. ;1 . B. 1 ;0 . C. 1;2 . D. 3; . NG CÔN Ờ N Câu 3.
Cho hàm số f x đồng biến trên đoạn 3 ; 1 thỏa mãn f 3
1, f 0 2 , f 1 3 . Ễ Y TRƢ
Mệnh đề nào dƣới đây đúng ? GU N A. 1 f 2 2 . B. 2 f 2 3. C. f 2 1. D. f 2 3. N Câu 4. Cho hàm số y
f x có đạo hàm f x 2
x x
1 x 4.u x với mọi x
và u x 0 2 ÁO VIÊ
với mọi x . Hàm số g x f x đồng biến trên khoảng nào trong các khoảng sau GI đây? A. 1;2 . B. 1 ; 1 . C. 2 ; 1 . D. ; 2 .
Câu 5. Cho hàm số y f x liên tục trên ( ;1
) và (1;)có bảng biến thiên nhƣ sau
Số nghiệm thực của phƣơng trình 2 f (x) 1 0 là A. 3 . B. 2 . C. 1. D. 4 . Câu 6. Cho hàm số y
f x . Hàm số y f
x có đồ thị nhƣ hình vẽ sau. Bất phƣơng trình 2 1 ex f x
m nghiệm đúng với mọi x 1;1 khi và chỉ khi
NGUYỄN CÔNG ĐỊNH | 95
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. m f 1 1. B. 2 m f 1 e . C. 2 m f 1 e . D. m f 1 1.
Câu 7. Cho hàm số y f x . Hàm số y f x có bảng biến thiên nhƣ sau: I Ơ M D
Bất phƣơng trình ex f x
m đúng với mọi x 1; 1 khi và chỉ khi: Ầ Đ
A. m f 1 1 .
B. m f 1 e .
C. m f 1 e .
D. m f 1 1 . NH e e Ị Đ Câu 8. Cho hàm số
y f x xác định trên và có đạo hàm G THPT
f ' x 1 x2 xsin x 2 2019 . Hàm số y f 1 x nghịch biến N.C.Đ 2019x 2018 NG CÔN
trên khoảng nào dƣới đây ? Ờ N 3; 0;3 1; Ễ A. . B. . C. ;3 . D. . Y
TRƢ Câu 9. Cho hàm số f x có đạo hàm xác định và liên tục trên thoả mãn GU N N f x .
x f x x x
1 x 2 , x
. Hàm số g x .x f x đồng biến trên khoảng nào? ÁO VIÊ A. ;0 . B. 1;2 . C. 2; . D. 0; 2 .
GI Câu 10. Cho hàm số y f x có đồ thị là đƣờng cong
trong hình vẽ bên. Số nghiệm thực của phƣơng
trình f x 2019 1 là A. 1. B. 2 . C. 3 . D. 4 .
Câu 11. Cho hàm số y f x có đồ thị nhƣ hình vẽ dƣới đây
NGUYỄN CÔNG ĐỊNH | 96
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Tìm tất cả các giá trị thực của tham số m để phƣơng trình f x log m có hai nghiệm 2 phân biệt. A. m 0.
B. 0 m 1; m 16 .
C. m 1; m 16 . D. m 4.
Câu 12. Cho hàm số y f x . Hàm số y f (
x) có bảng biến thiên nhƣ hình dƣới. Bất phƣơng trình .
x f x mx 1 nghiệm đúng với mọi x 1;2019 khi x ∞ 2 3 + ∞ + ∞ 4 f'(x) ∞ 0
A. m f 1 1.
B. m f 1 1.
C. m f 1 2019 .
D. m f 1 2019 . 2019 2019 I
Ơ Câu 13. Cho hàm số y
f x . Hàm số y
f x có đồ thị nhƣ sau: M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG
Bất phƣơng trình f x 2
x 2x m đúng với mọi x1;2 khi và chỉ khi CÔN Ờ N m f 2 m f m f 2 1 m f Ễ A. . B. 1 1. C. . D. 1 1. Y
TRƢ Câu 14. Cho hàm số y f x . Hàm số y f x có bảng biến thiên nhƣ sau: GU N N ÁO VIÊ GI Bất phƣơng trình 2 ( ) 3ex f x
m có nghiệm x 2 ;2 khi và chỉ khi:
A. m f 2 3.
B. m f 4 2 3e .
C. m f 4 2 3e .
D. m f 2 3.
Câu 15. Cho hàm số y f x có bảng xét dấu của đạo hàm nhƣ sau Bất phƣơng trình 2 x f x e
m đúng với mọi x 1 ; 1 khi và chỉ khi
A. m f 0 1 .
B. m f 1 e .
C. m f 0 1.
D. m f 1 e .
Câu 16. Có bao nhiêu số nguyên m để phƣơng trình log 2x m 2
2log x x 4x 2m 1 có 2 2
hai nghiệm thực phân biệt? A. 2. B. 3. C. 1. D. 4.
NGUYỄN CÔNG ĐỊNH | 97
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 3 2019 x x x 1 x ...
ex khi x 0
Câu 17. Cho hàm số f x 2! 3! 2019!
. Hỏi có bao nhiêu giá trị 2 x 10x khi x 0
nguyên dƣơng và chia hết cho 5 của tham số m để bất phƣơng trình m f x 0 có nghiệm? A. 25 . B. 0 . C. 6 . D. 5 .
Câu 18. Gọi S là tập tất cả các giá trị nguyên của tham số m 2
019;2019 để bất phƣơng trình 3 m 3 x 3 m 2 x 3 m m 3 1 3 2 13 3
x 10 m m 0 đúng với mọi x 1; 3 . Số phần
tử của tập S là A. 4038. B. 2021. C. 2022. D. 2020.
Câu 19. Cho hàm số y f x . Đồ thị hàm số y f x đƣợc cho nhƣ hình vẽ bên. Hàm số
g x f 4 2x
1 đồng biến trên khoảng nào sau đây? I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG 1 3 CÔN A. ; 1 . B. . C. .
D. 2; . Ờ ;1 1; N 2 2 Ễ Y 3 TRƢ 2019
Câu 20. Cho hàm số f x cos2x . Bất phƣơng trình f
x m đúng với mọi x ; 12 8 GU N N khi và chỉ khi A. 2019 m 2 . B. 2018 m . C. 2018 m 2 . D. 2019 m 2 . ÁO VIÊ 2019 3 GI
Do đó bất phƣơng trình f
x m đúng với mọi x ; khi và chỉ khi 12 8 2018 m 2 .
Câu 21. Cho hàm số y f (x) có đạo hàm đến cấp hai trên
. Bảng biến thiên của hàm số 1
y f '(x) nhƣ hình vẽ. Bất phƣơng trình 2 3
m x f (x)
x nghiệm đúng với mọi 3
x 0;3 khi và chỉ khi
A. m f 0 .
B. m f 3 .
C. m f 0 .
D. m f 2 1 . 3
NGUYỄN CÔNG ĐỊNH | 98
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 22. Tìm tất cả các giá trị thực của tham số m để phƣơng trình 2 x x
mx 2 5 12 16 2
x 2 có hai nghiệm thực phân biệt thoả mãn 2 x x 1 2 x 1 2018 2018 2019x 2019 . 11 3
A. m 2 6 ; .
B. m 2 6 ;3 3 . 3 I Ơ 11 3
C. m 2 6 ;3 3 . D. m 3 3 ; 2 6 . M D 3 Ầ Đ x 1
Câu 23. Có bao nhiêu số nguyên m để phƣơng trình 1 2 2
8 x m có 3 nghiệm thực phân NHỊ 2 Đ biệt? G THPT A. 8 . B. 9 . N.C.Đ C. 6 . D. 7 . NG 3 4 2 3 2 2 2 CÔN
Câu 24. Cho bất phƣơng trình
x x m 2x 1 x x
1 1 m . Tìm tất cả các giá trị Ờ N Ễ
thực của tham số m để bất phƣơng trình nghiệm đúng với mọi x 1 . Y TRƢ 1 m m 1 1 m m 1 GU N A. . B. . C. . D. . 2 2 N f 12x 1
Câu 25. Cho hàm số y f x . Đồ thị y f x nhƣ hình bên. Hàm số g x nghịch ÁO VIÊ 2 GI
biến trên khoảng nào trong các khoảng sau? A. 0 ;1 . B. ;0 . C. 1 ;0 . D. 1; .
Câu 26. Cho hàm số f x liên tục trên
có đồ thị nhƣ hình vẽ. Có bao nhiêu giá trị nguyên của
n để phƣơng trình sau có nghiệm x . f 2 16
sin x 6sin 2x 8 f nn 1
NGUYỄN CÔNG ĐỊNH | 99
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. 10. B. 6. C. 4. D. 8.
Câu 27 Cho hàm số y f x liên tục trên R và có đồ thị nhƣ hình vẽ dƣới đây . I Ơ M D Ầ Đ NH 3 2 Ị
f x 3 f x 4 f x 2 3 f x 2 Đ
Số nghiệm của phƣơng trình là:
3 f x 1 G THPT N.C.Đ A. 6 . B. 9 .
C. 7 . D. 8 . NG CÔN
Ờ Câu 28. Cho hàm số y f x liên tục trên và có đồ thị nhƣ hình vẽ dƣới đây. Tập hợp tất cả N Ễ
các giá trị thực của tham số m để phƣơng trình f 3 2 x x 2 3
2 m 3m có nghiệm Y TRƢ GU N
thuộc nửa khoảng 1; 3 là N ÁO VIÊ GI A. 1 ;
1 2;4 . B. 1; 2 4; . C. ;
1 2;4 . D. 1 ; 1 2;4 .
Câu 29. Cho hàm số y f x thỏa mãn f x 2 x 2 x
. Bất phƣơng trình f x m có
nghiệm thuộc khoảng 0 ;1 khi và chỉ khi
A. m f 1 .
B. m f 0 .
C. m f 0 .
D. m f 1 .
Câu 30. Cho cấp số cộng a , cấp số nhân b thoả mãn a a 0 , b b 1 và hàm số n n 2 1 2 1 f x 3
x 3x sao cho f a 2 f a và f log b 2 f log b . Tìm số nguyên 2 2 2 1 2 1
dƣơng n nhỏ nhất sao cho b 2019a n n A. 17. B. 14. C. 15. D. 16.
NGUYỄN CÔNG ĐỊNH | 100
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 31. Cho bất phƣơng trình 2
m 1 x 12 1 x 16x 3m 1 x 2m 15 . Có tất cả bao nhiêu
giá trị nguyên của tham số m 9 ;
9 để bất phƣơng trình có nghiệm đúng với mọi x 1 ; 1 ? A. 4 . B. 5 . C. 8 . D. 10 .
Câu 32. Tập hợp tất cả các giá trị của tham số m để phƣơng trình m m 1 1 sin x sin x có 1
nghiệm là đoạn a;b. Khi đó giá trị của biểu thức T 4a 2 bằng b A. 4 . B. 5 . C. 3 . D. 3 .
Câu 33. Có bao nhiêu giá trị nguyên của tham số m để phƣơng trình f f x m 3 3 ( )
x m có
nghiệm x 1;2 biết 5 3
f (x) x 3x 4m . A. 16. B. 15. C. 17. D. 18.
I Câu 34. Biết rằng tập hợp tất cả các giá trị thực của tham số m để bất phƣơng trình Ơ 4 2 4
x 1 x x 2mx 2m 0 đúng với mọi x là S ;
a b . Tính a 2 8b . M D A. 2 . B. 3. C. 6. D. 5. Ầ
a, ,b ,c d, e , a 0, b 0
Đ Câu 35. Biết rằng phƣơng trình 4 3 2
ax bx cx dx e 0 có 4 NHỊ
nghiệm thực phân biệt. Hỏi phƣơng trình sau có bao nhiêu nghiệm thực? Đ 2 3 2 2 4 3 2 G
4ax 3bx 2cx d 26ax 3bx c.ax bx cx dx e THPT 0 N.C.Đ NG A. 0 . B. 2 . C. 4 . D. 6 . CÔN Ờ N
Câu 36. Cho hàm số f x 3 2
x 4x x 4 có đồ thị nhƣ hình vẽ. Có tất cả bao nhiêu giá trị ỄY TRƢ
nguyên của m để phƣơng trình sau có bốn nghiệm thuộc đoạn 0;2 GU N 2 2 N
2019 f 15x 30x 16 m 15x 30x 16 m 0 ÁO VIÊ GI A. 4541. B. 4542 . C. 4543. D. 4540 .
Câu 37. Có bao nhiêu số nguyên x ( 1
00;100) thỏa mãn bất phƣơng trình 2 3 2019 2 3 2019 x x x x x x 1 x ... 1 x ... 1. 2! 3! 2019! 2! 3! 2019! A. 199 B. 0 C. 99 D. 198
Câu 38. Cho hàm số f x 3 3
7 3x 7 3x 2019x . Gọi S là tập hợp các giá trị nguyên của m
thỏa mãn điều kiện f 3 2
x x x m f 2 2 3
2x 2x 5 0, x 0 ;1 . Số phần tử của S là? A. 7 . B. 3 . C. 9 . D. 5 .
NGUYỄN CÔNG ĐỊNH | 101
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA I Ơ M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI
NGUYỄN CÔNG ĐỊNH | 102
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA HƢỚNG DẪN GIẢI Câu 1.
Cho hàm số y f (x) có bảng biến thiên nhƣ hình vẽ dƣới. Số nghiệm của phƣơng trình 2
f (x ) 4 là: x 0 4 y’ - 0 + 0 - y 5 1 A. 4 B. 6 C. 2 D. 8 Lời giải Chọn A
Ta thấy phƣơng trình f (x) 4 có 3 nghiệm phân biệt trong đó có 2 nghiệm dƣơng và I 1 nghiệm âm. Ơ Do đó phƣơng trình 2
f (x ) 4 có 4 nghiệm phân biệt.
M D Câu 2. Cho hàm số y f (x) có đạo hàm f x x 2 ' 3 x 1 2x , x . Hàm số Ầ Đ
g x f x 2
x 1 đồng biến trên khoảng nào trong các khoảng dƣới đây? NHỊ Đ A. ;1 . B. 1 ;0 . C. 1;2 . D. 3; . G THPT Lời giải N.C.Đ NG Chọn C CÔN Ờ N
Ta có: g ' x f ' x 2x . Ễ Y TRƢ x 3 GU N
g ' x 0
f 'x 2x 0 x 2 3 x 1 0 x 1 . N x 1 ÁO VIÊ
Ta có bảng biến thiên của hàm g x nhƣ sau: GI
Hàm số đồng biến trên các khoảng ;
1 và 1;3 . Suy ra hàm số đồng biến trên 1;2. Câu 3.
Cho hàm số f x đồng biến trên đoạn 3 ; 1 thỏa mãn f 3
1, f 0 2 , f 1 3 .
Mệnh đề nào dƣới đây đúng ? A. 1 f 2 2 . B. 2 f 2 3. C. f 2 1. D. f 2 3. Lời giải Chọn A
NGUYỄN CÔNG ĐỊNH | 103
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Do hàm số f x đồng biến trên đoạn 3 ; 1 và 3 2 0 nên f 3 f 2
f 01 f 2 2 . Câu 4. Cho hàm số y
f x có đạo hàm f x 2
x x
1 x 4.u x với mọi x
và u x 0
với mọi x . Hàm số 2 g x
f x đồng biến trên khoảng nào trong các khoảng sau đây? A. 1;2 . B. 1 ; 1 . C. 2 ; 1 . D. ; 2 . Lời giải Chọn C 2
Ta có g x x f 2
x x 2 x 2 x 2
x u 2 ' 2 . ' 2 . 1 4 . x . x 0
Thấy g ' x 0 x 1 . I x 2 Ơ
Bảng xét dấu g ' x nhƣ sau M D Ầ Đ NH Ị Đ
Do đó hàm số đồng biến trên khoảng 2; 1. G
THPT Câu 5. Cho hàm số y f x liên tục trên ( ;1
) và (1;)có bảng biến thiên nhƣ sau N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ
Số nghiệm thực của phƣơng trình 2 f (x) 1 0 là GI A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn B.
Ta có : f x f x 1 2 ( ) 1 0 . 2
Dựa vào bảng biến thiên thấy phƣơng trình có hai nghiệm. Câu 6. Cho hàm số y
f x . Hàm số y f
x có đồ thị nhƣ hình vẽ sau. Bất phƣơng trình 2 1 ex f x
m nghiệm đúng với mọi x 1;1 khi và chỉ khi
NGUYỄN CÔNG ĐỊNH | 104
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. m f 1 1. B. 2 m f 1 e . C. 2 m f 1 e . D. m f 1 1. Lời giải Chọn D 2 2 Ta có 1 ex f x
m đúng với mọi x 1;1 tƣơng đƣơng với 1 ex m f x 2 đúng với mọi x 1;1 . Xét 1 ex g x f x với x 1;1 . I 2 x x Ơ Ta có g x f 1 x 2 . x e f 1 x 2 e x . Nhận xét: M D 2 x Ầ +) Với 1 x 0 thì 1 1 x 2 nên f 1 x 0 và e x 0 suy ra g x 0 . Đ 2 NH x Ị +) Với 0 x
1 thì 0 1 x 1 nên f 1 x 0 và e x 0 suy ra g x 0 . Đ 2 x G x 0 1 x 1 e x 0 THPT +) Với thì nên f 1 x 0 và suy ra g x 0 . N.C.Đ NG Bảng biến thiên CÔN Ờ N Ễ Y TRƢ GU N N ÁO VIÊ GI 2 Để 1 ex m f x
nghiệm đúng với mọi x 1;1 suy ra m f 1 1.
Câu 7. Cho hàm số y f x . Hàm số y f x có bảng biến thiên nhƣ sau:
Bất phƣơng trình ex f x
m đúng với mọi x 1 ; 1 khi và chỉ khi:
A. m f 1 1 .
B. m f 1 e .
C. m f 1 e .
D. m f 1 1 . e e Lời giải Chọn D
NGUYỄN CÔNG ĐỊNH | 105
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Theo giả thiết ta có: ex m f x
g x, x 1 ; 1 * .
Xét hàm số g x trên 1 ;
1 ta có: ex g x f x . Ta có hàm số ex y đồng biến trên khoảng 1 ; 1 nên: x 1 1 e e 0, x 1
;1 . Mà f x 0, x 1 ; 1 . e
Từ đó suy ra ex g x f x 0, x 1 ;
1 . Nghĩa là hàm số y g x nghịch biến trên khoảng 1 ; 1 ** . Từ * và
** ta có: m g m f 1 1 1 . e Câu 8. Cho hàm số
y f x xác định trên và có đạo hàm
f ' x 1 x2 xsin x 2 2019 . Hàm số y f 1 x 2019x 2018 nghịch biến
trên khoảng nào dƣới đây ? A. 3; . B. 0;3 . C. ;3 . D. 1; . I Ơ Lời giải Chọn B M D
Xét hàm số y f 1 x 2019x 2018 xác định trên . Ầ Đ
y f 1 x 2019 NH Ta có Ị Đ 1
1 x.21 xsin
1 x 2 2019 2019 G THPT
x3 x sin 1 x 2 N.C.Đ . NG CÔN Ờ
Mặt khác sin 1 x 2 0 với mọi x . N Ễ x Y TRƢ
Do đó y 0 x 3 x 0 0 . x 3 GU N N
Dấu của y là dấu của biểu thức x 3 x . Ta có bảng biến thiên. ÁO VIÊ GI
Dựa vào bảng biến thiên ta thấy hàm số y f 1 x 2019x 2018 nghịch biến trên khoảng 0;3 .
Câu 9. Cho hàm số f x có đạo hàm xác định và liên tục trên thoả mãn f x .
x f x x x
1 x 2 , x
. Hàm số g x .x f x đồng biến trên khoảng nào? A. ;0 . B. 1;2 . C. 2; . D. 0; 2 .
NGUYỄN CÔNG ĐỊNH | 106
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Lời giải Chọn C
Ta có: g x . x f x f
x .xf x xx 1x 2 x 0
g x 0 x 1 . x 2 Bảng biến thiên: x 0 1 2 g x 0 0 0 g x
Từ bảng biến thiên ta thấy hàm số g x đồng biến trên khoảng 2; .
I Câu 10. Cho hàm số y f x có đồ thị là đƣờng cong Ơ
trong hình vẽ bên. Số nghiệm thực của phƣơng M D
trình f x 2019 1 là Ầ Đ A. 1. B. 2 . NHỊ C. 3 . D. 4 . Đ G THPT Lời giải N.C.Đ NG CÔN Ờ Chọn C N Ễ
Dựa vào đồ thị, ta có đƣờng thẳng y 1 cắt Y TRƢ
đồ thị tại ba điểm phân biệt , A B, C . GU N N Do đó
x 2019 xA ÁO VIÊ
f x 2019 1 x 2019 x B GI
x 2019 x C
x x 2019 A
x x 2019 B
x x 2019 C
Vậy số nghiệm thực của phƣơng trình f x 2019 1 là 3 .
Câu 11. Cho hàm số y f x có đồ thị nhƣ hình vẽ dƣới đây
Tìm tất cả các giá trị thực của tham số m để phƣơng trình f x log m có hai nghiệm 2 phân biệt.
NGUYỄN CÔNG ĐỊNH | 107
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA A. m 0.
B. 0 m 1; m 16 .
C. m 1; m 16 . D. m 4. Lời giải Chọn B
Số nghiệm của phƣơng trình f x log m chính là số giao điểm của đồ thị hàm số 2
y f x (hình vẽ) và đƣờng thẳng y log m. 2
Dựa vào hình vẽ ta có: phƣơng trình f x log m có hai nghiệm phân biệt khi và chỉ 2 khi log m 4 m 16 2 . log m 0 0 m 1 2
Câu 12. Cho hàm số y f x . Hàm số y f (
x) có bảng biến thiên nhƣ hình dƣới. Bất phƣơng trình .
x f x mx 1 nghiệm đúng với mọi x 1;2019 khi x ∞ 2 3 + ∞ I Ơ + ∞ 4 f'(x) M D Ầ ∞ Đ 0 NHỊ
A. m f 1 1.
B. m f 1 1. Đ G THPT
C. m f 1 2019 .
D. m f 1 2019 . 2019 N.C.Đ 2019 NG
Lời giải CÔN Ờ N Chọn B Ễ Y TRƢ Ta có .
x f x mx 1nghiệm đúng với mọi x 1;2019 GU N N 1 f x
m với mọi x1;2019 . x
Xét hàm số 1 h x f x
với mọi x 1;2019 . ÁO VIÊ x GI 1
Ta có h x f x . 2 x 1
Vì f x 0 với mọi x 1;2019 (dựa vào BBT) và
0 với mọi x1;2019 nên 2 x
h x 0 với mọi x 1;2019
hx đồng biến trên khoảng 1;2019
hx h
1 với mọi x 1;2019 .
Mà h x m với mọi x 1;2019 nên m h
1 m f 1 1 .
Câu 13. Cho hàm số y f x . Hàm số y f x có đồ thị nhƣ sau:
NGUYỄN CÔNG ĐỊNH | 108
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Bất phƣơng trình f x 2
x 2x m đúng với mọi x1;2 khi và chỉ khi
A. m f 2 .
B. m f 1 1.
C. m f 2 1 .
D. m f 1 1 . Lời giải Chọn A
Ta có f x 2
x 2x m, x
1;2 f x 2
x 2x m, x 1;2.
Xét hàm số g x f x 2
x 2x, x1;2
Ta có g x f x 2x 2 f x 2x 2
Vẽ đƣờng thẳng y 2x 2 I Ơ M D Ầ
Ta thấy f x 2x 2, x
1;2 do đó gx 0, x
1;2 suy ra hàm số g x nghịch Đ NH 1; 2 Ị biến trên khoảng . Đ
Vậy m g x, x
1;2 m g f 2 2
2 2 2.2 f 2 . G THPT N.C.Đ
Câu 14. Cho hàm số y
f x . Hàm số y
f x có bảng biến thiên nhƣ sau: NG CÔN Ờ N Ễ Y TRƢ GU N N Bất phƣơng trình 2 ( ) 3ex f x
m có nghiệm x 2 ;2 khi và chỉ khi: ÁO VIÊ GI A. m f 2 3 . B. m f 4 2 3e . C. m f 4 2 3e . D. m f 2 3. Lời giải Chọn B Ta có: x2 x2 f (x) 3e
m f (x) 3e m . Đặt h x x2 f x
hx f x x2 ( ) 3e 3e . Vì x 2
;2, f x 3 và x
x x2 e 4 2; 2 2 0; 4 3 3;3e
Nên h x f x x2 e x 4 3 0,
2; 2 f (2) 3e h x f ( 2 ) 3. Vậy bất phƣơng trình 2 ( ) 3ex f x
m có nghiệm x 2 ;2 khi và chỉ khi m f 4 2 3e .
Câu 15. Cho hàm số y f x có bảng xét dấu của đạo hàm nhƣ sau Bất phƣơng trình 2 x f x e
m đúng với mọi x 1 ; 1 khi và chỉ khi
NGUYỄN CÔNG ĐỊNH | 109
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
A. m f 0 1 .
B. m f 1 e .
C. m f 0 1.
D. m f 1 e . Lời giải Chọn C 2 Có x f x e , m x 1 ;1 2 x m g x
f x e , x 1 ;1 *
Ta có 2 2 . x g x f x
x e có nghiệm x 0 1 ; 1 và
g x 0, x 1
;0; gx 0, x 0; 1 . Bảng biến thiên: I Ơ
Do đó max g x g 0 f 0 1. M D 1 ; 1 Ầ Đ Ta đƣợc * m f 0 1. NHỊ
Câu 16. Có bao nhiêu số nguyên m để phƣơng trình log 2x m 2
2log x x 4x 2m 1 có 2 2 Đ G THPT
hai nghiệm thực phân biệt? N.C.Đ A. 2. B. 3. C. 1. D. 4. NG CÔN Ờ Lời giải N Ễ Chọn C Y TRƢ x 0 GU N Điều kiện: . N
2x m 0
Với điều kiện trên, phƣơng trình đã cho tƣơng đƣơng với phƣơng trình sau: ÁO VIÊ 2 2 log (2x )
m log x x 4x 2m 1 . 2 2 GI 2 2
log x x log 2x m 4x 2m 1. 2 2 2 2
log x x log (4x 2 )
m 4x 2m (1) . 2 2
Xét hàm số f (t) log t t trên D (0;) . 2 1
Ta có f '(t) 1 0 t
0 nên hàm số f (t) luôn đồng biến trên D . t ln 2
Suy ra phƣơng trình (1) tƣơng đƣơng với phƣơng trình: 2
x 4x 2m 2
x 4x 2m 0 (2) .
Yêu cầu bài toán tƣơng đƣơng với phƣơng trình (2) có hai nghiệm dƣơng phân biệt ' 0 4 2m 0 m 2
S 0 4 0 2 m 0. m 0 P 0 2 m 0
Vậy có duy nhất số nguyên m 1.
NGUYỄN CÔNG ĐỊNH | 110
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 3 2019 x x x 1 x ...
ex khi x 0
Câu 17. Cho hàm số f x 2! 3! 2019!
. Hỏi có bao nhiêu giá trị 2 x 10x khi x 0
nguyên dƣơng và chia hết cho 5 của tham số m để bất phƣơng trình m f x 0 có nghiệm? A. 25 . B. 0 . C. 6 . D. 5 . Lời giải. Chọn D x x x x
+) Với x 0 : f x 2 2018 1 x ...
ex ; f x 2 2017 1 x ... ex;... 2! 2018! 2! 2017! 2019 2018 1 ex f x 0, x 0 f x 2018 f 0 0, x 0 ;<
f x 0, x
0 f x f 0 0, x 0 . I Nên * m thì m
f x 0, x 0 . Ơ
Do đó bất phƣơng trình m f x 0 vô nghiệm trên 0; , * m . M D Ầ
+) Với x 0 : Bpt: 2 2 m x 10x 0 x 10x m . Đ Ta có bảng biến thiên NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ
Bất phƣơng trình có nghiệm m 2
5 m 25 m5;10;15;20;2 5 . GU N S m 2 019;2019 N
Câu 18. Gọi là tập tất cả các giá trị nguyên của tham số để bất phƣơng trình 3 m 3 x 3 m 2 x 3 m m 3 1 3 2 13 3
x 10 m m 0 đúng với mọi x 1; 3 . Số phần ÁO VIÊ
tử của tập S là GI A. 4038. B. 2021. C. 2022. D. 2020. Lời giải Chọn B 3 m 3 x 3 m 2 x 3 m m 3 1 3 2 13 3
x 10 m m 0, x 1;3 . x 3 2
x 2 m x 3 1 m x 1 , x 1; 3 . * Xét: f t 3
t t, t
, ta có f t 2
3t 1 0, t .
Hàm số f t luôn đồng biến trên . u x 2 Đặt . v m x 1
* f u f v u v x 2 m x 1 . x 2 ycbt m x x 2 5 ,
1;3 m Min m . x 1; 3 x 1 x 1 4
NGUYỄN CÔNG ĐỊNH | 111
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 5 m 20 19;2019 m 2 019; Mà nên 4 m 2 019; 2 018;..., 1 ;0 ;1 . m m
Vậy có 2021 giá trị cần tìm.
Câu 19. Cho hàm số y f x . Đồ thị hàm số y f x đƣợc cho nhƣ hình vẽ bên. Hàm số
g x f 4 2x
1 đồng biến trên khoảng nào sau đây? I 1 3 Ơ A. ; 1. B. ;1 . C. 1; .
D. 2; . 2 2 M D Lời giải Ầ Chọn B Đ NH Ị
Ta có g x f 4 x 3 x f 4 2 1 8 2x 1 0 Đ G THPT x 0 x 0 3 x 0 N.C.Đ 4 4 NG 2x 1 1 x 2 . 4 CÔN f ' 2x Ờ 1 0 4 4 N 2x 1 3 x 2 Ễ Y TRƢ
Dựa vào đồ thị hàm số f x và dấu của g x , ta có BBT nhƣ sau: GU N N ÁO VIÊ GI
g x đồng biến trên 4 ; 2 và 4 0; 2 . 1
Vậy g x đồng biến trên khoảng ;1 . 2 2019 3
Câu 20. Cho hàm số f x cos2x . Bất phƣơng trình f
x m đúng với mọi x ; 12 8 khi và chỉ khi A. 2019 m 2 . B. 2018 m . C. 2018 m 2 . D. 2019 m 2 . Lời giải. Chọn B
NGUYỄN CÔNG ĐỊNH | 112
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Ta có f x 2
sin 2x 2cos 2x
; f x 4
cos2x 2cos 2x 2 ;... 2 2 n 2019 2n f x cos 2x n . Do đó f x 2019 2019 2 cos 2x 2019 2 sin 2x . 2 2 3 3 1 3 x ; 2x ;
sin 2x sin , x ; 12 8 6 4 6 2 12 8 2019 f x 3 2018 2 , x ; . 12 8 2019 3
Do đó bất phƣơng trình f
x m đúng với mọi x ; khi và chỉ khi 12 8 2018 m 2 .
Câu 21. Cho hàm số y f (x) có đạo hàm đến cấp hai trên
. Bảng biến thiên của hàm số 1 I y
f '(x) nhƣ hình vẽ. Bất phƣơng trình 2 3 m x f (x)
x nghiệm đúng với mọi 3 Ơ
x 0;3 khi và chỉ khi M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N Ễ
A. m f 0 .
B. m f 3 .
C. m f 0 .
D. m f 2 1 . Y TRƢ 3 GU N Lời giải N Chọn C 1 1 2 3 ÁO VIÊ m x f (x) x 3 2 f (x) x x m . 3 3 GI 1
Đặt g x 3 2
f (x) x x . Theo bài ra, ta có: g x m, x 0;3(*). 3 Ta có 2 2 2
g '(x) f '(x) x 2x 1 x 2x (x 1) 0, x (0;3) .
Do đó g(0) g(x) g(3), x
(0;3) . Mà: g 0 f 0; g 3 f 3.
f (0) g(x) f (3), x (0;3)
Vì vậy (*) m f (0) .
Câu 22. Tìm tất cả các giá trị thực của tham số m để phƣơng trình 2 x x
mx 2 5 12 16 2
x 2 có hai nghiệm thực phân biệt thoả mãn
NGUYỄN CÔNG ĐỊNH | 113
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 x x 1 2 x 1 2018 2018 2019x 2019 . 11 3
A. m 2 6 ; .
B. m 2 6 ;3 3 . 3 11 3
C. m 2 6 ;3 3 . D. m 3 3 ; 2 6 . 3 Lời giải Chọn B Xét bất phƣơng trình 2x x 1 2 x 1 2018 2018 2019x 2019
(1) . Điều kiện: x 1 .
a 2x x 1 a b Đặt
a b 2(x 1) x 1 . 2 b 2 x 1
Bất phƣơng trình (1) thành: a b I
2018a 2018b 2019
0 2(2018)a 2019a 2(2018)b 2019b (2) . Ơ 2
Xét hàm số ( ) 2(2018)t f t
2019t liên tục trên . M D t Ầ f (
t) 2.2018 ln 2018 2019 0, t
nên f (t) đồng biến trên . Đ NH
Bất phƣơng trình (2) f (a) f ( )
b a b 2x x 1 2 x 1 1 x 1 . Ị Đ Với 1
x 1, ta có: G THPT 2 x x
mx 2 5 12 16 2 x 2 N.C.Đ NG CÔN 2 Ờ x x 2 2 2 2 2 N
3x 2 2x 2 mx 2 x 2 3 2 m (3) . 2 Ễ x x 2 2 Y TRƢ x 2 GU N Đặt t với x 1; 1 . 2 N x 2 2 2x 1 t 0, x 1
;1 nên hàm t đồng biến trên 1 ; 1 , suy ra t 3 . 3 ÁO VIÊ 2x 2 3 GI 1
Do hàm t đơn điệu trên 1 ;
1 nên ứng với mỗi giá trị của t ; 3 ta tìm đƣợc 3
đúng một giá trị của x 1 ; 1 và ngƣợc lại.
Viết lại phƣơng trình (3) theo ẩn t : 2 1 3t m 4 với t 3 . t 3
(3) có 2 nghiệm thực phân biệt x 1 ;
1 (4) có 2 nghiệm thực phân biệt 1 t ; 3 (*) . 3 2 1
Xét hàm số g(t) 3t liên tục trên ; 3 . t 3 2 2 2 1 g ( t) 3 . Cho 2 g (
t) 0 t t ; 3 . 2 t 3 3 3 Bảng biến thiên:
NGUYỄN CÔNG ĐỊNH | 114
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Dựa vào bảng biến thiên, ta có (*) m 2 6 ;3 3
Vậy m 2 6 ;3 3 thoả yêu cầu bài toán. x 1
Câu 23. Có bao nhiêu số nguyên m để phƣơng trình 1 2 2
8 x m có 3 nghiệm thực phân 2 I biệt? Ơ A. 8 . B. 9 . C. 6 . D. 7 . M D Lời giải Ầ Chọn A Đ NH x 1 Ị
Phƣơng trình đã cho tƣơng đƣơng với: 1 2 m 2 8 x (*). Đ 2 G THPT Xét hàm số: N.C.Đ NG x 1 1 2 CÔN 2
8 x (x 2) Ờ x 1 g x x x x 1 ( ) 2 ln 2 ( 2) 2 N 1 2 f (x) 2 8 x
f (x) . Ễ x 1 2 x 1 1 2 h(x) 2 ln 2 x (x 2) Y TRƢ 8 2 x (x 2) 2 GU N N
(Hàm số không có đạo hàm tại điểm x = 2). Ta có: x ÁO VIÊ 1 2 2 1 2 3 g (
x) 2 ln 2 1 2 ln 2 1 0, x 2 g( )
x g(2) 2 ln 2 0, x 2 (1). GI h( 1 ) ln 2 1 0 x 1 2 h ( x) 2 ln 2 1 0, x 2 và h(0).h( 1
) 0 do đó h(x) 0 h(0) 2 ln 2 0
có nghiệm duy nhất x ( 1
;0). Dùng máy tính tìm đƣợc x 0 ,797563 lƣu nghiệm 0 0
này vào biến nhớ A, ta có f x f ( ) A 6,53131. 0 Vậy ta có f (
x) 0 x x ( 1
;0). Bảng biến thiên: 0
Từ bảng biến thiên suy ra phƣơng trình có 3 nghiệm thực phân biệt khi và chỉ khi: 2
m f (x ) 6,53131. 0
NGUYỄN CÔNG ĐỊNH | 115
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Do m là số nguyên nên m 1 ,0,1,2,3,4,5, 6 .
Có tất cả 8 số nguyên thoả mãn yêu cầu.
Câu 24. Cho bất phƣơng trình 3 4 2 3 2 2
x x m
x x 2 2 1 x
1 1 m . Tìm tất cả các giá trị
thực của tham số m để bất phƣơng trình nghiệm đúng với mọi x 1 . 1 A. m . B. m 1 1. C. m . D. m 1. 2 2 Lời giải Chọn D Ta có: 3 4 2 3 2 2
x x m
x x 2 2 1 x 1 1 m 4 2
x x m 3 4 2 3 2
x x m x 2 2 1 2x 1 0 4 2
x x m 3 4 2 3 2
x x m x 2 2 1 2x 1 (1) I Xét hàm số 3
f t t t , t . Ơ Có f t 2
3t 1 0, t
nên hàm số f t đồng biến trên . M D 3 4 2 3 2 3 4 2 3 2 Ầ
Bất phƣơng trình (1) có dạng f x x m f 2x 1 x x m 2x 1 Đ NH 4 2 2 4 2 Ị
x x m 2x 1 m x x 1. Đ
Xét hàm số g x 4 2
x x 1 với x1; . G THPT N.C.Đ
Bất phƣơng trình đã cho nghiệm đúng với mọi x 1 m g x , x 1. NG CÔN Ờ 3 2 N g x 4x 2x 2x 2x 1 0, x 1. Ễ Y TRƢ Bảng biến thiên: GU N N ÁO VIÊ GI
Tập giá trị của hàm số g x trên 1; là ;1 .
Vậy m g x , x 1 m 1 . f 12x 1
Câu 25. Cho hàm số y f x . Đồ thị y f x nhƣ hình bên. Hàm số g x nghịch 2
biến trên khoảng nào trong các khoảng sau? A. 0 ;1 . B. ;0 . C. 1 ;0 . D. 1; .
NGUYỄN CÔNG ĐỊNH | 116
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA Lời giải Chọn D x
Từ đồ thị hàm số y f x ta có f x 1 0 . 1 x 2 f 12x 1 I
Xét hàm số g x . Ơ 2 f 12x f 12 x 1 1 1 M D
Ta có g x . 2
. f 1 2x.ln 2ln 2. . f 12x. Ầ 2 2 2 Đ NH x 1 Ị 1 2x 1 Đ
g x 0 f 1 2x 0 1 . 1 1 2x 2 x 0 G THPT 2 N.C.Đ NG
Vậy hàm số g x nghịch biến trên khoảng 1; . Chọn D. CÔN Ờ N
Câu 26. Cho hàm số f x liên tục trên
có đồ thị nhƣ hình vẽ. Có bao nhiêu giá trị nguyên của ỄY TRƢ
n để phƣơng trình sau có nghiệm x . f 2 16
sin x 6sin 2x 8 f nn 1 GU N N ÁO VIÊ GI A. 10. B. 6. C. 4. D. 8. Lời giải Chọn B
Nhìn vào đồ thị ta thấy hàm số f x luôn đồng biến trên , do đó f 2 x
x f nn 2 16 sin 6 sin 2 8 1 16
sin x 6sin 2x 8 nn 1 Ta xét 2 1
6sin x 6sin 2x 8 nn 1 8
1 cos 2x 6sin 2x 8 nn 1 0
8cos 2x 6sin 2x nn 1 0
NGUYỄN CÔNG ĐỊNH | 117
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Để phƣơng trình có nghiệm x thì
n n2 n n2 2 2 2 2 2 8 6 100 1
0 n n 10 1 41 1 41 2
n n 10 n (do 2 n n 1 0, n ). 2 2
Vì n nguyên nên n 3 ; 2 ; 1 ;0;1; 2 .
Câu 27 Cho hàm số y f x liên tục trên R và có đồ thị nhƣ hình vẽ dƣới đây . I 3 f x 2
3 f x 4 f x 2 Ơ
Số nghiệm của phƣơng trình
3 f x là: f x 2 3 1 M D A. 6 . B. 9 .
C. 7 . D. 8 . Ầ Đ Lời giải NHỊ Chọn B Đ G THPT
Đặt t f x đƣa phƣơng trình về hàm đặc trƣng t t t 3 3 1 1 3 1 3t 1 . N.C.Đ NG CÔN
Xét hàm đặc trƣng 3
f x x x đồng biến R nên ta đƣợc t 1 3t 1 t 0;t 1. Ờ N Ễ
Với t 0 ta có f x 0 từ đồ thị ta đƣợc số nghiệm là 3 . Y
TRƢ Với t 1 ta có f x 1 từ đồ thị ta đƣợc số nghiệm là 6 . GU N N
Vậy phƣơng trình có 9 nghiệm phân biệt.
Câu 28. Cho hàm số y f x liên tục trên và có đồ thị nhƣ hình vẽ dƣới đây. Tập hợp tất cả ÁO VIÊ
các giá trị thực của tham số m để phƣơng trình f 3 2 x x 2 3
2 m 3m có nghiệm GI
thuộc nửa khoảng 1; 3 là A. 1 ; 1 2;4 .
B. 1; 2 4; . C. ; 1 2;4 . D. 1 ; 1 2;4 . Lời giải Chọn D Đặt 3 2 2
t x 3x 2 t 3x 6x .
NGUYỄN CÔNG ĐỊNH | 118
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA x 01;3 t 0 . x 2 1;3 Ta có: t(2) 2
; t(1) 0; t(3) 2 t 2 ;2 . Khi đó f 3 2 x x 2 3
2 m 3m (1) trở thành: f t 2 m 3m (2) Phƣơng trình
1 có nghiệm thuộc 1; 3 khi phƣơng trình 2 có nghiệm t 2 ;2 . 1 m 4 2
m 3m 4 0 1 m 1 Dựa vào đồ thị ta có 2 2
m 3m 4 m 1 . 2
m 3m 2 0 2 m 4 m 2 Vậy phƣơng trình
1 có nghiệm thuộc 1; 3 khi m 1 ; 1 2;4 .
Câu 29. Cho hàm số y f x thỏa mãn f x 2 x 2 x
. Bất phƣơng trình f x m có
nghiệm thuộc khoảng 0 ;1 khi và chỉ khi I
A. m f 1 .
B. m f 0 .
C. m f 0 .
D. m f 1 . Ơ Lời giải M D Chọn D Ầ Đ f x 2
x 2 0 x
Hàm số nghịch biến trên nên f (0) f (1) NHỊ Đ Bảng biến thiên G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N
Từ bảng biến thiên ta có bất phƣơng trình f x m có nghiệm thuộc khoảng 0 ;1 m f ÁO VIÊ 1 .
GI Câu 30. Cho cấp số cộng a , cấp số nhân b thoả mãn a a 0 , b b 1 và hàm số n n 2 1 2 1 f x 3
x 3x sao cho f a 2 f a và f log b 2 f log b . Tìm số nguyên 2 2 2 1 2 1
dƣơng n nhỏ nhất sao cho b 2019a n n A. 17. B. 14. C. 15. D. 16. Lời giải Chọn D
Xét hàm số f x 3
x 3x với x [0, ) . Ta có f x 2
3x 3 0 x 1 từ đó ta suy
ra bảng biến thiên của f x trên [0, ) nhƣ sau: x 0 1 f x - 0 +
f x 0 2
Vì a 0 nên f a 2
f a f a 2 0 (1) 2 1 2 2
NGUYỄN CÔNG ĐỊNH | 119
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Giả sử a 1, vì f x đồng biến trên [1, ) nên f a f a suy ra f a 2 f a 1 1 2 1 1
vô lý. Vậy a [0,1) do đó f a 0 (2). 1 1 f a 0 a 0 1 Từ (1) và (2) ta có: 0 f a 1 a 1 2 1
Vậy số hạng tổng quát của dãy cấp số cộng a là a n . n 1 n
Một cách tƣơng tự, đặt t log b và t log b suy ra f t 2 f t , vì 1 b b nên 2 1 1 2 1 2 2 2 1 2 0 t t , 1 2
theo lập luận trên ta có: t 0 log b 0 b 1 1 2 1 1 t 1 log b 1 b 2 2 2 2 2
Vậy số hạng tổng quát của dãy cấp số nhân b là 1 b 2n . n n I Do đó n 1 b 2019a 2
2019 n (*). Trong 4 đáp án n 16 là số nguyên dƣơng n n 1 Ơ nhỏ nhất thỏa (*). M D
Ầ Câu 31. Cho bất phƣơng trình 2
m 1 x 12 1 x 16x 3m 1 x 2m 15 . Có tất cả bao nhiêu Đ
giá trị nguyên của tham số m 9 ;
9 để bất phƣơng trình có nghiệm đúng với mọi NHỊ Đ x 1 ; 1 ? G THPT A. 4 . B. 5 . N.C.Đ C. 8 . D. 10 . NG Lời giải CÔN Ờ N Chọn B Ễ Y TRƢ Bpt: 2
m 1 x 12 1 x 16x 3m 1 x 2m 15 GU N 2 N
m 1 x 3 1 x 2 28x6 1 x 15 (1).
Đặt t 1 x 3 1 x với x 1 ; 1 . ÁO VIÊ 1 3 GI t 0 x 1 ;1 . 2 1 x 2 1 x
Suy ra t nghịch biến trên 1 ; 1 . Nên t
1 t t 1 3 2 t 2 . Ta có 2 2
t 8x 10 6 1 x 2 t 2 2 5
2 8x 6 1 x 15.
Khi đó (1) trở thành: mt 2
2 2t 5 với t 3 2 ; 2 . 2 2t 5 m t (vì t 3 2 ; 2
nên t 2 0 ). t (2) với 3 2 ; 2 2 t
Xét hàm số f t 2 2 5 . t trên đoạn 3 2 ; 2 2
4t t 2 2 2t 5 f t 2 2t 8t 5 . t 22 t 22
NGUYỄN CÔNG ĐỊNH | 120
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 4 6 t (loại) 2
f t 0 4 6 t 2 (thỏa mãn) 62 93 2 2 2 4 6 f ( 3 2) 4 ,97 ; f ( 2) 1,7 ; f 8 2 6 3,1 14 2 2
(1) nghiệm đúng với mọi x 1 ;
1 (2) nghiệm đúng với mọi t 3 2 ; 2 m
f t f 62 93 2 min 3 2 4 ,97 . 3 2; 2 14 m
Kết hợp với điều kiện bài toán ta có: m 9 ;9 m 9 ;8; 7;6; 5 . I 62 93 2 Ơ m 4, 97 14 M D
Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán. Ầ
Đ Câu 32. Tập hợp tất cả các giá trị của tham số m để phƣơng trình m m 1 1 sin x sin x có NHỊ 1 Đ
nghiệm là đoạn a;b. Khi đó giá trị của biểu thức T 4a 2 bằng b G THPT A. 4 . B. 5 . N.C.Đ C. 3 . D. 3 . NG Lời giải CÔN Ờ N Chọn A Ễ Y TRƢ Ta có 1
sin x 1 0 1 sin x 2 0 1 sin x 2, x . GU N
Đặt t 1 sin x . Ta có 0 t 2 và 2
sin x t 1. N
Khi đó phƣơng trình có dạng: 2 2
m m 1 t t 1 m 1 t m 1 t t t * . ÁO VIÊ
Xét hàm số f t 2
t t, t 0 . GI
Ta có f t 2t 1 0, t 0 . Do đó hàm số 2
f t t t luôn đồng biến trên 0; . Vì thế 2
* t m 1 t m t t 1 **
Xét hàm số g t 2
t t 1, t 0; 2 .
gt 2t 1. gt 1
0 2t 1 0 t . 2
Bảng biến thiên của hàm số g t 2
t t 1, t 0; 2
NGUYỄN CÔNG ĐỊNH | 121
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 5
Phƣơng trình đề bài có nghiệm
** có nghiệm t 0; 2 m 1 2 . 4 5 5 Vậy m ;1 2
nên a ;b 1 2 T 4 . 4 4 I
Ơ Câu 33. Có bao nhiêu giá trị nguyên của tham số m để phƣơng trình f f x m 3 3 ( )
x m có M D
nghiệm x 1;2 biết 5 3 f (x) x 3x 4m . Ầ Đ A. 16. B. 15. C. 17. D. 18. NHỊ Lời giải Đ Chọn A G THPT Đặt 3 3 t
f (x) m t f (x) m . Ta đ N ƣ .C ợ .Đ c hệ phƣơng trình sau: NG 3 3 3 3 CÔN Ờ
f (t) x m
f (t) x m
f (t) t f (x) x (*) N . 3 3 Ễ
t f (x) m
f (x) t m f (x) t m Y TRƢ Vì 5 3 4 2
f (x) x 3x 4 ,
m f '(x) 5x 9x 0, x nên hàm số 3
h(x) f (x) x đồng GU N N biến trên
. Do đó: (*) x t . 1 2 Khi đó ta đƣợc: 3 5 3 5 3 5 3
f (x) x m x 3x 4m x 2x 3m g(x) x x m(**) ÁO VIÊ 3 3 GI . 1 2 Dễ thấy 5 3 g( x) x
x đồng biến trên 1;2 nên phƣơng trình (**) có nghiệm trên 3 3
đoạn 1;2 khi và chỉ khi: g(1) m g(2) 1 m 16.
Vì m thuộc số nguyên nên có 16 số thỏa mãn bài toán.
Câu 34. Biết rằng tập hợp tất cả các giá trị thực của tham số m để bất phƣơng trình 4 2 4
x 1 x x 2mx 2m 0 đúng với mọi x là S ;
a b . Tính a 2 8b . A. 2 . B. 3. C. 6. D. 5. Lời giải Chọn A Xét bất phƣơng trình: 4 2 4
x 1 x x 2mx 2m 0 * * xác định khi 4
2mx 2m 0 m 4 2 x
1 0 2m 0 m 0 .
NGUYỄN CÔNG ĐỊNH | 122
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 1 3 4 2 2
x 1 x x 0 Xét x 0 : 2 4 * luôn đúng. 4
x 2mx 2m 0 Xét x 0 : 4 x x 1
* trở thành: 2m . 4 1 x x x 4 1 x Đặt t , t
; t 0 x 1 4 x 1 x 3 4 1 BBT I Ơ M D Ầ Đ NHỊ 2 Đ t ; 0 . 2 G THPT N.C.Đ NG
* trở thành: 2m f t với 1 f t t CÔN Ờ t N Ễ 1 2 Y
f t 1 0 , t ; 0 TRƢ 2 t 2 GU N N 2 2 1
Yêu cầu bài toán 2m Min f t 2m f 2m m . 2 2 2 4 ;0 2 ÁO VIÊ GI 1 1 Do đó m 0;
a 0,b . 4 4
Vậy a 2 8b 2 .
Câu 35. Biết rằng phƣơng trình 4 3 2
ax bx cx dx e 0 a, , b ,
c d, e , a 0, b 0 có 4
nghiệm thực phân biệt. Hỏi phƣơng trình sau có bao nhiêu nghiệm thực?
ax bx cx d2 3 2 2
ax bx c 4 3 2 4 3 2 2 6 3
. ax bx cx dx e 0 A. 0 . B. 2 . C. 4 . D. 6 . Lời giải Chọn A
Gọi các hoành độ giao điểm của đồ thị hàm số y f x và trục hoành là x , x , x , x . 1 2 3 4
Suy ra: f x a x x x x x x x x . 1 2 3 4
f x a x x x x x x a x x x x x x 2 3 4 1 3 4
a x x x x x x a x x x x x x . 1 2 4 1 2 3
NGUYỄN CÔNG ĐỊNH | 123
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA 2 2
Ta có: g x f
x f
x . f x f
x 0, x i i i i i . i
g x 0 không có nghiệm x . i 1 1 1 1 1
Xét x x , ta có f x f x f x 4 . . i x x x x x x x x x x 1 2 3 4 i 1 i f x 4 1 f x 4 1 . f x x x f x x x i 1 i i 1 i
f x. f x f x 2 4 1 2 hay f
x f
x. f x 0, x x . i f x 0, x 2 i x xi2 1
Vậy trong mọi trƣờng hợp phƣơng trình g x 0 đểu vô nghiệm.
Câu 36. Cho hàm số f x 3 2
x 4x x 4 có đồ thị nhƣ hình vẽ. Có tất cả bao nhiêu giá trị I
nguyên của m để phƣơng trình sau có bốn nghiệm thuộc đoạn 0;2 Ơ f 2 x x 2 2019 15 30
16 m 15x 30x 16 m 0 M D Ầ Đ NHỊ Đ G THPT N.C.Đ NG CÔN Ờ N A. 4541. B. 4542 . C. 4543. D. 4540 . Ễ Y TRƢ Lời giải GU N Chọn B N ÁO VIÊ GI 15x 15
Đặt t x 2
15x 30x 16 tx
, t x 0 x 1. 2
15x 30x 16 Ta có bảng biến thiên
NGUYỄN CÔNG ĐỊNH | 124
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Vậy 1 t x 4 và mỗi t x1;4, tồn tại hai giá trị của x 0;2 Phƣơng trình trở thành: 3 2
t t t 3 2 2019 4
4 mt m 0 2019(t 4t t 4) t 1 m 3 2
t 4t t 4 m m Hay 2
t 5t 4
(*) (vì t 1 0 ). Phƣơng trình đã cho có 4 t 1 2109 2019
nghiệm khi và chỉ khi phƣơng trình (*) có 2 nghiệm phân biệt t (1; 4] 9 m Xét hàm 2
g(t) t 5t 4 trên 1;4 ta đƣợc
0 4542,75 m 0 . 4 2019
Vì m Z nên có 4542 giá trị thỏa mãn.
Câu 37. Có bao nhiêu số nguyên x ( 1
00;100) thỏa mãn bất phƣơng trình 2 3 2019 2 3 2019 x x x x x x 1 x ... 1 x ... 1. 2! 3! 2019! 2! 3! 2019! I A. 199 B. 0 C. 99 D. 198 Ơ Lời giải M D Chọn D Ầ Đặt Đ NH 2 3 2019 2 3 2018 2019 Ị x x x x x x x
u(x) 1 x ...
u '(x) 1 x ... u(x) Đ 2! 3! 2019! 2! 3! 2018! 2019! G THPT 2 3 2019 2 3 2018 2019 x x x x x x x
v(x) 1 x ... v '(xN ) .C .Đ 1 x ... v(x) NG 2! 3! 2019! 2! 3! 2018! 2019! CÔN Ờ N
Và đặt f x u x.v x . Ta có Ễ Y TRƢ 2019 2019 x x f x u (
x)v(x) v '(x)u(x) u(x)
v(x) v(x) u(x) GU N 2019! 2019! N 2019 x
u(x) v(x) 2019! ÁO VIÊ 2 4 2018 GI x x x
Nhận xét: u(x) v(x) 21 0, x nên suy ra 2! 4! 2018! 2019 x Suy ra 2019
f '(x) 0
(u(x) v(x)) 0 x
0 x 0. Do đó, ta có bảng biến 2019!
thiên của hàm số y f (x) là
Từ bảng biến thiên suy ra f (x) 1 x 0 x 9 9,..., 1 ,1,...,9 9 . Có tất cả 198 số nguyên thoả mãn.
NGUYỄN CÔNG ĐỊNH | 125
CHINH PHỤC ĐIỂM 8 – 9 – 10 KÌ THI THPT QUỐC GIA
Câu 38. Cho hàm số f x 3 3
7 3x 7 3x 2019x . Gọi S là tập hợp các giá trị nguyên của m
thỏa mãn điều kiện f 3 2
x x x m f 2 2 3
2x 2x 5 0, x 0 ;1 . Số phần tử của S là? A. 7 . B. 3 . C. 9 . D. 5 . Lời giải Chọn C Vì f x 3 3
7 3x 7 3x 2019x là hàm số lẻ và đồng biến trên nên ta có f 3 2
x x x m f 2 2 3
2x 2x 5 f 3 2
x x x m f 2 2 3
2x 2x 5 3 2 2
x 2x 3x m 2x 2x 5 3 2 2
x 2x 3x m 2x 2x 5 I 3 2 2 Ơ
x 2x 3x m 2
x 2x 5 3 2
x 4x 5x 5 m M D 3 Ầ
x x 5 m Đ NH Xét g x 3 2
x 4x 5x 5 và hx 3
x x 5trên 0
;1 có bảng biến thiên là Ị Đ G THPT N.C.Đ NG CÔN Ờ N Ễ Y TRƢ GU N N
Từ bảng biến thiên suy ra f 3 2
x x x m f 2 2 3
2x 2x 5 0, x 0 ;1 khi và chỉ ÁO VIÊ khi GI m 3 3 m 5 m 5
NGUYỄN CÔNG ĐỊNH | 126




