Bảng tham chiếu - Tài liệu hỗ trợ biến đổi Fourier và Laplace môn Tín hiệu và hệ thống | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616
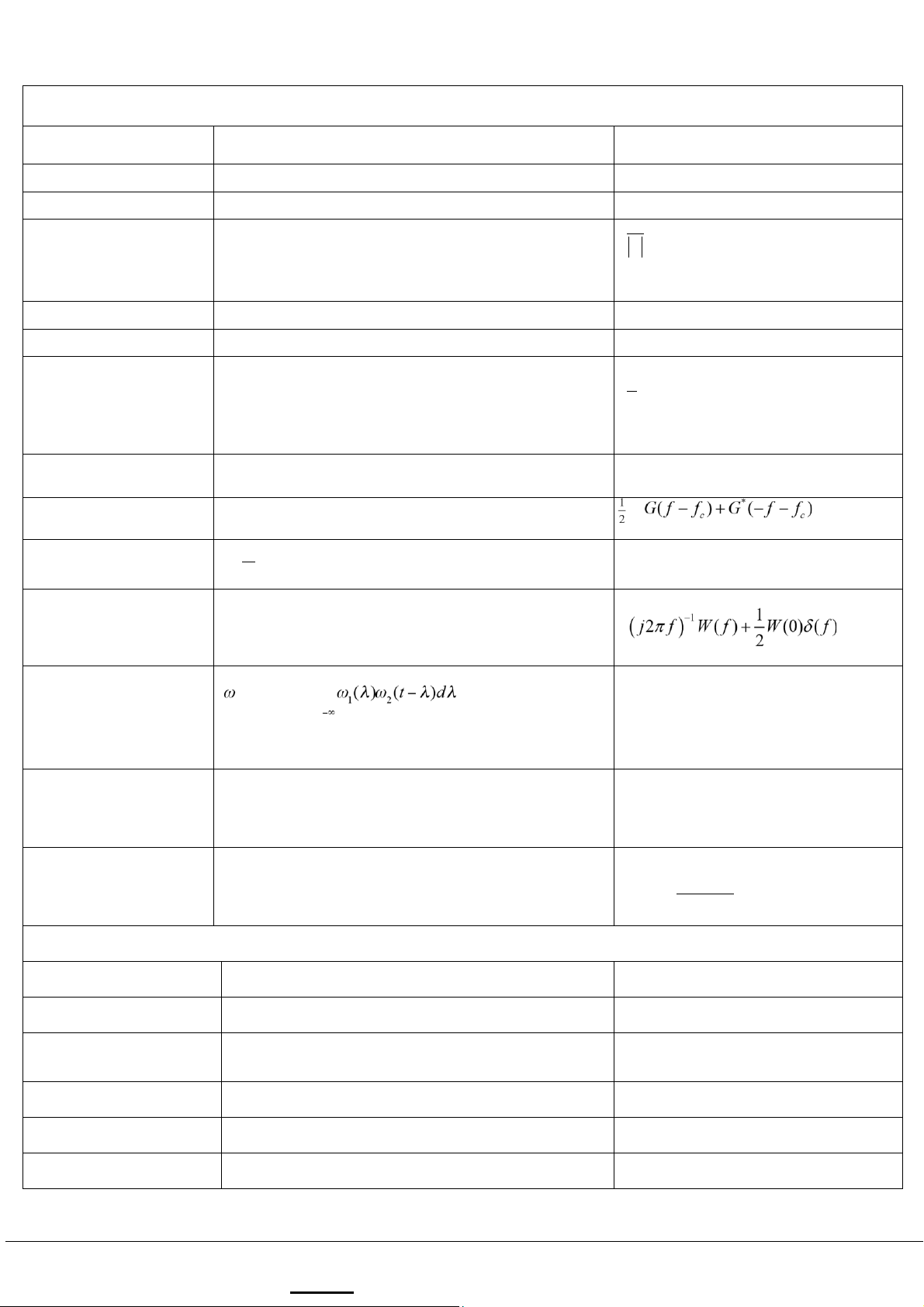
Các tính chất của biến đổi Fourier thời gian liên tục Operation Function Fourier transform Linearity
a1 1w w( )t + a2 2( )t
aW f1 1( )+a W2 2( )f Time delay w(t -Td)
W f e( ) - j Twd 1 W æ öç Scale change w( )at ÷af a è ø Conjugation w*( )t W*(-f ) Duality W t( ) w(-f ) Real signal frequency 1 translation
[w( )t w w q( )t cos(
ée W fjq ( - fc )+e- jqW f( + fc ct + ) isreal] )ûù 2ë Complex signal w frequency translation ( )t e jwct W f( - fc) Band-pass signal Re{g t e( ) } jwct éë ùû dnw( )t Differentiation
( j2pf )nW f( ) dt n t Integration òwll( )d -¥ ∞ (t)∗ω (t)= Convolution W f W 1 2 1( ) 2( )f ∫ ¥ Multiplicationb w w1( )t2( )t
W f1( )*W2( )f = òW1( )lW2( f -ll)d -¥ n Multiplication tnw( )t (- j2p)-n d W f( )n df
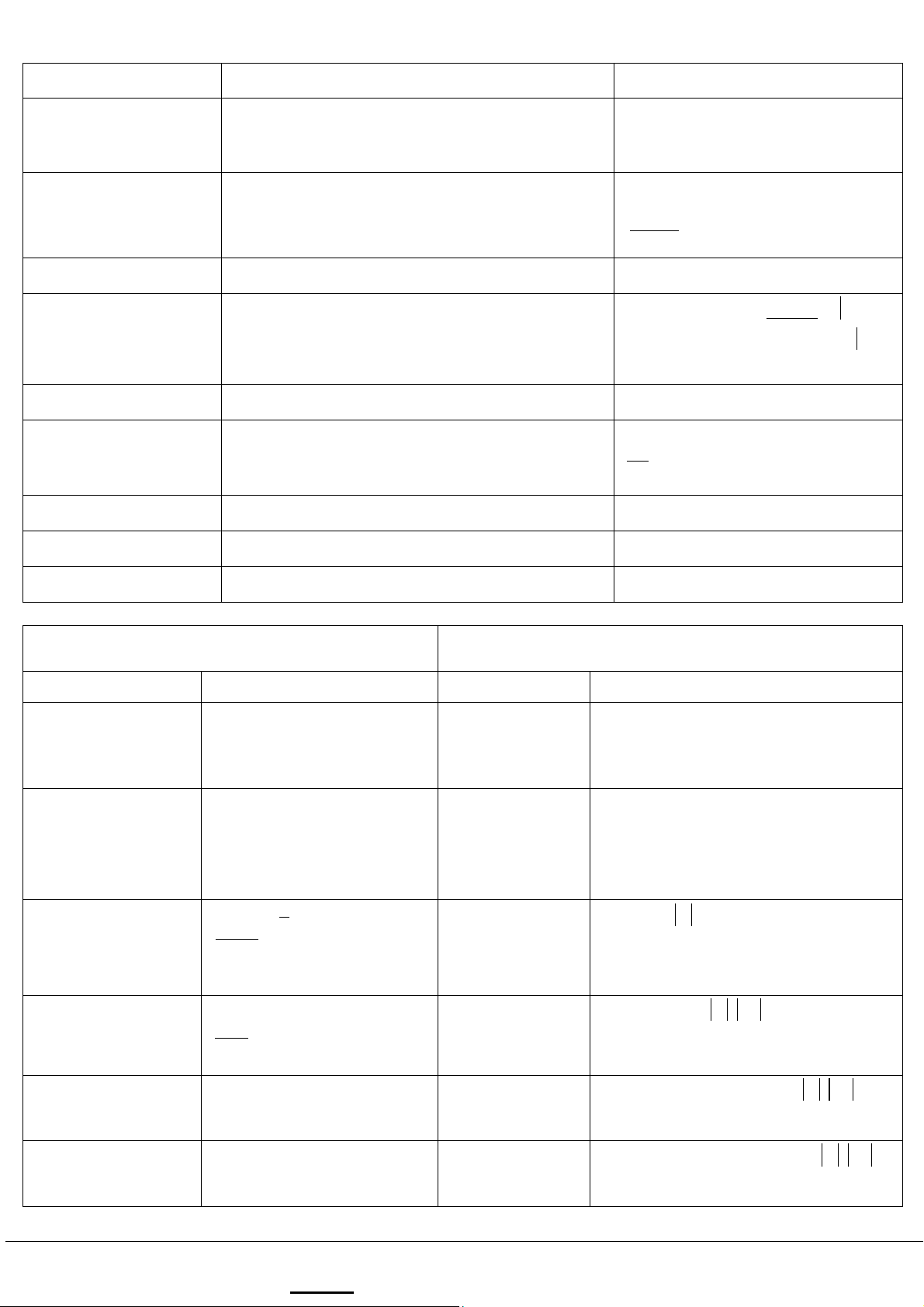
Các tính chất của biến đổi Fourier thời gian rời rạc Property Sequence Fourier Transform Periodicity x n[ ] X(W+2 )p=X( )W Linearity ax n a x n1 1[ ]+ 2
aX1 1( )W +a X2 2( )W 2[ ] Time shifting x n n[ - 0]
e- j nW 0 X( )W Frequency shifting ejW0nxn[ ] X(W-W0) Conjugation x n*[ ] X*(-W)
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào. lOMoAR cPSD| 59031616 Time reversal x n[- ] X(-W) Time scaling
ìx n m[ / ] if n = km X m( W)
x( )m [ ]n =í if n ¹ km î0 dX( )W j
Frequency differentiation nxn[ ] dW First difference xn xn[ ]- -[ 1]
(1-e- jW) ( )X W ¥ p dX ( ) ( )0 W + Accumulation å x k[ ] 1 W£p - jW X ( )W 1- k=-¥ e Convolution x n x n1[ ]* 2[ ] X1( )W WX2( ) 1 Multiplication x n x n1[ ] [ ]2 X ( )WÄ WX ( ) 2p 1 2 Real sequence
xn x n x n[ ]= e[ ]+ o[ ]
X( )W = A( )W + jB( )W Even component x ne[ ]
Re[ ( )]X W =A( )W Odd component x no[ ]
jIm[ ( )]X W = jB( )W
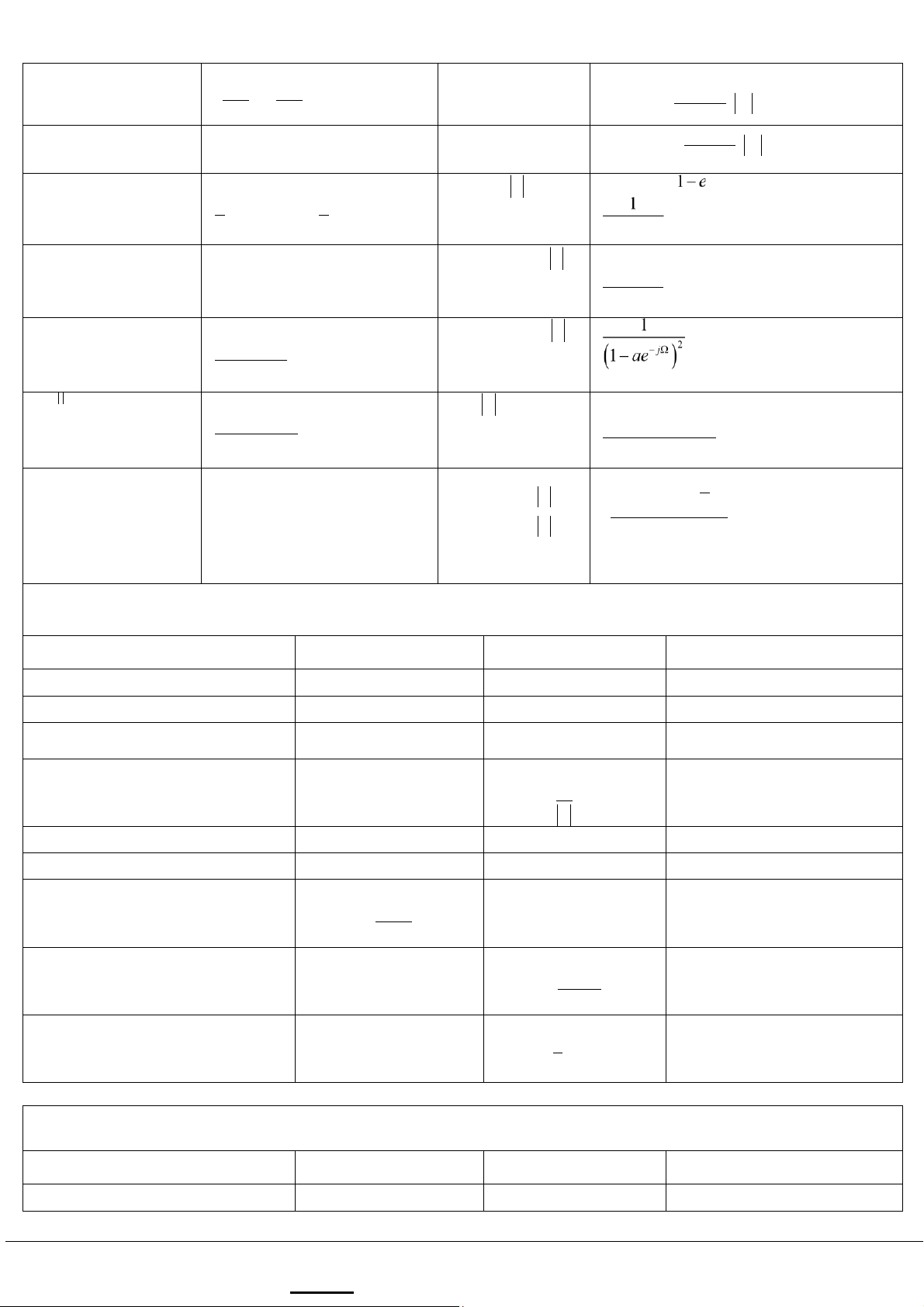
Các cặp biến đổi Fourier thời gian liên tục
Các cặp biến đổi Fourier thời gian rời rạc
Time Waveformw( )t Spectrum W(f) x n[ ] X( )W Pæ öç ] d[ ]n 1 ÷Tt T Sa[(pft) è ø Ùæ d T Sa[ (pft)]2 (n n- 0) e- j nW 0 öç ÷Tt è ø ì+ >1, t 1 1 d( )f + xn[ ] 1= 2pd( )W W£,p 0 u t( )=í < 0 2 j2pf î0, t ì+ >1, t 0 1 e jW0n 2pd(W-W W W £ ) p 0 , , 0
sgn( )t =í-1, t < 0 î jpf 1 d( )f cosW0n pd[ (W-W )+d(W+W W W £ ) 0 0 ], , p 0 d(t -to)
e- j2pft0 sinW0n
-jpd[ (W-W - W ) d( +W W W £ ) 0 0 ], , p 0
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào. lOMoAR cPSD| 59031616 Sa(2pWt) 1 æ f ö u n[ ] 2W Pçè2W ø÷
pd( )W + 1- jW , W£p 1-e e j(w j0t+ )
ejjd(f - f0) - - -u n[1] -pd( )W + 1- jW , W£p cos(w jct + ) a un an [ ],<1
1e jj( f - fc )+ 1e- jj( f + fc ) 2 2 1-ae- jW e-p(t t/ )2 1 0 t e0 -p( ft0)2 -au nn [- -1], a >1 1-ae- jW
ìe-t T/ , t > 0 T (n+1)a un an [ í ],<1 î0, t < 0 1 2+ j pfT e-t T/ 2T a an,<1 1-a2 1 (2+ pfT)2 1 2- acosW+a2 k=¥ n=¥ ì sinêWæçèN + å 1 d(t -kT)
xn[ ]=ïí1 n N£ f åd 1 ïî0 1 ö 0 ( f -nf0), 2 ø÷ùúû k=-¥ n N> n=-¥ 1 é ë where f0 =1/T sin(W / 2)
Tính chất của biến đổi Laplace Property Time Domain Laplace Domain ROC Linearity
a x t1 1( )+a x t2 2( )
a X s1 1( )+a X s2 2( ) Atleast R1 ÇR2 Time-Domain Shifting x t( -t0) e X s-st0 ( ) R
Laplace-Domain Shifting e x ts t0 ( ) X s s( - 0) R+Re{ }s0 1 s
Time/Frequency-Domain Scaling x at( ) X( ) aR a a Conjugation x t*( ) X s* *( ) R
Time-Domain Convolution x1*x t2( ) X s X s1( ). 2( ) Atleast R1 ÇR2 dx t( )
Time-Domain Differentiation sX s( ) AtleastR dt dX s( )
Laplace-Domain Differentiation -tx t( ) R ds t x d( 1 ò
Time-Domain Integration )t t X s( )
AtleastRÇ{Re{ }s >0} -¥ s
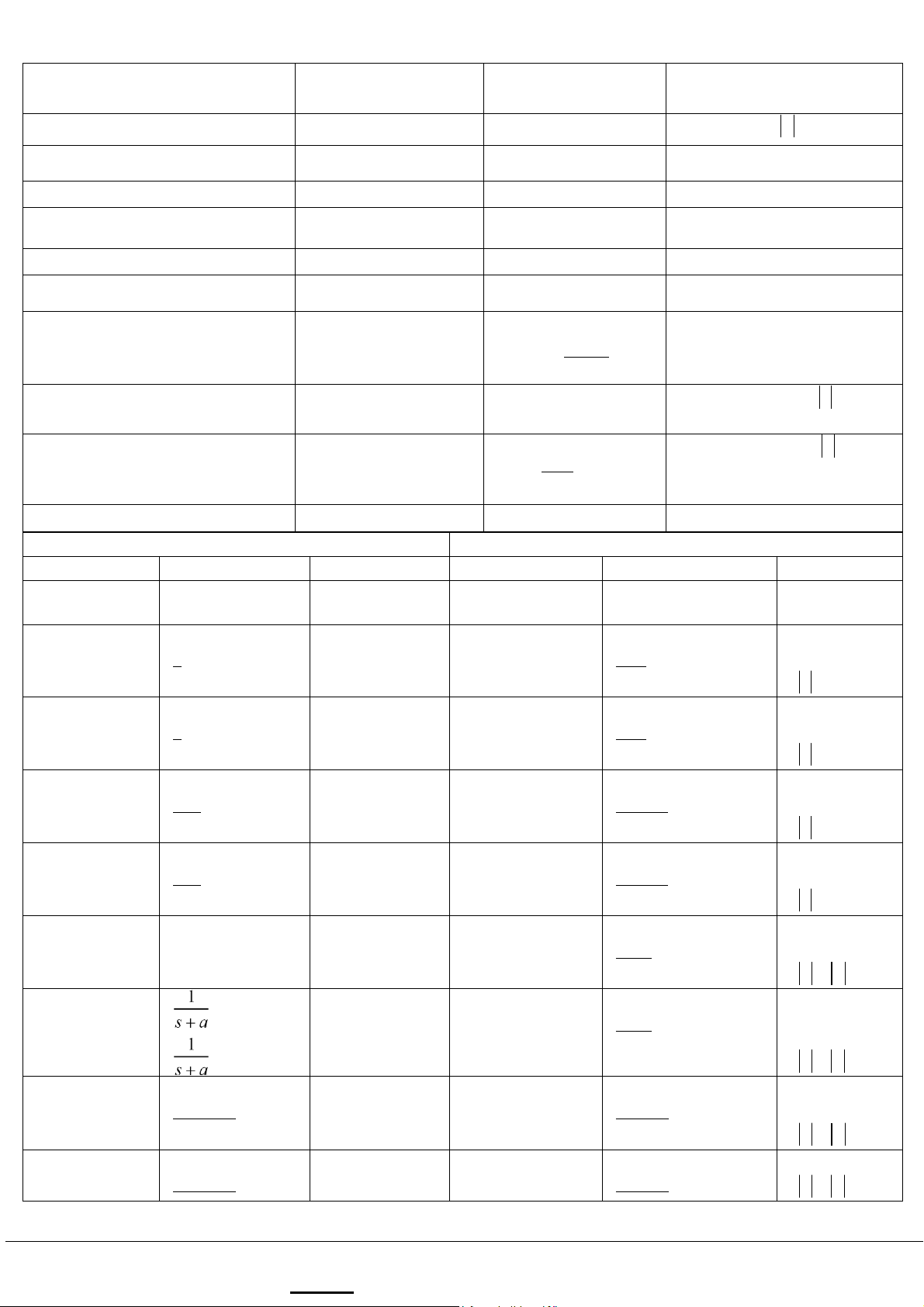
Tính chất của biến đổi z Property Time Domain z Domain ROC Linearity
ax n a x n1 1( )+ 2 2( )
a X z1 1( )+a X z2 2( ) Atleast R1 ÇR2
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào. lOMoAR cPSD| 59031616 Translation x n n( - R 0) z X z-n0 ( )
except possibleaddition deletion of/ 0 Z-Domain Scalling a x nn ( ) X a z( -1 ) a R ejW0nx n( )
X e( - jW0 z) R Time Reversal x n(- ) X(1/ z) R-1 Upsampling ( X z( M) ­ R1/M M x n) ( ) Conjugation x n*( ) X z* *( ) R Convolution x x n1 * 2( ) X z X z ( ) Atleast R1 ÇR2 1( ) 2 Z-Domain Diff nx n( ) -zdX z( ) R dz Differencing x n x n( )- ( -1) ( Ç 1-z- AtleastR z >0 1)X z( ) 1 Accumulation ¥ z
AtleastR Ç z >1 å 1 x k( ) X z( ) k=-¥ z-1 Linearity
ax n a x n1 1( )+ 2 2( )
a X z1 1( )+a X z2 2( ) Atleast R1 ÇR2
Các cặp biến đổi Laplace
Các cặp biến đổi z x(t) X(s) ROC x(n) X(z) ROC d( )t 1 Alls d( )n 1 All z 1 z u t( ) Re{ }s >0 s u n( ) z-1 z >1 1 z - -u( )t Re{ }s <0 s - - -u n(1) z-1 z <1 n! z t u tn ( ) Re{ }s >0 sn+1 nu n( ) (z-1)2 z >1 n! z - -t un ( )t Re{ }s <0 sn+1 - - -nu n(1) (z-1)2 z <1 z e-atu t( ) Re{ }s >-a a u nn ( ) z a- z > a z
-e-atu( )-t Re{ }s <-a z a- -au nn (- -1) z < a n! az t en -atu t( ) Re{ }s >-a (s a+ )n+1 nau nn ( ) (z a- )2 z > a n! az
-t en -atu( )-t Re{ }s <-a -nau nn (- -1) z < a
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào. lOMoAR cPSD| 59031616 (s a+ )n+1 (z a- )2 s z z( -cosW0) [coswot u t] ( ) Re{ }s >0 s2 +w02
cos(W0n u n) ( ) z2 -2zcosW + 0 1 z >1 w0 s2 zsinW0 [sinwot u t] ( ) +w02 Re{ }s >0 sin(W0n u n) ( ) z2 -2zcosW + 0 1 z >1 s a+ z z a( - cosW0)
[e-at coswot u t] ( Re{ }s >-a ) (s a+ )2 +w 2 + 0
(ancosW0nu n) ( )
z2 -2zcosW0 a2 z > a w0 azsinW0
[e-at sinwot u t] ( Re{ }s >-a ) (s a+ )2 +w 2
z2 -2zcosW +a2 0
(ansinW0nu n) ( ) 0 z > a
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào.