Bài giảng Chương 7 - Phân tích không gian trạng thái hệ thống LTI môn Tín hiệu và hệ thống | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616 CHƯƠNG 7 1 KH NG GIAN TRẠNG TH
I CỦA HỆ THỐNG LTI Ng Thu Trang 5/19/21
Chương 7 — Kh ng gian trạng th i của hệ thống LTI 2
▪ Kh i niệm về trạng th i
▪ Ph n t ch kh ng gian trạng th i của hệ thống LTI li n tục
- M h nh kh ng gian trạng th i
- Nghiệm trong miền tần số của phtr trạng th i
- Nghiệm trong miền thời gian của phtr trạng th i
- Biến đổi tuyến t nh của vector trạng th i
▪ Ph n t ch kh ng gian trạng th i của hệ thống LTI rời rạc
- M h nh kh ng gian trạng th i
- Nghiệm trong miền tần số của phtr trạng th i
- Nghiệm trong miền thời gian của phtr trạng th i lOMoAR cPSD| 59031616
C c kĩ thuật ph n t ch hệ thống 3 - Phương tr nh vi
¥ Tập trung x c định mối quan hệ giữa đầu ra theo đầu v o
ph n/ sai ph n ¥ Hiệu quả cho c c hệ thống tuyến t nh bất - T ch
chập/ Tổng chập biến theo thời gian
¥ Ph hợp với c c hệ thống một đầu v o — - H m truyền đạt một đầu ra
¥ Cho ph p x c định mối quan hệ b n trong
của hệ thống th ng qua c c biến b n
- Phương tr nh trong/ trung gian của hệ thống
¥ Hiệu quả cho cả c c hệ thống phi tuyến v
trạng th i ¥ biPh hến đổợi theo thp cho c c hời gian ệ thống nhiều đầu v o — nhiều đầu ra
Kh i niệm về trạng th i 4
▪ Định nghĩa 1: Đối với c c hệ thống nh n quả
- Trạng th i của hệ thống tại thời điểm t = t0 (hoặc n = n0)
l th ng tin tối thiểu đủ để x c định trạng th i v đầu ra của
hệ thống tại mọi thời điểm t ≥ t0 (hoặc n ≥ n0) khi biết
trước đầu v o của hệ thống tại mọi thời điểm t ≥ t0.
- C c biến chứa th ng tin n y được gọi l c c biến trạng th i lOMoAR cPSD| 59031616
Kh i niệm về trạng th i 5
▪ Định nghĩa 2: Đối với c c mạch điện SI - SO LTI
- Nếu biết được to n bộ th ng tin của đầu v o x(t) trong khoảng
(−∞, t) th sẽ đủ để x c định đầu ra y(t) trong khoảng (−∞, t)
- Nếu chỉ biết đầu v o x(t) của hệ thống trong khoảng (t0, t) th
cần biết c c biến trung gian tại thời điểm t0 (v dụ như d ng
diện qua điện trở, điện p tr n tụ,
) để c thể x c định được
đầu ra y(t) của hệ thống trong khoảng (t0, t)
- C c biến trung gian n y được gọi l trạng th i của hệ thống tại thời điểm t0 5/19/21
Lựa chọn biến trạng th i 6
▪ C rất nhiều c ch lựa chọn c c biến trạng th i cho một hệ thống cho trước
- C c biến trạng th i l đầu ra của c c phần tử c nhớ của hệ thống
- Hệ thống rời rạc gồm c c bộ trễ, bộ cộng, bộ khuếch đại → biến
trạng th i được chọn l đầu ra của bộ trễ
- Hệ thống li n tục gồm bộ t ch ph n, bộ cộng, bộ khuếch đại →biến
trạng th i được chọn l đầu ra của bộ t ch ph n
- Hệ thống li n tục c chứa c c bộ lưu giữ năng lượng vật lý (cuộn
cảm, tụ điện, ) →đầu ra của ch ng được chọn l m biến trạng th i
- C c biến trạng th i l c c biến đạo h m trung gian trong trường
hợp hệ thống được biểu diễn bởi phtr vi ph n/ sai ph n - lOMoAR cPSD| 59031616
th ố ng lin t ụ c 7
▪ Hệ thống Single Input - Single Output CT-LTI được m tả bởi phtr vi ph n sau
Tập c c điều kiện ban đầu l y(0), y(1)(0), , y(N)(0) với y(k)(t) = dky(t)/dtk
→ Định nghĩa N biến trạng th i g1(t), g2(t), , gN(t) như sau: g1(t) = y(t)
ġ1(t) = g2(t) g2(t) = y(1)(t) ġ với ġ1(t) = dgk(t)/d 2(t) = g3(t) t gN(t) = yN-1(t)
ġN(t) = —aNg1(t) — aN—1g2(t) — — a1gN(t) + x(t)
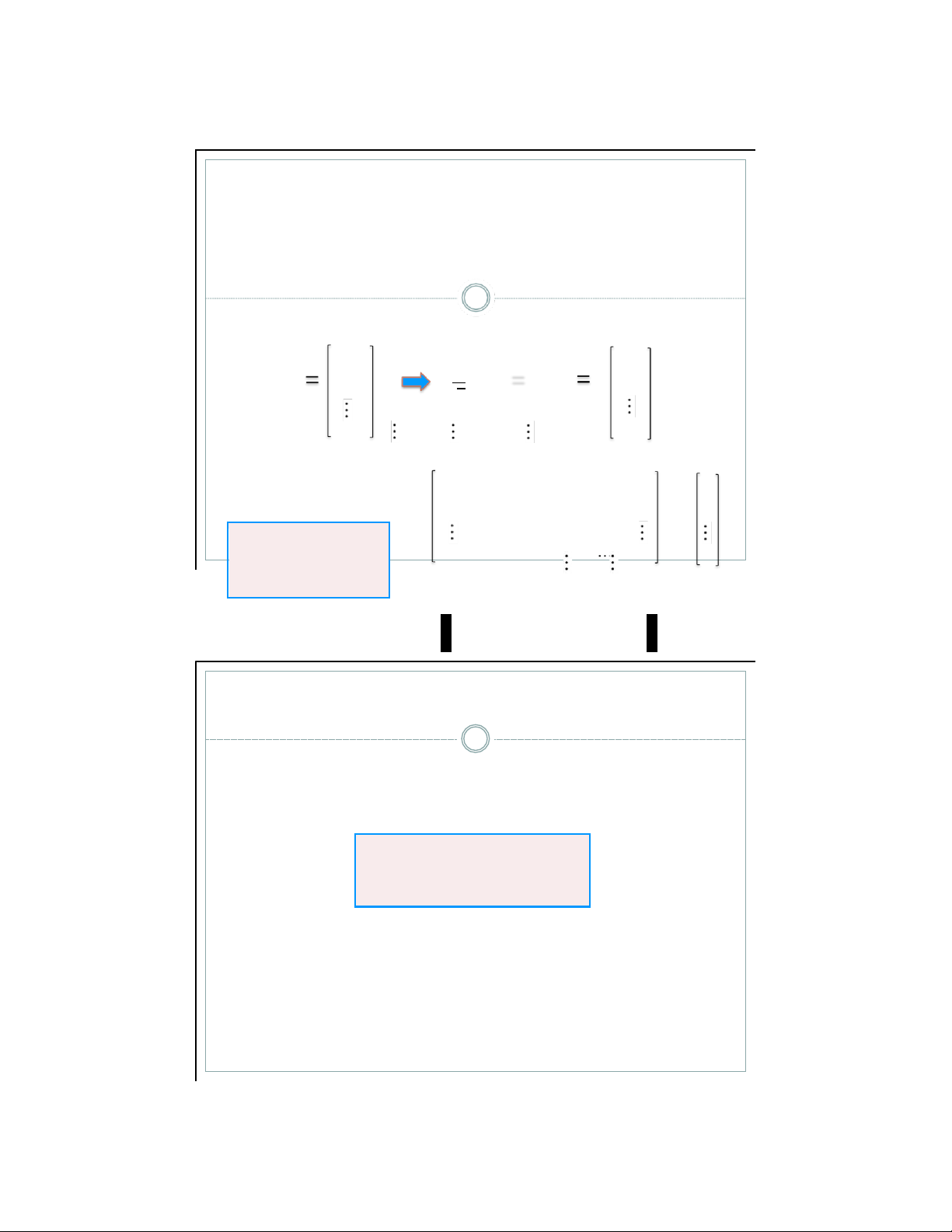
Ph n t ch kh ng gian trạng th i của hệ thống li n tục 8
▪ Viết lại mối quan hệ giữa c c biến trạng th i, đầu v o v đầu ra dưới dạng ma trận
ġ1(t) 0 1 0 0 0 ġ2(t) 0 0 1 0 g 1 ( t ) 0 x(t) g 2 ( t ) a (t ġ — 1 g N )
N(t) —aN — aN—1 — aN—2 1 g 1 ( t) g 2 (t) y(t) 1 0 0 0 g N ( t) lOMoAR cPSD| 59031616
Ph n t ch kh ng gian trạng th i của hệ thống li n tục 9
▪ Định nghĩa vector trạng th i N chiều như sau: g1(t) ġ1(t) g(t) g2(t) dg(t)/dt ġ(t) ġ2(t) gN(t) ġN(t)
→ Hệ thống SI-SO CT-LTI được m tả bởi phtr trạng th i 0 1 0 0 0 A = 0 0 1 ġ(t) = Ag(t) + bx(t) 0 b = 0 y(t) = cg(t) —aN — aN—1 — aN— 2 — a1 1 c = 1 0 0 0
Ph n t ch kh ng gian trạng th i của hệ thống li n tục 10
▪ Hệ thống SI-SO CT-LTI được m tả bởi kh ng gian trạng th i
tổng qu t, biểu diễn c c đại lượng ma trận, như sau ġ(t) = Ag(t) + bx(t) y(t) = cg(t) + dx(t)
Trong đ : Ma trận A(NxN) l ma trận hệ thống
b, c, d l c c vector hệ số gồm N phần tử
▪ Như vậy, c th m một c ch thức nữa để biểu diễn hệ thống
▪ Với mỗi tập điều kiện ban đầu kh c nhau sẽ c ma trận hệ thống kh c nhau
▪ Để x c định đầu ra của hệ thống từ đầu v o v ma trận hệ
thống, cần giải phtr trạng th i lOMoAR cPSD| 59031616
Ph n t ch kh ng gian trạng th i của hệ thống li n tục 11
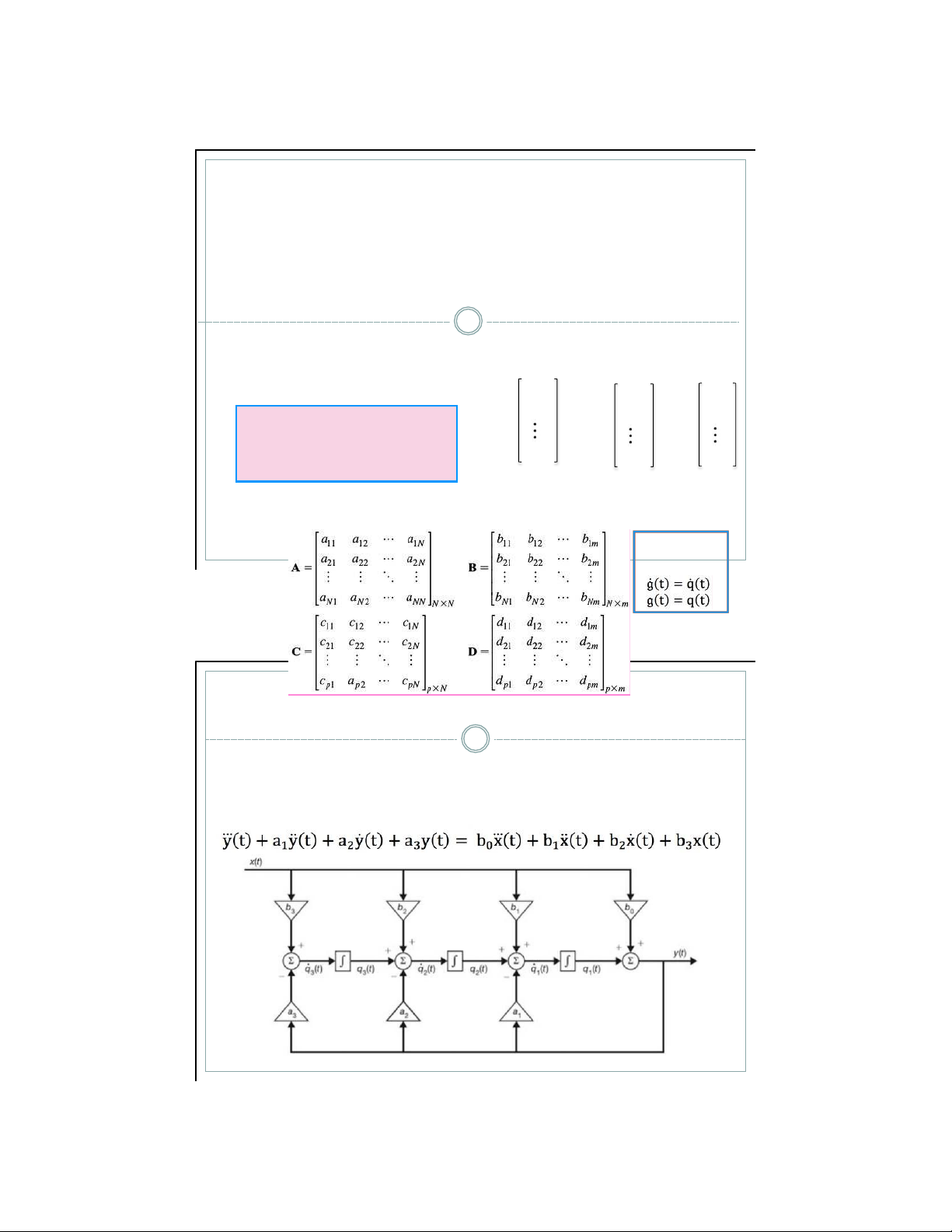
▪ Hệ thống Multi Input - Multi Output CT-LTI gồm m đầu v o, p đầu ra
được m tả bởi kh ng gian trạng th i tổng qu t, r t ra từ hệ thống SI-SO CT-LTI, như sau g1(t) x1(t) y1(t)
g(t) = g2(t) x(t) = x2(t) y(t) = Bx(t) y2(t) ġ(t) = Ag(t) + y(t) = Cg(t) + Dx(t) gN(t) xm(t) yp(t) Trong đ : cc k hi ệ u t ươ ng đươ ng V dụ 1 12
▪ Phtr vi ph n biểu diễn mối quan hệ giữa đầu v o v đầu ra
cho hệ thống li n tục sau lOMoAR cPSD| 59031616 V dụ 1 13
▪ Ch ọ n đầ u ra c ủ a cc b ộ tch phn lm bi ế n tr ạ ng thi q(t):
▪ Vi ế t l ạ i d ướ i d ạ ng ma tr ậ n A B C D 5 /19/21 V dụ 2 14
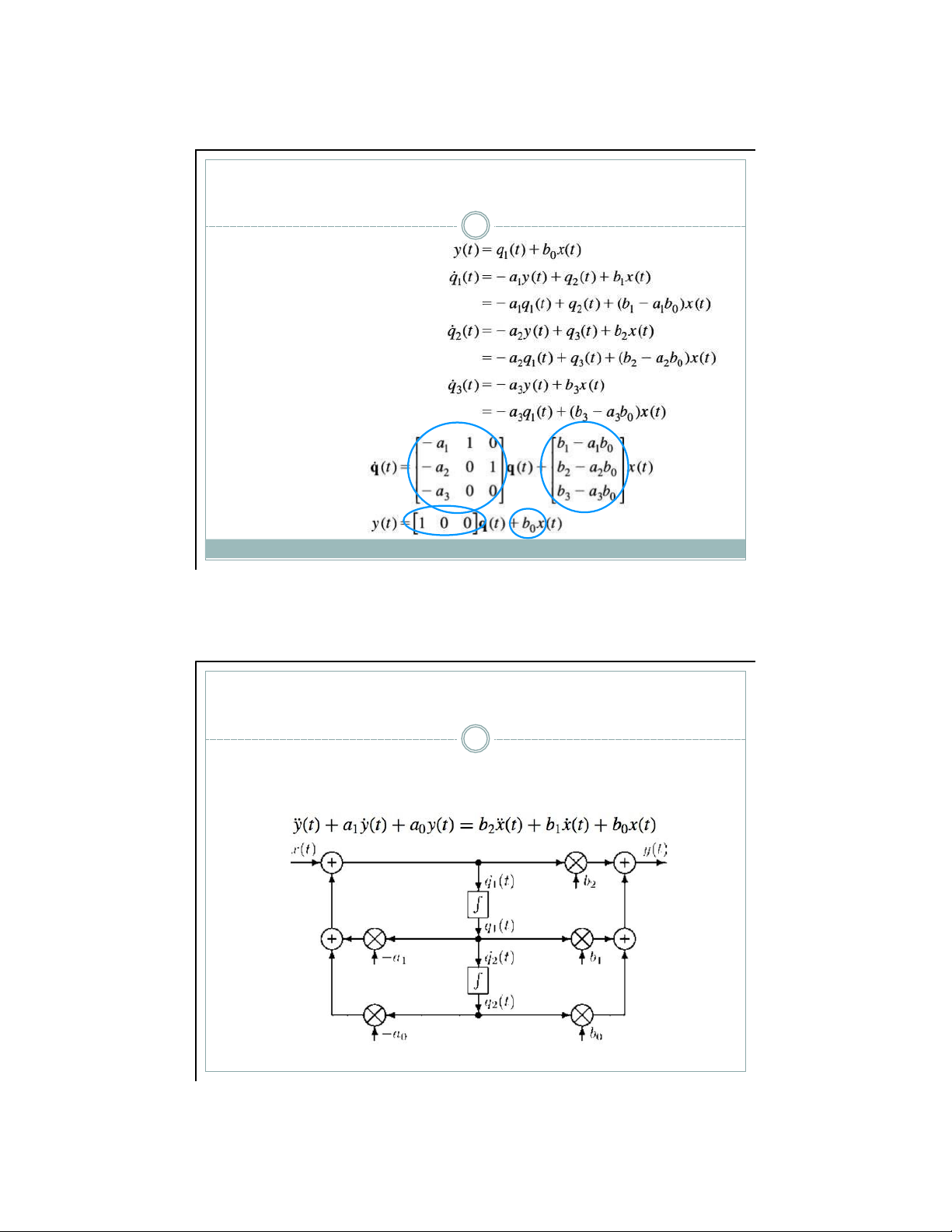
▪ Phtr vi ph n biểu diễn mối quan hệ giữa đầu v o v đầu ra
cho hệ thống li n tục sau lOMoAR cPSD| 59031616 V dụ 2 15
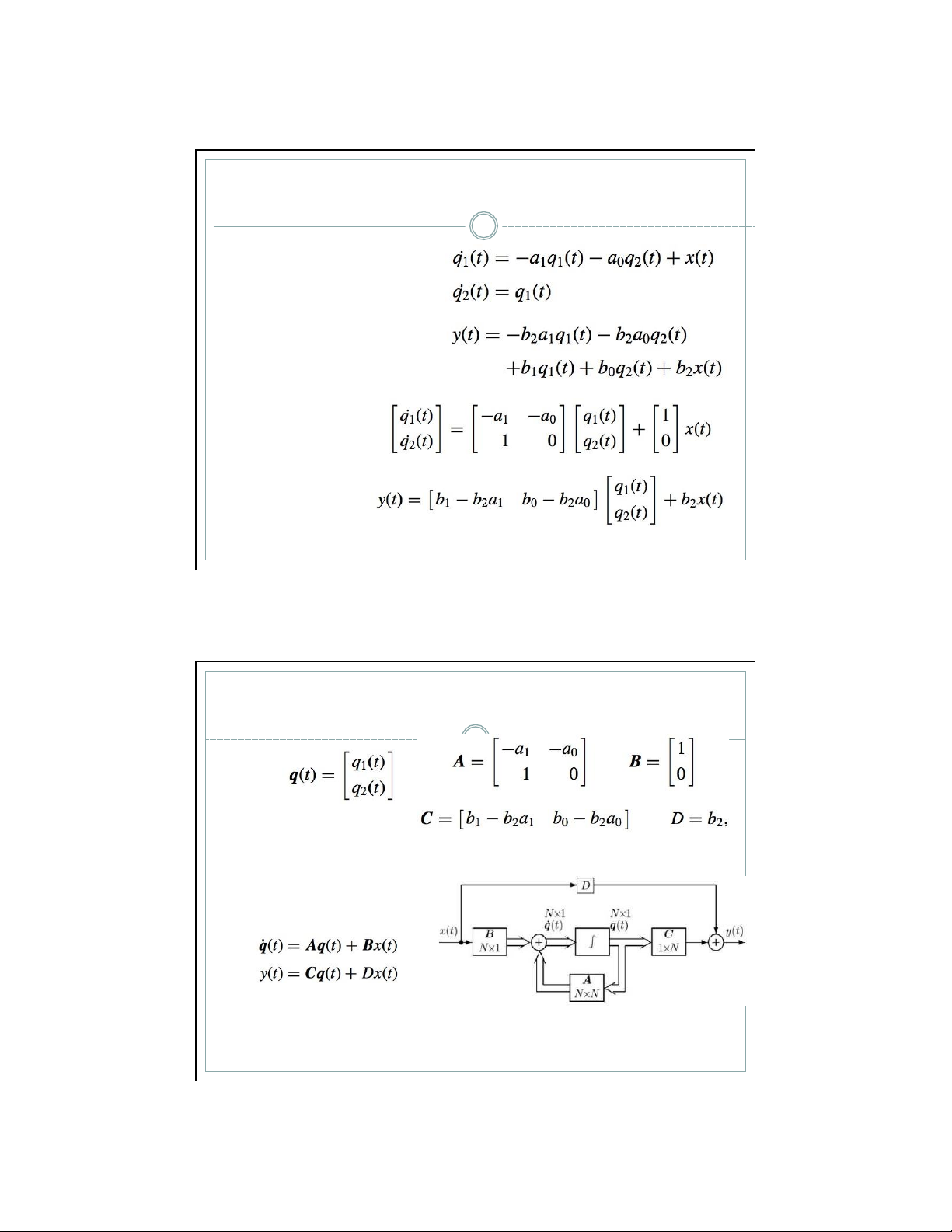
▪ Ch ọ n đầ u ra c ủ a cc b ộ tch phn lm bi ế n tr ạ ng thi q(t): ▪ Đầ u ra y(t) ▪ V ế t l ạ i d ướ i d ạ ng ma tr ậ n 5 /19/21 V dụ 2 16 ▪ M h nh kh ng gian
trạng th i của hệ thống lOMoAR cPSD| 59031616
Nghiệm trong miền tần số của phtr trạng th i 17
▪ Giải phtr trạng th i trong miền tần số → thu được nghiệm
trong miền tần số: p dụng biến đổi Laplace
Bi ế n đổ i Laplace m ộ t pha
K ch th ướ c c c ma tr ậ n: A(NxN), b(Nx1), c(1xN), d(1x1)
q(0): tr ạ ng th i ban đầ u
▪ Chuy ể n v ế phtr tr ạ ng thi v nhn hai v
ế v ớ i (s I — A ) — 1, thu đượ c Y(s) đ p ứ ng h ệ th ố ng
đ p ứ ng h ệ th ố ng ở khi đầ u vo b ằ ng 0 tr ạ ng thi 0
Nghiệm trong miền thời gian của phtr trạng th i 18
▪ Giải phtr trạng th i trong miền thời gian → thu được nghiệm trong miền thời gian.
▪ Định nghĩa h m mũ ma trận eAt v đạo h m của n như sau:
▪ p dụng chuỗi v hạn x c định h m mũ của số v hướng a cho trường hợp
h m mũ của ma trận A lOMoAR cPSD| 59031616
Nghiệm trong miền thời gian của phtr trạng th i 19
▪ p dụng c c t nh chất sau:
▪ Tại t = 0, ta c : e0 = I với 0 l ma trận 0 k ch thước NxN
▪ eA(t — τ) = eAte—Aτ = e— Aτ eAt → eAt e— At = e— At eAt = e0 = I
▪ Tồn tại nghịch đảo: e— At = (eAt)—1
▪ Lấy đạo h m cả hai ph a khai triển chuỗi eAt theo t eA t 5/19/21
Nghiệm trong miền thời gian của phtr trạng th i 20
▪ p d ụ ng đạ o hm t ừ ng ph ầ n
▪ Nhn hai v ế phtr tr ạ ng thi v ớ i e — A t 
▪ Tnh tch phn bi ể u th ứ c trn trong kho ả ng t t ừ 0 đế n t   lOMoAR cPSD| 59031616
Nghiệm trong miền thời gian của phtr trạng th i 21
▪ Nhn hai v ế c ủ a e — A tq(t) v ớ i e A t , thu đượ c vector tr ạ ng thi
▪ C vector tr ạ ng thi, tm đượ c nghi ệ m trong mi ề n th ờ i gian
y zi ( t): đ p ứ ng h ệ th ố ng
y zs ( t ) : đ p ứ ng h ệ khi đầ u vo b ằ ng 0 th ố ng ở tr ạ ng thi 0
e At : ma trận chuyển tiếp/ ma trận cơ bản của hệ thống
▪ Nếu trạng th i ban đầu của hệ thống l q(t0) v biết x(t) ∀ t ≥
t0 th vector trạng th i sẽ l (lấy t ch ph n từ t0 đến t) X c định eAt 22
▪ Phương ph p 1: dựa tr n định lý Cayley - Hamilton ▪ Từ
định lý Cayley — Hamilton, ta c :
▪ Nếu c c gi trị ri ng λk của ma trận A l ph n biệt, c c hệ số b0, b1, ,
bN-1 thu được từ phtr điều kiện sau b b 0 0 b b 1 1 b 3 b b N-1 4 Cc h ệ s ố b Cc h ệ s ố b l gi tr ị
k đượ c tnh t ừ N gi tr ị
k trong tr ườ ng h ợ p λ k
ring phn bi ệ t c ủ a ma tr ậ n A
ring kp b ậ c 2 (hng 2 c ủ a ma tr ậ n l đạ o hm theo λ k c ủ a hng 1) lOMoAR cPSD| 59031616
X c định eAt 23
▪ Phương ph p 2: dựa tr n đường ch o ho ma trận A
▪ Nếu tất cả gi trị ri ng λk của ma trận A l ph n biệt, ta c :
▪ Với ma trận P l ma trận đường ch o ho v xk (k = 1, 2, , N) l c c
vector ri ng của ma trận A, được t nh lần lượt như sau
X c định eAt 24
▪ Phương ph p 3: dựa tr n phương ph p ph n t ch phổ ma trận A
▪ Với N gi trị ri ng λk (k = 1, 2,
, N) ph n biệt của ma trận A, t
m c c ma trận cấu th nh Ek sao cho ▪ Khi đ, thu được lOMoAR cPSD| 59031616
X c định eAt 25
▪ Phương ph p 4: sử dụng biến đổi Laplace
▪ So s nh giữa nghiệm trong miền thời gian v miền tần số 5/19/21
Ph n t ch kh ng gian trạng th i của hệ thống li n tục 26
▪ H m truyền đạt hệ thống H(s)
▪ H m truyền đạt của hệ thống CT-LTI sẽ l H(s) = Y(s)/X(s) với
điều kiện ban đầu bằng 0, tức l q(0) = 0, do vậy ▪ Hệ thống ổn định
▪ Nếu c c gi trị ri ng λk của ma trận hệ thống A c phần thực m, tức l Re{λk} < 0 ∀k
th hệ thống được gọi l tiệm cận ổn định | 27
▪ Xc đị nh đầ u ra y(t) c ủ a h ệ th ố ng đượ c m t ả b ở i phtr vi
phn sau s ử d ụ ng ph ươ ng php trong mi ề n th ờ i gian v ớ i
đ i ề u ki ệ n ban đầ u y(0 — ) = 2 v ý (0 — ) = 3 v đầ u vo l u(t) ▪
p d ụ ng v d ụ 2, thu đượ c cc ma tr ậ n sau
▪ Thay đ i ề u ki ệ n ban đầ u vo vector tr ạ ng thi v phtr tr ạ ng thi: 5 /19/21 V dụ 3 28
▪ Ch ý rằng x(t) = u(t) → x(0—) = 0. Thay v o phtr đầu ra, ta c
▪ Gi ả i cc phtr trn, thu đượ c vector tr ạ ng thi ban đầ u
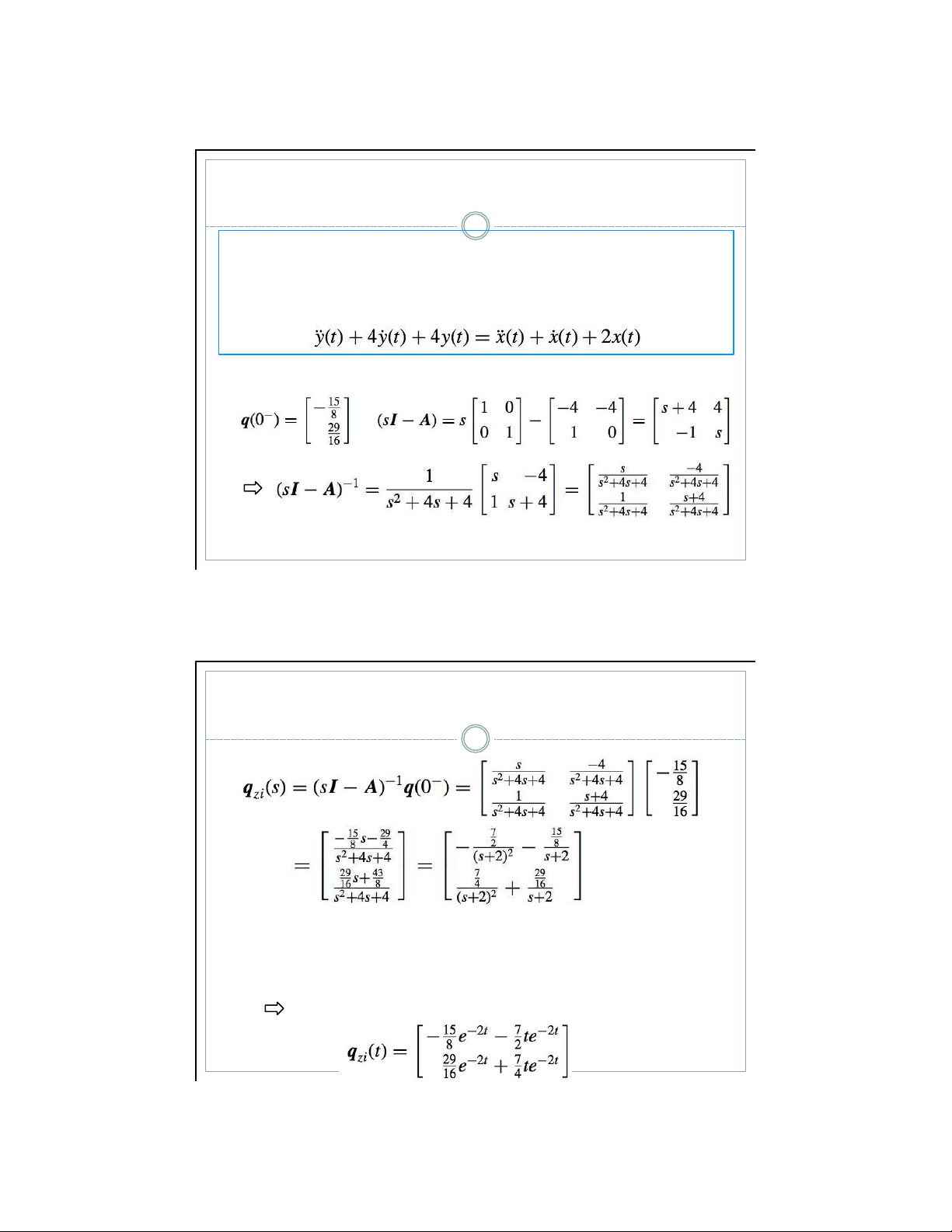
▪ Phtr đặc trưng của hệ thống thu được từ định thức của ma
trận (sI — A) như sau (cũng c thể thu được từ phtr sai ph n) Phtr đặ c tr ư ng
Với c ng một hệ thống c nhiều c ch lựa chọn biến trạng th i kh c nhau n n c thể
c nhiều ma trận A kh c nhau, tuy nhi n phtr đặc trưng lu n kh ng đổi | 29
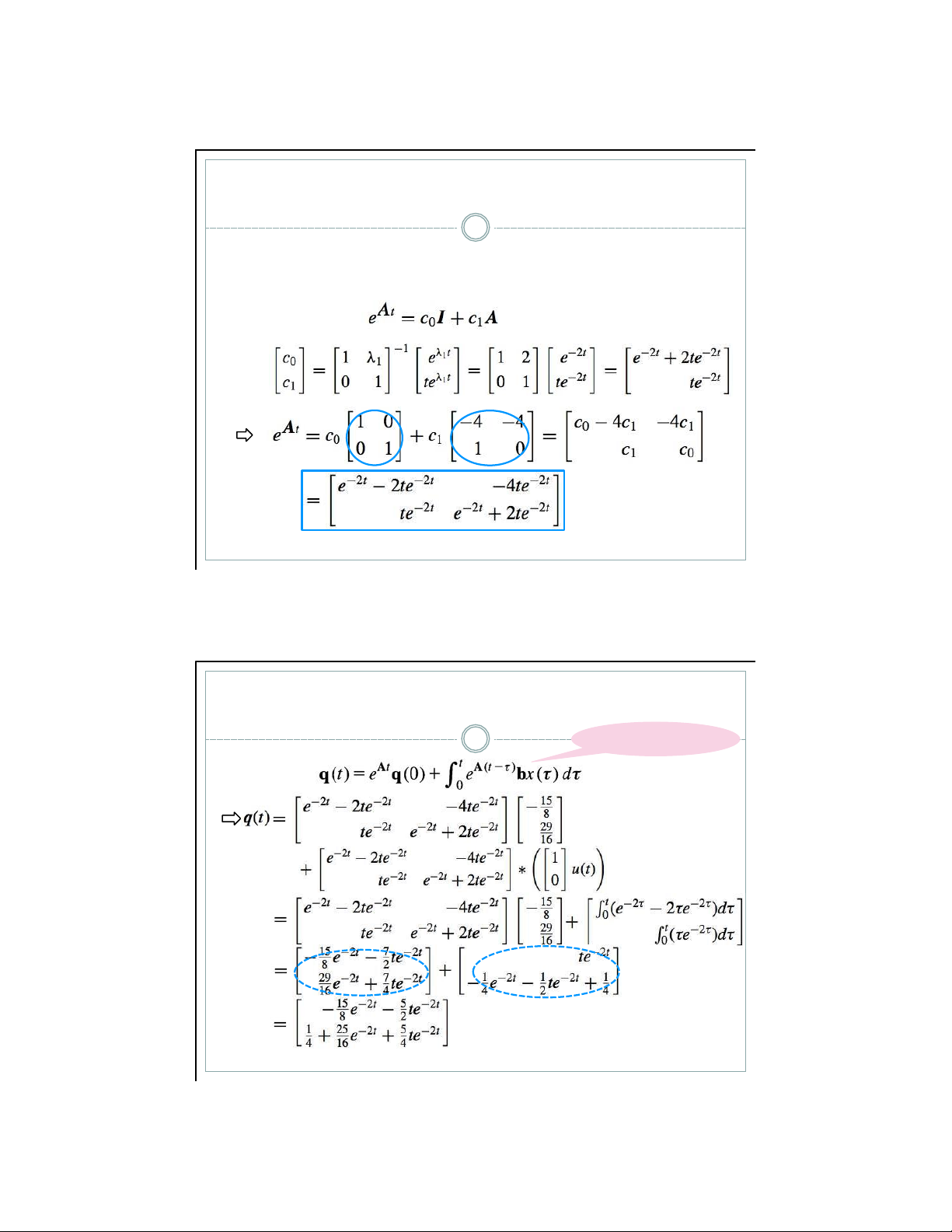
▪ Phtr đặc trưng c nghiệm k p λ1 = λ2 = —2, p dụng định lý
Caley — Hamilton để t m eAt, ta c v ớ i I A V dụ 3 30 ▪ Tch ch
Xc đị nh vector tr ạ ng thi ậ p e A t q (0)
Tch ch ậ p | 31
▪ Xc đị nh đầ u ra y(t)
y zi ( t): đ p ứ ng h ệ th ố ng
y zs ( t ) : đ p ứ ng h ệ khi đầ u vo b ằ ng 0 th ố ng ở tr ạ ng thi 0 5 /19/21 V dụ 4 32
▪ X c định đp ứng h(t) của hệ thống được m tả bởi phtr vi ph
n như trong v dụ 3 sử dụng phương ph p trong miền thời gian
▪ T nh tương tự v dụ 3 qua c c biến trạng th i, thu được
▪ Đầ u vo h ệ th ố ng l δ ( t) đầ u ra l đ p ứ ng h(t) c ủ a h ệ th ố ng: V dụ 5 33
▪ Xc đị nh đầ u ra y(t) c ủ a h ệ th ố ng đượ c m t ả b ở i phtr vi
phn nh ư trong v d ụ 3 s ử d ụ ng ph ươ ng php trong mi ề n t ầ n s ố
▪ Từ v dụ 3 thu được vector trạng th i ban đầu v ma trận (sI — A) 5 /19/21 V dụ 5 34
▪ Vector trạng th i khi đầu v o hệ thống bằng 0
▪ Thực hiện biến đổi Laplace ngược lOMoAR cPSD| 59031616 5 35
▪ Vector tr ạ ng thi khi khi h ệ th ố ng ở tr ạ ng thi 0
▪ Th ự c hi ệ n bi ế n đổ i Laplace ng ượ c
▪ Sử dụng phtr đầu ra, thay gi trị vector trạng th i v c c ma
trận hệ số A, B, C, D → thu được y(t) như trong v dụ 3 5/19/21 V dụ 6 36
▪ X c định đp ứng h(t) của hệ thống được m tả bởi phtr vi ph
n như trong v dụ 3 sử dụng phương ph p trong miền tần số
▪ Ta c hm truy ề n đạ t c ủ a h ệ th ố ng
▪ Th ự c hi ệ n bi ế n đổ i Laplace ng ượ c: lOMoAR cPSD| 59031616
Biến đổi tuyến t nh của vector trạng th i 37
▪ Với một hệ thống cho trước, c kh ng giới hạn c ch lựa chọn
biến trạng th i  với một hệ thống biết trước mối quan hệ
giữa đầu v o v đầu ra, c kh ng giới hạn cấu tr c b n trong kh c
nhau →c nhiều vector trạng th i kh c nhau cho c ng một hệ thống
▪ Biến đổi tuyến t nh của vector trạng th i: x c định vector
trạng th i mới từ vector trạng th i đ c
▪ Hệ thống c vector trạng th i q → x c định vector trạng th i
mới th ng qua ma trận kh ng suy biến bất k P (NxN) v tồn tại P—1, sao cho v 5/19/21
Biến đổi tuyến t nh của vector trạng th i 38
▪ Phương tr nh trạng th i mới thu được từ vector trạng th i mới
▪ Nhn c ả hai v ế v ớ i P , ta c ▪ Đặ t v
thu đượ c phtr tr ạ ng thi m ớ i
▪ Đặ t thu đượ c phtr đầ u ra
▪ Đị nh th ứ c c ủ a cc c ặ p ma tr ậ n (A v ) v ( ( s I — A ) v ) l nh ư
nhau → phtr đặ c tr ư ng khng đổ i
Biến đổi tuyến t nh lOMoAR cPSD| 59031616 V dụ 7 39
▪ Xc đị nh vector tr ạ ng thi m ớ i c ủ a h ệ th ố ng bi ế t
▪ Phtr tr ạ ng thi ban đầ u c ủ a h ệ th ố ng t ừ vector tr ạ ng thi ban đầ u
▪ M ố i quan h ệ gi ữ a vector tr ạ ng thi m ớ i v ớ i vector tr ạ ng thi c ũ
▪ Ch ứ ng minh r ằ ng hm truy ề n đạ t gi ố ng nhau trong hai tr ườ ng h ợ p 5 /19/21 V dụ 7 40 ▪ Ta c
▪ H m truyền đạt của hệ thống khi sử dụng vector trạng th i mới: V dụ 7