Bài giảng Chương 4 - Phân tích tín hiệu và biến đổi Fourier rời rạc môn Tín hiệu và hệ thống | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616 CHƯƠNG 4 1
PHÂN TÍCH TÍN HIỆU VÀ HỆ
THỐNG RỜI RẠC TRONG MIỀN TẦN SỐ Ngô Thu Trang 3/18/21
Chương 4 - Phân tích tín hiệu và
hệ thống rời rạc trong miền tần số 2
▪ Chuỗi Fourier rời rạc (Discrete – Time (DT) Fourier series)
- Biểu diễn tín hiệu rời rạc tuần hoàn bằng chuỗi Fourier
▪ Biến đổi Fourier tín hiệu rời rạc theo thời gian (Discrete
Time Fourier transform (DT – FT))
▪ Đáp ứng tần số của hệ thống LTI rời rạc
▪ Một số ví dụ về ứng dụng của biến đổi Fourier tín hiệu rời rạc theo thời gian
▪ Biến đổi Fourier rời rạc (Discrete Fourier Transform – DFT) lOMoAR cPSD| 59031616
DT - Fourier series vs CT - Fourier series 3
• Một cách biểu diễn tín hiệu khác trong miền thời
gian (vector không gian cơ sở là các hàm sin phức)
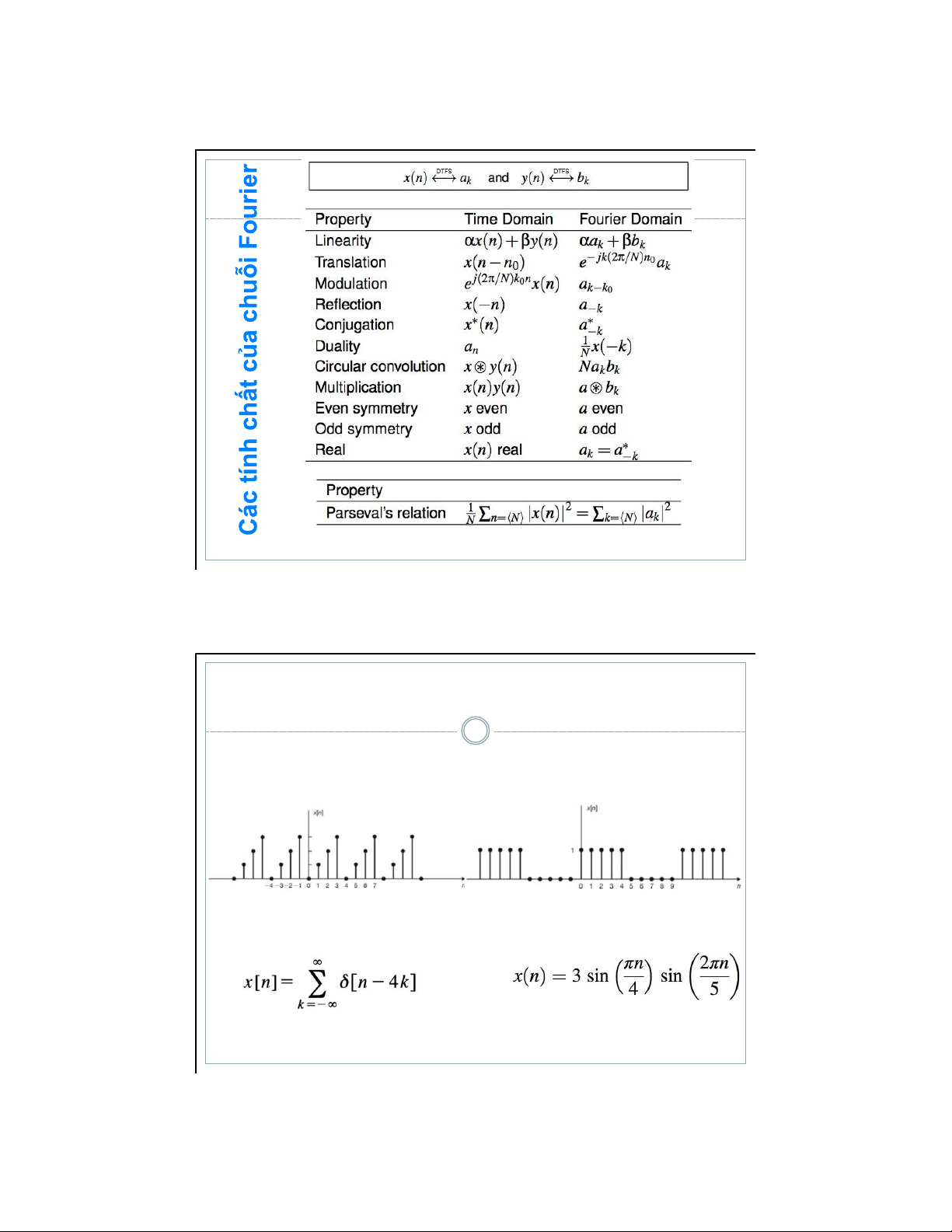
• Các tính chất của DT – Fourier series và CT – Fourier series
• DT – Fourier series biểu diễn cho một tín hiệu tuần
hoàn rời rạc theo thời gian có độ dài giới hạn →
không cần quan tâm đến điều kiện hội tụ
• CT – Fourier series biểu diễn cho một tín hiệu tuần
hoàn liên tục theo thời gian có độ dài vô hạn → cần
quan tâm đến điều kiện hội tụ 3/18/21
Chuỗi tuần hoàn rời rạc 4
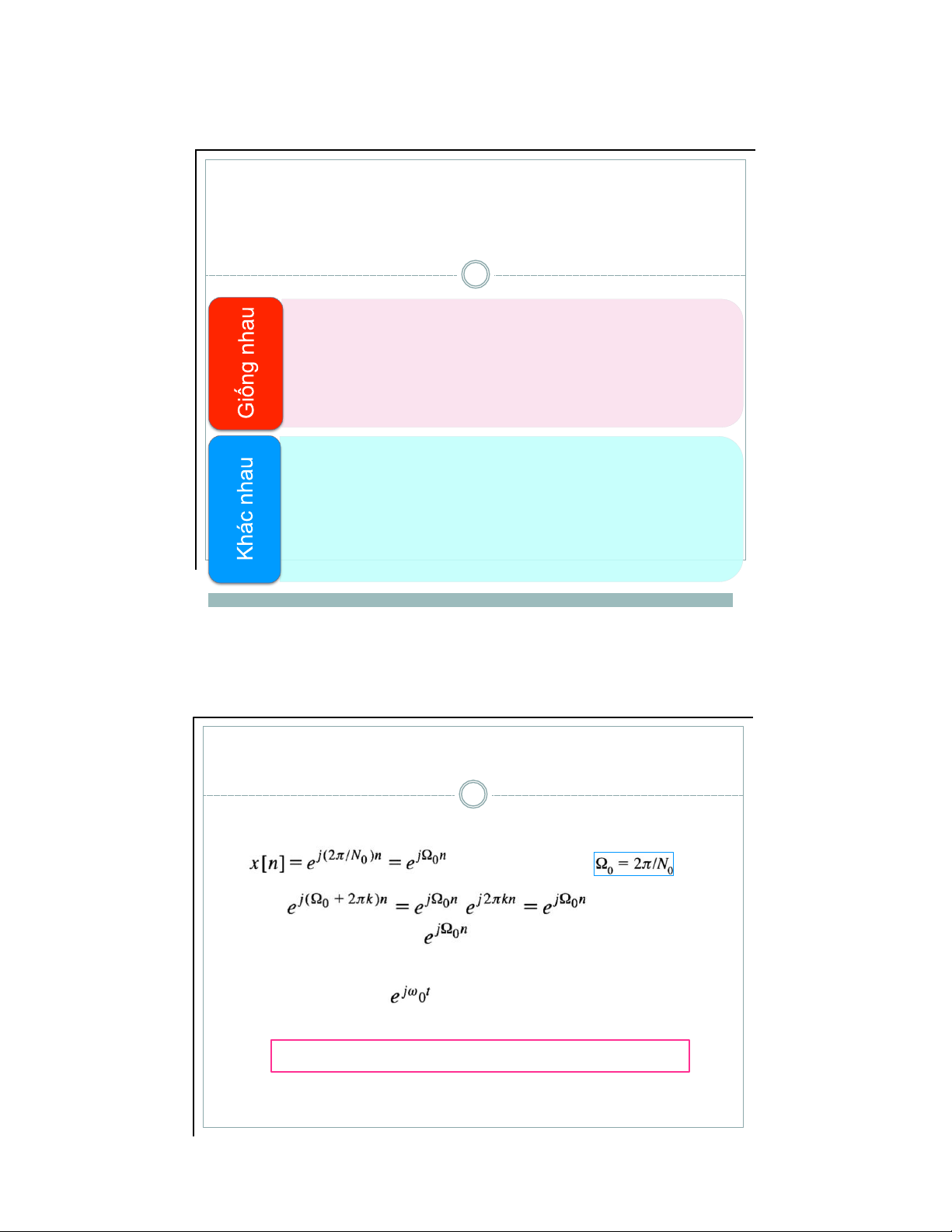
▪ Xét một chuỗi mũ phức tuần hoàn với chu kì cơ bản N0 với tần số cơ bản ta có ∀ k
nguyên → Các giá trị của chuỗi với tần số khác
nhau một số nguyên lần 2π là hoàn toàn giống nhau
Chú ý: Các tín hiệu là hàm cơ sở của chuỗi Fourier liên tục
có giá trị khác nhau tại các tần số ω0 khác nhau →
Khác biệt giữa hàm mũ rời rạc và liên tục lOMoAR cPSD| 59031616
Tập hàm sin phức đa hài rời rạc 5
▪ Một tập các hàm sin phức được gọi là hài của nhau nếu tồn tại
hằng số 2π/N sao cho tần số cơ bản của mỗi hàm sin phức là một
số nguyên lần của 2π/N.
▪ Tập các hàm sin phức đa hài có dạng với mọi k nguyên
▪ Trong tập , chỉ có N phần tử phân biệt, tức là k = i ÷ i+N-1 ∀ i
nguyên, do ∀ k nguyên → tập có độ dài hữu hạn là N
▪ Do tần số cơ bản của mỗi hàm sin phức trong tập các hàm sin
phức đa hài là một số nguyên lần của 2π/N nên tổ hợp tuyến tính
của các hàm sin phức này cũng là tuần hoàn với chu kì N 3/18/21 lOMoAR cPSD| 59031616
Dạng lượng giác của chuỗi Fourier 7
▪ Nếu x(n) là tín hiệu thực, chuỗi Fourier rời rạc của nó có thể
viết lại dưới dạng sau: với và
▪ Chú ý rằng ở biểu diễn chuỗi dưới dạng lượng giác chỉ chứa các giá trị thực 3/18/21 Tính
h ộ i t ụ c ủ a chu ỗ i Fourier 8
▪ Do chu ỗ i Fouirer r ờ i r ạ c là t ổ h ợ p c ủ a N xác đị nh hàm sin
ph ứ c ( t ổ ng h ữ u h ạ n )
→ Các h ệ s ố c ủ a chu ỗ i Fourier r ờ i r ạ c luôn t ồ n t ạ i và gi ớ i h ạ n
→ Chu ỗ i Fourier r ờ i r ạ c luôn h ộ i t ụ . lOMoAR cPSD| 59031616 9 3 /18/21 Bài t ậ p 10
Bài 26: Xác đị nh các h ệ s ố chu ỗ i Fourier c k c ủ a tín hi ệ u tu ầ n hoàn
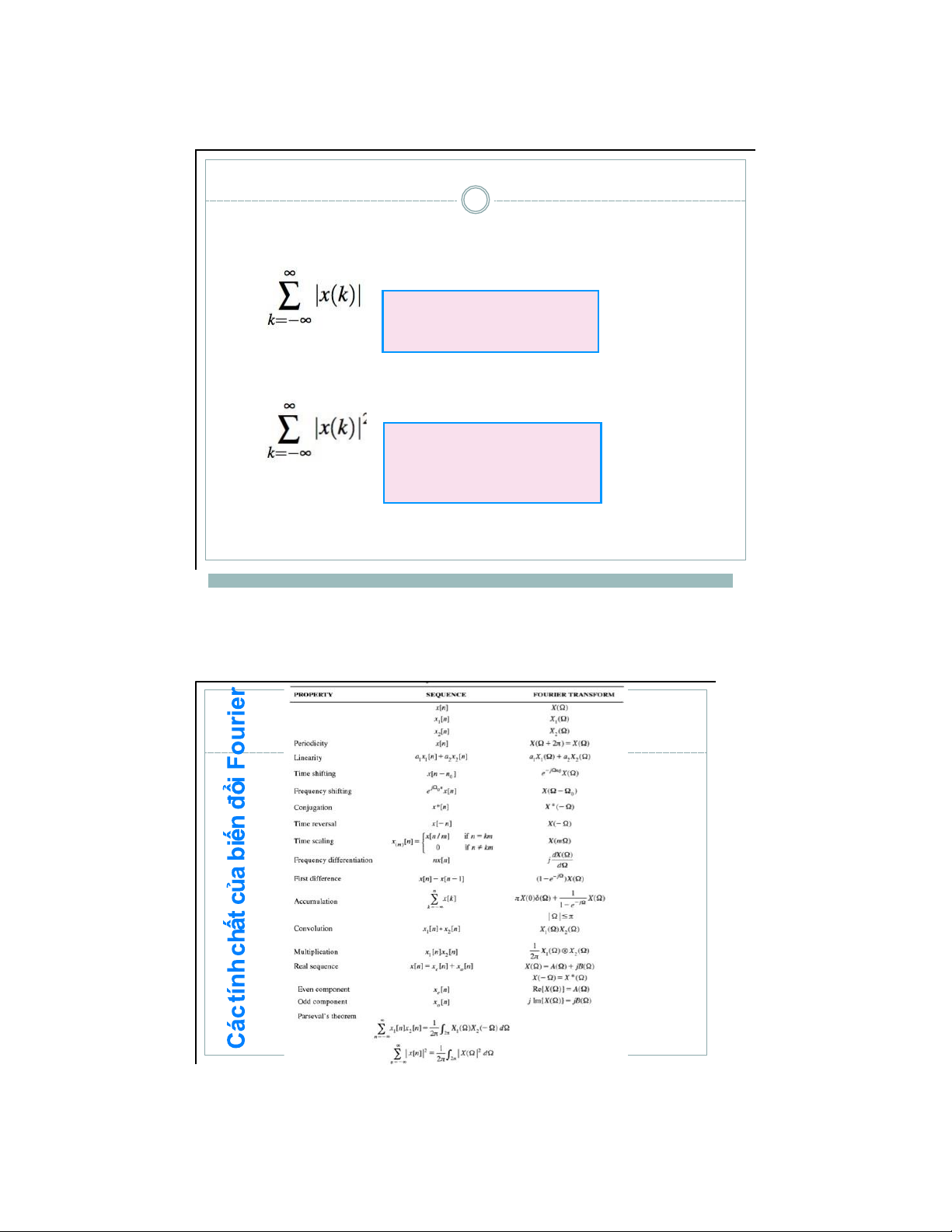
x(n) và v ẽ biên độ ph ổ c ủ a | c k | c ủ a nó a) b)
Bài 27: V ẽ d ạ ng xung và tìm các h ệ s ố chu ỗ i Fourier cho các tín hi ệ u sau a) b)
c) x(n) = n v ớ i 0 ≤ n ≤ 7 lOMoAR cPSD| 59031616
Chuỗi Fourier và phổ tần 11
▪ Mỗi hệ số của chuỗi Fourier định lượng lượng thông tin của
tín hiệu tại tần số tương ứng.
▪ Phân bố thông tin của tín hiệu tại các tần số khác nhau được
gọi là phổ tần (frequency spectrum) của tín hiệu
→ Các hệ số của chuỗi Fourier ck biểu diễn phổ tần
của tín hiệu rời rạc tuần hoàn
▪ Phổ của tín hiệu tuần hoàn chỉ tồn tại tại các tần số kΩ0 với k
là số nguyên với Ω0 = 2π/N.
▪ Các biên độ |ck| là phổ biên độ của tín hiệu x(t)
▪ Argument của ck là phổ pha của tín hiệu x(t) 3/18/21
Biến đổi Fourier tín hiệu thời gian rời rạc 12
▪ Biến đổi Fourier tín hiệu rời rạc theo thời gian
▪ Biến đổi Fourier thời gian rời rạc: Discrete time
Fourier transform (DT - Fourier Transform)
▪ Công cụ để biểu diễn một tín hiệu rời rạc trong miền
thời gian sang miền tần số
▪ Áp dụng đúng cách thức để xây dựng CT - FT từ
chuỗi Fourier cho việc xây dựng DT - FT lOMoAR cPSD| 59031616
Biến đổi Fourier thời gian rời rạc 13
▪ Đị nh ngh ĩ a 1: Bi ế n đổ i Fourier th ờ i gian r ờ i r ạ c ( DT-FT) c ủ a chu ỗ i x(n)
▪ Định nghĩa 2: Biến đổi Fourier ngược thời gian rời rạc (DT-IFT) của X(Ω)
x(n) và X(Ω) tạo nên cặp biến đổi Fourier 3/18/21
Biến đổi Fourier thời gian rời rạc 14
▪ x(n) là chuỗi tín hiệu rời rạc theo thời gian bất kì
(không cần phải là tín hiệu tuần hoàn) ▪ DT-FT
chính là phiên bản rời rạc của CT-FT → hầu
hết các tính chất của DT-FT và CT-FT là
tương tự nhau, ngoại trừ
▪ X(Ω) là tín hiệu tuần hoàn có chu kì 2π
▪ x(n) thu được nhờ tích phân trong khoảng hữu hạn
(2π) phổ tương ứng của nó lOMoAR cPSD| 59031616
Điều kiện thực hiện DT-FT – Điều kiện hội tụ 15
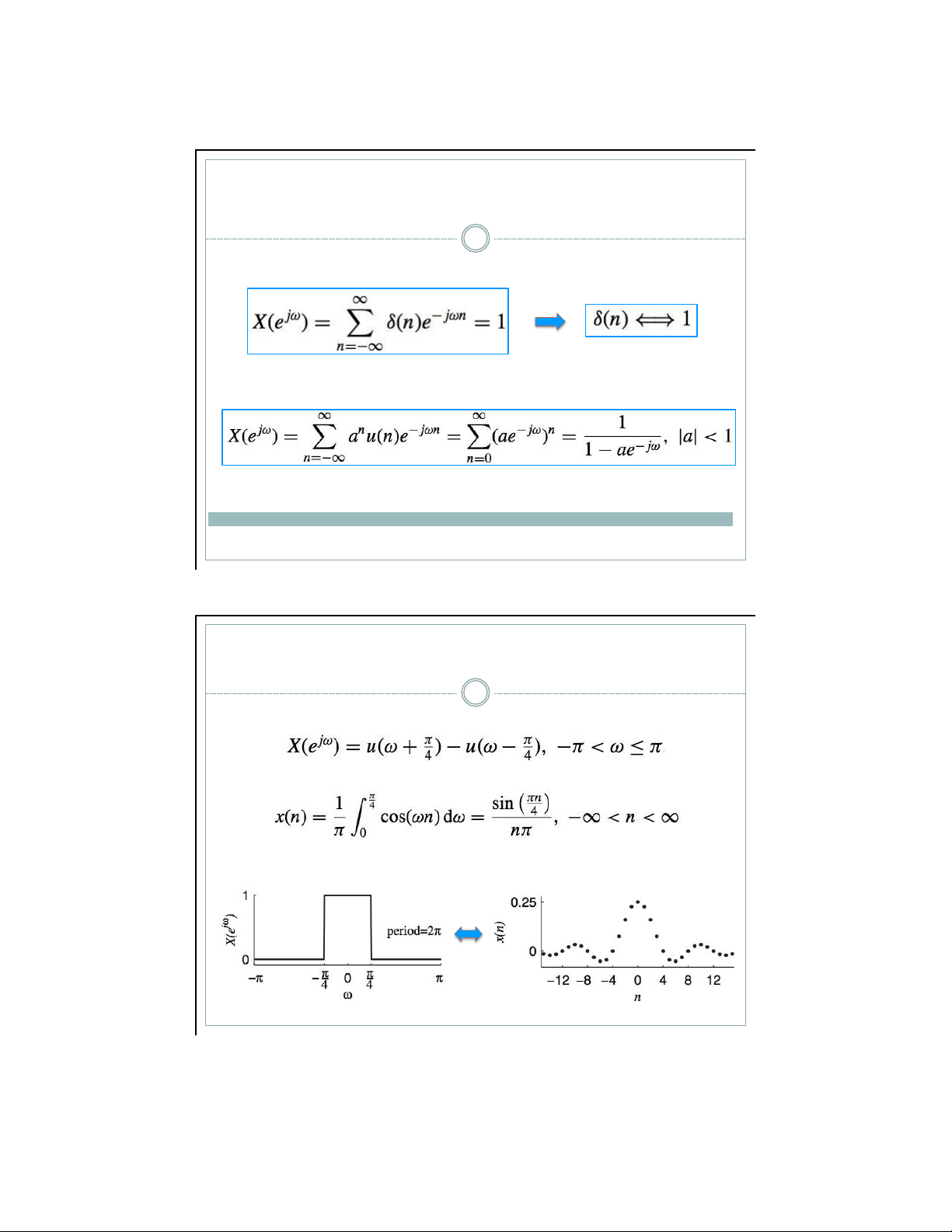
▪ Đối với chuỗi x(n), biến đổi Fourier thời gian rời rạc sẽ hội
tụ đều (uniformly) khi và chỉ khi x(n) có tổng hữu hạn (absolutely summable)
▪ Đối với chuỗi x(n), biến đổi Fourier thời gian rời rạc sẽ hội
tụ theo MSE khi và chỉ khi x(n) có tổng bình phương hữu hạn → x(n)
là tín hiệu năng lượng
▪ Nếu phổ X(Ω) là giới hạn, thì biến đổi Fourier ngược thời
gian rời rạc luôn luôn hội tụ do tích phân được lấy trong khoảng giới hạn 3/18/21 16 lOMoAR cPSD| 59031616
Phổ của một số tín hiệu cơ bản 17
▪ Phổ của xung đơn vị x(n) = δ(n)
▪ Phổ của chuỗi x(n) = anu(n), |a| < 1 3/18/21 Ph
ổ c ủ a m ộ t s ố tín hi ệ u c ơ b ả n 18
▪ Ph ổ c ủ a chu ỗ i x(n) có d ạ ng sau :
▪ Tìm chu ỗ i x(n) t ươ ng ứ ng : Do X( e j ω ) là hàm ch ẵ n nên
→ x(n) là tín hi ệ u n ă ng l ượ ng ch ỉ h ộ i t ụ theo MSE mà không h ộ i t ụ đề u lOMoAR cPSD| 59031616
Phổ của một số tín hiệu cơ bản 19
▪ Chu ỗ i x(n) = n → vi ph ạ m các đ i ề u ki ệ n h ữ u h ạ n
Ta có :x(n) = a n u ( n) → u(n) khi a → 1. Áp d ụ ng bi ể u th ứ c ph ổ c ủ a a n u ( n) 3 /18/21 lOMoAR cPSD| 59031616 21 3 /18/21 lOMoAR cPSD| 59031616
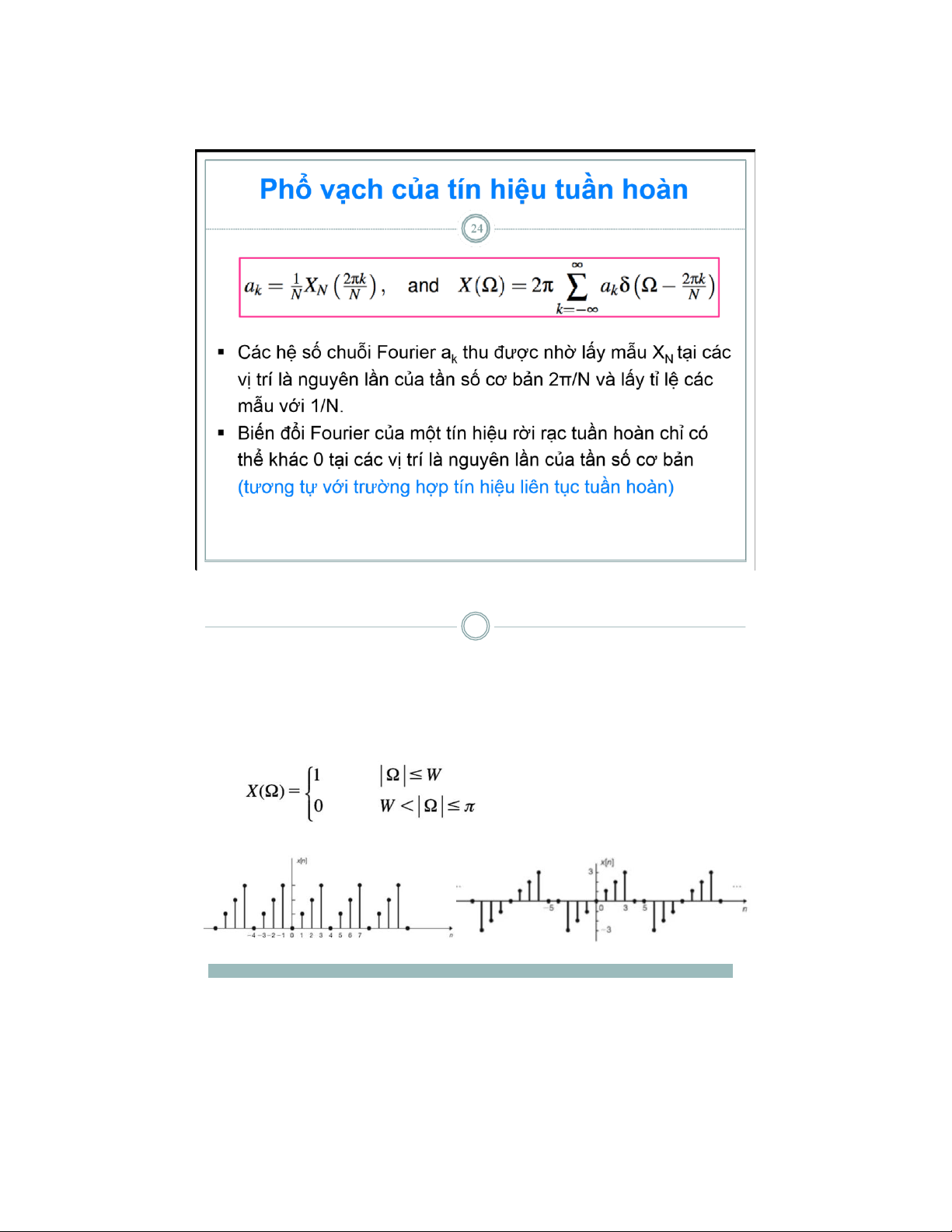
Phổ vạch của tín hiệu tuần hoàn 23
▪ Mối quan hệ giữa chuỗi Fourier và biến đổi Fourier
▪ Nếu chuỗi x(n) là tín hiệu tuần hoàn có chu kỳ N, định nghĩa chuỗi xN(n) như sau:
▪ Nếu ak là các hệ số chuỗi Fourier của x(n), X và XN lần lượt là biến
đổi Fourier của x(n) và xN(n) thì giữa chúng có mối quan hệ như sau 3/18/21 lOMoAR cPSD| 59031616 Bài tập 25
Bài 28: Tìm phổ của các tín hiệu sau: a) x[n] = a|n|, a<1
b) x[n] = sin(Ω0n), |Ω0|<π c) x[n] = u(– n – 1)
d) x[n] = u(n) – u(n – N)
Bài 29: Tìm biến đổi Fourier ngược của các tín hiệu sau a) b) X(Ω) = cos(2Ω) c) X(Ω) = jΩ
Bài 30: Tìm biến đổi Fourier của chuỗi x[n] sau a) b) 3/18/21 lOMoAR cPSD| 59031616 Đị
nh l ý Parseval 26 ▪
Đị nh l ý Perseval đư a ra m ộ t ph ươ ng pháp khác để xác
đị nh n ă ng l ượ ng trong mi ề n t ầ n s ố thay vì trong mi ề n th ờ i gian ▪
Hay nói cách khác n ă ng l ượ ng đượ c b ả o toàn trong c ả
2 mi ề n .
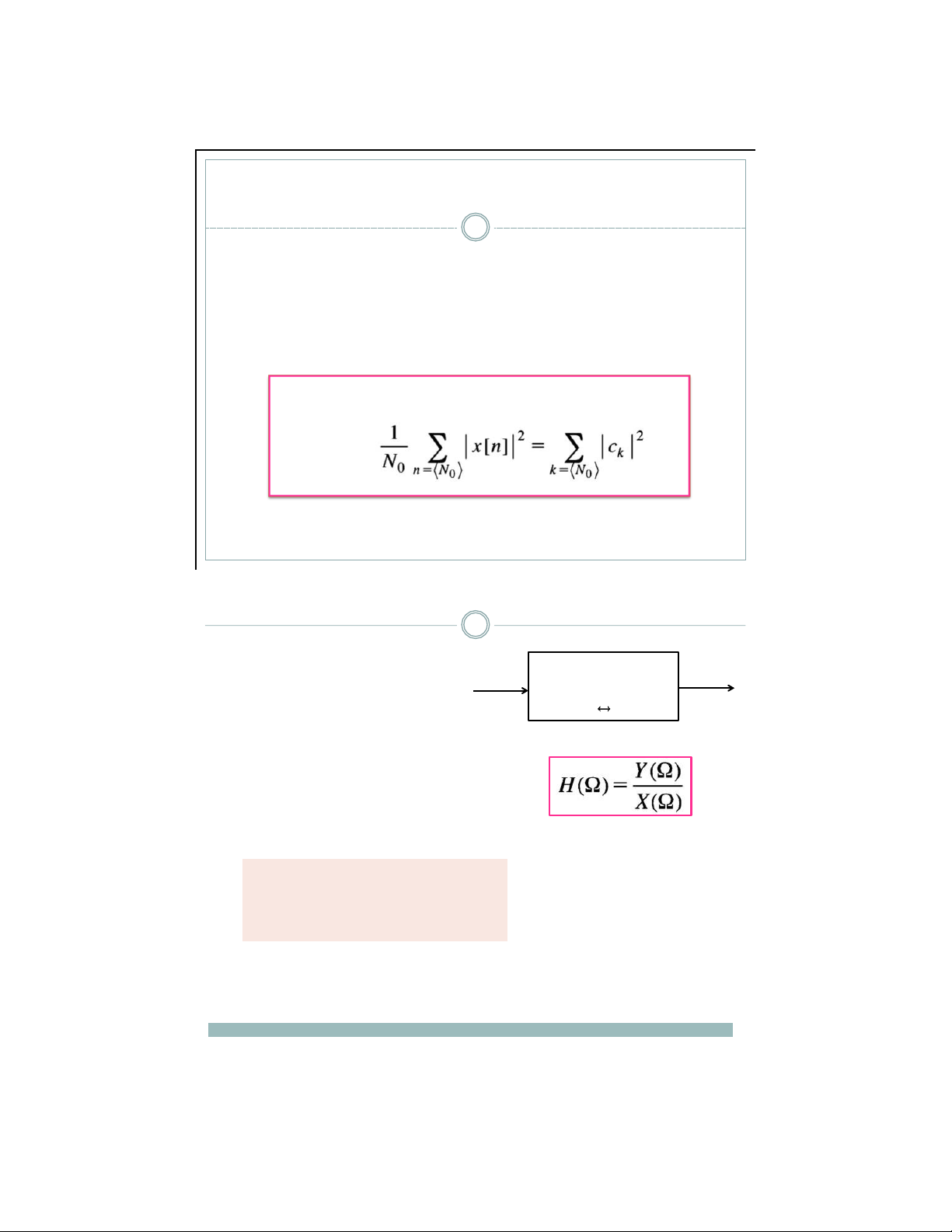
Đị nh l ý Parseval cho tín hi ệ u x(n) r ờ i r ạ c
c k là các h ệ s ố chu ỗ i Fourier c ủ a tín hi ệ u r ờ i r ạ c x(n)
Đáp ứng tần số của hệ thống DT-LTI 27
▪ Một hệ thống DT-LTI có mối x(n) H y(n)
quan hệ giữa đầu ra y(n) với ệ th ố ng DT-LTI h(n)
đầu vào x(n) và đáp ứng h(n) X( Ω )
H( Ω ) Y( Ω ) như sau y(n) = x(n) h(n) * ▪ Áp dụng
biến đổi Fourier Y(Ω) = X(Ω) H(Ω)
H(Ω): hàm truyền đạt hay đáp ứng
tần số của hệ thống DT-LTI. Đáp
ứng xung vs đáp ứng tần số: cặp biến đổi Fourier.
▪ Đáp ứng tần số của mọi hệ thống DT-LTI là tuần hoàn với chu kì
2π, chỉ cần quan sát đáp ứng tần số trong một chu kì → khác biêt so với hệ thống CT-LTI 3/18/21 lOMoAR cPSD| 59031616
Đáp ứng tần số của hệ thống DT-LTI 28
▪ H(Ω) là hàm phức, có thể được biểu
diễn dưới dạng toạ độ cực:
- |H(Ω)| là đáp ứng biên độ (chính là độ khuếch đại)
- Argument của H(Ω) là đáp ứng pha (chính là độ dịch pha)
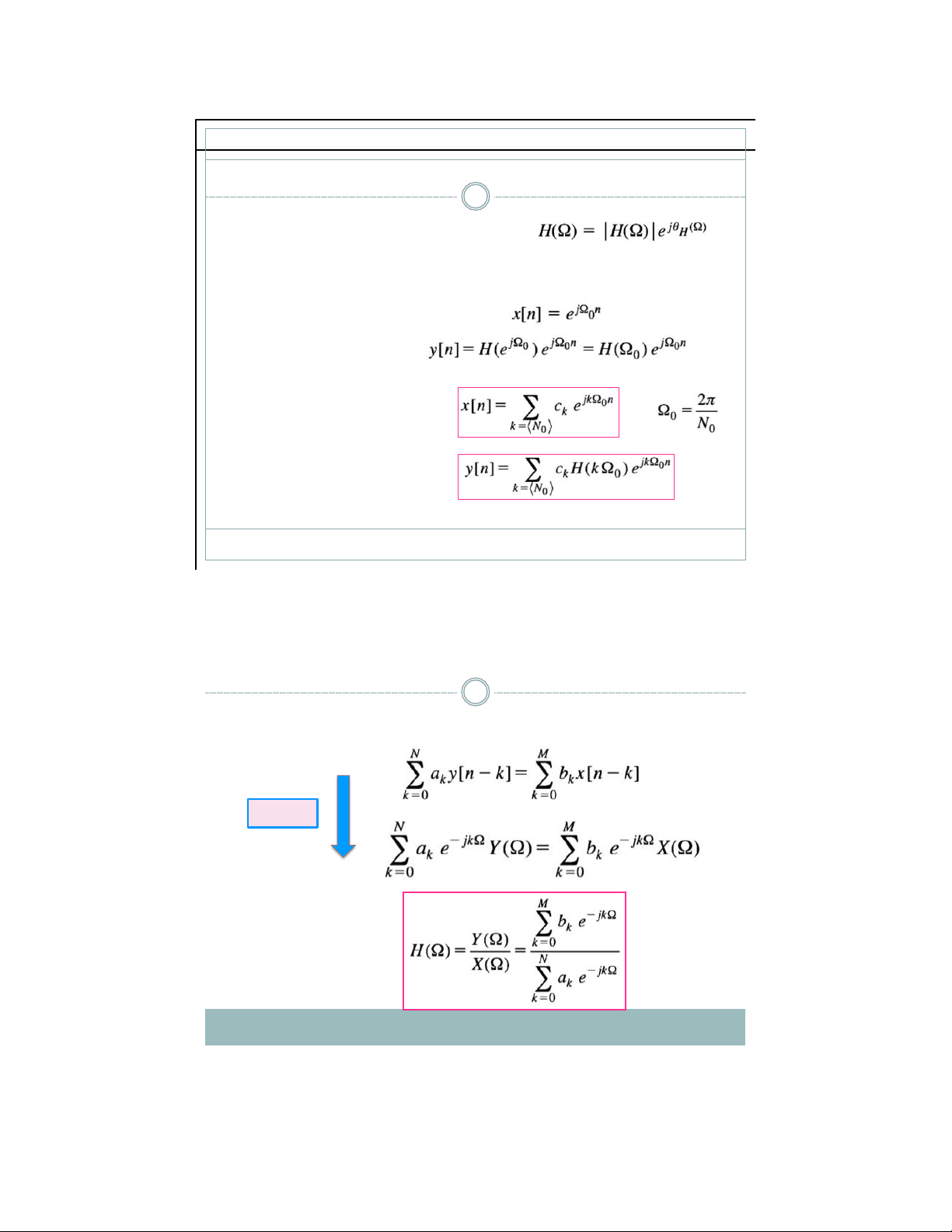
▪ Nếu tín hiệu đầu vào là chuỗi mũ phức
thì tín hiệu đầu ra cũng có dạng chuỗi mũ phức
▪ Nếu tín hiệu đầu vào x(n) là tuần hoàn
với chu kì N0 được biểu diễn dưới
dạng chuỗi Fourier rời rạc thì tín
hiệu đầu ra y(n) cũng là tuần hoàn với chu kì N0
Phtr sai phân của hệ thống DT-LTI 29
▪ Phtr sai phân đặ c tr ư ng cho h ệ th ố ng DT - LTI là : v ớ i MDT-FT → Đáp ứng tần số 3/18/21 lOMoAR cPSD| 59031616
Đáp ứng với tín hiệu đầu vào dạng sin 30
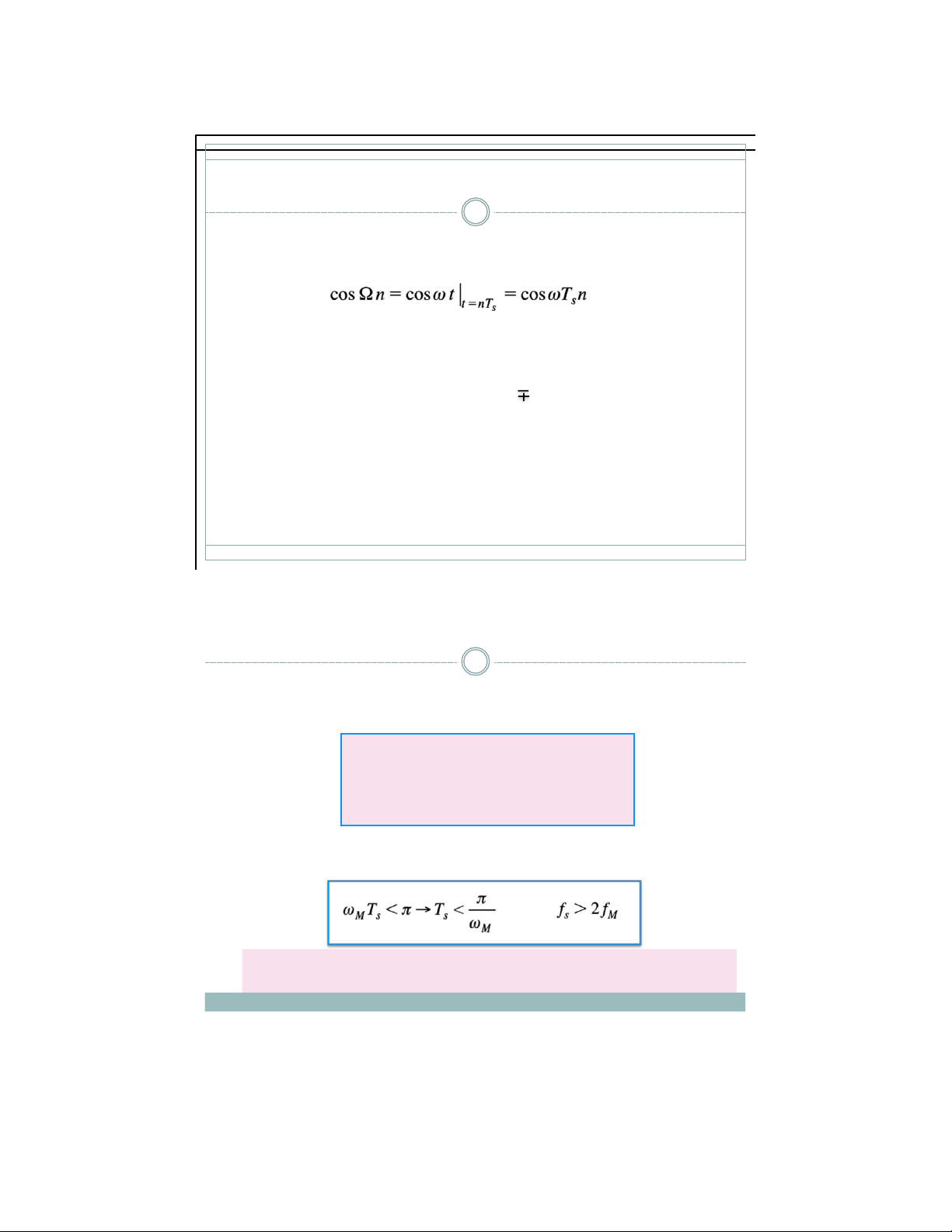
▪ Tín hiệu dạng sin rời rạc theo thời gian cos(Ωn) thu được từ tín
hiệu dạng sin liên tục theo thời gian cosωt với chu kì lấy mẫu Ts như sau: với Ω=ωTs -
Lưu ý 1: cos[(Ω + 2πm)n] = cos(Ωn + 2πmn) = cos(Ωn) ∀ m
nguyên → Tín hiệu dạng sin rời rạc cosΩn chỉ có dạng sóng duy nhất với
các giá trị Ω trong dải từ 0 đến 2π. -
Lưu ý 2: cos(π ± Ω)n = cos(πn)cos(Ωn) sin(πn)sin(Ωn) = (-
1)ncos(Ωn) Như vậy cos(π + Ω)n = cos(π - Ω)n → Tín hiệu dạng
sin rời rạc cosΩn chỉ có dạng sóng duy nhất với các giá trị Ω trong khoảng
0 ≤ Ω ≤ π: chỉ cần quan sát trong khoảng tần số này -
Lưu ý 3: Tín hiệu dạng sin liên tục cosωt có dạng sóng duy nhất với
mọi giá trị ω trong dải từ 0 đến ∞.
Đáp ứng với tín hiệu đầu vào dạng sin 31
▪ Khi tín hiệu đầu vào của hệ thống lần lượt là cos(Ωn), sin(Ωn) và ejΩn
với ejΩn=cos(Ωn) + jsin(Ωn) thì đáp ứng yc(n), ys(n) và y(n) tương ứng sẽ là
y(n) = yc(n) + jys(n) = H(Ω)ejΩn yc(n)
= Re{y(n)} = Re{H(Ω)ejΩn } ys(n) = Im{y(n)} = Im{H(Ω)ejΩn }
▪ Nếu ΩM = 2πfM là tần số lớn nhất của tín hiệu dạng sin liên tục thì điều
kiện để tín hiệu dạng sin rời rạc lấy mẫu có dạng sóng duy nhất là hay
T ố c độ l ấ y m ẫ u không đượ c nh ỏ h ơ n hai l ầ n t ầ n s ố l ớ n nh ấ t c ủ a
tín hi ệ u d ạ ng sin liên t ụ c 3 /18/21 lOMoAR cPSD| 59031616
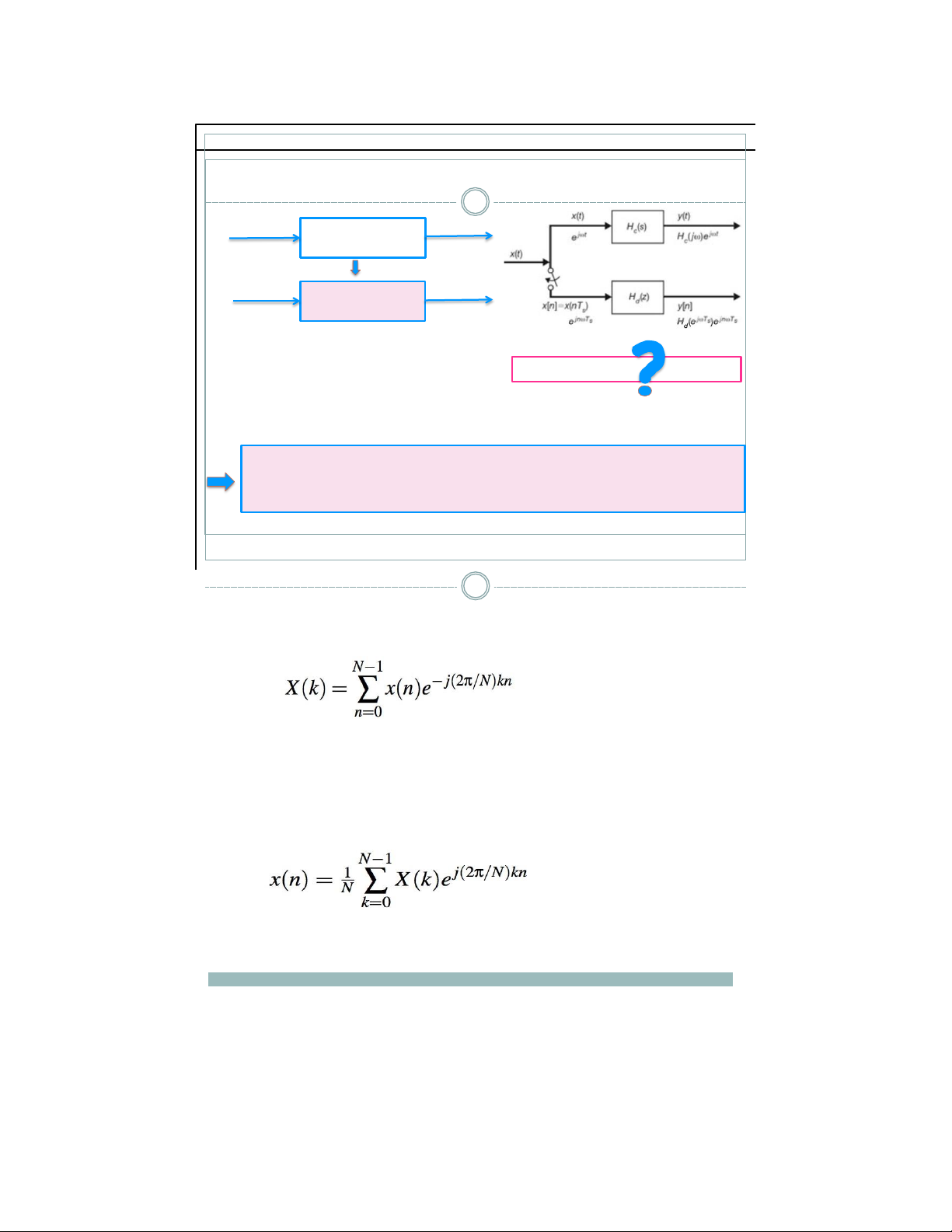
Mô phỏng CT-LTI bằng DT-LTI 32 x(t) Hệ thống CT-LTI y(t) Hc(s)
Lấy mẫu với chu kì Ts x[n] = x(nTs) Hệ thống
DT-LTI y[n] = y(nTs) Hd(z)
▪ Yêu cầu: y[n] = y(nTs) → Hc(jω)ejnωTs = Hd(ejωTs)ejnωTs  Hc(jω) = Hd(ejωTs)
→ Biểu diễn dưới dạng biến đổi Fourier: Hc(ω) = Hd(Ω) với Ω=ωTs (1)
▪ Hc(ω): đáp ứng của CT-LTI tồn tại duy nhất với mọi ω trong dải 0<ω<∞
▪ Hd(Ω): đáp ứng của DT-LTI là hàm tuần hoàn theo ω (chu kì là 2π/Ts)
✓ x(t) là tín hiệu có băng tần giới hạn, (1) thoả mãn ∀ω(-π/Ts, π/Ts) ✓
Có thể tìm được hệ thống DT-LTI thoả mãn (1) với độ chính xác
cho phép ∀ω trong dải tần của x(t)
Discrete Fourier Transform (DFT) 33
▪ Định nghĩa 1: Biến đổi Fourier rời rạc (DFT) của tín hiệu rời rạc x[n] có chiều dài N mẫu là với k = 0,1,2,…,N-1
▪ Định nghĩa 2: Biến đổi Fourier rời rạc ngược
(Inverse - DFT) của chuỗi phổ X có chiều dài N mẫu là với n = 0,1,2,…,N-1
x(n) và X(k) tạo nên cặp biến đổi Fourier rời rạc 3/18/21 lOMoAR cPSD| 59031616
Discrete Fourier Transform 34
▪ Đặc trưng quan trọng của DFT
- DFT ánh xạ một chuỗi tín hiệu N mẫu từ miền thời gian sang chuỗi tín
hiệu N mẫu trong miền tần số và ngược lại
- DFT có liên quan chặt chẽ với chuỗi Fourier và biến đổi Fourier - DFT
phù hợp thực hiện trên máy tính vì rời rạc và hữu hạn cả trong miền thời gian và tần số
- Thuật toán tính DFT cực nhanh → FFT
- X[k] của DFT chính là X(Ω) được lấy mẫu tại các Ω=k2π/N ∀k nguyên
Biến đổi thuận Biến đổi ngược Tín hiệu miền thời gian Tín hiệu miền tần số CT - FT Liên tục Liên tục Liên tục Liên tục DT - FT Rời rạc Liên tục Rời rạc Liên tục DFT Rời rạc Rời rạc Rời rạc Rời rạc
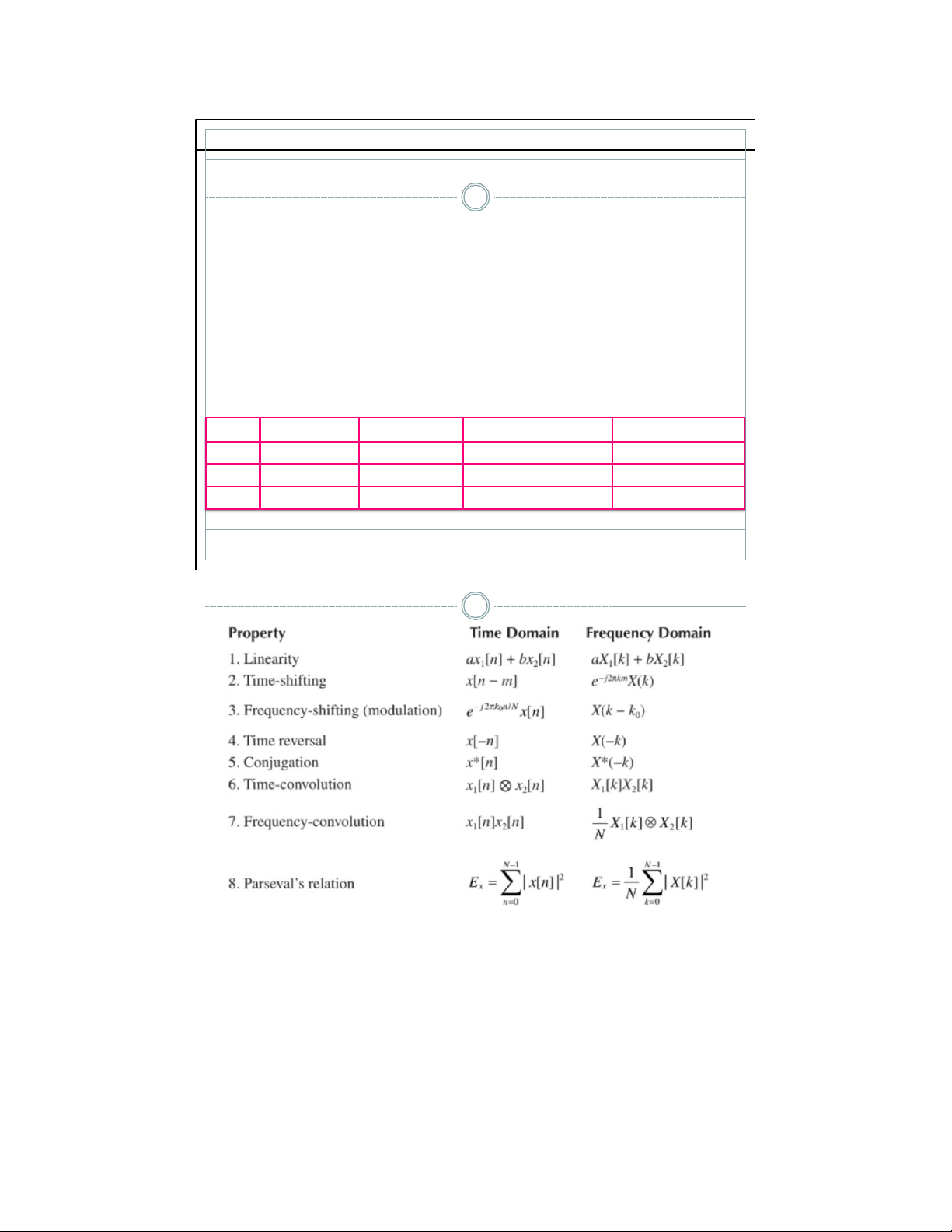
Các tính chất của DFT 35 3 /18/21 lOMoAR cPSD| 59031616 lOMoAR cPSD| 59031616 Bài tập 37
Bài 34: Tìm DFT N điểm cho các chuỗi x[n] sau a) x[n] = δ(n)
b) x[n] = u[n] – u[n – N]
Bài 35: Cho hai chuỗi x(n) và h(n) với số lượng mẫu bằng 4 như sau
theo l ý thuy ế t t ổ ng ch ậ p v ng
b) Tính y(n) s ử d ụ ng DFT a) Tính
Bài 36: Cho chuỗi mũ phức hữu hạn như sau a) Tìm X(Ω) của x(n) b) Tìm DFT N điểm X(k) của x(n) từ X(Ω) 3/18/21