Bài giảng Chương 6 - Biến đổi z và phân tích hệ thống LTI rời rạc môn Tín hiệu và hệ thống | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616 CH ƯƠ NG 6 1 BIẾN ĐỔI z Ngô Thu Trang 4/12/21
Chương 6 – Biến đổi z 2 ▪ Biến đổi z
- Biến đổi z một phía và hai phía
- Miền hội tụ của biến đổi z
- Các tính chất của biến đổi z
- Một số biến đổi z thông dụng ▪ Biến đổi z ngược
▪ Phân tích hệ thống LTI rời rạc bằng biến đổi z
- Biểu diễn hệ thống sử dụng biến đổi z
- Giải phtr sai phân tuyến tính hệ số hằng nhờ biến đổi z lOMoAR cPSD| 59031616 Biến đổi z 3
▪ Biến đổi z là một công cụ toán học quan trọng khác để nghiên cứu
về tín hiệu và hệ thống rời rạc.
▪ Biến đổi z có thể xem là tổng quát hoá biến đổi Fourier thời gian rời rạc
- Biến đổi z áp dụng cho đa dạng các tín hiệu rời rạc khác nhau, bao
gồm cả các tín hiệu không thực hiện được biến đổi Fourier
- Biến đổi z có thể coi là biến đổi Laplace rời rạc → Biến đổi z và biến
đổi Laplace có nhiều đặc trưng tương tự.
- Tuy nhiên, giữa chúng vẫn tồn tại một số khác biệt cơ bản do chúng
mô tả cho hai kiểu tín hiệu và hệ thống khác nhau: rời rạc và liên tục
▪ Biến đổi z chuyển dạng tín hiệu/ phtr sai phân của hệ
thống sang dạng phương trình đại số Biến đổi z 4
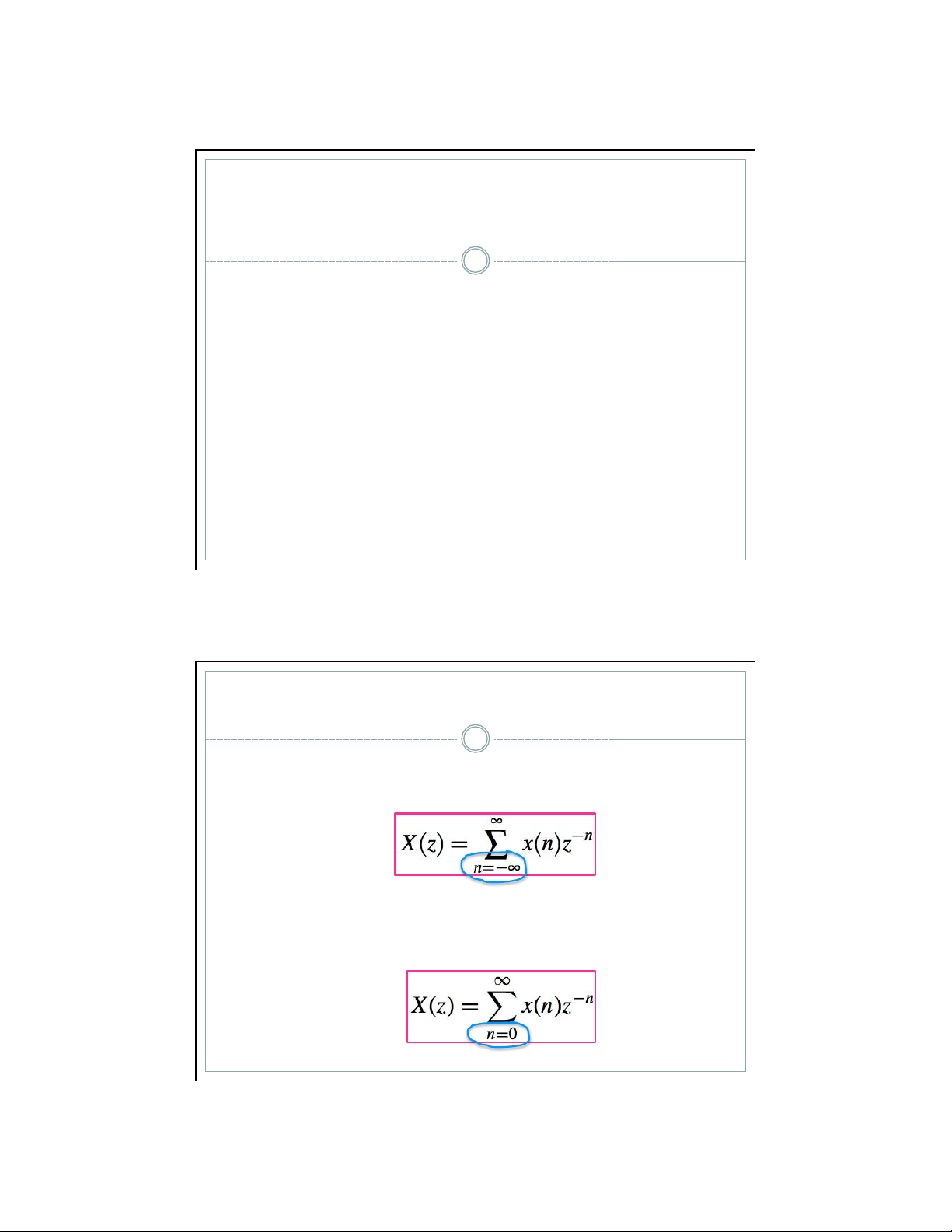
▪ Định nghĩa 1: Biến đổi z hai phía (Bilateral z transform) của tín hiệu x(n)
Biến z phức có dạng biểu diễn lượng giác: z = re jω
▪ Định nghĩa 2: Biến đổi z một phía (Unilateral z transform)
của tín hiệu x(n)
Biến đổi z một phía ứng dụng cho tín hiệu và hệ thống nhân quả x(n) = 0 với n < 0 lOMoAR cPSD| 59031616
Biến đổi z vs Biến đổi Fourier 5
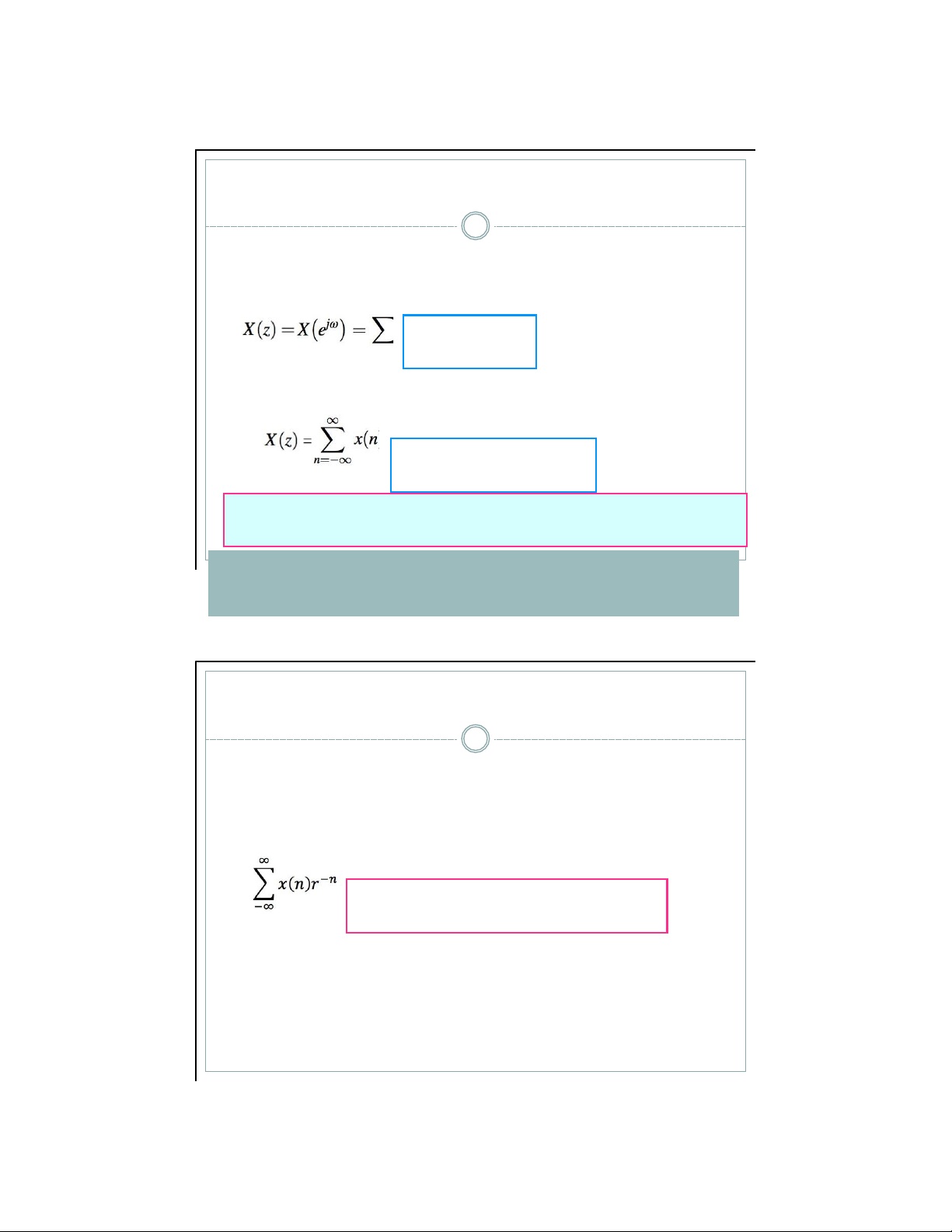
▪ Nếu biến phức z có biên độ r = 1, z = e jω, biến đổi z của x(n) là Biến đổi Fourier thời gian rời rạc
▪ Nếu biến phức z có biên độ r ≠ 1, z = re jω, biến đổi z của x(n) là Biến đổi Fo urier thời gian
rời rạc của x(n)r –n
Biến đổi z của x(n) chính là biến đổi Fourier thời gian rời rạc
của x(n)r –n , (phiên bản x(n) có biên độ tín hiệu thay đổi) 4/12/21 Vùng hội tụ - ROC 6
▪ Đối với một tín hiệu, biến đổi z hội tụ tại một vùng giá trị của z,
được gọi là vùng hội tụ (ROC – Range of Convergence)
▪ Để biến đổi z hội tụ  biến đổi Fourier của tín hiệu x(n)r –n hội tụ
Với mỗi x(n), điều kiện hội tụ xảy ra với ▪ z
một số giá trị r nhất định
được biểu diễn dưới dạng toạ độ cực, đặc trưng bởi bán kính
r và tần số góc ω → vùng hội tụ trên mặt phẳng z là tập các
đường tr n tâm tại gốc toạ độ và bán kính r thoả mãn điều
kiện xác định → điểm khác biệt so với biến đổi Laplace
▪ Biến đổI z suy biến thành biến đổi Fourier khi vùng hội tụ là
đường tr n đơn vị trên mặt phẳng z lOMoAR cPSD| 59031616 Vùng hội tụ - ROC 7
▪ Phương trình đại số mô tả biến đổi z X(z) của hai tín hiệu
x(n) khác nhau có thể hoàn toàn giống nhau ngoại trừ vùng hội tụ khác nhau.
▪ Vùng hội tụ là thành phần không thể thiếu của biến đổi z
để đảm bảo biến đổi z là ánh xạ duy nhất Bi ế n đổ i z X(z) LT x(n) là duy nh ấ t Vùng h ộ i t ụ 4/12/21 Ví dụ 1 8
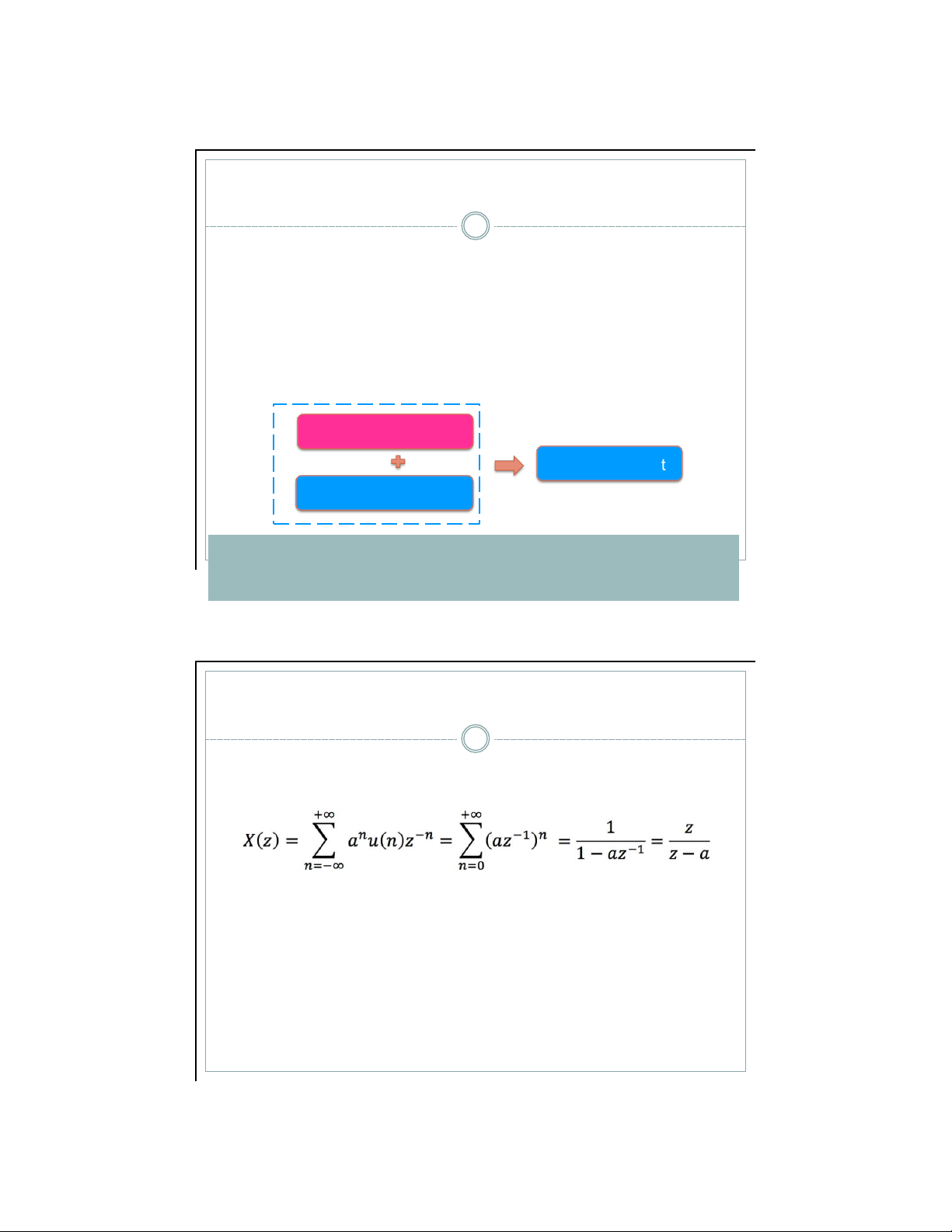
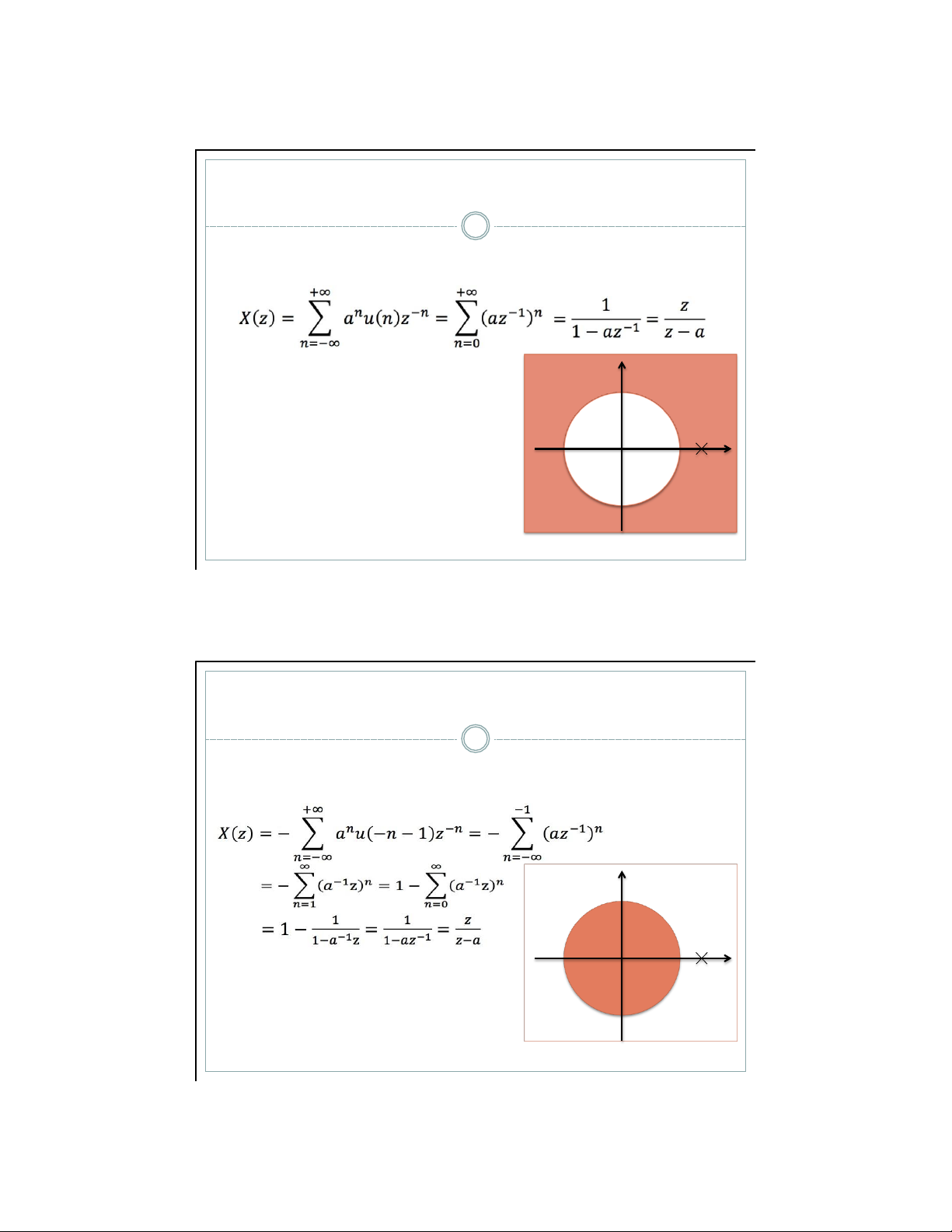
▪ Cho tín hiệu x(n) = a nu(n) với a thực (tín hiệu phía phải), biến đổi z của x(n) là Điểm zero: X(zzr) = toạ độ) Điểm 0 → zzr = 0 (gốc cực: X(zp) = ∞ → zp = a lOMoAR cPSD| 59031616 Ví dụ 1 9
▪ Cho tín hi ệ u x(n) = a n u(n) v ớ i a th ự c ( tín hi ệ u phía ph ả i ) , bi ế n đổ i z c ủ a x(n) là Để X(z) h ộ i t ụ thì Im ROC
| az – 1 | <1  |z| > |a|  r > |a|
• |a| = 1 → x(n) là xung nh ả y b ậ c đơ n v ị → Fourier transform Re
• |a| > 1: ROC không ch ứ a đườ ng tr n 0 |a | 1 zero
đơ n v ị → FT c ủ a x(n) không h ộ i t ụ pole
• |a| < 1: ROC có ch ứ a đườ ng tr n đơ n
v ị → FT c ủ a x(n) có h ộ i t ụ 4 /12/21 Ví dụ 2 10
▪ Cho tín hiệu x(n) = – a –nu(– n – 1) với a thực (tín hiệu phía
trái), biến đổi z của x(n) là Im ROC Re Để X(z) h ộ i t ụ thì 0 |a | 1 zero |a pole
– 1 z| < 1  |z| < |a|  r < |a| lOMoAR cPSD| 59031616 Ví dụ 3 11
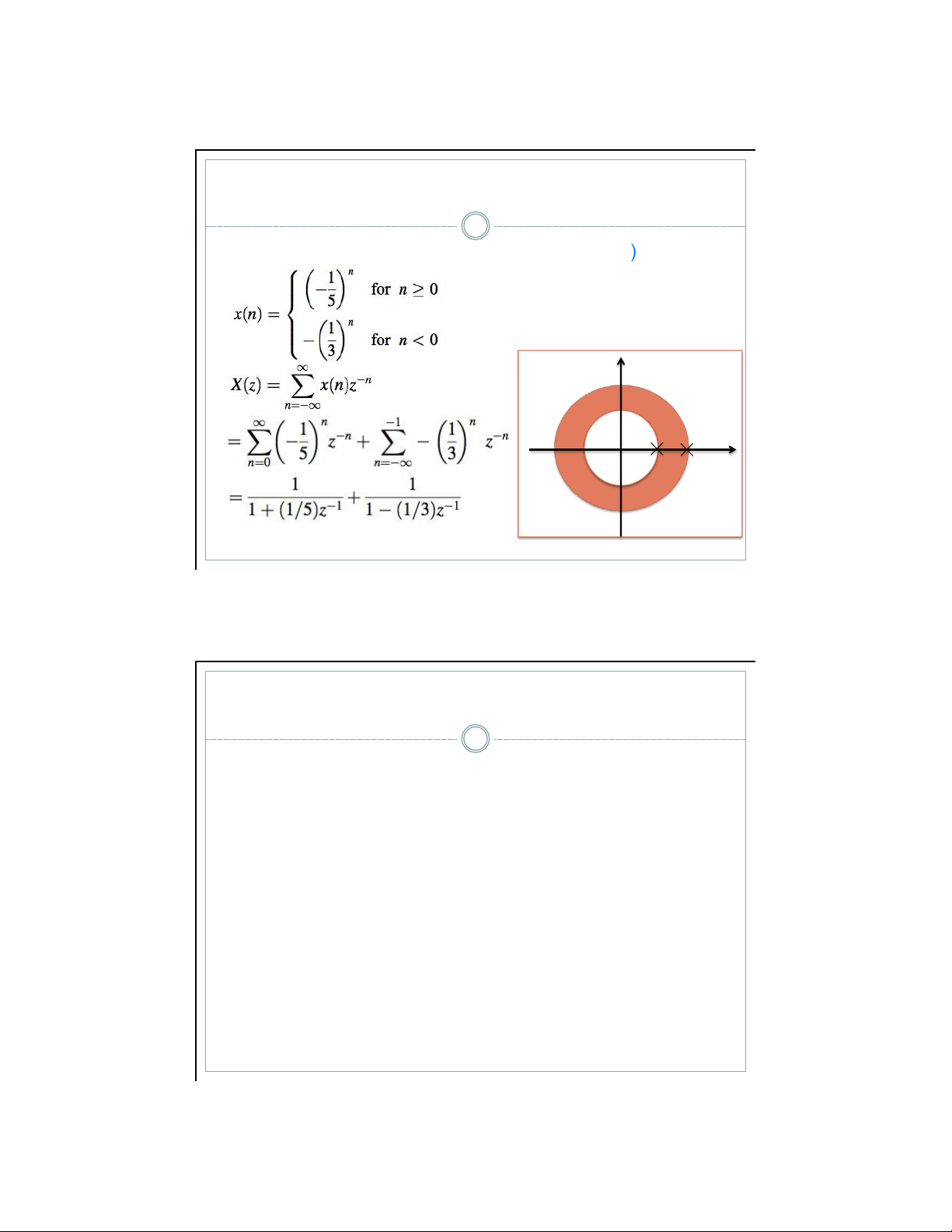
▪ Bi ế n đổ i z c ủ a tín hi ệ u hai phía ( two-side signa ) l x(n) s ẽ là Để X(z) h ộ i t ụ thì
|1/5| < |z| và |z| > |1/3| Im ROC 0 1 /5 1 /3 Re zero poles 4/12/ 21 Tính chất của ROC 12
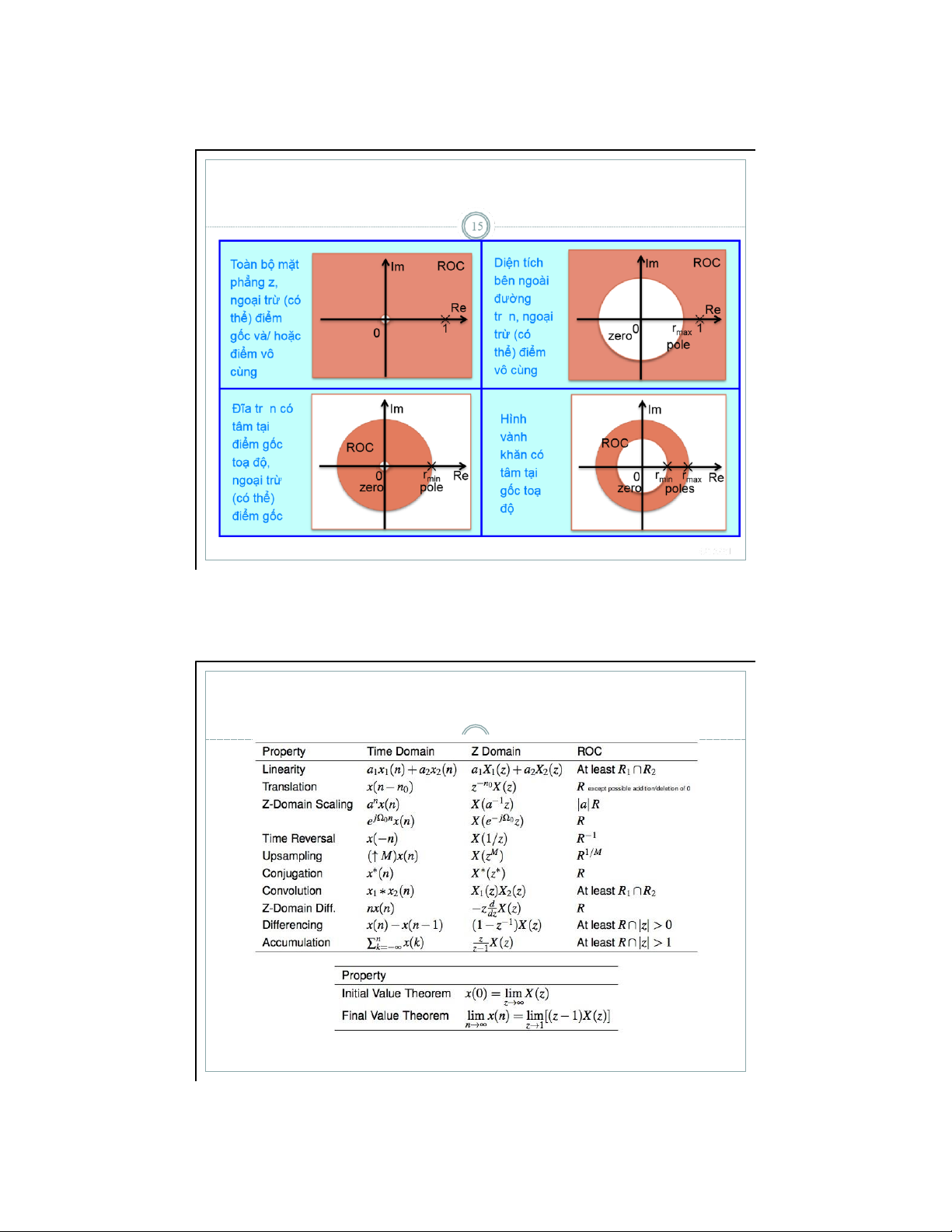
1. ROC của X(z) gồm các đường tr n đồng tâm có tâm tại gốc của mặt phẳng phức
2. ROC không chứa bất kì điểm cực nào.
3. Với x(n) là tín hiệu giới hạn, tức là x(n) ≠ 0 với N1 ≤ n ≤ N2, và
X(z) hội tụ tại một vài giá trị của z thì ROC là toàn bộ mặt phẳng z
ngoại trừ (có thể) z = 0 và/ hoặc z = ∞
4. Với x(n) là tín hiệu phía trái, tức là x(n) = 0 với t > N1 > -∞, và X(z) hội
tụ tại một vài giá trị của z thì ROC là phần diện tích bên trong đường tr
n |z| = rmin của mặt phẳng z ngoại trừ (có thể) z = 0, tức là ROC có
dạng: |z| < rmin hoặc 0 < |z| < rmin với rmin = min{abs(poles)} lOMoAR cPSD| 59031616 Tính chất của ROC 13
5. Với x(n) là tín hiệu phía phải, tức là x(n) = 0 với t < N2 < ∞, và
X(z) hội tụ tại một số giá trị của z thì ROC là phần diện tích
bên ngoài đường tr n |z| = rmax của mặt phẳng z ngoại trừ
(có thể) z = ∞, tức là ROC có dạng:
|z| > rmax hoặc ∞ > |z| > rmax với rmax = max{abs(poles)}
6. Với x(n) là tín hiệu hai phía và X(z) hội tụ tại một số giá trị
của z thì ROC là phần diện tích hình vành khăn trên mặt
phẳng z nằm giữa hai đường tr n |z| = rmax và |z| = rmin và
không chứa bất kì điểm cực nào, tức là ROC sẽ có dạng:
rmin < |z| < rmax với rmax,min = abs(poles) Tính chất của ROC 14
Nếu X(z) của x(n) có dạng phân số thì ROC của x(n) có các tính chất sau:
1. ROC bị giới hạn bởi các điểm cực hoặc mở rộng tới vô cùng
2. Nếu x(n) là tín hiệu phía phải thì ROC là vùng diện tích bên
ngoài đường tr n có bán kính là điểm cực lớn nhất. Và nếu
x(n) là nhân quả, x(n) = 0, n < 0, thì ROC có chứa z = ∞
3. Nếu x(n) là tín hiệu phía trái thì ROC là vùng diện tích bên
trong đường tr n có bán kính là điểm cực nhỏ nhất. Và nếu
x(n) là phản nhân quả, tức là x(n) = 0, n > 0, thì ROC có chứa z = 0 lOMoAR cPSD| 59031616 Các dạng của ROC
Tính chất của biến đổi z 16 lOMoAR cPSD| 59031616
Một số cặp biến đổi z 17 4 /12/21
Biến đổi z của một số tín hiệu 18
▪ Nếu x(n) là tín hiệu phức với biến đổi z là X(z) thì
Z[Re{x(n)}] = ½[X(z) + X*(z*)] với ROC không đổi
Do Re{x(n)} = ½[x(n) + x*(n)]; → áp dụng biến đổi z hai vế, áp
dụng tính chất tuyến tính → đpcm
▪ Nếu x(n) là tín hiệu phức với biến đổi z là X(z) thì
Z[Im{x(n)}] = (1/2j)[X(z) – X*(z*)] với ROC không đổi
Do Im{x(n)} = (1/2j)[x(n) – x*(n)];
→ áp dụng biến đổi z hai vế, áp dụng tính chất tuyến tính → đpcm lOMoAR cPSD| 59031616
Biến đổi z của một số tín hiệu 19
▪ Tìm bi ế n đổ i z c ủ a tín hi ệ u x(n) sau
▪ Áp d ụ ng đị nh ngh ĩ a , thu đượ c 4/12/21 Bài tập 20
Bài 48: Tìm biến đổi z, vẽ giản đồ cực - không và các giá trị
ban đầu, giá trị cuối cùng cho các tín hiệu sau a) x(n) = an + 1u(n + 1) b) x(n) = nan – 1u(n)
c) x(n) = – anu(– n – 1)
c) x(n) = (1/2)nu(n) + (1/3)nu(n) d) x(n) = a–nu(– n – 1)
e) x(n) = (1/3)nu(n) + (1/2)nu(– n –
1) Bài 49: Tìm biến đổi
z và vẽ giản đồ cực – không của tín hiệu x(n)
Bài 50: Cho tín hiệu x(n) = a|n| a > 0
a) Vẽ tín hiệu x(n) với a > 1 và a < 1
b) Tìm X(z) và vẽ giản đồ cực - không và ROC với a > 1 và a < 1 lOMoAR cPSD| 59031616
Biến đổi z ngược (Inverse z transform) 21
▪ Định nghĩa 3: Biến đổi z ngược (Inverse – z transform) của tín hiệu X(z)
Với Γ cho biết tích phân được tính theo đường bao tr n khép
kín ngược chiều kim đồng hồ có tâm tại gốc và bán kính r
sao cho Γ nằm trong ROC của X(z)
▪ Thực tế, để tìm x(n) từ X(z) thì công thức biến đổi z ngược ít được sử dụng.
▪ Nếu X(z) có dạng phân số thì triển khai phân số từng phần
được áp dụng để thực hiện biến đổi z ngược 4/12/21
Cách tính biến đổi z ngược 22
▪ Áp dụng lý thuyết phần dư Cauchy (Cauchy’s residue theorem)
▪ Áp dụng khai triển phân số từng phần (Partial fraction
expansion) cho X(z) có dạng tỉ số
▪ Áp dụng khai triển chuỗi công suất (Power series
expansion) bằng cách thực hiện “long division” của tử
số cho mẫu số, ta thu được dạng của X(z) như sau lOMoAR cPSD| 59031616
Lý thuyết phần dư Cauchy 23
▪ Theo lý thuyết phần dư Cauchy, trong trường hợp X(z) có
dạng tỉ số thì biến đổi z ngược của X(z) sẽ là:
Z– 1[X(z)] = x(n) = tổng của các phần dư của hàm [X(z)zn – 1]
tại tất cả các cực pi được bao bởi đường tr n C nằm trong
ROC của X(z) và có chứa gốc.
▪ Phần dư tại một điểm cực đơn có dạng
▪ Phân d ự t ạ i m ộ t đ i ể m c ự c có b ộ i b ậ c m có d ạ ng 4 /12/21 Ví dụ 4 24
▪ V ớ i x(n) là tín hi ệ u nhân qu ả có
▪ Do tín hi ệ u nhân qu ả → n > 0 ▪ X(z) z n – 1 có hai c ự c đơ n t ạ i z = 0.8 và z = – 0.4 T ạ i n = 0, có thêm c ự c t ạ i g ố c . → Tìm x(n) Ví dụ 5 25
▪ V ớ i x(n) là tín hi ệ u nhân qu ả có Tìm x(n)?
▪ Do tín hiệu nhân quả → n > 0 và X(z)zn –1 có cực bội bậc 3 tại z = 1
Cách tính biến đổi z ngược 26
▪ Khai triển phân số từng phần khi X(z) có dạng tỉ số
- Bước 1: Chia hai vế của X(z) cho z
- Bước 2: Đưa đa thức thu được ở bước 1 về dạng
tổng của các đa thức tỉ lệ bậc thấp có dạng cơ bản
- Bước 3: Tra bảng để tìm dạng tín hiệu trong miền
thời gian của từng đa thức thành phần
- Bước 4: Tổ hợp các kết quả để thu được tín hiệu
trong miền thời gian cần tìm
Khai triển phân số từng phần 27
▪ Bi ể u th ứ c X(z) v ớ i các đ i ể m c ự c đơ n có d ạ ng sau
▪ Áp d ụ ng khai tri ể n phân s ố t ừ ng ph ầ n , X(z) đượ c vi ế t l ạ i
▪ Khi đ ó , X(z) s ẽ là 4 /12/21
Khai triển phân số từng phần 28
▪ Biểu thức X(z) có điểm cực kép bậc r thì khai triển X(z)/z sẽ
bao gồm các đa thức bậc thấp sau với
▪ Biểu thức X(z) có bậc của tử số lớn hơn bậc của mẫu số
thì X(z) vẫn được áp dụng khai triển phân số từng phần và có dạng sau 6 29 4 /12/21 Ví dụ 7 30 lOMoAR cPSD| 59031616 Ví dụ 7 31 4 /12/21 Ví dụ 8 32 59031616 33 4 /12/21
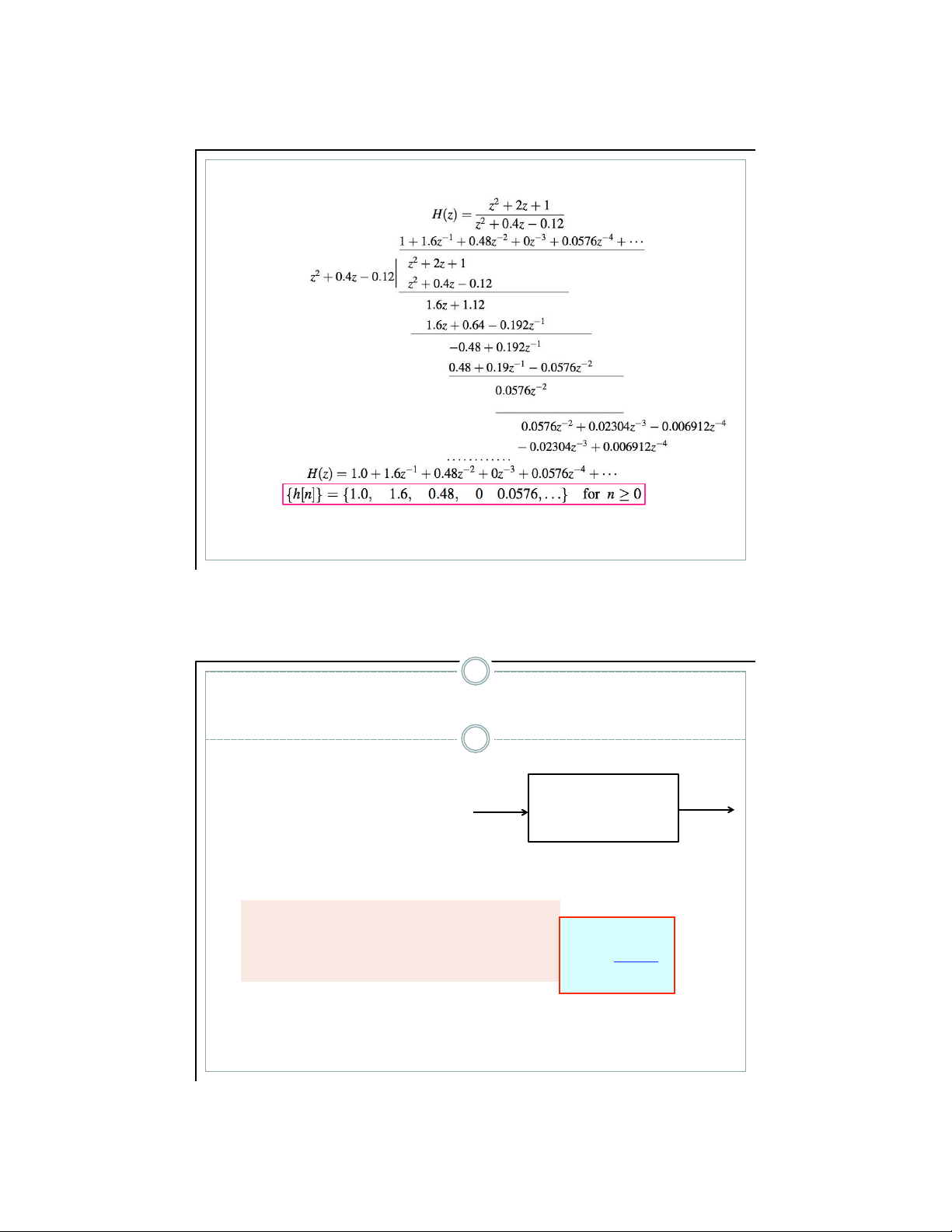
Khai triển chuỗi công suất 34 59031616
▪ V ớ i h(n) là nhân qu ả và có Tìm h(n)
Phân tích hệ thống LTI thời gian rời rạc 35 bằng biến đổi z
▪ Một hệ thống DT-LTI có mối quan hệ giữa đầu ra y(n) với đầu vào
x(n) và đáp ứng ứng h(n) như sau y(n) = x(n) h(n) * x(n) Hệ thống LTI y(n)
▪ Áp dụng biến đổi Laplace h(n) ↔ H(z) Y(z) X(z) Y(z) = X(z) H(z)
H(z): hàm truyền đạt hay hàm hệ thống
(system function) của hệ thống DT-LTI. Y(z)
Đáp ứng xung vs hàm truyền đạt: cặp H(z)= biến đổi z. X(z) 59031616
Phân tích hệ thống DT – LTI bằng biến đổi z 36 ▪
Hệ thống DT-LTI là nhân quả thì h(n) = 0 ∀n < 0
→ h(n) là tín hiệu phải nên ROC của H(z) phải là phần
diện tích bên ngoài đường tr n rmax trên mặt phẳng z |z| > rmax ▪
Hệ thống DT-LTI là ổn định thì →
ROC của H(z) phải chứa đường tr n đơn vị (|z| = 1)
Nếu hệ thống LTI thời gian rời rạc muốn là nhân quả và ổn
định thì tất cả các điểm cực của H(z) phải nằm bên trong
đường tr n đơn vị, tức là rmax < 1 với rmax = max(Re(poles)) lOMoAR cPSD| 59031616
Phân tích hệ thống DT – LTI bằng biến đổi z 37
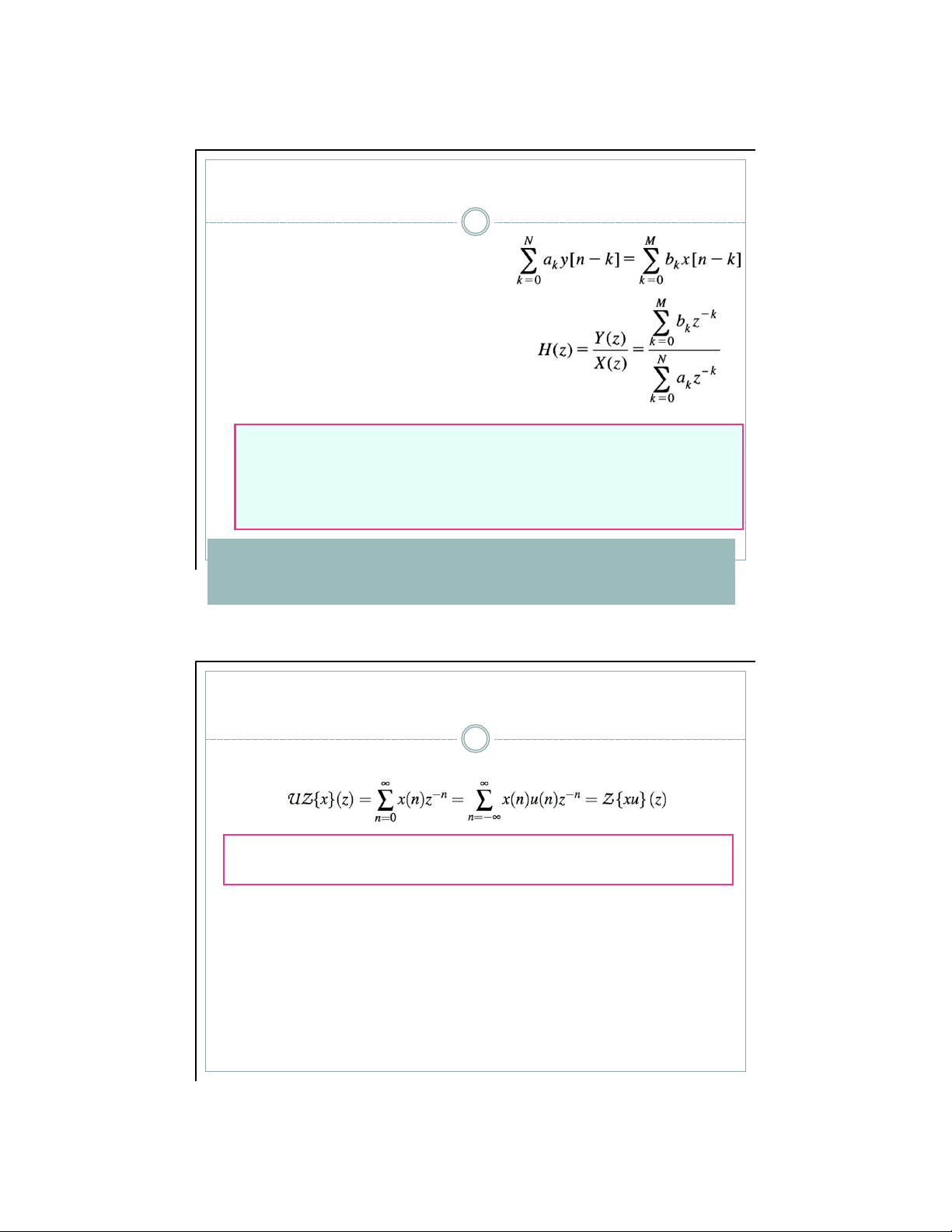
▪ H ệ th ố ng DT-LTI đượ c đặ c tr ư ng
b ở i phtr sai phân h ệ s ố h ằ ng
▪ Áp d ụ ng bi ế n đổ i z hai phía , thu
đượ c hàm truy ề n đạ t c ủ a h ệ th ố ng
Các bước giải phtr vi phân sử dụng biến đổi z
1. Áp dụng biến đổi z cho cả hai phía của phtr
2. Đưa ra phtr đại số đặc trưng cho Y(z) trong miền z
3. Tìm biến đổi Laplace ngược của Y(z) để thu được y(n) 4/12/21
Biến đổi z một phía 38
▪ Mối quan hệ giữa biến đổi z một phía và hai phía
Biến đổi z một phía của x(n) đơn giản là biến đổi z hai phía của tín hiệu x(n)u(n)
▪ x(n)u(n) là tín hiệu phải nên ROC của biến đổi z một phía luôn là phần
diện tích bên ngoài đường tr n rmax → không cần ghi ra ROC trong các biến đổi z một phía.
▪ Biến đổi z một phía ngược:
- Có cùng biểu thức như trong trường hợp biến đổi z hai phía
- Chỉ tồn tại biến đổi z một phía ngược cho tín hiệu nhân quả
- Nếu tín hiệu không nhân quả, chỉ tìm được biến đổi z ngược cho x(n) với n > 0