Đề kiểm tra giữa kỳ số 01 môn Tín hiệu và hệ thống | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616
HỌC VIỆN C NG NGHỆ BƯU CHÍNH VIỄN TH NG
ĐỀ KIỂM TRA GIỮA KỲ KHOA: Viễn th ng 1
(H nh thức thi viết)
BỘ M N: T n hiệu v hệ thống
Học phần: T n hiệu hệ thống Lớp:………..
Thời gian thi: 90 phœt
Hệ ào tạo: Đại học Đề số 01 C
u 1 (2 iểm): Cho t n hiệu sau: a) Vẽ dạng t n hiệu
b) T n hiệu x(t) l t n hiệu năng lượng hay c ng suất. Tính năng lượng v c ng suất của t n hiệu.
C u 2 (2 iểm): Thực hiện biến ổi Fourier v vẽ dạng phổ biên ộ của cÆc t n hiệu sau với a=2
a) Xung chữ nhật x(t) = П(2𝑡−𝑎)(sin2𝜋𝑎𝑡) 3
b)Xung tam giÆc x(t) = ˄(3𝑡−𝑎) 𝑎
C u 3 (3 iểm): Tìm áp ứng ầu ra của hệ thống bằng biến ổi Fourier ược ặc trưng bởi
phương trình sai phân sau:
y(n) - 2y(n-1) = 2x(n) + x(n-1) với x(n) = cos 𝜋n 4 C u 4 (3 iểm)
Cho hệ thống nh n quả ược m tả bởi phương trình sai phân sau biết áp ứng
xung của hệ thống l nh n quả v giÆ trị ban ầu y(-2) = y(-1) = 0 y(n-2) – 2y(n-1) + y(n) = x(n)
a) Xác ịnh áp ứng xung của hệ thống
b) Xác ịnh áp ứng ầu ra của hệ thống nếu ầu v o hệ thống
Ghi chœ: Sinh viên ược tham khảo Bảng t nh chất v cÆc biến ổi cơ bản.
H Nội, ngày…….tháng……năm 2024 lOMoAR cPSD| 59031616
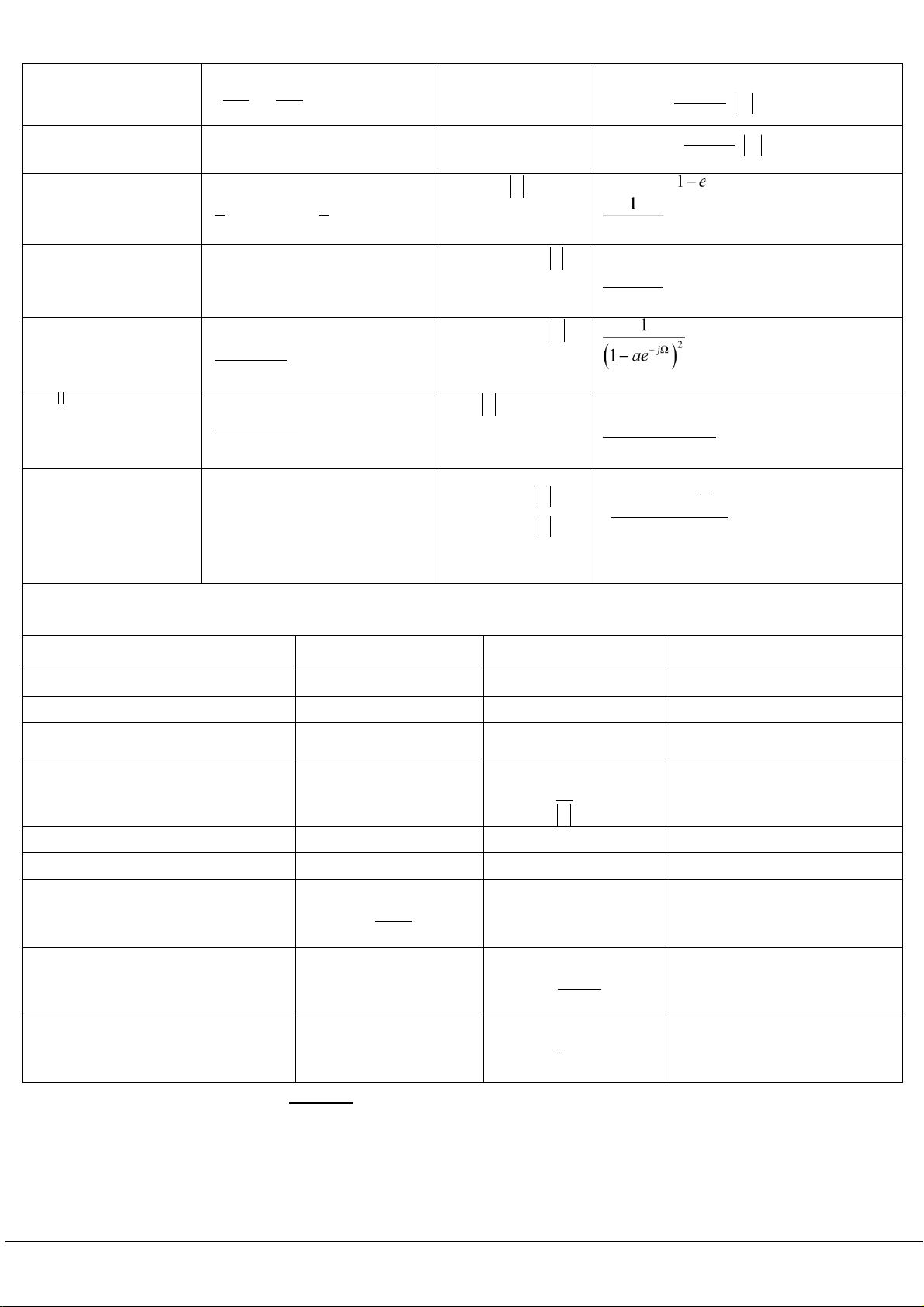
Các tính chất của biến đổi Fourier thời gian liên tục Operation Function Fourier transform Linearity
a1 1w w( )t + a2 2( )t
aW f1 1( )+a W2 2( )f Time delay w(t -Td)
W f e( ) - j Twd 1 W æ öç Scale change w( )at ÷af a è ø Conjugation w*( )t W*(-f ) Duality W t( ) w(-f ) Real signal frequency 1 translation
[w( )t w w q( )t cos(
ée W fjq ( - fc )+e- jqW f( + fc ct + ) isreal] )ûù 2ë Complex signal w frequency translation ( )t e jwct W f( - fc) Band-pass signal Re{g t e( ) } éë ùû jwct dnw( )t Differentiation
( j2pf )nW f( ) dt n t Integration òwll( )d -¥ ∞ (t)∗ω (t)= Convolution W f W 1 2 1( ) 2( )f ∫ ¥ Multiplicationb w w1( )t2( )t
W f1( )*W2( )f = òW1( )lW2( f -ll)d -¥ n Multiplication tnw( )t (- j2p)-n d W f( )n df
Các tính chất của biến đổi Fourier thời gian rời rạc Property Sequence Fourier Transform Periodicity x n[ ] X(W+2 )p=X( )W Linearity ax n a x n1 1[ ]+ 2
aX1 1( )W +a X2 2( )W 2[ ] Time shifting xn n[ - 0]
e- j nW 0 X( )W Frequency shifting e xnjW0n [ ] X(W-W0) Conjugation x n*[ ] X*(-W) Time reversal x n[- ] X(-W) lOMoAR cPSD| 59031616 Time scaling
ìx n m[ / ] if n = km X m( W)
x( )m [ ]n =í if n ¹ km î0 dX( )W j
Frequency differentiation nxn[ ] dW First difference xn xn[ ]- -[ 1]
(1-e- jW) ( )X W ¥ p dX ( ) ( )0 W + Accumulation å x k[ ] 1 W£p - jW X ( )W 1- k=-¥ e Convolution x n x n1[ ]* 2[ ] X1( )W WX2( ) 1 Multiplication x n x n1[ ] [ ]2 X ( )WÄ WX ( ) 2p 1 2 Real sequence
xn x n x n[ ]= e[ ]+ o[ ]
X( )W = A( )W + jB( )W Even component x ne[ ]
Re[ ( )]X W =A( )W Odd component x no[ ]
jIm[ ( )]X W = jB( )W
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào.
Các cặp biến đổi Fourier thời gian liên tục
Các cặp biến đổi Fourier thời gian rời rạc
Time Waveformw( )t Spectrum W(f) x n[ ] X( )W Pæ öç ] d[ ]n 1 ÷Tt T Sa[ (pft) è ø Ùæ T Sa[ (pft)]2 d(n n- 0) e- j nW 0 öç ÷Tt è ø ì+ >1, t 1 1 d( )f + xn[ ] 1= 2pd( )W W£,p 0 u t( )=í < 0 2 j2pf î0, t ì+ >1, t 0 1 e jW0n 2pd(W-W W W £ ) p 0 ,, 0
sgn( )t =í-1, t < 0 î jpf 1 d( )f cosW0n pd[ (W-W )+d(W+W W W £ ) 0 0 ], , p 0 d(t -to)
e- j2pft0 sinW0n
-jpd[ (W-W - W ) d( +W W W £ ) 0 0 ], , p 0 lOMoAR cPSD| 59031616 Sa(2pWt) 1 æ f ö un[ ] 2W Pçè2W ø÷
pd( )W + 1- jW , W£p 1-e e j(w j0t+ )
ejjd(f - f0) - - -u n[ 1] -pd( )W + 1- jW , W£p cos(w jct + ) a un an [ ],<1
1e jj( f - fc )+ 1e- jj( f + fc ) 2 2 1-ae- jW e-p(t t/ )2 1 0 t e0 -p( ft0)2 -au nn [- -1], a >1 1-ae- jW
ìe-t T/ , t > 0 T (n+1)a un an [ í ],<1 î 0, t < 0 1 2+ j pfT e-t T/ 2T a an,<1 1-a2 1 (2+ pfT)2 1 2- acosW+a2 k=¥ n=¥ ì sinêWæçèN + å 1 d(t -kT)
xn[ ]=ïí1 n N£ f åd 1 ïî0 1 ö 0 ( f -nf0), 2 ø÷ùúû k=-¥ n N> n=-¥ 1 é ë where f0 =1/T sin(W / 2)
Tính chất của biến đổi Laplace Property Time Domain Laplace Domain ROC Linearity
a x t1 1( )+a x t2 2( )
a X s1 1( )+a X s2 2( ) Atleast R1 ÇR2 Time-Domain Shifting x t( -t0) e X s-st0 ( ) R
Laplace-Domain Shifting e x ts t0 ( ) X s s( - 0) R+Re{ }s0 1 s
Time/Frequency-Domain Scaling x at( ) X( ) aR a a Conjugation x t*( ) X s* *( ) R
Time-Domain Convolution x1*x t2( ) X s X s1( ). 2( ) Atleast R1 ÇR2 dx t( )
Time-Domain Differentiation sX s( ) AtleastR dt dX s( )
Laplace-Domain Differentiation -tx t( ) R ds t x d( 1 ò
Time-Domain Integration )t t X s( )
AtleastRÇ{Re{ }s >0} -¥ s
Ghi chú: - Sinh viên không được trao đổi bài dưới bất kì hình thức nào.