Báo cáo bài tập lớn lý thuyết mật mã - Đề tài Triển khai hệ mật elgamal trên matlab | Trường Đại học Bách khoa Hà Nội

lOMoARcPSD| 41967345
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN ĐIỆN TỬ - VIỄN THÔNG ----- ----- BÁO CÁO BÀI TẬP LỚN LÝ THUYẾT MẬT MÃ Đề tài:
TRIỂN KHAI HỆ MẬT ELGAMAL TRÊN MATLAB Giảng viên hướng dẫn : TS. Hán T rọng Thanh
Nhóm sinh viên thực hiện : Nhóm số 7 .Lê B 1 á Tuấn Anh
MSSV: 20140088 – Điện tử 10 K59 2 .Tăng Bá Phương Duy
MSSV: 20140747 – Điện tử 10 K59 3 .Nguyễn Hữu Dương
MSSV: 20140873 – Điện tử 08 K59 4 .Phạm Bá Thông
MSSV: 20144316 – Điện tử 05 K59 5 .Nguyễn Quang Toàn
MSSV: 20144543 – Điện tử 02 K59 1 lOMoARcPSD| 41967345 Hà Nội – 05/2017 MỤC LỤC
MỤC LỤC ....................................................................................................................... 2
DANH MỤC HÌNH ẢNH ............................................................................................... 4
DANH MỤC BẢNG BIỂU ............................................................................................. 5
BẢNG PHÂN CÔNG CÔNG VIỆC ............................................................................... 6
LỜI NÓI ĐẦU ................................................................................................................. 6
Phần 1. Trình bày bài tập lớn ........................................................................................... 7
CHƯƠNG I – LÝ THUYẾT VỀ HỆ MẬT ELGAMAL ................................................ 7
1.1. Giới thiệu chung .................................................................................................... 7
1.1.1. Mục tiêu ......................................................................................................... 7
1.1.2. Giới thiệu về hệ mật mã ................................................................................. 7
1.2. Hệ mật mã Elgamal ............................................................................................... 8
1.2.1. Giới thiệu chung về hệ mật Elgamal ............................................................. 8
1.2.2. Mã hóa và giải mã hệ mật Elgamal ............................................................... 9
1.2.3. Thám mã hệ mật Elgamal ............................................................................ 10
1.2.4. Quản lý khóa ................................................................................................ 14
1.2.5. Độ an toàn .................................................................................................... 14
1.2.6. Ưu & nhược điểm của hệ mật Elgamal ....................................................... 15
CHƯƠNG II – TRIỂN KHAI HỆ MẬT ELGAMAL TRÊN MATLAB ..................... 16
2.1. Mô hình mô phỏng............................................................................................... 16
CHƯƠNG III – KẾT LUẬN ......................................................................................... 18
3.1. Kết quả đạt được : ................................................................................................ 18 lOMoARcPSD| 41967345
3.2. Kết quả chưa đạt được: ........................................................................................ 18
3.3. Thuận lợi : ............................................................................................................ 18
3.4. Khó khăn .............................................................................................................. 18
Phần 2. Tài liệu tham khảo ............................................................................................ 18
Phần 3. Phụ lục.............................................................................................................23 3 lOMoARcPSD| 41967345 DANH MỤC HÌNH ẢNH
[1] Hình 1. Quá trình mã hóa và giải mã............................................................Trang 09
[2] Hình 2: Sơ đồ mã hóa và giải mã hệ mật Elgamal........................................Trang 11
[3]Hình 3: Sơ đồ quản lý khóa............................................................................Trang 17
[4] Hình 4: Giao diện mô phỏng.........................................................................Trang 19
[5] Hình 5: Giao diện lập mã..............................................................................Trang 20
[6] Hình 6: Giao diện giải mã.............................................................................Trang 20 lOMoARcPSD| 41967345
DANH MỤC BẢNG BIỂU 5 lOMoARcPSD| 41967345
BẢNG PHÂN CÔNG CÔNG VIỆC STT Họ và tên MSSV Công việc được giao Điểm đánh giá của cả nhóm (thang 10) 1 Lê Bá Tuấn Anh
20140088 Tìm tài liệu và đọc hiểu 9 lý thuyết. 2
Tăng Bá Phương Duy 20140747 Module hóa lý thuyết 9 thành các sơ đồ. 3
Nguyễn Hữu Dương 20140873
Thiết kế lưu đồ thuật 9 toán dựa trên Module. 4 Phạm Bá Thông 20144316
Cài đặt thuật toán trên 9 Matlab. 5
Nguyễn Quang Toàn 20144543 Tổng hợp, hiệu chỉnh và 9 viết báo cáo LỜI NÓI ĐẦU
Trong mọi thời đại xã hội loài người, vấn đề bảo mật thông tin luôn được quan tâm
lớn. Từ xa xưa, con người đã sáng tạo ra các hệ mật mã cổ điển để đáp ứng nhu cầu bảo
mật thông tin. Mật mã học là một ngành có lịch sử từ hàng nghìn năm nay. Trong phần
lớn thời gian phát triển của mình (ngoại trừ vài thập kỷ trở lại đây), lịch sử mật mã học
chính là lịch sử của những phương pháp mật mã học cổ điển - các phương pháp mật mã
hóa với bút và giấy, đôi khi có hỗ trợ từ những dụng cụ cơ khí đơn giản.
Vào đầu thế kỷ 20, sự xuất hiện của các cơ cấu cơ khí và điện cơ, chẳng hạn như máy
Enigma, đã cung cấp những cơ chế phức tạp và hiệu quả hơn cho việc mật mã hóa. Sự
ra đời và phát triển mạnh mẽ của ngành điện tử và máy tính trong những thập kỷ gần
đây đã tạo điều kiện để mật mã học phát triển nhảy vọt lên một tầm cao mới. Rất nhiều
hệ mật mã hiện đại đã lần lượt ra đời dựa trên cơ sở đại số Modulo và các thuật toán
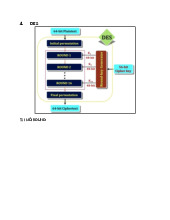
logarithm rời rạc… Năm 1975, IBM công bố Hệ mật DES, khởi đầu cho các hệ mật mã
hiện đại. Tiếp theo đó là sự ra đời của các hệ mật mã AES, RSA, DSA, Elgamal… Hệ
mật Elgamal được đề xuất vào năm 1984 trên cơ sở của bài toàn Logarit rời rạc, là một
hệ mật mã rất khó thám mã.
Dựa trên sự hướng dẫn của Thầy, các thành viên trong nhóm đã tiến hành tìm hiểu
về các thuật toán thám mã và giải mã hệ mật mã hóa Elgamal, nhóm tiến hành xây dựng
mô phỏng hệ mật Elgamal trên phần mềm Matlab. Báo cáo cũng như phần mô phỏng
của nhóm sẽ không tránh khỏi những thiếu sót, rất mong được sự góp ý chỉ dẫn của Thầy! lOMoARcPSD| 41967345
Phần 1. Trình bày bài tập lớn
CHƯƠNG I – LÝ THUYẾT VỀ HỆ MẬT ELGAMAL
1.1. Giới thiệu chung 1.1.1. Mục tiêu
1.1.2. Giới thiệu về hệ mật mã -
Ta biết rằng tin truyền trên mạng rất dễ bị lấy cắp. Để đảm bảo việc truyền
tin an toàn người ta thường mã hoá thông tin trước khi truyền đi. Việc mã hoá
thường theo quy tắc nhất định gọi là hệ thống mật mã. -
Một hệ thống mật mã là một hệ bao gồm 5 thành phần (P, C, K, E, D) thỏa mãn các tính chất sau:
• P (Plaintext) là tập hợp hữu hạn các bản rõ có thể.
• C (Ciphertext) là tập hợp những bản mã có thể.
• K (Key) là tập hợp các bản khóa có thể.
• E (Encrytion) là tập hợp các quy tắc mã hóa có thể.
• D (Decrytion) là tập hợp các quy tắc giải mã có thể. -
Quá trình mã hóa được tiến hành bằng cách áp dụng hàm toán học E lên thông
tin P, vốn được biểu diễn dưới dạng số, để trở thành thông tin đã mã hóa C. -
Quá trình giải mã được tiến hành ngược lại: áp dụng hàm D lên thông tin C để
được thông tin đã giải mã (P).
Hình 1: Quá trình mã hóa và giải mã. -
Thám mã (phá mã) là tìm những điểm yếu của hệ thống những điểm yếu hoặc
không an toàn trong phương thức mật mã hóa. Thám mã có thể được thực hiện
bởi những kẻ tấn công ác ý, nhằm làm hỏng hệ thống; hoặc bởi những người 7 lOMoARcPSD| 41967345
thiết kế ra hệ thống (hoặc những người khác) với ý định đánh giá độ an toàn của hệ thống. - Hệ mật mã gồm:
• Hệ mật mã đối xứng (hay còn gọi là mật mã khóa bí mật): là những hệ mật dùng
chung một khoá cả trong quá trình mã hoá dữ liệu và giải mã dữ liệu. Do đó khoá
phải được giữ bí mật tuyệt đối. Một số thuật toán nổi tiếng trong mã hoá đối xứng
là: DES, Triple DES(3DES), RC4, AES…
• Hệ mật mã bất đối xứng (hay còn gọi là mật mã khóa công khai): Các hệ mật
này dùng một khoá để mã hoá sau đó dùng một khoá khác để giải mã, nghĩa là
khoá để mã hoá và giải mã là khác nhau. Các khoá này tạo nên từng cặp chuyển
đổi ngược nhau và không có khoá nào có thể suy được từ khoá kia. Khoá dùng để
mã hoá có thể công khai nhưng khoá dùng để giải mã phải giữ bí mật. Do đó
trong thuật toán này có 2 loại khoá: Khoá để mã hoá được gọi là khóa công
khaiPublic Key, khoá để giải mã được gọi là khóa bí mật - Private Key. Một số
thuật toán mã hoá công khai nổi tiếng: Diffle-Hellman, RSA, Rabin, Elgamal…
1.2. Hệ mật mã Elgamal
1.2.1. Giới thiệu chung về hệ mật Elgamal
- Hệ Elgamal là một hệ mật mã công khai
- Hệ Elgamal dựa trên bài toán logarithm rời rạc. Tính an toàn của nó phụ thuộc
vào độ phức tạp của bài toán logarithm.
- Hệ Elgamal là 1 biến thể của sơ đồ phân phối khóa Diffie-Hellmal, được đưa ra năm 1984.
- So với RSA, Hệ Elgamal không có nhiều rắc rối về vấn đề quyền sử dụng. lOMoARcPSD| 41967345
1.2.2. Mã hóa và giải mã hệ mật Elgamal
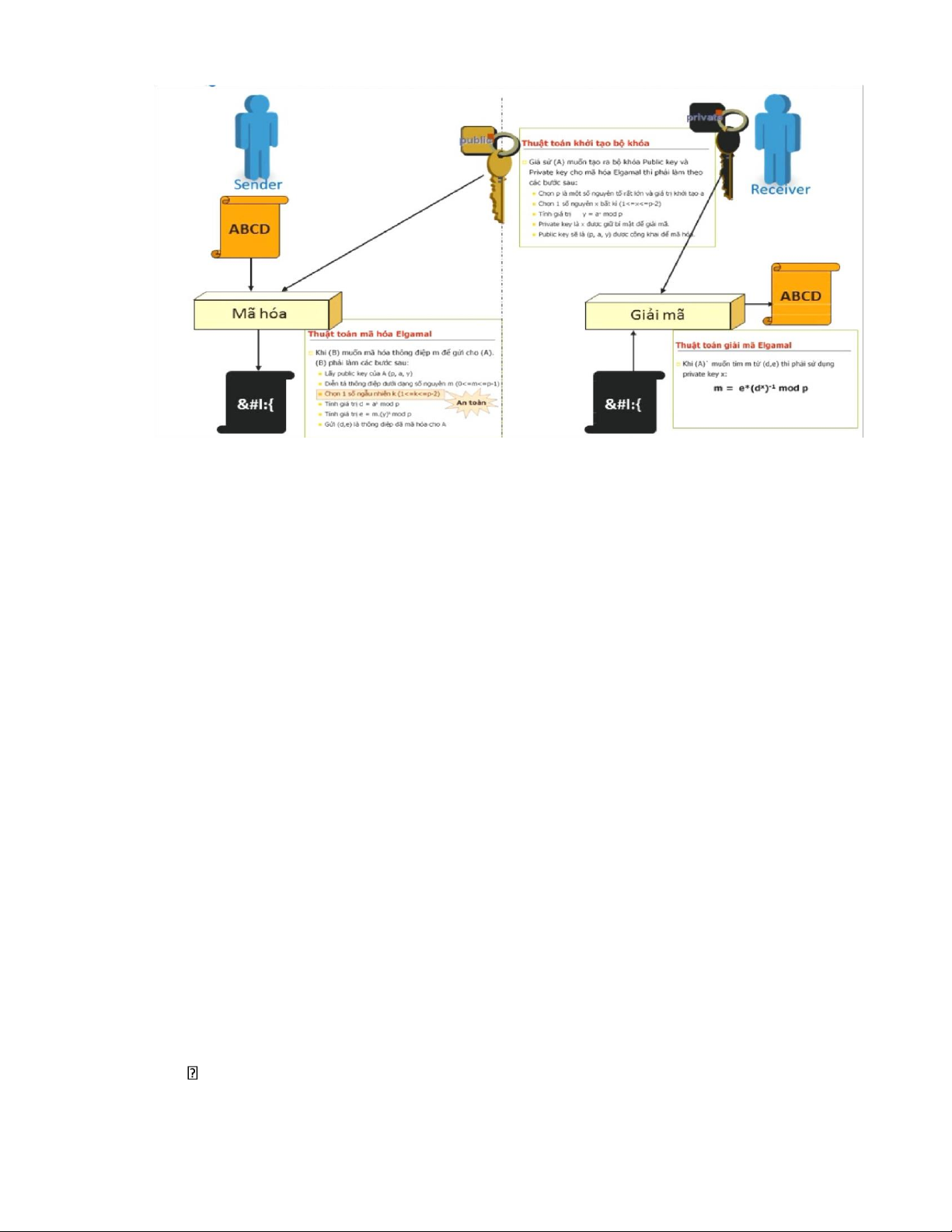
Hình 2: Sơ đồ mã hóa và giải mã hệ mật Elgamal -
Ban đầu người ta sẽ lựa chọn một số nguyên tố lớn p và 2 số nguyên tố nhỏ
hơn p là alpha ( một phần tử nguyên thủy của Z*p) và a ( khóa bí mật của
người nhận) sau đó tính khóa công khai:
beta =alphaa mod p
Lưu ý: Để tạo khó khăn cho việc phá mã thì nên chọn p có ít nhất 150 chữ số. -
Để mã hóa một thông điệp M (một số nguyên tố trên Zp) thành bản mã C
người gửi chọn một số ngẫu nhiên k nhỏ hơn p và tính cặp bản mã: C1 = alphak mod p C2 = (M*betak )mod p
Và gửi bản mã C=( C1,C2) đi (sau đó k sẽ bị hủy đi). -
Để giải mã thông điệp M đầu tiên ta dùng khóa bí mật a và tính theo công thức: M = (C a 2* (C1 ) -1) mod p Với: (C a (p-1-a) 1 ) -1) mod p = (C1 ) mod p Kết luận
Xây dựng được hệ mã Elgamal bộ khóa: K=(p, alpha, a, beta) với: 9 lOMoARcPSD| 41967345 -
Thành phần khóa công khai: KU = (alpha, beta, p) -
Thành phần khóa bí mật: KR= (a, p)
Ví dụ: Cho Hệ Elgamal có p = 2579; alpha = 2; a = 765; chọn k ngẫu nhiêu là 853. Bản rõ M = 1299.
Tìm khóa của hệ mã trên? Mã hóa:
Trước hết ta tính: beta = alphaa mod p = 2765 mod 2579 = 949 Để
mã hóa thông điệp M = 1299 ta tính theo k =853:
C1 = alphak mod p = 2853 mod 2579 =435
C2 = (M*betak )mod p = (1299*949853 ) mod 2579 =2396 Vậy
bản mã được gửi đi sẽ là C = (435, 2396). Giải mã: Với khóa bí mật a= 765:
(C1a) -1) mod p = (C1(p-1-a)) mod p = (435(2579-1-765)) mod 2579 = (4351813) mod 2579 = 1980 M = (C a
2* (C1 ) -1) mod p = (2396*1980) mod 2579 = 1299 Kết luận:
Xây dựng được hệ mã Elgamal bộ khóa:
K = (p, alpha, a, beta) = (2579, 2, 765, 949) với: -
Thành phần khóa công khai:
KU = (alpha, beta, p) -
Thành phần khóa bí mật:
KR = (a, p) = (765, 2579) -
Mã hóa M=1299 với C(C1, C2) = (435,2396)
1.2.3. Thám mã hệ mật Elgamal
Để thám mã hệ Hệ Elgamal, ta cần phải giải bài toán logarit rời rạc. Chúng
ta có 2 thuật toán để giải bài toán logarit rời rạc là: - Thuật toán Shank lOMoARcPSD| 41967345 - Thuật toán Pohlig_Hellman
Trong đó thuật toán thám mã Shank được sử dụng nhiều hơn cả nên nhóm chỉ
trình bài thuật toán Shank.
Bài toán logarith rời rạc:
Logarith rời rạc là sự kết nối của phép tính logarith trên trường số thực vào
các nhóm hữu hạn. Ta nhắc lại rằng với hai số thưc x,y và cơ số a>0, a#0, nếu ax
– y=0 thì x được gọi là logarith cơ số a của y, ký hiệu x = logay.
Logarith rời rạc là bài toán khó ( chưa biết thuật toán hiệu quả nào ). Trong
khi bài toán ngược lũy thừa rời rặc lại không khó ( có thể sử dụng thuật toán bình phương và nhân). Ví dụ:
Cho p là một số nguyên tố , xét nhóm nhân các số nguyên modulo p:
Z * = { 1,2….,p } với phép nhân modulo p. p
Nếu ta tính lũy thừa bậc k của một số trong nhóm rồi rút gọn theo modulo p
thì ta được một số trong nhóm đó . quá trình này được gọi là lũy thừa rời rạc
modulo p . Chẳng hạn với p = 17 , lấy a = 3, k = 4 ta có : 34 = 81 = 13 mod 17
Logarith rời rặc là phép tính ngược lại :
Biết : 3k = 13 (mod 17) hãy tìm k?
Thực hiện tương tự như thuật toán Shank => k = 4. Tuy nhiên đây là một bài
toán tương đối khó. Trong trường hợp p lớn ( có ít nhất 150 chữ số) thì bài
toán trở thành bất khả thi => an toàn. Thuật toán Shank:
Thuật toán này có tên gọi khác là thuật toán thời gian_bộ nhớ. Tư tưởng của
thuật toán là nếu ta có đủ bộ nhớ thì có thể sử dụng bộ nhớ đó để giảm thời gian
thực hiện của thuật toán.
Input : Số nguyên tố p, phần tử nguyên thủy a cua Z*p, số nguyên y.
Output : Cần tìm a sao cho beta =alphaa mod p. Thuật toán :
Gọi m = [(p-1)1/2] (lấy phần nguyên). 11 lOMoAR cPSD| 41967345
Bước 1: Tính alphamj mod p với 0 <= j <= m-1.
Bước 2: Sắp xếp các cặp (j, alphamj mod p) theo alphalmj mod p và lưu vào danh sách L1.
Bước 3: Tính beta*alpha-i mod p với 0 <= I <= m-1.
Bước 4: Sắp xếp các cặp (i, beta*alpha-i mod p) theo beta*alpha-i mod p
và lưu vào danh sách L2.
Bước 5: Tìm trong hai danh sách L1 và L2 xem có tồn tại cặp ( j, alphamj
mod p ) và ( i, beta*alpha-i mod p ) nào mà alphamj mod p = beta*alpha-
i mod p (tọa độ thứ hai của hai cặp bằng nhau ).
Lưu ý: Vì alphamj = beta*alpha-i => alphamj-i = beta nên bước 5 luôn thành công.
Bước 6: Tính a = logalpha beta = ( mj + i ) mod ( p - 1 ). Kết quả này có
thể kiểm chứng từ công thức:
alphamj mod p = beta*alpha-i mod p
=>alphamj+i mod p= beta mod p
=> logalpha beta = ( mj + i ) mod ( p – 1 ) = a
Ví dụ: Với bài toán trên người ta thám mã chỉ có khóa công khai:
Kp = ( p,a,y ) = ( 97,5,44 )
m = [(p-1)1/2] = [( 97-1)1/2] = 10
Bước 1: Tính alphamj mod p với 0 <= j <= m-1.
Bước 2: Sắp xếp các cặp (j, alphamj mod p) theo alphamj mod p và lưu vào danh sách L1. J(0<=j<=m-1) 510j mod 97(alphamj mod p) 0 1 1 53 2 93 3 79 4 16 5 72 6 33 7 3 lOMoAR cPSD| 41967345 8 62 9 85
Bước 3: Tính beta*alpha-i mod p với 0<=i<=m-1.
Bước 4: Sắp xếp các cặp (i, beta*alpha-i mod p) theo beta*alpha-i mod p và lưu vào danh sách L2. i(0<=j<=m-1)
44*5-i mod 97(beta*alpha-i mod p) 0 44 1 26 2 33 3 68 4 49 5 51 6 61 7 14 8 70 9 59
Bước 5: Tìm trong hai danh sách L1 và L2 xem có tồn tại cặp ( j, alphamj mod p )
và ( i, beta*alpha-i mod p ) nào mà alphamj mod p = beta*alpha-i mod p (tọa độ
thứ hai của hai cặp bằng nhau ).
Dựa vào hai bảng danh sách L1 và L2 khi j = 6 và i = 2 thì:
alphamj mod p = beta*alpha-i mod p = 33
Bước 6: Tính a = ( mj + i ) mod ( p - 1 ). Kết quả này có thể kiểm chứng từ công
thức alphamj mod p = beta*alpha-i mod p = alphamj+i mod p => a = ( mj + i ) mod ( p – 1 ).
Vậy ta có a = (10 * 6 +2) mod (97 – 1 ) = 62. 13 lOMoARcPSD| 41967345
1.2.4. Quản lý khóa
Hệ mật bất đối xứng khắc phục được tính chất phức tạp trong việc phân phối
khóa ở hệ mật đối xứng. Cho phép giao tiếp giữa các đối tượng một cách uyển chuyển , dễ dàng.
- Thông báo công khai khóa của người sử dụng.
- Thư mục truy cập công cộng.
- Phân phối khóa công khai từ tổ chức
- Chứng nhận khoá công khai: khoá công khai của người sử dụng được nơi
có thẩm quyền chứng nhận.
Hình 3: Sơ đồ quản lý khóa 1.2.5. Độ an toàn
Hệ thống elgamal dựa trên bài toàn logarit rời rạc. Tính an toàn của nó tùy
thuộc vào độ phức tạp của bài toán logarit.
Trong bài toán về hệ Elgamal:
- p là số nguyên tố, a là phần tử nguyên thủy của Z*p. (p và a là cố định).
- Bài toán logorit rời rạc có thể được phát biểu như sau: Tìm 1 số mũ x duy
nhất, 0<=x<=p-2 sao cho ax=y mod p, với y thuộc Z*p cho trước.
- Bài toán có thể giải được bởi phương pháp vét cạn ( tức là duyệt tất cả
phần tử x) để tìm x thỏa mãn. Bài toán có độ phức tạp là: O(p) (bỏ qua
thừa số logarit). Vấn đề đặt ra là nếu p lớn, rất lớn thì để thực hiện phương
pháp này cần thời gian rất lớn. Suy ra không khả thi.
Xét thuật toán Shank để thám mã hệ mã hóa Elgamal:
- Người thám mã chỉ có khóa công khai (p,a,y). lOMoARcPSD| 41967345
- Bài toán logarit rời rạc cũng được phát biểu như sau: Tìm 1 số mũ x duy
nhất, 0<=x<=p-2 sao cho ax=y mod p, với y thuộc Z*p cho trước.
- Độ phức tạp của bài toán là O([p-1]^1\2) và bộ nhớ O([p-1]^1\2)( bỏ qua
thừa số logarit), giảm rất nhiều so với phương pháp vét cạn.
- Chúng ta cần tính các phần tử thuộc 2 danh sách L1, L2 đều là phép toán
lũy thừa phụ thuộc và i, j; i và j lại phụ thuộc vào m nên ta nhận thấy bài
toán chỉ áp dụng với những trường hợp p nhỏ.
Đánh giá độ an toàn của hệ mã hóa Elgamal:
- Hệ mã hóa Elgamal áp dụng bài toán logarit rời rạc chính vì vậy độ an toàn
của hệ mã hóa là rất lớn vì bài toán logarit rời rạc chưa có phương pháp hiệu quả để tính.
- Với 1 số p đủ lớn, thuật toán mã hóa Elgamal không có phương pháp thám mã hiệu quả.
1.2.6. Ưu & nhược điểm của hệ mật Elgamal • Ưu điểm:
Độ phức tạp của bài toán logarith lớn nên đọ an toàn cao.
Bản mã phụ thuộc vào bản rõ x và giá trị ngẫu nhiên nên từ một bản rõ ta
có thể có nhiều bản ma khác nhau. • Nhược điểm:
Tốc độ chậm ( do phải xử lý số nguyên lớn ).
Dung lượng bộ nhớ dành cho việc lưu trữ khoa yêu cầu phải lớn.
Việc sinh khóa và quản lý khóa cũng khó khăn hơn các hệ mật mã khối do
việc sử dụng các số nguyên tố. 15 lOMoARcPSD| 41967345
CHƯƠNG II – TRIỂN KHAI HỆ MẬT ELGAMAL TRÊN MATLAB 2.
2.1. Mô hình mô phỏng
Dựa trên những kiến thức tìm hiểu được về hệ mật Elgamal, nhóm sinh viên đã triển
khai ý tưởng và mô phỏng hệ mật trên nền tảng của phần mềm Matlab.
Code mô phỏng nằm trong File đính kèm.
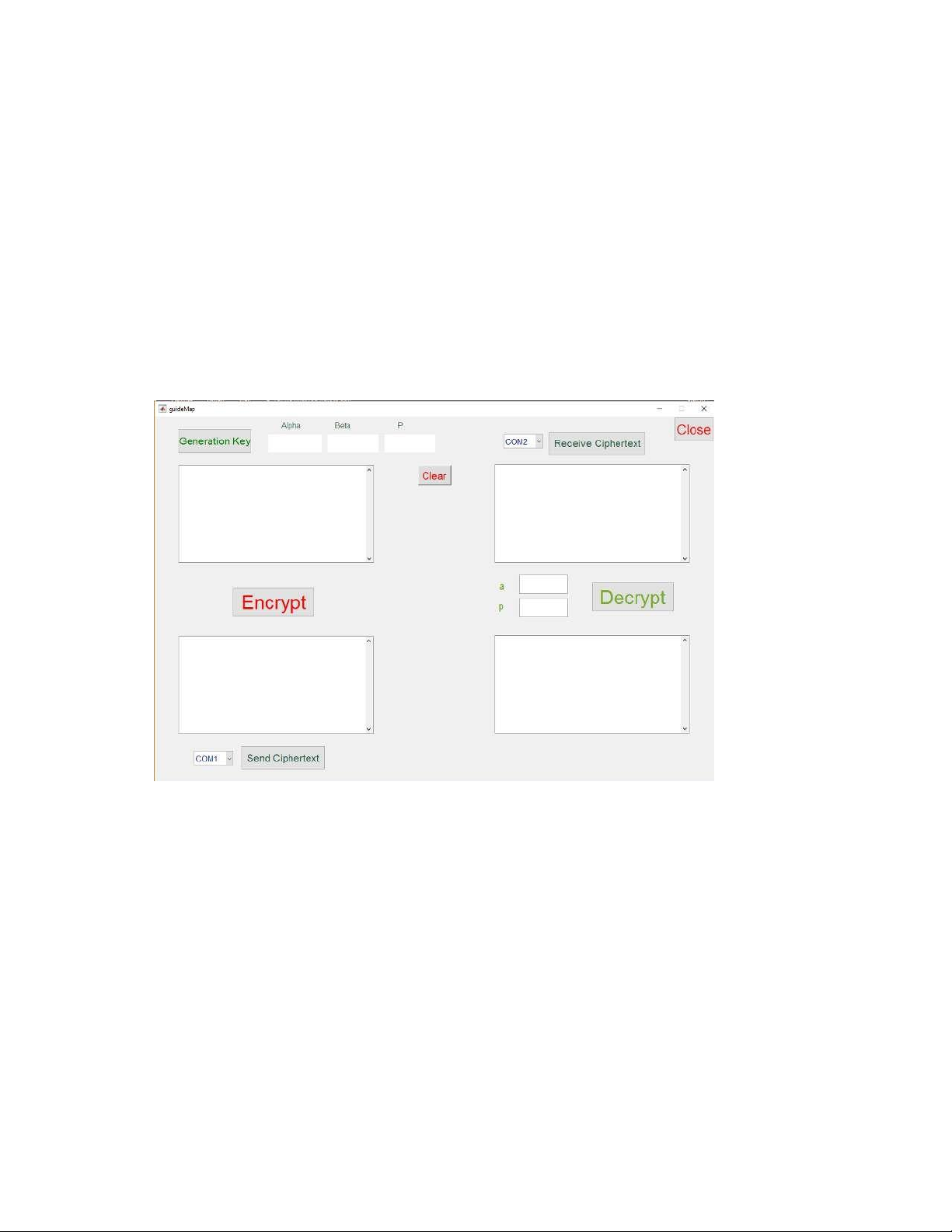
Giao diện mô phỏng:
Hình 4: Giao diện mô phỏng
Mã hóa: Mã hóa đoạn Plaintext "Lý thuyết mật mã" lOMoARcPSD| 41967345
Hình 5: Giao diện lập mã
Giải mã: Giải mã đoạn Ciphertext thu được
Hình 6: Giao diện giải mã
Kết quả: Thu được bản tin "Lý thuyết mật mã", chính là bản rõ ban đầu. 17 lOMoARcPSD| 41967345
CHƯƠNG III – KẾT LUẬN 3.
3.1. Kết quả đạt được :
Triển khai thành công hệ mã Elgamal trên phần mềm Matlab với dữ liệu đầu vào, ra là kí tự.
Xây dựng được chương trình mã hóa và mã giải, chuyển dữ liệu qua cổng COM trên PC.
Tăng thêm khả năng làm việc nhóm.
Có thêm kinh nghiệm về phần mềm matlab.
Học được thêm nhiều điều về bản thân mình.
3.2. Kết quả chưa đạt được:
Chưa mã hóa được hình ảnh. 3.3. Thuận lợi :
Công cụ Matlab đầy đủ, dễ triển khai thuật toán trên matlab.
Các thành viên có tinh thần trách nhiệm cao.
Khả năng làm việc cá nhân cũng như nhóm của các thành viên rất tốt. 3.4. Khó khăn
Tốn nhiều thời gian vào việc sửa lỗi và tối ưu chương trình.
Nguồn tài liệu còn hạn chế. 4.
Phần 2. Tài liệu tham khảo [1]
Bài giảng an toàn và bảo mật thông tin - Trần Minh Văn – Đại học Nha Trang [2]
Elgamal encryption - Wikipedia [3]
Bài giảng hệ mật mã Elgamal. Link: http://doc.edu.vn/tai-lieu/bai-giang-he- matelgamal-57863/ [4]
Tìm hiểu hệ mật mã Elgamal. Link: http://123doc.org/document/2556734-tim- hieuhe-mat-ma-elgamal.htm lOMoAR cPSD| 41967345 Phần 3. Phụ lục
Mã nguồn chương trình nằm trong File đính kèm. 19