Báo cáo Giải thuật FFT trong xử lý tín hiệu môn Technical Writing and Presentation SOICT | Trường Đại học Bách Khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN ĐÀO TẠO LIÊN TỤC ----- & ----- BÁOCÁOMÔNHỌC TECHNICALANDWRITING
Đề tài: Các giải thuật FFT trong xử lí tín hiệu Sinh viên thực hiện: Họ và tên MSSV Lý Minh Tiến 20249035P
Hà Nội,ngày 8 tháng 8 năm 2025 MỤC LỤC
MỤC LỤC..................................................................................................................2
GIỚI THIỆU...............................................................................................................3
TỔNG QUAN VỀ FFT.................................................................................................3
CÁC GIẢI THUẬT FFT PHỔ BIẾN.................................................................................4
SO SÁNH CÁC THUẬT TOÁN FFT...............................................................................4
ỨNG DỤNG THỰC TẾ................................................................................................5
KẾT LUẬN.................................................................................................................5
PHỤ LỤC...................................................................................................................5 1. Giới thiệu
Trong xử lý tín hiệu số, việc phân tích tín hiệu trong miền tần số là một bước không
thể thiếu. Biến đổi Fourier rời rạc (DFT) cho phép ta chuyển tín hiệu từ miền thời gian
sang miền tần số, giúp dễ dàng quan sát các thành phần tần số của tín hiệu. Tuy
nhiên, việc tính DFT theo định nghĩa có độ phức tạp thời gian là O(N²), gây ra sự chậm
trễ khi áp dụng trên tín hiệu có độ dài lớn.
Để giải quyết vấn đề này, các thuật toán FFT (Fast Fourier Transform) đã được phát
triển nhằm tăng tốc quá trình tính DFT. FFT không chỉ giúp tiết kiệm thời gian mà còn
mở rộng khả năng ứng dụng của xử lý tín hiệu vào thời gian thực và các hệ thống nhúng. 2. Tổng quan về FFT 2.1 Khái niệm:
FFT là tên gọi chung cho các thuật toán tối ưu hóa nhằm tính DFT và IDFT nhanh
hơn bằng cách khai thác tính chất tuần hoàn và đối xứng trong tính toán. Thay vì thực
hiện từng phép nhân và cộng một cách trực tiếp như DFT, FFT chia nhỏ bài toán và
tính toán song song, giúp rút gọn đáng kể số phép toán cần thực hiện. 2.2 Ứng dụng:
- Phân tích âm thanh: xác định cao độ, tần số nền, lọc tạp âm
- Xử lý ảnh: nén ảnh, nhận dạng đối tượng, phân tích kết cấu
- Truyền thông: điều chế OFDM, mã hóa tín hiệu trong Wi-Fi, 4G/5G
- Hệ thống radar và sonar: phân tích tín hiệu phản xạ để xác định vị trí
- Phát hiện lỗi trong thiết bị điện tử: kiểm tra phổ tín hiệu đầu ra 3
3. Các giải thuật FFT phổ biến
3.1 Giải thuật Cooley-Tukey:
Được phát triển năm 1965, thuật toán này chia DFT có kích thước N thành nhiều
DFT nhỏ hơn. Ví dụ, nếu N là lũy thừa của 2, ta có thể chia thành các DFT kích thước
2 rồi ghép kết quả lại. Sử dụng phương pháp chia để trị (divide and conquer), nó giúp
giảm độ phức tạp từ O(N²) xuống O(N log₂ N).
3.2 Giải thuật Prime Factor FFT:
Khi N không phải là lũy thừa của 2 nhưng là tích của các số nguyên tố khác nhau
(ví dụ: N = 3×5×7), ta có thể áp dụng thuật toán này để khai thác cấu trúc số học của
N. Nó sử dụng định lý số dư Trung Hoa để tách DFT lớn thành các DFT nhỏ tương
ứng với các nhân tử nguyên tố.
3.3 Giải thuật Bluestein (hoặc Chirp Z-transform):
Bluestein dùng một phương pháp rất thông minh để biến bài toán DFT thành bài
toán tích chập (convolution), có thể được giải nhanh bằng FFT thông thường. Đây là
thuật toán mạnh mẽ cho mọi giá trị N, bao gồm cả số nguyên tố.
4. So sánh các thuật toán FFT
Bảng so sánh dưới đây giúp ta đánh giá ưu nhược điểm của từng giải thuật: Thuật toán Điều kiện áp dụng Ưu điểm Nhược điểm Cooley-Tukey 𝑁 = 2𝑘 Đơn giản,hiệu quả Không áp dụng cho cao mọi N Prime Factor
𝑁 = 𝑝 ⋅ 𝑞,gcd(p,q) = 1 Khai thác tốt tính Cài đặt và tối ưu chất số học phức tạp Bluestein Mọi N Linh hoạt,hiệu quả Tốn bộ nhớ và phụ thuộc FFT chuẩn
5. Ứng dụng thực tế
Một số ví dụ thực tế cho thấy vai trò của FFT trong các hệ thống hiện đại:
- Trong hệ thống nhận diện giọng nói, FFT giúp phân tích âm thanh để tách từ, âm tiết.
- Trong chuẩn MP3, tín hiệu âm thanh được phân tích phổ bằng FFT để nén dữ liệu. -
Trong mạng 4G, tín hiệu được điều chế theo OFDM, trong đó FFT được dùng để
chuyển tín hiệu giữa miền tần số và thời gian.
- Trong y học, máy MRI và siêu âm sử dụng FFT để tái tạo hình ảnh từ tín hiệu thu được. 6. Kết luận
FFT là một trong những phát minh có ảnh hưởng lớn nhất trong lĩnh vực kỹ thuật
số. Từ một phép biến đổi toán học, nó đã trở thành công cụ kỹ thuật then chốt giúp xử
lý hàng tỷ tín hiệu mỗi ngày trong công nghệ hiện đại. Việc lựa chọn giải thuật FFT
phù hợp với kích thước dữ liệu và yêu cầu ứng dụng là yếu tố then chốt giúp tối ưu hiệu suất tính toán.
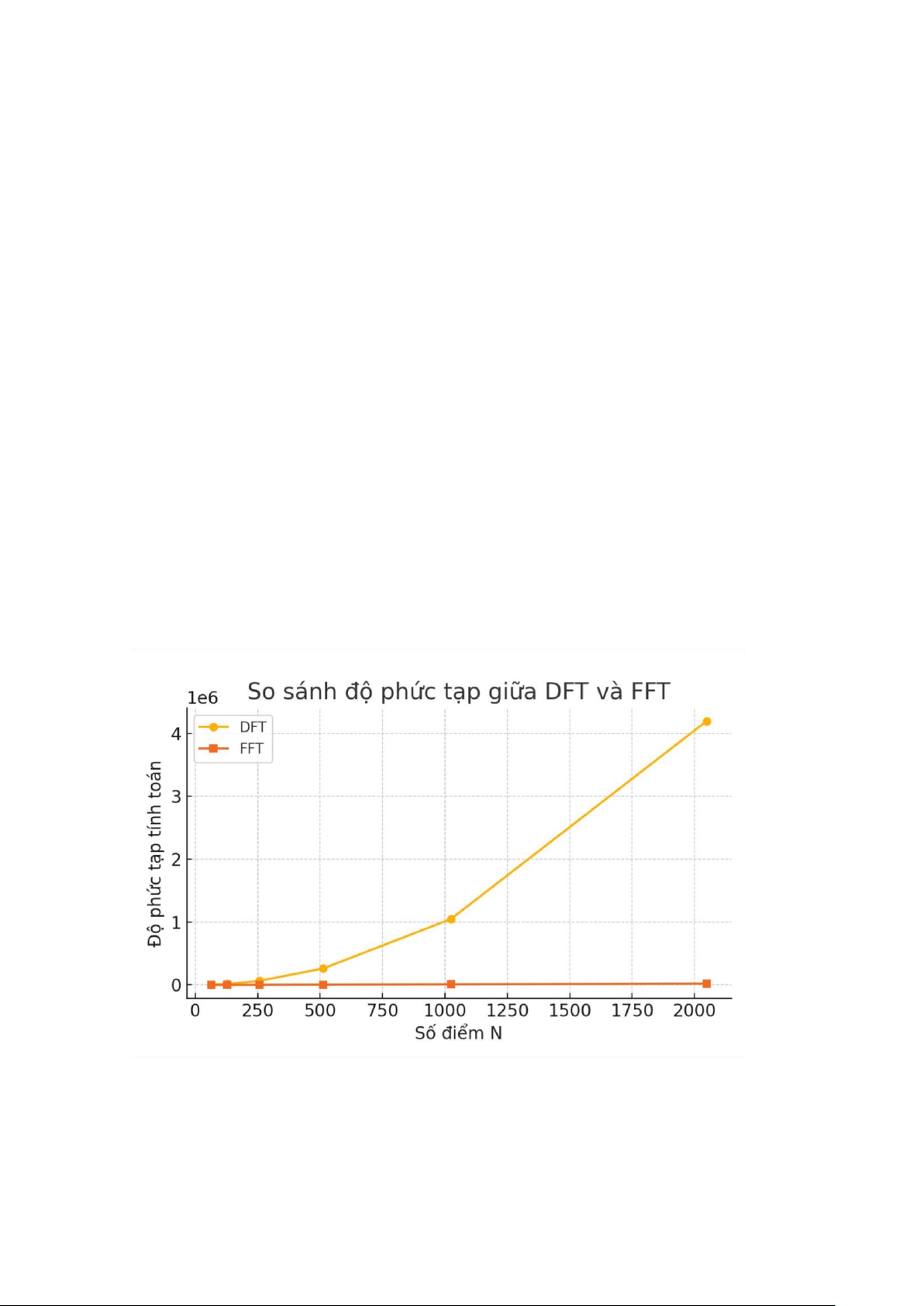
7. Phụ lục: Biểu đồ so sánh DFT và FFT
Hình: So sánh độ phức tạp tính toán giữa DFT (O(N²)) và FFT (O(N log N)) theo số điểm N 5