




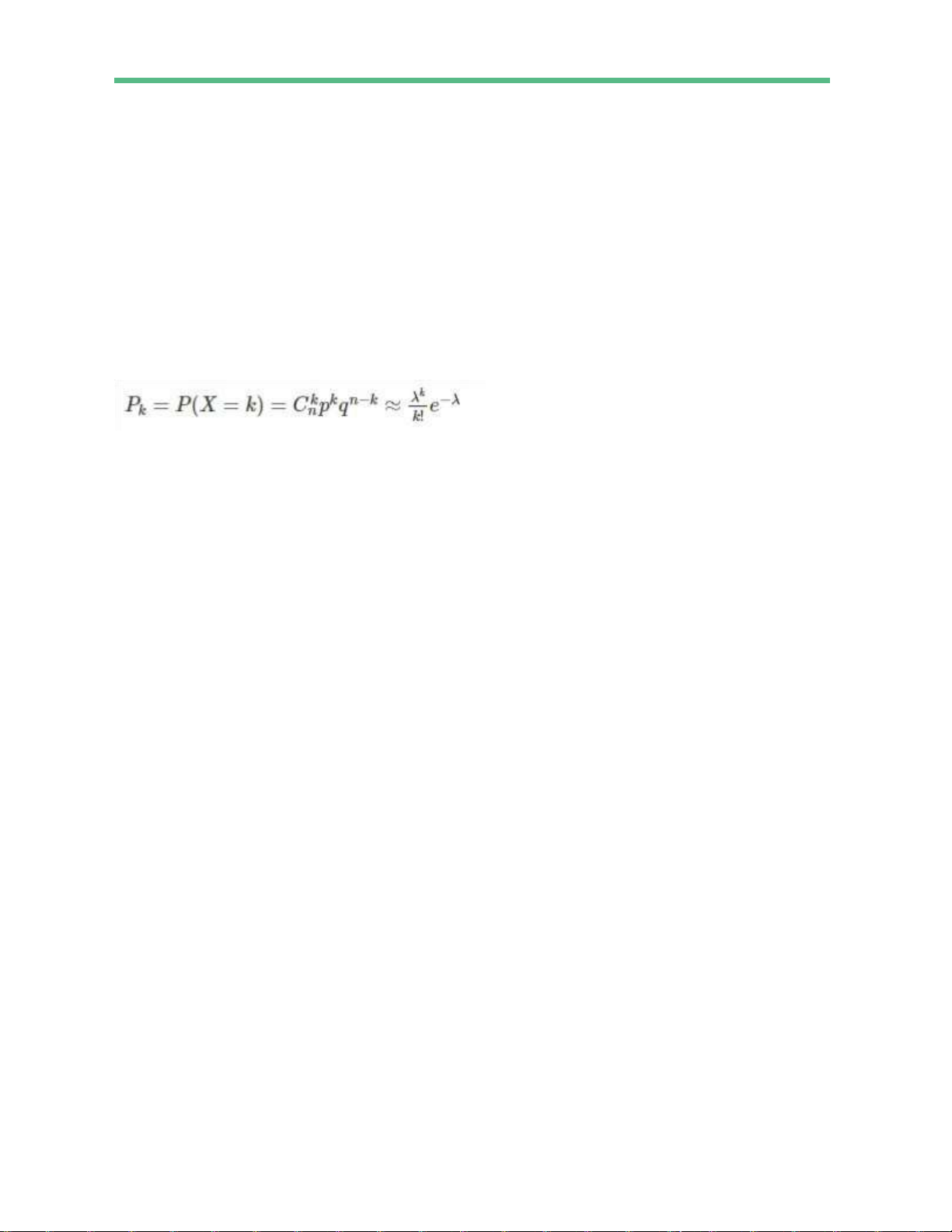










Preview text:
lOMoAR cPSD| 46672053
TRƯỜNG ĐẠI HỌC KINH DOANH VÀ CÔNG NGHỆ HÀ NỘI
KHOA CÔNG NGHỆ THÔNG TIN BÁO CÁO
MẠNG MÁY TÍNH NÂNG CAO
Tên đề tài: Tìm hiểu lý thuyết hàng đợi và ứng dụng trong
mạng máy tính
Nhóm học viên thực hiện: 1 Ngành: CNTT Lớp: K17.14
Hà Nội - Năm 2023 lOMoAR cPSD| 46672053
TRƯỜNG ĐẠI HỌC KINH DOANH VÀ CÔNG NGHỆ HÀ NỘI
KHO A CÔNG NGHỆ TH ÔNG TIN
TÊN ĐỀ TÀI
Tìm hiểu lý thuyết hàng ợi và ứng dụng
trong mạng máy tính
Nhóm học viên thực hiện: 1 Ngành : CNTT Lớp : K17.14
Hà Nội - Năm 2023 lOMoAR cPSD| 46672053 Tiểu luận
Mạng máy tính nâng cao HÀNG ĐỢI LÀ GÌ? Khái niệm
Hàng đợi thường là một thành phn quan trọng không thể thiếu khi mô hình hóa và nghiên cứu
hiệu suất của hệ thống sử dụng phương pháp toán học hoặc mô phỏng. Hàng đợi xuất hiện trong nhiều
lĩnh vực và ứng dụng khác nhau, từ quản lý dịch vụ khách hàng đến quản lý lưu lượng mạng, từ quản lý
chuỗi cung ứng đến quản lý vận tải, và nhiều lĩnh vực khác.
Việc sử dụng mô hình hàng đợi giúp đơn giản hóa phân tích và dự đoán hiệu suất của hệ thống
trong điều kiện thực tế, giúp người quản lý và nghiên cứu hiểu rõ hơn về cách hệ thống hoạt động và cách
tối ưu hóa nó. Mô hình hàng đợi có thể được sử dụng để đo lường các thông số quan trọng như thời gian
chờ đợi trung bình, tỷ lệ từ chối, tỷ lệ sử dụng tài nguyên, và nhiều thống kê khác để đưa ra quyết định quản lý thông minh.
Do đó, trong nghiên cứu và quản lý hệ thống, việc mô hình hóa hàng đợi là một công cụ quan
trọng để giúp tối ưu hóa và cải thiện hiệu suất của các quy trình và dịch vụ khác nhau.
Ví dụ về hàng đợi
Khi bạn đến sân bay để check-in, bạn thường thấy có một hàng đợi dài, và mọi người xếp hàng
chờ đến lượt của mình. Đây là một ứng dụng thực tế của nguyên tắc hàng đợi trong quản lý lưu lượng và
cung cấp dịch vụ cho hành khách. Trong ví dụ này:
▢ Hành khách đến sân bay theo lịch trình riêng của họ và muốn check-in để làm thủ tục trước khi lên máy bay.
▢ Hàng đợi trong trường hợp này là những người hành khách xếp hàng để chờ đến lượt của họ để
thực hiện việc check-in. Người đến trước sẽ được phục vụ trước, và người đến sau sẽ phải chờ
đợi cho đến khi đến lượt của họ. lOMoAR cPSD| 46672053
Hàng đợi đơn là gì?
Hàng đợi đơn là một loại hàng đợi đơn giản, bao gồm một tiến trình đến
(arrival process) và một tiến trình phục vụ (service process) theo cơ chế FIFO (First-In-First-Out). Điều
này có nghĩa là khách hàng đến trước sẽ được phục vụ trước và không có sự ưu tiên đối với bất kỳ khách hàng nào khác.
Dưới đây là mô tả chi tiết về các yếu tố trong một hàng đợi đơn với tiến trình tới và tiến trình phục vụ FIFO:
▢ Tiến trình tới (Arrival Process): Trong mô hình này, khách hàng đến hàng đợi theo một tiến trình
tới, thường là một quy trình Poisson với tốc độ đến λ (lambda). Điều này có nghĩa là khách hàng
đến theo một quy luật ngẫu nhiên, không đều đặn, với tốc độ trung bình là λ khách hàng mỗi đơn vị thời gian.
▢ Tiến trình phục vụ (Service Process): Tiến trình phục vụ trong mô hình hàng đợi đơn này cũng có
thể là một quy trình Poisson với tốc độ phục vụ μ ( mu ). Tốc độ này cho biết mức độ hoàn thành
của khách hàng trong hàng đợi. Mỗi khách hàng trong hàng đợi sẽ được phục vụ với tốc độ trung bình là μ.
▢ FIFO (First-In-First-Out): FIFO là nguyên tắc quản lý hàng đợi trong đó khách hàng đến trước sẽ được
phục vụ trước. Điều này đảm bảo tính công bằng và trái ngược với các nguyên tắc ưu tiên khác
nhau, như LIFO (Last- In-First-Out ) hoặc ưu tiên dựa trên loại dịch vụ.
Hàng đợi đơn với tiến trình tới và tiến trình phục vụ FIFO là một trường hợp đơn giản của mô hình
hàng đợi, thường được sử dụng để minh họa các khái niệm cơ bản về quản lý hàng đợi và lưu lượng. Mô
hình này có thể được sử dụng để tính toán các thông số quan trọng như thời gian chờ đợi trung bình, tỷ
lệ từ chối, và hiệu suất tổng thể của hệ thống hàng đợi.
Các tham số quan trọng để đánh giá hàng đợi
Để đánh giá hiệu suất và hiệu quả của một hệ thống hàng đợi, có một số tham số quan trọng cn
xem xét. Dưới đây là một số tham số quan trọng khi đánh giá một hệ thống hàng đợi:
▢ Thời gian chờ đợi trung bình (Average Waiting Time or Average Queueing Time - W): Đây là thời
gian trung bình mà một yêu cu hoặc khách hàng phải chờ trong hàng đợi trước khi được phục vụ.
Thời gian chờ đợi trung bình thấp hơn là một chỉ số quan trọng cho trải nghiệm của người sử dụng. lOMoAR cPSD| 46672053
ρ = λ / μ
▢ Thời gian phục vụ trung bình (Average Service Time - S): Đây là thời gian trung bình mà mỗi yêu cu
hoặc khách hàng phải dành để được phục vụ. Nó phụ thuộc vào tốc độ phục vụ của hệ thống.
▢ Tỷ lệ sử dụng tài nguyên (Resource Utilization - ρ): Tỷ lệ này đo lường mức độ sử dụng tài nguyên
(máy phục vụ) trong hệ thống. Nó được tính bằng tỷ lệ giữa thời gian tài nguyên thực sự được sử
dụng và thời gian tài nguyên tổng cộng có sẵn.
▢ Tỷ lệ từ chối (Blocking Probability - P_blocking): Đây là tỷ lệ của yêu cu hoặc khách hàng bị từ chối
và không được phục vụ khi hàng đợi đã đy.
▢ Số lượng yêu cu trong hàng đợi (Queue Length): Đây là số lượng yêu cu hoặc khách hàng hiện đang
đợi trong hàng đợi tại một thời điểm cụ thể.
▢ Thời gian dự kiến để xử lý yêu cu (Expected Response Time): Đây là thời gian trung bình mà một
yêu cu hoặc khách hàng phải dành để hoàn thành quy trình từ khi đến hàng đợi cho đến khi kết thúc dịch vụ.
▢ Sự biến động của thời gian chờ đợi và thời gian phục vụ (Variance of Waiting Time and Service
Time): Sự biến động này có thể ảnh hưởng đến sự dự đoán và quản lý của hệ thống.
▢ Hiệu suất tổng thể (Overall System Performance): Đánh giá tổng thể về hiệu suất của hệ thống hàng
đợi, đặc biệt là trong việc đáp ứng nhu cu của khách hàng và sử dụng tài nguyên một cách hiệu quả.
Các tham số trên cùng với việc thu thập dữ liệu thời gian đến và thời gian phục vụ thực tế có thể
giúp bạn hiểu rõ hơn về hoạt động của hệ thống hàng đợi và cải thiện nó để đáp ứng các mục tiêu kinh
doanh hoặc quản lý hàng đợi tốt hơn.
Thế nào là tải hàng đợi?
Tải hàng đợi, thường được ký hiệu bằng "ρ" (rho), đo lường mức độ sử dụng của hệ thống hàng
đợi và được tính toán bằng tỷ lệ giữa tốc độ đến (λ - lambda) và tốc độ phục vụ (μ - mu). Công thức tính tải hàng đợi như sau: Trong đó:
▢ ρ (rho): Tải hàng đợi (queue load), là tỷ lệ sử dụng của hệ thống hàng đợi. lOMoAR cPSD| 46672053
▢ λ (lambda): Tốc độ đến, tức là số yêu cu hoặc khách hàng đến hệ thống hàng đợi trong một đơn vị
thời gian (ví dụ: số yêu cu mỗi giờ).
▢ μ (mu): Tốc độ phục vụ, tức là số yêu cu hoặc khách hàng mà hệ thống có khả năng phục vụ trong một đơn vị thời gian.
Giá trị của ρ có thể nằm trong khoảng từ 0 đến 1. Khi ρ = 0, tức là hệ thống hoàn toàn không sử
dụng, không có yêu cu nào đến. Khi ρ = 1, tức là hệ thống đang hoạt động ở tối đa sức chứa của nó, và
hàng đợi có thể trở nên đy và dài lên vô hạn. Trong thực tế, một mục tiêu quan trọng trong quản lý hàng
đợi là duy trì ρ ở một mức chấp nhận được để đảm bảo rằng hệ thống không quá tải và khách hàng không
phải chờ đợi quá lâu. TIẾN TRÌNH POISSON
Tiến trình Poisson là gì?
Tiến trình Poisson là một loại tiến trình ngẫu nhiên trong lý thuyết xác suất và thống kê. Nó được
sử dụng để mô tả sự xuất hiện ngẫu nhiên của các sự kiện trong một khoảng thời gian hoặc không gian cố
định. Tiến trình Poisson không chỉ áp dụng cho sự đến của các gói liệu, mà còn cho nhiều loại sự kiện khác nhau, ví dụ:
▢ Sự đến của gói liệu: Tiến trình Poisson có thể được sử dụng để mô tả sự đến ngẫu nhiên của các gói
liệu tới một trạm hoặc hệ thống, chẳng hạn như sự đến của email, gói tin trong mạng máy tính,
hoặc bất kỳ dạng thông tin nào.
▢ Sự kiện giao thông: Tiến trình Poisson có thể được sử dụng để mô tả sự xuất hiện ngẫu nhiên của
các sự kiện liên quan đến giao thông, như tai nạn xe hơi hoặc yêu cu phải dừng lại tại một đèn đỏ.
▢ Khách hàng đến cửa hàng: Trong lĩnh vực dịch vụ, tiến trình Poisson có thể được sử dụng để mô tả
sự đến của khách hàng đến cửa hàng, ngân hàng, hoặc nhà hàng.
▢ Sự kiện trong khoa học tự nhiên: Tiến trình Poisson cũng có thể áp dụng cho nhiều sự kiện trong
khoa học tự nhiên, chẳng hạn như phân rã nguyên tử, xác suất mưa trong một khu vực cụ thể,
hoặc sự xuất hiện của các hạt phóng xạ.
Tiến trình Poisson được đặc trưng bởi tốc độ sự đến trung bình (lambda - λ), và nó có tính chất
quan trọng là sự đến của các sự kiện là ngẫu nhiên và độc lập trong khoảng thời gian hoặc không gian cố lOMoAR cPSD| 46672053
định. Nó là một công cụ quan trọng trong nhiều lĩnh vực, đặc biệt là trong mô hình hóa và dự đoán các sự
kiện xảy ra ngẫu nhiên.
Công thức tính xác suất của tiến trình Poisson
Công thức tính xác suất của tiến trình Poisson được sử dụng để tính xác suất xảy ra một số sự kiện
(k) cụ thể trong một khoảng thời gian hoặc không gian cố định dựa trên tốc độ sự đến trung bình (lambda
- λ). Công thức này được biểu diễn như sau: Trong đó:
▢ P(X=k) là xác suất xảy ra chính xác k sự kiện trong một khoảng thời gian hoặc không gian cố định.
▢ e là số Euler, khoảng giá trị xấp xỉ 2.71828.
▢ λ (lambda) là tốc độ sự đến trung bình, tức là số sự kiện trung bình xảy ra trong khoảng thời gian
hoặc không gian cố định.
▢ k là số sự kiện cụ thể bạn muốn tính xác suất.
▢ k! là giai thừa của k, tức là k giai thừa.
Công thức trên được sử dụng rộng rãi trong lý thuyết xác suất và thống kê để mô hình sự xuất
hiện ngẫu nhiên của các sự kiện.
HỆ THỐNG HÀNG ĐỢI M/M/1/0
Hệ thống hàng đợi M/M/1/0 là gì?
Hệ thống hàng đợi M/M/1/0 là một mô hình hàng đợi được đặc trưng bằng một chuỗi các tham
số, thường được sử dụng để mô phỏng và phân tích các hệ thống hàng đợi. Các chữ cái M/M/1/0 có ý nghĩa sau:
▢ M/M: Đây là viết tắt cho "Markovian arrivals" (sự đến theo quy luật Markov) và "Markovian
service" (dịch vụ theo quy luật Markov). Trong mô hình này, thời gian giữa các sự kiện đến (sự
đến của yêu cu hoặc khách hàng) và thời gian phục vụ (dịch vụ cho yêu cu hoặc khách hàng) được lOMoAR cPSD| 46672053
mô tả bằng quy luật Markov, nghĩa là các sự kiện xảy ra độc lập và không bị ảnh hưởng bởi lịch sử
hoặc sự kiện trước đó.
▢ 1: Đây là số lượng máy phục vụ (server) trong hệ thống. Trong hệ thống M/M/1/0, chỉ có một máy phục vụ duy nhất.
▢ 0: Đây biểu thị rằng không có sự phục hồi sau khi khách hàng hoặc yêu cu đã được phục vụ và rời
khỏi hệ thống. Không có hàng đợi dự phòng (overflow queue) trong hệ thống này, nghĩa là nếu
máy phục vụ đang bận, khách hàng mới sẽ bị từ chối và không được phục vụ.
Mô hình M/M/1/0 thường được sử dụng để nghiên cứu và dự đoán hiệu suất của một hệ thống
hàng đợi đơn giản với một máy phục vụ. Các tham số quan trọng trong mô hình này bao gồm tỷ lệ đến
(arrival rate - λ) và tỷ lệ phục vụ (service rate - μ), từ đó có thể tính được các thông số như thời gian chờ
đợi trung bình, tỷ lệ từ chối, và sử dụng tài nguyên (resource utilization). Mô hình này có thể được sử
dụng để đánh giá hiệu quả của một hệ thống hàng đợi đơn giản và giúp trong việc thiết kế và cải thiện quy trình phục vụ.
Đặc trưng của hệ thống hàng đợi M/M/1/0
▢ Số yêu cu đến tuân theo tiến trình Poisson với tham số là λ
▢ Thời gian phục vụ tuân theo phân số hàm mũ với tham số là μ ▢ Một trạm phục vụ
▢ Không có hàng đợi, như vậy hệ thống có thể chứa tối đa một yêu cu
▢ Phương thức phục vụ là FIFO
Nguyên lý của hàng đợi M/M/1/0
Nguyên lý của hệ thống hàng đợi M/M/1/0 (Markovian arrivals, Markovian service, 1 server, và
không có hàng đợi dự phòng) được xây dựng dựa trên một số nguyên tắc quan trọng:
▢ Tiến trình đến theo quy luật Poisson (Markovian Arrivals): Sự đến của yêu cu hoặc khách hàng vào
hệ thống tuân theo quy luật Poisson. Điều này có nghĩa là các yêu cu đến là ngẫu nhiên và độc lập
với nhau. Thời gian giữa các yêu cu đến cũng tuân theo quy luật mũ (exponential distribution). lOMoAR cPSD| 46672053
▢ Tiến trình phục vụ theo quy luật Poisson (Markovian Service): Thời gian phục vụ cho mỗi yêu cu
cũng tuân theo quy luật Poisson và độc lập với các yêu cu khác. Điều này đồng nghĩa với việc thời
gian phục vụ là ngẫu nhiên và không bị ảnh hưởng bởi lịch sử hoặc sự kiện trước đó.
▢ Chỉ có một máy phục vụ (1 Server): Trong hệ thống M/M/1/0, chỉ có một máy phục vụ duy nhất để
xử lý các yêu cu đến. Máy phục vụ này hoàn thành việc phục vụ một yêu cu trước khi bắt đu phục vụ yêu cu khác.
▢ Không có hàng đợi dự phòng (Zero Waiting Room): Hệ thống không có hàng đợi dự phòng (overflow
queue). Nếu máy phục vụ đang bận và có yêu cu mới đến, thì yêu cu mới sẽ bị từ chối và không được phục vụ.
▢ Tiến trình Markovian: Đặc trưng này nghĩa là các sự kiện xảy ra độc lập và không bị ảnh hưởng bởi
lịch sử hoặc sự kiện trước đó trong hệ thống. Thời gian giữa các sự kiện đến và thời gian phục vụ
là ngẫu nhiên và được xác định bởi quy luật Poisson và mũ.
Hệ thống M/M/1/0 được sử dụng để mô hình và phân tích các hệ thống hàng đợi đơn giản với một máy
phục vụ và tỷ lệ đến và tỷ lệ phục vụ là xác định bởi quy luật Poisson. Điều này giúp đánh giá hiệu suất của
hệ thống và có thể được áp dụng trong nhiều lĩnh vực khác nhau để dự đoán thời gian chờ đợi, tỷ lệ từ
chối, và sử dụng tài nguyên.
HỆ THỐNG HÀNG ĐỢI M/M/1/K
Hệ thống hàng đợi M/M/1/K là gì?
Hệ thống hàng đợi M/M/1/K là một mô hình hàng đợi sử dụng để mô phỏng và phân tích hiệu
suất của hệ thống hàng đợi với các đặc điểm sau: lOMoAR cPSD| 46672053 ▢
M/M: Đây là viết tắt cho "Markovian arrivals" (sự đến theo quy luật Markov) và "Markovian
service" (dịch vụ theo quy luật Markov). Trong mô hình này, thời gian giữa các sự kiện đến (sự
đến của yêu cu hoặc khách hàng) và thời gian phục vụ (dịch vụ cho yêu cu hoặc khách hàng) được
mô tả bằng quy luật Markov, nghĩa là các sự kiện xảy ra độc lập và không bị ảnh hưởng bởi lịch sử
hoặc sự kiện trước đó.
▢ 1: Đây là số lượng máy phục vụ (server) trong hệ thống. Trong hệ thống M/M/1/K, chỉ có một máy phục vụ duy nhất.
▢ K: Đây là giới hạn về kích thước hàng đợi. Tức là, hệ thống có thể chứa tối đa K yêu cu trong hàng
đợi. Nếu hàng đợi đã đy (chứa K yêu cu) và có yêu cu mới đến, thì yêu cu mới sẽ bị từ chối và không được phục vụ.
Hệ thống hàng đợi M/M/1/K thường được sử dụng khi bạn muốn mô phỏng một hệ thống hàng
đợi có giới hạn về dung lượng hoặc tài nguyên. Ví dụ, trong một trạm xăng, hàng đợi xe ô tô đến để nạp
xăng có thể được mô hình bằng hệ thống M/M/1/K với K là số lượng khoang nạp xăng có sẵn.
Trong mô hình này, bạn có thể đánh giá các thông số như thời gian chờ đợi trung bình, tỷ lệ từ
chối, và sử dụng tài nguyên trong một hệ thống hàng đợi có giới hạn về dung lượng.
Đặc trưng của hệ thống hàng đợi M/M/1/K
Hệ thống hàng đợi M/M/1/K có một số đặc trưng quan trọng cn được xem xét khi phân tích và
mô hình hệ thống hàng đợi này:
▢ Số lượng máy phục vụ (1 Server): Trong hệ thống M/M/1/K, chỉ có một máy phục vụ duy nhất để
xử lý yêu cu từ hàng đợi.
▢ Giới hạn về dung lượng hàng đợi (Queue Size - K): Hệ thống có một giới hạn về số lượng yêu cu có
thể được chứa trong hàng đợi. Nếu hàng đợi đã đy với K yêu cu và có yêu cu mới đến, thì yêu cu
mới sẽ bị từ chối và không được phục vụ.
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053 ▢
▢ Tiến trình đến theo quy luật Poisson (Markovian Arrivals): Sự đến của yêu cu vào hàng đợi tuân
theo quy luật Poisson, nghĩa là các yêu cu đến là ngẫu nhiên và độc lập với nhau. Thời gian giữa
các yêu cu đến cũng tuân theo quy luật mũ (exponential distribution).
Tiến trình phục vụ theo quy luật Poisson (Markovian Service): Thời gian phục vụ cho mỗi yêu cu
cũng tuân theo quy luật Poisson và độc lập với các yêu cu khác. Điều này đồng nghĩa với việc thời
gian phục vụ là ngẫu nhiên và không bị ảnh hưởng bởi lịch sử hoặc sự kiện trước đó.
▢ Thời gian chờ đợi trung bình (Average Waiting Time): Là thời gian trung bình mà một yêu cu phải
chờ đợi trong hàng đợi trước khi được phục vụ. Thời gian chờ đợi trung bình trong hệ thống
M/M/1/K có thể được tính toán và sẽ phụ thuộc vào tỷ lệ đến (λ), tỷ lệ phục vụ (μ), và kích thước hàng đợi ( K ).
▢ Tỷ lệ từ chối (Blocking Probability): Là xác suất mà một yêu cu mới sẽ bị từ chối nếu hàng đợi đã đy
(chứa K yêu cu). Tỷ lệ từ chối trong hệ thống M/M/1/K có thể được tính bằng cách so sánh số
lượng yêu cu đến với dung lượng hàng đợi.
▢ Sử dụng tài nguyên (Resource Utilization): Là tỷ lệ thời gian máy phục vụ đang hoạt động so với
tổng thời gian. Tỷ lệ này thường được tính bằng công thức
Hệ thống M/M/1/K thường được sử dụng để mô phỏng và đánh giá hiệu suất của các hệ thống
hàng đợi có giới hạn về dung lượng hoặc tài nguyên. Nó cho phép bạn đánh giá các thông số quan trọng
như thời gian chờ đợi, tỷ lệ từ chối, và sử dụng tài nguyên để đảm bảo rằng hệ thống có thể hoạt động
hiệu quả dưới tải làm việc cụ thể.
Nguyên lý của hàng đợi M/M/1/K
Nguyên lý của hệ thống hàng đợi M/M/1/K có thể được tóm lược như sau:
▢ Yêu cu đến hệ thống theo quy luật Poisson và được phục vụ bởi máy phục vụ theo quy luật Poisson.
▢ Nếu hàng đợi không đy (ít hơn K yêu cu), yêu cu mới sẽ được chấp nhận và chờ đợi trong hàng đợi để được phục vụ.
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053 ▢
▢ Nếu hàng đợi đã đy (đã có K yêu cu) và có yêu cu mới đến, yêu cu mới sẽ bị từ chối và không được phục vụ.
▢ Thời gian chờ đợi trung bình và tỷ lệ từ chối trong hệ thống này có thể được tính toán dựa trên tỷ
lệ đến (λ), tỷ lệ phục vụ (μ), và kích thước hàng đợi ( K ).
Hệ thống M/M/1/K thường được sử dụng để mô phỏng và đánh giá hiệu suất của các hệ thống
hàng đợi có giới hạn về dung lượng hoặc tài nguyên.
CÁC BÀI TOÁN THỰC TẾ Hàng đợi M/M/1/0
Bài toán: Giả sử bạn quản lý một mạng Wi-Fi công cộng tại một quán cà phê. Bạn muốn biết xem mạng
Wi-Fi của bạn có đủ hiệu suất để phục vụ số lượng khách hàng trong một khoảng thời gian cụ thể hoặc không.
Thông số cụ thể:
▢ Tốc độ đến (λ): Trong khoảng thời gian cao điểm buổi sáng, trung bình có 10 khách hàng đến quán
cà phê mỗi phút (λ = 10 khách hàng/phút).
▢ Tốc độ phục vụ (μ): Mạng Wi-Fi có khả năng xử lý trung bình 15 yêu cu kết nối mỗi phút (μ = 15 yêu cu/phút).
▢ Số lượng máy truyền (c): Trong trường hợp này, c = 1, tức là chỉ có một máy truyền Wi-Fi duy nhất.
Phân tích hiệu năng:
▢ Tính thời gian chờ đợi trung bình (Average Waiting Time - W):
Kết quả cho thấy rằng mỗi khách hàng phải chờ đợi trung bình 12 giây trước khi được kết nối vào mạng Wi-Fi.
▢ Tính tỷ lệ từ chối (Blocking Probability - Pb):
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053 ▢
Tỷ lệ từ chối là 0.33, nghĩa là có 33% khả năng một khách hàng mới sẽ bị từ chối nếu mạng Wi-Fi đã quá tải.
▢ Tính tỷ lệ sử dụng tài nguyên (Resource Utilization - U):
Tỷ lệ sử dụng tài nguyên là khoảng 67%, nghĩa là mạng Wi-Fi đang hoạt động ở mức tối ưu, không
quá tải hoặc không hoàn toàn chưa được sử dụng.
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053
Đánh giá hiệu năng:
Dựa trên phân tích trên, bạn có thể kết luận rằng trong khoảng thời gian cao điểm buổi sáng,
mạng Wi-Fi của bạn có thể phục vụ khách hàng tốt, với thời gian chờ đợi trung bình là 12 giây và tỷ lệ từ
chối là 33%. Tỷ lệ sử dụng tài nguyên đang ở mức tương đối tốt 67%. Tuy nhiên, bạn cn xem xét tăng
cường hiệu năng nếu tỷ lệ từ chối tăng lên quá cao hoặc thời gian chờ đợi trở nên không chấp nhận được đối với khách hàng. Hàng đợi M/M/1/K
Bài toán: Xét một quy dịch vụ khách hàng tại một ngân hàng. Ngân hàng này chỉ có một nhân viên (máy
phục vụ) để phục vụ khách hàng và có một số ghế (K ghế) để khách hàng có thể chờ đợi. Khách hàng đến
ngân hàng theo quy luật Poisson với tỷ lệ đến là λ (ví dụ, λ = 5 khách hàng/giờ), và thời gian phục vụ cho
mỗi khách hàng là một biến ngẫu nhiên theo phân phối mũ (exponential distribution) với tỷ lệ phục vụ là
μ (ví dụ, μ = 8 khách hàng/giờ).
Thông số cụ thể:
▢ Tỷ lệ đến (λ) = 5 khách hàng/giờ
▢ Tỷ lệ phục vụ (μ) = 8 khách hàng/giờ
▢ Số lượng ghế chờ (K) = 10 ghế
Phân tích hiệu năng:
▢ Tải hàng đợi (Traffic Intensity - ρ): Tải hàng đợi ρ là tỷ lệ giữa tỷ lệ đến (λ) và tỷ lệ phục vụ (μ), tức
là ρ = λ / μ. Trong ví dụ này, ρ = 5 / 8 = 0.625.
▢ Thời gian chờ đợi trung bình (Average Waiting Time - W): Thời gian chờ đợi trung bình cho mỗi
khách hàng có thể được tính bằng công thức W = 1 / (μ λ). Trong ví dụ này, W = 1 / (8 - 5) = 1/3
giờ, hoặc khoảng 20 phút.
▢ Tỷ lệ từ chối (Blocking Probability - Pb): Tỷ lệ từ chối là xác suất rằng một khách hàng mới sẽ không
thể chờ đợi và bị từ chối nếu tất cả ghế chờ đã đy. Trong ví dụ này, nếu có 10 khách hàng trong
hàng đợi, thì tỷ lệ từ chối sẽ là 0 , vì không còn chỗ trống cho khách hàng mới.
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053
▢ Sử dụng tài nguyên (Resource Utilization - U): Tỷ lệ sử dụng tài nguyên U là tỷ lệ thời gian máy phục
vụ đang hoạt động so với tổng thời gian. Trong ví dụ này, U = λ / μ = 5 / 8 = 0.625, nghĩa là máy
phục vụ đang được sử dụng 62.5 % thời gian.
Phân tích này giúp bạn đánh giá hiệu suất của quy dịch vụ khách hàng tại ngân hàng và có thể điều chỉnh
tham số như số lượng ghế chờ (K) hoặc tỷ lệ đến (λ) để cải thiện hiệu suất hoặc đảm bảo rằng hệ thống
đáp ứng được nhu cu khách hàng một cách hiệu quả.
Đánh giá hiệu năng:
Đánh giá hiệu năng của ví dụ trên được thể hiện thông qua các thông số sau:
▢ Tải hàng đợi (Traffic Intensity - ρ): Tải hàng đợi là 0.625, nghĩa là hệ thống đang hoạt động dưới tải
trung bình 62.5% của khả năng phục vụ của máy phục vụ. Điều này cho thấy hệ thống đang hoạt
động ổn định và không quá tải.
▢ Thời gian chờ đợi trung bình (Average Waiting Time - W): Thời gian chờ đợi trung bình cho mỗi
khách hàng là 1/3 giờ hoặc khoảng 20 phút. Điều này có nghĩa rằng trung bình mỗi khách hàng
phải chờ đợi trong khoảng thời gian này trước khi được phục vụ.
▢ Tỷ lệ từ chối (Blocking Probability - Pb): Tỷ lệ từ chối là 0, nghĩa là không có khách hàng nào bị từ
chối dịch vụ trong trường hợp này. Hệ thống đã đủ sức chứa và không có khách hàng nào bị từ chối khi hàng đợi đy.
▢ Sử dụng tài nguyên (Resource Utilization - U): Tỷ lệ sử dụng tài nguyên là 0.625, nghĩa là máy phục
vụ đang hoạt động 62.5% thời gian. Điều này cho thấy máy phục vụ được sử dụng một cách khá hiệu quả.
Dựa vào các thông số trên, hệ thống dịch vụ khách hàng tại ngân hàng có vẻ đang hoạt động tốt
dưới tải trung bình và không có sự từ chối dịch vụ. Tuy nhiên, thời gian chờ đợi trung bình (20 phút) có
thể cải thiện bằng cách tăng tỷ lệ phục vụ (μ) hoặc tăng số lượng ghế chờ (K) để giảm tải hàng đợi.
So sánh hàng đợi M/M/1/0 và M/M/1/K dựa trên hai ví dụ trên
Dựa vào hai ví dụ về hàng đợi M/M/1/0 và M/M/1/K, chúng ta có thể so sánh chúng như sau:
Hàng đợi M/M/1/0 (Zero Waiting Room):
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053
▢ Trong trường hợp này, không có hàng đợi dự phòng và mọi yêu cu mới sẽ bị từ chối nếu máy phục vụ đang bận.
▢ Thời gian chờ đợi trung bình là gn như bằng 0, vì không có khả năng chờ đợi cho khách hàng.
▢ Tỷ lệ từ chối (Blocking Probability) cao nếu máy phục vụ đã bận, nghĩa là một số yêu cu sẽ bị từ chối
nếu hệ thống quá tải.
▢ Thường được sử dụng trong các tình huống mà việc chờ đợi không được chấp nhận, và sự từ chối
của yêu cu mới là tùy chọn duy nhất.
Hàng đợi M/M/1/K (Limited Waiting Room):
▢ Trong trường hợp này, có một hàng đợi dự phòng với giới hạn K cho phép chứa K yêu cu mới nếu máy phục vụ đang bận.
▢ Thời gian chờ đợi trung bình có thể được tính và không bằng 0, nhưng nó có thể là một khoảng thời
gian ngắn hơn so với M/M/1/0 nếu hàng đợi chưa đy.
▢ Tỷ lệ từ chối thấp hơn so với M/M/1/0 nếu có hàng đợi dự phòng, vì yêu cu mới được chấp nhận và
đợi trong hàng đợi nếu máy phục vụ đang bận.
▢ Thường được sử dụng trong các hệ thống mà việc chờ đợi có thể được chấp nhận và hệ thống muốn
hạn chế tỷ lệ từ chối.
Tóm lại, điểm chính để so sánh giữa M/M/1/0 và M/M/1/K là sự có mặt hoặc vắng mặt của hàng
đợi dự phòng. M/M/1/0 không có hàng đợi dự phòng và từ chối yêu cu mới nếu máy phục vụ đang bận.
Trong khi đó, M/M/1/K có hàng đợi dự phòng với khả năng chứa K yêu cu mới và từ chối chỉ xảy ra khi
hàng đợi đã đy. Lựa chọn giữa hai loại hàng đợi phụ thuộc vào tình huống cụ thể và yêu cu của hệ thống.
TỔNG KẾT VỀ HÀNG ĐỢI M/M/1/0 và M/M/1/K Hàng đợi M/M/1/0 Ưu điểm:
▢ Đơn giản: Hệ thống M/M/1/0 đơn giản và dễ triển khai, không yêu cu quản lý hàng đợi dự phòng.
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn) lOMoAR cPSD| 46672053
▢ Tối ưu trong môi trường không thể chấp nhận chờ đợi: Phù hợp cho các ứng dụng mà việc chờ đợi
là không chấp nhận được, và việc từ chối yêu cu mới là tùy chọn chấp nhận được. Nhược điểm:
▢ Wasteful: Có thể là không hiệu quả về tài nguyên nếu một số yêu cu bị từ chối dù có khả năng phục vụ.
▢ Không phù hợp với các tình huống cn giữ yêu cu: Không phù hợp cho các tình huống mà việc giữ yêu
cu và chờ đợi là quan trọng. Hàng đợi M/M/1/K Ưu điểm:
▢ Hiệu quả tài nguyên: Tận dụng tốt tài nguyên bằng cách cho phép hàng đợi dự phòng, giảm tỷ lệ từ
chối và tận dụng các yêu cu khi máy phục vụ có sẵn.
▢ Phù hợp với mô hình hàng đợi: Thích hợp cho các tình huống mà việc chờ đợi là chấp nhận được và
hệ thống muốn hạn chế tỷ lệ từ chối.
▢ Quản lý tài nguyên: Hệ thống có khả năng quản lý tài nguyên một cách hiệu quả hơn bằng cách cho
phép một số yêu cu đợi trong hàng đợi. Nhược điểm:
▢ Phức tạp hơn: Hệ thống M/M/1/K có thể phức tạp hơn trong việc quản lý và cấu hình do sự tồn tại
của hàng đợi dự phòng.
▢ Thời gian chờ đợi có thể tăng: Dù có hàng đợi dự phòng, nhưng thời gian chờ đợi trung bình có thể
tăng so với M/M/1/0 nếu hàng đợi đã đy.
▢ Yêu cu dự đoán: Yêu cu ước tính và dự đoán để thiết lập kích thước hàng đợi (K) sao cho phù hợp
với mức tải đến và khả năng phục vụ.
Tùy thuộc vào yêu cu cụ thể của hệ thống và tình huống sử dụng, bạn có thể chọn M/M/1/0 hoặc
M/M/1/K để đáp ứng nhu cu của mình. M/M/1/0 thích hợp trong các tình huống mà việc chờ đợi không
được chấp nhận và từ chối yêu cu mới là tùy chọn, trong khi M/M/1/K thích hợp cho các tình huống mà
việc chờ đợi là chấp nhận được và tài nguyên cn được tận dụng hiệu quả hơn.
Downloaded by Anh Tr?n Th? Lan (anh.21d0003@huemed-univ.edu.vn)



