BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC NÔNG LÂM TP. HỒ CHÍ MINH KHOA KHOA HỌC
XÁC SUẤT THỐNG KÊ BÀI TẬP NHÓM
GIẢNG VIÊN PHỤ TRÁCH: BÙI ĐẠI NGHĨA Nhóm 13 STT Tên MSSV 1 NGUYỄN HOÀNG TUẤN 20113379 2 VŨ ĐÌNH ANH TUẤN 20126403 3 NGUYỄN HỮU TUYÊN 20126404 4 HUỲNH THỊ THANH TUYỀN 20126405 5 LÊ THỊ CẨM TUYỀN 20113179 6 ĐẶNG NGUYỄN HÀ VÂN 20126409 7 KIỀU TRỌNG VINH 20126412 8
HOÀNG NGUYỄN THỊ THẢO VY 20126415 9 VÕ HUỲNH THẢO VY 20126176 10 LÊ LAN XUÂN 20126419
BÀI 1: Một lô hàng có 5 sản phẩm tốt, 8 sản phẩm xấu. Có 2 người khách mỗi người lần
lượt lấy từ lô ra 1 sản phẩm để mua.
a) Tính xác suất người thứ 2 mua được sản phẩm tốt. Giải
Gọi A là biến cố người thứ i lấy được tốt i Ta có: 1 1 ( n )  = C .C 13 12
Gọi B là biến cố người thứ 2 mua được sản phẩm tốt 1 1 1 1 C .C C .C 5 5 4 8 5
P(B) = P( A .A ) + P( A .A ) = + = 1 2 1 2 13.12 13.12 13
b) Biết rằng người 2 mua được sản phẩm tốt tính xác suất người thứ nhất mua được sản phẩm tốt. P ( ) 1 1 C .C 5 5 4 = = 1 2 13.12 39
BÀI 2: Thời gian xếp hàng chờ phục vụ của khách hàng là biến liên tục X (đơn vị:phút)
có hàm phân phối xác suất:
a) Tìm hàm mật độ xác suất của X. Suy ra thời gian xếp hàng trung bình của khách hàng  0 khi x  3 
.Hàm mật độ xác suất: 2
P(t) = f (x) = F (x) ' 3  k.(x − 3)
khi 3  x  7  0 khi 7  7   0 khi x 3;7
Hay nói cách khác: p(t)=  2 3
 k.(x − 3) khi x 3;7  7 2
p(t)dt = 3k.(t − 3) dt = 1   Ta có : − 3 1
 64k =1 k = 64  3 2 = − =
Thời gian xếp hạng trung bình là: E( X ) . x .(x 3) dx 6  64 −
b) Tính xác suất trong 6 người xếp hàng thì có 4 người chờ không quá 5 phút: 3 3
P( X  5) = P(3  X  5) = F (5) − F (3) = − 0 = 16 16  3 
Gọi Y là số người chờ không quá 5 phút,Y ~ B 6,    16 
Vậy xác suất trong 6 người xếp hàng thì có 4 người chờ không quá 5 phút là: 4 2 3  3  4
P(Y = 4) = C . . 1− = 0,012 6   16  16 
BÀI 3 :Cho một máy sản xuất hai sản phẩm độc lập với xác suất được sản phẩm tốt ở
lần sản xuất thứ nhất là 0,9, xác suất sản xuất được sản phẩm tốt ở lần 2 là 0,6. Sau đó,
bán hai sản phẩm do máy sản xuất với sản phẩm tốt bán được 30(nghìn đồng); sản phẩm
xấu bán được 60(nghìn đồng). Hãy xác định số tiền trung bình khi bán hai sản phẩm do máy sản xuất. Giải
Gọi X là số sản phẩm tốt trong 2 sản phẩm lấy ra
X có bảng phân phối như sau: x 0 1 2 P(X) 0,04 0,42 0,54
E(X ) =  X .P =1.0,42 + 2.0,54 =1,5 i i
Tiền khi bán sản phẩm tốt trong 2 sản phẩm lấy ra: X.30000
Tiền khi bán sản phẩm xấu trong 2 sản phẩm lấy ra: (2-X).60000
Y = X.30000 + (2− X ).60000 = 90000X −120000
Số tiền trung bình sản phẩm bán ra là:
E(Y ) = E(90000.X −120000) = E( X ).90000 −120000 1,5.90000 −120000 = 15000
Vậy số tiền trung bình sản phẩm bán ra là 15 ngàn đồng.
Bài 4: Hộp I có 6 sản phẩm tốt, 5 sản phẩm xấu. Hộp II có 7 sản phẩm tốt, 6 sản phẩm xấu.
a) Lấy ngẫu nhiên từ mỗi hộp ra 1 sản phẩm.Tìm luật phân phối xác suất của số sản
phẩm tốt trong 2 sản phẩm lấy ra. Giải
Gọi X là số sản phẩm tốt trong số sản phẩm lấy ra
X nhân các giá trị nguyên 0,1,2. 5.6 30 P(X=0)= = 11.13 143 6.6 5.7 71 P(X=1)= + = 11.13 11.13 143 6.7 42 P(X=2)= = 11.13 143
Bảng phân phối xác suất của X X 0 1 2 30 71 42 P(X) 143 143 143
b) Lấy ngẫu nhiên từ hộp I ra 1 sản phẩm bỏ vaò hộp II sau đó từ hộp II lấy ngẫu
nhiên ra 2 sản phẩm. Tìm luật phân phối xác suất của số sản phẩm tốt trong 2 sản
phẩm lấy từ hộp II. Giải
Gọi X là số sản phẩm tốt trong 2 sản phẩm lấy ra từ hộp 2.
X nhận các giá trị nguyên 0,1,2 2 2 6.C 5.C 15 P(X=0)= 6 7 + = 2 2 11.C 11.C 77 14 14 1 1 1 1 6.C .C 5.C .C 41 P(X=1)= 6 8 7 7 + = 2 2 11.C 11.C 77 14 14 2 2 6.C 5.C 21 P(X=2)= 8 7 + = 2 2 11.C 11.C 77 14 14
Bảng phân phối xác suất của X: X 0 1 2 15 41 21 P(X) 77 77 77
Bài 5 :BÀI TẬP VỀ THỐNG
1) Khảo sát ngẫu nhiên 67 sinh viên trường đại học Nông Lâm TP.HCM
về thời gian học tập,ta được kết quả sau:
Thời gian học tập( phút ) Số sinh viên 0-20 30 20-40 22 40-60 11 60-80 4
Bảng 1: thời gian tập luyện TDTT của sinh viên Nông Lâm TP.HCM.
Dựa vào mẫu điều tra, ước lượng thời gian học tập trung bình của mỗi sinh viên, với độ tin cậy 95%. Giải
Gọi a là thời gian học tập trung bình của 1 sinh viên
𝑛 = 67; 𝑥̅ = 26,716; 𝑠𝑥 = 18,289
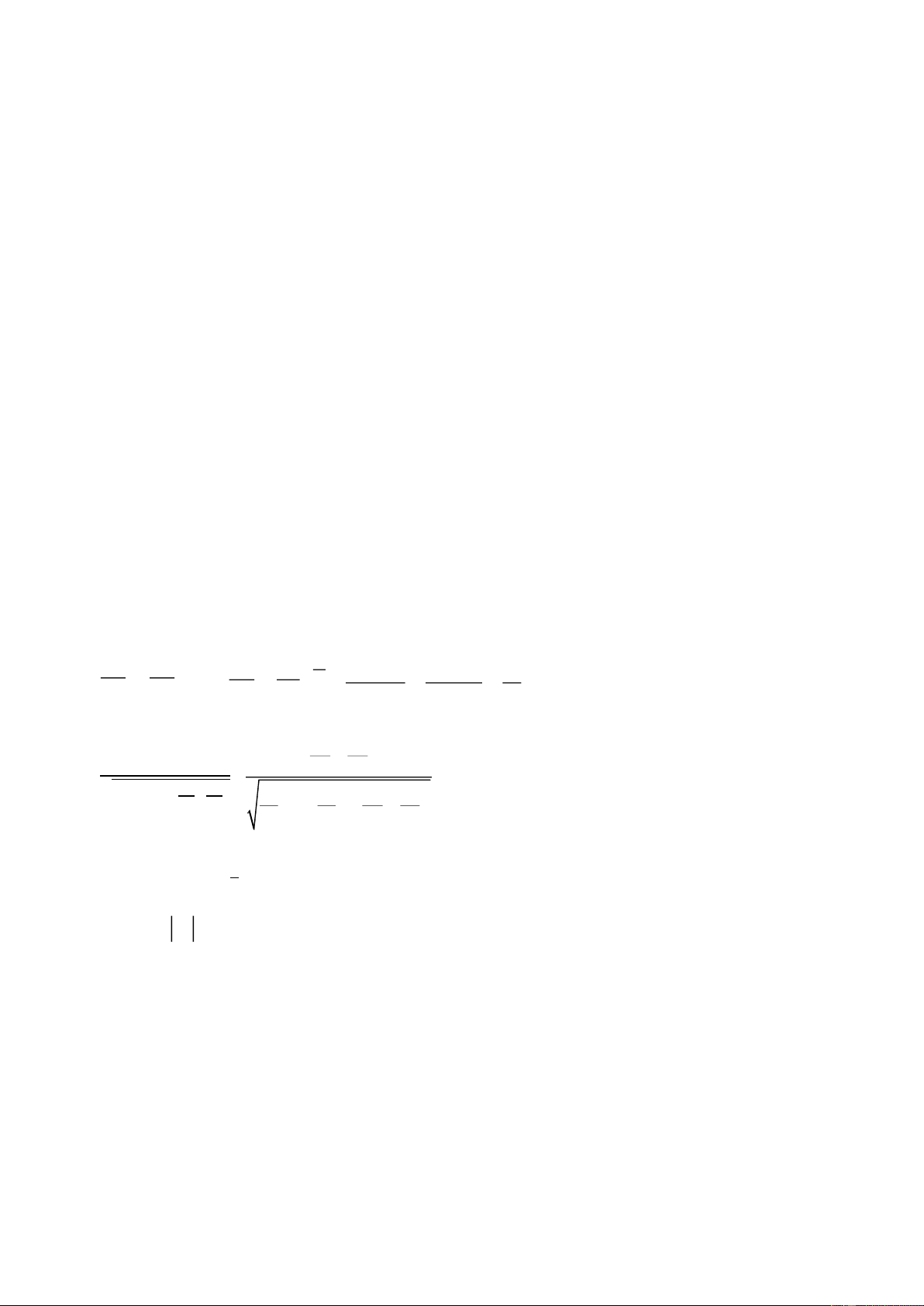
𝛾 = 95% → 𝛼 = 5% → 𝑧𝛼 = 1,96 2 𝑠 (𝑎 𝑥
1; 𝑎2) = 𝑥̅ ∓ 𝑧𝛼. 2 √𝑛 18,289 = 26,716 ∓ 1,96. √67 = (22,336; 31,095)
2) Khát sát 67 sinh viên của trường đại học Nông Lâm TP.HCM về thời gian
học tập, những sinh viên có thời gian học tập trên 40 phút trở lên được xem
là sinh viên chăm học. (sử dụng lại bảng 1)
a) Dựa vào mẫu điều tra ước lượng tỷ lệ sinh viên chăm học, với độ tin cậy 99%. Giải a) Ta có: m 15 A f = = n n 67
 = 99%   = 0,01 z = 2,58 0,005 𝑓 (𝑃 𝑛. (1 − 𝑓𝑛)
1; 𝑃2) = 𝑓𝑛 ∓ 𝑧 𝛼 . √ 2𝛼 𝑛 15 15 15 .(1− ) = ∓ 2,58. √67 67 67 67
= (0,092; 0,355)
b) Dựa vào mẫu điều tra, kiểm định giả thuyết cho rằng: tỷ lệ sinh viên chăm học nằm
dưới 50%, với mức ý nghĩa 2%.hãy cho kết luận về giả thuyết trên.
b) Gọi P là tỷ lệ sinh viên chăm học.
Đặt 𝐻0 = 𝑃 = 0,5 𝐻1 = 𝑃 < 0,5 15 𝑓 − 0,5 𝐾 = 𝑛 − 𝑃0 = 67 = −6,157 √𝑃0. (1 − 𝑃0) √. 0,5. (1 − 0,5) 𝑛 67  = 0,02  z = 2,0537 0,02  K  −z = 2 − ,0537 H H 0,02 ,Bác bỏ 0 ,Chấp nhận 1
Kết luận: với mức ý nghĩa 2% giả thuyết tỷ lệ sinh viên chăm học nằm dưới 50% là có thể chấp nhận được.
3) Kết quả khảo sát chiều cao (cm) của 20 sinh viên thuộc 2 khoa, khoa “Khoa học sinh
học” (I) và khoa”Cơ khí” (II) của trường đại học Nông Lâm TP.HCM. Số sinh viên 12 4 3 1 I 156 160 166 170 II 155 158 160 175
Dựa vào 2 mẫu điều tra, kiểm định giả thuyết cho rằng: chiều cao trung bình của sinh
viên khoa khoa học sinh học cao hơn khoa cơ khí, với mức ý nghĩa 5% hãy cho kết luận
về giả thuyết trên. Cho biết, dấu hiệu đang xét trên 2 đám đông có phân phối chuẩn, cùng phương sai. Giải  n = 20  n = 20 1  2 
KHSH(I) s = 4, 472 KCK(II)  s = 4,591 x y    x =159 y =157,35
H : a = a o 1 2
Đặt:  H :a  a  1 1 2
Gọi X là chiều cao trung bình của sinh viên khoa khoa học sinh học
Y là chiều cao trung bình của sinh viên khoa cơ khi
Vì X,Y có phương pháp chuẩn, cùng phương sai → 𝜎2 2 1 = 𝜎2 𝑥̅ − 𝑦̅ 𝐾 = (𝑛 2 + (𝑛 2 √ 1 − 1). 𝑠𝑥 2 − 1). 𝑠𝑦 1 1 𝑛 + ) 1 + 𝑛2 − 2 . (𝑛1 𝑛2 159 −157, 35 = =1,151 2 2 19.4, 472 +19.4, 591  1 1  . +   20 + 20 − 2  20 20  − ta có: n 1 19
 = 5% = 0,05  t = t =1,7291  0,05  19 K = 1,151  t
=1,7291.Bác bỏ H ,Chấp nhận H 0,05 1 0
Kết luận: với mức ý nghĩa 5% giả thuyết cho rằng:chiều cao trung bình của sinh viên khoa
khoa học sinh học cao hơn khoa cơ khí là chập nhận được.
4. Khảo sát thời gian ngủ một ngày của sinh viên 2 khoa, khoa khoa học sinh học và khoa Nông học.
 Khoa khoa học sinh học: khảo sát 40 sinh viên ta thấy 10 sinh viên ngủ đủ giấc(
thời gian ngủ nhiều hơn 8h )
 Khoa Nông học: khảo sát 35 sinh viên ta thấy có 25 sinh viên ngủ đủ giấc.
Dựa vào mẫu điều tra, kiểm định giả thuyết cho rằng: tỷ lệ phần tử có tính chất A của 2
đám đông này không như nhau, với mức ý nghĩa 1% có thể kết luận gì về giả thuyết trên. Giải
Gọi P1 là tỷ lệ sinh viên ngủ đủ giấc của khoa khoa học sinh học
P2 là tỷ lệ sinh viên ngủ dủ giấc của khoa Nông học
H :P = P 0 1 2
Đặt:  H :P  P  1 1 2 m 10 1 m 25 + + f = = f = = m m 10 25 7 = = = 1 ; 2 ; 1 2 f n 40 2 n 35 + + 1 n n 40 35 15 2 1 2 10 25 − 𝑓 𝐾 = 1−𝑓2 = 40 35 = −4,02 1 1 √𝑓. ̅ (1−𝑓̅).( + ) 7  7   1 1  𝑛1 𝑛2 . 1− . +     15  15   40 35 
Ta có: 𝛼 = 1% → 𝑧𝛼 = 2,58 2
 K = 4,02  z
= 2,58 Bác bỏ H ,Chấp nhận H 0,005 0 1
Kết luận: với mức ý nghĩa 1% , giả thuyết cho rằng tỷ lệ sinh viên ngủ đủ giấc của 2 khoa
Khoa học sinh học và khoa Nông học này không như nhau là chấp nhận được.