Báo cáo thí nghiệm - định luật malus môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

TR¯àNG ĐẠI HàC BÁCH KHOA HÀ NỘI ------------o0o------------ BÀI THÍ NGHIÞM VÀT LÝ 2 BÀI 4:
PHÂN CĀC ÁNH SÁNG. ĐÞNH LÝ MALUS. PHÂN CĀC TRÒN VÀ PHÂN CĀC ELIP
Giảng viên h°ßng d¿n: Lê Thß Hồng Liên Nhóm sinh viên thāc hißn: Há và tên MSSV Chuyên ngành Nguyễn Quang Anh 20207193
PFIEV Cơ Khí Hàng Không K65 Phạm Thị Tưßng Vi 20207228
PFIEV Cơ Khí Hàng Không K65 Hà Đăng Thắng 20200608
PFIEV Cơ Khí Hàng Không K65 Nguyễn Hữu Lực 20202834 PFIEV THCN & TĐH K65 Nguyễn Văn Thuận 20202837 PFIEV THCN & TĐH K65 Đỗ Hoài Nam 20202823 PFIEV THCN & TĐH K65 I. Mục đích thí nghißm
- Kiểm nghiệm định luật malus
- Kiểm nghiệm tính chất của bản một phần hai bước sóng và bản một phần tư bước sóng II. C¡ sở lý thuyết
1. Ánh sáng tā nhiên và ánh sáng phân cāc - Ánh sáng tự nhiên
Nguyên tử của nguồn sáng phát ánh sáng dưới dạng những đoàn sóng nối
tiếp nhau. Trong mỗi đoàn sóng, véc tơ điện trưßng E luôn luôn dao động theo
một phương xác định vuông góc với tia sáng. Do nguồn sáng chứa đựng vô số
các nguyên tử và do tính hỗn loạn của các vận động trong nguyên tử, véc tơ điện
trưßng E trong các đoàn sóng do nguốn sáng phát ra dao động theo mọi phương vuông góc với tia sáng.
Ánh sáng có véc tơ điện trưßng dao động đều đặn theo mọi phương vuông
góc với tia sáng được gọi là ánh sáng tự nhiên.
Để biểu diễn ánh sáng tự nhiên, ngưßi ta vẽ trong mặt phẳng vuông góc với
tia sáng các véc tơ điện trưßng có trị số bằng nhau phân bố đều đặn xung quanh tia sáng (hình 1). - Ánh sáng phân cực
Thực nghiệm chứng tỏ rằng khi cho một ánh sáng tự nhiên đi qua một môi
trưßng bất đẳng hướng về mặt quang học, ví dụ trong tinh thể tuamalin (allumini
silicoborat), trong một số trưßng hợp đặc biệt ánh sáng sau khi qua môi trưßng
chỉ còn dao động theo một phương xác định. Ánh sáng có véc tơ điện trưßng chỉ
dao động theo một phương xác định được gọi là ánh sáng phân cực thẳng hay ánh
sáng phân cực toàn phần. Thực nghiệm chứng tỏ rằng trong mỗi tinh thể tuamalin
có mặt phẳng chứa một phương đặc biệt gọi là quang trục, ánh sáng có véc tơ
điện trưßng nằm trong mặt phẳng đó sẽ truyền qua bản tinh thể, còn ánh sáng có
véc tơ điện trưßng vuông góc với mặt phẳng này sẽ không truyền qua bản.
Ánh sáng có véc tơ điện trưßng dao động theo mọi phương vuông góc với
tia sáng nhưng có phương dao động mạnh, có phương dao động yếu gọi là ánh
sáng phân cực một phần. 2. Đßnh luÁt Malus
Cho ánh sáng tự nhiên đi qua 2 bản tuamalin T1 và T2 có quang trục hợp với nhau một góc .
Cưßng độ ánh sáng sau bản T2 liên hệ với cưßng độ ánh sáng sau bản T1
theo hệ thức còn được gọi là định lý Malus: 2 I I 2 1co = s
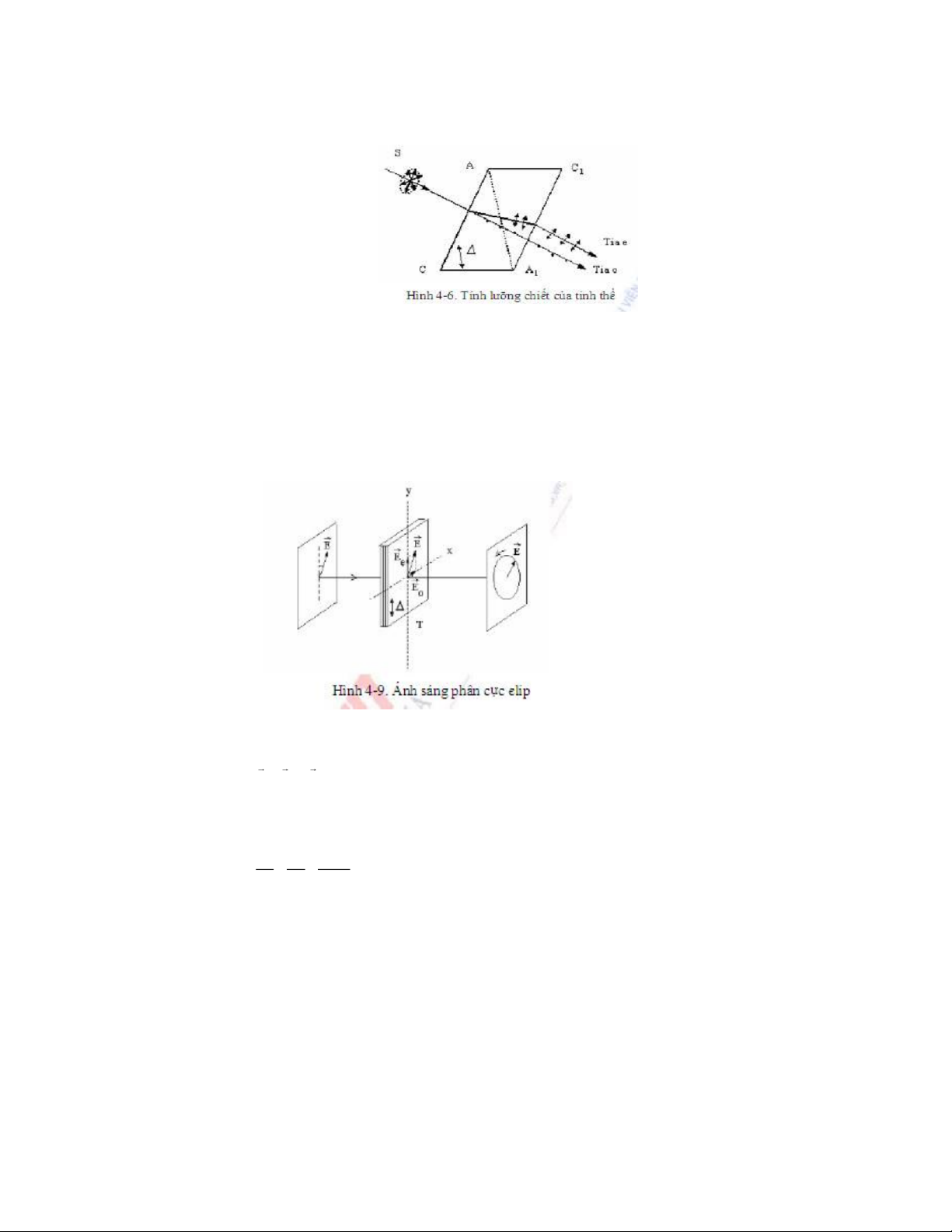
3. Phân cāc do l°ỡng chiết
Cho 1 tia sáng tự nhiên rọi vào tinh thể băng lan, ra khỏi tinh thể có 2 tia:
- Tia thưßng là tia phân cực toàn phần, phương phân cực vuông góc mp
chứa trục tinh thể và tia tới
- Tia bất thưßng là tia phân cực toàn phần, phương phân cực nằm trong mp
chứa trục tinh thể và tia tới
Chiết suất của tinh thể đối với hai tia trên là khác nhau, nethể lưỡng chiết, phân cực do lưỡng chiết. 4. Ánh sáng phân cāc elip
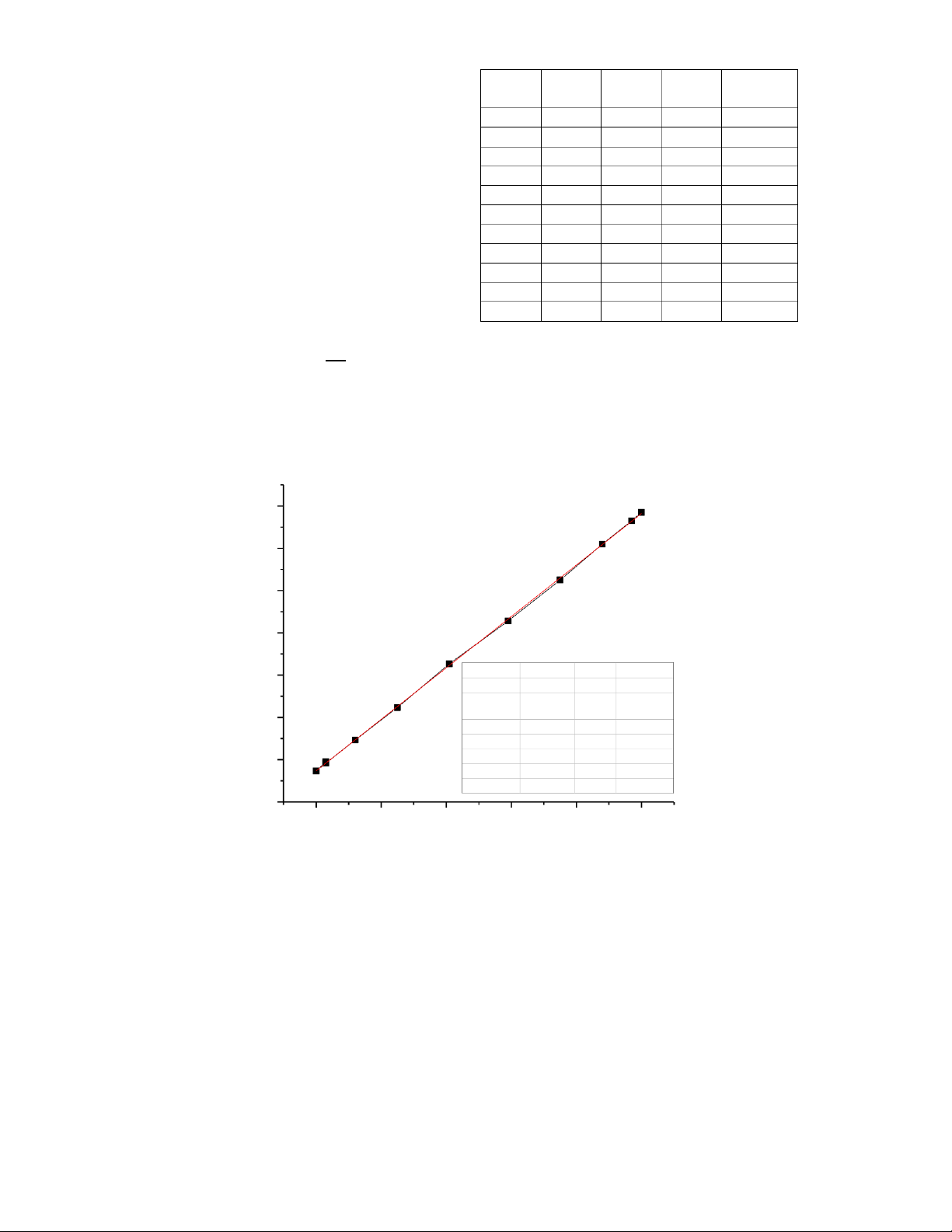
Chiếu 1 tia phân cực thẳng có Ei vào tinh thể lưỡng chiết. Vào bản tinh thể
tia này tách thành tia thưßng và tia bất thưßng có Eo và Ee. Véc tơ điện trưßng sau bản là: E = E + o eE
Các vectơ sáng E 0 và E e dao động theo 2 phương vuông góc nhau, do đó
đầu mút vector sáng tổng hợp sẽ chuyển động trên 1 đưßng elip xác định bái phương trình: 2 2 2 x y 2xy cos sin 2 2+ − = A A A A 1 2 1 2 Với A v 1 à A
2 lần lượt là biên độ và
= 0 e − là hiệu pha dao động của 2
vector sáng E 0 và E e. Nếu trước khi vào bản tinh thể, ánh sáng phân cực toàn
phần có biên độ là A thì A= Asin và A= Acos
. Như vậy ánh sáng phân cực 1 2
thẳng sau khi truyền qua bản tinh thể sẽ biến thành ánh sáng phân cực elip.
Chúng ta sẽ xét 1 vài trưßng hợp riêng phụ thuộc vào độ dày d của bản tinh thể.
- Bản phần tư bước sóng
Bản phần tư bước sóng là bản tinh thể có độ dày d sao cho hiệu quang lộ
của tia thưßng và tia bất thưßng truyền qua bản bằng 1 số lẻ lần của phần tư bước sóng: L= (n 0 e − n )d= (2k+ 1) 4
Khi đó hiệu pha của 2 tia bằng: ( = 2k 1 + ) 2 2 2
Và ta có được phương trình: x y 1 2 2+= A A 1 2
Trong trưßng hợp này, đầu mút của vector sáng tổng hợp E phía sau bản tinh
thể chuyển động trên 1 elip dạng chính tắc có 2 bán trục là A 1 và A2. Đặc biệt nếu α=45° thì A =
1 A2=A0 và phương trình trá thành x2+ y2= A0 2.
Khi đó đầu mút vector sáng tổng hợp E phía sau bản tinh thể chuyển động
trên đưßng tròn tâm O, bán kính A0 . Như vậy sau khi truyền qua bản 14 bước
sóng, ánh sáng phân cực thẳng đã bị biến đổi thành ánh sáng phân cực elip dạng
chính tắc hoặc phân cực tròn -Bản nửa bước sóng
Bản nửa bước sóng là bản tinh thể có độ dày d sao cho hiệu lộ quang của tia
thưßng và tia bất thưßng truyền qua bản bằng 1 số lẻ lần nửa bước sóng: L= (n − n )d= (2k+ 1) 2 0 e
Khi đó hiệu pha 2 tia bằng = (2k 1) + x y 0 Và phương trình +=
Đây là phươg trình của đưßng thẳng, mút 1 A 2A
vector sáng tổng hợp E phía sau bản sẽ chuyển động trên đưßng thẳn nằm trong
góc phâng tư thứ 2 và thứ 4 của hệ tạ độ Oxy, đưßng thẳng đó hợp với quang trục
1 góc α. Trước khi vào bản tinh thể mút vector sáng của ánh sáng phân cực thẳng
dao động trên đưßng thẳng. Như vậy sau khi truyền qua bản nửa bước sóng ánh
sáng phân cực thẳng vẫn là ánh sáng phân cực thẳng nhưng phương dao động đa
quay đi 1 góc 2α so với trước khi đi vào bản. III. Các b°ßc thí nghißm
1. Kiểm nghißm đßnh luÁt Malus:
1.1: Bố trí thí nghiệm:
- Nguồn sáng trắng tự nhiên (không phân cực), tấm chắn có lỗ há, 2 bản
tuamalin và luxmeter được đặt đồng trục với nhau trên giá đỡ. * Trình tự thí nghiệm: - Bật nguồn sáng
- Che chắn quang hệ để đảm bảo phần lớn ánh sáng chiếu vào luxmeter là từ nguồn.
- Đặt cho các quang trục của hai bản tuamalin trùng nhau (2 kim đều chỉ á vị trí 0).
- Đọc giá trị hiển thị trên luxmeter, ghi lại vào bảng số liệu.
- Giữ nguyên vị trí bản tuamalin thứ 1, thay đổi quang trục của bản tuamalin
thứ 2 lần lượt 5 độ một lần. à mỗi vị trí của bản tuamalin thứ 2, ghi lại giá
trị tương ứng trên luxmeter. Lấy lại vị trí bản tuamalin thứ 2 và đọc kết quả
(thực hiện 3 lần cho mỗi vị trí). 1.2 Yêu cầu:
- Vẽ đồ thị sự phụ thuộc của giá trị hiển thị trên luxmeter vào góc hợp bái
quang trục của hai bản tuamalin.
- Kiểm nghiệm lại định luật Malus. - Nhận xét
2. Tính chất của bản ½ b°ßc sóng: 2.1 Bố trí thí nghiệm:
- Chuẩn bị: nguồn sáng trắng tự nhiên, kính phân cực, bản ½ bước sóng, kính phân tích, luxmeter. * Trình tự thí nghiệm:
- Gọi góc giữa quang trục của kính phân cực và quang trục của bản ½ bước sóng là α.
- Trong khi làm thí nghiệm, giữ nguyên vị trí bản ½ bước sóng, chỉ quay
quang trục của kính phân cực để thay đổi góc α.
- Kiểm tra tính phân cực của chùm sáng phía sau bản ½ bước sóng. (Bằng
cách quay quang trục của kính phân tích và quan sát trên luxmeter). Đây sẽ
là chùm sáng phân cực thẳng.
- Gọi góc lệch giữa quang trục của kính phân tích so với quang trục của kính phân cực là β. * Yêu cầu: - Thay đổi góc α (
= 0;15;30; 45 ), ứng với mỗi giá trị α, cho β chạy từ 0 đến
360º (thay đổi 10 độ một).
- Kiểm tra mối quan hệ: β = 2 α. - Nhận xét
3. Tính chất của bản ¼ b°ßc sóng: 3.1 Bố trí thí nghiệm:
- Chuẩn bị: nguồn sáng trắng tự nhiên, kính phân cực, bản ¼ bước sóng, kính phân tích, luxmeter.
3.2 Trình tự thí nghiệm:
- Gọi góc giữa quang trục của kính phân cực và quang trục của bản ¼ bước sóng là α.
- Với các giá trị khác nhau của α, xác định tính chất phân cực của chùm tia
đi ra khỏi bản ¼ bước sóng bằng cách xoay quang trục của kính phân tích
và quan sát số chỉ trên luxmeter. * Yêu cầu:
- Khi α = 0 độ, chỉ ra rằng chùm sáng sau bản ¼ bước sóng là phân cực thẳng.
- Khi α = 45 độ, chỉ ra rằng chùm sáng sau bản ¼ bước sóng là phân cực tròn.
- Khi 0 < α < 45 độ (nên chọn α ≈ 30 độ), kiểm tra tính phân cực elip của
chùm sáng sau bản ¼ bước sóng.
Đo với các góc: = 0;15;30;45 , ứng với mỗi giá trị α, cho β chạy từ 0 đến
360º (thay đổi 10 độ một). VI. XỬ LÝ SÞ LIÞU 1. Đßnh luÁt malus
- Đo cưßng độ ánh sáng nền : I nền= 2(lux)
Sai số dụng cụ: ∆Idc = 1 (lux) ∆³dc = 1(°)
Sai số tuyệt đối ∆Inền = ∆Idc =1(lux)
Vậy cưßng độ ánh sáng nền : Inền = 2 ± 1(lux)
- Đo cưßng độ ánh sáng khi qua 2 bản tuamalin I ( bao gồm ánh sáng nền).
- Ta có bảng số liệu sau: Góc Đo I Đo I Đo I α lần lần lần I (lux) ∆I1 ∆I2 ∆I3 ∆I ∆I = ∆I + ∆Idc (°) 1(lux) 2(lux) 3(lux) 0° 139 138 140 139 0 1 1 1 2 10° 135 136 134 135 0 1 1 1 2 20° 124 123 125 124 0 1 1 1 2 30° 107 108 106 107 0 1 1 1 2 40° 87 88 88 88 1 0 0 0 1 50° 67 68 67 67 0 1 0 1 2 60° 47 46 47 47 0 1 0 1 2 70° 31 31 32 31 1 0 0 0 1 80° 20 21 20 20 0 1 0 0 1 90° 17 17 16 17 0 0 1 0 1 100° 20 22 21 21 0 1 1 1 2
- Cưßng độ ánh sáng khi qua 2 Góc α I bản tuamalin I 2 ∆I2 cos2³ ∆(cos2³) 2 (không bao (°) gồm ánh sáng nền): 0 137 3 1,00 0,00 Ta có: I 10 133 3 0,97 0,01 2 = I - Inền 20 122 3 0,88 0,01 → I 2= I 2 I nền 30 105 3 0,75 0,02 40 86 2 0,59 0,02 ∆I2= ∆I + ∆Inền 50 65 2 0,41 0,02 60 45 2 0,25 0,02 70 29 2 0,12 0,01
- Mặt khác, xét x = cos2³ 80 18 2 0,03 0,01 dx = - sin2α.dα 90 15 2 0,00 0,00 100 19 3 0,03 0,01 ∆(cos2³) = sin2³. ∆³
Trong đó ∆³ = 1.π180 ≈ 0,02 (rad)
- Vậy ta được bảng bên :
Ta có đồ thß mßi liên hß giÿa I
2 và �㔜�㔨�㔬�㗐�㗂 : 140 120 100 80 I2 60 Equation y = a + b*x Weight No Weighti Residual 3.27242 Sum of 40 Squares Pearson's r 0.99993 Adj. R-Squa 0.99984 20 Value Standard Er I2 Intercept 14.7307 0.28531 I2 Slope 121.662 0.48084 0 0.0 0.2 0.4 0.6 0.8 1.0 cos(anpha)2
- Nhận xét: theo công thức malus 2 I I 2 1co = s
, hệ số góc của đưßng fit linear
phải bằng I1=137 ± 3 nhưng thực tế chỉ gần đúng, nguyên nhân là do quang
trục của các kính phân tích bị lệch và khi chỉnh các kính phân tích không
hoàn toàn song song với nhau.
2. Tính chất bản 1/2 b°ßc sóng:
- Với mỗi giá trị của α ta tìm được các góc β sao cho cưßng độ ánh sáng tại đó là lớn nhất: α β Lần 1(°) Lần 2(°) Lần 3(°) Ā (°) ∆Ā 0° 1 0 3 1 2 15° 27 30 31 29 2 30° 55 57 56 56 1 45° 95 93 92 93 1
- Từ bảng rút ra nhận xét, Ā ≈ 2ÿ, tuy nhiên kết quả không trùng khớp
hoàn toàn do sai số dụng cụ và khi chỉnh các kính phân tích ta không làm
hoàn toàn song song với nhau . Vậy sau khi truyền qua bản nửa bước
sóng ánh sáng phân cực thẳng vẫn là ánh sáng phân cực thẳng nhưng
phương dao động đa quay đi 1 góc 2α so với trước khi đi vào bản.
3. Tính chất bản 1/4 b°ßc sóng: 2.1 Khi ³ = 45°:
Đo I lần Đo I lần Đo I lần ´(°) I 1 2 3 ∆I I 2 ∆I2 0 ±1 53 52 54 53 2 50 3 10 ±1 50 51 50 50 1 47 2 20 ±1 49 48 47 48 2 45 3 30 ±1 48 47 46 47 2 44 3 40 ±1 46 45 47 4 2 43 3 50 ±1 47 48 47 47 1 44 2 60 ±1 47 46 47 47 1 44 2 70 ±1 46 47 47 47 1 43 2 80 ±1 48 49 49 49 1 45 2 90 ±1 49 50 49 49 2 46 2 100 ±1 50 52 52 51 3 48 4 110 ±1 53 52 53 53 1 49 2 120 ±1 54 53 52 53 2 50 3 130 ±1 55 55 54 55 1 51 2 140 ±1 55 56 57 56 2 53 3 150 ±1 54 55 55 54 1 51 2 160 ±1 53 52 51 52 2 49 3 170 ±1 52 53 51 52 2 49 3 180 ±1 50 51 51 50 1 47 2 190 ±1 49 48 49 48 1 45 2 200 ±1 48 47 49 48 2 45 3 210 ±1 46 46 47 46 1 43 2 220 ±1 47 46 45 46 2 43 3 230 ±1 47 45 48 46 3 44 4 240 ±1 47 48 47 47 1 44 2 250 ±1 47 46 47 46 1 43 2 260 ±1 46 47 47 46 1 43 2 270 ±1 48 49 49 48 1 45 2 280 ±1 49 50 49 49 1 46 2 290 ±1 50 52 52 51 3 48 4 300 ±1 53 52 53 52 1 49 2 310 ±1 54 53 52 53 2 50 3 320 ±1 55 55 54 54 1 51 2 330 ±1 55 56 57 56 2 53 3 340 ±1 55 55 54 54 1 51 2 350 ±1 54 53 54 54 1 51 3
Đồ thị sự phân cực của ánh sáng khi ³ = 45° 90 100 80 110 70 120 60 50 130 50 40 140 40 30 150 30 20 160 20 10 170 10 C 0 180 0 10 190 350 20 200 340 30 210 330 40 220 320 230 310 50 240 300 250 260 270 280 290
- Nhận xét: đồ thị có dạng gần giống hình tròn, nên ánh sáng đã phân cực tròn. 2.2 Khi ³ = 0°:
Đo I lần Đo I lần Đo I lần ´(°) I 1 2 3 ∆I I 2 ∆I2 0 ±1 82 83 81 82 2 79 3 10 ±1 85 84 85 85 1 81 2 20 ±1 80 83 82 82 3 78 4 30 ±1 78 77 76 77 2 74 3 40 ±1 72 73 74 73 2 70 3 50 ±1 64 65 63 64 2 61 3 60 ±1 56 55 57 56 2 53 3 70 ±1 47 46 47 46 1 43 2 80 ±1 39 40 39 39 1 36 2 90 ±1 26 27 26 26 1 23 2 100 ±1 18 18 19 18 1 15 2 110 ±1 28 27 27 27 1 24 2 120 ±1 36 35 35 35 1 32 2 130 ±1 48 47 47 47 1 44 2 140 ±1 57 55 56 56 2 53 3 150 ±1 63 64 62 63 2 60 3 160 ±1 74 75 76 75 2 72 3 170 ±1 79 78 80 79 2 76 3 180 ±1 84 83 83 83 1 80 2 190 ±1 86 87 88 87 2 84 3 200 ±1 82 81 81 81 1 78 2 210 ±1 75 76 76 75 1 72 2 220 ±1 72 71 72 71 1 68 2 230 ±1 64 65 63 64 2 61 3 240 ±1 56 55 57 56 2 53 3 250 ±1 47 46 47 46 1 43 2 260 ±1 39 38 38 38 1 35 2 270 ±1 28 29 27 28 3 25 4 280 ±1 20 20 19 21 2 17 3 290 ±1 27 27 28 26 2 24 3 300 ±1 36 37 37 37 1 34 2 310 ±1 47 47 48 47 1 44 2 320 ±1 56 55 56 57 2 53 3 330 ±1 63 64 62 63 2 60 3 340 ±1 73 73 74 72 2 70 3 350 ±1 79 78 80 79 2 76 3
Đồ thị liên hệ giữa I và cos2´ 90 80 70 60 50 I 40 30 20 10 0.0 0.2 0.4 0.6 0.8 1.0 cos(beta)2
- Nhận xét: Ánh sáng qua bản ¼ bước sóng đã phân cực thẳng như tính
toán lý thuyết. Qua bản tuamalin thứ 2 cưßng độ sáng I2 mà ta đo được
tuân theo định luật malus I2 =I1cos2 ³ ( Đồ thị trên) với I1 là cưßng độ của
ánh sáng phân cực toàn phần (phân cực thẳng ) sau bản ¼ bước sóng. 2.3 Khi ³ = 30°:
Đo I lần Đo I lần Đo I lần ´(°) I 1 2 3 ∆I I 2 ∆I2 0 ±1 57 55 57 56 3 53 4 10 ±1 59 58 59 59 1 56 2 20 ±1 56 58 58 57 3 54 4 30 ±1 56 54 55 55 2 52 3 40 ±1 53 52 52 52 1 49 2 50 ±1 48 49 48 48 1 45 2 60 ±1 45 44 45 45 1 42 2 70 ±1 41 41 41 41 0 38 1 80 ±1 38 38 38 38 0 35 1 90 ±1 35 36 35 35 1 32 2 100 ±1 35 34 34 34 1 31 2 110 ±1 36 36 34 35 3 32 4 120 ±1 38 38 36 37 3 34 4 130 ±1 41 40 39 40 2 37 3 140 ±1 45 44 44 44 1 41 2 150 ±1 49 49 47 48 3 45 4 160 ±1 52 52 51 52 1 49 2 170 ±1 56 55 55 55 1 52 2 180 ±1 58 58 57 58 1 55 2 190 ±1 58 59 58 58 1 55 2 200 ±1 57 58 57 57 1 54 2 210 ±1 55 56 55 55 1 52 2 220 ±1 52 54 53 53 2 50 3 230 ±1 48 49 49 49 1 46 2 240 ±1 44 45 44 44 1 41 2 250 ±1 41 41 40 41 1 38 2 260 ±1 36 38 37 37 2 34 3 270 ±1 38 36 35 36 3 33 4 280 ±1 36 35 34 35 2 32 3 290 ±1 35 35 34 35 1 32 2 300 ±1 36 37 36 36 1 33 2 310 ±1 38 40 39 39 2 36 3 320 ±1 43 44 44 44 1 41 2 330 ±1 45 48 47 47 3 44 4 340 ±1 49 51 51 50 3 47 4 350 ±1 53 55 54 54 2 51 3
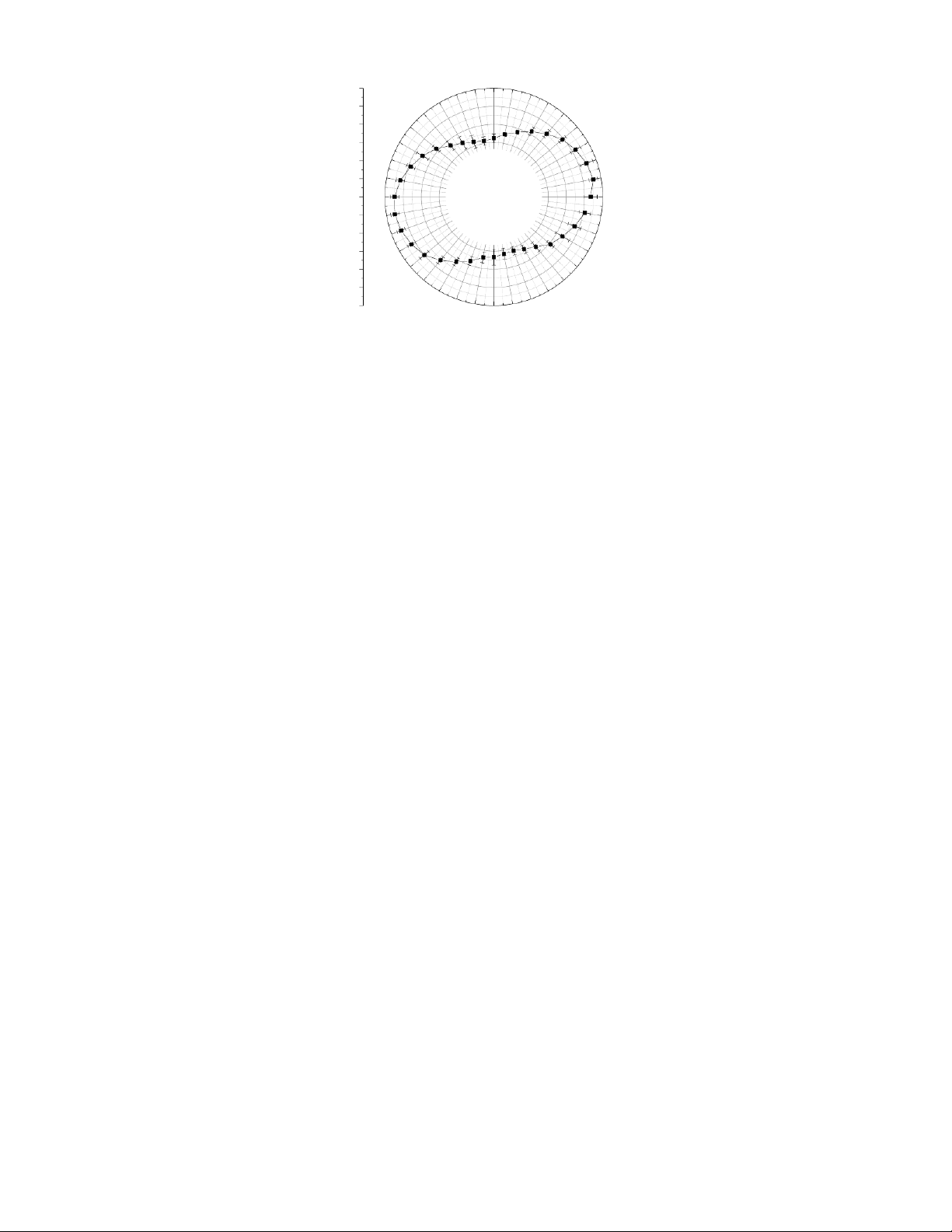
Đồ thị sự phân cực của ánh sáng khi ³ = 30° 90 100 80 60 110 70 120 60 50 130 50 40 140 40 30 150 30 20 160 20 10 170 10 B 0 180 0 10 190 350 20 200 340 30 210 330 40 220 320 50 230 310 240 300 60 250 260 270 280 290
- Nhận xét: đồ thị có dạng hình elip, nên ánh sáng đã phân cực elip.