Báo cáo thí nghiệm - giác kà đo góc môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

TR¯àNG Đ¾I HàC BÁCH KHOA HÀ NÞI VIÞN VÀT LÝ KỸ THUÀT ------------o0o------------
BÁO CÁO THÍ NGHIÞM VÀT LÝ 2 BÀI 2: GIÁC KÀ ĐO GÓC
Giảng viên h°ßng d¿n: Lê Thß Hồng Liên
Nhóm sinh viên thực hi n: ß Há và tên MSSV Chuyên ngành Nguyễn Quang Anh
20207193 PFIEV Cơ Khí Hàng Không K65 Phạm Thị Tường Vi
20207228 PFIEV Cơ Khí Hàng Không K65 Hà Đăng Thắng
20200608 PFIEV Cơ Khí Hàng Không K65 Nguyễn Hữu Lực 20202834 PFIEV THCN & TĐH K65 Nguyễn Văn Thuận 20202837 PFIEV THCN & TĐH K65 Đỗ Hoài Nam 20202823 PFIEV THCN & TĐH K65 1 I. Mục đích thí nghißm
- Kiểm nghiệm lại định luật Cauchy-Rayleigh về sự phụ thuộc chiết
suất của một chất trong suốt vào bước sóng ánh sáng: n(λ)= n0+a λ2
- Vẽ đường cong định chuẩn G(λ) của lăng kính, từ đó ta có thể xác
định được bước sóng của một ánh sáng bất kỳ bằng cách sử dụng giác
kế (người ta gọi phương pháp này là phương pháp quang phổ). II. Trình tự thí nghi m ß
1. Kiểm nghißm bằng thực nghißm đßnh luÁt Cauchy-Rayleigh
1.1: Điều chỉnh giác kế:
- Khi chưa chiếu sáng đèn. Điều chỉnh ống chuẩn trực:
+Điều chỉnh Thị kính để nhìn rõ dấu chữ thập.
+Xoay vòng 1 để điều chỉnh chữ thập thẳng đứng.
+Đặt gương phẳng sau ống chuẩn trực, quay núm 2 để nhận được
ảnh của chữ thập rõ nét.
- Sau khi bật đèn chiếu sáng Hg-Cd
+Nhìn thấy vết sáng màu vàng là ảnh của đèn.
+Để vệt sáng thẳng đứng: xoay vòng 3
+Để vệt sáng thanh mảnh, xoay vít nhỏ 6 cạnh vòng 3.
+Để vệt sáng nét: xoay vòng 2 hoặc vít 4.
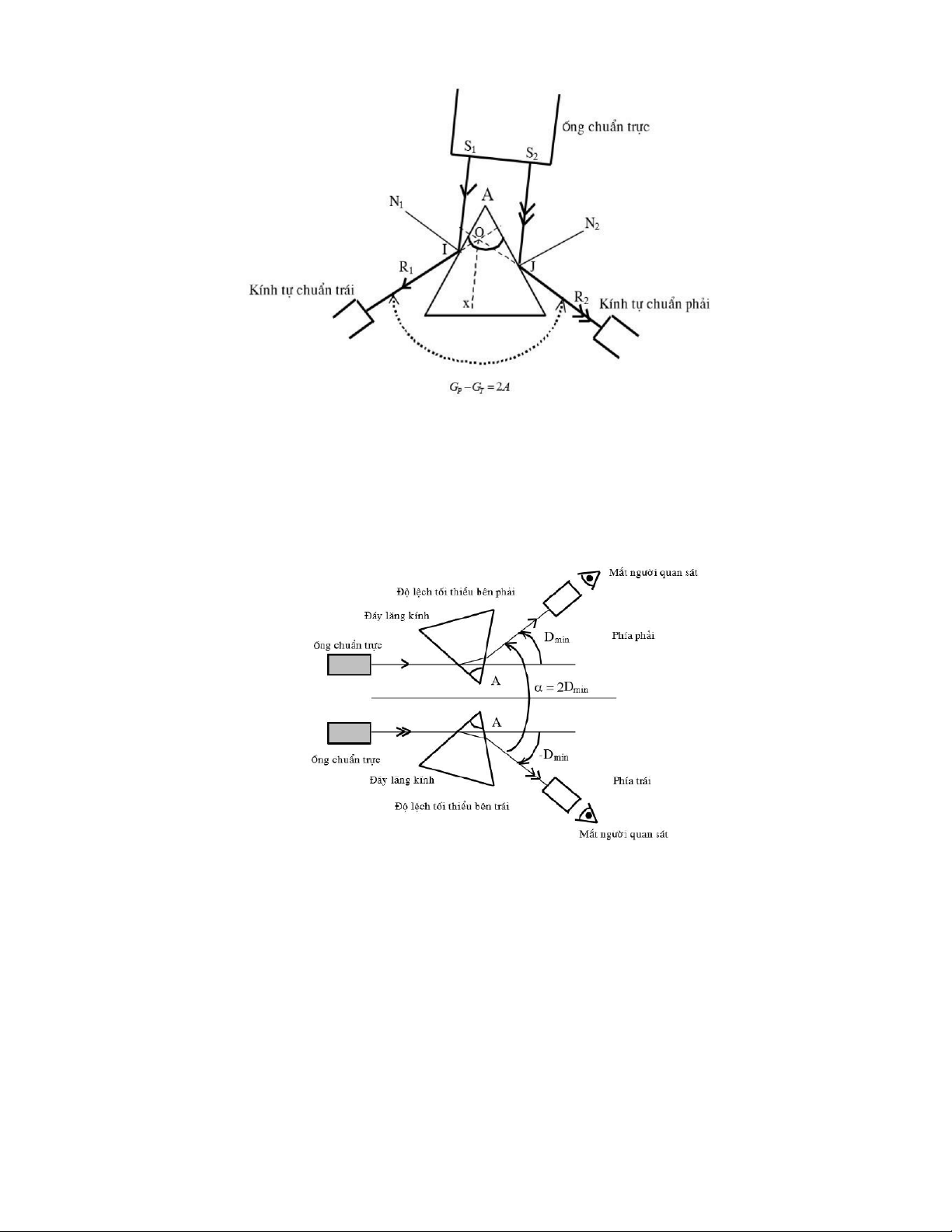
1.2: Đo góc A của lăng kính bằng phản xạ kép:
- Dùng đèn Hg-Cd sao cho tia tới chia thành 2 tia, 1 tia phản xạ trên
mặt trái và 1 tia phản xạ trên mặt phải của lăng kính. 2
Bằng kiến thức Toán học và sử dụng hình trên , ta có thể tính A:
Gp2 Gt=xOR1+xOR2 = 2. S1IA + 2. S2JA =2A
1.3: Đo chiết suất của lăng kính ứng với các vạch màu khác nhau bằng
phương pháp độ lệch tối thiểu: 3
Ta có : D = i1+ i22 A và có góc lệch cực tiểu khi i1= i2, do đó r1= r2=A 2 Dmin = 2i12 A ⇒ i1=Dmin + A 2
Theo định luật khúc xạ : 2)= n ⇒ n = sin (Dmin + A si s n i i n 1 r =sini1 2) sina(A sin (A2)
Từ đây ta thấy, sau khi tìm Dmin =|Gp2Gt|2, ta sẽ xác định được chiết
suất n của lăng kính. Bằng cách xác định n với các ánh sáng có bước sóng
khác nhau, ta nhận thấy rằng chiết suất n của một chất phụ thuộc vào bước
sóng ánh sáng tới. Sự phụ thuộc này được biểu diễn qua định luật Cauchy- Rayleigh: n(λ)= n0+a λ2
Do đó ta thấy rằng n(λ) sẽ là hàm tuyến tính theo 1/λ2 . Do đó bằng
cách xác định n(λ) đối với các ánh sáng có bước sóng xác định đã biết
trước, vẽ đồ thị của n(λ) theo 1/λ2 , ta có thể xác định được n 0 và a. Trong
thí nghiệm này, ta xác định n(λ) đối với 5 vạch màu mạnh nhất của đèn hơi Hg-Cd bằng cách đo Dmin: Cường độ
mạnh mạnh mạnh rất mạnh mạnh mạnh mạnh mạnh ánh sáng xanh lục- xanh xanh xanh Màu đỏ vàng vàng tím vàng lục lơ lam (nm) 643,8 579,1 577,0 546,1 508,6 480,0 435,8 404,7 Vạch 1 2 3 4 5 6 7 8 Chất phát ra Cd Hg Hg Hg Cd Cd Hg Hg
2. V¿ đ°áng cong đßnh chuẩn G(�㗌) của lăng kính
- Vẫn đang ở vị trí quan sát các vạch màu ở vị trí độ lệch tối thiểu.
- Bật thêm đèn của ống vi lượng, Điều chỉnh vị trí của ống vi lượng sao
cho tất cả 5 vạch màu của đèn Hg-Cd trên nằm trên thước đọc của ống vi lượng.
- Đọc vị trí các vạch màu này trên thước (gọi là G). Vẽ đường cong
định chuẩn G( ). Làm 3 lần lấy 3 giá trị của G cho mỗi vạch. 4
3. Đo b°ßc sóng của đèn Na
- Thay đèn Hg-Cd bằng đèn Na.
- Đọc vị trí vạch màu vàng của đèn Na trên thước của ống vi lượng.
- Nhờ đường cong định chuẩn G( ) đã xác định ở trên để xác định bước
sóng của vạch màu vàng của Na. III. XỬ LÝ SÞ LIÞU
1. Đo góc A của lăng kính bằng phản x¿ kép - Bảng số liệu: Lần đo Gt ∆Gt Gp ∆Gp Lần 1 81°02’ 0°32’ 200°58’ 0°42’ Lần 2 80°05’ 0°25’ 200°05’ 0°10’ Lần 3 80°09’ 0°21’ 200°04’ 0°11’ Lần 4 80°11’ 0°19’ 200°05’ 0°10’ Lần 5 81°03’ 0°33’ 200°05’ 0°10’ Trung bình Gt=80°30’ ∆Gt ≈0°26’
Gp =200°15’ ∆Gp =0°13’ - Xử lí:
+Sai số của dụng cụ (thước đo độ): ∆Gdc =0°01′
⇒ ∆Gt= ∆Gt + ∆Gdc =0°26′ +0°01′=0°27’a
⇒ ∆Gp= ∆Gp + ∆Gdc =0°13′ +0°01′=0°14’
Vậy Gt= Gt ± ∆Gt=80°30’ ± 0°27’aaa; ε = 0,56%
và Gp= Gp ± ∆Gp= 200°15’ ± 0°13’aa; ε = 0,11% +Tính A: A = |Gp2Gt| 2 =Gp 2 G = t 200°15’ 2 80°29’ ⇒ A 2=59°53’ ∆A = ∆Gp+ ∆ 2 G
=0 t°18′ +0°26’ 2=0°21′ εA=∆A =0°22’ 59°53’ ≈ 0,58% A
Vậy kết quả đo góc lăng kính: �㔀 = � ± 㔀
∆�㔀 = ÿă°ÿ�㗑’±0°21’aa; aaa�㗆 = ÿ, ÿĂ% 5
hayaaaaa�㔀 = ÿă,ĂĂ ± ÿ, �㗑ÿ(°); aaaaaa�㗆 = ÿ, ÿĂ%
2. Đo chiÁt suất của lăng kính ứng vßi các v¿ch màu khác nhau bằng
ph°¡ng pháp đß lßch tßi thiểu - Bảng số liệu: Góc Số lần đo Vạch màu đỏ 1 82°11′ 2 82°08′ Trái 3 82°12′ 4 82°05′ 5 82°12′ 1 206°15′ 2 206°10′ Phải 3 206°14′ 4 206°10′ 5 206°20′ - Xử lí:
+) Với vạch đỏ góc bên trái: =Gt1 + Gt2 + Gt3 + 5 G = t 8 42 + °1 G 1′ t5
+ 82°08′ + 82°12′+82°05′+ 82°12′ Gt 5≈ 82°10′ =|G12 G |+|G22 G |+|G32 G |+|G42 G |+|G52 G | ∆G 5
=|82°11′2 82°10′|+|82°08′ 2 82°10′|+|82°12′ 2 82°10′|+|82°05′ 2 82°10′|+|82°12′ 2 82°10′| 5 = 0°02′
+) Sai số dụng cụ: ∆Gdc = 0°01′
⇒ ∆G = ∆G + ∆Gdc = 0°02′ + 0°01′a = 0°03′ ε = ∆G=0°03′ 82°10′ ≈ 0,061% G
⇒ Gtađỏ = Gtađỏ ± ∆Gtađỏ =82°10′±a0°03′; aε = 0,061%
+) Tương tự với vạch đỏ góc bên phải:
Gpađỏ = Gpađỏ ± ∆Gpađỏ = 206°14′±a0°03'a; aε = 0,024% 6
+) Tương tự đối với các vạch màu khác: Gt ∆Gt Gp ∆Gp Đỏ 82°08′ 0°03′ 206°14′ 0°03′ Vàng 1 81°16′ 0°02′ 207°12′ 0°03′ Vàng 2 81°01′ 0°02′ 207°11′ 0°03′ Xanh lục 1 80°36′ 0°02′ 207°32′ 0°04′ Xanh lục 2 80°22′ 0°02′ 207°57′ 0°04′ Xanh lơ 1 79°48′ 0°01′ 208°18′ 0°04′ Xanh lơ 2 79°23′ 0°01′ 208°51′ 0°04′ Xanh lơ tím 78°41′ 0°01′ 209°48′ 0°05′ Tím 78°16′ 0°01′ 210°18′ 0°05′
+) Áp dụng công thức tính Dm , ta có: Dm=|Gp2 Gt| =Gp 2 Gt 2⇒ Dm 2 ∆Dm=∆Gt+ ∆G 2 p a⇒ εdm=∆Dm Dm
+) Tương tự với các vạch màu khác, ta có bảng: Vạch màu Dm ∆Dm ∆Dm(rad) εdm(%) Dm(°) Đỏ 62°02' 0°03' π/3600 0,08 62,03 ± 0,05 Vàng 1 62°58' 0°03' π/3600 0,08 62,97 ± 0,05 Vàng 2 63°05' 0°03' π/3600 0,08 63,08 ± 0,05 Xanh lục 1 63°28' 0°03' π/3600 0,08 63,47 ± 0,05 Xanh lục 2 63°47' 0°03' π/3600 0,08 63,78 ± 0,05 Xanh lơ 1 64°15' 0°03' π/3600 0,08 64,25 ± 0,05 Xanh lơ 2 64°44' 0°03' π/3600 0,08 64,73 ± 0,05 Xanh lơ tím 65°33' 0°03' π/3600 0,08 65,55 ± 0,05 Tím 66°01' 0°03' π/3600 0,07 66,02 ± 0,05 7
+) Tính chiết suất n của lăng kính: n = sin (Dm+ A 2)⇒ n = sin (Dm + A 2) 2) sin (A sin (A2) ln(n)=ln (sin (Dm+ A 2) sin (A2))a
⇒ d(ln(n)) = d (ln (sin (Dm+ A2)) 2ln (sin (A 2)))
⇒dn= cotg (Dm+ A2). d (Dm+ A 2)2 cotg (A 2). d (A2) ⇒dn=dDm2. cotg (Dm+ A2)+dA 2.[cotg (Dm+ A2)2 cotg (A 2)] Do Dm+2A
và A 2 trong khoảng 0 đến π/2, ta phải lấy dấu dương. Cho nên : Δn n =ΔDm 2. cotg (Dm + 2) A +ΔA 2.[cotg (A 2)2 cotg (Dm + A 2)]
+) Đối với vạch màu đỏ: n = sin (Dm + 2) A 2)=sin (62,03 +59,882) 2)≈ 1,75 sin (A sin (59,88 εn=Δnn =ΔDm 2. cotg (Dm + A 2) +ΔA2.[cotg (A 2)2 cotg (Dm + A 2)]
= π/3600.1 2. cotg (62,03 +59,88 2) +0,37.12.[cotg (59,88 2)2 cotg (62,03 +59,88 2)] ≈ 0,219 8
⇒ ∆n = εn. n ≈ 0,219.1,75 ≈ 0,38
+) Tương tự với các vạch màu khác ta có: Vạch màu n εn(%) ∆n Đỏ 1,75 22 0,38 Vàng 1 1,76 22 0,39 Vàng 2 1,76 22 0,39 Xanh lục 1 1,76 23 0,40 Xanh lục 2 1,76 23 0,40 Xanh lơ 1 1,77 23 0,40 Xanh lơ 2 1,77 23 0,40 Xanh lơ tím 1,78 23 0,40 Tím 1,78 23 0,41 +) Xử lí bước sóng:
Sai số tuyệt đối của λ: Δλ = 0,1a(nm)
Xét: y = 1λ2aaa ⇒ aa (lny)= d(2lnλ2)⇒ aa dyy= 22 dλ λaa ⇒ ∆y = 2y∆ λ λ aa ⇒ aaaaΔ (1 λ2)=2∆λ λ3 Vạch màu n ∆n λ(nm) 1/λ2.10212 Δ(1/λ2). 10212 Đỏ 1,75 0,38 643,8 2,413 0,00075 Vàng 1 1,76 0,39 579,1 2,982 0,00103 Vàng 2 1,76 0,39 577,0 3,004 0,00104 Xanh lục 1 1,76 0,40 546,1 3,353 0,00123 Xanh lục 2 1,76 0,40 508,6 3,866 0,00152 Xanh lơ 1 1,77 0,40 480,0 4,340 0,00180 Xanh lơ 2 1,77 0,40 467,8 4,569 0,00195 Xanh lơ tím 1,78 0,40 435,8 5,265 0,00242 Tím 1,78 0,41 404,7 6,106 0,00302 9 +) Đồ thị: 1.780 n Linear Fit of Sheet1 n 1.775 1.770 1.765 n Equation y = a + b*x Weight No Weighting 1.760 Residual Sum 6.81874E-5 of Squares Pearson's r 0.95764 Adj. R-Square 0.90522 Value Standard Error 1.755 nIntercept 1.7332 0.00382 nSlope 0.00811 9.22072E-4 1.750 1/λ2.10212(þ) 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 1/lamda^2.10^(-12) +) Đường y = A+Bx Parameter Value Error A 1,7332 0,00382 B 0,00811 9,22072E-4
+) Đồ thị thể hiện sự phụ thuộc của chiết suất lăng kính n vào 1/λ2a là
1 hàm bậc nhất. Đối chiếu với công thức Cauchy-Rayleigh: n(λ)= n0+a λ2 ta thu được:
n0= A = 1,7332 ± 0,0038a; aaϵ = 0,22%
a = B = 0,00811 ± 0,00073a; aε = 9%
+) Nhận xét: Đồ thị chỉ gần như tuyến tính chứ chưa thật hoàn hảo, lý
do là ta có sai số trong phép đo Dm, dẫn đến sai số trong việc xác định chiết 10
suất n(λ). Và định luật Cauchy chúng ta khảo sát là đơn giản, thực tế định
luật này có dạng n(λ)= n0+a λ2+�㕏
λ4. Vì vậy, thực nghiệm là chỉ có tính tương đối.
3. V¿ đ°áng cong đßnh chuẩn của lăng kính: - Bảng số liệu: Vạch màu Lần 1 Lần 2 Lần 3 Đỏ 27,9 27,9 27,8 Vàng 1 25,8 25,8 25,6 Vàng 2 25 25 24,9 Xanh lục 1 24 24 23,9 Xanh lục 2 23,2 23,2 23,1 Xanh lơ 1 21,4 21,4 21,5 Xanh lơ 2 20,6 20,6 20,6 Xanh lơ tím 13,3 13,2 13,1 Tím 8 8,2 8,1 - Xử lí:
+) Sai số dụng cụ: ∆Gdc=0,1 =G1+ G2+ G3 G 3 =|G12 G |+|G22 G |+|G32 G | ∆G 3 + ∆Gdc;aaεG=∆G ∆G = ∆G G +) Với tia đỏ ta có: =G1+ G2+3 G = 3 27,9 + 27,9 + 27,8 G 3=27,867
=|27,9 2 27,867|+|27,9 2 27,867|+|27,8 2 27,867| ∆G 3 ≈ 0,044 ∆G = 0,044 + 0,1 = 0,14 εG=∆G =0,14 27,87 ≈ 0,0052 G 11
+) Tương tự với các vạch màu khác: Vạch màu G(λ) ΔG(λ) ΔG(λ) εG(%) Đỏ 27.87 0.044 0.14 0.52 Vàng 1 25.73 0.089 0.19 0.73 Vàng 2 24.97 0.044 0.14 0.58 Xanh lục 1 23.97 0.044 0.14 0.60 Xanh lục 2 23.17 0.044 0.14 0.62 Xanh lơ 1 21.43 0.044 0.14 0.67 Xanh lơ 2 20.60 0.000 0.10 0.49 Xanh lơ tím 13.20 0.067 0.17 1.13 Tím 8.10 0.067 0.17 2.06
+) Tương tự đối với vạch màu vàng của đèn Na: Lần 1 Lần 2 Lần 3 G(λ) ΔG(λ) ΔG(λ) εG(%) G(λ) 25.5 25.7 25.6 25.6 0.067 0.17 0.65 +) Đồ thị: y = Intercept + 650 Equation B1*x^1 + B2*x ^2 Weight No W eighting Residual Sum 1594.70598 of Squares 600 Adj. R-Square 0.95518 Value Standard Error Lamda Intercept 523.89169 49.94638 Lamda B1 -20.32298 6.11493 550 Lamda B2 0.87727 0.16995 500 Lamda (nm) 450 400 Lamda
Polynomial Fit of Sheet1 Lamda 5 10 15 20 25 30 G(lamda) 12
+) Đường Polynomial Fit: Y = A + B X 1 + B2X2 Parameter Value Error A 523,89169 49,94638 B1 -20,32298 6,11493 B2 0,87727 0,16995
+ Bước sóng của ánh sáng vàng của đèn Na: �㔆 = 2 � ý 㕣+ þ1. �㔺 +� þ㕣 2 . �㔺�㕣
=523,89169 + (220,32298). 25,6 + 0,87727. 25,62 ≈578,55a(ÿþ)
ýÿ�㔆�㕣=ýÿ(ý + þ1�㔺�㕣+ þ2. �㔺�㕣2) �㕑 � � 㔆 㔆 �㕣 � = 㕣
�㕑(ý + þ1�㔺�㕣+ þ2. �㔺�㕣2)
ý + þ1�㔺�㕣+ þ2. �㔺�㕣2 =(þ1+ 2þ2)�㕑�㔺�㕣
ý + þ1�㔺�㕣+ þ2. �㔺�㕣2 ⇒ ∆�㔆�㕣= ∆�㔺 + � 2þ㕣 2 (þ ) 1 ≈ 3,16a(ÿþ) �㔀 = ∆� = 㔆 3,1 � 6 㕣 578,55 ≈ 0,55% �㔆�㕣
Vậy theo đường cong định chuẩn, bước sóng ánh sáng vàng của đèn Na là:
�㕀 = ÿāĂ,ÿÿ ± �㗑, ĀĀa(Āÿ)a; aa�㔺 = ÿ, ÿÿ%
+) Nhận xét: Kết quả thu được khá phù hợp với lý thuyết là vạch kép
vàng của Natri có bước sóng 589,6 nm và 589,0 nm. Nguyên nhân sai số là
ta đã lấy vạch lục vàng mạnh nhất của đèn Hg-Cd làm vị trí góc lệch cực
tiểu để xác định giá trị G, do đó có sai số vì vạch của Na nằm tương đối xa
so với vạch lục vàng đó. 13