Báo cáo thí nghiệm Lý thuyết mạch 1 | Đại học Bách Khoa Hà Nội

BÀI THÍ NGHIỆM LTM : 01
TÍNH CHẾ ĐỘ XÁC LẬP ĐIỀU HÒA TRONG MẠCH ĐIỆN TUYẾN
TÍNH BẰNG MÁY TÍNH DÙNG PHẦN MỀM MATLAB Bài 1: Phương pháp dòng vòng Code Matlab:
B = [1 0 1 1 0 0;0 1 1 0 1 0;0 0 0 -1 1 1]; j = sqrt(-1); pi = 3.1415;
E1 = 100; E2 = 220*exp(j*pi/3); Enh = [E1;E2;0;0;0;0]; J6 = 10*exp(j*pi/6); Jnh = [0;0;0;0;0;J6]; Z1 = 30+j*40; Z2 = 20+j*10; Z3 = 10+j*2*pi*60*0.2; Z4 = 15+j*2*pi*60*0.3; Z5 = 20+j*2*pi*60*0.4; Z6 = 10+j*20;
Z35 = j*2*pi*60*0.6*sqrt(0.2*0.4); Z53=Z35;
Znh = [Z1 0 0 0 0 0 ; 0 Z2 0 0 0 0 ; 0 0 Z3 0 Z35 0 ; 0 0 0 Z4 0 0 ; 0 0 Z53 0 Z5 0; 0 0 0 0 0 Z6]; Zv = B*Znh*B'; Ev = B*(Enh - Znh*Jnh); Iv = Zv\Ev; Inh = B'*Iv Unh = Znh*(Inh + Jnh) - Enh
Sng = (Inh + Jnh)'*Enh + Jnh'*Unh
Chạy đoạn code trên bằng chương trình Matlab ta thu được kết quả: Inh = -2.8620 - 3.0433i 3.9151 + 2.8309i 1.0531 - 0.2124i 1.2749 - 0.0992i -0.2218 - 0.1132i -4.1369 - 2.9441i Unh = 1.0e+02 * 2 -0.6413 - 2.0578i -0.6001 - 0.9475i 0.3379 + 0.6309i 0.3034 + 1.4269i 0.2622 + 0.3167i 0.0412 + 1.1103i Sng = 1.2746e+03 + 1.6798e+03i Bài 2:
Phương pháp dòng vòng: Code Matlab: B = [1 -1 0 1 0;0 1 -1 0 1]; j = sqrt(-1); pi = 3.1415; E1 = 200*exp(j*0); Enh = [E1;0;0;0;0]; Jnh = [0;0;0;0;0]; Z1 = 200; Z2 = 200; Z3 = 10; Z4 = 100; Z5 = 100;
Znh = [Z1 0 0 0 0;0 Z2 0 0 0; 0 0 Z3 0 0; 0 0 0 Z4 0; 0 0 0 0 Z5]; Zv = B*Znh*B'; Ev = B*(Enh - Znh*Jnh); Iv = Zv\Ev; Inh = B'*Iv Unh = Znh*(Inh + Jnh) - Enh
Chạy đoạn code trên bằng chương trình Matlab ta thu được kết quả: Inh = 0.5391 -0.1913 -0.3478 0.5391 0.3478 Unh = -92.1739 -38.2609 -3.4783 53.9130 34.7826 3
BÀI THÍ NGHIỆM LTM : 02
CÁC HIỆN TƯỢNG CƠ BẢN – PHẦN TỬ CƠ BẢN R, L, C TRONG
MẠCH ĐIỆN CÓ NGUỒN HÌNH SIN
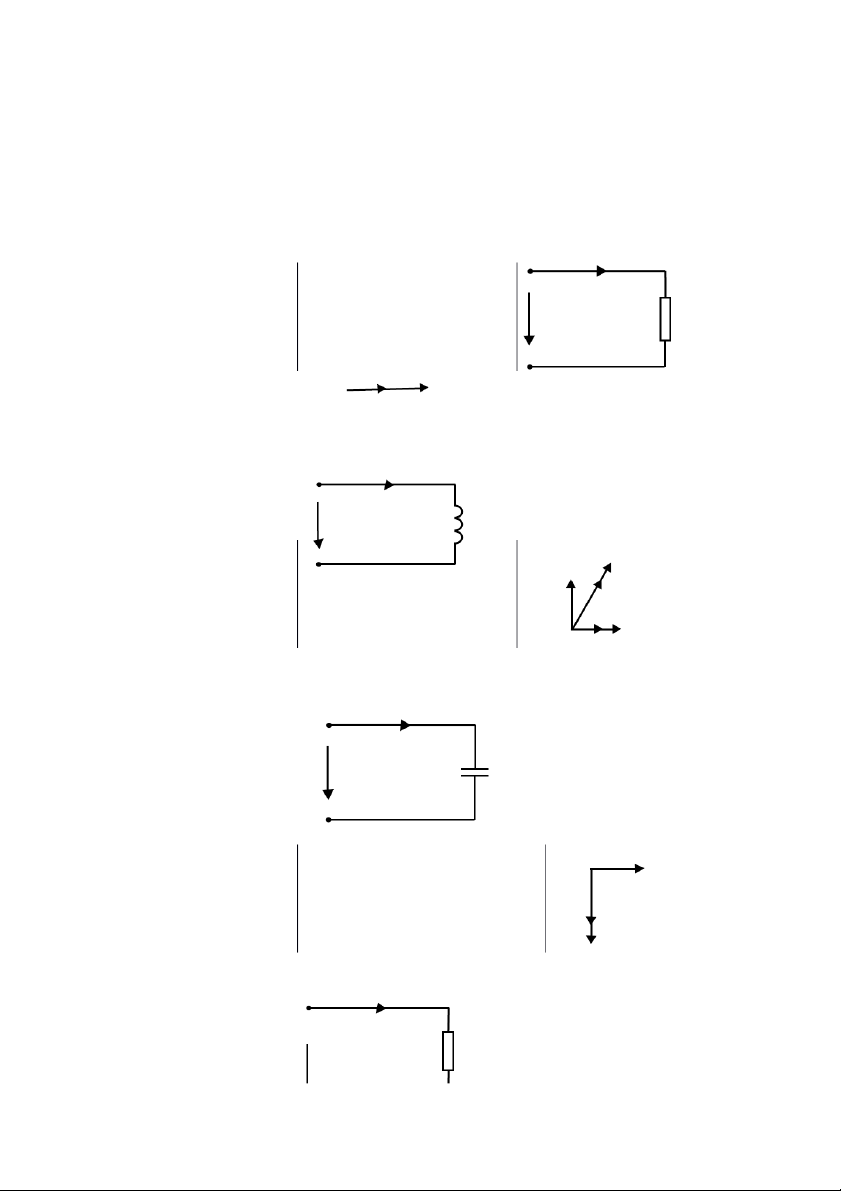
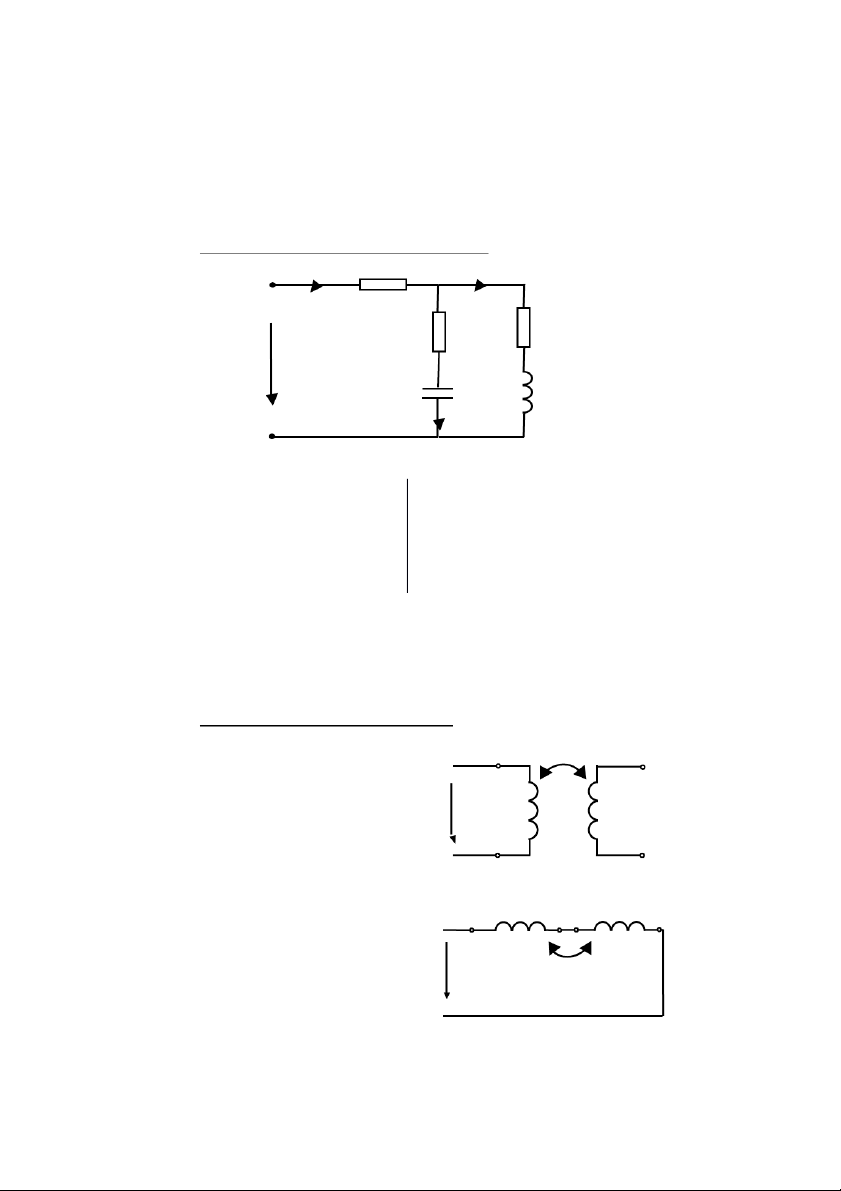
1. Mạch thuần điện trở: UR = 12.175 R = = 102.3 ( ) IR IR = 0.119
Theo lý thuyết, và cùng pha U R P nên có sơ đồ: R = 1.435 Cos = -1
2. Mạch thuần điện cảm: IL U L UL = 12.168 V ZL = = 33.2 () IL = 0.357 A L = 0.106 (H) QL = 4.21 J
Do cuộn cảm có điện trở Z Cos
trong rất nhỏ nên có giản đồ:  = -0.22 R
3. Mạch thuần điện dung: IC U C UC = 12.196 V ZC = = 160.5 () IC = 0.076 A C = 1.98* (F) QC = 0.9259 J
Tụ điện có chậm pha hơn một Cos góc nên có giản đồ:  = 0.008
4. Mạch R – L nối tiếp: I 4 R U L U = 12.217 V ZL = = 142.2 () UR = 6.768 V L = 0.453 (H) I = 0.067 A R = = 101 ( ) U UL = 9.53 V
Trong cuộn cảm có điện trở P = 0.541 W
trong rất nhỏ nên có giản đồ: S = 0.826 VA Cos = -0.644
5. Mạch R – C nối tiếp: I R U C U = 12.173 V ZC = = 106.6 () U -5 R = 4.939 V C = 3*10 (F) I = 0.104 A R = = 47.5 ( ) UC = 11.084 V
Trong mạch này, chậm pha hơn P = 0.528 W một góc  với S = 1.266 VA
tan = nên có giản đồ: U Cos = 0.416
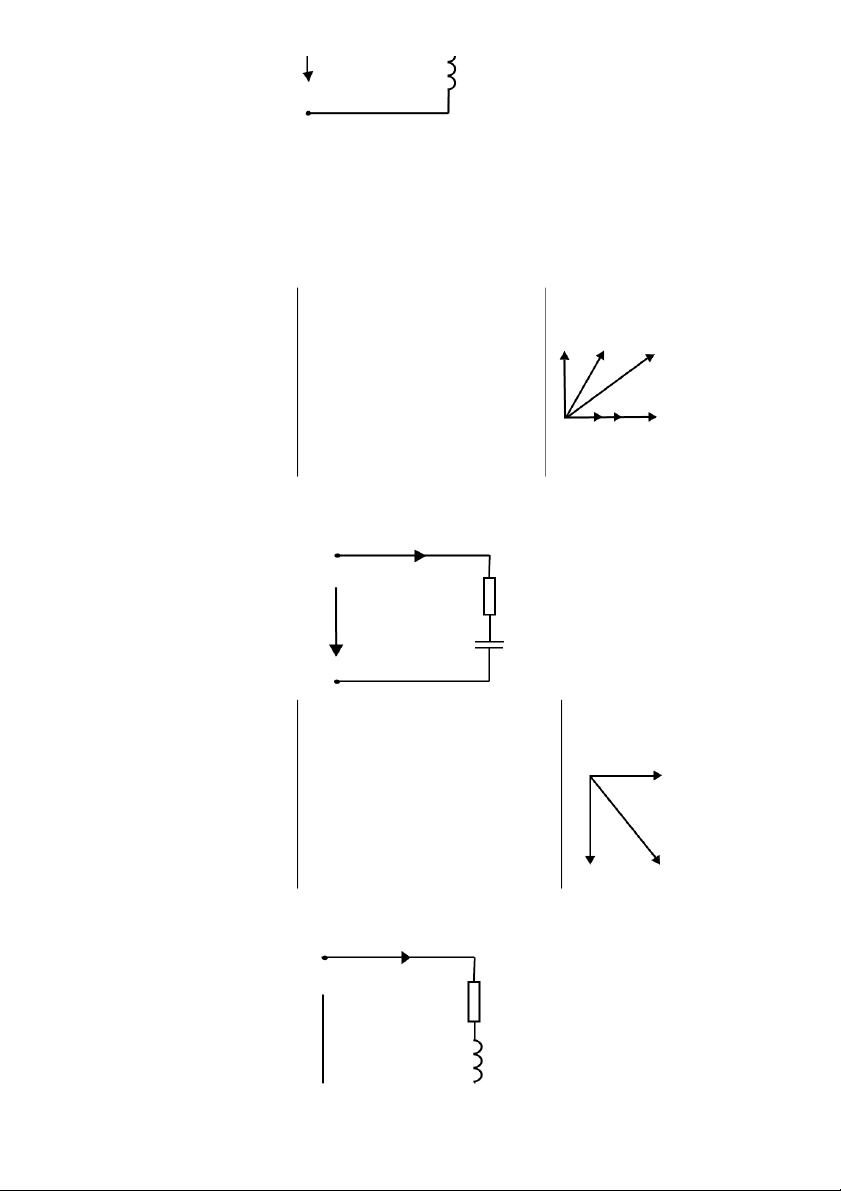
6. Mạch R - L – C nối tiếp: I R 5 U L C U = 12.152 V ZC = = 107.3 () I = 0.05 A C = 2.97*10-5 (F) UR = 4.951 V R = = 99 ( ) UL = 15.009 ZL = + ZC = 350.3 () UC = 5.366 V  L = 1.1 (H) P = 0.335 W Hoặc ZL = = 300.2 () S = 0.606 VA
2 giá trị ZL khác nhau nên mạch có Cos tính cảm kháng.  = -0.554 6
BÀI THÍ NGHIỆM LTM : 03
CÁC HIỆN TƯỢNG CƠ BẢN – PHẦN TỬ CƠ BẢN R, L, C – MẠCH
CÓ HỖ CẢM TRONG MẠCH ĐIỆN CÓ KÍCH THÍCH HÌNH SIN
1. Nghiệm chứng lại định luật Ki rchhoff 1 I1 I3 R1 R2 R3 U C L I2 U = 11.784 V; Cos o 1 = 1;
 1 = 0 : dòng cùng pha áp I o 1 = 0.077 A; Cos2 = 0.328;
2 = 70.85 : dòng sớm pha hơn áp I o 2 = 0.025 A; Cos3 = 0.968;
3 = -15.85 : dòng trễ pha áp I3 = 0.071 A;
 = 0.077 (A); = 0.0082 – j0.024 (A); = 0.0683 – j0.0194 (A)  - + + = 0
Qua kết quả thực nghiệm chứng minh được định luật Kirchhoff 1 đúng.
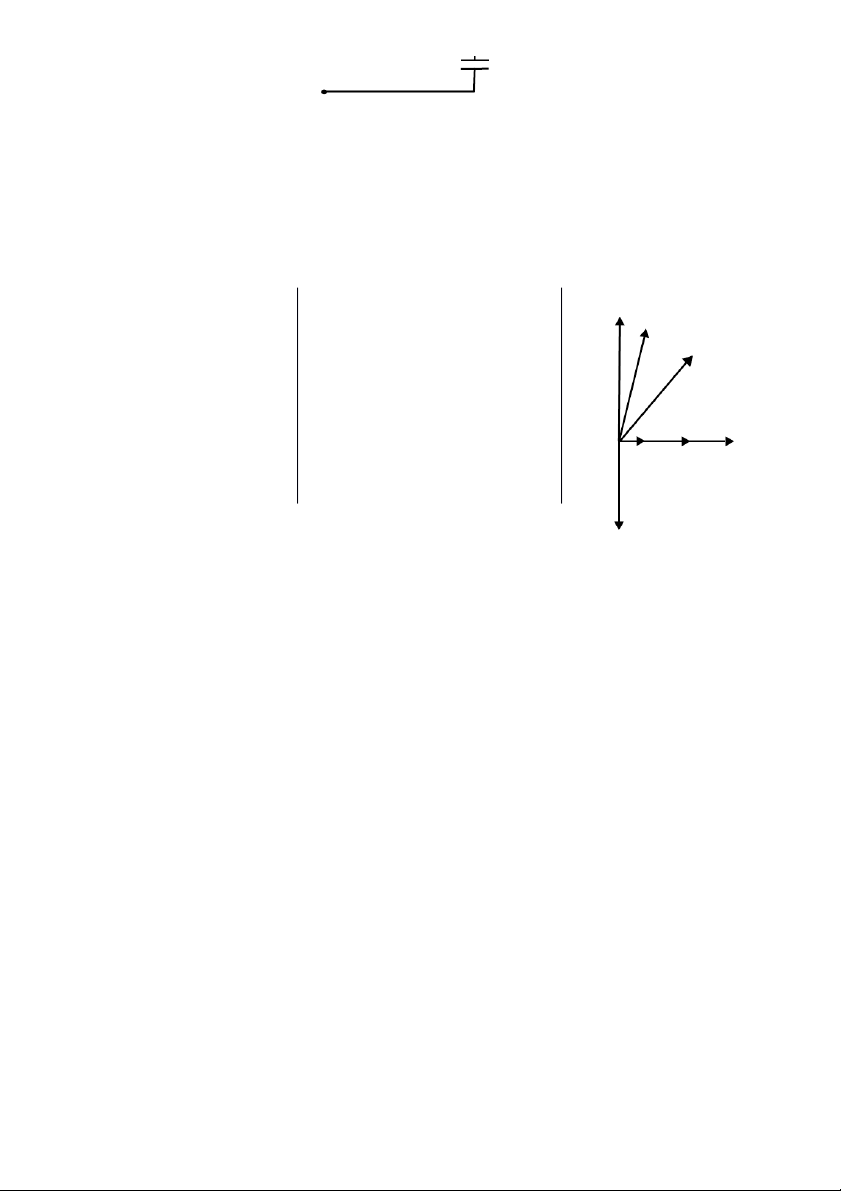
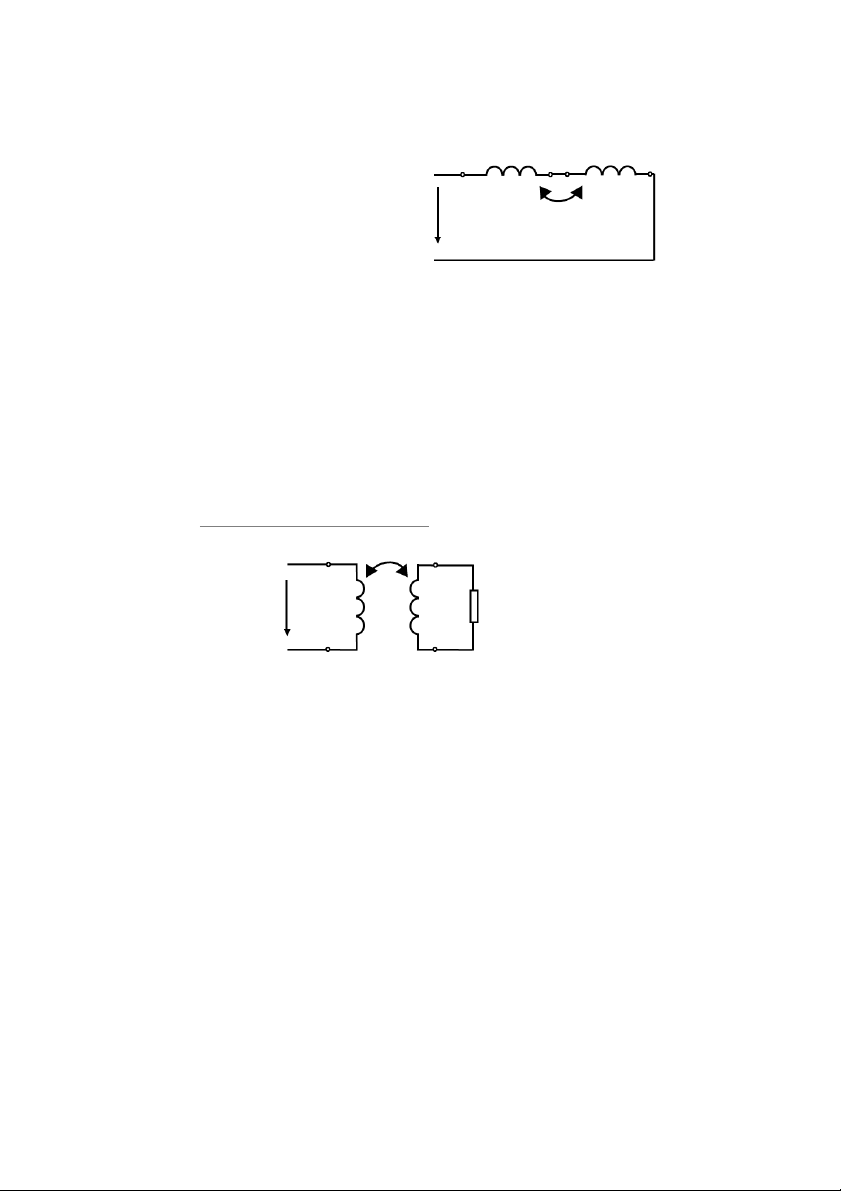
2. Nghiệm chứng hiện tượng hỗ cả m: M 1 2 U22’ = 11.87 V U 1’ 2’ 1’ 1 2 2’ * * U11’ = 12.375 V U M U22’ = 11.878 V 7 1’ 1 2’ 2 * * U11’ = 12.015 V U U M 2’2 = 11.551 V
Ta thấy U22’ > U2’2 nên
 Lần 1: 2 cuộn cảm cùng cực tính: o U11’ = UL1 + UM12 o U22’ = UL2 + UM21
 Lần 2: 2 cuộn cảm ngược cực tính o U11’ = UL1 - UM12 o U22’ = UL2 - UM21 3. T
ruyền công suất bằng hỗ cảm: M 2 1 U R 1’ 2’ U11’ = 11.7 V U22’ = 7.35 V
 Hệ số biến áp khi có tải R là: |K21| = = = 0.628 8