Bất phương trình lôgarit chứa tham số

Tài liệu gồm 20 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Bất phương trình lôgarit chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
BẤT PHƯƠNG TRÌNH LÔGARIT CHỨA THAM SỐ
Bài toán. Tìm
m
để bất phương trình
f x m
( , ) 0
hoặc
f x m
( , ) 0
có nghiệm trên
D
?
PHƯƠNG PHÁP
Bước 1. Tách tham số
m
ra khỏi
và đưa BPT về dạng
( ) ( )
A m f x
hoặc
( ) ( )
A m f x
.
Bước 2. Khảo sát sự biến thiên và dựa vào bảng biến thiên xác định các giá trị của tham số
m
để bất phương trình có nghiệm.
Lưu ý: Cho hàm số
y f x
xác định và liên tục trên
D
.
Trong trường hợp tồn tại
max ( )
x
f x
D
và
min ( )
x
f x
D
thì ta có:
Bất phương trình
( ) ( )
A m f x
có nghiệm trên
( ) max ( )
x
A m f x
D
D
.
Bất phương trình
( ) ( )
A m f x
có nghiệm trên
( ) min ( )
x
A m f x
D
D
.
Bất phương trình
( ) ( )
A m f x
nghiệm đúng
( ) min ( )
x
x A m f x
D
D
.
Bất phương trình
( ) ( )
A m f x
nghiệm đúng
( ) max ( )
x
x A m f x
D
D
.
Nếu
2
( ) 0
f x ax bx c a
thì
0
( ) 0,
0
a
f x x
.
0
( ) 0,
0
a
f x x
.
Câu 1. Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
2 2
log (7 7) log ( 4 )
x mx x m
nghiệm đúng với mọi giá trị thực của
x
?
A.
7
. B.
3
. C. Vô số. D.
4
.
Lời giải
Chọn B
Yêu cầu bài toán được thỏa mãn
2
2 2
4 0,
7 7 4 ,
mx x m x
x mx x m x
2
2
4 0,
7 4 7 0,
f x mx x m x
g x m x x m x
.
Ta thấy
0
m
;
7
m
không thỏa mãn điều kiện đề bài.
Với
0
m
và
7
m
. Khi đó ta có:
2
0
4 0
m
m
0
2
2
m
m
m
2
m
. (1)
2
7 0
4 7 0
m
m
2
7
14 45 0
m
m m
7
5
9
m
m
m
5
m
.
(2)
Từ (1) và (2) suy ra
2 5
m
. Do
m
nên
3;4;5
m
.
Câu 2. Tìm
m
để bất phương trình
2
2 2
log 2 2( 1)log 2 0
x m x
có nghiệm
( 2; ).
x

NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
(0; )
m
. B.
3
;0
4
m
. C.
3
;
4
m

. D.
( ;0)
m

.
Lời giải
Chọn C
Ta có
2
2 2
log 2 2( 1)log 2 0
x m x
2
2 2
1 log 2( 1)log 2 0
x m x
.
Đặt
2
log
t x
. Do
1
( 2; ) ;
2
x t
 
.
Khi đó
trở thành
2
1 2( 1) 2 0
t m t
2
1 2
1
2
t
m
t
2
1
2
t
f t m
t
(1).
Xét hàm
1
2 2
t
f t
t
liên tục trên
1
;
2

.
Ta có
2
1
;
2
1 1 1 1 3
0, ; min
2 2 2 2 4
f t t f t f
t


.
Khi đó (1) đúng với mọi
1
;
2
t

khi
1
;
2
min
f t m

3
4
m
.
Câu 3. Có tất cả bao nhiêu giá trị nguyên thuộc
100;100
của tham số
m
để bất phương trình
0,02 2 0,02
log log 3 1 log
x
m
nghiệm đúng với mọi
x
thuộc khoảng
;0

?
A.
99
. B.
98
. C.
100
. D.
101
.
Lời giải
Chọn C
Điều kiện:
2
log 3 1 0
0
0
x
m
m
.
Ta có
0,02 2 0,02 2
log log 3 1 log log 3 1
x x
m m
.
Xét hàm số
2
log 3 1
x
f x
. Ta có
3 .ln3
' 0
3 1 .ln 2
x
x
f x x
.
Suy ra hàm số luôn đồng biến trên tập xác định.
Dựa vào bảng biến thiên ta có bất phương trình nghiệm đúng với mọi
x
thuộc
;0

khi
1.
m
Do
m
nguyên và thuộc đoạn
100;100
nên
1;2;3;4;.....;100
m
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Câu 4. Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để bất phương trình
2 3
2 8
log 2 4 log 1
x m x
có nghiệm đúng với mọi
x
thuộc
16;

?
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn C
Điều kiện xác định:
2 2
2 2 2
0 0
log 2 4 0 log 2log 3 0
x x
x x x
2
2
0
1
0
log 1
8
2
log 3
x
x
x
x
x
.
Ta có :
2 3
2 8
log 2 4 log 1
x m x
2
2 2 2
log 2log 3 log 1 *
x x m x
.
Do
16;x

nên
2 2
log 4 log 1 0
x x
Suy ra
2
2 2
2
log 2log 3
*
log 1
x x
m
x
.
Đặt
2
log
t x
. Do
16;x

nên
4;t

.
Bất phương trình
*
trở thành
2
2 3
4;
1
t t
m t
t

.
Xét hàm
2
2 3
1
t t
f t
t
với
4;t

.
Ta có
2
2
2 2
' 0, 4;
2 3. 1
t
f t t
t t t

.
Suy ra hàm số
f t
nghịch biến trên khoảng
4;

.
Bảng biến thiên của hàm
f t
như sau:
Dựa vào bảng biến thiên ta thấy bất phương trình đã cho nghiệm đúng với mọi
x
thuộc
16;

khi
1
m
. Do
*
1
m m
.
Câu 5. Có tất cả bao nhiêu giá trị nguyên thuộc
10;10
của tham số
m
để bất phương trình
4 4
3 4 2 log 2
x
x x m
có nghiệm?
A.
8
. B.
5
. C.
6
. D.
7
.
Chọn A
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Điều kiện xác định:
0
4
0 4
4 4 1
4 4 0
x
x
x
x
x
.
Ta thấy
0 4
x
0 4 4 2 4 4 4
x x
. Suy ra
4 4
log 2 0
x
.
Khi đó bất phương trình
4 4
4 4
3 4
3 4 2 log 2
2.log 2
x
x
x x
x x m m
2
1
3 4 .log 4 4
2
m x x x
.
Xét hàm
2
1
3 4 .log 4 4
2
f x x x x
liên tục trên
0;4
.
Ta có
2
1 3 1 1 1
' .log 4 4 3 4 . 0 0;4
2 2
2 2 4
2 4 . 4 4 .ln2
f x x x x x
x x
x x
.
Suy ra hàm số
y f x
đồng biến trên
0;4
.
Để bất phương trình đã cho có nghiệm thì
1
m
.
Do
m
nguyên và thuộc khoảng
10;10
nên
2;3;...;9
m
.
Vậy có 8 giá trị
m
nguyên cần tìm là :
2;3;...;9
m
.
Câu 6. Cho bất phương trình
2 2
7 7
log 2 2 1 log 6 5
x x x x m
. Có bao nhiêu giá trị nguyên
của tham số
m
để bất phương trình trên có tập nghiệm chứa khoảng
1;3
?
A.
35
. B.
33
. C.
33
. D.
36
.
Lời giải
Chọn D
2
2 2
7 7
6 5 0
log 7 2 2 log 6 5
x x m
Bpt
x x x x m
2
2
6 5
6 8 9
m x x
x x m
.
Xét hàm
2
6 5
f x x x
liên tục trên đoạn
1;3
.
Ta có
2 6 0, 1;3
f x x x
f x
nghịch biến trên đoạn
1;3
1;3
max 1 12
f x f
.
Xét hàm
2
6 8 9
g x x x
liên tục trên đoạn
1;3
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
Ta có
12 8 0, 1;3g x x x
g x
đồng biến trên khoảng
1;3
1;3
min 1 23g x g
.
Yêu cầu bài toán được thỏa mãn khi
2
2
6 5
6 8 9
m x x
x x m
với mọi
1;3x
1;3
1;3
max
min
m f x
m g x
.
Khi đó ta có
12 23m
. Mà
m
nên
12; 11; 10; ...;22;23m
.
Vậy có tất cả
36
giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 7. Tìm tấtt cả các giá trị của tham số
m
để bất phương trình
2
2 1
4
4log 2log 0x x m
có
nghiệm với mọi
x
thuộc khoảng
0;1
.
A.
1
0;
4
m
. B.
1
;
4
m

. C.
;0m  . D.
1
;
4

.
Lời giải
Chọn D
Điều kiện:
0x
.
Ta có
2
2 1
4
4log 2log 0x x m
2
2 2
log log 0x x m .
Đặt
2
logt x
, do
0;1x
;0t 
.
Bất phương trình trở thành
2
0t t m
2
m t t
.
Xét hàm
2
f t t t với
;0t 
.
Ta có
2 1f t t
,
1
0
2
f t t
.
Bảng biến thiên của hàm
2
f t t t
như sau:
Dựa vào bảng biến thiên ta thấy ycbt được thỏa mãn
1
4
m .
Câu 8. Có bao nhiêu số nguyên m sao cho bất phương trình
2 2
ln 5 ln 1 ln 4x mx x m
có tập
nghiệm là
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta thấy
2
1 0,x x
.
Ta có
2 2 2 2
ln5 ln 1 ln 4 ln 5 5 ln 4x mx x m x mx x m
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
2 2
2
5 5 4
4 0
x mx x m
mx x m
2 2
2
5 5 4 1
1 4
x x m x
m x x
2
2
2
5 4 5
1
4
1
x x
m f x
x
x
m g x
x
.
Hàm số
f x
có bảng biến thiên như sau:
Hàm số
g x
có bảng biến thiên như sau:
Từ bảng biến thiên suy ra bất phương trình có tập nghiệm là
khi
2 3
m
.
Vậy có
1
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 9. Số giá trị nguyên của m để bất phương trình
2 2
3 3
1 log 1 log 2
x mx x m
có nghiệm
đúng với mọi số thực x là
A.
1
. B.
2
. C.
4
. D.
6
.
Lời giải
Chọn A
Điều kiện xác định:
2
2 0
mx x m
.
Ta có:
2 2 2 2
3 3 3 3
1 log 1 log 2 log 3 1 log 2
x mx x m x mx x m
2 2 2
3 1 2 3 2 3 0.
x mx x m m x x m
Ta thấy
0
m
;
3
m
không thỏa mãn điều kiện đề bài.
Với
0
m
và
3
m
. Khi đó:
Để bất phương trình nghiệm đúng với mọi x
thì
2
2
2 0
3 2 3 0
mx x m x
m x x m x
2
2
0
0
3 0
3
1 2
1 0
1; 1
2; 4
1 3 0
m
m
m
m
m
m
m m
m m
m
.
Mà m
nên
2
m
.
Câu 10. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc
2021;2021
sao cho bất
phương trình
3 2 2
3 3
1 log 3 log 3 1
x x x m x
nghiệm đúng với mọi
x
trên đoạn
0;3
. Tính số phần tử của tập hợp
S
.
A.
2020
. B.
2018
. C.
2022
. D.
4040
.
Lời giải
Chọn B
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Ta thấy
2
3 1 0,x x
.
Ta có:
3 2 2
3 3
1 log 3 log 3 1 ; 0;3
x x x m x x
3 2 2
3 3
log 3 3 9 3 log 3 1 ; 0;3
x x x m x x
3 2 2
3 3 9 3 3 1; 0;3
x x x m x x
3
3 3 9 1; 0;3
m x x x
.
Xét hàm số:
3
3 9 1
f x x x
trên
0;3
.
Ta có:
2
9 9
f x x
,
0
f x
1 0;3
1 0;3
x
x
.
Bảng biến thiên:
Từ bảng biến thiên ta có:
7
3 7
3
m m
.
Mà m
và
2021;2021
m
nên
{3; 4; ; 2020}
m
.
Câu 11. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc
2021;2021
sao cho bất
phương trình
2
2 2
3log 2 12log 1 0
x x m
nghiệm đúng với mọi
x
trên khoảng
2;

. Tính
số phần tử của tập hợp
S
.
A.
2018
. B.
2020
. C.
2022
. D.
4040
.
Lời giải
Chọn B
Ta có:
2
2 2
3log 2 12log 1 0
x x m
2
2 2 2
3 log 2log 1 12log 1 0
x x x m
2
2 2
3log 6 log 2 0
x x m
*
.
Đặt: log
x t
2
, với
1
2; ;
2
x t
 
.
Khi đó bất phương trình (*) trở thành
2
3 6 2 0
t t m
2
3 6 2
m t t
.
Xét hàm số
2
1
3 6 2, ;
2
f t t t t
.
Ta có:
6 6
f t t
;
0 6 6 0 1
f t t t
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy
1
m
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Mà m
và
2021;2021
m
nên
2020; 2019;...; 1
m
.
Câu 12. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2 2
log (5 1).log (2.5 2)
x x
m
có nghiệm
1
x
.
A. m
. B.
6
m
. C.
6
m
. D.
6
m
.
Lời giải
Chọn A
Với
1
x
thì
5 1 0; 2.5 2 0
x x
.
Ta có
2 2
log (5 1).log (2.5 2)
x x
m
2 2
log (5 1).log (2.5 2) m
x x
2 2
log (5 1). 1 log (5 1) m
x x
.
Đặt
2
log 5 1
x
t
do
1
x
2;t

.
BPT trở thành:
2
(1 )
t t m t t m
.
Đặt
2
( )
f t t t
ta có
( ) 2 1 0
f t t
với
2;t
nên hàm số
y f t
đồng biến và
liên tục trên
2;

. Suy ra
6;f t

khi
2;t

.
Do đó để để bất phương trình
2 2
log (5 1).log (2.5 2) m
x x
có nghiệm thỏa mãn
1
x
thì
m
Câu 13. Tổng tất cả các giá trị nguyên của tham số
m
sao cho khoảng
2;3
thuộc tập nghiệm của bất
phương trình
2 2
5 5
log 1 log 4 1
x x x m
là
A.
13
. B.
12
. C. 12. D. 13.
Lời giải
Chọn D.
Ta có
2
2
2
2
2
4
4 ( )
1
(1)
5
4 4 5 ( )
4 0
x x m
m x x f x
x
m x x g x
x x m
.
Hệ trên thỏa mãn
2;3
x
2;3
2;3
( ) 12
12 13
( ) 13
m Max f x
m
m Min g x
.
Câu 14 . Có bao nhiêu số nguyên dương
m
trong đoạn
2018;2018
sao cho bất phương trình
11
log
log
10
10
10 10
x
x
m
x
đúng với mọi
1;100
x
?
A. 2022. B. 2021. C. 2020. D. 2018.
Lời giải
Chọn D.
Điều kiện
0
x
.
Ta có
11
log
log
10
10
log
11
10 10 log 1 log
10 10
x
x
m
x
x m x x
2
log 10 log 1 11log 0 10 log 1 log 10log 0
x m x x m x x x
.
Vì
1;100
x
nên
log 0; 2
x
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Do đó
2
2
10log log
10 log 1 log 10log 0 10
log 1
x x
m x x x m
x
.
Đặt
log
t x
,
0; 2
t
.
Xét hàm số
2
10
1
t t
f t
t
liên tục trên đoạn
0;2
.
Ta có
2
2
10 2
0, 0; 2
1
t t
f t t
t
Hàm số
f t
đồng biến trên
0;2
.
Suy ra
0;2
16
max ( ) 2
3
f t f
.
Để bất phương trình
2
10log log
10
log 1
x x
m
x
đúng với mọi
1;100
x
thì
16 8
10
3 15
m m .
Do đó
8
; 2018
15
m
hay có
2018
số thỏa mãn.
Câu 15 . Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
3
1 1
2 2
log 1 log
x x x m
có nghiệm.
A.
2
m
. B. m
.
C.
2
m
. D. Không tồn tại
m
.
Lời giải
Chọn B
Điều kiện
3
1
0
x
x x m
.
Bất Phương trình đã cho
3 3 3
1 1
2 2
log 1 log 1 1 .
x x x m x x x m x m
Đặt
3
1
f x x
, ta có
2
3 , 0 0 1;f x x f x x

.
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy yêu cầu bài toán được thỏa mãn
m
.
Câu 16. Có tất cả bao nhiêu giá trị của tham số
m
để bất phương trình
2 2
2 2
log 2 log 2
x mx m x
nghiệm đúng với mọi
x
?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn D
Ta thấy
2
2 0x x
.
Do đó bất phương trình
2 2 2 2
2 2
log 2 log 2 2 2 0
x mx m x x mx m x mx m
.
Bất phương trình
2 2
2 2
log 2 log 2
x mx m x
nghiệm đúng với mọi
x
khi và chỉ
khi
0 0
mx m x m
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 16. Có tất cả bao nhiêu giá trị nguyên của
2021;2022
m
để bất phương trình
2 2
3 3 1
3
log 3 log 1 2log 2 2 0
x x x m
có nghiệm với mọi
x
thuộc đoạn
3
1; 3
?
A.
2021
. B.
2022
. C.
4043
. D.
4042
.
Lời giải
Chọn A
Điều kiện
0
x
. Ta có
2 2
3 3 1
3
log 3 log 1 2log 2 2 0
x x x m
2
2
3 3 3
1 log log 1 2log 2 2 0
x x x m
2
2
3 3
log log 1 2 1 0
x x m
.
Đặt
2
3
log 1 1
t x
, ta được bất phương trình
2 2
2 2 0 2 2 *
t t m t t m .
Ta có
3
1; 3
x
3
0 log 3
x
2
3
1 log 1 2 1;2
t x t
.
Xét hàm
2
f t t t
, với
1; 2
t . Ta có
2 1 0, 1;2
f t t t
.
Suy ra hàm số
f t
là hàm đồng biến và liên tục trên đoạn
1; 2
.
Ta thấy
1 2
f
và
2 6
f
.
Bất phương trình
2 2
f t m
có nghiệm với
1; 2
t
2 2 2 6 2 2 2
f m m m
.
Do
, 2021;2022
m m
nên
2,...,2022
m
. Vậy có 2021 giá trị nguyên của
m
thỏa
mãn yêu cầu bài toán.
Câu 18. Cho hàm số
2
2
2 3 7 4 3 ln 1
x x
f x x x
. Tìm các giá trị của tham số
m
để bất phương trình
2
3 2 2 2 0
f x m f x x
nghiệm đúng với mọi giá trị
x
.
A.
3
2
m
. B.
1 3
2 2
m
. C.
1
2
m
. D.
m
.
Lời giải
Chọn D
Ta có
2 2
1 1 0
x x x x
nên tập xác định của hàm số đã cho là
D
.
Với
x R
, ta có
2 2
2
2 3 2 3 ln 1
x x
f x x x
2 2
2
2 3 2 3 ln 1
x x
f x x x
2 2
2
2 3 2 3 ln 1
x x
x x f x
f x
là hàm số lẻ.
Lại có
2 2
2
1
2. 2 3 ln 2 3 2. 2 3 ln 2 3 0,
1
x x
f x x
x
Hàm số
f x
nghịch biến trên
.
Ta có
2 2
3 2 2 2 0 2 2 2 3
f x m f x x f x x f x m
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
2 2
2 2 2 3 2 2 1
x x x m x m x x
2
2
2 4 1
2 1
m x x
m x
,
x
.
Do
2 2
max( 4 1) 3, min( 1) 1
x x x
nên ta có
3
2
1
2
m
m
.
Vậy không có giá trị nào của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 19. Biết rằng
a
là số thực dương sao cho bất phương trình
2 5
5 2
log 3 log 6 9 0
x x x x
a
nghiệm đúng với mọi x
. Mệnh đề nào sau đây đúng?
A.
12;14
a
. B.
10;12
a
. C.
14;16
a
. D.
16;18
a
.
Lời giải
Chọn D
Ta có
2 5 2 5 2 5
5 2
log 3 log 6 9 0 log 3 log 6 9
x x x x x x x x
a a
3 6 9
x x x x
a
18 6 9 3 18
x x x x x x
a
18 3 2 1 9 2 1
x x x x x x
a
18 3 2 1 3 1
x x x x x
a
*
.
Ta thấy
2 1 3 1 0,
x x
x
3 2 1 3 1 0,
x x x
x
.
Do đó,
*
đúng với mọi mọi x
18 0,
x x
a x
1,
18
x
a
x
1 18 16;18
18
a
a
.
Câu 20. Cho hàm số
2
log 1 2 2
f x x x x
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc
10;10
để bất phương trình
2
2 4 6 0
f x m f x x
nghiệm đúng với mọi
x
thuộc
1;1
?
A.
8
. B.
4
. C.
11
. D.
3
.
Lời giải
Chọn A
Ta có
2
2
1 2 2 1 1 1 1 1 0,x x x x x x x x
Hàm số
2
log 1 2 2
f x x x x
xác định trên
.
Ta có
2
2
1
2 log 1 1 1 log
1 1 1
f x x x f x
x x
2
2 2
1
1
1 1
1
0,
1 1 1 ln10 1 1 ln10
x
x
f x x
x x x
hàm số
f x
đồng
biến trên
.
Ta có:
2 2
2 4 6 0 2 4 6
f x m f x x f x m f x x
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
2 2
2 4 8 2 4 8
f x m f x x x m x x
2 2
2 2
2 2 4 8 2 6 8
2 2 4 8 2 2 8
x m x x m x x
x m x x m x x
Xét các hàm số
2
6 8
u x x x
và
2
2 8
v x x x
trên
1;1
ta có bảng biến thiên
Dựa vào BBT ta thấy để bất phương trình đã cho nghiệm đúng với mọi
x
thuộc
1;1
thì
15
2
11
2
m
m
. Do
m
nguyên và
10;10
m
nên có
8
giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 21. Cho hàm số
2
2
1
1
x x
f x
x
. Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
2
4
5
4
2 log
f x f x
f x m
f x
có nghiệm
0;x

.
A.
9
8
m
. B.
1
2
m
. C.
9
8
m
. D.
1
2
m
.
Lời giải
Chọn C
Xét hàm số
2
2
1
1
x x
f x
x
trên khoảng
0;

.
Ta có
2
2
2
1
1
x
f x
x
;
2
1
0 1 0
1 0;
x
f x x
x
Bảng biến thiên
Dựa vào BBT ta thấy
3
1 , 0;
2
f x x

.
Xét hàm số
2
4
5
4
2 log
f x f x
g x f x
f x
trên
0;

Do
1
f x
nên hàm số
g x
xác định trên khoảng
0;

.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Ta có
2
2
4
4
1
. 2 4 .2 .ln 2
4
ln5
f x f x
f x
g x f x f x f x
f x
f x
2
4
3
2
2 2.2 .ln 2
4 ln5
f x f x
f x
g x f x f x
f x f x
.
Do
3
1
2
f x
nên
0 0 1
g x f x x
Ta có bảng biến thiên
Dựa vào BBT ta thấy để bất phương trình đã cho có nghiệm
0;x

thì
9
8
m
.
Câu 22. Cho các bất phương trình
2 2
2 4
log 4 2 log 4 8
x x m x x m
1
và
3 1 0
x x
2
. Có tất cả bao nhiêu giá trị nguyên của
m
thỏa mãn mọi nghiệm của
bất phương trình
2
đều là nghiệm của bất phương trình
1
.
A.
254
. B.
255
. C.
256
. D.
257
.
Lời giải
Chọn B
Bất phương trình
3
2
3 0
1
1 0
x
x
x
.
Suy ra tập nghiệm của bất phương trình
2
là:
1;3
S
.
Do đó mọi nghiệm của bất phương trình
2
đều là nghiệm của bất phương trình
1
khi và chỉ
khi bất phương trình
1
có nghiệm đúng với mọi
1;3
x
.
Điều kiện:
2
2
2
4
4 0
4 1
log 4 0
x x m
x x m
x x m
2
4 1
m x x
thỏa mãn
1;3
x
.
Khi đó
1;3
max
m f x
với
2
4 1
f x x x
.
Xét hàm số
2
4 1
f x x x
trên đoạn
1;3
2 4 0
f x x
2
x
.
Bảng biến thiên:
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Dựa vào bảng biến thiên ta có
1;3
max 5
m f x m
. (3)
Ta có
2 2
2 4
log 4 2 log 4 8
x x m x x m
2 2
2 2
1 1
log 4 2 log 4 8
2 2
x x m x x m
.
Đặt
2
2
1
log 4
2
t x x m
,
0
t
.
Bất phương trình trở thành:
2
2 8 0 4;2 0;2
t t t t
.
Với
2
t
ta có
2
2
1
log 4 4
2
x x m
2
4 256
m x x
với mọi
1;3
x
.
1;3
min
m g x
với
2
4 256
g x x x
.
Xét hàm số
2
4 256
g x x x với
1;3
x .
' 2 4 0 2
g x x x
.
Bảng biến thiên:
Dựa vào bảng biến thiên:
1;3
min 259
m g x m
. (4)
Từ
3
,
4
ta có
5;259
m
thỏa mãn yêu cầu bài toán.
Vậy có tất cả
255
giá trị nguyên của
m
thỏa mãn mọi nghiệm của bất phương trình
2
đều là
nghiệm của bất phương trình
1
.
Câu 23. Cho bất phương trình
2
2
2
2 2
2 .log 4 6 4 log 2 2
x m
x
x x x m
với
m
là tham số thực.
Biết rằng tập hợp tất cả các giá trị nguyên của
m
để bất phương trình có nghiệm đúng với mọi
0;2
x
là đoạn
;
a b
. Khi đó
2 2
a b
bằng:
A.
4
. B.
8
. C.
16
. D.
0
.
Lời giải
Chọn B
Điều kiện: x
.
Ta có
2
2
2
2 2
2 .log 4 6 4 log 2 2
x m
x
x x x m
2
2
22
2 2
2 .log 2 2 2 log 2 2 1
x mx
x x m
Xét hàm số
2
2 .log 2
t
y t
với
0
t
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
Hàm số
2
2 .log 2
t
y t
xác định và liên tục trên
0;
.
Ta có
2
2
2 .log 2 .ln 2 0, 0
2 ln 2
t
t
y t t
t
.
Vậy hàm số
2
2 .log 2
t
y t
đồng biến trên
0;
.
Khi đó
2 2
1 2 2 2 2
f x f x m x x m
2 2
2 2 2
x x m x
2
2
2 6 4
, 0;2
2 2 4
m x x
x
m x x
2
0;2
2
0;2
2 min 6 4
2 max 2 4
m x x
m x x
2 4
2 2
2 4
m
m
m
.
Vậy tập hợp tất cả các giá trị nguyên của
m
để bất phương trình có nghiệm đúng với mọi
0;2
x
là đoạn
2 2
2;2 2; 2 8
a b a b
.
Câu 24. Cho
,
a b
là các số nguyên dương nhỏ hơn
2022
. Biết rằng với mỗi giá trị của
b
luôn có ít nhất
1000
giá trị của
a
thỏa mãn
2
1
2 2 .log 4 1
a b b a b
a
b
. Số giá trị
b
là
A.
1021
. B.
1022
. C.
1020
. D.
1023
.
Lời giải
Chọn A
Đặt
1, 2
c a c
, khi đó
2
1
2 2 .log 4 1 2 2 .log 2 2 , 1
a b b a b c c b b
a c
b b
.
+)
1
b
, không thỏa mãn
1
.
+)
2
2 2 15
2 , 2
log 4
c c
b
c
.
)
2
c
, không thỏa mãn
2
.
)
3
c
, hàm
2
2
2 .ln 2.ln 1 .2 .ln 2.ln 2
2 2
, 0
log
.ln 2 log
c c c
c c
c
c c c c
f c f c
c
c c
.
Suy ra
15
3 , 3 2 2021
4
f c f c a
. Do đó
2
b
thỏa mãn.
+)
3
b
,
2 2 2 2
1 , 3
ln ln
c c b b
c b
.
Hàm số
2
2 2
log
t t
f t
t
đồng biến với mọi
3
t
và
2
c
không thỏa mãn
3
nên
3
c
.
Do đó
3
3 , 3 3 2021 3 1022
2021 1 1000
b
c b b b a b
b
.
Vậy
2 1022
b
.
Câu 25. Có bao nhiêu số nguyên
2022;2022
m
sao cho thỏa mãn bất
phương trình
ln 1 ln
1 1
x x m
x x x x
,
0, 1
x x
?
A. 2. B. 1. C. Vô số. D. 0.
Lời giải
Chọn C
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
Bất phương trình đã cho tương đương với
2
2 ln
1
1
x x
m
x
,
0, 1
x x
. (1)
Xét hàm số
2
2 ln
( )
1
x x
f x
x
,
0, 1
x x
.
Ta có
2
2
2 2
2 2 2 2 2
1
2 ln
1
2[( 1)ln 1]
( )
( 1) ( 1)( 1)
x
x
x
x x x
f x
x x x
.
Xét hàm số
2
2
1
( ) ln
1
x
g x x
x
,
0
x
.
Ta có
2 2
2 2
( 1)
( ) 0
( 1)
x
g x
x x
,
0
x
,
1
x
;
( ) 0 1
g x x
.
Suy ra
( ) (1) 0
g x g
khi
1
x
và
( ) (1) 0
g x g
khi
1
x
.
Do đó ta có bảng biến thiên
Từ bảng biến thiên suy ra
(1) 1 1 0
m m
.
Vậy có vô số giá trị nguyên của tham số
m
thỏa mãn.
Câu 26. Hỏi có tất cả bao nhiêu giá trị thực của tham số
m
để bất phương trình
2 2
2 ln 1 0
x
x e mx x e
đúng với
x
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A
Bất phương trình đã cho tương đương với:
2 2
2 ln 1 0
x
f x x e mx x e
. Nhận thấy nhanh rằng:
0 0
f
Suy ra hàm số trên thỏa mãn
0 0
0 0
f x f x R
f
hàm số đạt cực tiểu tại
0
x
Xét
2
2
2 2
x
x
f x x e m
x e
có
0 2 0 2
f m m
Thử lại với
2
m
thì
2 2
2 2 ln 1
x
f x x e x x e
2 2
2 1
2 2 2 2 1 2 1 0 0
x x
x
f x x e x e x
x e x e
Đến đây ta nhận thấy
0 0
f x f
nên suy ra
2
m
thỏa nên có đúng 1 giá trị
m
Câu 27. Hỏi có tất cả bao nhiêu giá trị thực của tham số
m
để bất phương trình
2 2 2 2 2
2 3
4 4 log 2 1 log 1 0
m m x mx m m x
có nghiệm thực
x
?
A.
1
. B.
2
. C.
3
. D.
6
.
Lời giải
Chọn B
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
Bất phương trình đã cho tương đương với:
2 2
2 2
2 3
0
0
0
2 log 1 log 1 0
m x m m x


Ta nhận thấy:
2 2
2 2
2 3
2 log 1 log 1 0
m x m m x
nên suy ra bất phương trình trên
chỉ có nghiệm khi xảy ra dấu bằng, tức là:
2 2
2
2 2
2 2
2 3
2 2
3
2
2
2
2
2
2
2
2
3
2 log 1 0
2 log 1 log 1 0
log 1 0
2 0
2 0
2 2
log 1 0
0
0
0 0
0
0
0 0
0
log 1 0
m x m
m x m m x
m x
m
m
m m
x m
x m x
x m
m m
m
m
x x
x
x
Suy ra có 2 giá trị thực
m
thỏa mãn bài toán
Câu 28. Gọi
S
là tập chứa tất cả các giá trị nguyên của tham số
m
để bất phương trình
2
ln 4 3 log
x x m
có đúng 3 nghiệm nguyên, vậy tổng phần tử của
S
là
A.
108
. B.
5
. C.Vô số D.
89
.
Lời giải
Chọn B
Bất phương trình đã cho tương đương với:
2 2
ln 4 3 log ln 4 3 log
x x m f x x x m
Xét hàm số
2 2
1
ln 4 3 ; 4 3 0
3
x
f x x x x x
x
Ta có:
2
1 1
2
3 3
22
2
2
2
lim lim ln 4 3 ln 0
lim lim ln 4 3 ln 0
2 4 4 34 3
0 2
4 3
4 3
x x
x x
f x x x
f x x x
x x xx x
f x x
x x
x x


Từ đó ta có bảng biến thiên như sau:
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Nhận thấy ngay 3 nghiệm nguyên thỏa mãn bài toán đó là:
0;2;4
x
. Lưu ý rằng hai nghiệm
nguyên
1; 3
x x
bị vi phạm điều kiện nên không được tính
Suy ra
4 log 5 ln3 log ln8 13 120
m Z
f m f m m

Như vậy có tất cả
120 13 1 108
giá trị nguyên
m
thỏa mãn bài toán.
Câu 29. Có tất cả bao nhiêu bộ số nguyên
; ; ;
a b c d
với
, , , 3;3
a b c d thỏa
mãn điều kiện bất phương trình
2 3
4 3 2
ln 1
2 3
x x
x ax bx cx dx
nghiệm đúng với
1;x

?
A.
43
B.
71
C.
37
D.
47
Lời giải
Chọn B
Ta để ý rằng 2 đồ thị
2 3
ln 1
2 3
x x
f x x
và
4 3 2
g x ax bx cx dx
cùng đi qua
gốc tọa độ. Do đó ta xét tiếp tuyến tại gốc tọa độ của
y f x
. Ta có
0 1; 0 0
f f
nên
tiếp
tuyến là
y x
.
TABLE ta có
2 3
ln 1 0
2 3
x x
x x
1;x

.
Do vậy đồ thị
2 3
ln 1
2 3
x x
f x x
luôn đứng dưới đường thẳng
y x
và tiếp xúc nhau
tại
O
.
Xét phương trình hoành độ giao điểm
4 3 2
1 0
ax bx cx d x
có nghiệm kép
0
x
nên
1
d
.
Đồ thị
4 3 2
g x ax bx cx dx
luôn đứng trên đường thẳng
y x
và tiếp xúc nhau tại
O
thì điều kiện cần và đủ là
2
0 1;ax bx c x

do đó
0
a
.
Trường hợp 1:
0
0 1;
a
bx c x

0
0
0
a
b
b c
. Có 10 bộ:
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 19
Trường hợp 2:
2
0
4
a
b ac
. Có tất cả 60 bộ:
Trường hợp 3:
2
0
4
a
b ac
khi đó
1 2
0 1;a x x x x x 
khi
1 2
1x x
.
Do đó
1 2
1 2
2
2
2
1 0
1 1 0
b
b a
x x
b a
a
c b
a c b
x x
a a
.
Có duy nhất 1 bộ thỏa mãn
1
3
2
a
b
c
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Kết luận: Có tất cả 71 bộ số cần tìm.
Câu 30. Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ.
Với điều kiện nào của tham số
m
thì bất phương trình
2
2019
5 2
1 28
1 .log 0
125 5
2020
f x m
x
f x
nghiệm đúng với mọi
4;5
x
?
A.
10
m
. B.
10
m
. C.
10
m
. D.
10
m
.
Lời giải
Chọn A
Ta có:
2
2
4 4, 4;5
28 7
, 4;5
27 28 28
125 5 5
, 4;5
5 125 5 5
f x x
x
f x x
x
x

.
2
2019
28
log 0, 4;5
125 5
x
f x x
(*).
Từ (*) ta có:
2
2019
5 2
1 28
1 .log 0, 4;5
125 5
2020
f x m
x
f x x
5 2
1
1 0, 4;5
2020
f x m
x
5 2
1
1, 4;5
2020
f x m
x
5 2 0, 4;5
f x m x
2
, 4;5
5
m
f x x
2
4 10
5
m m
.
_______________ TOANMATH.com _______________
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
BẤT PHƯƠNG TRÌNH LÔGARIT CHỨA THAM SỐ
Bài toán. Tìm m để bất phương trình f (x,m)  0 hoặc f (x,m)  0 có nghiệm trên D ? PHƯƠNG PHÁP
Bước 1. Tách tham số m ra khỏi x và đưa BPT về dạng (
A m)  f (x) hoặc A(m)  f (x) .
Bước 2. Khảo sát sự biến thiên và dựa vào bảng biến thiên xác định các giá trị của tham số m
để bất phương trình có nghiệm.
Lưu ý: Cho hàm số y  f  x xác định và liên tục trên D .
Trong trường hợp tồn tại max f (x) và min f (x) thì ta có: xD xD  Bất phương trình (
A m)  f (x) có nghiệm trên D  ( A m)  max f (x) . xD  Bất phương trình (
A m)  f (x) có nghiệm trên D  ( A m)  min f (x) . xD  Bất phương trình (
A m)  f (x) nghiệm đúng x  D  ( A m)  min f (x) . xD  Bất phương trình (
A m)  f (x) nghiệm đúng x  D  ( A m)  max f (x) . xD Nếu 2
f (x)  ax  bx  c a  0 thì a  0
f (x)  0, x     .   0 a  0
f (x)  0, x     .   0
Câu 1. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 2 2
log (7x  7)  log (mx  4x  m) nghiệm đúng với mọi giá trị thực của x ? 2 2 A. 7 . B. 3 . C. Vô số. D. 4 . Lời giải Chọn B 2 mx  4x  m  0, x   
Yêu cầu bài toán được thỏa mãn   2 2
7x  7  mx  4x  , m x     f x 2  mx  4x  m  0, x         . g
  x  7  m 2 x  4x  7  m  0, x    
Ta thấy m  0; m  7 không thỏa mãn điều kiện đề bài.
Với m  0 và m  7 . Khi đó ta có: m  0 m  0    
 m  2  m  2 . (1) 2   4  m  0  m  2 m  7     7 m 0 m  7       
 m  5  m  5. (2)   4  2  7  m2  0 m 14m  45  0  m  9
Từ (1) và (2) suy ra 2  m  5 . Do m   nên m 3;4;  5 .
Câu 2. Tìm m để bất phương trình 2
log 2x  2(m 1) log x  2  0 có nghiệm x  ( 2; ). 2 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC  3   3  A. m  (0; ) . B. m   ;0   . C. m   ;    . D. m  (;0) .  4   4  Lời giải Chọn C Ta có 2
log 2x  2(m 1) log x  2  0  1 log x  2(m 1) log x  2  0 .  2 2 2 2 2  1 
Đặt t  log x . Do x  ( 2; )  t  ;  . 2    2 
Khi đó  trở thành   t2 1  2(m 1)t  2  0  t2 1  2 2   t 1 1  m  f t   m (1). 2t 2t t 1  Xét hàm f t 1   liên tục trên ;  . 2 2t   2  1 1  1   1  3 Ta có f t    0, t   ;   min f t  f   . 2       1 2 2t  2   ;  2  4    2   1 
Khi đó (1) đúng với mọi t  ;  
 khi min f t   m  3 m   .  2  1  ; 4   2 
Câu 3. Có tất cả bao nhiêu giá trị nguyên thuộc  1
 00;100 của tham số mđể bất phương trình log log 3x 1  log
m nghiệm đúng với mọi x thuộc khoảng  ;  0 ? 0,02  2   0,02 A. 99. B. 98. C. 100 . D. 101. Lời giải Chọn C log 3x 1  0 2   Điều kiện:   m  0. m  0 Ta có log log 3x 1  log  log 3x m 1  m . 0,02  2   0,02 2   3x.ln 3 Xét hàm số   log 3x f x  1 . Ta có f 'x   0 x    . 2   3x  1.ln2
Suy ra hàm số luôn đồng biến trên tập xác định.
Dựa vào bảng biến thiên ta có bất phương trình nghiệm đúng với mọi x thuộc  ;  0 khi m  1.
Do m nguyên và thuộc đoạn  1
 00;100 nên m1;2;3;4;.....;10  0 . Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Câu 4. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 2 log 2x  4  m 3
log x 1 có nghiệm đúng với mọi x thuộc 16;? 2 8  A. 2 . B. 3. C. 1. D. 4 . Lời giải Chọn C x  0 x  0
Điều kiện xác định:    2 2 log 2x  4  0 log x  2log x  3  0  2  2 2 x  0  1  0  x   log x 1    . 2 8  log x  3  x  2 2 Ta có : 2 log 2x  4  m 3 log x 1 2
 log x  2log x  3  m log x 1 * . 2 2  2    2 8 
Do x 16; nên log x  4  log x 1  0 2 2 2 log x  2log x  3 Suy ra * 2 2   m . log x 1 2
Đặt t  log x . Do x 16; nên t 4; . 2 2 t  2t  3 Bất phương trình   * trở thành  m t  4;. t 1 2 t  2t  3 Xét hàm f t  với t 4; . t 1 2  2t Ta có f 't   0, t  4;. t  2t  3.t  2 2 1
Suy ra hàm số f t nghịch biến trên khoảng 4; .
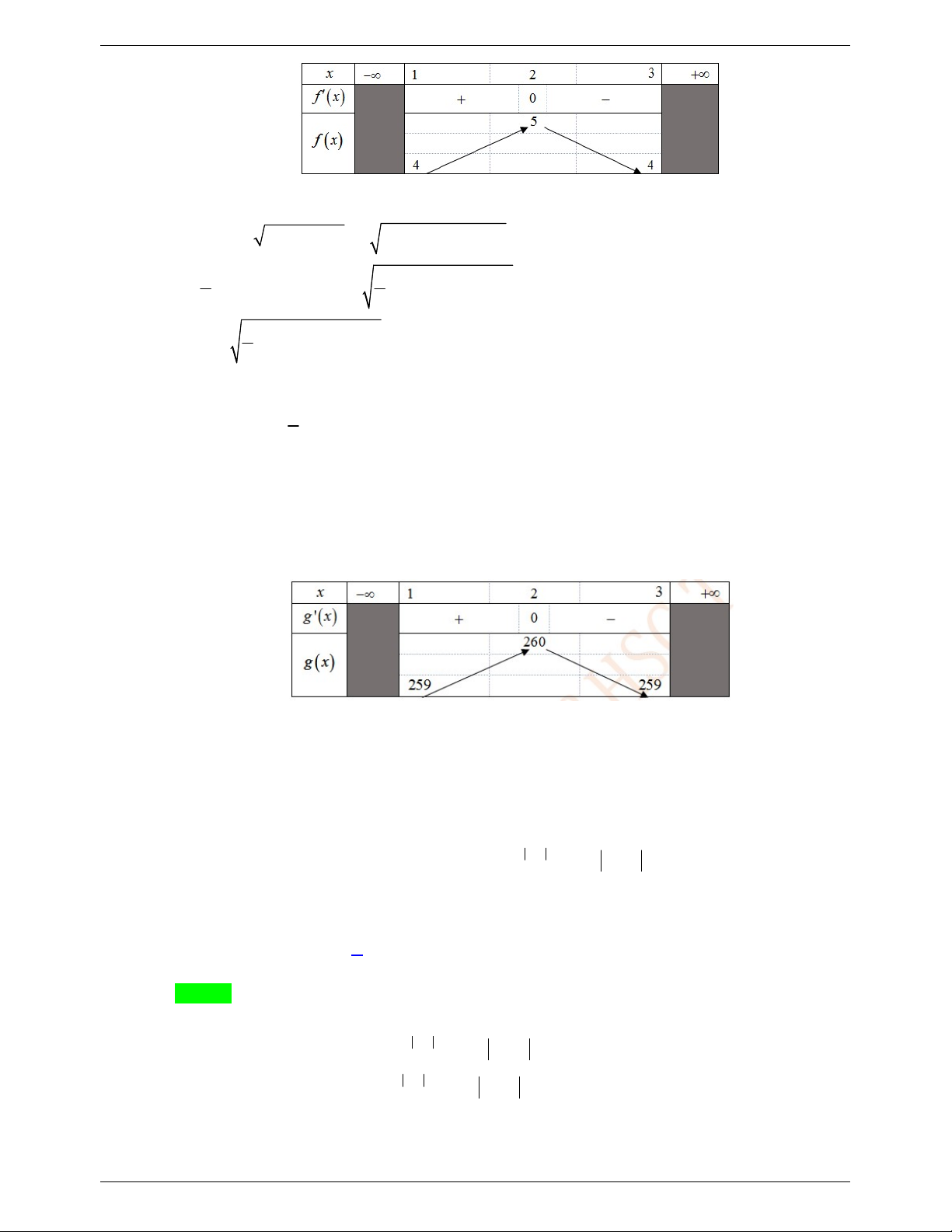
Bảng biến thiên của hàm f t như sau:
Dựa vào bảng biến thiên ta thấy bất phương trình đã cho nghiệm đúng với mọi x thuộc
16; khi m 1. Do * m  m 1. Câu 5.
Có tất cả bao nhiêu giá trị nguyên thuộc  1
 0;10 của tham số m để bất phương trình 3 x  x  4  2mlog 2 có nghiệm? 4 4x A. 8 . B. 5. C. 6 . D. 7 . Chọn A
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC x  0 x  4 
Điều kiện xác định:   0  x  4 . 4  4  x  1   4  4  x  0
Ta thấy 0  x  4  0  4  x  4  2  4  4  x  4 . Suy ra log 2  0 . 4 4x
Khi đó bất phương trình 3 x  x  4 3 x  x  4  2mlog 2  m  4 4x 2.log 2 4 4x 1
 m  3 x  x  4.log 4  4  x . 2   2 1
Xét hàm f  x  3 x  x  4.log 4  4  x liên tục trên 0;4. 2   2 Ta có   f   1 3 1 1 1 ' x  
.log 4 4x  3 x  x4 . 0 x   0;4   . 2     22 x 2 x4 2 2 4x .4 4x   .ln2
Suy ra hàm số y  f  x đồng biến trên 0;4.
Để bất phương trình đã cho có nghiệm thì m  1.
Do m nguyên và thuộc khoảng  1
 0;10 nên m2;3;...;  9 .
Vậy có 8 giá trị m nguyên cần tìm là : m 2;3;...;  9 .
Câu 6. Cho bất phương trình log  2
x  2x  2 1  log  2
x  6x  5  m . Có bao nhiêu giá trị nguyên 7 7 
của tham số m để bất phương trình trên có tập nghiệm chứa khoảng 1;3 ? A. 35 . B. 33. C. 33 . D. 36 . Lời giải Chọn D 2 x  6x  5  m  0  2 m  x  6x 5 Bpt     . log 7 2    2 x  2x  2  log   2x 6x5  m 6x 8x  9  m 7 7  Xét hàm f  x 2
 x  6x  5 liên tục trên đoạn 1;  3 . Ta có f  x  2  x  6  0, x
 1;3  f x nghịch biến trên đoạn 1;  3
 max f x  f   1  1  2 . 1; 3 Xét hàm g  x 2
 6x  8x  9 liên tục trên đoạn 1;  3 . Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Ta có g x 12x  8  0, x
 1;3  g  x đồng biến trên khoảng 1;  3
 min g x  g   1  23 . 1; 3 2  m  max f x m  x  6x  5  1;3
Yêu cầu bài toán được thỏa mãn khi 
với mọi x 1;3   . 2 6x  8x  9  m m  min g  x  1; 3
Khi đó ta có 12  m  23. Mà m   nên m 1  2; 1  1;10; ...;22;2  3 .
Vậy có tất cả 36 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 7. Tìm tấtt cả các giá trị của tham số m để bất phương trình 2 4log x  2log x  m  0 có 2 1 4
nghiệm với mọi x thuộc khoảng 0;  1 .  1   1  1  A. m  0;  . B. m   ;   . C. m   ;  0. D. ;   . 4    4     4  Lời giải Chọn D Điều kiện: x  0 . Ta có 2 4log
x  2log x  m  0  log x  log x  m  0 . 2 2 2 1 2 4
Đặt t  log x , do x 0;  1  t  ;  0. 2
Bất phương trình trở thành 2 t  t  m  0 2  m  t   t . Xét hàm   2
f t  t  t với t  ;  0 . Ta có f t  2  t 1, f t 1  0  t   . 2
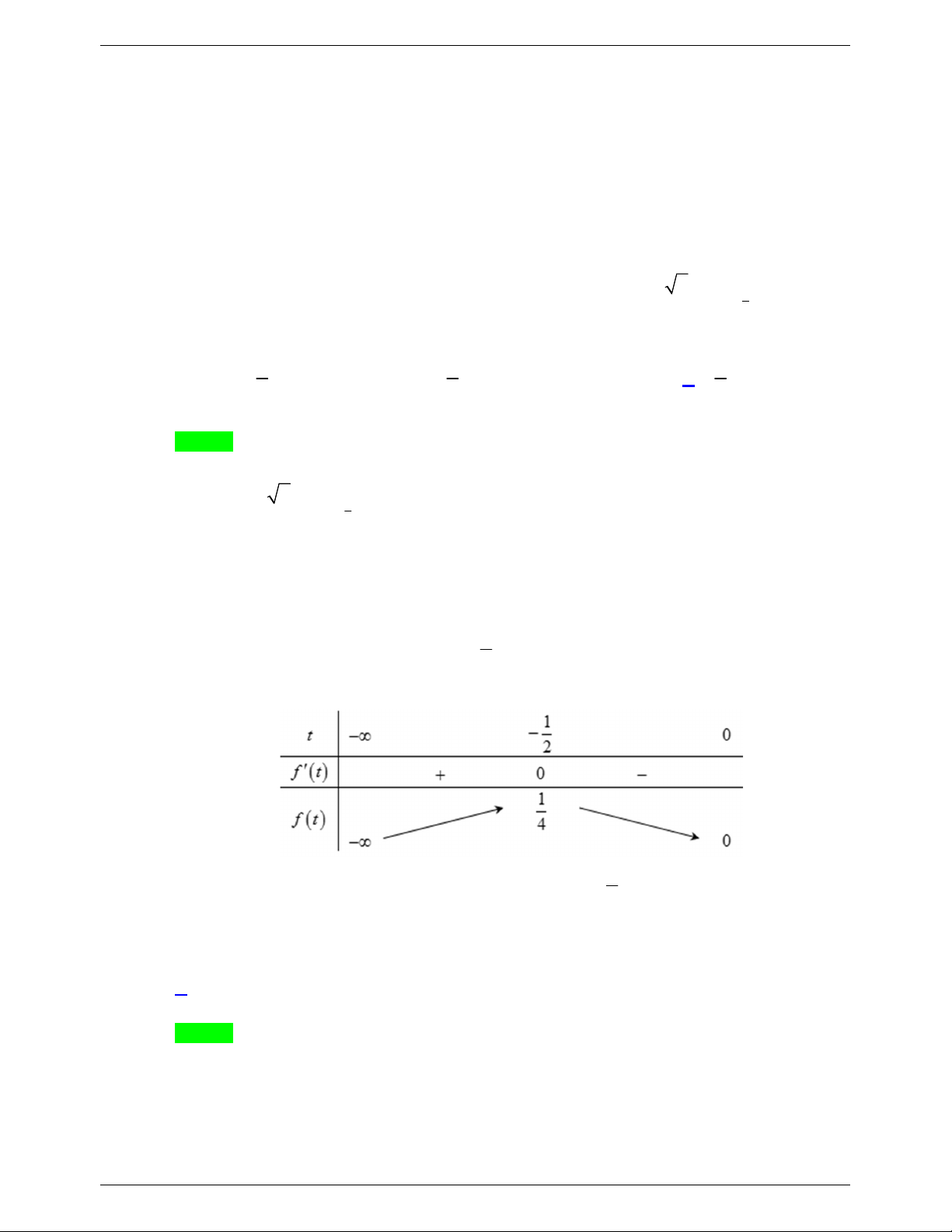
Bảng biến thiên của hàm   2 f t  t  t như sau: 1
Dựa vào bảng biến thiên ta thấy ycbt được thỏa mãn  m  . 4
Câu 8. Có bao nhiêu số nguyên m sao cho bất phương trình   2 x     2 ln 5 ln 1
ln mx  4x  m có tập nghiệm là  ? A.1 . B. 2 . C. 3 . D. 4 . Lời giải Chọn A Ta thấy 2 x 1  0, x    . Ta có   2 x     2 mx  x  m   2 x     2 ln5 ln 1 ln 4 ln 5 5 ln mx  4x  m
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2  5x  4x  5 2 2 2 2  m   f  x 5
 x  5  mx  4x  m 5x  5  4x  m x   1 2      x 1   . 2 mx  4x  m  0 m 4x   2 x   1  4x m    g x  2  x 1
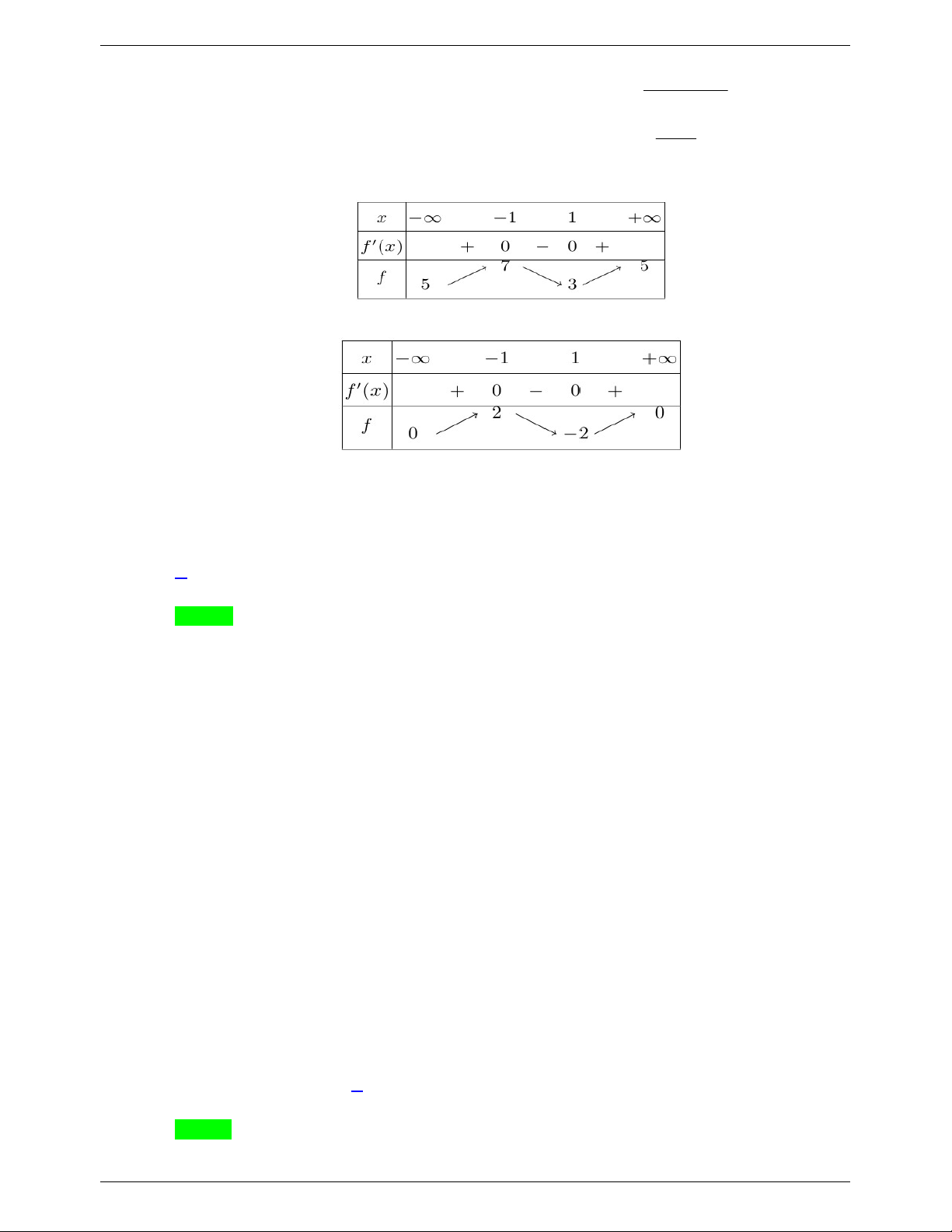
Hàm số f  x có bảng biến thiên như sau:
Hàm số g  x có bảng biến thiên như sau:
Từ bảng biến thiên suy ra bất phương trình có tập nghiệm là  khi 2  m  3.
Vậy có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 9. Số giá trị nguyên của m để bất phương trình 1 log  2 x   1  log  2 mx  2x  m có nghiệm 3 3 
đúng với mọi số thực x là A. 1. B. 2 . C. 4 . D. 6 . Lời giải Chọn A Điều kiện xác định: 2 mx  2x  m  0 . Ta có: 1 log  2 x   1  log  2
mx  2x  m  log 3 2 x   1  log  2 mx  2x  m 3 3 3 3    2 x   2
 mx  x  m    m 2 3 1 2 3 x  2x  3  m  0.
Ta thấy m  0; m  3 không thỏa mãn điều kiện đề bài.
Với m  0 và m  3. Khi đó: 2
mx  2x  m  0 x
Để bất phương trình nghiệm đúng với mọi x   thì   3 m 
 2x  2x 3 m  0 x    m  0 m  0 3  m  0   m  3      1 m  2 . 2 1 m  0 m  1;m  1   1    3 m2  0 m  2;m  4 Mà m nên m  2 .
Câu 10. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc  2  021;202  1 sao cho bất phương trình 1 log  3 2
x  x  3x  m  log  2
3x 1 nghiệm đúng với mọi x trên đoạn 0;  3 3 3 
. Tính số phần tử của tập hợp S . A. 2020 . B. 2018 . C. 2022 . D. 4040 . Lời giải Chọn B Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Ta thấy 2 3x 1  0, x    . Ta có: 1 log  3 2
x  x  3x  m  log  2 3x 1 ; x  0;3 3 3     log  3 2
3x  3x  9x  3m  log  2 3x 1 ; x   0;3 3 3    3 2 2
 3x  3x  9x  3m  3x 1; x  0;  3 3  3m  3  x  9x 1; x  0;  3 . Xét hàm số: f  x 3  3
 x  9x 1 trên 0;  3 .  x 10;3 Ta có: f  x 2  9
 x  9 , f x  0   . x  1    0;3 Bảng biến thiên: 7
Từ bảng biến thiên ta có: 3m  7  m  . 3 Mà m và m 2  021;202  1 nên m {3; 4;;2020}.
Câu 11. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc  2  021;202  1 sao cho bất phương trình 2
3log 2x 12log x 1 m  0 nghiệm đúng với mọi x trên khoảng  2; . Tính 2 2
số phần tử của tập hợp S . A. 2018 . B. 2020 . C. 2022 . D. 4040 . Lời giải Chọn B Ta có: 2
3log 2x 12log x 1 m  0  3 2
log x  2 log x 1 12 log x 1 m  0 2 2  2 2 2 2
 3log x  6log x  2  m  0 * . 2 2  
Đặt: log x  t , với x   1 2;  t  ;  . 2    2 
Khi đó bất phương trình (*) trở thành 2 3t  6t  2  m  0 2  m  3t  6t  2 .  1  Xét hàm số f t 2  3t  6t  2, t   ;   .  2 
Ta có: f t  6t  6; f t  0  6t  6  0  t  1. Bảng biến thiên:
Từ bảng biến thiên ta thấy m  1  .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Mà m và m 2  021;202  1 nên m 2  020; 2019;...;  1 .
Câu 12. Tìm tất cả các giá trị thực của tham số m để bất phương trình log (5x 1).log (2.5x  2)  m 2 2 có nghiệm x  1. A. m   . B. m  6. C. m  6 . D. m  6 . Lời giải Chọn A
Với x  1 thì 5x 1 0; 2.5x    2  0.
Ta có log (5x 1).log (2.5x  2)  m 2 2 log (5x 1).log (2.5x    2)  m 2 2
 log (5x 1). 1 log (5x  1)  m 2  2  . Đặt log 5x t 
1 do x  1  t 2;. 2   BPT trở thành: 2
t(1 t)  m  t  t  m . Đặt 2
f (t)  t  t ta có f (t)  2t 1 0 với t
 2; nên hàm số y  f t đồng biến và
liên tục trên 2; . Suy ra f t6; khi t 2; .
Do đó để để bất phương trình log (5x 1).log (2.5x 
 2)  m có nghiệm thỏa mãn x  1 2 2 thì m  
Câu 13. Tổng tất cả các giá trị nguyên của tham số m sao cho khoảng 2;3 thuộc tập nghiệm của bất phương trình log  2 x   1  log  2 x  4x  m 1 là 5 5  A. 1  3. B. 1  2. C. 12. D. 13. Lời giải Chọn D. 2  x  4x  m 2 2 x 1 
m  x  4x  f (x) Ta có (1)   5   . 2       2 m 4x 4x 5 g(x) x  4x  m  0 m  Max f (x)  12  2;3 Hệ trên thỏa mãn x  2;3    12  m  13 . m  Min g(x)  13  2;3
Câu 14 . Có bao nhiêu số nguyên dương m trong đoạn 2018;2018 
 sao cho bất phương trình  x logx 11 m x 10 10  log 10 10
đúng với mọi x 1;100 ? A. 2022. B. 2021. C. 2020. D. 2018. Lời giải Chọn D. Điều kiện x  0 . log x 11 m log x log x 11 Ta có 10x    10  10 10  m  log x  1  log x  10  10   x  m x    x   m x    2 log 10 log 1 11log 0 10 log 1 log x  10log x  0 .
Vì x 1;100 nên logx0;2 . Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2 x x Do đó m x     2 10log log 10 log
1 log x 10log x  0  10m  . log x  1
Đặt t  log x , t 0;2 . 2 10t t Xét hàm số f t  
liên tục trên đoạn 0;2 . t  1   10  2t  2 t Ta có f t   0, t  0;2
Hàm số f t đồng biến trên 0;2 . 2    t 1 16
Suy ra max f (t)  f 2  . 0;2 3 x  2 10log log x 16 8
Để bất phương trình 10m 
đúng với mọi x 1;100 thì 10m   m  . log x  1 3 15  8 
Do đó m   ;2018 hay có 2018 số thỏa mãn. 15 
Câu 15 . Tìm tất cả các giá trị thực của tham số m để bất phương trình log x  1  log  3x  xm 1 1  2 2 có nghiệm. A. m  2 . B. m   . C. m  2 . D. Không tồn tại m . Lời giải Chọn B x 1 Điều kiện  . 3 x   xm  0 
Bất Phương trình đã cho  log x  1  log  3x  xm 3 3
 x1 x  xm  x 1 . m 1 1 2 2 Đặt f  x 3
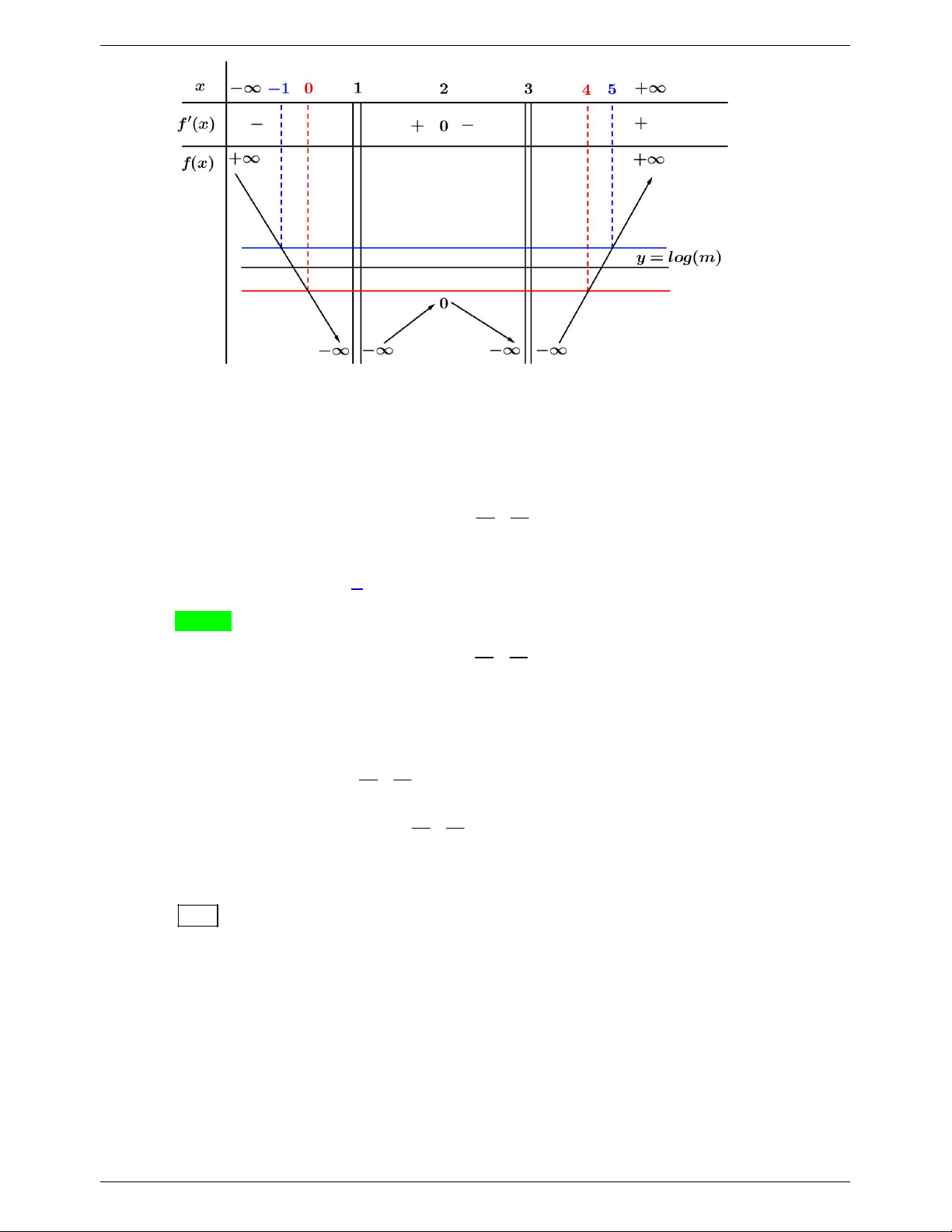
 x 1, ta có f x 2
 3x , f x 0  x  01;   . Bảng biến thiên
Dựa vào bảng biến thiên ta thấy yêu cầu bài toán được thỏa mãn  m   .
Câu 16. Có tất cả bao nhiêu giá trị của tham số m để bất phương trình log  2
x  mx  m  2  log  2
x  2 nghiệm đúng với mọi x   ? 2 2  A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn D Ta thấy 2 x  2  0 x  . Do đó bất phương trình log  2
x  mx  m  2  log  2 x  2 2 2
 x  mx  m  2  x  2  mx  m  0 . 2 2
Bất phương trình log  2
x  mx  m  2  log  2
x  2 nghiệm đúng với mọi x   khi và chỉ 2 2  khi mx  m  0 x     m  0 .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Câu 16. Có tất cả bao nhiêu giá trị nguyên của m 2  021;202  2 để bất phương trình 2 2
log 3x  log x 1  2log x  2m  2  0 có nghiệm với mọi x   3 3 1 thuộc đoạn 3 1; 3   ? 3 A. 2021. B. 2022 . C. 4043. D. 4042 . Lời giải Chọn A
Điều kiện x  0 . Ta có 2 2
log 3x  log x 1  2log x  2m  2  0 3 3 1 3  1 log x2 2
 log x 1  2log x  2m  2  0 3 3 3  log x2 2
 log x 1  2m 1  0 . 3 3 Đặt 2
t  log x 1  1, ta được bất phương trình 2 2
t  t  2m  2  0  t  t  2m  2 *. 3 Ta có 3 x  1  ; 3  2 
  0  log x  3  1  t  log x 1  2  t  1;2 . 3   3 Xét hàm   2
f t  t  t , với t 1; 2. Ta có f t  2t 1  0, t  1;2 .
Suy ra hàm số f t là hàm đồng biến và liên tục trên đoạn 1; 2. Ta thấy f   1  2 và f 2  6.
Bất phương trình f t  2m  2 có nghiệm với t  1; 2
 f 2  2m  2  6  2m  2  m  2. Do m ,  m 2  021;202  2 nên m2,...,202 
2 . Vậy có 2021 giá trị nguyên của m thỏa mãn yêu cầu bài toán. 2 x x
Câu 18. Cho hàm số f  x           2 2 3 7 4 3 ln
x 1  x. Tìm các giá trị của tham số m
để bất phương trình f   x  m   f  2 3 2
x  2x  2  0 nghiệm đúng với mọi giá trị x   . 3 1 3 1 A. m  . B.  m  . C. m  . D. m   . 2 2 2 2 Lời giải Chọn D Ta có 2 2
x 1  x  x 1  x  0 nên tập xác định của hàm số đã cho là D   .  2x 2 x
Với x  R , ta có f  x           2 2 3 2 3 ln x  x 1
      2x   2x f x   2 2 3 2 3 ln x 1  x  2 x 2 x       2 2 3 2 3 ln x x 1           f  x  
 f x là hàm số lẻ. 2 x 2 x 1 Lại có f  x  2
 .2  3 ln2 3  2.2  3 ln2 3   0, x    2 x 1
 Hàm số f x nghịch biến trên  .
Ta có f   x  m   f  2
x  x     f  2 3 2 2 2 0
x  2x  2  f 2 x  m  3 Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2 2m  x  4x 1 2 2
 x  2x  2  2 x  m  3  2 x  m  x  2x 1   , x   . 2 2m  x 1  3 m   Do 2 2
max(x  4x 1)  3, min(x 1)  1 nên ta có 2  .   1 m   2
Vậy không có giá trị nào của tham số m thỏa mãn yêu cầu bài toán.
Câu 19. Biết rằng a là số thực dương sao cho bất phương trình log 3x  x  log 6x  9x a  0 2 5   52
nghiệm đúng với mọi x . Mệnh đề nào sau đây đúng? A. a 12;14 . B. a 10;12 . C. a 14;16 . D. a 16;1  8 . Lời giải Chọn D Ta có log 3x  x  log 6x  9x  0  log 3x  x  log 6x  9x a a 2 5   52 2 5   2 5    3x  x  6x  9x a x 
18x  6x  9x  3x 18x a x  18x  3x 2x   1  9x 2x a   1 x  18x  3x  2x   1 3x a   1 * . Ta thấy 2x   1 3x  
1  0,x    3x 2x   1 3x   1  0, x    . x  a 
Do đó, * đúng với mọi mọi x x x  a 18  0, x     1,x     18  a 
 1  a  1816;18. 18
Câu 20. Cho hàm số f  x   2
log x 1 x  2x  2 . Có bao nhiêu giá trị nguyên của tham số m thuộc  1
 0;10 để bất phương trình f  x  m   f  2 2
x  4x  6  0 nghiệm đúng với mọi x thuộc  1  ;  1 ? A. 8 . B. 4 . C. 11. D. 3 . Lời giải Chọn A
Ta có x   x  x   x   x  2 2 1 2 2 1
1 1  x 1 x 1  0, x   Hàm số f  x   2
log x 1 x  2x  2  xác định trên  .     1 Ta có f 2 x log1 x 1 x2 1 log           f x      x  2 1 1  x 1   x 1 1 x 2  f  x 1 1 1  
 0,x   hàm số f x đồng  x 1 x 2 1 1ln10   x 2 1 1       ln10     biến trên  .
Ta có: f  x  m   f  2
x  x     f  x  m    f  2 2 4 6 0 2 x  4x  6
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
 f  x  m   f  2 x  x   2 2 4
8  2 x  m  x  4x  8 2 2
2x  2m  x  4x  8 2m  x  6x  8     2 2 2x
  2m  x  4x 8 2m   x  2x  8 Xét các hàm số u  x 2
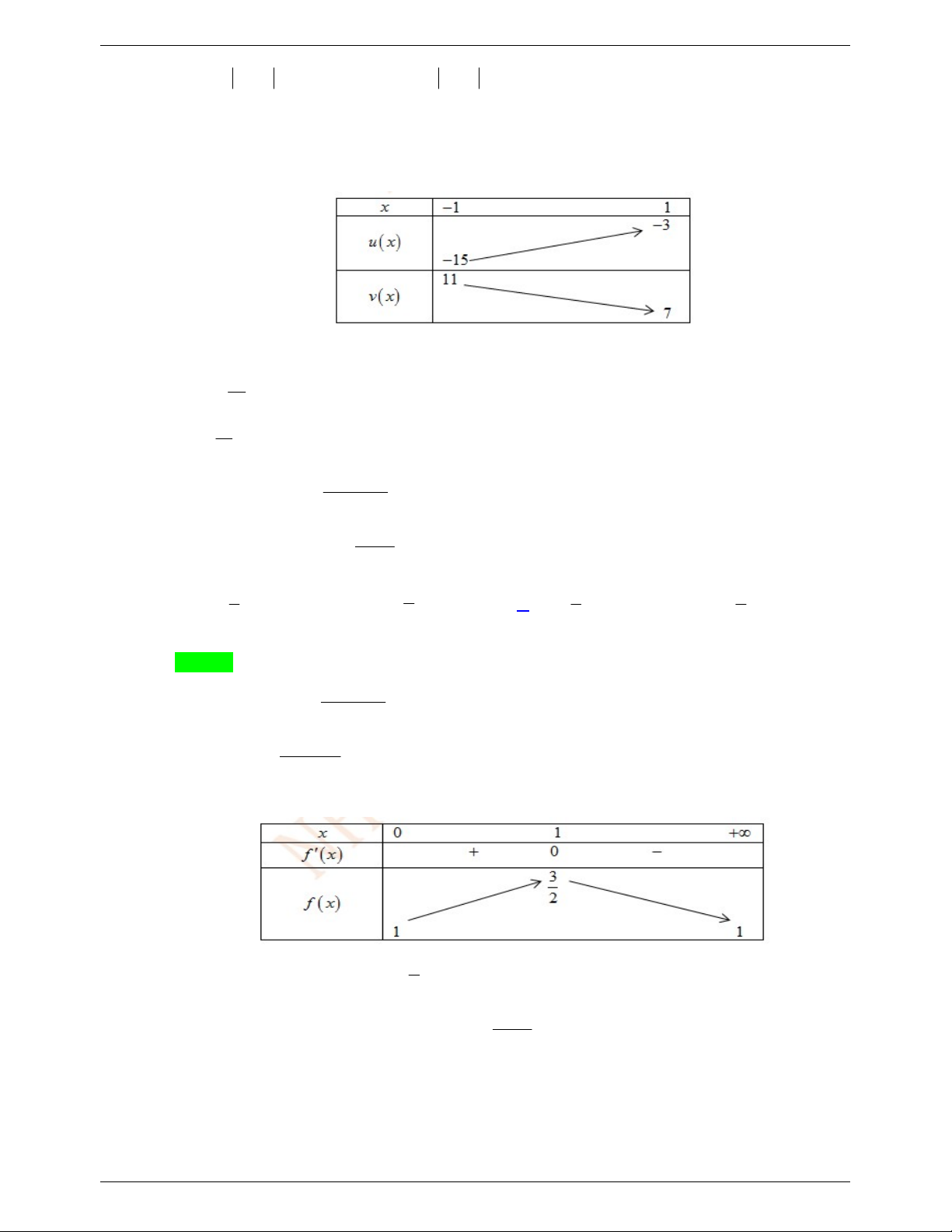
 x  6x 8 và vx 2  x  2x  8 trên  1  ;  1 ta có bảng biến thiên
Dựa vào BBT ta thấy để bất phương trình đã cho nghiệm đúng với mọi x thuộc  1  ;  1 thì  15 m    2  . Do m nguyên và m  1
 0;10 nên có 8 giá trị m thỏa mãn yêu cầu bài toán. 11 m   2 2 x  x 1
Câu 21. Cho hàm số f  x 
. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x 1   2 f  x4 f x 4 2  log  f x 
  m có nghiệm x 0; . 5    f  x 9 1 9 1 A. m  . B. m  . C. m  . D. m  . 8 2 8 2 Lời giải Chọn C 2 x  x 1 Xét hàm số f  x 
trên khoảng 0;. 2 x 1 2 x 1 x  1 Ta có f  x  2  
; f  x  0  x 1  0   x  2 2 1 x  1  0;   Bảng biến thiên 3
Dựa vào BBT ta thấy 1  f x  ,x 0; . 2   2 f x  f x 4 Xét hàm số g  x   4    2  log  f x   trên 0; 5    f x   
Do f  x 1 nên hàm số g  x xác định trên khoảng 0;. Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC  4   1  2 2   f x 
Ta có g x  f  x.2 f  x f  x 4 f  x  4.2 .ln 2  f   x        f x 4     f  x ln 5         
 gx  f  x  f x 2  f x f  x 2 4 f x    2 2.2 .ln 2    .    3
f  x  4 f  xln 5   Do  f  x 3 1
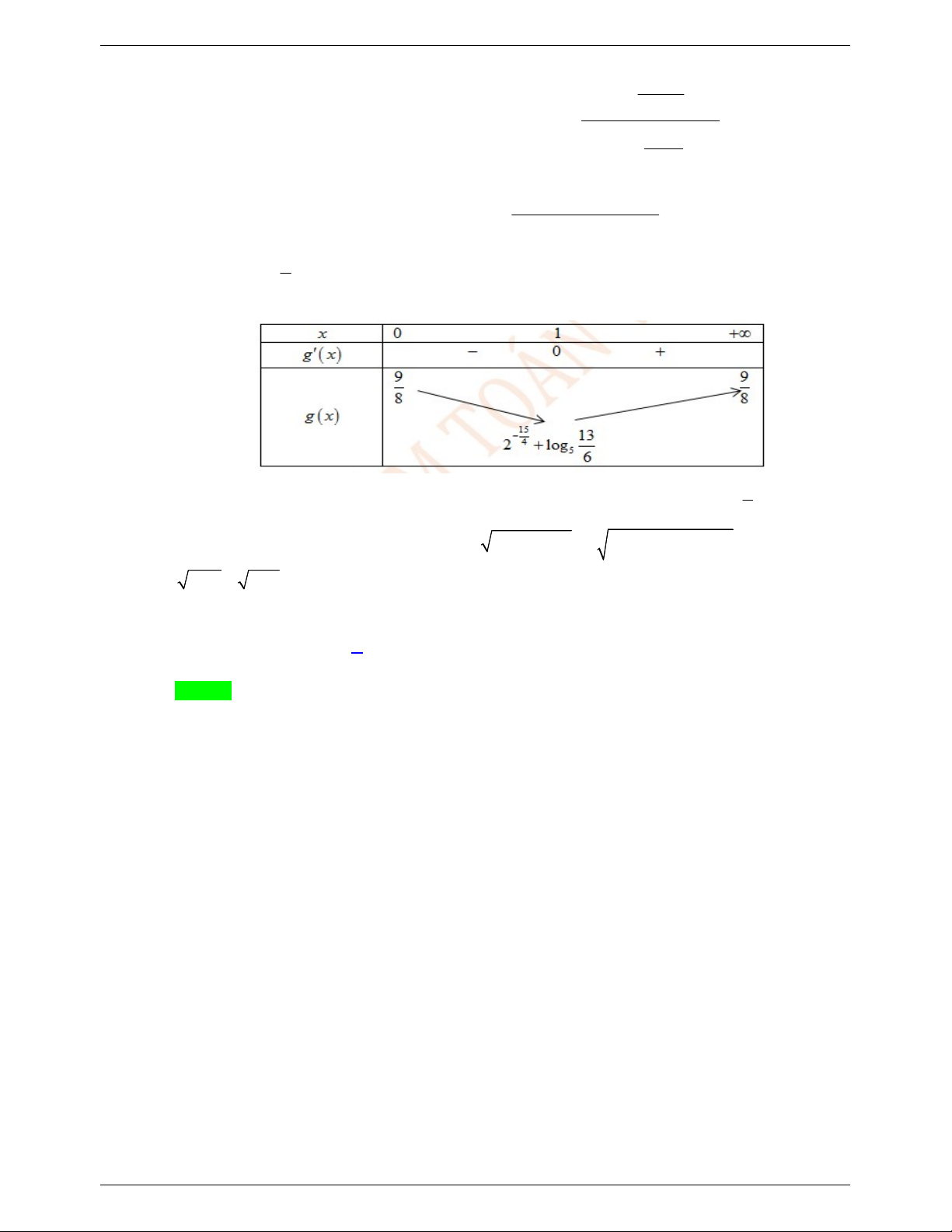
 nên g x  0  f  x  0  x 1 2 Ta có bảng biến thiên 9
Dựa vào BBT ta thấy để bất phương trình đã cho có nghiệm x 0; thì m  . 8
Câu 22. Cho các bất phương trình 2 log x  4x  m  2 log  2 x  4x  m  8   1 và 2 4 
3 x  x 1  0 2 . Có tất cả bao nhiêu giá trị nguyên của m thỏa mãn mọi nghiệm của
bất phương trình 2 đều là nghiệm của bất phương trình   1 . A. 254 . B. 255 . C. 256 . D. 257 . Lời giải Chọn B 3   x  0
Bất phương trình 2    1  x  3 . x 1 0
Suy ra tập nghiệm của bất phương trình 2 là: S  1;  3 .
Do đó mọi nghiệm của bất phương trình 2 đều là nghiệm của bất phương trình   1 khi và chỉ
khi bất phương trình  
1 có nghiệm đúng với mọi x 1;  3 . 2 x  4x  m  0  Điều kiện:   x  x  m  2
 m  x  4x 1 thỏa mãn x  1;  3 . log  x 4xm 2 4 1 2  0 4
Khi đó m  max f  x với f  x 2  x  4x 1. 1; 3 Xét hàm số f  x 2
 x  4x 1 trên đoạn 1;  3 f x  2
 x  4  0  x  2. Bảng biến thiên:
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Dựa vào bảng biến thiên ta có m  max f  x  m  5. (3) 1; 3 Ta có 2 log x  4x  m  2 log  2 x  4x  m  8 2 4  1  log  1 2 x  4x  m  2 log  2 x  4x  m  8 . 2 2  2 2 1 Đặt t  log  2 x  4x  m , t  0 . 2  2
Bất phương trình trở thành: 2
t  2t  8  0  t  4  ;2  t 0;2. 1 Với t  2 ta có log  2 x  4x  m  4 2
 m  x  4x  256 với mọi x 1;  3 . 2  2
 m  min g  x với g x 2  x  4x  256 . 1; 3 Xét hàm số g  x 2
 x  4x  256 với x1;  3 . g ' x  2
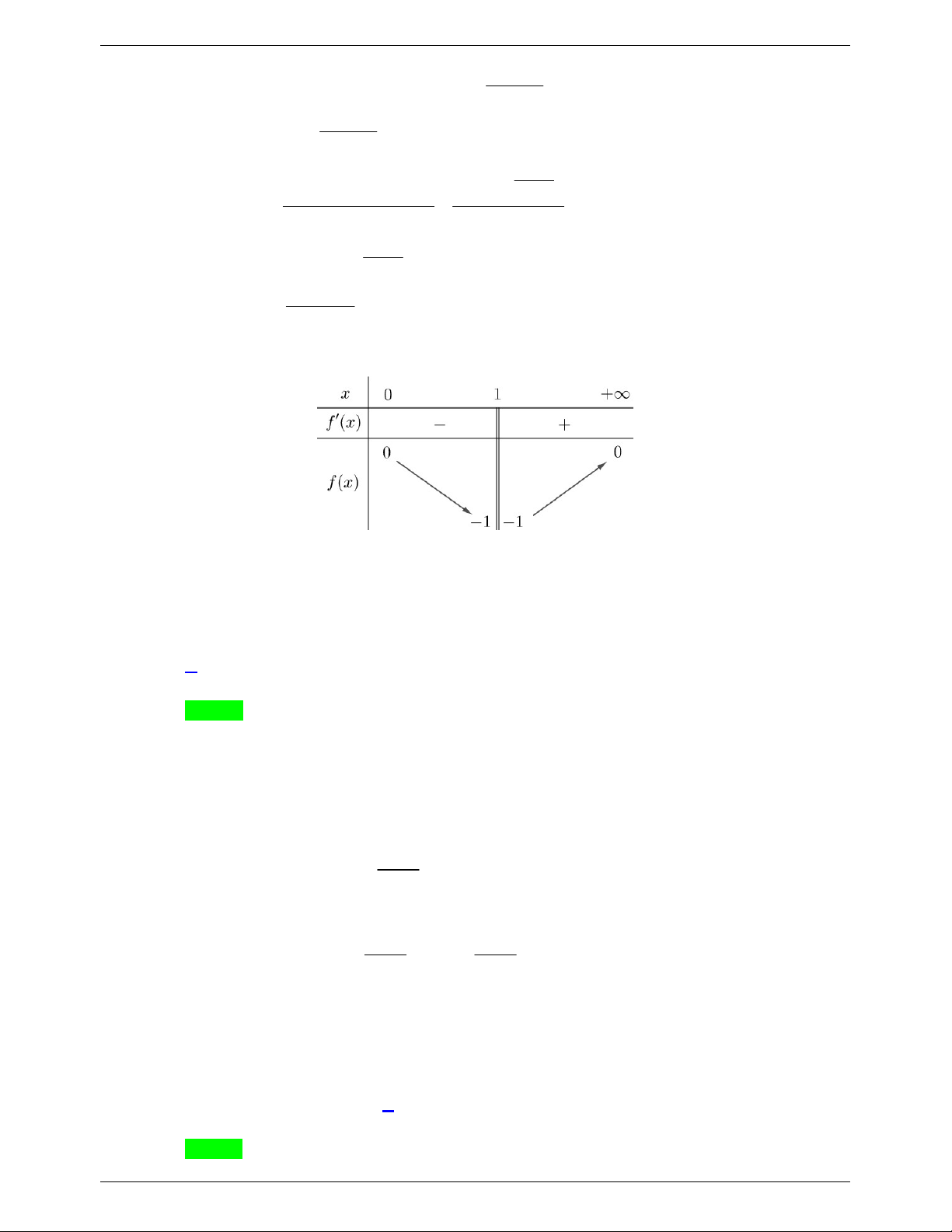
 x  4  0  x  2 . Bảng biến thiên:
Dựa vào bảng biến thiên: m  min g  x  m  259 . (4) 1; 3
Từ 3 , 4 ta có m 5;259 thỏa mãn yêu cầu bài toán.
Vậy có tất cả 255 giá trị nguyên của m thỏa mãn mọi nghiệm của bất phương trình 2 đều là
nghiệm của bất phương trình   1 . 2
Câu 23. Cho bất phương trình x2 2 .log  2
x  4x  6  4 xm log 2 x  m  2 với m là tham số thực. 2  2  
Biết rằng tập hợp tất cả các giá trị nguyên của m để bất phương trình có nghiệm đúng với mọi
x 0;2 là đoạn  ; a b . Khi đó 2 2 a  b bằng: A. 4 . B. 8 . C. 16. D. 0 . Lời giải Chọn B Điều kiện: x  . 2 Ta có x2 2 .log  2
x  4x  6  4 xm log 2 x  m  2 2  2   x22 2 2 xm      2 .log x 2 2  2 log 2 x  m  2 1 2   2       Xét hàm số  2t y .log t  2 với t  0. 2   Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Hàm số  2t y
.log t  2 xác định và liên tục trên 0;  . 2   t 2t
Ta có y  2 .log t  2 .ln 2   0, t   0 . 2   t  2ln 2 Vậy hàm số  2t y
.log t  2 đồng biến trên 0;  . 2  
Khi đó    f x  2   f  x  m   x  2 1 2 2 2  2 x  m
 x  2  x  m  x  2 2 2 2
2m  min  2x  6x  4 2 2m  x  6x  4 2m  4   0;2  , x  0;2      2   m  2 . 2 2m  x  2x  4 2m  max  2 x  2x  4 2m  4   0;2
Vậy tập hợp tất cả các giá trị nguyên của m để bất phương trình có nghiệm đúng với mọi
x 0;2 là đoạn   2 2 2; 2  a  2
 ;b  2  a  b  8.
Câu 24. Cho a,b là các số nguyên dương nhỏ hơn 2022 . Biết rằng với mỗi giá trị của b luôn có ít nhất
1000 giá trị của a thỏa mãn  ab2 2  2ba .log
b  4b 1. Số giá trị b là a 1  A. 1021. B. 1022 . C. 1020 . D. 1023 . Lời giải Chọn A
Đặt c  a 1,c  2 , khi đó  ab2 2  2ba .log
b  4b 1  2c  2c .log b  2b  2b, 1 . a 1    c  
+) b  1, không thỏa mãn   1 . 2c  2c 15 +) b  2   ,2 . log c 4 2
) c  2 , không thỏa mãn 2 . 2c  2c 2c . c ln 2.ln c 1  . c 2c.ln 2.ln c  2c
) c  3 , hàm f c  , f c     0 . log c . c ln 2log c c 2 2
Suy ra f c  f   15 3 
, c  3 2  a  2021. Do đó b  2 thỏa mãn. 4 2c  2c 2b  2b +) b  3 ,   1   ,3 . ln c ln b 2t  2t Hàm số f t 
đồng biến với mọi t  3 và c  2 không thỏa mãn 3 nên c  3 . log t 2 b  
Do đó    c  b b   3 3 ,
3  3  b  a  2021    3  b  1022. 2021 b 1 1000 Vậy 2  b  1022 .
Câu 25. Có bao nhiêu số nguyên m  2
 022;2022 sao cho thỏa mãn bất ln x 1 ln x m phương trình    , x  0, x  1 ? x 1 x x 1 x A. 2. B. 1. C. Vô số. D. 0. Lời giải Chọn C
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2  x ln x
Bất phương trình đã cho tương đương với
 m 1, x  0, x  1 . (1) 2 x 1 2x ln x Xét hàm số f (x)  , x  0, x  1. 2 x 1 2  x 1 2 ln x    2 2 2 2[(x 1) ln x  x 1] x  1 Ta có f (x)     . 2 2 2 2 2 (x 1) (x 1)(x 1) 2 x 1
Xét hàm số g(x)  ln x  , x  0 . 2 x 1 2 2 (x 1) Ta có g (  x) 
 0 , x  0 , x  1; g (x)  0  x  1. 2 2 x(x 1)
Suy ra g(x)  g(1)  0 khi x 1 và g(x)  g(1)  0 khi x  1.
Do đó ta có bảng biến thiên
Từ bảng biến thiên suy ra (1)  m 1  1  m  0 .
Vậy có vô số giá trị nguyên của tham số m thỏa mãn.
Câu 26. Hỏi có tất cả bao nhiêu giá trị thực của tham số m để bất phương trình 2 x x  e  mx   2 2
ln x  e 1  0 đúng với x   ? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn A
Bất phương trình đã cho tương đương với:   2 x
f x  x  e  mx   2 2
ln x  e 1 0 . Nhận thấy nhanh rằng: f 0  0
 f x  f 0  0 x   R
Suy ra hàm số trên thỏa mãn 
 hàm số đạt cực tiểu tại x  0  f  0  0 2x
Xét f  x  2x  2 x e  m 
có f 0  2  m  0  m  2 2 x  e
Thử lại với m  2 thì   2 x
f x  x  e  x   2 2 2 ln x  e 1    f  x x x 2 1  2x  2e  2   2x 1  2 x e 1  0  x  0 2  2    x  e  x  e 
Đến đây ta nhận thấy f  x  f 0  0 nên suy ra m  2 thỏa nên có đúng 1 giá trị m
Câu 27. Hỏi có tất cả bao nhiêu giá trị thực của tham số m để bất phương trình  2 m  4m  4log  2 2 x  2mx  m   2 1  m log  2
x 1  0 có nghiệm thực x ? 2 3  A. 1. B. 2 . C. 3 . D. 6 . Lời giải Chọn B Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Bất phương trình đã cho tương đương với:
 m  22 log  x  m2   2 1  m log  2 x 1  0 2 3       0 0 0
Ta nhận thấy: m  22 log  x  m2   2 1  m log  2
x 1  0 nên suy ra bất phương trình trên 2 3 
chỉ có nghiệm khi xảy ra dấu bằng, tức là: 2
 m  2 log x  m 1  0 2 2  2 2  2 2 
m  2 log x  m 1  m log x 1  0  2    3        2 m log   2x 1  0 3  m 22  0  
m  22  0 m  2 m  2  log 
 xm2  10    x  m2      2 0 x m x 0         2 2     m  0 m  0 m 0 m 0         x   x  log   2 0 0 x 1 0 x 0 3 
Suy ra có 2 giá trị thực m thỏa mãn bài toán
Câu 28. Gọi S là tập chứa tất cả các giá trị nguyên của tham số m để bất phương trình 2
ln x  4x  3  log m có đúng 3 nghiệm nguyên, vậy tổng phần tử của S là A. 108 . B. 5 . C.Vô số D. 89 . Lời giải Chọn B
Bất phương trình đã cho tương đương với: 2 x  x   m  f  x 2 ln 4 3 log
 ln x  4x  3  log m x  1 Xét hàm số f  x 2 2
 ln x  4x  3 ; x  4x  3  0   x  3   lim f x  lim 2
ln x  4x  3   ln0    x 1  x 1  
Ta có: lim f  x  lim 2
ln x  4x  3   ln0   x3 x3   2 x  4x  3
2x  4 2x  4x 3  f x    0  x  2 2 2  2 x  4x  3 x  4x  3 
Từ đó ta có bảng biến thiên như sau:
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Nhận thấy ngay 3 nghiệm nguyên thỏa mãn bài toán đó là: x  0; 2;4 . Lưu ý rằng hai nghiệm
nguyên x  1; x  3 bị vi phạm điều kiện nên không được tính Suy ra 4 log 5 ln3 log ln8 m Z f m f m        1  3  m 120
Như vậy có tất cả 120 13 1  108 giá trị nguyên m thỏa mãn bài toán.
Câu 29. Có tất cả bao nhiêu bộ số nguyên  ; a ; b ; c d  với a, , b c,d  3  ;  3 thỏa 2 3 x x
mãn điều kiện bất phương trình  x   4 3 2 ln 1  
 ax  bx  cx  dx nghiệm đúng với 2 3 x   1  ;? A. 43 B. 71 C. 37 D. 47 Lời giải Chọn B 2 3 x x
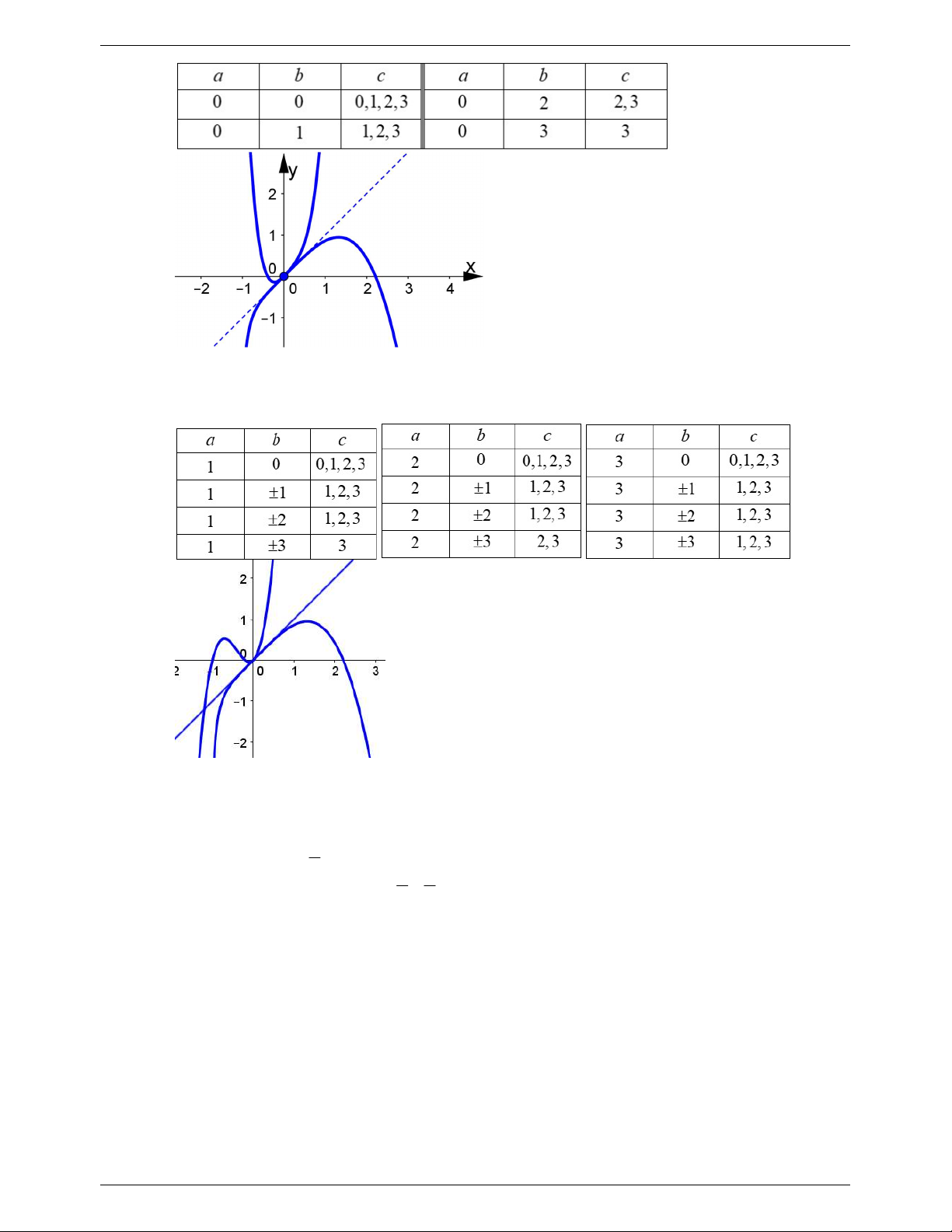
Ta để ý rằng 2 đồ thị f  x  ln  x   1   và   4 3 2
g x  ax  bx  cx  dx cùng đi qua 2 3
gốc tọa độ. Do đó ta xét tiếp tuyến tại gốc tọa độ của y  f  x . Ta có f 0 1; f 0  0 nên tiếp tuyến là y  x . 2 3 x x TABLE ta có ln  x   1    x  0 x   1  ;. 2 3 2 3 x x
Do vậy đồ thị f  x  ln  x   1  
luôn đứng dưới đường thẳng y  x và tiếp xúc nhau 2 3 tại O .
Xét phương trình hoành độ giao điểm 4 3 2
ax  bx  cx  d  
1 x  0 có nghiệm kép x  0 nên d 1 . Đồ thị   4 3 2
g x  ax  bx  cx  dx luôn đứng trên đường thẳng y  x và tiếp xúc nhau tại O
thì điều kiện cần và đủ là 2 ax  bx  c  0 x   1
 ; do đó a  0 . a  0 a   0  Trường hợp 1:   b   0 . Có 10 bộ: bx  c  0 x     1  ; b  c  0  Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC a  0 Trường hợp 2:  . Có tất cả 60 bộ: 2 b  4ac a  0 Trường hợp 3: 
khi đó a  x  x x  x  0 x   1  ; khi x  x  1  . 1   2    2 1 2 b  4ac  b b   2      2 a x x  b   2a Do đó 1 2  a   c b   .   1  0      a  c  b x 1 x 1 0  1  2  a a a  1 
Có duy nhất 1 bộ thỏa mãn b   3 . c  2 
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 19 NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Kết luận: Có tất cả 71 bộ số cần tìm.
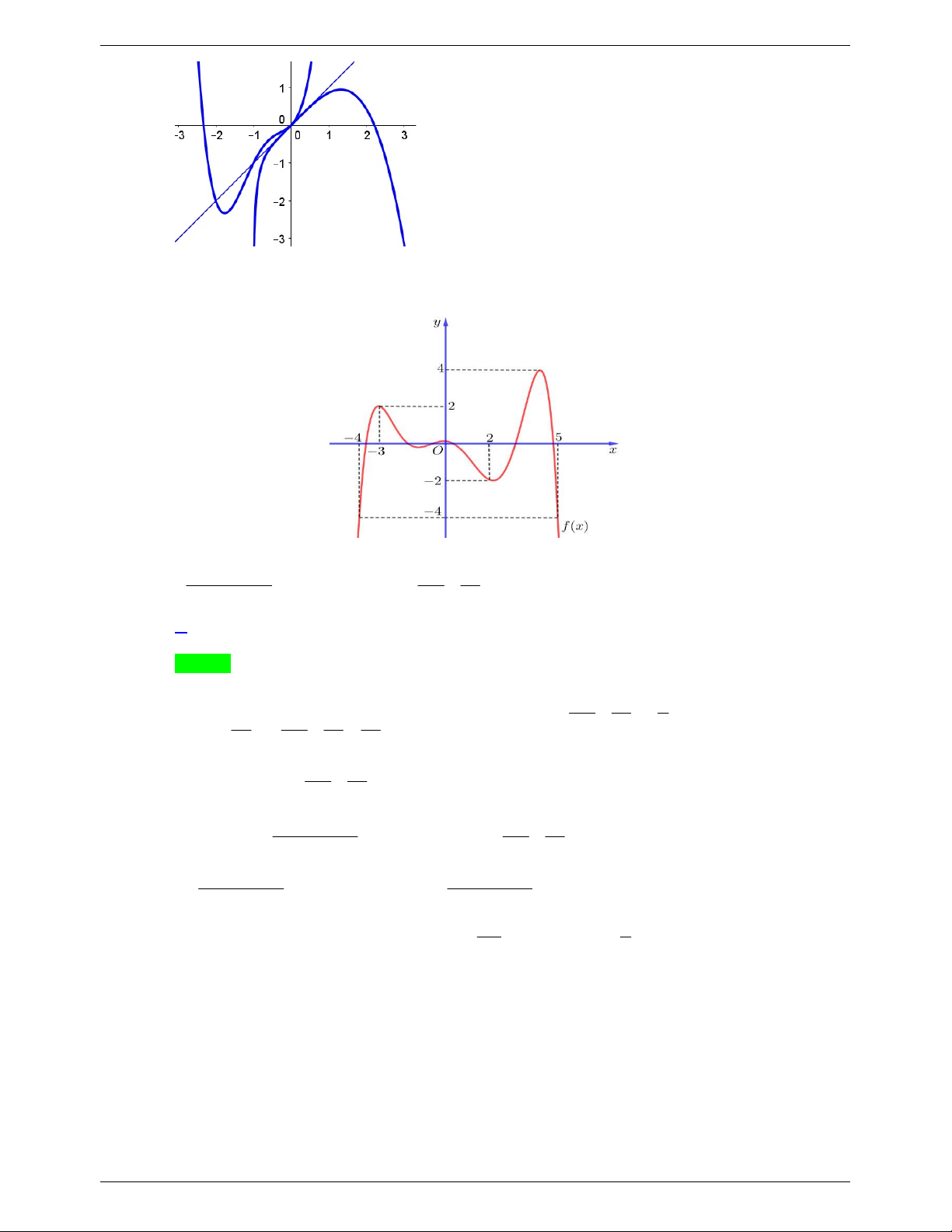
Câu 30. Cho hàm số f  x liên tục trên  và có đồ thị như hình vẽ. Với điều kiện nào của tham số m thì bất phương trình 2  1   x 28  1 .log    f x  
  0 nghiệm đúng với mọi x  4  ;5 ? 5 2 2019      2020 f x m   125 5  A. m  1  0 . B. m  1  0 . C. m  10 . D. m  10 . Lời giải Chọn A  4   f x  4, x   4  ;5 2   x 28  7 Ta có: 2   f x      , x x   4  ;5 27 28 28 .      , x   4  ;5  125 5  5  5 125 5 5 2  x 28   log  f x     0, x   4;5 (*). 2019      125 5  2  1   x 28  Từ (*) ta có: 1 .log    f x     0, x   4  ;5 5 2 2019        2020 f x m   125 5  1   1 1 0, x   4  ;5  1, x   4  ;5 5 2   5 2     2020 f x m   2020 f x m  2m 5 f  x  2m  0, x   4  ;5  f  x  , x   4  2
;5  m  4  m  1  0 . 5 5
_______________ TOANMATH.com _______________ Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA