Bất phương trình lôgarit không chứa tham số

Tài liệu gồm 22 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Bất phương trình lôgarit không chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

22 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
GIẢI BẤT PHƯƠNG TRÌNH LÔGARIT BẰNG PHƯƠNG PHÁP HÀM SỐ - ĐÁNH GIÁ
PHƯƠNG PHÁP HÀM SỐ
Dạng 1 : Bất phương trình có dạng
() 0
Fx≥
với
()Fx
là hàm số đồng biến hoặc nghịch biến
trên D.
Bước 1. Đưa bất phương trình về dạng
() 0Fx≥
Bước 2. Xét hàm số
()y Fx=
. Chỉ rõ hàm số
()y Fx
=
đồng biến hoặc nghịch biến trên D
Bước 3. Dự đoán
0
()0Fx
=
, từ đó kết luận nghiệm của bất phương trình.
Dạng 2 : Bất phương trình có dạng
() ()
Fu Fv≥
với
là hàm số đồng biến hoặc nghịch
biến trên D
Bước 1. Đưa bất phương trình về dạng
() ()
Fu Fv≥
Bước 2. Xét hàm số
()y Fx=
. Chỉ rõ hàm số
()y Fx=
đồng biến hoặc nghịch biến trên D
Bước 3. Bất phương trình
() ()Fu Fv u v
≥ ⇔≥
nếu
()y Fx=
là hàm đồng biến
và
() ()Fu Fv u v≥ ⇔≤
nếu
()y Fx=
là hàm nghịch biến.
Câu 1. Gọi
S
là tập hợp gồm tất cả các nghiệm nguyên của bất phương trình
73
log log ( 2)xx
<+
.
Tính tổng các phần tử của
S
.
A.
2176
. B.
1128
C.
1196
. D.
1176
.
Lời giải
Chọn D
Điều kiện:
0x >
.
Đặt
7
logtx=
7
t
x⇒=
và bất phương trình đã cho trở thành
2
3
log (7 2)
t
t <+
2
71
7 2 3 2 1 (*)
33
t
t
t
t


⇔ +> ⇔ + >





.
Vì hàm số
71
() 2
33
t
t
ft


= +





nghịch biến trên tập
mà
(2) 1f
=
nên suy ra bất phương
trình
(*)
trở thành
( ) (2)ft f>
2
t⇔<
.
Ta có
2t <
suy ra
7
log 2 0 49xx<⇔<<
.
Do đó tập nghiệm của bất phương trình đã cho là
(0;49)
suy ra
{ }
1, 2,3,...., 48S
=
.
Vậy tổng các phần tử của
S
bằng
1 2 3 ... 48 1176+++ + =
.
Câu 2. Số nghiệm nguyên của bất phương trình
22
22
log 3 log 4 1 0x xx x 
là
A.
5
. B.
7
. C.
4
. D.
3
.
Lời giải
Chọn D
Điều kiện:
0x
. Ta có
2 2 22
22 2 2
log 3 log 4 1 0 log 3 3 log 4 4 *x xx x x x x x 
.
Xét hàm số
2
logft t t
trên
0;D 
. Ta có
1
10
ln 2
ft t D
t

hàm số
f
đồng biến trên
D
.
Suy ra
22
* 3 4 34 1 3fx f x x x x 
. ( Thỏa mãn điều kiện)
Vậy bất phương trình có 3 nghiệm nguyên.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 3. Bất phương trình
2
2
3
2
31
log 2 0
2 23
xx
xx
xx
++
+ −−≤
++
có số nghiệm
nguyên là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn A
Điều kiện:
2
22
2
2
31
0
( 3 1 0, 2 2 3 0, )
2 23
2 2 30
xx
x do x x x x x
xx
xx
++
>
⇔∀∈ + +> + + > ∀∈
++
+ +≠

Ta có
( ) ( )
2
2 2 22
3 33
2
31
log 2 0 log 3 1 log 2 2 3 2 0
2 23
xx
xx xx x x xx
xx
++
+ −−≤⇔ ++ − + + + −−≤
++
( ) ( )
( )
22 2 2
33
log 3 1 3 1 log 2 2 3 2 2 3 *xx xx x x x x⇔ ++ + ++≤ + + + + +
.
Xét hàm số
( )
3
logft t t= +
với
0t
>
. Ta có
( )
1
1 0, 0
ln 3
ft t
t
′
= + > ∀>
.
Vậy hàm số đã cho đồng biến trên khoảng
(0; )+∞
.
Khi đó
( )
(
) ( )
22
* 3 1 2 23
fx x fx x⇔ ++ < + +
22
3 12 2 3xx x x⇔ + +≤ + +
2
20 1 2xx x
⇔ − − ≤ ⇔− ≤ ≤
Do
{
}
1; 0; 1; 2
xx∈ ⇒ ∈−
. Vậy bất phương trình đã cho có
4
nghiệm nguyên.
Câu 4. Bất phương trình
( )
22
ln 1 xx+<
có bao nhiêu nghiệm nguyên thuộc khoảng
( )
2021;2022−
?
A.
4042.
B.
4040.
C.
4041.
D.
4039.
Lời giải
Chọn C
Xét hàm số
( )
( )
22
ln 1
fx x x= +−
.
Ta có:
( )
22
21
2 0 2 1 0 0.
11
x
fx x x x
xx

′
= − =⇔ − =⇔=

++

Ta có bảng biến thiên:
Suy ra:
( )
( )
22
ln 1 0fx x x= + −<
,
0x∀≠
.
Vậy tập nghiệm của bất phương trình
( )
22
ln 1
xx+<
là
{ }
\0
do đó số nghiệm nguyên thuộc
khoảng
( )
2021;2022−
là 4041.
Câu 5. Cho bất phương trình
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
. Biết tập nghiệm của bất
phương trình là
(
;
−−
ab
. Khi đó
.ab
bằng
A.
15
16
. B.
12
5
. C.
16
15
. D.
5
12
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Lời giải
Chọn C
Ta có:
22
2
+−xx x
(
)
2
2= +−xx x
2
2
2
=
++
x
xx
.
Ta có:
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
2
2
2
2
log 4 2 2 1
2

⇔ + + + +≤

++

x
xx
xx
(
)
( )
2
2
2
2
23 2 2
log 2 2 1 1
2
xx
xx
xx
++
⇔ + + +≤
++
Ta có
2
20++>xx
,
x
∀∈
.
Điều kiện:
2
3 2 20+ +>xx
2
2 23⇔ + >−xx
22
0
0
4 89
≥
<
⇔
+>
x
x
xx
( )
8
,*
5
⇔ >−x
Với điều kiện
(
)
*
, ta có
( )
(
)
(
)
( )
2 2 22
22
1 log 3 2 2 3 2 2 log 2 2 , 2⇔ + + + + +≤ ++ + ++xx xx x xx x
Xét hàm số
(
)
2
log
= +ft t t
với
có
(
)
1
10
.ln 2
′
= +>ft
t
,
( )
0;∀ ∈ +∞t
.
Do hàm số
(
)
2
log= +
ft t t
đồng biến trên khoảng
( )
0; ,+∞
với điều kiện (*) thì các biểu thức
2
32 2xx++
và
2
2xx++
đều lấy giá trị trong khoảng
( )
0; +∞
nên ta có
( )
(
)
(
)
22
2 32 2 2⇔ + + ≤ ++fx x f x x
22
32 2 2⇔ + +≤ ++xx x x
2
22⇔ + ≤−xx
22
20
24
−≥
⇔
+≤
x
xx
2
0
32
≤
⇔
≥
x
x
2
3
⇔ ≤−x
.
Kết hợp với điều kiện ta có tập nghiệm bất phương trình là
82
;
53

−−

hay
16
.
15
=
ab
.
Câu 6. Gọi
S
là tổng tất cả các nghiệm nguyên không vượt quá
2022
của bất phương trình
( )
( ) ( )
32
3 33
log 3 25 log 1 3log 1 1xx x x− + + +≥ ++
. Tìm chữ số hàng đơn vị của
S
.
A.
3
. B.
8
. C.
0
. D.
5
.
Lời giải
Chọn A
Điều kiện:
3
10
1.
3 25 0
x
x
xx
+>
⇔ >−
−+>
Ta có:
( )( ) ( )
( )
2
2
4 2 0, 1 4 4 4 0 , 1x x x x xx x+ − ≥ ∀ >− ⇒ + − + ≥ ∀ >−
(
)
(
)
33
33
3 25 9 9, 1 log 3 25 log 9 9 , 1xx x x xx x x⇒ − + ≥ + ∀ >− ⇒ − + ≥ + ∀ >−
(
)
(
) ( ) (
) ( )
32 2
3 33 33
log 3 25 log 1 3log 1 1 log 1 2log 1 1, 1xx x x x x x⇒ − + + +− +−≥ +− ++∀>−
.
Mà
( ) ( ) ( )
( )
2
2
33 3
log 1 2 log 1 1 log 1 1 0, 1xx x x+− ++= +− ≥∀>−
do đó bất phương trình
( )
( ) ( )
32
3 33
log 3 25 log 1 3log 1 1xx x x− + + +≥ ++
nghiệm đúng với mọi
1.x >−
Suy ra bất phương trình
( )
( ) ( )
32
3 33
log 3 25 log 1 3log 1 1xx x x− + + +≥ ++
có tập nghiệm là
khoảng
( 1; )− +∞
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Vậy tập tất cả các nghiệm nguyên không vượt quá
2022
của bất phương trình đã cho là
{ }
0;1;2;3;...;2021; 2022A =
. Tổng
S
của tất cả các phần tử thuộc tập A là:
1 2 ... 2021 2022 2023.1011 2045253
S
=+++ + = =
.
Câu 7. Biết rằng bất phương trình
(
)
2 32
2
2 log 2 3 1 1 3 2 2 2 1. 1xx xxxx x x−++−+−−+≤ − −
có tập nghiệm
3
;
b
Sa
c

+
=

với
*
,,abc∈
. Tính tổng
2T abc= +−
.
A.
0
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn B
Điều kiện:
2
22
2
2 10
10
11
2 3 10
2 311 0 2 31 1
2 3 11 0
x
x
xx
xx
xx x xx x
xx x
−≥
−≥
≥≥


⇔⇔

− +≥
− ++−> − +>−


− ++− >
( ) ( )
22
11
1.
1. 2 1 1 1. 2 1 1
xx
x
xx x xx x
≥≥


⇔⇔⇔>

− −> − − −> −


Ta có:
(
)
2 32
2
2 log 2 3 1 1 3 2 2 2 1. 1xx xxxx x x
−++−+−−+≤ − −
(
)
2
2 32
2
log 2 3 1 1 3 2 2 2 1. 1xx xxxx x x⇔ −++− +−−+≤ − −
( )
( )
2
32
2
log 1 21 1 32221. 1x x x xx x x x

⇔ − −− − + − − + ≤ − −


(
)
( )
2
32
2
2
1
log 3 2 2 2 1. 1
21 1
xx
xx x x x
xx
−
⇔ + − − +≤ − −
−+ −
( )
(
)
32 2 32
22
log log 3 2 2 2 3 1 3 2 2 2 1. 1xx x x x xx x x x
⇔ − − −+ − + + − ≤ −+ − −
( ) ( )
(
)
(
)
32 32 2 2
22
log log 3 2 2 2 3 1 3 2 2 2 3 1xx xx x x x x x x⇔ − + − ≤ −+ − + + −+ − +
(*)
Xét hàm số
(
)
3
ft t t= +
trên
có
( )
2
' 3 10ft t t= + > ∀∈ ⇒
Hàm số đồng biến trên
.
Do vậy với điều kiện
1x >
, bất phương trình (*)
( )
( )
( )
( )
22
32 32
21 1 21 1 1 21 1fxxfxx xx xx xx xx⇔ − ≤ −+ − ⇔ − ≤ −+ − ⇔ −≤ −+ −
( )
32 2
35 35
112130310
22
x x x x xx x x x
−+
⇔ − −≤ −⇔ − +≤⇔ − +≤⇔ ≤≤
Kết hợp với điều kiện, ta được:
1
35
1 55
2
2
a
x bT
c
=
+
<≤ ⇒ =⇒=
=
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
GIẢI BPT LÔGARIT BẰNG PHƯƠNG PHÁP HÀM ĐẶC TRƯNG
(KHÔNG CHỨA THAM SỐ)
Lý thuyết:
Cho hàm số
()
y fx
=
đồng biến trên
( )
;ab
và
( )
,;uv ab∈
thì
( )
()f u fv u v≥ ⇔≥
Cho hàm số
()y fx=
nghịch biến trên
( )
;ab
và
( )
,;
uv ab∈
thì
( )
()f u fv u v≥ ⇔≤
Câu 1. Tập nghiệm của bất phương trình
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
là
(
;
−−
ab
.
Khi đó
.ab
bằng
A.
15
16
. B.
12
5
. C.
16
15
. D.
5
12
.
Lời giải
Chọn C
Ta có:
22
2+−xx x
(
)
2
2= +−xx x
2
2
2
=
++
x
xx
.
Ta có:
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
(
)
(
)
22
2
log 2 4 2 2 1⇔ +−++ + +≤xx x x x
2
2
2
2
log 4 2 2 1
2

⇔ + + + +≤

++

x
xx
xx
(
)
( )
2
2
2
2
23 2 2
log 2 2 1, 1
2
++
⇔ + + +≤
++
xx
xx
xx
Ta có
2
20++>xx
,
x
∀∈
.
Điều kiện:
2
3 2 20+ +>xx
2
2 23⇔ + >−
xx
22
0
0
4 89
≥
<
⇔
+>
x
x
xx
( )
8
,*
5
⇔ >−x
Với điều kiện
( )
*
, ta có
( )
(
)
(
)
( )
2 2 22
22
1 log 3 2 2 3 2 2 log 2 2 , 2⇔ + + + + +≤ ++ + ++xx xx x xx x
Xét hàm số
( )
2
log= +ft t t
với
0
>t
. Có
(
)
1
10
.ln 2
′
= +>ft
t
,
( )
0;∀ ∈ +∞t
.
Hàm số
( )
2
log= +ft t t
đồng biến trên
( )
0; ,+∞
(
)
( )
2
3 2 2 0;+ + ∈ +∞xx
và
(
)
(
)
2
2 0;+ + ∈ +∞xx
.
Nên
( )
(
)
(
)
22
2 32 2 2⇔ + + ≤ ++fx x f x x
22
32 2 2⇔ + +≤ ++xx x x
2
22⇔ + ≤−xx
22
20
24
−≥
⇔
+≤
x
xx
2
0
32
≤
⇔
≥
x
x
2
3
⇔ ≤−
x
.
Kết hợp với ĐK ta có tập nghiệm bất phương trình là
82
;
53

−−

hay
16
.
15
=ab
.
Câu 2. Tập nghiệm của bất phương trình
53
21 1
log 2 log
2
2
xx
x
x

+
≥−



là
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
(
1; 3 2 2
+
. B.
1; 3 2 2

+

. C.
( )
1; 2
. D.
1; 2


.
Lời giải
Chọn A
53 53
21 1 21 1
log 2 log log 2 log
2
22

+ +−
= −⇔ =



x x xx
xx
xx
Đk:
( )
0
1*
10
x
x
x
>
⇔>
−>
( )
( )
2
5 53 3
2
5 3 53
Pt log 2 1 log log ( 1) log 4
log 2 1 log 4 log log ( 1) (1)
x xx x
x xx x
⇔ +− ≥ − −
⇔ ++ ≥ + −
Đặt
(
)
2
2 14 1
= +⇒ = −
t x xt
.
(1)
trở thành
22
53 5 3
log log ( 1) log log ( 1) (2)
tt xx+ −≥ + −
Xét
2
53
( ) log log ( 1)=+−
fy y y
, do
13 1>⇒>⇒ >xt y
.
Xét
1>y
:
2
11
'( ) .2( 1) 0
ln 5 ( 1) ln 3
= + −>
−
fy y
yy
()⇒
fy
là hàm đồng biến trên miền
( )
1; +∞
(2)
có dạng
() ( ) 2 1 2 1 0ft fx t x x x x x
≥ ⇔≥⇔ +≥⇔− −≤
Đặt
,0u xu= ≥
,
( )
2
2
2 10 1 2 1 2uu u⇔ − −≤ ⇔− ≤ ≤+
(
)
1 2 3 223
xx⇒ ≤+ ⇔ ≤+
Từ
( ) ( )
3, * 1 3 2 2x⇒< ≤+
Câu 3. Tập nghiệm của bất phương trình
22
22
log 3 log 4 1 0
x xx x 
là
A.
(
] [
)
;1 3;S = −∞ ∪ +∞
. B.
[ ]
1; 3−
. C.
[
)
1; +∞
. D.
[ ]
1; 3S =
.
Lời giải
Chọn D
Điều kiện:
0x
.
Ta có
2 2 22
22 2 2
log 3 log 4 1 0 log 3 3 log 4 4 *x xx x x x x x

.
Xét hàm số
2
logft t t
trên
0;D

. Ta có
1
10
ln 2
ft t D
t

hàm số
f
đồng biến trên
D
.
Suy ra
22
* 3 4 34 1 3fx f x x x x 
.
Câu 4. Bất phương trình
( )
22
3
4 2 log 4 6 0xx xx−++ −+>
có tập nghiệm
( ) ( )
;;S ab= −∞ ∪ +∞
. Tính
2
T ab b= +
.
A.
12
. B.
15
. C.
13
. D.
21
.
Lời giải
Chọn A
Đặt
( )
2
2
4 2 2 2, 2tx x x t= − + = − − ≥−
. Ta có bất phương trình
( )
3
log 4 0.tt
+ +>
Đặt
( ) ( )
3
log 4 , 2ft t t t
= + + ≥−
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Ta có
( )
( )
1
' 1 0, 2
4 ln 3
ft t
t
= + > ∀ ≥−
+
. Suy ra
( )
ft
đồng biến trên
[
)
2;− +∞
.
Mặt khác
(
)
10
f −=
.
Do đó
( ) ( ) ( )
22
0 1421430 ;13;ft t xx xx x>⇒>−⇒ − +>−⇒ − +>⇒∈−∞ ∪ +∞
.
Vậy tập nghiệm của bất phương trình là
( ) ( )
;1 3;S = −∞ ∪ +∞
, khi đó
22
1; 3 1.3 3 12a b ab b= =⇒+= +=
.
Câu 5. Bất phương trình Cho bất phương trình
32
32
2
22
ln 3 0
2
xx
xx
x
−+
+− ≥
+
có tập nghiệm
S
. Tập
( )
;100
S ∩ −∞
có số phần tử nguyên là
A.
99
. B.
101
. C.
97
. D.
96
.
Lời giải
Chọn C
Điều kiện:
32
2
22
0
2
xx
x
−+
>
+
do
2
2
x +
nên
32
2 20
xx− +>
Bất phương trình
( ) ( ) ( )
32 2 32 2
ln 2 2 ln 2 2 2 2 0xx x xx x⇔ − +− ++− +− +≥
( ) (
)
32 32 2 2
ln 2 2 2 2 ln 2 2
xx xx x x
⇔ − ++− +≥ +++
( )
1
Xét hàm:
( )
lnft t t= +
trên
( )
0;
+∞
.
( )
1
' 10
ft
t
=+>
với
( )
0;t∀ ∈ +∞
(
)
ft⇒
là hàm đồng biến trên
( )
0; +∞
.
Do đó
( )
32 2
1 22 2xx x⇔ − +≥ +
32
03xx⇔≤ −
( )
2
0 33xx x⇔≤ − ⇔≥
suy ra
[
)
3;S = +∞
( )
[
)
;100 3;100TS⇒ = ∩ −∞ =
.
Tập các phần tử nguyên của
T
là
{ }
3;4;5;...;99
có
97
phần tử nguyên.
Câu 6. Tổng bình phương các nghiệm nguyên của bất phương trình
( )
( )
( )
2
1
2
2
22
2 .log 2 3 4 .log 2 2 2
x
x
xx x
−
−
− + ≤ −+
bằng
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn A
Xét hàm số
( )
( )
2
2 .log 2
t
ft t= +
,
( ) ( )
( )
2
1
2 .ln 2.log 2 2 . 0
2 ln 2
tt
ft t
t
′
= ++ >
+
,
0t∀≥
.
( )
ft
⇒
đồng biến trên
[
)
0; +∞
.
Ta có
( )
( )
( )
2
1
2
2
22
2 .log 2 3 4 .log 2 2 2
x
x
xx x
−
−
− + ≤ −+
( )
( )
( )
( )
2
2
1
22
22
2 .log 1 2 2 .log 2 2 2
x
x
xx
−
−
⇔ − + ≤ −+
( )
2
1 22fx f x


⇔ −≤ −


( )
2
122xx⇔− ≤ −
4
4
1 22xx
22
122.1220x xx x





22
4 5 3 0 3; 3 .xx x x




Vì
xZ
nên
1; 0;1x 
.
Khi đó
2
22
1 0 1 2. 
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 7. Số nghiệm nguyên của bất phương trình
2
2
7
4 41
log 4 1 6
2
xx
xx
x

−+
+ +<


là
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn A
Điều kiện
0
1
2
x
x
>
≠
.
Ta có
( )
2
2
22
77
21
4 41
log 4 1 6 log 4 4 1 2
22
x
xx
x x xx x
xx

−

−+
+ +< ⇔ + − +<





( )
( ) ( )
22
77
log 2 1 2 1 log 2 2 1x x xx⇔ −+ −< +
Xét hàm số
( ) ( )
7
1
log 1 0
ln 7
ft t t f t
t
′
= +⇔ = +>
với
0t >
.
Vậy hàm số đồng biến trên
( )
0; +∞
.
Bất phương trình
( )
1
trở thành
(
)
(
)
( ) ( )
22
2
21 2 21 2 4 610f x fx x x x x− < ⇔ − < ⇔ − +<
35 35
44
x


.
Kết hợp điều kiện ta được
3 53 5 1
; \.
4 42
x










Vì
xZ
nên
1x
.
Câu 8. Số nghiệm nguyên của bất phương trình
2
2
2
2
4 12 8
log 4 1
21
xx
xx
xx



trên khoảng
2021;2021
là
A.
4035
. B.
4034
. C.
4037
. D.
4036
.
Lời giải
Chọn B
Điều kiện:
2
2
2
4 12 8
0 4 12 8 0 ;1 2;
21
xx
xx x
xx

 

.
Khi đó
2
2
2
2
4 12 8
log 4 0
21
xx
xx
xx



2
22
2
2
22 22
22
32
log (2 1) ( 3 2)
21
log ( 3 2) 3 2 log 2 1 (2 1).(1)
xx
xx x x
xx
x x x x xx xx



 
Xét hàm
2
( ) logft t t

với
0t
có
1
( ) 1 0, 0
ln 2
ft t
t

. Vì vậy,
()ft
là hàm số
đồng biến trên
( )
0; +∞
.
Do đó
2 22
1 3 22 1 4 10x x xx x x 
; 2 5 2 5;x




.
Vì
xZ
,
2021;2021x 
và kết hợp điều kiện ta được
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
2020; 2019;...; 5 3;4;....;2020
x

.
Vây có
4034
số nguyên thỏa mãn yêu cầu.
Câu 9. Tập nghiệm của bất phương trình
33
log ( 1) log (2 ) 4(1 2 )+> −+ −x xx
là
A.
( )
1; 2−
. B.
1
;2
2



. C.
( 1; 2)
−
. D.
1
;
2

+∞


.
Lời giải
Chọn B
Điều kiện xác định
10
12
20
+>
⇔− < <
−>
x
x
x
.
Bất phương trình tương đương với:
( )
33
log ( 1) 4 1 log (2 ) 4(2 )xx xx++ +> − + −
(*).
Xét hàm số
3
( ) log 4= +ft t t
trên
(0; )+∞
. Ta có:
1
() 4 0
ln 3
′
= +>ft
t
với mọi
(0; )∈ +∞t
.
Do đó:
1
(*) ( 1) (2 ) 1 2
2
⇔ + > − ⇔ +> − ⇔ >fx f x x x x
.
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là
1
;2
2

=


S
.
Câu 10. Tập nghiệm của bất phương trình
22
log ( 5) log (4 2 ) 3(1 3 ) 0+− −++≥x xx
là
A.
1
;2
3

−

. B.
1
;2
3

−


. C.
( ;2)−∞
. D.
( )
5; 2−
.
Lời giải
Chọn A
Điều kiện xác định
50
52
42 0
+>
⇔− < <
−>
x
x
x
.
Bất phương trình tương đương với:
22
log ( 5) 3( 5) log (4 2 ) 3(4 2 )++ +≥ − + −xx x x
(*).
Xét hàm số
2
( ) log 3= +ft t t
trên
(0; )+∞
. Ta có:
1
() 3 0
ln 2
′
= +>
ft
t
với mọi
(0; )∈ +∞t
.
Do đó:
1
(*) ( 5) (4 2 ) 5 4 2
3
⇔ + ≥ − ⇔ + ≥ − ⇔ ≥−fx f x x x x
.
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là
1
;2
3

= −

S
.
Câu 11. Tập nghiệm của bất phương trình
22
log ( 5) log (4 ) 2 1 0+ − − + +≤x xx
là
A.
1
;2
5

−

. B.
1
5;
2

−


. C.
1
5;
2

−−

. D.
( )
5; 2−
.
Lời giải
Chọn C
Điều kiện xác định
50
54
40
+>
⇔− < <
−>
x
x
x
.
Bất phương trình tương đương với:
22
log ( 5) 5 log (4 2 ) 4+ ++≤ − +−xx xx
(*).
Xét hàm số
2
( ) log= +ft t t
trên
(0; )+∞
. Ta có:
1
() 1 0
ln 2
′
= +>ft
t
với mọi
(0; )∈ +∞t
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Do đó:
1
(*) ( 5) (4 ) 5 4
2
fx f x x x x
⇔ + ≤ − ⇔+≤−⇔≤
.
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là
1
5;
2
S

=−−

.
Câu 12. Tính tổng các nghiệm nguyên của bất phương trình
2
2
2
1
log 4 2 0
51
xx
xx
x
++
+ − +<
−
.
A.
6
. B.
7
. C.
8
. D.
5
.
Lời giải
Chọn A
Với điều kiện:
1
5
x >
, ta có:
( ) ( )
( ) ( )
2
2 22
2 22
11 1
log 4 2 0 log 1 1 log 5 1 5 1 .
51 2 2
xx
x x xx xx x x
x
++
+ − +<⇔ ++ + ++ < − + −
−
Xét hàm số
( ) ( )
2
11
log ; 1 0
2 2 ln 2
ft t tf t
t
′
= + = +>
với
(
)
0;t∀ ∈ +∞
.Vậy hàm số
( )
ft
đồng
biến trên
(
)
0; +∞
, suy ra
(
)
( )
(
) { }
22
1 51 151 2 2 2 2tmdk, 1;2;3fxx fx xx x x x x
++ < − ⇔ ++< −⇔− <<+ ∈⇒∈
Vậy tổng các nghiệm nguyên của bất phương trình là 6.
Câu 13. Tập nghiệm của bất phương trình
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
là
(
;
−−
ab
.
Khi đó
.
ab
bằng
A.
15
16
. B.
12
5
. C.
5
12
. D.
16
15
.
Lời giải
Chọn D
Ta có:
22
2+−xx x
(
)
2
2= +−xx x
2
2
2
=
++
x
xx
.
Theo bài
(
)
22 2
2
log 2 4 2 2 1++− + + + ≤xx x x x
(
)
(
)
22
2
log 2 4 2 2 1⇔ +−++ + +≤xx x x x
2
2
2
2
log 4 2 2 1
2

⇔ + + + +≤

++

x
xx
xx
(
)
( )
2
2
2
2
23 2 2
log 2 2 1, 1
2
++
⇔ + + +≤
++
xx
xx
xx
Ta có
2
20++>xx
,
x∀∈
.
Điều kiện:
2
3 2 20
+ +>xx
2
2 23⇔ + >−xx
22
0
0
4 89
≥
<
⇔
+>
x
x
xx
( )
8
,*
5
⇔ >−x
Với điều kiện
( )
*
, ta có
( )
(
)
(
)
( )
2 2 22
22
1 log 3 2 2 3 2 2 log 2 2 , 2⇔ + + + + +≤ ++ + ++xx xx x xx x
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Xét hàm số
( )
2
log
= +
ft t t
với
0>t
. Có
(
)
1
10
.ln 2
′
= +>ft
t
,
(
)
0;
∀ ∈ +∞t
.
Hàm số
( )
2
log= +ft t t
đồng biến trên
( )
0; ,+∞
(
)
(
)
2
3 2 2 0;
+ + ∈ +∞xx
và
(
)
( )
2
2 0;+ + ∈ +∞xx
Nên
( )
(
)
(
)
22
2 32 2 2⇔ + + ≤ ++fx x f x x
22
32 2 2⇔ + +≤ ++xx x x
2
22⇔ + ≤−xx
22
20
24
−≥
⇔
+≤
x
xx
2
0
32
≤
⇔
≥
x
x
2
3
⇔ ≤−x
.
Kết hợp với ĐK ta có tập nghiệm bất phương trình là
82
;
53

−−

hay
16
.
15
=ab
.
Câu 14. Biết bất phương trình
( )
2
2
2
1
log 2 1
16 3
xx
xx
x

++
+ − +≤

+

có tập nghiệm là
( )
;.
S ab=
Hãy tính
tổng
20 10T ab= +
.
A.
46 10 2T = −
. B.
45 10 2
T = −
. C.
46 11 2T = −
. D.
47 11 2T = −
.
Lời giải
Chọn B
Điều kiện:
0x ≥
.
( )
( )
( )
2
2
2
2 22
1
log 2 1 log 1 log 16 3 2 4 3 0
16 3
xx
x x xx x x x
x

++
+ − + ≤⇔ ++ − + + − +≤

+

( )
2
2
22
1 3 13 3 3
log 2 log 2 2 2
2 4 24 4 4
x x xx


 
⇔ + ++ ++≤ ++ +

 


 


Xét hàm số
( )
2
2
33
log 2
44
ft t t

= ++ +


với
0t
>
có
( )
2
2
20
3
ln 2
4
t
ft
t
′
= +>

+


,
0t∀>
nên
(
)
ft
đồng biến trên khoảng
( )
0; +∞
.
Suy ra
2
0
1 3 3 1 3 22 3 22
22
1
24 4 2 2 2
30
4
x
x x xx x
xx
≥
−+

+ +≤ +⇔ ≥+⇔ ⇔ ≤≤

− +≤

3 22 3 22
; 20 10 45 10 2
22
a b T ab
−+
⇒= = ⇒= + = −
.
Câu 15. Tập nghiệm của bất phương trình
2
22
11
3 log 2 1 2 2 log 2
xx x
xx

−+ −< − + −+ −


là
( ) ( )
;;S ab cd= ∪
với
,,,abcd
là các số thực. Khi đó giá trị
222 2
abcd+++
được quy tròn
bằng
A.
16
. B.
12
. C.
9
. D.
4
.
Lời giải
Chọn A
Bất phương trình
( )
2
22
11
3 log 2 1 2 2 log 2 1xx x
xx

−+ −< − + −+ −


NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Điều kiện
20
0
1
20
x
x
x
−>
≠
−>
2
0
0 0,5
x
x
xx
<
⇔≠
<∨>
(
)
0
2
0,5 2
x
x
<
⇔
<<
.
Bất phương trình
( )
1
trở thành:
(
)
( )
2
2
22
11
2 1 log 2 2 1 log 2 3xx
xx

 
−− + −< − − + −
 

 

Hàm đặc trưng
( ) ( )
2
2
1 logft t t=−+
.
Vì
( ) ( )
2
1 2ln 2. 2 ln 2. 1
2 1 0, 0
.ln 2 .ln 2
tt
ft t t
tt
−+
′
= − + = > ∀>
nên hàm số
(
)
ft
đồng biến trên
khoảng
( )
0; +∞
.
Do đó
( )
3
trở thành:
(
)
1
22 4x
x
−<−
Kết hợp
(
)
2
,
( )
4
, chúng ta được
( ) ( )
( )
32
2
; 0 0, 5; 2
3 13
; 0 1; 2
2 41
2
0
x
x
xx x
x
∈ −∞ ∪

−−
⇔∈ ∪

+ −+

>

Vậy
222 2
21 3 13
2
abcd
+
+++ =
.
Câu 16. Tập nghiệm của bất phương trình
( )
4
2
2
2
2
12 1 3 1
log 3 12 4 log
x
x xx
xx x
+
+++ < + +
là
( )
( )
;;S ab cd
= ∪
với
,,,abcd
là các số thực. Khi đó giá trị
222 2
abcd+++
bằng
A.
8
. B.
2
. C.
10
. D.
11
.
Lời giải
Chọn D
Bất phương trình
(
)
( )
4
2
2
2
2
12 1 3 1
log 3 12 4 log 1
x
x xx
xx x
+
+++ < + +
.
Điều kiện:
( )
30
1
3; 0;
31
3
0
x
x
x
x
+>

⇔ ∈ − − ∪ +∞
+

>

.
Bất phương trình
( )
1
trở thành
( )
( )
2
22
2
1 11
4log 3 12 4 log 3 12. 2x xx
x xx

+++ < ++ +


.
Hàm đặc trưng
( ) ( )
2
2
4log 3 12ft t t t= +++
.
Vì
( )
( ) ( )
( )
11
4. 2 12 4. 2 3 6 0, 3
3 .ln 2 3 .ln 2
ft t t t
tt
′
= + + = + + + > ∀ >−
++
nên hàm số
( )
ft
đồng biến trên khoảng
(
)
3;− +∞
.
Ngoài ra
3x >−
và
1
3
x
>−
.
Do đó
( ) ( ) ( )
2
11
2 0 ; 1 0;1
x
xx
xx
−
⇔ < ⇔ < ⇔ ∈ −∞ − ∪
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Đối chiếu với điều kiện, chúng ta được tập nghiệm
( )
(
)
3; 1 0;1S =−−∪
.
Vậy
( ) ( )
22
2 2 2 2 22
3 1 0 1 11abcd+++ =− +−++=
.
Câu 17. Tập nghiệm của bất phương trình
(
)
22 2
2
log 2 4 2 2 1xx x x x++− + + +≤
là
(
]
;ab
. Khi đó
22
ab+
bằng
A.
34
15
. B.
15
16
. C.
16
15
. D.
12
5
.
Lời giải
Chọn A
Bất phương trình
(
)
( )
22 2
2
log 2 4 2 2 1 1xx x x x++− + + +≤
Điều kiện:
(
)
( )
2
22 2
2
64 2
24 0 2 40 0 2
2
xx
xx x x x x
xx
++
++− >⇔ +− +>⇔ >
++
.
Vì
2
2
x xx+ > ≥−
nên
2
2 0,x xx++>∀∈
.
Dẫn đến
(
)
2
2 2 23
xx
⇔ + >−
( )
2
22
30
20
30
4 29
x
x
x
xx
− ≤
+≥
⇔
−>
+>
2
0
0
58
x
x
x
≥
⇔
<
<
8
5
x⇔ >−
.
(
)
(
)
(
)
(
)
(
)
(
)
( )
2
2
2
2
2 2 22
22
23 2 2
1 log 2 2 1
2
log 3 2 2 3 2 2 log 2 2 3
xx
xx
xx
xx xx x x x x
++
⇔ + + +≤
++
⇔ + + + + + ≤ ++ + ++
Hàm đặc trưng
( )
2
logft t t= +
.
Vì
( )
1
1 0, 0
.ln 2
ft t
t
′
= + > ∀>
nên hàm đặc trưng
( )
ft
đồng biến trên khoảng
( )
0; +∞
.
Do đó
( )
22 2
3 32 2 2 2 2xx x xx x⇔ + +≤ ++⇔ +≤−
2
22
20
20
24
x
x
xx
−≥
⇔ +≥
+≤
2
3
x
⇔ ≤−
.
Đối chiếu với điều kiện, chúng ta được tập nghiệm
82
;
53
S

=−−

.
Vậy
22
8 2 34
5 3 15
ab+ =+=
.
Câu 18. Cho
x
,
y
là các số thực dương thỏa mãn bất đẳng thức
( )
4 3 22 2
1
log 9 6 2 1
31
x
yyxyyx
y
+
≤+− −
+
. Biết
1000y ≤
, hỏi có bao nhiêu cặp số nguyên dương
( )
;xy
thỏa mãn bất đẳng thức
( )
1
?
A.
1501100
. B.
1501300
. C.
1501400
. D.
1501500
.
Lời giải
Chọn D
Ta có
4 3 22 2
1
log 9 6 2
31
x
yyxyyx
y
+
≤+− −
+
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
(
) (
)
4 3 2 22 2
2
log 9 6 2 .
3
xy y
y y y x y xy y y
yy
+
⇔ ≤ ++− + +
+
( )
( ) ( )
( )
2
2
22
log log 3 3xy y y y y y xy y⇔ +− +≤ + − +
( ) (
)
( ) ( )
( )
2
2
22
log log 3 3 *xy y xy y y y y y⇔ ++ + ≤ ++ +
Xét hàm
(
)
2
log
ft t t= +
với
(
)
0;
t
∈ +∞
(
)
1
20
ln10
ft t
t
′
= +>
,
( )
0;t
∀ ∈ +∞
. Suy ra
(
)
ft
là hàm đồng biến trên
(
)
0;t
∈ +∞
.
( )
( )
( )
2
*3f xy y f y y
⇔ +≤ +
2
33xy y y y x y⇔ +≤ +⇔≤
.
Vì
1000y
≤
nên ta có các trường hợp sau
1y =
{ }
1;2;3x⇒∈
.
{
}
2 1;2;3;4;5;6yx=⇒∈
.
.
{ }
1000 1; 2;.......;3000yx= ⇒∈
.
Vậy số cặp nghiệm thỏa mãn điều kiện đề bài là:
3 6 9 ... 3000 1501500+++ + =
.
Câu 19. Tập nghiệm của bất phương trình
( )
( )
2
41
log 2
2
+
>−
+
x
xx
x
là
;
2

+
=

bc
Sa
, trong đó
,,abc
là các số nguyên không âm. Tính
++
abc
.
A.
8
. B.
10
. C.
12
. D.
6
.
Lời giải
Chọn A
Điều kiện:
0≥x
( )
( )
( )
( )
( )
2 22
41
log 2 log 4 1 log 2 2
2
+
>−⇔ +− +>−
+
x
xx x x xx
x
( )
( ) ( )
22
2 log 1 log 2 2⇔+ + > + + −x x xx
( )
( )
(
)
22
log 1 2 log 1 1 2 1⇔ + − > ++ − +
xx x x
Xét hàm số
( ) ( )
2
log 1 2= +−fx x x
,
[
)
0;∈ +∞x
.
( )
( )
[
)
1
2 0 0;
1 ln 2
′
= − < ∀ ∈ +∞
+
fx x
x
. Do đó hàm số
( )
fx
nghịch biến trên
[
)
0; +∞
.
Khi đó
( )
( ) ( )
22
log 1 2 log 1 1 2 1
+ − > ++ − +xx x x
( )
( )
1 11⇔ > + ⇔ < +⇔ −<fx f x x x x x
( )
2
2
1
10
1
0
0
0
35
0
1
10
2
1
35 35
3 10
1
22
x
x
x
x
x
x
x
x
x
x
xx
xx
x
<
−< ⇔
<
≥
≥
≥
+
⇔ ⇔ ⇔ ⇔≤<
≥
−≥
≥


−+
− +<
−<
<<
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
Do đó
35
0;
2

+
=

S
. Vậy
035 8++=++=abc
Câu 20. Tập nghiệm của bất phương trình
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
là
(
;
−−
ab
với
,ab
∈
. Khi đó
.
ab
bằng
A.
15
16
. B.
12
5
. C.
16
15
. D.
5
12
.
Lời giải
Chọn C
Ta có
22
2+−xx x
(
)
2
2= +−xx x
2
2
2
=
++
x
xx
.
Khi đó
(
)
22 2
2
log 2 4 2 2 1++− + + +≤xx x x x
(
)
(
)
22
2
log 2 4 2 2 1
⇔ +−++ + +≤xx x x x
2
2
2
2
log 4 2 2 1
2

⇔ + + + +≤

++

x
xx
xx
(
)
(
)
2
2
2
2
23 2 2
log 2 2 1, 1
2
++
⇔ + + +≤
++
xx
xx
xx
Mà
2
20++>xx
,
x
∀∈
, nên điều kiện
2
3 2 20
+ +>
xx
2
2 23⇔ + >−xx
22
0
0
4 89
≥
<
⇔
+>
x
x
xx
( )
8
,*
5
⇔ >−x
Với điều kiện
( )
*
, ta có
( )
(
)
(
)
( )
2 2 22
22
1 log 3 2 2 3 2 2 log 2 2 , 2⇔ + + + + +≤ ++ + ++xx xx x xx x
Xét hàm số
( )
2
log
= +ft t t
trên
( )
0; +∞
.
Ta có
( )
1
10
.ln 2
′
= +>ft
t
,
( )
0;∀ ∈ +∞t
.
Nên hàm số
( )
2
log= +
ft t t
đồng biến trên
( )
0; ,+∞
(
)
( )
2
3 2 2 0;+ + ∈ +∞xx
và
(
)
( )
2
2 0;+ + ∈ +∞xx
Do đó
( )
(
)
(
)
22
2 32 2 2⇔ + + ≤ ++fx x f x x
22
32 2 2⇔ + +≤ ++xx x x
2
22⇔ + ≤−xx
22
20
24
−≥
⇔
+≤
x
xx
2
0
32
≤
⇔
≥
x
x
2
3
⇔ ≤−x
.
Kết hợp với ĐK ta có tập nghiệm bất phương trình là
82
;
53

−−

hay
16
.
15
=ab
.
Câu 21 Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn bất phương trình
( )
22
22 22
2
2 24 log 20 8 78 0
5 2 20
xy
xy x xy xy
xy


+
+−− ++− −+ <


+−


?
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
116
. B.
119
. C.
113
. D.
120
.
Lời giải
Chọn C
(
)
22
22 22
2
2 24 log 20 8 78 0
5 2 20
xy
xy x xy xy
xy


+
+−− ++− −+ <


+−


22
22
22
2
22
22
22
2
2 24 0
log 20 8 78 0
5 2 20
2 24 0
log 20 8 78 0
5 2 20
xy x
xy
xy xy
xy
xy x
xy
xy xy
xy
+−−>

+
++− −+<

+−

⇔
+−−<

+
++− −+>

+−

(
)
( )
( )
( )
( )
( )
( ) (
)
2
22
22 22
22
2
22
22 22
22
15
5 2 20 0
log log 5 2 20 4 5 2 20 2 0
15
5 2 20 0
log log 5 2 20 4 5 2 20 2 0
xy
xy
xy xy xy xy
xy
xy
xy xy xy xy
−+>
+−>
+ ++− +− − +− −<
⇔
−+<
+−>
+ ++− +− − +− −>
( )
( ) ( )
( )
( ) ( )
2
22
22
22
22
2
22
22
22
22
15
5 2 20 0
log log 5 2 20 4 5 2 20
4
15
5 2 20 0
log log 5 2 20 4 5 2 20
4
xy
xy
xy
xy xy xy
xy
xy
xy
xy xy xy
−+>
+−>

+
++< +− + +−


⇔
−+<
+−>

+
++> +− + +−


(I)
Xét bất phương trình
( ) (
)
22
22
22
log log 5 2 20 4 5 2 20
4
xy
xy xy xy

+
++> +− + +−


(a).
Xét hàm số
( )
2
log 4ft t t= +
trên
( )
0; +∞
.
Ta có ,
( )
1
4 0, 0
ln 2
ft t
t
′
= + > ∀>
.
Nên hàm số
(
)
2
log 4ft t t= +
đồng biến trên
( )
0; +∞
.
Mà (a)
( )
22 22
5 2 20 5 2 20
44
xy xy
f fxy xy

++
⇔ > +− ⇔ >+−


NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Do đó
( )
( )
( )
( )
2
22
22
2
22
22
15
5 2 20 0
4 5 2 20
(I)
15
5 2 20 0
4 5 2 20
xy
xy
xy xy
xy
xy
xy xy
−+>
+−>
+< +−
⇔
−+<
+−>
+> +−
( )
(
) ( )
( )
( ) ( )
2
22
22
2
2
22
22
2
15
5 2 20 0
10 4 6
15
5 2 20 0
10 4 6
xy
xy
xy
xy
xy
xy
−+>
+−>
− +− <
⇔
−+<
+−>
− +− >
.
Xét
(
)
( ) ( )
2
22
22
2
15
5 2 20 0
10 4 6
xy
xy
xy
−+<
+−>
− +− >
.
Do
(
)
{
}
{ }
2
22
15
3; 2; 1; 0; 4; 5
15 5
4;3;2;1;0
,
x
x
xy y
y
xy
−<
=±±±
− +<⇒ < ⇔

=±±±±
∈
.
Thay vào
5 2 20 0xy+−>
và
(
)
( )
22
2
10 4 6xy− +− >
Ta có
8
cặp số:
( ) (
) ( )
( ) (
) ( )
( ) ( )
5,0;5, 1;5, 2;4,1;4,2;4,3;3,3;3,4−−
thoả mãn .
Xét
(
)
( ) ( )
2
22
22
2
15
5 2 20 0
10 4 6
xy
xy
xy
−+>
+−>
− +− <
,
(
) (
)
22
2
10 6
4 16
10 4 6 4 6 2 10
,
,
x
x
xy y y
xy
xy
− <
<<
− + − < ⇒ − < ⇔−< <


∈
∈
.
Thử trực tiếp ta được các cặp số:
( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
5; 4 ,..., 5;7 , 6;1 ,..., 6;8 , 7; 1 ,..., 7;9 , 8; 1 ,
..., 8;9 ,−−
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
9; 1 ,..., 9;9 , 10; 1 ,..., 10;9 , 11; 1 ,..., 11;9 , 12; 1 ,..., 12;9 ,−−−−
( )
( ) ( ) ( ) (
) ( )
13; 1 ,..., 13;9 , 14;0 ,..., 14;8 , 15;1 ,..., 15;7
−
nên có 105 cặp số.
Vậy có
105 8 113+=
cặp số thoả mãn yêu cầu bài toán.
Câu 22. Cho
,xy
là các số thực thỏa mãn bất phương trình:
( )
2
log 2 2 3 8
y
x xy+ +− ≥
. Biết
0 20x≤≤
,
số các cặp
,xy
nguyên không âm thỏa mãn bất phương trình trên là
A.
2
. B.
33
. C.
35
. D.
5
.
Lời giải
Chọn C
Ta có:
( )
( )
(
)
2
log 1
3
22
log 2 2 3 8 2 log 1 2 3
x
yy
x xy x y
+
+ +− ≥ ⇔ + + ≥ +
. (1)
Xét hàm số
( )
2
t
ft t= +
.
Ta có
( )
2 ln 2 1 0,
t
ft t
′
= + > ∀∈
. Nên hàm số
( )
2
t
ft t= +
đồng biến trên
.
Khi đó
( )
( )
(
)
( ) ( )
3
22
1 log 1 3 log 1 3 2 1
y
f x fy x y x⇔ + ≥ ⇔ +≥ ⇔≥ −
.
Với
3
8
0 20 1 2 21 0 log 21
y
xy≤ ≤ ⇒≤ ≤ ⇒ ≤ ≤
. Vì
{ }
0;1yy∈⇒∈
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Với
0
y
=
thì
0x ≥
nên có 21 cặp số
( )
;xy
thỏa mãn.
Với
1y =
thì
7x ≥
nên có 14 cặp số
( )
;xy
thỏa mãn.
Vậy có tất cả 35 cặp
( )
;xy
thỏa mãn.
Câu 23. Số nghiệm nguyên của bất phương trình
( )( )
33
2 22 2
log log log 4 log 5x xx x+ ≤+ +
là
A.
17
. B.
15
. C.
16
. D.Vô số.
Lời giải
Chọn C
( )( )
33
2 22 2
log log log 4 log 5x xx x+ ≤+ +
(1)
ĐK:
2
log 0
1
0
x
x
x
≥
⇔≥
>
.
Đặt
2
logtx=
, điều kiện
0t ≥
.
Bất phương trình (1) trở thành
( )( ) ( )
2
33 33 2
4 5 4 ( 4)t tt t t tt t+ ≤+ + ⇔+ ≤+ + +
(2).
Xét hàm số
( )
fu u u= +
trên
[
)
0; +∞
.
Ta có
( )
1
' 1 0, 0
2
fu u
u
=+ > ∀>
. Nên hàm số
( )
fu u u= +
đồng biến trên
[
)
0; +∞
.
Mà
( )
(
)
( )
( )
2
3 32
2 4 8 16ft f t t t t⇔ ≤ + ⇔≤++
( )
( )
2
4 34 0 4t tt t
⇔ − + + ≤ ⇔≤
. Kết hợp với
0t ≥
ta được
04t≤≤
.
Với
04t≤≤
thì
2
0 log 4 1 16xx≤ ≤⇔≤≤
(thoả điều kiện).
Vì
x ∈
nên có 16 giá trị nguyên của
x
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
GIẢI PT LÔGARIT BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
(KHÔNG CHỨA THAM SỐ)
PHƯƠNG PHÁP
Đặt ẩn phụ
t
theo biểu thức logarit của ẩn
x
. Khi đó, thu được phương trình ẩn
t
.
Giải phương trình ẩn
t
ta được nghiệm
t
theo ẩn
x
.
Giải phương trình thu được nghiệm của phương trình.
Câu 01. Số nghiệm của phương trình
( )
2
22
log 4 3 log 8 2 0x x xx+ − − +=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Điều kiện:
0
x >
.
Đặt
2
logtx=
, phương trình trở thành:
( )
2
4 3 8 20t x tx+ − − +=
.
Ta có
( ) ( ) ( )
22
2
4 3 4 8 2 16 8 1 4 1x x xx x∆= − − − + = + + = +
( ) ( )
( )
43 41
41
2
4 341
2
2
xx
tx
xx
t
− −− +
= =−+
⇒
− −+ +
= =
.
Với
( )
2
2 log 2 4 ktx mđx t=⇒ =⇔=
.
Với
22
41log 41 log 410
t x x x xx
=−+⇒ =−+⇔ + −=
.
Xét hàm số
( )
2
log 4 1fx x x= +−
trên
( )
0;+∞
Có
( )
1
4 0, 0
ln 2
fx x
x
′
= +> ∀>⇒
hàm số
(
)
fx
đồng biến trên
( )
0;+∞
.
Mặt khác
( )
11
0
22
tmđk
fx

=⇒=


là nghiệm duy nhất của phương trình
2
log 4 1xx=−+
.
Vậy phương trình đã cho có
2
nghiệm phân biệt.
Câu 2. Cho phương trình
( )
22
21
4
log 5 log 6 2 0x xx x+ − +− =
. Tích các nghiệm của phương trình bằng
A.
4
. B.
8
. C.
6
. D.
2
.
Lời giải
Chọn B
Điều kiện:
0.x >
Ta có
( ) ( )
22 2
21 22
4
log 5 log 6 2 0 log 5 log 6 2 0x x x x xx x x+ − +− = ⇔ + − +− =
Đặt
2
logtx=
, phương trình trở thành:
( ) ( )( )
2
5 62 0 2 3 0t x t x t tx+ − +− = ⇔ − +− =
.
2
3
t
tx
=
⇔
= −
.
Với
( )
2
2
2 log 2 2 4t kmx đx t=⇒ =⇔==
.
Với
22
3 log 3 log 3 0t x x x xx=− ⇒ =− ⇔ +−=
.
Xét hàm số
( )
2
log 3fx x x= +−
trên
( )
0;+∞
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Có
( )
1
1 0, 0
ln 2
fx x
x
′
= +> ∀> ⇒
hàm số
(
)
fx
đồng biến trên
(
)
0;
+∞
.
Mặt khác
( ) ( )
20 2 kfxtmđ=⇒=
là nghiệm duy nhất của phương trình
2
log 3
xx= −
.
Vậy tích các nghiệm của phương trình bằng
4.2 8=
.
Câu 3. Cho phương trình
( ) ( ) ( )
2
33
log 1 5 .log 3 3 3 11 0xx x x++ − +− + =
. Lập phương của tổng các
nghiệm của phương trình bằng
A.
520
. B.
100
. C.
1000
. D.
10
.
Lời giải
Chọn C
Điều kiện:
10 1xx+ > ⇔ >−
Ta có:
( ) ( ) ( )
2
33
log 1 5 .log 3 3 3 11 0xx x x++ − +− + =
( ) ( ) ( )
2
33
log 1 5 .log 1 2 6 0xx x x⇔ ++ − +− +=
Đăt
(
)
3
log 1
tx
= +
, phương trình trở thành:
( )
2
5. 2 6 0t x tx+ − − +=
Mà
( ) (
)
( )
22
2
5 4.1. 6 2 1
3
t
x xx
tx
=
∆= − − − = − ⇒
= −
Với
( ) ( )
3
2 log 1 2 8 tmđkt xx=⇒ +=⇔=
Với
( )
( )
33
3 log 1 3 log 1 3 0
tx x x x x=−⇒ + =− ⇔ + +−=
.
Xét hàm số
( ) ( )
3
log 1 3fx x x= + +−
trên
( )
1;− +∞
Có
( )
( )
1
1 0, 1
1 ln 3
fx x
x
′
= + > ∀ >− ⇒
+
hàm số
( )
fx
đồng biến trên
(
)
1;− +∞
.
Mặt khác
( ) ( )
20 2 kfxtmđ=⇒=
là nghiệm duy nhất của phương trình
(
)
3
log 1 3
xx
+=−
.
Vậy lập phương của tổng các nghiệm bằng
( )
3
3
2 8 10 1000+==
.
Câu 4. Cho phương trình
( )
2
22
log 12 .log 11 0x x xx− + − +− =
. Tổng lập phương các nghiệm của
phương trình bằng
A.
4
. B.
520
. C.
100
. D.
230
.
Lời giải
Chọn B
Điều kiện:
0x >
. Đăt
2
logtx=
, phương trình trở thành:
( )
2
12 11 0t xt x−+ − +− =
.
Mà
( )
1
1 12 11 0
11
t
xx
tx
=
−+ − + − = ⇒
= −
.
Với
( )
2
1 log 1 2 k
tx mđx
t=⇒ =⇔=
.
Với
22
11 log 11 log 11 0t x x x xx= −⇒ = −⇔ +− =
.
Xét hàm số
(
)
2
log 11fx x x= +−
trên
( )
0;+∞
Có
( )
1
1 0, 0
ln 2
fx x
x
′
= +> ∀> ⇒
hàm số
( )
fx
đồng biến trên
( )
0;+∞
.
Mặt khác
( ) ( )
80 8 kfxtmđ=⇒=
là nghiệm duy nhất của phương trình
2
log 11xx= −
.
Vậy tổng lập phương các nghiệm là:
33
2 8 520+=
.
Câu 5. Tích các nghiệm của phương trình
( ) ( )
2
0,5 0,5
1 log 2 5 log 6 0x xx x+ + + +=
là
A.
4−
. B.
16
. C.
8
. D.
32
.
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Lời giải
Chọn C
Điều kiện:
0x >
.
Đặt
0,5
logtx=
, phương trình trở thành:
( ) ( )
2
1 2 5 60xt x t+ + + +=
.
Có
( ) ( )
(
)
22
2
2 5 4.6 1 4 4 1 2 1x xxxx∆= + − + = − + = −
( ) (
)
( )
(
)
( )
25 21
2
21
2 521
3
21 1
xx
t
x
xx
t
xx
− +− −
= = −
+
⇒
− ++ −
−
= =
++
.
Với
( )
0,5
2 log 2 4t kx mđx t=−⇒ =−⇔ =
.
Với
0,5 0,5
333
log log 0
11 1
tx x
xx x
−−
=⇒ =⇔ +=
++ +
.
Xét hàm số
( )
0,5
3
log
1
fx x
x
= +
+
trên
( )
0;+∞
có
( )
( )
2
13
0, 0
ln 0, 5
1
fx x
x
x
′
= − < ∀> ⇒
+
hàm số
( )
fx
nghịch biến trên
( )
0;+∞
.
Mặt khác,
( )
( )
20 2 kfxtmđ=⇒=
là nghiệm duy nhất của phương trình
0,5
3
log
1
x
x
−
=
+
.
Vậy tích các nghiệm của phương trình đã cho là
4.2 8=
.
Câu 6. Cho phương trình
( ) ( )
4
2
2
2
2 log 5 .log 2 3 18 0x xx x x+ −+ ++=
. Tích các nghiệm của phương
trình bằng:
A.
4
. B.
8
. C.
6
. D.
2
.
Lời giải
Chọn B
Điều kiện:
0x >
.
Ta có:
(
) ( )
4
2
2
2
2 log 5 .log 2 3 18 0
x xx x x+ −+ ++=
( ) ( )
2
22
2 log 2 5 .log (2 ) 3 18 0x x x xx⇔+ − + ++=
Đăt
2
logtx=
, phương trình trở thành:
( ) ( )
2
2 2 5. 8 0x t x tx+ − + ++=
(*)
Do
( ) ( ) ( )
2 2. 5 8 0x xx+− +++=
nên phương trình (*) có hai nghiệm
8
1, .
2
x
tt
x
+
= =
+
Với
(
)
2
1 log 1 2tx tm kx đ
=⇒ =⇔=
.
Với
22
88 6
log log 1 0
22 2
xx
t xx
xx x
++
= ⇒ = ⇔ −− =
++ +
.
Xét hàm số
( )
2
6
log 1
2
fx x
x
= −−
+
trên
( )
0;+∞
Có
( )
( )
2
16
0, 0
ln 2
2
fx x
x
x
′
= + > ∀> ⇒
+
hàm số
( )
fx
đồng biến trên
( )
0;+∞
.
Mặt khác
( ) ( )
40 4 kfxtmđ=⇒=
là nghiệm duy nhất của phương trình
2
8
log
2
x
x
x
+
=
+
.
Vậy tích các nghiệm bằng
2.4 8=
.
Câu 7. Cho phương trình
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
( ) ( )
2
31
3
3 1 log (2 1) 7 1 log (2 1) 2 10 0x x x xx+ −+ + −+ + =
. Tổng lập phương các nghiệm của
phương trình thuộc khoảng nào sau đây?
A.
(80;110)
. B.
(100;130)
C.
(110;140)
. D.
(140;160)
.
Lời giải
Chọn C
Điều kiện:
1
.
2
x >
Ta có:
(
)
( )
2
31
3
3 1 log (2 1) 7 1 log (2 1) 2 10 0
x x x xx
+ −+ + −+ + =
( ) ( )
2
33
3 1 log (2 1) 7 1 log (2 1) 2 10 0x x x xx⇔ + −− + −+ + =
Đặt
3
log ( 2 1)tx= −
, phương trình trở thành:
( ) ( )
2
3 1 7 1 2 10 0xt xtx+ − + ++=
(*)
Ta có:
( ) ( )( ) ( )
22
49 1 4 3 1 2 10 5 3 0x xx x∆= + − + + = − ≥
nên phương trình (*)
2
5
31
t
x
t
x
=
⇔
+
=
+
.
Với
( )
3
2 log ( 2 1) 2 5 tt mđkxx
=⇒ −=⇔=
.
Với
33
55 5
log ( 2 1) log ( 2 1) 0
31 31 31
xx x
tx x
xx x
++ +
= ⇒ −= ⇔ −− =
++ +
(**)
Xét hàm số
( )
3
5
log (2 1)
31
x
fx x
x
+
= −−
+
trên
1
;
2

+∞


Có
( )
( )
2
2 14 1
0,
(2 1). ln 3 2
31
fx x
x
x
′
= + > ∀>
−
+
nên hàm số
(
)
fx
đồng biến trên
1
;
2

+∞


.
Mặt khác
( ) ( )
20 2 kfxtmđ=⇒=
là nghiệm duy nhất của phương trình (**).
Vậy tổng lập phương các nghiệm bằng
33
5 2 133+=
(110;140)∈
.
_______________ TOANMATH.com _______________
| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
GIẢI BẤT PHƯƠNG TRÌNH LÔGARIT BẰNG PHƯƠNG PHÁP HÀM SỐ - ĐÁNH GIÁ
PHƯƠNG PHÁP HÀM SỐ
Dạng 1 : Bất phương trình có dạng F(x) ≥ 0 với F(x) là hàm số đồng biến hoặc nghịch biến trên D.
Bước 1. Đưa bất phương trình về dạng F(x) ≥ 0
Bước 2. Xét hàm số y = F(x) . Chỉ rõ hàm số y = F(x) đồng biến hoặc nghịch biến trên D
Bước 3. Dự đoán F(x ) = 0 , từ đó kết luận nghiệm của bất phương trình. 0
Dạng 2 : Bất phương trình có dạng F(u) ≥ F(v) với F(x) là hàm số đồng biến hoặc nghịch biến trên D
Bước 1. Đưa bất phương trình về dạng F(u) ≥ F(v)
Bước 2. Xét hàm số y = F(x) . Chỉ rõ hàm số y = F(x) đồng biến hoặc nghịch biến trên D
Bước 3. Bất phương trình F(u) ≥ F(v) ⇔ u ≥ v nếu y = F(x) là hàm đồng biến
và F(u) ≥ F(v) ⇔ u ≤ v nếu y = F(x) là hàm nghịch biến.
Câu 1. Gọi S là tập hợp gồm tất cả các nghiệm nguyên của bất phương trình log x < log ( x + 2) . 7 3
Tính tổng các phần tử của S . A. 2176 . B. 1128 C. 1196. D. 1176. Lời giải Chọn D
Điều kiện: x > 0 . t
Đặt t = log x ⇒ = 7t x
và bất phương trình đã cho trở thành 2 t < log (7 + 2) 7 3 t t   t 7  1 t 2 ⇔ 7 + 2 > 3 ⇔  + 2 >     1 (*) . 3    3  t t   Vì hàm số 7  1 f (t)   2  = + 
nghịch biến trên tập  mà f (2) =1 nên suy ra bất phương 3      3 
trình (*) trở thành f (t) > f (2) ⇔ t < 2 .
Ta có t < 2 suy ra log x < 2 ⇔ 0 < x < 49 . 7
Do đó tập nghiệm của bất phương trình đã cho là (0;49) suy ra S = {1,2,3,...., } 48 .
Vậy tổng các phần tử của S bằng 1+ 2 + 3+...+ 48 =1176 .
Câu 2. Số nghiệm nguyên của bất phương trình log  2 x   2
3 log x x 4x 1 0 là 2 2 A. 5. B. 7 . C. 4 . D. 3. Lời giải Chọn D
Điều kiện: x  0 . Ta có log  2 x   2
3 log x x 4x 1 0  log  2 x   2
3  x 3 log 4x  4x * . 2 2 2 2  
Xét hàm số f t log t t trên D 0; . Ta có 2 f t 1 
1 0 t D  hàm số f đồng biến trên D . t ln 2
Suy ra    f  2
x   f x 2 * 3
4  x 3 4x 1 x  3. ( Thỏa mãn điều kiện)
Vậy bất phương trình có 3 nghiệm nguyên.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2 + +
Câu 3. Bất phương trình 3x x 1 2 log
+ x − x − 2 ≤ 0 có số nghiệm 3 2 2x + 2x + 3 nguyên là A. 4 . B. 1. C. 3. D. 2 . Lời giải Chọn A 2  3x + x +1  > 0 Điều kiện: 2 2 2 2x + 2x + 3 ⇔ x
∀ ∈ (do 3x + x +1 > 0, 2x + 2x + 3 > 0, x ∀ ∈ )  2
2x + 2x + 3 ≠ 0 2 + + Ta có 3x x 1 2 log
+ x − x − 2 ≤ 0 ⇔ log 3x + x +1 − log 2x + 2x + 3 + x − x − 2 ≤ 0 2 ( 2 ) ( 2 ) 2 3 3 3 2x + 2x + 3 ⇔ log ( 2 3x + x + ) 2
1 + 3x + x +1≤ log ( 2 2x + 2x + 3) 2
+ 2x + 2x + 3 * . 3 3 ( )
Xét hàm số f (t) = log t + t với t > 0. Ta có f ′(t) 1 = +1 > 0, t ∀ > 0. 3 t ln 3
Vậy hàm số đã cho đồng biến trên khoảng (0;+ ∞) . Khi đó ( ) ⇔ f ( 2
x + x + ) < f ( 2 * 3 1 2x + 2x + 3) 2 2
⇔ 3x + x +1≤ 2x + 2x + 3 2
⇔ x − x − 2 ≤ 0 ⇔ 1 − ≤ x ≤ 2
Do x ∈ ⇒ x∈{ 1; − 0;1; }
2 . Vậy bất phương trình đã cho có 4 nghiệm nguyên.
Câu 4. Bất phương trình ( 2 + ) 2
ln 1 x < x có bao nhiêu nghiệm nguyên thuộc khoảng ( 2021 − ;2022) ? A. 4042. B. 4040. C. 4041. D. 4039. Lời giải Chọn C
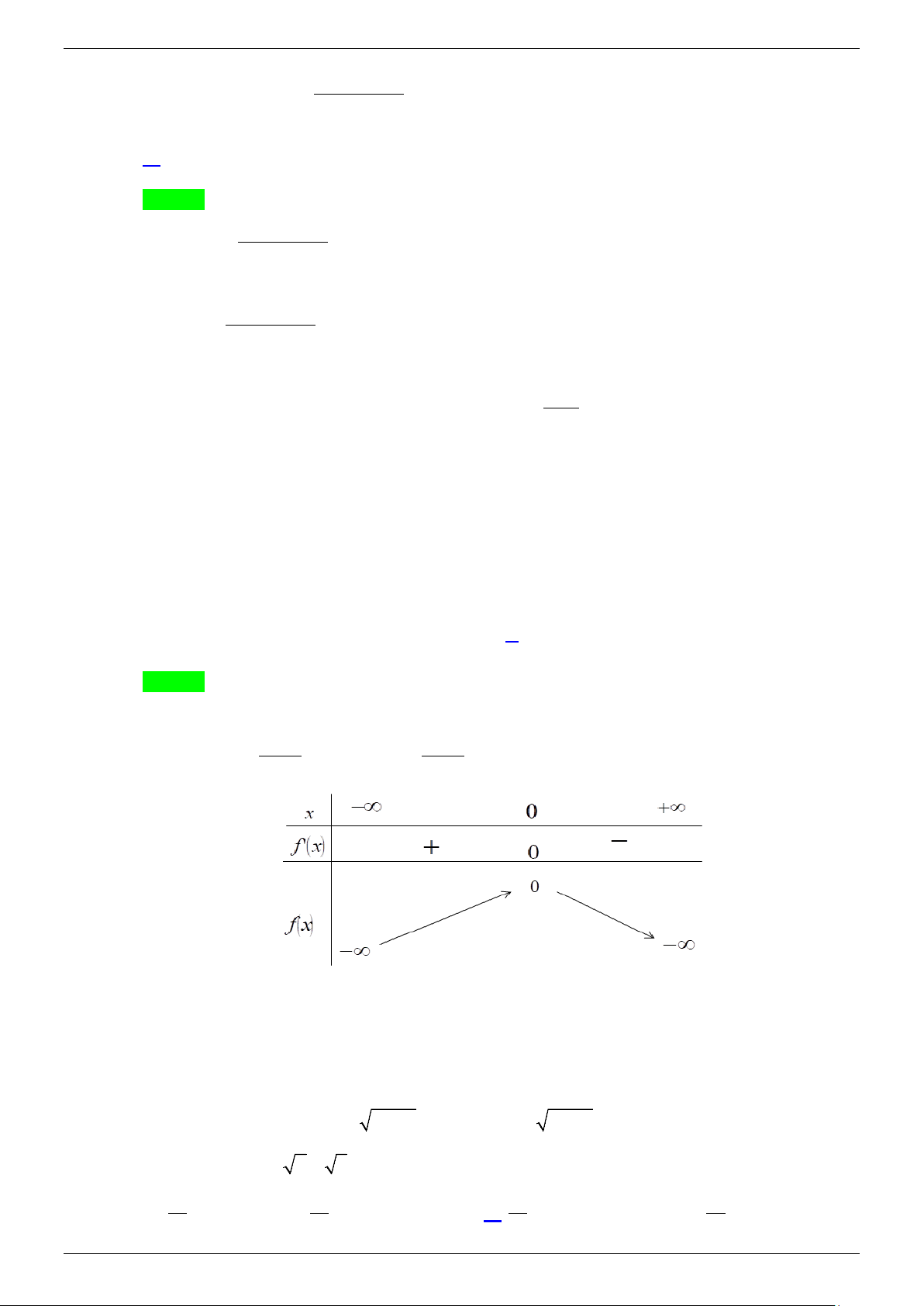
Xét hàm số f (x) = ( 2 + x ) 2 ln 1 − x . Ta có: f (x) 2x  1 2x 0 2x 1 ′ = − = ⇔ − = 0⇔ x =  
0. Ta có bảng biến thiên: 2 2 x +1  x +1 
Suy ra: f (x) = ( 2 + x ) 2 ln 1 − x < 0, x ∀ ≠ 0.
Vậy tập nghiệm của bất phương trình ( 2 + ) 2
ln 1 x < x là  \{ }
0 do đó số nghiệm nguyên thuộc khoảng ( 2021 − ;2022) là 4041.
Câu 5. Cho bất phương trình log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1. Biết tập nghiệm của bất 2
phương trình là (− a;− b. Khi đó .ab bằng A. 15 . B. 12 . C. 16 . D. 5 . 16 5 15 12 Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Lời giải Chọn C x Ta có: 2 2 2
x x + 2 − x = x( 2x + 2 − x) = . 2 x + 2 + x Ta có: log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 2 2  2(3x + 2 x + 2) 2x  2 ⇔ log 
+ 4 + 2x + x + 2 ≤1 2 ⇔ log
+ 2x + x + 2 ≤1 1 2 ( ) 2 2  x + 2 + x  2 x + 2 + x Ta có 2
x + 2 + x > 0, x ∀ ∈ . x ≥ 0 Điều kiện: 2
3x + 2 x + 2 > 0 2 ⇔ 2 x + 2 > 3 − x  8 ⇔ x < 0  ⇔ x > − ,(*)   5 2 2
4x + 8 > 9x
Với điều kiện (*) , ta có ( ) 1 ⇔ log ( 2 3x + 2 x + 2 ) 2
+ 3x + 2 x + 2 ≤ log ( 2x + 2 + x) 2 + x + 2 + x, 2 2 2 ( )
Xét hàm số f (t) = log t + t với t > 0 có f ′(t) 1 =
+1 > 0 , ∀t ∈(0;+∞) . 2 t.ln 2
Do hàm số f (t) = log t + t
0;+∞ , với điều kiện (*) thì các biểu thức 2
đồng biến trên khoảng ( ) 2
3x + 2 x + 2 và 2
x + 2 + x đều lấy giá trị trong khoảng (0;+∞) nên ta có ( ) ⇔ f ( 2 x + x + ) ≤ f ( 2 2 3 2 2 x + 2 + x)  2 − x ≥ 0 x ≤ 0 2 2
⇔ 3x + 2 x + 2 ≤ x + 2 + x 2 ⇔ x + 2 ≤ 2 − x 2 ⇔  ⇔  ⇔ x ≤ − . 2 2 x + 2 ≤ 4x 2 3  x ≥ 2 3  8 2 
Kết hợp với điều kiện ta có tập nghiệm bất phương trình là  − ;− hay 16 . a b = . 5 3     15
Câu 6. Gọi S là tổng tất cả các nghiệm nguyên không vượt quá 2022 của bất phương trình log ( 3 x − 3x + 25) 2
+ log x +1 ≥ 3log x +1 +1. Tìm chữ số hàng đơn vị của S . 3 3 ( ) 3 ( ) A. 3. B. 8 . C. 0 . D. 5. Lời giải Chọn A x +1 > 0 Điều kiện:  ⇔ x > 1. − 3
x − 3x + 25 > 0
Ta có: (x + )(x − )2 ≥ x
∀ > − ⇒ (x + )( 2 4 2 0, 1
4 x − 4x + 4) ≥ 0, x ∀ > 1 − 3
⇒ x − 3x + 25 ≥ 9x + 9, x ∀ > 1 − ⇒ log ( 3
x − 3x + 25 ≥ log 9x + 9 , x ∀ > 1 − 3 ) 3 ( ) ⇒ log ( 3 x − 3x + 25) 2 + log (x + ) 1 − 3log (x + ) 2
1 −1≥ log x +1 − 2log x +1 +1, x ∀ > 1 − . 3 3 3 3 ( ) 3 ( ) Mà log (x + ) 1 − 2log (x + ) 1 +1 = (log (x + ) 1 − )2 2 1 ≥ 0, x ∀ > 1
− do đó bất phương trình 3 3 3 log ( 3 x − 3x + 25) 2
+ log x +1 ≥ 3log x +1 +1 nghiệm đúng với mọi x > 1. − 3 3 ( ) 3 ( )
Suy ra bất phương trình log ( 3 x − 3x + 25) 2
+ log x +1 ≥ 3log x +1 +1 có tập nghiệm là 3 3 ( ) 3 ( ) khoảng ( 1; − + ∞) .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Vậy tập tất cả các nghiệm nguyên không vượt quá 2022 của bất phương trình đã cho là A = {0;1;2;3;...;2021; }
2022 . Tổng S của tất cả các phần tử thuộc tập A là:
S =1+ 2 +...+ 2021+ 2022 = 2023.1011 = 2045253.
Câu 7. Biết rằng bất phương trình  +  2log ( 2
2x − 3x +1 +1− x) 3 2
+ x − x − 3x + 2 ≤ 2 2x −1. x −1 có tập nghiệm 3 =  ; b S a 2 c     với *
a,b,c ∈ . Tính tổng T = 2a + b − c . A. 0 . B. 5. C. 3. D. 2 . Lời giải Chọn B 2x −1 ≥ 0 x −1 ≥0 x ≥ 1    x ≥ 1 Điều kiện:  ⇔  ⇔ 2  − + ≥ 2 2 2x 3x 1 0 
 2x − 3x +1 +1− x > 0
 2x − 3x +1 > x −1  2
 2x − 3x +1 +1− x > 0 x ≥ 1 x ≥ 1   ⇔  ⇔  ⇔ > x −
x − > ( x − )2 x −
x − > ( x −     )2 x 1. 1. 2 1 1 1. 2 1 1 Ta có: 2log ( 2
2x − 3x +1 +1− x) 3 2
+ x − x − 3x + 2 ≤ 2 2x −1. x −1 2
⇔ log ( 2x −3x +1+1− x)2 2 3 2
+ x − x − 3x + 2 ≤ 2 2x −1. x −1 2
⇔ log (x − ) 1 
( 2x−1− x−1)2 3 2
+ x − x − 3x + 2 ≤ 2 2x −1. x −1 2    (x − ) 2 1 x 3 2 ⇔ log
+ x − x − 3x + 2 ≤ 2 2x −1. x −1
2 ( 2x−1+ x−1)2 ⇔ log ( 3 2
x − x ) − log ( 2
3x − 2 + 2 2x − 3x +1) 3 2
+ x − x ≤ 3x − 2 + 2 2x −1. x −1 2 2 ⇔ log ( 3 2 x − x ) + ( 3 2
x − x ) ≤ log ( 2
3x − 2 + 2 2x − 3x +1)+( 2
3x − 2 + 2 2x − 3x +1 (*) 2 2 ) Xét hàm số ( ) 3
f t = t + t trên  có f (t) 2 ' = 3t +1 > 0 t
∀ ∈  ⇒ Hàm số đồng biến trên  .
Do vậy với điều kiện x >1, bất phương trình (*)
⇔ f (x − x ) ≤ f ( x− + x− )2) ⇔ x − x ≤ ( x− + x− )2 3 2 3 2 2 1 1 2 1
1 ⇔ x x −1 ≤ 2x −1 + x −1 ⇔ (x − ) 3 2 2 3− 5 3+ 5
1 x −1 ≤ 2x −1 ⇔ x − 3x + x ≤ 0 ⇔ x − 3x +1≤ 0 ⇔ ≤ x ≤ 2 2 a =1 +
Kết hợp với điều kiện, ta được: 3 5 1 x b  < ≤
⇒  = 5 ⇒ T = 5 . 2 c =  2 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
GIẢI BPT LÔGARIT BẰNG PHƯƠNG PHÁP HÀM ĐẶC TRƯNG
(KHÔNG CHỨA THAM SỐ) Lý thuyết:
Cho hàm số y = f (x) đồng biến trên ( ;
a b) và u,v∈( ;
a b) thì f (u) ≥ f (v) ⇔ u ≥ v
Cho hàm số y = f (x) nghịch biến trên ( ;
a b) và u,v∈( ;
a b) thì f (u) ≥ f (v) ⇔ u ≤ v
Câu 1. Tập nghiệm của bất phương trình log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 là (− a − . 2 ; b Khi đó . a b bằng A. 15 . B. 12 . C. 16 . D. 5 . 16 5 15 12 Lời giải Chọn C 2x Ta có: 2 2
x x + 2 − x = x( 2x + 2 − x) = . 2 x + 2 + x Ta có: log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 ⇔ log x x + 2 − x + 4 + 2x + x + 2 ≤1 2 ( ( 2 ) ) 2 2  2 2x  2(3x + 2 x + 2) 2 ⇔ log 
+ 4 + 2x + x + 2 ≤1 2 ⇔ log
+ 2x + x + 2 ≤1, 1 2 ( ) 2 2  x + 2 + x  2 x + 2 + x Ta có 2
x + 2 + x > 0, x ∀ ∈  . x ≥ 0 8 Điều kiện: 2
3x + 2 x + 2 > 0 2 ⇔ 2 x + 2 > 3 − x  ⇔ x < 0  ⇔ x > − ,(*)   5 2 2
4x + 8 > 9x
Với điều kiện (*) , ta có ( )1 ⇔ log ( 2 3x + 2 x + 2) 2
+ 3x + 2 x + 2 ≤ log ( 2x + 2 + x) 2 + x + 2 + x, 2 2 2 ( )
Xét hàm số f (t) = log t + t t > f ′ t = + > ∀t ∈ 0;+∞ 2 với 0. Có ( ) 1 1 0 , ( ). t.ln 2
Hàm số f (t) = log t + t 0;+∞ , 2
3x + 2 x + 2 ∈ 0;+∞ 2 đồng biến trên ( ) ( ) ( ) và
( 2x +2+x)∈(0;+∞). Nên ( ) ⇔ f ( 2 x + x + ) ≤ f ( 2 2 3 2 2 x + 2 + x) 2 2
⇔ 3x + 2 x + 2 ≤ x + 2 + x  2 − x ≥ 0 x ≤ 0 2 2 ⇔ x + 2 ≤ 2 − x ⇔  ⇔  ⇔ x ≤ − . 2 2 x + 2 ≤ 4x 2 3  x ≥ 2 3  
Kết hợp với ĐK ta có tập nghiệm bất phương trình là 8 2  − ;− hay 16 . a b = . 5 3     15 +  
Câu 2. Tập nghiệm của bất phương trình 2 x 1 x 1 log ≥ 2log  − là 5 3  x  2 2 x   
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC A. (1;3+ 2 2  +   . B. 1;3 2 2   . C. (1; 2) . D. 1;  2    . Lời giải Chọn A 2 x +1  x 1  2 x +1 x −1 log = 2log  −  ⇔ log = 2log 5 3 5 3  x 2 2   x x 2 xx > 0 Đk:  ⇔ x >1 (*) x −1 > 0 Pt ⇔ log (2 x + ) 2
1 − log x ≥ log (x −1) − log 4x 5 5 3 3 ⇔ log (2 x + ) 2
1 + log 4x ≥ log x + log (x −1) (1) 5 3 5 3 Đặt t =
x + ⇒ x = (t − )2 2 1 4 1 . (1) trở thành 2 2
log t + log (t −1) ≥ log x + log (x −1) (2) 5 3 5 3 Xét 2
f (y) = log y + log (y −1) , do x >1⇒ t > 3 ⇒ y >1. 5 3 Xét y >1: 1 1 f '(y) = + .2(y −1) > 0 2
y ln 5 (y −1) ln 3
⇒ f (y) là hàm đồng biến trên miền (1;+∞)
(2) có dạng f (t) ≥ f (x) ⇔ t ≥ x ⇔ 2 x +1≥ x ⇔ x − 2 x −1≤ 0
Đặt u = x,u ≥ 0, (2) 2
⇔ u − 2u −1≤ 0 ⇔ 1− 2 ≤ u ≤1+ 2
⇒ x ≤1+ 2 ⇔ x ≤ 3+ 2 2 (3)
Từ (3), (*) ⇒1< x ≤ 3+ 2 2
Câu 3. Tập nghiệm của bất phương trình log  2 x   2
3 log x x 4x 1 0 là 2 2 A. S = ( ;
−∞ ]1∪[3;+∞). B. [ 1; − ] 3 . C. [1;+∞) . D. S = [1; ] 3 . Lời giải Chọn D
Điều kiện: x  0 . Ta có log  2 x   2
3 log x x 4x 1 0  log  2 x   2
3  x 3 log 4x  4x * . 2 2 2 2  
Xét hàm số f t log t t D  0;  2 trên  . Ta có f t 1 
1 0 t D  hàm số f đồng biến trên D . t ln 2
Suy ra    f  2
x   f x 2 * 3
4  x 3 4x 1 x  3.
Câu 4. Bất phương trình 2
x − 4x + 2 + log ( 2
x − 4x + 6 > 0 có tập nghiệm S = ( ; −∞ a)∪( ; b +∞) . Tính 3 ) 2
T = ab + b . A. 12. B. 15. C. 13. D. 21. Lời giải Chọn A Đặt 2
t = x − 4x + 2 = (x − 2)2 − 2, t ≥ 2
− . Ta có bất phương trình t + log t + 4 > 0. 3 ( )
Đặt f (t) = t + log t + 4 ,t ≥ 2 − 3 ( ) Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Ta có f (t) 1 ' = 1+ (
> ∀ ≥ − . Suy ra f (t) đồng biến trên [ 2; − +∞). t + ) 0, t 2 4 ln 3 Mặt khác f (− ) 1 = 0. Do đó f (t) 2 2 > 0 ⇒ t > 1
− ⇒ x − 4x + 2 > 1
− ⇒ x − 4x + 3 > 0 ⇒ x∈(− ; ∞ ) 1 ∪(3;+∞) .
Vậy tập nghiệm của bất phương trình là S = ( ; −∞ ) 1 ∪(3;+∞) , khi đó 2 2
a =1;b = 3 ⇒ ab + b =1.3+ 3 =12 . 3 2 Câu 5. − +
Bất phương trình Cho bất phương trình x 2x 2 3 2 ln
+ x − 3x ≥ 0 có tập nghiệm S . Tập 2 x + 2 S ∩( ;
−∞ 100) có số phần tử nguyên là A. 99. B. 101. C. 97 . D. 96. Lời giải Chọn C 3 2 − +
Điều kiện: x 2x
2 > 0 do 2x +2 nên 3 2
x − 2x + 2 > 0 2 x + 2 Bất phương trình ⇔ ( 3 2
x − x + ) − ( 2 x + ) 3 2
+ x − x + − ( 2 ln 2 2 ln 2 2 2 x + 2) ≥ 0 ⇔ ( 3 2 x − x + ) 3 2
+ x − x + ≥ ( 2 x + ) 2 ln 2 2 2 2 ln 2 + x + 2 ( ) 1
Xét hàm: f (t) = ln t + t trên (0;+∞). f (t) 1 ' = +1 > 0 với t
∀ ∈(0;+∞) ⇒ f (t) là hàm đồng biến trên (0;+∞). t Do đó ( ) 3 2 2
1 ⇔ x − 2x + 2 ≥ x + 2 3 2
⇔ 0 ≤ x −3x 2
⇔ 0 ≤ x (x −3) ⇔ x ≥ 3 suy ra S = [3;+∞) ⇒ T = S ∩( ; −∞ 100) = [3;100) .
Tập các phần tử nguyên của T là {3;4;5;...; }
99 có 97 phần tử nguyên. Câu 6. Tổng bình phương các nghiệm nguyên của bất phương trình (x− )2 1 2 .log ( 2 2 3 4x x x − − + ≤
.log 2 x − 2 + 2 bằng 2 ) 2 2 ( ) A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn A t t 1 Xét hàm số ( ) = 2t f t
.log t + 2 f ′ t = 2 .ln 2.log t + 2 + 2 . > 0 2 ( ), ( ) 2 ( ) ( , t ∀ ≥ 0 . t + 2)ln 2
⇒ f (t) đồng biến trên [0;+∞) . Ta có (x− )2 1 2 .log ( 2 2 3 4x x x − − + ≤ .log 2 x − 2 + 2 2 ) 2 2 ( ) (x− )2 1 ⇔ 2 .log ((x − )2 1 + 2) 2x−2 ≤ 2
.log 2 x − 2 + 2 ⇔ f (x − )2
1  ≤ f 2 x − 2  2 2 ( )     ⇔ (x − )2
1 ≤ 2 x − 2  x 4
1 2x24 x 2 x  x 2 1 2 2 . 1 2x 2         0          2x x  2 4 5 x 3 0 x  3; 3         .  
Vì x Z nên x 1;0;  1 . Khi đó  2 2 2 1 0 1  2.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2  − + 
Câu 7. Số nghiệm nguyên của bất phương trình 4x 4x 1 2 log 
 + 4x +1 < 6x là 7  2xA. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn A x > 0 Điều kiện  1 . x ≠  2
 4x − 4x +1  2x −1  2 ( )2 2 Ta có 2 log 
 + 4x +1 < 6x ⇔ log 
 + 4x − 4x +1< 2x 7 7 2x  2x      ⇔ log (2x − )2 1 + (2x − )2
1 < log 2x + 2x 1 7 7 ( )
Xét hàm số f (t) 1
= log t + t ⇔ f ′ t = +1 > 0 với . 7 ( ) t > 0 t ln 7
Vậy hàm số đồng biến trên (0;+∞). Bất phương trình ( )
1 trở thành f ( x − )2) < f ( x) ⇔ ( x − )2 2 2 1 2 2
1 < 2x ⇔ 4x − 6x +1< 0 3 5 3 5   x  . 4 4         
Kết hợp điều kiện ta được 3 5 3 5 1 x  ;   \    .  4 4    2
Vì x Z nên x 1. 2
Câu 8. Số nghiệm nguyên của bất phương trình 4x 12x 8 2 log
x 4x 1 trên khoảng 2 2 2x x 1 2021;  2021 là A. 4035 . B. 4034 . C. 4037 . D. 4036 . Lời giải Chọn B 2
Điều kiện: 4x 12x 8 2
 0  4x 12x 8  0  x  ;   1 2;. 2 2x x 1 2 Khi đó 4x 12x 8 2 log
x 4x  0 2 2 2x x 1 2 x 3x  2 2 2  log
 (2x x 1)(x 3x  2) 2 2 2x x 1 2
 log (x 3x  2)  2 x 3x   2  log  2 2x x   2
1 (2x x 1).(1) 2 2
Xét hàm f (t)  log t t với t  0 có 1 f (t) 
1 0,  t  0. Vì vậy, f (t) là hàm số 2 t ln 2
đồng biến trên (0;+∞). Do đó   2 2 2
1  x 3x  2  2x x 1 x  4x1 0 x  ; 2 5        2 5;     .
Vì x Z , x 2021; 
2021 và kết hợp điều kiện ta được Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
x 2020;2019;...;  5 3;4;....;  2020 .
Vây có 4034 số nguyên thỏa mãn yêu cầu.
Câu 9. Tập nghiệm của bất phương trình log (x +1) > log (2 − x) + 4(1− 2x) là 3 3  1  A. ( 1; − 2) . B.    ;2 . C. ( 1; − 2) . D. 1  ;+∞ . 2    2    Lời giải Chọn B x +1 > 0
Điều kiện xác định  ⇔ 1 − < x < 2 . 2 − x > 0
Bất phương trình tương đương với: log (x +1) + 4 x +1 > log (2 − x) + 4(2 − x) 3 ( ) 3 (*).
Xét hàm số f (t) = log t + 4t +∞ f ′ t = + > t ∈ +∞ 3 trên (0; ). Ta có: 1 ( ) 4 0 với mọi (0; ) . t ln 3 Do đó: 1
(*) ⇔ f (x +1) > f (2 − x) ⇔ x +1 > 2 − x ⇔ x > . 2  1 
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là S =  ;2 . 2   
Câu 10. Tập nghiệm của bất phương trình log (x + 5) − log (4 − 2x) + 3(1+ 3x) ≥ 0 2 2 là  1  A.  1 ;2 −  . B. −  ;2. C. ( ; −∞ 2) . D. ( 5; − 2) .  3   3  Lời giải Chọn A x + 5 > 0
Điều kiện xác định  ⇔ 5 − < x < 2 . 4 − 2x > 0
Bất phương trình tương đương với: log (x + 5) + 3(x + 5) ≥ log (4 − 2x) + 3(4 − 2x) 2 2 (*).
Xét hàm số f (t) = log t + 3t +∞ f ′ t = + > t ∈ +∞ 2 trên (0; ). Ta có: 1 ( ) 3 0 với mọi (0; ) . t ln 2 Do đó: 1
(*) ⇔ f (x + 5) ≥ f (4 − 2x) ⇔ x + 5 ≥ 4 − 2x ⇔ x ≥ − . 3  1 
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là S = − ;2  .  3 
Câu 11. Tập nghiệm của bất phương trình log (x + 5) − log (4 − x) + 2x +1≤ 0 2 2 là  1   1 A.  1 ;2 −  . B. 5; −   . C. 5; − −  . D. ( 5; − 2) .  5   2  2   Lời giải Chọn C x + 5 > 0
Điều kiện xác định  ⇔ 5 − < x < 4 . 4 − x > 0
Bất phương trình tương đương với: log (x + 5) + x + 5 ≤ log (4 − 2x) + 4 − x 2 2 (*).
Xét hàm số f (t) = log t + t +∞ f ′ t = + > t ∈ +∞ 2 trên (0; ). Ta có: 1 ( ) 1 0 với mọi (0; ) . t ln 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Do đó: 1
(*) ⇔ f (x + 5) ≤ f (4 − x) ⇔ x + 5 ≤ 4 − x ⇔ x ≤ . 2 1
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là S  = 5; − −  . 2   2 Câu 12. + +
Tính tổng các nghiệm nguyên của bất phương trình x x 1 2 log
+ x − 4x + 2 < 0. 2 5x −1 A. 6 . B. 7 . C. 8 . D. 5. Lời giải Chọn A Với điều kiện: 1 x > , ta có: 5 2 x + x +1 2 1
+ x − x + < ⇔ ( 2x + x+ )+( 2 1 log 4 2 0 log 1
x + x +1 < log 5x −1 + 5x −1 . 2 2 ) 2 ( ) ( ) 5x −1 2 2
Xét hàm số f (t) 1 1 = log t + t; 1 f ′ t = + > 0 với t
∀ ∈(0;+∞) .Vậy hàm số f (t) đồng 2 ( ) 2 2t ln 2 biến trên (0;+∞), suy ra f ( 2
x + x + ) < f ( x − ) 2 1
5 1 ⇔ x + x +1< 5x −1 ⇔ 2 − 2 < x < 2 + 2 (tmdk), x∈ ⇒ x∈{1;2; } 3
Vậy tổng các nghiệm nguyên của bất phương trình là 6.
Câu 13. Tập nghiệm của bất phương trình log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 là (− a;− b . 2  Khi đó . a b bằng A. 15 . B. 12 . C. 5 . D. 16 . 16 5 12 15 Lời giải Chọn D Ta có: 2 2
x x + 2 − x = x( 2x + 2 − x) 2 = x . 2 x + 2 + x Theo bài log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 2
⇔ log (x( 2x + 2 − x)+ 4) 2
+ 2x + x + 2 ≤1 2  2 2x  2(3x + 2 x + 2) 2 ⇔ log 
+ 4 + 2x + x + 2 ≤1 2 ⇔ log
+ 2x + x + 2 ≤1, 1 2 ( ) 2 2  x + 2 + x  2 x + 2 + x Ta có 2
x + 2 + x > 0, x ∀ ∈  . x ≥ 0 8 Điều kiện: 2
3x + 2 x + 2 > 0 2 ⇔ 2 x + 2 > 3 − x  ⇔ x < 0  ⇔ x > − ,(*)   5 2 2
4x + 8 > 9x
Với điều kiện (*) , ta có ( )1 ⇔ log ( 2 3x + 2 x + 2) 2
+ 3x + 2 x + 2 ≤ log ( 2x + 2 + x) 2 + x + 2 + x, 2 2 2 ( ) Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Xét hàm số f (t) = log t + t t > f ′ t = + > ∀t ∈ 0;+∞ 2 với 0. Có ( ) 1 1 0 , ( ). t.ln 2 Hàm số
f (t) = log t + t 0;+∞ , 2 x + x + ∈ +∞ 2 đồng biến trên ( ) (3 2 2) (0; ) và
( 2x +2+x)∈(0;+∞) Nên ( ) ⇔ f ( 2 x + x + ) ≤ f ( 2 2 3 2 2 x + 2 + x)  2 − x ≥ 0 x ≤ 0 2 2
⇔ 3x + 2 x + 2 ≤ x + 2 + x 2 ⇔ x + 2 ≤ 2 − x 2 ⇔  ⇔  ⇔ x ≤ − . 2 2 x + 2 ≤ 4x 2 3  x ≥ 2 3  
Kết hợp với ĐK ta có tập nghiệm bất phương trình là 8 2  − ;− hay 16 . a b = . 5 3     15 2  + +  2
Câu 14. Biết bất phương trình x x 1 log   +
x − 2 + x ≤1 có tập nghiệm là S = ( ; a b). Hãy tính 2 ( )  16x + 3 
tổng T = 20a +10b .
A. T = 46 −10 2 .
B. T = 45 −10 2 .
C. T = 46 −11 2 .
D. T = 47 −11 2 . Lời giải Chọn B
Điều kiện: x ≥ 0 . 2  x + x +1 log 
 + ( x − 2)2 + x ≤1 ⇔ log ( 2
x + x +1 − log 16x + 3 + 2x − 4 x + 3 ≤ 0 2 2 ) 2 ( )  16x + 3  2  1  3   1  3  x    x        ( x)2 3  3 log 2 log 2  2 2 x  ⇔ + + + + + ≤ + + + 2 2  2  4    2  4   4   4 
Xét hàm số f (t)  2 3   3 log 2tt  2t  = + + +
với t > 0 có f ′(t) = + 2 > 0, t ∀ > 0 2 4 4       2 3 t  +  ln 2  4 
nên f (t) đồng biến trên khoảng (0;+∞). x ≥ 0    − + Suy ra 1 3 3 1 3 2 2 3 2 2  x + + ≤ 
2 x + ⇔ 2 x ≥ x + ⇔  ⇔ ≤ x ≤ 2 1  2  4 4 2
x − 3x + ≤ 0 2 2  4 3− 2 2 3+ 2 2 ⇒ a = ;b =
⇒ T = 20a +10b = 45 −10 2 . 2 2 2
Câu 15. Tập nghiệm của bất phương trình  1   1 3 x log 2 x 1  2 2 x log 2  − + − < − + − + − là 2 2 x x     
S = (a;b)∪( ;cd ) với a,b,c,d là các số thực. Khi đó giá trị 2 2 2 2
a + b + c + d được quy tròn bằng A. 16. B. 12. C. 9. D. 4 . Lời giải Chọn A 2 Bất phương trình  1   1 3 x log 2 x 1 2 2 x log 2  − + − < − + − + −     1 2 2 ( )  x   x
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 2− x > 0  x < 2  x < 0 Điều kiện  x ≠ 0 ⇔ x ≠ 0 ⇔  (2) .  0,5 < x < 2 1  2 − > 0
x < 0 ∨ x >  0,5  x Bất phương trình ( ) 1 trở thành: ( x ) 2 2  1    1 2 1 log 2 x  2 1 log 2  − − + − < − − + −     3 2 2 ( )  x    x
Hàm đặc trưng f (t) = (t − )2 1 + log t . 2 2 − +
Vì f ′(t) = (t − ) 1 2ln 2.t 2ln 2.t 1 2 1 + = > 0, t
∀ > 0 nên hàm số f (t) đồng biến trên t.ln 2 t.ln 2 khoảng (0;+∞). Do đó (3) trở thành: 1 2 − x < 2 − (4) xx ∈( ; −∞ 0) ∪(0,5;2)   3 − − 13 
Kết hợp (2) , (4) , chúng ta được 3 2  ⇔ + − + x∈ ;0 x x x  ∪(1;2 2 4 1 )  0  2  > 2  x   Vậy 2 2 2 2 21 3 13 a b c d + + + + = . 2
Câu 16. Tập nghiệm của bất phương trình 2 12 1 3 +1 log + 3 + +12 < + + 4log x x x x là 4 ( ) 2 2 2 x x x S = ( ;
a b)∪( ;cd ) với a,b,c,d là các số thực. Khi đó giá trị 2 2 2 2
a + b + c + d bằng A. 8 . B. 2 . C. 10. D. 11. Lời giải Chọn D Bất phương trình 2 12 1 3x +1 log
x + 3 + x +12x < + + 4log 1 . 4 ( ) 2 2 2 ( ) x x xx + 3 > 0 Điều kiện:   1  3x +1 ⇔ x ∈ 3 − ;− ∪  (0;+∞) . >  0  3   x Bất phương trình ( ) 1 trở thành (x + ) 2  1  1 1 4log
3 + x +12x < 4log + 3 + +   12. 2 . 2 2 2 ( )  xx x
Hàm đặc trưng f (t) = 4log (t + 3) 2 + t +12t 2 . Vì f ′(t) 1 1 = 4.( + + = +
+ + > ∀ > − nên hàm số f (t) t + ) 2t 12 4.(t + ) 2(t 3) 6 0, t 3 3 .ln 2 3 .ln 2
đồng biến trên khoảng ( 3 − ;+∞) . Ngoài ra x > 3 − và 1 > 3 − . x 2 − Do đó ( ) 1 x 1 2 ⇔ x < ⇔ < 0 ⇔ x ∈( ; −∞ − ) 1 ∪(0; ) 1 . x x Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Đối chiếu với điều kiện, chúng ta được tập nghiệm S = ( 3 − ;− ) 1 ∪(0; ) 1 . Vậy 2 2 2 2
a + b + c + d = (− )2 + (− )2 2 2 3 1 + 0 +1 =11.
Câu 17. Tập nghiệm của bất phương trình log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 là (a;b] . Khi đó 2 2 2 a + b bằng A. 34 . B. 15 . C. 16 . D. 12 . 15 16 15 5 Lời giải Chọn A
Bất phương trình log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 1 2 ( ) 2 + + Điều kiện: 2 2
x x + + − x > ⇔ x( 2x + − x) 6x 4 x 2 2 4 0 2 + 4 > 0 ⇔ > 0 (2) . 2 x + 2 + x Vì 2
x + 2 > x ≥ −x nên 2
x + 2 + x > 0, x ∀ ∈  .  3 − x ≤ 0  2 x ≥ 0 x + 2 ≥ 0 Dẫn đến ( ) 2 2 ⇔ 2 x + 2 > 3 − x 8 ⇔  
⇔ x < 0 ⇔ x > − .  3 − x > 0     5  2  5  x < 8  4  ( 2 x + 2) 2 >  9x 2( 2 3x + 2 x + 2) ( ) 2 1 ⇔ log
+ 2x + x + 2 ≤1 2 2 x + 2 + x ⇔ log ( 2 3x + 2 x + 2)+( 2
3x + 2 x + 2) ≤ log ( 2x + 2 + x)+( 2x + 2 + x 3 2 2 ) ( )
Hàm đặc trưng f (t) = log t + t 2 . Vì f ′(t) 1 = +1 > 0, t
∀ > 0 nên hàm đặc trưng f (t) đồng biến trên khoảng (0;+∞). t.ln 2  2 − x ≥ 0 Do đó ( ) 2 2 2
3 ⇔ 3x + 2 x + 2 ≤ x + 2 + x ⇔ x + 2 ≤ 2 − x  2 2
⇔ x + 2 ≥ 0 ⇔ x ≤ − .  3 2 2 x + 2 ≤  4x  
Đối chiếu với điều kiện, chúng ta được tập nghiệm 8 2 S = − ;− . 5 3     Vậy 2 2 8 2 34 a + b = + = . 5 3 15 Câu 18. + Cho x 1
x , y là các số thực dương thỏa mãn bất đẳng thức 4 3 2 2 2 log
≤ 9y + 6y − x y − 2y x ( ) 1 3y +1
. Biết y ≤1000 , hỏi có bao nhiêu cặp số nguyên dương (x; y) thỏa mãn bất đẳng thức ( ) 1 ? A. 1501100. B. 1501300. C. 1501400. D. 1501500. Lời giải Chọn D + Ta có x 1 4 3 2 2 2 log
≤ 9y + 6y − x y − 2y x 3y +1
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC + ⇔ log xy y ≤ ( 4 3 2
9y + 6y + y ) −( 2 2 2 x y + 2x . y y + y 2 ) 3y + y ⇔
(xy + y)− ( 2y + y) ≤ ( 2 log log 3
3y + y)2 −(xy + y)2 ⇔
(xy + y)+(xy + y)2 ≤ ( 2y + y)+( 2 log log 3 3y + y)2 (*)
Xét hàm f (t) 2
= logt + t với t ∈(0;+ ∞) f ′(t) 1 = + 2t > 0 , t
∀ ∈(0;+ ∞). Suy ra f (t) là hàm đồng biến trên t ∈(0;+ ∞) . t ln10
( ) ⇔ f (xy + y) ≤ f ( 2 * 3y + y) 2
⇔ xy + y ≤ 3y + y ⇔ x ≤ 3y .
Vì y ≤1000 nên ta có các trường hợp sau
y =1 ⇒ x∈{1;2; } 3 .
y = 2 ⇒ x ∈{1;2;3;4;5; } 6 . .
y =1000 ⇒ x ∈{1;2;.......; } 3000 .
Vậy số cặp nghiệm thỏa mãn điều kiện đề bài là: 3+ 6 + 9 +...+ 3000 =1501500 . 4(x + ) 1  b + c
Câu 19. Tập nghiệm của bất phương trình log
> 2 x − x là S =  ; a , trong đó 2 ( )  x + 2 2   
a,b,c là các số nguyên không âm. Tính a + b + c . A. 8 . B. 10. C. 12. D. 6 . Lời giải Chọn A
Điều kiện: x ≥ 0 4(x + ) 1 log
> 2 x − x ⇔ log 4 x +1 − log
x + 2 > 2 x − x 2 ( ) 2 ( ) 2 ( ) ( ) x + 2
⇔ 2 + log x +1 > log
x + 2 + 2 x − x 2 ( ) 2 ( ) ( )
⇔ log x +1 − 2x > log
x +1+1 − 2 x +1 2 ( ) 2 ( ) ( )
Xét hàm số f (x) = log x +1 − 2x x∈ 0;+∞ 2 ( ) , [ ). f ′(x) 1 = ( x
. Do đó hàm số f (x) nghịch biến trên [0;+∞) . x + ) − 2 < 0∀ ∈[0;+∞) 1 ln 2
Khi đó log x +1 − 2x > log
x +1+1 − 2 x +1 2 ( ) 2 ( ) ( )
⇔ f (x) > f ( x + )
1 ⇔ x < x +1 ⇔ x −1< x x <1 x −1< 0 ⇔ x <1     ≥  ≥ x ≥ 0 x 0 x 0 3+ 5 ⇔ ⇔ ⇔   x ≥ 1 ⇔ 0 ≤ x < x −1 ≥ 0   x ≥ 1  2    (     x −  )2 2 3− 5 3+ 5 1 < x
x −3x +1< 0  < x <  2 2 Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC  +  Do đó 3 5 S = 0;
 . Vậy a + b + c = 0 + 3 + 5 = 8 2   
Câu 20. Tập nghiệm của bất phương trình log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 là (− a;− b 2 
với a,b∈ . Khi đó . a b bằng A. 15 . B. 12 . C. 16 . D. 5 . 16 5 15 12 Lời giải Chọn C Ta có 2 2
x x + 2 − x = x( 2x + 2 − x) 2 = x . 2 x + 2 + x Khi đó log ( 2 2
x x + 2 + 4 − x ) 2
+ 2x + x + 2 ≤1 2  2x
⇔ log (x( 2x + 2 − x)+ 4) 2
+ 2x + x + 2 ≤1 2 ⇔ log 
+ 4 + 2x + x + 2 ≤1 2 2 2  x + 2 + x  2( 2 3x + 2 x + 2 ) 2 ⇔ log
+ 2x + x + 2 ≤1, 1 2 ( ) 2 x + 2 + x Mà 2
x + 2 + x > 0, x
∀ ∈  , nên điều kiện 2
3x + 2 x + 2 > 0 2 ⇔ 2 x + 2 > 3 − x x ≥ 0  ⇔ x < 0 8  ⇔ x > − ,(*)   5 2 2
4x + 8 > 9x
Với điều kiện (*) , ta có ( )1 ⇔ log ( 2 3x + 2 x + 2) 2
+ 3x + 2 x + 2 ≤ log ( 2x + 2 + x) 2 + x + 2 + x, 2 2 2 ( )
Xét hàm số f (t) = log t + t trên (0;+∞). 2 Ta có f ′(t) 1 =
+1 > 0 , ∀t ∈(0;+∞) . t.ln 2
Nên hàm số f (t) = log t + t 0;+∞ , ( 2
3x + 2 x + 2)∈(0;+∞) và 2 đồng biến trên ( )
( 2x +2+x)∈(0;+∞) Do đó ( ) ⇔ f ( 2 x + x + ) ≤ f ( 2 2 3 2 2 x + 2 + x)  2 − x ≥ 0 x ≤ 0 2 2
⇔ 3x + 2 x + 2 ≤ x + 2 + x 2 ⇔ x + 2 ≤ 2 − x ⇔ 2  ⇔  ⇔ x ≤ − . 2 2 x + 2 ≤ 4x 2 3  x ≥ 2 3  
Kết hợp với ĐK ta có tập nghiệm bất phương trình là 8 2  − ;− hay 16 . a b = . 5 3     15
Câu 21 Có bao nhiêu cặp số nguyên
( ;x y) thỏa mãn bất phương trình (   +  
x + y − 2x − 24) 2 2 2 2 x y 2 2 log 
 + x + y − 20x − 8y + 78 < 0 ? 2 
 5x + 2y − 20  
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC A. 116. B. 119. C. 113. D. 120. Lời giải Chọn C (   +  
x + y − 2x − 24) 2 2 2 2 x y 2 2 log 
 + x + y − 20x − 8y + 78 < 0 2 
 5x + 2y − 20   2 2 
x + y − 2x − 24 > 0  2 2   x + y  2 2 log 
 + x + y − 20x −8y + 78 < 0 2 
 5x + 2y − 20   ⇔  2 2 
x + y − 2x − 24 < 0  2 2   x + y  2 2 log 
 + x + y − 20x −8y + 78 > 0 2 
 5x + 2y − 20   (x − )2 2 2 1 + y > 5  
5x + 2y − 20 > 0  log  ( 2 2 x + y ) 2 2
+ x + y − log 5x + 2y − 20 − 4 5x + 2y − 20 − 2 < 0 2 2 ( ) ( ) ⇔   (x − )2 2 2 1 + y < 5  
5x + 2y − 20 > 0 log  ( 2 2 x + y ) 2 2
+ x + y − log 5x + 2y − 20 − 4 5x + 2y − 20 − 2 >  0 2 2 ( ) ( )   (x − )2 2 2 1 + y >  5  
5x + 2y − 20 > 0  2 2   x + y  2 2   log 
 + x + y < log 5x + 2y − 20 + 4 5x + 2y − 20 2 2 ( ) ( )    4  ⇔  (I)    (x − )2 2 2 1 + y < 5  
5x + 2y − 20 > 0  2 2  x + y  2 2 log 
 + x + y > log 5x + 2y − 20 + 4 5x + 2y − 20 2 2 ( ) ( )    4  2 2  +  Xét bất phương trình x y 2 2 log 
 + x + y > log 5x + 2y − 20 + 4 5x + 2y − 20 (a). 2 2 ( ) ( )  4 
Xét hàm số f (t) = log t + 4t trên (0;+∞). 2
Ta có , f ′(t) 1 = + 4 > 0, t ∀ > 0. t ln 2
Nên hàm số f (t) = log t + 4t đồng biến trên (0;+∞) . 2 2 2 2 2  +  + Mà (a) x y ⇔   > (5 + 2 − 20) x y f f x y ⇔
> 5x + 2y − 20  4  4 Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC  (x − )2 2 2 1 + y > 5  (x − )2 2 2 1 + y > 5   
5x + 2y − 20 > 0 
5x + 2y − 20 > 0  2 2
x + y < 4(5x + 2y − 20)   (   x −10  )2 +( y − 4)2 2 < 6 Do đó (I)  ⇔  ⇔  .   (x − )2 2 2 1 + y < 5   (x − )2 2 2 + y <  1 5    
5x + 2y − 20 > 0  
5x + 2y − 20 > 0   2 2
x + y > 4(5x + 2y − 20)  2 2   (  x −10  ) +( y − 4) 2 > 6  (x − )2 2 2 1 + y < 5  Xét 
5x + 2y − 20 > 0 . (   x −10  )2 +( y − 4)2 2 > 6  x −1 < 5  x = 3 ± ; 2; ± 1 ± ;0;4;5 2 { } Do (x − ) 2 2
1 + y < 5 ⇒  y < 5 ⇔  .  y =  { 4 ± ; 3 ± ; 2 ± ; 1 ± ; } 0 x, y ∈  
Thay vào 5x + 2y − 20 > 0 và (x − )2 + ( y − )2 2 10 4 > 6
Ta có 8 cặp số: (5,0);(5,− ) 1 ;(5, 2 − );(4, )
1 ;(4,2);(4,3);(3,3);(3,4) thoả mãn .  (x − )2 2 2 1 + y > 5  Xét 
5x + 2y − 20 > 0 , (   x −10  )2 +( y − 4)2 2 < 6  x −10 < 6 4 < x <16 (  x 10)2 ( y 4)2 2 6  y 4 6  − + − < ⇒ − < ⇔  2 − < y <10 . x, y  ∈ x, y ∈  
Thử trực tiếp ta được các cặp số:
(5;4),...,(5;7),(6; )1,...,(6;8),(7;− )1,...,(7;9),(8;− )1,...,(8;9),
(9;− )1,...,(9;9),(10;− )1,...,(10;9),(11;− )1,...,(11;9),(12;− )1,...,(12;9),
(13;− )1,...,(13;9),(14;0),...,(14;8),(15; )1,...,(15;7) nên có 105 cặp số.
Vậy có 105 + 8 =113 cặp số thoả mãn yêu cầu bài toán.
Câu 22. Cho x, y là các số thực thỏa mãn bất phương trình: log 2 + 2 + − 3 ≥ 8y x x y
. Biết 0 ≤ x ≤ 20, 2 ( )
số các cặp x, y nguyên không âm thỏa mãn bất phương trình trên là A. 2 . B. 33. C. 35. D. 5 . Lời giải Chọn C Ta có: log (2 + 2) y log2(x+ ) 1 + − 3 ≥ 8 ⇔ 2 + log ( + ) 3 1 ≥ 2 y x x y x + 3y . (1) 2 2 Xét hàm số ( ) = 2t f t + t . Ta có ′( ) = 2t f t ln 2 +1 > 0, t
∀ ∈  . Nên hàm số ( ) = 2t f t
+ t đồng biến trên  . Khi đó ( ) 1 ⇔ (log ( + ) 1 ) ≥ (3 ) ⇔ log ( + ) 3 1 ≥ 3 ⇔ ≥ 2 y f x f y x y x −1. 2 2 Với 3
0 ≤ ≤ 20 ⇒1≤ 2 y x
≤ 21⇒ 0 ≤ y ≤ log 21. Vì y ∈ ⇒ y ∈{0; } 1 . 8
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Với y = 0 thì x ≥ 0 nên có 21 cặp số ( ; x y) thỏa mãn.
Với y =1 thì x ≥ 7 nên có 14 cặp số ( ; x y) thỏa mãn.
Vậy có tất cả 35 cặp ( ; x y) thỏa mãn.
Câu 23. Số nghiệm nguyên của bất phương trình 3 3
log x + log x ≤ log x + 4 log x + 5 2 2 ( 2 )( 2 ) là A. 17 . B. 15. C. 16. D.Vô số. Lời giải Chọn C 3 3
log x + log x ≤ log x + 4 log x + 5 2 2 ( 2 )( 2 ) (1) log x ≥ 0 ĐK: 2  ⇔ x ≥1 . x > 0
Đặt t = log x , điều kiện t ≥ 0 . 2
Bất phương trình (1) trở thành 3 3
t + t ≤ (t + )(t + ) 3 3
⇔ t + t ≤ (t + )2 2 4 5 4 + (t + 4) (2).
Xét hàm số f (u) = u + u trên [0;+∞) . Ta có f (u) 1 ' = 1+ > 0, u
∀ > 0 . Nên hàm số f (u) = u + u đồng biến trên [0;+∞) . 2 u
Mà ( ) ⇔ f ( 3t) ≤ f ( t + )2 ) 3 2 2 4
⇔ t ≤ t + 8t +16 ⇔ (t − )( 2
4 t + 3t + 4) ≤ 0 ⇔ t ≤ 4. Kết hợp với t ≥ 0 ta được 0 ≤ t ≤ 4 .
Với 0 ≤ t ≤ 4 thì 0 ≤ log x ≤ 4 ⇔ 1≤ x ≤16 (thoả điều kiện). 2
Vì x ∈ nên có 16 giá trị nguyên của x . Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
GIẢI PT LÔGARIT BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Đặt ẩn phụ t theo biểu thức logarit của ẩn x . Khi đó, thu được phương trình ẩn t .
Giải phương trình ẩn t ta được nghiệm t theo ẩn x .
Giải phương trình thu được nghiệm của phương trình.
Câu 01. Số nghiệm của phương trình 2
log x + 4x − 3 log x −8x + 2 = 0 là 2 ( ) 2 A. 1. B. 2 . C. 0 . D. 3. Lời giải Chọn B
Điều kiện: x > 0 .
Đặt t = log x , phương trình trở thành: 2t + (4x − 3)t −8x + 2 = 0. 2
Ta có ∆ = ( x − )2 − (− x + ) 2 4 3 4 8
2 =16x + 8x +1 = (4x + )2 1 
−(4x − 3) − (4x + ) 1 t = = − 4x +  1 2 ⇒  . 
−(4x − 3) + 4x +1 t = =  2  2
Với t = 2 ⇒ log x = 2 ⇔ x = 4 tm k đ . 2 ( ) Với t = 4
− x +1⇒ log x = 4
− x +1⇔ log x + 4x −1 = 0 . 2 2
Xét hàm số f (x) = log x + 4x −1 trên (0;+∞) 2 Có f ′(x) 1 = + 4 > 0, x
∀ > 0 ⇒ hàm số f ( x) đồng biến trên (0;+ ∞) . x ln 2 Mặt khác  1  1 f = 0 ⇒ x =  
(tmđk) là nghiệm duy nhất của phương trình log x = 4 − x +1.  2  2 2
Vậy phương trình đã cho có 2 nghiệm phân biệt.
Câu 2. Cho phương trình 2
log x + (5 − x) 2
log x + 6 − 2x = 0 . Tích các nghiệm của phương trình bằng 2 1 4 A. 4 . B. 8 . C. 6 . D. 2 . Lời giải Chọn B
Điều kiện: x > 0. Ta có 2
log x + (5 − x) 2 2
log x + 6 − 2x = 0 ⇔ log x + x − 5 log x + 6 − 2x = 0 2 1 2 ( ) 2 4
Đặt t = log x , phương trình trở thành: 2t + (x − 5)t + 6 − 2x = 0 ⇔ (t − 2)(t + x − 3) = 0. 2 t = 2 ⇔  . t =3 − x Với 2
t = 2 ⇒ log x = 2 ⇔ x = 2 = 4 tmđk . 2 ( )
Với t = 3− x ⇒ log x = 3− x ⇔ log x + x − 3 = 0 . 2 2
Xét hàm số f (x) = log x + x − 3 trên (0;+∞) 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Có f ′(x) 1 = +1 > 0, x
∀ > 0 ⇒ hàm số f ( x) đồng biến trên (0;+∞) . x ln 2
Mặt khác f (2) = 0 ⇒ x = 2 (tm k
đ ) là nghiệm duy nhất của phương trình log x = 3− x . 2
Vậy tích các nghiệm của phương trình bằng 4.2 = 8 .
Câu 3. Cho phương trình 2
log x +1 + x − 5 .log 3x + 3 − 3x +11 = 0 . Lập phương của tổng các 3 ( ) ( ) 3 ( )
nghiệm của phương trình bằng A. 520. B. 100. C. 1000. D. 10. Lời giải Chọn C
Điều kiện: x +1 > 0 ⇔ x > 1 − Ta có: 2
log x +1 + x − 5 .log 3x + 3 − 3x +11 = 0 3 ( ) ( ) 3 ( ) 2
⇔ log x +1 + x − 5 .log x +1 − 2x + 6 = 0 3 ( ) ( ) 3 ( )
Đăt t = log x +1 , phương trình trở thành: 2
t + (x −5).t − 2x + 6 = 0 3 ( ) t = Mà ∆ = (x − )2 −
( − x) = (x − )2 2 5 4.1. 6 2 1 ⇒  t = 3 − x
Với t = 2 ⇒ log x +1 = 2 ⇔ x = 8 tmđk 3 ( ) ( )
Với t = 3− x ⇒ log x +1 = 3− x ⇔ log x +1 + x − 3 = 0 . 3 ( ) 3 ( )
Xét hàm số f (x) = log x +1 + x − 3 trên ( 1; − +∞) 3 ( ) Có f ′(x) 1 = ( + >
∀ > − ⇒ hàm số f (x) đồng biến trên ( 1; − +∞) . x + ) 1 0, x 1 1 ln 3
Mặt khác f (2) = 0 ⇒ x = 2 (tm k
đ ) là nghiệm duy nhất của phương trình log x +1 = 3− x . 3 ( )
Vậy lập phương của tổng các nghiệm bằng ( + )3 3 2 8 =10 =1000 .
Câu 4. Cho phương trình 2
−log x + 12 − x .log x + x −11 = 0 . Tổng lập phương các nghiệm của 2 ( ) 2 phương trình bằng A. 4 . B. 520. C. 100. D. 230 . Lời giải Chọn B
Điều kiện: x > 0 . Đăt t = log x 2 t − +
− x t + x − = 2
, phương trình trở thành: (12 ) 11 0 . t = Mà − + ( − x) 1 1 12 + x −11 = 0 ⇒  . t =11− x
Với t =1⇒ log x =1 ⇔ x = 2 tmđk . 2 ( )
Với t =11− x ⇒ log x =11− x ⇔ log x + x −11 = 0 . 2 2
Xét hàm số f (x) = log x + x −11 trên (0;+∞) 2 Có f ′(x) 1 = +1 > 0, x
∀ > 0 ⇒ hàm số f ( x) đồng biến trên (0;+∞) . x ln 2
Mặt khác f (8) = 0 ⇒ x = 8 (tm k
đ ) là nghiệm duy nhất của phương trình log x =11− x . 2
Vậy tổng lập phương các nghiệm là: 3 3 2 + 8 = 520 .
Câu 5. Tích các nghiệm của phương trình(x + ) 2
1 log x + 2x + 5 log x + 6 = 0 là 0,5 ( ) 0,5 A. 4 − . B. 16. C. 8 . D. 32. Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Lời giải Chọn C
Điều kiện: x > 0 .
Đặt t = log x , phương trình trở thành: (x + ) 2
1 t + (2x + 5)t + 6 = 0 . 0,5 Có ∆ = ( x + )2 − (x + ) 2 2 5 4.6
1 = 4x − 4x +1 = (2x − )2 1 
−(2x + 5) − (2x − ) 1 t = ( = − x + ) 2 2 1  ⇒  .
−(2x + 5) + 2x −1 3 t −  = =  2  (x + )1 x +1 Với t = 2 − ⇒ log x = 2
− ⇔ x = 4 tm k đ . 0,5 ( ) Với 3 − 3 − 3 t = ⇒ log x = ⇔ log x + = 0 . 0,5 0,5 x +1 x +1 x +1
Xét hàm số f (x) 3 = log x +
trên (0;+∞) có f ′(x) 1 3 = − < 0, x ∀ > 0 ⇒ 0,5 x +1 x ln 0,5 (x + )2 1
hàm số f (x) nghịch biến trên (0;+∞) .
Mặt khác, f (2) = 0 ⇒ x = 2 (tm k
đ ) là nghiệm duy nhất của phương trình 3 − log x = . 0,5 x +1
Vậy tích các nghiệm của phương trình đã cho là 4.2 = 8 .
Câu 6. Cho phương trình (x + 2) 2
log x − x + 5 .log
2x + 3x +18 = 0 . Tích các nghiệm của phương 2 ( ) 4 2 trình bằng: A. 4 . B. 8 . C. 6 . D. 2 . Lời giải Chọn B
Điều kiện: x > 0 . Ta có: (x + 2) 2
log x − x + 5 .log 2x + 3x +18 = 0 2 ( ) 4 2 ⇔ (x + 2) 2
log x − 2 x + 5 .log (2x) + 3x +18 = 0 2 ( ) 2 Đăt t = log x 2 + − + + + = 2
, phương trình trở thành: (x 2)t 2(x 5).t x 8 0 (*)
Do (x + 2) − 2.(x + 5) + (x + 8) = 0 nên phương trình (*) có hai nghiệm x + 8 t =1,t = . x + 2
Với t =1⇒ log x =1 ⇔ x = 2 tm k đ . 2 ( ) Với x + 8 x + 8 6 t = ⇒ log x = ⇔ log x −1− = 0. 2 2 x + 2 x + 2 x + 2
Xét hàm số f (x) 6 = log x −1− trên (0;+∞) 2 x + 2 Có f ′(x) 1 6 = + > 0, x
∀ > 0 ⇒ hàm số f (x) đồng biến trên (0;+∞) . x ln 2 (x + 2)2
Mặt khác f (4) = 0 ⇒ x = 4 (tm k
đ ) là nghiệm duy nhất của phương trình x + 8 log x = . 2 x + 2
Vậy tích các nghiệm bằng 2.4 = 8 .
Câu 7. Cho phương trình
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC (3x + ) 2
1 log (2x −1) + 7 x +1 log (2x −1) + 2x +10 = 0 . Tổng lập phương các nghiệm của 3 ( ) 1 3
phương trình thuộc khoảng nào sau đây? A. (80;110). B. (100;130) C. (110;140) . D. (140;160) . Lời giải Chọn C Điều kiện: 1 x > . 2 Ta có: (3x + ) 2
1 log (2x −1) + 7 x +1 log (2x −1) + 2x +10 = 0 3 ( ) 1 3 ⇔ (3x + ) 2
1 log (2x −1) − 7 x +1 log (2x −1) + 2x +10 = 0 3 ( ) 3
Đặt t = log (2x −1) , phương trình trở thành: ( x + ) 2
3 1 t − 7(x + )
1 t + 2x +10 = 0 (*) 3 t = 2 Ta có: ∆ =
(x + )2 − ( x + )( x + ) = ( x − )2 49 1 4 3 1 2 10 5
3 ≥ 0 nên phương trình (*)  ⇔ x + 5 . t =  3x +1
Với t = 2 ⇒ log (2x −1) = 2 ⇔ x = 5 tmđk . 3 ( ) Với x + 5 x + 5 x + 5 t = ⇒ log (2x −1) = ⇔ log (2x −1) − = 0 (**) 3 3 3x +1 3x +1 3x +1 x + 5
Xét hàm số f (x) = log (2x −1) − trên  1  ;  +∞ 3 3x +1 2    Có f ′(x) 2 14 1 = + > 0, x
∀ > nên hàm số f (x) đồng biến trên  1  ;  +∞ . (2x −1).ln 3 (  3x + )2 1 2  2 
Mặt khác f (2) = 0 ⇒ x = 2 (tm k
đ ) là nghiệm duy nhất của phương trình (**).
Vậy tổng lập phương các nghiệm bằng 3 3 5 + 2 =133 ∈(110;140).
_______________ TOANMATH.com _______________ Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
Document Outline

  • Đợt-10-Dạng-5-Giải-bất-phương-trình-lôgarit-bằng-phương-pháp-hàm-số-đánh-giá-PB2
  • Đợt-10-Dạng-6-Giải-bpt-logarit-bằng-phương-pháp-hàm-đặc-trưng-không-chứa-tham-số-PB2
  • Đợt-10-Dạng-7-Giải-pt-logarit-bằng-phương-pháp-đặt-ẩn-phụ-không-hoàn-toàn-không-chứa-tham-số-PB2