Bất phương trình lôgarit không chứa tham số

Tài liệu gồm 67 trang, được biên soạn bởi thầy giáo Hoàng Xuân Nhàn, hướng dẫn phương pháp giải các bài tập trắc nghiệm phương trình mũ và phương trình lôgarit mức độ vận dụng và vận dụng cao (Giải tích 12 chương 2).

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

67 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Hoàng Xuân Nhàn
1
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
1
MỤC LỤC:
A. TÓM TẮT LÍ THUYẾT: ....................................................................................................................... 1
B. PHÂN DẠNG BÀI TẬP: ........................................................................................................................ 5
Dạng 1. Phương trình mũ ....................................................................................................................... 5
Bài toán 1: Các phương trình mũ thường gặp ........................................................................ 5
Bài toán 2: Phương trình mũ dạng đặt ẩn phụ ........................................................................ 7
Bài toán 3: Phương trình mũ dạng tích ................................................................................... 9
Bài toán 4: Giải phương trình mũ bằng phương pháp đánh giá ............................................ 11
Bài toán 5: Giải phương trình mũ bằng phương pháp hàm đặc trưng .................................. 13
Dạng 2. Phương trình lôgarit ................................................................................................................. 15
Bài toán 1: Các phương trình lôgarit thường gặp ................................................................... 15
Bài toán 2: Phương trình lô garit dạng đặt ẩn phụ ................................................................. 17
Bài toán 3: Phương trình lôgarit dạng tích.............................................................................. 19
Bài toán 4: Giải phương trình lôgarit bằng phương pháp đánh giá ...................................... 21
Bài toán 5: Giải phương trình lôgarit bằng phương pháp hàm đặc trưng ............................. 24
Dạng 3. Phương trình mũ và lôgarit có chứa tham số ......................................................................... 26
Phương pháp giải toán .............................................................................................................. 26
Bài toán 1: Phương trình mũ, lôgarit quy về bậc hai có nghiệm đẹp ..................................... 28
Bài toán 2: Áp dụng định lí Vi-ét cho phương trình mũ, lôgarit quy về bậc hai .................... 30
Bài toán 3: Tìm điều kiện tham số thông qua miền giá trị hàm số ......................................... 32
Bài toán 4: Tìm điều kiện tham số thông qua bảng biến thiên của hàm số ........................... 34
Bài toán 5: Tìm điều kiện tham số dựa vào hàm đặc trưng .................................................... 37
Bài toán 6: Nghiệm đặc biệt của phương trình mũ, lôgarit chứa hàm đối xứng ................... 41
Bài toán 7: Tìm điều kiện tham số của phương trình mũ, lôgarit có chứa hàm ẩn ............... 42
Dạng 4. Nghiệm nguyên của phương trình mũ, lôgarit ....................................................................... 45
Phương pháp giải toán .............................................................................................................. 45
Bài toán 1: Nghiệm nguyên của phương trình mũ và lôgarit dạng tích ................................. 45
Bài toán 2: Nghiệm nguyên của phương trình mũ và lôgarit chứa hàm đặc trưng .............. 47
Bài toán 3: Phương pháp đánh giá và bài toán nghiệm nguyên phương trình ..................... 49
Bài toán 4: Xét nghiệm nguyên phương trình dựa vào đặc thù tổng, tích… các số nguyên. 52
Bài toán 5: Bài toán nghiệm nguyên phương trình mũ, lôgarit nhiều ẩn chứa tham số. ..... 53
C. BÀI TẬP THỰC HÀNH: ....................................................................................................................... 55
BÀI TẬP MỨC ĐỘ I: ............................................................................................................................. 55
Đáp án: ...................................................................................................................................... 57
BÀI TẬP MỨC ĐỘ II: ........................................................................................................................... 57
Đáp án: ...................................................................................................................................... 59
BÀI TẬP MỨC ĐỘ III: .......................................................................................................................... 60
Đáp án: ...................................................................................................................................... 62
BÀI TẬP MỨC ĐỘ IV: .......................................................................................................................... 63
Đáp án: ...................................................................................................................................... 66
2
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
2
A – TÓM TẮT LÍ THUYẾT:
I – PHƯƠNG TRÌNH MŨ:
1. Phương trình mũ cơ bản: Cho trước
0, 1aa
.
Phương trình mũ cơ bản có dạng
x
ab=
0b
log
x
a
a b x b= =
(nghiệm duy nhất)
0b
x
a b x=
(phương trình vô nghiệm)
2. Phương trình mũ dạng cùng cơ số: Cho trước
0, 1aa
.
Ta có:
( ) ( )
( ) ( )
f x g x
a a f x g x==
.
3. Phương trình mũ dạng lôgarit hóa hai vế: Cho trước
, 0, 1a b a
.
()
( ) ( )
( ) log
( ) ( ).log ( 1)
fx
a
f x g x
a
a b f x b
a b f x g x b b
= =
= =
.
4. Phương trình mũ dạng đặt ẩn phụ:
◼ Đặt
()
0
fx
ta=
.
◼ Đưa phương trình đã cho về dạng phương trình đa thức bậc
n
theo
t ⎯⎯→
Giải tìm
t
.
◼ Với
t
có được, thay vào
()fx
ta=
để tìm
x
.
a) Phương trình
2 ( ) ( )
. . 0
f x f x
m a n a p+ + =
với
0, 1aa
.
Đặt
()
0
fx
ta=
.
Phương trình trở thành:
2
0mt nt p+ + =
.
b) Phương trình
( ) ( ) ( )
. . . 0
g x g x g x
m a n b p c+ + =
với
, , 0, 1, 1, 1a b c a b c
.
Nhận dạng:
2 ( ) ( ) 2 ( )
( . ) . 0
f x f x f x
ma n a c p c+ + =
.
Chia hai vế phương trình cho
2 ( )
0
fx
c
, ta được:
2 ( ) ( )
0
f x f x
aa
m n p
cc
+ + =
.
Chú ý: Ta có thể chia hai vế của phương trình cho bất kỳ hàm mũ nào trong ba hàm
( ) ( ) ( )
;;
g x g x g x
abc
, kết quả sau cùng của bài toán không thay đổi.
c) Phương trình
( ) ( )
.( ) ( )
f x f x
m a b n a b p+ + − =
với
0, 1
0, 1
a b a b
a b a b
+ +
− −
.
Nhận dạng:
2
( )( ) 1a b a b a b+ − = − =
.
Đặt
( ) ( )
1
( ) , 0 ( )
f x f x
t a b t a b
t
= + = −
.
Phương trình trở thành:
2
0
n
mt p mt pt n
t
+ = − + =
.
5. Phương trình mũ dạng tích:
3
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
3
a) Dạng cơ bản:
0
0
0
0
a
ab
b
a
ab ac
bc
=
=
=
=
=
=
.
b) Dạng thường gặp:
( ) ( ) ( ) ( )
1
f x g x f x g x
a a a
+
+ = +
với
0, 1aa
.
Cách giải:
()
( ) ( ) ( ) ( ) ( ) ( ) ( )
()
10
1 1 .( 1)
1
fx
f x g x f x g x f x g x f x
gx
a
a a a a a a
a
+
−=
+ = + − = −
=
.
II – PHƯƠNG TRÌNH LÔGARIT:
1. Phương trình lôgarit cơ bản: Cho trước
0, 1aa
.
Ta có:
log
b
a
x b x a= =
(dạng này không cần đặt điều kiện cho x).
2. Phương trình lôgarit dạng cùng cơ số: Cho trước
0, 1aa
.
Ta có:
log ( ) log ( ) ( ) ( ) 0
aa
f x g x f x g x= =
.
3. Phương trình lôgarit dạng mũ hóa hai vế: Cho trước
0, 1aa
.
Ta có:
log ( ) ( )
b
a
f x b f x a= =
(dạng này không cần đặt điều kiện cho
( )
fx
).
4. Phương trình lôgarit dạng đặt ẩn phụ:
◼ Đặt
log ( )
a
t f x=
.
◼ Đưa phương trình đã cho về dạng phương trình đa thức bậc
n
theo
t ⎯⎯→
giải tìm
t
.
◼ Có
t
, thay vào
log ( )
a
t f x=
để tìm
x
.
a) Phương trình
2
log ( ) log ( ) 0
aa
m f x n f x p+ + =
với
0, 1aa
.
Đặt
log ( )
a
t f x=
.
Phương trình đã cho trở thành:
2
0mt nt p+ + =
.
b) Phương trình
()
.log ( ) .log 0
a f x
m f x n a p+ + =
với
0, 1aa
.
Điều kiện:
( ) 0, ( ) 1f x f x
.
Đặt
()
1
log ( ) log
a f x
t f x a
t
= =
.
Phương trình trở thành:
2
00
n
mt p mt pt n
t
+ + = + + =
.
c) Phương trình đơn giản chứa
log ( ), log ( )
ab
f x g x
với
0, 1, 0, 1a a b b
.
Điều kiện:
( ) ( )
0, 0f x g x
.
Đặt
log ( ) ( )
t
a
t f x f x a= =
(cô lập x nếu được).
Thay trở lại phương trình, ta có một phương trình mới đơn giản hơn (chứa ít logarit hơn).
5. Phương trình lôgarit dạng tích:
4
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
4
a) Dạng cơ bản:
0
0
0
0
a
ab
b
a
ab ac
bc
=
=
=
=
=
=
.
b) Dạng thường gặp:
( ) ( ) ( ) ( )
log log log log 1
a b a b
f x f x f x f x+ = +
với
0, 1
0, 1
aa
bb


.
Cách giải:
( ) ( ) ( ) ( )
log log log log 1
a b a b
f x f x f x f x+ = +
( ) ( ) ( )
( )
( )
1 log 0
log 1 log 1 log
log 1
b
a b b
a
fx
f x f x f x
fx
−=
− = −


=
.
III – GIẢI PHƯƠNG TRÌNH MŨ-LÔGARIT BẰNG CÁC ĐÁNH GIÁ NÂNG CAO
1. Phương pháp đánh giá hai vế:
a) Dạng 1: Phương pháp đối lập.
Xét phương trình
( ) ( )f x g x=
với
xD
.
Ta chứng minh:
()
()
f x M
g x M
với mọi
xD
. Do đó:
()
( ) ( )
()
f x M
f x g x
g x M
=
=
=
.
Chú ý:
22
00
00
a b a b
a b a b
+ = = =
+ = = =
.
b) Dạng 2: Dùng tính đơn điệu của hàm số (phương trình có nghiệm duy nhất).
Xét phương trình
( ) ( )f x g x=
có miền điều kiện là
.D
Bước 1: Nhận thấy
0
xx=
là một nghiệm của phương trình.
Bước 2: Chứng minh một trong các trường hợp sau:
•
( )
fx
đồng biến trên D,
( )
gx
nghịch biến trên D.
•
( )
fx
nghịch biến trên D,
( )
gx
đồng biến trên D.
•
( )
fx
đơn điệu trên D,
( )
gx
không đổi trên D.
•
( )
fx
không đổi trên D,
( )
gx
đơn điệu trên D.
Bước 3: Kết luận phương trình
( ) ( )f x g x=
có nghiệm duy nhất
0
xx=
.
c) Dạng 3: Dùng tính đơn điệu của hàm số (phương trình có hai nghiệm, ba nghiệm,…).
Với nguyên tắc làm tương tự Dạng 2, ta thực hiện:
• Nhận thấy
12
,x x x x==
là nghiệm của phương trình
( ) ( )f x g x=
.
• Mặt khác, hàm số
( ) ( )y f x g x=−
với đạo hàm
0y
=
có duy nhất một nghiệm. Suy ra
phương trình
( ) ( )f x g x=
có tối đa hai nghiệm.
• Kết luận: Vậy
1
2
( ) ( )
xx
f x g x
xx
=
=
=
.
5
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
5
Mở rộng: Xét phương trình
( ) ( )f x g x=
với hàm số
( ) ( )y f x g x=−
liên tục trên miền D;
trong đó
0y
=
có n nghiệm, ta suy ra phương trình
( ) ( )f x g x=
có tối đa n + 1 nghiệm.
2. Phương trình chứa hàm đặc trưng:
Xét phương trình dạng:
( )
()f u f v=
trên miền điều kiện D.
Nếu hàm
( )
y f t=
đơn điệu trên miền D (tức là đạo hàm chỉ mang một dấu duy nhất trên D)
thì:
( )
()f u f v u v= =
.
B – PHÂN DẠNG BÀI TẬP:
Phương pháp:
Bạn đọc cần Nắm vững phương pháp giải phương trình trong phần Tóm tắt lí thuyết gồm:
⎯ Phương trình mũ cơ bản.
⎯ Phương trình mũ dạng lôgarit hóa hai vế.
⎯ Phương trình mũ dạng đặt ẩn phụ.
⎯ Phương trình mũ dạng tích.
⎯ Đánh giá hai vế phương trình hoặc dựa vào tính đơn điệu của hàm số, chứng minh
phương trình vô nghiệm, có tối đa 1 nghiệm, 2 nghiệm...
Bài toán 1. Các phương trình mũ thường gặp
VÍ DỤ 1. Phương trình
21
2 32
x+
=
có nghiệm là
A.
5
.
2
x =
B.
2.x =
C.
3
.
2
x =
D.
3.x =
Hướng dẫn giải:
Ta có:
21
2 32
x+
=
2 1 5
22
x+
=
2 1 5x + =
2x=
.
Chọn B.
VÍ DỤ 2. Giải phương trình
2
3
2 1.
xx+
=
A.
0x =
,
3x =
. B.
1x =
,
3.x =−
C.
1x =
,
2.x =
D.
0x =
,
3.x =−
Hướng dẫn giải:
Ta có:
2
3
21
xx+
=
2
30
22
xx+
=
2
30xx + =
0
3
x
x
=
=−
.
6
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
6
Chọn D.
VÍ DỤ 3. Tìm tích số của tất cả các nghiệm thực của phương trình
2
3
2
7 49 7
xx−+
=
.
A.
1−
. B.
1
. C.
1
2
−
. D.
1
2
.
Hướng dẫn giải:
Ta có :
22
3 3 5
2
2 2 2
35
7 49 7 7 7
22
x x x x
xx
− + − +
= = − + =
2
15
2
10
15
2
x
xx
x
−
=
− − =
+
=
.
Khi đó tích các nghiệm là:
1 5 1 5
.1
22
−+
=−
. Chọn A.
VÍ DỤ 4. Cho phương trình
( ) ( )
2
12
7 4 3 2 3
x x x+ − −
+ = +
. Mệnh đề nào sau đây đúng?
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt.
Hướng dẫn giải:
Do
( )
2
7 4 3 2 3+ = +
nên phương trình ban đầu tương đương với
( )
( )
( )
2
2 1 2
2 3 2 3
x x x+ − −
+ = +
2
2 2 2 2x x x + − = −
2
20xx + =
0
1
2
x
x
=
=−
.
Vậy phương trình đã cho có hai nghiệm không dương. Chọn A.
VÍ DỤ 5. Nghiệm của phương trình
11
2 2 3 3
x x x x++
+ = +
là.
A.
3
4
3
log
2
. B.
1x =
. C.
3
2
3
log
4
x =
. D.
4
3
2
log
3
x =
.
Hướng dẫn giải:
Ta có:
11
2 2 3 3 2 2.2 3 3.3
x x x x x x x x++
+ = + + = +
3.2 4.3
xx
=
33
24
x

=


3
2
3
log
4
x=
.
Chọn C.
7
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
7
VÍ DỤ 6. Cho biết phương trình
2
3 2 2
53
x x x− + −
=
có một nghiệm không nguyên dạng
log
a
xb=
với
a
,
b
là các số nguyên dương nhỏ hơn
16
. Khi đó
2ab+
bằng:
A.
35
. B.
25
. C.
40
. D.
30
.
Hướng dẫn giải:
Xét phương trình :
2
3 2 2
53
x x x− + −
=
. Lấy logarit cơ số
5
cho hai vế, ta được :
( ) ( )( ) ( )
2
55
3 2 2 log 3 2 1 2 log 3 0x x x x x x− + = − − − − − =
( )( )
5
2 1 log 3 0xx − − − =
5
2
1 log 3
x
x
=
=+
5
2
log 15
x
x
=
=
.
Suy ra
5a =
,
15b =
. Vậy
2 35ab+=
. Chọn A.
Bài toán 2. Phương trình mũ dạng đặt ẩn phụ
VÍ DỤ 7. Cho phương trình
1
4 2 3 0.
xx+
+ − =
Khi đặt
2
x
t =
ta được phương trình nào sau đây:
A.
4 3 0.t −=
B.
2
3 0.tt+ − =
C.
2
2 3 0.tt+ − =
D.
2
2 3 0.tt−=
Hướng dẫn giải:
Ta có :
( )
2
1
4 2 3 0 2 2.2 3 0
x x x x+
+ − = + − =
.
Đặt
2 , 0.
x
tt=
Phương trình trở thành :
2
2 3 0.tt+ − =
Chọn C.
VÍ DỤ 8. Số nghiệm của phương trình
1
3 3 2
xx−
−=
là:
A.
3
. B.
1
. C.
2
. D.
0
.
Hướng dẫn giải:
Ta có:
1
3 3 2
xx−
−=
3
32
3
x
x
− =
2
3 2.3 3 0
xx
− − =
.
Đặt
3 , 0
x
tt=
. Phương trình trở thành :
2
2 3 0tt− − =
1 0 (loaïi)
3
t
t
.
Với
3t =
thì
3 3 1.
x
x= =
Vậy phương trình đã cho có một nghiệm. Chọn B.
VÍ DỤ 9. Tổng tất cả các nghiệm thực của phương trình
22
2 1 3 6 1
2 5.2 2 0
x x x x+ + +
− + =
bằng:
A.
6
. B.
10
. C.
3
. D.
5
.
Hướng dẫn giải:
8
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
8
Ta có:
2 2 2 2
2 1 3 6 1 2 3 6
2 5.2 2 0 2.2 5.2 2.2 0
x x x x x x x x+ + + +
− + = − + =
.
Chia hai vế phương trình cho
6
20
x
, ta được:
22
2 6 3
2.2 5.2 2 0
x x x x−−
− + =
.
Đặt
2
3
2 , 0
xx
tt
−
=
; suy ra
( )
2
23
2
2 , 0
xx
tt
−
=
. Phương trình trở thành:
2
2
2 5 2 0
1
2
t
tt
t
=
− + =
=
.
Với
2t =
thì
2
32
1,2
3 13
2 2 3 1
2
xx
x x x
−
= − = =
; suy ra
12
3xx+=
.
Với
1
2
t =
thì
2
32
3,4
1 3 5
2 3 1
22
xx
x x x
−
= − = − =
; suy ra
34
3xx+=
.
Vậy tổng các nghiệm phương trình là:
3 3 6.+=
Chọn A.
VÍ DỤ 10. Cho phương trình
5.49 3.35 14.25
x x x
+=
. Kết luận nào sau đây sai?
A. Phương trình vô nghiệm. B. Phương trình có một nghiệm.
C.
1x =
là nghiệm của phương trình. D. Phương trình không có nghiệm âm.
Hướng dẫn giải:
Chia hai vế phương trình cho
25 0
x
, ta có :
5.49 3.35 14.25
x x x
+=
49 35
5. 3. 14
25 25
xx
+ =
2
77
5. 3. 14 0
55
xx
+ − =
.
Đặt
7
0
5
x
t

=


. Phương trình trở thành:
2
5 3 14 0tt+ − =
7
0
5
2 0 (loaïi)
t
t
.
Với
7
5
t =
thì
77
1
55
x
x

= =


. Chọn A.
VÍ DỤ 11. Cho phương trình:
( ) ( )
3
3 5 16 3 5 2 (*)
xx
x+
+ + − =
. Phát biểu nào sau đây sai?
A.
(*)
có nghiệm là số vô tỉ. B.
(*)
có nghiệm dương.
C.
(*)
có nghiệm duy nhất.
D.
(*)
có hai nghiệm phân biệt.
Hướng dẫn giải:
Chia hai vế phương trình cho
20
x
, ta được :
3
3 5 3 5
16 2
22
xx
+−
+=
.
9
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
9
Nhận thấy:
3 5 3 5
.1
22
+−
=
. Đặt
3 5 1 3 5
0
22
xx
t
t
+−
= =
.
Phương trình trở thành:
2
16
8 0 8 16 0 4t t t t
t
+ − = − + = =
.
Với
4t =
thì
35
2
35
4 log 4
2
x
x
+

+
= =



. Chọn D.
VÍ DỤ 12. Gọi
0
x
là một nghiệm của phương trình
( )
2
2 2 2
22
4 2( 1) 3
2 2 2 2 1
x
x x x
+
+ + +
= + − +
. Khi đó
( )
2
0
log 3
a
x b c= + −
với
,,abc
. Tính
2 2 2
a b c−+
.
A.
2 2 2
95a b c− + = −
. B.
2 2 2
85a b c− + =
. C.
2 2 2
65a b c− + = −
. D.
2 2 2
75a b c− + =
.
Hướng dẫn giải:
Ta có:
( )
2
2 2 2 2 2 2 2
22
4 2( 1) 3 1 2( 1) 2( 1) 1
2 2 2 2 1 8.2 2 4.2 4.2 1
x
x x x x x x x
+
+ + + + + + +
= + − + = + − +
Đặt
2
1
2 ( 2).
x
tt
+
=
Phương trình trở thành:
( )
2
2 2 2
4 4 1 8 2 1 8t t t t t t t+ − + = + − =
( )
22
2 1 8 6 1 0 3 10t t t t t t
+
+ − = − − = =
; vì
2t
nên
3 10t =+
.
Với
3 10t =+
thì
( ) ( )
2
1 2 2
22
2 3 10 1 log 3 10 log 3 10 1
x
xx
+
= + + = + = + −
.
Ta có
0
x
là một nghiêm của phương trình và
( )
2
0
log 3 2, 10, 1
a
x b c a b c= + − = = =
.
Suy ra:
2 2 2
95a b c− + = −
. Chọn A.
Bài toán 3. Phương trình mũ dạng tích
VÍ DỤ 13. Gọi
( )
, a b a b
là các nghiệm của phương trình
11
6 6 2 3
x x x++
+ = +
. Tính giá trị của
23
ab
P =+
.
A.
17
. B.
7
. C.
31
. D.
5
.
Hướng dẫn giải:
Ta có:
( ) ( ) ( )( )
11
6 6 2 3 6 6 2.2 3.3 2 . 3 2 3. 3 2 3 2 2 3 0
x x x x x x x x x x x++
+ = + + = + − = − − − =
( )
3
23
2
log 2
32
log 3; log 2
log 3
23
x
x
x
a b a b
x
=
=
= =
=
=
.
Vậy
3
2
log 2
log 3
2 3 3 2 5P = + = + =
. Chọn D.
VÍ DỤ 14. Tính giá trị
T
là tổng tất cả nghiệm thực của phương trình:
2 2 2
3 2 6 5 2 3 7
4 4 4 1.
x x x x x x− + + + + +
+ = +
10
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
10
A.
3
. B.
5−
. C.
3−
. D.
5
.
Hướng dẫn giải:
Ta có :
2 2 2
3 2 6 5 2 3 7
4 4 4 1
x x x x x x− + + + + +
+ = +
2 2 2 2
3 2 6 5 3 2 6 5
4 4 4 .4 1
x x x x x x x x− + + + − + + +
+ = +
( ) ( )
2 2 2 2 2 2 2
22
22
3 2 3 2 6 5 6 5 3 2 6 5 3 2
3 2 3 2 0 2
2
6 5 6 5 0
4 1 4 .4 4 4 1 .1 4 4 1
4 1 0 4 4 3 2 0 1 2
.
15
6 5 0
4 1 4 4
x x x x x x x x x x x x x x
x x x x
x x x x
x x x x
xx
xx
− + − + + + + + − + + + − +
− + − +
+ + + +
− = − − = −

− = = − + = = =

= − = −
+ + =
==

Tổng các nghiệm của phương trình:
( ) ( )
1 2 1 5 3.T = + + − + − = −
Chọn C.
VÍ DỤ 15. Tìm tổng bình phương tất cả nghiệm thực của phương trình
( )
4 2 1 2
x x x
xx= + + −
.
A.
10
. B.
5
. C.
1
. D.
13
.
_____TRÍCH TỪ ĐỀ THI HSG 12, TP. HCM, 2021_____
Hướng dẫn giải:
Điều kiện:
20
x
x−
. Ta có:
( )
4 2 1 2
x x x
xx= + + −
( ) ( )( ) ( )
21
4 1 2 1 2 1 2 1 2 1 2 1
21
x
x x x x x x
x
x
x x x
x
−−
− = + + − − − + − + =
−+
( )( )
2 1 0 (1)
21
2 1 2 1
1
2 1 (2)
21
21
x
x
xx
x
x
x
x
x
x
x
x
− − =
−−
− − + =
+=
−+
−+
.
Giải phương trình (1): Xét hàm số
( )
21
x
f x x= − −
có
( ) ( )
1 0, 0 0ff==
.
Ngoài ra:
( )
2
1
2 ln2 1 0 log
ln2
x
f x x
= − = =
; vì
( )
0fx
=
chỉ có một nghiệm nên phương trình
( )
0fx=
có tối đa hai nghiệm. Vậy
( )
0
1
1
x
x
=
=
.
Giải phương trình (2): Ta có:
2 1 1
20
,,
1
1
2 1 1
21
x
x
x
x
xx
x
x
+

− +
−+
. Suy ra phương
trình (2) vô nghiệm.
Vậy phương trình ban đầu có đúng hai nghiệm là
0; 1xx==
. Suy ra
22
0 1 1+=
. Chọn C.
11
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
11
Bài toán 4. Giải phương trình mũ bằng phương pháp đánh giá
VÍ DỤ 16. Cho phương trình
( )
2
12
2023 1 .2024 1.
xx
x
−
+ − =
Mệnh đề nào sau đây đúng ?
A. Phương trình đã cho có nghiệm duy nhất.
B. Phương trình đã cho có nhiều hơn hai nghiệm.
C. Phương trình đã cho có tổng các nghiệm bằng
0
.
D. Phương trình đã cho có hai nghiệm dương phân biệt.
Hướng dẫn giải:
Xét phương trình (*):
( )
2
12
2023 1 .2024 1.
xx
x
−
+ − =
Ta thấy
1x =
là các nghiệm của (*).
Xét trường hợp:
2
1
10
1
x
x
x
−
−
. Khi đó:
( )
2
1
2
2023 1
1 .2024 0
x
x
x
−
−
Vế trái (*)
1
nên dấu đẳng
thức không thể xảy ra. Vậy trường hợp này không thỏa mãn.
Xét trường hợp:
2
1 0 1 1xx− −
. Khi đó:
( )
2
1
2
2023 1
1 .2024 0
x
x
x
−
−
Vế trái (*)
1
nên dấu đẳng
thức không thể xảy ra. Vậy trường hợp này cũng không thỏa mãn.
Tóm lại phương trình (*) có hai nghiệm
1x =
, suy ra tổng hai nghiệm bằng 0. Chọn C.
VÍ DỤ 17. Phương trình
( )
1 1 2
2 4 2
xx
xx
−+
+ = +
có tổng các nghiệm bằng
A.
5
. B.
3
. C.
6
. D.
7
.
Hướng dẫn giải:
Ta có:
( )
( ) ( )
( )
1 1 2 1 2 1 2 1
1
4
2 4 2 .2 2 .2 4 2 4 4
2*
x x x x x
x
x
x x x x x x x x
x
− + − − −
−
=
+ = + − = − − = −
=
.
Đặt
( ) ( )
11
2 2 .ln2 1
xx
f x x f x
−−
= − = −
;
( ) ( )
22
1
0 1 log 1 log ln2
ln2
f x x
= = + = −
.
Ta thấy
( )
0fx
=
có duy nhất 1 nghiệm nên phương trình
( )
0fx=
có tối đa 2 nghiệm.
Mặt khác:
( ) ( )
1 0; 2 0ff==
, suy ra phương trình
( )
*
có 2 nghiệm
1; 2xx==
.
Vậy phương trình đã cho có 3 nghiệm
1; 2; 4x x x= = =
.Tổng các nghiệm bằng
7
. Chọn D.
VÍ DỤ 18. Cho phương trình:
2
3
5
2025 2023 2024 2025
x
x+ = + +
. Tìm số nghiệm của phương trình
trên.
A.
1
. B.
2
. C.
3
. D.
4
.
_____Trích THTT Số 2-485 tháng 11, năm 2017_____
Hướng dẫn giải:
12
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
12
Ta có:
2
3
5
2025 2023 2024 2025
x
x+ = + +
2
3
5
2025 2023 2024 2025 0
x
x + − + + =
.
Đặt
( )
2
3
5
2025 2023 2024 2025
x
f x x= + − + +
,
D =
.
Ta có:
( )
2025 .ln 2025 2
x
f x x
=+
;
( )
2
2025 .ln 2025 2 0, .
x
f x x

= +
Do đó hàm
( )
fx
đồng biến trên mà
( ) ( )
1 . 0 0ff

−
nên
( )
0fx
=
có nghiệm duy nhất trong
khoảng
( )
1;0−
, suy ra phương trình
( )
0fx=
có tối đa hai nghiệm.
Tới đây, ta cần sự hỗ trợ của MTBT để dò khoảng nghiệm của phương trình :
Sử dụng chức năng Table của máy (thao tác sau đây được thực hiện trên VINACAL 680EX PLUS):
( )
2
3
5
8 2025 2023 2024 2025 : 10
NEXT NEXT NEXT
X
MODE F X X START⎯⎯⎯→ ⎯⎯⎯→ = + − + + ⎯⎯⎯→ −
:10 :1
NEXT NEXT NEXT
END STEP⎯⎯⎯→ ⎯⎯⎯→ ⎯⎯⎯→ =
. (Lưu ý trong quá trình nhập, nếu gặp
( )
GX
thì
ta nhấn dấu
=
để bỏ qua).
Kết quả hiển thị từ màn hình MTBT , ta thấy
( )
FX
đổi dấu hai lần khi x đi từ
7 6, 0 1− → − →
.
Ta có :
( ) ( )
( ) ( )
7 . 6 0
0 . 1 0
ff
ff
− −
. Vậy phương trình đã cho chỉ có hai nghiệm trên hai khoảng
( )
7; 6−−
và
( )
0;1
. Do đó số nghiệm phương trình đã cho bằng 2.
VÍ DỤ 19. Tổng lập phương tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23.
xx
xx
+
= + +
A.
5.
B.
6.
C.
8.
D.
0.
Hướng dẫn giải:
Ta có:
1
15 .5 5 27 23
+
= + +
xx
xx
( )
1
5 . 3 1 27 23 (1)
x
xx
+
− = +
.
Ta thấy
1
3
x =
không là nghiệm của
( )
1
. Với
1
3
x
, (1) trở thành:
( )
1
27 23
52
31
x
x
x
+
+
=
−
.
Trường hợp 1: Xét
1
;
3
x

+


. Ta thấy hàm số
1
5
x
y
+
=
(với
1
5 ln5 0
x
y
+
=
) đồng biến trên
1
;
3

+


, hàm số
27 23
31
x
y
x
+
=
−
(với
( )
2
96
0
31
y
x
= −
−
) nghịch biến trên
1
;
3

+


.
Mặt khác:
1
1;
3
x

= +


là một nghiệm của (2). Vậy (2) có nghiệm duy nhất
1
1;
3
x

= +


.
13
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
13
Trường hợp 2: Xét
1
;
3
x

−


ta có hàm số
1
5
x
y
+
=
đồng biến trên
1
;
3

+


, hàm số
27 23
31
x
y
x
+
=
−
nghịch biến trên
1
;
3

−


.
Mặt khác:
1
1;
3
x

= − −


là một nghiệm của (2). Vậy (2) có nghiệm duy nhất
1
1;
3
x

= − −


.
Vậy phương trình có hai nghiệm:
1, 1.xx= = −
Suy ra:
( )
3
3
1 1 0.+ − =
Chọn D.
VÍ DỤ 20. Số nghiệm của phương trình
( ) ( )
22
2 2 3 6 2 3
2 2 9 3 .8 3 6 .8
x x x x
x x x x x x
+ − − −
+ − = − − + + −
là
A.
1
. B.
3
. C.
2
. D.
4
.
_____THPT Chuyên Vĩnh Phúc, lần 3, 2018_____
Hướng dẫn giải:
Đặt
2
3u x x= − −
,
2
36v x x= + −
. Phương trình trở thành:
.8 .8
vu
u v u v+ = +
( )
*
.
Trường hợp 1:
0u =
,
( )
*
trở thành
vv=
(đúng). Ta có:
2
1,2
3 33
3 6 0
2
u x x x
−
= + − = =
.
Trường hợp 2:
0v =
,
( )
*
trở thành
uu=
(đúng). Ta có
2
3,4
1 13
30
2
v x x x
= − − = =
.
Trường hợp 3:
0uv
; khi đó:
8 8 1 1 8 1 8 1
.8 .8 0
v u v u
vu
u v u v
v u v u v u
−−
+ = + + = + + =
(**).
Xét
( )
81
v
fv
v
−
=
. Ta sẽ chứng minh
( )
81
0, 0
v
f v v
v
−
=
. Thật vậy:
⎯ Nếu
0v
thì
( )
0
81
8 8 8 1 0 0
v
vv
fv
v
−
− =
.
⎯ Nếu
0v
thì
( )
0
81
8 8 8 1 0 0
v
vv
fv
v
−
− =
.
Suy ra
( )
81
0, 0
v
f v v
v
−
=
. Hoàn toàn tương tự, ta cũng có
( )
81
0, 0
u
f u u
u
−
=
.
Ta thấy vế trái (**) luôn dương nên (**) vô nghiệm.
Vậy, phương trình đã cho có bốn nghiệm phân biệt. Chọn D.
Bài toán 5. Giải phương trình mũ bằng phương pháp hàm đặc trưng
VÍ DỤ 21. Số nghiệm của phương trình
2
2 3 2 3 2
2024 2024 2 3 1 0
x x x
x x x
− − −
− + − − + =
là
A. 3 B. 0. C. 1. D. 2.
Hướng dẫn giải:
14
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
14
Điều kiện:
(
2
3
2 3 0 ;0 ;
2
x x x

− − +

.
Phương trình đã cho tương đương với
( )
2
2 3 2 2 3
2024 2 3 2 2024 3 *
x x x
x x x
− − −
+ − − = + −
.
Xét hàm số
( )
2024
t
f t t=+
với
;t
( )
2024 ln2024 1 0,
t
f t t
= +
.
Suy ra hàm
( )
ft
đồng biến trên .
Do vậy:
( )
(
)
( )
22
* 2 3 2 3 2 3 2 3f x x f x x x x − − = − − − = −
2
2 3 1x x x − = −
2 2 2
1 0 1
2 3 2 1 1 0
xx
x x x x x x
−



− = − + − − =

1
15
15
2
2
x
x
x
+
=
=
(thỏa điều kiện).
Vậy phương trình có nghiệm duy nhất là
15
2
x
+
=
. Chọn C.
VÍ DỤ 22. Tìm số nghiệm của phương trình
22
2024 2023 2 2
. 2023 2024
xx
e x x
+ − +
+ = +
.
A. 0. B. 2. C. 4. D. 1.
Hướng dẫn giải:
Ta có :
22
2024 2023 2 2
. 2023 2024
xx
e x x
+ − +
+ = +
22
2024 2023
2
2
2024
2023
xx
ee
x
x
++
=
+
+
(1).
Nhận xét :
2
2023 1x +
và
2
2024 1x +
với mọi
x
.
Xét hàm số
( )
t
e
ft
t
=
với
1t
,
( )
2
.
tt
e t e
ft
t
−
=
( )
2
1
0
t
et
t
−
=
với mọi
1t
.
Suy ra hàm
( )
ft
đồng biến trên
( )
1; +
. Vì vậy
( )
( )
( )
22
1 2024 2023f x f x + = +
22
2024 2023xx + = +
( )
22
2023 2023 1 0xx + − + + =
(2).
Đặt
2
2023 2023tx= +
. Phương trình (2) trở thành:
2
10tt− + =
(vô nghiệm).
Vậy phương trình đã cho vô nghiệm. Chọn A.
VÍ DỤ 23. Gọi T là tổng tất cả các nghiệm của phương trình
22
2cos cos
2024 2024 2024
cos2 .
643 643 643
xx
x
−=
trên
đoạn
0; .
A.
.x
=
B.
.
4
x
=
C.
.
2
x
=
D.
3
.
4
x
=
Hướng dẫn giải:
15
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
15
Đặt
2024
1,002 1
643
a
=
. Phương trình trở thành:
22
2cos cos
cos2 .
xx
a a x a−=
2
22
2cos
cos cos
cos2
x
xx
aa
x
aa
− =
2 2 2 2
1 cos cos 2 2 sin 2 cos 2
cos sin sin cos
x x x x
a a x x a x a x
−
− = − + = +
(*).
Xét hàm số
( )
t
f t a t=+
với
0t
;
( )
1
ln 1 0, 0.
a
t
f t a a t
+
= +
Suy ra
( )
ft
đồng biến trên
.
Vì vậy:
( )
*
( ) ( )
2 2 2 2
sin cos sin cosf x f x x x = =
22
cos sin 0 cos2 0x x x − = =
, .
42
x k k

= +
Vì
0;x
nên
3
;
44
x


=


.
Suy ra
3
44
T

= + =
. Chọn A.
Phương pháp:
Bạn đọc cần Nắm vững phương pháp giải phương trình trong phần Tóm tắt lí thuyết gồm:
⎯ Phương trình lôgarit cơ bản.
⎯ Phương trình lôgarit dạng mũ hóa hai vế.
⎯ Phương trình lôgarit dạng đặt ẩn phụ.
⎯ Phương trình lôgarit dạng tích.
⎯ Đánh giá hai vế phương trình hoặc dựa vào tính đơn điệu của hàm số, chứng minh
phương trình vô nghiệm, có tối đa 1 nghiệm, 2 nghiệm...
Lưu ý: Với phương trình
( ) ( )
log
b
a
f x b f x a= =
thì ta không cần đặt điều kiện cho f(x),
tất cả phương trình lôgarit còn lại luôn cần điều kiện để lôgarit có nghĩa trước khi được giải.
Bài toán 1. Các phương trình lôgarit thường gặp
VÍ DỤ 24. Tập nghiệm của phương trình
2
3
log ( 7) 2x −=
là:
A.
{ 15; 15}.−
B.
{ 4;4}.−
C.
4 .
D.
.4−
Nhận xét: Với phương trình dạng
( ) ( )
log 0, 1
a
f x b a a=
thì ta không cần đặt điều kiện cho x.
Hướng dẫn giải:
Ta có:
2
3
log ( 7) 2x −=
2
79x − =
4
.
4
x
x
=
=−
Vậy tập nghiệm phương trình là
4;4S =−
.
16
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
16
Chọn B.
VÍ DỤ 25. Gọi
1
x
,
2
x
là các nghiệm của phương trình
( )
( )
2
22
log log 1x x x− = +
. Tính
22
12
P x x=+
.
A.
6P =
. B.
8P =
. C.
2P =
. D.
4P =
.
Hướng dẫn giải:
Ta có:
( )
( )
2
22
log log 1x x x− = +
2
1
10
x x x
x
−=+
+
2
2 1 0
1
xx
x
− − =
−
1
2
12
12
x
x
=+
=−
.
Do đó:
( ) ( )
22
22
12
1 2 1 2 6xx+ = + + − =
. Chọn B.
VÍ DỤ 26. Tìm tập nghiệm
S
của phương trình
( ) ( )
33
log 2 1 log 1 1xx+ − − =
.
A.
1.S =
B.
2.S =−
C.
3.S =
D.
4.S =
_____Đề thi THPT QG, năm 2017_____
Hướng dẫn giải:
Điều kiện :
1
2 1 0
1.
2
10
1
x
x
x
x
x
−
+

−
Ta có :
( ) ( )
3 3 3
21
log 2 1 log 1 1 log 1
1
x
xx
x
+
+ − − = =
−
21
34
1
x
x
x
+
= =
−
(thỏa mãn). Chọn D.
VÍ DỤ 27. Nghiệm của phương trình
3
log (3 8) 2
x
x− = −
là:
A. 1. B. 2. C. 0. D. 3.
Hướng dẫn giải:
Ta có:
2
2
3
3
log (3 8) 2 3 8 3 3 8
3
x x x x
x
x
−
− = − − = − =
( )
2
3 8.3 9 0
xx
− − =
3 1 0
39
x
x
= −
=
(loaïi)
(nhaän)
2
3 3 2.
x
x = =
Chọn B.
VÍ DỤ 28. Phương trình
( )
( )
2
2
49 7 7
3
1
log log 1 log log 3
2
xx+ − =
có bao nhiêu nghiệm?
A.
2
. B.
3
. C.
1
. D.
4
.
Hướng dẫn giải:
17
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
17
Điều kiện:
( )
2
2
0
0
1
10
x
x
x
x

−
.
Ta có :
( )
( )
2
2
49 7 7
3
1
log log 1 log log 3
2
xx+ − =
7 7 7
log log 1 log 2xx + − =
( ) ( )
77
log 1 log 2 1 2x x x x − = − =
( )
( )
12
12
xx
xx
−=
− = −
2
2
20
20
xx
xx
− − =
− + =
2
1
x
x
=
=−
(nhận).
Chọn A.
Bài toán 2. Phương trình lôgarit dạng đặt ẩn phụ
VÍ DỤ 29. Cho phương trình
2
5
log 2 log (*)
2
x
x+=
. Tìm mệnh đề đúng.
A.
(*)
có hai nghiệm dương. B.
(*)
vô nghiệm.
C.
(*)
có một nghiệm âm. D.
(*)
có hai nghiệm trái dấu.
Hướng dẫn giải:
Điều kiện:
01x
. Đặt
2
1
log log 2
x
tx
t
= =
.
Phương trình (*) trở thành:
2
2
1 5 5
10
1
22
2
t
t t t
t
t
=
+ = − + =
=
.
Với
2t =
thì
2
2
log 2 2 4.xx= = =
Với
1
2
t =
thì
1
2
2
1
log 2 2.
2
xx= = =
Vậy, tập nghiệm của phương trình (*) là:
2;4 .S =
Chọn A.
VÍ DỤ 30. Tổng các nghiệm của phương trình
( ) ( )
2
33
log 3 log 9 7 0xx+ − =
bằng
A.
84
. B.
28
81
. C.
244
81
. D.
244
3
.
Hướng dẫn giải:
Điều kiện:
0x
. Ta có:
( ) ( ) ( ) ( )
22
3 3 3 3 3
log 3 log 9 7 0 log 3 log 3 log 3 7 0x x x x+ − = + + − =
( ) ( )
2
33
log 3 log 3 6 0xx + − =
.
Đặt
( )
3
log 3tx=
. Phương trình trở thành:
2
60tt+ − =
3
2
t
t
=−
=
.
18
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
18
Khi đó:
( )
( )
3
3
log 3 3
log 3 2
x
x
=−
=
3
2
1
33
81
33
3
x
x
x
x
−
=
=

=
=
(thỏa điều kiện) .
Tổng các nghiệm của phương trình là
1 244
3
81 81
+=
. Chọn C.
VÍ DỤ 31. Tích các nghiệm của phương trình
( )
2
25
log 125 log 1
x
xx=
bằng:
A.
7
25
. B.
630
625
. C.
1
125
. D.
630
.
Hướng dẫn giải:
Điều kiện :
01x
.
Ta có :
( )
( )
( )
2
2 3 2 2
25 5
5
1
log 125 log 1 log 5 1 log 1 3log 5 1 log 1
4
x x x
x x x x= + = + =
.
Đặt
5
1
log log 5.
x
tx
t
= =
Phương trình trở thành:
22
1
3 1 3 1
1 . . 1 1 0 .
4
4 4 4
t
t t t
t
t
=

+ = + − =

=−

Với
1t =
thì
5
log 1 5.xx= =
Với
4t =−
thì
4
5
log 4 5 .xx
−
= − =
Tích hai nghiệm phương trình là
4
1
5.5
125
−
=
. Chọn C.
VÍ DỤ 32. Cho phương trình
( )
( )
2
2
2 1 1
log 2 1 log 2 1 4
xx
x x x
−+
+ − + − =
. Tìm tích hai nghiệm của phương
trình trên.
A.
3
. B.
2
. C.
5
4
. D.
5
2
.
Điều kiện:
2
2 1 0
1
0 2 1 1 1
2
0 1 1
xx
xx
x
+ −
−
+
.
Phương trình đã cho trở thành
( )( ) ( )
2 1 1
log 2 1 1 2log 2 1 4
xx
x x x
−+
− + + − =
( ) ( ) ( ) ( )
2 1 1 2 1 1
1 log 1 2log 2 1 4 log 1 2log 2 1 3 0 (*).
x x x x
x x x x
− + − +
+ + + − = + + − − =
Đặt
( ) ( )
2 1 1
1
log 1 log 2 1
xx
t x x
t
−+
= + = −
.
Khi đó (*) trở thành:
2
1
2
3 0 3 2 0 .
2
t
t t t
t
t
=
+ − = − + =
=
Với
1t =
thì
( )
21
log 1 1 1 2 1 2.
x
x x x x
−
+ = + = − =
Với
2t =
thì
( ) ( )
2
2
21
log 1 2 1 2 1 4 5 0
x
x x x x x
−
+ = + = − − =
0 (loaïi)
5
(nhaän)
4
x
x
.
19
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
19
Phương trình có hai nghiệm
5
2;
4
xx==
nên tích của chúng bằng
5
2
. Chọn D.
VÍ DỤ 33. Cho phương trình
( ) ( ) ( ) ( )
2
33
2 log 1 4 1 log 1 16 0x x x x+ + + + + − =
. Biết
,ab
là hai nghiệm
thực của phương trình đã cho với
ab
, hãy tính giá trị
27ab+
.
A.
49
2
−
. B.
74
3
−
. C.
1
. D.
0
.
Hướng dẫn giải:
Điều kiện:
1.x −
Đặt
( )
3
log 1tx=+
.
Phương trình trở thành:
( ) ( )
2
2 4 1 16 0 (*)x t x t+ + + − =
. Nhận xét:
2 0, 1.xx+ −
Ta có:
( ) ( ) ( )
22
2
4 1 16 2 4 24 36 2 6x x x x x
= + + + = + + = +
.
Khi đó, (*) có hai nghiệm:
( ) ( ) ( )
12
2 1 2 6 2 1 2 6 4 2
4
;4
2 2 2 2
x x x x x
tt
x x x x
− + + + − + − − − +
= = = = = −
+ + + +
.
Với
1
4
2
tt
x
==
+
thì
( )
3
4
log 1
2
x
x
+=
+
. Phương trình này chỉ có một nghiệm
2x =
vì vế trái là
hàm số đồng biến trên
( )
1;− +
, vế phải là hàm nghịch biến trên
( )
1;− +
.
Với
2
4tt= = −
thì
( )
3
1 80
log 1 4 1
81 81
x x x+ = − + = = −
.
Do vậy, ta có:
80 74
2, 27
81 3
a b a b= = − + = −
. Chọn B.
Bài toán 3. Phương trình lôgarit dạng tích
VÍ DỤ 34. Phương trình
( )
2 2 2
log 3 4 .log logx x x−=
có số nghiệm là:
A. 1. B. 5. C. 10. D. 17.
Hướng dẫn giải:
Điều kiện:
4
3
x
.
Ta có:
( ) ( )
2 2 2 2 2
log 3 4 .log log log . log 3 4 1 0x x x x x− = − − =


( )
2
2
log 0
11
log 3 4 1
3 4 2 2
x
xx
x
xx
=
==


−=
− = =

(loaïi)
(nhaän)
.
Vậy phương trình đã cho có đúng một nghiệm. Chọn A.
VÍ DỤ 35. Tổng các nghiệm của phương trình
( )
2
22
log log .log 4 2log 0x x x x− + =
là:
20
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
20
A. 100. B. 101. C. 102. D. 103
Hướng dẫn giải:
Điều kiện:
0x
.
Ta có:
( )
22
2 2 2 2
log log .log 4 2log 0 log 2log log .log 2log 0x x x x x x x x x− + = − − + =
( ) ( ) ( ) ( )
22
log log 2 log . log 2 0 log log . log 2 0x x x x x x x − − − = − − =
( )
2
22
2
log 1 log 10 0
log log 0 log log 10.log 0
1
100
log 2 0 log 2
10
x
x x x x
x
x
xx
x
− =
− = − =
=


=
− = =
=

(thỏa mãn).
Tổng các nghiệm của phương trình là 101. Chọn B.
VÍ DỤ 36. Cho biết
0
a
x
b
=
(với
,ab
và a là số nguyên tố) là một nghiệm của phương trình
3
3 2 3 2
31
log log log log
2
3
x
xx
x


− = +




. Tìm bội số chung nhỏ nhất của hai số a và b.
A.
16
. B.
24
. C. 12. D.
6
.
Hướng dẫn giải:
Điều kiện:
0.x
Ta có:
( )
3
3 2 3 2 3 2 3 2
3 1 1 1 1
log log log log 1 log log 3log log
2 2 2 2
3
x
x x x x x x
x

− = + − − − = +


( ) ( )
3 2 3 2 3 2 3 2 2
11
1 log log 3log log 0 1 log log 3log 2log log 0
22
x x x x x x x x − − − = − − − =
3
2
1
3log 2
2 3 3
2
33
1
log 0
1
log 1 log 3log 2 0 .
1
3
2
log 3log 2
3
2
8
x
x
xx
x
x
−+
=
=

− − − =

= − +

==
Vậy
0
3
3
8
8
a
a
x
b
b
=
= =
=
. Bộ số chung nhỏ nhất của 3 và 8 là 24. Chọn B.
VÍ DỤ 37. Cho phương trình
( ) ( )
( )
2
22
3 1 3 1
33
3log 2 2 2log 2 2 log 9 1 log 0x x x x x x

+ + − + + + − + − =


,
biết rằng
0
17a
x
b
=
(với
a
b
là phân số tối giản) là một nghiệm của phương trình trên. Giá trị
log
a
b
thuộc khoảng nào sau đây?
A.
( )
1;2
. B.
( )
0;1
. C.
( )
3;4
. D.
( )
2;3
.
_____Trích từ đề thi tự luận Kỳ thi THPT Quốc gia năm 2016_____
Hướng dẫn giải:
Điều kiện:
02x
.
21
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
21
Phương trình
( ) ( )
( ) ( )
22
2
3 3 3 3
3log 2 2 2log 2 2 log 3 1 log 0x x x x x x + + − − + + − + + =
( ) ( )
( ) ( )
22
3 3 3 3
3log 2 2 4log 2 2 log 3 log 3 0x x x x x x + + − − + + − + =
( ) ( )
( )
( )
( ) ( )
22
3 3 3 3 3 3
3log 2 2 3log 2 2 log 3 log 2 2 log 3 log 3 0x x x x x x x x x + + − − + + − − + + − + =
( ) ( )
( ) ( )
( )
( )
3 3 3 3 3 3
3log 2 2 log 2 2 log 3 log 3 log 2 2 log 3 0x x x x x x x x x
+ + − + + − − − + + − − =
( )
( )
( )
( )
3 3 3 3
log 2 2 log 3 . 3log 2 2 log 3 0x x x x x x
+ + − − + + − − =
( )
( )
( )
( )
( )
33
3
3
33
log 2 2 log 3
2 2 3 (1)
2 2 3 (2)
log 2 2 log 3
x x x
x x x
x x x
x x x
+ + − =
+ + − =

+ + − =
+ + − =
▪
( )
( )
2
2 2 2 2
2 4 2
9 4 0
1 2 2 2 4 9 2 4 9 4
4 4 81 72 16
x
x x x x x x
x x x
−
+ + − + − = − = −
− = − +
22
42
22
22
2 17
33
33
68
9
0
81 68 0
81
xx
xx
x
xx
xx
−
−

=


= =
−=
. So điều kiện, ta nhận
2 17
9
x =
.
▪ Xét phương trình (2): Ta có:
( )
(
2
2
2 2 4 2 4 4, 0;2x x x x+ + − = + −
; mặt khác
(
2 2 2, 0;2x x x+ + −
. Suy ra vế trái (2) =
( )( )
2
2 2 2 2 8x x x x+ + − + + −
.
Vế phải (2)
(
3 6, 0;2xx=
. Do vậy phương trình (2) vô nghiệm.
Vậy, phương trình đã cho có nghiệm duy nhất
( )
2
2
2 17 17
log 9 3,17 3;4
9
9
a
a
x
b
b
=
= =
=
.
Chọn C.
Bài toán 4. Giải phương trình lôgarit bằng phương pháp đánh giá
VÍ DỤ 38. Số nghiệm của phương trình
( )
9
log 1 log
2
x
x +=
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải:
Xét phương trình (*):
( )
9
log 1 log
2
x
x +=
. Điều kiện:
01x
.
Xét
1x
. Vế trái (*):
( )
9
log 1 log 1 log
2
xx
xx+ =
. Suy ra (*) không có nghiệm thuộc
( )
1; .+
22
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
22
Xét
01x
. Vế trái (*):
( )
9
log 1 log 1 0 log
4
xx
x + =
. Suy ra (*) không có nghiệm thuộc
( )
0;1
.
Vậy phương trình đã cho vô nghiệm. Chọn A.
VÍ DỤ 39. Số nghiệm của phương trình
( ) ( )
35
log 1 log 2 1 2xx+ + + =
là:
A. 1. B. 2. C. 0. D. 3.
Hướng dẫn giải:
Điều kiện:
1
2
x
−
. Xét hàm số
( ) ( ) ( )
35
log 1 log 2 1f x x x= + + +
với
1
;
2
x

− +


.
Ta có:
( )
( ) ( )
1 2 1
0, ;
1 ln3 2 1 ln5 2
f x x
xx
−

= + +

++

. Suy ra
( )
fx
đồng biến trên
1
;
2

− +


.
Mặt khác:
( )
22f =
nên
2x =
là một nghiệm của phương trình đã cho.
Vậy phương trình có nghiệm duy nhất là
2x =
. Chọn A.
VÍ DỤ 40. Xét phương trình
( )
46 2025
log 1 logxx+=
. Kết luận nào sau đây là đúng?
A. Phương trình có nghiệm là một số chính phương.
B. Phương trình vô nghiệm.
C. Phương trình có đúng hai nghiệm.
D. Phương trình có nghiệm là số thực nhỏ hơn 2024.
Hướng dẫn giải:
Đặt
( )
46 2025
1 46 (1)
log 1 log
2025 (2)
t
t
x
t x x
x
+=
= + =
=
.
Thay (2) vào (1):
1 45
1 2025 46 1 45 46 1 (*)
46 46
tt
t t t t
+ = + = + =
.
Đặt
( )
1 45
46 46
tt
ft
=+
; ta có
( )
11f =
;
( )
ft
là hàm nghịch biến trên (vì nó là tổng của hai
hàm nghịch biến trên ), vế phải của (*) là hằng số.
Vậy (*) chỉ có nghiệm duy nhật
1t =
; suy ra
2
2025
log 1 2025 45xx= = =
. Chọn A.
VÍ DỤ 41. Hỏi phương trình
( )
3
2
3 6 ln 1 1 0x x x− + + + =
có bao nhiêu nghiệm phân biệt?
A.
2
. B.
1
. C.
3
. D.
4
.
_____Đề tham khảo, Kỳ thi THPT QG năm 2017, lần 2_____
Hướng dẫn giải:
Điều kiện:
1x −
. Phương trình đã cho tương đương với
( )
2
3 6 3ln 1 1 0x x x− + + + =
.
23
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
23
Xét hàm số
( ) ( )
2
3 6 3ln 1 1g x x x x= − + + +
liên tục trên khoảng
( )
1;− +
.
Ta có:
( )
2
2
3 6 3 2
6 6 ; 0 2 1 0
1 1 2
x
g x x y x x
xx
−

= − + = = − = =
++
(thỏa điều kiện).
Vì
2
3,059 0
2
g

−



,
2
0,138 0
2
g

−



và
( )
lim
x
gx
→
= 
nên đồ thị hàm số
( )
y g x=
cắt trục hoành tại 3 điểm phân biệt. Vì vậy phương trình (*):
( )
0gx=
có ba nghiệm. Chọn C.
VÍ DỤ 42. Cho biết phương trình
( )
3
32
2
log 1 log
3
x x x+ + =
có nghiệm là
0
x
, hỏi
0
2
x
có tất cả bao
nhiêu chữ số?
A.
1234
. B.
4097
. C.
4096
. D.
1233
.
ơ
Nhận xét: Điều kiện bài toán là
0x
. Ta thấy trong lôgarit xuất hiện căn bậc hai và căn
bậc ba (có bội số chung là 6), thêm nữa ta muốn đổi biến sao cho
2
log x
được tính một
cách dễ dàng. Từ những lí do trên, ta nảy sinh ý tưởng đặt
6
2
y
x =
.
Hướng dẫn giải:
Điều kiện:
0x
. Đặt
6
2
y
x =
, phương trình trở thành:
(
)
3
6 6 6
32
2
log 1 2 2 log 2
3
y y y
+ + =
( ) ( )
3 2 3 3 2 3 2 2
3 2 3
2
log 1 2 2 .log 2 log 1 2 2 2 1 2 2 3
3
1 8 4
1 8 4 9 1 (*).
9 9 9
y y y y y y y y
y y y
y y y
y + + = + + = + + =
+ + = + + =
Đặt
( )
1 8 4
9 9 9
y y y
fy
= + +
; ta có
( )
21f =
và
( )
fy
là hàm số nghịch biến trên (vì nó là
tổng của các hàm số nghịch biến trên . Do vậy phương trình (*) có nghiệm duy nhất
2y =
.
Suy ra:
6.2 12
0
2 2 4096xx= = = =
. Khi đó:
0
4096
22
x
=
.
Số các chữ số của
4096
2
là
4096log2 1 1234+=
(chữ số).
24
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
24
Ghi nhớ: Số các chữ số của số tự nhiên rất lớn M là
log 1M +
; trong đó
log M
là phần
nguyên của logM.
Bài toán 5. Giải phương trình lôgarit bằng phương pháp hàm đặc trưng
VÍ DỤ 43. Phương trình
2
2
34
ln 4 2 0
2
xx
xx
x
++
+ + + =
−+
có hai nghiệm
12
,xx
. Khi đó
12
xx+
bằng
A.
4−
. B.
2
. C.
4
. D.
2−
.
Hướng dẫn giải:
Điều kiện:
2
34
0 2 0
2
xx
x
x
++
− +
−+
(do
2
3 4 0,x x x+ +
)
2.x
Ta có:
2
2
34
ln 4 2 0
2
xx
xx
x
++
+ + + =
−+
( ) ( )
( ) ( )
22
ln 3 4 3 4 ln 2 2x x x x x x + + + + + = − + + − +
(*).
Xét hàm số
( )
lnf t t t=+
với
( )
0;t +
.
Ta có:
( ) ( )
1
1 0, 0;f t t
t
= + +
nên hàm số
( )
ft
đồng biến trên khoảng
( )
0;+
.
Vậy (*)
( )
( )
2
3 4 2f x x f x + + = − +
2
3 4 2x x x + + = − +
2
22
4 2 0
22
x
xx
x
= − +
+ + =
= − −
(thỏa mãn điều kiện).
Khi đó:
12
4xx+ = −
. Chọn A.
VÍ DỤ 44. Biết phương trình
53
2 1 1
log 2log
2
2
xx
x
x
có một nghiệm dạng
2x a b
trong đó
,ab
là các số nguyên. Tính
2ab
.
A.
3
. B.
8
. C.
4
. D.
5
.
Hướng dẫn giải:
Điều kiện:
0
0
1
1
1
0
2
2
x
x
x
x
x
x
x


−

.
Ta có:
( )
( )
( )
5 3 5 5 3 3
2 1 1
log 2log log 2 1 log 2log 1 2log 2
2
xx
x x x x
x
x
+−

= + − = − −


( ) ( )
( ) ( )
5 3 5 3
log 2 1 2log 2 log 2log 1 *x x x x + + = + −
.
Xét hàm số:
( ) ( )
53
log 1 2logf t t t= + +
với
0t
.
Ta có:
( )
( )
12
0
1 ln5 ln3
ft
tt
= +
+
,
0t
. Suy ra
( )
ft
đồng biến trên
( )
0;+
.
25
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
HOÀNG XUÂN NHÀN
25
Vì vậy
( )
( )
( )
1 2 1
* 2 1 2 1 2 1 0
1 2 1
x
f x f x x x x x
x
= −
= − = − − − =
= +
.
Vậy
1 2 3 2 2 3, 2x x a b= + = + = =
. Ta có:
2 8.ab+=
Chọn B.
VÍ DỤ 45. Tính tổng tất cả các nghiệm của phương trình: .
A. . B. . C. . D. .
Hướng dẫn giải:
Điều kiện Phương trình tương đương
(1).
Xét hàm số
( )
ln 5 , 0f t t t t= +
;
( )
1
5 0, 0f t t
t
= +
. Suy ra đồng biến trên
( )
0;+
.
Vì vậy:
( )
1
.
Xét ,
( )
5 ln5 3 ln3 6
xx
gx
= + −
;
( )
22
1
5 ln 5 3 ln 3 0,
3
xx
g x x

= + −
.
Vì vậy phương trình
( )
0gx
=
có không quá một nghiệm, suy ra phương trình
( )
0gx=
có không
quá hai nghiệm.
Ta lại có:
( ) ( )
0 1 0gg==
. Vậy phương trình đã cho có hai nghiệm là
0; 1.xx==
Tổng hai nghiệm này bằng 1. Chọn A.
S
1
53
ln 5 5.3 30 10 0
62
xx
xx
x
x
+

+
+ + − − =

+

1S =
2S =
1S =−
3S =
1
.
3
x −
( )
( )
( )
( )
ln 5 3 ln 6 2 5 5 3 5 6 2 0
x x x x
xx+ − + + + − + =
( ) ( )
( ) ( )
ln 5 3 5 5 3 ln 6 2 5 6 2
x x x x
xx + + + = + + +
( )
ft
( )
( )
5 3 6 2
xx
f f x+ = +
5 3 6 2
xx
x + = +
5 3 6 2 0
xx
x + − − =
( )
5 3 6 2
xx
g x x= + − −
26
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
26
Phương pháp giải toán:
1. Biện luận nghiệm phương trình dựa vào tam thức bậc hai:
a) Dạng tam thức bậc hai:
( ) ( )
2
0f x ax bx c a= + +
.
22
4,
2
b
b ac b ac b

= − = − =


.
• Nếu
0
thì phương trình
( )
0fx=
vô nghiệm.
• Nếu
0=
thì phương trình
( )
0fx=
có nghiệm kép
12
2
b
xx
a
= = −
.
• Nếu
0
thì phương trình
( )
0fx=
có hai nghiệm phân biệt
1,2
2
b
x
a
−
=
(hoặc
1,2
b
x
a

−
=
).
b) Định lí Vi-ét: Xét phương trình
2
0ax bx c+ + =
với
0, 0a
. Ta có:
• Tổng hai nghiệm:
12
b
S x x
a
= + = −
.
• Tích hai nghiệm:
12
.
c
P x x
a
==
c) Điều kiện có nghiệm của phương trình
2
0ax bx c+ + =
với
( )
2
f x ax bx c= + +
.
• Phương trình có hai nghiệm dương phân biệt
0, 0
0, 0
a
SP

.
• Phương trình có hai nghiệm âm phân biệt
0, 0
0, 0
a
SP

.
• Phương trình có hai nghiệm trái dấu
0ac
.
• Phương trình có hai nghiệm phân biệt lớn hơn
( )
0, 0
0,
2
a
S
af


.
• Phương trình có hai nghiệm phân biệt bé hơn
( )
0, 0
0,
2
a
S
af


.
• Phương trình có hai nghiệm phân biệt thỏa
( )
12
0x x af

.
Chú ý: Những chỗ có điều kiện
0
, ta đều có thể thay bằng
0

.
2. Biện luận nghiệm phương trình dựa vào khảo sát hàm số:
27
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
27
a) Mối quan hệ giữa nghiệm phương trình và tương giao đồ thị:
Xét phương trình
( ) ( ) ( )
*f x g x=
, miền điều kiện D.
Khi đó: (*) có n nghiệm
Đồ thị hai hàm số
( ) ( )
,y f x y g x==
cắt nhau tại n điểm.
b) Phương pháp biện luận nghiệm dựa vào khảo sát hàm số:
Xét phương trình
( ) ( )
, 0 *f x m =
.
Bước 1: Cô lập m từ phương trình (*):
( )
g x m=
(hoặc
( ) ( )
g x h m=
, trong đó
( )
hm
là một hàm chỉ chứa tham số m).
Bước 2: Thực hiện một trong hai tình huống sau:
• Nếu đề bài chỉ đưa ra giả thiết: “phương trình có nghiệm”; ta chỉ cần tìm miền giá
trị
T
của hàm số
( )
gx
trên tập khảo sát của nó, sau đó cho
mT
(hoặc
( )
h m T
).
• Nếu đề bài đưa ra giả thiết: “Phương trình có n nghiệm (âm, dương, lớn hơn a, bé
hơn b…)”; ta lập bảng biến thiên của hàm số
( )
gx
trên tập khảo sát của nó.
Vì đường thẳng
( )
( )
hayy m y h m==
luôn là đường thẳng nằm ngang (vuông góc
trục tung), ta chọn m ứng với đường thẳng nằm ngang phù hợp đề bài.
3. Nghiệm đặc biệt của phương trình chứa biểu thức đối xứng:
a) Biểu thức đối xứng theo u, v:
Một biểu thức hai biến dạng
( )
,f u v
được gọi là biểu thức đối xứng nếu
( ) ( )
,,f u v f v u=
.
b) Phương trình đối xứng loại 1:
Xét một phương trình dạng
( )
,0f u v =
. Phương trình này được gọi là đối xứng loại 1
theo u, v nếu
( )
,f u v
là biểu thức đối xứng, tức là
( ) ( )
,,f u v f v u=
.
c) Nghiệm đặc biệt của phương trình đối xứng loại 1:
Xét phương trình chứa biểu thức đối xứng dạng:
( ) ( )
, 0 *f u v =
. Khi đó:
⎯ Nếu
( )
00
;uv
là một nghiệm của (*) thì
( )
00
;vu
cũng là một nghiệm của (*).
⎯ Nếu phương trình (*) có
( )
21nn+
nghiệm thì sẽ có một nghiệm dạng
( )
00
;uu
, tức là
00
uv=
.
⎯ Nếu
vu=−
thì (*) có dạng:
( )
,0f u u−=
.
Nếu phương trình này có nghiệm
0
x
thì nó cũng có một nghiệm là
0
x−
. Vì vậy,
phương trình có nghiệm duy nhất suy ra
0 0 0
0x x x= − =
.
28
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
28
Bài toán 1. Phương trình mũ, lôgarit quy về bậc hai có nghiệm đẹp
VÍ DỤ 46. Cho phương trình
( ) ( )
2
33
log 9 5 log 3 10 0x m x m− + + − =
. Số giá trị nguyên của tham số
m
để phương trình đã cho có hai nghiệm phân biệt thuộc
1;81
là
A.
3
. B.
5
. C.
4
. D.
2
.
Hướng dẫn giải:
Ta có:
( ) ( ) ( ) ( )
2
2
3 3 3 3
log 9 5 log 3 10 0 2 log 5 log 3 10 0x m x m x m x m− + + − = + − + + − =
(1).
Đặt
3
logtx=
; với
1;81x
thì
0;4t
.
Khi đó (1) trở thành (2):
( )
???
2
3
1 3 6 0
2
t
t m t m
tm
=
− + + − =
=−
.
Mỗi nghiệm t của (2) sẽ tương ứng với một nghiệm x của (1) trong điều kiện của chúng.
Theo đề: (1) có hai nghiệm phân biệt thuộc
( )
1;81 2
có hai nghiệm phân biệt thuộc
0;4
2 3 5
0 2 4 2 6
mm
mm
−



−

. Vì m nguyên nên
2;3;4;6m
. Chọn C.
Bình luận: Một phương trình bậc hai chứa tham số được gọi là có nghiệm đẹp khi biệt số
Δ của nó được biểu diễn ở dạng bình phương một đa thức theo tham số đó; vì vậy nghiệm
của phương trình được biểu diễn dễ dàng theo tham số đó.
Xét phương trình (2):
( )
2
1 3 6 0t m t m− + + − =
;
( ) ( ) ( )
22
2
1 4 3 6 10 25 5m m m m m = + − − = − + = −
.
Nhờ vậy mà phương trình có hai nghiệm đẹp là:
( ) ( )
12
1 5 1 5
2; 3
2.1 2.1
m m m m
t m t
+ + − + − −
= = − = =
.
Điều này giải đáp cho mục (???) trong lời giải trên.
Tuy vậy, trong trắc nghiệm, học sinh còn có một giải pháp hiệu quả hơn, đó là nhờ sự hỗ trợ của
máy tính bỏ túi, trong đó các em thay m = 100 để thử xem liệu phương trình có cho nghiệm đẹp?
Dùng chức năng giải phương trình
bậc hai với
1,a =
( )
100 1b = − +
,
3.100 6c =−
(tức thay
100m =
).
Kết quả thu được:
1
98 100 2 2xm= = − = −
Kết quả thu được:
2
3x =
Nhờ vậy, ta viết nhanh nghiệm của phương trình (2) là
3; 2t t m= = −
.
Tuy vậy, nếu máy tính không cho ra những kết quả lý tưởng như trên, ta buộc lựa chọn phương
pháp giải khác mà cuốn sách này sẽ đề cập đến trong các bài toán sau.
29
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
29
VÍ DỤ 47. Giả sử phương trình
2
22
log ( 2)log 2 0x m x m− + + =
có hai nghiệm thực phân biệt
12
,xx
thỏa
mãn
12
6xx+=
. Giá trị biểu thức
12
xx−
là
A. 4. B. 3. C. 8. D. 2.
Hướng dẫn giải:
Xét phương trình (1):
2
22
log ( 2)log 2 0x m x m− + + =
. Điều kiện:
0x
.
Đặt
2
logtx=
. Phương trình (1) tương đương với (2):
( )
2
2
2 2 0
t
t m t m
tm
=
− + + =
=
.
Mỗi nghiệm t của (2) sẽ tương ứng với một nghiệm x của (1) trong điều kiện của chúng.
Phương trình (1) có hai nghiệm phân biệt
Phương trình (2) có hai nghiệm phân biệt
2.m
Ta có:
2 1 1 2 2 2
log 2 4; log 2
m
x x x m x= = = =
.
Theo giả thiết:
12
6 2 4 6 1
m
x x m+ = + = =
. Vì vậy
2 1 2
22x x x= − =
. Chọn D.
VÍ DỤ 48. Tìm tất cả các giá trị của tham số
m
để phương trình
( ) ( )
2 2 2
2 2 1 2 4 2
4.4 2 2 6 6 3 3 0
x x x x x x
mm
+ + + + +
+ − − + =
có hai nghiệm thực phân biệt.
A.
4 3 2 4 3 2m− +
B.
4 3 2m +
hoặc
4 3 2m −
.
C.
1m −
hoặc
1
2
m
−
. D.
1
1
2
m
−
−
.
Hướng dẫn giải:
Ta có:
( ) ( )
2 2 2
2 2 1 2 4 2
4.4 2 2 6 6 3 3 0
x x x x x x
mm
+ + + + +
+ − − + =
( )
( )
( )
( )
( )
( )
( )
( )
( )
22
2 2 2
11
1 1 1
42
4 2 2 6 6 3 9 0 2 2 6 3 0 (1)
93
xx
x x x
m m m m
++
+ + +
+ − − + = + − − + =
Đặt
2
( 1)
2
3
x
t
+

=


; vì
( )
2
10x +
nên
01t
.
Phương trình (1) trở thành (2):
(
2
3 0;1
(2 2) 6 3 0
21
t
t m t m
tm
=
+ − − − =
= − −
.
Phương trình đã cho có hai nghiệm thực phân biệt
( )
???
2 1 0;1tm = − −
1
0 2 1 1 1 2 2 1
2
m m m − − − − −
. Chọn D.
Nhận xét: Khi
( )
0
0;1tt=
thì
( )
2
( 1)
2
0 2 0
3
2
1 log 0
3
x
t x t
+

= + =


, từ đây ta giải được hai
nghiệm phân biệt
12
,.xx
Nếu
1t =
thì
( )
2
( 1)
2
2
1 1 0 1
3
x
xx
+

= + = = −


(nghiệm kép). Vì vậy,
muốn phương trình ban đầu có hai nghiệm phân biệt
12
,,xx
ta cần
( )
0;1t
.
30
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
30
Bài toán 2. Áp dụng định lí Vi-ét cho phương trình mũ, lôgarit quy về bậc hai
VÍ DỤ 49. Tìm tất cả các giá trị thực của tham số
m
để phương trình
1
4 2 0
xx
m
+
− + =
có hai nghiệm
thực phân biệt
A.
( )
;1m −
. B.
(
0;1m
. C.
( )
0;1m
. D.
( )
0;m +
.
Hướng dẫn giải:
Phương trình đã cho tương đương với
( )
2
1
4 2 0 2 2.2 0
x x x x
mm
+
− + = − + =
( )
1
.
Đặt
20
x
t =
. Phương trình
( )
1
trở thành:
2
20t t m− + =
( )
2
.
Khi đó:
( )
1
có hai nghiệm thực phân biệt
( )
2
có hai nghiệm dương phân biệt
10
0
2
0 0 0 1
1
0
0
1
m
Sm
P
m
−

−

−


. Chọn C.
VÍ DỤ 50. Phương trình
1
4 3.2 0
xx
m
+
− + =
có hai nghiệm thực
12
,xx
thỏa mãn
12
1xx+ = −
. Giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;0−
. B.
( )
7; 5−−
. C.
( )
0;1
. D.
( )
5;7
.
Hướng dẫn giải:
Ta có:
( )
( )
2
1
4 3.2 0 2 6.2 0 1
x x x x
mm
+
− + = − + =
.
Đặt
2
x
t =
. Phương trình đã cho trở thành:
( )
2
6 0 2t t m−+=
.
Xét
1 2 1 2
1
12
1
2 .2 2 2
2
x x x x
tt
+
−
= = = =
. Theo đính lí Vi-ét:
( )
2
12
t t m=
. Suy ra
1
2
m =
.
Thử lại: Thay
1
2
m =
vào (2):
2
1,2
1 6 34
6 0 0
22
t t t
− + = =
. Như vậy, (2) có hai nghiệm
dương phân biệt nên (1) có hai nghiệm thực phân biệt
12
,xx
. Vậy
1
2
m =
thỏa mãn đề bài. Chọn C.
VÍ DỤ 51. Cho biết
m
là số thực để phương trình
2
33
log 3log 2 7 0x x m− + − =
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
( )( )
12
3 3 72xx+ + =
. Mệnh đề nào đúng?
A.
( )
4;5m
. B.
( )
3;4m =
. C.
( )
2;3m
. D.
( )
1;2m
.
Hướng dẫn giải:
Đặt
3
logtx=
. Phương trình đã cho trở thành
( )
2
3 2 7 0 *t t m− + − =
.
31
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
31
Ứng với mỗi nghiệm
t
của
( )
*
thì phương trình ban đầu sẽ có một nghiệm
0x
.
Phương trình đã cho có hai nghiệm phân biệt
( )
*
có hai nghiệm phân biệt
0
( ) ( )
2
37
3 4 2 7 0 9 8 28 0
8
m m m − − − − +
.
Gọi
1
t
,
2
t
là hai nghiệm phương trình
( )
*
. Theo định lí Vi-ét:
12
3tt+=
( )
3 1 3 2 3 1 2 1 2
log log 3 log . 3 . 27x x x x x x + = = =
.
Theo giả thiết:
( )( ) ( )
1 2 1 2 1 2 1 2
27
3 3 72 . 3 9 72 12x x x x x x x x
=
+ + = + + + = + =
.
Vậy ta có
1 2 1 1 1 1
12
1 2 2 2 2 2
12 9 3 2 1
.2
. 27 3 9 1 2
x x x x t t
tt
x x x x t t
+ = = = = =
=
= = = = =
.
Theo định lý Viét:
12
9
. 2 2 7 2
2
t t m m= − = =
(thỏa điều kiện). Chọn A.
VÍ DỤ 52. Xét các số nguyên dương
, ab
sao cho phương trình
2
ln ln 5 0a x b x+ + =
có hai nghiệm
phân biệt
12
, xx
và phương trình
2
5log log 0x b x a+ + =
có hai nghiệm phân biệt
34
, xx
thỏa mãn
1 2 3 4
x x x x
. Tìm giá trị nhỏ nhất của
23S a b=+
A.
min
33S =
. B.
min
30S =
. C.
min
17S =
. D.
min
25S =
.
Hướng dẫn giải:
Điều kiện để hai phương trình:
2
ln ln 5 0a x b x+ + =
và
2
5log log 0x b x a+ + =
có hai nghiệm
phân biệt là:
2
20 0ba−
.
Áp dụng định lí Vi-ét cho mỗi phương trình:
( )
( )
1 2 1 2
12
5
3 4 3 4
34
ln ln ln
log log log
10
5
b
a
b
b
x x x x
x x e
a
b
x x x x
xx
−
−
+ = = −
=



+ = = −
=
.
Theo giả thiết:
5
1 2 3 4
10
bb
a
x x x x e
−−
(*).
Lấy lôgarit cơ số e hai vế của (*):
ln10
5
bb
a
− −
**
1 1 5
ln10 2,17 3
5 ln10
ba
aa
a
(1)
Theo điều kiện:
*
22
20 0 20 60 8
b
b a b a b
−
(2).
Từ (1) và (2) suy ra:
min
2 3 2.3 3.8 30 30S a b S= + + = =
. Chọn B.
Dấu đẳng thức xảy ra khi và chỉ khi
3, 8.ab==
32
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
32
Bài toán 3. Tìm điều kiện tham số thông qua miền giá trị hàm số
VÍ DỤ 53. Tìm tất cả các giá trị của tham số
m
để phương trình
sin 1 sin
4 2 0
xx
m
+
+ − =
có nghiệm.
A.
5
8.
4
m
B.
5
9.
4
m
C.
5
7.
4
m
D.
5
8.
3
m
Hướng dẫn giải:
Đặt
sin
2
x
t =
; với
1 sin 1x−
thì
1
2.
2
t
Phương trình trở thành:
22
2 0 2t t m t t m+ − = + =
(*).
Xét hàm
( )
2
2f t t t=+
với
1
;2
2
t



, ta có:
( )
1
2 2 0, ;2 .
2
f t t t

= +


Ta lại có:
( )
15
, 2 8
24
ff

==


. Hơn nữa, hàm
( )
ft
liên tục trên đoạn
1
;2 .
2



Vậy miền giá trị của hàm số
( )
ft
trên
1
;2
2



là
5
;8
4
T

=


.
Phương trình đã cho có nghiệm x
Phương trình (*) có nghiệm
1
;2
2
t



5
8
4
m
. Chọn A.
VÍ DỤ 54. Cho phương trình
( )
22
1 1 1 1
25 2 5 2 1 0
xx
mm
+ − + −
− + + + =
với m là tham số thực. Tập hợp tất
cả giá trị m để phương trình trên có nghiệm là
;ab
. Tìm tích
.ab
.
A.
1500
.
11
ab =
B.
3072
.
25
ab =
C.
100.ab =
D.
3072
.
23
ab =
Hướng dẫn giải:
Điều kiện:
11x−
. Đặt
( )
22
1 1 1 1
2
5 ; 5 .ln5. 0 0 1;1
1
xx
x
t t x
x
+ − + −
−
= = = = −
−
.
Ta lại có:
( ) ( ) ( )
1 1 5, 0 25t t t− = = =
. Do vậy
5;25t
.
Phương trình đã cho trở thành:
( )
2
2 2 1 0t m t m− + + + =
( )
( )
2
2
2 1 1
2 1 2 do 5;25
22
tt
t t m t m t m t
tt
−+
− + = − = = +
−−
(*).
Đặt
( )
1
, 5;25
2
f t t t
t
= +
−
; ta có:
( )
( )
( )
2
2
3
1
1 0 2 1
1
2
t
f t t
t
t
=
= − = − =
=
−
(loại).
Mặt khác:
( ) ( )
16 576
5 , 25
3 23
ff==
; đồng thời hàm
( )
ft
liên tục trên đoạn
5;25
.
33
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
33
Vì vậy miền giá trị của
( )
ft
trên
5;25
là
16 576
;
3 23
T

=


.
Phương trình đã cho có nghiệm x
(*) có nghiệm
16 576
5;25 ;
3 23
tm



.
Do vậy
16 576 3072
,
3 23 23
a b ab= = =
. Chọn D.
VÍ DỤ 55. Tìm tất cả các giá trị thực của tham số
m
để phương trình
33
log log 1 2 1 0x x m+ + − − =
có ít nhất một nghiệm thực trong đoạn
1;27
.
A.
( )
0;2m
. B.
0;2m
. C.
2;4m
. D.
( )
0;4m
.
Hướng dẫn giải:
Đặt
2
33
log 1 1 logt x t x= + − =
; với
1;27x
thì
1;2t
.
Phương trình đã cho trở thành:
2
1 2 1 0t t m− + − − =
2
22t t m + = +
( )
*
.
Xét hàm số
( )
2
f t t t=+
trên
1;2
;
( )
2 1 0, 1;2f t t t
= +
.
Ta lại có:
( ) ( )
1 2, 2 6ff==
; đồng thời hàm
( )
ft
liên tục trên đoạn
1;2
.
Vì vậy miền giá trị của
( )
ft
là
2;6T =
.
Phương trình đã cho có nghiệm
( )
1;27 *x
có nghiệm
1;2 2 2 2 6 0 2t m m +
.
Chọn B.
VÍ DỤ 56. Có bao nhiêu số nguyên
m
để phương trình
( ) ( )
2
35
log 3 2 log 3
xx
mm+ = −
có nghiệm?
A.
3
. B.
4
. C.
2
. D.
5
.
Hướng dẫn giải:
Điều kiện:
2
3 2 0
30
x
x
m
m
+
−
. Đặt
( ) ( )
( )
2
35
2
3 2 3 1
log 3 2 log 3
3 5 (2)
xt
xx
xt
m
m m t
m
+=
+ = − =
−=
.
Trừ theo vế (1) và (2), ta được:
2
2 3 5
tt
mm+ = −
2
2 1 3 5 1
tt
mm + + = − +
(*).
Xét hàm số
( )
3 5 1
tt
ft= − +
với
t
.
Ta có:
( ) ( ) ( )
3 3 3 0 0
5
3 ln5
3.ln3 5.ln5 0 log 5 log log 5 ; 1,1396
5 ln3
t
tt
f t t t f t

= − = = = = =


.
Mặt khác:
( ) ( )
lim , lim 1
tt
f t f t
→+ →−
= − =
và hàm
( )
ft
liên tục trên .
Vì vậy miền giá trị của hàm
( )
ft
với
t
là
( )
0
1,1396
;T f t

= −

.
34
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
34
Phương trình đã cho có nghiệm
x
( )
*
có nghiệm
( )
2
0
21t m m f t + +
( ) ( ) ( ) ( ) ( ) ( ) ( )
2
0 0 0 0 0 0
2,0675 0,0675
1 1 1 1 1m f t m f t f t m f t f t m f t
−
+ + − + − − − +
.
Vì m nguyên nên
2; 1;0m − −
. Chọn A.
Bài toán 4. Tìm điều kiện tham số thông qua bảng biến thiên hàm số
VÍ DỤ 57. Gọi
( )
;ab
là tập các giá trị của tham số
m
để phương trình
2
2 8 0
xx
e e m− − =
có đúng hai
nghiệm thuộc khoảng
( )
0;ln5
. Tổng
ab+
là
A. 2. B. 4. C.
6−
. D.
14−
.
Hướng dẫn giải:
Đặt
x
te=
; với
( )
0;ln5x
thì
( )
1;5t
. Phương trình trở thành
2
2 8 (*)t t m−=
.
Xét hàm số
( )
2
28f t t t=−
với
( )
1;5t
;
( )
4 8 0 2.f t t t
= − = =
Bảng biến thiên:
Phương trình đã cho có hai nghiệm phân biệt thuộc khoảng
( )
0;ln5
( )
*
có hai nghiệm
( )
1;5t
86m − −
. Do vậy
( ) ( )
8; 6 ; 8, 6m a b a b − − = = − = −
. Suy ra
14ab+ = −
. Chọn D.
VÍ DỤ 58. Tìm số giá trị nguyên của tham số
( )
10;10m−
để phương trình
( ) ( )
22
2
1
10 1 10 1 2.3
xx
x
m
+
+ + − =
có đúng hai nghiệm phân biệt?
A.
14
. B.
15
. C.
13
. D.
16
.
Hướng dẫn giải:
Ta có:
( ) ( )
22
22
2
1
10 1 10 1
10 1 10 1 2.3 6
33
xx
xx
x
mm
+
+−
+ + − = + =
(1)
.
Đặt
22
10 1 10 1 1
33
xx
t
t
+−
= =
; với
2
0x
thì
1t
.
35
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
35
Khi đó (1) trở thành:
22
1
. 6 6 6t m t m t t t m
t
+ = + = − + =
(2).
Xét hàm số
2
( ) 6f t t t= − +
trên nửa khoảng
)
1; +
, ta có:
( )
2 6 0 3f t t t
= − + = =
.
Bảng biến thiên:
Nhận xét: (1) có đúng hai nghiệm phân biệt
( )
2
có đúng một nghiệm lớn hơn 1.
Dựa vào bảng biến thiên, ta được:
5m
hoặc
9m =
. Do
( )
10;10m −
nên
9; 8;...;3;4;9m − −
. Vậy có 15 giá trị
m
cần tìm. Chọn B.
VÍ DỤ 59. Gọi là tổng các giá trị nguyên của tham số để phương trình có
nghiệm . Chọn đáp án đúng.
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
2
4 8.2 7 6
xx
mm − + = +
(*).
Đặt
2
x
t =
; với thì
( )
2;8t
. Phương trình trở thành: .
Đặt
( ) ( )
2
8 7, 2;8f t t t t= − +
; ta có:
( )
2 8 0 4f t t t
= − = =
(nhận).
Bảng biến thiên:
Theo đó, phương trình (*) có nghiệm
2
2
69
71
71
67
m m m
m
m
mm
+ −
−

−
+
.
Vì nguyên nên . Suy ra tổng
21S =−
. Chọn D.
VÍ DỤ 60. Cho phương trình
( )
ln 1 2 0m x x+ − − =
. Biết rằng tập hợp tất cả các giá trị của tham số
m
để phương trình đã cho có hai nghiệm
1
x
,
2
x
thỏa mãn
12
0 2 4xx
là khoảng
( )
;a +
. Khi
đó
a
thuộc khoảng nào dưới đây?
A.
( )
3,7;3,8
. B.
( )
3,6;3,7
. C.
( )
3,8;3,9
. D.
( )
3,5;3,6
.
S
m
32
4 7 2 6
xx
mm
+
+ = + +
( )
1;3x
35S =−
20S =
25S =
21S =−
32
4 7 2 6
xx
mm
+
+ = + +
( )
1;3x
22
8 7 6t t m m− + = +
( )
1;3x
m
6; 5; 4; 3; 2; 1;0m − − − − − −
36
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
36
Hướng dẫn giải:
Điều kiện:
1x −
. Nhận xét:
0x =
không là nghiệm phương trình đã cho, vì vậy ta có:
( )
( )
2
ln 1 2 0
ln 1
x
m x x m
x
+
+ − − = =
+
(*).
Đặt
( )
( )
2
ln 1
x
fx
x
+
=
+
với
( )
1; \ 0x − +
. Ta có:
( )
( ) ( )
( )
2
1
ln 1 2
1
ln 1
xx
x
fx
x
+ − +
+
=
+
;
( ) ( )
2
0 ln 1 0
1
x
f x x
x
+
= + − =
+
.
Đặt
( ) ( ) ( )
( )
( )
2
2 1 1
ln 1 0, 1; \ 0
11
1
x
g x x g x x
xx
x
+
= + − = + − +
++
+
.
Mặt khác:
( ) ( )
45
2 . 3 ln3 ln4 0,032 0
34
gg
= − − −
nên
( )
0gx=
có một nghiệm
( )
0
2;3x
;
Vậy
( )
0fx
=
có nghiệm duy nhất
( )
0
2;3x
. Từ đây ta có bảng biến thiên:
Theo đó, phương trình (*) có hai nghiệm phân biệt thỏa
12
0 2 4xx
6
ln5
m
.
Vậy
6
;
ln5
m

+


thỏa mãn đề bài, nên
( )
6
3,728 3,7;3,8
ln5
a =
. Chọn A.
37
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
37
Bài toán 5. Tìm điều kiện tham số dựa vào hàm đặc trưng
VÍ DỤ 61. Biết rằng điều kiện cần và đủ của tham số
m
để phương trình
(
)
2
log 2 2
x
m m x+ + =
có
nghiệm là
a
m
b
−
với
,ab
là hai số nguyên dương và
7b
. Hỏi
2
a b b++
bằng bao nhiêu?
A.
31
. B.
32
. C.
21
. D.
23
.
Hướng dẫn giải:
Điều kiện:
20
x
m+
và
20
x
mm+ +
.
Ta có:
(
)
( ) ( )
2
2
2
log 2 2 2 2 2 2 2 2
x x x x x x x
m m x m m m m+ + = + + = + + + = +
(1).
Xét hàm
( ) ( )
2
0f t t t t= +
;
( )
2 1 0, 0f t t t
= +
, suy ra hàm
( )
ft
đồng biến trên
)
0;+
.
Vậy:
( )
(
)
( ) ( ) ( )
( )
2
22
11
1 2 2 2 2 2 2 2 2 2 2
24
x x x x x x x x x
f m f m m m m

+ = + = = + − = − = +


.
Xét hàm
( )
2
1
2
2
x
gx

=−


liên tục trên ; ta có:
2
1
2 0,
2
x
x

−


.
Vì vậy miền giá trị của
( )
gx
trên là
)
0;+
.
Phương trình đã cho có nghiệm
( )
2
có nghiệm
11
0
44
a
mm
b
+ − = −
.
Suy ra:
2
1
21.
4
a
a b b
b
=
+ + =
=
Chọn C.
VÍ DỤ 62. Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
(
)
(
)
3 2 2
2 1 1 1
mm
e e x x x x+ = + − + −
có nghiệm là
A.
1
0; ln2
2



. B.
1
; ln 2
2

−

. C.
1
0;
e



. D.
1
ln2;
2

+

.
Hướng dẫn giải:
Ta có:
(
)
(
)
(
)
(
)
3 2 2 3 2 2
2 1 1 1 1 2 2 1 (*)
m m m m
e e x x x x e e x x x x+ = + − + − + = + − + −
.
Đặt
( )
2 2 2 2 2
1 1 1 1 2 1 1 2 1t x x x t x x t x x= + − − = + − − = −
.
Ta có:
2
2
22
22
0
12
1 0 1 0
2
1
11
x
x x x
t x x x
xx
xx
−−
= − = = − − = =
−=
−−
.
Ta tính được:
( ) ( )
2
1 1, 1 1, 2
2
t t t

− = − = =



. Vì vậy ta có:
12t−
.
38
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
38
Khi đó (*) trở thành:
( )
32
1
mm
e e t t+ = +
33
(**)
mm
e e t t + = +
.
Xét hàm
( )
3
f u u u=+
( )
2
3 1 0,f u u u
= +
; suy ra hàm
( )
fu
luôn đồng biến trên .
Khi đó:
( )
( )
(**)
m
f e f t=
m
et=
.
Phương trình này có nghiệm
1
1 2 2 ln 2
2
mm
e e m −
. Chọn B.
VÍ DỤ 63. Tìm tất cả các giá trị của
m
để phương trình
( )
ln ln sin sinm m x x+ + =


có nghiệm.
A.
1
1 1.me
e
+ −
B.
1 1.me −
C.
1
1 1.m
e
+
D.
1 1.me −
Hướng dẫn giải:
Điều kiện:
( )
sin 0
ln sin 0
mx
m m x
+
+ +
. Ta có:
( )
ln ln sin sinm m x x+ + =


( ) ( ) ( ) ( ) ( )
ln ln sin ln sin ln sin sin 1m m x m m x m x m x + + + + + = + + +
.
Xét hàm
( ) ( )
ln 0f t t t t= +
;
( )
1
1 0, 0f t t
t
= +
. Suy ra hàm
( )
ft
đồng biến trên
( )
0;+
.
Vì vậy:
( ) ( )
( )
( ) ( )
1 ln sin sin ln sin sinf m m x f m x m m x m x + + = + + + = +
( )
sin sin
ln sin sin sin sin
xx
m x x m x e m e x + = + = = −
(2).
Đặt
sin 1;1ux= −
, (2) trở thành:
u
m e u=−
(3).
Xét hàm
( )
u
g u e u=−
với
1;1u −
;
( )
1 0 0 1;1
u
g u e u
= − = = −
.
Vì hàm
( )
gu
liên tục trên
1;1−
và
( ) ( ) ( )
1
1 1, 1 1, 0 1g g e g
e
− = + = − =
.
Do vậy tập giá trị của hàm
( )
gu
trên
1;1−
là
1; 1Te=−
.
Phương trình đã cho có nghiệm
( )
3
có nghiệm
1;1 1 1u m e − −
. Chọn B.
VÍ DỤ 64. Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
2
2
2
21
log 2 1 2
2
x mx
x mx x
x

++
+ + + = +


+

có hai nghiệm phân biệt?
A.
3
. B.
1
. C.
4.
D.
2
.
Hướng dẫn giải:
Điều kiện:
2
2
2
2 1 0
2 1 0
21
2
0
2
x mx
x mx
x mx
x
x
+ +
+ +

++
−
+
.
Phương trình đã cho tương đương với
( ) ( )
22
22
log 2 1 2 1 2 log 2 1x mx x mx x x+ + + + + = + + +
.
39
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
39
Xét hàm số
( )
2
logf t t t=+
,
( )
0;t +
;
( ) ( )
1
1 0, 0;
ln2
f t t
t
= + +
.
Suy ra
( )
ft
đồng biến trên
( )
0;+
.
Vì vậy:
( )
(
)
( )
22
1 2 1 2 2 1 2f x mx f x x mx x + + = + + + = +
2
22
2 1 4 4
x
x mx x x
−
+ + = + +
( ) ( )
2
4 3 0 2x m x + − − =
.
Phương trình đã cho có hai nghiệm phân biệt
( )
2
có hai nghiệm phân biệt lớn hơn
2−
( )
( ) ( )
( )
( )
2
2
4 4 3 0
0
4 12 0,
8
49
2 2 4 4
9
2 2 2
2 9 0
2
2 0 1. 4 2 8 3 0
m
mm
m
Sm
mm
m
m
af m
− − −

− +
−
− − − −
− +

− − + −
.
Do
*
1;2;3;4mm
. Vậy có bốn giá trị của
m
thỏa mãn. Chọn C.
VÍ DỤ 65. Cho phương trình
( )
( )
2
22
1
2
2
4 .log 2 3 2 .log 2 2 0
xm
xx
x x x m
−−
−
− + + − + =
với
m
là tham số.
Tổng tất cả các giá trị của tham số
m
để phương trình đã cho có ba nghiệm phân biệt là
A.
4
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải:
Phương trình đã cho tương đương với
( )
( )
( )
2
2
12
11
22
2 .log 1 2 2 .log 2 2 0
xm
x
x x m
−−
−−

− + − − + =

( )
( )
( )
2
12
11
2
2
2
22
log 2 2
log 1 2
xm
x
xm
x
−−
−−
=
−+

−+

(*).
Xét hàm số
( )
( )
( )
1
2
2
0
log 2
t
f t t
t
−
=
+
;
( )
( )
( )
( )
1
1
2
2
2
2
2 .ln 2.log 2
2 ln2
0, 0.
log 2
t
t
t
t
f t t
t
+
+
−
−
+
− + −
+
=
+


Suy ra hàm
( )
ft
nghịch biến trên
)
0;+
.
Vì vậy:
( )
( )
( )
( )
( )
2
22
2
2 1 2 2
* 2 1 1 2
2 1 2 2
x x x m
f x m f x x x m
x x x m
− + = −
− = − − = −
− + = − +
( )
2
2
4 1 2
**
12
x x m
xm
− + − =
+=
.
40
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
40
Nhận xét: Số nghiệm của (**) chính là số giao điểm giữa
đường thẳng nằm ngang
2ym=
với hợp hai đồ thị hàm
số
( ) ( )
22
12
4 1 , 1y x x C y x C= − + − = +
. Xem hình.
Phương trình đã cho có ba nghiệm phân biệt
( )
**
có ba
nghiệm phân biệt
1
21
2
2 2 1
2 3 3
2
m
m
mm
m
m
=
=
= =
=
=
.
Tổng các giá trị của m là:
13
1 3.
22
+ + =
Chọn D.
VÍ DỤ 66. Gọi
S
là tập hợp các giá trị của tham số
m
sao cho hai phương trình
2
2 1 3
m
x +=
và
2
3 2 1
x
m x x= − + −
có nghiệm chung. Tính tổng các phần tử của
S
.
A.
6
. B.
3
. C. 1. D.
5
2
.
Hướng dẫn giải:
Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm
(*).
Xét hàm
( )
3
t
f t t=+
,
t
;
( )
3 ln3 1 0
t
ft
= +
; suy ra hàm
( )
3
t
f t t=+
đồng biến trên .
Do vậy: (*)
( )
( )
( )
2
3
log 2 1f x f x + =
.
Xét hàm số xác định và liên tục trên .
Ta có:
( ) ( ) ( )
23
4 3 ln3, 4 3 ln 3, 3 ln 3 0,
x x x
g x x g x g x x
= − = − = −
.
Suy ra hàm số
( )
gx

nghịch biến trên nên
( )
0gx

=
có tối đa một nghiệm.
Suy ra
( )
0gx
=
có tối đa hai nghiệm; và vì thế phương trình
( )
0gx=
có tối đa là ba nghiệm.
Ta lại có:
( ) ( ) ( )
0 1 2 0g g g= = =
. Vì vậy: .
Tổng các giá trị m thu được bằng 3. Chọn B.
( )
( )
2
2
22
3
3
2
2
log 2 1
2 1 3
log 2 1 3 2 1
3 2 1
3 2 1
m
x
x
x
mx
x
x x x
m x x
m x x
=+
+=

+ = − + −

= − + −
= − + −
( )
( )
( )
2
3
log 2 1
2 2 2
33
log 2 1 2 1 3 3 log 2 1 3
x
xx
x x x x x
+
+ + + = + + + = +
( )
22
3
log 2 1 2 1 3
x
x x x+ = + =
( )
2
2 1 3
x
g x x= + −
2
00
2 1 3 1 1
22
x
xm
x x m
xm
==
+ = = =
==
41
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
41
Bài toán 6. Nghiệm đặc biệt của phương trình mũ, lôgarit chứa hàm đối xứng
VÍ DỤ 67. Cho biết có một giá trị của
m
để phương trình
1
4 2 0
xx
m
+
− − =
có nghiệm duy nhất, khi đó:
A.
3
2
2
m− −
. B.
1m
. C.
2m −
. D.
3
0
2
m−
.
Hướng dẫn giải:
Xét hàm số
( )
1
42
xx
f x m
+
= − −
xác định trên .
Ta có:
( ) ( )
11
4 2 4 2
x x x x
f x m m f x
− − + +
− = − − = − − =
.
Vì vậy
( )
fx
là hàm số chẵn. Nếu
0
x
là một nghiệm của phương trình
( )
0fx=
thì
0
x−
cũng là
một nghiệm của phương trình
( )
0fx=
.
Điều kiện cần: Phương trình
( )
0fx=
có nghiệm duy nhất suy ra
0 0 0
0x x x= − =
.
Thay vào phương trình ban đầu, ta có:
0 0 1
4 2 0 1mm
+
− − = = −
.
Điều kiện đủ: Thử lại với
1m =−
, thay vào phương trình đã cho:
( )
2
4 2.2 1 0 2 1 0 2 1 0
x x x x
x− + = − = = =
.
Vậy
1m =−
thỏa mãn đề bài. Chọn D.
VÍ DỤ 68. Cho phương trình
( )
2 .2 .cos 4
xx
mx
=−
, với
m
là tham số. Gọi
0
m
là giá trị của
m
sao cho
phương trình trên có đúng một nghiệm thực. Khẳng định nào sau đây là đúng?
A.
)
0
5; 1 .m − −
B.
0
5.m −
C.
)
0
1;0 .m −
D.
0
0.m
Hướng dẫn giải:
Phương trình đã cho tương đương với
( ) ( )
2
4 .2 .cos 4 2 2 .cos 0
x x x x
m x m x

−
= − + − =
(*).
Xét hàm
( ) ( )
2
2 2 .cos
xx
f x m x
−
= + −
với mọi
x
.
Ta có:
( )
( )
( )
22
2
2 2 2 cos 2
x
x
f x m x
−−
−
− = + − −
( ) ( ) ( )
22
2 2 cos 2 2 2 cos
x x x x
m x m x f x
−−
= + − − = + − =
.
Vậy
( ) ( )
2f x f x−=
nên hàm
f
đối xứng theo
x
và
2 x−
. Nếu
0
x
là một nghiệm của (*) thì
0
2 x−
cũng là một nghiệm của (*).
Điều kiện cần: Phương trình (*) có nghiệm duy nhất nên
0 0 0
21x x x= − =
.
Thay vào phương trình ta có:
( )
1 2 1
2 2 .cos 0 4mm
−
+ − = = −
.
Điều kiện đủ: Thử lại với
4m =−
, ta có:
( )
4 4.2 cos 4 0
xx
x
+ + =
( ) ( ) ( ) ( ) ( )
2
2 2 2
4 4.2 cos 4cos 4 4cos 0 2 2cos 4sin 0
x x x
x x x x x

+ + + − = + + =

42
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
42
( )
( )
( )
( )
( )
( )
2 2cos
2 2cos
22
1
cos 1
cos 1
sin 0
cos 1
x
x
x
x
x
x
x
x
x
x
=−
=−
=

=
=

=−
=
=−
.
Vậy
4m =−
thỏa mãn. Chọn A.
Bài toán 7. Tìm điều kiện tham số của phương trình mũ, lôgarit có chứa hàm ẩn
VÍ DỤ 69. Cho hàm số
()=y f x
có bảng biến thiên như sau:
Tìm giá trị lớn nhất của
m
để phương trình:
( ) ( ) ( )
32
13 3
27
22
e
f x f x f x
m
− + +
=
có nghiệm trên đoạn
0;2
.
A.
5
e
. B.
15
13
e
. C.
3
e
. D.
4
e
.
Hướng dẫn giải:
Ta có:
( ) ( ) ( )
32
13 3
27
22
e
f x f x f x
m
− + +
=
( ) ( ) ( )
32
13 3
2 7 ln
22
− + + =f x f x f x m
.
Đặt
( ) ( ) ( ) ( )
32
13 3
27
22
= − + +g x f x f x f x
;
( ) ( ) ( ) ( )
2
6 13 7 .g x f x f x f x


= − +

.
Ta có:
( )
( )
( ) ( )
13
0
0 1 3
7
1
0
6
xx
fx
g x x x a
f x f x
xb
= =
=
= = =
= =
=
.
Bảng biến thiên của
( )
gx
trên đoạn
0;2
:
Giá trị lớn nhất của
m
để phương trình có nghiệm trên
0;2
thỏa mãn:
4
ln 4 e= =mm
.
Chọn D.
43
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
43
VÍ DỤ 70. Cho cấp số cộng
( )
n
a
, cấp số nhân
( )
n
b
, thỏa mãn
21
0aa
,
21
1bb
và hàm số
3
( ) 3f x x x=−
sao cho
21
( ) 2 ( )f a f a+=
và
( ) ( )
2 2 2 1
log 2 logf b f b+=
. Tìm số nguyên dương
n
nhỏ nhất sao cho
( )
2022
nn
b a n − −
.
A. 17. B. 12. C. 15. D. 13.
Định hướng: Ta cần tìm công thức tổng quát của các dãy số
( )
n
a
và
( )
n
b
dựa vào những dữ
kiện đã cho trước khi tìm n thông qua
( )
2022
nn
b a n − −
.
Hướng dẫn giải:
Ta có:
21
21
21
0
0
d a a
aa
a a d
= −
=+
với d là công sai cập số cộng.
Khi đó:
( )
3
3
2 1 1 1 1 1 1 1
( ) 2 ( ) ( ) 2 ( ) 3( ) 2 3f a f a f a d f a a d a d a a+ = + + = + − + + = −
2
11
0
0
3 ( 1) ( 2) 0a d a d d d
++
+

+ + − + =



( )
1
1
2
0
0
1
10
a
a
d
d
=
=


=
−=
.
Do vậy:
1
( 1) 1
n
a a n d n= + − = −
.
Ta lại có:
2
1
21
21
1
1
b
q
b
bb
b b q
=
=
. Suy ra:
( )
2 2 2 1 2 1 2
log ( ) log log logb b q b q= = +
.
Đặt
2 2 2 1 2 1 2 2 1
log 0, log 0, log 0t b t b m q t t m= = = = +
.
Khi đó:
21
( ) 2 ( )f t f t+=
( ) ( )
3
3 3 3
2 2 1 1 1 1 1 1
3 2 3 3 2 3t t t t t m t m t t − + = − + − + + = −
2
11
0
0
3 . .( ) ( 1) ( 2) 0m t t m m m
++
+
+ + − + =
21
11
2
log 0
01
log 1
12
b
tb
q
mq
=
==

=
==

.
Do vậy:
11
1
.2
nn
n
b b q
−−
==
.
Ta có:
( )
11
2
2022 2 1 2022 2 2021 1 log 2021 10,98
nn
nn
b a n n n n
−−
− − − − + −
.
Suy ra
11,98n
. Vì n nguyên dương và nhỏ nhất nên
12n =
. Chọn B.
VÍ DỤ 71. Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
0;9
sao cho bất phương trình
( ) ( ) ( ) ( ) ( )
22
2 16.2 4 16 0
f x f x m f x f x m f x+ − − −
− − + =
có nghiệm
( )
1;1x−
.
44
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
44
A.
6
. B.
8
. C.
5
. D.
7
.
Hướng dẫn giải:
Ta có:
( ) ( ) ( ) ( ) ( )
22
2 16.2 4 16 0
f x f x m f x f x m f x+ − − −
− − + =
( ) ( ) ( ) ( ) ( )
22
2
16 16.2 2 2 0
f x f x m f x f x f x m− − + −
− − − =
( ) ( ) ( ) ( ) ( )
22
2
16 1 2 2 1 2 0
f x f x m f x f x f x m− − − −
− − − =
( ) ( ) ( )
2
2
1 2 16 2 0
f x f x m f x−−


− − =


(1).
Với
( )
1;1x−
thì
( ) ( ) ( ) ( )
( ) ( )
22
1
2;2 2 4;4 2 ;16 16 2 0
16
f x f x
f x f x

− − −


.
Khi đó:
( )
( ) ( )
( ) ( ) ( ) ( )
2
22
1 1 2 0 0
f x f x m
f x f x m m f x f x
−−
− = − − = = −
(2).
Đặt
( )
=t f x
,
( )
2;2t −
. Khi đó:
( )
2
trở thành
2
m t t = −
(3).
Xét hàm
( ) ( )
2
, 2;2g t t t t= − −
;
( )
1
2 1 0
2
g t t t
= − = =
.
Vậy phương trình đã cho có nghiệm
( )
1;1−x
(3) có nghiệm
( )
2;2−t
1
6
4
m −
.
Vì
, 0;9 0;1;2;3;4;5m m m
. Chọn A.
45
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
45
Phương pháp giải toán:
1. Phương trình nhiều ẩn:
• Một phương trình nhiều ẩn là một mệnh đề chứa biến có dạng:
( ) ( )
, , , ,... 0 *f x y z t =
trong đó
( )
, , , ,...f x y z t
là một biểu thức chứa nhiều biến số là
, , , ...x y z t
. Mỗi bộ số
( )
; ; ; ;...x y z t
làm cho mệnh đề (*) đúng thì chúng được gọi là một nghiệm của (*).
• Phương trình hai ẩn có dạng:
( ) ( )
, 0 **f x y =
. Mỗi bộ số
( )
;xy
làm cho (**) thỏa
mãn được gọi là một nghiệm của (**).
2. Tìm điều kiện của ẩn cho bài toán nghiệm nguyên:
Một cách tổng quát, ta xét bài toán phương trình hai biến dạng
( )
,0f x y =
.
Cách giải 1:
⎯ Cô lập một ẩn của phương trình, đưa về dạng:
( )
x g y=
hoặc
( )
y g x=
.
Trong bước giải này, ta có thể sử dụng phương trình tích hoặc các phương pháp đánh
giá hai vế bằng bất đẳng thức, hàm số; cũng có thể dùng hàm đặc trưng để làm.
⎯ Dựa vào điều kiện cho ẩn x hoặc y để giới hạn số nghiệm của phương trình.
Cách giải 2:
⎯ Tìm một mối liên hệ thu gọn của các biến.
⎯ Sử dụng điều kiện
0
để phương trình bậc hai có nghiệm (hoặc dùng điều kiện tương
giao giữa các đường cơ bản, hay các bất đẳng thức cơ bản đã học) để giới hạn phạm vi
một ẩn.
⎯ Suy ra phạm vi của ẩn còn lại dựa vào giả thiết của bài toán.
Cách giải 3:
⎯ Tìm một mối liên hệ thu gọn của các biến.
⎯ Dựa vào tính chất điểm có tọa độ nguyên thuộc các đường cong đã học (sử dụng thêm
các tính chất đặc thù của số nguyên đối với phép nhân, chia, tổng, tổng bình phương
v.v…) để suy ra phạm vi nghiệm phương trình.
Bài toán 1. Nghiệm nguyên của phương trình mũ và lôgarit dạng tích
VÍ DỤ 73. Có bao nhiêu số nguyên dương
a
nhỏ hơn
2021
sao cho tồn tại số nguyên
x
thỏa mãn
( ) ( )
3 2 3
2 2 1 2 2 1
a x a x
aa
++
− + = + −
?
A.
12
. B.
15
. C.
10
. D.
14
.
Hướng dẫn giải:
46
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
46
Ta có:
( ) ( ) ( ) ( )
3 2 3 3 2 3
2 2 1 2 2 1 2 2 1 2 . 2 1 0
a x a x a x a x
a a a a a
+ + + +
− + = + − − − + − − =
( ) ( )
33
2 2 1 2 1 0
a x x
a a a
++
− − − − − =
( )( )
3
2 2 1 0
ax
aa
+
− − − =
3
20
2 1 0
a
x
a
a
+
−=
− − =
.
Trường hợp 1:
20
a
a−=
. Xét hàm số
( )
2
a
f a a=−
với
0a
.
Ta có:
( ) ( )
20
1
2 ln2 1; 0 log
ln2
a
f a f a a a


= − = = =


.
Bảng biến thiên
Từ bảng biến thiên, suy ra
( ) ( )
0
0,914 0f a f a
.Suy ra phương trình
20
a
a−=
vô nghiệm.
Trường hợp 2:
33
2 1 0 2 1
xx
aa
++
− − = = −
.
Vì a dương và nhỏ hơn 2021 nên
3
3
22
3 0 3
2 1 0
.
3 log 2022 log 2022 3 7,98
2 1 2021
x
x
xx
xx
+
+
+ −
−


+ −
−

Mặt khác
2; 1;0;1;2;3;4;5;6;7x x A − − =
.
Với mỗi giá trị x thuộc tập A, ta tìm được một giá trị nguyên a tương ứng. Chọn C.
VÍ DỤ 74. Có bao nhiêu cặp số nguyên dương
( )
;xy
thoả mãn
( )
( )
23
3 3 1 1 3
x y x y
x x x
+
− − = + −
, với
2024x
?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
( )
( )
( ) ( )
2 3 2
3 3 1 1 3 3 3 1 3 1
x y x y y x x
x x x x x x
+
− − = + − − − = − −
( )( )
( )
( )
2
2
3 1 0 1
3 3 1 0
3 0 2
x
yx
y
x
xx
x
− − =
− − − =
−=
.
Giải phương trình (1): Đặt
( ) ( )
3 1, 0;2024
x
f x x x= − −
;
( ) ( )
3 ln3 1 0, 0;2024
x
f x x
= −
.
Suy ra
( ) ( ) ( )
0 0, 0;2024f x f x =
. Vì vậy phương trình (1) vô nghiệm.
Giải phương trình (2): Ta có:
1
0
22
2
3 0 3 3
x
y
yy
x x x
− = = =
.
13
15
6
7
47
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
47
Do
2024x
nên
1
2
33
1
3 2024 log 2024 2log 2024 13,86
2
y
yy
; mà y nguyên dương
nên
1;2;...;13y
. Vậy có 13 cặp số nguyên dương
( )
;xy
thỏa mãn đề bài. Chọn A.
Bài toán 2. Nghiệm nguyên của phương trình mũ và lôgarit chứa hàm đặc trưng
VÍ DỤ 75. Cho
0 2021x
và
( )
3
log 1 3 1 27
y
x x y+ + − + =
. Có bao nhiêu cặp số
( )
;xy
nguyên thỏa
mãn điều kiện trên?
A.
2021
. B.
2020
. C.
4
. D.
3
.
Hướng dẫn giải:
Với điều kiện
0 2021x
, phương trình đã cho tương đương:
( )
( )
( ) ( )
3
log 1
3
33
log 1 1 27 3 3 log 1 3 3 *
x
yy
x x y x y
+
+ + + = + + + = +
.
Xét hàm số
( )
3
t
f t t=+
với
t
;
( )
3.ln3 1 0,
t
f t t
= +
nên
( )
ft
đồng biến trên .
Vì vậy:
( ) ( )
( )
( ) ( )
33
* log 1 3 log 1 3 1 27 27 1
yy
f x f y x y x x + = + = + = = −
.
Theo giả thiết:
0 2021x
27
0 27 1 2021 1 27 2022 0 log 2022 2,31
yy
y −
.
Ta có
y
nên
0;1;2y
; suy ra
0;26;728x
.
Do đó có 3 cặp số nguyên
( )
;xy
thỏa mãn phương trình đã cho là:
( ) ( ) ( )
0;0 , 26;1 , 728;2
.
Chọn D.
VÍ DỤ 76. Có bao nhiêu cặp số
( )
;xy
sao cho y nguyên thuộc đoạn
2023;2023−
và x là số thực thỏa
mãn
( )
2
log 5 2 5 2
x
y y x− + + − =
?
A.
2019
. B.
2021
. C.
4041
. D.
2021
.
_____Thi thử Chuyên Lê Hồng Phong, TP.HCM, 2021_____
Hướng dẫn giải:
Điều kiện:
2 5 0
5 2 5 0
x
x
y
yy
+ −
− + + −
. Phương trình đã cho tương đương với:
2
5 2 5 2
xx
yy− + + − =
( )
2
2 5 2 5 2 2 1
x x x x
yy + − + + − = +
.
Xét hàm số
( )
2
f t t t=+
với
0t
;
( )
2 1 0, 0f t t t
= +
nên
( )
ft
đồng biến trên
( )
0;+
.
Vì vậy:
( )
( )
( )
( )
22
1 5 2 2 5 2 2 5 2 2 2 2 5 2
x x x x x x x x
f y f y y y − + = − + = − + = = − +
.
Xét hàm
( )
2
2 2 5
xx
gx= − +
với
x
;
48
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
48
( )
42
ln2 1 1
4 ln4 2 ln2 0 2 log 2 log 1
ln4 2 2
x x x
g x x

= − = = = = = = −


.
Bảng biến thiên:
Ta thấy: Phương trình đã cho có nghiệm
Phương trình
( )
2
có nghiệm
19
4
y
.
Do
y
và
2023;2023y−
nên
5;6;...;2023y
. Vậy có 2019 cặp (x;y) thỏa mãn. Chọn A.
VÍ DỤ 77. Cho phương trình
( )( )
( )
( )
2 4 7
4 7 2 1 2 2 7
xy x y y
xy y x e e x y y e
++
+ − − = − + +


. Hỏi có bao
nhiêu cặp số nguyên
( )
;xy
thỏa mãn phương trình đã cho?
A.
8
. B.
5
. C.
6
. D.
7
.
Hướng dẫn giải:
Ta có:
( )( )
( )
( )
2 4 7
4 7 2 1 2 2 7
xy x y y
xy y x e e x y y e
++
+ − − = − + +


( )( )
( )
( )
2 4 7
4 7 2 2 2 7
xy y x
x xy y e e x y y
−+
+ − − = − + +
(chia hai vế phương trình cho
0)
y
e
.
( )( )
( )
( ) ( )
2 4 7
4 7 2 . 4 7 2
xy y x
x xy y e e x xy y
−+
+ − − = + − −
( ) ( ) ( ) ( )
2 4 7
4 7 . 2 1 2 4 7 1
xy y x
x xy y e xy y x e
−+
+ − − = − + −
( ) ( )
2 4 7
2 1 4 7 1
2 4 7
xy y x
xy y e x e
xy y x
−+
− − + −
=
−+
(do x, y nguyên nên
71
, , 0
42
x x y −
)
2 4 7
11
2 4 7
xy y x
ee
xy y x
−+
− = −
−+
(*).
Xét hàm
( )
1
t
f t e
t
=−
với
0t
;
( )
2
1
0, 0
t
f t e t
t
= +
( )
ft
đồng biến trên các khoảng xác
định của nó.
Vì vậy: (*)
( ) ( )
4 7 9
2 4 7 2 4 7 2
2 1 2 1
x
f xy y f x xy y x y
xx
+
− = + − = + = = +
−−
.
Vì y nguyên nên
21x −
là ước số nguyên của 9, do vậy
2 1 1 1 0
2 1 3 2 1
2 1 9 5 4
x x x
x x x
x x x
− = = =


− = = = −


− = = = −

.
Vậy có 6 cặp số nguyên (x;y) thỏa mãn đề bài. Chọn C.
49
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
49
Bài toán 3. Phương pháp đánh giá và bài toán nghiệm nguyên phương trình mũ, lôgarit
VÍ DỤ 78. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;3
3
x



thỏa mãn
( )
2
39
27 1 27
x xy x
xy
+
=+
.
A.
27
. B.
9
. C.
11
. D.
12
.
_____Mã đề 101, Đề thi THPT Quốc Gia năm 2021_____
Ý tưởng:
• Tìm điều kiện cho y với
1
;3
3
x



. Biến đổi phương trình về
2
39
27 1 0
x xy x
xy
+−
− − =
.
• Xét hàm hai biến
( )
2
39
, 27 1
x xy x
f x y xy
+−
= − −
, đây là hàm liên tục với mọi
,xy
.
• Ta chứng minh
( )
3, 0fy
trên miền điều kiện của nó. Phương trình đã cho có nghiệm
( )
( )
3, 0
1 1 1
;3 , . 3, 0 , 0
3 3 3
fy
x f y f y f y
(ứng với đặc thù của hàm số đang xét).
Từ đây ta tìm điều kiện cho y.
Hướng dẫn giải:
Từ phương trình suy ra:
0
1
10
x
xy y
x
+ −
mà
1
;3
3
x



nên
3y −
; vì y nguyên nên
2.y −
Phương trình tương đương với
2
39
27 1 0
x xy x
xy
+−
− − =
(*).
Xét hàm hai biến
( )
2
39
, 27 1
x xy x
f x y xy
+−
= − −
, ta thấy hàm này liên tục với mọi
1
;3
3
x



,
2y −
.
Ta có:
( ) ( )
3
3, 27 3 1
y
f y y g y= − − =
với
( ) ( )
63
2 27 5 0, 1 27 2 0gg
−−
− = + − = +
(1);
( )
00g =
nên ta thay
0y =
vào phương trình đã cho:
2
39
1
0 ;3
3
27 27
1
3 ;3
3
xx
x
x

=


=

=


, do vậy
0y =
không thỏa mãn phương trình ban đầu (2).
Ta có:
( )
( )
33
3.27 ln27 3 3 27 ln27 1 0, 1
yy
g y y
= − = −
; suy ra
( ) ( )
3
1 27 4 0g y g = −
(3).
Từ (1), (2), (3) suy ra
( )
0, 2, , 0g y y y y −
.
50
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
50
Ta có:
( )
8
11
, 3 1
33
y
f y y h y
−

= − − =


với
2y −
; trong đó
( )
1
3 ln3 0
3
y
hy
= − =
30
1,856
1
log
3ln3
yy
−

= =


. Mặt khác
( ) ( )
3 . 2 0hh− −
và
( ) ( )
9 . 10 0hh
nên tồn tại
( ) ( )
12
3; 2 , 9;10yy − −
để
( )
0hy=
. Ta có bảng biến thiên:
Phương trình đã cho có nghiệm
1
;3
3
x



( ) ( )
( )
( ) ( )
( )
1 3,
,
3
. 0 0 do 0
fy
fy
g y h y h y g y



.
Dựa vào bảng biến thiên, kết hợp
,2yy
, ta có:
2; 1;1;2;...;9y − −
thỏa mãn. Chọn C.
VÍ DỤ 79. Có bao nhiêu số nguyên
y
nằm trong khoảng
( )
2027;− +
sao cho với mỗi giá trị của
y
tồn tại nhiều hơn hai số thực
x
thỏa mãn
( ) ( )
2
2 2 2
.2027 2 .2027
x y x x
x y x x x x y
+−
+ + − = − +
?
A.
2026
. B.
2027
. C.
2028
. D.
2029
.
Hướng dẫn giải:
Nhân hai vế phương trình đã cho với
2
2027
xx−
, ta được phương trình sau:
( ) ( ) ( ) ( )
22
2 2 2 2
.2027 .2027
x x x y
x y x x x x x y
−+
+ + − = − + +
( )
( )
( )
( )
22
22
. 2027 1 . 2027 1 0
x x x y
x y x x
−+
+ − + − − =
( )
1
.
Xét
( )( )
22
0x y x x+ −
. Khi đó:
( )
1
22
22
2027 1 2027 1
0
x x x y
x x x y
−+
−−
+=
−+
( )
2
• Nếu
2
0xx−
thì
2
2027 1 0
xx−
−
nên
2
2
2027 1
0
xx
xx
−
−
−
.
• Nếu
2
0xx−
thì
2
2027 1 0
xx−
−
nên
2
2
2027 1
0
xx
xx
−
−
−
. Vậy
2
2
2027 1
0
xx
xx
−
−
−
khi
2
0xx−
.
• Lý luận tương tự, ta có
2
2
2027 1
0
xy
xy
+
−
+
khi
2
0xy+
.
51
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
51
Vì vậy vế trái (2) luôn dương nên (2) vô nghiệm. Do đó: (1)
2
2
2
0
0
1
0
x
xx
x
xy
xy
=
−=
=
+=
=−
.
Nhận xét: Với mọi số thực y thì phương trình đã cho luôn có sẵn hai nghiệm 0; 1. Vì vậy ta cần
phương trình
2
xy=−
có không dưới một nghiệm khác 0; 1. Suy ra
0y−
0y
.
Do
y
nguyên thuộc
( )
2027;− +
nên
2026; 2025;...; 1y − − −
. Chọn A.
VÍ DỤ 80. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
( )
( )
22
34
log log 2x y x y+ = +
A.
3
. B.
2
. C. Vô số. D.
1
.
_____Thi thử THPT Quốc Oai, Hà Nội, 2021_____
Hướng dẫn giải:
Điều kiện :
22
0
20
xy
xy
+
+
. Đặt :
( )
( )
22
34
22
3
log log 2
24
t
t
xy
x y x y t
xy
+=
+ = + =
+=
.
Ta có:
( )
2
2
Cauchy-Schwarz
2
22
9
4
3
4
1 1 3 3 1
1. . 2 1 2 3 .4 log
2 2 2 2
2
t
t
tt
x y x y x y t






+ = + + + =







.
Mặt khác
1
2
2
4 4 2 2 2
t
xx = −
. Vì
1;0;1xx −
.
Với
1x =−
, ta có:
2
13
2 4 1
t
t
y
y
=+
=−
( )
2
4 1 2 1 3 2.9 4.3 3 4 0
t t t t t
− = + + + − =
(1).
• Nếu
0t
thì
2.9 4 0; 4.3 3 0
t t t
− +
Vế trái (1) luôn dương.
• Nếu
0t
thì
3 4 0; 2.9 4.3 0
t t t
− +
Vế trái (1) luôn dương.
Do vậy (1) không có nghiệm t nên không tồn tại y thỏa mãn đề bài.
Với
0x =
, ta có:
9
2
4
3
1
2.9 4 log
2
24
t
tt
t
y
t
y
=
= =
=
. Khi đó
9
4
1
log
2
3 0,391y =
(tồn tại số thực y).
Với
1x =
, ta có:
( )
2
2
31
4 1 2. 3 1 2.9 4.3 3 4 0
2 4 1
t
t t t t t
t
y
y
=−
− = − − + − =
=−
. Ta thấy phương trình
này có ít nhất một nghiệm
0t =
, suy ra
0y =
(tức là đã tồn tại y thỏa mãn phương trình ban đầu).
Vậy có
2
giá trị nguyên của
x
thỏa đề là
0x =
và
1x =
. Chọn B.
52
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
52
Bài toán 4. Xét nghiệm nguyên phương trình mũ, lôgarit dựa vào đặc thù của tổng, tích,
tổng bình phương… các số nguyên
VÍ DỤ 81. Có bao nhiêu cặp số nguyên dương
( )
;xy
thỏa mãn
log log log log 100x y x y+ + + =
và
log , log ,xy
log , logxy
cũng là các số nguyên dương?
A.
3
. B.
2
. C. 0. D.
1
.
_____Thi thử Sở GD-ĐT Hà Nội năm 2020_____
Hướng dẫn giải:
Ta có:
11
log log log log 100 log log log log 100
22
x y x y x y x y+ + + = + + + =
(1).
Đặt
22
log , log log , loga x b y a x b y= = = =
.
Khi đó (1) trở thành:
( ) ( ) ( ) ( )
2 2 2 2
2 2 2 2
11
100 1 1 202 1 1 9 11
22
a b a b a b a b+ + + = + + + = + + + = +
.
Vì
*
,ab
nên
1 9 1 11 8 10
1 11 1 9 10 8
a a a a
b b b b
+ = + = = =
+ = + = = =
.
• Với
8
10
a
b
=
=
thì
64
100
log 8
log 64 10
log 100
10
log 10
x
xx
y
y
y
=
==


=
=
=
.
• Với
10
8
a
b
=
=
thì
100
64
log 10
log 100 10
log 64
10
log 8
x
xx
y
y
y
=
==


=
=
=
.
Vậy có hai cặp số
( )
;xy
thỏa mãn đề bài. Chọn B.
VÍ DỤ 82. Có bao nhiêu số nguyên dương x sao cho tồn tại số nguyên dương y thỏa mãn điều kiện
( )( )
1
2
3
log 2 2 1 2 3.9 27 1?
xy
xy
x y x y
−
+
− + + + = +


A.
3
. B.
2
. C. 0. D.
1
.
Hướng dẫn giải:
Điều kiện:
*
,
2 2 1 0
xy
xy
− +
.
Phương trình đã cho tương đương với
( ) ( )
3
2 2 1
2
3 3 3
log 2 2 1 log 2 3 3 log 3
xy
xy
x y x y
−+
+
− + + + + = +
( )
3
2 2 1
2
33
3
log 2 2 1 3 log 3 (1).
2
xy
xy
xy
xy
−+
+
− + + = +
+
Đặt
( ) ( )
3
1
log 3 , 0; 3 ln3 0, 0
ln3
tt
f t t t f t t
t
= + = +
. Suy ra
( )
ft
đồng biến trên
( )
0;+
.
53
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
53
Vì vậy:
( ) ( ) ( )( ) ( )
33
1 2 2 1 2 2 1 2 2 1 2 3 * .
22
f x y f x y x y x y
x y x y

− + = − + = − + + =

++

Do điều kiện nên
*
*
2 2 1
2
xy
xy
− +
+
, (*) suy ra:
2 2 1 1 2 2 1 3
2 3 2 1
x y x y
x y x y
− + = − + =


+ = + =

1
1
x
y
=
=
(nhận) hoặc
1
0
x
y
=
=
(loại).
Vậy có duy nhất một cặp số
( ) ( )
; 1;1xy =
thỏa mãn đề bài. Chọn D.
Bài toán 5. Bài toán nghiệm nguyên phương trình mũ, lôgarit nhiều ẩn chứa tham số
VÍ DỤ 83. Có tất cả bao nhiêu giá trị thực của tham số sao cho phương trình
có nghiệm nguyên duy nhất?
A. . B. . C. . D. .
Hướng dẫn giải:
Nhận xét: Vì
,xy
có vai tr như nhau (đối xứng) nên nếu phương trình đã cho có một nghiệm
( )
00
;xy
thì
( )
00
;yx
cũng là một nghiệm của phương trình đó. Theo giả thiết, phương trình có nghiệm nguyên
duy nhất nên
00
xy=
.
Điều kiện:
10xy+ −
.
Điều kiện cn: Phương trình đã cho có nghiệm nguyên duy nhất
( )
00
;xy
00
xy=
.
Thay vào phương trình, ta được:
( )
( )
2
2
0 2 0
1
log 2 log 4 2 (*)
m
xx
+
=−
Vì
0 0 0
, 4 2 0 4 2 1x x x − −
. Hơn nữa:
( )
2
2
0
2 1 0x −
2
00
2 4 2xx−
Do đó (*):
( )
( )
( )
22
2
2 0 0 0
11
log 4 2 log 2 log 4 2
mm
x x x
++
+
+
− = −
( )
00
0
2
4 2 4 2
4 2 1
log 1 log 2
xx
x
m
−−
−
+
22
1 2 1mm +
mà
1;1 1mm − =
.
Điều kiện đủ: Với
1m =
thì phương trình đã cho trở thành
( )
( )
22
22
log log 2 2 2x y x y+ = + −
( ) ( )
22
22
1
2 2 2 1 1 0
1
x
x y x y x y
y
=
+ = + − − + − =
=
; ta thấy phương trình đã cho có nghiệm
nguyên duy nhất
( )
1;1
nên
1m =
thỏa mãn.
Vậy có hai giá trị m thỏa mãn đề bài. Chọn B.
1;1m−
( )
( )
2
22
2
1
log log 2 2 2
m
x y x y
+
+ = + −
( )
;xy
3
2
1
0
54
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
54
VÍ DỤ 84. Cho các số thực
,,x y z
thỏa mãn
( ) ( )
2 2 3 3
37
log 2 log 2 logx y x y z+ = + =
. Có bao giá trị
nguyên của
z
để có đúng hai cặp
( )
;xy
thỏa mãn đẳng thức trên.
A.
2
. B.
211
. C.
99
. D.
4.
Nhận xét:
Sau khi đặt
( ) ( )
( )
( )
( )
22
2 2 3 3 3 3
37
2 3 1
log 2 log 2 log 2 7 2
10 3
t
t
t
xy
x y x y z t x y
z
+=
+ = + = = + =
=
.
Phương trình (1) có vế trái là đẳng cấp bậc hai theo x, y; phương trình (2) có vế trái là đẳng cấp
bậc ba theo x, y. Bội số chung nhỏ nhất của 2 và 3 là 6, vì vậy ta lập phương hai vế của (1), bình
phương hai vế của (2), và sau đó tiến hành như lời giải sau.
Hướng dẫn giải:
Đặt:
( ) ( )
( )
( )
( )
22
2 2 3 3 3 3
37
2 3 1
log 2 log 2 log 2 7 2
10 3
t
t
t
xy
x y x y z t x y
z
+=
+ = + = = + =
=
.
Trường hợp 1:
0y =
.
Khi đó:
( )
3
27
t
x=
. Thay vào
( )
1
ta được:
3
2
3
3
49
2.7 3 log 2
t
t
t= =
; (3)
3
3
49
log 2
10z=
.
Trường hợp này không tồn tại hai cặp (x;y) thỏa mãn đề bài.
Trường hợp 2:
0y
.
Từ
( ) ( )
1 , 2
suy ra
( )
( )
( )
( )
( )
6
2
3
3
2
22
33
Chia
33
2
2
22
33
2
2 27
2
49 49
*
27 27
2
2 49
21
t
tt
y
t
x
xy
y
xy
xy
xy
x
y


+


+=
+



= =

+
+=

+





.
Đặt
x
u
y
=
. Xét hàm
( )
( )
( )
( )
( )
( )
( )
2
33
3
34
22
0
2 6 2 4
; 0 2
2 1 2 1
4
u
u u u u
f u f u u
uu
u
=
+ + −
= = = = −
++
=
.
Ta có bảng biến thiên:
55
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
55
Với mỗi giá trị
u
thỏa mãn (*), ta tìm được một cặp
( )
,xy
thỏa mãn đề bài.
Yêu cầu bài toán tương đương:
49 49
27 27
49 49
27 27
4
49
27
1
log log 4
8
1
log log 4
8
49 49
211,8
3,24.10
27 27
4
log
33
49
27
1
1 49
10 10
log log 4
4
8
10 10 10
8 27
4
49 4
log
0
0 10 10
33
27 33
t
t
t
t
z
t
t
−
























49
27
4
7
4
log
33
2,88.10
0 10z
−




.
Vì
z
nguyên nên
1;2;...;211z
. Vậy có
211
giá trị nguyên của z thỏa mãn. Chọn B.
C – BÀI TẬP THỰC HÀNH:
BÀI TẬP MỨC ĐỘ I:
Câu 1. Nghiệm của phương trình
21
1
3
27
x+
=
là
A.
1x =−
. B.
1x =
. C.
2x =−
. D.
3x =−
.
Câu 2. Phương trình
5
log (2 3) 1x−=
có nghiệm là
A.
2x =
. B.
4x =
. C.
5x =
. D.
3x =
.
Câu 3. Nghiệm của phương trình
( )
log 3 5 2x −=
A.
36x =
. B.
35x =
. C.
40x =
. D.
30x =
.
Câu 4. Nghiệm của phương trình
( )
3
log 1 2x −=
là
A.
10x =
. B.
9x =
. C.
8x =
. D.
11x =
.
Câu 5. Nghiệm của phương trình
1
28
x−
=
là
A.
2x =
. B.
3x =
. C.
4x =
. D.
5x =
.
Câu 6. Nghiệm của phương trình
1
5 125
x+
=
là
56
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
56
A.
2x=
. B.
3x=
. C.
0x=
. D.
1x=
.
Câu 7. Nghiệm của phương trình
( )
2
log 3 2 3x −=
là
A.
10
3
x =
. B.
8x =
. C.
1x =
. D.
1
3
x =
.
Câu 8. Phương trình
2
log ( 1) 3x +=
có nghiệm là
A.
5x =
. B.
7x =
. C.
8x =
. D.
10x =
.
Câu 9. Số nghiệm của phương trình
( )
2
22
log logx x x=−
là.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 10. Nghiệm của phương trình
1
28
x+
=
là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 11. Phương trình
( )
3
log 5 1 2x −=
có nghiệm là
A.
2
. B.
9
5
. C.
11
5
. D.
8
5
.
Câu 12. Nghiệm của phương trình
2
39
x+
=
là
A.
4x =
. B.
0x =
. C.
4x =−
. D.
3x =
.
Câu 13. Nghiệm của phương trình
24
39
x−
=
.
A.
3x =
. B.
2x =
. C.
1x =
. D.
1x =−
.
Câu 14. Nghiệm của phương trình
4
1
log (8 3 )
2
x−=
là
A.
3x =
. B.
2x =
. C.
2
2
36
10 4
2
x
x−
=+
. D.
3
.
Câu 15. Nghiệm của phương trình
1T =−
là
A.
6T =
. B.
5
6
T =
. C.
1
2
x =−
. D.
3
2
x =
.
Câu 16. Nghiệm của phương trình
( )
3
log 3 3x −=
là
A.
12x =
. B.
24x =
. C.
30x =
. D.
6x =
.
Câu 17. Số nghiệm của phương trình
1
3
1
7
7
x
x
+
−

=


là bao nhiêu
A. 1 B. 2 C. 3 D. 0
Câu 18. Tìm nghiệm của phương trình
45ab+
A.
6x =
. B.
21x =
. C.
13x =
. D.
9x =
.
57
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
57
Câu 19. Cho phương trình
2
45
39
xx−+
=
, tổng lập phương các nghiệm thực của phương trình là:
A.
25
. B.
28
. C.
26
. D.
27
.
Câu 20. Tìm tập nghiệm
S
của phương trình
4
log 3x =
.
A.
12S =
. B.
S =
. C.
64S =
. D.
81S =
.
Câu 21. Tập nghiệm của phương trình
2
log( 4) 1xx+ + =
là
A.
3; 2−
. B.
3−
. C.
2
. D.
2;3−
.
Câu 22. Tập nghiệm của phương trình
2
ln(2 1) 0xx− + =
là
A.
0
. B.
1
0;
2



. C.
1
2



. D.
.
Câu 23. Phương trình
( )
21
2
5 log 32
x−
=
có nghiệm là
A.
1x =
. B.
2
3
x =
. C.
3
2
x =
. D.
1
2
x =
.
Câu 24. Tìm tập nghiệm
S
của phương trình
32
x
=
.
A.
2
3
S

=


. B.
3
log 2S =
. C.
S =
. D.
2
log 3S =
.
Câu 25. Nghiệm của phương trình
( )
3
5 2 6 5 2 6
x
− = +
là
A.
1
. B.
1−
. C.
1
3
−
. D.
1
3
.
ĐÁP ÁN TRẮC NGHIỆM
1C
2B
3B
4A
5C
6A
7A
8B
9B
10C
11A
12B
13A
14B
15C
16C
17A
18B
19B
20C
21A
22B
23C
24B
25C
BÀI TẬP MỨC ĐỘ II:
Câu 26. Phương trình
2
23
x
x
=
có bao nhiêu nghiệm thực?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 27. Phương trình
2
2
36
10 4
2
x
x−
=+
có số nghiệm là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 28. Cho số thực
x
thoả mãn:
1
25 5 6 0
xx+
− − =
. Tính giá trị của biểu thức
55
x
T =−
.
58
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
58
A.
5T =
. B.
1T =−
. C.
6T =
. D.
5
6
T =
.
Câu 29. Số nghiệm thực của phương trình
( )
22
42
log log 2xx=−
là
A.
0
. B.
2
. C.
4
. D.
1
.
Câu 30. Phương trình
2
(ln 1) 0xx−=
có số nghiệm
là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 31. Số nghiệm thực của phương trình
2
33
xx−
=
là
A.
3.
B.
2.
C.
1.
D.
0.
Câu 32. Phương trình
( )
( )
2
2 5 log 3 0
x
x− − =
có hai nghiệm
12
,xx
(với
12
xx
). Tính giá trị của biểu
thức
12
3K x x=+
.
A.
3
32 log 2.K =+
B.
2
18 log 5.K =+
C.
2
24 log 5.K =+
D.
2
32 log 3.K =+
Câu 33. Biết
10
log 3 0,1
x
=−
. Mệnh đề nào sau đây đúng
A.
( )
1;0x−
. B.
( )
1;4x
. C.
( )
0;1x
. D.
( )
4; 1x − −
.
Câu 34. Tìm nghiệm phương trình
( )
42
2log log 3 2xx+ − =
.
A.
4x =
. B.
1x =
. C.
3x =
. D.
16x =
.
Câu 35. Tập nghiệm của phương trình
( )
2
2
1
log 2 1 0
2
x + − =
là
A.
1;0−
. B.
4−
. C.
0; 4−
. D.
0
.
Câu 36. Nghiệm của phương trình
1 ln81
9
x
e
−
=
là
A.
4.x =
B.
5.x =
C.
6.x =
D.
17.x =
Câu 37.
Với
,,a b x
là các số thực dương thỏa mãn
2 2 2
log 5.log 3.logx a b=+
. Mệnh đề nào sau đây
đúng?
A.
3 5 .x a b=+
B.
5 3 .x a b=+
C.
53
.x a b=+
D.
53
..x a b=
Câu 38. Gọi
1
x
,
2
x
là các nghiệm của phương trình
( )
( )
2
22
log log 1x x x− = +
. Tính
22
12
P x x=+
.
A.
6P =
. B.
8P =
. C.
2P =
. D.
4P =
.
Câu 39. Tổng tất cả các nghiệm của phương trình
( )
1
3
log 4.3 1 2 1
x
x
−
− = −
bằng
A.
1
. B.
2
. C.
7
. D.
3
.
Câu 40. Gọi
P
là tích tất cả các nghiệm của phương trình:
( ) ( )
32
22
log 1 log 2 1x x x+ + = +
. Tính .
P
..
59
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
59
A.
1P =
. B.
3P =
. C.
6P =
. D.
0P =
.
Câu 41. Nếu
2 2 2
log 5log 4logx a b=+
( )
,0ab
thì
x
bằng
A.
54
ab
. B.
45
ab
. C.
54ab+
. D.
45ab+
.
Câu 42. Nghiệm của phương trình
3 2020
42
x+
=
là
A.
2013x =
. B.
2023x =
. C.
1007x =
. D.
2017x =
.
Câu 43. Gọi
S
là tập hợp các giá trị của
x
để 3 số
( )
8
log 4x
;
4
1 log x+
;
2
log x
theo thứ tự lập thành
cấp số nhân. Số phần tử của
S
là
A. 2. B. 3. C. 1. D. 0.
Câu 44. Cho các số thực dương
,ab
thỏa mãn
( ) ( )
22
log 3 log .a b ab+ = +
Giá trị
11
ab
+
bằng
A.
3
. B.
1
3
. C.
1
8
. D.
8
.
Câu 45. Phương trình
2
31
4
1
3
9
x
x
−
−

=


có hai nghiệm
12
,.xx
Tính
12
.xx
A.
6
. B.
2−
. C.
5−
. D.
6−
.
Câu 46. Biết phương trình
4 5.2 3 0
xx
− + =
có hai nghiệm
12
,xx
. Tính
12
xx+
.
A.
3
. B.
2
log 3
. C.
5
. D.
2
log 5
.
Câu 47. Số nghiệm của phương trình
2
9 3 1 0
xx+
+ − =
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 48. Gọi
P
là tổng bình phương tất cả các nghiệm của phương trình
12
2 2 3
xx−−
+=
. Khi đó,
P
bằng
A.
3P =
. B.
5P =
. C.
9P =
. D.
1P =
.
Câu 49. Phương trình
3
log 1 2x
có tất cả bao nhiêu nghiệm?
A.
2
nghiệm. B. Vô nghiệm. C.
3
nghiệm. D.
1
nghiệm.
Câu 50. Tổng các nghiệm của phương trình
( ) ( )
2
3
3
log 2 log 4 0xx− + − =
là
2S a b=+
(với
a
;
b
là các số nguyên). Giá trị của biểu thức
Q ab=
bằng:
A.
0
. B.
3
. C.
9
. D.
6
.
ĐÁP ÁN TRẮC NGHIỆM
26A
27B
28B
29B
30C
31C
32C
33C
34A
35C
36B
37D
38A
39A
40D
41A
42C
43A
44D
45D
46B
47C
48B
49A
50D
60
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
60
BÀI TẬP MỨC ĐỘ III:
Câu 51. Tổng tất cả các nghiệm của phương trình
2 7 2 7
log 2log 2 log .logx x x x+ = +
bằng
A. 13. B. 11. C. 15. D. 10.
Câu 52. Tích tất cả các nghiệm của phương trình
(
)
(
)
2
5 21 5 21 5.2
x
xx
+ + − =
bằng:
A.
2−
. B.
4−
. C.
4
. D.
2
.
Câu 53. Tính
S
là tổng tất cả các nghiệm của phương trình
( ) ( )
22
4. 2 2 4. 2 2 7 0.
x x x x−−
+ − + − =
A.
1.S =
B.
1.S =−
C.
3.S =
D.
0.S =
Câu 54. Phương trình
( )
22
3.25 3 10 5 3 0
xx
xx
−−
+ − + − =
có tất cả bao nhiêu nghiệm?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 55. Cho phương trình
( ) ( )
5
3
22
2
11
x
x
x x x x
+
+
+ + = + +
. Tìm tổng tất cả các nghiệm của phương trình.
A.
17
4
−
. B.
13
4
−
. C.
15
4
−
. D.
11
4
−
.
Câu 56. Cho phương trình
( )
.16 2 2 .4 3 0
xx
m m m− − + − =
. Tập hợp tất cả các giá trị dương của
m
để
phương trình đã cho có hai nghiệm phân biệt là khoảng
( )
;.ab
Tổng
2T a b=+
bằng:
A.
14
. B.
10
. C.
11
. D.
7
.
Câu 57. Biết phương trình
( ) ( )
3
3 5 15 3 5 2
xx
x+
+ + − =
có hai nghiệm
12
,xx
và
1
2
log 1
a
x
b
x
=
, trong
đó
,ab
là các số nguyên tố, giá trị của biểu thức
2ab+
là:
A.
11
. B.
17
. C.
13
. D.
19
.
Câu 58. Tổng tất cả các nghiệm của phương trình
( )
4
2
3 1 1
3 81
1
log 5 6 log 2 log 3
2
x x x x− + + − = +
bằng
A.
10.
B.
3 10.
C. 0. D. 3.
Câu 59. Tìm tất cả các giá trị thực của tham số
m
để phương trình
33
log log 1 2 1 0x x m+ + − − =
có ít
nhất một nghiệm thực trong đoạn
1;27
.
A.
( )
0;2m
. B.
0;2m
. C.
2;4m
. D.
( )
0;4m
.
Câu 60. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
22
39
log log 2 0x m x m− + − =
có
nghiệm
1;9x
.
61
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
61
A.
1
. B.
5
. C.
3
. D.
2
.
Câu 61. Có bao nhiêu giá trị nguyên của
m
để phương trình
( ) ( )
2
2
log log 1mx x=+
vô nghiệm?
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 62. Tìm tất cả các giá trị của tham số
m
để phương trình
sin 1 sin
4 2 0
xx
m
+
+ − =
có nghiệm.
A.
5
8
3
m
. B.
5
8
4
m
. C.
5
7
4
m
. D.
5
9
4
m
.
Câu 63. Cho phương trình
( )
22
22
log 5 1 log 4 0x m x m m− + + + =
. Biết phương trình có 2 nghiệm phân
biệt
12
,xx
thỏa
12
165xx+=
. Giá trị của
12
xx−
bằng
A.
16
. B.
119
. C.
120
. D.
159
.
Câu 64. Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
3
3
log 3 log 9 16
x
xm
+
+ + =
có hai nghiệm
thỏa mãn
12
2 xx−
.
A.
17
. B.
16
. C.
14
. D.
15
.
Câu 65. Cho phương trình
( ) ( )
2
33
log 9 5 log 3 10 0x m x m− + + − =
. Số giá trị nguyên của tham số
m
để
phương trình đã cho có hai nghiệm phân biệt thuộc
1;81
là
A.
3
. B.
5
. C.
4
. D.
2
.
Câu 66. Phương trình
( )
( )
( )
2 3 1 2 2 3 4 0
xx
a+ + − − − =
có 2 nghiệm phân biệt
12
,xx
thỏa mãn
12
23
log 3xx
+
−=
. Khi đó
a
thuộc khoảng
A.
3
;
2

− −


. B.
( )
0;+
. C.
3
;
2

+


. D.
3
;
2

− +


.
Câu 67. Biết rằng
0
mm=
là giá trị của tham số
m
sao cho phương trình
( ) ( )
9 2 2 1 3 3 4 1 0
xx
mm− + + − =
có hai nghiệm thực
12
,xx
thỏa mãn
( )( )
12
2 2 12xx+ + =
. Khi
đó
0
m
thuộc khoảng nào sau đây
A.
(3;9)
. B.
( )
9;+
. C.
( )
1;3
. D.
( )
-2;0
.
Câu 68. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
16 2 1 4 3 8 0
xx
mm− + + − =
có
hai nghiệm trái dấu?
A.
6
. B.
7
. C.
0
. D.
3
.
Câu 69. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
12
16 .4 5 44 0
xx
mm
−
− + − =
có hai nghiệm đối nhau. Hỏi
S
có bao nhiêu phần tử?
A.
2
. B.
0
. C.
1
. D.
3
.
62
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
62
Câu 70. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
4 2 .2 6 0
xx
mm− − + =
có hai nghiệm thực
12
,xx
sao cho
12
3xx
. Tập hợp
S
có bao nhiêu phần tử?
A. Vô số. B.
3
. C.
2
. D.
1
.
Câu 71. Gọi
( ; )ab
là tập các giá trị của tham số
m
để phương trình
2
2e 8e 0− − =
xx
m
có đúng hai
nghiệm thuộc khoảng
(0;ln5).
Tổng
+ab
bằng
A.
2
. B.
4.
C.
6.−
D.
14.−
Câu 72. Giá trị thực của tham số
m
để phương trình
( )
4 2 3 .2 64 0
xx
m− + + =
có hai nghiệm thực
1
x
,
2
x
thỏa mãn
( )( )
12
2 2 24xx+ + =
thuộc khoảng nào sau đây?
A.
3
0;
2



. B.
3
;0
2

−


. C.
21 29
;
22



. D.
11 19
;
22



.
Câu 73. Gọi là tập hợp tất cả các giá trị nguyên của tham số để phương trình
có nghiệm duy nhất. Số tập con của là
A. . B. . C. . D. .
Câu 74. Tập các giá trị của để phương trình có nghiệm là
A. . B. . C. . D. .
Câu 75. Cho hàm số
( )
y f x=
liên tục trên và có đồ
thị như hình vẽ.
Tập hợp tất cả các giá trị thực của
m
để phương
trình
( )
2
x
f e m=
có đúng 2 nghiệm thực là
A.
0;4
. B.
0;4
.
C.
( )
0 4; +
. D.
)
4;+
.
ĐÁP ÁN TRẮC NGHIỆM
51B
52B
53D
54B
55A
56C
57A
58A
59B
60A
61A
62B
63D
64D
65C
66D
67C
68A
69B
70C
71D
72D
73C
74D
75C
S
m
5 10 25 4
xx
m+ = +
S
3
4
16
15
m
( )
22
1 1 1 1
4 2 2 2 1 0
xx
mm
+ − + −
− + + + =
9
;
2

−


9
4;
2



( )
;4−
)
4;+
63
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
63
BÀI TẬP MỨC ĐỘ IV:
Câu 76. Tổng tất cả các giá trị nguyên của để phương trình
có 3 nghiệm phân biệt.
A. . B. . C. . D. .
Câu 77. Gọi
0
m
là giá trị nhỏ nhất của tham số thực
m
sao cho phương trình
( ) ( ) ( ) ( )
2
11
22
1 log 2 5 log 2 1 0m x m x m− − − − − + − =
có nghiệm thuộc khoảng
( )
2;4
. Khẳng
định nào dưới đây đúng?
A.
0
4
1;
3
m

−


. B.
0
10
2;
3
m



. C.
0
16
4;
3
m



. D.
0
5
5;
2
m
−

−


.
Câu 78. Có bao nhiêu giá trị của tham số
m
để phương trình
2
36 6
4log log 2 0
6
x
xm− + =
có hai nghiệm
phân biệt
12
,xx
thỏa mãn
1 2 1 2
. 72 . 1296 0x x x x− +
A.
0.
B.
1.
C.
2.
D.
3.
Câu 79. Tập hợp các số thực m để phương trình
( )
( )
2
ln 3 1 ln 4 3x mx x x− + = − + −
có nghiệm là nửa
khoảng
)
;ab
. Tổng
ab+
bằng
A.
10
.
3
B.
4.
C.
22
.
3
D.
7.
Câu 80. Cho
,ab
là các số thực dương lớn hơn 1, thay đổi thỏa mãn
2019ab+=
để phương trình
5log .log 4log 3log 2019 0
a b a b
x x x x− − − =
luôn có hai nghiệm phân biệt
12
;xx
. Biết giá trị
lớn nhất của
( )
12
ln .xx
bằng
34
ln ln
5 7 5 7
mn
+
; với
,mn
là các số nguyên dương. Tính
2S m n=+
A.
22209
. B.
20190
. C.
2019
. D.
14133
.
Câu 81. Số các giá trị nguyên nhỏ hơn
2018
của tham số
m
để phương trình
( ) ( )
64
log 2018 log 1009x m x+=
có nghiệm là
A.
2018
. B.
2017
. C.
2020
. D.
2019
.
Câu 82. Có bao nhiêu số nguyên
m
để phương trình
( ) ( )
2
35
log 3 2 log 3
xx
mm+ = −
có nghiệm?
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 83. Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
5;5m−
sao cho phương trình
( )
( )
( )
( )
( ) ( )
32
21
2
2
log 1 log 1 2 8 log 1 2 0f x f x m f x m+ − + + − + + =
có nghiệm
( )
1;1x−
?
m
( )
3
3 3 3 2 3
3 9 24 .3 3 1
x m x x x
x x x m
− + − −
+ − + + = +
34
27
38
45
64
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
64
A.
7
. B.
5
. C.
6
. D. vô số.
Câu 84. Cho phương trình
( ) ( ) ( ) ( )
2
ln 1 2 ln 1 2 0 1 .m x x m x x+ − + − + − − =
Tập hợp tất cả các giá trị
của tham số
m
để phương trình
( )
1
có hai nghiệm phân biệt thoả mãn
12
0 2 4xx
là
khoảng
( )
;a +
. Khi đó
a
thuộc khoảng
A.
( )
3,8;3,9
B.
( )
3,6;3,7
. C.
( )
3,7;3,8
. D.
( )
3,5;3,6
.
Câu 85. Cho hàm số , khi phương trình
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số có dạng . Tính .
A. . B. . C. . D. .
Câu 86. Cho số thực và hàm số có đồ thị như hình vẽ dưới đây.
Phương trình có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn ?
A. . B. . C. . D. .
Câu 87. Xét các số nguyên dương
,ab
sao cho phương trình
.4 .2 50 0
xx
ab− + =
(1) có hai nghiệm phân
biệt
12
,xx
và phương trình
9 .3 50 0
xx
ba− + =
(2) có hai nghiệm
34
,xx
thỏa mãn điều kiện
3 4 1 2
x x x x+ +
. Tìm giá trị nhỏ nhất của biểu thức
34S a b=+
.
A.
109
. B.
51
. C.
49
. D.
87
.
Câu 88. Cho phương trình: . Tập các giá trị để bất phương trình có
ba nghiệm phân biệt có dạng . Tổng bằng:
( ) ( )
47
3 1 .2 – 6 3
xx
f x x x
−−
= + + +
(
)
2
7 4 6 9 3 1 0f x x m− − + − =
m
a
b
T a b=+
7T =
11T =
8T =
13T =
m
( )
y f x=
( )
22
xx
fm
−
+=
1;2−
2
3
4
5
3 2 2
23
2 2 3 0
x x x m x x
x x m
+ − + +
− + − + =
( )
;ab
2ab+
65
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
65
A. B. C. D.
Câu 89. Có bao nhiêu số nguyên để phương trình có
đúng 3 nghiệm thực phân biệt?
A. Vô số. B. . C. . D. .
Câu 90. Có bao nhiêu giá trị nguyên của tham số để phương trình
có đúng 3 nghiệm thực phân biệt?
A. . B. C. D. .
Câu 91. Có bao nhiêu số nguyên
( )
2mm
sao cho tồn tại số thực
x
thỏa mãn
( )
ln
ln
4 4 ?
m
x
mx+ + =
A.
8
. B.
9
. C.
1
. D. Vô số
Câu 92. Có bao nhiêu giá trị nguyên của
m
với
1m
sao cho tồn tại số thực
x
thỏa mãn:
( )
( )
5
5
log
log
3 3 1
m
x
mx+ = −
.
A.
4
. B.
3
. C.
5
. D.
8
.
Câu 93. Tổng tất cả các giá trị của tham số
m
sao cho phương trình:
( )
( )
( )
2
1
2
22
2 .log 2 3 4 .log 2 2
xm
x
x x x m
−
−
− + = − +
có đúng ba nghiệm phân biệt là:
A. 2. B.
3
.
2
C. 0. D. 3.
Câu 94. Cho phương trình
(
)
( )
(
)
2 2 2 2
2 3 2 3
log 1 2 log 1 1 0x x m x x
+−
+ + + − + − − =
với
m
là tham số
thực. Gọi
S
là tập hợp tất cả các giá trị của
m
để phương trình có 2 nghiệm phân biệt
12
;xx
thỏa mãn
2
11
2
22
1
7 4 3
1
xx
xx
+−
=+
++
. Tích các phần tử của
S
bằng
A.
4−
. B.
4
. C.
0
. D.
2
.
Câu 95. Có bao nhiêu số nguyên
y
nằm trong khoảng
( )
2021;− +
sao cho với mỗi giá trị của
y
tồn
tại nhiều hơn hai số thực
x
thỏa mãn
( ) ( )
2
2 2 2
.2020 2 .2020
x y x x
x y x x x x y
+−
+ + − = − +
?
A.
2020
. B.
2019
. C.
2021
. D.
2022
.
Câu 96. Cho hàm số bậc 4 có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
và
2021;2021m−
để phương trình
( )
( ) ( )
3
2
log
fx
x f x mx mx f x
mx
+ − = −


có hai nghiệm
dương phân biệt?
1.
2.
4.−
0.
m
(
)
22
4
9.3 4 2 1 3 3 3 1 0
xx
m x x m− + + + + + =
3
1
2
2019;2019m
2 1 2 1
2019 0
12
x
x mx m
xx
4038
2019.
2017.
4039
66
PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
HOÀNG XUÂN NHÀN
66
A.
2022
. B.
2020
. C.
2019
. D.
2021
.
Câu 97. Biết điều kiện cần và đủ của tham số
m
để phương trình
( ) ( )
2
2
11
22
1
log 2 4 5 log 8 4 0
2
x m m
x
+ + − − + =
+
có nghiệm thuộc
3
;6
2

−


là
(
)
;;m a b − +
. Tính giá trị biểu thức
T a b=+
.
A.
8
3
T =−
. B.
22
3
T =−
. C.
8
3
T =
. D.
22
3
T =
.
Câu 98. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
( )
( )
22
34
log log 2x y x y+ = +
A.
3
. B.
2
. C. Vô số. D.
1
.
Câu 99. Có bao nhiêu cặp số
,xy
là các số nguyên không âm thỏa mãn:
( )
( )
( )
( )
2
2
22
22
2 1 2 log 2 2log 2 2 4 4x y x y x y xy x x y x y+ + + + = + + + + + + +
A. 2. B. 3. C. 4. D. 5.
Câu 100. Có bao nhiêu số nguyên dương
a
nhỏ hơn
2021
sao cho tồn tại số nguyên
x
thỏa mãn
( ) ( )
3 2 3
2 2 1 2 2 1
a x a x
aa
++
− + = + −
?
A.
12
. B.
15
. C.
10
. D.
14
.
ĐÁP ÁN TRẮC NGHIỆM
76B
77D
78A
79D
80A
81C
82A
83A
84C
85C
86B
87A
88B
89C
90C
91C
92B
93D
94B
95A
96D
97D
98B
99B
100C
O
x
y
1−
1
1
| 1/67
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Hoàng Xuân Nhàn
1 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT MỤC LỤC:
A. TÓM TẮT LÍ THUYẾT: ....................................................................................................................... 1
B. PHÂN DẠNG BÀI TẬP: ........................................................................................................................ 5
Dạng 1. Phương trình mũ ....................................................................................................................... 5
Bài toán 1: Các phương trình mũ thường gặp ........................................................................ 5
Bài toán 2: Phương trình mũ dạng đặt ẩn phụ ........................................................................ 7
Bài toán 3: Phương trình mũ dạng tích ................................................................................... 9
Bài toán 4: Giải phương trình mũ bằng phương pháp đánh giá ............................................ 11
Bài toán 5: Giải phương trình mũ bằng phương pháp hàm đặc trưng .................................. 13
Dạng 2. Phương trình lôgarit ................................................................................................................. 15
Bài toán 1: Các phương trình lôgarit thường gặp ................................................................... 15
Bài toán 2: Phương trình lô garit dạng đặt ẩn phụ ................................................................. 17
Bài toán 3: Phương trình lôgarit dạng tích.............................................................................. 19
Bài toán 4: Giải phương trình lôgarit bằng phương pháp đánh giá ...................................... 21
Bài toán 5: Giải phương trình lôgarit bằng phương pháp hàm đặc trưng ............................. 24
Dạng 3. Phương trình mũ và lôgarit có chứa tham số ......................................................................... 26
Phương pháp giải toán .............................................................................................................. 26
Bài toán 1: Phương trình mũ, lôgarit quy về bậc hai có nghiệm đẹp ..................................... 28
Bài toán 2: Áp dụng định lí Vi-ét cho phương trình mũ, lôgarit quy về bậc hai .................... 30
Bài toán 3: Tìm điều kiện tham số thông qua miền giá trị hàm số ......................................... 32
Bài toán 4: Tìm điều kiện tham số thông qua bảng biến thiên của hàm số ........................... 34
Bài toán 5: Tìm điều kiện tham số dựa vào hàm đặc trưng .................................................... 37
Bài toán 6: Nghiệm đặc biệt của phương trình mũ, lôgarit chứa hàm đối xứng ................... 41
Bài toán 7: Tìm điều kiện tham số của phương trình mũ, lôgarit có chứa hàm ẩn ............... 42
Dạng 4. Nghiệm nguyên của phương trình mũ, lôgarit ....................................................................... 45
Phương pháp giải toán .............................................................................................................. 45
Bài toán 1: Nghiệm nguyên của phương trình mũ và lôgarit dạng tích ................................. 45
Bài toán 2: Nghiệm nguyên của phương trình mũ và lôgarit chứa hàm đặc trưng .............. 47
Bài toán 3: Phương pháp đánh giá và bài toán nghiệm nguyên phương trình ..................... 49
Bài toán 4: Xét nghiệm nguyên phương trình dựa vào đặc thù tổng, tích… các số nguyên. 52
Bài toán 5: Bài toán nghiệm nguyên phương trình mũ, lôgarit nhiều ẩn chứa tham số. ..... 53
C. BÀI TẬP THỰC HÀNH: ....................................................................................................................... 55
BÀI TẬP MỨC ĐỘ I: ............................................................................................................................. 55
Đáp án: ...................................................................................................................................... 57
BÀI TẬP MỨC ĐỘ II: ........................................................................................................................... 57
Đáp án: ...................................................................................................................................... 59
BÀI TẬP MỨC ĐỘ III: .......................................................................................................................... 60
Đáp án: ...................................................................................................................................... 62
BÀI TẬP MỨC ĐỘ IV: .......................................................................................................................... 63
Đáp án: ...................................................................................................................................... 66 HOÀNG XUÂN NHÀN 1
2 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
A – TÓM TẮT LÍ THUYẾT:
I – PHƯƠNG TRÌNH MŨ:
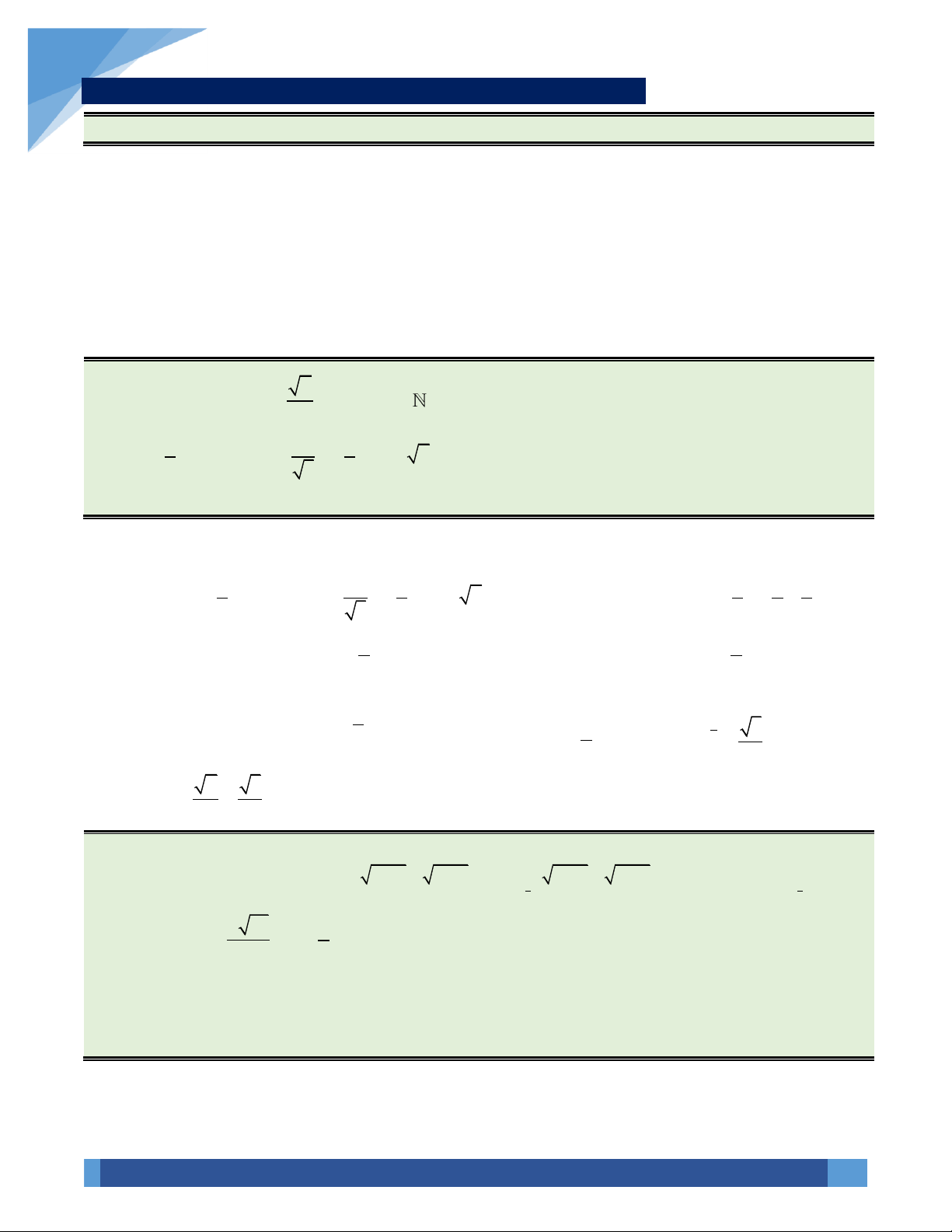
1. Phương trình mũ cơ bản: Cho trước a  0, a  1.
Phương trình mũ cơ bản có dạng x a = b b  0 x
a = b x = log b (nghiệm duy nhất) a b  0 x
a = b x  (phương trình vô nghiệm)
2. Phương trình mũ dạng cùng cơ số: Cho trước a  0, a  1. Ta có:
f ( x )
g( x ) a = a
f (x) = g(x) .
3. Phương trình mũ dạng lôgarit hóa hai vế: Cho trước ,
a b  0, a  1.
f ( x )a
= b f (x) = log b a .
f ( x )
g( x )a = b
f (x) = g(x).log b (b 1) a
4. Phương trình mũ dạng đặt ẩn phụ: ◼ Đặt f ( x) t = a  0 .
◼ Đưa phương trình đã cho về dạng phương trình đa thức bậc n theo t ⎯⎯ → Giải tìm t .
◼ Với t có được, thay vào f ( x) t = a để tìm x . a) Phương trình
2 f ( x )
f ( x )
m.a
+ n.a
+ p = 0 với a 0, a 1. Đặt f ( x) t = a  0 . Phương trình trở thành: 2
mt + nt + p = 0 . b) Phương trình
g( x )
g( x )
g( x )
m.a
+ n.b
+ p.c
= 0 với a, ,
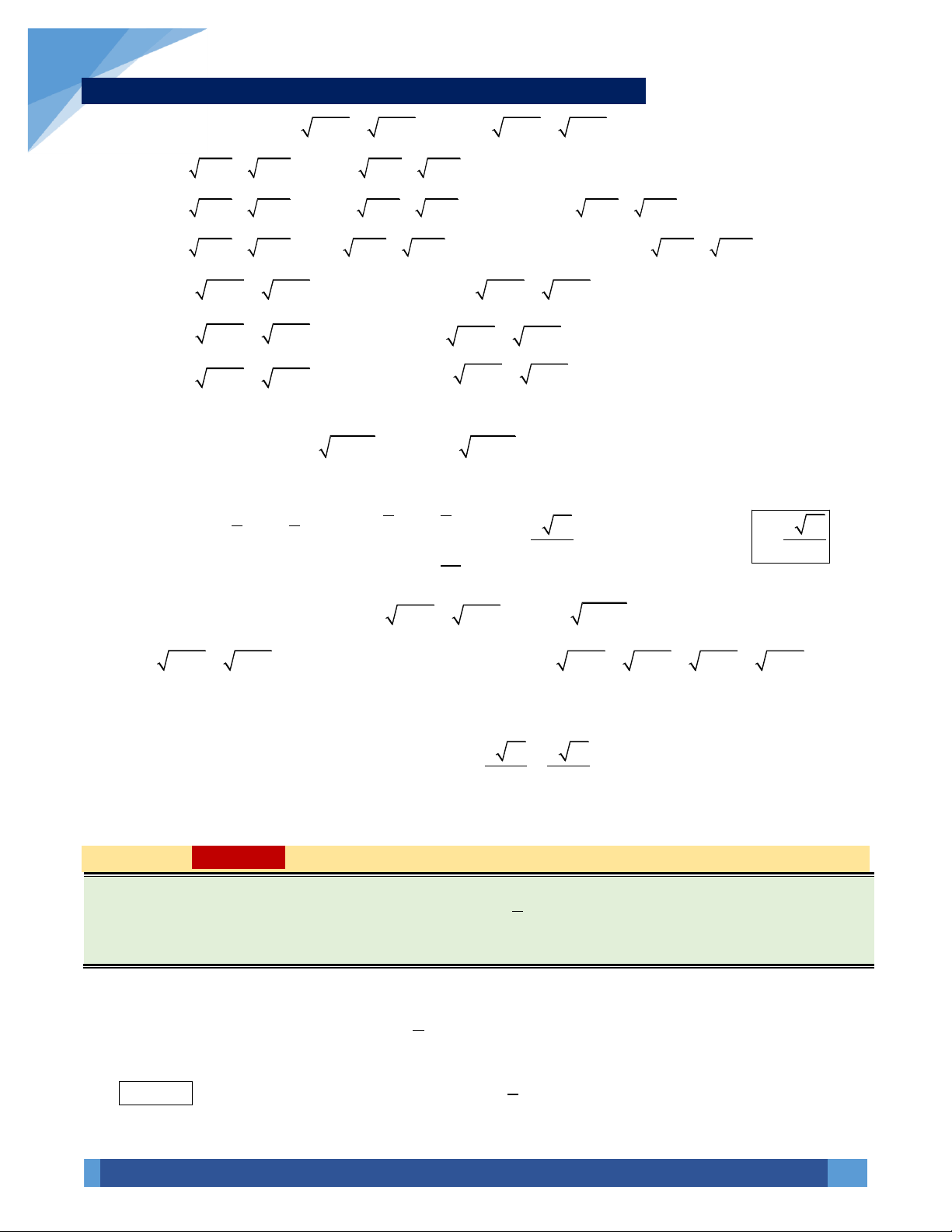
b c 0, a 1, b 1, c 1. Nhận dạng: 2 f ( x) f ( x) 2 f ( x) ma + ( n . a c) + . p c = 0 . 2 f ( x) f ( x)  a   a
Chia hai vế phương trình cho 2 f (x) c  0 , ta được: m + n + p = 0     .  c   c
Chú ý: Ta có thể chia hai vế của phương trình cho bất kỳ hàm mũ nào trong ba hàm
g(x) g(x) g(x) a ;b ; c
, kết quả sau cùng của bài toán không thay đổi.
a + b 0, a + b 1 c) Phương trình
f ( x )
f ( x )
m.(a + b ) + (
n a − b )
= p với  .
a − b 0, a − b 1 Nhận dạng: 2
(a + b )(a − b ) = a − b = 1. Đặ f x 1 t ( ) f ( x)
t = (a + b) , t  0  = (a − b) . t n Phương trình trở thành: 2 mt +
= p mt − pt + n = 0 . t
5. Phương trình mũ dạng tích: HOÀNG XUÂN NHÀN 2
3 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT a = 0
ab = 0  b = 0 a) Dạng cơ bản: . a = 0
ab = ac  b = c
b) Dạng thường gặp:
f ( x )
g( x )
f ( x ) g( x ) a a a + + =
+ 1 với a 0, a 1. f ( x) a −1 = 0 Cách giải: + f (x) g ( x)
f ( x) g ( x) f ( x) g ( x) f ( x) a + a = a +1  a −1 = a .(a −1)   . g ( x) a =1
II – PHƯƠNG TRÌNH LÔGARIT:
1. Phương trình lôgarit cơ bản: Cho trước a  0, a  1. Ta có: log b
x = b x = a (dạng này không cần đặt điều kiện cho x). a
2. Phương trình lôgarit dạng cùng cơ số: Cho trước a  0, a  1.
Ta có: log f ( x) = log g( x) f ( x) = g( x) 0 . a a
3. Phương trình lôgarit dạng mũ hóa hai vế: Cho trước a  0, a  1.
Ta có: log f ( x) = b f ( x) b
= a (dạng này không cần đặt điều kiện cho f ( x) ). a
4. Phương trình lôgarit dạng đặt ẩn phụ:
◼ Đặt t = log f (x) . a
◼ Đưa phương trình đã cho về dạng phương trình đa thức bậc n theo t ⎯⎯ → giải tìm t .
◼ Có t , thay vào t = log f (x) để tìm x . a a) Phương trình 2 m log
f ( x) + n log f ( x) + p = 0 với a 0, a 1. a a
Đặt t = log f (x) . a
Phương trình đã cho trở thành: 2
mt + nt + p = 0 .
b) Phương trình m. log f ( x) + n. log
a + p = 0 với a 0, a 1. a
f ( x ) Điều kiện: f ( ) x  0, f ( ) x  1. Đặ 1
t t = log f (x)  = log a . a f ( x) t n Phương trình trở thành: 2 mt +
+ p = 0  mt + pt + n = 0 . t
c) Phương trình đơn giản chứa log f ( x), log g( x) với a 0, a 1, b 0, b 1 . a b
Điều kiện: f ( x)  0, g ( x)  0 .
Đặt t = log f (x)  f (x) t
= a (cô lập x nếu được). a
Thay trở lại phương trình, ta có một phương trình mới đơn giản hơn (chứa ít logarit hơn).
5. Phương trình lôgarit dạng tích: HOÀNG XUÂN NHÀN 3
4 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT a = 0
ab = 0  b = 0 a) Dạng cơ bản: . a = 0
ab = ac  b = c
a 0, a 1
b) Dạng thường gặp: log f ( x) + log f ( x) = log f ( x) log f ( x) + 1 với  . a b a b
b 0, b 1
Cách giải: log f ( x) + log f ( x) = log f ( x)log f ( x) +1 a b a b 1  − log f x = b ( )  f x  − f x  = − f x     . a ( ) b ( ) b ( ) 0 log 1 log 1 log log f x =  a ( ) 1
III – GIẢI PHƯƠNG TRÌNH MŨ-LÔGARIT BẰNG CÁC ĐÁNH GIÁ NÂNG CAO
1. Phương pháp đánh giá hai vế:
a) Dạng 1: Phương pháp đối lập.
Xét phương trình f ( ) x = g( )
x với x D .
f (x)  M
f (x) = M Ta chứng minh: 
với mọi x D . Do đó: f (x) = g(x)   .
g(x)  M
g(x) = M 2 2
a + b = 0  a = b = 0  Chú ý: .
a + b = 0  a = b = 0
b) Dạng 2: Dùng tính đơn điệu của hàm số (phương trình có nghiệm duy nhất).
Xét phương trình f ( ) x = g( )
x có miền điều kiện là . D
Bước 1: Nhận thấy x = x là một nghiệm của phương trình. 0
Bước 2: Chứng minh một trong các trường hợp sau:
• f ( x) đồng biến trên D, g ( x) nghịch biến trên D.
• f ( x) nghịch biến trên D, g ( x) đồng biến trên D.
• f ( x) đơn điệu trên D, g ( x) không đổi trên D.
• f ( x) không đổi trên D, g ( x) đơn điệu trên D.
Bước 3: Kết luận phương trình f ( ) x = g( )
x có nghiệm duy nhất x = x . 0
c) Dạng 3: Dùng tính đơn điệu của hàm số (phương trình có hai nghiệm, ba nghiệm,…).
Với nguyên tắc làm tương tự Dạng 2, ta thực hiện:
• Nhận thấy x = x , x = x là nghiệm của phương trình f ( ) x = g( ) x . 1 2
• Mặt khác, hàm số y = f ( ) x − g( )
x với đạo hàm y = 0 có duy nhất một nghiệm. Suy ra phương trình f ( ) x = g( )
x có tối đa hai nghiệm.  = • x x Kết luận: Vậy 1
f (x) = g(x)   . x = x  2 HOÀNG XUÂN NHÀN 4
5 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Mở rộng: Xét phương trình f ( ) x = g( )
x với hàm số y = f ( ) x − g( )
x liên tục trên miền D;
trong đó y = 0 có n nghiệm, ta suy ra phương trình f ( ) x = g( )
x có tối đa n + 1 nghiệm.
2. Phương trình chứa hàm đặc trưng:
Xét phương trình dạng: f (u) = f (v) trên miền điều kiện D.
Nếu hàm y = f (t ) đơn điệu trên miền D (tức là đạo hàm chỉ mang một dấu duy nhất trên D)
thì: f (u) = f (v)  u = v .
B – PHÂN DẠNG BÀI TẬP: Phương pháp:
Bạn đọc cần Nắm vững phương pháp giải phương trình trong phần Tóm tắt lí thuyết gồm:
⎯ Phương trình mũ cơ bản.
⎯ Phương trình mũ dạng lôgarit hóa hai vế.
⎯ Phương trình mũ dạng đặt ẩn phụ.
⎯ Phương trình mũ dạng tích.
⎯ Đánh giá hai vế phương trình hoặc dựa vào tính đơn điệu của hàm số, chứng minh
phương trình vô nghiệm, có tối đa 1 nghiệm, 2 nghiệm...
Bài toán 1. Các phương trình mũ thường gặp
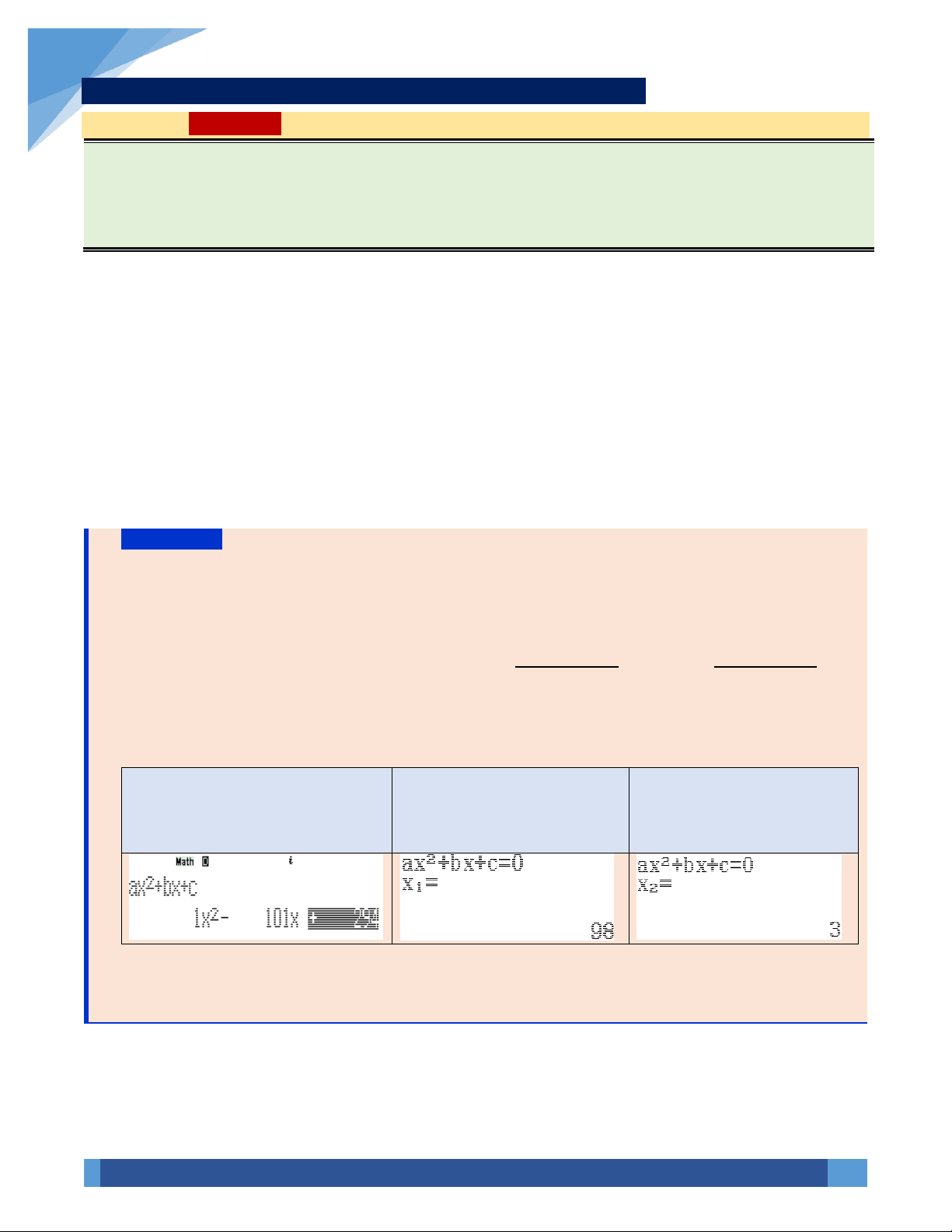
VÍ DỤ 1. Phương trình 2x 1 2 + = 32 có nghiệm là 5 3 A. x = . B. x = 2. C. x = .
D. x = 3. 2 2 Hướng dẫn giải: Ta có: 2x 1 2 + = 32 2x 1 + 5  2
= 2  2x +1= 5  x = 2. Chọn B. VÍ DỤ 2. + Giải phương trình 2 x 3 2 x =1.
A. x = 0 , x = 3 .
B. x = 1, x = 3. −
C. x = 1 , x = 2.
D. x = 0 , x = 3. − Hướng dẫn giải: x = 0 2 + Ta có: x +3 2 x = 2 1 x 3x 0  2 = 2 2
x + 3x = 0   . x = 3 − HOÀNG XUÂN NHÀN 5
6 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT Chọn D. 2 3 x − x+
VÍ DỤ 3. Tìm tích số của tất cả các nghiệm thực của phương trình 2 7 = 49 7 . 1 1 A. 1 − . B. 1. C. − . D. . 2 2 Hướng dẫn giải:  1− 5 x = 2 3 2 3 5 x −x+ x −x+ 3 5 2 Ta có : 2 2 2 2 7 = 49 7  7
= 7  x − x + = 2
x − x −1 = 0   . 2 2  1+ 5 x =  2 1− 5 1+ 5
Khi đó tích các nghiệm là: . = 1 − . Chọn A. 2 2 2 x + x 1 − x−2
VÍ DỤ 4. Cho phương trình (7 + 4 3)
= (2+ 3) . Mệnh đề nào sau đây đúng?
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt. Hướng dẫn giải: Do + = ( + )2 7 4 3 2 3
nên phương trình ban đầu tương đương với  = ( x 0 +
) ( 22x+x− )1 =( + )x−2 2 3 2 3 2  
2x + 2x − 2 = x − 2 2
 2x + x = 0  1  . x = −  2
Vậy phương trình đã cho có hai nghiệm không dương. Chọn A.
VÍ DỤ 5. Nghiệm của phương trình x x 1 + x x 1 2 2 3 3 + + = + là. 3 3 2 A. log . B. x = 1. C. x = log . D. x = log . 3 2 3 4 4 3 4 2 3 Hướng dẫn giải: x   3 Ta có: x x 1 + x x 1 2 2 3 3 + + = +
 2x + 2.2x = 3x +3.3x 3.2x 4.3x  = 3 3  =    x = log .  2  3 4 4 2 Chọn C. HOÀNG XUÂN NHÀN 6
7 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT VÍ DỤ 6. − + − Cho biết phương trình 2 x 3x 2 x 2 5
= 3 có một nghiệm không nguyên dạng x = log b với a , b a
là các số nguyên dương nhỏ hơn 16 . Khi đó a + 2b bằng: A. 35 . B. 25 . C. 40 . D. 30 . Hướng dẫn giải: Xét phương trình 2 − + − : x 3x 2 x 2 5
= 3 . Lấy logarit cơ số 5 cho hai vế, ta được : 2
x − 3x + 2 = ( x − 2) log 3  x − 2 x −1 − x − 2 log 3 = 0 5 ( )( ) ( ) 5  =  =  ( x 2 x 2
x − 2)( x −1− log 3 = 0   . 5 )   x = 1+ log 3  x = log 15 5  5
Suy ra a = 5 , b = 15 . Vậy a + 2b = 35 . Chọn A.
Bài toán 2. Phương trình mũ dạng đặt ẩn phụ
VÍ DỤ 7. Cho phương trình x x 1 4 2 + + −3 = 0. Khi đặt 2x t =
ta được phương trình nào sau đây:
A. 4t − 3 = 0. B. 2
t + t − 3 = 0. C. 2
t + 2t − 3 = 0. D. 2
2t − 3t = 0. Hướng dẫn giải: Ta có : x x+ + − =  ( x )2 1 4 2 3 0 2 + 2.2x − 3 = 0 . Đặt = 2x t
, t  0. Phương trình trở thành : 2
t + 2t − 3 = 0. Chọn C.
VÍ DỤ 8. Số nghiệm của phương trình x 1 3 − 3 −x = 2 là: A. 3 . B. 1. C. 2 . D. 0 . Hướng dẫn giải: Ta có: x 1 3 − 3 −x = x 3 2  3 − = 2 2 3 x 2.3x  − −3 = 0 . 3x t Đặt = 3x t
, t  0 . Phương trình trở thành : 2
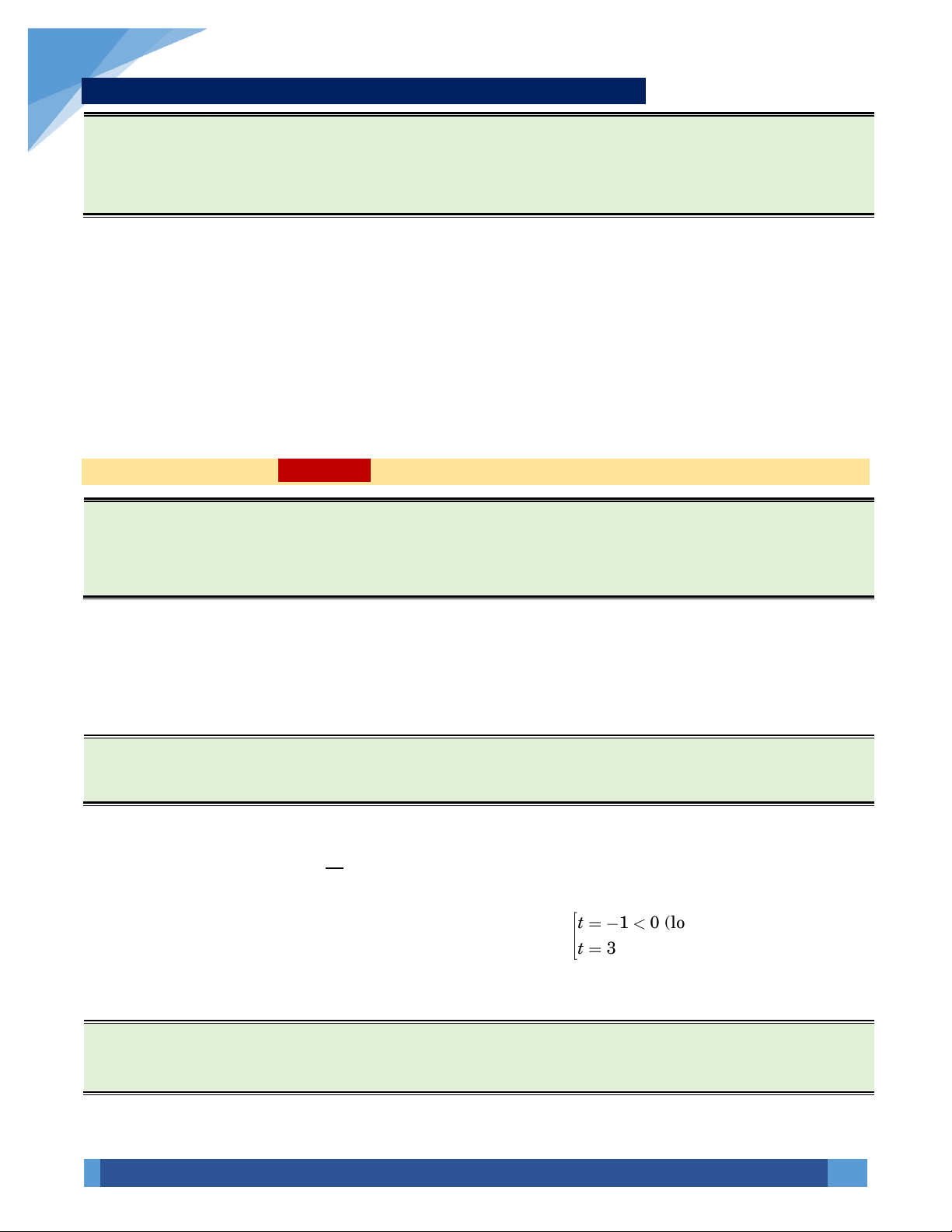
t − 2t − 3 = 0  1 0 (loaïi) . t 3
Với t = 3 thì 3x = 3  x = 1. Vậy phương trình đã cho có một nghiệm. Chọn B. VÍ DỤ 9. + + +
Tổng tất cả các nghiệm thực của phương trình 2 2 2x 1 x 3x 6x 1 2 −5.2 + 2 = 0 bằng: A. 6 . B. 10 . C. 3 . D. 5 . Hướng dẫn giải: HOÀNG XUÂN NHÀN 7
8 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT 2 2 2 2 + + + + Ta có: 2x 1 x 3x 6x 1 2x x 3x 6 2 −5.2 + 2 = 0  2.2 −5.2 + 2.2 x = 0 . 2 2 − −
Chia hai vế phương trình cho 6
2 x  0 , ta được: 2x 6x x 3 2.2 −5.2 x + 2 = 0 .  = ( t 2 2 2 x −3 2 x) Đặ 2 −  t x 3 = 2 x t
, t  0 ; suy ra t = 2
, t  0 . Phương trình trở thành: 2
2t − 5t + 2 = 0  1  . t =  2 2 x −  x 3 13 Với t = 2 thì 3 2 2
= 2  x − 3x =1  x =
; suy ra x + x = 3 . 1,2 2 1 2 1 2 x −  x 1 3 5 Với t = thì 3 2 2
=  x − 3x = 1 −  x =
; suy ra x + x = 3. 2 3,4 2 2 3 4
Vậy tổng các nghiệm phương trình là: 3 + 3 = 6. Chọn A.
VÍ DỤ 10. Cho phương trình 5.49x 3.35x 14.25x + =
. Kết luận nào sau đây sai?
A. Phương trình vô nghiệm.
B. Phương trình có một nghiệm.
C. x = 1 là nghiệm của phương trình.
D. Phương trình không có nghiệm âm. Hướng dẫn giải:
Chia hai vế phương trình cho 25x  0 , ta có : 5.49x 3.35x 14.25x + = x x  2 x x 49   35    7   7  5. + 3. =14      5. + 3. −14 = 0     .  25   25   5   5  x   7 t 0 Đặ 7 t t =  0  
. Phương trình trở thành: 2
5t + 3t −14 = 0  5 .  5  t 2 0 (loaïi) 7 x  7  7 Với t = thì =  x =1   . Chọn A. 5  5  5 x x
VÍ DỤ 11. Cho phương trình ( + ) + ( − ) : x+3 3 5 16 3 5 = 2
(*) . Phát biểu nào sau đây sai?
A. (*) có nghiệm là số vô tỉ.
B. (*) có nghiệm dương.
C. (*) có nghiệm duy nhất.
D. (*) có hai nghiệm phân biệt. Hướng dẫn giải: x x  3+ 5   3− 5  x  , ta đượ   +   =
Chia hai vế phương trình cho 2 0 c : 3 16 2     . 2 2     HOÀNG XUÂN NHÀN 8
9 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT x x 3 + 5 3 − 5  3+ 5  1  3− 5  Nhận thấy: . =1. Đặt t =    0  =   . 2 2     2 t 2     16 Phương trình trở thành: 2 t +
−8 = 0  t −8t +16 = 0  t = 4 . t x  3+ 5  Với t = 4 thì   = 4  x = log 4   . Chọn D. 3+ 5 2   2 + +4 2( 1) + ( 2 2 2 x x x ) VÍ DỤ 12. 2 2 2
Gọi x là một nghiệm của phương trình x +3 2 = 2 + 2 − 2 +1 . Khi đó 0 2 x = log
3 + b − c với , a , b c  . Tính 2 2 2
a − b + c . 0 a ( ) A. 2 2 2
a − b + c = 95 − . B. 2 2 2
a − b + c = 85 . C. 2 2 2
a − b + c = 65 − . D. 2 2 2
a − b + c = 75 . Hướng dẫn giải: 2 + x + x + ( 2 2 2 x 2 4 2( 1) ) 2 2 2 2 2 + + + + + Ta có: x 3 x 1 2( x 1) 2( x 1) x 1 2 = 2 + 2 − 2 +1  8.2 = 2 + 4.2 − 4.2 +1 Đặ 2 t x 1 t 2 + =
(t  2). Phương trình trở thành: t +
t − t + = t t + ( t − )2 2 2 2 4 4 1 8 2 1 = 8t 2
t + ( t − ) 2 2
1 = 8t t − 6t −1 = 0  t = 3  10 ; vì t  2 nên t = 3 + 10 . + 2
Với t = 3 + 10 thì x 1 + 2 2
= 3+ 10  x +1 = log (3+ 10) 2
x = log 3 + 10 −1. 2 2 ( )
Ta có x là một nghiêm của phương trình và 2 x = log
3 + b − c a = 2, b = 10, c = 1. 0 a ( ) 0 Suy ra: 2 2 2
a − b + c = 95 − . Chọn A.
Bài toán 3. Phương trình mũ dạng tích
VÍ DỤ 13. Gọi a, b (a b) là các nghiệm của phương trình x x 1 + x 1 6 6 2 3 + + = + . Tính giá trị của 2a 3b P = + . A. 17 . B. 7 . C. 31. D. 5 . Hướng dẫn giải: Ta có: x x 1 + x 1 6 6 2 3 + + = +
 6x + 6 = 2.2x + 3.3x  2 .x(3x − 2) = 3.(3x − 2)  (3x − 2)(2x −3) = 0 3x = 2 x = log 2 3   
a = log 3; b = log 2 a b  . 2 3 ( ) 2x = 3 x = log 3  2 log 3 log 2 Vậy 2 3 P = 2 +3 = 3+ 2 = 5 . Chọn D. VÍ DỤ 14. − + + + + +
Tính giá trị T là tổng tất cả nghiệm thực của phương trình: 2 2 2 x 3x 2 x 6x 5 2x 3x 7 4 + 4 = 4 +1. HOÀNG XUÂN NHÀN 9
10 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT A. 3 . B. 5 − . C. 3 − . D. 5 . Hướng dẫn giải: 2 2 2 − + + + − + + + Ta có : x 3 − x+2 x +6x+5 2x +3x+7 4 + 4 = 4 + 2 2 2 2 1 x 3x 2 x 6x 5 x 3x 2 x 6x 5  4 + 4 = 4 .4 +1 2 2 2 2 x −3x+2 x −3x+2 x +6 x+5 x +6 x+5  4 −1 = 4 .4 − 4  ( 2x−3x+2 4 − ) 2 x +6 x+5 1 .1 = 4 ( 2x−3x+2 4 − )1 2 2 x −3x+2 x −3x+2 0 2 4 −1 = 0 4 = 4
x − 3x + 2 = 0 x =1 x = 2        .  2 2 + + + + 2 x 6 x 5 x 6 x 5 0 4 =1 4 = 4
x + 6x + 5 = 0 x = 1 −  x = 5 −
Tổng các nghiệm của phương trình: T = 1+ 2 + (− )
1 + (−5) = −3. Chọn C.
VÍ DỤ 15. Tìm tổng bình phương tất cả nghiệm thực của phương trình 4x = (2x + ) 1 + 2x x − x . A. 10 . B. 5 . C. 1. D. 13 .
_____TRÍCH TỪ ĐỀ THI HSG 12, TP. HCM, 2021_____ Hướng dẫn giải:
Điều kiện: 2x − x  0 . Ta có: 4x = (2x + ) 1 + 2x x − x − −  − = x( + )+
− x −  ( − )( + )− x( + ) 2x x x x x x x x 1 4 1 2 1 2 1 2 1 2 1 2 1 = 2x − x +1
2x − x −1 = 0 (1) ( − −  
− − x)( + ) 2x x x x 1 2 1 2 1 =  . x 1  x 2 +1 = (2) 2 − x +1  2x − x +1
Giải phương trình (1): Xét hàm số ( ) = 2x f x
− x −1 có f ( ) 1 = 0, f (0) = 0 . x 1
Ngoài ra: f ( x) = 2 ln 2 −1 = 0  x = log
; vì f ( x) = 0 chỉ có một nghiệm nên phương trình 2 ln 2 x =
f ( x) = 0 có tối đa hai nghiệm. Vậy ( ) 0 1   . x =1 2x +  x 1 1 2  0  
Giải phương trình (2): Ta có:  , x     1 , x   . Suy ra phương x 1  2 − x +11   2x − x +1 trình (2) vô nghiệm.
Vậy phương trình ban đầu có đúng hai nghiệm là x = 0; x =1. Suy ra 2 2 0 +1 =1. Chọn C. HOÀNG XUÂN NHÀN 10
11 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Bài toán 4. Giải phương trình mũ bằng phương pháp đánh giá VÍ DỤ 16. 2 − Cho phương trình x 1 + ( 2 2023 − ) 1 .2024x x
=1. Mệnh đề nào sau đây đúng ?
A. Phương trình đã cho có nghiệm duy nhất.
B. Phương trình đã cho có nhiều hơn hai nghiệm.
C. Phương trình đã cho có tổng các nghiệm bằng 0 .
D. Phương trình đã cho có hai nghiệm dương phân biệt. Hướng dẫn giải: Xét phương trình (*): 2 x 1 − + ( 2 2023 − ) 1 .2024x x =1. Ta thấy x = 1
 là các nghiệm của (*).  2 − x  1 − x 1 2023   1 Xét trường hợp: 2 x −1  0   . Khi đó: 
 Vế trái (*) 1 nên dấu đẳng x 1 ( 2 −  )1.2024x x  0
thức không thể xảy ra. Vậy trường hợp này không thỏa mãn. 2 x 1 2023 −    1 Xét trường hợp: 2 x −1  0  1
−  x 1. Khi đó: (
Vế trái (*) 1 nên dấu đẳng 2 −  )1.2024x x  0
thức không thể xảy ra. Vậy trường hợp này cũng không thỏa mãn.
Tóm lại phương trình (*) có hai nghiệm x = 1
 , suy ra tổng hai nghiệm bằng 0. Chọn C.
VÍ DỤ 17. Phương trình x ( x 1− + ) x 1 + 2 2 4 = 2
+ x có tổng các nghiệm bằng A. 5 . B. 3 . C. 6 . D. 7 . Hướng dẫn giải: x = 4 − + − − − Ta có: x ( x 1 2 + 4) x 1 2 x 1 2 x 1 2 x 1 = 2 + x  . x 2
− 2 .2 = x − 4x  2 (x − 4) = x(x − 4)   . x 1 2 − = x  ( ) * Đặ − − 1 t f ( x) x 1 =
− x f (x) x 1 2
= 2 .ln 2 −1; f (x) = 0  x = 1+ log = 1− log ln 2 . 2 2 ( ) ln 2
Ta thấy f ( x) = 0 có duy nhất 1 nghiệm nên phương trình f ( x) = 0 có tối đa 2 nghiệm. Mặt khác: f ( )
1 = 0; f (2) = 0 , suy ra phương trình (*) có 2 nghiệm x = 1; x = 2 .
Vậy phương trình đã cho có 3 nghiệm x = 1; x = 2; x = 4 .Tổng các nghiệm bằng 7 . Chọn D.
VÍ DỤ 18. Cho phương trình: x 2 3 5
2025 + x = 2023 + 2024 + 2025 . Tìm số nghiệm của phương trình trên. A. 1. B. 2 . C. 3 . D. 4 .
_____Trích THTT Số 2-485 tháng 11, năm 2017_____ Hướng dẫn giải: HOÀNG XUÂN NHÀN 11
12 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT Ta có: x 2 3 5
2025 + x = 2023 + 2024 + 2025 x 2 3 5
 2025 + x − 2023 + 2024 + 2025 = 0 . Đặt f ( x) x 2 3 5
= 2025 + x − 2023+ 2024 + 2025 , D = .
Ta có: ( ) = 2025 .x f x
ln 2025 + 2x ; f ( x) x 2
= 2025 .ln 2025 + 2  0, x   .
Do đó hàm f ( x) đồng biến trên mà f (− )
1 . f (0)  0 nên f ( x) = 0 có nghiệm duy nhất trong
khoảng (−1;0) , suy ra phương trình f ( x) = 0 có tối đa hai nghiệm.
Tới đây, ta cần sự hỗ trợ của MTBT để dò khoảng nghiệm của phương trình :
Sử dụng chức năng Table của máy (thao tác sau đây được thực hiện trên VINACAL 680EX PLUS): NEXT NEXT MODE ⎯⎯⎯
→ ⎯⎯⎯→ F ( X ) X 2 3 5 8
= 2025 + X − 2023+ 2024 + 2025 NEXT
⎯⎯⎯→ START : −10 NEXT ⎯⎯⎯→ :10 NEXT ⎯⎯⎯→ :1 NEXT END STEP
⎯⎯⎯→ = . (Lưu ý trong quá trình nhập, nếu gặp G ( X ) thì
ta nhấn dấu = để bỏ qua).
Kết quả hiển thị từ màn hình MTBT , ta thấy F ( X ) đổi dấu hai lần khi x đi từ 7 − → 6 − , 0 →1.  f  ( 7 − ). f ( 6 − )  0 Ta có : 
. Vậy phương trình đã cho chỉ có hai nghiệm trên hai khoảng (−7; −6)  f  (0). f ( ) 1  0 và (0; )
1 . Do đó số nghiệm phương trình đã cho bằng 2.
VÍ DỤ 19. Tổng lập phương tất cả các nghiệm thực của phương trình x x 1 15 . x 5 5 + = + 27x + 23. A. 5. B. 6. C. 8. D. 0. Hướng dẫn giải: + Ta có: x x 1 15 . x 5 5 + = + 27x + 23 x 1  5 .(3x − ) 1 = 27x + 23 (1) . 1 1 + x + x 27 23 Ta thấy x = không là nghiệm của ( ) 1 . Với x  , (1) trở thành: 1 5 = (2). 3 3 3x −1   Trườ 1 + ng hợp 1: Xét x  ; +   . Ta thấy hàm số 1 5x y + = (với x 1 y = 5
ln 5  0 ) đồng biến trên  3   1  27x + 23 96  1  ; +   , hàm số y = y = −  0 ) nghịch biến trên ; +   .  3  3x − (với 1 (3x − )2 1  3   1   1  Mặt khác: x = 1 ; + 
 là một nghiệm của (2). Vậy (2) có nghiệm duy nhất x = 1 ; +   .  3   3  HOÀNG XUÂN NHÀN 12
13 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT  1   1 
Trường hợp 2: Xét x  − ;    ta có hàm số 1 5x y + = đồng biến trên ; +   , hàm số  3   3  27x + 23  1  y = ; −  . 3x − nghịch biến trên 1  3   1   1  Mặt khác: x = 1 −  − ;  
 là một nghiệm của (2). Vậy (2) có nghiệm duy nhất x = 1 −  − ;    .  3   3 
Vậy phương trình có hai nghiệm: x = 1, x = 1 − . Suy ra: + (− )3 3 1 1 = 0. Chọn D. VÍ DỤ 20. 2 2
Số nghiệm của phương trình 2 x + x − = ( 2
x − x − ) x +3x−6 + ( 2
x + x − ) x −x−3 2 2 9 3 .8 3 6 .8 là A. 1. B. 3 . C. 2 . D. 4 .
_____THPT Chuyên Vĩnh Phúc, lần 3, 2018_____ Hướng dẫn giải: Đặt 2
u = x − x − 3 , 2
v = x + 3x − 6 . Phương trình trở thành: + = .8v + .8u u v u v (*) . −  Trườ 3 33
ng hợp 1: u = 0 , (*) trở thành v = v (đúng). Ta có: 2
u = x + 3x − 6 = 0  x = . 1,2 2  Trườ 1 13
ng hợp 2: v = 0 , (*) trở thành u = u (đúng). Ta có 2
v = x − x − 3 = 0  x = . 3,4 2 v u v u − −
Trường hợp 3: uv  0 ; khi đó: v u 8 8 1 1 8 1 8 1 u + v = . u 8 + . v 8  + = +  + = 0 (**). v u v u v u v − v − Xét f (v) 8 1 =
. Ta sẽ chứng minh f (v) 8 1 =  0, v   0 . Thật vậy: v v v − ⎯ v v 8 1 Nếu v  0 thì 0
8  8  8 −1  0  f (v) =  0 . v v − ⎯ v v 8 1 Nếu v  0 thì 0
8  8  8 −1  0  f (v) =  0 . v v − u − Suy ra f (v) 8 1 =  0, v
  0 . Hoàn toàn tương tự, ta cũng có f (u) 8 1 =  0, u   0 . v u
Ta thấy vế trái (**) luôn dương nên (**) vô nghiệm.
Vậy, phương trình đã cho có bốn nghiệm phân biệt. Chọn D.
Bài toán 5. Giải phương trình mũ bằng phương pháp hàm đặc trưng VÍ DỤ 21. − − −
Số nghiệm của phương trình 2 2 x 3x 2 x 3 2 2024
− 2024 + 2x − 3x − x +1 = 0 là A. 3 B. 0. C. 1. D. 2. Hướng dẫn giải: HOÀNG XUÂN NHÀN 13
14 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT 3  Điều kiện: 2
2x − 3x  0  x (− ;  0 ;+   . 2 
Phương trình đã cho tương đương vớ 2 − − − i 2 x 3x 2 2 x 3 2024
+ 2x − 3x − 2 = 2024 + x − 3 (*) . Xét hàm số ( ) = 2024t f t
+ t với t  ; ( ) = 2024t f t ln 2024 +1  0, t   .
Suy ra hàm f (t ) đồng biến trên . Do vậy: ( )  f ( 2
x − x − ) = f (x − ) 2 * 2 3 2
3  2x − 3x − 2 = x − 3 2
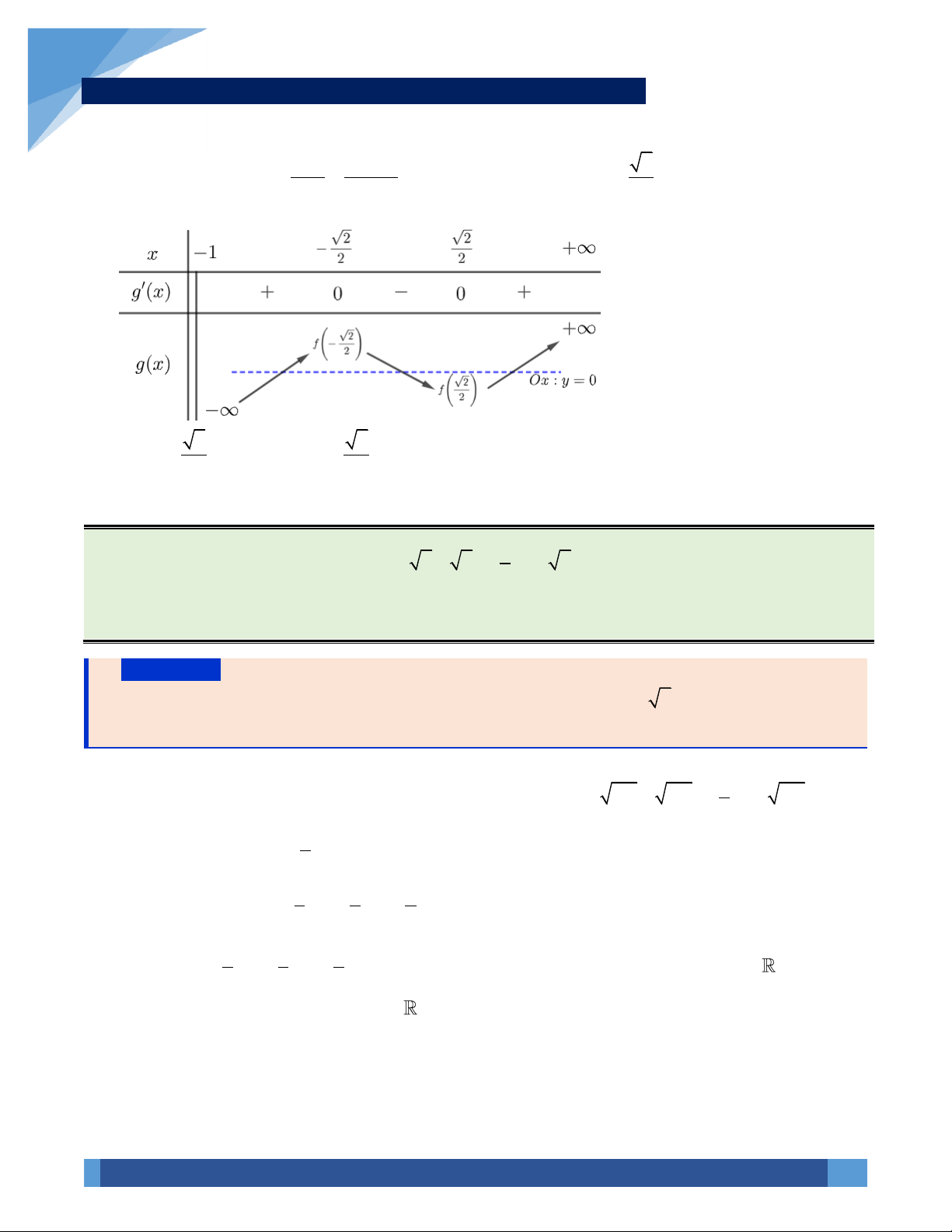
 2x − 3x = x −1 x 1 x −1 0 x 1  +  1 5       x =  (thỏa điều kiện). 2 2 2 1 5
2x − 3x = x − 2x +1
x − x −1 = 0 x = 2  2 1+ 5
Vậy phương trình có nghiệm duy nhất là x = . Chọn C. 2 VÍ DỤ 22. + − +
Tìm số nghiệm của phương trình 2 2 x 2024 x 2023 2 2 e
. x + 2023 = x + 2024 . A. 0. B. 2. C. 4. D. 1. Hướng dẫn giải: 2 2 x +2024 x +2023 2 2 + − + e e
Ta có : x 2024 x 2023 2 2 e
. x + 2023 = x + 2024  = (1). 2 2 x + 2024 x + 2023 Nhận xét : 2 x + 2023  1 và 2
x + 2024  1 với mọi x  . t e t . t e t − e t e (t − ) 1
Xét hàm số f (t ) =
với t  1, f (t ) = =
 0 với mọi t 1. t 2 t 2 t
Suy ra hàm f (t ) đồng biến trên (1; +) . Vì vậy ( )  f ( 2 x + ) = f ( 2 1 2024 x + 2023 ) 2 2
x + 2024 = x + 2023  ( 2 x + ) 2
2023 − x + 2023 +1 = 0 (2). Đặt 2 t =
x + 2023  2023 . Phương trình (2) trở thành: 2
t − t +1 = 0 (vô nghiệm).
Vậy phương trình đã cho vô nghiệm. Chọn A. 2 2 2cos x cos x 2024  2024   2024 
VÍ DỤ 23. Gọi T là tổng tất cả các nghiệm của phương trình − = cos 2 . x     trên 643  643   643  đoạn 0; .   3 A. x = . B. x = . C. x = . D. x = . 4 2 4 Hướng dẫn giải: HOÀNG XUÂN NHÀN 14
15 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT Đặ 2024 2 2 t a =
1,002 1. Phương trình trở thành: 2cos x cos − = cos2 . x a a x a 643 2 2cos x a a  − = 2 2 2 2 cos 2x 1−cos x cos x 2 2 sin x 2 cos x 2  a − a
= cos x −sin x a +sin x = a + cos x (*). 2 2 cos x cos x a a a Xét hàm số ( ) t
f t = a + t với t  0 ; ( ) 1 t f
t = a ln a +1  0, t
  0.Suy ra f (t) đồng biến trên . + Vì vậy: ( ) 2 2 2 2
*  f (sin x) = f (cos x)  sin x = cos x 2 2
 cos x −sin x = 0  cos2x = 0      3  x =
+ k , k  . Vì x 0;  nên x =  ;  . 4 2  4 4   3 Suy ra T = + =  . Chọn A. 4 4 Phương pháp:
Bạn đọc cần Nắm vững phương pháp giải phương trình trong phần Tóm tắt lí thuyết gồm:
⎯ Phương trình lôgarit cơ bản.
⎯ Phương trình lôgarit dạng mũ hóa hai vế.
⎯ Phương trình lôgarit dạng đặt ẩn phụ.
⎯ Phương trình lôgarit dạng tích.
⎯ Đánh giá hai vế phương trình hoặc dựa vào tính đơn điệu của hàm số, chứng minh
phương trình vô nghiệm, có tối đa 1 nghiệm, 2 nghiệm...
Lưu ý: Với phương trình log f ( x) = b f ( x) b
= a thì ta không cần đặt điều kiện cho f(x), a
tất cả phương trình lôgarit còn lại luôn cần điều kiện để lôgarit có nghĩa trước khi được giải.
Bài toán 1. Các phương trình lôgarit thường gặp
VÍ DỤ 24. Tập nghiệm của phương trình 2 log (x − 7) = 2 là: 3 A. {− 15; 15}. B. { 4 − ;4}. C.   4 . D. −  4 .
Nhận xét: Với phương trình dạng log f ( x) = b (a  0, a  )
1 thì ta không cần đặt điều kiện cho x. a Hướng dẫn giải: x = 4 Ta có: 2 log (x − 7) = 2 2  x − 7 = 9 
. Vậy tập nghiệm phương trình là S =  4 − ;  4 . 3  x = 4 − HOÀNG XUÂN NHÀN 15
16 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT Chọn B.
VÍ DỤ 25. Gọi x , x là các nghiệm của phương trình log ( 2 x − x = log x +1 . Tính 2 2
P = x + x . 2 ) 2 ( ) 1 2 1 2 A. P = 6 . B. P = 8 . C. P = 2 . D. P = 4 . Hướng dẫn giải: 2
x − x = x +1 2
x − 2x −1 = 0 x =1+ 2 Ta có: log ( 2 x − x = log x +1     1   . 2 ) 2 ( ) x +1  0 x  1 − x =1− 2  2 2 2 Do đó: 2 2 x + x = 1+ 2
+ 1− 2 = 6 . Chọn B. 1 2 ( ) ( )
VÍ DỤ 26. Tìm tập nghiệm S của phương trình log 2x +1 − log x −1 = 1. 3 ( ) 3 ( ) A. S =   1 .
B. S = −  2 . C. S =   3 . D. S =   4 .
_____Đề thi THPT QG, năm 2017_____ Hướng dẫn giải:  1 − 2x +1  0 x  Điều kiện :    2  x  1. x −1  0 x 1 2x +1 2x +1 Ta có : log 2x +1 − log x −1 = 1  log =1  = 3  x = 4 3 ( ) 3 ( ) 3 x −1 x −
(thỏa mãn). Chọn D. 1
VÍ DỤ 27. Nghiệm của phương trình log (3x − 8) = 2 − x là: 3 A. 1. B. 2. C. 0. D. 3. Hướng dẫn giải: 2 x x −x x 3 Ta có: 2
log (3 − 8) = 2 − x  3 − 8 = 3  3 −8 = ( x)2 3 8.3x  − − 9 = 0 3 3x 3x = 1 −  0 (loaïi)   x 2  3 = 3  x = 2. 3x = 9 (nhaän) Chọn B. VÍ DỤ 28. 1 2 Phương trình 2 log x + log x −1
= log log 3 có bao nhiêu nghiệm? 49 7 ( ) 7 ( 3 ) 2 A. 2 . B. 3 . C. 1. D. 4 . Hướng dẫn giải: HOÀNG XUÂN NHÀN 16
17 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT 2 x  0  x  0 Điều kiện:   (  .  x −  )2 1  0 x  1 1 2 Ta có : 2 log x + log x −1
= log log 3  log x + log x −1 = log 2 49 7 ( ) 7 ( 3 ) 2 7 7 7 x(x − ) 1 = 2 2  − − = x = 2  x x 2 0
log x x −1 = log 2  x x −1 = 2      (nhận). 7 ( ) 7 ( )  x  ( x − ) 1 = 2 − 2
x − x + 2 = 0 x = 1 − Chọn A.
Bài toán 2. Phương trình lôgarit dạng đặt ẩn phụ VÍ DỤ 29. 5
Cho phương trình log 2 + log x =
(*) . Tìm mệnh đề đúng. x 2 2
A. (*) có hai nghiệm dương. B. (*) vô nghiệm.
C. (*) có một nghiệm âm.
D. (*) có hai nghiệm trái dấu. Hướng dẫn giải: Điề 1
u kiện: 0  x  1. Đặt t = log x  = log 2 . 2 x tt = 2 Phương trình (*) trở 1 5 5  thành: 2
+ t =  t − t +1 = 0  1 . t 2 2 t =  2 1 1 1 Với t = 2 thì 2
log x = 2  x = 2 = 4. Với t = thì 2 log x =  x = 2 = 2. 2 2 2 2
Vậy, tập nghiệm của phương trình (*) là: S =  2;  4 . Chọn A.
VÍ DỤ 30. Tổng các nghiệm của phương trình 2 log
3x + log 9x − 7 = 0 bằng 3 ( ) 3 ( ) 28 244 244 A. 84 . B. . C. . D. . 81 81 3 Hướng dẫn giải:
Điều kiện: x  0 . Ta có: 2
log (3x) + log (9x) 2
− 7 = 0  log 3x + log 3x + log 3 − 7 = 0 3 3 3 ( ) 3 ( ) 3 2
 log 3x + log 3x − 6 = 0 . 3 ( ) 3 ( ) t = 3 −
Đặt t = log 3x . Phương trình trở thành: 2
t + t − 6 = 0  . 3 ( )  t = 2 HOÀNG XUÂN NHÀN 17
18 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT log 3x = 3 − 3 −  1  = = 3 ( ) 3x 3 x Khi đó:      81  (thỏa điều kiện) . log 3x = 2  2 3x = 3  3 ( ) x = 3 1 244
Tổng các nghiệm của phương trình là + 3 = . Chọn C. 81 81
VÍ DỤ 31. Tích các nghiệm của phương trình log (125x) 2 log x = 1 bằng: x 25 7 630 1 A. . B. . C. . D. 630 . 25 625 125 Hướng dẫn giải:
Điều kiện : 0  x 1. 1 Ta có : log x x =  + x =  + x = . x (125 ) 2 log 1 log 5 1 log 1 3log 5 1 log 1 25 ( 3 x ) 2 2 2 ( x ) 5 5 4  3  1 3 1 t =1 Đặ 1 t t = log x
= log 5. Phương trình trở thành: 2 2
+1 . .t =1  t + t −1 = 0  . 5 x    tt  4 4 4 t = 4 −
Với t = 1 thì log x =1  x = 5. Với t = 4 − thì 4 log x 4 x 5− = −  = . 5 5 − 1
Tích hai nghiệm phương trình là 4 5.5 = . Chọn C. 125
VÍ DỤ 32. Cho phương trình log x + x − + x −
= . Tìm tích hai nghiệm của phương x− ( 2 )1 logx+ (2 )2 2 1 4 2 1 1 trình trên. 5 5 A. 3 . B. 2 . C. . D. . 4 2 2
2x + x −1  0  Điề 1
u kiện: 0  2x −1  1   x  1. 2 0  x +11 
Phương trình đã cho trở thành log
2x −1 x +1 + 2 log 2x −1 = 4 2 x 1 − ( )( ) x 1 + ( )  1+ log x +1 + 2 log 2x −1 = 4  log x +1 + 2 log 2x −1 − 3 = 0 (*). 2 x 1 − ( ) x 1 + ( ) 2 x 1 − ( ) x 1 + ( ) Đặ 1 t t = log x +1  = log 2x −1 . 2 x 1 − ( ) x 1 + ( ) t 2 t =1 Khi đó (*) trở thành: 2 t +
− 3 = 0  t − 3t + 2 = 0  .  tt = 2 Với t = 1 thì log
x +1 = 1  x +1 = 2x −1  x = 2. 2 x 1 − ( ) x 0 (loaïi) Với t = 2 thì log x +
=  x + = x −
x − x =  . x− ( ) 1 2 1 (2 )2 2 1 4 5 0 2 1 5 x (nhaän) 4 HOÀNG XUÂN NHÀN 18
19 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Phương trình có hai nghiệ 5 5 m x = 2; x =
nên tích của chúng bằng . Chọn D. 4 2
VÍ DỤ 33. Cho phương trình ( x + 2) 2 log
x +1 + 4 x +1 log
x +1 −16 = 0 . Biết , a b là hai nghiệm 3 ( ) ( ) 3 ( )
thực của phương trình đã cho với a b , hãy tính giá trị a + 27b . 49 74 A. − . B. − . C. 1. D. 0 . 2 3 Hướng dẫn giải:
Điều kiện: x  1.
− Đặt t = log x +1 . 3 ( )
Phương trình trở thành: ( x + ) 2 2 t + 4 ( x + )
1 t −16 = 0 (*) . Nhận xét: x + 2  0, x   1 − . 2 2
Ta có:  = ( x + ) + (x + ) 2 4 1 16
2 = 4x + 24x + 36 = (2x + 6) . 2 − (x + ) 1 + 2x + 6 4 2 − (x + ) 1 − 2x − 6 4 − (x + 2)
Khi đó, (*) có hai nghiệm: t = = ; t = = = 4 − 1 2 x + 2 x + 2 x + 2 x + . 2 4 4 Với t = t = log x +1 =
. Phương trình này chỉ có một nghiệm x = 2 vì vế trái là 1 x + thì 3 ( ) 2 x + 2
hàm số đồng biến trên (−1; +) , vế phải là hàm nghịch biến trên (−1; +) . 1 80 Với t = t = 4 − thì log x +1 = 4 −  x +1 =  x = − . 3 ( ) 2 81 81 80 74
Do vậy, ta có: a = 2, b = −
a + 27b = − . Chọn B. 81 3
Bài toán 3. Phương trình lôgarit dạng tích
VÍ DỤ 34. Phương trình log 3x − 4 .log x = log x có số nghiệm là: 2 ( ) 2 2 A. 1. B. 5. C. 10. D. 17. Hướng dẫn giải: Điề 4 u kiện: x  . 3 Ta có: log
3x − 4 .log x = log x  log . x log 3x − 4 −1 = 0 2 ( ) 2 2 2  2 ( )  log x = 0  =  = (loaïi) 2 x 1 x 1       log 3x − 4 = 1  3x − 4 = 2 x = 2 (nhaän). 2 ( )
Vậy phương trình đã cho có đúng một nghiệm. Chọn A.
VÍ DỤ 35. Tổng các nghiệm của phương trình 2 log x − log . x log
4x + 2 log x = 0 là: 2 ( ) 2 HOÀNG XUÂN NHÀN 19
20 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT A. 100. B. 101. C. 102. D. 103 Hướng dẫn giải:
Điều kiện: x  0 . Ta có: 2 log x − log . x log (4x) 2
+ 2log x = 0  log x − 2log x − log .
x log x + 2 log x = 0 2 2 2 2
 log x(log x − 2) − log .x log x − 2 = 0  log x − log x . log x − 2 = 0 2 ( ) ( 2 ) ( )
log x − log x = 0
log x − log 10.log x = 0
log x 1− log 10 = 0 x =1 2 2 ( 2 )         (thỏa mãn). 2 log x − 2 = 0 log x = 2 x =10 x =100
Tổng các nghiệm của phương trình là 101. Chọn B. a
VÍ DỤ 36. Cho biết x = (với , a b
và a là số nguyên tố) là một nghiệm của phương trình 0 b 3  3   x  1 log log x − log     = + log
x . Tìm bội số chung nhỏ nhất của hai số a và b. 3 2 3 2  x   3  2 A. 16 . B. 24 . C. 12. D. 6 . Hướng dẫn giải:
Điều kiện: x  0. 3  3   x  1  1  1 1 Ta có: log log x − log     = + log
x  1− log x log x − 3log x − = + log x 3 2 3 2 ( 3 ) 2  3  2  x   3  2  2  2 2  ( 1 1
1− log x log x − 3log x −
log x = 0  1− log x log x − 3log 2 log x − log x = 0 3 ) 2 3 2 ( 3 ) 2 3 2 2 2 2 log x = 0 x =1 2  1    1
 log x 1− log x − 3log 2 − = 0  1    3 − log 2+ . 2 3 3 3 3     2 2 log x = 3 − log 2 + x = 3 = 3 3  2  8 a 3 a = 3 Vậy x = =  
. Bộ số chung nhỏ nhất của 3 và 8 là 24. Chọn B. 0 b 8 b  = 8 2  
VÍ DỤ 37. Cho phương trình 2
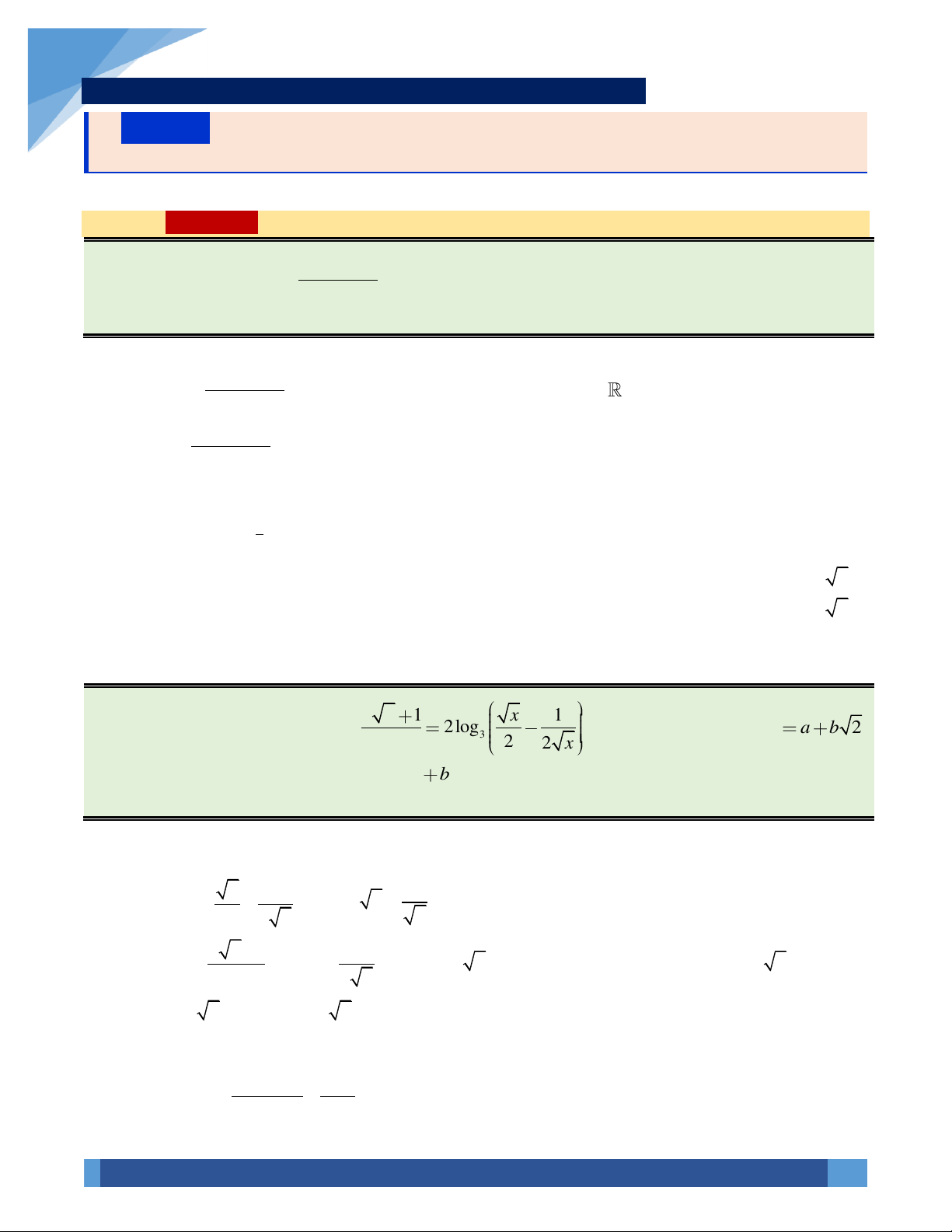
3log ( 2 + x + 2 − x ) + 2log ( 2 + x + 2 − x )log ( 2 9x
+ 1−log x = 0 , 3 1 3 ) 1 3  3  a 17 a biết rằng x = (với
là phân số tối giản) là một nghiệm của phương trình trên. Giá trị log b 0 b b a
thuộc khoảng nào sau đây? A. (1; 2) . B. (0; ) 1 . C. (3; 4) . D. (2;3) .
_____Trích từ đề thi tự luận Kỳ thi THPT Quốc gia năm 2016_____ Hướng dẫn giải:
Điều kiện: 0  x  2. HOÀNG XUÂN NHÀN 20
21 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Phương trình  3log ( 2 + x + 2 − x ) − 2log ( 2 + x + 2 − x )log (3x)2 + (1+ log x)2 2 = 0 3 3 3 3 2
 3log ( 2+ x + 2− x)−4log ( 2+ x + 2− x)log (3x) 2 + log 3x = 0 3 3 3 3 ( ) 2
 3log ( 2+ x + 2− x)−3log ( 2+ x + 2− x)log (3x)−log ( 2+ x + 2− x)log (3x) 2 + log 3x = 0 3 3 3 3 3 3 ( )  3log
2 + x + 2 − x log
2 + x + 2 − x − log 3x  − log 3x log
2 + x + 2 − x − log 3x  = 0 3 ( ) 3  ( ) 3( ) 3 ( ) 3   ( ) 3( )  log
2 + x + 2 − x − log 3x  . 3log
2 + x + 2 − x − log 3x  = 0 3  ( ) 3( ) 3   ( ) 3( ) log
2 + x + 2 − x = log 3x  + + − = 3 ( ) 3 ( ) 2 x 2 x 3x (1)       (  + x + − x ) = 
( x) ( 2+ x + 2− x)3 3 = 3x (2) log 2 2 log 3 3 3 2 9  x − 4  0  ▪ ( ) 2 2 2 2
1  2 + x + 2 − x + 2 4 − x = 9x  2 4 − x = 9x − 4  4  ( 2 4 − x ) 4 2
= 81x − 72x +16  2 2  2 2 x  −  x
x  −  x   3 3 2 17  2 17  3 3    x = 
. So điều kiện, ta nhận x = . 68 9 9 4 2 2 2   8
 1x − 68x = 0 x = 0  x =  81 2
▪ Xét phương trình (2): Ta có: ( + x + − x ) 2 2 2
= 4 + 2 4 − x  4, x  (0;2; mặt khác
2 + x + 2 − x  2, x
 (0;2. Suy ra vế trái (2) = ( + x + − x)( + x + − x)2 2 2 2 2  8.
Vế phải (2) = 3x  6, x
 (0;2 . Do vậy phương trình (2) vô nghiệm. 2 17 a 17 a = 2
Vậy, phương trình đã cho có nghiệm duy nhất x = =    log 9  3,17  3;4 . 2 ( ) 9 b b  = 9 Chọn C.
Bài toán 4. Giải phương trình lôgarit bằng phương pháp đánh giá
VÍ DỤ 38. Số nghiệm của phương trình x + = là: x ( ) 9 log 1 log 2 A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giải: Xét phương trình (*): x + =
. Điều kiện: 0  x  1. x ( ) 9 log 1 log 2
Xét x  1 . Vế trái (*): x +  x = 
. Suy ra (*) không có nghiệm thuộc (1; +). x ( ) 9 log 1 log 1 log x 2 HOÀNG XUÂN NHÀN 21
22 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Xét 0  x  1. Vế trái (*): x +  = 
. Suy ra (*) không có nghiệm thuộc (0; ) 1 . x ( ) 9 log 1 log 1 0 log x 4
Vậy phương trình đã cho vô nghiệm. Chọn A.
VÍ DỤ 39. Số nghiệm của phương trình log x +1 + log 2x +1 = 2 là: 3 ( ) 5 ( ) A. 1. B. 2. C. 0. D. 3. Hướng dẫn giải: −  1  Điề 1 u kiện: x
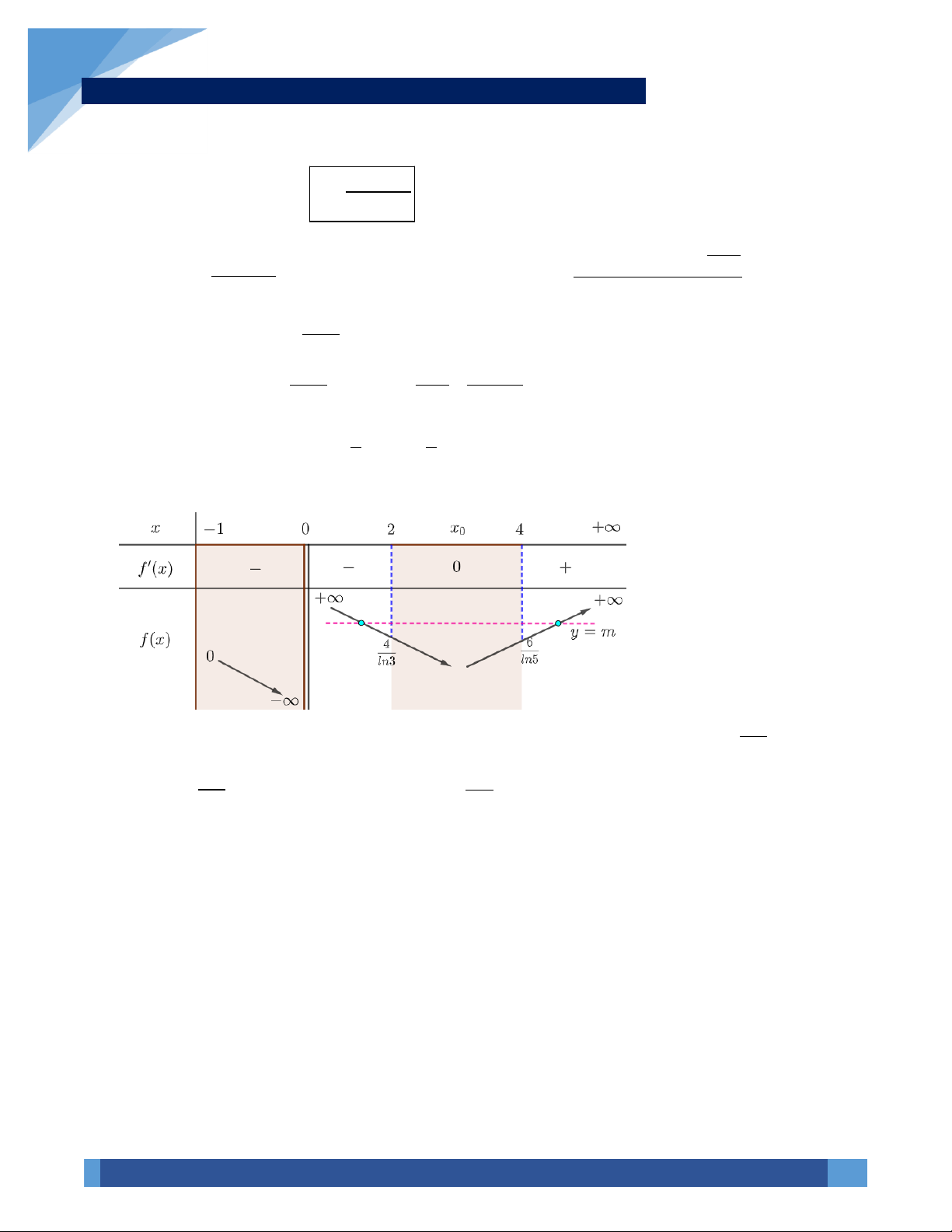
. Xét hàm số f ( x) = log x + 1 + log 2x + 1 với x  − ; +   . 3 ( ) 5 ( ) 2  2  1 2  1 −   1 
Ta có: f ( x) = ( +    + 
. Suy ra f ( x) đồng biến trên − ;+   . x + ) ( x + ) 0, x ; 1 ln 3 2 1 ln 5  2   2 
Mặt khác: f (2) = 2 nên x = 2 là một nghiệm của phương trình đã cho.
Vậy phương trình có nghiệm duy nhất là x = 2 . Chọn A.
VÍ DỤ 40. Xét phương trình log 1+ x = log
x . Kết luận nào sau đây là đúng? 46 ( ) 2025
A. Phương trình có nghiệm là một số chính phương.
B. Phương trình vô nghiệm.
C. Phương trình có đúng hai nghiệm.
D. Phương trình có nghiệm là số thực nhỏ hơn 2024. Hướng dẫn giải: 1
 + x = 46t (1) Đặt t = log 1+ x = log x   . 46 ( ) 2025 x = 2025t (2) t t     t t t t 1 45
Thay (2) vào (1): 1+ 2025 = 46  1+ 45 = 46  + =1 (*)     .  46   46  t t     Đặt f (t) 1 45 = +     ; ta có f ( )
1 = 1; f (t ) là hàm nghịch biến trên
(vì nó là tổng của hai  46   46  hàm nghịch biến trên
), vế phải của (*) là hằng số.
Vậy (*) chỉ có nghiệm duy nhật t = 1; suy ra 2 log
x = 1  x = 2025 = 45 . Chọn A. 2025
VÍ DỤ 41. Hỏi phương trình x − x + ( x + )3 2 3 6 ln
1 +1 = 0 có bao nhiêu nghiệm phân biệt? A. 2 . B. 1. C. 3 . D. 4 .
_____Đề tham khảo, Kỳ thi THPT QG năm 2017, lần 2_____ Hướng dẫn giải: Điều kiện: x  1
− . Phương trình đã cho tương đương với 2
3x − 6x + 3ln ( x + ) 1 +1 = 0 . HOÀNG XUÂN NHÀN 22
23 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Xét hàm số g ( x) 2
= 3x − 6x + 3ln (x + )
1 +1 liên tục trên khoảng (−1; +) . 3 6x − 3 2 Ta có: g( x) 2 2 = 6x − 6 + =
; y = 0  2x −1 = 0  x =  x +1 x + (thỏa điều kiện). 1 2  2   2  Vì g  −   3,059  0   , g    0 − ,138  0  
và lim g ( x) =  nên đồ thị hàm số y = g ( x) 2   2   x→
cắt trục hoành tại 3 điểm phân biệt. Vì vậy phương trình (*): g ( x) = 0 có ba nghiệm. Chọn C. VÍ DỤ 42. 2
Cho biết phương trình log ( 3 1+ x + x = log
x có nghiệm là x , hỏi 0 2x có tất cả bao 3 ) 2 3 0 nhiêu chữ số? A. 1234 . B. 4097 . C. 4096 . D. 1233 . ơ
Nhận xét: Điều kiện bài toán là x  0 . Ta thấy trong lôgarit xuất hiện căn bậc hai và căn
bậc ba (có bội số chung là 6), thêm nữa ta muốn đổi biến sao cho log
x được tính một 2
cách dễ dàng. Từ những lí do trên, ta nảy sinh ý tưởng đặt 6 2 y x = . Hướng dẫn giải: Điề y y 2
u kiện: x  0 . Đặt 6 2 y x =
, phương trình trở thành: log ( 6 3 6 1 2 2 ) 6 log 2 y + + = 3 2 3  log ( y y 2 3 2 1+ 2 + 2 ) 3 = .log 2 y  log ( 3 y 2 1+ 2 + 2 y ) 3 y 2 y 2
= 2y  1+ 2 + 2 = 3 y 3 2 3 3 y y y       y y y 1 8 4  1+ 8 + 4 = 9  + + = 1 (*).        9   9   9  y y y       Đặt f ( y) 1 8 4 = + +    
  ; ta có f (2) = 1 và f ( y) là hàm số nghịch biến trên (vì nó là  9   9   9 
tổng của các hàm số nghịch biến trên
. Do vậy phương trình (*) có nghiệm duy nhất y = 2 . Suy ra: 6.2 12 x = 2
= 2 = 4096 = x . Khi đó: 0x 4096 2 = 2 . 0
Số các chữ số của 4096 2
là 4096 log 2 +1 = 1234 (chữ số). HOÀNG XUÂN NHÀN 23
24 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
Ghi nhớ: Số các chữ số của số tự nhiên rất lớn M là log M  +1; trong đó log M  là phần nguyên của logM.
Bài toán 5. Giải phương trình lôgarit bằng phương pháp hàm đặc trưng 2 x + 3x + 4
VÍ DỤ 43. Phương trình 2 ln + x + 4x + 2 = 0 + −
x , x . Khi đó x x bằng x + có hai nghiệm 2 1 2 1 2 A. 4 − . B. 2 . C. 4 . D. 2 − . Hướng dẫn giải: 2 x + 3x + 4 Điều kiện:
 0  −x + 2  0 + +      − x x x ) x 2. x + (do 2 3 4 0, 2 2 x + 3x + 4 Ta có: 2 ln
+ x + 4x + 2 = 0  ( 2 x + x + ) + ( 2 ln 3 4
x + 3x + 4) = ln (−x + 2) + (−x + 2) − (*). x + 2
Xét hàm số f (t ) = t + ln t với t (0; +) . 1
Ta có: f (t ) = 1+  0, t
 (0;+) nên hàm số f (t) đồng biến trên khoảng (0;+). tx = 2 − + 2 Vậy (*)  f ( 2
x + 3x + 4) = f (−x + 2) 2
x + 3x + 4 = −x + 2 2
x + 4x + 2 = 0  x = 2−− 2 (thỏa mãn điều kiện).
Khi đó: x + x = 4 − . Chọn A. 1 2 VÍ DỤ 44. 2 x 1 x 1
Biết phương trình log 2 log
có một nghiệm dạng x a b 2 5 3 x 2 2 x trong đó ,
a b là các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5 . Hướng dẫn giải: x  0 x  0   Điều kiện:  x 1   1  x  1 . −  0 x     2 2 xx 2 x +1  x −1  Ta có: log = 2log
 log 2 x +1 − log x = 2log x −1 − 2log 2 x 5 3   5 ( ) 5 3 ( ) 3 ( ) x  2 x
 log 2 x +1 + 2log 2 x = log x + 2log x −1 * . 5 ( ) 3 ( ) 5 3 ( ) ( )
Xét hàm số: f (t ) = log t +1 + 2 log t với t  0 . 5 ( ) 3 1 2
Ta có: f (t ) = ( +  , t
  0 . Suy ra f (t) đồng biến trên (0;+). t + ) 0 1 ln 5 t ln 3 HOÀNG XUÂN NHÀN 24
25 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT x = −  Vì vậy ( )  f (
x ) = f (x − ) 1 2 1 * 2
1  2 x = x −1  x − 2 x −1 = 0   .  x =1+ 2 1
Vậy x = 1+ 2  x = 3 + 2 2  a = 3, b = 2 . Ta có: 2a + b = 8. Chọn B. x x  +  VÍ DỤ 45. 5 3 Tính tổng +
S tất cả các nghiệm của phương trình: x 1 ln 
 + 5 + 5.3x − 30x −10 = 0 .  6x + 2  A. S = 1. B. S = 2 . C. S = 1 − .
D. S = 3. Hướng dẫn giải: 1
Điều kiện x  − . Phương trình tương đương ln (5x + 3x ) − ln (6 + 2) + 5(5x + 3x x )−5(6x+2) = 0 3
 ln (5x + 3x ) + 5(5x + 3x ) = ln(6x + 2) +5(6x + 2) (1).
Xét hàm số f (t ) = ln t + 5t, t  0 ; f (t ) 1 = + 5  0, t
  0 . Suy ra f (t) đồng biến trên (0;+). t Vì vậy: ( ) 1  (5x +3x f
) = f (6x+2) 5x +3x =6x+2 5x +3x −6x−2=0. x x x x 1
Xét g ( x) = 5 + 3 − 6x − 2 , ( ) = 5x ln 5 + 3x g x
ln 3 − 6 ; g ( x) 2 2
= 5 ln 5 + 3 ln 3  0, x   − . 3
Vì vậy phương trình g( x) = 0 có không quá một nghiệm, suy ra phương trình g ( x) = 0 có không quá hai nghiệm.
Ta lại có: g (0) = g ( )
1 = 0 . Vậy phương trình đã cho có hai nghiệm là x = 0; x =1.
Tổng hai nghiệm này bằng 1. Chọn A. HOÀNG XUÂN NHÀN 25
26 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Phương pháp giải toán:
1. Biện luận nghiệm phương trình dựa vào tam thức bậc hai:
a) Dạng tam thức bậc hai: f ( x) 2
= ax + bx + c (a 0) . b  2 2
 = b − 4ac  = b − ac, b =   .  2 
• Nếu   0 thì phương trình f (x) = 0 vô nghiệm. • b
Nếu  = 0 thì phương trình f ( x) = 0 có nghiệm kép x = x = − . 1 2 2a −   • b
Nếu   0 thì phương trình f ( x) = 0 có hai nghiệm phân biệt x = (hoặc 1,2 2a b −    x = ). 1,2 a
b) Định lí Vi-ét: Xét phương trình 2
ax + bx + c = 0 với a  0,   0 . Ta có: • b
Tổng hai nghiệm: S = x + x = − . 1 2 a • c
Tích hai nghiệm: P = x x = . 1 2 a
c) Điều kiện có nghiệm của phương trình 2
ax + bx + c = 0 với ( ) 2
f x = ax + bx + c .     • a 0, 0
Phương trình có hai nghiệm dương phân biệt   .
S  0, P  0     • a 0, 0
Phương trình có hai nghiệm âm phân biệt   .
S  0, P  0
• Phương trình có hai nghiệm trái dấu  ac  0 . a  0,   0 
• Phương trình có hai nghiệm phân biệt lớn hơn    .  ( ) S af  0,    2 a  0,   0 • 
Phương trình có hai nghiệm phân biệt bé hơn    .  ( ) S af   0,    2
• Phương trình có hai nghiệm phân biệt thỏa x    x af   0 . 1 2 ( )
Chú ý: Những chỗ có điều kiện   0 , ta đều có thể thay bằng    0 .
2. Biện luận nghiệm phương trình dựa vào khảo sát hàm số: HOÀNG XUÂN NHÀN 26
27 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
a) Mối quan hệ giữa nghiệm phương trình và tương giao đồ thị:
Xét phương trình f ( x) = g ( x) (*) , miền điều kiện D.
Khi đó: (*) có n nghiệm  Đồ thị hai hàm số y = f ( x), y = g ( x) cắt nhau tại n điểm.
b) Phương pháp biện luận nghiệm dựa vào khảo sát hàm số:
Xét phương trình f ( x,m) = 0 (*) .
Bước 1: Cô lập m từ phương trình (*): g ( x) = m
(hoặc g ( x) = h (m) , trong đó h (m) là một hàm chỉ chứa tham số m).
Bước 2: Thực hiện một trong hai tình huống sau:
• Nếu đề bài chỉ đưa ra giả thiết: “phương trình có nghiệm”; ta chỉ cần tìm miền giá
trị T của hàm số g ( x) trên tập khảo sát của nó, sau đó cho mT (hoặc h (m) T ).
• Nếu đề bài đưa ra giả thiết: “Phương trình có n nghiệm (âm, dương, lớn hơn a, bé
hơn b…)”; ta lập bảng biến thiên của hàm số g ( x) trên tập khảo sát của nó.
Vì đường thẳng y = m (hay y = h(m)) luôn là đường thẳng nằm ngang (vuông góc
trục tung), ta chọn m ứng với đường thẳng nằm ngang phù hợp đề bài.
3. Nghiệm đặc biệt của phương trình chứa biểu thức đối xứng:
a) Biểu thức đối xứng theo u, v:
Một biểu thức hai biến dạng f (u, v) được gọi là biểu thức đối xứng nếu
f (u, v) = f (v,u) .
b) Phương trình đối xứng loại 1:
Xét một phương trình dạng f (u, v) = 0 . Phương trình này được gọi là đối xứng loại 1
theo u, v nếu f (u, v) là biểu thức đối xứng, tức là f (u, v) = f (v,u ) .
c) Nghiệm đặc biệt của phương trình đối xứng loại 1:
Xét phương trình chứa biểu thức đối xứng dạng: f (u,v) = 0 (*) . Khi đó:
⎯ Nếu (u ;v là một nghiệm của (*) thì (v ;u cũng là một nghiệm của (*). 0 0 ) 0 0 )
⎯ Nếu phương trình (*) có 2n +1 (n ) nghiệm thì sẽ có một nghiệm dạng (u ;u 0 0 )
, tức là u = v . 0 0 ⎯ Nếu v = u
− thì (*) có dạng: f (u, u − ) = 0.
Nếu phương trình này có nghiệm x thì nó cũng có một nghiệm là −x . Vì vậy, 0 0
phương trình có nghiệm duy nhất suy ra x = −x x = 0 . 0 0 0 HOÀNG XUÂN NHÀN 27
28 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 1. Phương trình mũ, lôgarit quy về bậc hai có nghiệm đẹp
VÍ DỤ 46. Cho phương trình 2 log
9x − m + 5 log x + 3m −10 = 0 . Số giá trị nguyên của tham số m 3 ( ) ( ) 3
để phương trình đã cho có hai nghiệm phân biệt thuộc 1;8  1 là A. 3 . B. 5 . C. 4 . D. 2 . Hướng dẫn giải: 2 Ta có: 2 log
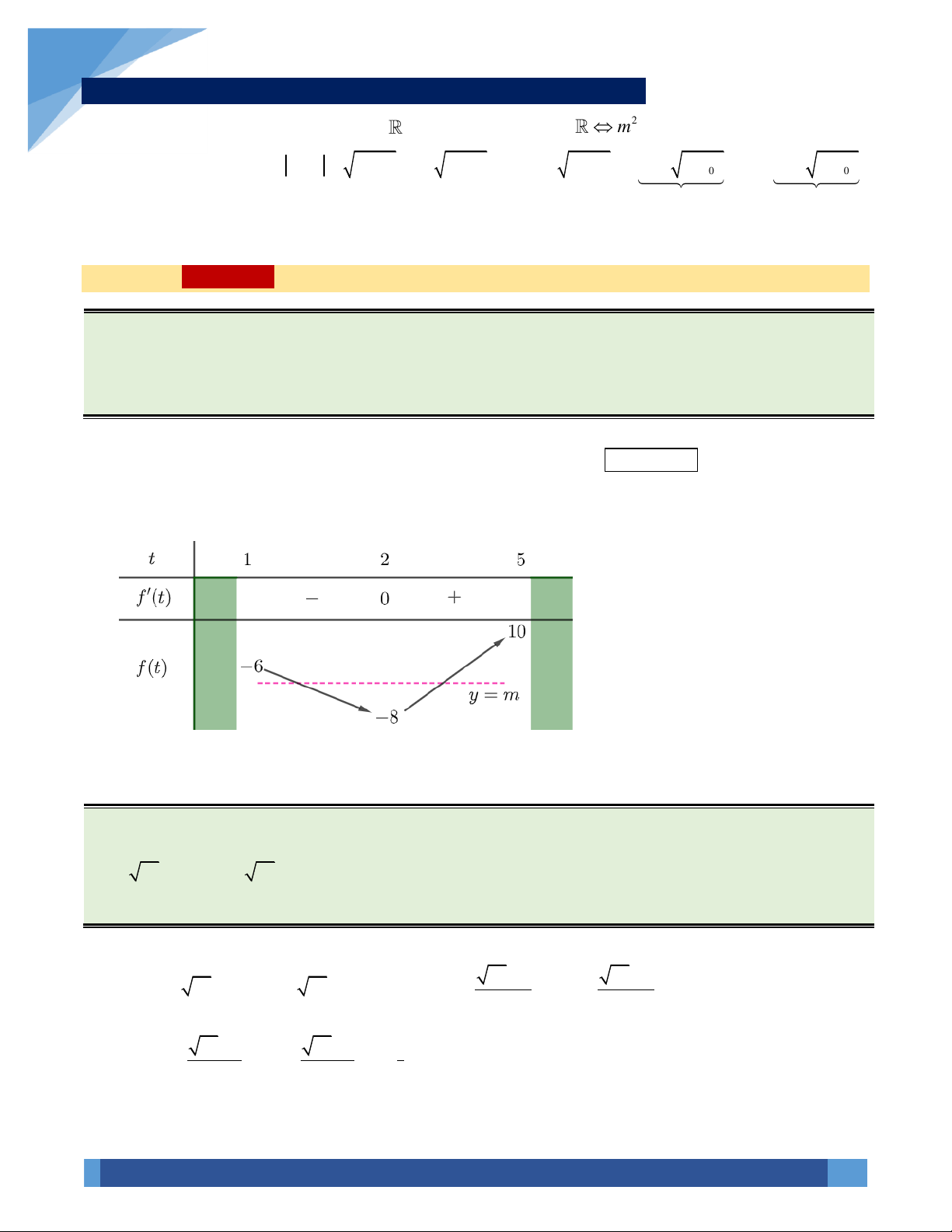
9x − m + 5 log x + 3m −10 = 0  2 + log x
− m + 5 log x + 3m −10 = 0 (1). 3 ( ) ( ) 3 ( 3 ) ( ) 3
Đặt t = log x ; với x 1; 
81 thì t 0; 4 . 3 t = 3
Khi đó (1) trở thành (2): t − (m + ) ??? 2
1 t + 3m − 6 = 0   . t = m − 2
Mỗi nghiệm t của (2) sẽ tương ứng với một nghiệm x của (1) trong điều kiện của chúng.
Theo đề: (1) có hai nghiệm phân biệt thuộc 1; 
81  (2) có hai nghiệm phân biệt thuộc 0; 4 m − 2  3 m  5    
. Vì m nguyên nên m 2;3; 4;  6 . Chọn C. 0  m − 2  4 2  m  6
Bình luận: Một phương trình bậc hai chứa tham số được gọi là có nghiệm đẹp khi biệt số
Δ của nó được biểu diễn ở dạng bình phương một đa thức theo tham số đó; vì vậy nghiệm
của phương trình được biểu diễn dễ dàng theo tham số đó. Xét phương trình (2) 2 2 : 2 t − (m + )
1 t + 3m − 6 = 0 ;  = (m + ) − ( m − ) 2 1 4 3
6 = m −10m + 25 = (m − 5) . m +1+ (m − 5)
m +1− (m − 5)
Nhờ vậy mà phương trình có hai nghiệm đẹp là: t = = m − 2; t = = 3 . 1 2 2.1 2.1
Điều này giải đáp cho mục (???) trong lời giải trên.
Tuy vậy, trong trắc nghiệm, học sinh còn có một giải pháp hiệu quả hơn, đó là nhờ sự hỗ trợ của
máy tính bỏ túi, trong đó các em thay m = 100 để thử xem liệu phương trình có cho nghiệm đẹp?
Dùng chức năng giải phương trình Kết quả thu được: Kết quả thu được:
bậc hai với a = 1, b = − (100 + ) 1 ,
x = 98 =100 − 2 = m − 2 x = 3 1 2
c = 3.100 − 6 (tức thay m = 100 ).
Nhờ vậy, ta viết nhanh nghiệm của phương trình (2) là t = 3; t = m − 2 .
Tuy vậy, nếu máy tính không cho ra những kết quả lý tưởng như trên, ta buộc lựa chọn phương
pháp giải khác mà cuốn sách này sẽ đề cập đến trong các bài toán sau. HOÀNG XUÂN NHÀN 28
29 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
VÍ DỤ 47. Giả sử phương trình 2
log x − (m + 2) log x + 2m = 0 có hai nghiệm thực phân biệt x , x thỏa 2 2 1 2
mãn x + x = 6 . Giá trị biểu thức x − x là 1 2 1 2 A. 4. B. 3. C. 8. D. 2. Hướng dẫn giải: Xét phương trình (1): 2
log x − (m + 2) log x + 2m = 0 . Điều kiện: x  0 . 2 2 t = 2
Đặt t = log x . Phương trình (1) tương đương với (2): 2
t − (m + 2)t + 2m = 0  . 2  t = m
Mỗi nghiệm t của (2) sẽ tương ứng với một nghiệm x của (1) trong điều kiện của chúng.
Phương trình (1) có hai nghiệm phân biệt  Phương trình (2) có hai nghiệm phân biệt  m  2. Ta có: log = 2  = 4; log =  = 2m x x x m x . 2 1 1 2 2 2 Theo giả thiết: + = 6  2m x x
+ 4 = 6  m = 1. Vì vậy x = 2  x − x = 2. Chọn D. 1 2 2 1 2 VÍ DỤ 48. Tìm tất cả các giá trị của tham số m để phương trình 2
x + x + ( m − ) 2x+ x+ − ( m + ) 2 2 2 1 2 x +4 x+2 4.4 2 2 6 6 3 3
= 0 có hai nghiệm thực phân biệt.
A. 4 − 3 2  m  4 + 3 2
B. m  4 + 3 2 hoặc m  4 − 3 2 . −1 1 − C. m  1 − hoặc m  . D. 1 −  m  . 2 2 Hướng dẫn giải: 2 2 2 Ta có:
x +2 x + ( m − ) x +2x 1
+ − ( m + ) 2x +4x+2 4.4 2 2 6 6 3 3 = 0 (x+ )2 1 (x+ )2 1 (x+ )2 1 ( + +      + m − ) (x )2 1
− ( m + ) (x )2 1 4 =  +   ( m− ) 2 4 2 2 6 6 3 9 0 2 2 −   (6m+3) = 0 (1)  9   3  2 ( x 1 + )   Đặ 2 t t =   ; vì ( x + )2 1
 0 nên 0  t 1.  3  t = 3 0;1 2 ( 
Phương trình (1) trở thành (2): t + (2m − 2)t − 6m − 3 = 0   . t = 2 − m −1 ???
Phương trình đã cho có hai nghiệm thực phân biệt  t = 2 − m −1(0; ) 1 1  0  2
− m −11  1 2
− m  2  −  m  −1. Chọn D. 2 2 ( x 1 + )    2 2
Nhận xét: Khi t = t  0;1 thì
= t x +1 = log t  0  
, từ đây ta giải được hai 0 ( ) 0 ( ) 2 0  3  3 2 ( x 1 + )  2  2
nghiệm phân biệt x , x . Nếu t = 1 thì =1   
(x + )1 = 0  x = 1
− (nghiệm kép). Vì vậy, 1 2  3 
muốn phương trình ban đầu có hai nghiệm phân biệt x , x , ta cần t  (0; ) 1 . 1 2 HOÀNG XUÂN NHÀN 29
30 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 2. Áp dụng định lí Vi-ét cho phương trình mũ, lôgarit quy về bậc hai
VÍ DỤ 49. Tìm tất cả các giá trị thực của tham số m để phương trình x x 1 4 2 + −
+ m = 0 có hai nghiệm thực phân biệt
A. m  (− ) ;1 . B. m  (0;  1 . C. m  (0; ) 1 .
D. m  (0; +) . Hướng dẫn giải:
Phương trình đã cho tương đương với x x+ − + =  ( x )2 1 4 2 0 2 − 2.2x m + m = 0 ( ) 1 . Đặt 2x t =  0. Phương trình ( ) 1 trở thành: 2
t − 2t + m = 0 (2) . Khi đó: ( )
1 có hai nghiệm thực phân biệt  (2) có hai nghiệm dương phân biệt  1  − m  0   0    2 −
 S  0  −
 0  0  m  1. Chọn C. 1   P  0  m  0  1
VÍ DỤ 50. Phương trình x x 1 4 3.2 + −
+ m = 0 có hai nghiệm thực x , x thỏa mãn x + x = 1 − . Giá trị của 1 2 1 2
m thuộc khoảng nào sau đây? A. (−5;0) . B. (−7; −5) . C. (0; ) 1 . D. (5;7) . Hướng dẫn giải: 2 Ta có: x x 1 4 3.2 + −
+ = 0  (2x ) − 6.2x m + m = 0 ( ) 1 . Đặt 2x t =
. Phương trình đã cho trở thành: 2
t − 6t + m = 0 (2) . (2) 1 x x x + x − 1 Xét 1 2 1 2 1 t t = 2 .2 = 2
= 2 = . Theo đính lí Vi-ét: t t = m . Suy ra m = . 1 2 2 1 2 2 1 1 6  34
Thử lại: Thay m = vào (2): 2 t − 6t + = 0  t =
 0 . Như vậy, (2) có hai nghiệm 1,2 2 2 2 dương phân biệ 1
t nên (1) có hai nghiệm thực phân biệt x , x . Vậy m =
thỏa mãn đề bài. Chọn C. 1 2 2
VÍ DỤ 51. Cho biết m là số thực để phương trình 2
log x − 3log x + 2m − 7 = 0 có hai nghiệm thực x , 3 3 1
x thỏa mãn ( x + 3 x + 3 = 72 . Mệnh đề nào đúng? 1 )( 2 ) 2
A. m  (4;5) .
B. m = (3; 4) .
C. m  (2;3) .
D. m  (1; 2) . Hướng dẫn giải:
Đặt t = log x . Phương trình đã cho trở thành 2
t − 3t + 2m − 7 = 0 (*) . 3 HOÀNG XUÂN NHÀN 30
31 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Ứng với mỗi nghiệm t của (*) thì phương trình ban đầu sẽ có một nghiệm x  0 .
Phương trình đã cho có hai nghiệm phân biệt  (*) có hai nghiệm phân biệt    0
 (− )2 − ( m − ) 37 3 4 2
7  0  9 − 8m + 28  0  m  . 8
Gọi t , t là hai nghiệm phương trình (*) . Theo định lí Vi-ét: t + t = 3 1 2 1 2
 log x + log x = 3  log x .x = 3  x .x = 27 . 3 1 3 2 3 ( 1 2 ) 1 2
Theo giả thiết: ( x + 3 x + 3 = 72  x .x + 3 x + x + 9 = 72  x + x = 12 . 1 )( 2 ) 1 2 ( 1 2 ) 1 2 =27 x + x =12
x = 9 x = 3 t  = 2 t  =1 Vậy ta có 1 2 1 1 1 1           t .t = 2. 1 2 x .x = 27 x = 3 x = 9 t = 1 t = 2  1 2  2  2  2  2 Theo đị 9
nh lý Viét: t .t = 2  2m − 7 = 2  m =
(thỏa điều kiện). Chọn A. 1 2 2
VÍ DỤ 52. Xét các số nguyên dương ,
a b sao cho phương trình 2
a ln x + b ln x + 5 = 0 có hai nghiệm
phân biệt x , x và phương trình 2
5log x + blog x + a = 0 có hai nghiệm phân biệt x , x thỏa mãn 1 2 3 4
x x x x . Tìm giá trị nhỏ nhất của S = 2a + 3b 1 2 3 4 A. S = 33. B. S = 30. C. S = 17 . D. S = 25. min min min min Hướng dẫn giải:
Điều kiện để hai phương trình: 2
a ln x + b ln x + 5 = 0 và 2
5log x + blog x + a = 0 có hai nghiệm phân biệt là: 2
b − 20a  0 .  b b
ln x + ln x = ln x x = −  −  1 2 ( 1 2) a  x x = e a
Áp dụng định lí Vi-ét cho mỗi phương trình: 1 2    . b b −
log x log x log(x x )  + = = − 5 = 3 4 3 4 x x 10   3 4  5 b b − − Theo giả thiết: a 5
x x x x e  10 (*). 1 2 3 4 * * b b b 1 1 5 a
Lấy lôgarit cơ số e hai vế của (*): −  − ln10   ln10  a
 2,17  a  3 (1) a 5 a 5 ln10 * b Theo điều kiện: 2 2
b − 20a  0  b  20a  60  b  8 (2).
Từ (1) và (2) suy ra: S = 2a + 3b  2.3 + 3.8 = 30  S = 30 . Chọn B. min
Dấu đẳng thức xảy ra khi và chỉ khi a = 3, b = 8. HOÀNG XUÂN NHÀN 31
32 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 3. Tìm điều kiện tham số thông qua miền giá trị hàm số VÍ DỤ 53. +
Tìm tất cả các giá trị của tham số x x
m để phương trình sin 1 sin 4 + 2
− m = 0 có nghiệm. 5 5 5 5 A. m  8. B. m  9. C. m  7. D. m  8. 4 4 4 3 Hướng dẫn giải: Đặ 1 t sin 2 x t = ; với 1
−  sin x 1 thì  t  2. 2
Phương trình trở thành: 2 2
t + 2t − m = 0  t + 2t = m (*). 1    Xét hàm f (t) 2
= t + 2t với t  ; 2 
 , ta có: f (t) 1
= 2t + 2  0, t   ; 2 .    2  2   1  5 1  Ta lại có: f = , f  
(2) = 8. Hơn nữa, hàm f (t) liên tục trên đoạn ;2 .    2  4 2  1  5 
Vậy miền giá trị của hàm số f (t ) trên ; 2   là T = ;8 .    2  4  1 
Phương trình đã cho có nghiệ 5
m x  Phương trình (*) có nghiệm t  ; 2 
   m  8 . Chọn A. 2  4 VÍ DỤ 54. 2 2 Cho phương trình 1+ 1− x − ( + ) 1+ 1 25 2 5 −x m
+ 2m +1 = 0 với m là tham số thực. Tập hợp tất
cả giá trị m để phương trình trên có nghiệm là a;b . Tìm tích . a b . 1500 3072 3072 A. ab = . B. ab = . C. ab =100. D. ab = . 11 25 23 Hướng dẫn giải: Điề 2 2 + − + − −x u kiện: 1 −  x 1. Đặt 1 1 x 1 1 t = 5 ; t = 5 x .ln 5. = 0  x = 0( 1 − ) ;1 . 2 1− x Ta lại có: t (− ) 1 = t ( )
1 = 5, t (0) = 25 . Do vậy t 5; 25 .
Phương trình đã cho trở thành: 2
t − (m + 2)t + 2m +1 = 0 t − t +
t − 2t +1 = m(t − 2) 2 2 1 1 2  m =
(do t5;25)  m = t + (*). t − 2 t − 2 1 t = 3 Đặ 1
t f (t ) = t +
, t 5; 25; ta có: f (t ) = 1−
= 0  t − 2 =1  (loại). 2 ( )2 t − 2 (t − 2) t =1 16 576 Mặt khác: f (5) = , f (25) =
; đồng thời hàm f (t) liên tục trên đoạn 5;25 . 3 23 HOÀNG XUÂN NHÀN 32
33 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT 16 576
Vì vậy miền giá trị của f (t ) trên 5; 25 là T = ;   .  3 23   
Phương trình đã cho có nghiệm x  (*) có nghiệm t   16 576 5; 25  m  ;   .  3 23  16 576 3072 Do vậy a = , b =  ab = . Chọn D. 3 23 23
VÍ DỤ 55. Tìm tất cả các giá trị thực của tham số m để phương trình log x + log x +1 − 2m −1 = 0 3 3
có ít nhất một nghiệm thực trong đoạn 1;27.
A. m  (0;2) .
B. m 0;2 .
C. m 2;4 .
D. m  (0;4) . Hướng dẫn giải: Đặt 2
t = log x +1  t −1 = log x ; với x 1; 27 thì t 1; 2 . 3 3
Phương trình đã cho trở thành: 2
t −1+ t − 2m −1 = 0 2
t + t = 2m + 2 (*) . Xét hàm số ( ) 2
f t = t + t trên 1; 2; f (t ) = 2t +1  0, t  1;2. Ta lại có: f ( )
1 = 2, f (2) = 6 ; đồng thời hàm f (t ) liên tục trên đoạn 1; 2.
Vì vậy miền giá trị của f (t ) là T = 2;6 .
Phương trình đã cho có nghiệm x 1;27  (*) có nghiệm t 1;2  2  2m + 2  6  0  m  2 . Chọn B.
VÍ DỤ 56. Có bao nhiêu số nguyên m để phương trình log (3x + 2m) = log ( x 2 3 − m có nghiệm? 3 5 ) A. 3 . B. 4 . C. 2 . D. 5 . Hướng dẫn giải: 3x  + 2m  0 3x  + 2m = 3t 1 Điều kiện: 
. Đặt log 3x + 2m = log 3x − m = t   . 3 ( ) 5 ( ) ( ) 2 x 2 3  − m  0 x 2 3
 − m = 5t (2)
Trừ theo vế (1) và (2), ta được: 2 2 + = 3t −5t m m 2 
+ 2 +1 = 3t − 5t m m +1 (*). Xét hàm số ( ) 3t 5t f t = − +1 với t  . t   t t 3 ln 5
Ta có: f (t ) = 3 .ln 3 − 5 .ln 5 = 0  =
= log 5  t = log log 5 = t ; f t 1,1396   . 3 3 ( 3 ) 0 ( 0)  5  ln 3 5
Mặt khác: lim f (t ) = −, lim f (t ) = 1 và hàm f (t ) liên tục trên . t →+ t→−  
Vì vậy miền giá trị của hàm f (t ) với t  là T =  − ;  f (t  . 0 )    1  ,1396  HOÀNG XUÂN NHÀN 33
34 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Phương trình đã cho có nghiệm x  (*) có nghiệm 2 t
m + 2m +1  f (t0 )  (m + )2
1  f (t m +1  f t
 − f t m +1 f t  1
− − f t m  1 − + f t . 0 ) ( 0) ( 0) ( 0) ( 0) ( 0)  2 − ,0675 0,0675
Vì m nguyên nên m −2; −1;  0 . Chọn A.
Bài toán 4. Tìm điều kiện tham số thông qua bảng biến thiên hàm số
VÍ DỤ 57. Gọi (a;b) là tập các giá trị của tham số m để phương trình 2 2 x −8 x e
e − m = 0 có đúng hai
nghiệm thuộc khoảng (0;ln 5) . Tổng a + b là A. 2. B. 4. C. 6 − . D. 14 − . Hướng dẫn giải: Đặt x
t = e ; với x  (0;ln 5) thì t  (1;5) . Phương trình trở thành 2
2t − 8t = m (*) .
Xét hàm số f (t ) 2
= 2t − 8t với t (1;5) ; f (t) = 4t − 8 = 0  t = 2. Bảng biến thiên:
Phương trình đã cho có hai nghiệm phân biệt thuộc khoảng (0;ln 5)  (*) có hai nghiệm t (1;5)  8 −  m  6 − . Do vậy m( 8 − ; 6 − ) = ( ;
a b)  a = −8, b = −6 . Suy ra a + b = 14 − . Chọn D.
VÍ DỤ 58. Tìm số giá trị nguyên của tham số m  (−10;10) để phương trình ( ) 2x m( ) 2x 2 x 1 10 1 10 1 2.3 + + + − =
có đúng hai nghiệm phân biệt? A. 14 . B. 15 . C. 13 . D. 16 . Hướng dẫn giải: 2 2 x x 2 2 x x  +   −  2 x + 10 1 10 1 Ta có: ( 10 + ) 1 + m( 10 − ) 1 1 = 2.3    + m  = 6 (1) . 3 3     2 2 x x  +   −  Đặ 10 1 10 1 1 t t =      = ; với 2 thì t  1.     x  0 3 3 t     HOÀNG XUÂN NHÀN 34
35 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT Khi đó (1) trở 1 thành: 2 2 t + . m
= 6  t + m = 6t t
− + 6t = m (2). t Xét hàm số 2 f (t) = t
− + 6t trên nửa khoảng 1;+) , ta có: f (t) = −2t + 6 = 0  t = 3 . Bảng biến thiên:
Nhận xét: (1) có đúng hai nghiệm phân biệt
 (2) có đúng một nghiệm lớn hơn 1.
Dựa vào bảng biến thiên, ta được: m  5
hoặc m = 9 . Do m  (−10;10) nên
m −9; −8;...;3; 4; 
9 . Vậy có 15 giá trị m cần tìm. Chọn B.
VÍ DỤ 59. Gọi S là tổng các giá trị nguyên của tham số m để phương trình x x 3 + 2 4 + 7 = 2 + m + 6m có
nghiệm x  (1;3) . Chọn đáp án đúng. A. S = 35 − .
B. S = 20 .
C. S = 25 . D. S = 21 − . Hướng dẫn giải: Ta có: x x 3 + 2 x x 2 4 + 7 = 2
+ m + 6m  4 −8.2 + 7 = m + 6m (*). Đặt 2x t =
; với x  (1;3) thì t  (2;8) . Phương trình trở thành: 2 2
t − 8t + 7 = m + 6m . Đặt f (t) 2
= t − 8t + 7, t (2;8); ta có: f (t) = 2t −8 = 0  t = 4 (nhận). Bảng biến thiên: 2
m + 6m  9 − m
Theo đó, phương trình (*) có nghiệm x  (1;3)      7 −  m 1. 2
m + 6m  7  7 −  m 1
Vì m nguyên nên m −6;−5;−4;−3;−2;−1; 
0 . Suy ra tổng S = 21 − . Chọn D.
VÍ DỤ 60. Cho phương trình m ln ( x + )
1 − x − 2 = 0 . Biết rằng tập hợp tất cả các giá trị của tham số m
để phương trình đã cho có hai nghiệm x , x thỏa mãn 0  x  2  4  x là khoảng (a;+) . Khi 1 2 1 2
đó a thuộc khoảng nào dưới đây? A. (3, 7;3,8) . B. (3, 6;3, 7) . C. (3,8;3,9) . D. (3,5;3, 6) . HOÀNG XUÂN NHÀN 35
36 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT Hướng dẫn giải: Điều kiện: x  1
− . Nhận xét: x = 0 không là nghiệm phương trình đã cho, vì vậy ta có: + m (x + ) x 2 ln
1 − x − 2 = 0  m = (*). ln ( x + ) 1
(x + )−(x + ) 1 ln 1 2 x + 2 Đặ + t f ( x) = với x  ( 1 − ;+) \ 
0 . Ta có: f ( x) x 1 = ; ln ( x + ) 1 2 ln ( x + ) 1 + f ( x) =  (x + ) x 2 0 ln 1 − = 0 . x +1 + Đặ x 2 1 1
t g ( x) = ln ( x + ) 1 −  g(x) = +  0, x   1 − ;+ \ 0 . 2 ( )   x +1 x +1 (x + ) 1   
Mặt khác: g ( ) g ( ) 4 5 2 . 3 = ln 3 − ln 4 −  0 − ,032  0   
nên g ( x) = 0 có một nghiệm x  2;3 ; 0 ( )  3  4 
Vậy f ( x) = 0 có nghiệm duy nhất x  2;3 . Từ đây ta có bảng biến thiên: 0 ( )
Theo đó, phương trình (*) có hai nghiệm phân biệt thỏa 0  x  2  4  6 x m  . 1 2 ln 5  6  6 Vậy m  ; + 
 thỏa mãn đề bài, nên a =
 3,728(3,7;3,8) . Chọn A.  ln 5  ln 5 HOÀNG XUÂN NHÀN 36
37 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 5. Tìm điều kiện tham số dựa vào hàm đặc trưng
VÍ DỤ 61. Biết rằng điều kiện cần và đủ của tham số m để phương trình log + + 2x m m = 2x có 2 ( ) a nghiệm là m  − với ,
a b là hai số nguyên dương và b  7 . Hỏi 2
a + b + b bằng bao nhiêu? b A. 31. B. 32 . C. 21. D. 23. Hướng dẫn giải: Điều kiện: 2x m +  0 và + + 2x m m  0 . Ta có: log ( + + 2x ) = 2  +
+ 2x = 2 x  ( + 2x )+ + 2x = (2x )2 2 + 2x m m x m m m m (1). 2 Xét hàm f (t ) 2
= t + t (t  0) ; f (t) = 2t +1 0, t
  0 , suy ra hàm f (t) đồng biến trên 0;+) . 2 2 2   x x x x x x x x x 1 1 Vậy: ( )
1  f ( m+ 2 ) = f (2 )  m+ 2 = 2  (2 ) = 2 + m  (2 ) − 2 = m  2 − = m +   (2) .  2  4 2   2   x 1 x 1
Xét hàm g ( x) = 2 − 
 liên tục trên ; ta có: 2 −  0, x     .  2   2 
Vì vậy miền giá trị của g ( x) trên là 0; +) .
Phương trình đã cho có nghiệ 1 1 a
m  (2) có nghiệm  m +
 0  m  − = − . 4 4 ba =1 Suy ra: 2 
a + b + b = 21. Chọn C. b  = 4
VÍ DỤ 62. Tập hợp tất cả các giá trị thực của tham số m để phương trình 3m m e + e = ( 2 x + − x )( 2 2 1
1+ x 1− x ) có nghiệm là  1   1   1  1  A. 0; ln 2   . B. ; − ln 2  . C. 0;   . D. ln 2; +   .   2   2   e  2  Hướng dẫn giải: Ta có: 3m m + = ( 2 + − )( 2 + − ) 3m m e e x x x xe + e = ( 2 x + − x )( 2 2 1 1 1 1
2 + 2x 1− x ) (*) . Đặt 2 t = x + − x (−  x  ) 2 2 2 2 1 1
1  t = 1+ 2x 1− x t −1 = 2x 1− x . 2 x 1− x − xx  0 2 Ta có: 2 t = 1− =
= 0  1− x − x = 0    x = . 2 2 2 2 1− x 1− x 1  − x = x 2  
Ta tính được: t (− ) = − t ( ) 2 1 1, 1 = 1, t   = 2   . Vì vậy ta có: 1 −  t  2 . 2   HOÀNG XUÂN NHÀN 37
38 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Khi đó (*) trở thành: 3m m e
+ e = t ( 2t + ) 1 3m m 3
e + e = t + t (**) . Xét hàm ( ) 3
f u = u + u f (u) 2 = 3u +1  0, u
  ; suy ra hàm f (u) luôn đồng biến trên . Khi đó: (**)  ( m
f e ) = f (t ) me = t . Phương trình này có m m 1 nghiệm  1
−  e  2  e  2  m  ln 2 . Chọn B. 2
VÍ DỤ 63. Tìm tất cả các giá trị của m để phương trình ln m + ln 
(m + sin x) = sin x  có nghiệm. 1 1
A. +1  m e −1.
B. 1  m e −1. C. 1  m  +1.
D. 1  m e −1. e e Hướng dẫn giải:
m + sin x  0  Điều kiện:  . Ta có: ln m + ln 
(m + sin x) = sin x  m + ln  (m +sin x)  0  ln m + ln 
(m +sin x) + m + ln  
(m +sin x) = ln 
(m +sin x)+ (m + sin x) ( ) 1 .
Xét hàm f (t ) = ln t + t (t  0) ; f (t ) 1 = +1  0, t
  0 . Suy ra hàm f (t) đồng biến trên (0;+). t Vì vậy: ( )
1  f (m + ln (m + sin x)) = f (m + sin x)  m + ln (m + sin x) = m + sin x  ( + ) sin x sin ln sin = sin  + sin x m x x m x = em = e − sin x (2).
Đặt u = sin x  1 − ;  1 , (2) trở thành: u
m = e − u (3). Xét hàm ( ) u
g u = e − u với u  1 − ;  1 ; ( ) u
g u = e −1 = 0  u = 0  1 − ;  1 . 1
Vì hàm g (u ) liên tục trên −1;  1 và g (− ) 1 = +1, g ( )
1 = e −1, g (0) = 1. e
Do vậy tập giá trị của hàm g (u ) trên −1; 
1 là T = 1;e −  1 .
Phương trình đã cho có nghiệm  (3) có nghiệm u  1 − 
;1  1  m e −1 . Chọn B.
VÍ DỤ 64. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2  2x mx 1  + + 2 log 
 + 2x + mx +1 = x + 2 có hai nghiệm phân biệt? 2  x + 2    A. 3 . B. 1. C. 4. D. 2 . Hướng dẫn giải: 2
2x + mx +1 0 2 
2x + mx +1  0 Điều kiện: 2   2x + mx +1  .   x  2 0 −  x + 2
Phương trình đã cho tương đương với 2 2 log
2x + mx +1 + 2x + mx +1 = x + 2 + log x + 2 1 . 2 2 ( ) ( ) HOÀNG XUÂN NHÀN 38
39 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT 1
Xét hàm số f (t ) = log t + t , t (0; +) ; f (t ) = +1  0, t  (0;+) . 2 t ln 2
Suy ra f (t ) đồng biến trên (0; +) . x 2 − Vì vậy: ( )  f ( 2
x + mx + ) = f (x + ) 2 1 2 1 2 
2x + mx +1 = x + 2 2 2
 2x + mx +1 = x + 4x + 4 2
x + (m − 4) x −3 = 0 (2) .
Phương trình đã cho có hai nghiệm phân biệt  (2) có hai nghiệm phân biệt lớn hơn 2 −    0 (m − 4)2 − 4( 3 − )  0  (
m − 4)2 +12  0, m    m  8 S 4 − m   9    2 −    2 −  4 − m  4 −   9  m  . 2 2 m  2     − +   af (− )   ( − m + − ) 2m 9 0 2 2 0 1. 4 2 8 3  0    Do * m   m1;2;3; 
4 . Vậy có bốn giá trị của m thỏa mãn. Chọn C. VÍ DỤ 65. 2 − −
Cho phương trình 4 x m.log ( 2 −2 +3) 2 + 2 x−x x x .log
2 x − m + 2 = 0 với m là tham số. 1 2 ( ) 2
Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là A. 4 . B. 1. C. 2 . D. 3 . Hướng dẫn giải: 2
Phương trình đã cho tương đương với 1−2 − − − 2
x m .log ( x − )2 1 ( x ) 1 1 + 2 − 2 .log
2 x − m + 2 = 0 2 2 ( )   − x−m −(x− )2 1 2 1 1 2 2  = (*).
log (2 x − m + 2) log ( x − )2 +  2 1 2 2   + + − −t 2 t
− 2 .ln 2.log t + 2 − 2 ( ) 1 1 1−t (t + 2)ln 2
Xét hàm số f (t) 2 =
t  0 ; f (t ) =  0, t   0. log t + 2 log t + 2   2 ( ) 2 2 ( ) ( )  +
Suy ra hàm f (t ) nghịch biến trên 0; +) . 2
x − 2x +1 = 2x − 2m Vì vậy: ( )
*  f (2 x − m ) = f ( x − )2 1 )  (x − )2 1
= 2 x − m   2
x − 2x +1 = 2 − x + 2m 2
−x + 4x −1 = 2m   ( ) ** . 2 x +1 = 2m HOÀNG XUÂN NHÀN 39
40 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Nhận xét: Số nghiệm của (**) chính là số giao điểm giữa
đường thẳng nằm ngang y = 2m với hợp hai đồ thị hàm số 2
y = −x + 4x −1 (C ) 2
, y = x +1 C . Xem hình. 1 ( 2)
Phương trình đã cho có ba nghiệm phân biệt  (**) có ba  1 m = 2m =1  2  
nghiệm phân biệt  2m = 2  m = 1   . 2m = 3  3  m =  2 Tổng các giá trị của 1 3 m là: +1+ = 3. Chọn D. 2 2
VÍ DỤ 66. Gọi S là tập hợp các giá trị của tham số m sao cho hai phương trình 2 2 1 3m x + = và x 2
m = 3 − 2x + x −1 có nghiệm chung. Tính tổng các phần tử của S . 5 A. 6 . B. 3 . C. 1. D. . 2 Hướng dẫn giải:
Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm 2  2x +1 = 3m
 m = log 2x +1 3 ( 2 )   
 log 2x +1 = 3x − 2x + x −1 x 2 3 ( 2 ) 2 x 2
m = 3 − 2x + x −1
m = 3 − 2x + x −1  log (2 + ) log ( 2 3 2 x x + )1 2 2 1 + 2 +1 = 3 +  3 + log ( 2 2 +1 = 3x x x x x + x 3 3 ) (*). Xét hàm ( ) = 3t f t
+ t , t  ; ( ) = 3t f t ln 3 +1  0 ; suy ra hàm ( ) = 3t f t
+ t đồng biến trên .
Do vậy: (*)  f (log ( 2 2x +1
= f x  log 2 +1 =  2 +1 = 3x x x x 3 ( 2 ) 2 . 3 ) ( ) Xét hàm số ( ) 2 = 2 +1− 3x g x x
xác định và liên tục trên . Ta có: g( x) x = x − g ( x) x 2 = − g( x) x 3 4 3 ln 3, 4 3 ln 3, = 3 − ln 3  0, x   .
Suy ra hàm số g( x) nghịch biến trên
nên g ( x) = 0 có tối đa một nghiệm.
Suy ra g( x) = 0 có tối đa hai nghiệm; và vì thế phương trình g ( x) = 0 có tối đa là ba nghiệm. x = 0 m = 0 2 x  
Ta lại có: g (0) = g ( )
1 = g (2) = 0 . Vì vậy: 2x +1 = 3  x = 1  m = 1 .  
x = 2 m = 2  
Tổng các giá trị m thu được bằng 3. Chọn B. HOÀNG XUÂN NHÀN 40
41 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 6. Nghiệm đặc biệt của phương trình mũ, lôgarit chứa hàm đối xứng VÍ DỤ 67. +
Cho biết có một giá trị của m để phương trình x x 1 4 − 2
− m = 0 có nghiệm duy nhất, khi đó: 3 3 A. 2
−  m  − .
B. m  1. C. m  2 − . D. −  m  0 . 2 2 Hướng dẫn giải: +
Xét hàm số f ( x) x x 1 = 4 − 2
− m xác định trên . − − + + Ta có: f (−x) x x 1 x x 1 = 4 − 2 − m = 4 − 2
− m = f (x).
Vì vậy f ( x) là hàm số chẵn. Nếu x là một nghiệm của phương trình f ( x) = 0 thì −x cũng là 0 0
một nghiệm của phương trình f ( x) = 0 .
Điều kiện cần: Phương trình f ( x) = 0 có nghiệm duy nhất suy ra x = −x x = 0 . 0 0 0
Thay vào phương trình ban đầu, ta có: 0 0 1 4 2 + −
− m = 0  m = 1 − .
Điều kiện đủ: Thử lại với m = 1
− , thay vào phương trình đã cho: x x − + =  ( x − )2 4 2.2 1 0 2 1
= 0  2 x =1  x = 0 . Vậy m = 1
− thỏa mãn đề bài. Chọn D.
VÍ DỤ 68. Cho phương trình 2x = .2 . x m
cos ( x) − 4 , với m là tham số. Gọi m là giá trị của m sao cho 0
phương trình trên có đúng một nghiệm thực. Khẳng định nào sau đây là đúng?
A. m  −5; −1 . B. m  5. − C. m  1 − ;0 . D. m  0. 0  ) 0  ) 0 0 Hướng dẫn giải:
Phương trình đã cho tương đương với x x = ( ) x 2 4 .2 .cos − 4  2 + 2 −x m x − .
m cos ( x) = 0 (*). − Xét hàm ( ) x 2 = 2 + 2 x f x − .
m cos ( x) với mọi x  . − − −
Ta có: f (2 − x) 2 x 2 (2 x) = 2 + 2
− mcos (2 − x) 2− x x = + − (  − ) 2 2 2 cos 2 = 2 −x + 2x m x
− mcos( x) = f (x) .
Vậy f (2 − x) = f ( x) nên hàm f đối xứng theo x và 2 − x . Nếu x là một nghiệm của (*) thì 0
2 − x cũng là một nghiệm của (*). 0
Điều kiện cần: Phương trình (*) có nghiệm duy nhất nên x = 2 − x x =1. 0 0 0
Thay vào phương trình ta có: 1 2 1 2 2 − + − .
m cos ( ) = 0  m = 4 − .
Điều kiện đủ: Thử lại với m = 4
− , ta có: 4x + 4.2x cos( x) + 4 = 0 x x  + ( )+ ( )+ − ( ) x x x x =   + ( x) 2 2 2 2 4 4.2 cos 4 cos 4 4 cos 0 2 2 cos  + 4sin ( x) = 0   HOÀNG XUÂN NHÀN 41
42 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT 2x = 2 − cos( x) 2x = 2 − cos( x) x   =    cos( x) 2 2 =    x = . sin  ( x) 1 = 0  cos  ( x) 1 = − cos  ( x) 1 = 1 − Vậy m = 4
− thỏa mãn. Chọn A.
Bài toán 7. Tìm điều kiện tham số của phương trình mũ, lôgarit có chứa hàm ẩn
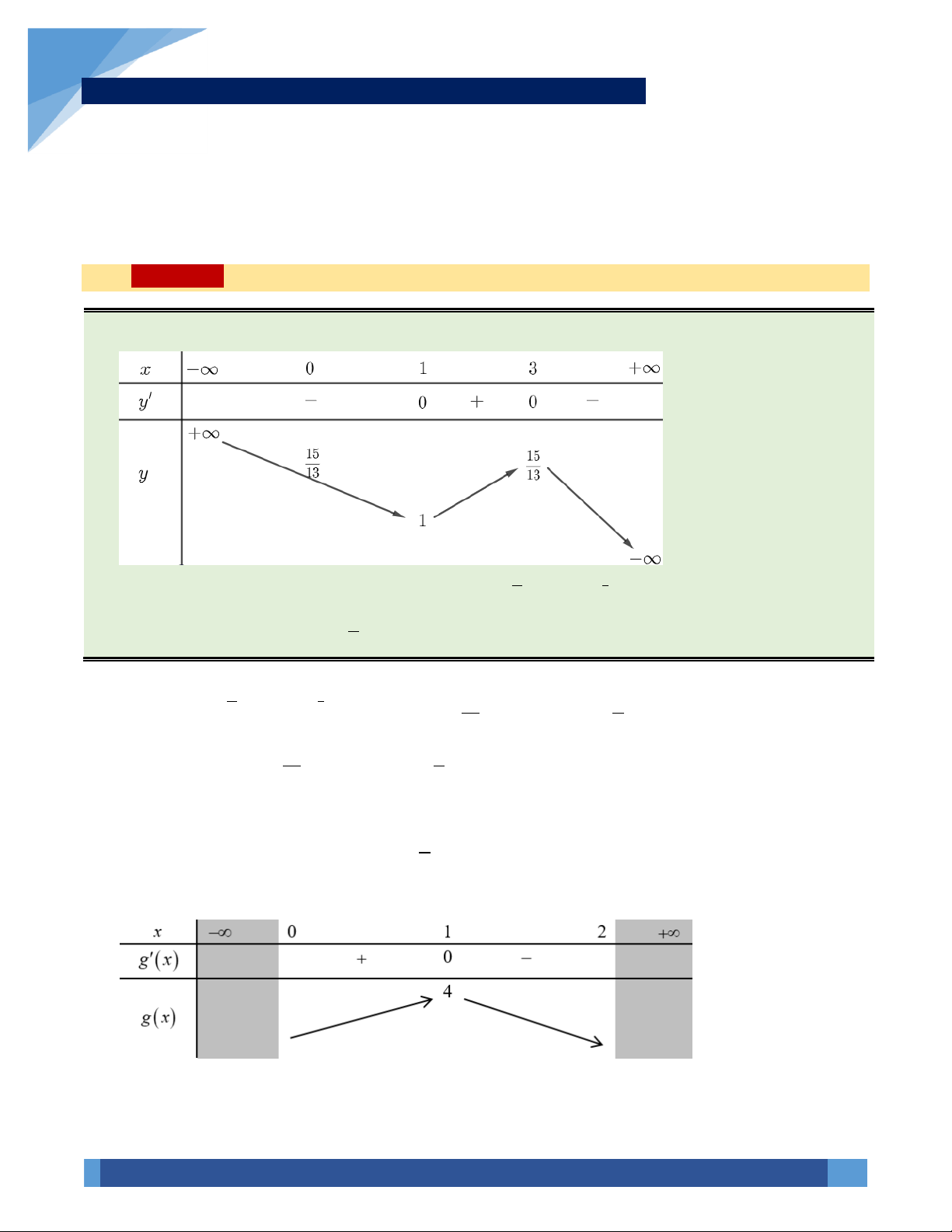
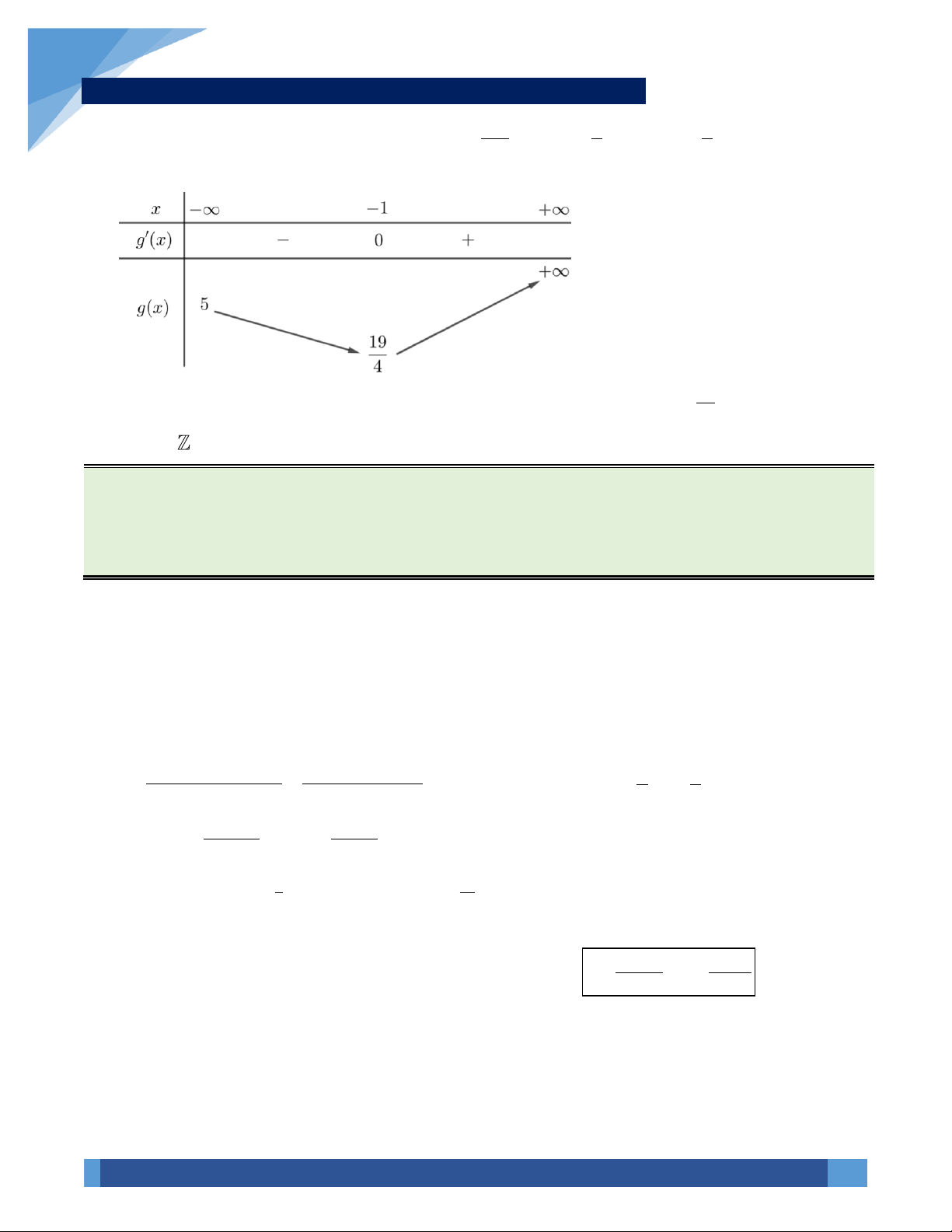
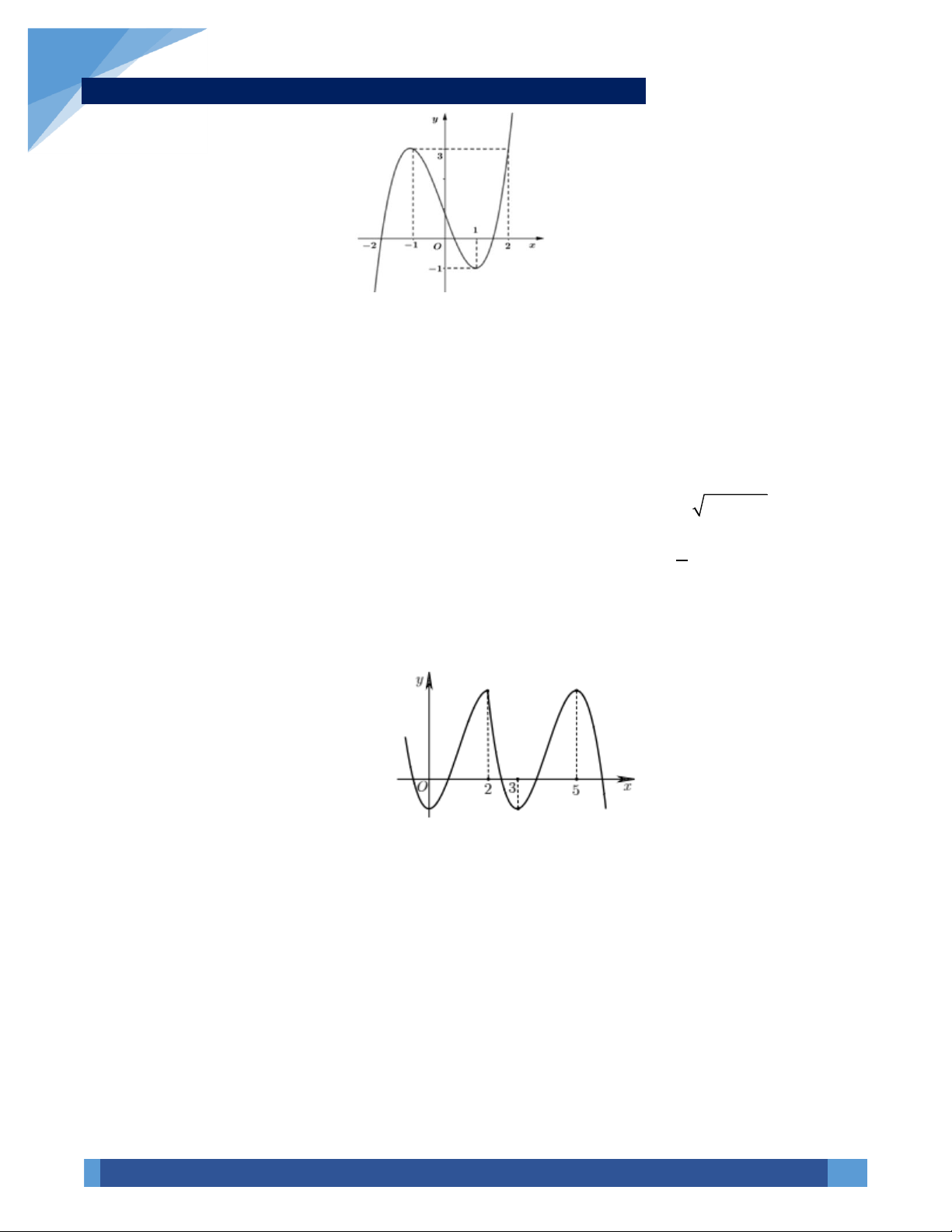
VÍ DỤ 69. Cho hàm số y = f (x) có bảng biến thiên như sau: 3 f ( x) 13 2 − f ( x) + f ( x) 3 2 7 +
Tìm giá trị lớn nhất của m để phương trình: 2 2 e
= m có nghiệm trên đoạn 0;2 . 15 A. 5 e . B. 13 e . C. 3 e . D. 4 e . Hướng dẫn giải: 3 f ( x) 13 2 − f ( x) + f ( x) 3 2 7 + 13 3 Ta có: 2 2 e = m 3  2 f (x) 2 −
f ( x) + 7 f ( x) + = ln m . 2 2 13 3 Đặt g ( x) 3 = 2 f (x) 2 −
f ( x) + 7 f ( x) + ; g( x) 2
= 6 f (x) −13 f (x) + 7. f (x)   . 2 2  f (x) = 0 x =1 x = 3  
Ta có: g( x) = 0   =  =    .
f ( x) =  f ( x) x 1 x a 3 7 1 =  6 x = b  0 
Bảng biến thiên của g ( x) trên đoạn 0; 2 :
Giá trị lớn nhất của m để phương trình có nghiệm trên 0; 2 thỏa mãn: 4
ln m = 4  m = e . Chọn D. HOÀNG XUÂN NHÀN 42
43 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
VÍ DỤ 70. Cho cấp số cộng (a , cấp số nhân (b , thỏa mãn a a  0 , b b  1 và hàm số n ) n ) 2 1 2 1 3
f (x) = x − 3x sao cho f (a ) + 2 = f (a ) và f (log b + 2 = f log b . Tìm số nguyên dương n 2 2 ) ( 2 1) 2 1
nhỏ nhất sao cho b a − (n − 2022 . n n ) A. 17. B. 12. C. 15. D. 13.
Định hướng: Ta cần tìm công thức tổng quát của các dãy số (a và (b dựa vào những dữ n ) n )
kiện đã cho trước khi tìm n thông qua b a − (n − 2022 . n n )
Hướng dẫn giải:
d = a − a  0 Ta có: 2 1
a a  0  
với d là công sai cập số cộng. 2 1 a = a + d  2 1
Khi đó: f (a ) + 2 = f (a )  f (a + d) + 2 = f (a )  (a + d )3 3
− 3(a + d) + 2 = a − 3a 2 1 1 1 1 1 1 1   a = 0  a = 0 2  1
3a d a + d  + (d −1) (d + 2) = 0 1     . 1 1   2 + +  d −1 = 0  d =1 0  +  ( ) 0
Do vậy: a = a + (n −1)d = n −1 . n 1  b2 q = 1 
Ta lại có: b b  1   b
. Suy ra: log (b ) = log
b q = log b + log q . 2 2 2 ( 1 ) 2 1 1 2 1 2 b = b q  2 1
Đặt t = log b  0, t = log b  0, m = log q  0  t = t + m . 2 2 2 1 2 1 2 2 1
Khi đó: f (t ) + 2 = f (t )  t − 3t + 2 = t − 3t t + m − 3 t + m + 2 = t − 3t 2 2 1 1 ( 1 )3 3 3 ( 1 ) 3 2 1 1 1 t  = 0 log b = 0 b  =1 2
 3m.t .(t + m) + (m −1) (m + 2) = 0 1 2 1 1       . 1 1 + + m =1 log q = 1  q = 2 0 + 0 2 − Do vậy: n 1 n 1
b = b .q − = 2 . n 1 − −
Ta có: b a − n − 
n − − n +    n −   . n n ( 2022) n 1 n 1 2 1 2022 2 2021 1 log 2021 10, 98 2
Suy ra n 11,98 . Vì n nguyên dương và nhỏ nhất nên n = 12 . Chọn B.
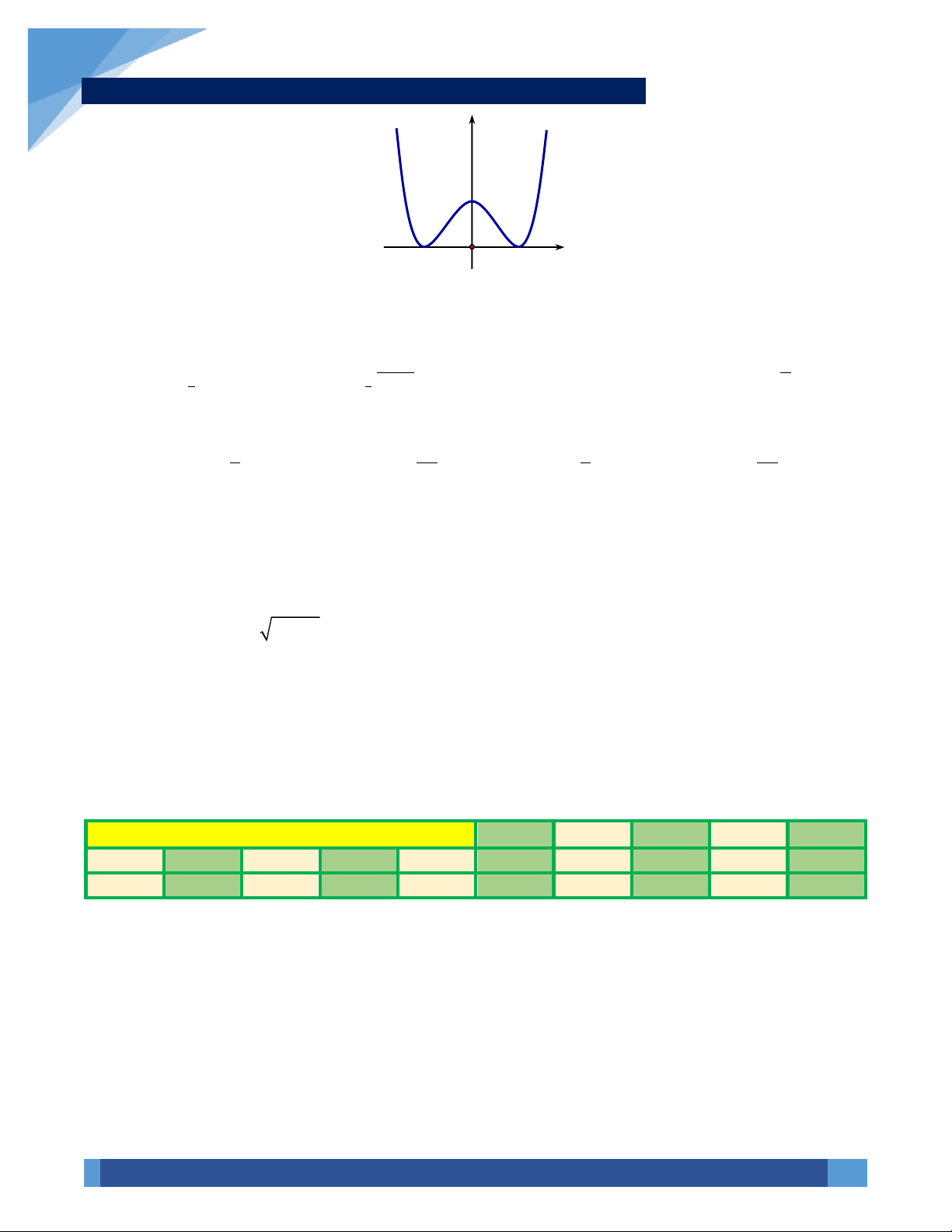
VÍ DỤ 71. Cho hàm số bậc ba y = f ( x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số 2 2 + − − −
m thuộc đoạn 0;9 sao cho bất phương trình f (x) f (x) m
f ( x) f (x) m f (x) 2 −16.2 − 4 +16 = 0 có nghiệm x  ( 1 − ; ) 1 . HOÀNG XUÂN NHÀN 43
44 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT A. 6 . B. 8 . C. 5 . D. 7 . Hướng dẫn giải: 2
f (x)+ f (x) 2 −m
f (x)− f (x)−m f (x) Ta có: 2 −16.2 − 4 +16 = 0 2
f ( x)− f ( x)−m f ( x) 2 2
f ( x)+ f ( x)−  1  6 −16.2  − 2 − 2 m  = 0     2
f ( x)− f ( x)−m f ( x) 2 2
f ( x)− f ( x)−  2
f ( x)− f ( x)−m 2 f ( x) 16 1  − 2  − 2 1  − 2 m  = 0   −   −      1 2 16 2 = 0     (1).   f x 1 Với x  ( 1 − ; )
1 thì f ( x) ( 2
− ;2)  2 f (x)( 4 − ;4) 2 ( ) 2 f ( x)  2  ;16  16 − 2  0   . 16  Khi đó: ( ) 2
f ( x)− f ( x)−m 2  −
=  f (x) − f (x) 2 1 1 2 0
− m = 0  m = f (x) − f (x) (2).
Đặt t = f ( x) , t ( 2
− ;2) . Khi đó: (2) trở thành 2
m = t − t (3). Xét hàm g (t ) 2
= t − t, t ( 2
− ;2) ; g(t) 1
= 2t −1 = 0  t = . 2 1
Vậy phương trình đã cho có nghiệm x  ( 1 − ; )
1  (3) có nghiệm t  ( 2
− ;2)  −  m  6 . 4
Vì m  , m 0;9  m 0;1; 2;3; 4;  5 . Chọn A. HOÀNG XUÂN NHÀN 44
45 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Phương pháp giải toán:
1. Phương trình nhiều ẩn:
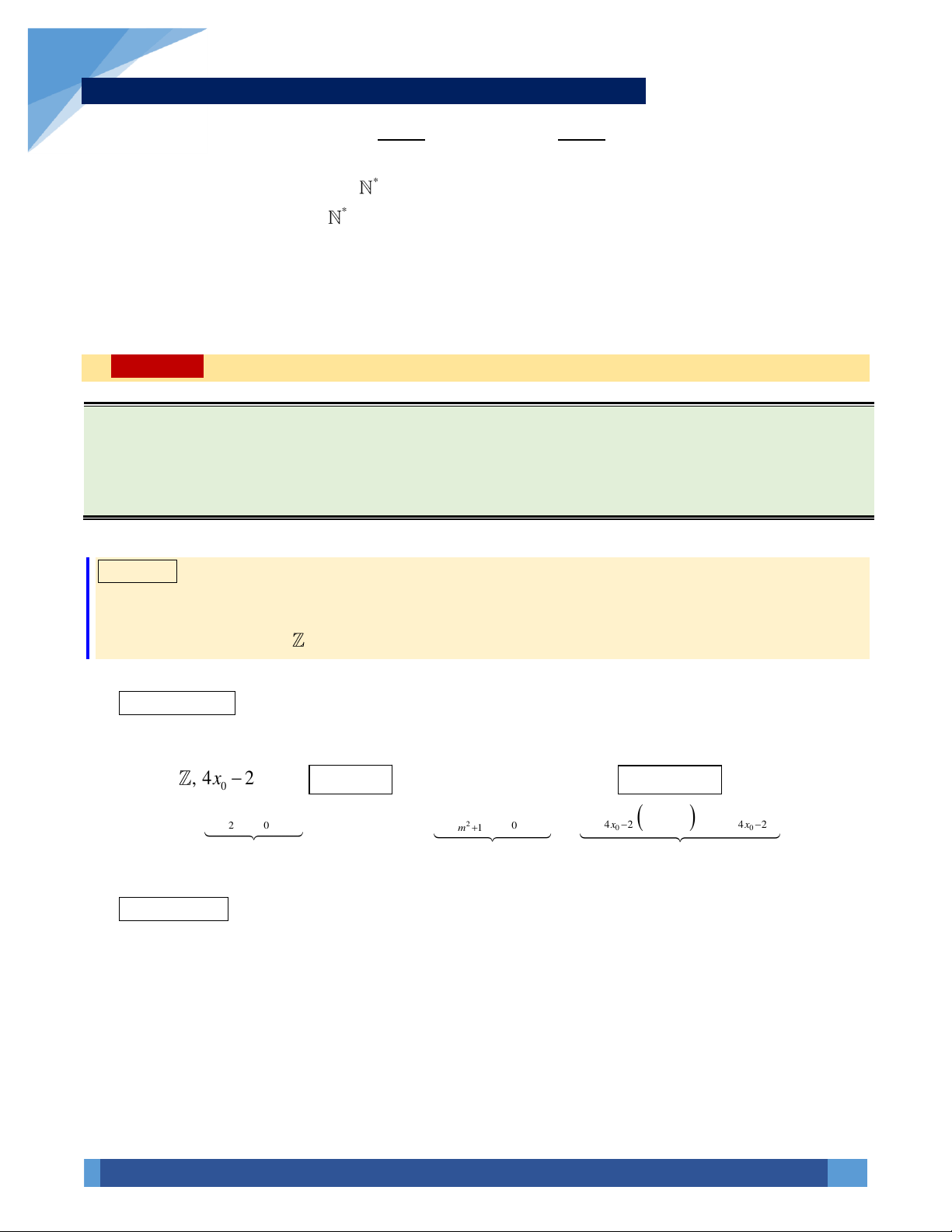
• Một phương trình nhiều ẩn là một mệnh đề chứa biến có dạng: f (x, y, z,t,...) = 0 (*)
trong đó f ( x, y, z,t,...) là một biểu thức chứa nhiều biến số là , x , y z, . t .. . Mỗi bộ số
( ;x y; z; t;...) làm cho mệnh đề (*) đúng thì chúng được gọi là một nghiệm của (*).
• Phương trình hai ẩn có dạng: f (x, y) = 0 (**) . Mỗi bộ số ( ;
x y ) làm cho (**) thỏa
mãn được gọi là một nghiệm của (**).
2. Tìm điều kiện của ẩn cho bài toán nghiệm nguyên:
Một cách tổng quát, ta xét bài toán phương trình hai biến dạng f ( x, y) = 0 .  Cách giải 1:
⎯ Cô lập một ẩn của phương trình, đưa về dạng: x = g ( y) hoặc y = g (x) .
Trong bước giải này, ta có thể sử dụng phương trình tích hoặc các phương pháp đánh
giá hai vế bằng bất đẳng thức, hàm số; cũng có thể dùng hàm đặc trưng để làm.
⎯ Dựa vào điều kiện cho ẩn x hoặc y để giới hạn số nghiệm của phương trình.  Cách giải 2:
⎯ Tìm một mối liên hệ thu gọn của các biến.
⎯ Sử dụng điều kiện   0 để phương trình bậc hai có nghiệm (hoặc dùng điều kiện tương
giao giữa các đường cơ bản, hay các bất đẳng thức cơ bản đã học) để giới hạn phạm vi một ẩn.
⎯ Suy ra phạm vi của ẩn còn lại dựa vào giả thiết của bài toán.  Cách giải 3:
⎯ Tìm một mối liên hệ thu gọn của các biến.
⎯ Dựa vào tính chất điểm có tọa độ nguyên thuộc các đường cong đã học (sử dụng thêm
các tính chất đặc thù của số nguyên đối với phép nhân, chia, tổng, tổng bình phương
v.v…) để suy ra phạm vi nghiệm phương trình.
Bài toán 1. Nghiệm nguyên của phương trình mũ và lôgarit dạng tích
VÍ DỤ 73. Có bao nhiêu số nguyên dương a nhỏ hơn 2021 sao cho tồn tại số nguyên x thỏa mãn a ( x+3 − ) 2
+ a = a ( a x+3 2 2 1 2 + 2 − ) 1 ? A. 12 . B. 15 . C. 10 . D. 14 .
Hướng dẫn giải: HOÀNG XUÂN NHÀN 45
46 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Ta có: a ( x+3 − ) 2
+ a = a ( a x+3 + − ) a  ( x+3 − ) a 2
− a + a − a ( x+3 2 2 1 2 2 1 2 2 1 2 . 2 − ) 1 = 0 2a − a = 0 a  ( x+3 − − +
a) − a ( x+3 2 2 1 2
−1− a) = 0  ( a − a)( x 3 2 2 −1− a) = 0   . x+3 2 −1− a = 0
Trường hợp 1: 2a − a = 0 . Xét hàm số ( ) = 2a f a
− a với a  0 .   a 1
Ta có: f (a) = 2 ln 2 −1; f (a) = 0  a = log = a . 2   0  ln 2  Bảng biến thiên
Từ bảng biến thiên, suy ra f (a)  f (a  0,914  0 .Suy ra phương trình 2a − a = 0 vô nghiệm. 0 ) Trường hợp 2: x+3 x+3 2
−1− a = 0  a = 2 −1. x+3 2 −1 0 x + 3  0 x  3 −
Vì a dương và nhỏ hơn 2021 nên      . x+3 2 −1 2021 x + 3  log 2022
x  log 2022 − 3  7,98  2  2 Mặt khác x
x −2;−1;0;1;2;3;4;5;6;  7 = A .
Với mỗi giá trị x thuộc tập A, ta tìm được một giá trị nguyên a tương ứng. Chọn C.
VÍ DỤ 74. Có bao nhiêu cặp số nguyên dương ( ;
x y ) thoả mãn x+y 2
− x ( x − ) = (x + ) y 3 3 3 1 1 3 − x , với x  2024 ? A. 13 . B. 15 . C. 6 . D. 7 .
Hướng dẫn giải: Ta có: x+ y 2
− ( x − ) = ( + ) y 3 y −  ( x − − ) 2 3 3 1 1 3 3 3 1 = (3x x x x x x −1− x)  (
3x − x −1 = 0 1 y 2
3 − x )(3x − x − ) ( ) 1 = 0   . y 2 3 − x = 0  (2)
Giải phương trình (1): Đặt ( ) = 3x f x
− x −1, x (0;2024) ; ( ) = 3x f x ln 3 −1  0, x  (0;2024) .
Suy ra f ( x)  f (0) = 0, x
 (0;2024) . Vì vậy phương trình (1) vô nghiệm. 1 x0 y
Giải phương trình (2): Ta có: y 2 2 y 2
3 − x = 0  x = 3  x = 3 . HOÀNG XUÂN NHÀN 46
47 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT 1 y 1 Do x  2024 nên 2 3
 2024  y  log 2024  y  2log 2024 13,86 ; mà y nguyên dương 3 3 2
nên y 1; 2;...;1 
3 . Vậy có 13 cặp số nguyên dương ( ;
x y ) thỏa mãn đề bài. Chọn A.
Bài toán 2. Nghiệm nguyên của phương trình mũ và lôgarit chứa hàm đặc trưng
VÍ DỤ 75. Cho 0  x  2021 và log +1 + − 3 +1 = 27y x x y
. Có bao nhiêu cặp số ( x ; y) nguyên thỏa 3 ( ) mãn điều kiện trên? A. 2021. B. 2020 . C. 4 . D. 3 .
Hướng dẫn giải:
Với điều kiện 0  x  2021, phương trình đã cho tương đương: + log ( + ) y log x 1 3 ( ) 1 + +1 = 27 + 3  3 + log ( + ) 3 1 = 3 y x x y x
+ 3y * . 3 3 ( ) Xét hàm số ( ) = 3t f t
+ t với t  ; ( ) = 3t f t .ln 3 +1  0 , t
  nên f (t) đồng biến trên . Vì vậy: (*) 
(log +1 = 3  log +1 = 3  +1= 27y  = 27y f x f y x y x x −1 . 3 ( )) ( ) 3 ( )
Theo giả thiết: 0  x  2021  0  27y −1  2021  1  27 y  2022  0  y  log 2022  2, 31 . 27
Ta có y  nên y 0;1; 
2 ; suy ra x 0; 26;72  8 .
Do đó có 3 cặp số nguyên ( x; y) thỏa mãn phương trình đã cho là: (0;0), (26; ) 1 , (728; 2) . Chọn D.
VÍ DỤ 76. Có bao nhiêu cặp số ( ;
x y ) sao cho y nguyên thuộc đoạn −2023; 202 
3 và x là số thực thỏa mãn log x − + + − = 2 ( y 5 y 2 5 ) 2x ? A. 2019 . B. 2021. C. 4041. D. 2021.
_____Thi thử Chuyên Lê Hồng Phong, TP.HCM, 2021_____
Hướng dẫn giải:
y + 2x −5  0  Điều kiện: 
. Phương trình đã cho tương đương với:
y − 5 + y + 2x − 5  0  x 2 − 5 + + 2 − 5 = 2 x y y x x 2  + 2 − 5 +
+ 2 − 5 = 2 x + 2x y y ( ) 1 . Xét hàm số ( ) 2
f t = t + t với t  0 ; f (t ) = 2t +1  0, t
  0 nên f (t) đồng biến trên (0;+). Vì vậy: ( )  ( x − + )= ( x) x x x 2x 2 1 5 2 2 
− 5 + 2 = 2  − 5 + 2 = 2  = 2 x − 2x f y f y y y + 5 (2) . x x Xét hàm g ( x) 2
= 2 − 2 + 5 với x ; HOÀNG XUÂN NHÀN 47
48 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT   g( x) x x x ln 2 1 1
= 4 ln 4 − 2 ln 2 = 0  2 = = log 2 =  x = log = 1 − . 4 2   ln 4 2  2  Bảng biến thiên: 19
Ta thấy: Phương trình đã cho có nghiệm  Phương trình (2) có nghiệm  y  . 4 Do y  và y  2023 − ; 
2023 nên y 5;6;...; 
2023 . Vậy có 2019 cặp (x;y) thỏa mãn. Chọn A.
VÍ DỤ 77. Cho phương trình ( +
)( − )( 2xy 4x+y+7 4 7 2 1 −
) = 2 (2− )+ +7 y xy y x e e x y ye  . Hỏi có bao nhiêu cặp số nguyên ( ;
x y ) thỏa mãn phương trình đã cho? A. 8 . B. 5 . C. 6 . D. 7 .
Hướng dẫn giải: Ta có: ( +
)( − )( 2xy 4x+y+7 4 7 2 1 −
) = 2 (2− )+ +7 y xy y x e e x y ye
 ( x + )( xy − y)( 2xy−y 4 x+7 4 7 2 e − e
) = 2x(2− y)+ y +7 (chia hai vế phương trình cho ye  0).
 ( x + )( xy − y) ( 2xy−y 4 x+7 4 7 2 . e − e
) = (4x+7)−(2xy − y)
 ( x + ) ( xy − y) 2xy−y e
−  = ( xy − y) ( x + ) 4x+7 4 7 . 2 1 2 4 7 e −1    
( xy − y) 2xy−y e − ( x + ) 4x+7 2 1 4 7 e −1  = 7 1 x  − , x  , y  0 ) 2xy − y 4x +
(do x, y nguyên nên 7 4 2 xy− y 1 x+ 1 2 4 7  e − = e − (*). 2xy − y 4x + 7 t 1 Xét hàm f (t ) t 1
= e − với t  0; f (t) = e +  0, t
  0  f (t) đồng biến trên các khoảng xác t 2 t định của nó. +
Vì vậy: (*)  f ( xy − y) = f ( x + ) 4x 7 9 2 4
7  2xy − y = 4x + 7  y = = 2 + . 2x −1 2x −1 2x −1 = 1  x =1 x = 0  
Vì y nguyên nên 2x −1 là ước số nguyên của 9, do vậy 2x −1 = 3
  x = 2  x = 1 −   . 2x −1 = 9 
x = 5 x = 4 −  
Vậy có 6 cặp số nguyên (x;y) thỏa mãn đề bài. Chọn C. HOÀNG XUÂN NHÀN 48
49 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 3. Phương pháp đánh giá và bài toán nghiệm nguyên phương trình mũ, lôgarit   VÍ DỤ 78. 1 2
Có bao nhiêu số nguyên +
y sao cho tồn tại x  ;3 
 thỏa mãn 3x xy = ( + ) 9 27 1 27 x xy .  3  A. 27 . B. 9 . C. 11. D. 12 .
_____Mã đề 101, Đề thi THPT Quốc Gia năm 2021_____ Ý tưởng: •  1  2
Tìm điều kiện cho y với + − x  ;3 
 . Biến đổi phương trình về 3x xy 9 27
x −1− xy = 0 .  3  • + − Xét hàm hai biến ( ) 2 3x xy 9 , = 27 x f x y
−1− xy , đây là hàm liên tục với mọi , x y  .
• Ta chứng minh f (3, y)  0 trên miền điều kiện của nó. Phương trình đã cho có nghiệm f (3, y)       x   f y f     ( y) 0 1 1 1 ;3 , . 3,  0  f , y  0  
(ứng với đặc thù của hàm số đang xét).  3   3   3 
Từ đây ta tìm điều kiện cho y.
Hướng dẫn giải: x0 1  1 
Từ phương trình suy ra: 1+ xy  0  y  − mà x  ;3   nên y  3
− ; vì y nguyên nên y  2. − x  3 
Phương trình tương đương vớ 2 i 3x + xy −9 27
x −1− xy = 0 (*). + −  1  Xét hàm hai biến ( ) 2 3x xy 9 , = 27 x f x y
−1− xy , ta thấy hàm này liên tục với mọi x  ;3   , y  2 − .  3  − − Ta có: ( ) 3 3, = 27 y f y
− 3y −1 = g ( y) với g (− ) 6 = +  g (− ) 3 2 27 5 0, 1 = 27 + 2  0 (1);   1  x = 0  ;3     3 
g (0) = 0 nên ta thay y = 0 vào phương trình đã cho: 2 3x 9 27 = 27 x   , do vậy y = 0  1  x = 3 ;3      3 
không thỏa mãn phương trình ban đầu (2). Ta có: ( ) 3 y = − = ( 3 3.27 ln 27 3 3 27 y g y ln 27 − ) 1  0, y
 1; suy ra g ( y)  g ( ) 3 1 = 27 − 4  0 (3).
Từ (1), (2), (3) suy ra g ( y)  0, y   2
− , y  , y  0 . HOÀNG XUÂN NHÀN 49
50 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT  1  y− 1 Ta có: 8 f , y = 3 − y −1 = h  
( y) với y  2
− ; trong đó h( y) y 1 = 3 ln 3 − = 0  3  3 3  1   y = log
= y . Mặt khác h( 3 − ).h( 2
− )  0 và h(9).h(10)  0 nên tồn tại 3   0  3ln 3  1 − ,856 y  3
− ;−2 , y  9;10 để h( y) = 0. Ta có bảng biến thiên: 1 ( ) 2 ( )  
Phương trình đã cho có nghiệ 1 m x  ;3 
  g ( y).h( y)  0  h( y)  0 (do g ( y)  0) .  3   1  f (3, y) f , y    3 
Dựa vào bảng biến thiên, kết hợp y  , y  2, ta có: y −2; −1;1; 2;...; 
9 thỏa mãn. Chọn C.
VÍ DỤ 79. Có bao nhiêu số nguyên y nằm trong khoảng (−2027;+ ) sao cho với mỗi giá trị của y + −
tồn tại nhiều hơn hai số thực x thỏa mãn + + ( − ) x y = ( − + ) 2 2 2 2 .2027 2 .2027x x x y x x x x y ? A. 2026 . B. 2027 . C. 2028 . D. 2029 .
Hướng dẫn giải: 2 −
Nhân hai vế phương trình đã cho với 2027x x , ta được phương trình sau: ( + ) 2
x − x + ( − ) 2 2 2 x + y x y x x = ( 2 x − x) + ( 2 .2027 .2027 x + y )  ( + ) ( 2
x − x − ) + ( − ) ( 2 2 2 . 2027 1 . 2027x +y x y x x − )1 = 0 ( )1 . 2 2 2027x −x −1 2027x +y −1 Xét ( 2 x + y )( 2
x − x)  0 . Khi đó: ( ) 1  + = 0 (2) 2 2 x − x x + y 2 x − x − • 2 2027 1 − Nếu 2
x − x  0 thì 2027x x −1  0 nên  0 . 2 x − x 2 x − x − 2 x − x − • 2 2027 1 2027 1 − Nếu 2
x − x  0 thì 2027x x −1  0 nên  0 . Vậy  0 khi 2 x − x  0 . 2 x − x 2 x − x 2 x + y − • 2027 1
Lý luận tương tự, ta có  0 khi 2 x + y  0 . 2 x + y HOÀNG XUÂN NHÀN 50
51 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT x = 0 2 x − x = 0 
Vì vậy vế trái (2) luôn dương nên (2) vô nghiệm. Do đó: (1)    x = 1  . 2 x + y = 0 2 x = −y
Nhận xét: Với mọi số thực y thì phương trình đã cho luôn có sẵn hai nghiệm 0; 1. Vì vậy ta cần phương trình 2
x = − y có không dưới một nghiệm khác 0; 1. Suy ra − y  0  y  0 .
Do y nguyên thuộc (−2027; + ) nên y  2026 − ; − 2025;...; −  1 . Chọn A.
VÍ DỤ 80. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log ( x + y) = log ( 2 2 x + 2 y 3 4 ) A. 3 . B. 2 . C. Vô số. D. 1.
_____Thi thử THPT Quốc Oai, Hà Nội, 2021_____
Hướng dẫn giải: x + y  0
x + y = 3t Điều kiện : 
. Đặt : log ( x + y) = log ( 2 2 x + 2 y = t   . 3 4 ) 2 2 x + 2y  0 2 2
x + 2y = 4t 2 2     Cauchy-Schwarz   2 1  1  t 3 t 3 1 Ta có: 2 2
x + y  = 1.x + . 2 y  1+
x + 2y    
(3 )  .4 t  log =   . 9        t 2 2 2 2 2 t 4  3   4  1 Mặt khác 2 t 2
x  4  4 = 2  − 2  x  2 . Vì x   x −1;0;  1 . y =1+ 3t Với x = 1 − , ta có:  t ( t )2 4 1 2 1 3 2.9t 4.3t 3 4t  − = +  + + − = 0 (1). 2
2y = 4t −1
• Nếu t  0 thì 2.9t 4t 0; 4.3t − 
+3  0  Vế trái (1) luôn dương.
• Nếu t  0 thì 3 4t 0; 2.9t 4.3t −  +
 0  Vế trái (1) luôn dương.
Do vậy (1) không có nghiệm t nên không tồn tại y thỏa mãn đề bài.  1 y = 3t log9 t t 1 2
Với x = 0 , ta có:   2.9 = 4  t = log . Khi đó 4 y = 3
 0,391 (tồn tại số thực y). 9 2 2y = 4t 2 4
y = 3t −1
Với x = 1 , ta có:   4t −1 = 2. −  −
+ − = . Ta thấy phương trình t (3t )2 1 2.9t 4.3t 3 4t 0 2 2y = 4 −1
này có ít nhất một nghiệm t = 0, suy ra y = 0 (tức là đã tồn tại y thỏa mãn phương trình ban đầu).
Vậy có 2 giá trị nguyên của x thỏa đề là x = 0 và x = 1. Chọn B. HOÀNG XUÂN NHÀN 51
52 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Bài toán 4. Xét nghiệm nguyên phương trình mũ, lôgarit dựa vào đặc thù của tổng, tích,
tổng bình phương… các số nguyên
VÍ DỤ 81. Có bao nhiêu cặp số nguyên dương ( ;
x y ) thỏa mãn log x + log y + log x + log y = 100 và log x,
log y , log x , log
y cũng là các số nguyên dương? A. 3 . B. 2 . C. 0. D. 1.
_____Thi thử Sở GD-ĐT Hà Nội năm 2020_____
Hướng dẫn giải: 1 1
Ta có: log x + log y + log x + log y = 100  log x + log y + log x + log y = 100 (1). 2 2 Đặt 2 2 a = log x, b =
log y a = log x, b = log y . Khi đó (1) trở 1 1 2 2 2 2 thành: 2 2 a + b +
a + b = 100  (a + ) 1 + (b + ) 1 = 202  (a + ) 1 + (b + ) 2 2 1 = 9 +11 . 2 2 a +1 = 9 a +1 =11 a = 8 a =10 Vì * a, b  nên        . b  +1 =11 b  +1 = 9 b  =10 b  = 8  = 64  log x = 8  =  = • a 8 log x 64 x 10 Với  thì      . b  = 10 100  = log y =100 log y 10   y =10  = 100  log x =10  =  = • a 10 log x 100 x 10 Với  thì      . b  = 8 64  = log y = 64 log y 8   y =10 Vậy có hai cặp số ( ;
x y ) thỏa mãn đề bài. Chọn B.
VÍ DỤ 82. Có bao nhiêu số nguyên dương x sao cho tồn tại số nguyên dương y thỏa mãn điều kiện 1 log (2 2 ) 1 ( 2 ) x y x 2  3.9 27 y x y x y − + − + + + = +1? 3  A. 3 . B. 2 . C. 0. D. 1.
Hướng dẫn giải: *  
Điều kiện: x, y  .
2x − 2y +1  0 3
Phương trình đã cho tương đương với log (2 2 ) 1 log ( 2 ) 2 x 2 y 1 x 2 3 3 y x y x y − + + − + + + + = + log 3 3 3 3 3  log (2 − 2 + ) x− y+ 3 2 2 1 x+2 1 + 3 = log + 3 y x y (1). 3 3 x + 2y Đặt ( ) t 1 = log + 3 ,  0;  = + 3t f t t t f t ln 3  0, t
  0 . Suy ra f (t) đồng biến trên (0;+). 3 ( ) tln3 HOÀNG XUÂN NHÀN 52
53 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT  
Vì vậy: ( )  f ( x − y + ) 3 3 1 2 2 1 = f
 2x − 2y +1 =   
(2x − 2y + )1(x + 2y) = 3 (*).  x + 2y x + 2 y *
2x − 2y +1
2x − 2y +1 =1 2x − 2y +1 = 3 Do điều kiện nên  , (*) suy ra:    * x + 2y  x + 2y = 3 x + 2y =1 x = 1  =  x 1  (nhận) hoặc  (loại).  y = 1  y = 0
Vậy có duy nhất một cặp số ( ; x y ) = (1; )
1 thỏa mãn đề bài. Chọn D.
Bài toán 5. Bài toán nghiệm nguyên phương trình mũ, lôgarit nhiều ẩn chứa tham số
VÍ DỤ 83. Có tất cả bao nhiêu giá trị thực của tham số m  1 − ;  1 sao cho phương trình 2 2 log x + y
= log 2x + 2y − 2 ( ;x y) 2 m 1 + ( ) 2 ( ) có nghiệm nguyên duy nhất? A. 3 . B. 2 . C. 1 . D. 0 . Hướng dẫn giải: Nhận xét: Vì ,
x y có vai trò như nhau (đối xứng) nên nếu phương trình đã cho có một nghiệm ( x ; y 0 0 )
thì ( y ; x cũng là một nghiệm của phương trình đó. Theo giả thiết, phương trình có nghiệm nguyên 0 0 )
duy nhất nên x = y  . 0 0
Điều kiện: x + y −1  0 .
Điều kiện cần: Phương trình đã cho có nghiệm nguyên duy nhất ( x ; y x = y . 0 0 ) 0 0
Thay vào phương trình, ta được: 2 log 2x = log 4x − 2 (*) 2 m 1 + ( 0 ) 2 ( 0 )
Vì x  , 4x − 2  0  4x − 2  1 . Hơn nữa: 2 ( x −1  0  2 2x  4x − 2 0 )2 2 0 0 0 0 0 Do đó (*): 2 log 4x − 2 = log 2x  log 4x − 2  log m +1  log 2 4 − − 0 x 2 ( ) 2 ( 0 ) 2 2 m 1 + ( 0 ) 2 ( + 0 ) m 1 4 0 x 2 + + 4 −  0 x 2 1 2 2
m +1 2  m 1 mà m  1 − ;  1  m = 1  .
Điều kiện đủ: Với m = 1
 thì phương trình đã cho trở thành log ( 2 2 x + y
= log 2x + 2y − 2 2 ) 2 ( ) x =
x + y = 2x + 2y − 2  (x − )2 1 + ( y − )2 1 2 2 1 = 0  
; ta thấy phương trình đã cho có nghiệm y =1 nguyên duy nhất (1; ) 1 nên m = 1  thỏa mãn.
Vậy có hai giá trị m thỏa mãn đề bài. Chọn B. HOÀNG XUÂN NHÀN 53
54 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
VÍ DỤ 84. Cho các số thực ,
x y, z thỏa mãn log ( 2 2
2x + y ) = log ( 3 3 x + 2 y
= log z . Có bao giá trị 3 7 )
nguyên của z để có đúng hai cặp ( ;
x y ) thỏa mãn đẳng thức trên. A. 2 . B. 211. C. 99 . D. 4. Nhận xét: 2 2
2x + y = 3t ( ) 1  Sau khi đặt log ( 2 2
2x + y ) = log ( 3 3 x + 2 y ) 3 3
= log z = t  x + 2y = 7t 2 . 3 7 ( )  z =10t (3) 
Phương trình (1) có vế trái là đẳng cấp bậc hai theo x, y; phương trình (2) có vế trái là đẳng cấp
bậc ba theo x, y. Bội số chung nhỏ nhất của 2 và 3 là 6, vì vậy ta lập phương hai vế của (1), bình
phương hai vế của (2), và sau đó tiến hành như lời giải sau. Hướng dẫn giải: 2 2
2x + y = 3t ( ) 1  Đặt: log ( 2 2
2x + y ) = log ( 3 3 x + 2 y ) 3 3
= log z = t  x + 2y = 7t 2 . 3 7 ( )  z =10t (3) 
Trường hợp 1: y = 0. t 2t log 3 2 Khi đó: ( ) 3
2  x = 7 . Thay vào ( ) 1 ta được: 3 2.7 = 3t t = log 2 ; (3) 3 49  z = 10 . 3 3 49
Trường hợp này không tồn tại hai cặp (x;y) thỏa mãn đề bài.
Trường hợp 2: y  0 . 2 3    x  (  +     2x + y
)3 = 27t (x +2y )2 2 2 2 3 3 t 6 t Chia  49 y   y      49  Từ ( ) 1 , (2) suy ra   =  = *     . 3 3 ( )
(x +2y )2 = 49t ( 2 2 3 3 x + y ) 2  27     27 2   x   2 +1      y     ( u = u + 2)2 0 3 6u ( 3 u + 2)(u − 4)  Đặ x t u =
. Xét hàm f (u) = ; f u = = 0  u = − 2  . 3 ( ) 3 y (2u + )1 (2u + )4 2 2 1 u = 4  Ta có bảng biến thiên: HOÀNG XUÂN NHÀN 54
55 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Với mỗi giá trị u thỏa mãn (*), ta tìm được một cặp ( x, y) thỏa mãn đề bài.
Yêu cầu bài toán tương đương:  1   log t 49 log   49 4   8 1  49    1    1  27 27   log        10  z 10 49 log 49 4 4 log t log 4    49   49  8  27 t 27        4 8 27 8 10 10 10 −  211,8 3,24.10 7 27 27        . t  4  4   4  log  49  4   49        log    49 33 t log t   33  27 0 49   0 10 10 27    33   0 z 10 27  33  27  4 −  2,88.10
Vì z nguyên nên z 1; 2;...; 21 
1 . Vậy có 211giá trị nguyên của z thỏa mãn. Chọn B.
C – BÀI TẬP THỰC HÀNH:
BÀI TẬP MỨC ĐỘ I: x+ 1 Câu 1.
Nghiệm của phương trình 2 1 3 = là 27 A. x = 1 − . B. x = 1. C. x = 2 − . D. x = 3 − . Câu 2.
Phương trình log (2x −3) =1có nghiệm là 5 A. x = 2 . B. x = 4 . C. x = 5. D. x = 3 . Câu 3.
Nghiệm của phương trình log (3x − 5) = 2 A. x = 36 . B. x = 35. C. x = 40 . D. x = 30 . Câu 4.
Nghiệm của phương trình log x −1 = 2 là 3 ( ) A. x = 10 . B. x = 9 . C. x = 8 . D. x = 11. Câu 5.
Nghiệm của phương trình x 1 2 − = 8 là
A. x = 2 . B. x = 3. C. x = 4 . D. x = 5 . Câu 6.
Nghiệm của phương trình x+1 5 =125 là HOÀNG XUÂN NHÀN 55
56 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT A. x = 2 . B. x =3 . C. x = 0 . D. x 1 = . Câu 7.
Nghiệm của phương trình log 3x − 2 = 3 là 2 ( ) 10 1 A. x = . B. x = 8 . C. x = 1. D. x = . 3 3 Câu 8.
Phương trình log (x +1) = 3 có nghiệm là 2
A. x = 5.
B. x = 7 .
C. x = 8 .
D. x = 10 . Câu 9.
Số nghiệm của phương trình log x = log ( 2 x − x là. 2 2 ) A. 0 . B. 1. C. 2 . D. 3 .
Câu 10. Nghiệm của phương trình x 1 2 + = 8 là A. 1. B. 3 . C. 2 . D. 4 .
Câu 11. Phương trình log 5x −1 = 2 có nghiệm là 3 ( ) 9 11 8 A. 2 . B. . C. . D. . 5 5 5
Câu 12. Nghiệm của phương trình x+2 3 = 9 là A. x = 4 . B. x = 0 . C. x = 4 − . D. x = 3 .
Câu 13. Nghiệm của phương trình 2x−4 3 = 9 . A. x = 3. B. x = 2 . C. x = 1. D. x = 1 − . 1
Câu 14. Nghiệm của phương trình log (8 − 3x) = là 4 2 36 x A. x = 3. B. x = 2 . C. 2 =10 + 4 . D. 3 . x−2 2
Câu 15. Nghiệm của phương trình T = 1 − là 5 1 3 A. T = 6 . B. T = . C. x = − . D. x = . 6 2 2
Câu 16. Nghiệm của phương trình log x − 3 = 3 là 3 ( ) A. x = 12 . B. x = 24 . C. x = 30 . D. x = 6 . x 1 +  x−  1
Câu 17. Số nghiệm của phương trình 3 7 =   là bao nhiêu  7  A. 1 B. 2 C. 3 D. 0
Câu 18. Tìm nghiệm của phương trình 4a +5b A. x = 6 . B. x = 21. C. x = 13. D. x = 9 . HOÀNG XUÂN NHÀN 56
57 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Câu 19. Cho phương trình 2 x −4 x+5 3
= 9, tổng lập phương các nghiệm thực của phương trình là: A. 25 . B. 28 . C. 26 . D. 27 .
Câu 20. Tìm tập nghiệm S của phương trình log x = 3 . 4 A. S =   12 . B. S =  . C. S =   64 . D. S =   81 .
Câu 21. Tập nghiệm của phương trình 2
log(x + x + 4) =1 là A. −3;  2 . B. −  3 . C.   2 . D. −2;  3 .
Câu 22. Tập nghiệm của phương trình 2
ln(2x − x +1) = 0 là  1  1  A.   0 . B. 0 ;  . C.   . D.  .  2  2 x−
Câu 23. Phương trình ( 5)2 1 = log 32 có nghiệm là 2 2 3 1
A. x = 1. B. x = . C. x = . D. x = . 3 2 2
Câu 24. Tìm tập nghiệm S của phương trình 3x = 2 . 2 A. S =  .
B. S = log 2 . C. S =  .
D. S = log 3 . 2  3  3 x
Câu 25. Nghiệm của phương trình ( − )3 5 2 6 = 5 + 2 6 là 1 1 A. 1. B. 1 − . C. − . D. . 3 3
ĐÁP ÁN TRẮC NGHIỆM 1C 2B 3B 4A 5C 6A 7A 8B 9B 10C 11A 12B 13A 14B 15C 16C 17A 18B 19B 20C 21A 22B 23C 24B 25C
BÀI TẬP MỨC ĐỘ II:
Câu 26. Phương trình 2
2x = 3x có bao nhiêu nghiệm thực? A. 2 . B. 3 . C. 0 . D. 1. 36 x
Câu 27. Phương trình 2
=10 + 4 có số nghiệm là x−2 2 A. 3 . B. 1. C. 0 . D. 2 .
Câu 28. Cho số thực x thoả mãn: x 1
25 − 5 +x − 6 = 0 . Tính giá trị của biểu thức 5 5x T = − . HOÀNG XUÂN NHÀN 57
58 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT 5 A. T = 5 . B. T = 1 − . C. T = 6 . D. T = . 6
Câu 29. Số nghiệm thực của phương trình 2 log x = log ( 2 x − 2 là 4 2 ) A. 0 . B. 2 . C. 4 . D. 1.
Câu 30. Phương trình 2
x(ln x −1) = 0 có số nghiệm là A. 3 . B. 0 . C. 2 . D. 1.
Câu 31. Số nghiệm thực của phương trình x 2 3 = 3 −x là A. 3. B. 2. C. 1. D. 0.
Câu 32. Phương trình (2x − 5)(log x − 3 = 0 có hai nghiệm x , x (với x x ). Tính giá trị của biểu 2 ) 1 2 1 2
thức K = x + 3x . 1 2
A. K = 32 + log 2.
B. K = 18 + log 5.
C. K = 24 + log 5.
D. K = 32 + log 3. 3 2 2 2 Câu 33. Biết 10 log 3 = 0
− ,1. Mệnh đề nào sau đây đúng x A. x  ( 1; − 0) .
B. x  (1; 4) . C. x  (0; ) 1 .
D. x  (−4; − ) 1 .
Câu 34. Tìm nghiệm phương trình 2 log x + log x − 3 = 2 . 4 2 ( )
A. x = 4 .
B. x = 1.
C. x = 3. D. x = 16 . 1
Câu 35. Tập nghiệm của phương trình
log ( x + 2)2 −1 = 0 là 2 2 A. −1;  0 . B. −  4 . C. 0; −  4 . D.   0 . −
Câu 36. Nghiệm của phương trình 1 ln 81 9 x = e là A. x = 4. B. x = 5. C. x = 6. D. x = 17. Câu 37. Với , a ,
b x là các số thực dương thỏa mãn log x = 5.log a + 3.log b . Mệnh đề nào sau đây 2 2 2 đúng?
A. x = 3a + 5 . b
B. x = 5a + 3 . b C. 5 3
x = a + b . D. 5 3
x = a .b .
Câu 38. Gọi x , x là các nghiệm của phương trình log ( 2 x − x = log x +1 . Tính 2 2
P = x + x . 2 ) 2 ( ) 1 2 1 2 A. P = 6 . B. P = 8 . C. P = 2 . D. P = 4 .
Câu 39. Tổng tất cả các nghiệm của phương trình log ( x 1
4.3 − −1 = 2x −1 bằng 3 ) A. 1. B. 2 . C. 7 . D. 3 .
Câu 40. Gọi P là tích tất cả các nghiệm của phương trình: log ( 3 x + x + ) 1 = log ( 2
2x +1 . Tính . P .. 2 2 ) HOÀNG XUÂN NHÀN 58
59 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT A. P =1 . B. P = 3 . C. P = 6 . D. P = 0 .
Câu 41. Nếu log x = 5log a + 4log b (a, b  0) thì x bằng 2 2 2 A. 5 4 a b . B. 4 5 a b .
C. 5a + 4b .
D. 4a + 5b .
Câu 42. Nghiệm của phương trình x+3 2020 4 = 2 là A. x = 2013 . B. x = 2023 . C. x = 1007 . D. x = 2017 .
Câu 43. Gọi S là tập hợp các giá trị của x để 3 số log 4x ; 1+ log x ; log x theo thứ tự lập thành 8 ( ) 4 2
cấp số nhân. Số phần tử của S là A. 2. B. 3. C. 1. D. 0. 1 1
Câu 44. Cho các số thực dương , a b thỏa mãn log a + b = 3 + log ab . Giá trị + bằng 2 ( ) 2 ( ) a b 1 1 A. 3 . B. . C. . D. 8 . 3 8 3x 1 −  x −  1
Câu 45. Phương trình 2 4 3
=   có hai nghiệm x , x . Tính x x .  1 2 9  1 2 A. 6 . B. 2 − . C. 5 − . D. 6 − .
Câu 46. Biết phương trình 4x 5.2x −
+3 = 0 có hai nghiệm x , x . Tính x + x . 1 2 1 2 A. 3 . B. log 3 . C. 5 . D. log 5 . 2 2
Câu 47. Số nghiệm của phương trình x x+2 9 + 3 −1= 0 là A. 3 . B. 2 . C. 1. D. 0 . − −
Câu 48. Gọi P là tổng bình phương tất cả các nghiệm của phương trình x 1 2 2
+ 2 x = 3. Khi đó, P bằng A. P = 3 . B. P = 5 . C. P = 9 . D. P =1.
Câu 49. Phương trình log x 1
2 có tất cả bao nhiêu nghiệm? 3 A. 2 nghiệm. B. Vô nghiệm. C. 3 nghiệm. D. 1 nghiệm.
Câu 50. Tổng các nghiệm của phương trình log
(x − 2)+ log (x −4)2 = 0 là S = a +b 2 (với a ; b 3 3
là các số nguyên). Giá trị của biểu thức Q = ab bằng: A. 0 . B. 3 . C. 9 . D. 6 .
ĐÁP ÁN TRẮC NGHIỆM 26A 27B 28B 29B 30C 31C 32C 33C 34A 35C 36B 37D 38A 39A 40D 41A 42C 43A 44D 45D 46B 47C 48B 49A 50D HOÀNG XUÂN NHÀN 59
60 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
BÀI TẬP MỨC ĐỘ III:
Câu 51. Tổng tất cả các nghiệm của phương trình log x + 2log x = 2 + log .
x log x bằng 2 7 2 7 A. 13. B. 11. C. 15. D. 10. x x x
Câu 52. Tích tất cả các nghiệm của phương trình ( + ) +( − ) 2 5 21 5 21 = 5.2 bằng: A. 2 − . B. 4 − . C. 4 . D. 2 .
Câu 53. Tính S là tổng tất cả các nghiệm của phương trình ( 2x 2 4. 2
+ 2− x ) − 4.(2x + 2−x ) − 7 = 0. A. S = 1. B. S = 1. − C. S = 3. D. S = 0. − −
Câu 54. Phương trình
x 2 + ( x − ) x 2 3.25 3 10 5
+ 3 − x = 0 có tất cả bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4. x+5 3
Câu 55. Cho phương trình ( 2 )x x x + + + = ( 2 2 1 x + x + )
1 . Tìm tổng tất cả các nghiệm của phương trình. 17 13 15 11 A. − . B. − . C. − . D. − . 4 4 4 4
Câu 56. Cho phương trình .16x − 2 ( − 2).4x m m
+ m − 3 = 0 . Tập hợp tất cả các giá trị dương của m để
phương trình đã cho có hai nghiệm phân biệt là khoảng (a;b). Tổng T = a + 2b bằng: A. 14 . B. 10 . C. 11. D. 7 . x x x
Câu 57. Biết phương trình ( + ) + ( − ) x+3 3 5 15 3 5
= 2 có hai nghiệm x , x và 1 = log b 1, trong 1 2 a x2 đó ,
a b là các số nguyên tố, giá trị của biểu thức 2a + b là: A. 11. B. 17 . C. 13 . D. 19 . 1
Câu 58. Tổng tất cả các nghiệm của phương trình log
x − 5x + 6 + log x − 2 = log ( x + 3)4 2 bằng 3 1 1 2 3 81 A. 10. B. 3 10. C. 0. D. 3.
Câu 59. Tìm tất cả các giá trị thực của tham số m để phương trình log x + log x +1 − 2m −1 = 0 có ít 3 3
nhất một nghiệm thực trong đoạn 1; 27 .
A. m  (0; 2) .
B. m 0; 2 .
C. m 2; 4 .
D. m  (0; 4) .
Câu 60. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
log x − m log x + 2 − m = 0 có 3 9
nghiệm x 1;9 . HOÀNG XUÂN NHÀN 60
61 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT A. 1. B. 5 . C. 3 . D. 2 .
Câu 61. Có bao nhiêu giá trị nguyên của m để phương trình log mx = log x +1 vô nghiệm? 2 ( ) ( ) 2 A. 4 . B. 6 . C. 3 . D. 5 .
Câu 62. Tìm tất cả các giá trị của tham số m để phương trình sin x 1+sin 4 + 2
x − m = 0 có nghiệm. 5 5 5 5 A. m  8 . B. m  8 . C. m  7 . D. m  9 . 3 4 4 4
Câu 63. Cho phương trình 2
log x − (5m + ) 2
1 log x + 4m + m = 0 . Biết phương trình có 2 nghiệm phân 2 2
biệt x , x thỏa x + x = 165 . Giá trị của x − x bằng 1 2 1 2 1 2 A. 16 . B. 119 . C. 120 . D. 159 .
Câu 64. Có bao nhiêu giá trị nguyên của m để phương trình log x + 3 + m log 9 = 16 có hai nghiệm 3 ( ) x+3
thỏa mãn −2  x x . 1 2 A. 17 . B. 16 . C. 14 . D. 15 .
Câu 65. Cho phương trình 2 log
9x − m + 5 log x + 3m −10 = 0 . Số giá trị nguyên của tham số m để 3 ( ) ( ) 3
phương trình đã cho có hai nghiệm phân biệt thuộc 1;8  1 là A. 3 . B. 5 . C. 4 . D. 2 . x x
Câu 66. Phương trình (2 + 3) + (1− 2a)(2 − 3) − 4 = 0 có 2 nghiệm phân biệt x , x thỏa mãn 1 2 x − x = log
3 . Khi đó a thuộc khoảng 1 2 2+ 3  3   3   3  A. − ; −   . B. (0; + ) . C. ; +   . D. − ; +    .  2   2   2  Câu 67. Biết rằng m = m là giá trị của tham số m 0 sao cho phương trình 9x − 2 (2 + ) 1 3x m + 3(4m − )
1 = 0 có hai nghiệm thực x , x thỏa mãn ( x + 2 x + 2 = 12 . Khi 1 )( 2 ) 1 2
đó m thuộc khoảng nào sau đây 0 A. (3;9) . B. (9; +) . C. (1;3) . D. (-2;0) .
Câu 68. Có bao nhiêu giá trị nguyên của tham số m để phương trình 16x − 2 ( + ) 1 4x m + 3m − 8 = 0 có hai nghiệm trái dấu? A. 6 . B. 7 . C. 0 . D. 3 .
Câu 69. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1 − 2 16 − . m 4
+5m − 44 = 0 có hai nghiệm đối nhau. Hỏi S có bao nhiêu phần tử? A. 2 . B. 0 . C. 1. D. 3 . HOÀNG XUÂN NHÀN 61
62 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
Câu 70. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 4x − 2 .2x m − m + 6 = 0
có hai nghiệm thực x , x sao cho x x  3 . Tập hợp S có bao nhiêu phần tử? 1 2 1 2 A. Vô số. B. 3 . C. 2 . D. 1. Câu 71. Gọi ( ; a )
b là tập các giá trị của tham số m để phương trình 2
2e x −8ex − m = 0 có đúng hai
nghiệm thuộc khoảng (0;ln 5). Tổng a + b bằng A. 2 . B. 4. C. 6. − D. 14. −
Câu 72. Giá trị thực của tham số m để phương trình 4x − (2 + 3).2x m
+ 64 = 0 có hai nghiệm thực x , 1
x thỏa mãn ( x + 2 x + 2 = 24 thuộc khoảng nào sau đây? 1 )( 2 ) 2  3   3   21 29  11 19  A. 0;  . B. − ; 0   . C. ;   . D. ;   .  2   2   2 2   2 2 
Câu 73. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 5x +10 = 25x m + 4
có nghiệm duy nhất. Số tập con của S là A. 3 . B. 4 . C. 16 . D. 15 . 2 2 + − + −
Câu 74. Tập các giá trị của m để phương trình 1 1 x − ( + ) 1 1 4 2 2 x m
+ 2m +1 = 0 có nghiệm là  9   9  A. − ;  . B. 4; .
C. (− ; 4) .
D. 4; + ) .    2   2
Câu 75. Cho hàm số y = f ( x) liên tục trên và có đồ thị như hình vẽ.
Tập hợp tất cả các giá trị thực của m để phương 2 trình ( x
f e ) = m có đúng 2 nghiệm thực là A. 0; 4 . B. 0;  4 . C.   0  (4; +) . D. 4; +) .
ĐÁP ÁN TRẮC NGHIỆM 51B 52B 53D 54B 55A 56C 57A 58A 59B 60A 61A 62B 63D 64D 65C 66D 67C 68A 69B 70C 71D 72D 73C 74D 75C HOÀNG XUÂN NHÀN 62
63 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
BÀI TẬP MỨC ĐỘ IV: Câu 76. Tổng tất cả các giá trị nguyên của m để phương trình 3
x−3+ m−3x + ( 3 2 − + + ) x−3 3 9 24 .3 = 3x x x x m
+1 có 3 nghiệm phân biệt. A. 34 . B. 27 . C. 38 . D. 45 .
Câu 77. Gọi m là giá trị nhỏ nhất của tham số thực m sao cho phương trình 0 (m − ) 2 1 log
x − 2 − m − 5 log
x − 2 + m −1 = 0 có nghiệm thuộc khoảng (2; 4) . Khẳng 1 ( ) ( ) 1 ( ) 2 2
định nào dưới đây đúng?  4   10   16   5 −  A. m  1 − ; . B. m  2; . C. m  4; . D. m  5; − . 0          3  0  3  0  3  0  2  x
Câu 78. Có bao nhiêu giá trị của tham số m để phương trình 2 4 log x − m log + 2 = 0 có hai nghiệm 36 6 6
phân biệt x , x thỏa mãn x .x − 72 x .x +1296  0 1 2 1 2 1 2 A. 0. B. 1. C. 2. D. 3.
Câu 79. Tập hợp các số thực m để phương trình
( x − mx + ) = ( 2 ln 3 1
ln −x + 4x − 3) có nghiệm là nửa
khoảng a;b) . Tổng a + b bằng 10 22 A. . B. 4. C. . D. 7. 3 3 Câu 80. Cho ,
a b là các số thực dương lớn hơn 1, thay đổi thỏa mãn a + b = 2019 để phương trình 5log .
x log x − 4log x − 3log x − 2019 = 0 luôn có hai nghiệm phân biệt x ; x . Biết giá trị a b a b 1 2 3
m  4  n
lớn nhất của ln ( x .x bằng ln + ln ; với ,
m n là các số nguyên dương. Tính 1 2 )     5  7  5  7 
S = m + 2n A. 22209 . B. 20190 . C. 2019 . D. 14133 .
Câu 81. Số các giá trị nguyên nhỏ hơn 2018 của tham số m để phương trình log
2018x + m = log 1009x có nghiệm là 6 ( ) 4 ( ) A. 2018 . B. 2017 . C. 2020 . D. 2019 .
Câu 82. Có bao nhiêu số nguyên m để phương trình log (3x + 2m) = log ( x 2 3 − m có nghiệm? 3 5 ) A. 3 . B. 4 . C. 2 . D. 5 .
Câu 83. Cho hàm số bậc ba y = f ( x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m  5 − ;5 sao cho phương trình 3 log ( f ( x) + ) 2 1 − log
f x +1 + 2m − 8 log
f x +1 + 2m = 0 có nghiệm x  ( 1 − ; ) 1 ? 2 2 ( ( ) ) ( ) 1 ( ) 2 HOÀNG XUÂN NHÀN 63
64 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT A. 7 . B. 5 . C. 6 . D. vô số.
Câu 84. Cho phương trình 2 m ln ( x + )
1 − ( x + 2 − m) ln ( x + ) 1 − x − 2 = 0 ( )
1 . Tập hợp tất cả các giá trị
của tham số m để phương trình ( )
1 có hai nghiệm phân biệt thoả mãn 0  x  2  4  x là 1 2
khoảng (a ; + ) . Khi đó a thuộc khoảng A. (3,8;3,9)
B. (3, 6;3, 7) . C. (3, 7;3,8) . D. (3,5;3, 6) . − − Câu 85. Cho hàm số ( ) x 4 = + ( + ) 7 3 1 .2 x f x x
– 6x + 3 , khi phương trình f ( 2
7 − 4 6x − 9x ) + 3m −1 = 0 a
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số m có dạng
. Tính T = a + b . b A. T = 7 . B. T = 11. C. T = 8 . D. T = 13 .
Câu 86. Cho số thực m và hàm số y = f ( x) có đồ thị như hình vẽ dưới đây.
Phương trình (2x + 2−x f
) = m có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn −1;2? A. 2 . B. 3 . C. 4 . D. 5 .
Câu 87. Xét các số nguyên dương ,
a b sao cho phương trình .4x − .2x a b
+50 = 0 (1) có hai nghiệm phân
biệt x , x và phương trình 9x − .3x b
+50a = 0 (2) có hai nghiệm x , x thỏa mãn điều kiện 1 2 3 4
x + x x + x . Tìm giá trị nhỏ nhất của biểu thức S = 3a + 4b . 3 4 1 2 A. 109 . B. 51. C. 49 . D. 87 . 3 2 2
Câu 88. Cho phương trình: x +x −2x+m x +x 3 2 − 2
+ x −3x + m = 0 . Tập các giá trị để bất phương trình có
ba nghiệm phân biệt có dạng (a ;b) . Tổng a + 2b bằng: HOÀNG XUÂN NHÀN 64
65 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT A. 1. B. 2. C. 4. − D. 0.
Câu 89. Có bao nhiêu số nguyên m để phương trình 2 9.3 x − ( 4 2 4 + 2 +1 + 3 + 3)3x m x x m +1 = 0 có
đúng 3 nghiệm thực phân biệt? A. Vô số. B. 3 . C. 1 . D. 2 .
Câu 90. Có bao nhiêu giá trị nguyên của tham số m
2019; 2019 để phương trình x mx m x 2 1 2 1 2019
0 có đúng 3 nghiệm thực phân biệt? x 1 x 2 A. 4038 . B. 2019. C. 2017. D. 4039 . m
Câu 91. Có bao nhiêu số nguyên m (m  2) sao cho tồn tại số thực x thỏa mãn ( x m + )ln ln 4 + 4 = x? A. 8 . B. 9 . C. 1. D. Vô số
Câu 92. Có bao nhiêu giá trị nguyên của m với m  1 sao cho tồn tại số thực x thỏa mãn: ( m log x m + 3)log5 5 = x − 3 ( ) 1 . A. 4 . B. 3 . C. 5 . D. 8 .
Câu 93. Tổng tất cả các giá trị của tham số m sao cho phương trình: (x− )2 1 − 2 .log ( 2
x − 2x + 3 = 4 x m.log
2 x − m + 2 có đúng ba nghiệm phân biệt là: 2 ) 2 ( ) 3 A. 2. B. . C. 0. D. 3. 2
Câu 94. Cho phương trình 2 log + + + −
+ − − = với m là tham số +
( 2x 1 x) ( 2m 2)log − ( 2x 1 x 1 0 2 3 2 3 )
thực. Gọi S là tập hợp tất cả các giá trị của m để phương trình có 2 nghiệm phân biệt x ; x 1 2 2 x +1 − x thỏa mãn 1
1 = 7 + 4 3 . Tích các phần tử của S bằng 2 x +1 + x 2 2 A. 4 − . B. 4 . C. 0 . D. 2 .
Câu 95. Có bao nhiêu số nguyên y nằm trong khoảng (−2021; + ) sao cho với mỗi giá trị của y tồn + −
tại nhiều hơn hai số thực x thỏa mãn + + ( − ) x y = ( − + ) 2 2 2 2 .2020 2 .2020x x x y x x x x y ? A. 2020 . B. 2019 . C. 2021. D. 2022 .
Câu 96. Cho hàm số bậc 4 có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m và f ( x) m  2021; −  2021 để phương trình log + x f  ( x) 3
− mx = mx − f x có hai nghiệm 2  ( ) mx dương phân biệt? HOÀNG XUÂN NHÀN 65
66 PHƯƠNG PHÁP TRẮC NGHIỆM VẬN DỤNG & VẬN DỤNG CAO
CHƯƠNG II. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT y 1 O x 1 − 1 A. 2022 . B. 2020 . C. 2019 . D. 2021. Câu 97. Biết điều kiện cần và đủ của tham số m để phương trình  3  log ( x + 2)2 1 2 + 4 m − 5 log −8m + 4 = 0 có nghiệm thuộc − ;6 là 1 ( ) 1   x + 2  2  2 2 m  ( ; − a ;
b + ) . Tính giá trị biểu thức T = a + b . 8 22 8 22 A. T = − . B. T = − . C. T = . D. T = . 3 3 3 3
Câu 98. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log ( x + y) = log ( 2 2 x + 2 y 3 4 ) A. 3 . B. 2 . C. Vô số. D. 1.
Câu 99. Có bao nhiêu cặp số ,
x y là các số nguyên không âm thỏa mãn:
2(1+ x + 2y )2 + log ( x + 2y) = 2log ( x + y + 2xy + x) + 2(x + y)2 2 2
+ 4x + 4y 2 2 A. 2. B. 3. C. 4. D. 5.
Câu 100. Có bao nhiêu số nguyên dương a nhỏ hơn 2021 sao cho tồn tại số nguyên x thỏa mãn a ( x+3 − ) 2
+ a = a ( a x+3 2 2 1 2 + 2 − ) 1 ? A. 12 . B. 15 . C. 10 . D. 14 .
ĐÁP ÁN TRẮC NGHIỆM 76B 77D 78A 79D 80A 81C 82A 83A 84C 85C 86B 87A 88B 89C 90C 91C 92B 93D 94B 95A 96D 97D 98B 99B 100C HOÀNG XUÂN NHÀN 66