



















Preview text:
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
GIẢI BPT MŨ BẰNG PHƯƠNG PHÁP HÀM SỐ - ĐÁNH GIÁ
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Nhắc lại kiến thức cũ :
Đạo hàm : ( u )′ = . u a
u′ a .ln a
Nếu hàm số f đồng biến trên khoảng D thì x
∀ , y ∈ D : f (x) > f ( y) ⇔ x > y
Nếu hàm số f nghịch biến trên khoảng D thì x
∀ , y ∈ D : f (x) > f ( y) ⇔ x < y
Bước 1 : Đặt điều kiện của bpt (nếu có)
Bước 2 : Các phương pháp giải
Phương pháp 1 : Dùng tính đơn điệu của hàm số
Phương pháp 2 : Dùng phương pháp đồ thị hàm số
Phương pháp 3 : Đánh giá
Câu 1. Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình 2x−25 + ( 2 x − ) x+2021 3 25 .4 ≤1 A. 10. B. 11. C. 8 . D. 9. Lời giải Chọn B
Xét bất phương trình 2x−25 + ( 2 x − ) x+2021 3 25 .4 ≤ 1( ) 1 Ta có: x+2021 4 > 0, x ∀ ∈ TH1: Xét 2
x − 25 = 0 ⇔ x = 5 ± ta có VT ( ) 1 =1≤1 (Đúng) nên bpt ( ) 1 có nghiệm x = 5 ± x < 5 − TH2: Xét 2 x − 25 > 0 ⇔ x > 5 2 x −25 0 3 > 3 =1 Ta có (
⇒ VT 1 >1 nên bpt ( ) 1 vô nghiệm. 2 x − 25 ) ( ) x+2021 .4 > 0 TH3: Xét 2 x − 25 < 0 ⇔ 5 − < x < 5 2 x −25 0 3 < 3 =1 Ta có (
⇒ VT 1 <1 nên bpt ( ) 1 có nghiệm 5 − < x < 5 2 x − 25 ) ( ) x+2021 .4 < 0
Vậy nghiệm của bpt đã cho là x ∈[ 5; − 5].
Vì x nguyên nên x ∈{ 5 ± ; 4 ± ; 3 ± ; 2 ± ; 1 ± ; } 0 có 11 giá trị x 1 + Câu 2. −
Giải bất phương trình 6 3 10 >
ta được tập nghiệm S = ( ;
a b) . Tính giá trị của biểu thức x 2x −1
P =10b − 3a
A. P = 5.
B. P = 4 .
C. P = 2 . D. P = 0 . Lời giải Chọn A Điều kiện 1
x ≠ 0; x ≠ (*) 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
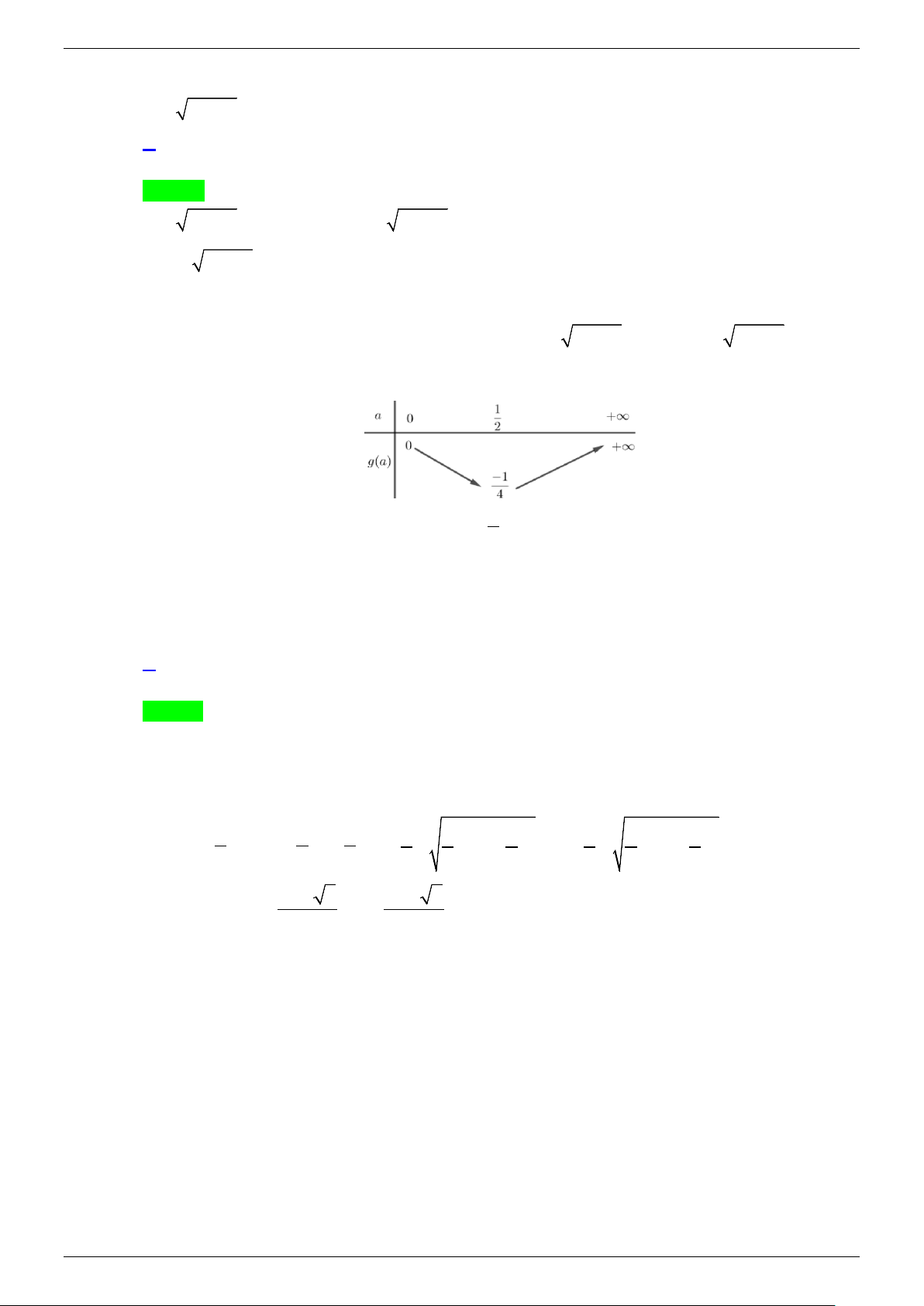
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC x > 0 x > 0 x+ 10x x+ 2x − 6 ( ) 1 1 1 − > < + 6 3 3 x 1 − − Với điều kiện ( − *) , ta có: 6 3 10 2x 1 2x 1 > ⇔ ⇔ x 2x 1 x 0 − < x < 0 x+ 10x x+ 2x − 6 (2) 1 1 6 − 3 < 3 > 2x 1 − 2x −1 − Gọi ( x
C) và (H ) theo thứ tự là đồ thị của hàm số ( ) 1 3x y g x + = =
và y = f (x) 2 6 = 2x −1
Dựa vào đồ thị, ta có: hệ bpt ( ) 1 có nghiệm 1
0 < x < ; hệ bpt (2) vô nghiệm. 2
Vậy tập nghiệm của bpt đã cho là 1 S 0; = suy ra 1
a = 0;b = nên P =10b − 3a = 5. 2 2 1−x Câu 3. − +
Tập nghiệm của bất phương trình 2 2x 1 ≥ 0 là 2x −1 A. [0; ] 1 . B. (0; ] 1 . C. ( 1; − 0]. D. (0;2]. Lời giải Chọn B
Điều kiện: 2x −1 ≠ 0 ⇔ x ≠ 0 .
Xét hàm số f (x) 1−x 2 = 2 − 2x +1 = 2 − x +1+ có f ′(x) 2.ln 2 = 2 − − < 0 , x ∀ . 2x 2x
Do đó hàm số này nghịch biến trên . Vậy 1
2 −x − 2x +1 > 0 ⇔ f (x) > f ( )
1 ⇔ x <1 ⇔ 1− x > 0 tức là f (x) cùng dấu với 1− x . Xét hàm số ( ) 2x g x = −1 có ′( ) = 2x g x .ln 2 > 0 , x
∀ . Do đó hàm số này đồng biến trên .
Vậy 2x −1 > 0 ⇔ g (x) > 0 ⇔ x > 0 tức là g (x) cùng dấu với x. −
Suy ra bất phương trình đã cho tương đương với 1 x ≥ 0 ⇔ 0 < x ≤1. x
Vậy tập nghiệm của BPT là S = (0; ] 1 .
Câu 4. Bất phương trình 2 2 2 sin x cos x sin 2 3 4.3 x + ≥
có bao nhiêu nghiệm nguyên trên [ 2021 − π;2022π ]. Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC A. 4043. B. 2021. C. 4044 . D. 2022 . Lời giải Chọn C Đặt 2
t = sin x (0 ≤ t ≤ )
1 thay vào bất phương trình đã cho ta có t t t 1
2 + 3 −t ≥ 4.3t t 3 ⇔ 2 + ≥ 4.3t t t 2 1 6 3 4.9 3 ⇔ + ≥ ⇔ + ≥ 4 (1). 3t 3 9 t t t t
Xét hàm số f (t) 2 1 3 = + , 0 ≤ t ≤ 2 2 1 1
1. Có f ′(t) = .ln + 3 ln < 0, t ∀ ∈ [0; ]1. 3 9 3 3 9 9
Suy ra hàm số f (t) nghịch biến trên [0; ] 1 . t t
Do đó luôn có f (t) ≤ f (0) hay 2 1 3 + ≤ 4 (2). 3 9 t t
Từ (1) và (2) suy ra: 2 1 2 + 3
= 4 ⇔ t = 0 ⇔ sin x = 0 ⇔ x = kπ (k ∈ ) 3 9 Do 2021 −
π ≤ x ≤ 2022π ⇒ 2021 −
π ≤ kπ ≤ 2022π ⇔ 2021 −
≤ k ≤ 2022(k ∈) Suy ra k ∈{ 2021 − ; 2020 − ;...;2021; }
2022 , có tất cả 4044 giá trị k
Vậy bất phương trình có tất cả 4044 nghiệm nguyên.
Câu 5. Cho hàm số ( ) 2 x 1 2 (2x 2 x f x + − = −
). Gọi S là tổng các giá trị xnguyên dương thỏa mãn bất
phương trình f (x ) 228 22 f + + ≤ 0 . Tính S ? x − 9
A. S = 36 .
B. S = 45 . C. 30. D. 8 . Chọn A Xét hàm số ( ) 2 2 x 1 x x 1 2 2 x f x + + + − = −
có tập xác định D = nên x
∀ ∈ ⇒ −x∈ . Ta có : (− ) 2 2 x 1 + −x x 1 = 2 − 2 + +x f x
= − f (x) nên hàm số đã cho là hàm số lẻ. Mặt khác ′( ) 2 + + x 2 x 1 x x 1 = 2 .ln 2. +1 − 2 + −x.ln 2 x f x −1 2 2 x +1 x +1 2 2 + + + − ′( ) 2 x + +x x 1 x 2 1 x 1 + −x x 1 = 2 ln 2 + 2 x f x .ln 2 > 0 2 2 x 1 x 1 + + ( Vì 2 2 2
x +1 > x = x ⇒ x +1 ± x > 0)
Do đó hàm số f (x) đồng biến trên .
Từ đó suy ra f (x ) 228 22 f + + ≤
0 ⇔ f ( x + ) 228 22 ≤ − f ⇔ f ( x + ) 228 22 ≤ f x − 9 x − 9 9 − x 2 228 x +13x + 30 x ≤ 10 − ⇔ x + 22 ≤ − ⇔ ≤ 0 ⇔ x − 9 x − 9 3 − ≤ x < 9
Vậy các số nguyên dương thỏa mãn bất phương trình là x ∈{1;2;3;4;5;6;7; }
8 ⇒ S =1+ 2 +. .+ 8 = 36 .
Câu 6. Có bao nhiêu cặp số nguyên ( ;
x y) thỏa mãn bất phương trình ( x + y) 2 2 2
5x +2xy+2 y −3 2 .2
+ (x − y)2 ≤ 3 ?
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn D
Từ ( x + y) 2 2 2
5x +2xy+2 y −3 2 .2
+ (x − y)2 ≤ 3 ⇔ ( x + y) (2x+y)2+(x−y)2 2 −3 2 .2
+ (x − y)2 − 3 ≤ 0 (∗) a = (2x + y)2 Đặt . b =
(x − y)2 −3 ≥ 3 −
Khi đó bất phương trình ( + b ∗) có dạng: .2a b a b 0 .2a a 0 .2a a b − + ≤ ⇔ + ≤ ⇔ ≤ − . b ( ).2 b 2
Vì a ≥ 0 ⇒ b
− ≥ 0 nên ta xét các trường hợp sau đây: a > b − ≥ 0
TH1: Nếu a > b − ≥ 0 ⇒ ⇒ .2a a > ( b
− ).2−b không thoả mãn bất phương trình.
2a > 2−b ≥ 0 0 ≤ a ≤ b −
TH2: Nếu 0 ≤ a ≤ b − ⇒ ⇒ .2a a ≤ ( b
− ).2−b thoả mãn bất phương trình.
0 < 2a ≤ 2−b
Vậy bất phương trình .2a ( ).2 b a b − ≤ − ⇔ a ≤ b
− ⇔ a + b ≤ 0
Suy ra ( x + y)2 + (x − y)2 − ≤ ⇔ ( x + y)2 + (x − y)2 2 3 0 2 ≤ 3.
Với giả thiết x, y ∈ Z nên ( + )2 2x y và ( − )2
x y chỉ có thể xảy ra các trường hợp sau:
Vậy có tất cả 3 cặp ( ; x y) thoả mãn.
Câu 7. Có bao nhiêu số nguyên trong đoạn [0; ]
2021 thỏa mãn bất phương
trình : x − x − ≤ ( x − ) 2 2 x −6x+2 + ( 2 x − x + ) 3x−4 3 2 3 4 .2021 6 2 .2021 A. 2016 . B. 2017 . C. 2020 . D. 2021. Lời giải Chọn B Đặt 2
a = x − 6x + 2 , b = 3x − 4 .
Bất phương trình có dạng :
+ ≤ .2021a + .2021b a b b a
⇔ .(1− 2021b ) ≤ .(2021a a b − ) 1 ( ) 1
TH1: a = 0 hoặc b = 0 thì nghiệm đúng bất phương trình đã cho. 2 x = 3± 7
x − 6x + 2 = 0
Bất phương trình đã cho tương với ⇔ 4 . 3x − 4 = 0 x = 3 a > 0 2021a −1> 0 TH2: Nếu ⇒ ⇒ VT( ) 1 < 0 ; VP( ) 1 > 0 . b > 0 1 − 2021b < 0 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Khi đó bất phương trình luôn đúng. x > 3+ 7 2 x 6x 2 0 − + >
Vậy bất phương trình tương đương với ⇔ x < 3 − 7 ⇔ x > 3+ 7 . 3 x − 4 > 0 4 x > 3 a < 0 2021a −1< 0 TH3: Nếu ⇒ ⇒ VT( ) 1 < 0 ; VP( ) 1 > 0 b < 0 1 − 2021b > 0
Khi đó bất phương trình luôn đúng.
Vậy bất phương trình tương đương với 2 3− 7 < x < 3+ 7
x − 6x + 2 < 0 4 ⇔ ⇔ 3− 7 4 < x < . 3 x − 4 < 0 x < 3 3 a > 0 2021a −1> 0 TH4: Nếu ⇒ ⇒ VT( ) 1 > 0 ; VP( ) 1 < 0 . b < 0 1 − 2021b > 0
Trường hợp này bất phương trình vô nghiệm. a < 0 2021a −1< 0 TH5: Nếu ⇒ ⇒ VT( ) 1 > 0 ; VP( ) 1 < 0 b > 0 1 − 2021b < 0
Trường hợp này bất phương trình vô nghiệm.
Từ các trường hợp trên, bất phương trình đã cho có tập nghiệm là 4 S = 3− 7; ∪ 3+ 7;+∞ ) 3
Các số nguyên thỏa mãn bất phương trình là x ∈{1;6;7;...;2020; } 2021 .
Vậy bất phương trình có 2017 nghiệm nguyên trong đoạn [0; ] 2021 .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
GIẢI PHƯƠNG TRÌNH MŨ BẰNG PHƯƠNG PHÁP ĐẶC TRƯNG
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Bước 1 : Biến đổi bất phương trình về dạng
f (a) < f (b) ( f (a) > f (b); f (a) ≤ f (b); f (a) ≥ f (b)) ( ) 1 .
Bước 2 : Xét hàm số y = f (x) , chứng minh hàm số luôn đồng biến, hoặc luôn nghịch biến
Bước 3 : Do hàm số y = f (x) luôn đồng biến, hoặc luôn nghịch biến suy ra
f (a) < f (b) ⇔ a < b hoặc f (a) < f (b) ⇔ a >
Câu 1. Số nghiệm nguyên của bất phương trình sau là: 2 2 2x 15 − x 100 + x 10 + x−50 2 2 − 2
+ x − 25x +150 < 0 là A. 4 . B. 6. C. 3. D. 5. Lời giải Chọn A Ta có 2 2 2x 15 − x 100 + x 10 + x−50 2 2 − 2
+ x − 25x +150 < 0 2 2 2x 15 − x 100 + x 10 + x−50 2 ⇔ − + x − x + − ( 2 2 2 2
15 100 x +10x − 50) < 0. Đặt 2
a = 2x −15x +100, 2
b = x +10x − 50 .
Khi đó bất phương trình trở thành: 2a − 2b + a − b < 0 ⇔ 2a − − > 2b a − − b ( ) 1 . Xét hàm số ( ) = 2t f t
− − t có ′( ) = 2t f t
− ln 2 −1< 0 với t ∀ ∈ .
Suy ra f (t) nghịch biến trên .
Bất phương trình ( ) ⇔ f (a) > f (b) 2 2 1
⇔ a < b ⇔ 2x −15x +100 < x +10x − 50 2
⇔ x − 25x +150 < 0 ⇔ 10 < x <15 .
Mà x ∈ nên x∈{11;12;13; } 14 .
Vậy bất phương trình có 4 nghiệm nguyên.
Câu 2. Cho bất phương trình 2 x +x 8 2 + x ≤
− x x + + . Số nghiệm x ( )1 3 2
nguyên dương của bất phương trình đã cho là A. 0 . B. 3 C. 1. D. 2 . Lời giải Chọn C
Tập xác định D = (−∞;− ] 1 ∪[0;+ ∞) . Ta có: 2 x +x 8 2 x x x + x − + ≤ − + + ⇔ + ≤ − x + x + x ( ) 2 x x 3 x 2 1 3 2 2 3 2 2 x +x 2 3 ⇔ 2 + + ≤ 2 −x x x + 3− x ( ) 1 . Xét hàm số ( ) = 2t f t
+ t , có ′( ) = 2t f t .ln 2 +1 > 0, t ∀ ∈ .
Vậy hàm số f (t) đồng biến trên .( ) ⇔ f ( 2x + x) ≤ f ( − x) 2 1 3
⇔ x + x ≤ 3− x
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC x ≤ 3 x ≤ 3 x ≤ 1 x ≥ 0 x ≥ 0 − ⇔ ⇔ ⇔ 9 . x ≤ 1 − x ≤ 1 − 0 ≤ x ≤ 7 2 x x ( x)2 + ≤ − 9 3 x ≤ 7
Do x nguyên dương, do đó x ∈{ } 1 .
Vậy bất phương trình đã cho có 1 nghiệm nguyên dương.
Câu 3. Tập nghiệm của bất phương trình 3x 3 3
5 x 3(3x 5x − + − ) > 0 là A. ( ;0 −∞ ). B. ( ;0 −∞ ] . C. (0;+∞). D. [0;+∞) . Lời giải Chọn A
Bất phương trình đã cho tương đương với 3x x 3
3 + 3.3 > 5 x + 3.5x ⇔ (3x ) > (5x f f ).
Xét hàm số f (t) 3
= t + 3t trên khoảng (0;+∞), ta có: f ′(t) 2
= 3t + 3 > 0, t ∀ > 0 .
Suy ra hàm số đồng biến trên khoảng (0;+∞). x
Do đó từ (3x ) > (5x f f ) ta có x x 5 3 5 > ⇔ <1 ⇔ x < 0 . 3
(*) Thử các giá trị là chọn được đáp án. Ta có: 3x 3 3
5 x 3(3x 5x VT = − + − )
Thử với x = 0 được VT = 0 ⇒ x = 0 không thỏa mãn bất phương trình. Do đó loại B và D.
Thử với x =1 được VT = 104 −
⇒ x =1 không thỏa mãn bất phương trình. Do đó loại C.
Vậy còn lại đáp án đúng là A.
Câu 4. Có bao nhiêu số nguyên x ∈( 2021 −
;2022) thỏa mãn bất phương trình 6x 4x 3x 2x x+2
2 − 2 − 2 + 2 − 2 − 3 < 0 A. 2021. B. 2020 . C. 2022 . D. 2019 . Lời giải Chọn A
Bất phương trình đã cho tương đương với x x x ( x x
) ( x ) ( x)3 ( x)2 3 2 2 2 2 2 2 3.2 3.2 1 2 2.2 1 3. 2 1 2 2 3.2 x + + + − + + + + > − +
⇔ ( x + )3 −( x + )2 + ( x + ) > ( x )3 −( x )2 2 2 2x + ⇔ ( x + ) > ( 2 2 1 2 1 3. 2 1 2 2 3.2 2 1 2 x f f ).
Xét hàm số f (t) 3 2
= t − t + 3t trên khoảng (0;+∞), ta có: f ′(t) 2
= 3t − 2t + 3 > 0, 0 t ∀ > .
Suy ra hàm số đồng biến trên khoảng (0;+∞). − +
Do đó từ f ( x + ) > f ( 2x ) x 2x 2x x 1 5 x 1 5 2 1 2
⇔ 2 +1 > 2 ⇔ 2 − 2 −1< 0 ⇔ < 2 < 2 2 1+ 5 ⇔ x < log ≈ 0,69 . 2 2 Mà x ∈( 2021 −
;2022) và x∈ nên ta có x∈{ 2020 − ; 2019 − ;...; } 0 .
Vậy có 2021 số nguyên x thỏa mãn ycbt. Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Câu 5. Tập nghiệm của bất phương trình 4 2x 2 + 5 −
− 5x − 2 > 0 là 2 5 x 5x x > log 2 x ≥ log 2
A. 0 < x < log 2 .
B. 0 ≤ x ≤ log 2 . C. 5 . D. 5 . 5 5 x < 0 x ≤ 0 Lời giải Chọn C
Bất phương trình đã cho tương đương với 2 2 x 2 x 2 2 5 5 3 3 f 5x + − + > − ⇔ + > f . x x x (3) 5 5 5 Xét hàm số ( ) 2
f t = t − t trên khoảng (2 2;+∞) , ta có: f ′(t) = 2t −1> 0, t ∀ > 2 2 .
Suy ra hàm số đồng biến trên khoảng (2 2;+∞) . 2 < x < x 2 5x 1 0 Do đó từ f + 5 > f ⇔ + > ⇔ − + > ⇔ ⇔ . x (3) x 2 5 3 5 x 3.5x 2 0 5 5x 5x > 2 x > log 2 5
(*) Cách 2: Đề xuất bởi GVPB2 2
Bất phương trình đã cho tương đương với 2 x 2 5 5x + − + − 6 > 0 5x 5x 2 5x <1 x < 0 x 2 ⇔
+ 5 > 3 ⇔ 5 x − 3.5x + 2 > 0 ⇔ ⇔ . 5x 5x > 2 x > log 2 5
Câu 6. Phương trình 2 2x −8+2 x 1 + 2 2021
− 2021 = x − 2x −8 −1 có nghiệm duy nhất x = a + b với
a,b∈ . Tính b − . a A. 9. B. 11 − . C. 11. D. 9 − . Lời giải Chọn C x ≤ 2 − Điều kiện: 2 2x −8 ≥ 0 ⇔ . x ≥ 2 2 2 2x −8+2 x 1 + 2 2x −8+2 2 x 1 2021 2021 x 2x 8 1 2021 2x 8 2 2021 + − = − − − ⇔ + − + = + x +1 ( ) 1
Xét hàm số ( ) = 2021t f t
+ t . Có ′( ) = 2021t f t ln 2021+1 > 0, t
∀ ⇒ hàm số đồng biến trên . Khi đó ( ) ⇔ f ( 2 1
2x −8 + 2) = f (x + )1 x ≥1 2
⇔ 2x −8 + 2 = x +1 ⇔ ⇔ x = 1 − + 10 . 2 2
2x − 8 = x − 2x +1 Do đó a = 1 − , 10
b = ⇒ b − a =11.
Câu 7. Tìm số nghiệm của phương trình 2 2 sin x cos x π −π
= cos 2x trong khoảng (0;10π ). A. 19. B. 15. C. 20 . D. 17. Lời giải Chọn C 2 2 2 2 2 2 sin x cos x sin x cos x 2 2 sin x 2 cos x 2 π −π = cos 2x ⇔ π −π
= cos x − sin x ⇔ π + sin x = π + cos x . Xét hàm số ( ) t
f t = π + t có ′( ) t
f t = π lnπ +1 > 0, t
∀ ∈ R ⇒ hàm số đồng biến trên .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC π π Khi đó ( ) ⇔ ( 2 ) = ( 2 ) 2 2 1 sin cos ⇔ sin = cos ⇒ cos 2 = 0 k f x f x x x x ⇒ x = + 4 2 π π Kết hợp với k x ∈(0;10π ) suy ra 1 39 0 < +
<10π ⇔ − < k < . 4 2 2 2
k ∈ ⇒ k ∈{0;1;2;...; }
19 . Vậy phương trình có 20 nghiệm.
Câu 8. Có bao nhiêu cặp số nguyên ( ;
x y) thỏa mãn 0 ≤ y ≤ 2021 và 2 x 1 + 2 2021 + = 2021y x + y −1. A. 45 . B. 89 . C. 11. D. 20 . Lời giải Chọn B 2 2 x 1 + 2 y x 1 + 2 2021 + = 2021 + −1 ⇔ 2021 + +1 = 2021y x y x + y ( ) 1 .
Xét hàm số ( ) = 2021t f t
+ t .Có ′( ) = 2021t f t ln 2021+1 > 0, t
∀ ⇒ hàm số đồng biến trên . Khi đó ( ) ⇔ f ( 2 1 x + ) 1 = f ( y) 2 ⇔ y = x +1
Ta có với x nguyên thì y nguyên. Mà 2
0 ≤ y ≤ 2021⇒ 0 ≤ x +1≤ 2021⇒ 44 − ≤ x ≤ 44. Vậy có 89 bộ ( ;
x y) nguyên thỏa mãn.
Câu 9. Tìm số nghiệm nguyên của bất phương trình 2x+x 3−x 2 2
+ 2x ≤ 2 − x + 3. A. 5. B. 6 . C. 7 . D. 8 . Lời giải Chọn A Ta có 2 2 x +x 3−x 2 x +x 2 3 2 + 2 ≤ 2 − + 3 ⇔ 2 + + ≤ 2 −x x x x x + 3− x ( ) 1 . Xét hàm số ( ) = 2t f t
+ t, t ∈ , có ′( ) = 2t f t .ln 2 +1 > 0, t ∀ ∈ .
Vậy hàm số f (t) đồng biến trên . Ta có ( ) ⇔ f ( 2
x + x) ≤ f ( − x) 2 1 3
⇔ x + x ≤ 3− x ⇔ 3 − ≤ x ≤1.
Vậy có 5 giá trị nguyên của x thỏa mãn ycbt.
Câu 10. Tổng tất cả các nghiệm nguyên dương nhỏ hơn 6 của bất phương trình:
27x 8x 3.4x 2.3x 5.2x − − + − − 3 ≥ 0 là A. 15. B. 12. C. 13. D. 19. Lời giải Chọn A
Ta có 27x 8x 3.4x 2.3x 5.2x 3 0
27x 2.3x (8x 3.4x 3.2x ) 1 2(2x − − + − − ≥ ⇔ + ≥ + + + + + ) 1 ( x)3 x ( x )3 3 2.3 2 1 2(2x ⇔ + ≥ + + + ) 1 ( ) 1 .
Xét hàm số f (t) 3
= t + 2t trên ta có f ′(t) 2
= 3t + 2 > 0, t
∀ ∈ . Vậy hàm số f (t) 3
= t + 2t đồng biến trên . x x Mà ( )
f ( x ) f ( x ) x x 2 1 1 3 2 1 3 2 1 ⇔ ≥ + ⇔ ≥ + ⇔ + ≤ 1 (2) . 3 3 x x x x
Xét hàm số g (x) 2 1 = + có g′(x) 2 2 1 1 = .ln + .ln < 0, x ∀ ∈ . 3 3 3 3 3 3 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC x x
Vậy hàm số g (x) 2 1 = + nghịch biến trên . 3 3
Mà (2) ⇔ g (x) ≤ g ( ) 1 ⇔ x ≥1
Vậy tập hợp các nghiệm nguyên dương nhỏ hơn 6 của bất phương trình là {1, 2, 3, 4, } 5 .
Tổng tất cả các nghiệm nguyên dương nhỏ hơn 6 của bất phương trình: 1+ 2 + 3+ 4 + 5 =15.
Câu 11. Tìm số nghiệm nguyên dương của bất phương trình sau: −x 3x( 3 5)1 2 x 1 2 − 3x +1≥ 3x − 6x . 5 A. 2022 . B. 1. C. 2 . D. 2021. Lời giải Chọn C
Theo đề ra ta có x ∈ và x > 0 . 1 −x
Bất phương trình 3x( 3 5) 2 x 1 2 − 3x +1≥ 3x − 6x 5 1 −x 2 − − 1 −x 1 ⇔ ( 3 ) 2 x x 1 x 1 1 x 1 3 6 1 5 − ≥ ⇔ ( 3 5) 2 − ≥ x − 2 − ⇔ 3x x−2 5 +
≥ 5 + x − 2 (∗) . 5 3x 5 3x 3x Xét hàm số ( ) = 5t g t
+ t có ′( ) = 5t g t
ln 5 +1 > 0 , t ∈ nên hàm số g (t) đồng biến trên . ( 1 − + ∗) ⇔ 1 g ≥ g(x− 2) ⇔ ≥ x − 2 2 3 2 3 3 2 3
⇔ 3x − 6x −1≤ 0 ⇔ ≤ x ≤ 3x 3x 3 3
Theo đề ra ta có x ∈ và x > 0 nên x∈{1; }
2 tức 2 nghiệm nguyên dương từ bpt trên
Câu 12. Tìm số nghiệm nguyên thuộc [ 2021 −
;2022] của bất phương trình 3 2x 1 − 2−x 3 3 2 2022
− 2022 + 2x −1 + x − 6x +15x −11≤ 0 A. 2024 . B. 2023. C. 2021. D. 2022 . Lời giải Chọn B
Từ giả thiết ta có bất phương trình tương đương với: 3 2x 1 − 2−x 3 3 2 2022
− 2022 + 2x −1 + x − 6x +15x −11≤ 0 3 2x 1 − 3 2−x 3 2 ⇔ 2022
+ 2x −1+ 2x −1 ≤ 2022 − x + 6x −13x +10 3 2x 1 ⇔ 2022 − + ( 3 2 −1)3 3 2 + 2 −1 ≤ 2022 −x x x
+ (2 − x)3 + 2 − x ( ) 1 .
Xét hàm số f (t) t 3 =
+ t + t ⇒ f ′(t) t 2 2022
= 2022 .ln 2022 + 3t +1 > 0, t
∀ ⇒ f (t) là hàm đồng
biến trên . Từ (1) ta có f ( 3 2x −1) ≤ f (2− x) 3
⇔ 2x −1 ≤ 2 − x 2 3
⇔ 2x −1≤ 8 −12x + 6x − x 3 2
⇔ x − 6x +14x − 9 ≤ 0 ⇔ (x − )( 2
1 x − 5x + 9) ≤ 0 ⇔ x ≤1
Vì x nguyên và x ∈[ 2021 − ;2022] ⇒ 2021 −
≤ x ≤1 nên có 2023 giá trị nguyên của x .
Câu 13. Có bao nhiêu giá trị nguyên của tham số m∈[ 2021 − ; ] 2021 để mọi
nghiệm của bất phương trình 2 2
2x+ −x +2x+3 4+ −x +2x+3 5 − 5
+ (x − 2)3 ≤ x(x − 3)2 − ( ) 2 1 đều là
nghiệm của bất phương trình 2
x − (m − 2) x − 2m + 4 ≤ ( 0 2) . A. 2019 . B. 2020 . C. 2021. D. 2018 .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Lời giải Chọn A 2 2
2x+ −x +2x+3 4+ −x +2x+3 5 − 5
+ (x − 2)3 ≤ x(x − 3)2 − ( ) 2 1 . Điều kiện 1 − ≤ x ≤ 3. ( ) 2 2
2x+ −x +2x+3 4+ −x +2x+3 1 ⇔ 5 − 5 + 3x − 6 ≤ 0 2 2
3 2x + −x + 2x + 3
3 4 + −x + 2x + 3 2
2x+ −x +2x+3 ( ) 2 4+ −x +2x+3 ( ) ⇔ 5 + ≤ 5 + (*). 2 2
Xét hàm số f (t) t 3
= + t t ∈ ⇒ f ′(t) t 3 5 , = 5 .ln 5 + > 0, t ∀ ∈ . 2 2
⇒ Hàm số đồng biến trên . ( ) ⇔ f ( 2
x + −x + x + ) ≤ f ( 2 * 2 2 3
4 + −x + 2x + 3) 2 2
⇔ 2x + −x + 2x + 3 ≤ 4 + −x + 2x + 3 ⇔ 1 − ≤ x ≤ 2 .
Theo yêu cầu bài toán thì 2
x − (m − 2) x − 2m + 4 ≤ 0, x ∀ ∈[ 1; − 2] 2 x + 2x + 4 + + ⇔ m ≥ x ∀ ∈[− ] 2 x 2x 4 , 1;2 ⇒ m ≥ max . + x [ ∈ 1; − 2] x 2 x + 2 2 + + 2 x + 4x x = 0∈[ 1; − 2]
Đặt g (x) x 2x 4 =
. Ta có g′(x) = = 0 ⇔ . x + 2 (x + 2)2 x = 4 − ∉ [ 1; − 2] 2 + + g ( x 2x 4 − ) 1 = 3 g ( ; 0) = 2 g ( ; 2) = 3, suy ra max = 3. x [ ∈ 1; − 2] x + 2
⇒ m ≥ 3 , vì m∈[ 2021 − ; ]
2021 ⇒ 3 ≤ m ≤ 2021. Vậy có 2019 giá trị nguyên của tham số m .
Câu 14. Có bao nhiêu cặp nghiệm nguyên ( ;
x y) thỏa mãn bất phương trình ( x − y) 2 2 2
10x −8xy+2 y −4 2 2 3 .3
≤ 4 − x + 2xy − y ? A. 8 . B. 6 . C. 5. D. 9. Lời giải Chọn D
Từ ( x − y) 2 2 2
10x −8xy+2 y −4 2 2 3 .3
≤ 4 − x + 2xy − y ⇔ ( x − y) (3x−y)2+(x−y)2 2 −4 3 .3
≤ 4 − (x − y)2 (*).
a = (3x − y)2 ≥ 0 Đặt
khi đó (*) đưa về: .3a+b ≤ − ⇔ .3a ≤ (− ).3−b a b a b . b =
(x − y)2 − 4 ≥ 4 −
Vì a ≥ 0 ⇒ b
− ≥ 0 .Xét hàm số ( ) = .3t f t
t , t ∈[0;+∞) có ′( ) = 3t + .3t f t
t .ln 3 > 0, t ∀ ∈[ 0;+∞)
Suy ra f (a) ≤ f ( b
− ) ⇔ a ≤ b
− ⇔ a + b ≤ 0 .
Suy ra ( x − y)2 + (x − y)2 − ≤ ⇔ ( x − y)2 + (x − y)2 3 4 0 3 ≤ 4 .
Với giả thiết x, y là các số nguyên nên ( − )2 3x y và ( − )2
x y đều nguyên nên chỉ có thể xảy ra các trường hợp sau: Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 3x − y 0 0 1 0 1 − 1 1 − 1 − 1 2 0 2 − 0 x − y 0 1 0 1 − 0 1 1 − 1 1 − 0 2 0 2 − x 0 1 − 1 1 1 − 0 0 1 1 − 1 − 1 1 − 1 2 2 2 2 y 0 3 − 1 3 1 − 1 3 − 1 − 3 1 − 1 2 − 2 2 2 2 2
Vậy có tất cả 9 cặp nghiệm thỏa mãn.
Câu 15. Tính tổng các nghiệm nguyên dương của bất phương trình sau 2 x 1 + 2 x+2 5
+ 2x − 4x − 6 ≤ 25 A. 6 . B. 5. C. 3. D. 7 . Chọn A Ta có 2 2 x 1 + 2 x+2 x 1 + x − x + − ≤ ⇔ + ( 2 x + ) 2(x+2) 5 2 4 6 25 5 2 1 ≤ 5 + 4(x + 2) (*) . Xét hàm số ( ) = 5t f t + 2t . TXĐ: D = . ′( ) = 5t f t ln 5 + 2 > 0 với t
∀ ∈ ⇒ f (t) là hàm số đồng biến trên (−∞;+ ∞). ( ) ⇔ f ( 2 * x + )
1 ≤ f (2(x + 2)) 2
⇔ x +1≤ 2(x + 2) 2
⇔ x − 2x − 3 ≤ 0 ⇔ 1 − ≤ x ≤ 3.
Mà x ∈ nên x∈{−1;0;1;2;3}.
Vậy tổng các nghiệm nguyên dương của phương trình đã cho bằng 6.
Câu 16. Hãy xác định số nghiệm nguyên âm của bất phương trình sau: 2 x −3x−7 x 10 + 2 9.3 − 3
+ 2x −8x ≤ 30 A. 2 . B. 3. C. 6 . D. 9. Lời giải Chọn A Ta có 2 2 x −3x−7 x 10 + 2 x −3x−5 x x ( 2x x ) x 10 9.3 3 2 8 30 3 2 3 5 3 + − + − ≤ ⇔ + − − ≤ + 2(x +10) (*) . Xét hàm số ( ) = 3t f t + 2t . TXĐ D = . ′( ) = 3t f t
ln 3+ 2 > 0,∀t ∈ .⇒ f (t) là hàm số đồng biến trên .
(*) ⇔ f ( 2x − x − ) ≤ f (x + ) 2 3 5
10 ⇒ x − 3x − 5 ≤ x +10 ⇔ 2 − 19 ≤ x ≤ 2 + 19 . ⇒ x ∈{ 2 − ;−1;0;...;5; } 6 .
Số nghiệm nguyên âm của bất phương trình đã cho là 2.
Câu 17. Tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất của bất phương trình 2 x 1 + 2 x+2 4
+ 2x − 4x − 6 >16 bằng bao nhiêu? A. 8 − . B. 3 − . C. 3. D. 2 . Lời giải Chọn A Ta có 2 2 x 1 + 2 x+2 x 1 + 2 2x+4 4
+ 2x − 4x − 6 >16 ⇔ 4 + 2(x +1) > 4 + 2(2x + 4) (1) .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC Xét hàm số ( ) = 4t f t + 2t . TXĐ D = . ′( ) = 4t f t
.ln 4 + 2> 0,∀t ∈ ⇒ f (t) đồng biến trên . x < 1 − ⇔ f ( 2 (1) x + )
1 > f (2x + 4) 2
⇔ x +1 > 2x + 4 2
⇔ x − 2x − 3 > 0 ⇔ . x > 3
Do đó nghiệm nguyên âm lớn nhất là 2
− và nghiệm nguyên dương nhỏ nhất là 4 . Tích của chúng bằng 8 − .
Câu 18. Gọi S là tập hợp tất cả các giá trị nguyên của x thỏa mãn bất phương trình 2 x −5x+2 5x+2 2 2021 − 2021
+ x − 5x + 2 ≤ 5x + 2. Tổng các phần tử của S bằng A. 55. B. 5. C. 6 . D. 25 . Lời giải Chọn A Ta có 2 x −5x+2 5x+2 2 2021 − 2021
+ x − 5x + 2 ≤ 5x + 2 2 x −5x+2 2 5x+2 ⇔ 2021
+ x − 5x + 2 ≤ 2021 + 5x + 2 (1).
Xét hàm số ( ) = 2021t + ⇒ ′( ) = 2021t f t t f t .ln 2021+1 > 0, t ∀ ∈ .
⇒ f (t) là hàm đồng biến trên .
Từ (1) ta có f ( 2x − x + ) ≤ f ( x + ) 2 5 2 5
2 ⇔ x − 5x + 2 ≤ 5x + 2 5 2 x + 2 ≥ 0 x ≥ − 2 5 x ≥ − 2
⇔ x −5x + 2 ≤ 5x + 2 ⇔ ⇔ 5 ⇔ x ∈[0;10] 2 .
x −10x ≤ 0 2 x∈ [0;10]
x − 5x + 2 ≥ 5 − x − 2 2 x + 4 ≥ 0 2 5 + 2 ≥ 0 x x ≥ − 5 2 x ≥ − 2 2
⇔ x −5x + 2 ≤ 5x + 2 ⇔ x −10x ≤ 0 ⇔ 5 ⇔ 0 ≤ x ≤10 . 2 2
x − x + ≥ − x − x + ≥ 0 ≤ x ≤ 10 5 2 5 2 4 0
Yêu cầu của bài toán x ∈ ⇒ S = {0;1;2;3;4;5;6;7;8;9;1 } 0 .
Vậy tổng các phần tử của S bằng 0 +1+ 2 + 3+ 4 + 5 + 6 + 7 + 8 + 9 +10 = 55 .
Câu 19. Gọi S là tập hợp tất cả các giá trị nguyên của x thỏa mãn bất phương trình 2 1+ x −3x 10 − x 1 − 2 2
− 2 + 2 x − 3x −10 < 2x − 4 . Số phần tử của S bằng A. 9. B. 5. C. 4 . D. 15. Lời giải Chọn A Ta có 2 1+ x −3x 10 − x 1 − 2 2
− 2 + 2 x − 3x −10 < 2x − 4 2 x −3x 10 − 2 x−2 ⇔ 2
+ x − 3x −10 < 2 + x − 2 (1). Xét hàm số ( ) = 2t f t
+ t có ′( ) = 2t f t ln 2 +1< 0 với t ∀ ∈ . Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Suy ra f (t) đồng biến trên . Bất phương trình ( )
1 ⇔ f ( 2x − x − ) < f (x − ) 2 3 10
2 ⇔ x − 3x −10 < x − 2 x ≤ 2 − 2
x − 3x −10 ≥ 0 x ≥ 5 ⇔ x − 2 > 0
⇔ x > 2 ⇔ 5 ≤ x <14 2
x − 3x −10 < < (x − 2)2 x 14
Mà x ∈ nên S = {5;6;7;8;9;10;11;12; }
13 .Vậy số phần tử của S bằng 9. 3 x −6x−4
Câu 20. Biết rằng bất phương trình 2 3 2 4 − 3 ⋅2 x x x
< 24x + 32 có tập nghiệm là S = ( 3 3
a;b + c + d ), với a,b,c,d ∈. Tính giá trị của biểu thức T = 4abcd . A. T = 75 . B. T = 80 . C. T = 81. D. T = 82 . Lời giải Chọn C Ta có 3 2 2
4x − 3x = x (4x − 3) .
Bất phương trình đã cho xác định với mọi 3 x ≥ . 4
Với điều kiện xác định trên, bất phương trình đã cho tương đương với 3 x −6x−4 24x 16 + + 4x− 12 + 2 3x 4 x x x − ⋅ < ⇔ x − ⋅ (4 ) 2x <(4 ) 3 4 4 3 2 8 4 3 2 2 x x 2 2 + + + − − ⇔ x − ⋅( x x x x + x + 4 ) 3x 4 < (4 )9 24 16 3 4 4 3 4 3 2 x x ⇔ x − ⋅ (4 ) 3 4 4 3 2 2 4 3 2 < ( 4 2) x . x x t
Xét hàm số f (t) = t ( ) 2 4 2 , với t ≥ 0 . 2 2 t t
Ta có f ′(t) = ( 4 2) 1 2
+ t ( 4 2) ln 2 > 0, 0 t
∀ ≥ nên f (t) là hàm số đồng biến trên (0;+∞). 2 Do đó 2 + − x − ⋅( ) x 3x + 4 < ( ) 3x 4 4 3 + 4 4 x x ⇔ f ( x − ) 3 4 4 3 2 2 4 3 < f x x 2 3x + 4 9x + 24x +16 3 4x 3 4x 3 do x ⇔ − < ⇔ − < ≥ 2 x x 4 3 2
⇔ 4x −12x − 24x −16 < 0 3 2 3 3 2
⇔ 2x − 6x −12x −8 < 0 ⇔ 3x < x + 6x +12x + 8 3
⇔ 3x < (x + 2)3 3 2 3 3
⇔ 3x < x + 2 ⇔ x < ⇔ x <1+ 3 + 9. 3 3 −1
Kết hợp với điều kiện xác định, phương trình đã cho có nghiệm 3 3 3 S ;1 3 9 = + + . 4 Suy ra 3 a = , b =1, c = 3,
d = 9 . Do đó T = 4abcd = 81. 4
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC 3 2 − x 16 + x −48x+36
Câu 21. Bất phương trình +1 ≤ (2 − 3) 2 .2 x x x x
có tập nghiệm S = a;b + c d với
a,b,c,d ∈ và c ≠1. Tính giá trị của biểu thức S = a + b + c + d . A. 17 . B. 16. C. 15. D. 18. Lời giải Chọn A Điều kiện: x ≥ 1
− và x ≠ 0 . Ta có: 3 2 − x 16 + x −48x+36
x x +1 ≤ (2x −3) 2 .2 x 2
16x −48x+36−x
⇔ 2x x +1 ≤ (4x − 6) 2 .2 x . (4x−6)2
⇔ 2x x +1.2x ≤ (4x − 6) 2 .2 x (*)
▸ TH-1: x > 0 : để bất phương trình (*) có nghiệm thì 4 − 6 > 0 3 x ⇔ x > . 2 2 2 4x−6 Khi đó: ( x 1+) 4x − 6 (*) x 1.2 ⇔ + ≤ .2 x . x Xét hàm số ( ) 2 = .2t f t t với t > 0 . Ta có ′( ) 2 2 t 2 = 2 + 2 ⋅2t f t t ⋅ln 2 > 0, t ∀ > 0.
Vậy f (t) là hàm đồng biến trên (0;+∞), từ bất phương trình ta có f ( x + ) 4x − 6 4x − 6 1 ≤ f ⇔ x +1 ≤ x x 2
⇔ x x +1 ≤ 4x − 6 ⇔ x (x + ) 2
1 ≤16x − 48x + 36 x ≤ 6 − 2 6 . 3 2 ⇔ x − 5
1 x + 48x − 36 ≤ 0 ⇔ (x − 3)( 2
x −12x +12) ≤ 0 ⇔ 3≤ x≤6+2 6
Kết hợp với điều kiện 3
x > suy ra TH-1 có nghiệm là: 3 ≤ x ≤ 6 + 2 6 . 2 2 2 4x−6 x+ 4x − 6 ▸ TH-2: 1 − ≤ x < 0 : ( 1) (*) x 1.2 ⇔ + ≥ .2 x x ⇔ f ( x + ) 4x − 6 4x − 6 1 ≥ f ⇔ x +1 ≥ x x 2 16x − 48x + 36 2 ⇔ x +1≥ ⇔ x (x + ) 2
1 ≥16x − 48x + 36 2 x
6 − 2 6 ≤ x ≤ 3 3 2
⇔ x −15x + 48x − 36 ≥ 0 ⇔ (x − 3)( 2
x −12x +12) ≤ 0 ⇔ . x ≥ 6 + 2 6
Kết hợp với điều kiện 1
− ≤ x < 0 suy ra TH-2 vô nghiệm.
Vậy tập nghiệm của bất phương trình là S = 3;6 + 2 6 . Suy ra a = 3, c = 2,
b = d = 6. Do đó a + b + c + d =17 . Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Câu 22. Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2018 để phương trình x 2 + + 2 > 2 x m m có nghiệm thực? A. 2017 . B. 2018 . C. 2016 . D. 2015 . Lời giải Chọn A x 2x + + > ⇔ ( x + ) x 2 2 2 2 +
+ 2 > 2 x + 2x m m m m (1) Ta có 2x 0, 2x m + ≥
> 0. Xét hàm đặc trưng ( ) 2
f t = t + t trên [0;+∞) .
f ′(t) = 2t +1≥ 0, t ∀ ∈[ 0;+∞)
⇒ f (t) đồng biến trên khoảng [0;+∞) do đó (1) ⇔ ( + 2x ) > (2x ) ⇔ + 2x > 2x f m f m 2
⇔ > 2 x − 2x m . Đặt = 2x a ,
a > 0 . Ta có ⇔ > ( ) 2
m g a = a − a .
Bất phương trình đã cho có nghiệm 1
⇔ m > − mà m nguyên dương nhỏ hơn 2018 nên 4 m∈{1;2;3; ; … }
2017 . Vậy có 2017 giá trị m thỏa mãn yêu cầu bài toán.
Câu 23. Có bao nhiêu số nguyên x sao cho tồn tại số thực dương y thỏa mãn 2 2
2x +y < 2.2y−x ? A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B Ta có: 2 2 2 2 x + y y−x x + y y−x 1 + 2 2 2 2 2 < 2.2 ⇔ 2 < 2
⇔ x + y < y − x +1 ⇔ y − y < −x − x +1 (*) . Yêu cầu bài toán x ∈ ; 0 y > x ∈ ; 0 y > 2 2 ⇔ 1 1 3 2 2 ⇔ 1 3 1 1 3 1 . x + + y − < − − x + < y < + − x + ( *) 2 2 2 2 2 2 2 2 2 − − − + Nhận xét: 1 6 1 6 x ∈ ; ≤ x ≤ suy ra x = 1 − hoặc x = 0 2 2
Thay vào thấy có tồn tại số thực y > 0.
Vậy có 2 số nguyên x thỏa mãn để phương trình (*) có nghiệm thực y > 0.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
GIẢI BPT MŨ BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP Đặt u(x)
T = a với T > 0 .
Bất phương trình biến đổi về dạng 2
AT + g (x)T + h(x) > 0 hoặc 2
AT + g (x)T + h(x) < 0
Bước 1 : Giải phương trình 2
AT + g (x)T + h(x) = 0
Bước 2 : Lập bảng xét dấu của 2
AT + g (x)T + h(x)
Bước 3 : Từ bảng kết luận.
Câu 1. Tập nghiệm của bất phương trình 9x − 2( + 5).3x x + 9(2x + ) 1 ≥ 0 là A. [0; ] 1 ∪[2;+ ∞) . B. ( ; −∞ ] 1 ∪[2;+ ∞) . C. [1;2]. D. ( ;
−∞ 0]∪[2;+ ∞) . Lời giải Chọn A
Đặt 3x = t , t > 0 bất phương trình trở thành 2t − 2(x + 5).t + 9(2x + ) 1 ≥ 0 (*) .
Xét phương trình: 2t − 2(x + 5)t + 9(2x + ) 1 = 0 ( ) 1 .
Ta có ∆′ = (x + )2 − ( x + ) 2 5 9 2
1 = x −8x +16 = (x − 4)2 . t = 2x +1 Do đó phương trình ( ) 1 luôn có nghiệm . t = 9
Khi đó (*) trở thành (3x −9)(3x − 2x − ) 1 ≥ 0 (**) .
Xét các phương trình 3x = 9 ⇔ x = 2 ( )
1 và 3x = 2 +1 ⇔ 3x x − 2x −1 = 0 (2) . Đặt ( ) = 3x f x
− 2x −1 là hàm số liên tục trên ; ta có f ′(x) x x 2 = 3 ln 3− 2 ⇒ f (
′′ x) = 3 ln 3 > 0, x ∀ ∈ .
Suy ra phương trình (2) có tối đa hai nghiệm phân biệt.
Lại có f (0) = f ( )
1 = 0. Vậy phương trình (2) có đúng hai nghiệm phân biệt x = 0 , x =1. Bảng xét dấu
Tập nghiệm của bất phương trình đã cho là: S = [0; ] 1 ∪[2;+ ∞) .
Câu 2. Tập nghiệm của bất phương trình 25x − (4 + 6).5x x
+ 20x + 5 ≤ 0 là A. [0; ] 1 . B. [1;+ ∞) . C. ( ;0 −∞ ] . D. ( ] ;1 −∞ . Lời giải Chọn C
Đặt 5x = t , t > 0, bất phương trình trở thành 2t − (4x + 6).t + 20x + 5 ≤ 0 (*) .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Xét phương trình: 2t − (4x + 6).t + 20x + 5 = 0 ( ) 1 .
Ta có ∆′ = ( x + )2 − ( x + ) 2 4 6 4 20
5 =16x − 32x +16 =16(x − )2 1 . t = 4x +1 Do đó phương trình ( ) 1 luôn có nghiệm . t = 5
Khi đó (*) trở thành (5x −5)(5x − 4x − ) 1 ≤ 0 (**) .
Xét các phương trình 5x = 5 ⇔ x =1 ( )
1 và 5x = 4 +1 ⇔ 5x x − 4x −1 = 0 (2) . Đặt ( ) = 5x f x
− 4x −1 là hàm số liên tục trên ; ta có f ′(x) x x 2 = 5 ln 5 − 4 ⇒ f (
′′ x) = 5 ln 5 > 0, x ∀ ∈ .
Suy ra phương trình (2) có tối đa hai nghiệm phân biệt.
Lại có f (0) = f ( )
1 = 0 nên phương trình 5x − 4x −1 = 0 có đúng hai nghiệm phân biệt x = 0 , x =1. Bảng xét dấu
Tập nghiệm của bất phương trình đã cho là: S = ( ; −∞ 0].
Câu 3. Cho bất phương trình 2x x x+2 2 − .2
x + 2x + 3 > 2 − x (*) có tập nghiệm là S = (a;b) ∪( ; c +∞) tính
T = a + 2b − c . A. 4 log . B. 2 log . C. 8 log . D. log 3. 2 3 2 3 2 3 2 Lời giải Chọn A Ta có 2x x x+2 2
2 − .2 + 2 + 3 > 2 − ⇔ 2 x − ( + 4).2x x x x x
+ 3x + 3 > 0 . Đặt 2x t = , t > 0.
Bất phương trình đã cho trở thành 2
t − (x + 4)t + 3(x + ) 1 > 0. Xét phương trình: 2
t − (x + 4)t + 3(x + ) 1 = 0 (2) .
Ta có ∆ = (x + )2 − (x + ) 2 4 12
1 = x − 4x + 4 = (x − 2)2 nên phương trình (2) luôn có nghiệm. t = x +1 2x = x +1 ⇔ . t = 3 2x = 3
+) 2x = 3 ⇔ x = log 3 . 2
+) Xét hàm số ( ) = 2x f x
− x −1, liên tục trên . Ta có f ′(x) x =
− ⇒ f ′′(x) x 2 2 ln 2 1 = 2 ln 2 > 0, x ∀ ∈ .
Suy ra phương trình f (x) = 0 , có không quá 2 nghiệm trên .
Mặt khác f (0) = f ( )
1 = 0 nên phương trình f (x) = 0 có đúng hai nghiệm x = 0 , x =1.
Vậy phương trình (2) có 3 nghiệm là x = 0 , x =1 và x = log 3. 2
Bảng xét dấu VT của bất phương trình đã là: Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC x - ∞ 0 1 log23 + ∞ VT(*) - 0 + 0 - 0 +
Tập nghiệm của bất phương trình (*) là S = (0; ) 1 ∪(log 3;+∞ . 2 ) Vậy 4
T = a + 2b − c = log . 2 3
Câu 4. Cho bất phương trình 3.4x − (7 + 9).2x x +14x + 6 ≥ 0 ( )
1 . Số nghiệm nguyên thuộc ( 2022 −
;2022) của bất phương trình ( ) 1 là A. 1011. B. 2022. C. 4042. D. 2021. Lời giải Chọn D
Đặt 2x = t , t > 0. ( ) 1 trở thành 2
3t − (7x + 9)t +14x + 6 ≥ 0 . Xét phương trình: 2
3t − (7x + 9)t +14x + 6 = 0 (2) .
Ta có ∆ = ( x + )2 − ( x + ) 2 7 9 12 14
6 = 49x − 42x + 9 = (7x − 3)2 nên phương trình (2) luôn có nghiệm. 7 x 7 t = x +1 2 = x +1 3 ⇔ 3 . t = 2 2x = 2
+) 2x = 2 ⇔ x =1.
+) Xét hàm số f (x) x 7
= 2 − x −1, liên tục trên . 3 Ta có f ′(x) x 7
= 2 ln 2 − ⇒ f ' (x) x 2 = 2 ln 2 > 0, x ∀ ∈ . 3
⇒ phương trình f (x) = 0 , có không quá 2 nghiệm trên .
Mặt khác f (0) = f (3) = 0 .
Suy ra phương trình f (x) = 0 có đúng hai nghiệm x = 0 , x = 3.
Vậy phương trình (2) có 3 nghiệm là x = 0 , x =1 và x = 3.
Bảng xét dấu VT của BPT ( ) 1 đã cho là:
Ta được tập nghiệm của bất phương trình ( )
1 là: T =[0; ]1∪[3;+∞).
Số nghiệm nguyên thuộc ( 2022 − ;2022) của BPT ( ) 1 là 2021.
Câu 5. Cho bất phương trình 2x
e − ( x + ) x 2
2 1 e + x + x ≥ 0 ( )
1 . Số nghiệm nguyên thuộc [ 20 − ;20] của bất phương trình ( ) 1 là
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC A. 41. B. 40. C. 20. D. 19. Lời giải Chọn A Đặt x
e = t , t > 0. Khi đó Bất phương trình (1) trở thành: 2 t − ( x + ) 2 2
1 t + x + x ≥ 0
Xét tam thức bậc hai f (t x) 2 = t − ( x + ) 2 ,
2 1 t + x + x .
Ta có ∆ = ( x + )2 − ( 2 2 1 4 x + x) =1. x ( t = x t ≥ x + e ≥ x +1
f t , x) = 0 ⇔ . Vậy f (t x) 1 , ≥ 0 ⇔ hay . t = x +1 t ≤ x x e ≤ x Xét hàm số ( ) x
g x = e − x −1, liên tục trên . Ta có: ′( ) x
f x = e −1 = 0 ⇔ x = 0 Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy: x ≥ +1 x e x
⇔ e − x −1≥ 0, x ∀ ∈ .
Vậy tập nghiệm của bất phương trình ( )
1 là T = nên số nghiệm nguyên thuộc [ 20 − ;20] của bất phương trình ( ) 1 là 41. Câu 6. Cho hàm số 2 ( ) ( ) 3f x f x y − =
liên tục trên và có đồ thị như hình vẽ y 9 3 1 O 1 2 x
Bất phương trình 2f(x)− f (x) 2
f (x)− f (x) 2
f (x)− f (x) 9 − 2 .3 x +18x ≥10.3
− 9 (*) có tập nghiệm là:
S = [a;b]∪[c;+ ∞). Tính a + b + c . Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC A. 3. B. 2 . C. 4 . D. 5. Lời giải Chọn A Đặt 2 ( ) ( ) 3f x f x t − =
, t > 0. Bất phương trình đã cho trở thành: 2t − 2(x + 5)t + 9(2x + ) 1 ≥ 0 .
Xét phương trình: 2t − 2(x + 5)t + 9(2x + ) 1 = 0 (**) .
Ta có ∆′ = (x + )2 − ( x + ) 2 5 9 2
1 = x −8x +16 = (x − 4)2 nên phương trình (**) luôn có nghiệm. 2
f (x)− f (x) t = 2x +1 3 = 2x +1 ( ) 1 ⇔ . 2 =
f (x)− f (x) t 9 3 = 9 (2) y 9 3 1 O 1 2 x
+ Nghiệm của (2) là hoành độ giao điểm của đồ thị hàm số 2 ( ) ( ) 3f x f x y − = và đường thẳng có phương trình y = 9.
Dựa vào đồ thị có 2f(x)− f (x) 3 = 9 ⇔ x = 2. +) Nghiệm của ( )
1 là hoành độ giao điểm của đồ thị hàm số 2 ( ) ( ) 3f x f x y − = và đường thẳng y = 2x +1. = − x f x f x 0
Dựa vào đồ thị có 2( ) ( ) 3 = 2x +1 ⇔ . x =1 Khi đó (*) trở thành 2
f (x)− f (x) (3
− 9) 2f(x)−f(x) (3 − 2x − )1 ≥ 0. Bảng xét dấu x - ∞ 0 1 2 + ∞
3f 2(x)-f (x)- 9 - - - 0 +
3f 2(x)-f (x)- 2x-1 + 0 - 0 + + VT(*) - 0 + 0 - 0 +
Tập nghiệm của bất phương trình (*) là S = [0; ] 1 ∪[2;+∞).
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Vậy a + b + c = 3.
Câu 7. Số nghiệm nguyên thuộc đoạn [ 20
− ;20] của bất phương trình sau: 4x+2 3x 1 + − + ( 2
x + x − + ) 2x − ( 2
x + x − + ) x 2 2 18.2 8 2 3 85 .2 9 4 2
3 2 2 + 8 x + 2x − 3 ≥ 0 là A. 36. B. 38. C. 18. D. 17 . Lời giải Chọn A x ≤ 3 − Điều kiện: 2
x + 2x − 3 ≥ 0 ⇔ . x ≥ 1
Biến đổi bất phương trình đã cho về dạng: ( x+ x − )2 2 1 + ( 2 + − + )( 2x 1+ x x x − ) 2 2 9.2 4 2 3 2 2
9.2 + 8 x + 2x − 3 ≥ 0 . Đặt 2x 1 2 9.2x t + = − ta có: 2 t + ( 2 x + x − + ) 2 4 2
3 2 t + 8 x + 2x − 3 ≥ 0 ⇔ ( 2
t + 4 x + 2x − 3)(t + 2) ≥ 0 (*).
+ TH1: Nếu 20 ≥ x ≥ 3 . Khi đó 2x 1 + x x x 1 t 2 9.2 2 (2 + = − =
− 9) > 0 ⇒ t + 2 > 0 và 2
t + 4 x + 2x − 3 > 0. Suy ra (*) luôn
đúng. Vậy trước mắt ta có được 18 nghiệm nguyên thỏa mãn bài toán.
+ TH2: Nếu x =1, suy ra t = 10 − thay vào (*) ta có 10 − ( 10
− + 2) ≥ 0 ⇔ 80 ≥ 0 luôn đúng
nên x =1 là nghiệm của bất phương trình ban đầu.
+ TH3: Với x = 2 suy ra t = 4
− thay vào (*) ta có 8 −8 5 ≥ 0 vô lý nên x = 2 không là
nghiệm của bất phương trình đã cho. + TH4: Với 20 − ≤ x ≤ 4 − ta có: 2
h(x) = x + 2x − 3 ⇒ h′(x) = 2x + 2 < 0, x ∀ ∈[ 2 − 0; 4 − ] thì
min h(x) = h( 4 − ) 2
= 5 ⇒ 4 x + 2x − 3 ≥ 4 5 , x ∀ ∈[ 2 − 0; 4 − ] . [ 20 − ; 4 − ] Mặt khác 2x 1
= 2 + − 9.2x ⇒ ′ = 2x (4.2x t t − 9)ln 2 < 0, x ∀ ∈[ 20 − ; 4 − ] . Suy ra t = t (− ) 71 − min 4 = . [ 20 − ; 4 − ] 128 Do đó 2 71
t + 4 x + 2x − 3 ≥ 4 5 − > 0 và 71 185 t + 2 > 2 − = > 0 nên (*) đúng. 128 128 128 Dễ thấy x = 3 − không là nghiệm.
Suy ra có 17 nghiệm nguyên thỏa mãn.
Vậy bất phương trình có 18 +1+17 = 36 nghiệm nguyên thỏa mãn yêu cầu đề bài.
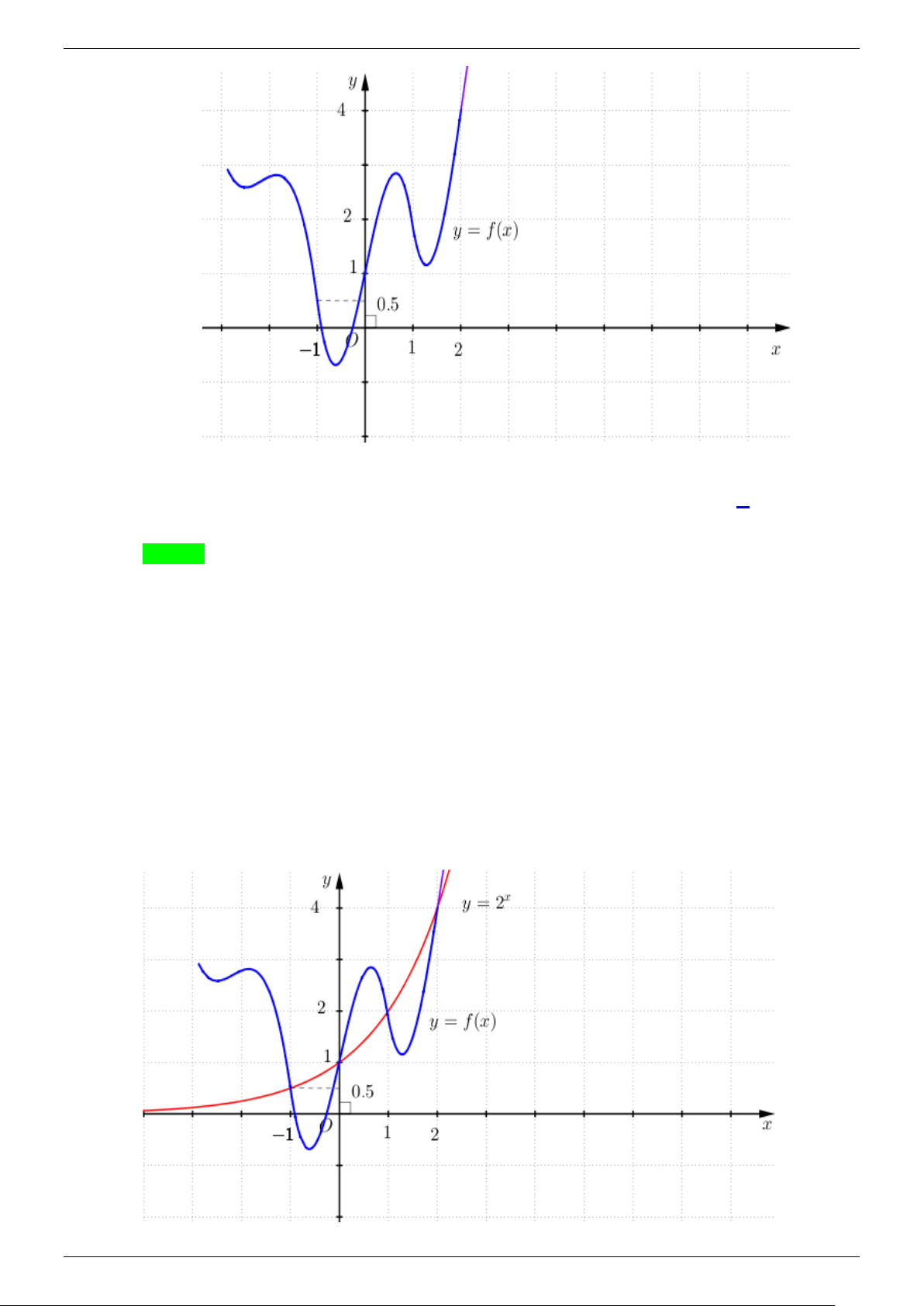
Câu 8. Cho hàm số y = f (x) liên tục trên có đồ thị như hình vẽ. Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
Tập nghiệm của bất phương trình 4x − ( + ( ) + ) 1 .2x x f x + (x + )
1 f (x) ≥ 0 (*) là A. ( ;
−∞ 0]∪[2; +∞) . B. [0; ] 1 . C. ( ; −∞ − ] 1 ∪[2; +∞) . D. [ 1; − 2]. Lời giải Chọn D Đặt 2x t = , t > 0.
Bất phương trình đã cho trở thành: 2
t − (x + f (x) + ) 1 .t + (x + ) 1 f (x) ≥ 0 .
t = f (x)
2x = f (x) ( ) 1 Xét phương trình: 2
t − (x + f (x) + ) 1 .t + (x + )
1 f (x) = 0 ⇔ ⇔ . t = x +1 2x = x +1 (2) + Nghiệm của ( )
1 là hoành độ giao điểm của đồ thị hàm số 2x
y = và đồ thị y = f (x) . x = 1 − x = 0
Dựa vào đồ thị có 2x = f (x) ⇔ . x =1 x = 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT- VD_VDC
+) Xét hàm số ( ) = 2x g x
− x −1, liên tục trên . Ta có g′(x) x =
− ⇒ g′′(x) x 2 2 ln 2 1 = 2 ln 2 > 0, x ∀ ∈ .
Suy ra phương trình g (x) = 0 , có không quá 2 nghiệm trên .
Mặt khác g (0) = g ( )
1 = 0 nên phương trình g (x) = 0 có đúng hai nghiệm x = 0 , x =1.
Khi đó (*) trở thành (2x − − ) 1 (2x x
− f (x)) ≥ 0. Bảng xét dấu x - ∞ - 1 0 1 2 + ∞ 2x- f (x) - 0 + 0 - 0 + 0 - 2x- x-1 + + 0 - 0 + + VT(*) - 0 + 0 + 0 + 0 -
Tập nghiệm của bất phương trình (*) là S = [ 1; − 2].
_______________ TOANMATH.com _______________ Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
Document Outline
- Đợt-10-Dạng-1-Giải-bpt-mũ-bằng-phương-pháp-hàm-số-đánh-giá-không-chứa-tham-số-PB3
- Đợt-10-Dạng-2-Giải-bpt-mũ-bằng-phương-pháp-hàm-đặc-trưng-không-chứa-tham-số-PB3
- Đợt-10-Dạng-3-Giải-bpt-mũ-bằng-phương-pháp-đặt-ẩn-phụ-không-hoàn-toàn-(không-chứa-tham-số)-PB3




