Bí kíp giải hệ phương trình chỉ trong 10 phút – Đỗ Duy Thành

Tài liệu trình bày phương pháp giải nhanh hệ phương trình chỉ trong 10 phút do thầy giáo – tiến sĩ Đỗ Duy Thành biên soạn.

Nội dung tài liệu:
Chuyên đề 1. Phương pháp miền giá trị giải hệ phương trình
+ Trường hợp 1: Hệ có 1 trong 2 phương trình là bậc 2 với x, y
Cách giải:
Coi phương trình là bậc 2 ẩn x, giải Δ ≥ 0 ⇒ điều kiện của y
Coi phương trình là bậc 2 ẩn y, giải Δ ≥ 0 ⇒ điều kiện của x

 

76 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 1. Phƣơng pháp miền giá trị giải hệ phƣơng trình
42
22
697
(1)
81
3 4 4 0 (2)
xy
x y xy x y

Coi (2) là phương trình bậc hai ẩn
x
:
22
( 3) 4 4 0x y x y y
Phương trình có nghiệm
0
22
22
2
( 3) 4( 4 4) 0
6 9 4 16 16 0
3 10 7 0
7
1
3
y y y
y y y y
yy
y
BÍ KÍP GIẢI HỆ PHƢƠNG TRÌNH CHỈ TRONG 10 PHÚT
- Khi máy tính casio bó tay
- Khi các kỹ năng phân tích nhân tử đưa về phương trình tích vô hiệu hóa
Các em học sinh sẽ phải xử lý thế nào ? Hãy áp dụng những phương
pháp cực hữu ích sau đây
1. Dấu hiệu nhận biết:
Trƣờng hợp 1: Hệ có 1 trong 2 phương trình là bậc 2 với
.
Cách giải: Coi phương trình là bậc 2 ẩn
x
, giải
0
điều kiện của
.y
Coi phương trình là bậc 2 ẩn
y
, giải
0
điều kiện của
.x
Dùng điều kiện của
để đánh giá phương trình còn lại.
Trƣờng hợp 2: Hệ có 2 phương trình cùng là bậc hai với
x
(hoặc cùng là
bậc hai với
y
).
Cách giải: Với phương trình (1), coi
x
là ẩn, giải
0
điều kiện của
.y
Với phương trình (2), coi
x
là ẩn, giải
0
điều kiện của
.y
So sánh điều kiện của ở 2 phương trình và rút ra kết luận.
Ví dụ 1: Giải hệ phương trình
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Coi (2) là phương trình bậc hai ẩn
y
:
22
( 4) 3 4 0y x y x x
Phương trình có nghiệm
0
22
22
2
( 4) 4( 3 4) 0
8 16 4 12 16 0
3 4 0
4
0
3
x x x
x x x x
xx
x
74
1, , 0,
33
yx
thì
42
42
4 7 697
3 3 81
xy
VT(1)
VP(1), do đó
VT(1)=VP(1) khi
47
,
33
xy
. Vậy hệ phương trình có nghiệm duy nhất
47
,
33



.
Ví dụ 2: Giải hệ phƣơng trình
22
22
7
(2 1)(2 1) (1)
2
7 6 14 0 (2)
x y xy
x y xy x y
Coi (2) là phương trình bậc hai ẩn
x
:
22
( 7) 6 14 0x y x y y
Phương trình có nghiệm
0
22
2
14 49 4 24 56 0
3 10 7 0
7
1
3
y y y y
yy
y
Coi (2) là phương trình bậc hai ẩn
y
:
22
( 6) 7 14 0y x y x x
Phương trình có nghiệm
0
22
2
12 36 4 28 56 0
3 16 20 0
10
2
3
x x x x
xx
x
0xy
không là nghiệm của hệ.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
1 1 7
(1) 2 2 (3)
2
xy
xy




Đặt
'
2
11
2 2 0f t t f t f t
tt
đồng biến trên
( ;0)
và
(0; )
.
Xét
11
7 1 89 7
1; 1 2 1; .
7 89
3 21 3
3 21
f
t y y
y
f



Xét
7
2
2
10 7 1 191 10
2; 2 2; .
10 191
3 2 30 3
3 30
f
t x x
x
f



7
VT (3) .
2

Dấu “=” xảy ra
1
2
x
y
Ví dụ 3: Giải hệ phƣơng trình
2 2 2
23
2 0 (1)
2 4 3 0 (2)
x y x y
x x y
Coi (1) là phương trình bậc hai ẩn
x
:
2 2 2
20x y x y
.
Phương trình có nghiệm
4
' 0 1 0 1 1yy
.
(3)
Coi (2) là phương trình bậc hai ẩn
x
:
23
2 4 3 0x x y
.
Phương trình có nghiệm
33
' 0 4 2 3 0 1 0 1y y y
. (4)
Từ (3) và (4)
1.y
Thay vào hệ ta được x=1. Vậy hệ có nghiệm (1;-1).
2. Bài tập tự luyện
32
22
2
0
xy
x xy y y

. Vậy hệ có nghiệm (1;2).
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 2. Phƣơng pháp nhân chia giải hệ phƣơng trình
Ví dụ 1: Giải hệ phƣơng trình
( ) (1)
2
( ) 3 (2)
x
x y y
x y x y


Điều kiện:
,0xy
+) Dễ thấy
0xy
là 1 nghiệm của hệ
+) Với
,0xy
, chia 2 vế của phương trình (1) và (2) cho nhau ta được:
()
( ) 6
x y y
x
x y x y
6 ( ) ( )y x y x x y
22
5 6 0x xy y
3
2
xy
xy
Với
3xy
, thay vào phương trình (1) ta được:
3
2
2
y
yy
3. Dấu hiệu nhận biết:
Trƣờng hợp 1: Hệ phương trình tích
Trƣờng hợp 2: Hệ phương trình chưa phải là hệ phương trình tích nhưng
có thể sử dụng các biến đổi đại số để đưa về hệ phương trình tích
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
3
3
2
0
3
4
3
4
4
16 3
(16 3) 0
y
y
y
y
yy
yy



Đối chiếu với điều kiện ta được:
3
4
y
33
4
x
Với
2xy
, thay vào phương trình (1) ta được:
2
2
y
yy
22y y y
3
42yy
2
0
2
2
2 (2 1) 0
y
y
yy
Đối chiếu với điều kiện ta được:
2
2
2
yx
Vậy hệ phương trình đã cho có nghiệm (0, 0);
3 3 3
( , )
44
;
2
( 2, ).
2
Ví dụ 2: Giải hệ phƣơng trình
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
2
2
( 1) 3
( 2) 1
x y x y
y x y x
2
2
( 1) ( 1) 2
( 2) ( 2) 1
x y x y
y x y x
2
2
( 1)( 1) 2 (1)
( 2)( 1) 1 (2)
x y y
y x x
+) Nhận thấy
1, 2xy
là nghiệm của hệ phương trình.
+) Với
1, 2xy
, nhân 2 vế của phương trình (1) và (2) cho nhau, ta được:
22
( 1)( 1) 1 (3)xy
Do
2
2
11
11
x
y


(3) (3)VT VP
Khi đó VT(3)=VP(3)
0xy
.
Thay
0xy
vào hệ ban đầu không thỏa mãn. Vậy hệ có nghiệm duy nhất (1,2).
Ví dụ 3: Giải hệ phƣơng trình
1
(4 ) 2 3
2
1
(4 ) 4
2
x
yx
y
yx


Điều kiện:
,0xy
Hệ phương trình
1 2 3
4 (1)
2
14
4 (2)
2
yx
x
yx
y


Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Cộng 2 vế của phương trình (1) và (2), trừ 2 vế của phương trình (1) và (2) ta được hệ :
2 3 4
8 (3)
2 2 3 4
(4)
2
xy
yx
xy


Nhân 2 vế của phương trình (3) và (4) ta được:
11 26
2
16
xxy y
22
8 2 3 0x xy y
1
2
xy
(thỏa mãn)
3
4
xy
(loại)
Với
2yx
, thế vào phương trình ban đầu ta được:
1
4 2 3
4
x
x




(16 1) 8 3x x x
16 1 8 3xx
2
(16 1) 192xx
2
5 2 6
16
5 2 6
16
256 160 1 0
x
x
xx
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Vậy hệ có 2 nghiệm
5 2 6 5 2 6
,
16 8




và
5 2 6 5 2 6
,
16 8




.
4. Bài tập tự luyện
Bài 1.
2
1
(1 ) 3 2
1
(1 ) 2 4
x
yx
y
yx


Bài 2.
12
12
(1 ) 2
3
(1 ) 6
3
x
yx
y
yx


Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 3. Phƣơng pháp thế hạng tử tự do
Ví dụ 1. Giải hệ phƣơng trình
32
22
2 0 (1)
8 1 (2)
x xy y
yx

Giải: Thế phương trình (2) vào phương trình (1) ta được:
3 2 2 2
3 2 2 3
2 (8 ) 0
2 8 0 (3)
x xy y x y
x xy x y y
Nhận thấy x=0 không là nghiệm của hệ phương trình.
Khi
0x
, chia cả 2 vế của phương trình (3) cho
3
0x
ta được:
:
23
1 2 8 0. (4)
y y y
x x x
Đặt
y
t
x
, thì phương trình (4) có dạng:
32
8 2 1 0t t t
2
(2 1)(4 1) 0
1
2
2
t t t
t x y
Thế vào phương trình (2) ta được
2
11
2 3 3
12 1
11
2 3 3
yx
y
yx

Vậy hệ phương trình đã cho có nghiệm
1 1 1 1
; ; , ;
3 2 3 3 2 3
xy

.
Chú ý:
Ở phương pháp này ta cần làm những bước sau để giải được bài toán:
Đưa các số hạng cùng bậc về cùng một nhóm
So sánh bậc của hai phương trình để tìm cách thế hợp lí.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Ví dụ 2. Giải hệ phƣơng trình
33
5 5 2 2
1 (1)
(2)
xy
x y x y

Giải: Thế phương trình (1) vào (2) ta được
5 5 2 2 3 3
2 3 3 2
22
( )( )
0
( ) 0
0
0
.
x y x y x y
x y x y
x y x y
x
y
xy


Nếu
0x
thì từ (1) suy ra
1y
.
Nếu
0y
thì từ (1) suy ra
1x
.
Nếu
xy
thì từ (1) suy ra
01
, dẫn tới phương trình vô nghiệm.
Vậy hệ phương trình có nghiệm là (x;y) = (0;1), (1;0).
Ví dụ 3. Giải hệ phƣơng trình
33
22
-8x = y +2y
x -3 = 3(y +1)
x
Giải:
3 3 3 3
2 2 2 2
-8x = y +2y 2(4 ) (1)
x -3 = 3(y +1) 3 6 (2)
x x y x y
xy




Thế phương trình (2) vào phương trình (1) ta đươc
3 3 2 2
3 3 3 2 2 3
3 2 2
22
3( ) ( 3 )(4 )
3 3 4 12 3
12 0
0
12 0 (3)
x y x y x y
x y x x y xy y
x x y xy
x
x xy y
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Nếu x=0 thì từ (2) suy ra phương trình vô nghiệm.
Nếu
0x
, thì chia cả 2 vế của phương trình (3) cho
2
0x
ta được:
2
1 12 0
yy
xx
.
Đặt
y
t
x
, ta có phương trình sau
2
1
3
3
1 12 0
4
1
4
t
xy
tt
xy
t

Với x=3y, thay vào phương trình (2) ta được
2
13
66
3
yx
y
y

Với x=-4y, thay vào phương trình (2) ta được
2
66
4
13 13
13 6
66
4
13 13
yx
y
yx

Vậy hệ phương trình có nghiệm
6 6 6 6
; ( 3; 1),(3;1), 4 ; , 4 ;
13 13 13 13
xy
.
Ví dụ 4: Giải hệ phƣơng trình (ĐHKA-2011)
2 2 3
2 2 2
5 4 3 2( ) 0 (1)
( ) 2 ( ) (2)
x y xy y x y
xy x y x y
Giải:
Ta có:
22
(2) ( 1)( 2) 0 1xy x y xy
hoặc
22
2.xy
Nếu
1xy
thì từ (1) suy ra:
42
2 1 0 1.y y y
Suy ra: (x;y)=(1;1) hoặc (x;y)=(-1;-1)
Nếu
22
2xy
thì từ (1) suy ra:
1 x
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
2 2 2 2
22
3 ( ) 4 2 2( ) 0
6 4 2 2( ) 0
1
(1 )(2 ) 0
2
y x y xy x y x y
y xy x y x y
xy
xy y x
xy
Với x=2y, từ
22
2xy
suy ra:
2 10 10
( ; ) ;
55
xy



hoặc
2 10 10
( ; ) ; .
55
xy



Vậy hệ có nghiệm:
2 10 10 2 10 10
(1;1),( 1; 1), ; , ; .
5 5 5 5
Bài tập tự luyện
Giải các hệ phƣơng trình sau:
Bài 1.
32
2
3 6 0
3
y y x x y
x xy

Bài 2.
8
5
x x y x y y
xy

Bài 3.
3 3 2
44
8 4 1
2 8 2 0
x y xy
x y x y
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 4. Phƣơng pháp hàm đặc trƣng
Ví dụ 1. Giải hệ phƣơng trình
3
3
(2 3 ) 1
( 2) 3
xy
xy


Giải:
Xét x=0 không là nghiệm của hệ phương trình.
Xét
0x
:
3
3
3
3
1
2 3 (1)
(2 3 ) 1
3
( 2) 3
2 (2)
y
xy
x
xy
y
x





Cộng 2 phương trình (1) và (2) ta được:
3
3
13
3yy
xx
.(3)
Xét hàm :
3
3f t t t
.
Ta có
2
' 3 3 0f t t
suy ra hàm
()ft
đồng biến trên .
5. Nội dung phƣơng pháp:
Phương pháp này ta sẽ sử dụng với hệ mà các phương trình có x và y độc lập
với nhau hoặc có thể biến đổi về hệ phương trình có x và y độc lập với nhau.
Sau đó xét một hàm số
ft
đồng biến (hoặc nghịch biến) trên
D
. Khi đó
phương trình
( ) ( ) .f u f v u v
Để xuất hiện hàm đặc trƣng cần chú ý:
Hàm đặc trưng sẽ xuất hiện từ (1) trong (2) phương trình của hệ thông qua
biến đổi đại số, đặt ẩn phụ hoặc chia cả hai vế của phương trình cho cùng
một biếu thức.
Hàm đặc trưng sẽ xuất hiện sau khi cộng hoặc trừ hai phương trình của hệ.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
1
(3) ( )
1
f f y
x
y
x





Thay vào phương trình (1) ta được:
3 3 2
1
2
3
(2 ) 1 2 3 1 0
2
11
xy
x x x
x
xy
Vậy hệ phương trình đã cho có nghiệm
1
; ;2 , 1; 1
2
xy



.
Ví dụ 2. Giải hệ phƣơng trình
21
21
2 2 3 1 (1)
2 2 3 1 (2)
y
x
x x x
y y y
Giải:
Trừ hai vế của 2 phương trình cho nhau ta đươc:
Xét hàm
2
( ) 1 3.
t
f t t t
Ta có
'
2
( ) 1 3 ln 0,
1
t
t
f t t t
t
suy ra hàm
()ft
đồng biến trên .
(3) 1 ( 1)f x f y
xy

Thay vào 1 trong 2 phương trình được:
22
11
1 1 1 3 1 1 1 3 (3)
xy
x x y y

2
1
21
21
2
1
1 1 1 3
2 2 3 1
2 2 3 1
1 1 1 3
y
y
x
x
xx
x x x
y y y
yy



Fanpage: Thầy Duy Thành – Tiến sĩ Toán
2
1
1 1 1 3
x
xx
Đặt
1ux
Ta được phương trình
2
2
13
3 1 1
u
u
uu
uu
Xét hàm:
2
2
3 1 ' 3 ln3. 1 0
1
uu
u
g u u u g u
u




.
Suy ra hàm
()gu
nghịch biến trên .
Mặt khác, g(0)=1, do đó phương trình có 1 nghiệm duy nhất u=0 suy ra hệ phương trình
có nghiệm duy nhất (x;y)=(1;1).
Ví dụ 3. Giải hệ phƣơng trình
5 4 10 6
2
(1)
4 5 8 6 (2)
x xy y y
xy
0
5
0y
5
5
(3)
xx
yy
yy



Ta xét hàm:
54
'( ) 5 1 0f t t t f t t
. Suy ra hàm
()ft
đồng biến trên .
Giải:
y
Nhận thấy không là nghiệm của hệ nên ta chia cả 2 vế phương trình (1) cho
:ta được:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
2
(3) ( )
x
f f y
y
x
y
y
xy






Thay vào phương trình (2):
4 5 8 6
4 5 3 8 3 0
4( 1) 1
0
4 5 3 8 3
41
( 1) 0
4 5 3 8 3
1
11
41
0
4 5 3 8 3
xx
xx
xx
xx
x
xx
x
xy
xx





Vậy hệ phương trình có nghiệm
; (1;1)xy
, (1;-1)
Ví dụ 4 (ĐHKA-2010). Giải hệ phƣơng trình
2
22
4 1 3 5 2 0 (1)
4 2 3 4 7 (2)
x x y y
x y x
Giải:
Đặt
2
5
5 2 ( 0)
2
t
y t t y
.
2
2
2
2
1
(1) 4 1 . 0
2
2 2 1 1 (3)
t
x x t
x x t t



Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Ta xét hàm:
22
( 1) '( ) 3 1 0f t t t f t t
. Suy ra hàm
()ft
đồng biến trên .
2
(3) 2x ( )
2x
2 5 2
0
5 4x
2
f f t
t
xy
x
y


Thế vào (2) ta được:
2
22
53
4 2 2 3 4 7 (4), 0
24
x x x x



Dễ thấy
3
0,
4
xx
không là nghiệm của
(4)
.
Xét
2
22
5
( ) 4 2 2 3 4
2
g x x x x



trên
3
0;
4



.
23
2
5 4 4
'( ) 8 8 2 12 16
2
3 4 3 4
43
4 4 3 0 0;
4
34
g x x x x x x
xx
x x x
x







Suy ra hàm
()gx
nghịch biến trên
3
0;
4



. Mặt khác
11
0
22
gx



là nghiệm duy
nhất của (4)
2.y
Vậy hệ đã cho có nghiệm
1
( ; ) ;2
2
xy



NOTE: Chúng ta chỉ xét hàm trên (a,b) chứ không xét hàm trên [a,b], vì trong một số
trường hợp tại các điểm mút a,b đạo hàm không xác định. Vì vậy các em nên tách 2
điểm đầu mút xét riêng xem có là nghiệm của phương trình không.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Ví dụ 5. Giải hệ phƣơng trình
2 1 (1)
1 (2)
x y x y
xy
e e x
e x y

Giải:
Đặt
, u x y v x y
. Hệ có dạng:
2 1 1
1
1
1
1 (3)
1 (4)
uv
u
u v u
u
v
u
e e u v u v
ev
e e u e
ev
eu
ev




Trừ 2 vế của (3) và (4) cho nhau ta được:
vu
e e u v
(5)
vu
e v e u
Ta xét hàm:
'( ) 1 0
tt
f t e t f t e
. Suy ra hàm
()ft
đồng biến trên .
(5) ( )f u f v
uv


0x y x y y
Từ (2)
11
xx
e x e x
. (6)
Đặt
()
x
g x e x
,
'( ) 1.
x
g x e
Nếu
'
0 ( ) 0 ( )x g x g x
đồng biến trên
(0; )
.
( ) (0) ( ) 1g x g g x
.
Suy ra (6) vô nghiệm.
Nếu
'
0 ( ) 0 ( )x g x g x
nghịch biến trên
( ;0)
( ) (0)g x g
.
( ) 1gx
. Suy ra (6) vô nghiệm.
Nếu
0 VT(6) VP(6) 1 0xx
là nghiệm duy nhất của (6).
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Vậy hệ đã cho có nghiệm
( ; ) (0;0).xy
6. Bài tập tự luyện
Giải các hệ phƣơng trình sau:
Bài 1.
3
2
2 2 1 3 1
2 1 2 1
y x x x y
y x xy x
Bài 2.
3
2 2 1 2 1 2 3 2
4 2 2 4 6
x x y y
xy
Bài 3.
3 3 2
2
3 4 2
1 2 1
y y x x x
x y y
Bài 4.
3
3 2 2 2 1 0
2 2 2 1 1
x x y y
xy
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 5. Phƣơng pháp đặt ẩn phụ
Ví dụ 1. Giải hệ phƣơng trình
22
2 2 2
6
15
y xy x
x y x


Giải:
Xét x=0 không là nghiệm của hệ phương trình.
Xét
0x
, chia cả 2 vế của hai phương trình cho
2
0x
ta được:
2
2
2
2
2
6
1
5
1
6
1
25
yy
xx
y
x
y
y
xx
y
y
xx









Đặt
1
;
y
u v y
xx
ta được hệ phương trình:
2
3
2
6
6
. 6 2
2 5 6 3
5 12 0
2 5 0
u
u v u
u
v
v
v u v
vv
v
v

Với u=2, v=3:
7. Nội dung phƣơng pháp: Sử dụng phƣơng pháp khi hệ phƣơng trình có vế
phải độc lập với x hoặc y. Khi đó ta khử x, y ở vế phải của cả hai phƣơng
trình và lựa chọn ẩn phụ cho phù hợp.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
2
1
2
2
2
2
1
1
1 2 3 1 0
23
3
2
1
x
y
y
yx
yx
x
xx
x
x
y
x
x
y


Vậy hệ phương trình đã cho có nghiệm
1
; 1;2 , ;1
2
xy



.
Ví dụ 2. Giải hệ phƣơng trình
22
22
2 3 0 (1)
2 0 (2)
xy y x
y x y x
Giải:
Ta có x=y=0 là một nghiệm của hệ phương trình.
Khi
0; 0xy
, chia 2 vế của phương trình (1) cho
2
x
, chia 2 vế của phương
trình 2 cho
2
y
ta được:
22
22
22
22
2 3 0 2 3
1 2 0 2 1
y y y y
x x x x
x x x x
y y y y




Đặt
22
;
yx
uv
xy

ta được hệ phương trình
2
1
2
32
2
3
1
2
3
3
1
2
6
2
1
2
3 2 0
1
2
2
3
3
3
u
uv
u
v
u
v
u
v
v
v
u
v
vv
v
v
u
v
v





Với u= -1,v=1 ta có:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
2
2
2
1
1
1
1
1
1
y
x
x
x
x
y
x
y
y






Với
2
6;
3
uv
ta có
2
3
2
3
2
6
3
6
2
3
9
y
x
x
x
y
y








Vậy hệ phương trình đã cho có nghiệm
33
26
; ; , 1;1
39
xy



.
Ví dụ 3. Giải hệ phƣơng trình
22
22
+y +xy+1 = 4y
y(x+y) = 2x 7 2
x
y

Giải:
2
2 2 2
2 2 2 2
2
2
1
4
+y +xy+1 = 4y ( ) ( 1) 4
y(x+y) = 2x 7 2 ( ) 2( 1) 7
1
( ) 2 7
x
xy
y
x y x y x y
y y x y x y
x
xy
y




Đặt
2
1
;
x
u x y v
y
ta được hệ phương trình
2 2 2
3
4
1
4 4 4
1
2 7 2 7 10 9 0
5
9
9
u
uv
v
u v u v u v
v
u v u v v v
u
v
v


Với
3; 1:uv
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
22
1
3
33
4
1
11
11
2
2
1
x
yx
x y y x
y
x
xx
x
x
yy
y








Với
5; 9uv
:
22
55
11
99
x y y x
xx
yy





(vô nghiệm)
Vậy hệ phương trình có nghiệm
; ( 1;4),(2;1)xy 
.
Ví dụ 4: Giải hệ phƣơng trình
3 3 3
22
(9 ) (1)
6 (2)
y x x
x y y x


Giải:
Nhận thấy x=y=0 là một nghiệm của hệ phương hệ phương trình.
Xét
0; 0xy
. Chia 2 vế của phương trình (1) cho
3
x
, chia 2 vế của phương
trình (2) cho x ta được:
2
3
3
2
2
3
3
2
2
[ -3y]=9
( ) 9
9
9
( ) 6
6
) 6
6
yy
yy
y
y
xx
x x y
x
x
xx
xx
x
y
y
y
y
yx
yx
xy
x
x
x
x















Đặt
;
y
u x v y
x
ta được hệ phương trình:
2
3
6
3
( 3 ) 9
3
.6
27
v
v
u u v
u
u
uv
u




Với u=3;v=3:
3
3
y
x
x
y

(hệ vô nghiệm)

x

(yx
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Vậy hệ phương trình có nghiệm: (x;y)=(0;0).
8. Bài tập tự luyện
Bài 1. Bài 6.
3 3 3
22
1 19
6
x y x
y xy x

3 3 3
22
8 27 18
46
x y x
xy x y


Bài 2. Bài 7.
3
3
(2 3 ) 8
( 2) 6
xy
xy


2 2 2
17
1 13
xy x y
x y xy x
Bài 3. Bài 8.
2
4 2 2 2
20
4 3 0
x xy x y
x x y x y
32
23
216
24
x xy y
x y y x


Bài 4.
3 3 3
22
1 19x y x
y xy x

Bài 5.
2
2
1 ( ) 4
( 1)( 2)
x y x y y
x y x y
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

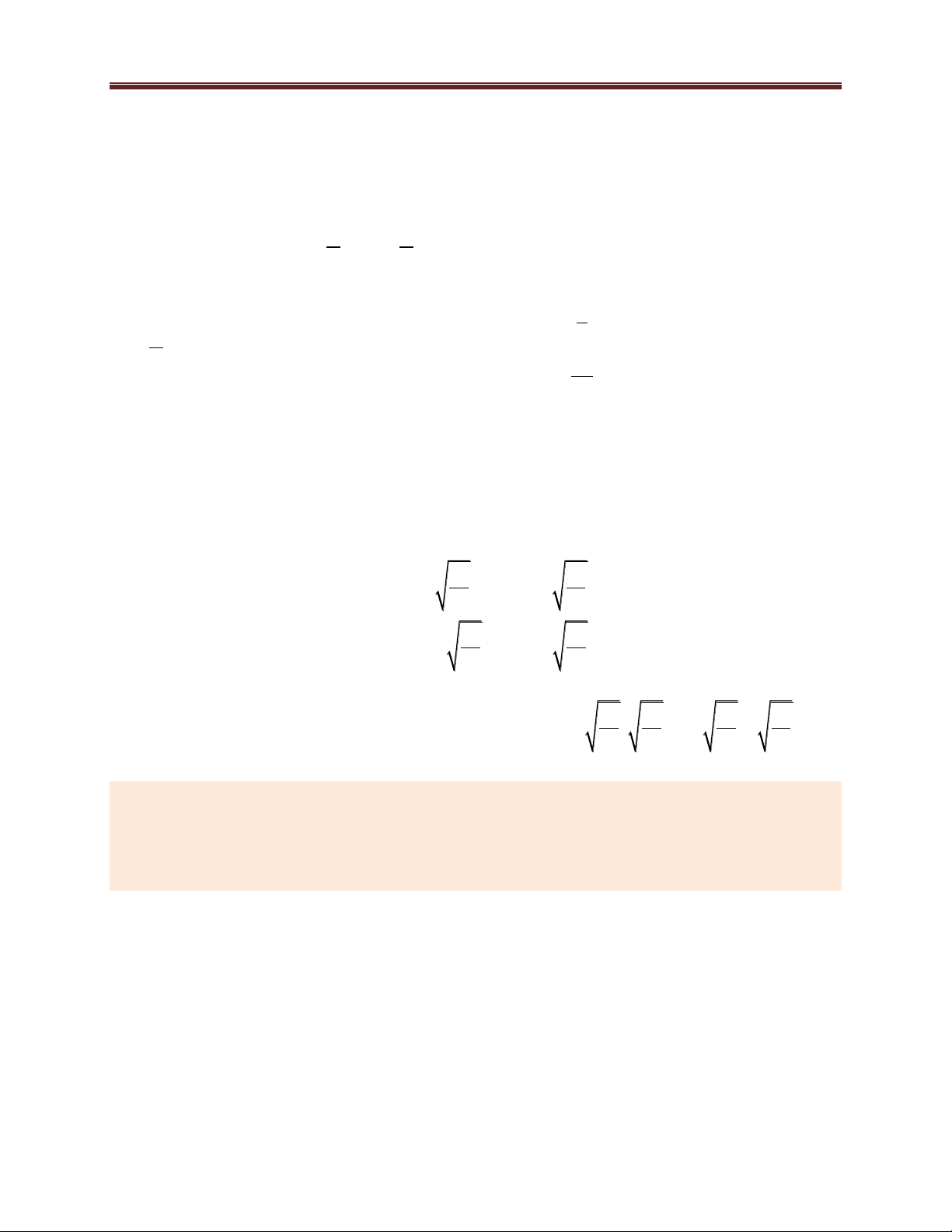
Preview text:

Fanpage: Thầy Duy Thành – Tiến sĩ Toán
BÍ KÍP GIẢI HỆ PHƢƠNG TRÌNH CHỈ TRONG 10 PHÚT - Khi máy tính casio bó tay -
Khi các kỹ năng phân tích nhân tử đưa về phương trình tích vô hiệu hóa
Các em học sinh sẽ phải xử lý thế nào ? Hãy áp dụng những phương
pháp cực hữu ích sau đây
Chuyên đề 1. Phƣơng pháp miền giá trị giải hệ phƣơng trình
1. Dấu hiệu nhận biết:
Trƣờng hợp 1: Hệ có 1 trong 2 p
hương trình là bậc 2 với , x y .
Cách giải: Coi phương trình là bậc 2 ẩn x , giải   0  điều kiện của . y
Coi phương trình là bậc 2 ẩn y , giải   0  điều kiện của . x Dùng điều kiện của , x y để
đánh giá phương trình còn lại.
Trƣờng hợp 2: Hệ có 2 phương trình cùng là bậc hai với x (hoặc cùng là bậc hai với y ).
Cách giải: Với phương trình (1), coi x là ẩn, giải   0  điều kiện của . y
Với phương trình (2), coi x là ẩn, giải   0  điều kiện của . y So sánh điều kiện của
ở 2 phương trình và rút ra kết luận.
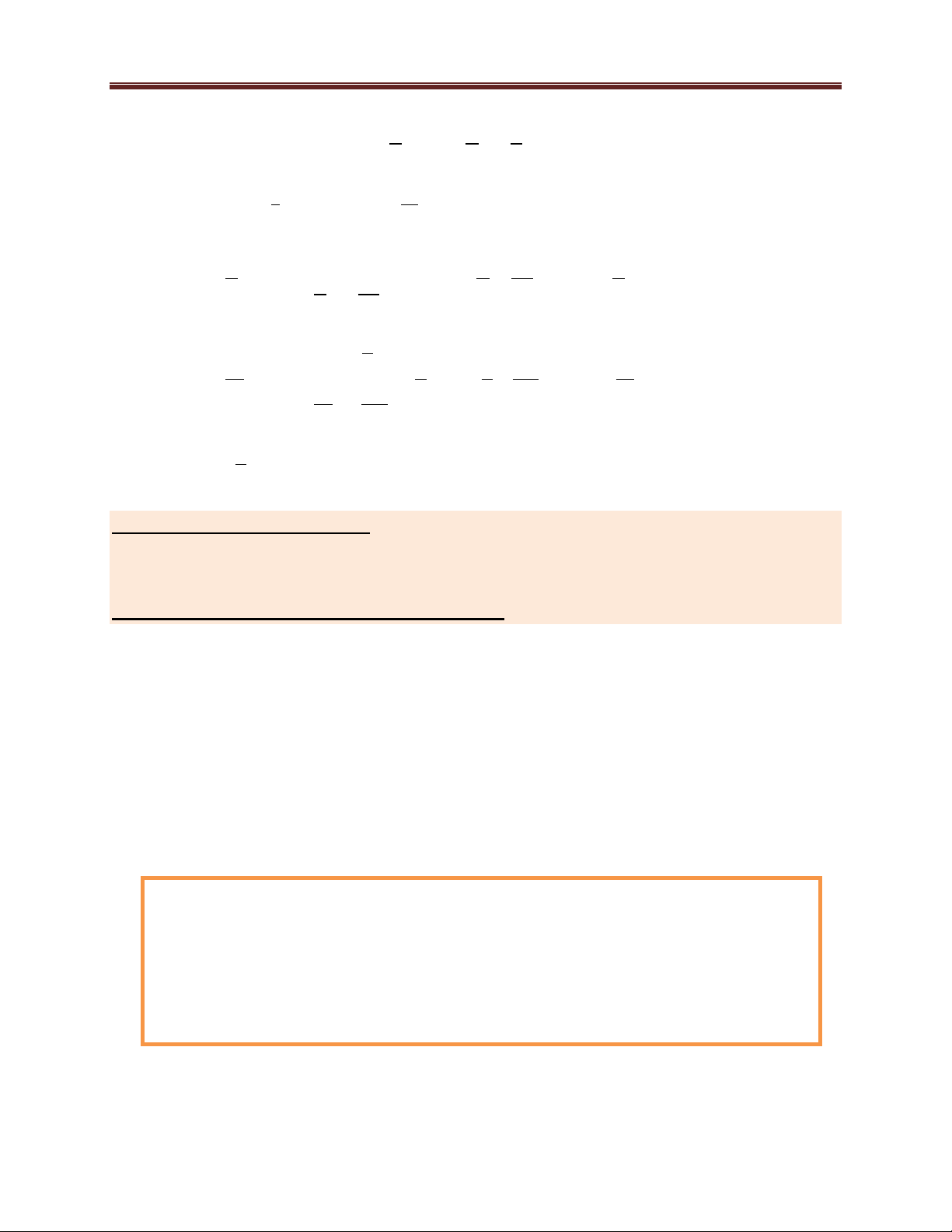
Ví dụ 1: Giải hệ phương trình  697 4 2  x y  (1)  81 2 2
x y xy 3x  4y  4  0 (2)
Coi (2) là phương trình bậc hai ẩn x : 2 2
x  ( y  3)x y  4y  4  0
Phương trình có nghiệm    0 2 2
 (y  3)  4(y  4y  4)  0 2 2
y  6y  9  4y 16y 16  0 2  3
y 10y  7  0 7  1  y  3
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Coi (2) là phương trình bậc hai ẩn y : 2 2
y  (x  4) y x  3x  4  0
Phương trình có nghiệm    0 2 2
 (x  4)  4(x  3x  4)  0 2 2
x  8x 16  4x 12x 16  0 2  3
x  4x  0 4  0  x  3  7  4 4 2  4   7  697 y   1, , x  0,     thì 4 2 x y     VT(1)  VP(1), do đó      3   3  3   3  81 4 7  4 7  VT(1)=VP(1) khi x  , y
. Vậy hệ phương trình có nghiệm duy nhất ,   . 3 3  3 3 
Ví dụ 2: Giải hệ phƣơng trình  7 2 2
(2x 1)(2y 1)  xy (1)  2 2 2
x y xy 7x 6y 14  0 (2)
Coi (2) là phương trình bậc hai ẩn x : 2 2
x  ( y  7)x y  6y 14  0
Phương trình có nghiệm    0 2 2
y 14y  49  4y  24y  56  0 2  3
y 10y  7  0 7  1  y  3
Coi (2) là phương trình bậc hai ẩn y : 2 2
y  (x  6) y x  7x 14  0
Phương trình có nghiệm    0 2 2
x 12x  36  4x  28x  56  0 2  3
x 16x  20  0 10  2  x  3
x y  0 không là nghiệm của hệ.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán  1  1  7 (1)  2x  2 y   (3)     x  y  2 Đặ 1 1 t f t  '
 2t   f t  2   0  f t đồng biến trên ( ;  0) và (0; )  . 2   t tf   1  1   7   1 89  7  Xét t  1;   
  7  89 1 2y   y   1; .    3 fy 21     3   3  21  f   7 2     10  2 7 1 191  10 Xét t  2;       2x   x   2; .    3  10  191 2 x 30   3  f      3  30 7    x 1 VT (3) 
. Dấu “=” xảy ra  
. Vậy hệ có nghiệm (1;2). 2 y  2
Ví dụ 3: Giải hệ phƣơng trình 2 2 2
x y  2x y  0 (1)  2 3
2x  4x  3  y  0 (2)
Coi (1) là phương trình bậc hai ẩn x : 2 2 2
x y  2x y  0. Phương trình có nghiệm 4
 '  0 1 y  0  1   y 1. (3)
Coi (2) là phương trình bậc hai ẩn x : 2 3
2x  4x  3  y  0 .
Phương trình có nghiệm       3  y  3 ' 0 4 2 3
 0 1 y  0  y  1  . (4)
Từ (3) và (4)  y  1.
 Thay vào hệ ta được x=1. Vậy hệ có nghiệm (1;-1).
2. Bài tập tự luyện 3 2
x y  2  2 2
x xy y y  0
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 2. Phƣơng pháp nhân chia giải hệ phƣơng trình
3. Dấu hiệu nhận biết:
Trƣờng hợp 1: Hệ phư ơng trình tích
Trƣờng hợp 2: Hệ phương trình chưa phải là hệ phương trình tích nhưng
có thể sử dụng các biến đổi đại số để đưa về hệ phương trình tích
Ví dụ 1: Giải hệ phƣơng trình x
(x y) y  (1)  2
(x y) x  3 y (2)  Điều kiện: , x y  0
+) Dễ thấy x y  0 là 1 nghiệm của hệ +) Với ,
x y  0 , chia 2 vế của phương trình (1) và (2) cho nhau ta được:
(x y) y x
(x y) x 6 y
 6y(x y)  ( x x y) 2 2
x 5xy 6y  0 x  3y
 x  2y
Với x  3y , thay vào phương trình (1) ta được: 3y 2y y  2
Fanpage: Thầy Duy Thành – Tiến sĩ Toán 3 3y  4y  4 3  16y  3y 2
y(16y 3)  0  y  0   3  y    4
Đối chiếu với điều kiện ta được: 3 y  3 3  x  4 4
Với x  2y , thay vào phương trình (1) ta được: 2 y y y  2  2y y  2y 3  4y  2y 2
 2y(2y 1)  0  y  0    2  y   2
Đối chiếu với điều kiện ta được: 2 y   x  2 2 3 3 3 2
Vậy hệ phương trình đã cho có nghiệm (0, 0); ( , ) ; ( 2, ). 4 4 2
Ví dụ 2: Giải hệ phƣơng trình
Fanpage: Thầy Duy Thành – Tiến sĩ Toán 2
 (x 1) y x y  3  2
 (y  2) x y x 1  2
 (x 1) y (x 1)  2 y   2
 (y  2) x  ( y  2)  x 1  2
 (x 1)(y 1)  2 y (1)   2
 (y  2)(x 1)  x 1 (2) 
+) Nhận thấy x  1, y 2 là nghiệm của hệ phương trình.
+) Với x 1, y  2 , nhân 2 vế của phương trình (1) và (2) cho nhau, ta được: 2 2
(x 1)( y 1) 1 (3) 2 x 1  1 Do 2 y 1  1
VT(3)  VP(3)
Khi đó VT(3)=VP(3)  xy 0 .
Thay x y 0 vào hệ ban đầu không thỏa mãn. Vậy hệ có nghiệm duy nhất (1,2).
Ví dụ 3: Giải hệ phƣơng trình  1 (4  ) x  2 3   y  2x  1  (4 ) y  4  y  2x  Điều kiện: , x y  0  1 2 3 4   (1)  y  2x x Hệ phương trình   1 4 4  (2)  y  2x y
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Cộng 2 vế của phương trình (1) và (2), trừ 2 vế của phương trình (1) và (2) ta được hệ :  2 3 4  8   (3)  x y   2 2 3 4   (4)  y  2x x y
Nhân 2 vế của phương trình (3) và (4) ta được: 16 12 16   2x y x y 2 2
 8x  2xy 3y  0  1   x y (thỏa mãn)  2   3  x   y (loại) 4
Với y  2x , thế vào phương trình ban đầu ta được:  1   4   x  2 3  4x   (16x 1  ) x  8x 3  16x 1   8 x 3 2  (16x 1  ) 192x 2  256x 16  0x10  5  2 6 x  16   52 6 x   16
Fanpage: Thầy Duy Thành – Tiến sĩ Toán  5  2 6 5  2 6   5  2 6 5  2 6  Vậy hệ có 2 nghiệm  ,  và  ,  . 16 8   16 8  
4. Bài tập tự luyện  1 (1 ) 3x  2   y x Bài 1.  1  (1 ) 2 y  4 2  y x   12 (1 ) x  2   y  3x Bài 2.  12  (1 ) y  6  y  3x
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 3. Phƣơng pháp thế hạng tử tự do Chú ý:
Ở phương pháp này ta cần làm những bước sau để giải được bài toán:
 Đưa các số hạng cùng bậc về cùng một nhóm
 So sánh bậc của hai phương trình để tìm cách thế hợp lí. 3 2
x  2xy y  0 (1)
Ví dụ 1. Giải hệ phƣơng trình  2 2 8  y x 1 (2)
Giải: Thế phương trình (2) vào phương trình (1) ta được: 3 2 2 2
x  2xy  (8y x ) y  0 3 2 2 3
x  2xy x y  8y  0 (3)
 Nhận thấy x=0 không là nghiệm của hệ phương trình.
 Khi x  0, chia cả 2 vế của phương trình (3) cho 3 x  0 ta được: 2 3  y   y   y  : 1 2   8  0. (4)        x   x   x  Đặ y t
t , thì phương trình (4) có dạng: x 3 2
8t  2t t 1 0 2
 (2t 1)(4t t 1)  0 1   t   x  2  y 2  1 1  y   x   2 3 3
Thế vào phương trình (2) ta được 2 12 y  1   1  1 y   x   2 3 3      
Vậy hệ phương trình đã cho có nghiệm  x y 1 1 1 1 ;  ; , ;     .  3 2 3   3 2 3 
Fanpage: Thầy Duy Thành – Tiến sĩ Toán 3 3  x y 1 (1)
Ví dụ 2. Giải hệ phƣơng trình  5 5 2 2
x y x y (2)
Giải: Thế phương trình (1) vào (2) ta được 5 5 2 2 3 3
x y  (x y )(x y ) 2 3 3 2
x y x y  0 2 2
x y (x y)  0 x  0   y  0  x   . y
Nếu x  0 thì từ (1) suy ra y  1 .
Nếu y  0 thì từ (1) suy ra x  1 .
Nếu x   y thì từ (1) suy ra 0  1, dẫn tới phương trình vô nghiệm.
Vậy hệ phương trình có nghiệm là (x;y) = (0;1), (1;0).
Ví dụ 3. Giải hệ phƣơng trình 3 3 x -8x = y +2y  2 2  x -3 = 3(y +1) Giải: 3 3 3 3  x -8x = y +2y
x y  2(4x y) (1)    2 2 2 2  x -3 = 3(y +1)
x  3y  6 (2)
Thế phương trình (2) vào phương trình (1) ta đươc 3 3 2 2
3(x y )  (x  3y )(4x y) 3 3 3 2 2 3
 3x  3y  4x x y 12xy  3y 3 2 2
x x y 12xy  0 x  0   2 2
x xy 12y  0 (3)
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Nếu x=0 thì từ (2) suy ra phương trình vô nghiệm.
Nếu x  0 , thì chia cả 2 vế của phương trình (3) cho 2 x  0 ta được: 2  y   y  1 12  0     .  x   x   1 t    x  3y Đặ y 3 t
t , ta có phương trình sau 2
1 t 12t  0     x 1   x  4  y t   4
y 1 x  3
Với x=3y, thay vào phương trình (2) ta được 2
6 y  6  y  1 x  3
Với x=-4y, thay vào phương trình (2) ta được  6 6  y   x  4  2 13 13 13y  6   6 6  y    x  4  13 13    
Vậy hệ phương trình có nghiệm  x y 6 6 6 6 ;  ( 3  ; 1  ),(3;1),  4  ; ,  4  ;  . 13 13 13 13    
Ví dụ 4: Giải hệ phƣơng trình (ĐHKA-2011) 2 2 3
5x y  4xy  3y  2(x y)  0 (1)  2 2 2
xy(x y )  2  (x y) (2) Giải: Ta có: 2 2
(2)  (xy 1)(x y  2)  0  xy  1 hoặc 2 2 x y  2.  Nếu xy 1       thì từ (1) suy ra: 4 2 y 2y 1 0 y 1.
Suy ra: (x;y)=(1;1) hoặc (x;y)=(-1;-1)  Nếu 2 2
x y  2 thì từ (1) suy ra:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán 2 2 2 2
3y(x y )  4xy  2x y  2(x y)  0 2 2
 6y  4xy  2x y  2(x y)  0  xy  1
 (1 xy)(2y x)  0  x  2y Với x=2y, từ 2 2
x y  2 suy ra:  2 10 10   2 10 10  ( ; x y)   ;  hoặc ( ; x y)    ;  . 5 5   5 5    2 10 10   2 10 10 
Vậy hệ có nghiệm: (1;1),( 1  ; 1  ), ; ,  ;  . 5 5 5 5     Bài tập tự luyện
Giải các hệ phƣơng trình sau: Bài 1. 3 2
y y x  3x  6y  0  2  x xy  3 Bài 2.
x x 8 y x y y   x y  5 Bài 3. 3 3 2
x  8y  4xy 1  4 4
2x  8y  2x y  0
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 4. Phƣơng pháp hàm đặc trƣng
5. Nội dung phƣơng pháp:
Phương pháp này ta sẽ sử dụng với h ệ mà các phương trình có x và y độc lập
với nhau hoặc có thể biến đổi về hệ phương trình có x và y độc lập với nhau.
Sau đó xét một hàm số f t đồng biến (hoặc nghịch biến) trên D . Khi đó phương trình
f (u)  f (v)  u  . v
Để xuất hiện hàm đặc trƣng cần chú ý:
 Hàm đặc trưng sẽ xuất hiện từ (1) trong (2) phương trình của hệ thông qua
biến đổi đại số, đặt ẩn phụ hoặc chia cả hai vế của phương trình cho cùng một biếu thức.
 Hàm đặc trưng sẽ xuất hiện sau khi cộng hoặc trừ hai phương trình của hệ. 3
x (2  3y) 1
Ví dụ 1. Giải hệ phƣơng trình  3
x(y  2)  3 Giải:
 Xét x=0 không là nghiệm của hệ phương trình.  1 2  3y  (1) 3     3  x (2 3y) 1  x Xét x  0 :    3
x(y  2)  3 3 3 y  2  (2)  x 1 3
Cộng 2 phương trình (1) và (2) ta được: 3
  y  3y .(3) 3 x x Xét hàm : f t  3  t  3t .
Ta có f t  2 '
 3t  3  0 suy ra hàm f (t) đồng biến trên .
Fanpage: Thầy Duy Thành – Tiến sĩ Toán  1  (3)  ff (y)    x  1   y x
Thay vào phương trình (1) ta được:  1 3 x   y  2 3 3 2 x (2 ) 1 2x 3x 1 0         2 x  x  1   y  1   1 
Vậy hệ phương trình đã cho có nghiệm  ; x y  ; 2 , 1  ;    1 .  2  2 y 1
 x x  2x  2  3  1 (1)
Ví dụ 2. Giải hệ phƣơng trình  2 x 1
y y  2y  2  3  1 (2)  Giải: y
x x  2x  2  3y 1 x  1 x  2 1 2 1 1 1  3    2 x 1
y y  2y  2  3  1    y   1   y  2 x 1 1 1  3  
Trừ hai vế của 2 phương trình cho nhau ta đươc:
x  x 2 x
y   y 2 1 y 1 1 1 1 3 1 1 1 3             (3) t Xét hàm 2 ( )   1  3t f t t t .Ta có ' f (t)  1
 3t lnt  0, t
 suy ra hàm f (t) 2 t 1 đồng biến trên .
(3)  f x  
1  f ( y 1)  x y
Thay vào 1 trong 2 phương trình được:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán  2 1 1 1 1 3x x x       Đặt u x 1 Ta được phương trình 2
u u 1  3u  3u  2
u u 1 1     u
Xét hàm: g u  3 u  2
u u 1  g 'u  3 u  ln3.1   0 . 2  u 1 
Suy ra hàm g(u) nghịch biến trên .
Mặt khác, g(0)=1, do đó phương trình có 1 nghiệm duy nhất u=0 suy ra hệ phương trình
có nghiệm duy nhất (x;y)=(1;1). 5 4 10 6
x xy y y (1) 
Ví dụ 3. Giải hệ phƣơng trình  2
 4x  5  y  8  6 (2)  Giải: Nhận thấy y  0 5
không là nghiệm của hệ nên ta chia cả 2 vế phương trình (1) cho y  0 :ta được: 5  x x 5
  y y (3)    y y Ta xét hàm: f t 5 4
t t f '(t)  5t 1 0 . Suy ra hàm f (t) đồng biến trên .
Fanpage: Thầy Duy Thành – Tiến sĩ Toánx  (3)  ff (y)    y x   y y 2  x y
Thay vào phương trình (2): 4x  5  x  8  6
  4x  5 3   x 8 3  0 4(x 1) x 1    0 4x  5  3 x  8  3  4 1   (x 1)   0    4x  5  3 x  8  3   x  1   4 1
x  1 y  1     0  4x  5  3 x  8  3
Vậy hệ phương trình có nghiệm  ;
x y  (1;1) , (1;-1)
Ví dụ 4 (ĐHKA-2010). Giải hệ phƣơng trình  2  4x  
1xy 3 52y  0 (1)  2 2
4x y  2 3 4x  7 (2) Giải: 2  Đặ 5 t
t 5  2 y t (t  0)  y  . 2   t (1)  4x   2 1 2 1 x  .t  0 2
 2x 2x2 1   2t   1 t (3)  
Fanpage: Thầy Duy Thành – Tiến sĩ Toán Ta xét hàm: f t  2 2
 (t 1)t f '(t)  3t 1 0. Suy ra hàm f (t) đồng biến trên .
(3)  f 2x  f (t)  2x  t
 2x  5  2yx  0  2   5  4x y   2 Thế vào (2) ta được: 2  5  3 2 2 4x   2x  2 3  4x  7 (4), 0  x     2  4 3
Dễ thấy x  0, x
không là nghiệm của (4) . 4 2  5   3  Xét 2 2
g(x)  4x   2x  2 3  4x   trên 0; .    2   4   5  4 4 2 3
g '(x)  8x  8x  2x   1
 2x 16x     2  3  4x 3  4x    4x 4 3 2 4x  3   0 x   0;   3  4x  4   3   1  1
Suy ra hàm g(x) nghịch biến trên 0;   . Mặt khác g  0  x    là nghiệm duy  4   2  2
nhất của (4)  y  2.  1  
Vậy hệ đã cho có nghiệm ( ; x y) ; 2    2 
NOTE: Chúng ta chỉ xét hàm trên (a,b) chứ không xét hàm trên [a,b], vì trong một số
trường hợp tại các điểm mút a,b đạo hàm không xác định. Vì vậy các em nên tách 2
điểm đầu mút xét riêng xem có là nghiệm của phương trình không.
Fanpage: Thầy Duy Thành – Tiến sĩ Toán xy xyee  2x   1 (1)
Ví dụ 5. Giải hệ phƣơng trình xyex y 1 (2) Giải:
Đặt u x y, v x y . Hệ có dạng: u v
e e u v  2  u   1  v   1  ue v 1 u v
e e  u   1 ue   ue v 1 v
e u 1 (3)   u
e v 1 (4)
Trừ 2 vế của (3) và (4) cho nhau ta được: v u
e e u v v u
e v e u (5) Ta xét hàm:   t    '( ) t f t e t
f t e 1  0 . Suy ra hàm f (t) đồng biến trên .
(5)  f u  f (v)  u v
x y x y y  0 Từ (2) x   1 x e x
e x 1. (6) Đặt ( ) x
g x e x , '( ) x g x e 1.  Nếu '
x  0  g (x)  0  g(x) đồng biến trên (0; )
 . g(x)  g(0)  g(x) 1. Suy ra (6) vô nghiệm.  Nếu '
x  0  g (x)  0  g(x) nghịch biến trên ( ;
 0)  g(x)  g(0)
.  g(x)  1. Suy ra (6) vô nghiệm.
 Nếu x  0  VT(6)  VP(6) 1 x  0 là nghiệm duy nhất của (6).
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Vậy hệ đã cho có nghiệm ( ; x ) y  (0;0).
6. Bài tập tự luyện
Giải các hệ phƣơng trình sau: Bài 1. 3
2y  2x 1 x  3 1 x y  2
y  2x 1 2xy 1 x Bài 2.   x  3 2 2
1  2x 1  2 y  3 y  2 
 4x  2  2y  4  6  Bài 3. 3 3 2
y y x  3x  4x  2   2
 1 x y  2  y 1  Bài 4.
 3 x 2  x  2y 2y 1  0  
 2 2  x  2y  3 1 1 
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Chuyên đề 5. Phƣơng pháp đặt ẩn phụ
7. Nội dung phƣơng pháp: Sử dụng phƣơng pháp khi hệ phƣơng trình có vế
phải độc lập với x hoặc y. Khi đó ta khử x, y ở vế phải của cả hai phƣơng
trình và lựa chọn ẩn phụ cho phù hợp. 2 2
y xy  6x
Ví dụ 1. Giải hệ phƣơng trình  2 2 2 1
  x y  5x Giải:
 Xét x=0 không là nghiệm của hệ phương trình.
 Xét x  0, chia cả 2 vế của hai phương trình cho 2
x  0 ta được: 2  y y   6  2  x x  1  2  y  5 2  xy  1   y  6     x x    2   1  yy  2  5     xx Đặ y 1 t u  ;v
y ta được hệ phương trình: x x   6 u   6  .uv  6   u u   2 v      v   2 v  2u  5 6    v  3 2 3 v  2  5  0
v  5v 12  0   v Với u=2, v=3:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán     x 1  y      2  y  2x  y  2    y  2x x   1     2  1 1  2x  3
2x  3x 1  0    x   y  3 x     2 x         y  1  
Vậy hệ phương trình đã cho có nghiệm  x y    1 ; 1; 2 , ;1  .  2  2 2
xy  2y  3x  0 (1)
Ví dụ 2. Giải hệ phƣơng trình  2 2
y x y  2x  0 (2) Giải:
 Ta có x=y=0 là một nghiệm của hệ phương trình.
 Khi x  0; y  0 , chia 2 vế của phương trình (1) cho 2
x , chia 2 vế của phương trình 2 cho 2 y ta được: 2 2  y yy y   2  3  0  2  3   2 2  x xx x    2 2 x x x x   1  2  0  2  1  2 2  y y    y y 2 2 Đặ y x t u  ;v
ta được hệ phương trình x yu   1    2 u      3   2 2 3 v u   u    3    2    v  1 v    u   3 v    v 1    2   v      u  6  2 v   1  2            2  v 1 2 3v v 2 0 v         2 u 3   3 v     v   3 Với u= -1,v=1 ta có:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán 2  y  1  x  1   x  x  1  2    x   2 x  1    y  1  1  y  y 2  Với u  6;  v  ta có 3 2  y  2  6  x     3  x  3    2 x 2 6     y   3  y 3  9  2 6 
Vậy hệ phương trình đã cho có nghiệm  ; x y   ;  ,    1  ;  1 . 3 3  3 9  2 2  x +y +xy+1 = 4y
Ví dụ 3. Giải hệ phƣơng trình  2 2
y(x+y) = 2x  7y  2 Giải: 2   x 1  x y   4  2 2 2  x +y +xy+1 = 4y
y(x y)  (x 1)  4yy      2 2 2 2 2
y(x+y) = 2x  7y  2
y(x y)  2(x 1)  7 y   x 1 2 (x y)  2  7     y 2  Đặ x 1
t u x y;v
ta được hệ phương trình yu   3 u   4  v  
 u v  4
u  4  vu  4  v   v  1        v 1  2 2 2 u   2v  7 u  2v  7  
v 10v  9  0    u   5   v  9   v  9
Với u  3;v  1:
Fanpage: Thầy Duy Thành – Tiến sĩ Toán    x  1 
x y  3
y  3  xy  3  x      y  4 2 2  x 1   x 1   x  1    1  1      x  2 y yx  2            y  1 Với u  5  ;v  9 : x y  5  y  5   x   2 2  x 1   x 1  (vô nghiệm) 9  9   y   y
Vậy hệ phương trình có nghiệm  ; x y  ( 1  ;4),(2;1). 3 3 3
y x (9  x ) (1)
Ví dụ 4: Giải hệ phƣơng trình  2 2
x y y  6x (2) Giải:
 Nhận thấy x=y=0 là một nghiệm của hệ phương hệ phương trình.
 Xét x  0; y  0 . Chia 2 vế của phương trình (1) cho 3
x , chia 2 vế của phương trình (2) cho x ta được:  3 2  3  2  y    y   y yy   y  3 3 2   9  x       x  9  x  (x y  )  9    x  [ x  -3y]=9     2  x   x   x x  x   x         2  yyy   y xy   6 y(x  )  6 y(x  )  6 y x   6       x x x      x  Đặ y t u x
;v y ta được hệ phương trình: x   6 2 u
 (u  3v)  9  v  v  3    u   . u v  6     3 u 3 u    27  yx   3
Với u=3;v=3: x
(hệ vô nghiệm)  y  3
Fanpage: Thầy Duy Thành – Tiến sĩ Toán
Vậy hệ phương trình có nghiệm: (x;y)=(0;0).
8. Bài tập tự luyện Bài 1. Bài 6. 3 3 3 1
  x y 19x 3 3 3 8
x y  27 18x   2 2
y xy  6  x 2 2
 4xy  6x y Bài 2. Bài 7. 3
x (2  3y)  8
xy x 1  7y   3
x(y  2)  6 2 2 2
x y xy 1 13x Bài 3. Bài 8. 2
x  2xy x y  0 3 2
x xy  216y   4 2 2 2
x  4x y  3x y  0 2 3
x y y  24x Bài 4. 3 3 3 1
  x y 19x  2 2
y xy  x Bài 5. 2
x 1 y(x y)  4y  2
(x 1)(y x  2)  y