Bộ 10 Đề Kiểm Tra Cuối Kỳ 2 Toán 7 Cấu Trúc Mới 2025 Có Đáp Án Ma Trận Đặc Tả
Trong một ống cắm bút có 1 bút vàng, 1 bút đỏ và 1 bút đen. Lần lượt lấy ra 2 bút từ ống. Gọi A là biến cố: ''Lấy được bút đỏ ở lần thứ nhất''. Hãy nêu tập hợp các kết quả làm cho biến cố A xảy ra? Gieo ngẫu nhiên xúc xắc một lần. Biến cố “Mặt xuất hiện của xúc xắc là mặt ba chấm” có xác suất bằng. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề HK2 Toán 7 234 tài liệu
Môn: Toán 7 2.2 K tài liệu
Tác giả:
Preview text:
thuvienhoclieu.com
ĐỀ KIỂM TRA CUỐI HỌC KỲ II ĐỀ 1 MÔN:TOÁN - LỚP 7
NĂM HỌC: 2025 – 2026
Thời gian làm bài: 90 phút
Phần I. Trắc nghiệm (5,0 điểm) Học sinh trả lời từ Câu 1 đến Câu 20. Mỗi câu
hỏi, học sinh chỉ chọn một phương án và ghi chữ cái đứng trước phương án đó vào bài làm x 4 Câu 1 (NB). Nếu thì ta có: 3 9 4 4 4 A. 4 x B. x C. x D. x 9 9 3 3
Câu 2 (NB). Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức? 8 12 3 6 0, 25 5 1 2 A. và . B. và . C. và . D. và . 12 10 5 10 1, 75 30 1, 5 5
Câu 3 (NB). Biểu thức đại số nào sau đây biểu thị chu vi của một hình chữ nhật có
chiều dài bằng 7(cm) và chiều rộng bằng x (cm)?
A. 7 x.2
B. 7 x : 2 C. 7x.2 D. 7x
Câu 4 (NB). Đa thức nào sau đây là đa thức một biến? A. 2
2x y 5 . B. 3 2
3x 2x x 1.
C. x y z . D. 2
x y y 3 .
Câu 5 (NB). Cho đa thức Q x 6x 6. Nghiệm của đa thức Q x là? A. x 1 B. x 2 . C. x 1 . D. x 2 .
Câu 6 (NB). Cho đa thức một biến Px 2 3
x 3x 5 2x . Cách biểu diễn nào sau đây
là sắp xếp theo lũy thừa tăng của biến?
A. Px 2 3
x 3x 2x 5
B. Px 3 2
2x 3x x 5
C. Px 2 3 5
x 3x 2x
D. Px 3 2 5
x 2x 3x
Câu 7 (TH). Bậc của đa thức P x 4 7 2 7
5x 7x x 3x 7x là? A. Bậc 1 B. Bậc 4 . C. Bậc 7 . D. Bậc 2 .
Câu 8 (TH). Giá trị của đa thức Ax 3 2
x 2x 3x 1 tại x = -1 là
A. -1 B. - 5 C. 1 D. -3
Câu 9 (VD): Cho x x 2 3 2
1 2x 5x 3 . Thương của phép chia đa thức 2
2x 5x 3 cho đa thức x 3 là:
A. x B. 2x C. 2x 1 D. x 3
Câu 10 (NB). Trong một ống cắm bút có 1 bút vàng, 1 bút đỏ và 1 bút đen. Lần lượt
lấy ra 2 bút từ ống. Gọi A là biến cố: ' Lấy được bút đỏ ở lần thứ nhất' . Hãy nêu tập
hợp các kết quả làm cho biến cố A xảy ra?
A. X = {đỏ - vàng, đỏ -
B. X = {đỏ - xanh, đỏ - vàng} đen}
C. X = {đỏ - hồng, đỏ -
D. X = {đỏ - vàng, đỏ - đỏ xanh} đen} Trang 1
Câu 11 (NB). Chọn ngẫu nhiên một số trong tập hợp S = {1; 3; 5; 7; 9}. Biến cố nào
là biến cố chắc chắn?
A. Biến cố A: “Số được chọn là số lẻ” B. Biến cố B: “Số được chọn là số 1”
C. Biến cố C: Số được chọn là số
D. Biến cố D: “Số được chọn là số chẵn” 3”.
Câu 12 (TH). Gieo ngẫu nhiên xúc xắc một lần. Biến cố “Mặt xuất hiện của xúc xắc
là mặt ba chấm” có xác suất bằng 1 1 1 2 A. . B. . C. . D. . 6 3 2 3
Câu 13 (TH): Lớp 7 A có 35 học sinh gồm 16 bạn nam và 17 bạn nữ, chọn ngẫu
nhiên một bạn nam và một bạn nữ để làm lớp trưởng và lớp phó học tập, trong các
biến cố sau đây biến cố nào là biến cố chắc chắn?
A. “Bạn nam làm lớp trưởng và bạn nữ làm lớp phó”.
B. “Bạn nam làm lớp phó và bạn nữ làm lớp trưởng”.
C. “Bạn nam hoặc bạn nữ sẽ làm lớp trưởng”.
D. “Không có bạn nam nào làm lớp trưởng cả”.
Câu 14 (NB). Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ
dài ba cạnh của một tam giác? A. 2c ; m 3c ; m 5cm B. 3c ; m 4c ; m 8cm C. 2c ; m 5c ; m 8cm D. 3c ; m 4c ; m 6cm
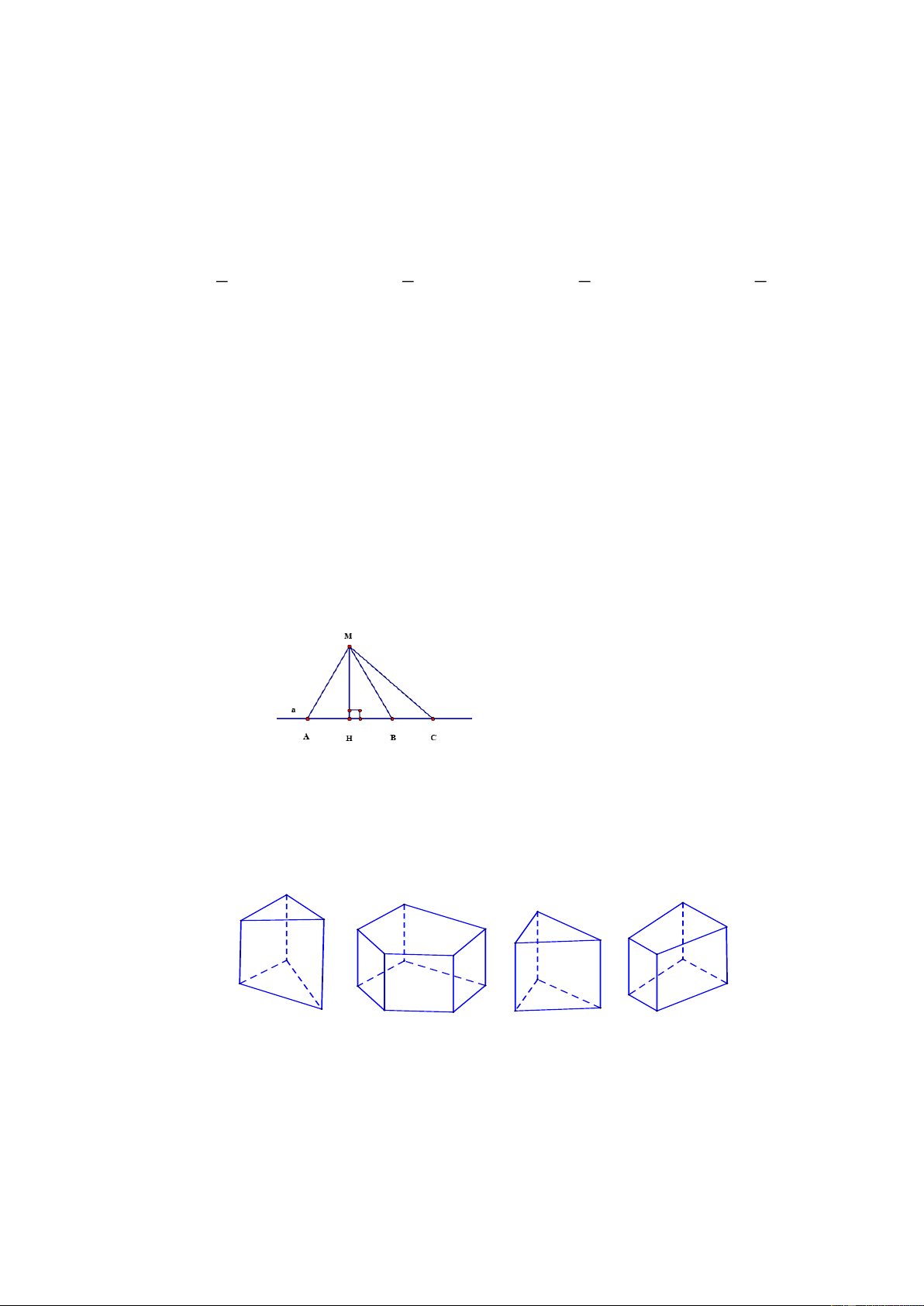
Câu 15 (NB). Đường vuông góc kẻ từ M xuống đường thẳng a là: A. MA B. MH C. MB D. MC
Câu 16 (NB). Cho M NP H
EF . Khi đó ta có:
A. Đỉnh M và đỉnh E là hai đỉnh tương ứng.
B. MN HE
C. MN EF
D. H E
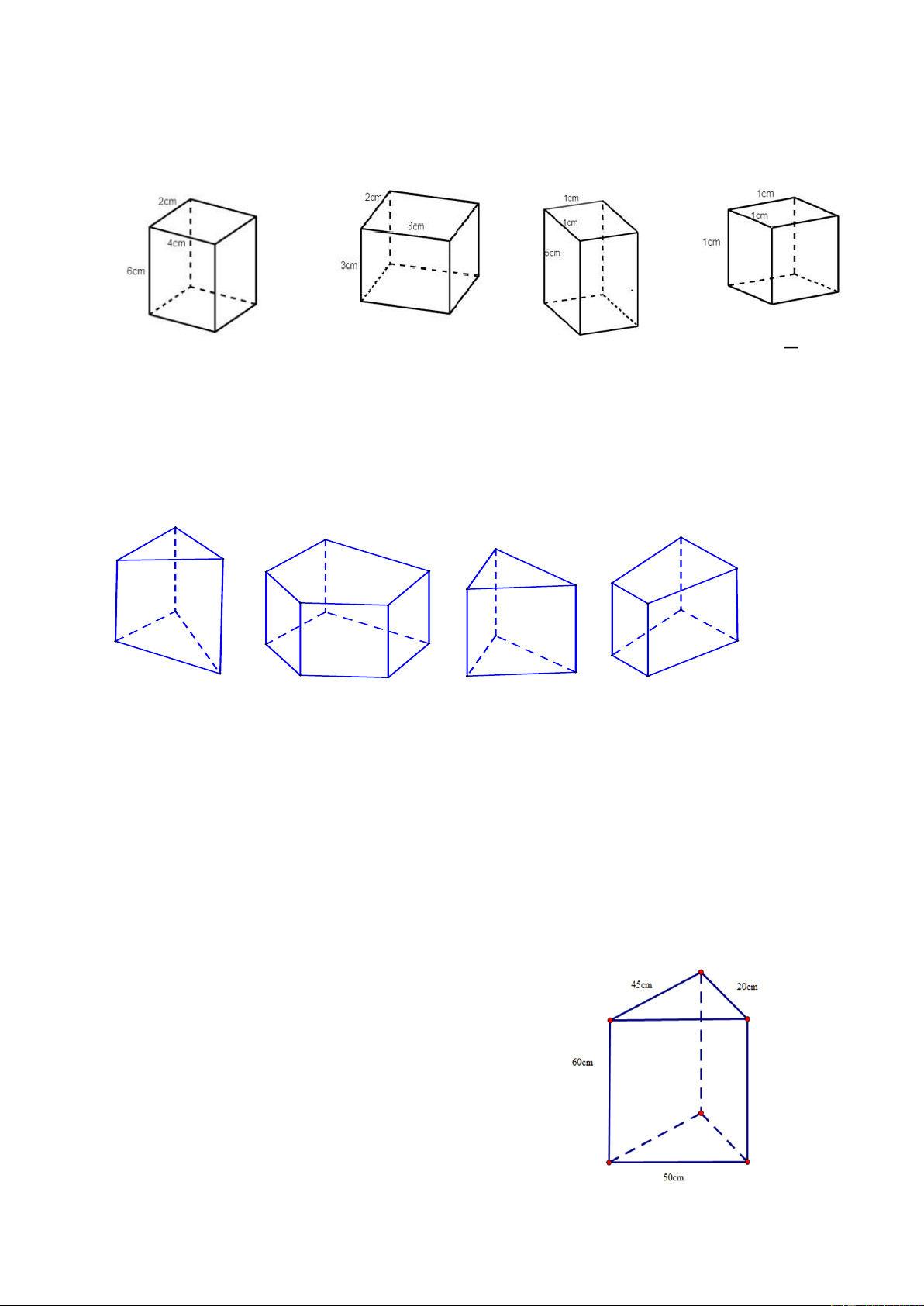
Câu 17 (NB). Trong các hình sau, hình nào là hình lăng trụ đứng tứ giác?
Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 3. B. Hình 2. C. Hình 1. D. Hình 4.
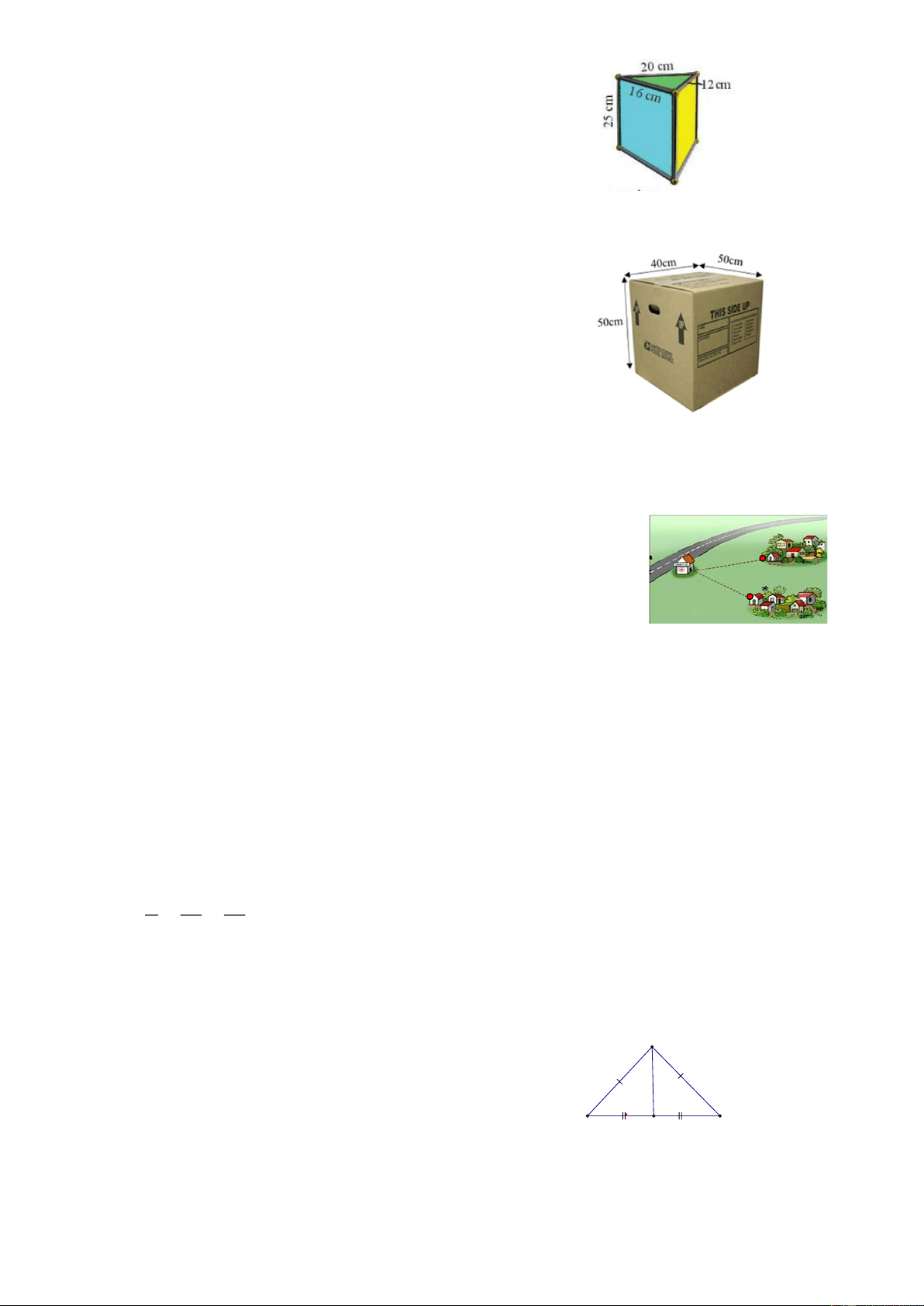
Câu 18 (TH). Một chiếc hộp đèn có dạng hình lăng trụ đứng tam giác có kích thước
như hình 4. Diện tích xung quanh của chiếc hộp là: Trang 2 A. 2 48 cm . B. 3 1200 cm . C. 2 1200 cm . D. 3 73 cm .
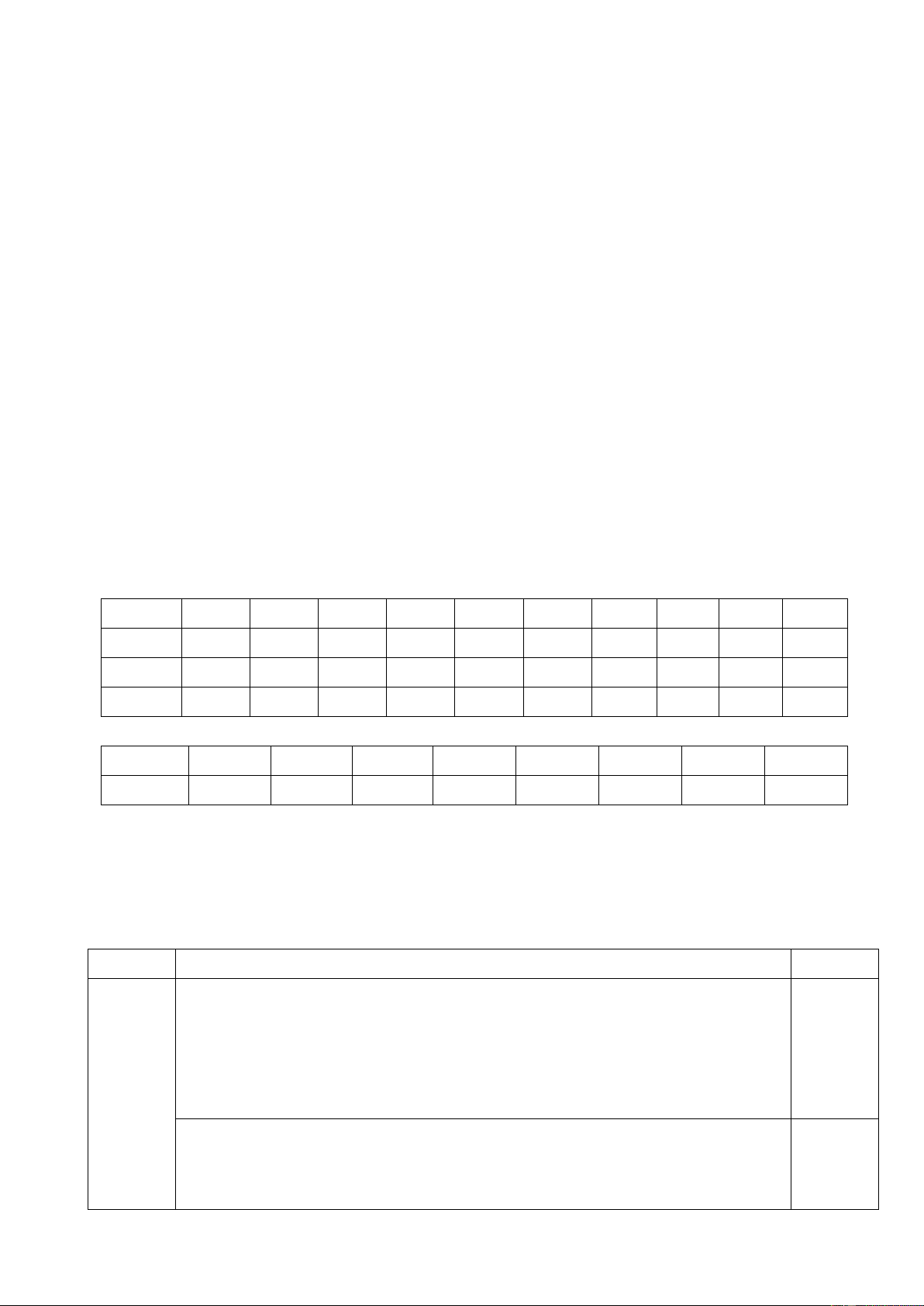
Câu 19 (TH): Một thùng carton có kích thước dài 50cm , rộng 40cm và cao 50cm .
Tính thể tích của thùng carton là : A. 3 100 000 cm B. 3 10 000 cm C. 3 20 000 cm D. 3 25 000 cm
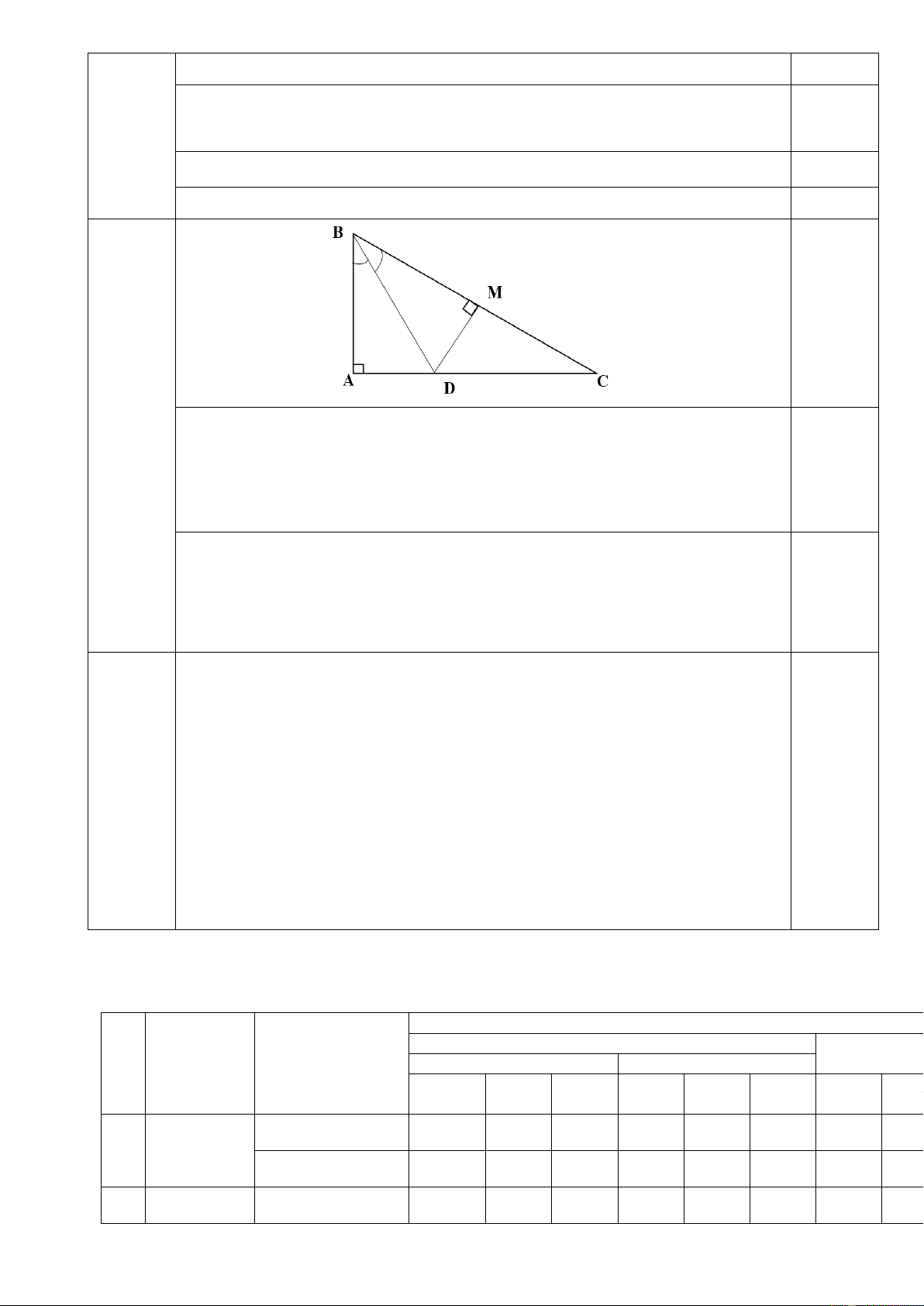
Câu 20 (VD): Một con đường quốc lộ cách không xa hai điểm dân cư A và B (hình
vẽ). Hãy tìm bên đường đó một địa điểm C để xây dựng một trạm y tế sao cho trạm
y tế này cách đều hai điểm dân cư.
A. C nằm trên đường trung trực của đoạn thẳng AB .
B. C nằm trên đường thẳng vuông góc với đoạn thẳng A AB .
C. C nằm trên đường thẳng song song với đoạn thẳng B AB .
D. C nằm trên đường tròn đi qua hai điểm A và B .
Phần II. Câu trắc nghiệm đúng sai (2,0 điểm). Học sinh trả lời từ Câu 21 đến Câu
22. Trong mỗi ý a), b), c), d) ở mỗi câu học sinh chỉ trả lời đúng hoặc sai và ghi chữ
"đúng" hoặc "sai" đó vào bài làm
Câu 21 (VD). Ba đô ̣i máy san đất có số lượng máy cày lần lượt là x, y, z ( máy,
x, y, z 0 ) làm ba khố i lươ ̣ng công viê ̣c như nhau. Đô ̣i thứ nhất hoàn thành công viê ̣c
trong 8 ngày, đô ̣i thứ hai trong 12 ngày và đô ̣i thứ ba trong 16 ngày. Biết rằ ng đô ̣i
thứ nhất có nhiều hơn đô ̣i thứ ba 6 máy. Khi đó x y z A. .
B. 8x 12 y 16z . 8 12 16
C. x y 6 .
D. x 12; y 8; z 6 .
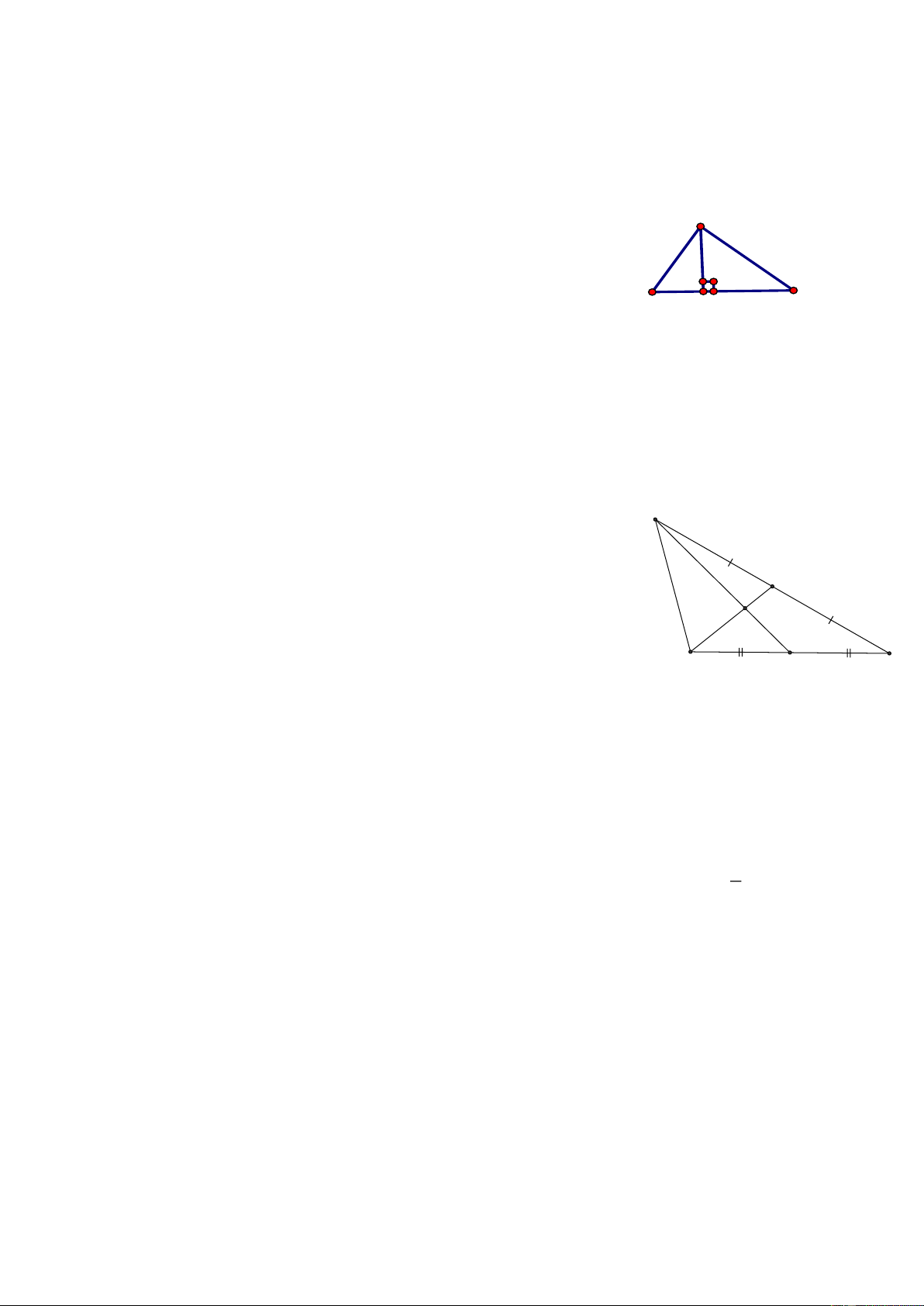
Câu 22 (NB). Gọi I là trung điểm của đoạn thẳng AB, M là điểm không nằm trên AB
sao cho MA = MB (tham khảo hình vẽ). Khi đó: A. M IA M IB. M
B. MI là đường trung trực của đoạn AB. C. MI vuông góc AB. A
D. Tam giác MAB đều I B
Phần III. Tự luận (3,0 điểm) Trang 3
Bài 1 (1,0 điểm). (TH) Cho các đa thức: P x 3 2
4x 7x 3x 12 ; Q x 3 2 4
x 5x 9x 12 và G(x) x
a) Tính P(x) Q(x) ?
b) Tính P(x).G(x) ?
Bài 2 (1,0 đ) Cho ABC
vuông tại A có AB AC , kẻ đường phân giác BD của
ABC, D AC . Kẻ DM vuông góc với BC tại M.
a) (TH) Chứng minh D AB D MB .
b) (VD) Chứng minh AD DC
Bài 3 (VDC). (1,0 điểm) Ba thành phố , A ,
B C trên một bản đồ là ba đỉnh của một
tam giác, trong đó AB 30km, AC 65km.
a) Nếu đặt ở B máy phát sóng có bán kính hoạt động là 34km thì trong hai thành
phố A và C thành phố nào nhận được tín hiệu? Vì sao?
b) Cũng câu hỏi như trên với máy phát sóng có bán kính hoạt động là 110km.
-------------------- HẾT -------------------- HƯỚNG DẪN CHẤM
Phần I. Trắc nghiệm nhiều lựa chọn (5,0 điểm). Mỗi câu đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C B A B A C B C C A Câu 11 12 13 14 15 16 17 18 19 20 Đáp án A A C D B B D C A A
Phần II. Trắc nghiệm câu đúng sai (2,0 điểm). Câu 21A) 21B) 21C) 21Dd) 22A) 22B) 22C) 22D) Đáp án Sai Đúng Sai Đúng Đúng Đúng Đúng Sai
Cách cho điểm câu 9 và câu 10 có tất cả 8 ý trả lời:
HS chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm; lựa chọn chính xác 02
ý được 0,25 điểm; lựa chọn chính xác 03 ý được 0,5 điểm; lựa chọn chính xác cả 04 ý được 1,0 điểm.
Phần III. Tự luận (3,0 điểm) BÀI ĐÁP ÁN ĐIỂM
Cho các đa thức: Px 3 2
4x 7x 3x 12 ; Q x 3 2 4
x 5x 9x 12 và G(x) x
a) Tính P(x) Q(x) ? Bài 1 (1,0đ
b) Tính P(x).G(x) ?
H x P x 3 2 3 2 ( ) (
Q x) (4x 7x 3x 12) ( 4
x 5x 9x 12) 0,25 Trang 4 3 2 3 2
4x 7x 3x 12 4x 5x 9x 12 2 2 x 6x 0,5 Vậy 2 H( ) x 2 x 6x
P(x).G(x) 3 2 (
x 4x 7x 3x 12) 4 3 2
4x 7x 3x 12x 0,25 Bài 2
a) X ét ∆DAB và ∆DMB có: (1,0đ) 0
A M 90 , ABD MBD (gt) 0,5 Ca ̣nh BD chung Vâ ̣y D AB D
MB (ca ̣nh huyền – góc nhọn)
b) Từ phần a ta có: D AB D
MB nên AD MD ( Hai cạnh tương ứng bằng nhau ). ; (1) 0,5 Vì D
MC vuông tại M nên DC DM ; (2)
Từ (1) và (2) suy ra AD DC .
Xét tam giác ABC, theo bất đẳng thức tam giác ta có:
AC AB BC AB AC 0,25
65 30 BC 65 30 35 BC 95 0,25 Bài 3
a) Nếu máy phát sóng ở B có bán kính hoạt động bằng 34km thì ở (1,0đ)
A nhận được tín hiệu ( vì 34km 30km ), còn ở C không nhận 0,25 đượ
c tín hiệu (vì 34km 35km BC )
b) Nếu máy phát sóng ở B có bán kính hoạt động bằng 110km thì ở 0,25
cả A và C đều nhận được tín hiệu.
KHUNG MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II - MÔN TOÁN 7
Mức độ đánh giá
Trắc nghiệm khách quan Chủ Nội dung/Đơn vị Tự luận TT đề/Chương Nhiều lựa chọn Đúng/Sai kiến thức Vận Vận Biết Hiểu Biết Hiểu Biết Hiểu dụng dụng
Chủ đề 1: Số Tỉ lệ thức và dãy tỉ số 2 bằng nhau (C1,2) 1 thư ̣c
Giải toán về đại 1
lượng tỉ lệ (C21) 1 2 Chủ đề 2:
Biểu thức đại số (C3) Trang 5 Biểu thức đại 3 2 1 1 số
Đa thức một biến (C4,5,6) (C7,8) (C9) (B1)
Tam giác. Tam giác
bằng nhau. Tam giác
cân. Quan hệ giữa 3 1 1 Chủ đề 3:
đường vuông góc và (C14,15, (C22)
đường xiên. (B2a) Các 16) Các hình
đường đồng quy của 3 hình ho ̣c cơ
tam giác bản
Giải bài toán có nội
dung hình học và
vận dụng giải quyết 1
vấn đề thực tiễn liên (C20)
quan đến hình học Chủ đề 4:
Hình hộp chữ nhật 1 Các hình
và hình lập phương (C19) 4 khối trong
Lăng trụ đứng tam thực tiễn 1 1
giác, lăng trụ đứng (C17) (C18) tứ giác
Làm quen với biến Chủ đề 5:
cố ngẫu nhiên. Làm 2 Một số yếu
quen với xác suất 2 5 (C12, tố xác suất
của biến cố ngẫu (C10, 11) 13)
nhiên trong một số ví
dụ đơn giản Tổng số câu 12 6 2 1 1 2 Tổng số điểm 5,0 2,0 3,0 Tỷ lệ % 50% 20% 30%
KHUNG BẢN ĐẶC TẢ ĐỀ KIỂM TRA HỌC KỲ II - MÔN TOÁN 7
Số câu hỏi/ý hỏi ở các mức độ đánh giá Trắc nghiệm khách quan Chủ Nội dung/Đơn TT đề/Chương Yêu cầu cần đạt Nhiều lựa chọn Đúng/Sai vị kiến thức Vận Biết Hiểu Biết Hiểu dụng - Nhâ ̣n biết: – Tỉ lệ thức và
Nhận biết đươ ̣c tỉ lệ 2 TN
thức và các tính chất của 1 dãy tỉ số bằng tỉ lệ thức. (C1,2) nhau –
Nhận biết đươ ̣c dãy tỉ số bằng nhau. Chủ đề 1: Vâ ̣n du ̣ng: Số thư ̣c
– Giải đươ ̣c một số bài toán đơn giản về
Giải toán về đại đại lượng tỉ lệ nghịch
lượng tỉ lệ
(ví dụ: bài toán về thời gian hoàn thành kế hoạch và năng suất lao động,...). Nhâ ̣n biết: Chủ đề 2:
– Nhận biết được biểu 1 TN 2 Biểu thức đại
Biểu thức đại số thức số. (C3) số Vâ ̣n du ̣ng: Trang 6
– Tính được giá trị của
một biểu thức đại số. Nhâ ̣n biết:
– Nhận biết đươ ̣c định nghĩa đa thức một biến.
– Nhận biết đươ ̣c cách
biểu diễn đa thức một biến;
– Nhận biết được khái niệm nghiệm của đa thức một biến. Thông hiểu:
– Xác định được bậc của đa thức một biến. 3TN
Đa thức một biến 2 TN 1 TN Vận dụng: (C4,5,6) (C7,8) (C9) – Tính được giá trị của đa thức khi biết giá trị của biến.
– Thực hiện được các phép tính: phép cộng, phép trừ, phép nhân, phép chia trong tập hợp các đa thức một
biến; vâ ̣n dụng được những tính chất của các phép tính đó trong tính toán. Nhận biết:
– Nhâ ̣n biết được liên hệ về độ dài của ba cạnh trong một tam giác.
– Nhận biết đươ ̣c khái niệm hai tam giác bằng nhau.
– Nhận biết đươ ̣c khái niệm: đường vuông Tam giác. Tam
giác bằng nhau. góc và đường xiên; Tam giác cân. khoảng cách từ một Chủ đề 3:
Quan hệ giữa
điểm đến một đường 3 TN Ca 1 TN 3 ́ c hình
đường vuông góc thẳng. (C14, 15, hình ho ̣c cơ
và đường xiên. – (C22) Nhâ ̣n biết đươ ̣c 16) bản
Các đường đồng đường trung trực của
quy của tam giác mô ̣t đoa ̣n thẳng và
tính chất cơ bản của đường trung trực.
– Nhâ ̣n biết được: các
đường đă ̣c biê ̣t trong tam giác (đường trung tuyến, đường cao, đường phân giác,
đường trung trực); sự đồng quy của các đường đặc biệt đó. Trang 7 Thông hiểu:
– Giải thích được quan hệ giữa đường vuông góc và đường xiên dựa trên mối quan hệ giữa cạnh và góc đối trong tam giác
(đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại).
– Giải thích được các
trường hợp bằng nhau của hai tam giác, của hai tam giác vuông. Vận dụng:
– Diễn đạt được lâ ̣p luâ ̣n và chứng minh hình ho ̣c trong những
trường hợp đơn giản (ví dụ: lập luận và
Giải bài toán có chứng minh được các
nội dung hình đoạn thẳng bằng nhau,
học và vận dụng các góc bằng nhau từ
giải quyết vấn đề các điều kiện ban đầu 1 TN
thực tiễn liên liên quan đến tam (C20)
quan đến hình giác,...). học Vận dụng cao:
– Giải quyết được một
số vấn đề thực tiễn
(phức hợp, không quen
thuộc) liên quan đến
ứng dụng của hình học
như: đo, vẽ, ta ̣o dựng các hình đã học. Nhận biết
Mô tả được mô ̣t số yếu
tố cơ bản (đỉnh, ca ̣nh,
góc, đường chéo) của hình hộp chữ nhật và hình lâ ̣p phương. Thông hiểu Chủ đề 4:
– Giải quyết được mô ̣t
Hình hộp chữ Ca
số vấn đề thực tiễn gắn 1 TN ́ c hình khối trong
nhật và hình lập với việc ti phương ́nh thể tích, (C19) thực tiễn diê ̣n tích xung quanh
của hình hộp chữ nhật,
hình lập phương (ví dụ:
tính thể tích hoặc diê ̣n tích xung quanh của một
số đồ vật quen thuộc có
dạng hình hộp chữ nhật, hình lập phương,...). Nhận biết
Lăng trụ đứng
– Mô tả được hình lăng 1 TN 1 TN
tam giác, lăng
tru ̣ đứng tam giác, hình (C17) (C18)
trụ đứng tứ giác lăng tru ̣ đứng tứ giác (ví
dụ: hai mặt đáy là song Trang 8
song; các mặt bên đều là hình chữ nhật, ...). Thông hiểu
– Tính được diện tích xung quanh, thể tích của hình lăng trụ đứng tam
giác, hình lăng trụ đứng tứ giác. Nhận biết:
– Làm quen với các khái
niệm mở đầu về biến cố Làm quen với
ngẫu nhiên và xác suất
biến cố ngẫu
của biến cố ngẫu nhiên Chủ đề 5:
nhiên. Làm quen trong các ví dụ đơn giản. 2 TN 2 TN Một số yếu
với xác suất của Thông hiểu: (C10, (C12, tố xác suất
biến cố ngẫu
– Nhận biết được xác 11) 13)
nhiên trong một
suất của một biến cố
số ví dụ đơn giản ngẫu nhiên trong một số
ví dụ đơn giản (ví dụ: lấy bóng trong túi, tung xúc xắc,...). Tổng số câu 12 6 2 1 Tổng số điểm 5 2 Tỷ lệ % 50% 20% thuvienhoclieu.com
ĐỀ KIỂM TRA CUỐI HỌC KỲ II ĐỀ 2 MÔN:TOÁN - LỚP 7
NĂM HỌC: 2024 – 2025
Thời gian làm bài: 90 phút
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. (Học sinh
trả lời câu hỏi từ câu 1 tới câu 20. Mỗi câu chọn 1 phương án đúng nhất)
Câu 1: (NB) Từ đẳng thức 8.6 = 4.12 ta lập được tỉ lệ thức là 12 6 A. 8 12 B. 4 8 C. 4 12 D. 4 8 4 6 12 6 8 6
Câu 2: (NB) Từ đẳng thức a.b = c.d với a, b, c, d 0 lập được nhiều nhất là mấy tỉ lệ thức? A. 4 B. 2 C. 6 D. 3 Câu 3: (TH) Với , a , b , c d Z; ,
b d 0;b d . Kết luận nào sau đây là đúng? a c a c a c a c A. . B. . b d b d b d d b a c a c a c a c C. . D. . b d b d b d b d a b c Câu 4: (TH) Cho
; a + b + c = 30 thì : 4 5 6
A. a = -8 ; b = -10 ; c = -12
B. a = 8 ; b = 12 ; c = 10
C. a = - 8 ; b = - 12 ; c = - 10
D. a = 8 ; b = 10 ; c = 12 Trang 9
Câu 5: (TH) Cho x và y là hai đại lượng tỉ lệ thuận. Biết khi x 5 thì y 10 . Hệ số tỉ lệ là A. -2 B. 50. C. 2. D. -50
Câu 6: (TH) Số điểm 10 trong kì kiểm tra học kì I của ba bạn Giang, Hoài , Thương
tỉ lệ với 3 ; 1 ;2 . Số điểm 10 của cả ba bạn đạt được là 12 . Số điểm 10 của bạn Giang đạt được là A. 6 B. 7 C. 8 D. 9
Câu 7: (NB) Có bao nhiêu đơn thức trong các biểu thức sau: 2x ; 8 4x ; 6 5x ; 1
5xy ; 3x ? 1 A. 3. B. 4. C. 1. D. 5.
Câu 8: (NB) Đa thức nào là đa thức một biến? A. 2
27x y 3xy 15. B. 3 2
x 6x 9 . C. 3
8x y 8 . D. 3
yz 2x y 5 .
Câu 9: (NB) Biểu thức biểu thị chu vi của hình chữ nhật có chiều dài 6cm và chiều rộng 5cm là
A. 5+6cm. B. 2.6 5 cm. C. 5.2 6 cm. D. 5 6.2 cm.
Câu 10: (TH) Bậc của đa thức 3 2
x 3x 4x 5 là A. 1. B. 2. C. 9 . D. 3
Câu 11: (TH) Hệ số tự do của đa thức 3 2
4x 6x 3x 11 là
A. 4. B. - 11. C. 11. D. 3.
Câu 12: (NB) Biến cố không thể có xác suất bằng bao nhiêu?
A. Bằng 1; B. Bằng 0;
C. Bằng 1 ; D. Một số bất kì. 2
Câu 13: (NB) Một hộp bút màu có nhiều màu: màu cam, màu vàng, màu đỏ, màu
hồng, màu xanh. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?
A. 3. B. 4. C. 2. D. 5.
Câu 14: (NB) Cho hình vẽ, chọn câu đúng? A
A. Đường vuông góc kẻ từ A đến MQ là AI
B. Đường vuông góc kẻ từ A đến MQ là AN
C. Đường xiên kẻ từ A đến MQ là AI
D. Đường vuông góc kẻ từ A đến MQ là AP . M N I P Q
Câu 15: (NB) Hãy chọn khẳng định sai. Hình hộp chữ nhật ABCD.A'B'C'D' có: Trang 10 A. 8 đỉnh; B. 4 mặt bên; C. 6 cạnh; D. 6 mặt.
Câu 16: (NB) Trong các hình hộp dưới đây hình nào là hình lập phương? A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 Hình 1 Hình 2 Hình 3 Hình 4 a
Câu 17: (TH) Hìn h hộp chữ nhật có ba kích thước lần lượt là 2a ; 3a ; . Thể 3
tích của hình hộp chữ nh ật đó là: A. 2 a . B. 2 4a . C. 2 2a . D. 3 2a .
Câu 18: (NB) Trong các hình sau, đâu là hình lăng trụ đứng tam giác?
A. Hình 3. B. Hình 2. C. Hình 1. D. Hình 4.
Hình 1 Hình 2 Hình 3 Hình 4
Câu 19: (NB) Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
B. Các mặt bên của hình lăng trụ đứng là các hình thang cân.
C. Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật.
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác.
Câu 20: (TH) Cho hình lăng trụ đứng tam giác với hai đáy là hai tam giác và các
kích thước như hình vẽ. Diện tích xung quanh của hình lăng trụ đứng tam giác đó bằng?
A. 7 200 cm2; B. 6 900 cm2;
C. 6 250 cm2; D. 7 900 cm2. Trang 11
PHẦN II. TRẮC NGHIỆM ĐÚNG/SAI. Thí sinh trả lời câu hỏi từ câu 1 và câu 2.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Bốn khối 6, 7, 8, 9 của trường lao động trồng cây đầu năm. Tổng số cây trồng
được là 72 cây. Mỗi lớp trồng được số cây theo tỉ lệ là 3: 4: 5: 6. Gọi số cây mỗi khối
trồng được lần lượt là a,b, c, d (cây).
a) a b c d 72
b) Mỗi lớp trồng được số cây theo tỉ lệ là 3: 4: 5: 6 nên ta có: 3a 4b 5c 6d
a b c d 72
c) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: 4 3 4 5 6 18
d) Số cây mỗi khối 9,8,7,6 trồng được lần lượt là: 12 cây, 16 cây, 20 cây, 24 cây. Câu 2. Cho A
BC có AB 4c ;
m AC 1cm. Khi đó ta có:
a) Góc đối diện với cạnh AB là C b) B C c) BC 5cm d) Chu vi A
BC nhỏ hơn 10cm.
PHẦN III. TỰ LUẬN
Câu 1. ( 1 điểm ): Cho A x 2 3
x 4x 1
a, Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b, Tìm B(x) biết A x B x 2 3
x 5x 4
Câu 2. ( 1,5 điểm ): Cho M NP cân tại M µ 0
M 90 . Kẻ NH MP HMP , PK MN KMN . NH và PK cắt nhau tại E. a) Chứng minh N HP P KN b) Chứng minh ENP cân.
Câu 3. (0,5 điểm ): Cho đa thức A (x) = 2
x 2x 2 . Chứng minh đa thức không có nghiệm.
MA TRẬN ĐỀ KIỂM TRA ĐỊNH KỲ MÔN TOÁN 7 – CUỐI HỌC KÌ II
Mức độ đánh giá
Trắc nghiệm khách quan Chủ Nội dung/Đơn vị Tự luận TT đề/Chương Nhiều lựa chọn Đúng/Sai kiến thức Vận Vận Biết Hiểu Biết Hiểu Biết Hiểu dụng dụng Chủ đề 1: Tỉ lệ thức và tính 2 2 1 Tỉ lệ thức chất của dãy tỉ số 0,5 0,5 Trang 12 và đại bằng nhau.
lượng tỉ lệ Giải toán về đại 2 ¼ 2/4 ¼ lượng tỉ lệ. 0,5 0,25 0,5 0,25 Chủ đề 2: Biểu thức đại số 1 Biểu thức 0,25 2 đại số và Đa thức một biến đa thức 2 2 1/2 một biến 0,5 0,5 0,5 Làm quen với biến cố ngẫu nhiên. Làm quen Chủ đề 3: 2 với xác suất của Biến cố biến cố 0,5 ngẫu nhiên trong một số ví dụ đơn giản Tam giác. Tam Chủ đề 3 giác bằng nhau. Tam giác Tam giác cân. bằng nhau Quan hệ giữa 1 ¼ 2/4 ¼ 3 và các yếu đường vuông góc 0,25 0,25 0,5 0,25 tố liên và đường xiên. quan Các đường đồng quy của tam giác Hình hộp chữ
Chủ đề 4: nhật và hình lập 2 1 Một số phương. 0,5 0,25 4 hình khối Hình lăng trụ
trong thực đứng tam giác, tứ 2 1 tiễn 0,5 0,25 giác. Tổng số câu Tổng số điểm 5 2 3 Tỷ lệ % 50% 20% 30%
BẢN ĐẶC TẢ ĐỀ KIỂM TRA ĐỊNH KỲ MÔN TOÁN 7 – CUỐI HỌC KÌ II
Số câu hỏi/ý hỏi ở các mức độ đánh giá Nội
Trắc nghiệm khách quan Chủ TT dung/Đơn vị đề/Chương
Yêu cầu cần đạt Nhiều lựa chọn Đúng/Sai kiến thức Vận Biết Hiểu Biết dụng
Tỉ lệ thức và - Biết: Nhận biết đươ ̣c
tính chất của tỉ lệ thức và các tính
dãy tỉ số chất của tỉ lệ thức. bằng nhau.
Nhận biết được dãy tỉ số bằng nhau. Chủ đề 1: 2
- Hiểu: Hiểu đươ ̣c tính 2 Tỉ lệ thức 1
chất của tỉ lệ thức trong và đại lượng tỉ lệ
giải toán. Hiểu đươ ̣c
tính chất của dãy tỉ số bằng nhau trong giải toán
Giải toán về - Biết: Lập biểu thức mối ¼ đại lượng tỉ 2
liên hệ giữa các đại lượng. 0,25 Trang 13 lệ.
- Hiểu: Mối quan hệ giữa
các đại lượng tỉ lệ.
-Vận dụng: Giải đươ ̣c một số bài toán đơn
giản về đại lượng tỉ lệ thuận, nghịch Biểu thức Nhận biết: đại số
– Nhận biết được biểu 1 thức số.
Đa thức một Nhâ ̣n biết: biến
– Nhận biết được định
nghĩa đa thức một biến.
– Nhận biết được cách
biểu diễn đa thức một biến;
– Nhận biết được khái niệm nghiệm của đa thức một biến. Thông hiểu: Chủ đề 2:
– Xác định được bậc, Biểu thức
hệ số của đa thức một 2 đại số và biến. đa thức một biến Vâ ̣n du ̣ng: 2 2
– Tính được giá trị của
đa thức khi biết giá trị của biến.
– Thực hiện được các phép tính: phép cộng, phép trừ, phép nhân, phép chia trong tập hợp các đa thức một
biến; vâ ̣n dụng được những tính chất của các phép tính đó trong tính toán. Tìm nghiệm của đa thức. Làm quen với biến cố Nhận biết:
ngẫu nhiên. – Làm quen với các Làm quen Chủ đề 3:
với xác suất khái niệm mở đầu về Một số yếu
của biến cố biến cố ngẫu nhiên và 2 tố xác suất
xác suất của biến cố ngẫu nhiên
trong một số ngẫu nhiên trong các ví dụ đơn giản ví dụ đơn . giản Chủ đề 4. ¼ 3 Tam giác. Nhận biết: 1 Tam giác 0,25 Trang 14 bằng nhau Tam giác
– Nhận biết được khái và các yếu
bằng nhau. niệm: đường vuông tố liên Tam giác góc và đường xiên; quan
cân. Quan hệ khoảng cách từ một
giữa đường điểm đến một đường
vuông góc và thẳng.
đường xiên. – Nhâ ̣n biết được: các
Các đường đường đă ̣c biê ̣t trong đồng quy tam giác (đường trung
của tam giác tuyến, đường cao,
đường phân giác, đường
trung trực); sự đồng quy
của các đường đặc biệt đó. Thông hiểu:
– Giải thích được các
trường hợp bằng nhau của hai tam giác, của hai tam giác vuông.
– Mô tả được tam giác
cân và giải thích được
tính chất của tam giác cân (ví dụ: hai cạnh bên bằng nhau; hai góc đáy bằng nhau). Vận dụng:
– Diễn đạt được lâ ̣p luâ ̣n và chứng minh hình ho ̣c trong những
trường hợp đơn giản (ví dụ: lập luận và chứng minh được các đoạn thẳng bằng nhau, các góc bằng nhau từ
các điều kiện ban đầu liên quan đến tam giác,...).
– Giải quyết được một
số vấn đề thực tiễn (đơn giản, quen
thuộc) liên quan đến
ứng dụng của hình học
như: đo, vẽ, ta ̣o dựng các hình đã học. Chủ đề 5: Hình
hộp Nhận biết 4 Một số
chữ nhật và Mô tả được mô ̣t số yếu 2 1 hình khối hình
lập tố cơ bản (đỉnh, ca ̣nh, Trang 15 trong thực phương.
góc, đường chéo) của tiễn hình hộp chữ nhật và hình lâ ̣p phương. Thông hiểu
– Giải quyết được mô ̣t
số vấn đề thư ̣c tiễn gắn
với việc tính thể tích, diê ̣n tích xung quanh
của hình hộp chữ nhật, hình lập phương (ví
dụ: tính thể tích hoặc diê ̣n tích xung quanh
của một số đồ vật quen
thuộc có dạng hình hộp chữ nhật, hình lập phương,...). Hình lăng Nhận biết trụ đứng
– Mô tả được hình lăng tam giác, tứ
tru ̣ đứng tam giác, hình giác.
lăng tru ̣ đứng tứ giác
(ví dụ: hai mặt đáy là song song; các mặt bên đều là hình chữ nhật, ...). 2 1 Thông hiểu
– Tính được diện tích xung quanh, thể tích
của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác. Tổng số câu Tổng số điểm 5 2 Tỷ lệ % 50% 20% thuvienhoclieu.com
ĐỀ KIỂM TRA CUỐI HỌC KỲ II ĐỀ 3 MÔN:TOÁN - LỚP 7
NĂM HỌC: 2024 – 2025
Thời gian làm bài: 90 phút
I. TRẮC NGHIỆM (7,0 điểm). Chọn phương án trả lời đúng của mỗi câu hỏi sau:
Câu 1. (NB)Từ đẳng thức 8.6 = 4.12 ta lập được tỉ lệ thức là 12 6 8 12 4 8 4 12 A. B. C. D. 4 8 4 6 12 6 8 6
Câu 2. (NB) Cho x, y là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ 2. Công thức biểu
diễn y theo x là Trang 16 2 x 1 A. y . B. y . C. y . x y x x 2 D. 2 . 2
Câu 3. (TH) Cho x và y tỉ lệ nghịch với nhau. Khi x 4 thì y 12 thì hệ số tỉ lệ bằng A. 3. B. 48. C. 4. D. 12.
Câu 4.( NB) Trong các biểu thức sau , biểu thức nào là đơn thức : A. 5x – 3 B. -4(x + y)3 C. -8 (x + y) D. 2022
Câu 5. (NB) Hệ số tự do của đa thức 3 2
4x 6x 3x 11 là A. 4. B. - 11. C. 11. D. 3.
Câu 6.(NB) Bậc của đa thức - 5x4y2 + 6x2y2 + 5y8 +1 là A. 8 B. 6 C. 5 D. 4
Câu 7.(TH) Kết quả của phép chia đa thức 3 2
8x 4x 2x cho 2x là A. 2 4x 2x 1. B. 2 4x 2x 1. C. 2 4
x 2x 1. D. 2 4x 2x 1.
Câu 8. (TH): Cho hai đa thức f(x) = 5x4 + x3 – x2 + 1 và g(x) = –5x4 – x2 + 2.
Tính h(x) = f(x) + g(x) và tìm bậc của h(x). Ta được:
A. h(x)= x3 – 1 và bậc của h(x) là 3
B. h(x)= x3 – 2x2 +3 và bậc của h(x) là 3
C. h(x)= x4 +3 và bậc của h(x) là 4
D. h(x)= x3 – 2x2 +3 và bậc của h(x) là 5
Câu 9. (TH): Sắp xếp đa thức 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
A. 6x3 + 5x4 – 8x6 – 3x2 + 4
B. –8x6 + 5x4 –3x2 + 4 + 6x3
C. –8x6 + 5x4 +6x3 + 4 –3x2
D. –8x6 + 5x4 +6x3 –3x2 + 4
Câu 10. (NB)Một hộp bút màu có nhiều màu: màu xanh, màu vàng, màu đỏ, màu
đen, màu hồng, màu cam. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả? A. 3. B. 4. C. 5. D. 6.
Câu 11. (NB)Sau khi gieo một con xúc xắc 10 lần liên tiếp thì thấy mặt 4 chấm xuất hiện
3 lần. Khi đó xác suất xuất hiện mặt 4 chấm là 4 3 7 3 A. . B. . C. . D. . 10 10 10 14
Câu 12 (TH): Chon ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn
được số chia hết cho 5 là: A. 0 B. 1 C. 2 D.4
Câu 13 (TH). Hoa và Mai mỗi người gieo một con xúc xắc. Xác suất hiệu giữa số
chấm xuất hiện trên hai con xúc xắc bằng 6 là: A. 0 B. 1 C. 2 D. 3 Trang 17
Câu 14 : (TH) Cho ABC cân tại A, có 0
BAC 50 khi đó ABC bằng A. 400 B. 500 C. 650 D. 550.
Câu 15.(TH) Cho tam giác nhọn ABC có B C . Kẻ AH vuông góc với BC tại H. Khi đó ta có
A. AC > AH > AB. A B. AH > AB > AC. C. AB > AC > AH D. AC > AB > AH B C H
Câu 16.(VD) Cho ΔABC có: µ
A = 350 . Đường trung trực của AC cắt AB ở D. Biết
CD là tia phân giác của · ACB . Số đo các góc · · ABC; ACB là: · 0 · · 0 ·
A. ABC = 72 ; ACB = 730
B. ABC = 73 ; ACB = 720 · 0 · · 0 ·
C. ABC = 75 ; ACB = 700
D. ABC = 70 ; ACB = 750
Câu 17.(VD) Cho hình vẽ sau.
Biết MG = 3cm. Độ dài đoạn thẳng MR bằng: M A. 4,5 cm S B. 2 cm G C. 3 cm D. 1 cm P N R
Câu 18(NB): Hãy chọn câu sai. Hình hộp chữ nhật ABCD. A'B'C'D' có: A. 6 cạnh B. 12 cạnh C. 8 đỉnh D. 6 mặt
Câu 19. (TH)Một bể cá cảnh có dạng hình hộp chữ nhật với các kích thước của đáy
dưới là 4cm, 5cm và chiều cao là 12cm . Thể tích của bể cá đó là A. 240cm3 B. 108cm3. C. 216cm3. D. 120cm3 a
Câu 20(NB): Hình hộp chữ nhật có ba kích thước lần lượt là: a, 2a, thể tích của 2
hình hộp chữ nhật đó là: A. 4a3. B. 3a3. C. 2a3. D. a3.
2. Dạng 2. Câu trắc nghiệm đúng sai (2 điểm). Thí sinh trả lời câu 21, 22. Trong
mỗi ý a).b).c).d) ở mỗi câu thí sinh chọn đúng hoặc sai.
Câu 21: Cho tam giác ABC vuông tại A có BD là tia phân giác, kẻ DE vuông góc với
BD ( E thuộc BC ). Gọi F là giao điểm của AB và DE . Khi đó ta có: Trang 18
a) BD là đường trung trực của AE . b) DF DC c) AD DC d) AE FC
Câu 22. Gieo một con xúc xắc sáu mặt cân đối. Khi đó ta có:
A : Biến cố “Mặt xuất hiện có số chấm nhỏ hơn 8 ”. là biến cố chắc chắn.
B : Biến cố “Mặt xuất hiện có số chấm chia hết cho 7 ” là biến cố ngẫu nhiên
C : Biến cố “Mặt xuất hiện có số chấm lớn hơn 3 ” là biến cố không thể
D : Biến cố “Mặt xuất hiện có số chấm nhỏ hơn 4 ” là biến cố ngẫu nhiên.
B. PHẦN TỰ LUẬN (3,0 điểm) x y
Bài 1(TH). (0,5 điểm) Tìm hai số x và y, biết: và x - y = -15 9 4
Bài 2(VD). (0,5 điểm) Trong một buổi lao động trồng cây, ba bạn Bình, An và Toàn
trồng được số cây tỉ lệ với các số 5; 3; 4. Tính số cây mỗi bạn trồng được, biết tổng
số cây trồng được của ba bạn là 48 cây.
Bài 3 (1,5 điểm).
Cho tam giác ABC vuông tại A có AB = 6cm; BC = 10 cm; AC = 8cm.
a) (TH) So sánh các góc của tam giác ABC.
b) (VD) Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng
BD. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AC tại M. Tính MC.
c) (VD) Đường trung trực d của đoạn thẳng AC cắt đường thẳng DC tại Q. Chứng
minh ba điểm B, M, Q thẳng hàng.
Bài 4 (VDC). (0,5 điểm) Cho hai đa thức sau: f(x) = ( x-1)(x+2) g(x) = x3 + ax2 + bx + 2
Xác định a và b biết nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x). HƯỚNG DẪN CHẤM I. TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 Trang 19 Đáp án B D B D B A A B D D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án B A A C D C A A A D
2. Dạng 2. Câu trắc nghiệm đúng sai
Biểu điểm mỗi câu
- HS đúng 01 ý đa ̣t 0,1 điểm.
- HS đúng 02 ý đa ̣t 0,25 điểm.
- HS đúng 0,3 ý đa ̣t 0,5 điểm.
- HS đúng 04 ý đa ̣t 1 điểm. ý Câu a b c d 21 Đúng Sai Sai Sai 22 Đúng Sai Sai Đúng
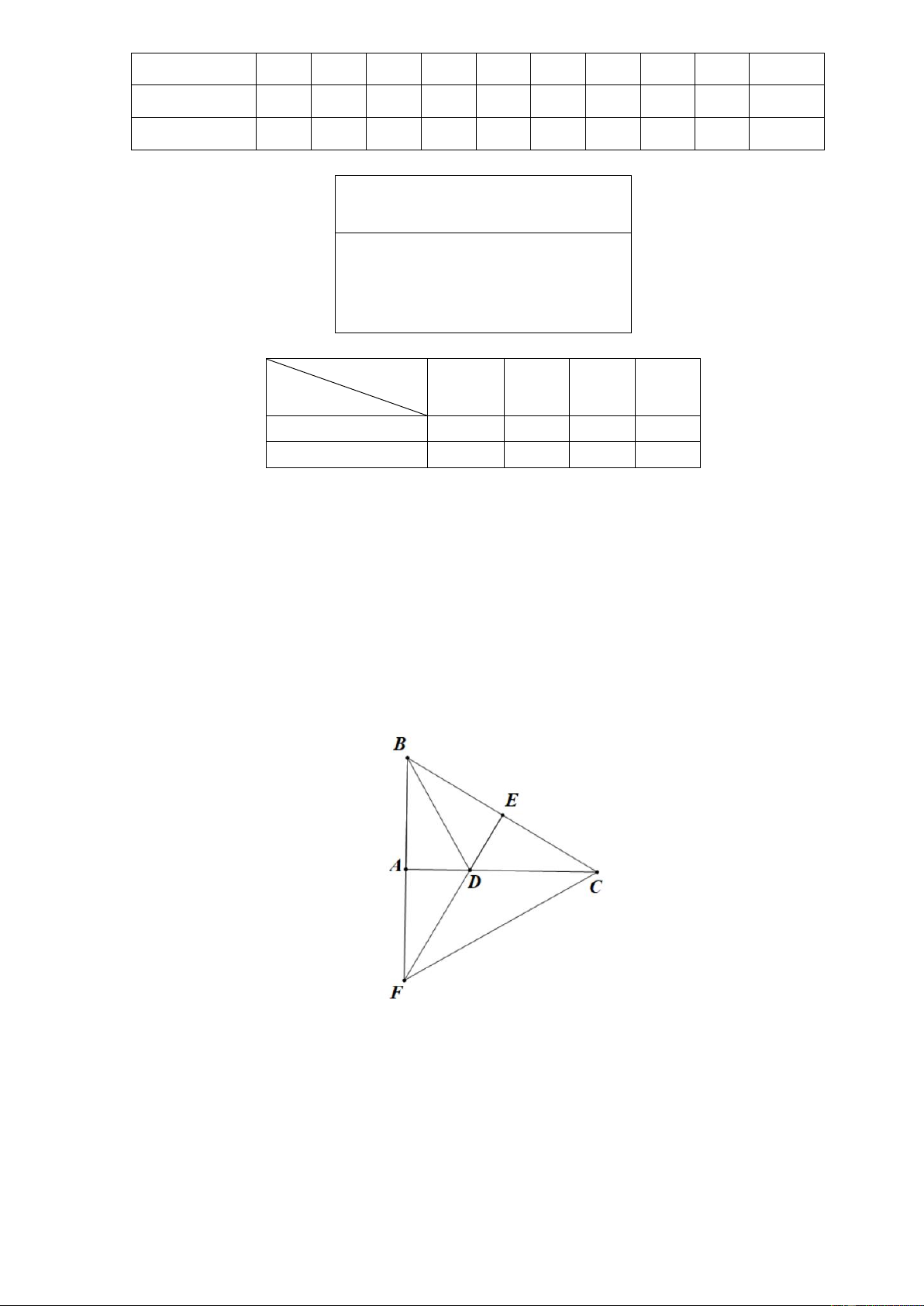
Câu 21: Cho tam giác ABC vuông tại A có BD là tia phân giác, kẻ DE vuông góc với BD ( E
thuộc BC ). Gọi F là giao điểm của AB và DE . Khi đó ta có:
a) BD là đường trung trực của AE . b.) DF DC , c) AD DC d) AE FC Lời giải a. Chứng minh A BD E
BDch gn
Suy ra AB BE A BE cân tại B
BD là phân giác của góc B
Suy ra BD là đường trung trực của AE b.Chứng minh D FA D
CEg c g
Suy ra DF DC Trang 20