








Preview text:
ĐỀ 1
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. n − 2 Câu 1. Cho dãy số ( = n u ) với u , n 1 n
. Tìm khẳng định sai. 3n +1 8 47 1 19 A. u = . u = . u = . u = . 10 B. 50 C. 3 D. 21 31 150 10 64
Câu 2. Phương trình cos x = cos có tất cả các nghiệm là 3 A. x =
+ k2 (k ) .
B. x = + k2 (k ) . 3 3 2 C. x =
+ k2 (k ) . D. x =
+ k (k ) . 3 3 2sin x −1
Câu 3. Tập xác định của hàm số y = là cos x A. D = \
k,k . B. D = \
k2,k . C. D = \
k ,k . D. D = \
+ k ,k . 2 2 3
Câu 4. Cho sin = . Tính cos 2 . 4 7 1 1 7 A. − . B. − . C. . D. . 4 8 8 4 1
Câu 5. Cho cấp số nhân (U có U = , U =16 . Khi đó công bội q là n ) 1 2 2 A. 8 . B. 32. C. 4 . D. 64 .
Câu 6. Giải phương trình tan (2x) = tan80. Kết quả thu được là
A. x = 40 + k90. B. x = 40 + 1 k 80.
C. x = 40+ k45 . D. x = 80 + 1 k 80 .
Câu 7. Cho tứ diện ABC .
D Gọi M , N, P, Q lần lượt là trung điểm của các cạnh AB, AD, CD, BC.
Mệnh đề nào sau đây sai? 1
A. MN BD và MN = BD .
B. MN PQ và MN = PQ . 2
C. MP và NQ chéo nhau.
D. MNPQ là hình bình hành.
Câu 8. Giá trị nhỏ nhất của hàm số y = 2sin x + 5 là A. 3 . B. 4 . C. 2 . D. 5 . 1
Câu 9. Cho sin a = với
a . Tính cosa . 3 2 8 8 2 2 2 2
A. cos a = .
B. cos a = − . C. cos a = − . D. cos a = . 9 9 3 3
Câu 10. Trong mặt phẳng ( ) , cho bốn điểm ,
A B,C, D trong đó không có ba điểm nào thẳng hàng. Điểm
S ( ) . Có bao nhiêu mặt phẳng tạo bởi S và hai trong bốn điểm nói trên? A. 8 . B. 5 . C. 6 . D. 4 . Trang 1
Câu 11. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi A , B lần lượt là trung điểm của , SA . SB
Đường thẳng AB song song với mặt phẳng nào sau đây?
A. (SCD) .
B. (SAB) .
C. (SAD).
D. (SBC). Câu 12. Cho
, tìm phát biểu đúng trong các phát biểu sau: 2
A. cot x 0.
B. sin x 0.
C. cos x 0.
D. tan x 0.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. 1
Câu 1. Cho phương trình lượng giác sin 2x = − (*). Khi đó: 2
a) Phương trình (*) tương đương sin 2x = sin 6 3
b) Tổng các nghiệm của phương trình trong khoảng (0; ) bằng 2 11
c) Trong khoảng (0; ) phương trình có nghiệm lớn nhất bằng 12
d) Trong khoảng (0; ) phương trình có 3 nghiệm
Câu 2. Cho tứ diện ABCD. Gọi M là điểm trên cạnh AB, N là điểm thuộc cạnh AC sao cho MN không
song song với BC . Gọi P là điểm nằm trong B
CD. Xét tính đúng sai của các khẳng định sau:
a) Giao tuyến của hai mặt phẳng (MNP),( ABD) là đường thẳng cắt AB và DC
b) Giao tuyến của hai mặt phẳng (MNP),(BCD) là đường thẳng cắt BC
c) Giao tuyến của hai mặt phẳng (MNP),( ACD) là đường thẳng cắt AB và DC
d) MN = (MNP) ( ABC)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Một vật được phóng lên theo phương ngang một góc , với 45 90
, có vận tốc ban đầu v 0
(tính bằng m / s ) từ chân một mặt phẳng nghiêng tạo với phương ngang góc 45 . (Xem hình minh họa.)
Nếu bỏ qua sức cản không khí, quãng đường R mà vật đi dọc theo mặt phẳng nghiêng, khi là hàm 2 v 2
của , được cho bởi 0 R( ) =
[sin(2 ) − cos(2 ) −1] 32
Khi đó R đạt giá trị dài nhất khi bằng bao nhiêu độ?
Câu 2. Cho hình chóp S ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O . Gọi I là trung
điểm của SO . Mặt phẳng (ICD) cắt S ,
A SB lần lượt tại M và N . Cho AB = 3 khi đó hãy tính độ
dài đoạn thẳng MN . Trang 2
Câu 3. Qui luật sinh sản của một đôi thỏ, được tuân thủ theo dãy số Fibonacci có hệ thức truy hồi là: F =1 1 F =1
, n 3, F là số lượng đôi thỏ được sinh ra ở tháng thứ n. 2 n
F = F + F n n 1 − n−2
Một người nông dân A, nuôi một đôi thỏ (gồm 1 thỏ đực và 1 thỏ cái) trong một chuồng. Hỏi sau
một năm người nông dân A đó sẽ thu được bao nhiêu con thỏ (giả sử thỏ con không chết trong 1 năm)?
Câu 4. Hằng ngày, Mặt trời chiếu sáng, bóng của một tòa chung cư cao 40m in trên mặt đất, độ dài bóng
của tòa nhà này được tính bằng công thức S(t) = 40 cot
t , ở đó S được tính bằng mét, còn t là số 12
giờ tính từ 6 giờ sáng đến 18 giờ chiều. Hãy cho biết có bao nhiêu giá trị của t thỏa điều kiện bóng
của tòa nhà bằng chiều cao của tòa nhà?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
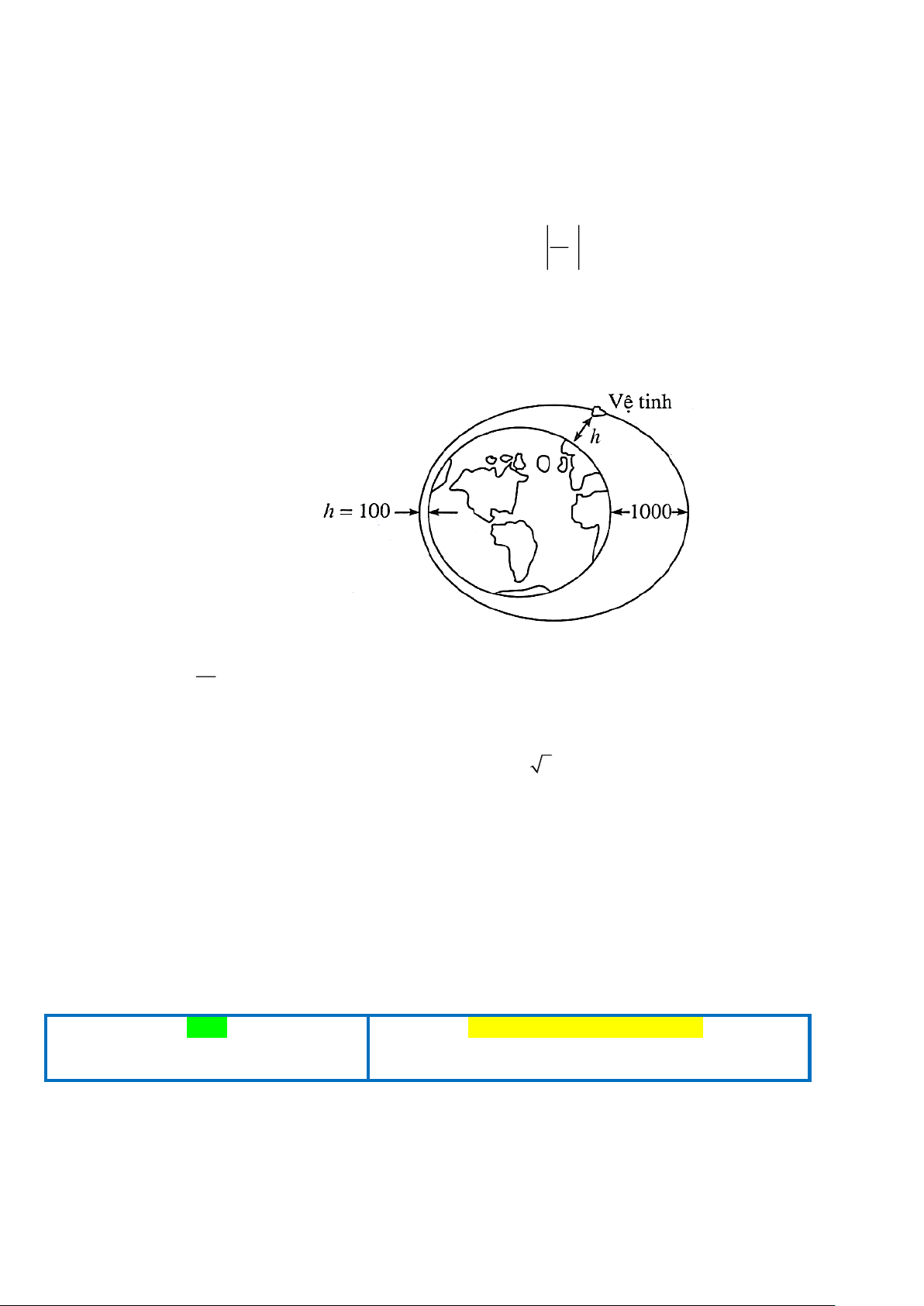
Câu 1. Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ):
Độ cao h (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức h = 550 + 450 cos
t . Trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người ta 50
cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất 250 km . Trong khoảng 60 phút đầu tiên kể từ
lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm để có thể thực hiện thí nghiệm đó?
Câu 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y = 3 sin 2x + 2sin x −1. Câu 3. Cho 4 điểm ,
A B,C, D không đồng phẳng. Gọi I , K theo thứ tự là 2 điểm nằm trong các tam giác ABC và BC .
D Giả sử IK cắt ( ACD) tại J. Xác định giao điểm đó.
Câu 4. Có hai cơ sở khoan giếng A và B . Cơ sở A giá mét khoan đầu tiên là 8000 đồng một mét và kể
từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 500 đồng so với giá của mét khoan ngay
trước đó. Cơ sở B : Giá của mét khoan đầu tiên là 6000 đồng một mét và kể từ mét khoan thứ hai,
giá của mỗi mét khoan sau tăng thêm 7% giá của mét khoan ngay trước đó. Một công ty giống cây
trồng muốn thuê khoan hai giếng với độ sâu lần lượt là 20(m) và 25(m) để phục vụ sản xuất. Giả
thiết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau. Công tý ấy nên chọn cơ sở nào
để tiết kiệm chi phí nhât? ĐỀ 2
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Tìm tập xác định D của hàm số y = tan x .
A. D = ¡ .
B. D = ¡ \k,k ¢ . Trang 3 C.
D = ¡ \ + k2 , k ¢ .
D. D = ¡ \ + k ,k ¢ . 2 2
Câu 2. Trong các phương trình sau, phương trình nào có nghiệm? 3 A. cos x = .
B. cos x = 3. C. cos x = .
D. cos3x = . 3
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đường thẳng AD song song với mặt
phẳng nào trong các mặt phẳng dưới đây?
A. (SAB) .
B. SAC) .
C. ( ABCD) . D. (SBC).
Câu 4. Tìm giá trị nhỏ nhất của hàm số y = sin 2x trên tập xác định của nó. A. 2 . B. −1. C. 1. D. 2 − .
Câu 5. Cho phương trình lượng giác tan 2x − = 1.
Nghiệm của phương trình là 6 k 5 A. x = + , k . B. x =
+ k , k . 8 2 12 5 k C. x = + , k . D. x =
+ k , k . 24 2 4
Câu 6. Trong mặt phẳng (P) cho ba điểm ,
A B, C phân biệt, không thẳng hàng. D là điểm nằm ngoài mặt
phẳng (P) . Khẳng định nào sau đây đúng khi nói về hai đường thẳng AD và BC? Mệnh đề nào sau
đây đúng khi nói về hai đường thẳng AD và BC ? A. Chéo nhau.
B. Song song hoặc cắt nhau. C. Song song. D. Cắt nhau.
Câu 7. Cho bốn điểm ,
A B,C, D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các
điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sao đây ?
A. ( ABD).
B. (CMN ).
C. (BCD).
D. ( ACD).
Câu 8. Cho cấp số nhân (u với u = 2 và công bội q = 3 . Tìm số hạng thứ 4 của cấp số nhân? n ) 1 A. 54. B. 48 . C. 162. D. 24 .
Câu 9. Cho dãy số (u , biết u = 1
− , u = u + 3, n
1. Ba số hạng đầu của dãy số đó là? n ) 1 n 1 + n A. 4; 7; 10 . B. 2; 5; 8 . C. 1; 4; 7 . D. 1 − ; 2; 5 .
Câu 10. Khẳng định nào dưới đây sai? A. 2
2sin a = 1− cos 2a .
B. sin 2a = 2sin acos a .
C. cos2a = 2cos a −1.
D. sin(a +b) = sin acosb +sinbcosa . 3 Câu 11. Cho sin =
. giá trị của cos bằng 5 2 2 4
A. cos = − .
B. cos = − . 5 5 2 4 C. cos = . D. cos = . 5 5
Câu 12. Cho 0 a . Kết quả đúng là 2
A. sin a 0, cos a 0 .
B. sin a 0, cos a 0 .
C. sin a 0, cos a 0 .
D. sin a 0, cos a 0 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Trang 4 1
Câu 1. Cho phương trình lượng giác cot 3x = − (*). Khi đó 3
a) Phương trình (*) có nghiệm x =
+ k (k ) 9 3 −5
b) Tổng các nghiệm của phương trình trong khoảng − ;0 bằng 2 9 −
c) Phương trình (*) tương đương cot 3x = cot 6 2
d) Phương trình có nghiệm dương nhỏ nhất bằng 9
Câu 2. Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh
AC , BC ; P là trọng tâm tam giác BCD. Các khẳng định sau đúng hay sai?
a) Ba điểm N , P , D thẳng hàng.
b) Mặt phẳng (MNP) cắt tứ diện theo một thiết diện là tam giác MNP .
c) Giao tuyến của mặt phẳng (ABC) và (BCD) là BC . 2 a 11
d) Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là . 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Số giờ có ánh sáng của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số y = 4sin (t −60) +10
, với t Z và 0 t 365. Gọi t là thời điểm ngày trong năm mà thành 178
phố A có nhiều giờ ánh sáng mặt trời nhất . Giá trị nhỏ nhất của biểu thức 2
P = a + 2a + t là bao nhiêu?
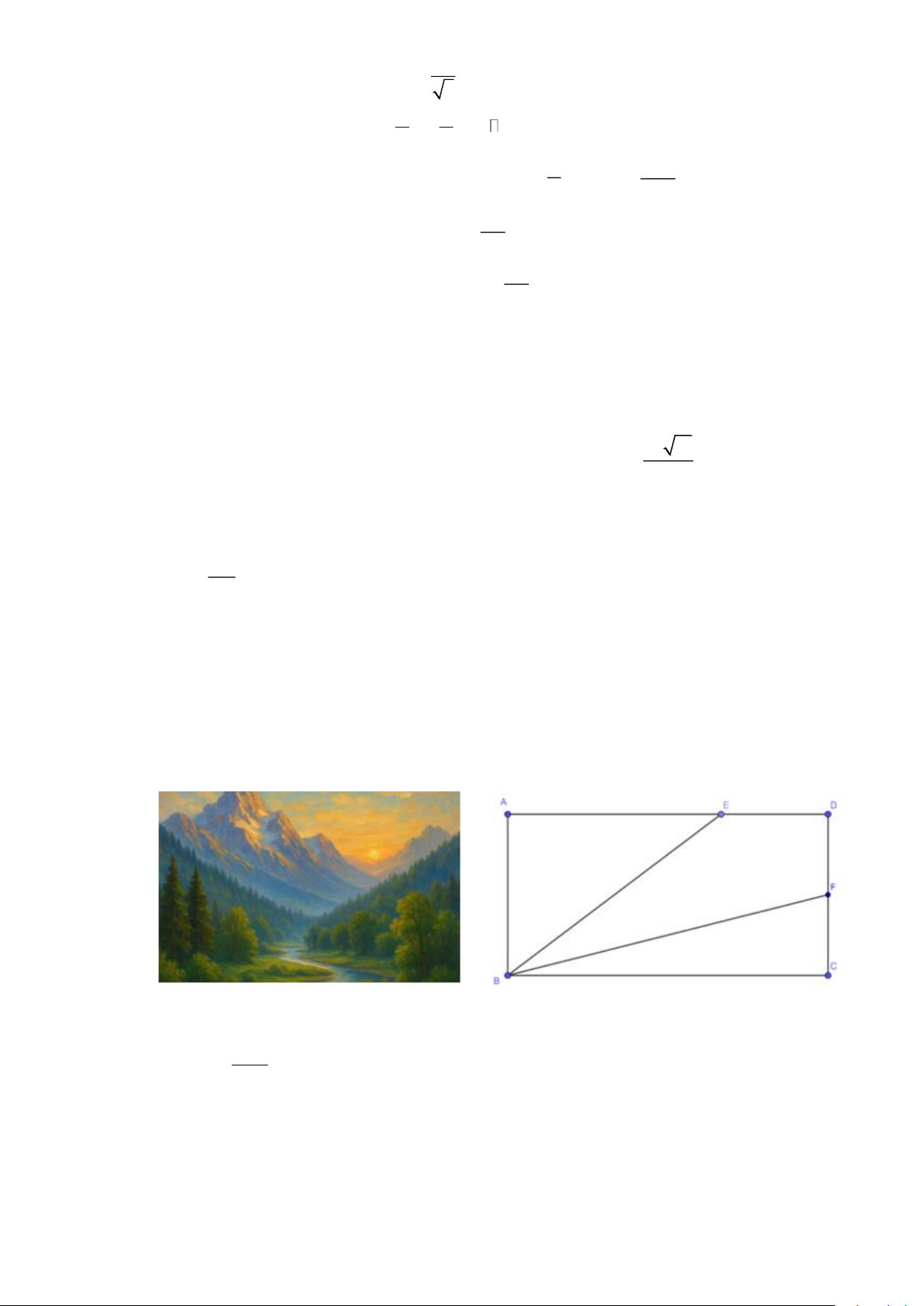
Câu 2. Bức tranh phong cảnh thiên nhiên là một cách gửi gắm thông điệp ý nghĩa và luôn có sức hấp dẫn
đối với nhiều người. Trong một buổi học mỹ thuật, thầy An hướng dẫn rằng để vẽ một bức tranh
phong cảnh đẹp thì ta cần phải phân bổ bố cục rõ ràng. Trên một bức tranh hình chữ nhật ABCD
có chiều dài gấp đôi chiều rộng, thầy An hướng dẫn 1 cách phân bố cục bằng việc lấy 2 điểm E, F
trên đoạn AD,CD rồi nối 2 đoạn BE, BF (như hình vẽ). Biết 3AE = 2AD,CF = FD , Giá trị của
cot EBF là bao nhiêu? (làm tròn kết quả đến hàng phần mười)
Câu 3. Ông Hùng gửi tiết kiệm 200 triệu đồng kì hạn 1 tháng với lãi suất 6% một năm theo hình thức tính
lãi kép. Số tiền (triệu đồng) của ông Hùng thu được sau n tháng được cho bởi công thức 0, 06 n T = 200 1+
. Số tiền ông Hùng nhận được sau 1 năm bằng bao nhiêu? (làm tròn kết quả n 12
đến hàng đơn vị) Trang 5
Câu 4. Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N lần lượt là trung SI a
điểm của SC , OB . Gọi I là giao điểm của SD và mặt phẳng ( AMN ) . Khi đó tỉ số = với DI b
a là phân số tối giản và a,b . Tính giá trị biểu thức a + b. b
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Tìm GTLN - GTNN của hàm số y = 2cos x + cos 2x − 8 trên đoạn − ; 2 4 Câu 2.
Hai nguồn sóng cơ A và B dao động trên mặt chất lỏng theo các phương trình lần lượt là
x = 5cos 50t −
cm / s và x = 5cos 50t +
cm / s . Hai sóng này giao thoa với nhau tạo nên một A 6 B 3 1 k
sóng tổng hợp x = x + x . Biết tại các thời điểm t = − + (giây) với *
k, S thì sóng tổng hợp cao nhất. A B S 25 Tìm S
Câu 3. Cho hình chóp S.ABCD có M là trung điểm của SC. Tìm giao điểm của AM với mặt phẳng (SBD).
Câu 4. Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kĩ sư theo phương thức như sau:
Mức lương của quý làm việc đầu tiên cho công ty là 24,5 triệu đồng/quý, và kể từ quý làm việc
thứ hai mức lương sẻ được tăng thêm 0, 7 triệu đồng so với quý trước đó. Hãy tính tổng số tiền
lương một kĩ sư nhận được sau 3 năm làm việc cho công ty. ĐỀ 3
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau: A. cos x = 1
− x = − + k2 .
B. sin x = 0 x = k2 . 2 3
C. cos x = 0 x = + k .
D. sin x = −1 x = − + k2 . 2 2
Câu 2. Trong không gian cho hai đường thẳng song song a và b . Kết luận nào sau đây đúng?
A. Nếu c cắt a thì c chéo b .
B. Nếu đường thẳng c song song với a thì c song song hoặc trùng b .
C. Nếu c cắt a thì c cắt b .
D. Nếu c chéo a thì c chéo b .
Câu 3. Tìm tất cả các nghiệm của phương trình tan x = m , (m ) .
A. x = arctan m + k , (k ) .
B. x = arctan m + k2 , (k ) .
C. x = arctan m+ k , (k ) . D.
x = arctan m + k hoặc
x = −arctan m+ k , (k ) .
Câu 4. Cho hình chóp S.ABC . Gọi M , N, K, E lần lượt là trung điểm của ,
SA SB, SC, BC . Bốn điểm nào
sau đây đồng phẳng?
A. M , K, , A C .
B. M , N, K, E .
C. M , N, , A C .
D. M , N, K,C . Trang 6
Câu 5. Cho tứ diện ABCD có M , N lần lượt là trung điểm của các cạnh AB, AC , Xét vị trí tương đối của
MN và mp (BCD). Khẳng định nào đúng?
A. MN song song với (BCD).
B. MN chứa trong (BCD).
C. Không xác định được vị trí tương đối.
D. MN cắt (BCD). 4
Câu 6. Biết sin = , (90 180). Khi đó giá trị cos bằng 5 3 1 1 3 A. − . B. − . C. . D. . 5 5 5 5
Câu 7. Tập giá trị của hàm số y = sin x là A. ( 1 − ; ) 1 . B. . C. 1 − ; 1 . D. 0; 1 . 2
Câu 8. Cho cấp số nhân có u = 3, q = . Chọn kết quả đúng: 1 3
A. (u là một dãy số tăng. n ) 2 n B. S = 9. − 9. n 3 4 8 16
C. Bốn số hạng tiếp theo của cấp số là: 2; ; ; . 3 3 3 n 1 2 − D. u = 3. . n 3
Câu 9. Xét bốn mệnh đề sau:
( )1: Hàm số y = sin x có tập xác định là R .
(2): Hàm số y = cos x có tập xác định là R .
(3): Hàm số y = tan x có tập giá trị là R .
(4): Hàm số y = cot x có tập xác định là R .
Tìm số phát biểu đúng. A. 2 . B. 4 . C. 3 . D. 1.
Câu 10. Cho dãy số (u có u = − n +
n . Số hạng thứ năm của dãy là n ( ) 1 n .(3 7), * n ) A. 22 . B. 24 − . C. 22 − . D. 24 .
Câu 11. Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a = cos a + sin a. B. 2
cos2a = 2cos a −1. C. 2 2
cos 2a = cos a −sin a . D. 2
cos 2a =1− 2sin a .
Câu 12. Cho góc (90 ;18
0 ) . Khẳng định nào sau đây đúng?
A. sin và tan cùng dấu.
B. Tích sin.cot mang dấu âm.
C. sin và cot cùng dấu.
D. Tích sin.cos mang dấu dương.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD, BC , M là một điểm trên cạnh AB, N
là một điểm trên cạnh AC . Khi đó:
a) NDlà giao tuyến của hai mặt phẳng (MND), ( ADC) .
b) BI là giao tuyến của hai mặt phẳng (BCI ), ( ABD) . Trang 7
c) IJ là giao tuyến của hai mặt phẳng (IBC), (JAD) .
d) Giao tuyến của hai mặt phẳng (IBC),(DMN ) song song với đường thẳng IJ .
Câu 2. Cho phương trình lượng giác 2cos x = 3 , khi đó:
a) Phương trình có nghiệm x =
+ k2 (k ) 3 5 25
b) Tổng các nghiệm của phương trình trong đoạn 0; bằng 2 6 5 13 c) Trong đoạn 0;
phương trình có nghiệm lớn nhất bằng 2 6 5 d) Trong đoạn 0;
phương trình có 4 nghiệm 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
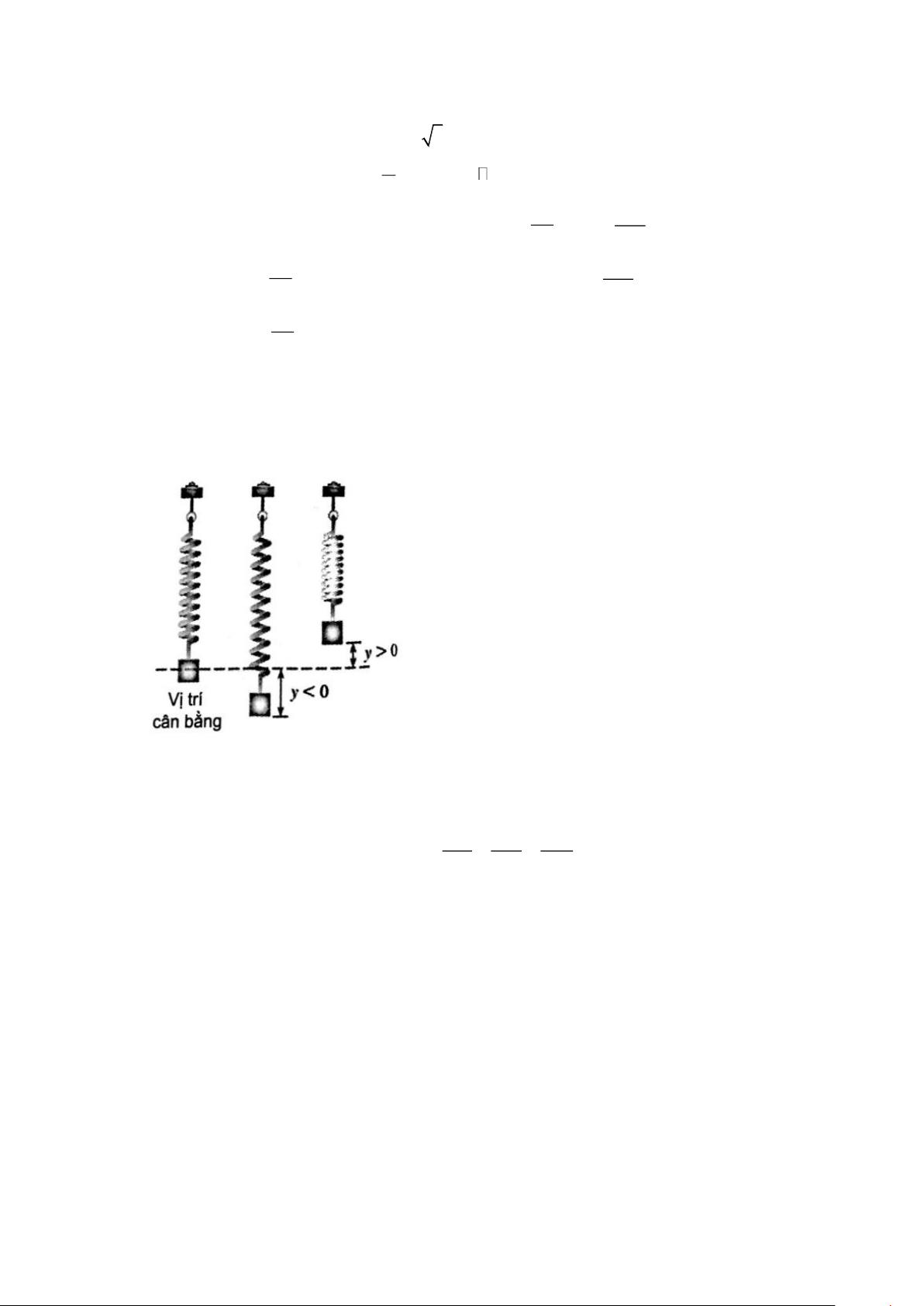
Câu 1. Một con lắc lò xo dao động điều hòa quanh vị trí cân bằng theo phương trình y = 25sin 4t , trong
đó y được tính bằng centimét, còn t được tính bằng giây. Hãy cho biết tần số giao động của con lắc
lò xo, tức là số lần dao động trong một giây?
Câu 2. Cho hình chóp S.ABC . Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các
đường thẳng lần lượt song song với ,
SA SB,SC và cắt các mặt phẳng (SBC),(SCA),(SAB) theo OA OB OC
thứ tự tại A , B ,C . Khi đó tổng tỉ số T = + + bằng bao nhiêu? SA SB SC
Câu 3. Đèo Hải Vân là ranh giới tự nhiên của thành phố Đà Nẵng và tỉnh Thừa Thiên-Huế. Hầm
được khởi công ngày 27/8/2000 và khánh thành ngày 5/6/2005. Đây là hầm đường bộ dài nhất, hiện
đại nhất Đông Nam Á và là một trong 30 đường hầm dài nhất trên thế giới. Trong kiến trúc, có hình
nửa đường tròn để có thể chịu lực tốt. Trong hình bên, cổng Đèo Hải Vân được ghép bởi sáu cung
vật liệu tốt chịu lực tốt hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một
cung vật liệu tốt chốt ở đỉnh. Cho AH = 18 ,
m BK = 4,3m . Biết rằng hình chữ nhật MNFC có MN
là khoảng cách hai làn xe, CM là chiều cao cho phép của các xe lưu thông ( Xem hình minh
họa).Tính chiều cao CM cho phép của các xe lưu thông. (Làm tròn đến một chữ số thập phân) Trang 8
Câu 4. Một sinh viên được gia đình gửi vào sổ tiết kiệm ngân hàng là 200 triệu đồng với lãi suất 0,5%
/tháng. Nếu mỗi tháng sinh viên đó đều rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì
hàng tháng anh ta rút ra bao nhiêu tiền (đơn vị nghìn đồng) để đúng sau 4 năm đại học sẽ vừa hết
số tiền cả vốn lẫn lãi (kết quả làm tròn đến hàng đơn vị).
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Ông X trồng cây cao su trên một khu đất hình tam giác đều có diện tích 2019 ( 2 m ) . Hàng thứ
nhất ông trồng 1 cây ở đỉnh, hàng thứ hai cách đỉnh 1 m ông trồng nhiều hơn hàng thứ nhất 2 cây
và cứ tiếp tục như vậy đến hàng cuối cùng (mỗi hàng cách đều nhau và song song với cạnh của khu
đất). Hỏi ông X trồng được bao nhiêu cây cao su? 2x 4x
Câu 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = sin + cos +1. 2 2 1+ x 1+ x
Câu 3. Cho tứ giác ABCD có AC và BD giao nhau tại O và một điểm S không thuộc mặt phẳng
(ABCD) . Trên đoạn SC lấy một điểm M không trùng với S và C . Xác định giao điểm của
đường thẳng SD với mặt phẳng ( ABM ).
Câu 4. Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình x = 2cos 5t − 6
Ở đây thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong khoảng
thời gian từ 0 đến 6 giây thì vật đi qua vị trí cân bằng bao nhiêu lần? ĐỀ 4
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Nghiệm của phương trình cos x = 1 là A. x =
+ k2 , k .
B. x = k , k . 2
C. x = + k2 , k .
D. x = k2 , k .
Câu 2. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Một điểm và một đường thẳng.
B. Bốn điểm phân biệt.
C. Hai đường thẳng cắt nhau.
D. Ba điểm phân biệt.
Câu 3. Giá trị lớn nhất của hàm số y = cos 2x trên là Trang 9 A. 1. B. 2 . C. −1. D. 2 − .
Câu 4. Trong các đẳng thức sau, đẳng thức nào sai? 1 1 A. sin . a sinb = cos
(a−b)−cos(a+b) cos .
a cosb = cos a −b + cos a + b 2 . B. ( ) ( ) 2 . 1 1 C. sin . a cosb = sin
(a−b)−sin(a+b) sin .
a cosb = sin a −b + sin a + b 2 . D. ( ) ( ) 2 . 1
Câu 5. Nếu cos = thì sin bằng: 7 5 2 4 3 4 3 A. . B. o 3 cos150 = . C. . D. . 7 5 7 7
Câu 6. Chọn cấp số nhân trong các dãy số sau: A. 1; 1; 1 − ; 1 − . B. 16; 8 − ; 4, 2 − ; 1.
C. 3; 9; 18; 27 D. 1; 2;4;16.
Câu 7. Phương trình lượng giác: 3 tan x − 3 = 0 có tất cả các nghiệm là:
A. x = 60 + k360 . B. x = 60 + 1 k 80. C. x = 6 − 0+ 1 k 80 . D. x = 6 0+ 1 k 80 .
Câu 8. Cho dãy số (u thỏa u = 2n +1, *
n . Giá trị của số hạng u bằng n ) n 2019 A. 4040 . B. 4039 . C. 4041. D. 4038 .
Câu 9. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng phân biệt không có điểm chung thì chéo nhau.
Câu A sai vì hai đường thẳng không có điểm chung thì chéo nhau hoặc song song với nhau.
Câu B sai vì hai đường thẳng phân biệt không có điểm chung thì chéo nhau hoặc song song với nhau.
Câu D sai vì hai đường thẳng phân biệt nằm trên hai mặt phẳng phân biệt thì có thể chéo nhau hoặc song song với nhau.
Câu 10. Cho góc x thỏa mãn 0 0
0 < x < 90 . Trong các mệnh đề sau, mệnh đề nào sai? A. cosx 0. B. sinx 0. C. tanx 0. D. cotx 0.
Câu 11. Cho ba đường thẳng đôi một chéo nhau a, b, c . Gọi (P) là mặt phẳng qua a , (Q) là mặt phẳng
qua b sao cho giao tuyến của (P) và (Q) song song với c . Có nhiều nhất bao nhiêu mặt phẳng
(P) và (Q) thỏa mãn yêu cầu trên?
A. Một mặt phẳng (Q) , vô số mặt phẳng (P).
B. Một mặt phẳng (P) , một mặt phẳng (Q).
C. Vô số mặt phẳng (P) và (Q).
D. Một mặt phẳng (P) , vô số mặt phẳng (Q).
Câu 12. Tập xác định của hàm số: y = tan 2x + ? 6 k A. \ + , k . B. \
+ k ,k . 6 2 6 − k C. \ + , k . D. \
+ k , k . 6 2 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho bốn điểm ,
A B,C, D không đồng phẳng. Gọi M , N lần lượt là trung điểm của AC và BC .
Trên đoạn BD lấy điểm P sao cho BP = 2PD , E = CD NP . Khi đó:
a) NM là giao tuyến của hai mặt phẳng (MNP) , (ABC) Trang 10
b) DC là giao tuyến của hai mặt phẳng (BCD),(ADC)
c) Giao điểm của đường thẳng CD và mặt phẳng (MNP) là điểm E
d) Giao điểm của đường thẳng AD và mặt phẳng (MNP) là giao điểm của đường thẳng AD với đường thẳng MP
Câu 2. Cho phương trình lượng giác 2sin x − + 3 = 0 , khi đó: 12
a) Số nghiệm của phương trình trong khoảng ( − ; ) là hai nghiệm
b) Phương trình tương đương sin x − = sin 12 3 7
c) Phương trình có nghiệm là: x = + k2; x =
+ k2 (k ) . 4 12
d) Phương trình có nghiệm âm lớn nhất bằng − 4
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. John đang có số dư 3000 đô trên thẻ Discover, với lãi suất 1% mỗi tháng áp dụng trên số dư chưa
thanh toán. Mỗi tháng John có thể trả 100 đô cho số dư. Số dư sau mỗi tháng, ngay sau khi thanh B = 3000
toán 100 đô, được cho bởi dãy truy hồi 0 B =1,01B −100 n n 1 −
Hãy xác định số dư của John sau lần thanh toán đầu tiên, tức là tìm B . 1
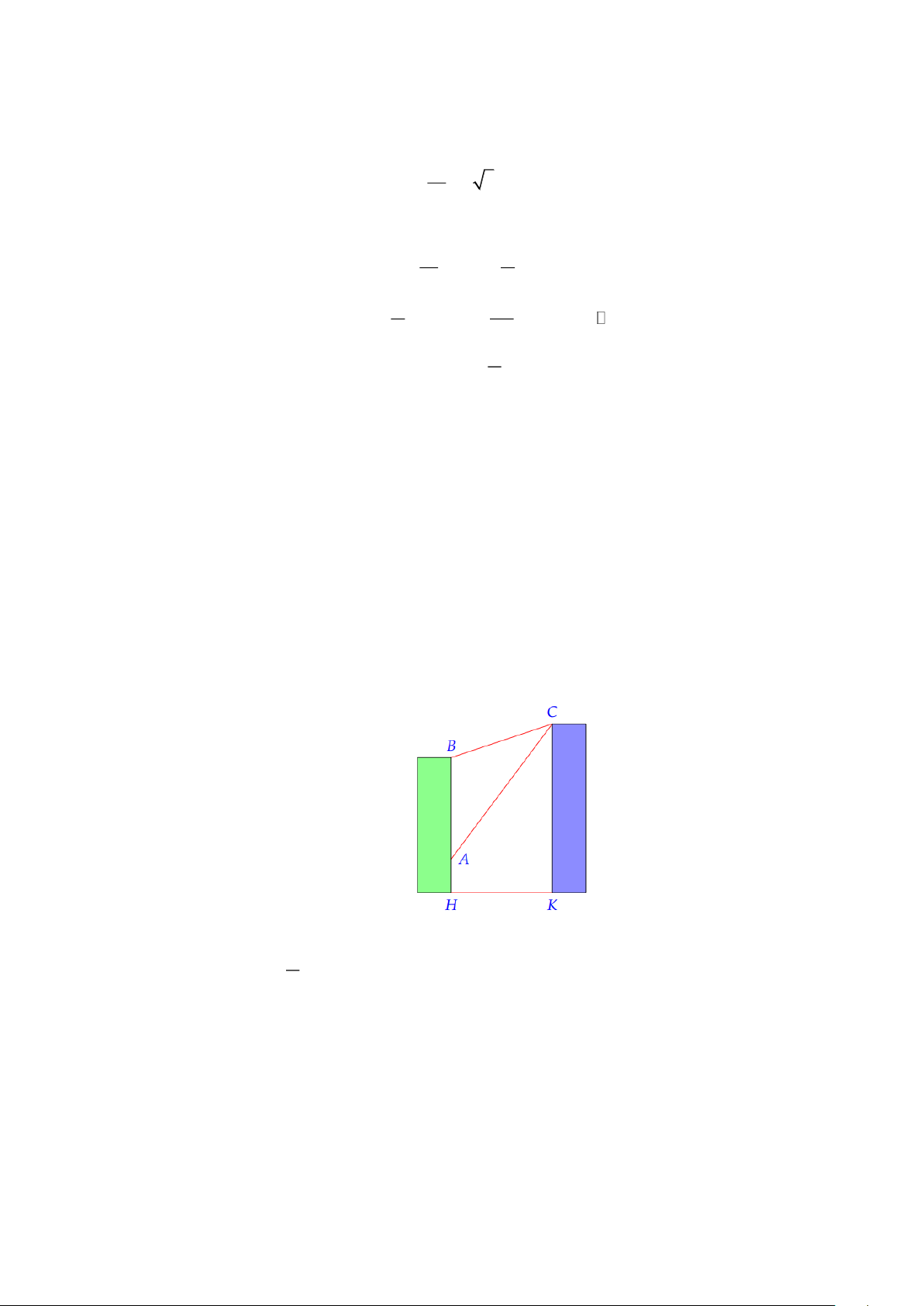
Câu 2. Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 25 m . Để đảm bảo
an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C . Gọi ,
A B lần lượt là vị trí thấp
nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (tham khảo hình vẽ). Hãy tính số đo góc
ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều
cao của chung cư thứ hai là CK = 32 ,
m AH = 6 m , BH = 24 m (làm tròn kết quả đến hàng phần
mười theo đơn vị độ).
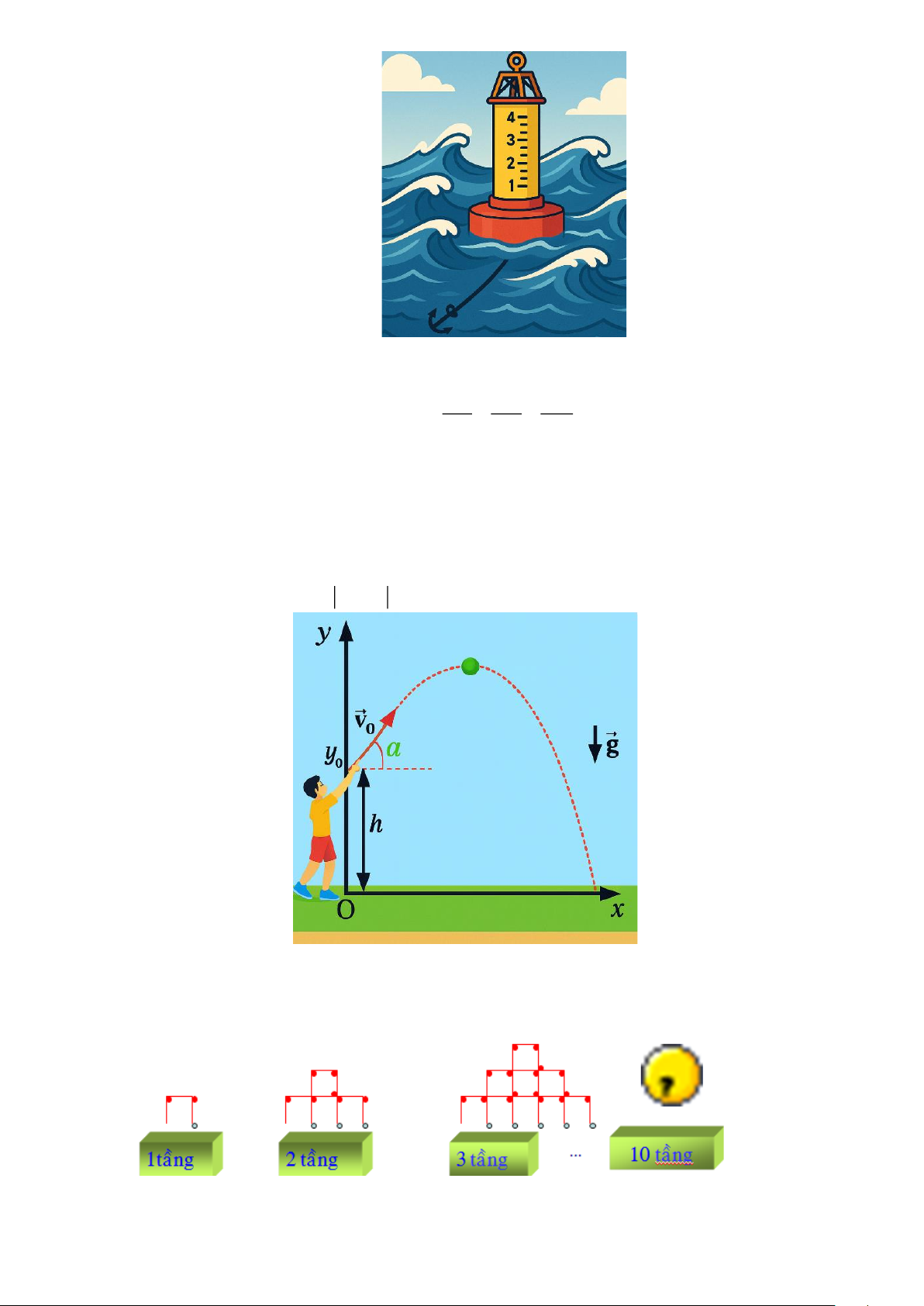
Câu 3. Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi
hàm số h (t) = 5sin t
, trong đó h(t) là độ cao tính bằng cetimét trên mực nước biển trung bình 5
tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao giây chiếc phao lại ở vị trí
đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). Trang 11
Câu 4. Cho hình chóp S.ABC . Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các
đường thẳng lần lượt song song với ,
SA SB,SC và cắt các mặt phẳng (SBC),(SCA),(SAB) theo OA OB OC
thứ tự tại A , B ,C . Khi đó tổng tỉ số T = + + bằng bao nhiêu? SA SB SC
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Cho N, P lần lượt là hai điểm thuộc miền trong tam giác ACD và tam giác ABC của tứ diện
ABCD. M là một điểm tùy ý trên cạnh DB . Tìm giao điểm của NP và mp( ACM ) .
Câu 2. Một vận động viên có chiều cao 1m75 thực hiện ném tạ với vận tốc ban đầu v = 30m / s . Đạt thành o
tích 15 m. Gọi là góc ném của vận động viên hợp với mặt đất (tham khảo hình vẽ). Coi gia tốc trọng trường 2
g =10m / s . Tính giá trị của cos 2
Câu 3. Tìm GTLN - GTNN của hàm số y = ( − x)2 2 2 1 cos − 2cos x +1
Câu 4. Bạn An và bạn Bình chơi trò xếp tháp bằng que diêm được mô tả như hình dưới đây.
Để xếp tháp 10 tầng hai bạn phải chuẩn bị ít nhất bao nhiêu que diêm ? Trang 12 ĐỀ 5
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt phẳng phân biệt
từ các điểm đó? A. 2 . B. 4 . C. 3 . D. 6 . 3
Câu 2. Cho sin = . Khi đó, cos 2 bằng 4 1 1 7 7 A. − . B. . C. − . D. . 8 8 4 4
Câu 3. Tập giá trị của hàm số y = cos x là ? A. ( ;0 − . B. .
C. 0;+) . D. 1 − ; 1 . u = 1 − , u = 3
Câu 4. Cho dãy số (u xác định bởi 1 2
với n 2 . Tìm 5 số hạng đầu của dãy. n )
u = u +2u n 1+ n n 1 − A. 1 − ,3,5,13,31.
B. −1,3,1, 7,9 . C. 1 − ,3, 2,5,7 . D. 1 − ,3,5, −1, −11.
Câu 5. Chọn khẳng định đúng.
A. cot ( − ) = cot .
B. sin ( − ) = −sin .
C. cos( − ) = −cos .
D. tan ( − ) = tan . Câu 6. Cho 0;
. Mệnh đề nào dưới đây sai? 2
A. sin 0.
B. tan 0.
C. cos 0.
D. sin 0.
Câu 7. Giải phương trình 1+ cos x = 0 được nghiệm: A. x =
+ k2 , k .
B. x = + k2 , k . 2
C. x = k2 , k . D. x =
+ k ,k . 2
Câu 8. Cho hai đường thẳng chéo nhau a và b . Khẳng định nào sau đây sai?
A. Có duy nhất một mặt phẳng qua a và song song với . b
B. Có vô số đường thẳng song song với a và cắt . b
C. Có duy nhất một mặt phẳng song song với a và . b
D. Có duy nhất một mặt phẳng qua điểm M , song song với a và b .
Câu 9. Cho tứ diện ABCD. Gọi M , N lần lượt là trung điểm của AB ,CD và điểm P thuộc cạnh BC
sao cho P không là trung điểm của BC . Cặp đường thẳng nào sau đây không cắt nhau? A M B D N P C
A. MN và BD .
B. MP và AC .
C. AP và CM .
D. PN và BD .
Câu 10. Tất cả các nghiệm của phương trình tan 2x = 3 là: A. x =
+ k ;k . B. x =
+ k ;k . 6 2 6 Trang 13 C. x =
+ k ;k . D. x =
+ k ;k . 3 6 3
Câu 11. Điều kiện xác định của hàm số y = tan x là
A. cos x 0. B. sin x 0.
C. sin x 0 .
D. cos x 0 .
Câu 12. Dãy số nào sau đây không phải là cấp số nhân?
A. 1; −1; 1; −1; 1.
B. 1; 2; 3; 4; 5.
C. 1; 2; 4; 8; 16 .
D. 1; − 2; 4; − 8; 16 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. 1
Câu 1. Cho phương trình lượng giác sin x = − , khi đó: 2
a) Phương trình tương đương sin x = sin 6
b) Phương trình có nghiệm âm lớn nhất bằng − 3 7
c) Phương trình có nghiệm là: x = − + k2 ; x =
+ k2 (k ) . 6 6
d) Số nghiệm của phương trình trong khoảng ( − ; ) là ba nghiệm
Câu 2. Cho hình bình hành ABCD và một điểm S không thuộc mặt phẳng (ABCD) , các điểm M , N lần
lượt là trung điểm của đoạn thẳng AB, SC . Gọi O = AC BD ;
a) SO giao tuyến của hai mặt phẳng (SAC) và (SBD) .
b) Giao điểm của I của đường thẳng AN và mặt phẳng (SBD) là điểm nằm trên đường thẳng SO
c) Giao điểm của J của đường thẳng MN và mặt phẳng (SBD) là điểm nằm trên đường thẳng SD
d) Ba điểm I, J , B thẳng hàng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M , N lần lượt là trung điểm của AB , AD SH
và G là trọng tâm tam giác SBD . Mặt phẳng (MNG) cắt SC tại điểm H . Tính SC
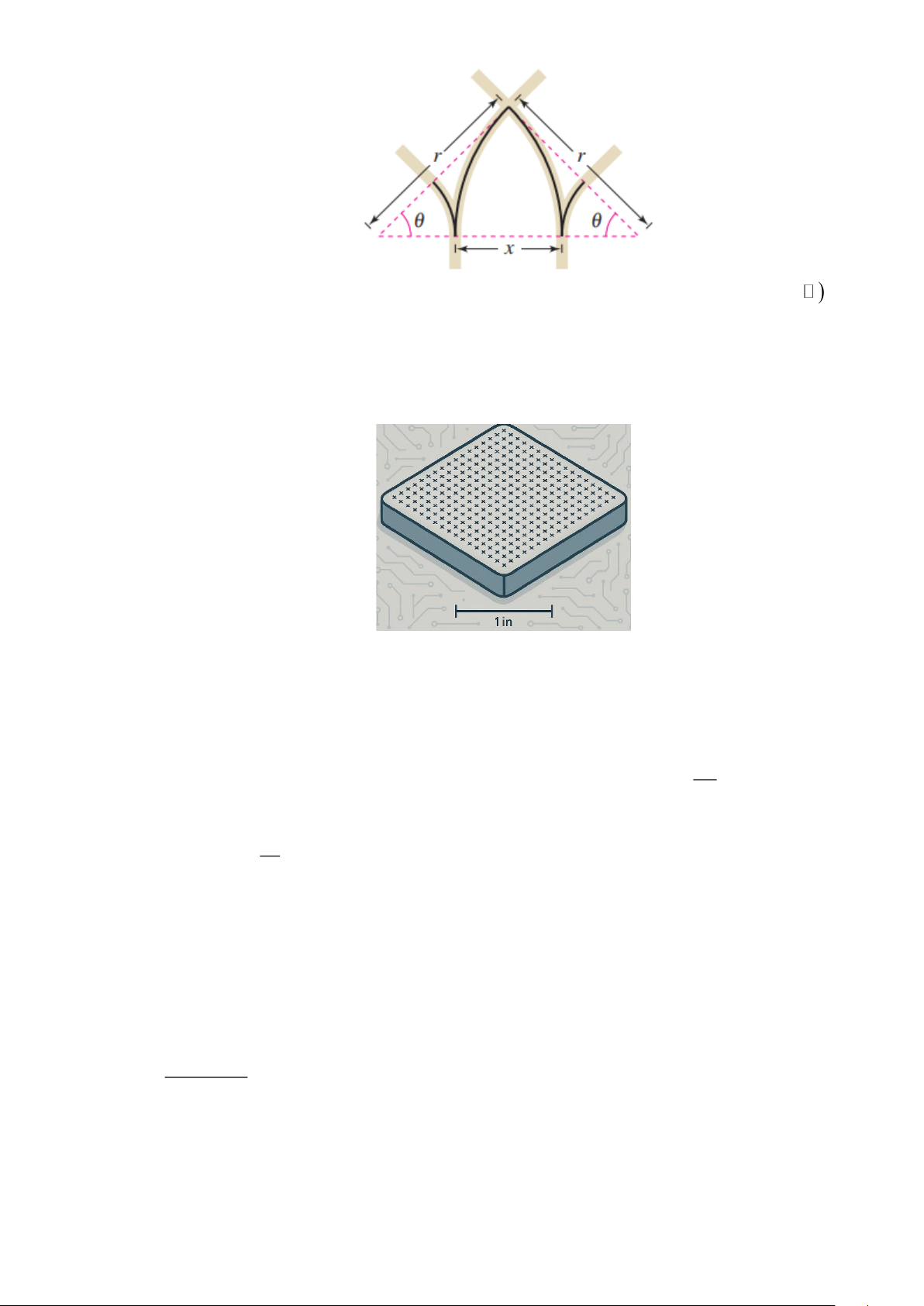
Câu 2. Khi hai đường ray đường sắt hợp nhất, phần chồng lên nhau của các đường ray có dạng là một cung
tròn (xem hình). Bán kính của mỗi cung là r (tính theo feet) và góc liên hệ với x qua đẳng thức x 2 = 2r sin 2 2 Trang 14
Viết lại công thức biểu diễn x theo cos ta được x = Qr(P + Rcos);( ; Q ; P R ). Tính
Q + P + R
Câu 3. Định luât Moore: "Số lượng transistor trên mỗi đơn vị inch vuông của chíp máy tính sẽ tăng lên gấp
đôi sau mỗi 24 tháng." (một inch vuông xấp xỉ 2
6,45 cm ). Biết năm 2000 số lượng transistor trên
mỗi inch vuông là khoảng 10 triệu. Ước lượng số lượng transistor trên mỗi inch vuông vào năm
2010 khoảng bao nhiêu triệu (làm tròn kết quả đến hàng đơn vị)
Câu 4. Huyết áp là áp lực cần thiết tác động lên thành động mạch để đưa máu từ tim đến nuôi dưỡng các
mô trong cơ thể. Huyết áp được tạo ra do co bóp của cơ tim và sức cản của thành động mạch. Mỗi
lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu
được gọi tương ứng là huyết tâm thu và huyết tâm trương. Chỉ số huyết áp của chúng ta được viết
là huyết áp tâm thu/huyết áp tâm trương. Chỉ số huyết áp 120 / 80 là bình thường. Giả sử huyết áp
của một người nào đó được mô hình hóa bởi hàm số p(t) 7 = 110 + 20sin t
, trong đó p(t) là 3
huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian tính theo giây. Tính huyết áp của 25 người đó khi t = . 14
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Tìm GTLN - GTNN của hàm số 2
y = 2sin x − sin x + 2 trên đoạn 0;
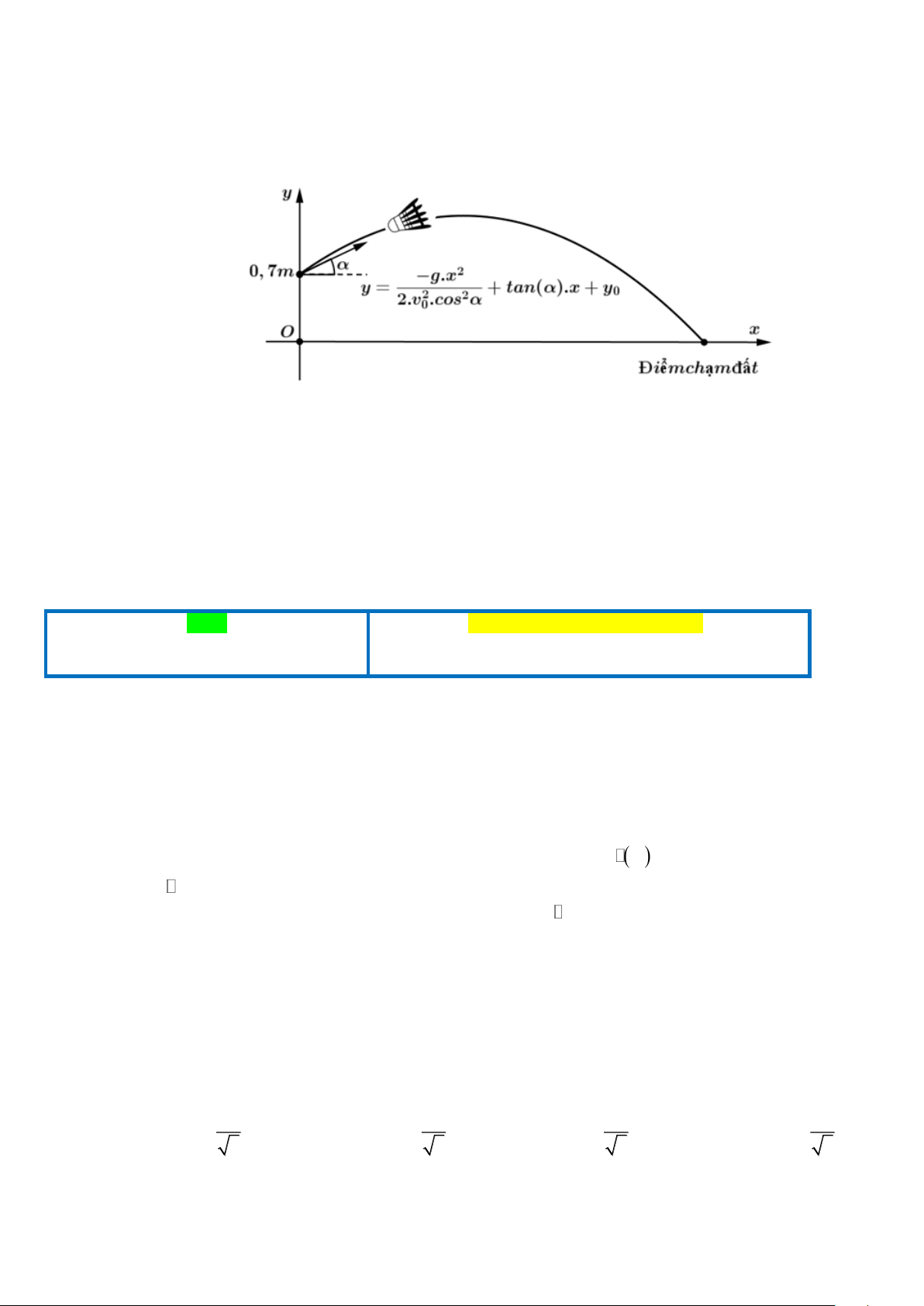
Câu 2. Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương
và không được để cho cầu rơi ngoài biên. Trong mặt phẳng toạ độ Oxy , chọn điểm có tọa độ ( ;
O y là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: 0 ) 2 −g.x y =
+ tan.x + y ; trong đó: 2 2 0 2.v .cos 0
g là gia tốc trọng trường (thường được chọn là 2 9,8 m / s )
là góc phát cầu (so với phương ngang của mặt đất)
v là vận tốc ban đầu của cầu 0
y là khoảng cách từ vị trí phát cầu đến mặt đất. 0 Trang 15
Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.
Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất
(tầm bay xa) là 6,68 m. Quan sát hình bên dưới, hỏi người chơi đã phát cầu góc khoảng bao nhiêu độ so với
mặt đất? ( biết cầu rời mặt vợt ở độ cao 0,7 m so với mặt đất và vận tốc xuất phát của cầu là 8 m/s, bỏ qua
sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng).
Câu 3. Công ty A đề xuất 2 phương án trả lương để người lao động chọn như sau:
Phương án 1: Người lao động sẽ nhận 45.000.000 đồng cho năm làm việc đầu tiên và kể từ
năm thứ hai, mức lương sẽ tăng thêm 3.000.000 đồng so với năm trước đó.
Phương án 2: Người lao động sẽ nhận mức lương 7.000.000 đồng cho qúy làm việc đầu và kể từ
qúy thứ hai mức lương sẽ tăng thêm 500.000 đồng so với qúy trước đó.
Hỏi sau 10 năm số tiền lương mà người lao động nhận được theo mỗi phương án là bao nhiêu?
Câu 4. Cho hình chóp S.ABCD . Gọi O là giao điểm của AC và BD . Lấy M , N, P lần lượt là các điểm trên ,
SA SB, SC . Tìm giao điểm Q của SC với mặt phẳng (MNP) . ĐỀ 6
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Chọn cấp số nhân trong các dãy số sau: A. 1; 4; 8; 16
B. 1; 0, 2; 0,04; 0,0008. C. 1; 2; 3; 4.
D. 2; 22; 222;2222.
Câu 2. Cho hai đường thẳng phân biệt a, b và mặt phẳng ( ) . Giả sử a (
) , b ( ) . Khi đó: A. a . b
B. a, b chéo nhau.
C. a, b cắt nhau. D. a b
hoặc a, b chéo nhau.
Câu 3. Đẳng thức nào sau đây Sai? A. 2
cos 2a = 2cos a −1.
B. cos2a = 2.sin . a cos a . C. 2 2
cos 2a = cos a − sin a . D. 2
cos 2a = 1− 2sin a .
Câu 4. Cho hai đường thẳng phân biệt a,b và mặt phẳng ( ) . Giả sử a// ( ), b ( ). Khi đó
A. a//b.
B. a//b hoặc a, b chéo nhau.
C. a, b cắt nhau.
D. a, b chéo nhau.
Câu 5. Biết tan = 2 và
− 0. Tính cos . 2 2 1 1 A. cos = . B. cos = − . C. cos = . D. cos = − . 5 5 5 5
Câu 6. Chọn khẳng định sai trong các khẳng định sau:
A. Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
B. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất. Trang 16
C. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Hai mặt phẳng có một điểm chung thì chúng còn vô số điểm chung khác nữ
Câu 7. Xét góc lượng giác (O ;
A OM ) = trong đó M là điểm không nằm trên các trục tọa độ Ox và Oy .
Khi đó M thuộc góc phần tư nào để sin và cos cùng dấu?
A. (II ) và (III ) .
B. (I ) và (IV ).
C. (I ) và (III ) .
D. (I ) và (II ) .
Câu 8. Tập giá trị của hàm số y = 4sin x là A. 4 − ; 4 . B. 2 − ; 2 . C. 1 − ; 1 . D. 6 − ; 6 .
Câu 9. Cho dãy số (u với u = 3n. Tính u ? n ) n n 1 + A. u = 3n + 3. B. u = 3 n +1 . C. u = 3n +1. D. u = 3.3 .n n 1 + ( ) n 1 + n 1 + n 1 +
Câu 10. Phương trình 3cot x − 3 = 0 có họ nghiệm là A. x =
+ k ,k .
B. vô nghiệm. 6 C. x =
+ k ,k . D. x =
+ k2 ,k . 3 3
Câu 11. Phương trình cos x = 2 có số nghiệm là A. 1. B. 2. C. 0. D. vô số.
Câu 12. Tập xác định của hàm số y = 2 cos x −1 là: A. D = \
+ k ,k . B. D = \
+ k,k . 2 1
C. D = .
D. D = \ . 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hai đồ thị hàm số y = sin x +
và y = sin x , khi đó: 4
a) Khi x [0;2 ] thì hai đồ thị hàm số cắt nhau tại ba điểm 5 5 7 7
b) Khi x [0;2 ] thì toạ độ giao điểm của hai đồ thị hàm số là: ;sin , ;sin . 8 8 8 8
c) Phương trình hoành độ giao điểm của hai đồ thị hàm số: sin x + = sin x 4 3
d) Hoành độ giao điểm của hai đồ thị là x =
+ k (k ) 8
Câu 2. Cho tứ diện SABC . Gọi M và N lần lượt là hai điểm trên hai cạnh AB và BC sao cho MN
không song song với AC . Khi đó:
a) Giao điểm của đường thẳng MN và mặt phẳng (SAC) là giao điểm của MN và AC .
b) Đường thẳng MN cắt đường thẳng AC
c) Giao tuyến của hai mặt phẳng (SMN) và (SAC) là đường thẳng đi qua giao điểm của MN và AC .
d) Giao tuyến của hai mặt phẳng (SAN ) và (SCM ) là đường thẳng đi qua giao điểm của MN và AC .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4. Trang 17
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A là điểm trên SA sao cho 1
AA = AS . Qua A kẻ đường thẳng song song với AC cắt SC tại C . Mặt phẳng ( ) chứa 2 SB SD A C
cắt các cạnh SB , SD lần lượt tại B, D . Tính giá trị của biểu thức T = + . SB SD
Câu 2. Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác = (O ,
x OM) theo hàm số v = 0,3sin (m / s) (Hình bên). Dựa vào đồ thị hàm số sin, biết trong x
vòng quay đầu tiên (0 2 ) góc thuộc các khoảng ( ; a ) b và ( ;
c d) thì v tăng. Hãy cho biết x
a + b + c + d có giá trị bằng bao nhiêu?
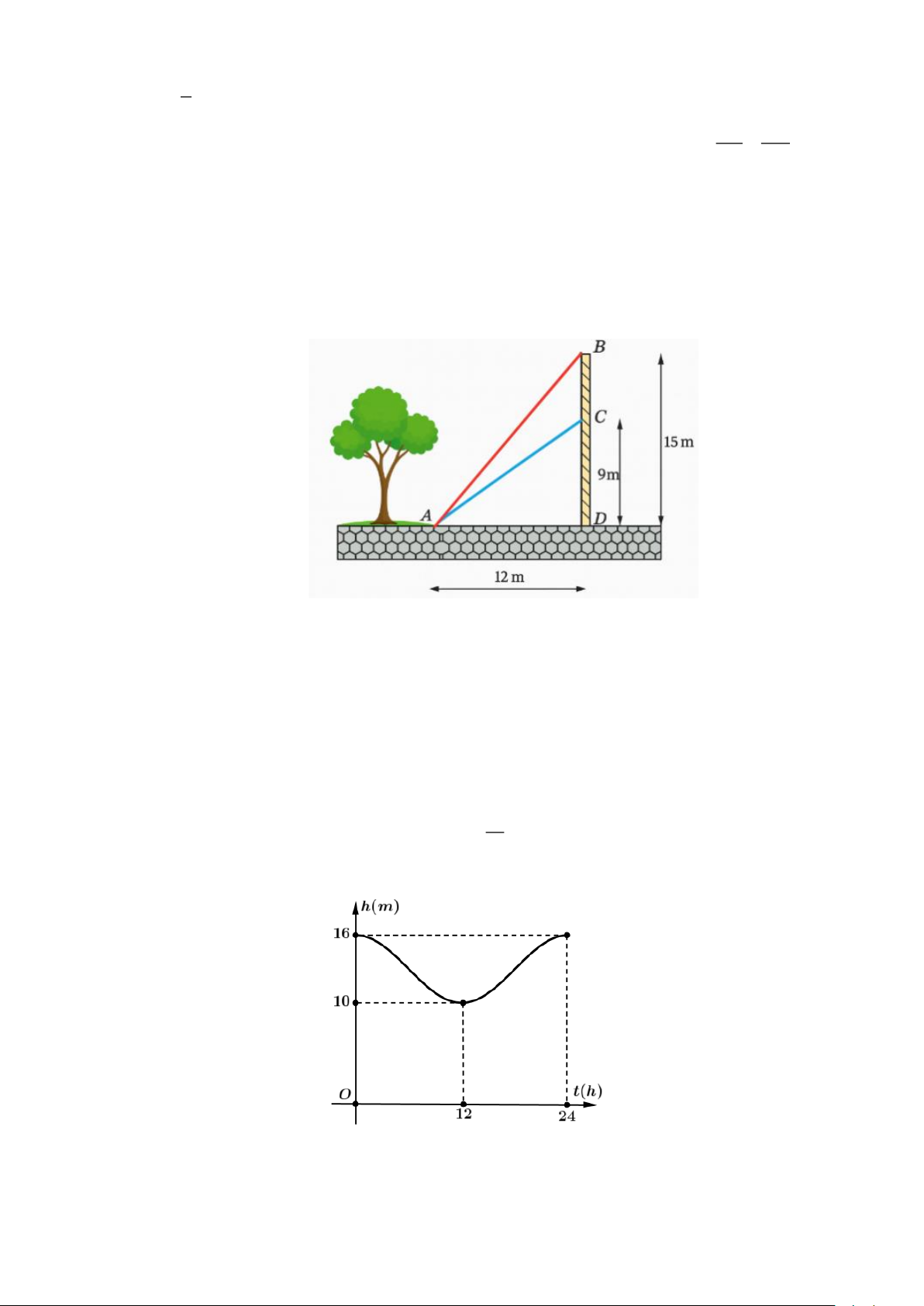
Câu 3. Từ một vị trí A , người ta buộc hai sợi cáp AB và AC đến một cái trụ cao 15 m, được dựng vuông
góc với mặt đất, chân trụ ở vị trí D . Biết CD = 9 m và AD =12 m . Tìm góc nhọn = BAC tạo bởi
hai sợi dây cáp đó, đồng thời tính gần đúng (làm tròn đến hàng phần chục, đơn vị độ).
Câu 4. Một người sử dụng xe có giá trị ban đầu là 80 triệu. Sau mỗi năm, giá trị xe giảm 10% so với năm
trước đó. Hỏi sau 5 năm thì giá trị của xe còn lại bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần mười)
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Tìm GTLN - GTNN của hàm số 2 y = 2
− sin x + 3sin x −1
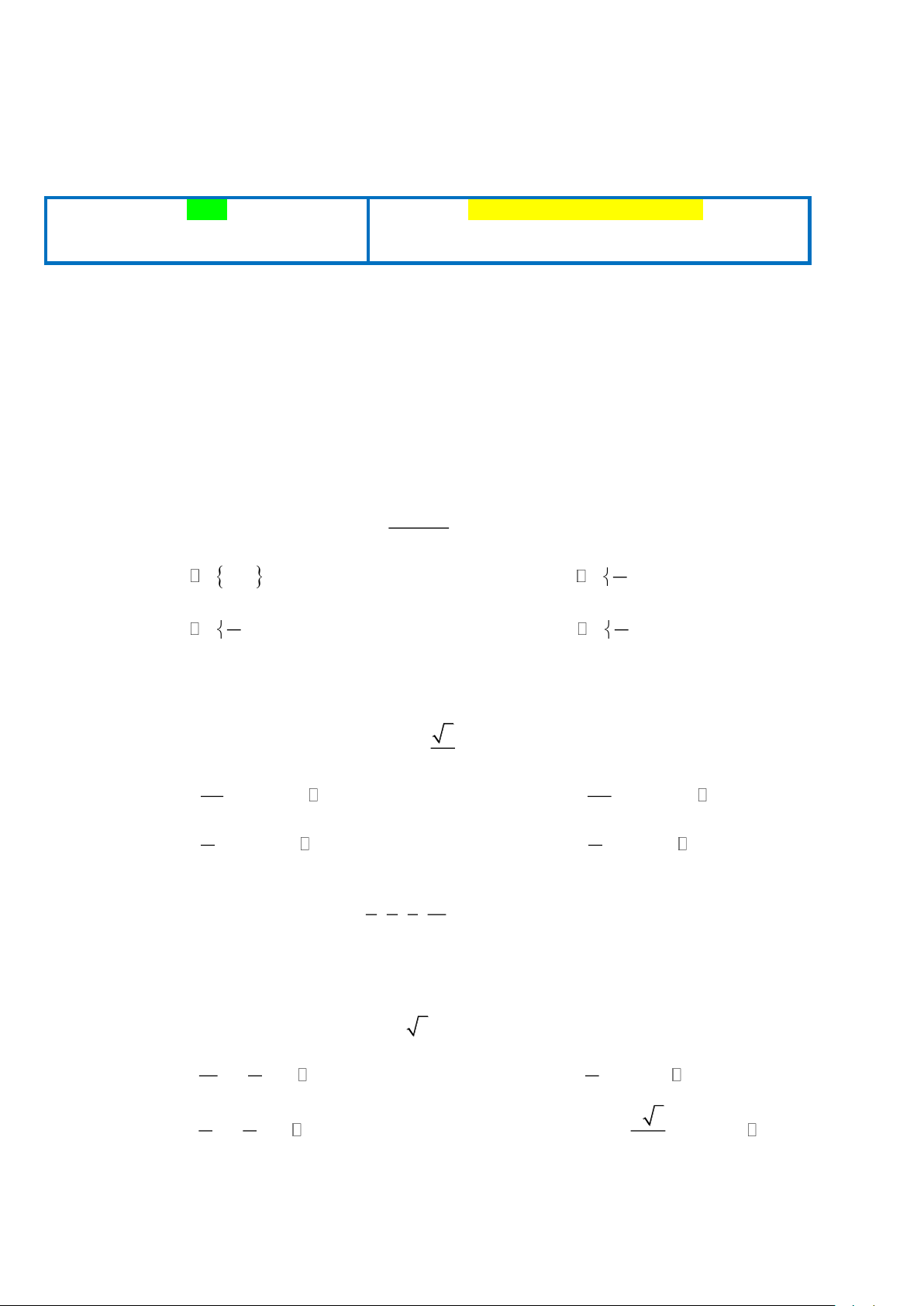
Câu 2. Mực nước cao nhất tại một cảng biển là 16 m khi thủy triều lên cao và sau 12 giờ khi thủy triều
xuống thấp thì mực nước thấp nhất là 10 m. Đồ thị ở hình dưới đây mô tả sự thay đổi chiều cao của mực
nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước h( m) theo thời gian
t ( h)(0 t 24) được cho bởi công thức h = m + acos t
với m,a là các số thực dương cho trước. Tìm 12
thời điềm trong ngày khi chiều cao của mực nước là 11,5 m và tính tổng các thời điểm đó.
Câu 3. Cho tứ diện ABCD, O là một điểm thuộc miền trong tam giác BCD , M là điểm trên đoạn AO
.Tìm giao điểm của mặt phẳng (MCD) với đường thẳng AB. Trang 18
Câu 4. An và Bình chơi bài. Người thua phải trả 1 cây kẹo cho người thắng trong ván đầu tiên; 2 cây kẹo
trong ván thứ 2; 4 cây kẹo trong ván thứ 3 và cứ thế số kẹo mỗi lần thua tăng gấp đôi so với lần
trước đó. Ban đầu An có 625 cây kẹo và sau 10 ván thì An thua hết kẹo (có ván thắng, có ván thua).
An nói với Bình: “Nếu chúng ta không chơi theo luật vừa rồi mà chơi theo luật khác: ván đầu người
thua trả 10 cây cho người thắng, ván 2 trả 20 cây, ván 3 trả 30 cây thì tớ vẫn còn chơi với cậu được
vài ván nữa”. Vậy, bạn An nói đúng hay sai? ĐỀ 7
ĐỀ ÔN TẬP GIỮA HỌC KÌ I
MÔN: TOÁN – LỚP 11
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Mệnh đề nào sau đây sai?
A. cos2a = 2sin acos a B. 2 2
cos 2a = cos a − sin a . C. 2
cos 2a = 2cos a −1. D. 2
cos 2a = 1− 2sin a .
Câu 2. Với mọi góc lượng giác và số nguyên k , mệnh đề nào sau đây sai?
A. sin( + k2) = sin .
B. tan( + k) = tan .
C. cot ( + k) = cot .
D. cos( + k) = cos . tan x
Câu 3. Tìm tập xác định của hàm số y = . cos x −1
A. D = \k2 .
B. D = \ + k2; x k . 2
C. D = \ + k;k2 .
D. D = \ + k2 . 2 2
Câu 4. Điểm cuối của cung trên đường tròn lượng giác thuộc góc phần tư thứ II. Chọn khẳng định đúng?
A. cos 0.
B. sin 0.
C. tan 0.
D. cot 0 . 3
Câu 5. Tập nghiệm của phương trình cos x = − là 2 5 2 A. x =
+ k2 ,k . B. x =
+ k2 , k . 6 3 C. x =
+ k2 ,k . D. x =
+ k ,k . 3 6
Câu 6. Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân? 5 5 5 5 A. 1; 2;3; 4;5. B. 5; ; ; ; .
C. 0; 4;8;12;16. D. 1;3;5;7;9 . 2 4 8 16
Câu 7. Cho tứ giác ABCD. Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh của tứ giác ABCD A. 3 . B. 2 . C. 4 . D. 1.
Câu 8. Nghiệm của phương trình cot 2x = − 3 là A. x = −
+ k ,k .
B. x = − + k ,k . 12 2 6 − 3
C. x = − + k ,k .
D. x = arccot
+ k ,k . 6 2 2
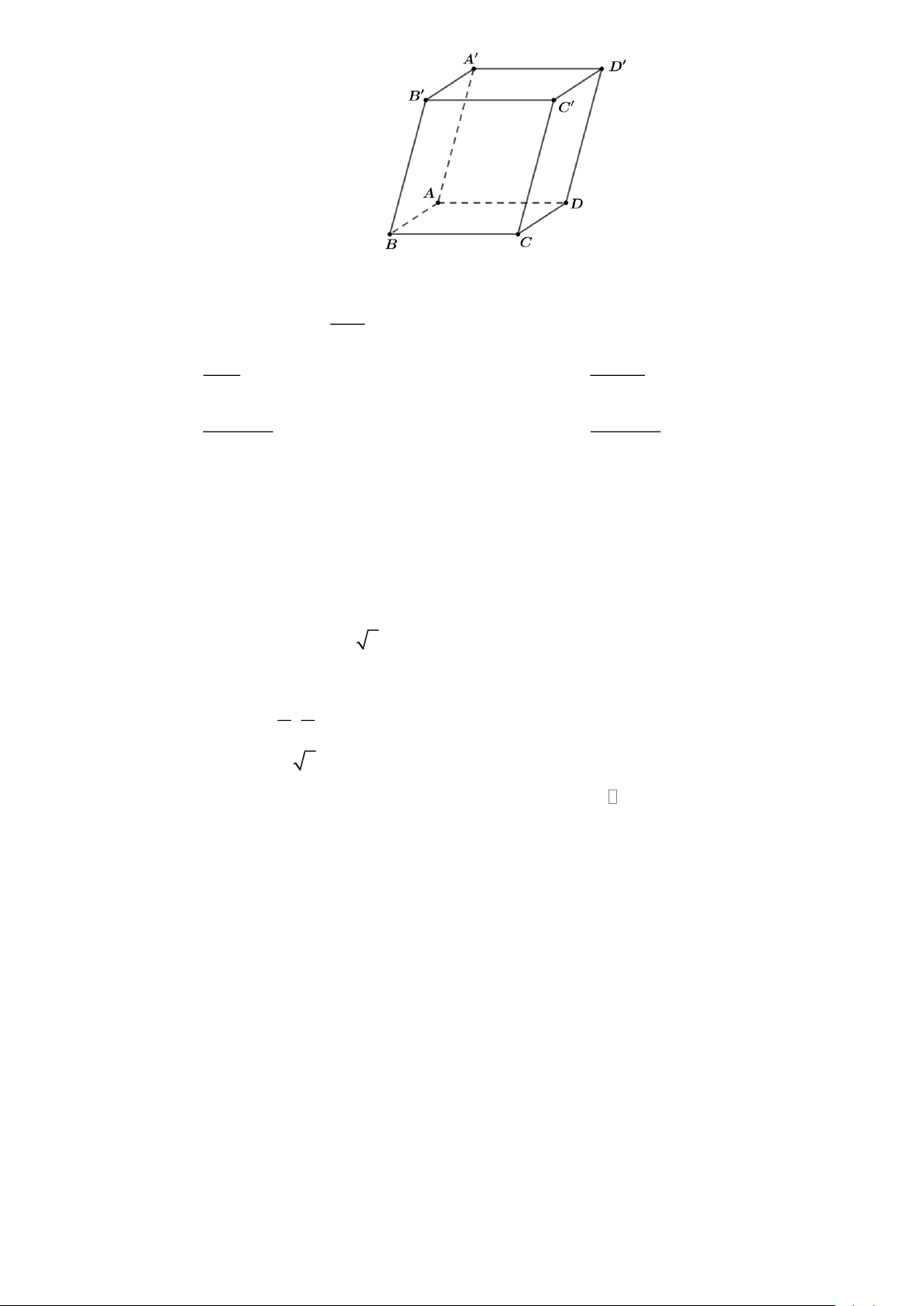
Câu 9. Cho hình hộp ABC . D A B C D
như hình vẽ. Đường thẳng nào sau đây không song song với đường thẳng BC ? Trang 19
A. Đường thẳng AD .
B. Đường thẳng B D .
C. Đường thẳng B C .
D. Đường thẳng AD . 2 an
Câu 10. Cho dãy số (u với u =
( a hằng số). Hỏi u là số hạng nào sau đây? n ) n n +1 n 1 + 2 an 2 . a n +1 A. u = . B. u = . n 1 + n + 2 n 1 + n +1 . a (n + )2 1 . a (n + )2 1 C. u = . D. u = . n 1 + n + 2 n 1 + n +1
Câu 11. Trong không gian có bao nhiêu vị trí tương đối của đường thẳng a và mặt phẳng (P) ? A. 2 . B. 3 . C. 4 . D. 1.
Câu 12. Hàm số y = 5 + 3sin x luôn nhận giá trị trong tập nào sau đây? A. 5; 8 . B. 3 − ; 3 . C. 2; 8 D. 1 − ; 1 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho phương trình lượng giác 2 2sin (45 −
− 2x) = 0 , vậy:
a) Phương trình tương đương với sin (45 2x) sin 45 − = b) Trên khoảng − ;
phương trình đã cho có một nghiệm 2 2
c) Đồ thị hàm số y 2 2sin (45 = −
− 2x) cắt trục hoành tại điểm gốc tọa độ
d) Phương trình có nghiệm là: x 1 k 80; x 45 1 k 80 = − = − − (k ) .
Câu 2. Cho tứ diện ABCD. Gọi M , N, P,Q, R, S lần lượt là trung điểm của AB,CD, BC, AD, AC, BD . Các
khẳng định sau đúng hay sai?
a) [VD] Ba đoạn MN, PQ, RS cắt nhau tại trung điểm của mỗi đoạn.
b) [NB] Mặt phẳng (ABC) cắt mặt phẳng (MNP) theo giao tuyến PM .
c) [TH] Tứ giác MPNQ là chữ nhật.
d) [NB] Đoạn thẳng BC và AD đồng phẳng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác
cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với
mặt đất tại một vị trí cách chân cột 15 m (Hình vẽ).Tính tan , ở đó là góc giữa hai sợi cáp trên (
làm tròn đến một chữ số thập phân) Trang 20




