






Preview text:
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Câu 1. Đa thức nào sau đây chưa thu gọn? 2 x + 2 y A. 2
4x + x − y . B. 4 4
x y + x − 2yx . C. 3 2
−x y + y . D. . 5 5
Câu 2. Đơn thức nào sau đây đồng dạng với đơn thức 2 3 − x y ? 1 A. 2 3x yz . B. xyx . C. 2 xy . D. 2 −3x z . 2 Câu 3. Đa thức 3 2 4 3
7x y z − 2x y chia hết cho đơn thức nào dưới đây? A. 4 3x . B. 4 −3x . C. 3 2 − x y . D. 3 2xy .
Câu 4. Giá trị của biểu thức 4 2
A = x + 4x y − 6z tại x = 4, y = 5 − , z = 2 − là A. 76 − . B. 52 − . C. 25 − . D. 37 .
Câu 5. Hằng đẳng thức 2 2
A − B = ( A− B)( A+ B) có tên là
A. bình phương của một tổng.
B. bình phương của một hiệu.
C. tổng hai bình phương.
D. hiệu hai bình phương. Câu 6. Cho x + x + x + = (x + a)3 3 2 12 48 64
. Giá trị của a là A. 64 − . B. 64. C. 4 − . D. 4.
Câu 7. Trong một tứ giác, hai cạnh kề nhau là hai cạnh
A. có chung một đỉnh.
B. không có đỉnh chung nào.
C. thuộc một đường thẳng.
D. có hai đỉnh chung.
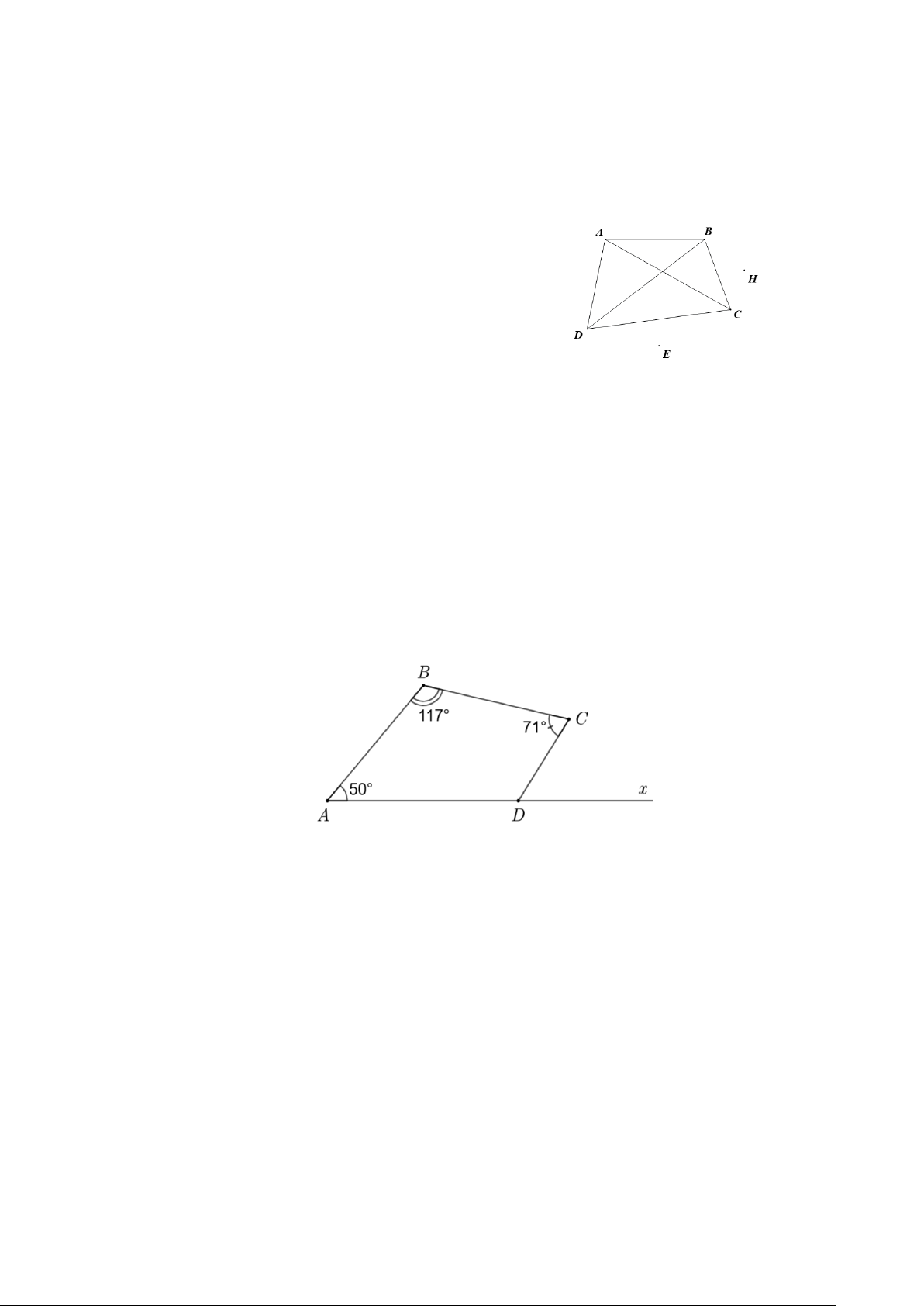
Câu 8. Cho hình vẽ bên. Khẳng định nào sau đây là sai?
A. Hai cạnh AB và BC kề nhau.
B. Hai cạnh BC và DA đối nhau.
C. Các cặp góc A và B ; C và D đối nhau.
D. Các điểm H và E nằm ngoài.
Câu 9. Cho tứ giác ABCD có A = 50 ; B =117 ;
C = 71 . Số đo góc ngoài tại đỉnh D bằng A. 58. B. 107 . C. 113 . D. 83 .
Câu 10. Cho hình thang cân ABCD có AB // CD và A =125 . Khi đó B bằng A. 65. B. 125 . C. 90 . D. 55 . Trang 1
Câu 11. Cho các hình sau. Khẳng định nào sau đây là đúng? A B A B A B D C D C D C Hình 1 Hình 2 Hình 3
A. Cả ba hình đều là hình thoi.
B. Hình 1 và hình 2 là hình thoi.
C. Chỉ hình 1 là hình thoi.
D. Cả ba hình đều không phải hình thoi.
Câu 12. Tứ giác ABCD là hình bình hành nếu thỏa mãn điều kiện nào dưới đây?
A. AB // CD, AC = BD . B. A = C .
C. AB = CD. D.
A = C; B = D .
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho hai đa thức 2
P = x − 4xy + 9 và 2 Q = 6
− xy − 4y + 9.
Đa thức A và M thỏa mãn P − A = Q
M = (x − y) 3 ; 2 A− x + 5.
a) Với x = 1; y = 1
− thì giá trị của biểu thức P bằng 10.
b) Đa thức Q có bậc là 2. c) 2 2
A = x + xy + 4y .
d) Giá trị của biểu thức M không phụ thuộc vào biến . x
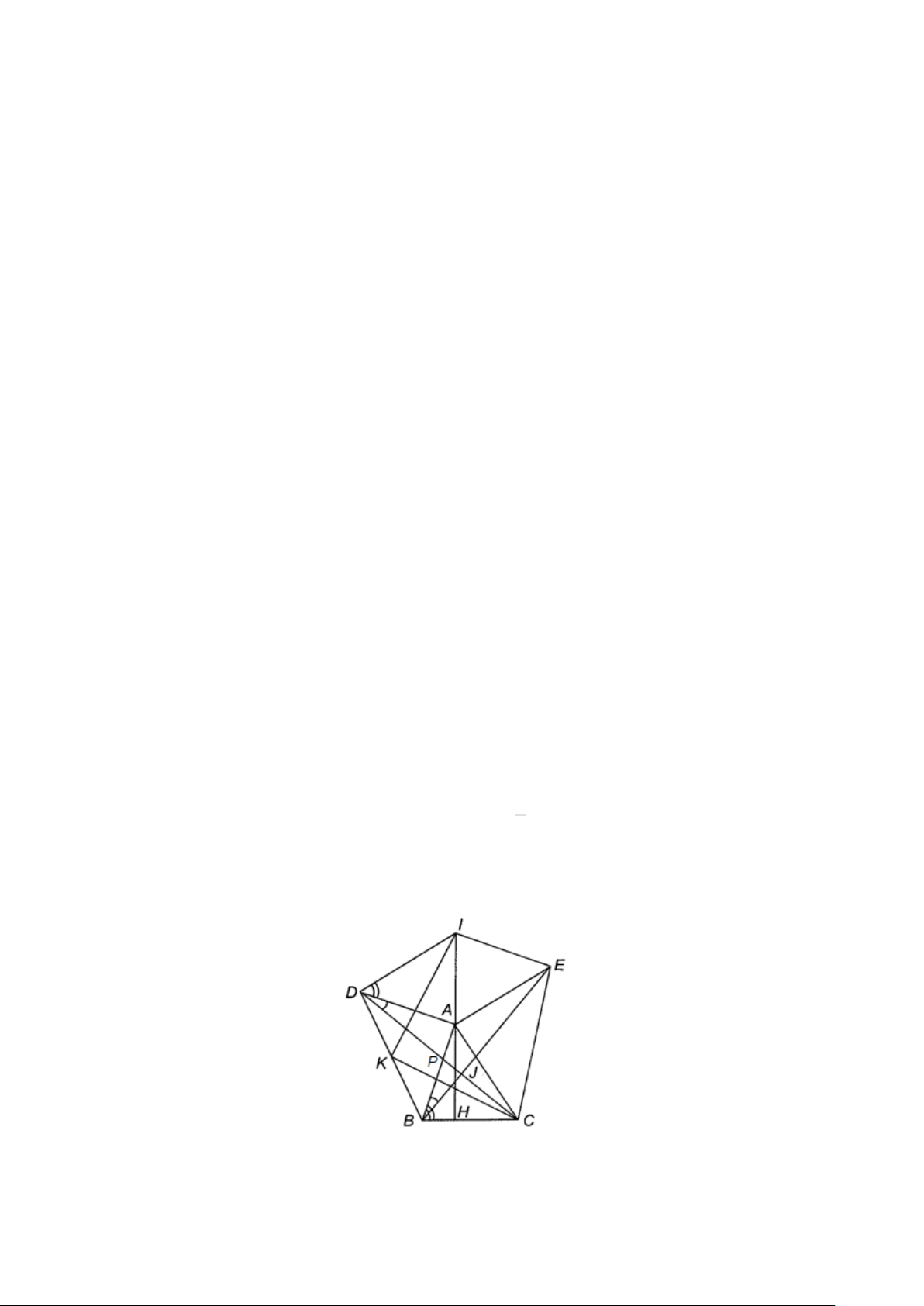
Câu 14. Cho tam giác ABC không vuông tại A . Dựng bên ngoài tam giác đó hai tam giác
ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID . Biết
DAI = ABC . Gọi K là trung điểm của . BD a)
DAI + BAH = 45 . b) AI ⊥ BC . 1 c) EBA = CDA. d) KAI = KBC . 2
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Cho B − ( 2 x − xyz) 2 5 2
= 2x + 2xyz +1. Hạng tử tự do của đa thức B là bao nhiêu?
Câu 16. Cho biểu thức 3 2
x − 9x + 27x − m là lập phương của một tổng. Tính giá trị của m .
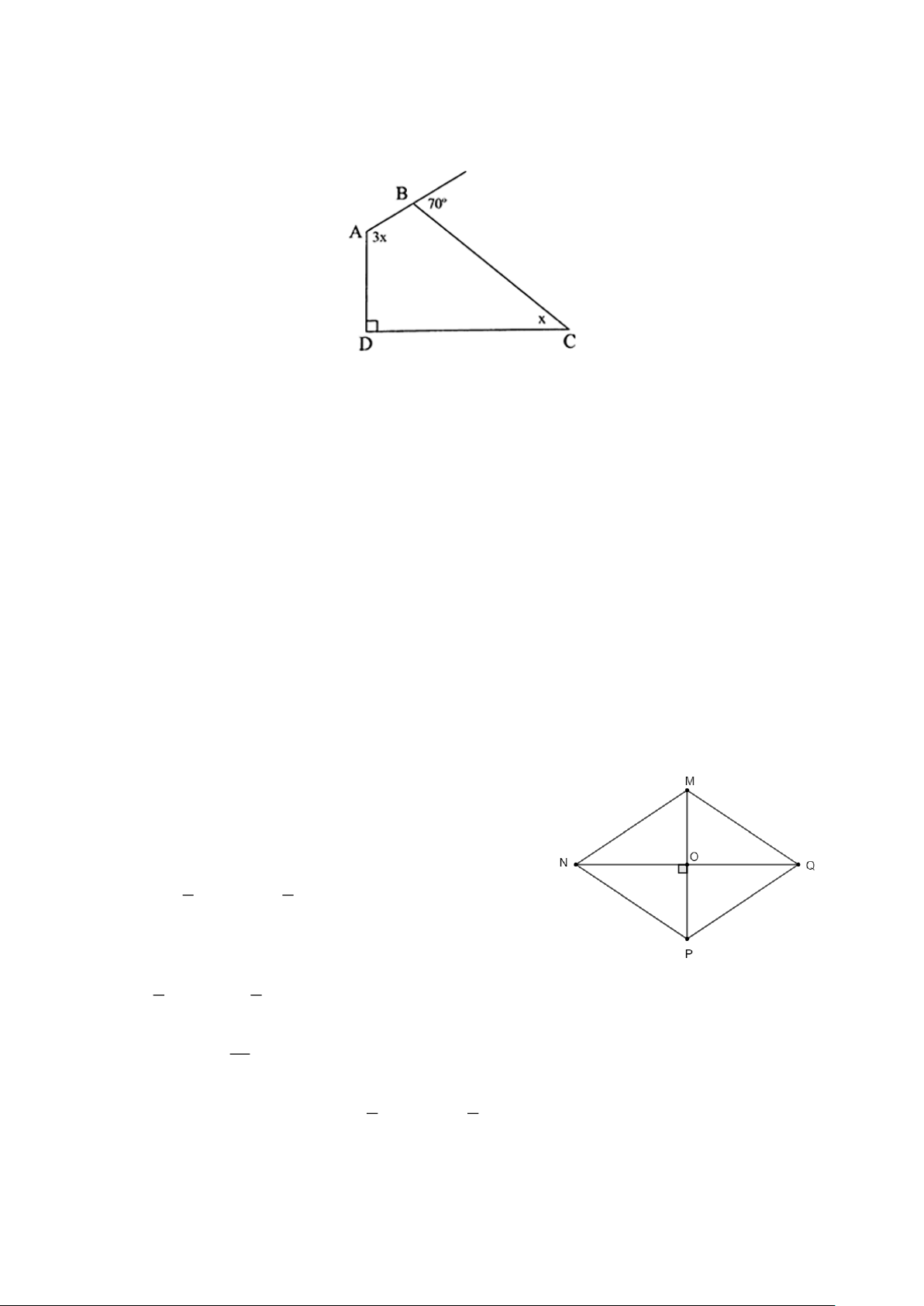
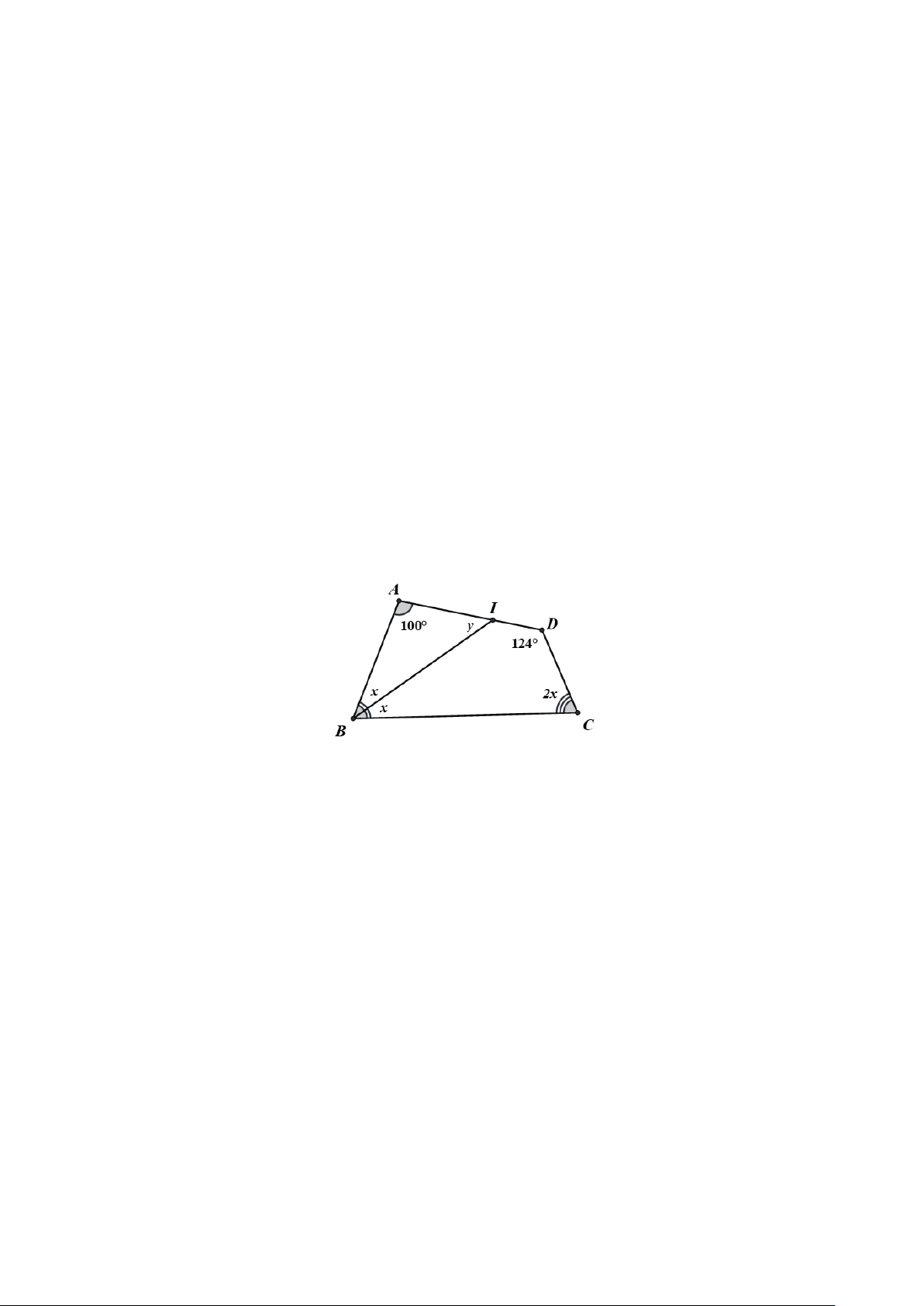
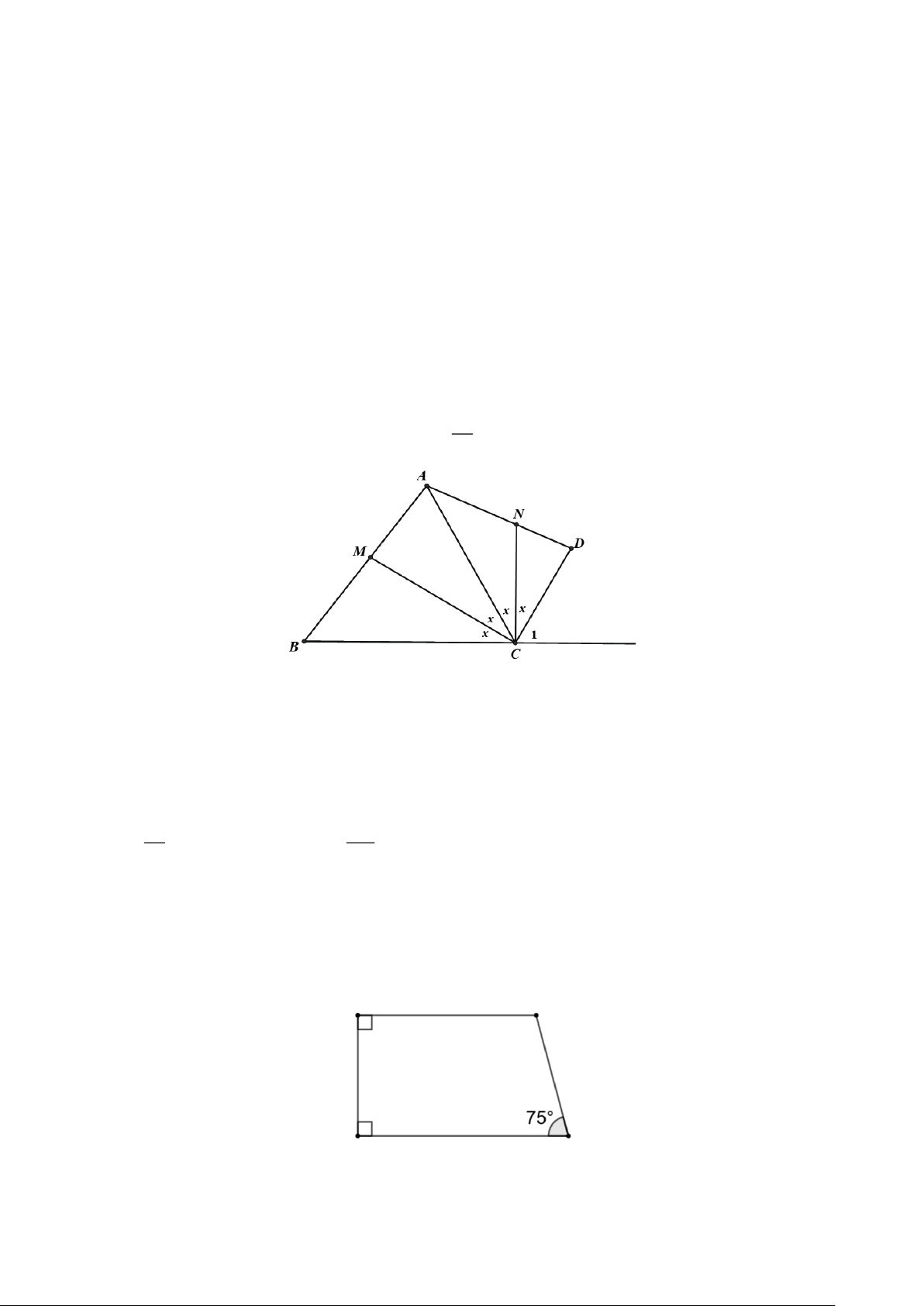
Câu 17. Cho hình vẽ dưới đây. Tính số đo góc A (đơn vị: độ). Trang 2
Câu 18. Cho hình thoi MNPQ có diện tích là 2
48 cm . Gọi O là giao điểm của hai đường chéo.
Tính diện tích tam giác MON (đơn vị: 2 cm ).
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm) Tìm x , biết: a) 3 2
x + 9x + 27x +19 = 0 ; b) (x + )2 25
3 + (1– 5x)(1+ 5x) = 8 ;
c) ( x + )2 + ( x − )2 3 2 2
1 − 7( x + 3)( x − 3) = 36 .
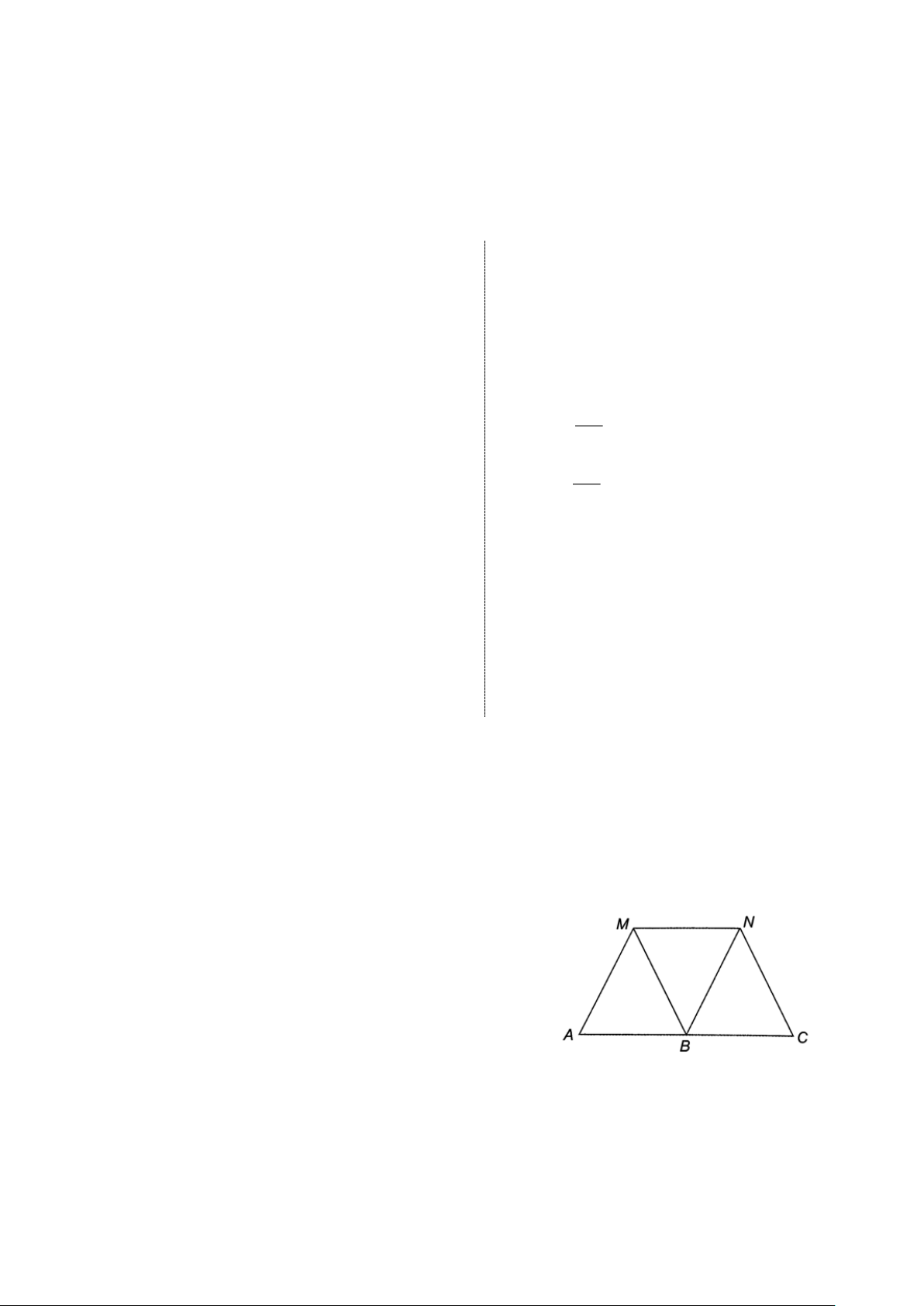
Bài 2. (1,5 điểm) Cho hai hình bình hành MNBA và MNCB .
a) Chứng minh B là trung điểm của AC .
b) Hỏi tam giác MAB thoả mãn điều kiện gì để MNCA là một hình thang cân?
c) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thoả mãn điều kiện gì để
MNDA là một hình thang cân? -----HẾT-----
ĐÁP ÁN VÀ LỜI GIẢI
A. TRẮC NGHIỆM (7,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B C C B D D A C A B C D Câu
13a 13b 13c 13d 14a 14b 14c 14d 15 16 17 18 Đáp án S Đ S Đ S Đ Đ S 1 27 120 12
Hướng dẫn giải chi tiết
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Câu 1. Đa thức nào sau đây chưa thu gọn? 2 x + 2 y A. 2
4x + x − y . B. 4 4
x y + x − 2yx . C. 3 2
−x y + y . D. . 5 5
Hướng dẫn giải
Đáp án đúng là: B Ta có 4 4 4 4 4
x y + x − 2yx = x y − 2x y + x = −x y + x . Trang 3 Vậy đa thức 4 4
x y + x − 2yx là đa thức chưa thu gọn.
Câu 2. Đơn thức nào sau đây đồng dạng với đơn thức 2 3 − x y ? 1 A. 2 3x yz . B. xyx . C. 2 xy . D. 2 −3x z . 2
Hướng dẫn giải
Đáp án đúng là: B 1 1 Ta có: 2
xyx = x y , đơn thức này đồng dạng với đơn thức 2 3 − x y . 2 2 Câu 3. Đa thức 3 2 4 3
7x y z − 2x y chia hết cho đơn thức nào dưới đây? A. 4 3x . B. 4 −3x . C. 3 2 − x y . D. 3 2xy .
Hướng dẫn giải
Đáp án đúng là: C Đa thức 3 2 4 3
7x y z − 2x y chia hết cho 3 2 − x y . Hạng tử 3 2
7x y z không chia hết cho đơn thức 4 4
3x ; − 3x và 3 2xy nên đa thức 3 2 4 3
7x y z − 2x y cũng không chia hết cho 4 4
3x ; − 3x và 3 2xy .
Câu 4. Giá trị của biểu thức 4 2
A = x + 4x y − 6z tại x = 4, y = 5 − , z = 2 − là A. 76 − . B. 52 − . C. 25 − . D. 37 .
Hướng dẫn giải
Đáp án đúng là: B
Thay x = 4, y = 5 − , z = 2
− vào biểu thức A ta được: 4 2 A = 4 + 4.4 .( 5 − ) −6.( 2 − ) = 256 −320 +12 = 5 − 2 .
Câu 5. Hằng đẳng thức 2 2
A − B = ( A− B)( A+ B) có tên là
A. bình phương của một tổng.
B. bình phương của một hiệu.
C. tổng hai bình phương.
D. hiệu hai bình phương.
Hướng dẫn giải
Đáp án đúng là: D Hằng đẳng thức 2 2
A − B = ( A− B)( A+ B) có tên là hiệu hai bình phương. Câu 6. Cho x + x + x + = (x + a)3 3 2 12 48 64
. Giá trị của a là A. 64 − . B. 64. C. 4 − . D. 4.
Hướng dẫn giải
Đáp án đúng là: D Ta có x + x + x + = (x + )3 3 2 12 48 64 4 . Vậy a = 4.
Câu 7. Trong một tứ giác, hai cạnh kề nhau là hai cạnh Trang 4
A. có chung một đỉnh.
B. không có đỉnh chung nào.
C. thuộc một đường thẳng.
D. có hai đỉnh chung. Hướng dẫn giải Đáp án đúng là: A
Trong một tứ giác, hai cạnh kề nhau là hai cạnh có chung một đỉnh.
Câu 8. Cho hình vẽ bên. Khẳng định nào sau đây là sai?
A. Hai cạnh AB và BC kề nhau.
B. Hai cạnh BC và DA đối nhau.
C. Các cặp góc A và B; C và D đối nhau.
D. Các điểm H và E nằm ngoài.
Hướng dẫn giải
Đáp án đúng là: C
Tứ giác ABCD có các cặp góc đối nhau là A và C , B và D.
Các cặp góc A và B , C và
D là hai cặp góc kề nhau.
Câu 9. Cho tứ giác ABCD có A = 50 ; B =117 ;
C = 71 . Số đo góc ngoài tại đỉnh D bằng A. 58. B. 107 . C. 113 . D. 83 .
Hướng dẫn giải
Đáp án đúng là: A Gọi
CDx là góc ngoài tại đỉnh D .
Tứ giác ABCD có:
ADC = 360 − (A+ B +C). Suy ra
ADC = 360 − (50 + 1 1 7 7 + 1) = 22 1 . Vì ADC và
CDx là hai góc kề bù nên CDx =1 0 8 ° − A C
D =180 −122 = 5 ° 8 .
Vậy số đo góc ngoài tại đỉnh D bằng 58 .
Câu 10. Cho hình thang cân ABCD có AB // CD và A =125 . Khi đó B bằng A. 65. B. 125 . C. 90 . D. 55 .
Hướng dẫn giải
Đáp án đúng là: B
Hình thang cân ABCD có AB // CD nên AB và CD là hai đáy. Trang 5
Theo tính chất của hình thang cân ta có A = B =125.
Câu 11. Cho các hình sau. Khẳng định nào sau đây là đúng? A B A B A B D C D C D C Hình 1 Hình 2 Hình 3
A. Cả ba hình đều là hình thoi.
B. Hình 1 và hình 2 là hình thoi.
C. Chỉ hình 1 là hình thoi.
D. Cả ba hình đều không phải hình thoi.
Hướng dẫn giải
Đáp án đúng là: C
• Hình 1 là hình thoi vì có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau.
• Hình 2 , Hình 3 không là hình thoi vì bốn cạnh không bằng nhau.
Câu 12. Tứ giác ABCD là hình bình hành nếu thỏa mãn điều kiện nào dưới đây?
A. AB // CD, AC = BD . B. A = C .
C. AB = CD. D.
A = C; B = D .
Hướng dẫn giải
Đáp án đúng là: D
• Tứ giác ABCD là hình bình hành nếu thỏa mãn điều kiện
A = C; B = D (các góc đối bằng nhau).
• Tứ giác ABCD có một cặp cạnh đối bằng nhau ( AB = CD) hoặc một cặp góc đối bằng nhau
(A=C) thì chưa đủ điều kiện để kết luận hình bình hành.
• Tứ giác ABCD có một cặp cạnh đối song song ( AB // CD) thì chưa đủ để kết luận hình bình hành
và hai đường chéo của hình bình hành có thể không bằng nhau.
Vậy ta chọn phương án D.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Câu 13. Cho hai đa thức 2
P = x − 4xy + 9 và 2 Q = 6
− xy − 4y + 9.
Đa thức A và M thỏa mãn P − A = Q
M = (x − y) 3 ; 2 A− x + 5.
a) Với x = 1; y = 1
− thì giá trị của biểu thức P bằng 10.
b) Đa thức Q có bậc là 2. c) 2 2
A = x + xy + 4y .
d) Giá trị của biểu thức M không phụ thuộc vào biến . x
Hướng dẫn giải Đáp án: a) Sai. b) Đúng. c) Sai. d) Đúng. Trang 6
⦁ Thay x = 1; y = 1
− vào biểu thức P , ta có: 2 P =1 − 4 1 (− ) 1 + 9 =1+ 4 + 9 =14.
Vậy với x = 1; y = 0 thì P = 14 . Do đó ý a) sai. ⦁ Đa thức 2 Q = 6
− xy − 4y + 9 có bậc là 2. Do đó ý b) đúng.
⦁ Ta có P − A = Q
Suy ra A = P − Q 2
= x − xy + − ( 2 4 9 6
− xy − 4y + 9) 2 2
= x − 4xy + 9 + 6xy + 4y −9 2 2
= x + 2xy + 4y . Như vậy 2 2
A = x + 2xy + 4y . Do đó ý c) sai.
⦁ Ta có: M = (x − y) 3 2 A− x + 5 = (x − y)( 2 2
x + xy + y ) 3 2 2 4 − x + 5 = x( 2 2
x + xy + y ) − y ( 2 2
x + xy + y ) 3 2 4 2 2 4 − x + 5 3 2 2 2 2 3 3
= x + 2x y + 4xy − 2x y − 4xy −8y − x + 5 3 3 3
= x −8y − x + 5 3 = 8 − y + 5.
Như vậy, giá trị của biểu thức M không phụ thuộc vào giá trị của biến .
x Do đó ý d) đúng.
Câu 14. Cho tam giác ABC không vuông tại A . Dựng bên ngoài tam giác đó hai tam giác
ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID . Biết
DAI = ABC . Gọi K là trung điểm của . BD a)
DAI + BAH = 45 . b) AI ⊥ BC . 1 c) EBA = CDA. d) KAI = KBC . 2 Hướng dẫn giải Đáp án: a) Sai.
b) Đúng. c) Đúng. d) Sai.
⦁ Giả sử AI cắt BC ở H . Trang 7 Ta có:
DAI + DAB + BAH =180 , mà
DAB = 90 (do DAB vuông cân tại A ). Suy ra
DAI + BAH = 90 . Do đó ý a) sai. ⦁ Mà
DAI = ABC (gt) nên
ABH + BAH = 90 . Trong ABH có:
ABH + BAH + AHB =180. Suy ra
AHB =180(ABH + BAH ) =180−90 = 90 hay AI ⊥ BC. Do đó ý b) đúng. ⦁ Ta có
BAE = BAC + CAE = BAC + 90 và
DAC = BAC + BAD = BAC + 90 . Do đó BAE = DAC . Xét BAE và D AC có: AB = A ; D BAE = DA ; C AC = AE ; Do đó B AE = D AC (c.g.c). Suy ra
EBA = CDA (hai góc tương ứng). Do đó ý c) đúng.
⦁ Tam giác ABD vuông cân tại A nên AK vừa là đường trung tuyến, vừa là đường cao, đường 1 phân giác. Do đó
DAK = BAD = 45 . 2 Khi đó
ABK = BAK = 45 nên ABK vuông cân tại K , do đó KA = KB . Ta có
KAI = DAK + DAI = 45 + DAI = 45 + ABC . Mặt khác
KBC = ABK + ABC = 45 + ABC (do ABD vuông cân tại A nên ABK = 45 ) . Do đó
KAI = KBC . Do đó ý d) sai.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Câu 15. Cho B − ( 2 x − xyz) 2 5 2
= 2x + 2xyz +1. Hạng tử tự do của đa thức B là bao nhiêu?
Hướng dẫn giải Đáp số: 1. Ta có B − ( 2 x − xyz) 2 5 2 = 2x + 2xyz +1 Suy ra B = ( 2
x + xyz + ) + ( 2 2 2 1 5x − 2xyz) 2 2
= 2x + 2xyz +1+ 5x − 2xyz = ( 2 2
x + x ) + ( xyz − xyz) 2 2 5 2 2 +1 = 7x +1.
Do đó, hạng tử tự do của đa thức B là 1.
Câu 16. Cho biểu thức 3 2
x − 9x + 27x − m là lập phương của một tổng. Tính giá trị của m .
Hướng dẫn giải Đáp số: 27. Ta có 3 2 3 2 2
x − 9x + 27x − m = x − 3 x 3 + 3 x 3 − m . Trang 8
Để biểu thức trên là lập phương của một tổng thì 3 m = 3 = 27 .
Khi đó, x − x + x −
= x − x + x − = (x − )3 3 2 3 2 2 3 9 27 27 3 3 3 3 3 3 .
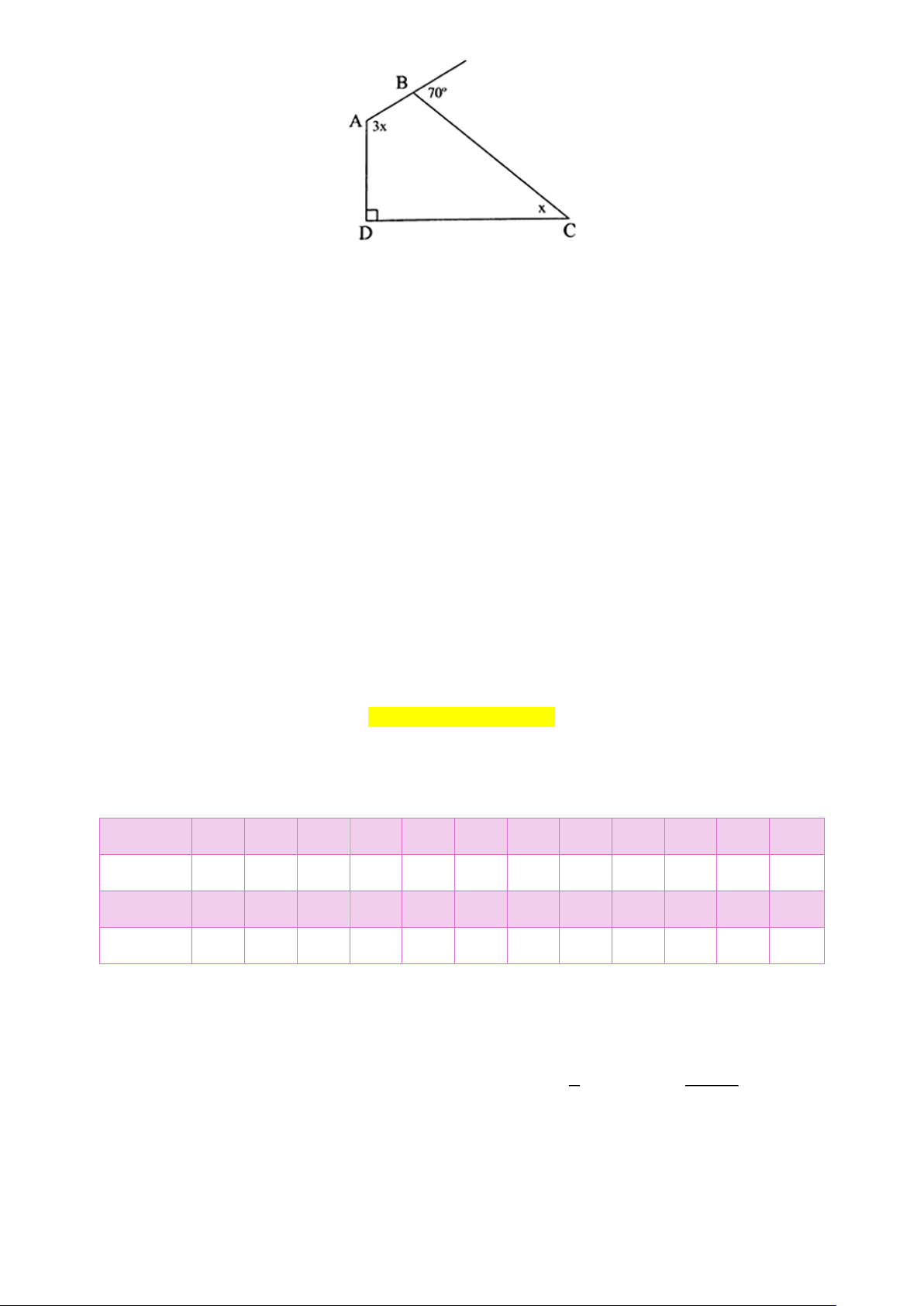
Câu 17. Cho hình vẽ dưới đây. Tính số đo góc A (đơn vị: độ). Hướng dẫn giải Đáp số: 120.
Góc ngoài tại đỉnh B có số đo bằng 70 nên góc trong tại đỉnh B có số đo bằng 180−70 =110 .
Xét tứ giác ABCD, ta có:
A + B + C + D = 360 .
Do đó 3x +110+ x +90 = 360 .
Suy ra 4x =160 nên x = 40 .
Vậy 3x = 340 =120 .
Câu 18. Cho hình thoi MNPQ có diện tích là 2
48 cm . Gọi O là giao điểm của hai đường chéo.
Tính diện tích tam giác MON (đơn vị: 2 cm ).
Hướng dẫn giải Đáp số: 12.
Tứ giác MNPQ là hình thoi nên hai đường chéo MP và
NQ vuông góc với nhau và cắt nhau tại trung điểm O của mỗi đường. 1 1
Suy ra OM = MP; ON = . NQ 2 2
Diện tích hình thoi MNPQ là: 1 1 S
= MP NQ = 2OM 2ON = 2OM ON = 48 MNPQ ( 2 cm ). 2 2 48
Suy ra OM ON = = 24. 2 1 1
Diện tích tam giác MON là: S
= OM ON = 24 = 12 MON ( 2 cm ). 2 2
Vậy diện tích tam giác MON là 2 12 cm .
B. TỰ LUẬN (3,0 điểm) Trang 9
Bài 1. (1,5 điểm) Tìm x , biết: a) 3 2
x + 9x + 27x +19 = 0 ; b) (x + )2 25
3 + (1– 5x)(1+ 5x) = 8 ;
c) ( x + )2 + ( x − )2 3 2 2
1 − 7( x + 3)( x − 3) = 36 .
Hướng dẫn giải a) 3 2
x + 9x + 27x +19 = 0 b) (x + )2 25
3 + (1– 5x)(1+ 5x) = 8 3 2
x + 9x + 27x + 27 − 8 = 0
(x + x+ )+ −( x)2 2 2 25 6 9 1 5 = 8 ( x + )3 3 = 8 2 2
25x +150x + 225 +1− 25x = 8 Suy ra x + 3 = 2 150x = 2 − 18 x = 1. − 109 Vậy x = 1. − x = − . 75
c) ( x + )2 + ( x − )2 3 2 2
1 − 7( x + 3)( x − 3) = 36 109 Vậy x = − . ( 75 2
3 x + 4x + 4) + ( 2 4x − 4x + ) 1 − 7 ( 2 x − 9) = 6 3 2 2 2
3x +12x +12 + 4x − 4x +1− 7x + 63 = 36 ( 2 2 2
3x + 4x − 7x ) + (12x − 4x) + (12 +1+ 63) = 36 8x = 4 − 0 x = 5. − Vậy x = 5. −
Bài 2. (1,5 điểm) Cho hai hình bình hành MNBA và MNCB .
a) Chứng minh B là trung điểm của AC .
b) Hỏi tam giác MAB thoả mãn điều kiện gì để MNCA là một hình thang cân?
c) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thoả mãn điều kiện gì để
MNDA là một hình thang cân?
Hướng dẫn giải
a) Do MNBA và MNCB là hình bình hành
Suy ra AB // MN, BC // MN nên theo tiên đề Euclid, hai
đường thẳng AB và BC trùng nhau. Do đó ba điểm ,
A B, C thẳng hàng.
Do MNBA và MNCB là hình bình hành nên
AB = MN, BC = MN . Suy ra AB = BC . Mà ,
A B, C thẳng hàng nên B là trung điểm của AC .
b) Từ câu a, ta suy ra MN // AC nên MNCA là hình thang. Trang 10
Do MNCB là hình bình hành nên NC // MB , từ đó
NCB = MBA (hai góc đồng vị). Điều kiện để
hình thang MNCA là hình thang cân là
MAB = NCB tức là MAB = MB . A
Vậy điều kiện để MNCA là hình thang cân là tam giác MAB cân tại M .
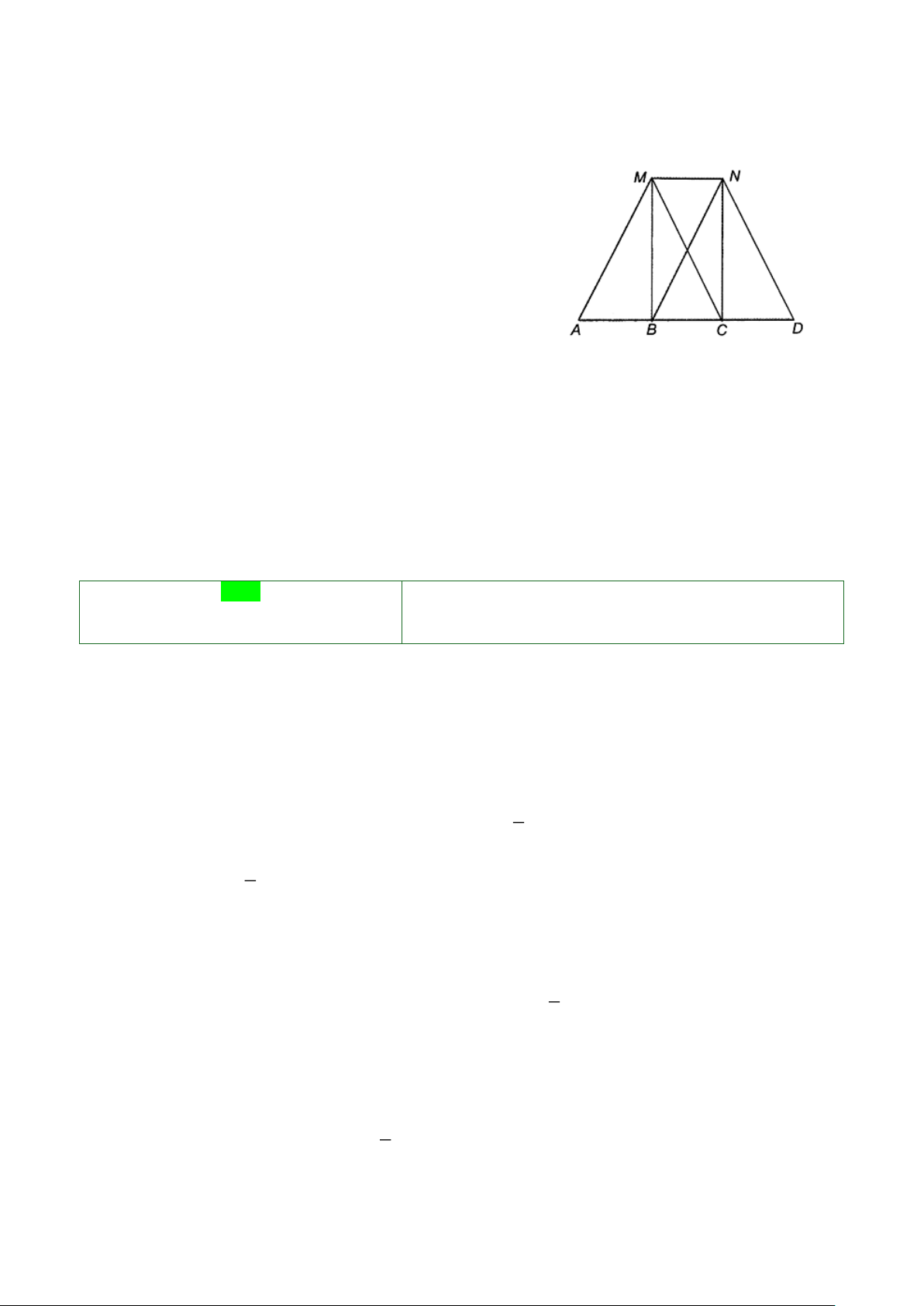
c) Chứng minh tương tự câu a, ta có MN // AD và bốn điểm ,
A B,C, D thẳng hàng. Do đó MNDA là hình thang.
Do MNDC là hình bình hành nên ND // MC , từ đó
NDC = MCA (hai góc đồng vị).
Điều kiện để hình thang MNDA là hình thang cân là NDC = MAC .
Khi đó điều kiện để MNDA là hình thang cân là
MCA = MAC tức là tam giác MAC cân tại M .
Do MB là đường trung tuyến của tam giác MAC nên điều kiện để tam giác MAC cân tại M là
MB vuông góc với AC .
Vậy điều kiện để hình thang MNDA là hình thang cân đó là tam giác MAB vuông tại B . -----HẾT----- ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 8
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm. 5
Câu 1. Trong các đơn thức sau: 2 2 2 2 2 2
− xy ; 3x y ; − 4x y ; x y ;12x . Có bao nhiêu đơn thức đồng 2 3 dạng với đơn thức 2 − x y ? 2 A. 1. B. 2 . C. 3 . D. 4 .
Câu 2. Đa thức nào sau đây không phải là đa thức bậc 4? 1 A. 2 4xy z . B. 4 5 x − 3 . C. 4 3 x − xy z . D. 2 xy + xyzt . 2
Câu 3. Điều kiện của số tự nhiên n để phép chia 5 n n 3
x y : x y là phép chia hết là
A. n = 3.
B. n = 4 .
C. n = 5.
D. n3; 4; 5 . 1
Câu 4. Giá trị của biểu thức 2 2 2
S = −6xy x yz + 2zxy x khi x = 2
− ; y = 1; z = 1 − là 2
A. S = 8. B. S = 8 − . C. S = 4 − . D. S = 4 . Trang 11
Câu 5. Đẳng thức nào sau đây là hằng đẳng thức? A. 2 2
x − x = −x + x .
B. x(x − ) 2
1 = x − x . C. (a b)2 (b a)2 − = − − .
D. a − 2 = 2− a . Câu 6. Đa thức 2 4
− x +12x − 9 được viết thành A. (2x − ) 3 (2x + 3).
B. − ( x − )2 2 3 . C. ( − )2 3 2x . D. − ( x + )2 2 3 .
Câu 7. Cho tứ giác ABCD. Khẳng định nào sau đây là sai?
A. AB và BC là hai cạnh kề nhau.
B. BC và AD là hai cạnh đối nhau. C. A và
B là hai góc đối nhau.
D. AC và BD là hai đường chéo.
Câu 8. Khẳng định nào sau đây là đúng?
A. Tứ giác có 4 đường chéo.
B. Tổng các góc của một tứ giác bằng 180 .
C. Tồn tại một tứ giác có 1 góc tù và 3 góc vuông.
D. Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
Câu 9. Giá trị số đo 2y − x trong hình vẽ là A. 46. B. 126 . C. 134 . D. 58 .
Câu 10. Khẳng định nào sau đây là sai?
A. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
B. Hình thang có hai cạnh bên song song là hình bình hành.
C. Hình thang có hai đường chéo bằng nhau là hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Câu 11. Khẳng định nào sau đây là sai? Tứ giác ABCD là hình chữ nhật khi A.
A = B = C = 90 . B.
A = B = C = 90 và AB // CD .
C. AB = CD = AD = BC . D. AB // ; CD AB = ;
CD AC = B . D
Câu 12. Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
A. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
B. Hình thoi có một góc vuông là hình vuông.
C. Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
D. Hình thoi có hai đường chéo vuông góc là hình vuông. Trang 12
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Trong câu 13 và câu 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Câu 13. Cho hai biểu thức A và B thỏa mãn 6 3 3 2
45x y : A = 5x y và ( 4 2 B + x y ) 2 7
: A = 3xy + 2x . y
a) Biểu thức A là đơn thức bậc 3. b) Với x = 1;
− y = 2 thì giá trị của biểu thức A bằng 18. −
c) Đa thức B có hai hạng tử.
d) Tích của hai biểu thức A và B là 7 5 7 3 36x y + 20x y .
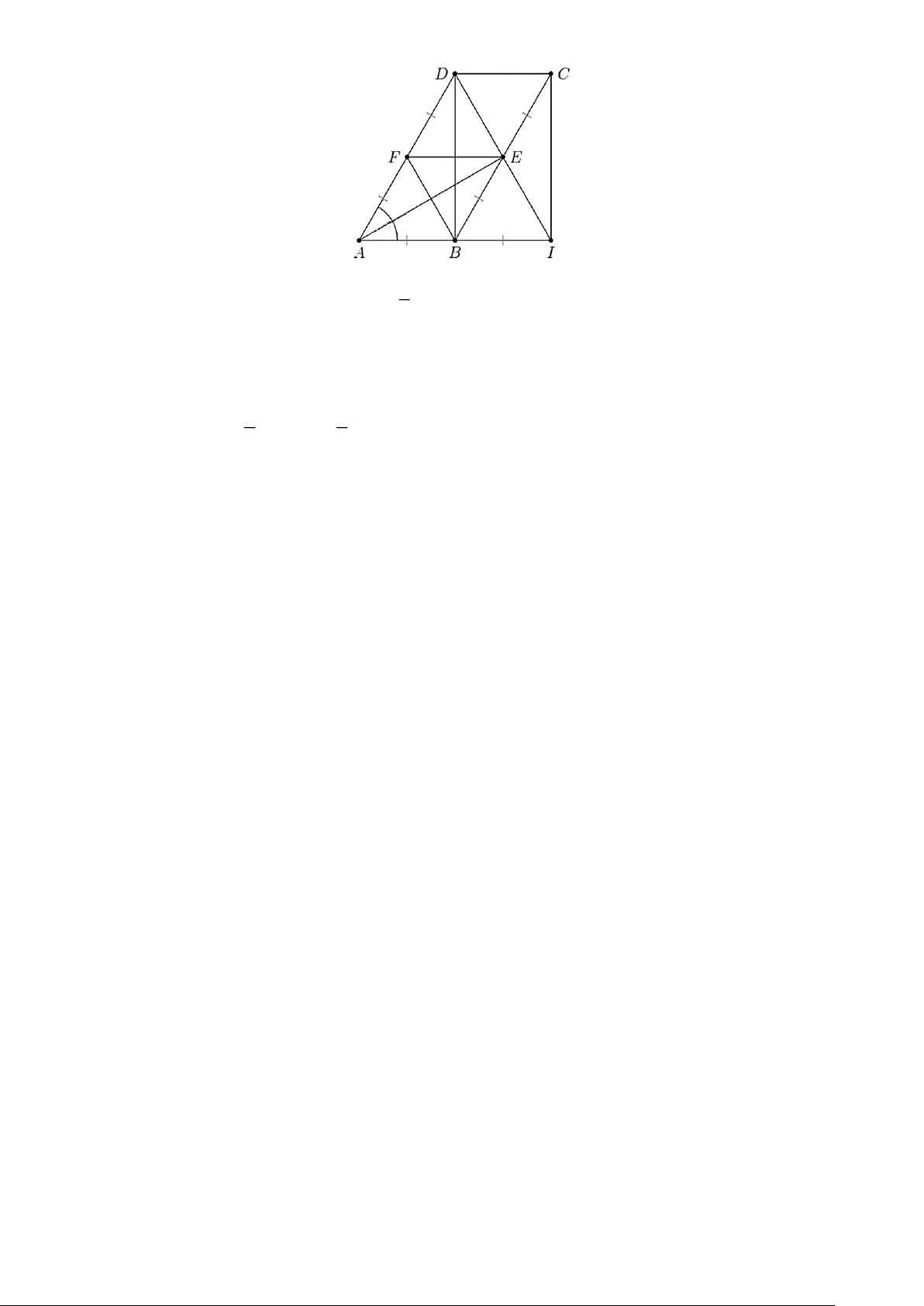
Câu 14. Cho hình bình hành ABCD có BC = 2AB, A = 60 . Gọi E , F theo thứ tự là trung điểm
của BC , AD . Trên tia AB lấy điểm I sao cho B là trung điểm của AI. 2 a) AB = BE .
b) Tứ giác ABEF là hình chữ nhật. 3
c) Tam giác ADI cân tại D . d) AED = 90 .
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Trong mỗi câu hỏi từ câu 15 đến câu 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày
lời giải chi tiết.
Câu 15. Xác định bậc của đa thức 2 3
3xyz − 5x y − 6xyz + 4x yz .
Câu 16. Giá trị của biểu thức A = ( x + )2 + ( x )2 3 1 3 –1 – 2(3x – ) 1 (3x + ) 1 bằng bao nhiêu? x
Câu 17. Cho hình vẽ, biết 7
B + D = 135, BAD = . 2 Tính số đo góc
C (đơn vị: độ). 1
Câu 18. Một hình thang vuông có một góc bằng 75 ,
tính số đo góc còn lại không vuông của hình
thang đó (đơn vị: độ).
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,5 điểm) Phân tích mỗi đa thức sau thành nhân tử: a) 3 2
8x yz +12x yz + 6xyz + yz ; b) 4 x ( 2 2 z y ) 2 2 81 − − z + y ; c) 4 2 x − 5x + 4 . Trang 13
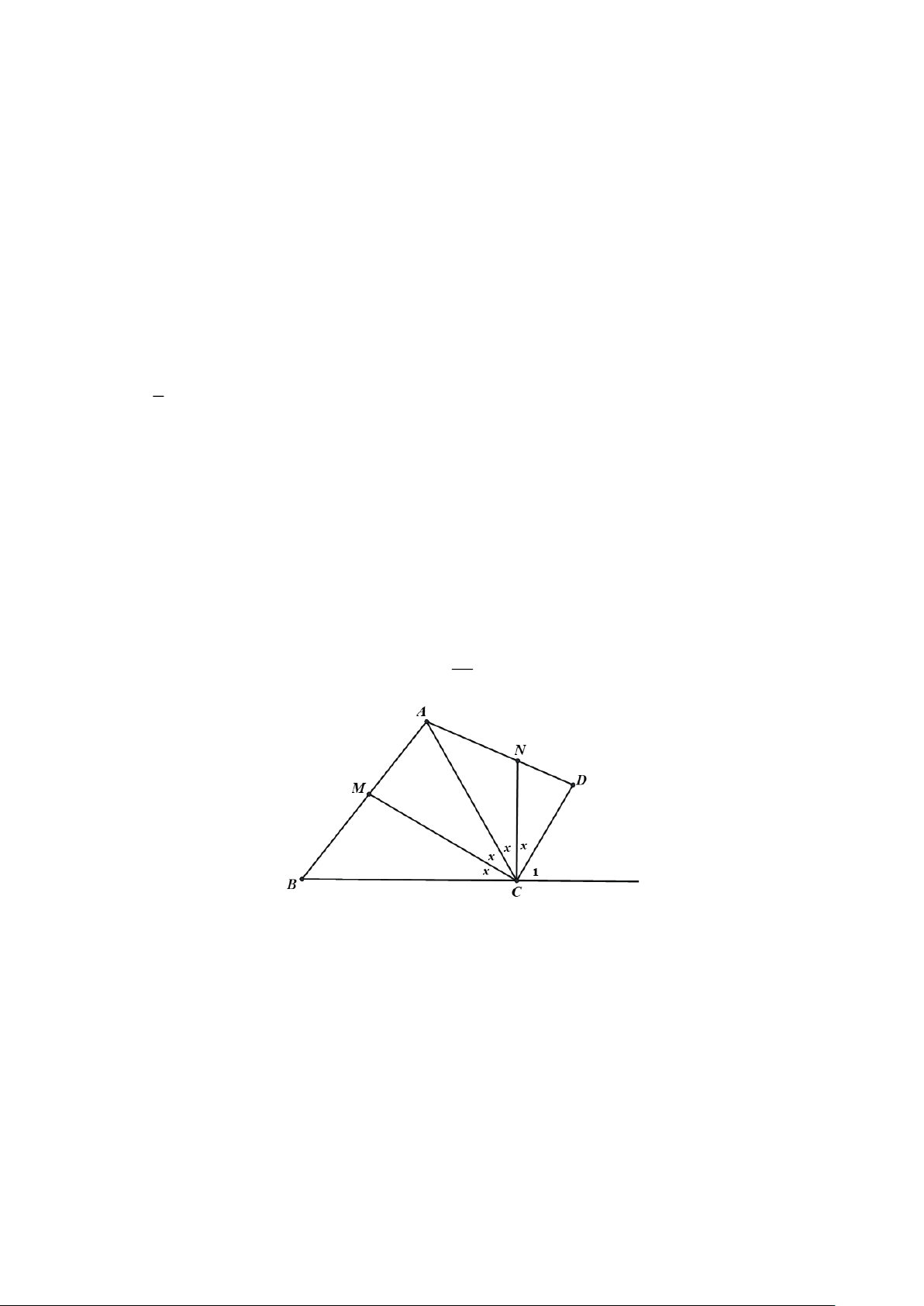
Bài 2. (1,5 điểm) Cho ABC cân tại ,
A trung tuyến AM , I là trung điểm AC. Gọi N là điểm
đối xứng của M qua I .
a) Tứ giác AMCN là hình gì? Vì sao?
b) Gọi E là trung điểm AM. Chứng minh E là trung điểm BN.
c) Gọi K là trung điểm của .
AB Tìm điều kiện của ABC
để tứ giác AKMI là hình vuông. -----HẾT-----
ĐÁP ÁN VÀ LỜI GIẢI
A. TRẮC NGHIỆM (7,0 điểm)
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B C D B A B C D D C C D Câu
13a 13b 13c 13d 14a 14b 14c 14d 15 16 17 18 Đáp án S Đ Đ S S S Đ Đ 5 4 30 105
Hướng dẫn giải chi tiết
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm) 5
Câu 1. Trong các đơn thức sau: 2 2 2 2 2 2
− xy ; 3x y ; − 4x y ; x y ;12x . Có bao nhiêu đơn thức đồng 2 3 dạng với đơn thức 2 − x y ? 2 A. 1. B. 2 . C. 3 . D. 4 .
Hướng dẫn giải
Đáp án đúng là: B 5 3 Các đơn thức 2 2
3x y ; x y đồng dạng với đơn thức 2
− x y vì đều có phần hệ số khác 0 và phần 2 2 biến đều là 2 x . y 3
Do đó, có 2 đơn thức đồng dạng với đơn thức 2 − x y . 2
Câu 2. Đa thức nào sau đây không phải là đa thức bậc 4? 1 A. 2 4xy z . B. 4 5 x − 3 . C. 4 3 x − xy z . D. 2 xy + xyzt . 2 Hướng dẫn giải Đáp án đúng là: C • Các đa thức 2 4xy z ; 4 5 x − 3 ; 2
xy + xyzt có bậc là 4. 1 • Đa thức 4 3 x −
xy z có bậc là 5. 2 Trang 14
Câu 3. Điều kiện của số tự nhiên n để phép chia 5 n n 3
x y : x y là phép chia hết là
A. n = 3.
B. n = 4 .
C. n = 5.
D. n3; 4; 5 .
Hướng dẫn giải
Đáp án đúng là: D Để phép chia 5 n n 3
x y : x y là phép chia hết thì 3 n 5, suy ra n3; 4; 5 . 1
Câu 4. Giá trị của biểu thức 2 2 2 S = 6
− xy x yz + 2zxy x khi x = 2
− ; y = 1; z = 1 − là 2
A. S = 8. B. S = 8 − . C. S = 4 − . D. S = 4 . Hướng dẫn giải Đáp án đúng là: B 1 Ta có 2 2 2 3 2 3 2 3 2 S = 6
− xy x yz + 2zxy x = 3
− x y z + 2x y z = −x y z . 2 Thay x = 2
− ; y = 1; z = 1 − vào biểu thức 3 2 −x y z ta được: S = −(− )3 2 2 1 (− ) 1 = 8. − Vậy khi x = 2
− , y = 1, z = 1 − thì S = 8. −
Câu 5. Đẳng thức nào sau đây là hằng đẳng thức? A. 2 2
x − x = −x + x .
B. x(x − ) 2
1 = x − x . C. (a b)2 (b a)2 − = − − .
D. a − 2 = 2 − a .
Hướng dẫn giải
Đáp án đúng là: A • Đẳng thức 2 2
x − x = −x + x là hằng đẳng thức.
• Đẳng thức x(x − ) 2
1 = x − x không là hằng đẳng thức vì khi ta thay x = 2 thì hai đẳng thức không bằng nhau.
• Đẳng thức (a b)2 (b a)2 − = − −
không là hằng đẳng thức vì khi ta thay a = 0, b = 1 thì hai đẳng thức không bằng nhau.
• Đẳng thức a − 2 = 2 − a không là hằng đẳng thức vì khi ta thay a = 0 thì hai đẳng thức không bằng nhau. Câu 6. Đa thức 2 4
− x +12x − 9 được viết thành A. (2x − ) 3 (2x + 3).
B. − ( x − )2 2 3 . C. ( − )2 3 2x . D. − ( x + )2 2 3 .
Hướng dẫn giải
Đáp án đúng là: B Ta có: − x +
x − = −( x − x + ) = −( x − )2 2 2 4 12 9 4 12 9 2 3 .
Câu 7. Cho tứ giác ABCD. Khẳng định nào sau đây là sai? Trang 15
A. AB và BC là hai cạnh kề nhau.
B. BC và AD là hai cạnh đối nhau. C. A và
B là hai góc đối nhau.
D. AC và BD là hai đường chéo.
Hướng dẫn giải
Đáp án đúng là: C
Tứ giác ABCD có các cặp góc đối nhau là A và C ; B và D .
Do đó phương án C là khẳng định sai.
Câu 8. Khẳng định nào sau đây là đúng?
A. Tứ giác có 4 đường chéo.
B. Tổng các góc của một tứ giác bằng 180 .
C. Tồn tại một tứ giác có 1 góc tù và 3 góc vuông.
D. Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
Hướng dẫn giải
Đáp án đúng là: D
Tứ giác có 2 đường chéo, tổng các góc bằng 360 .
Giả sử có tứ giác có 1 góc tù và 3 góc vuông khi đó tổng số đo các góc của tứ giác này là lớn hơn
90 + 3 90 = 360, điều này mâu thuẫn với định lí tổng các góc của một tứ giác.
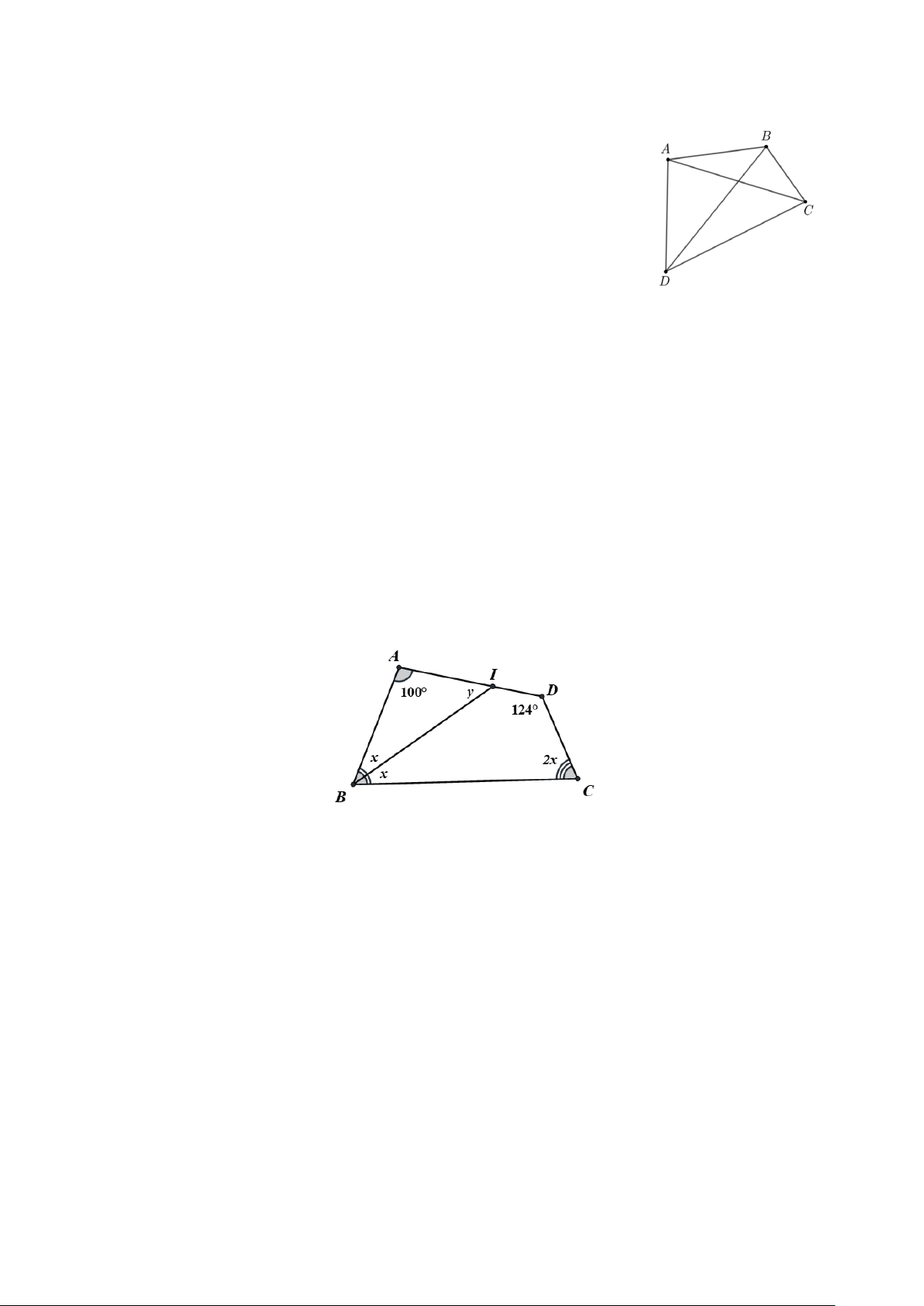
Câu 9. Giá trị số đo 2y − x trong hình vẽ là A. 46. B. 126 . C. 134 . D. 58 .
Hướng dẫn giải
Đáp án đúng là: D
• Xét tứ giác ABCD có
A + ABC + C + D = 360.
Suy ra 100+ x + x + 2x +124 = 360
Hay 4x + 224 = 360 nên x = 34.
• Xét tam giác ABI có
A + ABI + AIB =180.
Suy ra 100 + 34 + y = 180 nên y = 46 .
Do đó 2y − x = 2 46 − 34 = 58 .
Câu 10. Khẳng định nào sau đây là sai?
A. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
B. Hình thang có hai cạnh bên song song là hình bình hành. Trang 16
C. Hình thang có hai đường chéo bằng nhau là hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành. Hướng dẫn giải Đáp án đúng là: C
Áp dụng dấu hiệu nhận biết hình bình hành:
− Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên A đúng.
− Hình thang nên hai cạnh đối song song, thêm điều kiện hai cạnh bên song song tức có các cặp
cạnh đối song song nên hình thang này là hình bình hành nên B đúng.
− Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành nên D đúng.
− Hình thang cân có hai đường chéo bằng nhau nên không đủ dữ kiện khẳng định là hình bình hành.
Do đó phương án C là khẳng định sai.
Câu 11. Khẳng định nào sau đây là sai? Tứ giác ABCD là hình chữ nhật khi A.
A = B = C = 90 . B.
A = B = C = 90 và AB // CD .
C. AB = CD = AD = BC . D. AB // ; CD AB = ;
CD AC = B . D
Hướng dẫn giải
Đáp án đúng là: C
Ta thấy AB = CD = AD = BC thì ABCD chỉ có bốn cạnh bằng nhau nên ABCD chưa chắc là hình chữ nhật. − Nếu
A = B = C = 90 thì tứ giác ABCD có ba góc vuông nên ABCD là hình chữ nhật (do dấu
hiệu tứ giác có 3 góc vuông). − Nếu
A = B = C = 90 và AB // CD thì tứ giác ABCD có AD // BC; AB // CD nên ABCD là hình
bình hành, lại có A = 90 nên ABCD là hình chữ nhật (do dấu hiệu hình bình hành có một góc vuông).
− Nếu AB // C ;
D AB = CD và AC = BD thì ABCD là hình bình hành (do có cặp cạnh đối AB; CD
song song và bằng nhau), lại có hai đường chéo bằng nhau AC = BD nên ABCD là hình chữ nhật
(do dấu hiệu hình bình hành có hai đường chéo bằng nhau).
Câu 12. Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
A. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
B. Hình thoi có một góc vuông là hình vuông.
C. Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
D. Hình thoi có hai đường chéo vuông góc là hình vuông. Hướng dẫn giải Đáp án đúng là: D
Các phương án A, B, C là các khẳng định đúng theo dấu hiệu nhận biết hình vuông.
Phương án D sai vì hình thoi đã có sẵn hai đường chéo vuông góc, hình thoi cần có hai đường chéo
bằng nhau thì mới là hình vuông. Trang 17
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Câu 13. Cho hai biểu thức A và B thỏa mãn 6 3 3 2
45x y : A = 5x y và ( 4 2 B + x y ) 2 7
: A = 3xy + 2x . y
a) Biểu thức A là đơn thức bậc 3. b) Với x = 1;
− y = 2 thì giá trị của biểu thức A bằng 18. −
c) Đa thức B có hai hạng tử.
d) Tích của hai biểu thức A và B là 7 5 7 3 36x y + 20x y . Hướng dẫn giải Đáp án: a) Sai.
b) Đúng. c) Đúng. d) Sai. ⦁ Ta có 6 3 2
45x y : A = 5xy . Suy ra 6 3 3 2 3
A = 45x y : 5x y = 9x y .
Như vậy, biểu thức A là đơn thức bậc 4. Do đó ý a) sai. ⦁ Thay x = 1;
− y = 2 vào biểu thức A , ta có: A = (− )3 9 1 2 = 9 − 2 = 18 − . Vậy với x = 1;
− y = 2 thì A = 18 − . Do đó ý b) đúng. ⦁ Với 3
A = 9x y , ta có ( 4 2 B + x y ) 3 2 7
: 9x y = 3xy + 2xy Suy ra 4 2 3
B + x y = x y ( 2 xy + xy) 4 4 4 2 7 9 3 2
= 27x y +18x y . Do đó 4 4 4 2 4 2 4 4 4 2
B = 27x y +18x y − 7x y = 27x y +11x y .
Như vậy, đa thức B có hai hạng tử là 4 4 27x y và 4 2
11x y . Do đó ý c) đúng. ⦁ Ta có 3
A B = x y ( 4 4 4 2 9 27x y +11x y ) 3 4 4 3 4 2
= 9x y 27x y + 9x y 11x y 7 5 7 3
= 243x y + 99x y .
Như vậy, tích của hai biểu thức A và B là 7 5 7 3
243x y + 99x y . Do đó ý d) sai.
Câu 14. Cho hình bình hành ABCD có BC = 2AB, A = 60 . Gọi E , F theo thứ tự là trung điểm
của BC , AD . Trên tia AB lấy điểm I sao cho B là trung điểm của AI. 2 a) AB = BE .
b) Tứ giác ABEF là hình chữ nhật. 3
c) Tam giác ADI cân tại D . d) AED = 90 . Hướng dẫn giải Đáp án: a) Sai. b) Sai. c) Đúng. d) Đúng. Trang 18 1
⦁ Do E là trung điểm của BC nên BE = BC hay BC = 2B . E 2
Vì BC = 2AB và BC = 2BE nên AB = BE . Do đó ý a) là sai.
⦁ Theo đề bài, tứ giác ABCD là hình bình hành nên AD = BC, AD // BC . 1 1
Vì AD = BC ; BE = BC; AF = AD (do F là trung điểm của AD) nên BE = AF . 2 2
Tứ giác ABEF có BE = AF (cmt) và BE // AF (vì AD // BC ).
Suy ra, tứ giác ABEF là hình bình hành.
Hình bình hành ABEF có AB = BE nên ABEF là hình thoi. Do đó ý b) sai.
⦁ Ta thấy BD vừa là đường trung tuyến vừa là đường phân giác của tam giác ADI nên tam giác
ADI cân tại D .
Tam giác ADI cân tại D có
DAI = 60 nên tam giác ADI là tam giác đều.
Suy ra BD cũng là đường cao của tam giác ADI nên BD ⊥ BI hay DBI = 90 . Do đó ý c) đúng.
⦁ Vì tứ giác ABCD là hình bình hành nên AB = CD, AB // CD .
Vì AB = CD; AB = BI (do B là trung điểm của AI ) nên BI = CD .
Tứ giác BICD có BI // CD (vì AB // CD ) và BI = CD nên tứ giác BICD là hình bình hành.
Hình bình hành BICD có
DBI = 90 nên tứ giác BICD là hình chữ nhật.
Khi đó, E là trung điểm của DI .
Ta có tam giác ADI là tam giác đều có AE là đường trung tuyến nên đồng thời là đường cao.
Do đó, AE ⊥ DI hay
AED = 90 . Do đó ý d) đúng.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Câu 15. Xác định bậc của đa thức 2 3
3xyz − 5x y − 6xyz + 4x yz .
Hướng dẫn giải Đáp số: 5. Ta có 2 3 3 2
3xyz −5x y − 6xyz + 4x yz = 4x yz −5x y + (3xyz −6xyz) 3 2
= 4x yz − 5x y − 3xyz . Trang 19 Đơn thức 3
4x yz có bậc là 5; các đơn thức −3xyz và 2 5
− x y đều có bậc là 3. Do đó, đa thức 2 3
3xyz − 5x y − 6xyz + 4x yz có bậc là 5.
Câu 16. Giá trị của biểu thức A = ( x + )2 + ( x )2 3 1 3 –1 – 2(3x – ) 1 (3x + ) 1 bằng bao nhiêu?
Hướng dẫn giải Đáp số: 4.
Ta có A = ( x + )2 + ( x )2 3 1 3 –1 – 2(3x – ) 1 (3x + ) 1
= ( x + ) −( x − ) 2 3 1 3 1
= (3x +1−3x + )2 2 1 = 2 = 4 .
Vậy giá trị của biểu thức A bằng 4. x
Câu 17. Cho hình vẽ, biết 7
B + D = 135, BAD = . 2 Tính số đo góc
C (đơn vị: độ). 1
Hướng dẫn giải Đáp số: 30.
Xét tứ giác ABCD có
BAD + B + BCD + D = 360 . 7x 15x Suy ra
+ 4x +135 = 360 hay = 225 nên x = 30 . 2 2
Câu 18. Một hình thang vuông có một góc bằng 75 ,
tính số đo góc còn lại không vuông của hình
thang đó (đơn vị: độ).
Hướng dẫn giải Đáp số: 105.
Do hình thang đã cho là hình thang vuông nên nó có hai góc vuông.
Gọi số đo góc còn lại của hình vuông là . x Trang 20




