Bộ Câu Hỏi Lý Thuyết môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

CLB HỖ TRỢ HỌC TẬP VẬT BỘ LÍ CÂ UĐ H Ạ ỎII LÝ THUYẾT CƯƠNG 2
ĐẠI HỌC BÁCH KHOA HÀ NỘI
HANOI UNIVERSITY OF SCIENCE AND TECHNOLOGY
THẺ SINH VIÊN / Student ID card MSSV / ID No. IDOL HOBO SCAN ME + A
TÀI LIỆU ĐƯỢC TỔNG HỢP VÀ BIÊN SOẠN BỞI
CLB HỖ TRỢ HỌC TẬP BÁCH KHOA
BIÊNSOẠN BỞICLBHỖTRỢHỌC TẬPBÁCHKHOA CLB.HTHT-WEBSITE.COM
TàiliệulàmónquànhândịpnămmớiẤtTỵ2025củaCLBHỗtrợHọctậpdànhchocácbạnsinhviênĐạihọcBáchKhoa
HàNội.CLBxingửilờicảmơnchânthànhnhấtđếncácbạnvìđãtintưởngđồnghànhcùngCLBtrongsuốtthờigianvừa
qua.SựủnghộcủacácbạnchínhlànguồnđộnglựclớnnhấtđểchúngmìnhphấnđấuđưaCLBngàymộtpháttriểnhơn.
Cuốicùng,xinchúccácbạnmộtkỳhọctậphiệuquảvàthànhcông.
Bảninlầnthứnhất,tháng12năm2024 Mụclục
1Chương1-Điệntrườngtĩnh ............................................. 4
Câu1. PhátbiểuđịnhluậtCoulomb.Địnhnghĩađiệntrường.Nêuđặcđiểmcủavéctơcườngđộđiện
trường. Phát biểu nguyên lý chồng chất điện trường. .................................. 4
Câu2. Nêucáchxácđịnhvéctơcườngđộđiệntrườngcủađiệntíchđiểm,hệđiệntíchđiểmphânbố
giánđoạnvàhệđiệntíchphânbốliêntục. Ápdụngcholưỡngcựcđiện,dâydẫnthẳngdài(vôhạn),
vành tròn, đĩa tròn tích điện đều. ................................................. 5
Câu3. PhátbiểuvàchứngminhđịnhlýOstrogradski-Gauss(ĐịnhluậtGauss).Ápdụngchotrườnghợp
mặtcầumangđiệnđều,mặtphẳngvôhạnmangđiệnđều,haimặtphẳngmangđiệntíchđốinhau,
mặt trụ thẳng dài vô hạn mang điện đều. .......................................... 6
Câu4. Tính công của lực tĩnh điện. Từ đó chứng tỏ trường tĩnh điện là một trường thế. .......... 8
Câu5. Dẫnracôngthứctínhthế năngcủađiệntíchtrongđiệntrường.Nêuđịnhnghĩa,ýnghĩacủa
điện thế và hiệu điện thế. Nếu định nghĩa và các tính chất của mặt đẳng thế. ................ 8
Câu6. Trìnhbàyvềmốiliênhệgiữacườngđộđiệntrườngvàđiệnthế.Ápdụngchohaimặtphẳng
songsongvôhạnmangđiện đều,tráidấu;mặtcầumangđiệnđều;mặttrụthẳngdàivôhạnmang
điệnđều................................................................... 9
2Chương2-Vậtdẫn .................................................... 12
Câu7. Nêuđiềukiệncânbằngtĩnhđiệnvàtínhchấtcủavậtdẫntíchđiện.Nêuđịnhnghĩavàcông
thức tính điện dung của vật dẫn cô lập. .......................................... 12
Câu8. Địnhnghĩahiệntượngđiệnhưởng.Thếnàolàđiệnhưởngmộtphần,điệnhưởngtoànphần?
Định nghĩa tụ điện. Tính điện dung của tụ phẳng, tụ trụ, và tụ cầu......................... 13
Câu9. Chứngminhcôngthứctínhnănglượngtươngtácđiệncủahệđiệntíchđiểm,vậtdẫncôlập
tích điện, năng lượng tụ điện phẳng và năng lượng điện trường. .................. ....... 15
3Chương3-Điệnmôi ................................................... 17
Câu10. Sựphâncựcđiệnmôilàgì?Giảithíchhiệntượngphâncựcđiệnmôi.Địnhnghĩavàcôngthức
tínhđộlớncủavéctơphâncựcđiệnmôi.Trìnhbàyvềmốiliênhệgiữavéctơphâncựcđiệnmôivàmật
độđiệnmặtcủacácđiệntíchliênkết.Nêucôngthứctínhcườngđộđiệntrườngvàđiệncảmtrong
điệnmôi..................................................................17
4Chương4-Từtrường .................................................. 20
Câu11. Nêuđịnhnghĩa,đặcđiểm,ýnghĩavậtlýcủavéctơmậtđộdòngđiện.Chứngminhcông
thứcđịnhluậtOhmdạngviphân.Tìmbiểuthứcsuấtđiệnđộngcủanguồnđiệntrongtrườnghợptổng
quát.....................................................................20
Câu12. Tươngtáctừlàgì?NêunộidungcủađịnhluậtAmpere.Địnhnghĩatừtrường.Nêuđặcđiểm
của véctơ cảm ứng từ............................... ......................... 21
Câu13.Phátbiểunguyênlýchồngchấttừtrường.Ápdụngchodòngđiệnthẳng,dòngđiệntròn. 22 2
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
Câu14.Địnhnghĩatừthông.NêunộidungđịnhlýOstrogradski-Gauss(ĐịnhluậtGauss)đốivớitừ
trường. ..................................................................24
Câu15.ChứngminhđịnhlýAmperevềdòngđiệntoànphần.Ápdụngchocuộndâyhìnhxuyến,bên
trong ống dây điện thẳng dài vô hạn. ............................................ 24
Câu16.Nêuđặcđiểmcủalựctừ(lựcAmpere).Trìnhbàyvềtácdụng củatừtrườngđềulênmộtmạch
điện kín. Tính công của lực từ. .................................................. 26
Câu17.NêuđặcđiểmcủalựcLorentz.Nêukếtquảkhảosátchuyểnđộngcủahạttíchđiệntrongtừ
trườngđều(xétcảtrườnghợphạtmangđiệnbayvàtừtrườngtheophươngkhôngvuônggócvới
đường sức từ trường đều).... ................................................. 27
5Chương5-Hiệntượngcảmứngđiệntừ ................................ 29
Câu18.Địnhnghĩahiệntượngcảmứngđiệntừ.Nêunộidungcácđịnhluậtvềhiệntượngcảmứng
điệntừ.Hiệntượngtựcảmlàgì?Nêuđịnhnghĩa,côngthứctínhđộtựcảm;côngthứctínhsuấtđiện
động tự cảm. Giải thích định tính hiệu ứng bề mặt. ................................... 29
Câu19.DẫnracôngthứctínhnănglượngtừtrườngcủamạchđiệncóđộtựcảmL,nănglượngcủatừ
trườngbấtkỳ..............................................................30
6Chương6-Vậtliệutừ .................................................. 32
Câu20.Sựtừhóalàgì?Phânbiệtcácloạivậtliệutừ.Nêuđặcđiểmcủamômentừvàmômenđộng
lượng của nguyên tử. Giải thích hiệu ứng nghịch từ. .................................. 32
Câu21.Nêuđặcđiểmcủavéctơtừđộ.Giảithíchđịnhtínhhiệntượngnghịchtừvàthuậntừ.Nêucác
tínhchấtcủavậtliệusắttừ(nhiệtđộCurie,hiệntượngtừtrễ,Ferittừ).Trìnhbàysơlượcvềthuyếtmiền
từhóatựnhiên. ............................................................3
7Chương 7 - Trường điện từ.............................................. 35
Câu22.Nêuđịnhnghĩavàđặcđiểmcủađiệntrườngxoáy.PhátbiểuluậnđiểmIcủaMaxwel .Thành
lậpphươngtrìnhMaxwel -Faraday.Nêuđịnhnghĩavàbiểuthứccủadòngđiệndịch.Phátbiểuluận
điểm I của Maxwel . Thành lập phương trình Maxwel -Ampere. .......................... 35
Câu23.Trườngđiệntừlàgì?ViếthệphươngtrìnhMaxwel .Trìnhbàyvềnănglượngcủatrườngđiện
từ.......................................................................37
8Chương8,9-Daođộngđiệntừ-Sóngđiệntừ .......................... 39
Câu24.Trình bàyvềdaođộngđiệntừđiềuhòa,daođộngđiệntừtắtdần,vàdaođộngđiệntừcưỡng
bức. ....................................................................39
Câu25.Địnhnghĩasóngđiệntừ.Nêucáctínhchấttổngquátcủasóngđiệntừ.Nêuđặcđiểm,phương
trìnhcủasóngđiệntừphẳng,đơnsắc.Trìnhbàyvềnănglượngvànăngthôngsóngđiệntừ. . . . . 41 3
1.Chương1-Điệntrườngtĩnh Câu1
PhátbiểuđịnhluậtCoulomb.Địnhnghĩađiệntrường.Nêuđặcđiểmcủavéctơcườngđộđiệntrường.Phátbiểu
nguyênlýchồngchấtđiệntrường. ■ [Lờigiải]
+)ĐịnhluậtCoulomb:lựctươngtáctĩnhđiệngiữa2điệntíchcóphươngnằmtrênđườngnối2điệntích,cóchiềunhư
hình1(haiđiệntíchcùngdấuthìđẩynhau,tráidấuthìhútnhau),cóđộlớntỉlệthuậnvớitíchđộlớncủa2điệntíchvàtỉlệ
nghịchvớibìnhphươngkhoảngcáchgiữa2điệntíchđó.
Hình1.1:Lựctươngtácgiữa2điệntích
+)Côngthứctínhđộlớnlựctươngtácgiữa2điệntích: F=q1q 4 2
πε0ε.r2=kq1q2 ε.r2 trongđó:
•q1,q2làđộlớn2điệntíchđangxét(đơnvị: C) •ε0=8,86.10−12 C2 N.m2
•ε:hằngsốđiệnmôicủamôitrường.Đốivớimôitrườngchânkhông,ε=1
+)Điệntrường:làkhoảngkhônggiantồntạixungquanhđiệntích,cóđặctrưnglàgâyralựcđiệnlêncácđiệntíchđặt trongnó.
+)Đặcđiểmvectơcườngđộđiệntrường:
•Phương:trênđườngnốitừđiệntíchqđếnđiểmcầnxét
•Chiều:hướngraxađiệntíchqnếuqdương,hướnglạigầnđiệntíchqnếuqâm
•Độlớn:E=k|Q|ε.r2=|Q|4πεε0.r2 4
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+)Nguyênlýchồngchấtđiệntrường:Vectocườngđộđiệntrườngcủamộthệđiệntíchđiểmbằngtổngcácvectocường
độđiệntrườnggâyrabởitừngđiệntíchđiểmcủahệ n 
E=E1+E2+· · · +En= ∑ Ei i=1 Câu2
Nêucáchxácđịnhvéctơcườngđộđiệntrườngcủađiệntíchđiểm,hệđiệntíchđiểmphânbốgiánđoạnvàhệ
điệntíchphânbốliêntục.Ápdụngcholưỡngcựcđiện,dâydẫnthẳngdài(vôhạn),vànhtròn,đĩatròntích điệnđều. ■ [Lờigiải]
+)Xácđịnhvectơcườngđộđiệntrườngcủađiệntíchđiểm:
•CôngthứcxácđịnhvectơcườngđộđiệntrườngtạimộtđiểmMbấtkìcáchđiệntíchđiểmqmộtkhoảngr: E= 
F =q4πεε0r2.r q0 r
trongđó:rlàvectơcóđộlớnbằngkhoảngcáchtừqđếnM,phươnglàđoạnnốiqvàM,chiềutừqđếnM.
+)Xácđịnhvectơcườngđộđiệntrườngcủamộthệđiệntíchđiểm:
• Đốivớihệđiệntíchđiểmphânbốgiánđoạn:Vectocườngđộđiệntrườngdohệđiệntíchđiểmtạimộtđiểmbấtkì
chínhbằngtổngvectơcườngđộđiệntrườngcủatừngđiệntíchđiểmtácdụnglênđiểmấy 
E=E1+E2+E3+· · · +En.
• Đốivớihệđiệntíchphânbốliêntục:Tiếnhànhchiavậtthànhnhữngphần rấtnhỏchứađiệntích dq,sauđótính
vectơcườngđộđiệntrườngcủatừngphầnnhỏấyrồitiếnhànhlấytíchphânđểthuđượcvectơcườngđộđiệntrường củahệphânbốliêntục:   E=ˆ dq r d E=ˆ 4πεε0r2 r toànbộvật toànbộvật
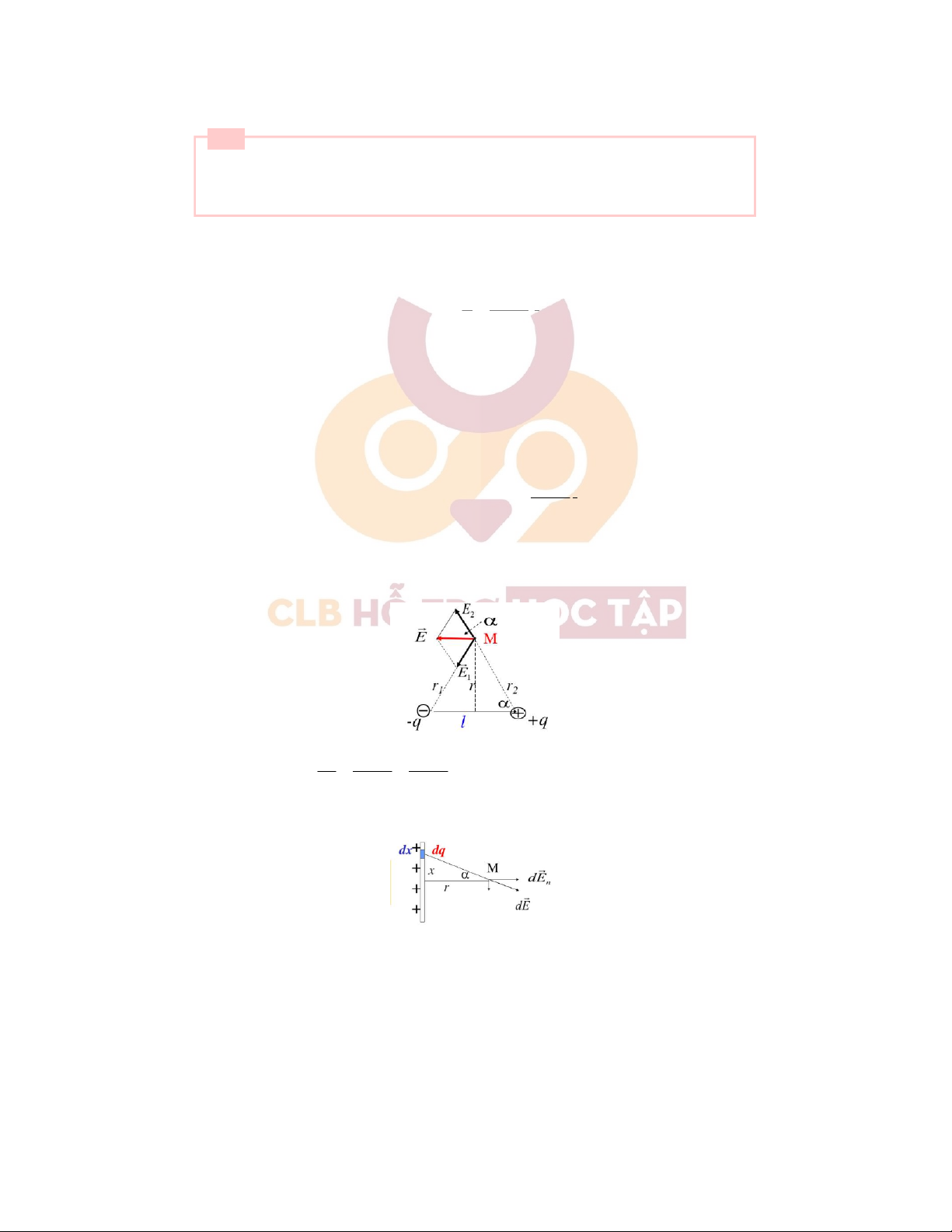
+)Lưỡngcựcđiện:lưỡngcựcđiệnlàmộthệgồm2điệntíchtráidấu,cùngđộlớn,cáchnhaumộtkhoảng d rấtnhỏsovới
khoảngcáchtừđiểmcầnxétđếnlưỡngcựcđiện.
Mômenlưỡngcựcđiện: Pe=q. l
Vectocườngđộđiệntrườngnằmtrêntrungtrựccủalưỡngcực:
Khiđóta có: E=E1+E2
Độlớn:E=2E1.cosα=E1.l =ql =P e r1 4πεε0r3 4πεε0r3 1 1
+)Dâydẫnthẳngdàivôhạn:XétmộtđoạndâydẫncóchiềudàirấtnhỏcócườngđộđiệntrườngdE tạimộtđiểmcách dâymộtkhoảngr 5
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
Có:Exđốixứngtừngđôi⇒dE =dEy=dE.cosα=dq.cosα4πεε0R2 •dq =λdx
•x=rtanα⇒dx =rdα cos2α π π ⇒dE =λ.r c d o α s2co α. s4 α
πεε0.R2⇒E=ˆ 2 c λ os .2rd α.α 4 c πo εsεα 0.R2=ˆ 2 λdα 4πco ε s ε0 α .r=λ −π −π 2πεε0r 2 2
+)Vànhtròntíchđiệnđều:Chiavànhtrònthànhnhữngđoạnnhỏmangđiệntíchdq.
Tacó: Exđốixứngtừngđôimột⇒dE =dEy=dE cosϕ.Mặtkháctalạicó:
•dq =λ.rdϕ=q 2πrrdϕ=q 2πdϕ •cosϕ=h r2+h2 p
⇒dE =q.hdϕ 2⇒E=ˆ2π q.hdϕ =q.h
8π2εε0(r2+h2)3 0
8π2εε0(r2+h2)3 4πεε 2 0(r2+h2)3 2
+)Đĩatròntíchđiệnđều:
Chiađĩatrònthànhcácvànhtrònnhưhìnhvẽ
Có:dE =dq.h
4πεε0(r2+h2)3 2 Mặtkhác:
•dS=π(r+dr)2−πr2=2πrdr →dq =σdS =σ.2πrdr r ˆ 2εε  0
⇒dE =σ.2πhrdr σ.2πhrdr =σ  1−1  2⇒E= 4πεε  0(r2+h2)3 4πεε0(r2+h2)3 1+r2 2 q 0 h2
Lưuý:Khi r→+∞ ,mặttrêntrởthànhmặtphẳngvôhạn tíchđiệnđều.Côngthứcđiệntrườngtrênmặtphẳngtíchđiện đều:E=σ 2εε0 Câu3
PhátbiểuvàchứngminhđịnhlýOstrogradski-Gauss(ĐịnhluậtGauss).Ápdụngchotrườnghợpmặtcầumangđiện
đều,mặtphẳngvôhạnmangđiệnđều,haimặtphẳngmangđiệntíchđốinhau,mặttrụthẳngdàivôhạnmangđiện đều.■ [Lờigiải]
+)ĐịnhlýOstrogradski-Gauss:ĐiệnthôngquamộtmặtkínScógiátrịbằngtổngđạisốcácđiệntíchchứatrongmặtkín ấy.
˛S Dds =∑qi
+)ChứngminhđịnhlýO-G:xétthônglượngcảmứngđiệnđượcgửiquamộtdiệntíchdS có:
dφe= Dd S
=D.ds.cosα(vớiαlàgóc tạo bởi
Dvàvectopháptuyến n)
=Dn.ds (DnlàhìnhchiếucủaDtrên n)
XétmộtmặtkínlàmộtmặtcầutâmO,bánkínhRcó:
φe=ˆS Dnds =q4πr2.4πr2=q
Vậytừthônggửiquamộtmặtkíncógiátrịbằngtổngđiệntíchchứatrongmặtấy 6
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+)ĐịnhluậtGaussđốivớimặtcầumangđiệnđều:Chomặtcầutâm
O,bánkính R.Xácđịnhđiệntrườngtạiđiểmcách Omộtkhoảngr>R S R r M
•TạomộtmặtSlàmặtcầutâmOđiquaM.Khiđó,Slàmặtkín.
•ÁpdụngđịnhlýO-GđốivớimặtStacó:
˛S Dds =∑qi⇔D.˛S ds =q ⇔D.4π.r2=q ⇔D=q 4πr2 ⇒E=D =q εε0 4πεε0r2
ĐốivớiđiểmMnằmtrongmặtcầu,tacócườngđộđiệntrườngtổnghợpbằng0.
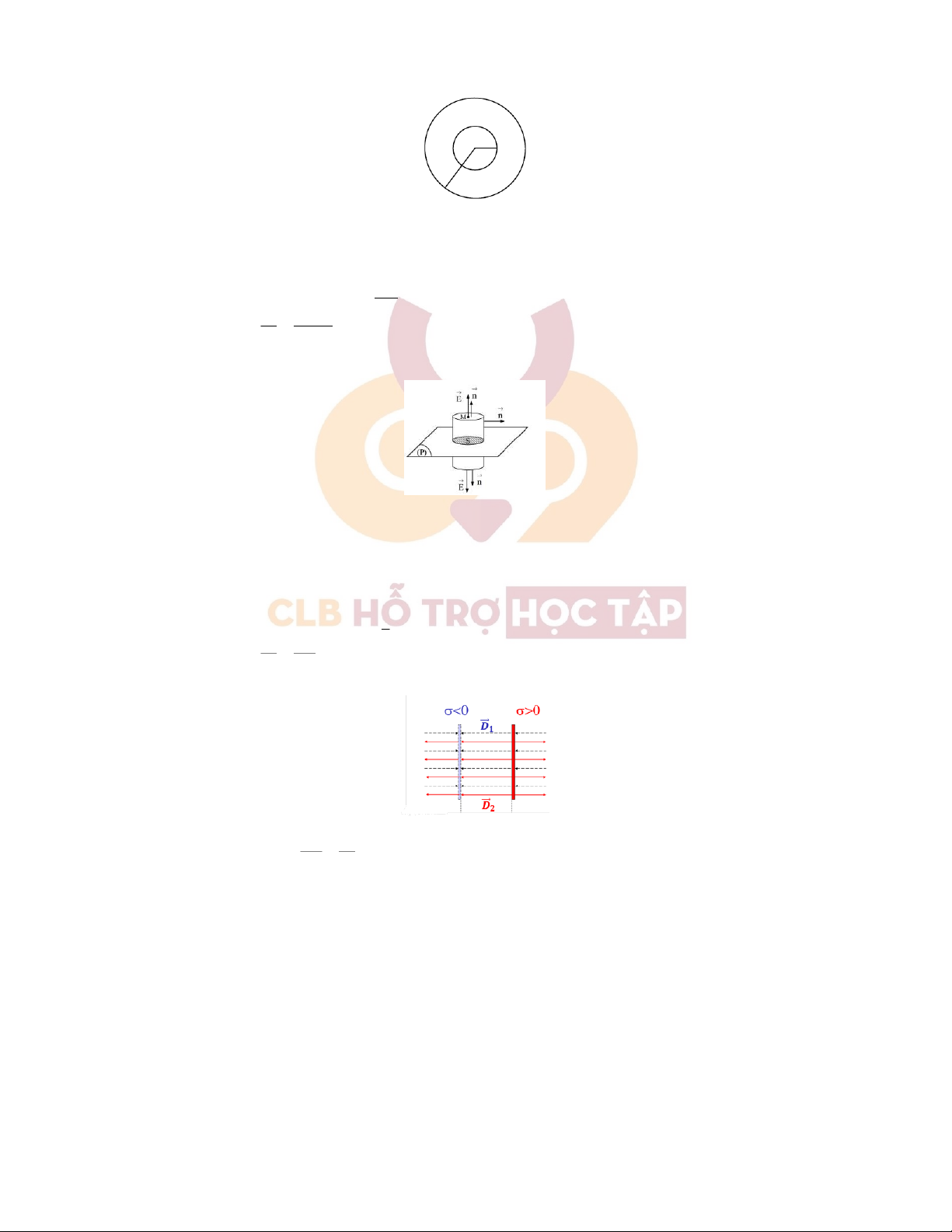
+)ĐịnhlýO-Gđốivớimặtphẳngvôhạntíchđiệnđều:
•Chọnmặtkínlàmặttrụnhưhìnhvẽ.Khiđótacóthônglượngquamặttrụlà:
φ=ˆhaiđáyDds +ˆmặtbênDds
Mặtkhác,thônglượngcủamặtbênbằng0.ÁpdụngđịnhlýO-G,tacó:
φ=ˆhaiđáyDds =σ.2πr⇔2Dˆmộtđáyds =σ.2πr ⇔4πrD =σ.2πr ⇔D=σ 2 ⇒E=D =σ εε0 2εε0
+)Điệntrườngcủahaimặtphẳngmangđiệntíchđốinhau:
•Ởkhoảnggiữa2mặtphẳng,tathấy 
D1vàD2cùngchiều ⇒D=2D1=2σ =σ 2εε0 εε0
•Ởbênngoài2mặtphẳng:E=0 7
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+)Điệntrườngcủamặttrụthẳngdàimangđiệnđều:
•ChọnmặtGausslàmặttrụbánkínhr,chiềudàil.Tacóđiệnthôngquamặttrụ:
φ=ˆhaiđáyDds +ˆmặtbênDds
•Dễthấy,ˆhai đáyDds =0
⇒ˆmặtbênDds =q⇔D.2πrl =Q
•Qlàđiệntíchtrênmặttrụ,vàgiảsửmậtđộđiệndàicủamặttrụlàλ,tacó:
D.2πrl =λ.l⇔D=λ 2πr⇒E=D =λ εε0 2πεε0r Câu4
Tínhcôngcủalựctĩnhđiện.Từđóchứngtỏtrườngtĩnhđiệnlàmộttrườngthế. ■ [Lờigiải]
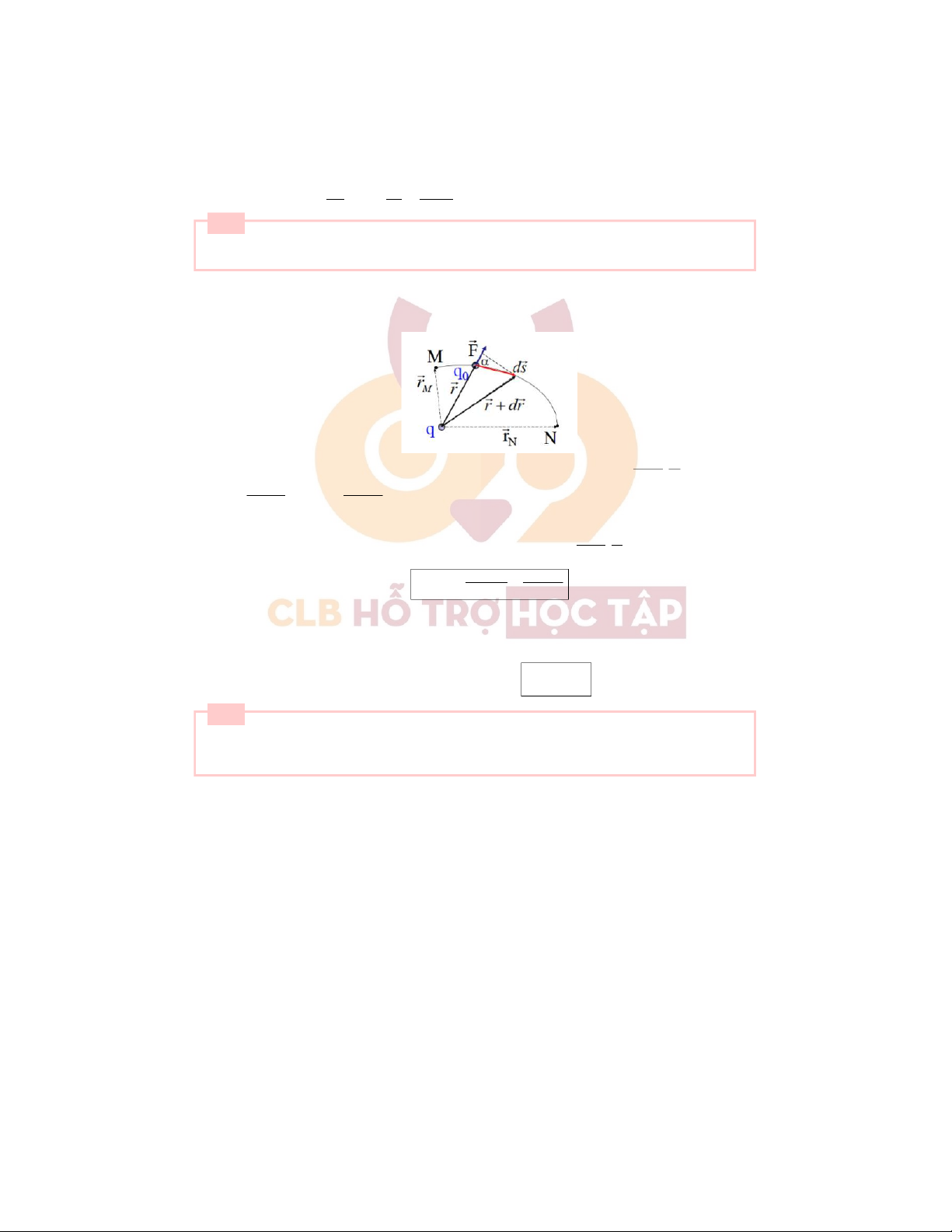
+ Xétđiệntíchthửq0dịchchuyểntừMđếnNtrongđiệntrườnggâybởiq(đứngyêntạiO).Lựctácdụnglênq0là − → F=q0− →E(−
→E:điệntrườngdoqgâyratạivịtríq0) .− →
+ Côngcủalựctĩnhđiệntrongchuyểndờivôcùngnhỏ s=q r d− → s:dA =− → 0− →E d r F d − → s=q0.q 3d− →s 4πεε0 4π q
εε0r2.ds.cosα=q0q.dr =q0 4πεε0r2
(ds.cosα=dr:hìnhchiếucủads lên− → r) N ˆ rN ˆ
+ Côngcủalựctĩnhđiệntrongchuyểndời q0q .dr
q0từMđếnN:AMN = dA = 4πεε0 r2 M rM
⇒AMN =q0q
4πεε0rM−q0q 4πεε0rN
→Côngcủalựctĩnhđiệntrongsựdịchchuyểnmộtđiệntíchđiểmq0trongmộtđiệntrườngbấtkỳkhôngphụthuộcvào
mộtdạngđườngcongdịchchuyểnmàchỉphụthuộcvàođiểmđầuvàđiểmcuốicủachuyểndời.
Haynếudịchchuyểnq0theomộtđườngcongkínthìcôngcủalựctĩnhđiệntrongdịchchuyểnđóbằngkhông→Trường
tĩnhđiệnlàmộttrườngthế. A=˛− → s=q0˛− → F d E d− → s=0⇒˛− → E d− → s=0 Câu5
Dẫnracôngthứctínhthếnăngcủađiệntíchtrongđiệntrường.Nêuđịnhnghĩa,ýnghĩacủađiệnthếvàhiệuđiệnthế.
Nếuđịnhnghĩavàcáctínhchấtcủamặtđẳngthế. ■ [Lờigiải]
a)Dẫnracôngthứctínhthếnăngtrongcủađiệntíchtrongđiệntrường:
+ Vìđiệntrườnglàmộttrườngthếnêncôngcủalựctĩnhđiệntrongdịchchuyểnq0bằngđộgiảmthếnăngcủađiện
tíchđótrongđiệntrường: N ˆ AMN = q0
Eds=WM−WN M 8
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+ Thếnăngcủaq0trongđiệntrườngcủamộtđiệntíchđiểmq:
Xétq0dịchchuyểntrongđiệntrườngcủaq.Khiđó: AMN =q0q
4πεε0rM−q0q =WM−WN 4πεε0rN
→ Biểuthứcthếnăngcủa
q0 đặttrongđiệntrườngcủađiệntíchđiểm
q vàcáchđiệntíchnày mộtkhoảngbằng r là W=q0q 4πεε0r+C
Quy ước chọnWcủaq0khinóởxaqvôcùngbằngkhông: W∞=0→C=0→W=q0q 4πεε0r
+ Thếnăngcủaq0trong điện trường của hệ điện tích điểm:W=∑Wi=∑q0qi 4πεε0ri
+ Thếnăngcủaq0trongđiệntrườngbấtkỳ: WM=ˆ∞
q0Eds M
b)Địnhnghĩa,ýnghĩacủađiệnthếvàhiệuđiệnthế:
+ Địnhnghĩa:Tỷsố W/q0 khôngphụthuộcvàođiệntích
q0 màchỉphụthuộcvàocácđiệntíchgâyrađiệntrườngvà
vàovịtríđiểmđangxéttrongđiệntrường.Vậytacóthểdùngtỷsốđóđểđặctrưngchođiệntrườngtạiđiểmđang
xét.V=W/q0đượcgọilàđiệnthếcủađiệntrườngtạiđiểmđangxét. +Ýnghĩa:
+)Điệnthếtạimộtđiểmtrongđiệntrườnglàmộtđạilượngvềtrịsốbằngcôngcủalựctĩnhđiệntrongsựdịch
chuyểnmộtđơnvịđiệntíchdươngtừđiểmđóraxavôcùng.
+)Hiệuđiệnthếgiữahaiđiểm
M và N trongđiệntrườnglàmộtđạilượngvềtrịsốbằngcôngcủalựctĩnhđiệntrong
sựdịchchuyểnmộtđơnvịđiệntíchdươngtừđiểmMtớiđiểmN
c)Địnhnghĩavàcáctínhchấtcủamặtđẳngthế:
+Địnhnghĩa:Mặtđẳngthếlàquỹtíchcủanhữngđiểmcócùngđiệnthế V=C=const
+Ýnghĩacủamặtđẳngthế:
+)Cácmặtđẳngthếkhôngcắtnhau
+)Côngcủalựctĩnhđiệntrongsựdịchchuyểnđiệntích
q0 trênmặtđẳngthếbằngkhông:
AMN =q0(VM−VN) = 0
+)Vectơcườngđộđiệntrườngtạimộtđiểmtrênmặtđẳngthếvuônggócvớimặtđẳngthếtạiđiểmđó E n ds M Câu6
Trìnhbàyvềmốiliênhệgiữacườngđộđiệntrườngvàđiệnthế.Ápdụngchohaimặtphẳngsongsongvôhạnmang
điệnđều,tráidấu;mặtcầumangđiệnđều;mặttrụthẳngdàivôhạnmangđiệnđều. ■ [Lờigiải]
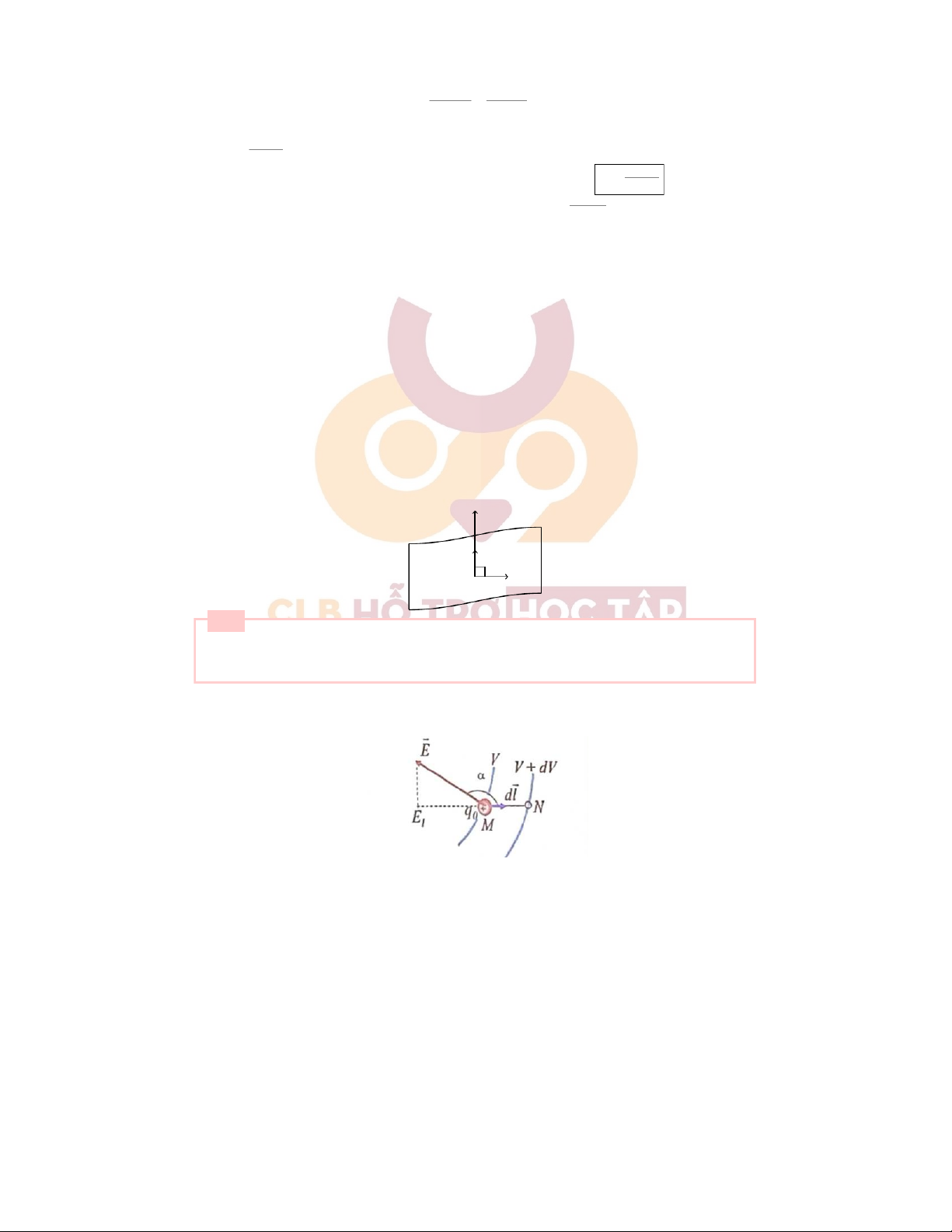
a)Mốiliênhệgiữacườngđộđiệntrườngvàđiệnthế:
+ Theođịnhnghĩatacó:dA =q0 Eds
+ MàdA =q0[V−(V+dV )] = −q0dV
Dođó,ta có: Eds=dV haydV =− Eds=−E.ds.cos(α)vớiα= ( E,ds)
* Kếtluận1:Vectorcườngđộđiệntrườngluônhướngtheochiềuđiệnthếgiảm. 9
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
* Kếtluận2:Hìnhchiếuvectorcườngđộđiệntrườngtrênmộtphươngnàođóvềtrịsốbằngđộgiảmđiệnthếtrênđơn vịdàicủaphươngđó.
b)Ápdụngchohaimặtphẳngsongsongvôhạnmạngđiệnđều;mặtcầumangđiệnđều;mặttrụthẳngdàivôhạn mangđiệnđều
+ Xácđịnhhiệuđiệnthếgiữahaimặtphẳngsongsongvôhạnmangđiệnđều,tráidấu: V1V2 +- +- +-  E +- +- +- (1) (2) d
+)TacódV =− E.dscos (I) +)Theo(I),tacó: V2 ˆ (2) ˆ (2) ˆ (2) ˆ
−dV =V1−V2=  Eds= Eds =E ds =Ed V1 (1) (1) (1) MàE=σ
nênV1−V2=σd εε0 εε0
+ Xácđịnhhiệuđiệnthếgiữahaiđiểmtrongđiệntrườngcủamộtmặtcầumangđiệnđều: R2 R1  E dr q + O R1R2
Giảsửtamuốnxéthiệuđiệnthếgiữa2điểmcáchtâmquảcầunhữngđoạn
R1 và R2 (với R2>R1>R ; R làbánkính củaquảcầu)
+)Tacó−dV = E.dr=E.dr.cos(α) = En.dr (Enlà hình chiếucủa Elênphươngpháptuyếnncủamặtcầu)
+)Màmặtcầulàmộtmặtđẳngthếnên
E↑↑EnnênEn=E=q 4πεε0r2
⇒−dV =q4πεε0r2.dr . V2 ˆ R2 ˆ Từđó: q.dr −dV = 4πεε0r2 V1 R1 HayV 1R
1−V2=q 4πεε0 1−1 R2  
+)Trongtrườnghợp R1=R vàR2=∞(V2=0) ,tasẽtìmđượcbiểuthứctínhđiệnthếVcủamộtmặtcầumangđiện đềuV=q 4πεε0R 10
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+ Xácđịnhhiệuđiệnthếgiữahaiđiểmtrongđiệntrườngcủamộtmặttrụthẳngdàivôhạnmangđiệnđều ∆ R R1 (1) (2) l dr  E R2
+)Đãbiết:En=E=Q 2πεε0lr =λ2πεε0r=σRεε0r V2 ˆ R2 ˆ R2 ˆ +)Từđó,tasuyra σ ε R
ε0rdr =σR ln R2 R1 V   1−V2= −dV = Endr = εε0 V1 R1 R1 +) VậyV R2 R1 =λ ln R2 R1 =σR ln R2 R1
1−V2=Q 2πεε0lln       2πεε0 εε0 11 2.Chương2-Vậtdẫn Câu7
Nêuđiềukiệncânbằngtĩnhđiệnvàtínhchấtcủavậtdẫntíchđiện.Nêuđịnhnghĩavàcôngthứctínhđiện
dungcủavậtdẫncôlập. ■ [Lờigiải]
•Điềukiệncânbằngtĩnhđiện:
1.Vectocườngđộđiệntrườngtạimọiđiểmbêntrongvậtdẫnbằngkhông:  Etr =0
2.Thànhphầntiếptuyếncủavectocườngđộđiệntrườngtạimọiđiểmtrênmặtvậtdẫnphảibằngkhông: 
Et=0,E=En Nếu 
Etr =0,Et=0 thìcácelectrontựdobêntrongvàtrênbềmặtvậtdẫnsẽchuyểndờicóhướng −→ tráivớiđiều kiệncânbằngđãđặtra.
•Tínhchấtcủavậtdẫnmangđiện:
Tínhchất1:Vậtdẫnlàvậtđẳngthể
-XéthaiđiểmM,Nbấtkýtrênvậtdẫn.Hiệuđiệnthểgiữa2điểmđólà: N ˆ N ˆ VM−VN=  Eds= Esds M M
1.Bêntrong vậtdẫn: E=0−→ Vtạimọiđiểmbêntrongvậtdẫnđềubằngnhau.
Hình2.1:Eslàhìnhchiếucủa
Etrênphươngchuyểndời
2.Trênbềmặtvậtdẫn:Et=0−→ Vtạimọiđiểmvậtdẫnđềubằngnhau.
3.DoVcótínhliêntục−→điệnthếtạimọiđiểmcủavậtdẫnđềubằngnhau. 12
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
Tínhchất2:Khivậtdẫnởtrạngtháicânbằngtĩnhđiện,điệntíchchỉphânbốtrênbềmặtvậtdẫn.Bêntrong
vậtdẫnđiệntíchbằng0
-Giảsửtruyềncho vậtdẫnmộtđiệntíchqnàođó.Tưởngtượnglấymộtmặtkín
(S) bấtkỳtrongvậtdẫn.TheoO-G,
tổngđạisốđiệntíchnằmtrongmặtkín(S)là:
∑qi=˛ DdS S
-Bên trong vậtdẫn: D=ε0εE=0⇒∑qi=0
-Vìmặtkín(S)đượcchọnbấtkỳ⇒Takếtluận:Tổngđạisốđiệntíchbêntrongvậtdẫnbằngkhông.
-Nếutatruyềnchovậtdẫnmộtđiệntíchqthìđiệntíchnàysẽchuyểnrabềmặtvậtdẫnvàphânbốtrênbềmặtvật dẫnđó.
-Đốivớivậtdẫnrỗngđãởtrạngtháicânbằngtinhđiện,điệntrườngởphầnrỗngvàtrongthànhcủavậtdẫnrỗng cũngluônbằngkhông.
-Nếuđemmộtquảcầukimloạimangđiệntíchqchotiếpxúcvớimặttrongcủavậtdẫnrỗngthìqsẽtruyềnhếtra
mặtngoaivậtdẫnrỗng→NguyêntắcmáypháttĩnhđiệnVandeGraf
-Vìđiệntrườngbêntrongvậtdẫnrỗngbằngkhông
→ Vậtdẫnrỗngcótácdụngnhư1mànbảovệ → Vậtdẫnrỗng đượcgọilàmànđiện
Tínhchất3:Sựphânbốđiệntíchtrênmặtvậtdẫnchỉthuộcvàohìnhdạngcủamặtđó.
-Điệntíchtậptrungởnhữngchỗcómũinhọn.Ởnhữngchỗlõmđiệntíchrấtít,hầunhưbằngkhông
-Hiệuứngmũinhọn,gióđiện:Giảiphóngđiệntíchtrênmáybay,phóngđiệnbảovệmáyđiện,cộtthulôi.
•Địnhnghĩađiệndungcủavậtdẫncôlập:
1.Vậtdẫncôlập:Mộtvâtdẫnđượcgọilàcôlậpvềđiệnnếugầnnókhôngcómộtvậtnàokháccóthểgâyraảnh
hưởngđếnsựphânbốđiệntíchtrênvậtdẫnđangxét.
2.Địnhnghĩađiệndung:Điệndungcủamộtvậtdẫncôlập làmộtđạilượngvềtrịsốbằngđiệntíchcầntruyềncho
vậtdẫnđểđiệnthếcủavậttănglên1đơnvịđiệnthế.
3.Côngthứctínhđiệndungcủavậtdẫncôlập:
TínhđiệndungcủaquảcầukimloạibánkinhRđặttrongmôitrườngcóh/sđiệnmôi
ε -Gọi Q làđiệntíchquảcầu.
-Vlà điện thế của quả cầu:V=Q 4πε0εR⇒C=Q V=4πε0εR(1)
-Nếutrong(1)chọnC=1F,ε=1 ⇒R=C
=14π.8,86.10−12 =9.109m=1500Rđất 4πε0 Câu8
Địnhnghĩahiệntượngđiệnhưởng.Thếnàolàđiệnhưởngmộtphần,điệnhưởngtoànphần?Địnhnghĩatụ
điện.Tínhđiệndungcủatụphẳng,tụtrụ,vàtụcầu. ■ [Lờigiải]
•Địnhnghĩahiệntượngđiệnhưởng: 1.Hiệntượng:
-ĐặtvậtdẫntrunghòatrongđiệntrườngngoàiE0haiphíacủavậtdẫnxuấthiệncácđiệntíchtráidấugọilàcác
điệntíchcảmứng.Hiệntượngnàygọilàhiệntượngđiệnhưởng. 13
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập 2.Giảithích:
-Dướitácdụngcủađiệntrườngngoàicácetựdotrongvậtdẫnchuyểnđộngngượchướngvớiđiệntrườngngoài.Kết
quảlàmặt B tíchđiện“-”,mặt C tíchđiện“+”,chúngcóđộlớnbằngnhau,tạonênđiệntrường
E’bêntrongvậtdẫn
•Điệnhưởngmộtphầnvàđiệnhưởngtoànphần:
1.Điệnhưởngmộtphần:
Chỉmộtphầnsốđườngcảmứngđiệncủavậtmangđiệngặpvặtbịđiệnhưởng,dođóđộlớncủađiệntíchcảmứng
nhỏhơnđộlớncủađiệntíchtrênvậtmangđiện: |q′|<|q|
2.Điệnhưởngtoànphần:
-Khivậtdẫn (BC) baobọchoàntoànvậtmangđiện
A,toànbộđườngcảmứngđiệnxuấtpháttừ A đếntậncùngtrên
vậtdẫn(BC),tacóhiệntượngđiệnhưởngtoànphần.
Ápdụngđịnhlývềcácphầntửtươngứng→độlớncủađiệntíchcảmứngbằngđộlớncủađiệntíchtrênvậtmang điện. |q′|=|q| •Địnhnghĩatụđiện: 1.Địnhnghĩa:
-TụđiệnlàmộthệhaivậtdẫnAvàBsaochovậtdẫnBbaobọchoàntoànvậtdẫnA.Khiđóhaivậtdẫnởtrạngthái điệnhưởngtoànphần. 2.Tínhchất:
a)Tínhchất1:q1+q2=0(dođiệnhưởngtoànphần)
b) Tính chất 2: GọiV1,V2làđiệnthếcủaAvàB:
q1=C11V1+C12V2 (
q2+q′2=C21V1+C22V2
-Khisửdụngtụđiện,2bảnthườngđượcnốivớinguồn,nóichungq′ 2khôngxuấthiện.
q1=C11V1+C12V2
( q2=C21V1+C22V2→q1+q2= (C11 +C21)V1+ (C12 +C22)V2=0
- DoV1,V2tùyý→C11 +C21 =0vàC12 +C22 =0 DoC12 =C21 11
→C =C22 =C,C12 =C21 =−C
q1=C(V1−V2) (
q2=−C(V1−V2) c)Tínhchất3:
q1=C(V1−V2) (
q2=−C(V1−V2)(3)
-VìC>0,từ(3)suyrakhiq1>0thìV1>V2
-Vậytrongtụđiện,điệnthếcủabảntíchđiệndươngcaohơnđiệnthếcủabảntíchđiệnâm
q=q1=−q2 đượcgọilà điệntíchcủatụđiện
q=C(V1−V2) = CU
•Tínhđiệndungcủamộtsốtụđiện: 1.Tụđiệnphẳng:
U=V1−V2=E.d=σ
ε0εd=Qε0εSd C=Q =ε0εS V1−V2 d 2.Tụđiệncầu:
U=V1−V2=E.d=Q 4πε0ε(1R1−1
) = Q(R2−R1) R2 4πε0εR1R2 C=Q =4πε0εR1R2 V1−V2 R2−R1 3.Tụđiệntrụ
U=V1−V2=λ 2πε0εln R2 =Q2πε0εlln R2 R1 R1 →C=Q =2πε0εl . V1−V2 ln R2 R1 14
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu9
Chứngminhcôngthứctínhnănglượngtươngtácđiệncủahệđiệntíchđiểm,vậtdẫncôlậptíchđiện,năng
lượngtụđiệnphẳngvànănglượngđiệntrường. ■ [Lờigiải]
a)Nănglượngtươngtácđiệncủahệđiệntíchđiểm
+)Hệhaiđiệntíchđiểm
Khiđiệntíchđiểmq2đặttrongđiệntrườngcủađiệntíchđiểmq1thếnăngcủaq2là: Wt=1 q1q2
Vớir12làkhoảngcáchgiữa2điệntích 4πε0ε r12
Wt cũnglàthếnăngcủa
q1 trongđiệntrườngcủa q2.Tanói Wt làthếnăngtươngtáchaynăng lượngtươngtácđiệncủahệ
2điệntíchq1vàq2,kýhiệulà: W12 =W21 =1 q1q2 4πε0ε r12 ⇔W q2 4πε0εr12 +12q2 q1 4πε0εr12 12 =W21 =1 2q1 ! ! Màtacó q2
=V1=Điệnthếdoq2gâyratạivịtríq1  4πε0εr12 q1 
=V2=Điệnthếdoq1gâyratạivịtríq2 4πε0εr12 Vậy
W12 =W21 =1 2(q1V1+q2V2) +)Hệ3điệntíchđiểm r W=W q1q2 31
12 +W23 +W31 =1 4πε0ε
+q2q3 +q3q1 ! r12 r23
⇔W=1 2q1 q2 4πε0εr31 +12q2 q3 4πε0εr12 +12q3 q1 4πε0εr23 +q3 ! +q1 ! +q2 ! 4πε0εr12 4πε0εr23 4πε0εr31
⇔W=1 2(q1V1+q2V2+q3V3)
(V1,V2,V3làđiệnthếtạivịtrícủaq1,q2,q3dohaiđiệntíchkiagâyra) Vậy
W=1 2(q1V1+q2V2+q3V3) +)Hệnđiệntíchđiểm W=1 2(q n
1V1+q2V2+... +qnVn) = 1 ∑qiVi 2 i=1
b)Nănglượngđiệncủamộtvậtdẫncôlậptíchđiện
q:điệntíchvậtdẫn.
Chiavậtdẫnthànhnhữngđiệntíchđiểmdq
W=1 2ˆV dq =1 2Vˆdq =1 2qV
W=1 2qV =12CV 2=q2 2C 15
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập c)Nănglượngtụđiện
Hệnvậtdẫncóđiệntích:q1,q2,...,qnvà điện thế tương ứng:V1,V2,..,Vn
Nănglượnghệvậtdẫnlà: W=1 n ∑ qiVi 2 i=1 Tụđiện
W=1 2(q1V1+q2V2)
Doq1=−q2=q
→W=1 2q(V1−V2) = 12qU Vậy
W=1 2qU =q2 2C=1 2CU2
d)Nănglượngđiệntrường
Xét1tụđiệnphẳng.Nănglượngcủatụđiệnlà: W=CU2 2=1 ε0εS dU2 2 MàU=Ed
→W=1 2(ε0εE2)Sd LạicóSd =∆V
→W=1 2(ε0εE2)∆V Mậtđộnănglượng
We=W∆V=1 2ε0εE2=1 D2 ε0ε=1 2DE(∗) 2
(∗)đúngvớiđiệntrườngbấtkì:
NănglượngđiệntrườngtrongkhônggianV
W=ˆV WedV =12ˆε0εE2dV 16 3.Chương3-Điệnmôi Câu10
Sựphâncựcđiệnmôilàgì?Giảithíchhiệntượngphâncựcđiệnmôi.Địnhnghĩavàcôngthứctínhđộlớncủa
véctơphâncựcđiệnmôi.Trìnhbàyvềmốiliênhệgiữavéctơphâncựcđiệnmôivàmậtđộđiệnmặtcủacác
điệntíchliênkết.Nêucôngthứctínhcườngđộđiệntrườngvàđiệncảmtrongđiệnmôi. ■ [Lờigiải]
1.Sựphâncựcđiệnmôilàgì?
–Hiệntượngtrênthanhđiệnmôiđặttrongđiệntrườngcóxuấthiệnđiệntíchđượcgọilàhiệntượngphâncựcđiệnmôi.
–Trênthanhđiệnmôi,điệntíchxuấthiệnởđâusẽđịnhxứtạiđó,khôngdịchchuyểntựdođượcnênđượcgọilàđiệntích
liênkết.CácđiệntíchliênkếtsinhrađiệntrườngphụE′.
–Điệntrườngtổnghợptrongđiệnmôi: 
E=E0+E′
2.Giảithíchhiệntượngphâncựcđiệnmôi
a)Điệnmôicấutạotừphântửkhôngphâncực:
-Khi E0=0 : pei =0
-Khi E0=0 : cácphântửbịphâncựcthànhcáclưỡngcựcđiệncó pe=αε0 E
•Mômenđiệncủacácphântửđềuhướngtheochiềuđiệntrường;
•Trênmặtgiớihạncủakhốiđiệnmôixuấthiệncácđiệntíchliênkếttráidấu.
b)Điệnmôicấutạotừphântửphâncực:
-Khi E0=0 : pei =0.Nhưngdochuyểnđộngnhiệtnên∑pei =0 -Khi E0=0:
•pexoaytheochiềuđiệntrườngngoài  E0;
•Dochuyểnđộngnhiệt petungrahaiphíasovớiphươngcủađiệntrườngngoài;
•Tronglòngđiệnmôi:∑qi=0;
•Trênmặtgiớihạn:xuấthiệncácđiệntíchtráidấu.
3.Véctơphâncựcđiệnmôi
–Giảsửtrongthểtích∆Vcủakhốiđiệnmôiđồngchấtcónphântử.
–Véctơphâncựcđiệnmôilàmộtđạilượngđobằngtổngcácmômenlưỡngcựcđiệncủacácphântửcótrongmộtđơnvị
thểtíchcủakhốiđiệnmôi. n ∑  Pei  P i=1 e= ∆V 17
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
a)Điệnmôicóphântửkhôngphâncực
-Khiđặttrongđiệntrườngđều,mọiphântửđiệnmôiđềucócùngvéctơ pe
e=npe P
∆V=n0pe
n0=n ∆Vlàmậtđộphântử
-GọiElàvéctơcườngđộđiệntrườngtổnghợptrongđiệnmôi  Pe=n0
pe=n0ε0α E=ε0χe E
χe=n0αlàđộcảmđiệnmôi,khôngthứnguyên,khôngphụthuộcvàoE
b)Điệnmôicóphântửphâncực
-Nếuđiệntrườngngoàiyếu,đãchứngminhđược: 
Pe=ε0χe Evớiχe=n0pe23ε0kT
k=1,38.10−23J/K,T:nhiệtđộtuyệtđốicủakhốiđiệnmôi
-Nếuđiệntrườngngoàimạnh,Tthấp:
Pekhôngtỷlệbậcnhấtvới
Enữa.Nếutăng Etớimộtgiátrịđủlớn,tấtcảcác
mômenđiệnđềusongsongvới E.Hiệntượngphâncựcđiệnmôiđãđạttrạngtháibãohòa. c)Điệnmôitinhthể 
Pe=ε0χeEĐơn vị:C/m2
4.Liênhệgiữavéctơphâncựcđiệnmôivớimậtđộđiệnmặtcủacácđiệntíchliênkết
-Táchratrongđiệnmôimộtkhốitrụxiêncó:
•Đườngsinhsong song E(tứclàsongsong Pe,cóchiềudàiL;
•Haiđáysongsong,mỗiđáycódiệntích∆S;
•+σ′,−σ′làmậtđộđiệnmặttrênmỗiđáy;
•nlàpháptuyếnngoàicủađáymangđiệntíchdương;
•Cóthểcoitoànbộkhốitrụnhưmộtlưỡngcựcđiệntạorabởicácđiệntíchliênkết−σ′∆Svà+σ′∆Strênhaiđáy
cáchnhaumộtđoạnL.Mômenđiệncủanócóđộlớnσ′∆SL. n e|=| ∑  pei| ∆V=σ′∆SL ∆SL cos α=σ′ Pe=| P i=1 cos α
→σ′=P ecos α=P en
-Kếtluận:Mậtđộđiệnmặt
σ′ củacácđiệntíchliênkếtxuấthiệntrênmặtgiớihạncủakhốiđiệnmôicótrịsốbằnghình
chiếucủavéctơphâncựcđiệnmôitrênpháptuyếncủamặtgiớihạnđó.
-ĐơnvịP e:C/m2
5.Côngthứctínhcườngđộđiệntrườngvàđiệncảmtrongđiệnmôi
a)Cườngđộđiệntrường
•Giảsửcómộtđiệntrườngđều 
E0giữahaimặtphẳngmangđiệnđềubằngnhautráidấu
•Chấtđiệnmôilấpđầykhoảngkhônggiangiữahaimặtphẳng
•Khốiđiệnmôibịphâncực
•Trênmặtđiệnmôixuấthiệncácđiệntíchliênkết+σ′,−σ′
•Cácđiệntíchliênkếtnàygâyrađiệntrườngphụ  E′
Điệntrườngtổnghợptrongđiệnmôi: 
E=E0+E′
VìE0ngượcchiều E′nêntacóE=E0−E′  E′=σ′ 
en =ε0χeEn=ε0χeE⇒E′=σ′ ε0 =χeE ε0  σ′=P 18
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Từđó,tacó:
E=E0−E′=E0−χeE⇒E=E0 =E0 1+χe ε
ε=1+χegọilàhằngsốđiệnmôicủamôitrường
Cườngđộđiệntrườngtrongđiệnmôigiảmđiεlầnsovớicườngđộđiệntrườngtrongchânkhông
b)Điệncảmtrongđiện D=ε0ε ( E ε=1+χe
⇒D=ε0(1+χe) E=ε0E+ε0χeE=ε0E+Pe 19