Bộ đề ôn thi tốt nghiệp thpt 2021 môn toán có đáp án lời giải chi tiết (bộ 2)

Bộ đề ôn thi tốt nghiệp thpt 2021 môn toán có đáp án lời giải chi tiết (bộ 2) được soạn dưới dạng file PDF. Đề thi bao có 83 trang, bao gồm bộ câu trắc nghiệm. Tài liệu có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mờicác bạn cùng đón xemở dưới.

 

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

83 trang 7 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 6
ĐỀ THI THỬ THPT QUỐC GIA 2021
MÔN TOÁN
Thời gian: 90 phút
Câu 1. c 5 chic gh xp thành mt hàng ngang. S cách xp ba bn
,,A B C
vào 5 chic gh
i bn ngi mt gh là
A.
3
5
.C
B.
6.
C.
3
5
.A
D.
15.
Câu 2. Cho cp s cng
n
u
có s hu
và công sai
3.d
Giá tr ca
5
u
bng
A.
14
. B.
5
. C.
11
. D.
15
.
Câu 3. 
32
4 16
x
có nghim là
A.
3
4
x
. B.
5x
. C.
4
3
x
. D.
3x
.
Câu 4. Khi chóp
.S ABCD

()SA ABCD
có th tích bng
A.
1
..
3
SA AB AD
. B.
1
..
3
SA AC BD
. C.
1
..
6
SA AB AD
. D.
1
..
6
SA AC BD
.
Câu 5. Hàm s
2
log 2 3yx
có tnh là
A.
D
. B.
3
;
2
D



. C.
3
\
2
D



. D.
3
;
2
D




.
Câu 6. Tìm h nguyên hàm ca hàm s
cosf x x
.
A.
2
1
cos .
2
xC
B.
sinxC
. C.
sinxC
. D.
2
1
cos
2
xC
.
Câu 7. Cho khi   dài hai cnh góc vuông là
3 ,4aa
và chiu
cao kh là
6a
. Th tích ca kh bng
A.
3
27Va
. B.
3
12Va
. C.
3
72Va
. D.
3
36Va
.
Câu 8. Tính chiu cao
h
ca hình tr bit chiu cao
h
b tích ca khi tr 
8
.
A.
2h
. B.
22
. C.
3
32
. D.
3
4
.
Câu 9. 
6cm

A.
216
. B.
288
. C.
432
. D.
864
.
Câu 10. Cho hàm s
y f x
có bng bi
x

2
0

y
0
0
y

2
2

Hàm s
y f x
nghch bin trên khong
A.
2;0
. B.
2;
. C.
2;2
. D.
;2
.
Câu 11. Vi
;ab
là hai s 
32
log ab
có giá tr bng biu th
A.
1
3 log log
2
ab



. B.
2log 3logab
. C.
1
3log log
2
ab
. D.
3log 2logab
.
Câu 12. Cho kh ng sinh bng 10 và din tích xung quanh bng
60
. Th tích ca
khng
A.
360
. B.
288
. C.
120
. D.
96
.
Câu 13. Cho hàm s
y f x
 th  bên. Tìm giá tr ci ca hàm s.
Trang2
A.
0
CD
y
. B.
2
CD
y 
. C.
4
CD
y
. D.
2
CD
y
.
Câu 14. Bng bia hàm s nào?
A.
42
23y x x
. B.
42
23y x x
.
C.
42
23y x x
. D.
42
23y x x
.
Câu 15. Cho hàm s
()y f x

\1


A.
1
. B.
2
. C.
3
. D.
4
.
Câu 16. Tìm tp nghim
S
ca b
11
22
log 1 log 2 1xx
.
A.
2;S 
. B.
1;2S 
. C.
;2S 
. D.
1
;2
2
S



.
Câu 17. Cho hàm s
y f x
có bng bi
S nghim thc c
2 3 0fx
là
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 18. Cho hàm s
fx
liên tc trên
và có
24
02
d 9; d 4f x x f x x

. Tính
4
0
dI f x x
?
A.
9
4
I
. B.
36I
. C.
13I
. D.
5I
.
4
O
2
2
2
2
y
x
Trang3
Câu 19. Cho s phc
12zi
. Tìm phn o ca s phc
z
.
A.2. B.
2
. C.
1
. D.1.
Câu 20. Cho s phc
12zi
. Tìm tng phn thc và phn o ca s phc
2w z z
.
A.3. B.5. C.1. D.2.
Câu 21. Cho s phc
12zi
. S phc
z
c biu din bt phng ta
?
A.
1; 2Q 
. B.
1;2P
. C.
1; 2N
. D.
1;2M
.
Câu 22. Trong không gian
Oxyz
m
2;1;3A
. Hình chiu vuông góc ca
A
lên trc
Ox
có ta
 là:
A.
0;1;0
. B.
2;0;0
. C.
0;0;3
. D.
0;1;3
.
Câu 23. Trong không gian
Oxyz
, mt cu
2 2 2
: 5 1 2 3S x y z
có bán kính bng
A.
3
. B. 2
3
. C. 9. D. 3.
Câu 24. Trong không gian
Oxyz
, cho mt phng
P
:
2 1 0xz
.T mn ca
mt phng
P
là
A.
2;0;1n
. B.
2;0; 1n 
. C.
2; 1;1n 
. D.
2; 1;0n 
.
Câu 25. 
Oxyz

3 2 1
:
2 1 4
x y z
d

không 
d
.
A.
1; 1; 5M 
. B.
1; 1;3M
. C.
3; 2; 1M 
. D.
5; 3;3M
.
Câu 26. Cho hình chóp
.S ABC
 
ABC
là tam giác vuông cân ti
B
cnh
AB a
, cnh
SA
vuông góc vi mt ph  
2SA a
. Tính
cosin
ca góc
là góc gia mt phng
ABC
và mt phng
SBC
.
A.
2
cos
3
. B.
1
cos
3
. C.
1
cos
5
. D.
1
cos
5
.
Câu 27. Cho hàm s
()y f x
o hàm
2
( ) ( 1) (2 3)f x x x x
. Hàm s m
cc tr?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 28. 

fx


1;3
 .

,Mm
l









y f x
trên
1;3
. 
Mm
.
A.
3
. B.
4
.
C.
5
. D.
1
.
Câu 29. Vi
,,abc
là các s th      
log ,log
ab
c x c y
     ca
log
c
ab
là
A.
xy
. B.
xy
xy
. C.
. D.
1
xy
.
Câu 30. S m c th hàm s
42
54y x x
vi trc hoành là:
Trang4
A.1. B.2. C.3. D.4.
Câu 31. B
21
3 7.3 2 0
xx
có nghim là
A.
2
1
log 3
x
x

. B.
2
2
log 3
x
x

. C.
3
1
log 2
x
x

. D.
3
2
log 2
x
x

.
Câu 32. u
ABC
cnh bng
a
. Tính th tích khi nón nhc khi
quay tam giác
ABC
quanh mng cao ca nó.
A.
3
3
24
a
V
. B.
3
3
72
a
V
. C.
3
4
a
V
. D.
3
3
4
a
V
.
Câu 33. Cho
2
2
1
2 1dI x x x
và
2
1ux
. M sai ?
A.
3
0
dI u u
. B.
2
27
3
I
. C.
2
1
dI u u
. D.
3
2
2
3
3
I
.
Câu 34. Din tích hình phng gii hn b  th hàm s
3
yx
, tr    ng thng
1, 2xx
là
A.
2
3
1
S x dx
B.
2
3
1
S x dx

C.
2
3
1
S x dx
D.
2
3
1
S x dx
Câu 35. Cho hai s phc
1
1zi
và
2
1zi
. Giá tr ca biu thc
12
z iz
bng
A.
22i
. B.
2i
. C.
2
. D.
22i
.
Câu 36. Gi
0
z
là nghim phc có phn 
2
6 34 0zz
. Tính
0
2zi
?
A.
17
. B.
17
. C.
2 17
. D.
37
.
Câu 37. Trong không gian
Oxyz
mt phng
P
  c t  và vuông góc v ng thng
11
:
2 1 2
x y z
d


A.
2 2 0x y z
. B.
2 2 0x y z
. C.
2 2 3 0x y z
. D.
2 2 1 0x y z
.
Câu 38. Trong không gian
Oxyz
ng thm
3;1;2A
,
1; 1;0B
là
A.
11
2 1 1
x y z


. B.
3 1 2
2 1 1
x y z

.
C.
3 1 2
2 1 1
x y z

. D.
11
2 1 1
x y z


.
Câu 39. Có 8 hc sinh nam, 5 hc sinh n và 1 thc sp xp ngng thành mt vòng
tròn. Tính xác su thng gia 2 hc sinh nam.
A.
7
.
39
P
B.
14
.
39
P
C.
28
.
39
P
D.
7
.
13
P
Câu 40. Cho hình l
.ABCD A B C D
cnh
a
. Tính khong cách ging thng
BC
và
CD
.
A.
2a
. B.
2a
. C.
3
3
a
. D.
2
3
a
.
Câu 41. Có bao nhiêu giá tr
m
nguyên thu n
2018 ; 2019
 hàm
s
32
2 2 5 5y x x m x
ng bin trên khong
0 ; +
?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Câu 42. i ta th mt s lá bèo vào mt h c, sau
10
gi s ng lá bèo s sinh sôi kín c mt
h. Bit rng sau mi gi s p 10 ln s 
i. Hi sau khong thi gian bao lâu s ng lá bèo ph kín ti thiu mt ph
h?
A.
10 log4
. B.
10log 4
. C.
1 10log4
. D.
10 10log4
.
Trang5
Câu 43. Cho hàm s
42
1 2 1y a x b x c
 th  bên
M 
A.
1a
,
2b 
,
1c
. B.
1a
,
2b 
,
1c
.
C.
1a
,
2b 
,
1c
. D.
1a
,
2b
,
1c
.
Câu 44. nh
S
ng tròn tâm
O
bán kính
R
ng tròn
O
ly hai
m
,AB
sao cho tam giác
OAB
vuông. Bit din tích tam giác
SAB
bng
2
2R
. Th tích
ng
A.
3
14
12
R
. B.
3
14
2
R
. C.
3
14
6
R
. D.
3
14
3
R
.
Câu 45. Cho
8
3
11
d ln
2
1
ac
Ix
bd
x x x

vi
, , ,a b c d
là các s 
,
ac
bd
ti gin.
Giá tr ca
abc d
bng
A.
6
. B.
18
. C.
0
. D.
3
.
Câu 46. Cho hàm s
y f x
 th  bên. Có bao nhiêu giá tr nguyên ca tham s
m


0f f x m


m phân bit.
A.
1.
B.
2.
C.
3.
D.
4.
Câu 47. 
,ab

22
1ab
và
22
log 1
ab
ab


2 4 3P a b
là
A.
10
. B.
10
2
. C.
2 10
. D.
1
10
.
Câu 48. Cho hàm s
4 3 2
44f x x x x a
. Gi
,Mm
l t là giá tr ln nht và giá tr nh
nht ca hàm s n
0;2
. Có bao nhiêu s nguyên
a
thun
3;2
sao cho
2?Mm
A.
7
. B.
5
. C.
6
. D.
4
.
Câu 49. Cho hình chóp
.S ABC
có các cnh
3SA BC
;
4SB AC
;
25SC AB
. Tính th tích
khi chóp
.S ABC
.
A.
390
12
. B.
390
4
. C.
390
6
. D.
390
8
.
Trang6
Câu 50. Cho
0 2021x
và
2
log (2 2) 3 8
y
x x y
.Có bao nhiêu cp s
( ; )xy
nguyên tha mãn
u kin trên ?
A.2021. B.2022. C.1. D.4.
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1. c 5 chic gh xp thành mt hàng ngang. S cách xp ba bn
,,A B C
vào 5 chic gh
i bn ngi mt gh là
A.
3
5
.C
B.
6.
C.
3
5
.A
D.
15.
Lời giải
Chọn C
Cách 1: Mi cách xp tha mãn yêu cu bài toán chính là mt chnh hp chp 3 ca 5 phn t
nên s cách xp là
3
5
A
.
Cách 2: Có 5 cách xp bn A, vi mi cách xp bn A thì có 4 cách xp bn B, vi mi cách
xp bn A và B thì có 3 cách xp bn C. Vy theo qui tc nhân có
5.4.3 60
.
Câu 2. Cho cp s cng
n
u
có s hu
và công sai
3.d
Giá tr ca
5
u
bng
A.
14
. B.
5
. C.
11
. D.
15
.
Lời giải
Chọn A
Cp s s cng
n
u
có s hu
1
u
và công sai
d
có công thc s hng tng quát là:
1
1
n
u u n d
. Suy ra
51
4 2 4.3 14u u d
.
Vy s giá tr ca
5
u
bng 14.
Câu 3. 
32
4 16
x
có nghim là
A.
3
4
x
. B.
5x
. C.
4
3
x
. D.
3x
.
Lời giải
Chọn C
Ta có:
32
4
4 16 3 2 2
3
x
xx
.
Vm là:
4
3
x
.
Câu 4. Khi chóp
.S ABCD

()SA ABCD
có th tích bng
A.
1
..
3
SA AB AD
. B.
1
..
3
SA AC BD
. C.
1
..
6
SA AB AD
. D.
1
..
6
SA AC BD
.
Lời giải
Chọn D
Ta có hình v
Khi chóp
.S ABCD

ABCD
và nhn
SA
ng cao.
Din tích hình thoi
ABCD
là
1
.
2
S AC BD
.
Trang7
Th tích khi chóp là
1
..
6
V SA AC BD
.
Câu 5. Hàm s
2
log 2 3yx
có tnh là
A.
D
. B.
3
;
2
D



. C.
3
\
2
D



. D.
3
;
2
D




.
Lời giải
Chọn D
Hàm s
2
log 2 3yx
nh
3
2 3 0
2
xx
.
Vy tnh ca hàm s là:
3
;
2
D




.
Câu 6. Tìm h nguyên hàm ca hàm s
cosf x x
.
A.
2
1
cos .
2
xC
B.
sinxC
. C.
sinxC
. D.
2
1
cos
2
xC
.
Lời giải
Chọn B
Ta có:
d cos d sin .f x x x x x C

Câu 7. Cho khi   dài hai cnh góc vuông là
3 ,4aa
và chiu
cao kh là
6a
. Th tích ca kh bng
A.
3
27Va
. B.
3
12Va
. C.
3
72Va
. D.
3
36Va
.
Lời giải
Chọn D
Th tích kh
.BVh
.

6ha
.
Di
2
1
.3 .4 6
2
B a a a
.
Vy
23
6 .6 36V a a a
Câu 8. Tính chiu cao
h
ca hình tr bit chiu cao
h
b tích ca khi tr 
8
.
A.
2h
. B.
22
. C.
3
32
. D.
3
4
.
Lời giải
Chọn A
Th tích khi tr là
2 3 3
8 8 2V r h h h h
.
Câu 9. 
6cm

A.
216
. B.
288
. C.
432
. D.
864
.
Lời giải
Chọn B
Ta có th tích khi cu :
33
44
6 288
33
VR
3
cm
.
Câu 10. Cho hàm s
y f x
có bng bi
x

2
0

Trang8
y
0
0
y
/

2
2

Hàm s
y f x
nghch bin trên khong
A.
2;0
. B.
2;
. C.
2;2
. D.
;2
.
Lời giải
Chọn A
Da vào bng bin thiên ca hàm s suy ra hàm s
y f x
nghch bin trên khong
2;0
.
Câu 11. Vi
;ab
là hai s 
32
log ab
có giá tr bng biu th
A.
1
3 log log
2
ab



. B.
2log 3logab
. C.
1
3log log
2
ab
. D.
3log 2logab
.
Lời giải
Chọn D
Vi
;ab
là hai s  :
3 2 3 2
log log log 3log 2loga b a b a b
.
Câu 12. Cho kh ng sinh bng 10 và din tích xung quanh bng
60
. Th tích ca
khng
A.
360
. B.
288
. C.
120
. D.
96
.
Lời giải
Chọn D
/
Ta có:
10l
60 60 10 60 6
xq
S rl r r
.
2 2 2 2
10 6 64 8h l r
.
.
 tích kh
22
11
.6 .8 96
33
V r h
.
Câu 13. Cho hàm s
y f x
 th  bên. Tìm giá tr ci ca hàm s.
A.
0
CD
y
. B.
2
CD
y 
. C.
4
CD
y
. D.
2
CD
y
.
Lời giải
Chọn C
D th hàm s, ta thy giá tr ci ca hàm s là
4
CD
y
ti
2x 
.
Câu 14. Bng bia hàm s nào?
/
A.
42
23y x x
. B.
42
23y x x
.
C.
42
23y x x
. D.
42
23y x x
.
Lời giải
Chọn C
T bng bin thiên suy ra h s
0a
.
Mt khác hàm s m cc tr suy ra các h s
,ab
trái du.
4
O
2
2
2
2
y
x
Trang9
Câu 15. Cho hàm s
()y f x

\1


/
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Tbng bin thiên ta thy:
lim ( ) 5
x
fx


5y
.
lim ( ) 3
x
fx


3y
.
1
1
lim ( )
lim ( )
x
x
fx
fx



1x
.
3 .
Câu 16. Tìm tp nghim
S
ca b
11
22
log 1 log 2 1xx
.
A.
2;S 
. B.
1;2S 
. C.
;2S 
. D.
1
;2
2
S



.
Lời giải
Chọn D
Ta có
11
22
log 1 log 2 1xx
1 2 1
2 1 0
xx
x

1
2
2
x
.
Câu 17. Cho hàm s
y f x
có bng bi
/
S nghim thc c
2 3 0fx
là
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn A

2 3 0fx
3
2
fx
.
S nghim cng s m ca  th hàm s
y f x
vng
thng
3
2
y
.
T bng bin thiên suy ra s nghim thc c
2 3 0fx
là
2
.
Câu 18. Cho hàm s
fx
liên tc trên
và có
24
02
d 9; d 4f x x f x x

. Tính
4
0
dI f x x
?
A.
9
4
I
. B.
36I
. C.
13I
. D.
5I
.
Lời giải
Chọn C
Ta có
4 2 4
0 0 2
d d d 9 4 13f x x f x x f x x
.
Trang10
Câu 19. Cho s phc
12zi
. Tìm phn o ca s phc
z
.
A.2. B.
2
. C.
1
. D.1.
Lời giải
Chọn A
Ta có
1 2 1 2z i z i
.
Vy
z
có phn o
2b
.
Câu 20. Cho s phc
12zi
. Tìm tng phn thc và phn o ca s phc
2w z z
.
A.3. B.5. C.1. D.2.
Lời giải
Chọn B
Ta có
1 2 1 2z i z i

2 2 1 2 1 2 3 2w z z i i i
.
Phn thc ca s phc
w
là 3, phn o ca s phc
w
là 2.
Tng phn thc và phn o là:
3 2 5
.
Câu 21. Cho s phc
12zi
. S phc
z
c biu din bt phng ta
?
A.
1; 2Q 
. B.
1;2P
. C.
1; 2N
. D.
1;2M
.
Lời giải
Chọn A
Ta có
1 2 1 2z i z i
.
Vy s phc
z
c biu din bm
1; 2Q 
.
Câu 22. Trong không gian
Oxyz
m
2;1;3A
. Hình chiu vuông góc ca
A
lên trc
Ox
có ta
 là:
A.
0;1;0
. B.
2;0;0
. C.
0;0;3
. D.
0;1;3
.
Lờigiải
Chọn B
Chiu vuông góc mm bt k lên trc
Ox
   và cao
 bng
0
.
Vy hình chiu vuông góc ca
A
lên trc
Ox
có t là:
2;0;0
.
Câu 23. Trong không gian
Oxyz
, mt cu
2 2 2
: 5 1 2 3S x y z
có bán kính bng
A.
3
. B. 2
3
. C. 9. D. 3.
Lời giải
ChọnA
T t cu
2 2 2
: 5 1 2 3S x y z
.
Suy ra, bán kính ca mt c
3R
.
Câu 24. Trong không gian
Oxyz
, cho mt phng
P
:
2 1 0xz
.T mn ca
mt phng
P
là
A.
2;0;1n
. B.
2;0; 1n 
. C.
2; 1;1n 
. D.
2; 1;0n 
.
Lời giải
Chọn B
Mt phng
P
có mn là
2;0 ; 1n 
.
Câu 25. 
Oxyz

3 2 1
:
2 1 4
x y z
d

không 
d
.
A.
1; 1; 5M 
. B.
1; 1;3M
. C.
3; 2; 1M 
. D.
5; 3;3M
.
Trang11
Lời giải
ChọnB
Th c:
1 3 1 2 5 1
1
2 1 4
. Suy ra
M
thung thng
d
.
Th c:
1 3 1 2 3 1
2 1 4

. Suy ra
M
không thung thng
d
.
Th c:
3 3 2 2 1 1
0
2 1 4
. Suy ra
M
thung thng
d
.
Th c:
5 3 3 2 3 1
1
2 1 4
. Suy ra
M
thung thng
d
.
Câu 26. Cho hình chóp
.S ABC
 
ABC
là tam giác vuông cân ti
B
cnh
AB a
, cnh
SA
vuông góc vi mt ph  
2SA a
. Tính
cosin
ca góc
là góc gia mt phng
ABC
và mt phng
SBC
.
A.
2
cos
3
. B.
1
cos
3
. C.
1
cos
5
. D.
1
cos
5
.
Lời giải
Chọn C
/
Vì
BC AB
BC SAB BC SB
BC SA
.
Suy ra góc gia 2 mt phng
ABC
và mt phng
SBC
là góc
SBA
.
Xét tam giác vuông
SBA
có
22
1
cos
5
AB AB
SB
SA AB
.
Câu 27. Cho hàm s
()y f x
o hàm
2
( ) ( 1) (2 3)f x x x x
. Hàm s m
cc tr?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
D thy:
()fx
liên tc trên
.
0
( ) 0 1
3
2
x
f x x
x


2
nghi
0x
và
3
2
x 
và mt nghim bi 2 là
1x
.
Lp bng xét du
()fx
/
fx
i du 2 ln nên hàm s
fx
m cc tr.
Câu 28. 

fx


1;3
 . 
,Mm
l

y f x
trên
1;3
. 
Mm
.
A.
3
. B.
4
.
C.
5
. D.
1
.
/
Lời giải
Chọn C




y f x





1;3

1

1x 

1;3

4

3x
. 
4, 1Mm
.
Trang12

4 1 5Mm
.
Câu 29. Vi
,,abc
là các s th      
log ,log
ab
c x c y
     ca
log
c
ab
là
A.
xy
. B.
xy
xy
. C.
. D.
1
xy
.
Lời giải
Chọn C
Ta có:
1 1 1 1
log log log
log log
c c c
a
ab a b c
c b x y
.
Câu 30. S m c th hàm s
42
54y x x
vi trc hoành là:
A.1. B.2. C.3. D.4.
Lời giải
Chọn D
 m c th hàm s và trc
Ox
là:
42
5 4 0xx
2
2
1
4
x
x
1
2
x
x


.
Vy s m chung c th hàm s
42
54y x x
vi trc hoành là 4.
Câu 31. B
21
3 7.3 2 0
xx
có nghim là
A.
2
1
log 3
x
x

. B.
2
2
log 3
x
x

. C.
3
1
log 2
x
x

. D.
3
2
log 2
x
x

.
Lời giải
Chọn C
Ta có
21
3 7.3 2 0
xx
2
3.3 7.3 2 0
xx
1
3
3
32
x
x
3
3
1
log
3
log 2
x
x
3
1
log 2
x
x

.
Câu 32. u
ABC
cnh bng
a
. Tính th tích khi nón nhc khi
quay tam giác
ABC
quanh mng cao ca nó.
A.
3
3
24
a
V
. B.
3
3
72
a
V
. C.
3
4
a
V
. D.
3
3
4
a
V
.
Lời giải
Chọn A
/
Ta có th tích khi nón
2
1
3
V r h
.

3
2
a
h AH
;
2
a
r HB
.

2
3
1 3 3
3 2 2 24
a a a
V




.
Câu 33. Cho
2
2
1
2 1dI x x x
và
2
1ux
. M sai ?
A.
3
0
dI u u
. B.
2
27
3
I
. C.
2
1
dI u u
. D.
3
2
2
3
3
I
.
Lời giải
Chọn C
t
2
1 d 2 du x u x x
i cn: Vi
1x
thì
0u
; vi
2x
thì
3u
.
Trang13

23
33
2
22
10
3
2 2 2
2 1d d 3 27
0
3 3 3
I x x x u u u


2
1
dI u u
sai.
Câu 34. Din tích hình phng gii hn b  th hàm s
3
yx
, tr    ng thng
1, 2xx
là
A.
2
3
1
S x dx
B.
2
3
1
S x dx

C.
2
3
1
S x dx
D.
2
3
1
S x dx
Lời giải
Chọn C
Theo công thc tính din tích hình phng ta có
2
3
1
S x dx
Câu 35. Cho hai s phc
1
1zi
và
2
1zi
. Giá tr ca biu thc
12
z iz
bng
A.
22i
. B.
2i
. C.
2
. D.
22i
.
Lời giải
ChọnC
Ta có
11
11z i z i
;
22
11z i iz i
.
Suy ra
12
2z iz
.
Câu 36. Gi
0
z
là nghim phc có phn 
2
6 34 0zz
. Tính
0
2zi
?
A.
17
. B.
17
. C.
2 17
. D.
37
.
Lời giải
Chọn A
2
6 34 0zz
35
35
zi
zi

0
35zi
0
2 1 4 17z i i
.
Câu 37. Trong không gian
Oxyz
mt phng
P
  c t  và vuông góc v ng thng
11
:
2 1 2
x y z
d


A.
2 2 0x y z
. B.
2 2 0x y z
. C.
2 2 3 0x y z
. D.
2 2 1 0x y z
.
Lời giải
Chọn A
11
:
2 1 2
x y z
d


Vì
Pd
nên chn
2; 1;2
P
n 
P
qua gc t nên
:2 2 0P x y z
Câu 38. Trong không gian
Oxyz
ng thm
3;1;2A
,
1; 1;0B
là
A.
11
2 1 1
x y z


. B.
3 1 2
2 1 1
x y z

.
C.
3 1 2
2 1 1
x y z

. D.
11
2 1 1
x y z


.
Lời giải
Chọn D
Ta có:
4; 2; 2AB
ng thng
AB
nhn vecto
1
2; 1; 1
2
n AB
làm vecto ch 
Trang14
Vì
B AB
ng thng
AB
là:
11
2 1 1
x y z


.
Câu 39. Có 8 hc sinh nam, 5 hc sinh n và 1 thc sp xp ngng thành mt vòng
tròn. Tính xác su thy ng gia 2 hc sinh nam.
A.
7
.
39
P
B.
14
.
39
P
C.
28
.
39
P
D.
7
.
13
P
Lời giải
Chọn B
S phn t ca không gian mu là:
13!.
Gi A là bin chng gia 2 hc sinh nam
c 1: Xp hai hng cnh thy giáo có
2
8
A
.
Coi hai hng cnh thy giáo và thy giáo là mi.
c 2: Xi quanh mt bàn tròn có
11!
cách.
S kt qu thun li ca bin c A là:
2
8
.11!.A
Vy
2
8
.11!
14
.
13! 39
A
PA
Câu 40. Cho hình l
.ABCD A B CD
cnh
a
. Tính khong cách ging thng
BC
và
CD
.
A.
2a
. B.
2a
. C.
3
3
a
. D.
2
3
a
.
Lời giải
Chọn C
/
.ABCD A B C D
là hình l
// // ;BC AD BC ACD CD ACD
; ; ; ;d BC CD d BC ACD d B ACD d D ACD h
.
.
T din
.D ACD
có
,,DA DC DD
t vuông góc.
2 2 2 2 2
1 1 1 1 3 3
3
a
h
h DA DC DD a
.
Câu 41. Có bao nhiêu giá tr
m
nguyên thu n
2018 ; 2019
 hàm
s
32
2 2 5 5y x x m x
ng bin trên khong
0 ; +
?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Lời giải
Chọn A
Ta có
2
3 4 2 5y x x m
Hàm s ng bin trên khong
0;+
0, 0;+yx
2
3 4 2 5 0 , 0;+x x m x
2
3 4 2 5 , 0;+x x m x
Xét hàm s
2
34f x x x
trên
0;+
, ta có
2
6 4 0
3
f x x x
Ta có bng bin thiên
/
T bng trên suy ra
2
3 4 2 5 , 0;+x x m x
4 11
25
36
mm
.
Do
m
nguyên và
2018 ; 2019m
2018; 2017; 2016,....,0,1m
.
Vy có
2020
giá tr
m
th bài.
Câu 42. i ta th mt s lá bèo vào mt h c, sau
10
gi s ng lá bèo s sinh sôi kín c mt
h. Bit rng sau mi gi s p 10 ln s 
i. Hi sau khong thi gian bao lâu s ng lá bèo ph kín ti thiu mt ph
h?
Trang15
A.
10 log4
. B.
10log 4
. C.
1 10log4
. D.
10 10log4
.
Lời giải
Chọn A
Gi
0
S
là s c th xung h.
Sau 1 gi thì s ng lá bèo có trong h là
10
10SS
;
Sau 2 gi thì s ng lá bèo có trong h là
2
20
10SS
;

Sau
n
gi thì s ng lá bèo có trong h là
0
10
n
n
SS
.
Sau 10 gi s ng lá bèo ph kín mt h nên ta có
10
10 0
10SS
.
Gi s sau
k
gi (
0 10k
) thì s ng lá bèo ph kín ti thiu mt ph

10 10
10
10 0 0
1 1 10 10
10 .10 10 log 10 log4
4 4 4 4
kk
k
S S S S k



.
Câu 43. Cho hàm s
42
1 2 1y a x b x c
 th  bên
/
M 
A.
1a
,
2b 
,
1c
. B.
1a
,
2b 
,
1c
.
C.
1a
,
2b 
,
1c
. D.
1a
,
2b
,
1c
.
Lời giải
Chọn B
 th 
x
nên
1 0 1aa
.
 th m
0; 1c
 nm phía trên trc hoành nên
1 0 1cc
.
 th hàm s m cc tr nên
1 . 2 0ab
mà
1a
nên
2 0 2bb
.
Câu 44. Cho nh
S
ng tròn tâm
O
bán kính
R
ng tròn
O
ly hai
m
,AB
sao cho tam giác
OAB
vuông. Bit din tích tam giác
SAB
bng
2
2R
. Th tích
ng
A.
3
14
12
R
. B.
3
14
2
R
. C.
3
14
6
R
. D.
3
14
3
R
.
Lời giải
Chọn C
/
Gi
H
m cn
.AB
Nhn thy:
+) Tam giác
OAB
vuông cân ti
O
.
+)
OH AB
,
SH AB
nên góc gia hai mt phng
()SAB
,
()OAB
bng
SHO
.
Ta có:
.cos
OAB SAB
SS

22
1
2.cos
2
RR

1
cos .
22

Mà
1
cos
22
OH
SH

2
1
2
22
R
SH

2
.2 2 2 .
2
R
SH R
22
SO SH OH
2
2
2
4
2
R
R





14
2
R
Vy th tích ca khi nón bng
3
22
1 1 14 14
. . .
3 3 2 6
RR
V R SO R

Câu 45. Cho
8
3
11
d ln
2
1
ac
Ix
bd
x x x

vi
, , ,a b c d
là các s 
,
ac
bd
ti gin.
Giá tr ca
abc d
bng
Trang16
A.
6
. B.
18
. C.
0
. D.
3
.
Lời giải
Chọn A
t
2
1 1 2 d dt x t x t t x
.
Khi
32xt
; Khi
83xt
.
 
3 3 3
2
2 2 2
2 2 2
1 2 2
.2 d d d
1 1 1 1
11
tt
I t t t t
t t t t t
tt

33
2 2 2
22
1 1 1 1
dd
1 1 1 1 1 1
t t t t
tt
t t t t t t





33
22
22
11
1 1 1 1
d . d
1 1 2 1 1
11
tt
tt
t t t t
tt


3
3
2
2
2
1 1 1 1 1 1
d ln 1 ln 1
2 1 1 2 1
1
t t t
t t t
t






3
2
1 1 1 1 1 1 1 1 1
ln ln ln
2 1 1 2 2 4 2 3 3
t
tt






1 1 1 1 1 1 1 3 1
ln ln ln
2 2 2 3 4 3 2 2 12
3a
,
2b
,
1c
,
12d
.
Vy
3.2.1 12 6abc d
.
Câu 46. Cho hàm s
y f x
 th  bên. Có bao nhiêu giá tr nguyên ca tham s
m


0f f x m


m phân bit.
/
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn A
t
*f x t

/
Nhn xét: +) Vi
3t 

*
có mt nghim
1x
.
+) Vi
3t

*
có hai nghim
1
xx
và
2
xx
vi
12
1; 1.xx
Ta có:
0f f x m


0
22
t m t m
t m t m




.
Vì
2,m m m
nên
0f f x m


m phân bit khi và ch khi:
33
3
2 3 5
mm
m
mm



.
Vy có 1 giá tr nguyên ca
m
tha mãn yêu cu bài toán.
Câu 47. 
,ab

22
1ab
và
22
log 1
ab
ab


2 4 3P a b
là
A.
10
. B.
10
2
. C.
2 10
. D.
1
10
.
Lời giải
Trang17
ChọnA
Do
22
1ab
nên t
22
22
log 1 1
ab
a b a b a b
.
Suy ra:
22
22
1
1 1 1
2 2 2
ab
ab

 
22
22
1 1 1 1 1
2 4 3 2 4 2 4 . 20. 10
2 2 2 2 2
P a b a b a b




ng thc xy ra khi
22
22
11
22
0
11
24
2
10
1 1 1
12
2 2 2
2
10
1
ab
a
ab
b
ab









Vy
max
10P
khi
11
2
10
12
2
10
a
b


.
Câu 48. Cho hàm s
4 3 2
44f x x x x a
. Gi
,Mm
l t là giá tr ln nht và giá tr nh
nht ca hàm s n
0;2
. Có bao nhiêu s nguyên
a
thun
3;2
sao cho
2?Mm
A.
7
. B.
5
. C.
6
. D.
4
.
Lời giải
Chọn D
Xét hàm s
4 3 2
44f x x x x a
n
0;2
, có:
32
' 4 12 8f x x x x
.
32
0
' 0 4 12 8 0 1
2
x
f x x x x x
x
.
Vì
0fa
,
1 1 4 4 1f a a
,
4 3 2
2 2 4.2 4.2f a a
n
0;2
giá tr ln nht và giá tr nh nht ca hàm s
4 3 2
44f x x x x a
ln
t là
1,aa
.
Suy ra
0;2
max ; 1M a a
;
0;2
min ; 1m a a
nu
10aa
.
0m
nu
10aa
.
TH1:
1
;2
2
a




1Ma
;
ma
  
2
1
2 1 2 3 2 1 0
3
1
a
M m a a a a
a

, vì
a
nên chn
1;2a
TH2:
1
3;
2
a


Trang18
Ma
;
1ma
  
2
2
2 2 1 3 8 4 0
3
2
a
M m a a a a
a


, vì
a
nên chn
3; 2a
Vy có
4
giá tr
a
tha yêu cu.
Câu 49. Cho hình chóp
.S ABC
có các cnh
3SA BC
;
4SB AC
;
25SC AB
. Tính th tích
khi chóp
.S ABC
.
A.
390
12
. B.
390
4
. C.
390
6
. D.
390
8
.
Lời giải.
Chọn B
/
/
+ Dng hình chóp
. ' ' 'S A B C
m
''BC
,
B
m
''AC
,
C
là
m
''AB
.
  
' ' 4SB AC BA BC
nên
''SA C
vuông ti
S
và
2
22
' ' 2. 64 (1)SA SC SB
.

''SB C
,
''SA B
vuông ti
S
và
22
22
' ' 80 (2)
' ' 36 (3)
SA SB
SB SC


.
+ T
1 ; 2 ; 3
ta suy ra
' 10SC
;
' 26SB
;
' 54SA
.
c
. ' ' '
11
'. . '. ' 390
32
S A B C
V SC SA SB
và
. . ' ' '
1 390
44
S ABC S A B C
VV
.
Câu 50. Cho
0 2021x
và
2
log (2 2) 3 8
y
x x y
.Có bao nhiêu cp s
( ; )xy
nguyên tha mãn
u kin trên ?
A.2021. B.2022. C.1. D.4.
Lời giải
Chọn D
Do
0 2021x
nên
2
log (2 2)x
luôn .
Ta có
2
log (2 2) 3 8
y
x x y
3
2
log ( 1) 1 3 2
y
x x y
2
log ( 1)
3
2
log ( 1) 2 3 2
x
y
xy
(1)
Xét hàm s
( ) 2
t
f t t
.
Tnh
D
và
( ) 1 2 ln 2
t
ft

( ) 0ft
t
.
Suy ra hàm s
()ft
ng bin trên

2
(1) log ( 1) 3xy
3
12
y
x
8
log ( 1)yx
.
Ta có
0 2021x
nên
1 1 2022 x
suy ra
88
0 log ( 1) log 2022 x
.
Li có
8
log 2022 3,66
nên nu
y
thì
0;1;2;3y
.
Vy có 4 cp s
( ; )xy
nguyên tha yêu cu bài toán là các cp
(0;0)
,
(7;1)
,
(63;2)
,
(511;3)
.
-----------------HT-----------------
Trang19
www.thuvienhoclieu.com
ĐỀ 7
ĐỀ THI THỬTHPT QUỐC GIA 2021
MÔN TOÁN
Thời gian: 90 phút
Câu 1: T các s 1, 2, 3, 4, 5, 6 có th lc bao nhiêu s t nhiên có hai ch s?
A.
2
6
A
. B. 36. C.
2
6
C
. D.
6
2
.
Câu 2: Cho cp s cng
n
u
vi
1
2u
, công sai
3d
. Tính
5
u
.
A. 14. B. 17. C. 162. D. 20.
Câu 3:Nghim c
37
2 32
x
là
A.
2
.
3
x
B.
23
.
3
x
C.
4.x
D.
4.x 
Câu 4: Tính th tích khi hp ch nhc
4, 5, 6a b c
A. 15.B. 40. C. 120.D. 60.
Câu 5: Tnh ca hàm s
2
log 2yx
là
A.
2; 
.B.
2; 
.C.
;2
. D.
;2
.
Câu 6:Vi
( ), ( )f x g x
là hai hàm s liên tc trên khong
K
và
0k ¹
thì m 
sai?
A.
( ) ( ) ( ) ( ) .f x g x dx f x dx g x dx=
ò ò ò
B.
( ) ( ) ( ) ( ) .f x g x dx f x dx g x dx
éù
+ = +
êú
ëû
ò ò ò
C.
( ) ( ) .f x dx f x C
¢
=+
ò
D.
( ) ( ) .kf x dx k f x dx=
òò
Câu 7:Cho khi chóp
.S ABCD

ABCD
là hình vuông cnh
a
,
2SA a
và
SA
vuông góc
vi mt ph tích khi chóp
.S ABCD
.
A.
3
3
a
. B.
3
4
3
a
. C.
3
2
3
a
. D.
3
2a
.
Câu 8:Cho khi nón có chiu cao
5h

3r
. Tính th tích ca kh
A.
25 .
B.
45
.
3
C.
45 .
D.
25
.
3
Câu 9:Tính din tính mt cu bán kính
2ra
.
A.
2
.a
B.
2
8.a
C.
2
4.a
D.
2
16 .a
Câu 10:Cho hàm s
()fx
có bng bin thiên sau
Hàm s   ng bin trên
kho  i 
A.
( ;0)
.B.
( 2;0)
.C.
( 4; ) 
D.
( ; 2)
.
Câu 11: Vi
, ab
là các s th
23
2
log ab
bng
A.
22
2log 3logab
.B.
22
11
log log
23
ab
. C.
22
2log 3logab
. D.
22
5 log logab
.
Câu 12:Tính din tích xung quanh ca hình tr  ng sinh
5l

4r
.
A.
40
.B.
20
.C.
48
.D.
16
.
Câu 13:Cho hàm s
()fx
có bng bin thiên sau
x

2
0

'( )fx
+ 0 - 0 +
()fx
0

-4

Trang20
Giá tr cc tiu
ca hàm s 
cho bng
A. 2.B. 0.C.
2
.D. 16.
Câu 14: th ca hàm s nào có dng cong i?
A.
42
21y x x
. B.
42
21y x x
C.
42
1y x x
.D.
32
31y x x
Câu 15: Tìm tim cng c th hàms
2021
1
x
y
x
.
A.
1.x 
B.
1.y 
C.
1y
.D.
2021x 
Câu 16:Gii b
3
log 2 5 2x
.
A.
7x
. B.
7x
. C.
5
7
2
x
. D.
7x
.
Câu 17:Cho hàm s
y f x
có bng bi    . S nghim c  
10fx
là:
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 18:Nu
3
1
( ) 4f x dx

và
3
2
( ) 3f x dx
thì
2
1
()f x dx
bng
A. -7.B. 7.C. -1.D. -12.
Câu 19:a s phc
65i
bng
A. 11.B.
11
.C. 61. D.
61
.
Câu 20: Gi
12
,zz
là hai nghim phc c
2
2 3 3 0zz
. Giá tr ca biu thc
22
12
zz
bng
A.
3
18
.B.
9
8
.C.
3
.D.
9
4
.
Câu 21:Tìm s phc liên hp
z
ca s phc
(3 2 )(2 3 ).z i i
A.
5.zi
B.
6 6 .zi
C.
12 5zi
D.
6 6 .zi
Câu 22:Trong không gian
Oxyz
, hình chiu cm
(2; 2;1)M
trên mt phng
()Oyz
có t
là
A.
(0; 2;1)
. B.
(2; 2;0)
.C.
(2;0;0)
.D.
(0; 2;0)
.
Câu 23:Trong không gian
Oxyz
, cho mt cu
2 2 2
( ):( 2) ( 1) ( 5) 25S x y z
. Tìm t
tâm ca mt cu
()S
.
A.
(2; 1;5)
.B.
( 2;1; 5)
.C.
(2;1;5)
.D.
( 2; 1; 5)
.
x

2
0 2

'( )fx
+ 0 - 0 + 0 -
()fx
1616
0


y
O
x
Trang21
Câu 24:Trong không gian
Oxyz
, cho mt phng
( ): 3 5 0P x y
t
n ca mt phng
()P
?
A.
1
(1;3; 5)n 

.B.
2
( 1;3; 5)n
. C.
3
(1; 3;0)n 
.D.
4
(1;3;0)n
.
Câu 25: Trong không gian
Oxyz
      ng thng
3 1 2
( ):
2 3 1
x y z
d


?
A.
(3; 1;2)M
.B.
( 3;1; 2)N 
. C.
(2; 3; 1)P 
.D.
( 3;1;2)Q
.
Câu 26: Cho hình chóp S.ABCD nh
2a
, SA vuông góc vi mt phng

23SA a
. Góc gia SC và mt phng (ABCD) bng
C
A
D
B
S
A.
0
30
.B.
0
60
.C.
0
45
.D.
0
90
.
Câu 27:Cho hàm s
y f x
có bng xét d
Hàm s m cc tr?
A. 1.B. 2.C.3.D. 4.
Câu 28:Giá tr nh nht ca hàm s
32
3 9 35y x x x
n
4;4


bng:
A. 41. B. 41. C. 8. D. 15.
Câu 29: Cho
23
log 5 ; log 5ab
. Tính
6
log 5
theo a và b .
A.
1
ab
. B.
ab
ab
. C.
ab
. D.
22
ab
.
Câu 30: Cho hàm s
()y f x
có bng bi
Tp tt c các giá tr ca tham s
m
 
()f x m
có ba nghim phân bit là
A.
(4; )
. B.
( ; 2)
. C.
[ 2;4]
. D.
( 2;4)
.
Trang22
Câu 31: B
22
log (3 2) log (6 5 ) xx
có tp nghim là
( ; )ab
. Tng
ab
bng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Câu 32: M ng sinh ba
hình nónbng
9π
ng cao
h
ca hình nón.
A.
3
2
. B.
33
. C.
3
3
. D.
3
.
Câu 33:Cho hàm s
y f x
liên tc trên
và
2
0
2 16, d 4f f x x
. Tính
4
0
d
2
x
xf x



.
A.
144I
. B.
12I
. C.
112I
. D.
28I
.
Câu 34. 








3
32f x x x
;
2g x x
:
A.
8S
. B.
4S
. C.
12S
. D.
16S
.
Câu 35. Cho hai s phc
1
23zi
và
2
35zi
. Tính tng phn thc và phn o ca s phc
12
w z z
.
A.
3
. B.
0
. C.
12i
. D.
3
.
Câu 36: Tp hm biu din s phc
z
thu kin
1 2 1 zi
là
ng tròn
1;2I
, bán kính
1R
.  ng tròn
1; 2I
, bán kính
1R
.
ng tròn
1;2I
, bán kính
1R
. ng tròn
1; 2I
, bán kính
1R
.
Câu 37: Trong không gian
Oxyz
m
3;1; 1A
,
2; 1;4B
t phng
OAB
(
O
là gc ta ) là
A.
3 14 5 0 x y z
. B.
3 14 5 0 x y z
. C.
3 14 5 0 x y z
. D.
3 14 5 0 x y z
.
Câu 38:Trong không gian vi h trc t
(Ox )yz
ng thng
d
m
1;2;1A
và vuông góc vi mt phng
: 2 1 0P x y z
có dng
A.
1 2 1
:
1 2 1
x y z
d

. B.
22
:
1 2 1
x y z
d


.
C.
1 2 1
:
1 2 1
x y z
d

. D.
22
:
2 4 2
x y z
d


.
Câu 39:Kt qu
;bc
ca vic gieo mt con súc sng cht hai ln liên tip, trong

b
là s chm xut hin ca ln gieo th nht,
c
là s chm xut hin ca ln gieo th c
thay vc hai
2
0x bx c
. Xác su m là
A.
7
12
. B.
17
36
. C.
23
36
. D.
5
36
.
Câu 40: Cho hình chóp
.S ABC

ABC
là tam giác vuông ti
A
,
BC SB a
. Hình chiu
vuông góc ca
S
lên mt phng
ABC
trùng vm ca
BC
. Góc ging thng
SA
và mt phng
ABC
bng
A.
0
60
. B.
0
75
. C.
0
30
. D.
0
45
.
Câu 41:   th hàm s
42
31y x m x m
m cm cc tiu
thì tt c các giá tr thc ca tham s
m
là
A.
3m
.B.
3m
.C.
3.m
D.
3m
.
Câu 42:M i vay ngân hàng 500 tri ng vi lãi sut 1,2%/   mua xe ô tô.
Saut tháng k t u tr n n c m
s tr cho ngân hàng 20 trin khi ht n (tháng cui cùng có th tr i 20 triu
Trang23
ng). H tr c ht n ngân hàng? Bit rng lãi sut không
i.
A. 30 tháng. B. 26 tháng. C. 29 tháng. D. 32 tháng.
Câu 43: Cho hàm s
4 3 2
y f x mx nx px qx r

, , , ,m n p q r
. Bit
hàm s
y f x
 th i.
y
x
4
-1
O
1
S nghim c
16 8 4 2f x m n p q r
là
Câu 44:Mt bác th gm làm mt cái l có dng khc to thành khi quay hình
phng gii hn bng
1yx
và trc
Ox
, quay quanh trc
Ox
. Bi và ming l
ng kính lt là
2dm
và
4dm
 tích ca l là :
A.
3
8 dm
. B.
3
15
dm
2
. C.
3
14
dm
3
. D.
3
15
dm
2
.
Câu 45: Cho tích phân
1
0
7
2 ln 1 d ln 2I x x x a
b

a
,
b
là các s 
Tng
2
ab
bng
A.
8
. B.
16
. C.
12
. D.
20
.
Câu 46:Cho hàm s
y f x
có bng xét du ca
fx

0
0
+
+
∞
-
+
3
-1
-
∞
f'(x)
x
Xét hàm s
2
1f x x
g x e

, tp nghim ca b
0gx
là
A.
1
;
2




. B.
1
; 1 ;2
2




. C.
1
;
2




. D.
1
1; 2;
2




.
Câu 47: Cho
x
,
y
tha mãn
3
22
log 9 9
2
xy
x x y y xy
x y xy
. Tìm giá tr ln nht
ca
3 2 9
10
xy
P
xy


khi
x
,
y
i.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 48. Cho hàm s
4 3 2
44f x x x x a
. Gi
M
,
m
là giá tr ln nht và giá tr nh nht
ca hàm s 
0;2
. Có bao nhiêu s nguyên
a
thuc
4;4
sao cho
2Mm
?
A.
7
. B.
5
. C.
6
. D.
4
.
Câu 49:Cho t din
ABCD
có
90DAB CBD
;
; 5; 135AB a AC a ABC
. Bit góc gia
hai mt phng
ABD
,
BCD
bng
30
. Th tích ca t din
ABCD
là
A.
3
23
a
. B.
3
2
a
. C.
3
32
a
. D.
3
6
a
.
Câu 50:Cho hai s thc
x
,
y
tha mãn
Trang24
2
2
2
2 3 2
3
54
log 8 16 log 5 1 2log log 2 8 .
3
xx
y y x x y



Gi
S
là tp các giá tr nguyên ca tham s
m
 giá tr ln nht ca biu thc
22
P x y m
t quá
10
. Hi
S
có bao nhiêu tp con không phi là tp rng?
A.
2047
. B.
16383
. C.
16384
. D.
32
.
------------- HT -------------
BẢNG ĐÁP ÁN
1B
2A
3CD
4D
5A
6A
7A
8B
9D
10D
11C
12A
13B
14A
15A
16A
17B
18A
19D
20D
21C
22A
23B
24D
25B
26B
27C
28A
29B
30D
31D
32B
33B
34A
35D
36C
37A
38D
39B
40A
41A
42A
43A
44B
45D
46A
47C
48A
49D
50B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: T các s 1, 2, 3, 4, 5, 6 có th lc bao nhiêu s t nhiên có hai ch s?
A.
2
6
A
. B. 36. C.
2
6
C
. D.
6
2
.
Li gii
lp s t nhiên có hai ch s ta thc hi
Chn s th nht: có 6 cách chn
Chn s th hai: có 6 cách chn
Theo quy tc nhân ta có 6.6=36 s
Câu 2: Cho cp s cng
n
u
vi
1
2u
, công sai
3d
. Tính
5
u
.
A. 14. B. 17. C. 162. D. 20.
Li gii
Theo công thc tính s hng tng quát
51
4 2 4.3 14u u d
Câu 3:Nghim c
37
2 32
x
là
A.
2
.
3
x
B.
23
.
3
x
C.
4.x
D.
4.x 
Li gii
3 7 3 7 5
2 32 2 2 3 7 5 4
xx
xx

Câu 4: Tính th tích khi hp ch nhc
4, 5, 6a b c
A. 15.B. 40.C.120.D. 60.
Li gii
4.5.6 120V abc
Câu 5:Tnh ca hàm s
2
log 2yx
là
A.
2; 
.B.
2; 
.C.
;2
. D.
;2
.
Li gii
u kin
2 0 2 xx
Câu 6:Vi
( ), ( )f x g x
là hai hàm s liên tc trên khong
K
và
0k ¹
thì m 
sai?
A.
( ) ( ) ( ) ( ) .f x g x dx f x dx g x dx=
ò ò ò
B.
( ) ( ) ( ) ( ) .f x g x dx f x dx g x dx
éù
+ = +
êú
ëû
ò ò ò
C.
( ) ( ) .f x dx f x C
¢
=+
ò
D.
( ) ( ) .kf x dx k f x dx=
òò
Li gii
Trang25
Nguyên hàm không có tính cht nguyên hàm ca tích bng tích các nguyên hàm.
Câu 7:Cho khi chóp
.S ABCD

ABCD
là hình vuông cnh
a
,
2SA a
và
SA
vuông góc
vi mt ph tích khi chóp
.S ABCD
.
A.
3
3
a
. B.
3
4
3
a
. C.
3
2
3
a
. D.
3
2a
.
Li gii
Ta có di
ABCD
:
2
ABCD
Sa
.
ng cao
2SA a
.
Vy th tích khi chóp
.S ABCD
là
1
.
3
ABCD
V S SA
2
1
. .2
3
aa
3
2
3
a
.
Câu 8:Cho khi nón có chiu cao
5h

3r
. Tính th tích ca kh
A.
25 .
B.
45
.
3
C.
45 .
D.
25
.
3
Li gii
2
1 45
.3 .5 .
33
V
Câu 9:Tính din tính mt cu bán kính
2ra
.
A.
2
.a
B.
2
8.a
C.
2
4.a
D.
2
16 .a
Li gii
Áp dng công thc tính din tích mt cu
2 2 2
4 4 .(2 ) 16S r a a
Câu 10:Cho hàm s
()fx
có bng bin thiên sau
Hàm s   ng bin trên
kho  i 
A.
( ;0)
.B.
( 2;0)
.C.
( 4; )
D.
( ; 2)
.
Li gii
Da vào bng bin thiên ta thy hàm s ng bin trên các khong
( ; 2)
và
(0; )
Câu 11: Vi
, ab
là các s thc 
23
2
log ab
bng
A.
22
2log 3logab
.B.
22
11
log log
23
ab
.C.
22
2log 3logab
. D.
22
5 log logab
.
Li gii
2 3 2 3
2 2 2 2 2
log log log 2log 3loga b a b a b
Câu 12:Tính din tích xung quanh ca hình tr  ng sinh
5l

4r
.
x

2
0

'( )fx
+ 0 - 0 +
()fx
/// 0

-4

Trang26
A.
40
.B.
20
.C.
48
.D.
16
.
Li gii
2 2 .4.5 40 .
xq
S rl
Câu 13:Cho hàm s
()fx
có bng bin thiên sau
Giá tr cc tiu
ca hàm s 
cho bng
A. 2 B. 0C.
2
D. 16
Li gii
Da vào bng bin thiên ta có
0
CT
y
Câu 14: th ca hàm s nào có dng cong i?
/A.
42
21y x x
. B.
42
21y x x
C.
42
1y x x
.D.
32
31y x x
Li gii
 th (
0a
,
0ab
)
 th (
0a
)
 th (
0, 0a ab
)
 th (Hàm s bc ba)
Câu 15: Tìm tim cng c th hàms
2021
1
x
y
x
.
A.
1.x 
.B.
1.y 
C.
1y
.D.
2020x
.
Li gii
Tìm tim cng c th hàms
2021
1
x
y
x
là
1.x 
Câu 16:Gii b
3
log 2 5 2x
.
A.
7x
. B.
7x
. C.
5
7
2
x
. D.
7x
.
Li gii
3
5
log 2 5 2 7
2
2 5 9

x
xx
x
Câu 17:Cho hàm s
y f x
có bng bi    . S nghim c  
10fx
là:
/
A.
0
. B.
3
. C.
2
. D.
1
.
Li gii
S nghim c  
1 0 ( ) 1 f x f x
bng s  m c  th hàm
s
y f x
ng thng
1y
x

2
0 2

'( )fx
+ 0 - 0 + 0 -
()fx
////1616
0


Trang27
//
Da vào bng bin thiên ta th th hàm s
y f x
cng thng
1y
tm phân
bim.
Câu 18:Nu
3
1
( ) 4f x dx

và
3
2
( ) 3f x dx
thì
2
1
()f x dx
bng
A. -7B. 7C. -1D. -12
Li gii
Ta có
2 3 3 2 3 3
1 2 1 1 1 2
( ) ( ) ( ) ( ) ( ) ( ) 4 3 7f x dx f x dx f x dx f x dx f x dx f x dx
Câu 19:a s phc
65i
bng
A. 11.B.
11
.C. 61. D.
61
.
Li gii
Ta có
22
6 5 6 ( 5) 61i
Câu 20: Gi
12
,zz
là hai nghim phc c
2
2 3 3 0zz
. Giá tr ca biu thc
22
12
zz
bng
A.
3
18
. B.
9
8
. C.
3
. D.
9
4
.
Li gii
Ta có
2
2 3 3 0zz
1
2
3 21
4
3 21
4
i
z
z


Suy ra
22
12
9
4
zz
.
Câu 21: Tìm s phc liên hp
z
ca s phc
(3 2 )(2 3 ).z i i
A.
5.zi
B.
6 6 .zi
C.
12 5zi
D.
6 6 .zi
Li gii
(3 2 )(2 3 ) 12 5 12 5 z i i i z i
Câu 22:Trong không gian
Oxyz
, hình chiu cm
(2; 2;1)M
trên mt phng
()Oyz
có t
là
A.
(0; 2;1)
. B.
(2; 2;0)
.C.
(2;0;0)
.D.
(0; 2;0)
.
Li gii
Ta có hình chiu cm
0 0 0
( ; ; )M x y z
trên mt phng
()Oyz
m
00
'(0; ; )M y z
Vy hình chiu cm
(2; 2;1)M
trên mt phng
()Oyz
có t là
(0; 2;1)
.
Câu 23:Trong không gian
Oxyz
, cho mt cu
2 2 2
( ):( 2) ( 1) ( 5) 25S x y z
. Tìm t
tâm ca mt cu
()S
.
A.
(2; 1;5)
.B.
( 2;1; 5)
.C.
(2;1;5)
.D.
( 2; 1; 5)
.
Li gii
Mt cu
2 2 2 2
( ):( ) ( ) ( )S x a y b z c r
có tâm
( ; ; )I a b c
t cu
()S
có tâm
( 2;1; 5)I 
.
Câu 24:Trong không gian
Oxyz
, cho mt phng
( ): 3 5 0P x y
t
n ca mt phng
()P
?
A.
1
(1;3; 5)n 

.B.
2
( 1;3; 5)n
. C.
3
(1; 3;0)n 
.D.
4
(1;3;0)n
.
Trang28
Li gii
Mt phng
()P
n là
()
(1;3;0)
P
n
Câu 25: Trong không gian
Oxyz
      ng thng
3 1 2
( ):
2 3 1
x y z
d


?
A.
(3; 1;2)M
.B.
( 3;1; 2)N 
. C.
(2; 3; 1)P 
.D.
( 3;1;2)Q
.
Li gii
Thay t ng thng ta thm
( 3;1; 2)N 
tha mãn
3 3 1 1 2 2
0
2 3 1

. Vy m
( 3;1; 2)N 
thung thng
3 1 2
( ):
2 3 1
x y z
d


Câu 26: Cho hình chóp S.ABCD nh
2a
, SA vuông góc vi mt phng

23SA a
. Góc gia SC và mt phng (ABCD) bng
/
A.
0
30
.B.
0
60
.C.
0
45
.D.
0
90
.
Li gii
Ta có
()SA ABCD
nên góc ging thng SC và mt phng (ABCD) bng
SCA
Xét tam giác vuông SAC,
23
tan 3
2 . 2
SA a
SCA
AC
a
Vy
0
60SCA
Câu 27:Cho hàm s
y f x
có bng xét d
/
Hàm s m cc tr?
B. 1B. 2C.3 D. 4
Li gii
T bng bin thiên ta thy
'fx
i du 3 ln khi qua
2; 0; 1x x x
nên hàm s m
cc tr.
Câu 28:Giá tr nh nht ca hàm s
32
3 9 35y x x x
n
4;4


bng:
A. 41. B. 41. C. 8.D. 15.
Li gii
Hàm s nh và liên tc n
4;4


2
' 3 6 9y x x
;
1 4;4
'0
3 4;4
x
y
x





( 4) 41; ( 1) 40; (3) 8; (4) 15y y y y
4;4
min 41y



Câu 29: Cho
23
log 5 ; log 5ab
. Tính
6
log 5
theo a và b .
A.
1
ab
. B.
ab
ab
. C.
ab
. D.
22
ab
.

5
6
5 5 5
log 5
11
log 5
11
log 6 log 2 log 3
ab
ab
ab

Trang29
Câu 30: Cho hàm s
()y f x
có bng bi
/
Tp tt c các giá tr ca tham s
m
 
()f x m
có ba nghim phân bit là
A.
(4; )
. B.
( ; 2)
. C.
[ 2;4]
. D.
( 2;4)
.
Li gii
S nghim c
()f x m
chính là s m c th hàm s
()y f x
ng
thng
ym
.
Da vào bng bi
()f x m
có ba nghim phân bit khi
24 m
.
Vm phân bit khi
( 2;4)m
.
Câu 31: B
22
log (3 2) log (6 5 ) xx
có tp nghim là
( ; )ab
. Tng
ab
bng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Li gii
Ta có:
22
1
3 2 6 5
6
log (3 2) log (6 5 ) 1
6
6 5 0
5
5


x
xx
x x x
x
x
.
Tp nghim ca b
6
(1; )
5
.
Vy
6 11
1
55
ab
.
Câu 32: M ng sinh ba
hình nónbng
9π
. ng cao
h
ca hình nón.
A.
3
2
. B.
33
. C.
3
3
. D.
3
.
Li gii
/
Gi
,lR
l ng sinh và a hình nón.
Theo bài ra ta có
2
2
26
33
9
lR
l R l
RR
πR π





.
ng cao ca hình nón là
22
36 9 3 3h l R
.
Câu 33: Cho hàm s
y f x
liên tc trên
và
2
0
2 16, d 4f f x x
. Tính
4
0
d
2
x
xf x



.
A.
144I
. B.
12I
. C.
112I
. D.
28I
.
Li gii
t
2 d 2d
2
x
t x t x t
.
i cn:
0 0; 4 2x t x t
.

4 2 2 2
2
0
0 0 0 0
d 4 d 4 4 d 4.2. 2 4. d
2
x
xf x tf t t tf t f t t f f x x




4.2.16 4.4 112
Câu 34. 








3
32f x x x
;
2g x x
:
A.
8S
. B.
4S
. C.
12S
. D.
16S
.
Lời giải
Trang30






33
0
3 2 2 4 0
2
x
x x x x x
x





02
33
20
4 d 4 dS x x x x x x

02
33
20
4 d 4 dx x x x x x

44
22
02
2 2 8
20
44
xx
xx
.
Câu 35. Cho hai s phc
1
23zi
và
2
35zi
. Tính tng phn thc và phn o ca s phc
12
w z z
.
A.
3
. B.
0
. C.
12i
. D.
3
.
Lời giải
12
2 3 3 5 1 2w z z i i i
. Vy tng phn thc và phn o ca s phc
w
là
3
.
Câu 36: Tp hm biu din s phc
z
thu kin
1 2 1 zi
là
ng tròn
1;2I
, bán kính
1R
.  ng tròn
1; 2I
, bán kính
1R
.
Cng tròn
1;2I
, bán kính
1R
. ng tròn
1; 2I
, bán kính
1R
.
Li gii
t
;, z x yi x y R

1 2 1 1 2 1 z i x y i
22
1 2 1 xy
22
1 2 1 xy
Vy tp hm biu din s phc
z
ng tròn
1;2I
, bán kính
1R
.
Câu 37: Trong không gian
Oxyz
m
3;1; 1A
,
2; 1;4B
t phng
OAB
(
O
là gc t) là
A.
3 14 5 0 x y z
. B.
3 14 5 0 x y z
. C.
3 14 5 0 x y z
. D.
3 14 5 0 x y z
.
Lời giải
Ta có
3;1; 1OA 
,
2; 1; 4OB 
.
t phng
OAB
n là
, 3; 14; 5n OA OB


.
Vt phng
OAB
là
3 14 5 0 x y z
.
Câu 38:Trong không gian vi h trc t
(Ox )yz
ng thng
d
m
1;2;1A
và vuông góc vi mt phng
: 2 1 0P x y z
có dng
A.
1 2 1
:
1 2 1
x y z
d

. B.
22
:
1 2 1
x y z
d


.
C.
1 2 1
:
1 2 1
x y z
d

. D.
22
:
2 4 2
x y z
d


.
Lời giải
Mt phng
P
có vecto pháp tuyn
1; 2;1
P
n 
. Vì
dP
nên
1; 2;1
P
n 

ng thng
d
ng thng
d
ng gp là
Trang31
1 2 1
1 2 1
x y z

. So vng thng
d
ng có vecto ch
i
P
n
m
1;2;1A
. Thay t m
1;2;1A

B, D tha mãn.
Câu 39: Kt qu
;bc
ca vic gieo mt con súc sng cht hai ln liên tip, trong

b
là s chm xut hin ca ln gieo th nht,
c
là s chm xut hin ca ln gieo th c
c hai
2
0x bx c
. Xác su c hai m là
A.
7
12
.B.
17
36
.C.
23
36
.D.
5
36
.
Li gii
S phn t ca không gian mu là
36
.

2
0x bx c
có
2
4bc
, vi
, 1,6bc
.
m
02bc
.
Ta có bng sau
/
Suy ra có
17
 m.
Vy xác sut cn tìm là
17
36
P
.
Câu 40: Cho hình chóp
.S ABC

ABC
là tam giác vuông ti
A
,
BC SB a
. Hình chiu
vuông góc ca
S
lên mt phng
ABC
trùng vm ca
BC
. Góc ging
thng
SA
và mt phng
ABC
bng
A.
0
60
. B.
0
75
. C.
0
30
. D.
0
45
.
Li gii
/
Gi
H
m cnh
BC SH ABC
.
Góc gia
SA
và mt phng
ABC
là
;SA HA SAH
.
22
3
2
a
SH SB HB
và
1
22
a
AH BC
Xét tam giác
SHA
ta có
0
tan 3 60
SH
SAH SAH
AH
.
Câu 41:   th hàm s
42
31y x m x m
m cm cc tiu
thì tt c các giá tr thc ca tham s
m
là
A.
3m
. B.
3m
. C.
3.m
D.
3m
.
Li gii
32
' 4 2 3 2 2 3y x m x x x m
.
2
0
'0
3
2
x
y
m
x

.
Vì hàm s i
10a
nên hàm s m ci mà không có
m cc tiu
'0y
m bng
0
3
0
2
m

3.m
Câu 42:Mi vay ngân hàng 500 tring vi lãi su mua xe ô tô. Sau
t tháng k t u tr n n c mi tháng
 tr cho ngân hàng 20 trin khi ht n (tháng cui cùng có th
Trang32
tr i 20 triu ng). H        c ht n ngân
hàng? Bit rng lãi sui.
A. 30 tháng. B. 26 tháng. C. 29 tháng. D. 32 tháng.
Li gii
 là:
1
1N N r m
vi
N
=500 triu ng ,
0,012r
,
m
=20 tring.
 là:
2
21
1 1 1 1N N r m N r m r


.

Sau tháng th
n
 là:
21
1 1 1 1 ... 1
nn
n
N N r m r r r


1. 1 1
11
11
n
nn
r
mm
N r m N r
r r r









.
 ht n  bng 0 nên ta có:
20 10
1 0 1 1,012 1,012
20 500.0,012 7
nn
nn
m m m
N r r
r r m Nr




1,012
10
log 29,90
7
nn
. V ht n ngân hàng.
Câu 43: Cho hàm s
4 3 2
y f x mx nx px qx r

, , , ,m n p q r
. Bit
hàm s
y f x
 th i.
/
S nghim c
16 8 4 2f x m n p q r
là
A.
4
. B.
5
. C.
2
. D.
3
.
Li gii
Da vào  th hàm s
y f x
, ta có bng bin thiên:
/
 th ta có
1 4 1 4
1 1 1 1
d d d d

f x x f x x f x x f x x
0 1 1 1 4 1 4 f f f f f f
.
 th ta có
1 2 1 2
1 1 1 1
d d d d

f x x f x x f x x f x x
0 1 1 1 2 1 2 f f f f f f
. Suy ra:
4 1 2 f f f
S nghim c
16 8 4 2f x m n p q r
là s m c th hàm
s
y f x
vng thng
2yf
.
Da vào bn bi
4
nghim phân bit.
Câu 44:Mt bác th gm làm mt cái l có dng khc to thành khi quay hình
phng gii hn bng
1yx
và trc
Ox
, quay quanh trc
Ox
. Bi và
ming l ng kính lt là
2dm
và
4dm
 tích ca l là :
A.
3
8 dm
. B.
3
15
dm
2
. C.
3
14
dm
3
. D.
3
15
dm
2
.
Li gii
/
Trang33
 ng kính bng
2dm
 bng
1dm

1 1 1 0y x x
Ta có ming l ng kính bng
4dm
suy ra bán kính ming l bng
2dm

2 1 2 3y x x

3
2
0
15
1 dx=
2
Vx


Câu 45: Cho tích phân
1
0
7
2 ln 1 d ln 2I x x x a
b

a
,
b
là các s 
Tng
2
ab
bng
A.
8
. B.
16
. C.
12
. D.
20
.
Li gii
t
2
1
dd
ln 1
1
1
d 2 d
43
2
ux
ux
x
v x x
v x x




.

1
1
2
0
0
11
4 3 ln 1 3 d
22
I x x x x x
11
22
00
11
4 3 ln 1 6
24
x x x x x
7
4ln 2
4

4ab
. Vy
2
20ab
.
Câu 46:Cho hàm s
y f x
có bng xét du ca
fx

/
Xét hàm s
2
1f x x
g x e

, tp nghim ca b
0gx
là
A.
1
;
2




. B.
1
; 1 ;2
2




. C.
1
;
2




. D.
1
1; 2;
2




.
Li gii
Ta có
2
1
2
1 2 1 .


f x x
g x x f x x e
, và
2
2
13
10
24
x x x x



2
1
22
0 1 2 1 . 0 1 2 1 0

f x x
g x x f x x e x f x x
2
2
10
1 2 0
10
1 2 0


f x x
x
f x x
x
2
2
13
1
1 2 0
1
2
13
2
1 2 0
xx
x
x
x
xx
x



Trang34
Câu 47:Cho
x
,
y
tha mãn
3
22
log 9 9
2
xy
x x y y xy
x y xy
. Tìm giá tr ln nht ca
3 2 9
10
xy
P
xy


khi
x
,
y

A.
2
. B.
3
. C.
1
. D.
0
.
Li gii
u kin:
0xy
(do
2
2
22
3
2 2 0
24
yy
x y xy x



).
ng thi
3
22
9
log 9 9 2 *
2
xy
x x y y xy
x y xy
.

22
20u x y xy
,
9 9 0v x y
, ta có.
3 3 3
* log log log
v
u v u u v v
u
.

3
logf t t t

0; 
nên suy ra
22
* 9 9 2 0u v x y xy x y
.
Ta có
2
2
2 2 2
3 9 3 19
9 9 2 0 9 2 3
2 2 4 2 4 4
yy
x y xy x y x x y y y
.

2
19 1 19
9 1 2 19
2 2 4 2 2 2
y y y
x x x x y
.
Suy ra
3 2 9 10 2 19 2 19
11
10 10 10
x y x y x y x y
P
x y x y x y
.
2 19 8
1
33
x y x
P
yy




.

max 1P
.
Cách 2:
T gi thit, ta có
22
9 9 2 0 *x y xy x y
Ta thy
8, 3xy
tha mãn
*
t
8, 3x a y b

2 2 2 2 2 2
9 9 2 0 10a 5 0 10a 5
10a 5 0 2a 0
x y xy x y a b ab b a ab b
bb
Ta có:
3 2 9 3 2 21 2
11
10 21 21
x y a b a b
P
x y a b a b
Dy ra khi và ch khi
8, 3xy
. Vy
P
t giá tr ln nht bng 1.
Câu 48. Cho hàm s
4 3 2
44f x x x x a
. Gi
M
,
m
là giá tr ln nht và giá tr nh nht
ca hàm s 
0;2
. Có bao nhiêu s nguyên
a
thuc
4;4
sao cho
2Mm
?
A.
7
. B.
5
. C.
6
. D.
4
.
Hướng dẫn giải
Xét hàm s
3 3 2
44g x x x x a
trên
0;2
.
Trang35
32
4 12 8g x x x x
;
0gx
0
1
2
x
x
x

;
0ga
,
11ga
,
2ga
.
Suy ra:
1a g x a
.
TH1:
04a
10aa
0;2
maxM f x
1a
;
0;2
minm f x
a
.
Suy ra:
04
12
a
aa


14a

4
giá tr ca
a
tha mãn.
TH2:
41a
11aa
1aa
0;2
maxM f x
a
a
;
0;2
minm f x
1a
1a
.
Suy ra:
41
22
a
aa
42a

3
giá tr ca
a
tha mãn.
Vy có tt c
7
giá tr tha mãn.
Câu 49:Cho t din
ABCD
có
90DAB CBD
;
; 5; 135AB a AC a ABC
. Bit góc gia
hai mt phng
ABD
,
BCD
bng
30
. Th tích ca t din
ABCD
là
A.
3
23
a
. B.
3
2
a
. C.
3
32
a
. D.
3
6
a
.
Li gii
/
V
AH BCD
,
H BCD
.
V
//HK BC
,
K BD
, có
BD BC
HK BD
, mà
AH BD
.
BD AHK
BD AK
.
Nên
, 30ABD BCD AKH
V
//HM BD
,
M BD
, có
BC BD
HM BC
, mà
AH BC
.
BC AM
, có góc
135ABC 
.
Suy ra
45ABM 
(nên
B
gia
M
và
C
).
ΔAMB
vuông ti
M
có
45ABM 
.
Suy ra
ΔAMB
vuông cân ti
B
22
AB a
AM MB
.
T giác
BKHM
là hình ch nht, nên
BM HK
.
ΔAHK
vuông ti
H
có
30AKH 
, nên
36
HK a
AH 
,
2
2
6
a
AK AH
.
ΔBAD
vuông ti
A
có
AK
ng cao nên
222
1 1 1
AK AB AD

.
2 2 2
3 1 1
2a a AD
22
11
2AD a

2AD a
và
22
3BD AB AD a
.
Có
BC CM BM
,
22
2 2 2 2
9
5
22
aa
CM CA AM a
3
2
22
aa
BC a
Có
11
. . .
36
BCD
V AH S AH BD BC
1
. 3. 2
6
6
a
aa
3
6
a
Trang36
Vy
3
6
a
V
.
Câu 50:Cho hai s thc
x
,
y
tha mãn
2
2
2
2 3 2
3
54
log 8 16 log 5 1 2log log 2 8 .
3
xx
y y x x y



Gi
S
là tp các giá tr nguyên ca tham s
m
 giá tr ln nht ca biu thc
22
P x y m
t quá
10
. Hi
S
có bao nhiêu tp con không phi là tp rng?
A.
2047
. B.
16383
. C.
16384
. D.
32
.
Li gii

15x
,
4y 
. Ta có:
2
2
2
2 3 2
3
54
log 8 16 log 5 1 2log log 2 8 .
3
xx
y y x x y



2 2 2 2
3 3 2 2
2log 8 16 2log 5 4 log 8 16 log 5 4y y x x y y x x
22
3 2 3 2
log 4 1 .log 8 16 log 4 1 .log 5 4y y x x
22
8 16 5 4y y x x
(vì hàm
32
log 4 1 .logf t t
ng bin trên
0;
).
2
2
2 2 2 2
11 4 8 80x y x y x y 
2
2 2 2 2
58 121 0x y x y
22
29 12 5 29 12 5xy
22
29 12 5 29 12 5xy
.
t
29 12 5a 
,
29 12 5b 
, ta có:
;
max max ,
ab
P a m b m
.

;
10
max 10
10
ab
am
P
bm



10 10
10 10
a m a
b m b
10 10b m a
.
Vì
m
nên
2; 1;0;1;2;3;4;5;6;7;8;9;10;11S
.
Vy stp con không phi là tp rng ca tp
S
là
14
2 1 16383
.
www.thuvienhoclieu.com
ĐỀ 8
ĐỀ THI THỬ THPT QUỐC GIA 2021
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Trong không gian
Oxyz,

3 2 0 1 4 3A( ; ; ),B( ; ; ).

AB
là
A.
2 2 3( ; ; ).
B.
4 6 3( ; ; ).
C.
4 6 3( ; ; ).
D.
4 6 3( ; ; ).
Câu 2: Cho
0; 1aa
. Tính
3
log .
a
Pa
A.
3.P
B.
1
.
3
P
C.
3.P 
D.
3.P
Câu 3: 
3
1y x x
hoành có bao nhiêu m chung?
A.
3.
B.
2.
C.
0.
D.
1.
Câu 4: 
A.
45.
B.
90.
C.
5.
D.
20.
Câu 5: 
,Oxyz

12
:.
2 3 2
x y z


là:
A.
( 2;3; 2).u
B.
(2;3; 2).u 
C.
(1; 2;0).u 
D.
( 1;2;0).u 
Trang37
Câu 6: 
l

r

A.
.rl
B.
4.l
C.
2
4.rl
D.
2.rl
Câu 7: 

2d 


 8 

8
72s
 hu
?
A.
1
1
.
16
u 
B.
1
1
.
16
u
C.
1
16.u
D.
1
16.u 
Câu 8: 
()y f x

()fx
ng
A.
( 2; ). 
B.
( ; 23).
C.
( ;4).
D.
(1; ).
Câu 9: 
x
2
y
3
Hide Luoi
vuong
-2
O
1
A.
3.
B.
2.
C.
0.
D.
2.
Câu 10: 
2
36cm

A.
3
120 .cm
B.
3
36 .cm
C.
3
360 .cm
D.
3
12 .cm
Câu 11:  
A. 864
. B. 36
. C. 216
. D. 288
.
Câu 12: 
1
53
x
là
A.
5
log 3 1.x 
B.
3
log 5 1.x 
C.
3
log 5 1.x 
D.
5
log 3 1.x 
Câu 13: 
1 3 .zi
A.
3.i
B.
1 3 .i
C.
1 3 .i
D.
1 3 .i
Câu 14: Trong không gian
,Oxyz

(2; 1;2)I
bán kính
2R

A.
2 2 2
( 2) ( 1) ( 2) 2.x y z
B.
2 2 2
( 2) ( 1) ( 2) 2.x y z
C.
2 2 2
( 2) ( 1) ( 2) 2.x y z
D.
2 2 2
( 2) ( 1) ( 2) 2.x y z
Câu 15: 
M

y
x
-3
2
Hide Luoi
M
Trang38
A.
3 2 .zi
B.
3 2 .zi
C.
3 2 .zi
D.
2 3 .zi
Câu 16: 
A. 24. B. 135. C. 504. D. 252.
Câu 17: 
h

r

A.
2
.hr
B.
3
1
.
3
hr
C.
2
1
.
3
hr
D.
2
4
.
3
hr
Câu 18: 
,Oxyz

(2;5; 3)M

,,A B C


M

, , .Ox Oy Oz

()ABC

A.
1.
3 5 2
x y z
B.
1.
2 5 3
x y z
C.
1.
5 2 3
x y z
D.
0.
2 5 3
x y z
Câu 19: 
2
3
9
x
y
x
là
A. 3. B. 0. C. 2. D. 1.
Câu 20: 
2
log 4yx
là:
A.
; 2 2; .D  
B.
2;2 .D 
C.
; 2 2; .D  
D.
2;2 .D 
Câu 21: Trong không gian
Oxyz
m
1;2; 1A
và mt phng
P x y z
ng thng

A
và vuông góc vi mt phng
P

A.
1 2 1
.
1 1 2
x y z

B.
1 2 1
.
1 1 2
x y z

C.
1 2 1
.
1 1 2
x y z

D.
1 2 1
.
1 1 2
x y z

Câu 22: Cho số phức
z
thỏa mãn điều kiện
(1 ) 2 3 .i z i i
Môđun của số phức
z
bằng
A.
5.
B.
9.
C.
3.
D.
3.
Câu 23: 
,Oxyz

12
:.
2 3 2
x y z


?
A.
1;5;2 .Q
B.
1;2; 2 .M
C.
1;5; 2 .N
D.
1;5; 2 .P 
Câu 24: 
12
3 , 1 i.z a i z

a
sao cho
12
3.zz
A.
2.
B.
1.
C.
0.
D.
3.
Câu 25: 
2
3
log ( 3 1) 2xx
là
A.
3 41 3 41
;.
22





B.
3 29 3 29
;.
22





C.
3 41
.
2






D.
3 29
.
2






Câu 26: 
Trang39
A.
3
3.y x x
B.
3
3.y x x
C.
32
3.y x x
D.
32
3 1.y x x
Câu 27: 
y f x

R


,Mm

2;1 .

Mm

A.
6.
B.
4.
C.
3.
D.
4.
Câu 28: Tính
1
0
1
.
51
I dx
x
A.
1
ln6.
5
I
B.
1
5ln .
6
I
C.
5ln6.I
D.
11
ln .
56
I
Câu 29: Cho
2
log 3 a

2
log 54 m na

;mn
. Tính
22
.S m n
A.
8.S
B.
5.S
C.
10.S
D.
13.S
Câu 30: 
m

ym

32
2 3 1y x x

A.
1 0.m
B.
0 1.m
C.
2 2.m
D.
1 1.m
Câu 31: Một người gửi tiết kiệm
150
triệu đồng vào một ngân hàng với lãi suất
6,55%
/năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi được nhập vào vốn
để tính lãi cho năm tiếp theo. Hỏi ít nhất bao nhiêu năm người đó thu được(cả số tiền gửi ban
đầu và lãi) không dưới
200
triệu đồng, giả định trong khoảng thời gian này lãi suất ngân hàng
không thay đổi và người đó không rút tiền ra?
A.
5
 B.
7
 C.
6
 D.
4

Câu 32: 
1
z

2
4 8 0.zz


1
7.w z i
là
A.
2; 2 .
B.
9;2 .
C.
5;2 .
D.
2;2 .
Câu 33: 
6h

8.r

Trang40

A.
48 .
B.
80 .
C.
64 .
D.
60 .
Câu 34: Cho
1
0
2f x dx
và
1
0
1.g x dx
Tính
1
0
2.I f x g x dx

A.
1.I
B.
3.I
C.
5.I
D.
1.I 
Câu 35: Tính th tích vt th tròn xoay to bi khi quay hình phng gii hn bng
2
2y x x
,
0y
,
0x
,
1x
quay quanh trc
Ox
.
A.
8
.
15
B.
15
.
8
C.
8
.
7
D.
8
.
15
Câu 36: 
y f x
(Hình 1). 
A.
3
3 2.y x x
B.
32
3x 5 .y x x
C.
32
3x 3.yx
D.
32
3x 3.yx
Câu 37: 

0
. Tính 
A. B. . C. D.
Câu 38: P
1
(7 45) 7(7 45) 4.2
x x x

12
,xx
và
22
12
.T x x
Khi

A.
(3;5).T
B.
(10;15).T
C.
(1;3).T
D.
(5;8).T
Câu 39: 


A.
1
.
30
B.
3
.
5
C.
1
.
120
D.
1
.
5
Câu 40: 

()fx


R

1
0
(1) 2 (0) 1, ( ) 5.f f f x dx

3
/
0
(6 ) ( ) .
3
x
I x f dx
A.
64.I
B.
66.I
C.
54.I
D.
56.I
Câu 41: 
y f x

\0

+
-
0
+
0
-
1
-3
Hình 1
Trang41
S nghim c
2 3 5 7 0fx
là
A.
4.
B.
3.
C.
1.
D.
2.
Câu 42: C
. ' ' 'ABC A B C

ABC
là tam giác vuông cân 
,A
6,BC

'A BC
và
ABC

0
60 .

'A

.ABC

'AA
và
'.BC
A.
65
.
5
B.
3 21
.
7
C.
4 15
.
5
D.
5 14
.
2
Câu 43: Cho hàm s
32
( ) 2 1y f x x mx
. Tìm tt c các giá tr thc ca tham s
m
 hàm
s
()y f x
m cc tr.
A.
;0 3;m 
. B.
03m
. C.
3m
. D.
3m
.
Câu 44: 
a


( ) 5v t t a

t


160 
a

A. 16 (m/s). B. 80 (m/s). C. 40 (m/s). D. 160 (m/s).
Câu 45: 



 
3


A. 90 bao. B. 120 bao. C. 100 bao. D. 110 bao.
Câu 46: Gọi
M
là giá trị lớn nhất của hàm số
2
2
x m m
y
x

trên đoạn
[1;2]
. Giá trị nhỏ nhất
của
M
bằng
A.
1
.
7
B.
1
.
5
C.
1
.
4
D.
1
.
6
Câu 47: C
,ab

22
12
log log .
2
a
b

3 3 3 3
2
4 5log 4P a b a b
là
min 2
logP x y z

,,x y z

z


.S x y z
A.
9.S
B.
11.S
C.
10.S
D.
8.S
Câu 48: Cho hàm s
32
3 2,y mx x x m
m
là tham s. Tp hp tt c các giá tr
m
 hàm s
ng bin trên khong
2;0
là
;
a
b



vi
a
b
là phân s ti gin và
0b
. Giá tr
ab
là:
A.
4.
B.
12.
C.
5.
D.
8.
Câu 49: 
,xy

1xy
và
22
1 0.x y xy x y

,Mm


.
1
xy
P
xy


2019 2020 .S M m
A.
1347.S 
B.
2483.S
C.
2530.
xq
S 
D.
1521.S
Câu 50: 
SABCD

2 , .SA a AB a

()P

AB


SAC

,SC SD

và MN

.NMABCD
Trang42
A.
3
5 14
.
48
a
B.
3
57
.
24
a
C.
3
5 14
.
8
a
D.
3
5 14
.
16
a
------ HẾT ------
ĐÁP ÁN
1
D
11
D
21
C
31
A
41
B
2
D
12
A
22
C
32
B
42
B
3
D
13
B
23
C
33
B
43
C
4
A
14
B
24
A
34
B
44
C
5
B
15
B
25
A
35
A
45
B
6
D
16
C
26
C
36
D
46
C
7
C
17
C
27
B
37
B
47
C
8
B
18
B
28
A
38
C
48
C
9
C
19
C
29
C
39
D
49
A
10
A
20
D
30
A
40
C
50
A
www.thuvienhoclieu.com
ĐỀ 9
ĐỀ THI THỬ THPT QUỐC GIA 2021
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Có bao nhiêu cách ch󰉭n 3 h󰉭c sinh t󰉾 nhóm có 7 h󰉭c sinh?
A.
3
7
.C
B.
3
7
.A
C.
7
3.
D.
3
7.
Câu 2: Cho c󰉙p s󰉯 c󰉳ng
n
u
v󰉵i
1
3u
và
2d
. Tính
3
?u
A.
7.
B.
6.
C.
5.
D.
12.
Câu 3: Nghi󰉪m c󰉻󰉼󰉴
28
x
là:
A.
1.x
B.
2.x
C.
3.x
D.
4.x
Câu 4: Th󰉨 tích c󰉻a kh󰉯i l󰉝󰉼󰉴󰉗nh b󰉟ng 1 là:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 5: Tìm nguyên hàm c󰉻a hàm s󰉯
tanf x x
A.
ln cosf x dx x C
B.
ln cosf x dx x C
C.
ln sinf x dx x C
D.
ln sinf x dx x C
Câu 6: Tìm nguyên hàm c󰉻a hàm s󰉯
2
1
.
4
fx
x
A.
12
ln
22
x
f x dx C
x

B.
12
ln
22
x
f x dx C
x

C.
12
ln
42
x
f x dx C
x

D.
12
ln
42
x
f x dx C
x

Câu 7: Tìm nguyên hàm c󰉻a hàm s󰉯
2
1
.
sin
fx
x
A.
( ) cot .f x dx x C
B.
( ) tan .f x dx x C
C.
( ) cot .f x dx x C
D.
( ) tan .f x dx x C
Câu 8: Tìm nguyên hàm c󰉻a hàm s󰉯
3
x
fx
A.
( ) 3 ln3 .
x
f x dx C
B.
3
( ) .
ln3
x
f x dx C
C.
( ) 3 ln3 .
x
f x dx C
D .
3
( ) .
ln3
x
f x dx C
Câu 9: Tìm ph󰉚n 󰉘o c󰉻a s󰉯 ph󰉽c z th󰉮a
(2 3 ) (4 )(2 ).z i i i
A. Ph󰉚n 󰉘o b󰉟ng
1
. B. Ph󰉚n 󰉘o b󰉟ng
1
.
Trang43
C. Ph󰉚n 󰉘o b󰉟ng
2
. D. Ph󰉚n 󰉘o b󰉟ng
2
.
Câu 10:Tìm modun c󰉻a s󰉯 ph󰉽c
3 2 .zi
A.
5.z
B.
13.z
C.
10.z
D.
2.z
Câu 11: Cho s󰉯 ph󰉽c
10 2zi
. Tìm ph󰉚n th󰊁c và ph󰉚n 󰉘o c󰉻a s󰉯 ph󰉽c
z
.
A. Ph󰉚n th󰊁c b󰉟ng
10
và Ph󰉚n 󰉘o b󰉟ng
2
.
B. Ph󰉚n th󰊁c b󰉟ng
10
và Ph󰉚n 󰉘o b󰉟ng
2i
.
C. Ph󰉚n th󰊁c b󰉟ng
10
và Ph󰉚n 󰉘o b󰉟ng
2
.
D. Ph󰉚n th󰊁c b󰉟ng
10
và Ph󰉚n 󰉘o b󰉟ng
2i
.
Câu 12:󰉴
1;2;1 , 2; 1;3ab
. Tính
.ab
.
A.
. 1.ab
B.
. 1.ab
C.
. 3.ab
D.
. 3.ab
Câu 13: Trong không gian Oxyz, cho m󰉢t c󰉚u
2 2 2
: 1 3 2 4S x y z
. 󰉬nh t󰉭󰉳 tâm I và
bán kính
R
c󰉻a m󰉢t c󰉚u
S
.
A.
1;3;2 , 2.IR
B.
1;3;2 , 4.IR
C.
1; 3; 2 , 2.IR
D.
1;3;2 , 4.IR
Câu 14:Trong không gian
Oxyz
, cho mp
: 2 2 1 0P x y z
󰉴không 󰉴
tuy󰉦n c󰉻a mp
P
?
A.
1; 2;2 .n 
B.
2;4; 4 .n
C.
1; 2; 2 .n
D.
3; 6;6 .n 
Câu 15:Trong không gian
Oxyz
cho tam giác
ABC
có
(1;0;0), (0;0;1), (2;1;1)A B C
. Kh󰉠󰉬

A.Tam giác
ABC
vuông t󰉗i
A
. B. Tam giác
ABC
cân t󰉗i
A
.
C. Tam giác
ABC
vuông cân t󰉗i
A
. D. Tam giác
ABC
󰉧u.
Câu 16:M󰉢t ph󰉠󰉨m
2; 3;1A
và ch󰉽a tr󰉺c
Ox
󰉼󰉴
A.
2 1 0.yz
B.
3 0.xy
C.
2 0.xz
D.
3 0.yz
Câu 17:Trong các m󰉢t ph󰉠ng sau, m󰉢t ph󰉠ng nào song song v󰉵i mp
Oxz
?
A.
0.y
B.
1 0.z 
C.
2 3 0.xz
D.
3 1 0.y 
Câu 18: Vi󰉦󰉼󰉴
P

1;1;0M
và song song v󰉵i mp
: 2 10 0Q x y z
.
A.
: 2 3 0.P x y z
B.
: 2 3 0.P x y z
C.
: 2 1 0.P x y z
D.
: 2 1 0.P x y z
Câu 19: Cho 󰉼󰉶ng th󰉠ng
1
: 2 2 ,
3
xt
y t t
zt


󰉨󰉳c
?
A.
1; 2;1 .
B.
2;0;4 .
C.
1;2; 3 .
D.
2;1;3 .
Câu 20: Trong các hàm s󰉯 󰉼󰉵󰉯 nào ngh󰉬ch bi󰉦n trên t󰉝p s󰉯 th󰊁c
?
A.
3
x
y



. B.
1
2
logyx
. C.
2
4
log 2 1yx

. D.
2
x
y
e



.
Câu 21:󰉝󰉬nh 󰉻󰉯
3
2
27yx

là
A.
3;D 
. B.
\2D
. C.
D
. D.
3;D 
.
Câu 22: Tìm nghi󰉪m c󰉻󰉼󰉴
2
log 5 4x 
.
A.
3x
. B.
13x
. C.
21x
. D.
11x
.
Trang44
Câu 23: 󰉗o hàm c󰉻a hàm s󰉯
2
log e
x
yx
.
A.
1e
ln 2
x
. B.
1e
e ln2
x
x
x
. C.
1e
e
x
x
x
. D.
1
e ln2
x
x
.
Câu 24: Nghi󰉪m c󰉻a b󰉙󰉼󰉴
2
3 243
x
là:
A.
27x
. B.
7x
. C.
7x
. D.
7x
.
Câu 25: Cho hàm s󰉯
y f x
liên t󰉺c trên
󰉰 th󰉬 󰉼󰉥 󰉼󰉵i. Kh󰉠󰉬

A. Hàm s󰉯 󰉰ng bi󰉦n trên kho󰉘ng
1;3
.
B. Hàm s󰉯 ngh󰉬ch bi󰉦n trên kho󰉘ng
6;
.
C. Hàm s󰉯 󰉰ng bi󰉦n trên kho󰉘ng
;3
.
D. Hàm s󰉯 ngh󰉬ch bi󰉦n trên kho󰉘ng
3;6
.
Câu 26: Cho hàm s󰉯
ax b
fx
cx d
󰉬nh trên t󰉝p
\1
󰉰 th󰉬 󰉼󰉼󰉵i.
Xét các m󰉪󰉧 sau:
(I) Hàm s󰉯 󰉰ng bi󰉦n trên m󰉲i kho󰉘ng
;1
và
1; 
.
(II) Hàm s󰉯 ngh󰉬ch bi󰉦n trên m󰉲i kho󰉘ng
;1
và
1; 
.
(III) Hàm s󰉯 󰉰ng bi󰉦n trên t󰉝󰉬nh.
S󰉯 các m󰉪󰉧 
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 27: Cho hàm s󰉯
y f x
󰉰 th󰉬 󰉼󰉥 bên. M󰉪󰉧 󰉧 hàm s󰉯 
A. 󰉰ng bi󰉦n trên kho󰉘ng
0;2
. B. Ngh󰉬ch bi󰉦n trên kho󰉘ng
3;0
.
C. 󰉰ng bi󰉦n trên kho󰉘ng
1;0
. D. Ngh󰉬ch bi󰉦n trên kho󰉘ng
0;3
.
O
x
y
3
1
2
3
O
x
y
2
7
Trang45
Câu 28:󰉼󰉶󰉼󰉵󰉰 th󰉬 c󰉻a m󰉳t hàm s󰉯 trong b󰉯n
hàm s󰉯 󰉼󰉵󰉮i hàm s󰉯 󰉯 nào?
A.
32
3 1.y x x
B.
42
2.y x x
C.
42
2 2.y x x
D.
42
2 2.y x x
Câu 29: Cho hàm s󰉯
y f x
có b󰉘ng bi󰉦󰉼
M󰉪󰉧 󰉼󰉵
A. Hàm s󰉯 󰉗t c󰊁󰉗i t󰉗i
3x
.
B. Hàm s󰉯 󰉗t c󰊁c ti󰉨u t󰉗i
2x 
.
C. Hàm s󰉯 có
CĐ
y
3
.
D. Hàm s󰉯 ngh󰉬ch bi󰉦n trên các kho󰉘ng
( ; 2)
và
(2; )
.
Câu 30:Ti󰉦p tuy󰉦n v󰉵󰉰 th󰉬 hàm s󰉯
32
1y x x
t󰉗󰉨m
󰉳
0
1x
󰉼󰉴
A.
.yx
B.
2.yx
C.
2 1.yx
D.
2.yx
Câu 31:󰉯 th󰉬
C
:
21
.
1
x
y
x
G󰉭󰉨m c󰉻a
2
󰉼󰉶ng ti󰉪m c󰉝n, t󰉭󰉳 󰉨m
I
?
A.
1;2 .I
B.
2;1 .I
C.
2; 1 .I
D.
1;2 .I
Câu 32: Cho hàm s󰉯 có b󰉘ng bi󰉦󰉼󰉭n kh󰉠󰉬
x

0


0
y
1
0 0
A. Hàm s󰉯 có giá tr󰉬 l󰉵n nh󰉙t b󰉟ng 1 và giá tr󰉬 nh󰉮 nh󰉙t b󰉟ng 0.
B. Hàm s󰉯 có giá tr󰉬 l󰉵n nh󰉙t b󰉟ng 0.
C. Hàm s󰉯 có giá tr󰉬 l󰉵n nh󰉙t b󰉟ng 1.
D. Hàm s󰉯 không có giá tr󰉬 l󰉵n nh󰉙t và giá tr󰉬 nh󰉮 nh󰉙t.
Câu 33:󰉼󰉶ng th󰉠ng
1yx
c󰉞󰉰 th󰉬 (C) c󰉻a hàm s󰉯
25
1
x
y
x
t󰉗󰉳 󰉨m là:
A.
2x 
. B.
2x 
. C.
4x 
. D.
2x
.
Câu 34:Cho hàm s󰉯
3
3
x
y
x
. Ti󰉪m c󰉝n ngang c󰉻󰉰 th󰉬 hàm s󰉯 là:
A.
1.y 
B.
1.x 
C.
3.x 
D.
1.y
Câu 35:Cho kh󰉯i nón có chi󰉧󰉼󰉶󰉼󰉶󰉟ng r. Th󰉨 tích c󰉻a
kh󰉯i nón là:
A.
2
V r h
B.
2
3V r h
C.
2
1
3
V rh
D.
2
1
3
V r h
Câu 36:Cho m󰉳t kh󰉯i tr󰉺 có kho󰉘ng cách gi󰊀󰉟ng 10, bi󰉦t di󰉪n tích xung quanh c󰉻a kh󰉯i
tr󰉺 b󰉟ng
80
. Th󰉨 tích c󰉻a kh󰉯i tr󰉺 là:
A.
160
B.
164
C.
64
D.
144
Câu 37:Th󰉨 tích V c󰉻a m󰉳t m󰉢t c󰉚󰉼󰉹󰉬nh b󰉷i công th󰉽
A.
4
3
r
V
B.
22
4
3
r
V
C.
3
4
3
r
V
. D.
23
4
3
r
V
Câu 38:Th󰉨 tích kh󰉯󰉺 󰉧u có t󰉙t c󰉘 các c󰉗nh b󰉟ng
a
là :
A.
3
2
3
a
. B.
3
2
4
a
. C.
3
3
2
a
. D.
3
3
4
a
.
4
2
-2
-4
-10
-5
5
10
x
y
f
x
= -
x
4
+2
x
2
Trang46
Câu 39: 󰉺 󰉧u
. ' ' 'ABC A B C
có c󰉗󰉟ng
a
, m󰉢t ph󰉠ng
( ' )A BC
h󰉹p v󰉵i m󰉢t
ph󰉠ng
()ABC
m󰉳t góc
60
o
. Th󰉨 tích c󰉻a kh󰉯󰉺
. ' ' 'ABC A B C
tính theo
a
b󰉟ng:
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
23
3
a
. D.
3
3
3
a
.
Câu 40:T󰉾 các ch󰊀 s󰉯 0,1,2,3,4,5,6 có th󰉨 l󰉝󰉼󰉹c bao nhiêu s󰉯 ch󰉡n, m󰉲i s󰉯 có 5 ch󰊀 s󰉯 khác nhau
󰊀 s󰉯 l󰉤 và 2 ch󰊀 s󰉯 l󰉤 󰉽ng c󰉗nh nhau?
A. 360 B. 280 C. 310 D. 290
Câu 41: Hàm s󰉯
()y f x
󰉗o hàm trên
󰉰 th󰉬 hàm s󰉯
'( )fx
󰉼󰉹󰉼󰉥. Hàm
s󰉯
()y f x
ngh󰉬ch bi󰉦n trên kho󰉘󰉼󰉵
A.
1
;1
3



. B.
0;
. C.
1
;
3




. D.
;0
.
Câu 42: Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 th󰊁c
m
󰉨 hàm s󰉯
32
12y mx mx m m x
󰉰ng bi󰉦n
trên
.
A.
4
3
m
. B.
4
3
m
và
0m
. C.
0m
ho󰉢c
4
3
m
. D.
4
3
m
.
Câu 43: Cho m󰉳t t󰉙m nhôm hình ch󰊀 nh󰉝t
ABCD
có
60cmAD
và
AB
có 󰉳 dài
󰉱i. Ta g󰉝p t󰉙m nhôm theo
2
c󰉗nh
MN
và
PQ
󰉦n khi
AB
và
DC
trùng
󰉼󰉥 󰉨 󰉼󰉹c m󰉳 tr󰉺
khuy󰉦t
2

x
󰉨 th󰉨 tích kh󰉯󰉺 t󰉗o
thành l󰉵n nh󰉙t?
A.
20x
. B.
25x
. C.
10x
. D.
30x
.
Câu 44: Cho hàm s󰉯 b󰉝c ba
y f x
󰉰 th󰉬 󰉼
󰈖󰈨󰈖
m 󰈜󰈘
y f x m
󰈜󰉼󰈨 󰈨
A.
1m
󰈨
3m
. B.
1m
󰈨
3m
.
C.
3m
󰈨
1m
. D.
13m
.
Câu 45: G󰉭i
,xy
là các s󰉯 th󰊁 󰉼󰉴 󰉮  󰉧u ki󰉪n
9 6 4
log log logx y x y
và
2
x a b
y

, v󰉵i
a
,
b
là hai s󰉯 󰉼󰉴
ab
.
A.
6ab
. B.
11ab
. C.
4ab
. D.
8ab
.
Câu 46: 
 󰉬 nguyên c󰉻a tham s󰉯
m
󰉨 󰉼󰉴
2
2
log 1 log 8x mx
có hai
nghi󰉪m phân bi󰉪t là
A.
3
. B.
4
. C.
5
. D.Vô s󰉯.
x
y
O
3
1
Trang47
Câu 47: Tìm t󰉙t c󰉘 các gúa tr󰉬 tham s󰉯
m
󰉰 th󰉬 hàm s󰉯
4 2 2
21y x m x m
󰉨m
c󰊁c tr󰉬 n󰉳i ti󰉦󰉼󰉶ng tròn bán kính b󰉟ng
1
.
A.
35
1;
2
mm

. B.
35
0;
2
mm


.
C.
35
0;
2
mm

. D.
35
1;
2
mm

.
Câu 48: Cho hàm s󰉯
y f x
󰉗o hàm liên t󰉺c trên
và hàm s󰉯
y f x
󰉰 th󰉬 󰉼󰉥.
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
x
y
H󰉮i hàm s󰉯
2
21g x f x x
󰉰ng bi󰉦n trên kho󰉘ng nào trong các kho󰉘ng sau?
A.
3;
. B.
1;3
. C.
3;1
. D.
;3
.
Câu 49: Cho
,ab
là s󰉯 th󰊁 󰉼󰉴 󰉮a mãn
22
12
log log
2
a
b
. Giá tr󰉬 nh󰉮 nh󰉙t c󰉻a bi󰉨u th󰉽c
3 3 3 3
2
4 4log 4P a b a b
là
A.
2
4log 6
. B.
2
44
4log
ln 2 ln 2
. C.
2
4 1 log 3
. D.
4
.
Câu 50: Cho hình h󰉳p
.ABCD A BC D
 
ABCD
là hình ch󰊀 nh󰉝t c󰉗nh
,2AB a AD a
,
3A B a
. G󰉭i
I
là tr󰉭ng tâm tam giác
A C D
,
là góc gi󰊀󰉼󰉶ng th󰉠ng
ID
và m󰉢t ph󰉠ng
ICB
. Giá tr󰉬 c󰉻a
sin
b󰉟ng
A.
9
253
. B.
6
11 2
. C.
6
253
. D.
23
11
.
Trang48
HƯỚNG DẪN GIẢI
Câu 40:T󰉾 các ch󰊀 s󰉯 0,1,2,3,4,5,6 có th󰉨 l󰉝󰉼󰉹c bao nhiêu s󰉯 ch󰉡n, m󰉲i s󰉯 có 5 ch󰊀 s󰉯 khác nhau
󰊀 s󰉯 l󰉤 và 2 ch󰊀 s󰉯 l󰉤 󰉽ng c󰉗nh nhau?
A. 360 B. 280 C. 310 D. 290
Hướng dẫn giải:
Chọn A.
G󰉭i
A
là s󰉯 t󰊁 nhiên có hai ch󰊀 s󰉯 l󰉤 khác nhau l󰉙y t󰉾 các s󰉯
0,1,2,3,4,5,6
s󰉯 cách ch󰉭󰉼󰉹c
A
là
2
3
6A
. S󰉯 ch󰉡n có 5 ch󰊀 s󰉯 mà hai s󰉯 l󰉤 󰉽ng k󰉧 nhau ph󰉘i ch󰉽a
A
và ba trong 4 ch󰊀 s󰉯 0;2;4;6. G󰉭i
; , , , { ,0,2,4,6}abcd a b c d A
là s󰉯 th󰉮a mãn yêu c󰉚u bài toán.
*TH1: N󰉦u
aA
có 1 cách ch󰉭n
a
và
3
4
A
ch󰉭n
,,b c d
.
* TH 2:
aA
có 3 cách ch󰉭n
a
+ N󰉦u
bA
có 1 cách ch󰉭n
b
và
2
3
A
cách ch󰉭n
,cd
.
+ N󰉦u
cA
có 1 cách ch󰉭n
c
và
2
3
A
cách ch󰉭n
,bd
.
V󰉝y có
2 3 2 2
3 4 3 3
3 1. 1. 360A A A A
s󰉯 th󰉮a mãm yêu c󰉚u bài toán.
Câu 41: Hàm s󰉯
()y f x
󰉗o hàm trên
󰉰 th󰉬 hàm s󰉯
'( )fx
󰉼󰉹󰉼󰉥. Hàm
s󰉯
()y f x
ngh󰉬ch bi󰉦n trên kho󰉘󰉼󰉵
A.
1
;1
3



. B.
0;
. C.
1
;
3




. D.
;0
.
Hướng dẫn giải :
Chọn D
0
0
1
x
fx
x

Ta có b󰉘ng bi󰉦n thiên c󰉻a hàm s󰉯
()fx
:
x

0
1

y
-
0
0
+
y
CT
y
T󰉾 b󰉘ng bi󰉦n thiên ta th󰉙y hàm s󰉯 ngh󰉬ch bi󰉦n trên
;0 .
Câu 42: Tìm t󰉙t c󰉘 các giá tr󰉬 c󰉻a tham s󰉯 th󰊁c
m
󰉨 hàm s󰉯
32
12y mx mx m m x
󰉰ng bi󰉦n
trên
.
A.
4
3
m
. B.
4
3
m
và
0m
. C.
0m
ho󰉢c
4
3
m
. D.
4
3
m
. Hướng dẫn
giải :
Chọn D.
TH1:
02my
là hàm h󰉟ng nên lo󰉗i
0m
TH2:
0m
. Ta có:
2
3 2 1y mx mx m m
.
Trang49
Hàm s󰉯 󰉰ng bi󰉦n trên
22
4
3 1 0
4
3
3
30
0
m
m m m
m
m
m

Câu 43: Cho m󰉳t t󰉙m nhôm hình ch󰊀 nh󰉝t
ABCD
có
60cmAD
và
AB
có 󰉳 dài
󰉱i. Ta g󰉝p t󰉙m nhôm theo
2
c󰉗nh
MN
và
PQ
󰉦n khi
AB
và
DC
trùng
󰉼󰉥 󰉨 󰉼󰉹c m󰉳 tr󰉺
khuy󰉦t
2

x
󰉨 th󰉨 tích kh󰉯󰉺 t󰉗o
thành l󰉵n nh󰉙t?
A.
20x
. B.
25x
. C.
10x
. D.
30x
.
Lơ i giai
Chọn A
+ Ta có:
AN PD x
(
cm, 0 30x
)
 NP x
+ Th󰉨 󰉺 t󰉗o thành b󰉟ng:
2
2
1
. . . .
22
NPA
NP
V AB S AB PA NP



2
23
60 2
. . 60 2 2 15. . 30 15 cm
22
AB x
x x AB x x



󰉱i nên ta ch󰉫 c󰉚n tìm x sao cho
30 15f x x x
󰉗t giá tr󰉬 l󰉵n nh󰉙t.
+ Xét hàm s󰉯
fx
trên
15;30
󰉼󰉹c
15;30
max 20 10 5 20f x f x
Câu 44: Cho hàm s󰉯 b󰉝c ba
y f x
󰉰 th󰉬 󰉼
󰈖󰈨󰈖
m 󰈜󰈘
y f x m
󰈜󰉼󰈨 󰈨
A.
1m
󰈨
3m
. B.
1m
󰈨
3m
.
C.
3m
󰈨
1m
. D.
13m
.
Lời giải
Chọn A.
- S󰉯 󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯
y f x m
b󰉟ng s󰉯 󰉨m c󰊁c tr󰉬 c󰉻a hàm s󰉯
( ) my f x
và s󰉯
nghi󰉪󰉴󰉻󰉼󰉴
( ) m 0fx
.
- D󰊁a vào hình v󰉥, hàm s󰉯
( ) my f x
󰉨m c󰊁c tr󰉬 
y f x m
󰈜󰉼󰈨 
󰈨
1m
󰈨
3m
.
Câu 45: G󰉭i
,xy
là các s󰉯 th󰊁 󰉼󰉴 󰉮  󰉧u ki󰉪n
9 6 4
log log logx y x y
và
2
x a b
y

, v󰉵i
a
,
b
là hai s󰉯 󰉼󰉴
ab
.
A.
6ab
. B.
11ab
. C.
4ab
. D.
8ab
.
Lờigiải
x
y
O
3
1
Trang50
ChọnA
󰉢t
9
log xt
󰉧 ra có
96
94
9 (1)
6 (2)
log log
4 (3)
log log
3
(4)
2
t
t
t
t
x
y
x y t
xy
x x y t
x
y







T󰉾 (1), (2), và (3) ta có
2
2
3 1 5
()
22
33
9 6 4 3 3.2 4 0 1 0
22
3 1 5
()
22
t
tt
t
t t t t t
t
TM
L








Th󰉦 󰉼󰉹c
3 1 5
1; 5
2 2 2
t
x a b
ab
y



Th󰉿 l󰉗i ta th󰉙y
1; 5ab
th󰉮a mãn d󰊀 ki󰉪n bài toán. Suy ra
6.ab
Câu 46: 
 󰉬 nguyên c󰉻a tham s󰉯
m
󰉨 󰉼󰉴
2
2
log 1 log 8x mx
có hai
nghi󰉪m phân bi󰉪t là
A.
3
. B.
4
. C.
5
. D.Vô s󰉯.
Lờigiải.
ChọnA
2
2
2
2
1
1
log 1 log 8
2 9 0
18
x
x
x mx
x m x
x mx


.
󰉨 󰉼󰉴󰉪m th󰊁c l󰉵󰉴
1
󰉧u ki󰉪n sau th󰉮a mãn.
2
12
12
12
8
4
4 32 0
0
1 1 0 0 4 8
1
80
1 1 0
m
m
mm
x x m m
xx
m
xx




Vì
5,6,7mm
.
Câu 47: Tìm t󰉙t c󰉘 các giá tr󰉬 tham s󰉯
m
󰉰 th󰉬 hàm s󰉯
4 2 2
21y x m x m
󰉨m
c󰊁c tr󰉬 n󰉳i ti󰉦󰉼󰉶ng tròn bán kính b󰉟ng
1
.
A.
35
1;
2
mm

. B.
35
0;
2
mm


.
C.
35
0;
2
mm

. D.
35
1;
2
mm

.
Lời giải
Chọn B.
Ta có
32
2
0
4 4 1 4 1 0
1
x
y x m x x x m
xm

1
󰉰 th󰉬 hàm s󰉯 󰉨m c󰊁c tr󰉬
0y

có ba nghi󰉪m phân bi󰉪t
1m
.

2
22
2
0
1
1 1 2 1 2 1
x y m
x m y m m m m
.
Nên ta có
2
0;Am
,
1; 2 1B m m
,
1; 2 1C m m
󰉨m c󰊁c tr󰉬 c󰉻󰉰 th󰉬 hàm s󰉯 
Trang51
Ta có
2
2
1; 2 1
1; 2 1
AB m m m
AC m m m
4
4
11
11
AB m m
AC m m
AB AC
.
G󰉭i
H
󰉨m c󰉻a c󰉗nh
BC
AH BC
và
0; 2 1Hm
2
22
0; 2 1 2 1 1AH m m AH m m m
.
Mà
1 . .
.
24
ABC
AB AC BC
S AH BC
R

2 . .R AH AB AC
.
Nên
1R
và
2 1;0 2 1BC m BC m
24
2 1 1 1m m m
3
1 1 2 1mm
32
30m m m
0m
,
35
2
m

.
Câu 48: Cho hàm s󰉯
y f x
󰉗o hàm liên t󰉺c trên
và hàm s󰉯
y f x
󰉰 th󰉬 󰉼󰉥.
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
x
y
H󰉮i hàm s󰉯
2
21g x f x x
󰉰ng bi󰉦n trên kho󰉘ng nào trong các kho󰉘ng sau?
A.
3;
. B.
1;3
. C.
3;1
. D.
;3
.
Lời giải
Chọn B
T󰉝󰉬nh c󰉻a
gx
là
. Ta có
21g x f x x



.
Hàm s󰉯 󰉰ng bi󰉦n khi và ch󰉫 khi
1f x x
, (d󰉙u b󰉟ng ch󰉫 x󰉘y ra t󰉗i h󰊀u h󰉗󰉨m).
V󰉥 󰉰 th󰉬
y f x
và
1yx
trên cùng m󰉳t h󰉪 tr󰉺󰉼
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-6
-5
-4
-3
-2
-1
1
2
3
x
y
T󰉾 󰉰 th󰉬 ta có
1f x x
3
13
x
x


.
Câu 49: Cho
,ab
là s󰉯 th󰊁 󰉼󰉴 󰉮a mãn
22
12
log log
2
a
b
. Giá tr󰉬 nh󰉮 nh󰉙t c󰉻a bi󰉨u th󰉽c
3 3 3 3
2
4 4log 4P a b a b
là
Trang52
A.
2
4log 6
. B.
2
44
4log
ln 2 ln2
. C.
2
4 1 log 3
. D.
4
.
Lời giải
Chọn C
Ta có
2 2 2 2
2
1 2 2 2 4
log log log log
2
a a a a
b b b b
󰉢t
33
3 3 3
3
66
256 256
4 3 . . 12 12;
22
bb
t a b b t
bb


2
4logP f t t t
,có
4
1 0, 2
ln2
f t t
t
Suy ra
ft
󰉰ng bi󰉦n trên
12; 12f t f
V󰉝y giá tr󰉬 nh󰉮 nh󰉙t c󰉻a
P
là
min 2 2
12 4log 12 4 1 log 3P
Câu 50: Cho hình h󰉳p
.ABCD A B CD
 
ABCD
là hình ch󰊀 nh󰉝t c󰉗nh
,2AB a AD a
,
3A B a
. G󰉭i
I
là tr󰉭ng tâm tam giác
A C D
,
là góc gi󰊀󰉼󰉶ng th󰉠ng
ID
và m󰉢t ph󰉠ng
ICB
. Giá tr󰉬 c󰉻a
sin
b󰉟ng
A.
9
253
. B.
6
11 2
. C.
6
253
. D.
23
11
.
Lời giải
G󰉭i
là góc t󰉗o b󰉷󰉼󰉶ng th󰉠ng
ID
và m󰉢t ph󰉠ng
ICB
,
H
là tr󰉭ng tâm tam giác
ACD
. Ta có:
;;
3
sin .
2
d D ICB d H ICB
ID ID

.
G󰉭i
E
là hình chi󰉦u c󰉻a
H
lên
CB
,
K
là hình chi󰉦u c󰉻a
H
lên
IE
, ta ch󰉽  󰉼󰉹c
;d H ICB HK
.
Ta có:
22
2 2 1 1 5
;4
3 3 3 3 3
aa
HE DC D I D B a a
.
Mà
2 2 2 2
3 2 2A A A B AB a a a HI a

.
2
2 2 2
5 23
2
93
aa
DI DD D I a

2 2 2
2
.2
.2
3
;
11
22
9
a
a
HE HI a
d H ICB HK
HE HI a
9
sin
253

.
Trang53
www.thuvienhoclieu.com
ĐỀ 10
ĐỀ THI THỬ THPT QUỐC GIA 2021
MÔN TOÁN
Thời gian: 90 phút
Câu 1: [1D2-1.2-1] Lp 11A có
20
hc sinh nam và
25
hc sinh n. Có bao nhiêu cách chn mt
m
1
nam và
1
n?
A.
45
. B.
2
45
C
. C.
2
45
A
. D.
500
.
Câu 2: [1D3-3.3-1] Cho cp s cng
n
u
có s hu
1
2u
, công sai
3d
. S hng th
5
ca
n
u
bng
A.
14
. B.
10
. C.
162
. D.
30
.
Câu 3: [2H2-1.2-1] Din tích xung quanh ca hình tr  ng sinh
l

r
bng
A.
4 rl
. B.
2 rl
. C.
rl
. D.
1
3
rl
.
Câu 4: [2D1-1.2-1] Cho hàm s
( )
fx
có bng bi
Hàm s nghch bin trên kho
A.
0;4
. B.
;1
. C.
1;1
. D.
0;2
.
Câu 5: [2H1-3.2-1]Cho hình hnh bng
a
và chiu cao
3a
. Th tích ca
hình hng
A.
3
a
. B.
3
3a
. C.
3
9a
. D.
3
1
3
a
.
Câu 6: [2D2-5.1-1] 
48
2021 1
x
có nghim là
A.
7
4
x
. B.
2x 
. C.
9
4
x
. D.
2x
.
Câu 7: [2D3-2.1-1] Nu
2
1
d5f x x
và
2
1
2 d 13f x g x x


thì
2
1
dg x x
bng
A.
3
. B.
1
. C.
1
. D.
3
.
Câu 8: [2D1-1.2-1] Cho hàm s
y f x
có bng bi
Trang54
Kh
A. Hàm s t cc tiu ti
4x 
.
B. m ci c th hàm s là
0x
.
C. Giá tr cc tiu ca hàm s bng
1
.
D.m ci c th hàm s là
0; 3A
.
Câu 9: [2D1-5.1-1]  th ca hàm s 
A.
2
21y x x
. B.
3
21y x x
. C.
42
21y x x
. D.
3
21y x x
.
Câu 10: [2D2-3.2-1] Vi s th
a
tùy ý,
3
log a
bng
A.
3
2 log a
. B.
3
1
log
2
a
. C.
3
2log a
. D.
3
1
log
2
a
.
Câu 11: [2D3-1.1-1] H tt c các nguyên hàm ca hàm s
2
sin 6f x x x
là
A.
3
cos 2x x C
. B.
3
cos 2x x C
. C.
3
cos 18x x C
. D.
3
cos 18x x C
.
Câu 12: [2D4-1.1-1] Gi
z
là s phc liên hpca s phc
34zi
. Tìm phn thc và phn o ca
s phc
z
.
A. S phc
z
có phn thc bng
3
và phn o bng
4
.
B. S phc
z
có phn thc bng
3
và phn o bng
4
.
C.S phc
z
có phn thc bng
3
và phn o bng
4
.
D. S phc
z
có phn thc bng
3
và phn o bng
4
.
Câu 13: [2H3-1.1-1] Trong không gian
Oxyz
, hình chiu vuông góc c m
1;2;3A
trên mt
phng
Oyz
có tlà
A.
0;2;3
. B.
1;0;3
. C.
1;0;0
. D.
0;2;0
.
Câu 14: [2H3-1.3-1] Trong không gian
Oxyz
      
2 2 2
: 2 4 6 0S x y z x y
là
A.
2;4;0
. B.
1;2;0
. C.
1;2;3
. D.
2;4;6
.
Trang55
Câu 15: [2H3-2.2-1] Trong không gian
Oxyz
, cho mt phng
:
2 3 1 0xz
. 
là mn ca
?
A.
2;3; 1n 
. B.
2;3;0n
. C.
2;0; 3n
. D.
2;0; 3n 
.
Câu 16: [2H3-3.3-1] Trong không gian
Oxyz
ng thng
12
:3
3
xt
d y t
zt


?
A.
1;3;0M
. B.
1;3;3N
. C.
2; 1;0P
. D.
2; 1;3Q
.
Câu 17: [1H3-3.3-2] Cho hình chóp
.S ABCD

O
,
ABD
u cnh
2a
,
SA
vuông góc vi mt ph
32
2
a
SA
(minh h
Góc ging thng
SO
và mt phng
ABCD
bng
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 18: [2D1-2.2-2] Cho hàm s
y f x
, bng xét du ca
fx

S m cc tiu ca hàm s 
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 19: [2D1-3.1-2] 
42
10 1f x x x

3;2

A.
1
. B.
23
. C.
24
. D.
8
.
Câu 20: [2D2-3.2-2] 
a
và
b

2
3 27
log loga a b


A.
2
ab
. B.
3
ab
. C.
ab
. D.
2
ab
.
Câu 21: [2D2-6.2-2] 
2
log log
99
9 18
xx
x
là
A.
1;9
. B.
1
;9
9



. C.
0;1 9;
. D.
1
0; 9;
9


.
Câu 22: [2H2-2.1-2] Cho mt cu
S
. Bit rng khi ct mt cu
S
bi mt mt phng cách tâm mt
kho dài là
3
c giao tuyng tròn
T
có chu vi là
12
. Din tích ca
mt cu
S
bng
Trang56
A.
180
. B.
180 3
. C.
90
. D.
45
.
Câu 23: [2D1-5.3-2] Cho hàm s bc ba
fx
 th . S giá tr nguyên ca tham s
m
 
1f x m
có
3
nghim phân bit là
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 24: [2D3-1.1-2] 
2
1
cos
x
x
e
ye
x




là
A.
tan
x
e x C
. B.
tan
x
e x C
. C.
1
cos
x
eC
x

. D.
1
cos
x
eC
x

.
Câu 25: [2D2-4.1-2] Tìm tnh ca hàm s
2
log 3xx
ye

.
A.
D
. B.
0;3D
.
C.
3;D 
. D.
;0 3;D 
Câu 26: [2H1-3.2-2] Cho kh   ng
.ABCD A B CD
     bình hành cnh
AB a
,
3AD a
,
120BAD 
và
2AB a
(minh h    ). Th tích ca
kh ng
A.
3
33
2
a
. B.
3
33
4
a
. C.
3
33
6
a
. D.
3
3a
.
Câu 27: [2D1-4.1-2] Gi
k
và
l
lt là s ng tim cn ngang và s ng tim cng ca
 th hàm s
2
1
x
y
xx
. Kh
A.
0k
;
2l
. B.
1k
;
2l
. C.
1k
;
1l
. D.
0k
;
1l
.
Câu 28: [2D1-5.1-2] Cho hàm s
42
y ax bx c
,
,,abc
 th  nh
 
Trang57
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
Câu 29: [2D3-3.1-2] Hãy tính din tích phm trong hình v 
A.
4
3
. B.
3
4
. C. 1. D.
2
.
Câu 30: [2D4-2.2-2] Cho
1
42zi
. Hãy tìm phn o ca s phc
2
21
12z i z
.
A.
6i
. B.
2i
. C.
2
. D.
6
.
Câu 31: [2D4-2.4-2] Cho s phc
,z x yi x y
có phn thc khác 0. Bit s phc
2
2w iz z
là s thun o. Tp hm biu din ca
z
là mng thi

A.
0;1M
. B.
2; 1N
. C.
1;3P
. D.
1;1Q
.
Câu 32: [2H3-1.1-2] Trong không gian
Oxyz
   
2;1;2a 
,
1; 1;0b 
. Tích vô
ng
.a b b
bng
A.
3
. B.
1
. C.
5
. D.
12
.
Câu 33: [2H3-3.7-2] Trong không gian
Oxyz
  ng thng
12
:
2 2 1
x y z
và mt phng
:2 3 0P x y z
. Gi
S
là mt cu có tâm
I
thuc
và tip xúc vi
P
tm
1; 1;0H
. a
S
là
A.
2 2 2
3 2 1 36x y z
. B.
2 2 2
3 2 1 36x y z
.
C.
2 2 2
3 2 1 6x y z
. D.
2 2 2
3 2 1 6x y z
.
Trang58
Câu 34: [2H3-2.3-2] Trong không gian
Oxyz
, mt phm
1;2;3M
và song song vi mt
phng
: 2 3 0P x y z

A.
2 3 0x y z
. B.
230x y z
.
C.
20x y z
. D.
2 8 0x y z
.
Câu 35: [2H3-3.1-1] Trong không gian
Oxyz
ng thng
21
:
1 2 1
x y z
d


nh
 
A.
1
1;2;1u
. B.
2
2;4;2u
. C.
3
2; 4;2u
. D.
4
1;2;1u 
.
Câu 36: [1D2-5.2-3] Gi
S
là tp hp các s t nhiên có
4
ch s khác nhau. Chn ngu nhiên mt s
t tp
S
. Tìm xác su s c chn có các ch s sp xp theo th t n và không
cha hai ch s nguyên nào liên tip nhau.
A.
1
36
. B.
2
3
. C.
5
63
. D.
5
1512
.
Câu 37: [1H3-5.4-3] Cho hình chóp
.S ABCD
 
ABCD
là hình thang vuông ti
A
và
D
,
3 , .AB a AD DC a
Gi
I
m ca
AD
, bit hai mt phng
SBI
và
SCI
cùng vuông góc vt phng
SBC
to vt góc
0
60 .
Gi
M
m trên
AB
sao cho
2AM a
, tính khong cách gia
MD
và
SC
.
A.
17
5
a
. B.
15
10
a
. C.
6
19
a
. D.
3
15
a
.
Câu 38: [2D3-2.4-3] Cho hàm s
fx
có
2
2
f



và
sinf x x x
.
Gi s rng
2
2
0
cos . d
a
x f x x
bc

(vi
,,abc
là các s 
a
b
ti gin).

abc
bng
A.
23
. B.
5
. C.
20
. D.
27
.
Câu 39: [2D1-1.3-3] Cho hàm s
1 2 3 1
()
2
23
mx
fx
x
m
(
0m
và là tham s thc). Tp hp
m

hàm s ch bin trên khong
1
;1
2



có dng
; ; ;S a b c d 
, vi
, , ,a b c d
là các s thc. Tính
P a b c d
.
A.
3-
. B.
1-
. C.
0
. D.
2
.
Câu 40: [2H2-1.1-3] 
S

O
. Mt mt phnh ca
hình nón và ct hình nón theo thit din là tam giác vuông có din tích bng
4
. 
thit din 
30
. Th tích ca khc gii hn
bng
A.
5
. B.
10 2
3
. C.
83
3
. D.
53
3
.
Câu 41: [2D2-5.3-3] Cho các s thc
,,abc
thuc khong
1; 
và tha mãn
Trang59
2
2
log log .log 9log 4log
b b a a
a
c
b c c b
b



. Giá tr ca biu thc
2
log log
ab
bc
bng:
A.
1
. B.
1
2
. C.
2
. D.
3
.
Câu 42: [2D1-3.1-3] Cho hàm s bc bn
y f x
 th  bên.
Có bao nhiêu giá tr nguyên ca tham s
m
thun
0;20
sao cho giá tr nh nht ca hàm
s
2 4 ( ) 3g x f x m f x
n
2;2

1
?
A.
18
. B.
19
. C.
20
. D.
21
.
Câu 43: [2D2-5.5-3]   
2
3 3 3
log 4log 5 log 1x x m x

m
   

m

27;
.
A.
02m
. B.
02m
. C.
01m
. D.
01m
.
Câu 44: [2D3-2.4-3] Cho hàm s
fx
o hàmliên tctrên
tho mãn
21
x
f x f x x e
và
02f 
. Tng tt c các nghim thc c
0fx
có giá trlà
A.
2
. B.
2
. C.
1
. D.
1
.
Câu 45: [2D1-5.3-3] Cho hàm s
y f x
liên tc trên
 th . Tng tt c giá tr
nguyên ca tham s
m
 
2 cosf f x m
có nghim
;.
2
x


A.
1
. B.
0
. C.
1
. D.
2
.
1
1
2
2
O
y
1
2
x
1
2
Trang60
Câu 46: [2D1-2.6-4] Cho hàm s  c bc bn
y f x
        
3, 3, 5 x x x
           
m
   
32
3

xx
g x f e m

7

A.
3
B.
4
C.
5
D.
6
Câu 47: [2D2-5.5-4] Có tt c bao nhiêu cp s
;ab
vi
,ab
là các s   a mãn:
3
22
3
log 3 3 1 1a b a b a b ab a b
.
A.
2
. B.
3
. C.
1
. D. vô s.
Câu 48: [2D3-2.4-4] Cho hàm s
fx


43
2
2 2 4 4
1 2 , 0, 1



x x x x
x f x f x x
xx

1
1
d
f x x

A.
0
. B.
1
. C.
1
2
. D.
3
2
.
Câu 49: [2H1-3.2-4] Cho hình chóp
.S ABC
    
ABC
có
;2AB a AC a
và
135CAB 
, tam giác
SAB
vuông ti
B
và tam giác
SAC
vuông ti
A
. Bit góc gia hai mt
phng
SAC
và
SAB
bng
30
. Tính th tích khi chóp
.S ABC
.
A.
3
6
a
. B.
3
3
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Câu 50: [2D1-1.3-4] Cho hàm s
y f x
và
0, f x x
. Bit hàm s
y f x
có bng bin
 và
1 137
2 16



f
.
Có bao nhiêu giá tr nguyên ca
2021; 2021m
 hàm s
2
45
.
x mx
g x e f x
ng
bin trên
1
1;
2



.
A.
4040
. B.
4041
. C.
2020
. D.
2021
.
HẾT
HƯỚNG DẦN GIẢI CHI TIẾT
Câu 1. [1D2-1.2-1] Lp 11A có
20
hc sinh nam và
25
hc sinh n. Có bao nhiêu cách chn m
song ca gm
1
nam và
1
n?
A.
45
. B.
2
45
C
. C.
2
45
A
. D.
500
.
Lời giải
Chọn D
 chc mm mt nam và mt n ta thc hin liên tin:
Trang61
Công đoạn 1: Chn
1
hc sinh nam t
20
hc sinh nam
có
20
cách chn.
Công đoạn 2: Chn
1
hc sinh n t
25
hc sinh na
có
25
cách chn.
Theo quy tc nhân ta có
20.25 500
cách chn.
Câu 2. [1D3-3.3-1] Cho cp s cng
n
u
có s hu
1
2u
, công sai
3d
. S hng th
5
ca
n
u
bng
A.
14
. B.
10
. C.
162
. D.
30
.
Lời giải
S hng tng quát ca cp s cng có s hu
1
u
và công sai bng
d
là
1
1
n
u u n d
.
Vy
51
4 2 4.3 14u u d
.
Câu 3. [2H2-1.2-1] Din tích xung quanh ca hình tr  ng sinh
l

r
bng
A.
4 rl
. B.
2 rl
. C.
rl
. D.
1
3
rl
.
Lời giải
Chọn B
Din tích xung quanh ca hình tr  ng sinh
l

r
là
2
xq
S rl
.
Câu 4. [2D1-1.2-1] Cho hàm s
( )
fx
có bng bi
Hàm s nghch bin trên kho
A.
0;4
. B.
;1
. C.
1;1
. D.
0;2
.
Lời giải
Chọn C
Da vào bng bin thiên, hàm s nghch bin trên khong
( )
1;1-
.
Câu 5. [2H1-3.2-1]Cho hình hnh bng
a
và chiu cao
3a
. Th tích ca
hình hng
A.
3
a
. B.
3
3a
. C.
3
9a
. D.
3
1
3
a
.
Lời giải
Th tích ca hình h
23
. .3 3V B h a a a
.
Câu 6. [2D2-5.1-1] 
48
2021 1
x
có nghim là
A.
7
4
x
. B.
2x 
. C.
9
4
x
. D.
2x
.
Lời giải
Chọn D
Ta có
4 8 4 8 0
2020 1 2020 2020 4 8 0 2
xx
xx

.
Vm
2x
.
Trang62
Câu 7. [2D3-2.1-1] Nu
2
1
d5f x x
và
2
1
2 d 13f x g x x


thì
2
1
dg x x
bng
A.
3
. B.
1
. C.
1
. D.
3
.
Lời giải
Chọn D
Ta có
2
1
2 d 13f x g x x


22
11
2. d d 13f x x g x x

22
11
d 13 2. dg x x f x x

2
1
d 13 2.5g x x
2
1
d3g x x
.
Vy
2
1
d3g x x
.
Câu 8. [2D1-1.2-1] Cho hàm s
y f x
có bng bi
Kh
A. Hàm s t cc tiu ti
4x 
.
B. m ci c th hàm s là
0x
.
C. Giá tr cc tiu ca hàm s bng
1
.
D. m ci c th hàm s là
0; 3A
.
Lời giải
Chọn D
Da vào bng bin thiên ta thy m ci c th hàm s là
0; 3A
n D.
Câu 9. [2D1-5.1-1]  th ca hàm s 
A.
2
21y x x
. B.
3
21y x x
. C.
42
21y x x
. D.
3
21y x x
.
Lời giải
Chọn B
+) T  th hàm s trên, ta th th là dng ca hàm bc ba nên loA, C.
+) T  th hàm s trên, ta thy gii hn ca hàm s khi
x
là

nên h s ca
3
x
D.
Trang63
V
Câu 10. [2D2-3.2-1] Vi s th
a
tùy ý,
3
log a
bng
A.
3
2 log a
. B.
3
1
log
2
a
. C.
3
2log a
. D.
3
1
log
2
a
.
Lời giải
Chọn D
Vi
a
là s th
1
2
3 3 3
1
log log log
2
a a a
.
Câu 11. [2D3-1.1-1] H tt c các nguyên hàm ca hàm s
2
sin 6f x x x
là
A.
3
cos 2x x C
. B.
3
cos 2x x C
. C.
3
cos 18x x C
. D.
3
cos 18x x C
.
Lời giải
Chọn A
Ta có
2 2 3
d sin 6 d sin d 2 3 d cos 2f x x x x x x x x x x x C
.
Câu 12. [2D4-1.1-1] Gi
z
là s phc liên hpca s phc
34zi
. Tìm phn thc và phn o ca
s phc
z
.
A. Sphc
z
có phn thc bng
3
và phn o bng
4
.
B. S phc
z
có phn thc bng
3
và phn o bng
4
.
C.S phc
z
có phn thc bng
3
và phn o bng
4
.
D. S phc
z
có phn thc bng
3
và phn o bng
4
.
Lời giải
Chọn C
S phc
34zi
có s phc liên hp là
34zi
.
Vy s phc
z
có phn thc bng
3
và phn o bng
4
.
Câu 13. [2H3-1.1-1] Trong không gian
Oxyz
, hình chiu vuông góc c m
1;2;3A
trên mt
phng
Oyz
có tlà
A.
0;2;3
. B.
1;0;3
. C.
1;0;0
. D.
0;2;0
.
Lời giải
Chọn A
Theo lý thuyt ta có : hình chiu vuông gócc m
;;M x y z
lên mt phng
Oyz
là
0; ;M y z
suy rahình chiu vuông góc cm
1;2;3A
trên mt phng
Oyz
có tlà
0;2;3
.
Câu 14. [2H3-1.3-1] Trong không gian
Oxyz
      
2 2 2
: 2 4 6 0S x y z x y
là
A.
2;4;0
. B.
1;2;0
. C.
1;2;3
. D.
2;4;6
.
Lời giải
Chọn B
Ta có
22
2
: 1 2 11S x y z
nên t tâm mt cu là
1;2;0
.
Câu 15. [2H3-2.2-1] [Mức độ 1] Trong không gian
Oxyz
, cho mt phng
:
2 3 1 0xz

n ca
?
A.
2;3; 1n 
. B.
2;3;0n
. C.
2;0; 3n
. D.
2;0; 3n 
.
Lời giải
Chọn C
Mt phng
0ax by cz d
n dng
; ; , , 0n ka kb kc k k
.
Trang64
Suy ra
có mn là
2;0; 3n
.
Câu 16. [2H3-3.3-1] Trong không gian
Oxyz
ng thng
12
:3
3
xt
d y t
zt


?
A.
1;3;0M
. B.
1;3;3N
. C.
2; 1;0P
. D.
2; 1;3Q
.
Lời giải
Chọn A
T ng thng
d
ta thng thm
1;3;0M
.
Câu 17. [1H3-3.3-2] Cho hình chóp
.S ABCD

O
,
ABD
u cnh
2a
,
SA
vuông góc vi mt ph
32
2
a
SA
(minh h
Góc ging thng
SO
và mt phng
ABCD
bng
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải
Chọn C
Do
SA ABCD
nên hình chiu ca
SO
lên mt phng
ABCD
là
AO
a
ng thng
SO
và mt phng
ABCD
là góc
SOA
.
ABD
u cnh
2a
nên
3 3 6
2.
2 2 2
a
AO AB a
.
SOA
vuông ti
A
có
32
2
a
SA
,
6
2
a
AO
nên
3 2 6
tan : 3 60
22
SA a a
SOA SOA
OA
.
Trang65
Vy góc ging thng
SO
và mt phng
ABCD
bng
60
.
Câu 18. [2D1-2.2-2] Cho hàm s
y f x
, bng xét du ca
fx

S m cc tiu ca hàm s 
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
  vào bng xét du ca
fx
ta thy
fx
i du t    ti các
m
1x 
và
1x
nên hàm s m cc tiu.
Câu 19. [2D1-3.1-2] Giá trị nhỏ nhất của hàm số
42
10 1f x x x
trên đoạn
3;2
bằng
A.
1
. B.
23
. C.
24
. D.
8
.
Lời giải
Chọn C
Hàm s
42
10 1f x x x
nh trên
3;2
.
Ta có
3
4 20f x x x

.
0 3;2
0 5 3;2 .
5 3;2
x
f x x
x
3 8; 5 24; 0 1; 2 23f f f f
.
Vy giá tr nh nht ca hàm s n
3;2
bng
24
ti
5x 
.
Câu 20. [2D2-3.2-2] Xét tất cả các số thực dương
a
và
b
thỏa mãn
2
3 27
log loga a b
. Mệnh đề nào dưới đây
đúng?
A.
2
ab
. B.
3
ab
. C.
ab
. D.
2
ab
.
Lời giải
Chọn D
Ta có
2
3 27
log loga a b
2
33
1
log log
3
a a b
2
33
3log loga a b
32
33
log loga a b
32
a a b
ab
2
ab
.
Câu 21. [2D2-6.2-2] 
2
log log
99
9 18
xx
x
là
A.
1;9
. B.
1
;9
9



. C.
0;1 9; 
. D.
1
0; 9;
9


.
Lời giải
Chọn B
2
log log
99
9 18 1
xx
x
.
u kin
0x
.
log .log log
9 9 9
1 9 18
x x x
x
9
9
log
log
log
9
9 18
x
x
x
x
log
9
2 18
x
x
log
9
9
x
x
9 9 9
log .log log 9xx
2
9
log 1x
9
1 log 1x
1
9
9
x
(tha mãn).
Trang66
Vy tp nghim ca b
1
;9
9
S



.
Câu 22. [2H2-2.1-2] Cho mt cu
S
. Bit rng khi ct mt cu
S
bi mt mt phng cách tâm mt
kho dài là
3
c giao tuyng tròn
T
có chu vi là
12
. Din tích ca
mt cu
S
bng
A.
180
. B.
180 3
. C.
90
. D.
45
.
Lời giải
Chọn A
A
J
I
Gi
I
là tâm mt cu
S
,
J
ng tròn
T
,
A
m thung tròn
T
ng tròn
T
là
r JA
,
3IJ
.
ng tròn
T
là
2 12Pr


6r
.
Gi
R
là bán kính mt cu thì
22
35R r IJ
.
Din tích mt cu
S
là
2
4 180SR


.
Vy
180S
.
Câu 23. [2D1-5.3-2] Cho hàm s bc ba
fx
 th . S giá tr nguyên ca tham s
m
 
1f x m
có
3
nghim phân bit là
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn D
+) Ta có
1f x m
1*f x m
.
+) S nghim c
*
bng s m c th hàm s
y f x
ng
thng
1ym
.
+) T  th ng thng
1ym
c th hàm s
y f x
tm phân bit khi
và ch khi
1 1 3 0 4mm
.
+) Vì
m
nên
1 ; 2 ;3m
.
Vy có 3 giá tr nguyên ca tham s
m
th bài.
Trang67
Câu 24. [2D3-1.1-2] 
2
1
cos
x
x
e
ye
x




là
A.
tan
x
e x C
. B.
tan
x
e x C
. C.
1
cos
x
eC
x

. D.
1
cos
x
eC
x

.
Lời giải
Chọn B
Ta có
22
1
1 d d tan
cos cos
x
x x x
e
e x e x e x C
xx







.
Câu 25. [2D2-4.1-2] Tìm tnh ca hàm s
2
log 3xx
ye

.
A.
D
. B.
0;3D
.
C.
3;D 
. D.
;0 3;D 
Lời giải
Chọn B
u kinh:
2
3 0 0 3x x x
.
Vy tnh ca hàm s là
0;3D
.
Câu 26. [2H1-3.2-2] Cho kh   ng
.ABCD A B CD
     bình hành cnh
AB a
,
3AD a
,
120BAD 
và
2AB a
(minh h    ). Th tích ca
kh ng
A.
3
33
2
a
. B.
3
33
4
a
. C.
3
33
6
a
. D.
3
3a
.
Lời giải
Chọn A
Din tích hình bình hành
ABCD
là
2
3
. .sin
2
ABCD
S AB AD BAD a
.
Tam giác
ABB
vuông ti
B
có
22
3BB AB AB a

.
Vy
23
.
3 3 3
. 3.
22
ABCD A B C D ABCD
V BB S a a a
.
Câu 27. [2D1-4.1-2] Gi
k
và
l
lt là s ng tim cn ngang và s ng tim cng c
th hàm s
2
1
x
y
xx
. Kh
A.
0k
;
2l
. B.
1k
;
2l
. C.
1k
;
1l
. D.
0k
;
1l
.
Lời giải
Chọn A
Trang68
Tnh
0;2 \ 1D
.
+ Do tnh ca hàm s là
0;2 \ 1D
nên không tn ti gii hn ca hàm s khi
x 
 th hàm s không có tim cn ngang.
+
1
1
2
lim lim
1
x
x
x
fx
xx


;
11
2
lim lim
1
xx
x
fx
xx



, suy ra
1x
là tim cn
ng c th hàm s.
+
00
2
lim lim
1
xx
x
fx
xx



, suy ra
0x
là tim cng c th hàm s.
 th hàm s ng tim cn ngang ng tim cng.
Vy
0k
;
2l
.
Câu 28. [2D1-5.1-2]Cho hàm s
42
y ax bx c
,
,,abc
 th  nh
 
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
Lời giải
Chọn B
+ D th ta có
0a
.
 th hàm s m cc tr suy ra
,ab
trái du, mà
0a
suy ra
0b
.
 th ct trc tung t âm, suy ra
0c
.
Vy
0a
,
0b
,
0c
.
Câu 29. [2D3-3.1-2] Hãy tính din tích phm trong hình v 
A.
4
3
. B.
3
4
. C. 1. D.
2
.
Lời giải
Chọn A
Cách 1: Ta có
2
1 0, 1;1xx
.
Trang69
n tích phm là
1
2
1
1dxSx

1
2
1
1 dxx

1
3
1
3
x
x




4
3
.
Cách 2: Công thc nhanh tính din tích
2
3
S Bh=
Áp dng công thc vi
2B =
,
1h=
ta có:
2 2 4
.2.1
3 3 3
S Bh= = =
.
Câu 30. [2D4-2.2-2] Cho
1
42zi
. Hãy tìm phn o ca s phc
2
21
12z i z
.
A.
6i
. B.
2i
. C.
2
. D.
6
.
Lời giải
Chọn C
Ta có
2
21
12z i z
3 4 4 2ii
12i
.
Vy phn o ca s phc
2
z
là
2
.
Câu 31. [2D4-2.4-2] Cho s phc
,z x yi x y
có phn thc khác 0. Bit s phc
2
2w iz z
là s thun o. Tp hm biu din ca
z
là mng thi

A.
0;1M
. B.
2; 1N
. C.
1;3P
. D.
1;1Q
.
Lời giải
Chọn D
Ta có
, ; 0z x yi x y x
Mt khác
2
2 2 2
2 2 2 2w iz z i x yi x yi x xy x y y i
.
Vì
w
là s thun o nên
0x xy

0 kh«ngtháa m·n ®iÒu kiÖn
1 0 (tháa m·n ®iÒu kiÖn)
x
y
.
Vy tp hm biu din s phc
z
ng th
10y 
(tr m
0;1M
ng thm
1;1Q
.
Câu 32. [2H3-1.1-2] Trong không gian
Oxyz

2;1;2a 
,
1; 1;0b 
ng
.a b b
bng
A.
3
. B.
1
. C.
5
. D.
12
.
Lời giải
Chọn C
Ta có
3;2;2 . 5a b a b b
.
Câu 33. [2H3-3.7-2] Trong không gian
Oxyz
  ng thng
12
:
2 2 1
x y z
và mt phng
:2 3 0P x y z
. Gi
S
là mt cu có tâm
I
thuc
và tip xúc vi
P
tm
1; 1;0H
a
S
là
A.
2 2 2
3 2 1 36x y z
. B.
2 2 2
3 2 1 36x y z
.
Trang70
C.
2 2 2
3 2 1 6x y z
. D.
2 2 2
3 2 1 6x y z
.
Lời giải
Chọn C
ng thng
12
:
2 2 1
x y z
c vit li là
12
: 2 ,
2
xt
y t t
zt


.
Theo gi thit
I 
1 2 ;2 ;2I t t t
.
Ta có
2 ;2 1; 2HI t t t
.
Mt phng
P
có mn là
2; 1;1n 
.
Vì mt cu
S
tip xúc vi
P
tm
H
nên
HI
và
n

Ta có
HI
và
n
     khi
2 2 1 2
2 1 1
t t t

21
2 1 2
tt
tt

1 3; 2;1tI
.
Bán kính mt cu
S
là :
2 2 2
1 3 1 2 0 1 6R IH
.
Vt cu
S
là :
2 2 2
3 2 1 6x y z
.
Câu 34. [2H3-2.3-2] Trong không gian
Oxyz
, mt phm
1;2;3M
và song song vi mt
phng
: 2 3 0P x y z

A.
2 3 0x y z
. B.
230x y z
.
C.
20x y z
. D.
2 8 0x y z
.
Lời giải
Chọn C
Gi
Q
là mt phm
1;2;3M
và song song vi mt phng
P
.
Vì
//QP
nên
Q
nhpháp tuyn
1; 2;1
P
n 
uuur
ca mt phng
P

pháp tuyn.
a mt phng
Q
là :
1. 1 2. 2 1. 3 0 2 0x y z x y z
.
Vy t phng
: 2 0Q x y z
.
Câu 35. [2H3-3.1-1] Trong không gian
Oxyz
ng thng
21
:
1 2 1
x y z
d


nh 
 
A.
1
1;2;1u
. B.
2
2;4;2u
. C.
3
2; 4;2u
. D.
4
1;2;1u 
.
Trang71
Lời giải
Chọn C
+) ng thng
d
có m  là
1;2; 1
d
u 
.
Mà
3
2
d
uu
suy ra
3
2; 4;2u
là m ng thng
d
.
Câu 36. [1D2-5.2-3] Gi
S
là tp hp các s t nhiên có
4
ch s khác nhau. Chn ngu nhiên mt s
t tp
S
. Tìm xác su s c chn có các ch s sp xp theo th t n và không
cha hai ch s nguyên nào liên tip nhau.
A.
1
36
. B.
2
3
. C.
5
63
. D.
5
1512
.
Lời giải
Chọn D
Xét phép thn ngu nhiên mt s t tp
S

S phn t ca không gian mu là:
3
9
9. 4536nA
.
Gi
A
là bin c c chn có các ch s sp xp theo th t n và không cha hai
ch s nguyên nào liên ti
Gi s c chn là
abcd
.
+) Vì ch s sp xp theo th t n nên:
19a b c d
.
+) Trong s c chn không cha hai ch s nguyên nào liên tip nhau nên:
1 1 2 3 6a b c d
.
t:
1
aa
;
1
1bb
;
1
2cc
;
1
3dd
.

1 1 1 1
16a b c d
.
S cách chn b bn s
1 1 1 1
;;;a b c d
là:
4
6
C
( cách)
có
4
6
C
cách chn
a
;
b
;
c
;
d
.
Mi cách chn
; ; ;a b c d
ch có mt cách sp xp tha mãn yêu cu bài toán nên to ra mt s.
Suy ra:
4
6
15n A C
.
Xác sut cn tìm là:
5
1512
nA
PA
n

Câu 37. [1H3-5.4-3] Cho hình chóp
.S ABCD
 
ABCD
là hình thang vuông ti
A
và
D
,
3 , .AB a AD DC a
Gi
I
m ca
AD
, bit hai mt phng
SBI
và
SCI
cùng vuông góc vt phng
SBC
to vt góc
0
60 .
Gi
M
m trên
AB
sao cho
2AM a
, tính khong cách gia
MD
và
SC
.
A.
17
5
a
. B.
15
10
a
. C.
6
19
a
. D.
3
15
a
.
Lời giải
a
2
a
E
I
M
A
B
D
C
S
K
H
Chọn B
Trang72
+) Theo gi thit ta có
()
( ) ( )
SBI
SCI
SBI
C
C
SCI
AB D
ABCD SI AB D
SI
+) V
IK BC BC SIK SKI
là góc gia mt phng
SBC
vi m
60SKI 
.
+) Vì
22
13
.,
2 4 4
IDC IAB
aa
S DI DC S

. Suy ra
2
-
BIC ABCD ICD IAB
S S S S a
.
+) Mt khác
2
2
5BC AB CD AD a
và
1
..
2
IBC
S IK BC
Suy ra
25
5
a
IK
+) Trong tam giác vuông
SIK
ta có
2a 15
.tan60
5
SI IK
.
+)Vì
2AM a=
nên
//BM a MD BC=Þ

( ) ( )
( )
( )
( )
, , ,d MD SC d MD SBC d D SBC==
.
+) Gi
E
m ca
AD
vi
BC
, ta có
11
32
ED DC
ED AD ID
EA AB
= = Þ = =
.

( )
( )
( )
( )
1
,,
2
d D SBC d I SBC=
.
+) Gi
H
là hình chiu ca
I
lên
SK
ta có
( )
( )
,d I SBC IH=
.
Trong tam giác vuông
SIK
, ta có:
2 2 2 2 2 2
1 1 1 5 5 5 15
.
12 4 3 5
a
IH
IH SI IK a a a
= + = + = Þ =
Vy
( )
15
,
10
a
d MD SC =
.
Nhận xét:  tính và , ta có th 
1)Tính : Ta có
. .2 2
( , ) ( ; )
55
AI AM a a a
IK d I BC d A DM
DM
a
.
2)Tính : Ta có
2 15
.sin .sin60
15
5 15
a a a
IH IK SKI
.
Câu 38. [2D3-2.4-3] Cho hàm s
fx
có
2
2
f



và
sinf x x x
.
Gi s rng
2
2
0
cos . d
a
x f x x
bc

(vi
,,abc
là các s 
a
b
ti gi
abc
bng
A.
23
. B.
5
. C.
20
. D.
27
.
Lời giải
Chọn D
Do
sinf x x x
nên
df x f x x
sin d dcosx x x x x

cos cos dx x x x
cos sinx x x C
.
Theo gi thit
2 1 2 1
2
f C C



.
Suy ra
sin cos 1f x x x x
.
Trang73
2 2 2
2
0 0 0
cos . d cos sin cos 1 d sin cos cos cos dx f x x x x x x x x x x x x x
2 2 2
0 0 0
11
sin2 d 1 cos2 d cos d
22
x x x x x x x
22
00
1 1 1
cos2 sin d dsin 2
22
4 2 4
00
x x x x x x



2 2 2
2
0
1 1 1 3 1 7
1 sin 2 sin 2 d cos2
2 2 2
2 4 4 4 2 16 8 4 16
0 0 0
x
x x x x x

.
Vy
7, 4, 16abc
. Suy ra
27abc
.
Câu 39. [2D1-1.3-3] Cho hàm s
1 2 3 1
()
2
23
mx
fx
x
m
(
0m
và là tham s thc). Tp hp
m

hàm s ch bin trên khong
1
;1
2



có dng
; ; ;S a b c d 
, vi
, , ,a b c d
là các s thc. Tính
P a b c d
.
A.
3-
. B.
1-
. C.
0
. D.
2
.
Lời giải
Chọn A
u kinh:
3
2
2
2 3 0
x
x
m
.
t
11
2 3 0, ;1
2
23
u x u x
x




, suy ra hàm s
23ux
nghch bin
trên khong
1
;1
2



.
Vi
1
;1 1; 2
2
xu



.
Yêu cu bài toán tr thành tìm
m
 hàm s
11
2
mu
gu
u
m


ng bin trên khong
1; 2 .
Ta có
2
2
11
2
,
2
m
m
g u u
m
u
m






.
Hàm s
gu
ng bin trên khong
1; 2
khi và ch khi
0, 1; 2
2
1; 2
g u u
m
Trang74
2
1 1 0
2
1
2
2
m
m
m
m
2
0
2
0
1
0
m
m
m
m
m
m
0
2
2
0
01
m
m
m
m
m



0
2
2
1
m
m
m
m



2
01
2
m
m
m

.
Vy
; 2 0;1 2;S 
2; 0; 1; 2a b c d
.

2 0 1 2 3P
.
Câu 40. [2H2-1.1-3] 
S

O
. Mt mt phnh ca hình
nón và ct hình nón theo thit din là tam giác vuông có din tích bng
4
. 
thit din 
30
. Th tích ca khc gii hn bi hình
ng
A.
5
. B.
10 2
3
. C.
83
3
. D.
53
3
.
Lời giải
Chọn D
Mt phnh ca hình nón và ct hình nón theo thit din là tam giác vuông
SAB
.
Gi
SA l
ng sinh,
OA R
là bán kính và
SO h
ng cao c
Gi
I
m ca
AB
và
K
là hình chiu ca
O
lên
SI
.
Góc ging cao ca hình nón và mt phng thit din là
; 30SO SAB OSK
.
SAB
vuông cân ti
S
nên
22
11
. 4 2 2
22
SAB
S SA l l
.
. 2 4AB l
ng trung tuyn
11
. .4 2
22
SI AB
.
vuông ti
O
:
3
cos .cos30 2. 3 3
2
SO
OSI SO SI h
SI
.
Ta có:
22
22
2 2 3 5R l h
.
Vy th tích ca khi nón là
2
1 1 5 3
.5. 3
3 3 3
V R h

.
Câu 41. [2D2-5.3-3] Cho các s thc
,,abc
thuc khong
1; 
và tha mãn
2
2
log log .log 9log 4log
b b a a
a
c
b c c b
b



. Giá tr ca biu thc
2
log log
ab
bc
bng:
A.
1
. B.
1
2
. C.
2
. D.
3
.
Lời giải
Chọn A
Trang75
Ta có:
2
2
log log .log 9log 4log
b b a a
a
c
b c c b
b



2
4log log . 2log log 9log 4log
a b b b a a
b c c b c b
22
4log 2log log 9log 4log *
a b b a a
b c c c b
.
t
log
log
a
b
bx
cy
(
,0xy
vì
, , 1abc
).
Ta có
log log .log
a a b
c b c xy
.
Thay vào
*
 c:
22
4 2 9 4x y y xy x
22
4 8 2 4 0x xy xy y x y
4 2 1 0x y x y


4 0 ¹
21
x y lo i
xy
.
Vy
2
log log log 2log 2 1
a b a b
b c b c x y
.
Câu 42. [2D1-3.1-3] Cho hàm s bc bn
y f x
 th  bên.
Có bao nhiêu giá tr nguyên ca tham s
m
thun
0;20
sao cho giá tr nh nht ca hàm
s
2 4 ( ) 3g x f x m f x
n
2;2

1
?
A.
18
. B.
19
. C.
20
. D.
21
.
Lời giải
Chọn B
Da vào hình v ta có:
2 ( ) 2, 2;2f x x
*
.
2 4 0, 2;2f x x
.
Vì
0;20m
nên
2 4 0f x m
suy ra
2 4 2 4, 2;2f x m f x m x
.
Ta có:
2 4 ( ) 3g x f x m f x
2 4 3f x m f x
1f x m
,
2;2x
.
+) Vi
0m
1g x f x
,
2;2x
.
*
1 1 3, 2;2f x x
.
0 1 3, 2;2f x x
0 3, 2;2g x x
.
2;2
0min g x
0m
không tha yêu cu bài toán.
+) Vi
1;20m
1 0 1f x m g x f x m
.
Trang76
T
*
ta có:
11f x m m
2;2
1ming x m
.
Yêu cu bài toán:
2;2
1min g x

1 1 2mm
2;20m
.
Vy có
19
giá tr nguyên ca tham s
m
tha yêu cu bài toán.
Câu 43. [2D2-5.5-3]   
2
3 3 3
log 4log 5 log 1x x m x

m
   

m

27;
.
A.
02m
. B.
02m
. C.
01m
. D.
01m
.
Lời giải
Chọn D

3
logtx

27 3xt
.

2
4 5 1 .t t m t
*

1
5
t
t

.

0m

2
4 5 0
, 5.
10
tt
t
t



0m
, ta có
2
4 5 0tt

1 ( )
.
5 ( )
t loaïi
t thoûamaõn

0m
thì
2
22
* 4 5 1t t m t
2 2 2 2
1 2 4 5 0m t m t m
. (**)

11mt


1m
, ta có (**)
22
1 1 5 0t m t m



2
2
1 ( )
5
1
t loaïi
m
t
m
.

22
22
56
5 0 1 1
11
mm
m
mm


0m
suy ra
01m
.

01m

[27; )
.
Câu 44. [2D3-2.4-3] Cho hàm s
fx
o hàmliên tc trên
tho mãn
21
x
f x f x x e
và
02f 
. Tng tt c các nghim thc c
0fx
có giá trlà
A.
2
. B.
2
. C.
1
. D.
1
.
Lời giải
Chọn D
Ta có
21
x
f x f x x e
. 2 1
x
f x f x e x


. . 2 1
xx
f x e f x e x

. 2 1
x
f x e x
2
. 2 1 d .
xx
f x e x x f x e x x C

(1).
Do
02f 
nên t (1) ta có
02
2. 0 0 2e C C
.

2
2.
x
f x x x e
.
22
0 2 . 0 2 0
x
f x x x e x x
1
2
x
x

.
Vy tng tt c các nghim thc c
0fx
là
1 2 1
.
Trang77
Câu 45. [2D1-5.3-3] Cho hàm s
y f x
liên tc trên
 th . Tng tt c giá tr
nguyên ca tham s
m
 
2 cosf f x m
có nghim
;.
2
x


A.
1
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn D
+) t
costx
, do
;
2
x


nên suy ra
1;0 .t 
Trên khong
1;0
hàm s nghch bin nên suy ra
Vi
1;0t 
thì
01f f t f
hay
0 2.ft
+) t
2 cosu f x
thì
2 , 0;2 .u f t u
 thành:
Tìm
m
 
f u m
có nghim
0;2 .u
 th ta thy rng vi
0;2u
thì
2;2 2 2.f u m
Vì
2; 1;0;1 .mm
Vy có 4 giá tr ca
.m
Tng các giá tr ca
m
tha mãn yêu cu bài toán là
2
.
Câu 46. [2D1-2.6-4] Cho hàm s  c bc bn
y f x
        
3, 3, 5 x x x
           
m
   
32
3

xx
g x f e m

7

A.
3
B.
4
C.
5
D.
6
Lời giải
Chọn D
Ta có
3 2 3 2
2 3 3
3 6 .


x x x x
g x x x e f e m
3 2 3 2
2 3 3
0 3 6 . 0


x x x x
g x x x e f e m
32
32
32
3
3
3
0
2
3
3
5


xx
xx
xx
x
x
em
em
em
32
32
32
3
3
3
0
2
3, 1
3, 2
5, 3



xx
xx
xx
x
x
em
em
em
.
1
1
2
2
O
y
1
2
x
1
2
Trang78
Hàm s
gx
có
7
 tng s nghii l, khác
0
và
2
ca

1 , 2 , 3
là
5
.
Xét hàm s
32
3
xx
h x e
có
32
23
36

xx
h x x x e
.
Ta có
0
0
2


x
hx
x
.


3

Trường hợp 1:

44
44
3 3 51,6
1 3 4 3 57,6



m e m e
m e m e
Do
m
nguyên nên
52;53;54;55;56;57m
.
Trường hợp 2:

44
44
5 5 49,6
1 3 2 3
0 3 1 3 4





m e m e
m e m e m
mm
.
Trường hợp 3:
Trang79

4
15
3 1
3 0


me
m
m
4
4 5 49,6
2
3
me
mm
m
.

6

m

Câu 47. [2D2-5.5-4] Có tt c bao nhiêu cp s
;ab
vi
,ab
là các s   a mãn:
3
22
3
log 3 3 1 1a b a b a b ab a b
.
A.
2
. B.
3
. C.
1
. D.vô s.
Lời giải
Chọn A
Cách 1:
Vi
,ab
là các s 
3
22
3
log 3 3 1 1a b a b a b ab a b
33
3 3 2 2
3
22
log 3 3 3 1
ab
a b ab a b a b ab ab a b
a b ab

3 3 3 3 2 2 2 2
33
log log 3 3 1a b a b a b ab a b ab


Xét hàm s:
3
logf t t t
trên
0;
.
1
' 1 0, 0
ln3
f t t
t
nên hàm s
ft
ng bin trên
0;
.

1
tr thành :
3 3 2 2 3 3 2 2 2 2
22
3 3 3 0
0*
30



f a b f a b ab a b a b ab a b ab a b
a b ab
ab
Do
*
, ab

*
vô nghim. Suy ra:
3ab
.
Mà
,ab
là các s 
*
2
03
1
03
3
1
,
2
a
a
b
b
ab
a
ab
b





Vy có hai cp s
;ab
tha mãn yêu cu bài toán.
Cách 2: (Vi
,ab
là các s 
3
22
3
3 3 2 2
3
22
3
log 3 3 1 1
log 3 3 3
3
log 3 1
3
a b a b a b ab a b
ab
a b ab a b a b ab ab a b
ab
a b ab a b
Trang80
ng hp 1:
2ab

3
2
1 log 4 3
3
ab
loi do
*
,ab
.
ng hp 2:
3
3 log 0
3
ab
ab
và
22
3 0, , *a b ab a b a b
nên
1
không xy ra.
ng hp 3:
3ab

1
tha mãn.
Mà
,ab
là các s 
2
1
1
2
a
b
a
b

.
Vy có hai cp s
;ab
tha mãn yêu cu bài toán.
Câu 48. [2D3-2.4-4] Cho hàm s
fx


43
2
2 2 4 4
1 2 , 0, 1



x x x x
x f x f x x
xx

1
1
d
f x x

A.
0
. B.
1
. C.
1
2
. D.
3
2
.
Lời giải
Chọn A
T gi thit suy ra
43
23
2 2 2 4 4
1



x x x x
f x f
x x x
Ta có:
2 2 2
43
23
1 1 1
2 2 2 4 4
1 d . d d
x x x x
f x x f x x
x x x



2 2 2
23
1 1 1
2 2 2 2 4 4
1 d 1 d 1 d

xx
f x x f x x
x x x x
11
2
2
00
2
42
dd
1
2




x
f t t f t t x
xx
01
10
d d 0

f t t f t t
1
1
d0

f t t
.
Vy
1
1
d0
f x x
.
Cách trắc nghiệm( Thy Hoàng Gia Hng)
Ta có :
43
2
2 2 4 4
1 2 , 0, 1
x x x x
x f x f x x
xx



43
2
2 2 4 4
1 2 , 0, 1
x x x x
x f x f x x
x x x



22
2 2 2 2
1 2 1 2 , 0, 1
xx
x f x f x x x x
xx

Chn
11
11
.d .d 0f x x f x x x x


.
Trang81
Câu 49. [2H1-3.2-4] Cho hình chóp
.S ABC
    
ABC
có
;2AB a AC a
và
135CAB 
, tam giác
SAB
vuông ti
B
và tam giác
SAC
vuông ti
A
. Bit góc gia hai mt
phng
SAC
và
SAB
bng
30
. Tính th tích khi chóp
.S ABC
.
A.
3
6
a
. B.
3
3
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Lời giải
Chọn A
Gi
D
là hình chiu vuông góc ca
S
xung mt phng
ABC
.
AB SB
AB SBD AB BD
AB SD
.
AC SA
AC SAD AC AD
AC SD
.
Tam giác
ABC
có
135 45CAB BAD
.
Tam giác
ABD
vuông ti
B
có
45BAD 
suy ra tam giác
ABD
vuông cân và
2AD a
.
T 
ACD
vuông cân ti
A
t giác
ABDC
là hình thang vuông ti
B
và
D
.
Trong mt phng
SBD
, h
DH SB H SB
. D chng minh
DH SAB
.
Trong mt phng
SAD
, h
DK SA K SA
. D chng minh
DK SAC
.
Gi
là góc gia hai mt phng
SAB
và
SAC
ta có:
, 30DH DK HDK
do tam
giác
DHK
vuông ti
H
.
t
SD x
,
0x
.
Tam giác
DHK
vuông ti
H
có
22
22
32
cos .
2
2.
HD ax a x
HDK
DK
ax
ax
2 2 2 2 2 2 2 2
6 2 2 6 6 8 4a x a x a x a x x a
.
3
.
1
. . . .sin
66
S ABC
a
V SD AB AC BAC
.
Vy th tích khi
.S ABC
bng
3
6
a
.
Câu 50. [2D1-1.3-4] Cho hàm s
y f x
và
0, f x x
. Bit hàm s
y f x
có bng bin
thiên  và
1 137
2 16



f
.
Trang82
Có bao nhiêu giá tr nguyên ca
2021; 2021m
 hàm s
2
45
.
x mx
g x e f x
ng
bin trên
1
1;
2



.
A.
4040
. B.
4041
. C.
2020
. D.
2021
.
Lời giải
Chọn D
Ta có
22
4 5 4 5
2 4 . . .

x mx x mx
g x x m e f x e f x
2
45
2 4 . .



x mx
g x x m f x f x e
.
Yêu cu bài toán
1
0, 1;
2



g x x
và
0gx
ch xy ra ti mt s hu hm
thuc
1
1;
2



.
1
2 4 . 0, 1;
2



x m f x f x x
(vì
2
45
0
x mx
e
)
1
2 4 , 1;
2
fx
x m x
fx



, ( vì
0, f x x
)
1
4 2 , 1;
2



fx
m x x
fx
*
.
Xét
1
2 , 1;
2



fx
h x x x
fx
. Ta có
2
2
.
2



f x f x f x
hx
fx
.
Mà
0
1
, 1;
2
0




fx
x
fx
2
2
.
1
0, 1;
2





f x f x f x
x
fx
.
T 
1
0, 1;
2



h x x
. Vy hàm s
hx
ng bin trên
1
1;
2



.
Bng bin thiên
Vu kin
*
1
1 1 225 225
2
4 4 2. 4
1
2 2 137 548
2






f
m h m m m
f
.
Trang83
Li có
2021;2021

m
m
1;2;3;...;2021m
.
Vy có
2021
giá tr nguyên ca
m
tha mãn yêu cu bài toán.
HẾT
| 1/83
| | Tải xuống

Có thể bạn quan tâm:

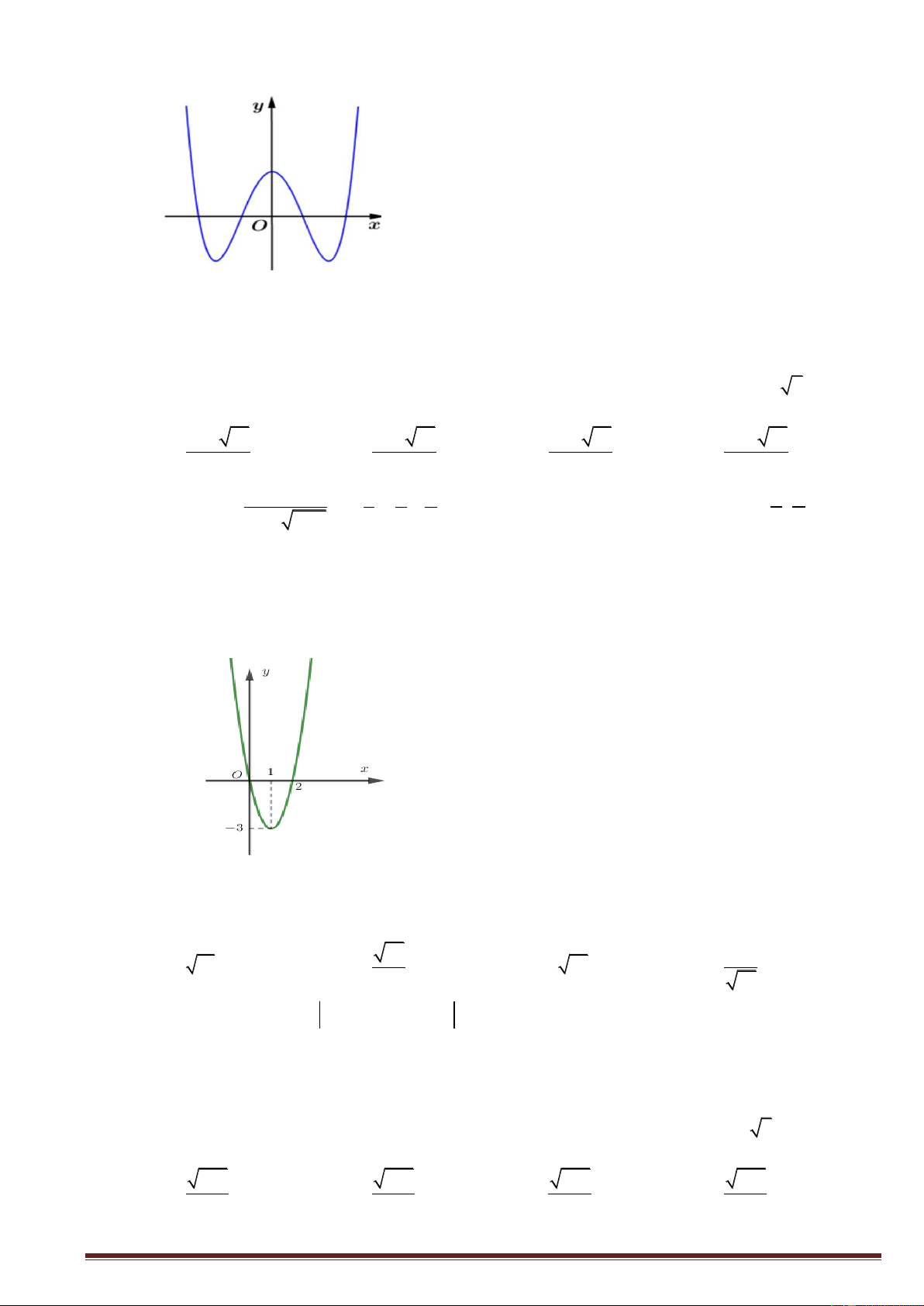
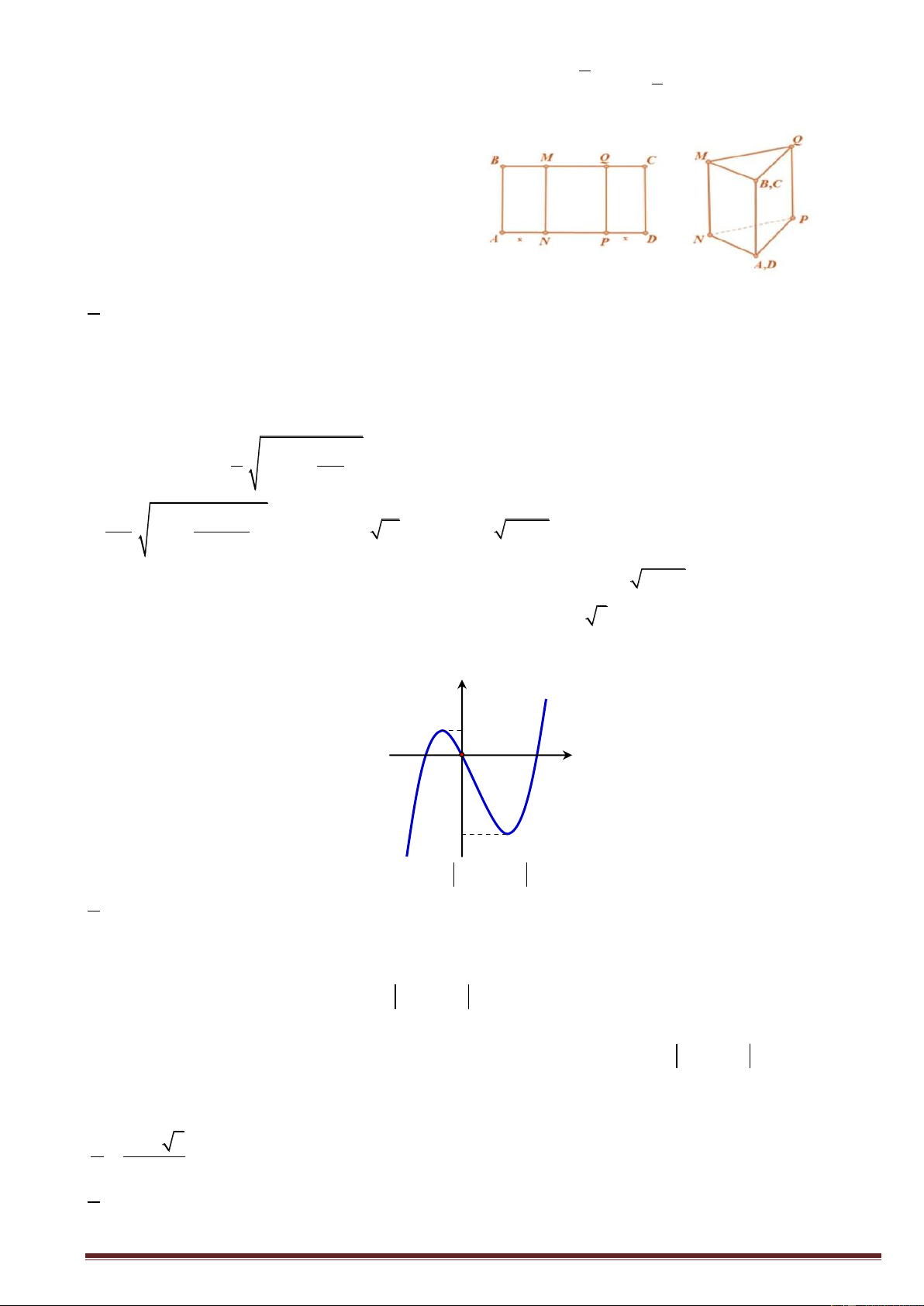
Preview text:


ĐỀ THI THỬ THPT QUỐC GIA 2021 ĐỀ 6 MÔN TOÁN Thời gian: 90 phút Câu 1.
Cho trước 5 chiếc ghế xếp thành một hàng ngang. Số cách xếp ba bạn ,
A B, C vào 5 chiếc ghế
đó sao cho mỗi bạn ngồi một ghế là A. 3 C . B. 6. C. 3 A . D.15. 5 5 Câu 2.
Cho cấp số cộng u có số hạng đầu u  2 và công sai d  3. Giá trị của u bằng n  1 5 A. 14 . B. 5 . C.11. D.15 . Câu 3. Phương trình 3x2 4
 16 có nghiệm là 3 4 A. x  .
B. x  5. C. x  . D. x  3. 4 3 Câu 4.
Khối chóp S.ABCD có đáy là hình thoi và SA  ( ABCD) có thể tích bằng 1 1 1 1 A. . SA . AB AD . B. S .
A AC.BD . C. S . A A . B AD . D. S . A AC.BD . 3 3 6 6 Câu 5. Hàm số y  log
2x  3 có tập xác định là 2   3  3  3 
A. D   . B. D  ;    .
C. D   \   . D. D  ;    . 2  2  2  Câu 6.
Tìm họ nguyên hàm của hàm số f x  cos x . 1 1 A. 2 cos x C.
B. sin x C .
C. sin x C . D. 2
 cos x C . 2 2 Câu 7.
Cho khối lăng trụ đứng có đáy là tam giác vuông, độ dài hai cạnh góc vuông là 3a, 4a và chiều
cao khối lăng trụ là 6a . Thể tích của khối lăng trụ bằng A. 3
V  27a . B. 3
V  12a . C. 3
V  72a . D. 3 V  36a . Câu 8.
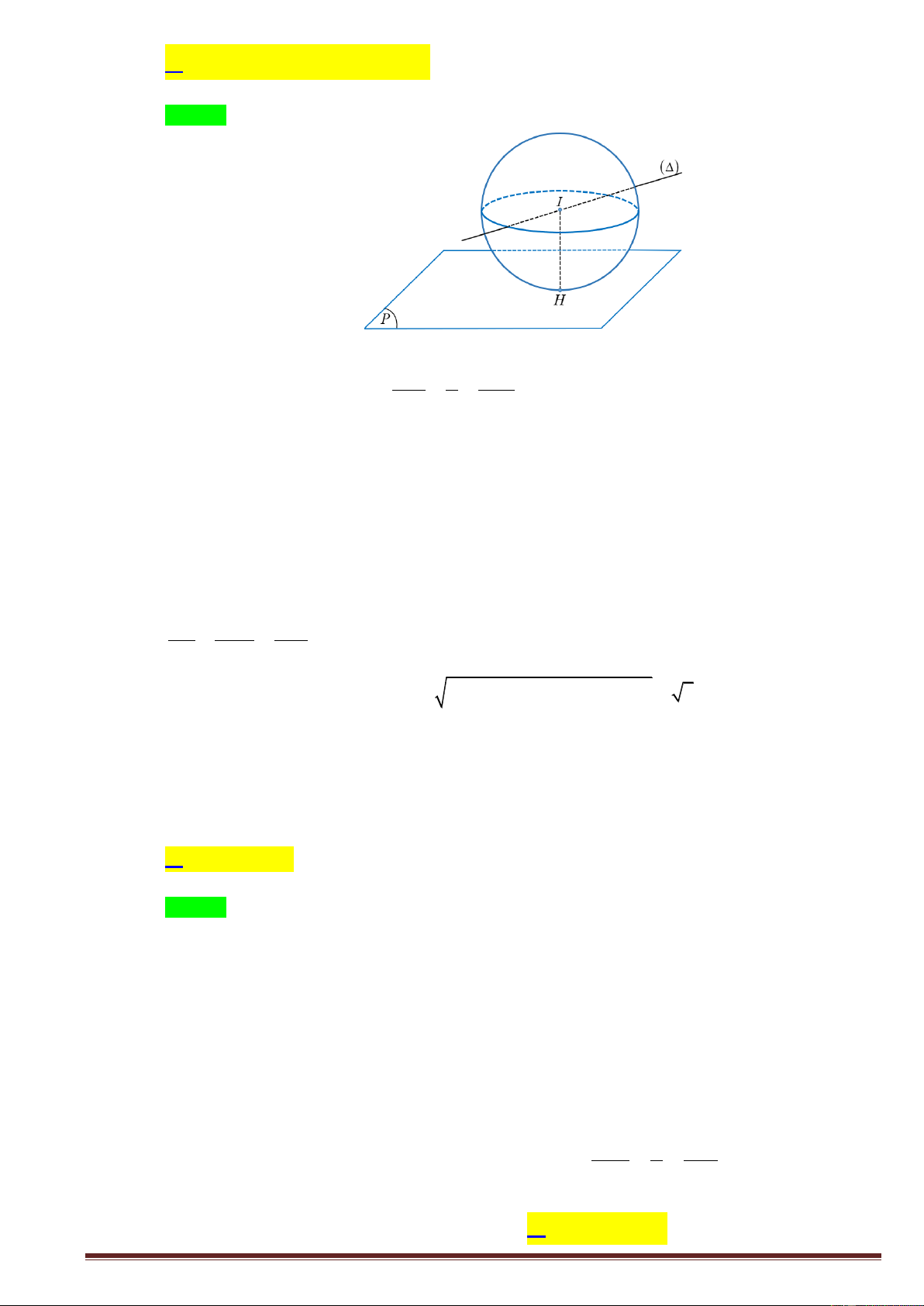
Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích của khối trụ đó là 8 .
A. h  2 . B. 2 2 . C. 3 32 . D. 3 4 . Câu 9.
Thể tích khối cầu có bán kính 6cm bằng A. 216 . B. 288 . C. 432 . D. 864 .
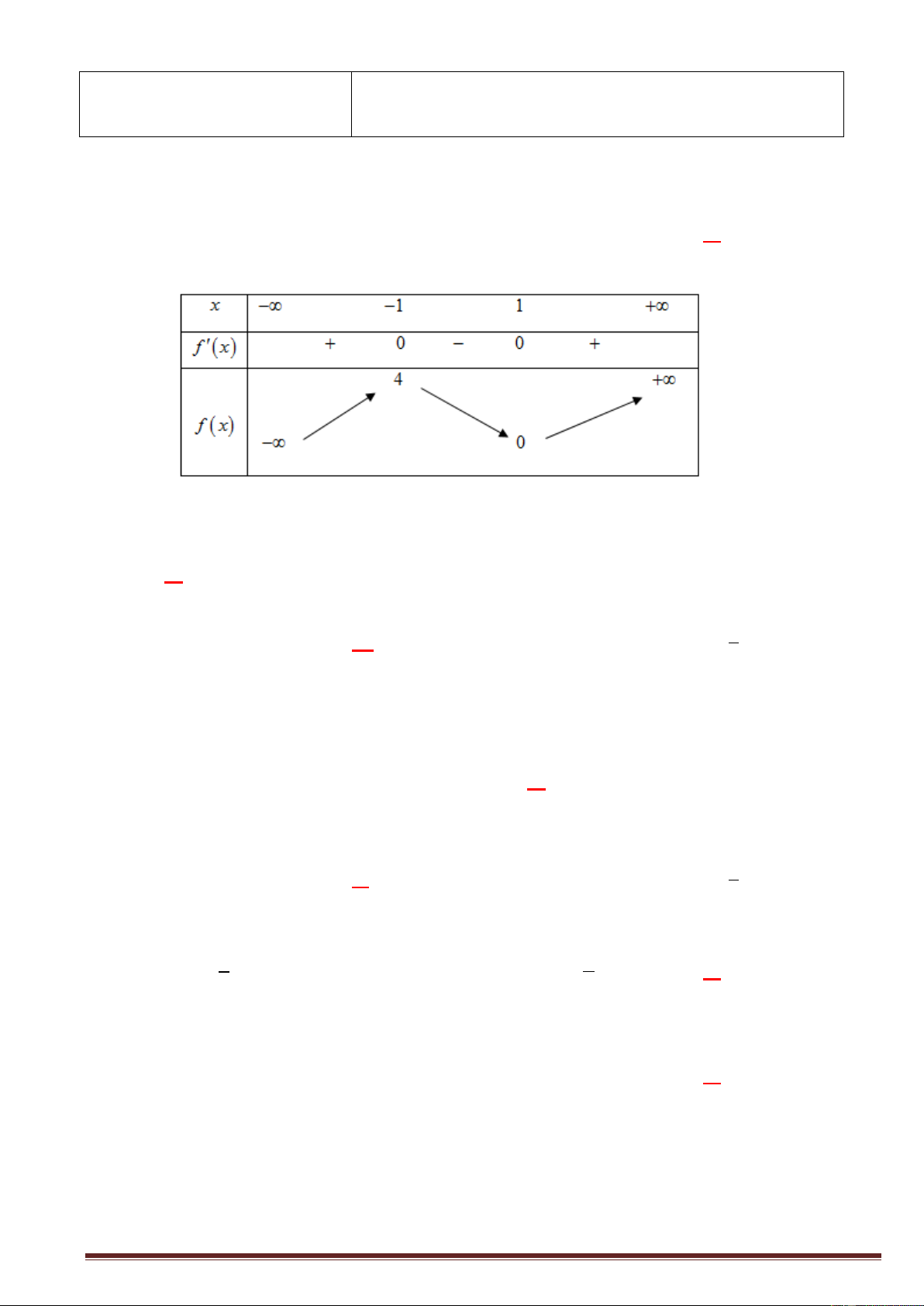
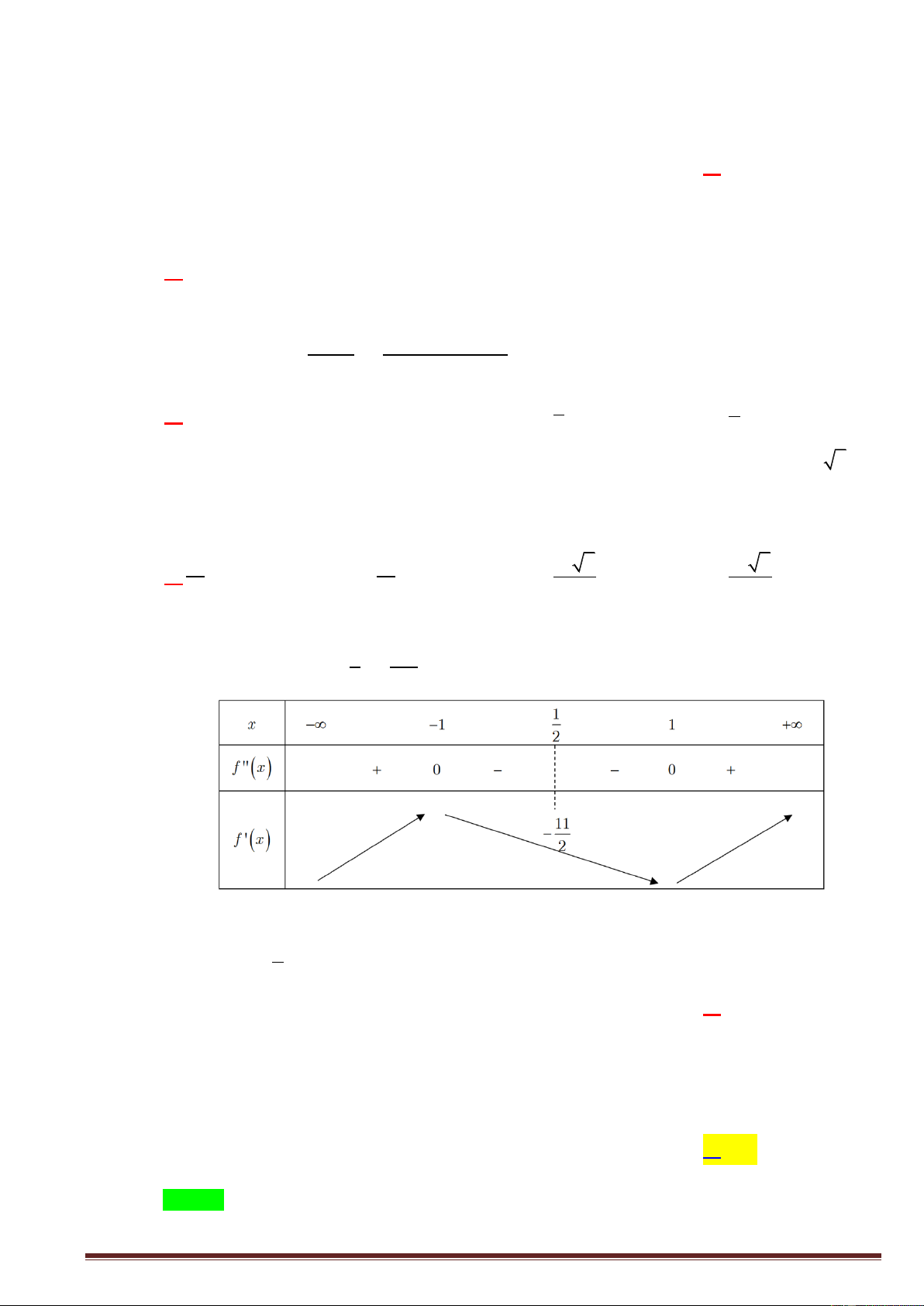
Câu 10. Cho hàm số y f x có bảng biến thiên như sau: x  2  0  y  0  0  y  2  2 
Hàm số y f x nghịch biến trên khoảng A.  2  ;0 .
B. 2;   . C.  2  ;2 .
D. ;  2 .
Câu 11. Với a;b là hai số dương tùy ý thì  3 2
log a b  có giá trị bằng biểu thức nào sau đây?  1  1 A. 3 log a  log b
 . B. 2log a  3logb . C. 3log a  log b .
D. 3log a  2 log b .  2  2
Câu 12. Cho khối nón có độ dài đường sinh bằng 10 và diện tích xung quanh bằng 60 . Thể tích của
khối nón đã cho bằng A. 360 . B. 288 . C.120 . D. 96 .
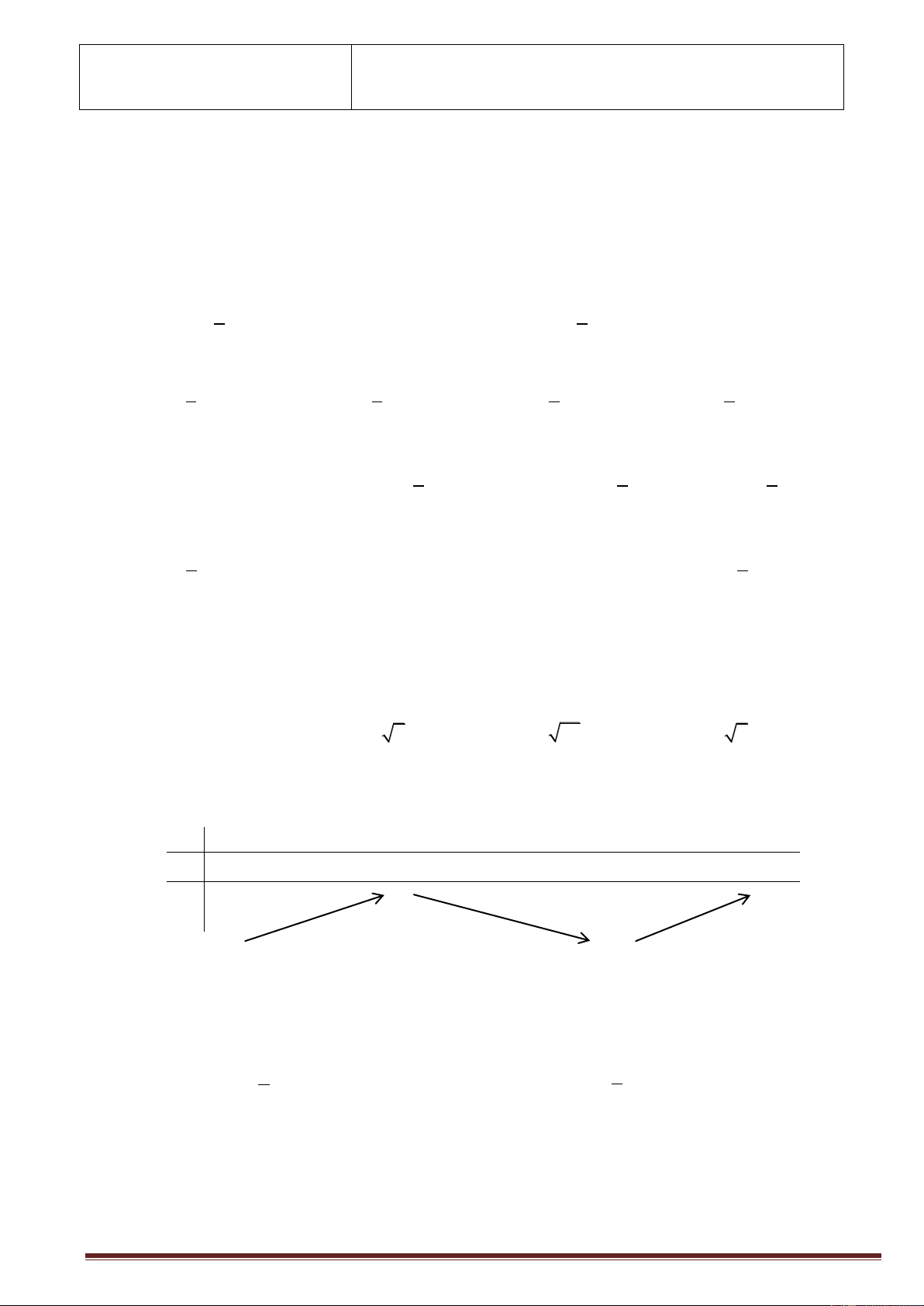
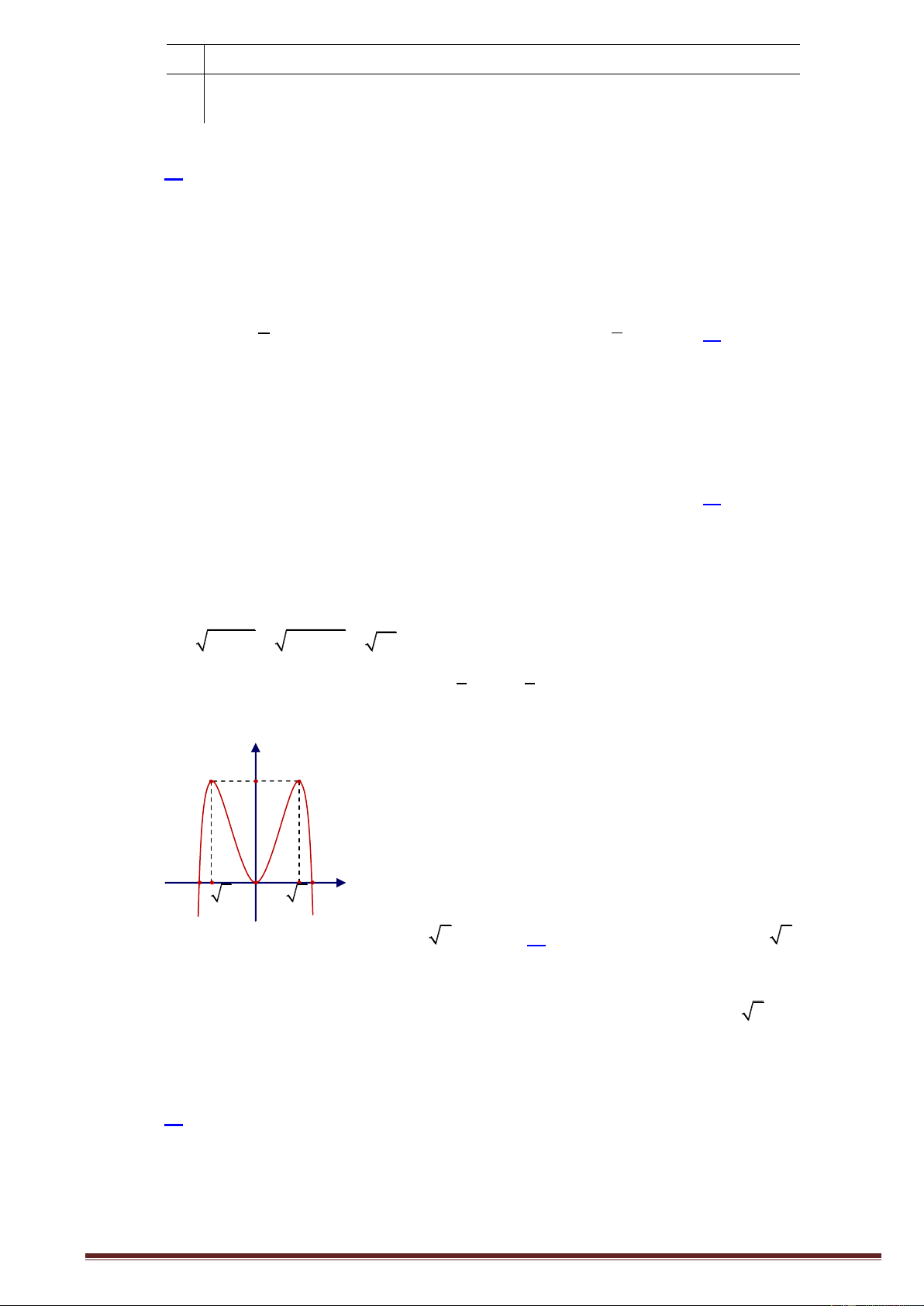
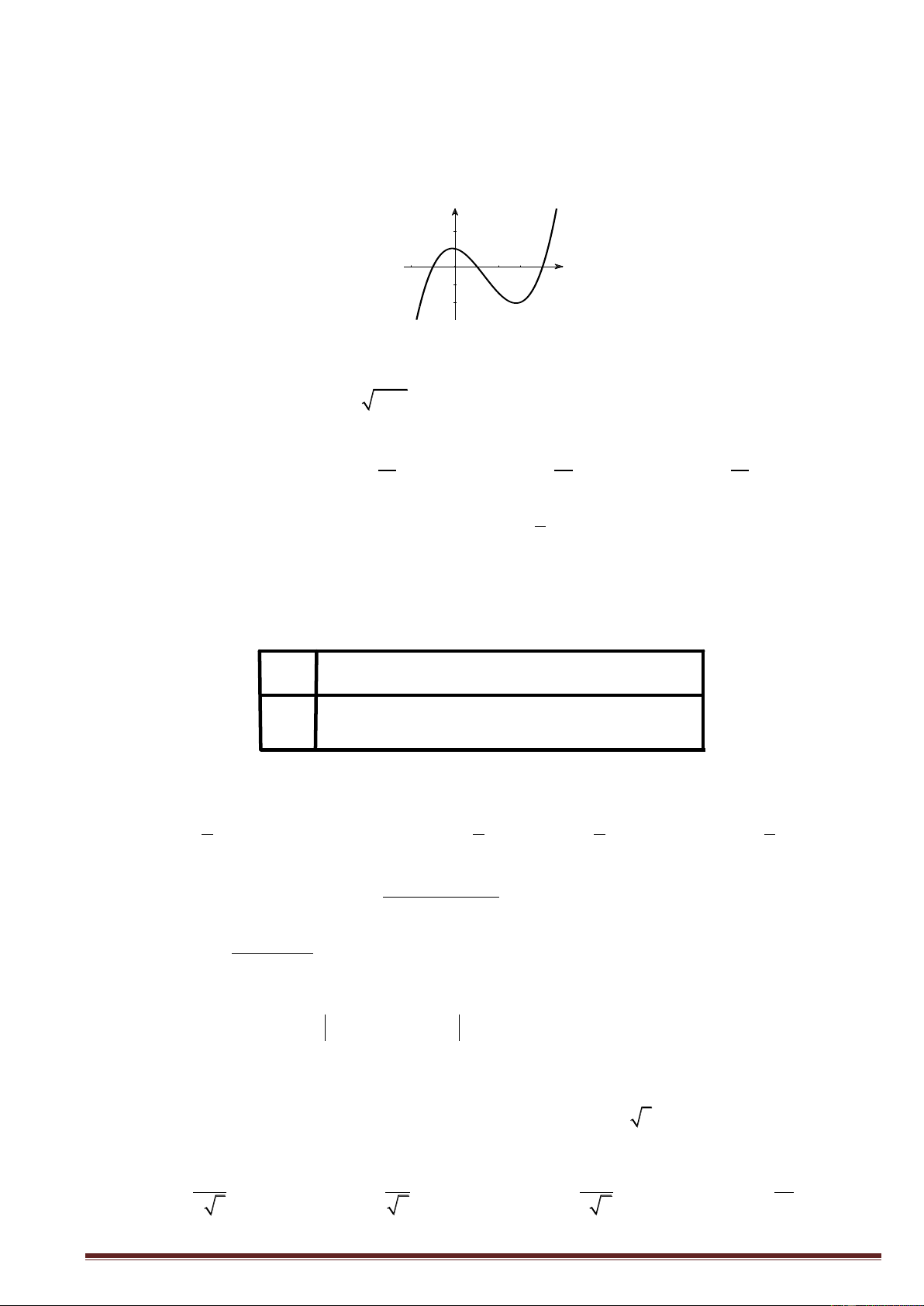
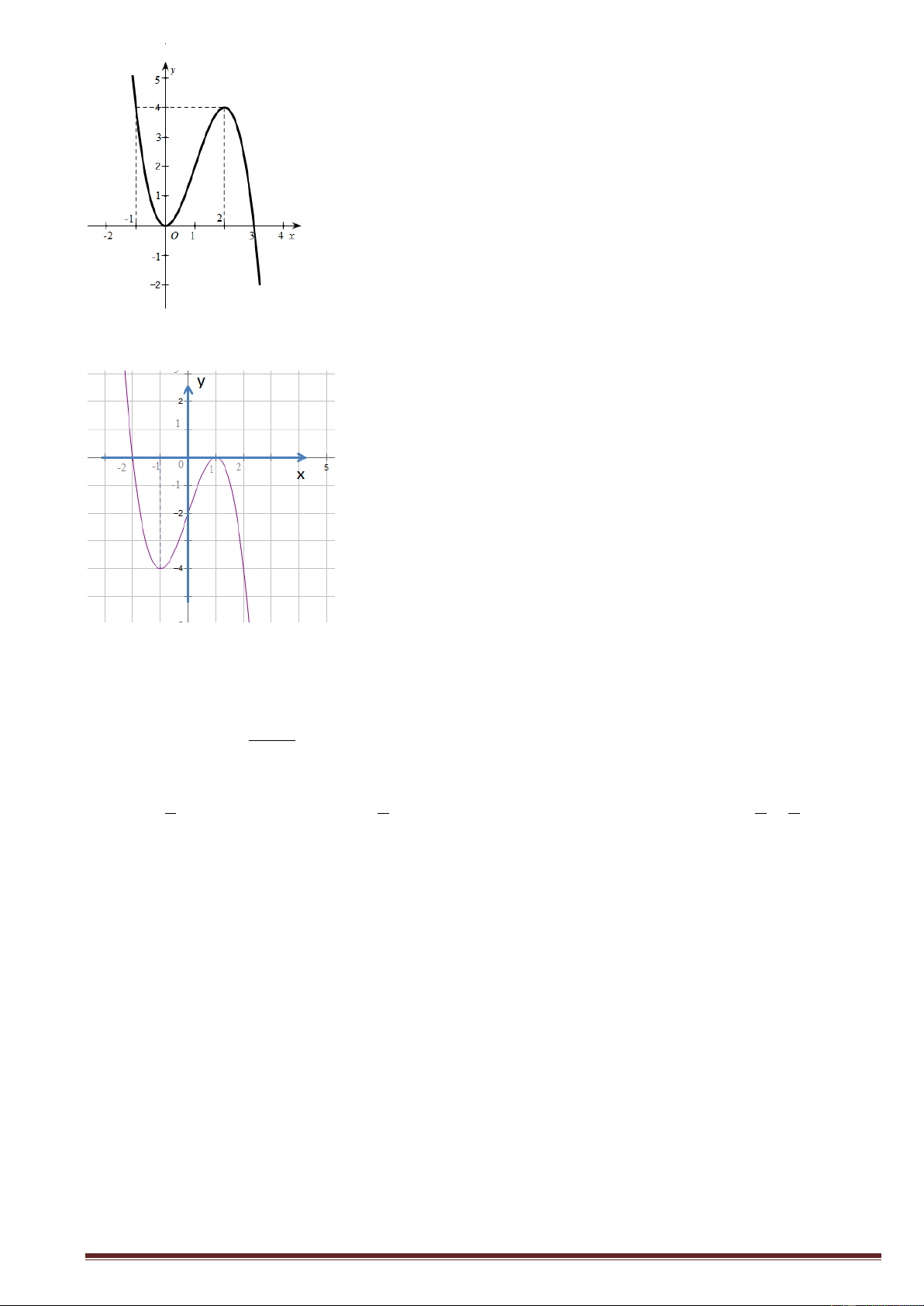
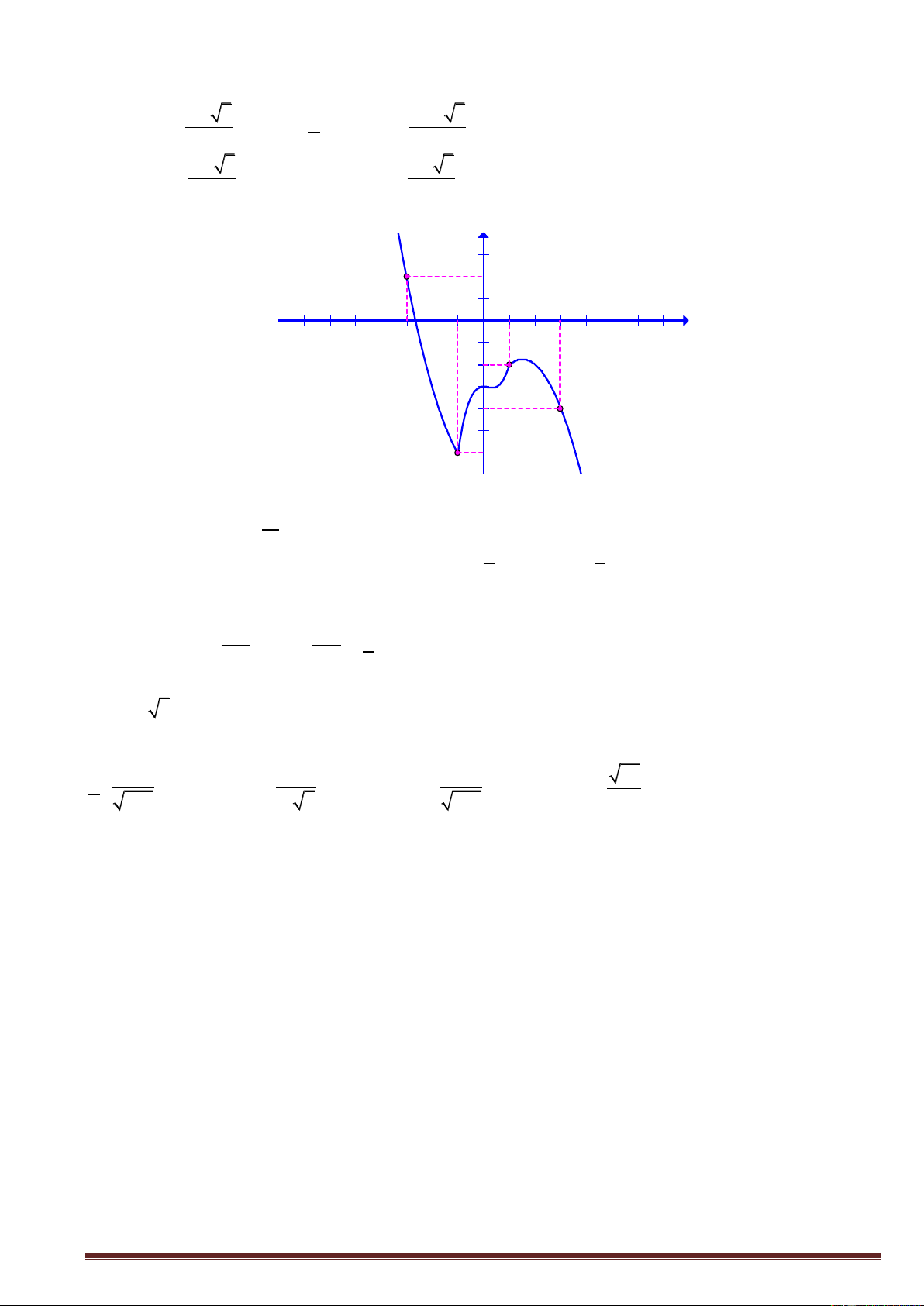
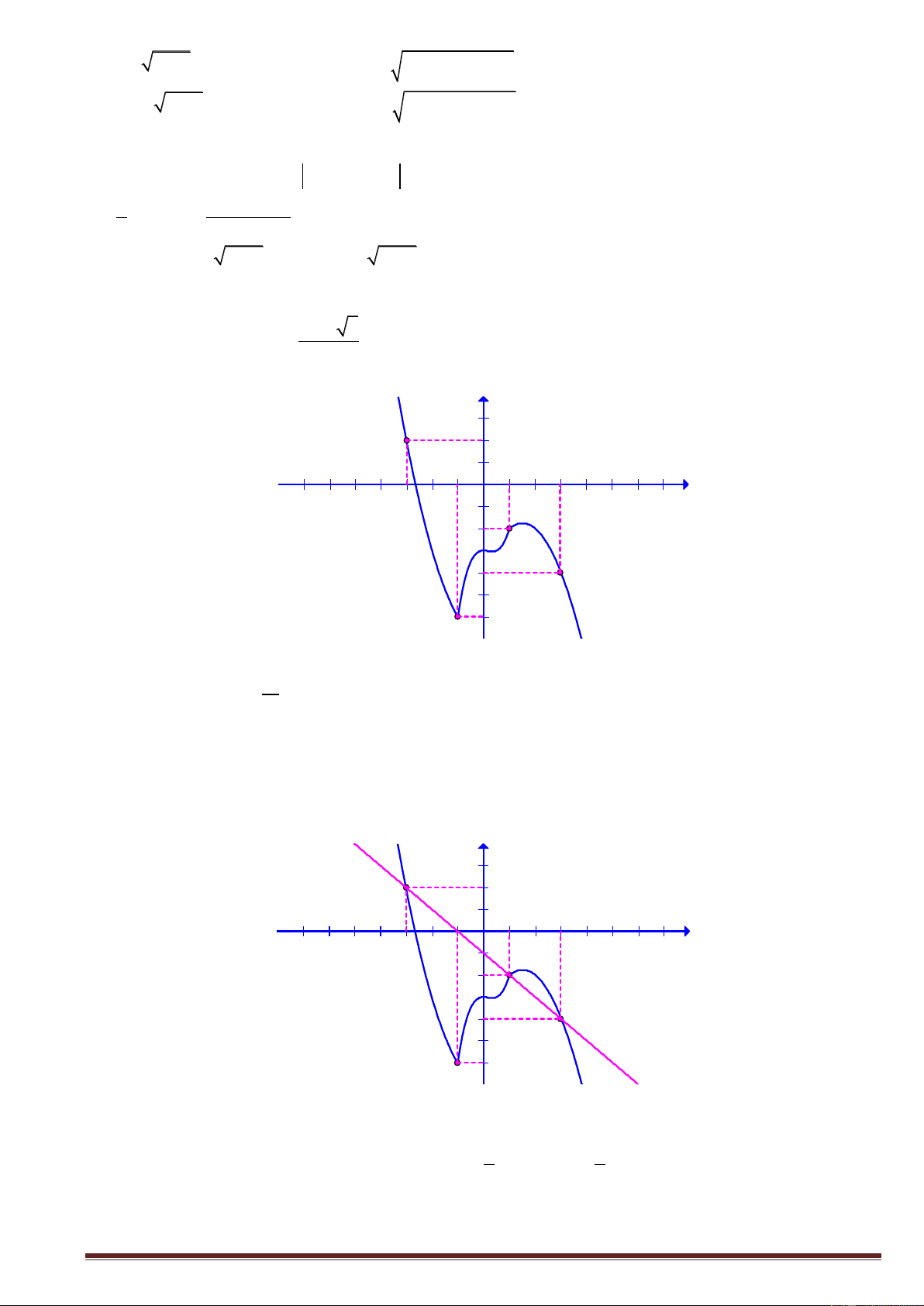
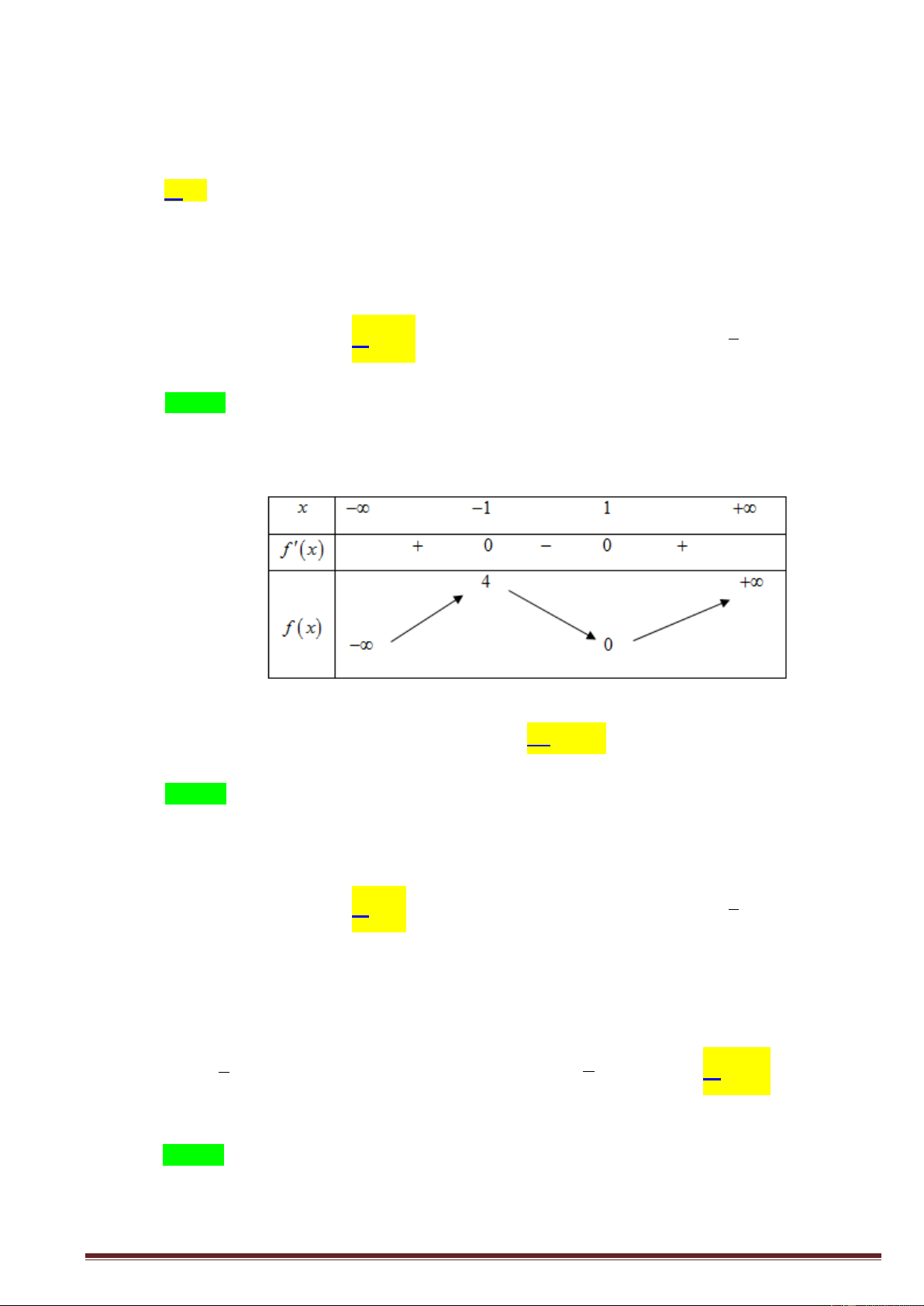
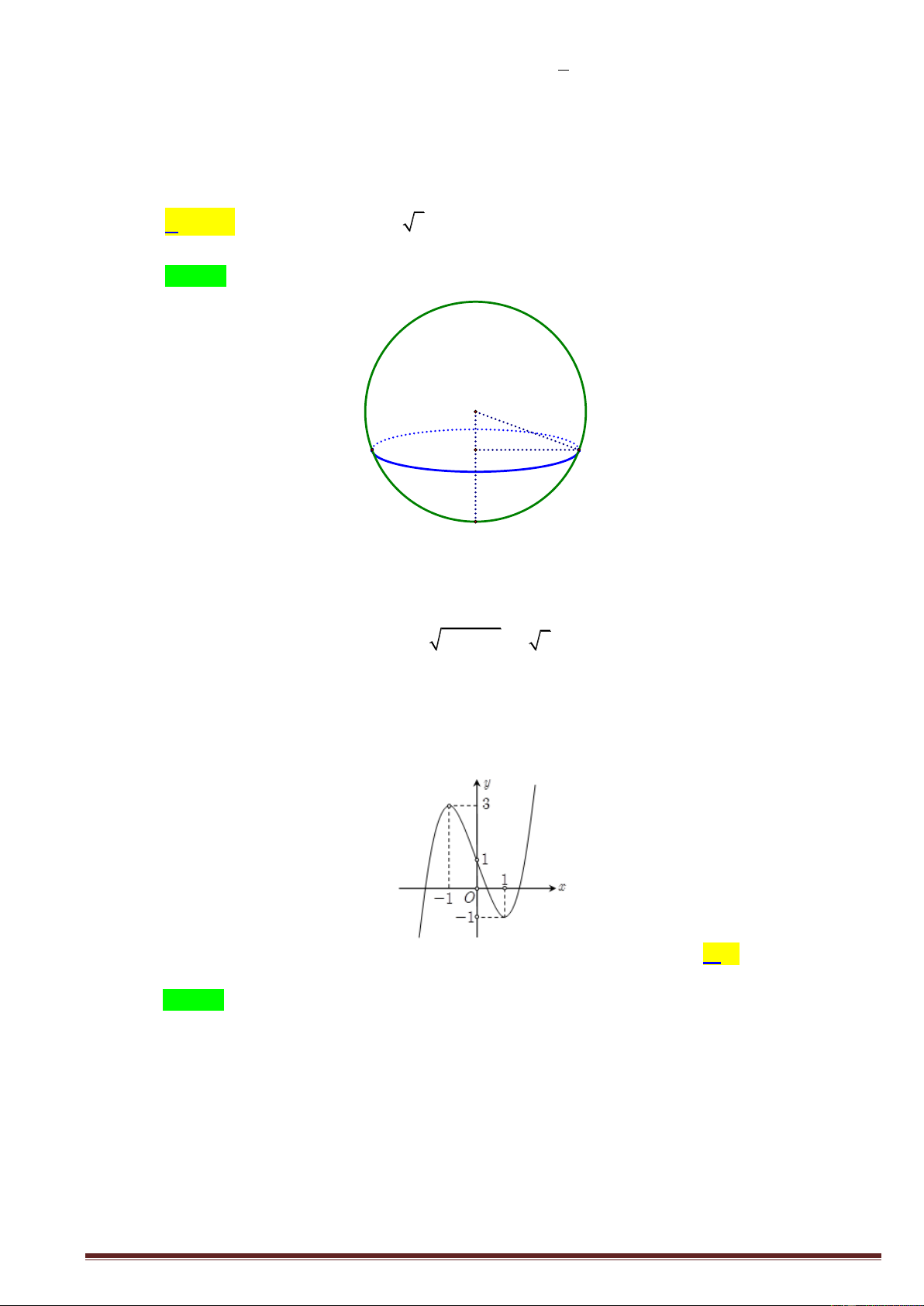
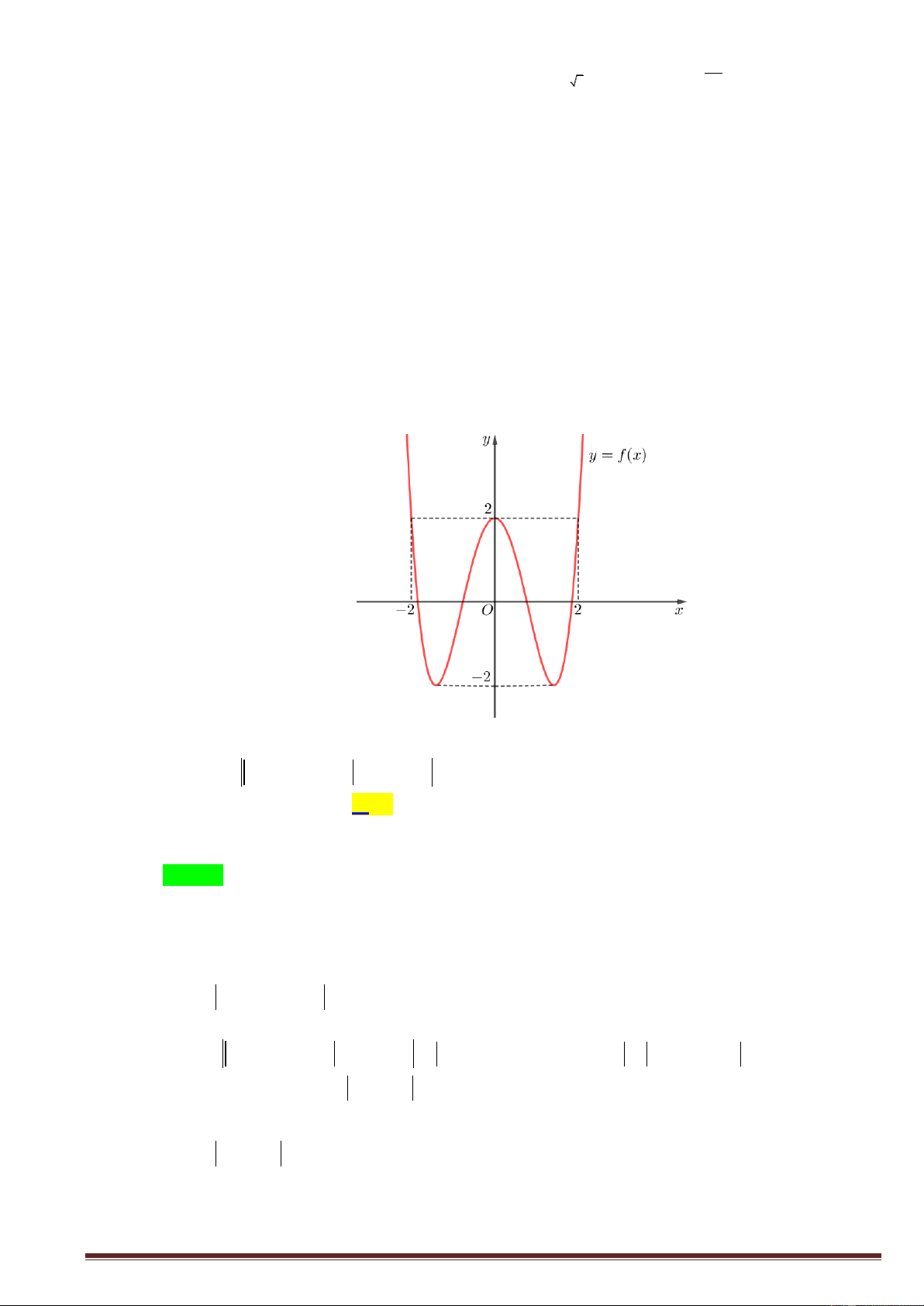
Câu 13. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm giá trị cực đại của hàm số. Trang1 y 4 x 2  2  O 2 2 A. y  0 . B. y   2 . C. y  4 . D. y  2 . CD CD CD CD
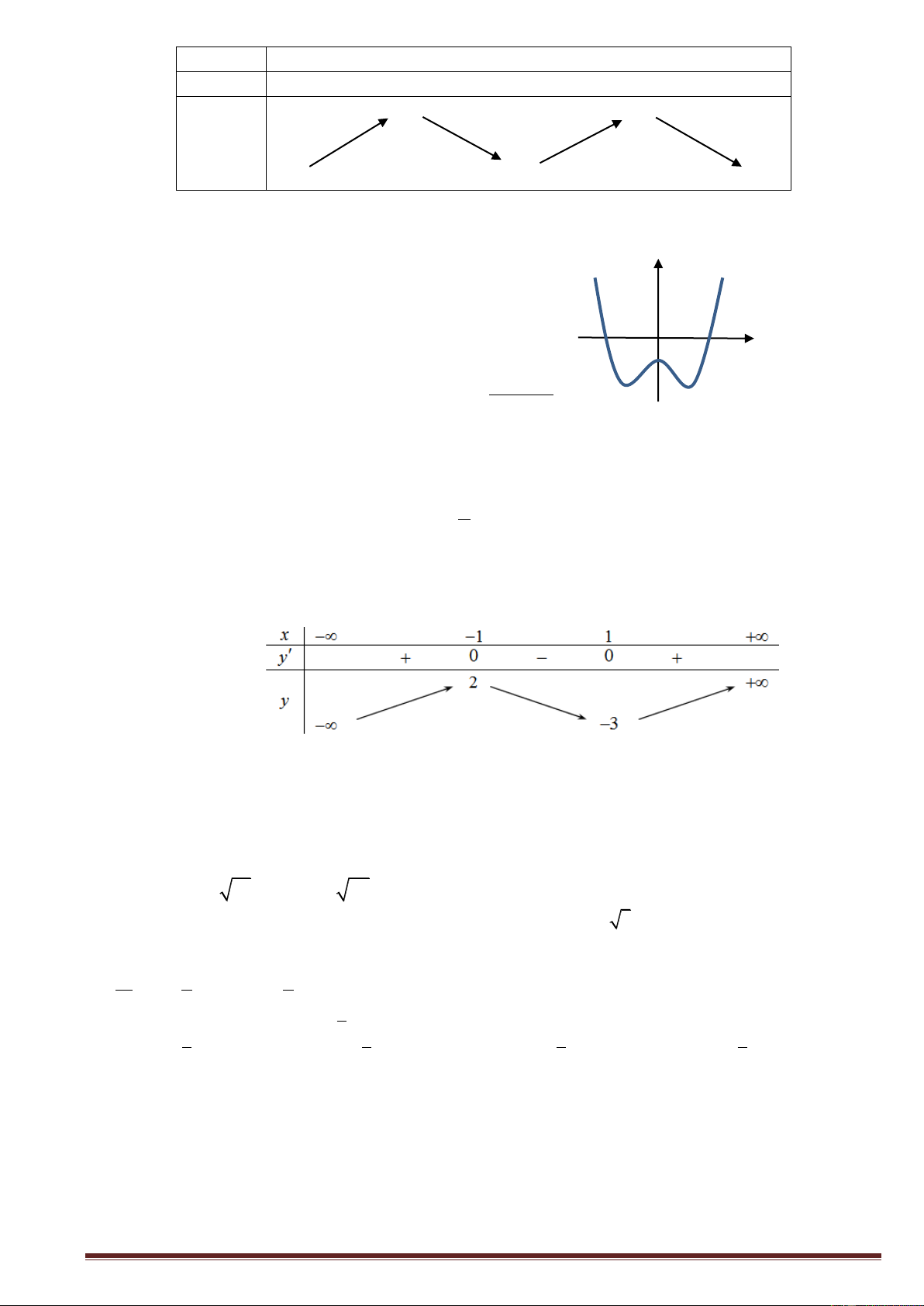
Câu 14. Bảng biến thiên dưới đây là của hàm số nào? A. 4 2
y x  2x  3 . B. 4 2
y  x  2x  3 . C. 4 2
y x  2x  3 . D. 4 2
y x  2x  3 .
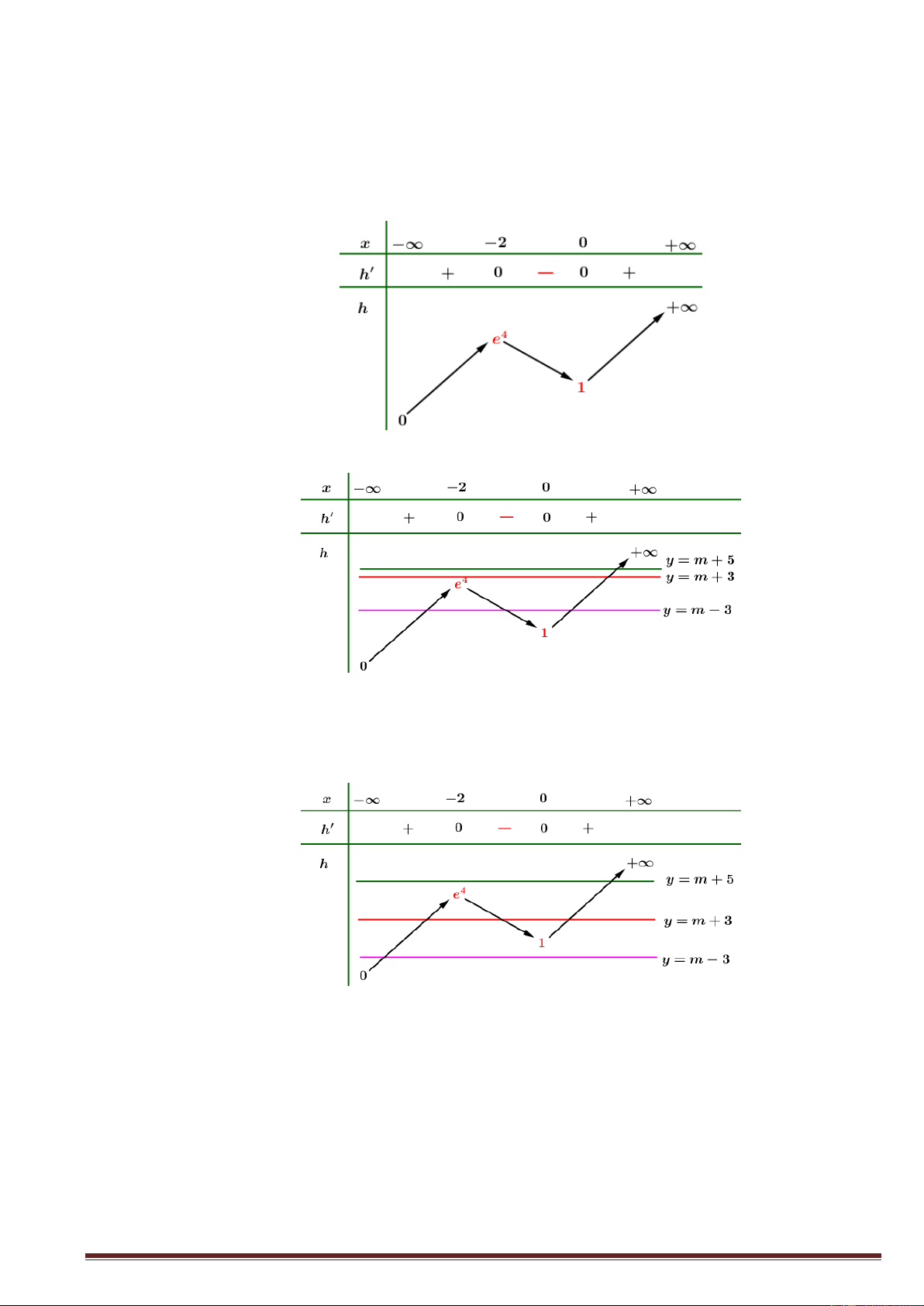
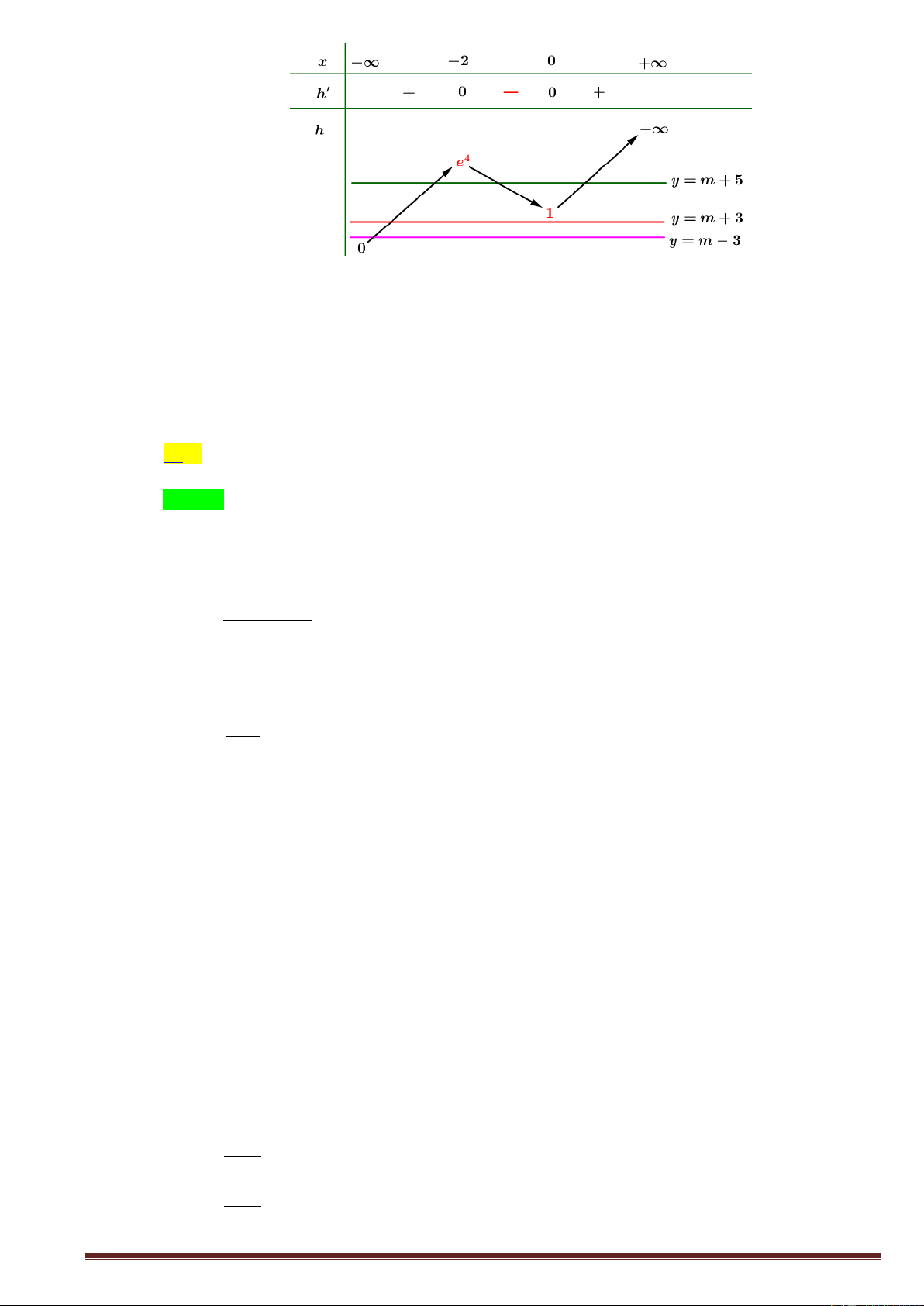
Câu 15. Cho hàm số y f (x) xác định trên  \  
1 , liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình dưới đây. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? A.1. B. 2 . C. 3 . D. 4 .
Câu 16. Tìm tập nghiệm S của bất phương trình log x 1  log 2x 1 . 1   1   2 2  1 
A. S  2;  . B. S   1  ;2.
C. S   ;  2 . D. S  ; 2  .  2 
Câu 17. Cho hàm số y f x có bảng biến thiên như sau
Số nghiệm thực của phương trình 2 f x  3  0 là A. 2 . B. 4 . C. 3 . D.1. 2 4 4
Câu 18. Cho hàm số f x liên tục trên  và có f
 xdx  9; f
 xdx  4. Tính I f
 xdx ? 0 2 0 9 A. I  .
B. I  36 .
C. I 13 . D. I  5 . 4 Trang2
Câu 19. Cho số phức z 1 2i . Tìm phần ảo của số phức z . A.2. B. 2  . C. 1. D.1.
Câu 20. Cho số phức z 1 2i . Tìm tổng phần thực và phần ảo của số phức w  2z z . A.3. B.5. C.1. D.2.
Câu 21. Cho số phức z  1
  2i . Số phức z được biểu diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ? A. Q  1  ; 2   .
B. P 1; 2 . C. N 1; 2   . D. M  1  ;2 .
Câu 22. Trong không gian Oxyz cho điểm A 2
 ;1;3 . Hình chiếu vuông góc của A lên trục Ox có tọa độ là: A. 0;1;0 . B.  2  ;0;0 .
C. 0;0;3 . D. 0;1;3 . 2 2 2
Câu 23. Trong không gian Oxyz , mặt cầu S  :  x  5   y  
1   z  2  3 có bán kính bằng A. 3 . B. 2 3 . C. 9. D. 3.
Câu 24. Trong không gian Oxyz , cho mặt phẳng  P : 2x z 1 0 .Tọa độ một vectơ pháp tuyến của
mặt phẳng  P là    
A. n  2;0;  1 .
B. n  2;0;  1 .
C. n  2; 1;  1 .
D. n  2; 1;0 . x  3 y  2 z 1
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   2 1  4
Điểm nào sau đây không thuộc đường thẳng d .
A. M 1; 1;  5 .
B. M 1; 1;3 .
C. M 3;  2;   1 .
D. M 5;  3;3 .
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B cạnh AB a , cạnh SA
vuông góc với mặt phẳng đáy và SA  2a . Tính cosin của góc  là góc giữa mặt phẳng
ABC và mặt phẳng SBC. 2 1 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 5 5
Câu 27. Cho hàm số y f (x) có đạo hàm 2 f (
x)  x(x 1) (2x  3) . Hàm số đã cho có bao nhiêu điểm cực trị? A. 2 . B. 3 . C. 0 . D.1.
Câu 28. Cho hàm số
f x liên tu ̣c trên  1  ; 
3 và có đồ thị như hình vẽ bên .
Gọi M , m lần lượt là giá tri ̣ lớn nhất và giá tri ̣ nhỏ nhất của hàm số y f x trên  1  ; 
3 . Tính M m . A. 3 . B. 4 . C. 5 . D.1.
Câu 29. Với a, b, c là các số thực dương tùy ý khác 1 và log c x, log c y . Khi đó giá trị của a b log ab là c   xy 1 1 1
A. x y . B.  . D. . x  . C. y x y xy
Câu 30. Số giao điểm của đồ thị hàm số 4 2
y x  5x  4 với trục hoành là: Trang3 A.1. B.2. C.3. D.4. 
Câu 31. Bất phương trình 2x 1 3
 7.3x  2  0 có nghiệm là x  1 x  2 x  1 x  2 A.  . B.  . C.  . D.  . x  log 3  x  log 3  x  log 2 x  log 2 2 2  3  3
Câu 32. Trong không gian, cho tam giác đều ABC cạnh bằng a . Tính thể tích khối nón nhận được khi
quay tam giác ABC quanh một đường cao của nó. 3 a 3 3 a 3 3  a 3 3 a A.V  . B.V  . C.V  . D.V  . 24 72 4 4 2 Câu 33. Cho 2
I  2x x 1dx  và 2
u x 1. Mệnh đề nào dưới đây sai ? 1 3 2 2 3 2 A. I udu  . B. I  27 . C. I udu  . D. 2 I  3 . 3 3 0 1
Câu 34. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục hoành và hai đường thẳng
x  1, x  2 là 2 2 2 2 A. 3 S x dx B. 3 S  x dx C. 3 S x dx D. 3 S x dx  1  1  1  1
Câu 35. Cho hai số phức z  1 i và z  1 i . Giá trị của biểu thức z iz bằng 1 2 1 2
A. 2  2i . B. 2i . C. 2 . D. 2  2i .
Câu 36. Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z  34  0 . Tính z  2  i ? 0 0 A. 17 . B.17 . C. 2 17 . D. 37 .
Câu 37. Trong không gian Oxyz mặt phẳng  P đi qua gốc tọa độ và vuông góc với đường thẳng x 1  y 1 z d : 
 có phương trình là: 2 1 2
A. 2x y  2z  0 .
B. 2x y  2z  0 .
C. 2x y  2z  3  0 . D. 2x y  2z 1  0 .
Câu 38. Trong không gian Oxyz , phương trình đường thẳng đi qua hai điểm A 3  ;1;2 , B1; 1  ;0 là x 1 y 1 z x  3 y 1 z  2 A.     2  1  . B. 1 2 1  . 1 x  3 y 1 z  2 x 1 y 1 z C.     2 1  . D. 1 2 1  . 1
Câu 39. Có 8 học sinh nam, 5 học sinh nữ và 1 thầy giáo được sắp xếp ngẫu nhiên đứng thành một vòng
tròn. Tính xác suất để thầy giáo đứng giữa 2 học sinh nam. 7 14 28 7 A. P  . B. P  . C. P  . D. P  . 39 39 39 13
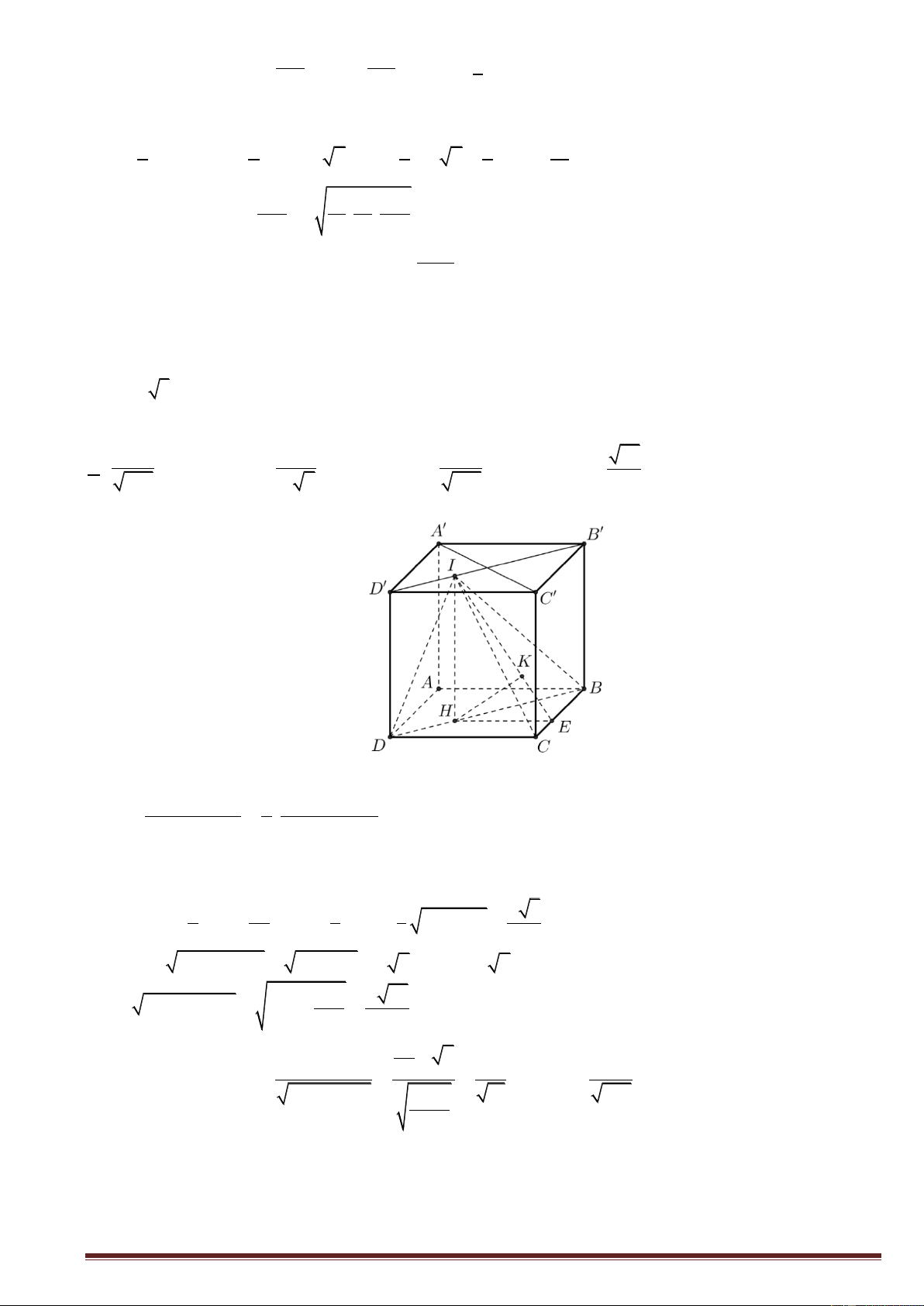
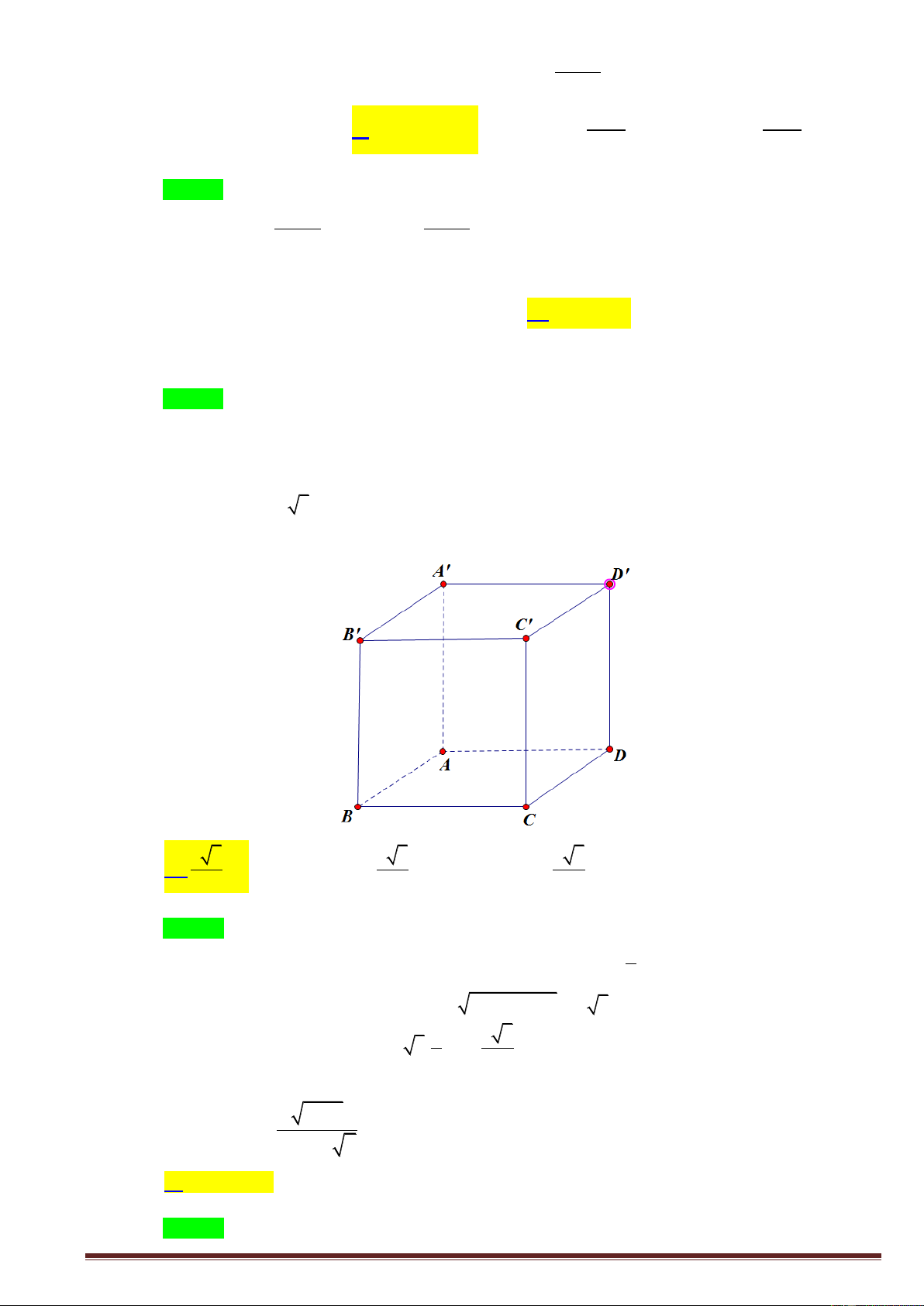
Câu 40. Cho hình lập phương ABC . D A BCD
  cạnh a . Tính khoảng cách giữa hai đường thẳng BC và CD . a 3 a 2 A. a 2 . B. 2a . C. . D. . 3 3 Câu 41. Có bao nhiêu giá trị m nguyên thuộc đoạn  2  018 ; 2019 để hàm số 3 2
y x  2x  2m  5 x  5 đồng biến trên khoảng 0 ; + ? A. 2020 . B. 2022 . C. 2021. D. 2019 .
Câu 42. Người ta thả một số lá bèo vào một hồ nước, sau 10 giờ số lượng lá bèo sẽ sinh sôi kín cả mặt
hồ. Biết rằng sau mỗi giờ số lượng lá bèo tăng gấp 10 lần số lượng lá bèo trước đó và tốc độ
tăng không đổi. Hỏi sau khoảng thời gian bao lâu số lượng lá bèo phủ kín tối thiểu một phần tư hồ? A.10  log 4 . B.10 log 4 .
C.110 log 4 . D.10 10 log 4 . Trang4
Câu 43. Cho hàm số y  a   4
x  b   2 1
2 x c 1 có đồ thị như hình vẽ bên
Mệnh đề nào dưới đây là đúng?
A. a 1, b  2
 , c 1. B. a 1, b  2  , c 1.
C. a 1, b  2
 , c 1. D. a 1, b  2, c 1.
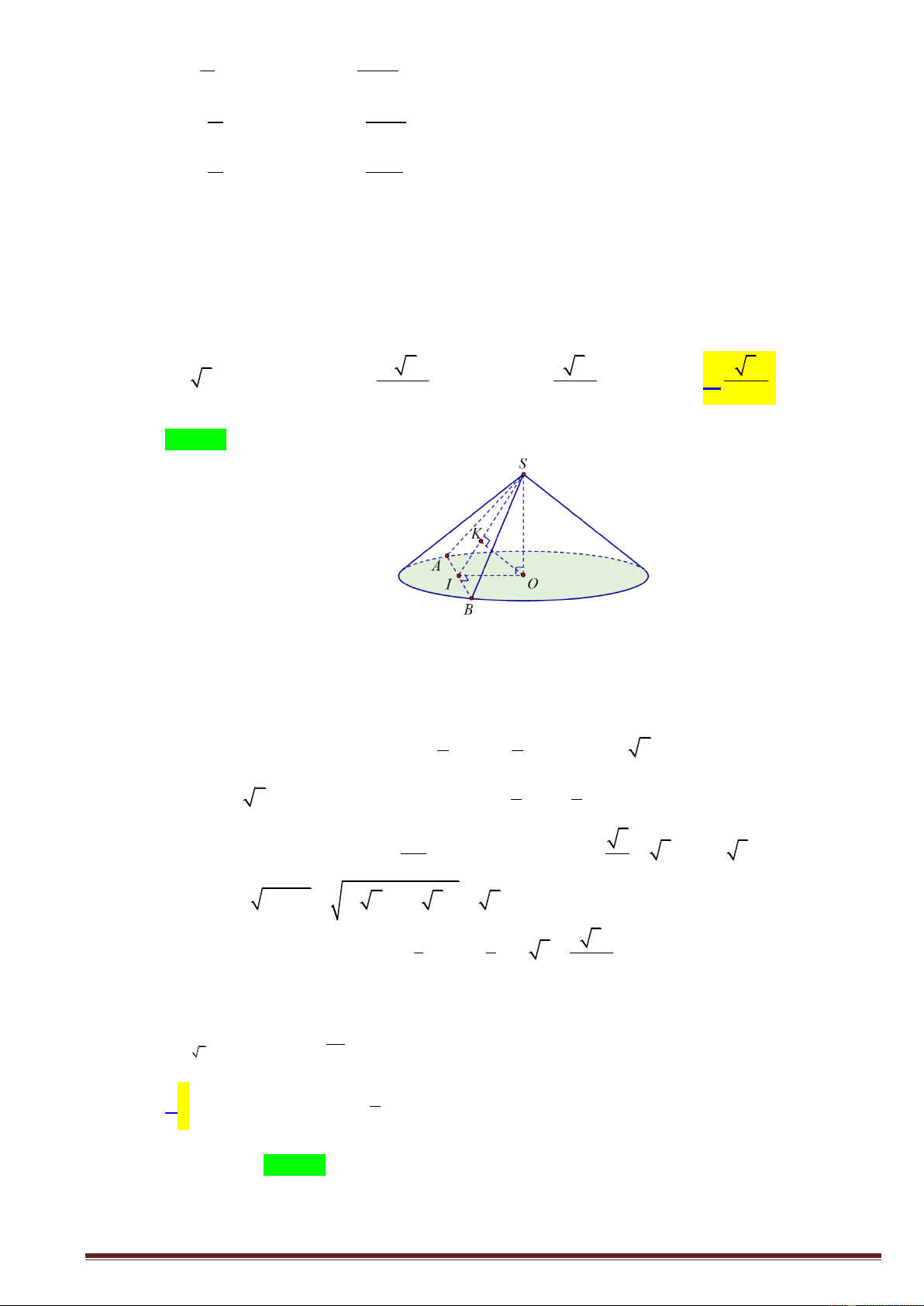
Câu 44. Cho hình nón đỉnh S có đáy là đường tròn tâm O bán kính R . Trên đường tròn O lấy hai điểm ,
A B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng 2 R 2 . Thể tích
hình nón đã cho bằng 3  R 14 3  R 14 3  R 14 3  R 14 A. . B. . C. . D. . 12 2 6 3 8 1 1 a c a c
Câu 45. Cho I  dx  ln  
với a, b, c, d là các số nguyên dương và , tối giản. x x x 1 2 b d b d 3
Giá trị của abc d bằng A. 6  . B.18 . C. 0 . D. 3  .
Câu 46. Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để
phương trình f f
 x  m  0 
có đúng 3 nghiệm phân biệt. A.1. B. 2. C. 3. D. 4.
Câu 47. Cho hai số thực a , b thỏa mãn 2 2
a b  1 và log
a b  1. Giá trị lớn nhất của biểu thức 2 2   a b
P  2a  4b  3 là 10 1 A. 10 . B. . C. 2 10 . D. . 2 10
Câu 48. Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số đã cho trên đoạn 0; 2 . Có bao nhiêu số nguyên a thuộc đoạn 3; 2 sao cho
M  2 m ? A. 7 . B. 5 . C. 6 . D. 4 .
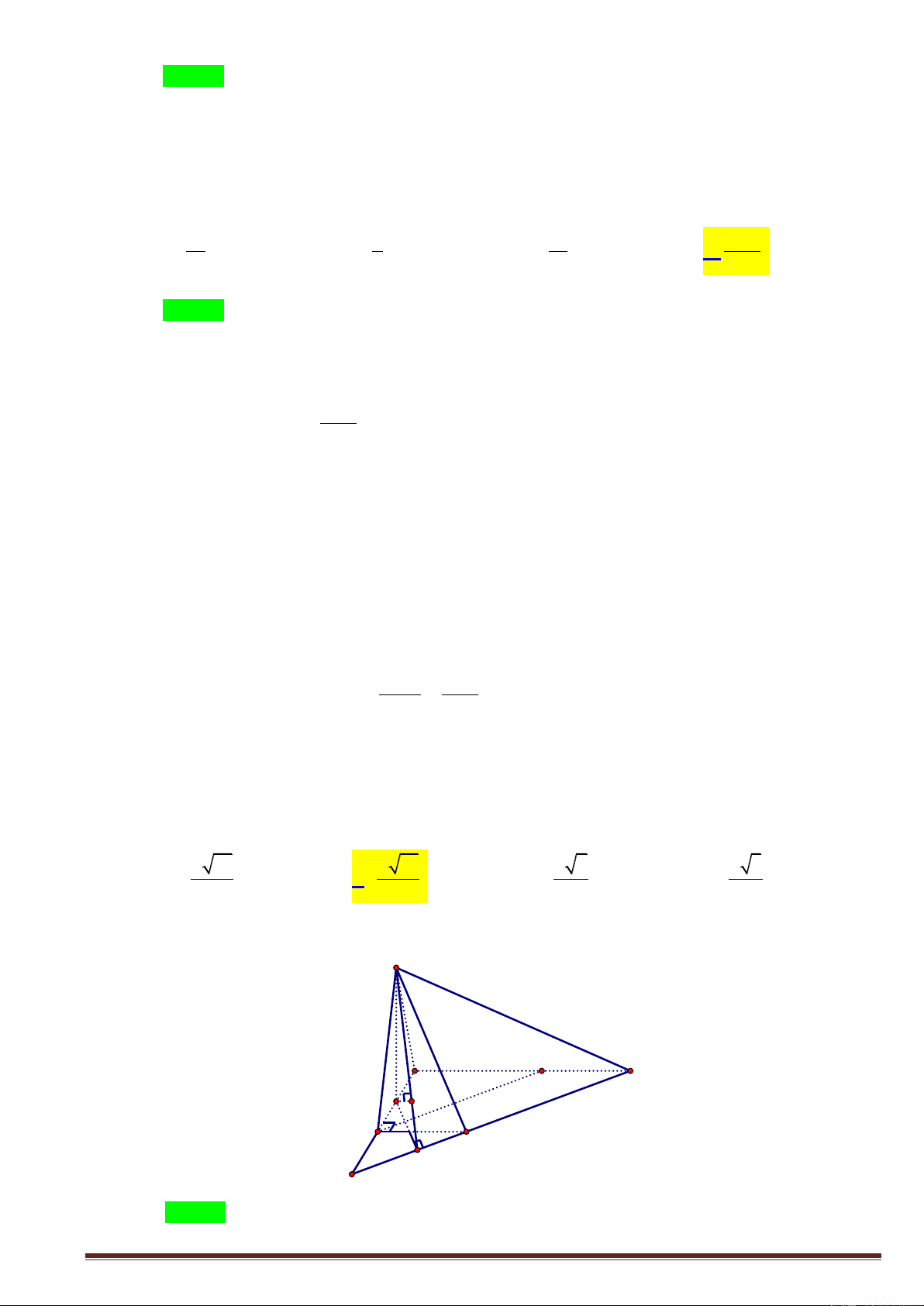
Câu 49. Cho hình chóp S.ABC có các cạnh SA BC  3 ; SB AC  4 ; SC AB  2 5 . Tính thể tích
khối chóp S.ABC . 390 390 390 390 A. . B. . C. . D. . 12 4 6 8 Trang5
Câu 50. Cho 0  x  2021 và log (2  2)   3  8y x x y
.Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn 2
các điều kiện trên ? A.2021. B.2022. C.1. D.4.
ĐÁP ÁN VÀ LỜI GIẢI Câu 1.
Cho trước 5 chiếc ghế xếp thành một hàng ngang. Số cách xếp ba bạn ,
A B, C vào 5 chiếc ghế
đó sao cho mỗi bạn ngồi một ghế là A. 3 C . B. 6. C. 3 A . D.15. 5 5 Lời giải Chọn C
Cách 1: Mỗi cách xếp thỏa mãn yêu cầu bài toán chính là một chỉnh hợp chập 3 của 5 phần tử nên số cách xếp là 3 A . 5
Cách 2: Có 5 cách xếp bạn A, với mỗi cách xếp bạn A thì có 4 cách xếp bạn B, với mỗi cách
xếp bạn A và B thì có 3 cách xếp bạn
C. Vậy theo qui tắc nhân có 5.4.3  60 . Câu 2.
Cho cấp số cộng u có số hạng đầu u  2 và công sai d  3. Giá trị của u bằng n  1 5 A. 14 . B. 5 . C.11. D.15 . Lời giải Chọn A
Cấp số số cộng u có số hạng đầu u và công sai d có công thức số hạng tổng quát là: n  1
u u n 1 d . Suy ra u u  4d  2  4.3  14 . n 1   5 1
Vậy số giá trị của u bằng 14. 5 Câu 3. Phương trình 3x2 4
 16 có nghiệm là 3 4 A. x  .
B. x  5. C. x  . D. x  3. 4 3 Lời giải Chọn C x 4 Ta có: 3 2 4
 16  3x  2  2  x  . 3 4
Vậy phương trình có nghiệm là: x  . 3 Câu 4.
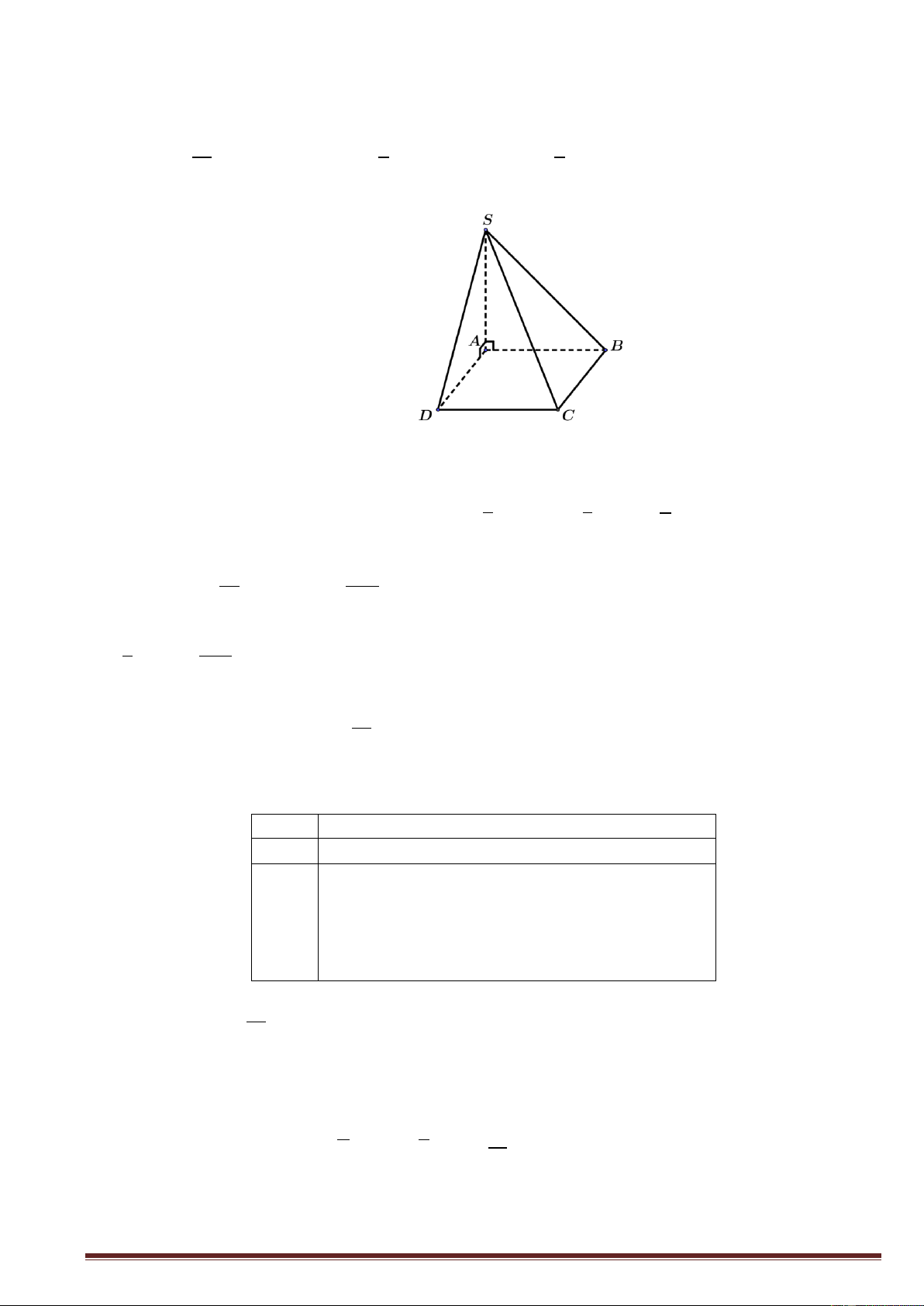
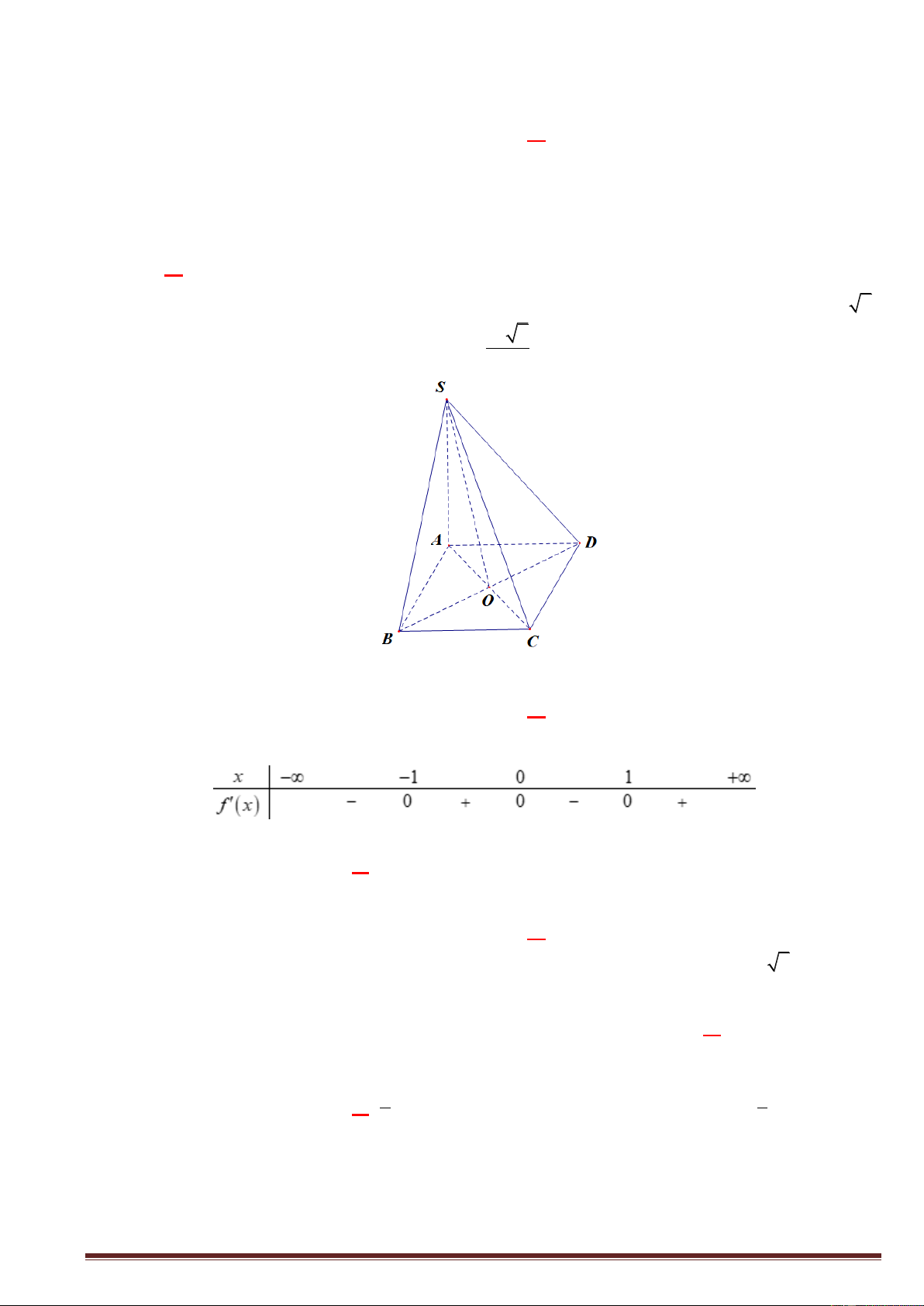
Khối chóp S.ABCD có đáy là hình thoi và SA  ( ABCD) có thể tích bằng 1 1 1 1 A. . SA . AB AD . B. S .
A AC.BD . C. S . A A . B AD . D. S . A AC.BD . 3 3 6 6 Lời giải Chọn D Ta có hình vẽ
Khối chóp S.ABCD có đáy là hình thoi ABCD và nhận SA làm đường cao. 1
Diện tích hình thoi ABCD là S AC.BD . 2 Trang6 1
Thể tích khối chóp là V S . A AC.BD . 6 Câu 5. Hàm số y  log
2x  3 có tập xác định là 2   3  3  3 
A. D   . B. D  ;    .
C. D   \   . D. D  ;    . 2  2  2  Lời giải Chọn D 3 Hàm số y  log
2x  3 xác định  2x  3  0  x  . 2   2  3 
Vậy tập xác định của hàm số là: D  ;    .  2  Câu 6.
Tìm họ nguyên hàm của hàm số f x  cos x . 1 1 A. 2 cos x C.
B. sin x C .
C. sin x C . D. 2
 cos x C . 2 2 Lời giải Chọn B Ta có: f
 xdx  cos d
x x  sin x  . C Câu 7.
Cho khối lăng trụ đứng có đáy là tam giác vuông, độ dài hai cạnh góc vuông là 3a, 4a và chiều
cao khối lăng trụ là 6a . Thể tích của khối lăng trụ bằng A. 3
V  27a . B. 3
V  12a . C. 3
V  72a . D. 3 V  36a . Lời giải Chọn D
Thể tích khối lăng trụV  .B h .
Trong đó h  6a . 1 Diện tích đáy 2 B  .3 .4 a a  6a . 2 Vậy 2 3 V  6 .6 a a  36a Câu 8.
Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích của khối trụ đó là 8 .
A. h  2 . B. 2 2 . C. 3 32 . D. 3 4 . Lời giải Chọn A Thể tích khối trụ là 2 3 3
V   r h   h  8  h  8  h  2 . Câu 9.
Thể tích khối cầu có bán kính 6cm bằng A. 216 . B. 288 . C. 432 . D. 864 . Lời giải Chọn B 4 4
Ta có thể tích khối cầu : 3 3 V
R   6  288  3 cm  . 3 3
Câu 10. Cho hàm số y f x có bảng biến thiên như sau: x  2  0  Trang7 y  0  0  / y  2  2 
Hàm số y f x nghịch biến trên khoảng A.  2  ;0 .
B. 2;   . C.  2  ;2 .
D. ;  2 . Lời giải Chọn A
Dựa vào bảng biến thiên của hàm số suy ra hàm số y f x nghịch biến trên khoảng  2  ;0 .
Câu 11. Với a;b là hai số dương tùy ý thì  3 2
log a b  có giá trị bằng biểu thức nào sau đây?  1  1 A. 3 log a  log b
 . B. 2log a  3logb . C. 3log a  log b .
D. 3log a  2 log b .  2  2 Lời giải Chọn D
Với a;b là hai số dương tùy ý, ta có :  3 2 a b  3 2 log
 log a  logb  3loga  2logb .
Câu 12. Cho khối nón có độ dài đường sinh bằng 10 và diện tích xung quanh bằng 60 . Thể tích của
khối nón đã cho bằng A. 360 . B. 288 . C.120 . D. 96 . Lời giải Chọn D / Ta có: l 10
S  60   rl  60 10 r  60  r  6 . xq 2 2 2 2
h l r  10  6  64  8 .. 1 1
Do đó thể tích khối nón đã cho là: 2 2
V   r h   .6 .8  96 . 3 3
Câu 13. Cho hàm số y f x có đồ thị như hình vẽ bên. Tìm giá trị cực đại của hàm số. y 4 x 2  2  O 2 2 A. y  0 . B. y   2 . C. y  4 . D. y  2 . CD CD CD CD Lời giải Chọn C
Dựa vào đồ thị hàm số, ta thấy giá trị cực đại của hàm số là y
 4 tại x   2 . CD
Câu 14. Bảng biến thiên dưới đây là của hàm số nào? / A. 4 2
y x  2x  3 . B. 4 2
y  x  2x  3 . C. 4 2
y x  2x  3 . D. 4 2
y x  2x  3 . Lời giải Chọn C
Từ bảng biến thiên suy ra hệ số a  0 .
Mặt khác hàm số có 3 điểm cực trị suy ra các hệ số a, b trái dấu. Trang8
Câu 15. Cho hàm số y f (x) xác định trên  \  
1 , liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình dưới đây. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? / A.1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Từbảng biến thiên ta thấy:
lim f (x)  5  Đồ thị hàm số có đường tiệm cận ngang: y  5 . x
lim f (x)  3  Đồ thị hàm số có đường tiệm cận ngang: y  3 . x
lim f (x)    x 1  
 Đồ thị hàm số có đường tiệm cận đứng: x 1.
lim f (x)     x 1 
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Câu 16. Tìm tập nghiệm S của bất phương trình log x 1  log 2x 1 . 1   1   2 2  1 
A. S  2;  . B. S   1  ;2.
C. S   ;  2 . D. S  ; 2  .  2  Lời giải Chọn D
x   x  1 Ta có log x 1  log 2x  1 2 1 1     x  2 . 1   1   2x10 2 2 2
Câu 17. Cho hàm số y f x có bảng biến thiên như sau /
Số nghiệm thực của phương trình 2 f x  3  0 là A. 2 . B. 4 . C. 3 . D.1. Lời giải Chọn A
Phương trình 2 f x  3  0  f x 3  . 2
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y f x với đường 3 thẳng y  . 2
Từ bảng biến thiên suy ra số nghiệm thực của phương trình 2 f x  3  0 là 2 . 2 4 4
Câu 18. Cho hàm số f x liên tục trên  và có f
 xdx  9; f
 xdx  4. Tính I f
 xdx ? 0 2 0 9 A. I  .
B. I  36 .
C. I 13 . D. I  5 . 4 Lời giải Chọn C 4 2 4 Ta có f
 xdx f
 xdxf
 xdx  94 13. 0 0 2 Trang9
Câu 19. Cho số phức z 1 2i . Tìm phần ảo của số phức z . A.2. B. 2  . C. 1. D.1. Lời giải Chọn A
Ta có z  1 2i z  1 2i .
Vậy z có phần ảo b  2 .
Câu 20. Cho số phức z 1 2i . Tìm tổng phần thực và phần ảo của số phức w  2z z . A.3. B.5. C.1. D.2. Lời giải Chọn B
Ta có z  1 2i z  1 2i , khi đó w  2z z  2 1 2i  1 2i  3  2i .
Phần thực của số phức w là 3, phần ảo của số phức w là 2.
 Tổng phần thực và phần ảo là: 3 2  5.
Câu 21. Cho số phức z  1
  2i . Số phức z được biểu diễn bởi điểm nào dưới đây trên mặt phẳng tọa độ? A. Q  1  ; 2   .
B. P 1; 2 . C. N 1; 2   . D. M  1  ;2 . Lời giải Chọn A Ta có z  1
  2i z  1   2i .
Vậy số phức z được biểu diễn bởi điểm Q  1  ; 2   .
Câu 22. Trong không gian Oxyz cho điểm A 2
 ;1;3 . Hình chiếu vuông góc của A lên trục Ox có tọa độ là: A. 0;1;0 . B.  2  ;0;0 .
C. 0;0;3 . D. 0;1;3 . Lờigiải Chọn B
Chiếu vuông góc một điểm bất kỳ lên trục Ox khi đó giữ nguyên hoành độ còn tung độ và cao độ bằng 0 .
Vậy hình chiếu vuông góc của A lên trục Ox có tọa độ là:  2  ;0;0 . 2 2 2
Câu 23. Trong không gian Oxyz , mặt cầu S  :  x  5   y  
1   z  2  3 có bán kính bằng A. 3 . B. 2 3 . C. 9. D. 3. Lời giải ChọnA 2 2 2
Từ phương trình mặt cầu S  :  x  5   y  
1   z  2  3.
Suy ra, bán kính của mặt cầu đó là R  3 .
Câu 24. Trong không gian Oxyz , cho mặt phẳng  P : 2x z 1 0 .Tọa độ một vectơ pháp tuyến của
mặt phẳng  P là    
A. n  2;0;  1 .
B. n  2;0;  1 .
C. n  2; 1;  1 .
D. n  2; 1;0 . Lời giải Chọn B
Mặt phẳng  P có một vectơ pháp tuyến là n  2;0 ;   1 . x  3 y  2 z 1
Câu 25. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   2 1  4
Điểm nào sau đây không thuộc đường thẳng d .
A. M 1; 1;  5 .
B. M 1; 1;3 .
C. M 3;  2;   1 .
D. M 5;  3;3 . Trang10 Lời giải ChọnB 1 3 1 2 5 1
Thử đáp án A ta được:    1 2 1 
. Suy ra M thuộc đường thẳng d . 4 1 3 1   2 3 1
Thử đáp án B ta được:   2 1 
. Suy ra M không thuộc đường thẳng d . 4 3  3 2   2 1  1
Thử đáp án C ta được:    0 2 1 
. Suy ra M thuộc đường thẳng d . 4 5  3 3  2 3 1
Thử đáp án D ta được:    1 2 
. Suy ra M thuộc đường thẳng d . 1 4
Câu 26. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B cạnh AB a , cạnh SA
vuông góc với mặt phẳng đáy và SA  2a . Tính cosin của góc  là góc giữa mặt phẳng
ABC và mặt phẳng SBC. 2 1 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 5 5 Lời giải Chọn C / BC AB Vì 
BC  SAB  BC SB . BC SA
Suy ra góc giữa 2 mặt phẳng  ABC  và mặt phẳng SBC  là góc    SBA. AB AB 1
Xét tam giác vuông SBA có cos    . 2 2 SB SA AB 5
Câu 27. Cho hàm số y f (x) có đạo hàm 2 f (
x)  x(x 1) (2x  3) . Hàm số đã cho có bao nhiêu điểm cực trị? A. 2 . B. 3 . C. 0 . D.1. Lời giải Chọn A Dễ thấy: f (
x) liên tục trên  .  x  0  3 f (
x)  0  x 1 
. Trong đó có 2 nghiệm đơn là x  0 và x   và một nghiệm bội 2 là  2 3 x    2 x 1.
Lập bảng xét dấu f (  x) /
f  x đổi dấu 2 lần nên hàm số f x có hai điểm cực trị.
Câu 28. Cho hàm số f x liên tu ̣c trên  1  ; 
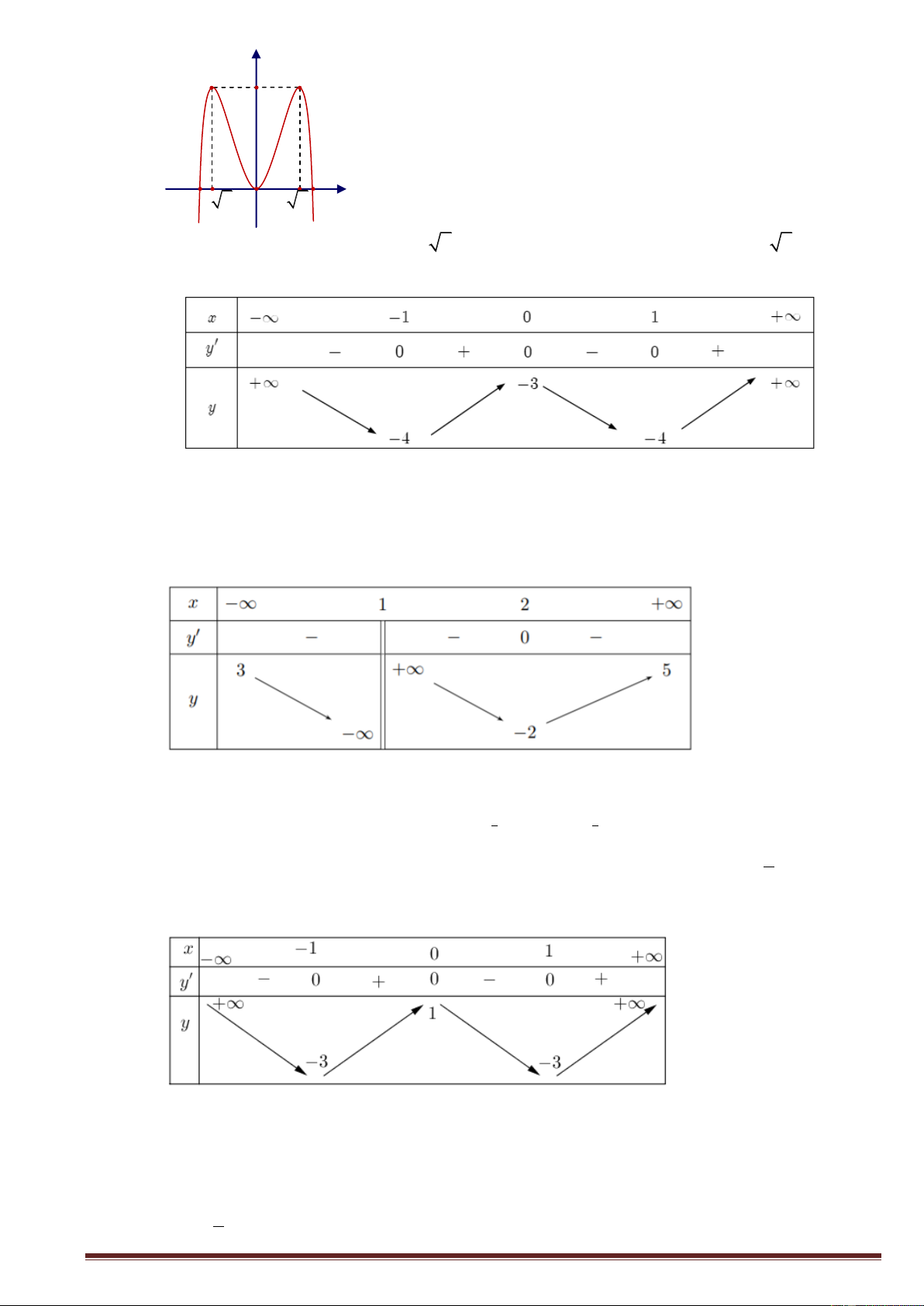
3 và có đồ thị như hình vẽ bên . Gọi M , m lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của hàm số y f x trên  1  ; 
3 . Tính M m . A. 3 . B. 4 . C. 5 . D.1. / Lời giải Chọn C
Quan sát đồ thi ̣ ta thấy hàm số y f x đa ̣t giá tri ̣ nhỏ nhất trên  1  ; 
3 là 1 tại điểm x  1 
và đạt giá trị lớn nhất trên  1  ; 
3 là 4 tại điểm x  3. Do đó M  4, m  1  . Trang11
Giá trị M m  4    1  5 .
Câu 29. Với a, b, c là các số thực dương tùy ý khác 1 và log c x, log c y . Khi đó giá trị của a b log ab là c   xy 1 1 1
A. x y . B. . C.  . D. . x y x y xy Lời giải Chọn C Ta có: ab a b   c   . c   1 1 1 1 log log log c c log c log b x y a
Câu 30. Số giao điểm của đồ thị hàm số 4 2
y x  5x  4 với trục hoành là: A.1. B.2. C.3. D.4. Lời giải Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số và trục Ox là: 2 x 1 x  1  4 2
x  5x  4  0     . 2 x  4 x  2 
Vậy số điểm chung của đồ thị hàm số 4 2
y x  5x  4 với trục hoành là 4. 
Câu 31. Bất phương trình 2x 1 3
 7.3x  2  0 có nghiệm là x  1 x  2 x  1 x  2 A.  . B.  . C.  . D.  . x  log 3  x  log 3  x  log 2 x  log 2 2 2  3  3 Lời giải Chọn C   x 1  1      3  x log  x 1 Ta có 2x 1 3  7.3x  2  0 2 3.3 x 7.3x    2  0  3 3   3     .  x log 2  3x  2 x  log 2  3 3
Câu 32. Trong không gian, cho tam giác đều ABC cạnh bằng a . Tính thể tích khối nón nhận được khi
quay tam giác ABC quanh một đường cao của nó. 3 a 3 3 a 3 3  a 3 3 a A.V  . B.V  . C.V  . D.V  . 24 72 4 4 Lời giải Chọn A / 1
Ta có thể tích khối nón 2 V   r h . 3 a 3 a
Trong đó h AH  ; r HB  . 2 2 2 3  Do đó: 1 a a 3 3 a V        . 3  2  2 24 2 Câu 33. Cho 2
I  2x x 1dx  và 2
u x 1. Mệnh đề nào dưới đây sai ? 1 3 2 2 3 2 A. I udu  . B. I  27 . C. I udu  . D. 2 I  3 . 3 3 0 1 Lời giải Chọn C Đặt 2
u x 1  du  2 d x x
Đổi cận: Với x 1 thì u  0 ; với x  2 thì u  3. Trang12 2 3 3 3 2 3 2 Khi đó 2 2 2 2 2
I  2x x 1dx udu u  3  27  
do đó mệnh đề I udu  sai. 3 0 3 3 1 0 1
Câu 34. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục hoành và hai đường thẳng
x  1, x  2 là 2 2 2 2 A. 3 S x dx B. 3 S  x dx C. 3 S x dx D. 3 S x dx  1  1  1  1 Lời giải Chọn C 2
Theo công thức tính diện tích hình phẳng ta có 3 S x dx  1 
Câu 35. Cho hai số phức z  1 i và z  1 i . Giá trị của biểu thức z iz bằng 1 2 1 2
A. 2  2i . B. 2i . C. 2 . D. 2  2i . Lời giải ChọnC
Ta có z  1 i z  1 i ; z  1 i iz  1 i . 1 1 2 2
Suy ra z iz  2 . 1 2
Câu 36. Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z  34  0 . Tính z  2  i ? 0 0 A. 17 . B.17 . C. 2 17 . D. 37 . Lời giải Chọn A
z    i 2
z  6z  34  3 5 0   z  3   5i Do đó z  3
  5i z  2  i  1 4i  17 . 0 0
Câu 37. Trong không gian Oxyz mặt phẳng  P đi qua gốc tọa độ và vuông góc với đường thẳng x 1  y 1 z d : 
 có phương trình là: 2 1 2
A. 2x y  2z  0 .
B. 2x y  2z  0 .
C. 2x y  2z  3  0 . D. 2x y  2z 1  0 . Lời giải Chọn A x 1 y 1 z d :   2  1 2 
Vì  P  d  nên chọn n  2; 1; 2 P
P qua gốc tọa độ nên P:2x y  2z  0
Câu 38. Trong không gian Oxyz , phương trình đường thẳng đi qua hai điểm A 3  ;1;2 , B1; 1  ;0 là x 1 y 1 z x  3 y 1 z  2 A.     2  1  . B. 1 2 1  . 1 x  3 y 1 z  2 x 1 y 1 z C.     2 1  . D. 1 2 1  . 1 Lời giải Chọn D   1  Ta có: AB  4; 2  ; 2
  nên phương trình đường thẳng AB nhận vecto n AB  2; 1  ;  1 2 làm vecto chỉ phương. Trang13 x 1 y 1 z
Vì B AB nên ta suy ra phương trình đường thẳng AB là:   2 1  . 1
Câu 39. Có 8 học sinh nam, 5 học sinh nữ và 1 thầy giáo được sắp xếp ngẫu nhiên đứng thành một vòng
tròn. Tính xác suất để thầy giáo đứng giữa 2 học sinh nam. 7 14 28 7 A. P  . B. P  . C. P  . D. P  . 39 39 39 13 Lời giải Chọn B
Số phần tử của không gian mẫu là: 13!.
Gọi A là biến cố: “Thầy giáo đứng giữa 2 học sinh nam”
Bước 1: Xếp hai học sinh nam đứng cạnh thầy giáo có 2 A . 8
Coi hai học sinh nam đứng cạnh thầy giáo và thầy giáo là một người.
Bước 2: Xếp 12 người quanh một bàn tròn có 11! cách.
Số kết quả thuận lợi của biến cố A là: 2 A .11!. 8 A .11! 14 Vậy P A 2 8   . 13! 39
Câu 40. Cho hình lập phương ABC . D A BCD
  cạnh a . Tính khoảng cách giữa hai đường thẳng BC và CD . a 3 a 2 A. a 2 . B. 2a . C. . D. . 3 3 Lời giải Chọn C / ABC . D A BCD
  là hình lập phương  BC// AD  BC //  ACD; CD   ACD
d BC;CD  d BC; ACD  d B; ACD  d D; ACD  h . . Tứ diện . D ACD có D ,
A DC, DD đôi một vuông góc. 1 1 1 1 3 a 3       h  2 2 2 2 2 h DA DC DD . a 3 Câu 41. Có bao nhiêu giá trị m nguyên thuộc đoạn  2  018 ; 2019 để hàm số 3 2
y x  2x  2m  5 x  5 đồng biến trên khoảng 0 ; + ? A. 2020 . B. 2022 . C. 2021. D. 2019 . Lời giải Chọn A Ta có 2
y  3x  4x  2m  5
Hàm số đồng biến trên khoảng 0;+  y  0, x   0;+ 2
 3x  4x  2m  5  0 , x  0;+ 2
 3x  4x  2m  5 , x  0;+
Xét hàm số f x 2
 3x  4x trên 0;+, ta có f x 2
 6x  4  0  x  3 Ta có bảng biến thiên / 4 11 Từ bảng trên suy ra 2
3x  4x  2m  5 , x
  0;+  2m  5    m  . 3 6
Do m nguyên và m  2
 018 ; 2019  m 2  018; 2  017; 2  016,....,0,  1 .
Vậy có 2020 giá trị m thỏa mãn đề bài.
Câu 42. Người ta thả một số lá bèo vào một hồ nước, sau 10 giờ số lượng lá bèo sẽ sinh sôi kín cả mặt
hồ. Biết rằng sau mỗi giờ số lượng lá bèo tăng gấp 10 lần số lượng lá bèo trước đó và tốc độ
tăng không đổi. Hỏi sau khoảng thời gian bao lâu số lượng lá bèo phủ kín tối thiểu một phần tư hồ? Trang14
A.10  log 4 . B.10 log 4 .
C.110 log 4 . D.10 10 log 4 . Lời giải Chọn A
Gọi S là số lượng lá bèo ban đầu được thả xuống hồ. 0
Sau 1 giờ thì số lượng lá bèo có trong hồ là S  10S ; 1 0
Sau 2 giờ thì số lượng lá bèo có trong hồ là 2 S 10 S ; 2 0 ……….
Sau n giờ thì số lượng lá bèo có trong hồ là S 10n S . n 0
Sau 10 giờ số lượng lá bèo phủ kín mặt hồ nên ta có 10 S  10 S . 10 0
Giả sử sau k giờ ( 0  k 10 ) thì số lượng lá bèo phủ kín tối thiểu một phần tư hồ 10 10   Khi đó: 1 k 1 k 10 10 10 S S  10 S  .10 S  10   k  log    10  log 4 . k 10 0 0 4 4 4  4 
Câu 43. Cho hàm số y  a   4
x  b   2 1
2 x c 1 có đồ thị như hình vẽ bên /
Mệnh đề nào dưới đây là đúng?
A. a 1, b  2
 , c 1. B. a 1, b  2  , c 1.
C. a 1, b  2
 , c 1. D. a 1, b  2, c 1. Lời giải Chọn B
Đồ thị đi lên khi x   nên a 1 0  a 1.
Đồ thị đi qua điểm 0;c  
1 có tung độ nằm phía trên trục hoành nên c 1  0  c 1 .
Đồ thị hàm số có 3 điểm cực trị nên a  
1 .b  2  0 mà a 1 nên b  2  0  b  2  .
Câu 44. Cho hình nón đỉnh S có đáy là đường tròn tâm O bán kính R . Trên đường tròn O lấy hai điểm ,
A B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng 2 R 2 . Thể tích
hình nón đã cho bằng 3  R 14 3  R 14 3  R 14 3  R 14 A. . B. . C. . D. . 12 2 6 3 Lời giải Chọn C /
Gọi H là trung điểm của đoạn . AB Nhận thấy:
+) Tam giác OAB vuông cân tại O .
+) OH AB , SH AB nên góc giữa hai mặt phẳng (SAB) , (OAB) bằng    SHO . 1 Ta có: SS .cos 2 2  R  1 R 2.cos  cos  . OAB SAB 2 2 2 R 2 OH 1 1 R Mà cos   2   2  SH  .2 2  2 . R SH 2 2 SH 2 2 2 2  R 2  R 14 2 2
SO SH OH 2  4R       2   2 3 1 1 R 14  R 14
Vậy thể tích của khối nón bằng 2 2
V   R .SO   R .  . 3 3 2 6 8 1 1 a c a c
Câu 45. Cho I  dx  ln  
với a, b, c, d là các số nguyên dương và , tối giản. x x x 1 2 b d b d 3
Giá trị của abc d bằng Trang15 A. 6  . B.18 . C. 0 . D. 3  . Lời giải Chọn A Đặt 2 t
x 1  t x 1  2 d t t  dx .
Khi x  3  t  2 ; Khi x  8  t  3. Khi đó 3 3 3 1 2t 2t I  .2 d t t  dt  dt    2 t 1  2 t   1 t
 2t 1 t 1 t 1 t 1 2 2   2   2 3 t   1  t   3 1  t   1 t   1          t tt 1 t  d d 2 1   t  1 t 2 1 t  1 t 2 1        2 2  3 3  1 1   1 t   1  t   1 1          t     t t 1 t   1 t   d . d 2 1   2 t   1 t   1 t     2 1  2 2  3 3  1 1 1 1    1 1      d     t
ln t 1  ln t 1  2    
2  t 1 t 1 t 1  2 t 1 2    2  3 1 t 1 1  1 1 1  1 1 1   ln   ln   ln      2 t 1 t 1 2 2 4  2 3 3  2 1 1 1 1 1 1 1 3 1
 ln  ln    ln 
a  3, b  2 , c 1, d 12 . 2 2 2 3 4 3 2 2 12
Vậy abc d  3.2.1 1  2  6  .
Câu 46. Cho hàm số y f x có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để
phương trình f f
 x  m  0 
có đúng 3 nghiệm phân biệt. / A.1. B. 2. C. 3. D. 4. Lời giải Chọn A
Đặt f x  t   * . Khi đó: /
Nhận xét: +) Với t  3
  phương trình * có một nghiệm x 1. +) Với t  3
  phương trình * có hai nghiệm x x và x x với x 1; x 1. 1 2 1 2 t m  0  t  m Ta có: f f
 x  m  0      . t   m  2 t   2  m
Vì 2  m  m, m  nên f f
 x  m  0 
có đúng 3 nghiệm phân biệt khi và chỉ khi:  m  3  m  3     m  3. 2  m  3  m  5
Vậy có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 47. Cho hai số thực a , b thỏa mãn 2 2
a b  1 và log
a b  1. Giá trị lớn nhất của biểu thức 2 2   a b
P  2a  4b  3 là 10 1 A. 10 . B. . C. 2 10 . D. . 2 10 Lời giải Trang16 ChọnA Do 2 2
a b  1 nên từ 2 2 log
a b  1  a b a b  1. 2 2   a b 2 2 a b 1  Suy ra: 2 2  1   1  1  a   b         2   2  2 Khi đó: 1 1            
P  2a  4b  3  2 a   4 b       2 4  2 2 1 1 1 2 2 .  a   b        20.  10    2   2    2   2     2    1 1 a b   2 2    0  1 1 2 4  a    2 2   Đẳ 2 10 ng thức xảy ra khi  1   1  1   a b          1 2  2   2  2 b      2 10   2 2 a b 1  1 1 a    2 10 Vậy P  10 khi  . max 1 2 b    2 10
Câu 48. Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số đã cho trên đoạn 0; 2 . Có bao nhiêu số nguyên a thuộc đoạn 3; 2 sao cho
M  2 m ? A. 7 . B. 5 . C. 6 . D. 4 . Lời giải Chọn D
Xét hàm số f x 4 3 2
x  4x  4x a trên đoạn 0;2 , có: f x 3 2 '
 4x 12x 8x . x  0  f ' x 3 2
 0  4x 12x  8x  0  x 1  . x  2 
Vì f 0  a , f  
1  1 4  4  a a 1, f   4 3 2
2  2  4.2  4.2  a a
nên trên đoạn 0;2 giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 4 3 2
x  4x  4x a lần
lượt là a 1, a .
Suy ra M  max  a ; a 1 ; m  min a ; a 1 nếu a a  
1  0 . m  0 nếu a a   1  0 . 0;2 0;2  1  TH1: a   ; 2    2   1 a   
M a 1 ; m a . Khi đó 2
M  2 m a 1  2 a  3a  2a 1  0  3  , vì a  a 1
nên chọn a 1;  2  1  TH2: a  3;      2  Trang17  2 a   
M a ; m a 1 . Khi đó 2
M  2 m a  2 a 1  3a  8a  4  0  3  , vì a  a  2  nên chọn a  3  ;  2
Vậy có 4 giá trị a thỏa yêu cầu.
Câu 49. Cho hình chóp S.ABC có các cạnh SA BC  3 ; SB AC  4 ; SC AB  2 5 . Tính thể tích
khối chóp S.ABC . 390 390 390 390 A. . B. . C. . D. . 12 4 6 8 Lời giải. Chọn B / /
+ Dựng hình chóp S.A' B'C ' sao cho A là trung điểm B 'C ' , B là trung điểm A'C ' , C là
trung điểm A' B ' . + Khi đó
SB AC BA'  BC '  4 nên SA'C 'vuông tại S và SA SC   SB2 2 2 ' ' 2.  64 (1) . 2 2
SA'  SB'  80 (2) + Tương tự S
B'C' , S
A'B' vuông tại S và  . 2 2
SB'  SC '  36 (3) + Từ  
1 ;2;3 ta suy ra SC '  10 ; SB '  26 ; SA'  54 . 1 1 + Ta tính đượ 1 390 c V
SC '. .SA'.SB '  390 và VV  .
S . A' B 'C ' 3 2 S.ABC
S. A' B'C ' 4 4
Câu 50. Cho 0  x  2021 và log (2  2)   3  8y x x y
.Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn 2
các điều kiện trên ? A.2021. B.2022. C.1. D.4. Lời giải Chọn D
Do 0  x  2021 nên log (2x  2) luôn có nghĩa. 2
Ta có log (2  2)   3  8y x x y 2 3
 log ( 1)  1 3  2 y x x y 2 log  2 ( x 1) 3  log ( 1)  2  3  2 y x y (1) 2
Xét hàm số ( )   2t f t t .
Tập xác định D   và (  ) 1 2t f t ln 2  f (  t)  0 t   .
Suy ra hàm số f (t) đồng biến trên  . Do đó (1)  log (x 1)  3y 3  1  2 y x 2
y  log (x 1) . 8
Ta có 0  x  2021 nên 1 x 1 2022 suy ra 0  log (x 1)  log 2022 . 8 8
Lại có log 2022  3, 66 nên nếu y   thì y 0;1;2;  3 . 8
Vậy có 4 cặp số (x ; y) nguyên thỏa yêu cầu bài toán là các cặp (0 ; 0) , (7 ;1) , (63; 2) , (511;3) .
-----------------HẾT----------------- Trang18 www.thuvienhoclieu.com
ĐỀ THI THỬTHPT QUỐC GIA 2021 ĐỀ 7 MÔN TOÁN Thời gian: 90 phút
Câu 1: Từ các số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có hai chữ số? A. 2 A . B. 36. C. 2 C . D. 6 2 . 6 6
Câu 2: Cho cấp số cộng u với u  2, công sai d  3. Tính u . n  1 5 A. 14. B. 17. C. 162. D. 20.
Câu 3:Nghiệm của phương trình 3x7 2  32 là 2 23 A. x  .B. x
.C. x  4.D. x  4.  3 3
Câu 4: Tính thể tích khối hộp chữ nhật có ba kích thước a  4, b  5, c  6 A. 15.B. 40. C. 120.D. 60.
Câu 5: Tập xác định của hàm số y  log x  2 là 2  
A. 2;   .B. 2;   .C.  ;  2 . D.  ;  2.
Câu 6:Với f (x ), (
g x ) là hai hàm số liên tục trên khoảng K và k ¹ 0 thì mệnh đề nào sau đây là sai? A. f (x) ( g x)dx = f (x)dx ( g x)dx. ò ò ò B. f é (x) ( g x)d ù + x = f (x)dx + ( g x)dx. ò êë úû ò ò C. f (
¢x)dx = f (x) + C . ò D.
kf (x)dx = k f (x)dx. ò ò
Câu 7:Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA  2a và SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD . 3 a 4 2 A. . B. 3 a . C. 3 a . D. 3 2a . 3 3 3
Câu 8:Cho khối nón có chiều cao h  5, bán kính đáy r  3. Tính thể tích của khối nón đã cho. 45 25 A. 25.B. .C. 45.D. . 3 3
Câu 9:Tính diện tính mặt cầu bán kính r  2a . A. 2 a .B. 2 8 a .C. 2 4 a .D. 2 16 a .
Câu 10:Cho hàm số f (x) có bảng biến thiên sau x  2 0 
f '(x) + 0 - 0 + 0  Hàm số đã cho đồng biến trên f (x) khoảng nào dưới đây? -4 A. ( ;  0) .B.  (2; 0) .C. (4; ) D. ( ;  2) . Câu 11: Với ,
a b là các số thực dương tùy ý, 2 3 log a b bằng 2 1 1
A. 2log a  3log b .B.
log a  log b . C. 2log a  3log b. D. 5  log a  log b . 2 2 2 2 2 3 2 2 2 2
Câu 12:Tính diện tích xung quanh của hình trụ có độ dài đường sinh l  5 bán kính đáy r  4.
A. 40 .B. 20 .C. 48 .D. 16 .
Câu 13:Cho hàm số f (x) có bảng biến thiên sau Trang19 x  2 0 2  f '(x) + 0 - 0 + 0 - 1616 f (x) Giá trị cực tiểu 0 của hàm số đã   cho bằng A. 2.B. 0.C. 2.D. 16.
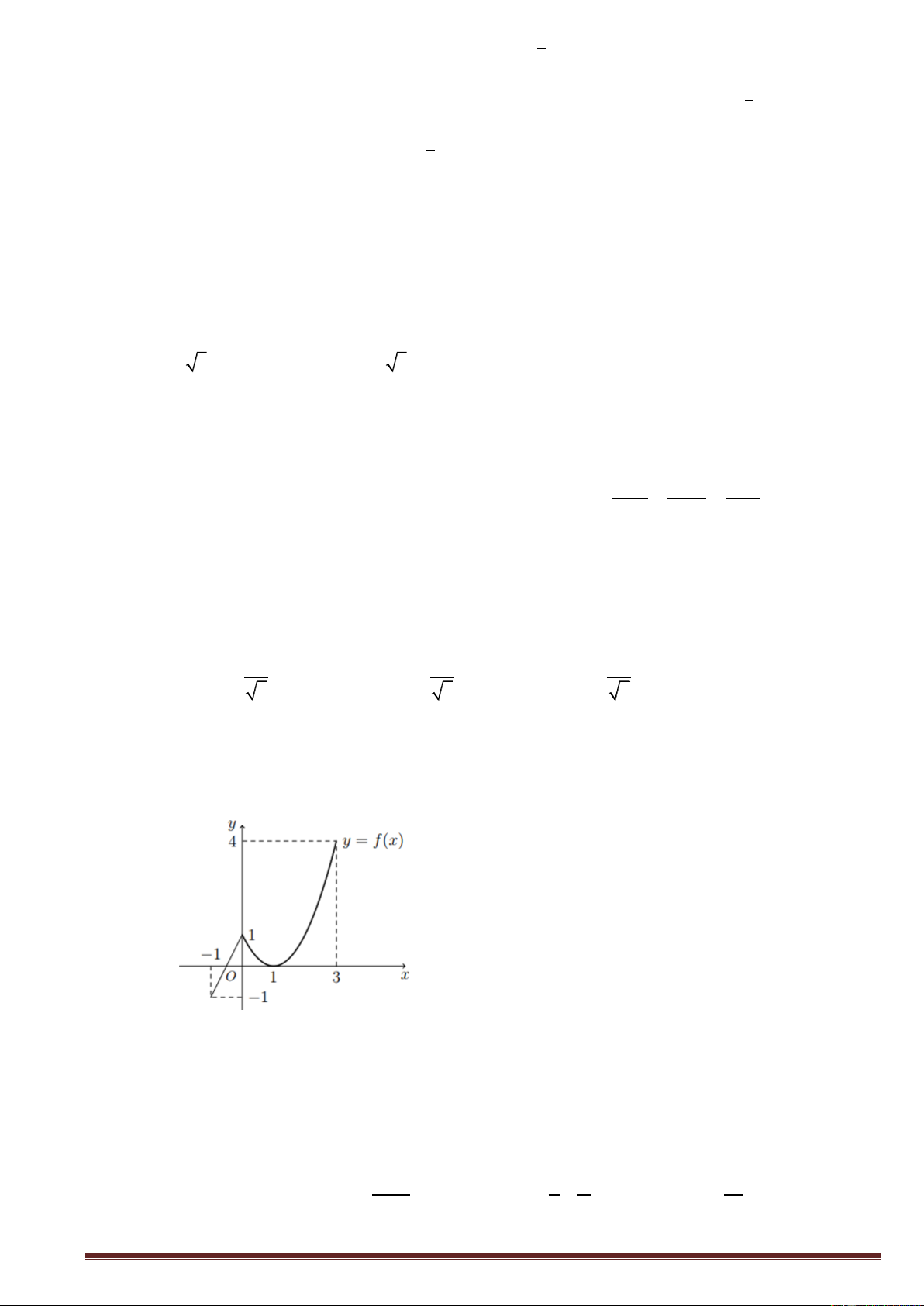
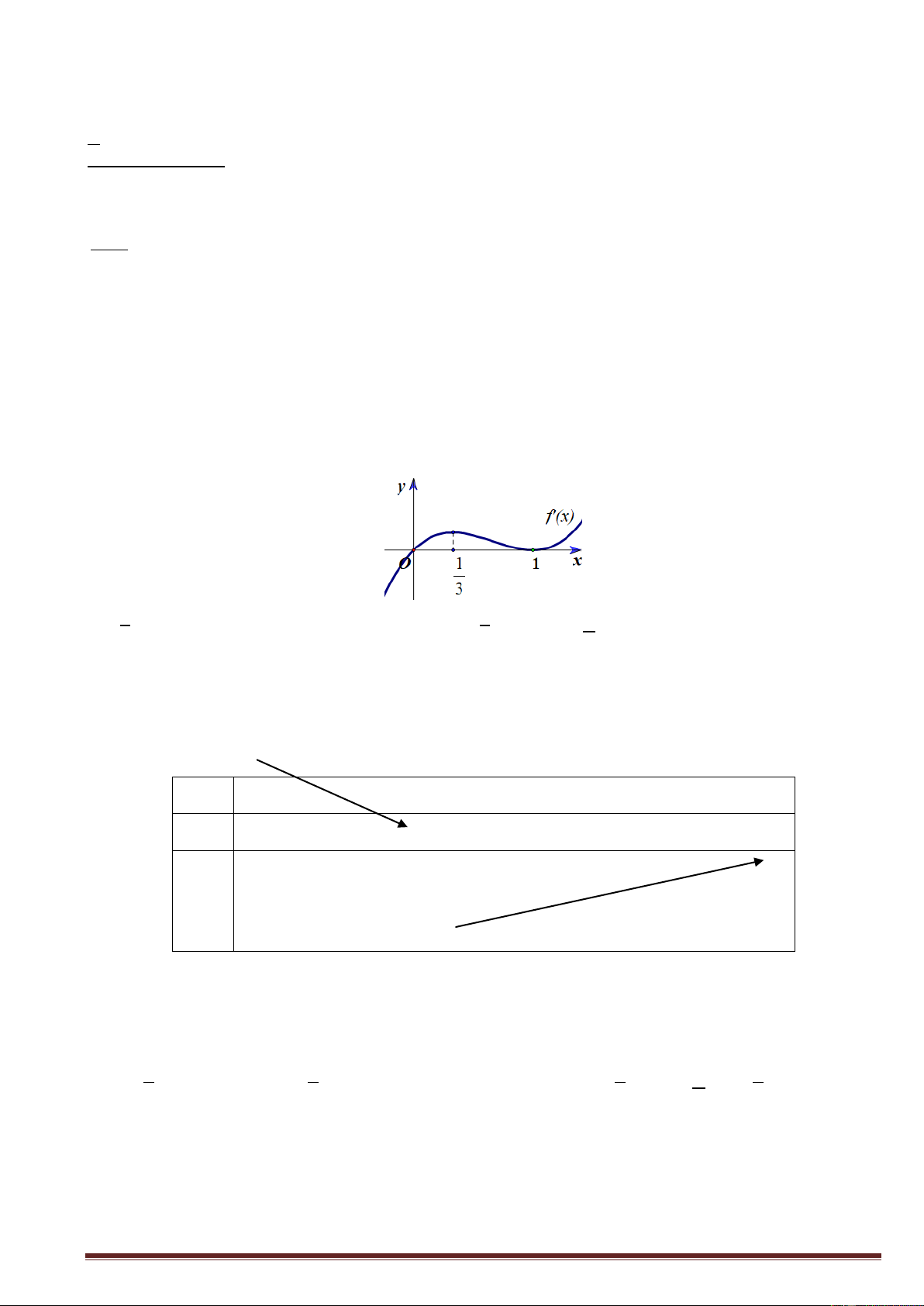
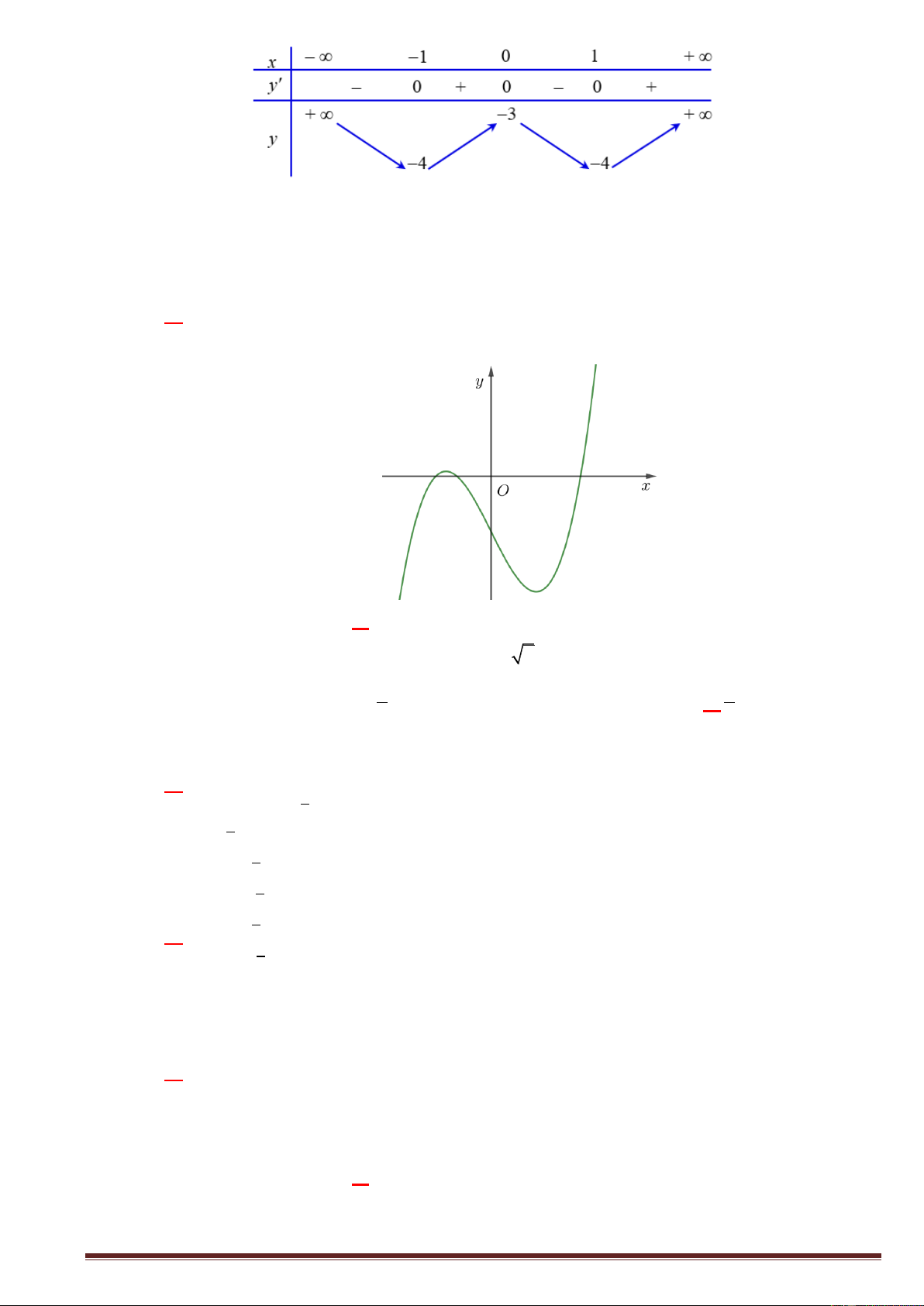
Câu 14:Đồ thị của hàm số nào có dạng như đường cong ở hình dưới? A. 4 2
y x  2x 1. B. 4 2
y  x  2x 1 y C. 4 2
y x x 1.D. 3 2
y x  3x 1 O x x
Câu 15: Tìm tiệm cận đứng của đồ thị hàmsố 2021 y  . x 1 A. x  1.
 B. y  1.C. y  1.D. x  2021 
Câu 16:Giải bất phương trình log 2x  5  2 . 3   5
A. x  7 . B. x  7 . C.
x  7 . D. x  7 . 2
Câu 17:Cho hàm số y f x có bảng biến thiên như hình bên. Số nghiệm của phương trình
f x 1  0 là: A. 0 . B. 3 . C. 2 . D. 1. 3 3 2 Câu 18:Nếu f ( ) x dx  4   và f ( ) x dx  3  thì f ( ) x dx  bằng 1  2 1  A. -7.B. 7.C. -1.D. -12.
Câu 19:Môđun của số phức 6  5i bằng A. 11.B. 11 .C. 61. D. 61 .
Câu 20: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Giá trị của biểu thức 1 2 2 2
z z bằng 1 2 3 9 9 A. .B.  .C. 3 .D.  . 18 8 4
Câu 21:Tìm số phức liên hợp z của số phức z  (3  2i)(2  3i). A. z  5
 .i B. z  66 .i
C. z 12 5i D. z  6  6 . i
Câu 22:Trong không gian Oxyz, hình chiếu của điểm M(2; 2
 ;1) trên mặt phẳng (Oy ) z có tọa độ là A. (0; 2  ;1) . B. (2; 2  ;0) .C. (2;0;0) .D. (0; 2  ;0) .
Câu 23:Trong không gian Oxyz, cho mặt cầu 2 2 2 ( )
S : (x  2)  (y  1)  (z 5)  25. Tìm tọa độ tâm của mặt cầu ( ) S . A. (2; 1  ;5) .B. ( 2  ;1; 5  ) .C. (2;1;5) .D. ( 2  ; 1  ; 5  ) . Trang20
Câu 24:Trong không gian Oxyz, cho mặt phẳng ( )
P : x  3y  5  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng ( ) P ?     A. n  (1;3; 5  ) .B. n  ( 1  ;3; 5  ) . C. n  (1; 3
 ;0) .D. n  (1;3;0) . 1 2 3 4
Câu 25: Trong không gian
Oxyz, điểm nào dưới đây thuộc đường thẳng x  3 y 1 z 2 (d) :   2 3  1  ?
A. M(3; 1;2) .B. N( 3  ;1; 2  ) . C. ( P 2; 3  ; 1  ).D. ( Q 3  ;1;2) .
Câu 26: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a , SA vuông góc với mặt phẳng
đáy và SA  2 3a . Góc giữa SC và mặt phẳng (ABCD) bằng S A B D C A. 0 30 .B. 0 60 .C. 0 45 .D. 0 90 .
Câu 27:Cho hàm số y f x có bảng xét dấu đạo hàm như sau
Hàm số đã cho có bao nhiêu điểm cực trị? A. 1.B. 2.C.3.D. 4.
Câu 28:Giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn  4  ;4   bằng:
A. – 41. B. 41. C. 8. D. 15.
Câu 29: Cho log 5  ;
a log 5  b . Tính log 5theo a và b . 2 3 6 1 ab A.  . D. 2 2 a b . a  . B. b a  . C. a b b
Câu 30: Cho hàm số y f (x) có bảng biến thiên như sau:
Tập tất cả các giá trị của tham số m để phương trình f (x)  m có ba nghiệm phân biệt là A. (4;  ) . B. ( ;  2) . C. [  2; 4] . D. ( 2  ;4) . Trang21
Câu 31: Bất phương trình log (3x  2)  log (6  5x) có tập nghiệm là (a ;b) . Tổng a b bằng 2 2 8 28 26 11 A. . B. . C. . D. . 3 15 5 5
Câu 32: Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của
hình nónbằng 9π . Tính đường cao h của hình nón. 3 3 A. . B. 3 3 . C. . D. 3 . 2 3 2 4  x
Câu 33:Cho hàm số y f x liên tục trên  và f 2  16, f
 xdx  4. Tính xf  dx    .  2  0 0 A. I  144 . B. I  12 . C. I  112 . D. I  28.
Câu 34. Diê ̣n tích hình phẳng giới ha ̣n bởi hai đồ thi ̣ f x 3
x 3x  2 ; g x  x  2 là: A. S  8. B. S  4 . C. S 12 . D. S 16 .
Câu 35. Cho hai số phức z  2  3i và z  3
  5i . Tính tổng phần thực và phần ảo của số phức 1 2
w z z . 1 2 A. 3 . B. 0 . C. 1   2i . D. 3  .
Câu 36: Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện z 1 2i  1 là
A. đường tròn I 1;2, bán kính R 1.
B. đường tròn I  1  ; 2   , bán kính R  1 .
C. đường tròn I  1
 ;2, bán kính R 1.
D. đường tròn I 1; 2
  , bán kính R 1.
Câu 37: Trong không gian Oxyz , cho hai điểm A3;1; 1   , B2; 1
 ;4 . Phương trình mặt phẳng
OAB (O là gốc tọa độ) là
A. 3x 14 y  5z  0 .
B. 3x 14 y  5z  0 . C. 3x 14 y  5z  0 . D. 3x 14 y  5z  0 .
Câu 38:Trong không gian với hệ trục tọa độ (Oxyz) , phương trình đường thẳng d đi qua điểm
A1;2;1 và vuông góc với mặt phẳng  P : x  2y z 1  0 có dạng x 1 y  2 z 1 x  2 y z  2 A. d :   d :   1  . B. 2 1 1 2  . 1 x 1 y  2 z 1 x  2 y z  2 C. d :   . D. d :   1 2 1 2 4  . 2
Câu 39:Kết quả  ;
b c của việc gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp, trong
đó b là số chấm xuất hiện của lần gieo thứ nhất, c là số chấm xuất hiện của lần gieo thứ hai được
thay vào phương trình bậc hai 2
x bx c  0 . Xác suất để phương trình bậc hai đó vô nghiệm là 7 17 23 5 A. . B. . C. . D. . 12 36 36 36
Câu 40: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , BC SB a. Hình chiếu
vuông góc của S lên mặt phẳng  ABC  trùng với trung điểm của BC . Góc giữa đường thẳng SA
và mặt phẳng  ABC  bằng A. 0 60 . B. 0 75 . C. 0 30 . D. 0 45 .
Câu 41: Để đồ thị hàm số 4
y  x  m   2
3 x m 1 có điểm cực đại mà không có điểm cực tiểu
thì tất cả các giá trị thực của tham số m là
A. m  3 .B. m  3 .C. m  3.D. m  3 .
Câu 42:Một người vay ngân hàng 500 triệu đồng với lãi suất 1,2%/ tháng để mua xe ô tô.
Sauđúng một tháng kể từ ngày vay thì người đó bắt đầu trả nợ và đều đặn cứ mỗi tháng người đó
sẽ trả cho ngân hàng 20 triệu đồng cho đến khi hết nợ (tháng cuối cùng có thể trả dưới 20 triệu Trang22
đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng? Biết rằng lãi suất không thay đổi. A. 30 tháng. B. 26 tháng. C. 29 tháng. D. 32 tháng. Câu 43: Cho hàm số    4 3 2 y
f x mx nx px qx r , trong đó , m , n , p , q r   . Biết
hàm số y f   x có đồ thị như hình bên dưới. y -1 1 4 x O
Số nghiệm của phương trình f x  16m  8n  4 p  2q r là
Câu 44:Một bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y x 1 và trục Ox , quay quanh trục Ox . Biết đáy lọ và miệng lọ
có đường kính lần lượt là 2 dm và 4 dm , khi đó thể tích của lọ là : 15 14 15 A. 3 8 dm . B. 3  dm . C. 3  dm . D. 3 dm . 2 3 2 1 7
Câu 45: Cho tích phân I   x  2 ln  x  
1 dx a ln 2  
trong đó a , b là các số nguyên dương. b 0 Tổng 2 a b bằng
A. 8 . B. 16 . C. 12 . D. 20 .
Câu 46:Cho hàm số y f x có bảng xét dấu của f   x như sau. x -∞ -1 3 +∞ f'(x) + 0 - 0 + 2
f 1xx
Xét hàm số g x    e
, tập nghiệm của bất phương trình g  x  0 là  1     1   1  A. ;   . B.    1 ; 1  ; 2   . C. ;    . D. 1  ;  2;    .  2   2   2   2  x y
Câu 47: Cho x , y thỏa mãn log
x x  9  y y  9  xy 3 2 2    
x y xy
. Tìm giá trị lớn nhất 2 3x  2 y  9 của P
khi x , y thay đổi. x y 10 A. 2 . B. 3 . C. 1. D. 0 .
Câu 48. Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số đã cho trên 0;2 . Có bao nhiêu số nguyên a thuộc 4; 4 sao cho M  2m ? A. 7 . B. 5 . C. 6 . D. 4 .
Câu 49:Cho tứ diện ABCD có  
DAB CBD  90 ;  AB  ;
a AC a 5; ABC  135 . Biết góc giữa
hai mặt phẳng  ABD,  BCD bằng 30 . Thể tích của tứ diện ABCD là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 3 2 3 2 6
Câu 50:Cho hai số thực x , y thỏa mãn Trang23    y y  
  x  x 2 5 4x x log 8 16 log 5 1   2log  log  2y 82 2 . 2 3 2 3 3
Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức 2 2 P
x y m
không vượt quá 10 . Hỏi S có bao nhiêu tập con không phải là tập rỗng? A. 2047 . B. 16383. C. 16384. D. 32 .
------------- HẾT ------------- BẢNG ĐÁP ÁN 1B 2A 3CD 4D 5A 6A 7A 8B 9D 10D 11C 12A 13B 14A 15A 16A 17B 18A 19D 20D 21C 22A 23B 24D 25B 26B 27C 28A 29B 30D 31D 32B 33B 34A 35D 36C 37A 38D 39B 40A 41A 42A 43A 44B 45D 46A 47C 48A 49D 50B
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Từ các số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có hai chữ số? A. 2 A . B. 36. C. 2 C . D. 6 2 . 6 6 Lời giải
Đểlập số tự nhiên có hai chữ số ta thực hiện như sau:
Chọn số thứ nhất: có 6 cách chọn
Chọn số thứ hai: có 6 cách chọn
Theo quy tắc nhân ta có 6.6=36 số
Câu 2: Cho cấp số cộng u với u  2, công sai d  3. Tính u . n  1 5 A. 14. B. 17. C. 162. D. 20. Lời giải
Theo công thức tính số hạng tổng quát
u u  4d  2  4.3  14 5 1
Câu 3:Nghiệm của phương trình 3x7 2  32 là 2 23 A. x  .B. x
.C. x  4.D. x  4.  3 3 Lời giải 3x7 3x7 5 2  32  2
 2  3x  7  5  x  4
Câu 4: Tính thể tích khối hộp chữ nhật có ba kích thước a  4, b  5, c  6 A. 15.B. 40.C.120.D. 60. Lời giải
V abc  4.5.6  120
Câu 5:Tập xác định của hàm số y  log x  2 là 2  
A. 2;   .B. 2;   .C.  ;  2 . D.  ;  2. Lời giải
Điều kiện x  2  0  x  2
Câu 6:Với f (x ), (
g x ) là hai hàm số liên tục trên khoảng K và k ¹ 0 thì mệnh đề nào sau đây là sai? A. f (x) ( g x)dx = f (x)dx ( g x)dx. ò ò ò B. f é (x) ( g x)d ù + x = f (x)dx + ( g x)dx. ò êë úû ò ò C. f (
¢x)dx = f (x) + C . ò D.
kf (x)dx = k f (x)dx. ò ò Lời giải Trang24
Nguyên hàm không có tính chất nguyên hàm của tích bằng tích các nguyên hàm.
Câu 7:Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA  2a và SA vuông góc
với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD . 3 a 4 2 A. . B. 3 a . C. 3 a . D. 3 2a . 3 3 3 Lời giải
Ta có diện tích đáy ABCD : 2 Sa . ABCD
Đường cao SA  2a . 1 1 2
Vậy thể tích khối chóp S.ABCD là V S .SA 2  .a .2a 3  a . 3 ABCD 3 3
Câu 8:Cho khối nón có chiều cao h  5, bán kính đáy r  3. Tính thể tích của khối nón đã cho. 45 25 A. 25.B. .C. 45.D. . 3 3 Lời giải 1 45 2 V  .3 .5  . 3 3
Câu 9:Tính diện tính mặt cầu bán kính r  2a . A. 2 a .B. 2 8 a .C. 2 4 a .D. 2 16 a . Lời giải
Áp dụng công thức tính diện tích mặt cầu 2 2 2
S 4r  4 .(2 ) a  16 a
Câu 10:Cho hàm số f (x) có bảng biến thiên sau x  2 0 
f '(x) + 0 - 0 + /// 0 f (x)  Hàm số đã cho đồng biến trên -4 khoảng nào dưới đây?  A. ( ;  0) .B.
(2; 0) .C. (4; ) D. ( ;  2) . Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên các khoảng ( ;  2) và (0;) Câu 11: Với ,
a b là các số thực dương tùy ý, 2 3 log a b bằng 2 1 1
A. 2log a  3log b .B.
log a  log b .C. 2log a  3log b. D. 5  log a  log b . 2 2 2 2 2 3 2 2 2 2 Lời giải 2 3 2 3
log a b  log a  log b  2log a  3log b 2 2 2 2 2
Câu 12:Tính diện tích xung quanh của hình trụ có độ dài đường sinh l  5 bán kính đáy r  4. Trang25
A. 40 .B. 20 .C. 48 .D. 16 . Lời giải
S  2rl  2 .4.5  40 . xq
Câu 13:Cho hàm số f (x) có bảng biến thiên sau x  2 0 2  f '(x) + 0 - 0 + 0 - ////1616 f (x) Giá trị cực tiểu 0 của hàm số đã   cho bằng A. 2 B. 0C. 2D. 16 Lời giải
Dựa vào bảng biến thiên ta có y  0 CT
Câu 14:Đồ thị của hàm số nào có dạng như đường cong ở hình dưới? /A. 4 2
y x  2x 1. B. 4 2
y  x  2x 1 C. 4 2
y x x 1.D. 3 2
y x  3x 1 Lời giải
Câu A: Đúng dạng đồ thị ( a  0, ab  0)
Câu B: Không đúng dạng đồ thị ( a  0)
Câu C: Không đúng dạng đồ thị ( a  0,ab  0 )
Câu D: Không đúng dạng đồ thị (Hàm số bậc ba) x
Câu 15: Tìm tiệm cận đứng của đồ thị hàmsố 2021 y  . x 1 A. x  1.
 .B. y  1.C. y  1.D. x  2020  . Lời giải x
Tìm tiệm cận đứng của đồ thị hàmsố 2021 y  là x  1.  x 1
Câu 16:Giải bất phương trình log 2x  5  2 . 3   5
A. x  7 . B. x  7 . C.
x  7 . D. x  7 . 2 Lời giải  5 x  log 2x  5  2   2  x  7 3   2x 5  9
Câu 17:Cho hàm số y f x có bảng biến thiên như hình bên. Số nghiệm của phương trình
f x 1  0 là: / A. 0 . B. 3 . C. 2 . D. 1. Lời giải
Số nghiệm của phương trình f x 1  0  f (x)  1
 bằng số giao điểm của đồ thị hàm
số y f x và đường thẳng y  1 Trang26 //
Dựa vào bảng biến thiên ta thấy đồ thị hàm số y f x cắt đường thẳng y  1 tại 3 điểm phân
biệt suy ra phương trình đã cho có 3 nghiệm. 3 3 2 Câu 18:Nếu f ( ) x dx  4   và f ( ) x dx  3  thì f ( ) x dx  bằng 1  2 1  A. -7B. 7C. -1D. -12 Lời giải Ta có 2 3 3 2 3 3 f ( ) x dx f ( ) x dx f ( ) x dx f ( ) x dx f ( ) x dx f ( )
x dx   4  3  7        1  2 1  1  1  2
Câu 19:Môđun của số phức 6  5i bằng A. 11.B. 11 .C. 61. D. 61 . Lời giải Ta có 2 2 6  5i  6  ( 5  )  61
Câu 20: Gọi z , z là hai nghiệm phức của phương trình 2
2z  3z  3  0 . Giá trị của biểu thức 1 2 2 2
z z bằng 1 2 3 9 9 A. . B.  . C. 3 . D.  . 18 8 4 Lời giải   3  21iz  1 Ta có 2 4
2z  3z  3  0     3  21  z  2  4 9 Suy ra 2 2 z z   . 1 2 4
Câu 21: Tìm số phức liên hợp z của số phức z  (3  2i)(2  3i). A. z  5
 .i B. z  66 .i
C. z 12 5i D. z  6  6 . i Lời giải
z  (3  2i)(2  3i) 12  5i z  12  5i
Câu 22:Trong không gian Oxyz, hình chiếu của điểm M(2; 2
 ;1) trên mặt phẳng (Oy ) z có tọa độ là A. (0; 2  ;1) . B. (2; 2  ;0) .C. (2;0;0) .D. (0; 2  ;0) . Lời giải
Ta có hình chiếu của điểm M(x ; y ; z ) trên mặt phẳng (Oy )
z là điểm M '(0; y ; z ) 0 0 0 0 0
Vậy hình chiếu của điểm M(2; 2
 ;1) trên mặt phẳng (Oy )
z có tọa độ là (0; 2  ;1) .
Câu 23:Trong không gian Oxyz, cho mặt cầu 2 2 2 ( )
S : (x  2)  (y  1)  (z 5)  25. Tìm tọa độ tâm của mặt cầu ( ) S . A. (2; 1  ;5) .B. ( 2  ;1; 5  ) .C. (2;1;5) .D. ( 2  ; 1  ; 5  ) . Lời giải Mặt cầu 2 2 2 2 ( ) S : (x  ) a  (y  ) b  (z )
c r có tâm I ( ; a ; b ) c Do đó mặt cầu ( )
S có tâm I (2;1; 5) .
Câu 24:Trong không gian Oxyz, cho mặt phẳng ( )
P : x  3y  5  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng ( ) P ?     A. n  (1;3; 5  ) .B. n  ( 1  ;3; 5  ) . C. n  (1; 3
 ;0) .D. n  (1;3;0) . 1 2 3 4 Trang27 Lời giải  Mặt phẳng ( )
P có vec tơ pháp tuyến là n  (1;3;0) (P)
Câu 25: Trong không gian
Oxyz, điểm nào dưới đây thuộc đường thẳng x  3 y 1 z 2 (d) :   2 3  1  ?
A. M(3; 1;2) .B. N( 3  ;1; 2  ) . C. ( P 2; 3  ; 1  ).D. ( Q 3  ;1;2) . Lời giải
Thay tọa độ các điểm vào phương trình đường thẳng ta thấy điểm N( 3  ;1; 2  ) thỏa mãn 3   3 11 2   2       x 3 y 1 z 2 0 N
 thuộc đường thẳng (d) :   2 3  1  . Vậy điểm ( 3;1; 2) 2 3  1 
Câu 26: Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a , SA vuông góc với mặt phẳng
đáy và SA  2 3a . Góc giữa SC và mặt phẳng (ABCD) bằng / A. 0 30 .B. 0 60 .C. 0 45 .D. 0 90 . Lời giải
Ta có SA  (ABCD) nên góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng SCA SA 2 3a
Xét tam giác vuông SAC, tan SCA    3 AC 2 . a 2 Vậy 0 SCA  60
Câu 27:Cho hàm số y f x có bảng xét dấu đạo hàm như sau /
Hàm số đã cho có bao nhiêu điểm cực trị? B. 1B. 2C.3 D. 4 Lời giải
Từ bảng biến thiên ta thấy f ' x đổi dấu 3 lần khi qua x  2
 ; x  0; x  1 nên hàm số có 3 điểm cực trị.
Câu 28:Giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x  35 trên đoạn  4  ;4   bằng: A.– 41. B. 41. C. 8.D. 15. Lời giải
Hàm số đã cho xác định và liên tục trên đoạn  4  ;4   x  1    4  ;4   2
y'  3x  6x  9; y'  0   x  3  4  ;4    ( y 4  )  4  1; ( y 1  )  40; ( y 3)  8; ( y 4)  15 min y  4  1  4  ;4  
Câu 29: Cho log 5  ;
a log 5  b . Tính log 5theo a và b . 2 3 6 1 ab A.  . D. 2 2 a b . a  . B. b a  . C. a b b Lời giải log 5 1 1 ab 5 log 5     6 log 6 log 2  log 3 1 1 a b 5 5 5  a b Trang28
Câu 30: Cho hàm số y f (x) có bảng biến thiên như sau: /
Tập tất cả các giá trị của tham số m để phương trình f (x)  m có ba nghiệm phân biệt là A. (4;  ) . B. ( ;  2) . C. [  2; 4] . D. ( 2  ;4) . Lời giải
Số nghiệm của phương trình f (x)  m chính là số giao điểm của đồ thị hàm số y f (x) và đường
thẳng y m .
Dựa vào bảng biến thiên thì phương trình f (x)  m có ba nghiệm phân biệt khi 2   m  4 .
Vậy phương trình có ba nghiệm phân biệt khi m  ( 2  ;4) .
Câu 31: Bất phương trình log (3x  2)  log (6  5x) có tập nghiệm là (a ;b) . Tổng a b bằng 2 2 8 28 26 11 A. . B. . C. . D. . 3 15 5 5 Lời giải x 1 3
x  2  6  5x  6
Ta có: log (3x  2)  log (6  5x)     6  1  x  . 2 2 6  5x  0 x  5  5
Tập nghiệm của bất phương trình là 6 (1; ) . 5 6 11
Vậy a b  1  . 5 5
Câu 32: Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của
hình nónbằng 9π . Tính đường cao h của hình nón. 3 3 A. . B. 3 3 . C. . D. 3 . 2 3 Lời giải /
Gọi l, R lần lượt là độ dài đường sinh và đường kính đáy của hình nón. l   2R l   2R l   6 Theo bài ra ta có      . 2 πR  9πR  3 R  3
Đường cao của hình nón là 2 2
h l R  36  9  3 3 . 2 4  x
Câu 33: Cho hàm số y f x liên tục trên  và f 2  16, f
 xdx  4. Tính xf  dx    .  2  0 0 A. I  144 . B. I  12 . C. I  112 . D. I  28. Lời giải Đặ x t
t x  2t  dx  2dt . 2
Đổi cận: x  0  t  0; x  4  t  2. 4 2 2 2 Khi đó  x xf  dx  4 tf    
 tdt  4tf t2 4 f
 tdt  4.2.f 24. f  xdx 0  2  0 0 0 0  4.2.164.4 112
Câu 34. Diê ̣n tích hình phẳng giới ha ̣n bởi hai đồ thi ̣ f x 3
x 3x  2 ; g x  x  2 là: A. S  8. B. S  4 . C. S 12 . D. S 16 . Lời giải Trang29
Phương trình hoành đô ̣ giao điểm của hai đồ thi ̣ x  0 3 3
x  3x  2  x  2  x  4x  0   x  2  Diê ̣n tích cần tìm 0 2 0 2 3 3 S
x  4x dx
x  4x dx  
   3x 4xdx   3x 4xdx 2  0 2  0 4 4  x  0  x  2 2 2    2x
   2x   8. 4 2     4 0 
Câu 35. Cho hai số phức z  2  3i và z  3
  5i . Tính tổng phần thực và phần ảo của số phức 1 2
w z z . 1 2 A. 3 . B. 0 . C. 1   2i . D. 3  . Lời giải
w z z  2  3i  3  5i  1
  2i . Vậy tổng phần thực và phần ảo của số phức w là 3  . 1 2
Câu 36: Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện z 1 2i  1 là
A. đường tròn I 1;2, bán kính R 1.
B. đường tròn I  1  ; 2   , bán kính R  1 .
C. đường tròn I  1
 ;2, bán kính R 1.
D. đường tròn I 1; 2
  , bán kính R 1. Lời giải
Đặt z x y ;ix, y R Khi đó: 2 2
z 1 2i  1   x  
1  y  2i 1   x  
1   y  2  1
 x  2  y  2 1 2 1
Vậy tập hợp điểm biểu diễn số phức z là đường tròn I  1
 ;2, bán kính R 1.
Câu 37: Trong không gian Oxyz , cho hai điểm A3;1; 1   , B2; 1
 ;4 . Phương trình mặt phẳng
OAB (O là gốc tọa độ) là
A. 3x 14 y  5z  0 .
B. 3x 14 y  5z  0 . C. 3x 14 y  5z  0 . D. 3x 14 y  5z  0 . Lời giải   Ta có OA  3;1; 1
  , OB  2; 1  ;4 .   
Phương trình mặt phẳng OAB có vectơ pháp tuyến là n  O , A OB  3; 1  4; 5     .
Vậy phương trình mặt phẳng OAB là 3x 14y  5z  0 .
Câu 38:Trong không gian với hệ trục tọa độ (Oxyz) , phương trình đường thẳng d đi qua điểm A1; 2 
;1 và vuông góc với mặt phẳng  P : x  2y z 1  0 có dạng x 1 y  2 z 1 x  2 y z  2 A. d :   d :   1  . B. 2 1 1 2  . 1 x 1 y  2 z 1 x  2 y z  2 C. d :   . D. d :   1 2 1 2 4  . 2 Lời giải  
Mặt phẳng P có vecto pháp tuyến n  1; 2  ; 
1 . Vì d   P nên n   cũng là vecto chỉ P 1; 2;  1 P
phương của đường thẳng d . Suy ra phương trình đường thẳng d thường gặp là Trang30 x 1 y  2 z 1   1 
. So với đáp án không có, nên đường thẳng d theo bài là đường có vecto chỉ 2 1 
phương cùng phương với n và đi qua điểm A1;2 
;1 . Thay tọa độ điểm A1;2;1 vào 3 đáp án A, P
B, D thấy đáp án D thỏa mãn. Câu 39: Kết quả  ;
b c của việc gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp, trong
đó b là số chấm xuất hiện của lần gieo thứ nhất, c là số chấm xuất hiện của lần gieo thứ hai được
thay vào phương trình bậc hai 2
x bx c  0 . Xác suất để phương trình bậc hai đó vô nghiệm là 7 17 23 5 A. .B. .C. .D. . 12 36 36 36 Lời giải
Số phần tử của không gian mẫu là 36 . Xét phương trình 2
x bx c  0 có 2
  b  4c , với , b c 1  ,6 .
Phương trình vô nghiệm    0  b  2 c . Ta có bảng sau /
Suy ra có 17 cách gieo để phương trình vô nghiệm. 17
Vậy xác suất cần tìm là P  . 36
Câu 40: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , BC SB a. Hình chiếu
vuông góc của S lên mặt phẳng  ABC  trùng với trung điểm của BC . Góc giữa đường
thẳng SA và mặt phẳng  ABC  bằng A. 0 60 . B. 0 75 . C. 0 30 . D. 0 45 . Lời giải /
Gọi H là trung điểm cạnh BC SH   ABC .
Góc giữa SA và mặt phẳng  ABC  là  SA HA  ;  SAH . a 3 1 a 2 2
SH SB HB  và AH BC  2 2 2 SH
Xét tam giác SHA ta có   0 tan SAH   3  SAH  60 . AH
Câu 41: Để đồ thị hàm số 4
y  x  m   2
3 x m 1 có điểm cực đại mà không có điểm cực tiểu
thì tất cả các giá trị thực của tham số m là A. m  3 . B. m  3 . C. m  3. D. m  3 . Lời giải 3
y   x  m   x   x  2 ' 4 2 3 2
2x m  3 . x  0 y ' 0    3  m . 2 x   2
Vì hàm số đã cho là hàm trùng phương với a  1
  0 nên hàm số có điểm cực đại mà không có  điể 3 m
m cực tiểu  y '  0 có đúng 1 nghiệm bằng 0   0  m  3. 2
Câu 42:Một người vay ngân hàng 500 triệu đồng với lãi suất 1,2%/ tháng để mua xe ô tô. Sau
đúng một tháng kể từ ngày vay thì người đó bắt đầu trả nợ và đều đặn cứ mỗi tháng
người đó sẽ trả cho ngân hàng 20 triệu đồng cho đến khi hết nợ (tháng cuối cùng có thể Trang31
trả dưới 20 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân
hàng? Biết rằng lãi suất không thay đổi. A. 30 tháng. B. 26 tháng. C. 29 tháng. D. 32 tháng. Lời giải
Sau 1 tháng dư nợ là: N N 1 r m với N =500 triệu đồng , r  0,012 , m =20 triệu đồng. 1   Sau 2 tháng dư nợ 2
là: N N 1 r m N 1 rm 1   1 r  2 1        . ………….. n 2 n 1 
Sau tháng thứ n dư nợ là: N N
r m    r   r    rn 1  1 1  1  ... 1    n          rn 1.1 r  1 m n m N 1  m    N   1 r  .  1 r 1   r r  
Người đó trả hết nợ ngân hàng khi dư nợ bằng 0 nên ta có:  m N   rn m
     rn m n 20 n 10 1 0 1  1,012  1,012     r r m Nr 20  500.0, 012 7 10  n  log
n  29,90 . Vậy sau 30 tháng người đó trả hết nợ ngân hàng. 1,012 7 Câu 43: Cho hàm số    4 3 2 y
f x mx nx px qx r , trong đó , m , n , p , q r   . Biết
hàm số y f   x có đồ thị như hình bên dưới. /
Số nghiệm của phương trình f x  16m  8n  4 p  2q r là A. 4 . B. 5 . C. 2 . D. 3 . Lời giải
Dựa vào đồ thị hàm số y f  x , ta có bảng biến thiên: / 1 4 1 4 Nhìn vào đồ thị ta có f
 xdx f
 xdx f
 xdx   f   xdx 1  1 1  1  0  f   1  f   1  f  
1  f 4  f   1  f 4 . 1 2 1 2 Nhìn vào đồ thị ta có f
 xdx f
 xdx f
 xdx   f   xdx 1  1 1  1  0  f   1  f   1  f  
1  f 2  f  
1  f 2 . Suy ra: f 4  f   1  f 2
Số nghiệm của phương trình f x  16m  8n  4 p  2q r là số giao điểm của đồ thị hàm
số y f x với đường thẳng y f 2 .
Dựa vào bản biến thiên suy ra phương trình đã cho có 4 nghiệm phân biệt.
Câu 44:Một bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y x 1 và trục Ox , quay quanh trục Ox . Biết đáy lọ và
miệng lọ có đường kính lần lượt là 2 dm và 4 dm , khi đó thể tích của lọ là : 15 14 15 A. 3 8 dm . B. 3  dm . C. 3  dm . D. 3 dm . 2 3 2 Lời giải / Trang32
Ta có đáy lọ có đường kính bằng 2 dm suy ra bán kính đáy lọ bằng 1dm . Do đó
y 1 x 1 1  x  0
Ta có miệng lọ có đường kính bằng 4 dm suy ra bán kính miệng lọ bằng 2 dm . Do đó
y  2  x 1  2  x  3 3 2
Khi đó V    x    15 1 dx=  2 0 1 7
Câu 45: Cho tích phân I   x  2 ln  x  
1 dx a ln 2  
trong đó a , b là các số nguyên dương. b 0 Tổng 2
a b bằng A. 8 . B. 16 . C. 12 . D. 20 . Lời giải  1       du  d ln 1 x u x  Đặ  t x 1    . d  v   x  2dx 1 v    2
x  4x  3  2 1 1 Do đó, 1 I   1 2
x  4x  3 ln  x   1  x  3dx  2 0 2 0 1 1 1   1 2
x  4x  3 ln  x   1   2 x  7 6x  4 ln 2  2 4 0 4 0
a b  4. Vậy 2
a b  20 .
Câu 46:Cho hàm số y f x có bảng xét dấu của f   x như sau. / 2
f 1xx
Xét hàm số g x    e
, tập nghiệm của bất phương trình g  x  0 là  1     1   1  A. ;   . B.    1 ; 1  ; 2   . C. ;    . D. 1  ;  2;    .  2   2   2   2  Lời giải 2 2  
f 1 xx 1 3
Ta có g x    xf  2 1 2
1  x x    .e , và 2
1  x x x    0 x       2  4
g  x 
   xf   x x f  2 1 x 2 x e
    xf  2 0 1 2 1 . 0 1 2
1  x x   0  2   f  2
1  x x   0
1  x x  3   x  1  1   2x  0 1   2x  0      1     f  2
1  x x   0 2
1  x x  3 2   x      2  1   2x  0  1   2x  0 Trang33 x y
Câu 47:Cho x , y thỏa mãn log
x x  9  y y  9  xy 3 2 2    
x y xy
. Tìm giá trị lớn nhất của 2 3x  2 y  9 P
khi x , y thay đổi. x y 10 A. 2 . B. 3 . C. 1. D. 0 . Lời giải 2 2   Điề y 3y
u kiện: x y  0 (do 2 2
x y xy  2  x    2  0   ).  2  4
Đẳng thức đã cho tương đương với 9 x y log
x x  9  y y  9  xy  2 * 3 2 2      
x y xy  . 2 Đặt 2 2
u x y xy  2  0 , v  9x  9 y  0 , ta có.  v *  log
u v u  log u v  log v . 3 3 3 u
Mà hàm số f t  t  log t đồng biến trên 0;   nên suy ra 3   2 2
*  u v x y xy  9x  9y  2  0 . Ta có 2  y   y  3 9 3
x y xy  9x  9 y  2  0  x   9 x
  y y  2    y 32 19 2 2 2      .  2   2  4 2 4 4 Dẫn đến 2  y   y  19 1 y 19 x   9 x      x    1
  2x y 19     .  2   2  4 2 2 2 Suy ra 3x  2 y  9
x y 10  2x y 19 2x y 19 P   1  1. x y 10 x y 10 x y 10
2x y 19 x  8 P  1     . y  3 y  3 Vậy max P 1. Cách 2: Từ giả thiết, ta có 2 2
x y xy  9x  9 y  2  0  *
Ta thấy x  8, y  3 thỏa mãn * , đặt x a  8, y b  3 khi đó: 2 2 2 2
x y xy x y  
a b ab      b   2 2 9 9 2 0 10a 5 0 10a 5
a ab b
10a  5b  0  2a  b  0 3x  2 y  9 3a  2b  21 2a b P    1  1 Ta có: x y 10 a b  21 a b  21
Dấu “=” xảy ra khi và chỉ khi x  8, y  3 . Vậy P đạt giá trị lớn nhất bằng 1.
Câu 48. Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số đã cho trên 0;2 . Có bao nhiêu số nguyên a thuộc 4; 4 sao cho M  2m ? A. 7 . B. 5 . C. 6 . D. 4 . Hướng dẫn giải
Xét hàm số g x 3 3 2
x  4x  4x a trên 0;2 . Trang34 x  0  g x 3 2
 4x 12x  8x ; gx  0  x 1 
; g 0  a , g  
1  a 1, g 2  a . x  2 
Suy ra: a g x  a 1.
TH1: 0  a  4  a 1 a  0  M  max f x  a 1; m  min f x  a . 0;2 0;2 0   a  4 Suy ra: 
1 a  4 . Do đó: có 4 giá trị của a thỏa mãn. a 1 2a TH2: 4   a  1
  a a 1 1
  a 1  a
M  max f x  a  a ; m  min f x  a 1  a  1. 0;2 0;2  4   a  1  Suy ra:   4   a  2
 . Do đó: có 3 giá trị của a thỏa mãn. a  2  a  2
Vậy có tất cả 7 giá trị thỏa mãn.
Câu 49:Cho tứ diện ABCD có  
DAB CBD  90 ;  AB  ;
a AC a 5; ABC  135 . Biết góc giữa
hai mặt phẳng  ABD,  BCD bằng 30 . Thể tích của tứ diện ABCD là 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 3 2 3 2 6 Lời giải /
Vẽ AH   BCD , H  BCD .
Vẽ HK // BC , K BD , có BD BC HK BD , mà AH BD .
BD   AHK   BD AK . Nên 
ABD BCD  ,  AKH  30
Vẽ HM // BD , M BD , có BC BD HM BC , mà AH BC .
BC AM , có góc  ABC  135 . Suy ra 
ABM  45 (nên B ở giữa M và C ).
ΔAMB vuông tại M có  ABM  45 . AB a
Suy ra ΔAMB vuông cân tại B AM MB   . 2 2
Tứ giác BKHM là hình chữ nhật, nên BM HK . Δ HK a 2a
AHK vuông tại H có 
AKH  30 , nên AH   , AK  2AH  . 3 6 6 Δ 1 1 1
BAD vuông tại A có AK là đường cao nên   . 2 2 2 AK AB AD 3 1 1    1 1  
AD a 2 và 2 2 BD
AB AD a 3 . 2 2 2 2a a AD 2 2 AD 2a 2 2 a 9a
Có BC CM BM , 2 2 2 2
CM CA AM  5a   2 2 3a aBC    a 2 2 2 1 1 a 3 a Có V AH .S  1 AH . . BD BC  .a 3.a 2  3 BCD 6 6 6 6 Trang35 3 a Vậy V  . 6
Câu 50:Cho hai số thực x , y thỏa mãn    y y  
  x  x 2 5 4x x log 8 16 log 5 1   2log  log  2y 82 2 . 2 3 2 3 3
Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức 2 2 P
x y m
không vượt quá 10 . Hỏi S có bao nhiêu tập con không phải là tập rỗng? A. 2047 . B. 16383. C. 16384. D. 32 . Lời giải ĐK: 1
  x  5 , y  4 . Ta có:    y y  
  x  x 2 5 4x x log 8 16 log 5 1   2log  log  2y 82 2 . 2 3 2 3 3  2log  2
y  8y 16  2log  2
5  4x x   log  2
y  8y 16  log  2 5  4x x 3 3 2 2   log 4   1 .log  2
y  8y 16  log 4   1 .log  2 5  4x x 3 2 3 2  2 2
y  8y 16  5  4x x (vì hàm f t  log 4 1 .log t đồng biến trên 0; ). 3  2   2 x y
2   x y2 2 2   2 2 11 4 8
80 x y    2 2 x y    2 2
58 x y  121  0 2 2
 29 12 5  x y  29 12 5 2 2
 29 12 5  x y  29 12 5 .
Đặt a  29 12 5 , b  29 12 5 , ta có: maxP  max a m , b m. a;b
a m 10 
a 10  m a 10
Do đó, maxP 10    
b 10  m a 10. a;b
b m 10  b
 10  m b 10
Vì m nên S   2  ; 1
 ;0;1;2;3;4;5;6;7;8;9;10;1  1 .
Vậy sốtập con không phải là tập rỗng của tập S là 14 2 1  16383 . www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2021 ĐỀ 8 MÔN TOÁN Thời gian: 90 phút 
Câu 1: Trong không gian Oxyz, cho hai điểm A( 3  ; 2
;0 ),B(1;4; 3
). Tọa độ vectơ AB là A. ( 2  ;2; 3  ).
B. ( 4;6;3 ). C. ( 4  ; 6  ;3 ).
D. ( 4;6; 3  ).
Câu 2: Cho a  0; a  1. Tính 3 P  log a . a 1 A. P  3. B. P  . C. P  3.  D. P  3. 3
Câu 3: Đồ thị hàm số 3
y x x 1 và trục hoành có bao nhiêu điểm chung? A. 3. B. 2. C. 0. D. 1.
Câu 4: Từ một nhóm có 10 học sinh, có bao nhiêu cách chọn hai bạn làm trực nhật? A. 45. B. 90. C. 5. D. 20. x y z
Câu 5: Trong không gian tọa độ Oxyz, cho đường thẳng 1 2  :   . Một vectơ chỉ 2 3 2  phương của  là:    
A. u  (2;3; 2).
B. u  (2;3; 2). 
C. u  (1; 2;0). D. u  ( 1  ;2;0). Trang36
Câu 6: Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng A.  . rl B. 4 l. C. 2 4 r l. D. 2 rl.
Câu 7: Cho cấp số cô ̣ng có d  2
 và tổng của 8 số ha ̣ng đầu là s  72 . Khi đó số hạng đầu 8 bằng bao nhiêu? 1 1 A. u   . B. u  . C. u  16. D. u  1  6. 1 16 1 16 1 1
Câu 8: Cho hàm số y f (x) có bảng biến thiên như bên. Hàm số f (x) nghịch biến trên khoảng v uong Hide Luoi A. (2; ). B. ( ;  2  3). C. ( ;  4). D. (1; ).
Câu 9: Cho hàm số có đồ thị như hình vẽ. Tìm điểm cực đại của hàm số. y 3 1 2 x O -2 A. 3. B. 2.  C. 0. D. 2.
Câu 10: Tính thể tích của khối chóp tứ giác biết đáy có diện tích 2
36cm và có chiều cao là 1dm. A. 3 120cm . B. 3 36cm . C. 3 360cm . D. 3 12cm .
Câu 11: Tính thể tích khối bi sắt có dạng hình cầu biết bán kính bằng 6 cm. A. 864 . B. 36 . C. 216 . D. 288 .
Câu 12: Nghiệm của phương trình x 1 5   3 là
A. x  log 3 1.
B. x  log 5 1.
C. x  log 5 1.
D. x  log 3 1. 5 3 3 5
Câu 13: Tìm số phức liên hợp của số phức z  1  3 . i A. 3  . i B. 1  3 . i C. 1   3 .i D. 1  3 . i
Câu 14: Trong không gian Oxyz, mặt cầu tâm I (2; 1
 ;2) bán kính R  2 có phương trình là Hide Luoi A. 2 2 2
(x  2)  ( y 1)  (z  2)  2. B. 2 2 2
(x  2)  ( y 1)  (z  2)  2. C. 2 2 2
(x  2)  ( y 1)  (z  2)  2. D. 2 2 2
(x  2)  ( y 1)  (z  2)  2.
Câu 15: Điểm M là điểm biểu diễn của số phức nào sau đây? y M 2 -3 x Trang37
A. z  3  2 . i B. z  3   2 .i C. z  3   2 .i
D. z  2  3 . i
Câu 16: Tính thể tích khối hộp chữ nhật có ba kích thước là 7, 8, 9. A. 24. B. 135. C. 504. D. 252.
Câu 17: Thể tích khối nón có độ dài đường cao bằng h và bán kính đáy r bằng 1 1 4 A. 2 hr . B. 3 hr . C. 2 hr . D. 2 hr . 3 3 3
Câu 18: Trong không gian tọa độ Oxyz, cho điểm M (2;5; 3  ) . Gọi , A ,
B C lần lượt là hình chiếu
của M trên các trục tọa độ Ox,Oy,Oz. Mặt phẳng (ABC) có phương trình: x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    0. 3  5 2 2 5 3  5 2 3  2 5 3  x  3
Câu 19: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x  9 A. 3. B. 0. C. 2. D. 1.
Câu 20: Tập xác định của hàm số y   2 log 4  x  là:
A. D   ;  2   2;. B. D   2  ;2.
C. D   ;  2  2;. D. D   2  ;2.
Câu 21: Trong không gian Oxyz , cho điểm A1;2; 1
  và mặt phẳng P : x – y  2z – 3  0 . Đường thẳng
đi qua A và vuông góc với mặt phẳng P có phương trình là x 1 2  y z 1 x 1 y  2 z 1 x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . C.   . D.   . 1 1  2 1 1  2 1 1  2 1 1 2
Câu 22: Cho số phức z thỏa mãn điều kiện (1 i)z  2i  3  .
i Môđun của số phức z bằng A. 5. B. 9. C. 3. D. 3. x y z
Câu 23: Trong không gian tọa độ Oxyz, cho đường thẳng 1 2  :   . Trong các điểm 2 3 2 
sau, điểm nào thuộc ?
A. Q 1;5; 2. B. M 1;2; 2  . C. N 1;5; 2  . D. P  1  ;5; 2  .
Câu 24: Cho hai số phức z a  3i, z  1 i. Có bao nhiêu giá trị thực a sao cho z z  3. 1 2 1 2 A. 2. B. 1. C. 0. D. 3.
Câu 25: Tập nghiệm của phương trình 2
log (x  3x 1)  2 là 3  3   41 3   41  3   29 3   29  A.  ; . B.  ; .  2 2    2 2    3   41  3   29  C.  . D.  .  2    2  
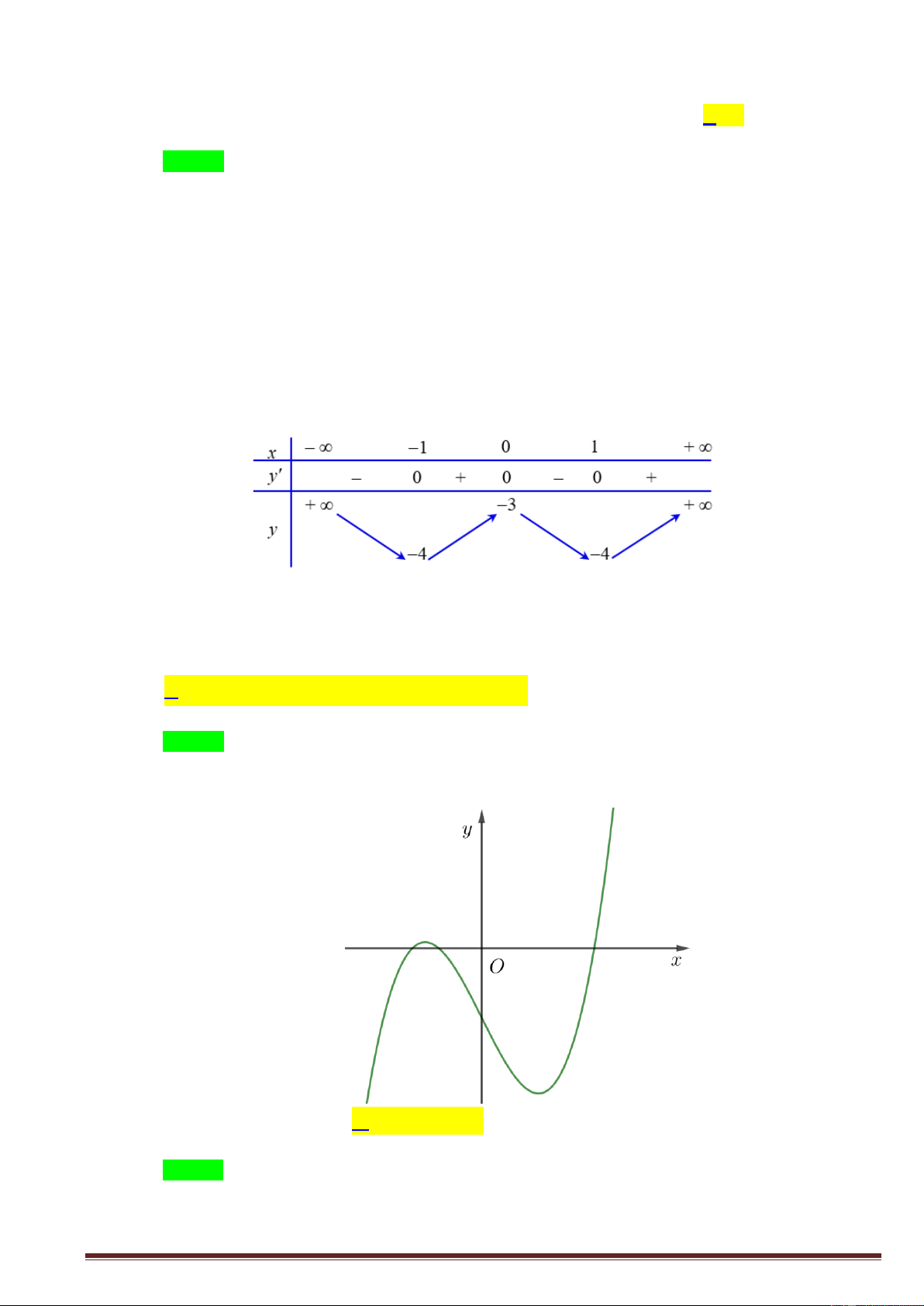
Câu 26: Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây? Trang38 A. 3
y  x  3 . x B. 3 y x  3 . x C. 3 2
y  x  3x . D. 3 2
y x  3x 1.
Câu 27: Cho hàm số y f x xác định và liên tục trên R và có đồ thị như hình vẽ.
Gọi M ,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên  2  ; 
1 . Khi đó M m bằng A. 6.  B. 4.  C. 3. D. 4. 1 1
Câu 28: Tính I d . x  5x 1 0 1 1 1 1 A. I  ln 6. B. I  5 ln . C. I  5ln 6. D. I  ln . 5 6 5 6
Câu 29: Cho log 3  a , biết log 54  m na , với ; m n   . Tính 2 2
S m n . 2 2 A. S  8. B. S  5. C. S 10. D. S 13.
Câu 30: Tìm tất cả các giá trị của tham số m để đường thẳng y m cắt đồ thị hàm số 3 2
y  2x  3x 1 tại 3 điểm phân biệt. A. 1   m  0.
B. 0  m 1. C. 2   m  2. D. 1   m 1.
Câu 31: Một người gửi tiết kiệm 150 triệu đồng vào một ngân hàng với lãi suất 6,55% /năm.
Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi được nhập vào vốn
để tính lãi cho năm tiếp theo. Hỏi ít nhất bao nhiêu năm người đó thu được(cả số tiền gửi ban
đầu và lãi) không dưới 200 triệu đồng, giả định trong khoảng thời gian này lãi suất ngân hàng
không thay đổi và người đó không rút tiền ra? A. 5 năm. B. 7 năm. C. 6 năm. D. 4 năm.
Câu 32: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  4z  8  0. Tọa độ điểm 1
biểu diễn của số phức w  7  z .i là 1 A.  2  ; 2  . B. 9; 2. C. 5; 2. D. 2; 2.
Câu 33: Cho khối nón có chiều cao h  6 và bán kính đáy r  8. Diện tích xung quanh của khối Trang39 nón đã cho bằng A. 48. B. 80. C. 64. D. 60. 1 1 1 Câu 34: Cho f
 xdx  2 và g
 xdx 1. Tính I  2 f
 x gxd .x  0 0 0 A. I  1. B. I  3. C. I  5. D. I  1. 
Câu 35: Tính thể tích vật thể tròn xoay tạo bởi khi quay hình phẳng giới hạn bởi các đường 2
y x  2x ,
y  0 , x  0 , x  1 quay quanh trục Ox . 8 15 8 8 A. . B. . C. . D. . 15 8 7 15
Câu 36: Cho bảng biến thiên của hàm số y f x(Hình 1). Hãy xác định hàm số đó. + - 0 + 0 - 1 -3 Hình 1 A. 3
y x  3x  2. B. 3 2
y  x  3 x  5 . x C. 3 2
y  x  3 x  3. D. 3 2
y  x  3 x  3.
Câu 37: Cho hình chóp S.ABC có SA vuông góc với mặt đáy (ABC). Biết AB=5, BC=7,
và mặt phẳng (SBC) tạo với mặt đáy một góc 450. Tính thể tích của khối chóp S.ABC. A. B. . C. D.
Câu 38: Phương trình x x x 1 (7 45) 7(7 45) 4.2     
có hai nghiệm x , x và 2 2
T x x . Khi 1 2 1 2 đó:
A. T  (3;5).
B. T  (10;15). C. T  (1;3). D. T  (5;8).
Câu 39: Có 6 chiếc ghế được kê thành hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3
nữ, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để 3 học sinh nữ luôn ngồi gần nhau bằng 1 3 1 1 A. . B. . C. . D. . 30 5 120 5 1
Câu 40: Cho hàm số f (x) liên tu ̣c trên R và f (1)  2 f (0)  1, f (x)dx  5.  Tính 0 3 x /
I  (6  x) f ( )d . x  3 0 A. I  64. B. I  66. C. I  54. D. I  56.
Câu 41: Cho hàm số y f x xác định trên  \ 
0 có bảng biến thiên như sau Trang40
Số nghiệm của phương trình 2 f 3x  5  7  0 là A. 4. B. 3. C. 1. D. 2.
Câu 42: Cho hình lăng trụ AB .
C A' B'C ' , đáy ABC là tam giác vuông cân tại ,
A BC  6, góc giữa
A'BC và ABC bằng 0
60 . Hình chiếu vuông góc của A ' lên mặt đáy là trọng tâm của tam giác .
ABC Tính khoảng cách giữa hai đường thẳng AA' và BC '. 6 5 3 21 4 15 5 14 A. . B. . C. . D. . 5 7 5 2 Câu 43: Cho hàm số 3 2
y f (x)  2x mx 1. Tìm tất cả các giá trị thực của tham số m đề hàm
số y f (x) có 5 điểm cực trị.
A. m  ;  0 3;  .
B. 0  m  3 . C. m  3 . D. m  3 .
Câu 44: Một ô tô đang chạy đều với vận tốc a (m/s) thì người lái đạp phanh. Từ thời điểm đó ô
tô chuyển động chậm dần đều với vận tốc v(t)  5
t a (m/s), trong đó t là khoảng thời gian
tính bằng giây kể từ lúc bắt đầu đạp phanh đến khi dừng lại. Biết từ lúc đạp phanh đến khi dừng
hẳn ô tô chạy được quảng đường 160 (m). Hỏi vận tốc ban đầu a bằng bao nhiêu? A. 16 (m/s). B. 80 (m/s). C. 40 (m/s). D. 160 (m/s).
Câu 45: Một đội xây dựng cần hoàn thiện một một hệ thống cột trụ tròn gồm 10 chiếc của một
ngôi nhà. Trước khi hoàn thiện mỗi chiếc cột là một khối bê tông cốt thép hình lăng trụ tứ giác
đều có cạnh đáy 20 cm; sau khi hoàn thiện một cột là một khối trụ tròn có đường kính đáy bằng
60 cm. Chiều cao mỗi cột trước và sau khi hoàn thiện là 4 m. Biết lượng xi măng cần dùng chiếm
40% lượng vữa và cứ một bao xi măng 50 kg thì tương ứng với 65000 cm3 xi măng. Hỏi cần ít
nhất bao nhiêu bao xi măng loại 50 kg để hoàn thiện toàn bộ hệ thống cột theo yêu cầu? A. 90 bao. B. 120 bao. C. 100 bao. D. 110 bao. 2
x m m
Câu 46: Gọi M là giá trị lớn nhất của hàm số y
trên đoạn [1; 2] . Giá trị nhỏ nhất x  2 của M bằng 1 1 1 1 A. . B. . C. . D. . 7 5 4 6 1 2
Câu 47: Cho 2 số thực dương a,b thỏa mãn log a  log
. Giá trị nhỏ nhất của biểu thức 2 2 2 b 3 3
P  4a b  5log  3 3 4a b là P
x y log z với ,
x y, z là các số thực, z là số nguyên tố. Tính 2  min 2
tổng S x y  . z A. S  9. B. S 11. C. S 10. D. S  8. Câu 48: Cho hàm số 3 2
y mx x  3x m  2, m là tham số. Tập hợp tất cả các giá trị m để hàm số đồ  aa ng biến trên khoảng  2  ;0 là ; 
 với là phân số tối giản và b  0. Giá trị a b là:  bb A. 4.  B. 12. C. 5. D. 8.
Câu 49: Cho hai số thực ,
x y thỏa mãn x y  1  và 2 2
x y xy x y 1  0. Gọi M , m lần lượt
là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức xy P
. Tính giá trị S  2019M  2020 . m x y 1 A. S  1347.  B. S  2483. C. S  2530.  D. S 1521. xq
Câu 50: Cho hình chóp đều SABCD biết SA  2a, AB  .
a Mặt phẳng (P) chứa AB và đi qua
trọng tâm của tam giác SAC cắt SC, SD lần lượt tại M và N . Tính thể tích khối đa diện NMABC . D Trang41 3 5a 14 3 5a 7 3 5a 14 3 5a 14 A. . B. . C. . D. . 48 24 8 16
------ HẾT ------ ĐÁP ÁN 1 D 11 D 21 C 31 A 41 B 2 D 12 A 22 C 32 B 42 B 3 D 13 B 23 C 33 B 43 C 4 A 14 B 24 A 34 B 44 C 5 B 15 B 25 A 35 A 45 B 6 D 16 C 26 C 36 D 46 C 7 C 17 C 27 B 37 B 47 C 8 B 18 B 28 A 38 C 48 C 9 C 19 C 29 C 39 D 49 A 10 A 20 D 30 A 40 C 50 A www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2021 ĐỀ 9 MÔN TOÁN Thời gian: 90 phút
Câu 1: Có bao nhiêu cách chọn 3 học sinh từ nhóm có 7 học sinh? A. 3 C . B. 3 A . C. 7 3 . D. 3 7 . 7 7
Câu 2: Cho cấp số cộng u với u  3 và d  2. Tính u ? n  1 3 A. 7. B. 6. C. 5. D. 12.
Câu 3: Nghiệm của phương trình 2x  8 là: A. x 1. B. x  2. C. x  3. D. x  4.
Câu 4: Thể tích của khối lập phương cạnh bằng 1 là: A. 1. B. 2. C. 3. D. 4.
Câu 5: Tìm nguyên hàm của hàm số f x  tan x A. f
 xdx  ln cosx C B. f
 xdx  ln cosx C C. f
 xdx  ln sin x C D. f
 xdx  ln sin x C
Câu 6: Tìm nguyên hàm của hàm số f x 1  . 2 x  4   A. x f  x 1 x 2 dx  ln
C B. f  x 1 2 dx  ln  C 2 x  2 2 x  2   C. x f  x 1 x 2 dx  ln
C D. f  x 1 2 dx  ln  C 4 x  2 4 x  2
Câu 7: Tìm nguyên hàm của hàm số f x 1  . 2 sin x
A. f (x)dx cot x  . C
B. f (x)dx   tan x  . C
C. f (x)dx   cot x C. 
D. f (x)dx  tan x  . C
Câu 8: Tìm nguyên hàm của hàm số   3x f x x x A. ( ) 3x f x dx  ln 3  C.  B. 3
f (x)dx   C.  C. ( )   3x f x dx ln 3  C.  D . 3
f (x)dx    C.  ln 3 ln 3
Câu 9: Tìm phần ảo của số phức z thỏa z  (2  3i)  (4  i)(2  i).
A. Phần ảo bằng 1.
B. Phần ảo bằng 1. Trang42 C. Phần ảo bằng 2  .
D. Phần ảo bằng 2 .
Câu 10:Tìm modun của số phức z  3 2 .i A. z  5. B. z  13. C. z  10.
D. z  2.
Câu 11: Cho số phức z 10  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 10 và Phần ảo bằng 2 .
B. Phần thực bằng 10 và Phần ảo bằng 2i .
C. Phần thực bằng 10  và Phần ảo bằng 2  .
D. Phần thực bằng 10  và Phần ảo bằng 2  i .  
Câu 12:Trong không gian Oxyz, cho c|c vectơ   a  1; 2;  1 , b  2; 1
 ;3 . Tính a.b .     A.     . a b  1  . B. . a b  1. C. . a b  3. D. . a b  3  .
Câu 13: Trong không gian Oxyz, cho mặt cầu S x  2   y  2  z  2 : 1 3 2
 4 . X|c định tọa độ tâm I và
bán kính R của mặt cầu S  . A. I  1
 ;3;2, R  2. B. I  1
 ;3;2, R  4. C. I 1; 3  ; 2
 , R  2.
D. I 1;3;2, R  4.
Câu 14:Trong không gian Oxyz , cho mp P : x  2y  2z 1 0. Vectơ n{o sau đ}y không l{ vectơ ph|p
tuyến của mp P ? A.     n  1; 2  ;2. B. n   2  ;4; 4
 . C. n  1; 2  ; 2  . D. n  3; 6  ;6.
Câu 15:Trong không gian Oxyz cho tam giác ABC có (
A 1; 0; 0), B(0; 0;1), C(2;1;1) . Khẳng định n{o sau đ}y đúng?
A.Tam giác ABC vuông tại A .
B. Tam giác ABC cân tại A .
C. Tam giác ABC vuông cân tại A .
D. Tam giác ABC đều.
Câu 16:Mặt phẳng đi qua điểm A2; 3  ; 
1 và chứa trục Ox có phương trình l{
A. y  2z 1  0.
B. x  3y  0.
C. x  2z  0.
D. y  3z  0.
Câu 17:Trong các mặt phẳng sau, mặt phẳng nào song song với mp Oxz ?
A. y  0.
B. z 1 0.
C. 2x 3z  0.
D. 3y 1  0.
Câu 18: Viết phương trình mp P đi qua M  1
 ;1;0 và song song với mpQ: x  2y z 10  0 .
A. P : x  2y z 3  0.
B. P : x  2y z  3  0.
C. P : x  2y z 1 0.
D. P : x  2y z 1 0. x 1 t
Câu 19: Cho đường thẳng  : y  2  2t , t  . Điểm n{o sau đ}y thuộc  ? z  3tA. 1; 2   ;1 .
B. 2;0;4. C. 1;2; 3  .
D. 2;1;3.
Câu 20: Trong các hàm số dưới đ}y, h{m số nào nghịch biến trên tập số thực  ? x   x A.    y    .
B. y  log x .
C. y  log  2 2x    1. D. 2 y   .  3  1  e  2 4 
Câu 21:Tập x|c định của h{m số y   3 x  2 27 là
A. D  3;. B. D   \ 
2 . C. D   .
D. D  3;.
Câu 22: Tìm nghiệm của phương trình log x  5  4 . 2   A. x  3. B. x 13. C. x  21. D. x 11. Trang43
Câu 23: Tính đạo hàm của hàm số  log  ex y x . 2   xxxA. 1 e . B. 1 e . C. 1 e . D. 1 . ln 2  ex x ln2  ex x  ex x  ln2
Câu 24: Nghiệm của bất phương trình x2 3  243 là:
A. 2  x  7 . B. x  7 . C. x  7 . D. x  7 .
Câu 25: Cho hàm số y f x liên tục trên  v{ có đồ thị như hình vẽ bên dưới. Khẳng định n{o sau đ}y l{ đúng? y 7 O x 2
A. Hàm số đồng biến trên khoảng 1;3 .
B. Hàm số nghịch biến trên khoảng 6; .
C. Hàm số đồng biến trên khoảng  ;3   .
D. Hàm số nghịch biến trên khoảng 3;6 . 
Câu 26: Cho hàm số   ax b f x
x|c định trên tập  \ 
1 v{ có đồ thị như hình bên dưới. cx d Xét các mệnh đề sau:
(I) Hàm số đồng biến trên mỗi khoảng   ;1  và 1; .
(II) Hàm số nghịch biến trên mỗi khoảng  ;    1 và 1; .
(III) Hàm số đồng biến trên tập x|c định.
Số các mệnh đề đúng l{: A. 2 . B. 1. C. 0 . D. 3 .
Câu 27: Cho hàm số y f x có đồ thị như hình vẽ bên. Mệnh đề n{o sau đ}y đúng về hàm số đó? y 3 2 1 O x 3 
A. Đồng biến trên khoảng 0;2 .
B. Nghịch biến trên khoảng  3  ;0 .
C. Đồng biến trên khoảng  1  ;0 .
D. Nghịch biến trên khoảng 0;3 . Trang44 fx = -x4+2x2 4
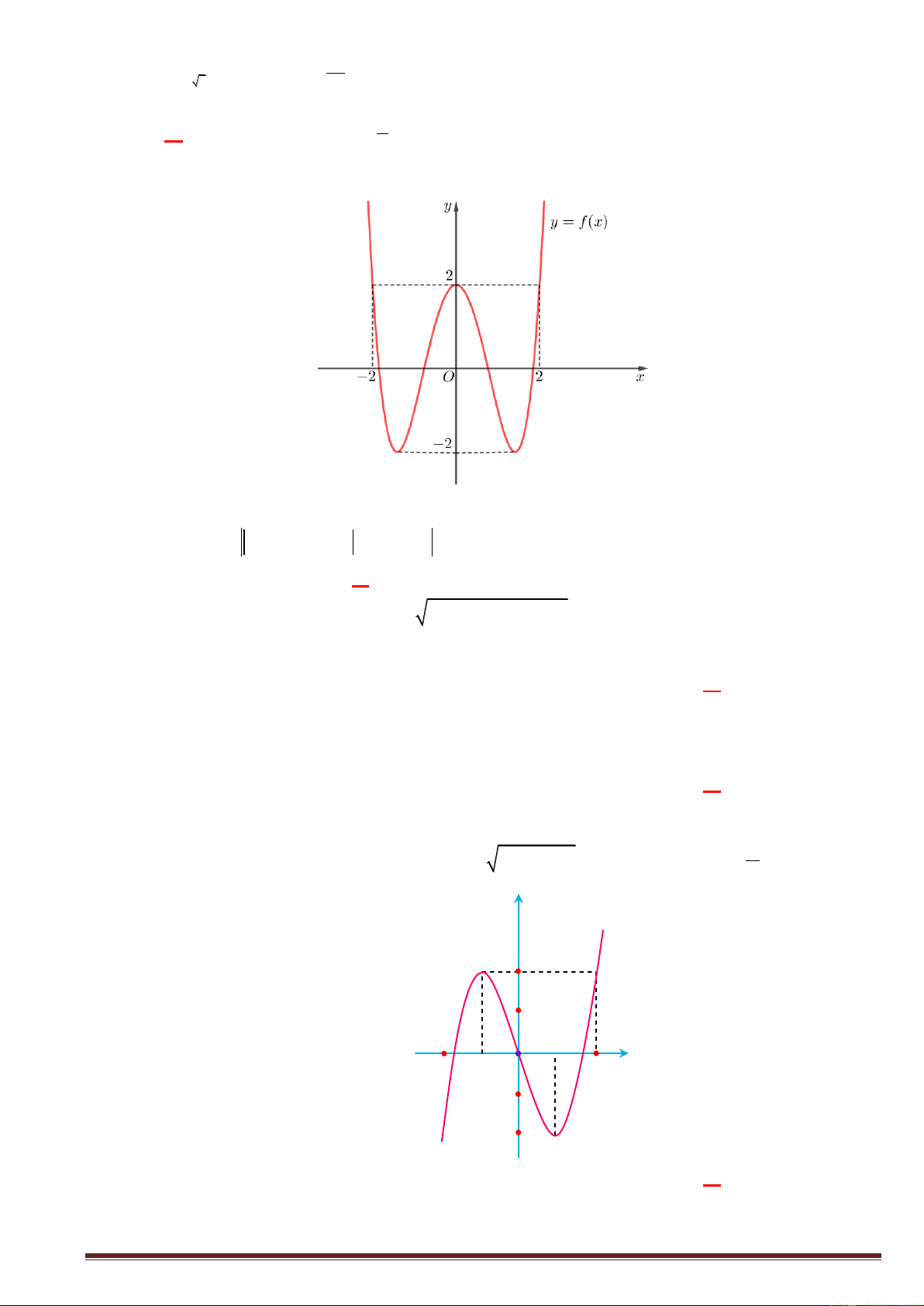
Câu 28:Đường cong trong hình dưới l{ đồ thị của một hàm số trong y bốn
hàm số dưới đ}y. Hỏi hàm số đó l{ h{m số nào? 2 A. 3 2
y  x  3x 1. x B. 4 2
y  x  2x . -10 -5 5 10 C. 4 2
y x  2x  2. -2 D. 4 2
y x  2x  2. -4
Câu 29: Cho hàm số y f x có bảng biến thiên như sau
Mệnh đề n{o dưới đ}y đúng?
A. Hàm số đạt cực đại tại x  3.
B. Hàm số đạt cực tiểu tại x  2  .
C. Hàm số có y  3 . CĐ
D. Hàm số nghịch biến trên các khoảng (;2) và (2;) .
Câu 30:Tiếp tuyến với đồ thị hàm số 3 2
y x x 1 tại điểm
có ho{nh độ x  1 có phương trình: 0 A. y  . x B. y  2 . x
C. y  2x 1.
D. y x  2. 
Câu 31:Cho đố thị  x C  : 2 1 y
. Gọi I l{ giao điểm của 2 đường tiệm cận, tọa độ điểm I ? x 1 A. I  1  ;2. B. I 2  ;1 .
C. I 2;  1 .
D. I 1;2.
Câu 32: Cho hàm số có bảng biến thiên như sau. H~y chọn khẳng định đúng. x  0  y’ 0 y 1 0 0
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Hàm số có giá trị lớn nhất bằng 1.
D. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất. 
Câu 33:Đường thẳng x
y x 1 cắt đồ thị (C) của hàm số 2 5 y
tại c|c ho{nh độ giao điểm là: x 1 A. x  2  . B. x  2  . C. x  4  . D. x  2 .  Câu 34:Cho hàm số 3 x y
. Tiệm cận ngang của đồ thị hàm số là: x  3 A. y  1.  B. x  1.  C. x  3.  D. y  1.
Câu 35:Cho khối nón có chiều cao h, đường sinh l v{ b|n kính đường tròn đ|y bằng r. Thể tích của khối nón là: A. 1 1 2 V   r h B. 2 V  3 r h C. 2 V   rh D. 2 V   r h 3 3
Câu 36:Cho một khối trụ có khoảng cách giữa hai đ|y bằng 10, biết diện tích xung quanh của khối
trụ bằng 80 . Thể tích của khối trụ là: A. 160 B. 164 C. 64 D. 144
Câu 37:Thể tích V của một mặt cầu có b|n kính r được x|c định bởi công thức n{o sau đ}y:  2 2  3  2 3  A. 4 r 4 r 4 r 4 r V B. V C. V  . D. V  3 3 3 3
Câu 38:Thể tích khối lăng trụ tam gi|c đều có tất cả các cạnh bằng a là : 3 3 3 3 A. 2a . B. 2a . C. 3a . D. 3a . 3 4 2 4 Trang45
Câu 39: Cho hình lăng trụ đều AB .
C A' B'C ' có cạnh đ|y bằng a , mặt phẳng ( A' BC) hợp với mặt
phẳng (ABC) một góc 60o . Thể tích của khối lăng trụ AB .
C A' B'C ' tính theo a bằng: 3 3 3 3 A. 3a . B. 3a .
C. 2 3a . D. 3a . 4 2 3 3
Câu 40:Từ các chữ số 0,1,2,3,4,5,6 có thể lập được bao nhiêu số chẵn, mỗi số có 5 chữ số khác nhau
trong đó có đúng hai chữ số lẻ và 2 chữ số lẻ đứng cạnh nhau? A. 360 B. 280 C. 310 D. 290
Câu 41: Hàm số y f (x) có đạo hàm trên  v{ có đồ thị hàm số f '(x) được cho như hình vẽ. Hàm
số y f (x) nghịch biến trên khoảng n{o dưới đ}y? A.  1    ;1   . B. 0; . C. 1 ;    . D.  ;0  .  3   3 
Câu 42: Tìm tất cả các giá trị của tham số thực m để hàm số 3 2
y mx mx m m  
1 x  2 đồng biến trên  . A. 4 m  . B. 4 m  và m  0 .
C. m  0hoặc 4 m  . D. 4 m  . 3 3 3 3
Câu 43: Cho một tấm nhôm hình chữ nhật
ABCD có AD  60 cm và AB có độ dài
không đổi. Ta gập tấm nhôm theo 2 cạnh MN và
PQ v{o phía trong đến khi AB và DC trùng
nhau như hình vẽ bên để được một hình lăng trụ
khuyết 2 đ|y. Tìm x để thể tích khối lăng trụ tạo thành lớn nhất? A. x  20. B. x  25. C. x 10 . D. x  30 .
Câu 44: Cho hàm số bậc ba y f x có đồ thị như hình bên. y 1 O x 3 
Ta ́t cả các giá trị của tham so ́ m đẻ hàm só y f x  m có ba điẻm cực trị là A. m  1  hoa ̣c m  3. B. m  1
 hoa ̣c m  3. C. m  3  hoa ̣c m 1 .
D.1 m  3 .
Câu 45: Gọi x, y là các số thực dương thỏa m~n điều kiện log x  log y  log x y và 9 6 4   xa b
, với a , b là hai số nguyên dương. Tính a b . y 2
A. a b  6.
B. a b 11.
C. a b  4 .
D. a b  8.
Câu 46: So ́ các giá tr ị nguyên của tham số m để phương trình log  x   1  log mx  8 có hai 2   2 nghiệm phân biệt là A. 3 . B. 4 . C. 5 . D.Vô số. Trang46
Câu 47: Tìm tất cả các gúa trị tham số m sao cho đồ thị hàm số 4
y x  m   2 2 2
1 x m có ba điểm
cực trị nội tiếp đường tròn bán kính bằng 1.    A. 3 5 m  1; m  . B. 3 5 m  0; m  . 2 2   C. 3 5 m  0; m  . D. 3 5 m  1; m  . 2 2
Câu 48: Cho hàm số y f x có đạo hàm liên tục trên  và hàm số y f x có đồ thị như hình vẽ. y 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6
Hỏi hàm số g x  f x x  2 2
1 đồng biến trên khoảng nào trong các khoảng sau?
A. 3;  . B.1;3 . C.  3  ; 
1 . D. ;3 . Câu 49: Cho 1 2
a, b là số thực dương thỏa mãn log a  log
. Giá trị nhỏ nhất của biểu thức 2 2 2 b 3 3
P  4a b  4log  3 3 4a b là 2  A. 4 4 4 log 6 . B.  4log . C. 41 log 3 . D. 4  . 2  2 2 ln 2 ln 2
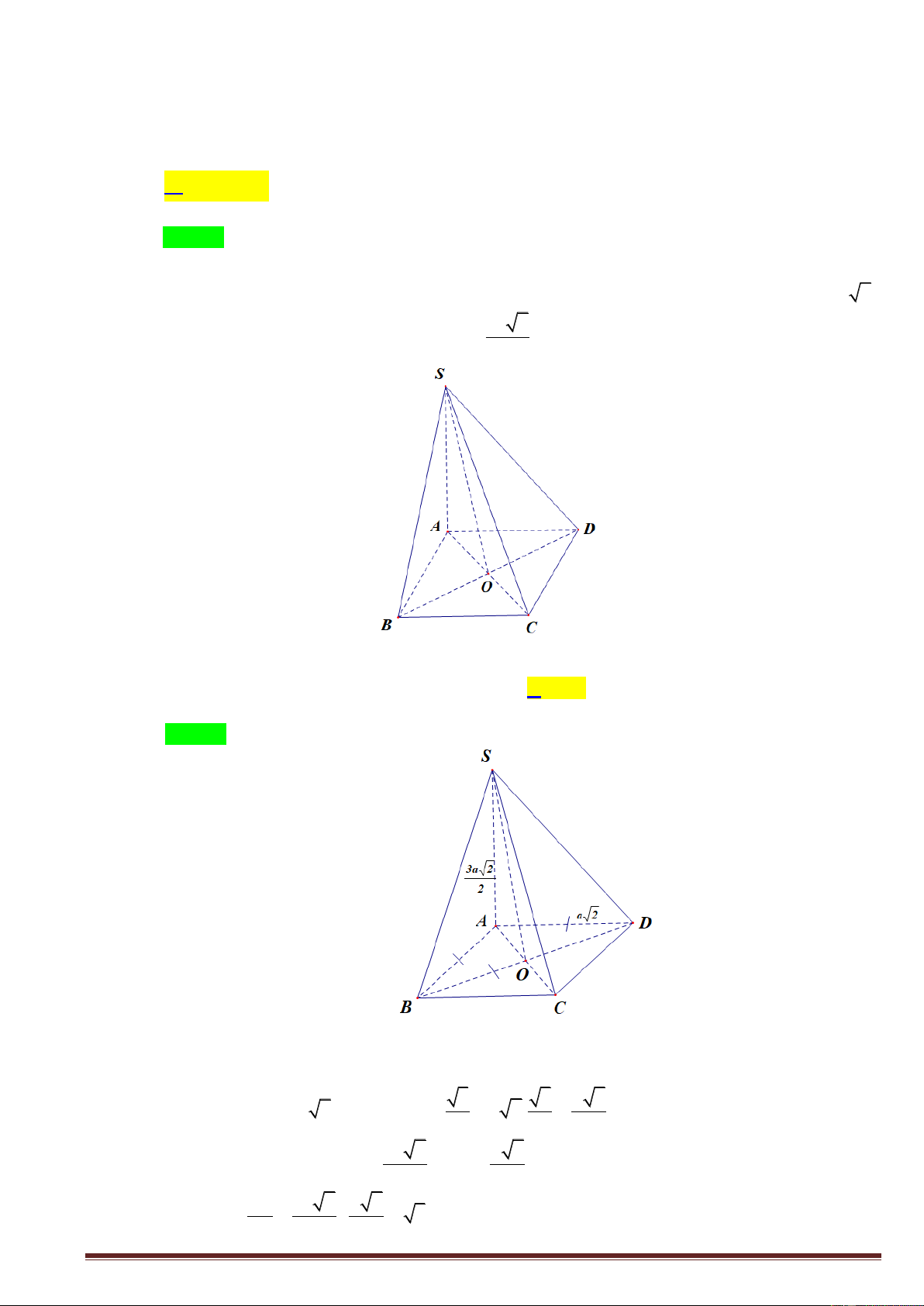
Câu 50: Cho hình hộp ABC . D AB CD
  có đ|y ABCD là hình chữ nhật cạnh AB a, AD  2a ,
AB a 3 . Gọi I là trọng tâm tam giác  A CD
  ,  là góc giữa đường thẳng ID và mặt phẳng
ICB . Giá trị của sin bằng A. 9 . B. 6 . C. 6 . D. 23 . 253 11 2 253 11 Trang47 HƯỚNG DẪN GIẢI
Câu 40:Từ các chữ số 0,1,2,3,4,5,6 có thể lập được bao nhiêu số chẵn, mỗi số có 5 chữ số khác nhau
trong đó có đúng hai chữ số lẻ và 2 chữ số lẻ đứng cạnh nhau? A. 360 B. 280 C. 310 D. 290
Hướng dẫn giải: Chọn A.
Gọi A là số tự nhiên có hai chữ số lẻ khác nhau lấy từ các số 0,1, 2,3, 4,5,6 số cách chọn được A là 2
A  6 . Số chẵn có 5 chữ số mà hai số lẻ đứng kề nhau phải chứa A và ba trong 4 chữ số 0;2;4;6. Gọi 3 abcd; , a , b , c d {  ,
A 0, 2, 4, 6} là số thỏa mãn yêu cầu bài toán.
*TH1: Nếu a Acó 1 cách chọn a và 3 A chọn , b c, d . 4
* TH 2: a Acó 3 cách chọn a
+ Nếu b A có 1 cách chọn b và 2
A cách chọn c, d . 3
+ Nếu c Acó 1 cách chọn c và 2 A cách chọn , b d . 3 Vậy có 2 A  3 A  3 2 2 1.A 1.A
 360 số thỏa mãm yêu cầu bài toán. 3 4 3 3 
Câu 41: Hàm số y f (x) có đạo hàm trên  v{ có đồ thị hàm số f '(x) được cho như hình vẽ. Hàm
số y f (x) nghịch biến trên khoảng n{o dưới đ}y? A.  1    ;1   . B. 0; . C. 1 ;    . D.  ;0  .  3   3 
Hướng dẫn giải : Chọn D   f  xx 0  0   x 1
Ta có bảng biến thiên của hàm số f (x) : x  0 1  y - 0  0 + y y CT
Từ bảng biến thiên ta thấy hàm số nghịch biến trên  ;  0.
Câu 42: Tìm tất cả các giá trị của tham số thực m để hàm số 3 2
y mx mx m m  
1 x  2 đồng biến trên  . A. 4 m  . B. 4 m  và m  0 .
C. m  0hoặc 4 m  . D. 4 m  . Hướng dẫn 3 3 3 3 giải : Chọn D.
TH1: m  0  y  2 là hàm hằng nên loại m  0
TH2: m  0 . Ta có: 2
y  3mx  2mx m m   1 . Trang48  4 2 2
  m  3m m     
Hàm số đồng biến trên 1 0 m 4      3  m   3m  0 3 m  0
Câu 43: Cho một tấm nhôm hình chữ nhật
ABCD có AD  60 cm và AB có độ dài
không đổi. Ta gập tấm nhôm theo 2 cạnh MN và
PQ v{o phía trong đến khi AB và DC trùng
nhau như hình vẽ bên để được một hình lăng trụ
khuyết 2 đ|y. Tìm x để thể tích khối lăng trụ tạo thành lớn nhất? A. x  20. B. x  25. C. x 10 . D. x  30 . Lời giải Chọn A
+ Ta có: AN PD x ( cm, 0  x  30 )  NP  60 – 2xcm
+ Thể tích hình lăng trụ tạo thành bằng: 2 1  NP  2 V A . B SA . B . PA  .NP NPA   2  2  2 AB  60  2x  2  . x  . 
 60  2x  2 15.A .
B 30  xx 15  3 cm  2  2 
+ Trong đó AB không đổi nên ta chỉ cần tìm x sao cho f x  30  xx 15 đạt giá trị lớn nhất.
+ Xét hàm số f x trên 15;30 ta được max f x  f 20 10 5  x  20 15;30
Câu 44: Cho hàm số bậc ba y f x có đồ thị như hình bên. y 1 O x 3 
Ta ́t cả các giá trị của tham so ́ m đẻ hàm só y f x  m có ba điẻm cực trị là A. m  1  hoa ̣c m  3. B. m  1
 hoa ̣c m  3. C. m  3  hoa ̣c m 1 .
D.1 m  3 . Lời giải Chọn A.
- Số điểm cực trị của đồ thị hàm số y f x  m bằng số điểm cực trị của hàm số y f (x)  m và số
nghiệm đơn của phương trình f (x)  m  0 .
- Dựa vào hình vẽ, hàm số y f (x)  m có hai điểm cực trị ne n hàm so ́ y f x  m có ba điẻm cực trị kvck m  1  hoa ̣c m  3.
Câu 45: Gọi x, y là các số thực dương thỏa m~n điều kiện log x  log y  log x y và 9 6 4   xa b
, với a , b là hai số nguyên dương. Tính a b . y 2
A. a b  6.
B. a b 11.
C. a b  4 .
D. a b  8. Lờigiải Trang49 ChọnA
Đặt log x t 9 x  9t (1) y  6t (2) 
log x  log y t   Theo đề ra có 9 6 
 x y  4t (3)
log x  log x y t  9 4    tx  3   (4)    y  2  Từ (1), (2), và (3) ta có t  3  1   5   (TM ) t t   t      
9t  6t  4t  3t  2 2  3.2 t 3 3 2 2  4  0   1  0       2   2  t   3  1   5   (L)    2  2 t      
Thế v{o (4) ta được x 3 1 5 a b   
a 1;b  5   y  2  2 2
Thử lại ta thấy a  1;b  5 thỏa mãn dữ kiện bài toán. Suy ra a b  6.
Câu 46: So ́ các giá tr ị nguyên của tham số m để phương trình log  x   1  log mx  8 có hai 2   2 nghiệm phân biệt là A. 3 . B. 4 . C. 5 . D.Vô số. Lờigiải. ChọnA        x   x 1 x 1 log 1  log mx  8     . 2   2   x   2 2 1  mx 8 x  
m 2 x 9  0
Để phương trình đ~ cho có hai nghiệm thực lớn hơn 1 thì điều kiện sau thỏa mãn. m  8   2
m  4m  32  0 m  4   0    
  x 1  x 1  0  m  0  4  m  8 1   2  1  x x  1 2       8  m  0 x 1 x 1 0  1  2   
Vì m  m5,6,  7 .
Câu 47: Tìm tất cả các giá trị tham số m sao cho đồ thị hàm số 4
y x  m   2 2 2
1 x m có ba điểm
cực trị nội tiếp đường tròn bán kính bằng 1.    A. 3 5 m  1; m  . B. 3 5 m  0; m  . 2 2   C. 3 5 m  0; m  . D. 3 5 m  1; m  . 2 2 Lời giải Chọn B. x  0 Ta có 3
y  4x  4 m   1 x  4x  2 x m   1  0     1 2 x m 1
Đồ thị hàm số đ~ cho có ba điểm cực trị  y  0 có ba nghiệm phân biệt  m  1  . 2
x  0  y m Khi đó   1   .
x   m 1  y   m 2 1  2m  2 2 1  m  2  m 1 Nên ta có A 2
0; m  , Bm 1; 2  m  
1 , C  m 1; 2  m  
1 l{ ba điểm cực trị của đồ thị hàm số đ~ cho. Trang50  AB   2
m 1; m  2m    1
AB m 1 m   4 1 Ta có     AB AC . AC  4   2
m 1;m  2m  1 AC m1m 1 
Gọi H l{ trung điểm của cạnh BC AH BC và H 0; 2  m   1 
AH   m m    AH  m m   m  2 2 2 0; 2 1 2 1 1 . Mà 1 . AB AC.BC SAH.BC   2 . R AH A . B AC . ABC 2 4R 
Nên R  1 và BC   2
m 1;0  BC  2 m1   3
m  2  m   m  4 2 1 1 1  m  
1 1  2m   1   3 2
m  3m m  0  m  0 , 3 5 m  . 2
Câu 48: Cho hàm số y f x có đạo hàm liên tục trên  và hàm số y f x có đồ thị như hình vẽ. y 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6
Hỏi hàm số g x  f x x  2 2
1 đồng biến trên khoảng nào trong các khoảng sau?
A. 3;  . B.1;3 . C.  3  ; 
1 . D. ;3 . Lời giải Chọn B
Tập x|c định của g x là  . Ta có gx  2 f x  x 1   .
Hàm số đồng biến khi và chỉ khi f x  x 1, (dấu bằng chỉ xảy ra tại hữu hạn điểm).
Vẽ chung đồ thị y f x và y  x 1 trên cùng một hệ trục như sau: y 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 x  
Từ đồ thị ta có f x  x  3 1   . 1   x  3 Câu 49: Cho 1 2
a, b là số thực dương thỏa mãn log a  log
. Giá trị nhỏ nhất của biểu thức 2 2 2 b 3 3
P  4a b  4log  3 3 4a b là 2  Trang51 A. 4 4 4 log 6 . B.  4log . C. 41 log 3 . D. 4  . 2  2 2 ln 2 ln 2 Lời giải Chọn C Ta có 1 2 2 2 4 log a  log  log a  log
a   a  2 2 2 2 2 2 b b b b 3 3 Đặt 256 b b 256 3 3 3 3
t  4a b b   3 . .
12  t  12; 6 6   b 2 2 b
Khi đó P f t  t  4log t ,có f t 4  1  0, t   2 2 t ln 2
Suy ra f t l{ h{m đồng biến trên 12;  f t  f 12
Vậy giá trị nhỏ nhất của P là P 12  4log 12  4 1 log 3 min 2  2 
Câu 50: Cho hình hộp ABC . D AB CD
  có đ|y ABCD là hình chữ nhật cạnh AB a, AD  2a ,
AB a 3 . Gọi I là trọng tâm tam giác  A CD
  ,  là góc giữa đường thẳng ID và mặt phẳng
ICB . Giá trị của sin bằng A. 9 . B. 6 . C. 6 . D. 23 . 253 11 2 253 11 Lời giải
Gọi  là góc tạo bởi đường thẳng ID và mặt phẳng ICB , H là trọng tâm tam giác  ACD . Ta có: d  ; D ICB
3 d H ; ICB sin   . . ID 2 ID
Gọi E là hình chiếu của H lên CB , K là hình chiếu của H lên IE , ta chứng minh được
d H; ICB  HK . Ta có: 2 2a 1 1 a 5 2 2 HE DC  ; D I   D B    4 a a  . 3 3 3 3 3 Mà 2 2 2 2 A A   A B
  AB  3a a a 2  HI a 2 . 2 5a a 23 2 2 2 DI DD  D I   2a   9 3 2a .a 2    9 ICB HE.HI 2 3 a d H ;  HK     sin  . 2 2 2 HE HI 22 a 11 253 9 Trang52 www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2021 ĐỀ 10 MÔN TOÁN Thời gian: 90 phút Câu 1:
[1D2-1.2-1] Lớp 11A có 20 học sinh nam và 25 học sinh nữ. Có bao nhiêu cách chọn một
đôi song ca gồm 1 nam và 1 nữ? A. 45 . B. 2 C . C. 2 A . D. 500 . 45 45 Câu 2:
[1D3-3.3-1] Cho cấp số cộng u có số hạng đầu u  2 , công sai d  3. Số hạng thứ 5 của n  1 u bằng n A.14 . B. 10 . C. 162 . D. 30 . Câu 3:
[2H2-1.2-1] Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng 1 A. 4 rl . B. 2 rl . C. rl . D. rl . 3 Câu 4:
[2D1-1.2-1] Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng nào dưới đây? A. 0; 4 . B.  ;    1 . C.  1   ;1 . D. 0; 2 . Câu 5:
[2H1-3.2-1]Cho hình hộp có đáy là hình vuông cạnh bằng a và chiều cao 3a . Thể tích của hình hộp đã cho bằng 3 3 3 1 A. a . B. 3a . C. 9a . D. 3 a . 3 xCâu 6:
[2D2-5.1-1] Phương trình 4 8 2021 1 có nghiệm là 7 9 A. x  . B. x  2  . C. x  . D. x  2 . 4 4 2 2 2 Câu 7: [2D3-2.1-1] Nếu f
 xdx 5 và 2f
 x gxdx 13 
thì g xdx  bằng 1 1 1 A. 3  . B. 1. C. 1. D. 3 . Câu 8:
[2D1-1.2-1] Cho hàm số y f x có bảng biến thiên như sau: Trang53
Khẳng định nào sau đây đúng
A. Hàm số đạt cực tiểu tại x  4  .
B. Điểm cực đại của đồ thị hàm số là x  0 .
C. Giá trị cực tiểu của hàm số bằng 1.
D.Điểm cực đại của đồ thị hàm số là A0 ;  3 . Câu 9:
[2D1-5.1-1] Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới đây? A. 2
y x  2x 1 . B. 3
y x  2x 1 . C. 4 2
y x  2x 1. D. 3
y  x  2x 1 .
Câu 10: [2D2-3.2-1] Với số thực dương a tùy ý, log a bằng 3 1 1
A. 2  log a . B.  log a . C. 2 log a . D. log a . 3 3 2 3 3 2
Câu 11: [2D3-1.1-1] Họ tất cả các nguyên hàm của hàm số f x 2
 sin x  6x là A. 3
 cos x  2x C . B. 3
cos x  2x C . C. 3
 cos x 18x C . D. 3
cos x 18x C .
Câu 12: [2D4-1.1-1] Gọi z là số phức liên hợpcủa số phức z  3
  4i . Tìm phần thực và phần ảo của số phức z .
A. Số phức z có phần thực bằng 3
 và phần ảo bằng 4 .
B. Số phức z có phần thực bằng 3 và phần ảo bằng 4 .
C.Số phức z có phần thực bằng 3  và phần ảo bằng 4  .
D. Số phức z có phần thực bằng 3 và phần ảo bằng 4  .
Câu 13: [2H3-1.1-1] Trong không gian Oxyz , hình chiếu vuông góc của điểm A1; 2;3 trên mặt
phẳng Oyz có tọa độlà
A. 0; 2;3 .
B. 1;0;3 .
C. 1;0;0 . D. 0; 2;0 . Câu 14: [2H3-1.3-1] Trong không gian Oxyz , tọa độ tâm của mặt cầu S 2 2 2
: x y z  2x  4y  6  0 là A. 2; 4;0 .
B. 1; 2;0 .
C. 1; 2;3 . D. 2; 4;6 . Trang54
Câu 15: [2H3-2.2-1] Trong không gian Oxyz , cho mặt phẳng   : 2x  3z 1 0 . Vectơ nào dưới đây
là một vectơ pháp tuyến của   ?    
A. n  2;3;   1 .
B. n  2;3;0 .
C. n  2;0;  3 .
D. n  2;0;  3 . x 1 2t
Câu 16: [2H3-3.3-1] Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :  y  3  t ? z  3t
A. M 1;3;0 .
B. N 1;3;3 .
C. P 2;1;0 .
D. Q 2; 1;3 .
Câu 17: [1H3-3.3-2] Cho hình chóp S.ABCD có đáy là hình hình thoi tâm O , ABD  đều cạnh a 2 , a
SA vuông góc với mặt phẳng đáy và 3 2 SA
(minh họa như hình bên). 2
Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng A. 45. B. 30 . C. 60 . D. 90 .
Câu 18: [2D1-2.2-2] Cho hàm số y f x , bảng xét dấu của f  x như sau
Số điểm cực tiểu của hàm số đã cho là A. 0 . B. 2 . C. 1. D. 3 .
Câu 19: [2D1-3.1-2] Giá trị nhỏ nhất của hàm số f x 4 2
x 10x 1trên đoạn 3;2 bằng A. 1. B. 23  . C. 24 . D. 8  .
Câu 20: [2D2-3.2-2] Xét tất cả các số thực dương a và b thỏa mãn log a  log  2 a b . Mệnh đề 3 27  nào dưới đây đúng? A. 2 a b . B. 3 a b .
C. a b . D. 2 a b . 2 log x log x
Câu 21: [2D2-6.2-2] Tập nghiệm của bất phương trình 9 9 9  x  18 là 1   1 A. 1;9 . B. ;9   . C. 0;  1 9; . D. 0; 9;  .   9   9
Câu 22: [2H2-2.1-2] Cho mặt cầu  S  . Biết rằng khi cắt mặt cầu  S  bởi một mặt phẳng cách tâm một
khoảng có độ dài là 3 thì được giao tuyến là đường tròn T  có chu vi là 12 . Diện tích của
mặt cầu  S  bằng Trang55 A.180 . B. 180 3 . C. 90 . D. 45 .
Câu 23: [2D1-5.3-2] Cho hàm số bậc ba f x có đồ thị như hình vẽ. Số giá trị nguyên của tham số m
để phương trình f x 1  m có 3 nghiệm phân biệt là A. 4 . B. 5 . C. 2 . D. 3 .  xe
Câu 24: [2D3-1.1-2] Họ nguyên hàm của hàm số x y e 1    là 2  cos x x 1 x 1 A. x
e  tan x C . B. x
e  tan x C . C. e   C . D. e   C . cos x cos x  2
log  x 3x
Câu 25: [2D2-4.1-2] Tìm tập xác định của hàm số y e . A. D   .
B. D  0;3 .
C. D  3;  .
D. D   ;  03;
Câu 26: [2H1-3.2-2] Cho khối lăng trụ đứng ABC . D A BCD
  , có đáy là hình bình hành cạnh
AB a , AD a 3 , 
BAD  120 và AB  2a (minh họa như hình dưới đây). Thể tích của
khối lăng trụ đã cho bằng 3 3 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 2 4 6
Câu 27: [2D1-4.1-2] Gọi k và l lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của 2  đồ x
thị hàm sốy  
. Khẳng định nào sau đây đúng x   1 x
A. k  0 ; l  2.
B. k 1; l  2.
C. k 1; l 1.
D. k  0 ; l 1.
Câu 28: [2D1-5.1-2] Cho hàm số 4 2
y ax bx c , a, ,
b c    có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng? Trang56
A. a  0 , b  0 , c  0 .
B. a  0 , b  0 , c  0 .
C. a  0 , b  0, c  0 .
D. a  0 , b  0 , c  0 .
Câu 29: [2D3-3.1-2] Hãy tính diện tích phần tô đậm trong hình vẽ dưới đây. 4 3  A. . B. . C. 1. D. . 3 4 2
Câu 30: [2D4-2.2-2] Cho z  4  2i . Hãy tìm phần ảo của số phức z  1 2iz . 2  2 1 1 A. 6  i . B. 2  i . C. 2  . D. 6  .
Câu 31: [2D4-2.4-2] Cho số phức z x yi x, y    có phần thực khác 0. Biết số phức 2
w iz  2z
là số thuần ảo. Tập hợp các điểm biểu diễn của z là một đường thẳng đi qua điểm nào dưới đây? A. M 0  ;1 .
B. N 2;  1 .
C. P 1;3 . D. Q 1  ;1 .  
Câu 32: [2H3-1.1-2] Trong không gian Oxyz , cho các vectơ a  2;1; 2 , b  1; 1  ;0 . Tích vô   
hướng a b.b bằng A. 3  . B. 1. C. 5  . D. 12 . x 1 y z  2
Câu 33: [2H3-3.7-2] Trong không gian Oxyz , cho đường thẳng  :   và mặt phẳng 2  2 1
P:2x y z 3  0 . Gọi Slà mặt cầu có tâm I thuộc  và tiếp xúc với P tại điểm H 1;1; 
0 . Phương trình của S  là 2 2 2 2 2 2
A. x  3   y  2   z   1  36.
B. x  3   y  2   z   1  36 . 2 2 2 2 2 2 C. x  
3   y  2   z   1  6 . D. x  
3   y  2   z   1  6 . Trang57
Câu 34: [2H3-2.3-2] Trong không gian Oxyz , mặt phẳng đi qua điểm M 1; 2;3 và song song với mặt
phẳng  P : x  2y z  3  0 có phương trình là
A. x  2 y z  3  0 .
B. x  2 y  3z  0 .
C. x  2 y z  0 .
D. x  2 y z  8  0 . x  2 y z  1
Câu 35: [2H3-3.1-1] Trong không gian Oxyz , đường thẳng d :   nhận vectơ nào sau 1 2 1 
đây làm vectơ chỉ phương?    
A. u  1; 2;1 .
B. u  2; 4; 2 . C. u  2  ; 4  ;2 .
D. u  1; 2;1 . 4   3   2   1  
Câu 36: [1D2-5.2-3] Gọi S là tập hợp các số tự nhiên có 4 chữ số khác nhau. Chọn ngẫu nhiên một số
từ tập S . Tìm xác suất để số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không
chứa hai chữ số nguyên nào liên tiếp nhau. 1 2 5 5 A. . B. . C. . D. . 36 3 63 1512
Câu 37: [1H3-5.4-3] Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D ,
AB  3a, AD DC  .
a Gọi I là trung điểm của AD , biết hai mặt phẳng  SBI  và SCI
cùng vuông góc với đáy và mặt phẳng SBC  tạo với đáy một góc 0
60 . Gọi M điểm trên AB
sao cho AM  2a , tính khoảng cách giữa MD và SC . a 17 a 15 a 6 a 3 A. . B. . C. . D. . 5 10 19 15   
Câu 38: [2D3-2.4-3] Cho hàm số f x có f  2  
và f  x  x sin x .  2   2 a  Giả sử rằng cos . x f x 2 dx   
(với a, b, c là các số nguyên dương, a tối giản). b c b 0
Khi đó a b c bằng A. 23. B. 5 . C. 20 . D. 27 . m   1 2  x  3 1
Câu 39: [2D1-1.3-3] Cho hàm số f (x) 
( m  0 và là tham số thực). Tập hợp m để 2  2
x  3  m  1 
hàm số đã cho nghịch biến trên khoảng  ; 1 
 có dạng S   ;  a ;
b cd;   , với  2 
a, b, c, d là các số thực. Tính P a b c d . A. - 3 . B. - 1. C. 0 . D. 2 .
Câu 40: [2H2-1.1-3] Cho hình nón đỉnh S có đáy là hình tròn tâm O . Một mặt phẳng qua đỉnh của
hình nón và cắt hình nón theo thiết diện là tam giác vuông có diện tích bằng 4 . Góc giữa
đường cao của hình nónvà mặt phẳng thiết diện bằng 30 . Thể tích của khối nón được giới hạn
bởi hình nón đã cho bằng 10 2 8 3 5 3 A. 5 . B. . C. . D. . 3 3 3
Câu 41: [2D2-5.3-3] Cho các số thực a, b, c thuộc khoảng 1;  và thỏa mãn Trang58 2  c  2 log b  log . c log 
  9log c  4log b . Giá trị của biểu thức 2
log b  log c bằng: b b a a ab a b 1 A.1. B. . C. 2 . D. 3 . 2
Câu 42: [2D1-3.1-3] Cho hàm số bậc bốn y f x có đồ thị như hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0; 20 sao cho giá trị nhỏ nhất của hàm
số g x  2 f x  m  4  f (x)  3 trên đoạn 2; 2 không bé hơn 1? A. 18. B.19 . C. 20 . D. 21 .
Câu 43: [2D2-5.5-3] Cho phương trình 2
log x  4 log x  5  m log x 1 với m là tham số thực. 3 3  3 
Tìm tất cả các giá trị của m để phương trình có nghiệm thuộc 27; .
A. 0  m  2 .
B. 0  m  2 .
C. 0  m 1.
D. 0  m 1.
Câu 44: [2D3-2.4-3] Cho hàm số f x có đạo hàmliên tụctrên  thoả mãn       2   1 x f x f x x e và f 0  2
 . Tổng tất cả các nghiệm thực của phương trình f x  0 có giá trịlà A. 2  . B. 2 . C. 1. D. 1.
Câu 45: [2D1-5.3-3] Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Tổng tất cả giá trị  
nguyên của tham số m để phương trình f  2 f cos x   m có nghiệm x  ; .    2  y 2 1 2 1 x 1  O 2 1  2 A. 1. B. 0 . C. 1. D. 2  . Trang59
Câu 46: [2D1-2.6-4] Cho hàm số đa thức bậc bốn y f x , biết hàm số có ba điểm cực trị x  3
 , x  3, x  5 . Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số     3 2 x 3x g x f e
m có đúng 7 điểm cực trị A. 3 B. 4 C. 5 D. 6
Câu 47: [2D2-5.5-4] Có tất cả bao nhiêu cặp số a;b với a, b là các số nguyên dương thỏa mãn:
log a b  a b3  3 2 2 a b
 3ab a b 1 1. 3    A. 2 . B. 3 . C. 1. D. vô số.
Câu 48: [2D3-2.4-4] Cho hàm số f x liên tục trên  thỏa mãn 1 x f
x   x x x  1 x 4 3 2 2 4 4 2  2 f
,x  0, x  1  
. Khi đó  f xdx có giá trị là  x x 1  1 3 A. 0 . B. 1. C. . D. . 2 2
Câu 49: [2H1-3.2-4] Cho hình chóp S.ABC , đáy là tam giác ABC có AB  ;
a AC a 2 và 
CAB  135 , tam giác SAB vuông tại B và tam giác SAC vuông tại A . Biết góc giữa hai mặt
phẳng SAC  và SAB bằng 30 . Tính thể tích khối chóp S.ABC . 3 a 3 a 3 a 6 3 a 6 A. . B. . C. . D. . 6 3 3 6
Câu 50: [2D1-1.3-4] Cho hàm số y f x và f x  0,x   . Biết hàm số y f  x có bảng biến   thiên như hình vẽ 1 137 và f    .  2  16 2   
Có bao nhiêu giá trị nguyên của m  2  021; 202  1 để hàm số   4 5  x mx g x e
. f x đồng  1  biến trên 1  ;  .  2  A. 4040 . B. 4041. C. 2020 . D. 2021. HẾT
HƯỚNG DẦN GIẢI CHI TIẾT Câu 1.
[1D2-1.2-1] Lớp 11A có 20 học sinh nam và 25 học sinh nữ. Có bao nhiêu cách chọn một đôi
song ca gồm 1 nam và 1 nữ? A. 45 . B. 2 C . C. 2 A . D. 500 . 45 45 Lời giải Chọn D
Để chọn được một đôi song ca gồm một nam và một nữ ta thực hiện liên tiếp 2 công đoạn: Trang60
Công đoạn 1: Chọn 1 học sinh nam từ 20 học sinh nam  có 20 cách chọn.
Công đoạn 2: Chọn 1 học sinh nữ từ 25 học sinh nữa  có 25 cách chọn.
Theo quy tắc nhân ta có 20.25  500 cách chọn. Câu 2.
[1D3-3.3-1] Cho cấp số cộng u có số hạng đầu u  2 , công sai d  3. Số hạng thứ 5 của n  1 u bằng n A.14 . B. 10 . C. 162 . D. 30 . Lời giải
Số hạng tổng quát của cấp số cộng có số hạng đầu u và công sai bằng d là u u n 1 d . n 1   1
Vậy u u  4d  2  4.3  14 . 5 1 Câu 3.
[2H2-1.2-1] Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng 1 A. 4 rl . B. 2 rl . C. rl . D. rl . 3 Lời giải Chọn B
Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r là S  2 xq rl . Câu 4.
[2D1-1.2-1] Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng nào dưới đây? A. 0; 4 . B.  ;    1 . C.  1   ;1 . D. 0; 2 . Lời giải Chọn C
Dựa vào bảng biến thiên, hàm số nghịch biến trên khoảng (- 1 ) ;1 . Câu 5.
[2H1-3.2-1]Cho hình hộp có đáy là hình vuông cạnh bằng a và chiều cao 3a . Thể tích của hình hộp đã cho bằng 3 3 3 1 A. a . B. 3a . C. 9a . D. 3 a . 3 Lời giải
Thể tích của hình hộp đã cho là 2 3 V  .
B h a .3a  3a . xCâu 6.
[2D2-5.1-1] Phương trình 4 8 2021 1 có nghiệm là 7 9 A. x  . B. x  2  . C. x  . D. x  2 . 4 4 Lời giải Chọn D 4x 8  4x 8  0 Ta có 2020 1 2020
 2020  4x 8  0  x  2.
Vậy phương trình đã cho có nghiệm x  2 . Trang61 2 2 2 Câu 7. [2D3-2.1-1] Nếu f
 xdx 5 và 2f
 x gxdx 13 
thì g xdx  bằng 1 1 1 A. 3  . B. 1. C. 1. D. 3 . Lời giải Chọn D 2 2 2 Ta có 2 f
 x gxdx 13   2. f
 xdxg
 xdx 13 1 1 1 2 2 2  g
 xdx 132. f
 xdx g
 xdx 132.5 1 1 1 2  g
 xdx 3. 1 2 Vậy g
 xdx 3. 1 Câu 8.
[2D1-1.2-1] Cho hàm số y f x có bảng biến thiên như sau :
Khẳng định nào sau đây đúng
A. Hàm số đạt cực tiểu tại x  4  .
B. Điểm cực đại của đồ thị hàm số là x  0 .
C. Giá trị cực tiểu của hàm số bằng 1.
D. Điểm cực đại của đồ thị hàm số là A0 ;  3 . Lời giải Chọn D
Dựa vào bảng biến thiên ta thấy điểm cực đại của đồ thị hàm số là A0 ;  3 do đó chọn D. Câu 9.
[2D1-5.1-1] Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới đây? A. 2
y x  2x 1 . B. 3
y x  2x 1 . C. 4 2
y x  2x 1. D. 3
y  x  2x 1 . Lời giải Chọn B
+) Từ đồ thị hàm số trên, ta thấy đồ thị là dạng của hàm bậc ba nên loại đáp án A, C.
+) Từ đồ thị hàm số trên, ta thấy giới hạn của hàm số khi x   là  nên hệ số của 3 x
dương, loại đáp ánD. Trang62 Vậy B là đáp án đúng.
Câu 10. [2D2-3.2-1] Với số thực dương a tùy ý, log a bằng 3 1 1
A. 2  log a . B.  log a . C. 2 log a . D. log a . 3 3 2 3 3 2 Lời giải Chọn D 1 1
Với a là số thực dương tùy ý, ta có 2 log a  log a  log a . 3 3 3 2
Câu 11. [2D3-1.1-1] Họ tất cả các nguyên hàm của hàm số f x 2
 sin x  6x là A. 3
 cos x  2x C . B. 3
cos x  2x C . C. 3
 cos x 18x C . D. 3
cos x 18x C . Lời giải Chọn A Ta có f
 xx   2 x x  2 3 d sin 6 dx  sin d
x x  2 3x dx   cos x  2x C   .
Câu 12. [2D4-1.1-1] Gọi z là số phức liên hợpcủa số phức z  3
  4i . Tìm phần thực và phần ảo của số phức z .
A. Sốphức z có phần thực bằng 3
 và phần ảo bằng 4 .
B. Số phức z có phần thực bằng 3 và phần ảo bằng 4 .
C.Số phức z có phần thực bằng 3  và phần ảo bằng 4  .
D. Số phức z có phần thực bằng 3 và phần ảo bằng 4  . Lời giải Chọn C Số phức z  3
  4i có số phức liên hợp là z  3   4i .
Vậy số phức z có phần thực bằng 3  và phần ảo bằng 4  .
Câu 13. [2H3-1.1-1] Trong không gian Oxyz , hình chiếu vuông góc của điểm A1; 2;3 trên mặt
phẳng Oyz có tọa độlà
A. 0; 2;3 . B. 1;0;  3 .
C. 1;0;0 . D. 0; 2;0 . Lời giải Chọn A
Theo lý thuyết ta có : hình chiếu vuông góccủa điểm M  ;
x y; z  lên mặt phẳng Oyz là M 0; ;
y z suy rahình chiếu vuông góc của điểm A1;2;3 trên mặt phẳng Oyz có tọa độlà 0;2;3 . Câu 14. [2H3-1.3-1] Trong không gian Oxyz , tọa độ tâm của mặt cầu S 2 2 2
: x y z  2x  4y  6  0 là A. 2; 4;0 .
B. 1; 2;0 .
C. 1; 2;3 . D. 2; 4;6 . Lời giải Chọn B 2 2
Ta có S   x     y   2 : 1 2
z 11 nên tọa độ tâm mặt cầu là 1;2;0 .
Câu 15. [2H3-2.2-1] [Mức độ 1] Trong không gian Oxyz , cho mặt phẳng   : 2x  3z 1 0 . Vectơ
nào dưới đây là một vectơ pháp tuyến của   ?    
A. n  2;3;   1 .
B. n  2;3; 0 .
C. n  2;0;  3 .
D. n  2;0;  3 . Lời giải Chọn C
Mặt phẳng ax by cz d  0 có các vectơ pháp tuyến dạng n  ka ; kb; kc, k   , k  0 . Trang63
Suy ra   có một vectơ pháp tuyến là n  2;0;  3 . x 1 2t
Câu 16. [2H3-3.3-1] Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :  y  3  t ? z  3t
A. M 1;3;0 .
B. N 1;3;3 .
C. P 2;1;0 .
D. Q 2; 1;3 . Lời giải Chọn A
Từ phương trình đường thẳng d ta thấy đường thẳng đi qua điểm M 1;3;0 .
Câu 17. [1H3-3.3-2] Cho hình chóp S.ABCD có đáy là hình hình thoi tâm O , ABD  đều cạnh a 2 , a
SA vuông góc với mặt phẳng đáy và 3 2 SA
(minh họa như hình bên). 2
Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng A. 45. B. 30 . C. 60 . D. 90 . Lời giải Chọn C
Do SA   ABCD nên hình chiếu của SO lên mặt phẳng  ABCD là AO . Khi đó góc giữa
đường thẳng SO và mặt phẳng  ABCD là góc  SOA . 3 3 a 6 ABD
đều cạnh a 2 nên AO ABa 2.  . 2 2 2 3a 2 a 6 S
OA vuông tại A có SA  , AO  nên 2 2  SA 3a 2 a 6  tan SOA   :
 3  SOA  60. OA 2 2 Trang64
Vậy góc giữa đường thẳng SO và mặt phẳng  ABCD bằng 60 .
Câu 18. [2D1-2.2-2] Cho hàm số y f x , bảng xét dấu của f  x như sau
Số điểm cực tiểu của hàm số đã cho là A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B
Căn cứ vào bảng xét dấu của f x ta thấy f x đổi dấu từ âm sang dương tại các điểm x  1
 và x 1nên hàm số đã cho có 2 điểm cực tiểu. Câu 19.
[2D1-3.1-2] Giá trị nhỏ nhất của hàm số f x 4 2
x 10x 1trên đoạn 3;2 bằng A. 1. B. 23  . C. 24 . D. 8  . Lời giải Chọn C
Hàm số f x 4 2
x 10x 1 xác định trên 3;2.
Ta có f  x 3
 4x  20x . x  0  3  ;2 
f  x  0  x  5  3  ;2 .  x   5    3  ;2 f   3  8
 ; f  5  2
 4; f 0 1; f 2  2  3.
Vậy giá trị nhỏ nhất của hàm số trên đoạn 3; 2 bằng 24 tại x   5 . Câu 20.
[2D2-3.2-2] Xét tất cả các số thực dương a và b thỏa mãn log a  log  2 a
b . Mệnh đề nào dưới đây 3 27  đúng? A. 2 a b . B. 3 a b .
C. a b . D. 2 a b . Lời giải Chọn D 1
Ta có log a  log  2 a
b  log a  log  2 a
b  3log a  log  2 a b 3 3  3 3  3 27  3 3  log a  log  2 a b 3 2
a a b a b 2  a b . 3 3  2 log x log x
Câu 21. [2D2-6.2-2] Tập nghiệm của bất phương trình 9 9 9  x  18 là 1   1 A. 1;9 . B. ;9   . C. 0;  1 9; . D. 0; 9;  .   9   9 Lời giải Chọn B 2 log x log 9 9 9 xx  18   1 .
Điều kiện x  0 . x x x log x   log .log log 9 9 9 1  9 x log x log xx  18   log  9 9 9 9  x  18 9  2x 18 log9 xx  9  log .
x log x  log 9  log x 1 9 2 9 9 9  1   log x  1 1 
x  9 (thỏa mãn). 9 9 Trang65  
Vậy tập nghiệm của bất phương trình đã cho là 1 S  ;9   . 9 
Câu 22. [2H2-2.1-2] Cho mặt cầu  S  . Biết rằng khi cắt mặt cầu  S  bởi một mặt phẳng cách tâm một
khoảng có độ dài là 3 thì được giao tuyến là đường tròn T  có chu vi là 12 . Diện tích của
mặt cầu  S  bằng A. 180 . B. 180 3 . C. 90 . D. 45 . Lời giải Chọn A I J A
Gọi I là tâm mặt cầu  S  , J là tâm đường tròn T  , A là điểm thuộc đường tròn T
Có bán kính đường tròn T  là r JA, IJ  3.
Có chu vi đường tròn T  là P  2r 12  r  6.
Gọi R là bán kính mặt cầu thì 2 2
R r IJ  3 5 .
Diện tích mặt cầu  S  là 2
S  4 R  180 . Vậy S 180 .
Câu 23. [2D1-5.3-2] Cho hàm số bậc ba f x có đồ thị như hình vẽ. Số giá trị nguyên của tham số m
để phương trình f x 1  m có 3 nghiệm phân biệt là A. 4 . B. 5 . C. 2 . D. 3 . Lời giải Chọn D
+) Ta có f x 1  m f x  m 1  * .
+) Số nghiệm của phương trình  
* bằng số giao điểm của đồ thị hàm số y f x và đường
thẳng y m  1.
+) Từ đồ thị ta có, đường thẳng y m  1 cắt đồ thị hàm số y f x tại 3 điểm phân biệt khi và chỉ khi 1
  m 1 3  0  m  4 .
+) Vì m nên m 1 ; 2 ;  3 .
Vậy có 3 giá trị nguyên của tham số m thỏa mãn đề bài. Trang66 xe
Câu 24. [2D3-1.1-2] Họ nguyên hàm của hàm số x y e 1    là 2  cos x x 1 x 1 A. x
e  tan x C . B. x
e  tan x C . C. e   C . D. e   C . cos x cos x Lời giải Chọn B xe    x x 1 Ta có e 1  dx e  d x
x e  tan x C      . 2 2  cos x   cos x   2
log  x 3x
Câu 25. [2D2-4.1-2] Tìm tập xác định của hàm số y e . A. D   .
B. D  0;3 .
C. D  3;  .
D. D   ;  03; Lời giải Chọn B
+ Điều kiện xác định: 2
x  3x  0  0  x  3 .
Vậy tập xác định của hàm số là D  0;3 .
Câu 26. [2H1-3.2-2] Cho khối lăng trụ đứng ABC . D A BCD
  , có đáy là hình bình hành cạnh
AB a , AD a 3 , 
BAD  120 và AB  2a (minh họa như hình dưới đây). Thể tích của
khối lăng trụ đã cho bằng 3 3 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 3a . 2 4 6 Lời giải Chọn A 3
Diện tích hình bình hành ABCD là  2 S  . AB . AD sin BAD a . ABCD 2
Tam giác ABB vuông tại B có 2 2 BB 
AB  AB a 3 . 3 3 3 Vậy 2 3 V         BB .S a 3. a a . ABCD. A B C D ABCD 2 2
Câu 27. [2D1-4.1-2] Gọi k và l lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ 2  x
thị hàm sốy  
. Khẳng định nào sau đây đúng x   1 x
A. k  0 ; l  2.
B. k 1; l  2.
C. k 1; l 1.
D. k  0 ; l 1. Lời giải Chọn A Trang67
Tập xác định D  0;2 \  1 .
+ Do tập xác định của hàm số là D  0;2 \ 
1 nên không tồn tại giới hạn của hàm số khi
x   , do đó đồ thị hàm số không có tiệm cận ngang. 2  x 2  x
+ lim f x  lim
  ; lim f x  lim
  , suy ra x 1 là tiệm cận    x 1  x 1    x   1 x x 1  x 1   x   1 x
đứng của đồ thị hàm số. 2  x
+ lim f x  lim
  , suy ra x  0 là tiệm cận đứng của đồ thị hàm số.   x0
x0  x   1 x
Do đó đồ thị hàm số không có đường tiệm cận ngang và có hai đường tiệm cận đứng.
Vậy k  0 ; l  2.
Câu 28. [2D1-5.1-2]Cho hàm số 4 2
y ax bx c , a, ,
b c    có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
A. a  0 , b  0 , c  0 .
B. a  0 , b  0 , c  0 .
C. a  0 , b  0, c  0 .
D. a  0 , b  0 , c  0 . Lời giải Chọn B
+ Dựa vào hình dáng đồ thị ta có a  0 .
+ Đồ thị hàm số có ba điểm cực trị suy ra a, b trái dấu, mà a  0 suy ra b  0.
+ Đồ thị cắt trục tung tại điểm có tung độ âm, suy ra c  0 .
Vậy a  0 , b  0 , c  0 .
Câu 29. [2D3-3.1-2] Hãy tính diện tích phần tô đậm trong hình vẽ dưới đây. 4 3  A. . B. . C. 1. D. . 3 4 2 Lời giải Chọn A Cách 1: Ta có 2 x 1  0, x   1   ;1 . Trang68 1 3 1 1   Do đó diệ x 4 n tích phần tô đậm là 2 S x 1dx     2
1 x dx   x    . 1 1  3  3 1  2
Cách 2: Công thức nhanh tính diện tích S = Bh 3 2 2 4
Áp dụng công thức với B = 2 , h = 1 ta có: S = Bh = .2.1 = . 3 3 3
Câu 30. [2D4-2.2-2] Cho z  4  2i . Hãy tìm phần ảo của số phức z  1 2iz . 2  2 1 1 A. 6  i . B. 2  i . C. 2  . D. 6  . Lời giải Chọn C
Ta có z  1 2i2  z  3
  4i  4 2i 1 2i . 2 1
Vậy phần ảo của số phức z là 2  . 2
Câu 31. [2D4-2.4-2] Cho số phức z x yi x, y    có phần thực khác 0. Biết số phức 2
w iz  2z
là số thuần ảo. Tập hợp các điểm biểu diễn của z là một đường thẳng đi qua điểm nào dưới đây? A. M 0  ;1 .
B. N 2;  1 .
C. P 1;3 . D. Q 1  ;1 . Lời giải Chọn D
Ta có z x yi  ,
x y   ; x  0 2 Mặt khác 2
w iz z i x yi   x yi   x xy   2 2 2 2 2
x y  2 y i .
x  0 kh«ngtháa m·n ®iÒu kiÖn 
Vì w là số thuần ảo nên x xy  0   .
y 1  0 (tháa m·n ®iÒu kiÖn)
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình y 1  0 (trừ điểm M 0 
;1 ), do đó đường thẳng này đi qua điểm Q 1  ;1 .  
Câu 32. [2H3-1.1-2] Trong không gian Oxyz , cho các vectơ a  2;1; 2 , b  1; 1
 ;0 . Tích vô hướng   
a b.b bằng A. 3  . B. 1. C. 5  . D.12 . Lời giải Chọn C     
Ta có a b   3
 ;2;2  ab.b  5  . x 1 y z  2
Câu 33. [2H3-3.7-2] Trong không gian Oxyz , cho đường thẳng  :   và mặt phẳng 2  2 1
P:2x y z 3  0 . Gọi Slà mặt cầu có tâm I thuộc  và tiếp xúc với P tại điểm H 1;1; 
0 . Phương trình của S  là 2 2 2 2 2 2
A. x  3   y  2   z   1  36.
B. x  3   y  2   z   1  36 . Trang69 2 2 2 2 2 2 C. x  
3   y  2   z   1  6 . D. x  
3   y  2   z   1  6 . Lời giải Chọn Cx 1 2t    Phương trình đườ x 1 y z 2 ng thẳng  :  
được viết lại là  :  y  2t , t  . 2  2 1  z  2t
Theo giả thiết I    I 1 2t ;2t ;2  t    . 
Ta có HI  2t; 2t 1;t  2 . 
Mặt phẳng  P có một vectơ pháp tuyến là n  2; 1   ;1 .  
Vì mặt cầu  S  tiếp xúc với  P tại điểm H nên HI và n cùng phương.   Ta có HI và n cùng phương khi và chỉ khi
2t 2t 1 t  2      t 2t 1    t  1   I 3; 2  ;  1 . 2 1  1 2t 1  t   2 2 2 2
Bán kính mặt cầu  S  là : R IH  1 3   1   2  0   1  6 . 2 2 2
Vậy phương trình mặt cầu  S  là :  x  
3   y  2   z   1  6 .
Câu 34. [2H3-2.3-2] Trong không gian Oxyz , mặt phẳng đi qua điểm M 1; 2;3 và song song với mặt
phẳng  P : x  2y z  3  0 có phương trình là
A. x  2 y z  3  0 .
B. x  2 y  3z  0 .
C. x  2 y z  0 .
D. x  2 y z  8  0 . Lời giải Chọn C
Gọi Q là mặt phẳng đi qua điểm M 1; 2;3 và song song với mặt phẳng  P . uuur
Vì Q //  P nên Q nhận vectơ pháp tuyến n  1; 2  ;   
1 của mặt phẳng  P làm vectơ P pháp tuyến.
Phương trình của mặt phẳng Q là :1. x  
1  2. y  2 1. z  3  0  x  2y z  0 .
Vậy phương trình mặt phẳng Q : x  2y z  0 . x  2 y z  1
Câu 35. [2H3-3.1-1] Trong không gian Oxyz , đường thẳng d :   1 2 1  nhận vectơ nào sau
đây làm vectơ chỉ phương?    
A. u  1; 2;1 .
B. u  2; 4; 2 . C. u  2  ; 4  ;2 .
D. u  1; 2;1 . 4   3   2   1   Trang70 Lời giải Chọn C 
+) Đường thẳng d có một vectơ chỉ phương là u  1; 2;   1 . d    Mà u  2
u suy ra u  2  ; 4
 ;2 cũnglà một vectơ chỉ phương của đường thẳng d . 3   3 d
Câu 36. [1D2-5.2-3] Gọi S là tập hợp các số tự nhiên có 4 chữ số khác nhau. Chọn ngẫu nhiên một số
từ tập S . Tìm xác suất để số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không
chứa hai chữ số nguyên nào liên tiếp nhau. 1 2 5 5 A. . B. . C. . D. . 36 3 63 1512 Lời giải Chọn D
Xét phép thử: “ Chọn ngẫu nhiên một số từ tập S ”.
Số phần tử của không gian mẫu là: n  3  9.A  4536 . 9
Gọi A là biến cố: “ Số được chọn có các chữ số sắp xếp theo thứ tự tăng dần và không chứa hai
chữ số nguyên nào liên tiếp nhau”.
Gọi số được chọn là abcd .
+) Vì chữ số sắp xếp theo thứ tự tăng dần nên: 1  a b c d  9 .
+) Trong số được chọn không chứa hai chữ số nguyên nào liên tiếp nhau nên:
1  a b 1  c  2  d  3  6 .
Đặt: a a ; b b 1; c c  2 ; d d  3 . 1 1 1 1
Khi đó: 1  a b c d  6. 1 1 1 1
Số cách chọn bộ bốn số a ;b ;c ; d là: 4 C ( cách)  có 4
C cách chọn a ; b ; c ; d . 1 1 1 1  6 6 Mỗi cách chọn  ; a ; b ;
c d  chỉ có một cách sắp xếp thỏa mãn yêu cầu bài toán nên tạo ra một số.
Suy ra: n A 4  C  15 . 6 n A 5
Xác suất cần tìm là: P A     n  1512
Câu 37. [1H3-5.4-3] Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D ,
AB  3a, AD DC  .
a Gọi I là trung điểm của AD , biết hai mặt phẳng  SBI  và SCI
cùng vuông góc với đáy và mặt phẳng SBC  tạo với đáy một góc 0
60 . Gọi M điểm trên AB
sao cho AM  2a , tính khoảng cách giữa MD và SC . a 17 a 15 a 6 a 3 A. . B. . C. . D. . 5 10 19 15 Lời giải S A 2a M a B I H D C K E Chọn B Trang71
SBI   (A C B D) 
+) Theo giả thiết ta có 
SCI   (ABCD)  SI  (A C B D) SI  
SBI SCI  +) Vẽ       IK BC BC
SIK SKI là góc giữa mặt phẳng SBC  với mặt đáy nên  SKI  60 . 2 2 1 a 3a +) Vì SDI.DC  , S  . Suy ra SS SSa . BIC ABCDICD IAB  2 - IDC  2 4 IAB 4 1 2a 5
+) Mặt khác BC   AB CD2 2
AD a 5 và S
IK.BC. Suy ra IK IBC 2 5 2a 15
+) Trong tam giác vuông SIK ta có SI IK.tan 60  . 5
+)Vì AM = 2a nên BM = a Þ MD // BC , do đó
d (MD, SC)= d (MD,(SBC))= d (D,(SBC)). ED DC 1 1
+) Gọi E là giao điểm của AD với BC , ta có = = Þ ED = AD = ID . EA AB 3 2 Do đó 1
d (D ,(SBC))=
d (I ,(SBC)). 2
+) Gọi H là hình chiếu của I lên SK ta có d (I , (SBC))= IH .
Trong tam giác vuông SIK , ta có: 1 1 1 5 5 5 a 15 = + = + = Þ IH = . 2 2 2 2 2 2 IH SI IK 12a 4a 3a 5 a 15 Vậy d (M , D SC)= . 10
Nhận xét: Để tính và , ta có thể làm như sau: AI.AM .2 a a 2a 1)Tính
: Ta có IK d (I , BC)  d ( ; A DM )    . DM a 5 5 a a a 2)Tính : Ta có  2 15
IH IK.sin SKI  .sin 60   . 5 15 15   
Câu 38. [2D3-2.4-3] Cho hàm số f x có f  2  
và f  x  x sin x .  2   2 a  Giả sử rằng cos . x f x 2 dx   
(với a, b, c là các số nguyên dương, a tối giản). Khi đó b c b 0
a b c bằng A. 23. B. 5 . C. 20 . D. 27 . Lời giải Chọn D
Do f  x  x sin x nên f x  f
 xdx xsin d x x   d x cos x   
xcos x  cos d x x
 xcos x sin x C .    Theo giả thiết f
 2 1 C  2  C 1   .  2 
Suy ra f x  sin x x cos x 1. Trang72    2 cos . x f  x 2 dx  cos x
sin x xcos x   2 1 dx   2
sin x cos x x cos x  cos xdx 0 0 0    2 2 1 1  sin 2 d x x x   1cos2x 2 dx  cos d x x  2 2 0 0 0     2 2 1 1 1
  cos 2x 2  sin x 2  d x x  d x sin 2x   4 2 4 0 0 0 0     2 2 2 2 1 x 1 1 3  1 7   1 2  x sin 2x 2  sin 2 d x x    cos 2x 2    . 2 4 4 4 2 16 8 4 16 0 0 0 0
Vậy a  7, b  4, c 16 . Suy ra a b c  27 . m   1 2  x  3 1
Câu 39. [2D1-1.3-3] Cho hàm số f (x) 
( m  0 và là tham số thực). Tập hợp m để 2  2
x  3  m  1 
hàm số đã cho nghịch biến trên khoảng  ; 1 
 có dạng S   ;  a ;
b cd;   , với  2 
a, b, c, d là các số thực. Tính P a b c d . A. - 3 . B. - 1. C. 0 . D. 2 . Lời giải Chọn A  3 x   2
Điều kiện xác định:  . 2  2  x  3   0  m 1   1  Đặt u  2
x  3  u   0, x    ; 1 
 , suy ra hàm số u  2
x  3 nghịch biến 2  x  3  2   1  trên khoảng  ; 1   .  2   1 
Với x   ; 1  u    1; 2 .  2  m u
Yêu cầu bài toán trở thành tìm m để hàm số g u   1 1 
đồng biến trên khoảng 1; 2. 2 u   m 2 m  11 2 Ta có   m g u  , u  . 2  2  m u      m
gu  0, u  1; 2 
Hàm số g u đồng biến trên khoảng 1; 2 khi và chỉ khi  2  1; 2 m Trang73  2  m  2   m   1 1  0   0  m 0   m  m 0  m  m  2   m  2   2 m  2  m  2      1     0   m  2    0  m 1  . m  m   m  2  m  0 m  2  2       m 1    2  m 1   0      m   m 0 m 1 
Vậy S  ;  2 0; 1 2;     a  2; b  0; c  1; d  2 . Do đó P  2  01 2  3  .
Câu 40. [2H2-1.1-3] Cho hình nón đỉnh S có đáy là hình tròn tâm O . Một mặt phẳng qua đỉnh của hình
nón và cắt hình nón theo thiết diện là tam giác vuông có diện tích bằng 4 . Góc giữa đường cao
của hình nónvà mặt phẳng thiết diện bằng 30 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng 10 2 8 3 5 3 A. 5 . B. . C. . D. . 3 3 3 Lời giải Chọn D
Mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông SAB .
Gọi SA l là đường sinh, OA R là bán kính và SO h là đường cao của hình nón đã cho.
Gọi I là trung điểm của AB và K là hình chiếu của O lên SI . 
Góc giữa đường cao của hình nón và mặt phẳng thiết diện là  SO SAB   ;  OSK  30 . 1 1 S
AB vuông cân tại S nên 2 2 S
 .SA l  4  l  2 2  . SAB 2 2  1 1
AB l. 2  4  Đường trung tuyến SI  .AB  .4  2 . 2 2 SO S
OI vuông tại O :  3 cosOSI
SO SI.cos30  2.  3  h  3 . SI 2 2 2 Ta có: 2 2
R l h  2 2   3  5 . 1 1 5 3
Vậy thể tích của khối nón là 2
V   R h  .5. 3  . 3 3 3
Câu 41. [2D2-5.3-3] Cho các số thực a, b, c thuộc khoảng 1;  và thỏa mãn 2  c  2 log b  log . c log 
  9log c  4log b . Giá trị của biểu thức 2
log b  log c bằng: b b a a ab a b 1 A.1 . B. . C. 2 . D. 3 . 2 Lời giải Chọn A Trang74 2  c  2 Ta có: log b  log . c log 
  9log c  4log b b b a a ab  2  4log b  log .
c 2log c  log b  9log c  4log b a b b b a a 2 2
 4log b  2log c  log c  9log c  4log b * . a b b a a  log b x Đặt a
( x, y  0 vì a, , b c  1 ). log c yb Ta có log c  log .
b log c xy . a a b Thay vào * ta được: 2 2
4x  2 y y  9xy  4x 2 2
 4x xy 8xy  2y 4x y  0
4x y  0 lo¹i
 4x yx  2y   1  0   .
x  2y  1 Vậy 2
log b log c log b 2log c x 2  y 1  . a b a b
Câu 42. [2D1-3.1-3] Cho hàm số bậc bốn y f x có đồ thị như hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0; 20 sao cho giá trị nhỏ nhất của hàm
số g x  2 f x  m  4  f (x)  3 trên đoạn 2; 2 không bé hơn 1? A. 18. B.19 . C. 20 . D. 21 . Lời giải Chọn B
Dựa vào hình vẽ ta có: 2
  f (x)  2, x   2  ;2 * .
 2 f x  4  0, x   2  ;2.
Vì m 0; 20 nên 2 f x  m  4  0
suy ra 2 f x  m  4  2 f x  m  4, x   2  ;  2 . Ta có:
g x  2 f x  m  4  f (x)  3  2 f x  m  4  f x  3  f x  m 1 , x   2  ;2.
+) Với m  0  g x  f x 1 , x   2  ;2.   *  1
  f x 1 3, x   2  ;2.
 0  f x 1  3, x   2
 ;2  0  g x  3, x   2  ;2.
min g x  0  m  0 không thỏa yêu cầu bài toán.  2  ;2
+) Với m 1; 20  f x  m 1  0  g x  f x  m 1. Trang75
Từ * ta có: f x  m 1  m 1  min g x  m 1.  2  ;2
Yêu cầu bài toán: min g x  1  m 11 m  2  m2;20 .  2  ;2
Vậy có 19 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 43. [2D2-5.5-3] Cho phương trình 2
log x  4 log x  5  m log x 1 với m là tham số thực. 3 3  3 
Tìm tất cả các giá trị của m để phương trình có nghiệm thuộc 27; .
A. 0  m  2 .
B. 0  m  2 .
C. 0  m 1.
D. 0  m 1. Lời giải Chọn D
Đặt t  log x , với x  27  t  3. 3 Phương trình trở thành 2
t  4t  5  m t   1 . * t   1 
Điều kiện xác định:  . t   5 2     +) Với t 4t 5 0
m  0 thì phương trình vô nghiệm, do  , t   5. t  1 0
t  1 (loaïi)
+) Với m  0, ta có 2
t  4t  5  0   .
t  5 (thoûamaõ) n
+) Với m  0 thì    t t   m t  2 2 2 * 4 5 1   2
m  2t  2 m   2 1 2
4 t  5  m  0 . (**)
Nếu m 1 t  1  không thỏa mãn.
t  1 (loaïi) Nếu 
m  1, ta có (**)  t    2   m  2 1 1
t m  5  0    2 m   . t  5  1 2 m 2 2 
Do đó, phương trình đã cho có nghiệm m 5 6m   5   0  1
  m  1, kết hợp m  0 2 2 1 m 1 m suy ra 0  m 1.
Vậy với 0  m 1 thì phương trình đã cho có nghiệm thuộc [27;  ) .
Câu 44. [2D3-2.4-3] Cho hàm số f x có đạo hàmliên tục trên  thoả mãn       2   1 x f x f x x e và f 0  2
 . Tổng tất cả các nghiệm thực của phương trình f x  0 có giá trịlà A. 2  . B. 2 . C. 1. D. 1. Lời giải Chọn D  Ta có
      2   1 x f x f x x e   
     . x f x f x e  2x 1 
  . x   .   x f x e f x
e   2x 1    .   x
f x e   2x 1
f x x e
  x  x f x x 2 . 2 1 d .e
x x C (1). Do f 0  2  nên từ (1) ta có 0 2 2.
e  0  0  C C  2  .
Khi đó     2   2. x f x x x e . x
f x    2
x x   x 2 0
2 .e  0  x x  2  1 0   . x  2 
Vậy tổng tất cả các nghiệm thực của phương trình f x  0 là 1 2  1  . Trang76
Câu 45. [2D1-5.3-3] Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Tổng tất cả giá trị  
nguyên của tham số m để phương trình f  2 f cos x   m có nghiệm x ; .    2  y 2 1 2 1 x 1  O 2 1  2 A. 1. B. 0 . C. 1. D. 2  . Lời giải Chọn D  
+) Đặt t  cos x , do x  ; 
 nên suy ra t  1  ;0.  2  Trên khoảng  1
 ;0 hàm số nghịch biến nên suy ra Với t   1
 ;0 thì f 0  f t  f  
1 hay 0  f t   2. +) Đặt u
2 f cos x thì u  2 f t ,u 0; 2. Khi đó bài toán trở thành:
Tìm m để phương trình f u  m có nghiệm u 0; 2.
Quan sát đồ thị ta thấy rằng với u 0;2 thì f u 2  ;2  2   m  2.
Vì m    m  2  ; 1  ;0; 
1 . Vậy có 4 giá trị của m.
Tổng các giá trị của m thỏa mãn yêu cầu bài toán là 2  .
Câu 46. [2D1-2.6-4] Cho hàm số đa thức bậc bốn y f x , biết hàm số có ba điểm cực trị x  3
 , x  3, x  5 . Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số     3 2 x 3x g x f e
m có đúng 7 điểm cực trị A. 3 B. 4 C. 5 D. 6 Lời giải Chọn D 3 2 3 2 x x x
Ta có     2   3  3 3 6 . x g x x x e f em        3 2 x x  3 2 2 3 x 3 0 3 6 . x g x x x e f em  0   x  0 x  0   x  2   x  2   3 2  x 3  x 3 2 x em  3 3x   em  3 ,  1 .  3 2  x 3x 3 2 em  3 x 3x  em  3 , 2  3 2 x 3  x em  5 3 2 x 3  x em  5  , 3 Trang77
Hàm số g x có 7 điểm cực trị khi và chỉ khi tổng số nghiệm đơn và bội lẻ, khác 0 và 2  của các phương trình   1 , 2,3 là 5 .  Xét hàm số   3 2 3  x x h x e có     3 2 2 3 3 6     x x h x x x e .  x  Ta có  h x 0  0   . x  2  Bảng biến thiên:
Khi đó có 3 trường hợp sau: Trường hợp 1: 4 4 m   e
m e   Khi đó: 3 3 51, 6    4 4
 1  m  3  e
 4  m e  3  57,6
Do m nguyên nên m 52;53;54;55;56;5  7 . Trường hợp 2: 4 4 m  5  e
m e  5  49,6   Khi đó: 4 4 1
  m  3  e   2
  m e  3  m .   0  m  3  1 3  m  4   Trường hợp 3: Trang78 4
 1 m  5  e 4  4
  m e  5  49,6  
Khi đó: m  3 1  m  2  m .   m  3  0  m  3 
Vậy có 6 giá trị nguyên của tham số m thỏa yêu cầu bài toán.
Câu 47. [2D2-5.5-4] Có tất cả bao nhiêu cặp số a;b với a, b là các số nguyên dương thỏa mãn:
log a b  a b3  3 2 2 a b
 3ab a b 1 1. 3    A. 2 . B. 3 . C. 1. D.vô số. Lời giải Chọn A Cách 1:
Với a, b là các số nguyên dương, ta có:
log a b  a b3  3 2 2 a b
 3ab a b 1 1 3    3 3 a b 3 3  log
a b  3aba b  3 2 2
a b ab  3ab a b 1 3 2 2    a b ab  log  3 3 a b  3 3
a b  log 3   2 2
a b ab  3   2 2
a b ab 1 3 3   
Xét hàm số: f t   log t t trên 0;  . 3 f t  1 '  1  0, t
  0 nên hàm số f t đồng biến trên 0; . t ln 3
Khi đó, phương trình   1 trở thành : f  3 3
a b   f 3   2 2
a b ab 3 3
  a b  3   2 2
a b ab   2 2
a b aba b  3  0 2 2
a b ab  0   *
 ab30 Do * ,
a b  nên phương trình * vô nghiệm. Suy ra: a b  3. 0  a  3 a  2   0  b  3 b  1
Mà a, b là các số nguyên dương nên   a b  3   a 1  * a,b  b   2
Vậy có hai cặp số a;b thỏa mãn yêu cầu bài toán.
Cách 2: (Với a, b là các số nguyên dương, ta có:
log a b  a b3  3 2 2 a b
 3ab a b 1 1 3    a b 3 3  log
a b  3aba b  3 2 2
a b ab  3ab a b 3    3 a b  log  2 2
a b ab 3  a b 1 3    3 Trang79 Trườ 2
ng hợp 1: a b  2 . Khi đó:   1  log
 4  3ab loại do * a, b   . 3 3  Trườ a b
ng hợp 2: a b  3  log  0 và  2 2
a b ab3 a b  0, a  ,b * 3 3 nên   1 không xảy ra.
Trường hợp 3: a b  3, khi đó   1 thỏa mãn. a  2 b  1
Mà a, b là các số nguyên dương nên  . a 1   b   2
Vậy có hai cặp số a;b thỏa mãn yêu cầu bài toán.
Câu 48. [2D3-2.4-4] Cho hàm số f x liên tục trên  thỏa mãn
 2x  2  x x  4x  4 1 x f 1 x 4 3 2  2 f
,x  0, x  1  
. Khi đó  f xdx có giá trị là  x x 1  1 3 A. 0 . B. 1. C. . D. . 2 2 Lời giải Chọn A 2
 2x  2  x x  4x  4
Từ giả thiết suy ra f 1 x 4 3  f    2 3 xx x 2 2 2 4 3  2x  2  2
x x  4x  4 Ta có: f
 1 xdxf . dx  dx     2 3  x x x 1 1 1 2 2 2
f   x   x
 2x  2   2x  2   4 4    1 d 1  f d  x 1  d        x 2 3
x   x   x x  1 1 1 1  1  f t  x   
dt   f t 2 4 2 2 dt     x    2  2 x x 1  0 0 0 1
  f tdt   f tdt  0 1  0 1
  f tdt  0. 1  1
Vậy  f xdx  0 . 1 
Cách trắc nghiệm( Thầy Hoàng Gia Hứng)
 2x  2  x x  4x  4
Ta có : x f 1 x 4 3 2  2 f  , x   0, x  1    x x  
x   x x x x f 1 x 4 3 2 2 4 4 2  2 f   , x   0, x  1    x x x  2x  2   2x  2  2
x f 1 x 2  2 fx   1 x 2 , x   0, x 1    x   x  1 1
Chọn f x  x f
 x.dx  .xdx  0  . 1  1  Trang80
Câu 49. [2H1-3.2-4] Cho hình chóp S.ABC , đáy là tam giác ABC có AB  ;
a AC a 2 và 
CAB  135 , tam giác SAB vuông tại B và tam giác SAC vuông tại A . Biết góc giữa hai mặt
phẳng SAC  và SAB bằng 30 . Tính thể tích khối chóp S.ABC . 3 a 3 a 3 a 6 3 a 6 A. . B. . C. . D. . 6 3 3 6 Lời giải Chọn A
Gọi D là hình chiếu vuông góc của S xuống mặt phẳng  ABC  . AB SB
AB  SBD  AB BD . AB SD AC SA
AC  SAD  AC AD . AC SD Tam giác ABC có  
CAB  135  BAD  45 .
Tam giác ABD vuông tại B có 
BAD  45 suy ra tam giác ABD vuông cân và AD a 2 .
Từ đó có tam giác ACD vuông cân tại A  tứ giác ABDC là hình thang vuông tại B và D .
Trong mặt phẳng SBD , hạ DH SB H SB . Dễ chứng minh DH  SAB .
Trong mặt phẳng SAD , hạ DK SA K SA . Dễ chứng minh DK  SAC  . 
Gọi  là góc giữa hai mặt phẳng SAB và SAC  ta có:    DH DK   ,
HDK  30 do tam
giác DHK vuông tại H .
Đặt SD x ,  x  0 . 2 2 HD 3 ax 2a x
Tam giác DHK vuông tại H có  cos HDK    . DK 2 2 2 2.ax a x 2 2 2 2 2 2 2 2
 6 a x  2 2a x  6a  6x  8a  4x x a . 3 1  a   S V . .S . D A . B AC.sin ABC BAC . 6 6 3 a
Vậy thể tích khối S.ABC bằng . 6
Câu 50. [2D1-1.3-4] Cho hàm số y f x và f x  0,x   . Biết hàm số y f  x có bảng biến  1  137
thiên như hình vẽ và f    .  2  16 Trang81 2   
Có bao nhiêu giá trị nguyên của m  2  021; 202  1 để hàm số   4 5  x mx g x e
. f x đồng  1  biến trên 1  ;  .  2  A. 4040 . B. 4041. C. 2020 . D. 2021. Lời giải Chọn D 2 2 x mx x mx
Ta có g x   x m 4 5 e f x 4 5 2 4 . .  e . f x
           2 4 5 2 4 . .       x mx g x x m f x f x e .  
Yêu cầu bài toán  g x 1  0,x 1  ; 
 và g x  0 chỉ xảy ra tại một số hữu hạn điểm  2   1  thuộc 1  ;  .  2    2  x mx
x mf x  f  x  1  2 4 .  0,x 1  ;   (vì 4 5 e  0)  2  f  x  1   2
x  4m      
 , ( vì f x  0,x )
f x , x 1;  2  f  x  1 
 4m  2x  * .
f x ,x  1  ;    2  2 f x  1 
f x . f x   f x    Xét h x    2x  . Ta có  h x        2  .
f x ,x  1  ;    2  2 f x  2 f   x  0  1 
f   x. f x   f   x  1  Mà  x   0,x 1  ;   .  f x ,   1  ;    0  2  2 f x  2     1  Từ đó suy ra  h x 1  0,x  1  ; 
 . Vậy hàm số hx đồng biến trên 1  ;  .  2   2  Bảng biến thiên  1  f    1   1   2  225 225
Vậy điều kiện *  4m h  4m  2.   4m   m      .  2   2   1  137 548 f    2  Trang82 m   Lại có 
m1;2;3;...;202  1 . m   2  021;202  1
Vậy có 2021 giá trị nguyên của m thỏa mãn yêu cầu bài toán. HẾT Trang83