






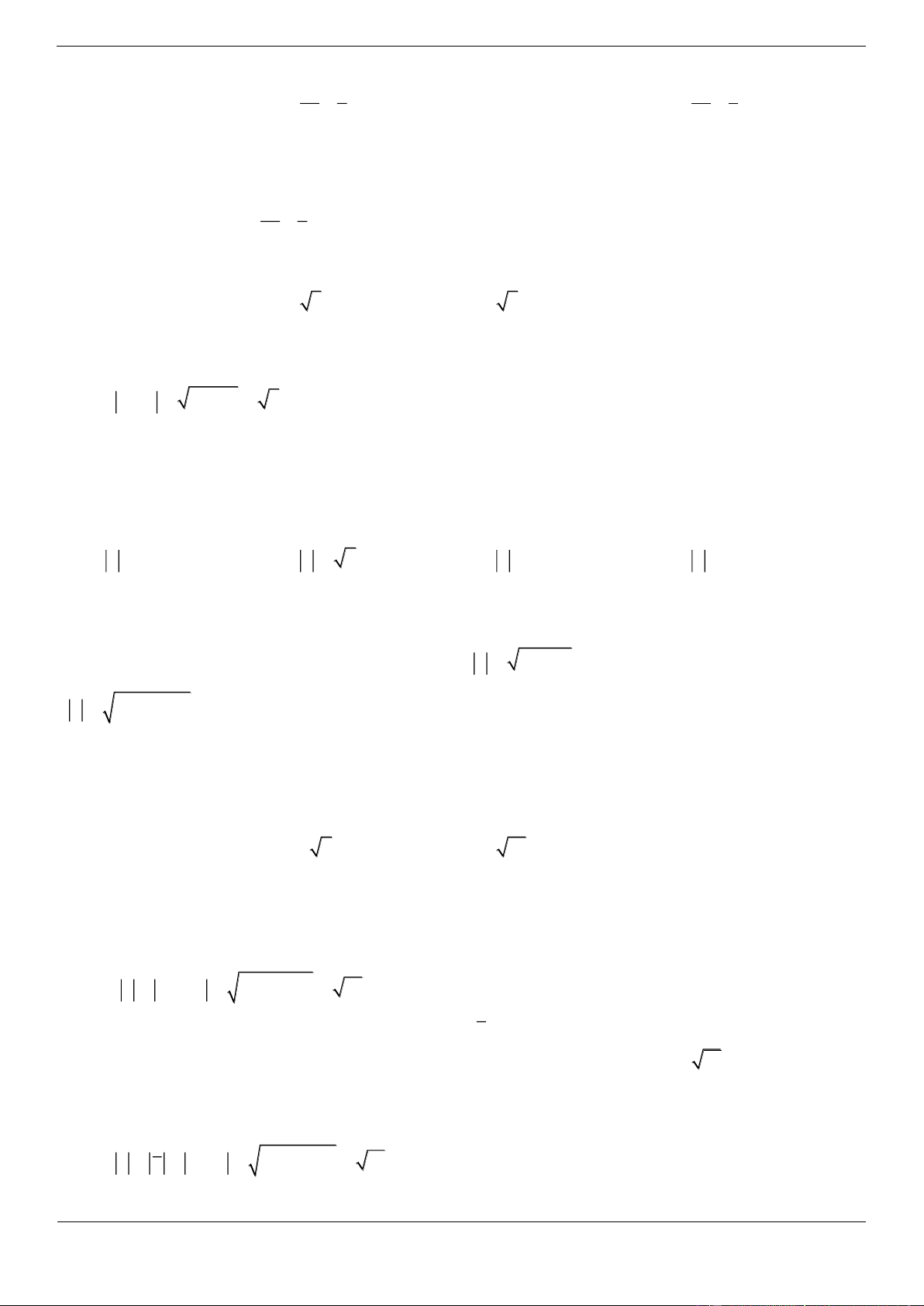




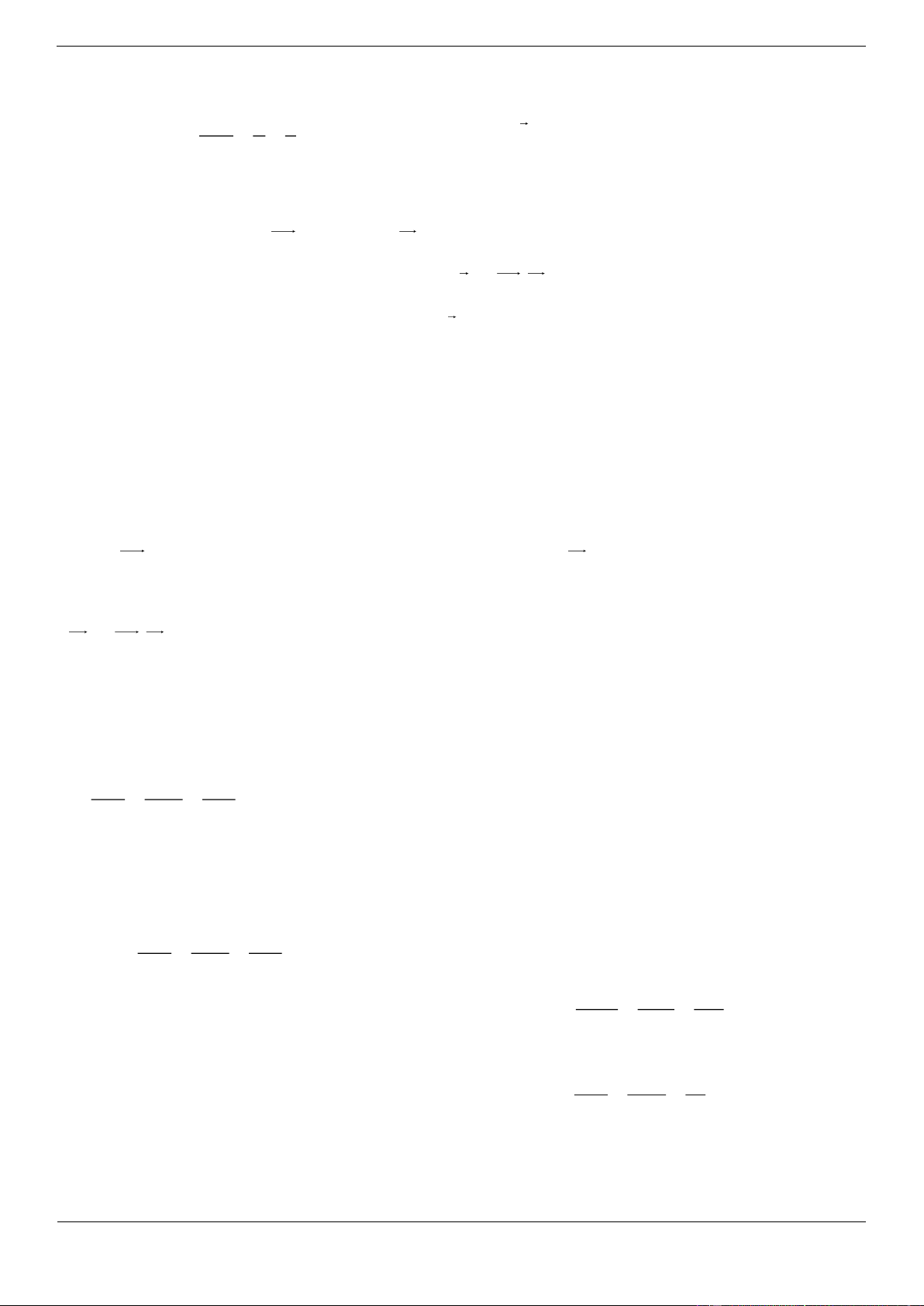










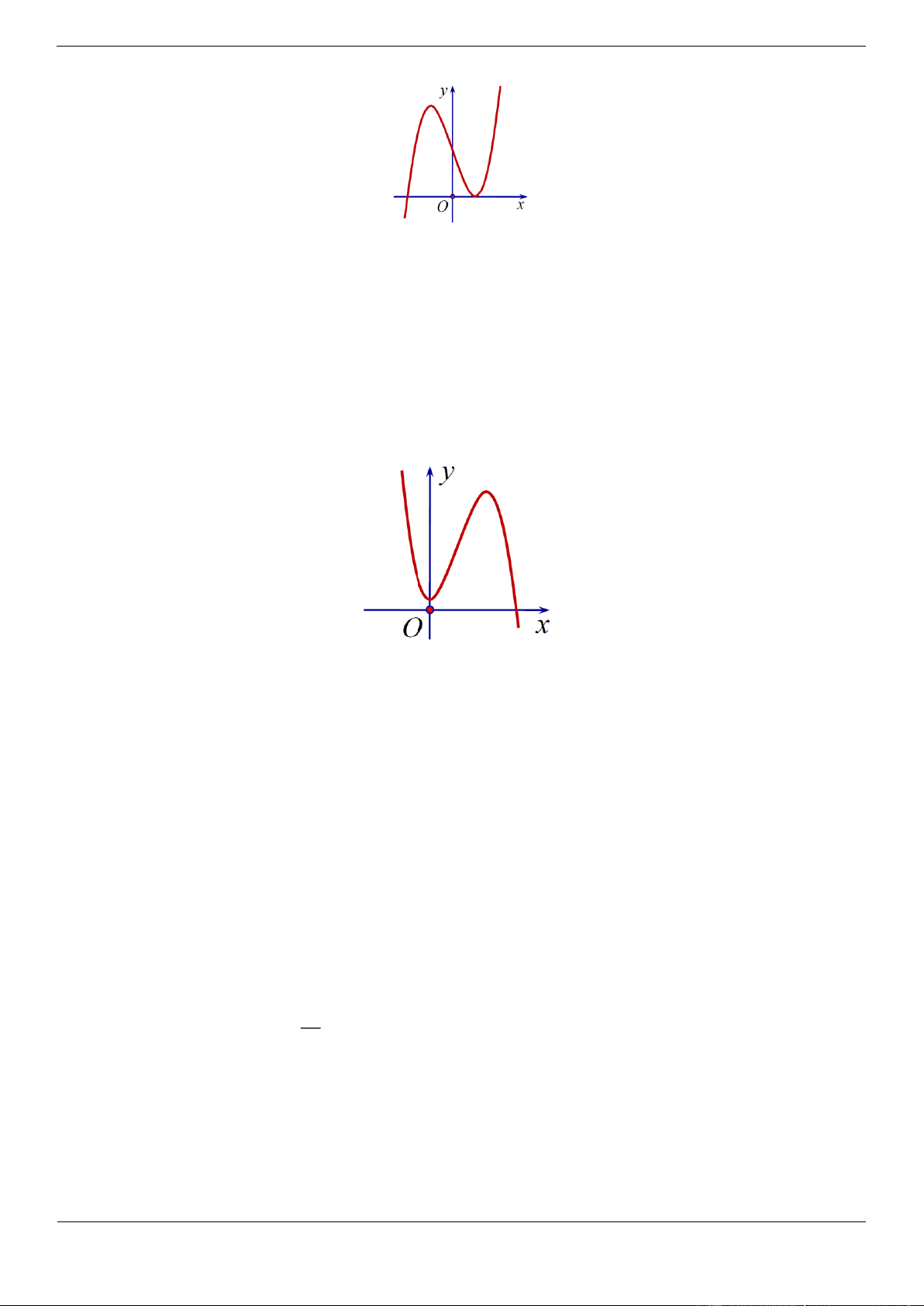

























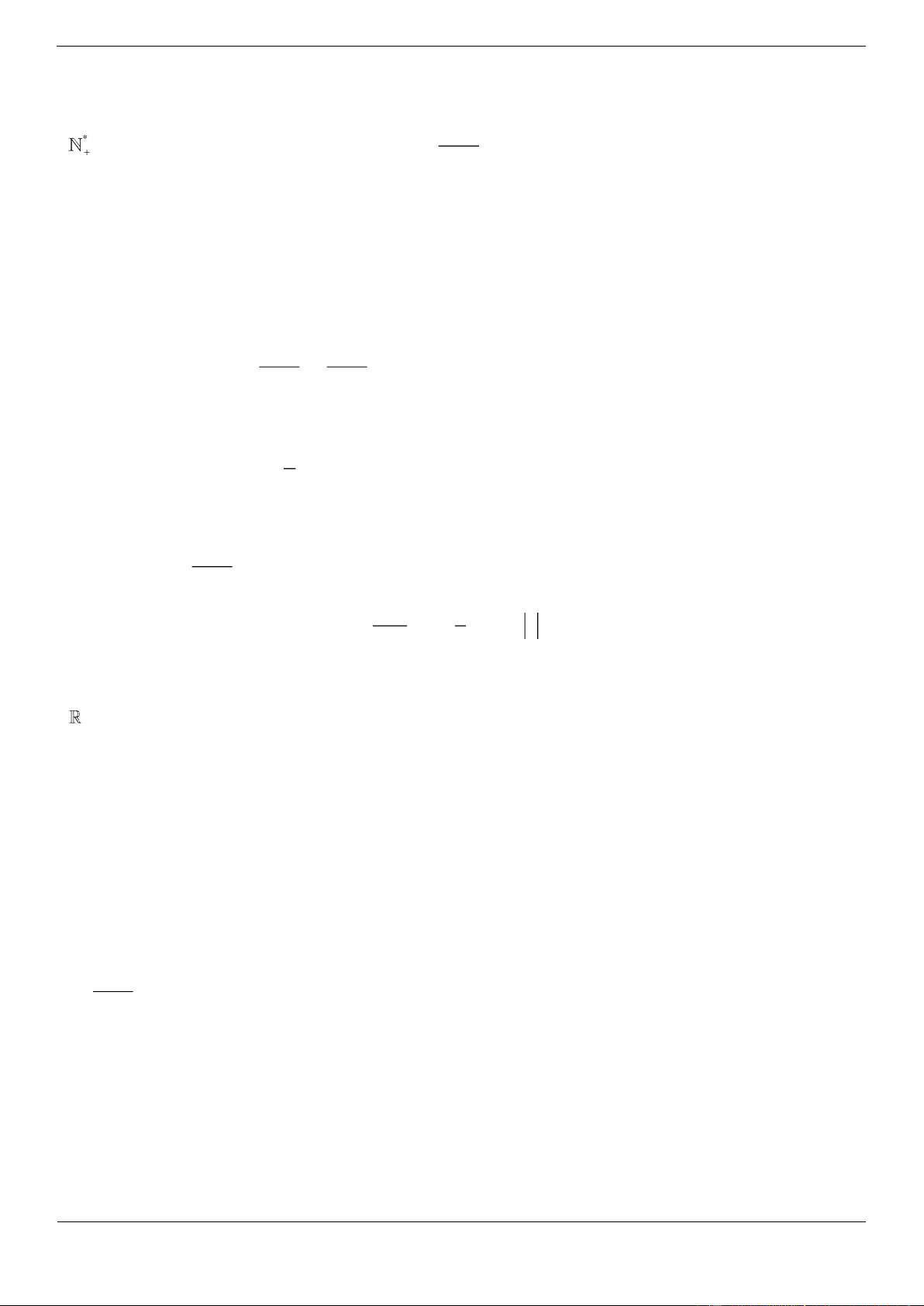

















Preview text:
A B C ☑ D
PHÁT TRIỂN ĐỀ THI THAM KHẢO CỦA BGD –2020 Môn: TOÁN
Câu 1. [ĐỀ THI THAM KHẢO] Từ một nhóm học sinh gồm 10 nam và 15 nữ, có bao nhiêu cách chọn ra một học sinh? A. 25. B. 150. C. 10 D. 15. Lời giải Chọn A
Để chọn ra một học sinh ta có 2 phương án thực hiện:
Phương án 1: Chọn một học sinh nam, có 10 cách chọn.
Phương án 2: Chọn một học sinh nữ, có 15 cách chọn.
Theo quy tắc cộng, ta có: 10 + 15 = 25 cách chọn ra một học sinh.
Câu hỏi phát triển tương tự câu 1:
Câu 1.1 (Câu tương tự câu1 ) Một nhóm học sinh gồm 9 học sinh nam và x học sinh nữ. Biết rằng có 15
cách chọn ra một học sinh từ nhóm học sinh trên, khi đó giá trị của x là A. 24 B. 6 C. 12 D. 25 Lời giải Chọn B
Để chọn ra một học sinh ta có 2 phương án thực hiện:
Phương án 1: Chọn một học sinh nam, có 9 cách chọn.
Phương án 2: Chọn một học sinh nữ, có x cách chọn.
Theo quy tắc cộng, ta có: 9 x cách chọn ra một học sinh.
Theo bài ra, ta có: 9 x 15 x 6
Câu 1.2 (Câu phát triển câu1 ) Từ một nhóm học sinh gồm 6 nam và 8 nữ, có bao nhiêu cách chọn
ra 3 học sinh có cả nam và nữ? A. 120 B. 168 C. 288 D. 364 Lời giải Chọn C
Phương án 1: Chọn 2 học sinh nam và 1 học sinh nữ, có 2 1
C .C 120 cách thực hiện. 6 8
Phương án 2: Chọn 1 học sinh nam và 2 học sinh nữ, có 1 2
C .C 168 cách thực hiện. 6 8
Theo quy tắc cộng, ta có: 120 + 168 = 288 cách chọn ra 3 học sinh có cả nam và nữ.
Câu 1.3 (Câu phát triển câu1 ). Một lớp có 30 học sinh gồm 20 nam và 10 nữ. Hỏi có bao nhiêu cách
chọn ra một nhóm 3 học sinh sao cho nhóm đó có ít nhất một học sinh nữ? A. 1140 B. 2920 C. 1900 D. 900 Lời giải Chọn B Cách 1:
Để chọn ra 3 học sinh trong đó có ít nhất một học sinh nữ ta có các phương án sau: 1
Phương án 1: Chọn 1 học sinh nữ và 2 học sinh nam, có 1 2
C .C cách thực hiện. 10 20
Phương án 2: Chọn 2 học sinh nữ và 1 học sinh nam, có 2 1
C .C cách thực hiện. 10 20
Phương án 3: Chọn 3 học sinh nữ, có 3
C cách thực hiện. 10
Theo quy tắc cộng, ta có: 1 2 2 1 3
C .C C .C C 2920 cách chọn ra một nhóm 3 học sinh sao cho nhóm 10 20 10 20 10
đó có ít nhất một học sinh nữ. Cách 2: Có 3
C cách chọn ra 3 học sinh từ 30 học sinh, trong đó có 3
C cách chọn ra 3 học sinh, không có học 20 30 sinh nữ. Suy ra có 3 3
C C 2920 cách chọn ra một nhóm 3 học sinh sao cho nhóm đó có ít nhất một học sinh 30 20 nữ.
Câu 2. [ĐỀ THI THAM KHẢO] Cho cấp số nhân u với u 3 và u 15 . Công bội của cấp số n 1 2 nhân đã cho bằng 1 A. 5 B. 12 C. 12 D. 5 Lời giải Chọn A u
Công bội của cấp số nhân đã cho là 2 q 5 . u1
Câu hỏi phát triển tương tự câu 2:
Câu 2.1 (Câu phát triển câu2 ) Cho cấp số nhân u với u 2 và công bội q 3. Tìm số hạng thứ 4 n 1 của cấp số nhân. A. 24. B. 54. C. 162. D. 48. Lời giải Chọn B
Số hạng thứ 4 của cấp số nhân là 3 3
u u .q 2.3 54 . 4 1
Câu 2.2 (Câu phát triển câu2 ) Cho cấp số nhân u với u 9 và u 243 . Công bội của cấp số nhân n 3 6 đã cho bằng 1 A. 3 B. 27 C. D. 126. 27 Lời giải Chọn A 2 u u .q u
Gọi q là công bội của cấp số nhân đã cho, ta có: 3 1 3 6 q 27 q 3 5 u u .q u 3 6 1
Câu 2.3 (Câu phát triển câu2 ) Dãy số u với u 2n là một cấp số nhân với n n
A. Công bội là 2 và số hạng đầu tiên là 1.
B. Công bội là 2 và số hạng đầu tiên là 2.
C. Công bội là 4 và số hạng đầu tiên là 2.
D. Công bội là 1 và số hạng đầu tiên là 2. Trang 2 Lời giải Chọn B u 2 1
Cấp số nhân đã cho là: 2; 4; 8; 16; .... u . 2 q 2 u 1
Câu 3. [ĐỀ THI THAM KHẢO] Diện tích xung quanh của hình nón có độ dài đường sinh 4a và bán kính đáy a bằng 4 A. 2 16 a B. 2 8 a C. 2 4 a D. 2 a 3 Lời giải Chọn C
Diện tích xung quanh của hình nón có độ dài đường sinh l 4a và bán kính đáy r a là 2 S rl . .
a 4a 4 a . xq
Câu hỏi phát triển tương tự câu 3:
Câu 3.1 (Câu phát triển câu3 ) Cho hình nón có diện tích xung quanh bằng 2
6 a và đường kính đáy
bằng 2a . Tính độ dài đường sinh hình nón đã cho. A. 3a B. 2a C. 6a D. 6a Lời giải Chọn C Bán kính đáy 2a r a 2
Diện tích xung quanh của hình nón 2 S rl . .
a l 6 a l 6a xq
Câu 3.2 (Câu phát triển câu3 ) Cho hình nón có thiết diện qua trục là tam giác đều cạnh bằng 2a . Diện
tích xung quanh của hình nón bằng 2 A. 2 2 a B. 2 8 a C. 2 4 a D. 2 a 3 Lời giải Chọn A Trang 3 l 2a l 2a
Vì thiết diện qua trục của hình nón là tam giác đều cạnh bằng 2a nên 2r 2a r a
Diện tích xung quanh của hình nón đã cho là 2 S rl . .
a 2a 2 a xq
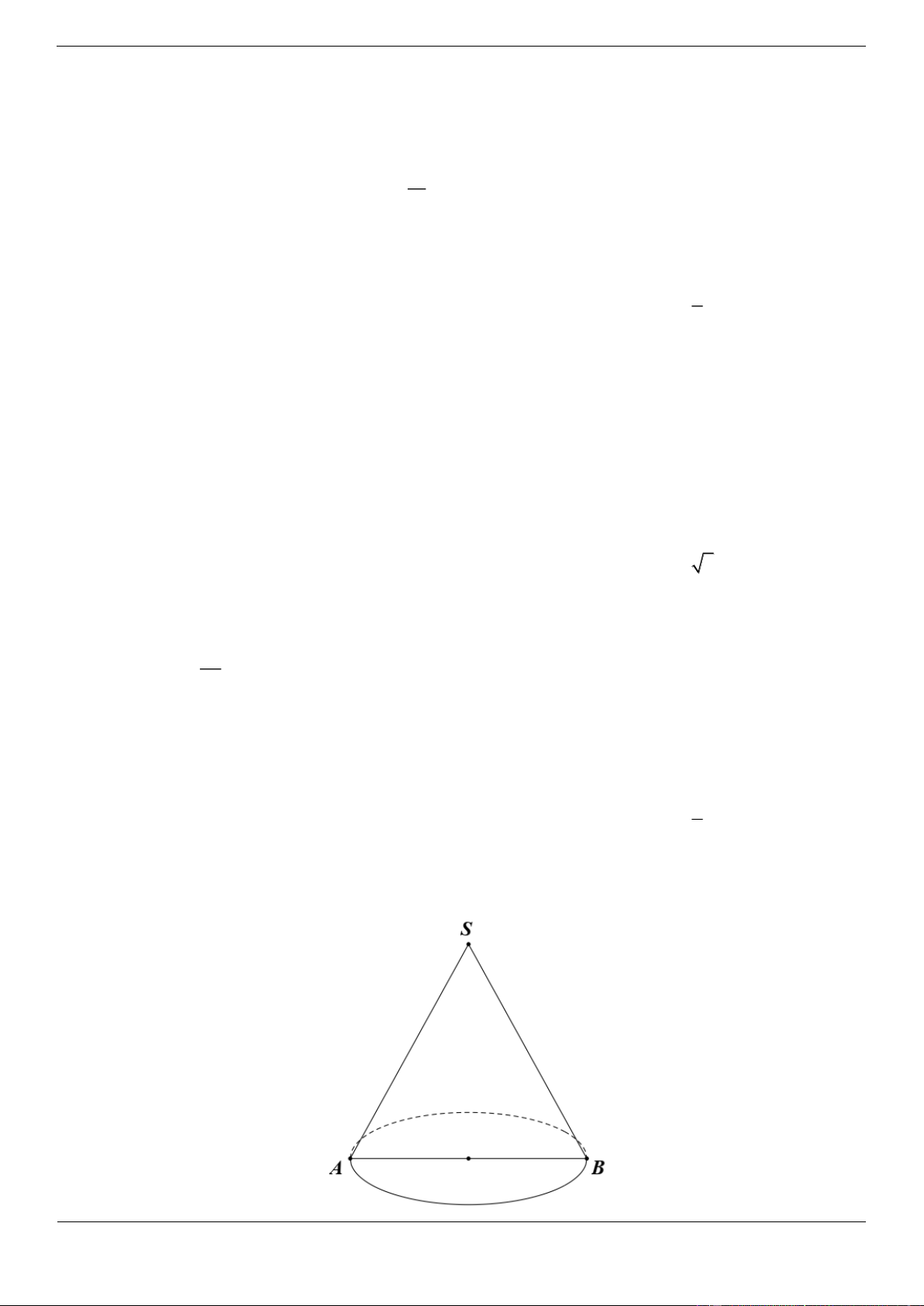
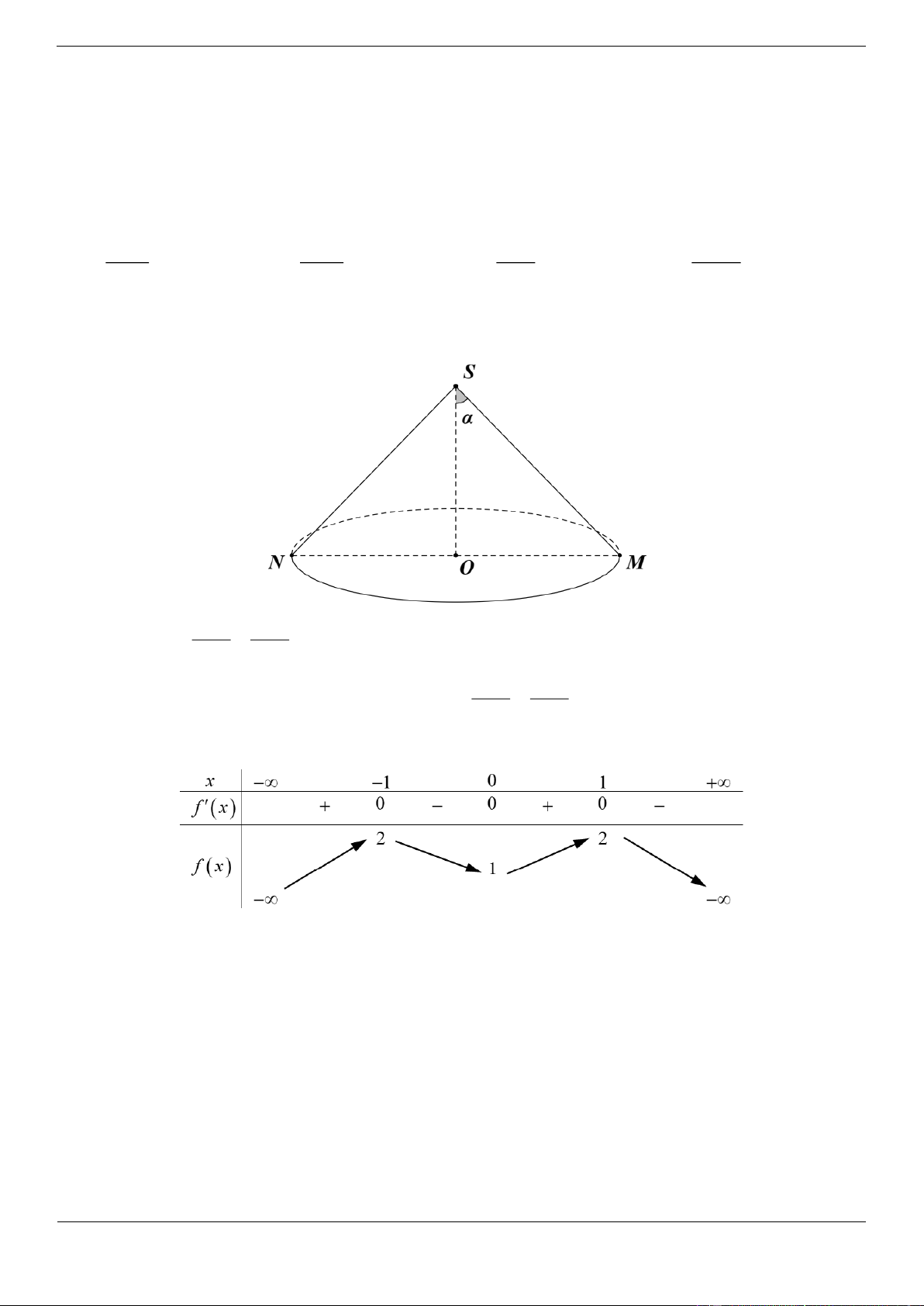
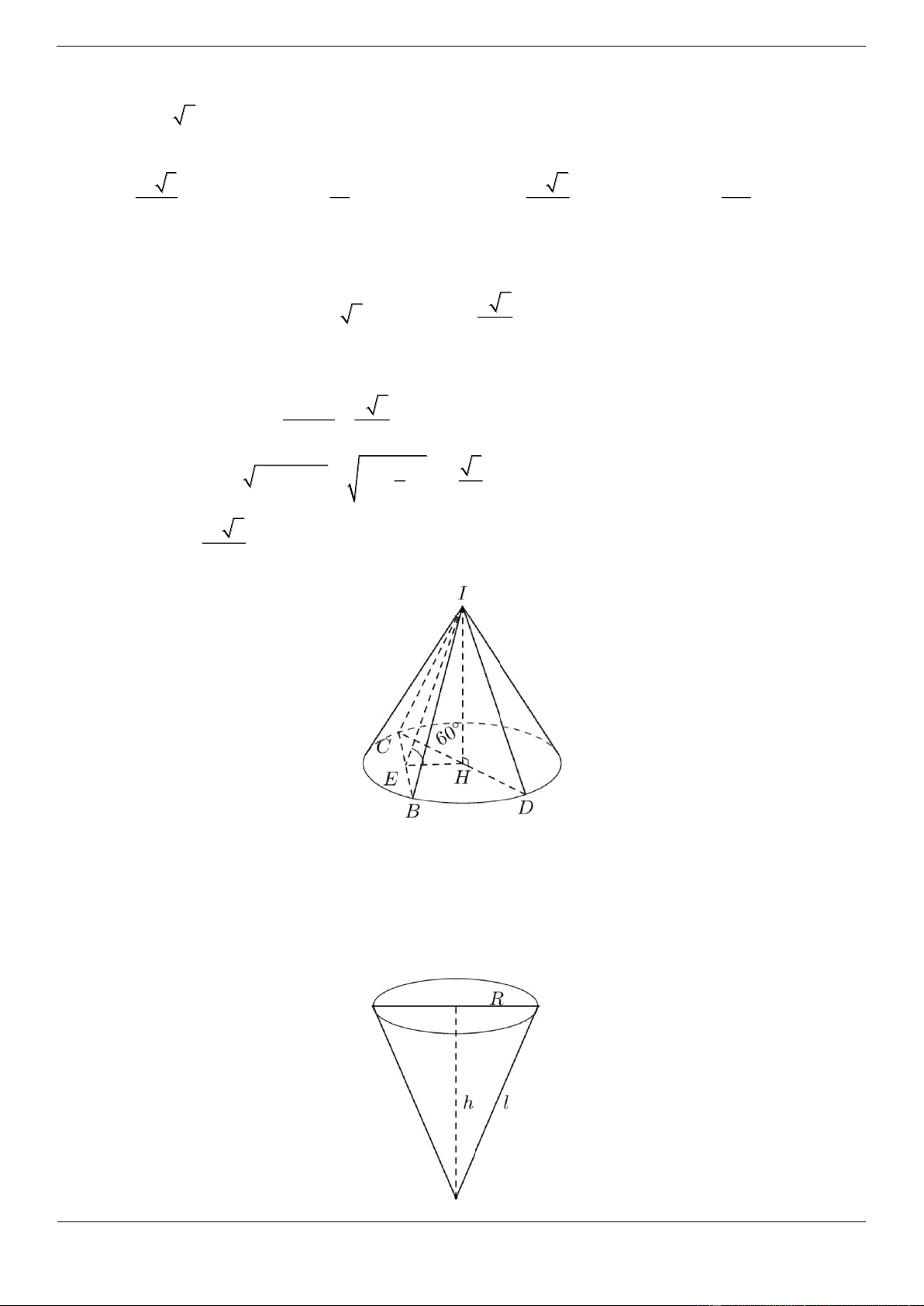
Câu 3.3 (Câu phát triển câu3 ) Cho hình nón có bán kính đáy R , góc ở đỉnh là 2 với 45 90.
Tính diện tích xung quanh của hình nón theo R và . 2 4 R 2 2 R 2 R 2 R A. sin B. sin C. sin D. 3sin Lời giải Chọn C OM R
Ta có: l SM sin sin 2 R R
Diện tích xung quanh của hình nón là S rl . . R xq sin sin
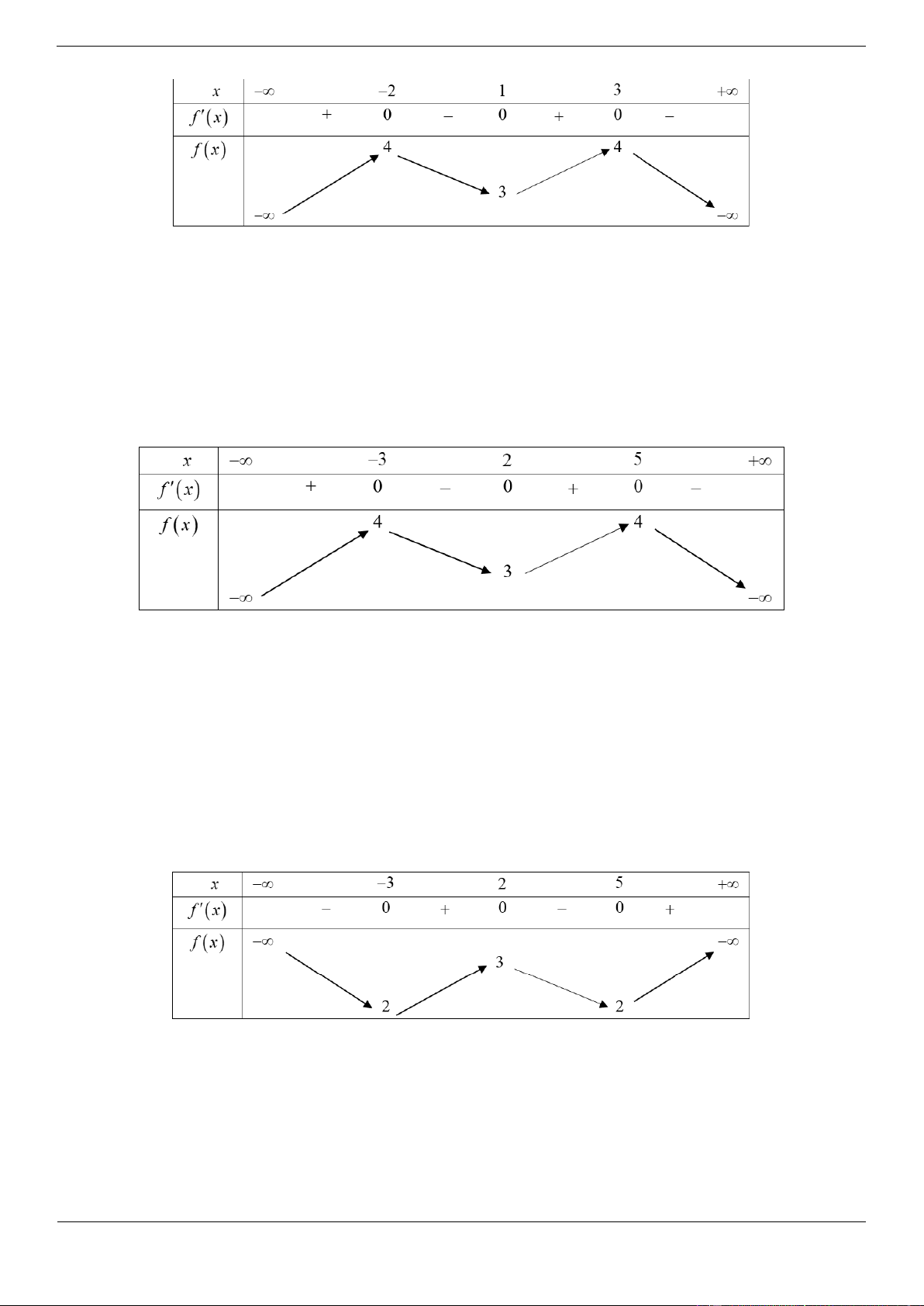
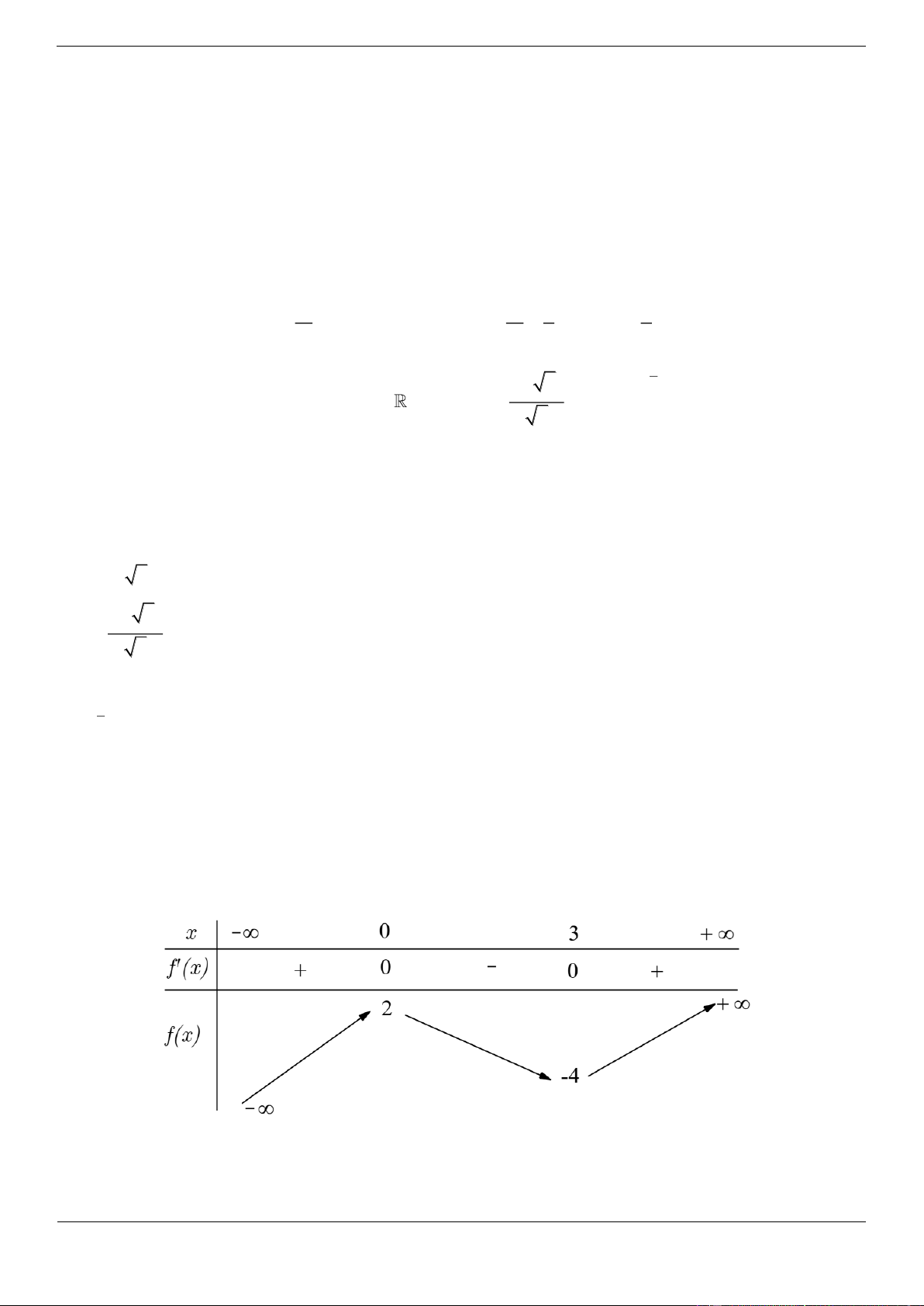
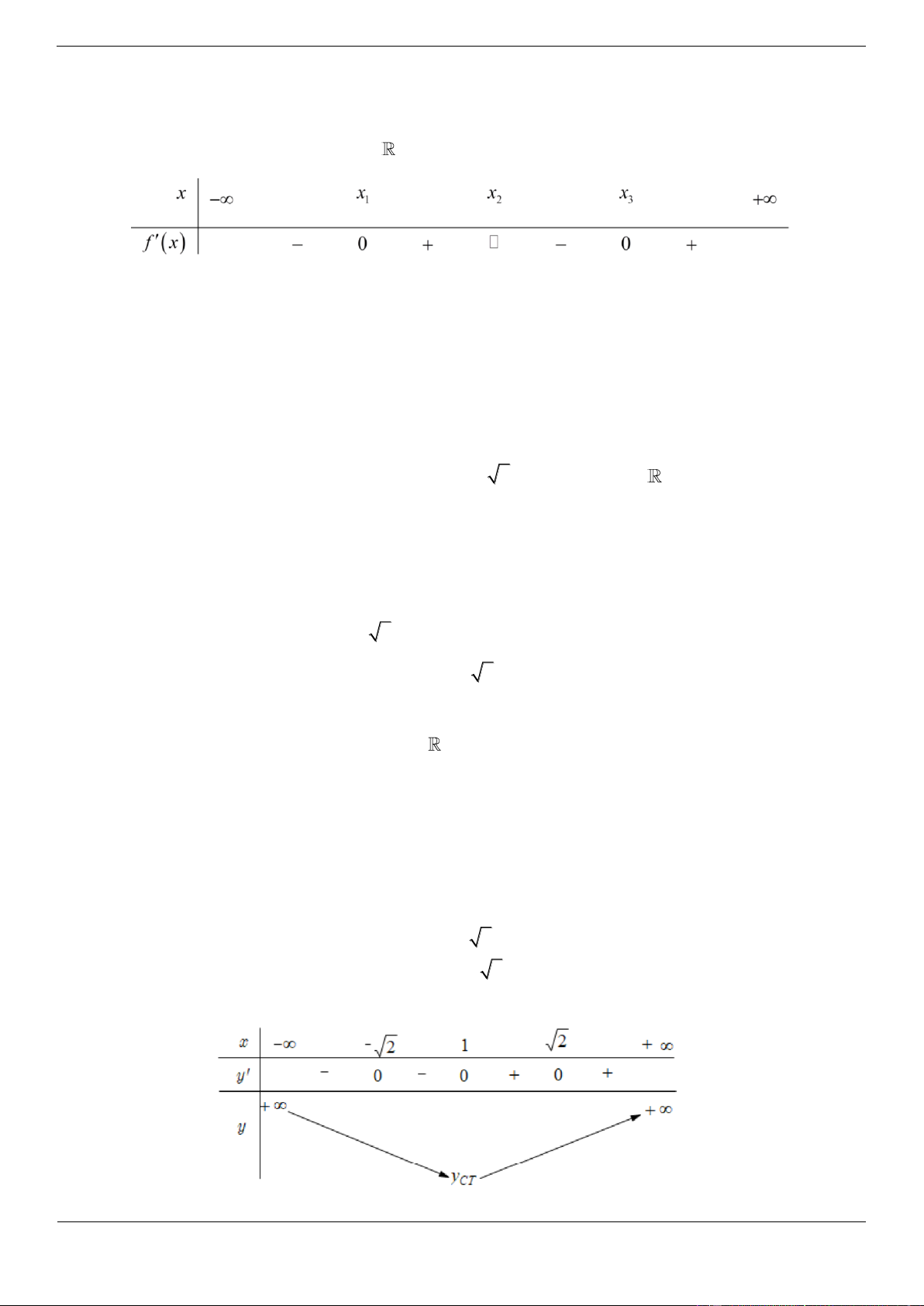
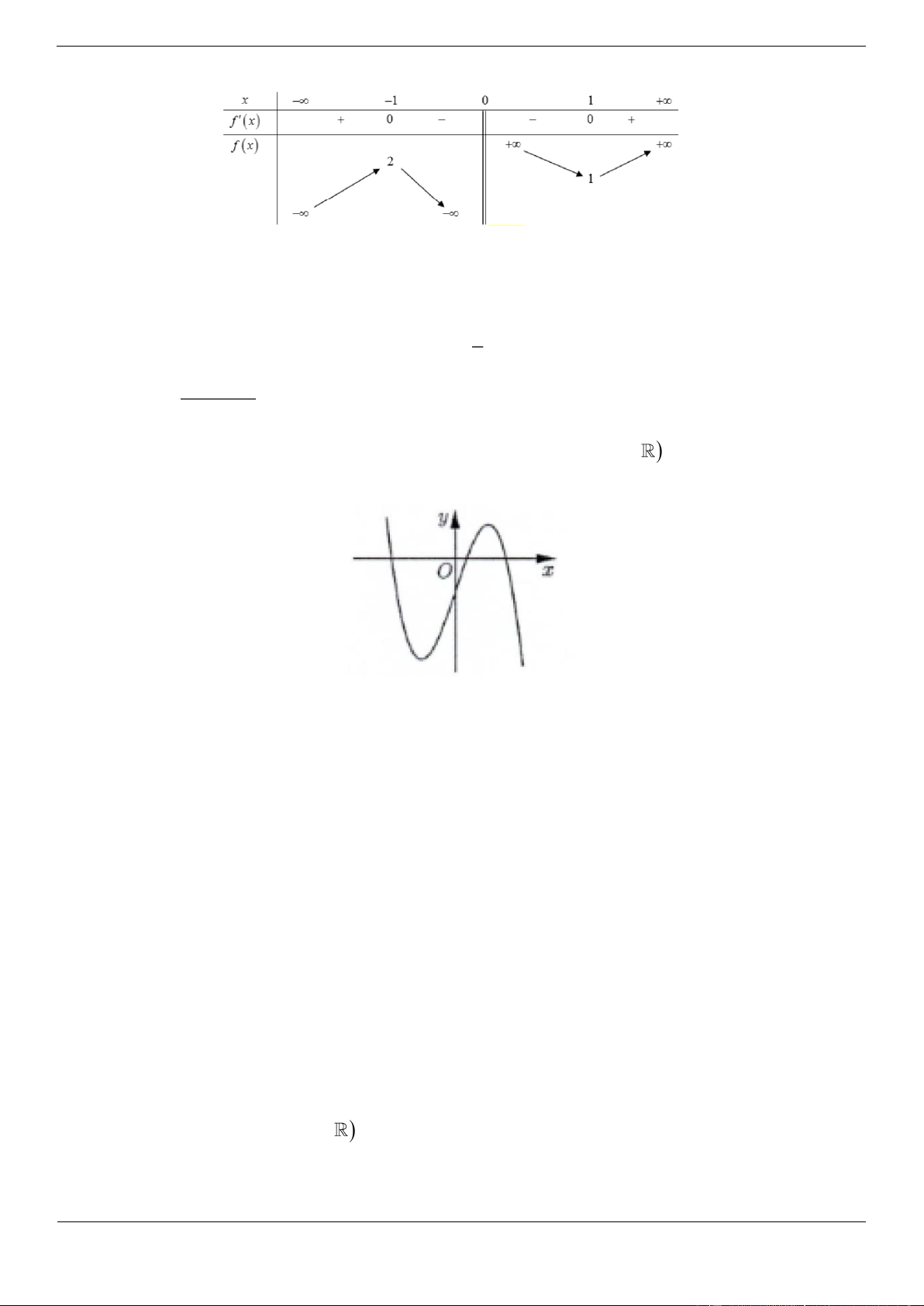
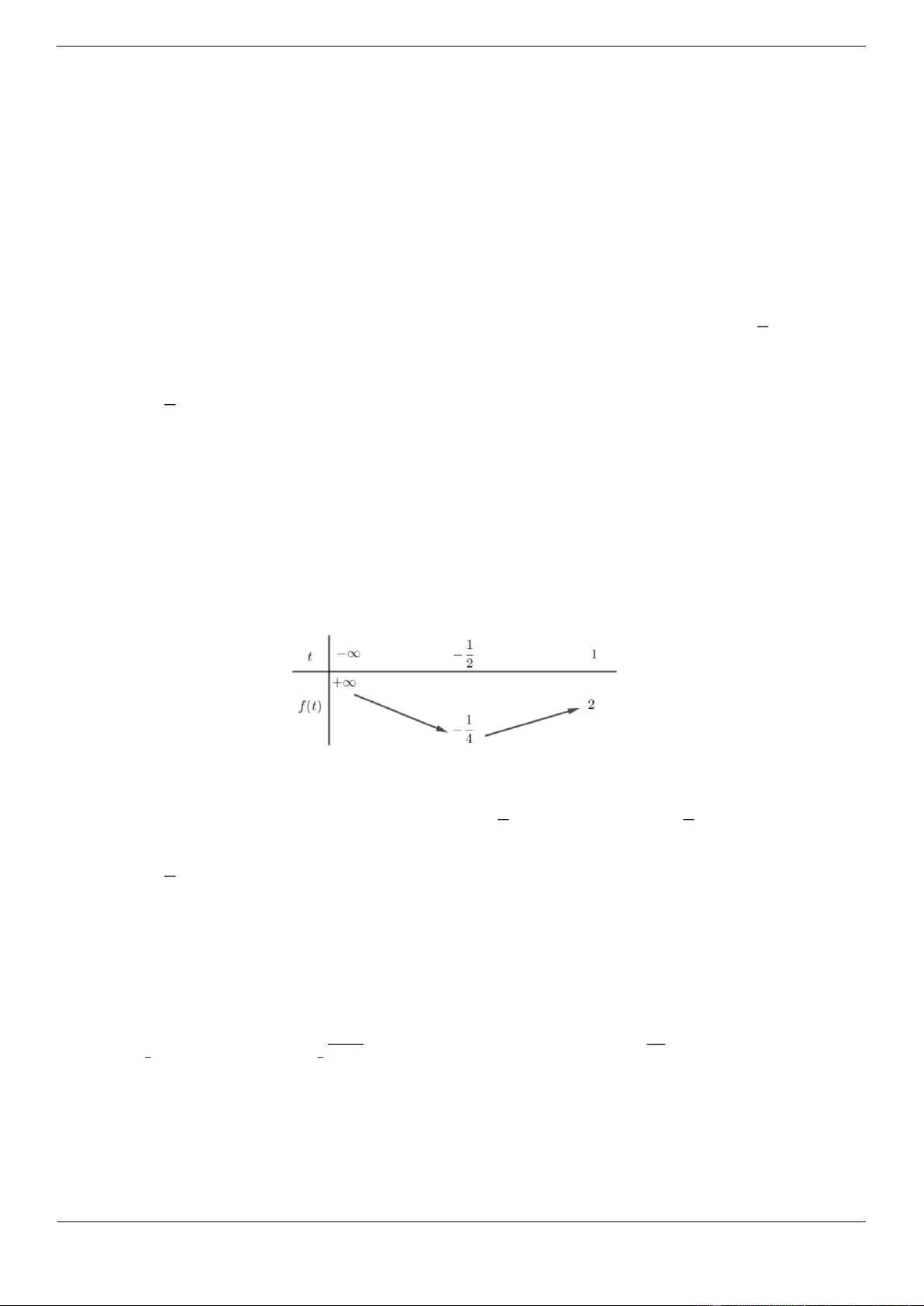
Câu 4. [ĐỀ THI THAM KHẢO] Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 1; B. 1 ;0 C. 1 ;1 D. 0 ;1 Lời giải Chọn D
Hàm số đã cho đồng biến trên mỗi khoảng ; 1 và 0 ;1 .
Câu hỏi phát triển tương tự :
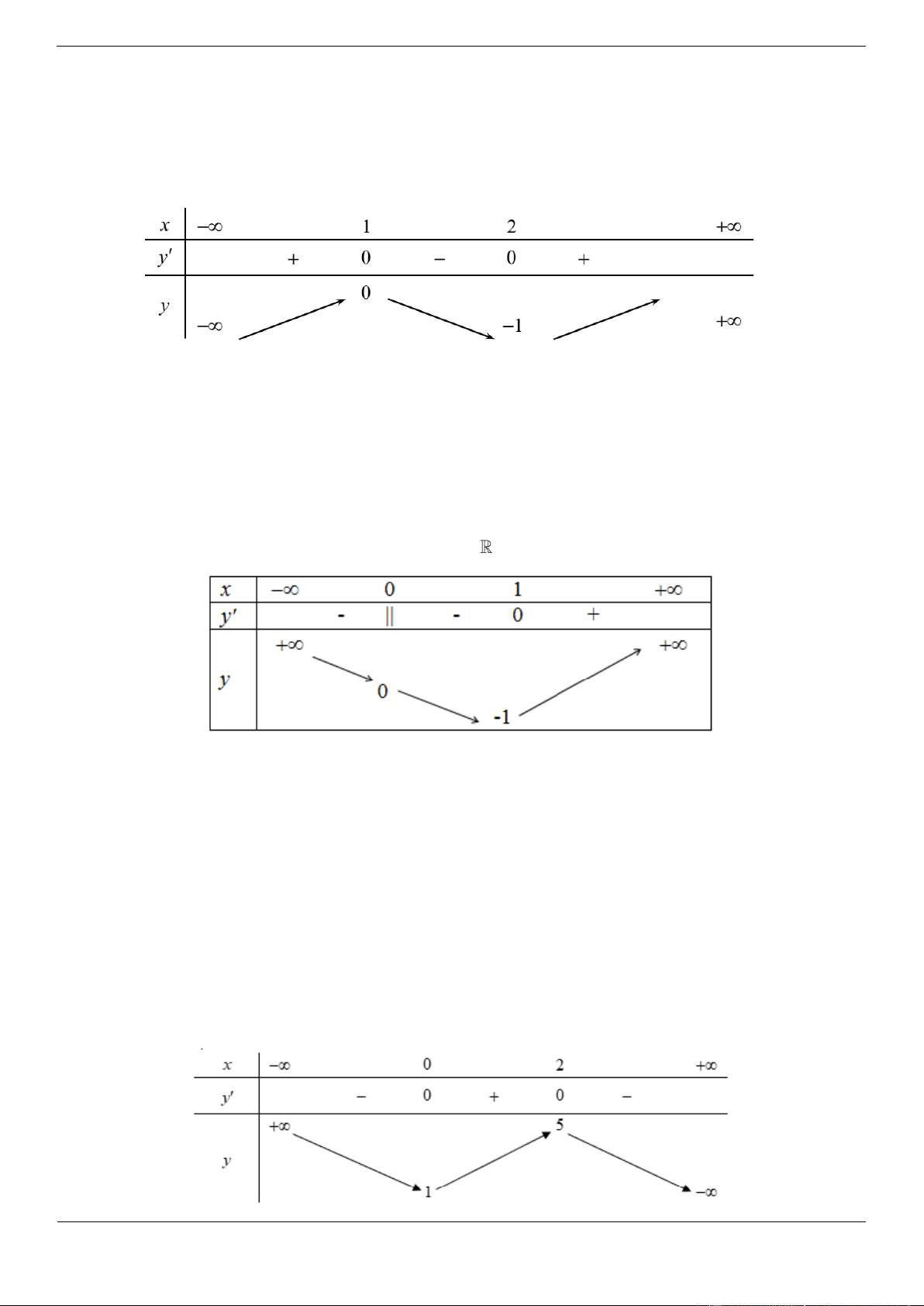
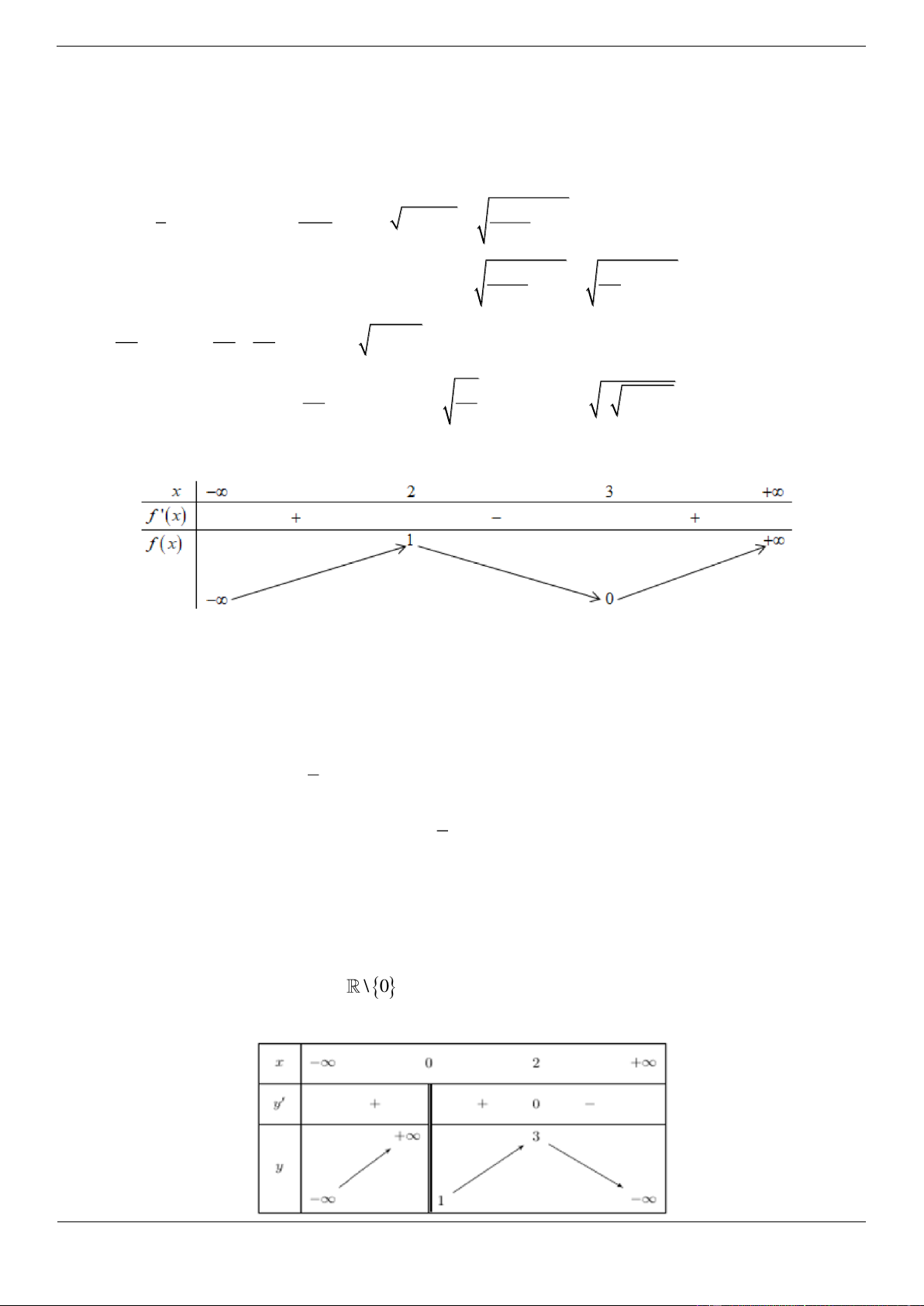
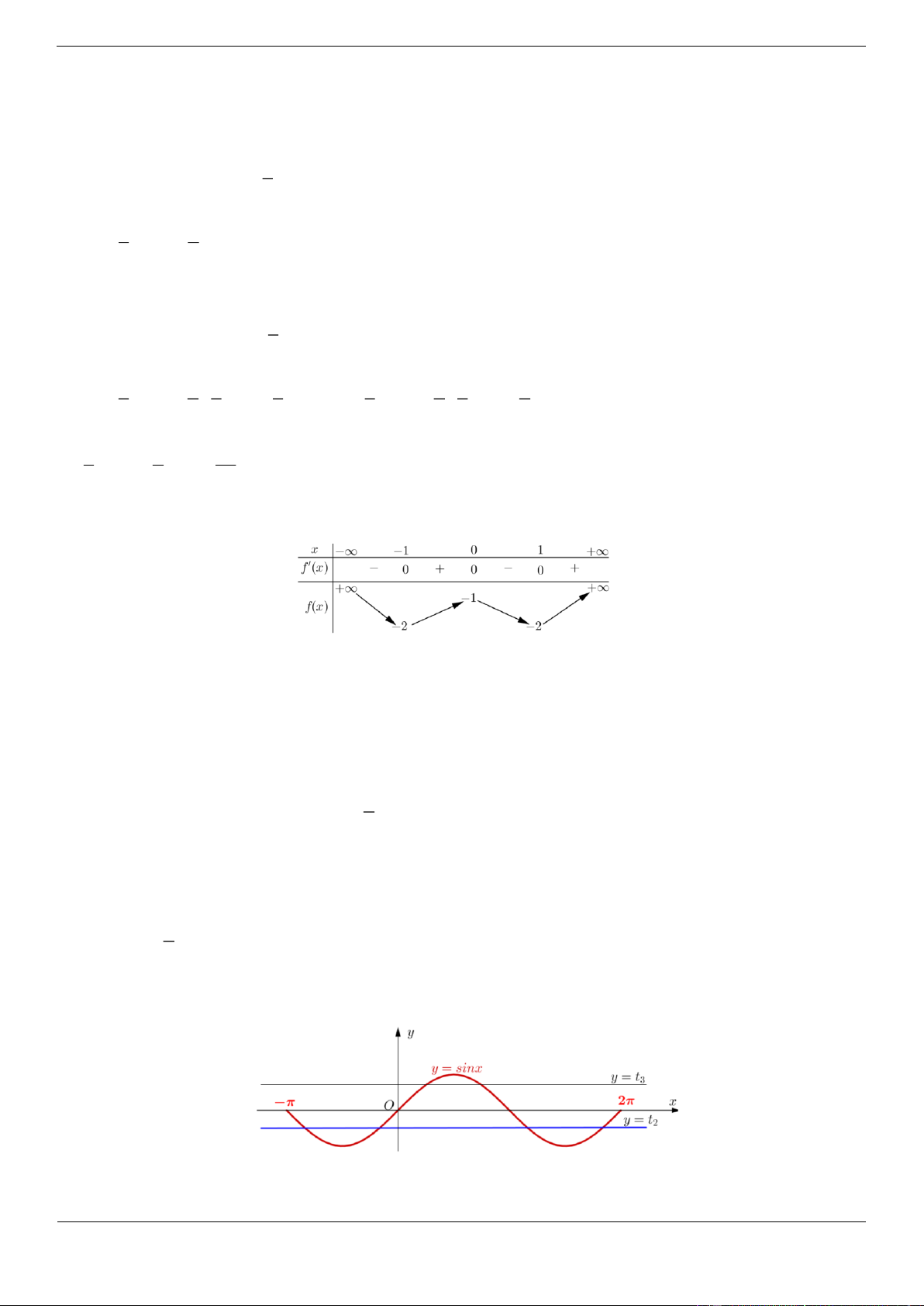
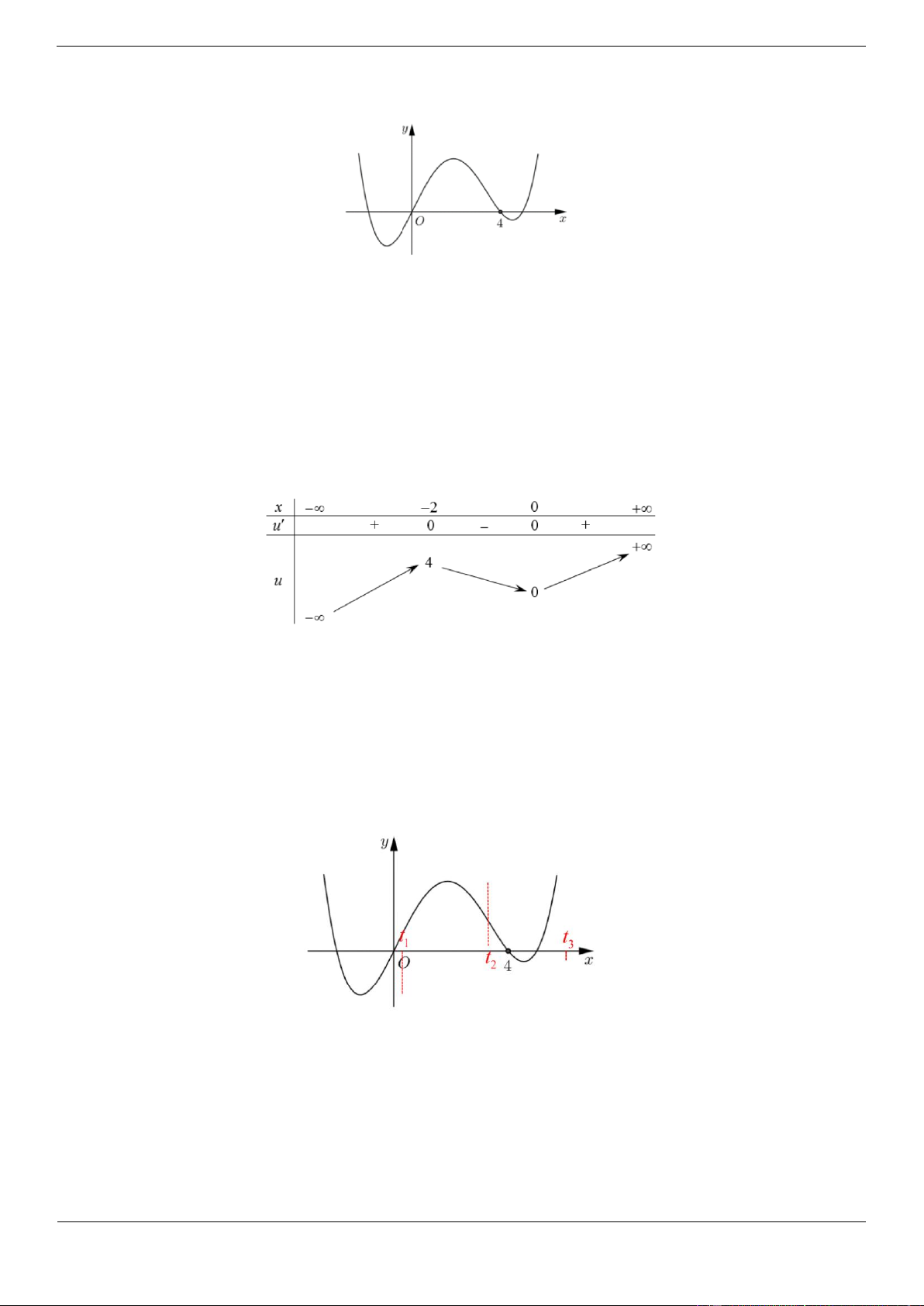
Câu 4a: Cho hàm số f x có bảng biến thiên như sau: Trang 4
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 1; B. 1;3
C. 3; D. ; 0 Lời giải Chọn B
Hàm số đã cho đồng biến trên mỗi khoảng ; 2 và 1;3 .
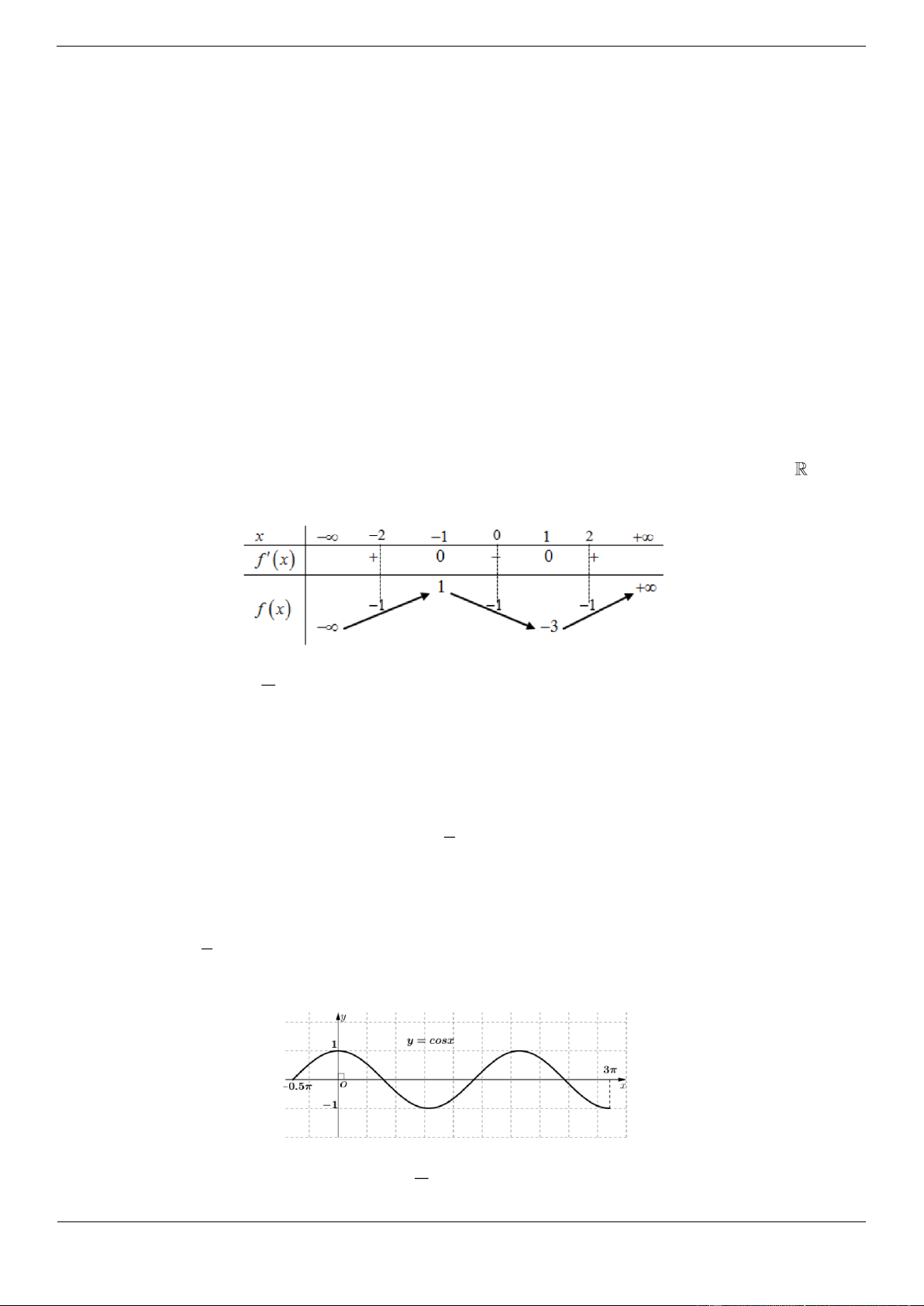
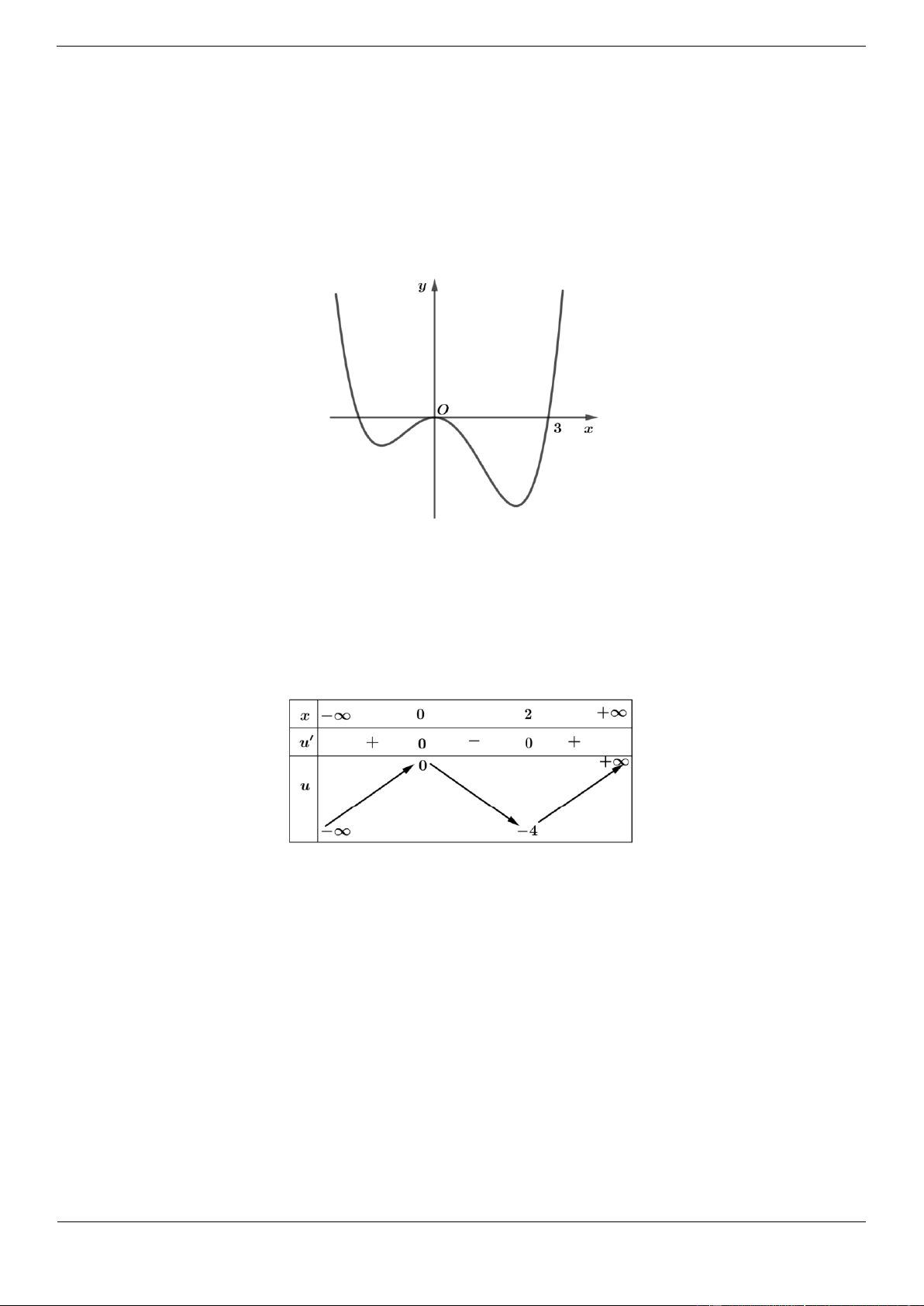
Câu 4b: Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ; 4 B. 3 ;5
C. 2; D. ; 4 Lời giải Chọn A
Hàm số đã cho đồng biến trên mỗi khoảng ; 3 và 2;5 .
Do đó hàm số cũng đồng biến trên khoảng ; 4.
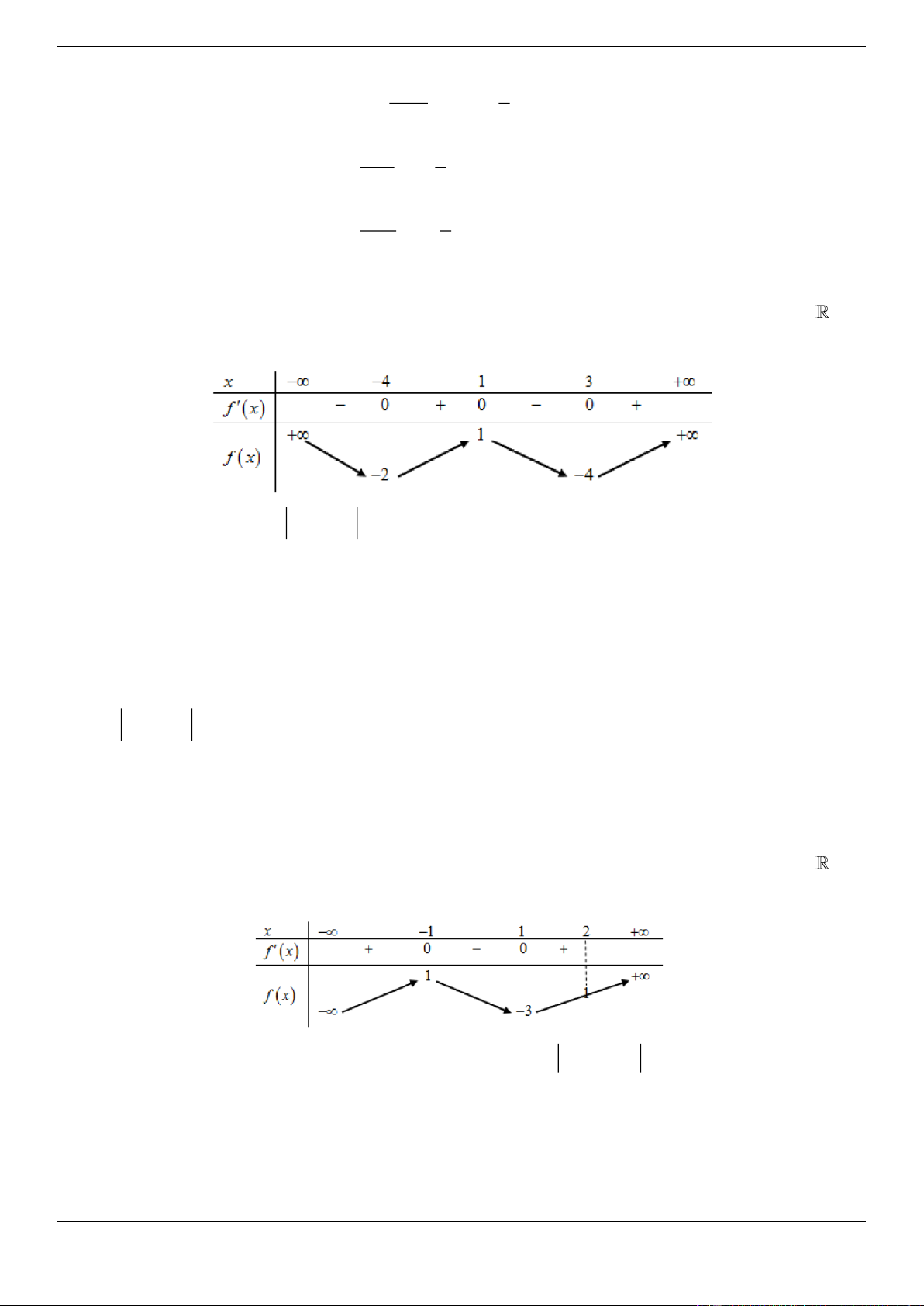
Câu 4c: Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ; 2 B. 3 ;2 C. 2;3 D. 2;6 Lời giải Chọn C
Hàm số đã cho nghịch biến trên mỗi khoảng ; 3 và 2;5 Trang 5
Do đó hàm số cũng nghịch biến trên khoảng 2;3.
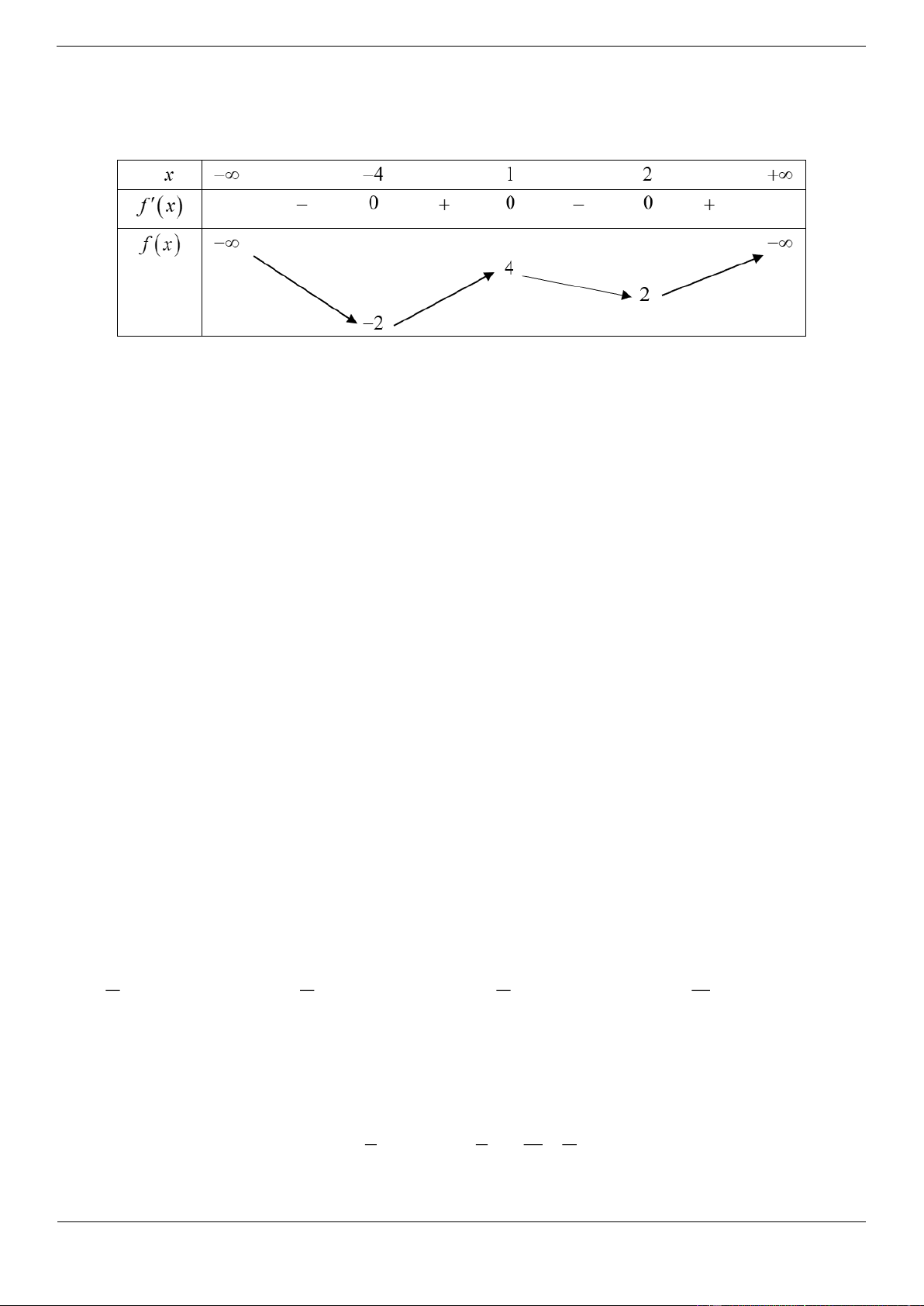
Câu 4d: Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ; 2
B. 1; C. 4 ; 2 D. 2 ;4 Lời giải Chọn C
Hàm số đã cho đồng biến trên mỗi khoảng 4 ;1 và 2; .
Do đó hàm số cũng đồng biến trên khoảng 4 ; 2.
Câu 5. [ĐỀ THI THAM KHẢO] Cho khối lập phương có cạnh bằng 6. Thể tích của khối lập phương đã cho bằng A. 216 B. 18 C. 36 D. 72 Lời giải Chọn A
Thể tích khối lập phương đã cho là 3 V 6 216 .
Câu hỏi phát triển tương tự :
Câu 5a: Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng A. 12 B. 32 C. 16 D. 64 Lời giải Chọn D
Thể tích khối lập phương đã cho là 3 V 4 64 .
Câu 5b: Cho khối lập phương có thể tích bằng V . Thể tích của khối lập phương có cạnh bằng một nửa
cạnh của khối lập phương đã cho bằng V V V V A. B. C. D. 2 4 8 16 Lời giải Chọn C
Gọi cạnh của khối lập phương ban đầu là 3
a a V 3 a 3 a a V
Thể tích khối lập phương có cạnh bằng sẽ là: V 2 2 8 8 Trang 6
Câu 5c: Cho khối lập phương có cạnh bằng a. Chia khối lập phương thành 64 khối lập phương nhỏ có thể
tích bằng nhau. Độ dài cạnh của mỗi khối lập phương nhỏ bằng a a a a A. B. C. D. 4 8 16 64 Lời giải Chọn A
Thể tích khối lập phương lớn là: 3 V a
Gọi chiều dài cạnh hình lập phương nhỏ là x => thể tích khối lập phương nhỏ là: 3 V x a Từ giả thiết 3 3
V 64V a 64x x 4
Câu 5d: Biết diện tích toàn phần của một khối lập phương bằng 96. Tính thể tích khối lập phương A. 32 B. 64 C. 16 D. 128 Lời giải Chọn B
Gọi độ dài cạnh hình lập phương bằng 2
a 6a 96 a 4
Thể tích khối lập phương: 3 V 4 64 .
Câu 6. [ĐỀ THI THAM KHẢO] Nghiệm của phương trình log 2x 1 2 là 3 9 7 A. x 3 B. x 5 C. x D. x 2 2 Lời giải Chọn B
Ta có: log 2x 2
1 2 2x 1 3 2x 1 9 x 5. 3
Câu hỏi phát triển tương tự:
Câu 6a: Nghiệm của phương trình log 3x 2 2 là 4 10 7 A. x 6 B. x 3 C. x D. x 3 2 Lời giải Chọn A
Ta có: log 3x 2 2
2 3x 2 4 3x 2 16 x 6 . 4 x 1
Câu 6b: Nghiệm của phương trình log 2 là 2 x 2 10 7 A. x 2 B. x 6 C. x D. x 3 3 Lời giải Chọn D x 1 x 1 7 Ta có: log 2
4 x 1 4x 8 x 2 x 2 x 2 3 Trang 7
Câu 6c: Nghiệm của phương trình log x
1 log x 2 1 6 là 2 2 10 A. x 6 B. x 3 C. x
D. x 5 3 Lời giải Chọn D
Ta có: log x
1 log x 2 1 6 (đk: x 1) 2 2
log x 1 2log x 1 6 2 2
log x 1 2 x 5 2
Câu 6d: Nghiệm của phương trình log 2 x 9 2 là 4 A. x 5 B. x 3 C. x 5 D. x 3 Lời giải Chọn C Ta có: log 2 x 9 2 2 2
2 x 9 4 x 25 x 5 4 2 3 3
Câu 7. [ĐỀ THI THAM KHẢO]
f x dx 2 và f
xdx 1 thì f xdx bằng: 1 2 1 A. 3 B. 1 C. 1 D. 3 Lời giải Chọn B 3 2 3 Ta có
f x dx f x dx f x dx 1 . 1 1 2 Câu tƣơng tự: 10 7 10
Cho hàm số f x liên tục trên . Biết f
xdx 7 và f xdx 5 thì
f x dx bằng 0 0 7 A. 2 B. 12 C. 12 D. 2 Lời giải b c c
Áp dụng công thức f
xdx f
xdx f
xdx ta có: a b a 10 0 10 7 10 f
xdx f
xdx f
xdx f
xdx f
xdx 5 7 12 7 7 0 0 0 Chọn C Câu phát triển 2 5 10 10 Câu 7.1: Cho f
xdx 2; 2 f
xdx 6; f
xdx 5. Tính I f xdx? 0 2 5 0 A. I 13 B. I 10 C. I 16
D. I 4 Lời giải Trang 8 10 2 5 10 I f
xdx f
xdx f
xdx f
xdx 235 10. 0 0 2 5 Chọn B. 4 2 Câu 7.2: Cho f
xdx 16. Tính I f 2x x d . 0 0 A. I 32 B. I 8 C. I 16
D. I 4 Lời giải 4 4 Đặ dt dt 1 1
t t 2x dt 2dx dx
. Khi đó ta có: I f
t f
tdt .16 8 2 2 2 2 0 0 9 f x 2
Câu 7.3: Cho hàm số f x liên tục trên thỏa mãn dx 4 và f
sin xcosxdx 2. Tính x 1 0 3 tích phân I f xdx ? 0 A. I 2 B. I 6 C. I 4
D. I 10 Lời giải Đặt 2 t
x t x 2tdt dx . Khi đó 9 f x 3 3 3 3 4 dx f
t2dt 2 f
tdt 2 f
xdx f
xdx 2 x 1 1 1 1 1
Đặt t sin x dt cos xdx . Khi đó 2 1 1 1 2 f
sin xcosxdx f
tdt f
xdx f
xdx 2 0 0 0 0 3 1 3
Từ đây ta suy ra I f
xdx f
xdx f
xdx 4. 0 0 1 Chọn C
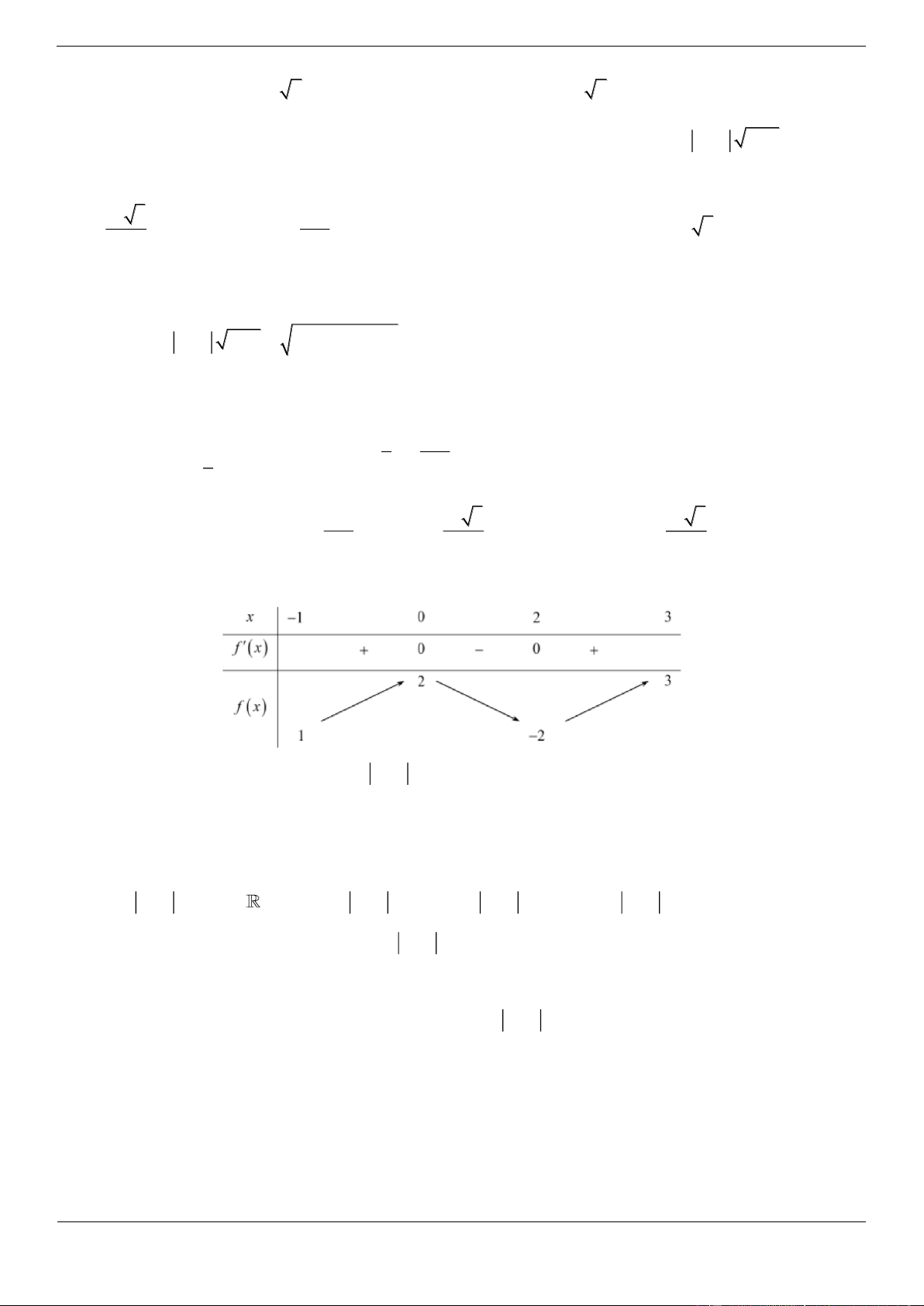
Câu 8. [ĐỀ THI THAM KHẢO] Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 B. 3 C. 0 D. 4 Lời giải Trang 9 Chọn D
Từ bảng biến thiên ta có giá trị cực tiểu của hàm số bằng 4 Câu tƣơng tự:
Cho hàm số y f x có bảng biến thiên như hình vẽ
Hàm số có giá trị cực đại bằng A. 1 B. 0 C. 2 D. 1 Lời giải Chọn B
Hàm số có giá trị cực đại bằng 0 . Câu phát triển
Câu 8.1: Cho hàm số y f x xác định, liên tục trên
và có bảng biến thiên.
Khẳng định nào sau đây là khẳng định sai?
A. Hàm số có giá trị cực tiểu bằng 1 .
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại x 0 và đạt cực tiểu tại x 1 .
D. Hàm số có giá trị nhỏ nhất bằng 1 . Lời giải Chọn C
Khi qua x 0 đạo hàm không đổi dấu nên hàm số không thể đạt cực trị tại x 0 .
Vậy khẳng định câu C là sai.
Câu 8.2: Cho hàm số y f x có bảng biến thiên như hình vẽ Trang 10
Hàm số y 2 f x 1 đạt cực tiểu tại điểm A. x 5 B. x 2 C. x 0
D. x 1 Lời giải Chọn C
Ta có: y 2 f x 1 y 2 f x
Suy ra: Điểm cực tiểu của hàm số y f x cũng chính là điểm cực tiểu của hàm số y 2 f x 1
Vậy: Hàm số y 2 f x 1 đạt cực tiểu tại điểm x 0 .
Câu 8.3: Số điểm cực trị của hàm số y x x 2 1 2 là: A. 3 B. 1 C. 4 D. 2 Lời giải Chọn A
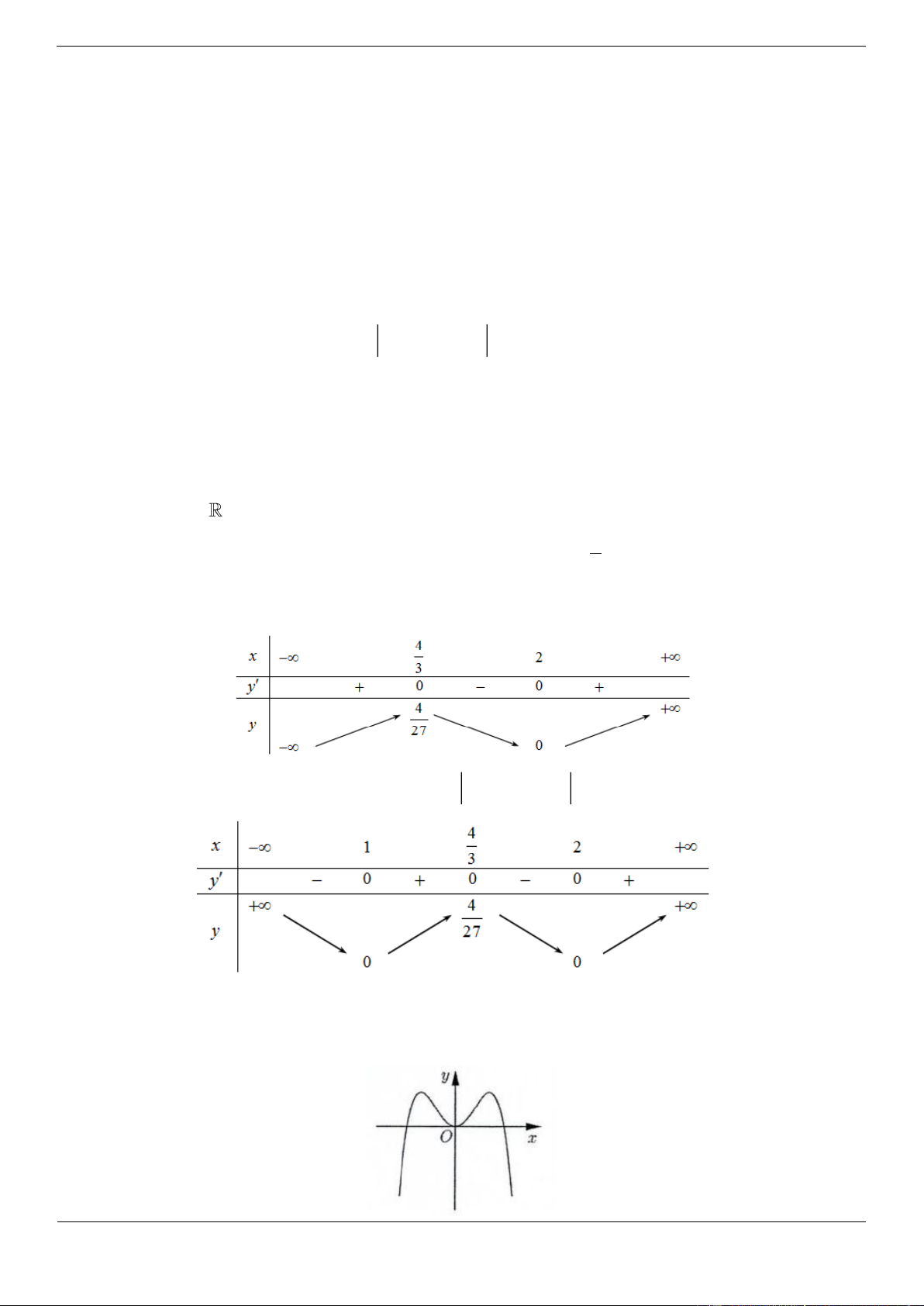
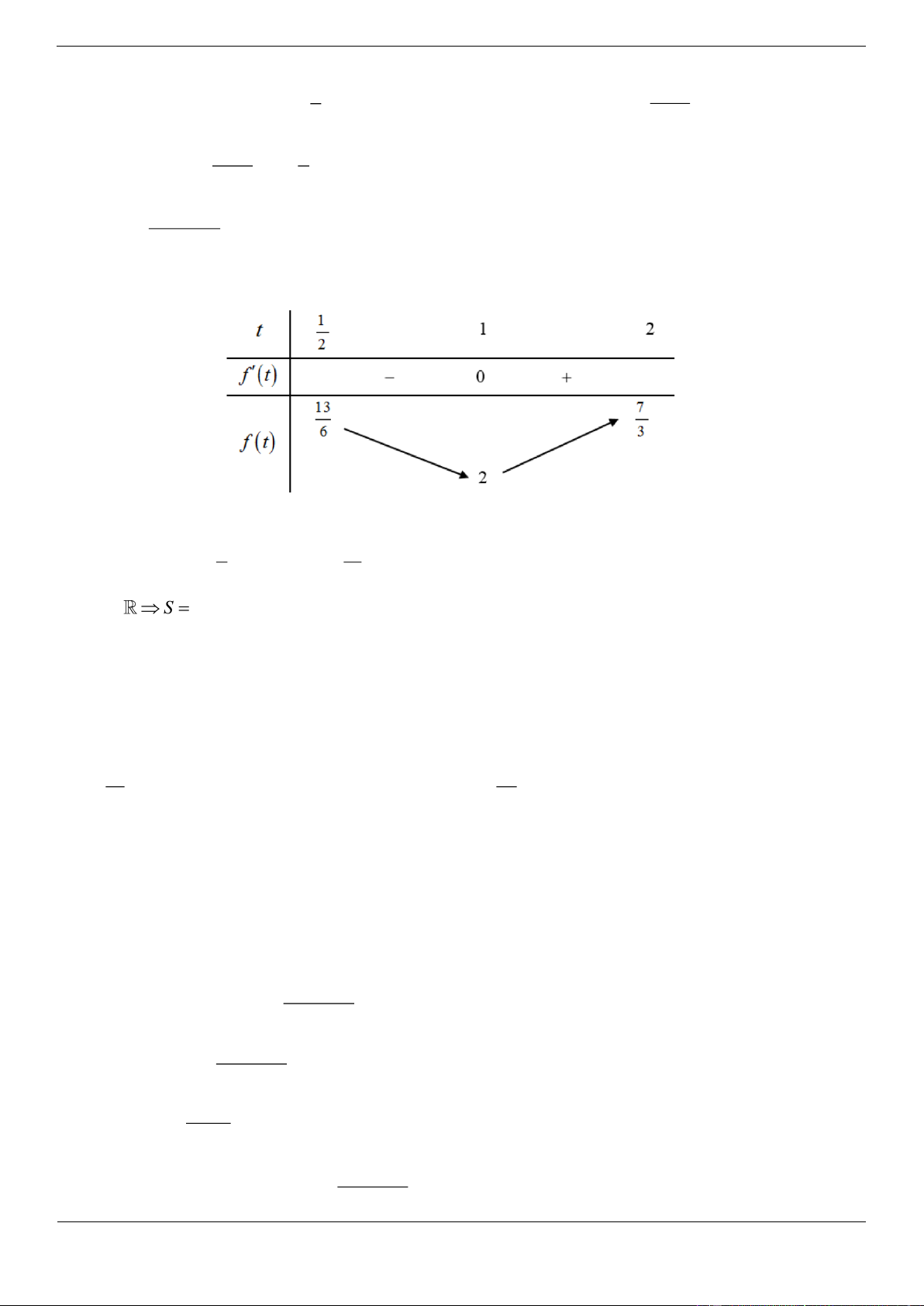
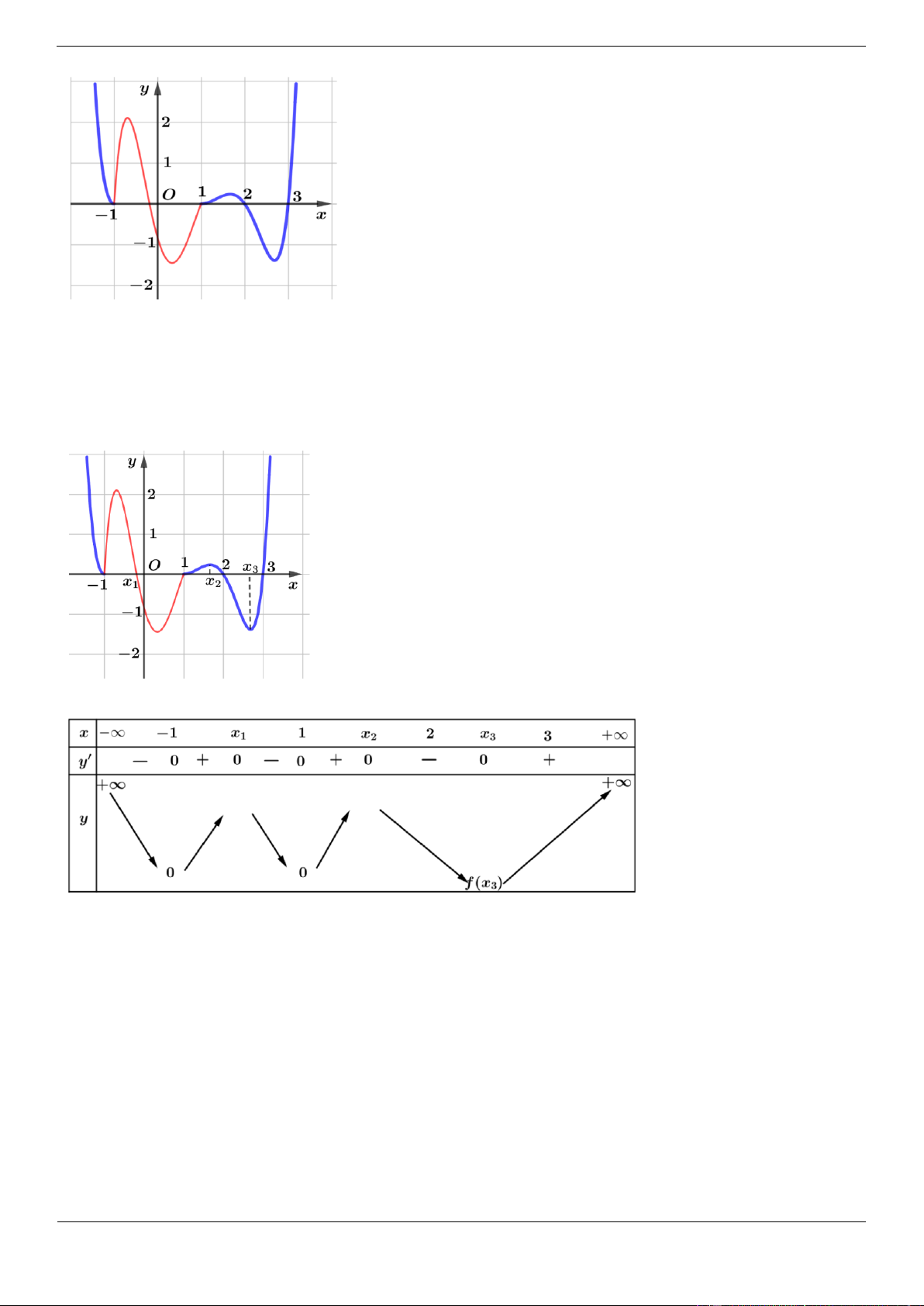
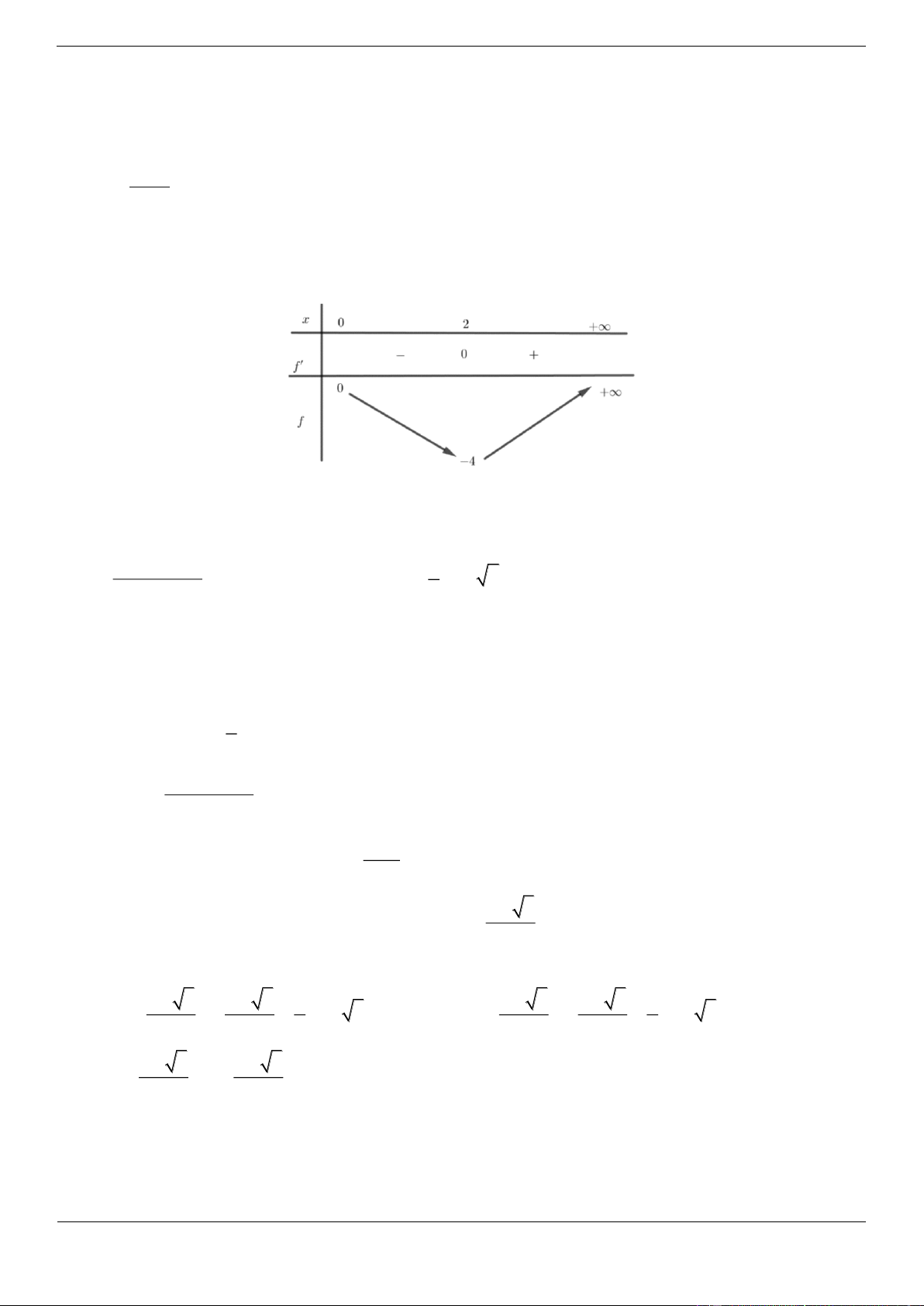
Xét hàm số y x x 2 3 2 1 2
x 5x 8x 4
Tập xác định: D 4 Ta có: 2 2
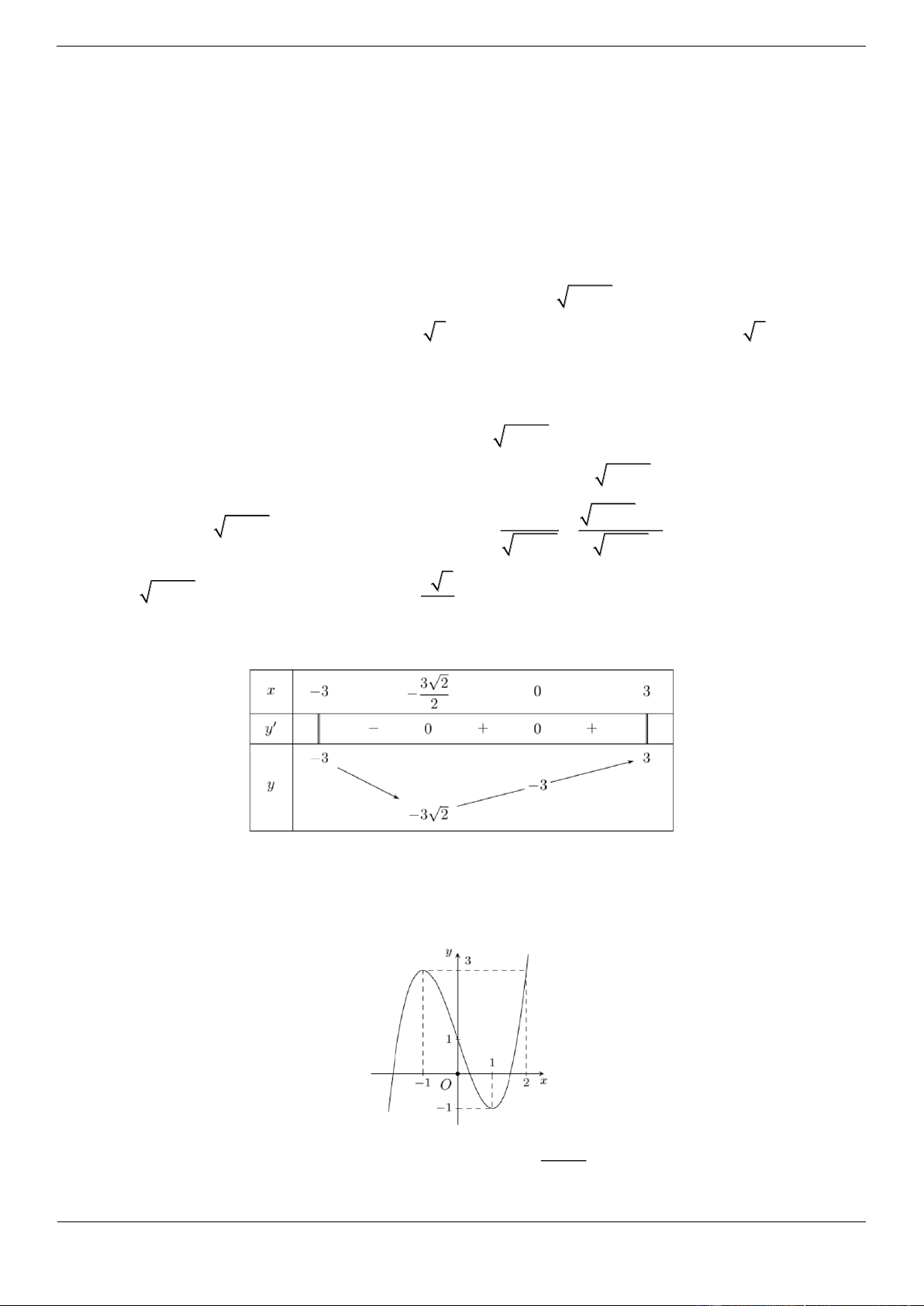
y 3x 10x 8; y 0 3x 10x 8 0 x 2 hoặc x 3 Bảng biến thiên.
Từ BBT của y x x 2 1
2 suy ra BBT của y x x 2 1 2 :
Vậy hàm số đã cho có 3 điểm cực trị.
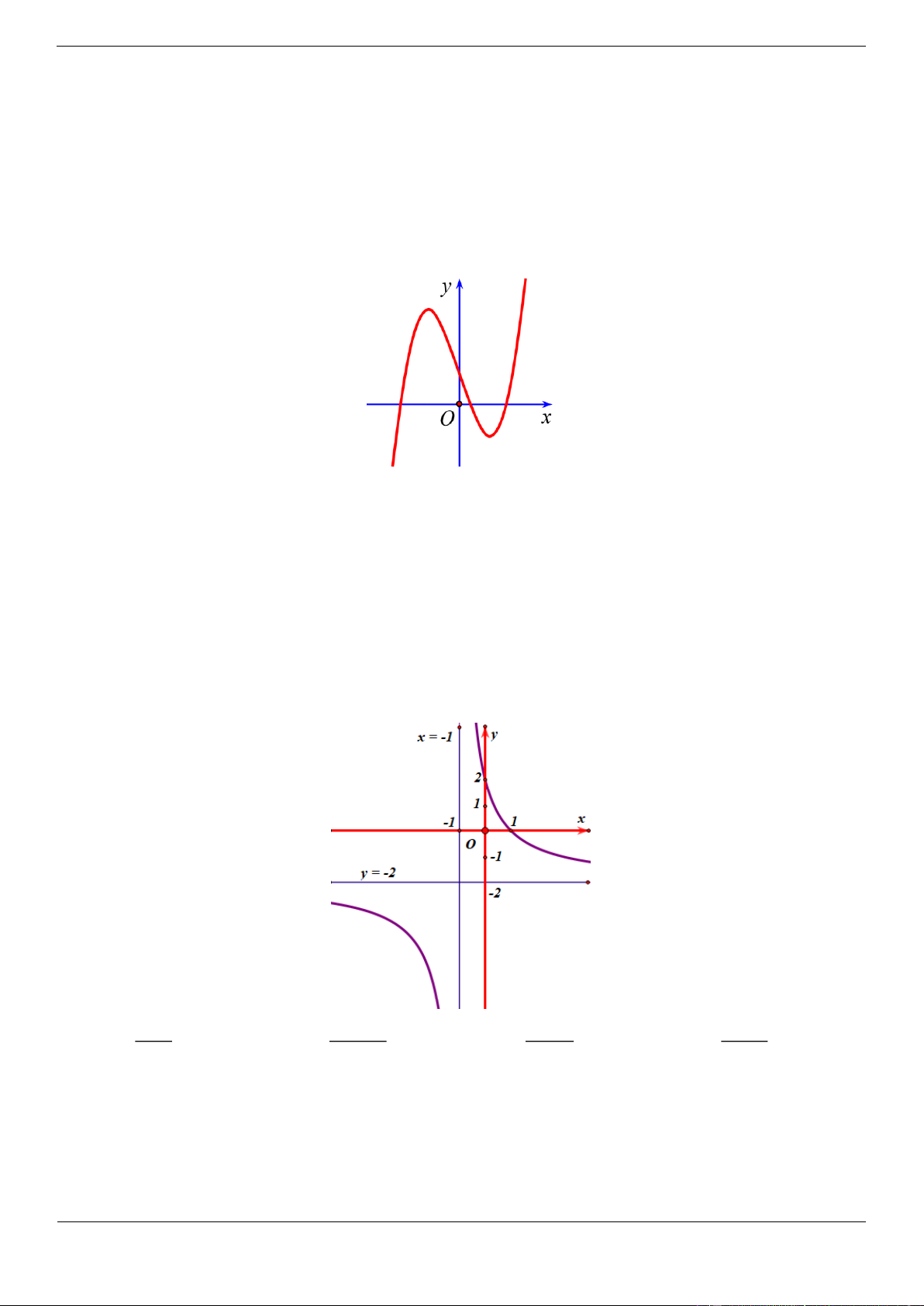
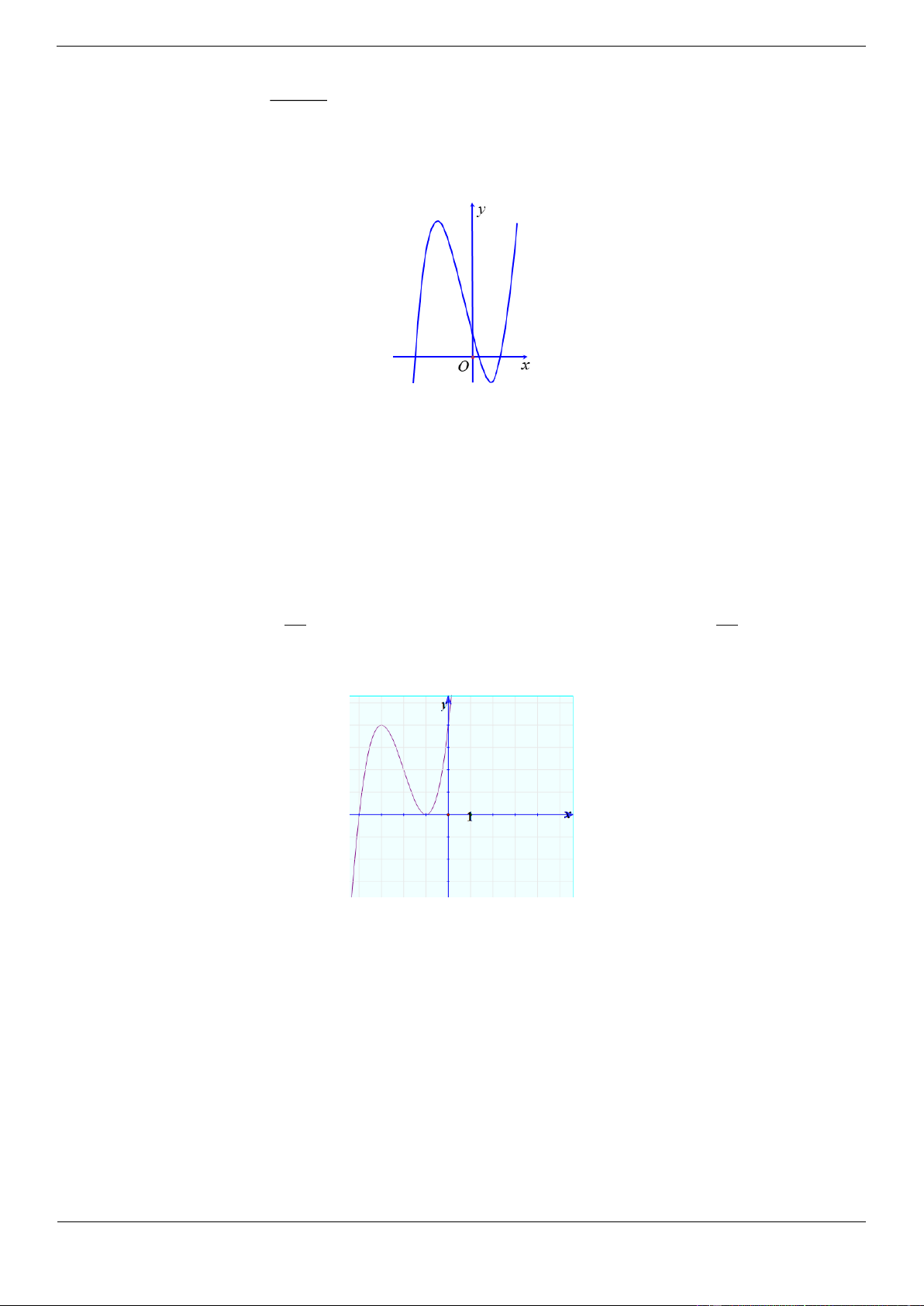
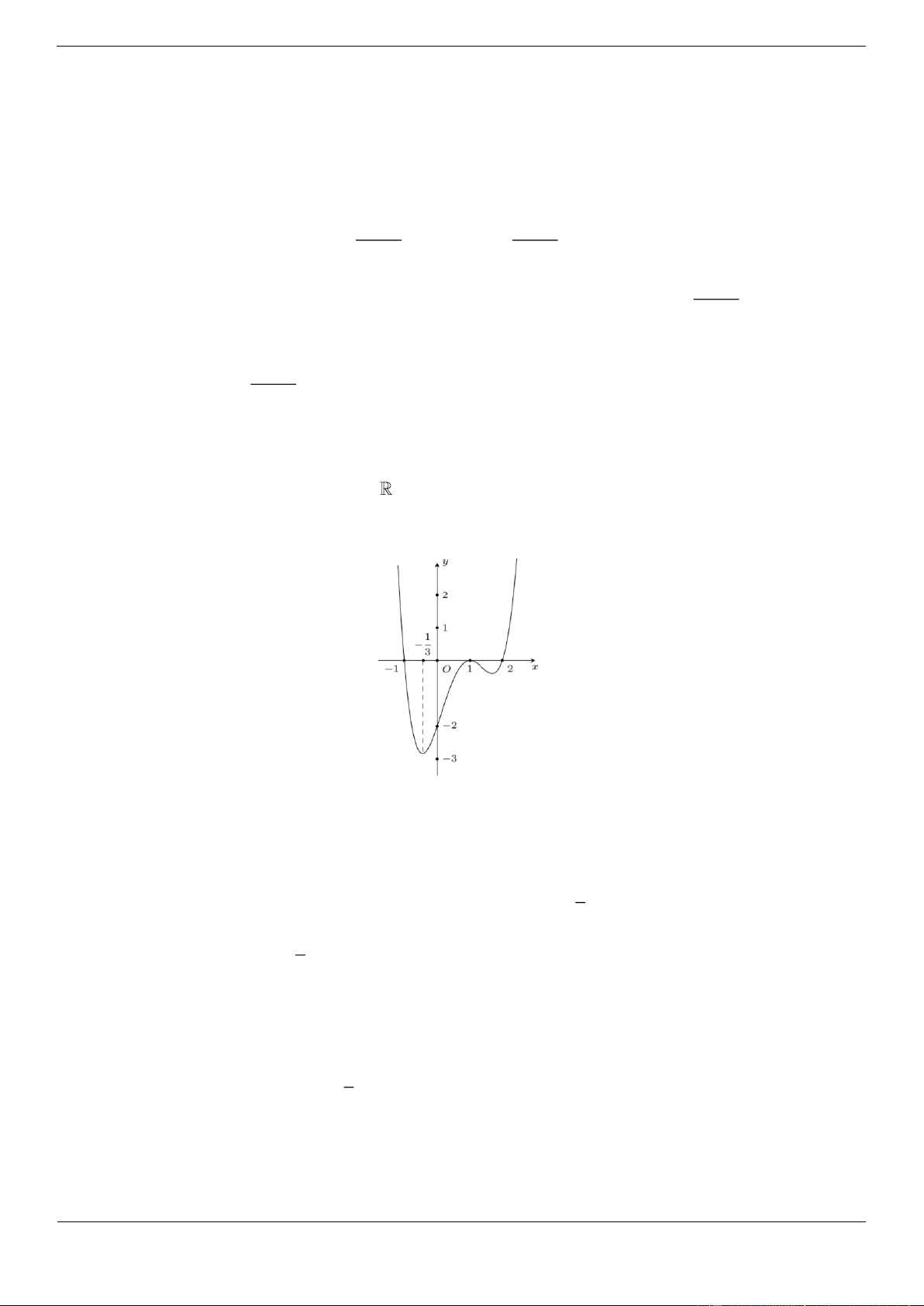
Câu 9. [ĐỀ THI THAM KHẢO] Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? Trang 11 A. 4 2
y x 2x B. 4 2
y x 2x C. 3 2
y x 3x D. 3 2
y x 3x Lời giải Chọn A
Đồ thị trên là đồ thị của hàm số dạng 4 2
y ax bx c với a 0 . Câu tƣơng tự:
Câu 9.1 Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào ? A. 3
y x 3x 1 B. 3
y x 3x 1 C. 3
y x 3x 1 D. 4 2
y x 4x 1 Lời giải Chọn C
Đây là đồ thị hàm bậc ba có hệ số a dương nên loại đáp án B, D.
Đồ thị hàm bậc ba có hai điểm cực trị nên loại A. Câu phát triển
Câu 9.2: Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau x 2 2 x 2 x 2 2x 2 A. y B. y C. y D. y x 1 x 1 x 2 x 1 Lời giải Chọn B
Ta có từ đồ thị hàm số ta thấy hàm số giảm, có tiệm cận ngang là y 2
, tiệm cận đứng là x 1 , giao
với Ox tại điểm 1;0 , giao với Oy tại điểm 0; 2 . Trang 12 2 x 2
Vậy hàm số cần tìm là y . x 1
Câu 9.3: Cho hàm số 3 2
f x ax bx cx d có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?
A. a 0,b 0, c 0, d 0
B. a 0,b 0, c 0, d 0
C. a 0,b 0, c 0, d 0
D. a 0,b 0, c 0, d 0 Lời giải Chọn A
lim y a 0 x
Xét f x 2
3ax 2bx ,
c f x 0 có hai nghiệm phân biệt trái dấu nên suy ra .
a c 0 c 0 . b b
Xét y 6ax 2b 0 x
, dựa vào đồ thị ta thấy hoành độ của điểm uốn âm 0 b 0 . 3a 3a
Câu 9.4: Cho hàm số y f x 3 2
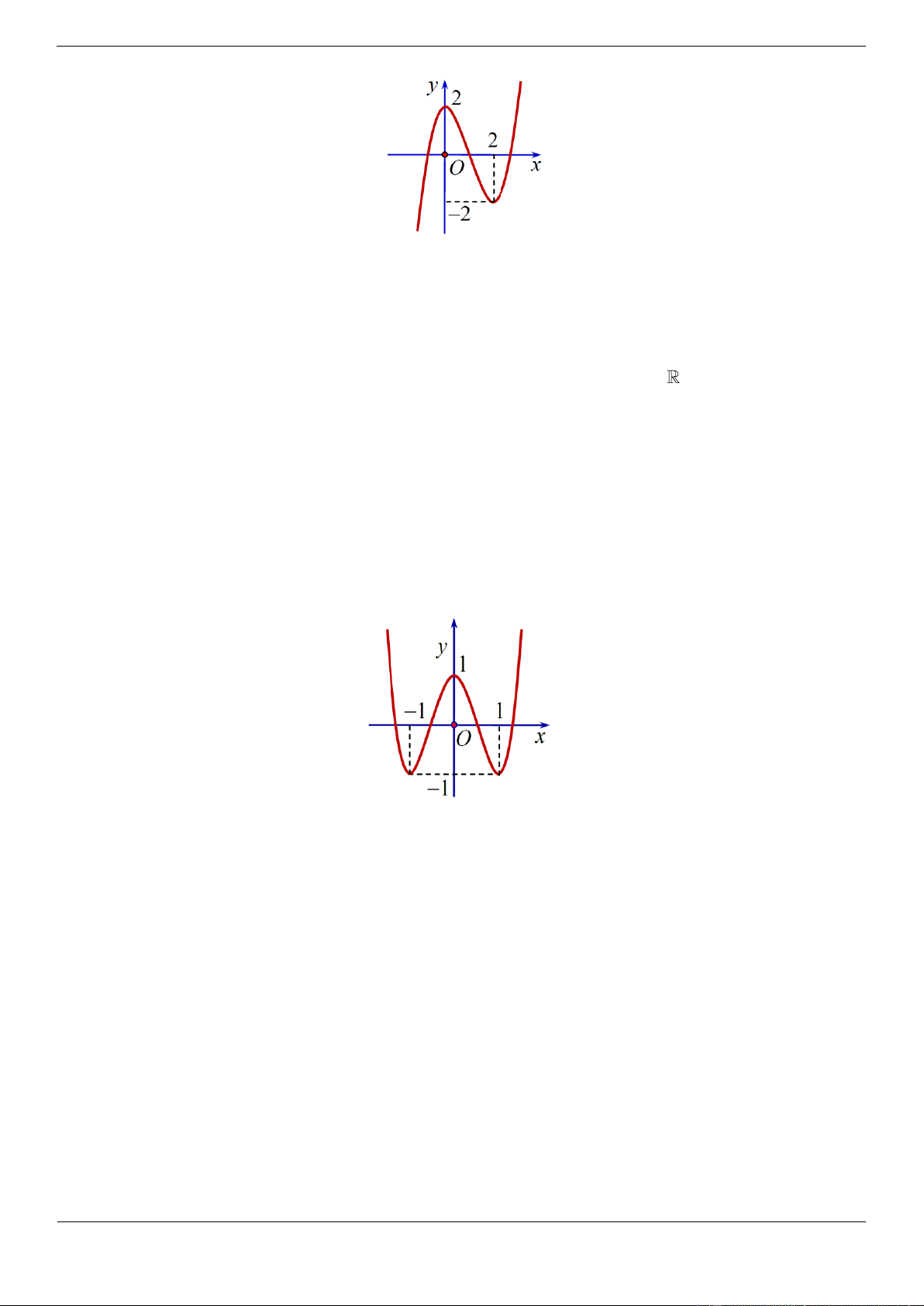
x ax bx 4 có đồ thị như hình vẽ.
Hàm số y f x là hàm số nào trong bốn hàm số sau: A. 3 2
y x 3x 2. B. 3 2
y x 3x 2. C. 3 2
y x 6x 9x 4. D. 3 2
y x 6x 9x 4. Lời giải Chọn C
Vì đồ thị hàm số y f x 3 2
x ax bx 4 đi qua các điểm 0;4, 1 ;0, 2 ;2 nên ta có 3 2
0 6.0 9.0 4 0 3 2 a b 3 a 6 hệ: 1 . a 1 b 1 4 0
4a 2b 6 b 9 2 2 .a 2 2 b 2 4 2 Vậy 3 2
y x 6x 9x 4 . Trang 13
Câu 10. [ĐỀ THI THAM KHẢO] Với a là số thực dương tùy ý, log 2 a bằng 2 1 1
A. 2 log a B. log a C. 2 log a D. log a 2 2 2 2 2 2 Lời giải Chọn C Ta có: log 2 a 2log a 2 2
Phân tích: sử dụng các công thức về logarit.
Câu tƣơng tự câu 10
Câu 10.1 Với a là số thực dương tùy ý, log 4 a bằng 3 1 1
A. 4 log a B. log a
C. 4 log a D. log a 3 3 4 3 3 4 Lời giải Chọn C Ta có: log 4 a 4log a 3 3 Phát triển
Câu 10.2 Với a là số thực dương tùy ý, log 3 log 100a bằng 1 1
A. 6 log a
B. 3 3log a C. log a
D. 2 3log a 2 3 Lời giải Chọn D Ta có 3 a 2 3 log 100
log10 log a 2 3log a a
Câu 10.3 Cho các số thực ,
a b 0 thoả mãn 3a 4b . Giá trị của bằng b A. log 3 B. ln12 C. ln 0, 75 D. log 4 4 3 Lời giải Chọn D a b ln 4 Ta có: 3 4 . a ln 3 . b ln 4 log 4 3 b ln 3 1
Câu 10.4 Cho log 3 a . Giá trị của bằng? log 1000 81 3a 4a 1 A. B. C. D. 12a 4 3 12a Lời giải Chọn B 1 4 4a Ta có 4 log 81 log 3 log 3 3 1000 10 log 1000 3 3 81 Trang 14
Câu 11. [ĐỀ THI THAM KHẢO] Họ tất cả các nguyên hàm của hàm số f x cos x 6x là A. 2
sin x 3x . C B. 2
sin x 3x C C. 2
sin x 6x C
D. sin x C Lời giải Chọn A Ta có: x x 2 cos 6
dx sin x 3x C
Phân tích: Sử dụng các nguyên hàm cơ bản. Câu tƣơng tự
Câu 11.1 Họ tất cả các nguyên hàm của hàm số f x 2x sin x là A. 2
x cos x C B. 2
x cos x C C. 2
2x cos x C D. 2
2x cos x C Lời giải Chọn B f
x x x 2 2 sin
dx x cos x C Phát tiển
Câu 11.2 Họ tất cả các nguyên hàm của hàm số 2 x f x x e là A. 2 x e C B. 2 x x e C C. 2 x
x e C D. 2 x x e C Lời giải Chọn C 2 2 x x x e
dx x e C
Câu 11.3 Họ tất cả các nguyên hàm của hàm số 3x f x sin8x là 3x 3x 1 3x 1 x 1 A.
cos8x C B.
cos8x C C.
cos8x C
D. 3 ln 3 cos8x C ln 3 ln 3 8 ln 3 8 8 Lời giải Chọn B x 3x x 1 3 sin 8 dx
cos8x C ln 3 8
Câu 11.4 Họ tất cả các nguyên hàm của hàm số f x 2x cos 2x là 1 1 A. 2
x sin 2x C B. 2 x sin 2x C C. 2 x sin 2x C D. 2
x 2sin 2x C 2 2 Lời giải Chọn B f
x 2xcos2x 1 2 dx x sin 2x C 2
Câu 11.5 Họ tất cả các nguyên hàm của hàm số f x 3
x sin3x là Trang 15 4 x 1 4 x 1 A. 2
3x 3cos 3x C B.
cos3x C C. 4
x cos 3x C D.
cos3x C 4 3 4 3 Lời giải Chọn D x 1
Ta có: x sin3x 4 3 dx
cos3x C 4 3
Câu 12. [ĐỀ THI THAM KHẢO] Mô-đun của số phức 1 2i bằng A. 5 B. 3 C. 5 D. 3 Lời giải Chọn C Ta có 2 2
1 2i 1 2 5
Phân tích: xác định các yếu cơ bản của số phức như: Số phức liên hợp, mo đun của số phức,
điểm biểu diễn số phức,… Câu tƣơng tự
Câu 12.1 Tính modul của số phức z 4 3i : A. z 25 B. z 7 C. z 7
D. z 5 Lời giải Chọn D
Áp dụng công thức tính thể modul số phức 2 2
z a bi : z a b . Theo đầu bài ta có: z 2 2 4 3 5 Phát triển
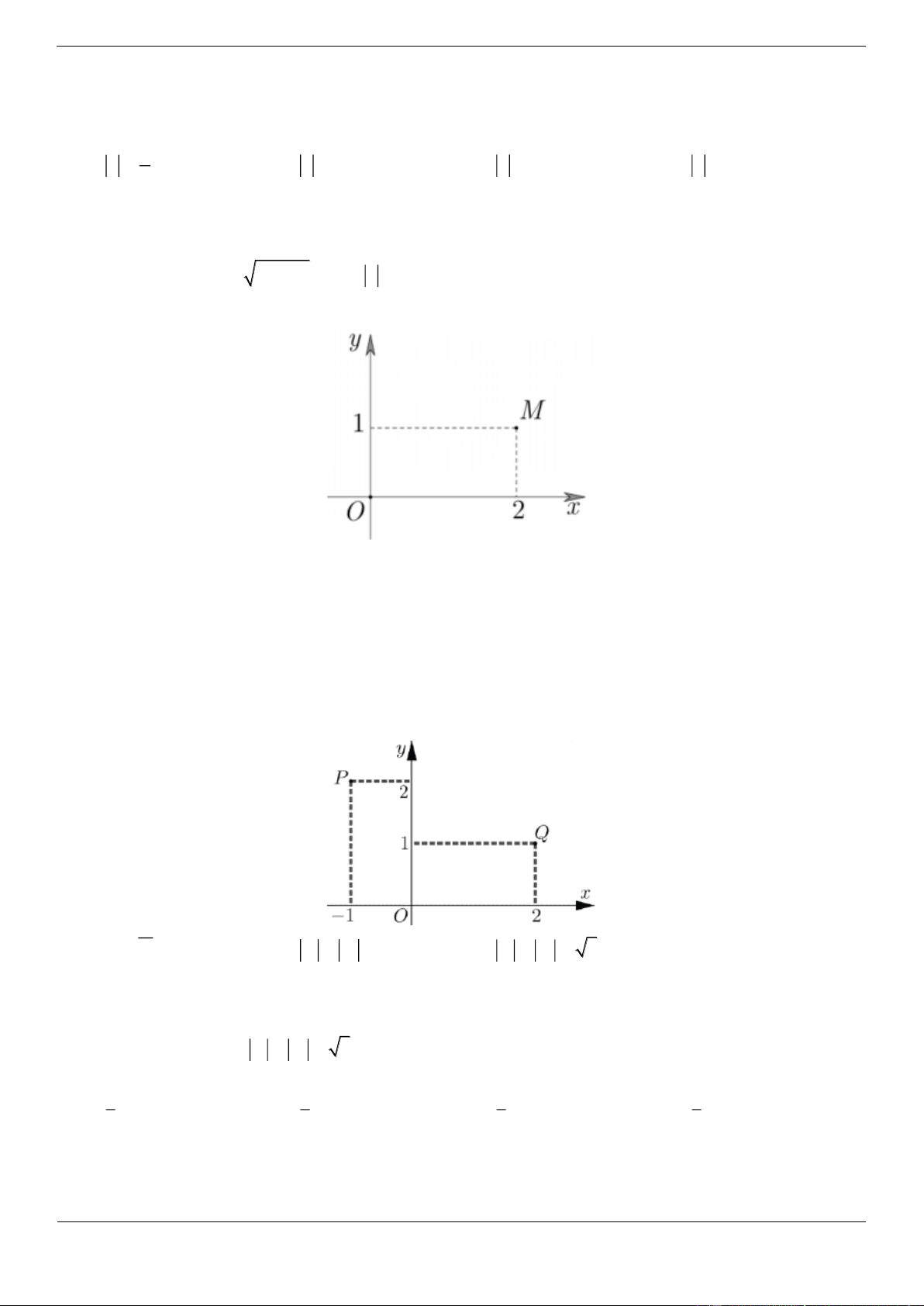
Câu 12.2 Cho số phức z được biểu diễn bởi điểm M 1
;3 trên mặt phẳng tọa độ. Môđun
của số phức z bằng A. 10. B. 2 2 C. 10 D. 8. Lời giải Chọn C
Số phức z được biểu diễn bởi điểm M 1 ;3 z 1 3i .
Ta có: z i 2 2 1 3 1 3 10 .
Câu 12.3 Cho số phức z 2 3i . Môđun của số phức z là A. 1 B. 1 C. 2 3i D. 13 Lời giải Chọn D
Ta có z z i 2 2 2 3 2 3 13 Trang 16
Câu 12.4 Nếu điểm M ;
x y là điểm biểu diễn hình học của số phức z trong mặt phẳng tọa độ Oxy thoả mãn OM 4 thì 1 A. z B. z 4 C. z 16
D. z 2 4 Lời giải Chọn B Theo bài ra 2 2 OM 4
x y 4 z 4
Câu 12.5 Trong hình vẽ bên dưới, điểm M biểu diễn cho số phức z. Số phức z là A. 2 i B. 1 2i C. 1 2i
D. 2 i Lời giải Chọn D Ta có M 2;
1 z 2 i
Câu 12.6 Trong hình vẽ bên, điểm P biểu diễn số phức z , điểm Q biểu diễn số phức z . 1 2
Mệnh đề nào dưới đây đúng?
A. z z
B. z z 5
C. z z 5
D. z z 1 2 1 2 1 2 1 2 Lời giải Chọn C z 1
2 ;i z 2 i z z 5 1 2 1 2
Câu 12.7. Số phức liên hợp của số phức z 5 6i là A. z 5 6i B. z 5 6i
C. z 6 5i
D. z 5 6i Lời giải Chọn D Trang 17
Số phức liên hợp của số phức z x yi, , x y
là số phức z x yi . Do đó số phức liên hợp của số
phức z 5 6i là z 5 6i .
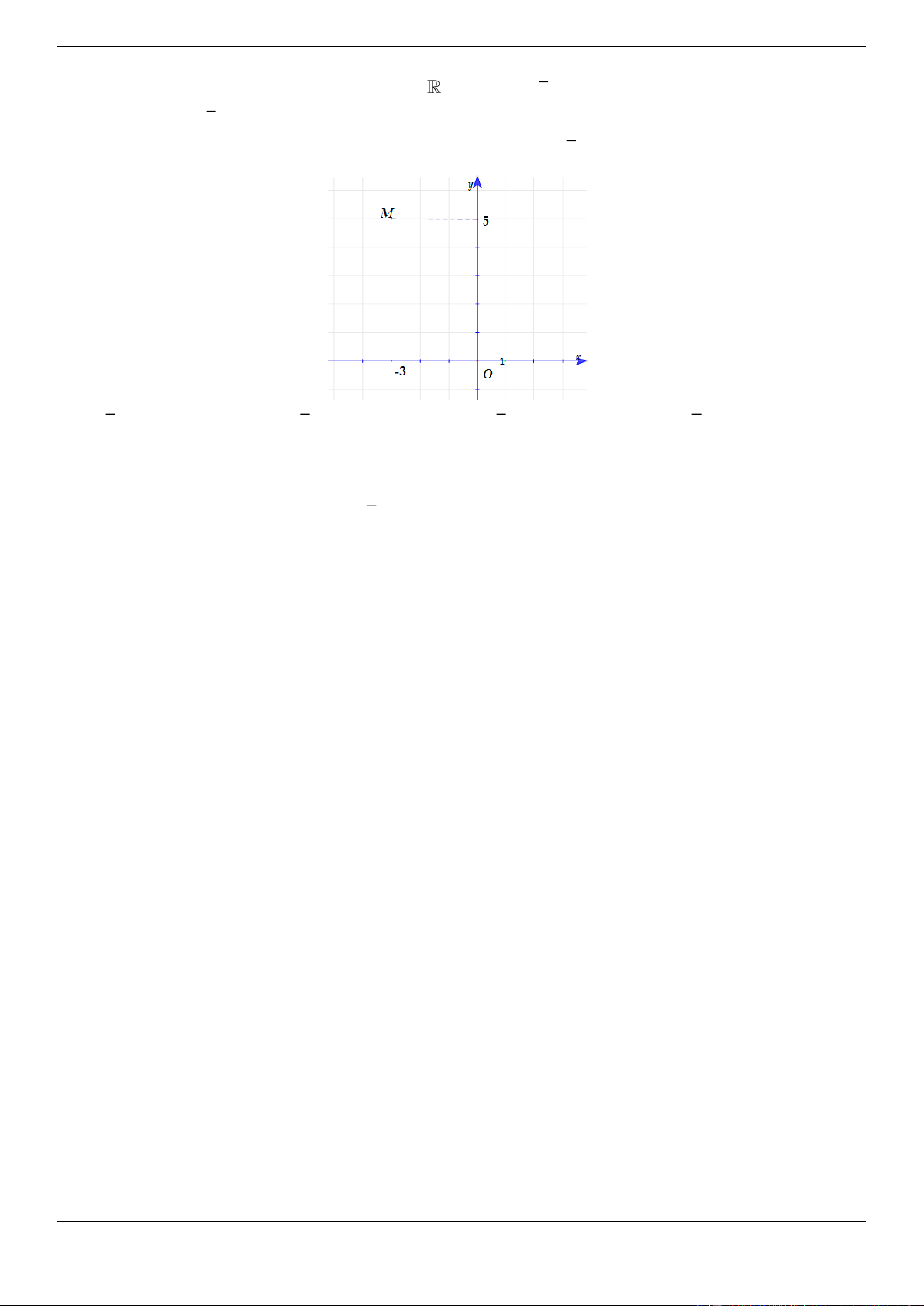
Câu 12.8 Điểm M trong hình vẽ bên biểu diễn số phức z. Số phức z là
A. z 3 5i B. z 3 5i
C. z 3 5i D. z 3 5i Lời giải Chọn D
Tọa độ điểm M 3 ;5 z 3
5i z 3 5i
Câu 13. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2; 2;
1 trên mặt phẳng Oxy có tọa độ là A. 2;0; 1 B. 2; 2; 0 C. 0; 2; 1 D. 0;0; 1 Lời giải Chọn B
Hình chiếu của M 2; 2;
1 lên mặt phẳng Oxy thì cao độ bằng 0
Phân tích ý tƣởng câu hỏi:
Đây là dạng toán tìm tọa độ các điểm trên mặt phẳng tọa độ hoặc các trục tọa độ. Đây là dạng toán cơ
bản. Nằm trong mạch kiến thức của khái niệm hệ trục tọa độ của hình học không gian Oxyz
Cho điểm M ; a ; b c khi đó
+ Hình chiếu của điểm M trên mặt phẳng Oxy là ; a ; b 0
+ Hình chiếu của điểm M trên mặt phẳng Oyz là 0; ; b c
+ Hình chiếu của điểm M trên mặt phẳng Oxz là ; a 0;c
+ Hình chiếu của điểm M trên trục Ox là ; a 0;0
+ Hình chiếu của điểm M trên trục Oy là 0; ; b 0
+ Hình chiếu của điểm M trên trục Oz là 0;0;c
Các bài toán khai thác phát triển từ bài toán này là: Xác định điểm đối xứng của một điểm qua mặt
phẳng tọa độ, qua trục tọa độ, khoảng cách một điểm đến mặt phẳng tọa độ, trục tọa độ; phương trình mặt
cầu tiếp xúc mặt phẳng tọa độ, trục tọa độ…v.v. Trang 18
Bài tập tƣơng tự:
Câu 13.1. Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2; 2;
1 trên mặt phẳng Oyz có tọa độ là A. 2;0; 1 B. 2; 2;0 C. 0; 2; 1 D. 0;0; 1 Lời giải Chọn C
Hình chiếu của M 2; 2;
1 lên mặt phẳng Oyz là một điểm có hoành độ bằng 0 nên hình
chiếu là điểm 0; 2; 1 .
Bài tập phát triển
Câu 13.2. Trong không gian Oxyz , điểm đối xứng với điểm M 2; 2;
1 qua mặt phẳng Oyz có tọa độ là A. 2;0; 1 B. 2 ; 2; 1 C. 0; 2; 1 D. 0;0; 1 Lời giải Chọn B
Gọi điểm H 0; 2;
1 là hình chiếu của M trên mặt phẳng Oyz . Điểm đối xứng với điểm M 2; 2;
1 qua mặt phẳng Oyz : x 0 là điểm M ; a ;
b c sao cho M M nhận H làm trung điểm. Suy 1 1 ra M 2 ; 2;1 . 1
Câu 13.3. Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2; 2;
1 trên trục Ox là điểm có tọa độ là A. 2;0; 1 B. 2;0;0 C. 0; 2; 1 D. 0;0; 1 Lời giải Chọn B
Hình chiếu của M trên trục Ox là điểm có tọa độ 2;0;0
Câu 13.4. Trong không gian với hệ tọa độ Oxyz cho điểm A 3
;1;2 . Tọa độ điểm A’ đối xứng
với điểm A qua trục Oy là A. 3 ;1;2 B. 3;1; 2
C. 3; 1; 2
D. 3; 1; 2 Lời giải Chọn B
Gọi M là hình chiếu của điểm A lên trục Oy M 0;1;0
Ta có A đối xứng với điểm A qua trục Oy nên M là trung điểm của AA x 2x x x 0 3 3 A M A A y 2 y y y 2.1 1 1 A A M A A 3;1; 2 z 2z z z 0 2 2 A M A A Trang 19
Câu 13.5 Trong không gian Oxyz , cho hai điểm A 1
;2;6, B5; 4;2 , đường thẳng AB cắt mặt phẳng
Oxz tại M và MA k MB . Tính k . 1 1 A. k B. k C. k 2 D. k 2 2 2 Lời giải Chọn A
Dễ nhận thấy hai điểm A B , nằm khác phía so với mặt phẳng Oxz : y 0
Suy ra điểm M nằm trong đoạn AB nên MA kM , B k 0 . MA d , A Oxz 2 1 1 Ta có . Suy ra k MB
d B,Oxz 4 2 2 Câu 14.
[ĐỀ THI THAM KHẢO] Trong không gian Oxyz , cho mặt cầu
S x 2 y 2 z 2 : 1 2 3
16 . Tâm của S có tọa độ là A. 1 ; 2;3 B. 1; 2;3 C. 1 ;2;3
D. 1; 2;3 Lời giải Chọn D
Phân tích ý tƣởng câu hỏi:
Đây là dạng xác định tâm và bán kính mặt cầu, xác định một phương trình có phải là phương trình mặt
cầu hay không? Đây là dạng toán rất cơ bản.
Cho mặt cầu S có tâm I ; a ;
b c bán kính R thì ta có + Phương trình mặ 2 2 2
t cầu là S x a y b z c 2 : R
+ Ngược lại mọi phương trình có dạng 2 2 2
x y z 2ax 2by 2cz d 0 là phương trình mặt cầu khi và chỉ khi 2 2 2
a b c d 0 . Khi đó tâm mặt cầu là I ; a ; b c , bán kính 2 2 2 2
R a b c d .
Các bài toán khai thác phát triển từ bài toán này là xác định một phương trình có phải là phương trình
mặt cầu hay không? Tập hợp điểm là mặt cầu.
Bài tập tƣơng tự: 2 2 2
Câu 14.1 Trong không gian Oxyz , cho mặt cầu S : x
1 y 2 z 3 5. Tâm của S có tọa độ là A. 1 ; 2;3 B. 1; 2;3 C. 1 ;2;3 D. 1; 2; 3 Lời giải Chọn D
Bài tập phát triển
Câu 14.2. Trong không gian Oxyz , mặt cầu S 2 2 2
: x y z 4x 2y 2z 3 0 có tâm và bán kính là
A. I 2;1; 1 ; R 9 B. I 2 ;1; 1 ; R 3
C. I 2;1; 1 ; R 3 D. I 2 ;1; 1 ; R 9 Lời giải Trang 20 Chọn B 2 2 2
Mặt cầu S có tâm I 2 ;1;
1 và bán kính R 2 2 1 1 3 3 2 2
Câu 14.3. Trong không gian Oxyz , cho mặt cầu S x 2 :
1 y z 3 4 . Tìm tâm I và bán kính r
của mặt cầu S
A. I 1;0; 3, r 4 B. I 1 ;0;3,r 2 C. I 1 ;0;3,r 4
D. I 1;0; 3, r 2 Lời giải Chọn B
Mặt cầu (S) có tâm là điểm I 1
;0;3 và bán kính r 2
Câu 14.4. Trong không gian Oxyz , phương trình nào dưới đây là phương trình mặt cầu? A. 2 2 2
x y z x 1 0 B. 2 2 2
x y z 6x 9 0 C. 2 2 2
x y z 9 0 D. 2 2 2
x y z 2 0 Lời giải Chọn D
Ta có x y z
x y z 2 2 2 2 2 2 2 2 0 0 0 0 2
. Mặt cầu có tâm O 0;0;0 , bán kính R 2 .
Câu 14.5. Trong không gian Oxyz , tìm điều kiện của tham số m để phương trình 2 2 2 2
x y z 2mx 4y 2mz m 5m 0 là phương trình mặt cầu m 1 m 1 A. m 4 B. C. m 1 D. m 4 m 4 Lời giải Chọn D Ta có phương trình
x y z mx y mz m m
x m2 y 2 z m2 2 2 2 2 2 2 4 2 5 0 2
m 5m 4 m 1
Để thỏa mãn bài toán khi 2
m 5m 4 0 . m 4
Câu 14.6. Trong không gian Oxyz , cho mặt cầu S 2 2 2
: x y z 2x 4y 4z m 0 (m là tham số).
Biết mặt cầu có bán kính bằng 5. Tìm m. A. m 25 B. m 11 C. m 16 D. m 16 Lời giải Chọn C
R 5 1 4 4 m 5 m 16
Câu 15. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz , cho mặt phẳng : 3x 2y 4z 1 0 .
Vectơ nào dưới đây là một vectơ pháp tuyến của ? Trang 21
A. n 3; 2; 4 B. n 2; 4 ;1 C. n 3; 4 ;1 D. n 3; 2; 4 4 1 3 2 Lời giải Chọn D
Mặt phẳng : 3x 2y 4z 1 0 có một vec tơ pháp tuyến là n3;2; 4 .
Phân tích bài toán:
Đây là dạng toán căn bản xác định véc-tơ pháp tuyến của mặt phẳng.
Véc tơ pháp tuyến của mặt phẳng là véc-tơ khác véc-tơ không và có giá vuông góc với mặt phẳng.
Nếu hai véc tơ a và b không cùng phương có giá song song hoặc nằm trong mặt phẳng thì tích có
hướng của chúng bằng véc tơ pháp tuyến của mặt phẳng.
Nếu n là véc-tơ pháp tuyến của mặt phẳng thì véc tơ kn cũng là véc-tơ pháp tuyến, k 0 .
Trong không gian mọi mặt phẳng phương trình luôn có dạng . A x . B y .
C z D 0 trong đó 2 2 2
A B C 0 . Khi đó véc tơ pháp tuyến là n ; A ; B C .
Bài tập tƣơng tự:
Câu 15.1 Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P : z 2x 3 0 . Một véc-tơ pháp tuyến của (P) là
A. u 0;1; 2 B. v 1; 2 ;3
C. n 2;0; 1 D. w 1; 2 ;0 Lời giải
Ta viết lại phương trình mặt phẳng P : 2x z 3 0 và thấy P có một véc-tơ pháp tuyến là n 2;0; 1
Bài tập phát triển
Câu 15.2 Trong không gian Oxyz , mặt phẳng nào sau đây nhận n 1; 2;3 làm véc-tơ pháp tuyến?
A. x 2y 3z 1 0
B. 2x 4y 6z 1 0
C. 2x 4z 6 0
D. x 2y 3z 1 0 Lời giải
Ta có mặt phẳng 2x 4y 6z 1 0 có một véc-tơ pháp tuyến là n 2;4;6 21;2;3
Câu 15.3. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P đi qua điểm A1; 3;2 và chứa b c
trục Oz . Gọi n ; a ;
b c là một véc-tơ pháp tuyến của mặt phẳng P . Tính M . a 1 1 A. M B. M 3 C. M D. M 3 3 3 Lời giải
(P) chứa Oz nên k 0;0;
1 nằm trên P .
Ngoài ra, (P) chứa O và A nên véc-tơ OA 1; 3;2 nằm trên (P). 1 Vậy ta có n P k,OA 3;1;0 . Do đó M . 3 Trang 22
Câu 15.4. Trong không gian với hệ tọa độ Oxyz . Phương trình mặt phẳng đi qua điểm A1;2;0 và chứa đườ x 1 y z ng thẳng : d :
có một véc-tơ pháp tuyến là n1; ;
a b . Tính a b . 2 3 1
A. a b 2
B. a b 0
C. a b 3
D. a b 3 Lời giải Lấy B 1
;0;0d . Ta có AB 2 ; 2
;0,u 2;3; 1 d
Mặt phẳng đi qua A và chứa d có véc-tơ pháp tuyến n A , B u 2 ;2; 2 d
Một trong các véc-tơ pháp tuyến của mặt phẳng là n 1; 1 ; 1 a 1 ,b 1
Vậy a b 0 .
Câu 15.5. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A2;4; 1 , B 1 ;1;3 và mặt phẳng
P: x 3y 2z 5 0. Một mặt phẳng Q đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có
dạng là ax by cz 11 0 . Tính a b c .
A. a b c 10
B. a b c 3
C. a b c 5
D. a b c 7 Lời giải Ta có: AB 3 ; 3
;2 và véc-tơ pháp tuyến của mặt phẳng (P) là n 1; 3 ;2 P
Mặt phẳng Q đi qua hai điểm A, B và vuông góc với mặt phẳng P có một véc-tơ chỉ phương là n A ,
B n 0;8;12 40;2;3 Q P
Phương trình mặt phẳng Q là 0.x 2 2. y 4 3.z 1 0
Hay Q : 2y 3z 11 0 . Từ đó suy ra a 0,b 2,c 3. Do đó a b c 0 2 3 5 .
Câu 16. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng x 1 y 2 z 1 d : ? 1 3 3 A. P 1 ;2; 1 B. Q 1; 2 ; 1 C. N 1 ;3;2 D. M 1;2; 1 Lời giải Chọn A x 1 y 2 z 1 Ta có d : . 1 3 3 1 1 2 2 11
Thay tọa độ điểm P 1 ;2;
1 vào phương trình đường thẳng d ta có
ta thấy P d và 1 3 3 các điểm ,
Q N, M , không thuộc đường thẳng d. x y z
Câu 16.1. Trong không gian với hệ trục tọa độ , đường thẳng 1 2 :
không đi qua điểm 2 1 1 nào dưới đây? A. A 1 ;2;0 B. B 1 ; 3 ; 1 C. C 3; 1 ; 1 D. D 1; 2 ;0 Lời giải Trang 23 Chọn A 1 1 2 2 0 Ta có nên điểm A 1
;2;0 không thuộc đường thẳng . 2 1 1 x t
Câu 16.2. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : y 1 t . Đường thẳng d đi z 2t qua điểm nào sau đây? A. K 1; 1 ; 1
B. H 1;2;0
C. E 1;1; 2
D. F 0;1;2 Lời giải Chọn D
Đường thẳng d đi qua điểm F 0;1;2
Câu 16.3. Trong không gian với hệ trục toạ độ Oxyz , cho hai mặt phẳng P : 2x y 2z 3 0 ;
Q: x y z 3 0. Giao tuyến của hai mặt phẳng P và Q là đường thẳng đi qua điểm nào dưới đây?
A. P 1;1; 1 B. M 2; 1 ;0 C. N 0; 3 ;0 D. Q 1 ;2; 3 Lời giải Chọn A Cách 1:
Giả sử giao tuyến của hai mặt phẳng P,Q là một đường thẳng đi qua điểm I. I P Khi đó: . I Q
Kiểm tra các điểm M , N, ,
P Q . Ta thấy chỉ có điểm P cùng thuộc hai mặt phẳng P,Q . Vậy P 1;1; 1 là điểm cần tìm. Cách 2:
P có vectơ pháp tuyến là n 2; 1 ;2 . 1
Q có vectơ pháp tuyến là n 1;1;1 . 2
Gọi P Q
Ta có qua điểm I 0;1; 2 và có vectơ chỉ phương là u n , n 3 ;0;3 1 2 x t
Phương trình đường thẳng : y 1 z 2t
Dễ thấy P 1;1; 1 . Trang 24 x 1 2t
Câu 16.4. Trong không gian với hệ trục toạ độ Oxyz , cho đường thẳng d : y 2 t
t và điểm z 2 2t
M 1;2; m . Tìm tất cả các giá trị của tham số m để điểm M thuộc đường thẳng d. A. m 2 B. m 1 C. m 2 D. m 0 Lời giải Chọn C x 1 2t 1 2t 1 t 0
Điểm M 1;2;m thuộc đường thẳng d : y 2 t khi và chỉ khi 2 t 2 . m 2 z 2 2t 2 2t m
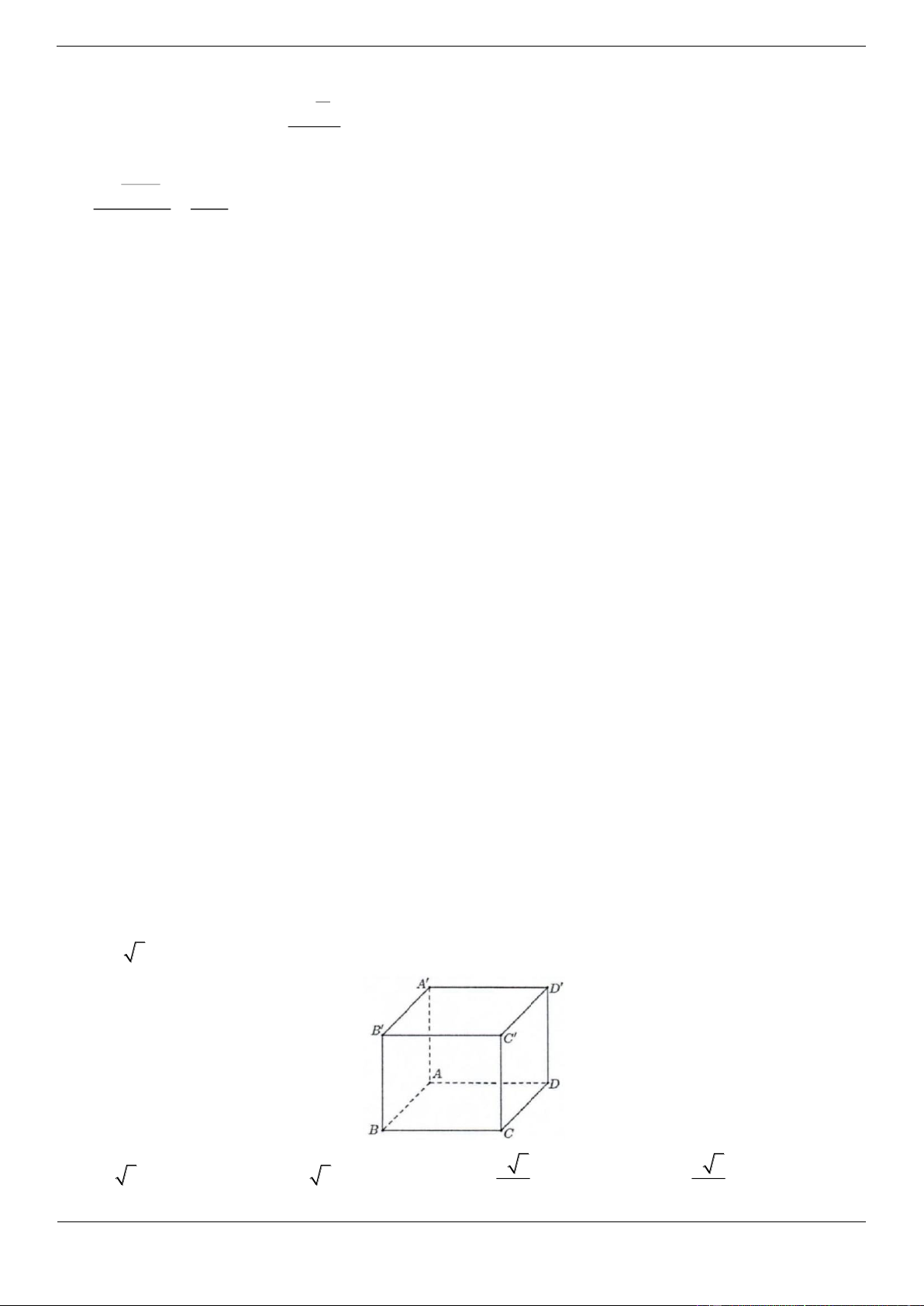
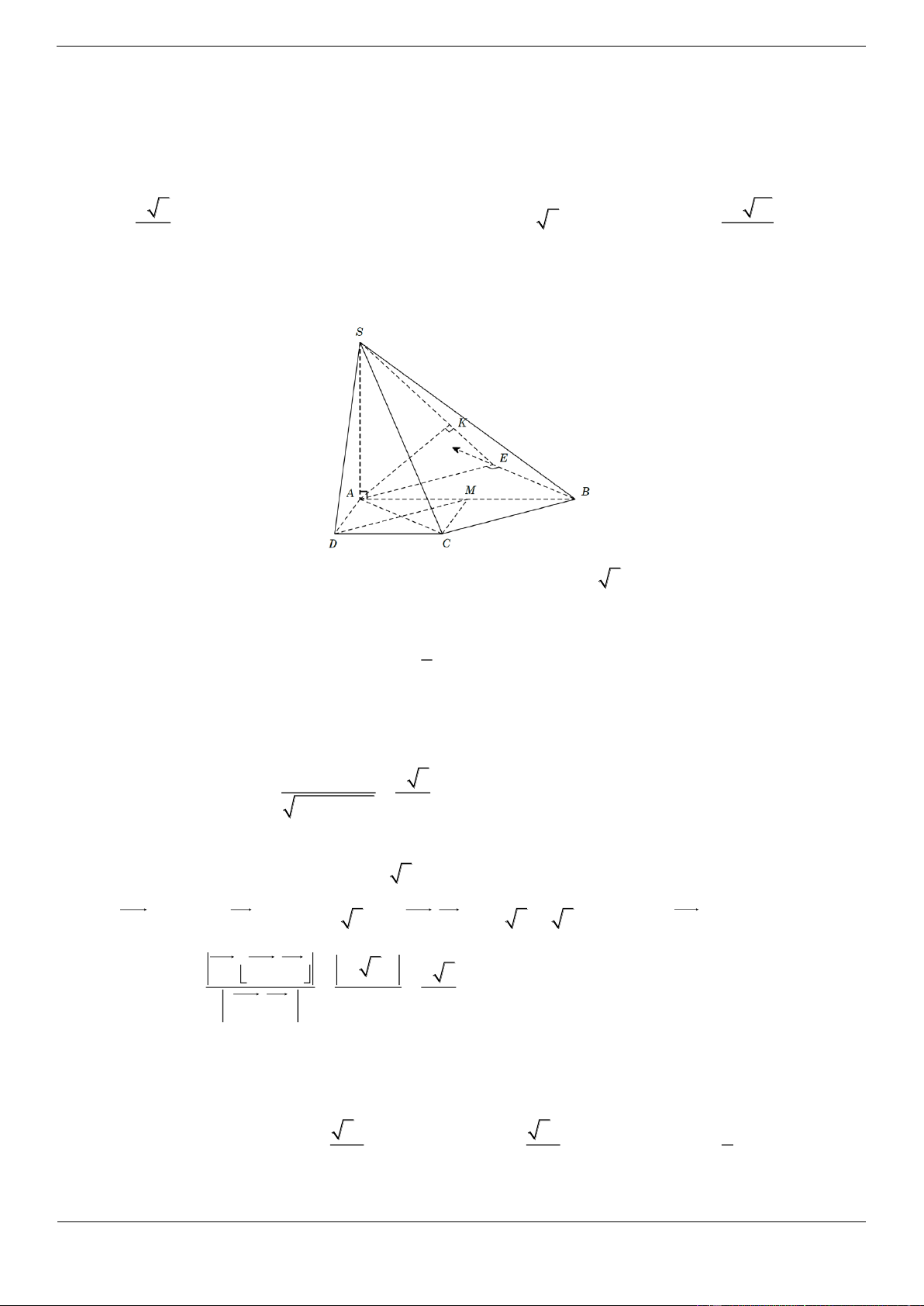
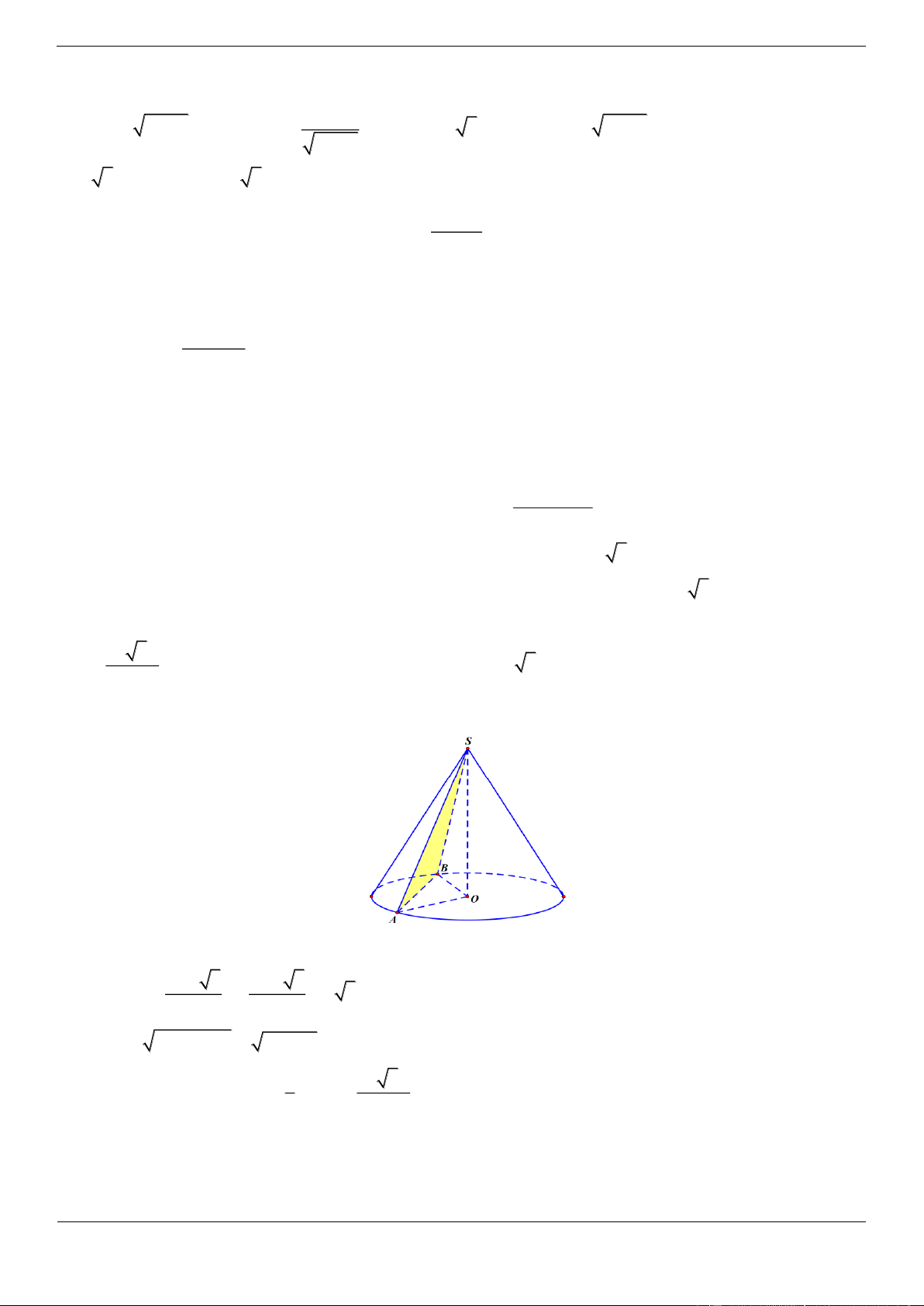
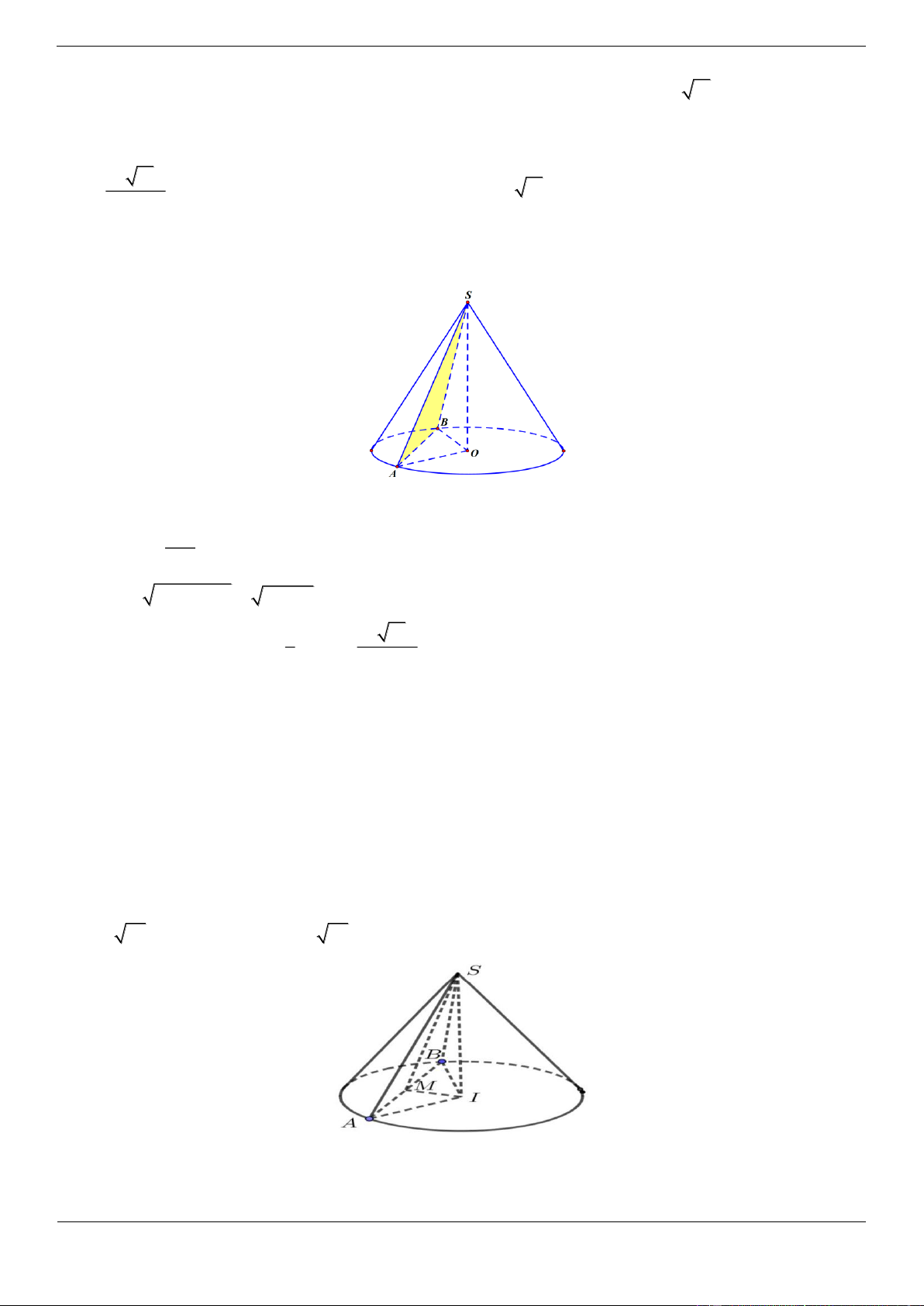
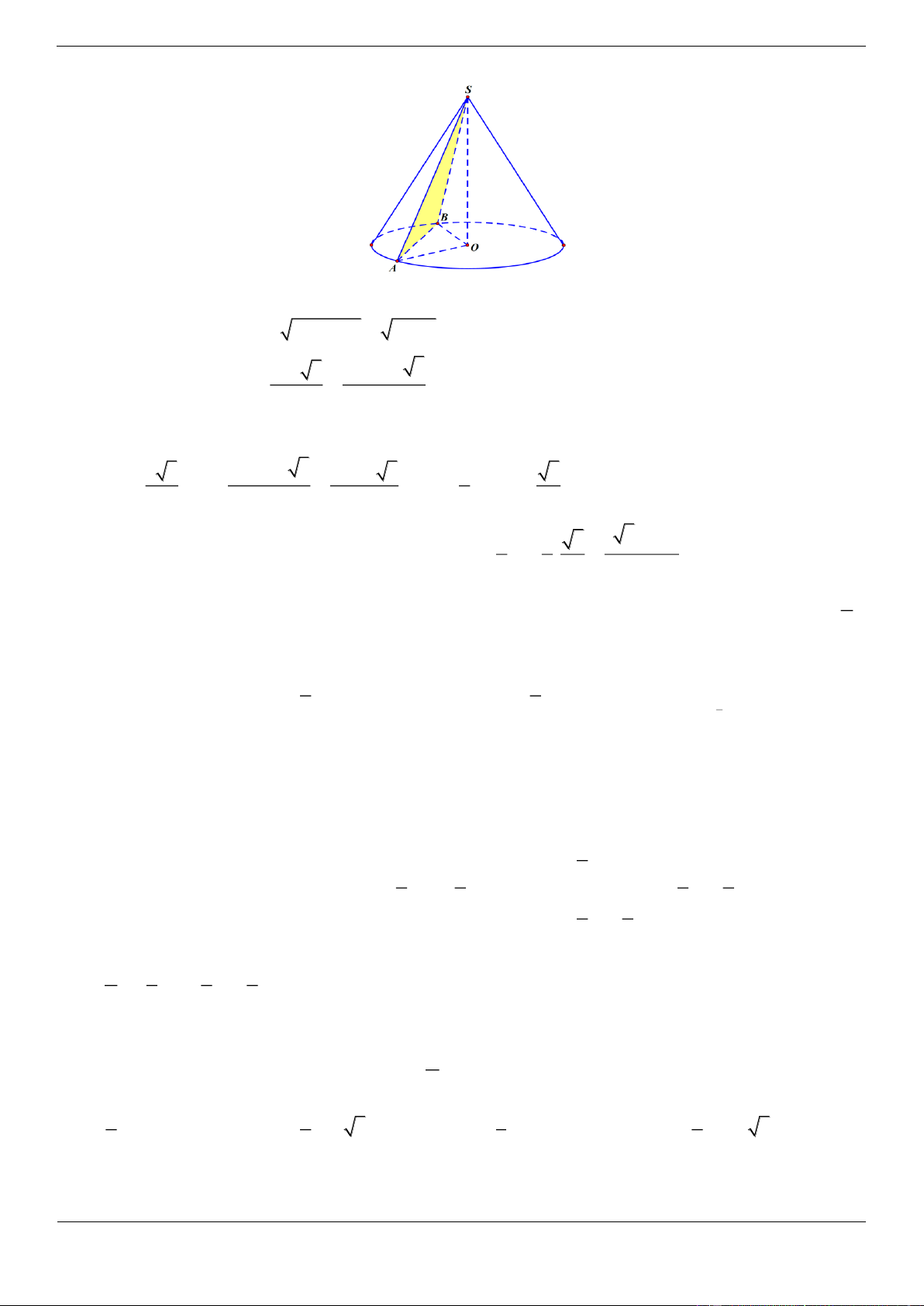
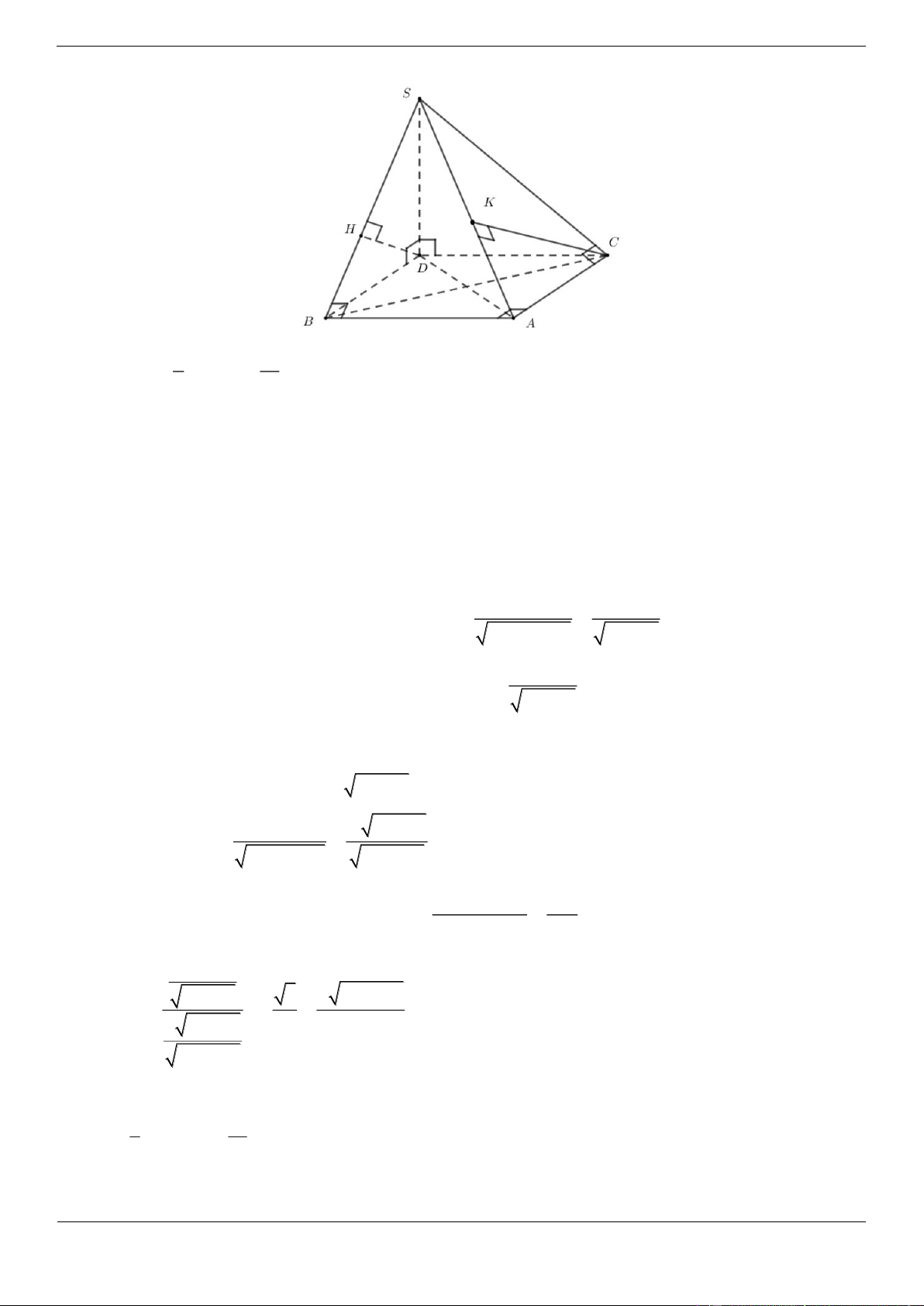
Câu 17. [ĐỀ THI THAM KHẢO] Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3, SA vuông
góc với mặt phẳng đáy và SA a 2 (minh họa như hình vẽ bên dưới). Góc giữa SC và mặt phẳng ABCD bằng A. 45 B. 30 C. 60 D. 90 Lời giải Chọn B
Góc giữa đường thẳng SC và mặt phẳng ABCD là SCA SA a 2 1 Ta có tan SCA SCA 30 . AC a 3. 2 3
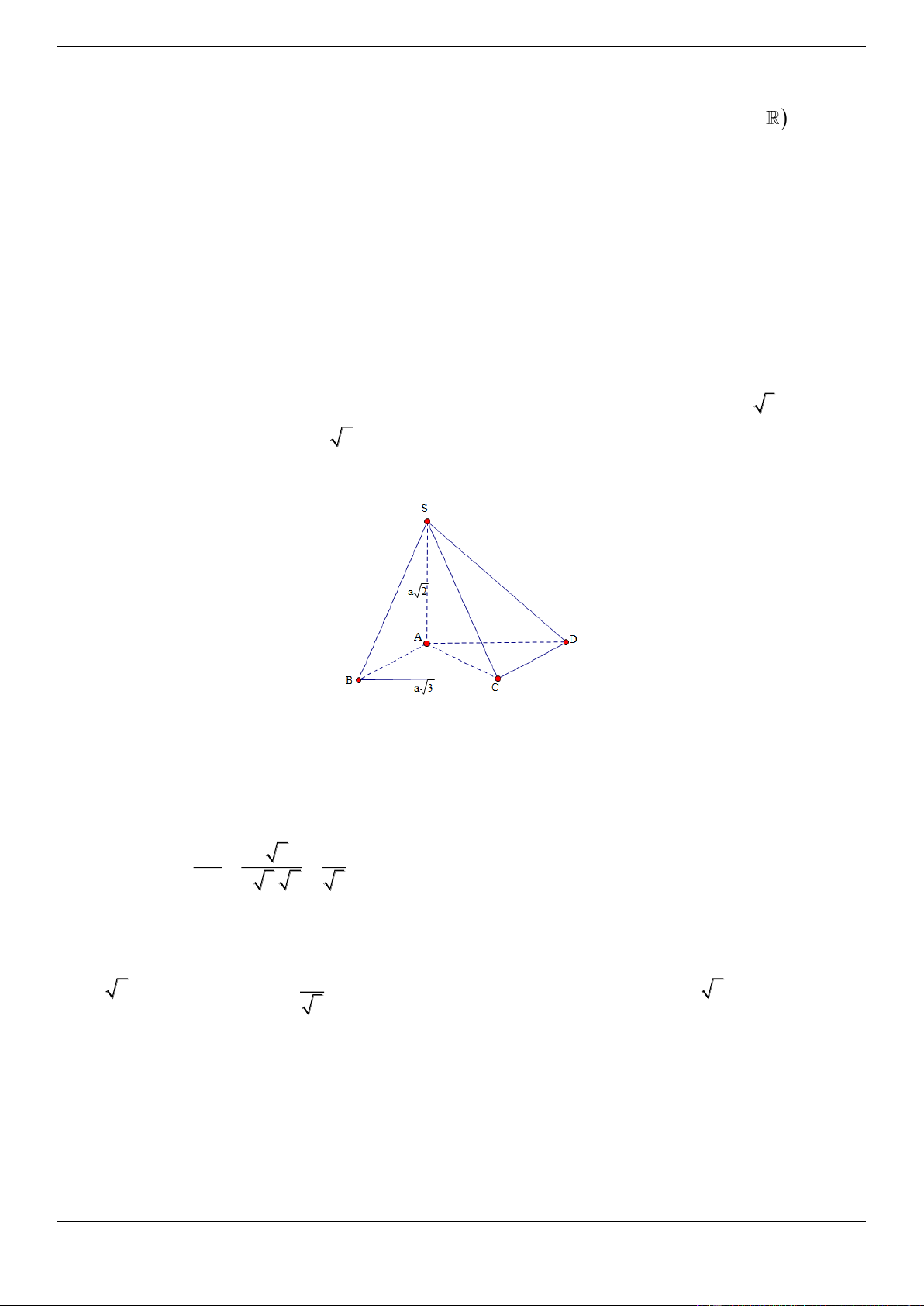
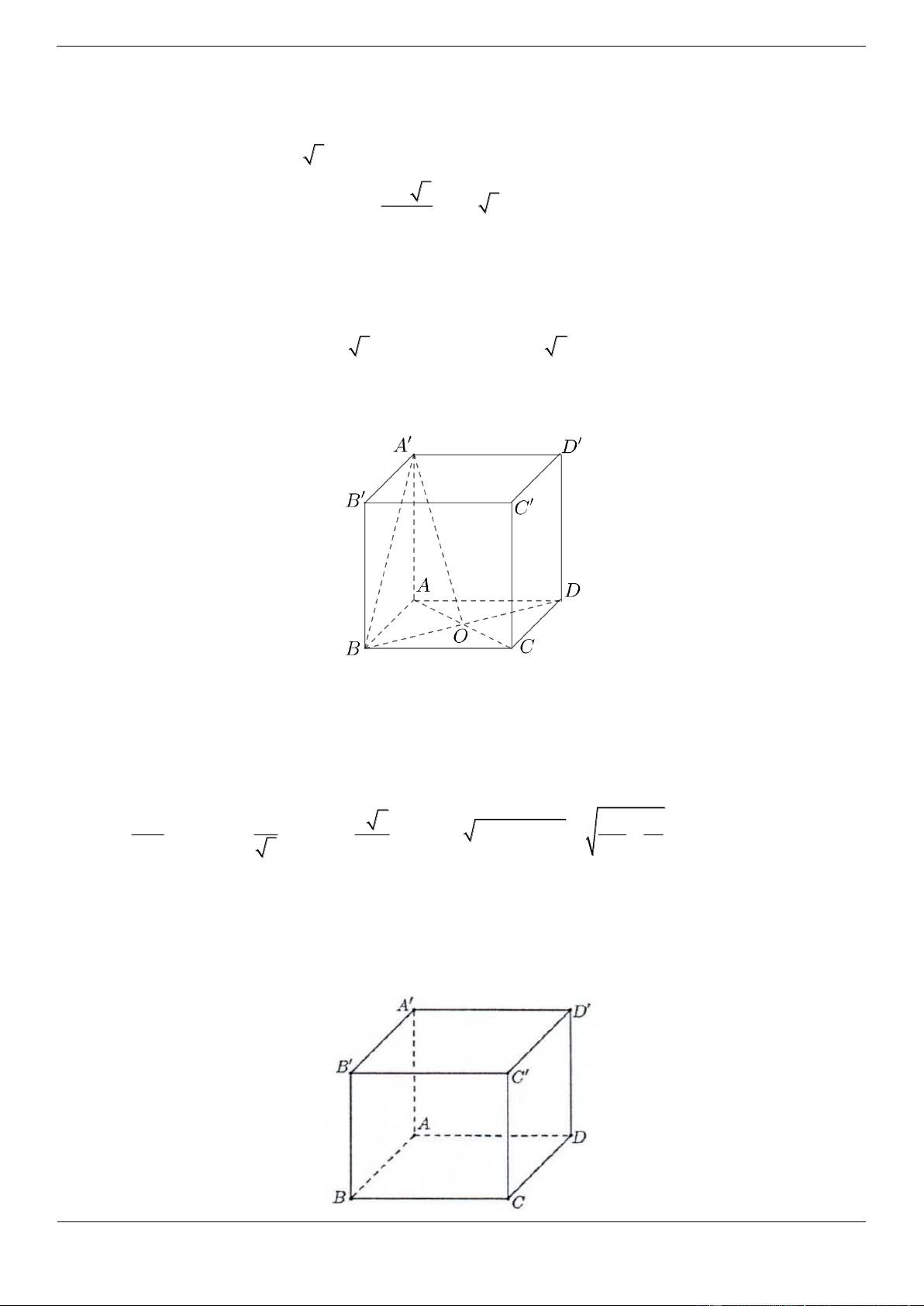
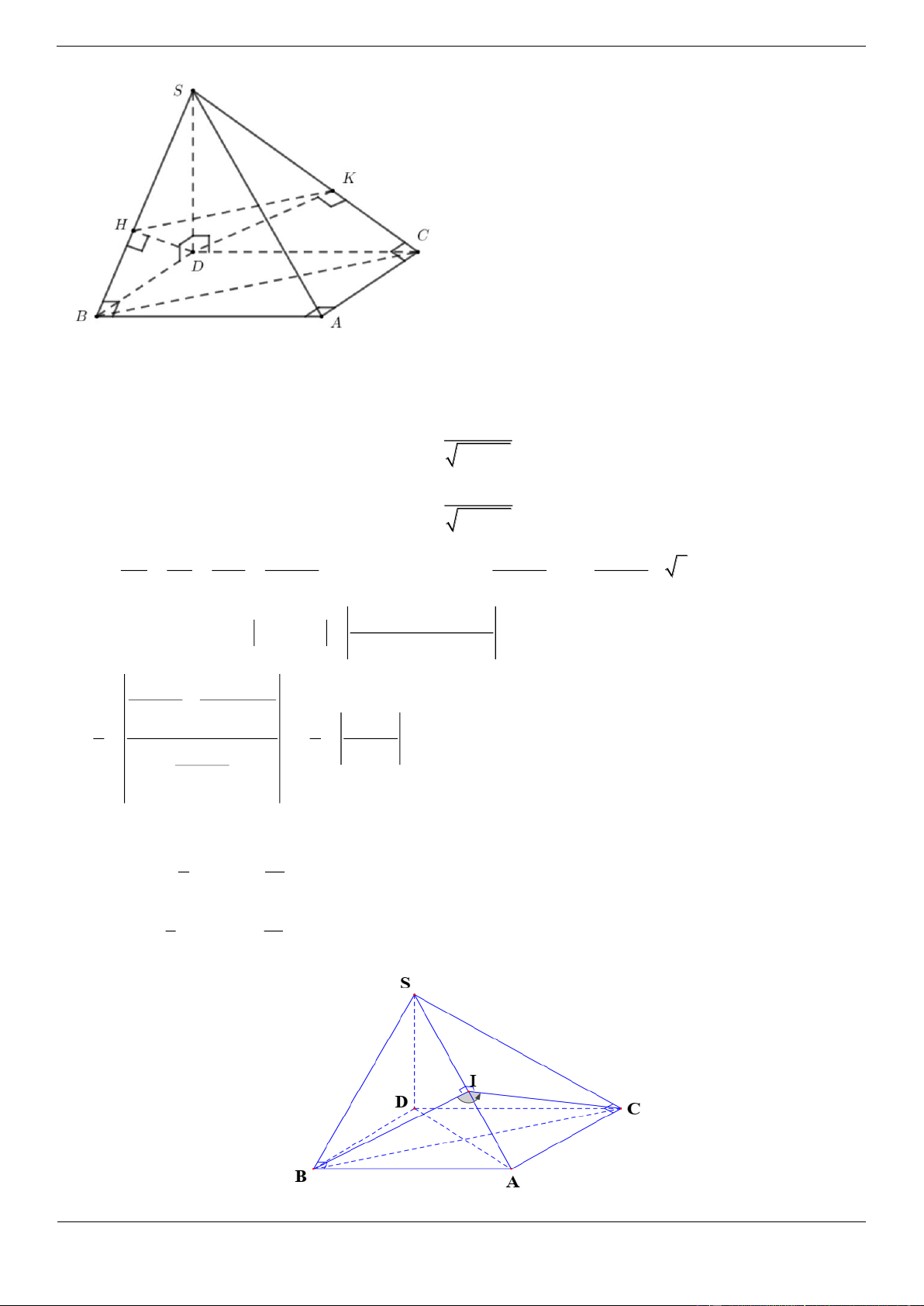
Câu 17.1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA vuông góc với
mặt phẳng đáy và SA 2a . Góc giữa đường thẳng SC và mặt phẳng ABCD là a. Khi đó tan bằng 2 A. 2 B. C. 2 D. 2 2 3 Lời giải Chọn A Trang 25
Góc giữa đường thẳng SC và mặt phẳng ABCD là . Suy ra SCA SA 2a tan 2 AC a 2
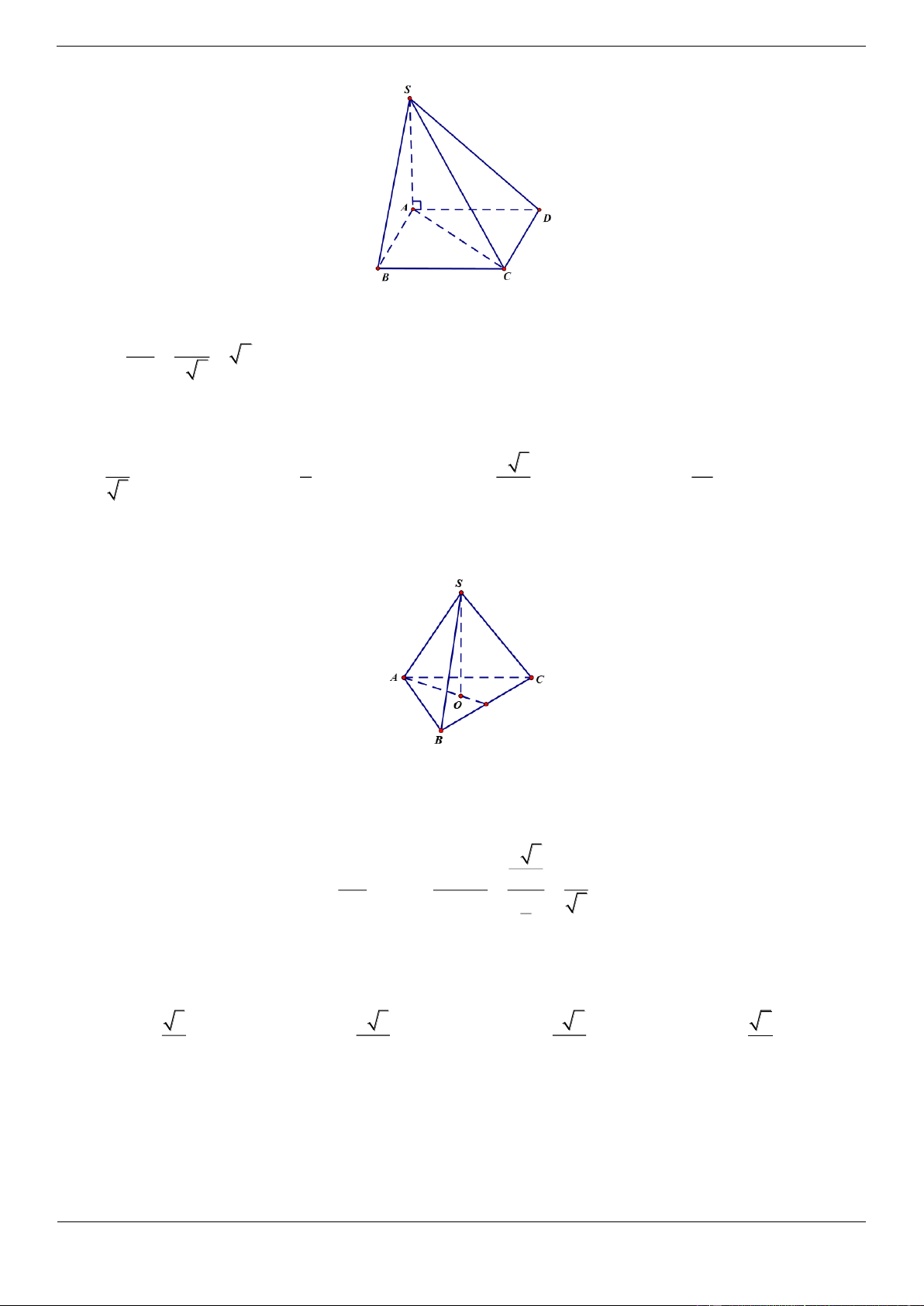
Câu 17.2. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a . Độ dài cạnh bên của hình
chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 60 ? 2a a a 3 2a A. B. C. D. 3 6 6 3 Lời giải Chọn A
Gọi O là tâm của tam giác đều ABC SO ABC .
Hình chiếu của SA trên mặt phẳng ABC là AO => góc giữa cạnh bên SA và mặt đáy là góc SAO 60 a 3 AO AO 2a Xét tam giác vuông SAO: 3 cos 60 SA SA cos 60 1 3 2
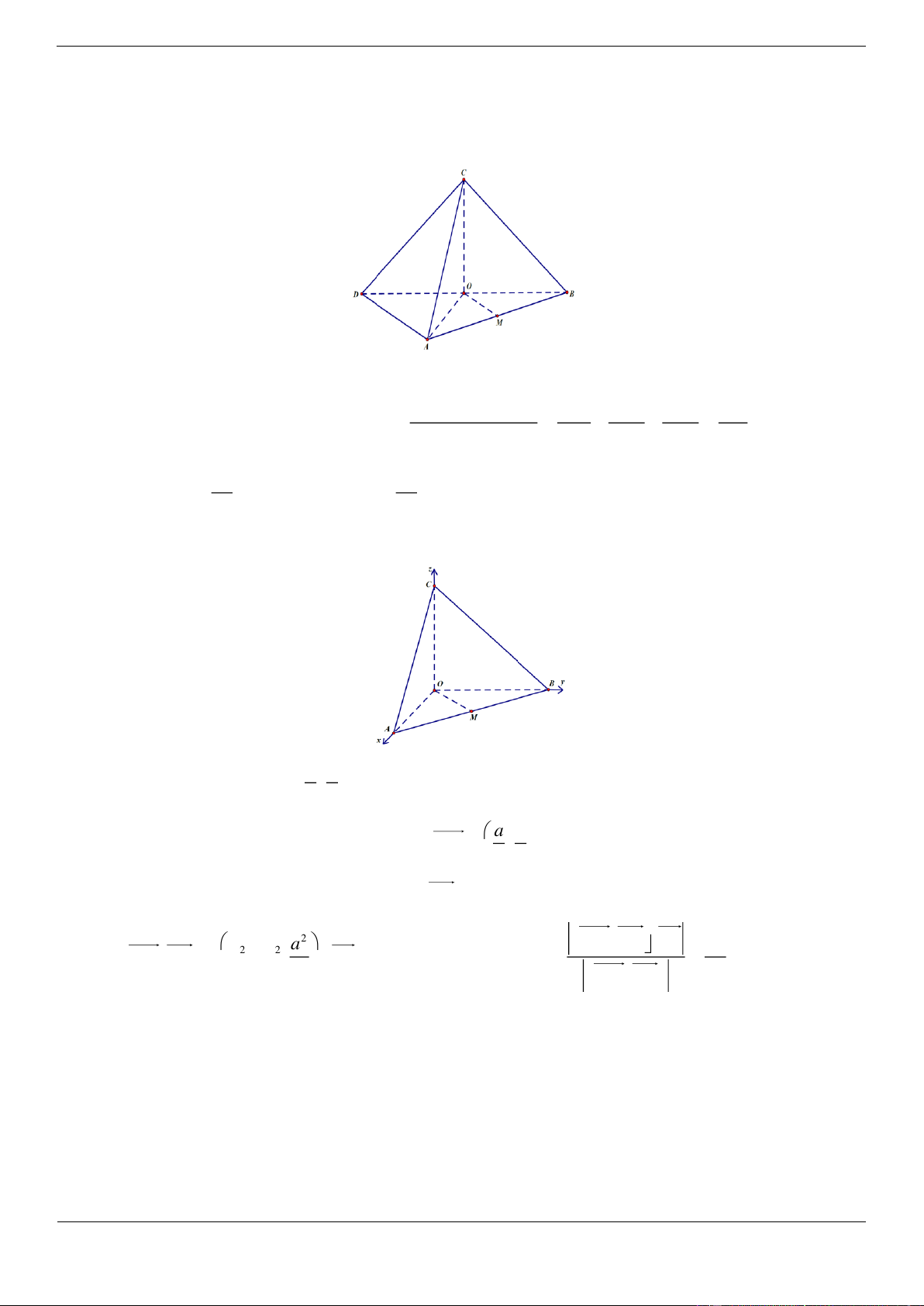
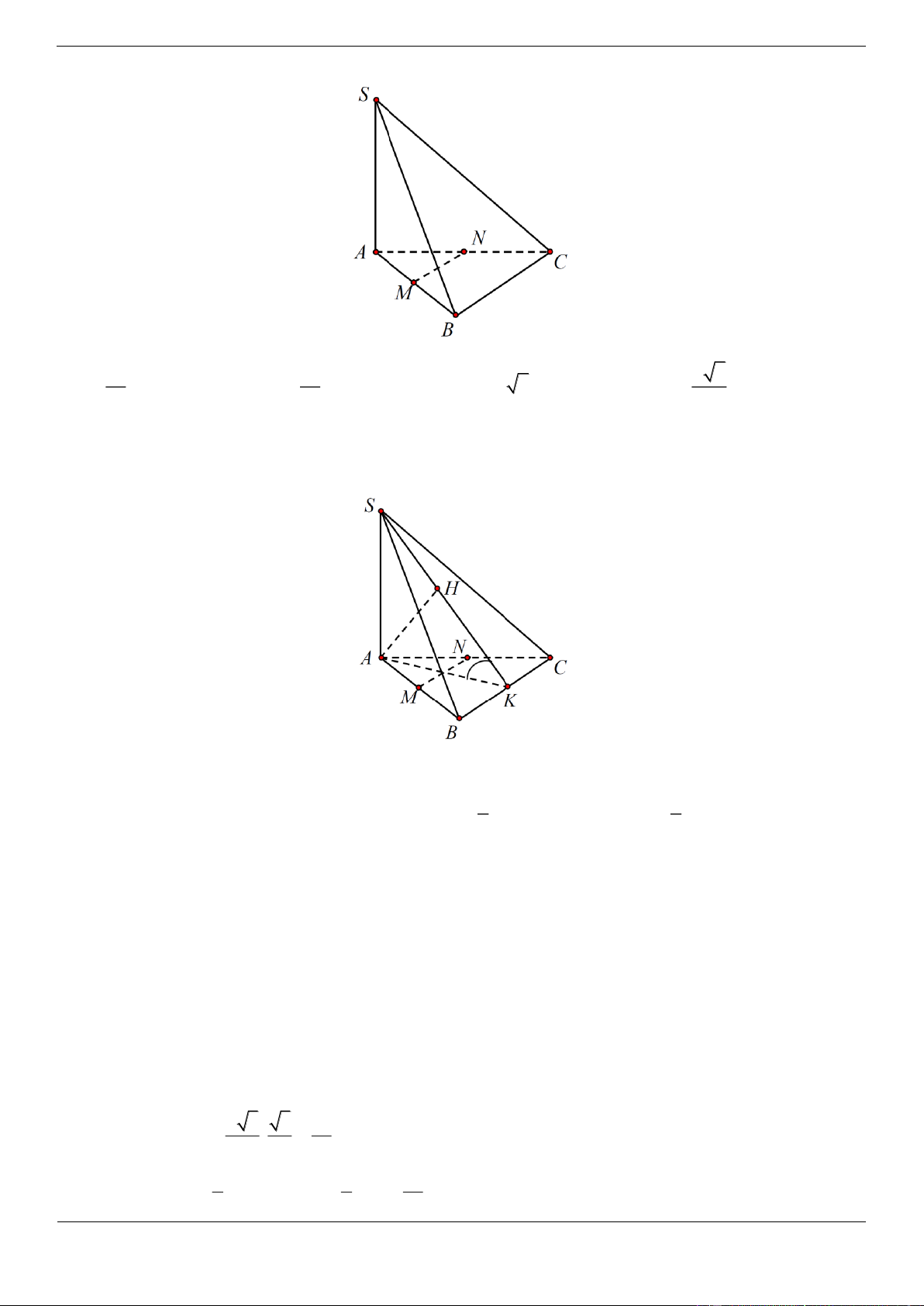
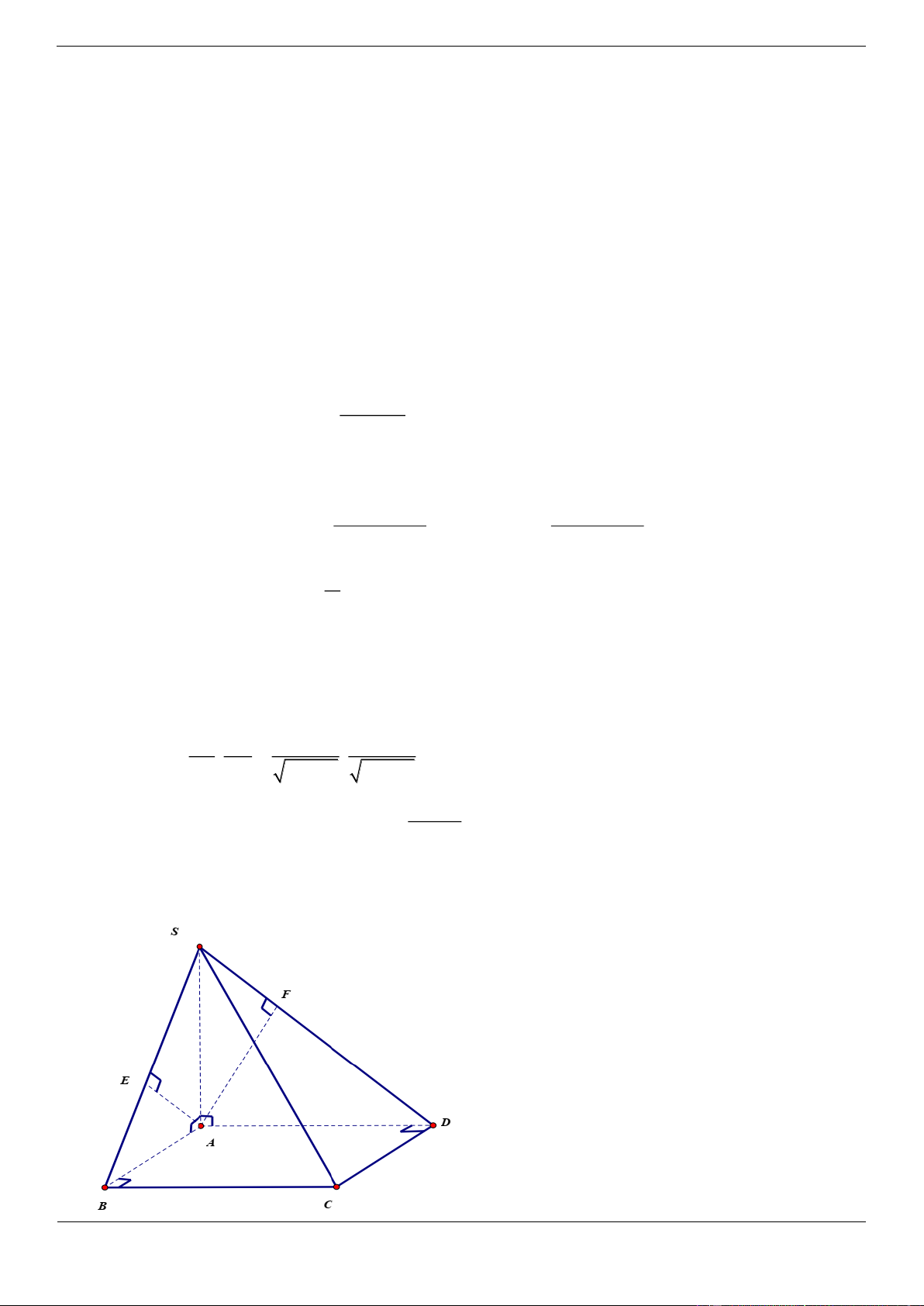
Câu 17.3. Cho tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng
BCD, AB 2a . M là trung điểm đoạn AD , gọi là góc giữa CM với mặt phẳng BCD , khi đó 3 2 3 3 2 6 A. tan B. tan C. tan D. tan 2 3 2 3 Lời giải Trang 26
Gọi N là trung điểm BD, suy ra MN / / AB MN BCD , do đó góc giữa CM với mp BCD bằng góc MCN . AB a 3 MN 2 2 3 MN a,CN tan . a . 2 2 CN a 3 3
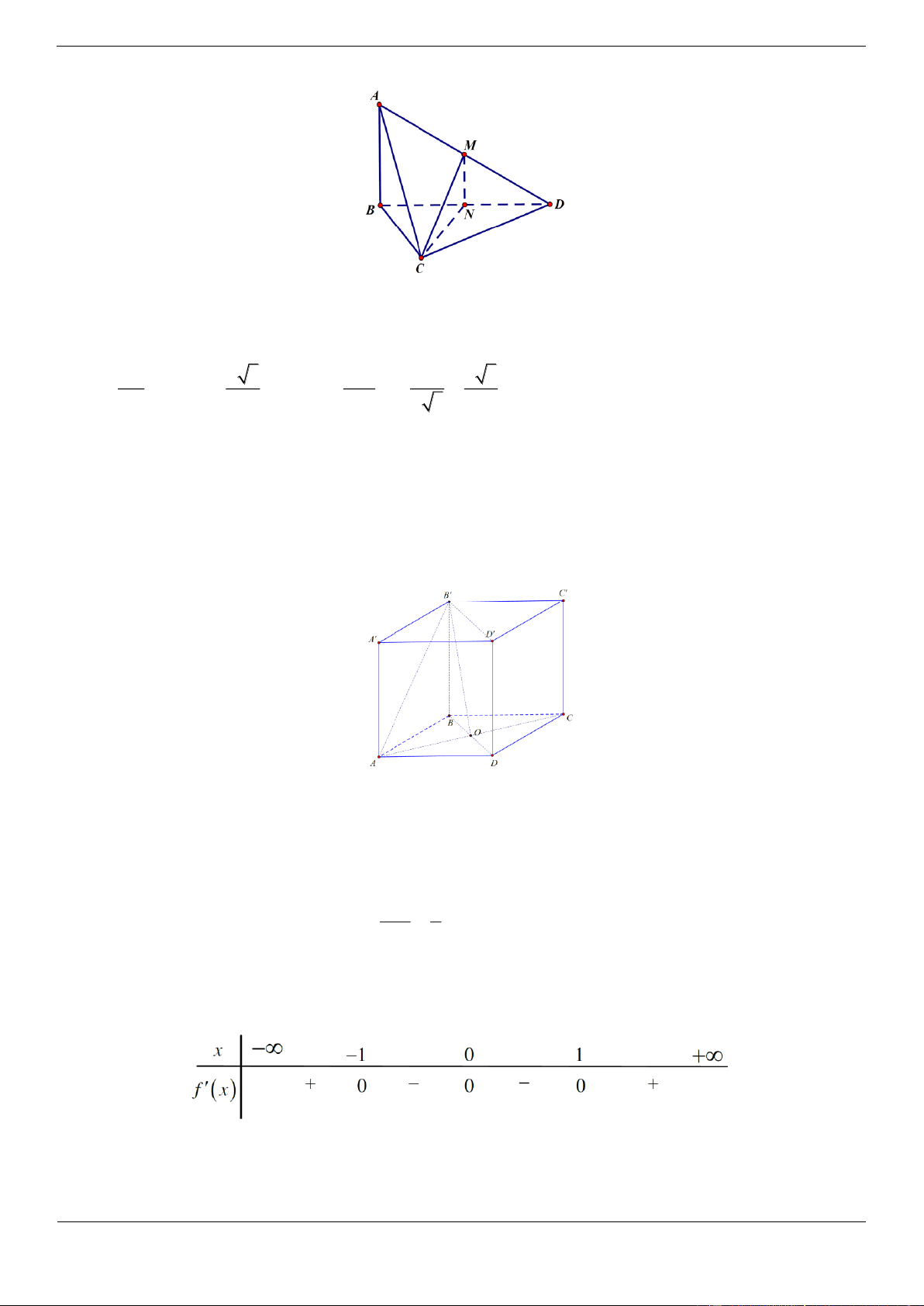
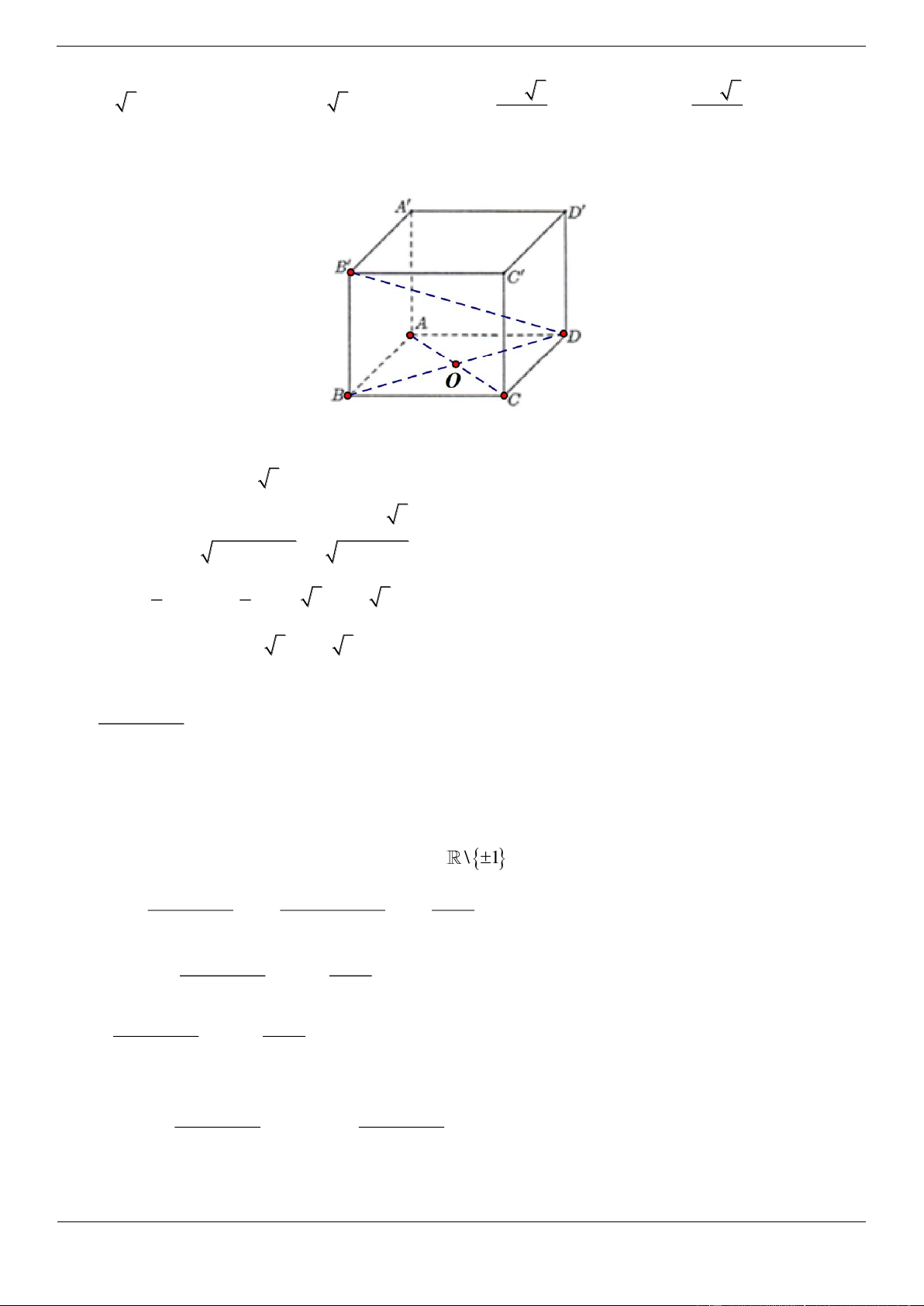
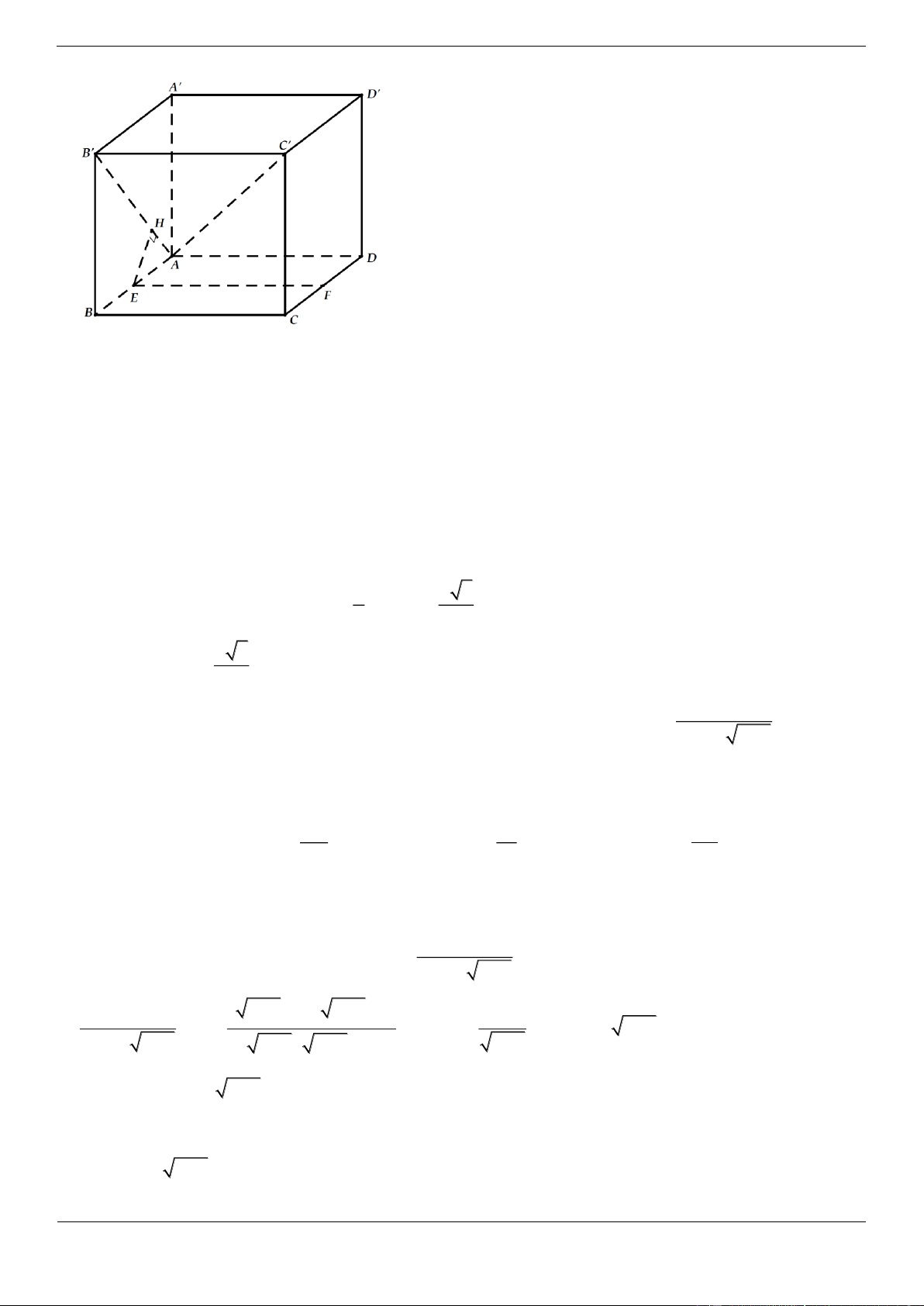
Câu 17.4. Cho hình lập phương ABC . D A B C D
. Tính góc giữa đường thẳng AB và mặt phẳng BDD B A. 60 B. 90 C. 45 D. 30 Lời giải Chọn D
Gọi O là tâm của hình vuông ABCD khi đó ta có AO BD 1 .
Mặt khác ta lại có ABC . D A B C D
là hình lập phương nên BB ABCD BB AO 2.
Từ (1) và (2) ta có AO BDD B
AB ,ABCD AB ,B O AB O . AO 1
Xét tam giác vuông AB O có sin AB O AB O 30 AB . 2
Vậy AB , ABCD 30 .
Câu 18. [ĐỀ THI THAM KHẢO] Cho hàm số f x , bảng xét dấu của f x như sau:
Số điểm cực trị của hàm số đã cho là A. 0 B. 2 C. 1 D. 3 Lời giải Trang 27 Chọn B
Vì đạo hàm của hàm số đã cho đổi dấu 2 lần qua x 1
nên hàm số đã cho có điểm 2 cực trị
Câu 18.1. Cho hàm số f x liên tục trên
, bảng xét dấu của f x như sau:
Khi đó số điểm cực trị của hàm số y f x là: A. 3 B. 2 C. 4 D. 1 Lời giải Chọn A
Do hàm số xác định trên và có biểu thức đạo hàm đổi dấu ba lần tại x ; x ; x nên hàm số y f x có ba 1 2 3 điểm cực trị.
Câu 18.2. Cho hàm số f x có đạo hàm f x x
x x 3 2 2 2 2 , x
. Số điểm cực trị của hàm số là A. 1 B. 2 C. 3 D. 4 Lời giải Chọn C
Ta có f x có 4 nghiệm phân biệt là 4 2;0; 2
Tuy nhiên f x chỉ đổi dấu khi đi qua các nghiệm 4 2 và 2
nên hàm số f x có 3 điểm cực trị.
Câu 18.3. Cho hàm số y f x liên tục trên
, có đạo hàm f x x 2 x 4 1 2
x 4 . Số điểm
cực trị của hàm số y f x là A. 4 B. 2 C. 1 D. 3 Lời giải Chọn C x 1 2
Cho f x 0 x 1 2 x 2 2
x 2 0 x 2 x 2 Bảng biến thiên Trang 28
Vậy hàm số có 1 điểm cực trị.
Câu 18.4. Đường cong của hình vẽ bên là đồ thị hàm số y f x
Số điểm cực trị của hàm số y f x là? A. 4 B. 3 C. 5 D. 2 Lời giải Chọn D
Từ hình vẽ ta thấy f x 0 và đổi dấu tại đúng hai điểm nên hàm số có hai điểm cực trị.
Câu 19. [ĐỀ THI THAM KHẢO] Giá trị lớn nhất của hàm số f x 4 2
x 12x 1 trên đoạn 1 ;2 bằng A. 1 B. 37 C. 33 D. 12 Lời giải Chọn C
Hàm số liên tục và xác định trên 1 ;2. x 0
Ta có: f x 3 4
x 24x f x 3 0 4
x 24x 0 x 6 1 ;2 x 6 1 ;2
Ta có f 0 1; f
1 12; f 2 33 . Vậy max f x 33 . 1 ;2 Phát triển
Câu 19.1: (Tƣơng tự) Tìm giá trị lớn nhất của hàm số y f x x 1 5 x trên đoạn 1;5
A. max f x 3 2
B. max f x 2
C. max f x 2 2
D. max f x 2 1; 5 1; 5 1; 5 1; 5 Lời giải Chọn C
Hàm số đã cho liên tục trên đoạn 1;5 x x
Ta có: f x 1 1 5 1 2 x 1 2 5 x
2. x 1. 5 x
Do đó f x 0 5 x x 1 x 31; 5 Trang 29 Mặt khác f
1 2; f 3 2 2; f 5 2. Vậy max f x f 3 2 2 . 1; 5
Câu 19.2: Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x x 3 x 1 trên đoạn
0;4. Tính M 2N 16 3 256 A. B. C. 3 D. 5 9 27 Lời giải Chọn A 2 2
Ta có f x x 3 x 1 x 3 x
1 . Xét hàm số g x x 3 x
1 , với x 0;4 .
g x x x x 2 2 3 1 3
x 32x
1 x 3 x 33x 1 . x 30;4
g x g 1 256 0 ; 0 0; g
; g 3 0; g 4 ; x 0;4 5 1 3 27 3 Khi đó 256 16 3 16 3
min g x 0; max g x . Hay M
; N 0 . Vậy M 2N . 0;4 0;4 27 9 9
Câu 19.3: Cho hàm số f x liên tục trên đoạn 1 ;
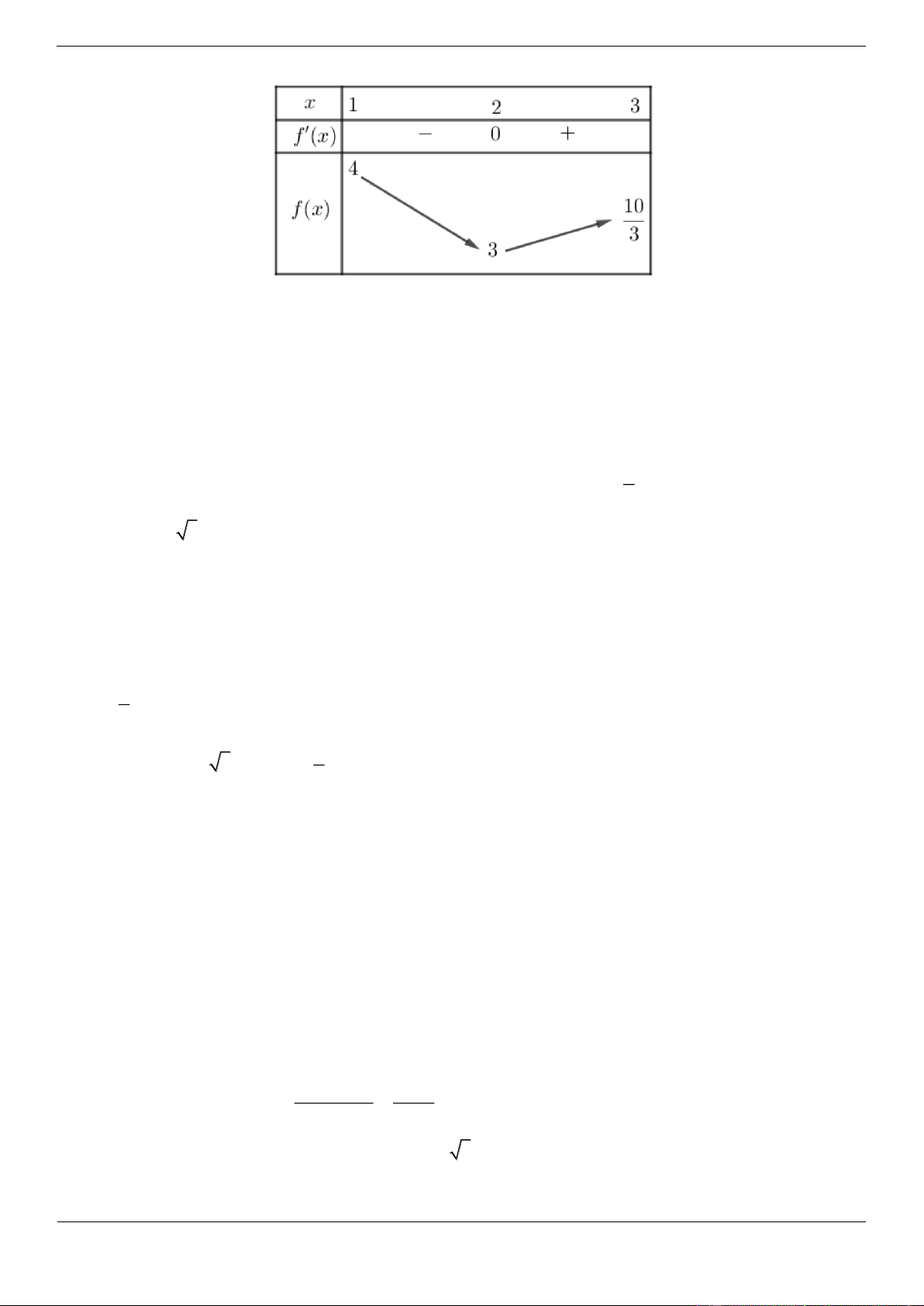
3 và có bảng biến thiên như sau
Tìm giá trị lớn nhất của hàm số y f 3 sin x 1 A. 4 B. 3 C. 2 D. 1 Lời giải Chọn C
Đặt t 3 sin x 1, x
. Ta có 0 sin x 1 0 3 sin x 3 1
3 sin x 1 2. Vậy t 1 ;2 .
Do đó, giá trị lớn nhất của hàm số y f 3 sin x
1 chính là giá trị lớn nhất của hàm số y f t trên đoạn 1 ;2.
Dựa vào bảng biến thiên của hàm số f x ta có max f 3 sin x
1 max f t f 0 2 1 ; 2
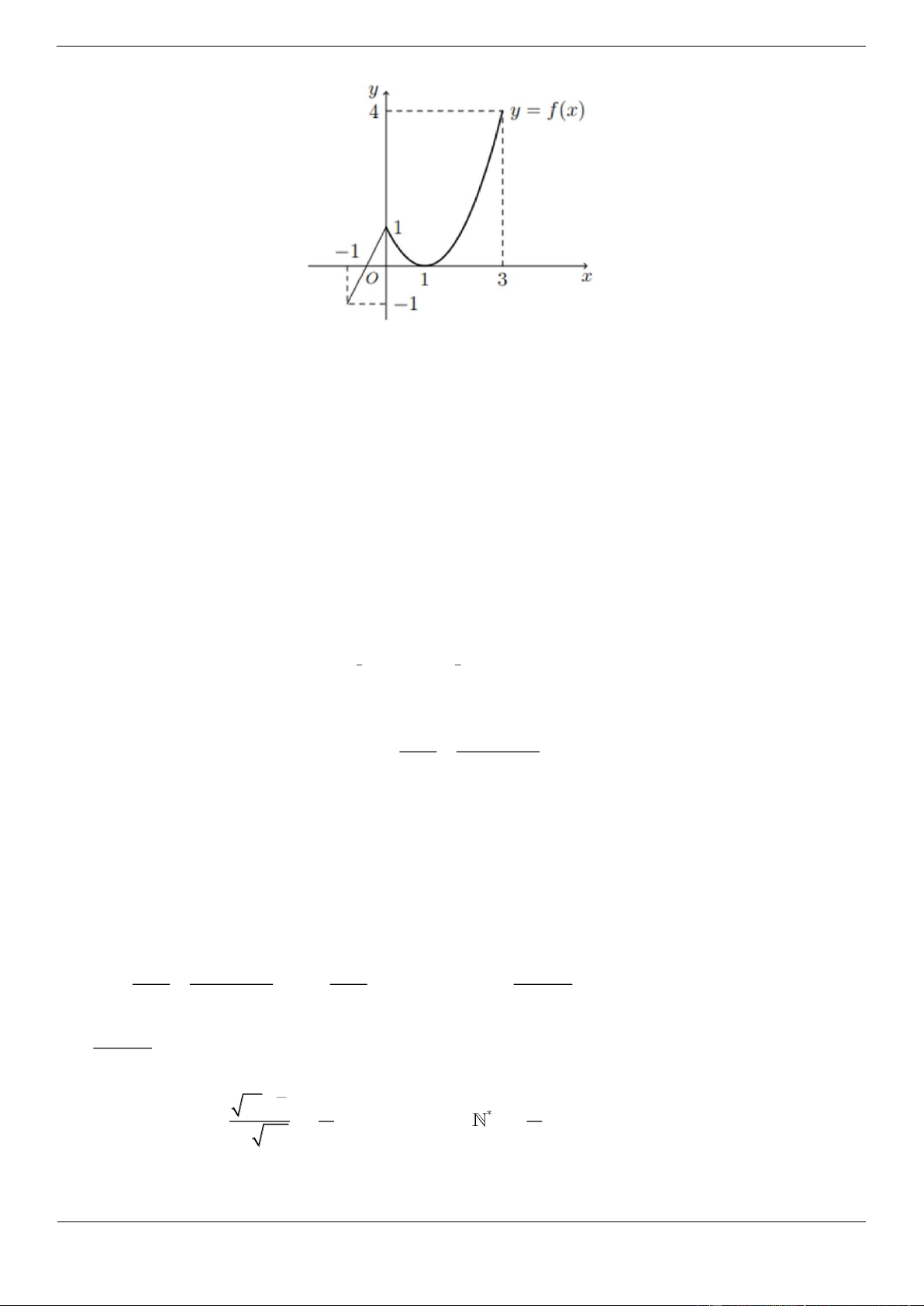
Câu 19.4: Cho hàm số f x liên tục trên 1 ;
3 và có đồ thị như hình vẽ bên. Gọi M , m lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f x trên 1 ;
3 . Tính M m . Trang 30 A. 2 B. 5 C. 3 D. 4 Lời giải Chọn B
Quan sát đồ thị ta thấy hàm số y f x đạt giá trị nhỏ nhất trên 1 ; 3 là 1
tại điểm x 1 và đạt giá trị lớn nhất trên 1 ;
3 là 4 tại điểm x 3 . Do đó M 4, m 1
, nên M m 4 1 5
Câu 20. [ĐỀ THI THAM KHẢO] Xét tất cả các số thực dương a và b thỏa mãn log a log ab . 2 8
Mệnh đề nào dưới đây đúng? A. 2 a b B. 3 a b
C. a b D. 2 a b Lời giải Chọn D
log a log ab log a log ab1 a ab1 2 3 3 a b 2 8 2 2 Phát triển câu 20 a b 2 ln a ln b
Câu 20.1: (Tƣơng tự) Cho a 0,b 0 ln
. Chọn mệnh đề đúng trong các mệnh đề 3 3 sau: A. 3 3 2 2
a b 8a b ab B. 3 3
a b 2 2
3 8a b ab C. 3 3
a b 2 2
3 a b ab D. 3 3
a b 2 2
3 8a b ab Lời giải Chọn D a b 2 ln a ln b a b a b3 Ta có ln 3ln
2ln a ln b ln ln 2 a b 3 3 3 27 a b3
a b a b3 2 2 3 2 2 3 2 3 3
a b a a b ab b
a b a b 2 2 27 3 3 27
3 8a b ab 27 11 3 7 3
a .a m m Câu 20.2: Cho log với * a 0; , m n và
là phân số tối giản. Khẳng định nào sau a 4 7 5 . n a a n đây đúng? Trang 31 A. 2 2 m n 312 B. 2 2 m n 543 C. 2 2 m n 312 D. 2 2 m n 409 Lời giải Chọn A 11 7 11 3 7 6 19 3 3 3 19 Đặ a .a a .a a 19 t 7 A a , suy ra 7 log A log a 5 23 a a 4 7 5 a . a 7 4 7 7 a .a a m 19 m Vậy , mà * , m n và
là phân số tối giản nên 2 2
m 19, n 7 m n 312 . n 7 n b 16
Câu 20.3: Cho a 0,b 0 và a 1 thỏa mãn log b ;log a
. Tính tổng a b . a 2 4 b A. 12 B. 18 C. 16 D. 10 Lời giải 16 16 b b log 2 b a a suy ra log b log log b
ta được b 16 a 2 2 16 b a 2 2 b 16 4
Vậy a b 18 . a Câu 20.4: Nếu 2
log a log b 5 và 2
log a log b 7 thì giá trị của là 8 4 4 8 b A. 2 B. 18 2 C. 8 D. 9 2 Lời giải Chọn C
Điều kiện a 0,b 0 1 2 log a log b 5 6 2 2 log a log b 5 log a 6 a 2 8 4 3 2 a . Vậy 3 2 8 2 3
log a log b 7 1 log b 3 b 2 b 2 4 8
log a log b 7 2 2 3 2
Câu 21. [ĐỀ THI THAM KHẢO] Tập nghiệm của bất phương trình x 1 x x9 5 5 là A. 2 ;4 B. 4 ;2 C. ;
24; D. ; 4
2; Lời giải
Chọn A. Ta có bất phương trình 2 2
x 1 x x 9 x 2x 8 0 2 x 4
Vậy tập nghiệm của bất phương trình đã cho là S 2 ;4 . Phát triển 3 x 3x2 1
Câu 21.1: (Tƣơng tự) Tập nghiệm của bất phương trình 4 là 2 A. ; 03; B. ; 0 C. 3; D. 0; 3 Lời giải Chọn D Trang 32 2 2 x 3x2 x 3x2 2 1 1 1 Ta có 2 4
x 3x 0 0 x 3 . 2 2 2
Câu 21.2: Tập nghiệm của bất phương trình 2
log x 3log x 2 0 là 2 2 A. 4; B. 2; 4
C. 0;24; D. 0; 2 Lời giải Chọn B
Điều kiện xác định x 0 Ta có 2 2
log x 3log x 2 0 1 log x 2 2 x 4 2 2 2
Vậy tập nghiệm của bất phương trình là S 2;4
Câu 21.3: Số nghiệm nguyên của bất phương trình log 1,5x 4 log 13x 8 là 0,8 0,8 A. 1 B. 4 C. 3 D. 2 Lời giải Chọn D x 2 1
5x 4 13x 8 2x 4 Ta có log 15x 4 log 13x 8 0,8 0,8 4 1 5x 4 0 1 5x 4 x 15 4 x 2 15
Nghiệm nguyên của bất phương trình đã cho là x 0; 1 . 2 2
Câu 21.4: Tổng tất cả các nghiệm nguyên không âm của bất phương trình x x 1 2
.3x x 18 bằng A. 3 B. 2 C. 4 D. 1 Lời giải Chọn A x x Ta có x x x x x x x x 2 2 2 2 2 2 1 x x 2 2 2 .3 18 2 .3 36 2.3 36 6
6 x x 2 0 . 1 x 2
Như vậy các nghiệm nguyên không âm của bất phương trình là x 0;1; 2 .
Do đó tổng tất cả các nghiệm nguyên không âm của bất phương trình đã cho bằng 3 .
Câu 22. [ĐỀ THI THAM KHẢO] Cho hình trụ có bán kính đáy bằng 3 . Biết rằng khi cắt hình trụ đã
cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng A. 18 B. 36 C. 54 D. 27 Lời giải Chọn B
Ta có hình trụ có bán kính đáy R 3 .
Thiết diện qua trục thu được là một hình vuông nên hình trụ có chiều cao h 2R 6 . Trang 33 Vậy S
2 Rh 36 . xq
Nhận xét. Đây là một dạng toán cơ bản, học sinh phải hình dung được hình dạng của thiết diện
tạo thành khi cắt hình trụ, hình nón, hình cầu bởi một mặt phẳng.
Câu hỏi tương tự
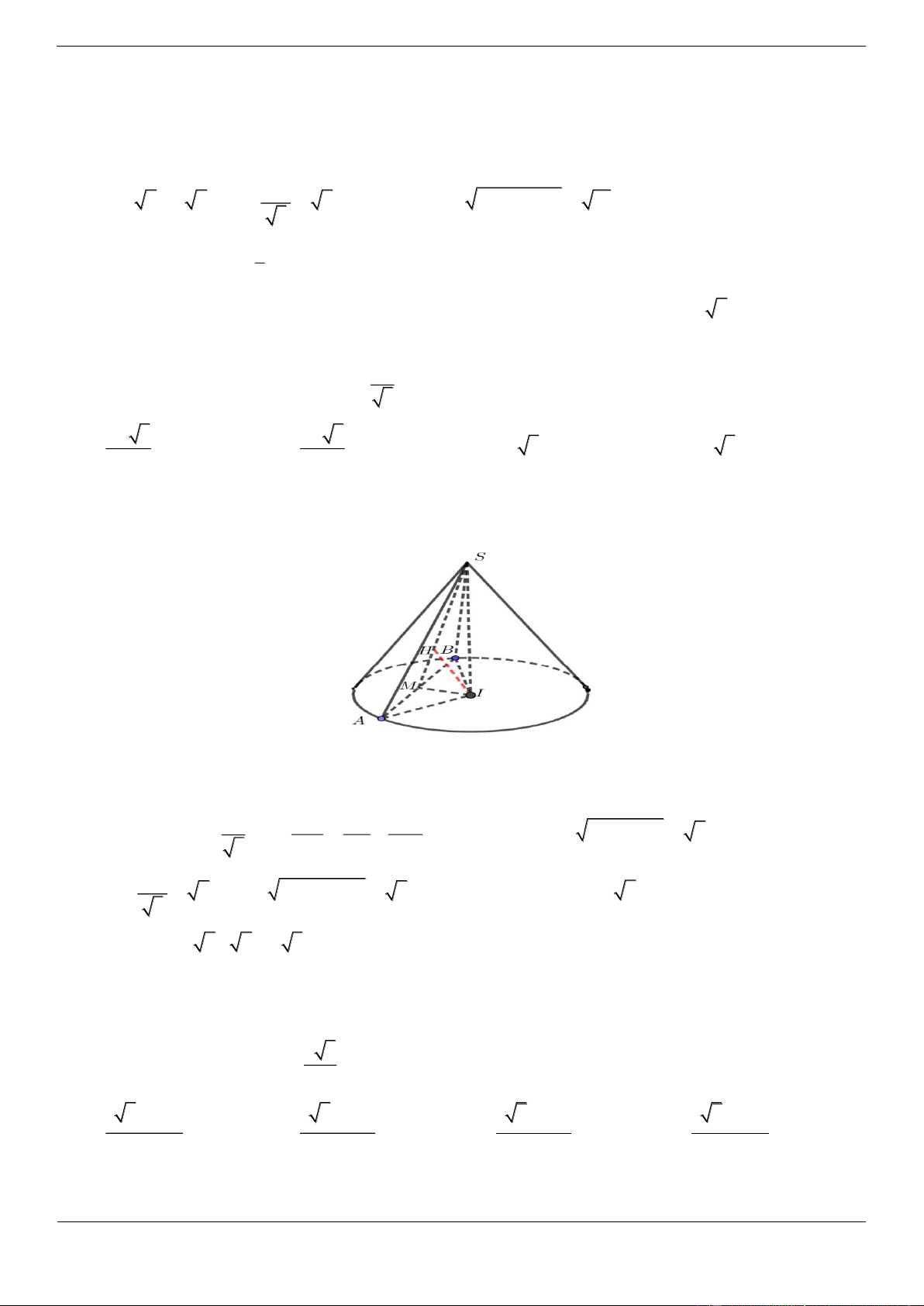
Cho hình nón đỉnh S , đáy là hình tròn tâm O , bán kính R 3, góc ở đỉnh của hình nón là 120. Cắt
hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB , trong đó A, B thuộc đường tròn đáy.
Diện tích của tam giác SAB bằng A. 6 3 B. 6 C. 3 3 D. 3 Lời giải Chọn C 2R
Do góc ở đỉnh của hình nón 120 , gọi l là độ dài đường sinh ta có l 2 3 SA 3 Khi đó, diệ 3
n tích của tam giác SAB bằng 2 S SA 3 3 . 4
Câu 22: (Phát triển 1)
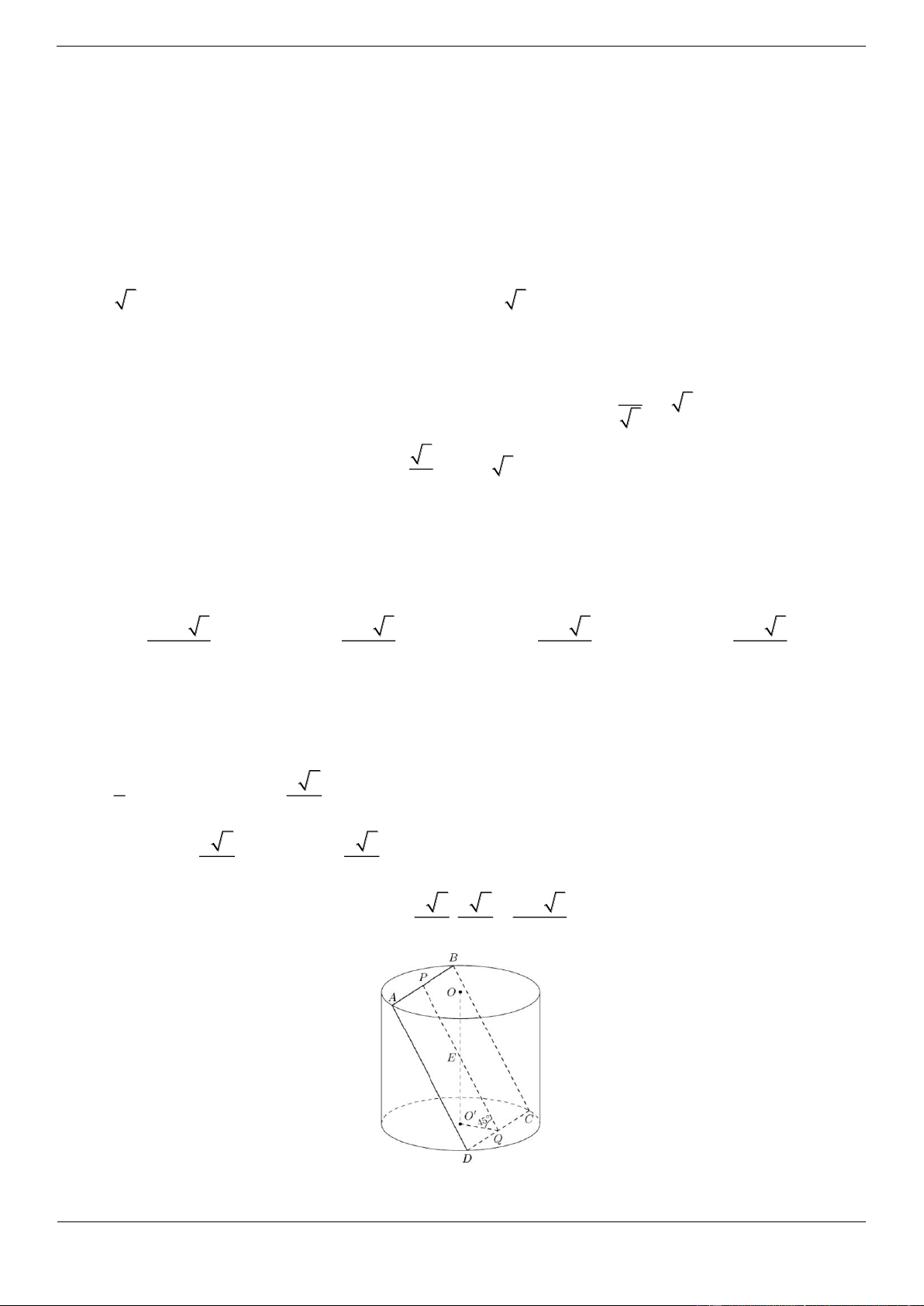
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn
đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng
ABCD tạo với đáy hình trụ góc 45 . Tính diện tích xung quanh hình trụ? 2 2 a 3 2 a 3 2 a 3 2 a 3 A. S B. S C. S D. S xq 5 xq 3 xq 4 xq 2 Lời giải Chọn D Gọi , P ,
Q E lần lượt là trung điểm A , B C ,
D OO . Góc giữa ABCD và mặt đáy là O Q
E 45 . Ta có a a EQ , do đó 2 O Q EO 2 4 a 2 a 6
Suy ra h OO và r O C 2 4 2 a 6 a 2 a 3
Diện tích xung quanh của hình trụ là S 2. . . xq 4 2 2
Câu 22: (Phát triển 2) Trang 34
Cắt hình nón đỉnh I bởi một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông cân có cạnh
huyền bằng a 2 , BC là dây cung của đường tròn đáy hình nón sao cho mặt phẳng IBC tạo với mặt
phẳng chứa đáy hình nón một góc 60 . Tính theo a diện tích S của tam giác IBC . 2 a 3 2 a 2 a 2 2 2a A. S B. S C. S D. S 3 3 3 3 Lời giải Chọn C a 2
Tam giác IDC vuông cân có DC a 2 IH HC và IC a . 2
Gọi E là trung điểm cạnh BC , góc giữa mặt phẳng IBC và BCD là IEH 60 . IH a 6
Trong tam giác IHE có IE . sin 60 3 2 3 Tam giác IEC có 2 2 2 2 CE
IC IE a a a 3 3 2 a 2
Vậy S EI.EC 3
Câu 22: (Phát triển 3)
Khi sản xuất cái phễu hình nón (không có nắp) bằng nhôm, các nhà thiết kế luôn đạt mục tiêu sao cho chi
phí nguyên liệu làm phểu ít nhất, tức là diện tích xung quanh của hình nón là nhỏ nhất. Hỏi nếu ta muốn
sản xuất cái phễu có thể tích là 2 dm3 thì diện tích xung quanh của cái phễu sẽ có giá trị nhỏ nhất gần với
giá trị nào sau đây nhất? Trang 35 A. 6,85 dm2. B. 6,75 dm2. C. 6,65 dm2. D. 6,25 dm2. Lời giải Chọn C
Gọi R, h, l lần lượt là bán kính đáy, chiều cao và độ dài đường sinh của cái phễu. Khi đó 1 6 36 2
V R .h 2 h và 2 2 2
l h R R . 2 3 R 2 4 R 36 36
Diện tích xung quanh của hình nón là 2 2 4 S . . R l R R R . xq 2 4 2 R R 36 18 18 Ta có R
R 3 18 2 2 4 2 4 3 . 2 2 2 R R R 18 18
Dấu bằng xảy ra khi và chỉ khi 2 4 6
R R . Suy ra S . xq 2 3 3 18 6, 65 2 2 R
Câu 23. [ĐỀ THI THAM KHẢO] Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm của phương trình 3 f x 2 0 là A. 2 B. 6 C. 3 D. 1 Lời giải Chọn C
Ta có: f x f x 2 3 2 0 3 2
Từ bảng biến thiên ta thấy đường thẳng : d : y
cắt đồ thị hàm số y f x tại 3 điểm phân biệt nên 3
phương trình đã cho có 3 nghiệm phân biệt.
Nhận xét. Dạng toán ở mức độ thông hiểu. Học sinh cần kĩ năng quan sát và đọc bảng biến thiên, từ đó
biện luận được số nghiệm phương trình thông qua sự tương giao giữa hai đồ thị. Câu 23 (Tƣơng tự)
Cho hàm số f x m xác định trên \
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau Trang 36
Tìm tất cả giá trị thực của tham số m để phương trình f x m có ba nghiệm thực phân biệt.
A. m 1;3
B. m 1; 3
C. m 1; 3
D. m 1;3 Lời giải Chọn A
Dựa vào biến thiên, phương trình có ba nghiệm thực phân biệt khi m 1;3 .
Câu 23 (Phát triển 1)
Tìm tất cả các giá trị của tham số m để phương trình 2
x m 9 x 0 có đúng 1 nghiệm dương? A. m 3 ; 3 B. m 3 ; 3 3
2 C. m0; 3 D. m 3 2 Lời giải Chọn A Điều kiện 3
x 3. Phương trình tương đương với 2
x 9 x m .
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số 2
y x 9 x và đường thẳng y m . 2 x 9 x x Xét hàm số 2
y x 9 x với 3
x 3. Ta có y 1 . 2 2 9 x 9 x x 0 3 2 2
y 0 9 x x x 3 ; 3 . 2 2 9 x x 2 Bảng biến thiên
Dựa vào bảng biến thiên phương trình có đúng một nghiệm khi 3 m 3 .
Câu 23 (Phát triển 2)
Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ sau m x 1
Số các giá trị nguyên của tham số m để phương trình f 7 2 1
0 có hai nghiệm phân biệt là 8 A. 6 B. 4 C. 7 D. 5 Trang 37 Lời giải Chọn D
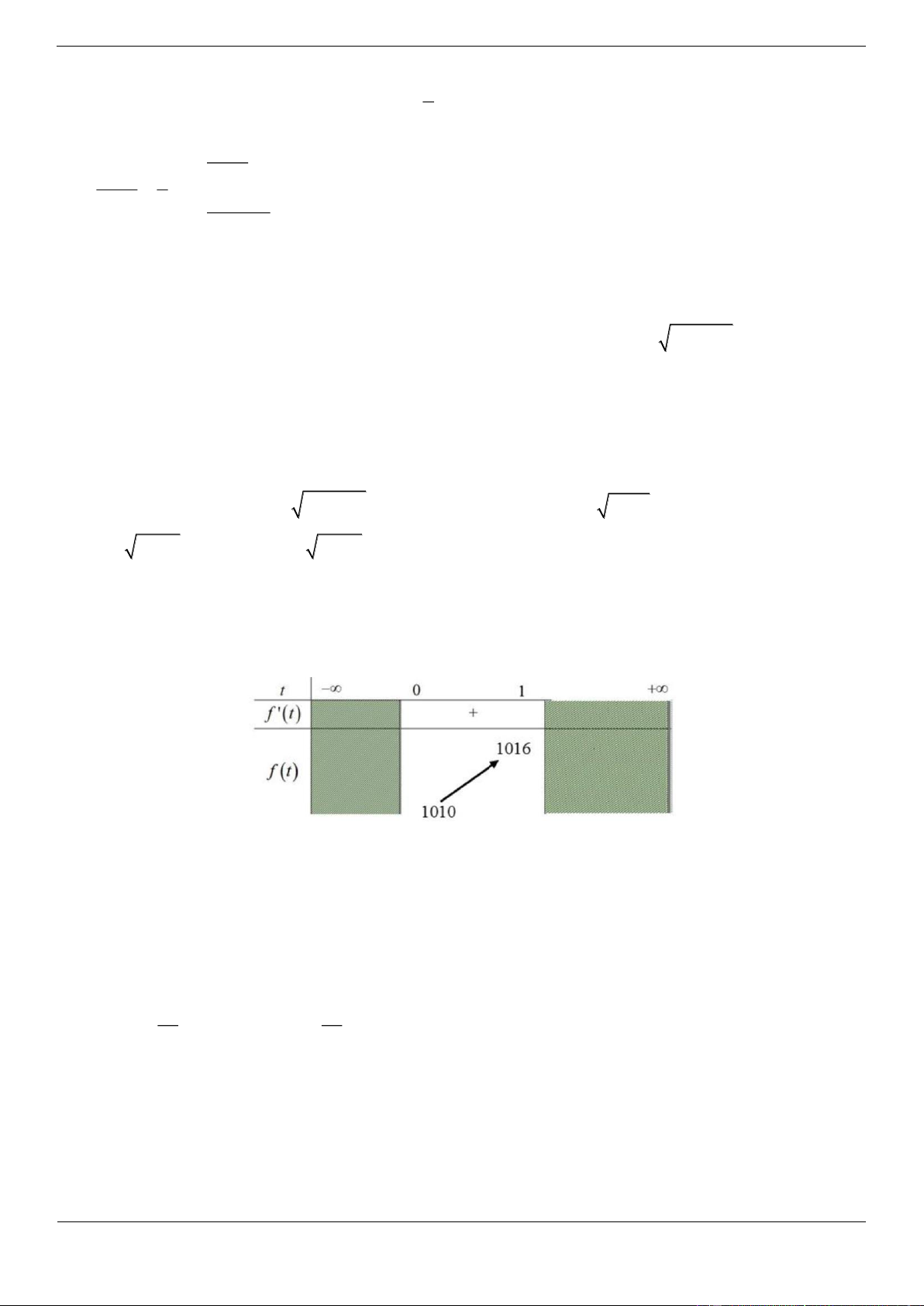
Từ đồ thị ta suy ra hàm số y f x có phương trình 3
y x 3x 1. Đặt x 1 t 7
,t 0 . Khi đó ta có phương trình f t 2 m
f t 2 1 m 1 0 ,t 0 . 8 8 m
Dựa vào đồ thị hàm số y f x như hình vẽ. Với t 0 để phương trình f t 2 1 có hai nghiệm 8 khi và chỉ khi 2 m 1 2 2 1 1 8
m 1 8 7
m 9 m0; 1 ; 2 . 8
Vậy có 5 giá trị nguyên của tham số m để phương trình có 2 nghiệm phân biệt.
Câu 23 (Phát triển 3)
Cho hàm số y f x có đạo hàm trên
và có đồ thị như hình vẽ. Đặt g x f f x 1 . Tìm số
nghiệm của phương trình g x 0 . A. 3 B. 4 C. 9 D. 8 Lời giải Chọn C 1
Từ đồ thị, ta thấy hàm số y f x có ba điểm cực trị x , x 1 và x a 1 a 2 . Do đó 3 1
f x 0 có ba nghiệm x , x 1 và x a 1 a 2 . 3
f x 0 1
Ta có g x 0 f x. f f x 1 0 f
f x 1 0 2
Phương trình (1) có ba nghiệ 1
m x , x 1 và x a 1 a 2 . 3 Trang 38 f x 1 f x 2 1 3 3 3
Phương trình (2) f x 1 1 f x 2 4 .
f x 1 a
f x a 1 5
Nghiệm của phương trình f x m là phương trình hoành độ giao điểm của đồ thị hàm số
y f x với đường thẳng y m. Từ đồ thị của hàm số y f x , ta vẽ thêm các đường thẳng 2 y 2, y
và y a 1 (với 2 a 1 3) như sau 3 2
Từ đồ thị trên, ta thấy các đường thẳng y 2, y
và y a 1 (với 2 a 1 3) lần lượt cắt đồ thị tại 3 hai điể 1
m phân biệt khác nhau và khác với , 1, a . Do đó các phương trình (3),(4),(5) 3 1
lần lượt có hai nghiệm phân biệt khác nhau và khác với , 1, a . 3
Vậy phương trình g x 0 có 9 nghiệm phân biệt x
Câu 24. Họ tất cả các nguyên hàm của hàm số f x 2
trên khoảng 1; là x 1 3 3
A. x 3ln x 1 C
B. x 3ln x 1 C C. x D. x C x C 2 1 x 2 1 Lời giải x
Ta có: f x 2 3 1 x 1 x 1 f x 3 1 dx 1 dx dx 3 dx x 3ln x
1 C với x 1; x 1 x 1
Nhận xét. Đây là một dạng toán cơ bản về nguyên hàm, mức độ thông hiểu. Học sinh biết chia đa thức để
tách phân thức hữu tỉ đưa về các nguyên hàm quen thuộc. Câu 24 (Tƣơng tự) Trang 39 4 2x 3 Cho hàm số y
trên khoảng 0; . Khẳng định nào sau đây là đúng? 2 x x x A. f x 3 2 3 dx C B. f x 3 2 3 dx C 3 2x 3 x 3 x C. f x 3 dx 2x C D. f x 3 2 3 dx C x 3 x Lời giải Chọn D 2x 3 3 2x 3 Ta có f x 4 3 2 dx dx 2x dx C 2 2 x x 3 x
Câu 24 (Phát triển 1) 2 cos x 1
Cho hàm số F x là một nguyên hàm của hàm số f x
trên khoảng 0; . Biết rằng giá trị 2 sin x
lớn nhất của F x trên khoảng 0; là 3 . Chọn mệnh đề đúng trong các mệnh đề sau. 2 3 5 A. F 3 3 4 B. F C. F 3 D. F 3 3 6 3 2 3 6 Lời giải Chọn A 2 cos x 1 2 cos x 1 1 1 Ta có : f
xdx dx dx dx 2 d sin x dx 2 2 2 2 2 sin x sin x sin x sin x sin x
Do đó F x f x 2 dx
cot x C sin x 2 cos x 1 1
Ta có F x f x
0 cos x x 0; . 2 sin x 2 3
Hàm F x đạt giá trị lớn nhất tại x . Suy ra 3 2 4 3 3
cot C 3
C 3 C 2 3 3 3 3 sin 3
Do đó F x 2
cot x 2 3 nên F 3 3 4 . sin x 6
Câu 24 (Phát triển 2) Trang 40
Cho hàm số f x có đạo hàm liên tục trên 1
; . Biểu thức x x
2 f x x 1 f x 2 1 2 được thỏa mãn x 1
;. Tính giá trị f 0 . 2 x 3 A. 3 3 B. 2 3 C. 3 D. 3 Lời giải Chọn B x x 1
Vì 2 f x x 1 f x 2 2 được thỏa mãn x 1
; nên f 1 1 2 x 3 Trên khoảng 1 ; , ta có: x x
2 f x x 1 f x 2 1 2 2 x 3 2 x 1 x f x f x 2 x 2 1 x 1 x 3 x 1 . f x 2x 3 . x 1
Do đó x 1. f x 2
x 3 C x 1 0
Khi x 1 ta có . f 2
1 1 3 C C 2
. Vậy f 0 2 3 . 2
Câu 24 (Phát triển 3) 1 2
Cho hàm số f x có đạo hàm liên tục trên đoạn 0
;1 thỏa mãn f 1 0, f
x dx 7 và 0 2 1 1 2 sin . x cos .
x f sin x dx . Tính tích phân
f x dx bằng 3 0 0 7 7 A. B. 4 C. D. 1 5 4 Lời giải Chọn A 2 Xét tích phân 2 I sin . x cos . x f sin x dx 1 0
Đặt t sin x dt cos .
x dx . Ta có: x 0 t 0; x t 1. 2 1 1 1 Ta có: 2
I t f t 2
dt x f x dx
(tính chất không phục thuộc biến số). 3 0 0 Trang 41 1 1 1 1 1 1 1 Ta có 2 x f x 3 dx x f x 3 x f x 3 dx
x f xdx 1 . 3 3 3 0 0 0 0 1 1 1 1 2 2 Ta có f x 3
7x dx f x 3
dx 14 x f x 6
dx 49 x dx 7 14 7 0 . 0 0 0 0 1 Do đó 2 7 f x 3
7x dx 0 f x 3
7x 0 f x 3 7
x f x 4 x C . 4 0 1 1 7 7 7 7
Theo giả thiết f 1 0 C f x 4 dx x dx . 4 4 4 5 0 0 1 7 Vậy
f x dx 5 0
Câu 25. [ĐỀ THI THAM KHẢO] Để dự báo dân số của một quốc gia, người ta sử dụng công thức . nr S
A e , trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ gia tăng dân
số hằng năm. Năm 2017, dân số Việt Nam là 93.671.600 người (Tổng cục Thống kê, Niên giám thống
kê 2017, Nhà xuất bản Thống kê, Tr.79 ). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,81%, dự báo
dân số Việt Nam năm 2035 là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)?
A. 109.256.100. B. 108.374.700. C. 107.500.500. D. 108.311.100. Lời giải Chọn B
Từ năm 2017 đến năm 2035 có 18 năm. Áp dụng công thức nr 18.0,81% S .
A e 93.671.600.e 108.374.700 .
Câu 25.1 (câu tƣơng tự).
Để dự báo dân số của một quốc gia, người ta sử dụng công thức . nr S
A e , trong đó A là dân số của năm
lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ gia tăng dân số hằng năm. Năm 2017, dân số Việt Nam
là 93.671.600 người (Tổng cục Thống kê, Niên giám thống kê 2017, Nhà xuất bản Thống kê, Tr.79 ). Giả
sử tỉ lệ tăng dân số hàng năm không đổi là 0,79% , dự báo dân số Việt Nam năm 2040 là bao nhiêu người
(kết quả làm tròn đến chữ số hàng trăm)? A. 112.336.100. B. 112.336.075. C. 112.336.080. D. 112.366.100. Lời giải Chọn A
Từ năm 2017 đến năm 2040 có 23 năm. Áp dụng công thức nr 23.0,79% S .
A e 93.671.600.e 112.336.100
Câu 25.2 (phát triển)
Số lượng của một loại vi khuẩn được nuôi cấy trong phòng thí nghiệm tăng lên theo công thức . rt S A e ,
trong đó A là số lượng ban đầu, t là thời gian (tính bằng giờ), r là tỉ lệ tăng trưởng, S là số lượng sau t giờ.
Biết rằng A 1000 con, r 10% , hỏi cần khoảng mấy giờ để đạt được 20000 con? A. 29 giờ. B. 30 giờ. C. 31 giờ. D. 32 giờ. Lời giải Chọn B Trang 42 S ln A
Từ công thức S . rt A e t , thay số ta được: r 2000 ln 1000 ln 20 t
29,96 , hay cần khoảng 30 giờ để đạt được số lượng cần thiết. 10% 0,1
Câu 25.3 (phát triển).
Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất là 7% /năm. Biết rằng nếu không rút
ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ nhập vào vốn ban đầu (người ta gọi là lãi kép). Để
người đó lãnh được số tiền 250 triệu thì người đó cần gửi trong khoảng thời gian là ít nhất bao nhiêu
năm? (nếu trong khoảng thời gian này không rút tiền và lãi suất không thay đổi) A. 12 năm. B. 15 năm. C. 14 năm. D. 13 năm. Lời giải Chọn C n
Gọi n là số năm cần gửi, bài toán thuộc lãi kép gửi một lần tính theo công thức T M 1 r với M , r là n
số tiền ban đầu và lãi suất định kì. Thế thì ta có 250 1001 0,07 suy ra n 13,5 nên người đó gửi ít
nhất là 14 năm mới đủ số tiền.
Câu 25.4 (phát triển)
Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quý), lãi suất 6% một quý theo hình
thưc lãi kép. Sau đúng 6 tháng, người đó lại gửi thêm 100 triệu đồng với hình thức và lãi suất như trên.
Hỏi sau 1 năm tính từ lần gửi đầu tiên người đó nhận số tiền gần với kết quả nào nhất?
A. 224,7 triệu đồng.
B. 243,5 triệu đồng
C. 236.2 triệu đồng
D. 238,6 triệu đồng. Lời giải Chọn D
Sau 6 tháng đầu thì người đó gửi được hai kì hạn nên tổng cả vốn và lãi lúc đó là A 2 100. 1, 06 triệu đồng.
Người đó gửi thêm 100 triệu thì số tiền gửi là B A100 triệu. 2 4 2
Vậy sau một năm thì được số tiền là B 1,06 100.1,06 100.1,06 238,6 triệu đồng.
Câu 26. [ĐỀ THI THAM KHẢO] Cho khối lăng trụ đứng ABC . D A B C D
có đáy là hình thoi cạnh
BD a 3 và AA 4a (minh họa như hình bên dưới). Thể tích của khối lăng trụ đã cho bằng 2 3 4 3 A. 3 2 3a B. 3 4 3a C. 3 a D. 3 a 3 3 Trang 43 Lời giải Chọn A 3
Vì ABCD là hình thoi cạnh a, có 2 2
BD a 3 AC 2.AO 2. a
a a , với O là trung điểm AC. 4 2 a 3 Suy ra S AC.BD . ABCD 2 Vậy 3
V AA .S 2 3a ABCD
Câu 26.1 (câu tƣơng tự)
Tính thể tích khối lăng trụ đứng ABC . D A B C D
có đáy là hình vuông cạnh a và đường chéo A C 2a A. 3 a B. 3 a 3 C. 3 a 2 D. 3 2a Lời giải Chọn C Ta có 2 2 2 2
AC a 2, AA A C
AC 4a 2a a 2 2 S a ABCD Vậy 2 3
V a .a 2 a 2 .
Câu 26.2 (phát triển)
Cho hình lăng trụ tam giác đều AB . C A B C
có AB 2a , góc giữa hai mặt phẳng A B
C và ABC
bằng 60 . Tính thể tích của khối lăng trụ đã cho. 3 3a 3 3 3a 3 A. 3 3a 3 B. C. 3 3a 6 D. 8 6 Lời giải Chọn A Trang 44
Gọi M là trung điểm của BC . Tam giác ABC đều nên AM BC , vì AA là đường cao lăng trụ nên
BC AA . Do đó, BC AA M nên A B
C; ABC AMA 60 .
Suy ra AA AM.tan AMA a 3.tan 60 3a . 2 4a 3
Vậy thể tích cần tìm là 3
V AA .S 3 . a 3a 3 . ABC 4
Câu 26.3 (phát triển)
Cho hình lăng trụ tứ giác đều ABC . D A B C D
có cạnh đáy bằng a và góc giữa A B và mặt phẳng A A
CC bằng 30. Tính thể tích V của khối lăng trụ đã cho. A. 3 V a B. 3 V a 3 C. 3 V a 2 D. 3 V 2a Lời giải Chọn A
Gọi O AC BD BO AC Ta có:
BO ACC A
tại O. Do đó góc giữa A B
và mặt phẳng A A CC là BO A A BA O BA O 30. 2 2 BO 1 a 6 3a a Suy ra : 2 2 tan 30 A O A A A O AO a A O 3 2 2 2
Vậy thể tích V của khối lăng trụ đã cho là 2 3
V AA .S . a a a . ABCD
Câu 26.4 (phát triển)
Cho khối lăng trụ đứng ABC . D A B C D
có đáy là hình thoi cạnh 2 ,
a AA 2a , góc giữa B D và mặt
đáy bằng 30 (minh họa như hình bên dưới). Thể tích của khối lăng trụ đã cho bằng Trang 45 3 2a 3 3 4a 3 A. 3 2 3a B. 3 4a 3 C. D. 5 3 Lời giải Chọn B
Vì BD là hình chiếu của B D
trên mặt phẳng ABCD nên B D
B 30 là góc giữa B D và mặt đáy
BD B .
B cot 30 2a 3
Vì ABCD là hình thoi cạnh 2a có BD 2a 3 2 2 2 2
AC 2AO 2 AB BO 2 4a 3a 2a 1 1 2 S
AC.BD .2 .
a 2a 3 2a 3 ABCD 2 2 2 3
V AA .S 2 . a 2a 3 4a 3 ABCD
Câu 27. [ĐỀ THI THAM KHẢO] Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 5x 4x 1 y là 2 x 1 A. 0 B. 1 C. 2 D. 3 Lời giải Chọn C Điều kiện: 2
x 1 0 x 1
. Suy ra: TXĐ: D \ 1 2 5x 4x 1 x 1 5x 1 5x 1 Ta có: lim lim lim 3 2 x 1 x 1 x 1 x 1 x x 1 1 x 1 2 5x 4x 1 5x 1 + Ta có: lim lim x 2 1 x 1 x 1 x 1 2 5x 4x 1 5x 1 lim lim x 2 1 x 1 x 1 x 1
=> Đồ thị hàm số có một tiệm cận đứng x 1 2 5x 4x 1 2 5x 4x 1 + Ta có: lim 5 và lim
5 => Đồ thị hàm số có một đường tiệm cận ngang 2 x x 1 2 x x 1 y 5 .
Vậy tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là 2. Trang 46
Câu 27.1 (câu tƣơng tự) 2 x 6x 8
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số f x 2
x 4x 3 x 2 A. 5 B. 2 C. 4 D. 3 Lời giải Chọn B 2
x 4x 3 0 x 2 Điều kiện:
. Suy ra: D 2; \ 3 . x 3 x 2 0 6 8 2 1 2 x 6x 8 + Ta có: lim lim x x f x x x lim 0 2
x 4x 3 x 2 x 4 3 1 x 2 2 x x
Suy ra đồ thị hàm số có tiệm cận ngang là: y 0. 2 x 6x 8
x 2x 4
x 2 x 4
+ Ta có: lim f x lim . x x lim lim 0 2
x 4x 3 x 2 x 2 2 2 2
x 4x 3 x2 x 2
2x 4x3 + Ta có: x x x x lim f x 2 6 8 1 2 4 lim x x lim . 2 3 3
x 4x 3 x 3 x 2 x 3 x 1
Suy ra đồ thị hàm số có tiệm cận đứng là: x 3.
Vậy đồ thị hàm số có 2 tiệm cận 2 x 1
Câu 27.2 (phát triển) Đồ thị hàm số y có bao nhiêu tiệm cận? x 1 A. 3 B. 1 C. 0 D. 2 Lời giải Chọn A TXĐ: D \ 1 . Ta có: 2 2 x 1 x 1 + lim y lim , lim y lim x 1 x 1 x 1 x 1 x 1 x 1
Suy ra x 1 là tiệm cận đứng 1 1 2 x 1 1 2 2 x 1 x x + lim y lim lim lim 1 x x x 1 x 1 x 1 x 1 1 x x
Suy ra y 1 là tiệm cận ngang Trang 47 1 1 2 x 1 1 2 2 x 1 x x + lim y lim lim lim 1 x x x 1 x 1 x 1 x 1 1 x x Suy ra y 1 là tiệm cận ngang.
Vậy đồ thị hàm số có 3 tiệm cận.
Câu 27.3 (phát triển) x 2
Số đường tiệm cận của đồ thị hàm số y là 2 x 4 A. 2 B. 1 C. 3 D. 4 Lời giải Chọn C TXĐ: D ; 22; 2 1 x 2 +) Ta có lim lim lim x y 1. x x 2 x 4 x 4 1 2 x 2 1 x 2 x lim y lim lim 1 . x x 2 x 4 x 4 1 2 x
Suy ra đồ thị hàm số có hai tiện cận ngang. x 2 x 22 x 2
+) Ta lại có: lim y lim lim lim 0 . 2 x 2 x 2 x2 x
x 2x 2 x2 x 2 4
lim x 2 4 0 x 2 x 2 lim y lim do 2 lim x 4 0 . x x 2 2 2 x 4 x 2 2 x 4 0, x 2 Suy ra x 2
là một đường tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Câu 27.4 (phát triển)
Cho hàm số y f x liên tục trên \
0 và có bảng biến thiên như hình vẽ dưới. Số đường tiệm cận đứ 2020
ng của đồ thị hàm số y là
3 2 f x Trang 48 A. 2 B. 3 C. 4 D. 1 Lời giải Chọn C
Dựa vào BBT, phương trình f x f x 3 3 2 0
có 4 nghiệm phân biệt và tử số là hằng số nên đồ 2 2020 thị hàm số y
có 4 đường tiệm cận đứng.
3 2 f x
Câu 28. [ ĐỀ THI THAM KHẢO ] Cho hàm số 3
y ax 3x d , a d
, có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A. a 0, d 0
B. a 0, d 0
C. a 0, d 0
D. a 0; d 0 Lời giải Chọn D
Do nhánh tiến đến của đồ thị hàm số đi xuống a 0 .
Do đồ thị cắt trục tung tại điểm có tung độ nhỏ hơn 0 d 0. Phát triển câu 28.
Nhận xét: Đây là câu mức độ vận dụng, dạng cho đồ thị hàm số đa thức, tìm dấu các hệ số Phƣơng pháp:
+ Tính lim y để tìm dấu hệ số có lũy thừa cao nhất. lim y a 0; lim y a 0 . x x x
Nhận diện nhanh: Nhánh ngoài cùng của đồ thị đi lên từ trái qua phải a 0 , đi xuống từ trái
qua phải a 0 .
+ Xét giao điểm đồ thị với trục hoành, trục tung.
+ Dựa vào điểm cực trị. Câu tƣơng tự: Cho hàm số 3
y ax 3x d , a d
có đồ thị như hình bên. Mệnh đề nào sau đây đúng? Trang 49
A. a 0, d 0
B. a 0, d 0
C. a 0, d 0
D. a 0, d 0 Lời giải Chọn A.
Ta có lim y a 0 x
Đồ thị hàm số cắt trục Oy là điểm nằm phía trên trục Ox nên d 0 . Phát triển
Câu 28.1. Cho hàm số 3 2 y
f x ax bx cx d có đồ thị hàm số như hình bên.
Khẳng định nào sau đây là đúng ?
A. a 0;b 0;c 0; d 0
B. a 0, c 0, d 0;b 0
C. a 0;b 0;c 0, d 0
D. a 0;b 0; d 0;c 0 Lời giải Chọn D.
Ta có lim lim y a 0 . x
Đồ thị hàm số cắt trục Oy là điểm nằm phía trên Ox nên d 0 .
Ta lại có hàm số có hai điểm cực trị trong đó có một điểm đạt cực tiểu tại điểm x 0 và một điểm cực
đại đạt tại điểm x 0 .
Suy ra phương trình f x 2
3ax 2bx c 0 có hai nghiệm x 0 x . 1 2 f c c 0 0 0 0 Khi đó ta có b
a 0 . Đáp án D. x x 0 0 1 2 3a b 0
Câu 28.2. Cho hàm số 3 2
f x ax bx cx d có đồ thị là đường cong như hình vẽ. Trang 50
Tính tổng S a b c d . A. S 0 . B. S 6 C. S 4 D. S 2 Lời giải Chọn A
Ta có f x 2
3ax 2bx c . Hàm số 3 2
f x ax bx cx d liên tục trên
; đồ thị hàm số có hai
điểm cực trị là 2; 2 và 0;2 . f 2 2 8
a 4b 2c d 2 a 1 f 2 0 1
2a 4b c 0 b 3 . f S 0 0 2 d 2 c 0 f c 0 d 2 0 0
Câu 28.3. Biết rằng hàm số 4 2
f x ax bx c có đồ thị là đường cong hình vẽ bên
Tính giá trị f 3a 2b c.
A. f 3a 2b c 1 25
B. f 3a 2b c 1 44
C. f 3a 2b c 1 13
D. f 3a 2b c 1 Lời giải Chọn A
Ta có f x 3
4ax 2bx
Dựa vào đồ thị ta thấy đồ thị hàm số đi qua hai điểm 0; 1 ,1; 1
và có điểm cực trị 1; 1 nên f 0 1 c 1 c 1
ta có hệ phương trình: f 1 1
a b c 1 a 2 f 4a 2b 0 b 4 1 0
Ta có hàm số f x 4 2 2
x 4x 1. Trang 51
Khi đó f 3a 2b c f 3 1 25
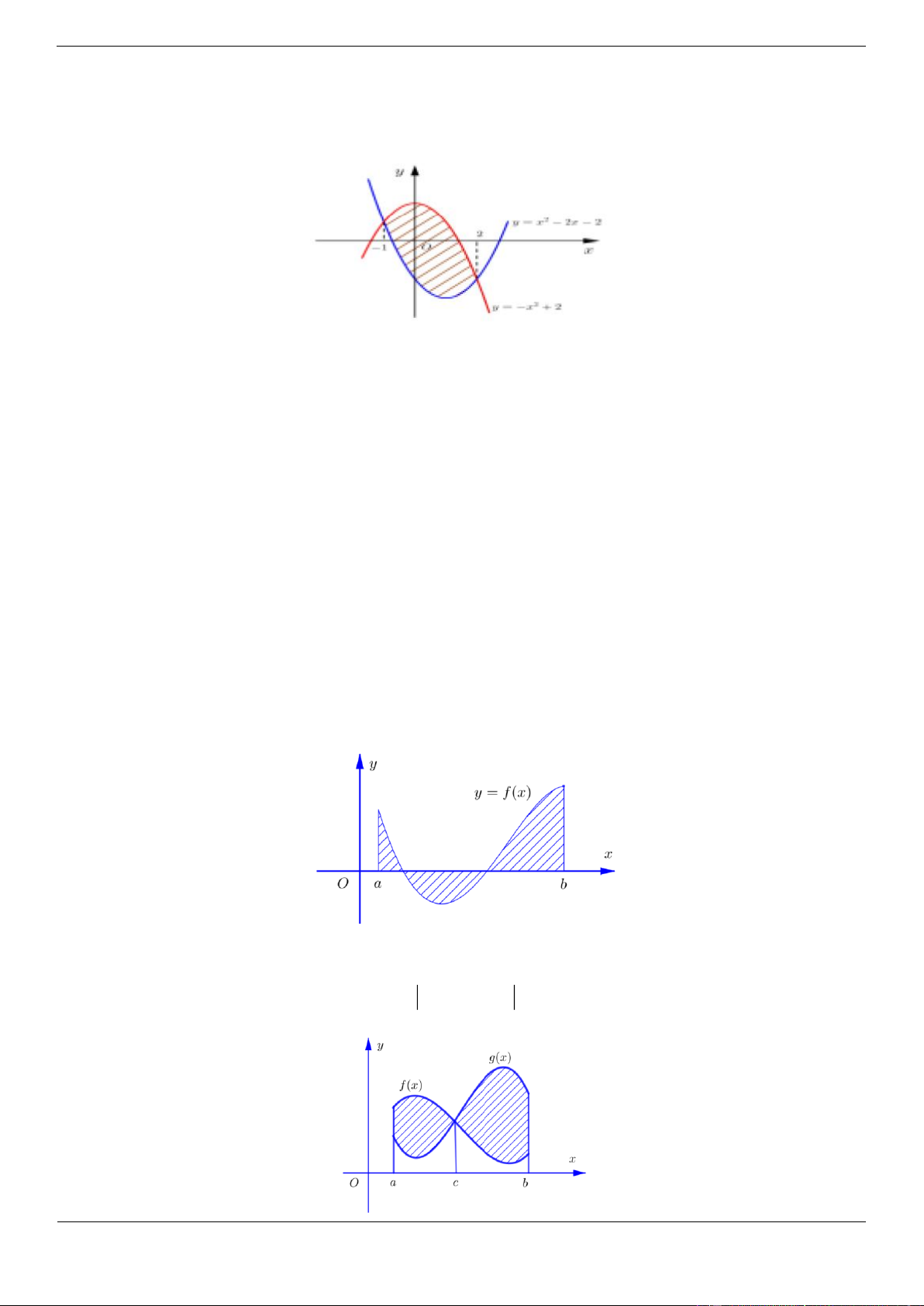
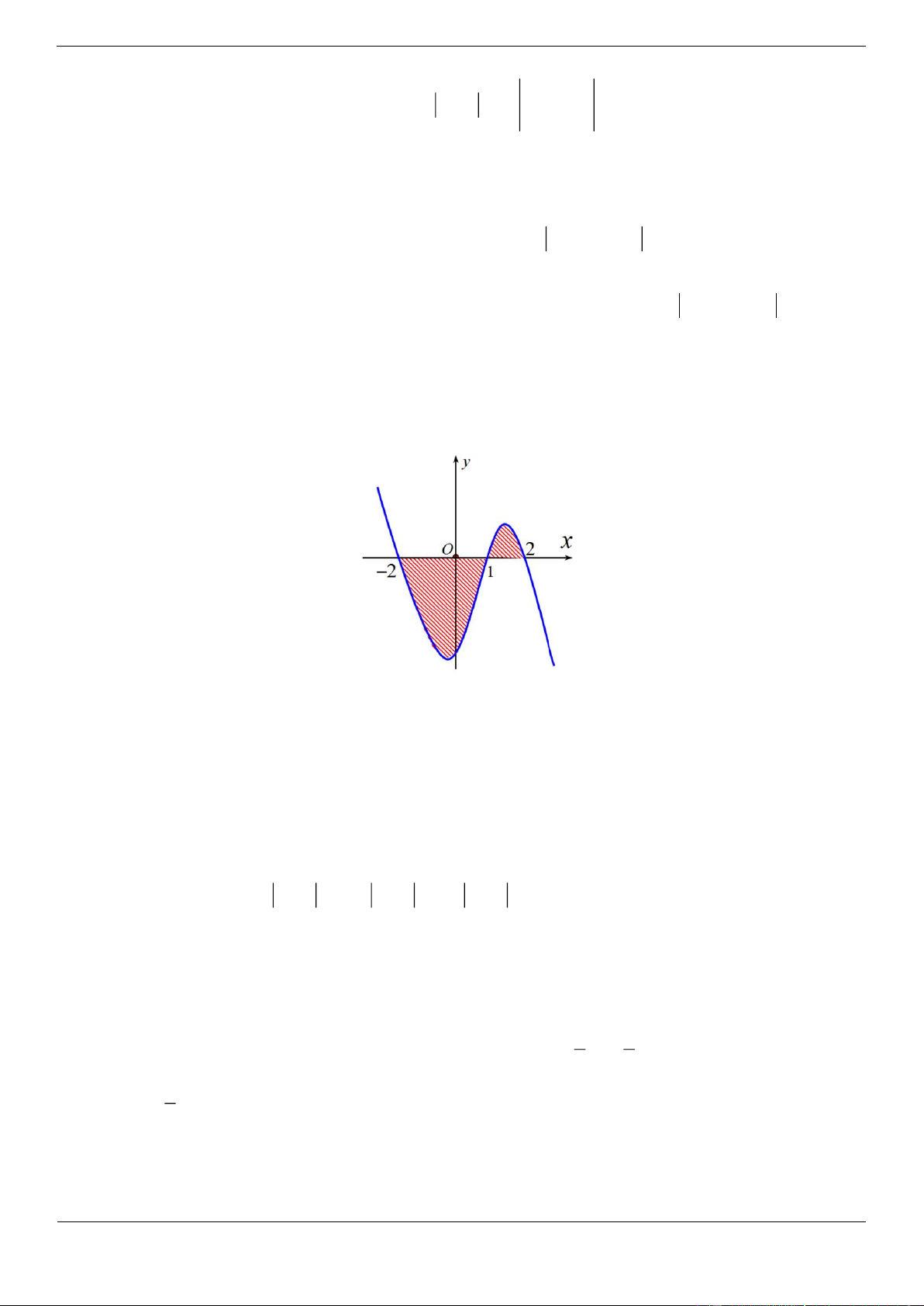
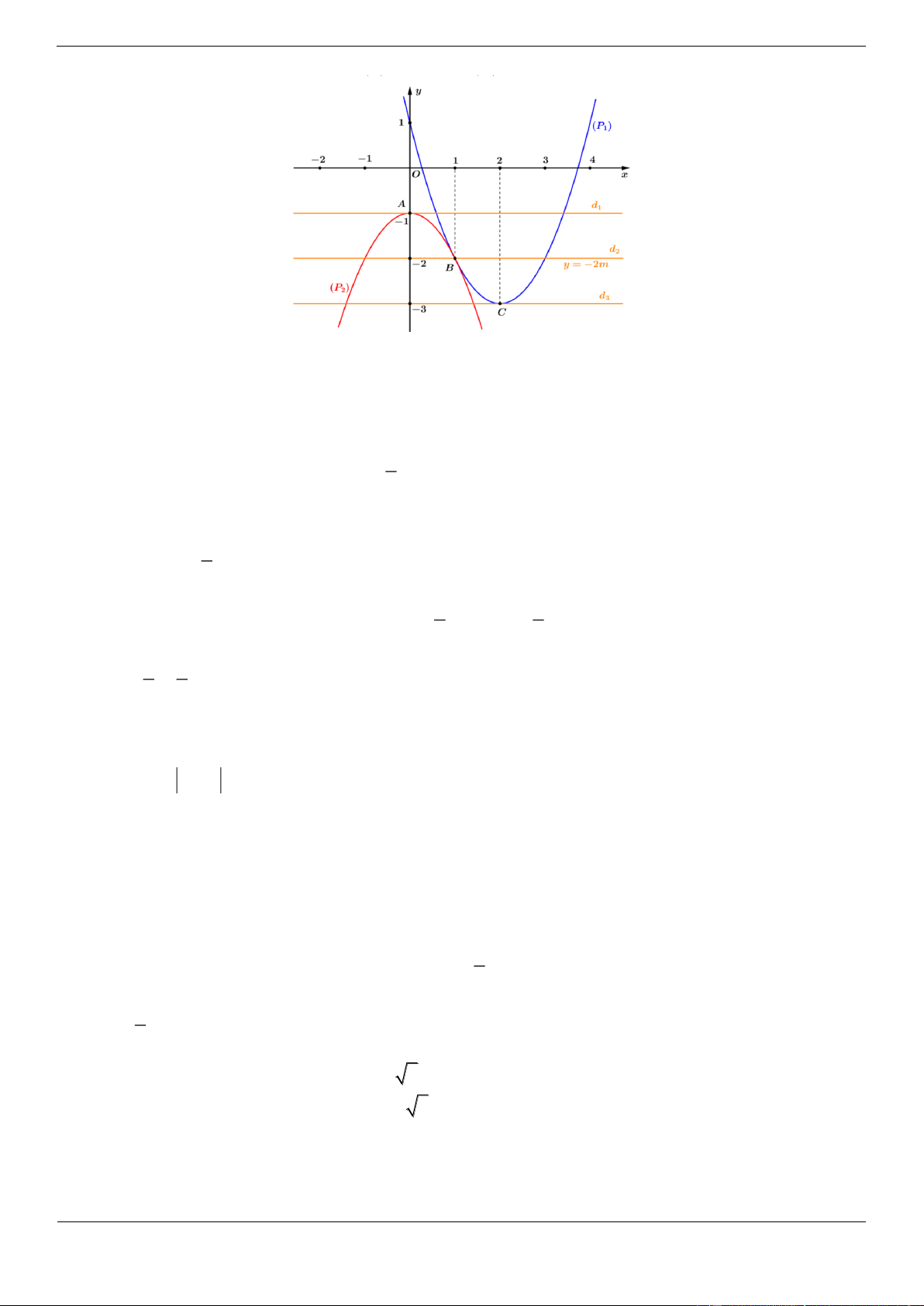
Câu 29: [ ĐỀ THI THAM KHẢO ] Diện tích hình phẳng được gạch chéo trong hình dưới đây bằng 2 2 2 2 A. 2 2
x 2x 4dx B. 2
2x 2x 4 dx C. 2 2
x 2x 4dx D. 2
2x 2x 4 dx 1 1 1 1 Lời giải Chọn A
Ta có diện tích hình phẳng được gạch chéo bằng 2 S
x 2x 2x2 2 2 2 dx 2 2
x 2x 4dx 1 1 Phát triển câu 29.
Nhận xét: Câu hỏi ở mức độ vận dụng Phƣơng pháp:
1) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x liên tục trên đoạn ;
a b , trục hoành và hai b
đường thẳng x ,
a x b được xác định: S f xdx a
2) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x, y g x liên tục trên đoạn ; a b và hai b
đường thẳng x ,
a x b được xác định: S f
x gx dx. a Trang 52 b b Trên ;
a b hàm số f x không đổi dấu thì: f
x dx f xdx a a
Nắm vững cách tính tích phân của hàm số chứa giá trị tuyệt đối
Diện tích của hình phẳng giới hạn bởi các đường x g y , d
x h y và hai đường thẳng y ,
c y d được xác định: S g
yhy dy c xn
3) Diện tích hình phẳng giới hạn bởi 2 đồ thị C : f x , C : f x là: S f
x gx dx . Trong 1 1 2 2 x1
đó: x , x tương ứng là nghiệm nhỏ và lớn nhất của phương trình f x g x. 1 n
Câu tƣơng tự: Cho đồ thị y f x như hình vẽ sau đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi. 2 1 2 A. S f xdx B. S f
xdx f xdx 2 2 1 2 2 1 2 C. S f
xdx f xdx D. S f
xdx f xdx 1 1 2 1 Lời giải Chọn C 2 1 2
Diện tích cần tích là: S f
x dx f
x dx f x dx 2 2 1 1 2 2 2 f
xdx f
xdx f
xdx f xdx 2 1 1 1 Phát triển CÂU 29 1 1
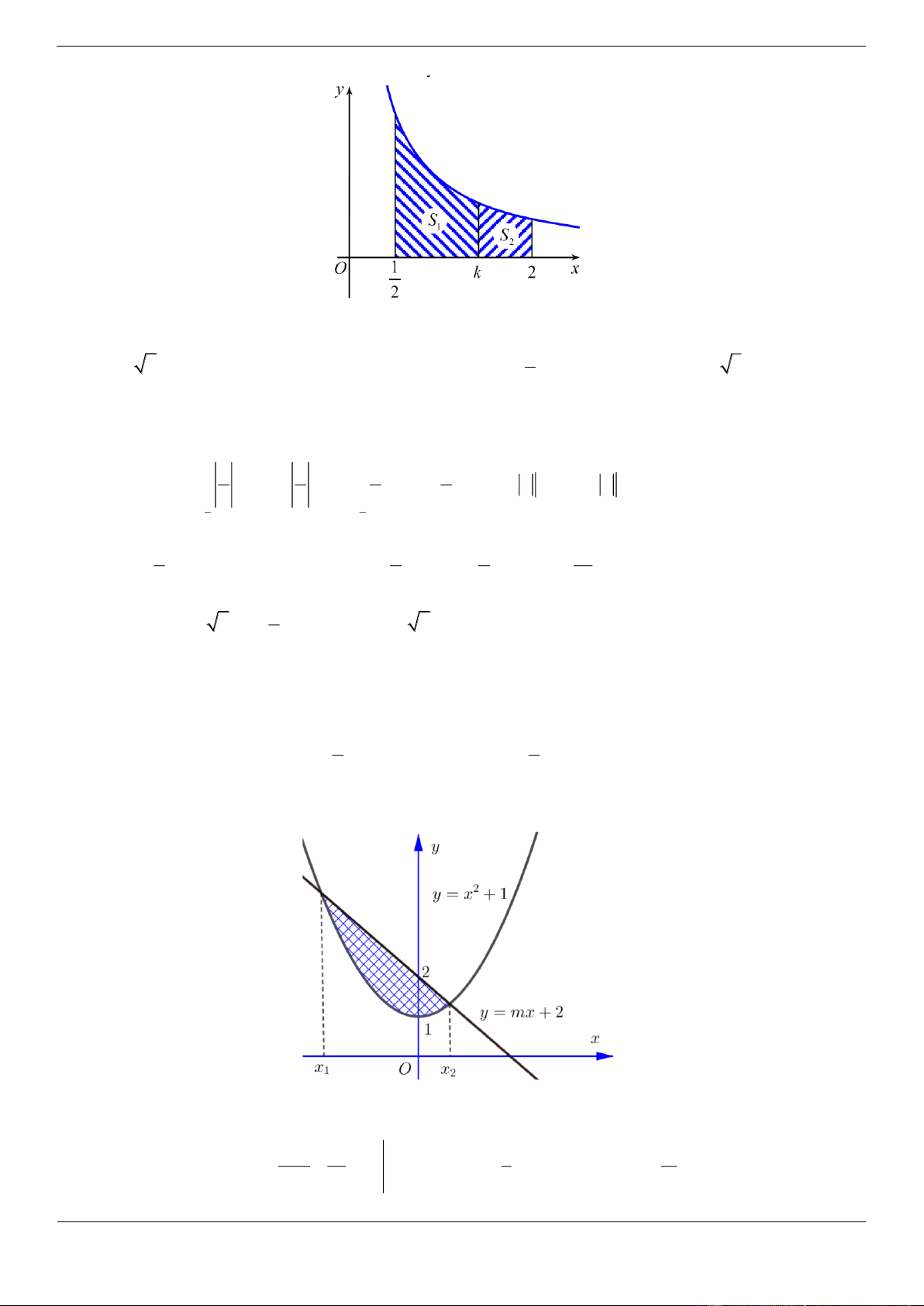
Câu 29.1. Cho hình thang cong H giới hạn bởi các đường y , x , x 2 và trục hoành. Đường x 2 1 thẳng x k k 2
chia H thành hai phần có diện tích là S và S như hình vẽ dưới đây. 2 1 2 Trang 53
Tìm tất cả giá trị thực của k để S 3S 1 2 7 A. k 2 B. k 1 C. k D. k 3 5 Lời giải Chọn A k 2 k 2 1 1 1 1 k 2
Ta có S 3S dx 3 dx dx 3 dx ln x 3ln x 1 2 1/ 2 k x x x x 1 k 1 k 2 2 3 1 k k 2 2 8 ln ln 3 ln 2 ln
ln 2k 3ln 2k 2k 3 2 k k k 1 4
k 4 k 2 mà k 2 nên k 2 . 2
Câu 29.2. Với mọi m thì đường thẳng d : y mx 2 luôn cắt parabol P 2
: y x 1 tại hai điểm phân
biệt có hoành độ x , x . Tìm m để diện tích của hình phẳng giới hạn bởi d và P là nhỏ nhất. 1 2 4 3 A. m 0 B. m C. m D. m 4 3 4 Lời giải
Ta có x , x là hai nghiệm của phương trình 2
x mx 1 0 . Khi đó: 1 2 x x x 2 2 2 3 mx x dx
x x x 1 m S mx 2 1 x x 2 2 x x x x 1 2 1 1 2 1 2 1 2 2 3 3 2 1 x 1 x Trang 54 1
m 4 2m 1 1 3m 6
m 4 m 4 3 4 2 2 2 2 2 6 6 6 S m 0 min 1
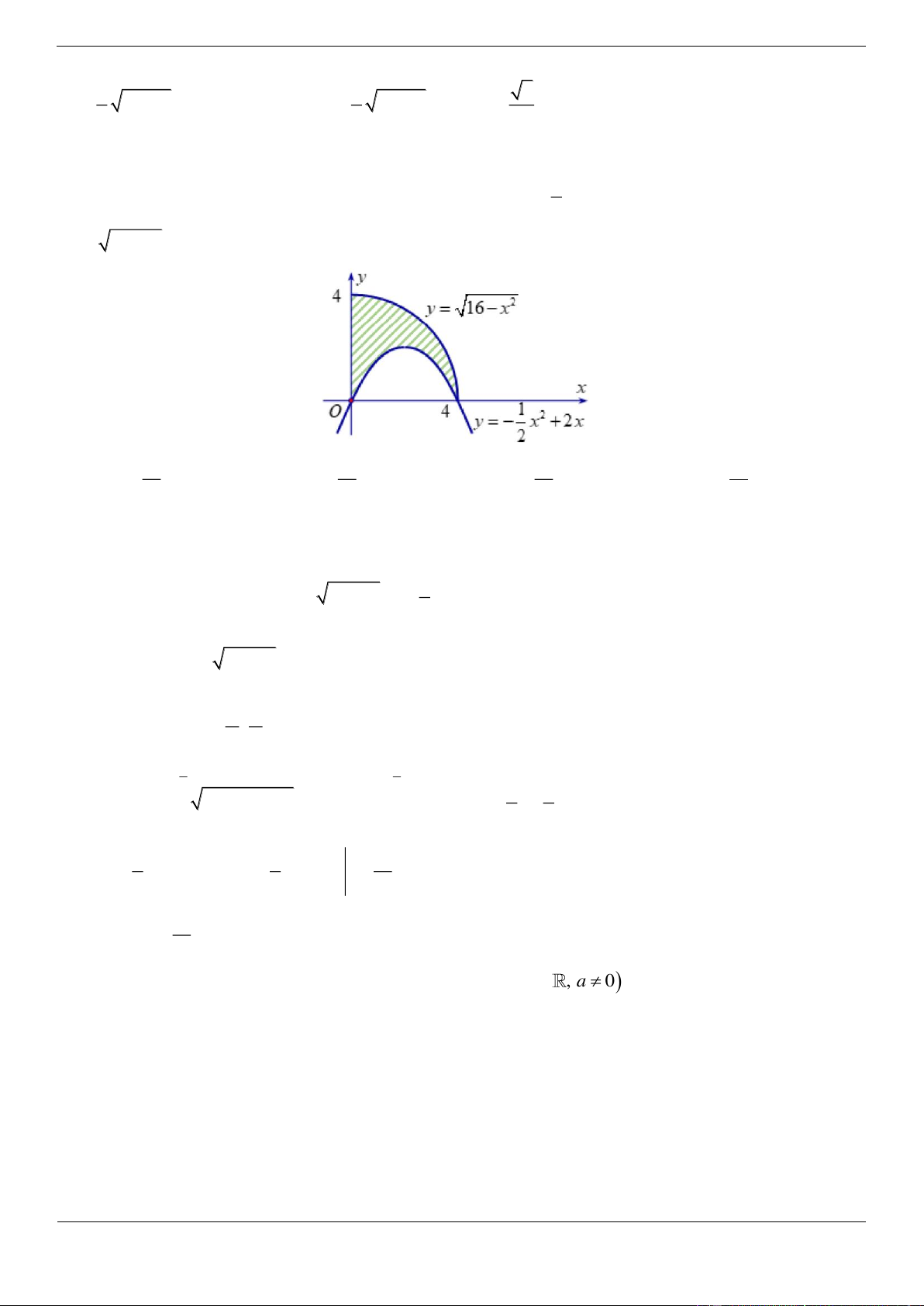
Câu 29.3. Cho hình phẳng D giới hạn bởi parabol 2 y
x 2x , cung tròn có phương trình 2 2
y 16 x , với 0 x 4 , trục tung (phần tô đậm trong hình vẽ). Tính diện tích của hình D. 16 16 16 16 A. 8 B. 2 C. 4 D. 4 3 3 3 3 Lời giải Chọn D 4 1
Diện tích hình phẳng D là 2 2 S 16 x x 2x dx 2 0 4 Xét tích phân 2 I 16 x dx 0
Đặt x 4sin t, t ; . 2 2 2 2 Khi đó 1 1 2 2 I dt
16 16sin t .4 cos tdt 16 cos tdt 16 t sin 2t 4 2 2 0 0 4 4 1 1 16 2 3 2 J
x 2x dx x x 2 6 3 0 16 Vậy S 4 . 3
Câu 29.4. Cho hàm số y f x 3 2
ax bx cx d, , a , b ,
c d , a 0 có đồ thị (C). Biết rằng đồ thị
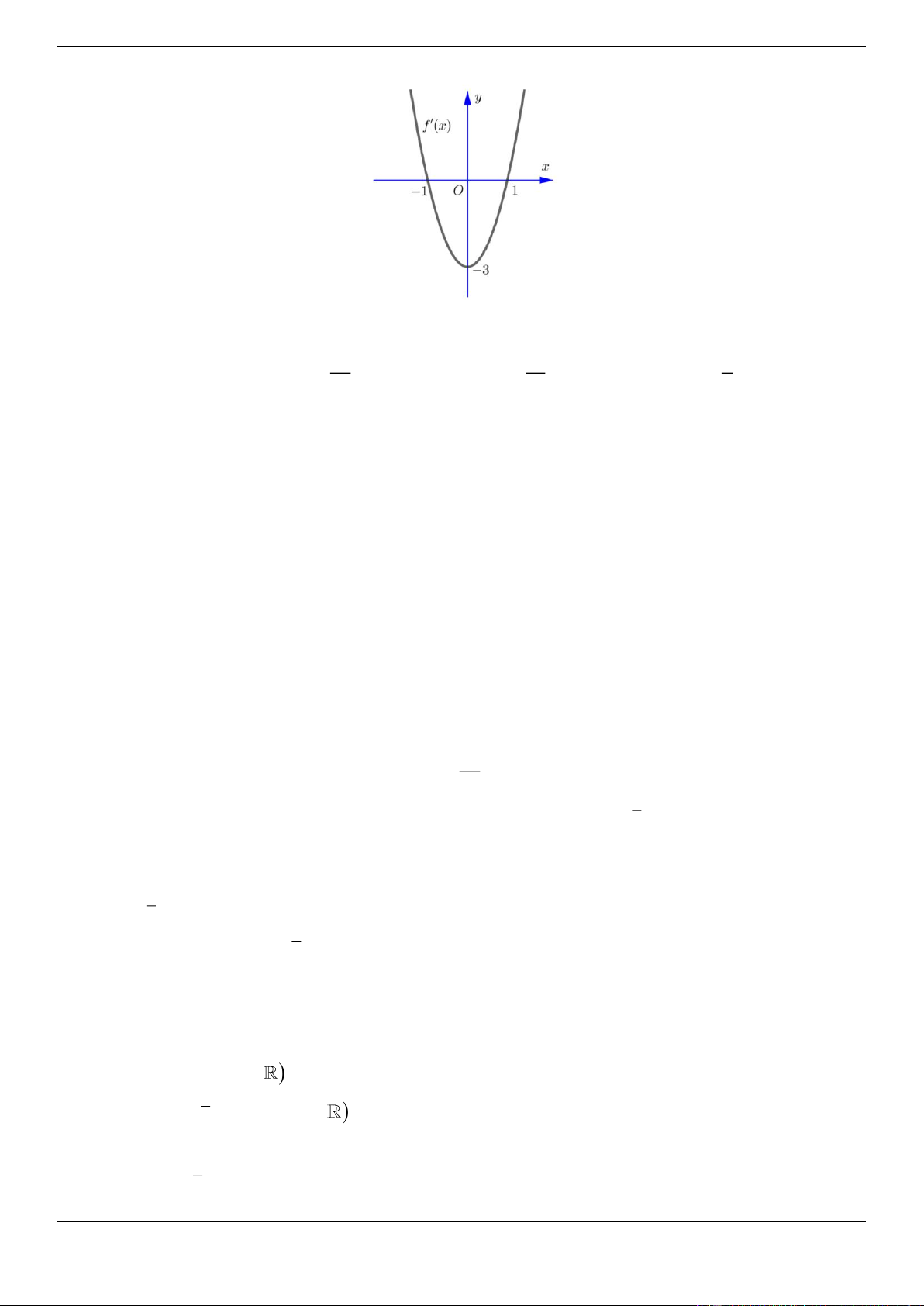
(C) tiếp xúc với đường thẳng y 4 tại điểm có hoành độ âm và đồ thị của hàm số y f x cho bởi hình vẽ dưới đây. Trang 55
Tính diện tích S của hình phẳng giới hạn bởi đồ thị C và trục hoành 27 21 5 A. S 9 B. S C. S D. S 4 4 4 Lời giải Chọn B.
Từ đồ thị suy ra f x 2 3x 3.
f x f
xdx 2x 3 3
3 dx x 3x C .
Do C tiếp xúc với đường thẳng y 4 tại điểm có hoành độ x âm nên 0 f x 2
0 3x 3 0 x 1 . 0 0 0 Vậy f
1 4 nên có ngay C 2 . Vậy phương trình đường cong C là 3
y x 3x 2 . x 2 Xét phương trình 3
x 3x 2 0 . x 1 1 27
Diện tích hình phẳng cần tìm là
3x 3x2dx . 2 4
Câu 30. Cho hai số phức z 3
i và z 1 i . Phần ảo của số phức z z bằng 1 2 1 2 A. 2 B. 2i C. 2 D. 2 i Lời giải
Ta có z z 3
i 1 i 2 2i 1 2
Vậy phần ảo của số phức z z bằng 2. 1 2 Phát triển câu 30
Nhân xét : Câu hỏi ở mức độ thông hiểu : Phƣơng pháp
Số phức z a bi, ; a b
, a là phần thực, b là phần ảo.
Số phức liên hợp z a bi, ; a b .
Câu tƣơng tự (Phát triển câu 30- Đề thi tham khảo) Cho hai số phức z 5 i và z 7 2i . Phần ảo 1 2
của số phức z z bằng 1 2 Trang 56 A. 3 B. 3i C. 3 D. 3 i Lời giải Chọn C
Ta có: z z 5 i 7 2i 12 3i 1 2
Vậy phần ảo của số phức z z bằng 3 . 1 2 Câu phát triển
Câu 30.1. Cho hai số phức z 2 4i và z 1 3i . Phần ảo của số phức z iz bằng 1 2 1 2 A. 5 B. 5 i C. 3 D. 3i Lời giải Chọn C
Ta có z iz 2 4i i 1 3i 1 3i 1 2
Vậy phần ảo của số phức z iz bằng 3 1 2
Câu 30.2. Cho hai số phức z 5 6i và z 1 8i . Phần ảo của số phức liên hợp w z iz bằng 1 2 1 2 A. 5 i B. 5 C. 5i D. 5 Lời giải Chọn B
Ta có w z iz 5 6i i 1 8i 3
5i w 3 5i 1 2
Vậy phần ảo của số phức w z iz bằng 5 . 1 2
Câu 30.3. Cho hai số phức z 2019 2020i và z 2002i . Phần ảo của số phức iz z bằng 1 2 1 2 A. 2020. B. 4021 C. 2020 D. 4021 Lời giải Chọn D
Ta có iz z i 2019 2020i 2 002i 2 020 4021i 1 2
Vậy phần ảo của số phức iz z bằng 4021. 1 2 1
Câu 30.4. Nếu số phức z 1 thỏa mãn z 1 thì phần thực của bằng 1 z 1 1 A. B. C. 2 D. 2 2 2 Lời giải Chọn A Cách 1:
Gọi z a bi, , a b ,z 1. Vì 2 2
z 1 a b 1. 1 1 1abi 1 a b 1 b Ta có i i z. 1 z
1abi 1a2 2 b 2 2a 2 2a 2 2 2a 1 1
Vậy phần thực của số phức là . 1 z 2 Trang 57 Cách 2: 2 Ta có: . z z z 1 Khi đó: 1 1 1 1 1 1 1 2 Re
1 z 1 z 1 z 1 z 1 z 1 z 1 z 2 z z 2 z z 1
1 z z . z z
1 z z 1 1 1 Suy ra: Re 1 z 2
Câu 31. [ ĐỀ THI THAM KHẢO ] Trong không gian Oxyz, cho mặt cầu S có tâm I 0;0; 3 và đi
qua điểm M 4;0;0 . Phương trình của S là
A. x y z 2 2 2 3 25
B. x y z 2 2 2 3 5
C. x y z 2 2 2 3 25
D. x y z 2 2 2 3 5 Lời giải Chọn A
Bán kính mặt cầu r IM 2 2 2 4 0 3 5
Phương trình mặt cầu là: x y z 2 2 2 3 25
Câu 31.1. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z i 3 2i là điểm nào dưới đây?
A. M 3; 2 B. N 3; 2 C. P 2 ;3 D. Q 2; 3 Lời giải Chọn C
Ta có z i i 2
3 2 3i 2i 3i 2 2 3i .
Vậy điểm biểu diễn cho số phức z trong mặt phẳng phức là điểm có tọa độ 2 ;3 .
Phát triển câu 31, tìm điểm biểu diễn cho số phức w biết số phức w tính thông qua z và z thỏa mãn một
biểu thức cho trước
Câu 2. (Phát triển câu 31) Cho số phức z thỏa mãn 2 i z 3 4i . Tìm phần thực của số phức
w 2 iz 3z . A. 9 B. 5 C. 1 D. 6 Lời giải Chọn A 3 4i
Từ giả thiết z
2 i . Suy ra w 2 iz 3z 2 i2i 32i 95i . 2 i
Vậy phần thực của số phức w là 9.
Phát triển câu 31, kết hợp việc tìm tọa độ điểm biểu diễn cho số phức với kiến thức tính diện tích tam
giác khi biết tọa độ 3 đỉnh ở lớp 10 Trang 58
Câu 3. (Phát triển câu 31) Trong mặt phẳng tọa độ, cho A, B, C là ba điểm biểu diễn lần lượt cho ba số
phức z 5 i, z 4 i2 và z 2i . Diện tích của tam giác ABC là kết quả nào dưới đây? 3 3 1 2 25 185 A. 25. B. C. D. 185 2 2 Lời giải Chọn B
Ta có: z 5 i A 5; 1 1
z 4 i2 2
16 8i i 16 8i 1158i B 15;8 2
z 2i3 8
i C 0;8 3 1 25
Diện tích tam giác ABC khi biết tọa độ 3 đỉnh là S 5 (đvdt). ABC 8 8 15 8 1 0 1 8 2 2
Phát triển câu 31, ý tưởng điểm biểu diễn gắn với hình học phẳng. Sử dụng vectơ bằng nhau và tích
vô hướng để tìm điều kiện cho một tứ giác là hình chữ nhật
Câu 4. (Phát triển câu 31) Cho số phức z a bi (với , a b
) và số phức liên hợp của nó là z có
điểm biểu diễn trong mặt phẳng phức là A và D . Số phức 2 5i z và liên hợp của nó có điểm biểu diễn
là B và C . Biết rằng tứ giác ABCD là hình chữ nhật và z 3 i đạt giá trị nhỏ nhất. Tìm tích . a b . 80 80 16 16 A. B. C. D. 169 169 169 169 Lời giải Chọn A
Ta có z a bi A ;
a b; z a bi D ; a b
25iz 25iabi 2a5b5a 2bi B2a5 ;b5a 2b
Điểm biểu diễn cho số phức liên hợp của số phức 2 5i z là C 2a 5 ;
b 5a 2b .
Ta có AB a 5 ;
b 5a b, AD 0; 2
b, DC a 5 ;
b 5a b a,b 0 a,b 0
a 5b a 5b a,b 0
Để tứ giác ABCD là hình chữ nhật thì AB DC 5a b 5 a 5b b 5 a A . B AD 0 2 b
5a b 0
Khi đó số phức z a bi a 5ai . 2 2 2 4 98 98
Xét z 3 i a 5ai 3 i a 3 5a 2 1
26a 16a 10 26 a 13 13 13 98 4 20
Vậy z 3 i đạt giá trị nhỏ nhất là
đạt được khi a , b (thỏa mãn) 13 13 13 Do đó 4 20 80 z i , suy ra: . a b . 13 13 169 Trang 59
Câu 32. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz, mặt phẳng đi qua điểm M 1;1; 1 và vuông x 1 y 2 z 1
góc với đường thẳng : có phương trình là 2 2 1
A. 2x 2y z 3 0
B. x 2y z 0
C. 2x 2y z 3 0
D. x 2y z 2 0 Lời giải Chọn C
Đường thẳng có vecto chỉ phương u 2;2; 1 .
Mặt phẳng cần tìm đi qua điểm M 1;1;
1 , nhận u 2;2;
1 làm vtpt nên có phương trình 2 x 1 2 y 1 1 z
1 0 2x 2y z 3 0 .
Câu 1. (Tƣơng tự câu 32) Trong không gian Oxyz , cho các vectơ a 2;7; 3
, b 2;1;4. Tính tích
vô hướng a a b bằng A. 21 B. 63 C. 53 D. 52 Lời giải Chọn B
a b 0;6; 7
Vậy a a b 2.0 7.6 3. 7 63.
Phát triển câu 32, sử dụng ứng dụng của tích vô hướng vào việc tìm tham số để một tam giác trong không
gian là tam giác vuông
Câu 2. (Phát triển câu 32) Trong không gian Oxyz, cho ba điểm A2;0; 1 , B 1 ;4;3 và C ; m 2m 3;
1 . Tìm m để tam giác ABC vuông tại B. A. 7 B. 4 C. 7 D. 4 Lời giải Chọn C BA 3; 4 ; 2
, BC m 1;2m 7; 2
Để tam giác ABC vuông tại B thì B .
A BC 0 3m
1 42m 7 4 0 5
m 35 0 m 7 .
Phát triển câu 32, sử dụng ứng dụng của tích vô hướng vào việc quỹ tích điểm M thỏa mãn đẳng thức cho
trước, bài toán có sử dụng việc khai thác điểm trung gian
Câu 3. (Phát triển câu 32) Trong không gian Oxyz , cho A2;0;4 và B 0; 6
;0, M là một điểm bất kỳ 561 thỏa mãn 2 2 2 3MA 2MB
AB . Khi đó M thuộc mặt cầu có bán kính là giá trị nào dưới đây? 280 A. 3 B. 9 C. 56 D. 56 Lời giải Trang 60 Chọn A 6
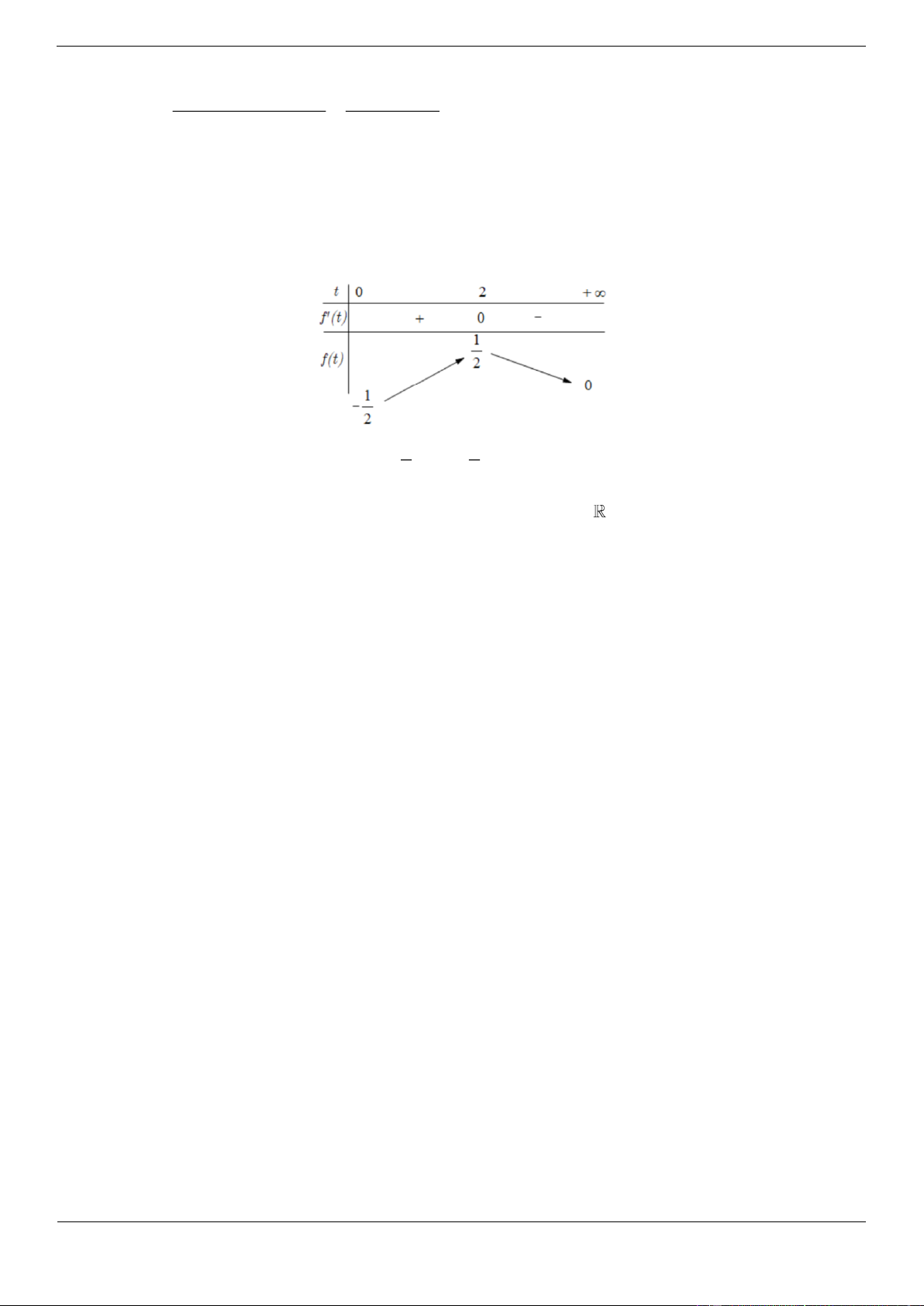
x x x 5 3 2 2 0 0 Xét điể 12 m I ;
x y thỏa mãn 3IA 2IB 0 3
0 y 2 6
y 0 y .
z z 5 3 4 2 0 0 12 z 5 6 12 12 I ; ; 5 5 5 Mà 2 2 2 2
AB 2 6 4 56 2 2 561 561 Xét 2 2 3MA 2MB
3MI IA 2MI IB 5 5 3 561 2 2
MI 2MI.IA IA 2 2 2
MI 2MI.IB IB 5 561 672 1008 561 2 2 2 2 2
5.MI 2MI.3.IA 2.IB 3IA 2.IB 5.MI MI 9 5 25 25 5 0 6 12 12
Vậy M luôn chạy trên mặt cầu tâm I ; ; và có bán kính là 3. 5 5 5
Phát triển câu 32, sử dụng kiến thức về độ dài vectơ, điểm trên tia để lấy tọa độ không âm, áp dụng biến
dạng của bất đẳng thức BunhiaCopxki vào đánh giá GTNN
Câu 4. (Phát triển câu 32) Trong không gian Oxyz , trên các tia Ox, Oy, Oz lấy ba điểm không trùng O là 1 4 9
A, B, C. Biết OA OB OC 1 và biểu thức
đạt giá trị nhỏ nhất. Tính OA OB OC
OAOBOBOC. 5 1 A. 1. B. . C. 0. D. . 6 9 Lời giải Chọn D
Vì A, B, C thuộc các tia O ,
x Oy,Oz nên gọi tọa độ các điểm là A ;
a 0;0, B0; ;
b 0 , C 0;0;c , suy ra OA ;
a 0;0,OB 0; ;
b 0,OC 0;0;c, , a , b c 0 .
Theo giả thiết OA OB OC 1 a b c 1. 1 4 9 2 1 2 3 36 Xét 36 . OA OB OC
OA OB OC
a b c 1 a 6 1 2 3 1 4 9 1 Biểu thức
đạt giá trị nhỏ nhất là 36 xảy ra khi a b c b . OA OB OC 3
a b c 1 1 c 2 Trang 61 1 1 1 1 1 Suy ra OA
;0;0 ,OB 0; ;0 , OC 0;0;
; OB OC 0; ; 6 3 2 3 2 1 1 OA OB ; ;0 6 3
Vậy OA OB OB OC 1 1 1 1 1 . .0 . 0. . 6 3 3 2 9
Câu 33. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương
của đường thẳng đi qua hai điểm M 2;3; 1 và N 4;5;3 ?
A. u 1;1; 1
B. u 1;1;2
C. u 3;4; 1
D. u 3;4;2 Lời giải Chọn B
Ta có vectơ MN 2;2;4 là một vec tơ chỉ phương của đường thẳng đi qua hai điểm MN
mà MN 21;1;2 2 ;
u u 1;1;2 nên chọn B
Câu 1. (Tƣơng tự câu 33) Trong không gian Oxyz, cho mặt cầu S có tâm I 8;0;0 và đi qua điểm M 0; 6
;0. Phương trình của S là
A. x 2 2 2 8
y z 100
B. x 2 2 2 8
y z 10
C. x 2 2 2 8
y z 100
D. x 2 2 2 8
y z 10 Lời giải Chọn A 2 2 2
Vì M S nên bán kính mặt cầu là R IM 8 0 0 6 0 0 100 10 . 2 2 2 2
Vậy phương trình mặt cầu cần tìm là x y z 2 x 2 2 8 0 0 10 8
y z 100.
Phát triển câu 33, sử dụng công thức tính khoảng cách để tìm bán kính mặt cầu trong trường hợp tiếp xúc.
Câu 2. (Phát triển câu 33) Trong không gian Oxyz, cho mặt cầu S có tâm I 1;0; 4 và tiếp xúc với
mặt phẳng Oxy . Phương trình mặt cầu S là 2 2 2 2
A. x 2
1 y z 4 4. B. x 2
1 y z 4 16. 2 2 2 2
C. x 2
1 y z 4 1 D. x 2
1 y z 4 2 Lời giải Chọn B
Phương trình mặt phẳng Oxy là z 0. Vậy bán kính mặt cầu S là R d I Oxy 4 , 4 1 Phương trình mặ 2 2 2 2 2
t cầu cần tìm là x y z 2 x 2 1 0 4 4
1 y z 4 16. Trang 62
Phát triển câu 33, mặt cầu đi qua 2 điểm thì tâm mặt cầu phải thuộc mặt phẳng trung trực của đoạn
thẳng tạo bởi hai điểm đó.
Câu 3. (Phát triển câu 33) Trong không gian Oxyz, cho mặt cầu S có tâm I thuộc đường thẳng x 4 y z 3 d :
và S đi qua hai điểm A 3
;0;5 và B1;4;
1 . Khi đó bán kính mặt cầu S là 2 1 1
giá trị nào dưới đây? A. 290 B. 3 C. 2 17 D. 299 Lời giải Chọn D
Gọi M là trung điểm của AB , tọa độ điểm M 1 ;2;2 .
Gọi là mặt phẳng trung trực của AB , khi đó M và một vectơ pháp tuyến của là MA MA 2 ; 2 ; 3 .
Phương trình mặt phẳng : 2 x
1 2 y 2 3 z 2 0 2x 2y 3z 8 0 .
Mà I d suy ra tọa độ I 4 2t;t; 3
t,t
I suy ra 24 2t 2t 3 3
t 8 0 t 3 I 10;3; 6 . 2 2 2
Vậy bán kính mặt cầu là R IA 3
10 0 3 5 6 299 .
Phát triển câu 33, mặt cầu ngoại tiếp khối tứ diện thì tâm mặt cầu phải nằm trên đường thẳng đi qua tâm
của đường tròn ngoại tiếp một trong các mặt phẳng của tứ diện và vuông góc với mặt phẳng đó. Để thể
tích đạt giá trị lớn nhất thì đỉnh còn lại của tứ diện phải thuộc đường thẳng đi qua tâm mặt cầu và vuông
góc với mặt phẳng đối diện. Điểm còn lại tìm được tính khoảng cách đến mặt phẳng đã cho mà có giá trị
lớn hơn thì đó là đỉnh còn lại của tứ diện 2 2
Câu 4. (Phát triển cầu 33) Trong không gian Oxyz, cho mặt cầu S 2
: x y
1 z 2 9 và tam
giác BCD với tọa độ các đỉnh là B 3;1; 2 , C0; 2 ; 2 , D0;1;
1 . Tìm tọa độ điểm A thuộc mặt cầu
S sao cho thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
A. A 3; 1 3; 2 3
B. A 3;1 3; 2 3
C. A0;2; 2 2 2 D. A0;2; 2 2 2 Lời giải Chọn A Dễ thấy ba điểm ,
B C, D đều thuộc mặt cầu S . Để AS mà thể tích khối tứ diện ABCD đạt giá trị
lớn nhất thì A là một trong 2 giao điểm của đường thẳng với mặt cầu; trong đó là đường thẳng đi
qua tâm I của mặt cầu và vuông góc với mặt phẳng BCD . Ta có: BC 3 ; 3 ;0, BD 3
;0;3 . Tọa độ tâm mặt cầu S là I 0;1; 2 .
Một vectơ pháp tuyến của mặt phẳng BCD là n BC, BD 9 ; 9 ; 9 . Trang 63
Vì vuông góc với nên 1 vectơ chỉ phương của là u 1;1; 1 . x t
Phương trình đường thẳng : y 1 t , t . z 2 t 2 2
Vì A At;1 t; 2 t , mà AS 2
t t t 2 1 1 2 2 9 t 3
t 3 A 3;1 3; 2 3 1 .
t 3 A 3;1 3; 2 3 2
Phương trình mặt phẳng BCD : 1 x 0 1 y 1 1 z
1 0 x y z 2 0 3 1 3 2 3 2
* Xét A : d A , BCD 3 3 . 1 1 3
3 1 3 2 3 2
* Xét A : d A , BCD 3 3 . 2 2 3
Dễ thấy d A , BCD d A , BCD A 3;1 3; 2
3 là điểm cần tìm. 2 1
Câu 34. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz , mặt phẳng đi qua điểm M 1;1; 1 và x 1 y 2 z 1
vuông góc với đường thẳng : có phương trình là 2 2 1
A. 2x 2y z 3 0
B. x 2y z 0
C. 2x 2y z 3 0
D. x 2y z 2 0 Lời giải Chọn C
Đường thẳng có vecto chỉ phương u 2;2; 1 .
Mặt phẳng cần tìm đi qua điểm M 1;1;
1 , nhận u 2;2;
1 làm vtpt nên có phương trình 2 x 1 2 y 1 1 z
1 0 2x 2y z 3 0
Phân tích : Một câu viết phương trình mặt phẳng khi cho véc tơ pháp tuyến và điểm đi qua.
Câu 1 : (Phát triển câu 34- Đề thi tham khảo) Trong không gian Oxyz, cho ba điểm A1;2; 3 ; B2; 2 ; 1 ;C 1
;3;4 mặt phẳng đi qua điểm A và vuông góc với BC có phương trình là
A. 3x 5y 3z 2 0
B. x 4y 4z 3 0
C. 3x 5y 3z 2 0
D. 2x y 7z 3 0 Lời giải Chọn A Ta có BC 3 ;5;3
Mặt phẳng cần tìm đi qua điểm A1;2; 3
, nhận n 3; 5 ; 3
làm vtpt nên có phương trình 3 x
1 5 y 2 3 z 3 0 3x 5y 3z 2 0 Trang 64
Câu 2 : (Phát triển câu 34- Đề thi tham khảo) Trong không gian Oxyz, mặt phẳng đi qua ba điểm A1;2; 1 ; B 1 ;3;
1 ;C 3;4;3 có phương trình là
A. x 2y 3z 2 0
B. x 2y 3z 2 0
C. x 2y 3z 6 0
D. x 2y 3z 10 0 Lời giải Chọn B Ta có AB 2
;1;0;BC 4;1;2 A ; B BC 2;4; 6 21;2; 3
Mặt phẳng cần tìm đi qua ba điểm A1; 2;
1 nhận n 1;2; 3
làm vtpt nên có phương trình x
1 2 y 2 3 z
1 0 x 2y 3z 2 0
Câu 3 : (Phát triển câu 34- Đề thi tham khảo) Trong không gian Oxyz, mặt phẳng P chứa đường x 1 y z 1 x 2 y 1 z 3 thẳng : d : và song song với : : có phương trình là 1 2 2 2 1 3
A. 4x 7 y 5z 9 0
B. 4x 7 y 5z 9 0
C. x 2y 2z 3 0
D. 4x 7 y 5z 9 0 Lời giải Chọn D x 1 y z 1 d :
u 1;2;2 là véctơ chỉ phương của d 1 1 2 2 x 2 y 1 z 3 : u 2; 1 ; 3
là véctơ chỉ phương của 2 2 1 3
Mặt phẳng P chứa đường thẳng d và song song với nên nhận u ,u là VTCP 1 2 n u ;u 4 ;7; 5 A 1;0;1 . 1 2 là vtptvà qua điểm P: 4 x
1 7 y 0 5 z
1 0 4x 7 y 5z 9 0
Câu 4 : (Phát triển câu 34- Đề thi tham khảo) Trong không gian Oxyz, mặt phẳng P đi qua x 2 y 1 z 1 A2; 3
;3 và chứa d : có phương trình là 1 2 3
A. 4x y z 10 0
B. 5x y z 10 0
C. 5x y z 10 0
D. 5x y z 10 0 Lời giải Chọn D x 2 y 1 z 1 d :
u 1;2;3 là véctơ chỉ phương của d 1 2 3 B 2;1;
1 d AB 0;4; 4
Mặt phẳng P đi qua A2; 3
;3 và nhận u, AB là VTCP n ; u AB 2 0;4;4 4 5; 1 ; 1 là VTPT Trang 65
và qua điểm A2; 3 ;
3 P : 5 x 2 y 3 z 3 0 5x y z 10 0
Câu 35. [ĐỀ THI THAM KHẢO] Trong không gian Oxyz , vectơ nào dưới đây là một vectơ chỉ
phương của đường thẳng đi qua hai điểm M 2;3; 1 và N 4;5;3 ?
A. u 1;1; 1
B. u 1;1;2
C. u 3;4; 1
D. u 3;4;2 Lời giải Chọn B
Ta có vectơ MN 2;2;4 là một vec tơ chỉ phương của đường thẳng đi qua hai điểm MN
mà MN 21;1;2 2 ;
u u 1;1;2 nên chọn B
Phân tích : Một câu về xác định các yếu tố cơ bản của đường thẳng trong không gian.
Câu 1 : (Phát triển câu 35- Đề thi tham khảo) Trong không gian Oxyz, cho ba điểm A1;1; 3 ; B 2;3; 1 ;C 2 ; 1
;4 một vectơ chỉ phương của đường thẳng d qua A và song song với BC là vectơ nào sau đây
A. u 4;4; 3
B. u 4; 4;3
C. u 1;1; 1
D. u 2;2; 1 Lời giải Chọn A Ta có BC 4 ; 4
;3 là một vectơ chỉ phương của đường thẳng d
Một vectơ chỉ phương của đường thẳng d là u BC 4;4; 3
Câu 2 : (Phát triển câu 35- Đề thi tham khảo) Trong không gian Oxyz, cho ba điểm A1;2; 1 ; B 1 ;3;
1 ;C 3;4;3 đường thẳng d đi qua A và vuông góc với mặt phẳng đi qua ba điểm A, B,
C có phương trình là x 1 y 2 z 1 x 1 y 2 z 1 A. B. 1 2 3 1 2 3 x 1 y 2 z 1 x 1 y 2 z 1 C. D. 1 2 3 1 2 3 Lời giải Chọn B Ta có AB 2
;1;0;BC 4;1;2 A ; B BC 2;4; 6 21;2; 3
Đường thẳng d đi qua A1;2;
1 nhận u 1;2; 3 làm VTCP
nên có phương trình x 1 y 2 z 1 1 2 3
Câu 3 : (Phát triển câu 35- Đề thi tham khảo) Trong không gian Oxyz, một vectơ chỉ phương của
đường thẳng d là giao tuyến của hai mặt phẳng P : x 2y 3z 2 0 và Q : 2x y 3z 4 0 là
A. u 3;3; 1 B. u 3; 3 ; 1 C. u 3;3 ;1 D. u 3; 3 ; 1 Lời giải Chọn D Trang 66
P: x 2y 3z 2 0 n 1;2; 3
là véctơ pháp tuyến của P 1
Q:2x y 3z 4 0 n 2;1;3 là véctơ pháp tuyến của Q 2
Đường thẳng d là giao tuyến của hai mặt phẳng P và Q nên nhận
n ;n 9; 9 ; 3 3 3; 3 ; 1 1 2
là một vectơ chỉ phương Vậy u 3; 3 ;
1 là một vectơ chỉ phương của đường thẳng d.
Câu 4: (Phát triển câu 35- Đề thi tham khảo) Trong không gian Oxyz, đường thẳng d song song với x y 2 z 1
mặt phẳng P : x y z 2 0 và vuông góc với : :
có một vectơ chỉ phương là 1 2 2
A. u 1;0; 1 B. u 0; 1 ; 1 C. u 1; 1 ;0
D. u 0;1; 1 Lời giải Chọn D
P: x y z 2 0 n1;1;
1 là véctơ pháp tuyến của P x y 2 z 1 : u
1; 2; 2 là một vectơ chỉ phương của . 1 2 2
Vectơ u n ;u 0;1;1 1
là là một vectơ chỉ phương của đường thẳng d.
Câu 36. [ ĐỀ THI THAM KHẢO ] Chọn ngẫu nghiên một số từ tập các số tự nhiên có ba chữ số đôi
một khác nhau. Xác suất để số được chọn có tổng các chữ số là chẵn bằng 41 4 1 16 A. B. C. D. 81 9 2 81 Lời giải Chọn A
Ta có: n 9.9.8 648
Gọi N abc (với , a ,
b c 0;1;2;3;4;5;6;7;8; 9 ; , a ,
b c đôi một khác nhau, a 0 và a b c là số chẵn)
+ Trường hợp 1: Ba chữ số a, ,
b c đều chẵn, có: 4.4.3 48 (số).
+ Trường hợp 2: Ba chữ số a, ,
b c trong đó có hai chữ số lẻ và một chữ số chẵn:
Chọn 1 chữ số chẵn có 1 C cách, 5 Chọn 2 chữ số lẻ có 2 C cách, 5
hoán vị 3 chữ số được chọn có 3! cách. Loại đi 2
A cách có chữ số 0 đứng đầu. 5
Vậy trường hợp này có: 1 2 2
C .C .3! A 280 số. 5 5 5
Vậy có tất cả 48 280 328 (số). 328 41
Suy ra xác suất cần tìm: P 648 81
PHÁT TRIỂN THÊM CÂU 36: Trang 67
Câu 36.1. Chọn ngẫu nghiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để
số được chọn có tổng các chữ số hàng trăm và hàng đơn vị bằng hai lần chữ số hàng chục 5 1 5 2 A. B. C. D. 81 81 162 81 Lời giải Chọn B
Ta có: n 9.9.8 648
Gọi N abc (với , a ,
b c 0;1;2;3;4;5;6;7;8; 9 ; , a ,
b c đôi một khác nhau, a 0 và a c 2b ).
Vì a c 2b nên a c là số chẵn khác 0, ta có các trường hợp sau: + Trường hợp 1: , a c 1;3;5;7;
9 , mỗi cách chọn a, c có duy nhất 1 cách chọn b nên có: 2 A 20 (số). 5 + Trường hợp 2: , a c 0;2;4;6;
8 , a 0 , mỗi cách chọn a, c có duy nhất 1 cách chọn b nên có: 2 A 4 16 (số) 5
Vậy có tất cả 20 16 36 (số) 36 1
Suy ra xác suất cần tìm là: P 648 18
Câu 36.2. Chọn ngẫu nghiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để
số được chọn có chữ số hàng trăm, chữ số hàng đơn vị và tổng các chữ số theo thứ tự tạo thành 1 cấp số cộng có công sai dương 5 4 1 16 A. B. C. D. 162 9 2 81 Lời giải Chọn A
Ta có: n 9.9.8 648
Gọi N abc (với , a ,
b c 0;1;2;3;4;5;6;7;8; 9 ; , a ,
b c đôi một khác nhau, a 0 và , a ,
c a b c theo
thứ tự tạo thành 1 cấp số cộng có công sai d dương).
c a d
c a d
c a d
a b c a 2d
b d a b d a Ta có: 1 a 9
a d 9 a .
a d 9 a 0 . b c 9
a d 9 a 1 a 4 d 0 1 a 9
Với mỗi 1 a 4 có 9 a a 1 10 2a cách chọn d. 4
Suy ra có tất cả: 10 2a 20 (số) a 1 20 5
Vậy xác suất cần tìm là: P 648 162
Câu 36.3. Chọn ngẫu nghiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để
số được chọn có tích các chữ số là số dương và chia hết cho 6 Trang 68 55 23 13 49 A. B. C. D. 108 54 27 108 Lời giải Chọn A
Ta có: n 9.9.8 648
Gọi N abc (với , a ,
b c 0;1;2;3;4;5;6;7;8; 9 ; , a ,
b c đôi một khác nhau, a 0 và abc là số dương và chia hết cho 6).
Ta có: abc là số dương chia hết cho 6 nên abc 0 , chia hết cho 2 và 3.
abc chia hết cho 2 thì ít nhất một trong các số a, ,
b c thuộc 2; 4;6; 8 .
abc chia hết cho 3 thì ít nhất một trong các số a, , b c 3;6; 9 .
Do đó ta có các trường hợp sau:
+ Trường hợp 1: N có mặt số 6 , có: 2 3.A 168 (số). 8
+ Trường hợp 2: N có mặt số 3 hoặc 9 , không có mặt số 6 và có ít nhất một trong các số a, , b c thuộc 2;4; 8 , có: 2. 1 1 2
C .C .3! C .3 1
! C .3! 162 (số). 3 3 3 3
Vậy có tất cả: 168 162 330 (số). 330 55
Suy ra xác suất cần tìm là: P . 648 108
Câu 36.4. Chọn ngẫu nghiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để
số được chọn có tích các chữ số là số chia hết cho 15. 13 10 7 13 A. B. C. D. 36 27 18 27 Lời giải Chọn C
Ta có: n 9.9.8 648
Gọi N abc (với , a ,
b c 0;1;2;3;4;5;6;7;8; 9 ; , a ,
b c đôi một khác nhau, a 0 và abc là số dương và chia hết cho 15).
Ta có: abc là số chia hết cho 15 nên abc chia hết cho 3 và 5 .
abc chia hết cho 5 thì ít nhất một trong các số a, , b c thuộc 5; 0 .
abc chia hết cho 3 thì ít nhất một trong các số a, ,
b c thuộc 0;3;6; 9 .
Do đó ta có các trường hợp sau:
+ Trường hợp 1: N có mặt số 0 , có: 2 2.A 144 (số). 9
+ Trường hợp 2: N có mặt số 5 , không có mặt số 0 và có ít nhất một trong các số a, ,
b c thuộc 3;6; 9 , có: 1 1 2
C .C .3! C .3! 108 (số). 3 5 3
Vậy có tất cả: 144 108 252 (số) Trang 69 252 7
Suy ra xác suất cần tìm là: P 648 18
Câu 36.5. Chọn ngẫu nghiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để
số được chọn có tổng các chữ số là số chia hết cho 3. 1 1 19 11 A. B. C. D. 36 9 54 108 Lời giải Chọn C
Ta có: n 9.9.8 648
Gọi N abc (với , a ,
b c 0;1;2;3;4;5;6;7;8; 9 ; , a ,
b c đôi một khác nhau, a 0 và a b c là số chia hết cho 3 )
Gọi A 0;3;6; 9 , B 1;4; 7 ,C 2;5; 8
Để a b c chia hết cho 3 ta có các trường hợp sau: Trường hợp 1: a, ,
b c thuộc A hoặc B hoặc C , có: 2
3.A 3! 30 (số). 3
+ Trường hợp 2: 3 số a, ,
b c thuộc 3 tập khác nhau , A , B C Có: 1 1 1 1 1
2.C .C .2! C .C .C .3! 198 (số) 3 3 3 3 3
Vậy có tất cả: 30 198 228 (số). 228 19
Suy ra xác suất cần tìm là: P . 648 54 mx
Câu 37. [ ĐỀ THI THAM KHẢO ] Cho hàm số hàm số f x 4
( m là tham số thực). Có bao x m
nhiêu giá trị nguyên của m để hàm số đã cho đồng biến trên khoảng 0; ? A. 5 B. 4 C. 3 D. 2 Lời giải Chọn D
Điều kiện xác định: x m 2 m 4 Ta có y . x m2
Để hàm số đồng biến trên khoảng 0; thì 2 y 0 m 4 0 2 m 2 m 2 m 0 0; m 0 m 0
Do m nguyên nên m 1
;m 0 . Vậy có 2 giá trị nguyên của m thỏa mãn.
Câu 37-1. [Tƣơng tự câu 37-MH-2020] Cho hình chóp S.ABC . có đáy là tam giác đều cạnh a , SA
vuông góc với mặt phẳng đáy và SA 2a (minh họa như hình bên). Gọi M , N lần lượt là trung điểm của A ,
B AC . Khoảng cách giữa hai đường thẳng SB và MN bằng Trang 70 a 3 a 3 2 57a a 57 A. B. C. D. 4 2 19 19 Lời giải Chọn D
Ta có MN // BC MN // SBC Do đó 1
d MN SB d MN SBC d M SBC 1 , , , d ,
A ABC (vì MB AB ) 2 2 BC AK
Kẻ AK BC, AH SK , ta có:
BC SAK AH BC . BC SA AH SK Khi đó
AH SBC d ,
A SBC AH . AH BC
Xét tam giác SAK vuông tại A, có đường cao AH , ta có 1 1 1 1 1 19 2a 57 AH . 2 2 2 2 2 2 AH SA AK 4a 12a 19 a 3 2 1 1 a 57
Vậy d DM , SB d ,
A SBC AH . 2 2 19
Câu 37-2. [Phát triển câu 37-MH-2020 theo hƣớng thay đổi đa giác đáy] Cho tứ diện OABC có OA,
OB, OC đôi một vuông góc, OA OB ,
a OC 2a . Gọi M là trung điểm của AB. Khoảng cách giữa hai
đường thẳng OM và AC bằng 2 5a a 2 a 2 2a A. B. C. D. 5 2 3 3 Trang 71 Lời giải Chọn D
Cách 1: Gọi D đối xứng với B qua O.
Ta có: OM // AD OM // CAD d OM , AC d OM, ACD d ,
O ACD . 1 1 1 1 9 Vì O ,
A OC,OD đôi một vuông góc nên ta có 2 2 2 2 2 4 , OA OC OD a d O ACD a
O ACD 2a d ,
. Vậy d OM AC 2 , . 3 3
Cách 2: Chọn hệ trục tọa độ Oxyz sao cho O0;0;0; A ;
a 0;0; B0; ;
a 0;C 0;0;2a a a
M là trung điểm của AB M ; ; 0 . 2 2 Đườ a a
ng thẳng OM qua O và có vectơ chỉ phương OM ; ; 0 2 2
Đường thẳng AC qua A và có vectơ chỉ phương AC ; a 0;c . 2
OM , AC .OA a 2a Ta có: 2 2
OM , AC
a ;a ; ; OA ;
a 0; 0 d OM , AC . 2 3 OM , AC
Câu 37-3. [Phát triển câu 37-MH-2020 theo hƣớng giúp học sinh khắc sâu thêm cách xác định góc
giữa hai mặt phẳng] Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA vuông góc với mặt
phẳng đáy, góc giữa mặt phẳng SBC và mặt đáy là 60 (minh họa như hình bên). Gọi M , N lần lượt là trung điểm của A ,
B AC . Khoảng cách giữa hai đường thẳng SB và MN bằng Trang 72 3a 3a a 6 A. B. C. a 6 D. 8 4 2 Lời giải Chọn A
Ta có: MN // BC MN // SBC Do đó 1
d MN SB d MN SBC d M SBC 1 , , , d ,
A SBC (vì MB AB ) 2 2 BC AK
Kẻ AK BC, AH SK , ta có:
BC SAK AH BC . BC AC AH SK Khi đó
AH SBC d ,
A SBC AH . AH BC
SBC ABC BC
Ta lại có BC AK
SBC, ABC SKA 60. BC SK
BC SAK
Xét tam giác AKH vuông tại H, ta có: a 3 3 3a
AH AK.sin SKA . 2 2 4 1 1 3a
Vậy d DM , SB d ,
A SBC AH 2 2 8 Trang 73
Câu 37-4. [Phát triển câu 37-MH-2020 theo hƣớng giúp học sinh khắc sâu thêm cách xác định góc
giữa dƣờng thẳng và mặt phẳng] Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB 2 ,
a AD DC a . Hai mặt phẳng SAB và SAD cùng vuông góc với đáy. Góc giữa SC
và mặt đáy bằng 60 . Tính khoảng cách d giữa hai đường thẳng AC và SB . a 6 2a 15 A. d
B. d 2a
C. d a 2 D. d 2 5 Lời giải Chọn A
Xác định 60 SC, ABCD SC, AC SCA và SA A .
C tan SCA a 6
Gọi M là trung điểm AB, suy ra ADCM là hình vuông nên CM AD a 1
Xét tam giác ACB, ta có trung tuyến CM a
AB nên tam giác ACB vuông tại C. 2
Lấy điểm E sao cho ACBE là hình chữ nhật, suy ra AC // BE .
Do đó d AC, SB d AC,SBE d , A SBE
. Kẻ AK SE Do đó d A SBE S . A AE a 6 , AK 2 2 2 SA AE
Cách khác: Hệ tọa độ hóa trong không gian.
Chọn hệ trục tọa độ với A0;0;0, S 0;0;a 6,C ; a ; a 0, B 2 ; a 0;0 .
Ta có: AC a a SB a a AC SB 2 2 2 ; ;0 , 2 ;0; 6 , 6a ; 6a ; 2
a và AB 2 ; a 0;0 3 A .
B AC, SB 2 6a a 6
Vậy d AC; SB . 4a 2 AC, SB
Câu 37-5. [Phát triễn câu 37-MH-2020 theo hƣớng giúp học sinh khắc sâu thêm cách tính khoảng
cách giữa hai đƣờng thẳng chéo nhau] Cho hình lập phương ABC . D A B C D
có cạnh bằng a. Gọi E,F
lần lượt là trung điểm của AB, CD. Khoảng cách d giữa hai đường thẳng EF và AC' là 2a 2a a
A. d a B. d C. d D. d 4 2 2 Lời giải Trang 74
Ta có EF // B C
EF // AC B
Nên d EF; AC d EF; AC B
d E;AC B
Kẻ EH ABH AB Do C B ABB A nên B C EH
Suy ra EH AC B
Do đó d E; AC B EH a a 2 Xét AEH
vuông cân tại H có: EA EH 2 4 a
Vậy d EF AC 2 ; 4 x
Câu 38. [ ĐỀ THI THAM KHẢO ] Cho hàm số f x có f 3 3 và f x với x 0 . x 1 x 1 8
Khi đó f x dx bằng 3 197 29 181 A. 7 B. C. D. 6 2 6 Lời giải Chọn B x
f x là một nguyên hàm của hàm số f x x 1 x 1 x
x 1 1 x 1 1 1 dx dx dx x x C x x
x 1 x 1 1 2 1 1 1 1 x 1
Suy ra f x x 2 x 1 C
f 3 3 C 4
f x x 2 x 1 4 Trang 75 8 197
Dùng máy tính bấm x 2 x 1 4dx 6 3
Bình luận. Bài này hoàn toàn có thể đặt t
x 1 để tìm nguyên hàm của hàm số.
Câu 1. [Phát triển câu 38 tƣơng tự dùng liên hiệp ]. Cho hàm số f x có f 0 1 và 1 f x 1
với x 0 . Khi đó
f x dx bằng x 1 x x x 1 0 17 8 17 8 A. 32 12 1 B. 2 C. 32 12 1 D. 2 3 3 3 3 Lời giải Chọn B 1 x 1 x x x 1 dx dx x 1 x x x 1 x 2 2
1 x x x 1 x 1 x x x 1 1 1 dx
dx 2 x 2 x 1 C x x 1 x x 1
Suy ra f x 2 x 2 x 1 C
Mà f 0 1 C 3. 1 17 8
Bấm máy tính 2 x 2 x 1 3dx 2 3 3 0 9 16 1 a b ln 2
Câu 2. Phát triển 2 câu 38 [ Nâng cao đổi biến ] Cho dt với a, , b c là các x 1 x 1 c 0 a số nguyên dương và
tối giản. Giá trị của biểu thức a b c bằng c A. 43 B. 48 C. 88 D. 33 Lời giải Chọn D
x 1 x t 2 2 1 1 4t 1
Đặt t x 1 x
2 x t 4x t 4 1 dx dt
x 1 x t t t t Đổ 9
i cận: x 0 t 1; x t 2. 16 9 16 4 2 2 2 t 1 t t 2 3 2 1 1 1 1
1 t t t 1 Suy ra dt dt dt dt 3 x 1 x 1 2t t 3 3 1 2 t 2 t 0 1 1 1 2 2 1 1 1 1 1 1 1 9 8ln 2 1 dt
t ln t 2 3 2 t t t 2 t 2t 16 1 1
Vậy a 9;b 8;c 16 a b c 33 . Trang 76
Câu 3. Phát triển 3 câu 38[ nâng cao, kết hợp liên hiệp ] 2 4 3x 3x 3 Cho
dx a b c
, với a, b, c là các số nguyên dương. Giá trị biẻu thức a b c bằng 2 x x 1 1 A. 59 B. 104 C. 111 D. 147 Lời giải Chọn D Ta có 4 3 3 3 3 4 2 2 x x x x 2 1 3 2 x x 1 2 x x 1 dx dx dx 2 2 2 x x 1 x x 1 x x 1 1 1 1 2
3x 3 x 1dx 2
x 2 x 3 2 3
1 86 314 2 1 1
7 6 3 4 2 7 32 108
Vậy a 7;b 32;c 108 a b c 147 .
Câu 4. Phát triển 4 câu 38 [ nâng cao, kết hợp lƣơng hiêp và đổi biến ] 2 dx Cho
a b 2 c 3 d ln 3 2 3 với , a , b ,
c d là các số hữu tỷ. Giá trị của biểu thức 2 1 1 x 1 x
a b c d bằng 1 5 A. 0 B. 3 C. D. 2 2 Lời giải Chọn A 3 3 2 3 2 dx
1 x 1 x
1 x 1 x Vì x 1 ; 3 nên I dx dx 2
1 x 1 x 1 x 1 x 2x 1 1 2 2 1 3 3 3 3 2 1 dx 1 1 1 x 1 1 x 3 2 1 1 x dx xdx ln 3 1 xdx 2 2 2 x 2 2 x 2 2 2 x 1 1 1 1 1 Đặt 2 t x t 2 2 1,
0 x t 1 xdx tdt
Đổi cận: - Với x 1 t 2
- Với x 3 t 2 1 1 2 1 t I ln 3 3 1 tdt 2 2 2 2 t 1 2 2 2 2 2 2 t 1 1 1 1 1 t 1 Ta có: dt 1 dt 1 dt 1 ln 2 2 t 1 t 1
2 t 1 t 1 2 t 1 2 2 2 2 2 1 1 2 1 1 1 1 2 2 ln ln 2 2 ln ln 2 1 2 3 2 1 2 3 2 Trang 77 I 2 1 1 1 1 1 1 ln 3 3 1 2 2 ln ln 2 1 2 2 2 2 3 2 3 1 1 1 3 2 ln 3 2 3 2 2 2 2 3 1 1 1
a ,b ,c ,d 2 2 2 2
a b c d 0 mx
Câu 39. [ ĐỀ THI THAM KHẢO ] Cho hàm số f x 4
(với m là tham số thực). Có bao nhiêu x m
giá trị nguyên của m để hàm số đã cho đồng biến trên khoảng 0; ? A. 5 B. 4 C. 3 D. 2 Lời giải Chọn D
Điều kiện xác định: x m 2 m 4 Ta có: y x m2 2 y 0, x m m 4 0
Hàm số đồng biến trên khoảng 0; . m 2 m 0 0; m 0
Do m nguyên nên m 1 ; 0
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu đề bài. Phân tích:
Đây là bài toán “Xét tính đơn điệ ax b
u của hàm số phân thức hữu tỉ y
, với ad bc 0 ”. cx d
Kiến thức này ở bài học “Tính đơn điện của hàm số” thuộc Chương I – Giải tích 12.
Để nắm vững các bài toán kiểu này, các em học sinh cần ghi nhớ các kiến thức cơ bản sau đây: ax b
Bài toán 1: Đối với hàm số y
, với ad bc 0 . cx d d
+ Tập xác định của hàm số là D \ . c + Đạ ad bc o hàm y
cx d , x D 2
Kiến thức 1: Hàm số đã cho đồng biến trên từng khoảng xác định khi và chỉ khi y 0 , với mọi
x D ad bc 0 .
Kiến thức 2: Hàm số đã cho nghịch biến trên từng khoảng xác định khi và chỉ khi y 0 , với mọi
x D ad bc 0 .
Kiến thức 3: Hàm số đã cho đồng biến trên K khi và chỉ khi y 0 , với mọi x K Trang 78
ad bc 0
ad bc 0 d
. (Ở đây, K có thể là một khoảng, nửa khoảng hoặc đoạn) K D K c
Kiến thức 4: Hàm số đã cho nghịch biến trên K khi và chỉ khi y 0 , với mọi x K
ad bc 0
ad bc 0 d . K D K c Chú ý rằng: d d d + Nếu
; thì ta phải có hoặc . c c c d d + Nếu
; thì ta phải có c c d d + Nếu ;
thì ta phải có c c
+ Các em có thể áp dụng cho các trường hợp tương tự. Bên cạnh đó, cần nắm vững các phép toán tập hợp
để tránh những nhầm lẫn đáng tiếc. .
a u x b
Bài toán 2: Đối với hàm số y
, với ad bc 0 . Trong đó, u x là hàm số theo biến x. .
c u x d
+ Bƣớc 1: Đặt u u x , ta có u ux . .
a u x b
+ Bƣớc 2: Đưa hàm số đã cho về dạng y
, với ad bc 0 . Đến đây, ta thấy bài toán đã cho .
c u x d
trở về bài toán giống như “Bài toán 1”. Tuy nhiên, ở đây ta cần chú ý cụ thể đến tính đồng biến hoặc
nghịch biến của hàm số u x để xử lí bài toán 2 cho chuẩn xác, cụ thể: .
a u x b
Trƣờng hợp 1: Nếu u u x là hàm đồng biến trên khoảng ; thì hàm số y đồng .
c u x d . a u b
biến (hoặc nghịch biến) trên khoảng ; khi và chỉ khi hàm số y
đồng biến (hoặc nghịch . c u d
biến) trên khoảng u ;u . .
a u x b
Trƣờng hợp 2: Nếu u u x là hàm nghịch biến trên khoảng ; thì hàm số y đồng .
c u x d . a u b
biến (hoặc nghịch biến) trên khoảng ; khi và chỉ khi hàm số y
nghịch biến (hoặc đồng . c u d
biến) trên khoảng u ;u .
Ta sẽ tìm hiểu chi tiết qua các câu hỏi tương tự sau đây:
CÂU HỎI TƢƠNG TỰ: 2x m
Câu 1: Tìm tất cả các giá trị thực của tham số m để hàm số y
đồng biến trên các khoảng xác x 1 định của nó. Trang 79 A. m 2 B. m 2 C. m 2 D. m 2 Lời giải Chọn C
Tập xác định: D \ 1 m 2 Ta có: y x , x D 2 1
YCBT y 0, x
D m 2 0 m 2. mx 2
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số y
nghịch biến trên các khoảng ác x m 3 định của nó.
A. 1 m 2
B. 1 m 2.
C. m 2 hoặc m 1
D. m 2 hoặc m 1 Lời giải Chọn A
Tập xác định: D \ 3 m 2 m 3m 2 Ta có: y x D
x m 3 , 2 2
YCBT y 0, x
D m 3m 2 0 1 m 2. x 2
Câu 3: Có bao nhiêu giá trị nguyên của tham số m để hàm số y
đồng biến trên khoảng x 5m ; 10 ? A. 2 B. Vô số C. 1 D. 3 Lời giải Chọn A
Tập xác định: D \ 5 m 5m 2 Ta có: y x D x 5m , 2 2 y 0, x D 5 m 2 0 m 2 YCBT m ; 10 D 5 m ; 1 0 5 2 5 5 m 1 0 Vì m nên m 1;
2 . Vậy có 2 giá trị của m thỏa mãn yêu cầu đề bài m 1 x 2m 2
Câu 4: Có bao nhiêu giá trị nguyên của tham số m để hàm số y nghịch biến trên x m 1 ; ? A. 2 B. Vô số C. 1 D. 3 Lời giải Chọn C Trang 80
Tập xác định: D \ m 2 m m 2 Ta có: y
x m , x D 2 2 y 0, x D
m m 2 0 1 m 2 YCBT m m D 1 ; 1 2 1; m 1 Vì m
nên m 1. Vậy có 1 giá trị của m thỏa mãn yêu cầu đề bài mx 2m 3
Câu 5: Cho hàm số y
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để x m
hàm số đồng biến trên các khoảng xác định. Tính tổng bình phương các phần tử của S . A. 5 B. 15 C. 9 D. 3 Lời giải Chọn B
Tập xác định: D \ m 2
m 2m 3 Ta có: y x m , x D 2 2
YCBT y 0, x
D m 2m 3 0 1 m 3
Do đó, S 0;1;
2 . Vậy tổng bình phương các phần tử của S bằng 5 mx 4m
Câu 6: Cho hàm số y
với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của m x m
để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S . A. 5 B. 4 C. Vô số. D. 3 Lời giải Chọn D
Tập xác định: D \ m 2 m 4m Ta có: y
x m , x D 2 2
YCBT y 0, x
D m 4m 0 0 m 4.
Do đó, S 1;2;
3 . Vậy số phần tử của S là 3. tan x 2
Câu 7: Có bao nhiêu giá trị nguyên của tham số m để hàm số y
đồng biến trên khoảng tan x m 0; ? 4 A. 0 B. 2 C. 1 D. Vô số. Lời giải Chọn C Trang 81 Đặ 1
t u tan x , ta có u 0, x 0;
. Do đó u tan x đồng biến trên khoảng 0; . Và khi 2 cos x 4 4 x 0;
ta có u 0; 1 . 4 Bài toán đã cho trở u
thành: “Tìm tất cả các giá trị thực của tham số m để hàm số f u 2 đồng biến u m trên khoảng 0; 1 ” 2 m
Ta có: f u u m2 m 2 2 m 0 + YCBT m m m 0; 0 1 2 1 m 1 2cos x 1
Câu 8: Tìm tất cả các giá trị thực của tham số m để hàm số y
nghịch biến trên khoảng cos x m 0; . 2 A. m 0 B. m 0 C. m 1 D. m 1 Lời giải Chọn A
Đặt u cos x , ta có u sin x 0, x 0;
. Do đó u cos x nghịch biến trên khoảng 0; . Và 2 2 khi x 0;
ta có u 0; 1 . 2
Bài toán đã cho trở u
thành: “Tìm tất cả các giá trị thực của tham số m để hàm số f u 2 1 đồng u m
biến trên khoảng 0; 1 ” 2 m 1
Ta có: f u u m2 1 m 2 m 1 0 2 + YCBT m m 0; 0 1 m 0 m 1 2 2 9 x m
Câu 9: Cho hàm số y
, với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m 2 9 x m
không vượt quá 2020 để hàm số đồng biến trên khoảng 0; 5. Tính tổng các phần tử của tập hợp S. A. 2041205. B. 2039190. C. 2039191. D. 2041210. Lời giải Trang 82 Chọn D Đặ x t 2
u 9 x , ta có u 0, x 0; 5 . Do đó 2
u 9 x nghịch biến trên khoảng 2 9 x
0; 5. Và khi x0; 5 ta có u2;3.
Bài toán đã cho trở thành: “Cho hàm số 2u m f u
, với m là tham số. Gọi S là tập hợp tất cả các giá u m
trị nguyên của m không vượt quá 2020 để hàm số nghịch biến trên khoảng 2;3 . Tính tổng các phần tử của tập hợp S ”. m
Ta có: f u u m2 m 0 m 0 + YCBT . m m m 2;3 2 0;2 3; m 3 + Do đó 2020.2021
S 1;2;3;4;....,202
0 . Tổng phần tử của S là T 2041210. 2
Câu 40: [ ĐỀ THI THAM KHẢO ] Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh
hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối
nón được giới hạn bởi hình nón đã cho bằng 32 5 A. B. 32 C. 32 5 D. 96 3 Lời giải Chọn A 2 2 AB 3 AB 3 Ta có 2 2 S
9 3 AB 36 SA 36 . SAB 4 4 2 2 R OA
SA SO 36 20 4 . 1 32 5
Thể tích của khối nón là 2
V R h 3 3 Câu tương tự Trang 83
Câu 40.1 ( Câu tương tự 40 đề thi tham khảo) Cho hình nón có chiều cao bằng 11 . Một mặt phẳng đi
qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác vuông cân có diện tích bằng 18. Thể
tích của khối nón được giới hạn bởi hình nón đã cho bằng 25 11 A. B. 150 C. 25 11 D. 50 3 Lời giải Chọn A Theo giả thiết, S
AB vuông cân tại S. 2 SA Ta có 2 S 18 SA 36 . SAB 2 2 2 R OA
SA SO 36 11 5. 1 25 11
Thể tích của khối nón là 2
V R h . 3 3
Các câu phát triển
Ý tưởng: Ta biết rằng với hình nón, ta có công thức: 2 2 2
R h l . Trong ba đại lượng ,
R l, h nếu biết hai
đại lượng thì tính được đại lượng còn lại. Nếu cho một trong ba đại lượng và ẩn giấu đại lượng thứ hai
trong một giả thiết nào đó thì bài toán sẽ khó hơn cho luôn hai đại lượng.
Câu 40.2 (Phát triển đề thi tham khảo câu 40) Cho hình nón có chiều cao bằng 3. Một mặt phẳng
đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều. Biết góc giữa đường thẳng chứa
trục của hình nón và mặt phẳng là 45. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng A. 5 24 B. 15 24 C. 45 D. 15 Lời giải Chọn D Trang 84
Gọi thiết diện của hình nón cắt bởi là tam giác đều SAB, I là tâm của đáy, M là trung điểm của AB.
Ta có góc giữa đường thẳng chứa trục của hình nón và mặt phẳng là 45.
MSI 45 M
SI vuông cân tại I. SM 2 2
SM SI 2 3 2, MB
6, MI SI 3, R MB MI 15 . 3 1 Thể tích khối nón là 2
V R h 15 . 3
Câu 40.3 ( Phát triển đề thi tham khảo câu 40) Cho hình nón có chiều cao bằng 2 . Một mặt phẳng
đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều. Biết khoảng cách từ tâm 2
của đáy hình nón đến mặt phẳng là
. Diện tích xung quanh của hình nón đã cho bằng 3 4 3 8 3 A. B. C. 8 3 D. 4 3 3 3 Lời giải Chọn D
Gọi thiết diện của hình nón cắt bởi là tam giác đều SAB, I là tâm của đáy, M là trung điểm của AB.
Kẻ IH SM tại H. 1 1 1
d I 2 , IH . Mà 2 2
IM 2 SM SI IM 6 3 2 2 2 IH SI IM SM 2 2 MB
2 R IM MB 6 và l SB AB 2MB 2 2 3
S Rl 6.2 2 4 3 . xq
Câu 40.4 ( Phát triển đề thi tham khảo câu 40) Cho hình nón có chiều cao bằng 1. Một mặt phẳng
đi qua đỉnh hình nón và cắt hình nón theo một thiết diện là tam giác đều có diện tích S. Gọi S là diện d tích đáy củ 5 3
a hình nón. Biết S
S . Diện tích toàn phần của hình nón đã cho bằng 4 d 53 5 1 5 1 53 A. B. C. D. 6 2 4 12 Lời giải Trang 85
Gọi R là bán kính đáy của hình nón.
Cạnh của thiết diện là: 2 2 2 SA
SO R 1 R . 2 2 1 R SA 3 3
Diện tích thiết diện là: S . 4 4
Diện tích đáy hình nón: 2 S R . d 2 R 2 1 3 5 3 R .5 3 1 5 Ta có S S
R SA l 4 d 4 4 2 2 5 1 1 1 5 2
Diện tích toàn phần của hình nón là: S R Rl . . . . tp 4 2 2 4 Câu 41: [ ĐỀ x
THI THAM KHẢO ] Cho ,
x y 0 thỏa log x log y log 2x y . Giá trị của 9 6 4 y bằng 1 3 A. 2. B. C. log D. log 2 2 2 2 3 2 Lời giải Chọn B
Đặt log x log y log 2x y t 9 6 4 t 3 1 t t 2
x 9 , y 6 t t t t t t 3 3 2 3 1 Suy ra 2.9 6 4 2. 1 0 .
2x y 4t 2 2 t 2 2 3 1 2 2 t t x 9 3 1 Vậy . y 6 2 2
Câu 41.1. (Phát triển Tương tự câu 41 đề thi tham khảo) Giả sử p, q là các số thực dương thỏa mãn p
log p log q log
p q . Tìm giá trị của ? 16 20 25 q 4 1 8 1 A. B. 1 5 C. D. 1 5 5 2 5 2 Lời giải Chọn D Trang 86 log p t p 16t 16
Ta có: log p log q log
p q log q t q 20t
16t 20t 25t 16 20 25 20 log
p q t
p q 25t 25 t 4 1 5 vn t t 16 4 5 2 1 0 25 5 t 4 1 5 5 2 t p 16 4 1 5 Từ đó ta được . q 20t 5 2
Câu 41.2. (Phát triển Tương tự câu 41 đề thi tham khảo :nâng độ khó, khi tính tổng tỷ lệ) Cho các 1 1 số ,
a b 0 thỏa mãn log a log b log a b . Giá trị bằng 3 6 2 2 2 a b A. 18. B. 45. C. 27. D. 36. Lời giải Chọn B a 3t t Đặ t t t t 3
t t log a log b log
a b b 6 3 6 2 3t 1 1 3 6 2 2
a b 2t t t 3 3 Xét hàm số 3 3t f t trên , có .ln 3t f t .ln 3 0, t f
t đồng biến trên 2 2 2 1 1 1 1 và
1 f t f 1 t 1
a ,b 45 . 2 2 3 6 a b
Câu 41.3. (Phát triển Tương tự câu 41 đề thi tham khảo: Phát triển cho 3 số với giả thiết hàm a 4b a
logarit) Cho hai số thực a , b thỏa mãn log
a log b log . Giá trị bằng 100 40 16 12 b A. 4. B. 12. C. 6. D. 2. Lời giải Chọn C a 4b a b t t 4
Đặt log a log b log
t . Ta có a 100 ,b 40 , 16t . 100 40 16 12 12 t 2 1 t t t t t 4 2 5 6
Suy ra 100 4.40 12.16 12. 4. 1 0 25 5 t 2 1 5 2 t t t Do đó 2 1 a 100 5 6 . 5 6 b 40 2 Trang 87
Câu 41.4. (Phát triển Tương tự câu 41 đề thi tham khảo: Phát triển cho 3 số với giả thiết hàm mũ) n n
Cho các số m 0, n 0, p 0 thỏa mãn 4m 10n 25p
. Tính giá trị biểu thức T . 2m 2 p 5 1 A. T 1 B. T C. T 2 D. T 2 10 Lời giải Chọn A n m n log 4
Vì 4 10 n mlog 4 log 2 . 2m 2 n n p log 25
Vì 10 25 n p log 25 log5. 2 p 2 n n Suy ra T
log 2 log5 log10 1. 2m 2 p
Câu 42: [ ĐỀ THI THAM KHẢO ] Gọi S là tập hợp tất cả các giá trị thực của tham số thực m sao cho
giá trị lớn nhất của hàm số 3
y x 3x m trên đoạn 0;
3 bằng 16 . Tính tổng các phần tử của S bằng A. 16 B. 16 C. 12 D. 2 Lời giải Chọn A
Nhận xét: Hàm số g x 3
x 3x m là hàm số bậc ba không đơn điệu trên đoạn 0; 3 nên ta sẽ đưa
hàm số này về hàm bậc nhất để sử dụng các tính chất cho bài tập này. Đặt 3
t x 3x , do 0;
3 nên ta tìm được miền giá trị t 2 ;1
8 . Khi đó y t m đơn điệu trên 2 ;1 8 . Ta có y t m
m m m 2 m 18 m 2 m 18 max max max 2 ; 18 . m 8 10 x 0; 3 t 2 ;1 8 2 m 2
Từ giả thiết ta có max y 16 m 8 10 16 m 8 6 . x 0; 3 m 14
a b a b
Chú ý: Cách giải trên ta đã sử dụng tính chất của hàm số bậc nhất là max a ; b 1 2
Tuy nhiên có thể trình bày phần sau bài toán như sau mà không cần công thức (1). Ta có
max y max t m max m 2 ; m 18 x 0; 3 t 2 ;1 8 m 18 16
+ Trường hợp 1: max y m 18 16 m 2 . x 0; 3 m 2 16 m 2 16
+ Trường hợp 2: max y m 2 16 m 1 4 . x 0; 3 m 18 16 Trang 88 CÂU TƯƠNG TỰ
Câu 42.1: (Phát triển Tương tự câu 42 đề thi tham khảo) Gọi S là tập hợp tất cả các giá trị thực của
tham số m sao cho giá trị lớn nhất của hàm số 2
y x 2x m trên đoạn 0;
3 bằng 5. Tổng tất cả các phần tử của S bằng A. 2 B. 2 C. 12 D. 8 Lời giải Chọn A
Xét hàm số f x 2
x 2x m trên đoạn 0; 3 .
f x 2x 2
f x 0 2x 2 0 x 1 f 0 , m f
1 m 1, f 3 m 3
max f x maxm 1; ; m m 3 m 3 x 0; 3
min f x maxm 1; ; m m 3 m 1 x 0; 3 m 1 5 y f x m m m 3 5 m 4 max max max 1 ; 3 5 . x 0; 3 x 0; 3 m 3 5 m 2 m 1 5 Vậy S 4 ;
2 . Tổng tất cả các phần tử của S bằng 2 .
CÂU PHÁT TRIỂN 1. Phát triển theo ý tưởng so sánh giữa max và min của hàm chứa ẩn trong
dấu giá trị tuyệt đối.
Câu 42.2: (Phát triển Tương tự câu 42 đề thi tham khảo) Cho hàm số 4 3 2
y 3x 4x 12x a . Gọi
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn 1
;2. Có bao nhiêu số
nguyên dương a thuộc đoạn 0;100 sao cho M 2m ? A. 36 B. 37 C. 40 D. 38. Lời giải Chọn B
Xét hàm số f x 4 3 2
3x 4x 12x a trên đoạn 1 ;2. f x 3 2
12x 12x 24x x 1 f x 3 2
0 12x 12x 24x 0 x 0 x 2 f 0 , a f
1 a 5, f 2 a 32 Trang 89
Để có được M 2m thì m 0 (có nghĩa là phần đồ thị hàm số f x 4 3 2
3x 4x 12x a trên đoạn 1
;2 không cắt trục hoành). a 0 a 0 Vậy ta suy ra . a 32 0 a 32
Vì a 0;100 nên ta chỉ loại trường hợp a 0
Với a 32 , ta có: m a 32 a 32, M a a
Vậy M 2m a 2a 32 a 64 (thỏa mãn).
Kết luận: Trong đoạn 0;100 có 37 số nguyên dương a thỏa mãn.
CÂU PHÁT TRIỂN 2. Phát triển theo ý tưởng tìm min của hàm số chứa ẩn trong dấu giá trị tuyệt đối.
Câu 42.3: (Phát triển Tương tự câu 42 đề thi tham khảo) Gọi S là tập hợp tất cả các giá trị thực của
tham số m sao cho giá trị nhỏ nhất của hàm số 3 2
y x 3x m trên đoạn 1;
3 bằng 3. Tổng tất cả các
phần tử của S bằng A. 3 B. 2 C. 4 D. 7 Lời giải Chọn C
Xét hàm số f x 3 2
x 3x m trên đoạn 1; 3 f x 2 3x 6x f x x 0 2
0 3x 6x 0 x 2 f
1 m 2, f 2 m 4, f 3 m
Gọi A, a lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x 3 2
x 3x m trên đoạn 1; 3 . Ta có:
A max f x maxm 4;m 2; m m x 1; 3
a min f x minm 4;m 2; m m 4 x 1; 3
+ Nếu a 0 m 4 0 m 4 thì min y m 4 m 4 3 m 7 (thỏa mãn) x 1; 3
+ Nếu A 0 m 0 thì min y m m 3 m 3 (thỏa mãn). x 1; 3
+ Nếu Aa 0 thì min y 0 (loại) x 1; 3 Trang 90 Vậy S 3 ;
7 . Tổng tất cả các phẩn tử của S bằng 4.
CÂU PHÁT TRIỂN 3. Phát triển theo ý tưởng tìm max của hàm số chứa ẩn trong dấu giá trị tuyệt đối
chứa hai tham số khác nhau.
Câu 42.4: (Phát triển Tương tự câu 42 đề thi tham khảo) Cho hàm số 4 2
y 8x ax b . Trong đó
a,b là các hệ số thực. Tìm mối liên hệ giữa a và b để giá trị lớn nhất của hàm số đã cho trên đoạn 1 ; 1 bằng 1?
A. b 8a 0
B. b 4a 0
C. b 4a 0
D. b 8a 0 Lời giải Chọn D Đặt 2
t x , suy ra t 0; 1 2 a a Xét g t 2
8t at b , đây là đồ thị Parabol có bề lõm quay lên và tọa độ đỉnh là I ; b 16 32 Trườ a ng hợp 1. 0; 1 16
Để thỏa mãn yêu cầu của bài toán, ta phải có: 1 g 0 1 1 b 1 3 2 32b 32 1 g 1 1 1
a b 8 1 3
2 32a 32b 256 32 2 2 2 a 3
2 a 32b 32 3
2 a 32b 32 1 b 1 32 2 6 4 a 64 8 a 8 8 a 8 a 8 2 2 6
4 a 32a 256 64
a 32a 192 0 2 4 a 8 1 b 1 1 b 1 1 b 1 Với a 8 thay vào hệ 1
a b 8 1 , ta được: b 1 3 2 6 4 32b 32 1 b 3 2 3
2 a 32b 32
Thử lại: g t 2
8t 8t 1 với t 0; 1
gt 16t 8 gt 1
0 16t 8 0 t 2 g 1 0 1, g 1 , g 1 1 2 a 8
Vậy max y max g t 1, suy ra thỏa mãn. 1 ; 1 0; 1 b 1 Trang 91 a 0 a 0 Trườ 16 ng hợp 2. a a 16 1 16
Để thỏa mãn yêu cầu của bài toán, ta phải có: 1 g 0 1 1 b 1 1 b 1 1 g 1 1 1
a b 8 1 1
a b 8 1 2
a 8 2 1 0 a 6 (loại)
Câu 43 : [ ĐỀ THI THAM KHẢO ] Cho phương trình 2 log
2x m 1 log x m 2 0 ( m là tham 2 2
số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1;2 là A. 1;2 B. 1;2 C. 1;2 D. 2; Lời giải Chọn C Phương tr 2 ình: 2 log
2x m 2 log x m 2 0 1 log x
m 2 log x m 2 0 2 2 2 2 log x 1 0 2
log x mlog x m 1 0 log x 1 log x 1 m 0 . 2 2 2 2 2
log x m1 2
Ta có: log x 1 0 x 2 (thỏa mãn). 2 Yêu cầu bài toán 1 log 1 2m x m x
có nghiệm duy nhất trên 1;2 . 2 m 1 1 2
2 0 m111 m 2. Bình luận:
Dạng toán: Tìm điều kiện của m để phương trình có dạng Plog ;
x m 0 với m là tham số thực có k a
nghiệm thực phân biệt trên K. Phương pháp chung:
Bước 1: Đặt t log x , khi x K t K . a 1
Bước 2: Phương trình Plog ;
x m 0 Pt;m 0 * . a
Phương trình đã cho có k nghiệm trên K
* có k nghiệm trên K . 1
Câu 43.1.(Bài toán tương tự) (Phát triển Tương tự câu 43 đề thi tham khảo)
Định hướng xây dựng bài toán: Tương tự như câu 43 giữ nguyên dạng phương trình và cách đặt vấn đề
cũng như yêu cầu của bài toán. Cho phương trình log 2
log 3x log x m 1 0 ( m là tham số thực). Tập hợp tất cả các giá trị của m để 3 3
phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng 0; 1 9 1 9 9 A. m B. 0 m C. 0 m D. m 4 4 4 4 Lời giải Trang 92 Chọn C
Cách 1: Phương trình đã cho 2
log 3x log 3x m 2 0 1 . 3 3
Đặt t log 3x , thì phương trình (1) có dạng: 2
t t m 2 0 2 . 3 Khi x 0;
1 0 3x 3 log 3x 1 t 1. 3
Yêu cầu đề bài tương đương với tìm tham số m đề phương trình (2) có đúng hai nghiệm phân biệt t ,t 1 2 nhỏ hơn 1. 0 0 1 4m 8 0 9 4m 0 9
t 1 t 1 0 t
t t t 1 0 m 2 11 0 0 m . 1 2 1 2 1 2 m 0 4
t t 2 0
t t 2 0 1 2 0 1 2 1 2 9 Vậy 0 m . 4
Cách 2: Phương trình đã cho 2
log 3x log 3x m 2 0 1 . 3 3
Đặt t log 3x , thì phương trình (1) có dạng: 2 2
t t m 2 0 t t 2 m 2 . 3 Khi x 0;
1 0 3x 3 log 3x 1 t 1. 3 Xét hàm số 2
f t t t với t ;1 .
Bảng biến thiên của f t :
Số nghiệm của phương trình (2) bằng số giao điểm của đồ thị y f t và đường thẳng y 2 m .
Phương trình (2) có hai nghiệm phân biệt nhỏ hơn 1 1 9
2 m 2 0 m . 4 4 9 Vậy 0 m . 4
Câu 43.2.(Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Định hướng xây dựng bài toán: Bài toán giữ nguyên ý tưởng câu 43 thay đổi cách đặt vấn đề và hướng tiếp cận bài toán. Gọi S là tập tất cả giá trị nguyên của tham số m để phương trình 10 m 1 log x 32 1 2 4 m 5 log
4 m 1 0 có nghiệm trên đoạn
;6 . Số phần tử của tập S 1 1 x 3 3 3 3 bằng A. 5 B. 3 C. 6 D. 4 Lời giải Chọn C Trang 93 2 1
Cách 1: Ta có m 2 1 log x 3 4 m 5 log 4 m 1 0 1 1 x 3 3 3 4m 2 1 log
x 3 4 m 5 log
x 3 4 m 1 0 1 1 3 3 m 2 1 log
x 3 m 5 log
x 3 m 1 0 1 1 3 3 Đặ 10 t t log
x 3 khi x ;6 t 1 ; 1 . 1 3 3
Phương trình trở thành: m 2
1 t m 5t m 1 0 .
Bài toán trở thành tìm giá trị nguyên của m để phương trình: m 2
1 t m 5t m 1 0 * có nghiệm t 1 ; 1 . 2 t 5t 1 * m
có nghiệm t 1 ;
1 min g t m max g t . 2 t t 1 1 ; 1 1 ; 1 4 2 t t 5t 1 1
Xét hàm: g t 2
. Ta có: gt 0, t 1 ;1 2 2 t t 1
2t t 1
Lại có hàm số g t liên tục trên 1 ; 1 .
Suy ra, g t nghịch biến trên đoạn 1 ; 1 .
g t g
g t g 7 min 1 3; max 1 . 1 ; 1 1 ; 1 3 7 3
m và m m 3 ; 2 ; 1 ;0;1; 2 . 3 Cách 2: 2 1
Với điều kiện x 3 thì m 2 1 log x 3 4 m 5 log 4 m 1 0 1 . 1 1 x 3 3 3 4m 2 1 log
x 3 4 m 5 log
x 3 4 m 1 0 . 1 1 3 3 m 2 1 log
x 3 m 5 log
x 3 m 1 0 . 1 1 3 3 Đặ 10 t t log
x 3 , khi đó x ;6 t 1 ; 1 . 1 3 3 10 Vậy (1) có nghiệm trên
;6 f t m 2
1 t m 5t m 1 0 2 có nghiệm trên 1 ; 1 . 3
+ Với m 1 2 t 0 1 ;
1 , vậy m 1 thỏa mãn điều kiện bài toán (3). 2 2 7
+ Với m 1 2 có nghiệm khi m 5 4m
1 0 m 33m 7 0 3 m . 3 7 Vậy m 3 ; \ 1 thì (2) có nghiệm. 3 Trang 94 7
Xét thấy f 1 . f
1 3m 7m 3 0 đúng với m 3 ; \ 1 3 7 Nên m 3 ; \ 1
thì (2) luôn có đúng 1 nghiệm 1 ; 1 4 3 7 10
Từ (3) và (4) suy ra m 3;
thì (2) có nghiệm trên 1 ; 1 1 có nghiệm trên ;6 3 3
Vì m nguyên nên m 3 ; 2 ; 1 ;0;1; 2 10
Vậy có 6 giá trị nguyên của m để (1) có nghiệm trên ;6 . 3
Câu 43.3. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Định hướng xây dựng bài toán: Bài toán giữ nguyên ý tưởng câu 43 (sử dụng phương pháp đặt ẩn phụ)
thay đổi cách đặt vấn đề và hướng tiếp cận bài toán. Cho phương trình 2 2
log x log x 3 m 2
log x 3 , (m là tham số thực). Tập tất cả các giá trị thực 2 1 4 2
của tham số m để phương trình đã cho có nghiệm thuộc 8 2;
là ;ab. Khẳng định nào sau đây là đúng?
A. 2a b 3
B. 2a b 4
C. 2a b 0
D. 2a b 5 Lời giải Chọn D Ta có 2 2
log x log x 3 m 2 log x 3 2
log x 2log x 3 m log x 3 * . 2 1 4 2 2 2 2 Đặ 7 7
t t log x , khi x 8 2;
log x t ; . 2 2 2 2 m 0 m 0 Suy ra phương trình 2
* t 2t 3 mt 3 t 1 . 2 2 t
2t 3 m t 32 2 m t 3 t
Xét hàm số f t 1 7 , t ; . t 3 2 4 7
Ta có f t t . t 3 0, 2 2 Bảng biến thiên Trang 95 m 0 a 1 Yêu cầu bài toán
1 m 3
2a b 5 . 2 1 m 9 b 3
Câu 43.4. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Định hướng xây dựng bài toán: Bài toán giữ nguyên ý tưởng câu 43 (sử dụng phương pháp đặt ẩn phụ)
thay đổi cách đặt vấn đề và phương trình mũ thay cho phương trình logarit.
Tính tổng T các giá trị nguyên của tham số m để phương trình x 2 3 3x m m
2m có đúng hai nghiệm phân biệt nhỏ hơn 1 . log 3 A. T 28 B. T 20 C. T 21 D. T 27 Lời giải Chọn D m m
3x m m x x 2 2 3 2m 3 2m 0 . x 1 3 Đặt 3x t ,t 0 2 2
1 t 2mt m m 0 2
Phương trình (1) có 2 nghiệ 1
m phân biệt x ; x thỏa mãn x x
phương trình (2) có hai nghiệm 1 2 1 2 log 3
phân biệt t ;t thỏa mãn 0 t t 10 . 1 2 1 2 m0; 0 m 0 m S 0;10 0 10 0 m 10 2
m ;0 1; m m 0 P 0 t t 2 21 41 21 41 m 21m 100 0 m ; ; 10 10 0 1 2 2 2 21 41 1 m , vì m
m2;3;4;5;6; 7 . 2
Vậy T 2 3 4 5 6 7 27 .
Câu 43.5. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Định hướng xây dựng bài toán: Bài toán giữ nguyên ý tưởng câu 43 (sử dụng phương pháp đặt ẩn phụ)
thay đổi cách đặt vấn đề và phương trình mũ thay cho phương trình logarit.
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình 4x .2x m
m 3 0 có hai nghiệm
phân biệt thuộc khoảng 1 ;
1 . Số tập con của tập hợp S là A. 1 B. 0 C. 2 D. 3 Lời giải Chọn A Phương trình đã cho 2x 2 .2x m
m 3 0 1 Trang 96 2 Đặ t 3 t 2x t khi x 1 1;1 t ; 2 , ta có: 2
1 t mt m 3 0 m 2 . 2 t 1 t
Xét hàm số f t 2 3 1 , t ;2 . t 1 2 f t 2 t 2t 3 t 3
; f t 0 2 t 1 t 1 Bảng biến thiên
Phương trình (1) có hai nghiệm phân biệt thuộc khoảng 1 ;
1 Phương trình (2) có hai nghiệm phân 1 13 biệt thuộc khoảng ; 2 2 m . 2 6 Vì m S .
Vậy tập S có 1 tập con là chính nó.
Câu 43.6. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Tập hợp các số thực m để phương trình
x mx 2 ln 3 1
ln x 4x 3 có nghiệm là nửa khoảng
;ab. Tổng a b bằng 10 22 A. B. 4 C. D. 7 3 3 Lời giải Chọn D
x 4x 3 0
Phương trình ln 3x mx
1 ln x 4x 3 2 2 . 2 3
x mx 1 x 4x 3 1 x 3 1 x 3 2 2 x x 4
x x 4 mx m * x x x
Xét hàm số f x 2 4 với 1 x 3 . x 2 x 4 x 2
Khi đó f x
; f x 0 . 2 x x 2 x x
Bẳng biến thiên của hàm số f x 2 4 trên khoảng 1;3 . x Trang 97
Nhận xét: Phương trình ban đầu có nghiệm khi và chỉ khi phương trình (*) có nghiệm trên khoảng 1;3 .
Dựa vào bảng biến thiên ta thấy phương trình (*) có nghiệm trên khoảng 1;3 khi và chỉ khi 3 m 4
hay m 3;4 . Do đó a 3,b 4 .
Vậy a b 7 .
Câu 43.7. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo) x
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2 m ln
2 mln x 4 có nghiệm e thuộc đoạn 1 ; e ? A. 0 B. 4 C. 3 D. 2 Lời giải Chọn C Điều kiện x 0 x 2 m
m x 2 m m 2 ln 2 ln 4
2 ln x m 4 1 e Đặ 1 t t ln , x x 1
; e t 0; 2
Phương trình (1) trở thành 2 m m 2
2 t m 4 2 m 1 TH1: 2
m m 2 0 m 2
Với m 1, phương trình 2 0t 3
m 1 (Loại). Với m 2
, phương trình 2 0t 0 Phương trình (2) vô số nghiệm. m 2 (Thỏa mãn). m 1 TH2: 2
m m 2 0 m 2 2 Phương trình (2) trở m 4 m 2 thành t . 2 m m 2 m 1
Để phương trình ban đầu có nghiệm thuộc đoạn 1 ; e . Trang 98 1
Phương trình (2) có nghiệm thuộc đoạn 0; 2 m 2 0 m 2 m 2 1 m 1 0
m 1 m2; 3 1 . m 1 2 m 3 m 0 1 m 3 2 1 Vậy m 2; 3 2 ;
1 . Vậy số giá trị nguyên dương của tham số m là 3.
Câu 43.8. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình 4 8
2log x 2log x 2m 2020 0 2 2
có ít nhất một nghiệm thuộc đoạn 1;2. Số phần tử của S là A. 7 B. 9 C. 8 D. 6 Lời giải Chọn A
Khi x 1;2 ta có 4 8
2log x 2log x 2m 2020 0 4log x 2 log x 1010 m . 2 2 2 2
Đặt t log x . Vì x 1;2 log x 0;1 . 2 2 f t 2
4t 2t 1010 m có nghiệm thuộc 1;2.
Ta có f t 8t 2 0, t 0; 1 . Bảng biến thiên:
1010 m 1016 S 1010;1011;1012;1013;1014;1015;10 16
Số phần tử của S là 7.
Câu 43.9. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Cho phương trình 3x 5 2 log
x m 9x 19 log
x m 12 với m là tham số. Tìm tất cả các giá trị 3 3
của m để phương trình đã cho có nghiệm thuộc khoảng 2; 53 53 A. ; B. ;79 C. 7 9; D. ; 79 27 27 Lời giải Chọn D TXĐ: D ; m
Đặt t log x m . Phương trình đã cho trở 2
3x 5 t 9x 19 t 12 0 3 thành Trang 99 x 2 3
5 t 9x 15t 4t 12 0 3x 5tt 34t 3 0 t 3 3x 5 t4 0 t 3 t 3 0 x 4 3 5 t 4 0 t do x 2 3x 5 1 1 +) Với t 3
log x m 3
x m x m 3 27 27 . 1 1 1 53 Để x m 2; m 2 m 2 m . 27
là nghiệm thuộc khoảng thì 27 27 27 4 4 +) Với t
log x m 3 3x 5 3x 5 4 4 3x 5 3x 5 x m 3 m 3 x 4 4 12 Đặt 3 5 3 x f x
x với x 2 f x 3x5 3 . .ln31 0 x 2 . 3x 52
f x nghịch biến trên 2; f x f 2 f x 79.
Phương trình có nghiệm thuộc từ 2; thì m 79 .
Kết hợp hai trường hợp trên ta được m ; 79.
Câu 43.10. (Bài toán phát triển) (Phát triển Tương tự câu 43 đề thi tham khảo)
Tìm tất cả các giá trị của tham số m đề đồ thị hàm số 2
y mlog x 2log x 2m 1 2 2 cắt trục hoành tại
một điểm duy nhất có hoành độ thuộc khoảng 1 ; . 1 1 1 1 1 1 1 1 A. m ;
. B. m ;0
C. m ;
. D. m ;0 . 2 2 2 2 2 2 2 2 Lời giải Chọn D
Xét phương trình hoành độ giao điểm 2
mlog x 2log x 2m 1 0 1 . 2 2
Ycbt Phương trình (1) có duy nhất một nghiệm thuộc khoảng 1 ; .
Đặt t log x 0 x 1 ; 2 . 2t 1 Phương trình 2
1 mt 2t 2m 1 0 m 2 2 t 2
Ycbt Phương trình (2) có duy nhất một nghiệm t 0; . 2t 1
Xét hàm số f t trên 0; . 2 t 2 Trang 100 2 t t t 2 2 2 2 2 1 2
t 2t 4
Ta có f t t 2 1 t 2 2 2 1 f t t 1 0; 2 0 2
t 2t 4 0 t . 2 0; Bảng biến thiên 1 1
Từ bảng biến thiên ta suy ra: ybct m ; 0 . 2 2
Câu 44: [ ĐỀ THI THAM KHẢO ] Cho hàm số f x liên tục trên . Biết cos2x là một nguyên hàm
của hàm số x
f x e , họ tất cả các nguyên hàm của hàm số x f x e là
A. sin 2x cos2x C B. 2
sin2x cos2x C C. 2
sin2x cos2x C
D. 2sin 2x cos2x C
Phân tích ý tưởng: Bài toán sử dụng định nghĩa nguyên hàm: F x là một nguyên hàm của f x thì
Fx f x . + Tính chất: f
xdx f xC
+ Bản chất của dạng toán là tìm được hàm f x từ dữ kiện ban đầu. + Nguyên hàm từng phần. Lời giải Chọn C x x
Theo giả thiết cos2x f xe f xe 2 sin2x . Xét x I f x e dx x x u e
du e dx Đặt dv . f xdx v f x
x x I f x e f x e dx 2
sin2x 2 sin2xdx 2
sin2x cos2x C Phát triển câu 44 Trang 101
Câu 44.1 ( Tương tự Phát triển Tương tự câu 44 đề thi tham khảo) Cho hàm số f x liên tục trên f x * f x x
. Biết sin 2x là một nguyên hàm của hàm số
x , họ tất cả các nguyên hàm của hàm số ln
trên khoảng 0; là A. 2x cos2 .
x ln x sin2x C B. 2x sin 2 .
x ln x cos2x C C. 2x cos2 .
x ln x sin2x C D. 2 x cos2 .
x ln x sin2x C Lời giải Chọn C f x f x
Theo giả thiết sin 2x
2cos2x f x 2x cos2x x x Xét I f
xlnxdx 1 u ln x du dx Đặt x dv f x dx v f x
I f x f x ln x
dx 2x cos2x.ln x 2 cos2.xdx 2x cos2x.ln x sin2x C x n 1 n u 1
Phát triển hướng 1 : Áp dụng u du ; C
du ln u C. n 1 u
Câu 44.2. (Phát triển Tương tự câu 44 đề thi tham khảo) Cho hàm số f x có đạo hàm liên tục trên và f 1 0, 2020 2020 F x
f x là một nguyên hàm của 2020 . x
x e . Họ các nguyên hàm của f x là x
A. 2020 2 x x e C
B. xe C
C. 2020 2 x x e C
D. 2 x x e C Lời giải Chọn D Ta có: x 2019 x 2019 2020 2020. . 2020 . . . x F x xe f x f x x e f x f x x e .
2019 x 2019 . .
1. x f x f x dx x de f x df x x e C 1 . 2020
1. x 2020 2020 1. x f x x e C f x x e 2020C . 2020 2020 x Do f
1 0 C 0 hay f x 2020x 1.e . Do đó 2020 1 x I f x dx x e dx .
u x 1 du dx Đặt x x
dv e dx v e 1 x x 2 x I x e e dx x e C. Trang 102
Phát triển hướng 2: Áp dụng . u v u v . u v.
Câu 44.3 : (Phát triển Tương tự câu 44 đề thi tham khảo) Cho hàm số f x có đạo hàm liên tục trên
và f 0 1. x F x
f x e x là một nguyên hàm của f x . Họ các nguyên hàm của f x là A. 1 x x e C. B. 1 x x
e x C.
C. 2 x x
e x C. D. 1 x x
e x C Lời giải Chọn B
Ta có x F x f x
f x e 1 f x x 1 x x 1 x f x f x e e f x e f x e x 1 x x x x 1 x e f x e e f x x e C f x xe C e .
Do 0 1 2 2 x f C f x x e 1.
Do đó 2 x 1 2 x I f x dx x e dx x e dx dx.
u x 2 du dx Đặt x x
dv e dx v e 2 x x 2 x x 1 x I x e e dx dx x e e x C x
e x C. u v
uv u
Phát triển hướng 3: Áp dụng . 2 v v
Câu 44.4 : (Phát triển Tương tự câu 44 đề thi tham khảo) Cho hàm số f x có đạo hàm liên tục trên 3x 3x
và f 0 0, 3 . x F x
f x e là một nguyên hàm của e .6 f
x2xe . Họ các nguyên hàm của f x là
1 2 3x 2 3x 2 3x
1 2 3x 2 3x 2 3x A. x e xe e C x e xe e C 3 9 27 B. 3 9 27
1 2 3x 1 3x 1 3x
1 2 3x 1 3x 1 3x C. x e xe e C. x e xe e C. 3 9 27 D. 3 9 27 Lời giải Chọn A 3x 3x 3x 3x 3x 6x
Ta có F x e .6 f
x2xe f
xe 3f xe 6e f x2xe 3x 3x f x f x e 3 f x e 3x
e 3 f x 3x 6x e xe x x e 2 3 f x f x 2 2x x C 3x 3x e e
Do 2 3 0 0 0 x f C f x x e Trang 103 Do đó 2 3x I
f x dx x e dx. 2 du 2xdx 2 u x Đặt 1 3x 1 3x dv e dx v e 1 2 3 1 2 3x 2 3x
I x e xe dx. 3 3 du dx 2 u x 2 Đặt 3x 1 3x dv e dx v e 2 2 3 1 2 3x 2 1 3x 1 3x
1 2 3x 2 1 3x 1 3x
I x e xe e dx x e xe e C. 3 3 3 3 3 3 3 9
1 2 3x 2 3x 2 3x
x e xe e C 3 9 27
Câu 45: [ ĐỀ THI THAM KHẢO ] Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm thuộc đoạn ;2
của phương trình 2 f sin x 3 0 là A. 4 B. 6 C. 3 D. 8 Lời giải Chọn B Ta có f
x f x 3 2 sin 3 0 sin 2
Dựa vào bảng biến thiên ta có:
sin x t ; 1 1 1 x t f sin x sin 1;0 2 3 2 2
sin x t 0;1 3 3
sinx t 1; 4 4
Phương trình (1) và (4) vô nghiệm.
Phương trình (2) có 4 nghiệm phân biệt Trang 104
Phương trình (3) có hai nghiệm phân biệt khác các nghiệm của (2).
Do đó tổng số nghiệm của phương trình đã cho là 6.
Phân tích: Bài toán là sự kết hợp giữa kiến thức
1) Dựa vào BBT xác định số nghiệm phương trình f x M lớp 12
2) Xác định số nghiệm phương trình sin x m trên một đoạn ; a b lớp 11
Hướng phát triển:
1) Thay BBT thành đồ thị của hàm số y f x xác định số nghiệm f x a , f x ax b, 2
f x ax bx c .
2) Thay phương trình f u m thành phương trình chứa dấu trị tuyệt đối, căn thức, phương trình chứa tham số.
Bài tập : Tương tự
Câu 45.1 (Phát triển Tương tự câu 45 đề thi tham khảo) Cho hàm số y f x liên tục trên và có
bảng biến thiên như hình vẽ.
Số nghiệm thuộc đoạn ;3
2 f 2cos x 1 3 0 2 của phương trình là A. 6 B. 7 C. 11 D. 12 Lời giải Chọn B Ta có: f
x f x 3 2 2cos 1 3 0 2cos 1 2 Dựa vào BBT ta có:
2cos x 1 m ; 2 1 f x 3 2cos 1 1
2cos x 1 n0; 1 2 2
2 cos x 1 p 1;2 3
Dựa vào đồ thị hàm số y cos x trên đoạn ;3 2 ta có: Trang 105
x m m 1 3 1 2cos 1 ; 2 cos x ;
phương trình vô nghiệ 2 2 m
x n n 1 1 2 2cos 1 0;1 cos x ;0 2
2 phương trình có 3 nghiệm phân biệt
x p p 1 1 3 2cos 1 1;2 cos x 0; 2
2 phương trình có 4 nghiệm phân biệt
Phát triển theo hướng phương trình chứa dấu trị tuyệt đối.
Câu 45.2 (Phát triển Tương tự câu 45 đề thi tham khảo) Cho hàm số y f x liên tục trên có
bảng biến thiên như hình vẽ.
Số nghiệm của phương trình f f x 2 A. 4 B. 5 C. 7 D. 9 Lời giải Chọn C
f x a 4
f f x
f x b 3 2
Ta có: f f x 2
phương trình có 7 nghiệm phân biệt f f x f x 4 2
f x c 1;3
f x d 3
Phát triển theo hướng phương trình chứa tham số.
Câu 45.3 (Phát triển Tương tự câu 45 đề thi tham khảo) Cho hàm số y f x liên tục trên có
bảng biến thiên như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 f x m 1 có đúng 2 nghiệm trên 1 ;1 . A. 13 B. 9 C. 4 D. 5 Lời giải Chọn D Trang 106
2 f x m 1 VN
Ta có: f 2 f x m 1
2 f x m 2 f x f x m 2 m 2 2 2
2 f x m 2 f x 2 m 2
Dựa vào BBT ta có trên 1 ;1
, để phương trình f 2 f x m 1 có đúng 2 nghiệm thì 2 m 3 1 2 0 m 8
0 m 4 có 5 giá trị nguyên của tham số m. 2 m 4 m 4 3 1 2
Phát triển theo hướng đồ thị và phương trình chứa tham số
Câu 45.4 (Phát triển Tương tự câu 45 đề thi tham khảo) Cho hàm số y f x liên tục trên có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f f x m 1 f x m có đúng 3
nghiệm phân biệt trên 1 ;1 . A. 1 B. 2 C. 3 D. 4 Lời giải Chọn A
Ta có: f f x m 1 f x m f t t 1 với t f x m f t
x m2 2
Dựa vào đồ thị ta có: f t t 1 t 0 f
x m t 2 f
x m 2
Dựa vào đồ thị trên 1 ;1
, phương trình f f x m 1 f x m có đúng 3 nghiệm phân biệt khi 3
m 2 1 3 m 1 3 m 1 1
m 3 m 1. 3 m 2 1 1 m 5 Trang 107
Câu 46: [ ĐỀ THI THAM KHẢO ] Cho hàm số bậc bốn y f x có đồ thị như hình dưới đây 3 2
Số điểm cực trị của hàm số g x f x 3x là A. 5 B. 3 C. 7 D. 11 Lời giải Chọn C x 2 3 2 2
Xét hàm số u x 3x ta có u 3x 6x 0 . x 0 Bảng biến thiên 3 2 2 3 2
Xét hàm số g x f x 3x , ta có gx 3x 6x f x 3x 2 gx 3x 6x 0 0 f 3 2
x 3x 0 Phương trình 2
3x 6x 0 có hai nghiệm phân biệt x 2 , x 0 .
Từ đồ thị hàm số y f x . 3 2
x 3x t ; 0 1 1
Suy ra: Phương trình f 3 2 x 3x 3 2
0 x 3x 5 0;4 2 2 3 2
x 3x t 4; 3 3 3 2
Dựa vào bảng biến thiên của hàm số u x 3x ta thấy:
(1) có 1 nghiệm duy nhất.
(2) có 3 nghiệm duy nhất. Trang 108
(3) có 1 nghiệm duy nhất.
Suy ra g x 0 có 7 nghiệm phân biệt và g x đổi dấu qua các nghiệm này nên hàm số y f x có 7 điểm cực trị.
Bài tương tự câu 46:
Câu 46.1 (Phát triển Tương tự câu 46 đề thi tham khảo) Cho hàm số bậc bốn y f x có đồ thị như hình dưới đây. 3 2
Số điểm cực trị của hàm số g x f x 3x là A. 5 B. 6 C. 7 D. 9 Lời giải Chọn C 3 2
Xét hàm số u x 3x có bảng biến thiên như sau: 2 3 2
Ta có g x 3x 6x f x 3x 2 g x 3x 6x 0 x 0 x 2 ' 0 f ' 2 3
x 3x 0 Trang 109
Từ đồ thị hàm số y f x ta có: 3 2 x 3x 0 1 f 3 2 x 3x 3 2
0 x 3x x 3 ;0 2 1 3 2
x 3x x 1;3 3 2 3 2
Dựa vào bảng biến thiên của hàm số u x 3x ta thấy:
(1) có 2 nghiệm phân biệt, trong đó x 0 là nghiệm kép.
(2) có 3 nghiệm phân biệt khác với các nghiệm trên.
(3) có nghiệm duy nhất khác với tất cả các nghiệm trên.
Suy ra g x 0 có 7 nghiệm phân biệt và g x đổi dấu qua các nghiệm này (trong đó x 0 là nghiệm
bội 3) nên hàm số g x có 7 điểm cực trị.
Bài phát triển câu 46
Câu 46.2 (Phát triển Tương tự câu 46 đề thi tham khảo) Cho hàm số bậc bốn y f x có đồ thị như hình dưới đây 3 6 4 3 2
Số điểm cực trị của hàm số g x 8 f x 3x 3 2x 12x 16x 18x 48x 1 là A. 5 B. 3 C. 7 D. 9 Lời giải Chọn A 2 3 5 3 2
Ta có g x 83x 3 f x 3x 3 12x 48x 48x 36x 48 Trang 110 3
x x 24 3 3 1 2 x 1 f 3
x 3x 3 2 2
x 1 0 x 1 gx 3 0 f x 3x 3 1 3
x 3x 3 * 2
Từ đồ thị hàm số y f x , ta có: Đặ 3
t: x 3x 3 t t 1 t 1
Phương trình (*) trở thành: f x t 1 2 t 5 3 +) Với t 1
ta có: x 3x 3 1
( phương trình này có 1 nghiệm không nguyên) x 1 3
+) Với t 1 ta có: x 3x 3 1
, trong đó x 1 là nghiệm bội hai. x 2 x 2 3
+) Với t 5 ta có: x 3x 3 5 , trong đó x 1 là nghiệm bội hai. x 1
Suy ra g x 0 có 5 nghiệm phân biệt và g x đối dấu qua các nghiệm này (trong đó x 1 là
nghiệm bội 3) nên hàm số g x có 5 điểm cực trị.
Phân tích hướng phát triển: tìm số điểm cực trị của hàm số gx f u ux trong đó ux là hàm
cụ thể và f x là hàm đã cho sẵn đồ thị
Câu 46.3 (Phát triển Tương tự câu 46 đề thi tham khảo) Cho hai hàm số bậc bốn y f x và
y gx có các đồ thị như hình dưới đây (2 đồ thị chỉ có đúng 3 điểm chung). Trang 111
Số điểm cực trị của hàm số h x 2 f x 2
g x2 f x.gx là A. 5 B. 4 C. 6 D. 3 Lời giải Chọn A 2
Ta có: h x f
x gx h
x 2f xgxf
x gx hx
f x gx 0 1 0 f
x g x 0 2
Từ đồ thị ta thấy phương trình (1) có đúng 3 nghiệm phân biệt là x 1
; x x 1;3 x 1 ; 3 và đa thức
f x gx đổi dấu khi qua các nghiệm này. Do đó các nghiệm trên là các nghiệm bội lẻ của (1) . Mà
f x và gx đều là đa thức bậc 4 nên bậc của phương trình (1) nhỏ hơn hoặc bằng 4. Từ đó suy ra
phương trình (1) là phương trình bậc 3.
Do phương trình (1) là phương trình bậc 3 có 3 nghiệm phân biệt nên phương trình (2) phải có 2 nghiệm
phân biệt không trùng các nghiệm của phương trình (1).
Suy ra h x 0 có 5 nghiệm phân biệt và h x đổi dấu qua các nghiệm này nên hàm số h x có 5 điểm cực trị.
Phân tích hướng phát triển: tìm số điểm cực trị của hàm số hx u f
x;gx trong đó g x và
f x là hàm đã cho sẵn đồ thị
Câu 46.4 (Phát triển Tương tự câu 46 đề thi tham khảo) Cho hàm số bậc bốn y f x . Trong hình
vẽ dưới đây, gồm đồ thị y f x trên ; 1 và 1 ;
(đậm hơn), đồ thị y fx trên 1 ;1 .
Biết max f x 1. 1;1 Trang 112
Số điểm cực trị của hàm số g x f f
x 2 là A. 9 B. 7 C. 13 D. 11 Lời giải Chọn C
Dựa vào đồ thị ta có bảng biến thiên sau:
max f x f x 1 1 1;1
Chú ý rằng: f x 0;0,5 2 min f
x f x 1 ,5 3
Ta có: g x f x. f f
x 2
f x 0 gx 1 0 f f
x 2 0 2 1 x 1
x x x x x x 1 2 3 Trang 113
f x 2 1 3
f x 2 x 0 ,5;0 4 1
2 f x 2 1 5
f x2 x 1,5;2 6 2
f x2 x 2,5;3 7 3
Dựa vào đồ thị và bảng biến thiên ta có: (3) và (4) vô nghiệm.
5 f x 1
: có 2 nghiệm phân biệt
6 f x x 2 0 ,5;0 2
: có 2 nghiệm phân biệt.
7 f x x 2 0,5;1 3
: có 4 nghiệm phân biệt.
Suy ra g x 0 có 13 nghiệm phân biệt và g x đổi dấu qua các nghiệm này nên hàm số g x điểm cực trị.
Phân tích hướng phát triển: tìm số điểm cực trị của hàm số gx f f x trong đó là hằng số
và cho sẵn 1 phần đồ thị của f x và của f x .
Câu 47. [ ĐỀ THI THAM KHẢO ] Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 x 2020 và
log 3 3 2 9y x x y 3 ? A. 2019. B. 6 C. 2020 D. 4 Lời giải Chọn D Điều kiện x 1
Ta có: log 3 3 2 9y log 1 2 1 2 3 y x x y x x y 3 3 (*) Xét hàm số 3t f t t
,t có 13t f t
ln3 0,t , tức hàm số luôn đồng biến . Khi đó
* log 1 2 log 1 2 9y f x f y x y x 1 3 3 y
Vì 0 x 2020 nên 0 9 1 2020 0 y log 2021. 9
Do y nguyên nên y 0;1;2; 3 . ; x y
0;0;8, 1;80;2;728;3 nên tổng cộng có 4 cặp số nguyên ;xy thỏa đề.
Bài tập tương tự
Câu 47.1 (Phát triển Tương tự câu 47 đề thi tham khảo) Cho x, y là các số thực thỏa mãn
log 2 2 3 8y x x y x ; x y 2 . Biết 0
2018, số cặp nguyên thỏa mãn đẳng thức là A. 2 B. 3 C. 4 D. 5 Lời giải Chọn C Trang 114 y log x 1 Ta có log 2 2 2 3 8 2 log 3 1 2 y x x y x 3y 1 2 2 . Xét hàm số 2t f t
t có 2t f t ln2 1 0 Nên 1 log 3 1 3 2 y x y x 1 2 . Với 0 2018 1 8y x
2019 0 y log 2019,y y 0;1;2;3 8
Bài tập phát triển:
Biến đổi phương trình đưa về hàm đặc trưng. Là điểm mấu chốt bài toán từ đó suy ra f u f v
Vấn đề khó nhất trong lời giải là tìm ra được hàm đặc trưng từ đó xét tính đồng biến, nghịch biến của hàm
số trên tập xác định của nó, suy ra f u f v , muốn làm được dạng này học sinh phải thành thạo các kĩ
năng biến đổi phương trình mũ, phương trình logarit. từ đó suy ra hàm đặc trưng.
Câu 47.2 (Phát triển Tương tự câu 47 đề thi tham khảo) Cho phương trình 4 xm log
2 3 2x x x x
log 2 x m 2 0. Gọi S là tập hợp tất cả các giá trị của để m 2 2 2 2 1 2
phương trình có 3 nghiệm thực phân biệt. Tổng các phần tử của S bằng 1 3 A. 3 B. C. 2 D. 2 2 Lời giải Chọn A
Điều kiện xác định: x 2
Xét phương trình 4 xm log
2 3 2x x x x
log 2 x m 2 0 1 2 2 2 1 2 2 xm 1 1 2
.log 2x 2x1 2 2 x x .log 2 xm 2 2 2 2 1 1 2 2 x 2x 1 2 .log 2
x 2x 1 2 2 xm.log 2 x m 2 2 2 2 2
Xét hàm số: 2t f t
log t 2 ,t 0 2 t t 1
Ta có: f t 2 .ln 2.log t 2 2 . 0 t 0. 2 t 2ln2
Mà f t liên tục trên 0;
suy ra f t đồng biến trên 0; . 2 Phương trình (2) có dạ 2
ng f x 2x
1 f 2 x m và 2
x 2x 1 x
1 0; 2 x m 0 x 2 2
x 2x 1 2 x m
x 4x 2 m * 2 Do đó 2
x 2x 1 2 x m . 2
x 2x 1 2 , m x 2 x 1 2 m **
Phương trình (1) có 3 nghiệm thực phân biệt Phương trình (2) có 3 nghiệm thực phân biệt. Dựng các Parabol: 2
y x 4x 1P 2
y x 1 P 1 và
2 trên cùng 1 hệ trục tọa độ (xem hình vẽ). Trang 115
Số lượng nghiệm của (*) và (**) bằng số giao điểm của đường thẳng d : y 2
m lần lượt với các đồ thị P P
1 và 2 . Dựa vào đồ thị có thể thấy phương trình đã cho có đúng 3 nghiệm phân biệt thì d phải nằm
ở các vị trí của d ,d ,d 1 2 3 . 1
Tương ứng khi đó ta có: 2m 1 m 2 2 m 2 m 1; 3 2 m 3 m 2 . 1 3
Do đó có ba giá trị của m thỏa mãn yêu cầu: m ;m 1;m 2 2 . 1 3 Vậy S ;1; 2
2 suy ra tổng các phần tử của S bằng 3. Cách 2. 2
x 2x 1 2 x m x
4x 1 2m 0 a 2
2
x 2x 1 2 x m 2
x 2x 1 2
2m x x 12m 0 b
Phương trình (1) có 3 nghiệm thực phân biệt Phương trình (2) có 3 nghiệm thực phân biệt. Xảy ra 3 khả năng:
KN1: Phương trình (a) có nghiệm kép, phương trình (b) có hai nghiệm phân biệt khác nghiệm kép của phương trình (a). 3
Phương trình (a) có nghiệm kép 3 2m 0 m 2 . 3 Với m , Phương trình ( x 2 a) có nghiệm kép 2 x 2 2
Phương trình (b) thành x 2 0
(Thỏa mãn x 2 ). x 2
KN2: Phương trình (b) có nghiệm kép, phương trình (a) có hai nghiệm phân biệt khác nghiệm kép của phương trình (b) . Trang 116 1
Phương trình (b) có nghiệm kép 1 2m 0 m 2 1 Với m
, phương trình (b) có nghiệ x 2 m kép 0. x 2 2 2
Phương trình (a) thành x 4x 2 0
(thỏa mãn x 0 ). x 2 2
KN3: Phương trình (a) và phương trình (b) đều có hai nghiệm phân biệt và chúng có đúng 1 nghiệm chung.
Gọi x0 là nghiệm chung của phương trình (a) và phương trình (b). 2
x 4x 1 2m 0 Khi đ 0 0 2 2 2 ó:
x 4x 1 x 1 2x 4x 2 0 x 1 2 x 1 2m 0 0 0 0 0 0 0 0 x 1 2m 2 m 1 0
là nghiệm chung của (a) và (b) . Với m 1 x 1 Phương trình a 2
: x 4x 3 0 x . 3 x 1 Phương trình b 2
: x 1 0 x . 1
Khi đó phương trình (1) có 3 nghiệm phân biệt x 1; x 1; x 3 1 3
Từ đó suy ra có ba giá trị của m thỏa mãn yêu cầu: m ;m 1;m 2 2 1 3
Vậy S ;1; nên tổng các phần tử của S bằng 3 . 2 2
Câu 47.3 (Phát triển Tương tự câu 47 đề thi tham khảo) Có bao nhiêu số nguyên của m để phương trình log 2x m 2log x x 4x 2m 1 2 2 2
có hai nghiệm thực phân biệt. A. 2 B. 3 C. 1 D. 4 Lời giải Chọn C x 0 Điều kiện m x 2
log 2x m 2log x x 4x 2m 1 2 2 2 log 2x m 2log x x 2 x 2m 1 2 2 2
log 2x m 2x 2m1 2 log x 2 x 2 2
log 22x m 2x 2m 2 log x 2 x 2 2 Trang 117
f u f v
Xét f u log u , u u 0 2 f u 1 1 0 u ln2
Suy ra f u f v u v x m 2 x 2 2 2
x 4x 2m
Xét hàm số f x 2
x 2x,x 0
Phương trình có 2 nghiệm dương khi 4 2m 0 2 m 0 suy ra có 1 giá trị nguyên.
Câu 47.4 (Phát triển Tương tự câu 47 đề thi tham khảo) Biết x , x 1
2 là hai nghiệm của phương trình 2
4x 4x 1 log 4x 1 6x 1 x 2x a b a b 7 2 với ,
a b là hai số nguyên dương. Tính . 2x và 1 2 4
A. a b 13
B. a b 11
C. a b 16
D. a b 14 Lời giải Chọn C 1
Điều kiện: x 0, x 2 2
4x 4x 1 2 2 2 Ta có: log 4x 1 6x log 4x 4x 1 4x 4x 1 log 2x 2x 7 7 7 2x 1
Xét hàm số f t log t t f t 1 0 t 0 0; 7 có tln7
nên là hàm số đồng biến trên . 2 2 3 5
Do đó ta có 4x 4x 1 2x 4x 6x 1 0 x . 4 Khi đó 3 5 3 5 1 x 3 5 3 5 1 2x 2 9 5 x 2x 2 9 5 1 2 4 4 4 hoặc 1 2 4 4 4 3 5 3 5 Vậy x ; x
. Do đó a 9;b 5 a b 9 5 14 1 2 4 4 và . Trang 118
Câu 47.5 (Phát triển Tương tự câu 47 đề thi tham khảo) Biết phương trình 2 x 1 x 1 log 2log x a b 5 3 x 2
có một nghiệm dạng 2 trong đó ,
a b là các số nguyên. 2 x Tính 2a b A. 3 B. 8 C. 4 D. 5 Lời giải Chọn B 2 x 1 x 1 2 x 1 x 1 Ta có log 2log log 2log 1 . 5 3 5 3 x 2 2 x x 2 x ĐKXĐ: x 1
1 log 2 x 12log 2 x log x2log x1 * 5 3 5 3
Xét hàm số f t log t 2log t 1 t 5 3 , với 1 . f t 1 2 0 t f t 1; t.ln5 t với mọi 1 , suy ra
đồng biến trên khoảng . 1ln3 2
Từ (*) ta có f 2 x
1 f x nên suy ra 2 x 1 x x 2 x 1 0 x 1 2 (do x 1)
Suy ra x 3 2 2 a 3; b 2 2a b 8 . Nhận xét:
Câu này dùng Casio với chức năng SOLVE, ta tìm được nghiệm và STO .
Tức là A a b 2 a A b 2
Dùng chức năng T BLE với f x A x 2 , start 10, end 10, step 1. Ta tìm được a b , như cách giải tự luận.
Câu 48: [ ĐỀ THI THAM KHẢO ] Cho hàm số f x liên tục trên thỏa mãn xf 3
x f 2 x 10 x 6 1
x 2x,x . 0
Khi đó f xdx bằng 1 17 13 17 A. 20 B. 4 C. 4 D. 1 Lời giải 1
Gọi F x là một nguyên hàm của hàm f x trên . Với x ta có: xf 3
x f 2 x 10 x 6 1 x 2x Trang 119 2 x f 3
x xf 2 x 11 x 7 x 2 1 2x * 2 x f 3
x dx xf 2
x dx 11 x 7 x 2 1 2x dx 12 8 3 1 1 x x 2x f 3 x d 3 x f 1 2 x d 1 2 x C 3 2 12 8 3 12 8 3 1 1 x x 2x F 3
x F1 2 x C 3 3 12 8 3 1 1
Thay x 0 ta được
F 0 F 1 C 1 3 2 1 1 5
Thay x 1 ta được F
1 F 0 C2 3 2 8 1 1 17
Thay x 1 ta được F 1 F 0 C 3 3 2 24 5 5 3 Từ
1 ,2 suy ra F
1 F 0 F 1 F 0 6 8 4 1 32 Từ (2), (3) suy ra F 1 F 1 F 1 F 1 4. 3 24 0 3 13 Vậy
f xdx F0 F 1 4 . 4 4 1 Lời giải 2: 3 2 10 6 2 3 2 2 11 7
Từ xf x f 1 x x x 2x x f x xf 1 x 2x x x ,x . 1 1 2 3 2 2 11 7
Suy ra, hàm số x f x xf 1 x 2x là hàm lẻ. Ta có x x dx 24 0 0 1 2 3 2 2 2 3 2 2 1 Do đó
x f x xf 1 x 2x dx
x f x xf 1 x 2x . 24 1 0 0 0
1 f 3x 3 1 dx f 2 1 x 2 2 d 1 x 3 2 3 1 1 1 1 1 3 3 1 2 2 2 1
f x dx
f 1 x d 1 x 3 2 3 24 0 0 0 1 1 1 1 1 4 1 1 15
f xdx
f xdx
f xdx
f xdx 3 2 3 3 2 24 1 0 0 0 0 1 1 15
2 f xdx 3 f xdx 8 5 f xdx 4 1 0 0 0 1 13
f xdx 4 f xdx 4 1 0 Lời giải 3: Trang 120 Ta có xf 3
x f 2 x 10 x 6 1
x 2x,x 1 3 2 10 6
Thay x bằng x ta được xf x f 1 x x x 2x,x 2 3 3 3 3
Từ (1), (2) suy ra xf x x f x 4x,x f x f x 4,x 3
Thay x bởi x ta được f x f x 4 Do đó, 0 0 1 0 1
f x f xdx f xdx f xdx 4dx 4
f xdx 4 1 1 0 1 1 2 3 2 11 7 2
Từ (1) x f x xf 1 x x x 2x 1 1 1 1 1 5 f 3 x d 3 x f 1 2 x d 1 2 x 11 x 7 x 2 2x dx 3 2 8 0 0 0 1 1 1 1 1 5 3
f xdx
f xdx f xdx 3 2 8 4 0 0 0 0 3 13
Do đó, f xdx 4 4 4 1 Lời giải 4: 3 2 10 6 Với x
ta có xf x f 1 x x x 2x 2 x f 3
x xf 2 x 11 x 7 x 2 1 2x * 1 1 1 2 x f 3
x dx xf 1 2
x dx 11 x 7 x 2 2x dx 0 0 0 1 1 1 1 5 f 3 x d 3 x f 1 2 x d 1 2 x 3 2 8 0 0 1 1 1 1 1 5 3
f xdx
f xdx f xdx 3 2 8 4 0 0 0 0 0 0 Mặt khác * 2 x f 3
x dx xf 1 2
x dx 11 x 7 x 2 2x dx 1 1 1 0 0 1 1 17 * f 3 x 3 dx f 1 2 x d 1 2 x 3 2 24 1 1 0 1 0 1 1 17 1 3 17 13
f xdx f xdx f x dx 3 . 3 2 24 2 4 24 4 1 0 1
Lời giải 5: Đi tìm hàm f x Ban đầ 3 2 3 2
u ta sẽ nghĩ đến có f x , f 1 x thì bên vế phải có thể đưa liên quan gì đến x ,1 x không? Trang 121 3 Ta có xf 3 10 x x x 3 3 2 x f x x 2 3 2 2 4 6
Vậy thì nghĩ thêm việc cũng tạo tiếp cái 1 x 2 33x 3x x 3 2 2 2 4 6
Hay f 1 x 1 x 2 33x 3x x Như thế ta sẽ có: 3 3 3 2 2 2 4 6 6
x f x x
2 f 1 x 1 x
2 3 3x 3x x x
x f x x 3 2
f 1 x 1 x 3 3 3 2 2 2 3 2 3x 4 3x
x f x x 3 x f x x 3 3 3 4 2 2 2 2 3 1 1 2 3 1 x 0 x f x x 3 x f x x 3 3 3 3 2 2 2 3 2 1 1 3 1 x 2 0 Đặ 3 3 2
t g x f x x 3x 2 ta được xgx g1 x 0
Thay x bởi x ta được xg 3
x g 2 1 x 0 3 3
hay xgx xgx ,x
Do đó gx là hàm lẻ. Như vậ 3 2 3 2
y xgx g1 x 0 xgx gx 1 ,x
Từ giả thiết ta có: g 0 g 1 0
Vì f x liên tục trên 1;0
nên g x liên tục trên 1;0 .
Đặt M max gx 0,x 1;0 1;0
Giả sử M 0 khi đó a 1;0 : ga M
Chọn x b 1 a 1;0 Ta được g a
3 ga g 3 b M bg b M b 0;1 b b do
Điều này mẫu thuẫn do M max gx 1;0
Do vậy max g x 0,x 1;0 . 1;0
Hay g x x 1;0 3 0,
f x x 3x 2,x1;0 . Trang 122 0 0 13 Vậy
f xdx 3
x 3x 2dx 4 1 1 Nhận xét chung:
Ở 5 cách trên, khi giải quyết bài toán dạng này ta thường hướng tới:
Biến đổi giả thiết đi đến tính chất
u f udx
f udu.
Dựa theo tính chất hàm chẵn, hàm lẻ.
Sử dụng các phép thế xác định hàm số f x .
* Với lời giải 1, 2, 3, 4: Ta đều sử dụng đến tính chất ub b
u f udx
f udu hay ux f uxdx
f xdx a ua 3 2
Vì thế ta mới nghĩ đến việc tạo ra đạo hàm của x ;1 x bằng việc nhân hai vế của giả thiết với x để tạo ra 0 x f x 0 1 1 2 3 1 1 dx f x 2 d ; x x f 3 x dx
f xdx 3 3 ; 1 1 0 0 0 1 1 xf 1 1 1 1 2 x dx
f xdx xf 1 2 x dx f x dx 2 và 2 . 1 0 0 0 1 1
Trong các đổi biến này xuất hiện f xdx buộc ta phải đi tính thêm f xdx . Ở đây, nếu cận không 0 0 3 phải là 1;0;
1 thì các cách làm này sẽ bị phá sản, ví dụ yêu cầu tính f xdx , lúc này chắc chỉ còn 0
cách đi tìm f x 3 2
. Vì thế, các cận 1;0;
1 phải được liên hệ mật thiết với x ,1 x .
Ngoài ra, với hai tính chất: 2 3 2 2
Hàm số x f x xf 1 x 2x là hàm lẻ;
Hàm số f x f x 4 là hàm chẵn.
cũng hữu ích cho việc tính toán nhanh hơn. 17 17
* Lỗi sai có thể mắc dẫn đến các phương án nhiễu ,
20 4 đều sai dấu khi tính 0 1 1 xf 1 1 1 1 2 x dx
f xdx xf 1 2 x dx f x dx 2 và 2 . 1 0 0 0
* Với lời giải 5: Việc tìm f x khá khó khăn, không nói là mò. Nếu f x là những hàm quen thuộc thì
rất có thể đoán bằng việc thử các giá trị và cân bằng hệ số.
Khi đó, mục đích khai thác tính chất
u f udx
f udu coi như phá sản.
2. Các bài toán tương tự
Dựa theo những phân tích trên ta có một số bài toán tương tự như sau: Trang 123
Hướng 1: Dựa theo tính chất
u f udx
f udu
Câu 48.1 (Phát triển Tương tự câu 48 đề thi tham khảo) : Cho hàm f x liên tục trên \ 0 thỏa mãn 2 xf 2
x f x 3 1 2 x
2,x \ 0 f x dx 2x
. Giá trị nằm trong khoảng nào? 1 A. 5;6 B. 3;4 C. 1;2 D. 2;3 Lời giải Chọn D 2 3 1
Ta có xf x f 2x x
2,x \ 0 2x 2 2 1
xf 2x f 2x 3 dx x 2 dx 2x 1 1 2 2 4 2
1 f 2xd 2x 1 f 2xd2x x 1
ln x 2x 2 2 4 2 1 1 1 4 4 2 1 1 7 1 1 7 1
f xdx
f xdx ln2
f xdx ln2 2 2 4 2 2 4 2 1 2 1 2 7
f xdx ln2 2;3 2 1
Câu 48.2 (Phát triển Tương tự câu 48 đề thi tham khảo) Cho hàm số y f x liên tục trên đoạn 0;4 2 2
và thỏa mãn điều kiện 4xf x 6 f 2x 4 x ,x 0;2 . 4
Giá trị f xdx bằng 0 A. 5 B. 2 C. 20 D. 10 Lời giải Chọn A 2 2
Ta có 4xf x 6 f 2x 4 x 2 2 4xf 2
x 6 f 2xdx 4 2 x dx 0 0 2 2
2 f 2x 2 dx
3 f 2xd 2x 0 0 4 4 4
2 f xdx 3 f xdx f x dx 5 0 0 0 Trang 124
Hướng 2: Dựa theo hướng đi tìm f x bằng biến đổ.
Câu 48.3 (Phát triển Tương tự câu 48 đề thi tham khảo) Cho hàm số y f x liên tục và có đạo hàm 1 a 2 a trên
thỏa mãn 5 f x 7 f 1 x 3x 2x,x . Biết rằng x. f xdx
b , với b là phân số 0
tối giản. Giá trị của 8a 3b là A. 1 B. 0 C. 16 D. 16 Lời giải Chọn B 2 2
Từ 5 f x 7 f 1 x 3x 2x thay x bởi 1 x ta được 5 f 1 x 7 f x 3x 1
5f x7f 1 x 3 2x 2x Do đó ta có hệ
7 f x 5 f 1 x 2 3x 1 2 2 2
Suy ra 25 f x 49 f x 15x 2x 21x
1 24 f x 36x 30x 21 1 2 1
Hay f x 12x 10x 7 f x 12x 5 8 4 1 1 a 1 3 a 3
Do đó x.f xdx x12x 5 dx b 4 8 b 8 0 0
Vậy 8a 3b 0 2
Câu 48.4 (Phát triển Tương tự câu 48 đề thi tham khảo) Cho hàm số f x liên tục trên đoạn ;1 3 2 2 1
và thỏa mãn 2 f x 3 f 5 ; x x ; 1 ln xf x dx bằng 3x . Tích phân 3 2 3 5 2 1 5 2 1 5 2 1 5 2 1 A. ln ln ln ln 3 3 3 B. 3 3 3 C. 3 3 3 D. 3 3 3 Lời giải Chọn D Cách 1: 2 2 2 10
Từ 2 f x 3 f 5x 2 f 3 f x 3x thay x bởi 3x ta được 3x 3x . 10 2 2
Do đó 4 f x 9 f x 10x
f x 2x f x 2 2 x x x 1 1 xf x 2 5 2 1 ln dx
2 ln xdx ln 2 x 3 3 3 2 2 3 3 Cách 2: Trang 125 1 1 1 f x dx
Ta có ln xf x dx f x ln x 2 x . 2 3 2 3 3 2 2
Từ 2 f x 3 f 5x,x ; 1 3x 3 2 2 f 1 3 f 5 f 1 0 2 3
Thay x 1 và x 3 vào (1) ta được hệ 2 5 . 2 2 f 3 f 10 f 1 3 3 3 3 1 f x Xét I dx x 2 3 2 x t 2 2 1 Đặ 3 t x dx dt , đổi cận 2 3t 3t 2 x 1 t 3 2 2 1 2 2 f . dt f dt f dx 3 2 1 1 2 3t t 3t 3x Khi đó I 3 2 t x . 1 2 2 3 3 3t 2 2 f dx 2 f x 3 f 1 f x 1 1 dx 3x 3x 1 5 1
Ta có 2I 3I 2 3 5I
dx 5dx I x x x 3 3 2 2 2 2 3 3 3 3 1 1 1 f x dx 2 2 1 5 2 1
Vậy ln xf xdx f x ln x ln1.f1 ln f ln 2 x 3 3 3 3 3 3 . 2 3 2 3 3
Hướng 3: Kết hợp với tính chẵn, lẻ, đối xứng của hàm số.
Câu 48.5 (Phát triển Tương tự câu 48 đề thi tham khảo) Cho hàm y f x liên tục trên đoạn 0; 1 1
và thỏa mãn f x f x 2 1
2x 2x 1,x 0;
1 . Giá trị của f xdx bằng 0 4 2 1 1 A. 3 B. 3 C. 2 D. 3 Lời giải Chọn D
Ta có f x f x 2 1 2x 2x 1 1 1 1 1
I f 1 xdx 2 2x 2x
1dx I f 1 x 2 3 2 dx x x x 3 0 0 0 0 Trang 126 1 2
I f 1 xdx 1 3 0 1 Xét f 1
xdx , đặt t 1 x dt dx 0
Đổi cận x 0 t 1; x 1 t 0 . 1 0 1 Ta có
f 1 xdx f tdt f tdt I 2 0 1 0 1 1 2 1 Từ
1 ;2 2 f xdx f xdx . 3 3 0 0
Câu 48.6 (Phát triển Tương tự câu 48 đề thi tham khảo) Cho hàm số f x xác định, liên tục trên và 1 3 3 6 4 2
thoả mãn f x x
1 f x x
1 6 12x 6x 2,x . Giá trị của f xdx bằng 3 A. 32 B. 4 C. 36 D. 20 Lời giải Chọn D 2 Đặ 3
t a x x 1, khi đó ta có f a f a 2 6a 1 2
1 . Hàm số f a liên tục và xác định trên . 1
Lúc đó ycbt trở thành tính giá trị của tích phân f ada . 3 1 1 1 2
Lấy tích phân hai vế của (1) ta được
f ada f a 2da 6a1 2da 40 2. 3 3 3 1 Từ tích phân f a
2da ta đặt t a2 dt da. 3
Khi a 3 t 1; a 1 t 3 1
Tích phân trên chuyển thành f tdt , kết hợp với (2) ta suy ra 3 1 2 f a 1
da 40 f ada 20 3 3
Câu 49: [ ĐỀ THI THAM KHẢO ] Cho khối chóp .
S ABC có đáy ABC là tam giác vuông cân tại , A AB ,
a SBA SCA 9
0 , góc giữa hai mặt phẳng SAB và SAC bằng
60 . Thể tích khối chóp đã cho bằng 3 3 3 3 a a a A. a B. 3 C. 2 D. 6 Lời giải Trang 127 2 1 a Ta có S A . B AC ABC 2 2
Gọi D là hình chiếu vuông góc của S lên mặt phẳng (ABC). AB SB Ta có
AB SBD AB BD AB SD .
Tương tự, ta có AC CD
ABDC là hình vuông cạnh a.
Đặt SD x, x 0 D . B DS ax
Gọi H là hình chiếu vuông góc của D lên SB DH . 2 DB 2 2 DS a 2 x DH SB ax Ta có
DH SAB d D,SAB DH . DH 2 AB a 2 x
Lại có CD / / AB CD / / SAB d C,SAB d D,SAB DH . SCA 2 2
vuông tại C, có AC ,
a SC x a . 2 C . A CS . a x 2 a
Kẻ CK SA CK . 2 CA 2 2 CS x 2 2a
d C, SAB DH
Vì SAB SAC SA sin SAB,SAC
dC,SA CK . ax a 2 x 3 x x 2 2 2 2 2a sin 60 3 2 x 2 a 2 4x 2 x 2 2a x a 2 2 2 a x 2 2 a x a 2 x 2 2a DH a . 3 1 a V S .SD S.ABC 3 ABC 6 . Cách 2: Trang 128
Dựng hình vuông ABCD SD ABCD .
Đặt SD x, x 0 ax Kẻ DH S ,
B H SB DH SAB và DH . 2 x 2 a ax
Kẻ DK SC,K SC DK SAC và DK . 2 x 2 a 2 2 2 2 SH SK SD x x x Ta có:
HK // BD HK BD .a 2 . 2 2 SB SC SB x 2 2 a x 2 2 a x 2 a 2 2 2 DH DK HK Ta có: cosSA , B SAC cosHDK 2DH.DK 2 2 2 4 2x a 2a x 2 x 2 a 1 2 2 x 2 a 2 1 a x a 2 2 2 2 2x a 2 x 2 a 2 x 2 a SD a 2 1 a Lại có S A . B AC . ABC 2 2 3 1 a Vậy V S .SD S.ABC 3 ABC 6 Trang 129
Ta có hai tam giác vuông SAB và SAC bằng nhau và chung cạnh huyền S .
Kẻ BI SA CI SA và góc giữa hai mặt phẳng SAB và SAC là góc giữa hai đường thẳng BI
và CI BI;CI 6 0 .
Có BC a 2 , BIC cân tại I. Do BI CI AC a a 2 BC nên BIC không đều. a 6 a 3 BIC
120 BI CI 2 AI ; AB AI.SA SA a 3 3 . Từ đó 3 .
Dựng hình vuông ABDC SD ABDC 3 2 2 2 1 a
Có: SD SA AD ; a S a V S .SD ABC S.ABC 3 ABC 6 .
Cách 4: Sau khi đã tính được SA ta có thể tính 1 1 V S
. SI AI S .SA S.ABC IBC 3 3 IBC 2 2 3 1 a 3 1 a 3 a Với S . . IB IC.sin12 0 V . .a 3 IBC S. 2 6 ABC 3 6 6 .
Cách 4 trắc nghiệm
CÔNG THỨC TÍNH NHANH :(Sẽ được chứng minh sau trong phần phát triển)
Gọi D là hình chiếu vuông góc của S lên mặt phẳng ABC AB SB Ta có
AB SBD AB BD AB SD .
Tương tự, ta có AC CD ABDC là hình vuông cạnh a. 2 2 a a 1 Đặt SD , h h 0.cos
h a SD a 2 h 2 2 a h 2 a 2 3 1 a
Từ đây tiếp tục tính thể tích V S .SD S.ABC 3 ABC 6
PHÂN TÍCH Ý TƯỞNG CÂU 49
Bài toán góc giữa hai mặt phẳng luôn là bài toán khó nhất trong các bài toán hình học không gian. Ở câu
49 này Bộ đã đưa ra hai vấn đề khó thường gặp :
Khó thứ nhất là cái khó chung của bài toán hình học không gian, là hình trong
bài không có đường cao cho trước.
Khó thứ hai là cái khó riêng của bài toán góc giữa hai mặt phẳng. Ở đây câu
49 này còn kết hợp hết cái khó của bài toán góc: Cho góc giữa hai mặt bên vào giả thiết. Muốn
giải quyết được bài toán này phải khai thác được giả thiết góc.
Tuy nhiên đây đã là bài toán quen , ý tưởng không có gì mới. Nên chúng ta
chỉ cần lần lượt giải quyết hai vấn đề trên.
Giải quyết vấn đề 1: Trang 130
Tìm đường cao của hình : học sinh phải tìm đường cao bằng cách suy ra từ các quan hệ vuông góc giữa
đường với đường để chứng mình được đường vuông góc với mặt, hay phục dựng hình ẩn để xác định đường cao.
Giải quyết vấn đề 2:
Để khai thác được giả thiết góc ta thường làm :
+ Xác định được góc. Trong quá trình xác định góc phải tránh bẫy khi đưa về góc giữa hai đường thẳng
cắt nhau nó là góc không tù.
+ Cần chọn ẩn ( Là chiều cao hay cạnh đáy nếu giả thiết chưa có) sau đó sử dụng giả thiết góc để tìm ẩn.
Và có thể sử dụng nhiều phương pháp khác ngoài hai cách truyền thống để tính góc giữa hai mặt bên
Phương pháp khoảng cách : giả sử là góc giữa hai mặt bên và d M, sin
ở đây d , M
d M,d
Phương pháp diện tích hai mặt bên : giả sử là góc giữa hai mặt bên ABC và ABD 2S .S 3.V .AB ABC V
ABD .sin sin ABCD ABCD 3AB 2S .S . ABC ABD S
Công thức đa giác chiếu : cos S
Ta đi chứng minh công thức tính nhanh cho bài toán này : Cho hình chóp . S ABCD có
SA ABCD , đáy ABCD là hình chữ nhật, biết SA , h AB , a AD b.
Gọi SBC,SDC AB AD a b Khi đó: cos . . 1 2 SB SD h 2 2 a h 2 b 2 a
Đặt biệt khi ABCD là hình vuông thì cos 2 2 2 h a Thật vậy : Cách c/m 1: Trang 131
Gọi E, F lần lượt là hình chiếu của A lên S ,
B SD khi đó ta có AE SBC và AF SDC , do đó
SBC,SDCAE,AF . AE.AF Khi đó cos 3 AE.AF A . B SA 2 SA 2 2 2 SA SA AB Ta có AE * SE SE SB AE AB AS SB và SB suy ra 2 2 2 SB SB SB 2 A . D SA SA Tương tự, AF * *,SF SD SD 2 2 2 SA SA AD Suy ra SF SD AF AD AS 2 2 2 SD SD SD 2 2 AB .AD
Do đó AE.AF 2 .AS *** . 2 2 SB .SD
Thay (*), (**), (***) vào (3) ta được công thức (1). Cho a b ta được (2). Cách c/m 2:
Gọi K là hình chiếu của D lên SC, khi đó
d D,SBC d , A SBC AE AS.AB SC AS.SC sin . DK DK DK SB S . D DC S . B SD 2 2 SB .SD 2 . SA 2 SA 2 AB 2 2 2 AD AS SC cos 1 2 2 2 2 SB .SD SB .SD 2 SA 2 AB . 2 SA 2 AD 2 SA 2 SA 2 AB 2 AD A . D AB 2 2 SB .SD S . D SB
Cách c/m 3: PP Toạ độ hoá
CÁC CÂU TƯƠNG TỰ VÀ PHÁT TRIỂN CÂU 49.
Câu 1: 49.1 ( Tương tự câu 49 – Đề thi tham khảo) Cho hình chóp .
S ABC có đáy ABC là tam giác
vuông cân tại B với BA BC 5 ;
a SAB SCB 9
0 . Biết góc giữa hai mặt phẳng SBC và SBA 9
bằng với cos 16 . Thể tích của khối chóp .SABC bằng 3 50a 3 125 7a 3 125 7a 3 50a A. 3 B. 9 C. 18 D. 9 Lời giải Chọn C Trang 132
Ta có hai tam giác vuông SAB và SBC bằng nhau và chung cạnh huyền SB.
Kẻ AI SB CI SB và góc giữa hai mặt phẳng SBA và SBC là góc giữa hai đường thẳng AI và
CI AI;CI . 9 Do CBA 9 0 18 0 AIC 9 0 AIC 18
0 cos AIC 16 Có AC 5 2 ,
a AIC cân tại I nên có: 2 2AI 2 2 AC 2AI 2 AC 9 cos AIC 2 AI 2
16a AI 4a 2 2 2AI 2AI 16 2 AI 16 25a
BI 3a SI a SB IB 3 3 Cách 1 : BA SA
Dựng SD ABC tại D. Ta có:
BA AD . Tương tự BC CD BA SD 2 2 5 7
Nên tứ giác ABCD là vuông cạnh 5a BD 5 2a SD SB BD a 3 3 1 1 2 1 5 7 1 3 125 7a Vậy V S . D BA . . .25a SABC 3 2 3 3 2 18 1 1 1 Cách 2: V V V SI.S BI.S S . B S S.ABC S.ACI B.ACI 3 ACI 3 ACI 3 ACI 2 1 1 5 7 5 7a AIC 2 2
cân tại I, nên S
AI sin .16a . ACI 2 2 16 2 2 3 1 25a 5 7a 125 7a Vậy V . . S.ABC 3 3 2 18
ÁP DỤNG CT TÍNH NHANH KHI GIẢI TN :
Gọi D là hình chiếu vuông góc của S lên mặt phẳng ABC AB SB Ta có
AB SBD AB BD AB SD . Trang 133
Tương tự, ta có AC CD ABDC là hình vuông cạnh a. 2 2 5a 25a 9 5 7a Đặt SD , h h 0.cos h SD 2 h 2 2 5a h 2 25a 16 3 3 1 125 7a
Từ đây tiếp tục tính thể tích V S .SD S.ABC 3 ABC 18
Câu 2: 49.2 ( Phát triển câu 49 – Đề thi tham khảo) Cho hình chóp .
S ABC có BC 2BA 4a ,
ABC BAS
90 . Biết góc giữa hai mặt phẳng SBC và SBA bằng
60 và SC SB . Thể tích của khối chóp . S ABC bằng: 3 32a 3 8a 3 16a 3 16a A. 3 B. 3 C. 3 D. 9 Lời giải Chọn B
Tam giác SBC cân cạnh đáy BC 4a . Gọi E là trung điểm BC thì ta có SEB vuông tại E,
BE 2a BA. Đưa về bài toán gốc với chóp . S ABE .
Ta có hai tam giác vuông SAB và SEB bằng nhau và chung cạnh huyền SB.
Kẻ AI SB EI SB và góc giữa hai mặt phẳng SBA và SBC góc giữa hai mặt phẳng SBA và
SBE là góc giữa hai đường thẳng Aivà EI AI;EI 6 0. 1 Do CBA 9 0 18 0 AIE 9 0 AIE 12
0 cos AIE 2 Có AE 2 2 ,
a AIE cân tại I, nên có 2 2AI 2 2 AE 2AI 2 2 AE 1 8a 2 2 cos AIC 2 AI AI a 2 2 2AI 2AI 2 3 3 2 2a AI 4a 6a BI SI SB . 3 IB 3 3 Cách 1: Trang 134 BA SA
Dựng SD ABC tại D. Ta có:
BA AD . Tương tự BE ED BA SD
Nên tứ giác ABED là hình vuông cạnh 2a. BD a SD 2 SB 2 2 2 BD 2a 3 1 1 1 2 8a Thể tích V S .
D BC.BA .2 .4 a a SABC 3 2 3 3 1
Cách 2: V S .2 B S SABC 3 AEI 2 2 1 1 8a 3 4 3a S 2 AI sin . . ACI 2 2 3 2 3 2 3 1 6a 4 3a 8a Vậy V . . S.ABC 3 . 3 3 3 2 2 4a 4a 1
Cách tính nhanh: cos 2 4a 2
h h 2a SD 2 h 2 2 4a h 2 4a 2 3 1 1 1 2 8a Thể tích V S .
D BC.BA .2 .4 a a SABC 3 2 3 3
Câu 3: 49.3 ( Phát triển câu 49 – Đề thi tham khảo) Cho hình chóp .
S ABC có đáy ABC là tam giác
đều cạnh a, SAB SCB
90 góc giữa hai mặt phẳng SAB và SCB bằng 60 . Thể tích của khối chóp . S ABC bằng 3 3a 3 2a 3 2a 3 2a A. 24 B. 24 C. 8 D. 12 Lời giải Chọn B
Gọi M là trung điểm của SB. Và G là trọng tâm của tam giác đều ABC.
Theo giả thiết SAB SCB
90 MS MB MA MC M thuộc trục đường tròn ngoại tiếp
ABC MG ABC .
Gọi D là điểm đối xứng với G qua cạnh AC thì SD ABC .
Từ giả thiết suy ra hai tam giác vuông bằng nhau (SAB) và (SCB). Trang 135
Do đó từ A kẻ AI S ,
B I SB thì CI SB .
Nên góc giữa hai mặt phẳng SAB và SCB bằng góc AI,CI 6 0 2 2AI 2 AC 1 a Do ABC 6 0 AIC 12 0 AI 2 2AI 2 3 2a a 3 BI SB 3 2 2 2 4 3 2 2 2 3a 4a a Ta có BD . a
SD SB BD 3 2 3 2 3 6 3 1 1 1 3 3 2a Thể tích V S . D S . . a SABC 3 ABC 3 . 6 4 24 1
Cách tính khác: V S .2 B S SABC 3 AEI 2 2 1 1 a 3 3a S 2 AI sin . . ACI 2 2 3 2 12 2 3 1 a 3 3a 2a V . SABC 3 2 12 24
Câu 4: 49.4 ( Phát triển câu 49 – Đề thi tham khảo- Sở Bắc Ninh lần 2-2018-2019) Cho tứ diện ABCD
có DAB CBD 90 ; AB ;
a AC a 5; ABC 13
5 . Biết góc giữa hai mặt phẳng ABD,BCD bằng
30 . Thể tích của tứ diện ABCD bằng 3 a 3 a 3 a 3 a A. B. C. D. 2 3 2 3 2 6 Lời giải Chọn D
Dựng DH ABC Trang 136 BA DA BC DB Ta có
BA AH . Tương tự BC BH BA DH BC DH
Tam giác AHB có AB a , ABH
45 HAB vuông cân tại A AH AB a
Áp dụng định lý cosin, ta có BC a 2 . 2 1 1 2 a Vậy S .B .
A BC.sinCBA . . a a 2. ABC 2 2 2 2 HE DA Dựng
HE DAB HF DBC HE DB và
Suy ra DBA,DBC HE,HF EHF và tam giác HEF vuông tại E. ax xa 2
Đặt DH x , khi đó HE ,HF 2 a 2 2 x 2a 2 x 2 HE 3 x 2 2a Suy ra cos EHF x a 2 HF 4 2x 2 2a 3 1 a Vậy V .DH.S ABCD 3 ABC 6 .
Câu 5: 49.5 ( Phát triển câu 49 – Đề thi tham khảo) Cho hình chóp . S ABC có AB 2 , a AC , a BC 3 ,
a SBA SCA 9
0 . Và hai mặt phẳng SAB và SAC tạo với nhau một 1 góc sao cho cos
. Thể tích của khối chóp . S ABC bằng 3 3 2a 3 2a 3 2a 3 2a A. 12 B. 2 C. 3 D. 6 Lời giải Chọn D 2 2 2 2 2 2
Từ giả thiết : AB 2 , a AC ,
a BC 3a BC 3a 2a a AB AC
ABC vuông tại A
Dựng SD ABC ABDC hình chữ nhật. DB AC ,
a DC AB 2a . Gọi SD h . Áp dụng công thức tính nhanh: Trang 137 DB DC Ta có: . cos a SB SC
. Coi 1 để tiện tính toán ta có: 1 2 1 . 4 h 2 3h 4 0 2
h 1 h 1 h a SD . 2 h 2 1 h 2 3 3 1 1 2a V .S . D A . B AC SABC 3 2 6
Câu 50: [ ĐỀ THI THAM KHẢO ] Cho hàm số f x . Hàm số y f x có đồ thị như hình sau.
Hàm số g x f x 2 1 2
x x nghịch biến trên khoảng nào dưới đây? 3 1 A. 1; 0; 2;1 D. 2;3 2 B. 2 C. Lời giải Chọn A Ta có
g x 2 f 12x 2x 1 g x 2x 1
0 2 f 12x 2x 1 0 f 12x * 2 t
Đặt t 1 2x , ta có đồ thị hàm số y f t và y 2 như hình vẽ sau : t 1 3 Trên đoạn 2; 4 thì
* f t 2 t 0 2 12x 0 x 2 2 2 . 1 3
=> Hàm số nghịch biến trên khoảng ; 2 2 . Trang 138 3 1 3
Đối chiếu với các phương án suy ra chọn đáp án A vì 1; ; 2 2 2 .
Câu 50.1 ( Tương tự Câu 50 ): Cho hàm số f x . Hàm số y f x có đồ thị như hình sau.
Hàm số g x f x 3 x 2 3 1 2 8
21x 6x đồng biến trên khoảng nào dưới đây? A. 1;2 B. 3; 1 C. 0; 1 D. 1;2 Lời giải Chọn A Ta có
g x f x 2 6 1 2
24x 42x 6
g x f x 2 0 1 2
4x 7x 1 * 1 t
Đặt 1 2x t x 2 1 t 2 1 t 3 3
Ta có (*) trở thành f t 4. 7.
1 f t 2t t . 2 2 2 2 2 3 3
Ta vẽ parapol P : y x x
y f x 2
2 trên cùng hệ trục Oxy với đồ thị
như hình vẽ sau ( đường 3 33
nét đứt), ta thấy P có đỉnh I ;
và đi qua các điểm 3;3,1;2,1; 1 . 4 16 Trang 139 2 3 3
Từ đồ thị hàm số ta thấy trên khoảng 3;
1 ta có f t t t 3 t 1 2 2 .
3 12x 11 x 2
Vậy hàm số g x nghịch biến trên khoảng 1;2 .
Câu 50.2 ( Phát triển Câu 50). Cho hàm số f x . Hàm số y f x có đồ thị như hình sau.
Có tất cả bao nhiêu giá trị nguyên dương của tham số m đề hàm số g x f x m 2 4
x 2mx 2020
đồng biến trên khoảng 1;2 A. 2 B. 3 C. 0 D. 1 Lời giải Chọn A Ta có
g x 4 f x m 2x 2m x m
g x 0 f x m * 2 t
Đặt t x m thì * f t 2 x
Vẽ đường thẳng y
y f x
2 trên cùng hệ trục Oxy với đồ thị như hình vẽ sau Trang 140 t 2 t 0
m 2 x m
Từ đồ thị ta có f t 2 t 4 x m 4
Hàm số g x đồng biến trên khoảng 1;2
g x 0 x 1;2
m 2 1 2 m 2 m 3 m 4 1 m 3
Vì m nguyên dương nên m 2; 3
Vậy có hai giá trị nguyên dương của m đề hàm số g x đồng biến trên khoảng 1;2 .
Câu 50.3 ( Phát triển Câu 50). Cho hàm số đa thức f x có đạo hàm tràm trên R. Biết f 0 0 và đồ
thị hàm số y f x như hình sau.
Hàm số g x f x 2 4
x đồng biến trên khoảng nào dưới đây ? A. 0;4 B. 2;0 C. 4; D. ;2 Lời giải Chọn A
Xét hàm số h x f x 2 4
x , x R x Có
h x 4 f x 2x
h x 0 f x 2 x
Vẽ đường thẳng y
y f x
2 trên cùng hệ trục Oxy với đồ thị như hình vẽ sau Trang 141
Từ đồ thị ta có BBT của h x như sau :
Chú ý ở đây h 0 4 f 0 0
Từ đó ta có BBT của như sau :
Từ BBT ta suy ra g x đồng biến trên khoảng 0;4
Câu 50.4 ( Phát triển Câu 50). Cho hàm số y f x có bảng xét dấu đạo hàm như sau 3 2
Biết rằng 1 f x 5,x R . Hàm số g x f f x
1 x 3x 2020 nghịch biến trên khoảng nào dưới đây A. 0;5 B. 2;0 C. 2;5 D. ;2 Lời giải Chọn B 2 Ta có
g x f x.f f x
1 3x 6x
Vì 1 f x 5,x R 0 f x 1 4
Từ bảng xét dấu của f x f f x 1 0 Trang 142
Từ đó ta có bảng xét dấu như sau
Do đó hàm gx nghịch biến trên khoảng 2;0 Trang 143
Document Outline
- bia ôn 20 đề Tn 2020-Duong Hung
- BỘ PHÁT TRIỂN ĐỀ MINH HỌA BGD 2020




