






Preview text:
filename VM003.pdf2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN VIETNAM - MATHS & LATEX
ÔN TẬP HỌC KỲ I, NĂM HỌC 2025-2026 Đề số 1
ĐỀ THAM KHẢO - BỘ SÁCH KNTT
Biên soạn: Nguyên Thái Hoàng Môn: TOÁN 11
Phản biện: Nguyễn Tiến Dũng
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh: Số báo danh: Mã đề: 0101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi, thí sinh chỉ lựa chọn một phương án.
Câu 1. Phát biểu đúng khi nói về “đường tròn lượng giác” là
A. Mỗi đường tròn là một đường tròn lượng giác.
B. Mỗi đường tròn có bán kính R = 1 là một đường tròn lượng giác.
C. Mỗi đường tròn có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác.
D Mỗi đường tròn định hướng có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác. Lời giải.
Mỗi đường tròn định hướng có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 2. Trong không gian, số vị trí tương đối giữa hai đường thẳng a và b phân biệt là A. 4. B. 2. C 3. D. 1. Lời giải.
Vì hai đường thẳng a và b phân biệt nên hai đường thẳng có 3 vị trí tương đối: cắt nhau, song song, chéo nhau.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
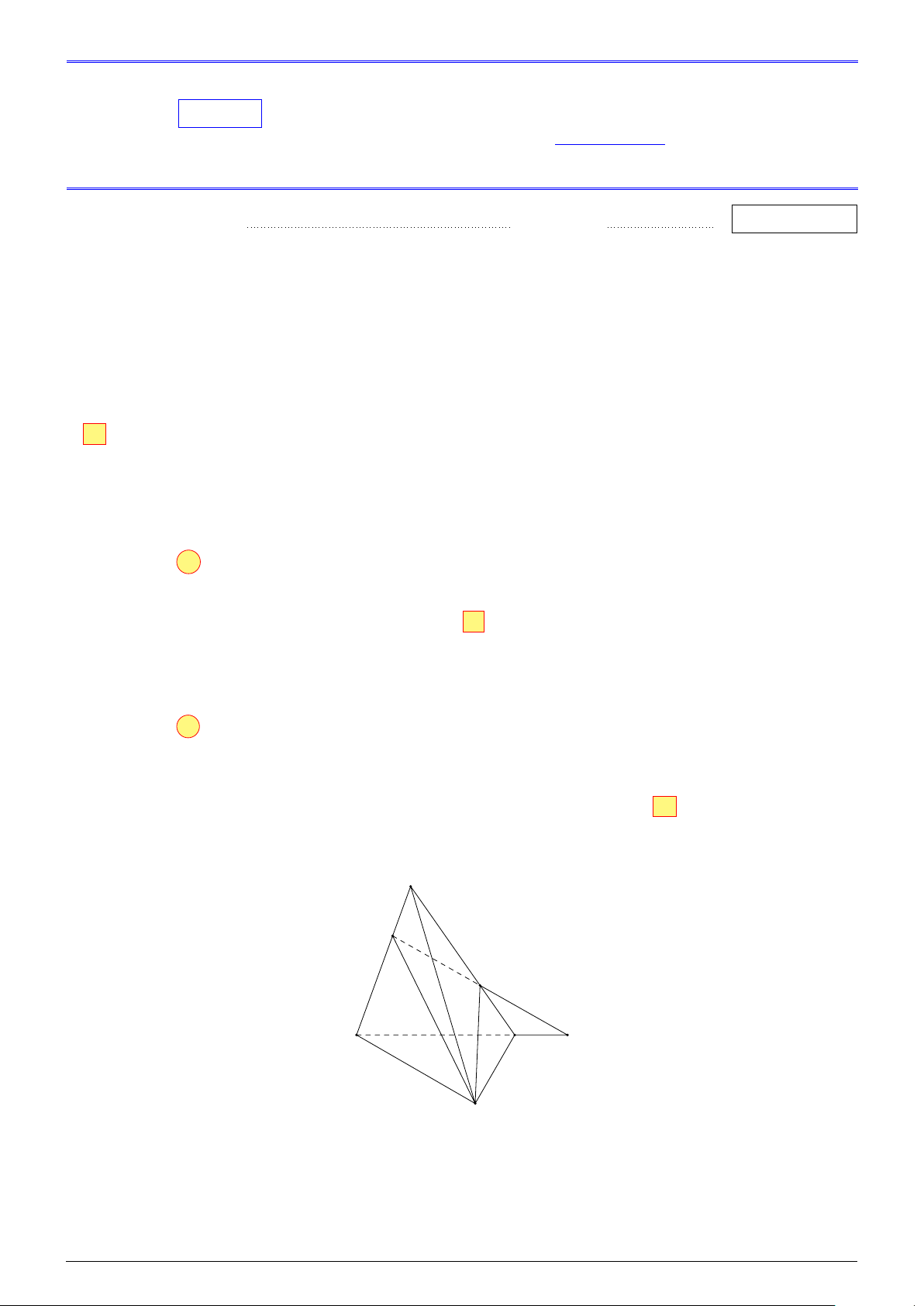
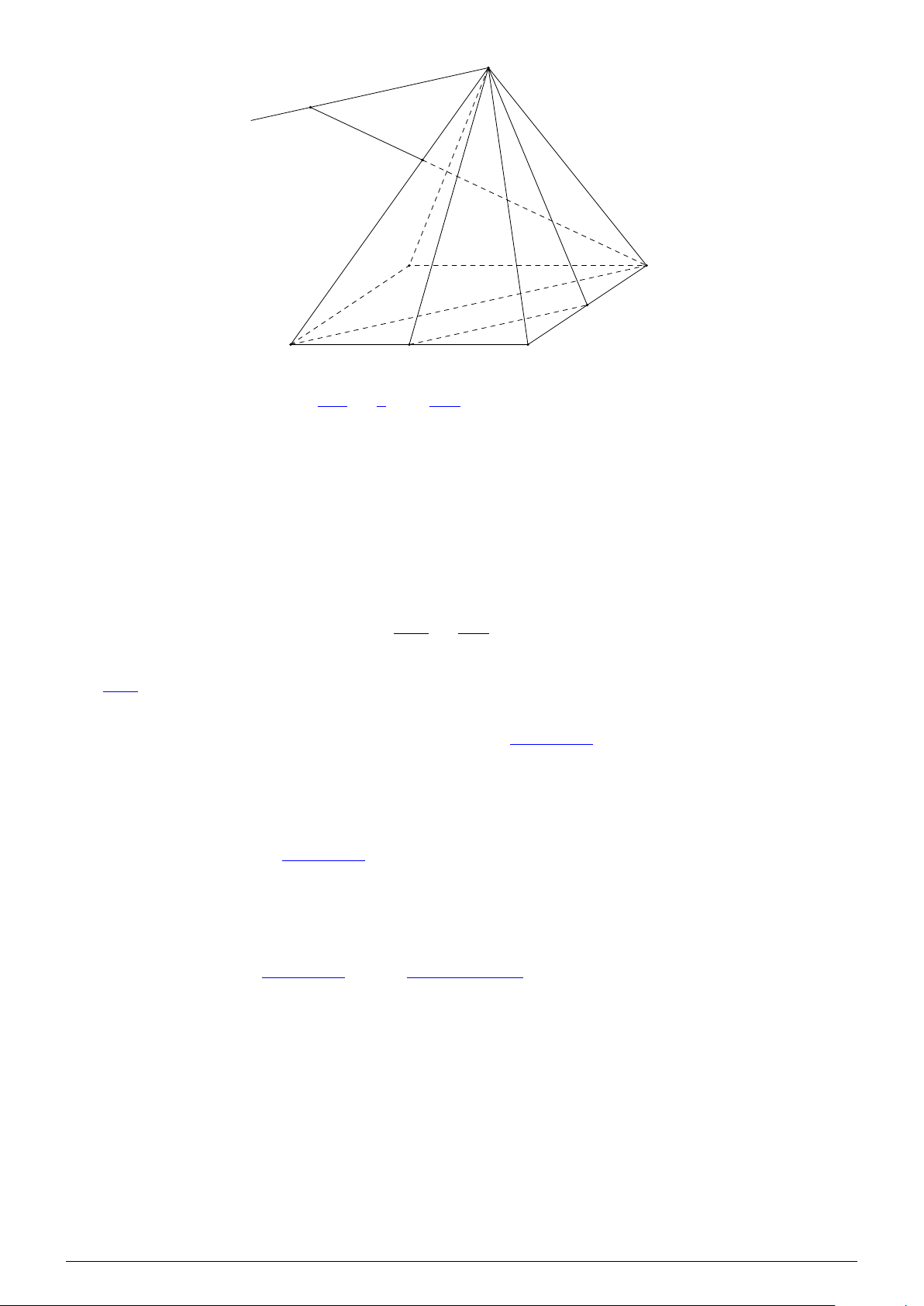
Câu 3. Cho tứ diện S.ABC. Trên SA, SC lần lượt lấy các điểm M và N sao cho MN cắt AC tại E.
Mặt phẳng không chứa điểm E là A. (ABC). B. (SAC). C. (BMN). D (SBC). Lời giải. S M N C A E B Ta có
• E ∈ AC ⊂ (SAC) ⇒ E ∈ (SAC).
• E ∈ AC ⊂ (ABC) ⇒ E ∈ (ABC). NHÓM VN - MATHS & LATEX − 249 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM
• E ∈ MN ⊂ (BMN) ⇒ E ∈ (BMN). • E / ∈ (SBC).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 4. Cho hai mặt phẳng (P) và (Q) song song với nhau. Phát biểu sai là
A. Nếu đường thẳng ∆ cắt (P) thì ∆ cũng cắt (Q).
B. Mọi đường thẳng đi qua điểm A ∈ (P) và song song với (Q) đều nằm trong (P).
C Đường thẳng a ⊂ (P) và đường thẳng b ⊂ (Q) thì a ∥ b.
D. Nếu đường thẳng a ⊂ (Q) thì a ∥ (P). Lời giải.
Nếu (P) ∥ (Q) và đường thẳng a ⊂ (P); b ⊂ (Q) thì a và b có thể chéo nhau.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 5. Nghiệm của phương trình 2 cos x = −1 là π kπ π A. x = + , k ∈ Z. B. x = + kπ, k ∈ Z. 3 2 3 kπ 2π C. x = − π + , k ∈ Z. D x = ± + k2π, k ∈ Z. 3 3 3 Lời giải. 1 2π
Ta có 2 cos x = −1 ⇔ cos x = − ⇔ x = ± + k2π, k ∈ Z. 2 3
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 6. Trong các dãy số sau, dãy số là một cấp số cộng là
A. 1; −3; −6; −9; −12.
B 1; −3; −7; −11; −15.
C. 1; −3; −5; −7; −9.
D. 1; −2; −4; −6; −8. Lời giải.
Ta có dãy số 1; −3; −7; −11; −15 là một cấp số cộng với công sai d = −4.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 7. Cho dãy số (un) với un = 2n + 5. Số 19 là số hạng thứ bao nhiêu của dãy số đã cho? A. 12. B. 19. C. 5. D 7. Lời giải.
Ta có un = 19 ⇔ 2n + 5 = 19 ⇔ 2n = 14 ⇔ n = 7.
Vậy 19 là số hạng thứ 7 của dãy số đã cho.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ 1
Câu 8. Cho hai dãy số (un) và (vn) với un = 2n + 1, vn = . Khi đó lim (u 1 − n n · vn) bằng n→+∞ A. 0. B. 2. C −2. D. +∞. Lời giải. 1 2n + 1 Ta có un · vn = (2n + 1) · = . 1 − n 1 − n 1 2n + 1 2 + Khi đó lim (u n n · vn) = lim = lim = −2. n→+∞ n→+∞ 1 − n n→+∞ 1 − 1 n Vậy lim (un · vn) = 2. n→+∞
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ NHÓM VN - MATHS & LATEX − 250 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN
Câu 9. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút) [0; 10) [10; 20) [20; 30) [30; 40) [40; 50) [50; 60) Số học sinh 7 13 9 18 22 6 Nhóm chứa trung vị là A [30; 40). B. [10; 20). C. [20; 30). D. [40; 50). Lời giải.
Ta có cỡ mẫu là n = 7 + 13 + 9 + 18 + 22 + 6 = 75.
Gọi x1; x2; . . .; x75 lần lượt là thời gian tập thể dục trong ngày của 75 học sinh khối 11 và giả sử
dãy này đã sắp xếp theo thứ tự không giảm.
Khi đó, trung vị là x38 thuộc nhóm [30; 40) nên nhóm này chứa trung vị Me.
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 10. Lượng nước tiêu thụ trong một tháng của các hộ gia đình trong một khu chung cư được ghi lại như sau: Lượng nước m3 [0; 20) [20; 40) [40; 60) [60; 80) [80; 100) [100; 120) Số hộ gia đình 6 12 10 7 4 2
Giá trị đại diện của nhóm chứa mốt của mẫu số liệu trên là A 30. B. 40. C. 50. D. 60. Lời giải.
Tần số lớn nhất của mẫu số liệu là 12 nên nhóm chứa mốt của mẫu số liệu là nhóm [20; 40). 20 + 40
Suy ra giá trị đại diện của nhóm này là = 30. 2
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
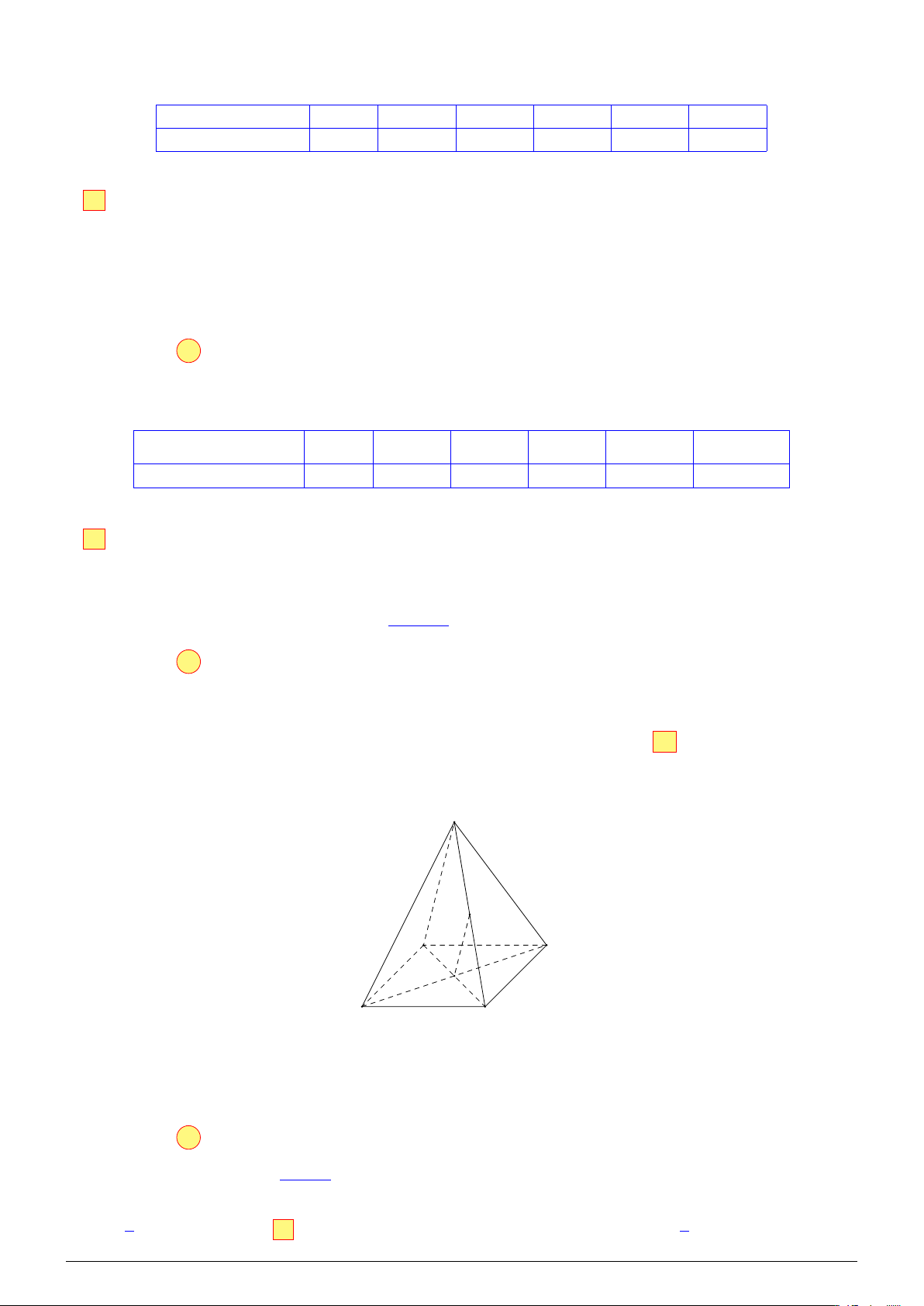
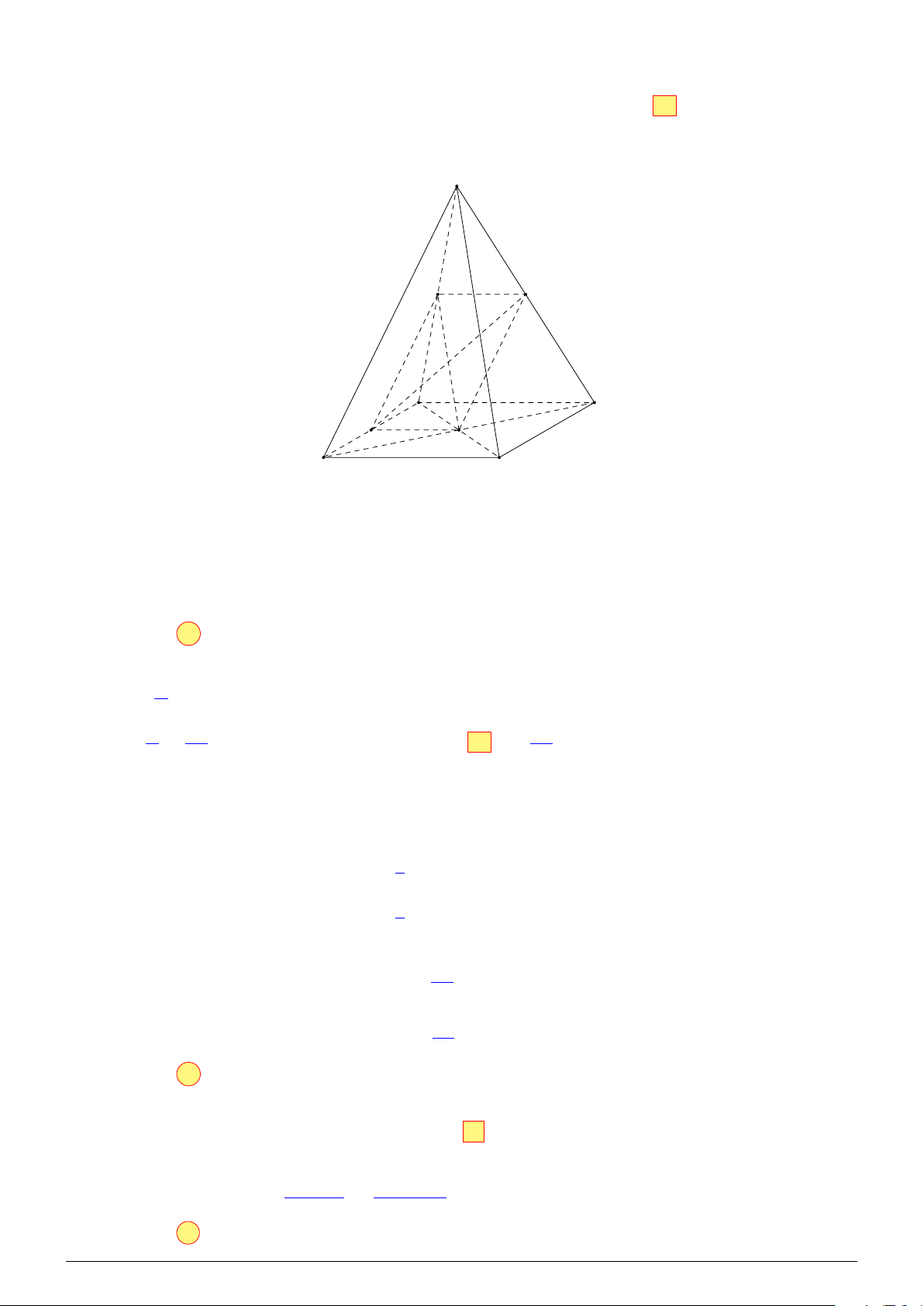
Câu 11. Cho hình chóp S.ABCD, đáy là hình bình hành. Gọi O là giao điểm của AC và BD, M là
trung điểm SC. Phát biểu đúng là A. OM ∥ (ABCD). B. OM ∥ (SBD). C. OM ∥ (SAC). D OM ∥ (SAD). Lời giải. S M A D O C B
Vì M và O lần lượt là trung điểm của SC và AC nên OM là đường trung bình tam giác SAC. Suy ra OM ∥ SA.
Mà SA ⊂ (SAD) và OM ̸⊂ (SAD) nên OM ∥ (SAD).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ 3 + 2x Câu 12. Giới hạn lim bằng x→(−3)+ x + 3 1 7 A. − . B −∞. C. +∞. D. . 4 4 NHÓM VN - MATHS & LATEX − 251 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM Lời giải. Ta có lim (3 + 2x) = −3,
lim (x + 3) = 0 và x + 3 > 0 với ∀x > −3. x→(−3)+ x→(−3)+ 3 + 2x Suy ra lim = −∞. x→(−3)+ x + 3
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d)
ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho cấp số cộng (un) với số hạng đầu u1 = 5 và công sai d = 2. a u6 = 15.
b Số hạng tổng quát của cấp số cộng là un = 2n + 3.
c Tổng n số hạng đầu tiên của cấp số cộng là Sn = n2 + 4n.
d) S = u10 + u11 + · · · + u20 = 310. Lời giải.
a) Đ Ta có u6 = u1 + 5d = 5 + 5 · 2 = 15.
b) Đ Ta có un = u1 + (n − 1)d = 5 + (n − 1) · 2 = 2n + 3. n [2u n [2 · 5 + (n − 1) · 2] c) Đ Ta có S 1 + (n − 1)d] n = = = n2 + 4n. 2 2
d) S Ta có S20 = 202 + 4 · 20 = 480 và S9 = 92 + 4 · 9 = 117. Khi đó S = u10 + u11 + · · · + u20
= (u1 + u2 + · · · + u20) − (u1 + u2 + · · · + u9) = S20 − S9 = 480 − 117 = 363.
Chọn đáp án a đúng b đúng c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 2. Một bảng xếp hạng đã tính điểm chuẩn hoá cho chỉ số nghiên cứu của một số trường đại
học ở Việt Nam và thu được kết quả sau: Điểm [10; 20) [20; 30) [30; 40) [40; 50) [50; 60) [60; 70) Số trường 4 19 6 2 3 1
a Số liệu đã cho có 35 giá trị.
b) Số trung bình của mẫu số liệu đã cho là 28.
c) Số trung vị của mẫu số liệu đã cho là Me = 12.
d 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam là những trường có điểm chuẩn
hóa lớn hơn hoặc bằng 35,42. Lời giải.
a) Đ Ta có cỡ mẫu n = 4 + 19 + 6 + 2 + 3 + 1 = 35.
b) S Bảng giá trị đại diện như sau: Điểm [10; 20) [20; 30) [30; 40) [40; 50) [50; 60) [60; 70) Giá trị đại diện 15 25 35 45 55 65 Số trường 4 19 6 2 3 1
Số trung bình của mẫu số liệu là
15 · 4 + 25 · 19 + 35 · 6 + 45 · 2 + 55 · 3 + 65 · 1 213 x = = ≈ 30,4. 35 7 NHÓM VN - MATHS & LATEX − 252 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN
c) S Gọi x1, x2, . . ., x35 là điểm chuẩn hóa cho chỉ số nghiên cứu của một số trường đại học ở
Việt Nam và giả sử dãy trên được sắp xếp theo thứ tự không giảm. Khi đó, trung vị là x18.
Do x18 thuộc nhóm [20; 30) nên nhóm này chứa trung vị.
Do đó p = 2, a2 = 20, a3 = 30, m2 = 19, m1 = 4, a3 − a2 = 10. Vậy n − m 1 + · · · + mp−1 M 2 e = ap + · a m p+1 − ap p 35 − 4 515 = 20 + 2 · 10 = ≈ 27,1. 19 19
d) Đ Điểm ngưỡng để đưa ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt
Nam là tứ phân vị thứ ba.
Tứ phân vị thứ ba của mẫu số liệu gốc là x27 mà x27 thuộc nhóm [30; 40) nên nhóm này chứa Q3.
Do đó p = 3, a3 = 30, m3 = 6, m1 + m2 = 4 + 19 = 23, a4 − a3 = 10 và ta có 3 · 35 − 23 425 Q 4 3 = 30 + · 10 = ≈ 35,42. 6 12
Vậy 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam là những trường có điểm
chuẩn hóa lớn hơn hoặc bằng 35,42.
Chọn đáp án a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Một bánh xe của người đi xe ô tô quay được 12 vòng trong 6 giây. Hỏi trong 1 giây, bánh
xe quay được một góc bao nhiêu rađian (làm tròn kết quả đến hàng phần mười)? Đáp án: 1 2 , 6 Lời giải. 12
Trong 1 giây, bánh xe quay được
= 2 (vòng), tức là quay được một góc 4π ≈ 12,6 (rad). 6
Đáp án: 12,6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 2. Một người xếp chồng những khúc gỗ có kích thước như nhau thành 10 hàng. Sau khi xếp
xong người đó nhận thấy mỗi hàng nằm liền phía trên ít hơn hàng dưới 1 khúc gỗ và hàng trên
cùng có 1 khúc gỗ. Hỏi người đó có tổng cộng bao nhiêu khúc gỗ? Đáp án: 5 5 Lời giải.
Mỗi hàng liền phía trên ít hơn hàng dưới 1 khúc gỗ và hàng trên cùng có 1 khúc gỗ nên ta có đây
là một cấp số cộng với u1 = 1, d = 1, n = 10.
Khi đó, tổng số khúc gỗ là n [2u 10 [2 · 1 + (10 − 1) · 1] S 1 + (n − 1)d] 10 = = = 55. 2 2
Đáp án: 55 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 3. Thống kê tiền điện tháng 9/2024 của các hộ gia đình xóm Chùa cho bởi bảng số liệu sau: Số tiền (nghìn đồng) [350; 400) [400; 450) [450; 500) [500; 550) [550; 600) Số hộ gia đình 6 14 21 17 2 NHÓM VN - MATHS & LATEX − 253 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM
Tiền điện trung bình của các hộ gia đình trong xóm Chùa bằng bao nhiêu (làm tròn kết quả đến nghìn đồng)? Đáp án: 4 7 1 Lời giải.
Ta có giá trị đại diện của các nhóm lần lượt là: 375; 425; 475; 525; 575.
Trung bình cộng của bảng số liệu trên là
375 · 6 + 425 · 14 + 475 · 21 + 525 · 17 + 575 · 2 x = ≈ 471 (nghìn đồng). 60
Đáp án: 471 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 4. Một cái hồ chứa 600 lít nước ngọt. Người ta bơm nước biển có nồng độ muối 30 gam/lít
vào hồ với tốc độ 15 lít/phút. Gọi t là số phút bơm nước biển vào hồ chứa. Nồng độ muối trong
hồ dần về bao nhiêu gam/lít sau thời gian dài (giả sử hồ nước chứa được lượng nước vô hạn)? Đáp án: 3 0 Lời giải.
Sau t phút bơm nước vào hồ thì lượng nước là 600 + 15t (lít) và lượng muối có được là 30 · 15t (gam). 30 · 15t 30t
Nồng độ muối của nước là C(t) = = (gam/lít). 600 + 15t 40 + t
Sau thời gian dài, tức là t dần tới dương vô cùng, ta có 30t 30t 30 lim C(t) = lim = lim = lim = 30 (gam/lít). t→+∞ t→+∞ 40 + t t→+∞ 40 t→+∞ 40 t + 1 + 1 t t
Đáp án: 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày bài giải từ câu 1 đến câu 3. 2x2 − ax + 4 Câu 1. Biết lim
= b (với a, b ∈ R). Tính a2 + b2. x→2 x2 − 3x + 2 Lời giải.
Xét thấy x = 2 là nghiệm của phương trình x2 − 3x + 2 = 0 (mẫu số) và kết quả của giới hạn là
một số thực nên x = 2 cũng là một nghiệm của phương trình 2x2 − ax + 4 = 0 (tử số).
Vậy suy ra 2 · 22 − 2a + 4 = 0 ⇔ a = 6. Khi đó 2x2 − ax + 4 2x2 − 6x + 4 2 x2 − 3x + 2 lim = lim = lim = lim 2 = 2. x→2 x2 − 3x + 2 x→2 x2 − 3x + 2 x→2 (x2 − 3x + 2) x→2 Suy ra a = 6; b = 2. Vậy a2 + b2 = 36 + 4 = 40.
Câu 2. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, K lần lượt là trung điểm các cạnh SM 1
BC, CD và M là điểm trên cạnh SB sao cho =
. Gọi N là giao điểm của MD và mặt phẳng SB 3 ND (SIK). Tính tỉ số . N M Lời giải. NHÓM VN - MATHS & LATEX − 254 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN S N x M A D K B I C SM 1 MB
Ta có M là điểm trên cạnh SB, = nên = 2. SB 3 MS
Do I và K lần lượt là trung điểm của BC và CD nên IK ∥ BD. S ∈ (SIK) ∩ (SBD) Ta có IK ⊂ (SIK), BD ⊂ (SBD) IK ∥ BD.
⇒ (SBD) ∩ (SIK) = Sx với Sx ∥ IK ∥ BD.
Trong mặt phẳng (SBD), DM ∩ Sx = N, vậy N chính là giao điểm của DM và (SIK).
Trong mặt phẳng (SBD) có Sx ∥ BD nên áp dụng hệ quả của định lý Thalès ta có MD MS = = 2. MN MB ND Vậy = 3. N M x2 − x − 2 khi x ̸= 2
Câu 3. Tìm giá trị của tham số m để hàm số f (x) = x − 2 liên tục trên R. m khi x = 2 Lời giải.
Tập xác định D = R. x2 − x − 2 Với x ̸= 2, ta có f (x) =
là hàm số phân thức hữu tỷ nên liên tục trên các khoảng x − 2 (−∞; 2) và (2; +∞).
Do đó để hàm số liên tục trên R thì hàm số f (x) liên tục tại x = 2. f (2) = m Ta có x2 − x − 2 (x + 1)(x − 2) lim f (x) = lim = lim = lim(x + 1) = 3. x→2 x→2 x − 2 x→2 x − 2 x→2
Hàm số f (x) liên tục trên R khi và chỉ khi f (2) = lim f (x) ⇔ m = 3. x→2 NHÓM VN - MATHS & LATEX − 255 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM BẢNG ĐÁP ÁN PHẦN I. 1. D 2. C 3. D 4. C 5. D 6. B 7. D 8. C 9. A 10. A 11. D 12. B PHẦN II. Câu 1. a Đ b Đ c Đ d S Câu 2. a Đ b S c S d Đ PHẦN III. Câu 1. 1 2 , 6 Câu 2. 5 5 Câu 3. 4 7 1 Câu 4. 3 0 NHÓM VN - MATHS & LATEX − 256 −
L Ôn tập học kỳ I, 2025-2026 filename VM003.pdf2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN VIETNAM - MATHS & LATEX
ÔN TẬP HỌC KỲ I, NĂM HỌC 2025-2026 Đề số 2
ĐỀ THAM KHẢO - BỘ SÁCH KNTT
Biên soạn: Nguyễn Tiến Dũng Môn: TOÁN 11
Phản biện: Phạm Quốc Toàn
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh: Số báo danh: Mã đề: 0101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi, thí sinh chỉ lựa chọn một phương án. 25π Câu 1. Giá trị sin bằng 4 √ √ √ 2 3 1 2 A . B. . C. − . D. − . 2 2 2 2 Lời giải. √ 25π π π 2 Ta có sin = sin + 3 · 2π = sin = . 4 4 4 2
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 2. Phát biểu nào sau đây đúng?
A. Trong không gian, hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Trong không gian, hai đường cùng song song với một đường thẳng thứ ba thì trùng nhau.
C Trong không gian, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
D. Trong không gian, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chéo nhau. Lời giải.
Trong không gian, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
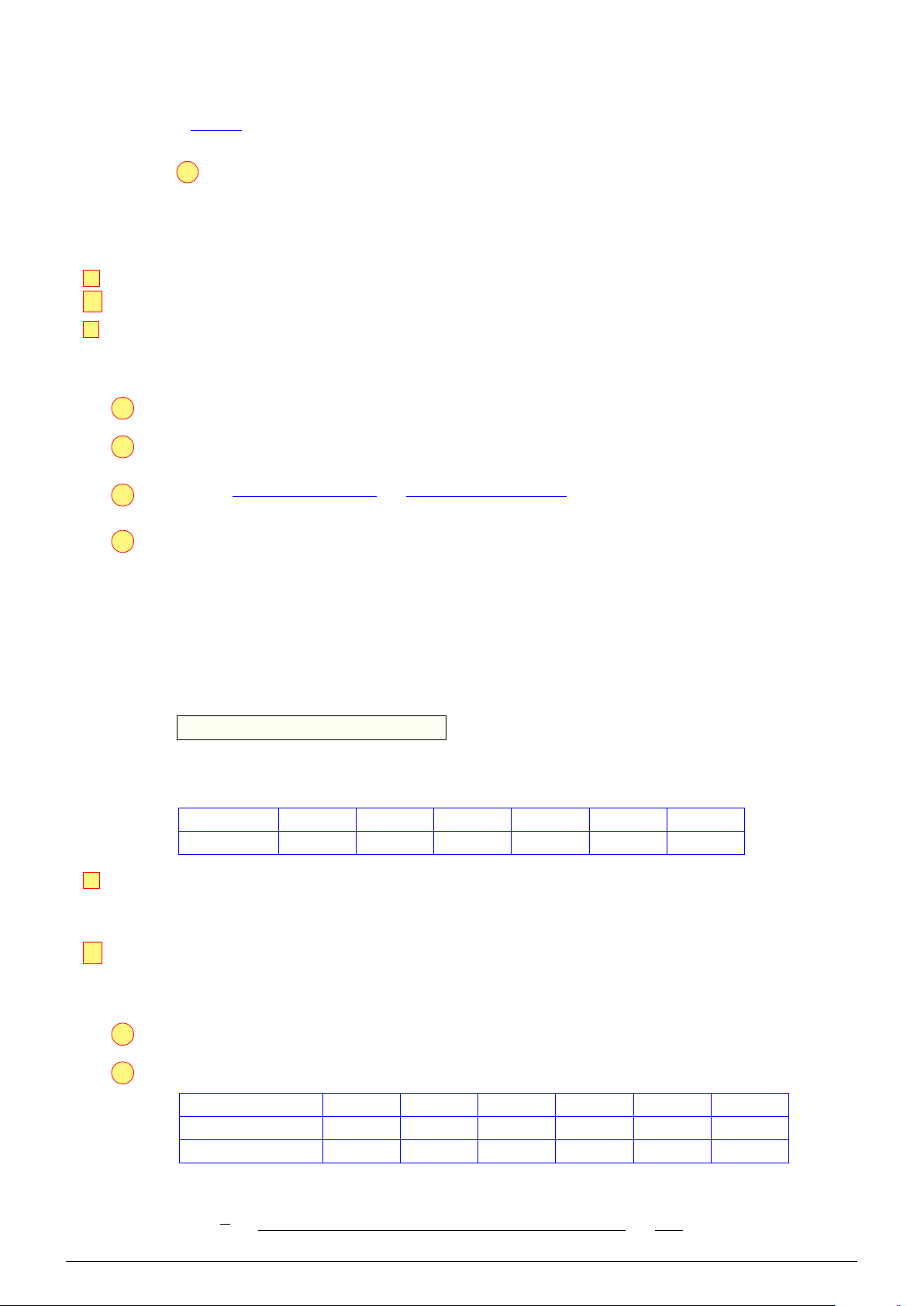
Câu 3. Cho tứ diện ABCD có M, Q lần lượt là các điểm A
nằm trên cạnh AC, AD sao cho MQ không song song với
CD. Gọi I là giao điểm của MQ và CD. Điểm N nằm trên
cạnh BC và IN cắt BD tại P (tham khảo hình vẽ). Khẳng
định nào sau đây sai? M Q I A. I ∈ (MNQ). B I ∈ (ABD). C. I ∈ (BCD). D. I ∈ (ACD). B P D N C Lời giải. Ta có • I ∈ MQ nên I ∈ (MNQ);
• I ∈ CD nên I ∈ (BCD) và I ∈ (ACD).
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ NHÓM VN - MATHS & LATEX − 257 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM
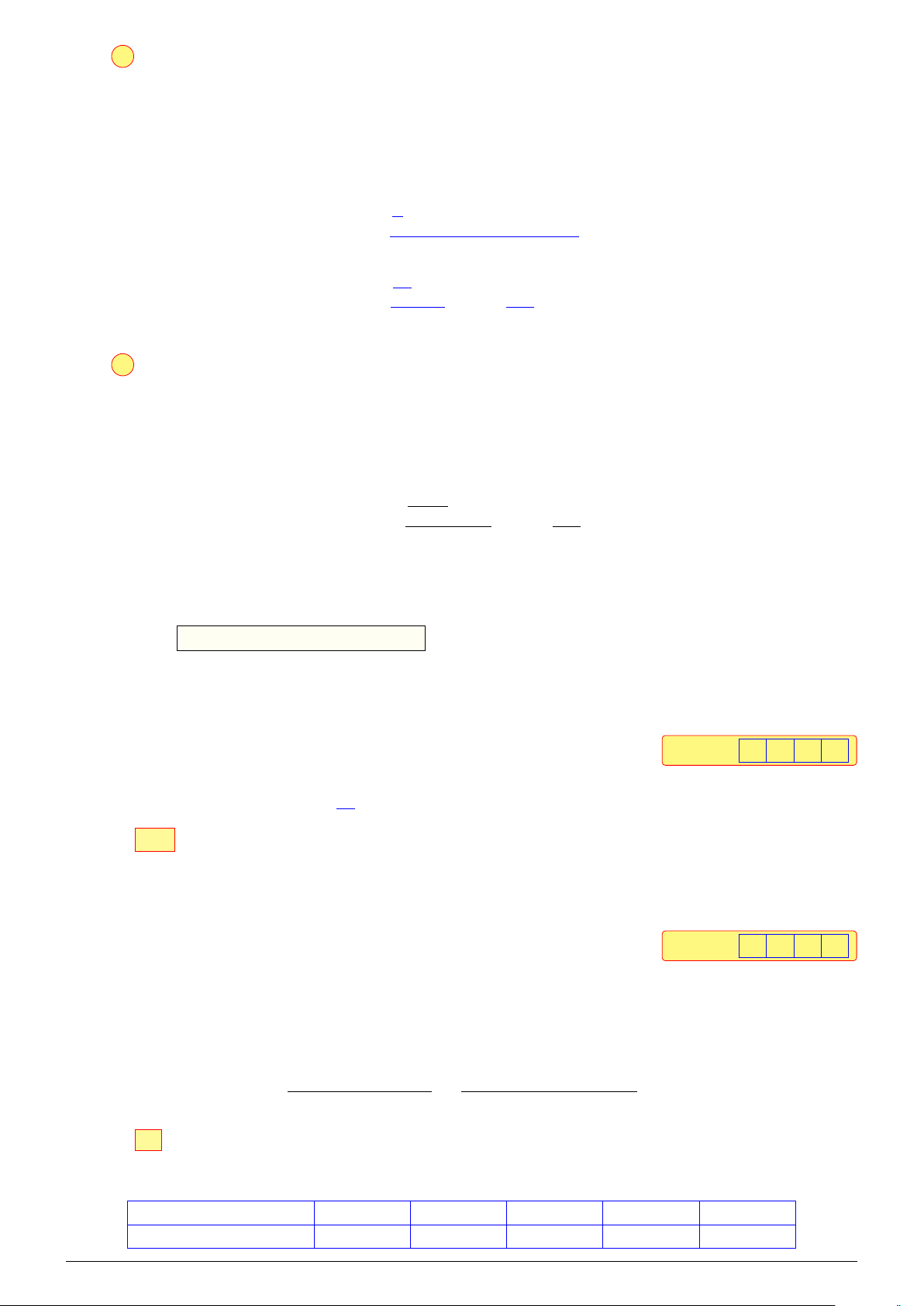
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là
trung điểm của SA, SD và AB. Phát biểu nào sau đây đúng?
A. (MON) ∥ (OPM). B. (SBD) ∥ (MNP). C. (PON) ∥ (MNP). D (MON) ∥ (SBC). Lời giải. S M N D A P O B C
Ta có OM là đường trung bình của △SAC nên OM ∥ SC.
Mà SC ⊂ (SBC) suy ra OM ∥ (SBC). (1)
Đồng thời ON là đường trung bình của △SBD nên ON ∥ SB.
Mà SB ⊂ (SBC) suy ra ON ∥ (SBC). (2)
Từ (1) và (2) suy ra (MON) ∥ (SBC).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 5. Nghiệm của phương trình sin x · cos x · cos 2x = 0 là π A. x = k (k ∈ Z).
B. x = kπ (k ∈ Z). 2 π kπ kπ C. x = + (k ∈ Z). D x = (k ∈ Z). 8 4 4 Lời giải. Ta có sin x · cos x · cos 2x = 0 1 ⇔ sin 2x · cos 2x = 0 2 1 ⇔ sin 4x = 0 4 ⇔ 4x = kπ k ⇔ π x = (k ∈ Z). 4 kπ
Vậy nghiệm của phương trình đã cho là x = (k ∈ Z). 4
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 6. Cho cấp số cộng (un), biết u5 = −3 và u7 = 9. Công sai của cấp số cộng (un) là A. d = −6. B. d = 12. C d = 6. D. d = −12. Lời giải. u 9 − (−3) Ta có u 7 − u5 7 = u5 + 2d ⇒ d = = = 6. 2 2
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ NHÓM VN - MATHS & LATEX − 258 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN 3n + 1 61
Câu 7. Cho dãy số (un) có số hạng tổng quát là un = . Khi đó
là số hạng thứ mấy của n2 + 2 402 dãy số? A. 19. B 20. C. 17. D. 18. Lời giải. n = 20 3n + 1 61 Ta có =
⇔ 61n2 − 1206n − 280 = 0 ⇔ 14 n2 + 2 402 n = − . 61
Do n ∈ N∗ nên n = 20. 61 Vậy số
là số hạng thứ 20 của dãy số. 402
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ 5 · 2n+2 − 2 · 3n+2
Câu 8. Giới hạn lim bằng n→+∞ 7 + 3n+1 2 5 A. − . B. . C. 6. D −6. 7 7 Lời giải. 2 n 20 · − 18 5 · 2n+2 − 2 · 3n+2 20 · 2n − 18 · 3n 3 −18 Ta có lim = lim = lim = = −6. n→+∞ 7 + 3n+1 n→+∞ 7 + 3 · 3n n→+∞ 1 n 3 7 · + 3 3
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 9. Cho mẫu số liệu ghép nhóm về độ tuổi và số lượng khách hàng của một cửa hàng như sau: Khoảng tuổi [17; 22) [22; 27) [27; 32) [32; 37) [37; 42) Số người 8 7 14 8 7
Giá trị đại diện của nhóm [32; 37) bằng A. 37. B. 17,25. C. 32. D 34,5. Lời giải. 32 + 37
Giá trị đại diện của nhóm [32; 37) là = 34,5. 2
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 10. Cho mẫu số liệu ghép nhóm về cân nặng và số người như sau: Cân nặng [45; 51) [51; 57) [57; 63) [63; 69) [69; 75) [75; 81) Số người 25 2 9 34 34 9
Nhóm chứa trung vị của mẫu số liệu ghép nhóm là A. [57; 63). B [63; 69). C. [69; 75). D. [51; 57). Lời giải.
Cỡ mẫu là n = 25 + 2 + 9 + 34 + 34 + 9 = 113.
Gọi x1, x2, . . . , x113 là cân nặng của 113 người được sắp xếp theo thứ tự không giảm.
Khi đó, trung vị của mẫu số liệu gốc là x57 thuộc nhóm [63; 69) nên trung vị của mẫu số liệu ghép nhóm thuộc nhóm [63; 69).
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 11. Cho tứ diện ABCD có M, N lần lượt là trọng tâm của tam giác ABC và tam giác ACD.
Đường thẳng MN song song với mặt phẳng nào sau đây? A. (ABC). B. (ABD). C (BCD). D. (AEF). Lời giải. NHÓM VN - MATHS & LATEX − 259 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM A M N B D E F C
Gọi E, F lần lượt là trung điểm của BC và CD. AM AN 2
Do M, N lần lượt là trọng tâm của tam giác ABC và tam giác ACD nên = = . AE AF 3
Áp dụng định lý Thalès đảo, ta có MN ∥ EF.
Mà EF ⊂ (BCD), MN ̸⊂ (BCD) nên MN ∥ (BCD).
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ √3x − 2 − 2
Câu 12. Giới hạn lim bằng x→2 x2 − 4 3 1 3 A. 0. B . C. . D. . 16 16 4 Lời giải. Ta có √ √ 3x − 2 − 2 3x − 22 − 22 lim = lim √ x→2 x2 − 4 x→2 (x2 − 4) 3x − 2 + 2 3(x − 2) = lim √ x→2 (x − 2)(x + 2) 3x − 2 + 2 3 = lim √ x→2 (x + 2) 3x − 2 + 2 3 = √ (2 + 2) 3 · 2 − 2 + 2 3 = . 16
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d)
ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Thời gian (đơn vị: phút) để nhân viên y tế đo mắt cho học sinh khối 11 ở một trường THPT
được được cho bởi bảng sau: Thời gian [0,25; 0,75) [0,75; 1,25) [1,25; 1,75) [1,75; 2,25) [2,25; 2,75) Số lần 25 32 14 12 4
a Nhóm chứa mốt của mẫu số liệu ghép nhóm trên là [0,75; 1,25).
b) Giá trị đại diện của nhóm [1,25; 1,75) là 1,25. NHÓM VN - MATHS & LATEX − 260 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN
c) Thời gian trung bình để nhân viên y tế đo mắt cho học sinh lớn hơn 1,15 phút. 133
d Trung vị của mẫu số liệu ghép nhóm trên là Me = . 128 Lời giải.
a) Đ Nhóm [0,75; 1,25) có tần số bằng 32 lớn nhất nên nhóm [0,75; 1,25) chứa mốt của mẫu số liệu ghép nhóm. 1,25 + 1,75
b) S Giá trị đại diện của nhóm [1,25; 1,75) là = 1,50. 2
c) S Cỡ mẫu là 25 + 32 + 14 + 12 + 4 = 87.
Bảng giá trị đại diện của mẫu số liệu ghép nhóm Thời gian [0,25; 0,75) [0,75; 1,25) [1,25; 1,75) [1,75; 2,25) [2,25; 2,75) Giá trị đại diện 0,5 1 1,5 2 2,5 Số lần 25 32 14 12 4
Thời gian trung bình để nhân viên y tế đo mắt cho học sinh là
0,5 · 25 + 1 · 32 + 1,5 · 14 + 2 · 12 + 2,5 · 4 199 t0 = = ≈ 1,143. 87 174
Vì 1,143 < 1,15 nên thời gian đo mắt trung bình nhỏ hơn 1,15.
d) Đ Gọi x1, x2, . . . , x87 lần lượt là thời gian đo mắt của nhân viên y tế với từng học sinh sắp
xếp theo thứ tự không giảm.
Khi đó, trung vị x44 của mẫu số liệu gốc thuộc nhóm [0,75; 1,25) nên trung vị của mẫu số
liệu ghép nhóm thuộc [0,75; 1,25).
Do đó, p = 2, a2 = 0,75, m2 = 32, m1 = 25, a3 − a2 = 0,5 và ta có 87 − 25 133 M 2 e = 0,75 + · 0,5 = . 32 128 133 Vậy Me = . 128
Chọn đáp án a đúng b sai c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung
điểm của các cạnh SB, BC và SD.
a Đường thẳng SA là giao tuyến của hai mặt phẳng (SAB) và (SAC).
b) Hai đường thẳng MP và SC cắt nhau.
c Giao tuyến của mặt phẳng (MNP) và mặt phẳng (ABCD) là đường thẳng đi qua N và song
song với đường thẳng BD. SK 1
d Biết rằng đường thẳng SA cắt mặt phẳng (MNP) tại điểm K, khi đó = . SA 4 Lời giải. S K P M D A I Q B N C NHÓM VN - MATHS & LATEX − 261 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM
a) Đ Ta có S và A là hai điểm chung của hai mặt phẳng (SAB) và (SAC) nên đường thẳng SA
là giao tuyến của hai mặt phẳng (SAB) và (SAC). b) S Ta có C /
∈ (SMP) nên hai đường thẳng SC và MP không cùng nằm trong một mặt phẳng,
suy ra hai đường thẳng SC và MP chéo nhau.
c) Đ Ta có N là một điểm chung của hai mặt phẳng (MNP) và (ABCD). (1)
Mặt khác MP ⊂ (MNP), BD ⊂ (ABCD) và MP ∥ BD (do MP là đường trung bình của tam giác SBD). (2)
Từ (1) và (2) suy ra giao tuyến của hai mặt phẳng (MNP) và (ABCD) là đường thẳng đi
qua N đồng thời song song với BD, MP và cắt CD tại trung điểm Q của CD.
d) Đ Trong mặt phẳng (ABCD), gọi I là giao điểm của hai đường thẳng AC và NQ.
Từ giả thiết, ta có ba mặt phẳng (MNP), (SBC) và (SAC) đôi một cắt nhau theo ba giao
tuyến là MN, SC và IK; trong đó có MN ∥ SC (do MN là đường trung bình của △SBC).
Suy ra MN, SC và IK đôi một song song. SK CI 1
Xét tam giác SAC có IK ∥ SC, áp dụng định lý Thalès ta có = = . SA CA 4
Chọn đáp án a đúng b sai c đúng d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
Câu 1. Một con lắc lò xo dao động điều hòa quanh vị trí cân bằng theo thời gian t được xác định
bởi hàm số y = 25 sin 4πt, trong đó y được tính bằng centimét, t được tính bằng giây như hình vẽ sau: y > 0 y < Vị trí 0 cân bằng
Tần số dao động của con lắc lò xo (số lần dao động trong một giây) bằng bao nhiêu? Đáp án: 2 Lời giải. 2π 1
Hàm số y = 25 sin 4πt tuần hoàn với chu kỳ T = = (giây). 4π 2 1
Vì chu kỳ dao động của con lắc là T =
giây nên trong một giây con lắc dao động được 2 lần. 2
Đáp án: 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .□
Câu 2. Cho mẫu số liệu ghép nhóm về chiều cao (đơn vị: cm) của 25 cây dừa giống như sau: Chiều cao [0; 10) [10; 20) [20; 30) [30; 40) [40; 50) Số cây 4 6 7 5 3 a a
Trung vị của mẫu số liệu ghép nhóm trên là Me = (a, b ∈ N∗ và
là phân số tối giản). Giá trị b b a − 5b bằng bao nhiêu? Đáp án: 1 3 0 Lời giải.
Cỡ mẫu n = 4 + 6 + 7 + 5 + 3 = 25.
Ta có x1, x2, . . . , x25 là chiều cao của 25 cây dừa giống được sắp xếp theo thứ tự không giảm. NHÓM VN - MATHS & LATEX − 262 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN
Khi đó, trung vị là x13. Do x13 thuộc nhóm [20; 30) nên nhóm này chứa trung vị.
Ta xác định được n = 25, p = 3, a3 = 20, m3 = 7, m1 + m2 = 10, a4 − a3 = 10. Do đó 25 − 10 165 M 2 e = 20 + · 10 = . 7 7 a Mà Me = nên a = 165 và b = 7. b
Vậy a − 5b = 165 − 5 · 7 = 130.
Đáp án: 130 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 3. Một ruộng bậc thang có thửa thấp nhất (bậc thứ nhất) nằm ở độ cao 950 m so với mực
nước biển, độ cao chênh lệch trung bình giữa thửa trên và thửa dưới liền kề là 1,4 m. Khi đó, thửa
ruộng ở bậc thứ 16 có độ cao bao nhiêu mét so với mực nước biển? Đáp án: 9 7 1 Lời giải.
Kí hiệu un là chiều cao so với mực nước biển của thửa ruộng ở bậc thứ n.
Khi đó dãy số (un) là cấp số cộng với u1 = 950 và d = 1,4.
Ta có u16 = u1 + 15d = 950 + 15 · 1,4 = 971.
Vậy thửa ruộng ở bậc thứ 16 có độ cao 971 m so với mực nước biển.
Đáp án: 971 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ f (x) − 20
Câu 4. Cho f (x) là đa thức thỏa mãn lim
= 10. Giá trị của biểu thức x→2 x − 2 3 p6 f (x) + 5 − 5 T = lim x→2 x2 + x − 6 bằng bao nhiêu? Đáp án: 0 , 1 6 Lời giải. f (x) − 20 Do lim(x − 2) = 0 và lim
= 10 nên lim f (x) − 20 = 0 hay lim f (x) = 20. x→2 x→2 x − 2 x→2 x→2 Khi đó 3 p6 f (x) + 5 − 5 T = lim x→2 x2 + x − 6 6 f (x) + 5 − 125 = lim x→2 2 (x2 + x − 6) 3 p6 f (x) + 5 + 5 3 p6 f (x) + 5 + 25 6 [ f (x) − 20] = lim x→2 2 (x − 2)(x + 3) 3 p6 f (x) + 5 + 5 3 p6 f (x) + 5 + 25 f (x) − 20 6 = lim · x→2 x − 2 2 (x + 3) 3 p6 f (x) + 5 + 5 3 p6 f (x) + 5 + 25 6 = 10 · 5 · 75 4 = 25 = 0,16.
Đáp án: 0,16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ NHÓM VN - MATHS & LATEX − 263 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày bài giải từ câu 1 đến câu 3.
Câu 1. Tìm số thực dương x để ba số hạng x; x + 2; 2x + 1 theo thứ tự lập thành một cấp số nhân. Lời giải.
Để ba số hạng x; x + 2; 2x + 1 thì (x + 2)2 = x(2x + 1) ⇔ x2 + 4x + 4 = 2x2 + x ⇔ x2 − 3x − 4 = 0 "x = −1 ⇔ x = 4.
Vì x là số thực dương nên x = 4 thoả mãn yêu cầu bài toán.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SN
BC, (α) là mặt phẳng qua A, M và song song với SD. Mặt phẳng (α) cắt SB tại N. Tính tỉ số . NB Lời giải. S N A D I O B M C
Trong mặt phẳng (ABCD), gọi O là giao điểm của hai đường thẳng AC và BD, I là giao điểm của
hai đường thẳng AM và BD.
Xét tam giác ABC, ta có O, M lần lượt là trung điểm của hai cạnh AC, BC nên I là trọng tâm tam giác ABC. BI 2 Suy ra = . BO 3 1 BI 1 ID 2 Mặt khác BO = BD nên = suy ra = . 2 BD 3 BD 3
Ta có (α) và mặt phẳng (SBD) có chung điểm I, (α) ∥ SD, SD ⊂ (SBD)
Suy ra giao tuyến của (α) và mặt phẳng (SBD) là đường thẳng qua I song song với SD cắt SB tại N. SN ID
Áp dụng định lý Thalès trong tam giác SBD, ta có N I ∥ SD nên = = 2. NB IB √ ax2 + 1 − bx − 2 1 khi x ̸=
Câu 3. Cho hàm số f (x) = 4x3 − 3x + 1
2 (a, b, c ∈ R). Biết hàm số f (x) liên c 1 khi x = 2 2 1
tục tại x = . Giá trị của biểu thức S = abc bằng bao nhiêu? 2 Lời giải. NHÓM VN - MATHS & LATEX − 264 −
L Ôn tập học kỳ I, 2025-2026 2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN Ta có √ √ 2 ax2 + 1 − bx − 2 ax2 + 1 − (bx + 2)2 = √ 4x3 − 3x + 1 (2x − 1)2(x + 1) ax2 + 1 + bx + 2 a − b2 x2 − 4bx − 3 = √ . (2x − 1)2(x + 1) ax2 + 1 + bx + 2 1 1 c
Hàm số liên tục tại x =
khi và chỉ khi lim f (x) = f = ∈ R. 2 2 2 x→ 1 2
Nghĩa là biểu thức a − b2 x2 − 4bx − 3 phải được phân tích thành m(2x − 1)2. Do đó
a − b2 x2 − 4bx − 3 = m(2x − 1)2, ∀x ∈ R r a b + + 1 + 2 ̸= 0 4 2
a − b2 x2 − 4bx − 3 = 4mx2 − 4mx + m ⇔ r a b + + 1 + 2 ̸= 0 4 2 a − b2 = 4m ⇔ − 4b = −4m m = −3 m = −3 ⇔ b = −3 a = −3. Khi đó √ax2 + 1 − bx − 2 −12x2 + 12x − 3 lim = lim √ 4x3 − 3x + 1 x→ 1 (2x − 1)2(x + 1) −3x2 + 1 − 3x + 2 2 x→ 1 2 −3 = lim √ x→ 1 (x + 1) −3x2 + 1 − 3x + 2 2 −3 = = −2. 3 2 1 c c Do lim f (x) = f = ⇔ = −2 ⇔ c = −4. 2 2 2 x→ 1 2
Vậy S = abc = (−3) · (−3) · (−4) = −36. NHÓM VN - MATHS & LATEX − 265 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM BẢNG ĐÁP ÁN PHẦN I. 1. A 2. C 3. B 4. D 5. D 6. C 7. B 8. D 9. D 10. B 11. C 12. B PHẦN II. Câu 1. a Đ b S c S d Đ Câu 2. a Đ b S c Đ d Đ PHẦN III. Câu 1. 2 Câu 2. 1 3 0 Câu 3. 9 7 1 Câu 4. 0 , 1 6 NHÓM VN - MATHS & LATEX − 266 −
L Ôn tập học kỳ I, 2025-2026 filename VM003.pdf2025-2026 HỌC NĂM I, KỲ HỌC CUỐI TẬP ÔN VIETNAM - MATHS & LATEX
ÔN TẬP HỌC KỲ I, NĂM HỌC 2025-2026 Đề số 3
ĐỀ THAM KHẢO - BỘ SÁCH KNTT
Biên soạn: Phạm Quốc Toàn Môn: TOÁN 11
Phản biện: Nguyễn Thái Hoàng
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh: Số báo danh: Mã đề: 0101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi, thí sinh chỉ lựa chọn một phương án.
Câu 1. Đổi số đo của góc α = 90◦ sang đơn vị radian ta được 2π π π π A. . B. . C . D. . 3 6 2 3 Lời giải. π
Ta có α = 90 · π = . 180 2
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ π
Câu 2. Cho hai góc α, β thỏa mãn α + β = . Phát biểu đúng là 2
A. sin α = sin β.
B sin α = cos β.
C. sin α = − cos β.
D. sin α = − sin β. Lời giải. π π Vì α + β = nên sin α = sin − β = cos β. 2 2
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 3. Phát biểu đúng là
A. cos 2x = sin2 x − cos2 x.
B. cos 2x = 2 sin2 x − 1. 1 C. sin 2x = sin x · cos x.
D sin 2x = 2 sin x · cos x. 2 Lời giải.
Ta có sin 2x = 2 sin x · cos x.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □ 1
Câu 4. Nghiệm của phương trình sin x = là 2 π π x = + k2π x = + k2π A. 6 3 , (k ∈ Z). B. , (k ∈ Z).
x = − π + k2π
x = − π + k2π 6 3 π π x = + k2π x = + k2π 6 3 C , (k ∈ Z). D. , (k ∈ Z). 5π 2π x = + k2π x = + k2π 6 3 Lời giải. π π x = + k2 1 x = + k2π π π 6 Ta có sin x = ⇔ sin x = sin ⇔ 6 ⇔ , (k ∈ Z). 2 6 5 x = π
π − π + k2π x = + k2 6 π 6
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 5. Trong các dãy số sau, dãy số tăng là A 1; 5; 7; 8; 9.
B. −1; 1; −1; 1; −1. C. 7; 7; 7; 7; 7. D. 1; 5; 7; 4; 8. NHÓM VN - MATHS & LATEX − 267 −
L Ôn tập học kỳ I, 2025-2026 X T EAL & THS MA - VN NHÓM Lời giải.
Dãy 1; 5; 7; 8; 9 là dãy số tăng vì 1 < 5 < 7 < 8 < 9.
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 6. Cho cấp số nhân (un) có số hạng đầu tiên u1 = 3 và công bội q = 2. Số hạng tổng quát của cấp số nhân trên là A. un = 3 · 2n. B. un = 1 + 2n. C. un = 2 · 3n−1. D un = 3 · 2n−1. Lời giải.
Ta có un = u1 · qn−1 = 3 · 2n−1.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 7. Cho bảng khảo sát về số tiền trả cho việc tiêu thụ điện của một số hộ gia đình Số tiền (nghìn đồng) [350; 400) [400; 450) [450; 500) [500; 550) [550; 600) Số hộ gia đình 6 14 21 17 2
Dựa vào mẫu số liệu trên, số hộ gia đình được khảo sát là A 60. B. 50. C. 350. D. 250. Lời giải.
Số hộ gia đình được điều tra là 6 + 14 + 21 + 17 + 2 = 60 (hộ gia đình).
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 8. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau Thời gian (phút) [0; 20) [20; 40) [40; 60) [60; 80) [80; 100) Số học sinh 5 9 12 10 6
Nhóm chứa mốt của mẫu số liệu này là A. [20; 40). B [40; 60). C. [60; 80). D. [80; 100). Lời giải.
Nhóm có tần số lớn nhất là [40; 60).
Do vậy, nhóm này là nhóm chứa mốt.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . □
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I, J lần lượt là trung
điểm của SA và SC. Đường thẳng song song với đường thẳng I J là A. SO. B AC. C. BC. D. BD. Lời giải. S I J A D O B C NHÓM VN - MATHS & LATEX − 268 −
L Ôn tập học kỳ I, 2025-2026




