

















Preview text:
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
BỘ ĐỀ THI CUỐI KỲ MÔN GIẢI TÍCH 1 ĐỀ CK GIẢI TÍCH 1
Dành cho sinh viên trường Đại học Bách khoa Hà Nội
Biên soạn: Tài liệu HUST DANH SÁCH ĐỀ THI
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 2 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 4 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 6 (Nhóm ngành 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 7 (Nhóm ngành 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 7 (Nhóm ngành 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .24
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 8 (Nhóm ngành 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20192 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20192 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20193 – ĐỀ 2 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 1 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .42
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 2 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 2 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .47
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 3 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 3 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .49
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 4 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 1
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 4 (Nhóm ngành 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .54
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 5 (Nhóm ngành 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 5 (Nhóm ngành 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .56
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 6 (Nhóm ngành 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 7 (Nhóm ngành 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 7 (Nhóm ngành 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . .62
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20181 – ĐỀ 8 (Nhóm ngành 3). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 (TaiLieuHust, 2022)
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 2
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: 1 a) li
x m ln(1 x) x 0 x . x3 y b) lim . 6 ( 3 x, y) y2 (0,0) 2x
Câu 2 (1 điểm). Tính gần đúng nhờ vi phân A 2,022 3,042 3 . x2
Câu 3 (1 điểm). Chứng minh rằng cos x 1 ,x 0 . 2
Câu 4 (1 điểm). Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường y x2 3x
và y 0 quanh trục Oy một vòng. 1
Câu 5 (1 điểm). Tính
2x 3 1 x2 2 dx .
Câu 6 (1 điểm). Hàm số f (x) x3 x có hàm ngược là y g(x) . Tính g (2) .
2 z 2 z 3 z 1
Câu 7 (1 điểm). Tính P với z .
x2 y2 y y x2 y23
Câu 8 (1 điểm). Không khí được bơm vào một quả bóng bay hình cầu vói tốc độ 100cm3 / s .
Tính tốc độ tăng lên của bán kính quả bóng khi bán kính quả bóng bằng 50cm.
Câu 9 (1 điểm). Tính 2 cot x dx. 0
Tai liệu được chia sẻ miễn phí tại website Tailieuhst.com 3
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 1 (Nhóm ngành 1) 1 ln ln(1 x)
Câu 1: L lim ln(1 x) x x lim e x . x0 x x0 ln(1 x) ln(1 x) ln 1 x ln 1 x
Xét giới hạn K lim lim x0 x x0 x
lim ln(1 x) 1 11 0 ln(1 x)
x0 ln(1 x) Vì x0 x , nên ln 1 1 1 x ~ x . ln(1 x) 1
1 x2 ox2 K lim x
(VCB) lim ln(1 x) x = lim 2 (Khai triển Maclaurin) x0 x x0 x2 x0 x2 1 x2 1 lim 2 x0 x2 2
Giới hạn đã cho bằng L eK e1/2 . x3 y
b) f (x, y)
, (x, y) 0. 2x6 3y2 +) Chọn M
1 a, a3 . Khi a 0 thì M
1 a, a3 (0, 0) .
f a,a 1 3 Ta có: f M a3a3 6 6 1 2a 3a 5
f M 1 khi M1 (0,0) (1) 1 5 +) Chọn M 2
b,b3 . Khi b 0 thì M b,b3 (0,0). 2
Ta có: f M (b)3b3 1 2
f b,b 3 6 6 2(b) 3b 5
f M 1 khi M2 (0,0) (2) 2 5 x3 y
Từ (1) và (2) f (x, y) không cùng tiến tới một giá trị khi (x, y) (0,0) lim
( x, y)(0,0) 2x 6 3y2 không tồn tại.
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 4
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Câu 2. Xét hàm số f (x, y) x2 y2 3 . Ta có:
f (x, y) x
, f (x, y) y
. Chọn x0 2, x 0,02 . x x y 2 y2 3 x2 y2 3
y 3, y 0,04 0
Áp dụng công thức tính gần đúng: A
f x x, y y f x , y f x , y x f x , y y 2,022 3,042 3 0 0 0 0 x 0 0 y 0 0 1 3
f (2,3) f (2,3)0,02 f (2,3)0,04 4 0,02 0,04 4,04 x y 2 4 Vậy A 4,04 . x2 x2
Câu 3. Chứng minh: cos x 1
,x 0 cos x 1 0,x 0 . 2 2 x2
Xét f (x) cos x
1 trên [0;). Ta có: f (x) sin x x, f (x) cos x 1 0,x 0 2
f (x) đồng biến trên [0;) f (x) f (0) 0,x 0
f (x) đồng biến trên [0;) f (x) f (0) 0,x 0
Từ đó ta có được điều phải chứng minh. Dấu bằng xảy ra khi x = 0
Câu 4. Quay miền D là hình phẳng giới hạn bởi các
đường y x2 3x, y 0, x 0, x 3 quay quanh trục
Oy thì thu được vật thể có thể tích là:
V 2 3 xx2 3xdx 2 x3x x2 dx (vì 0
x2 3x 0,x [0,3]) 27
= 2 3x x dx 2 x 3 (đvtt) 3 2 3 3 x4 0 4 2 0 3
Câu 5. Điều kiện: 2x 3 0 x 1 x2 0 1 x2 x2 1 , do đó: 2 1 1
I 2x 3 1 x2 2 dx
2x 3 x2 1 2 dx 1 1
2x 3dx dx
(2x 3)3 ln x x2 1 C x2 1 3
Tai liệu được chia sẻ miễn phí tại website Tailieuhst.com 5
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Câu 6. Ta có: f (x) 3x21. Với y 2 x3 x 2 x 1. 0 0 0 0
Vì y g(x) là hàm ngược của f (x) x3 x nên: g y 1 1 1 . 0
f 0x f (1) 4 1 Vậy g (2) . 4
Câu 7. Điều kiện xác định P là y 0 . 2 z 12x2 3y2
Do sự đối xứng của $x, y$ trong hàm z(x, y) nên: . x2 x2 y27
2 z 2 z 3 z 12x2 3y2 12 y2 3x2 3 3y P x2 y2 y y x2 y27 y x2 y25 9 9 0,y 0.
x2 y25 x2 y25
Câu 8. Gọi thể tích của quả bóng tại thời điểm t(s) là V(t)cm3.
Theo bài ra, tốc độ bơm không khí vào quả bóng là 100cm3 / s V(t) 100cm3 / s .
Tại thời điểm t0 nào đó, Rt0 50(cm) . Ta có: 4
V (t) (R(t))3 . Lấy đạo hàm hai vế theo t , ta có: V (t) 4 (R(t))2 R(t) 3
Tại t t , ta có: V t 4
2 R t 100 4 (50)2 R t 0 0
R t0 0 0
R t 100 1 (cm/s). 0 4 (50)2 100
Khi bán kính quà bóng bằng 50cm, tốc độ tăng lên của bán kính quả bóng khi bán kính là 1 (cm / s) . 100 /2
Câu 9. I cot x dx. 0 Xét /2 L (
cot x)dx /2 sin x cosx tan x
/2sinxcosxdx. 0 0 dx cos x sin x 0 sin x cos x
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 6
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Đặt t sin x cos x dt (cos x sin x)dx . 2 2 1 t2
t (sin x cos x) 1 2sin x cos x sin x cos x . 2
Đổi cận: - Khi x 0 thì t 1; Khi x thì t 1 2 dt 1 0 2 1 2 L dt dt 1 1t2 1 1t2 0 1t2 2 0 2 B 2 lim dt lim dt A(1) A B1 0 1 t 2 1 t 2 0 B
lim ( 2 arcsin t) lim( 2 arcsin t) A(1) A B1 0
lim ( 2 arcsin A) lim( 2 arcsin B) 2 2 2 A(1) B1 2 2 /2 Giờ xét
cot x dx, với f (x) cot x 0 liên tục trên 0, . 0 2 cos x x0 1 x0 1 1 cot x ~ ~ , sin x sin x x1/2 x mà /2 1
hội tụ (vì 1 (0,1) /2 cot x dx hội tụ. dx 0 x1/2 2 0 Đổi biến
t x x t , ta có: 2 2 /2 cot 0 x dx /2 /2 cot
t ( dt) tan t dt tan x dx. 0 /2 0 0 2 /2 1 /2 1 cot x dx
( tan x cotx)dx L . 0 2 0 2 2
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 7
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 2 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: 1 ex 1x a) lim . x0 x b) lim xy4 2 8
(x,y)(0,0) 4x 3y
Câu 2 (1 điểm). Tính gần đúng nhờ vi phân A 4,032 2,022 5 . 2 x x
Câu 3 (1 điểm). Chứng minh rằng e 1 x ,x 0 . 2
Câu 4 (1 điểm). Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường y x2 4x
và y 0 quanh trục Oy một vòng. 1
Câu 5 (1 điểm). Tính
4 3x 1 x2 2 dx .
Câu 6 (1 điểm). Hàm số f (x) x5 x có hàm ngược là y g(x) . Tính g (2) .
2 z 2 z 5 z 1
Câu 7 (1 điểm). Tính P với z .
x2 y2 y y x2 y25
Câu 8 (1 điểm). Không khí được bơm vào một quả bóng bay hình cầu với tốe độ 200cm3 / s .
Tính tốc độ tăng lên của bán kính quả bóng khi bán kính quả bóng bằng 60cm.
Câu 9 (1 diểm). Tính 2 tan x dx. 0
Cách giải tham khảo đề số 1
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 8
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: a) lim x . x sin x 2y2 ln x b) lim .
( x, y)(1,0) (x 1)2 y2
Câu 2 (1 điểm). Phương trình x3 3x2y y5 5 0 xác định hàm ẩn y y(x) . Tính y(1) .
Câu 3 (1 điểm). Tính đạo hàm của hàm số y arctan 2x , x 1. 1 x2
Câu 4 (1 điểm). Tìm khai triển Maclaurin của y ln(1 2x) đến x3 . x
Câu 5 (1 điểm). Tìm các tiệm cận của đồ thị hàm số y . ex 1
Câu 6 (2 điểm). Tính các tích phân sau:
a) tan(2x)dx . b) dx 0 .
(x 3)x2 x 1 3 3
Câu 7 (1 điểm). Quay đường x2 y2 4 quanh trục Ox một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8 (1 điểm). Tìm cực trị của hàm số z x3 y3 (x y)2 .
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 9
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 3 (Nhóm ngành 1) Câu 1. 1
lim x lim 1
1. (dạng vô định nên ta dùng L’Hospital) x sin x x cos x cos
Vậy lim x 1. x sin x 2y2 ln x
b) Đặt f (x, y) (x1)2 y2 2y2 ln1
+) Nếu x 1 và y 0 thì f (x, y)
0 0 khi y 0 . (1) 02 y2
+) Nếu x 1 và (x, y) (1,0) thì: lim 2y2 ln x lim ln x lim 2 y2(x 1) 2 2 2 2
(x,y)(1,0) (x 1) y x1
x(x1,y)(1,0) x 1 (x,y)(1,0) (x 1) y x1
Ta có: lim ln x lim ln x VCB x 1 lim 1
( x, y )(1,0) x 1 x1 x 1 x1 x 1
0 2 y2 (x 1) 2 | (x 1)y | (x 1)2 y2 | y | | y | , mà lim | y | 0 | y | (x 1)2 y2 (x 1)2 y2 (x 1)2 y2 ( x, y)(1,0) 2 y2 (x 1) lim
2 y2 (x 1) 0 theo nguyên lý kẹp lim 0
( x, y)(1,0) (x 1)2 y2
( x, y )(1,0) (x 1)2 y2 x1 x1 lim
2y2 ln x 1.0 0 (2)
( x, y)(1,0) (x 1)2 y2 x ̀ 2y2 ln x Tù (1) và (2) lim 0
(x, y)(1,0) (x 1)2 y2 Câu 2.
+) Với x 1 thì 1 3y y5 5 0 y5 3y 4 y 1 y(1) 1.
Theo bài ra: x3 3x2 y(x) [ y(x)]5 5 0
+) Lấy đạo hàm hai vế theo x , ta có: 3x2 6xy(x) 3x2y(x) 5y(x)[ y(x)]4 0
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 10
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST Thay x 1, ta có:
3 6y(1) 3y(1) 5y(1)[y(1)]4 0 3 6 3y(1) 5y(1) 0 ( do y(1) 1) y(1) 98 9 Vậy y(1) 8
Cách giải khác: Đặt F(x, y) x3 3x2y y5 5. F (x, y) Ta có: y (x) x
3x2 6xy.(*)
F(x, y) 3x2 5y4 y
Với x 1 thì 13y y5 5 0 y5 3y 4 y 1 y(1) 1.
Thay x 1, y 1 vào (*), ta có: y(1) (3 6) 9 . 3 5 8
21 x2 2x (2x) 2x2 2 1 x2 2 1 x2 2 2x2 1 2 Câu 3. y ,x 1. 2x 2 x4 2x2 1
x2 12 x2 1
1 1 x2 1 x2 2 2 Vậy y ,x 1. x2 1 x2 x3 3
Câu 4. Ta có khai triển Maclaurin: ln(1 x) x o x . 2 3
Khi x 0 thì 2x 0, thay x bởi 2 x , ta có khai triển Maclaurin của y đến cấp 3 là: (2x)2 (2x)3 3 2 8 3 3
y ln(1 2x) 2x
o(2x) 2x 2x x ox 2 3 3
Vậy khai triển cần tìm là y 8
2x 2x2 x3 o x3 . 3 Câu 5.
+) Tập xác định D
Đồ thị hàm số không có tiệm cận đứng. +) Khi x : 1 lim y lim LHospital x lim 0 (Dạng vô định) x
x ex 1 x ex
y 0 là tiệm cận ngang bên phải của đồ thị hàm số.
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 11
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST +) Khi x : x
a lim y lim ex 1 lim 1 1 0 vì lim ex 0 Khi x không có tiệm cận x x x x x 0 1 x ngang.
b lim (y ax) lim x x lim xex lim x dạng x x x x x e 1
x e 1 x 1 e L'Hospital lim
1 0 do lim ex
x ex x
y x là tiệm cận xiên bên trái của đồ thị hàm số.
Vậy đồ thị hàm số không có tiệm cận đứng, và có y 0 là tiệm cận ngang bên phải, y là tiệm cận xiên bên trái. Câu 6.
a)tan(2x)dx sin(2
x)dx 1 2sin(2
x)dx 1 d(cos(2x)) 1ln|cos2x|C cos(2x) 2 cos(2x) 2 cos(2x) 2 Vậy 1
tan(2x)dx ln | cos 2x | C. 2 b) dx lim A dx 0
(x 3)x2 x 1 A 0 (x 3)x2 x 1 1 lim A 1 1 2x 1 7 1 dx
A 0 13 x 3
26 x2 x 1 26 1 2 3 x 2 4 1 A
ln | x 3| ln x2 x1 7 2 x 2 lim arctan A 13 26 26 3 3 2 0
ln | A3| ln A2 A1 7 2A 1 ln 3 7 lim arctan A 13 26 13 3 3 13 78 3
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 12
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST 1 | A 1|2 7 2A 1 ln 3 7 lim ln arctan A 26 13 A 78 3 2 A 1 13 3 3 1 ln1 7 ln3 7 14 ln3 26 13 3 2 13 78 3 39 3 13 14 ln 3
Vậy tích phân suy rộng cần tính bằng . 39 3 13 2 3 3 2 3 3 Câu 7. x2 y2 4 x y 1 2 2
x(t) 8cos3 t
Tham số hoá đường cong: (0 t 2 )
y(t) 8sin3 t
Do tính đối xứng qua trục Ox và trục Oy , diện tích vật thể cần tính bằng 2 lần diện tích vật
thể thu được, khi quay phần ứng với 0 t quanh trục Ox. 2 Diện tícch cần tính là:
2 2 /2|y(t)| x' (t)2 y(t)2 dt 4 /2 8sin3 t 24sin t cos2 t2 24cost sin2 t 2 dt 0 0
768 /2sin3t sin2 tcos2 tcos2 t sin2 tdt 768 /2sin4t costdt 0 0 /2
768 /2 sin4td(cost) 768 sin5 t 768 (dvdt) 0 5 0 5
Vậy diện tích cần tính là 768 (dvdt). 5 Câu 8.
Tập xác định: D 2 Tìm điểm dừng: x y
z 3x2 2(x y) 0 y2 x2 { 2 0 x y 0 x 3x 4
z 3y2 2(x y) 0 3x 2x2y 0 x y x y 2 y { 3 2
3x 4x 0
hàm số có 2 điểm dừng là M 4 , 4 (0,0) 1 và M . 3 3 2
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 13
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
+) Ta có: A z 6x 2, B z 2, C z 6y 2 xx xy yy
B2 AC 4 (6x 2)(6y 2).
- Tại điểm M 4 , 4 , ta có 1
32 0 và A 6 0 3 3
z(x, y) đạt cực tiểu tại M (1,1), z z M 1 CT 1 64 . 27
- Tại điểm M2(0,0).
Xét z z(0 x,0 y) f (0,0) (x)3 (y)3 (x y)2
Khi x y 0 ta có: z 0, điều này chứng tỏ zM2 zM3 , với
M (x,y) 3
thuộc lân cận của M2
hàm số không đạt cực trị tại M 2
Vậy hàm số đạt cực trị duy nhất tại một điểm là M 4 , 4 (cực tiểu), giá trị cực tiểu là 1 3 3
z z M 64 . CT 1 27
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 14
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 4 (Nhóm ngành 1)
Câu 1 (2 điểm). Tìm các giới hạn sau: a) lim 2x . x cos x 2 2x3 ln y b) lim . 2 ( ( x, y) y 1)2 (0,1) x
Câu 2 (1điểm). Phương trình x4 4xy3 3y5 8 0 xác định hàm ẩn y y(x) . Tính y(1) .
Câu 3 (1điểm). Tính đạo hàm của hàm số y arcsin 2x , x 1. 1 x2
Câu 4 (1 điểm). Tìm khai triển Maclaurin của y ln(13x) đến x3 .
Câu 5 (1 điểm). Tìm các tiệm cận của đồ thị hàm số y x . 2ex 1
Câu 6 (2 điểm). Tính các tích phân sau:
a) cot(3x)dx . b) dx 0
(x 4) x2 x 1 3 3
Câu 7 (1 điểm). Quay đường x2 y2 9 quanh trục Ox một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8 (1 điểm). Tìm cực trị của hàm số z x3 y3 (x y)2 .
Cách giải tham khảo đề số 3
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 15
Downloaded by Nguyen Linh (vjt19@gmail.com)
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2)
Câu 1 (1 điểm). Tìm giới hạn lim 2 x0
e2x 1 1 x .
Câu 2 (1 điểm). Cho hàm số
xác định bởi x t t3 . Tính .
y f (x)
f (x), f (x)
y 2t2 3t4
Câu 3 (1 điểm). Tìm cực trị của hàm số y 3 x(x 3)2 . 2 2
Câu 4 (1 điểm). Chứng minh rằng vói mọi x 0 , ta có ln1 x 2 x .
Câu 5 (1 điểm). Tìm giới hạn
16 26 n6 . lim 7 n n
Câu 6 (2 điểm). Tính các tích phân sau: sin3 xdx
a) sinxcosx . b) 3
arccot 3 x dx . 2
Câu 7 (1 điểm). Tính tích phân suy rộng dx . 1 x3x4 2
Câu 8 (1 điểm). Tính diện tích mặt tròn xoay tạo bởi đường tròn x2 (y 2)2 1 quanh trục Ox .
Câu 9 (1 điểm). Cho hàm số: f (x) x arctan 3x, x 0
ae3x b sin x, x 0
Tìm a và b để hàm số f (x) khả vi tại x 0 .
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 16
Downloaded by Nguyen Linh (vjt19@gmail.com)
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
ĐÁP ÁN ĐỀ CUỐI KỲ GIẢI TÍCH 1 20191 – ĐỀ 5 (Nhóm ngành 2) 2 1
2x e2x 1
Câu 1. L lim 2x lim 2x
x0 e 1 x x0 e 1 x
Dùng VCB: e2x 1x0 ~ 2x cho mẫu số, ta có: VCB L 2
lim x e2x 1 (dạng 0 ) x0 2x x 0 LHospital
lim 2 2e2x (dạng 0 ) L Hospital
lim 4e2x 4e0 1. x0 4x 0 x0 4 4
Vậy giới hạn cần tính bằng 1.
Cách giải 2: Dùng khai triển Maclaurin: (2x)2 2
2x e2x 1
2x 2x 2! o x L lim = lim (Khai triển Maclaurin) x0
e2x 1 x x0 2x x
2x2 ox2 lim
lim 2x2 1. x0 2x2 x0 2x2 Câu 2.
x x(t)
Ta có công thức: Với y y(t) Xác định hàm y = f (x)
y(t)x(t) y(t)x(t)
f (x) y(t) và f (x) . x(t) x (t)3
Áp dụng công thức trên ta có: dy
y(t) 4t 12t3 f (x) 4t. dx x(t) 1 3t2 d2 y d dy d 1 d 1 4 f (x) (4t) (4t) 4 .
dx2 dx dx x(t)dt x (t) dt 1 3t2 1 3t2 Câu 3.
+) Tập xác định: D .
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 17
Downloaded by Nguyen Linh (vjt19@gmail.com)
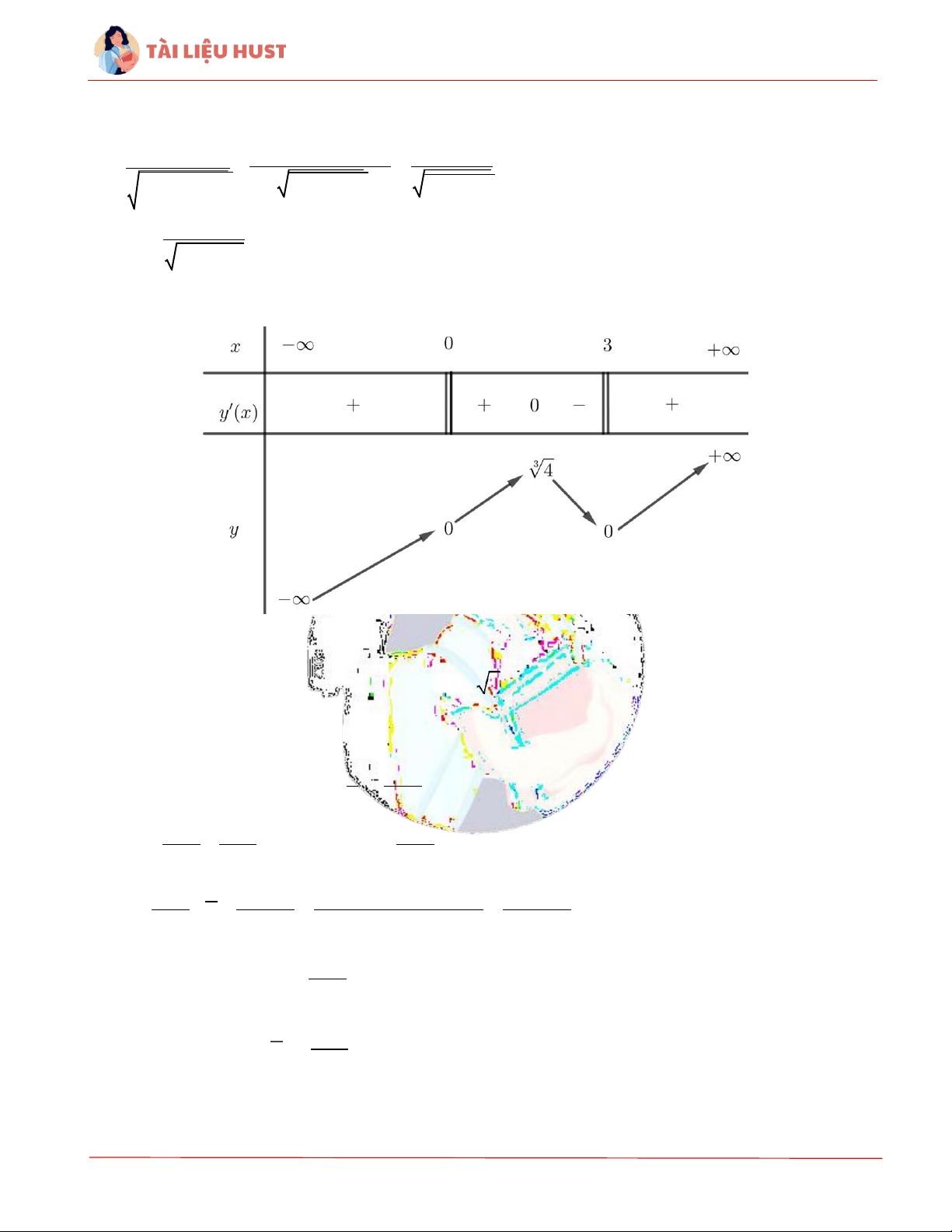
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST +) Sự biến thiên:
x(x3)2 y
(x 3)2 2(x 3)x x 3 2x ,x 0, x 3. 3 3 x2(x 3) 3 x2(x 3)4
x(x 3)22 $
y 0 x 3 2x 0 x 1. 3 x2(x 3) Lập bảng biến thiên:
Dựa vào bàng biến thiên, ta kết luận hàm số có 2 điểm cực trị: 3 4
- Hàm số đạt cực đại tại điểm x 1, yCD y(1) .
- Hàm số đạt cực tiểu tại điểm x 3, y y(3) 0 CT . 2
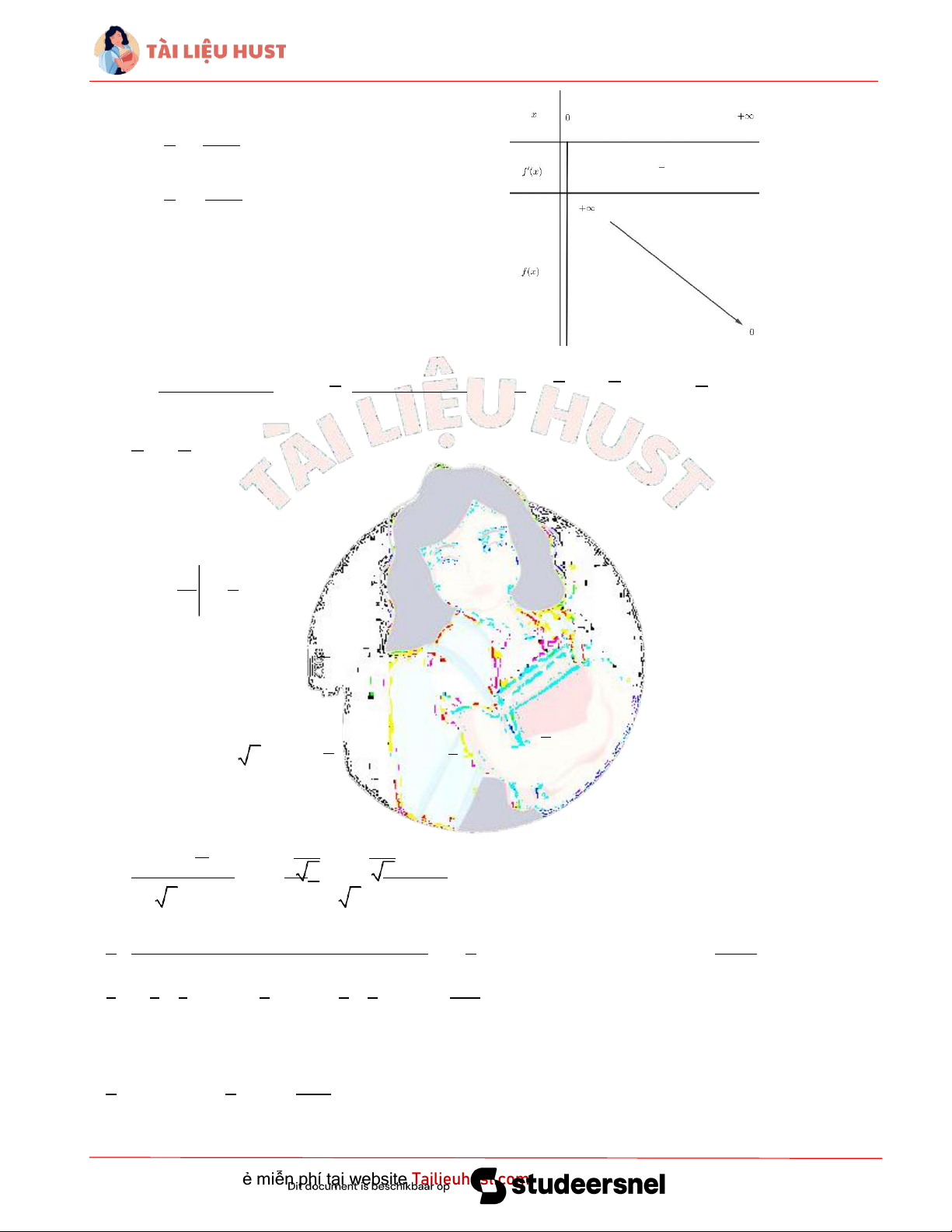
Câu 4. Xét hàm số f (x) ln(1 ) 2 trên (0, ) x 2 x 2
f (x) ln x 2 2 ln(x 2) ln x ( do x 0) x 2 x 2 x 1 1 2
(x 2)x (x 2)2 2x 4 f (x) 0,x 0.
x 2 x (x 2)2 x(x 2)2 x(2 x)2 lim f (x) 2 2 lim ln 1 x0 x0
x 2 x 2 lim f (x) 2 ln(1 0) 0 0 lim ln 1 x x
x 2 x Ta có bảng biến thiên:
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 18
Downloaded by Nguyen Linh (vjt19@gmail.com)
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
Từ bảng biến thiên, suy ra: f (x) 0,x 0 2 2 ln 1 0,x 0 x 2 x 2 2 ln1 ,x 0 (đpcm) x 2 x Câu 5.
16 26 n6
1 16 26 n6 1 1 6 2 6 n 6 L lim 7 lim
lim n n n n n6
n n n n n 1 n k 6 lim
n n k1 n 1
f (x)dx, trong đó f (x) x6 hàm liên tục, khả tích trên [0,1]. 0 1 1 x7
x6 dx 1 . 0 7 7 0
Vậy giới hạn cần tính bằng 1 . 7 Câu 6.
Giải: sin x cos x 2 sin
x . Đặt t x x t
dx dt . Tích phân cần tính trở 4 4 4 thành: 3 1 1 3 sin t 4 sin t cost 2 I dt 2 dt 2 sin t 2 sin t
1 sin3 t 3sin2 t cos t 3sin t cos2 t cos3 t 1 2 2 cos3 t 4 sin t
dt 4 sin t 3sintcost 3cos t sint dt 1 1 3 3 cost
1 cos2t sin 2t 3 cos2t 1 2 4 2 2 2 2 2 sin t sin t dt
1 2 cos 2t 3 sin 2t cost cost sin t dt 4 2 sin t
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 19
Downloaded by Nguyen Linh (vjt19@gmail.com)
Bộ đề thi cuối kỳ môn Giải tích 1 - HUST
1 2 cos 2t sin 2t cost dt 1 2t 1 sin 2t 1 cos 2t ln | sin t | C 4 sin t 2 2 2 2
Thay t x 4 sin3 xdx 1 1 1 sin cos sin x cos x 4 2x 2 2
2x 2 2 2x 2 ln sin x 4 C
x cos(2x) sin(2x) 1 ln sin 2 8 4 x 4 C 1 b) Xét nguyên hàm
arccot 3 x dx arccot 3 x d(x4) (x 4)arccot 3 x (x 4)d(arccot 3 x) 1 1 (x 4)arccot
3 x (x 4) dx
1 ( 3 x)2 2 3 x
(x 4) arccot 3 x
1 dx(x4)arccot 3 x 3 x C. 2 3 x 3 3
arccot 3 x dx [(x4)arccot 2
3 x 3 x] 1 1 2 2 2 Câu 7. 1 f (x)
là hàm dương và liên tục trên [1,) .
x 3x4 2 dx
là tích phần suy rộng loại 1 với điểm bất thường 1 x3x4 2 1 x
1 1 , mà 1 dx hội tụ (do 5 1)
x3x4 2 ~ x 3x4 3x5 1 3x5 dx
hội tụ theo tiêu chuẩn so sánh. 1 x3x4 2
Câu 8. Tham số hoá đường tròn x2 (y 2)2 1: x cos t (0 t 2 ) .
y 2 sin t
Diện tích mặt tròn xoay tạo bởi đường tròn x2 (y 2)2 1 quanh trục Ox là:
2 2|y(t) | 2
x (t)2 y (t)2 dt 2
(sin t)2 (cos t)2 |2sint | dt 0 0
Tai liệu được chia sẻ miễn phí tại website Tailieuhust.com 20
Downloaded by Nguyen Linh (vjt19@gmail.com)




