Bộ Đề Thi Giữa HK1 Toán 9 Cánh Diều Có Đáp Án Ma Trận Đặc Tả

ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
I. PHẦN TRẮC NGHIỆM
Câu 1: Trong các phương trình sau, phương trình là phương trình bậc nhất hai ẩn là A. 5
− x + 0y = 6 .
B. 0x + 0y = 1.
C. 5x − 3 = 0 .
D. 5 − 3y = 10 .
ax + by = c  ( ) 1
Câu 2: Cặp số ( x ; y là một nghiệm của hệ phương trình nếu 0 0 )  ' ' '
a x + b y = c  (2)
A. ( x ; y là nghiệm của phương trình ( ) 1 . 0 0 )
B. ( x ; y là nghiệm của phương trình (2) . 0 0 )
C. ( x ; y là nghiệm của một trong hai phương trình. 0 0 )
D. ( x ; y là nghiệm chung của hai phương trình ( ) 1 và (2) . 0 0 )
Câu 3: Hệ thức 5  10
A. là một đẳng thức.
B. là một bất đẳng thức với 5 là vế phải của bất đẳng thức.
C. là một bất đẳng thức với 5 là vế trái và 10 là vế phải của bất đẳng thức.
D. là một bất đẳng thức với 5 là vế phải và 10 là vế trái của bất đẳng thức.
Câu 4: Bất phương trình dạng ax + b  0 (hoặc ax + b  0, ax + b  0, ax + b  0 ) là bất phương trình bậc
nhất một ẩn (ẩn là x) với điều kiện:
A. a, b là hai số đã cho.
B. a, b là hai số đã cho và a khác 0. C. a khác 0. D. a và b khác 0.
Câu 5: Cho góc nhọn  . Xét tam giác ABC vuông tại A có ABC =  thì tỉ số giữa cạnh đối và cạnh huyền được gọi là A. sin . B. cos . C. tan . D. cot .
Câu 6: Tâm đối xứng của đường tròn là.
A. một điểm nằm trên đường tròn.
B. tâm đường tròn.
C. đường kính của đường tròn.
D. mọi đường thẳng đi qua tâm của đường tròn. 2x + y = 5
Câu 7: Nghiệm của hệ phương trình  là. x − 3y = 1 − Trang 1 A. (2; ) 1 . B. (1;2) . C. (−1;7) . D. (−1;0) . −x + 2y = 4
Câu 8: Cặp số nào là nghiệm của hệ phương trình  . x − y = 2 − A. (−2; ) 1 . B. (−2;0) . C. (0;2) . D. (−2;3) .
Câu 9: Với 3 số a, b, c và a  b thì.
A. Nếu c > 0 thì a.c  b.c.
B. Nếu c < 0 thì a.c > b.c.
C. Nếu c < 0 thì a.c  b.c.
D. Nếu c > 0 thì a.c  b.c.
Câu 10: Cho tam giác ABC vuông tại A có BC = 10 cm, 0
C = 30 . Độ dài AB là A. 5,5cm . B. 5cm. C. 5 3 cm . D. 5 2 cm.
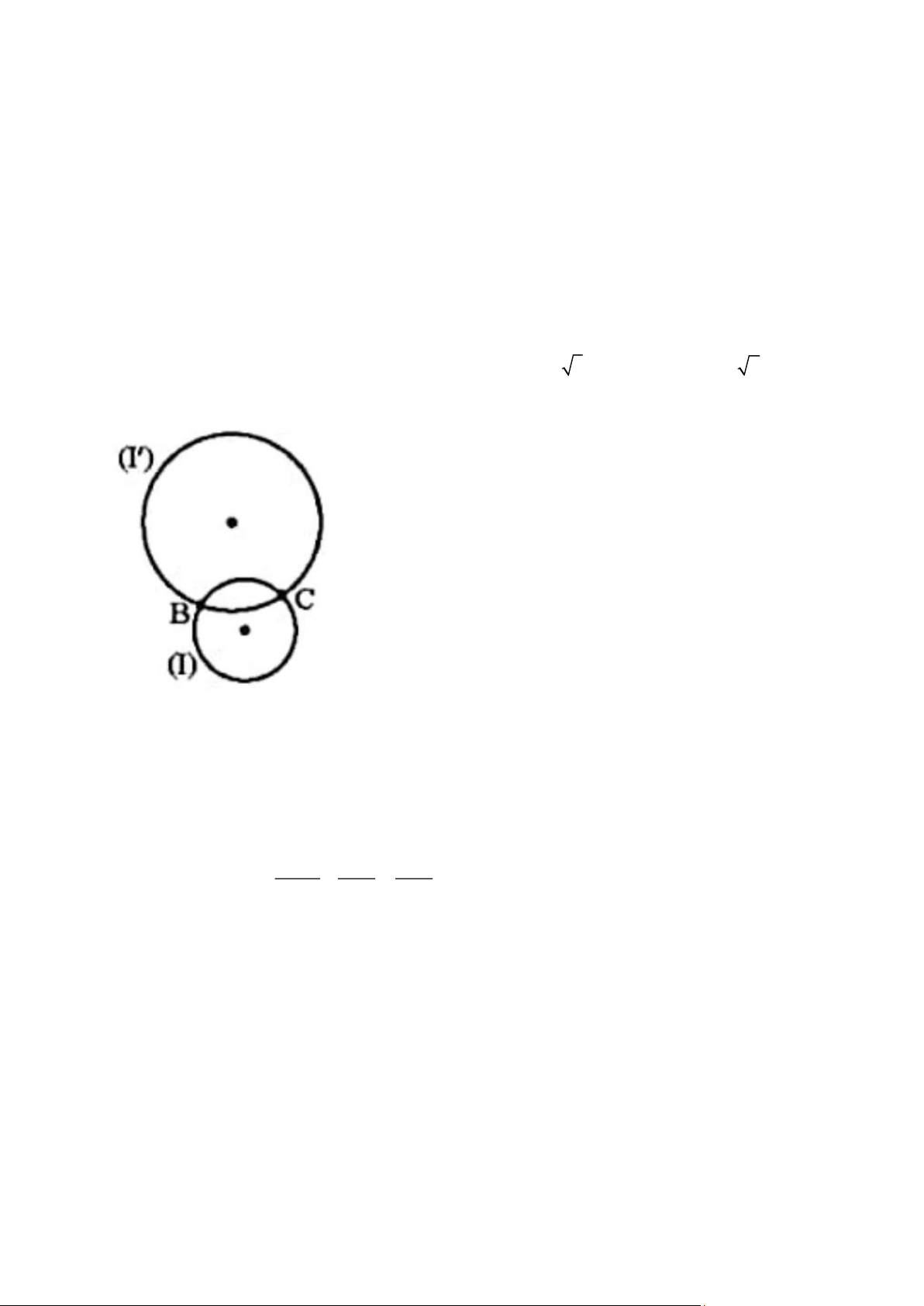
Câu 11: Cho hình vẽ.
A. Hai đường tròn ( I ) và ( ' I ) tiếp xúc nhau.
B. Hai đường tròn ( I ) và ( '
I ) cắt nhau; B và C là tiếp điểm; đoạn thẳng BC là dây chung.
C. Hai đường tròn ( I ) và ( '
I ) cắt nhau; B và C là giao điểm; đoạn thẳng BC là dây chung.
D. Hai đường tròn ( I ) và ( ' I ) không giao nhau. 16 x + 2 2 − x
Câu 12: Phương trình + = có nghiệm là. 2 x − 4 2 − x x + 2 A. x = 2. B. −2 . C. Vô số nghiệm. D. Vô nghiệm. II. PHẦN TỰ LUẬN
Câu 13: Cho phương trình 2x + y = 4 . Trong hai cặp số (1;2) và (−1;2) , cặp số nào là nghiệm của phương trình đã cho? 2x + y = 1 −
Câu 14: Giải hệ phương trình  .  2 − x + 3y = 5
Câu 15: Hai bạn An và Bình có tất cả 93 viên bi. Biết số bi của An nhiều hơn Bình là 33 viên. Tính số viên bi của mỗi bạn?
Câu 16: Viết bất đẳng thức diễn tả mỗi khẳng định sau:. a) x nhỏ hơn 7.
b) y lớn hơn hoặc bằng 3. Trang 2
c) m nhỏ hơn hoặc bằng −10 . Câu 17:
a) Không thực hiện phép tính, hãy so sánh 99.( 1 − 5) và 100.( 15 − ) . 2x + 3 1− x
b) Giải bất phương trình sau:  +1 2 3 Câu 18:
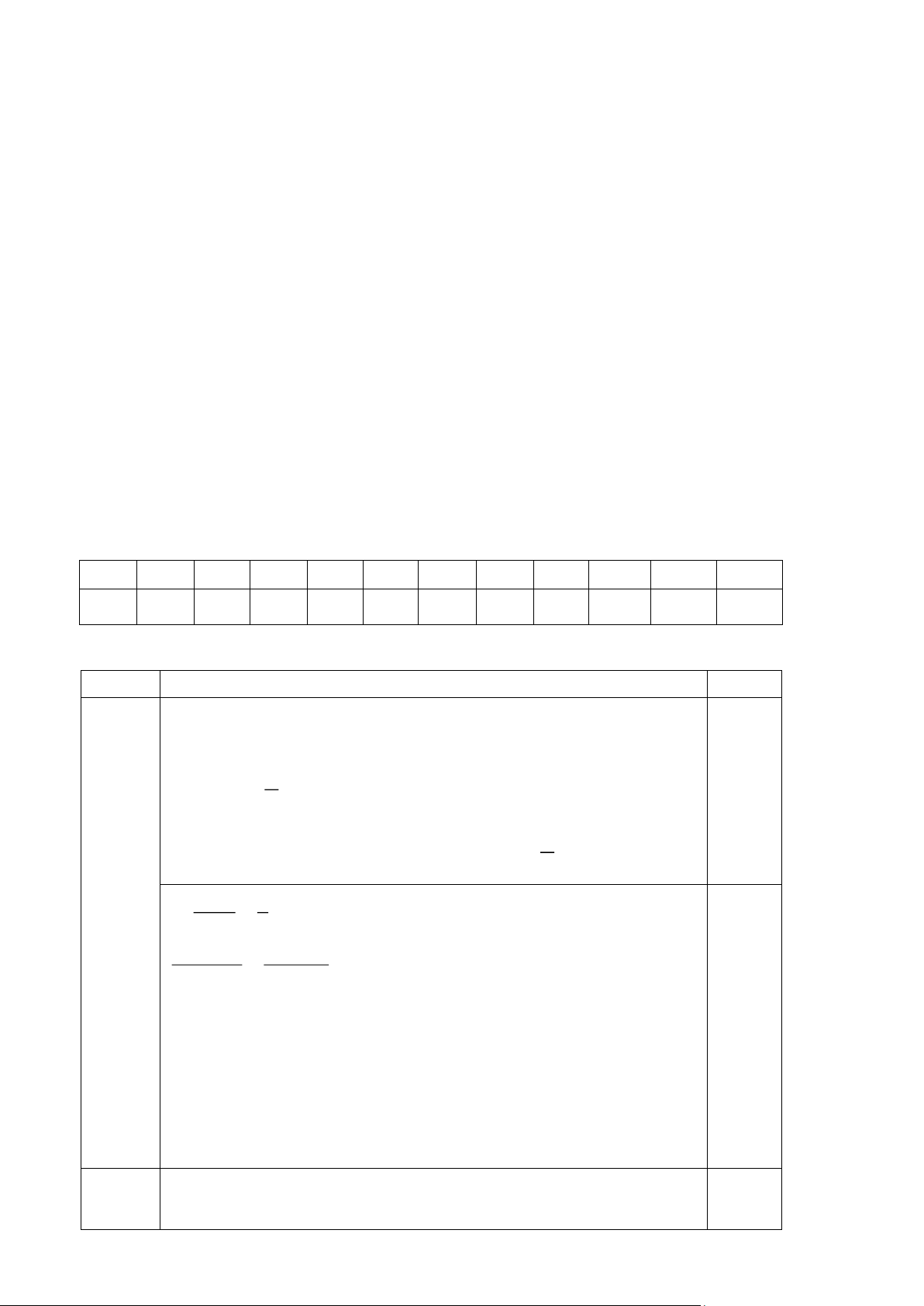
a) Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. Tính các tỉ số lượng giác sin C và tan B . cos B
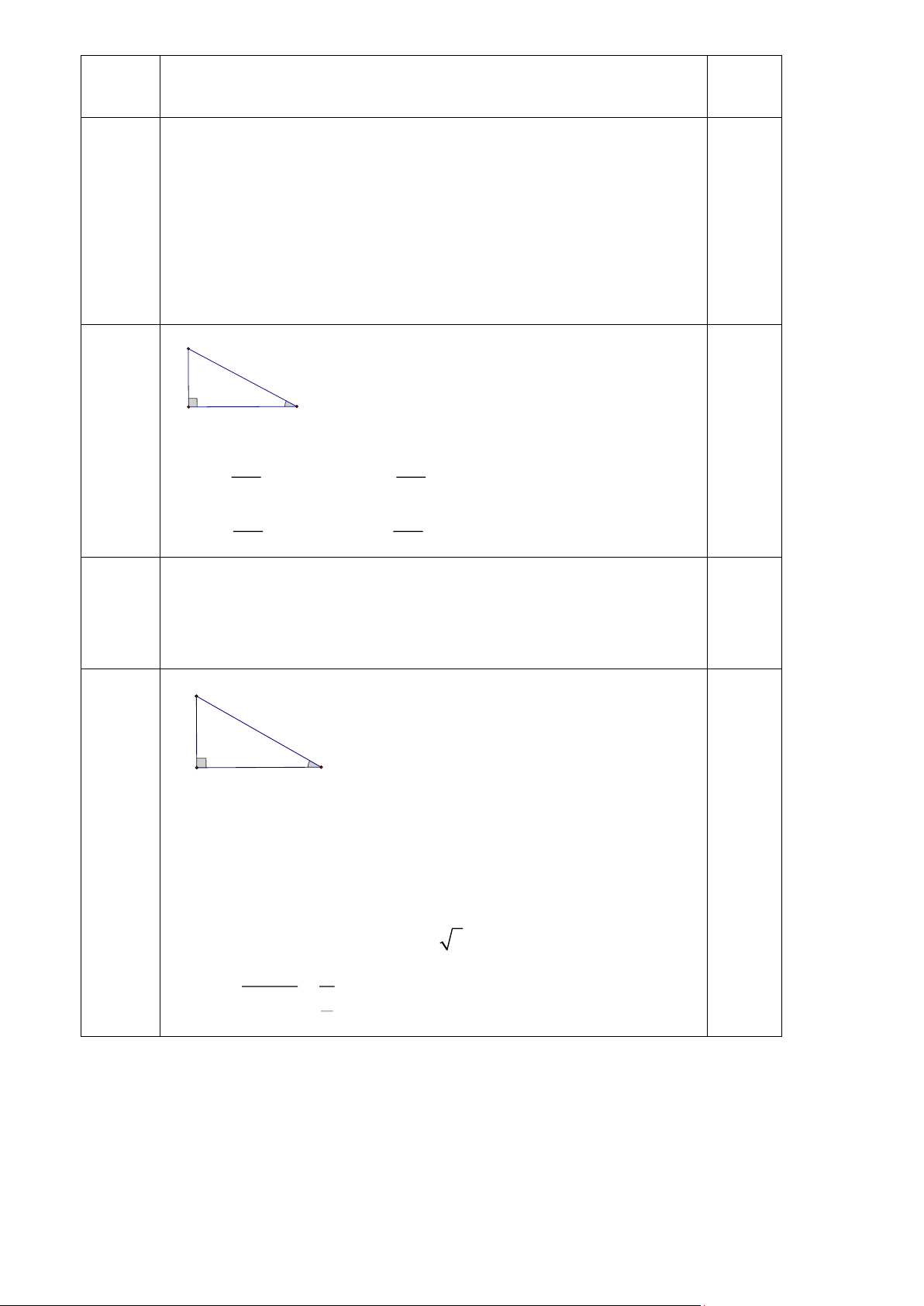
b) Cho tam giác ABC vuông tại A. Chứng minh rằng cot B = cosC 1 1 1
Câu 19: Cho tam giác ABC cân tại A, đường cao AH và BK. Chứng minh: = + 2 2 2 BK BC 4AH
ĐÁP ÁN – BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM
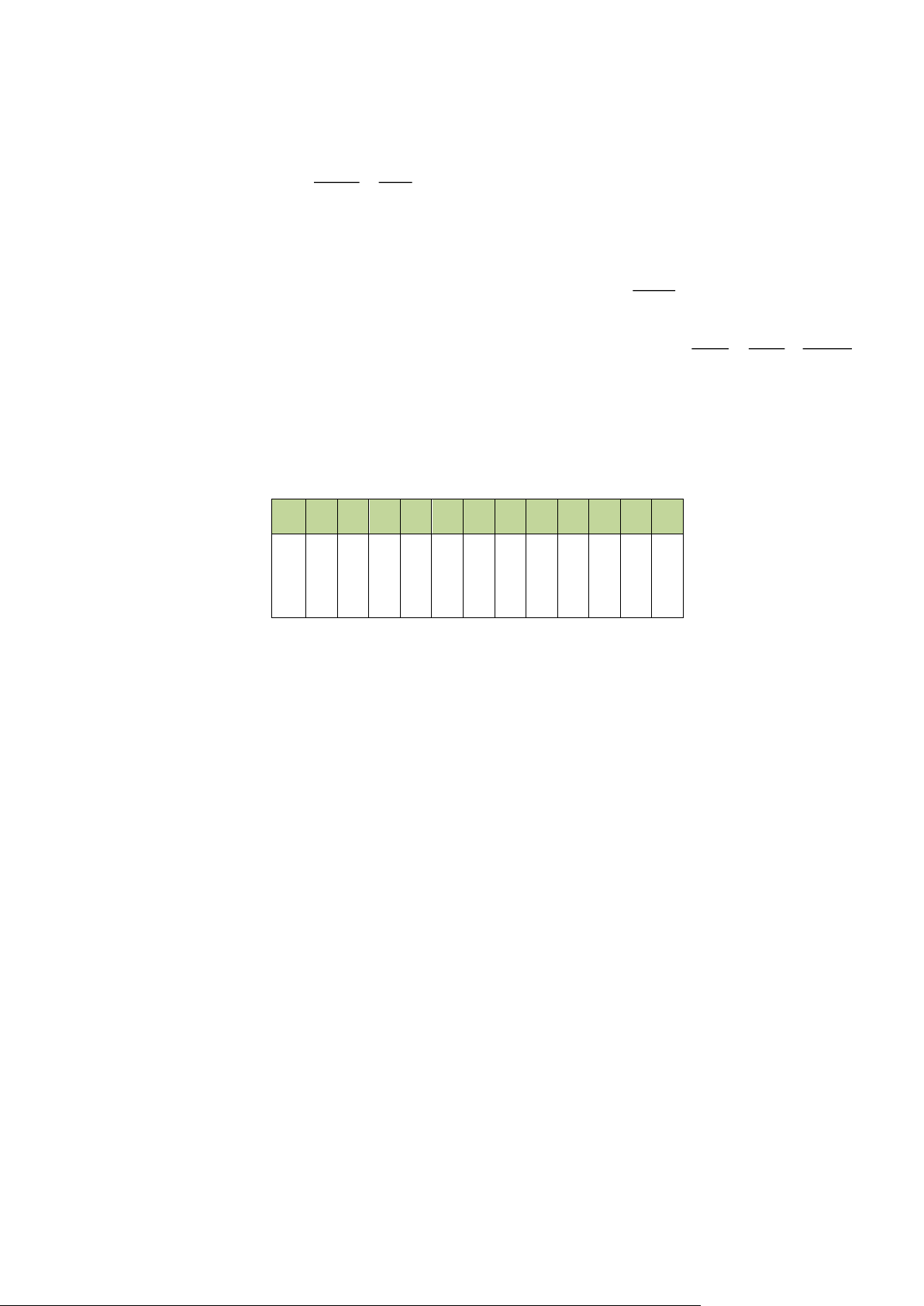
Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp C D á A D C B A B A C D B n II. PHẦN TỰ LUẬN Câu 13:
- Cặp số (1;2) là nghiệm của phương trình đã cho vì 2.1+ 2 = 4
- Cặp số (−1;2) không là nghiệm của phương trình đã cho vì 2.(− ) 1 + 2 = 0  4 Câu 14
Cộng từng vế hai phương trình của hệ, ta được 4 y = 4 . Suy ra y = 1.
Thay y = 1 vào phương trình thứ hai của hệ, ta được −2x + 3.1 = 5 . Do đó x = −1 .
Vậy hệ phương trình có nghiệm duy nhất là (−1; ) 1 . Câu 15:
Gọi số bi của An và Bình lần lượt là x, y (viên, 93 > x > y > 0, x, y ∈ ℕ) x + y = 93
Lập luận có hệ phương trình  x − y = 33 x = 63 Tìm được  y = 30
Kết luận số bi của An và Bình lần lượt là 63 và 30 viên bi Câu 16: a) x  7 . Trang 3 b) y  3 . c) m  −10 . Câu 17:
a) Ta có 99  100 . Nhân hai vế của bất đẳng thức với (−15) , ta được: 99.( 15 − ) 100.( 15 − ) . b) Ta có 2x + 3 1− x  +1 2 3
3.(2x + 3)  2.(1− x) +1.6
6x + 9  2 − 2x + 6
6x + 2x  2 + 6 − 9 4x  1 − 1 − x  4 1 −
Vậy nghiệm của bất phương trình là x  . 4 Câu 18: AB 3 a) Ta có sin C = = BC 5 2 2 2 2
AC = BC − AB = 5 − 3 = 4(cm) AC 4 Vậy tan B = = AB 5 b) Ta có : AB cot B = AC cos B AB AC AB = : = cosC BC BC AC cos B Vậy cot B = cosC
Câu 19: Kẻ tia Bx vuông góc với BC tại B cắt AC tại E
Chứng minh được BE = 2AH 1 1 1 Chứng minh được = + 2 2 2 BK BC 4AH ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN: TOÁN 9 Thời gian: 90 phút
PHẦN I. TRẮC NGHIỆM (3,0 điểm) Chọn câu trả lời đúng trong mỗi câu sau:  1 
Câu 1. (VD) Nghiệm của phương trình x +  (x − 3) = 0 là  3  1 A. x = −  3 Trang 4 1 B. x =  3 1 C. x = − và x = 3. 3 1
D. x = − và x = −3. 3 7 3
Câu 2. (VD) Nghiệm của phương trình = là x + 2 x − 5 41 A. x =  3 B. x = −2. 41 C. x =  4 D. x = 5.
Câu 3. (NB) Phương trình nào sau đây là phương trình bậc nhất hai ẩn? A. 2 2x + 3y = 0 . B. 3 x + y = 5. C. xy − x = 1. D. 2x − 3y = 4 .
Câu 4. (NB) Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ hai phương trình bậc nhất hai ẩn? 2  x − 2y = 0 A.  2x + 3y = 1.  x − 2y = 0 B.  2x + 3y =1. 2  x − 2y = 0 C.  2x + 3y = 1. 2  x − 2y = 0 D.  2 2x + 3y = 1.  2 
Câu 5. (NB) Trong các cặp số (−1; 2) ; (2;2) ;(3; −3) ; 1; 
 , cặp số nào là nghiệm của phương  3  trình 4x + 3y = 2 ? A. (−1; 2) . B. (2;2) . C. (3; −3) .  2  D. 1;  .  3 
Câu 6. (NB) Hệ phương trình nào sau đây có vô số nghiệm?  x − 2y = 5  A.  1 − x + y = 3.  2 Trang 5  x − 2y = 5 B. 1 x + y = 3. 2  x − 2y = 5 C.  1 5 − x + y = − .  2 2  x − 2y = 5 D.  1 − x − y = 3.  2 3x + 5y = 2
Câu 7. (TH) Với điều kiện nào của a, b thì hệ  nhận (−1; ) 1 là nghiệm? 2x + by = a A. a  , b  . B. a − b = 2 − . C. a + b = 2 − . D. a + b = 2 . 4x − y = 2
Câu 8. (TH) Cho hệ phương trình 
. Cặp số nào dưới đây là nghiệm của hệ x + 3y = 7 phương trình đã cho? A. (2;2) . B. (1;2) . C. (−1;−2). D. (2;−2).
Câu 9. (NB) Nếu tam giác ABC vuông tại A , AB =3, BC = 5 thì sin C bằng B A C A. 5  3 B. 3  5 C. 4  5 D. 3  4
Câu 10. (NB) Cho tam giác ABC vuông tại A , AB = 4 và AC = 3 . Khẳng định đúng là C A B 4 A. sin B =  5 Trang 6 3 B. cosB =  5 3 C. tan B =  4 3 D. cot B =  4
Câu 11. (NB) Cho tam giác ABC vuông tại A có AC = 3; AB = 1 thì cot C bằng C A B 3 A.  3 B. 1 . C. − 3 . D. 3 .
Câu 12. (NB) Cho tam giác ABC vuông tại A như hình vẽ. Khẳng định nào sau đây là sai? A C B A. tan B = cot C . sin B B. tan B =  cos B C. sin B = cos C . 1 D. tan B =  cot C
PHẦN II. TỰ LUẬN (7,0 điểm).
Câu 13. VD (1,5 điểm) Giải các phương trình sau: x + 2 1 a) (2x − ) 1 (x + 3) = 0; b) =  x − 2 5
Câu 14. NB (0,75 điểm) Trong hai phương trình: 0, 2x + 0y = 1 − ,5 và 2 x − 2y = 0 , phương
trình nào là phương trình bậc nhất hai ẩn? Tìm hệ số a, b, c của phương trình bậc nhất hai ẩn đó.
Câu 15. NB (0,75điểm) Chứng tỏ cặp số (1;1) là nghiệm của phương trình 4x + 3y = 7.
Câu 16. VDC (1,0 điểm)
Tập thể dục, thể thao là những hoạt động rất
có ích cho sức khỏe con người. Bạn Hùng trung
bình tiêu thụ 12 calo cho mỗi phút chạy bộ, và 4
calo cho mỗi phút đi bộ. Hôm nay Hùng mất 1
giờ cho cả hai hoạt động trên và tiêu thụ hết 560 Trang 7
calo. Hỏi hôm nay Hùng mất bao nhiêu phút cho mỗi hoạt động?
Câu 17. NB (0,5 điểm) Cho tam giác ABC vuông tại A, viết các tỉ số lượng giác của góc B.
Câu 18. TH (1,0 điểm)
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°: a) sin 60o; b) cos 75o; c) tan 80o; d) cot 50 .o
Câu 19. (TH) (1,5 điểm) Cho tam giác ABC vuông tại A. Có 0
C = 30 . Cạnh AB = 8cm . Tính: a) Số đo góc B; b) Tính cạnh AC; c) Tính cạnh BC. --------Hết-------
HƯỚNG DẪN CHẤM, ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM (3,0 điểm). Mỗi câu đúng được 0,25 điểm. 1 2 3 4 5 6 7 8 9 10 11 12 C C D B A C B B B C D D
PHẦN II. TỰ LUẬN (7,0 điểm). Câu Nội dung Điểm a) Ta có: (2x − ) 1 (x + 3) = 0 2x −1 = 0 hoặc x + 3 = 0 0,25 1 x = hoặc x = −3. 0,25 2 1
Vậy phương trình đã cho có 2 nghiệm là x = và x = −3. 0,25 2 x + 2 1 b) = ĐKXĐ: x  2 13 x − 2 5 0,25 (1,5đ) 5.(x + 2) 1(x − 2) = 5.(x − 2) 5(x − 2) 5(x + 2) = x − 2 5x +10 = x − 2 0,25 5x − x = 2 − −10 4x = 12 −
x = −3 (thỏa mãn điều kiện xác định) 0,25
Vậy phương trình đã cho có 2 nghiệm là x = −3. 14
Phương trình: 0, 2x + 0y = 1
− ,5 là phương trình bậc nhất hai ẩn. 0,25
(0,75đ) Với a = 0, 2; b = 0; c = 1 − ,5. 0,5 Trang 8 15
Do 4.1+ 3.1 = 7 là một khẳng định đúng nên cặp số (1;1) là
(0,75đ) nghiệm của phương trình 4x + 3y = 7. 0,75 Đổi 1 giờ = 60 phút
Gọi thời gian hôm nay cho hoạt động chạy bộ và hoạt động đi bộ 0,25
của Hùng lần lượt là x (phút) và y (phút). ĐK: x, y >0 x + y = 60 16 0,25 Theo đề bài ta có :  (1,0đ) 1  2x + 4y = 560
Giải HPT, ta được : x = 40, y = 20 (thỏa điều kiện) 0,25
Vậy hôm nay Hùng mất 40 phút chạy bộ và 20 phút đi bộ. 0,25 C A B 17 (0,5đ) AC AB sin B =  cos B =  0,25 BC BC AC AB tan B =  cot B =  0,25 AB AC a) 0 0 sin 60 = cos30 . 0,25 18 b) 0 0 cos75 = sin15 . 0,25 (1,0đ) c) 0 0 tan80 = cot10 . 0,25 d) 0 0 cot 50 = tan 40 . 0,25 B 8cm 30° A C
a) Xét tam giác ABC vuông tại A, ta có: 19 (1,5đ) 0
B + C = 90 (tổng hai góc nhọn của tam giác vuông) 0,5 Suy ra 0 0 0 0 B = 90 − C = 90 − 30 = 60 b) 0
AC = AB.tan B = 8.tan 60 = 8 3 (cm) 0,5 AB 8 c) BC = = = 16 cm 0,5 0 ( ) sin 30 1 2
Ghi chú: Mọi cách giải khác đúng, phù hợp với chương trình đều chấm điểm tối đa. Trang 9
MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ I MÔN TOÁN – LỚP 9-ĐỀ 1
Mức độ đánh giá Tổng % điểm Chương/ TT
Nội dung/đơn vị kiến thức Vận dụng Chủ đề Nhận biết Thông hiểu Vận dụng cao TNK TNKQ TL TNKQ TL TL TNKQ TL Q
- Phương trình quy về phương trình bậc nhất một ẩn. 2 1 1 1 Phương trình và
-Phương trình bậc nhất hai ẩn hệ hai 0,5 1 0,25 hệ phương
phương trình bậc nhất hai ẩn 40% trình
-Hệ hai phương trình bậc nhất hai ẩn 2 1 1
-Giải hệ hai phương trình bậc nhất hai ẩn 0,5 0,75 1 Bât đẳng thức, -Bất đẳng thức 1 1 1 Bất phương trình 0,25 0,75 0,25 25% 2
bậc nhất một ẩn
Bất phương trình bậc nhất một ẩn 1 1 1 0,25 0,5 0,5 Hệ thức lượng
Tỉ số lượng giác của góc nhọn 1 1 1 3trong tam giác 0,25 0,75 0,5 30% 4 vuông
Hệ thức giữa cạnh và góc của tam giác 1 1 1 3 vuông 0,25 0,5 0,75 4 Đường tròn Đường tròn 1 1 5% 0,25 0,25 Trang 10 Tổng 7 40 6 10 5 8 1 1, 3 10 1,5 2,5 1,25 2 0,25 7 0,75 5 Tỉ lệ % 40% 32,5% 20% 7,5% 100 Tỉ lệ chung 70% 30% 100
MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ I MÔN TOÁN – LỚP 9-ĐỀ 2
I. BẢNG TRỌNG SỐ VÀ NỘI DUNG CẦN KIỂM TRA
Nội dung kiến thức từ tuần 1 - tuần 8: 32 tiết.
Kiểm tra vào tuần 9: 02 tiết. TT Chủ đề/ Chương Số tiết Tỷ lệ trọng số Số điểm 1
Chương I. Phương trình và hệ phương trình bậc nhất 17 (17/30)*100% 56,7% 6,0đ 2
Chương IV. Hệ thức lượng trong tam giác vuông 13 (13/30)*100%  43,3% 4,0đ
ÔN VÀ KIỂM TRA GIỮA KÌ I 4 Không tính
II. BẢNG ĐẶC TẢ MỨC ĐỘ ĐÁNH GIÁ ĐỀ KIỂM TRA GIỮA KÌ I - MÔN TOÁN – LỚP 9 TT Chương/ Nội dung/
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức Trang 11 Chủ đề Đơn vị kiến Vận Thông Vận thức Nhận biêt dụng hiểu dụng cao Phương Vận dụng:
trình quy về -Giải được phương trình tích có dạng (a 1TN 1x + b1).(a2x + b2) = 0. phương
-Giải được phương trình chứa ẩn ở mẫu quy về phương trình C1 trình bậc bậc nhất. 1TN
nhất một ẩn C2 Phương Nhận biết : trình và hệ 2TN C3,4
– Nhận biết được khái niệm phương trình bậc nhất hai ẩn, hệ phương 2TN C5,6
hai phương trình bậc nhất hai ẩn. Phương trình bậc 2TL
– Nhận biết được khái niệm nghiệm của hệ hai phương trình trình và nhất C14,15 bậc nhất hai ẩn. hệ phương hai ẩn 1 Thông hiểu: trình bậc 2TN nhất (13
– Tính được nghiệm của hệ hai phương trình bậc nhất hai ẩn C7,8 tiết) bằng máy tính cầm tay. Vận dụng:
– Giải được hệ hai phương trình bậc nhất hai ẩn.
– Giải quyết được một số vấn đề thực tiễn (đơn giản, quen
thuộc) gắn với hệ hai phương trình bậc nhất hai ẩn (ví dụ: các
bài toán liên quan đến cân bằng phản ứng trong Hoá học,...). Vận dụng cao:
– Giải quyết được một số vấn đề thực tiễn (phức hợp, không 1TL
quen thuộc) gắn với hệ hai phương trình bậc nhất hai ẩn. C16 Hệ thức Nhận biết 4TN
Tỉ số lượng lượng C9,10, 2 giác của
Nhận biết được các giá trị sin (sine), côsin (cosine), tang trong tam 11,12 góc nhọn
(tangent), côtang (cotangent) của góc nhọn. giác vuông 1TL Trang 12 (10 tiết) C17 Thông hiểu
– Giải thích được tỉ số lượng giác của các góc nhọn đặc biệt
(góc 30o, 45o, 60o) và của hai góc phụ nhau. 1TL
– Giải thích được một số hệ thức về cạnh và góc trong tam C18a,b Một số hệ
giác vuông (cạnh góc vuông bằng cạnh huyền nhân với sin ,c,d thức về
góc đối hoặc nhân với côsin góc kề; cạnh góc vuông bằng 1TL cạnh và góc
cạnh góc vuông kia nhân với tang góc đối hoặc nhân với C19a,b trong tam côtang góc kề). ,c,d
giác vuông Tính được giá trị (đúng hoặc gần đúng) tỉ số lượng giác của
góc nhọn bằng máy tính cầm tay. Vận dụng
Giải quyết được một số vấn đề thực tiễn gắn với tỉ số lượng
giác của góc nhọn (ví dụ: Tính độ dài đoạn thẳng, độ lớn góc
và áp dụng giải tam giác vuông,...). Tổng 8 (TN) 2 (TN) 2(TN) 3 (TL)
2(TL) 1(TL) 1(TL) Tỉ lệ % 40% 30% 20% 10% Tỉ lệ chung 70% 30% Trang 13 III. MA TRẬN
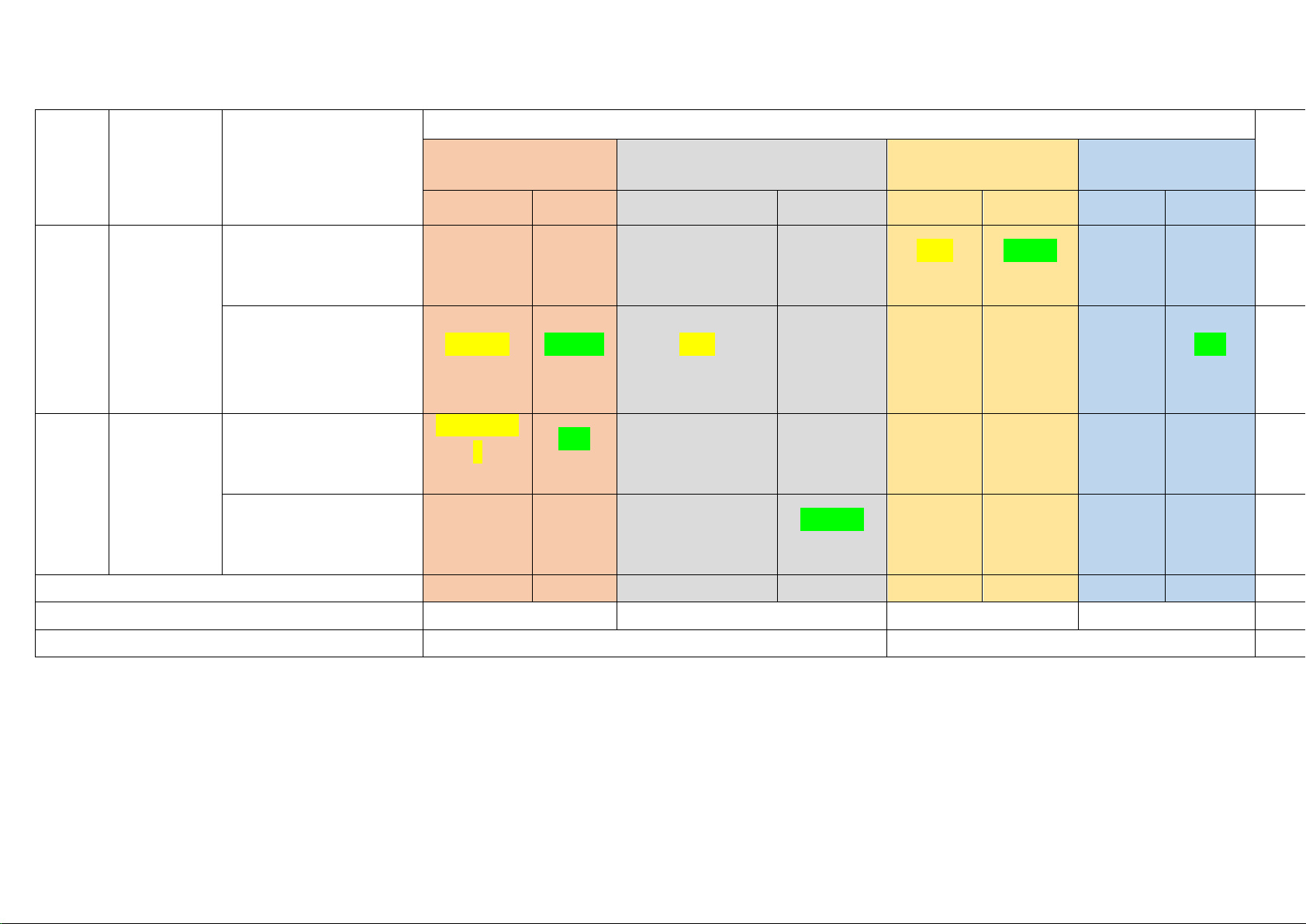
Mức độ đánh giá Tổng Chương/
Nội dung/đơn vị kiến % TT Nhận biết Thông hiểu Vận dụng Vận dụng cao Chủ đề thức điểm TNKQ TL TNKQ TL TNKQ TL TNKQ TL
Phương trình quy về Phương C1,2 C13a,b 2đ
phương trình bậc trình và hệ 0,5đ 1,5đ 20%
nhất một ẩn phương 1
trình bậc Phương trình và hệ C3,4,5,6 C14, 15 C7,8 C16 4đ nhất
phương trình bậc 1đ 1,5đ 0.5đ 1,0đ 40% (13 tiết) nhất hai ẩn C9,10,11,1 Hệ thức
Tỉ số lượng giác của C17 1,5đ 2 lượng góc nhọn 0,5đ 15% 1đ 2
trong tam Một số hệ thức về giác vuông C18, 19 2,5đ
cạnh và góc trong (10 tiết) 2,5đ 25%
tam giác vuông Tổng 8 02 02 02 02 01 0 01 18 Tỉ lệ % 40% 30% 20% 10% 100 Tỉ lệ chung 70% 30% 100 Trang 14