Bộ đề thi ma trận k70 | Đại học Sư phạm Hà Nội
với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.
Môn: Nhập môn lý thuyết ma trận
Trường: Đại học Sư Phạm Hà Nội
Thông tin:
Tác giả:
Preview text:
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
ĐỀ THI KẾT THÚC HỌC PHẦN Khoa Toán - Tin
Môn thi: Nhập môn lý thuyết ma trận ————–
Thời gian làm bài: 60 phút
Câu 1. (3,5 điểm) Cho các ma trận 3 1 ! −1 4 2 A = 1 0 , B = 1 2 0 , −2 m
trong đó m là tham số thực.
(a) Tính tổng tất cả các phần tử của ma trận BA.
(b) Tìm tất cả các số thực m để định thức của ma trận AB + 2I bằng 4,
trong đó I là ma trận đơn vị cấp 3.
Câu 2. (3,0 điểm) Cho ma trận 2 −4 1 ! A = 1 −3 1 . −2 2 −1
(a) Tìm tất cả các giá trị riêng và các véctơ riêng của ma trận A.
(b) Tính định thức của ma trận A2020 − I, trong đó I là ma trận đơn vị cấp 3.
Câu 3. (2,0 điểm) Giải hệ phương trình tuyến tính
−2x1 + 3x2 − 3x3 + x4 = −1 3x1 + 2x2 + x3 − 5x4 = 1 x1 + 4x3 + 2x4 = 7 2x1 + 5x2 + x3 − 3x4 = 5.
PHẦN TỰ CHỌN: Sinh viên chỉ cần làm một trong hai bài sau
Câu 4A. (1,5 điểm) Cho ma trận vuông cấp n (n ≥ 3) 1 2 3 · · · n 0 1 2 · · · n − 1 X = 0 0 1 · · · n − 2 . · · · · · · · · · · · · · · · 0 0 0 · · · 1
Hãy tính phần tử nằm ở dòng 2, cột 3 của ma trận nghịch đảo của X.
Câu 4B. (1,5 điểm) Trong phân tử M2X có tổng số hạt (p, n, e) là 140 hạt,
trong đó số hạt mang điện nhiều hơn số hạt không mang điện là 44 hạt.
Số khối của nguyên tử M lớn hơn số khối của nguyên tử X là 23. Tổng số
hạt (p, n, e) trong nguyên tử M nhiều hơn trong nguyên tử X là 34 hạt.
Xác định công thức phân tử của hợp chất M2X.
———— Hết ———–
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
ĐỀ THI KẾT THÚC HỌC PHẦN Khoa Toán - Tin
Môn thi: Nhập môn lý thuyết ma trận ————–
Thời gian làm bài: 60 phút
Câu 1. (3,5 điểm) Cho các ma trận 1 0 ! 1 A = −1 3 −1 −1 , B = , 0 2 2 1 m
trong đó m là tham số thực.
(a) Tính tổng tất cả các phần tử của ma trận BA.
(b) Tìm tất cả các số thực m để định thức của ma trận AB − I bằng 7,
trong đó I là ma trận đơn vị cấp 3.
Câu 2. (3,0 điểm) Cho ma trận 1 2 3 ! A = 2 5 7 . −2 −4 −6
(a) Tìm tất cả các giá trị riêng và các véctơ riêng của ma trận A.
(b) Tính định thức của ma trận A2021 + I, trong đó I là ma trận đơn vị cấp 3.
Câu 3. (2,0 điểm) Giải hệ phương trình tuyến tính x1 + x2 − x3 + 2x4 = 1 2x1 + x3 − x4 = −4 x1 − x2 + 3x3 − 5x4 = −8
−x1 + 3x2 − 6x3 + 10x4 = 14.
PHẦN TỰ CHỌN: Sinh viên chỉ cần làm một trong hai bài sau
Câu 4A. (1,5 điểm) Cho ma trận Y = (1 2 3 · · · 2021) và X là một ma
trận bất kì cỡ 2021 × 1. Chứng minh rằng ma trận XY không khả nghịch.
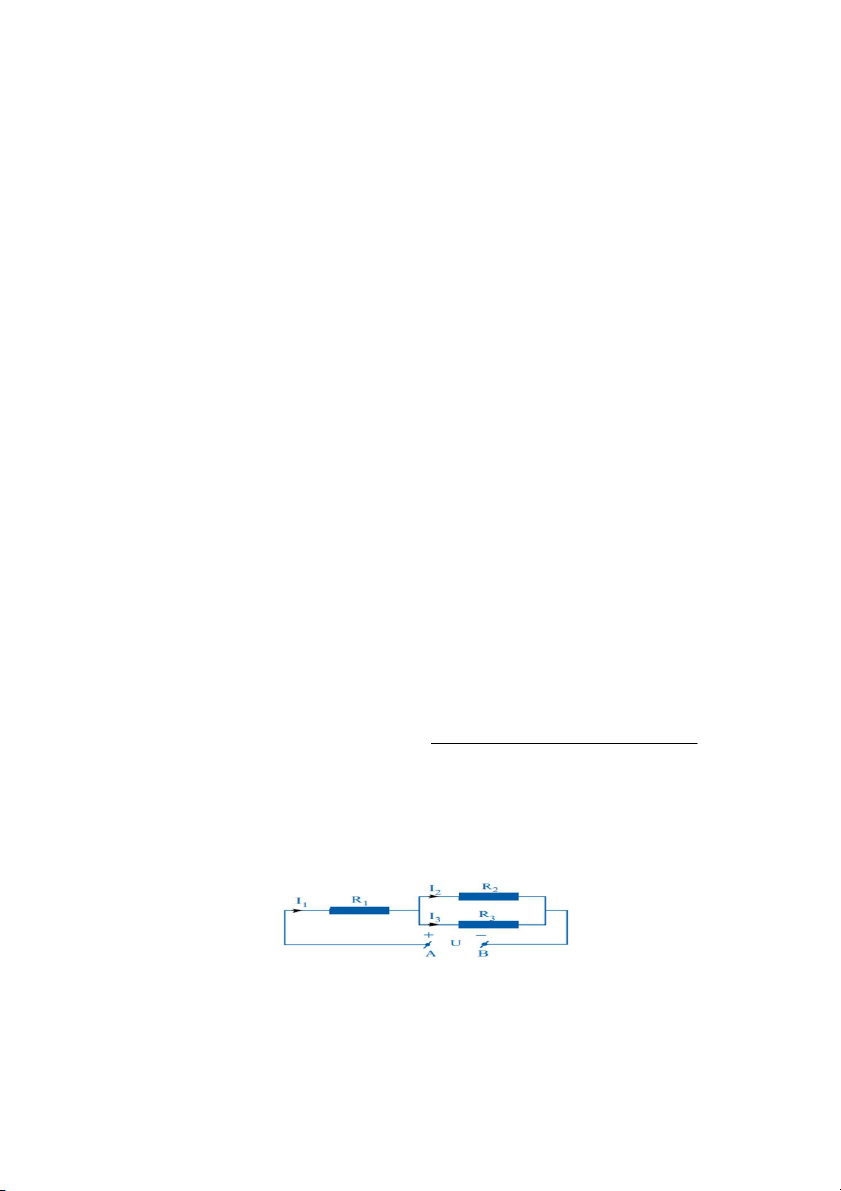
Câu 4B. (1,5 điểm) Cho một đoạn mạch điện như Hình A. Biết R1 = 36Ω, R
là cường độ dòng điện của 2
= 90Ω, R3 = 60Ω và U = 60V . Gọi I1 mạch chính, I và
là cường độ dòng điện của hai mạch rẽ. Tính I1, I2, I3. 2 I3 Hình A
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
ĐỀ THI KẾT THÚC HỌC PHẦN Khoa Toán - Tin
Môn thi: Nhập môn lý thuyết ma trận ————–
Thời gian làm bài: 60 phút
Câu 1. (2,5 điểm) Cho các ma trận ! 2 −1 1 2 A = −1 1 0 3 −2 , 3 2 a , B = , C = 1 3 1 4
trong đó a là tham số thực.
(a) Hãy xác định ma trận AB − 2C khi a = 1.
(b) Tìm tất cả các số thực a để định thức của ma trận BA bằng 0.
Câu 2. (3,5 điểm) Cho ma trận −3 −1 1 ! A = 10 4 3 − . 4 2 −1
(a) Tìm tất cả các giá trị riêng và các véctơ riêng của ma trận A.
(b) Tìm tất cả các giá trị riêng của ma trận A2021.
Câu 3. (2,5 điểm) Giải hệ phương trình tuyến tính 2x + 3x + 2 = 6 1 2 − x3 x4 −3x + 5x + 4 = 1 3 x4 −7 x + 4 = 1 − 2x2 x3 − x4 −2 4x + 2x + 3 = 5 1 2 x4 .
PHẦN TỰ CHỌN: Sinh viên chỉ cần làm một trong hai bài sau
Câu 4A. (1,5 điểm) Cho X là một ma trận khả nghịch cỡ 3 × 3. Để tìm ma
trận nghịch đảo của X bằng phương pháp Gauss-Jordan, người ta đã biến 1 2 3! đổi ma trận X về dạng 0 1 3
bằng các phép biến đổi sơ cấp theo 0 0 1 1 0 0 !
dòng. Khi đó ma trận đơn vị trở thành 3 0 1 − . Giả sử rằng các 2 −1 0
biến đổi đều đúng, hãy tìm ma trận nghịch đảo của ma trận X.
Câu 4B. (1,5 điểm) Hòa tan hoàn toàn 13, 4 g hỗn hợp X gồm Mg, Al, F e vào dung dịch H
đặc nóng dư thu được 12 (trong điều 2S O4 , 32 lít khí SO2
kiện tiêu chuẩn). Mặt khác, nếu cho 13, 4 g hỗn hợp trên tác dụng với
dung dịch HCl dư thì thu được 11, 2 lít H (trong điều kiện tiêu chuẩn). 2
Tính khối lượng M g, Al, F e trong hỗn hợp X.
———— Hết ———–