Bộ đề thi thử tốt nghiệp môn toán 2020 phát triển từ đề minh họa - tập 3

Bộ đề thi thử tốt nghiệp môn toán 2020 phát triển từ đề minh họa - tập 3 được soạn dưới dạng file PDF. Đề thi bao có 80 trang, bao gồm 5 bộ đề câu hỏi trắc nghiệm. Đề thi có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mờicác bạn cùng đón xem ở dưới.

63 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2020

Môn: Toán

Thông tin:

80 trang 7 tháng trước

Tác giả:

Profile ha phan
Trang 1
ĐỀ 11
PHÁT TRIỂN TỪ ĐỀ MINH
HỌA LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Cho tp hp
A
gm có 9 phn t. S tp con gm có 4 phn t ca tp hp
A
là
A.
4
9
A
. B.
4
P
. C.
4
9
C
. D.
49
.
Câu 2: Cho mt cp s cng có
4
2u
,
2
4u
. Hi
1
u
và công sai
bng bao nhiêu?
A.
1
6u
và
1.d
B.
1
1u
và
1.d
C.
1
5u
và
1.d 
D.
1
1u 
và
1.d 
Câu 3: 
21
5 125
x
có nghim là
A.
5
2
x
. B.
1x
. C.
3x
. D.
3
2
x
.
Câu 4: Hình chóp
.S ABCD
nh
a
; chi dày bng
6.a
Tính th tích
khi chóp
.S ABCD
A.
2
2a
. B.
3
6a
. C.
3
2a
. D.
2
6a
.
Câu 5: Tìm tnh
D
ca hàm s
2
3
log 4 3y x x
A.
2 2;1 3;2 2D
. B.
1;3D
.
C.
;1 3;D  
. D.
;2 2 2 2;D
Câu 6: M 
A.
1
lndx x C
x

. B.
2
1
tan
cos
dx x C
x

.
C.
2
1
cot
sin
dx x C
x

. D.
cos sinxdx x C
.
Câu 7: Cho kh có ding
2
3a
và khong cách ging
a
. Tính th tích
V
ca kh 
A.
3
3
.
2
Va
B.
3
3.Va
C.
3
.Va
D.
3
9.Va
Câu 8: Th tích ca khi nón có chiu cao bng
3
2
a
ng
2
a
là
A.
3
3
6
a
. B.
3
3
24
a
. C.
3
3
8
a
. D.
3
3
8
a
.
Câu 9: Cho khi cu
S
có th tích là
288
. Hi din tích khi cu bng bao nhiêu?
A.
48S
. B.
72S
. C.
36S
. D.
144S
.
Câu 10: Cho hàm s
y f x
nh, liên tc trên
và có bng bin thiên
Kh
A. Hàm s nghch bin trên
. B. Hàm s nghch bin trên khong
;0
.
C. Hàm s nghch bin trên khong
1; 
. D. Hàm s nghch bin trên khong
0;1
.
Trang 2
Câu 11: Vi
,ab
là s thc tùy ý khác
0
, ta có
2
log ab
bng:
A.
22
log logab
. B.
22
log .logab
. C.
2
logba
. D.
22
log logab
.
Câu 12: Hình tr có thit din qua trc là hình vuông cnh a thì có th tích bng:
A.
3
1
.
4
a
B.
3
1
.
3
a
C.
3
1
.
2
a
D.
3
.a
Câu 13: Giá tr ln nht ca hàm s
3
32y x x
n
0;2
bng
A.
4.
B.
2.
C.
9.
D.
3.
Câu 14:  th ca hàm s ng cong trong hình bên?
.
A.
32
3y x x
. B.
32
3y x x
. C.
42
2y x x
. D.
42
2y x x
.
Câu 15: Tng s ng tim cng và tim cn ngang c th hàm s
xx
y
x

2
1
1
là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 16: Tp nghim ca b
44
log 1 log 2 5xx

là
A.
1;6
. B.
5
;6
2



. C.
;6
. D.
6;
.
Câu 17: Cho hàm s
y f x
 th i
S nghim c
2 3 0fx
là:
A.
4
. B.
2
. C.
0
. D.
3
.
Trang 3
Câu 18: Cho hàm s
fx
liên t  n
0;3
và
2
0
d1f x x
,
3
2
d4f x x
. Tính
3
0
dI f x x
.
A.
5I
B.
3I 
C.
3I
D.
4I
Câu 19: S phc liên hp ca s phc
31zi
là
A.
13zi
. B.
13zi
. C.
13zi
. D.
3zi
.
Câu 20: Cho s phc
3zi
. Phn thc ca s phc
21zi
bng
A.
6.
B.
7.
C.
3.
D.
2.
Câu 21: Cho hai s phc
1
13zi
và
2
22zi
. a s phc
12
2z z z
là
A.
2
. B.
22
. C.
10
. D.
23
.
Câu 22: Trong không gian vi h trc to 
Oxyz
m
2;3;4A
,
8; 5;6B
. Hình chiu
vuông góc cm
I
cn
AB
trên mt phng
Oyz

A.
0; 1;5M
. B.
0;0;5Q
. C.
3;0;0P
. D.
3; 1;5N
.
Câu 23: Trong không gian
Oxyz
, mt cu
S
có tâm
(1,1, 2)I
, tip xúc vi mt phng t
()Oxz
.
t cu
S
là:
A.
2 2 2
2 2 4 1 0x y z x y z
B.
2 2 2
2 2 4 5 0x y z x y z
C.
2 2 2
2 2 4 1 0x y z x y z
D.
2 2 2
2 2 4 5 0x y z x y z
Câu 24: Trong không gian
Oxyz
, cho mt phng
: 2 1 0P x y z
thuộc
P
?
A.
1; 2;1M
. B.
2;1;1N
. C.
0; 3;2P
. D.
3;0; 4Q
.
Câu 25: Trong không gian vi h t
Oxyz
, cho mt phng
:2 2 2017 0P x y z
, véc-
trong các véc-t véc-n ca
P
?
A.
2;2;1n 
. B.
4; 4;2n 
. C.
1; 2;2n 
. D.
1; 1;4n 
.
Câu 26: Cho hình chóp
.S ABC
có
SA SB CB CA
, hình chiu vuông góc ca
lên mt phng
ABC
trùng v  m
I
ca cnh
AB
. Góc gi ng thng
SC
và mt phng
ABC
bng.
A.
0
45
. B.
0
90
. C.
0
60
. D.
0
30
.
I
C
B
A
S
Trang 4
Câu 27: Cho hàm s
fx
, bng xét du ca
fx

x

1
1
2

fx
+
0
0
0
+
S m cc tr ca hàm s 
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 28: Giá tr ln nht ca hàm s
2
5y x x
bng
A.
0
. B.
5
2
. C.
6
. D.
2
.
Câu 29: Xét các s thc
a
và
b
tha mãn
3
1
3
27
9
log log 3
3
b
a



. M 
A.
1
2
18
ab
. B.
1
2
18
ab
. C.
1
2
18
ba
. D.
1
2
18
ab
.
Câu 30: S m c th hàm s
1
1
x
y
x
ng thng
2y
là
A.
1
. B.
2
. C.
4
. D.
6
.
Câu 31: Tp nghim
c
2
22
log 2log 4 7 0xx
là
A.
S 
. B.
3;1S 
.
C.
2S
. D.
1
;2
8
S



.
Câu 32: Cho tam giác
ABC
vuông ti
A

AB a
,
2BC a
. Quay tam giác
ABC
quanh trc
AB
c mt hình nón có th tích là
A.
3
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
4
3
a
.
Câu 33: Xét
2
sin
0
cos . d
x
x e x
, nt
sinux
thì
2
sin
0
cos . d
x
x e x
bng:
A.
1
0
2 e d
u
u
. B.
1
0
ed
u
u
. C.
1
2
0
ed
u
u
. D.
2
0
ed
u
u
.
Câu 34: Din tích
ca hình phng gii hn b th các hàm s
yx
,
e
x
y
,
1x
và trc tung
c tính bi công th
A.
1
0
e 1 d
x
Sx
. B.
1
0
ed
x
S x x
.
C.
1
0
ed
x
S x x
. D.
1
1
ed
x
S x x

.
Câu 35: Cho hai s phc
1
24zi
và
2
1 3 .zi
Phn o ca s phc
12
z iz
bng
A.
5
. B.
3i
. C.
5i
. D.
3
.
Câu 36: Kí hiu
12
,zz
là hai nghim phc c  
2
2 10 0zz
. Tính giá tr biu thc
22
12
A z z
.
A.
20A
. B.
10A
. C.
2 10A
. D.
16A
.
Trang 5
Câu 37: Trong không gian
Oxyz
m
1; 2;1K
. Mt phng
P

K
và vuông góc vi
trc
Oy

A.
20y 
.
B.
10x
.
C.
20y 
.
D.
10z 
.
Câu 38: Trong không gian
Oxyz
m
1;0;1M
và
3;2; 1N
. Gi
H
là hình chiu vuông
góc ca
N
lên trc
Oz
ng thng
MH
 là
A.
1
0
12
xt
y
zt


. B.
1
0
12
xt
y
zt


. C.
1
12
xt
yt
zt

. D.
12
12
xt
yt
zt


.
Câu 39:  th t cho 20 bn hc sinh lt t s th t
1
n s th t
20
. Chn ngu nhiên
ba bn hc sinh t
20
bn h ba bc chn không có hai bn
 th t liên tip.
A.
799
1140
. B.
139
190
. C.
68
95
. D.
27
95
.
Câu 40: Cho hình chóp
.S ABCD

ABCD
là hình ch nht,
,2AB a AD a
,
SA
vuông góc vi
mt ph
SA a
(tham kho hình v). Gi
M
m ca
CD
. Khong cách
ging thng
,SD BM
bng
A.
21
21
a
. B.
2 21
21
a
. C.
27
7
a
. D.
7
7
a
.
Câu 41: Tng tt c các giá tr nguyên ca tham s
10;10m
 hàm s
21xm
y
xm

nghch bin
trên
1;5
.
A.
30
. B.
4
. C.
36
. D.
45
.
Câu 42: Dân s th gic d c
.e
Nr
SA

A
: là dân s cy làm
mc tính,
S
là dân s sau
N

r
là t l   Theo s liu thc t, dân s
th gi
1950
là
2560
trii; dân s th gi
1980
là
3040
trii. Hãy d
 th gi
2020
?
A.
3823
triu. B.
5360
triu. C.
3954
triu. D.
4017
triu.
Câu 43: Cho hàm s
32
y ax bx cx d
 th  bên. M i

Trang 6
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 44: Khi ct khi tr
T
bi mt mt phng song song vi trc và cách trc ca tr
T
mt
khong bng
3a
c thit din là hình vuông có din tích bng
2
4a
. Tính th tích
V
ca
khi tr
T
.
A.
3
77Va
. B.
3
77
3
Va
. C.
3
8
3
Va
. D.
3
8Va
.
Câu 45: Cho hàm s
fx
có
27
28
f



và
2
12sin2 .cos 3 ,f x x x x

0
df x x
bng
A.
27
64
. B.
87
64
. C.
0
. D.
87
64
.
Câu 46: Cho hàm s
fx
có bng bi
S nghim thun
0;3
c
sin 1fx
là
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 47: Cho hai s th
a
và
b
tha mãn
81
4 .2
ab a b
ab
ab
. Giá tr ln nht ca biu thc
2
2P ab ab
bng
A.
3
. B.
1
. C.
51
2
. D.
3
17
.
Câu 48: Cho hàm s
( )
32
3f x x x m= - +
. Gi
S
là tp hp tt c các giá tr ca
m
sao cho
1;3
1;3
max 2minf x f x
. S phn t ca
S
là
A.
2
. B.
3
. C.
4
. D.
1
.
Trang 7
Câu 49: 
.ABC AB C
. Gi
M
,
N
,
P
lm thuc các cnh
AA
,
BB
,
CC
sao cho
2AM MA
,
2NB NB
,
PC PC
. Gi
1
V
,
2
V
lt là th tích ca hai khi
n
ABCMNP
và
ABC MNP
. Tính t s
1
2
V
V
.
A.
1
2
2
V
V
B.
1
2
1
2
V
V
C.
1
2
1
V
V
D.
1
2
2
3
V
V
Câu 50: Cho
0 2020x
và
2
log (2 2) 3 8
y
x x y
.Có bao nhiêu cp s
( ; )xy
nguyên tha mãn
u kin trên?
A. 2019. B. 2018. C. 1. D. 4.
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1: Cho tp hp
A
gm có 9 phn t. S tp con gm có 4 phn t ca tp hp
A
là
A.
4
9
A
. B.
4
P
. C.
4
9
C
. D.
49
.
Lời giải
Chọn C
S tp con gm có 4 phn t ca tp hp
A
là
4
9
C
.
Câu 2: Cho mt cp s cng có
4
2u
,
2
4u
. Hi
1
u
và công sai
bng bao nhiêu?
A.
1
6u
và
1.d
B.
1
1u
và
1.d
C.
1
5u
và
1.d 
D.
1
1u 
và
1.d 
Lời giải
Chọn C
Ta có:
1
1
n
u u n d
.Theo gi thit ta có h 
4
2
2
4
u
u
1
1
32
4
ud
ud


1
5
1
u
d

.
Vy
1
5u
và
1.d 
Câu 3: 
21
5 125
x
có nghim là
A.
5
2
x
. B.
1x
. C.
3x
. D.
3
2
x
.
Lời giải
Chọn B
Ta có:
21
5 125
x
2 1 3
55
x

2 1 3x
1x
.
Câu 4: Hình chóp
.S ABCD
nh
a
; chi dày bng
6.a
Tính th tích
khi chóp
.S ABCD
A.
2
2a
. B.
3
6a
. C.
3
2a
. D.
2
6a
.
Lời giải
Chọn C
23
11
. .6 2
33
V Bh a a a
.
Câu 5: Tìm tnh
D
ca hàm s
2
3
log 4 3y x x
A.
2 2;1 3;2 2D
. B.
1;3D
.
C.
;1 3;D  
. D.
;2 2 2 2;D 
Lời giải
Chọn C
Trang 8
u kin:
2
3
4 3 0 .
1
x
xx
x
Vy
;1 3;D  
Câu 6: M 
A.
1
lndx x C
x

. B.
2
1
tan
cos
dx x C
x

.
C.
2
1
cot
sin
dx x C
x

. D.
cos sinxdx x C
.
Lời giải
Chọn B
T bn ta chB.
Câu 7: Cho kh có ding
2
3a
và khong cách ging
a
. Tính th tích
V
ca kh 
A.
3
3
.
2
Va
B.
3
3.Va
C.
3
.Va
D.
3
9.Va
Lờigiải
ChọnC
Ta có th tích
V
ca kh 
23
.3 3V a a a
.
Câu 8: Th tích ca khi nón có chiu cao bng
3
2
a
ng
2
a
là
A.
3
3
6
a
. B.
3
3
24
a
. C.
3
3
8
a
. D.
3
3
8
a
.
Lời giải
Chọn B
Th tích khi nón là:
2
3
1 3 3
3 2 2 24
a a a
V




.
Câu 9: Cho khi cu
S
có th tích là
288
. Hi din tích khi cu bng bao nhiêu?
A.
48S
. B.
72S
. C.
36S
. D.
144S
.
Lời giải
Chọn D
Th tích ca khi cu là
3
4
288
3
VR


6R
.
n tích khi c
2
4 144SR


.
Câu 10: Cho hàm s
y f x
nh, liên tc trên
và có bng bin thiên
Kh
A. Hàm s nghch bin trên
. B. Hàm s nghch bin trên khong
;0
.
C. Hàm s nghch bin trên khong
1; 
. D.Hàm s nghch bin trên khong
0;1
.
Lời giải
Chọn D
Trang 9
Da vào bng bin thiên ta thy
0
fx
trên khong
0;1
hàm s nghch bin trên
0;1
.
Câu 11: Vi
,ab
là s thc tùy ý khác
0
, ta có
2
log ab
bng:
A.
22
log logab
. B.
22
log .logab
. C.
2
logba
. D.
22
log logab
.
Lờigiải
ChọnA
Ta có:
2 2 2
log log log .ab a b
Câu 12: Hình tr có thit din qua trc là hình vuông cnh a thì có th tích bng:
A.
3
1
.
4
a
B.
3
1
.
3
a
C.
3
1
.
2
a
D.
3
.a
Lời giải.
Chọn A
Hình tr có thit din qua trc là hình vuông cnh a ng cao a 
2
a
nên có th
tích
3
1
.
4
Va
Câu 13: Giá tr ln nht ca hàm s
3
32y x x
n
0;2
bng
A.
4.
B.
2.
C.
9.
D.
3.
Lời giải
Chọn A.
Hàm s nh và liên tn
0;2
.
3
2
' 3 3
' 0 3 3 0
1 0;2
1 0;2
0 2, 1 4, 2 0.
yx
yx
x
x
y y y

Vy:
0;2
max 4y
c ti
1.x
Câu 14:  th ca hàm s ng cong trong hình bên?
.
A.
32
3y x x
. B.
32
3y x x
. C.
42
2y x x
. D.
42
2y x x
.
Lời giải
Chọn A
 th ta th  th ca hàm s bc 4
Loi C, D.
Khi
x 
thì
y 
0a
.
32
3y x x
.
Trang 10
Câu 15: Tng s ng tim cng và tim cn ngang c th hàm s
xx
y
x

2
1
1
là
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn B
Tnh:
1\D 
.
Ta có:
2
11
1
lim lim
1
xx
xx
y
x



;
2
11
1
lim lim
1
xx
xx
y
x



.
 th hàm s nhng thng
1x 
ng tim cng.
Li có:
2
1
lim lim 0
1
xx
xx
y
x
 


;
2
1
lim lim 2
1
xx
xx
y
x
 


.
  th hàm s nh ng thng
0y
 ng thng
2y
  ng tim cn
ngang.
Câu 16: Tp nghim ca b
44
log 1 log 2 5xx

là
A.
1;6
. B.
5
;6
2



. C.
;6
. D.
6;
.
Lời giải
Chọn B
Ta có
44
log 1 log 2 5xx

10
5
2 5 0 6
2
1 2 5
x
xx
xx

.
Vy tp nghim ca b
5
;6
2



.
Câu 17: Cho hàm s
y f x
 th i
S nghim c
2 3 0fx
là:
A.
4
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn A
Trang 11
Ta có
3
2 3 0
2
f x f x
. D th, nhn thng thng
3
2
y 
c th
hàm s
y f x
ti
4
m phân bi
4
nghim.
Câu 18: Cho hàm s
fx
liên t  n
0;3
và
2
0
d1f x x
,
3
2
d4f x x
. Tính
3
0
dI f x x
.
A.
5I
B.
3I 
C.
3I
D.
4I
Lờigiải
ChọnA
Ta có
3
0
dI f x x
=
23
02
d d 1 4 5f x x f x x

.
Câu 19: S phc liên hp ca s phc
31zi
là
A.
13zi
. B.
13zi
. C.
13zi
. D.
3zi
.
Lời giải
Chọn B.
Ta có
3 1 1 3z i i
S phc liên hp ca s phc
13zi
là
13zi
.
Câu 20: Cho s phc
3zi
. Phn thc ca s phc
21zi
bng
A.
6.
B.
7.
C.
3.
D.
2.
Lời giải
Chọn B
Ta có
2 1 2 3 1 7 3z i i i i
. Vy phn thc ca s phc
21zi
bng
7
.
Câu 21: Cho hai s phc
1
13zi
và
2
22zi
. a s phc
12
2z z z
là
A.
2
. B.
22
. C.
10
. D.
23
.
Lời giải
Chọn A
Ta có:
12
2 1 3 2( 2 2 ) 3z z z i i i
.
a s phc
12
2z z z
là:
2
2
3 1 10z
.
Câu 22: Trong không gian vi h trc to 
Oxyz
m
2;3;4A
,
8; 5;6B
. Hình chiu
vuông góc cm
I
cn
AB
trên mt phng
Oyz

A.
0; 1;5M
. B.
0;0;5Q
. C.
3;0;0P
. D.
3; 1;5N
.
Lời giải
Trang 12
Chọn A
To  m ca
AB
là
3; 1;5I
.
Suy ra hình chiu vuông góc cm
I
lên mt phng
Oyz
là
0; 1;5M
.
Câu 23: Trong không gian
Oxyz
, mt cu
S
có tâm
(1,1, 2)I
, tip xúc vi mt phng t
()Oxz
.
t cu
S
là:
A.
2 2 2
2 2 4 1 0x y z x y z
B.
2 2 2
2 2 4 5 0x y z x y z
C.
2 2 2
2 2 4 1 0x y z x y z
D.
2 2 2
2 2 4 5 0x y z x y z
Lời giải
Chọn B
t phng t
()Oxz
:
0y
Do mt cu
S
tip xúc vi mt phng t
()Oxz
2
1.0 1.1 2.0
;1
1
R d I Oxz

t cu
S
có tâm
(1,1, 2)I
và bán kính
1R
là:
2 2 2
1 1 2 1x y z
2 2 2
2 2 4 5 0x y z x y z
.
Câu 24: Trong không gian
Oxyz
, cho mt phng
: 2 1 0P x y z
thuộc
P
?
A.
1; 2;1M
. B.
2;1;1N
. C.
0; 3;2P
. D.
3;0; 4Q
.
Lời giải
Chọn B
Lt thay to  m
M
,
N
,
P
,
Q

P
, ta thy to  m
N
tho 
P
. m
N
thuc
P
. Ch B.
Câu 25: Trong không gian vi h t
Oxyz
, cho mt phng
:2 2 2017 0P x y z
, véc-
trong các véc-t véc-n ca
P
?
A.
2;2;1n 
. B.
4; 4;2n 
. C.
1; 2;2n 
. D.
1; 1;4n 
.
Lời giải
Chọn B
    ng quát ca mt phng suy ra vecto pháp tuyn ca
P
là
4; 4;2n 
.
Câu 26: Cho hình chóp
.S ABC
có
SA SB CB CA
, hình chiu vuông góc ca
lên mt phng
ABC
trùng v  m
I
ca cnh
AB
. Góc gi ng thng
SC
và mt phng
ABC
bng.
A.
0
45
. B.
0
90
. C.
0
60
. D.
0
30
.
I
C
B
A
S
Trang 13
Lời giải
ChọnA
Vì
SI ABC
suy ra
IC
là hình chiu ca
SC
lên mt phng
ABC
.
ng thng
SC
và mt phng
ABC
là góc gia
SC
và
IC
hay góc
SCI
.
Li có,
SAB CAB
suy ra
CI SI
, nên tam giác
SIC
vuông cân ti
I
.

0
45SCI
.
Vy góc ging thng
SC
và mt phng
ABC
bng
0
45
.
Câu 27: Cho hàm s
fx
, bng xét du ca
fx

x

1
1
2

fx
+
0
0
0
+
S m cc tr ca hàm s 
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn C
T bng xét du ta thy
fx
i du khi qua
1x 
và
2x
nên hàm s hai m
cc tr.
Câu 28: Giá tr ln nht ca hàm s
2
5y x x
bng
A.
0
. B.
5
2
. C.
6
. D.
2
.
Lời giải
Chọn B
Tnh
0;5D
.
Ta có
2
25
'
25
x
y
xx


;
' 0 2 5 0yx
5
2
x
Có
0 5 0yy
;
55
22
y



.
Vy
[0;5]
55
max
22
yy




.
Câu 29: Xét các số thực
a
và
b
thỏa mãn
3
1
3
27
9
log log 3
3
b
a



. Mệnh đề nào dưới đây đúng?
A.
1
2
18
ab
. B.
1
2
18
ab
. C.
1
2
18
ba
. D.
1
2
18
ab
.
Lời giải
Chọn A
3
1
3
27
9
log log 3
3
b
a



13
2
1
2
3
3
3
log 3 log 3
ba

11
2 2 .
33
ba
1
2
18
ab
.
Câu 30: S m c th hàm s
1
1
x
y
x
ng thng
2y
là
A.
1
. B.
2
. C.
4
. D.
6
.
Lời giải
Chọn A
Xét hàm s
1
1
x
y
x
:
\1D
Trang 14
2
2
';
( 1)
y x D
x
Ta có bng bin thiên ca hàm s
1
1
x
y
x
T  m ca
1
1
x
y
x
và
2y
m.
Câu 31: Tp nghim
c
2
22
log 2log 4 7 0xx
là
A.
S 
. B.
3;1S 
.
C.
2S
. D.
1
;2
8
S



.
Lời giải
Chọn B
u kin
0*x
Ta có
22
2 2 2 2
log 2log 4 7 0 log 2log 3 0x x x x
2
2
log 1
log 3
x
x

2
1
8
x
x
.
i chiu vu kin
*
c
1
2;
8
xx
.
Vp nghim là
1
;2
8
S



.
Câu 32: Cho tam giác
ABC
vuông ti
A

AB a
,
2BC a
. Quay tam giác
ABC
quanh trc
AB
c mt hình nón có th tích là
A.
3
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
4
3
a
.
Lời giải
Chọn A
Xét tam giác
ABC
vuông ti
A
, ta có:
2 2 2
AC BC AB
2
22
23a a a
3AC a
.
2
a
a
A
B
C
Trang 15
Th tích hình nón khi quay trc
AB
:
2
1
3
V R h
2
23
1
3.
3
a a a


vi
3R AC a
và
h AB a
.
Vy
3
Va
(đvtt).
Câu 33: Xét
2
sin
0
cos . d
x
x e x
, nt
sinux
thì
2
sin
0
cos . d
x
x e x
bng:
A.
1
0
2 e d
u
u
. B.
1
0
ed
u
u
. C.
1
2
0
ed
u
u
. D.
2
0
ed
u
u
.
Lời giải
Chọn B
t
sin d cos du x u x x
.
Vi
00xu
Vi
1
2
xu
Vy
1
2
sin
00
cos . d
xu
x e x e du

.
Câu 34: Din tích
ca hình phng gii hn b th các hàm s
yx
,
e
x
y
,
1x
và trc tung
c tính bi công th
A.
1
0
e 1 d
x
Sx
. B.
1
0
ed
x
S x x
.
C.
1
0
ed
x
S x x
. D.
1
1
ed
x
S x x

.
Lời giải
Chọn B
Din tích cn tìm là:
11
00
e d e d
xx
S x x x x

.
Câu 35: Cho hai s phc
1
24zi
và
2
1 3 .zi
Phn o ca s phc
12
z iz
bng
A.
5
. B.
3i
. C.
5i
. D.
3
.
Lời giải
Chọn D
Ta có:
2
2 2 2
1 3 1 3 1 3 3 3z i z i iz i i i i i
Suy ra
12
2 4 3 1 3z iz i i i
.
Vy phn o ca s phc
12
z iz
là
3
.
Câu 36: Kí hiu
12
,zz
là hai nghim phc c  
2
2 10 0zz
. Tính giá tr biu thc
22
12
A z z
.
A.
20A
. B.
10A
. C.
2 10A
. D.
16A
.
Lời giải
Chọn A.
2
2 10 0zz
13
1 3
zi
zi
Trang 16
2 2 2 2
12
1 3 1 3 20A z z i i
nên chn A.
Câu 37: Trong không gian
Oxyz
m
1; 2;1K
. Mt phng
P

K
và vuông góc vi
trc
Oy

A.
20y 
.
B.
10x
.
C.
20y 
.
D.
10z 
.
Lời giải
Chọn C
Trc
Oy
 là
0;1;0j
.
Vì
P
vuông góc vi trc
Oy
nên
P
nhn
j
là mn.
Suy ra
:0 1 2 0 1 0P x y z
hay
20y 
.
Vy
: 2 0Py
.
Câu 38: Trong không gian
Oxyz
m
1;0;1M
và
3;2; 1N
. Gi
H
là hình chiu vuông
góc ca
N
lên trc
Oz
ng thng
MH
 là
A.
1
0
12
xt
y
zt


. B.
1
0
12
xt
y
zt


. C.
1
12
xt
yt
zt

. D.
12
12
xt
yt
zt


.
Lời giải
Chọn B.
Vì
H
là hình chiu vuông góc ca
N
lên trc
Oz
nên
(0;0; 1)H
.
M ng thng
MH
là
(1;0;2)HM
.
Vy
1
( ): 0
12
xt
MH y
zt


.
Câu 39:  th t cho 20 bn hc sinh lt t s th t
1
n s th t
20
. Chn ngu nhiên
ba bn hc sinh t
20
bn h ba bc chn không có hai bn
 th t liên tip.
A.
799
1140
. B.
139
190
. C.
68
95
. D.
27
95
.
Lời giải
Chọn C
Gi
là không gian mu. S phn t ca không gian mu là
3
20
1140.nC

A

A


18 2.17 17.16 324nA

A
là
324 68
1 1 1 .
1140 95
nA
p A p A
n
Câu 40: Cho hình chóp
.S ABCD

ABCD
là hình ch nht,
,2AB a AD a
,
SA
vuông góc vi
mt ph
SA a
(tham kho hình v). Gi
M
m ca
CD
. Khong cách
ging thng
,SD BM
bng
Trang 17
A.
21
21
a
. B.
2 21
21
a
. C.
27
7
a
. D.
7
7
a
.
Lời giải
Chọn B
Gi
N
m ca
AB

//BM DN
nên
//BM SDN
; ; ; ;d BM SD d BM SDN d B SDN d A SDN
.
K
AH DN
ti
H
. Ta có mt phng
SAH SDN
. Trong
mp SAH
k
AK SH
ti
K

;;d BM SD d A SDN AK
.
2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 4 1 1 21
44AK AH SA AN AD SA a a a a
. Suy ra
2 21
21
a
AK
.
Câu 41: Tng tt c các giá tr nguyên ca tham s
10;10m
 hàm s
21xm
y
xm

nghch bin
trên
1;5
.
A.
30
. B.
4
. C.
36
. D.
45
.
Lời giải
Chọn C
Tnh
\Dm
.
Ta có
2
31
' ,
m
y x D
xm

Hàm s ng bin trên
1;5
khi và ch khi hàm s nh trên
1;5
và
' 0 x 1;5y
Trang 18
1
1
1;5
1
5
3
3 1 0
1
5
3
m
m
m
m
m
m
m




Mà
m
nguyên và
10;10m
nên
1;5;6;7;8;9m
.
ng các giá tr ca
m
th bài là 36.
Câu 42: Dân s th gic d c
.e
Nr
SA

A
: là dân s cy làm
mc tính,
S
là dân s sau
N

r
là t l   Theo s liu thc t, dân s
th gi
1950
là
2560
trii; dân s th gi
1980
là
3040
trii. Hãy d
 th gi
2020
?
A.
3823
triu. B.
5360
triu. C.
3954
triu. D.
4017
triu.
Lời giải
Chọn A
Ta có:
1950. 6
61980.
1950 . 2560.10
1980 . 3040.10
r
r
S Ae
S Ae


Suy ra:
0
30
3
304 19
256 16
rr
ee
và
6
1950
2560.10
r
A
e
Vy:
2020
70
2020. 66
1950
6
2560.10 .
2020 . 2560.10 . 3823.10
r
rr
r
e
S Ae e
e
.
Câu 43: Cho hàm s
32
y ax bx cx d
 th  bên. M i

A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải
Chọn A
Do nhánh cui c th 
0a
.
Ta có
2
32y ax bx c
. Do cc tiu ca hàm s thuc trc tung và có giá tr âm nên
0d
và
0x
là nghim c
00yc
. Li có
2
0
2
3 2 0 0 0, 0
2
3
3
x
b
ax bx a b
b
a
x
a


.
Trang 19
Câu 44: Khi ct khi tr
T
bi mt mt phng song song vi trc và cách trc ca tr
T
mt
khong bng
3a
c thit din là hình vuông có din tích bng
2
4a
. Tính th tích
V
ca
khi tr
T
.
A.
3
77Va
. B.
3
77
3
Va
. C.
3
8
3
Va
. D.
3
8Va
.
Lời giải
Chọn D
Thit din là hình vuông
ABCD
.
2
42
ABCD
S a AD CD a
Gi
H
  m
CD
3OH CD OH ABCD OH a
2 2 2 2
32OD DH OH a a a
.
23
2 , 2 8h AD a r OD a V r h a

.
Câu 45: Cho hàm s
fx
có
27
28
f



và
2
12sin2 .cos 3 ,f x x x x

0
df x x
bng
A.
27
64
. B.
87
64
. C.
0
. D.
87
64
.
Lơ
i gia
i
Chọn C
Ta có
2
12sin2 .cos 3 ,f x x x x
nên
fx
là mt nguyên hàm ca
fx
.
Có
2
1 cos6
d 12sin 2 .cos 3 d 12.sin 2 . d 6.sin 2 d 6sin 2 .cos6 d
2
x
f x x x x x x x x x x x x
33
6 sin 2 d 3 sin8 sin 4 d 3cos2 cos8 cos4
84
x x x x x x x x C

.
Suy ra
33
3cos2 cos8 cos4
84
f x x x x C
. Mà
27
0
28
fC



.

00
0
3 3 3 3 3
d 3cos2 cos8 cos4 d sin2 sin8 sin4 0
8 4 2 64 16
f x x x x x x x x x


Câu 46: Cho hàm s
fx
có bng bi
Trang 20
S nghim thun
0;3
c
sin 1fx
là
A.
2
. B.
4
. C.
6
. D.
8
.
Lơ
i gia
i
ChọnC
Ta có
sin 1
sin 1
sin 1
fx
fx
fx


T bng bic
1
22
3
sin ; 1 ( )
sin 1 sin 1;0 sin 1;0 (1)
sin 1; ( )
x t VN
f x x t x t
x t VN


.
Dm nn
0;3
.
4
55
6
sin ; 1 ( )
sin 1 sin 0;1 sin 0;1 (2)
sin 1; ( )
x t VN
f x x t x t
x t VN


.
Dm nn
0;3
.
Vu có tt c 6 nghim.
Câu 47: Cho hai s th
a
và
b
tha mãn
81
4 .2
ab a b
ab
ab
. Giá tr ln nht ca biu thc
2
2P ab ab
bng
A.
3
. B.
1
. C.
51
2
. D.
3
17
.
Lời giải
Chọn B
T gi thit suy ra
10ab
.
81
4 .2
ab a b
ab
ab
2
81
.2
2
ab
ab
ab
ab
22
.2 2 2 .2
a b ab
a b ab

(1).
Xét hàm s
.2
t
f t t
vi
0;tD 
. D thy hàm s
ft
liên tc trên
D
và
2 .2 .ln2 0,
tt
f t t t D
suy ra
ft
là hàm s ng bin trên
D
.
(1)
22a b ab
1 2 2a b b
(2). T (2), suy ra
2 0 2bb
.
c
2
2
2 1 2 2P ab ab ba b b b
.
Theo bng thc Cô c
2
2
21
2
bb
P b b




.
Trang 21
Vy
max 1P
c khi và ch khi
1
3
1
a
b
.
Câu 48: Cho hàm s
( )
32
3f x x x m= - +
. Gi
S
là tp hp tt c các giá tr ca
m
sao cho
1;3
1;3
max 2minf x f x
. S phn t ca
S
là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn A
Ta có
2
36f x x x

,
0
0
2
x
fx
x

Ta có bng bin thiên ca
( )
32
3f x x x m= - +
trên
1;3
TH1:
4 0 0 4m m m

1;3
1;3
min 0 max 0f x f x
(vô lí)
TH2:
0m
, ta có:
[ ]
( )
[ ]
( )
1;3
1;3
min ,max 4 4f x m m f x m m= = - = - = -

4 2 4 2 4m m m m m
. Vy
4m 
TH3:
4 0 4mm- > Û >
, ta có:
[ ]
( )
[ ]
( )
1;3
1;3
min 4 4,maxf x m m f x m m= - = - = =
.

2 4 2 4 8m m m m m
. Vy
8m
Câu 49: 
.ABC AB C
. Gi
M
,
N
,
P
lm thuc các cnh
AA
,
BB
,
CC
sao cho
2AM MA
,
2NB NB
,
PC PC
. Gi
1
V
,
2
V
lt là th tích ca hai khi
n
ABCMNP
và
ABC MNP
. Tính t s
1
2
V
V
.
A.
1
2
2
V
V
B.
1
2
1
2
V
V
C.
1
2
1
V
V
D.
1
2
2
3
V
V
Lời giải
Chọn C
Trang 22
Gi
V
là th tích kh
.ABC A B C
. Ta có
1 . .M ABC M BCPN
V V V
.
.
1 1 2 2
. , . . ,
3 3 3 9
M ABC ABC ABC
V S d M ABC S d A ABC V
.
.
1 1 1 1
. , . . ,
3 3 3 9
M A B C A B C A B C
V S d M A B C S d M A B C V
.
Do
BCCB

là hình bình hành và
2NB NB
,
PC PC
nên
7
5
B C PN BCPN
SS

.
Suy ra
..
7
5
M B C PN M BCPN
VV

, T 
. . . .M ABC M BCPN M A B C M B C PN
V V V V V
. . .
2 1 7 5
9 9 5 18
M BCPN M BCPN M BCPN
V V V V V V V
.
y
12
2 5 1 1
9 18 2 2
V V V V V V
. Bi vy:
1
2
1
V
V
.
Câu 50: Cho
0 2020x
và
2
log (2 2) 3 8
y
x x y
.Có bao nhiêu cp s
( ; )xy
nguyên tha mãn
u kin trên?
A. 2019. B. 2018. C. 1. D.4.
Lời giải
Chọn D
Do
0 2020x
nên
2
log (2 2)x
luôn .
Ta có
2
log (2 2) 3 8
y
x x y
3
2
log ( 1) 1 3 2
y
x x y
2
log ( 1)
3
2
log ( 1) 2 3 2
x
y
xy
(1)
Xét hàm s
( ) 2
t
f t t
.
Tnh
D
và
( ) 1 2 ln2
t
ft

( ) 0ft
t
.
Suy ra hàm s
()ft
ng bin trên

2
(1) log ( 1) 3xy
8
log ( 1)yx
.
Ta có
0 2020x
nên
1 1 2021x
suy ra
8 8 8
0 log ( 1) log 2021 0 log 2021xy
.
Vì
y
nên
0;1;2;3y
.
Vy có 4 cp s
( ; )xy
nguyên tha yêu cu bài toán là các cp
(0;0)
,
(7;1)
,
(63;2)
,
(511;3)
.
P
C
B
A'
C'
B'
A
M
N
Trang 23
www.thuvienhoclieu.com
ĐỀ 12
PHÁT TRIỂN TỪ ĐỀ MINH
HỌA LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1:(NB) Có bao nhiêu cách chn 2 hc sinh nam t mt t gm 5 nam và 6 n ?
A.
2
5
.
C
B.
2
11
.
C
C.
2
6
.
C
D.
2
5.
Câu 2:(NB) S hng th
n
ca cp s cng là
23
n
un
. Tng ca s hng th nht và th hai bng:
A.
B.
1.
C.
0.
D.
2.
Câu 3:(NB) Tìm tp nghim c
2
1
28
x
.
A.
3;3
B.
3;2
C.
2;2
D.
2;3
Câu 4:(NB) Cho kh có di
2
3a
,th tích là
3
12a
. Tính chiu cao ca kh

A.
12ha
B.
5
36ha
C.
3
36ha
D.
4ha
Câu 5:(NB) Hàm s
2
3
5
xx
y
o hàm là
A.
2
3
2 3 5 .ln5
xx
x
B.
2
3
5 ln5.
xx
C.
2
3
2 3 5 .
xx
x
D.
2
2 3 1
3 5 .
xx
xx

Câu 6:(NB). Gi S là din tích ca hình phng gii hn b th ca hàm s
y f x
liên tc trên
;ab
, trng thng
,x a x b
. M 
A.
.
b
a
S f x dx
B.
.
b
a
S f x dx
C.
0
0
.
b
a
S f x dx f x dx

D.
0
0
.
b
a
S f x dx f x dx

Câu7:(NB)   dài tt c các cnh bng
3
. Th tích kh ng
A.
93
4
. B.
27 3
4
. C.
27 3
2
. D.
93
2
.
Câu8:(NB) Cho kh
3r
và chiu cao
4h
. Tính th tích
V
ca kh
cho.
A.
16 3V
. B.
12V
. C.
4V
. D.
4V
.
Câu 9:(NB). 


 . 




:
A.
3
4VR
. B.
3
4
3
VR
. C.
3
1
3
VR
. D.
2
4
3
VR
.
Câu 10:(NB) Cho hàm s
fx
có bng bi
x

1

()fx
()fx

2
2

Hàm s ng bin trên kho
A.
; 1 .
B.
2; . 
C.
;2 .
D.
; 1 1; .
Câu 11:(NB) 





2
2
y log x 2x 3
A.
D 1;3
B.
D ; 1 3; 
R
Trang 24
C.
D 1;3
D.
D ; 1 3;  
Câu12:(NB) Khi tr 
2a
, chiu cao là
2ha
có th tích là:
A.
3
Va
. B.
2
2V a h
. C.
2
2Va
. D.
3
2Va
.
Câu 13:(NB).Cho hàm s
fx
có bng bi
Hàm s t cc tiu ti
A.
2.x
B.
1.x
C.
1.x 
D.
3.x 
Câu 14:(TH)  th  th ca hàm s 
A. y = x
3
+ 3x
2
x 1
B. y = - x
3
2x
2
+ x 2
C. y = - x
3
+ 3x + 1
D. y = x
3
+ 3x
2
x 1
Câu 15:(NB) Tim cng c th ca hàm s là
A. x = - 1 B. x = 1 C. x = 2 D.
1
.
2
x
Câu 16:(NB) Nghim ca b
2
1
5
log 5 7 0xx
là
A.
2.x
B.
2x
hoc
3x
.
C.
23x
.
D.
3x
.
Câu 17:(TH) Cho hàm s
y f x
 nh,
liên tc trên R và có bng bi   
bên. S nghim ca p
3fx
là:
A. 1 B. 2 C. Vô nghim D. 3
Câu 18:(NB) Cho
5
2
10f x dx

2
5
24f x dx


bng:
A.
32.
B.
34.
C.
36.
D.
40.
Câu 19:(NB) Cho s phc
67zi
. S phc
z
m biu din trên h trc t Oxy là:
A.
6; 7
B.
6;7
C.
6; 7
D.
6;7
Câu 20:(NB) Tìm s phc liên hp ca s phc
2 3 3 2z i i
.
A.
12 5zi
. B.
12 5zi
. C.
12 5zi
. D.
12 5zi
.
Câu 21:(NB) Phn o ca s phc
23zi
là:
A.
3i
. B.
3
. C.
3
. D.
3i
.
1
22
x
y
x
-1
-1
1
3
1
y
x
O
Trang 25
Câu22:(TH)Trong không gian vi h trc ta 
Oxyz
 m thuc trc
Ox
    m
4;2; 1A
và
2;1;0B
là
A.
4;0;0M
. B.
5;0;0M
. C.
4;0;0M
. D.
5;0;0M
.
Câu 23:(NB) Trong không gian vi h t , cho mt cu . Tìm
t tâm và bán kính ca
A. và . B. và .
C. và . D. và .
Câu 24:(NB) c mt phng ?
A.
2; 1;3Q 
B.
2;3;1M
C.
1;2;3P
D.
2;1;3N
Câu 25:(NB) Cho hình chóp  , và . Tính
góc gia và .
A.
0
30
B.
0
45
C.
0
60
D.
0
90
Câu 26:(TH)ng thng
12
:
2 1 3
x y z
d


 dài c 
u
bng:
A.
6.
B.
14.
C.
14.
D.
6.
Câu 27:(TH) S m cc tiu ca hàm s
42
1
21
4
y x x
là:
A.
B.
2.
C.
3.
D.
0.
Câu 28:(TH) Hiu ca giá tr ln nht và giá tr nh nht ca hàm s
1
2
x
fx
x
n
3;5
là:
A.
5 3 .ff
B.
2.
C.
6.
D.
5 3 .ff
Câu 29:(TH) Cho a và b là hai s tha mãn
2
8.ab
Giá tr ca
2
22
4log logab
bng
A.
16.
B.
4.
C.
6.
D.
8.
Câu 30:(TH) Cho hàm s f(x) có bng bi
S nghim thc c
2 3 0fx
là
A.
2.
B.
C.
4.
D.
3.
Câu 31:(TH) 
2
3
log 4 9 2xx
là:
A.
;0 4; 
B.
0; 4
C.
0;4
D.
;0 4; 
Câu 32:(TH) Thit din qua trc ca mt hình nón là mt tam giác vuông cân có cnh huyn là
23
.
Th tích ca khi nón này bng:
Oxyz
2 2 2
: 1 2 1 9S x y z
I
R
S
1;2;1I
3R
1; 2; 1I 
3R
1;2;1I
9R
1; 2; 1I 
9R
: 2 3 0x y z
.S ABCD
a
SA ABCD
6
3
SA a
SC
ABCD
Trang 26
A.
3
. B.
32
. C.
3
. D.
33
.
Câu 33:(TH) Cho hàm s n [-1;2], f(-1) = -2 và f(2) = 1. Tính
2
1
'( )I f x dx
.
A. -3 B. 3 C. -1 D. 1
Câu 34:(TH) Din tích hình phng gii hn b th ca hàm s
3
yx
, trng thng
1, 2xx
bng:
A.
17
4
. B.
17
5
. C.
16
3
. D.
15
4
.
Câu 35:(TH) Cho hai s phc
1
12 zi
,
2
12 zi
. Giá tr ca biu thc
22
12
zz
bng:
A.
10
. B.
10
. C.
6
. D.
4
.
Câu 36:(TH) Tìm tng phn thc và phn o ca s phc
22
12
w z z
bit
1
z
,
2
z
là hai nghim phc ca

2
4 5 0zz
.
A.
4
. B.
6
. C.
8
. D.
5
.
Câu37:(TH) Trong không gian t 
Oxyz
, cho mt cu
S
 ng kính
AB
, vi
6;2; 5A
,
4;0;7B
. Vimt phng
P
tip xúc vi mt cu
S
ti
A
.
A.
 P x y z
. B.
P x y z
.
C.
P x y z
. D.
:5 6 62 0 P x y z
.
Câu 38:(TH) Trong không gian vi h t ng thng và
. Gi s sao cho n vuông góc chung cng
thng và . Tính
A.
5; 5;10MN 
. B.
2; 2;4MN 
. C.
3; 3;6MN 
. D.
1; 1;2MN 
.
Câu 39:(VD)Mt nhóm hc sinh c gm 7 hc sinh lp 10 và 4 hc sinh lp
ng thành m chp bc m sau bui l nhng k thi Olympic
t khi các hc sinh lng cnh nhau?
A.
7
.
33
B.
11
.
630
C.
1
.
5940
D.
1
.
105
Câu 40:(VD)S.ABC aG ABC.
SA (ABC) 
0
60
GC và SA

A.
5
5
a
B.
5
a
C.
5
10
a
D.
2
5
a
Câu 41:(VD)m 
2
3
x
y
xm

;6
?
A. 1 B. 3 C. 0 D. 2
Câu 42.(VD)Sau mt tháng thi công thì công trình xây dng Nhà hc th dc ca mc
hic mt khng công vic. Nu vn tip tc vi ti vy thì d ki
23 tháng na công trình s  sm hoàn thành công trình và k dng,
công ty xây dng quynh t tháng th hai, mng công vic so vi
tháng k c. Hi công trình s hoàn thành tháng th my sau khi khi công?
Oxyz
1
4 1 5
:
3 1 2
x y z

2
23
:
1 3 1
x y z
12
, MN
MN
1
2
.MN
uuur
Trang 27
A. 19. B.18. C. 17. D. 20.
Câu 43:(VD) Cho hàm s
()y f x
liên tc trên R,
(2) 3f

th  bên.Có bao nhiêu s nguyên
( 20;20)m
 
trình
3f x m
có 4 nghim thc phân bit.
A. 2 B. 18
C. 4. D. 19.
Câu 44:(VD)Mt bn hình tr a dm ngang, có
chiu dài bi np bt trên mt nm
ngang ca mt trdu trong bng vi 0,5 m
c tích gt ca khi du còn li trong b m
3
)
A.12,637m
3
. B.11,923 m
3
. C.11,781 m
3
D.
3
8,307m
.
Câu45:(VD)Cho
2
1
d2f x x
. Tính
4
1
d
fx
Ix
x
bng
A.
1I
. B.
2I
. C.
4I
. D.
1
2
I
.
Câu 46:(VDC) Cho hàm s  th . Xét hàm s
. M 
A. B.
C. D.
Câu47:(VDC) Có tt c bao nhiêu cp s nguyên chn
;xy
tha mãn
2 3 55
xy
?
A.
8
. B.
2
. C.
16
. D.
1
.
Câu 48. (VDC) Cho hàm s
()y f x
nghch bin trên
và tha mãn
6 4 2
( ) ( ) 3 2 ,f x x f x x x x x
. Gi M và m lt là giá tr ln nht và giá tr nh
nht ca hàm s
()y f x
n
1;2
. Giá tr ca
3Mm
bng:
A.
4.
B.
28.
C.
3.
D.
33.
Câu 49 :(VDC)   u cnh bng a, hình
chiu vuông góc cm BC. Bit khong cách ging
3
4
a
.
Tính th tích khi lng tr 
A.
3
33
8
a
V
B.
3
32
8
a
V
C.
3
3
8
a
V
D.
3
33
6
a
V
Câu 50: (VDC)   
2
2 2 2
2
log 2 2 2 2
y
x x y x x
. Có bao nhiêu cp s nguyên

; , 0 500x y x
th cho ?
A.
4.
B.
2.
C.
3.
D.
1.
Hết
y f x
'y f x
32
1 3 3
2018
3 4 2
g x f x x x x
3;1
ming x g 1

3;1
ming x g 1
3;1
ming x g 3

3;1
g 3 g 1
ming x
2

Trang 28
www.thuvienhoclieu.com
ĐỀ 13
PHÁT TRIỂN TỪ ĐỀ MINH
HỌA LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Bn An có 2 loi sách truyn truyn tranh và 5 quyn truyn ngn. Bn An
chn ngu nhiên 1 quy c. Hi bn An có my cách chn?
A. . B. . C. . D. .
Câu 2: Cho cp s nhân vi và . Công bi ca cp s ng
A. . B. . C. . D. .
Câu 3: là
A. . B. . C. . D. .
Câu 4: Th tích ca khi hp ch nhc có công thc là
A. B. C. D.
Câu 5: Cho . Hi khsai?
A. Hàm s có tnh là .
B. Hàm s o hàm .
C.  th hàm s nm phía trên trc hoành.
D.  th hàm s nhn trc Oy làm tim cn ngang.
Câu 6: H nguyên hàm ca hàm s là
A. . B. . C. . D. .
Câu 7: Cho khcnh , chiu cao bng . Th tích ca kh
là
A. . B. . C. . D. .
Câu 8:  ng sinh T s gia din tích xung quanh và
dia hình nón bng
A. B. C. D.
Câu 9: Cho mt cu có bán kính . Th tích ca khi cu có công thc là
A. B. C. D.
Câu 10: Cho hàm s có bng bi
2
15
50
5
n
u
4
3u
5
1u
2
2
1
3
3
log 1 2 1x
9
2
x 
9
2
x
11
2
x
11
2
x 
a,b,c
abc++
2 2 2
abc
abc
3 3 3
abc
x
y a (0 a 1)
x
y a lna
2
sin 6f x x x
3
cos 2x x C
3
cos 2x x C
3
cos 6x x C
cosxC
a
2a
3
4a
3
2
3
a
3
2a
3
4
3
a
,r
.
.
r
2
.
r
.
r
2
.
r
R
2
4
V R .
3
4
V R .
3
4
3
V R .
2
4
3
V R .
y f x
Trang 29
Hàm s nghch bin trên kho
A. B. C. D.
Câu 11: Vi s thc
a

4
3
log a
bng:
A.
3
4 log a
B.
3
4log a
C.
3
4
log
3
a
D.
3
log 4a
Câu 12: Th tích ca khi tr tròn xoay có chiu cao
a

a
bng
A.
3
1
3
a
B.
3
a
C.
3
2 a
D.
3
3 a
Câu 13: Cho hàm s
y f x
có bng bi
x

1
2

'fx
+ 0
0 +
fx

4
3

Giá tr cc tiu ca hàm s ng
A.
1
B.
3
C.
2
D.
4
Câu 14:  th ca hàm s ng cong trong hình bên?
A.
42
2y x x
B.
42
2y x x
C.
32
3y x x
D.
32
3y x x
Câu 15: Tim cng c th hàm s
22
1
x
y
x
là
A.
2y
B.
1x 
C.
1y 
D.
2x 
Câu 16: Tp nghim ca b
28
x
là
A.
;3
B.
4;
C.
3; 
D.
0;
Câu 17: Cho hàm s
y f x
 th trong hình bên.
y f x
10 ;
1 ;
01;
11 ;
Trang 30
S nghim c
20fx
là
A.
0
B.
2
C.
3
D.
4
Câu 18: Nu
3
1
3f x dx 
và
4
3
1f x dx
thì
4
1
f x dx
bng
A.
3
B.
2
C.
4
D.
1
Câu 19: a s phc
32zi
bng
A.
1z
B.
13z
C.
13z
D.
5z
Câu 20: Cho hai s phc
1
12zi
và
2
3zi
. Phn o ca s phc
12
2zz
bng
A.
5
B.
3
C.
2
D.
4
Câu 21. Cho hai s phc
1
2 zi
và
2
1zi
. Trên mt phng t m biu din s phc
12
2 zz
có t là
A.
3; 3
B.
2; 3
C.
3; 3
D.
3; 2
Câu 22. Trong không gian Oxyz, hình chiu vuông góc cm
2;1; 1M
trên trc Oz có t là.
A.
2;1;0 .
B.
0;0; 1 .
C.
2;0;0 .
D.
0;1;0 .
Câu 23. Trong không gian Oxyz, cho mt cu
2 2 2
: 2 2 7 0.S x y z x z
Bán kính ca mt cu
ng
A.
7.
B. 9.. C. 3. D.
15.
Câu 24: 
Oxyz

: 3 2 6 0x y z
. Vecto nào
không phải 
?
A.
2;6;4n 
. B.
1; 3; 2n
. C.
1;3;2n 
. D.
1;3;2n
.
Câu 25: Oxyz, 
d

13
2
2
xt
y
zt



A.
1; 0; 2 .d

B.
6; 0; 4 .a
C.
3; 2; 2 .b
D.
1; 2; 2 .c
Câu 26. Cho hình chóp S.ABC có SA vuông góc vi mt phng
,ABC
2,SA a
tam giác ABC vuông ti
B,
3AB a
và
BC a
(minh h bên). Góc ging thng SC và mt phng
ABC
bng
A.
90 .
B.
45 .
C.
30 .
D.
60 .
Trang 31
Câu 27 : Cho hàm s
y f x
liên tc trên
và có bng xét xét du c
Hàm s c tr ?
A.
1.
B. 2. C. 3. D. 4.
Câu 28. Giá tr ln nht ca hàm s
3
32f x x x
n
3;3
là
A.
16.
B. 20. C. 0. D. 4.
Câu 29. Cho a và b là hai s tha mãn
4
16.ab
Giá tr ca
22
4log logab
bng
A. 4. B. 2. C. 16. D. 8.
Câu 30. Tìm s m c th hàm s y = x
3
3x
2
+ 3x  th hàm s y = x
2
x 1
A. 1. B. 2. C. 3. D. 4.
Câu 31: Tp nghim ca b
22
log log 8xx
là:
A.
8;S
B.
;4S 
C.
4;8S
D.
0;4S
Câu 32: Mt cu
S
có din tích bng
20
, th tích khi cu
S
bng
A.
20 5
3
B.
20 5
C.
20
3
D.
45
3
Câu 33. Cho hàm s
fx
liên tc trên
và
8
2
( ) 10f x dx
. Tính
3
1
3
(3 1)
2
I f x dx
A. 30 B. 10 C. 20 D. 5
Câu 34. 

y f x





. 






A.
dd
bc
ab
f x x f x x

. B.
dd
bc
ab
f x x f x x

.
C.
dd
bc
ab
f x x f x x

. D.
dd
bb
ac
f x x f x x

.
Câu 35. Tìm s phc liên hp ca s phc
(3 1)z i i
A.
3zi
B.
3zi
C.
3zi
D.
3zi
Câu 36: Gi
0
z
là nghim phc có phn 
2
4 4 37 0zz
. Trên mt phng
tm biu din ca s phc
0
w iz
?
O
x
y
c
b
a
y f x
Trang 32
A.
2
1
3;
2
M



B.
3
1
3;
2
M



C.
4
1
3;
2
M



D.
1
1
3;
2
M




Câu 37. Vit phm
0; 1;2A
, song song vi trc Ox và vuông góc
vi mt phng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0 B. (P) : y + z - 1 = 0 C. (P) : y - z + 3 = 0 D. (P) : 2x + z - 2 = 0
Câu 38: Trong không gian
Oxyz
m
1;2;2M
ng th
M
và song song vi trc
Oy

A.
1
2
2
x
yt
zt



B.
1
2
2
xt
yt
z

C.
1
2
2
xt
yt
zt


D.
1
2
2
x
y t t
z

Câu 39: Chn ngu nhiên 5 hc sinh trong mt lp hc gm 25 nam và 20 n. Gi
A
là bin c
5 hc chn có ít nht 1 hc sinh nt ca bin c
A
là:
A.
5
20
5
45
C
PA
C
B.
4
25
5
45
20.C
PA
C
C.
4
44
5
45
20.C
PA
C
D.
5
25
5
45
1
C
PA
C

Câu 40: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh bng
a
. Hai mt phng
SAB
và
SAC
cùng vuông góc v  
khong cách ging thng
SA
và
BC
?
A.
2a
B.
a
C.
2
2
a
D.
2
a
Câu 41. Tìm giá tr thc ln nht ca tham s  hàm s
32
y x 3mx x
ng bin trên
.
A.
1.
B.
1
.
3
C.
1
.
3
D.
2.
Câu 42. Dân s th gic tính theo công thc
r.N
S A.e
 cy mc tính,
S là dân s  l  h vit nam có khong
i và t l  hu t l  hi
n nc ta có khong 120 trii?
A. 2020. B. 2024. C. 2026. D. 2022.
Câu 43. Cho hàm s
ax 1
y
bx c
 th  bên. Tính tng
S a b c.
Trang 33
A.
S 2.
B.
S 0.
C.
S 1.
D.
S 3.
Câu 44: Cho hình tr t mt phng không
vuông góc v   t hai m       
AB,A 'B'
mà
AB A'B' 6cm
(hình v). Bit din tích t giác
ABB'A'
bng 60 cm
2
. Tính chiu cao ca hình tr 
A.
62
cm. B.
43
cm.
C.
82
cm. D.
53
cm.
Câu 45: 
y f(x)


f(0) 1
và
2
f (x) x 1
f '(x).e 2x, x 0;1 .


1
0
f(x)dx.
A.
2.
B.
4
.
3
C.
4
.
3
D.
2
Câu 46. Cho hàm s
y f(x)
liên tc trên
 th :
Có bao nhiêu giá tr nguyên ca tham s  
2
3sinx cosx 1
f f m 4m 4 (1)
2cosx sinx 4



có nghim?
A. 1. B. 2. C. 3. D. 4.
Trang 34
Câu 47. Cho hai s thi tha mãn
22
x 4y 1.
Tìm giá tr ln nht ca biu thc
22
P log (x 2y).log (2x 4y).
A.
1
.
4
B.
1
.
2
C.
1
.
3
D.
1
.
6
Câu 48. Tìm tt c giá tr thc ca tham s  giá tr ln nht ca hàm s
3
y x 3x 2m 1
trên
n
0;2
t giá tr nh nht. Giá tr ca m thuc khong nào?
A.
3
; 1 .
2




B.
2
;2 .
3



C.
1;0 .
D.
0;1 .
Câu 49. Cho hình lnh a. Gi M, N lm ca các cnh
t phng (DMN) chia hình l thành hai phn. Gi
1
V
là th tích ca phn cha
nh A,
2
V
là th tích ca phn còn li. Tính t s
1
2
V
.
V
A.
55
.
89
B.
37
.
48
C.
1
.
2
D.
2
.
3
Câu 50.
2
2 y 2 2
2
log (2x 2x 2) 2 y x x.
Hi có bao nhiêu cp s 
(x,y), (0<x<500) th
A. 1. B. 2. C. 3. D. 4.
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
1-B
2-C
3-A
4-C
5-D
6-A
7-B
8-C
9-C
10-A
11-B
12-B
13-B
14-A
15-B
16-C
17-C
18-B
19-B
20-D
21-C
22-B
23-C
24-D
25-B
26-B
27-D
28-B
29-A
30-B
31-C
32-A
33-D
34-A
35-D
36-D
37-B
38-D
39-D
40-B
41-B
42-C
43-A
44-A
45-B
46-C
47-A
48-D
49-A
50-D
Câu 1: Bn An có 2 loi sách truyn truyn tranh và 5 quyn truyn ngn. Bn An
chn ngu nhiên 1 quy c. Hi bn An có my cách chn?
A. . B. . C. . D. .
Giải
Chn 1 quyn truyn tranh t 10 quyn truyn tranh có 10 cách chn.
Chn 1 quyn truyn ngn t 5 quyn truyn ngn có 5 cách chn.
Áp dng quy tc cng có: cách chn.
Đáp án B
Câu 2: Cho cp s nhân vi và . Công bi ca cp s ng
A. . B. . C. . D. .
Giải
Công bi ca cp s nhân là .
Đáp án C
Câu 3: là
A. . B. . C. . D. .
Giải
2
15
50
5
10 5 15+=
n
u
4
3u
5
1u
2
2
1
3
3
5
4
1
3
u
q
u

log 1 2 1x
9
2
x 
9
2
x
11
2
x
11
2
x 
Trang 35
Ta có .
Đáp án A
Câu 4: Th tích ca khi hp ch nhc có công thc là
A. B. C. D.
Giải
Công thc tính th tích khi hp ch nht là:
Đáp án C
Câu 5: Cho . Hi khsai?
A. Hàm s có tnh là .
B. Hàm s o hàm .
C.  th hàm s nm phía trên trc hoành.
D.  th hàm s nhn trc Oy làm tim cn ngang.
Giải
 th hàm s nhn trục Ox làm tim cn ngang
Đáp án D
Câu 6: H nguyên hàm ca hàm s là
A. . B. . C. . D. .
Giải
.
Đáp án A
Câu 7: Cho khnh , chiu cao bng . Th tích ca kh
là
A. . B. . C. . D. .
Giải
Din tích hình vuông:
Th tích khi chóp là: 
Đáp án B
Câu 8:  ng sinh T s gia din tích xung quanh và
dia hình nón bng
A. B. C. D.
Giải
Ta có
Đáp án C
Câu 9: Cho mt cu có bán kính . Th tích ca khi cu có công thc là
A. B. C. D.
Giải
Th tích ca khi cu có công thc là:
Đáp án C
Câu 10: Cho hàm s có bng bi
log 1 2 1x
1 2 10x
9
2
x
a,b,c
abc++
2 2 2
abc
abc
3 3 3
abc
V abc=
x
y a (0 a 1)
x
y a lna
x
y a (0 a 1)
2
sin 6f x x x
3
cos 2x x C
3
cos 2x x C
3
cos 6x x C
cosxC
3
23
sin 6 cos 6. cos 2
3
x
f x dx x x dx x C x x C

a
2a
3
4a
3
2
3
a
3
2a
3
4
3
a
2
Sa
3
2
1 1 2
. .2
3 3 3
a
V B h a a
,r
.
.
r
2
.
r
.
r
2
.
r
xq
xq
2
2
day
day
.
Sr
S
r
S r r
Sr

R
2
4
V R .
3
4
V R .
3
4
3
V R .
2
4
3
V R .
3
4
3
V R .
y f x
Trang 36
Hàm s nghch bin trên kho
A. . B. . C. . D. .
Giải
T bng bin thiên ta có hàm s nghch bin trên khong .
Đáp án A
Câu 11: Vi s thc
a

4
3
log a
bng:
A.
3
4 log a
B.
3
4log a
C.
3
4
log
3
a
D.
3
log 4a
Gii
Lý thuyt: Cho hai s 
, ;b 1ab
. Vi mi
, ta có:
log log .
bb
aa
Áp dng:
4
33
log 4log .aa

Câu 12: Th tích ca khi tr tròn xoay có chiu cao
a

a
bng
A.
3
1
3
a
B.
3
a
C.
3
2 a
D.
3
3 a
Gii
Th tích ca khi tr tròn xoay có chiu cao
a

a
bng
2 2 3
.V r h a a a

Câu 13: Cho hàm s
y f x
có bng bi
x

1
2

'fx
+ 0
0 +
fx

4
3

Giá tr cc tiu ca hàm s ng
A.
1
B.
3
C.
2
D.
4
Gii
Giá tr cc tiu ca hàm s ng
3
.

Câu 14:  th ca hàm s ng cong trong hình bên?
y f x
1;0
;1
0;1
1;1
1;0
Trang 37
A.
42
2y x x
B.
42
2y x x
C.
32
3y x x
D.
32
3y x x
Gii
Chn câu A.
Câu 15: Tim cng c th hàm s
22
1
x
y
x
là
A.
2y
B.
1x 
C.
1y 
D.
2x 
Gii
Tim cng ca  th hàm s
22
1
x
y
x
là
1x 

Câu 16: Tp nghim ca b
28
x
là
A.
;3
B.
4;
C.
3; 
D.
0;
Gii
Ta có:
3
2 8 2 2 3
xx
x
Chn câu C.
Câu 17: Cho hàm s
y f x
 th trong hình bên.
S nghim c
20fx
là
A.
0
B.
2
C.
3
D.
4
Gii
2 0 2f x f x
S nghim c m c th hàm s
y f x
ng thng
2y
.
Suy ra m.
Chn câu C.
Câu 18: Nu
3
1
3f x dx 
và
4
3
1f x dx
thì
4
1
f x dx
bng
A.
3
B.
2
C.
4
D.
1
Gii
Trang 38
Ta có:
4 3 4
1 1 3
3 1 2.f x dx f x dx f x dx
Chn câu B.
Câu 19: a s phc
32zi
bng
A.
1z
B.
13z
C.
13z
D.
5z
Gii
a s phc z là
2
2 2 2
3 2 13z a b
Chn câu B.
Câu 20: Cho hai s phc
1
12zi
và
2
3zi
. Phn o ca s phc
12
2zz
bng
A.
5
B.
3
C.
2
D.
4
Gii
Ta có:
12
2 1 2 6 2 5 4z z i i i
Phn o ca s phc
12
2zz
bng 4.
Chn câu D.
Câu 21: Cho hai s phc
1
2 zi
và
2
1zi
. Trên mt phng t m biu din s phc
12
2 zz
có t là
A.
3; 3
B.
2; 3
C.
3; 3
D.
3; 2
Giải
Ta có:
12
2 4 2 1 3 3 z z i i i
. Vm biu din s phc
12
2 zz
có t là
3; 3
.
Đáp án C
Câu 22 : Trong không gian Oxyz, hình chiu vuông góc cm
2;1; 1M
trên trc Oz có t là.
A.
2;1;0 .
B.
0;0; 1 .
C.
2;0;0 .
D.
0;1;0 .
Giải
Hình chiu vuông góc cm
2;1; 1M
trên trc Oz có t là
0;0; 1 .
Đáp án B.
Câu 23 : Trong không gian Oxyz, cho mt cu
2 2 2
: 2 2 7 0.S x y z x z
Bán kính ca mt cu
ng
A.
7.
B. 9.. C. 3. D.
15.
Giải
2 2 2 2 2 2
2 2 7 0 : 2. 1 . 2.0. 2.1. 7 0.x y z x z S x y z x y z
a 1,b 0,c 1,d 7.
Tâm mt cu
1;0;1I
bán kính
2
2 2 2 2 2
1 0 1 7 3.R a b c d
Đáp án C
Câu 24 :
Oxyz

: 3 2 6 0x y z
. Vecto nào
không phải 
?
A.
2;6;4n 
. B.
1; 3; 2n
. C.
1;3;2n 
. D.
1;3;2n
.
Giải
Đáp án D
Câu 25 : Oxyz, 
d

13
2
2
xt
y
zt



Trang 39
A.
1; 0; 2 .d

B.
6; 0; 4 .a
C.
3; 2; 2 .b
D.
1; 2; 2 .c
Giải
Đáp án B
Câu 26. Cho hình chóp S.ABC có SA vuông góc vi mt phng
,ABC
2,SA a
tam giác ABC vuông ti
B,
3AB a
và
BC a
(minh h bên). Góc ging thng SC và mt phng
ABC
bng
A.
90 .
B.
45 .
C.
30 .
D.
60 .
Giải
Ta có
SA ABC
nên AC là hình chiu ca SC lên mt phng
.ABC

, , .SC ABC SC AC SCA
Tam giác ABC vuông ti B,
3AB a
và
BC a
nên
2 2 2
4 2 .AC AB BC a a
SAC vuông cân ti A nên
45 .SCA 
Vy
, 45 .SC ABC 
Đáp án B
Câu 27 : Cho hàm s
y f x
liên tc trên
và có bng xét xét du c
Hàm s c tr ?
A.
1.
B. 2. C. 3. D. 4.
Giải
Da vào bng xét du ta tho hàm ca hàm s có 4 li du nên hàm s m cc tr
Đáp án D
Câu 28. Giá tr ln nht ca hàm s
3
32f x x x
n
3;3
là
A.
16.
B. 20. C. 0. D. 4.
Giải
Ta có
2
0 3 3 0 1 3;3 .f x x x
1 0; 1 4; 3 20; 3 16.f f f f
T 
3;3
max 3 20.f x f

Cách khác:
S dng table bm Mode 7 nhp
3
32f x x x
chn Start?
3
End? 3 Step? 0.2 s th c
3;3
max 3 20.f x f

Đáp án B
Câu 29. Cho a và b là hai s tha mãn
4
16.ab
Giá tr ca
22
4log logab
bng
A. 4. B. 2. C. 16. D. 8.
Giải
4 4 4
2 2 2 2 2 2 2
4log log log log log log 16 log 2 4.a b a b a b
Cách khác
Chn
2, 1ab
tha mãn
4
16ab
ri thay vào
22
4log logab
c kt qu.
Đáp án A
Câu 30. Tìm s m c th hàm s y = x
3
3x
2
+ 3x  th hàm s y = x
2
x 1
Trang 40
A. 1. B. 2. C. 3. D. 4.
Giải
 m : x
3
3x
2
+ 3x 1= x
2
x 1
x
3
4x
2
+ 4x = 0
x = 0 hoc x = 2
Đáp án B
Câu 31: Tp nghim ca b
22
log log 8xx
là:
A.
8;S
B.
;4S 
C.
4;8S
D.
0;4S
Giải
u kin:
08x
.
Ta có:
22
log log 8 8 4 4 8x x x x x x
. Chọn C.
Câu 32: Mt cu
S
có din tích bng
20
, th tích khi cu
S
bng
A.
20 5
3
B.
20 5
C.
20
3
D.
45
3
Giải
23
4 20 5
4 20 5
33
S R R V R
. Chọn A.
Câu 33. Cho hàm s
fx
liên tc trên
và
8
2
( ) 10f x dx
. Tính
3
1
3
(3 1)
2
I f x dx
A. 30 B. 10 C. 20 D. 5
Giải
Phương pháp:
S di bin tính tích phân.
Cách giải:
t
3 1 3
3
dt
t x dt dx dx
i cn
1 2, 3 8.x t x t

3 8 8
1 2 2
3 3 ( ) 1 1
(3 1) ( ) .10 5.
2 2 3 2 2
ft
I f x dx dt f t dt
Chọn D.
Câu 34. 

y f x





. 






O
x
y
c
b
a
y f x
Trang 41
A.
dd
bc
ab
f x x f x x

. B.
dd
bc
ab
f x x f x x

.
C.
dd
bc
ab
f x x f x x

. D.
dd
bb
ac
f x x f x x

.
Giải
Chn A
Câu 35. Tìm s phc liên hp ca s phc
(3 1)z i i
A.
3zi
B.
3zi
C.
3zi
D.
3zi
Giải
Phương pháp
S phc liên hp ca s phc z = a + bi (a, b R) là
z a bi
Cách giải:
Ta có
2
(3 1) 3i 3z i i i i
S phc liên hp ca z là
3zi
Chọn D.
Câu 36: Gi
0
z
là nghim phc có phn 
2
4 4 37 0zz
. Trên mt phng
tm biu din ca s phc
0
w iz
?
A.
2
1
3;
2
M



B.
3
1
3;
2
M



C.
4
1
3;
2
M



D.
1
1
3;
2
M




Giải
2
2
0
1 6 6 1
2 1 36 36 3
2 2 2
ii
z i z w i
. Chọn D.
Câu 37. Vit phm
0; 1;2A
, song song vi trc Ox và vuông góc
vi mt phng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0 B. (P) : y + z - 1 = 0 C. (P) : y - z + 3 = 0 D. (P) : 2x + z - 2 = 0
Giải
Phương pháp
(P) // Ox và (P) (Q) thì
()
( ) ( )
P
PQ
ni
nn
Cách giải:
Gi
()P
n
là VTPT ca (P). Do (P) // Ox và (P) (Q) nên
()
( ) ( )
P
PQ
ni
nn
.
Ox có VTPT
1;0;0i
và (Q) : x + 2y - 2z + l = 0 có VTPT
()
1;2; 2
Q
n 
Có
()
, 0;2;2
Q
in


nên chn
(P)
0;1;1n
.
-1; 2) và nhn
(P)
0;1;1n
làm VTPT nên
(P) : 0(x - 0) +1(y +1) +1(z - 2) = 0 y + z - 1 = 0.
Chọn B.
Trang 42
Câu 38: Trong không gian
Oxyz
m
1;2;2M
ng th
M
và song song vi trc
Oy

A.
1
2
2
x
yt
zt



B.
1
2
2
xt
yt
z

C.
1
2
2
xt
yt
zt


D.
1
2
2
x
y t t
z

Giải
ng th  
M
và song song vi trc Oy nhn
0;1;0j
      
1
2
2
x
y t t
z

. Chọn D.
Câu 39: Chn ngu nhiên 5 hc sinh trong mt lp hc gm 25 nam và 20 n. Gi
A
là bin c
5 hc chn có ít nht 1 hc sinh nt ca bin c
A
là:
A.
5
20
5
45
C
PA
C
B.
4
25
5
45
20.C
PA
C
C.
4
44
5
45
20.C
PA
C
D.
5
25
5
45
1
C
PA
C

Giải
Xác su trong 5 hc sinh không có hc sinh n nào là
5
25
5
45
C
C
.
Xác su trong 5 hc sinh có ít nht 1 hc sinh n là
5
25
5
45
1
C
C
. Chọn D.
Câu 40: Cho hình chóp
.S ABCD

ABCD
là hình vuông cnh bng
a
. Hai mt phng
SAB
và
SAC
cùng vuông góc v  
khong cách ging thng
SA
và
BC
?
A.
2a
B.
a
C.
2
2
a
D.
2
a
Giải
Do
SAB ABC
SA ABC
SAC ABC

.
Mt khác
,AB BC SA AB AB
n vuông góc chung ca
SA
và
BC
.

;d SA BC AB a
. Chọn B.
Câu 41. Tìm giá tr thc ln nht ca tham s  hàm s
32
y x 3mx x
ng bin trên
.
Trang 43
A.
1.
B.
1
.
3
C.
1
.
3
D.
2.
Giải
 :
D
Ta có
2
y' 3x 6mx 1
Hàm s ng bin trên
khi
y' 0, x
Hay
2
3x 6mx 1 0, x
11
m
33
Vy giá tr ln nht ca m là
1
.
3
Đáp án B
Câu 42. Dân s th gic tính theo công thc
r.N
S A.e
 cy mc tính,
S là dân s  l  h vit nam có khong
i và t l  hu t l  hni
c ta có khong 120 trii?
A. 2020. B. 2024. C. 2026. D. 2022.
Giải
Áp dng công thc ta có:
1,7
.N
100
120000000 78685000.e N 24,83
Vy cn ít nh dân s t 120 trii.
Suy ra dân s s t 120 tri
Đáp án C.
Câu 43. Cho hàm s
ax 1
y
bx c
 th  bên. Tính tng
S a b c.
A.
S 2.
B.
S 0.
C.
S 1.
D.
S 3.
Giải
T  th ta thy
b0
x
ax 1 a
lim
bx c b

suy ra:
a
2
b
(1)
cc
xx
bb
ax 1
lim y lim
bx c

suy ra
c
1
d
(2)
 th hàm s ct trc Oy tm (0;1) nên
1
1 c 1
c
(3)
T (1) (2) (3) suy ra:
c 1, b 1, a 2.
Trang 44
Vy
S 2.
Đáp án A
Câu 44: Cho hình tr   t mt phng không
vuông góc v   t hai m       
AB,A 'B'
mà
AB A'B' 6cm
(hình v). Bit din tích t giác
ABB'A'
bng 60 cm
2
. Tính chiu cao ca hình tr 
A.
62
cm. B.
43
cm.
C.
82
cm. D.
53
cm.
Giải
Dng sinh
B'C
và
A'D
, ta có t giác
A'B'CD
là hình ch nht
nên
CD//A'B'
và
CD A'B' 6cm
. Vy
CD//AB
và
CD AB 6cm
.
 giác
ABCD
là hình bình hành và ni tic nên là hình ch
nht. T t khác
AB B'C
nên
AB (BCB') AB BB'
Vy
ABB'A'
là hình bình hành có mt góc vuông nên là hình ch nht.
Ta có
ABB'A'
S AB.BB'
nên
60
BB' 10cm
6

.
Xét tam giác
BB'C
vuông ti
C
có
2 2 2
B'C BB' BC
mà
2 2 2
BC AC AB 64 36 28
nên:
2
B'C 100 28 72 B'C 6 2cm
.
Vy chiu cao hình tr là
6 2cm
.
Đáp án A
Câu 45:   
y f(x)
          
f(0) 1
và
2
f (x) x 1
f '(x).e 2x, x 0;1 .


1
0
f(x)dx.
A.
2.
B.
4
.
3
C.
4
.
3
D.
2
Giải
Ta có
2 2 2
f (x) x 1 f (x) x 1 f (x) ' x 1
f '(x).e 2x f '(x).e 2x.e (e ) 2x.e
22
f (x) x 1 f (x) x 1
e 2xe dx e e C.

Mt khác:
2
f (x) x 1 2
f(0) 1 C 0 e e f(x) x 1.

1
11
23
00
0
14
f(x)dx x 1 dx x x .
33




Đáp án B
Câu 46. Cho hàm s
y f(x)
liên tc trên
 th :
Trang 45
Có bao nhiêu giá tr nguyên ca tham s  
2
3sinx cosx 1
f f m 4m 4
2cosx sinx 4



có nghim?
A. 1. B. 2. C. 3. D. 4.
Giải
2
3sinx cosx 1
f f m 4m 4 (1)
2cosx sinx 4



Ta có:
2cosx sin x 4 0, x
t
3sin x cosx 1
t
2cosx sin x 4


2t 1 cosx (t 3)sinx 1 4t (*).

*
có nghim:
2 2 2
9
(2t 1) (t 3) ( 1 4t) t 1
11
Suy ra:
0 t 1.
T  th hàm s
y f(x)
ta có:
y f(x)
ng bin trên
0; .
22
m 4m 4 (m 2) 0; ). 
t 0;1
nên:
22
2
3sin x cosx 1
f f m 4m 4 f t f m 4m 4
2cosx sin x 4
t m 4m 4 4



m khi
2
0 m 4m 4 1
2
m 4m 4 1 3 m 1
Do
m m 3; 2; 1 .
Đáp án C
Câu 47. Cho hai s thi tha mãn
22
x 4y 1.
Tìm giá tr ln nht ca biu thc
22
P log (x 2y).log (2x 4y).
A.
1
.
4
B.
1
.
2
C.
1
.
3
D.
1
.
6
Giải
Theo gi thit ta có:
22
1
x 4y (x 2y)(x 2y) 1 x 2y
x 2y
Trang 46
Vy:
2 2 2 2
2
P log (x 2y).log (2x 4y) log (x 2y).log
x 2y
22
log (x 2y). 1 log x 2y


2
2
1 1 1
log (x 2y) .
2 4 4



Du bng xy ra khi:
2
3
1
x
x 2y
x 2y 2
x 2y
22
.
1
1
x 2y
1
y
log (x 2y)
2
42
2






Đáp án A
Câu 48. Tìm tt c giá tr thc ca tham s  giá tr ln nht ca hàm s
3
y x 3x 2m 1
trên
n
0;2
t giá tr nh nht. Giá tr ca m thuc khong nào?
A.
3
; 1 .
2




B.
2
;2 .
3



C.
1;0 .
D.
0;1 .
Giải
Xét hàm s
3
y x 3x 2m 1
n [0;2].
Ta có:
2
x 1 0;2
f '(x) 3x 3; f '(x) 0
x1
Ta có:
f(0) 2m 1; f(1) 2m 3; f(2) 2m 1
Suy ra:
0;2
max f(x) max 2m 1; 2m 3 ; 2m 1 max 2m 3 ; 2m 1 P
TH1:
1
2m 3 2m 1 4(4m 2) 0 m .
2

1
P 2m 3 2, m .
2
Suy ra:
min
1
P 2 m .
2
TH2:
1
2m 3 2m 1 4(4m 2) 0 m .
2

1
P 2m 1 2, m .
2
Suy ra
min
P
không tn ti.
Vy
1
m.
2
Đáp án D
Câu 49. Cho hình lnh a. Gi M, N lm ca các cnh
t phng (DMN) chia hình lng thành hai phn. Gi
1
V
là th tích ca phn cha
nh A,
2
V
là th tích ca phn còn li. Tính t s
1
2
V
.
V
A.
55
.
89
B.
37
.
48
C.
1
.
2
D.
2
.
3
Giải
Trang 47
Gi
H AB DN
;
MH
ci K, ci S; SD ci E.
Thit di
Phn cha A có th tích là:
1 S.ADH S.A'EM K.BNH
V V V V .
D th
1
SA' B'K A'A.
3

 dài cnh hình lng 1 thì:
12
SA' ; KB .
33

Ta có:
S.ADH
1 1 4
V . AD.AH.SA
3 2 9

S.A'EM S.ADH K.BNH S.ADH
1 1 1 1
V V ;V V .
64 144 8 18
Vy th tích phn cha A là:
1
4 1 1 55
V.
9 144 18 144
Th tích phn không cha A là:
55 89
1.
144 144

1
2
V
55
.
V 89

Đáp án A
Câu 50.
2
2 y 2 2
2
log (2x 2x 2) 2 y x x.
Hi có bao nhiêu cp s 
(x,y), (0<x<500) th cho.
A. 1. B. 2. C. 3. D. 4.
Giải
Ta có:
22
2 y 2 2 2 2 y 2
22
log 2x 2x 2 2 y x x log x x 1 x x 1 2 y
2
2
2
log (x x 1)
2 y 2
2
22
2
2 log (x x 1) 2 y
log (x x 1) y

Do
22
2
0 x 500 y log (x x 1) 0;18 0 y 5.
Vy có 4 giá tr nguyên ca y tha mãn yêu c p s (x;y) th

Đáp án D
--------------------------------------------------
www.thuvienhoclieu.com
ĐỀ 14
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Trang 48
PHÁT TRIỂN TỪ ĐỀ MINH
HỌA LẦN 2 NĂM 2020
Thời gian: 90 phút
Câu 1:(NB) Có bao nhiêu s có 2 ch s, mà tt c các ch s u l?
A. 25. B. 60. C. 20. D. 10.
Câu 2: (NB) Cho cp s nhân
n
u
có
21
4; 2.uu
Công bi
q
là:
A.
2
.
B.
2
.
C.
1
2
.
D.
1
2
.
Câu 3:
(NB)  
A
. .
B
. .
C
. .
D.
.
Câu 4: (NB)   

A.
3
2
3
a
. B.
3
2a
. C.
3
3
a
. D.
3
a
.
Câu 5:
(NB) 
sai

A. 
B. 
C. 
D. 
Câu 6:(NB) Tìm nguyên hàm ca hàm s .
A. . B. .
C. . D. .
Câu 7:(NB) Cho khi chóp  u cnh , vuông góc vi mt phng
 . Tính th tích khi chóp .
A. . B. . C. . D. .
Câu 8:(NB)   

A. . B. . C. . D. .
Câu 9:(NB) 


 . 




A. .
B. . C. . D. .
Câu 10: (NB)  

A. B. C. D.
Câu 11:
(NB)  là:
A. . B. . C. . D. .
Câu 12:(NB)  , bán kính  
A. . B. . C. . D. .
11
3 .2 24

xx
3x
2x
5x
2x 
a
2.a
7
x
fx
7 7 ln7
xx
dx C
1
77
xx
dx C

7
7
ln7
x
x
dx C
1
7
7
1
x
x
dx C
x

.S ABC
ABC
a
SA
2SA a
.S ABC
3
3
3
a
3
3
2
a
3
3
12
a
3
3
6
a
5a
.a
3
2 a
3
45
3
a
3
2
3
a
3
4
3
a
R
3
4VR
3
4
3
VR
3
1
3
VR
2
4
3
VR
y f x
0;1 .
1; .
1;0 .
0; .
2
( 3 2)
e
y x x
( ;1) (2; )D  
\{1;2}D
(0; )D 
(1;2)D
3
2
12
18
10
40
Trang 49
Câu 13:(NB)  

A. B. C. D.
Câu 14: (TH)
A. B. C. D.
Câu 15:(NB) đúng?
A. 
y = 3
. B. 
C. 
x = 2
. D. 
x = 3
.
Câu 16:(NB) là
A. B. C. D.
Câu 17:(TH)  là
A. B.
C. D.
Câu 18: (NB) Cho . Tính
A. . B. . C. . D. .
Câu 19: (NB) Cho s phc a s phc z .
A. B. C. D.
Câu 20:(NB) Cho 2 s phc
12
2 , 5 7z i z i
.Tìm phn thc a ca s phc
12
.z z z
fx
2.x
1.x
1.x 
3.x 
1
.
1
x
y
x
1
.
1
x
y
x
21
.
22
x
y
x
.
1
x
y
x
32
1
x
y
x
15
44
x
6; .
6; .
5;1 .
;6 .
y f x
1fx
x
y
-2
2
-1
1
O
1.
2.
3.
4.
2
0
5f x dx
2
0
2sinI f x x dx



7I
5
2
I

3I
5I

43zi
7.z
3.z
5.z
7.z
Trang 50
A.
7.a
B.
6.a
C.
6.a
D.
5.a
Câu 21: (NB) S phm biu dim hình bên?
A. B. C. D.
Câu 22: (TH)Trong không gian
Oxyz
m
1;2; 1 ;A
2; 1;3 .B

󰇍
󰇍
󰇍
󰇍
󰇍
có t là:
A.
1; 3;4
. B.
1;3; 4
. C.
3;1;2
. D.
1; 3;2
.
Câu 23: (NB) Trong không gian
Oxyz
, cho mt c   
.x y z x y z+ + + - + - =
2 2 2
2 2 4 1 0
Tâm và bán kính ca mt cu là:
A.
1;1; 2 , 7.IR
B.
1; 1; 2 , 7.IR
C.
1;1; 2 , 7.IR
D.
1;1; 2 , 7.IR
Câu 24: (NB) Trong không gian
Oxyz
, mt ph    m
( )
; ; ,Aa00
( )
; ; ,Bb00
( ; ; )Cc00
có

A.
x y z
a b c
+ + = 1
. B.
x y z
bac
+ + = 1
. C.
x y z
c b a
++=1
. D.
x y z
c b a
++=0
.
Câu 25: (TH)Trong không gian
Oxyz
    c ng th  
( )
;;M 5 4 1
có
VTCP
2; 3;1a
r

là:
A.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=-
í
ï
ï
=+
ï
ï
î
52
43
1
B.
xt
yt
zt
ì
=+
ï
ï
ï
ï
= - +
í
ï
ï
=+
ï
ï
î
25
34
1
. C.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=-
í
ï
ï
=-
ï
ï
î
25
43
1
. D.
xt
yt
zt
ì
=+
ï
ï
ï
ï
= - -
í
ï
ï
=-
ï
ï
î
52
43
1
.
Câu 26:(TH)Cho hình nh a, và
(minh h Gi là góc gia SC và (ABCD). Tính .
A. B. C. D.
Câu 27:(TH)  
cho là
A. 2. B. 1. C. 0. D. 3.
Câu 28:(TH)    và 
  
K
1
3 2 .zi=-
2
3 2 .zi=+
3
2 3 .zi= - -
4
2 3 .zi= - +
SA ABCD
SA a 6
cos
3
cos .
2

3
cos .
3

2
cos .
2

1
cos .
2

y f x
2
2,
f x x x x
y f x
2;2
M
m
2;2
Mm
Trang 51
A. 3. B. 6. C. 4. D. 8.
Câu 29:
(TH) 
1;1


.
A. . B. . C. . D.
Câu 30: (TH) và 
A.
B.
C.
D.
Câu 31:(TH) là
A. B. C. D.
Câu 32:(TH)  
quanh 
A. . B.
24S
.
C. . D. .
Câu 33: (TH)Cho các tích phân . Tính .
A. . B. . C. . D. .
Câu 34: (TH) th hàm s . Din tích hình phng S (phc xác
nh bng công thc:
A. . B. .
C. . D.
( ) ( )
S f x dx f x dx
-
= - +
òò
02
20
.
Câu 35: (TH) 
 
A.2. B.3. C.1. D.4.
Câu 36: (TH) Gi là hai nghim c Tính
A.
B.
C. D.
2
()
x
f x x e
e
1
e
2e
0
32
34y x x
0.
1.
2.
3.
2
33
log log 2 0xx
2;1 .
1
;1 .
9



1
;9 .
3



1
;3 .
9



3r
4l
S
83S
16 3S
43S
25
33
2; 4f x dx f t dt



5
2
f y dy
2I
6I
2I 
6I 
y f x
02
20


S f x dx f x dx
02
20


S f x dx f x dx
02
20


S f x dx f x dx
7 17
5
i
z
i
12
,zz
2
2 10 0.zz+ + =
22
12
.T z z=+
4.T =
6.T =
10.T =
20.T =
Trang 52
Câu 37: (TH)Trong không gian
Oxyz
t phng

3;1; 1 ;A
2; 1;4B
và
vuông góc vi mt phng
:2 3 1 0P x y z
là:
A.
13 5 5 0x y z
. B.
13 5 5 0x y z
. C.
13 5 5 0x y z
. D.
13 5 5 0x y z
.
Câu 38: (TH)Trong không gian
Oxyz
     c ng thng
 
1;2;3 ,A
4;4;4B
là:
A.
xt
yt
zt
ì
=-
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
13
22
3
. B.
xt
yt
zt
ì
= - +
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
3
22
13
. C.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
13
22
3
. D.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
13
22
32
.
Câu 39: (VD) Cho tp hp . Gi là tp hp các s có ch s c
lp thành t các ch s ca tp . Chn ngu nhiên mt s t , xác su s c chn là s chia ht
cho 9 là:
A. . B. . C. . D. .
Câu 40: (VD)Cho hình chóp S.ABCD  ABCD là hình vuông tâm O, cnh 4 . Hình chiu ca S
trên mt phng m H thuc AB sao cho . Góc gia cnh bên SC và mt 
bng . Khong cách t O n mt phng theo a là
A. . B. . C. . D. .
Câu 41:(VD)      m      
 ?
A. 2020. B. 2022. C. 2021. D. 2023.
Câu 42:
(VD) , k
đúng
?
A. . B. . C. . D. .
Câu 43:(VD) 

, , , a b c d

A. B. C. D.
Câu 44: (VD) 


                    
  và 
 
1; 2; 3; 4; 5;6A
S
3
A
S
7
20
3
20
1
20
9
20
a
ABCD
3HB HA
45
SBC
5 34a
5 34
17
a
5 34
34
a
5 17
2
a
2020;2020
32
3 (2 5) 5 y x x m x
(0; )
1
y ln
x1
'1
y
xy e
'1
y
xy e
'1
y
xy e
'1
y
xy e
32
a,b,c,df x ax bx cx d
x

1
1

()fx
0
0
()fx

4
0

1.
2.
3.
4.
22
3 ( )cm
2
()
c
a
S cm
b
, , *abc
a
b
20ab c
Trang 53
A.
18.
B.
5.
C.
33.
D.
15.
Câu 45:(VD)Cho hàm s
fx
o hàm liên tn tha mãn và
.  bng
A. . B. . C. . D. .
Câu 46:(VDC) có :
 . là
A. B. C. D.
Câu 47:(VDC)Mi có 10 tring gi vào ngân hàng vi k hn 3 tháng (1 quý là 3 tháng), lãi
sut 6% / 1 quý theo hình thc lãi kép (sau 3 tháng s tính lãi cng vào gi 
gi thêm vào 20 tring cùng vi hình thc lãi suy. H ln gu tiên,
c s tin gn nht vi kt qu nào?
A

B

C

D

Câu 48:(VDC)Cho ,     
 .
A. . B. . C. . D. .
Câu 49:   , 
 ,  , .
A. . B. . C. . D. .
Câu 50:(VDC)Ch M vay ngân hàng 300 tric tr  mua nhà. Nu cui mi
tháng, bu t tháng th nht ch M tr 5,5 tring và chu lãi s ti là 0,5% mi tháng
(bit lãi sui) thì sau bao lâu, ch M tr ht s tin trên?
A.
64 tháng.
B.
54 tháng.
C.
63 tháng.
D.
55 tháng.
---------- HẾT ----------
0;2
f(0) 3
2
(2x 3)f '(x) 2f(x) 4x 3x
f (2)
1
9
7
1
5
1
7
y f x
g x f f x
'0gx
5.
6.
7.
8.
, 0;xy
1xy
;m a b
22
5 4 5 4 40x y y x xy m
25 16T a b
829T
825T
816T
820T
.ABC AB C
2a
M
N
AB

BB
MC N
ACC A

2
4
6
4
3
4
3
4
x

1
3

()fx
0
0
()fx
4


2
Trang 54
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1: Có bao nhiêu s có 2 ch s, mà tt c các ch s u l?
A. 25. B. 60. C. 20. D. 10.
Hướng dẫn giải
Chọn A
Câu 2: Cho cp s nhân
n
u
có
21
4; 2.uu
Công bi
q
là:
A
.
2
B
.
2
C.
1
2
D.
1
2
Hướng dẫn giải
Chọn B
Câu 3:
 
A
.
B
.
C
.
D.
Chọn B.

11
3 .2 24

xx
có nghim là
A.
3x
B.
2x
C.
5x
D.
2x 
Hướng dẫn giải
Cách 1: Ta có
1 1 2
1
3 .2 24 3 .2 .2. 24 2 .3 36 6 6 2
3
x x x x x x x
x

.
Cách 2:Sử dụng máy tính cầm tay.
Nhp vào màn hình
11
3 2 24
XX

n CALC th các giá tr ca x  cho, thì
thy khi
2x
giá tr ca biu thc bng 0 nên ta chn B.
Câu 4: 
a

2.a


A.
3
2
3
a
B.
3
2a
C.
3
3
a
D.
3
a
Hướng dẫn giải
Chọn B

2
Ba
khi  là:
23
.2 2V a a a
Câu 5:

sai

A. hoành.
B. 
C. 
D.

Hướng dẫn giải
Chọn A

Câu 6:Tìm nguyên hàm ca hàm s
A. B.
C. D.
Hướng dẫn giải
11
3 .2 24

xx
3x
2x
5x
2x 
7
x
fx
7 7 ln7
xx
dx C
1
77
xx
dx C

7
7
ln7
x
x
dx C
1
7
7
1
x
x
dx C
x

Trang 55
Chọn C
Áp dng công thc
x
a dx
.
Câu 7:Cho khi chóp  u cnh , vuông góc vi mt ph
và . Tính th tích khi chóp .
A.
3
3
3
a
B.
3
3
2
a
C.
3
3
12
a
D.
3
3
6
a
Hướng dẫn giải
Chọn D

2
3
4
a
B
khi chóp S.ABC là:
23
1 1 3 3
. . . .2
3 3 4 6
ABC
aa
V S SA a
Câu 8:  

A.
3
2 a
B.
3
45
3
a
C.
3
2
3
a
D.
3
4
3
a
Hướng dẫn giải
Chọn D
Ta có
2 2 2 2
( 5) 2R l h a a a
.

3
22
1 1 4
(2 ) .
3 3 3
a
V R h a a

Câu 9: 


 . 




A.
3
4VR
B.
3
4
3
VR
. C.
3
1
3
VR
. D.
2
4
3
VR
.
Hướng dẫn giải
Chọn B
 là
Câu 10: 

A. B. C. D.
Hướng dẫn giải
Chọn A

Câu 11:

2
( 3 2)
e
y x x
là:
A.
( ;1) (2; )D  
B.
\{1;2}D
C.
(0; )D 
D.
(1;2)D
Hướng dẫn giải
Chọn A
Vì
e

2
2
3x 2 0
1
x
x
x
.
.S ABC
ABC
a
SA
2SA a
.S ABC
5a
.a
R
R
3
4
3
VR
y f x
0;1 .
1; .
1;0 .
0; .
Trang 56
Câu 12: 
3
, bán kính 
2

A.
12
. B.
18
. C.
10
. D.
40
.
Hướng dẫn giải
Chọn A
là
22
.2 .3 12V r h
Câu 13: 

A. B. C. D.
Hướng dẫn giải
Chọn C

1.x 
Câu 14: 
A.
1
.
1
x
y
x
B.
1
.
1
x
y
x
C.
21
.
22
x
y
x
D.
.
1
x
y
x
Hướng dẫn giải
Chọn A

1x


0; 1

Câu 15: đúng?
A. 
y = 3
. B. 
C. 
x = 2
. D. 
x = 3
.
Hướng dẫn giải
Chọn A
Do
32
lim lim 3
1
xx
x
y
x
 

và
32
lim lim 3
1
xx
x
y
x
 



Câu16: 
15
44
x
là
A.
6; .
B.
6; .
C.
5;1 .
D.
;6 .
Hướng dẫn giải
Chọn B
Ta có:
15
4 4 1 5 6
x
xx
.
fx
2.x
1.x
1.x 
3.x 
32
1
x
y
x
Trang 57

6;x 
.
Câu 17: 
y f x

1fx
là
A.
1.
B.
2.
C.
3.
D.
4.
Hướng dẫn giải
Chọn C
+ pt
1fx

1y
.
+ 
1y


1fx

Câu 18:Cho . Tính
A. B. C. D.
Hướng dẫn giải
Chọn A.
Ta có
2
0
22
00
2sin
2 sin
I f x x dx
f x dx xdx






.
2
2
0
0
2cos
7
f x dx x

Hướng dẫn giải
Câu 19: Cho s phc a s phc z .
A. B. C. D.
Hướng dẫn giải
Chọn C
Câu 20:Cho 2 s phc
12
2 , 5 7z i z i
.Tìm phn thc a ca s phc
12
.z z z
A.
7.a
B.
6.a
C.
6.a
D.
5.a
Hướng dẫn giải
Chọn A
m biu dim hình
Câu 21: S phc
bên?
2
0
5f x dx
2
0
2sinI f x x dx



7I
5
2
I

3I
5I

43zi
7.z
3.z
5.z
7.z
K
x
y
-2
2
-1
1
O
Trang 58
A.
B.
C.
D.
Hướng dẫn giải
Chọn D
Câu 22: m:
1;2; 1 ;A
2; 1;3 .B

󰇍
󰇍
󰇍
󰇍
󰇍
có t là:
A.
1; 3;4
B.
1;3; 4
C.
3;1;2
D.
1; 3;2
Hướng dẫn giải
Chọn A
Câu 23: Trong không gian Oxyz cho mt c
2
+
2
+
2
+ 2 2 + 4 1 =
0. Tâm và bán kính ca mt cu là:
A. I(1,1,-2), R =
7 B. I(1,-1,-2), R =
7C. I(-1,1,-2), R = 7 D. I(-1,1,-2), R =
7
Hướng dẫn giải
Chọn D
a = -1,b = 1, c = -2, d= -1
Tâm I(-1,1,-2)
R =
2
+
2
+
2
=
7
Câu 24: Trong không gian Oxyz mt phm
( )
; ; ,Aa00
( )
; ; ,Bb00
( ; ; )Cc00

trình:
A.
x y z
a b c
+ + = 1
B.
x y z
bac
+ + = 1
C.
x y z
c b a
++=1
D.
x y z
c b a
++=0
Hướng dẫn giải
Chọn C
Câu 25: Trong h t  cng th
( )
;;M 5 4 1
có VTCP
2; 3;1a
r

là:
A.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=-
í
ï
ï
=+
ï
ï
î
52
43
1
B.
xt
yt
zt
ì
=+
ï
ï
ï
ï
= - +
í
ï
ï
=+
ï
ï
î
25
34
1
C.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=-
í
ï
ï
=-
ï
ï
î
25
43
1
D.
xt
yt
zt
ì
=+
ï
ï
ï
ï
= - -
í
ï
ï
=-
ï
ï
î
52
43
1
Chọn A
Câu 26:           nh a, và
(minh h Gi là góc gia SC và (ABCD). Tính .
A.
B.
C.
1
3 2 .zi=-
2
3 2 .zi=+
3
2 3 .zi= - -
4
2 3 .zi= - +
SA ABCD
SA a 6
cos
3
cos .
2

3
cos .
3

2
cos .
2

Trang 59
D.
Hướng dẫn giải
Chọn D.
·
·
SA ABCD SC; ABCD SCA.
Do ABCD là hình vuông cnh a
AC a 2.
Tam giác SAC vuông ti S nên
22
SC SA AC 2a 2.

AC 1
cos
SC 2
.
Câu 27:  
A. 2 B. 1 C. 0 D. 3.
Hướng dẫn giải
Chọn B.
2
20
f x x x

0x

Câu 28:   và 
  
A. 3. B. 6. C. 4. D. 8.
Hướng dẫn giải
Chọn C

2;2 2;2
max 2 2, min 2 6

M f x f m f x f
2 6 4 Mm
.
Câu 29:

2
()
x
f x x e
-1 ; 1] ?
A.
e
B.
1
e
C.
2e
D.
0
Hướng dẫn giải
Chọn A

1;1
, ta có:
/
2
x
f x xe x
;
/
00f x x

2x 

Ta có:
1
1 ; 0 0; 1f f f e
e
Suy ra:
1;1
max f x e
Câu 30: 
32
34y x x
và 
A.
0.
B.
1.
C.
2.
D.
3.
1
cos .
2

y f x
2
2,
f x x x x
y f x
2;2
M
m
2;2
Mm
Trang 60
Hướng dẫn giải
Chọn B

0x
4y
.

0;4A
.
Câu 31:
2
33
log log 2 0xx
là
A.
2;1 .
B.
1
;1 .
9



C.
1
;9 .
3



D.
1
;3 .
9



Hướng dẫn giải
Chọn D
+ 
0x
.
+ Ta có:
2
33
log log 2 0xx
3
1
2 log 1 3
9
xx
.

1
;3 .
9
x



Câu 32:   

A.
83S
. B.
24S
. C.
16 3S
. D.
43S
Hướng dẫn giải
Chọn D
D là:
. 3.4 4 3S rl
Câu 33:Cho các tích phân . Tính
A. B. C. D.
Chọn A.
Ta có:
2 2 5 5
3 3 3 3
2; 4f x dx f y dy f t dt f y dy
(tích phân không ph thuc vào bin)
Li có:
2 5 5
3 2 3
4 2 2f y dy f y dy f y dy I

.
Câu 34:  th hàm s . Din tích hình phng S (phnh
bng công thc
3r
4l
S
25
33
2; 4f x dx f t dt



5
2
f y dy
2I
6I
2I 
6I 
y f x
Trang 61
A.
B.
C.
D.
( ) ( )
S f x dx f x dx
-
= - +
òò
02
20
Hướng dẫn giải
Chọn A.
D th hàm s ta có
02
20


S f x dx f x dx
.
Câu 35: 
 
A.2. B.3. C.1. D.4.
Hướng dẫn giải
Chọn A
Câu 36: Gi là hai nghim c Tính
A. B. C. D.
Hướng dẫn giải
Chọn D
Câu 37: t phng
-1) ; B(2,-1,4) và vuông góc vi mt phng (P):
2x-y+3z -
A. x 13y + 5z + 5 = 0 B. x 13y - 5z + 5 = 0
C. x + 13y + 5z - 5 = 0 D. x 13y + 5z + 5 = 0
Hướng dẫn giải
Chọn B

󰇍
󰇍
󰇍
󰇍
󰇍
= (-1,-2,5)
()
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
= (2,-1,3)
=>
󰇍
= ;
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍

󰇍
󰇍
󰇍
󰇍
= (-1,13,5)
Mà
󰇛
󰇜
qua A(3,1,-1) nên pt
󰇛
󰇜
: x 13y 5z + 5 = 0
Câu 38: Trong h t  cng th
1;2;3 ,A
4;4;4B
là:
A.
xt
yt
zt
ì
=-
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
13
22
3
B.
xt
yt
zt
ì
= - +
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
3
22
13
C.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
13
22
3
D.
xt
yt
zt
ì
=+
ï
ï
ï
ï
=+
í
ï
ï
=+
ï
ï
î
13
22
32
.
Hướng dẫn giải
Chọn C
Câu 39:(VD) Cho tp hp
1; 2; 3; 4; 5;6A
. Gi
S
là tp hp các s có
3
ch s c
lp thành t các ch s ca tp
A
. Chn ngu nhiên mt s t
S
, xác su s c chn là s chia ht
cho 9 là:
A.
7
20
. B.
3
20
. C.
1
20
. D.
9
20
.
02
20


S f x dx f x dx
02
20


S f x dx f x dx
02
20


S f x dx f x dx
7 17
5
i
z
i
12
,zz
2
2 10 0.zz+ + =
22
12
.T z z=+
4.T =
6.T =
10.T =
20.T =
Trang 62
Hướng dẫn giải
Chọn B
G c chn là s chia ht cho 
S chia hc to nên t các tp sau:
1;2;6 ; 1;3;5 ; 2;3;4
83
18
120 20
n B P B
Câu 40: Cho hình chóp S.ABCD  ABCD là hình vuông tâm O, cnh 4 . Hình chiu ca S trên mt
phng m H thuc AB sao cho . Góc gia cnh bên SC và mt ng .
Khong cách t O n mt phng theo a là
A. B. C. D.
Hướng dẫn giải
Chọn B
K
HK SB(K SB) HK (SBC)
Vì
HB HA HA a,HB a HC BH BC a
22
3 3 5
Ta có
)
)
)
SC;(ABCD) SC;HC SCH SH HC a 45 5
o
Tam giác SBH vuông ti H, có ng cao
22
SH.HB 15a 34
HK
34
SH HB


d H;(SBC)
BH a
d A;(SBC)
d A;(SBC) AB
3 10 34
4 17
Vy
aa
d O;(SBC) d A;(SBC) .
1 1 10 34 5 34
2 2 17 17
Câu 41:m  
 ?
A. 2020 B. 2022 C. 2021 D. 2023
Hướng dẫn giải
Chọn B
Cách 1: Ta có
2
3 6 2 5
y x x m

(0; ) 0, (0; )
 yx
22
3 6 2 5 0, (0; ) 3( 1) 2 2, (0; )  x x m x x m x
Vì
2
( 1) 0, (0; ) xx

1x
) nên
2
3( 1) 2 2, (0; ) 2 2 0 1  x m x m m
.
Do m nguyên và
2020;2020 2020; 2019; 2018;...;0;1 mm
.
m 
Cách 2: Ta có
2
3 6 2 5; 9 6 15 6 6

y x x m a a
.

01
m
thì
0,
yx

(0; )
.

01
m

0
y

1 2 1 2
; ( )x x x x
.

1
( ; ) x
và
2
( ; )x
.

(0; )
thì
12
12
12
20
0
0
25
0
0
3



xx
xx
m
xx

a
ABCD
3HB HA
45
SBC
5 34a
5 34
17
a
5 34
34
a
5 17
2
a
2020;2020
32
3 (2 5) 5 y x x m x
(0; )
3
6
120n S A
Trang 63

1m

Mà m nguyên và
2020;2020 2020; 2019; 2018;...;0;1 mm
.
m 
Câu 42:

1
y ln
x1
, 
A.
'1
y
xy e
B.
'1
y
xy e
C.
'1
y
xy e
D.
'1
y
xy e
Hướng dẫn giải
Chọn A
/
11
ln ln 1
11
y x y
xx

Ta có:
11
' 1 1 1
1 1 1
x
xy x
x x x



,
1
ln
1
1
1
y
x
ee
x

.
Câu 43:
32
a,b,c,df x ax bx cx d
:
x

1
1

()fx
0
0
()fx

4
0


A.
1.
B.
2.
C.
3.
D.
4.
Hướng dẫn giải
Chọn A
+ 
1;0
và
1;4
nên:
0
4
a b c d
a b c d
+ Ta có:
2
' 3 2f x ax bx c

1x 
và
1x
nên:
' 1 0
3 2 0
3 2 0
' 1 0
f
a b c
a b c
f



1a 
,
0b
,
3c
,
2d
.

Câu 44: 



22
3 ( )cm
.
      
2
()
c
a
S cm
b

, , *abc
và
a
b
     
20ab c

Trang 64
A.18. B. -5 C. 33. D.15.
Hướng dẫn giải
Chọn A

()x cm
.

22
3 3 ( ).
xq
S x x cm


3 3 3 3
.,
2 2 4
h



2 3 3
..
3 2 3
R



2 2 3
3 3 3 3 13
2 2 2 . . 2 ( ) .
3 4 3 6
S Rh R
.

13; 6; 3 20 78 60 18.a b c ab c
Câu 45:Cho hàm s f(x) o hàm liên tn tha mãn và
.  bng
A. B. C. D.
Hướng dẫn giải
Chọn B.
Ta có:
22
(2x 3)f '(x) 2f(x) 4x 3x (2x 3)f(x) 4x 3x
Ly nguyên hàm 2 v c:
2 2 3
(2x 3)f(x) (4x 3x )dx 2x x C
Do
f(0) 3 3f(0) C C 9
Thay
9
x 2 7f(2) 8 8 9 f(2)
7
.
Câu 46:
y f x
có :

g x f f x

'0gx
là
A.
5.
B.
6.
C.
7.
D.
8.
Hướng dẫn giải
Chọn D
+ Ta có:
' ' . 'g x f x f f x

'0gx
0
0
0
' 0 1, x=3 2n
1 3n
'0
3 3n
f x x
fx
f f x
fx



'0gx

Câu 47:
Mi có 10 tring gi vào ngân hàng vi k hn 3 tháng (1 quý là 3 tháng), lãi sut 6% / 1 quý
theo hình thc lãi kép (sau 3 tháng s tính lãi cng vào gi thêm vào 20
tring cùng vi hình thc lãi suy. H ln gi n
c s tin gn nht vi kt qu nào?
0;2
f(0) 3
2
(2x 3)f '(x) 2f(x) 4x 3x
f (2)
1
9
7
1
5
1
7
x

1
3

()fx
0
0
()fx
4


2
Trang 65
A. 35 triu B. 37 triu C. 36 triu D. 38 triu
Hướng dẫn giải
Chọn C.
Sau k hn th nht, s tin nhc là:
1
1A a amr a mr
Sau k hn th hai, s tin nhc là:
2
2
1 1 . 1A a mr a mr mr a mr

Sau k hn th n, s tin nhc là :
1
n
n
A a mr
Sau quý th nht, s tin trong tài khon c
10. 1 6% 20 30,6
trii thêm vào 20 triu).
Sau quý th hai s tin có trong tài khon c
30,6 30,6.6% 30,6 1 6%
tring.
 tic là
3
30,6. 1 6% 36,445
tring.
Do  thp phân nh n 36 tring là gn nht.
Câu 48:Cho ,  
 .
A. . B. . C. . D.
Hướng dẫn giải
Chọn B
Ta có:
2 2 3
33
25 20 56 25 20 3 56m xy x y xy xy x y xy x y xy


2
2
25 4 20 25 4 20xy xy t t
, vi
2
1
44
xy
t xy
.
Xét hàm s
2
25 4 20f t t t
n
1
0;
4



.
Ta có:
50 4f t t

. Xét
2
0
25
f t t
.
Ta có:
0 20f
,
2 496
25 25
f



và
1 329
4 16
f



.

496 329
;
25 16
m



496 329
,
25 16
ab
suy ra
825T
.
Câu 49:
.ABC A B C

2a

M
,
N


AB

,
BB

MC N
,
ACC A

.
A.
2
4
. B.
6
4
. C.
3
4
. D.
3
4
.
Hướng dẫn giải
Chọn B
, 0;xy
1xy
;m a b
22
5 4 5 4 40x y y x xy m
25 16T a b
829T
825T
816T
820T
Trang 66

I

AC

.
Ta có
( )
( )
1
B I A C
B I ACC A
B I AA
ì
¢ ¢ ¢
^
ï
ï
¢ ¢ ¢
Þ^
í
ï
¢¢
^
ï
î
.
+) Xét tam giác
A BB
¢¢
có
,M
N

AB
¢¢
và
BB
¢
MNÞ

A BB
¢¢
D
//MN A B
¢
Þ
.
Trong
( )
AA B B
¢¢
có
//
A B AB
AB MN
A B MN
ì
¢¢
^
ï
ï
¢
Þ^
í
ï
¢
ï
î
.

( )
C M A B
C M AA B B C M AB
C M AA
ì
¢ ¢ ¢
^
ï
ï
¢ ¢ ¢ ¢ ¢
Þ ^ Þ ^
í
ï
¢¢
^
ï
î
.
+) Ta có
( )
( )
2
AB MN
AB C MN
AB C M
ì
¢
^
ï
ï
¢¢
Þ^
í
ï
¢¢
^
ï
î
.

( )
1
và
( )
2

MC N
,
ACC A


BI
¢
và
AB
¢
.
+) Xét tam giác
AA B
¢¢

A
có
2 2 2 2
4 4 2 2AB AA A B a a a
¢ ¢ ¢ ¢
= + = + =
.

ABC
¢ ¢ ¢

2a
có
BI
¢

23
3
2
a
B I a
¢
Þ = =
.
Xét tam giác vuông
AA I
¢
có
2 2 2 2
45AI AA A I a a a
¢¢
= + = + =
.
+) Xét
AB I
¢
D
có
2 2 2 2 2 2
3 8 5 6
cos 0
2 . 4
2. 3.2 2
B I AB AI a a a
AB I
B I AB
aa


.

BI
¢
và
AB
¢

6
4
.

MC N
,
ACC A


6
4
.
Câu 50: Ch M vay ngân hàng 300 tric tr  mua nhà. Nu cui mi tháng,
bu t tháng th nht ch M tr 5,5 tring và chu lãi s ti là 0,5% mi tháng (bit lãi
sui) thì sau bao lâu, ch M tr ht s tin trên?
A
. 64 tháng
B
. 54 tháng
C
. 63 tháng
D
. 55 tháng
Hướng dẫn giải
Chọn A
Cui tháng th nht, s ti là
1
1N A r a
ng
Cui tháng th hai, s ti là
2
21
. 1 1 1N N r a A r a r a
Cui tháng th ba, s ti là:
Trang 67
32
32
1 1 1 . 1N N r a A r a r a r a
Cui tháng th n s ti là:
21
1 1 1 1 ... 1
nn
n
N A r a r r r
11
1.
n
n
r
A r a
r

 ht n sau n tháng thì s tin còn n sau n tháng là 0, tc là ta gi  
1 1 1 .
1 . 0
11
nn
n
n
r A r r
A r a a
r
r

(s tin phi tr mi tháng).
Lời giải
Áp dng công thc va thit lp bài toán t
1 0,5% 1
300. 1 0,5% 5,5. 0 300.1,005 1100. 1,005 1 0
0,5%
n
n
nn

1,005
11
log 63,84984073
8
n
.
www.thuvienhoclieu.com
ĐỀ 15
PHÁT TRIỂN TỪ ĐỀ MINH
HỌA LẦN 2 NĂM 2020
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Có bao nhiêu cách chn 5 hc sinh t 20 hc sinh lp 11A ?
A. 18640480 cách. B. 120 cách.
C. 15504 cách. D. 100 cách.
Câu 2: Cho cp s cng có
1
0u
và công sai d = 3. Tng ca 26 s hu tiên ca cp s c
bng bao nhiêu ?
A. 975. B. 775.
C. 875. D. 675.
Câu 3: Tìm nghim c
2
log 3 2 3x 
A.
8
3
x
. B.
10
3
x
.
C.
16
3
x
. D.
11
3
x
.
Câu 4: Tính th tích khi lnh a
A.
3
3
a
. B.
3
2
a
.
C.
3
a
. D.
3
6
a
.
Câu 5: Tnh ca hàm s
2
32y x x
là
A.
\ 1;2
. B.
;1 2; 
.
C.
1;2
. D.
;1 2;
.
Câu 6: Tìm h nguyên hàm F(x) ca hàm s
1
()
54
fx
x
Trang 68
A.
1
ln 5 4
ln5
F x x C
. B.
ln 5 4F x x C
.
C.
1
ln 5 4
5
F x x C
. D.
1
ln 5 4
5
F x x C
.
Câu 7: Cho khi chóp S.ABCD có c nht, AB = a,
AD = 2a, SA = 3a. Th tích khi chóp S.ABCD bng:
A.
3
6a
. B.
3
2a
.
C.
3
3
a
. D.
3
a
.
Câu 8: Cho kh
3r
và chiu cao h = 4. Tính th tích V ca khi nón 
A.
16 3.
B.
12 .
C. 4. D.
4.
Câu 9: Th tích ca khi cu có bán kính bng
2
a
là:
A.
3
.
2
a
B.
2
.
4
a
C.
3
.
6
a
D.
2
.a
Câu 10: Cho hàm s
32
34y x x
có bng bi
A.
, 2.ab 
B.
; 4.ab 
C.
; 1.ab 
D.
, 3.ab 
Câu 11: Vi a, b là hai s th
4
ln
ae
b
bng:
A.
4ln ln 1ab
. B.
4ln ln 1.ba
C.
4ln ln 1.ab
D.
4ln ln 1.ab
Câu 12: Cho hình tr ng 5 và chiu cao bng 7. Din tích xung quanh ca hình tr
ng:
A.
17
3
. B.
175 .
C.
70 .
D.
35 .
Câu 13: Cho hàm s y = f(x) liên tc trên
và có bng bi
M 
Trang 69
A. Hàm s m cc tr. B. Hàm s m cc tr.
C. Hàm s  cc tiu. D. Hàm s  không có giá tr ci.
Câu 14:  th ca hàm s 
A.
21
1
x
y
x
. B.
1
.
1
x
y
x
C.
42
1.y x x
D.
3
31y x x
.
Câu 15: ng tim cng c th hàm s
35
2
x
y
x
là:
A.
2.x
B.
2.y
C.
3.x
D.
3.y
Câu 16: Tp nghim ca b
39
x
là:
A.
2;
. B.
0;2 .
C.
0; .
D.
2; . 
Câu 17: Cho hàm s
()y f x
 th . S nghim c
3 ( ) 8 0fx
bng:
A. 1. B. 2.
C. 3. D. 4.
Câu 18: Nu
25
12
3, 1f x dx f x dx

thì
5
1
f x dx
bng:
A. 3. B. 4.
C.2. D.
2.
Câu 19: Cho s phc z tha mãn
32zi
. Tìm phn thc và phn o ca s phc z
A. Phn thc bng
3
, phn o bng 2.
B. Phn thc bng
3
, phn o bng 2.
C. Phn thc bng 3, phn o bng
2.
D. Phn thc bng
3
, phn o bng
2.
Câu 20: Cho hai s phc
12
1 2 , 3 9z i z i
m M biu din s phc
12
zz
trên mt phng
t
A.
2;11 .M
B.
2; 11 .M 
C.
11; 2 .M
D.
11;2M
.
Trang 70
C
B
A
S
Câu 21: Trên mt phng tm M (2;-m bin din ca s ph
A.z = 2+ 3i B.z = 2- 3i C.z = 3+2i D.z = 3-2i
Câu 22: Trong không gian Oxyz, hình chiu vuông góc cm
(2;1; 1)M
trên mt phn
()Ozy
có
t là:
A.
(0;1;0)
B.
(2;1;0)
C.
(0;1; 1)
D.
(2;0; 1)
Câu 23: Trong không gian Oxyz, cho mt cu (
):
2 2 2
( 3) ( 2) ( 1) 4.x y z
Tâm ca
()S
có
t là:
A.
( 3;2; 1)
B.
(3; 2; 1)
C.
(3; 2;1)
D.
( 3; 2;1)
Câu 24: Trong không gian Oxyz, cho mt phng (
P
m A(1;0;0), B(0;-2;0), C( 0;0;3).
a (
P
)?
A.
1
1 2 3
x y z
B.
1
1 2 3
x y z
C.
1
1 2 3
x y z
D.
1
1 2 3
x y z
Câu 25: ng thng d:
1 2 1
.
2 3 1
x y z


a d ?
A.
(2;3; 1)u 
B.
( 1; 2;1)u
C.
( 2; 3; 1)u
D.
(1;2; 1)u 
Câu 26: Cho hình chóp S.ABC có SA vuông góc vi mt phng (ABC), tam
giác ABC vuông ti
B
(minh ha mt phng
(SBC) và mt phng
()ABC
là :
A.
SBC
B
SCB
C.
SCA
D.
SBA
Câu 27: Cho hàm s
()y f x
nh, liên tc trên
và có
 th 
hình
bên. Khnh sai?
A th hàm s m
(0; 1)A
.
B. Hàm s có giá tr cc tiu bng -1.
C. Hàm s m cc tr.
D. Hàm s t ci ti
0x
Câu 28: Giá tr ln nht ca hàm s
1
2
x
y
x
n [0;2]là:
A.
1
4
B. 0 C.
1
2
D. 2
Câu 29: Vi mi a, b, x là các s th mãn
2 2 2
log 5log 3logx a b
. M i

A.
35x a b
B.
53x a b
C.
53
x a b
D.
53
x a b
Câu 30: S m c th hàm s
32
25y x x
và
51yx
là:
A. 3. B. 0 C. 2. D. 1.
Câu 31: Tp nghim ca b
2.2 3 04
xx
là
Trang 71
A.
[0; )
B.
(0; )
C.
( ;0)
D.
( ;0]
Câu 32: Trong không gian, cho tam giác ABC vuông ti A, AB = a và BC = 2a. Khi quay tam giác
ABC xung quanh cng gp khúc CBA to thành mt hình nón. Th tích
khng:
A.
3
2
3
a
B.
3
3
3
a
C.
3
6
3
a
D.
2
3
3
a
Câu 33: Cho tích phân:
1
1 ln
d.
2
e
x
Ix
x
t
1 ln .ux

I
bng :
A.
0
2
1
dI u u
B.
0
2
1
dI u u
C.
2
0
1
d.
2
u
Iu
D.
1
2
0
dI u u
Câu 34: Din tích hình phc gii hn b th hàm s
2
,
x
ye
trng
thng
0, 3xx
là
A.
6
1
22
e
B.
6
1
22
e
C.
6
1
33
e
D.
6
1
33
e
Câu 35: Cho hai s phc z
1
= 3-i và z
2
= 2+3i. Phn o ca s phc w = 2z
1
- z
2
là:
A. 4 B.5i C. -5i D.-5
Câu 36: Kí hiu z
1
, z
2
là hai nghim phc c
2
2 10 0zz
. Gi a
1
, a
2
lt là
phn thc ca z
1
, z
2
Tính
12
3 2 .M a a
A.
5.M
B.
3.M 
C.
2.M
D.
6M 
Câu 37: m
(2; 1;0)M
ng thng
4
: 2 2 ( )
3
xt
y t t
zt

.
Mt phi

A.
2 3 4 0x y z
B.
2 3 4 0x y z
C.
2 3 7 0x y z
D.
2 3 7 0x y z
Câu 38: m M( 1;0;-ng thi mt
phng
(P):
2 3 2 0x y z
, có phurong trinh tham s là:
A.
2
3
12
xt
y
zt



B.
2
3
12
xt
y
zt



C.
12
3
2
xt
yt
zt


D.
12
3
2
xt
yt
zt


Câu 39: Có 8 bn hc sinh lc xp ngu nhiên theo mt hang ngang.
Tính xác sut
P
 A và B ngi cnh nhau.
A.
1
8
P
. B.
1
4
P
. C.
1
64
P
. D.
1
25
P
.
Câu 40: Cho hình chóp
.S ABCD

ABCD
là hình ch nht,
,2AB a AD a
,
SA
vuông góc
vi mt ph
SA a
(tham kho hình v). Gi
M
m ca
CD
. Khong cách
ging thng
,SD BM
bng
Trang 72
A.
21
21
a
. B.
2 21
21
a
. C.
27
7
a
. D.
7
7
a
.
Câu 41: Có bao nhiêu giá tr nguyên ca tham s
2020;2020m
 hàm s
32
1 3 4 4 1y m x mx m x
ng bin trong khong
; 
?
A. 2020. B. 2018. C. 2019. D. 4040.
Câu 42: Mi th mt lá bèo vào mt h c. Sau 24 gi, bèo sinh sôi ph kín mc trong
h. Bit rng c sau mi gi p 20 l 
i. Hi sau my gi thì bèo ph kín
1
5
mc trong h (kt qu n hàng phn chc).
A.
23,5
gi. B.
22,5
gi. C.
21,4
gi. D.
20,3
gi.
Câu 43: ng cong  th hàm s
32
y ax bx cx d
.
Xét các m sau:
I
1a
.
II
0ad
.
III
1d
.
IV
1 a c b
.
Tìm s m đúng.
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 44: Cho 






ABCD

a

,AB








, 









. 


()ABCD

0
45
. 


xq
S


V
:
A.
23
3 3 2
;
38
xq
aa
SV

. B.
23
2 3 2
;
3 32
xq
aa
SV

.
C.
23
3 3 3
;
4 16
xq
aa
SV

. D.
23
3 3 2
;
2 16
xq
aa
SV

.
Trang 73
Câu 45:   
y f x
       
2
. . ' ,x f x f x f x x x
và có
21f
. Tích phân
2
2
0
.f x dx
A. B. C. D.
Câu 46: Cho hàm s
fx
có bng bi
S nghim thun
9
0;
2



c
2sin 1 1fx
là
A.
6
. B.
4
. C.
5
. D.
7
.
Câu 47: Cho hai s thc
,1ab
. Tìm giá tr nh nht ca biu thc
4
11
log log
ab
ab
S
ab

.
A.
2
min .
9
S
B.
9
min .
4
S
C.
4
min .
3
S
D.
1
min .
4
S
Câu 48: Gi
là tp hp tt c các giá thc ca tham s
m
sao cho giá tr ln nht ca hàm s
2
1
x mx m
y
x

n
1;2
bng 2. S phn t ca
là
A. 1. B. 2. C. 3. D. 4.
Câu 49: Cho hình chóp
.S ABCD

ABCD
là hình thang va mãn
23CD AB
. Bit
th tích ca khi chóp
.S ABD
bng
4V
và th tích ca khi chóp
.S CDMN
bng
126
25
V

,MN
lt nm trên cnh
,SA SB
sao cho
MN
song song vi
.AB
T s
SM
MA
bng:
A.
2
3
. B.
3
2
. C.
3
4
. D.
4
3
.
Câu 50: Có bao nhiêu giá tr nguyên ca tham s
m
2020m
  
1
4
2 log 2
x
x m m
có nghim ?
A.
2020
. B.
2019
. C.
2018
. D.
4040
.
Đáp án:
1. C
2.A
3.B
4.C
5.B
6.C
7.C
8.D
9.C
10.B
11. A
12.C
13.A
14.B
15.A
16.A
17.B
18.C
19.C
20.B
21.B
22.C
23.C
24.D
25.A
26.D
27.D
28.A
29.C
30.A
31.C
32.B
33.B
34.B
35.D
36.A
37.B
38.C
39.B
40.B
41.C
42.A
43.D
44.D
45.C
46.D
47.B
48.B
49.B
50.A
3
2
4
3
2
4
Trang 74
Câu 39: Có 8 bn hc sinh lc xp ngu nhiên theo mt hang ngang. Tính
xác sut
P
 A và B ngi cnh nhau.
A.
1
8
P
. B.
1
4
P
. C.
1
64
P
. D.
1
25
P
.
HƯỚNG DẪN GIẢI
chn B.
8!n 
S cách xp 8 hi cnh nhau là:
2!7!
.
2!7! 1
8! 4
P 
.
Câu 40: Cho hình chóp
.S ABCD

ABCD
là hình ch nht,
,2AB a AD a
,
SA
vuông góc
vi mt ph
SA a
(tham kho hình v). Gi
M
m ca
CD
. Khong cách gia
ng thng
,SD BM
bng
A.
21
21
a
. B.
2 21
21
a
. C.
27
7
a
. D.
7
7
a
.
HƯỚNG DẪN GIẢI
Chọn B
Gi
N
m ca
AB

//BM DN
nên
//BM SDN
; ; ; ;d BM SD d BM SDN d B SDN d A SDN
.
K
AH DN
ti
H
. Ta có mt phng
SAH SDN
. Trong
mp SAH
k
AK SH
ti
K

;;d BM SD d A SDN AK
.
2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 4 1 1 21
44AK AH SA AN AD SA a a a a
. Suy ra
2 21
21
a
AK
.
Trang 75
Câu 41: Có bao nhiêu giá tr nguyên ca tham s
2020;2020m
 hàm s
32
1 3 4 4 1y m x mx m x
ng bin trong khong
; 
?
A. 2020. B. 2018. C. 2019. D. 4040.
HƯỚNG DẪN GIẢI
Chọn C.

D
.
2
' 3 1 6 4 4y m x mx m
.
 hàm s ng bin trên khong
; 
thì
' 0,yx
TH1:
1 0 1mm
thì
4
' 0 6 8 0
3
y x x
(không tha mãn)
TH2:
2
2
'
1
10
1
'0
9 3 1 4 4 0
3 12 0
y
m
m
m
m m m
m



1
2
2
2
m
m
m
m

Do
m
là s nguyên và
2020;2020 2;3;...;2020mm
.
Vy có 2019 s nguyên m cn tìm.
Câu 42: Mi th mt lá bèo vào mt h c. Sau 24 gi, bèo sinh sôi ph kín mc trong h.
Bit rng c sau mi gi p 20 l i. Hi sau
my gi thì bèo ph kín
mc trong h (kt qu n hàng phn chc).
A.
23,5
gi. B.
22,5
gi. C.
21,4
gi. D.
20,3
gi.
HƯỚNG DẪN GIẢI
Chọn A.
Gi s mt lá bèo chim
x
phn mc trong h
01x
.
Sau 24 gi, bèo sinh sôi ph kín mc trong h nên ta có:
24
24
1
20 1
20
xx
.
Gi s sau
t
gi thì bèo bao ph kín
mc trong h , ta có:
24
20
24
1 1 1 1
.20 20 log 24 23,5
20 5 5 5
tt
t
gi.
Câu 43: ng cong  th hàm s
32
y ax bx cx d
.
Xét các m sau:
I
1a
.
II
0ad
.
III
1d
.
IV
1 a c b
.
Trang 76
Tìm s m đúng.
A.
3
. B.
1
. C.
4
. D.
2
.
HƯỚNG DẪN GIẢI
Chọn D.
D th ta thy
0a
. M
I
sai.
 th hàm s m
0;1
10 d
0ad
. M
II

III
sai.
 th hàm s m
1;0
1 a c b
. M
IV

Vy có hai m 
II
và
IV
.
Câu 44: Cho 






ABCD

a

,AB








, 









. 



()ABCD

0
45
. 


xq
S

V

:
A.
23
3 3 2
;
38
xq
aa
SV

. B.
23
2 3 2
;
3 32
xq
aa
SV

.
C.
23
3 3 3
;
4 16
xq
aa
SV

. D.
23
3 3 2
;
2 16
xq
aa
SV

.
Hướng dẫn giải:
Chọn D.
* 
,MN





AB

CD
. 
:
OM AB

'O N DC
.

I

MN

'OO
. 
, 'R OA h OO
.
* Trong
IOM
vuông 
I
nên:
2
2
OM OI IM
.
22
.
2 2 2 2
ha
ha
.
* 
:
2 2 2 2
R OA AM MO
2
2
2 2 2
23
2 4 4 8 8
a a a a a






.
2 2 3
2
3 2 3 3 2 3 2
2 2 . ; .
2 2 8 2 16
22
xq
a a a a a a
S Rh V R h
.
Câu 45: 
y f x
 
2
. . ' ,x f x f x f x x x
và có
21f
. Tích phân
2
2
0
.f x dx
A. B. C. D.
Hướng dẫn giải:
Chọn C.
3
2
4
3
2
4
Trang 77
Câu 46: Cho hàm s
fx
có bng bi
S nghim thun
9
0;
2



c
2sin 1 1fx
là
A.
6
. B.
4
. C.
5
. D.
7
.
Hướng dẫn giải:
Chọn D.
Da vào bng bin thiên, ta có
1
1 1;3
3;
x
f x x a
xb


.
y
sin 1 1
2sin 1 1
1
2sin 1 1 2sin 1 1;3 sin , 1;3 2
2
2sin 1 3;
1
sin , 3; 3
2
x
x
a
f x x a x a
xb
b
xb



.
n
9
0; ,
2




sin 1x 
có 2 nghim
37
,
22
xx


.
Vi
1
1 3 0 1 2 0 1
2
a
aa
 
1
sin
2
a
x
có 5 nghim phân bit thuc
9
0;
2



, các nghiu khác
3
2
và
7
2
.
Vi
1
3 1 2 1
2
b
bb

1
sin
2
b
x
vô nghim.
Vn
9
0;
2




2sin 1 1fx
có 7 nghim.
Câu 47: Cho hai s thc
,1ab
. Tìm giá tr nh nht ca biu thc
4
11
log log
ab
ab
S
ab

.
A.
2
min .
9
S
B.
9
min .
4
S
C.
4
min .
3
S
D.
1
min .
4
S
Hướng dẫn giải:
Chọn B.
22
2 2 2
2 2 2 2
0 0 0
2
. ( ). '( ) ( ) 2 . ( ). '( ) 2 ( ) 2
2 . ( ). '( ) ( ) 3 ( ) 2 . ( ) ' x 3 ( ) 2
2
. ( ) 3 4 2 3 4 2
0
x f x f x f x x x f x f x f x x
x f x f x f x f x x x f x d f x dx xdx
x f x I I I
Trang 78
1 1 1
log log 1 log log
4 4 4
51
log
4 4log
a b a b
a
a
S ab ab b a
b
b
Do
1, 1 log 0
a
a b b
. Áp dụng BĐT Cô-si, ta có :
5 1 5 1 5 9
log 2 log . 1
4 4log 4 4log 4 4
aa
aa
S b b
bb
Du « = » xy ra
1
log
1
2
log
1
4log
log
2
a
a
a
a
b tm
b b a
b
bl
Câu 48: Gi
S
là tp hp tt c các giá thc ca tham s
m
sao cho giá tr ln nht ca hàm s
2
1
x mx m
y
x

n
1;2
bng 2. S phn t ca
là
A. 1. B. 2. C. 3. D. 4.
Hướng dẫn giải:
Chọn B.
Xét hàm s
2
1
x mx m
fx
x

n
1;2
.
Ta có
'fx
liên tc trên
1;2
và
2
2
2
' 0, 1;2
1
xx
f x x
x
.
fx
ng bin trên
1;2
1;2
34
max 2
3
m
f x f
;
1;2
21
min 1
2
m
f x f

.

1;2
3 4 2 1
max max ;
32
mm
fx


.
Ta có
22
3 4 2 1 11
4 3 1 9 2 1
3 2 12
mm
m m m

.
Vi
11
12
m 
, ta có
1;2
2
34
3
max 2
10
3
3
m tm
m
fx
ml

Vi
11
12
m 
, ta có
1;2
5
21
2
min 2
3
2
2
m tm
m
fx
ml

Vy
52
;
23
S



S phn t ca
là 2.
Câu 49: Cho hình chóp
.S ABCD

ABCD
là hình thang va mãn
23CD AB
. Bit th
tích ca khi chóp
.S ABD
bng
4V
và th tích ca khi chóp
.S CDMN
bng
126
25
V

,MN
ln
t nm trên cnh
,SA SB
sao cho
MN
song song vi
.AB
T s
SM
MA
bng:
A.
2
3
. B.
3
2
. C.
3
4
. D.
4
3
.
Hướng dẫn giải:
Trang 79
Chọn B.
t
,0
SM SN
xx
SA SB
.
Nhn thy hai tam giác
,ABD BCD
 ng cao bng nhau và c 
3
2
CD AB
..
33
6
22
BCD DAB S BCD S DAB
S S V V V

.
Ta có t s th tích:
2 2 2
.
..
.
. . . 4 .
S DMN
S DMN S DAB
S DAB
V
SD SM SN
x V x V x V
V SD SA SB
.
.
..
.
. . . 6 .
S DNC
S DNC S DBC
S DBC
V
SD SN SC
x V xV xV
V SD SB SC
.
T gi thit
22
. . .
126 126
4 6 . 4 6 0
25 25
S CDMN S DMN S DNC
V V V x x V V x x
3
5
21
10
xn
xl

33
52
SM SN SM
SA SB MA
.
Vy
3
2
SM
MA
Câu 50: Có bao nhiêu giá tr nguyên ca tham s
m
2020m
  
1
4
2 log 2
x
x m m
có nghim ?
A.
2020
. B.
2019
. C.
2018
. D.
4040
.
Hướng dẫn giải:
Chọn A.

20xm
Ta có
1
4
2 log 2
x
x m m
2
2 log 2 2
x
x m m
t
2
log 2t x m
ta có
22
22


x
t
tm
xm
22
xt
xt
1
Do hàm s
2
u
f u u
ng bin trên
, nên ta có
1 tx

2 2 2 2
xx
x m m x
.
Xét hàm s
2
x
g x x
gx
2 ln2 1 0
x
2
log ln2 x
.
Bng bin thiên:
Trang 80
T       m khi và ch khi
2
2
log ln2
2 log ln2
2
g
m g m
0,457
(các nghiu thu kin vì
2 2 0
x
xm
)
Do
m
nguyên và
2020m
, nên
1;2;...;2020m
.
| 1/80
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 11
ĐỀ THI THỬ THPT QUỐC GIA 2020
PHÁT TRIỂN TỪ ĐỀ MINH MÔN TOÁN
HỌA LẦN 2 NĂM 2020 Thời gian: 90 phút Câu 1:
Cho tập hợp A gồm có 9 phần tử. Số tập con gồm có 4 phần tử của tập hợp A là A. 4 A . B. P . C. 4 C . D. 49 . 9 4 9 Câu 2:
Cho một cấp số cộng có u  2 , u  4 . Hỏi u và công sai d bằng bao nhiêu? 4 2 1
A. u  6 và d 1.
B. u  1và d 1.
C. u  5 và d  1.
D. u  1và d  1.  1 1 1 1 Câu 3: Phương trình 2x 1
5   125 có nghiệm là 5 3 A. x  . B. x 1. C. x  3. D. x  . 2 2 Câu 4:
Hình chóp S.ABCD có đáy là hình vuông cạnh a ; chiều cao có độ dày bằng 6 . a Tính thể tích
khối chóp S.ABCD A. 2 2a . B. 3 6a . C. 3 2a . D. 2 6a . Câu 5:
Tìm tập xác định D của hàm số y  log  2
x  4x  3 3 
A. D  2  2;  1 3;2  2 .
B. D  1;3 .
C. D   ;   1  3; .
D. D   ;
 2  22 2; Câu 6:
Mệnh đề nào sau đây đúng 1 1 A.
dx  ln x C  . B.
dx  tan x C  . x 2 cos x 1 C.
dx  cot x C  .
D. cos x dx  sin x C  . 2 sin x Câu 7:
Cho khối lăng trụ có diện tích đáy bằng 2
3a và khoảng cách giữa hai đáy bằng a . Tính thể tích
V của khối lăng trụ đã cho. 3 A. 3 V a . B. 3 V  3a . C. 3 V a . D. 3 V  9a . 2 a 3 a Câu 8:
Thể tích của khối nón có chiều cao bằng
và bán kính đường tròn đáy bằng là 2 2 3 3 a 3 3 a 3 3 a 3 3 a A. . B. . C. . D. . 6 24 8 8 Câu 9:
Cho khối cầu  S  có thể tích là 288 . Hỏi diện tích khối cầu bằng bao nhiêu?
A. S  48 .
B. S  72 .
C. S  36 .
D. S 144 .
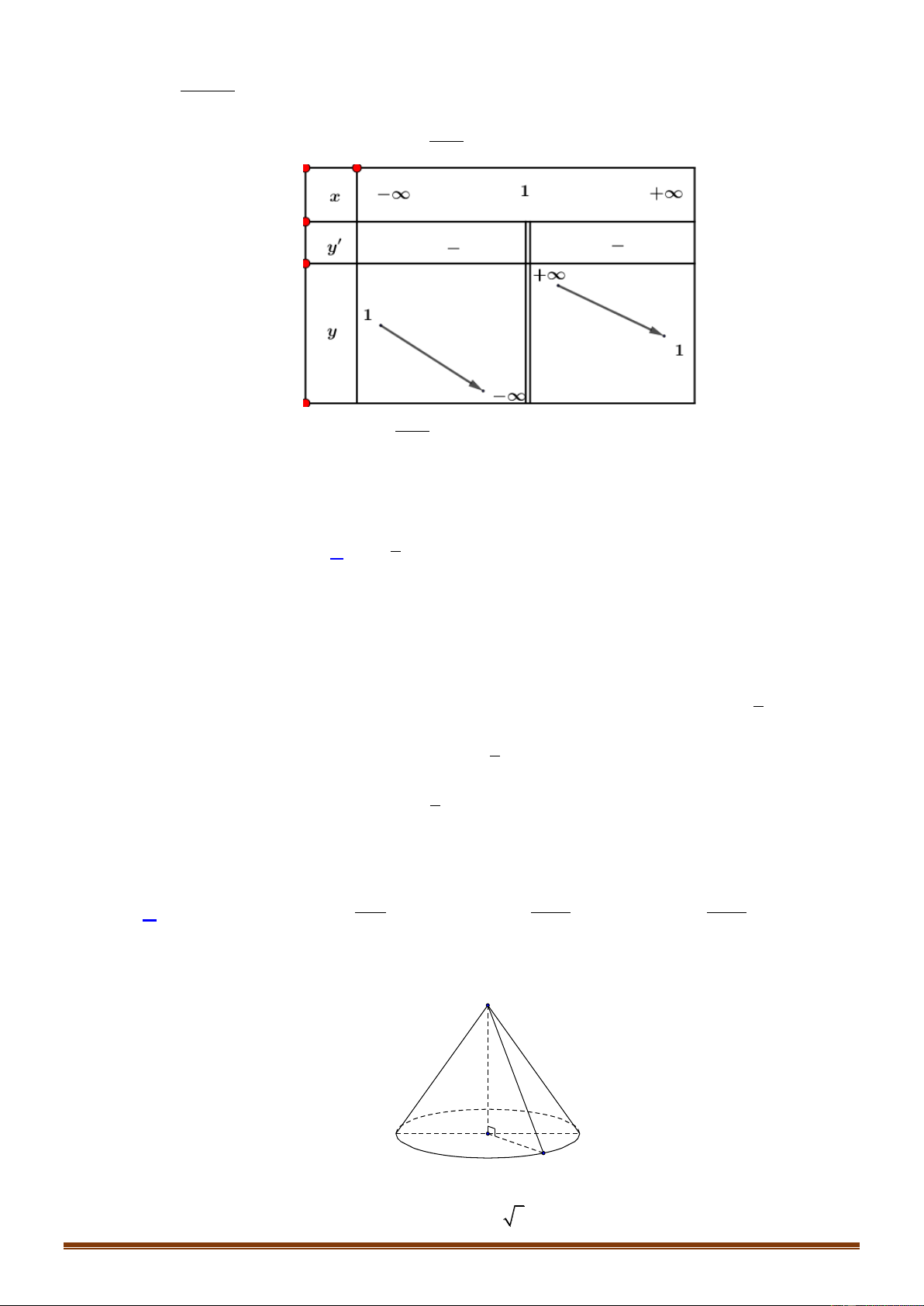
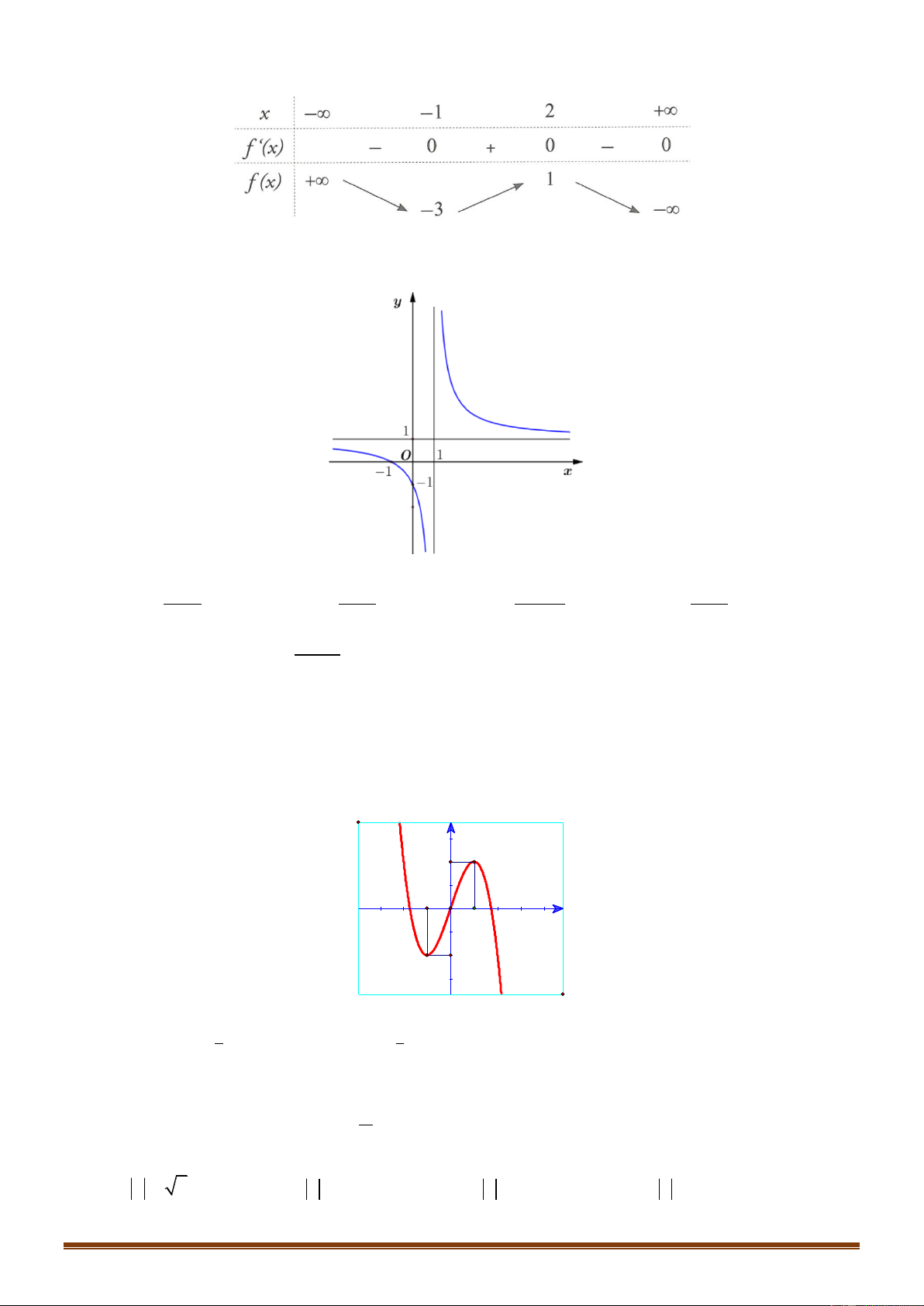
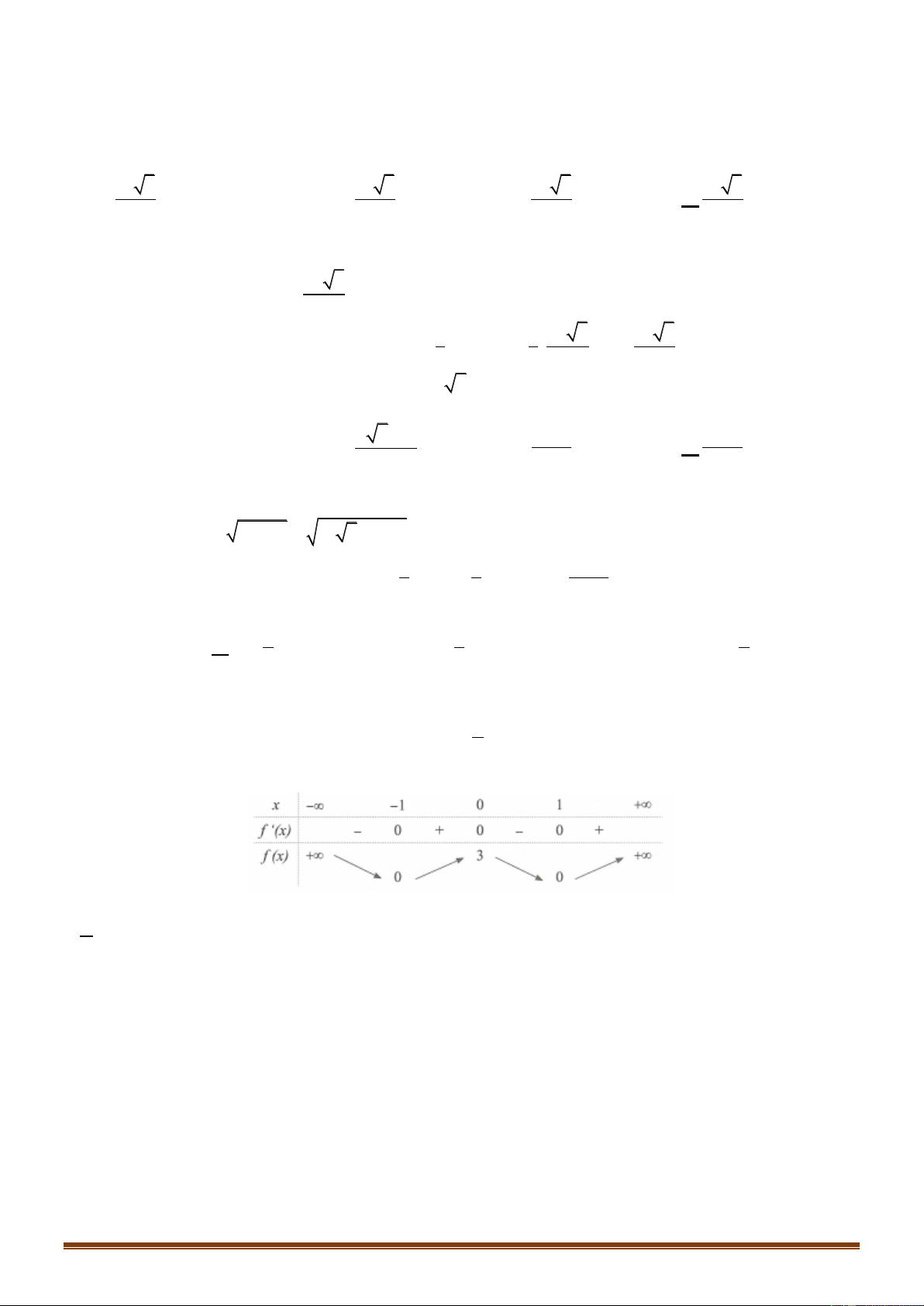
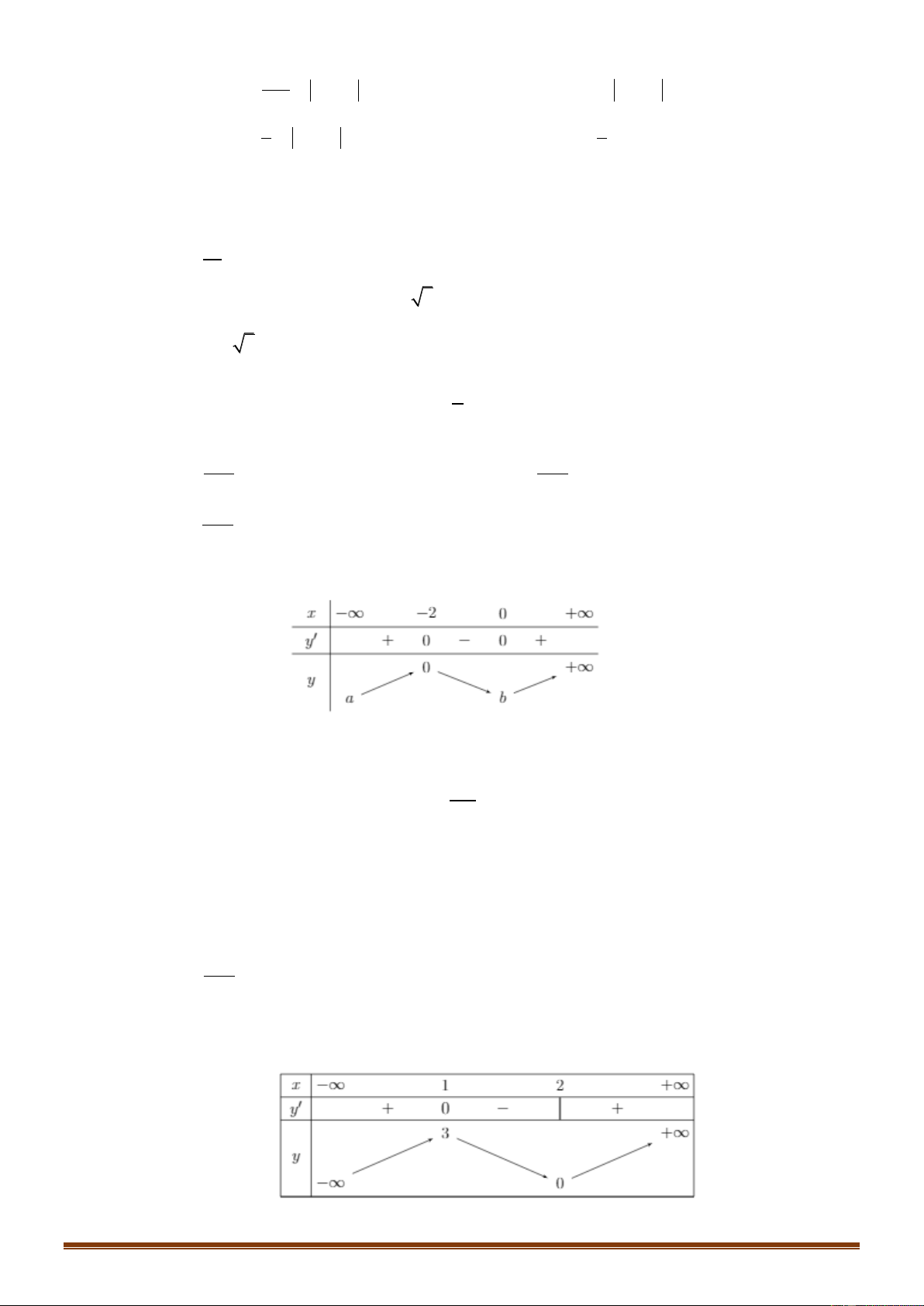
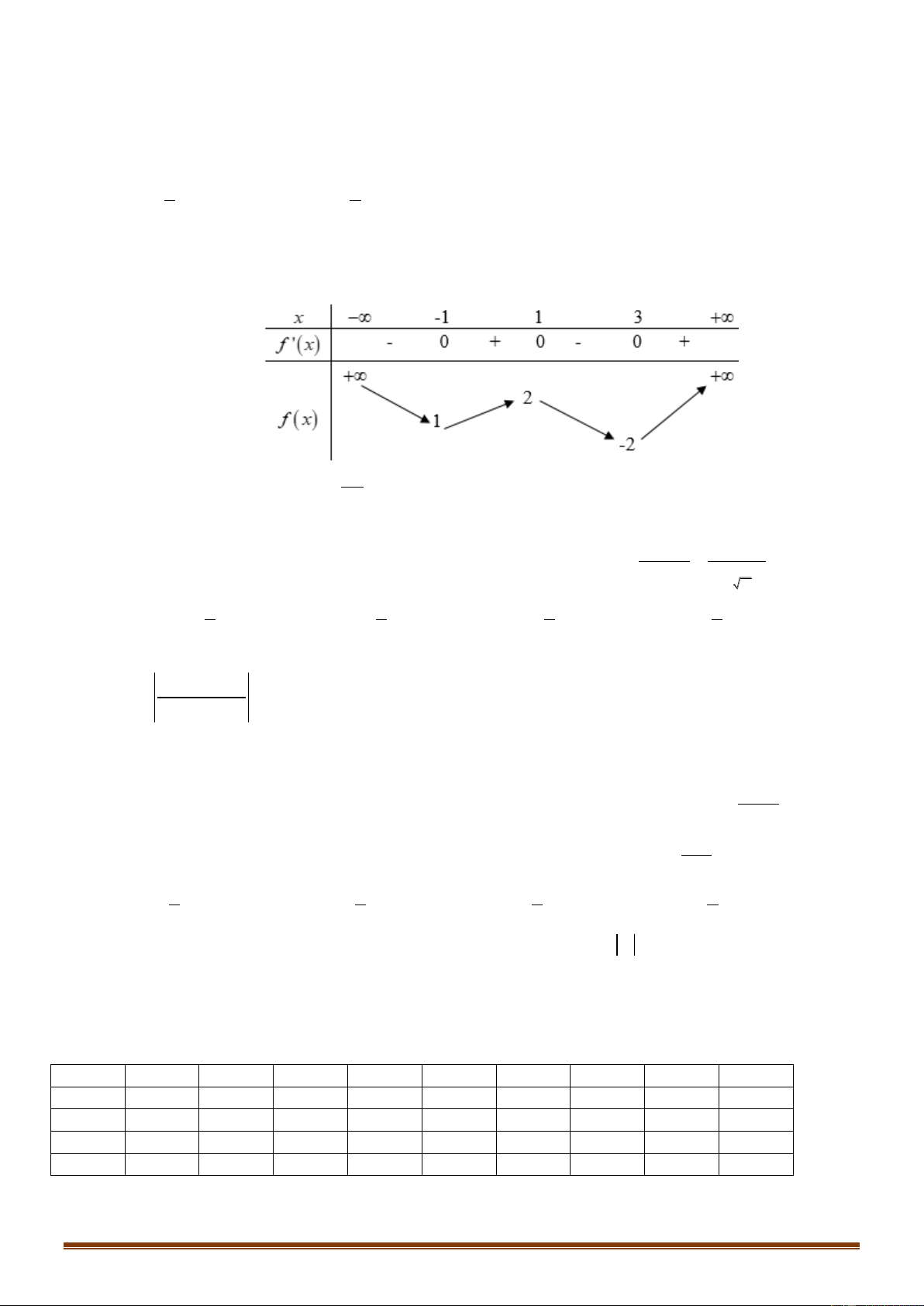
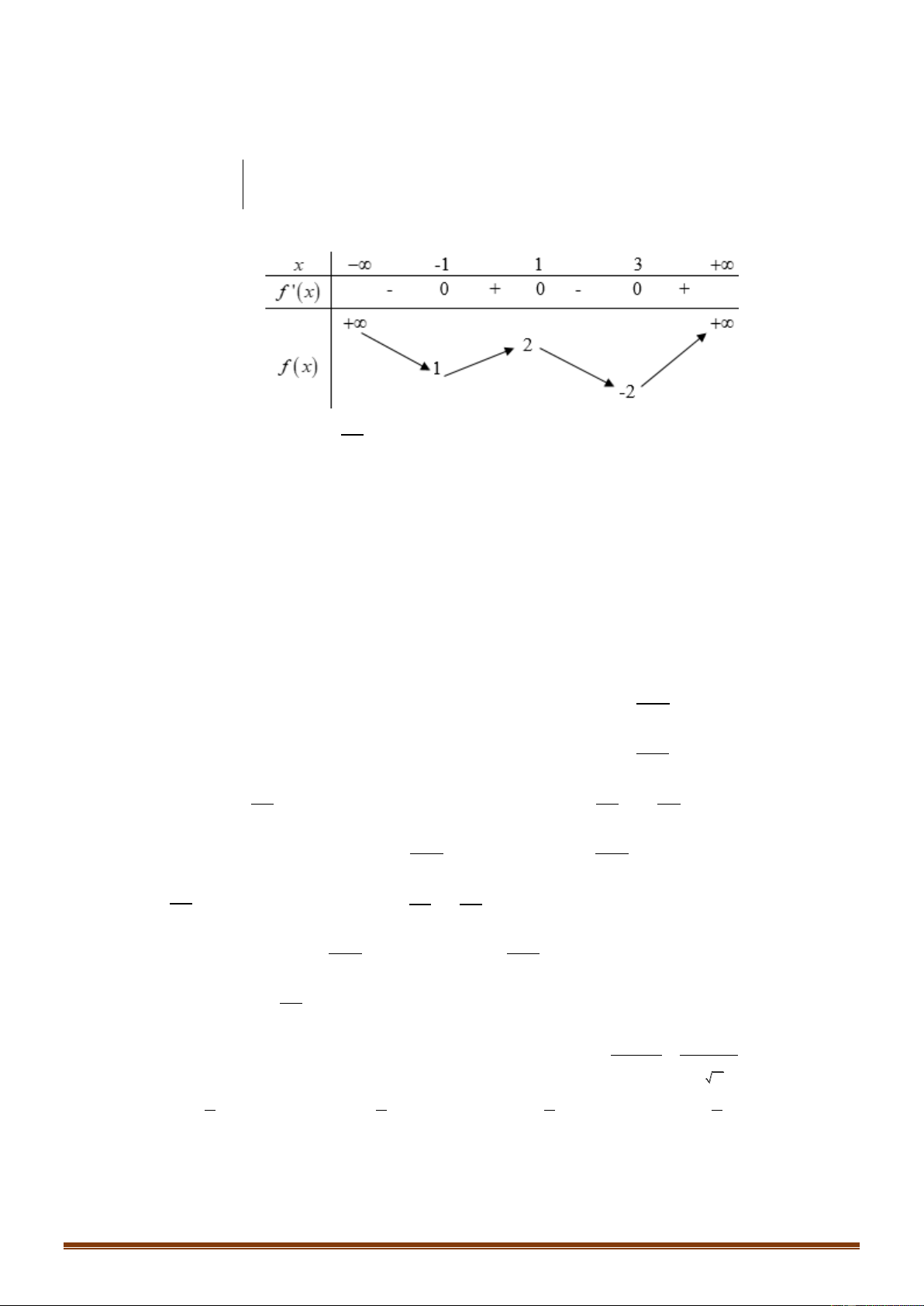
Câu 10: Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên  .
B. Hàm số nghịch biến trên khoảng  ;0  .
C. Hàm số nghịch biến trên khoảng 1;  .
D. Hàm số nghịch biến trên khoảng 0;  1 . Trang 1
Câu 11: Với a, b là số thực tùy ý khác 0 , ta có log ab bằng: 2  
A. log a  log b . B. log . a log b .
C. b log a .
D. log a  log b . 2 2 2 2 2 2 2
Câu 12: Hình trụ có thiết diện qua trục là hình vuông cạnh a thì có thể tích bằng: 1 1 1 A. 3  a . B. 3  a . C. 3  a . D. 3  a . 4 3 2
Câu 13: Giá trị lớn nhất của hàm số 3
y  x  3x  2 trên đoạn 0;2 bằng A. 4. B. 2. C. 9.  D. 3.
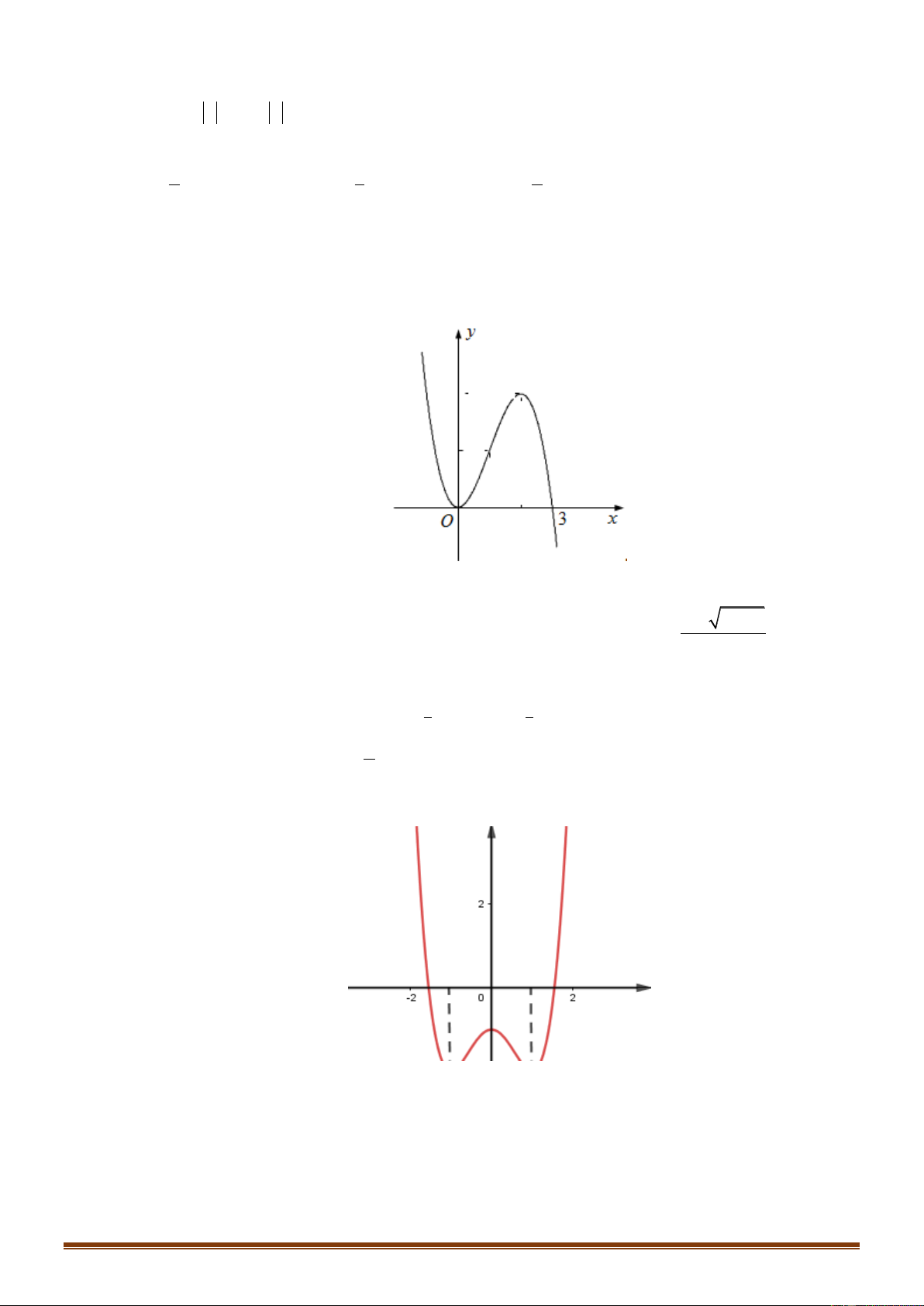
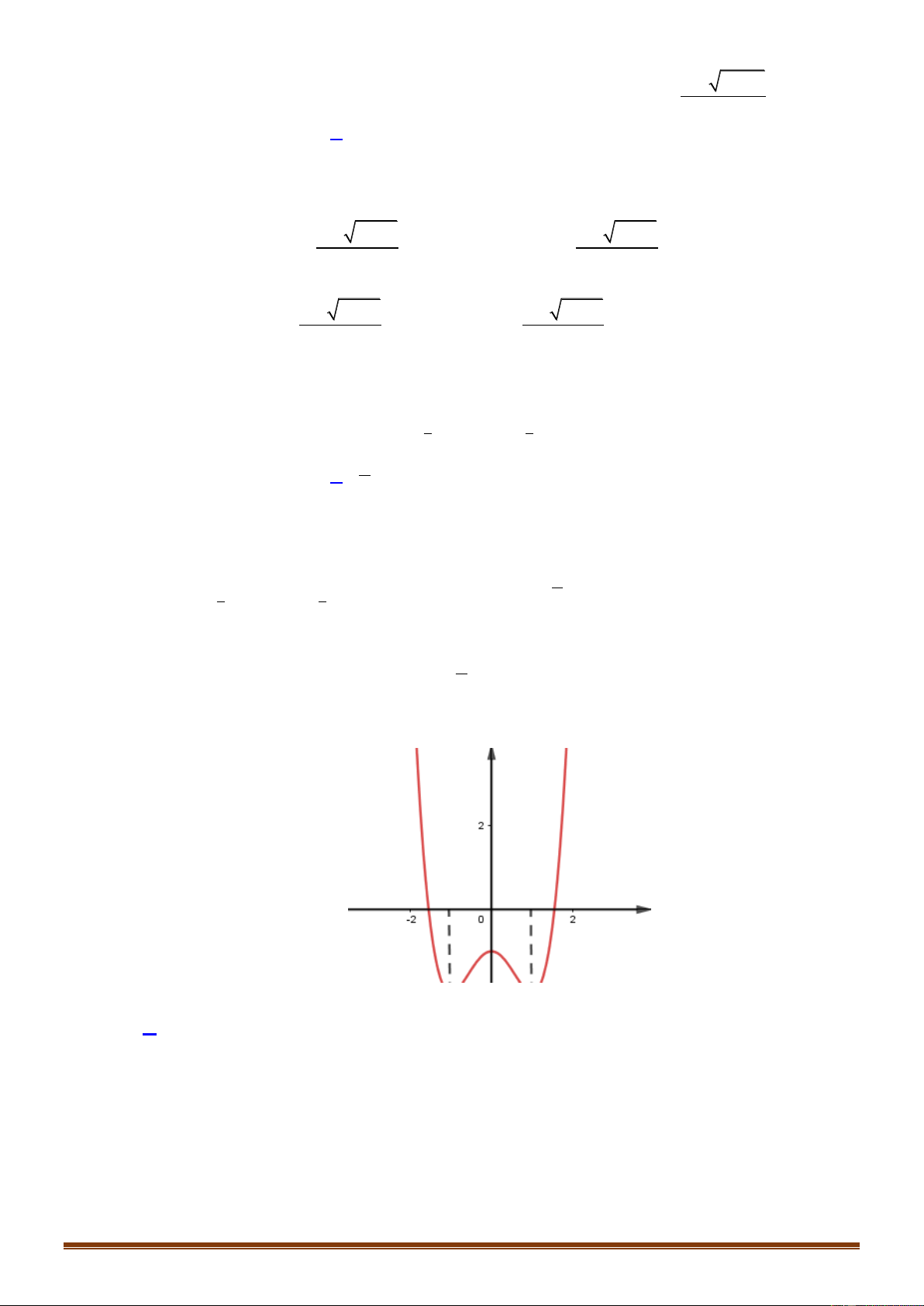
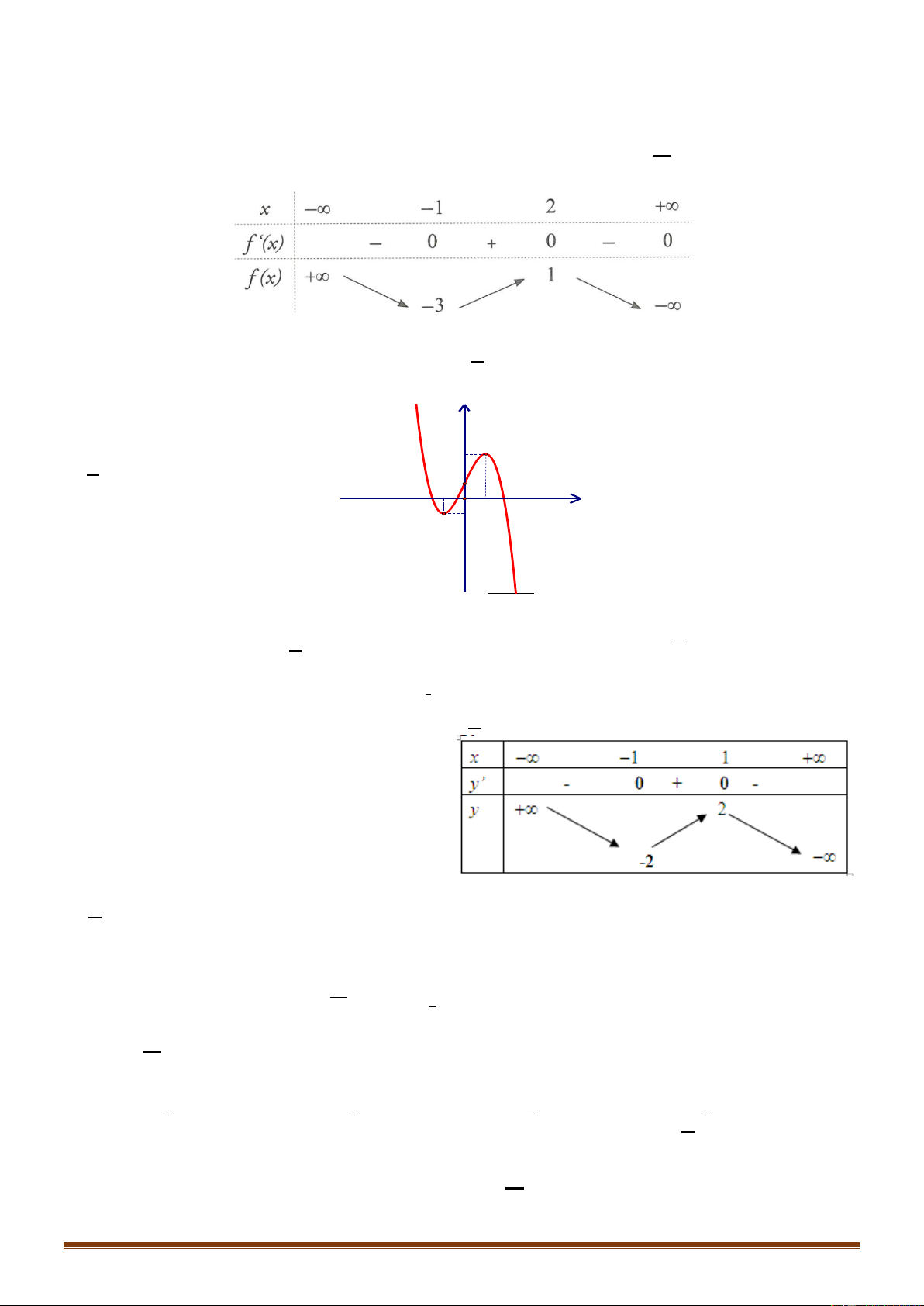
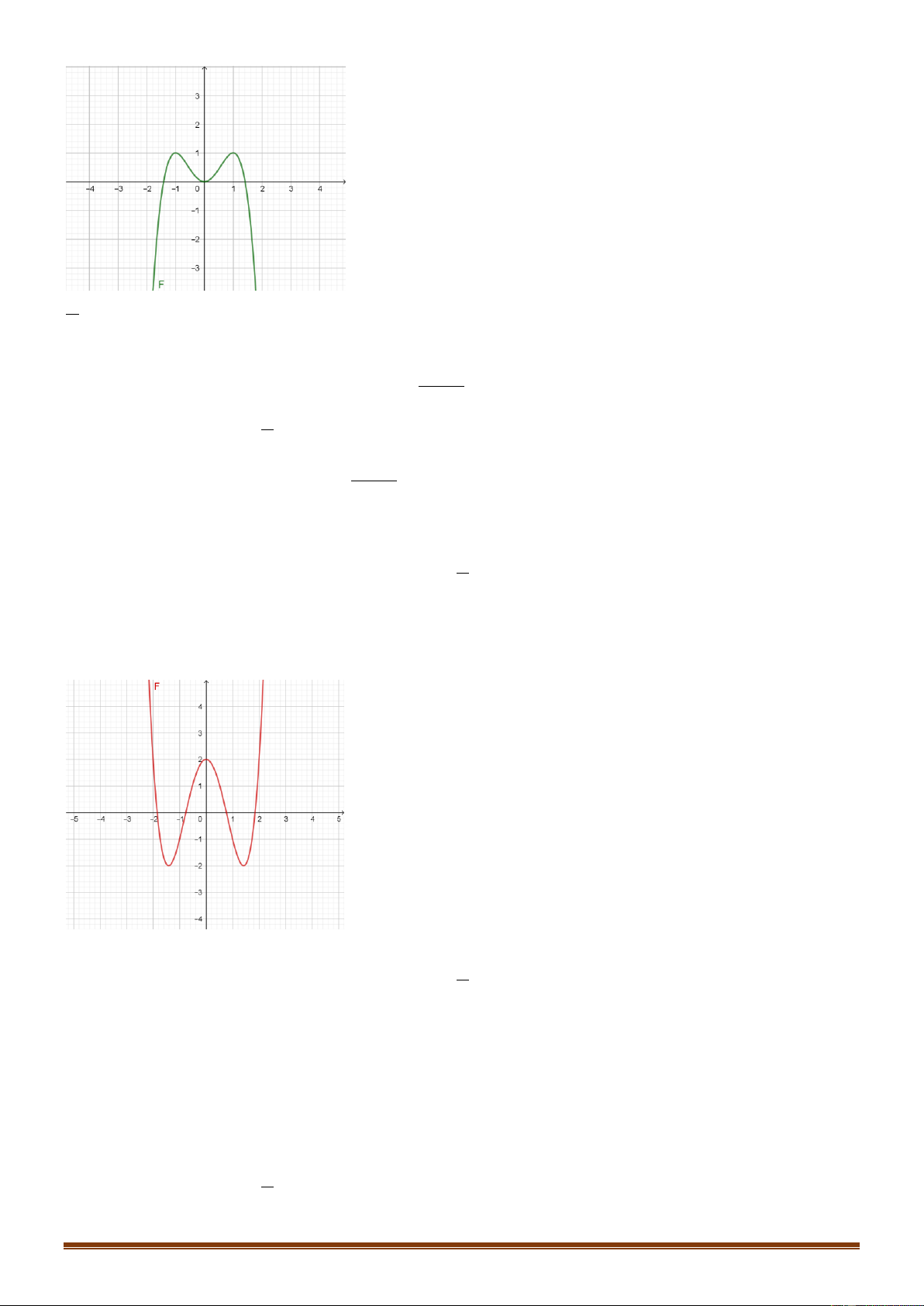
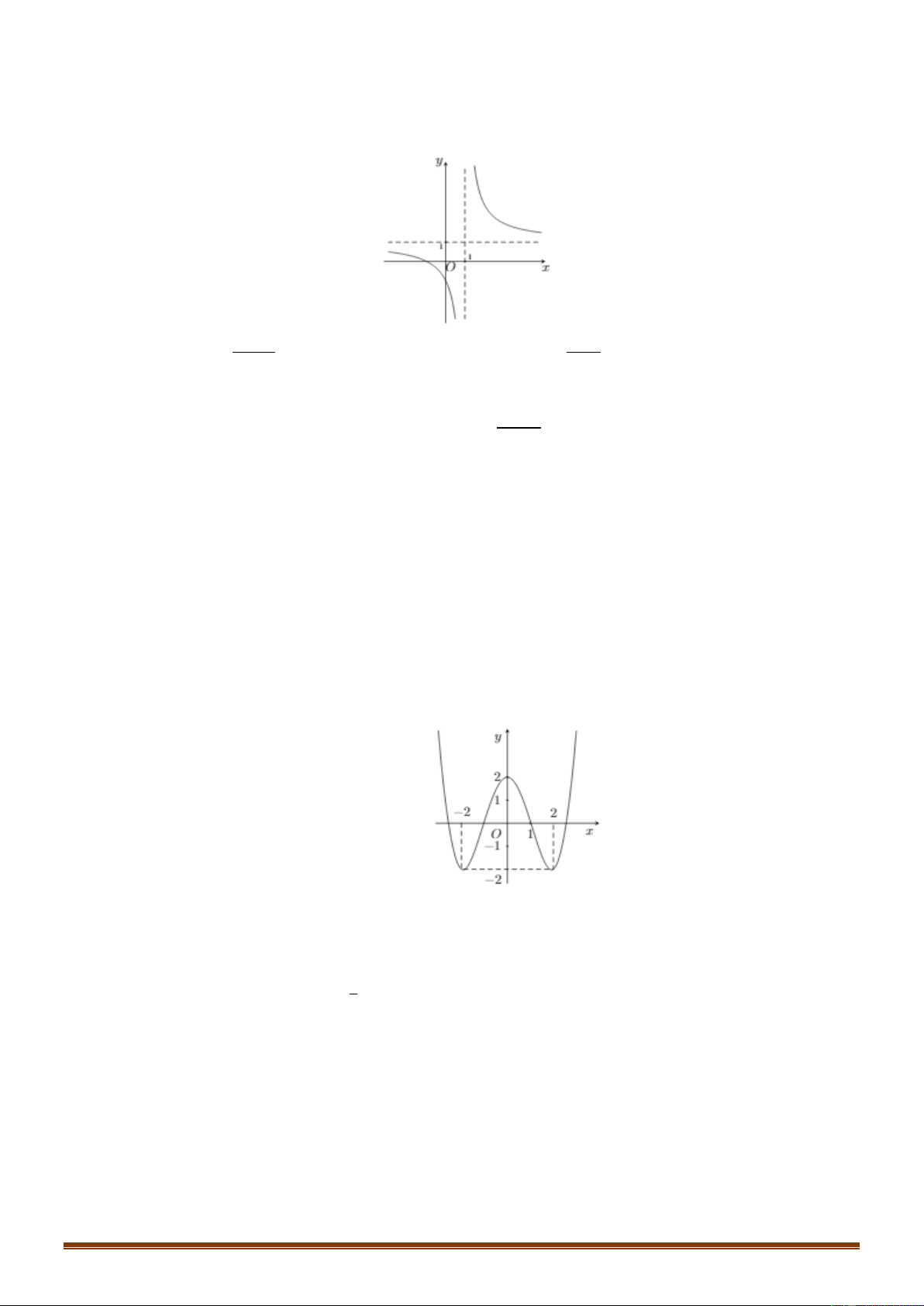
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? . A. 3 2
y  x  3x . B. 3 2
y x  3x . C. 4 2
y x  2x . D. 4 2
y  x  2x . x x2  1
Câu 15: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là x  1 A. 1. B. 3 . C. 2 . D. 0 .
Câu 16: Tập nghiệm của bất phương trình log      x
1 log 2x 5 là 4 4  5  A.  1  ;6 . B. ;6   . C.  ;6  . D. 6;  .  2 
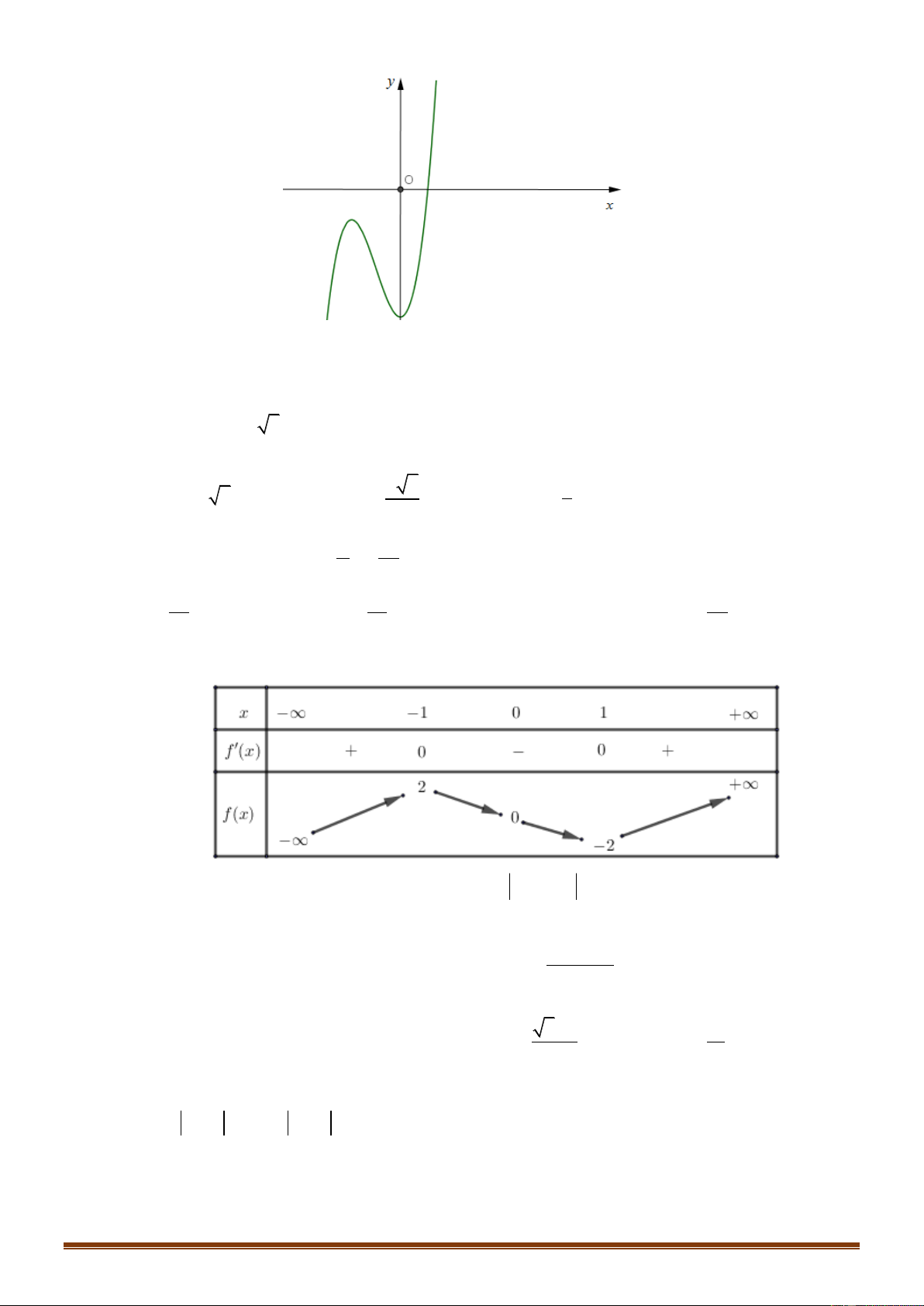
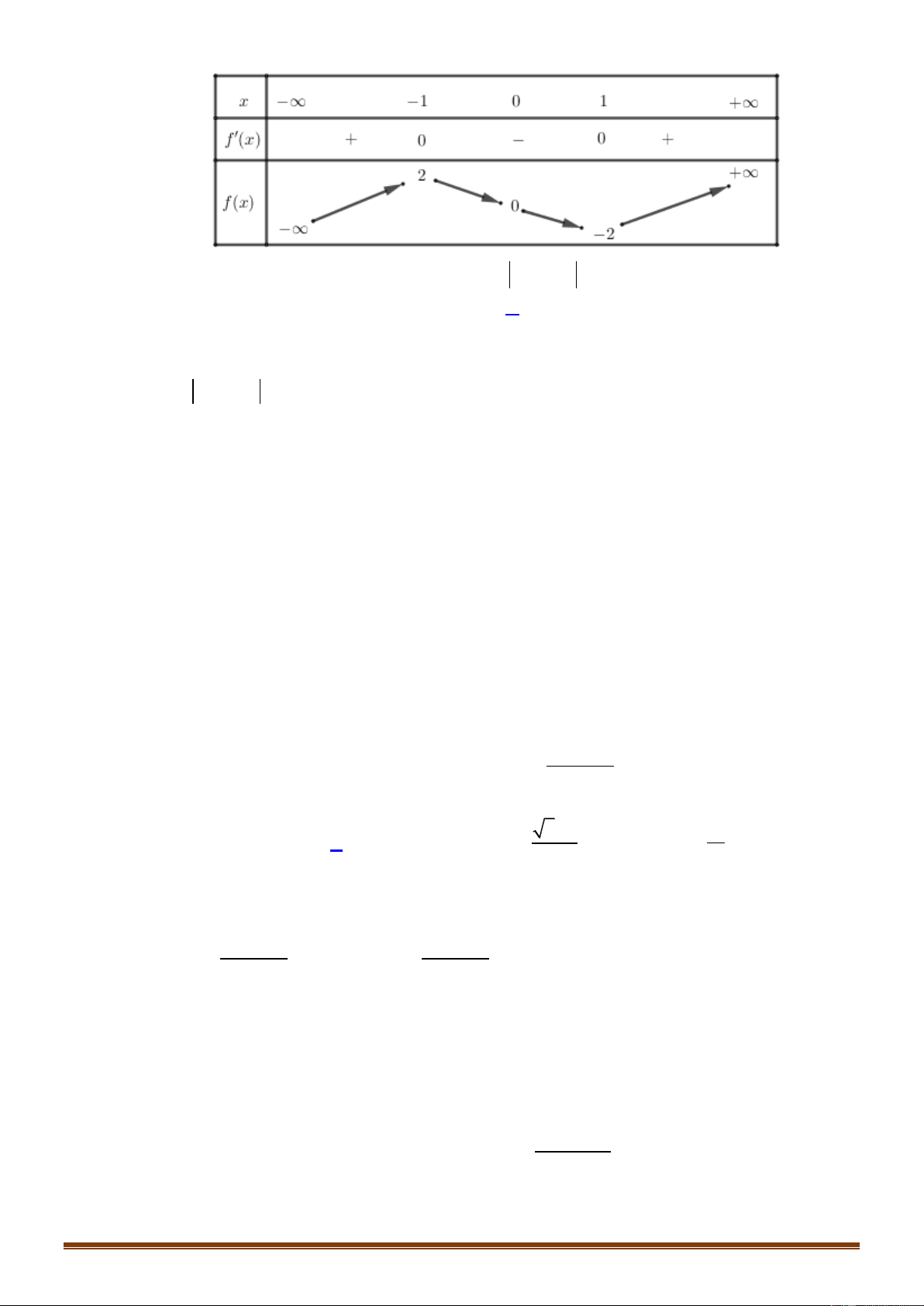
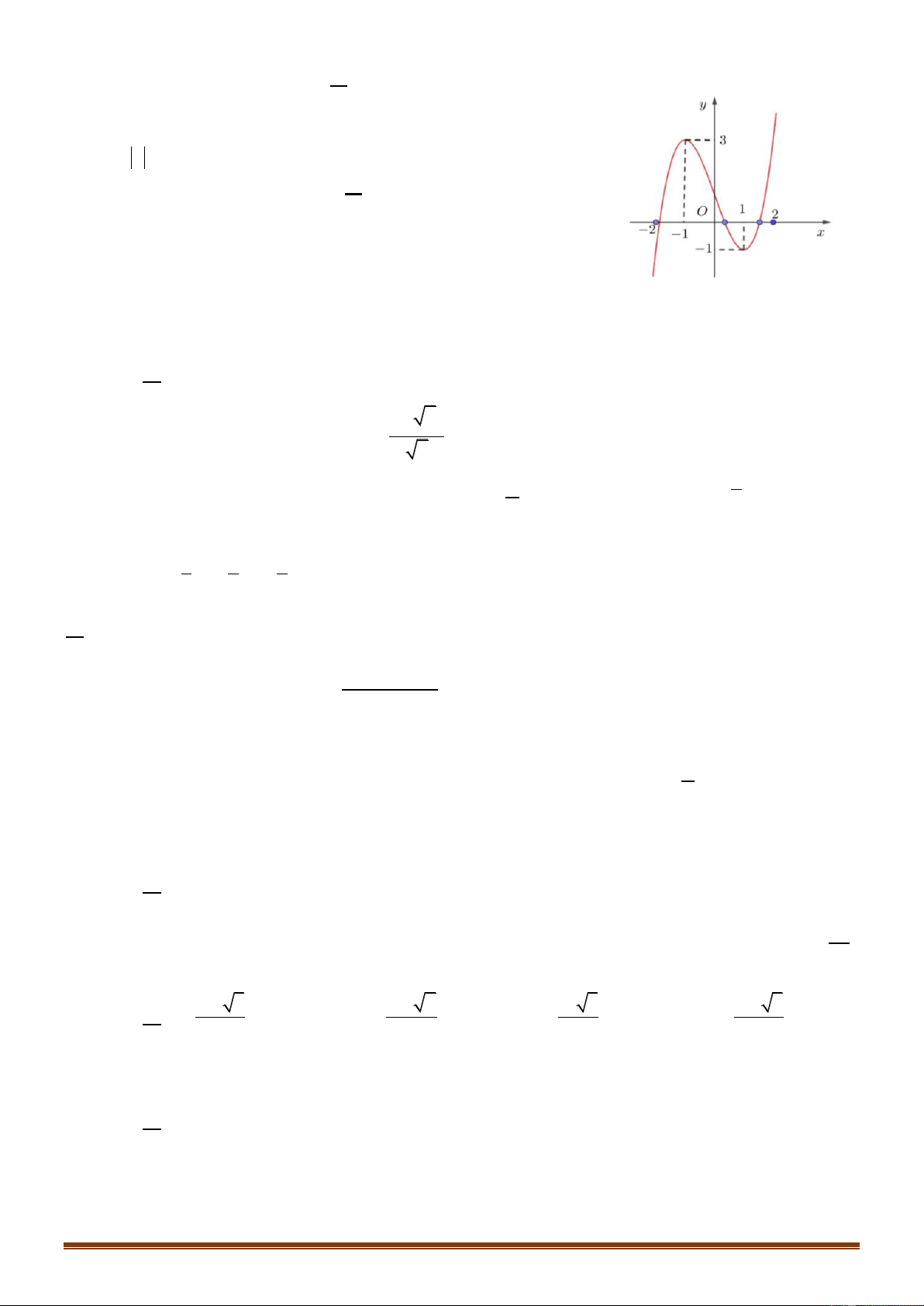
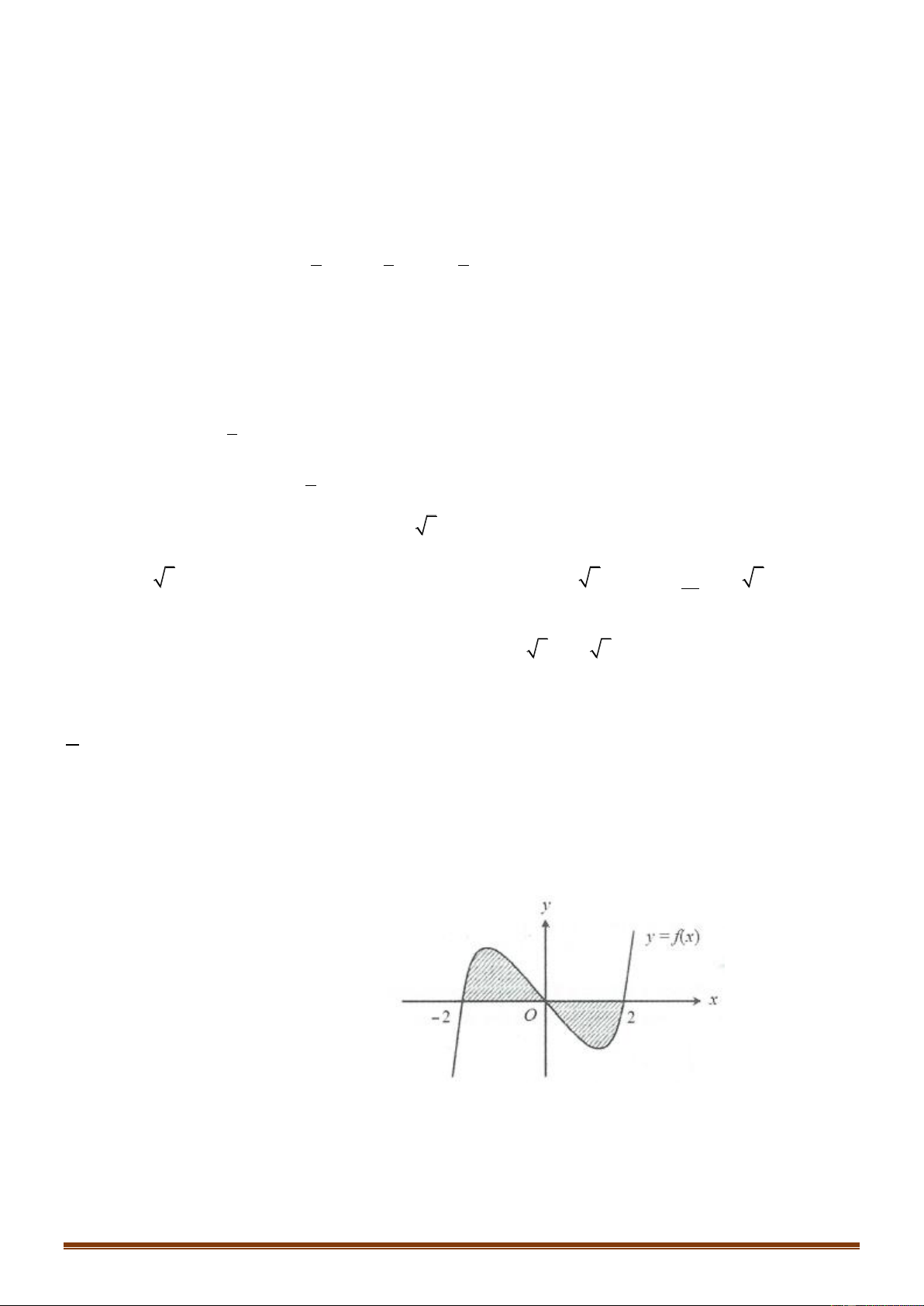
Câu 17: Cho hàm số y f x có đồ thị như hình bên dưới
Số nghiệm của phương trình 2 f x  3  0 là: A. 4 . B. 2 . C. 0 . D. 3 . Trang 2 2 3
Câu 18: Cho hàm số f x liên tục trên đoạn 0;  3 và f
 xdx 1, f
 xdx  4. Tính 0 2 3 I f  xdx . 0 A. I  5 B. I  3  C. I  3 D. I  4
Câu 19: Số phức liên hợp của số phức z  3i 1 là
A. z  1 3i . B. z  1  3i .
C. z  1 3i .
D. z  3  i .
Câu 20: Cho số phức z  3 i . Phần thực của số phức 2z 1 i bằng A. 6. B. 7. C. 3. D. 2. z  1 3i z  2   2i
z z  2z
Câu 21: Cho hai số phức 1 và 2 . Môđun của số phức 1 2 là A. 2 . B. 2 2 . C. 10 . D. 2 3 .
Câu 22: Trong không gian với hệ trục toạ độ Oxyz cho hai điểm A 2  ;3;4 , B8; 5  ;6 . Hình chiếu
vuông góc của trung điểm I của đoạn AB trên mặt phẳng Oyz là điểm nào dưới đây A. M 0; 1  ;5 .
B. Q 0;0;5 .
C. P 3;0;0 . D. N 3; 1  ;5.
Câu 23: Trong không gian Oxyz , mặt cầu S  có tâm I (1,1, 2) , tiếp xúc với mặt phẳng tọa độ (Oxz) .
Phương trình mặt cầu S  là: A. 2 2 2
x y z  2x  2 y  4z 1  0 B. 2 2 2
x y z  2x  2 y  4z  5  0 C. 2 2 2
x y z  2x  2 y  4z 1  0 D. 2 2 2
x y z  2x  2 y  4z  5  0
Câu 24: Trong không gian Oxyz , cho mặt phẳng  P : x  2y z 1  0 . Điểm nào dưới đây thuộc P ? A. M 1; 2   ;1 . B. N 2;1;  1 . C. P 0; 3  ;2 . D. Q 3;0; 4  .
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : 2x  2y z  2017  0 , véc-tơ nào
trong các véc-tơ được cho dưới đây là một véc-tơ pháp tuyến của  P ?    
A. n  2; 2;  1 .
B. n  4; 4; 2 .
C. n  1; 2; 2 . D. n  1; 1  ;4 .
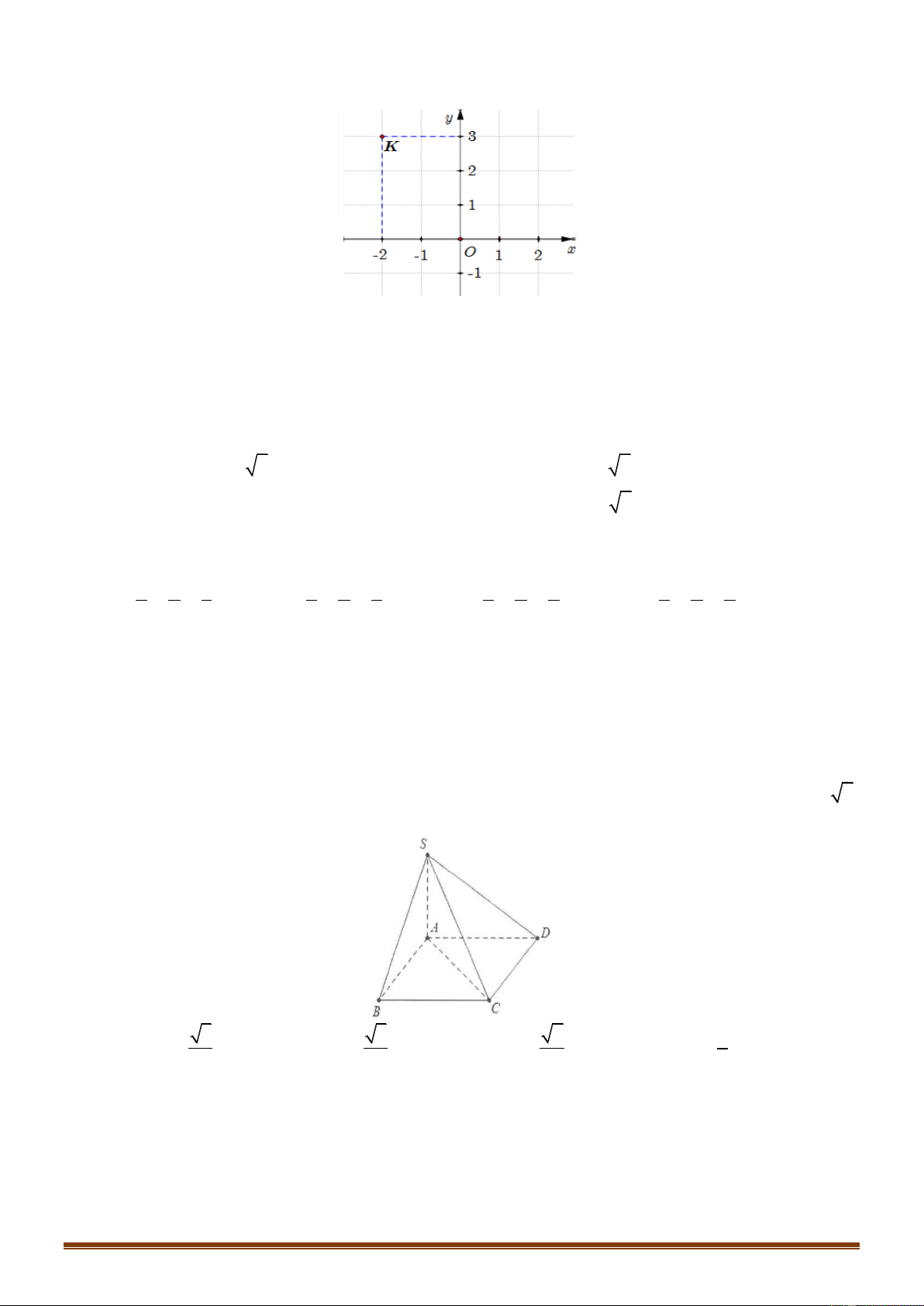
Câu 26: Cho hình chóp S.ABC có SA SB CB CA, hình chiếu vuông góc của S lên mặt phẳng
ABC trùng với trung điểm I của cạnh AB . Góc giữa đường thẳng SC và mặt phẳng ABC bằng. S B C I A A. 0 45 . B. 0 90 . C. 0 60 . D. 0 30 . Trang 3
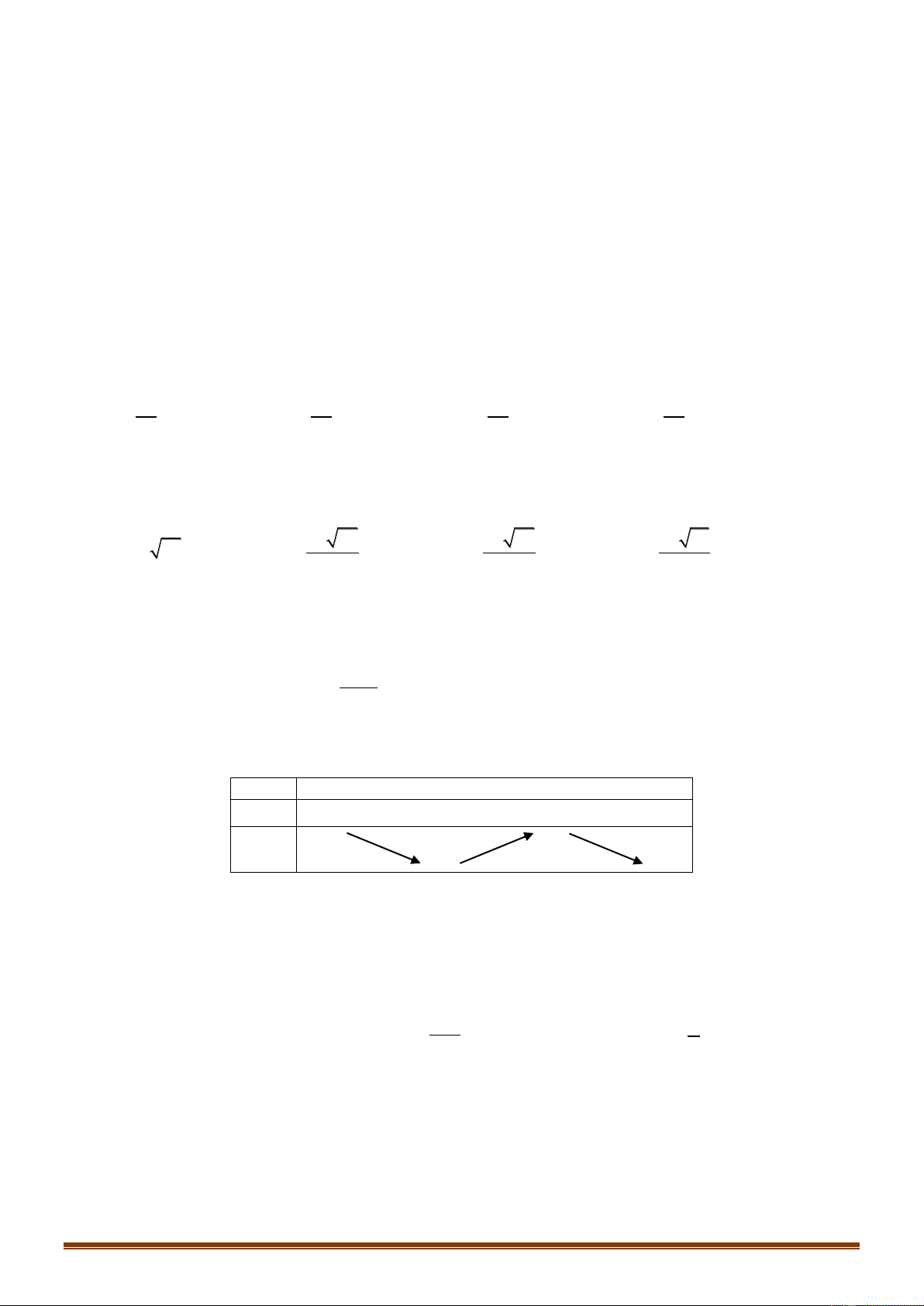
Câu 27: Cho hàm số f x , bảng xét dấu của f  x như sau: x  1 1 2  f  x + 0  0  0 +
Số điểm cực trị của hàm số đã cho là A. 3 . B. 0 . C. 2 . D. 1.
Câu 28: Giá trị lớn nhất của hàm số 2 y
x  5x bằng 5 A. 0 . B. . C. 6 . D. 2 . 2  9b
Câu 29: Xét các số thực a và b thỏa mãn 3 log    log
3 . Mệnh đề nào dưới đây đúng? a 1 3 3   27 1 1 1 1
A. a  2b  .
B. a  2b  .
C. 2b a  .
D. 2a b  . 18 18 18 18 x 1
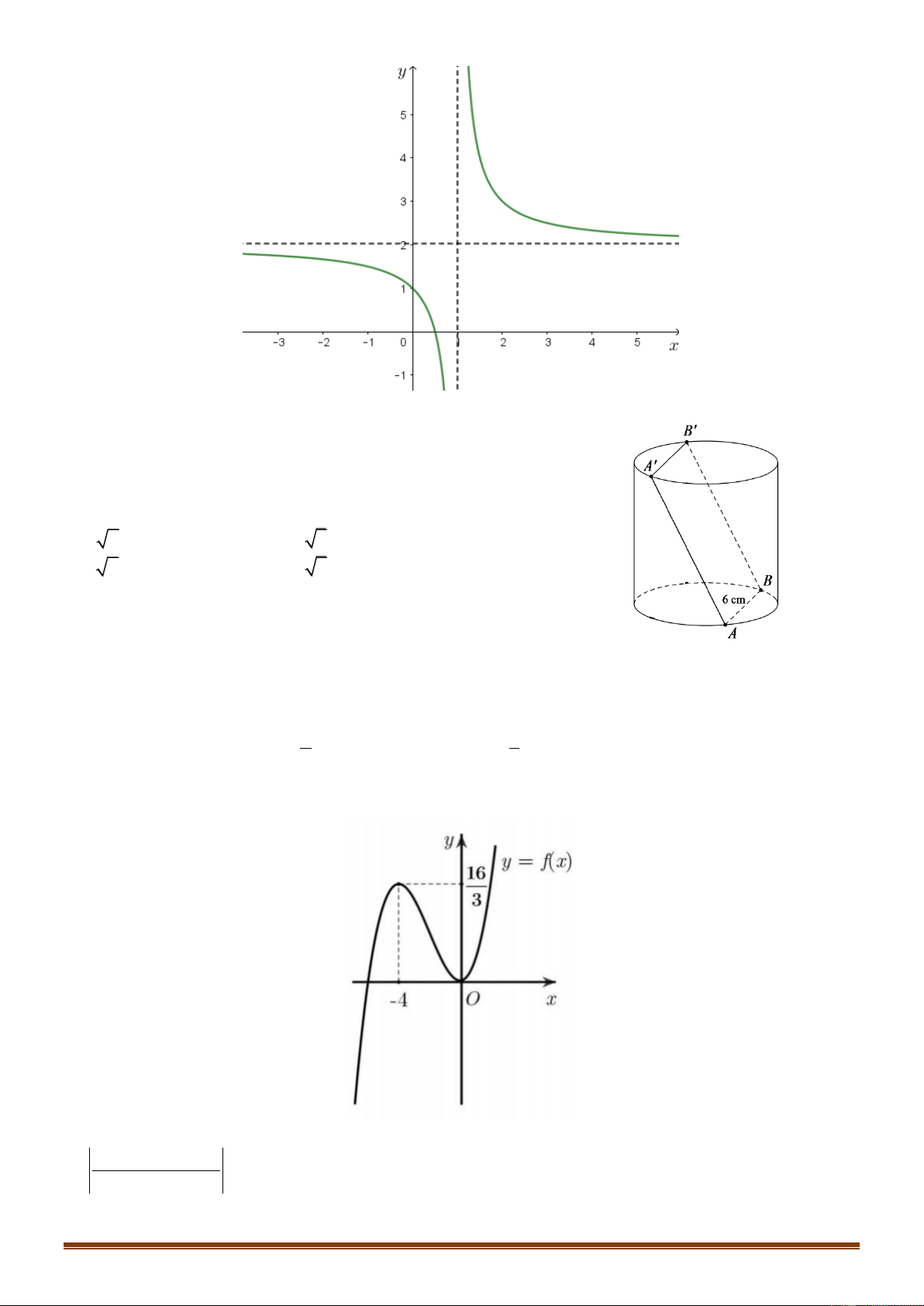
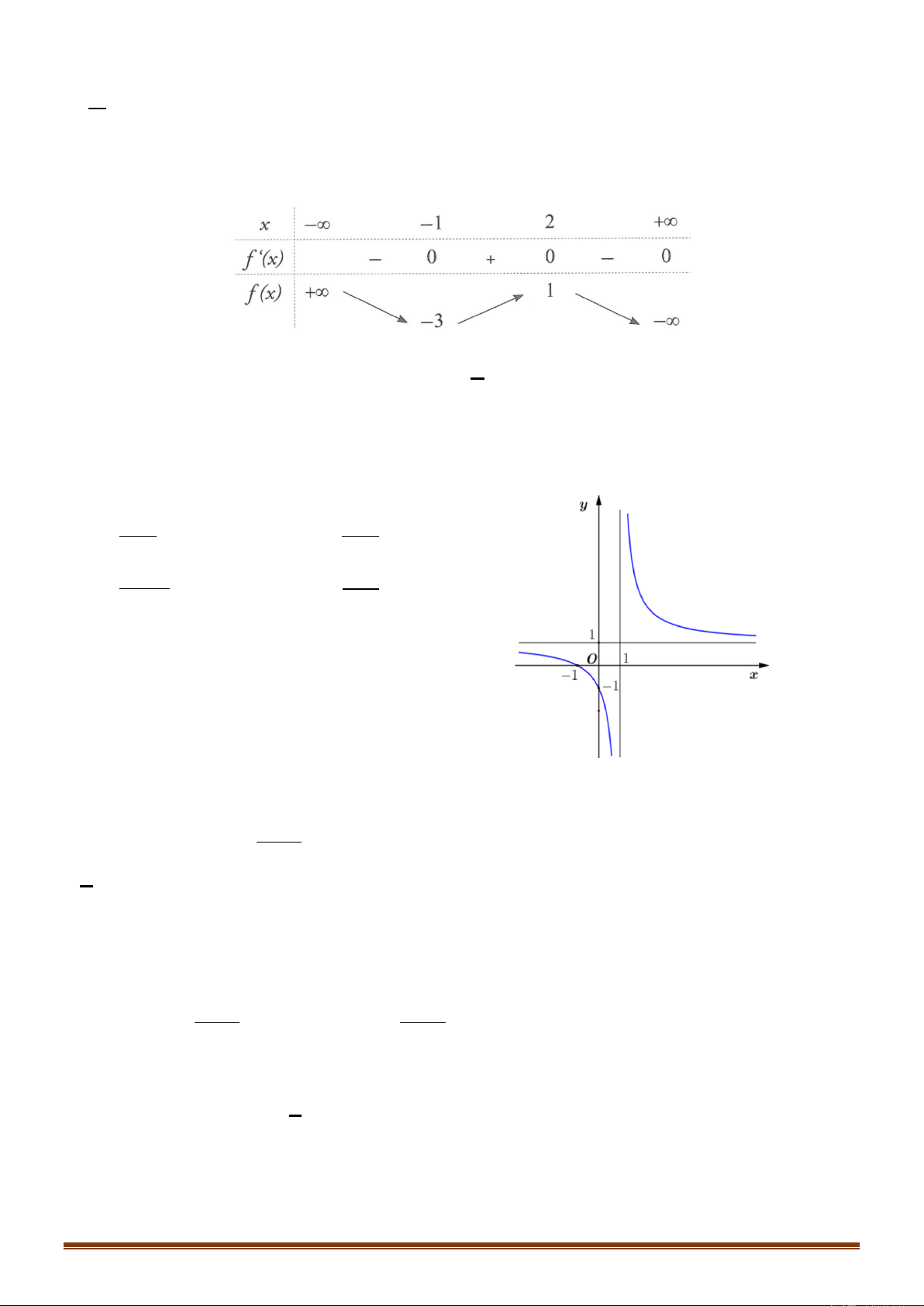
Câu 30: Số giao điểm của đồ thị hàm số y y  là
x  và đường thẳng 2 1 A. 1. B. 2 . C. 4 . D. 6 .
Câu 31: Tập nghiệm S của phương trình 2
log x  2log 4x  7  0 là 2 2 A. S   . B. S   3  ;  1 . 1  C. S    2 .
D. S   ;2 . 8 
Câu 32: Cho tam giác ABC vuông tại A , trong đó AB a , BC  2a . Quay tam giác ABC quanh trục
AB ta được một hình nón có thể tích là 3  a 3 2 a 3 4 a A. 3  a . B. . C. . D. . 3 3 3   2 2 Câu 33: Xét sin cos . x x e dx
, nếu đặt u  sin x thì sin cos . x x e dx  bằng: 0 0 1  1 1 2 2 A. 2 eudu  . B. eudu  . C. eudu  . D. eudu  . 0 0 0 0
Câu 34: Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y x , ex y
, x 1và trục tung
được tính bởi công thức nào dưới đây? 1 1 A.  ex S 1 dx  . B.  ex Sxdx. 0 0 1 1 C.   ex S x
dx. D.  ex Sx dx  . 0 1 
Câu 35: Cho hai số phức z  2  4i và z  1 3 .
i Phần ảo của số phức z i z bằng 1 2 1 2 A. 5 . B. 3i . C. 5  i . D. 3  .
Câu 36: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Tính giá trị biểu thức 1 2 2 2 A zz . 1 2 A. A  20 . B. A  10 . C. A  2 10 . D. A  16. Trang 4
Câu 37: Trong không gian Oxyz , cho điểm K 1;  2; 
1 . Mặt phẳng  P đi qua K và vuông góc với
trục Oy có phương trình là
A. y  2  0 .
B. x 1  0 .
C. y  2  0 .
D. z 1  0 .
Câu 38: Trong không gian Oxyz , cho hai điểm M 1;0  ;1 và N 3;2; 
1 . Gọi H là hình chiếu vuông
góc của N lên trục Oz . Đường thẳng MH có phương trình tham số là x 1 tx 1 tx tx 1 2t     A. y  0 . B. y  0 .
C. y  1 t .
D. y t .     z  1 2tz  1 2tz  1   2tz  1 2t
Câu 39: Đánh số thứ tự cho 20 bạn học sinh lần lượt từ số thứ tự 1đến số thứ tự 20 . Chọn ngẫu nhiên
ba bạn học sinh từ 20 bạn học sinh đó. Tính xác suất để ba bạn được chọn không có hai bạn
nào được đánh số thứ tự liên tiếp. 799 139 68 27 A. . B. . C. . D. . 1140 190 95 95
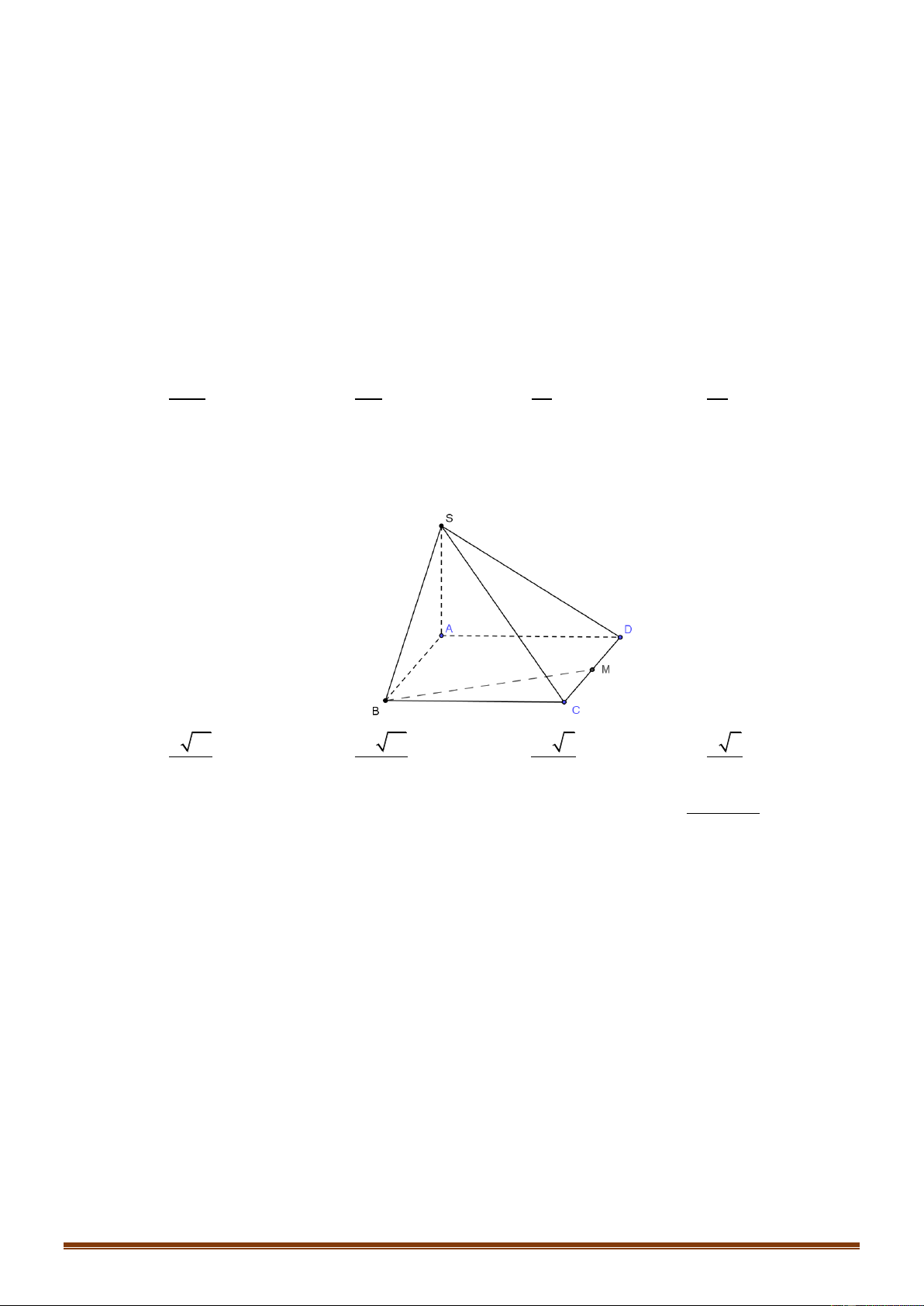
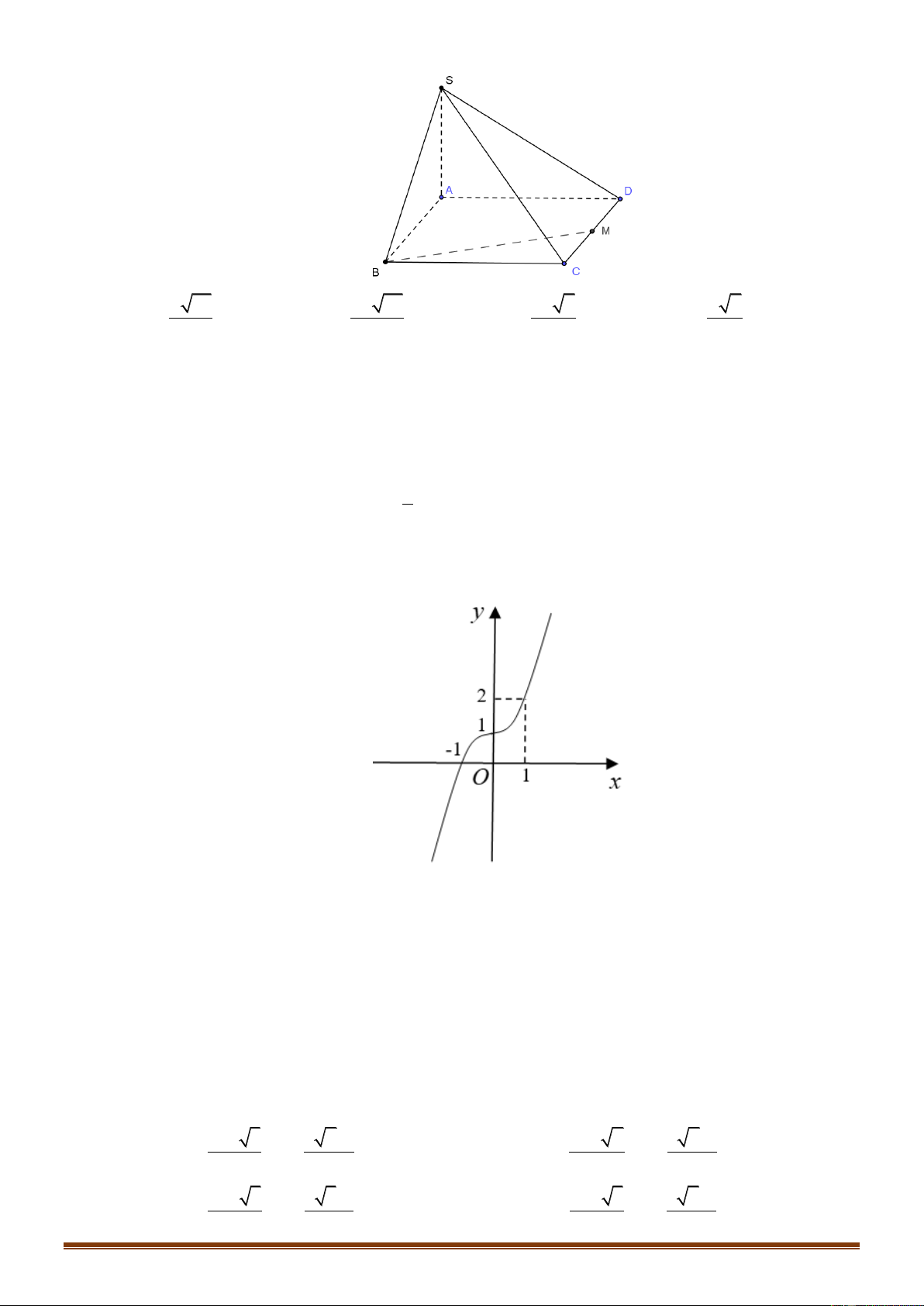
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD  2a , SA vuông góc với
mặt phẳng đáy và SA a (tham khảo hình vẽ). Gọi M là trung điểm của CD . Khoảng cách
giữa hai đường thẳng SD, BM bằng a 21 2a 21 2a 7 a 7 A. . B. . C. . D. . 21 21 7 7 2x m 1
Câu 41: Tổng tất cả các giá trị nguyên của tham số m  1
 0;10 để hàm số y  nghịch biến x m trên 1;5 . A. 30 . B. 4 . C. 36 . D. 45  .
Câu 42: Dân số thế giới được dự đoán theo công thức  .eNr S A
(trong đó A : là dân số của năm lấy làm
mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Theo số liệu thực tế, dân số
thế giới năm 1950 là 2560 triệu người; dân số thế giới năm 1980 là 3040 triệu người. Hãy dự
đoán dân số thế giới năm 2020 ? A. 3823triệu. B. 5360triệu. C. 3954triệu. D. 4017 triệu. Câu 43: Cho hàm số 3 2
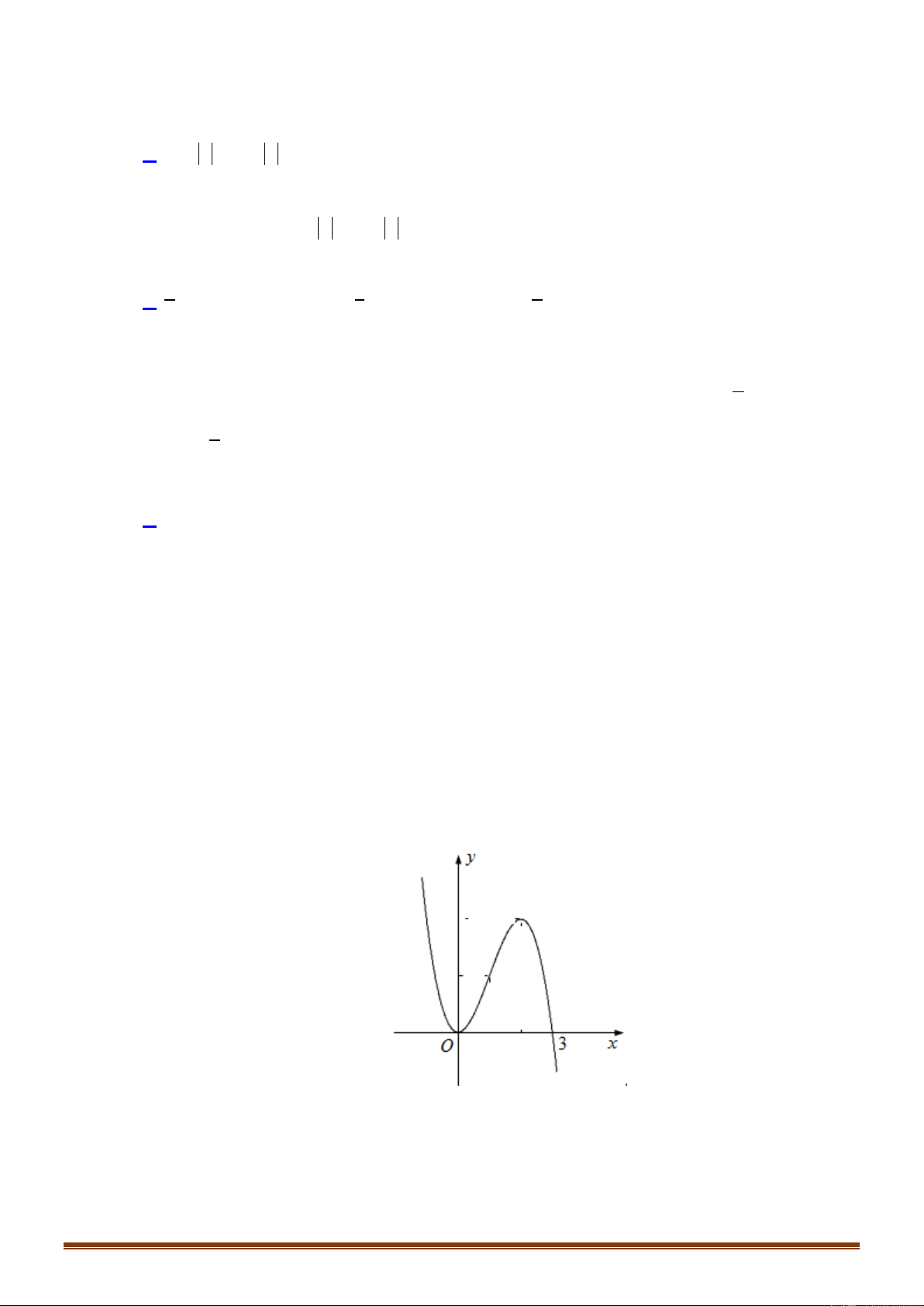
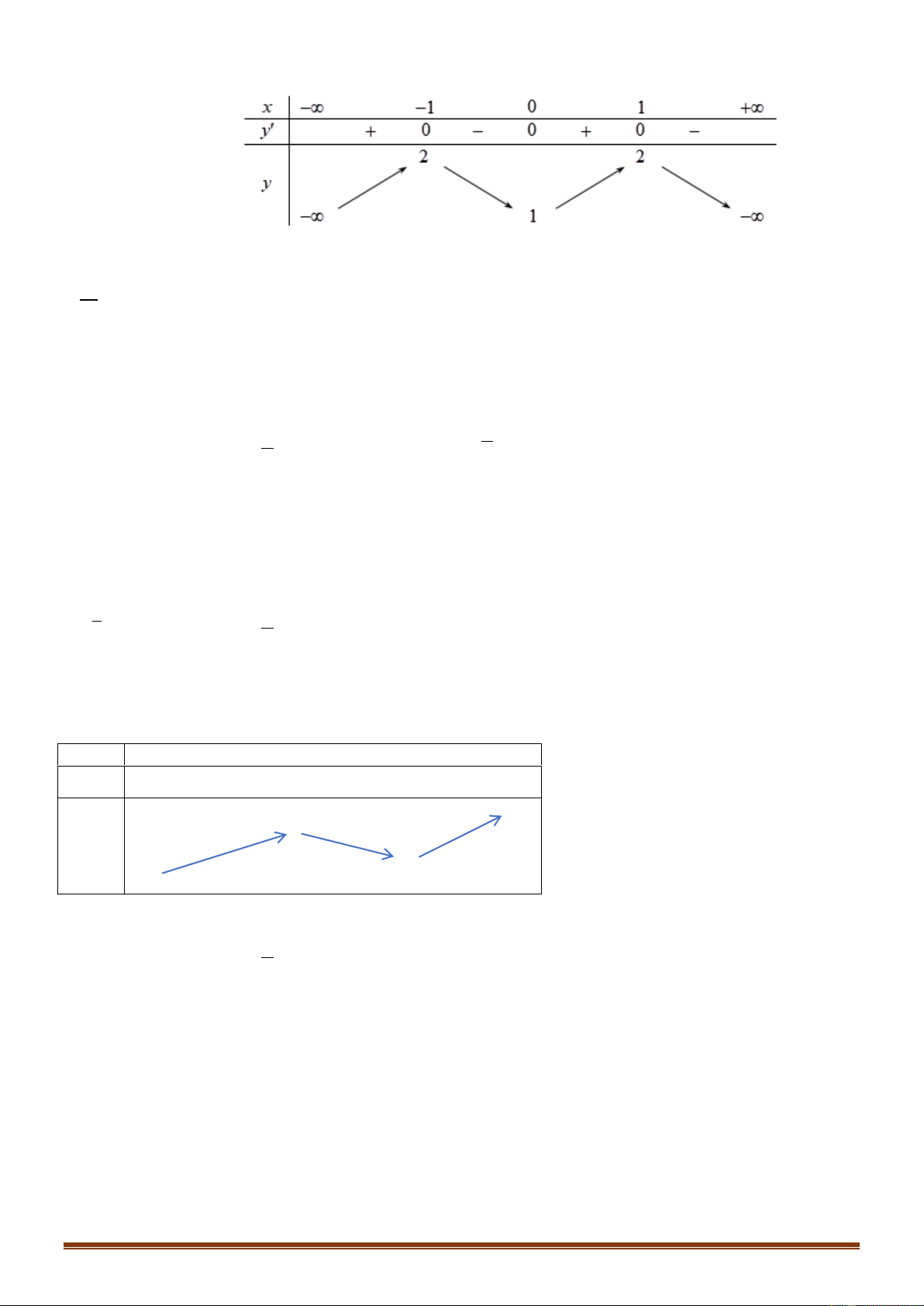
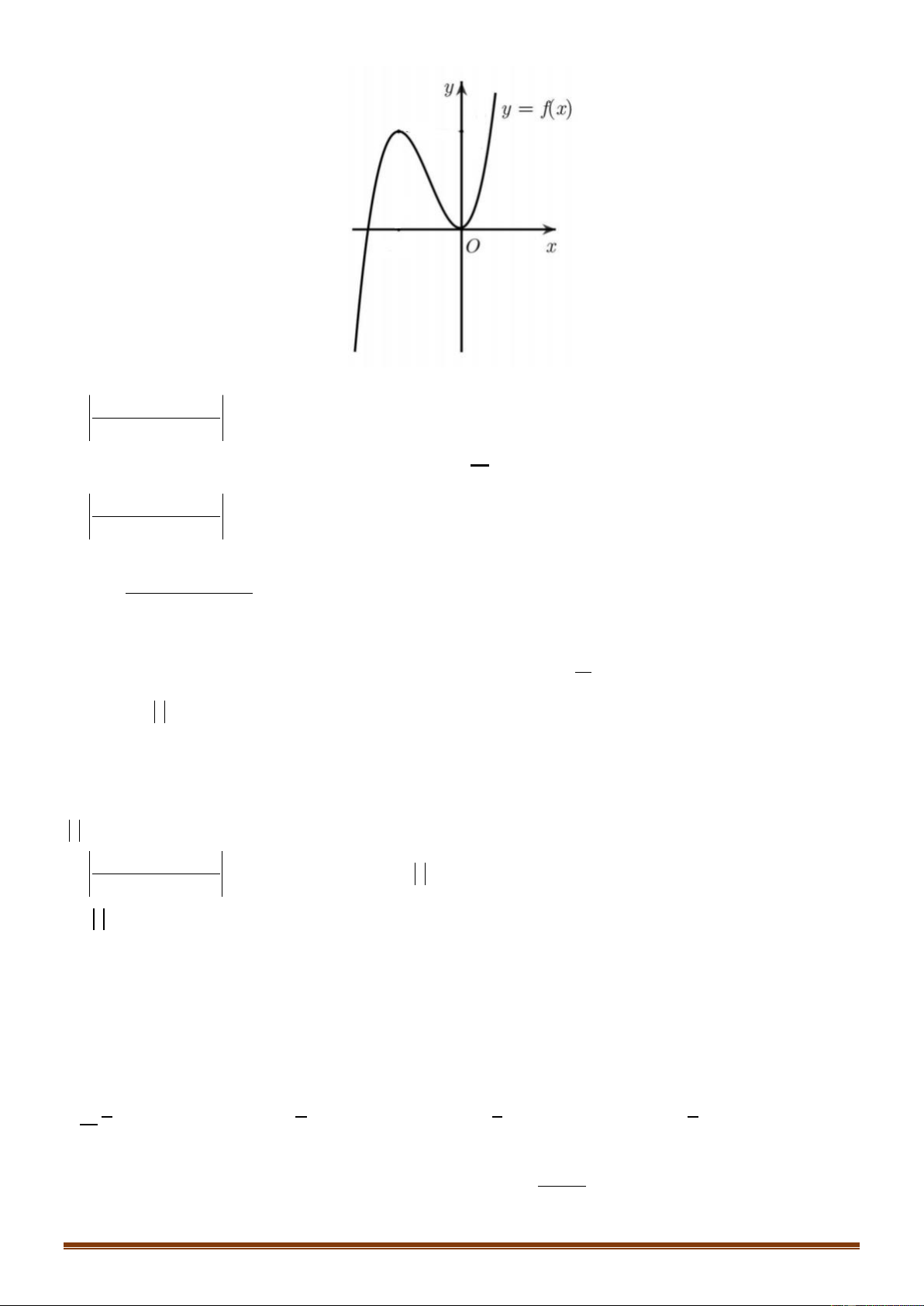
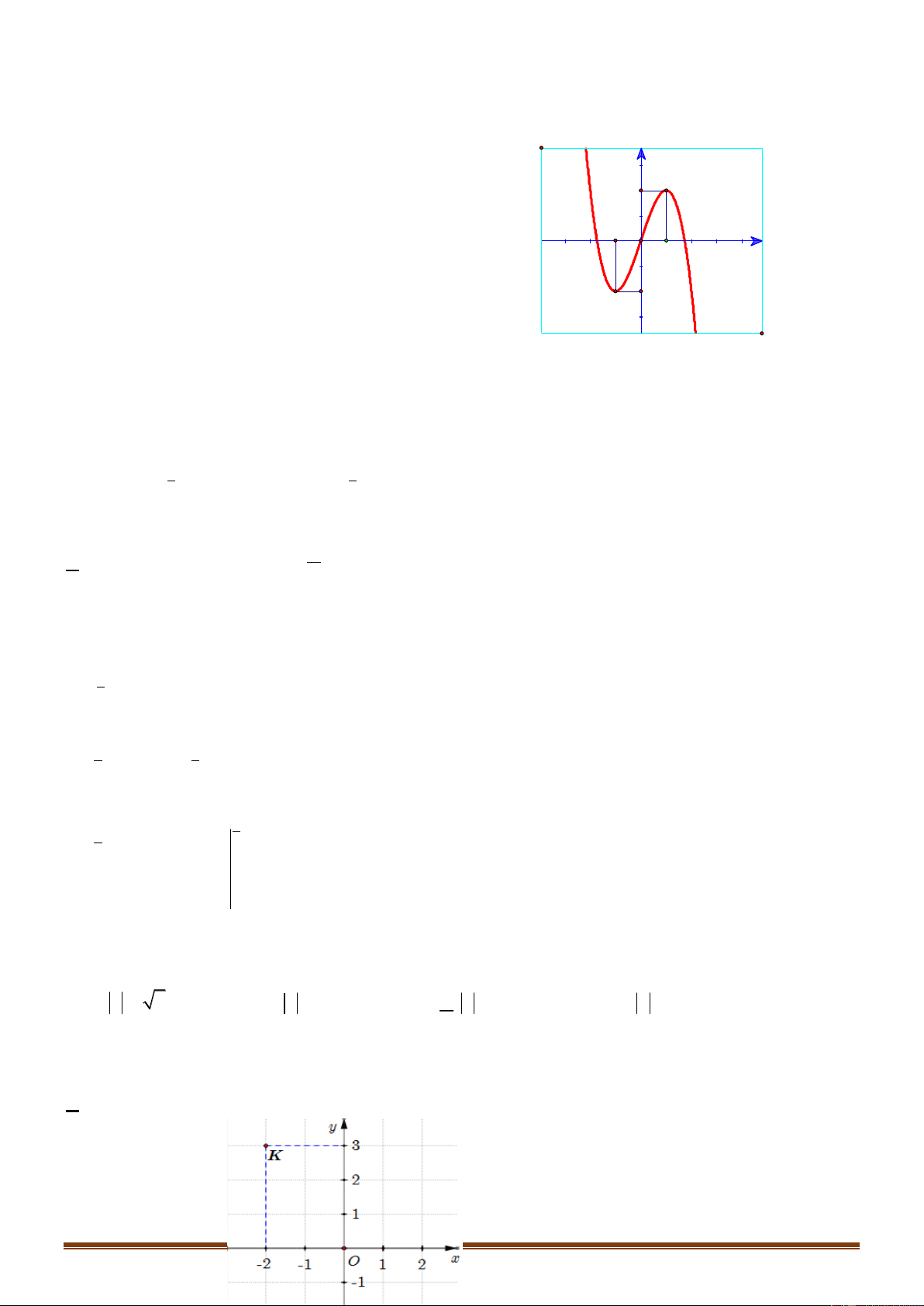
y ax bx cx d có đồ thị là đường cong như hình vẽ bên. Mệnh đề nào dưới đây đúng? Trang 5
A. a  0, b  0, c  0, d  0 .
B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 .
D. a  0, b  0, c  0, d  0 .
Câu 44: Khi cắt khối trụ T  bởi một mặt phẳng song song với trục và cách trục của trụ T  một
khoảng bằng a 3 ta được thiết diện là hình vuông có diện tích bằng 2
4a . Tính thể tích V của
khối trụ T  . 7 7 8 A. 3
V  7 7 a . B. 3 V  a . C. 3 V   a . D. 3 V  8 a . 3 3     27
Câu 45: Cho hàm số f x có f   
và f  x 2 12sin 2 . x cos 3 , x x   . Khi đó f
 xdx bằng  2  8 0 27 87 87 A. . B.  . C. 0 . D. . 64 64 64
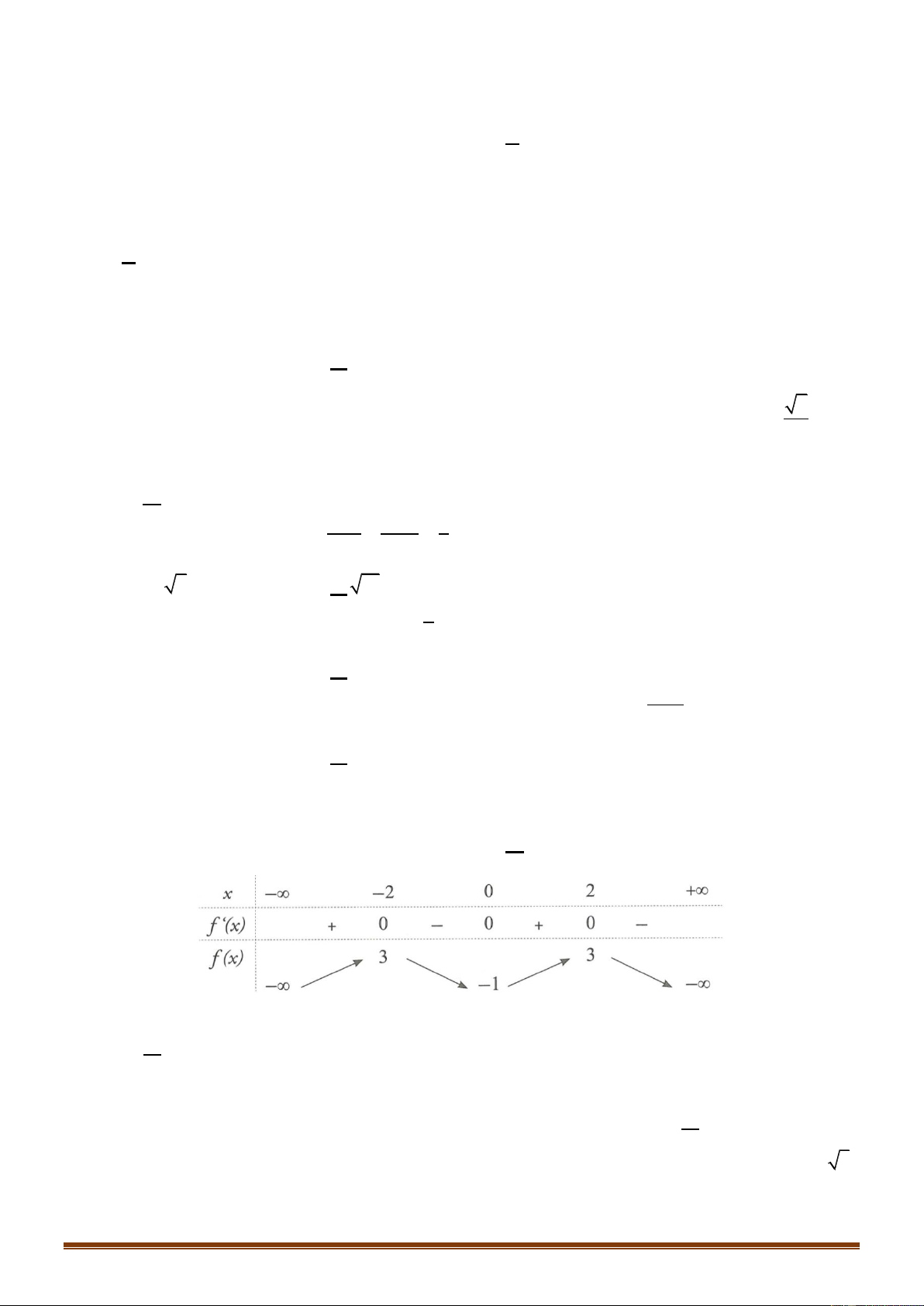
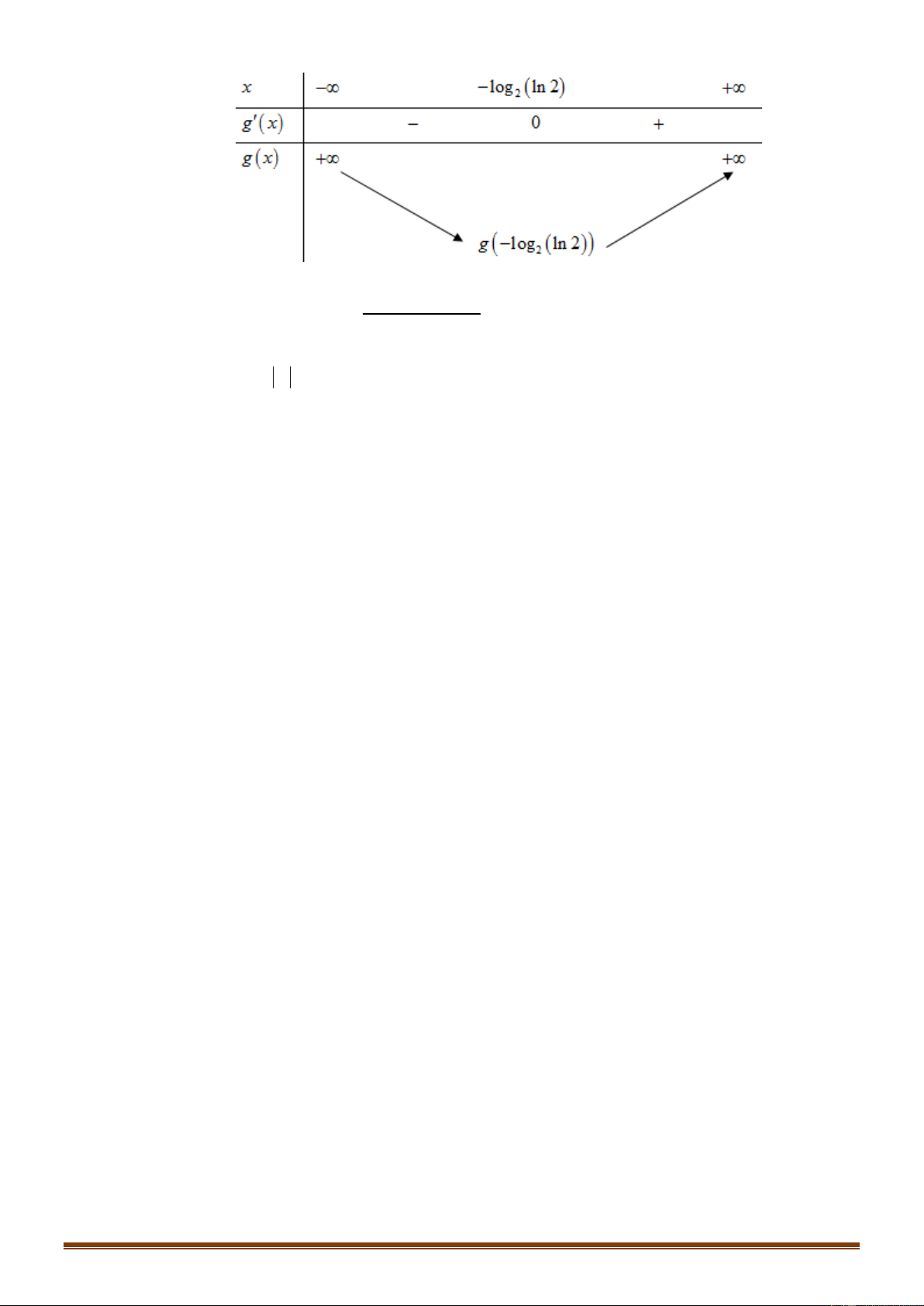
Câu 46: Cho hàm số f x có bảng biến thiên như sau:
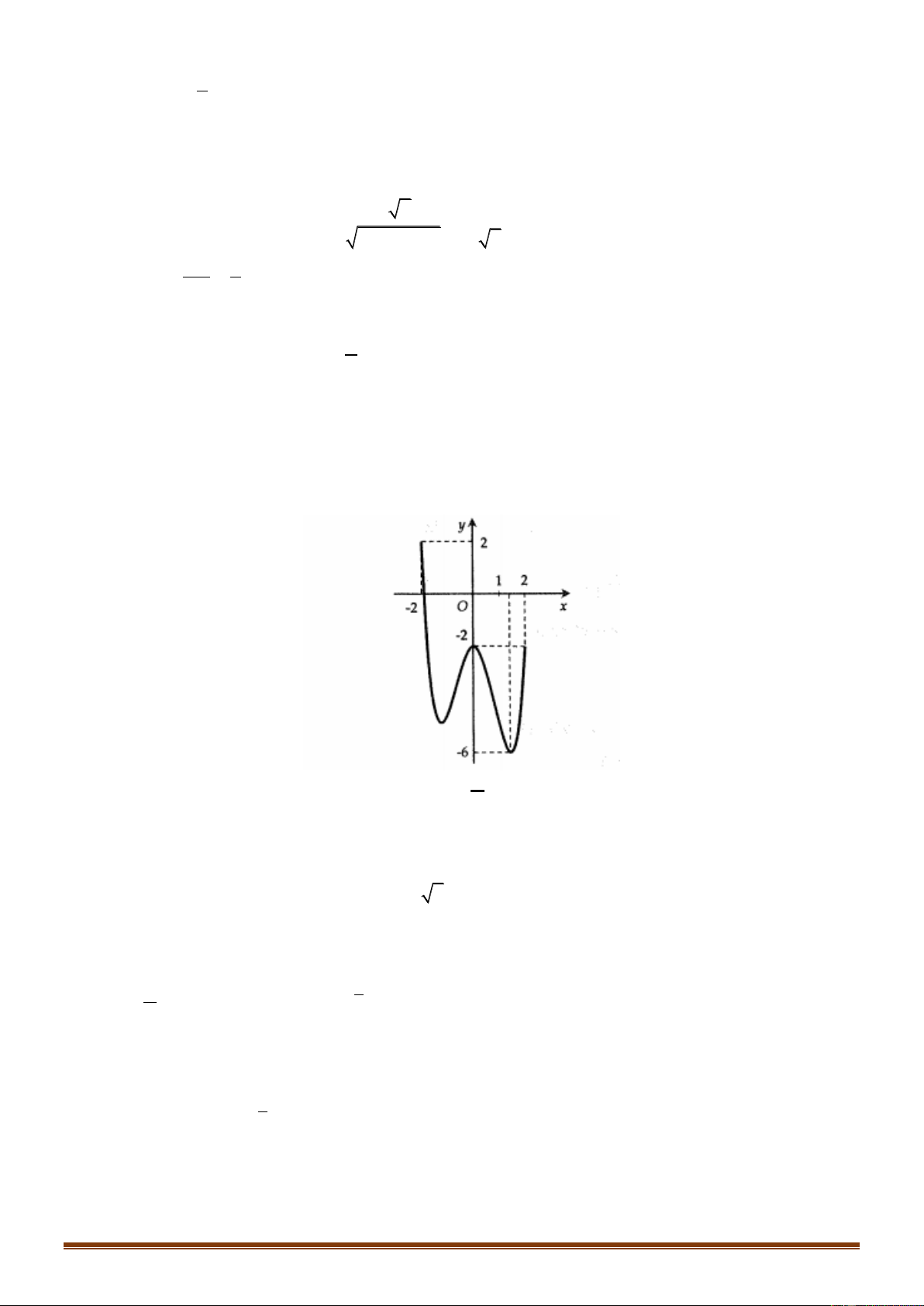
Số nghiệm thuộc đoạn 0;3  của phương trình f sin x  1 là A. 2 . B. 4 . C. 6 . D. 8 . 8   1 ab
Câu 47: Cho hai số thực dương a và b thỏa mãn 4 .2 ab a b a
. Giá trị lớn nhất của biểu thức b 2
P ab  2ab bằng 5 1 3 A. 3 . B. 1. C. . D. . 2 17
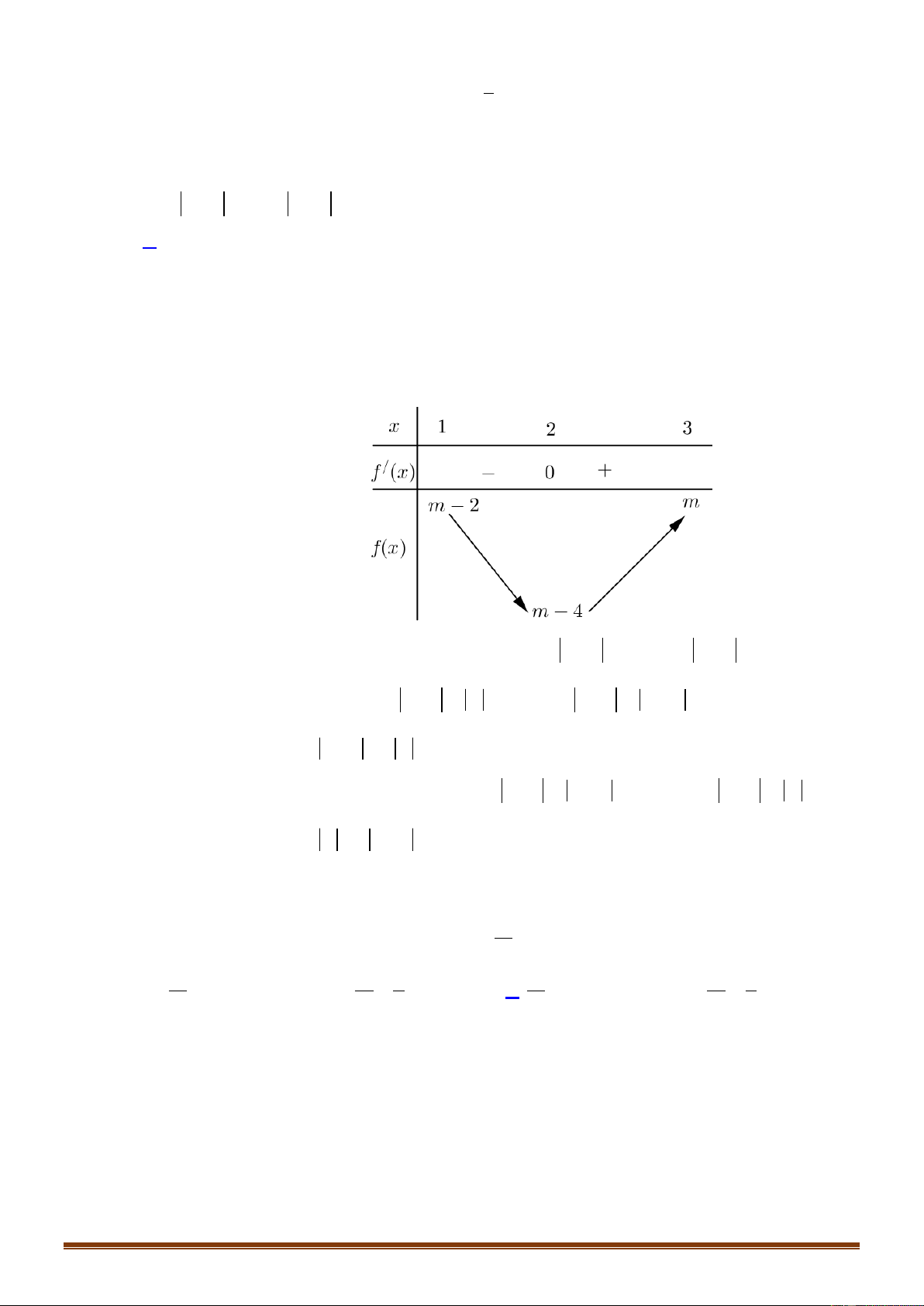
Câu 48: Cho hàm số f (x) 3 2
= x - 3x + m . Gọi S là tập hợp tất cả các giá trị của m sao cho
max f x  2 min f x . Số phần tử của S là 1  ;3 1  ;3 A. 2 . B. 3 . C. 4 . D. 1. Trang 6
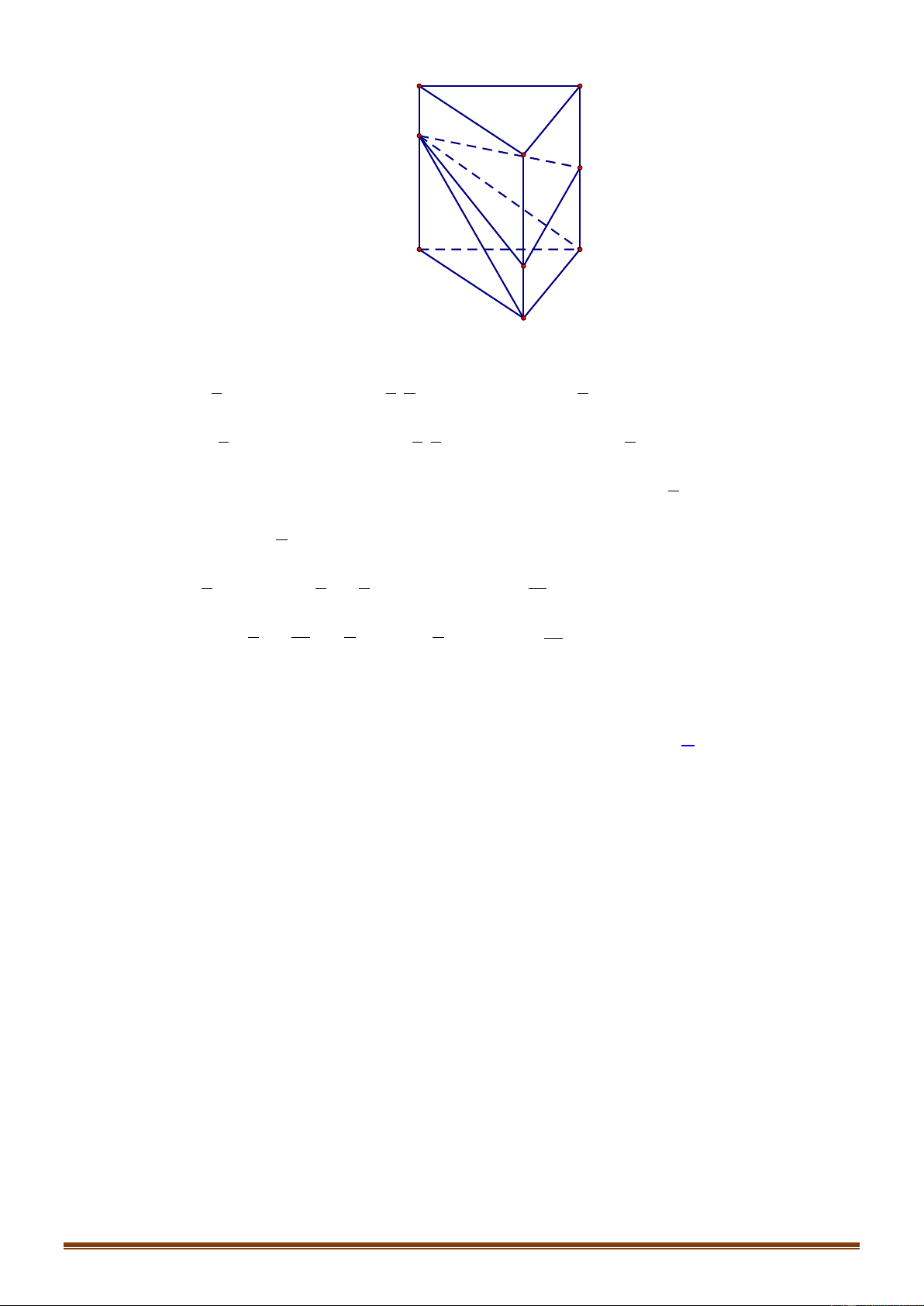
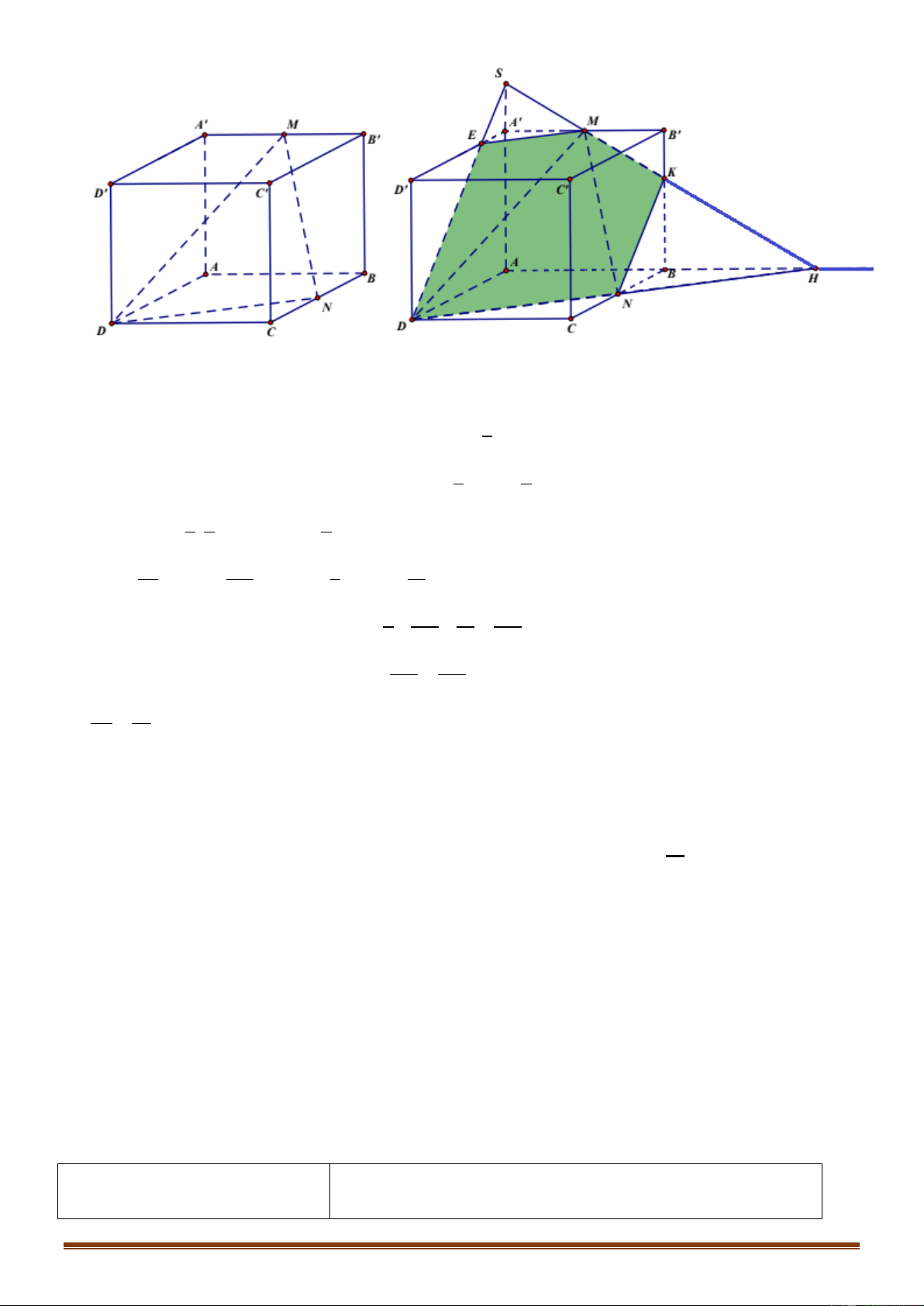
Câu 49: Cho hình lăng trụ AB . C A BC
 . Gọi M , N , P lần lượt là các điểm thuộc các cạnh AA , BB ,
CC sao cho AM  2MA , NB  2NB , PC PC . Gọi V , V lần lượt là thể tích của hai khối 1 2 đa diệ V
n ABCMNP và A BCM
NP . Tính tỉ số 1 . V2 V V 1 V V 2 A. 1  2 B. 1  C. 1  1 D. 1  V V 2 V V 3 2 2 2 2
Câu 50: Cho 0  x  2020 và log (2  2)   3  8y x x y
.Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn 2 các điều kiện trên? A. 2019. B. 2018. C. 1. D. 4.
ĐÁP ÁN VÀ LỜI GIẢI Câu 1:
Cho tập hợp A gồm có 9 phần tử. Số tập con gồm có 4 phần tử của tập hợp A là A. 4 A . B. P . C. 4 C . D. 49 . 9 4 9 Lời giải Chọn C
Số tập con gồm có 4 phần tử của tập hợp A là 4 C . 9 Câu 2:
Cho một cấp số cộng có u  2 , u  4 . Hỏi u và công sai d bằng bao nhiêu? 4 2 1
A. u  6 và d 1.
B. u  1và d 1.
C. u  5 và d  1. 
D. u  1 và d  1.  1 1 1 1 Lời giải Chọn C
Ta có: u u n 1 d .Theo giả thiết ta có hệ phương trình n 1   u  2 u   3d  2 u   5 4  1   1   . u  4  u d  4  d  1  2 1
Vậy u  5 và d  1.  1 Câu 3: Phương trình 2x 1
5   125 có nghiệm là 5 3 A. x  . B. x 1. C. x  3. D. x  . 2 2 Lời giải Chọn B Ta có: 2x 1 5   125 2 x 1  3  5
 5  2x 1 3  x 1. Câu 4:
Hình chóp S.ABCD có đáy là hình vuông cạnh a ; chiều cao có độ dày bằng 6 . a Tính thể tích
khối chóp S.ABCD A. 2 2a . B. 3 6a . C. 3 2a . D. 2 6a . Lời giải Chọn C 1 1 2 3 V Bh
.a .6a  2a . 3 3 Câu 5:
Tìm tập xác định D của hàm số y  log  2
x  4x  3 3 
A. D  2  2;  1 3;2  2 .
B. D  1;3 .
C. D   ;  
1  3; . D. D   ;
 2  22 2; Lời giải Chọn C Trang 7 x  3 Điều kiện: 2
x  4x  3  0  .  x 1
Vậy D  ;  1  3;  Câu 6:
Mệnh đề nào sau đây đúng 1 1 A.
dx  ln x C  . B.
dx  tan x C  . x 2 cos x 1 C.
dx  cot x C  .
D. cos x dx  sin x C  . 2 sin x Lời giải Chọn B
Từ bảng nguyên hàm cơ bản ta chọn đáp án B. Câu 7:
Cho khối lăng trụ có diện tích đáy bằng 2
3a và khoảng cách giữa hai đáy bằng a . Tính thể tích
V của khối lăng trụ đã cho. 3 A. 3 V a . B. 3 V  3a . C. 3 V a . D. 3 V  9a . 2 Lờigiải ChọnC
Ta có thể tích V của khối lăng trụ đã cho là: 2 3 V  .3 a a  3a . a 3 a Câu 8:
Thể tích của khối nón có chiều cao bằng
và bán kính đường tròn đáy bằng là 2 2 3 3 a 3 3 a 3 3 a 3 3 a A. . B. . C. . D. . 6 24 8 8 Lời giải Chọn B 2 3 1 a a 3 3 a
Thể tích khối nón là: V        . 3  2  2 24 Câu 9:
Cho khối cầu  S  có thể tích là 288 . Hỏi diện tích khối cầu bằng bao nhiêu?
A. S  48 .
B. S  72 .
C. S  36 .
D. S 144 . Lời giải Chọn D 4
Thể tích của khối cầu là 3 V
R  288  R  6. 3
Do đó diện tích khối cầu đã cho là: 2
S  4 R  144 .
Câu 10: Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên  .
B. Hàm số nghịch biến trên khoảng  ;0  .
C. Hàm số nghịch biến trên khoảng 1;  .
D.Hàm số nghịch biến trên khoảng 0;  1 . Lời giải Chọn D Trang 8
Dựa vào bảng biến thiên ta thấy f  x  0 trên khoảng 0; 
1  hàm số nghịch biến trên 0;  1 .
Câu 11: Với a, b là số thực tùy ý khác 0 , ta có log ab bằng: 2  
A. log a  log b . B. log . a log b .
C. b log a .
D. log a  log b . 2 2 2 2 2 2 2 Lờigiải ChọnA Ta có: log
ab  log a  log b . 2   2 2
Câu 12: Hình trụ có thiết diện qua trục là hình vuông cạnh a thì có thể tích bằng: 1 1 1 A. 3  a . B. 3  a . C. 3  a . D. 3  a . 4 3 2 Lời giải. Chọn A a
Hình trụ có thiết diện qua trục là hình vuông cạnh a nên có đường cao a và bán kính đáy nên có thể 2 1 tích 3 V   a . 4
Câu 13: Giá trị lớn nhất của hàm số 3
y  x  3x  2 trên đoạn 0;2 bằng A. 4. B. 2. C. 9.  D. 3. Lời giải Chọn A.
Hàm số xác định và liên tục trên đoạn 0;2 . 3 y '  3  x  3 2 y '  0  3  x  3  0
x  10;2  x 1  0;2
y 0  2, y  
1  4, y 2  0.
Vậy: max y  4 đạt được tại x  1. 0;2
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? . A. 3 2
y  x  3x . B. 3 2
y x  3x . C. 4 2
y x  2x . D. 4 2
y  x  2x . Lời giải Chọn A
Nhìn vào đồ thị ta thấy đây không thể là đồ thị của hàm số bậc 4  Loại C, D.
Khi x   thì y    a  0 . 3 2
y  x  3x . Trang 9 x x2  1
Câu 15: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là x  1 A. 1. B. 3 . C. 2 . D. 0 . Lời giải Chọn B
Tập xác định: D   \  1 . 2 x x 1 2 x x 1 Ta có: lim y  lim
  ; lim y  lim   .     x     1 x     1 x 1 x     1 x     1 x 1
Do đó đồ thị hàm số nhận đường thẳng x  1
 làm đường tiệm cận đứng. 2 x x 1 2 x x 1
Lại có: lim y  lim  0 ; lim y  lim  2. x x x 1 x x x 1
Do đồ thị hàm số nhận đường thẳng y  0 và đường thẳng y  2 làm hai đường tiệm cận ngang.
Câu 16: Tập nghiệm của bất phương trình log      x
1 log 2x 5 là 4 4  5  A.  1  ;6 . B. ;6   . C.  ;6  . D. 6;  .  2  Lời giải Chọn B x 1  0  5 Ta có log             x 1 log 2x 5 2x 5 0 x 6 . 2 4 4
x 1 2x 5   
Vậy tập nghiệm của bất phương trình là 5 ;6   .  2 
Câu 17: Cho hàm số y f x có đồ thị như hình bên dưới
Số nghiệm của phương trình 2 f x  3  0 là: A. 4 . B. 2 . C. 0 . D. 3 . Lời giải Chọn A Trang 10 3 Ta có
f x    f x 3 2 3 0
  . Dựa vào đồ thị, nhận thấy đường thẳng y   cắt đồ thị 2 2
hàm số y f x tại 4 điểm phân biệt nên phương trình đã cho có 4 nghiệm. 2 3
Câu 18: Cho hàm số f x liên tục trên đoạn 0;  3 và f
 xdx 1, f
 xdx  4. Tính 0 2 3 I f  xdx . 0 A. I  5 B. I  3  C. I  3 D. I  4 Lờigiải ChọnA 3 2 3 Ta có I f
 xdx = f
 xdxf
 xdx 14  5. 0 0 2
Câu 19: Số phức liên hợp của số phức z  3i 1 là
A. z  1 3i . B. z  1  3i .
C. z  1 3i .
D. z  3  i . Lời giải Chọn B.
Ta có z  3i 1  1  3i
Số phức liên hợp của số phức z  1
 3i là z  1  3i .
Câu 20: Cho số phức z  3 i . Phần thực của số phức 2z 1 i bằng A. 6. B. 7. C. 3. D. 2. Lời giải Chọn B
Ta có 2z 1 i  23  i 1 i  7  3i . Vậy phần thực của số phức 2z 1 i bằng 7 . z  1 3i z  2   2i
z z  2z
Câu 21: Cho hai số phức 1 và 2 . Môđun của số phức 1 2 là A. 2 . B. 2 2 . C. 10 . D. 2 3 . Lời giải Chọn A
Ta có: z z  2z  1 3i  2( 2   2i)  3   i . 1 2
Môđun của số phức z z  2z là: z   2 2 3 1  10 . 1 2
Câu 22: Trong không gian với hệ trục toạ độ Oxyz cho hai điểm A 2  ;3;4 , B8; 5  ;6 . Hình chiếu
vuông góc của trung điểm I của đoạn AB trên mặt phẳng Oyz là điểm nào dưới đây A. M 0; 1  ;5 .
B. Q 0;0;5 .
C. P 3;0;0 . D. N 3; 1  ;5. Lời giải Trang 11 Chọn A
Toạ độ trung điểm của AB là I 3; 1  ;5 .
Suy ra hình chiếu vuông góc của điểm I lên mặt phẳng Oyz là M 0; 1  ;5 .
Câu 23: Trong không gian Oxyz , mặt cầu S  có tâm I (1,1, 2) , tiếp xúc với mặt phẳng tọa độ (Oxz) .
Phương trình mặt cầu S  là: A. 2 2 2
x y z  2x  2 y  4z 1  0 B. 2 2 2
x y z  2x  2 y  4z  5  0 C. 2 2 2
x y z  2x  2 y  4z 1  0 D. 2 2 2
x y z  2x  2 y  4z  5  0 Lời giải Chọn B
Phương trình mặt phẳng tọa độ (Oxz) : y  0 1.0 1.1 2.0
Do mặt cầu S  tiếp xúc với mặt phẳng tọa độ (Oxz)  R d I;Oxz  1 2 1
Phương trình mặt cầu S  có tâm I(1,1, 2) và bán kính R 1 là:
x  2  y  2 z  2 1 1 2 1 2 2 2
x y z  2x  2y  4z  5  0 .
Câu 24: Trong không gian Oxyz , cho mặt phẳng  P : x  2y z 1  0 . Điểm nào dưới đây thuộc P ? A. M 1; 2   ;1 . B. N 2;1;  1 . C. P 0; 3  ;2 . D. Q 3;0; 4  . Lời giải Chọn B
Lần lượt thay toạ độ các điểm M , N , P , Q vào phương trình  P , ta thấy toạ độ điểm N
thoả mãn phương trình  P . Do đó điểm N thuộc  P . Chọn đáp án B.
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : 2x  2y z  2017  0 , véc-tơ nào
trong các véc-tơ được cho dưới đây là một véc-tơ pháp tuyến của  P ?    
A. n  2; 2;  1 .
B. n  4; 4; 2 .
C. n  1; 2; 2 . D. n  1; 1  ;4 . Lời giải Chọn B
Theo định nghĩa phương tổng quát của mặt phẳng suy ra vecto pháp tuyến của P là
n  4;4;2.
Câu 26: Cho hình chóp S.ABC có SA SB CB CA, hình chiếu vuông góc của S lên mặt phẳng
ABC trùng với trung điểm I của cạnh AB . Góc giữa đường thẳng SC và mặt phẳng ABC bằng. S B C I A A. 0 45 . B. 0 90 . C. 0 60 . D. 0 30 . Trang 12 Lời giải ChọnA
Vì SI   ABC  suy ra IC là hình chiếu của SC lên mặt phẳng  ABC  . Khi đó góc giữa đườ 
ng thẳng SC và mặt phẳng  ABC  là góc giữa SC và IC hay góc SCI . Lại có, SAB C
ABsuy ra CI SI , nên tam giác SIC vuông cân tại I . Khi đó  0 SCI  45 .
Vậy góc giữa đường thẳng SC và mặt phẳng  ABC  bằng 0 45 .
Câu 27: Cho hàm số f x , bảng xét dấu của f  x như sau: x  1 1 2  f  x + 0  0  0 +
Số điểm cực trị của hàm số đã cho là A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn C
Từ bảng xét dấu ta thấy f  x đổi dấu khi qua x  1
 và x  2 nên hàm số đã cho có hai điểm cực trị.
Câu 28: Giá trị lớn nhất của hàm số 2 y
x  5x bằng 5 A. 0 . B. . C. 6 . D. 2 . 2 Lời giải Chọn B
Tập xác định D  0;  5 . 2  x  5 Ta có y '  ; y '  0  2  x  5  5 0  x  2 2 x  5x 2  5  5
Có y 0  y 5  0 ; y    .  2  2  5  5
Vậy max y y    . [0;5]  2  2  9b
Câu 29: Xét các số thực a và b thỏa mãn 3 log    log
3 . Mệnh đề nào dưới đây đúng? a 1 3 3   27 1 1 1 1
A. a  2b  .
B. a  2b  .
C. 2b a  .
D. 2a b  . 18 18 18 18 Lời giải Chọn A  9b  1 3 log    log 3 2ba 3  log 3  log
 22b a 1 1   1     3 . a 2b . a 1 3 3   1 3 3 2 3 3 18 27 3 x 1
Câu 30: Số giao điểm của đồ thị hàm số y y  là
x  và đường thẳng 2 1 A.1. B. 2 . C. 4 . D. 6 . Lời giải Chọn A x 1
Xét hàm số y x  : 1 D   \   1 Trang 13 2  y '  ; x   D 2 (x 1) x 1
Ta có bảng biến thiên của hàm số y x 1 x 1
Từ đó ta có số giao điểm của y y  là 1 giao điểm. x  và 2 1
Câu 31: Tập nghiệm S của phương trình 2
log x  2log 4x  7  0 là 2 2 A. S   . B. S   3  ;  1 . 1  C. S    2 .
D. S   ;2 . 8  Lời giải Chọn B
Điều kiện x  0   *  x  2 log x  1 Ta có 2 2 
log x  2log 4x  7  0  log x  2log x  3  0 2    . 2 2 2 2 1 log x  3   x  2  8 Đố 1
i chiếu với điều kiện  
* ta được x  2;x  . 8 1 
Vậy phương trình đã cho có tập nghiệm là S   ;2 . 8 
Câu 32: Cho tam giác ABC vuông tại A , trong đó AB a , BC  2a . Quay tam giác ABC quanh trục
AB ta được một hình nón có thể tích là 3  a 3 2 a 3 4 a A. 3  a . B. . C. . D. . 3 3 3 Lời giải Chọn A B a 2a A C
Xét tam giác ABC vuông tại A , ta có: 2 2 2
AC BC AB   a2 2 2 2
a  3a AC a 3 . Trang 14
Thể tích hình nón khi quay trục AB : 1 1 2 V
R h   a 32 2 3
.a   a với R AC a 3 và h AB a . 3 3 Vậy 3
V   a (đvtt).   2 2 sin cos . x x e dx  sin cos . x x e dxCâu 33: Xét 0
, nếu đặt u  sin x thì 0 bằng: 1  1 1 2 2 A. 2 eudu  . B. eudu  . C. eudu  . D. eudu  . 0 0 0 0 Lời giải Chọn B
Đặt u  sin x  du  cos d x x .
Với x  0  u  0  Với x   u  1 2  2 1 Vậy sin cos . xd u x e x e du   . 0 0
Câu 34: Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y x , ex y
, x 1và trục tung
được tính bởi công thức nào dưới đây? 1 1 A.  ex S 1 dx  . B.  ex Sxdx. 0 0 1 1 C.   ex S x
dx. D.  ex Sx dx  . 0 1  Lời giải Chọn B 1 1 Diện tích cần tìm là:  ex  d   ex S x xxdx . 0 0 z  2  4i z  1 3 . i z i z
Câu 35: Cho hai số phức 1 và 2
Phần ảo của số phức 1 2 bằng A. 5 . B. 3i . C. 5  i . D. 3  . Lời giải Chọn D
Ta có: z  1 3i z  1 3i i z i 1 3i 2
 3i i  3   i 2 2 2
Suy ra z i z  2  4i  3
  i  1 3i . 1 2  
Vậy phần ảo của số phức z i z là 3  . 1 2
Câu 36: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Tính giá trị biểu thức 1 2 2 2 A zz . 1 2 A. A  20 . B. A  10 . C. A  2 10 . D. A  16. Lời giải Chọn A.
z    i 2
z  2z 10  1 3 0   z  1  3i Trang 15 2 2 2 2 A zz  1   3i  1
 3i  20 nên chọn A. 1 2
Câu 37: Trong không gian Oxyz , cho điểm K 1;  2; 
1 . Mặt phẳng  P đi qua K và vuông góc với
trục Oy có phương trình là
A. y  2  0 .
B. x 1  0 .
C. y  2  0 .
D. z 1  0 . Lời giải Chọn C
Trục Oy có vectơ đơn vị là j  0;1;0 . 
Vì  P vuông góc với trục Oy nên  P nhận j là một vectơ pháp tuyến.
Suy ra  P : 0 x  
1   y  2  0 z  
1  0 hay y  2  0 .
Vậy  P : y  2  0 .
Câu 38: Trong không gian Oxyz , cho hai điểm M 1;0  ;1 và N 3;2; 
1 . Gọi H là hình chiếu vuông
góc của N lên trục Oz . Đường thẳng MH có phương trình tham số là x 1 tx 1 tx tx 1 2t     A. y  0 . B. y  0 .
C. y  1 t .
D. y t .     z  1 2tz  1 2tz  1   2tz  1 2tLời giải Chọn B.
Vì H là hình chiếu vuông góc của N lên trục Oz nên H (0;0; 1) . 
Một vectơ chỉ phương của đường thẳng MH là HM  (1;0;2) . x 1 t
Vậy (MH ) : y  0 . z 1 2t
Câu 39: Đánh số thứ tự cho 20 bạn học sinh lần lượt từ số thứ tự 1đến số thứ tự 20 . Chọn ngẫu nhiên
ba bạn học sinh từ 20 bạn học sinh đó. Tính xác suất để ba bạn được chọn không có hai bạn
nào được đánh số thứ tự liên tiếp. 799 139 68 27 A. . B. . C. . D. . 1140 190 95 95 Lời giải Chọn C
Gọi  là không gian mẫu. Số phần tử của không gian mẫu là n  3  C 1140. 20
Gọi A là biến cố cần tìm thì A là biến cố chọn được ba bạn học sinh trong đó có 2 hoặc 3 bạn
được đánh số tự nhiên liên tiếp.
n A 18  2.17 17.16  324 n A Xác suất của biến cố 324 68
A là p A  1 p A   1    n  1 . 1140 95
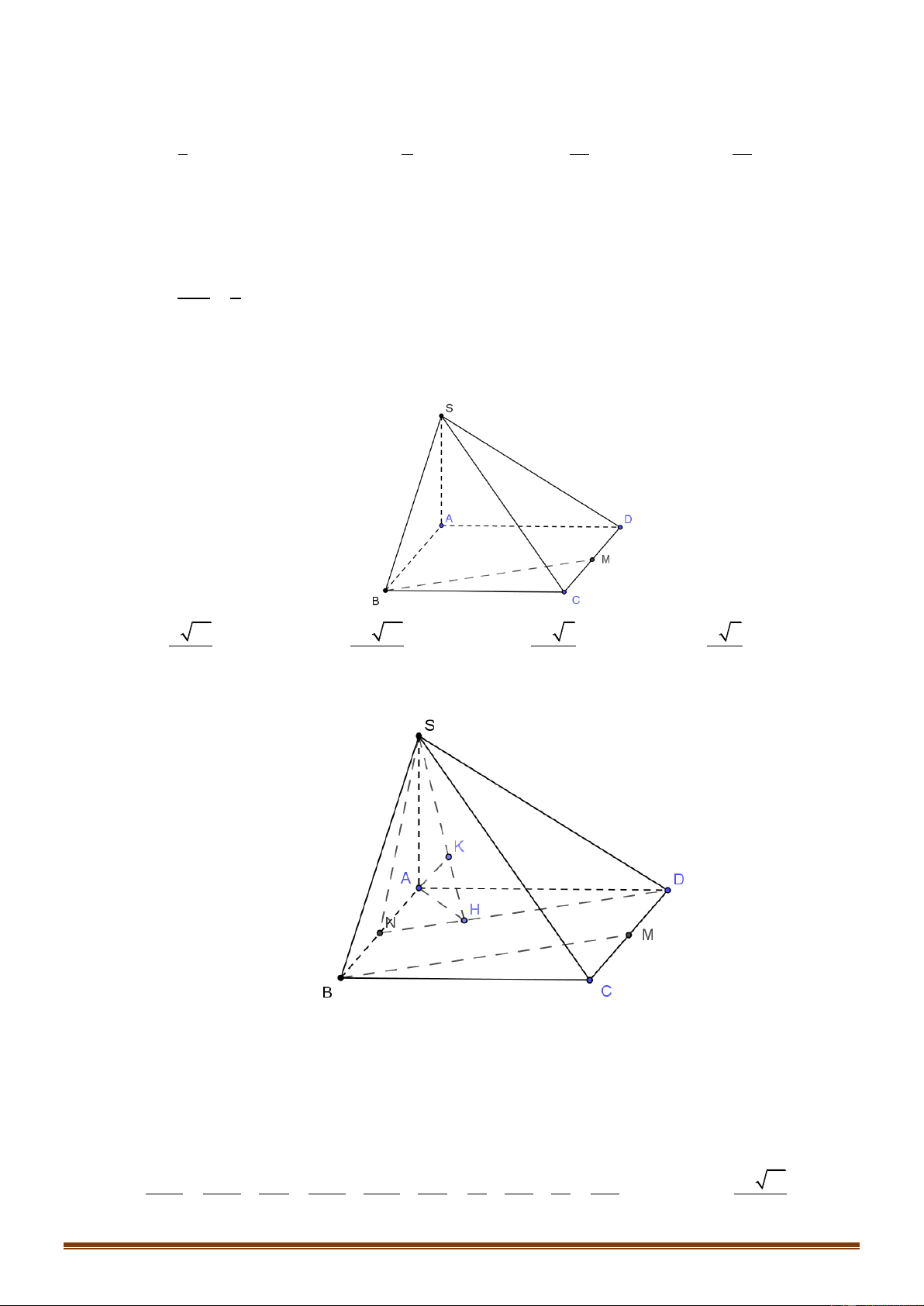
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD  2a , SA vuông góc với
mặt phẳng đáy và SA a (tham khảo hình vẽ). Gọi M là trung điểm của CD . Khoảng cách
giữa hai đường thẳng SD, BM bằng Trang 16 a 21 2a 21 2a 7 a 7 A. . B. . C. . D. . 21 21 7 7 Lời giải Chọn B
Gọi N là trung điểm của AB khi đó BM / /DN nên BM / / SDN
d BM ; SD  d BM ;SDN   d  ;
B SDN   d  ;
A SDN  .
Kẻ AH DN tại H . Ta có mặt phẳng SAH   SDN  . Trong mp SAH  kẻ AK SH tại K . Khi đó
d BM ; SD  d  ;
A SDN   AK . 1 1 1 1 1 1 4 1 1 21          2a 21 . Suy ra AK  . 2 2 2 2 2 2 2 2 2 2 AK AH SA AN AD SA a 4a a 4a 21 2x m 1
Câu 41: Tổng tất cả các giá trị nguyên của tham số m  1
 0;10 để hàm số y  nghịch biến x m trên 1;5 . A. 30 . B. 4 . C. 36 . D. 45  . Lời giải Chọn C
Tập xác định D   \   m . 3  m 1 Ta có y '    
x m , x D 2
Hàm số đồng biến trên 1;5 khi và chỉ khi hàm số xác định trên 1;5 và y '  0 x  1;5 Trang 17 m 1   m  1 1;5 m  5  m 1       3  3  m 1 0   1  m  5 m  3
Mà m nguyên và m  1
 0;10 nên m1;5;6;7;8;  9 .
Do đó tổng các giá trị của m thỏa mãn đề bài là 36.
Câu 42: Dân số thế giới được dự đoán theo công thức  .eNr S A
(trong đó A : là dân số của năm lấy làm
mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Theo số liệu thực tế, dân số
thế giới năm 1950 là 2560 triệu người; dân số thế giới năm 1980 là 3040 triệu người. Hãy dự
đoán dân số thế giới năm 2020 ? A. 3823triệu. B. 5360triệu. C. 3954triệu. D. 4017 triệu. Lời giải Chọn A S  1950 1950.r 6  . A e  2560.10 Ta có:  S  1980 1980.r 6  . A e  3040.10 6 2560.10 r 304 r 19 Suy ra: 30 0 3 e   e  và A  256 16 1950r e 6 2560.10 . r e 2020.r  2020 70 Vậy: S 2020 6  . A e   2560.10 . r e  3823.10 . 1950   6  re Câu 43: Cho hàm số 3 2
y ax bx cx d có đồ thị là đường cong như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. a  0, b  0, c  0, d  0 .
B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 .
D. a  0, b  0, c  0, d  0 . Lời giải Chọn A
Do nhánh cuối của đồ thị đi lên nên ta có a  0 . Ta có 2
y  3ax  2bx c . Do cực tiểu của hàm số thuộc trục tung và có giá trị âm nên d  0 và
x  0 là nghiệm của phương trình y  0  c  0 . Lại có x  0 2b 2 
3ax  2bx  0 2b  
 0  a  0,b  0  . x   3a  3a Trang 18
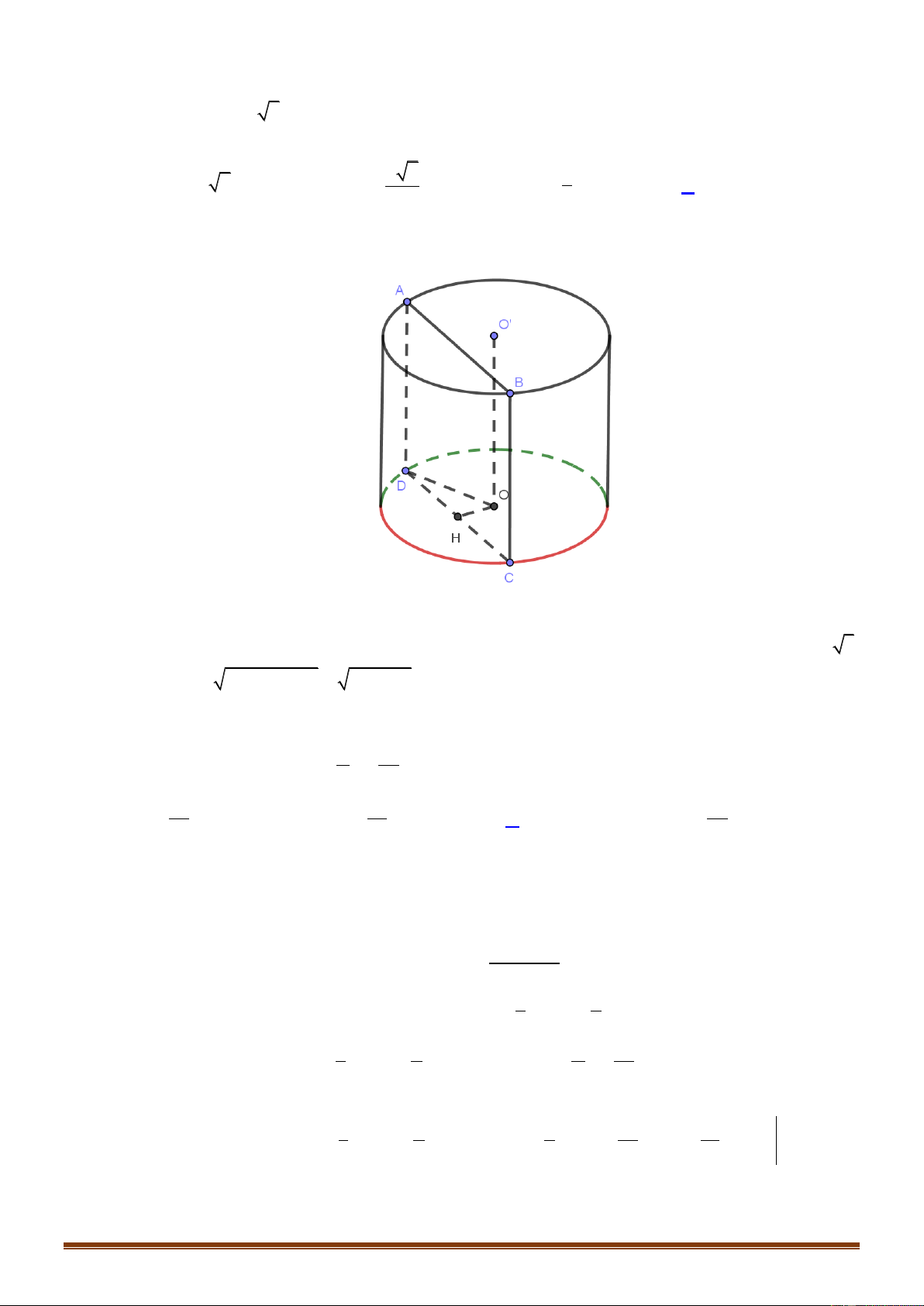
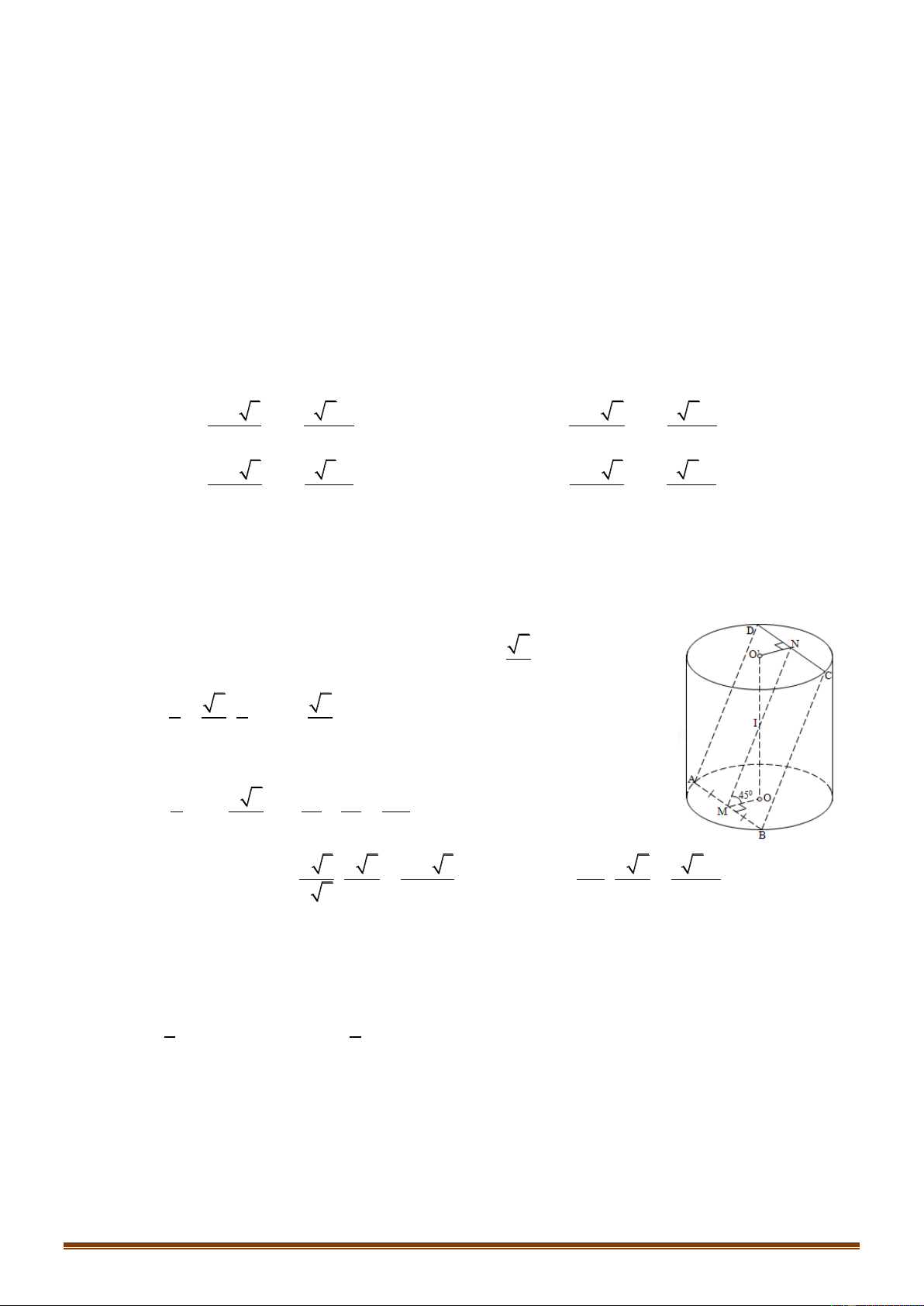
Câu 44: Khi cắt khối trụ T  bởi một mặt phẳng song song với trục và cách trục của trụ T  một
khoảng bằng a 3 ta được thiết diện là hình vuông có diện tích bằng 2
4a . Tính thể tích V của
khối trụ T  . 7 7 8 A. 3
V  7 7 a . B. 3 V  a . C. 3 V   a . D. 3 V  8 a . 3 3 Lời giải Chọn D
Thiết diện là hình vuông ABCD . 2 S
 4a AD CD  2a ABCD Gọi H là trung điểm
CD OH CD OH   ABCD  OH a 3 2 2 2 2
OD DH OH a  3a  2a . 2 3
h AD  2a, r OD  2a V   r h  8 a .     27
Câu 45: Cho hàm số f x có f   
và f  x 2 12sin 2 . x cos 3 , x x   . Khi đó f
 xdx bằng  2  8 0 27 87 87 A. . B.  . C. 0 . D. . 64 64 64 Lời giải Chọn C
Ta có f  x 2 12sin 2 . x cos 3 , x x
  nên f x là một nguyên hàm của f x . Có  f   x 1 cos 6x 2 dx  12 sin 2 . x cos 3 d x x  12.sin 2 . x dx  6.sin 2 d x x  6 sin 2 . x cos 6 d x x     2  x x    x x 3 3 6 sin 2 d 3 sin 8 sin 4 dx  3
 cos 2x  cos8x  cos 4x C . 8 4    27
Suy ra f x 3 3
 3cos 2x  cos8x  cos 4x C . Mà f   C  0   . 8 4  2  8 Do đó. Khi đó:        f  x 3 3 3 3 3 dx  3
 cos 2x  cos8x  cos 4x dx   sin 2x  sin 8x  sin 4x  0      8 4   2 64 16  0 0 0
Câu 46: Cho hàm số f x có bảng biến thiên như sau: Trang 19
Số nghiệm thuộc đoạn 0;3  của phương trình f sin x  1 là A. 2 . B. 4 . C. 6 . D. 8 . Lời giải ChọnC
f sin x 1
Ta có f sin x  1    f  sin x  1 
Từ bảng biến thiên ta được
sin x t   ;  1  (VN) 1   
f sin x  1  sin x t  1  ;0
 sin x t  1  ;0 (1) . 2   2  
sin x t  1; (VN)  3  
Dựa vào đường tròn lượng giác, phương trình (1) có 2 nghiệm nằm trong đoạn 0;3 .
sin x t   ;  1  (VN) 4   
f sin x  1
  sin x t  0;1
 sin x t  0;1 (2) . 5   5  
sin x t  1; (VN)  6  
Dựa vào đường tròn lượng giác, ta được phương trình (2) có 4 nghiệm nằm trong đoạn 0;3 .
Vậy phương trình ban đầu có tất cả 6 nghiệm. 8   1 ab
Câu 47: Cho hai số thực dương a và b thỏa mãn 4 .2 ab a b a
. Giá trị lớn nhất của biểu thức b 2
P ab  2ab bằng 5 1 3 A. 3 . B.1. C. . D. . 2 17 Lời giải Chọn B
Từ giả thiết suy ra 1 ab  0 . 8    1 ab 8 1 ab   4 .2 ab a b
 a bab   .2 
    a b     2 2 .2 2 2 .2 ab a b ab (1). a b 2 2 ab Xét hàm số    .2t f t t
với t 0;   D . Dễ thấy hàm số f t  liên tục trên D và
   2t  .2t f t t .ln 2  0, t
  D suy ra f t là hàm số đồng biến trên D .
(1)  a b  2  2ab a 1 2b  2  b (2). Từ (2), suy ra 2 b  0  b  2. 2 Ta được 2
P ab  2ab ba 1 2b  b 2  b  . b   b
Theo bất đẳng thức Cô – si, ta được P b   b   2 2 2     1. 2   Trang 20  1 a
Vậy max P 1, đạt được khi và chỉ khi  3 . b  1
Câu 48: Cho hàm số f (x) 3 2
= x - 3x + m . Gọi S là tập hợp tất cả các giá trị của m sao cho
max f x  2 min f x . Số phần tử của S là 1  ;3 1  ;3 A. 2 . B. 3 . C. 4 . D. 1. Lời giải Chọn A x
Ta có f  x 2
 3x  6x , f x 0  0   x  2
Ta có bảng biến thiên của f (x) 3 2
= x - 3x + m trên 1;  3
TH1: mm  4  0  0  m  4 , khi đó min f x  0  max f x  0 (vô lí) 1  ;3 1  ;3
TH2: m  0 , ta có: min f (x) = m = - m, max f (x) = m - 4 = 4- m [1; ] 3 [1 ] ;3
Khi đó ta có m  4  2 m  4  m  2
m m  4  . Vậy m  4 
TH3: m- 4 > 0 Û m > 4 , ta có: min f (x) = m - 4 = m - 4, max f (x) = m = m . [1; ] 3 [1 ] ;3
Khi đó ta có m  2 m  4  m  2m  4  m  8. Vậy m  8
Câu 49: Cho hình lăng trụ AB . C A BC
 . Gọi M , N , P lần lượt là các điểm thuộc các cạnh AA , BB ,
CC sao cho AM  2MA , NB  2NB , PC PC . Gọi V , V lần lượt là thể tích của hai khối 1 2 đa diệ V
n ABCMNP và A BCM
NP . Tính tỉ số 1 . V2 V V 1 V V 2 A. 1  2 B. 1  C. 1  1 D. 1  V V 2 V V 3 2 2 2 2 Lời giải Chọn C Trang 21 A' C' M B' P A C N B
Gọi V là thể tích khối lăng trụ AB . C A BC
 . Ta có V VV . 1 M . ABC M .BCPN 1 1 2 2 VS .d M , ABC  . S .d A ,  ABC V . M . ABC ABC    ABC    3 3 3 9 1 1 1 1 V            
S   .d M , A B C
. S   .d M , A B C V . M . A B C A B C    A B C    3 3 3 9 7 Do BCC B
  là hình bình hành và NB  2NB, PC PC nên S    S . B C PN 5 BCPN 7 Suy ra V    V
, Từ đó V VVV     V M .B C PN M .   5 BCPN M . ABC M .BCPN M . A B C M .B C PN 2 1 7 5
V V VV VVV . M .BCPN M .BCPN M . 9 9 5 BCPN 18 2 5 1 1 Như vậ V y V V V V V
V . Bởi vậy: 1  1. 1 2 9 18 2 2 V2
Câu 50: Cho 0  x  2020 và log (2  2)   3  8y x x y
.Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn 2 các điều kiện trên? A. 2019. B. 2018. C. 1. D.4. Lời giải Chọn D
Do 0  x  2020 nên log (2x  2) luôn có nghĩa. 2
Ta có log (2  2)   3  8y x x y 2 3
 log ( 1)  1 3  2 y x x y 2 log ( x 1  ) 2 3  log ( 1)  2  3  2 y x y (1) 2
Xét hàm số ( )   2t f t t . Tập xác định t
D   và f (
t) 1 2 ln 2  f (t)  0 t   .
Suy ra hàm số f (t) đồng biến trên  . Do đó (1)  log (x 1)  3y y  log (x 1) . 2 8
Ta có 0  x  2020 nên 1 x 1 2021 suy ra 0  log (x 1)  log 2021  0  y  log 2021. 8 8 8
Vì y   nên y 0;1;2;  3 .
Vậy có 4 cặp số (x ; y) nguyên thỏa yêu cầu bài toán là các cặp (0 ; 0) , (7 ;1) , (63; 2) , (511;3) . Trang 22 www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 12 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH Thời gian: 90 phút
HỌA LẦN 2 NĂM 2020
Câu 1:(NB) Có bao nhiêu cách chọn 2 học sinh nam từ một tổ gồm 5 nam và 6 nữ ? 2 2 2 A. . C B. . C C. . C D. 2 5 . 5 11 6
Câu 2:(NB) Số hạng thứ n của cấp số cộng là u  2n  3 . Tổng của số hạng thứ nhất và thứ hai bằng: n A.1. B. 1.  C. 0. D. 2. 
Câu 3:(NB) Tìm tập nghiệm của phương trình 2 x 1 2   8 . A. 3  ;  3 B. 3  ;  2 C. 2  ;  2 D.2;  3
Câu 4:(NB) Cho khối lăng trụ có diện tích đáy là 2 3a ,thể tích là 3
12a . Tính chiều cao của khối lăng trụ đó?
A. h 12a B. 5 h  36a C. 3 h  36a
D. h  4a 2 Câu 5:(NB) Hàm số 3 5x x y   có đạo hàm là 2   A.   2x 3  2 3 5 . x x   ln 5 B. x 3 5 x ln 5. C.   2x 3 2 3 5 . x x  
D. x x 2 2 x 3x 1 3 5 .
Câu 6:(NB). Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số y f x liên tục trên
a;b, trục hoành và hai đường thẳng x a,x b. Mệnh đề nào sau đây đúng? b b A. S f
 xd .x B. S f  xdx. a a 0 b 0 b C. S f
 xdx f
 xd .x D. S f
 xdx f
 xd .x a 0 a 0
Câu7:(NB) Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng 9 3 27 3 27 3 9 3 A. . B. . C. . D. . 4 4 2 2
Câu8:(NB) Cho khối nón có bán kính đáy r  3 và chiều cao h  4 . Tính thể tích V của khối nón đã cho.
A.V  16 3 . B.V 12 . C.V  4 . D.V  4 .
Câu 9:(NB). Cho khối cầu có bán kính R . Thể tích của khối cầu đó là: 4 1 4 A. 3 V  4 R . B. 3 V   R . C. 3 V   R . D. 2 V   R . 3 3 3
Câu 10:(NB) Cho hàm số f x có bảng biến thiên như sau: x  1  f (  x)    2 f (x) 2 
Hàm số đã cho đồng biến trên khoảng nào sau đây ? A.  ;    1 . B.  2  ;. C.  ;  2. D.  ;    1   1  ;.
Câu 11:(NB) Tâ ̣p xác đi ̣nh D của hàm số y  log  2 x  2x  3 2  A. D   1  ;3 B. D   ;    1  3; Trang 23 C. D   1  ;  3 D. D   ;    1 3;
Câu12:(NB) Khối trụ tròn xoay có đường kính đáy là 2a , chiều cao là h  2a có thể tích là: A. 3 V   a . B. 2
V  2 a h . C. 2 V  2 a . D. 3 V  2 a .
Câu 13:(NB).Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại A. x  2. B. x  1. C. x  1.  D. x  3. 
Câu 14:(TH) Đồ thị ở hình bên là đồ thị của hàm số nào sau đây: y A. y = x3 + 3x2 – x – 1 B. y = - x3 – 2x2 + x – 2 3 C. y = - x3 + 3x + 1 1 D. y = x3 + 3x2 – x – 1 -1 O 1 x -1 x 1
Câu 15:(NB) Tiệm cận đứng của đồ thị của hàm số y  là 2x  2 1 A. x = - 1 B. x = 1 C. x = 2 D. x  . 2
Câu 16:(NB) Nghiệm của bất phương trình log  2
x  5x  7  0 là 1  5 A. x  2.
B. x  2 hoặc x  3 . C. 2  x  3 . D. x  3 .
Câu 17:(TH) Cho hàm số y f x xác định,
liên tục trên R và có bảng biến thiên như hình
bên. Số nghiệm của phương trình f x  3 là: A. 1 B. 2 C. Vô nghiệm D. 3 5 2 Câu 18:(NB) Cho f
 xdx 10 . Khi đó 24 f  xdx  bằng: 2 5 A. 32. B. 34. C. 36. D. 40.
Câu 19:(NB) Cho số phức z  6  7i . Số phức z có điểm biễu diễn trên hệ trục tọa độ Oxy là: A. 6; 7   B. 6;7 C.  6  ; 7   D.  6  ;7
Câu 20:(NB) Tìm số phức liên hợp của số phức z  2  3i3  2i .
A. z  12  5i . B. z  1  2  5i . C. z  1  2 5i .
D. z  12  5i .
Câu 21:(NB) Phần ảo của số phức z  2  3i là: A. 3  i . B. 3 . C. 3 . D. 3i . Trang 24
Câu22:(TH)Trong không gian với hệ trục tọa độ Oxyz , điểm thuộc trục Ox và cách đều hai điểm A4; 2; 
1 và B 2;1;0 là A. M  4  ;0;0.
B. M 5;0;0 .
C. M 4;0;0 . D. M  5  ;0;0. 2 2 2
Câu 23:(NB) Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  :  x  
1   y  2  z   1  9 . Tìm
tọa độ tâm I và bán kính R của  S A. I  1  ;2  ;1 và R  3 . B. I 1; 2  ;  1 và R  3 . C. I  1  ;2  ;1 và R  9 . D. I 1; 2  ;  1 và R  9 .
Câu 24:(NB) Trong không gian, điểm nào dưới đây thuộc mặt phẳng   :  x y  2z  3  0 ? A. Q  2  ; 1  ;3 B. M 2;3  ;1
C. P 1;2;3 D. N  2  ;1;3 6
Câu 25:(NB) Cho hình chóp S.ABCD có đáy là hình vuông canh a , SA   ABCD và SA a . Tính 3
góc giữa SC và  ABCD. A. 0 30 B. 0 45 C. 0 60 D. 0 90 x 1 y  2 z
Câu 26:(TH)Cho đường thẳng d : 
 .Độ dài của véc tơ chỉ phương u bằng: 2 1 3 A. 6. B. 14. C.14. D. 6. 1
Câu 27:(TH) Số điểm cực tiểu của hàm số 4 2 y
x  2x 1 là: 4 A.1. B. 2. C. 3. D. 0. x
Câu 28:(TH) Hiệu của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x 1  trên đoạn 3;  5 là: x  2
A. f 5  f 3. B. 2. C. 6.
D. f 5  f 3.
Câu 29:(TH) Cho a và b là hai số thực dương thỏa mãn 2
a b  8. Giá trị của 2
4log a  log b bằng 2 2 A.16. B. 4. C. 6. D. 8.
Câu 30:(TH) Cho hàm số f(x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f x  3  0 là A. 2. B.1. C. 4. D. 3.
Câu 31:(TH) Tập nghiệm của bất phương trình log  2
x  4x  9  2 là: 3  A.  ;  04; B.0;  4 C.0;4 D.  ;  04;
Câu 32:(TH) Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền là 2 3 .
Thể tích của khối nón này bằng: Trang 25 A. 3 . B. 3 2 . C. 3 . D. 3 3 . 2
Câu 33:(TH) Cho hàm số f(x) có đạo hàm trên đoạn [-1;2], f(-1) = -2 và f(2) = 1. Tính I f '(x)dx  . 1  A. -3 B. 3 C. -1 D. 1
Câu 34:(TH) Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 3
y x , trục hoành và hai đường thẳng
x  1, x  2 bằng: 17 17 16 15 A. . B. . C. . D. . 4 5 3 4 2 2
Câu 35:(TH) Cho hai số phức z  1
  2i , z  1
  2i . Giá trị của biểu thức z z bằng: 1 2 1 2 A. 10 . B. 10 . C. 6  . D. 4 .
Câu 36:(TH) Tìm tổng phần thực và phần ảo của số phức 2 2
w z z biết z , z là hai nghiệm phức của 1 2 1 2 phương trình: 2
z  4z  5  0 . A. 4 . B. 6 . C. 8 . D. 5 .
Câu37:(TH) Trong không gian tọa độ Oxyz , cho mặt cầu S  có đường kính AB , với A6; 2; 5   , B  4
 ;0;7. Viết phương trình mặt phẳng P tiếp xúc với mặt cầu S  tại A .
A. P : 5x y – 6z  62  0 .
B. P : 5x y – 6z  62  0 .
C. P : 5x y – 6z  62  0 .
D. P : 5x y  6z  62  0 . x  4 y 1 z  5
Câu 38:(TH) Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng  :   1 và 3 1  2  x  2 y  3 z  :  
M   , N   MN 2 . Giả sử sao cho
là đoạn vuông góc chung của hai đường 1 3 1 1 2 uuur
thẳng  và  . Tính MN. 1 2   
A. MN  5; 5  ;10 .
B. MN  2; 2; 4 .
C. MN  3; 3  ;6 .
D. MN  1; 1; 2 .
Câu 39:(VD)Một nhóm học sinh của trường Hùng Vương gồm 7 học sinh lớp 10 và 4 học sinh lớp
11cùng đứng thành một hàng ngang để chụp bức ảnh lưu niệm sau buổi lễ nhận thưởng ở kỳ thi Olympic
năm 2019.Tính xác suất khi các học sinh lớp 11 không đứng cạnh nhau? 7 11 1 1 A. . B. . C. . D. . 33 630 5940 105
Câu 40:(VD)Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi G là trọng tâm tam giác ABC.
Góc giữa đường thẳng SA với mặt phẳng (ABC) bằng 0
60 . Khoảng cách giữa hai đường thẳng GC và SA bằng: a 5 a a 5 a 2 A. B. C. D. 5 5 10 5 x
Câu 41:(VD)Có tất cả bao nhiêu giá trị nguyên của m để hàm số 2 y  đồng biến trên  ;  6   ? x  3m A. 1 B. 3 C. 0 D. 2
Câu 42.(VD)Sau một tháng thi công thì công trình xây dựng Nhà học thể dục của một trường đã thực
hiện được một khối lượng công việc. Nếu vẫn tiếp tục với tiến độ như vậy thì dự kiến sau đúng
23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công trình và kịp đưa vào sử dụng,
công ty xây dựng quyết định từ tháng thứ hai, mỗi tháng tăng 4% khối lượng công việc so với
tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công? Trang 26 A. 19. B.18. C. 17. D. 20.
Câu 43:(VD) Cho hàm số y f (x) liên tục trên R, f (2)  3 và có đồ
thị như hình vẽ bên.Có bao nhiêu số nguyên m  (20; 20) để phương
trình f x m  3 có 4 nghiệm thực phân biệt. A. 2 B. 18 C. 4. D. 19.
Câu 44:(VD)Một bồn hình trụ đang chứa dầu được đăt nằm ngang, có
chiều dài bồn là 5m, có bán kính đáy 1m,với nắp bồn đặt trên mặt nằm
ngang của mặt trụ.Người ta đã rút dầu trong bồn tương ứng với 0,5 m
của đường kính đáy.Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn( theo đơn vị m3) A.12,637m3. B.11,923 m3. C.11,781 m3 D. 3 8, 307m . 2 4 f x Câu45:(VD)Cho f
 xdx  2. Tính I  dx  bằng x 1 1 1 A. I  1. B. I  2 . C. I  4 . D. I  . 2
Câu 46:(VDC) Cho hàm số y f x có đồ thị y f ' x như hình vẽ. Xét hàm số
g x  f x 1 3 3 3 2
x x x  2018. Mệnh đề nào dưới đây đúng? 3 4 2
A. min g x  g   1
B. min g x  g   1  3  ;  1  3  ;  1 g 3   g 1
C. min g x   g  3   D. min gx       3  ;  1  3  ;  1 2
Câu47:(VDC) Có tất cả bao nhiêu cặp số nguyên chẵn  ;
x y thỏa mãn 2x  3y  55 ? A. 8 . B. 2 . C.16 . D.1. Câu 48. (VDC) Cho hàm số
y f (x) nghịch biến trên  và thỏa mãn  f x x 6 4 2 ( )
f (x)  x  3x  2x , x
  . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số y f (x) trên đoạn 1; 2. Giá trị của 3M m bằng: A. 4. B. 28.  C. 3.  D. 33.
Câu 49 :(VDC) Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy làm tam giác đều cạnh bằng a, hình 3a
chiếu vuông góc của A’ lên mp(ABC) là trung điểm BC. Biết khoảng cách giữa BC và AA’ bằng . 4
Tính thể tích khối lẳng trụ đã cho. 3 3a 3 3 3a 2 3 a 3 3 3a 3 A.V B. V C.V D.V 8 8 8 6
Câu 50: (VDC) Cho phương trình log 2  2  2 2 2 2 2  2y x x
y x x . Có bao nhiêu cặp số nguyên 2 dương  ;
x y,0  x  500 thỏa mãn phương trình đã cho ? A. 4. B. 2. C. 3. D.1. Hết Trang 27 www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 13 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH Thời gian: 90 phút
HỌA LẦN 2 NĂM 2020
Câu 1: Bạn An có 2 loại sách truyện, trong đó có 10 quyển truyện tranh và 5 quyển truyện ngắn. Bạn An
chọn ngẫu nhiên 1 quyển để đọc. Hỏi bạn An có mấy cách chọn? A. 2 . B. 15 . C. 50 . D. 5 .
Câu 2: Cho cấp số nhân u u  3 u  1 n  với và
. Công bội của cấp số nhân đã cho bằng 4 5 1 A. 2  . B. 2 . C. . D. 3 . 3
Câu 3:Nghiệm của phương trình log 1 2x  1 là 9 A. x   9 . B. x  11 . C. x  11 . D. x   . 2 2 2 2
Câu 4: Thể tích của khối hộp chữ nhật có ba kích thước a,b,c có công thức là
A. a + b + c B. 2 2 2 a b c C. abc D. 3 3 3 a b c Câu 5: Cho x
y  a (0  a  1) . Hỏi khẳng định nào dưới đây là sai?
A. Hàm số có tập xác định là  .
B. Hàm số có đạo hàm x y  a ln a .
C. Đồ thị hàm số nằm phía trên trục hoành.
D. Đồ thị hàm số nhận trục Oy làm tiệm cận ngang.
Câu 6: Họ nguyên hàm của hàm số f x 2
 sin x  6x là A. 3
 cos x  2x C . B. 3
cos x  2x C . C. 3
cos x  6x C .
D. cos x C .
Câu 7: Cho khối chóp có đáy là hình vuông cạnh a , chiều cao bằng 2a . Thể tích của khối chóp đã cho là 2 4 A. 3 4a . B. 3 a . C. 3 2a . D. 3 a . 3 3
Câu 8: Cho hình nón có bán kính đường tròn đáy là r, đường sinh .
 Tỉ số giữa diện tích xung quanh và
diện tích đáy của hình nón bằng r 2r  2 A. . B. . C. . D. .   r r
Câu 9: Cho mặt cầu có bán kính R . Thể tích của khối cầu có công thức là 4 4 A. 2 V  4 R . B. 3 V  4 R . C. 3 V   R . D. 2 V   R . 3 3
Câu 10: Cho hàm số y f x có bảng biến thiên như sau Trang 28
Hàm số y f x nghịch biến trên khoảng nào dưới đây? A.  1  ; 0
B. ;   1 C. 0;  1 D.  1  ;  1
Câu 11: Với số thực a dương tùy ý, log  4 a bằng: 3  4 A. 4  log a B. 4 log a C. log a D. log 4a 3   3 3 3 3
Câu 12: Thể tích của khối trụ tròn xoay có chiều cao a và bán kính đáy a bằng 1 A. 3  a B. 3  a C. 3 2 a D. 3 3 a 3
Câu 13: Cho hàm số y f x có bảng biến thiên như sau: x  1 2  f ' x + 0  0 +  f x 4 3  
Giá trị cực tiểu của hàm số đã cho bằng A. 1 B. 3  C. 2 D. 4
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y  x  2x B. 4 2
y x  2x C. 3 2
y x  3x D. 3 2
y  x  3x 2x  2
Câu 15: Tiệm cận đứng của đồ thị hàm số y  là x 1 A. y  2 B. x  1  C. y  1 D. x  2 
Câu 16: Tập nghiệm của bất phương trình 2x  8 là A.  ;3   B. 4;  C. 3;  D. 0; 
Câu 17: Cho hàm số y f x có đồ thị trong hình bên. Trang 29
Số nghiệm của phương trình f x  2  0 là A. 0 B. 2 C. 3 D. 4 3 4 4 Câu 18: Nếu
f xdx  3   và f
 xdx 1 thì f xdx  bằng 1 3 1 A. 3  B. 2  C. 4 D. 1
Câu 19: Mô đun của số phức z  3 2i bằng A. z  1 B. z  13 C. z  13 D. z  5
Câu 20: Cho hai số phức z  1 2i và z  3
  i . Phần ảo của số phức z  2z bằng 1 2 1 2 A. 5  B. 3 C. 2  D. 4
Câu 21. Cho hai số phức z  2
  i và z  1 i . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là 1 2 A. 3;  3 B. 2;  3 C.  3  ; 3 D.  3  ; 2
Câu 22. Trong không gian Oxyz, hình chiếu vuông góc của điểm M 2;1;  
1 trên trục Oz có tọa độ là. A. 2;1;0. B. 0;0;  1 . C. 2;0;0. D. 0;1;0.
Câu 23. Trong không gian Oxyz, cho mặt cầu S  2 2 2
: x y z  2x  2z  7  0. Bán kính của mặt cầu đã cho bằng A. 7. B. 9.. C. 3. D. 15.
Câu 24: Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng   : x  3y  2z  6  0 . Vecto nào
không phải là vecto pháp tuyến của   ?     A. n   2  ;6;4 .
B. n  1;  3;  2 . C. n   1  ;3;2.
D. n  1;3; 2 . x 1 3t
Câu 25: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình  y  2 . Khi đó z  2t
vecto nào sau đây là một vecto chỉ phương của đường thẳng (d)?    
A. d  1; 0; 2. B. a   6  ; 0; 4. C. b   3  ; 2; 2.
D. c  1; 2; 2.
Câu 26. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA  2a, tam giác ABC vuông tại
B, AB a 3 và BC a (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng A. 90 .  B. 45 .  C. 30 .  D. 60 .  Trang 30
Câu 27 : Cho hàm số y f x  liên tục trên  và có bảng xét xét dấu của đạo hàm như sau :
Hàm số đã cho có bao nhiêu cực trị ? A.1. B. 2. C. 3. D. 4.
Câu 28. Giá trị lớn nhất của hàm số f x 3
x 3x  2 trên đoạn  3  ;  3 là A. 16.  B. 20. C. 0. D. 4.
Câu 29. Cho a và b là hai số thực dương thỏa mãn 4
a b  16. Giá trị của 4 log a  log b bằng 2 2 A. 4. B. 2. C. 16. D. 8.
Câu 30. Tìm số giao điểm của đồ thị hàm số y = x3 – 3x2 + 3x – 1 và đồ thị hàm số y = x2 – x – 1 A. 1. B. 2. C. 3. D. 4.
Câu 31: Tập nghiệm của bất phương trình log x  log 8  x là: 2 2  
A. S  8; 
B. S   ;  4
C. S  4;8
D. S  0;4
Câu 32: Mặt cầu  S  có diện tích bằng 20 , thể tích khối cầu  S  bằng 20 5 20 4 5 A. B. 20 5 C. D. 3 3 3 8 3 3
Câu 33. Cho hàm số f x liên tục trên  và f (x)dx  10  . Tính I
f (3x 1)dx  2 2 1 A. 30 B. 10 C. 20 D. 5
Câu 34. Cho hàm số y f x liên tục trên  và có đồ thi ̣ như hình vẽ bên. Hình phẳng được đánh dấu
trong hình vẽ bên có diê ̣n tích là y
y f xb a O c x b c b c A. f
 xdxf
 xdx . B. f
 xdxf
 xdx . a b a b b c b b C. f
 xdxf
 xdx. D. f
 xdxf  xdx . a b a c
Câu 35. Tìm số phức liên hợp của số phức z i(3i 1)
A. z  3  i B. z  3   i
C. z  3  i D. z  3  i
Câu 36: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
4z  4z  37  0 . Trên mặt phẳng 0
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0 Trang 31  1   1   1   1  A. M 3;  B. M 3; C. M 3;  D. M 3;   2          2  3  2  4  2  1  2 
Câu 37. Viết phương trình mặt phẳng (P) đi qua điểm A0; 1
 ;2 , song song với trục Ox và vuông góc
với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0 B. (P) : y + z - 1 = 0 C. (P) : y - z + 3 = 0
D. (P) : 2x + z - 2 = 0
Câu 38: Trong không gian Oxyz , cho điểm M  1
 ;2;2 . Đường thẳng đi qua M và song song với trục
Oy có phương trình là: x  1  x  1   tx  1   tx  1      A. y  2
t   B.y  2 t   C. y  2 t  
D. y  2  t t        z  2  tz  2  z  2  tz  2 
Câu 39: Chọn ngẫu nhiên 5 học sinh trong một lớp học gồm 25 nam và 20 nữ. Gọi A là biến cố: “Trong
5 học sinh được chọn có ít nhất 1 học sinh nữ”. Xác suất của biến cố A là: C 20.C 20.C C
A. P A 5 20 
B. P A 4 25 
C. P A 4 44 
D. P A 5 25 1 5 C 5 C 5 C 5 C 45 45 45 45
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng
a . Hai mặt phẳng SAB và SAC  cùng vuông góc với đáy. Tính
khoảng cách giữa hai đường thẳng SA và BC ? A. a 2 B. a a 2 a C. D. 2 2
Câu 41. Tìm giá trị thực lớn nhất của tham số m để hàm số 3 2
y  x  3mx  x đồng biến trên  . 1 1 A.1. B. . C.  . D. 2. 3 3
Câu 42. Dân số thế giới được tính theo công thức r.N S  A.e
trong đó: A là dân số của năm lấy mốc tính,
S là dân số sau N năm, r là tỷ lệ tăng dân số hằng năm. Cho biết năm 2001, dân số việt nam có khoảng
78.685.000 người và tỷ lệ tăng dân số hằng năm là 1,7%/năm. Nếu tỷ lệ tăng dân số hằng năm không đổi
thì đến năm bao nhiêu nước ta có khoảng 120 triệu người? A. 2020. B. 2024. C. 2026. D. 2022. ax 1
Câu 43. Cho hàm số y 
có đồ thị như hình vẽ bên. Tính tổng S  a  b  c. bx  c Trang 32 A. S  2. B. S  0. C. S  1  . D. S  3.
Câu 44: Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không
vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song
AB, A ' B ' mà AB  A'B'  6cm (hình vẽ). Biết diện tích tứ giác
ABB' A ' bằng 60 cm2. Tính chiều cao của hình trụ đã cho. A. 6 2 cm. B. 4 3 cm. C. 8 2 cm. D. 5 3 cm.
Câu 45: Cho hàm số y  f (x) có đạo hàm và liên tục trên đoạn [0;1] 1 thỏa mãn 2 f (0)  1 và f (x )x 1 f '(x).e   2x, x  0; 
1 . Tính giá trị của f (x)dx.  0 4 4 A. 2. B. . C.  . D. 2  3 3
Câu 46. Cho hàm số y  f (x) liên tục trên  và có đồ thị như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số m để phương trình:  3sin x  cos x 1  f  f    2
m  4m  4 (1) có nghiệm?  2cos x sin x  4  A. 1. B. 2. C. 3. D. 4. Trang 33
Câu 47. Cho hai số thực dương x, y thay đổi thỏa mãn 2 2
x  4y  1. Tìm giá trị lớn nhất của biểu thức
P  log (x  2y).log (2x  4y). 2 2 1 1 1 1 A. . B. . C. . D. . 4 2 3 6
Câu 48. Tìm tất cả giá trị thực của tham số m để giá trị lớn nhất của hàm số 3
y  x  3x  2m 1 trên
đoạn 0;2 đạt giá trị nhỏ nhất. Giá trị của m thuộc khoảng nào?  3   2  A.  ; 1  .   B. ; 2 .   C. 1  ;0. D. 0  ;1 .  2   3 
Câu 49. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của các cạnh
A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành hai phần. Gọi V là thể tích của phần chứa 1 V
đỉnh A, V là thể tích của phần còn lại. Tính tỉ số 1 . 2 V2 55 37 1 2 A. . B. . C. . D. . 89 48 2 3
Câu 50.Cho phương trình 2 2 y 2 2 log (2x  2x  2)  2
 y  x  x. Hỏi có bao nhiêu cặp số nguyên dương 2 (x,y), (0 A. 1. B. 2. C. 3. D. 4.
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT 1-B 2-C 3-A 4-C 5-D 6-A 7-B 8-C 9-C 10-A 11-B 12-B 13-B 14-A 15-B 16-C 17-C 18-B 19-B 20-D 21-C 22-B 23-C 24-D 25-B 26-B 27-D 28-B 29-A 30-B 31-C 32-A 33-D 34-A 35-D 36-D 37-B 38-D 39-D 40-B 41-B 42-C 43-A 44-A 45-B 46-C 47-A 48-D 49-A 50-D
Câu 1: Bạn An có 2 loại sách truyện, trong đó có 10 quyển truyện tranh và 5 quyển truyện ngắn. Bạn An
chọn ngẫu nhiên 1 quyển để đọc. Hỏi bạn An có mấy cách chọn? A. 2 . B.15 . C. 50 . D. 5 . Giải
Chọn 1 quyển truyện tranh từ 10 quyển truyện tranh có 10 cách chọn.
Chọn 1 quyển truyện ngắn từ 5 quyển truyện ngắn có 5 cách chọn.
Áp dụng quy tắc cộng có: 10+ 5 = 15 cách chọn. Đáp án B
Câu 2: Cho cấp số nhân u u  3 u  1 n  với và
. Công bội của cấp số nhân đã cho bằng 4 5 1 A. 2  . B. 2 . C. . D. 3 . 3 Giải u 1
Công bội của cấp số nhân là 5 q   . u 3 4 Đáp án C
Câu 3:Nghiệm của phương trình log 1 2x  1 là 9 A. x   9 . B. x  11 . C. x  11 . D. x   . 2 2 2 2 Giải Trang 34
Ta có log 1 2x  1 1 2x  9 10  x   . 2 Đáp án A
Câu 4: Thể tích của khối hộp chữ nhật có ba kích thước a,b,c có công thức là
A. a + b + c B. 2 2 2 a b c C. abc D. 3 3 3 a b c Giải
Công thức tính thể tích khối hộp chữ nhật là: V = abc Đáp án C Câu 5: Cho x
y  a (0  a  1) . Hỏi khẳng định nào dưới đây là sai?
A. Hàm số có tập xác định là  .
B. Hàm số có đạo hàm x y  a ln a .
C. Đồ thị hàm số nằm phía trên trục hoành.
D. Đồ thị hàm số nhận trục Oy làm tiệm cận ngang. Giải Đồ thị hàm số x
y  a (0  a  1) nhận trục Ox làm tiệm cận ngang Đáp án D
Câu 6: Họ nguyên hàm của hàm số f x 2
 sin x  6x là A. 3
 cos x  2x C . B. 3
cos x  2x C . C. 3
cos x  6x C .
D. cos x C . Giải f
 xdx   xx  3 2 x 3 sin 6
dx   cos x  6.
C  cos x  2x C . 3 Đáp án A
Câu 7: Cho khối chóp có đáy là hình vuông cạnh a , chiều cao bằng 2a . Thể tích của khối chóp đã cho là 2 4 A. 3 4a . B. 3 a . C. 3 2a . D. 3 a . 3 3 Giải Diện tích hình vuông: 2 S a 3 1 1 2a 2
Thể tích khối chóp là: V  . B h a .2a  (đvtt). 3 3 3 Đáp án B
Câu 8: Cho hình nón có bán kính đường tròn đáy là r, đường sinh .
 Tỉ số giữa diện tích xung quanh và
diện tích đáy của hình nón bằng r 2r  2 A. . B. . C. . D. .   r r Giải S   r   xq Sr  Ta có xq     . 2 2 S   r Sr r  day day Đáp án C
Câu 9: Cho mặt cầu có bán kính R . Thể tích của khối cầu có công thức là 4 4 A. 2 V  4 R . B. 3 V  4 R . C. 3 V   R . D. 2 V   R . 3 3 Giải 4
Thể tích của khối cầu có công thức là: 3 V   R . 3 Đáp án C
Câu 10: Cho hàm số y f x có bảng biến thiên như sau Trang 35
Hàm số y f x nghịch biến trên khoảng nào dưới đây? A.  1  ;0 . B.  ;    1 . C. 0;  1 . D.  1   ;1 . Giải
Từ bảng biến thiên ta có hàm số nghịch biến trên khoảng  1  ;0 . Đáp án A
Câu 11: Với số thực a dương tùy ý, log  4 a bằng: 3  4 A. 4  log a B. 4 log a C. log a D. log 4a 3   3 3 3 3 Giải
Lý thuyết: Cho hai số dương  a, ;
b b  1 . Với mọi  , ta có: log a    log . a b b Áp dụng: log  4 a  4log . a 3  3 Đáp án B.
Câu 12: Thể tích của khối trụ tròn xoay có chiều cao a và bán kính đáy a bằng 1 A. 3  a B. 3  a C. 3 2 a D. 3 3 a 3 Giải
Thể tích của khối trụ tròn xoay có chiều cao a và bán kính đáy a bằng 2 2 3
V   r h   a .a   a Đáp án B.
Câu 13: Cho hàm số y f x có bảng biến thiên như sau: x  1 2  f ' x + 0  0 +  f x 4 3  
Giá trị cực tiểu của hàm số đã cho bằng A. 1 B. 3  C. 2 D. 4 Giải
Giá trị cực tiểu của hàm số đã cho bằng 3  . Đáp án B.
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? Trang 36 A. 4 2
y  x  2x B. 4 2
y x  2x C. 3 2
y x  3x D. 3 2
y  x  3x Giải Chọn câu A. 2x  2
Câu 15: Tiệm cận đứng của đồ thị hàm số y  là x 1 A. y  2 B. x  1  C. y  1 D. x  2  Giải 2x  2
Tiệm cận đứng của đồ thị hàm số y  là x  1  x 1 Đáp án B.
Câu 16: Tập nghiệm của bất phương trình 2x  8 là A.  ;3   B. 4;  C. 3;  D. 0;  Giải Ta có: x x 3
2  8  2  2  x  3 Chọn câu C.
Câu 17: Cho hàm số y f x có đồ thị trong hình bên.
Số nghiệm của phương trình f x  2  0 là A. 0 B. 2 C. 3 D. 4 Giải
f x  2  0  f x  2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y f x và đường thẳng y  2 .
Suy ra có 3 giao điểm hay phương trình đã cho có 3 nghiệm. Chọn câu C. 3 4 4 Câu 18: Nếu
f xdx  3   và f
 xdx 1 thì f xdx  bằng 1 3 1 A. 3  B. 2  C. 4 D. 1 Giải Trang 37 4 3 4 Ta có: f
 xdx f
 xdxf
 xdx  3  1  2  . 1 1 3 Chọn câu B.
Câu 19: Mô đun của số phức z  3 2i bằng A. z  1 B. z  13 C. z  13 D. z  5 Giải
Mô đun của số phức z là z a b    2 2 2 2 3 2  13 Chọn câu B.
Câu 20: Cho hai số phức z  1 2i và z  3
  i . Phần ảo của số phức z  2z bằng 1 2 1 2 A. 5  B. 3 C. 2  D. 4 Giải
Ta có: z  2z  1 2i  6   2i  5   4i 1 2    
Phần ảo của số phức z  2z bằng 4. 1 2 Chọn câu D.
Câu 21: Cho hai số phức z  2
  i và z  1 i . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là 1 2 A. 3;  3 B. 2;  3 C.  3  ; 3 D.  3  ; 2 Giải
Ta có: 2z z  4
  2i 1 i  3
  3i . Vậy điểm biểu diễn số phức 2z z có tọa độ là  3  ; 3 . 1 2 1 2 Đáp án C
Câu 22 : Trong không gian Oxyz, hình chiếu vuông góc của điểm M 2;1;  
1 trên trục Oz có tọa độ là. A. 2;1;0. B. 0;0;  1 . C. 2;0;0. D. 0;1;0. Giải
Hình chiếu vuông góc của điểm M 2;1;  
1 trên trục Oz có tọa độ là 0;0;   1 . Đáp án B.
Câu 23 : Trong không gian Oxyz, cho mặt cầu S  2 2 2
: x y z  2x  2z  7  0. Bán kính của mặt cầu đã cho bằng A. 7. B. 9.. C. 3. D. 15. Giải 2 2 2
x y z x z    S 2 2 2 2 2 7 0
: x y z  2. 
1 .x  2.0.y  2.1.z  7  0.  a  1  , b  0,c  1,d  7. 
 Tâm mặt cầu I  1  ;0 
;1 bán kính R a b c d   2 2 2 2 2 2 1  0 1  7  3. Đáp án C
Câu 24 :Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng   : x  3y  2z  6  0 . Vecto nào
không phải là vecto pháp tuyến của   ?     A. n   2  ;6;4 .
B. n  1;  3;  2 . C. n   1  ;3;2.
D. n  1;3; 2 . Giải Đáp án D x 1 3t
Câu 25 : Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình  y  2 . Khi đó z  2t
vecto nào sau đây là một vecto chỉ phương của đường thẳng (d)? Trang 38    
A. d  1; 0; 2. B. a   6  ; 0; 4. C. b   3  ; 2; 2.
D. c  1; 2; 2. Giải Đáp án B
Câu 26. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA  2a, tam giác ABC vuông tại
B, AB a 3 và BC a (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng A. 90 .  B. 45 .  C. 30 .  D. 60 .  Giải
Ta có SA   ABC  nên AC là hình chiếu của SC lên mặt phẳng ABC.
Do đó SC ABC  SC AC  , ,  SC . A
Tam giác ABC vuông tại B, AB a 3 và BC a nên 2 2 2 AC
AB BC  4a  2 . a
Do đó tam giác SAC vuông cân tại A nên  SCA  45 . 
Vậy SC, ABC   45 .  Đáp án B
Câu 27 : Cho hàm số y f x  liên tục trên  và có bảng xét xét dấu của đạo hàm như sau :
Hàm số đã cho có bao nhiêu cực trị ? A.1. B. 2. C. 3. D. 4. Giải
Dựa vào bảng xét dấu ta thấy đạo hàm của hàm số có 4 lần đổi dấu nên hàm số có 4 điểm cực trị Đáp án D
Câu 28. Giá trị lớn nhất của hàm số f x 3
x 3x  2 trên đoạn  3  ;  3 là A. 16.  B. 20. C. 0. D. 4. Giải
Ta có f  x 2
 0  3x 3  0  x  1   3  ;  3 . f   1  0; f  
1  4; f 3  20; f  3    1  6.
Từ đó suy ra max f x  f 3  20.  3   ;3 Cách khác:
Sử dụng table bấm Mode 7 nhập f x 3
x 3x  2 chọn Start? 3
 End? 3 Step? 0.2 sẽ thấy được
max f x  f   3  20.  3   ;3 Đáp án B
Câu 29. Cho a và b là hai số thực dương thỏa mãn 4
a b  16. Giá trị của 4 log a  log b bằng 2 2 A. 4. B. 2. C. 16. D. 8. Giải 4
4 log a  log b  log a  log b  log  4 a b 4
 log 16  log 2  4. 2 2 2 2 2 2 2 Cách khác
Chọn a  2, b  1 thỏa mãn 4
a b  16 rồi thay vào 4 log a  log b được kết quả. 2 2 Đáp án A
Câu 30. Tìm số giao điểm của đồ thị hàm số y = x3 – 3x2 + 3x – 1 và đồ thị hàm số y = x2 – x – 1 Trang 39 A. 1. B. 2. C. 3. D. 4. Giải
Phương trình hoành độ giao điểm : x3 – 3x2 + 3x – 1= x2 – x – 1  x3 – 4x2 + 4x = 0  x = 0 hoặc x = 2 Đáp án B
Câu 31: Tập nghiệm của bất phương trình log x  log 8  x là: 2 2  
A. S  8; 
B. S   ;  4
C. S  4;8
D. S  0;4 Giải
Điều kiện: 0  x  8 . Ta có: log x  log
8  x x  8  x x  4  4  x  8 . Chọn C. 2 2  
Câu 32: Mặt cầu  S  có diện tích bằng 20 , thể tích khối cầu  S  bằng 20 5 20 4 5 A. B. 20 5 C. D. 3 3 3 Giải 4 20 5 2 3
S  4 R  20  R  5  V   R  . Chọn A. 3 3 8 3 3
Câu 33. Cho hàm số f x liên tục trên  và f (x)dx  10  . Tính I
f (3x 1)dx  2 2 1 A. 30 B. 10 C. 20 D. 5 Giải Phương pháp:
Sử dụng phương pháp đổi biến tính tích phân. Cách giải: Đặ dt
t t  3x 1  dt  3dx dx  3
Đổi cận x  1 t  2, x  3  t  8. 3 8 8 Khi đó 3 3 f (t) 1 1 I
f (3x 1)dx dt
f (t)dt  .10  5.    2 2 3 2 2 1 2 2 Chọn D.
Câu 34. Cho hàm số y f x liên tục trên  và có đồ thi ̣ như hình vẽ bên. Hình phẳng được đánh dấu
trong hình vẽ bên có diê ̣n tích là y
y f xb a O c x Trang 40 b c b c A. f
 xdxf
 xdx . B. f
 xdxf
 xdx . a b a b b c b b C. f
 xdxf
 xdx. D. f
 xdxf  xdx . a b a c Giải Chọn A
Câu 35. Tìm số phức liên hợp của số phức z i(3i 1)
A. z  3  i B. z  3   i
C. z  3  i D. z  3  i Giải Phương pháp
Số phức liên hợp của số phức z = a + bi (a, b  R) là z a bi Cách giải: Ta có 2
z i(3i 1)  3i  i  3   i
Số phức liên hợp của z là z  3  i Chọn D.
Câu 36: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
4z  4z  37  0 . Trên mặt phẳng 0
tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0  1   1   1   1  A. M 3;  B. M 3; C. M 3;  D. M 3;   2          2  3  2  4  2  1  2  Giải    i   i 2z  2 1 6 6 1 2 1  36 
 36i z   w
 3 i . Chọn D. 0 2 2 2
Câu 37. Viết phương trình mặt phẳng (P) đi qua điểm A0; 1
 ;2 , song song với trục Ox và vuông góc
với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0 B. (P) : y + z - 1 = 0 C. (P) : y - z + 3 = 0
D. (P) : 2x + z - 2 = 0 Giải Phương pháp   n i  (P)
(P) // Ox và (P)  (Q) thì   n n  (P) (Q) Cách giải:    n i  (P) Gọi n
là VTPT của (P). Do (P) // Ox và (P)  (Q) nên   . ( P ) n n  (P) (Q)  
Ox có VTPT i  1;0;0 và (Q) : x + 2y - 2z + l = 0 có VTPT n  1;2;2 (Q )      Có i
 ,n   0;2;2 nên chọn n  0;1;1 . (P)   (Q)     
(P) đi qua A(0; -1; 2) và nhận n  0;1;1 làm VTPT nên (P)  
(P) : 0(x - 0) +1(y +1) +1(z - 2) = 0  y + z - 1 = 0. Chọn B. Trang 41
Câu 38: Trong không gian Oxyz , cho điểm M  1
 ;2;2 . Đường thẳng đi qua M và song song với trục
Oy có phương trình là: x  1  x  1   tx  1   tx  1      A. y  2
t   B.y  2 t   C. y  2 t  
D. y  2  t t        z  2  tz  2  z  2  tz  2  Giải
Đường thẳng đi qua M và song song với trục Oy nhận j  0;1;0 là 1 VTCP nên có phương trình x  1  
y  2  t t   . Chọn D. z  2 
Câu 39: Chọn ngẫu nhiên 5 học sinh trong một lớp học gồm 25 nam và 20 nữ. Gọi A là biến cố: “Trong
5 học sinh được chọn có ít nhất 1 học sinh nữ”. Xác suất của biến cố A là: C 20.C 20.C C
A. P A 5 20 
B. P A 4 25 
C. P A 4 44 
D. P A 5 25 1 5 C 5 C 5 C 5 C 45 45 45 45 Giải 5 C
Xác suất để trong 5 học sinh không có học sinh nữ nào là 25 . 5 C45 5 C
Xác suất để trong 5 học sinh có ít nhất 1 học sinh nữ là 25 1 . Chọn D. 5 C45
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng
a . Hai mặt phẳng SAB và SAC  cùng vuông góc với đáy. Tính
khoảng cách giữa hai đường thẳng SA và BC ? A. a 2 B. a a 2 a C. D. 2 2 Giải   SAB    ABC Do 
SA   ABC  .  SAC    ABC
Mặt khác AB BC, SA AB AB là đoạn vuông góc chung của SA và BC . Do đó d S ;
A BC   AB a . Chọn B.
Câu 41. Tìm giá trị thực lớn nhất của tham số m để hàm số 3 2
y  x  3mx  x đồng biến trên  . Trang 42 1 1 A.1. B. . C.  . D. 2. 3 3 Giải TXĐ : D   Ta có 2 y '  3x  6mx 1
Hàm số đồng biến trên  khi y '  0, x    Hay 2 3x  6mx 1  0, x    1 1    m  3 3 1
Vậy giá trị lớn nhất của m là . 3 Đáp án B
Câu 42. Dân số thế giới được tính theo công thức r.N S  A.e
trong đó: A là dân số của năm lấy mốc tính,
S là dân số sau N năm, r là tỷ lệ tăng dân số hằng năm. Cho biết năm 2001, dân số việt nam có khoảng
78.685.000 người và tỷ lệ tăng dân số hằng năm là 1,7%/năm. Nếu tỷ lệ tăng dân số hằng năm không đổi
thì đến năm bao nhiêu nước ta có khoảng 120 triệu người? A. 2020. B. 2024. C. 2026. D. 2022. Giải 1,7 .N
Áp dụng công thức ta có: 100 120000000  78685000.e  N  24,83
Vậy cần ít nhất 25 năm để dân số đạt 120 triệu người.
Suy ra dân số sẽ đạt 120 triệu người vào năm 2026. Đáp án C. ax 1
Câu 43. Cho hàm số y 
có đồ thị như hình vẽ bên. Tính tổng S  a  b  c. bx  c A. S  2. B. S  0. C. S  1  . D. S  3. Giải
Từ đồ thị ta thấy b  0 ax 1 a a lim  suy ra:  2 (1) x bx  c b b ax 1 c lim y  lim   suy ra  1 (2)  c   c   x  x  bx c     d  b   b   Đồ 1
thị hàm số cắt trục Oy tại điểm (0;1) nên  1 c  1 (3) c
Từ (1) (2) (3) suy ra: c  1, b  1, a  2. Trang 43 Vậy S  2. Đáp án A
Câu 44: Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không
vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song
AB, A ' B ' mà AB  A'B'  6cm (hình vẽ). Biết diện tích tứ giác
ABB' A ' bằng 60 cm2. Tính chiều cao của hình trụ đã cho. A. 6 2 cm. B. 4 3 cm. C. 8 2 cm. D. 5 3 cm. Giải
Dựng đường sinh B'C và A ' D , ta có tứ giác A'B'CD là hình chữ nhật nên CD//A'B' và CD  A ' B '  6 cm . Vậy CD//AB và CD  AB  6 cm .
Do đó tứ giác ABCD là hình bình hành và nội tiếp được nên là hình chữ
nhật. Từ đó , mặt khác AB  B'C nên AB  (BCB ')  AB  BB '
Vậy ABB'A ' là hình bình hành có một góc vuông nên là hình chữ nhật. 60 Ta có S  AB.BB' nên BB'   10cm . ABB'A ' 6
Xét tam giác BB'C vuông tại C có 2 2 2 B 'C  BB '  BC mà 2 2 2
BC  AC  AB  64  36  28 nên: 2
B'C 100  28  72  B'C  6 2 cm .
Vậy chiều cao hình trụ là 6 2 cm . Đáp án A
Câu 45: Cho hàm số y  f (x) có đạo hàm và liên tục trên đoạn [0;1] thỏa mãn f (0)  1 và 1 2 f (x )x 1 f '(x).e   2x, x  0; 
1 . Tính giá trị của f (x)dx.  0 4 4 A. 2. B. . C.  . D. 2  3 3 Giải 2 2 2     Ta có f (x ) x 1 f (x ) x 1 f (x ) ' x 1 f '(x).e  2x  f '(x).e  2x.e  (e )  2x.e 2 2 f ( x ) x 1  f ( x ) x 1 e 2xe dx e e       C.  2  Mặt khác: f (x ) x 1 2 f (0)  1  C  0  e  e  f (x)  x 1.   Do đó: f (x)dx   x   1 1 1 1 4 2 3 1 dx  x  x  .    3  3 0 0 0 Đáp án B
Câu 46. Cho hàm số y  f (x) liên tục trên  và có đồ thị như hình vẽ: Trang 44
Có bao nhiêu giá trị nguyên của tham số m để phương trình:  3sin x  cos x 1  f  f    2
m  4m  4 có nghiệm?  2cos x sin x  4  A. 1. B. 2. C. 3. D. 4. Giải  3sin x  cos x 1  f  f    2 m  4m  4 (1)  2cos x sin x  4 
Ta có: 2 cos x  sin x  4  0, x      Đặ 3sin x cos x 1 t t  2 cos x  sin x  4  2t  
1 cos x  (t  3) sin x  1   4t (*). Phương trình  9 * có nghiệm: 2 2 2
 (2t 1)  (t  3)  (1 4t)    t  1 11 Suy ra: 0  t  1.
Từ đồ thị hàm số y  f (x) ta có:
y  f (x) đồng biến trên 0; . 2 2
m  4m  4  (m  2) 0;  )  . t 0  ;1 nên:  3sin x  cos x 1  f  f    2
m  4m  4  f  t   f  2 m  4m  4  2cos x  sin x  4  2  t  m  4m  4  4
Phương trình (1) có nghiệm khi 2 0  m  4m  4  1 2  m  4m  4 1  3   m  1  Do m    m  3  ; 2  ;  1 . Đáp án C
Câu 47. Cho hai số thực dương x, y thay đổi thỏa mãn 2 2
x  4y  1. Tìm giá trị lớn nhất của biểu thức
P  log (x  2y).log (2x  4y). 2 2 1 1 1 1 A. . B. . C. . D. . 4 2 3 6 Giải 1 Theo giả thiết ta có: 2 2
x  4y  (x  2y)(x  2y)  1  x  2y  x  2y Trang 45 2
Vậy: P  log (x  2y).log (2x  4y)  log (x  2y).log 2 2 2 2 x  2y  log (x  2y). 1   log x  2y  2  2   2  1  1 1   log (x  2y)    .  2   2  4 4  1  3 x  2y  x  2y  2 x     x  2y   2 2 Dấu bằng xảy ra khi:      . 1 1 x  2y  1    log (x  2y)  y  2  2  2  4 2 Đáp án A
Câu 48. Tìm tất cả giá trị thực của tham số m để giá trị lớn nhất của hàm số 3
y  x  3x  2m 1 trên
đoạn 0;2 đạt giá trị nhỏ nhất. Giá trị của m thuộc khoảng nào?  3   2  A.  ; 1  .   B. ; 2 .   C. 1  ;0. D. 0  ;1 .  2   3  Giải Xét hàm số 3
y  x  3x  2m 1 trên đoạn [0;2]. x  1   0;2 2  
Ta có: f '(x)  3x  3; f '(x)  0   x 1
Ta có: f (0)  2m 1; f (1)  2m  3; f (2)  2m 1
Suy ra: max f (x)  max  2m 1 ; 2m  3 ; 2m 1  max  2m  3 ; 2m 1  P 0;2 1
TH1: 2m  3  2m 1  4(
 4m  2)  0  m  . 2 Khi đó: 1 1 P  2m  3  2, m
  . Suy ra: P  2  m  . 2 min 2 1
TH2: 2m  3  2m 1  4(
 4m  2)  0  m  . 2 Khi đó: 1 P  2m 1  2, m
  . Suy ra P không tồn tại. 2 min 1 Vậy m  . 2 Đáp án D
Câu 49. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của các cạnh
A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành hai phần. Gọi V là thể tích của phần chứa 1 V
đỉnh A, V là thể tích của phần còn lại. Tính tỉ số 1 . 2 V2 55 37 1 2 A. . B. . C. . D. . 89 48 2 3 Giải Trang 46
Gọi H  ABDN ; MH cắt B’B tại K, cắt A’A tại S; SD cắt A’D’ tại E.
Thiết diện tương ứng là ngũ giác DNKME.
Phần đa diện chứa A có thể tích là: V  V  V  V . 1 S.ADH S.A 'EM K.BNH
Dễ thấy BA=BH, AH=4A’M, AD=4A’E, 1 SA '  B ' K  A ' A. 3 Cho độ 1 2
dài cạnh hình lập phương bằng 1 thì: SA '  ; KB  . 3 3 1 1 4 Ta có: V  . AD.AH.SA  S.ADH 3 2 9 1 1 1 1 V  V  ; V  V  . S.A 'EM S.ADH K.BNH S.ADH 64 144 8 18 4 1 1 55
Vậy thể tích phần đa diện chứa A là: V     . 1 9 144 18 144 55 89
Thể tích phần đa diện không chứa A là: 1  . 144 144 V 55 1   . V 89 2 Đáp án A
Câu 50.Cho phương trình 2 2 y 2 2 log (2x  2x  2)  2
 y  x  x. Hỏi có bao nhiêu cặp số nguyên dương 2 (x,y), (0 A. 1. B. 2. C. 3. D. 4. Giải 2 2 Ta có: log  2 2x  2x  2 y 2 2
 2  y  x  x  log  2 x  x   2 y 2 1  x  x 1  2  y 2 2 2 2 log ( x x 1  ) 2 2 y 2  2
 log (x  x 1)  2  y 2 2 2  log (x  x 1)  y 2 Do 2 2
0  x  500  y  log (x  x 1)  0;18  0  y  5. 2  
Vậy có 4 giá trị nguyên của y thỏa mãn yêu cầu đề bài, đồng nghĩa có 4 cặp số (x;y) thỏa mãn phương trình đã cho. Đáp án D
-------------------------------------------------- www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 14 MÔN TOÁN Trang 47
PHÁT TRIỂN TỪ ĐỀ MINH Thời gian: 90 phút
HỌA LẦN 2 NĂM 2020
Câu 1:(NB) Có bao nhiêu số có 2 chữ số, mà tất cả các chữ số đều lẻ? A. 25. B. 60. C. 20. D. 10.
Câu 2: (NB) Cho cấp số nhân u có u  4;u  2
 .Công bội q là: n  2 1 1 1 A. 2 . B. 2  . C. . D.  . 2 2
Câu 3: (NB) Phương trình x 1  x 1
3 .2   24 có nghiệm là A. x  3. B. x  2 . C. x  5. D. x  2  .
Câu 4: (NB) Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2 .
a Thể tích của khối lăng trụ đã cho bằng 3 2a 3 a A. . B. 3 2a . C. . D. 3 a . 3 3
Câu 5:(NB) Chọn phát biểu sai trong các phát biểu sau:
A. Đồ thị hàm số logarit nằm bên trên trục hoành.
B. Đồ thị hàm số mũ không nằm bên dưới trục hoành.
C. Đồ thị hàm số lôgarit nằm bên phải trục tung.
D. Đồ thị hàm số lũy thừa với số mũ âm luôn có hai tiệm cận.
Câu 6:(NB) Tìm nguyên hàm của hàm số   7x f x  .  A. 7x  7x dx ln 7  C . B. x x dx   C .  1 7 7  7x x 1  x 7 x C. 7 dx   C . D. 7 dx   C .   ln 7 x 1
Câu 7:(NB) Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng
đáy và SA  2a . Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 3 2 12 6
Câu 8:(NB) Cho khối nón có độ dài đường sinh bằng a 5 và chiều cao bằng a. Thể tích của khối nón đã cho bằng 3 4 5 a 3 2 a 3 4 a A. 3 2 a . B. . C. . D. . 3 3 3
Câu 9:(NB) Cho khối cầu có bán kính R . Thể tích của khối cầu đó là 4 1 4 3   3   3   2   A.V 4 R . B. V R . C. V R . D. V R . 3 3 3
Câu 10: (NB) Cho hàm số y f x có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đâỵ? A. 0  ;1 .
B. 1; . C.  1  ;0.
D. 0; .
Câu 11:(NB) Tập xác định của hàm số 2 ( 3 2)    e y x x là: A. D  ( ;
 1)  (2;) . B. D   \{1;2}.
C. D  (0; ) .
D. D  (1; 2) .
Câu 12:(NB) Một hình trụ có chiều cao bằng 3 , bán kính đáy bằng 2 . Tính thể tích của khối trụ? A. 12 . B. 18 . C. 10 . D. 40 . Trang 48
Câu 13:(NB) Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại A. x  2. B. x  1. C. x  1.  D. x  3. 
Câu 14: (TH)Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình? x 1 x 1 2x 1 x A. y  . B. y  . C. y  . D. y  . x 1 x 1 2x  2 1 x 3x  2
Câu 15:(NB)Cho hàm số y
có đồ thị là (C). Mệnh đề nào sau đây đúng? x 1
A. (C) có tiệm cận ngang là y = 3 .
B. (C) chỉ có 1 tiệm cận.
C. (C) có tiệm cận ngang là x = 2 .
D. (C) có tiệm cận đứng là x = 3. 
Câu 16:(NB)Tập nghiệm của bất phương trình x 1 5 4  4 là A. 6;. B.6;. C. 5;  1 . D.  ;  6.
Câu 17:(TH)Cho hàm số bậc ba y f x có đồ thị như hình sau. Số nghiệm của phương trình f x  1 là y 2 -1 O x 1 -2 A.1. B. 2. C. 3. D. 4.   2 2 Câu 18: (NB) Cho f
 xdx  5 . TínhI   f
 x2sin xdx  0 0 
A. I  7 . B. I  5  .
C. I  3 .
D. I  5  . 2
Câu 19: (NB) Cho số phức z  4  3i . Tính môđun của số phức z . A. z  7. B. z  3. C. z  5. D. z  7.
Câu 20:(NB) Cho 2 số phức z  2  i, z  5  7i .Tìm phần thực a của số phức z z z . 1 2 1 2 Trang 49 A. a  7. B. a  6.  C. a  6. D. a  5. 
Câu 21: (NB) Số phức nào dưới đây có điểm biểu diễn là điểm K ở hình bên?
A. z = 3 - 2i.
B. z = 3 + 2i.
C. z = - 2 - 3i.
D. z = - 2 + 3i. 1 2 3 4
Câu 22: (TH)Trong không gian Oxyz , cho hai điểm A1;2;  1 ; B2; 1  ;  3 .Vectơ 𝐴 𝐵 có tọa độ là: A. 1; 3  ;4 . B.  1  ;3;  4 .
C. 3;1;2 . D. 1; 3  ;2 . Câu 23: (NB) Trong không gian Oxyz , cho mặt cầu có phương trình
x2 + y2 + z2 + 2x - 2 y + 4 z - 1 = 0. Tâm và bán kính của mặt cầu là:
A. I 1;1;  2 , R  7. B. I 1; 1  ;  2 , R  7. C. I  1  ;1;  2 , R  7. D. I  1  ;1;  2 , R  7.
Câu 24: (NB) Trong không gian Oxyz , mặt phẳng đi qua 3 điểm A( ; 0 ; 0 a), B( ; 0 ;
b 0), C(c;0;0) có phương trình: x y z x y z x y z x y z A. + + = 1 . B. + + = 1 . C. + + = 1 . D. + + = 0 . a b c b a c c b a c b a
Câu 25: (TH)Trong không gian Oxyz , phương trình tham số của đường thẳng d đi qua M ( ; 5 4; ) 1 có r VTCP a  2; 3  ;  1 là: ìï x = 5+ 2t ì ì ì ï ï x = 2 + t 5 ï x = 2 + t 5 ï x = 5 + 2t ï ï ï ï ï ï ï ï
A. í y = 4 - t 3
B. í y = - 3 + 4t .
C. í y = 4 - t 3 .
D. í y = - 4 - t 3 . ïï ï ï ï ï ï ï ï z = 1+ t ïî ï z = 1+ t ïî ï z = 1- t ïî ï z = 1- t ïî
Câu 26:(TH)Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA  ABCD và SA  a 6
(minh họa như hình bên). Gọi  là góc giữa SC và (ABCD). Tính cos  . 3 A. cos   3 . B. cos   2 . C. cos   1 . D. cos   . 2 3 2 2
Câu 27:(TH)Cho hàm số y f x có đạo hàm f  x  xx  2 2
, x   . Số cực trị của hàm số đã cho là A. 2. B. 1. C. 0. D. 3.
Câu 28:(TH) Cho hàm số y f x  liên tục trên đoạn 2;2 và có đồ thị dưới đây. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 2;2 . Giá trị của M m bằng Trang 50 A. – 3. B. – 6. C. – 4. D. – 8.
Câu 29:(TH)Tìm giá trị lớn nhất củahàm số 2 ( )  x f x
x e trên đoạn  1  ;1   . 1 A. e . B. . C. 2e . D. 0 e
Câu 30: (TH)Số giao điểmcủa đồ thị hàm số 3 2
y x  3x  4 và trục tung là A. 0. B.1. C. 2. D. 3.
Câu 31:(TH)Tập nghiệm của bất phương trình 2
log x  log x  2  0 là 3 3    1   1  A.  2  1 ;  1 . B.  ;1. C.  ;9. D.  ;3.  9   3   9 
Câu 32:(TH)Cho hình nón có bán kính đáy là r  3 và độ dài đường sinh l  4 . Tính diện tích xung
quanh S của hình nón đã cho.
A. S  8 3 . B. S 24     . C. S 16 3 . D. S 4 3 . 2 5 5
Câu 33: (TH)Cho các tích phân f
 xdx  2; f
 tdt  4 . Tính f  ydy . 3  3  2 A. I  2 . B. I  6 . C. I  2 . D. I  6  .
Câu 34: (TH)Cho đồ thị hàm số y f x . Diện tích hình phẳng S (phần tô đậm trong hình) được xác định bằng công thức: 0 2 0 2 A. S
f xdx  
f xdx . B. S
f xdx  
f xdx . 2  0 2  0 0 2 0 2 C. S
f xdx  
f xdx . D. S = - f (x)dx + f (x)dx ò ò . 2  0 - 2 0 7 17i
Câu 35: (TH) Số phức z  có phần thực là 5  i A.2. B.3. C.1. D.4. 2 2
Câu 36: (TH) Gọi z , z 2
là hai nghiệm của phương trình z + 2z + 10 = 0. Tính T = z + z . 1 2 1 2 A.T = 4. B.T = 6. C.T = 10. D.T = 20. Trang 51
Câu 37: (TH)Trong không gian Oxyz , phương trình mặt phẳng  đi qua A3;1;  1 ; B2; 1  ;4 và
vuông góc với mặt phẳng P : 2x y  3z1 0 là:
A. x 13y  5z 5  0 . B. x 13y  5z 5  0 . C. x  13y  5z 5  0 . D. x 13y  5z 5  0 .
Câu 38: (TH)Trong không gian Oxyz , phương trình tham số của đường thẳng d đi qua A1;2;  3 , B4;4;4 là: ìï x = 1- t ì ì ì ï 3 ï x = - 3 + t ï x = 1+ t 3 ï x = 1+ t 3 ï ï ï ï ï ï ï ï
A. í y = 2 + 2t .
B. í y = 2 + 2t .
C.í y = 2 + 2t .
D.í y = 2 + 2t . ïï ï ï ï ï ï ï ï z = 3 + t ïî ï z = 1+ t ïî 3 ï z = 3 + t ïî ï z = 3 + 2t ïî
Câu 39: (VD) Cho tập hợp A   1; 2; 3; 4; 5; 
6 . Gọi S là tập hợp các số có 3 chữ số khác nhau được
lập thành từ các chữ số của tập A . Chọn ngẫu nhiên một số từ S , xác suất để số được chọn là số chia hết cho 9 là: 7 3 1 9 A. . B. . C. . D. . 20 20 20 20
Câu 40: (VD)Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 4 a . Hình chiếu của S
trên mặt phẳng  ABCD là điểm H thuộc AB sao cho HB  3HA . Góc giữa cạnh bên SC và mặt đáy
bằng 45. Khoảng cách từ O đến mặt phẳng SBC  theo a là 5a 34 5a 34 5a 17 A. 5a 34 . B. . C. . D. . 17 34 2
Câu 41:(VD) Có bao nhiêu giá trị m nguyên thuộc đoạn  2
 020;2020 để hàm số 3 2
y x  3x  (2m  5)x  5 đồng biến trên khoảng (0; ) ? A. 2020. B. 2022. C. 2021. D. 2023. 1
Câu 42:(VD)Đối với hàm số y  ln
, khẳng định nào sau đây là khẳng định đúng? x  1 A. '1 y xye . B. '1 y xy  e . C. '1 y xy  e . D. '1 y xye .
Câu 43:(VD)Cho hàm số f x 3 2
ax bx cx d a,b,c,d  có bảng biến thiên sau: x  1 1  f (  x)  0  0   4 f (x) 0 
Trong các số a, b, c, d có bao nhiêu số âm? A. 1. B. 2. C. 3. D. 4.
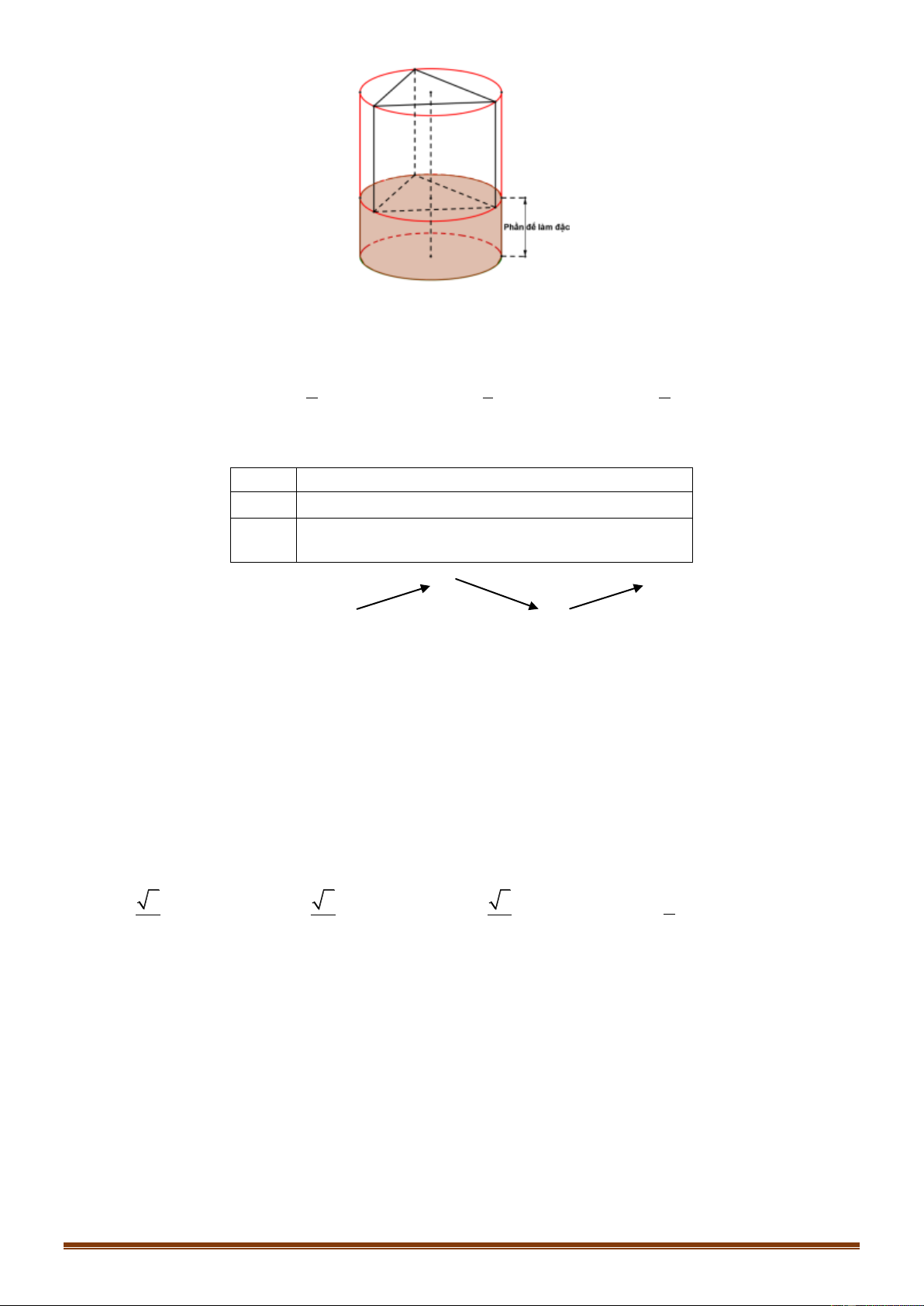
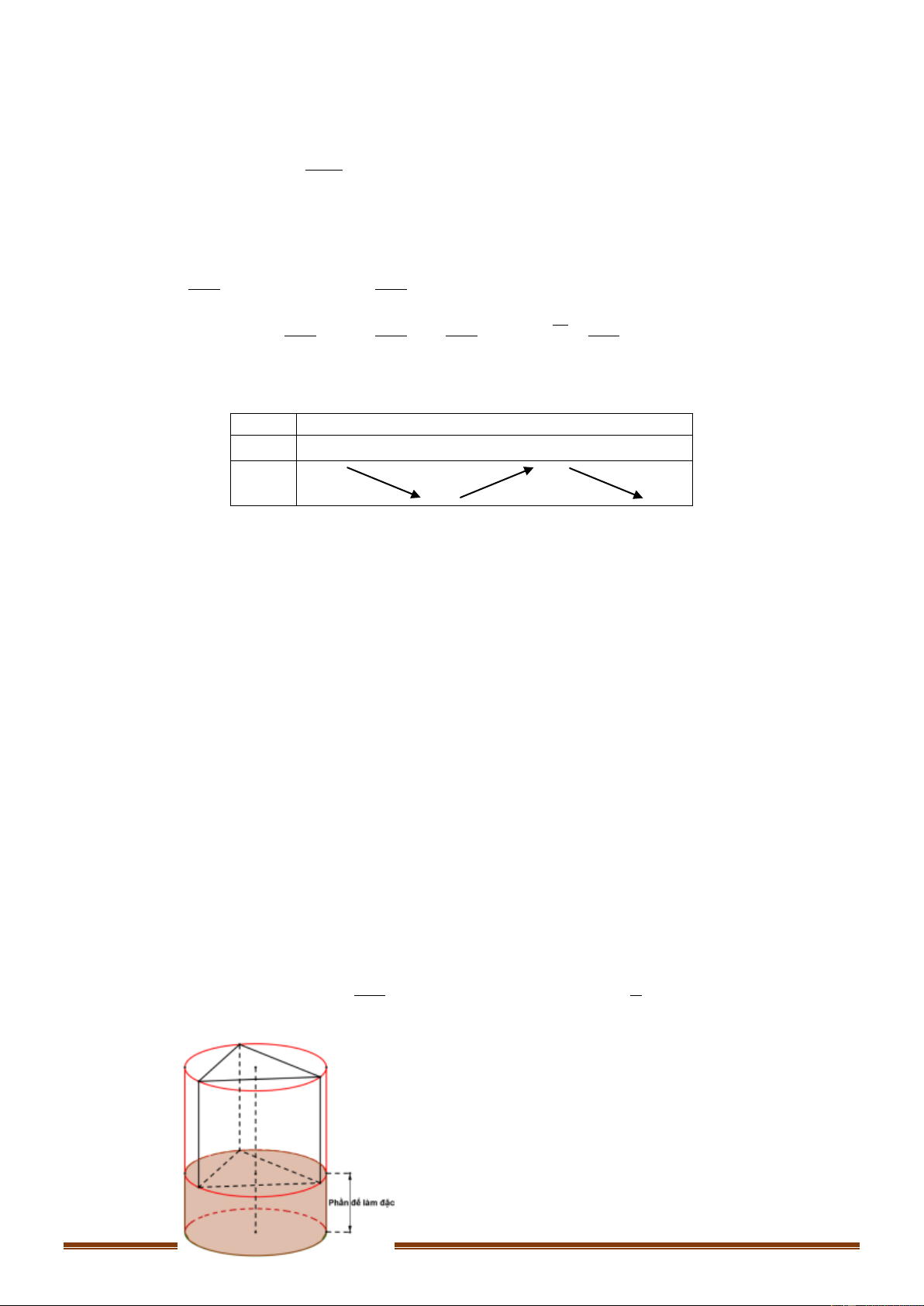
Câu 44: (VD) Bé Khải có 1 bộ đồ chơi là các khối hình không gian có thể lắp ráp lồng vào nhau gồm 1
hình trụ (có một phần đế làm đặc) và 1 hình lăng trụ tam giác đều có tất cả các cạnh bằng nhau (khối
hình trụ người ta đã làm sẵn 3 rãnh nhỏ để ráp khít vào 3 cạnh bên của lăng trụ tam giác đều như hình vẽ).
Biết hình trụ có chiều cao gấp rưỡi đường cao đáy lăng trụ và diện tích xung quanh lăng trụ bằng c a 2 2 a
3 (cm ) . Diện tích toàn phần hình trụ là 2 S
(cm ) , với a,b, c   * và là phân số tối giản. b b
Hỏi ab  20c bằng bao nhiêu? Trang 52 A. 18. B. 5.  C. 33. D. 15.
Câu 45:(VD)Cho hàm số f x có đạo hàm liên tục trên đoạn 0;2 thỏa mãn f (0)  3 và 2
(2x  3)f '(x)  2 f(x)  4x  3x . Khi đó f (2) bằng 9 1 1 A.1 . B. . C. . D. . 7 5 7
Câu 46:(VDC)Cho hàm số y f x có bảng biến thiên sau: x  1 3  f (  x)  0  0  4  f (x)  2 
Xét hàm số g x  f f x .Số nghiệm của phương trình g ' x  0 là A. 5. B. 6. C. 7. D. 8.
Câu 47:(VDC)Một người có 10 triệu đồng gửi vào ngân hàng với kỳ hạn 3 tháng (1 quý là 3 tháng), lãi
suất 6% / 1 quý theo hình thức lãi kép (sau 3 tháng sẽ tính lãi cộng vào gốc). Sau đúng 3 tháng, người đó
gửi thêm vào 20 triệu đồng cùng với hình thức lãi suất như vậy. Hỏi sau 1 năm, tính từ lần gửi đầu tiên,
người đó nhận được số tiền gần nhất với kết quả nào? A. 35 triệu. B. 37 triệu. C. 36 triệu. D. 38 triệu. Câu 48:(VDC)Cho ,
x y 0;  , x y  1 . Biết
m a ;b thì phương trình
 2x y 2 5 4
5y  4x  40xy m có nghiệm thực. Tính T  25a 16b . A. T  829 .
B. T  825 . C. T  816 . D. T  820 .
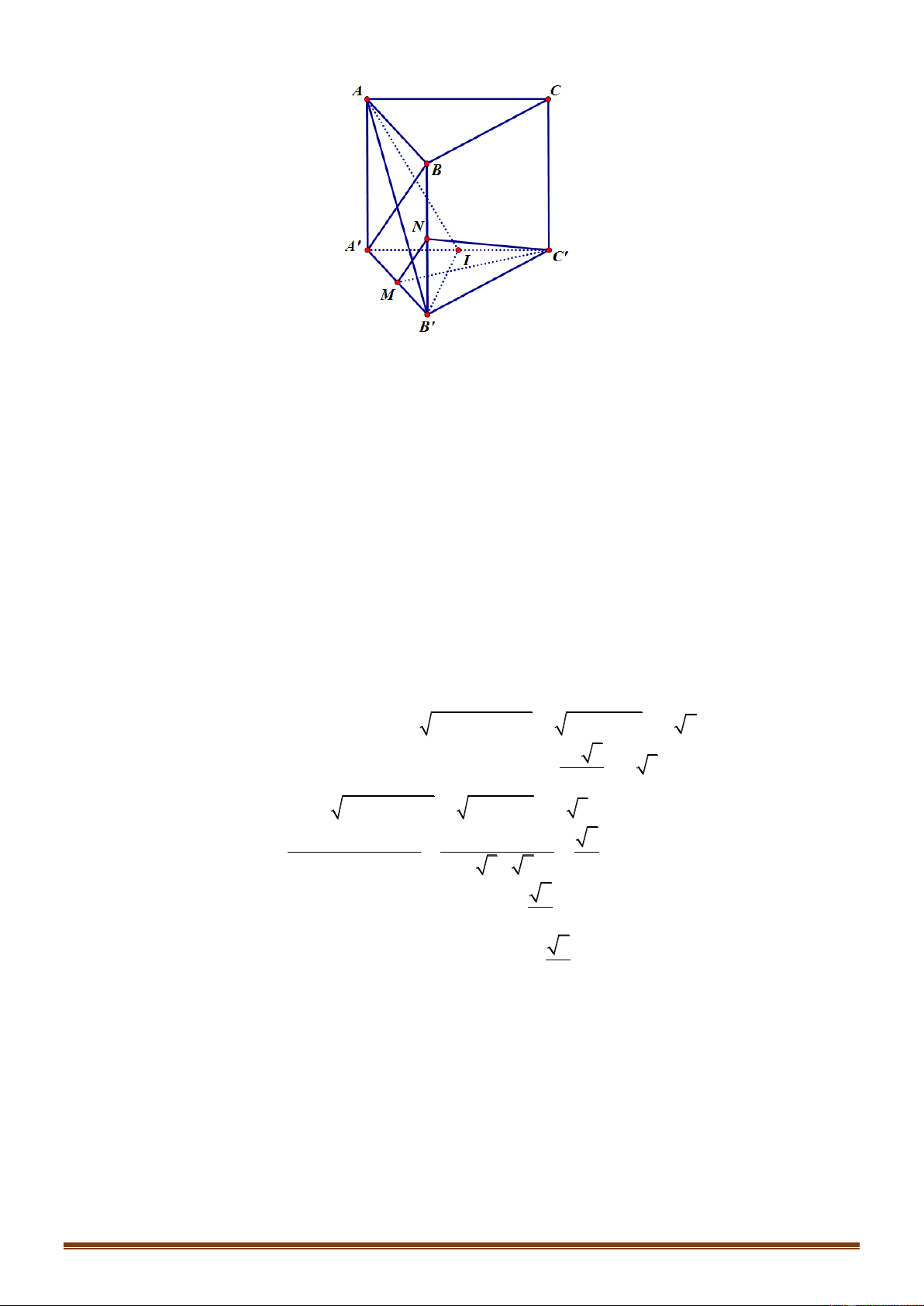
Câu 49:Cho lăng trụ đều AB . C A BC
  có tất cả các cạnh đều bằng 2a . Gọi M , N lần lượt là trung
điểm cạnh AB , BB . Tính cosin góc hợp bởi hai mặt phẳng MC N   , ACC A   . 2 6 3 3 A. . B. . C. . D. . 4 4 4 4
Câu 50:(VDC)Chị M vay ngân hàng 300 triệu đồng theo phương thức trả góp để mua nhà. Nếu cuối mỗi
tháng, bắt đầu từ tháng thứ nhất chị M trả 5,5 triệu đồng và chịu lãi số tiền chưa trả là 0,5% mỗi tháng
(biết lãi suất không thay đổi) thì sau bao lâu, chị M trả hết số tiền trên? A. 64 tháng. B. 54 tháng. C. 63 tháng. D. 55 tháng.
---------- HẾT ---------- Trang 53
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1: Có bao nhiêu số có 2 chữ số, mà tất cả các chữ số đều lẻ? A. 25. B. 60. C. 20. D. 10. Hướng dẫn giải Chọn A
Câu 2: Cho cấp số nhân u có u  4;u  2
 . Công bội q là: n  2 1 1 1 A. 2 B. 2  C. D.  2 2 Hướng dẫn giải Chọn B
Câu 3:Phương trình x 1  x 1
3 .2   24 có nghiệm là A. x  3 B. x  2 C. x  5 D. x  2  Chọn B. Phương trình x 1  x 1
3 .2   24 có nghiệm là A. x  3 B. x  2 C. x  5 D. x  2  Hướng dẫn giải xxx x 1 Cách 1: Ta có 1 1 x x x 2 3 .2
 24  3 .2 .2.  24  2 .3  36  6  6  x  2 . 3
Cách 2:Sử dụng máy tính cầm tay.
Nhập vào màn hình X 1  X 1 3 2  
 24 sau đó ấn CALC thử các giá trị của x trong 4 phương án đề cho, thì
thấy khi x  2 giá trị của biểu thức bằng 0 nên ta chọn B.
Câu 4: Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2 .
a Thể tích của khối lăng trụ đã cho bằng 3 2a 3 a A. B. 3 2a C. D. 3 a 3 3 Hướng dẫn giải Chọn B Diện tích đáy là: 2 B a
Vây thể tích khối lăng trụ là: 2 3
V a .2a  2a
Câu 5:Chọn phát biểu sai trong các phát biểu sau?
A. Đồ thị hàm số logarit nằm bên trên trục hoành.
B. Đồ thị hàm số mũ không nằm bên dưới trục hoành.
C. Đồ thị hàm số lôgarit nằm bên phải trục tung.
D. Đồ thị hàm số lũy thừa với số mũ âm luôn có hai tiệm cận. Hướng dẫn giải Chọn A
Đồ thị hàm số lôgarit nằm bên phải trục tung và cả dưới, cả trên trục hoành.
Câu 6:Tìm nguyên hàm của hàm số   7x f x   A. 7x  7x dx ln 7  C B. x x dx   C  1 7 7  7x x 1  x 7 x C. 7 dx   C D. 7 dx   C   ln 7 x 1 Hướng dẫn giải Trang 54 Chọn C Áp dụng công thức x a dx  .
Câu 7:Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng đáy
và SA  2a . Tính thể tích khối chóp S.ABC . 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 3 2 12 6 Hướng dẫn giải Chọn D 2 Diện tích đáy là: a 3 B  4 2 3 Vây thể tích 1 1 a 3 a 3
khối chóp S.ABC là: V  .S .SA  . .2a  3 ABC 3 4 6
Câu 8:Cho khối nón có độ dài đường sinh bằng a 5 và chiều cao bằng a. Thể tích của khối nón đã cho bằng 3 4 5 a 3 2 a 3 4 a A. 3 2 a B. C. D. 3 3 3 Hướng dẫn giải Chọn D Ta có 2 2 2 2
R l h  (a 5)  a  2a . 3 
Vậy thể tích của khối nón là: 1 1 4 a 2 2
V   R h   (2a) .a  3 3 3
Câu 9: Cho khối cầu có bán kính R . Thể tích của khối cầu đó là 4 1 4 A. 3
V  4 R B. 3 V   R . C. 3 V   R . D. 2 V   R . 3 3 3 Hướng dẫn giải Chọn B 4
Thể tích của khối cầu có bán kính R là 3 V   R 3
Câu 10:Cho hàm số y f x có bảng biến thiên như sau:
Hỏi hàm số nghịch biến trên khoảng nào sau đâỵ? A. 0  ;1 .
B. 1; . C.  1  ;0.
D. 0; . Hướng dẫn giải Chọn A
Vì trên (0; 1) hàm số có đạo hàm mang dấu âm.
Câu 11:Tập xác định của hàm số 2 ( 3 2)    e y x x là: A. D  ( ;  1)  (2;)
B. D   \ {1; 2}
C. D  (0; ) D. D  (1; 2) Hướng dẫn giải Chọn A x  2 Vì e
  nên hàm số xác định khi 2
x  3x  2  0   . x 1 Trang 55
Câu 12: Một hình trụ có chiều cao bằng 3 , bán kính đáy bằng 2 . Tính thể tích của khối trụ? A.12 . B. 18 . C. 10 . D. 40 . Hướng dẫn giải Chọn A
Thể tích của khối trụ là 2 2
V   r h   .2 .3  12
Câu 13:Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại A. x  2. B. x  1. C. x  1.  D. x  3.  Hướng dẫn giải Chọn C
Theo bảng biến thiên thì hàm số đạt cực tiểu tại điểm x  1. 
Câu 14: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? x 1 x 1 A. y  . B. y  . x 1 x 1 2x 1 x C. y  . D. y  . 2x  2 1 x Hướng dẫn giải Chọn A
+ ĐT có TCĐ: x 1 (Loại B)
+ ĐT cắt Oy tại điểm 0; 1  (Loại C, D) 3x  2
Câu 15:Cho hàm số y
có đồ thị là (C). Mệnh đề nào sau đây đúng? x 1
A. (C) có tiệm cận ngang là y = 3 .
B. (C) chỉ có 1 tiệm cận.
C. (C) có tiệm cận ngang là x = 2 .
D. (C) có tiệm cận đứng là x = 3. Hướng dẫn giải Chọn A 3x  2 3x  2 Do lim y  lim  3 và lim y  lim
 3 nên đường thẳng y = 3 là đường tiệm cận ngang x x x 1 x x x 1 của (C). 
Câu16: Tập nghiệm của bất phương trình x 1 5 4  4 là A. 6;. B.6;. C. 5;  1 . D.  ;  6. Hướng dẫn giải Chọn B  Ta có: x 1 5 4
 4  x 1 5  x  6 . Trang 56
Vậy x 6; .
Câu 17: Cho hàm số bậc ba y f x có đồ thị như hình bên. Số nghiệm của phương trình f x  1là A.1. B. 2. y C. 3. D. 4. 2 -1 O x 1 -2 Hướng dẫn giải Chọn C
+ pt f x  1là pthđgđ của ĐT và đt y  1.
+ Đường thẳng y  1cắt ĐT tại 3 điểm pb.
Vậy pt f x  1có 3 nghiệm.   2 2 Câu 18:Cho f
 xdx  5 . TínhI   f
 x2sin xdx  0 0  A. I  7 B. I  5  C. I  3
D. I  5  2 Hướng dẫn giải Chọn A. Ta có  2 I   f
  x 2sin xdx  0 .   2  f  x 2 dx  2 sin xdx  0 0   2 2  f
 xdx2cosx 0 0  7 Hướng dẫn giải
Câu 19: Cho số phức z  4  3i . Tính môđun của số phức z . A. z  7. B. z  3. C. z  5. D. z  7. Hướng dẫn giải Chọn C
Câu 20:Cho 2 số phức z  2  i, z  5  7i .Tìm phần thực a của số phức z z z . 1 2 1 2
A. a  7. B. a  6.
C. a  6. D. a  5.  Hướng dẫn giải Chọn A Câu 21: Số phức
nào dưới đây có điểm biểu diễn là điểm K ở hình bên? Trang 57
A. z = 3 - 2i. 1
B. z = 3 + 2i. 2
C. z = - 2 - 3i. 3
D. z = - 2 + 3i. 4 Hướng dẫn giải Chọn D
Câu 22: Trong không gian Oxyz cho hai điểm: A1;2;  1 ; B2; 1  ;  3 .Vectơ 𝐴 𝐵 có tọa độ là: A. 1; 3  ;4 B.  1  ;3;  4 C. 3;1;2 D. 1; 3  ;2 Hướng dẫn giải Chọn A
Câu 23: Trong không gian Oxyz cho mặt cầu có phương trình: 𝑥2 + 𝑦2 + 𝑧2 + 2𝑥 − 2𝑦 + 4𝑧 − 1 =
0. Tâm và bán kính của mặt cầu là:
A. I(1,1,-2), R = 7 B. I(1,-1,-2), R = 7C. I(-1,1,-2), R = 7 D. I(-1,1,-2), R = 7 Hướng dẫn giải Chọn D a = -1,b = 1, c = -2, d= -1 Tâm I(-1,1,-2)
R = 𝑎2 + 𝑏2 + 𝑐2 − 𝑑 = 7
Câu 24: Trong không gian Oxyz mặt phẳng đi qua 3 điểm A( ; 0 ; 0 a), B( ; 0 ;
b 0), C(c;0;0) có phương trình: x y z x y z x y z x y z A. + + = 1 B. + + = 1 C. + + = 1 D. + + = 0 a b c b a c c b a c b a Hướng dẫn giải Chọn C
Câu 25: Trong hệ tọa độ Oxyz phương trình tham số của đường thẳng d đi qua M ( ; 5 4; ) 1 có VTCP r a  2; 3  ;  1 là: ìï x = 5+ 2t ì ì ì ï ï x = 2 + t 5 ï x = 2 + t 5 ï x = 5 + 2t ï ï ï ï ï ï ï ï
A.í y = 4 - t 3
B. í y = - 3 + 4t
C.í y = 4 - t
3 D.í y = - 4 - t 3 ïï ï ï ï ï ï ï ï z = 1+ t ïî ï z = 1+ t ïî ï z = 1- t ïî ï z = 1- t ïî Chọn A
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA  ABCD và SA  a 6
(minh họa như hình bên). Gọi  là góc giữa SC và (ABCD). Tính cos  . 3 A. cos   . 2 3 B. cos   . 3 2 C. cos   . 2 Trang 58 1 D. cos   . 2 Hướng dẫn giải Chọn D.      ·  · SA ABCD SC; ABCD  SCA.
Do ABCD là hình vuông cạnh a  AC  a 2.
Tam giác SAC vuông tại S nên 2 2 SC  SA  AC  2a 2. Khi đó AC 1 cos    . SC 2
Câu 27:Cho hàm số y f x có đạo hàm f  x  xx  2 2
, x   . Số cực trị của hàm số đã cho là A. 2 B. 1 C. 0 D. 3. Hướng dẫn giải Chọn B.
f  x  x x  2 2
 0 có nghiệm đơn là x  0 nên có một cực trị
Câu 28:Cho hàm số y f x  liên tục trên đoạn 2;2 và có đồ thị dưới đây. Gọi M và m lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 2;2 . Giá trị của M m bằng A. – 3. B. – 6. C. – 4. D. – 8. Hướng dẫn giải Chọn C
Từ đồ thị ta thấy
M  max f x  f  2
   2,m  min f x  f      2 6  2;2  2;2
M m  26  4  .
Câu 29:Tìm giá trị lớn nhất củahàm số 2 ( )  x f x
x e trên đoạn [ -1 ; 1] ? 1 A. e B. C. 2e D. 0 e Hướng dẫn giải Chọn A Trên đoạn 1;  1 , ta có: /   x f
x xe x  2 ; /
f x  0  x  0 hoặc x  2  (loại). 1 Ta có: f  
1  ; f 0  0; f   1  e e
Suy ra: max f x  e  1  ;  1
Câu 30: Số giao điểmcủa đồ thị hàm số 3 2
y x  3x  4 và trục tung là A. 0. B.1. C. 2. D. 3. Trang 59 Hướng dẫn giải Chọn B
Trục Oy: x  0  y  4 .
ĐT cắt Oy tại A0; 4 .
Câu 31:Tập nghiệm của bất phương trình 2
log x  log x  2  0 là 3 3  1   1   1  A.  2  ;  1 .
B.  ;1.C. ;9.D. ;3.  9   3   9  Hướng dẫn giải Chọn D + ĐK: x  0 . + Ta có: 2
log x  log x  2  0 3 3 1  2
  log x 1  x  3. 3 9  
Kết hợp với ĐK ta được 1 x  ;3.  9 
Câu 32: Cho hình nón có bán kính đáy là r  3 và độ dài đường sinh l  4 . Tính diện tích xung quanh
S của hình nón đã cho A. S  8 3 .
B. S  24 .
C. S  16 3 . D. S  4 3 Hướng dẫn giải Chọn D
Diện tích xung quanh của hình nón là: S   rl   . 3.4  4 3 2 5 5
Câu 33:Cho các tích phân f
 xdx  2; f
 tdt  4 . Tính f  ydy 3  3  2 A. I  2 B. I  6 C. I  2 D. I  6  Chọn A. 2 2 5 5 Ta có: f
 xdx f
 ydy 2; f
 tdt f
 ydy  4 (tích phân không phụ thuộc vào biến) 3  3  3  3  Lại có: 2 5 5 f
 ydy f
 ydy f
 ydy I  42  2 . 3  2 3 
Câu 34: Cho đồ thị hàm số y f x . Diện tích hình phẳng S (phần tô đậm trong hình) được xác định bằng công thức Trang 60 0 2 A. S
f xdx  
f xdx 2  0 0 2 B. S
f xdx  
f xdx 2  0 0 2 C. S
f xdx  
f xdx 2  0 0 2 D. S = - f (x)dx + f (x)dx ò ò - 2 0 Hướng dẫn giải Chọn A. 0 2
Dựa vào đồ thị hàm số ta có S
f xdx  
f xdx . 2  0 7 17i
Câu 35: Số phức z  có phần thực là 5  i A.2. B.3. C.1. D.4. Hướng dẫn giải Chọn A
Câu 36: Gọi z , z 2
là hai nghiệm của phương trình z + 2z + 10 = 0. Tính 1 2 2 2 T = z + z . 1 2 A.T = 4. B.T = 6. C.T = 10. D.T = 20. Hướng dẫn giải Chọn D
Câu 37: Phương trình mặt phẳng  đi qua A(3,1,-1) ; B(2,-1,4) và vuông góc với mặt phẳng (P):
2x-y+3z -1=0. Có phương trình là:
A. x – 13y + 5z + 5 = 0 B. x – 13y - 5z + 5 = 0 C. x + 13y + 5z - 5 = 0 D. x – 13y + 5z + 5 = 0 Hướng dẫn giải Chọn B 𝐴 𝐵
= (-1,-2,5) 𝑛 ( 𝑝 ) = (2,-1,3) =>𝑛 = 𝐴 𝐵 ; 𝑛 𝑝 = (-1,13,5)
Mà ∝ qua A(3,1,-1) nên pt ∝ : x – 13y – 5z + 5 = 0
Câu 38: Trong hệ tọa độ Oxyz phương trình tham số của đường thẳng d đi qua A1;2;  3 , B4;4;4 là: ìï x = 1- t ì ì ì ï 3 ï x = - 3 + t ï x = 1+ t 3 ï x = 1+ t 3 ï ï ï ï ï ï ï ï
A. í y = 2 + 2t
B. í y = 2 + 2t
C. í y = 2 + 2t D.í y = 2 + 2t . ïï ï ï ï ï ï ï ï z = 3 + t ïî ï z = 1+ t ïî 3 ï z = 3 + t ïî ï z = 3 + 2t ïî Hướng dẫn giải Chọn C
Câu 39:(VD) Cho tập hợp A   1; 2; 3; 4; 5; 
6 . Gọi S là tập hợp các số có 3 chữ số khác nhau được
lập thành từ các chữ số của tập A . Chọn ngẫu nhiên một số từ S, xác suất để số được chọn là số chia hết cho 9 là: 7 3 1 9 A. . B. . C. . D. . 20 20 20 20 Trang 61 Hướng dẫn giải Chọn B n S  3  A 120 6
Gọi B: “Số được chọn là số chia hết cho 9 ”
Số chia hết cho 9 được tạo nên từ các tập sau:1; 2;  6 ;1;3;  5 ;2;3;  4
nB   PB 8 3 18   120 20
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 4 a . Hình chiếu của S trên mặt
phẳng  ABCD là điểm H thuộc AB sao cho HB  3HA . Góc giữa cạnh bên SC và mặt đáy bằng 45.
Khoảng cách từ O đến mặt phẳng SBC  theo a là 5a 34 5a 34 5a 17 A. 5a 34 B. C. D. 17 34 2 Hướng dẫn giải Chọn B
Kẻ HK  SB(K SB)  HK  (SBC)
Vì HB  HA  HA  a, HB  a  HC  BH2  BC2 3 3  a 5 ) Ta có    ) ) SC;(ABCD)
SC; HC  SCH  45o  SH  HC  a 5
Tam giác SBH vuông tại H, có HK là đường cao SH.HB 15a 34 HK   2 2  34 SH HB dH;(SBC) Khi đó BH 3 1 a     0 34 dA;(SBC) dA;(SBC) AB 4 17 1 1 10 34 5 34 Vậy      a a d O;(SBC) d A;(SBC)  .  2 2 17 17
Câu 41:Có bao nhiêu giá trị m nguyên thuộc đoạn  2  3 2
020; 2020 để hàm số y x  3x  (2m  5)x  5
đồng biến trên khoảng (0; ) ? A. 2020 B. 2022 C. 2021 D. 2023 Hướng dẫn giải Chọn B Cách 1: Ta có 2
y  3x  6x  2m  5
Hàm số đồng biến trên khoảng (0; )  y  0,x  (0; ) 2 2
 3x  6x  2m  5  0,x (0;)  3(x 1)  2m  2,x (0;) Vì 2
(x 1)  0, x  (0; ) (dấu bằng xảy ra khi x 1) nên 2
3(x 1)  2m  2, x  (0; )  2m  2  0  m  1.
Do m nguyên và m  2
 020;2020  m 2  020; 2  019; 2  018;...;0;  1 .
Vậy có 2022 giá trị m thỏa mãn đề bài. Cách 2: Ta có 2
y  3x  6x  2m  5;   9  6a 15  6a  6 . +) Nếu 
  0  m 1 thì y  0,x   do đó, hàm số đồng biến trên (0;). +) Nếu 
  0  m 1 thì phương trình y  0 có hai nghiệm phân biệt x ; x (x x ) . 1 2 1 2
Khi đó, hàm số đồng biến trên ( ;
 x ) và (x ;) . 1 2 2  0 x x  0 
Để hàm số đồng biến trên (0; ) thì 1 2
x x  0     m  (vô nghiệm). 1 2 2 5 x x  0   0 1 2  3 Trang 62
Do vậy, m 1 thỏa mãn bài toán.
Mà m nguyên và m  2
 020;2020  m 2  020; 2  019; 2  018;...;0;  1 .
Vậy có 2022 giá trị m thỏa mãn đề bài. 1
Câu 42: Đối với hàm số y  ln
, Khẳng định nào sau đây là khẳng định đúng? x  1 A. '1 y xye B. '1 y xy  e C. '1 y xy  e D. '1 y xye Hướng dẫn giải Chọn A 1 y  ln  lnx   1 / 1  y   x 1 x 1  1  x 1 1 ln y 1
Ta có: xy '1  x  1  1   , x 1 e e    .  x 1 x 1 x 1 x  1
Câu 43:Cho hàm số f x 3 2
ax bx cx d a,b,c,d  có bảng biến thiên sau: x  1 1  f (  x)  0  0   4 f (x) 0 
Trong các số a, b, c và d có bao nhiêu số âm? A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải Chọn A 0
  a b c d + ĐT đi qua  1
 ;0 và 1;4 nên: 
4  a b c d
+ Ta có: f x 2 '
 3ax  2bx c f '    1  0 3
a  2b c  0
+ ĐT có 2 cực trị x  1
 và x 1 nên:     f '    1  0 3
a  2b c  0
Giải hệ 4 ẩn ta được: a  1
 , b  0, c  3, d  2.
Vậy có 1 giá trị a là số âm.
Câu 44: Bé Khải có 1 bộ đồ chơi là các khối hình không gian có thể lắp ráp lồng vào nhau gồm 1 hình trụ
(có một phần đế làm đặc) và 1 hình lăng trụ tam giác đều có tất cả các cạnh bằng nhau (khối hình trụ
người ta đã làm sẵn 3 rãnh nhỏ để ráp khít vào 3 cạnh bên của lăng trụ tam giác đều như hình vẽ). Biết
hình trụ có chiều cao gấp rưỡi đường cao đáy lăng trụ và diện tích xung quanh lăng trụ bằng 2 2 3 (cm ) . c aa
Diện tích toàn phần hình trụ là 2 S
(cm ) (với a, b, c   * và
là phân số tối giản). Hỏi b b
ab  20c bằng Trang 63 A.18. B. -5 C. 33. D.15. Hướng dẫn giải Chọn A
Gọi lăng trụ có các cạnh bằng x (cm) . Theo giả thiết ta có 2 2 S
 3x  3  x   (c ) m . xq
Ta có chiều cao hình trụ là 3 3 3 3 h  .  
,bán kính đáy hình trụ là 2 3 3 R  .   . 2 2 4 3 2 3
Diện tích toàn phần hình trụ là 3 3 3 3 13 2 2 3
S  2 Rh  2 R  2. .   2 (  )   . . 3 4 3 6
Vậy a  13; b  6; c  3  ab  20c  78  60  18.
Câu 45:Cho hàm số f(x) có đạo hàm liên tục trên đoạn 0;2 thỏa mãn f (0)  3 và 2
(2x  3)f '(x)  2 f(x)  4x  3x . Khi đó f (2) bằng 9 1 1 A.1 B. C. D. 7 5 7 Hướng dẫn giải Chọn B.  Ta có: 2         2 (2x 3)f '(x) 2 f(x) 4x 3x (2x 3)f (x)  4x  3x
Lấy nguyên hàm 2 vế ta được: 2 2 3
(2x  3)f (x)  (4x  3x )dx  2x  x  C 
Do f (0)  3  3f(0)  C  C  9 9
Thay x  2  7f (2)  8  8  9  f (2)  . 7
Câu 46:Cho hàm số y f x có bảng biến thiên sau: x  1 3  f (  x)  0  0  f (x) 4   2 
Xét hàm số g x  f f x .Số nghiệm của phương trình g ' x  0 là A. 5. B. 6. C. 7. D. 8. Hướng dẫn giải Chọn D
+ Ta có: g 'x  f 'x. f ' f x
f 'x  0  x 1, x=3 2n0  
+ Do đó: g ' x  0    f x f '
  f x   1 3n0  0     f
  x  3 3n0 
Vậy pt g ' x  0 có tất cả là 8 nghiệm. Câu 47:
Một người có 10 triệu đồng gửi vào ngân hàng với kỳ hạn 3 tháng (1 quý là 3 tháng), lãi suất 6% / 1 quý
theo hình thức lãi kép (sau 3 tháng sẽ tính lãi cộng vào gốc). Sau đúng 3 tháng, người đó gửi thêm vào 20
triệu đồng cùng với hình thức lãi suất như vậy. Hỏi sau 1 năm, tính từ lần gửi đầu tiên, người đó nhận
được số tiền gần nhất với kết quả nào? Trang 64 A. 35 triệu B. 37 triệu C. 36 triệu D. 38 triệu Hướng dẫn giải Chọn C.
Sau kỳ hạn thứ nhất, số tiền nhận được là: A a amr a 1 mr 1  
Sau kỳ hạn thứ hai, số tiền nhận được là:
A a 1 mr   a 1 mr .mr a 1 mr 2 2 …… n
Sau kỳ hạn thứ n, số tiền nhận được là : A amr n 1 
Sau quý thứ nhất, số tiền trong tài khoản của người đó là:
10.1 6%  20  30,6 triệu đồng (do người đó gửi thêm vào 20 triệu).
Sau quý thứ hai số tiền có trong tài khoản của người đó là
30, 6  30, 6.6%  30, 6 1 6% triệu đồng.
Sau 1 năm số tiền người đó thu được là   3 30, 6. 1 6%  36,445 triệu đồng.
Do ở đây số thập phân nhỏ hơn phẩy 5 do đó ta chọn 36 triệu đồng là gần nhất. Câu 48:Cho ,
x y 0;  , x y  1 . Biết m a ;b thì phương trình  2 x y 2 5 4
5y  4x  40xy m
có nghiệm thực. Tính T  25a 16b .
A. T  829 . B. T  825 . C. T  816 . D. T  820 Hướng dẫn giải Chọn B 2 2 3 Ta có: m  xy   3 3 25
20 x y   56xy  25 xy  20  x y  3xy x y  56xy   x y2   1 xy2 2 25
 4xy  20  25t  4t  20, với t xy   . 4 4  1 
Xét hàm số f t  2
 25t  4t  20 trên đoạn 0;   .  4
Ta có: f t   50t  4 . Xét f t  2  0  t  . 25  2  496  1  329
Ta có: f 0  20 , f    và f    .  25  25  4  16  
Do đó để phương trình có nghiệm thực thì 496 329 496 329 m  ;    a  , b
suy ra T  825.  25 16  25 16
Câu 49:Cho lăng trụ đều AB . C A BC
  có tất cả các cạnh đều bằng 2a . Gọi M , N lần lượt là trung
điểm cạnh AB , BB . Tính cosin góc hợp bởi hai mặt phẳng MC N   , ACC A   . 2 6 3 3 A. . B. . C. . D. . 4 4 4 4 Hướng dẫn giải Chọn B Trang 65
+) Gọi I là trung điểm của A C   . ìï B I¢ ^ A C ¢ ¢ ï Ta có í Þ B I ¢ ^ (ACC A ¢ ) ¢ ( ) 1 . ï B I¢ ^ AA¢ ïî +) Xét tam giác A B
¢ B¢ có M , N lần lượt là trung điểm của A B ¢ ¢ và BB¢
Þ MN là đường trung bình của DA B
¢ B¢Þ MN//A B ¢ . ìï A B ¢ ^ AB¢ ï Trong (AA B ¢ B ¢ ) có í Þ AB¢^ MN ï . A B ¢ //MN ïî ìï C M ¢ ^ A B ¢ ¢ +) Mặt khác ïí Þ C M ¢ ^ (AA B ¢ B ¢ )Þ C M ¢ ^ AB¢ ï . C M ¢ ^ AA¢ ïî ìï AB¢^ MN ï +) Ta có í Þ AB¢^ (C M ¢ N) (2). ï AB¢^ C M ¢ ïî Từ ( )
1 và (2) suy ra góc giữa hai mặt phẳng MC N   , ACC A
  là góc giữa hai đường thẳng B I¢ và AB¢. +) Xét tam giác AA B
¢ ¢ vuông tại A có 2 2 2 2 AB¢= AA¢ + A B
¢ ¢ = 4a + 4a = 2 2a . Xét tam giác đều a A B ¢ C
¢ ¢ cạnh 2a có B I¢ là đường cao 2 3 Þ B I ¢ = = a 3 . 2
Xét tam giác vuông AA I ¢ có 2 2 2 2 AI = AA¢ + A I
¢ = 4a + a = a 5 . 2 2 2 2 2 2 B I
  AB  AI
3a  8a  5a 6 +) Xét DAB I ¢ có  cos AB I      0 2B I  .AB . 2.a 3.2 2a 4
Do đó cosin của góc giữa hai đường thẳng B I ¢ và AB¢ bằng 6 . 4
Vậy cosin góc hợp bởi hai mặt phẳng MC N   , ACC A   bằng 6 . 4
Câu 50: Chị M vay ngân hàng 300 triệu đồng theo phương thức trả góp để mua nhà. Nếu cuối mỗi tháng,
bắt đầu từ tháng thứ nhất chị M trả 5,5 triệu đồng và chịu lãi số tiền chưa trả là 0,5% mỗi tháng (biết lãi
suất không thay đổi) thì sau bao lâu, chị M trả hết số tiền trên? A. 64 tháng B. 54 tháng C. 63 tháng D. 55 tháng Hướng dẫn giải Chọn A
Cuối tháng thứ nhất, số tiền người đó còn nợ là N A 1 r a đồng 1  
Cuối tháng thứ hai, số tiền người đó còn nợ là
N N .1 r  a A1 r 2  a 1 r a 2 1  
Cuối tháng thứ ba, số tiền người đó còn nợ là: Trang 66
N N 1 r  a A1 r 3  a 1 r 2  .
a 1 r a 3 2   …
Cuối tháng thứ n số tiền người đó còn nợ là:  N A
r a   r   r    r n  n     2  n 1 1 1 1 1 ... 1  n  
A  rn 1 r 1 1  . a r
Để hết nợ sau n tháng thì số tiền còn nợ sau n tháng là 0, tức là ta giải phương trình n n      rn 1 r 1
A1 r  .r A 1  . a  0  a
(số tiền phải trả mỗi tháng). rn 1 r  1 Lời giải
Áp dụng công thức vừa thiết lập ở bài toán tổng quát thì ta có phương trình n      n 1 0,5% 1 300. 1 0, 5%  5,5.
 0  300.1,005n 1100.1,005n   1  0 0, 5% 11  n  log  63,84984073. 1,005 8 www.thuvienhoclieu.com
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 15 MÔN TOÁN
PHÁT TRIỂN TỪ ĐỀ MINH Thời gian: 90 phút
HỌA LẦN 2 NĂM 2020
Câu 1: Có bao nhiêu cách chọn 5 học sinh từ 20 học sinh lớp 11A ? A. 18640480 cách. B. 120 cách. C. 15504 cách. D. 100 cách.
Câu 2: Cho cấp số cộng có u  0 và công sai d = 3. Tổng của 26 số hạng đầu tiên của cấp số cộng đó 1 bằng bao nhiêu ? A. 975. B. 775. C. 875. D. 675.
Câu 3: Tìm nghiệm của phương trình log 3x  2  3 2   8 10 A. x  . B. x  . 3 3 16 11 C. x  . D. x  . 3 3
Câu 4: Tính thể tích khối lập phương cạnh a 3 a 3 a A. . B. . 3 2 3 a C. 3 a . D. . 6 
Câu 5: Tập xác định của hàm số y   2
x  3x  2 là A.  \ 1;  2 . B.   ;1  2; . C. 1; 2 . D.   ;1 2; . 1
Câu 6: Tìm họ nguyên hàm F(x) của hàm số f (x)  5x  4 Trang 67 A. F x 1 
ln 5x  4  C .
B. F x  ln 5x  4  C . ln 5 1 C. F x 1
 ln 5x  4  C .
D. F x  ln 5x  4  C . 5 5
Câu 7: Cho khối chóp S.ABCD có cạnh bên SA vuông góc đáy, ABCD là hình chữ nhật, AB = a,
AD = 2a, SA = 3a. Thể tích khối chóp S.ABCD bằng: A. 3 6a . B. 3 2a . 3 a C. . D. 3 a . 3
Câu 8: Cho khối nón có bán kính đáy r  3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho A. 16 3. B. 12. C. 4. D. 4 . a
Câu 9: Thể tích của khối cầu có bán kính bằng là: 2 3  a 2  a A. . B. . 2 4 3  a C. . D. 2  a . 6 Câu 10: Cho hàm số 3 2
y x  3x  4 có bảng biến thiên như sau, tìm a và b.
A. a  , b  2. B. a  ;  b  4. C. a  ;  b  1.
D. a  , b  3. 4 a e
Câu 11: Với a, b là hai số thực dương tùy ý, ln bằng: b
A. 4ln a  ln b 1.
B. 4ln b  ln a 1.
C. 4ln a  ln b 1.
D. 4ln a  ln b 1.
Câu 12: Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7. Diện tích xung quanh của hình trụ đã cho bằng: 17 A. . B. 175. 3 C. 70. D. 35.
Câu 13: Cho hàm số y = f(x) liên tục trên  và có bảng biến thiên như hình vẽ
Mệnh đề nào sau đây là đúng ? Trang 68
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho có đúng một điểm cực trị.
C. Hàm số đã cho không có giá trị cực tiểu. D. Hàm số đã cho không có giá trị cực đại.
Câu 14: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây ? 2x 1 x 1 A. y  . B. y  . x 1 x 1 C. 4 2
y x x 1. D. 3
y x  3x 1 . 3x  5
Câu 15: Đường tiệm cận đứng của đồ thị hàm số y  là: x  2 A. x  2. B. y  2. C. x  3. D. y  3.
Câu 16: Tập nghiệm của bất phương trình 3x  9 là: A. 2;  . B. 0; 2. C. 0; . D.  2  ;.
Câu 17: Cho hàm số y f (x) có đồ thị như hình vẽ. Số nghiệm của phương trình 3 f (x)  8  0 bằng: A. 1. B. 2. C. 3. D. 4. 2 5 5 Câu 18: Nếu
f xdx  3, f xdx  1    thì
f xdx  bằng: 1 2 1 A. 3. B. 4. C.2. D. 2. 
Câu 19: Cho số phức z thỏa mãn z  3  2i . Tìm phần thực và phần ảo của số phức z A. Phần thực bằng 3  , phần ảo bằng 2.
B. Phần thực bằng 3 , phần ảo bằng 2.
C. Phần thực bằng 3, phần ảo bằng 2.  D. Phần thực bằng 3  , phần ảo bằng 2. 
Câu 20: Cho hai số phức z  1 2i, z  3  9i . Tìm điểm M biểu diễn số phức z z trên mặt phẳng 1 2 1 2 tọa độ A. M  2  ;1  1 . B. M  2  ; 1   1 . C. M 11; 2  . D. M 11; 2 . Trang 69
Câu 21: Trên mặt phẳng tọa độ, điểm M (2;-3) là điểm biển diễn của số phức z nào dưới đây ? A.z = 2+ 3i B.z = 2- 3i C.z = 3+2i D.z = 3-2i
Câu 22: Trong không gian Oxyz, hình chiếu vuông góc của điểm M (2;1; 1) trên mặt phằn (Ozy) có tọa độ là: A. (0;1; 0) B. (2;1; 0) C. (0;1; 1  )
D. (2; 0; 1)
Câu 23: Trong không gian Oxyz, cho mặt cầu ( S ): 2 2 2
(x  3)  ( y  2)  (z 1)  4. Tâm của (S ) có tọa độ là:
A. (3; 2; 1) B. (3; 2; 1  ) C. (3; 2;1)
D. (3; 2;1)
Câu 24: Trong không gian Oxyz, cho mặt phẳng ( P ) đi qua 3 điểm A(1;0;0), B(0;-2;0), C( 0;0;3).
Phương trình nào sau đây là phương trình của ( P )? x y z x y z A.    1 B.    1 1 2 3 1 2 3 x y z x y z C.    1 D.    1 1 2 3 1 2 3 x 1 y  2 z 1
Câu 25: Trong không gian Oxyz, cho đường thẳng d:  
. Vectơ nào là vectơ chỉ 2 3 1  phương của d ?     A. u  (2;3; 1  ) B. u  ( 1  ; 2  ;1) C. u  ( 2  ; 3  ; 1  )
D. u  (1; 2; 1  )
Câu 26: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam S
giác ABC vuông tại B (minh họa như hình bên). Góc giữa mặt phẳng
(SBC) và mặt phẳng ( ABC) là : A. SBC B SCB A C C. SCA D. SBA B
Câu 27: Cho hàm số y f (x) xác định, liên tục trên  và có đồ thị như hình
bên. Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị hàm số đi qua điểm ( A 0; 1) .
B. Hàm số có giá trị cực tiểu bằng -1.
C. Hàm số có ba điềm cực trị.
D. Hàm số đạt cực đại tại x  0 x 1
Câu 28: Giá trị lớn nhất của hàm số y  trên đoạn [0;2]là: x  2 1 1 A. B. 0 C. D. 2 4 2
Câu 29: Với mọi a, b, x là các số thực dương thoả mãn log x  5log a  3log b . Mệnh đề nào dưới 2 2 2 đây đúng?
A. x  3a  5b
B. x  5a  3b C. 5 3
x a b D. 5 3
x a b
Câu 30: Số giao điểm của hai đồ thị hàm số 3 2
y x  2x  5 và y  5x 1là: A. 3. B. 0 C. 2. D. 1.
Câu 31: Tập nghiệm của bất phương trình: 4x 2.2x   3  0 là Trang 70 A. [0; ) B. (0; ) C. (; 0) D. (; 0]
Câu 32: Trong không gian, cho tam giác ABC vuông tại A, AB = a và BC = 2a. Khi quay tam giác
ABC xung quanh cạnh góc vuông AC thì đường gấp khúc CBA tạo thành một hình nón. Thể tích khối nón đó bằng: 3 a 2 3  a 3 3  a 6 2  a 3 A. B. C. D. 3 3 3 3 e 1 ln x
Câu 33: Cho tích phân: I  d . x
Đặt u  1 ln x. Khi đó I bằng : 1 2x 2 0 0 0 u 1 A. 2 I u du B. 2 I   u du C. I  d . u D. 2
I   u du 1 1 1 2 0
Câu 34: Diện tích hình phẳng được giới hạn bởi đồ thị hàm số 2 x
y e , trục hoành và hai đường
thẳng x  0, x  3 là 6 e 1 6 e 1 6 e 1 6 e 1 A. B. C. D. 2 2 2 2 3 3 3 3
Câu 35: Cho hai số phức z1 = 3-i và z2 = 2+3i. Phần ảo của số phức w = 2z1- z2 là: A. 4 B.5i C. -5i D.-5 Câu 36: Kí hiệu z   
1, z2là hai nghiệm phức của phương trình 2 z 2z 10
0 . Gọi a1, a2 lần lượt là phần thực của z   1, z2Tính M 3a 2a . 1 2
A. M  5. B. M  3. 
C. M  2. D. M  6  x  4  t
Câu 37: Trong không gian Oxyz, cho điểm M (2; 1
 ;0) và đường thẳng  : y  2 2t (t   ) . z  3t
Mặt phẳng đi qua M và vuông góc với  có phương trình là:
A. x  2 y  3z  4  0
B. x  2 y  3z  4  0
C. x  2 y  3z  7  0
D. x  2 y  3z  7  0
Câu 38: Trong không gian Oxyz, cho điểm M( 1;0;-2). Đường thẳng đi qua M và vuông góc với mặt phẳng
(P): 2x  3y z  2  0 , có phurong trinh tham số là: x  2  tx  2  tx 1 2tx  1   2t     A. y  3  B. y  3  C. y  3  t D. y  3  t     z  1 2tz  1 2tz  2   tz  2  t
Câu 39: Có 8 bạn học sinh lớp 12C trong đó có A và B được xếp ngẫu nhiên theo một hang ngang.
Tính xác suất P để A và B ngồi cạnh nhau. 1 1 1 1 A. P  . B. P  . C. P  . D. P  . 8 4 64 25
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD  2a , SA vuông góc
với mặt phẳng đáy và SA a (tham khảo hình vẽ). Gọi M là trung điểm của CD . Khoảng cách
giữa hai đường thẳng SD, BM bằng Trang 71 a 21 2a 21 2a 7 a 7 A. . B. . C. . D. . 21 21 7 7
Câu 41: Có bao nhiêu giá trị nguyên của tham số m  2
 020;2020 để hàm số
y  m   3 2
1 x  3mx  4m  4 x 1 đồng biến trong khoảng  ;   ? A. 2020. B. 2018. C. 2019. D. 4040.
Câu 42: Một người thả một lá bèo vào một hồ nước. Sau 24 giờ, bèo sinh sôi phủ kín mặt nước trong
hồ. Biết rằng cứ sau mỗi giờ lượng bèo tăng gấp 20 lần lượng bèo trước đó và tốc độ tăng không đổ 1
i. Hỏi sau mấy giờ thì bèo phủ kín
mặt nước trong hồ (kết quả làm tròn đến hàng phần chục). 5 A. 23, 5 giờ. B. 22, 5 giờ. C. 21, 4 giờ. D. 20, 3 giờ.
Câu 43: Đường cong hình bên dưới là đồ thị hàm số 3 2
y ax bx cx d . Xét các mệnh đề sau: I a  1  .
II ad  0.
III d  1  .
IV ac b1.
Tìm số mệnh đề đúng. A. 3 . B. 1. C. 4 . D. 2 .
Câu 44: Cho mô ̣t hình tru ̣ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp , A B nằm trên
đường tròn đáy thứ nhất của hình tru ̣ , hai đỉnh còn la ̣i nằm trên đường tròn đáy thứ hai của hình
trụ. Mă ̣t phẳng ( ABCD) tạo với đ áy hình trụ góc 0
45 . Diê ̣n tích xung quanh S hình trụ và thể xq
tích V của khối trụ là: 2 3 a 3 3 2a 2 3 a 2 3 2a A. S  ;V  . B. S  ;V  . xq 3 8 xq 3 32 2 3 a 3 3 3a 2 3 a 3 3 2a C. S  ;V  . D. S  ;V  . xq 4 16 xq 2 16 Trang 72 Câu 45: Cho hàm số
y f x có đạo hàm liên tục trên  thỏa mãn 2
x f xf x 2 . . '
f x  , x x
  và có f 2 1. Tích phân 2
f xd . x  0 3 4 A. B. C. 2 D. 4 2 3
Câu 46: Cho hàm số f x có bảng biến thiên như sau:  9 
Số nghiệm thuộc đoạn 0; 
 của phương trình f 2sin x   1  1là  2  A. 6 . B. 4 . C. 5 . D. 7 . 1 1
Câu 47: Cho hai số thực a, b  1 . Tìm giá trị nhỏ nhất của biểu thức S   . log a log b 4 ab ab 2 9 4 1 A. min S  . B. min S  . C. min S  . D. min S  . 9 4 3 4
Câu 48: Gọi S là tập hợp tất cả các giá thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m y
1; 2 bằng 2. Số phần tử của S là x  trên đoạn   1 A. 1. B. 2. C. 3. D. 4.
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình thang với hai đáy thỏa mãn 2CD  3AB . Biết 126V
thể tích của khối chóp S.ABD bằng 4V và thể tích của khối chóp S.CDMN bằng , trong đó 25 SM
M , N lần lượt nằm trên cạnh S ,
A SB sao cho MN song song với . AB Tỉ số bằng: MA 2 3 3 4 A. . B. . C. . D. . 3 2 4 3
Câu 50: Có bao nhiêu giá trị nguyên của tham số m m  2020 để phương trình x 1 2   log
x  2m m có nghiệm ? 4   A. 2020 . B. 2019 . C. 2018 . D. 4040 . Đáp án: 1. C 2.A 3.B 4.C 5.B 6.C 7.C 8.D 9.C 10.B 11. A 12.C 13.A 14.B 15.A 16.A 17.B 18.C 19.C 20.B 21.B 22.C 23.C 24.D 25.A 26.D 27.D 28.A 29.C 30.A 31.C 32.B 33.B 34.B 35.D 36.A 37.B 38.C 39.B 40.B 41.C 42.A 43.D 44.D 45.C 46.D 47.B 48.B 49.B 50.A Trang 73
Câu 39: Có 8 bạn học sinh lớp 12C trong đó có A và B được xếp ngẫu nhiên theo một hang ngang. Tính
xác suất P để A và B ngồi cạnh nhau. 1 1 1 1 A. P  . B. P  . C. P  . D. P  . 8 4 64 25 HƯỚNG DẪN GIẢI chọn B. n   8!
Số cách xếp 8 học sinh trong đó A và B ngồi cạnh nhau là: 2!7!. 2!7! 1 P   . 8! 4
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD  2a , SA vuông góc
với mặt phẳng đáy và SA a (tham khảo hình vẽ). Gọi M là trung điểm của CD . Khoảng cách giữa
hai đường thẳng SD, BM bằng a 21 2a 21 2a 7 a 7 A. . B. . C. . D. . 21 21 7 7 HƯỚNG DẪN GIẢI Chọn B
Gọi N là trung điểm của AB khi đó BM / /DN nên BM / / SDN
d BM ; SD  d BM ;SDN   d  ;
B SDN   d  ;
A SDN  .
Kẻ AH DN tại H . Ta có mặt phẳng SAH   SDN  . Trong mp SAH  kẻ AK SH tại K . Khi đó
d BM ; SD  d  ;
A SDN   AK . 1 1 1 1 1 1 4 1 1 21          2a 21 . Suy ra AK  . 2 2 2 2 2 2 2 2 2 2 AK AH SA AN AD SA a 4a a 4a 21 Trang 74
Câu 41: Có bao nhiêu giá trị nguyên của tham số m  2
 020;2020 để hàm số
y  m   3 2
1 x  3mx  4m  4 x 1 đồng biến trong khoảng  ;   ? A. 2020. B. 2018. C. 2019. D. 4040. HƯỚNG DẪN GIẢI Chọn C.
TXĐ: D   . y  m   2 ' 3
1 x  6mx  4m  4 .
Để hàm số đồng biến trên khoảng  ;
  thì y '  0, x      4
TH1: m 1  0  m 1 thì y '  0  6x  8  0  x  (không thỏa mãn) 3 m 1  0 m 1  m 1  TH2:      2  '  0   m m m       y 9 3  1 4 4 2 0 ' 3m 12 0 m 1   m  2   m  2  m  2
Do m là số nguyên và m  2
 020;2020  m2;3;...;202  0 .
Vậy có 2019 số nguyên m cần tìm.
Câu 42: Một người thả một lá bèo vào một hồ nước. Sau 24 giờ, bèo sinh sôi phủ kín mặt nước trong hồ.
Biết rằng cứ sau mỗi giờ lượng bèo tăng gấp 20 lần lượng bèo trước đó và tốc độ tăng không đổi. Hỏi sau 1
mấy giờ thì bèo phủ kín
mặt nước trong hồ (kết quả làm tròn đến hàng phần chục). 5 A. 23, 5 giờ. B. 22, 5 giờ. C. 21, 4 giờ. D. 20, 3 giờ. HƯỚNG DẪN GIẢI Chọn A.
Giả sử một lá bèo chiếm x phần mặt nước trong hồ 0  x   1 . 1
Sau 24 giờ, bèo sinh sôi phủ kín mặt nước trong hồ nên ta có: 24
20 x  1  x  . 24 20 1
Giả sử sau t giờ thì bèo bao phủ kín
mặt nước trong hồ , ta có: 5 1 t 1 t  1 1 24 .20   20   t  log  24  23,5giờ. 24 20 20 5 5 5
Câu 43: Đường cong hình bên dưới là đồ thị hàm số 3 2
y ax bx cx d . Xét các mệnh đề sau: I a  1  .
II ad  0.
III d  1  .
IV ac b1. Trang 75
Tìm số mệnh đề đúng. A. 3 . B. 1. C. 4 . D. 2 . HƯỚNG DẪN GIẢI Chọn D.
Dựa vào đồ thị ta thấy a  0 . Mệnh đề  I  sai.
Đồ thị hàm số đi qua điểm 0 
;1  d 1  0  ad  0. Mệnh đề  II  đúng, mệnh đề  III  sai.
Đồ thị hàm số đi qua điểm  1
 ;0  a c b1. Mệnh đề IV  đúng.
Vậy có hai mệnh đề đúng là  II  và  IV  .
Câu 44: Cho mô ̣t hình tru ̣ tròn xoay và hình vuông
ABCD cạnh a có hai đỉnh liên tiếp , A B nằm trên
đường tròn đáy thứ nhất của hình tru ̣ , hai đỉnh còn la ̣i nằm trên đường tròn đáy thứ hai của hình tru ̣ . Mă ̣t
phẳng ( ABCD) tạo với đáy hình trụ góc 0
45 . Diê ̣n tích xung quanh S hình trụ và thể tích V của khối xq trụ là: 2 3 a 3 3 2a 2 3 a 2 3 2a A. S  ;V  . B. S  ;V  . xq 3 8 xq 3 32 2 3 a 3 3 3a 2 3 a 3 3 2a C. S  ;V  . D. S  ;V  . xq 4 16 xq 2 16 Hướng dẫn giải: Chọn D.
* Gọi M, N theo thứ tự là trung điểm của AB và CD . Khi đó: OM AB vàO ' N DC .
Giả sử I là giao điểm của MN vàOO ' . Đặt R O ,
A h OO ' . 2 * Trong I
OM vuông cân ta ̣i I nên: OM OI IM . 2 h 2 a 2   .  h a . 2 2 2 2 * Ta có: 2 2 2 2
R OA AM MO 2 2 2 2 2  a   a 2  a a 3a          .  2  4 4 8 8   2 2 3 a 3 a 2 a 3 3a a 2 3 2a 2
S  2 Rh  2 . 
; V   R h   .  . xq 2 2 2 2 8 2 16
Câu 45: Cho hàm số y f x có đạo hàm liên tục trên  thỏa mãn x f xf x 2 . . '
f x  , x x   2
và có f 2  1. Tích phân 2
f xd . x  0 3 4 A. B. C. 2 D. 4 2 3 Hướng dẫn giải: Chọn C. Trang 76 2 2 .
x f (x). f '(x)  f (x)  x  2 .
x f (x). f '(x)  2 f (x)  2x 2  2 .
x f (x). f '(x)  f (x)  3 f (x)  2x   .x f (x) 2 2 2 2 2 2 ' x
d  3 f (x)dx  2xdx   0 0 0   2 2 .
x f (x)  3I  4  2  3I  4  I  2 0
Câu 46: Cho hàm số f x có bảng biến thiên như sau:  9 
Số nghiệm thuộc đoạn 0; 
 của phương trình f 2sin x   1  1là  2  A. 6 . B. 4 . C. 5 . D. 7 . Hướng dẫn giải: Chọn D. x  1  
Dựa vào bảng biến thiên, ta có f x  1  x a 1;3 .
x b3;    sin x  1  1 2sin x 1   1     Như vậ a 1 y f 2sin x 1   1  2  sin x 1
  a 1;3   sin  x
, a  1;3  2   . 
x   b      2 2sin 1 3;  b 1 sin x
, b  3;  3   2      Trên đoạ 9 3 7 n 0; , 
 phương trình sin x  1
 có 2 nghiệm x  , x  .  2  2 2 a 1 a
Với 1  a  3  0  a 1  2  0   1. Do đó 1 sin x
có 5 nghiệm phân biệt thuộc 2 2  9  3 7 0; 
 , các nghiệm này đều khác và .  2  2 2 b 1 b
Với b  3  b 1  2   1 . Do đó 1 sin x  vô nghiệm. 2 2  9  Vậy trên đoạn 0; 
 phương trình f 2sin x   1  1có 7 nghiệm.  2  1 1
Câu 47: Cho hai số thực a, b  1 . Tìm giá trị nhỏ nhất của biểu thức S   . log a log b 4 ab ab 2 9 4 1 A. min S  . B. min S  . C. min S  . D. min S  . 9 4 3 4 Hướng dẫn giải: Chọn B. Trang 77 S ab ab   b a a   1 b   1 1 log log 1 log log 4 a 4 b 4 5 1   log b  4 a 4 log b a
Do a  1, b  1  log b  0 . Áp dụng BĐT Cô-si, ta có : a 5 1 5 1 5 9 S   log b    2 log . b  1  4 a 4 log b 4 a 4 log b 4 4 a a  1 log b tma   1  2
Dấu « = » xảy ra  log b     b a a 4 log b 1  a log b l a    2
Câu 48: Gọi S là tập hợp tất cả các giá thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m y
1; 2 bằng 2. Số phần tử của S là x  trên đoạn   1 A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải: Chọn B.
x mx m
Xét hàm số f x 2  1; 2 . x  trên đoạn   1 2 x  2x
Ta có f ' x liên tục trên 1; 2 và f ' x   0, x   1;2 . 2   x   1  3m  4 2m 1
f x đồng biến trên 1; 2  max f x  f 2 
; min f x  f   1  . 1;2 3 1;2 2     Khi đó, f x 3m 4 2m 1 max  max  ; . 1;2  3 2  3m  4 2m 1 2 2 11 Ta có   43m   1  92m   1  m   . 3 2 12  2 m  tm    11 3m 4 3 Với m  
, ta có max f x   2   12 1;2 3 10
m   l  3  5
m   tm    11 2m 1 2 Với m  
, ta có min f x   2   12 1;2 2 3 m  l  2  5 2
Vậy S   ;  Số phần tử của S là 2.  2 3
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình thang với hai đáy thỏa mãn 2CD  3AB . Biết thể 126V
tích của khối chóp S.ABD bằng 4V và thể tích của khối chóp S.CDMN bằng
, trong đó M , N lần 25 lượ SM
t nằm trên cạnh S ,
A SB sao cho MN song song với . AB Tỉ số bằng: MA 2 3 3 4 A. . B. . C. . D. . 3 2 4 3 Hướng dẫn giải: Trang 78 Chọn B. Đặ SM SN t 
x,  x  0 . SA SB Nhận thấy hai tam giác ABD, B
CD có đường cao bằng nhau và cạnh đáy 3 CD AB 2 3 3  SSVV  6V . BCD DAB S .BCD S . 2 2 DAB Ta có tỉ số thể tích: V SD SM SN S.DMN 2 2 2  . .  x Vx .V  4x .V . S.DMN S.DAB V SD SA SB S.DAB V SD SN SC S.DNC  . .  x V  . xV  6 . xV . S.DNC S.DBC V SD SB SC S.DBC 126 126
Từ giả thiết  VVV
x x V
V x x   S CDMN S DMN S DNC  2 4 6  2 . 4 6 0 . . . 25 25  3 x  n  5   SM SN 3 SM 3      . 21  SA SB 5 MA 2 x   l  10 SM 3 Vậy  MA 2
Câu 50: Có bao nhiêu giá trị nguyên của tham số m m  2020 để phương trình x 1 2   log
x  2m m có nghiệm ? 4   A. 2020 . B. 2019 . C. 2018 . D. 4040 . Hướng dẫn giải: Chọn A.
ĐK: x  2m  0 x Ta có 1 2
 log x  2m m  2x  log x  2m  2m 2   4  
2x t  2m
Đặt t  log x  2m ta có 
 2x   2t xt   1 2  
2t x  2m Do hàm số    2u f u
u đồng biến trên  , nên ta có  
1  t x . Khi đó: 2x   2  2  2x x m mx .
Xét hàm số    2x g x
x gx  2x ln 2 1  0  x  log ln 2 . 2   Bảng biến thiên: Trang 79 Từ đó phương trình đã cho có nghiệm khi và chỉ khi g  2m g   log ln2 2  log ln 2  m   0, 457 2     2
(các nghiệm này đều thỏa mãn điều kiện vì  2  2x x m  0 )
Do m nguyên và m  2020 , nên m 1; 2;...; 202  0 . Trang 80