-
Thông tin
-
Hỏi đáp
Bộ điều khiển động cơ bàn máy X theo PID | lý thuyết môn SPSS | trường Đại học Huế
Xây dựng hàm truyền của hệ thông.Tìm hàm truyền đạt G(s). Kiểm tra tính ổn định của hàm truyền G(s):Kiểm tra sự ổn định của hệ hở.Kiểm tra sự ổn định của hệ kín:Kiểm tra đáp ứng của hệ.Thiết kế bộ điều khiển PID: Những kiến thức cơ sở về bộ điều khiển PID: Vai trò các khâu tỉ lệ, tích phân, vi phân:Thiết kế PID controller theo phương pháp thực nghiệm (phương pháp Ziegler- Nichols thứ nhất).Tìm hàm truyền của bàn Y.Tìm hàm truyền đạt G(s).Kiểm tra tính ổn định của hàm truyền G(s):Kiểm tra sự ổn định của hệ hở.Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
SPSS(ĐHH) 4 tài liệu
Đại học Huế 272 tài liệu
Bộ điều khiển động cơ bàn máy X theo PID | lý thuyết môn SPSS | trường Đại học Huế
Xây dựng hàm truyền của hệ thông.Tìm hàm truyền đạt G(s). Kiểm tra tính ổn định của hàm truyền G(s):Kiểm tra sự ổn định của hệ hở.Kiểm tra sự ổn định của hệ kín:Kiểm tra đáp ứng của hệ.Thiết kế bộ điều khiển PID: Những kiến thức cơ sở về bộ điều khiển PID: Vai trò các khâu tỉ lệ, tích phân, vi phân:Thiết kế PID controller theo phương pháp thực nghiệm (phương pháp Ziegler- Nichols thứ nhất).Tìm hàm truyền của bàn Y.Tìm hàm truyền đạt G(s).Kiểm tra tính ổn định của hàm truyền G(s):Kiểm tra sự ổn định của hệ hở.Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: SPSS(ĐHH) 4 tài liệu
Trường: Đại học Huế 272 tài liệu
Thông tin:
Tác giả:
Preview text:
lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT lO M oARcPSD| 47704698
CHƯƠNG 6. BỘ ĐIỂU KHIỂN ĐỘNG CƠ BÀN MÁY X THEO PID
6.1. Xây dựng hàm truyền của hệ thông
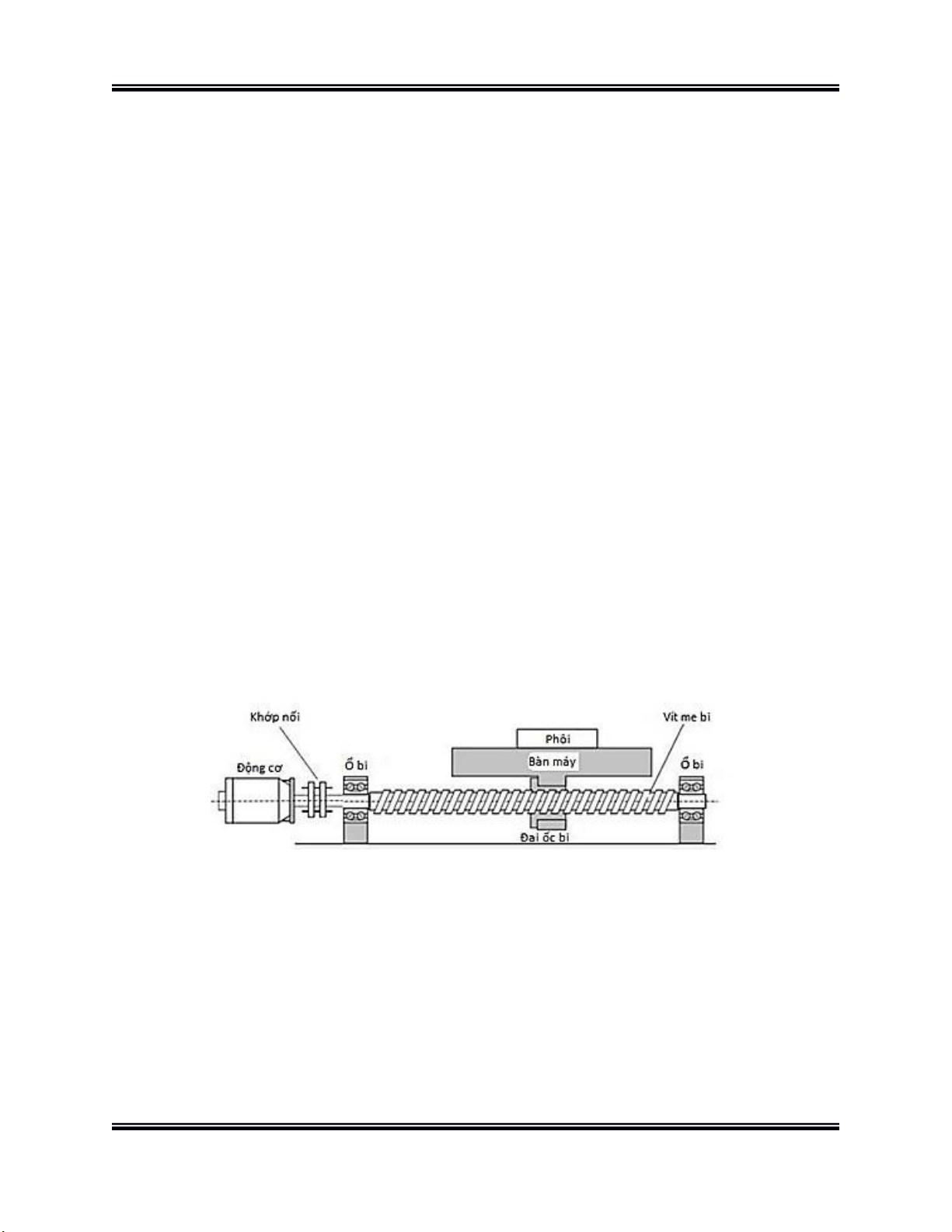
Bàn máy được lắp vít me, vít me được nối với động cơ qua khớp nối. Khi động cơ
quay thì làm vít mẹ quay, nhờ đó bàn máy di chuyển tịnh tiến trên vít me. Vậy nên,
ta điều khiển bàn máy cũng chính là điều khiển động cơ. Hình 1.
Mô hình bàn máy X của máy CNC
Từ đó ta có mô hình hóa hệ bàn máy như hình 6.2 bên dưới: SVTH: Đặng Văn Danh Trang | 1 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
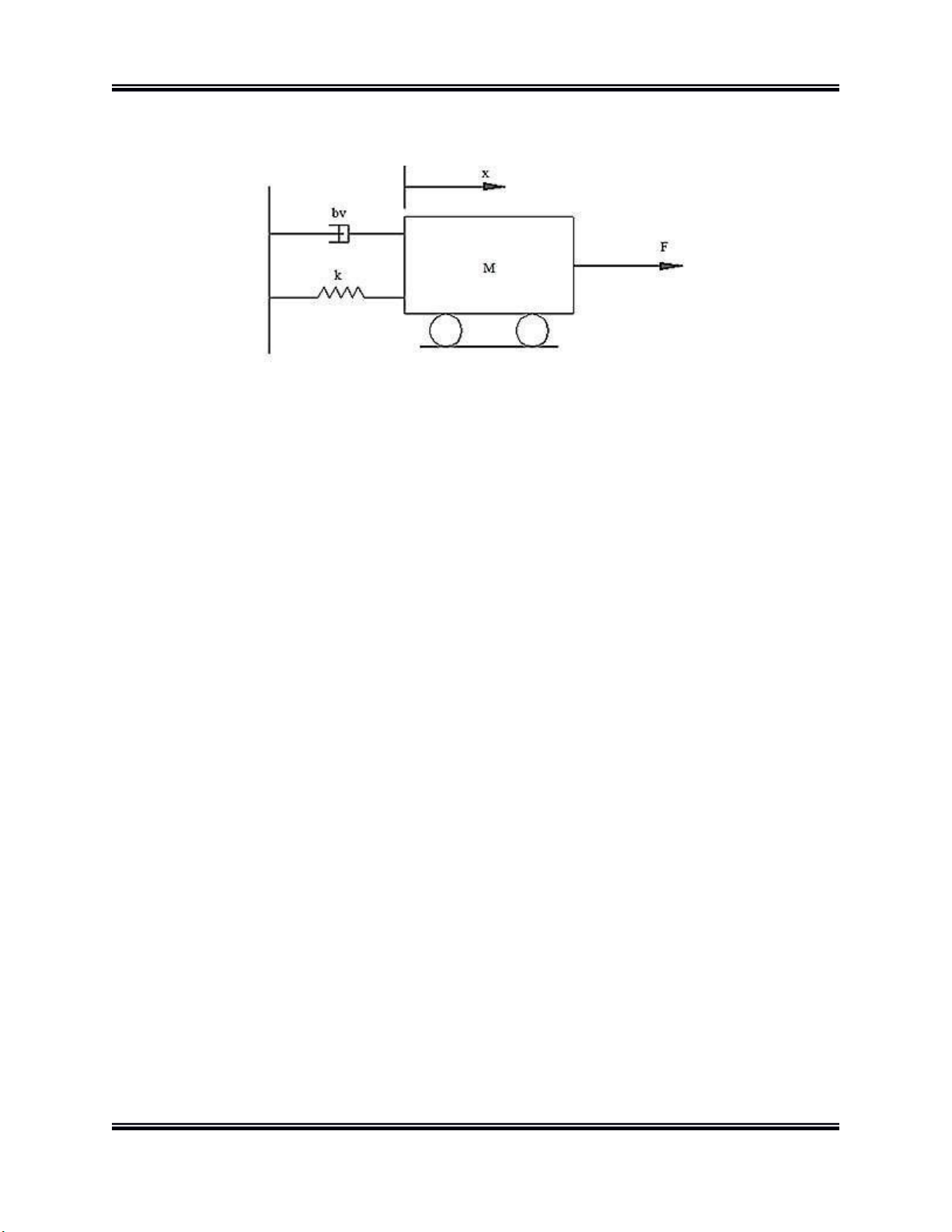
Hình 2. Mô hình hóa hệ bàn máy X Trong đó: -
M: Khối lượng bàn máy và phôi -
k: Hệ số độ cứng của vít me, ổ bi, nối trục, ray dẫn hướng - B: Hệ số giảm chấn -
: Các lực tác dụng gồm lực động cơ và lực ma sát -
: Khoảng dịch chuyển của bàn máy Thông số có ban đầu: -
Khối lượng phôi: =500 kg -
Khối lượng bàn X : =150 kg -
Khối lượng phôi và bàn máy : M = 500 + 150 = 650 kg - Hệ số ma sát: = 0.01 - Bước vít me: l = 10 mm -
Chiều dài vít me: L = 1269 mm Phương trình toán học: M(t) + B(t) +Kx = Lực động cơ: SVTH: Đặng Văn Danh Trang | 2 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT -
Góc quay của động cơ cần để có thể tạo ra một dịch chuyển x(t)- Bước vít me
Lực ma sát: với = 0.01là hệ số ma sát Hệ số độ cứng: Trong đó:
Chọn kiểu nối trục Single Flexing Coupling với kích thước đường kính trong
40mm. Độ cứng của nó là 205,9x(Nm/rad). Tài liệu coupling 2 trang 14. -
Độ cứng của nối trục - Độ cứng của ổ bi -
Độ cứng ray dẫn hướng - Độ cứng trục vít me - Độ cứng càng cua -
: Độ cứng của bi trong trục vít me = ==20,8 () Trong đó: -
A: Diện tích mặt cắt ngang trục vít me , A= -
E : Hệ số module Young, E=2,1.(kgf/) -
x : Khoảng cách gá đặt x = L = 1269 mm =0,8k.= 65,7. (N/m) SVTH: Đặng Văn Danh Trang | 3 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
Trong đó k=151, tải trọng động = 5220 kgf, lực dọc trục =266,5 kgf Từ đó ta có bảng sau: 205,9. 222. 3. 20 , 8. 65 , 7.
Ta tính được: K= 1,82. (N/m)
Hệ số giảm chấn: B=2=2.0,35. = 7,673.
6.2 Tìm hàm truyền đạt G(s) M(t) + B(t) +Kx = -
Sử dụng toán tử Laplace 2 vế của phương trình ta được: MX(s) + BsX(s) + KX(s) = =>[ M+(B+= => G(s)= = =
6.3. Kiểm tra tính ổn định của hàm truyền G(s):
6.3.1. Kiểm tra sự ổn định của hệ hở:
Nếu tất cả các nghiệm của biểu thức A(s) đều nằm phía bên trái trục ảo hay khi đó
A(s) được gọi là đa thức Hurwitz, ta dung lệnh roots A(s) được bộ nghiệm sau đây: -5,9048 + 15,6567i = -5,9048 + 15,6567i
Do đó, Hệ hở ổn định. SVTH: Đặng Văn Danh Trang | 4 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
6.3.2 Kiểm tra sự ổn định của hệ kín: Dùng tiêu chuẩn Nyquist
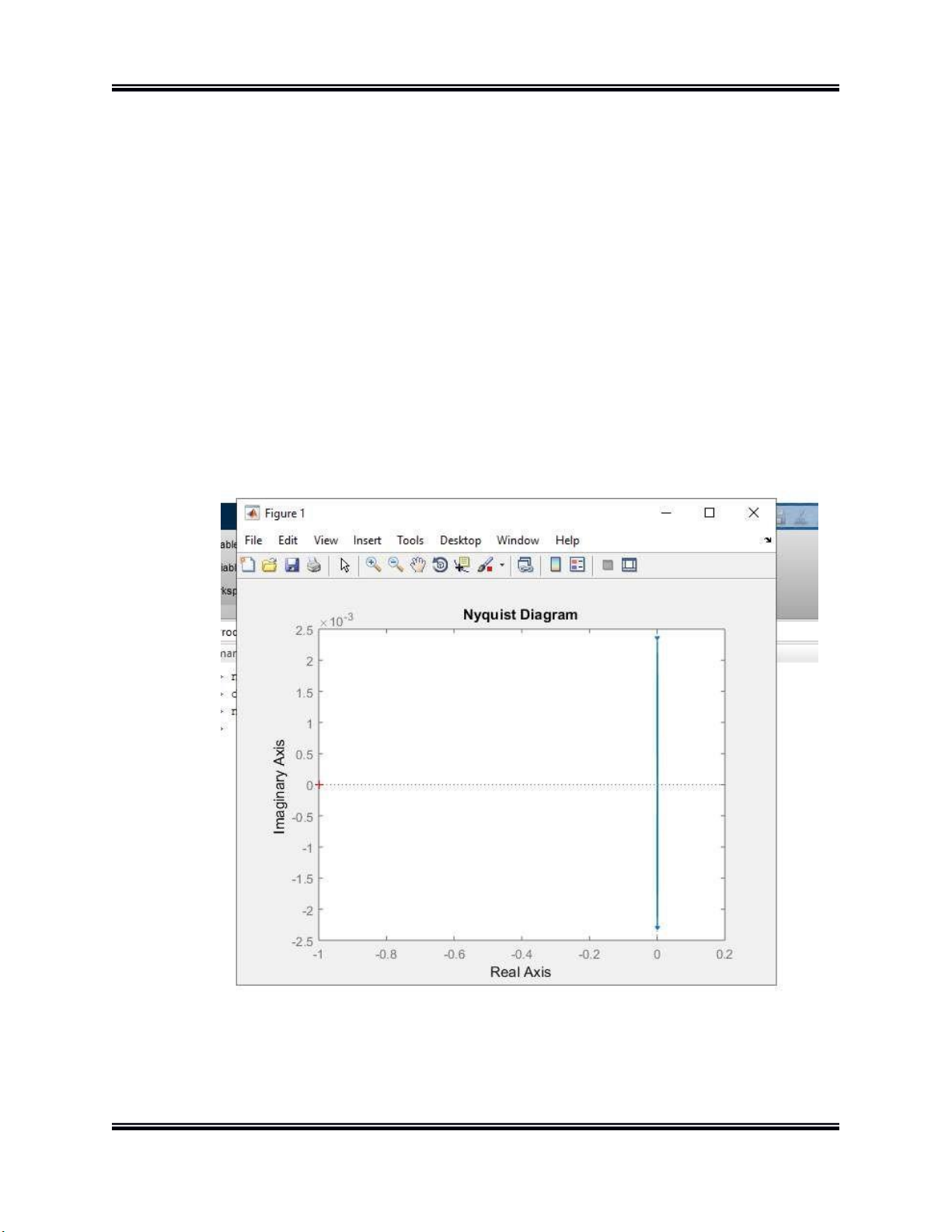
Từ dấu nhắc của cửa sổ Matlab ta nhập: » num = 290; » den = [650 7676.3 182000]; » nyquist(num,den)
Ta được đồ thị như hình bên dưới: SVTH: Đặng Văn Danh Trang | 5 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT Hình 3.
Đồ thị Nyquist của hệ
Dựa vào đồ thị bên dưới qua đồ thị ta nhận thấy rằng: Điểm (-1+j0) được đánh dấu
(+) trên hình vẽ không bị bao bởi đường đồ thị Nyquist nên hệ kín ổn định Đồ thị Bode.
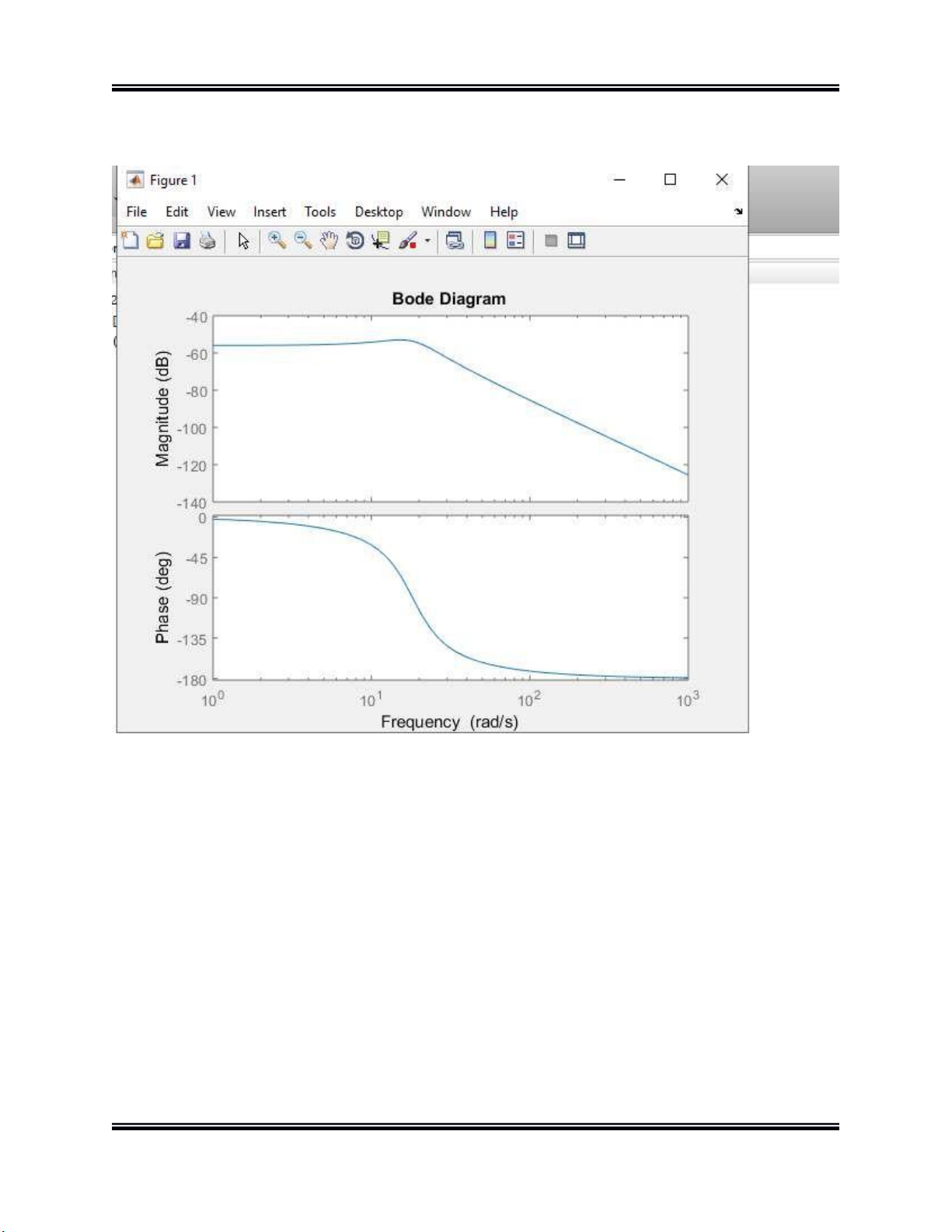
Từ dấu nhắc của cửa sổ Matlab ta nhập: » num = 290; » den = [650 7676.3 182000]; » bode(num,den)
Ta được đồ thị như hình bên dưới: SVTH: Đặng Văn Danh Trang | 6 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT Hình 4.
Đồ thị bode của hệ
Từ đồ thị ta nhận xét đường pha ở trên đường nên hệ kín ổn định
6.3.3.Kiểm tra đáp ứng của hệ SVTH: Đặng Văn Danh Trang | 7 lO M oARcPSD| 47704698
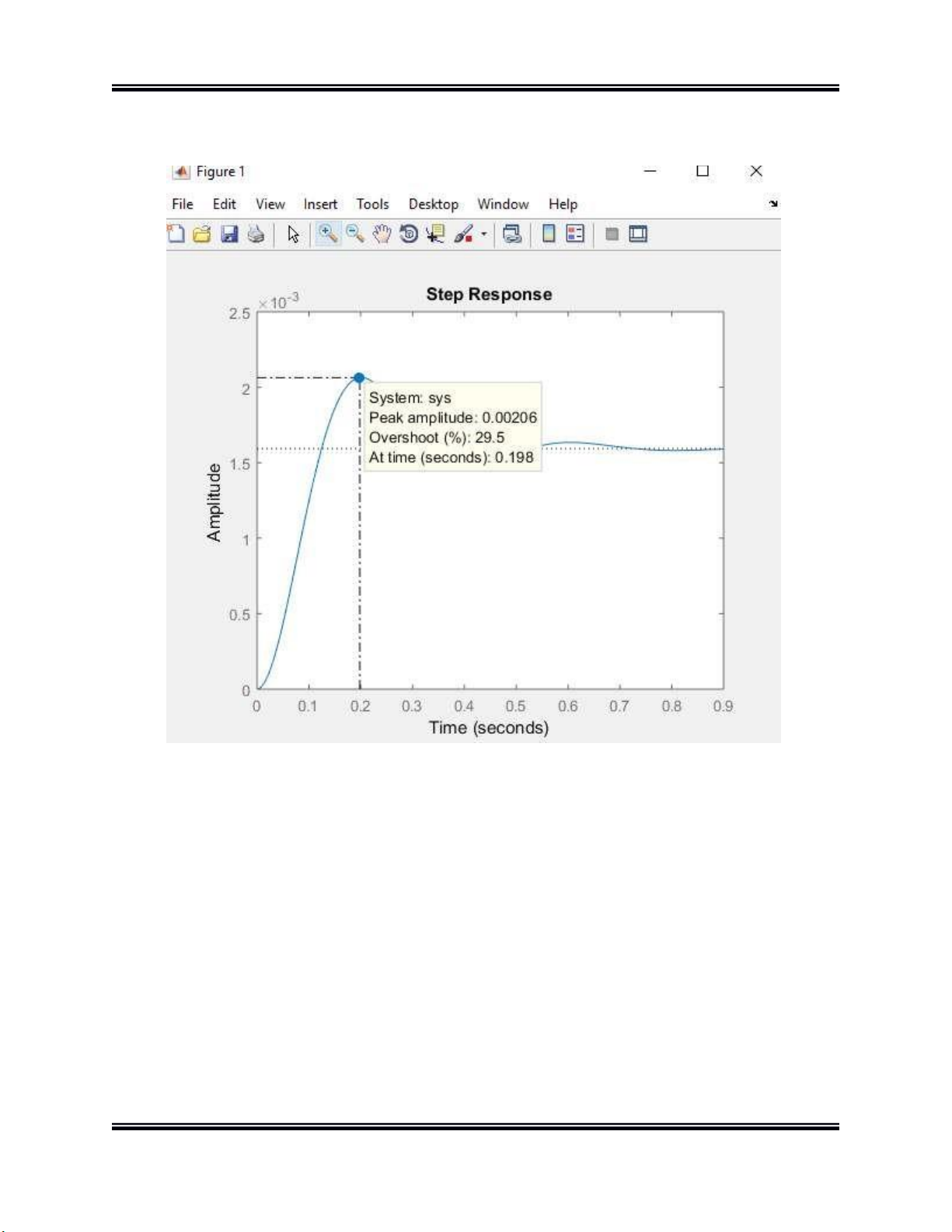
Đồ án thiết kế hệ thống CĐT Hình 5.
Đáp ứng khi đầu vào là hình bậc thang
Nhận xét: Với độ nhảy vọt (overshoot) lên đến =29.5%, =0.198s
Điều này là không chấp nhận được với hệ thống khi mà yêu cầu đặt ra độ quá độ
chỉ nằm trong khoảng 2%. Hơn nữa, ở đây chúng ta cho hệ kích thích bằng tín hiệu
l(t) nhưng hệ không bám lấy đầu vào
6.4. Thiết kế bộ điều khiển PID:
6.4.1. Những kiến thức cơ sở về bộ điều khiển PID:
Bộ PID có nhiệm vụ đưa sai lệch e(t) của hệ thống về 0 sao cho quá trình quá độ
thỏa mãn các yêu cầu cơ bản về chất lượng. SVTH: Đặng Văn Danh Trang | 8 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
- Nếu sai lệch e(t) thì thông qua khâu khuếch đại, tín hiệu u(t) càng lớn.
- Nếu sai lệch e(t) chưa bằng 0 thì thông qua khâu tích phân, PID vẫn còn tạo tín hiệu điều chỉnh.
- Nếu thay đổi sai lệch e(t) càng lớn thì thông qua thành phần vi phân, phản
ứng thích hợp của u(t) sẽ càng nhanh.
Bộ điều khiển PID được mô tả bằng mô hình vào – ra: ]
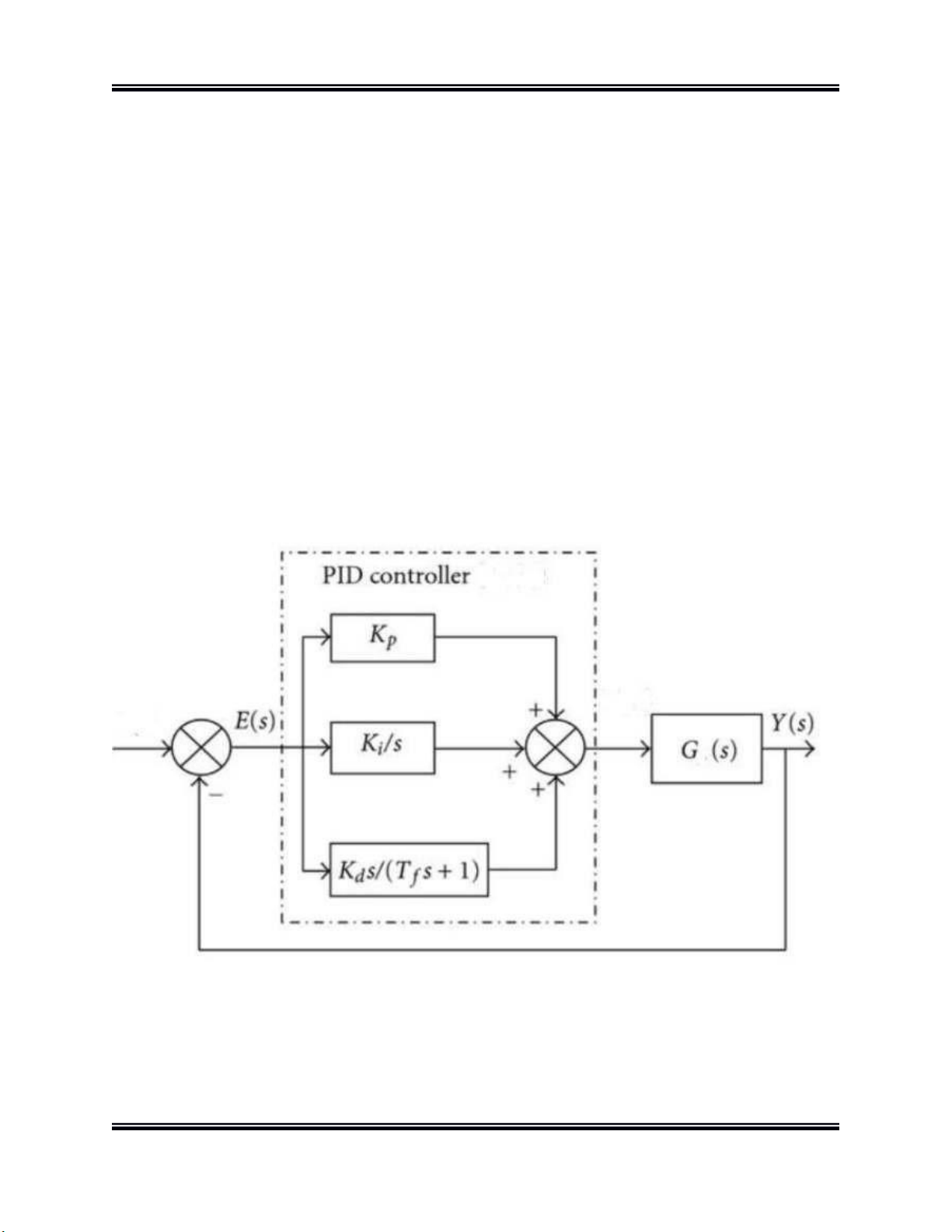
Hàm truyền đạt của bộ điều khiển PID: Hình 6.
Sơ đồ phản hồi vòng kín với bộ điều khiển PID
6.4.2. Vai trò các khâu tỉ lệ, tích phân, vi phân: - Khâu tỉ lệ: SVTH: Đặng Văn Danh Trang | 9 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
Giá trị càng lớn thì tốc độ đáp ứng càng nhanh, do đó sai số càng lớn, bù khâu tỉ lệ
càng lớn. Nếu độ lớn của khâu tỉ lệ quá cao, hệ thống sẽ không ổn định. Độ lớn
nhỏ là do đáp ứng đầu ra nhỏ trong khí sai số đầu vào lớn, và làm cho bộ điều
khiển kém nhạy, hoặc đáp ứng chậm. Nếu độ lợi của khâu tỉ lệ quá thấp, tác động
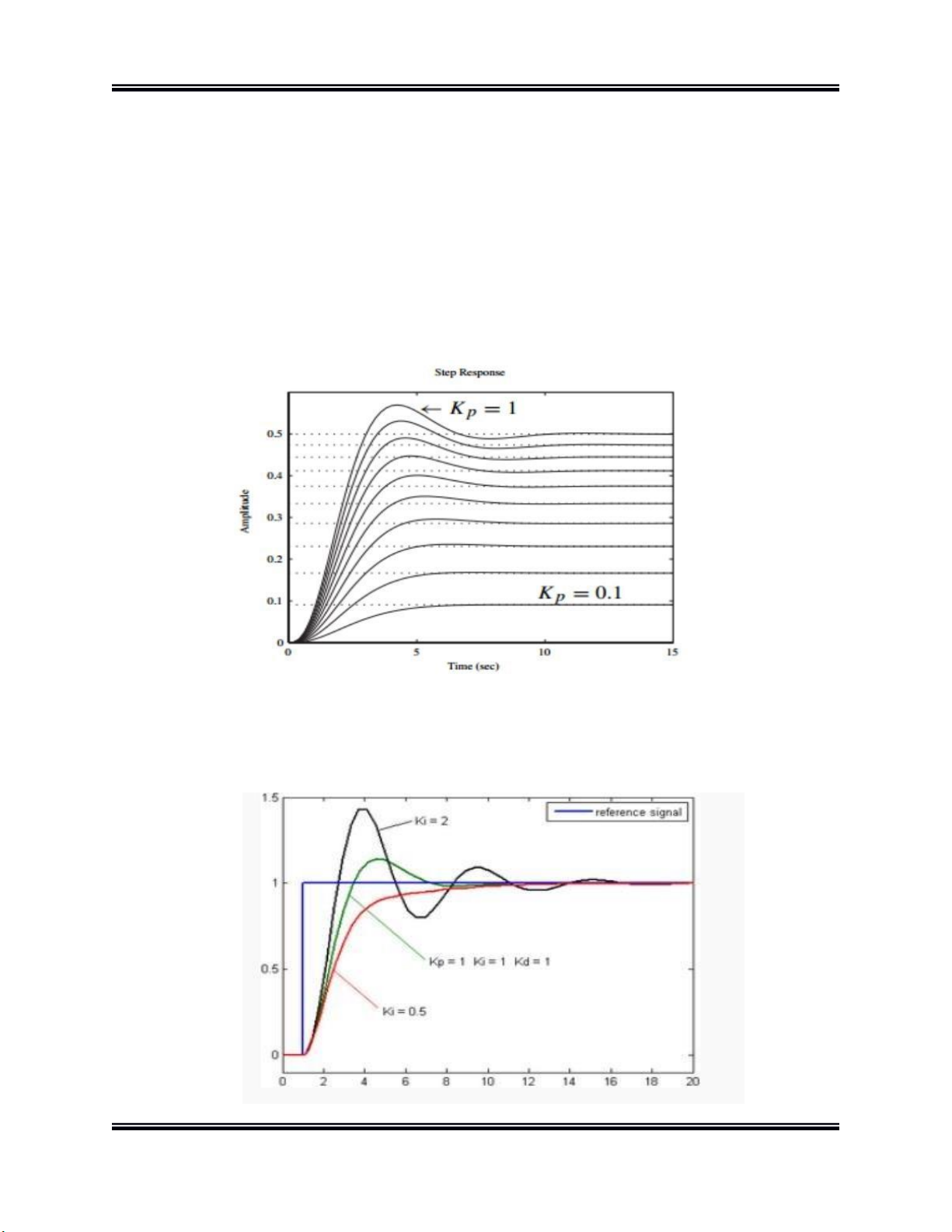
điều khiển có thể sẽ quá bé khi đáp ứng với các nhiễu của hệ thống. Hình 7.
Vai trò của khâu tỉ lệ trong bộ điều khiển PID - Khâu tích phân: SVTH: Đặng Văn Danh Trang | 10 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT Hình 8.
Vai trò của khâu tích phân trong bộ điều khiển PID
Phân phối của khâu tích phân (đôi khi còn gọi là reset) tỉ lệ thuận với cả biên độ sai
số lẫn quãng thời gian xảy ra sai số. Tổng sai số tức thời theo thởi gian
(tích phân hai số) cho ta tích lũy bù đã được hiệu chỉn trước đó. Tích lũy sai số sau
đó được nhân với độ lợi tích phân và cộng với tín hiệu đầu ra của bộ điều khiển.
Biên độ phân phối của khâu tích phân trên tất cả tác động điều chỉnh được xác định
bởi độ lợi tích phân, Ki.
Giá trị càng lớn kéo theo sai số bị khử càng nhanh. Đổi lại là độ vọt lố càng lớn:
bất kỳ sai số âm nào được tích phân trong suốt đáp ứng quá độ phải được triệt tiêu
tích phân bằng sai số dương trước khi tiến tới trạng thái ổn định. - -Khâu vi phân:
Khâu vi phân làm giảm tốc độ thay đổi của đầu ra bộ điều khiển và đặc tính này là
đáng chú ý nhất để đạt tới điểm đặt của bộ điều khiển. Từ đó điều khiển vi phân
được sử dụng để làm giảm biên độ vọt số được tạo ra bởi thành phần tích phân và
tăng cường độ ổn định của bộ điều khiển hỗn hợp. Tuy nhiên, phép vi phân của
một tín hiệu sẽ khuếch đại nhiễu và do đó khâu này sẽ nhạy hơn đối với nhiễu
trong sai số và có thể khiến quá trình trở nên không ổn định nếu nhiễu và độ lợi vi phân đủ lớn. SVTH: Đặng Văn Danh Trang | 11 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
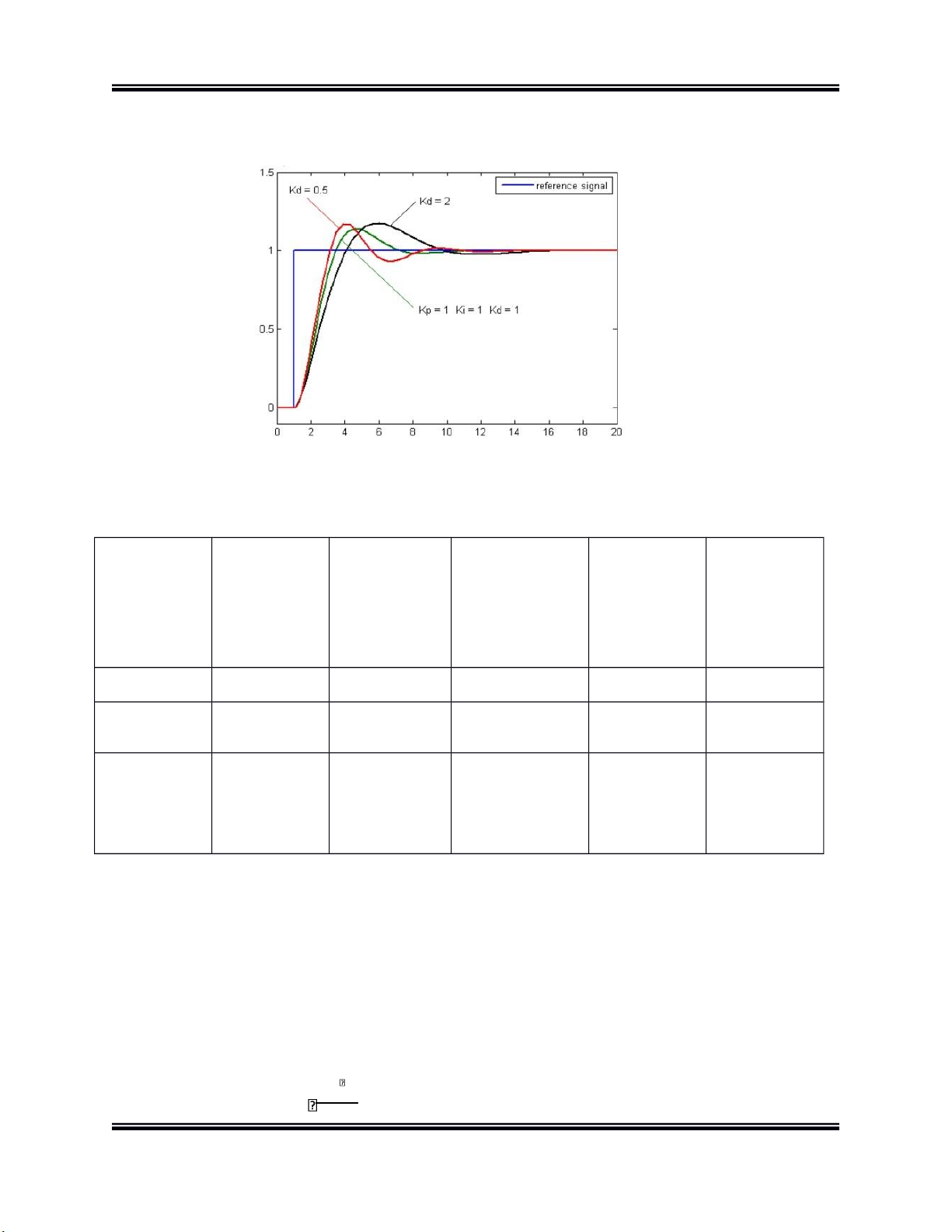
Hình 9. Vai trò của khâu vi phân trong bộ điều khiển PID Tác
động của việc tăng giảm một số thông số độc lập: Thông Số Thời gian Quá độ
Thời gian xác Sai số ổn Độ ổn định khởi động lập định Rise Time O ( vershoot ( Settlingtime ) ) Giảm Tăng Thay đổi nhỏ Giảm Giảm cấp Giảm Tăng Tăng Giảm đáng Giảm cấp kể Giảm ít Giảm ít Giảm Về lý Cải thiện thuyết nếu không tác nhỏ động
6.4.3.Thiết kế PID controller theo phương pháp thực nghiệm (phương pháp
Ziegler- Nichols thứ nhất)
Phương pháp Ziegler-Nichols thứ nhất sử dụng mô hình xấp xỉ quán tính bậc nhất
có trễ của đối tượng điều khiển. Ke Is G s( ) SVTH: Đặng Văn Danh Trang | 12 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT 1 Ts (1)
Phương pháp thực nghiệm có nhiệm vụ xác định các tham số KP, TI, TD cho bộ
điều khiển PID trên cơ sở xấp xỉ hàm truyền đạt G(s) về dạng (1), để hệ kín nhanh
chóng trở về chế độ xác lập và độ quá điều chỉnh không vượt quá một giới hạn h lim ( )h t
cho phép ,khoảng 40% so với t
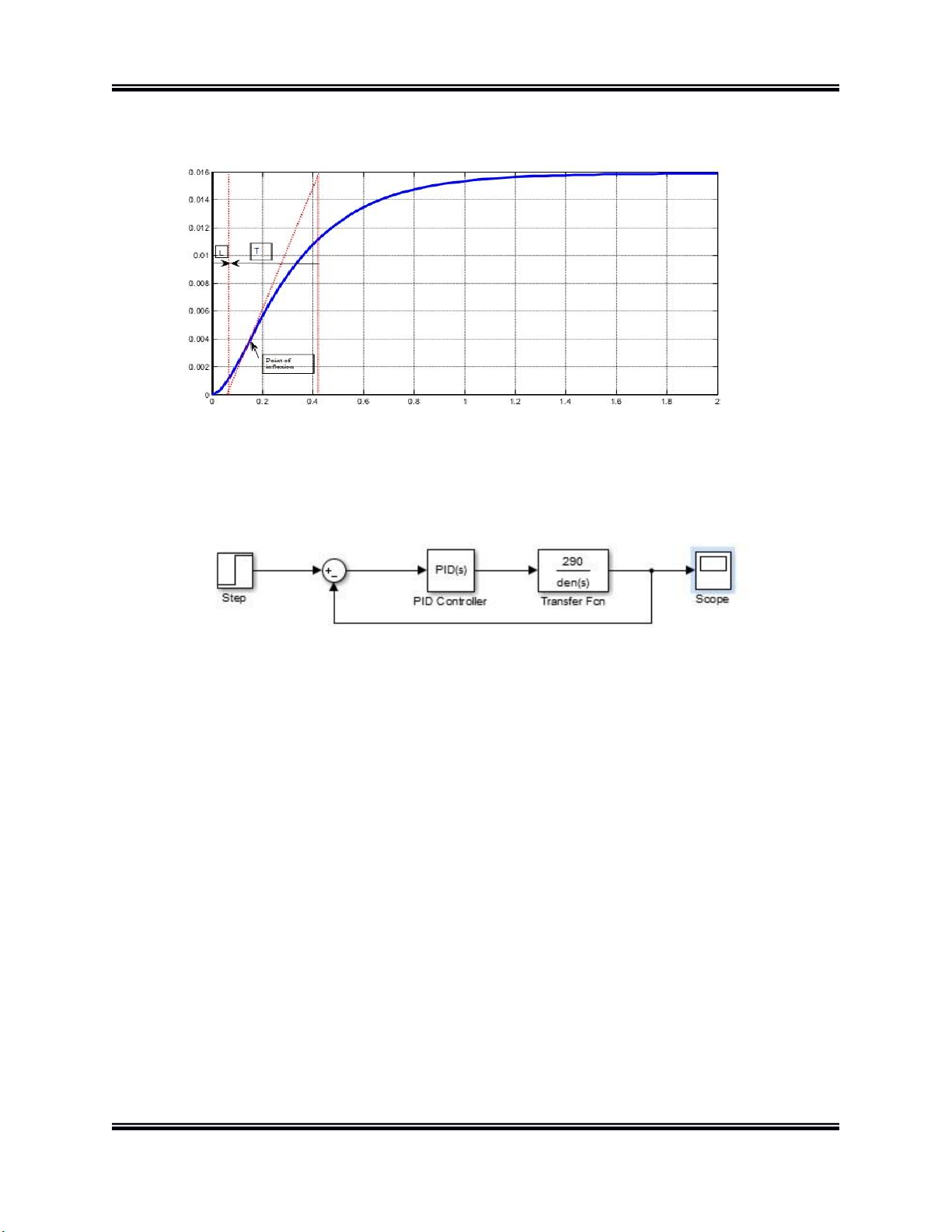
Ba tham số L( hằng số thời gian trễ) ,k(hệ số khuếch đại) và T( hằng số thời gian
quán tính) của mô hình sấp xỉ(1) có thể xác định gần đúng từ hàm quá độ h(t).
L là khoảng thời gian đầu ra h(t) chưa có phản ứng ngay với kích thích l(t) tại đầu vào. h lim ( )h t K là giá trị giới hạn t .
Gọi A là điểm kết thúc khoảng thời gian trễ, tức là điểm trên trục hoành có độ dài
bằng L. Khi đó T là khoảng thời gian cần thiết sau L để tiếp tuyến của h(t) tại A đạt giá trị k.
Sau khi đã tính được các thông số trên, bộ điều khiển PID có dạng: 1 S ) R s( ) K p (1 T1s TD L 1,2T kp với KL K p
.TI 2L hay KI 2L ,TD
2 hay KD 0,5k Lp
Áp dụng lý thuyết trên để thiết kế bộ điều khiển PID như sau: SVTH: Đặng Văn Danh Trang | 13 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT Hình 10.
Tìm các thông số L, T, k cho bộ điều khiển PID Hình 11.
Bộ điều khiển PID cho bàn X Thông
số ban đầu Kp=1, KI=1, KD=0:
Việc sử dụng công cụ mô phỏng số Matlab đã tích hợp sẵn công cụ thiết kế bộ điều
khiển PID. Kết quả của việc thiết kế bộ PID tự động dùng Matlab & Simulink như sau với:
Chọn bộ số PID tối ưu: = 1168 = 9985,48 = 33,82 SVTH: Đặng Văn Danh Trang | 14 lO M oARcPSD| 47704698
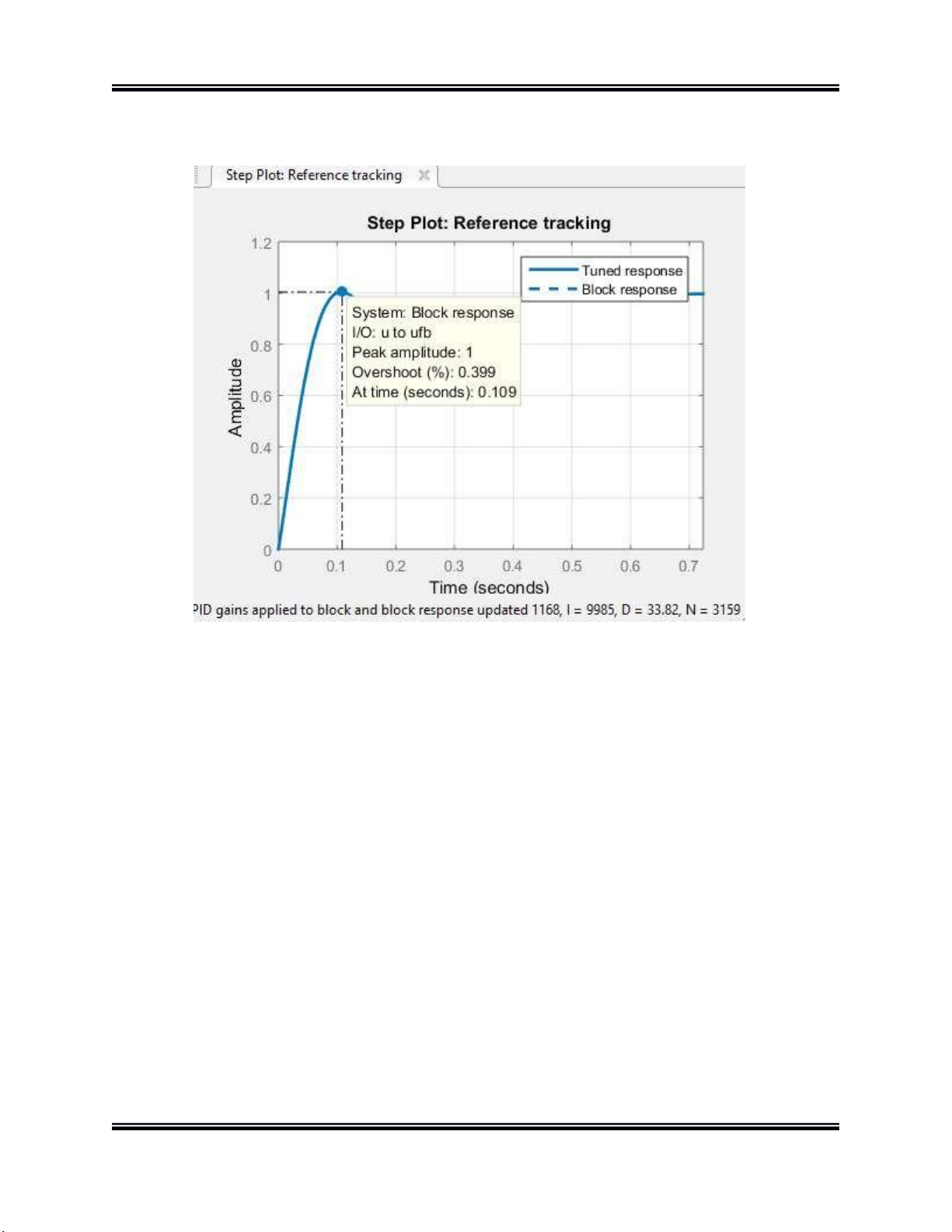
Đồ án thiết kế hệ thống CĐT Hình 12.
Đáp ứng khi có bộ điều khiển PID SVTH: Đặng Văn Danh Trang | 15 lO M oARcPSD| 47704698
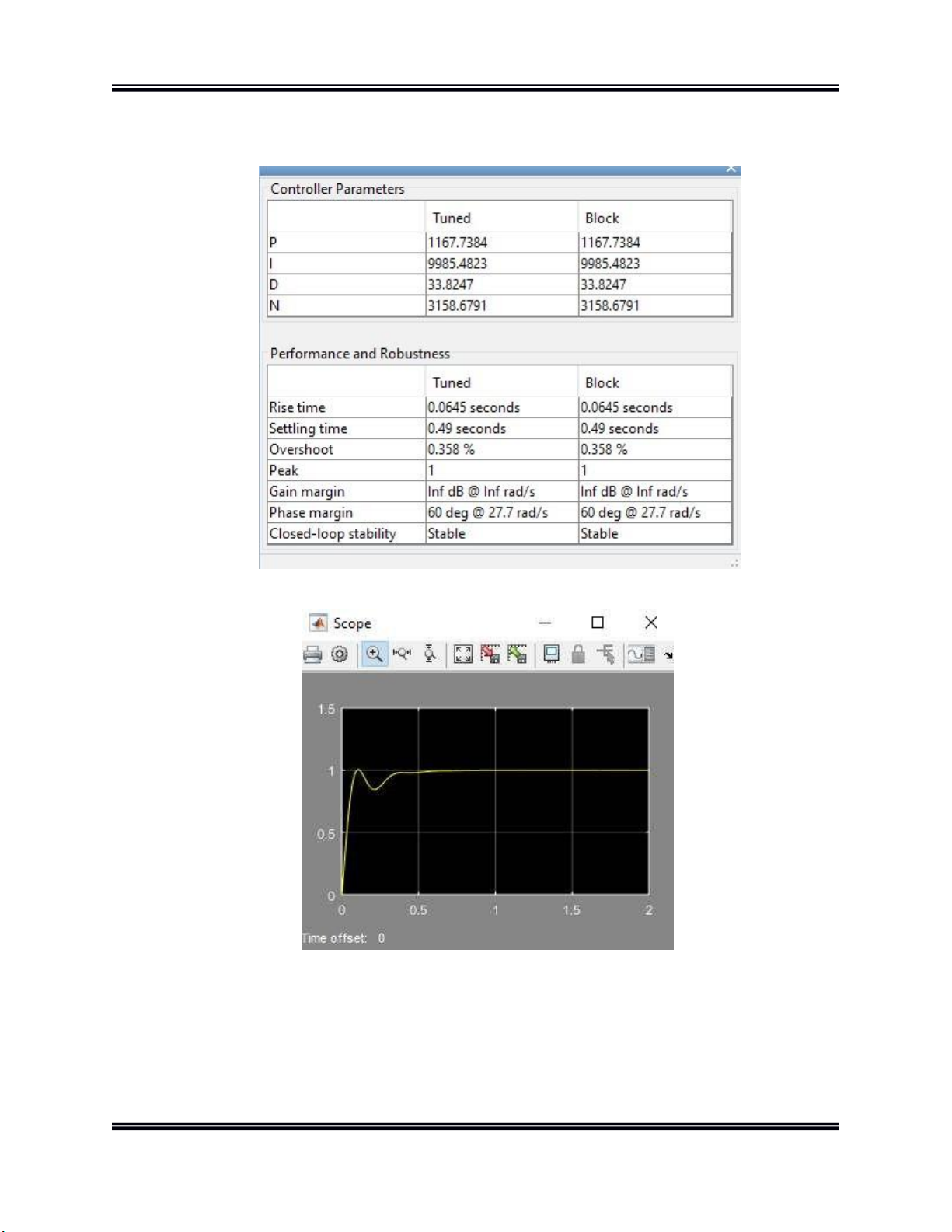
Đồ án thiết kế hệ thống CĐT Hình 13.
Bảng thông số bộ điều khiển PID
Nhìn vào đồ thị trên đáp ứng bước nhảy của bàn máy X khi có bộ điều khiển PID
ta thấy cơ hệ bám tốt tính hiệu đầu vào SVTH: Đặng Văn Danh Trang | 16 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
CHƯƠNG 7. BỘ ĐIỂU KHIỂN ĐỘNG CƠ BÀN MÁY Y THEO PID
7.1. Tìm hàm truyền của bàn Y: -
M: Khối lượng bàn máy và phôi -
k: Hệ số độ cứng của vít me, ổ bi, nối trục, ray dẫn hướng - B: Hệ số giảm chấn -
: Các lực tác dụng gồm lực động cơ và lực ma sát -
: Khoảng dịch chuyển của bàn máy Thông số có ban đầu: -
Khối lượng phôi: =500 kg -
Khối lượng bàn X : =150 kg -
Khối lượng bàn Y : =250 kg -
Khối lượng phôi và bàn máy : M = 500 + 150 + 250 = 900 kg - Hệ số ma sát: = 0.01 - Bước vít me: l = 10 mm -
Chiều dài vít me: L = 969 mm Phương trình toán học: M(t) + B(t) +Kx = Lực động cơ: -
Góc quay của động cơ cần để có thể tạo ra một dịch chuyển x(t)- Bước vít me
Lực ma sát: với = 0.01là hệ số ma sát Hệ số độ cứng: SVTH: Đặng Văn Danh Trang | 17 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT Trong đó:
Chọn kiểu nối trục Single Flexing Coupling với kích thước đường kính trong
40mm. Độ cứng của nó là 205,9x(Nm/rad). Tài liệu coupling 2 trang 14. -
Độ cứng của nối trục - Độ cứng của ổ bi -
Độ cứng ray dẫn hướng - Độ cứng trục vít me - Độ cứng càng cua -
: Độ cứng của bi trong trục vít me = ==27,24 () Trong đó: -
A: Diện tích mặt cắt ngang trục vít me , A= -
E : Hệ số module Young, E=2,1.(kgf/) -
x : Khoảng cách gá đặt x = L = 969 mm =0,8k.= 74,61. (N/m)
Trong đó k=151, tải trọng động = 5220 kgf, lực dọc trục =369 kgf Từ đó ta có bảng sau: 205,9. 222. 3. 27,24. 74,61. SVTH: Đặng Văn Danh Trang | 18 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
Ta tính được: K= 1,82. (N/m)
Hệ số giảm chấn: B=2=2.0,35. = 9042,2.
7.2 Tìm hàm truyền đạt G(s) M(t) + B(t) +Kx = -
Sử dụng toán tử Laplace 2 vế của phương trình ta được: MX(s) + BsX(s) + KX(s) = =>[ M+(B+= => G(s)= = =
7.3. Kiểm tra tính ổn định của hàm truyền G(s):
7.3.1. Kiểm tra sự ổn định của hệ hở:
Nếu tất cả các nghiệm của biểu thức A(s) đều nằm phía bên trái trục ảo hay khi đó
A(s) được gọi là đa thức Hurwitz, ta dung lệnh roots A(s) được bộ nghiệm sau đây: -5,023 + 13,3036i = -5,023 + 13,3036i
Do đó, Hệ hở ổn định.
7.3.2. Kiểm tra sự ổn định của hệ kín: Dùng tiêu chuẩn Nyquist
Từ dấu nhắc của cửa sổ Matlab ta nhập: » num = 290; » den = [900 9042,2 182000]; » nyquist(num,den) SVTH: Đặng Văn Danh Trang | 19 lO M oARcPSD| 47704698
Đồ án thiết kế hệ thống CĐT
Ta được đồ thị như hình bên dưới:
Hình 14. Đồ thị Nyquist của hệ
Dựa vào đồ thị bên dưới qua đồ thị ta nhận thấy rằng: Điểm (-1+j0) được đánh dấu
(+) trên hình vẽ không bị bao bởi đường đồ thị Nyquist nên hệ kín ổn định Đồ thị Bode.
Từ dấu nhắc của cửa sổ Matlab ta nhập: » num = 290; SVTH: Đặng Văn Danh Trang | 20