BỔ SUNG LÝ THUYẾT VÀ BÀI TẬP ĐIỆN - QUANG

lOMoARcPSD| 45650917
BỔ SUNG LÝ THUYẾT VÀ BÀI TẬP ĐIỆN - QUANG
A. PHẦN LÝ THUYẾT
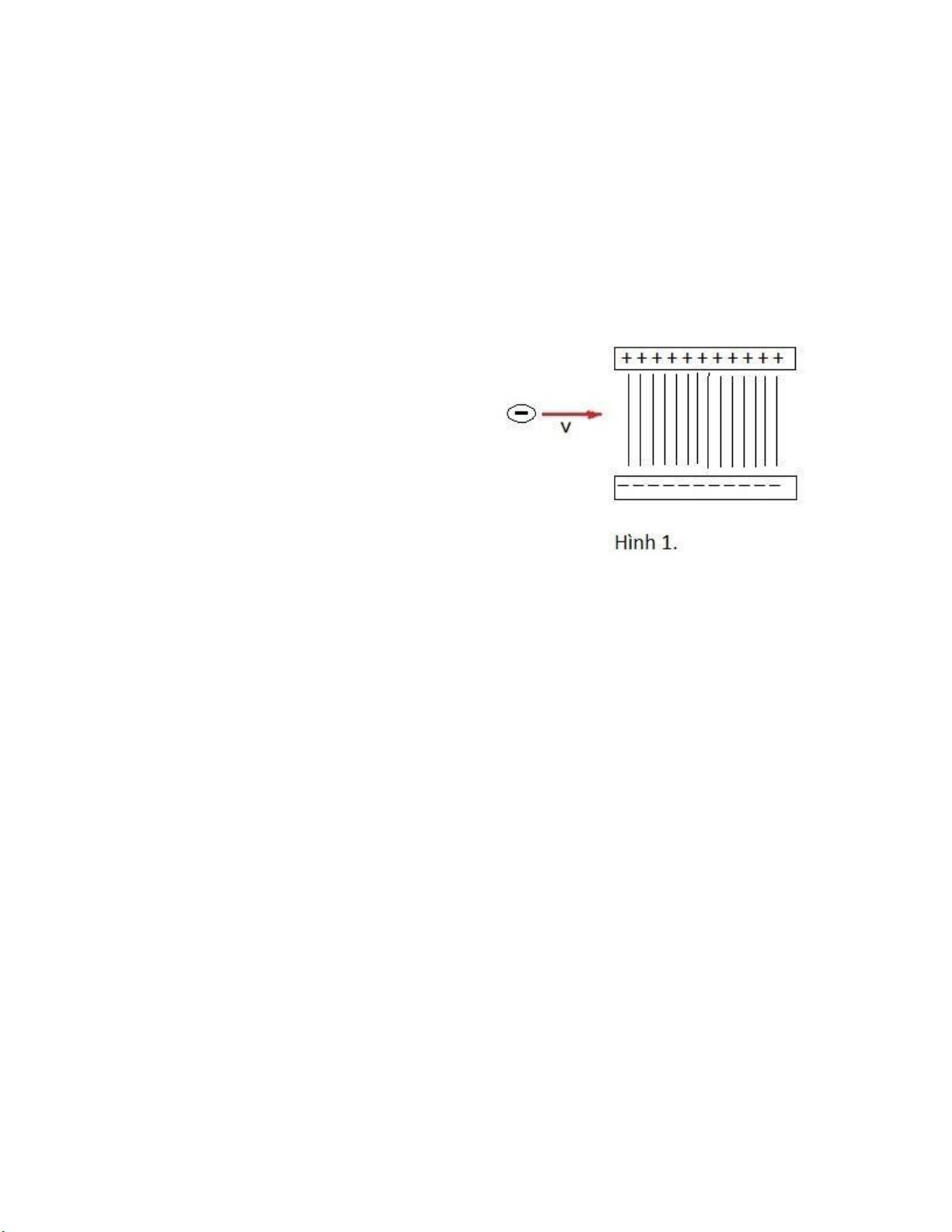
1. Một electron chuyển ộng theo phương nằm
ngang i vào khu vực của iện trường ồng nhất có
hướng vuông góc với phương chuyển ộng của
electron như trên Hình 1. Hãy mô tả quỹ ạo
chuyển ộng của electron. Cho biết quỹ ạo
chuyển ộng sẽ như thế nào khi thay thế iện tử bằng proton?
2.Viết biểu thức xác ịnh thế năng (U) của hệ gồm một cặp iện tích (q1, q2) ặt cách nhau một
khoảng r12. Giải thích ý nghĩa vật lí khi cặp iện tích cùng dấu thì thế năng của hệ là dương và khi
cặp iện tích trái dấu thì thế năng của hệ là âm?
3. Một iện tích âm chuyển ộng theo hướng của iện trường ồng nhất. Hỏi: thế năng của hệ ( iện
tích – iện trường) tăng hay giảm? Điện tích ó ang ược chuyển ộng về phía iện thế cao hay thấp?
4. Trình bày (phát biểu và biểu thức) ịnh lý O-G và nêu ứng dụng.
5. Cho ba quả cầu kim loại giống hệt nhau A, B, C. Hai quả cầu A và B tích iện bằng nhau, ặt
cách nhau một khoảng lớn hơn rất nhiều so với kích thước của chúng. Lực tác dụng giữa hai
quả cầu này là F. Quả cầu C không tích iện. Người ta cho quả cầu C tiếp xúc với quả cầu A,
sau ó cho tiếp xúc với quả cầu B, rồi cuối cùng ưa C ra rất xa A và B. Bây giờ xác ịnh lực tĩnh iện giữa A và B.
6.Điện trường trong khí quyển có hướng thẳng ứng xuống dưới (ở các ộ cao hợp lí). Cường ộ của
nó bằng 60 V/m ở ộ cao 300m và bằng 100 V/m ở ộ cao 200m. Tính lượng iện tích chứa trong 1 lOMoARcPSD| 45650917
khối không khí hình lập phương có cạnh bằng 100 m, nằm giữa hai ộ cao ó. Tính số ion (hóa trị
1) trung bình chứa trong 1 m3 không khí. Nêu nhận xét về kết quả thu ược. 7.
Khoảng cách giữa hai bản của một tụ iện phẳng không khí là cm. Người ta ặt vào
hai bản một hiệu iện thế
V. Hỏi tụ iện có bị “ ánh thủng” không? Cho biết không
khí trở thành dẫn iện khi cường ộ iện trường lớn hơn giá trị V/m ( thường ược
gọi là iện trường ánh thủng). Nếu sau ó, người ta ặt vào giữa hai bản tụ một tấm thủy tinh dày
3mm, với hằng số iện môi thì tụ iện có bị hỏng không? Biết rằng iện trường ánh thủng ối với thủy tinh là V/m. 8.
Định nghĩa và nêu ý nghĩa vật lý của iện thế, hiệu iện thế. Công thức liên hệ giữa véc tơ
cường ộ iện trường và iện thế.
9.Cho một quả cầu iện môi bán kính R tích iện ều trong toàn bộ thể tích của nó với tổng iện tích
Q . Diễn giải biểu thức tính iện trường do quả cầu gây ra tại iểm cách tâm cầu một khoảng r (chia
hai trường hợp r R và r R ).
10.Diễn giải quá trình ưa ra công thức iện dung của tụ iện phẳng, tụ iện trụ và tụ iện cầu.
11. Hai dòng iện thẳng vô hạn song song ngược chiều, ặt cạnh nhau thì hút nhau hay ẩy nhau?
Giải thích, vẽ hình minh họa.
12. Phát biểu ịnh lý dòng toàn phần (Định lý Ampere).
13. Phát biểu ịnh luật Biot-Savart-Laplace.
14. Mô tả chuyển ộng của một hạt mang iện tích dương q , chuyển ộng với vận tốc ban ầu    
v trong từ trường ều B , với góc tạo bởi giữa v và B là 90  . 15. 2 lOMoARcPSD| 45650917 
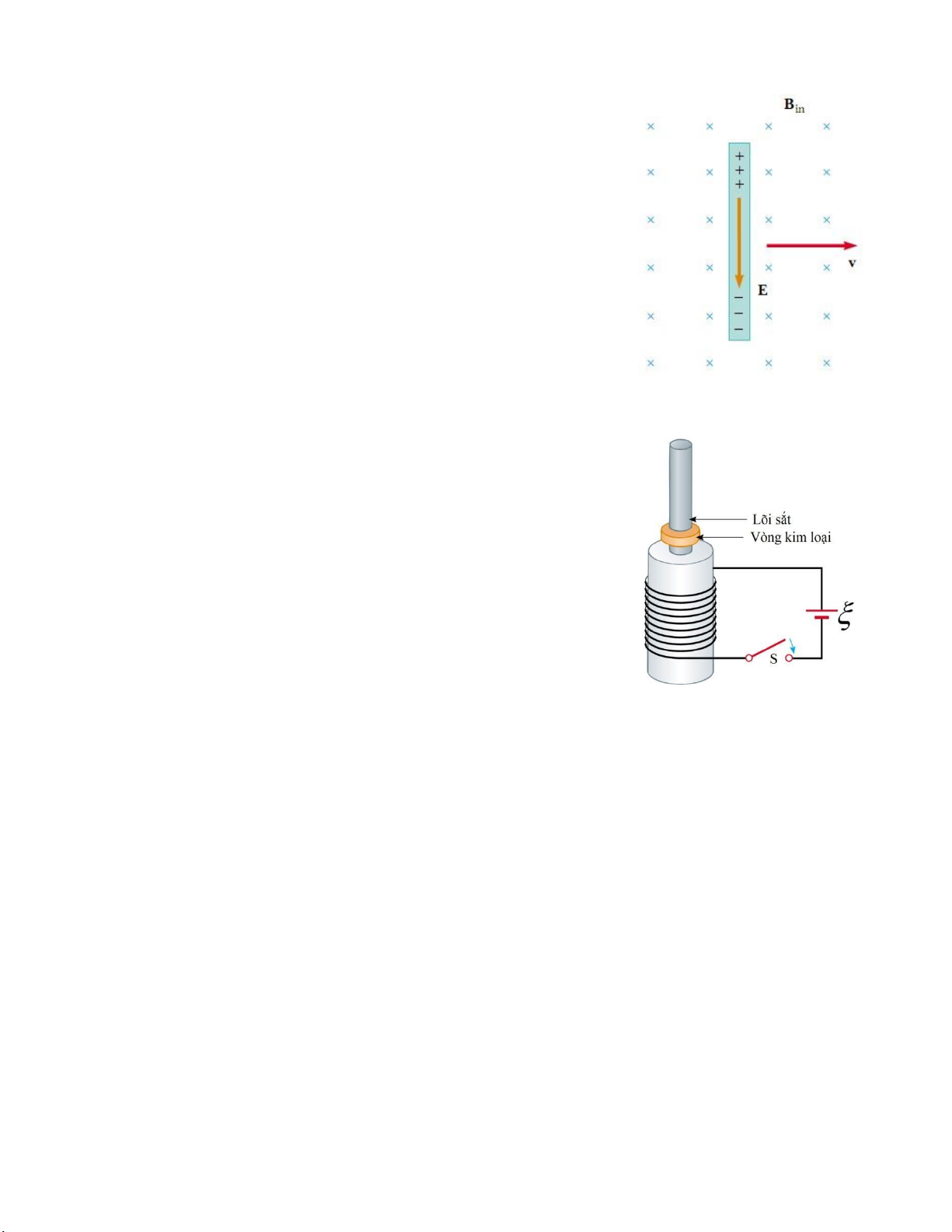
Khi một thanh vật dẫn chuyển ộng sang bên phải với vận tốc v 
trong từ trường ều B như hình vẽ,
một iện trường E ược thiết lập giữa hai ầu của thanh. Hãy giải
thích vì sao iện trường có chiều như vậy? 16.
Trong thí nghiệm mô tả trong hình vẽ, khi óng khóa S, vòng kim
loại nhảy bật lên. Hãy giải thích hiện tượng này? 17.
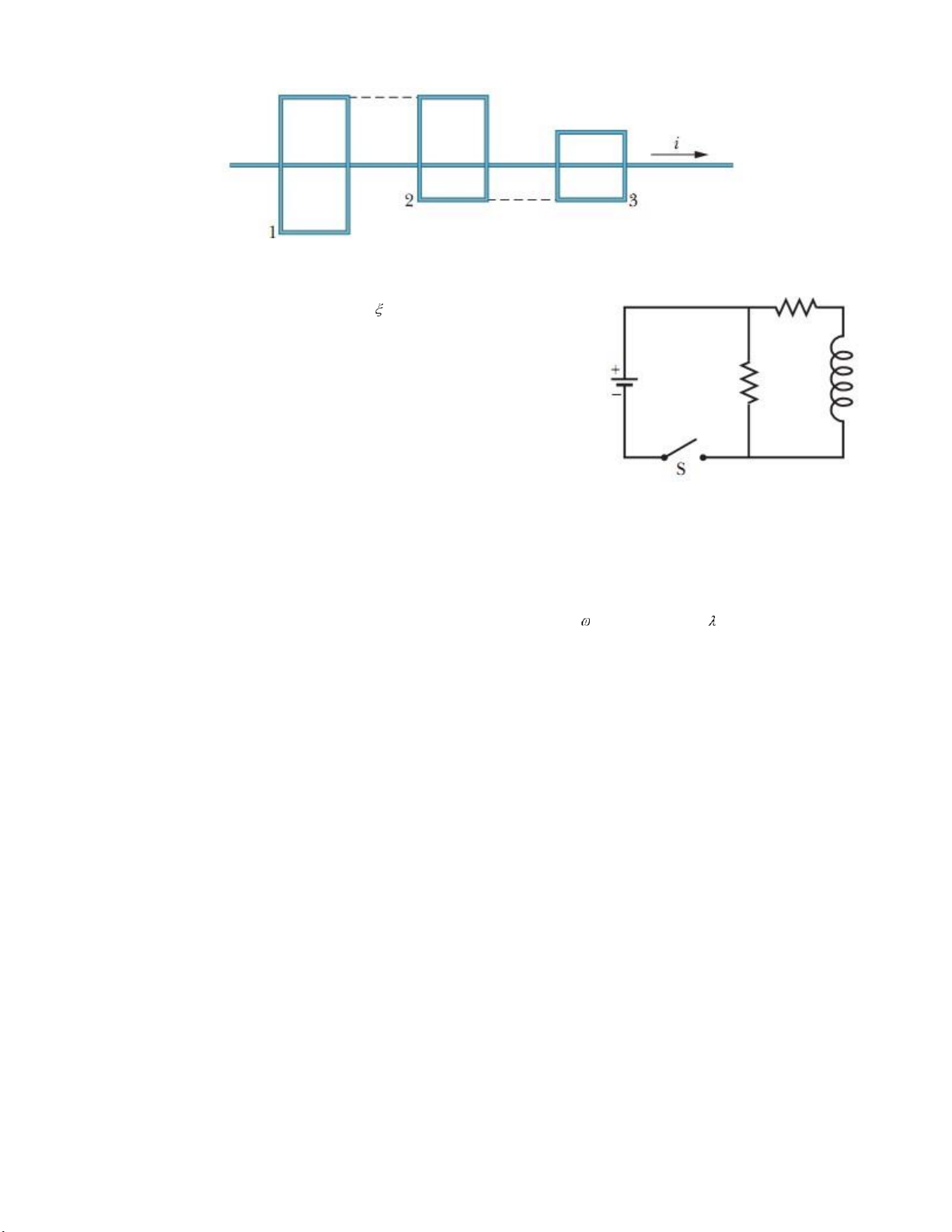
Trên hình vẽ, một dây dẫn thẳng dài vô hạn ược ặt cạnh (nhưng không chạm) vào 3 khung dây
dẫn hình chữ nhật với chiều rộng là L , chiều dài tương ứng là 2L , 1, 5 L , và L . Các dây ược ặt xa
nhau ể không ảnh hưởng ến nhau. Các khung dây 1 và 3 ược ặt ối xứng so với dây dẫn thẳng.
Hãy xếp thứ tự các khung dây theo ộ lớn dòng iện cảm ứng xuất hiện trong chúng nếu dòng iện i : a) Là hằng số. b) Tăng dần 3 lOMoARcPSD| 45650917 18.
Trên hình vẽ, mạch iện gồm nguồn , 2 iện trở R giống nhau và
một cuộn cảm lý tưởng (có iện trở không áng kể), có ộ tự cảm
L . So sánh cường ộ dòng iện chạy qua hai iện trở trong các trường hợp sau: a) Ngay sau khi óng khóa S.
b) Sau khi ã óng khóa S một thời gian dài.
c) Ngay sau khi mở khóa S lại sau ó một thời gian dài.
d) Một thời gian dài sau khi mở khóa lại.
19. Phát biểu 2 luận iểm của Maxwell (phương trình Maxwell-Faraday và phương trình Maxwell- Ampere).
20.Viết phươngtrình sóng iện từ phẳng ối với thành phần iện trường E và từ trường B , tốc ộ truyền
sóng, nghiệm ơn giản, mà hệ thức giữa số sóng k , tần số góc và bước sóng .
21. Giả sử thí nghiệm giao thoa với hai khe Young ược thực hiện trong nước, các vân giao thoa
sẽ thay ổi thế nào so với thí nghiệm trên nhưng ược thực hiện trong không khí? Hãy giải thích?
22.Tại các vũng nước khi có dầu loang, tại sao ta thấy tương tự như màu sắc cầu vồng?
23. Trình bày Nguyên lý Huygens – Fresnel.
24. Giải thích hiện tượng nhìn thấy màu sắc cầu vồng khi quan sát ánh sáng phản xạ trên ĩa CD, DVD.
25. Trình bày hiện tượng nhiễu xạ tia X trên mạng tinh thể, diễn giải công thức Bragg và nêu
ứng dụng trong thực tiễn của công thức này.
26. Để kiểm tra chất lượng của bề mặt một gương phẳng bằng cách ứng dụng hiện tượng giao
thoa ánh sáng người ta làm như thế nào?
27. Trong thí nghiệm khe ôi Young, tại sao chúng ta sử dụng ánh sáng ơn sắc. Nếu sử dụng ánh
sáng trắng, hình ảnh giao thoa sẽ thay ổi như thế nào. 4 lOMoARcPSD| 45650917
28. Phát biểu các ịnh luật về bức xạ nhiệt: Ðịnh luật Stéfan–Boltzmann, Ðịnh luật Wien.
29. Trong thí nghiệm nhiễu xạ qua khe hẹp ơn, ộ rộng của cực ại trung tâm thay ổi như nào khi ộ rộng khe hẹp giảm?
30. Một tấm kim loại ược chiếu bởi ánh sáng với tần số ã biết. Điều gì dưới ây sẽ xác ịnh việc
iện tử có bị bắn ra hay không? Giải thích tại sao?
a) Cường ộ của ánh sáng.
b) Thời gian chiếu của ánh sáng.
c) Độ dẫn nhiệt của tấm kim loại.
d) Diện tích của tấm kim loại.
e) Vật liệu tạo thành tấm kim loại. B. PHẦN BÀI TẬP
1.Hai iện tích iểm Q1 5 nC và Q 2
3 nC nằm cách nhau một khoảng r = 35 cm.
a) Tính thế năng tương tác tĩnh iện giữa 2 iện tích iểm này. Ý nghĩa của dấu của kết quả?
b) Tính iện thế tại iểm nằm chính giữa 2 iện tích iểm. HD:
Thế năng tương tác tĩnh iện giữa hai iện tích: QQ 7 1 2 3.852 10 U 4 r 0
Điện thế tại iểm nằm chính giữa hai iện tích: Q 1 Q 2 102.71 V V V 1 2 4 2 r 4 2 r 0 0
2.Hai hạt nhỏ mang iện tích 3q và
q ược gắn chặt vào
một thanh cách iện và cách nhau một
khoảng d . Một hạt
mang iện thứ 3 có thể trượt tự do dọc theo thanh. Xác ịnh vị trí cân bằng của hạt thứ 3 này. Cân bằng ó có bền không? 5 lOMoARcPSD| 45650917 HD:
Gọi khoảng cách từ hạt thứ 3 (mang iện tích q ) ến hạt mang iện tích 3q là x . Ở vị trí cân bằng, lực tác
dụng từ hạt mang iện tích 3q bằng và ngược hướng với hạt mang iện tích q : 3 qq qq 2 2 4 x 4 d x 0 0 Từ ó: 1 d x d x 3 x 1 13
…. Kết luận: cân bằng là bền. 3. Bốn mặt kín từ S ến cùng các iện tích 1 S 4
2Q , Q , và Q ược cho trong
hình vẽ. Hãy tìm iện thông qua từng mặt kín ó. HD:
Điện thông qua mặt S : 1 2 Q QS QS 1 1 1
Điện thông qua mặt S : 2 Q QS 2 2 0
Điện thông qua mặt S : 3 6 lOMoARcPSD| 45650917 2 2 Q Q Q S QS 3 3 3
Điện thông qua mặt S : 4
4 0 , do không có iện tích nào bên trong mặt S 4
4.Một quả cầu ặc bán kính R 40 cm mang iện tích Q 26 µC phân bố ều trong toàn bộ thể tích của nó. Tính
giá trị của iện trường tại iểm cách tâm cầu (a) 0 cm, (b) 10 cm, (c) 40 cm, và (d) 60 cm. HD:
Chọn mặt Gauss là mặt cầu bán kính r . Với r
R , iện tích nằm bên trong mặt cầu ó là: 3 4 3 r . q 3 Q r 3 R Áp dụng ịnh lý O-G:   2 q . E .4 dS E r r R r R  0 Q E r r R 3 4 0 R Với r
R , iện tích nằm bên trong mặt cầu ó là Q . Áp dụng ịnh lý O-G: 2 Q .4 E r r R 0 Q E r R 2 4 0 r
Thay các dữ liệu của ề bài.
5.Trong phân hạch hạt nhân, một hạt nhân nguyên tử Uranium-238 gồm 92 proton phân rã thành 2 hạt
nhân nhỏ hơn (hình cầu) gồm 46 proton và có bán kính R 5.9
10 –15 m. Tính lực ẩy tĩnh iện giữa hai hạt nhân nhỏ này. HD:
Giả sử ở trạng thái ban ầu, hai hạt nhân nhỏ hình cầu nằm sát nhau, khoảng cách giữa tâm của chúng là
2R . Lực ẩy tĩnh iện giữa chúng là: 2 2 7 lOMoARcPSD| 45650917 Z e 2 F 4 2 R , với 46 d Z 0 Thay dữ liệu. 6.
a) Tính vận tốc của proton ược gia tốc từ trạng thái nghỉ bởi hiệu iện thế U 120 V.
b) Tính vận tốc của electron ược gia tốc từ trạng thái nghỉ bởi hiệu iện thế U 120 V. 27
Cho khối lượng của proton là m p
1.6726219× 10 kg, khối lượng electron là m e 9 .1 × 1 0 31 kg.
Điện tích của proton là q p
1.6× 10 19 C, iện tích của electron là q e 1 .6 × 1 0 19 C. HD:
a) Động năng của proton thu ược sau khi gia tốc: 1 qU 2 2 p 151518.87 mv qU v (m/s) p p p p 2 W m p
Động năng của proton thu ược sau d p, khi gia tốc: 1 2 2 qU e 6495983.54 mv qU v ee e e 2 W m d e, e 7.
Hai vỏ cầu vật dẫn ồng tâm có bán kính là a 0.4 m và b 0.5 m, ược nối với
nhau bởi một dây dẫn. Nếu ặt lên hệ một iện tích Q 1 0 µC thì iện tích
ược phân bố trên mỗi vỏ cầu là bao nhiêu? HD:
Gọi iện tích trên mỗi vỏ cầu là q và . Do hai vỏ cầu ược nối với nhau bằng dây dẫn nên iện thế trên 2 1 q 2 vỏ cầu bằng nhau: 8 lOMoARcPSD| 45650917 q 1 q 2 q 1 q 2 Q V 4 4 a 4 b 4 a b a b 0 0 0 0
Vậy iện tích trên từng quả cầu là: 40 a 50 b Q Q q 9 a b µC và 9 a b µC 1 q 2 8.
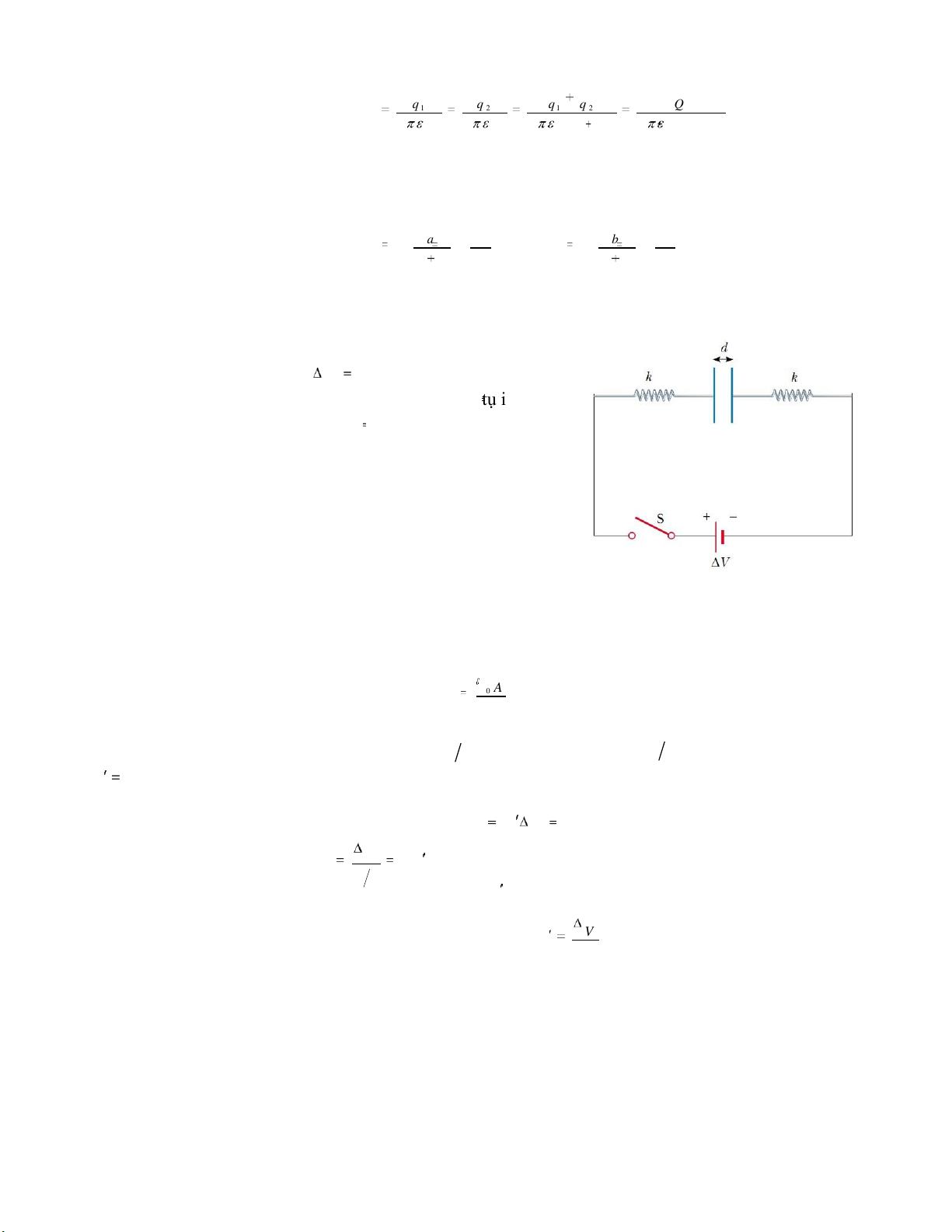
Hai bản kim loại giống nhau ược nối với hai lò xo kim loại có ộ
cứng k và nối với nguồn 100 V. Khi khóa S mở, hai bản không tích V
iện, khoảng cách giữa hai bản là d 8 mm và tạo thành tụ iện có iện
dung C 2 µF. Khi óng khóa S, khoảng cách giữa hai bản giảm i còn một nửa.
a) Tính iện tích trên mỗi bản kim loại.
b) Độ cứng của mỗi lò xo là bao nhiêu? HD:
Gọi A là diện tích của một bản kim loại. Hai bản kim loại tạo thành một tụ iện phẳng với iện dung: 0 A C d
Khi óng khóa S, khoảng cách giữa hai bản là d 2 , mỗi lò xo giãn một oạn d 4 , iện dung của tụ là C 2C . Điện tích trên tụ là: q C V 4 0 0 µC V
Điện trường giữa hai bản tụ là E 2 d
2 E , với E là iện trường do một bản kim loại gây ra: E V d
Lực hút giữa hai bản kim loại là: 9 lOMoARcPSD| 45650917 2 2 F d 2 C V C V qE d d 2 8 C V
Ở trạng thái cân bằng: T ừ ó: 2500 k d F F k d dh 2 4 d 9.
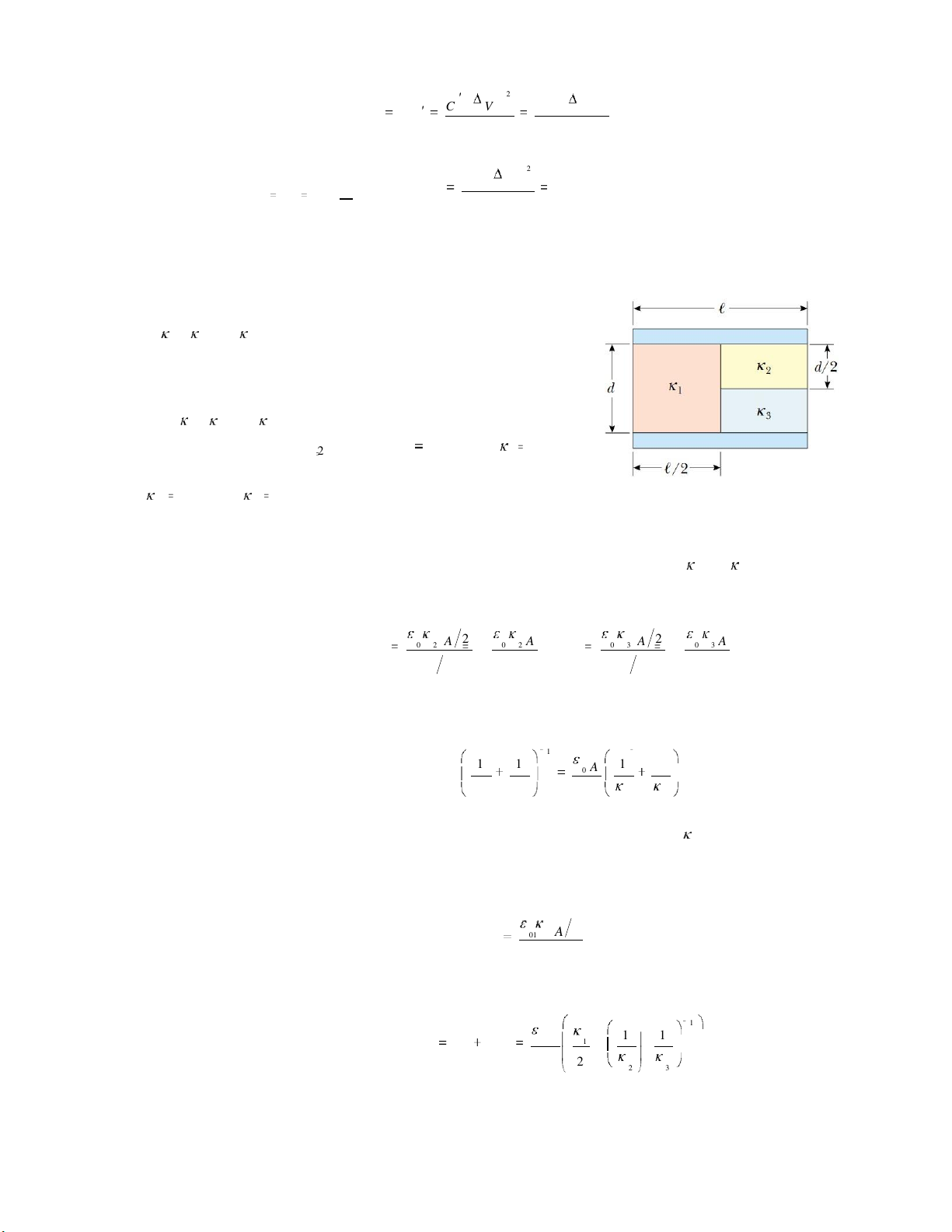
Một tụ iện phẳng sử dụng 3 chất iện môi với các hằng số iện môi , và . Coi 1 2 3 l d .
a) Xây dựng công thức iện dung của tụ theo
diện tích bản tụ A , khoảng cách giữa 2 bản tụ
d , và các hằng số iện môi , và . 1 2 3
b) Tính kết quả với A 1 cm2, d 2 mm, 1 4.9 , 2 5.6 , và 3 2.1 . HD:
Giả sử ặt một lá kim loại mỏng có ộ dày không áng kể vào giữa hai chất iện môi và . Khi ó lá kim 2 3
loại này sẽ óng vai trò là iện cực trung gian và tạo thành 2 tụ iện mắc nối tiếp với iện dung tương ứng là: 2 A 2 A 0 2 0 2 A A và 0 3 0 3 C 3 C 2 d d 2 d d 2
Điện dung tương ương là: 1 1 1 1 1 A 1 0 C 23 C 2 C 3 d 2 3
Tụ iện tương ương C tiếp tục mắc song song với tụ iện có iện 23 C 1
môi do cùng tiếp xúc với hai bản cực của tụ iện chính. Điện dung của tụ : 1 C 1 A C 01 2 1 d
Vậy iện dung của tụ iện chính là: 1 1 A 1 0 1 C 1 C 23 2 d C 2 3 Thay dữ liệu. 10 lOMoARcPSD| 45650917 10.
Tính công suất nhiệt tỏa ra trên từng iện trở trong mạch trên hình vẽ. Đáp án:
Hai iện trở 4 Ω mắc song song nên tương ương 1 iện trở 2 Ω.
Gọi dòng iện chạy qua nguồn 50 V và iện trở R 2 là , chạy qua nguồn 20 V và iện trở 1 I 1 R
2 là (quy ước chạy từ cực dương của các nguồn), dòng iện chạy qua iện trở tương ương 2 Ω là 2 I 2
I (quy ước chạy từ trên xuống dưới). Chiều dương của các ô mạng theo chiều kim ồng hồ. Các phương 3
trình ịnh luật Kirchhoff: 0 I I I 1 2 3 2 2 I 50 I 0 1 3 2 2 I 20 I 0 2 3
Giải hệ phương trình trên thu ược: 20 I A 1 15 I A 2 5 I A 3
Công suất tỏa nhiệt trên từng iện trở: 2 800 P RI W 1 1 1 2 450 P RI W 2 2 2 2 50 P RI W 3 3 3
Công suất tỏa nhiệt trên từng iện trở 4 Ω là P 31 2 P P 32 25 W 3 11 lOMoARcPSD| 45650917
11.Sử dụng các ịnh luật Kirchhoff, hãy tìm:
a) Dòng iện qua mỗi nhánh trên mạch iện trên Hình vẽ.
b) Hiệu iện thế giữa iểm c và iểm f. Điểm nào có iện thế cao hơn? HD:
Giả sử chiều dòng iện từ f ến a, từ c ến f, từ d ến c.
Giả sử chiều dương trong 2 ô mạng abcf và cdef ều theo chiều kim ồng hồ.
Áp dụng ịnh luật Kirchhoff thứ 1: (1)
Áp dụng ịnh luật Kirchhoff thứ 2 cho 2 ô mạng abcf và cdef: (2) (3)
Thay số vào ta có hệ phương trình:
Giải hệ phương trình trên thu ược:
Hiệu iện thế giữa 2 iểm c và f:
Điểm c có iện thế cao hơn iểm f. 12 lOMoARcPSD| 45650917
12.Một proton chuyển ộng gia tốc trong iện trường 640 N/C từ trạng thái dừng (vận tốc ban ầu bằng
không). Sau một khoảng thời gian, vận tốc của nó ạt giá trị là 1,20 × 106 m/s. Cho biết: Khối lượng của
proton m = 1,67 × 10-27 kg, iện tích của proton q = 1,6 × 10-19 C. Tính: a) Gia tốc chuyển ộng của proton.
b) Thời gian ể proton ạt ược vận tốc trên
c) Quãng ường proton i ược trong khoảng thời gian ó.
d) Động năng của proton tại thời iểm ó? HD:
a) Áp dụng công thức: a = qE/m.
Thay số tính ược a ~ 6,13 x 1010 m/s2
b) Thời gian ể proton ạt ược vận tốc trên là:
t = v/a = 1,20 × 106 m/s : 6,13 x 1010 m/s2 = 1,96 x 10-5 s hay 0.196 µs.
c) Quãng ường proton i ược trong khoảng thời gian ó là: S = at2/2 = ½ × 6,13× 1010
m/s2× (1,96 x 10-5 s)2 = 11.77 m
d) Động năng của proton tại thời iểm ó là:
mv2/2 = (1,67 × 10-27 kg) × (1,20 × 106 m/s)2/2 = 1,2 x 10-15 J
13.Một quả cầu nhỏ bằng thủy ngân bán kính R, tích iện ều với mật ộ iện khối là ρ và ặt trong không khí.
Tính cường ộ iện trường tại iểm cách tâm quả cầu một oạn là r.Giả sử có N giọt thủy ngân giống nhau và
tích iện ều, iện thế bề mặt mỗi quả là V. Nhập các giọt này thành một giọt hình cầu lớn. Tìm iện thế V0
trên bề mặt giọt lớn này. HD:
Đường sức iện trường là những ường thẳng hướng dọc theo bán kính quả cầu. Độ lớn cường ộ iện trường
tại các iểm trên cùng mặt cầu có giá trị như nhau
Chọn mặt Gaus là mặt cầu ồng tâm với quả cầu tích iện. Ta chia bài toán làm 2 trường hợp như sau:
- Trường hợp 1: Điểm M nằm bên trong quả cầu, tức là r<R. Ta có
Điện thông qua mặt cầu bán kính 2 r là: .4 E
r . Áp dụng ịnh lý O-G ta có q i 0 4 2 3 .4 E r V r Suy ra, 3 0 13 lOMoARcPSD| 45650917 r
Vậy iện trường tại iểm M (cách tâm quả cầu một khoảng r < R) sẽ là: E 3 0
- Trường hợp 2: Điểm N nằm ngoài hoặc nằm trên quả cầu: r ≥ R Áp dụng ịnh lý O-
G tương tự như trường hợp 1 ta có: 4 2 3 .4 E r V R 3 0
Vậy, iện trường tại iểm N (cách tâm quả cầu một khoảng r ≥ R) sẽ là: 3 R 2 E 3 r 0
Giả sử iện tích của một giọt thủy ngân là q, bán kính của giọt thủy ngân là R thì iện thế bề mặt của một giọt thủy ngân nhỏ là kq V R
Giả sử bán kính của giọt thủy ngân lớn là kq
R0 thì iện thế bề mặt của giọt thủy ngân lớn V N 0 R 0
Mặt khác, thể tích của giọt thủy ngân lớn bằng thể tích của N giọt thủy ngân nhỏ nên ta có: 3 3 4 4 R N R 0 3 3 3 Do ó, R R N 0 kq kq 2 / 3 N N VN Điện thế 3
trên mặt giọt thủy ngân lớn sẽ là: V R 0 R N 0
14.Giả sử có một nguyên tử mà trong ó một iện tử ở cách proton một khoảng là r = 5,2×10–9 cm chịu sức
hút tĩnh iện của proton. Muốn iện tử ó thoát khỏi sức hút tĩnh iện của proton thì nó cần ược chuyển ộng
với vận tốc tối thiểu là bao nhiêu? (Biết iện tích của iện tử bằng 1,6×10–19 C, khối lượng của iện tử bằng 9,1×10–31 kg). HD:
Công của iện trường tác dụng lên iện tử là: 2 14 lOMoARcPSD| 45650917 A . ke ke qV e r r
Để iện tử thoát khỏi sức hút của proton thì ộng năng của nó phải lớn hơn công của iện trường. Nói cách khác, ta có: 2 mv W d A 2 2 2 2 2 ke Ta có: mv ke , hay v=3,12×106 (m/s) mr 2 r
Như vậy, ể iện tử thoát khỏi sức hút tĩnh iện của proton thì iện tử phải có vận tốc tối thiểu là v = 3,12×106 (m/s).
15.Tụ phẳng không khí C = 6µF ược tích iện ến hiệu iện thế U = 600V rồi ngắt khỏi nguồn. Nhúng tụ vào iện môi lỏng (
) ngập 2/3 diện tích mỗi bản. Tính hiệu iện thế của tụ. Tính công cần thiết ể nhấc
tụ iện ra khỏi iện môi. Bỏ qua trọng lượng tụ. HD:
Khi nhúng một phần tụ vào iện môi, tụ có thể ược xem là hai phần tụ mắc song song là C1||C2. Ta có iện
dung của tụ không khí là: S 3 C 9 C 9.10.4 3 d 1
Điện dung của phần tụ lấp ầy iện môi: 2 S 8 3 C 9 C 9.10.4 3 d 2
Điện dung tương ương của C1, C2 là: C’ = C1 + C2 = 3C
Khi ngắt tụ khỏi nguồn thì iện tích của tụ không ổi: Q’ = Q nên CU = C’U’
Do ó, U’ = UC/C’ = UC/3C = U/3 = 200 V
Công ể nhấc tụ khỏi iện môi.
Năng lượng của tụ trong không khí là W1 = U2C/2 = 1,08J 15 lOMoARcPSD| 45650917
Năng lượng của tụ sau khi nhúng vào iện môi là W2 = U’2C’/2 = 0.36J
Công cần thiết ể nhấc tụ ra khỏi iện môi làA = W1 – W2
16.Cho một hình cầu iện môi rỗng tạo bởi 2 mặt cầu ồng tâm với bán kính trong là R1 15 cm, bán kính
ngoài là R 2 20 cm, tích iện ều theo toàn bộ thể tích của nó (phần không rỗng) với iện tích là Q 20
C . Hãy tính cường ộ iện trường tại:
a) Điểm cách tâm cầu 18 cm.
b) Điểm cách tâm cầu 25 cm. HD:
Mật ộ iện tích khối là: Q 4 3 3 R 2 R 1 3
Chọn mặt Gauss là mặt cầu với bán kính r . a) Với R r
, iện tích nằm trong mặt cầu ó là: 1 R 2 3 3 4 Q Q r R 1 3 3 r R 1 3 3 4 3 3 3 R 2 R 1 R 2 R 1 Q 3 1 Điện trường là: 3 3 r R 1 Q 1 Q 2 3 2 3 E 1 4 4 r R R r 2 1 0 0 Với r 18 cm, E1 2 .9 4 7 1 0 6 (V/m). b) Với r
R , iện tích nằm trong mặt cầu ó là Q 2 Q 2 Điện trường là: Q 2 E 4 r 2 0 16 lOMoARcPSD| 45650917 Với r 25 cm, E 2 2 .8 7 9 1 0 6 (V/m). 17.
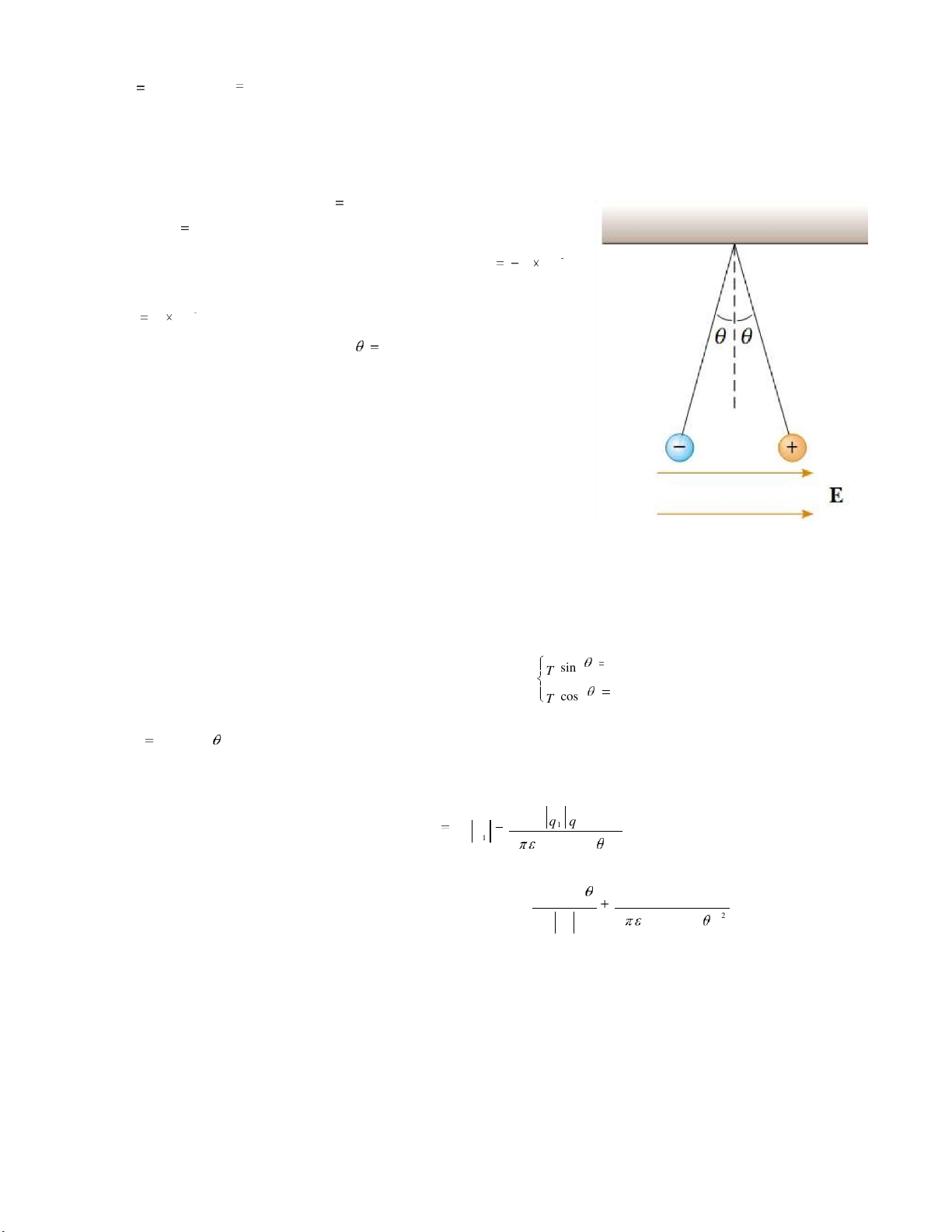
Hai quả cầu nhỏ khối lượng m 2 g, ược treo bằng dây
nhẹ chiều dài l 10 cm. Một iện trường ều ược ặt vào
theo phương x. Điện tích của các quả cầu tương ứng 8 5 10 là q 1 8 C và q 5 10
C. Hãy xác ịnh ộ lớn iện trường 2 E ể 
các quả cầu có thể cân bằng ở góc lệch 10 . HD:
Áp dụng ịnh luật II Newton ối với quả cầu 1 (bên trái, mang iện tích âm) và chiếu lên các phương x và ythu ược: sin T F d cos T mg Từ ó: F tan mg
. Lực tĩnh iện gồm lực do iện trường d Fd
E gây ra và lực hút tĩnh iện của iện tích dương q . 2 q 1 q 2 F Eq 1 d 2 4 2 0 sin l tan mg T ừ ó: q 2 441740 E (V/m). 2 q 4 2 sin l 1 0 18. 17 lOMoARcPSD| 45650917
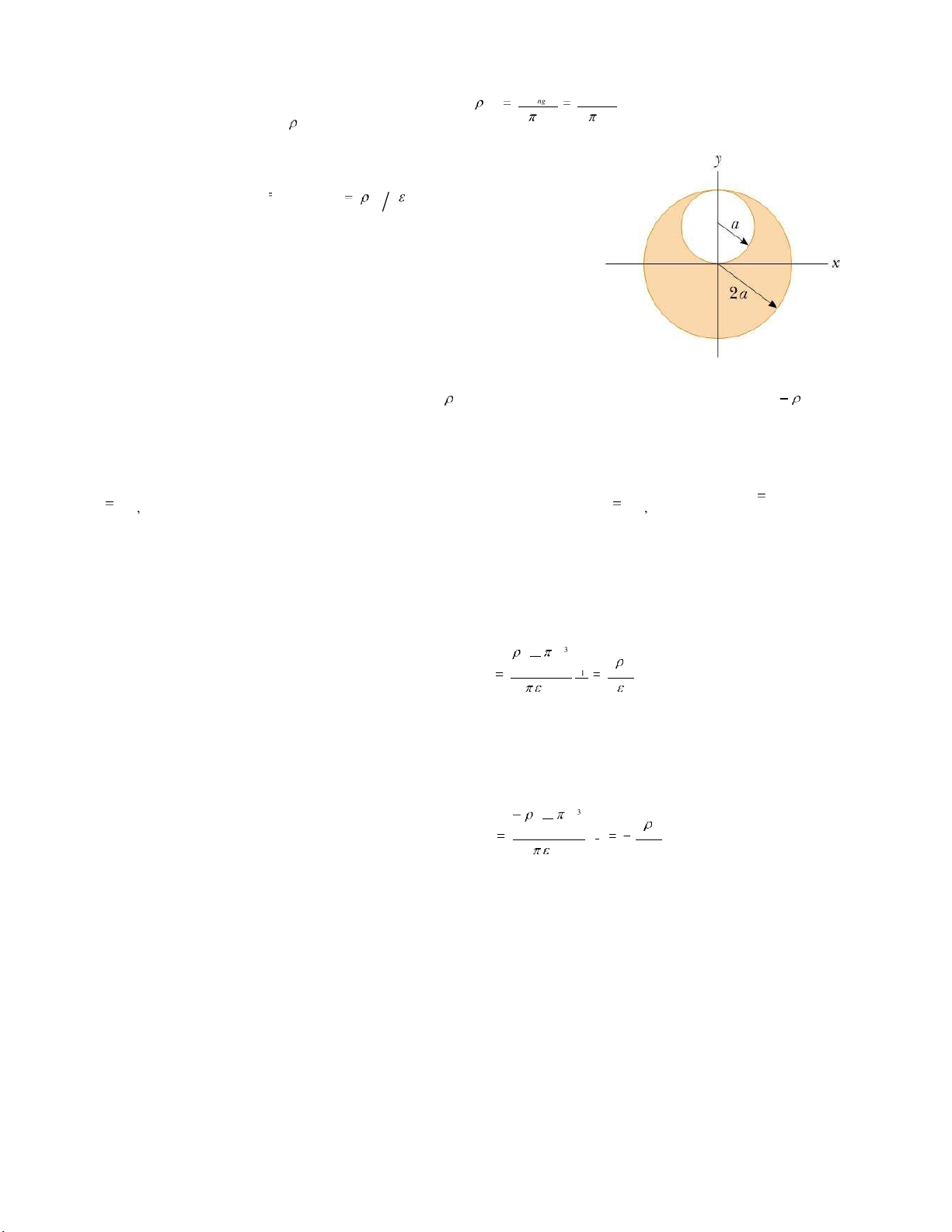
Một quả cầu iện môi ặc bán kính a tích iện ều
với mật ộ iện tích và tổng iện tích là Q . Quả
cầu ược ặt ồng tâm bên trong một vỏ cầu làm
bằng vật dẫn có bán kính trong là b và bán kính
ngoài là c . Vỏ cầu trung hòa về iện.
a) Tìm cường ộ iện trường tại các iểm cách a , a r b ,
tâm cầu khoảng r với các trường hợp r b r c , và r c .
b) Tính iện tích trên một ơn vị diện tích ở mặt trong và
mặt ngoài của vỏ cầu vật dẫn. HD:
a) Chọn mặt Gauss là mặt cầu bán kính r . Với r
a , iện tích nằm bên trong mặt cầu ó là: 3 4 3 r q . r 3 Q 3 a Áp dụng ịnh lý O-G:   2 q . E .4 dS E r r a r a  0 Q E r r a 3 4 0 a Với a r
b , iện tích nằm bên trong mặt cầu ó là Q . Áp dụng ịnh lý O-G: 18 lOMoARcPSD| 45650917 Với 2 Q b r
c , iện tích nằm bên trong mặt cầu ó là .4 E Q Q , với là iện tích nằm ở tr Q tr r a r b 0 Q
E a r b 2 4 r
mặt trong của vỏ cầu vật dẫn. Áp dụng ịnh lý O 0 -
G: trung hòa về iện nên iện tích Q
nằm ở mặt ngoài của vỏ cầu vật dẫn là Q Q . Với r
c , iện tích nằm bên trong mặt cầu ó là Q
b) Mật ộ iện tích mặt trong vỏ cầu là: Q Q tr tr 2 2 4 4 b b
Mật ộ iện tích mặt ngoài vỏ cầu là: 19 lOMoARcPSD| 45650917
19.Một quả cầu iện môi bán kính 2 Q a ược tích iện ng Q
ều với mật ộ iện tích khối . Quả cầu ược khoét i ng 2 2 4 4 c c
một hốc hình cầu bán kính a như hình vẽ. Chứng
minh rằng iện trường bên trong hốc là ều với 3 a E 0 . x 0 và E y HD:
Coi quả cầu ược khoét i là sự chồng chập của 1 quả
cầu bán kính 2 a nguyên vẹn với mật ộ iện khối và 1 quả cầu bán kính a với mật ộ iện khối , nằm ở úng vị trí của hốc.
Xét một iểm P trong hốc có tọa ộ là x y, . Bán kính véc-tơ vẽ từ tâm O1 của quả cầu lớn ến P là:  . Bán 1 , xy , xy
kính véc-tơ vẽ từ tâm O  
2 của quả cầu nhỏ ến P là: r . 2 a .
Đặt a O O1 2 r
Điện trường do quả cầu lớn gây ra tại P: 4 3 .   1 r 3 1 r  1 r 2 E 1 4 3 r r 0 1 1 0
Điện trường do quả cầu nhỏ gây ra tại P: 4 3  . r  2 r  E 3 2 2 r 2 2 4 3 r r 0 2 2 0
Điện trường tổng hợp tại iểm P:  E 20