BTTCC22023 (1)_250225_094903

STRY AND TRAD U E D - IN EL F E O CT Y R R I T C S I P N O I W M ER . Y U T I N S R E V I EPU BÀI TẬP T TOÁN CAO CẤP 2 Sư tầm tầm từ đề đề thi Toán T 2 các năm Biên tập tập lại th t eo heo trình tự tự bài giản giả g ng lý thu th y uyết Tài T liệu lưu hành nội bộ HÀ NỘI – 9/2023 Chương 1:
PHÉP TÍNH VI PHÂN, TÍCH PHÂN CỦA HÀM MỘT BIẾN Bài tập 1:
a. Xét sự liên tục của hàm số sau tại x = 1 : √  2x − 1 − 1  , x 6= 1 f (x) = x2 − 1 .  a , x = 1
b. Xét sự liên tục của hàm số sau tại x = 0 : √ √  3x + 1 − 3 5x + 1  f (x) = , x 6= 0 x .  a , x = 0
c. Xét sự liên tục của hàm số sau tại x = 0: √ √  2αx + 1 − βx + 1   , x 6= 0   x f (x) = .  β    , x = 0 2 Bài tập 2: Cho hàm số
f (x) = x(x − 1)(x − 2) . . . (x − 11). Tính f 0(0)?
Bài tập 3: Tìm vi phân của các hàm số: √ 5x x + 3 x a. y = 1 + x2 . b. y = . x
Bài tập 4: Tính đạo hàm của các hàm số: a a x b x b a. y =
, a > 0, b > 0, x > 0. b x a b. f (x) = x2 + 5x − 1cos x. c. f (x) = x2 + 4x + 3sin x.
Bài tập 5: Dùng công thức tính gần đúng vi phân, tính gần đúng giá trị của biểu thức a. A = arctan 1, 02. b. A = 3 p1, 06.
Bài tập 6: Xét sự hội tụ của các tích phân suy rộng Z +∞ dx Z +∞ dx a. I = . c. I = √ √ . x2 + x − 8 3 0 1 + 2x · 3 1 + x2 Z +∞ dx Z +∞ dx b. I = √ . d. I = √ . 3 3 x4 − 1 3 e−x( x − 1)
Bài tập 7: Tính tích phân suy rộng Z +∞ I = xe−5xdx 0 Chương 2: CHUỖI SỐ
Bài tập: Xét sự hội tụ của các chuỗi số ∞ n2 +∞ X 3n + 5 X 2n + 8n a. . g. . 7n − 3 7n n=1 n=1 ∞ ∞ n2 X 3n + 5 X nn b. . h. . 3n − 2 n! n=1 n=1 +∞ ∞ n2 (n + 5)2 X n + 5 X c. . i. . n − 3 73n+4 n=1 n=1 ∞ ∞ n X 2n − sin n + 1 X 2.4.6 . . . .(2n) d. √ . j. . 5n + 1 + n nn n=1 n=1 ∞ ∞ X 31/n − 1 X 1 e. √ . k. . n (n2 + 1) 6n n=1 n=1 ∞ X 3n + 5n f. . 8n n=1 Chương 3: HÀM SỐ NHIỀU BIẾN SỐ Bài tập 1: Cho hàm số z = ln x2 + xy + y2.
Chứng minh rằng xz0 + yz0 = 2. x y
Bài tập 2: Tìm các đạo hàm riêng z0 ; z0 và vi phân toàn phần cấp một dz của các x y hàm số: a. z = arctan(xy). x d. z = arctan . y b. z = ln y2 − 5x + 7 . p e. z = x3y − xy. p c. z = x2y − y2x.
Bài tập 3: Tìm vi phân toàn phần cấp một của hàm số x z = e y . Bài tập 4: Cho hàm số z = xy − ln y + 5.
Tìm các đạo hàm riêng cấp một và cấp hai của hàm số đã cho?
Bài tập 5: Tìm cực trị của các hàm số a. z = x2 + y2 − xy + x + y.
d. z = x3 + 3xy2 − 15x − 12y.
b. z = 4(x − y) − x2 − y2. e. z = 3xy − x2 − 2y2 + 9.
c. z = 2xy − 3x2 − 2y2 + 15.
f. z = 2x2 + y2 − 2xy − 2x + 7. Chương 4:
TÍCH PHÂN BỘI – TÍCH PHÂN ĐƯỜNG
Bài tập 1: Tính các tích phân kép Z Z a. I =
(x + 2y)dxdy, với D là miền giới hạn bởi {0 ≤ x ≤ 1; 0 ≤ y ≤ x}. D Z Z b. I =
x2 + y2 dxdy, trong đó D là miền giới hạn bởi {1 ≤ y ≤ 3; y − 1 ≤ x ≤ y}. D Z Z c. I =
(2x − y)dxdy, với D là miền giới hạn bởi 0 ≤ x ≤ 2; x2 ≤ y ≤ 4 . D Z Z d. I =
(x − 2y − 5)dxdy, với D là miền giới hạn bởi {0 ≤ x ≤ 1; 0 ≤ y ≤ x}. D Z Z y n √ o e. I =
dxdy, trong đó D là miền được xác định bởi 0 ≤ x ≤ 1; 0 ≤ y ≤ 1 − x2 . x2 + 1 D Z Z f. I =
x ln ydxdy, với D là miền giới được xác định bởi {0 ≤ x ≤ 4; 1 ≤ y ≤ e}. D Z Z dxdy g. I =
, trong đó D là miền giới hạn bởi x ≥ 0; y ≥ 0; x2 + y2 ≤ 1 . p1 + x2 + y2 D Z Z h. I =
e−x2−y2dxdy, trong đó D là miền xác định bởi x ≥ 0; y ≥ 0; x2 + y2 ≤ 1 . D Z Z x2 y2 k. I =
xydxdy, với D là miền elip + ≤ 1 . a2 b2 D
Bài tập 2: Tính các tích phân đường loại hai Z a. I =
cos ydx + (x + 2y)dy từ điểm (1; 0) đến (0; 1) dọc theo đường thẳng x + y = 1. C Z √ b. I =
ydx + (2x + 1)dy dọc theo đường y = x2 từ điểm O(0; 0) đến A(1; 1). C Z c. I =
(x + y)dx − (x − y)dy, với L là parabol y = x2 lấy từ điểm O(0; 0) đến A(1; 1). L Z d. I =
ydx − (x + y)dy, với L là đường thẳng y = 2x lấy từ điểm O(0; 0) đến A(1; 2). L Z e. I =
(2 − y)dx + xdy trong đó L là đường {x = t − sin t; y = 1 − cos t; 0 ≤ t ≤ 2π}. L Z f. I =
ydx − y + x2 dy trong đó L là một phần đường Parabol y = 2x − x2 nằm phía trên trục L
hoành chạy từ điểm O(0; 0) đến A(2; 0). I g. I =
(xy + x + y)dx + (xy + x − y)dy, trong đó L là đường tròn x2 + y2 = R2 lấy theo chiều dương. L Chương 5: PHƯƠNG TRÌNH VI PHÂN
Bài tập 1: Giải các phương trình vi phân với biến số phân ly a. x(1 − y)y0 = −5y. c. e6x + 1 ydy = e3xdx. b. xy0 = y − 3.
Bài tập 2: Giải các phương trình vi phân đẳng cấp y y a. y0 = − 5. c. y0 = + 7. x x y y b. y0 = e x + . x
Bài tập 3: Giải phương trình vi phân y xy0 − y = x tan , x π
với điều kiện đầu y(1) = . 2
Bài tập 4: Giải phương trình vi phân dạng biến số phân ly 1 + e2x y2dy = exdx, với điều kiện y(0) = 0.
Bài tập 5: Giải phương trình vi phân tuyến tính cấp một a. xy0 − y = x2 sin x. b. xy0 − y = x2 arctan x.
Bài tập 6: Giải các phương trình vi phân a. y00 − y = x + 1. d. y00 + y0 = sin x. b. y00 − 2y0 − 3y = e4x. e. y00 + y0 = x. c. y00 + y0 = 4 sin x. BÀI TẬP ỨNG DỤNG Bài tập 1:
Giả sử rằng mất t năm, một khoản đầu tư sẽ tạo ra lợi nhuận với tốc độ P 0(t) = 50 + t2 trăm đô la mỗi 1
năm, trong khi khoản đầu tư thứ hai sẽ tạo ra lợi nhuận với tốc độ P 0(t) = 200 + 5t trăm đô la mỗi năm. 2
a. Mất bao nhiêu năm để tốc độ sinh lời của khoản đầu tư thứ nhất vượt quá tốc độ sinh lời khoản đầu tư thứ hai?
b. Tính lợi nhuận vượt trội ròng của khoản đầu tư thứ hai so với khoản đầu tư thứ nhất trong khoảng
thời gian được xác định trong phần (a). Bài tập 2:
Một nhà sản xuất lốp xe ước tính rằng q (nghìn) lốp tròn sẽ được mua (yêu cầu) bởi người bán buôn với
giá mỗi lốp là p = D(q) = −0, 1q2 + 90 (đô la) và với cùng một số lượng lốp q, giá bán cho mỗi lốp là
p = S(q) = 0, 2q2 + q + 50 (đô la).
a. Tìm giá cân bằng (khi cung bằng cầu) và lượng cung và cầu ở mức giá đó.
b. Xác định thặng dư của người tiêu dùng và nhà sản xuất ở mức giá cân bằng. Bài tập 3: 3 2
Một nhà máy có sản lượng được cung cấp bởi hàm sản xuất Q(K, L) = 40K 5 L 3 trong đó K là đơn vị tư
bản và L là đơn vị lao động. Giả sử đơn vị tư bản hàng tháng thay đổi từ 10 nghìn đô la đến 12 nghìn đô
la, còn đơn vị lao động hàng tháng dao động từ 2800 đến 3200 . Tính sản lượng trung bình hàng tháng của nhà máy. Bài tập 4: 1 1
Một nhà máy có sản lượng mỗi ngày là Q = 60K 2 L 3 (sản phẩm), ở đó K là đơn vị tư bản và L là đơn vị
lao động. Đơn vị tư bản hiện tại K = 900 nghìn đô la và đơn vị lao động mỗi ngày L = 1000. Ước lượng
sự gia tăng sản lượng đầu ra nếu đơn vị tư bản tăng thêm 2 nghìn đô la và đơn vị lao động tăng thêm 5. Bài tập 5:
Một doanh nghiệp sản xuất hai loại chi tiết máy với giá bán lần lượt là p1 = 1600, p2 = 1200 (đồng). Gọi
x, y lần lượt là số chi tiết máy của mỗi loại cần sản xuất, khi đó chi phí mà doanh nghiệp cần bỏ ra là
C = 3x2 + 2xy + y2. Hãy xác định cơ cấu sản xuất (x, y) đề lợi nhuận doanh nghiệp thu được là tối đa. Bài tập 6:
Tìm mô men quán tính đối với gốc tọa độ của miền tròn D xác định bởi x2 + y2 − 2Rx ≤ 0 biết khối p lượng riêng ρ(x, y) = x2 + y2. Bài tập 7:
Tìm mô men quán tính đối với gốc tọa độ của miền tròn D xác định bởi x2 + y2 − 2Ry ≤ 0 biết khối p lượng riêng ρ(x, y) = x2 + y2. Bài tập 8: − → Tìm công của lực ~
F = 2x i − (x + y)~j khi di chuyển chất điểm M dọc theo đường gấp khúc BCD từ
B(0, 2) đến C(1, 1) rồi đến D(0, 1). Bài tập 9:
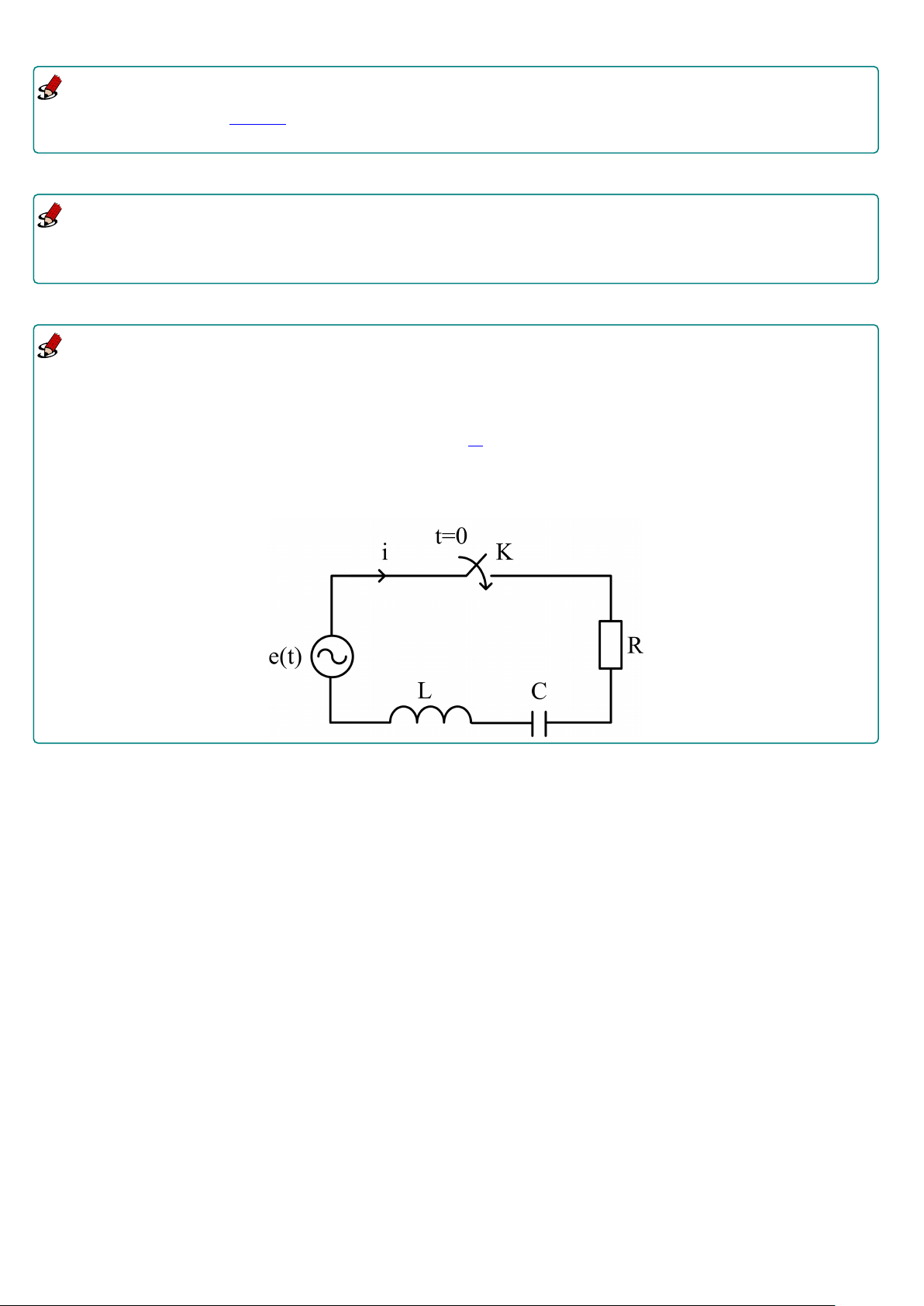
Cho mạch điện như hình vẽ dưới. Áp dụng Định luật Kirchhoff 2 (Tổng giá trị điện áp của các phần tử
trong một vòng kín bất kỳ bằng 0) cho mạch điện ta có phương trình 1 LQ00 + RQ0 + Q = e(t). C
Hãy tìm điện tích tại thời điểm t trong mạch điện biết R = 40Ω, L = 1H, C = 16·10−4F, e(t) = 100 cos 10t.